德兴一中2010-2011学年下学期第一次月考高二文科数学试卷
德兴一中2010-2011学年下学期第5次周考高二文科数学试卷

德兴一中2010-2011学年下学期第五次周考高二文科数学试卷一、选择题:本题共有10个小题,每小题5分,共50分;在每小题给出的四个选项中只有一项是正确的.1.函数()()4f x x x =+的零点是( )A. 0,-4B.0C.点(0,0)D. 点(0,0)与点(-4,0) 2.已知全集U R =,{|21}x A y y ==+,{|ln 0}B x x =<,则()U C A B =( )A .φB .1{|1}2x x <≤ C .{|1}x x < D .{|01}x x << 3.在以下区间中,存在函数f (x )=x 3+3x -3的零点的是( )A .[2,3]B .[1,2]C .[0,1]D .[-1,0]4.已知函数()f x 在R 上单调递减,则满足)1()2(f x f <-的x 取值范围是( )A . (-3, -1 )B .(3,∞+) C. (1, 3) D. (∞-,3) 5.设20.34log 4,log 3,0.3a b c -===,则( )A.b c a <<B.a b c <<C.c b a <<D.c a b <<6.满足2721()log 42x ->成立的x 的取值范围是 ( ) (A ){}|1x x >- (B ){}|3x x < (C ){}|3x x > (D ){}|1x x <-7. 设⎭⎬⎫⎩⎨⎧---∈3,2,1,21,31,21,1,2α,则使αx y =为奇函数且在()+∞,0上单调递减的α值的个数为( )A .1B .2C .3D .48.过点(0,1-)曲线13+=x y 的切线方程为( )A .1-=xB .033=--y xC .013=++y xD .013=--y x 9.计算 00cos15sin15cos 45-sin45的值等于( )A.12B.3C.22D. 310. 若实数y x ,满足01lg|1|=--yx ,则y 关于x 的函数的图象形状大致是( )二、填空题:本大题共5小题,每小题5分,共25分. 11.不等式lg(1)0x +≤的解集是__________________.12.已知函数()f x 为R 上的奇函数,当0x ≥时,2()f x x =. 若()2f a =-,则实数a = .13.地震的震级R 与地震释放的能量E 的关系为2(lg 11.4)3R E =-.2008年5月12日,中国汶川发生了8.0级特大地震,2011年3月11日,日本宫城发生里氏9.0级地震,那么日本宫城地震能量是2008年汶川地震能量的 倍.14. 抛物线24x y =上一点到直线54-=x y 的距离最短,则该点的坐标是 。
江西省德兴市第一中学高二下学期第一次月考试题(9科13份)(江西省德兴市第一中学高二下学期第一次月考

德兴一中2015-2016学年下学期第一次月考高二年级化学试卷(零班、重点班)分值 100 时间 90分钟命题人江文胜审题人董丽萍可能用到的相对原子质量H-1 C-12 N-14 O-16 Na—23一、选择题(每小题只有一个选项符合题意,共16小题,每小题3分,共48分)1. .某市高速公路发生苯酚槽罐车泄漏事故,导致部分苯酚泄漏并造成污染。
下列对于苯酚的叙述中,错误的是A.苯酚是一种弱酸,滴加指示剂不变色B.其浓溶液对皮肤有强烈的腐蚀性,如果不慎沾在皮肤上,应立即用酒精擦洗C.碳酸氢钠溶液中滴入苯酚的水溶液后会放出二氧化碳D.其在水中的溶解度随温度的升高而增大,超过65℃可以与水以任意比互溶2.下列有机物系统命名正确的是3.用一种试剂鉴别苯酚、己烯、碘化钾溶液、苯四种液体,可选用A.盐酸B.FeCl3溶液C.溴水D.四氯化碳4.取两份质量相等的有机物M,一份与足量的钠反应放出气体V1升,另一份与足量Na2CO3溶液反应放出气体V2升;若同温同压下V1>V2>0,则M可能是A.CH3COOH B.HOOC—COOH C.HO(CH2)2CHO D.HO--COOH5.属于同系物的一组物质是( )A.35Cl2、37Cl2、35Cl37Cl B.-OH、-CH2OH、-CH2CH2OHC.CH4、CH3CH(CH3)2、(CH3)3CCH2CH3 D.一氯甲烷、二氯甲烷、三氯甲烷6.下列化合物中,既能发生消去反应生成烯烃,又能发生水解反应的是 ( )7.酒后驾车是引发交通事故的重要原因。
交警对驾驶员进行呼气酒精检测的原理是:橙色的K2Cr2O7 酸性水溶液遇乙醇迅速生成蓝绿色Cr3+。
下列对乙醇的描述与此测定原理有关的是①乙醇沸点低②乙醇密度比水小③乙醇有还原性④乙醇是烃的含氧化合物( )A.②④B.②③C.①③ D.①④8.我国支持“人文奥运”的一个重要体现是:坚决反对运动员服用兴奋剂。
某种兴奋剂的结构简式如右图所示,有关该物质的正确的是A.该物质与苯酚属于同系物,遇FeCl3溶液呈紫色B.滴入酸性KMnO4溶液振荡,紫色褪去,能证明其结构中存在碳碳双键C.1mol该物质分别与浓溴水和H2反应时,最多消耗Br2 和H2分别为4mol和7molD.该分子中的所有碳原子不可能共平面9.用括号中的试剂除去各组中的杂质,正确的是( )A、苯中的苯酚(溴水)B、乙醇中的水(新制CaO)C、乙醇中的乙酸(水)D、乙酸乙酯中的乙酸(苛性钠溶液)10. 有机物A可用B式表示,则有机物C的许多同分异构体中,属于芳香醇的共有A.5种B.4种C. 3种D. 2种11.下列实验操作或实验方案设计不正确...的有①实验室制乙炔时用饱和食盐水与电石反应,并用硫酸铜溶液除杂质②重结晶法提纯苯甲酸时,为了析出更多晶体,热滤液用冰盐水充分冷却③只用水一种试剂可以鉴别乙醇、甲苯、硝基苯④用己烯萃取碘酒中的碘⑤检验溴乙烷中的溴元素:向NaOH水溶液中先加几滴溴乙烷,加热,充分反应后,冷却,再加入AgNO3溶液,观察现象。
江西省德兴一中2010-2011学年高二下学期第一次月考(数学文)

德兴一中2010—2011学年下学期第一次月考高二文科数学试卷共计150分,时间120分钟.一、选择题:本题共有10个小题,每小题5分,共50分;在每小题给出的四个选项中只有一项是正确的。
1.设全集U={1,2,3,4,5},集合A={1,a—2,5},∁U A={2,3},则a的值为( )A。
3 B。
4 C。
5 D.62.已知复数i bi ia-=-)2((,a b R∈),则a b+= ( )A. 14B。
12C. 1D. 23.如图所示,U是全集,M、N、S是U的子集,则图中阴影部分所示的集合是( )A。
(∁U M∩∁U N)∩S B.(∁U(M∩N))∩SC.(∁U N∩∁U S)∪MD.(∁U M∩∁U S)∪N4.若A、B、C为三个集合,A B B C⋃=⋂,则一定有( )A.A C⊆B。
C A⊆C。
A C≠B。
Aφ=5.使不等式2x2-5x—3≥0成立的一个充分不必要条件是( )A。
x≥0 B。
x<0或x>2 C. x≤-12或x≥3D。
x∈{-1,3,5}6。
已知命题p :“若a>b 〉0,则log11221a log <+b”,其命题p 的原命题、逆命题、否命题、逆否命题中为真命题的个数为( ) A 。
0 B 。
1 C 。
2 D.47. 已知集合A={(x,y)|y=lg(x+1)-1},B={(x ,y )|x=m },若A∩B=∅,则实数m 的取值范围是( )A 。
m 〈1B 。
m≤1 C.m 〈-1 D 。
m≤—1 8. 已知函数()()()40,40.x x x f x x x x +<⎧⎪=⎨-≥⎪⎩,,则函数()f x 的零点个数为 ( )A .1B .2 C.3 D.49。
设定义在R 上的函数()f x 满足()()213f x f x ⋅+=,若()12f =,则()99f =( ) A.13 B.132C.2 D.21310.设p:y=c x 是R 上的单调递减函数;q :函数g (x )=lg (2cx 2+2x+1)的值域为R .如果“p 且q”为假命题,“p 或q”为真命题,则正实数c 的取值范围是( )1.,12A ⎛⎫⎪⎝⎭1.,2B ∞⎛⎫+ ⎪⎝⎭C 。
江西省德兴市第一中学高二数学下学期第一次月考试题

德兴一中2015---2016学年下学期第一次月考高二年级数学试卷(文科)分值:150分 时间:120分钟一、选择题(共12个小题,每题5分,共60分) 1.复数2i1i --= ( ) A.3i 2+ B.1i 2- C.3i 2- D.3i 2--2.已知集合P ={1,m},Q ={1,3,5},则“m=5”是“P ⊆ Q ”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要条件 3.下列结论正确的是( ) A .xx5)'5(=B .5ln 5)'5(xx =C .xax a ln )'(log =D .xa x a =)'(log 4.已知函数x x x f ln 2)(-=的单调递减区间为( )A .)21,0(B .),0(+∞C .),21(+∞D .)21,(-∞5.已知曲线方程f(x)=sin 2x +2ax(a ∈R),若对任意实数m,直线l :x +y +m =0都不是曲线y =f(x)的切线,则a 的取值范围是 ( )A .(-∞,-1)∪(-1,0)B .(-∞,-1)∪(0,+∞)C .(-1,0)∪(0,+∞)D .a ∈R 且a≠0,a≠-1 6.下列说法正确的是 ( ). A . “”是“”的充分不必要条件B .“”是“”的必要不充分条件.C .命题“∈∃x R,使得012<++x x ”的否定是:“R x ∈∀,均有012<++x x ”.D .命题“若βαβαsin sin ==,则,”的逆否命题为真命题.7.已知a ≥0,函数f (x )=(x 2-2ax )e x,若f (x )在[-1,1]上是单调减函数,则a 的取值范围是( )A .0<a <34 B.12<a <34 C .a ≥34D .0<a <128.已知函数()2xf x e =,函数g (x )=k (x+1),若函数()f x 图象恒在函数g (x )图像的上方(没有交点),则实数是的取值范围是 ( )A .k>2B .k ≥2C .0≤k ≤2D .0≤k<29.一个机器人每一秒钟前进一步或后退一步,程序设计师设计的程序是让机器人以先前进3步,然后再后退2步的规律移动.如果将机器人放在数轴的原点,面向正的方向在数轴上移动(1步的距离为1个单位长度).令()P n 表示第n 秒时机器人所在位置的坐标,且记(0)0P =,则下列结论中错误的是( )A .(3)3P =B .(5)1P =C .(2007)(2006)P P >D .(2003)(2006)P P <10.已知定义在R 上的函数g(x)的导函数为g′(x),满足g′(x)-g(x)<0,若函数g(x)的图象关于直线x =2对称,且g(4)=1,则不等式xe x g )(>1的解集为( ) A .(-2,+∞) B .(0,+∞) C .(-∞,0) D .(-∞,2)11.关于x 的不等式|x -1|+|x -2|≤a 2+a +1的解集是空集,则a 的取值范围是( ) A .(0,1) B .(-1,0) C .(1,2) D .(-∞,-1) 12.当a>0时,函数f(x)=(x 2+2ax)e x的图象大致是( )二、填空题(4小题,每题5分,共20分)13.设曲线y =e x在点(0,1)处的切线与曲线y =1x (x>0)上点P 处的切线垂直,则P 的坐标为________.14.复数2(23)(21)z a a a i =--+--是纯虚数,则实数a 的取值是________.15.已知函数()(1)(2)(3)f x x x x =---,且在点(,())i f i 处的切线的斜率为(1,2,3)i k i =.则123111k k k ++=________. 16.定义域为R 的函数()f x ,满足(0)1f =,()()1f x f x '<+,则不等式()12x f x e +<的解集为________________________三、解答题 (6个小题,共70分)17.(本小题满分10分)已知f (x )=x 3+3ax 2+bx +a 2在x =-1时有极值0,求常数a ,b 的值.并求函数的单调减区间.18.(本小题满分12分)已知函数()21f x x =+,()g x x a =+ (1)当a =0时,解不等式 f (x )≥g (x );(2)若x R ∃∈,使得 f (x )≤g (x )成立,求实数a 的取值范围.19. (本小题满分12分)已知命题p :f (x )=x +a x在区间[1,+∞)上是增函数;命题q :f (x )=x 3+ax 2+3x +1在R 上有极值.若命题“p ∨q ”为真命题,求实数a 的取值范围.20.(本小题满分12分)已知函数f (x )=ax 3+bx+c 在点x=2处取得极值c ﹣16. (Ⅰ)求a ,b 的值;(Ⅱ)若f (x )有极大值28,求f (x )在[﹣3,3]上的最小值.21. (本小题满分12分)已知()()ln 1f x x a x =+-. (I )讨论()f x 的单调性;(II )当()f x 有最大值,且最大值大于22a -时,求a 的取值范围.22.(12分)已知函数()ln f x x ax =-在点()()2,2A f 处的切线l 的斜率为32. (Ⅰ)求实数a 的值;(Ⅱ)证明:函数()f x 的图象恒在直线l 的下方(点A 除外);(Ⅲ)设点()()()()1122,,,P x f x Q x f x ,当211x x >>时,直线PQ 的斜率恒大于k ,试求实数k 的取值范围.高二文科数学试卷第一次月考答案一、选择题(共12个小题,每题5分,共60分) 1 2 3 4 5 6 7 8 9 10 11 12 AABABDCDDCBB二、填空题(4小题,每题5分,共20分)13. (1,1) 14. -1 15.0 16.{0}x R x ∈> 三、解答题 (6个小题,共70分) 17、(本小题满分10分)解:∵f (x )在x =-1时有极值0,且f ′(x )=3x 2+6ax +b ,∴⎩⎪⎨⎪⎧f ′-1=0,f-1=0,即⎩⎪⎨⎪⎧3-6a +b =0,-1+3a -b +a 2=0,解得⎩⎪⎨⎪⎧a =1,b =3,或⎩⎪⎨⎪⎧a =2,b =9.(5分)当a =1,b =3时,f ′(x )=3x 2+6x +3=3(x +1)2≥0,∴f (x )在R 上为增函数,无极值,故舍去.∴a =2,b =9……………………7分 当a =2,b =9时,f ′(x )=3x 2+12x +9=3(x +1)(x +3),当x ∈(-3,-1)时,f (x )为减函数;……………………………10分 18.(本小题满分12分) 每问6分19(本小题满分12分).解 命题p :f ′(x )=1-a x 2.∵f (x )=x +a x在区间[1,+∞)上是增函数, 则f ′(x )=1-a x2≥0在[1,+∞)上恒成立,即a ≤x 2在[1,+∞)上恒成立, ∴a ≤(x 2)min ,∴a ≤1……………………………………………………………..5分 命题p :A ={a |a ≤1}. 命题q :f ′(x )=3x 2+2ax +3. 要使得f (x )=x 3+ax 2+3x +1在R 上有极值, 则f ′(x )=3x 2+2ax +3=0有两个不相等的实数解,Δ=4a 2-4×3×3>0,解得a <-3或a >3.命题q :B ={a |a <-3,或a >3}. …………………………………………..10分 ∵命题“p ∨q ”为真命题, ∴A ∪B ={a |a ≤1,或a >3}.∴所求实数a 的取值范围为(-∞,1]∪(3,+∞)…………………………12分 20(本小题满分12分)解:(Ⅰ)由题f (x )=ax 3+bx+c ,可得f′(x )=3ax2+b , 又函数在点x=2处取得极值c ﹣16∴, 即, 化简得解得a=1,b=﹣12 … ………6分(II )由(I )知f (x )=x 3﹣12x+c ,f′(x )=3x 2﹣12=3(x+2)(x ﹣2)令f′(x )=3x 2﹣12=3(x+2)(x ﹣2)=0,解得x 1=﹣2,x 2=2 当x∈(﹣∞,﹣2)时,f′(x )>0,故f (x )在∈(﹣∞,﹣2)上为增函数; 当x∈(﹣2,2)时,f′(x )<0, 故f (x )在(﹣2,2)上为减函数; 当x∈(2,+∞)时,f′(x )>0, 故f (x )在(2,+∞)上为增函数;由此可知f (x )在x 1=﹣2处取得极大值f (﹣2)=16+c , f (x )在x 2=2处取得极小值f (2)=c ﹣16, 由题设条件知16+c=28得,c=12此时f (﹣3)=9+c=21,f (3)=﹣9+c=3,f (2)=﹣16+c=﹣4因此f (x )在[﹣3,3]上的最小值f (2)=﹣4 …………12分21. (本小题满分12分)每问6分22. (本小题满分12分) (Ⅰ)因为()1f x a x'=-,又因为函数()f x 在点()()2,2A f 处的切线斜率为32,所以()322f '=,所以1a =-; 3分(Ⅱ)因为()ln f x x x =+,所以()2,ln 22A +,所以l 的方程为:3ln 212y x =+-, 令()()3ln 212g x f x x ⎡⎤=-+-⎢⎥⎣⎦1ln ln 212x x =--+, 则()112g x x '=-22xx -=,又因为0x >, 所以当()0,2x ∈时,()0g x '>;当()2,x ∈+∞时,()0g x '<, 所以函数()g x 在()0,2单调递增,在()2,+∞单调递减, 所以当2x =时,()g x 取得最大值()20g =,所以()0g x ≤, 所以()3ln 212f x x ≤+-,即函数()f x 的图象恒在其切线l 的下方(切点除外).7分 (Ⅲ)因为()()2121PQ f x f x k x x -=-,所以当211x x >>时,()()2121f x f x k x x ->-,即()()()2121f x f x k x x ->-,()()2211f x kx f x kx ->-. 令()()ln h x f x kx x x kx =-=+-()0x >, 所以()h x 在()1,+∞单调递增, 所以()110h x k x'=+-≥在()1,+∞恒成立, 所以11k x≤+在()1,+∞恒成立,所以1k ≤………………………………12分。
江西省德兴市第一中学高二数学下学期第一次月考试题

德兴一中2013-2014学年高二下学期第一次月考命题人:王 春 审题人:黄和林数 学 试 题(文科)第Ⅰ卷一、选择题(本题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一项是符合 题目要求的,请把正确答案的代号填在题后的括号内.)1.设全集U={1,2,3,4,5},集合A={1,2},B={2,3},则A ()U C B I = A .{1}B .{3}C .{4,5}D .{2,3}2.集合}032|{2<--=x x x M ,}|{a x x N >=,若N M ⊆,则实数a 的取值范围是( ) A .),3[+∞ B .),3(+∞ C .]1,(--∞ D .)1,(--∞ 3.已知R b a ∈,,条件p :“a>b ”,条件q :“122->ba”,则p 是q 的( ) A .充分不必要条件 B .必要不充分条件C .充分必要条件D .既不充分也不必要条件4.已知命题0,:;25sin ,:2>++∈∀=∈∃x x R x q x R x p 都有命题使R ,.01:25sin ,:2>++∈∀=∈∃x x R x q x R x p 都有命题使01,:;5sin ,:2>++∀=∈∃x x R q x R x p 都有命题使,.01,:;25sin ,:2>∀=∈∃x q x R x p 都有命题使给出下列结论: ①命题“q p ∧”是真命题②命题“q p ⌝∧”是假命题③命题“q p ∨⌝”是真命题 ④命题“q p ⌝∨⌝”是假命题, 其中正确的是( )A.②④B.②③C.③④D.①②③5.集合=P {x ,1},=Q {y ,1,2},其中∈y x ,{1, 2,3,4,5},则满足条件Q P ⊆的事件的概率为( )A.12 B.13 C.14 D.156.已知集合}{lg M x y x ==,集合()()22311x x N x y x x ⎧⎧>⎫⎪⎪==⎨⎨⎬-+<⎪⎭⎩⎪⎩,则M ∩N =( )A .(0,1)B .(2,+∞)C .(0,+∞)D .(0,1)∪(2,+∞) 7.已知函数211()log ,(),()12x f x f a f a x -==-+若则=( ) A .12B .—12C .2D .—28.已知双曲线2215x y m -=(0m >)的右焦点与抛物线212y x =的焦点相同,则此双曲线的离心率为( )A .6B .32 D .349.下面四个命题,真命题是( )A.若“p 或q ”为真命题,则p 、q 均为真命题B.设a 、b R ∈,若6a b +≠,则33a b ≠≠或;C.命题“a ∀、22,2(1)b R a b a b ∈+≥--”的否定是:“a ∃、22,2(1)b R a b a b ∈+≤--” D.“关于x 的方程01=-+k xx 在(0,1)x ∈有实数根”的充要条件是“2k ≥”; 10. 已知+∈R y x ,,312()2x y -=,若1,(0)m m x y +>的最小值为3,则m 等于( )A .2B .3C .D .4第Ⅱ卷二、填空题(每小题5分,共 25分) 11.已知函数2,2()(2),2x x f x f x x ≥⎧=⎨+<⎩,则函数( 2.5)f -的值为___________。
江西省德兴一中高二第一学期第一次月考数学

江西省德兴一中高二第一学期第一次月考数学试卷1、若a<b<0,则下列不等式中不一定能成立的是( )A>a 1b1B. |a|> |b|C.>-b a 1a 1 D.a ²>b ² 2、与不等式xx --23≥0同解的不等式是( )A 、)2)(3(x x --≥0B 、)2)(3(x x -->0C 、32--x x≥0D 、0<2-x ≤13、已知x 、y 是两个正数,且x 2+y 2=1,那么(1-xy)(1+xy)有( )A 、最小值34而无最大值 B 、最大值1而无最小值 C 、最小值12和最大值1 D 、最小值34和最大值14、设数集32{|0},{|1}43M x x N x x =≤≤=≤≤,如果把b a -叫做集合{|,}x a x b ba ≤≤≥的“长度”。
那么集合M N 的长度是( ) A 、112 B 、14 C 、13 D 、235、设0x >,0,1y x y >+=a ≤恒成立的a 的最小值是( )A 、2BC 、2D 、6、点(,)P x y 是直线320x y +-=上的动点,则代数式327xy+有( ) A 、最大值8 B 、最小值8 C 、最小值6 D 、最大值67、若直线0x =的倾斜角为α,则α( )A 、等于0B 、等于4πC 、等于2πD 、不存在8、圆422=+y x 截直线0323=-+y x 所得的弦长是( )A 、2B 、1C 、3D 、329、若不等式组022x y x y x y ay 0≥⎧-⎪+⎪⎨≥⎪⎪+<⎩≤表示的平面区域是一个三角形,则a 取值范围是( )A 、43a ³B 、01a <?C 、413a # D 、4013a a <3或 10、过点(1,1)P 作直线l ,与两坐标相交,所得三角形面积为2,则这样的直线l 有( ) A 、1条B 、2条C 、3条D 、4条110y +-与圆12cos 32sin x y q q=+=+(θ为参数)的位置关系是 ( )A 、相离B 、相切C 、相交但不过圆心D 、相交且过圆心12、已知,,,,,a b c R m n R +挝且满足222a b c +=,20am bn c ++=,则22m n +的最小值是( ) A 、2 B 、4 C 、6 D 、813、若x>4,函数y=-x+x-41,当x=________时,函数有最大值为___________________。
江西德兴一中2010-2011学年第一学期第一次月考高二数学文科试卷

江西德兴一中2010-2011学年第一学期第一次月考高二数学文科试卷考试时间120分钟,满分120+30分 命题人:王 春 审题人:雷大放一、(本大题共12小题,每小题5分,共60分,只有一项是符合题目要求的) 1.实数系的结构图为右图所示其中1、2、3三个方格中的内容分别为( ) A .有理数、零、整数 B .有理数、整数、零 C .零、有理数、整数 D .整数、有理数、零 2.由以下数据得到的回归直线必定过点( )A .(110),B .(26),C .(59),D .(2.59),3. 利用“直接插入排序法”给8,1,2,3,5,7按从大到小的顺序排序,当插入第四个数3时,实际是插入哪两个数之间 ( )A .5与2B .5与1C .8与2D .8与14.从一批产品中取出三件产品,设A=“三件产品全不是次品”,B=“三件产品全是次品”,C=“三件产品至少有一件是次品”,则下列结论正确的是( )A. A 与C 互斥B.任何两个均互斥C. B 与C 互斥D.任何两个均不互斥 5.小强和小华两位同学约定下午在钟楼公园喷水池旁见面,约定谁先到后必须等10分钟,这时若另一人还没有来就可以离开.如果小强是1:40分到达的,假设小华在1点到2点内到达,且小华在 1点到2点之间何时到达是等可能的,则他们会面的概率是 ( )A. 16B.12C. 14D.16.右图所示的算法流程图中,输出的S A .1+2+…+99 B .1+2+…+100C .99211+⋅⋅⋅++D .001211+⋅⋅⋅++7.为了解某校高三学生的视力情况,随机地抽查了该校200名高三学生的视力情况,得到频率分布直方图,如上图,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,设最多一组学生数为a ,视力在4.6到5.1之间的频率为b ,则a 、b 的值分别为( )A .85, 0.27B .27, 0.78C . 54 , 0.78D .54, 0.858.设有一个回归方程ˆ2 2.5yx =-,变量x 增加一个单位时,变量ˆy 平均 ( ) A.增加2.5 个单位 B.增加2个单位 C.减少2.5个单位 D.减少2个单位9. 用简单随机抽样法从120个零件中,抽取容量为20的样本,.则每个个体被抽取到的概率与某个个体第三次被抽取到的概率分别是( )A .61,61 B .601 ,1181 C .61 ,1181 D .61 ,120110.下列说法中正确的有:①若0r >,则x 增大时,y 也相应增大;②若0r <,则x 增大时,y 也相应增大;③若1r =,或1r =-,则x 与y 的关系完全对应(有函数关系),在散点图上各个点均在一条直线上( ) A .①②B .②③C .①③D .①②③11.甲、乙、丙三人参加数学竞赛,三人获奖的概率分别为0.6, 0.7和0.8, 那么他们三人中至少一人获奖的概率为( )A.0.788B.0.452C.0.9D.0.97612.半径为r 的圆的面积公式为2r s π=,当5=r 时,则计算面积的流程图为( )德兴一中2010-2011学年第一学期第一次月考二、填空题:本题共4小题,每小题4分,共16分.把答案填在题中的横线上.13.正方形被平均分成9个部分,向大正方形区域随机地投掷一个点(每次都能投中),设投中最左侧3个小正方形区域的事件记为A ,投中最上面3个小正方形或正中间的1个小正方形区域的事件记为B ,则()P A B =14.由1、2、3三个数字组成可以有重复数字的三位数,如果组成的个位数字是1,且恰有两个数字相同,这样的数称为“好数”,在所有三位数中,好数的概率是 . 15.已知如下算法语句输入t;If t<5 Then y=t 2+1;Else if t<8 Then y=2t-1;1+;End If End if输出y若输入t=8,则下列程序执行后输出的结果是16.已知bxy ae =线性转化为'''y a bx =+,其中'ln a a =则=/y ,=/x三、解答题:本大题共4小题,共44分,解答应写出文字说明、证明过程或演算步骤.17.(本题满分10分)为了参加奥运会,对自行车运动员甲、乙两人在相同的条件下进行了6次测试,测得他们的最大速度的数据如表所示:请判断:谁参加这项重大比赛更合适,并阐述理由。
江西省德兴一中2017-2018学年高二下学期第一次月考数学试卷(文科)Word版含答案

江西省德兴一中2017-2018学年高二下学期第一次月考数学试卷(文科)一、选择题:(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.如图所示,在“推理与证明”的知识结构图中,如果要加入“综合法”,则应该放在( )A.“合情推理”的下位B.“演绎推理”的下位C.“直接证明”的下位D.“间接证明”的下位2.用反证法证明数学命题时首先应该做出与命题结论相矛盾的假设.否定“自然数c b a ,, 中恰有一个偶数”时正确的反设为 ( )A .自然数c b a ,,都是奇数B .自然数c b a ,,都是偶数C .自然数c b a ,,中至少有两个偶数D .自然数c b a ,,中至少有两个偶数或都是奇数 3.若0>>b a ,则下列不等式中一定成立的是( )A.a b b a 11+>+B.11++>a b a bC.bb a a 11+>+ D.b ab a b a >++22 4.执行如图所示的程序框图,则输出的=S ( )A .512B .511C .1024D .10235.复数1z ,2z 在复平面内对应的点关于直线y x =对称,且132z i =+,则12z z ⋅=( ) A .1213i + B .1312i + C .13i - D .13i6.以下四个命题①从匀速传递的产品生产流水线上,质检员每5分钟从中抽取一件产品进行某项指标检测,这样的抽样是分层抽样;②样本方差反映了样本数据与样本平均值的偏离程度;③在回归分析模型中,残差平方和越小,说明模型的拟合效果越好;④在回归直线方程101.0+=∧x y 中,当解释变量x 每增加一个单位时,预报变量∧y 增加1.0个单位. 其中正确的是( )A.②③④B.①③④C.①②③D.①②④7.面积为S 的平面凸四边形的第i 条边的边长记为(1,2,3,4)i a i =,此四边形内任一点P 到第i 条边的距离记为(1,2,3,4)i h i =,若31241234a a a a k ====,则12342234S h h h h k+++=.类比以上性质,体积为V 的三棱锥的第i 个面的面积记为(1,2,3,4)i S i =,此三棱锥内任一点Q 到第i 个面的距离记为(1,2,3,4)i H i =,若31241234S S S S K ====,则1234234H H H H +++等于( ) A .2V K B .3V K C .2V K D .3V K8.定义运算:()()x x y x y y x y ≥⎧⊗=⎨<⎩,例如344⊗=,则下列等式不成立的是( )A .x y y x ⊗=⊗B .()()x y z x y z ⊗⊗=⊗⊗C .222()x y x y ⊗=⊗ D .()()()(0)c x y c y c x c ⋅⊗=⋅⊗⋅>9.在极坐标系中,曲线)20(2sin cos πθθρθρ≤≤=+与4πθ=的交点的极坐标是( )A.()1,1B.⎪⎭⎫ ⎝⎛4,1πC.⎪⎭⎫ ⎝⎛4,2π D.⎪⎭⎫ ⎝⎛-4,2π 10.复数212m iz i-=+(R m ∈,i 为虚数单位)在复平面内对应的点不可能位于( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限11.点集()3cos ,,0,3sin ,x M x y y θθθπθ⎧⎫=⎧⎪⎪=<<⎨⎨⎬=⎩⎪⎪⎩⎭是参数, (){}b x y y x N +==,, 若φ≠⋂N M ,则b 应满足( )A .2323≤≤-bB .323-<<-bC .230≤≤bD .233≤<-b12.设AB C D 为xoy 平面的一个正方形,其顶点是(0,0),(1,0),(1,1),(0,1)A B C D ,2u xy =,22v x y =-是xoy平面到uov 平面的变换,则正方形ABCD 像(,)u v 的点集是( )A. B. C. D. 二、填空题(本大题共4小题,每小题5分,共20分) 13.复数mi()12iz m R =∈+,其中i 为虚数单位,若||zm 的值为 . 14.在极坐标系中,直线()sin cos a ρθθ-=与曲线2cos 4sin ρθθ=-相交于A 、B 两点,若AB =a 的值为 .15.下表给出了一个“三角形数阵”:1411,24333,,48161111,,,248依照表中数的分布规律,可猜得第10行第6个数是 .16.在直角坐标系中,以原点为极点,x 轴的正半轴为极轴建立极坐标系,已知曲线2:sin 2cos (0)C k k ρθθ=>.过点(2,4)P --的直线l 的参数方程为24x ty t =-+⎧⎨=-+⎩(t 为参数).设直线l 与曲线C 分别交于,M N 两点.若||,||,||PM MN PN 成等比数列,则k 的值为______.三、解答题:(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤) 17.(本小题满分10分)证明下列命题:(1)若实数2≥a ,则211---<-+a a a a ;(2)若,a b 为两个不相等的正数,且1a b +=,则114a b+>.18.(本小题满分12分)为了研究“教学方式”对教学质量的影响,某高中数学老师分别用两种不同的教学方式对入学数学平均分数和优秀率都相同的甲、乙两个高一新班进行教学(勤奋程度和自觉性都一样).以下茎叶图为甲、乙两班学生的数学期末考试成绩.学校规定:成绩不低于75分的为优秀.(1)(2下面临界表仅供参考:(参考公式:χ2=))()()(()(d b c a d c b a bc ad n ++++-)19.(本小题满分12分)在直角坐标系xoy 中,曲线1C 的参数方程为sin x y αα⎧=⎪⎨=⎪⎩,(α为参数),以原点O 为极点,x 轴正半轴为极轴,建立极坐标系,曲线2C 的极坐标方程为sin()4πρθ+=(1)求曲线1C 的普通方程与曲线2C 的直角坐标方程;(2)设P 为曲线1C 上的动点,求点P 到曲线2C 的距离的最小值.20.(本小题满分12分)某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:(1)求回归直线方程y ^=bx +a ,其中b =-20;(2)预计在今后的销售中,销量与单价仍然服从(1)中的关系,且该产品的成本是4元/件,为使工厂获得最大利润,该产品的单价应定为多少元?21.(本小题满分12分)在平面直角坐标系中,已知直线l 过点(),12P - ,倾斜角6πα=,再以原点O 为极点,x 轴的正半轴为极轴建立极坐标系,曲线C 的极坐标方程为3ρ=. (1)写出直线l 的参数方程(标准式)和曲线C 的直角坐标方程; (2)若直线l 与曲线C 分别交于M N 、两点,求PM PN ⋅的值.22.(本小题满分12分)已知定理:对于任意的多项式()f x 与任意复数z ,()0f z =⇔x z -整除()f x .(1)在复数范围内分解因式21x x ++;(2)利用(1)和上述定理解决问题:求所有满足21x x ++整除21n nx x ++的正整数n 所构成的集合A .江西省德兴一中2017-2018学年高二下学期第一次月考数学试卷(文科)答案13.5± 14.15-或- 15.56416.1 三、计算题(本大题共有6小题,共70分) 17.(本小题10分)(1)分析法,先移项,再两边平方,即得;(2)综合法,乘一法,即得。
德兴一中2010-2011学年度第二学期第一次月考高一数学试卷

德兴一中2010-2011学年度第二学期第一次月考高一数学试卷一、 选择题(本大题共10小题,每小题5分,共50分,在每小题列出的四个选项中,选出符合题目要求的一项。
) 1.若数列{}n a 的前n 项和为2n S n =,则()A .12-=n a nB .12+=n a nC .12--=n a nD .12+-=n a n2.如果五个角依次成等差数列,最小的角为25°,最大的角为105°,则该等差数 的公差的:()A 、16°B 、15°C 、20°D 、13°20第一节 下列说法中不正确的是:()A 、在等比数列中,所有奇数项或者所有偶数项一定同号B 、常数列一定是等比数列C 、首项为正,公比大于1的等比数列一定是递增数列D 、首项为负,公比大于1的等比数列一定是递减数列 4.已知等比数列{}n a 中,42a =,64a =,则8a 的值为()A .B .±C .8D .8±5.设n S 为数列{}n a 的前n 项和,若数列满足12n n a a -=+(2n ≥), 且93=S ,则=1a ()A .1-B .1C .3D .56.已知:∆A B C a b A 中,,,c o s ===-3336,则边长c= ()A.2B.1C.-3D.37.在△ABC 中,若2cos B sin A =sinC ,则△ABC 的形状一定是()A.等腰直角三角形B.直角三角形C.等腰三角形D.等边三角形8.已知△ABC 中,3BC = ,4CA =,且BC CA ⋅=- △ABC 的面积是()A .3B ..6D .9.若函数()sin f x x x ωω=(0ω>,x R ∈),满足()2f α=-,()0f β=,且||βα-的最小值等于π43,则函数)(x f 的一个单调递增区间是()A .)2,2(ππ-B .),4(ππC .),2(ππ- D .)4,2(ππ-10.已知数列{a n }(n ∈N )中,a 1 = 1,a n +1 = a n2a n+ 1 ,则a n 为 ( )(A) 2n -1 (B) 2n + 1 (C)12n -1(D) 12n + 1 二、 填空题(本大题共5小题,每小题5分,共25分。
高二上册数学第一次月考文科试卷

第一次月考高二文科数学注意事项:1、本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
2、本堂考试120分钟,满分150分。
3、答题前,考生务必先将自己的姓名、学号填写在答题卡上,并使用2B 铅笔填涂。
4、考试结束后,将答题卡交回。
第Ⅰ卷(选择题,共60分)一、选择题(本大题12个小题,每题5分,共60分,请将答案涂在答题卡上) 1、已知复数(是虚数单位),则( )A.B.C.D.2、已知集合{}2|20A x x x =-≤,{}1,0,2,3B =-,则A ⋂B =( )A .{}0,1,2B .{}0,2C .{}1,3-D .{}1,0,1,2,3-3、命题“1sin ,≤∈∀x R x ”的否定是 ( )1sin ,.00≤∈∃x R x A 1sin ,.00>∈∃x R x B 1sin ,.>∈∀x R x C 1sin ,.00≥∈∃x R x D4、某篮球队甲、乙两名运动员练习投篮,每人练习10组,每组投篮40个.命中个数的茎叶图如下图,则下面结论中错误的一个是( )A. 甲的极差是29B. 乙的众数是21C. 甲的命中率比乙高D. 甲的中位数是245、已知直线b a 、是平面α内的两条直线,l 是空间中一条直线. 则“b l a l ⊥⊥,”是 “α⊥l ”的 ( ).A 充分不必要条件 .B 必要不充分条件 .C 充要条件 .D 既不充分也不必要条件 6、某市政府调查市民收入与旅游欲望时,采用独立性检验法抽取3 000人,计算发现χ2=6.023,则根据这一数据查阅下表,市政府断言市民收入增减与旅游欲望有关系的把握是( )……C .97.5%D .99.5%7、古希腊数学家阿基米德用穷竭法建立了这样的结论:“任何由直线和抛物线所包围的弓形,其面积都是其同底同高的三角形面积的三分之四.”如图,已知直线x =2交抛物线y 2=4x 于A ,B 两点.点A ,B 在y 轴上的射影分别为D ,C .从长方形ABCD 中任取一点,则根据阿基米德这一理论,该点位于阴影部分的概率为( )A.12 B .13 C.23 D .258、在极坐标系中,点)4,2(π到直线23)3sin(-=-πθρ的距离是 ( ▲ )1.A 21.B 31.C 41.D 9、若连续抛掷两次骰子得到的点数分别为m ,n ,则点P (m ,n )在直线x +y =4上的概率是( )A.13 B.14 C.16 D.11210、11、设1F ,2F 是双曲线()2222:10,0x y C a b a b-=>>的两个焦点,P 是C 上一点,若126PF PF a +=,且12PF F △的最小内角为30︒,则C 的离心率为( )A B .32C D 12、甲、乙、丙三人中,一人是工人,一人是农民,一人是知识分子。
江西省德兴-高二数学下学期第一次月考 文 新人教A版
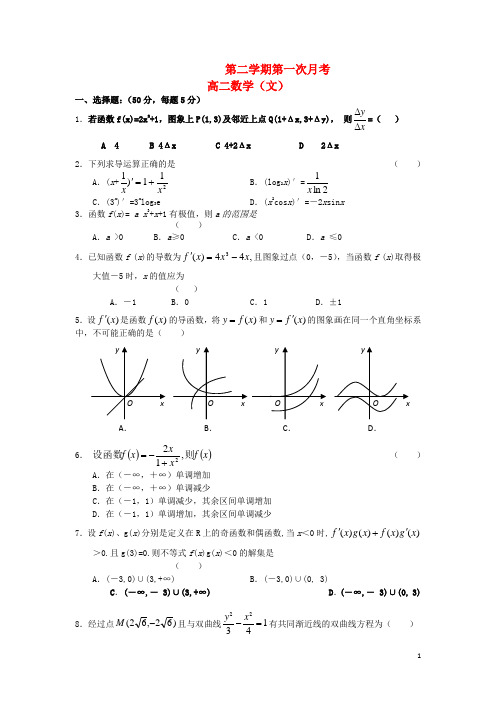
第二学期第一次月考 高二数学(文)一、选择题:(50分,每题5分)1.若函数f(x)=2x 2+1,图象上P(1,3)及邻近上点Q(1+Δx,3+Δy), 则xy∆∆=( ) A 4 B 4Δx C 4+2Δx D 2Δx 2.下列求导运算正确的是( )A .(x +211)1x x +=' B .(log 2x )′=2ln 1x C .(3x)′=3xlog 3e D .(x 2cos x )′=-2x sin x3.函数f (x )= a x 3+x +1有极值,则a 的范围是( )A .a >0B .a ≥0C .a <0D .a ≤04.已知函数f (x )的导数为,44)(3x x x f -='且图象过点(0,-5),当函数f (x )取得极大值-5时,x 的值应为( ) A .-1 B .0C .1D .±15.设()f x '是函数()f x 的导函数,将()y f x =和()y f x '=的图象画在同一个直角坐标系中,不可能正确的是( )6.()()x f x xx f 则设函数,122+-= ( )A .在(-∞,+∞)单调增加B .在(-∞,+∞)单调减少C .在(-1,1)单调减少,其余区间单调增加D .在(-1,1)单调增加,其余区间单调减少7.设f (x )、g(x )分别是定义在R 上的奇函数和偶函数,当x <0时,()()()()f xg x f x g x ''+>0.且g(3)=0.则不等式f (x )g(x )<0的解集是 ( )A .(-3,0)∪(3,+∞)B .(-3,0)∪(0, 3)C .(-∞,- 3)∪(3,+∞)D .(-∞,- 3)∪(0, 3)8.经过点)62,62(-M 且与双曲线22134y x -=有共同渐近线的双曲线方程为( ) A . B . C . D .A .18622=-x yB .16822=-x y C .16822=-y x D . 18622=-y x 9.已知椭圆125222=+y ax )5(>a 的两个焦点为1F 、2F ,且8||21=F F ,弦AB 过点1F ,则△2ABF 的周长为( )(A )10 (B )20 (C )241(D ) 41410.若存在过点(1,0)的直线与曲线3y x =和21594y ax x =+-都相切,则a 等于 (( ) A .1-或25-64 B .1-或214 C .74-或25-64D .74-或7二、填空题(25分,每题5分)11.函数y=2x 3-3x 2-12x+5在[0,3]上的最大值与最小值分别是 , 12.与直线250x y -+=平行的抛物线2y x =的切线方程为13.若f(x)=x 3+3ax 2+3(a +2)x +1有极大值和极小值,则a 的取值范围是_________. 14.离心率35=e ,一条准线为3=x 的椭圆的标准方程是________. 15.若曲线3()lnf x ax x =+存在垂直于y 轴的切线,则实数a 取值范围是_____________. 三、解答题: 16.(12分)设f(x)=x 3+3x,求函数f(x)的单调区间及其极值;17.(12分)设函数y =x 3+ax 2+bx +c 的图象如图所示,且与y =0在原点相切,若函数的极小值为-4,(1)求a 、b 、c 的值;(218.(12分)已知函数f(x)=4x 3+ax 2+bx +5在x=-1与x=32处有极值。
2011高二下第一次月考数学文科试题

2011高二下第一次月考数学文科试题江西省白鹭洲中学2010-2011学年度下学期第一次月考高二年级文科数学一、选择题(本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一项符合题目的要求。
) 1.“0m n >>”是“方程221mxny +=”表示焦点在y 轴上的椭圆”的 ( )A 充分而不必要条件B 必要而不充分条件C 充要条件D 既不充分也不必要条件 2.复数41(1)i+的值是( ) A .4i B .4i - C .4 D .-43.下列结论错误的是( )A .若“p 且q”与“⌝p 或q”均为假命题,则p 真q 假B .命题“存在0,2>-∈x x R x ”的否定是“对任意的0,2≤-∈x x R x ”C .“x =1”是“0232=+-x x”的充分不必要条件D .若“ba bm am <<则,22”的逆命题为真4.抛物线xy122=的准线与双曲线13922=-y x 的两条渐近线所围成的三角形的面积等于( )A .33 B .32C .2D .35.用火柴棒按下图的方法搭三角形:按图示的规律搭下去,则所用的火柴棒数na 与所搭三角形的个数n 之间的关系式可以是( C ) A.,3n a n= B. 13-=n anC. 12+=n anD. 12-=n an6.若椭圆经过原点,且焦点为)0,3(),0,1(21F F ,则离心率为 (C ) A .43 B .32 C .21 D .41 7. 设()ln f x x x =,若0()2f x '=,则0x =( B )A .2e B . e C .ln 2D . ln 22 8.函数51232)(23+--=x x xx f 在[0,3]上的最大值和最若y 对x 呈线性相关关系,则线性回归方程ˆybx a =+表示的直线一定过定点(4,5) .12.已知函数)(x f y =的图象在点))1(,1(f M 处的切线方程是221+=x y ,则)1()1(f f '+=__________ 13.复数Z 满足12,Z Z i +=+,那么Z=310.14.椭圆上点)3,2(M ,且两个焦点1F (-2,0),和2F (2,0),那么椭圆的标准方程是_______14822=+y x ___________15.类比平面内正三角形的“三边相等,三内角相等”的性质,可推出正四面体的下列哪些性质: (A )若各棱长相等,则同一顶点上的任两条棱的夹角都相等;(B )若各个面都是全等的正三角形,则相邻两个面所成的二面角都相等;(C )若各个面都是全等的正三角形,则同一顶点上的任两条棱的夹角都相等。
高二数学下学期第一次月考试题文00015

卜人入州八九几市潮王学校一中高二下学期第一次月考数学试卷〔文〕考试时长:120分钟总分值是:150分第I 卷〔选择题一共60分〕一、选择题〔本大题一一共12小题,每一小题5分,一共60分,在每一小题给出的四个选项里面,只有一项为哪一项哪一项符合题目要求的〕1.复数i i-1(i 是虚数单位)的实部是() A .21-B .21C .1-D .12.R,x ∃∈使得210xx ++<〞的否认是()A .R,x ∀∈均有210x x ++<B .R,x ∀∈均有210x x ++≥ C .R,x ∃∈使得210xx ++≥D .R,x ∀∈均有210x x ++>3.x,y 的取值如下表所示,假设y 与x 线性相关,且a x y +=5.0^,那么=a ()x0 1 3 4 y2.24.34.86.7A .5.3B .2.2C .8.4D .2.3 4.执行如下列图的程序框图,假设输入2x =,那么输出y 的值是()A .2B .5C .11D .235.袋中装有完全一样的5个小球,其中有红色小球3个,黄色小球2个,假设不放回地依次摸出2个小球,那么在第一次摸出红球的条件下,第二次摸出红球的概率是()A .310B .35C .12D .14 6.由“正三角形的内切圆切于三边的中点〞可类比猜想:正四面体的内切球切于四个面() A .各正三角形内一点B .各正三角形的某高线上的点 C .各正三角形的中心D .各正三角形外的某点7.等差数列{}n a 满足92742724=++a a a a ,那么其前10项之和为()A .-9B .-15C .15D .±152352<+--x x 的解集为〔〕A.∅B.⎪⎭⎫⎝⎛25,0 C.()5,0 D.()10,0 9.“3≥m 〞是“关于x 、y 的不等式组020100x x y x y x y m ≥⎧⎪-≤⎪⎨-+≥⎪⎪+-≤⎩表示的平面区域为三角形〞的〔〕不必要条件不充分条件 C.充要条件充分也不必要条件10.四个小动物换座位,开场是鼠、猴、兔、猫分别坐1、2、3、4号位上〔如图〕,第一次前后排动物互换座位,第二次左右列动物互换座位,这样交替进展下去,那么第202次互换座位后,小兔坐在第几号座位上 A.1B.2C.3D.411.双曲线)0,0(12222>>=-b a by a x 的左、右焦点分别为21,F F ,假设P 为其上一点,且212PF PF =,321π=∠PF F ,那么双曲线的离心率为()A .2B .2C .3D .312.函数()k x x x f 2ln +-=,在区间1[,]e e上任取三个数,,a b c 均存在以()f a ,()f b ,()f c 为边长的三角形,那么k 的取值范围是〔〕A .(1)-+∞,B .()1,∞-C .()3,-∞-e D .⎪⎭⎫⎝⎛+∞-,23e 第II 卷〔非选择题一共90分〕二、填空题〔本大题一一共4个小题,每一小题5分,一共20分〕iiz -+=131〔i 为虚数单位〕,那么z =.14.0,0x y >>,221=+yx ,那么2x y +的最小值为. x y 42=,直线l 的方程为04=+-y x ,抛物线上有一动点P 到y 轴的间隔为1d ,到直线l 的间隔为2d ,那么21d d +的最小值为.16.()x x x f +=331,R x ∈,假设至少存在一个实数x 使得()()012<-+-ax f x a f 成立,那么a 的取值范围为.三、解答题〔一共70分,请在答题卡指定区域内答题。
江西省德兴一中2010-2011学年高二下学期第一次月考(英语)

学必求其心得,业必贵于专精2010—2011学年度第二学期第一次月考高二英语试卷第一部分:听力(共两节,满分30分)第一节(共5小题;每小题1。
5分,满分7。
5分)请听下面5段对话,选出最佳选项。
1. What are the two speakers probably doing?A. Playing a ball game。
B. Cheering for the Nanjing team.C. Watching a ball game.2. What was the score at the end of the game?A. 35:17.B. 35:70。
C.53:70。
3。
Who is the man probably talking to?A. A teacher. B。
A doctor. C。
A mailman。
4。
Why won't the woman go to the concert?A. She will go to work.B. She will visit her friend。
C。
She will look after her sister.5。
What does the woman mean?A。
The transportation for the trip is free.B. The whole class enjoy going on the trip。
C. Some people may not go on the trip。
第二节(共15小题;每小题1.5分,满分7.5分)请听下面第5段对话或独白,选出最佳选项。
请听第6段材料,回答第6—7题。
6。
What does the man want to do?A。
Have dinner with the woman. B. Work overtime. C. Go home early。
7. When will the man pick up the woman on Friday?A。
江西省德兴一中、横峰中学、铅山一中、弋阳一中四校2012-2013学年高二下学期第一次月考数学(文)试题

一、选择题:(本题包括10小题,共50分,每小题只有一个选项符合题意)1.已知全集{1,2,3,4,5},{1,2,3},{3,4},()U U A B C A B ===⋃=则 ( )A .{3}B .{5}C .{1,2,4,5}D .{1,2,3,4}2.一组数据中,每一个数都减去80,得到一组新数据,若求得新数据的平均数是12.,方差是44.,则原来数据的平均数和方差分别为( ) A .812., 44. B .788., 44. C .812., 844. D .788.,756. 3.已知流程图如右图所示,该程序运行后,为使输出b 的值为16,则循环体的判断框内①处应填的是 ( )A .2B .3C .4D .164.已知3()z =⋅-,那么复数z 在平面内对应的点位于 ( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限5.θ是第三象限角,方程x 2+y 2sin θ=cos θ 表示的曲线是( ) A .焦点在y 轴上的双曲线 B . 焦点在y 轴上的椭圆 C . 焦点在x 轴上的双曲线 D .焦点在x 轴上的椭圆6.已知命题p :关于x 的函数234y x ax =-+在[1,+∞)上是增函数,命题q :关于x 的函数(21)xy a =-在R 上为减函数,若p 且q 为真命题,则a 的取值范围是 ( )A .23a ≤B .102a << C .1223a <≤ D .112a << 7.下列判断正确的是( )A. 若命题p 为真命题,命题q 为假命题,则命题“p 且q ”为真命题B. 命题“若0xy =,则0x =”的否命题为“若0xy =,则0x ≠”C. “1sin 2α=”是“ 6πα=”的充分不必要条件 D. 命题“对任意的x ∈R,2x >0”的否定是“存在x 002,x R ∈≤0”8.设双曲线22221(0,0)x y a b a b-=>>的左、右焦点分别是1F 、2F ,过点2F 的直线交双曲线右支于不同的两点M 、N .若△1MNF 为正三角形,则该双曲线的离心率为 ( )ABCD9.已知函数()f x 的导函数为()f x ',且满足2()2(1)f x xf x '=+,则(1)f '=( ) A .1- B .2- C .1 D .2 10.已知函数,10,ln )(<<<<=t s r x x g 则( )A . 无法确定B .rr g s s g t t g )()()(<< C . t t g s s g r r g )()()(<< D . rr g t t g s s g )()()(<< 二、填空题:(共5小题,每题5分,共25分) 11.如图所示,函数()y f x =的图象在点P 处的切线方程是8y x =-+,则(5)(5)f f '+= 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
德兴一中2010-2011学年下学期第一次月考高二文科数学试卷共计150分,时间120分钟.一、选择题:本题共有10个小题,每小题5分,共50分;在每小题给出的四个选项中只有一项是正确的.1.设全集U={1,2,3,4,5},集合A={1,a-2,5},∁U A={2,3},则a 的值为( ) A.3 B.4 C.5 D.62.已知复数i b i i a -=-)2((,a b R ∈),则a b += () A.14 B. 12C. 1D. 2 3.如图所示,U 是全集,M 、N 、S 是U 的子集,则图中阴影部分所示的集合是( ) A.(∁U M ∩∁U N)∩SB.(∁U (M ∩N))∩SC.(∁U N ∩∁U S)∪MD.(∁U M ∩∁U S)∪N4.若A 、B 、C 为三个集合,A B B C ⋃=⋂,则一定有() A.A C ⊆ B.C A ⊆ C.A C ≠ B.A φ=5.使不等式2x 2-5x-3≥0成立的一个充分不必要条件是( ) A.x≥0 B.x<0或x>2C. x≤-12或x≥3 D. x∈{-1,3,5}6. 已知命题p:“若a>b>0,则log 11221a log <+b”,其命题p 的原命题、逆命题、否命题、逆否命题中为真命题的个数为( ) A.0 B.1 C.2 D.47. 已知集合A={(x,y)|y=lg(x+1)-1},B={(x,y)|x=m},若A∩B=∅,则实数m 的取值范围是( )A.m<1B.m≤1C.m<-1D.m≤-18. 已知函数()()()40,40.x x x f x x x x +<⎧⎪=⎨-≥⎪⎩,, 则函数()f x 的零点个数为 ( )A .1B .2 C.3 D.49.设定义在R 上的函数()f x 满足()()213f x f x ⋅+=,若()12f =,则()99f =( )A.13 B.132 C.2 D.21310.设p:y=c x 是R 上的单调递减函数;q:函数g(x)=lg(2cx 2+2x+1)的值域为R .如果“p 且q”为假命题,“p 或q”为真命题,则正实数c 的取值范围是()1.,12A ⎛⎫ ⎪⎝⎭1.,2B ∞⎛⎫+ ⎪⎝⎭C.10,2⎛⎤ ⎥⎝⎦∪[1,+∞) 1.0,2D ⎛⎫⎪⎝⎭二、填空题:本大题共5小题,每小题5分,共25分.11.已知则12.已知f(x+9)=4x 2+4x+3(x ∈R),那么函数f(x)的最小值为____. 13.在平面直角坐标系xOy 中,点P 在曲线C :y =x 3-10x +3上,且在第二象限内,已知曲线C 在点P 处的切线的斜率为2,则点P 的坐标为________. 14. 若函数g(x)=lg(x 2-ax+3a)在[2, +∞)是增函数,则实数a 的取值范围是. 15.下列命题:①若定义D 内任意实数x 都有f(x+1)=f(x-1),则y=f(x)是周期函数;②1y x=-在定义域内是增函数;③函数()f x =④既是奇函数又是偶函数的函数一定是f (x)=0 ()R x ∈;⑤函数f (x )若在定义D 内的任意实数x 都有f (x +2)= f (2-x ),则f (x )图象关于直线x =2对称;其中正确命题是。
三、解答题:本大题共6小题,共75分,解答题应写出文字说明、证明过程或演算步骤。
16.(本小题满分12分)21,0,,0,0,)0,(f x x x x x π+>⎧=<=⎪⎨⎪⎩(){[1]}________.f f f -=已知函数f(x)=ax2+a2x+2b-a3,当x∈(-2,6)时,f(x)>0,当x∈(-∞,-2)∪(6,+∞)时,f(x)<0,(1)求f(x)的解析式.(2)求f(x)在区间[1,10]上的最值。
17.(本小题满分12分)已知f(x)、g(x)分别为奇函数、偶函数,且f(x)+g(x)=2x+2x,求f(x)、g(x)的解析式.18.(本小题满分12分)已知命题p:函数f(x)=loga|x|在(0,+∞)上单调递增,命题q:关于x的方程x2+2x+loga 32=0的解集只有一个子集,p∨q为真,(¬p)∨(¬q)也为真,求实数a的取值范围.19.(本小题满分12分)已知函数f(x)=-13x3+x2+ax+b(a,b∈R).(1)若a=3,试确定函数f(x)的单调区间;(2)若函数f(x)在其图象上任意一点(x0,f(x0))处切线的斜率都小于2a2,求a的取值范围.20.(本小题满分13分)已知双曲线C:2222x y a b=1(a>0,b>0)(1)求双曲线C 的方程;(2)已知直线x-y+m=0与双曲线C 交于不同的两点A,B,且线段AB 的中点在抛物 线y 2=4 x 上,求m 的值.21.(本小题满分14分)已知f(x)=x 2+bx +c 为偶函数,曲线y =f(x)过点(2,5),g(x)=(x +a)f(x). (1)求f(x)的解析式;(2)若曲线y =g(x)有斜率为0的切线,求实数a 的取值范围; (3)若当x =1时,函数y =g(x)取得极值,确定y =g(x)的单调区间.德兴一中2010-2011学年下学期第一次月考高二文科数学试卷参考答案一、 选择题(本大题共10小题,每小题5分,共50分)二、填空题11.2π+1 12. 2 13.P(-2,15). 14.(]4,4- 15.①③⑤三.解答题 16.解:(1)由题意得a<0,且x =-2,x =6是方程f(x)=0的两个根,由韦达定理得326226ab aa -+=-⎧⎪⎨--=⨯⎪⎩得48a b =-⎧⎨=-⎩ ∴.f(x)=-4x 2+16x +48…………………6分(2)f(x)=-4x 2+16x +48=-4(x -2)2+64∴f max (x)=f(2)=64f min (x)=f(10)=-192 …………………12分17.解:∵f (x )+g (x )=2x +2x ①∴f (-x )+g (-x )=2-x -2x ,…………………3分又f (x )为奇函数,g (x )为偶函数, ∴-f (x )+g (x )=2-x -2x ②…………………6分将①②联立,得g (x )=2x +2-x 2,f (x )=2x -2-x2+2x.…………………12分18.解:当命题p 是真命题时,应有a>1;…………………2分当命题q 是真命题时,关于x 的方程x 2+2x+log a32=0无解, 所以Δ=4-4log a32<0,解得1<a<32.…………………6分由于p∨q 为真,所以p 和q 中至少有一个为真,又(¬p)∨(¬q)也为真,所以¬p 和¬q 中至少有一个为真,即p 和q 中至少有一个为假,故p 和q 中一真一假.…………………8分p 假q 真时,a 无解;…………………10分p 真q 假时,a≥32.综上所述,实数a 的取值范围是[32,+∞).…………………12分 19.解:(1)f (x )=-13x 3+x 2+3x +b .f ′(x )=-x 2+2x +3,令f ′(x )>0,得-1<x <3, 令f ′(x )<0得x <-1或x >3.故f (x )的单调增区间为(-1,3),减区间为(-∞,-1),(3,+∞).…………6分 (2)∵f ′(x )=-x 2+2x +a ,由题意得 -x 2+2x +a <2a 2对任意x ∈R 成立. 即x 2-2x >a -2a 2对任意x ∈R 恒成立. 设g (x )=x 2-2x =(x -1)2-1,∴g (x )min =-1, ∴-1>a -2a 2,得a>1或a<-12.…………………12分20解:(1)由题意,得b c a⎧=⎪⎨=⎪⎩…………………3分∵b 2=c 2-a 2=2,∴a 2=1,∴所求双曲线C 的方程为x 2-21.2y =…………………6分(2)设A 、B 两点的坐标分别为(x 1,y 1),(x 2,y 2),线段AB 的中点为M(x 0,y 0),由22120y x x y m ⎧-=⎪⎨⎪-+=⎩得x 2-2mx-m 2-2=0(判别式Δ>0), ∴x 0=122x x +=m,y 0=x 0+m=2m,…………………10分 ∵点M(x 0,y 0)在抛物线y 2=4x 上, ∴m=1或m=0…………………13分21.解:(1)∵f(x)为偶函数,∴b =0.…………………2分 又f(x)过(2,5),∴4+c =5,得c =1.∴f(x)=x 2+1 …………………4分 (2)又g(x)=(x +a)f(x)=(x +a)(x 2+1)=x 3+ax 2+x +a. 由题意得g ′(x)=3x 2+2ax +1=0有解,∴Δ=4a 2-12>0,得a>3或a<- 3.…………………9分(3)由(1)知g ′(x)=3x 2+2ax +1,由题意得g ′(1)=0,得a =-2,经检验当a =-2时,y =g(x)取得极值符合题意,由g ′(x)=3x 2-4x +1>0,得x>1或x<13,由g ′(x)<0,得13<x<1,故g(x)的单调增区间为⎝⎛⎭⎫-∞,13,(1,+∞),单调减区间为⎝⎛⎭⎫13,1.…………………14分。
