阿氏圆专项训练-答案

合集下载

中考数学阿氏圆问题专项训练

阿氏圆问题专项训练1．如图，在Rt△ABC中，∠ACB＝90°，CB＝4，CA＝6，⊙C半径为2，P为圆上一动点，连接AP，BP，则AP+BP的最小值为（）A．B．6 C．2 D．4【答案】A【解答】解：如图1，连接CP，在CB上取点D，使CD＝1，则有＝＝，又∵∠PCD＝∠BCP，∴△PCD∽△BCP，∴＝，∴PD＝BP，∴AP+BP＝AP+PD．要使AP+BP最小，只要AP+PD最小，当点A，P，D在同一条直线时，AP+PD 最小，即：AP+BP最小值为AD，在Rt△ACD中，CD＝1，AC＝6，∴AD＝＝，AP+BP的最小值为，故选：A．2．如图，在正方形ABCD中．AB＝8，点P是正方形ABCD内部的一点，且满足BP＝4，则PD+PC的最小值是（）A．6 B．8 C．10 D．12【答案】C【解答】解：在BC边上取一点E，使BE＝2，连接DE，如图∵ABCD是正方形，AB＝8∴AB＝BC＝CD＝8，∠BCD＝90°∵BP＝4∴，∴且∠PBC＝∠PBC∴△PBE∽△BCP∴∴PE＝PC∴PD+PC＝PD+PE在Rt△DCE中，CD＝8，CE＝BC﹣BE＝6∴DE＝＝10∵PD+PE≥DE∴PD+PE≥10∴PD+PC的最小值是10故选：C．3．如图，在扇形COD中，∠COD＝90°，OC＝3，点A是OC中点，OB＝2，点P 是为CD上一点，则PB+2PA的最小值为．【答案】【解答】连接OP，延长OC至点E，使得OE＝6，则＝，，∴，∵∠AOP＝∠AOP，∴△AOP∽△POE，∴，即2PA＝PE，∴PB+2PA＝PB+PE，∴当E、P、B三点共线时，PB+PE最小，∴PB+2PA的最小值为BE＝＝．故答案为：．4．【新知探究】新定义：平面内两定点A，B，所有满足＝k（k为定值）的P点形成的图形是圆，我们把这种圆称之为“阿氏圆”【问题解决】如图，在△ABC中，CB＝4，AB＝2AC，则△ABC面积的最大值为．【答案】网版权所有【解答】解：以A为顶点，AC为边，在△ABC外部作∠CAP＝∠ABC，AP与BC 的延长线交于点P，∵∠CAP＝∠ABC，∠BPA＝∠APC，AB＝2AC，∴△APC∽△BPA，，∴BP＝2AP，CP＝AP，∵BP﹣CP＝BC＝4，∴2AP﹣AP＝4，解得：AP＝，∴BP＝，CP＝，即点P为定点，∴点A的轨迹为以点P为圆心，为半径的圆上，如图，过点P作BC的垂线，交圆P与点A1，此时点A1到BC的距离最大，即△ABC的面积最大，S＝BC•A1P＝×4×＝．△ABC故答案为：．5．如图①，在正方形ABCD中，AB＝1，点E，F为AD边上的两点，且AE＝DF，连接CF交BD于点G，连接AG交BE于点H．（1）求证：AG⊥BE；（2）如图②，点M为DC的中点，连接DH，M，求DH+HM的最小值；（3）连接BM，当点E与点F重合时，求tan∠EBM的值．【解答】（1）证明：∵四边形ABCD是正方形，∴AD＝CD，∠ADG＝∠CDG＝45°，∵DG＝DG，∴△ADG≌△CDG（SAS），∴∠DAG＝∠DCG，∵四边形ABCD是正方形，∴AB＝CD，∠BAE＝∠CDF＝90°，∵AE＝DF，∴△ABE≌△CDF（SAS），∴∠ABE＝∠DCF，∴∠DAG＝∠ABE，∵∠BAE＝90°，∴∠ABE+∠AEB＝90°，∴∠DAG+∠AEB＝90°，∴∠AHE＝90°，∴AG⊥BE；（2）如图1，∵∠ABH＝90°，∴点H在以AB的中点O为圆心，为半径的圆上运动，连接OH，OM，在OM上截取ON＝，连接HN，∵OA＝，DM＝，AB＝CD，∴OA＝DM，∵AB∥CD，∴四边形AOMD是平行四边形，∵∠BAD＝90°，∴▱AOMD是矩形，∴OM＝BC，∠DMN＝90°，∴OM＝AB＝2OA，∴，∵∠HON＝∠MOH，∴△HON∽△MOH，∴＝，∴HN＝，∴DH+＝DH+HN，∴当D、H、N共线时，DH+HN最小，最小值为DN的长，∵DN＝＝＝，∴DH+的最小值为：；（3）如图2，在Rt△CBM和Rt△DCE中，tan∠CBM＝，tan∠DCE＝，∴∠CBM＝∠DCE，∵∠BCM＝90°，∴∠CBM+∠CMB＝90°，∴∠DCE+∠CMB＝90°，∴∠BQE＝∠CQM＝90°，设CM＝DE＝DM＝a，则CE＝BM＝a，∴sin∠DEC＝，∴QM＝CM•sin∠DEC＝a，∴CQ＝2QM＝a，∴EQ＝CE﹣CQ＝a﹣＝a，BQ＝BM＝QM＝﹣a＝a，∴tan∠EBM＝．6．如图，已知抛物线y＝﹣x2+x+3与x轴交于A，B两点（A在点B的左侧），与y轴交于点C，⊙O与x轴交于点E（2，0），点P是⊙O上一点，连接CP，BP，求BP+CP的最小值．【解答】解：如图，在OC上取一点T，使得OT＝，连接PT，BT，OP．由题意C（0，3），E（2，0），A（﹣1，0），B（4，0）∴OE＝2，OC＝3，OB＝4，OA＝1，∴OP2＝OT•OB，∴＝，∵∠POT＝∠COP，∴△POT∽△COP，∴＝＝＝，∴PT＝PC，∴PB+PC＝BP+PT≥BT，在Rt△BOT中，OB＝4，OT＝，∴BT＝＝＝，∴ABP+PC≥，∴BP+PC的最小值为．。

最值系列6之阿氏圆问题(一)-学生版

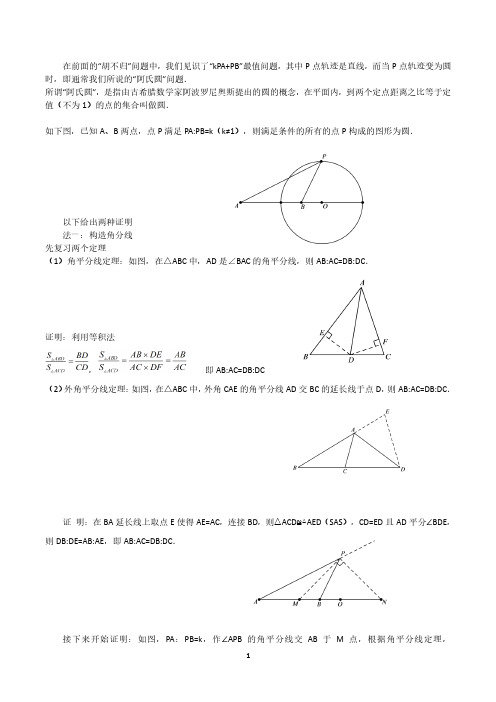
在平面上，到线段两端距离相等的点，在线段的垂直平分线上，即对于平面内的定点A、B，若平面内有一动点P 满足PA:PB＝1，则P 点轨迹为一条直线（即线段AB 的垂直平分线），如果这个比例不为1，P 点的轨迹又会是什么呢？两千多年前的阿波罗尼斯在其著作《平面轨迹》一书中，便已经回答了这个问题。

接下来，让我们站在巨人的肩膀上，一起探究PA：PB＝k（k ≠1）时P 点的轨迹.对于平面内的定点A、B，若在平面内有一动点P 且P 满足PA：PB＝k（k≠1），则动点P 的轨迹就是一个圆，这个圆被称为阿波罗尼斯圆，简称“阿氏圆”，如图所示：借助画板工具我们发现，动点P 在运动过程中，PA、PB 的长度都在变化，但是PA：PB 的比值始终保持不变，接下来我们在深入研究一下！法一：首先了解两个定理（1）角平分线定理：如图，在△ABC 中，AD 是∠BAC 的角平分线则AB DBAC DC=．（2）外角平分线定理：如图，在△ABC 中，外角CAE 的角平分线AD 交BC 的延长线于点D，则AB DBAC DC=．证明：在BA 延长线上取点E 使得AE=AC，连接BD，则△ACD≌△AED（SAS），CD=ED 且AD 平分∠BDE，则DB AB DE AE =，即AB DBAC DC=．接下来开始证明步骤：如图，PA：PB=k，作∠APB的角平分线交AB于M点，根据角平分线定理，MA PA kMB PB==，故M 点为定点，即∠APB的角平分线交AB于定点；作∠APB外角平分线交直线AB于N点，根据外角平分线定理，NA PA kNB PB==，故N点为定点，即∠APB外角平分线交直线AB于定点；又∠MPN=90°，定边对定角，故P点轨迹是以MN为直径的圆．法二：建系不妨将点A、B两点置于x轴上且关于原点对称，设A（-m，0），则B（m，0），设P（x，y），PA=kPB，即：()()()()()()()()222222222222222222222122102201x m y k x m yx m y k x m k yk x y m k m x k mm k mx y x mk++=-+++=-+-+-++-=++-+=-解析式满足圆的一般方程，故P点所构成的图形是圆，且圆心与AB共线．例1.如图，正方形ABCD的边长为4，圆B的半径为2，点P是圆B上一动点，则的最小值为，的最大值为.【答案】最小值为5，最大值为5例2.如图，在Rt△ABC 中，∠C=90°，AC=4，BC=3，以点C 为圆心，2为半径作圆C，分别交AC、BC 于D、E 两点，点P 是圆C 上一个动点，则12PA PB +的最小值为__________．【分析】注意到圆C 半径为2，CA=4，连接CP，构造包含线段AP 的△CPA，在CA 边上取点M 使得CM=2，连接PM，可得△CPA∽△CMP，故PA：PM=2:1，即PM=12PA ．【总结】（1）这里为什么是12PA ？答：因为圆C 半径为2，CA=4，比值是1:2，所以构造的是12PA ，也只能构造12PA ．（2）如果问题设计为PA+kPB 最小值，k 应为多少？答：根据圆C 半径与CB 之比为2:3，k 应为23．例3.如图，在ABC ∆中，∠ACB=90°，BC=12，AC=9，以点C 为圆心，6为半径的圆上有一个动点D．连接AD、BD、CD，则2AD+3BD 的最小值是．【分析】首先对问题作变式2AD+3BD=233AD BD ⎛⎫+ ⎪⎝⎭，故求23AD BD +最小值即可．考虑到D 点轨迹是圆，A 是定点，且要求构造23AD ，条件已经足够明显．当D 点运动到AC 边时，DA=3，此时在线段CD 上取点M 使得DM=2，则在点D 运动过程中，始终存在23DM DA =．问题转化为DM+DB 的最小值，直接连接BM，BM 长度的3倍即为本题答案．例4.如图，半圆的半径为1，AB为直径，AC、BD为切线，AC＝1，BD＝2，点P为弧AB上一动的最小值.解：如图所示，连接PB、CO，AD与CO相交于点M，当A、P、D的值最小.∵AB＝BD＝2,BD是⊙O的切线,∴∠ABD＝90º,∠BAD＝∠D＝45º,∵AB是⊙O直径,∴∠APB＝90º,∴∠PAB＝∠PBA＝45º,∴PA＝PB,PO⊥AB,∵AC是⊙O的切线,∴AC⊥AB,∴AC∥PO,∠CAO＝90º∵AC＝PO＝1,∴四边形AOPC是平行四边形,而OA＝OP,∠CAO＝90º,∴四边形AOPC是正方形,PC＋PD＝PM＋PD＝DM,∵DM⊥OC,PC＋PD的值最小，最小值为.练习题部分：1.如图，在平面直角坐标系中，点A（4，0），B（4，4），点P在半径为2的圆O上运动，则的最小值是.，，MO＝2，∠POM＝90º，Q则的最小值为.3.如图，在平面直角坐标系中，A（2，0）、B（0，2）、C（4，0）、D（3，2），P是△AOB外部的第一象限内一动点，且∠BPA＝135º，则2PD＋PC的最小值是.4．（1）如图1，已知正方形ABCD的边长为4，圆B的半径为2，点P是圆B上的一个动点，的最小值为，PD﹣PC的最大值为.（2）如图2，已知正方形ABCD的边长为9，圆B的半径为6，点P是圆B上的一个动点，那么PD＋的最小值为，PD﹣PC的最大值为．（3）如图3，已知菱形ABCD的边长为4，∠B＝60°，圆B的半径为2，点P是圆B上的一个动点，那么PD＋PC的最小值为，PD﹣PC的最大值为．5．如图，在△ACE中，CA＝CE，∠CAE＝30°，⊙O经过点C，且圆的直径AB在线段AE上．（1）证明：CE是⊙O的切线；（2）若△ACE中AE边上的高为h，试用含h的代数式表示⊙O的直径AB；（3）设点D是线段AC上任意一点（不含端点），连接OD，当CD＋OD的最小值为6时，求⊙O的直径AB的长．6.如图，在Rt△ABC中，∠A＝30°，AC＝8，以C为圆心，4为半径作⊙C．（1）试判断⊙C与AB的位置关系，并说明理由；（2）点F是⊙C上一动点，点D在AC上且CD＝2，试说明△FCD∽△ACF；（3）点E是AB边上任意一点，在（2）的情况下，试求出EF＋FA的最小值.7.如图，点A、B上，且OA＝OB＝6，且OA⊥OB，点C是OA的中点，点D在OB上，且OD＝4，动点P（1）求2PC＋PD的最小值；（2）求2PC＋3PD的最小值.8.问题提出：如图1，在等边△ABC中，AB＝12，⊙C半径为6，P为圆上一动点，连结AP，BP，求AP＋BP的最小值．（1）尝试解决：为了解决这个问题，下面给出一种解题思路：如图2，连接CP，在CB上取点D，使CD＝3，则有＝＝，又∵∠PCD＝∠BCP，∴△PCD∽△BCP，∴＝，∴PD＝BP，∴AP＋BP＝AP＋PD．请你完成余下的思考，并直接写出答案：AP＋BP的最小值为．（2）在“问题提出”的条件不变的情况下，AP＋BP的最小值为．（3）自主探索：如图3，矩形ABCD中，BC＝7，AB＝9，P为矩形内部一点，且PB＝3，AP ＋PC的最小值为．（4）拓展延伸：如图4，扇形COD中，O为圆心，∠COD＝120°，OC＝4，OA＝2，OB＝3，点P是上一点，求2PA＋PB的最小值，画出示意图并写出求解过程．（5）拓展延伸：已知扇形COD中，∠COD＝90°，OC＝6，OA＝3，OB＝5，点P是上一点，求2PA＋PB的最小值．。

专题4：阿氏圆练习

专题4 阿氏圆练习1．如图，在Rt △ABC 中，∠ACB ＝90°，CB ＝7，CA ＝9，⊙C 半径为3，P 为⊙C 上一动点，连结AP ，BP ，则13AP ＋BP 的最小值为（） A . 7 B . 5 2 C . 4＋10 D . 2132．如图，在Rt △ABC 中，CB ＝4，CA ＝5，⊙C 半径为2，P 为圆上一动点，连结AP ，BP ，则AP ＋12BP 的最小值为__________．PC BA3．如图，正方形ABCD 边长为22，内切圆O 上一动点P ，连接AP 、DP ，则AP +22PD 的最小值为______． O PDC BAP CB A 专题小结：所谓阿圆，就是动点到两定点距离之比为定值，那么动点的轨迹就是圆，这个圆，称为阿波罗尼斯圆，简称为阿圆．其本质就是通过构造母子相似，化去比例系数，转化为两定一动将军饮马型求最值，难点在于如何构造母子相似．4．如图，等边三角形ABC 边长为43，圆O 是△ABC 的内切圆，P 是圆O 上一动点，连接PB 、PC ，则BP ＋12CP 的最小值为______________．5．如图，在平面直角坐标系中，M (6，3)，N (10，0)，A (5，0)，点P 为以OA 为半径的圆O 上一动点，则PM ＋12PN 的最小值为_______________ yxO A N MP6．（反向操作）如图，∠AOB =90°，OA =OB =1，圆O 的半径为2，P 是圆O 上一动点，求P A +2PB 的最小值．B A PO7．（反向操作）已知扇形COD 中，∠COD =90°，OC =6，OA =3，OB =5，点P 是弧CD 上一点，求2P A +PB 的最小值．O DAB P CP O CB A8．(2019日照)如图1,在平面直角坐标系中,直线y=-5x+5与x 轴,y 轴分别交于A,C 两点,抛物线y=x 2+bx+c 经过A,C 两点,与x 轴的另一交点为B(1)求抛物线解析式及B 点坐标;(2)若点M 为x 轴下方抛物线上一动点,连接MA 、MB 、BC,当点M 运动到某一位置时,四边形AMBC 面积最大,求此时点M 的坐标及四边形AMBC 的面积(3)如图2,若P 点是半径为2的⊙B 上一动点,连接PC 、PA,当点P 运动到某一位置时,PC+21PA 的值最小,请求出这个最小值,并说明理由（1）（2）S=，m=3,即M(3,-4)时,四边形AMBC 面积最大,最大面积等于18 （3）9.（2017•兰州）如图，抛物线y=﹣x2+bx+c与直线AB交于A（﹣4，﹣4），B（0，4）两点，直线AC：y=﹣x﹣6交y轴于点C．点E是直线AB上的动点，过点E作EF⊥x轴交AC 于点F，交抛物线于点G．（1）求抛物线y=﹣x2+bx+c的表达式；（2）连接GB，EO，当四边形GEOB是平行四边形时，求点G的坐标；（3）①在y轴上存在一点H，连接EH，HF，当点E运动到什么位置时，以A，E，F，H为顶点的四边形是矩形？求出此时点E，H的坐标；②在①的前提下，以点E为圆心，EH长为半径作圆，点M为⊙E上一动点，求AM+CM它的最小值．10.（2016•济南）如图1，抛物线y=ax2+（a+3）x+3（a≠0）与x轴交于点A（4，0），与y轴交于点B，在x轴上有一动点E（m，0）（0＜m＜4），过点E作x轴的垂线交直线AB于点N，交抛物线于点P，过点P作PM⊥AB于点M．（1）求a的值和直线AB的函数表达式；（2）设△PMN的周长为C1，△AEN的周长为C2，若=，求m的值；（3）如图2，在（2）条件下，将线段OE绕点O逆时针旋转得到OE′，旋转角为α（0°＜α＜90°），连接E′A、E′B，求E′A+E′B的最小值．11.（2018•东台市一模）如图，抛物线y=﹣x2+bx+c（b为常数）与x轴交于A、C两点，与y轴交于B点，直线AB的函数关系式为y=x+．（1）求该抛物线的函数关系式与C点坐标；（2）已知点M（m，0）是线段OA上的一个动点，过点M作x轴的垂线l分别与直线AB 和抛物线交于D、E两点，当m为何值时，△BDE恰好是以DE为底边的等腰三角形？（3）在（2）问条件下，当△BDE恰好是以DE为底边的等腰三角形时，动点M相应位置记为点M′，将OM′绕原点O顺时针旋转得到ON（旋转角在0°到90°之间）；①探究：线段OB上是否存在定点P（P不与O、B重合），无论ON如何旋转，始终保持不变，若存在，试求出P点坐标；若不存在，请说明理由；②试求出此旋转过程中，（NA+NB）的最小值．阿波罗尼斯圆在前面的“胡不归”问题中，我们见识了“kPA+PB ”最值问题，其中P 点轨迹是直线，而当P 点轨迹变为圆时，即通常我们所说的“阿氏圆”问题．所谓“阿氏圆”，是指由古希腊数学家阿波罗尼奥斯提出的圆的概念，在平面内，到两个定点距离之比等于定值（不为1）的点的集合叫做圆．【在初中阶段的应用】阿氏圆主要应用于求系数不相同的线段和的最小值【基本解法】：构造相似阿氏圆一般解题步骤：PC+kPD1、连接动点至圆心O(将系数不为1的线段的两个端点分别与圆心相连接)，则连接OP 、OD ；2、计算出所连接的两条线段OP 、OD 长度3、计算两条线段长度的比m OD OP =；4、在OD 上取点M 使得m OP=OM ；5、连接CM ，与圆O 的交点即为点P.【例题】（2017·南山十校联考）如图，若⊙O 的半径为，PO=，MO=2，∠POM=90°，点Q 在⊙O 上运动，求PQ+QM 的最小值.【简释】：连接QO 、QM ，有22=OM OQ ，在OM 上取M ’使得22'Q =OQ M 显然有△QM'O ～△MQO ，∴QM'=QM∴PQ+QM ≧PM'==（1）在Rt △OAB 中，OA=8，OB=6，⊙O 的半径为4，P 为⊙O 上一动点，求PA+PB 的最小值.（2）如图，⊙O 是正方形ABCD 的内切圆，AB=4，点P 是⊙O 上一动点，则AP+DP 的最小值是________变式：如图，正方形ABCD 的边长为4，其内切圆上有一点E ，求DE+AE 的最小值（3）如图，AB=BD=2AC=2，AC、BD分别切半圆于A、B，求CF+DF的最小值（4）如图，正方形ABCD的边长为4，P是BD上一点，BG⊥AP，点M、N分别是线段CD、BC的中点，求NG+MG的最小值.（5）正方形ABCD的边长为4，以D为圆心，2为半径作圆，①求2BE+AE的最小值②此时△ABE的面积（6）菱形ABCD 边长为2，∠ABC=60°，圆A 的半径为3，BC 与圆相切于点E ，点P 在圆A 上运动，求PB+23PD 的最小值专题小结：所谓阿圆，就是动点到两定点距离之比为定值，那么动点的轨迹就是圆，这个圆，称为阿波罗尼斯圆，简称为阿圆．其本质就是通过构造母子相似，化去比例系数，转化为两定一动型求最值，难点在于如何构造母子相似．（7）【结合隐形圆】已知A（4，0），B(0，4)，C（8，0），D（6，4），点P是△AOB外部第一象限一动点，∠BPA=135°，求2PD+PC的最小值【点在圆内，反向操作】（8）如图，圆O半径为2，AO=BO=1，∠AOB=90°，求BP+2AP的最小值【练习】1.如图，在Rt △ABC 中，∠C=90°，AC=4，BC=3，以点C 为圆心，2为半径作圆C ，分别交AC 、BC于D 、E 两点，点P 是圆C 上一个动点，则12PA PB +的最小值为__________． E A B C D P2.如图，在ABC ∆中，∠ACB=90°，BC=12，AC=9，以点C 为圆心，6为半径的圆上有一个动点D ．连接AD 、BD 、CD ，则2AD+3BD 的最小值是．A B C D3.如图，已知正方ABCD 的边长为4，圆B 的半径为2，点P 是圆B 上的一个动点，则12PD PC -的最大值为_______．A B CDP【分析】当P 点运动到BC 边上时，此时PC=2，根据题意要求构造12PC ，在BC 上取M 使得此时PM=1，则在点P 运动的任意时刻，均有PM=12PC ，从而将问题转化为求PD-PM 的最大值连接PD ，对于△PDM ，PD-PM ＜DM ，故当D 、M 、P 共线时，PD-PM=DM 为最大值．A B CDPM M PD C B A【附加题·2018江西】在正方形ABCD 中，AB=6，连接AC,BD,P 是正方形边上或对角线上一点，若PD=2PA,则AP 的长为A B C D P M M P D C B A。

阿氏圆问题知识点例题含答案(全面非常好)

PC OPC O点 P 在圆上运动-----“阿氏圆”问题如图所示 2-1-1，⊙O 的半径为 r ,点 A 、B 都在⊙O 外，P 为⊙O 上的动点，已知 r =k ·OB.连接 P A 、PB ，则当“PA+k ·PB ”的值最小时，P 点的位置如何确定？A》BB图 2-1-1图 2-1-2 图 2-1-31、“阿氏圆”构造共边共角型相似构造△PAB ∽△CAP 推出PA 2=AB ·AC即：半径的平方=原有线段 ×构造线段 2、“阿氏圆”一般解题步骤：第一步：连接动点至圆心 O （将系数不为 1 的线段的两个端点分别与圆心相连接），则连接 O P 、OB ；第二步：计算出所连接的这两条线段 O P 、OB 长度；第三步：计算这两条线段长度的比k OB OP= 第四步：在 O B 上取点 C ，使得OBOPOP OC = 第五步：连接 A C ，与圆 O 交点即为点 P ．APBO1、（2016江阴期中）如图，在 Rt△ABC 中，∠ACB＝90°，CB＝4，CA＝6，⊙C 半径为 2，P 为圆上一动点，连结 AP，BP，求BPAP21的最小值．根号372、如图，在RT △ABC 中，B ∠=90°，AB=CB=2，以点B 为圆心做圆B 与AC 相切，P 为圆B 上一动点，则PC PA 22+的最小值为_____.根号53、如图，菱形ABCD 的边长为2，锐角大小为60°，⊙A 与BC 相切于点E ，在⊙A 上任意取一点P ，则PD PB 23的最小值为_____.二分之根号37AF=3/24、已知扇形COD 中，∠COD=90°，OC=6，OA=3，OB=5，点P 是弧CD 上一点，求2PA+PB 的最小值．135、如图，在边长为4的正方形中，内切圆记为圆O ，P 为圆O 上一动点，PC PB 2最小值为多少？ 666、边长为6的正三角形，内切圆记为圆O ，P 为圆O 上的动点，2PB+PC 最小值为多少3倍根号72倍根号77、如图，半圆的半径为1，AB 为直径，AC 、BD 为切线，AC=1，BD=2,P 为弧AB 上一动点，求PD PC 22的最小值2分之3倍根号28、在平面直角坐标系中，A(2，0),B(0，2),C(4，0),D(3，2),P是三角形AOB外部的第一象限内一动点，且 BPA=135°，则2PD+PC的最小值为4倍根号29．（2016济南）如图1，抛物线y=ax 2+（a+3）x+3（a ≠0）与x 轴交于点A （4，0），与y 轴交于点B ，在x 轴上有一动点E （m ，0）（0＜m ＜4），过点E 作x 轴的垂线交直线AB 于点N ，交抛物线于点P ，过点P 作PM ⊥AB 于点M ．（1）求a 的值和直线AB 的函数表达式；43-=a ,AB: 343+-=x y（2）设△PMN 的周长为C 1，△AEN 的周长为C 2，若=，求m 的值；（3）如图2，在（2）条件下，将线段OE 绕点O 逆时针旋转得到OE ′，旋转角为α（0°＜α＜90°），连接E ′A 、E ′B ，求E ′A+E ′B 的最小值．（2）m=2或4（舍）（3）3分之4倍根号1010．（1）如图1，已知正方形ABCD的边长为4，圆B的半径为2，点P是圆B上的一个动点，求PD+的最小值和PD﹣的最大值； 5,5（2）如图2，已知正方形ABCD的边长为9，圆B的半径为6，点P是圆B上的一个动点，那么PD+的最小值为，PD﹣的最大值为．根号106，根号106（3）如图3，已知菱形ABCD的边长为4，∠B=60°，圆B的半径为2，点P是圆B上的一个动点，那么PD+的最小值为，PD﹣的最大值为．根号37，根号3711、如图所示，抛物线y=-x 2+bx+c 与直线AB 交于(-4,-4),b(0,4)两点，直线AC ：y=-21x-6交y 轴于点C 。

阿氏圆专题训练

阿氏圆应用举例例1、（2020山西期末）阅读以下材料，并按要求完成相应的任务．已知平面上两点A、B，则所有符合＝k（k＞0且k≠1）的点P会组成一个圆．这个结论最先由古希腊数学家阿波罗尼斯发现，称阿氏圆．阿氏圆基本解法：构造三角形相似．【问题】如图1，在平面直角坐标中，在x轴，y轴上分别有点C（m，0），D（0，n），点P是平面内一动点，且OP＝r，设＝k，求PC+kPD的最小值．图1 图2 图3 阿氏圆的关键解题步骤：第一步：如图1，在OD上取点M，使得0M：OP＝OP：OD＝k；第二步：证明kPD＝PM；第三步：连接CM，此时CM即为所求的最小值．下面是该题的解答过程（部分）：解：在OD上取点M，使得OM：OP＝OP：OD＝k，又∵∠POD＝∠MOP，∴△POM～△DOP．任务：（1）将以上解答过程补充完整．（2）如图2，在Rt△ABC中，∠ACB＝90°，AC＝4，BC＝3，D为△ABC内一动点，满足CD＝2，利用（1）中的结论，请直接写出AD+BD的最小值．解（1）在OD上取点M，使得OM：OP＝OP：OD＝k，又∵∠POD＝∠MOP，∴△POM～△DOP．∴MP：PD＝k，∴MP＝kPD，∴PC+kPD＝PC+MP，当PC+kPD取最小值时，PC+MP有最小值，即C，P，M三点共线时有最小值，利用勾股定理得．（2）∵AC＝m＝4，＝，在CB上取一点M，使得CM＝CD＝，图3∴的最小值为．例2、（2017秋•滨湖区期末）如图，在Rt△ABC中，∠ACB＝90°，CB＝7，AC＝9，以C为圆心、3为半径作⊙C，P为⊙C上一动点，连接AP、BP，则AP+BP的最小值为（）A．7 B．5 C． D．解：如图，在CA上截取CM，使得CM＝1，连接PM，PC，BM．∵PC＝3，CM＝1，CA＝9，∴PC2＝CM•CA，∴＝，∵∠PCM＝∠ACP，∴△PCM∽△ACP，∴＝＝，∴PM＝PA，∴AP+BP＝PM+PB，∵PM+PB≥BM，在Rt△BCM中，∵∠BCM＝90°，CM＝1，BC＝7，∴BM＝＝5，∴AP+BP≥5，∴AP+BP的最小值为5．故选：B．练习1、（2019•郫都区模拟）在△ABC中，∠ACB＝90°，BC＝8，AC＝6，以点C为圆心，4为半径的圆上有一动点D，连接AD，BD，CD，则BD+AD的最小值是 2．解：如图，在CB上取一点F，使得CF＝2，连接FD，AF．∴CD＝4，CF＝2，CB＝8，∴CD2＝CF•CB，∴＝，∵∠FCD ＝∠DCB ，∴△FCD ∽△DCB ，∴＝＝，∴DF ＝BD ，∴BD +AD ＝DF +AF ，∵DF +AD ≥AF ，AF ＝＝2，∴BD +AD 的最小值是2，2、如图，在Rt △ABC 中，∠ACB ＝90°，CB ＝4，CA ＝6，⊙C 半径为2，P 为圆上一动点，连结AP ，BP ，则AP +BP 的最小值为（） A ．B ．6C ．2D ．4解：如图1，连接CP ，在CB 上取点D ，使CD ＝1，则有＝＝，又∵∠PCD ＝∠BCP ，∴△PCD ∽△BCP ，∴＝，∴PD ＝BP ，∴AP +BP ＝AP +PD ．要使AP +BP 最小，只要AP +AD 最小，当点A ，P ，D 在同一条直线时，AP +AD 最小，即：AP +BP 最小值为AD ，在Rt △ACD 中，CD ＝1，AC ＝6，∴AD ＝＝，AP +BP 的最小值为，故选：A ．3、如图，在Rt △ABC 中，∠ABC=90°，BC=4，AB=6，在线段AB 上有一点M ，且BM=2.在线段AC 上有一动点N ，连接MN ，BN.将BMN ∆沿BN 翻折得到BM N '∆.连接AM '、.CM '则223CM AM ''+的最小值为 . 解：在BM 上截取BQ=23， 2,3BQ BM QBM M BA BM BA '''==∠=∠'，.BQM BM A ''∴∆∆∠ 1,3QM BQ M A BM '∴==''1,3QM M A ''∴= 2122()2()33CM AM CM AM CM QM ''''''∴+=+=+当Q M C '、、三点共线时，=CM QM QC ''+有最小值为：3QC ==223CM AM ''∴+的最小值为3.4、（2019•路桥区一模）如图，在扇形OCD 中，∠COD ＝90°，OC ＝3，点A 在OD 上，AD ＝1，点B 为OC 的中点，点E 是弧CD 上的动点，则AE +2EB 的最小值是 2．解：如图，延长OC 至F ，使得CF ＝OC ＝3．连结EF ，OE ， ∵，∠EOB 为公共角，∴△OBE ∽△OEF ，∴，∴2BE ＝EF∴AE +2BE ＝AE +EF ，即A 、E 、F 三点共线时取得最小值.即由勾股定理得：AF ＝＝.例3、如图，在△ABC 中，∠ACB ＝90°，BC ＝12，AC ＝9，以点C 为圆心，6为半径的圆上有一个动点D ．连接AD 、BD 、CD ，则2AD+3BD 的最小值是 4．分析：首先对问题作变式2AD+3BD=233AD BD ⎛⎫+ ⎪⎝⎭，故求23AD BD +最小值即可．解：在CA 上截取CM ，使得CM ＝4，连接DM ，BM ．∵CD ＝6，CM ＝4，CA ＝9，∴CD 2＝CM •CA ，∴＝，∵∠DCM ＝∠ACD ，∴△DCM ∽△ACD ，∴＝＝，∴DM ＝AD ，∴AD +BD ＝DM +BD ，∵DM +BD ≥BM ，在Rt △CBM 中，∵∠CMB ＝90°，CM ＝4，BC ＝12，∴BM ＝＝4，∴AD +BD ≥4，∴AD +BD 的最小值为4．例4、（1）如图1，已知正方形ABCD 的边长为4，圆B 的半径为2，点P 是圆B 上的一个动点，求PD +的最小值和PD﹣的最大值；（2）如图2，已知正方形ABCD的边长为9，圆B的半径为6，点P是圆B上的一个动点，那么PD+的最小值为，PD﹣的最大值为．（3）如图3，已知菱形ABCD的边长为4，∠B＝60°，圆B的半径为2，点P是圆B上的一个动点，那么PD+的最小值为，PD﹣的最大值为．解：（1）如图1中，在BC上取一点G，使得BG＝1．∵＝＝2，＝＝2，∴＝，∵∠PBG＝∠PBC，∴△PBG∽△CBP，∴＝＝，∴PG＝PC，∴PD+PC＝DP+PG，∵DP+PG≥DG，∴当D、G、P共线时，PD+PC的值最小，最小值为DG＝＝5．∵PD﹣PC＝PD﹣PG≤DG，当点P在DG的延长线上时，PD﹣PC的值最大（如图2中），最大值为DG＝5．（2）如图3中，在BC上取一点G，使得BG＝4．∵＝＝，＝＝，∴＝，∵∠PBG＝∠PBC，∴△PBG∽△CBP，∴＝＝，∴PG＝PC，∴PD+PC＝DP+PG，∵DP+PG≥DG，∴当D、G、P共线时，PD+PC的值最小，最小值为DG＝＝．∵PD﹣PC＝PD﹣PG≤DG，当点P在DG的延长线上时，PD﹣PC的值最大，最大值为DG＝．（3）如图4中，在BC上取一点G，使得BG＝1，作DF⊥BC于F．∵＝＝2，＝＝2，∴＝，∵∠PBG＝∠PBC，∴△PBG∽△CBP，∴＝＝，∴PG＝PC，∴PD+PC＝DP+PG，∵DP+PG≥DG，∴当D、G、P共线时，PD+PC的值最小，最小值为DG，在Rt△CDF中，∠DCF＝60°，CD＝4，∴DF＝CD•sin60°＝2，CF＝2，在Rt△GDF中，DG＝＝∵PD﹣PC＝PD﹣PG≤DG，当点P在DG的延长线上时，PD﹣PC的值最大（如图2中），最大值为DG＝．练习：1、（1）初步思考：如图1，在△PCB中，已知PB＝2，BC＝4，N为BC上一点且BN＝1，试证明：PN＝PC（2）问题提出：如图2，已知正方形ABCD的边长为4，圆B的半径为2，点P是圆B上的一个动点，求PD+PC的最小值．（3）推广运用：如图3，已知菱形ABCD的边长为4，∠B＝60°，圆B的半径为2，点P是圆B上的一个动点，求PD﹣PC的最大值．（1）证明：如图1，∵PB＝2，BC＝4，BN＝1，∴PB2＝4，BN•BC＝4．∴PB2＝BN•BC．∴＝．又∵∠B＝∠B，∴△BPN∽△BCP．∴＝＝．∴PN＝PC；（2）如图2，在BC上取一点G，使得BG＝1，（3）同（2）中证法，如图3，取BG＝1，，当点P在DG的延长线上时，PD﹣PC 的最大值，最大值为．2、（2018•常熟市二模）如图，已知正方形ABCD的边长为4，⊙B的半径为2，点P是⊙B上的一个动点，则PD﹣PC的最大值为 5．解：在BC上取一点G，使得BG＝1，如图，∵＝2，＝2，∴，∵∠PBG＝∠PBC，∴△PBG∽△CBP，∴，∴PG＝PC，当点P在DG的延长线上时，PD﹣PC的值最大，最大值为DG＝＝5．例5、（2019•清江浦区一模）问题提出：如图1，在Rt△ABC中，∠ACB＝90°，CB＝4，CA＝6，⊙C半径为2，P为圆上一动点，连结AP、BP，求AP+BP的最小值．（1）尝试解决：为了解决这个问题，下面给出一种解题思路：如图2，连接CP，在CB上取点D，使CD＝1，则有＝＝，又∵∠PCD＝∠BCP，∴△PCD∽△BCP．∴＝，∴PD＝BP，∴AP+BP＝AP+PD．请你完成余下的思考，并直接写出答案：AP+BP的最小值为．（2）自主探索：在“问题提出”的条件不变的情况下，AP+BP的最小值为．（3）拓展延伸：已知扇形COD中，∠COD＝90°，OC＝6，OA＝3，OB＝5，点P是上一点，求2PA+PB的最小值．解：（1）如图1，连结AD，∵AP+BP＝AP+PD，要使AP+BP最小，∴AP+AD最小，当点A，P，D在同一条直线时，AP+AD最小，即：AP+BP最小值为AD，在Rt△ACD中，CD＝1，AC＝6，∴AD＝＝，AP+BP的最小值为.（2）如图2，连接CP，在CA上取点D，使CD＝，∴，∵∠PCD＝∠ACP，∴△PCD∽△ACP，∴，∴PD＝AP，∴AP+BP＝BP+PD，∴同（1）的方法得出AP+BP的最小值为BD＝＝．（3）如图3，延长OA到点E，使CE＝6，∴OE＝OC+CE＝12，连接PE、OP，∵OA＝3，∴，∵∠AOP＝∠AOP，∴△OAP∽△OPE，∴，∴EP＝2PA，∴2PA+PB＝EP+PB，∴当E、P、B三点共线时，取得最小值为：BE＝＝13.练习1、（2018秋•惠山区校级期中）问题提出：如图1，在等边△ABC中，AB＝12，⊙C半径为6，P为圆上一动点，连结AP，BP，求AP+BP的最小值．（1）尝试解决：为了解决这个问题，下面给出一种解题思路：如图2，连接CP，在CB上取点D，使CD＝3，则有＝＝，又∵∠PCD＝∠BCP，∴△PCD∽△BCP，∴＝，∴PD＝BP，∴AP+BP＝AP+PD．请你完成余下的思考，并直接写出答案：AP+BP的最小值为．（2）自主探索：如图3，矩形ABCD中，BC＝7，AB＝9，P为矩形内部一点，且PB＝3，AP+PC 的最小值为．（3）拓展延伸：如图4，扇形COD中，O为圆心，∠COD＝120°，OC＝4，OA＝2，OB＝3，点P 是上一点，求2PA+PB的最小值，画出示意图并写出求解过程．解：（1）解：（1）如图1，连结AD，过点A作AF⊥CB于点F，∵AP+BP＝AP+PD，要使AP+BP最小，∴AP+AD最小，当点A，P，D在同一条直线时，AP+AD最小，即：AP+BP最小值为AD， ∵AC＝12，AF⊥BC，∠ACB＝60°∴CF＝6，AF＝6∴DF＝CF﹣CD＝6﹣3＝3，∴AD＝＝3，∴AP+BP的最小值为3（2）如图，在AB上截取BF＝1，连接PF，PC，∵AB＝9，PB＝3，BF＝1∴，且∠ABP＝∠ABP，∴△ABP∽△PBF，∴∴PF＝AP∴AP+PC＝PF+PC，∴当点F，点P，点C三点共线时，AP+PC的值最小，∴CF＝＝＝5，∴AP+PC的值最小值为5，（3）如图，延长OC，使CF＝4，连接BF，OP，PF，过点F作FB⊥OD于点M，∵OC＝4，FC＝4，∴FO＝8，且OP＝4，OA＝2，∴，且∠AOP＝∠AOP，∴△AOP∽△POF，∴∴PF＝2AP，∴2PA+PB＝PF+PB，∴当点F，点P，点B三点共线时，2AP+PB的值最小，∵∠COD＝120°，∴∠FOM＝60°，且FO＝8，FM⊥OM∴OM＝4，FM＝4，∴MB＝OM+OB＝4+3＝7，∴FB＝＝∴2PA+PB的最小值为．2、（2019秋•江北区期末）问题提出：如图1，在等边△ABC中，AB＝9，⊙C半径为3，P为圆上一动点，连结AP，BP，求AP+BP的最小值（1）尝试解决：为了解决这个问题，下面给出一种解题思路，通过构造一对相似三角形，将BP转化为某一条线段长，具体方法如下：（请把下面的过程填写完整）如图2，连结CP，在CB上取点D，使CD＝1，则有又∵∠PCD＝∠BCP，∴△ PCD∽△ BCP，∴，∴PD＝BP，∴AP+BP＝AP+PD ∴当A，P，D三点共线时，AP+PD取到最小值.请你完成余下的思考，并直接写出答案：AP+BP的最小值为．（2）自主探索：如图3，矩形ABCD中，BC＝6，AB＝8，P为矩形内部一点，且PB＝4，则AP+PC的最小值为 2．（请在图3中添加相应的辅助线）（3）拓展延伸：如图4，在扇形COD中，O为圆心，∠COD＝120°，OC＝4．OA＝2，OB＝3，点P是上一点，求2PA+PB的最小值，画出示意图并写出求解过程．解：（1）如图1，连结AD，过点A作AF⊥CB于点F，∵AP+BP＝AP+PD，要使AP+BP最小，∴AP+AD最小，当点A，P，D在同一条直线时，AP+AD最小，即：AP+BP最小值为AD，∵AC＝9，AF⊥BC，∠ACB＝60°，∴CF＝，AF＝，∴DF＝CF﹣CD＝3﹣＝2，∴AD＝＝，∴AP+BP的最小值为；（2）如图2，在AB上截取BF＝2，连接PF，PC，∵AB＝8，PB＝4，BF＝2，∴＝＝，且∠ABP＝∠ABP，∴△ABP∽△PBF，∴＝＝，∴PF＝AP，∴AP+PC＝PF+PC，∴当点F，点P，点C三点共线时，AP+PC的值最小，∴CF＝＝＝2，∴AP+PC的值最小值为2，（3）如图3，延长OC，使CF＝4，连接BF，OP，PF，过点F作FB⊥OD于点M，∵OC＝4，FC＝4，∴FO＝8，且OP＝4，OA＝2，∴＝＝，且∠AOP＝∠AOP∴△AOP∽△POF，∴＝＝，∴PF＝2AP，∴2PA+PB＝PF+PB，∴当点F，点P，点B三点共线时，2AP+PB的值最小，∵∠COD＝120°，∴∠FOM＝60°，且FO＝8，FM⊥OM，∴OM＝4，FM＝4∴MB＝OM+OB＝4+3＝7，∴FB＝＝，∴2PA+PB的最小值为．。

高中数学圆锥曲线系统讲解第5讲《阿氏圆》练习及答案

第5讲阿氏圆知识与方法1.阿氏圆：设A 、B 是平面上的两个定点，若平面内的动点P 满足PA PBλ=（0λ>且1λ≠），则点P 的轨迹是圆，该圆叫做阿氏圆. 2．考题中常用的阿氏圆性质：（1）圆心位置：当1λ>时，圆心M 在AB 的延长线上；当01λ<<时，圆心M 在BA 的延长线上.（2）半径公式：21dr λλ=−，其中d 为两定点A 、B 之间的距离. （3）找定点：如右图所示，设圆M 的半径为r ，对于圆M 外任意一点A ，连接AM 交圆M 于点N ，则在线段MN 上必定存在点B ，使得对于圆M 上任意一点P ，都有PA PBλ=，可以根据2MA MB r ⋅=找到点B λ=求出λ.典型例题【例题】已知两个定点()2,0A −，()4,0B ，若动点C 满足2CB CA =，则点C 的轨迹方程为______.【解析】设(),C x y ，因为2CB CA =，所以=，化简得：()22416x y ++=【答案】()22416x y ++=变式1 已知圆()22:416M x y ++=，点()2,0A −，若x 轴上的定点B 满足对圆M 上的任意一点C ，都有PA PBλ=恒成立，其中λ为常数，则点B 的坐标为______，常数______.【解析】设(),0B a ，()00,C x y ，则()2200416x y ++=，所以()22200001648y x x x =−+=−−，故CA CB===，要使CA CB为定值，应有24428a a−=+−，解得：4a =或2−（舍去），所以点B 的坐标为()2,0−，此时12CA CB==，即12λ=.解法2：如图，由阿氏图性质，点B 在MA 的延长线上，且2MA MB r ⋅=，所以216MB =，故8MB =，显然()4,0M −，从而点B 的坐标为()4,0，12λ==.【答案】()2,0−，12变式2 在ABC 中，6AB =，2BC AC =，则ABC 的面积的最大值为______. 【解析】解法1：设AB c =，BC a =，AC b =，则6c =，2a b =，由余弦定理，22222536cos 24a b c b Cab b +−−==，所以21sin sin 2ABCSab C b C b b =====所以当b =时，ABC 的面积取得最大值12.解法2：以AB 中点O 为原点建立如图1所示的平面直角坐标系，则()3,0A −，()3,0B ，设(),C xy ，因为2BC AC==，化简得：()22516x y ++=()0y ≠。

中考数学阿氏圆专题含答案

阿氏圆基本解法：构造相似，A+kB 型第一步：连接动点至圆心O （将系数不为1的线段的两个端点分别与圆心相连接，）则连接OP 、OD ；第二步：计算出所连接的这两条线段OP 、OD 长度；第三步：计算这两条线段长度的比m OD OP =；第四步：在OD 上取点M ，使得m OPOM =；第五步：连接CM ，与圆O 交点即为点P.先动心，构相似，定联姻【经典例题1—A+21B 型】（1）如图，已知正方形ABCD 的边长为4，⊙B 的半径为2，点P 是⊙B 上的一个动点，则PD+21PC 的最小值为 .PD−21PC 的最大值为；（2）如图，已知正方形ABCD 的边长为9，⊙B 的半径为6，点P 是⊙B 上的一个动点，则PD+32PC 的最小值为 .PD−32PC 的最大值为；（3）如图，已知菱形ABCD 的边长为4，⊙B=60°，⊙B 的半径为2，点P 是⊙B上的一个动点，求PD+21PC 的最小值为；求PD -21PC 的最大值为 . 【解析】由PD -21PC=PD -PG≤DG ，当点P 在DG 的延长线上时，PD -21PC 的值最大，最大值为DG=5．解答在BC 上取一点G ，使得BG=1，如图， ⊙12=BG PB ，224==PB BC ， ⊙PB BC BG PB =，⊙⊙PBG=⊙PBC ，⊙⊙PBG⊙⊙CBP ，⊙21==PB BG PC PG ，⊙PG=21PC ， ∴PD+21PC=DP+PG ， ∵DP+PG ≥DG∴当D 、G 、P 共线时，PD+21PC 的值最小，最小值为DG=53422=+. ∵PD -21PC=PD -PG ≤DG 当点P 在DG 的延长线上时，PD−21PC 的值最大，最大值为DG=53422=+. 故答案为：5(2)如图3中，在BC 上取一点G ，使得BG=4.⊙PB/BG=6/4=3/2，BC/PB=9/6=3/2，⊙PB/BG=BC/PB ，⊙⊙PBG=⊙PBC ，⊙⊙PBG⊙⊙CBP ，⊙PG/PC=BG/PB=32， ⊙PG=32PC ， ⊙PD+32PC=DP+PG ，⊙DP+PG⊙DG ，⊙当D 、 G 、P 共线时，PD+32PC 的值最小，最小值为DG=1069522=+. ⊙PD−32PC=PD−PG⊙DG ，当点P 在DG 的延长线上时，PD−12PC 的值最大，最大值为DG=106. 故答案为106，106(3)如图4中，在BC 上取一点G ，使得BG=4，作DF⊙BC 于F.⊙PB/BG=2/1=2，BC/PB=4/2=2，⊙PB/BG=BC/PB ，⊙⊙PBG=⊙PBC ，⊙⊙PBG⊙⊙CBP ，⊙PG/PC=BG/PB=21， ⊙PG=21PC ， ⊙PD+21PC=DP+PG ，⊙DP+PG⊙DG ，⊙当D 、G 、P 共线时，PD+21PC 的值最小，最小值为DG ，在Rt⊙CDF 中，⊙DCF=60⊙，CD=4， ⊙DF=CD⊙sin60⊙=23，CF=2，在Rt⊙GDF 中，DG=37)5()32(22=+ ⊙PD−21PC=PD−PG⊙DG ，当点P 在DG 的延长线上时，PD−21PC 的值最大(如图2中)，最大值为DG=37. 故答案为37.练习1-1如图，正方形ABCD 的边长AB=8，E 为平面内一动点，且AE=4，F 为CD 上一点，CF=2，连接EF 、ED ，则EF+21ED 的最小值 . 【解析】如图，当点E 运动到点E′时，在AD 边上取AH=2，⊙AE′=AE=4，⊙AH AE '=2，⊙AD=8，⊙'AE AD =2， ⊙AH AE '='AE AD，⊙⊙DAE′=⊙E′AH ，⊙⊙DAE′⊙⊙E′AH ， ⊙H E DE ''=2， ⊙E′H=21DE'， ⊙EF+21ED=EF+21E′D=EF+E′H=HF ， ⊙EF+21ED 的最小值为HF 的值， ⊙DH=AD -AH=6，DF=DC -CF=6，在Rt⊙DHF 中，根据勾股定理，得 HF=2622=+DF DH ，故选：A ．练习1-2在矩形ABCD 中，AB=1，BC=3，P 为AD 上任意一点，求PB+21PD 最小值.【解析】如图，连接BD ，在矩形ABCD 中，AB=DC=1.BC=3， ⊙tan⊙DBC=DCBC=33⊙⊙DBC=30⊙ 作⊙DBN=⊙DBC=30⊙，过点D 作DM⊙BN 于点M ，BN 交AD 于点P.⊙⊙MDB=60⊙⊙AD⊙BC⊙⊙PDB=⊙DBC=30⊙ ⊙⊙MDP=30⊙⊙PM=21PD 此时BP+21PD=BP+PM 最小，最小值为BM 的长， ⊙⊙MBD=⊙CBD⊙BMD=⊙C=90⊙BD=BD⊙⊙BMD⊙⊙BCD(AAS) ⊙BM=BC=3答：PB+21PD 的最小值为3. 故选：C.练习1-3如图，P 是边长为8的正方形ABCD 内部一点，且满足BP=4，则PD+21PC 的最小值是 .【解析】在BC 边上取一点E ，使BE=2，连接DE ，如图⊙ABCD 是正方形，AB=8⊙AB=BC=CD=8，⊙BCD=90⊙⊙BP=4 ⊙2142==BP BE ，2184==BC BP ⊙BP BE =BC BP且⊙PBC=⊙PBC⊙⊙PBE⊙⊙BCP ⊙21==BC BP PC PE ⊙PE=21PC ⊙PD+21PC=PD+PE 在Rt⊙DCE 中，CD=8，CE=BC−BE=6 ⊙DE=1022=+CE CD ⊙PD+PE⊙DE⊙PD+PE⊙10 ⊙PD+21PC 的最小值是10 故选：C.练习1-4已知在△ABO 中，∠AOB=90°，AO=21，BO=8，以点O 为圆心，4为半径作圆，点D 是圆上一个动点，连接AD 、BD ，则AD+21BD 的最小值 .【解析】如图，在CB 上取一点E ，使CE=2，连接CD 、DE 、AE.∵AC=6，BC=8，AB=10，所以AC 2+BC 2=AB 2，∴∠ACB=90∘，∵CD=4，∴CE/CD=CD/CB=21， ∴△CED ∽△CDB ，∴ED/DB=CE/CD=21， ∴ED=21BD ， ∴AD+21BD=AD+ED⊙AE ，当且仅当E 、D 、A 三点共线时，AD+21BD 取得最小值AE=10222=+AC CE .练习1-5如图，在⊙ACE 中，CA=CE ，⊙CAE=30°，O 经过点C ，且圆的直径AB 在线段AE 上。

专题：阿氏圆最值问题

专题：阿氏圆最值问题一．填空题（共3小题）1．如图，四边形ABCD为边长为4的正方形，⊙B的半径为2，P是⊙B上一动点，则PD+PC 的最小值为；PD+4PC的最小值为．2．如图，在平面直角坐标系中，点A（4，0），B（4，4），点P在半径为2的圆O上运动，则AP+BP的最小值是．3．如图，正方形ABCD的边长为4，⊙B的半径为2，P为⊙B上的动点，则PD+PC的最小值等于．二．解答题（共8小题）4．问题提出：如图1，在Rt△ABC中，∠ACB＝90°，CB＝4，CA＝6，⊙C半径为2，P 为圆上一动点，连结AP、BP，求AP+BP的最小值．（1）尝试解决：为了解决这个问题，下面给出一种解题思路：如图2，连接CP，在CB 上取点D，使CD＝1，则有＝＝，又∵∠PCD＝∠BCP，∴△PCD∽△BCP．∴＝，∴PD＝BP，∴AP+BP＝AP+PD．请你完成余下的思考，并直接写出答案：AP+BP的最小值为．（2）自主探索：在“问题提出”的条件不变的情况下，AP+BP的最小值为．（3）拓展延伸：已知扇形COD中，∠COD＝90°，OC＝6，OA＝3，OB＝5，点P是上一点，求2P A+PB的最小值．5．问题提出：如图1，在等边△ABC中，AB＝12，⊙C半径为6，P为圆上一动点，连结AP，BP，求AP+BP的最小值．（1）尝试解决：为了解决这个问题，下面给出一种解题思路：如图2，连接CP，在CB 上取点D，使CD＝3，则有＝＝，又∵∠PCD＝∠BCP，∴△PCD∽△BCP，∴＝，∴PD＝BP，∴AP+BP＝AP+PD．请你完成余下的思考，并直接写出答案：AP+BP的最小值为．（2）自主探索：如图3，矩形ABCD中，BC＝7，AB＝9，P为矩形部一点，且PB＝3，AP+PC的最小值为．（3）拓展延伸：如图4，扇形COD中，O为圆心，∠COD＝120°，OC＝4，OA＝2，OB＝3，点P是上一点，求2P A+PB的最小值，画出示意图并写出求解过程．6．问题背景如图1，在△ABC中，BC＝4，AB＝2AC．问题初探请写出任意一对满足条件的AB与AC的值：AB＝，AC＝．问题再探如图2，在AC右侧作∠CAD＝∠B，交BC的延长线于点D，求CD的长．问题解决求△ABC的面积的最大值．7．如图，半圆的半径为1，AB为直径，AC、BD为切线，AC＝1，BD＝2，P为上一动点，求PC+PD的最小值．8．如图，在Rt△ABC中，∠A＝30°，AC＝8，以C为圆心，4为半径作⊙C．（1）试判断⊙C与AB的位置关系，并说明理由；（2）点F是⊙C上一动点，点D在AC上且CD＝2，试说明△FCD～△ACF；（3）点E是AB边上任意一点，在（2）的情况下，试求出EF+F A的最小值．9．（1）如图1，已知正方形ABCD的边长为4，圆B的半径为2，点P是圆B上的一个动点，求PD+的最小值和PD﹣的最大值；（2）如图2，已知正方形ABCD的边长为9，圆B的半径为6，点P是圆B上的一个动点，那么PD+的最小值为，PD﹣的最大值为．（3）如图3，已知菱形ABCD的边长为4，∠B＝60°，圆B的半径为2，点P是圆B 上的一个动点，那么PD+的最小值为，PD﹣的最大值为．10．如图，抛物线y＝﹣x2+bx+c与直线AB交于A（﹣4，﹣4），B（0，4）两点，直线AC：y＝﹣x﹣6交y轴于点C．点E是直线AB上的动点，过点E作EF⊥x轴交AC于点F，交抛物线于点G．（1）求抛物线y＝﹣x2+bx+c的表达式；（2）连接GB，EO，当四边形GEOB是平行四边形时，求点G的坐标；（3）在（2）的前提下，y轴上是否存在一点H，使∠AHF＝∠AEF？如果存在，求出此时点H的坐标，如果不存在，请说明理由．11．如图1，抛物线y＝ax2+（a+3）x+3（a≠0）与x轴交于点A（4，0），与y轴交于点B，在x轴上有一动点E（m，0）（0＜m＜4），过点E作x轴的垂线交直线AB于点N，交抛物线于点P，过点P作PM⊥AB于点M．（1）求a的值和直线AB的函数表达式；（2）设△PMN的周长为C1，△AEN的周长为C2，若＝，求m的值；（3）如图2，在（2）条件下，将线段OE绕点O逆时针旋转得到OE′，旋转角为α（0°＜α＜90°），连接E′A、E′B，求E′A+E′B的最小值．专题：阿氏圆最值问题参考答案与试题解析一．填空题（共3小题）1．如图，四边形ABCD为边长为4的正方形，⊙B的半径为2，P是⊙B上一动点，则PD+PC 的最小值为5；PD+4PC的最小值为10．【分析】①如图，连接PB、在BC上取一点E，使得BE＝1．只要证明△PBE∽△CBP，可得＝＝，推出PD+PC＝PD+PE，再根据三角形的三边关系PE+PD≤DE即可解决问题；②连接DB，PB，在BD上取一点E，使得BE＝，连接EC，作EF⊥BC于F．只要证明△PBE∽△DBP，可得＝＝，推出PE＝PD，推出PD+4PC＝4（PD+PC）＝4（PE+PC），根据三角形的三边关系PE+PC≤EC即可解决问题；【解答】解：①如图，连接PB、在BC上取一点E，使得BE＝1．∵PB2＝4，BE•BC＝4，∴PB2＝BE•BC，∴＝，∵∠PBE＝∠CBP，∴△PBE∽△CBP，∴＝＝，∴PD+PC＝PD+PE，∵PE+PD≤DE，在Rt△DCE中，DE＝＝5，∴PD+PC的最小值为5．②连接DB，PB，在BD上取一点E，使得BE＝，连接EC，作EF⊥BC于F．∵PB2＝4，BE•BD＝×4＝4，∴BP2＝BE•BD，∴＝，∵∠PBE＝∠PBD，∴△PBE∽△DBP，∴＝＝，∴PE＝PD，∴PD+4PC＝4（PD+PC）＝4（PE+PC），∵PE+PC≥EC，在Rt△EFC中，EF＝，FC＝，∴EC＝，∴PD+4PC的最小值为10．故答案为5，10．【点评】本题考查轴对称最短问题、正方形的性质、相似三角形的判定和性质等知识，解题的关键是学会利用数形结合的思想解决问题，学会根据相似三角形解决问题，属于中考填空题中的压轴题．2．如图，在平面直角坐标系中，点A（4，0），B（4，4），点P在半径为2的圆O上运动，则AP+BP的最小值是5．【分析】如图，取点K（1，0），连接OP、PK、BK．由△POK∽△AOP，可得＝＝，推出PK＝P A，在△PBK中，PB+PK≥BK，推出PB+P A＝PB+PK的最小值为BK的长．【解答】解：如图，取点K（1，0），连接OP、PK、BK．∵OP＝2，OA＝4，OK＝1，∴＝＝，∵∠POK＝∠AOP，∴△POK∽△AOP，∴＝＝，∴PK＝P A，∴PB+P A＝PB+PK，在△PBK中，PB+PK≥BK，∴PB+P A＝PB+PK的最小值为BK的长，∵B（4，4），K（1，0），∴BK＝＝5．故答案为5．【点评】本题考查坐标与图形的性质、相似三角形的判定和性质、三角形的三边关系、两点之间的距离公式等知识，解题的关键是灵活运用所学知识解决问题，学会用转化的思想思考问题，属于中考填空题中的压轴题．3．如图，正方形ABCD的边长为4，⊙B的半径为2，P为⊙B上的动点，则PD+PC的最小值等于5．【分析】在BC上截取BE＝1，连接BP，PE，由正方形的性质可得BC＝4＝CD，BP＝2，EC＝3，可证△PBE∽△CBP，可得PE＝PC，即当点D，点P，点E三点共线时，PD+PE 有最小值，即PD+PC有最小值，【解答】解：如图，在BC上截取BE＝1，连接BP，PE，∵正方形ABCD的边长为4，⊙B的半径为2，∴BC＝4＝CD，BP＝2，EC＝3∵，且∠PBE＝∠PBE∴△PBE∽△CBP∴∴PE＝PC∴PD+PC＝PD+PE∴当点D，点P，点E三点共线时，PD+PE有最小值，即PD+PC有最小值，∴PD+PC最小值为DE＝＝5故答案为：5【点评】本题考查了正方形的性质，圆的有关知识，相似三角形的判定和性质，添加恰当的辅助线构造相似三角形是本题的关键．二．解答题（共8小题）4．问题提出：如图1，在Rt△ABC中，∠ACB＝90°，CB＝4，CA＝6，⊙C半径为2，P 为圆上一动点，连结AP、BP，求AP+BP的最小值．（1）尝试解决：为了解决这个问题，下面给出一种解题思路：如图2，连接CP，在CB 上取点D，使CD＝1，则有＝＝，又∵∠PCD＝∠BCP，∴△PCD∽△BCP．∴＝，∴PD＝BP，∴AP+BP＝AP+PD．请你完成余下的思考，并直接写出答案：AP+BP的最小值为．（2）自主探索：在“问题提出”的条件不变的情况下，AP+BP的最小值为．（3）拓展延伸：已知扇形COD中，∠COD＝90°，OC＝6，OA＝3，OB＝5，点P是上一点，求2P A+PB的最小值．【分析】（1）利用勾股定理即可求出，最小值为AD＝；（2）连接CP，在CA上取点D，使CD＝，则有，可证△PCD∽△ACP，得到PD＝AP，即：AP+BP＝BP+PD，从而AP+BP的最小值为BD；（3）延长OA到点E，使CE＝6，连接PE、OP，可证△OAP∽△OPE，得到EP＝2P A，得到2P A+PB＝EP+PB，当E、P、B三点共线时，得到最小值．【解答】解：（1）如图1，连结AD，∵AP+BP＝AP+PD，要使AP+BP最小，∴AP+AD最小，当点A，P，D在同一条直线时，AP+AD最小，即：AP+BP最小值为AD，在Rt△ACD中，CD＝1，AC＝6，∴AD＝＝，AP+BP的最小值为，故答案为：；（2）如图2，连接CP，在CA上取点D，使CD＝，∴，∵∠PCD＝∠ACP，∴△PCD∽△ACP，∴，∴PD＝AP，∴AP+BP＝BP+PD，∴同（1）的方法得出AP+BP的最小值为BD＝＝．故答案为：；（3）如图3，延长OA到点E，使CE＝6，∴OE＝OC+CE＝12，连接PE、OP，∵OA＝3，∴，∵∠AOP＝∠AOP，∴△OAP∽△OPE，∴，∴EP＝2P A，∴2P A+PB＝EP+PB，∴当E、P、B三点共线时，取得最小值为：BE＝＝13．【点评】此题是圆的综合题，主要考查了勾股定理，相似三角形的判定和性质，极值的确定，还考查了学生的阅读理解能力，解本题的关键是根据材料中的思路构造出△PCD ∽△ACP和△OAP∽△OPE，也是解本题的难点．5．问题提出：如图1，在等边△ABC中，AB＝12，⊙C半径为6，P为圆上一动点，连结AP，BP，求AP+BP的最小值．（1）尝试解决：为了解决这个问题，下面给出一种解题思路：如图2，连接CP，在CB 上取点D，使CD＝3，则有＝＝，又∵∠PCD＝∠BCP，∴△PCD∽△BCP，∴＝，∴PD＝BP，∴AP+BP＝AP+PD．请你完成余下的思考，并直接写出答案：AP+BP的最小值为．（2）自主探索：如图3，矩形ABCD中，BC＝7，AB＝9，P为矩形部一点，且PB＝3，AP+PC的最小值为．（3）拓展延伸：如图4，扇形COD中，O为圆心，∠COD＝120°，OC＝4，OA＝2，OB＝3，点P是上一点，求2P A+PB的最小值，画出示意图并写出求解过程．【分析】（1）由等边三角形的性质可得CF＝6，AF＝6，由勾股定理可求AD的长；（2）在AB上截取BF＝1，连接PF，PC，由，可证△ABP∽△PBF，可得PF＝AP，即AP+PC＝PF+PC，则当点F，点P，点C三点共线时，AP+PC的值最小，由勾股定理可求AP+PC的值最小值；（3）延长OC，使CF＝4，连接BF，OP，PF，过点F作FB⊥OD于点M，由，可得△AOP∽△POF，可得PF＝2AP，即2P A+PB＝PF+PB，则当点F，点P，点B三点共线时，2AP+PB的值最小，由勾股定理可求2P A+PB的最小值．【解答】解：（1）解：（1）如图1，连结AD，过点A作AF⊥CB于点F，∵AP+BP＝AP+PD，要使AP+BP最小，∴AP+AD最小，当点A，P，D在同一条直线时，AP+AD最小，即：AP+BP最小值为AD，∵AC＝12，AF⊥BC，∠ACB＝60°∴CF＝6，AF＝6∴DF＝CF﹣CD＝6﹣3＝3∴AD＝＝3∴AP+BP的最小值为3（2）如图，在AB上截取BF＝1，连接PF，PC，∵AB＝9，PB＝3，BF＝1∴，且∠ABP＝∠ABP，∴△ABP∽△PBF，∴∴PF＝AP∴AP+PC＝PF+PC，∴当点F，点P，点C三点共线时，AP+PC的值最小，∴CF＝＝＝5∴AP+PC的值最小值为5，（3）如图，延长OC，使CF＝4，连接BF，OP，PF，过点F作FB⊥OD于点M，∵OC＝4，FC＝4，∴FO＝8，且OP＝4，OA＝2，∴，且∠AOP＝∠AOP∴△AOP∽△POF∴∴PF＝2AP∴2P A+PB＝PF+PB，∴当点F，点P，点B三点共线时，2AP+PB的值最小，∵∠COD＝120°，∴∠FOM＝60°，且FO＝8，FM⊥OM∴OM＝4，FM＝4∴MB＝OM+OB＝4+3＝7∴FB＝＝∴2P A+PB的最小值为．【点评】此题是圆的综合题，主要考查了圆的有关知识，勾股定理，相似三角形的判定和性质，极值的确定，还考查了学生的阅读理解能力，解本题的关键是根据材料中的思路构造出相似三角形，也是解本题的难点．6．问题背景如图1，在△ABC中，BC＝4，AB＝2AC．问题初探请写出任意一对满足条件的AB与AC的值：AB＝6，AC＝3．问题再探如图2，在AC右侧作∠CAD＝∠B，交BC的延长线于点D，求CD的长．问题解决求△ABC的面积的最大值．【分析】问题初探：设AC＝x，则AB＝2x，根据三角形三边间的关系知2x﹣x＜4且2x+x ＞4，解之得出x的围，在此围确定AC的值即可得出答案；问题再探：设CD＝a、AD＝b，证△DAC∽△DBA得＝＝，据此知，解之可得；问题解决：设AC＝m、则AB＝2m，根据面积公式可得S△ABC＝2m，由余弦定理可得cos C，代入化简S△ABC＝，结合m的取值围，利用二次函数的性质求解可得．【解答】解：问题初探，设AC＝x，则AB＝2x，∵BC＝4，∴2x﹣x＜4且2x+x＞4，解得：＜x＜4，取x＝3，则AC＝3、AB＝6，故答案为：6、3；问题再探，∵∠CAD＝∠B，∠D＝∠D，∴△DAC∽△DBA，则＝＝，设CD＝a、AD＝b，∴，解得：，即CD＝；问题解决，设AC＝m、则AB＝2m，根据面积公式可得S△ABC＝AC•BC sin C＝2m sin C＝2m，由余弦定理可得cos C＝，∴S△ABC＝2m＝2m＝＝＝由三角形三边关系知＜m＜4，所以当m＝时，S△ABC取得最大值．【点评】本题主要考查三角形三边关系、相似三角形的判定与性质及二次函数的应用，解题的关键是熟练掌握相似三角形的判定与性质、三角形的面积公式、余弦定理及二次函数的性质．7．如图，半圆的半径为1，AB为直径，AC、BD为切线，AC＝1，BD＝2，P为上一动点，求PC+PD的最小值．【分析】如图当A、P、D共线时，PC+PD最小，根据PC+PD＝PM+PD＝DM＝AD﹣AM即可计算．【解答】解：如图当A、P、D共线时，PC+PD最小．理由：连接PB、CO，AD与CO交于点M，∵AB＝BD＝4，BD是切线，∴∠ABD＝90°，∠BAD＝∠D＝45°，∵AB是直径，∴∠APB＝90°，∴∠P AB＝∠PBA＝45°，∴P A＝PB，PO⊥AB，∵AC＝PO＝2，AC∥PO，∴四边形AOPC是平行四边形，∴OA＝OP，∠AOP＝90°，∴四边形AOPC是正方形，∴PM＝PC，∴PC+PD＝PM+PD＝DM，∵DM⊥CO，∴此时PC+DP最小＝AD﹣AM＝2﹣＝．【点评】本题考查切线的性质、轴对称﹣最短问题、正方形的判定和性质、等腰直角三角形的判定和性质等知识，解题的关键是找到点P的位置，学会通过特殊点探究问题，找到解题的突破口，属于中考常考题型．8．如图，在Rt△ABC中，∠A＝30°，AC＝8，以C为圆心，4为半径作⊙C．（1）试判断⊙C与AB的位置关系，并说明理由；（2）点F是⊙C上一动点，点D在AC上且CD＝2，试说明△FCD～△ACF；（3）点E是AB边上任意一点，在（2）的情况下，试求出EF+F A的最小值．【分析】（1）结论：相切．作CM⊥AB于M．，只要证明CM＝4，即可解决问题；（2）由CF＝4，CD＝2，CA＝8，推出CF2＝CD•CA，推出＝，由∠FCD＝∠ACF，即可推出△FCD∽△ACF；（3）作DE′⊥AB于E′，交⊙C于F′．由△FCD∽△ACF，可得＝＝，推出DF＝AC，推出EF+AF＝EF+DF，所以欲求EF+AF的最小值，就是要求EF+DF 的最小值；【解答】（1）解：结论：相切．理由：作CM⊥AB于M．在Rt△ACM中，∵∠AMC＝90°，∠CAM＝30°，AC＝8，∴CM＝AC＝4，∵⊙O的半径为4，∴CM＝r，∴AB是⊙C的切线．（2）证明：∵CF＝4，CD＝2，CA＝8，∴CF2＝CD•CA，∴＝，∵∠FCD＝∠ACF，∴△FCD∽△ACF．（3）解：作DE′⊥AB于E′，交⊙C于F′．∵△FCD∽△ACF，∴＝＝，∴DF＝AC，∴EF+AF＝EF+DF，∴欲求EF+AF的最小值，就是要求EF+DF的最小值，当E与E′，F与F′重合时，EF+DF的值最小，最小值＝DE′＝AD＝3．【点评】本题考查圆综合题、切线的判定和性质、相似三角形的判定和性质，垂线段最短等知识，解题的关键是学会添加常用辅助线，正确切线的证明方法，学会正确寻找相似三角形解决问题，学会利用垂线段最短解决问题，属于中考压轴题．9．（1）如图1，已知正方形ABCD的边长为4，圆B的半径为2，点P是圆B上的一个动点，求PD+的最小值和PD﹣的最大值；（2）如图2，已知正方形ABCD的边长为9，圆B的半径为6，点P是圆B上的一个动点，那么PD+的最小值为，PD﹣的最大值为．（3）如图3，已知菱形ABCD的边长为4，∠B＝60°，圆B的半径为2，点P是圆B 上的一个动点，那么PD+的最小值为，PD﹣的最大值为．【分析】（1）如图1中，在BC上取一点G，使得BG＝1．由△PBG∽△CBP，推出＝＝，推出PG＝PC，推出PD+PC＝DP+PG，由DP+PG≥DG，当D、G、P共线时，PD+PC的值最小，最小值为DG＝＝5．由PD﹣PC＝PD﹣PG≤DG，当点P在DG的延长线上时，PD﹣PC的值最大（如图2中），最大值为DG＝5；（2）如图3中，在BC上取一点G，使得BG＝4．解法类似（1）；（3）如图4中，在BC上取一点G，使得BG＝4，作DF⊥BC于F．解法类似（1）；【解答】解：（1）如图1中，在BC上取一点G，使得BG＝1．∵＝＝2，＝＝2，∴＝，∵∠PBG＝∠PBC，∴△PBG∽△CBP，∴＝＝，∴PG＝PC，∴PD+PC＝DP+PG，∵DP+PG≥DG，∴当D、G、P共线时，PD+PC的值最小，最小值为DG＝＝5．∵PD﹣PC＝PD﹣PG≤DG，当点P在DG的延长线上时，PD﹣PC的值最大（如图2中），最大值为DG＝5．（2）如图3中，在BC上取一点G，使得BG＝4．∵＝＝，＝＝，∴＝，∵∠PBG＝∠PBC，∴△PBG∽△CBP，∴＝＝，∴PG＝PC，∴PD+PC＝DP+PG，∵DP+PG≥DG，∴当D、G、P共线时，PD+PC的值最小，最小值为DG＝＝．∵PD﹣PC＝PD﹣PG≤DG，当点P在DG的延长线上时，PD﹣PC的值最大，最大值为DG＝．故答案为，（3）如图4中，在BC上取一点G，使得BG＝1，作DF⊥BC于F．∵＝＝2，＝＝2，∴＝，∵∠PBG＝∠PBC，∴△PBG∽△CBP，∴＝＝，∴PG＝PC，∴PD+PC＝DP+PG，∵DP+PG≥DG，∴当D、G、P共线时，PD+PC的值最小，最小值为DG，在Rt△CDF中，∠DCF＝60°，CD＝4，∴DF＝CD•sin60°＝2，CF＝2，在Rt△GDF中，DG＝＝∵PD﹣PC＝PD﹣PG≤DG，当点P在DG的延长线上时，PD﹣PC的值最大（如图2中），最大值为DG＝．故答案为，．【点评】本题考查圆综合题、正方形的性质、菱形的性质、相似三角形的判定和性质、两点之间线段最短等知识，解题的关键是学会构建相似三角形解决问题，学会用转化的思想思考问题，把问题转化为两点之间线段最短解决，题目比较难，属于中考压轴题．10．如图，抛物线y＝﹣x2+bx+c与直线AB交于A（﹣4，﹣4），B（0，4）两点，直线AC：y＝﹣x﹣6交y轴于点C．点E是直线AB上的动点，过点E作EF⊥x轴交AC于点F，交抛物线于点G．（1）求抛物线y＝﹣x2+bx+c的表达式；（2）连接GB，EO，当四边形GEOB是平行四边形时，求点G的坐标；（3）在（2）的前提下，y轴上是否存在一点H，使∠AHF＝∠AEF？如果存在，求出此时点H的坐标，如果不存在，请说明理由．【分析】（1）把A、B点的坐标分别代入代入y＝﹣x2+bx+c得关于b、c的方程组，然后解方程组求出b、c，从而得到抛物线的解析式；（2）先利用待定系数法求出直线AB的解析式为y＝2x+4，设G（x，﹣x2﹣2x+4），则E （x，2x+4），根据平行四边形的判定，当GE＝OB时，且点G在点E的上方，四边形GEOB为平行四边形，从而得到﹣x2﹣2x+4﹣（2x+4）＝4，然后解方程即可得到此时G 点坐标；（3）先确定C（0，﹣6），再利用勾股定理的逆定理证明△BAC为直角三角形，∠BAC ＝90°，接着根据圆周角定理，由∠AHF＝∠AEF可判断点H在以EF为直径的圆上，EF的中点为M，如图，设H（0，t），由于E（﹣2，0），F（﹣2，﹣5），则M（﹣2，﹣），然后根据HM＝EF得到22+（t+）2＝×52，最后解方程即可得到H点的坐标．【解答】解：（1）把A（﹣4，﹣4），B（0，4）代入y＝﹣x2+bx+c得，解得，∴抛物线的解析式为y＝﹣x2﹣2x+4；（2）设直线AB的解析式为y＝kx+m，把A（﹣4，﹣4），B（0，4）代入得，解得，∴直线AB的解析式为y＝2x+4，设G（x，﹣x2﹣2x+4），则E（x，2x+4），∵OB∥GE，∴当GE＝OB时，且点G在点E的上方，四边形GEOB为平行四边形，∴﹣x2﹣2x+4﹣（2x+4）＝4，解得x1＝x2＝﹣2，此时G点坐标为（﹣2，4）；（3）存在．当x＝0时，y＝﹣x﹣6＝﹣6，则C（0，﹣6），∵AB2＝42+82＝80，AC2＝42+22＝20，BC2＝102＝100，∴AB2+AC2＝BC2，∴△BAC为直角三角形，∠BAC＝90°，∵∠AHF＝∠AEF，∴点H在以EF为直径的圆上，EF的中点为M，如图，设H（0，t），∵G（﹣2，4），∴E（﹣2，0），F（﹣2，﹣5），∴M（﹣2，﹣），∵HM＝EF，∴22+（t+）2＝×52，解得t1＝﹣1，t2＝﹣4，∴H点的坐标为（0，﹣1）或（0，﹣4）．【点评】本题考查了二次函数的综合题：熟练掌握二次函数图象上点的坐标特征和平行四边形的判定；会利用待定系数法求函数解析式；会利用勾股定理的逆定理证明直角三角形，能运用圆周角定理判断点在圆上；理解坐标与图形的性质，记住两点间的距离公式．11．如图1，抛物线y＝ax2+（a+3）x+3（a≠0）与x轴交于点A（4，0），与y轴交于点B，在x轴上有一动点E（m，0）（0＜m＜4），过点E作x轴的垂线交直线AB于点N，交抛物线于点P，过点P作PM⊥AB于点M．（1）求a的值和直线AB的函数表达式；（2）设△PMN的周长为C1，△AEN的周长为C2，若＝，求m的值；（3）如图2，在（2）条件下，将线段OE绕点O逆时针旋转得到OE′，旋转角为α（0°＜α＜90°），连接E′A、E′B，求E′A+E′B的最小值．【分析】（1）令y＝0，求出抛物线与x轴交点，列出方程即可求出a，根据待定系数法可以确定直线AB解析式．（2）由△PNM∽△ANE，推出＝，列出方程即可解决问题．（3）在y轴上取一点M使得OM′＝，构造相似三角形，可以证明AM′就是E′A+E′B的最小值．【解答】解：（1）令y＝0，则ax2+（a+3）x+3＝0，∴（x+1）（ax+3）＝0，∴x＝﹣1或﹣，∵抛物线y＝ax2+（a+3）x+3（a≠0）与x轴交于点A（4，0），∴﹣＝4，∴a＝﹣．∵A（4，0），B（0，3），设直线AB解析式为y＝kx+b，则，解得，∴直线AB解析式为y＝﹣x+3．（2）如图1中，∵PM⊥AB，PE⊥OA，∴∠PMN＝∠AEN，∵∠PNM＝∠ANE，∴△PNM∽△ANE，∴＝，∵NE∥OB，∴＝，∴AN＝（4﹣m），∵抛物线解析式为y＝﹣x2+x+3，∴PN＝﹣m2+m+3﹣（﹣m+3）＝﹣m2+3m，∴＝，解得m＝2．（3）如图2中，在y轴上取一点M′使得OM′＝，连接AM′，在AM′上取一点E′使得OE′＝OE．∵OE′＝2，OM′•OB＝×3＝4，∴OE′2＝OM′•OB，∴＝，∵∠BOE′＝∠M′OE′，∴△M′OE′∽△E′OB，∴＝＝，∴M′E′＝BE′，∴AE′+BE′＝AE′+E′M′＝AM′，此时AE′+BE′最小（两点间线段最短，A、M′、E′共线时），最小值＝AM′＝＝．【点评】本题考查相似三角形的判定和性质、待定系数法、最小值问题等知识，解题的关键是构造相似三角形，找到线段AM′就是E′A+E′B的最小值，属于中考压轴题．。

部编数学九年级下册专题18阿氏圆小题(解析版)含答案

答卷时应注意事项１、拿到试卷，要认真仔细的先填好自己的考生信息。

２、拿到试卷不要提笔就写，先大致的浏览一遍，有多少大题，每个大题里有几个小题，有什么题型，哪些容易，哪些难，做到心里有底；３、审题，每个题目都要多读几遍，不仅要读大题，还要读小题，不放过每一个字，遇到暂时弄不懂题意的题目，手指点读，多读几遍题目，就能理解题意了；容易混乱的地方也应该多读几遍，比如从小到大，从左到右这样的题；４、每个题目做完了以后，把自己的手从试卷上完全移开，好好的看看有没有被自己的手臂挡住而遗漏的题；试卷第１页和第２页上下衔接的地方一定要注意，仔细看看有没有遗漏的小题；５、中途遇到真的解决不了的难题，注意安排好时间，先把后面会做的做完，再来重新读题，结合平时课堂上所学的知识，解答难题；一定要镇定，不能因此慌了手脚，影响下面的答题；６、卷面要清洁，字迹要清工整，非常重要；７、做完的试卷要检查，这样可以发现刚才可能留下的错误或是可以检查是否有漏题，检查的时候，用手指点读题目，不要管自己的答案，重新分析题意，所有计算题重新计算，判断题重新判断，填空题重新填空，之后把检查的结果与先前做的结果进行对比分析。

亲爱的小朋友，你们好!经过两个月的学习，你们一定有不小的收获吧，用你的自信和智慧，认真答题，相信你一定会闯关成功。

相信你是最棒的！专题18 阿氏圆小题1．如图，在ABC D 中，90A Ð=°，4AB AC ==，点E 、F 分别是边AB 、AC 的中点，点P 是以A 为圆心、以AE 为半径的圆弧上的动点，则12PB PC +的最小值等于( )A ．4B ．CD 【解答】解：在AB 上截取1AQ =，连接AP ，PQ ，CQ ，Q 点E 、F 分别是边AB 、AC 的中点，点P 是以A 为圆心、以AE 为半径的圆弧上的动点，\12AP AB =，2AP =Q ，1AQ =，\12AQ AP =，PAQ BAP Ð=ÐQ ，APQ ABP \D D ∽，12PQ PB \=，\12PB PC PC PQ CQ +=+…，在Rt ACQ D 中，4AC =，1AQ =，QB \==，\12PB PC +故选：C ．2．如图，已知菱形ABCD 的边长为8，60B Ð=°，圆B 的半径为4，点P 是圆B 上的一个动点，则12PD PC -的最大值为【解答】解：连接PB ，在BC 上取一点G ，使得2BG =，连接PG ，DG ，过点D 作DH BC ^交BC 的延长线于H ．4PB =Q ，2BG =，8BC =，2PB BG BC \=×，\PB BC BG PB=，PBG CBP Ð=ÐQ ，PBG CBP \D D ∽，\12PG PB PC BC ==，12PG PC \=，Q 四边形ABCD 是菱形，//AB CD \，8AB CD BC ===，60DCH ABC \Ð=Ð=°，在Rt CDH D 中，cos604CH CD =×°=，sin 60DH CD =×°=6410GH CG CH \=+=+=，DG \===，12PD PC PD PG DG -=-Q …，12PD PC \-…，12PD PC \-的最大值为3．如图，正方形ABCD 的边长为4，E 为BC 的中点，以B 为圆心，BE 为半径作B e ，点P 是B e上一动点，连接PD 、PC ，则12PD PC +的最小值为 5　．【解答】解：如图，在BC 上取一点T ，使得1BT =，连接PB ，PT ，DT ．Q 四边形ABCD 是正方形，90DCT \Ð=°，4CD =Q ，3CT =，5DT \===，2PB =Q ，1BT =，4BC =，2PB BT BC \=×，\PB BC BT PB=，PBT PBC Ð=ÐQ ，PBT CBP \D D ∽，\12PT PB PC CB ==，12PT PC \=，152PD PC PD PT DT +=+=Q …，12PD PC \+的最小值为5，故答案为：5．4．如图，扇形AOB 中，90AOB Ð=°，6OA =，C 是OA 的中点，D 是OB 上一点，5OD =，P 是¶AB 上一动点，则12PC PD +的最小值为【解答】解：如图，延长OA 使AE OB =，连接EC ，EP ，OP ，6AO OB ==Q ，C 分别是OA 的中点，12OE \=，6OP =，3OC AC ==，\12OP OC OE OP ==，且COP EOP Ð=ÐOPE OCP\D D ∽\12PC OP PE OE ==，2EP PC \=，111(2)()222PC PD PC PD PD PE \+=+=+，\当点E ，点P ，点D 三点共线时，12PC PD +的值最小，13DE ===Q ，13PD PE DE \+=…，PD PE \+的最小值为13，12PC PD \+的值最小值为132．故答案为：132．5．如图所示的平面直角坐标系中，(0,4)A ，(4,0)B ，P 是第一象限内一动点，2OP =，连接AP 、BP ，则12BP AP +的最小值是【解答】解：如图，取点(0,1)T ，连接PT ，BT ．(0,1)T Q ，(0,4)A ，(4,0)B ，1OT \=，4OA =，4OB =，2OP =Q ，2OP OT OA \=×，\OP OA OT OP=，POT AOP Ð=ÐQ ，POT AOP \D D ∽，\12PT OP PA OA ==，12PT PA \=，12PB PA PB PT \+=+，BT ==QPB PT \+12BP AP \+12BP PB \+．6．如图，在O e 中，点A 、点B 在O e 上，90AOB Ð=°，6OA =，点C 在OA 上，且2OC AC =，点D 是OB 的中点，点M 是劣弧AB 上的动点，则2CM DM +的最小值为【解答】解：延长OB 到T ，使得BT OB =，连接MT ，CT ．6OM =Q ，3OD DB ==，12OT =，2OM OD OT \=×，\OM OT OD OM=，MOD TOM Ð=ÐQ ，MOD TOM \D D ∽，\12DM OM MT OT ==，2MT DM \=，2CM DM CM MT CT +=+Q …，又Q 在Rt OCT D 中，90COT Ð=°，4OC =，12OT =，CT \===，2CM DM \+…2CM DM \+的最小值为\答案为7．如图，边长为4的正方形，内切圆记为圆O ，P 为圆O 上一动点，则PB +的最小值为【解答】解：设O e 半径为r ，122OP r BC ===，OB ==，取OB 的中点I ，连接PI ，OI IB \===，，\OP OB OI OP=，O Ð是公共角，BOP POI \D D ∽，\PI OI PB OP ==PI \=，AP AP PI \=+，\当A 、P 、I 在一条直线上时，AP +最小，作IE AB ^于E ，45ABO Ð=°Q ，1IE BE \===，3AE AB BE \=-=，AI \==，AP PB \最小值AI ==，Q )PB PA +=+，\PB +==．故答案是8．如图，在Rt ABC D 中，90C Ð=°，9AC =，4BC =，以点C 为圆心，3为半径做C e ，分别交AC ，BC 于D ，E 两点，点P 是C e 上一个动点，则13PA PB +的最小值为【解答】解：在AC 上截取1CQ =，连接CP ，PQ ，BQ ，9AC =Q ，3CP =，\13CP AC =，3CP =Q ，1CQ =，\13CQ CP =，ACP PCQ \D D ∽，13PQ AP \=，\13PA PB PQ PB BQ +=+…，\当B 、Q 、P 三点共线时，13PA PB +的值最小，在Rt BCQ D 中，4BC =，1CQ =，QB \=，\13PA PB +9．如图，在Rt ABC D 中，90ACB Ð=°，6AC =，8BC =，D 、E 分别是边BC 、AC 上的两个动点，且4DE =，P 是DE 的中点，连接PA ，PB ，则14PA PB +的最小值为【解答】解：如图，在CB 上取一点F ，使得12CF =，连接PF ，AF ．90DCE Ð=°Q ，4DE =，DP PE =，122PC DE \==，Q14CF CP =，14CP CB =，\CF CP CP CB=，PCF BCP Ð=ÐQ ，PCF BCP \D D ∽，\14PF CF PB CP ==，14PF PB \=，14PA PB PA PF \+=+，PA PF AF +Q …，AF ===，14PA PB \+…，14PA PB \+，．10．如图，在ABC D 中，6BC =，60BAC Ð=°，则2AB AC +的最大值为【解答】解：122()2AB AC AB AC +=+Q ，\求2AB AC +的最大值就是求12()2AB AC +的最大值，过C 作CE AB ^于E ，延长EA 到P ，使得AP AE =，60BAC Ð=°Q ，12EA AC AP \==，12AB AC AB AP \+=+，EC =Q ，2PE AE =，由勾股定理得：PC =，sin CE P CP \===，P \Ð为定值，6BC =Q 是定值，\点P 在CBP D 的外接圆上，AB AP BP +=Q ，\当BP 为直径时，AB AP +最大，即BP ¢，sin sin BC P P BP ¢\===¢，解得BP ¢=AB AP \+=，22()AB AC AB AP \+=+=，故答案为：．11．如图，O e 与y 轴、x 轴的正半轴分别相交于点M 、点N ，O e 半径为3，点(0,1)A ，点(2,0)B ，点P 在弧MN 上移动，连接PA ，PB ，则3PA PB +的最小值为．【解答】解：如图，在y 轴上取点(0,9)H ，连接BH ，Q 点(0,1)A ，点(2,0)B ，点(0,9)H ，1AO \=，2OB =，9OH =，Q 1339OA OP OP OH===，AOP POH Ð=Ð，AOP POH \D D ∽，\13AP OP HP OH ==，3HP AP \=，3PA PB PH PB \+=+，\当点P 在BH 上时，3PA PB +有最小值为HB 的长，BH \===，．12．【新知探究】新定义：平面内两定点A ，B ，所有满足(PA k k PB=为定值）的P 点形成的图形是圆，我们把这种圆称之为“阿氏圆”【问题解决】如图，在ABC D 中，4CB =，2AB AC =，则ABC D 面积的最大值为【解答】解：以A 为顶点，AC 为边，在ABC D 外部作CAP ABC Ð=Ð，AP 与BC 的延长线交于点P ，CAP ABC Ð=ÐQ ，BPA APC Ð=Ð，2AB AC =，APC BPA \D D ∽，12AP CP AC BP AP AB ===，2BP AP \=，12CP AP =，4BP CP BC -==Q ，1242AP AP \-=，解得：83AP =，163BP \=，43CP =，即点P 为定点，\点A 的轨迹为以点P 为圆心，83为半径的圆上，如图，过点P 作BC 的垂线，交圆P 与点1A ，此时点1A 到BC 的距离最大，即ABC D 的面积最大，11181642233ABC S BC A P D =×=´´=．故答案为：163．13．如图所示，60ACB Ð=°，半径为2的圆O 内切于ACB Ð．P 为圆O 上一动点，过点P 作PM 、PN 分别垂直于ACB Ð的两边，垂足为M 、N ，则2PM PN +的取值范围为 626PM PN -++…　．【解答】解：作MH NP ^于H ，作MF BC ^于F ，PM AC ^Q ，PN CB ^，90PMC PNC \Ð=Ð=°，360120MPN PMC PNC C \Ð=°-Ð-Ð-Ð=°，18060MPH MPN \Ð=°-Ð=°，1cos cos602HP PM MPH PM PM \=×Ð=×°=，12PN PM PN HP NH \+=+=，MF NH =Q ，\当MP 与O e 相切时，MF 取得最大和最小，如图1，连接OP ，OG ，可得：四边形OPMG 是正方形，2MG OP \==，在Rt COG D 中，tan 60CG OG =×°=，2CM CG GM \=+=+，在Rt CMF D 中，cos (23MF CM C =×=+=，3HN MF \==+，122()262PM PN PM PN HN +=+==+如图2，由上知：CG =，2MG =，2CM \=，2)3HM \=-=-122()262PM PN PM PN HN \+=+==-，626PM PN \-++…．三．解答题（共2小题）14．如图，在每个小正方形的边长为1的网格中，OAB D 的顶点O ，A ，B 均在格点上，点E 在OA 上，且点E 也在格点上．()OE I OB （Ⅱ）¶DE是以点O 为圆心，2为半径的一段圆弧．在如图所示的网格中，将线段OE 绕点O 逆时针旋转得到OE ¢，旋转角为(090)a a °<<°连接E A ¢，E B ¢，当23E A E B ¢¢+的值最小时，请用无刻度的直尺画出点E ¢，并简要说明点E ¢的位置是如何找到的（不要求证明）．【解答】解：（1）由题意2OE =，3OB =，\23OE OB =，故答案为：23．（2）如图，取格点K ，T ，连接KT 交OB 于H ，连接AH 交¶DE于E ¢，连接BE ¢，点E ¢即为所求．故答案为：通过取格点K 、T ，使得:2:3OH OD =，构造相似三角形将23E B ¢转化为E H ¢，利用两点之间线段最短即可解决问题．15．阅读以下材料，并按要求完成相应的任务．已知平面上两点A 、B ，则所有符合(0PA k k PB=>且1)k ¹的点P 会组成一个圆．这个结论最先由古希腊数学家阿波罗尼斯发现，称阿氏圆．阿氏圆基本解法：构造三角形相似．【问题】如图1，在平面直角坐标系中，在x 轴，y 轴上分别有点(,0)C m ，(0,)D n ，点P 是平面内一动点，且OP r =，设OP k OD=，求PC kPD +的最小值．阿氏圆的关键解题步骤：第一步：如图1，在OD上取点M，使得::OM OP OP OD k==；第二步：证明kPD PM=；第三步：连接CM，此时CM即为所求的最小值．下面是该题的解答过程（部分）:解：在OD上取点M，使得::OM OP OP OD k==，又POD MOPÐ=ÐQ，POM DOP\D D∽．任务：（1）将以上解答过程补充完整．（2）如图2，在Rt ABCD中，90ACBÐ=°，4AC=，3BC=，D为ABCD内一动点，满足2CD=，利用（1）中的结论，请直接写出23AD BD+的最小值．【解答】解（1）在OD上取点M，使得::OM OP OP OD k==，又POD MOPÐ=ÐQ，POM DOP\D D∽．:MP PD k\=，MP kPD\=，PC kPD PC MP\+=+，当PC kPD+取最小值时，PC MP+有最小值，即C，P，M三点共线时有最小值，利用勾股定理得CM===．（2）4AC m==Q，23CDBC=，在CB上取一点M，使得2433CM CD==，\23AD BD +=．。

专题01 中考数学专题复习最值问题(阿氏圆)练习

中考数学专题复习最值问题（阿氏圆）练习1．如图，在Rt△ABC中，∠ACB＝90°，CB＝7，AC＝9，以C为圆心、3为半径作⊙C，P为⊙C上一动点，连接AP、BP，则13AP＋BP的最小值为（）A．7B．C．4D．【答案】B【解析】思路引领：如图，在CA上截取CM，使得CM＝1，连接PM，PC，BM．利用相似三角形的性质证明MP13=PA，可得13AP+BP＝PM+PB≥BM，利用勾股定理求出BM即可解决问题．答案解析：如图，在CA上截取CM，使得CM＝1，连接PM，PC，BM．∵PC＝3，CM＝1，CA＝9，∴PC2＝CM•CA，∴PC CM CA CP=，∵∠PCM＝∠ACP，∴△PCM∽△ACP，∴13 PM PCPA AC==，∴PM13=PA，∴13AP+BP＝PM+PB，∵PM+PB≥BM，在Rt△BCM中，∵∠BCM＝90°，CM＝1，BC＝7，∴BM==∴13AP +BP ，∴13AP +BP 的最小值为．故选：B ．2．如图，边长为4的正方形，内切圆记为⊙O ，P 是⊙O ＋PB 的最小值为________．【答案】【分析】＋PB （PA PB ）PB 即可解答．【解析】解：设⊙O 半径为r ，OP ＝r ＝12BC ＝2，OB r ＝，取OB PI ，∴OI ＝IB∵OP OI =，OB OP ==，∴OP OBOI OP= ，∠O 是公共角，∴△BOP ，∴PI PB =，∴PI ，∴AP ＝AP ＋PI ，∴当A 、P 、I 在一条直线上时，AP 最小，作IE ⊥AB 于E ，∵∠ABO ＝∴IE ＝BE ＝1，∴AE ＝AB −BE ＝3，∴AI =∴AP 最小值＝AI＋PB （PA PB ），＋=．故答案是【点睛】本题是“阿氏圆”问题，解决问题的关键是构造相似三角形．3．如图，已知正方ABCD 的边长为6，圆B 的半径为3，点P 是圆B 上的一个动点，则12PD PC -的最大值为_______．【答案】152【分析】如图，连接BP ，在BC 上取一点M ，使得BM =32，进而证明BPM BCP △∽△,则在点P 运动的任意时刻，均有PM =12PC ，从而将问题转化为求PD -PM 的最大值．连接PD ，在△PDM 中，PD -PM ＜DM ，故当D 、M 、P 共线时，PD -PM =DM 为最大值，勾股定理即可求得DM ．【解析】如图，连接BP ，在BC 上取一点M ，使得BM =32，31232BM BP ==Q ，3162BP BC ==BM BPBP BC\=PBM CBP Ð=ÐQ \BPM BCP△∽△12MP BM PC BP \==12MP PC \=12PD PC PD MD\-=-在△PDM 中，PD -PM ＜DM ，当D 、M 、P 共线时，PD -PM =DM 为最大值，Q 四边形ABCD 是正方形90C \Ð=°在Rt CDM V 中，152DM ===故答案为：152．【点睛】本题考查了圆的性质，相似三角形的性质与判定，勾股定理，构造12PC 是解题的关键．4．如图，在V 90,2B AB CB Ð=°==，以点B 为圆心作圆B 与AC 相切，点P 为圆B 上任一动点，则PA +的最小值是___________．【分析】作BH ⊥AC 于H ，取BC 的中点D ，连接PD ，如图，根据切线的性质得BH等腰直角三角形的性质得到BH 12=AC =接着证明△BPD ∽△BCP 得到PD =，所以PAPC ＝PA +PD ，而PA +PD ≥AD （当且仅当A 、P 、D 共线时取等号），从而计算出AD 得到PA 的最小值．【解析】解：作BH ⊥AC 于H ，取BC 的中点D ，连接PD ，如图，∵AC 为切线，∴BH 为⊙B 的半径，∵∠90°＝CB ＝2，∴AC =＝∴BH 12=AC∴BP =∵PB BC BD BP ==，而∠PBD ＝∠CBP ，∴△BPD∴PD PC ∴PD =，∴PA ＝PA +PD ，而PA +PD ≥AD （当且仅当A 、P 、D 共线时取等号），而AD =∴PA+即PA【点睛】：圆的切线垂直于经过切点的半径．解决问题的关键是利用相似比确定线段PD=．也考查了等腰直角三角形的性质．5．如图，在Rt ABCD中，AB＝AC＝4，点E，F分别是AB，AC的中点，点P是扇形AEF的 E F上任意一点，连接BP，CP，则12BP+CP的最小值是_____．．【分析】在AB上取一点T，使得AT＝1，连接PT，PA，CT．证明PAT BAPD D∽，推出PTPB＝APAB＝12，推出PT＝12PB，推出12PB+CP＝CP+PT，根据PC+PT≥TC，求出CT即可解决问题．【解析】解：在AB上取一点T，使得AT＝1，连接PT，PA，CT．∵PA＝2．AT＝1，AB＝4，∴PA2＝4=AT•AB，∴PAAT＝ABPA，∵∠PAT＝∠PAB，∴PAT BAPD D∽，∴PTPB＝APAB＝12，∴PT＝12PB，∴12PB+CP＝CP+PT，∵PC+PT≥TC，在Rt ACTD中，∵∠CAT＝90°，AT＝1，AC＝4，∴CT，∴12PB+PC，∴12PB+PC．．【点睛】本题考查等腰直角三角形的性质，三角形相似的判定与性质，勾股定理的应用，三角形的三边关系，圆的基本性质，掌握以上知识是解题的关键．6．如图，已知正方形ABCD的边长为4，⊙B的半径为2，点P是⊙B上的一个动点，则PD﹣12 PC的最大值为_____．【答案】5【解析】分析: 由PD−12PC＝PD−PG≤DG，当点P在DG的延长线上时，PD−12PC的值最大，最大值为DG＝5．解析: 在BC上取一点G，使得BG＝1，如图，∵221PBBG==，422BCPB==，∴PB BC BG PB=，∵∠PBG＝∠PBC，∴△PBG∽△CBP，∴12 PG BGPC PB==，∴PG＝12PC，当点P在DG的延长线上时，PD−12PC的值最大，最大值为DG＝5．故答案为5点睛: 本题考查圆综合题、正方形的性质、相似三角形的判定和性质等知识，解题的关键是学会构建相似三角形解决问题，学会用转化的思想思考问题，把问题转化为两点之间线段最短解决，题目比较难，属于中考压轴题．7．如图1所示，⊙O的半径为r，点A、B都在⊙O外，P为⊙O上的动点，已知r＝k·OB．连接PA、PB，则当“PA＋k·PB”的值最小时，P点的位置如何确定？【解析】1：连接动点至圆心0（将系数不为1的线段两端点分别与圆心相连接），即连接OP 、OB ；2：计算连接线段OP 、OB 长度；3：计算两线段长度的比值k OPOB=；4：在OB 上截取一点C ，使得OC OPOP OB=构建母子型相似：5：连接AC ，与圆0交点为P ，即AC 线段长为PA ＋K *PB 的最小值．本题的关键在于如何确定“k ·PB ”的大小，（如图 2）在线段 OB 上截取 OC 使 OC ＝k ·r ，则可说明△BPO 与△PCO 相似，即 k ·PB ＝PC ．∴本题求“PA ＋k ·PB ”的最小值转化为求“PA ＋PC ”的最小值，即 A 、P 、C 三点共线时最小（如图 3），时AC 线段长即所求最小值．8．如图，点A 、B 在O e 上，且OA ＝OB ＝6，且OA ⊥OB ，点C 是OA 的中点，点D 在OB 上，且OD ＝4，动点P 在O e 上．求2PC ＋PD 的最小值．【答案】【分析】连接OP ，在射线OA 上截取AE =6，连接PE ．由题意易证OPC OEP V :V ，即得出2PE PC =，从而得出2PC PD PE PD +=+，由此可知当P 、D 、E 三点共线时，PE PD +最小，最小值为DE 的长，最后在Rt OED △中利用勾股定理求出DE 的长即可．【解析】如图，连接OP ，在射线OA 上截取AE =6，连接PE ．∵C 是OA 的中点，∴1122OC OA OP ==．∴在△OPC 和△OEP 中，12COP POE OC OP OP OE Ð=Ðìïí==ïî，∴OPC OEP V :V ，∴1=2PC PE ，即2PE PC =，∴2PC PD PE PD +=+，.∴当P 、D 、E 三点共线时，PE PD +最小，最小值即为DE 的长，如图，在Rt OED △中，DE ===，∴2PC PD +的最小值为．【点睛】本题考查同圆半径相等、三角形相似的判定和性质和勾股定理等知识．正确作出辅助线并理解当P 、D 、E 三点共线时，PE PD +最小，最小值为DE 的长是解答本题的关键．9．如图，Rt △ABC ，∠ACB ＝90°，AC ＝BC ＝2，以C CDEF （C 、D 、E 、F 四个顶点按逆时针方向排列）可以绕点C 自由转动，且CD ，连接AF ，BD（1）求证：△BDC ≌△AFC（2）当正方形CDEF 有顶点在线段AB 上时，直接写出BD AD 的值；（3）直接写出正方形CDEF 旋转过程中，BD 的最小值．【答案】（1）见解析；（21 ；（3【分析】（1）利用SAS ，即可证明△FCA ≌△DCB ；（2）分两种情况当点D ，E 在AB 边上时和当点E ，F 在边AB（3）取AC 的中点M ．连接DM ，BM ．则CM ＝1，可证得△DCM ∽△ACD ，可得DM ，从而得到当B ，D ，M 共线时，BD 的值最小，即可求解．【解析】（1）证明： ∵四边形CDEF 是正方形，∴CF ＝CD ，∠DCF ＝∠ACB ＝90°，∴∠ACF ＝∠DCB ，∵AC ＝CB ，∴△FCA ≌△DCB （SAS ）；（2）解：①如图2中，当点D ，E 在AB 边上时，∵AC ＝BC ＝2，∠ACB ＝90°，∴sin 45ACAB ==°∵CD ⊥AB ，∴AD AC =´=∴BD ＝1==；②如图3中，当点E ，F 在边AB 上时．BD ＝CF ＝sin 452BC ´°==AD∴BD =综上所述，BD 1+（3）如图4中．取AC 的中点M ．连接DM ，BM ．则CM ＝1，∵CD CM ＝1，CA ＝2，∴CD 2＝CM •CA ，∴CD CA ＝CMCD，∵∠DCM ＝∠ACD ，∴△DCM ∽△∴DM AD ＝CD AC ，∴DM ，∴BD ＝BD +DM ，∴当B ，D ，M 共线时，BD 的值最小，最小值BM ==【点睛】本题主要考查了相似三角形的判定和性质，全等三角形的判定和性质，正方形的性质，锐角三角函数，熟练掌握相关知识点是解题的关键．10．已知抛物线y ＝ax 2＋bx ＋c 与x 轴交于A （﹣1，0），B （5，0）两点，C 为抛物线的顶点，抛物线的对称轴交x 轴于点D ，连接BC ，且tan∠CBD 4=3，如图所示．（1）求抛物线的解析式；（2）设P 是抛物线的对称轴上的一个动点．①过点P 作x 轴的平行线交线段BC 于点E ，过点E 作EF ⊥PE 交抛物线于点F ，连接FB 、FC ，求△BCF 的面积的最大值；②连接PB ，求35PC ＋PB 的最小值．【答案】（1）241620999x x -++；（2）①32；②245【解析】思路引领：（1）设抛物线的解析式为：y ＝a （x +1）（x ﹣5），可得对称轴为直线x ＝2，由锐角三角函数可求点C 坐标，代入解析式可求解析式；（2）①先求出直线BC 解析式，设P （2，t ），可得点E （534-t ，t ），点2315244F t t t æö--ç÷èø，，可求EF 的长，由三角形面积公式和二次函数性质可求解；②根据图形的对称性可知∠ACD ＝∠BCD ，AC ＝BC ＝5，过点P 作PG ⊥AC 于G ，可得PG 35=PC ，可得35PC PB PG PB +=+，过点B 作BH ⊥AC 于点H ，则PG +PB ≥BH ，即BH 是35PC +PB 的最小值，由三角形面积公式可求解．答案解析：（1）根据题意，可设抛物线的解析式为：y ＝a （x +1）（x ﹣5），∵抛物线的对称轴为直线x ＝2，∴D （2，0），又∵43CDtan CBD DBÐ==，∴CD ＝BD •tan∠CBD ＝4，即C （2，4），代入抛物线的解析式，得4＝a （2+1）（2﹣5），解得 49a =-，∴二次函数的解析式为 ()()441599y x x =-+-=-x 2162099x ++；（2）①设P （2，t ），其中0＜t ＜4，设直线BC 的解析式为 y ＝kx +b ，∴0542.k b k b =+ìí=+î，，解得 4320.3k b ì=-ïïíï=ïî即直线BC 的解析式为 42033y x =-+，令y ＝t ，得：354x t =-，∴点E （534-t ，t ），把354x t =- 代入()()4159y x x =-+-，得 24t y t æö=-ç÷èø，即2315244F t t t æö--ç÷èø，，∴221244t EF t t t t æö=--=-ç÷èø，∴△BCF 的面积12=´EF ×BD 32=（t 24t -）()223334(2)882t t t =--=--+，∴当t ＝2时，△BCF 的面积最大，且最大值为32；②如图，据图形的对称性可知∠ACD ＝∠BCD ，AC ＝BC ＝5，∴35AD sin ACD AC Ð==，过点P 作PG ⊥AC 于G ，则在Rt△PCG 中，35PG PC sin ACD PC =×Ð=，∴35PC PB PG PB +=+，过点B 作BH ⊥AC 于点H ，则PG +PB ≥BH ，∴线段BH 的长就是35PC PB +的最小值，∵11641222ABC S AB CD =´´=´´=V ，又∵1522ABC S AC BH BH =´´=V ，∴5122BH =，即245BH =，∴35PC PB +的最小值为245．11．问题提出：如图①，在Rt ABC △中，90C =o ∠，4CB =，6CA =，⊙C 的半径为2，P 为圆上一动点，连接AP 、BP ，求12AP BP +的最小值．（1）尝试解决：为了解决这个问题，下面给出一种解题思路：如图①，连接CP ，在CB 上取一点D ，使1CD =，则12CD CP CP CB ==．又PCD BCP Ð=Ð，所以PCD D ∽BCP D ．所以12PD CD BP CP ==．所以12PD PB =，所以12AP BP AP PD +=+．请你完成余下的思考，并直接写出答案：12AP BP +的最小值为________；（2）自主探索：在“问题提出”的条件不变的前提下，求13AP BP +的最小值；（3）拓展延伸：如图②，已知在扇形COD 中，90COD Ð=o ，6OC =，3OA =，5OB =，P 是 CD上一点，求2PA PB +的最小值．【答案】（1；（2（3）13．【分析】（1）根据题意可知最小值为AD 长度，利用勾股定理即可求出AD 长度．（2）连接CP ，在CA 上取一点D ，使23CD =，即可证明PCD V ∽ACP △，得到13PD AP =，即13AP BP PD BP +=+，所以13AP BP +的最小值为BD 长度，利用勾股定理即可求出BD 长度．（3）延长OC 到E ，使6CE =，连接PE ，OP ，即可证明OAP △∽OPE V ，得到2EP PA =，即2PA PB EP PB +=+，所以2PA PB +的最小值为BE 长度，利用勾股定理即可求出BE 长度．【解析】（1）根据题意可知，当A 、P 、D 三点共线时，12AP BP +最小，最小值AD ====．（2）连接CP ，在CA 上取一点D ，使23CD =，则有13CD CP CP CA ==，∵PCD ACP Ð=Ð，∴PCD D ∽ACP △，得13PD CD AP CP ==，∴13PD AP =，故13AP BP PD BP +=+，仅当B 、P 、D 三点共线时，13AP BP +的最小值BD ====．（3）延长OC 到E ，使6CE =，连接PE ，OP ，则12OA OP OP OE ==，∵AOP POE Ð=Ð，∴OAP △∽OPE D ，∴12OA OP AP OP OE EP ===，∴2EP PA =，∴2PA PB EP PB +=+，仅当E 、P 、B 三点共线时，13EP PB BE +====，即2PA PB +的最小值为13．【点睛】本题考查圆的综合，勾股定理，相似三角形的判定和性质．根据阅读材料的思路构造出PCD V ∽ACP △和OAP △∽OPE V 是解题的关键．本题较难．12．如图，抛物线2y ax bx c =++与x 轴交于A 0)，B 两点（点B 在点A 的左侧），与y 轴交于点C ，且3OB OA =，OAC Ð的平分线AD 交y 轴于点D ，过点A 且垂直于AD 的直线l 交y 轴于点E ，点P 是x 轴下方抛物线上的一个动点，过点P 作PF x ^轴，垂足为F ，交直线AD 于点H ．（1）求抛物线的解析式；（2）设点P 的横坐标为m ，当FH HP =时，求m 的值；（3）当直线PF 为抛物线的对称轴时，以点H 为圆心，12HC 为半径作⊙H ，点Q 为⊙H 上的一个动点，求14AQ EQ +的最小值．【答案】（1）y 13=x 2﹣3；（2）；（3【分析】对于（1），结合已知先求出点B 和点C 的坐标，再利用待定系数法求解即可；对于（2），在Rt△OAC 中，利用三角函数的知识求出∠OAC 的度数，再利用角平分线的定义求出∠OAD 的度数，进而得到点D 的坐标；接下来求出直线AD 的解析式，表示出点P ，H ，F 的3），首先求出⊙H 的半径，在HA 上取一点K ，使得HK=14，此时K （15-8）；然后由HQ 2=HK·HA ，得到△QHK∽△AHQ，再利用相似三角形的性质求出KQ=14AQ ，进而可得当E 、Q 、K 共线时，14AQ+EQ 的值最小，据此解答.【解析】（1）由题意A 0），B 0），C （0，﹣3），设抛物线的解析式为y ＝a （x（x ，把C （0，﹣3）代入得到a 13=，∴抛物线的解析式为y 13=x 2﹣3．（2）在Rt△AOC 中，tan∠OAC OCOA==，∴∠OAC ＝60°．∵AD OAC ，∴∠OAD ＝30°＝D （0，﹣1），∴直线AD 的解析式为y =﹣1，由题意P （m ，13m 2，H （m ﹣1），F （m ，0）．∵FH ＝PH ，∴1=﹣1﹣（13﹣3）解得m =，∴当时，m ．（3）如图，∵PF 是对称轴，∴F 0），H （．∵AH ⊥AE ，∴∠EAO ＝60°，∴EO =＝3，∴E （0，3）．∵C （0，﹣3），∴HC ==2，AH ＝2FH ＝4，∴QH 12=CH ＝1，在HA 上取一点K ，使得HK14=，此时K （158-）．∵HQ 2＝1，HK •HA ＝1，∴HQ 2＝HK •HA ，∴HQ KHAH HQ=．∵∠QHK ＝∠AHQ ，∴△QHK ∽△AHQ ，∴14KQ HQ AQ AH ==，∴KQ 14=AQ ，∴14AQ +QE ＝KQ +EQ ，∴当E 、Q 、K 共线时，14AQ +QE 的值最小，最小值==．【点睛】本题考查了相似三角形对应边成比例、两边成比例且夹角相等的两个三角形相似、待定系数法求二次函数的表达式、二次函数的图象与性质、数轴上两点间的距离公式，熟练掌握该知识点是本题解题的关键.。

阿氏圆 (隐圆压轴三)(解析版)--初中数学专项训练

阿氏圆阿氏圆问题问题：求解“AP+nPB”类加权线段和最小值方法：①定：定系数，并确定是半径和哪条线段的比值②造：根据线段比，构造母子型相似③算：根据母子型结论，计算定点位置④转：“AP+nPB”转化为“AP+PM”问题关键：①可解性：半径长与圆心到加权线段中定点距离比等于加权系数②系数小于1：内部构造母子型③系数大于1：外部构造母子型1阅读以下材料，并按要求完成相应的任务．已知平面上两点A、B，则所有符合PAPB=k(k>0且k≠1)的点P会组成一个圆．这个结论最先由古希腊数学家阿波罗尼斯发现，称阿氏圆．阿氏圆基本解法：构造三角形相似．【问题】如图1，在平面直角坐标系中，在x轴，y轴上分别有点C(m，0)，D(0，n)，点P是平面内一动点，且OP=r，设OPOD=k，求PC+kPD的最小值．阿氏圆的关键解题步骤：第一步：如图1，在OD上取点M，使得OM：OP=OP：OD=k；第二步：证明kPD=PM；第三步：连接CM，此时CM即为所求的最小值．下面是该题的解答过程(部分)：解：在OD上取点M，使得OM：OP=OP：OD=k，又∵∠POD=∠MOP，∴△POM∽△DOP．任务：(1)将以上解答过程补充完整．(2)如图2，在Rt△ABC中，∠ACB=90°，AC=4，BC=3，D为△ABC内一动点，满足CD=2，利用(1)中的结论，请直接写出AD+23BD的最小值．【解答】解(1)在OD上取点M，使得OM：OP=OP：OD=k，又∵∠POD=∠MOP，∴△POM∽△DOP．∴MP：PD=k，∴MP=kPD，∴PC+kPD=PC+MP，当PC+kPD取最小值时，PC+MP有最小值，即C，P，M三点共线时有最小值，利用勾股定理得CM=OC2+OM2=m2+kr2=m2+k2r2．(2)∵AC=m=4，CDBC =23，在CB上取一点M，使得CM=23CD=43，∴AD +23BD 的最小值为42+43 2=4103．1如图，在Rt △ABC 中，∠ABC =90°，AB =6，BC =9，⊙B 的半径为3，点P 是⊙B 上一点，连接AP ，CP ，则AP +13CP 的最小值为．【答案】37【解答】解：连接BP ，在BC 上截取BQ =1，连接PQ ，AQ ，∴BQ BP =13，BP BC =39=13，∴BQ BP =BP BC，∵∠PBQ =∠CBP ，∴△BPQ ∽△BCP ，∴PQ CP =BP BC =13，∴PQ =13CP ，∴AP +13CP =AP +PQ ≥AQ ，当A 、P 、Q 三点依次在同一直线上时，AP +13CP =AQ =AB 2+BQ 2=37的值最小，故答案为：37．2如图，在Rt △ABC 中，∠ACB =90°，CB =4，CA =6，⊙C 半径为2，P 为圆上一动点，连接AP ，BP ，则AP +12BP 的最小值为()A.37B.6C.217D.4【答案】A【解答】解：如图1，连接CP ，在CB 上取点D ，使CD =1，则有CD CP =CP CB =12，又∵∠PCD =∠BCP ，∴△PCD ∽△BCP ，∴PD BP =12，∴PD =12BP ，∴AP +12BP =AP +PD ．要使AP +12BP 最小，只要AP +PD 最小，当点A ，P ，D 在同一条直线时，AP +PD 最小，即：AP +12BP 最小值为AD ，在Rt △ACD 中，CD =1，AC =6，∴AD =AC 2+CD 2=37，AP +12BP 的最小值为37，故选：A ．3如图，在正方形ABCD 中．AB =8，点P 是正方形ABCD 内部的一点，且满足BP =4，则PD +12PC 的最小值是()A.6B.8C.10D.12【答案】C 【解答】解：在BC 边上取一点E ，使BE =2，连接DE ，如图∵ABCD 是正方形，AB =8∴AB =BC =CD =8，∠BCD =90°∵BP =4∴BE BP=24=12，BP BC =48=12∴BE BP =BP BC且∠PBC =∠PBC ∴△PBE ∽△BCP∴PE PC =BP BC =12∴PE =12PC ∴PD +12PC =PD +PE 在Rt △DCE 中，CD =8，CE =BC -BE =6∴DE =CD 2+CE 2=10∵PD +PE ≥DE∴PD +PE ≥10∴PD +12PC 的最小值是10故选：C ．4如图，已知抛物线y =-34x 2+94x +3与x 轴交于A ，B 两点(A 在点B 的左侧)，与y 轴交于点C ，⊙O 与x 轴交于点E (2，0)，点P 是⊙O 上一点，连接CP ，BP ，求BP +23CP 的最小值．【解答】解：如图，在OC 上取一点T ，使得OT =43，连接PT ，BT ，OP ．由题意C (0，3)，E (2，0)，A (-1，0)，B (4，0)∴OE =2，OC =3，OB =4，OA =1，∴OP 2=OT •OB ，∴OP OT =OB OP，∵∠POT =∠COP ，∴△POT ∽△COP ，∴PTPC =OP OC =23，∴PT =23PC ，∴PB +23PC =BP +PT ≥BT ，在Rt △BOT 中，OB =4，OT =43，∴BT =OB 2+OT 2=42+43 2=4103，∴ABP +23PC ≥4103，∴BP +23PC 的最小值为4103．5(西峡县期末)如图，在△ABC 中，∠A =90°，AB =AC =4，点E 、F 分别是边AB 、AC 的中点，点P 是以A 为圆心、以AE 为半径的圆弧上的动点，则12PB +PC 的最小值等于()A.4B.32C.17D.15【答案】C 【解答】解：在AB 上截取AQ =1，连接AP ，PQ ，CQ ，∵点E 、F 分别是边AB 、AC 的中点，点P 是以A 为圆心、以AE 为半径的圆弧上的动点，∴AP AB=12，∵AP =2，AQ =1，∴AQAP=12，∵∠PAQ =∠BAP ，∴△APQ ∽△ABP ，∴PQ =12PB ，∴12PB +PC =PC +PQ ≥CQ ，在Rt △ACQ 中，AC =4，AQ =1，∴QB =AC 2+AQ 2=17，∴12PB +PC 的最小值17，故选：C ．6(2022春•长顺县月考)如图，在Rt △ABC 中，∠ACB =90°，AC =6，BC =8，D 、E 分别是边BC 、AC 上的两个动点，且DE =4，P 是DE 的中点，连接PA ，PB ，则PA +14PB 的最小值为　1452　．【答案】见试题解答内容【解答】解：如图，在CB 上取一点F ，使得CF =12，连接PF ，AF ．∵∠DCE =90°，DE =4，DP =PE ，∴PC =12DE =2，∵CF CP =14，CP CB =14，∴CF CP =CP CB，∵∠PCF =∠BCP ，∴△PCF ∽△BCP ，∴PF PB =CF CP =14，∴PF =14PB ，∴PA +14PB =PA +PF ，∵PA +PF ≥AF ，AF =CF 2+AC 2=12 2+62=1452，∴PA +14PB ≥1452，∴PA +14PB 的最小值为1452，故答案为1452．7(龙凤区期末)如图，在Rt △ABC 中，∠C =90°，AC =9，BC =4，以点C 为圆心，3为半径做⊙C ，分别交AC ，BC 于D ，E 两点，点P 是⊙C 上一个动点，则13PA +PB 的最小值为．【答案】17．【解答】解：在AC 上截取CQ =1，连接CP ，PQ ，BQ ，∵AC =9，CP =3，∴CP AC=13，∵CP =3，CQ =1，∴CQ CP=13，∴△ACP ∽△PCQ ，∴PQ =13AP ，∴13PA +PB =PQ +PB ≥BQ ，∴当B 、Q 、P 三点共线时，13PA +PB 的值最小，在Rt △BCQ 中，BC =4，CQ =1，∴QB =17，∴13PA +PB 的最小值17，故答案为：17．8如图，在Rt △ABC 中，∠ACB =90°，AC =4，BC =3，点D 为△ABC 内一动点，且满足CD =2，则AD +23BD 的最小值为　4103　．【答案】4103．【解答】解：如图，在CB 上取一点T ，使得CT =43，连接DT ，AT ．∵CD =2，CT =43，CB =3，∴CD 2=CT •CB ，∴CD CT =CB CD，∵∠DCT =∠BCD ，∴△DCT ∽△BCD ，∴DT DB =CD CB =23，∴DT =23BD ，∴AD +23BD =AD +DT ≥AT ，在Rt △ACT 中，AC =4，CT =43，∴AT =AC 22+CT 2=42+43 2=4103，∴AD +23BD ≥4103，∴AD +23BD 的最小值为4103．9如图，正方形ABCD 的边长为4，E 为BC 的中点，以B 为圆心，BE 为半径作⊙B ，点P 是⊙B 上一动点，连接PD 、PC ，则PD +12PC 的最小值为5．【答案】5．【解答】解：如图，在BC 上取一点T ，使得BT =1，连接PB ，PT ，DT ．∵四边形ABCD 是正方形，∴∠DCT =90°，∵CD =4，CT =3，∴DT =CD 2+CT 2=42+32=5，∵PB =2，BT =1，BC =4，∴PB 2=BT •BC ，∴PB BT =BC PB，∵∠PBT =∠PBC ，∴△PBT ∽△CBP ，∴PT PC =PB CB =12，∴PT =12PC ，∵PD +12PC =PD +PT ≥DT =5，∴PD +12PC 的最小值为5，故答案为：5．2如图，在扇形AOB 中，∠AOB =90°，OA =4，C ，D 分别为OA ，OB 的中点，点P 是上一点，则2PC +PD 的最小值为．【答案】217．版权所有【解答】解：如图，延长OA 使AE =OA ，连接ED ，EP ，OP ，∵AO =OB =4，C ，D 分别是OA ，OB 的中点，∴OE =8，OP =4，OD =OC =2，∴OC OP =12=OP OE，且∠COP =∠EOP ，∴△OPE ∽△OCP ，∴PCPE =OP OE=12，∴EP =2DC ，∴2PC +PD =PE +PD ，∴当点E ，点P ，点D 三点共线时，2PC +PD 的值最小，∴2PC +PD 最小值=22+82=217．10如图，在扇形COD 中，∠COD =90°，OC =3，点A 是OC 中点，OB =2，点P 是为CD 上一点，则PB +2PA 的最小值为．【答案】210【解答】连接OP ，延长OC 至点E ，使得OE =6，则OA OP =323=12，OP OE =36=12，∴OA OP =OP OE，∵∠AOP =∠AOP ，∴△AOP ∽△POE ，∴PA PE=12，即2PA =PE ，∴PB +2PA =PB +PE ，∴当E 、P 、B 三点共线时，PB +PE 最小，∴PB +2PA 的最小值为BE =62+22=210．故答案为：210．11(梁溪区校级期中)如图，⊙O 与y 轴、x 轴的正半轴分别相交于点M 、点N ，⊙O 半径为3，点A (0，1)，点B (2，0)，点P 在弧MN 上移动，连接PA ，PB ，则3PA +PB 的最小值为　85　．【答案】85．【解答】解：如图，在y 轴上取点H (0，9)，连接BH ，∵点A (0，1)，点B (2，0)，点H (0，9)，∴AO =1，OB =2，OH =9，∵OA OP =13=39=OP OH，∠AOP =∠POH ，∴△AOP ∽△POH ，∴AP HP =OP OH=13，∴HP =3AP ，∴3PA +PB =PH +PB ，∴当点P 在BH 上时，3PA +PB 有最小值为HB 的长，∴BH =OB 2+OH 2=4+81=85，故答案为：85．12(溧阳市一模)如图，在⊙O 中，点A 、点B 在⊙O 上，∠AOB =90°，OA =6，点C 在OA 上，且OC =2AC ，点D 是OB 的中点，点M 是劣弧AB 上的动点，则CM +2DM 的最小值为　410　．【答案】410．【解答】解：延长OB 到T ，使得BT =OB ，连接MT ，CT ．∵OM =6，OD =DB =3，OT =12，∴OM 2=OD •OT ，∴OM OD =OT OM，∵∠MOD =∠TOM ，∴△MOD ∽△TOM ，∴DM MT =OM OT=12，∴MT =2DM ，∵CM +2DM =CM +MT ≥CT ，又∵在Rt △OCT 中，∠COT =90°，OC =4，OT =12，∴CT =OC 2+OT 2=42+122=410，∴CM +2DM ≥410，∴CM +2DM 的最小值为410，∴答案为410．13如图，边长为4的正方形，内切圆记为圆O ，P 为圆O 上一动点，则2PA +PB 的最小值为25　．【答案】25【解答】解：设⊙O 半径为r ，OP =r =12BC =2，OB =2r =22，取OB 的中点I ，连接PI ，∴OI =IB =2，∵OP OI =222=2，OB OP =222=2，∴OP OI =OB OP ，∠O 是公共角，∴△BOP ∽△POI ，∴PI PB =OI OP =22，∴PI =22PB ，∴AP +22PB =AP +PI ，∴当A 、P 、I 在一条直线上时，AP +22PB 最小，作IE ⊥AB 于E ，∵∠ABO =45°，∴IE =BE =22BI =1，∴AE =AB -BE =3，∴AI =32+12=10，∴AP +22PB 最小值=AI =10，∵2PA +PB =2(PA +22PB )，∴2PA +PB 的最小值是2AI =2×10=25．故答案是25．。

阿氏圆专题练习(含答案)

阿氏圆基础练习[类型一、向内构造]1. △ABC中，AC=6，BC=8，AB=10圆C的半径为4，点D是圆C上一动点，连接AD、BD，AD+!"BD的最小值为______，BD+"#BD的最小值为______2. 在Rt△ABC中，∠ACB=90°，AC=4,BC=3，点D是△ABC内一动点，且满足CD=2，则AD+"#BD 的最小值为______。

3. ∠O=90°,圆O的半径为 √2，PO=√10,MO=2,Q为圆O上一点，PQ+√""QM的最小值为______。

4. 如图，已知菱形ABCD的边长为4，圆B的半径为2，∠B=60∘,P为圆B上一动点, PD+!"PC的最小值为______。

5. 如图，四边形ABCD是边长为4的正方形，圆B的半径为2,P是圆B上一动点，则√2PD+4PC的最小值为______。

6. 如图，边长为4的正方形的内切圆记为圆O，P是圆O上一动点，则√2PA+PB的最小值______7. 如图，等边△ABC的边长为6，内切圆记为圆O，P是圆O上一动点，则2PB+PC的最小值为______8. 如图，△ABC中AB=9，BC=8，∠ABC=60°,圆A的半径为6，P是圆A上一动点，连接PB、PC，则3PC+2PB的最小值为______。

9. 如图，在△ABC中∠B=90∘,AB=BC=2,以B为圆心作圆与AC相切，点P为圆B上任意一点，2PA+√2PC的最小值是______10.如图，已知P是边长为6的正方形ABCD内部的一个动点，PA=3，2PC+PD的最小值是______11.如图，在矩形ABCD中，AB=18，BC=25，点M是矩形内部一个动点，MA=15，则5MC+3MD的最小值是______[类型二、向外构造]9上一点，2PA+PB的最小值是______ 12.如图，已知扇形COD,∠COD=90°,OC=6,OA=3,OB=5,点P是CD#一动点(不与C,B重合)，则2PD+PB的最13.如图，在扇形CAB中，CA=4,∠CAB=120°,D为CA的中点,P为BC小值为_____14.如图，AB是⊙O的直径，且AB=4,C是OA中点,过C作CD⊥AB交圆于D点,DE是⊙O的另一条直径,P是圆上的动点,2PC+PE的最小值为[类型三、两次构造]15. 如图，△ABC中AC=BC=4，∠ACB=90°,圆C的半径为2，D是圆C上一动点，E在CB上，CE=1，AD+2DE的最小值为______。

中考专题训练阿氏圆.pdf

在前面的“胡不归”问题中，我们见识了“kPA+PB”最值问题，其中P点轨迹是直线，而当P点轨迹变为圆时，即通常我们所说的“阿氏圆”问题．所谓“阿氏圆”，是指由古希腊数学家阿波罗尼奥斯提出的圆的概念，在平面内，到两个定点距离之比等于定值（不为1）的点的集合叫做圆．如下图，已知A、B两点，点P满足PA:PB=k（k≠1），则满足条件的所有的点P构成的图形为圆．以下给出两种证明法一：构造角分线先复习两个定理（1）角平分线定理：如图，在△ABC中，AD是∠BAC的角平分线，则AB:AC=DB:DC．证明：利用等积法，即AB:AC=DB:DC（2）外角平分线定理：如图，在△ABC中，外角CAE的角平分线AD交BC的延长线于点D，则AB:AC=DB:DC．证明：在BA延长线上取点E使得AE=AC，连接BD，则△ACD≌△AED（SAS），CD=ED且AD平分∠BDE，则DB:DE=AB:AE，即AB:AC=DB:DC．接下来开始证明：如图，PA：PB=k，作∠APB的角平分线交AB于M点，根据角平分线定理，MA:MB=PA:PB=k ，故M 点为定点，即∠APB 的角平分线交AB 于定点；作∠APB 外角平分线交直线AB 于N 点，根据外角平分线定理，NA:NB=PA:PB=k ，故N 点为定点，即∠APB 外角平分线交直线AB 于定点；又∠MPN=90°，定边对定角，故P 点轨迹是以MN 为直径的圆．中考专题训练阿氏圆模型阿氏圆（阿波罗尼斯圆）：已知平面上两定点A 、B ，则所有满足）（1≠=k k PBPA的点P 的轨迹是一个圆，这个轨迹最先由古希腊数学家阿波罗尼斯发现，故称阿氏圆. 在初中的题目中往往利用逆向思维构造“斜A ”型相似（也叫“母子型相似”）＋两点间线段最短，解决带系数两线段之和．．．．．．．．的最值问题. 观察下面的图形，当P 在⊙O 上运动时，用PA 、PB 的长在不断的发生变化，但PBPA的比值却始终保持不变.解决阿氏圆问题，首先要熟练掌握母子型相似三角形的性质和构造方法.那么如何应用“阿氏圆”的性质解答带系数的两条线段和的最小值呢？我们来看一道基本题目：例.已知∠ACB=90°，CB=4，CA=6，⊙C 半径为2，P 为圆上一动点.（1）求BP AP21+的最小值为 . （2）求BP AP +31的最小值为 .阿氏圆基本解法：构造相似阿氏圆一般解题步骤：AP+k BP第一步：连接动点和圆心C （将系数不为．．．．1．的线段．．．的两个端点分别与圆心相连接），即连接CP 、CB ；第二步：计算这两条线段长度的比）圆心到定点的距离半径（k CB CP =；第三步：在CB （即定边）上取点M ，使得k CPCM= 第四步：连接 AM ，与圆C 交点即为点P ；第五步：计算AM 的长度，即为AP+k BP 的最小值.实战演练：1.在△ABC 中，∠ACB=90°，AC=4，BC=3，点D 为△ABC 内一动点，且满足CD=2，则BD AD 32+的最小值为 .2.已知点A （4，0），B （4，4），点P 在半径为2的⊙O 上运动，则BP AP +21的最小值是 .3.已知点A(-3，0)，B （0，3），C （1，0），若点P 为⊙C 上一动点，且⊙C 与y 轴相切. （1）求BP AP +41的最小值；（2）求△ABP 面积的最小值.4.在平面直角坐标系中，A （2，0），B （0，2），C （4，0），D （3，2），P 是△AOB 外部的第一象限内一动点，且∠BPA=135°，则2PD+PC 的最小值是__________.5.已知⊙O 半径为1，AC 、BD 为切线，AC=1，BD=2，P 为弧AB 上一动点，试求PD PC +22的最小值.巩固练习：1.如图，在△ABC 中，∠B ﹦90°，AB ﹦CB ﹦2，以点B 为圆心作⊙B 与AC 相切，点P 为圆B 上任一动点，则PC PA 22+的最小值是．2. 如图，菱形ABCD 的边长为2，∠ABC=60°，⊙A 与BC 相切于点E ，在⊙A 上任取一点P ，求PD PB 23+的最小值.3.（1）如图1，已知正方形ABCD 的边长为4，⊙B 的半径为2，点P 是⊙B 上的一个动点，则PD+21PC 的最小值；（2）如图2，已知正方形ABCD 的边长为9，⊙B 的半径为6，点P 是⊙B 上的一个动点，那么PD+32PC 的最小值为；（3）如图3，已知菱形ABCD 的边长为4，∠B=60°，圆B 的半径为2，点P 是圆B 上的一个动点，那么PD+21PC 的最小值为 .4.如图1，抛物线y=ax 2+(a +3)x +3(a ≠0)与x 轴交于点A(4，0)，与y 轴交于点B ，在x 轴上有一动点E(m ，0)(0<m<4)，过点E 作x 轴的垂线交直线AB 于点N ，交抛物线于点P ，过点P 作PM ⊥AB 于点M. （1）求a 的值和直线AB 的函数表达式；（2）设△PMN 的周长为C 1，△AEN 的周长为C 2，若5621=C C ，求m 的值；（3）如图2，在(2)条件下，将线段OE 绕点O 逆时针旋转得到OE′，旋转角为α(0°<α<90°)，连接E′A 、E′B ，求E′A+32E′B 的最小值.问题提出：如图1,在Rt△ABC中,∠ACB=90∘,CB=4,CA=6,C半径为2,P为圆上一动点,连结AP、BP,求AP+1/2BP的最小值。

阿氏圆竞赛题

阿氏圆竞赛题阿氏圆，又称为阿基米德圆，是一个具有广泛应用的数学概念。

它的名字来源于古希腊数学家阿基米德，他首先发现了这一性质并将其应用于解决几何问题。

下面我们将详细介绍阿氏圆的定义、性质、应用以及求解方法。

一、阿氏圆的定义和性质阿氏圆是指：在平面直角坐标系中，已知一个点P（a，b）和一条直线l，求直线l与点P的距离最小的点Q的轨迹。

这个轨迹就是一个阿氏圆。

阿氏圆的半径等于点P到直线l的距离。

阿氏圆具有以下性质：1.阿氏圆的圆心是点P，半径等于点P到直线l的距离。

2.阿氏圆的方程为：(x - a) + (y - b) = r，其中r为半径。

3.阿氏圆对称于直线l，即直线l是阿氏圆的轴。

二、阿氏圆的应用阿氏圆在几何、代数、物理等领域具有广泛的应用。

例如，在解决几何问题时，通过找到阿氏圆的圆心和对称轴，可以简化问题并提高求解效率。

此外，阿氏圆还可以应用于解决生活中的实际问题，如测量、建筑等。

三、阿氏圆问题的求解方法求解阿氏圆问题的一般步骤如下：1.确定点P的坐标和直线l的方程。

2.计算点P到直线l的距离，得到阿氏圆的半径。

3.根据半径和点P的坐标，写出阿氏圆的方程。

4.根据需要，进一步求解阿氏圆与其他几何图形的位置关系、交点坐标等。

四、典型例题解析例1：已知点P（2，3），直线l的方程为x - 2 = 0，求阿氏圆的方程。

解：直线l的方程可化为x = 2，点P到直线l的距离为0，因此阿氏圆的半径为0。

故阿氏圆的方程为(x - 2) + (y - 3) = 0，即(x - 2) + (y - 3) = 0。

例2：已知点P（0，0），直线l的方程为y = x，求阿氏圆的方程。

解：直线l的方程可化为y = x，点P到直线l的距离为√2/2。

因此阿氏圆的半径为√2/2。

故阿氏圆的方程为(x - 0) + (y - 0) = (√2/2)，即x + y =2/2。

五、练习题及答案解析1.求解以下阿氏圆问题：已知点P（3，-1），直线l的方程为x - 3 = 0，求阿氏圆的方程。

2024学年初中数学几何(阿氏圆模型)模型专项练习(附答案)

12024学年初中数学几何（阿氏圆模型）模型专项练习1．阅读以下材料，并按要求完成相应的任务．已知平面上两点A 、B，则所有符合＝k（k ＞0且k ≠1）的点P 会组成一个圆．这个结论最先由古希腊数学家阿波罗尼斯发现，称阿氏圆．阿氏圆基本解法：构造三角形相似．【问题】如图1，在平面直角坐标系中，在x 轴，y 轴上分别有点C （m ，0），D （0，n ），点P 是平面内一动点，且OP ＝r ，设＝k ，求PC +kPD 的最小值．阿氏圆的关键解题步骤：第一步：如图1，在OD 上取点M ，使得OM ：OP ＝OP ：OD ＝k ；第二步：证明kPD ＝PM ；第三步：连接CM ，此时CM 即为所求的最小值．下面是该题的解答过程（部分）：解：在OD 上取点M ，使得OM ：OP ＝OP ：OD ＝k ，又∵∠POD ＝∠MOP ，∴△POM ∽△DOP ．任务：（1）将以上解答过程补充完整．（2）如图2，在Rt △ABC 中，∠ACB ＝90°，AC ＝4，BC ＝3，D 为△ABC 内一动点，满足CD ＝2，利用（1）中的结论，请直接写出AD+BD 的最小值．2．（1）如图1，已知正方形ABCD 的边长为4，圆B 的半径为2，点P 是圆B 上的一个动点，求PD+的最小值和PD ﹣的最大值；2的一个动点，那么PD +的最小值为，PD ﹣的最大值为．（3）如图3，已知菱形ABCD的边长为4，∠B＝60°，圆B的半径为2，点P是圆B上的一个动点，那么PD +的最小值为，PD ﹣的最大值为．3．【问题背景】如图1，△ABC中，∠BAC＞∠B，点D在边BC上，若∠CAD＝∠B，则可得△CAB∽△CAD ，进而可得，进一步变形有AC2＝CD•CB．【简单运用】（1）如图1，若AC＝2，BC＝4，则BD长为；＝．（2）如图2，⊙O中，弦AD、BC相交于点E，已知AB＝2AE，BE＝15，且C是劣弧AD的中点，求CD的长．【灵活运用】如图3，平面直角坐标系中，直线y＝﹣x+9交于坐标轴于A、B两点，点P坐标为（m，n），且m2+n2＝36，连接P A，PB，则3PB+2P A的最小值为．3动点，则PD ﹣PC 的最大值为．5．【新知探究】新定义：平面内两定点A ，B ，所有满足＝k （k 为定值）的P 点形成的图形是圆，我们把这种圆称之为“阿氏圆”【问题解决】如图，在△ABC 中，CB ＝4，AB ＝2AC ，则△ABC 面积的最大值为．参考答案1．阅读以下材料，并按要求完成相应的任务．已知平面上两点A、B，则所有符合＝k（k＞0且k≠1）的点P会组成一个圆．这个结论最先由古希腊数学家阿波罗尼斯发现，称阿氏圆．阿氏圆基本解法：构造三角形相似．【问题】如图1，在平面直角坐标系中，在x轴，y轴上分别有点C（m，0），D（0，n），点P是平面内一动点，且OP＝r，设＝k，求PC+kPD的最小值．阿氏圆的关键解题步骤：第一步：如图1，在OD上取点M，使得OM：OP＝OP：OD＝k；第二步：证明kPD＝PM；第三步：连接CM，此时CM即为所求的最小值．下面是该题的过程解答过程（部分）：解：在OD上取点M，使得OM：OP＝OP：OD＝k，又∵∠POD＝∠MOP，∴△POM∽△DOP．任务：（1）将以上过程解答过程补充完整．（2）如图2，在Rt△ABC中，∠ACB＝90°，AC＝4，BC＝3，D为△ABC内一动点，满足CD＝2，利用（1）中的结论，请直接写出AD+BD的最小值．【过程解答】解（1）在OD上取点M，使得OM：OP＝OP：OD＝k，又∵∠POD＝∠MOP，∴△POM∽△DOP．∴MP：PD＝k，∴MP＝kPD，∴PC+kPD＝PC+MP，当PC+kPD取最小值时，PC+MP有最小值，即C，P，M三点共线时有最小值，利用勾股定理得．（2）∵AC＝m＝4，＝，在CB上取一点M，使得CM＝CD＝，∴的最小值为．2．（1）如图1，已知正方形ABCD的边长为4，圆B的半径为2，点P是圆B上的一个动点，求PD+的最小值和PD﹣的最大值；（2）如图2，已知正方形ABCD的边长为9，圆B的半径为6，点P是圆B上的一个动点，那么PD+的最小值为，PD﹣的最大值为．（3）如图3，已知菱形ABCD的边长为4，∠B＝60°，圆B的半径为2，点P是圆B上的一个动点，那么PD+的最小值为，PD﹣的最大值为．【过程解答】解：（1）如图1中，在BC上取一点G，使得BG＝1．∵＝＝2，＝＝2，∴＝，∵∠PBG＝∠PBC，∴△PBG∽△CBP，∴＝＝，∴PG＝PC，∴PD+PC＝DP+PG，∵DP+PG≥DG，∴当D、G、P共线时，PD+PC的值最小，最小值为DG＝＝5．∵PD﹣PC＝PD﹣PG≤DG，当点P在DG的延长线上时，PD﹣PC的值最大（如图2中），最大值为DG＝5．（2）如图3中，在BC上取一点G，使得BG＝4．∵＝＝，＝＝，∴＝，∵∠PBG＝∠PBC，∴△PBG∽△CBP，∴＝＝，∴PG＝PC，∴PD+PC＝DP+PG，∵DP+PG≥DG，∴当D、G、P共线时，PD+PC的值最小，最小值为DG＝＝． ∵PD﹣PC＝PD﹣PG≤DG，当点P在DG的延长线上时，PD﹣PC的值最大，最大值为DG＝．故答案为，（3）如图4中，在BC上取一点G，使得BG＝1，作DF⊥BC于F．∵＝＝2，＝＝2，∴＝，∵∠PBG＝∠PBC，∴△PBG∽△CBP，∴＝＝，∴PG＝PC，∴PD+PC＝DP+PG，∵DP+PG≥DG，∴当D、G、P共线时，PD+PC的值最小，最小值为DG，在Rt△CDF中，∠DCF＝60°，CD＝4，∴DF＝CD•sin60°＝2，CF＝2，在Rt△GDF中，DG＝＝∵PD﹣PC＝PD﹣PG≤DG，当点P在DG的延长线上时，PD﹣PC的值最大（如图2中），最大值为DG＝．故答案为，．3．【问题背景】如图1，△ABC中，∠BAC＞∠B，点D在边BC上，若∠CAD＝∠B，则可得△CAB∽△CAD，进而可得，进一步变形有AC2＝CD•CB．【简单运用】（1）如图1，若AC＝2，BC＝4，则BD长为3；＝．（2）如图2，⊙O中，弦AD、BC相交于点E，已知AB＝2AE，BE＝15，且C是劣弧AD的中点，求CD的长．【灵活运用】如图3，平面直角坐标系中，直线y＝﹣x+9交于坐标轴于A、B两点，点P 坐标为（m，n），且m2+n2＝36，连接P A，PB，则3PB+2P A的最小值为3．【过程解答】解：（1）∵AC2＝CD•BD，∴4CD＝4，∴BD＝BC﹣CD＝3，∵△CAB∽△CAD，∴＝＝＝，故答案是3，；（2）如图1，∵＝，∴∠B＝∠CAE，由上知，∴△ACE∽△BCA，∴＝＝＝＝， AC2＝CE•BC，∴AC＝2CE，∴4CE2＝CE•（CE+15），∴CE＝5，∴CD＝AC＝2CE＝10；【灵活运用】如图2，由题意得，∵且m2+n2＝36，∴OP＝6，在OA上截取OC＝4，∴＝，又∵∠AOP是公共角，∴△AOP∽△POC，∴＝，∴P A＝PC，∴PB+P A＝PB+PC≥BC，当B、P、C共线时，（PB+PC）最小＝BC＝＝，∵3PB+2P A＝3（PB+P A），∴（3PB+2P A）最小＝3，故答案是3．4．如图，已知正方形ABCD的边长为4，⊙B的半径为2，点P是⊙B上的一个动点，则PD﹣PC的最大值为 5．【过程解答】解：在BC上取一点G，使得BG＝1，如图，∵＝2，＝2，∴，∵∠PBG＝∠PBC，∴△PBG∽△CBP，∴，∴PG＝PC，当点P在DG的延长线上时，PD﹣PC的值最大，最大值为DG＝＝5．故答案为：55．【新知探究】新定义：平面内两定点A，B，所有满足＝k（k为定值）的P点形成的图形是圆，我们把这种圆称之为“阿氏圆”【问题解决】如图，在△ABC中，CB＝4，AB＝2AC，则△ABC面积的最大值为．【过程解答】解：以A为顶点，AC为边，在△ABC外部作∠CAP＝∠ABC，AP与BC 的延长线交于点P，∵∠CAP＝∠ABC，∠BP A＝∠APC，AB＝2AC，∴△APC∽△BP A，，∴BP＝2AP，CP＝AP，∵BP﹣CP＝BC＝4，∴2AP﹣AP＝4，解得：AP＝，∴BP＝，CP＝，即点P为定点，∴点A的轨迹为以点P为圆心，为半径的圆上，如图，过点P作BC的垂线，交圆P 与点A1，此时点A1到BC的距离最大，即△ABC的面积最大，S△ABC＝BC•A1P＝×4×＝．故答案为：．1．（2021•黔西南州中考真题）古希腊数学家毕达哥拉斯认为：“一切平面图形中最美的是圆”．请研究如下美丽的圆．如图，线段AB是⊙O的直径，延长AB至点C，使BC＝OB，点E是线段OB的中点，DE⊥AB交⊙O于点D，点P是⊙O上一动点（不与点A，B重合），连接CD，PE，PC．（1）求证：CD是⊙O的切线；（2）小明在研究的过程中发现是一个确定的值．回答这个确定的值是多少？并对小明发现的结论加以证明．【过程解答】解：（1）如图1中，连接OD、DB，∵点E是线段OB的中点，DE⊥AB交⊙O于点D，∴DE垂直平分OB，∴DB＝DO，OE＝BE．解法一：∵在⊙O中，DO＝OB，∴DB＝DO＝OB，∴△ODB是等边三角形，∴∠BDO＝∠DBO＝60°，∵BC＝OB＝BD，且∠DBE为△BDC的外角，∴∠BCD＝∠BDC＝∠DBO．∵∠DBO＝60°，∴∠CDB＝30°．∴∠ODC＝∠BDO+∠BDC＝60°+30°＝90°，∴CD是⊙O的切线；解法二：∵BC＝OB，OB＝OD，∴＝＝＝，又∵∠DOE＝∠COD，∴△EOD∽△DOC，∴∠CDO＝∠DEO＝90°，∴CD为圆O的切线；（2）答：这个确定的值是．连接OP，如图2中：由已知可得：OP＝OB＝BC＝2OE．∴＝＝，又∵∠COP＝∠POE，∴△OEP∽△OPC，∴＝＝。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

阿氏圆类题目专项训练
1.在正方形ABCD 中，G 为正方形内一点，AD ＝4,P 为BC 中点，且BG=BP,则DG+2
1
GC 的最小值是_____.
简析：取BP 中点M ，则ΔBMG ∽ΔBGC ，∴GM=(1/2)GC ，∴DG+2
1
GC=DG+GM ≥DM=52.
如图，在△ABC 中，∠B=90°，AB=CB=2,以B 为圆心作圆B 与AC 相切，点P 为圆B 上
任一动点，则PA+
2
2
PC 的最小值是.
简析：如图取BM=1,则，△BMP ∽△BPC ，∴PM=22PC ，∴PA+2
2PC=PA+PM ≥AM=53.如图，已知P 是边长为6的正方形ABCD 内部的一个动点，PA ＝3，求PC+
2
1
PD 的最小值.
简析：如图，取AM ＝1.5，则△AMP ∽△APD ，∴PM=
21PD ，∴PC+2
1
PD=PC+PM ≥CM=7.5
4.如图，在矩形ABCD 中，AB=18，BC=25,点M 是矩形内部一个动点，MA=15,当MC+
5
3
MD 的值最小时，画出点M 的位置，并求出MC+
5
3
MD 的最小值.
简析：如图以点A 为圆心、AM 为半径画弧取AN=9,则M 点在所画弧与CN 连线交点处时MC+
53MD 的值最小，如图所示。

∵△ANM ∽△AMD ，∴MN=53MD ∴MC+
5
3
MD=MC+MN ≥CN=14525.如图，在平面直角坐标系xoy 中，A(-2,0),B(0,1),C(0,3),以O 为圆心，OC 为半径画圆，P 为圆O 上一动点，则
2
3
PA+PB 的最小值为___.
简析：在x 轴的负半轴上取一点E ，使得OE=4.5，△OAP ∼△OPE ，PE=
23PA ，2
3
PA+PB=PE+PB ≥EB=
2
85
6.如图，在△ABC 中，BC=4,AB=2AC,则△ABC 的面积的最大值为____.
简析：∵AC:AB=1:2，延长BC 到O ，连接OA ，设CO 为x,OA 为2x ，4+x=2×2x ，x=
34，OA=3
8S △ABC =
21BC ·AH ≤21BC ·AO=2
1
×4×38=316。

7.如图，△ABC 中，AC=6,BC=8,AB=10,圆C 的半径为4，点D 是圆上一动点，连接AD,BD,则AD+
2
1
BD 的最小值为_____.
简析：取半径中点M ，则△CMD ∽△CDB ，∴DM=
21BD ，∴AD+2
1
BD=AD+MD ≥AM=1028.如图，在Rt △ABC 中，∠ACB=90°,AC=4,BC=3,点D 是△ABC 内一动点，且满足CD=2，则AD+
3
2
BD 的最小值为_____.
简析：取CM=
34,则△CMD ∽△CDB ，∴DM=32BD ，∴AD+3
2
BD=AD+MD ≥AM=
31049.如图，已知菱形ABCD 的边长为4，∠B=60°,圆B 的半径为2，P 为圆B 上一动点，则PD+
2
1
PC
的最小值为_____.
简析：取BM=1,则△BMP ∽△BPC ∴PM=
21PC ∴DM=37∴PD+2
1
PC=PD+PM ≥DM=3710.如图，圆O 的半径为2，PO=10,MO=2,∠O=90°,Q 为圆O 上一动点，则PQ+2
2
QM 的最小值为_____.
简析：取ON=1,则△ONQ ∽△OQM ∴QN=
22QM ∴PQ+2
2
QM=PQ+QN ≥PN=1111.如图，四边形ABCD 是边长为4的正方形，圆B 的半径为2，P 是圆B 上一动点，则2PD+4PC 的最小值为____.
简析：转化为求4（PC+
42PD ）的最小值连接BD ，取BM ＝
2
2
，则△BMP ∽△BPD ∴PM=
42PD ∴PC+42PD=PC+PM ≥CM=225，4（PC+4
2
PD ）≥102
12.如图，边长为4的正方形的内切圆记为圆O ，P 是圆O 上一动点，则2PA+PB 的最小值为____.
简析：转化为求2（PA+
2
2
PB ）的最小值，连接BD ，OP,取OM ＝2，则△OMP ∽△OPB ∴PM=
22PB ∴PA+22PB=PA+PM ≥AM=10∴2（PA+2
2PB ）≥25，即2PA+PB ≥25
13.如图，等边△ABC 的边长为6，内切圆记为圆O ，P 是圆O 上一动点，则2PB+PC 的最小
值为____.
解析：转化为求2（PB+
21PC ）的最小值,连接CO ，OP,取OM ＝
2
3
，则△OMP ∽△OPC,∴PM=
21PC ，∴PB+21PC=PB+PM ≥BM=2
63
,∴2(PB+21PC)≥7363=14.如图,△ABC 中，AB=9,BC=8,∠ABC=60°,圆A 的半径为6，P 是圆A 上一动点,连接PB 、PC,则3PC+2PB 的最小值为____.
解析：转化为求3（PC+
32PB ）的最小值,连接AP ，取AM ＝4，则△AMP ∽△APB,∴PM=3
2
PB,
∴PC+
32PB=PC+PM ≥CM=7，∴3(PB+3
2
PB)≥2115.如图,△ABC 中，AC=BC=4,∠ACB=90°,圆C 的半径为2，D 是圆C 上一动点，E 在CB 上，CE=1,连接AD 、DE,则
2
1
AD+2DE 的最小值为____.
解析：取CM=1，连接MD,CD,DB.则△CMD ∽△CDA,△CED ∽△CDB.∴DM=
2
1
AD,BD=2DE.∴2
1
AD+2DE=DM+BD ≥BM=1716.如图，矩形ABCD 中，AB=34,BC=4,以C 为圆心，AC 的长为半径画圆，P 为圆C 上一动点，求DP+2BP 的最小值.
简析：延长CB 到E ，连接PE ，则△CBP ∽△CPE ，相似比为1:2，∴2BP=PE ，DP+2BP=DP+PE ≥DE=419
17.如图，在平面直角坐标系中，以点C(1,1)为圆心，5为半径的圆与x 轴、y 轴分别交于
点A 和点B ，点D 为弧AB 上的动点，则BD+
2
10
OD 的最小值为_____.
简析：连接DC ，延长CO 到E ，使得OE=
2
2
3，连接DE ，DB ，作EF ⊥y 轴于F 则△COD ∽△CDE ，
52===DE OD CE CD CD CO ,OD OD DE 210
2
5==，
2
10
3210=≥+=+
BE DE BD OD BD。