八年级数学梯形 同步练习3华师版
2021年八年级数学梯形教案(III)华师版
2021年八年级数学梯形教案(III)华师版教学目标 1.知道梯形、等腰梯形、直角梯形的有关概念;能说出并证明等腰梯形的两个性质;等腰梯形同一底上的两个角相等;两条对角线相等。
2.会运用梯形的有关概念和性质进行有关问题的论证和计算。
3.通过添加辅助线,把梯形的问题转化成平行四边形或三角形问题,使学生体会图形变换的方法和转化的思想。
教学模式问题解决教学教学过程想一想:什么样的四边形是平行四边形?平行四边形有哪些性质?学生回答后,教师板书以下关系图中的有关部分:画一画:画一个梯形,并指出梯形的上、下底,画出梯形的高。
问题教学问题1:根据刚才的画图,请给梯形下一个定义,并说说梯形与平行四边形的区别和联系。
(说明与建议:(l)让学生自己给梯形下定义,有助于训练学生观察、概括和语言表述的能力。
如果学生定义时,遗漏了“另一组对边不平行”教师可举及例(2)对梯形的定义,还可以让学生讨论以下问题:一组对边平行且这组对边不相等的四边形是梯形吗?为什么?教师可用反证法的思想说理。
然后,板书完成“想一想”中的关系图,并结合图表指出:梯形和平行四边形的区别和联系。
(3)梯形的高是指夹在两底间的公垂线段,在计算面积时高即为上下两底(平行线)间的距离,也就是夹在两底间的公垂线段的长度。
画高时可以从上底任一点向下底作垂线段,一般常从上底的两端向下底作垂线段可方便地构造直角三角形,便于计算。
)问题2:如图4.9-1,在(1)中:四边形ABCD的AD∥BC,ABCD,且CD⊥BC;在(2)中,四边形ABCD的AD∥BC,ABCD,且AB=CD。
请你给这两种四边形命名。
(说明与建议:学生说出图(l)的四边形是直角梯形,图(2)是等腰梯形,通常不会有困难;教师应进一步引导学生讨论,在图(1)中CD⊥BC,那么CD⊥AD吗?(CD⊥AD,且指出:CD就是直角梯形的高)当CD⊥BC时,另一腰AB可以垂直BC吗?为什么?(若AB⊥BC,那么四边形ABCD就成为矩形了,不再是梯形。
【优选】华师大版数学八下《等腰梯形的判定》同步测试

20.5 等腰梯形的判定A卷一、选择题1.下列结论中,正确的是()A.等腰梯形的两个底角相等 B.两个底角相等的梯形是等腰梯形C.一组对边平行的四边形是梯形 D.两条腰相等的梯形是等腰梯形2.如图所示,等腰梯形ABCD的对角线AC,BD相交于点O,则图中全等三角形有()A.2对 B.3对 C.4对 D.5对3.课外活动课上,•老师让同学们制作了一个对角线互相垂直的等腰梯形形状的风筝,其面积为450cm,则两条对角线所用的竹条长度之和至少为()A.2cm B.30cm C.60cm D.2二、填空题4.等腰梯形上底,下底和腰分别为4,•10,•5,•则梯形的高为_____,•对角线为______.5.一个等腰梯形的上底长为5cm,下底长为12cm,一个底角为60°,则它的腰长为____cm,周长为______cm.6.在四边形ABCD中,AD∥BC,但AD≠BC,若使它成为等腰梯形,则需要添加的条件是__________(填一个正确的条件即可).三、解答题7.如图所示,AD是∠BAC的平分线,DE∥AB,DE=AC,AD≠EC.求证:•四边形ADCE是等腰梯形.四、思考题8.如图所示,四边形ABCD中,有AB=DC,∠B=∠C,且AD<BC,四边形ABCD是等腰梯形吗?为什么?参考答案一、1.D 点拨:梯形的底角分为上底上的角和下底上的角,•因此在等腰梯形的性质和判别方法中必须强调同一底上的两个内角(•指上底上的两个内角或下底上的两个内角),否则就会出现错误,因此A,B选项都不正确,而C选项中漏掉了限制条件另外一组对边不平行,若平行该四边形就形成了平行四边形了,因此应选D.2.B 点拨:因为△ABC≌△DCB,△BAD≌△CDA,△AOB≌△DOC,所以共有3对全等的三角形.3.C 点拨:设该等腰梯形对角线长为Lcm,因为两条对角线互相垂直,•所以梯形面积为12L2=450,解得L=30,所以所用竹条长度之和至少为2L=2×30=60(cm).二、4.4:65点拨:如图所示,连结BD,过A,D分别作AE⊥BC,DF⊥BC,垂足分别为E,F.易知△BAE≌△CDF,在四边形AEFD为矩形,所以BE=CF=3,AD=EF=4.在Rt△CDF中,FC2+DF2=CD2,即32+DF2=52,所以DF=4,在Rt△BFD中,BF2+DF2=BD2,即72+42=BD2,所以BD=65.5.7;31点拨:如图所示,过点D作DE∥AB交BC于E.因为AD∥BC,AB ∥DE,所以四边形ABED是平行四边形.所以BE=AD=5(cm),AB=DE.又因为AB=CD,所以DE=•DC,又因为∠C=60°,所以△DEC是等边三角形,所以DE=DC=EC=7(cm),所以周长为5+•12+7+7=31(cm).6.AB=CD(或∠A=∠D,或∠B=∠C,或AC=BD,或∠A+∠C=180°,或∠B+∠D=180°)三、7.证明:因为AB∥ED,所以∠BAD=∠ADE.又因为AD是∠BAC的平分线,所以∠BAD=∠CAD,所以∠CAD=∠ADE,所以OA=OD.又因为AC=DE,所以AC-OA=DE-OD即OC=OE,•所以∠OCE=∠OEC,又因为∠AOD=∠COE,所以∠CAD=∠OCE.所以AD∥CE,而AD≠CE,故四边形ADCE是梯形.又因为∠CAD=∠ADE,AD=DA,AC=DE,所以△DAC≌△ADE,所以DC=•AE,所以四边形ADCE是等腰梯形.点拨:证明一个四边形是等腰梯形时,应先证其是梯形而后再证两腰相等或同一底上的两个角相等.四、8.解:四边形ABCD是等腰梯形.理由:延长BA,CD,相交于点E,如图所示,由∠B=∠C,可得EB=EC.又AB=DC,所以EB-AB=EC-DC,即AE=DE,所以∠EAD= ∠EDA.因为∠E+∠EAD+∠EDA=180°,∠E+∠B+∠C=180°,所以∠EAD=∠B.故AD∥BC.•又AD<BC,所以四边形ABCD是梯形.又AB=DC,所以四边形ABCD是等腰梯形.点拨:由题意可知,只要推出AD∥BC,再由AD<BC就可知四边形ABCD为梯形,再由AB=DC,即可求得此四边形是等腰梯形,由∠B=∠C联想到延长BA,CD,即可得到等腰三角形,从而使AD∥BC.20.5 等腰梯形的判定B卷一、七彩题1.(一题多解题)如图所示,等腰梯形ABCD中,AD∥BC,AB=CD=•12cm,•上底AD=15cm,∠BAD=120°,求下底BC的长.二、知识交叉题2.(科内交叉题)如图所示,在矩形ABCD中,AC,BD相交于点O,E,•F•分别是OA,OD的中点,且EF≠AD,试判断四边形EBCF的形状,并说明你的理由.三、实际应用题3.如图所示,小军将两根长度相等的木条AC,BD•交叉摆放,•并使木条AC,BD分别与水平线所成的夹角∠1,∠2相等,然后在交点O处钉一个钉子固定,OA<OC,•再用一根彩带沿AD,DC,CB,BA围起来,小军得到的四边形ABCD是等腰梯形吗?请说明你的理由.四、经典中考题4.(连云港,)如图所示,在直角梯形纸片ABCD中,AB ∥DC, ∠A=90°,CD>AD,将纸片沿过点D的直线折叠,使点A落在边CD上的点E,折痕为DF,连结EF并展开纸片.(1)求证:四边形ADEF是正方形;(2)取线段AF的中点G,连结EG,结果BG=CD,试说明四边形GBCE是等腰梯形.五、探究学习篇1.(翻折变换题)如图20-5-8所示,等腰梯形ABCD中,AD∥BC,∠DBC=45°,翻折梯形ABCD,使点B重合于点D,折痕分别交边AB,BC于点F,E,若AD=2,BC=8,求BE 的长.2.如图所示,在等腰梯形ABCD中,AD∥BC,M,N分别为AD,BC的中点,E,F•分别是BM,CM的中点.(1)试说明△ABM≌△DCM;(2)四边形MENF是什么图形?请说明理由.(3)若四边形MENF是正方形,则梯形的高与底边BC的长有何数量关系?请说明理由.3.阅读:下面是某同学解一道有关等腰梯形的问题的过程.已知:•在四边形ABCD 中,AB=DC,AC=BD,AD≠BC.试说明四边形ABCD是等腰梯形.解:过点D作DE∥AB,交BC于点E,如图20-5-10所示.则∠ABE=∠1 ①.•因为AB=DC,AC=DB,BC=CB ②,所以△ABC≌△DCB,所以∠ABC=∠DCB ③,所以∠1=∠DCB ④,所以AB=DC=DE ⑤,所以四边形ABCD是平行四边形⑥,所以AD∥BC ⑦.又因为AD≠BC,所以四边形ABCD是梯形⑧.因为AB=CD,所以四边形ABCD是等腰梯形⑨.•阅读填空:(1)说明过程是否有错误?错在第几步?答:_______.(2)有人认为第⑧步是多余的,你认为呢?为什么?答:___________.(3)若题目中没有AD ≠BC,•那么四边形ABCD•一定是等腰梯形吗?•为什么?• 答:___________.参考答案一、1.解法一:如图1所示,过A,D分别作AE⊥BC,DF⊥BC,垂足分别为E,•F,在梯形ABCD中,因为AD∥BC,所以∠B+∠BAD=180°,因为∠BAD=120°,所以∠B= 60°.在Rt△ABE中,∠BAE=90°-∠B=30°,所以BE=12AB=6cm.因为梯形ABCD是等腰梯形,所以∠C=∠B=60°,所以CF=12CD=6cm.因为四边形AEFD是矩形,所以EF=AD=15cm,所以BC=BE+EF+CF=27cm.图1 图2 图3 解法二:如图2所示,过A作AE∥CD交BC于E点,因为AD ∥BC,•所以四边形AECD是平行四边形.所以EC=AD=15cm,AE=CE.又因为AD∥BC,所以∠B+∠BAD=180°,•因为∠BAD=120°,所以∠B=60°,因为AB=CD,所以AB=AE,所以△ABE是等边三角形,•所以BE=AB=12cm,所以BC=BE+EC=15+12=27(cm).解法三:如图3所示,延长BA和CD交于点P,在梯形ABCD中,AB=CD,所以∠B=∠C,因为AD∥BC,所以∠PAD=∠B,∠PDA=∠C,∠BAD+∠B=180°.因为∠BAD=120 °,所以∠B=∠PAD=∠C=∠PDA=60°,所以△PAD和△PB C都是等边三角形.所以PA=AD=•15cm,PB=PA+AB=12+15=27(cm),所以BC=PB=27cm.点拨:以上三种辅助线的方法在梯形中运用相当广泛,•通过它们把梯形的问题转化为平行四边形,三角形等的问题来解决,体现了“转化”的数学思想.二、2.解:四边形EBCF是等腰梯形.理由如下:因为四边形ABCD是矩形,所以AC=•BD,AD=BC.又因为AO=OC,OB=OD,所以OA=OD=OC=OB.又因为E,F分别是OA,OD的中点,所以OE=OF,所以∠OEF=∠OFE.因为OB=OC,所以∠OBC=∠OCB.又因为∠EOF=∠BOC,所以∠OEF+∠OFE=∠OBC+∠OCB,即2∠OFE=2∠OBC,所以∠OFE=∠OBC,所以EF∥BC.•因为EF≠AD,所以EF≠BC.所以四边形EBCF是梯形.因为OE=OF,OB=OC,∠EOB=∠FOC,•所以△OEB≌△OFC,所以BE=CF,所以四边形EBCF是等腰梯形.点拨:本题是等腰梯形的判定与矩形的性质的知识交叉题.要说明一个四边形为等腰梯形,需先说明这个四边形为梯形(这一条很容易被忽略),再说明这个梯形为等腰梯形.三、3.解:小军得到的四边形ABCD是等腰梯形,理由如下:如图所示,延长DA,CB交于点E,因为AC=BD,∠1=∠2,CD=DC.所以△ADC≌△BCD(S.A.S.),所以AD=•BC,∠ADC=∠BCD.所以ED=EC,所以ED-AD=EC-BC,即EA=EB.所以∠3=∠4,因为∠3+∠4+∠E=180°,∠ADC+∠BCD+∠E=180°,所以∠3=1802E︒-∠,∠ADC=1802E︒-∠,所以∠3=∠ADC.所以AB∥CD,又因为OA<OC,故四边形ABCD必不为平行四边形,所以四边形ABCD是等腰梯形.点拨:要想使四边形ABCD是等腰梯形,关键是求得AB∥DC和AD=BC,可通过同位角相等和三角形全等分别求出.四、4.证明:如图所示,(1)因为∠A=90°,AB∥DC,所以∠ADE=90°.由沿DF折叠后△DAF与△DEF重合,知AD=DE,∠DEF=90°.所以四边形ADEF是矩形,且邻边AD,DE相等.所以四边形ADEF是正方形.(2)因为CE∥BG,且CE≠BG,所以四边形GBCE是梯形,因为四边形ADEF是正方形,•所以AD=FE,∠A=∠GFE=90°,又点G为AF的中点,所以AG=FG,连结DG.在△AGD 与△FGE中,因为AD=FE,∠A=∠GFE,AG=FG,所以△AGD≌△FGE,所以∠DGA=∠EGB.因为BG=•CD,BG∥CD,所以四边形BCDG是平行四边形.所以DG∥CD.所以∠DGA=∠B.所以∠EGB= ∠B.所以四边形GBCE是等腰梯形.五、探究学习1.解:因为△BFE与△DFE关于EF对称,所以△BFE≌△DFE.所以BE=DE.•又因为∠DBC=45°,所以∠EBD=∠EDB=45°,所以∠BED=90°.过A作AH⊥BC于H,•如图所示.因为AD∥BC,所以∠BED=∠ADE=90°.又因为∠AHE=90°,•所以四边形ADEH是矩形.所以AD=HE,AH=DE.在Rt△ABH和Rt△DCE中,因为AB=DC,AH=DE,所以Rt △ABH≌Rt△DCE,所以BH=EC.所以EC=12×(BC-AD)=12×(8-2)=3,所以BE=BC-EC=8-3=5.点拨:要求BE的长,因为BC已知,只需求EC的长,由已知条件可得∠DEC=90°,•故联系梯形常作辅助线,易求EC的长.2.解:(1)因为四边形ABCD为等腰梯形,所以AB=CD,∠A=∠D.因为M是AD的中点,所以AM=DM,所以△ABM≌△DCM.(2)四边形MENF是菱形.理由:由△ABM≌△DCM,得MB=MC.连结MN,因为N是BC的中点,所以MN⊥BC,而E,F分别是MB,MC的中点,所以ME=12MB,MF=12MC,NE=12MB,NF=12MC(直角三角形的斜边上的中线等于斜边的一半),所以ME=MF=•NF=NE,所以四边形MENF是菱形.(3)梯形的高等于底边BC的长的一半;理由:•因为四边形MENF是正方形,所以∠BMC=90°.由(2)知MN是梯形的高,因为N是中点,所以MN=12 BC.点拨:在(2)的解答过程中,易只判断出是平行四边形的情况,出现说理不彻底不全面的错误,这也是解此类题的难点.3.解:(1)没有错误;(2)第⑧步不是多余的,•因为如果没有第⑧步就不符合梯形的定义;(3)不一定,因为当AD=BC时,四边形ABCD是矩形.点拨:•做这种阅读材料的题时,一定要耐心,仔细地一步步读题.。
华师版八年级数学梯形 同步练习

梯形 同步练习一、填空题1.等腰梯形ABCD 的对角线相交于O 点,∠BOC =120°,∠BDC =80°,则∠DAB =________.2.若等腰梯形的上底与一条腰长的和等于下底的长,则腰长与上底的夹角为________.3.一梯形是上底为4cm ,过上底的一顶点,作—直线平行于一腰,并与下底相交组成一个三角形,若三角形的周长为12cm ,则梯形的周长是________.4.等腰梯形ABCD 中,AD ∥BC ,∠A =120°,两底分别为15cm 和49cm ,则其腰长为________.5.梯形ABCD 的面积是24,AD ∥BC ,且AD =5,BC =7,那么梯形的高是________.6.在梯形ABCD 中,AD ∥BC ,∠B =50°,∠C =80°,BC =5,AC =3,则CD =________.7.在梯形ABCD 中,AD ∥BC ,AD =3,AB =4,BC =5,那么腰CD 的取值X 围是________.8.在梯形ABCD 中,AD ∥BC ,∠B =90°,AD =1,△DBC 是等边三角形,则BC =________.9.在等腰梯形ABCD 中,AD ∥BC ,∠B =60°,则∠D =________.二、选择题10.下列结论正确的是( ).A .四边形可以分成平行四边形和梯形两类B .梯形可分为直角梯形和等腰梯形两类C .平行四边形是梯形的特殊形式D .直角梯形和等腰梯形都是梯形的特殊形式11.四边形ABCD 中,若∠A ︰∠B ︰∠C ︰∠D =2︰2︰1︰3,那么这个四边形是( ).A .梯形B .等腰梯形C .直角梯形D .任意四边形12.一等腰梯形上底为9cm ,下底为17cm ,一底角为60°,则它的腰长为( ).A .8cmB .9cmC .cm 28D .8.5cm13.等腰梯形ABCD 中,对角线AC =BC +AD ,则∠DBC 的度数是( ).A .30°B .45°C .60°D .90°三、解答题14.如图12-3-11,已知△ABC中,∠B=∠C,点D、E分别在边AB、AC上,且AD =AE,试说明四边形BCED是等腰梯形.15.如图12-3-12,在梯形ABCD中,AD∥BC,∠B=40°,∠C=70°,试说明AB+AD=BC.16.梯形ABCD中,AB∥CD,AB>CD,CE∥DA,交AB于E,且△BCE的周长为7cm,CD为3cm,求梯形ABCD的周长.17.如图12-3-13所示,在梯形ABCD中,上底AD=1 cm,下底BC=4cm,对角线BD ⊥AC,且BD=3cm,AC=4cm.求梯形ABCD的面积.参考答案一、1.110°2.120°3.20 cm4.34 cm 5.4 6.27.2<CD<6 8.2 9.120°二、10.D 11.C 12.A 13.C14.略.15.过A作AE∥DC交BC于E,EC=AD,AB=BE.BE+EC=BC,所以AB+AD=BC.16.周长为13cm.17.解:过点D作DE∥AC交BC的延长线于点E.因为在梯形ABCD中,AD∥BC,所以四边形ACED是平行四边形,则AC=DE,AD=CE.又因为AC⊥BD.所以BD⊥DE,即△BDE是直角三角形.因为△BDE与梯形ABCD同高,且梯形ABCD中(AD+BC)=BC+CE=BE,所以)cm(64321SS2BDEABCD=⨯⨯==∆梯形.。
华师大版数学八上163梯形梯形的性质同步测试

梯形的性质◆随堂检测一、等腰梯形的两腰,同一底上的两个角,对角线 .二、如图,在梯形ABCD中,∠B=50°,∠C=80°,则∠D= ,∠A .3、如图,在梯形ABCD中,AD∥BC,AD=4,AB=2,BC=6,∠B=60°,则CD= .4、一等腰梯形的上底为9cm,下底为17cm,一底角为60°,则它的腰长为()五、等腰梯形的上底与高相等,下底是上底的3倍,则其底角的度数为()°或150°°或135°°或120°°或105°六、如图,在梯形ABCD中,AB∥CD,DE∥BC交AB于点E,梯形周长为30cm,CD=5cm,则△ADE的周长为多少?◆典例分析如图,在梯形ABCD中,AD∥BC,AD=4cm,BC=10cm,∠DBC=45°,求梯形ABCD的面积.分析:已知梯形的上底和下底,要求梯形的面积,需要求出梯形的高,为此,可过上底的一个极点作梯形的高,将梯形分成矩形和直角三角形.解:作AE⊥BC,DF⊥BC,别离交BC于E、F.因为梯形为等腰梯形,因此BE=CF=1042=3cm,因此BF=10-3=7cm. 又∠DBC=45°,因此△DBF为等腰直角三角形,因此DF=BF=7cm,因此梯形ABCD的面积为12ABCD S =梯形(AD+BC )×DF=12(4+10)×7=49(2cm ).◆课下作业●拓展提高一、下列说法正确的是( )A.对角线相等的四边形是等腰梯形B.一组对边平行,另一组对边相等的四边形是等腰梯形C.两组对角别离互补的四边形是等腰梯形D.等腰梯形是轴对称图形,通过两底中点的直线是它的对称轴二、若是等腰梯形的两底之差等于一腰长,那么那个等腰梯形的锐角是( )° ° ° °3、等腰梯形有一角为120°,腰长为3cm ,一底边长为4cm ,则另一底边长为( )D. 1cm 或7cm4、已知直角梯形的一条腰长为5cm ,这腰与底边成30°角,则这梯形另一腰的长为()D.五、如图,在梯形ABCD 中,AB ∥CD ,∠D=2∠B ,AD=a ,CD=b ,则AB 等于( )A. 2ba + B. 2ab +C. a b +D. 2a b +六、如图,在梯形ABCD 中,AD ∥BC ,∠B=50°,∠C=80°,试说明CD=BC-AD.●体验中考一、(2009年山东威海)在梯形ABCD 中,AB ∥CD ,∠A=60°,∠B=30°,AD=CD=6,则AB 的长度为( )A .9B .12C .18D .633+二、(2009年重庆市江津区)如图,在梯形ABCD 中,AD ∥BC,AB =AD =DC,∠B =60º.(1)求证:AB ⊥AC ; 第6题(2)若DC=6,求梯形ABCD的面积 .参考答案:◆随堂检测一、相等相等相等.二、100° 130°.依照梯形上底和下底平行,可知∠A与∠B互补,∠C与∠D互补.3、2. 过A点作AE∥CD交BC于E,可得四边形AECD为平行四边形,因此∠AEC=∠C.又因为∠B=60°,因此∠AEC=∠B=60°,因此CD=AB=2.4、A. 能够等腰梯形上底的一极点向下底作垂线,如此垂线和腰还有下底组成直角三角形,再依照30°的直角边等于斜边的一半即可求得.五、B. 要分为上底较长和下底较长两种情形去考虑.六、20cm.解:因为梯形周长为30cm,因此AB+BC+CD+DA=30cm,又因为DE∥BC,因此四边形DEBC为平行四边形,因此EB=CD=5cm,因此△ADE的周长为AD+AE+DE=AD+AE+BC=AB+BC+CD+DA-2CD=30-2×5=20cm.◆课下作业●拓展提高一、D. 依照等腰梯形的性质可得.二、A. 依照30°的直角边等于斜边的一半即可求得.3、D. 要分底边长4cm为上底和下底两种情形来做.4、C. 依照30°的直角边等于斜边的一半即可求得.五、C. 过D作DE∥CB交AB于E,则四边形DEBC为平行四边形,因此∠DEB=∠B,又因为∠D=2∠B,因此∠ADE=∠AED,因此AD=AE,因此AB=AD+CD=a+b.六、解:过点D作DE∥AB交BC于E,则四边形ABED为平行四边形,AD=BE,因为∠DEC=∠B=50°,∠C=80°,因此∠EDC=50°,因此以∠EDC=∠DEC,因此DC=EC. 因为EC=BC-BE,因此DC=BC-AD.●体验中考一、C. 依照等腰梯形的性质可得.二、证明:(1)∵AD∥BC,AB=DC ∠B=60°∴∠DCB=∠B=60°∠DAC=∠ACB.又∵AD=DC ∴∠DAC=∠DCA ∴∠DCA=ACB=0602=30° ∴∠B+∠ACB=90°∴∠BAC=90°∴AB ⊥AC(2)过点A 作AE ⊥BC 于E ∵∠B=60°∴∠BAE=30°又∵AB=DC=6 ∴BE=3∴AE ===∵∠ACB=30°,AB ⊥AC∴BC=2AB=121()2ABCD S AD BC AE =+梯形1(612)2=+⋅=。
初中数学华师大版八年级下册试题 梯形 课后练习及详解
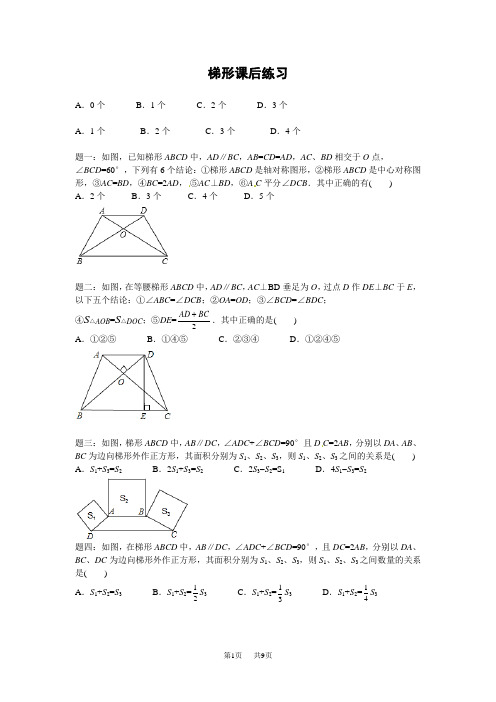
梯形课后练习A .0个B .1个C .2个D .3个A .1个B .2个C .3个D .4个题一:如图,已知梯形ABCD 中,AD ∥BC ,AB =CD =AD ,AC 、BD 相交于O 点,∠BCD =60°,下列有6个结论:①梯形ABCD 是轴对称图形,②梯形ABCD 是中心对称图形,③AC =BD ,④BC =2AD ,⑤AC ⊥BD ,⑥A C 平分∠DCB .其中正确的有( )A .2个B .3个C .4个D .5个题二:如图,在等腰梯形ABCD 中,AD ∥BC ,AC ⊥BD 垂足为O ,过点D 作DE ⊥BC 于E ,以下五个结论:①∠ABC =∠DCB ;②OA =OD ;③∠BCD =∠BDC ;④S △AOB =S △DOC ;⑤DE =2AD BC +.其中正确的是( ) A .①②⑤ B .①④⑤ C .②③④ D .①②④⑤题三:如图,梯形ABCD 中,AB ∥DC ,∠ADC +∠BCD =90°且D C =2AB ,分别以DA 、AB 、BC 为边向梯形外作正方形,其面积分别为S 1、S 2、S 3,则S 1、S 2、S 3之间的关系是( )A .S 1+S 3=S 2B .2S 1+S 3=S 2C .2S 3-S 2=S 1D .4S 1-S 3=S 2题四:如图,在梯形ABCD 中,AB ∥DC ,∠ADC +∠BCD =90°,且DC =2AB ,分别以DA 、BC 、DC 为边向梯形外作正方形,其面积分别为S 1、S 2、S 3,则S 1、S 2、S 3之间数量的关系是( )A .S 1+S 2=S 3B .S 1+S 2=12S 3C .S 1+S 2=13S 3 D .S 1+S 2=14S 3题五:如图,梯形纸片ABCD中,AD∥BC,∠B=30°.折叠纸片使BC经过点A,点B落在点B′处,EF是折痕,且BE=EF=4,AF∥CD.(1)求∠BAF的度数;(2)当梯形的上底AD多长时,线段DF恰为该梯形的高?题六:如图,在直角梯形ABCD中,∠A=∠B=90°,∠C= 45°,AB= 4,AD=5,把梯形沿过点D的直线折叠,使点A刚好落在BC边上,求此时折痕的长.题七:如图,四边形ABCD是轴对称图形,直线MN为对称轴,P为MN上一点.若使PC+PD 的值最小,则这个最小值是线段_________的长.题八:如图,直角梯形ABCD中,AD∥BC,∠B=90°,∠DCB= 45°,AD=3.5,DC=点P为腰AB上一动点,连结PD、PC,求PD+PC的最小值.题九:如图,在四边形ABCD中,DB平分∠ADC,∠ABC=120°,∠C=60°,∠BDC=30°;延长CD到点E,连接AE,使得∠E=12∠C.(1)求证:四边形ABDE是平行四边形;(2)若DC=16,求AD的长.题十:如图所示,已知在梯形ABCD中,AD∥BC,∠ABC=60°,BD平分∠ABC,且BD ⊥DC.(1)求证:梯形ABCD是等腰梯形;(2)当CD=1时,求等腰梯形ABCD的周长.题十一:如图,是用4个全等的等腰梯形镶嵌成的图形,则这个图形中等腰梯形上下两底边的比是.题十二:如图,四边形ABCD由4个全等的等腰梯形镶嵌而成,则线段AB与BC的大小关系为()A.AB B.AB=2BC C.2AB=4BC D.2AB=3BC梯形课后练习参考答案题一:4B.详解:解:根据梯形的性质和等腰梯形的判定可判断:①根据平行四边形的判定,一定是平行四边形,错误;②根据梯形的定义“一组对边平行而另一组对边不平行的四边形”,而一组对边平行但不相等的四边形的另一组对边肯定不平行,正确;③如平行四边形也符合这样的条件,错误;④也可以分为两个矩形,错误.故选B.题二:答案:B.④一组对边平行,另一组对边相等的四边形是等腰梯形错误,如平行四边形.故选:B.题三:答案:C.详解:①符合等腰梯形的性质,故此结论正确;②等腰梯形是轴对称图形而非中心对称图形,故此结论不正确;③等腰梯形的对角线相等,故此结论正确;④过点D作DE⊥BC,过点A作AF⊥BC,则四边形AFED是矩形,∵∠BCD=60°,∴∠EDC=30°,∴CE=BF=12 CD,∵AB=CD=AD,∴BC=2AD,故此结论正确;⑤∵CD=AD,∴∠DAC=∠DCA,∵AD∥BC,∴∠DAC=∠ACB,∴∠DCA=∠ACB,∵∠BCD=60°,∴∠DCA=∠ACB=30°,∴∠DBC=30°,∴∠BOC=120°,故此结论不正确;⑥∵CD=AD,∴∠DAC=∠DCA,∵AD∥BC,∴∠DAC=∠ACB,∴∠DCA=∠ACB,∴AC平分∠DCB,故此结论正确.所以正确的是①③④⑥.故选C.题四:答案:D.详解:∵四边形ABCD是等腰梯形,∴可得:①∠ABC=∠DCB;②OA=OD;∵BD≠BC,∴∠BCD≠∠BDC,即③不正确;在△AOD和△DOC中,OA=OD,OB=OC,∠AOD=∠DOC,∴△AOB≌△DOC,∴S△AOB=S△DOC;即④正确;∴△BDF是等腰直角三角形,故DE=12BF=2AD BC.即⑤正确.故选D.详解:过点A 作AE ∥BC 交CD 于点E ,∵AB ∥DC ,∴四边形AECB 是平行四边形,∴AB =CE ,BC =AE ,∠BCD =∠AED ,∵∠ADC +∠BCD =90°,DC =2AB ,∴AB =DE ,∠ADC +∠AED =90°,∴∠DAE =90°那么AD 2+AE 2=DE 2,∵S 1=AD 2,S 2=AB 2=DE 2,S 3=BC 2=AE 2,∴S 2=S 1+S 3.故选A .题五: 答案:D .详解:过点A 作AE ∥BC 交CD 于点E ,∵AB ∥DC ,∵∠ADC +∠BCD =90°,DC =2AB ,∴AB =DE ,∠ADC +∠AED =90°,∴∠DAE =90°,那么AD 2+AE 2=DE 2,∵S 1=AD 2,S =AB 2=DE 2,S 2=BC 2=A E 2,∴S =S 1+S 2.又∵DC =2AB ,∴S =14S 3.∴S 1+S 2=14S 3. 故选D .题六: 答案:见详解.详解:(1)∵BE =EF ,∴∠EFB =∠B ,∵△B ′EF ≌△BEF ,∴∠EFB ′=∠EFB =∠B =30°,∴∠BAF =180°-30°-30°-30°=90°;(2)连接DF ,∵在△AEF 中,∠EAF =90°,∠EF A =30°,EF = 4,∴AE =12EF =2,AF AE ∵AD ∥BC ,AF ∥CD ,∴四边形AFCD 是平行四边形,∴∠C =∠AFB =60°,CD =AF ,∵DF ⊥BC ,∴FC =12DC AD =FC即梯形的上底AD DF 恰为该梯形的高.题七: 详解:如图,过点D 作DF ⊥BC 于F ,∵∠A =∠B =90°,∠C = 45°,∴四边形ABFD 是矩形,△CDF 是等腰直角三角形,∴DF =AB = 4,CF =DF = 4,①如图1,折痕与AB 相交时,根据翻折的性质,A ′D =AD =5,在Rt △A ′DF 中,A ′F 2=A ′D 2-DF 2=52- 42=32,即A ′F =3,设AE =x ,则A ′E =x ,BE = 4-x ,又∵A ′B =BF -A ′F =5-3=2,∴在Rt △A ′BE 中,A ′E 2=A ′B 2+BE 2,即x 2=22+(4-x )2,解得x =52,所以,折痕DE 2=AD 2+AE 2=52+(52)2,即DE ②如图2,折痕与BC 相交时,根据翻折的性质,A ′D =AD =5,在Rt △A ′DF 中,A ′F 2=A ′D 2-DF 2=52-42=32,即A ′F =3,∴A ′B =BF +A ′F =5+3=8,设A ′E =x ,则BE =8-x ,根据翻折的性质求出B ′E =BE =8-x ,在Rt △A ′B ′E 中,A ′E 2=A ′B ′2+B ′E 2,即x 2=42+(8-x )2,解得x =5,∴EF =A ′E -A ′F =5-3=2,∴在Rt △DEF 中,折痕DE 2=DF 2+EF 2=42+22=20,即DE =题八: 答案:AC 或BD .详解:∵四边形ABCD 是轴对称图形,直线MN 为对称轴,∴点A 与点D 关于直线MN 对称,∴连接AC (BD ),则线段AC 或BD 的长即为PC +PD 的最小值.详解:如图,过点D 作DF ⊥BC 于点F ,作D 点与AB 的对称点D ′,过点D ′向BC 作垂线于点E ,∵∠DCB =45°,DC =DF =FC ×,∵AD =3.5,∴AD ′=BF =BE =3.5,∴CD ′==13,∴PD +PC 的最小值为13.题九: 答案:见详解.详解:(1)∵∠ABC =120°,∠C =60°,∴∠ABC +∠BCD =180°,∴AB ∥DC ,即AB ∥ED ,又∠C =60°,∠E =12∠C ,∠BDC =30°, ∴∠E =∠BDC =30°,∴AE ∥BD ,∴四边形AB DE 是平行四边形;(2)∵AB ∥DC ,∴四边形ABCD 是梯形,∵DB 平分∠ADC ,∠BDC =30°,∴∠ADC =∠BCD =60°, ∴四边形ABCD 是等腰梯形,∴BC =AD ,∵在△BCD 中,∠C =60°,∠BDC =30°,∴∠DBC =90°,又DC =16,∴AD =BC =12DC =8. 题十: 答案:见详解.详解:(1)证明:∵BD 平分∠ABC ,∴∠ABD =∠CBD ,∵∠ABC =60°,∴∠CBD =30°,∵BD ⊥DC ,∴∠BDC =90°,∴∠C =60°,(2)解:过点D 作DE ∥AB ,∵AD ∥BC ,∴四边形ABED 为平行四边形,∵CD =1,∴B C =2,∵∠C =60°,∴△DCE 为等边三角形,∴CE =BE =1,AD =1, ∴等腰梯形ABCD 的周长为AD +AB +CD +BC =1+1+1+2=5.题十一: 答案:12. 详解:延长CE 交AM 于D ,∵∠CEA =∠AEF =∠CEF =13×360°=120°, ∴∠AED =∠EAD =60°,∴△AED 是等边三角形, ∴AE =DE =CE ,AB ∥AD ,BC ∥AD ,∴四边形ABCD 是平行四边形, ∴AB =CD =CE +ED =2CE ,即等腰梯形上下两底边的比是2CE CE =12.题十二: 答案:D .详解:由图形可得等腰梯形的腰和较短的底边相等,设较短底边为a , 延长EG 交AB 于点F ,如图所示,可得DE =AF =2a ,即较长底边=2a ,则AB=AH+BH=3a,BC=2a,故可得:2AB=3BC.故选D.。
八年级数学梯形 同步练习1华师版 试题

梯形(1)一. 填空题1. 等腰梯形上底为6cm,下底为8 cm,高为3cm,则腰长为_______________.2. 若等腰梯形的锐角为60°,它的两底分别为11 cm, 35 cm, 则它的腰长为______ cm.3. 若直角梯形的一腰长为18 cm,这条腰和一个底所成的角是30°,则另一条腰长是______.4. 同一底上两个角相等的梯形是________形.5. 如图4.5-1,五边形ABCDE是正五边形,AC, AD, BD, BE, CE是对角线,则图形中共有等腰梯形_____________个.6. 如图4.5-2,在梯形ABCD中,DC∥AB,AC平分∠DAB, ∠DAB=∠CBA=60°,若梯形周长为80 cm,则AD=___________.7. 梯形ABCD中,对角线AC=BD,则ABCD是_________形,若延长两腰BA, CD相交于E,则△EBC是_________形.D CBA图4.5-1 图4.5-2二. 选择题8. 如图4.5-3,在梯形ABCD中,AB∥CD,将BC平移到DE的位置,若∠A=55°, ∠C=120°,则∠ADE等于 ( )A. 75°B. 65°C. 55°D. 45°CBA图4.5-39. 在梯形ABCD中,AD∥BC,那么四个叫之比可以成立的是 ( )A. 3:5:6:4B. 3:4:6:5C. 6:5:4:3D. 4:5:6:310. 若一底给定,一腰与底的夹角是90°时,等腰梯形 ( )A. 一定可以作出B. 一定作不出C. 可能作出D. 可以作出两个11. 以线段a=16, b=13, c=10, d=6为边作梯形,其中a,c作为梯形的两底,这样的梯形( )A. 可以作一个B. 可以作二个C. 可以作无数个D. 不能作12. 在直线梯形ABCD中,AD∥BC, AB⊥BC, E是CD的中点,则 ( )A. AE=BE B. AE>BE C. AE<BE D. AE,BE大小不确定三. 解答题13. 如图4.5-4,四边形ABCD中,AB=CD, AC=BD,且AB不平行于CD,试问: 四边形ABCD是等腰体梯形吗?为什么?B图4.5-414.(1) 在等腰梯形ABCD中,AD∥BC,E是BC的中点,连结AE, DE, AE与DE相等吗?请说明理由.(2) 上题中,若添加条件BC=2AD,图4.5-5中有平行四边形吗?请指出来,并说明理由.EDCBA图4.5-5四. 应用题15. (1) 如图4.5-6(1),四边形ABCD是平行四边形,AE=EF=FD, BG=GH=HC,问四边形EGFH的面积与平行四边形ABCD的面积有什么关系?(2) 如图4.5-6(2),四边形ABCD是梯形,E,F是AD的三等分点,G,H是BC的三等分点,问四边形EGHF的面积与梯形ABCD的面积有什么关系?(3) 如图4.5-6(3),当四边形ABCD是任意四边形时,其余条件不变,四边形EGHF的面积与四边形ABCD的面积间存在某种关系吗?说明你的探索结果.G H FE DCB AHG F E DCBAHG F E DCBA图4.5-6(1) 图4.5-6(2) 图4.5-6(3)16. 如图4.5-7,已知在四边形ABCD 中,有AB=CD,∠B=∠C,AD<BC.求证: 四边形ABCD 为等腰梯形.DCB A图4.5-7五. 综合能力提高题17. 如图4.5-8为一直角梯形,上底为a,下底为2a,高为a,请动手试一试能不能将它分割为若干个与原图形形状一样的小直角梯形?至少可分成几个?a2aa图4.5-818. 根据要求编拟一道新题.已知: 如图4.5-9,在矩形ABCD 平面内有一点P,且PA=PD.求证: PB=PC.PDCB A图4.5-9请你将上述条件中的”矩形ABCD ”改为另一种四边形,其余条件不变,使结论”PB=PC ”仍然成立,再根据改编后的题目画出图形,并说明理由.。
八年级数学第十六章第3节梯形的性质同步练习华东师大版

【模拟试题】(答题时间:45分钟)一. 选择题1. 如图,在等腰梯形ABCD 中,AD ∥BC ,∠C =60°,则∠1=( )A B C D1A. 35°B. 40°C. 60°D. 80°2. 等腰梯形的上底与高相等,下底是上底的3倍,则一个底角是( )A. 30°B. 45°C. 60°D. 75°3. 如图,在梯形ABCD 中,AD ∥BC ,CA 平分∠BCD ,CD =5,则AD 的长是( )A. 6B. 5C. 4D. 3A B CD4. 下列四边形:①等腰梯形,②正方形,③矩形,④菱形的对角线一定相等的是( )A. ①②③B. ①②③④C. ①②D. ②③*5. 如图,设M ,N 分别是直角梯形ABCD 两腰AD ,CB 的中点,DE ⊥AB 于点E ,将△ADE 沿DE 翻折,M 与N 恰好重合,则AE ∶BE 等于( )A. 2∶1B. 1∶2C. 3∶2D. 2∶3*6. 梯形ABCD 中,AD ∥BC ,∠B =50°,∠C =80°,BC =8cm ,AD =5cm ,则DC 长为( )A. 3cmB. 2cmC. 4cmD. cm*7. 梯形的两底长分别是16cm 和24cm ,下底角分别是60°和30°,则较短腰长为( )A. 3cmB. 83cmC. 12cmD. 4cm**8. 已知:如图所示,AB ∥CD ,AE ⊥DC ,AE =12,BD =15,AC =20,则梯形ABCD 的面积是( )A. 130B. 140C. 150D. 160A B CD E二. 填空题1. 梯形ABCD 中,AB ∥CD ,周长为30cm ,DE ∥BC 且交AB 于E ,CD =5cm ,则△ADE 的周长为_________.2. 已知直角梯形的两腰之比为1∶2,那么这个梯形的最大角为__________度.3. 等腰梯形的上底为6cm ,下底为8cm ,高为3cm .则腰长为__________cm .4. 等腰梯形有一角为120•°,•腰长为3cm ,•一底边长为4cm ,•则另一底边长为_______.5. 如图,在等腰梯形ABCD 中,AD ∥BC ,AE ∥DC ,AB =6cm ,则AE =__________cm . A B C E D*6. 如图所示,在梯形ABCD 中,AD ∥BC ,∠B 与∠C 互余,AD =5,BC =13,∠C =60°,则该梯形的面积为__________.A B C D三. 解答题1. 如图,等腰梯形ABCD 中,AD ∥BC ,AD =3,AB =4,BC =7,求∠B•的度数.A B CD2. 如图,E 、F 是梯形ABCD 的两底AD 、BC 的中点,且EF ⊥BC ,•试证明梯形ABCD 是等腰梯形.A BC D E F3. 已知:梯形ABCD 中,AD ∥BC ,AB =4,BC =9,CD =5,DA =6.(1)求证:AB ⊥BC ;(2)求梯形ABCD 的面积.**4. 如图,梯形ABCD 中,AD ∥BC ,∠BAD =90°,E 是DC 的中点,•证明∠AEB =2∠CBE .A B C DE【试题答案】一. 选择题1. C2. B3. B4. A5. A6. A7. D8. C二. 填空题1. 20cm2. 1503. 24. 1cm 或7cm5. 66. 183(过A 或D 作一腰的平行线)三. 解答题1. 60° 提示:过A 作AE ∥CD ,得平行四边形AECD ,分析可知△ABE 为等边三角形.2. 提示:分别过E 作EG ∥AB 交BC 于G ,EH ∥DC 交BC•于H ,•可证得EG =•EH ,所以梯形ABCD 是等腰梯形可证得.3. (1)过点D 作DE ∥AB 交BC 于点E ,则AB =DE =4,∠DEC =∠ABC ,AD =BE =6,CE =9-6=3.在△DEC 中,DC =5,DC 2=25,DE 2+CE 2=42+32=25,所以DC 2=DE 2+CE 2.所以△DCE 是直角三角形,所∠DEC =90°.所以∠ABC =90°,即AB ⊥BC ;(2)梯形ABCD 的面积=12(AD +BC )·AB =30. 4. 由于DE =EC ,AD ∥BC ,如果延长AE 交BC 的延长线于F ,就构造出△ADE 和△FCE 全等.从而AE =EF .这时BE 为R t △ABF 斜边上的中线.由此知∠EBF =∠F .由∠AEB =∠CBE +∠F 可得结论.。
八年级下华东师大版等腰梯形的判定同步练习

等腰梯形的判定同步练习目标与方法1.会证明等腰梯形的性质定理与判定定理.2.能运用等腰梯形的性质定理和判定定理进行简单的计算与证明.基础与巩固1.如图1,请写出等腰梯形ABCD(AD∥BC,AB=CD)特有而一般梯形不具备的3个特殊性质:(1)_________________;(2)_________________;(3)_________________.B ACDBACD(1) (2) (3)2.如图2,在梯形ABCD中,AD∥BC.•若再加上一个条件:•________,•则可得到梯形ABCD是等腰梯形.3.等腰梯形的一角为120°,两底分别为10和30,则它的腰长为().A.10 B.20 C.3 D.34.已知:如图3,在梯形ABCD中,AD∥BC,BD⊥DC,且BD平分∠ABC,∠C=60°,求证:•梯形ABCD是等腰梯形.拓展与延伸5.若等腰梯形的三条边长分别为3、4、11,则这个等腰三角形的周长为().A.21 B.29 C.21或29 D.21或22或296.已知:如图,在梯形ABCD中,AB∥DC,AD=BC,点E在边AB延长线上,且BE=DC.求证:AC=CE.后花园BACE D智力操已知:如图,在四边形ABCD中,AB∥CD,AE⊥DC,BD⊥AC,AE=12,•BD=•15,AC=20,求梯形ABCD的面积.参考答案:1.(1)∠A=∠D;(2)∠B=∠C;(3)AC=BD.BACED2.AB=CD或∠ABC=∠DCB或∠BAD=∠ADC.3.B4.∵BD⊥DC,∴∠BDC=90°.在△BCD中,∵∠C=60°,∴∠DBC=30°.又∵BD平分∠ABC,∴∠ABC=2∠DBC=60°.∴∠C=∠ABC.在梯形ABCD中,AD∥BC,且∠C=∠ABC,∴梯形ABCD是等腰梯形.5.B6.在梯形ABCD中,∵AB∥DC,AD=BC,∴∠ADC+∠DAB=180°,∠DAB=∠CBA.又∵∠CBA+∠CBE=180°,∴∠ADC=∠CBE.又∵BE=DC,AD=BC,∴△ADC≌△CBE.∴AC=CE.智力操 150.提示:过点B作BF∥AC,交DC的延长线于点F,则CF=AB.在Rt△DBF中,求得DF=25,于是DC+AB=25,代入梯形面积公式即可.。
2013-2014学年华东师大版八年级数学上册例题讲解+练习梯形的辅助线课后练习及详解

梯形的辅助线课后练习主讲教师:傲德题一:(1)如图,直角梯形ABCD中,AD∥BC,∠B=90°,腰AB= 4,两底之差为2,求另一腰CD的长;(2)在梯形ABCD中,AD∥BC,AB=CD,∠B=60°,AD=8,BC=14,求梯形ABCD的周长;(3)如图所示,在等腰梯形ABCD中,AB∥CD,DC=AD=BC,且对角线AC垂直于腰BC,求这个梯形各内角的度数;(4)如图,在梯形ABCD中,AD∥BC,∠B+∠C=90°,AD=1,BC=3,E、F分别是AD、BC的中点,则EF= .(1)如图,在梯形ABCD中,AD∥BC,∠B=30°,∠C=60°,E、F、M、N分别为AB、CD、BC、DA的中点,已知BC=7,MN=3,则EF= ;(2)如图,在梯形ABCD中,AD=DC,AB=DC,∠D=120°,对角线CA平分∠BCD,且梯形的周长为20,则梯形ABCD的面积为;(3)如图,等腰梯形ABCD中,AD∥BC,AD=3,AB= 4,BC=7,求∠B的度数;(4)如图,梯形ABCD中,AD∥BC,AC⊥BD,AD=3,BC=7,E在BC上,CE=2,则DE= .题二:已知:等腰梯形的上底是2cm,腰长是4cm,一个底角是60°,则等腰梯形的下底是cm.题三:已知:等腰梯形的一个底角等于60°,它的两底分别为4cm和7cm,则它的周长为cm.题四:如图所示,在梯形ABCD中,AD∥BC,AB=CD,AC⊥BD,且AD= 4,BC=8,求AC的长.题五:如图,在梯形ABCD中,AD∥BC,对角线AC⊥BD,若AD=3,BC=7,求梯形ABCD面积的最大值.题六:如图,梯形ABCD中,AD∥BC,点E在BC上,AE=BE,点F是CD的中点,且AF⊥AB,若AD=2.7,AF=4,AB=6,求CE的长.题七:如图,在梯形ABCD中,AB∥CD,∠A+∠B=90°,CD=5,AB=11,点M、N分别为AB、CD的中点,求线段MN的长.题八:如图,在梯形ABCD中,AD∥BC,∠ABC=90°,AB= 4,AD=3,BC=5,点M是边CD 的中点,连接AM、BM.求△ABM的面积.题九:如图,已知直角梯形ABCD中,AD∥BC(AD<BC),∠B=90°,AB=AD+BC.点E是CD 的中点,点F是AB上的点,∠ADF= 45°,FE=a,梯形ABCD的面积为m.(1)求证:BF=BC;(2)求△DEF的面积(用含a、m的代数式表示).题十:以线段a=16,b=13为梯形的两底,c=10,d=6为腰画梯形,这样的梯形() A.只能画出一个B.能画出2个C.能画出无数个D.不能画出题十一:以线段a=5,b=10,c=15,d=20做梯形四边形,这样的梯形(不全等的)() A.至少能做3个B.恰好能做2个C.仅仅只能做1个D.一个也不能做梯形的辅助线课后练习参考答案题一:(2)34;(3)60°,60°,120°,120°;(4)1.详解:(1)过D作DE⊥BC于E,∵AB⊥BC,DE⊥BC,AD∥BC,∴四边形ADEB是个矩形,∴AB=DE= 4,CE=BC-AD=2,Rt△DEC中,CD;(2)过A、D点作AE⊥BC于E,DF⊥BC于F,∵AB=CD,∠B=∠C,AE=DF,∴△ABE≌△DCF,∴BE=CF,∵AD=8,BC=14,BE=CF=3,又∵在Rt△ABE中,∠B=60°,∴AB=2BE=6,∴梯形ABCD的周长为8+14+6+6=34;(3)如图所示,过点C作CE∥AD,又DC∥AE,∴四边形AECD为平行四边形,又DC=AD=BC,∴四边形AECD为菱形,∴AE=CE=BC,∴∠EAC=∠ECA,∠CEB=∠B,∵∠B+∠CAB=90°,即3∠CAE=90°,∴∠CAE=30°,∴∠B=60°=∠DAB,∠D=∠DCB=120°;(4)过点E作AB、CD的平行线,与BC分别交于G,H,∵∠B+∠C=90°,∴∠EGH=∠B,∠EHG=∠C,∴∠EGH+∠EHG=90°,∴四边形ABGE和四边形CDEH都是平行四边形,△EGH为直角三角形,∵E、F分别是AD、BC的中点,∴BG=CH=0.5,GH=2,根据直角三角形中斜边上的中线是斜边的一半知,EF=12GH=1,∴EF=1.题二: (1)4;;(3)60°;(4)5.详解:(1)过点N 分别作NG ∥AB ,NH ∥CD ,得平行四边形ABGN 和平行四边形DCHN ,∴∠NGM +∠NHM =∠B +∠C =90°,GH =BC -AD ,MG =MH ,∴GH =2MN =6,∴AD =7-6=1,∴EF = 4;(2)∵在梯形ABCD 中,AB =DC ,∴梯形ABCD 是等腰梯形,∴∠D +∠DCB =180°,∵∠D =120°,∴∠B =∠DCB =60°,∵对角线CA 平分∠BCD ,∴∠ACB =30°,∵AD =DC ,∴∠DAC =∠ACD =30°,∴∠BAC =90°,∴BC =2AB ,∵梯形的周长为AD +DC +BC +AB =5AB =20,∴AB = 4,∴AC =4BC =8,过点A 作AE ⊥BC 于点E ,∵AB = 4,AC ,BC =8,∴AE ,∴梯形ABCD 的面积为(4+8)×12(3)过点A 作AE ∥DC 交BC 于E ,∵AD ∥BC ,∴四边形AECD 是平行四边形,∴EC =AD =3,DC =AE ,∴BE =BC -CE =7-3= 4,∴CD =AB = 4,∴AE =AB =BE = 4,∴△ABE 是等边三角形,∴∠B =60°;(4)过D 作DF ∥AC 交BC 的延长线于F ,∵AD ∥BC ,∴四边形ACFD 是平行四边形,∴CF =AD =3,∵BC =7,∴BF =BC +CF =7+3=10,∵CE =2,∴BE =7-2=5,EF =2+3=5,∴BE =EF ,又∵AC ⊥BD ,DF ∥AC ,∴∠BDF =90°,∴DE =12BF =5.题三: 6cm .详解:过D 作DE ∥AB 交BC 于E ,∵DE ∥AB ,AD ∥BC ,∴四边形ABED是平行四边形,∴AD=BE=2cm,DE=AB=4cm,∠DEC=∠B=60°,AB=DE=DC,∴△DEC是等边三角形,∴EC=CD= 4cm,∴BC= 4cm+2cm=6cm.题四:17cm.详解:过上底顶点D作DE∥AB交BC于E,则四边形ABED是平行四边形,∴DE=AB,AD=BE,∵梯形的一个底角是60°,∴∠C=60°,又∵腰长AB=CD=DE,∴△CDE是等边三角形,∴CD=CE=BC-BE=7-4=3cm,∴它的周长为3+7+3+4=17cm.题五:详解:过D作DE∥AC交BC的延长线于E,∵AD∥BC,AB=CD,∴四边形ABCD是等腰梯形,∴ADEC是平行四边形,∴AD=CE,AC=DE,即可得出BE=BC+CE=BC+AD=12,又∵AC=BD,∴BD=ED,∴△BDE为等腰直角三角形,∴AC=BD=题六:25.详解:过D作DE∥AC交BC延长线于E,∵AD∥BC,DE∥AC,∴四边形ACED是平行四边形,∴AD=CE,∴根据等底等高的三角形面积相等得出△ADC的面积等于△DCE的面积,即梯形ABCD的面积等于△BDE的面积,∵AC⊥BD,DE∥AC,∴∠BDE=90°,BE=3+7=10,∴此时△BDE的边BE边上的高越大,它的面积就越大,即当高是12BE时最大,即梯形的最大面积是12×10×12×10=25.题七: 2.3.详解:延长AF、BC交于点G,∵AD∥BC,∴∠D=∠FCG,∠DAF=∠G,又DF=CF,∴△AFD≌△GFC,∴AG=2AF=8,CG=AD=2.7,∵AF⊥AB,AB=6,∴BG=10,∴BC=BG-CG=7.3,∵AE=BE,∴∠BAE=∠B,∴∠EAG=∠AGE,∴AE=GE,∴BE=12BG=5,∴CE=BC-BE=2.3.题八:3.详解:如图,过D作DE∥BC,DF∥MN,∵在梯形ABCD中,AB∥CD,DE∥BC,∴CD=BE=5,AE=AB-BE=11-5=6,∵M为AB的中点,∴MB=AM=12AB=12×11=5.5,ME=MB-BE=5.5-5=0.5,∵N为DC的中点,∴DN=12DC=12×5=2.5,在四边形DFMN中,DC∥AB,DF∥MN,∴FM=DN=2.5,∴FE=FM+ME=2.5+0.5=3=12AE,∴F为AE的中点,又∵DE∥BC,∴∠B=∠AED,∵∠A+∠B=90°,∴∠A+∠AED=90°,∴∠ADE=90°,即△ADE是直角三角形,∴DF=MN=12AE=12×6=3.题九:8.详解:延长AM交BC的延长线于点N,∵AD∥BC,∴∠DAM=∠N,∠D=∠MCN,∵点M是边CD的中点,∴DM=CM,∴△ADM≌△NCM(AAS),∴CN=AD=3,AM=MN=12AN,∴BN=BC+CN=5+3=8,∵∠ABC=90°,∴S△ABN=12×AB•BN=12×4×8=16,∴S△ABM=12S△ABN=8,即△ABM的面积为8.题十:见详解.详解:(1)∵四边形ABCD是直角梯形,∴∠A=90°,∵∠ADF=45°,∴∠AFD= 45°,∴AD=AF,∵AB=AF+BF,AB=AD+BC,∴BF=BC;(2)连接FC,设AD=AF=x,BC=BF=y,连接CF,作DH⊥BC于H,易证四边形ABHD为矩形、△CDF为直角三角形,又∵E是CD中点,∴CD=2EF=2a,由勾股定理得x2+y2=2a2…①,由直角梯形的面积公式可得:(x+y)2=2m…②,由②-①,得xy=m-a2,∵S△DFC=S梯形ABCD-S△AFD-S△BFC=12(x+y)2 -12x2 -12y2 = xy,∴S△DEF=12S△DFC=12m-12a2.题十一:D.详解:如图,过点B作BE∥AD,则出现平行四边形ABED和一个△BEC,∵AB=13,CD=16,AD=10,BC=6∴CE=3,BE=10,∵3+6<10,∴BE,CE,BC不能构成三角形∴这样的梯形一个也不能作.故选D.题十二:C.详解:作DE∥AB,则DE=AB,①当a=5为上底,b=10为下底,c、d为腰时,10-5=5,与15,20不能构成三角形,故不满足题意;②当a=5为上底,b=15为下底,b、d为腰时,15-5=10,与10,20不能构成三角形,故不满足题意;③当a=5为上底,d=20为下底,b、c为腰时,20-5=15,与10,15可以构成三角形,故满足题意;④当b=10为上底,c=15为下底,a、d为腰时,15-10=5,与5,20不能构成三角形,故不满足题意;⑤当b=10为上底,d=20为下底,a、c为腰时,20-10=10,与5,15不能构成三角形,故不满足题意;⑥当c=15为上底,d=20 为下底,a、b为腰时,20-15=5,与5,10不能构成三角形,故不满足题意;综上可得只有当a=5为上底,d=20为下底,b、c为腰时,满足题意,即以线段a=5,b=10,c=15,d=20做梯形四边形,这样的梯形(不全等的)只能做一个.故选C.。
初中数学华师大版八年级下册试题 梯形-讲义

梯形
重难点易错点辨析
题一:下列叙述中,正确的是()
A.只有一组对边平行的四边形是梯形
C.梯形有两个内角是锐角,其余两个角是钝角
D.梯形是轴对称图形
等腰梯形的性质和判定
题二:如图,在等腰梯形AB CD中,AD∥BC,对角线AC、BD相交于点O,以下四个结论:
①∠ABC=∠DCB
②OA=OD
③∠BCD=∠BDC
④S△AOB=S△D O C
其中正确的是( )
A.①②B.①④C.②③④D.①②④
金题精讲
题一:如图所示,已知梯形ABCD,AD∥BC,E为CD的中点,若用S1、S2、S3分别表示△ADE、△EBC、△ABE的面积,则S1、S2、S3的关系是()
A.S1+S2>S3B.S1+S2=S3C.S1+S2<S3D.以上都不对
题二:如图,直角梯形纸片ABCD中,AD∥BC,∠A=90°,∠C=30°,折叠纸片使BC经过点D,点C落在点E处,BF是折痕,且BF=CF=8.
(1)求∠BDF的度数;
(2)求AB的长.
题三:如图,梯形ABCD中,AD∥BC,AB=C D=AD=1,∠B=60°,直线MN为梯形ABCD的对称轴,P为MN上一点,那么PC+PD的最小值为.
思维拓展
题一:如图,平行四边形ABCD是用12个全等的等腰梯形镶嵌成的图形,这个图形中等腰梯形的上底长与下底长的比是.
讲义参考答案
重难点易错点辨析
题一:A.题二:D.
金题精讲
题一:B.题二:(1)90°;(2)6.题四:(1)略;(2)10.
思维拓展
题一:1:2.。
华师大版八年级数学上册同步练习题及问题详解(全套)

12.1.1 平方根(第一课时)◆随堂检测1、若x 2= a ,则 叫 的平方根,如16的平方根是 ,972的平方根是 2、3±表示 的平方根,12-表示12的 3、196的平方根有 个,它们的和为 4、下列说法是否正确?说明理由 (1)0没有平方根; (2)—1的平方根是1±; (3)64的平方根是8; (4)5是25的平方根; (5)636±= 5、求下列各数的平方根(1)100 (2))8()2(-⨯- (3)1.21 (4)49151◆典例分析例 若42-m 与13-m 是同一个数的平方根,试确定m 的值◆课下作业●拓展提高一、选择1、如果一个数的平方根是a+3和2a-15,那么这个数是( )A 、49B 、441C 、7或21D 、49或441 2、2)2(-的平方根是( )A 、4B 、2C 、-2D 、2± 二、填空3、若5x+4的平方根为1±,则x=4、若m —4没有平方根,则|m —5|=5、已知12-a 的平方根是4±,3a+b-1的平方根是4±,则a+2b 的平方根是 三、解答题6、a 的两个平方根是方程3x+2y=2的一组解 (1) 求a 的值 (2)2a 的平方根7、已知1-x +∣x+y-2∣=0 求x-y 的值● 体验中考1、(09)若实数x ,y 满足2-x +2)3(y -=0,则代数式2x xy -的值为2、(08)在小于或等于100的非负整数中,其平方根是整数的共有 个3、(08)下列说确的是( )A 、64的平方根是8B 、-1 的平方根是1±C 、-8是64的平方根D 、2)1(-没有平方根12.1.1平方根(第二课时)◆随堂检测1、259的算术平方根是 ;___ __ 2、一个数的算术平方根是9,则这个数的平方根是3x 的取值围是 ,若a ≥04、下列叙述错误的是( )A 、-4是16的平方根B 、17是2(17)-的算术平方根 C 、164的算术平方根是18 D 、0.4的算术平方根是0.02◆典例分析例:已知△ABC 的三边分别为a 、b 、c 且a 、b |4|0b -=,求c 的取值围 分析:根据非负数的性质求a 、b 的值,再由三角形三边关系确定c 的围◆课下作业●拓展提高一、选择12=,则2(2)m +的平方根为( )A 、16B 、16±C 、4±D 、2±2 )A 、4B 、4±C 、2D 、2± 二、填空3、如果一个数的算术平方根等于它的平方根,那么这个数是42(4)y +=0,则xy =三、解答题5、若a 是2(2)-的平方根,b 2a +2b 的值6、已知a b-1是400●体验中考1.(2009年潍坊)一个自然数的算术平方根为a ,则和这个自然数相邻的下一个自然数是( )A .1a +B .21a +CD 12、(08的整数部分是 ;若<b ,(a 、b 为连续整数),则a= , b=3、(08年)如图,实数a 、b 在数轴上的位置,化简 =4、(08年随州)小明家装修用了大小相同的正方形瓷砖共66块铺成10.56米2的房间,小明想知道每块瓷砖的规格,请你帮助算一算.12.1.2 立方根◆随堂检测1、若一个数的立方等于 —5,则这个数叫做—5的 ,用符号表示为 ,—64的立方根是 ,125的立方根是 ; 的立方根是 —5.2、如果3x =216,则x = . 如果3x =64, 则x = .3、当x 为 时,.4、下列语句正确的是( )A 、64的立方根是2B 、3-的立方根是27C 、278的立方根是32± D 、2)1(-立方根是1- 典例分析例 若338x 51x 2+-=-,求2x 的值.◆课下作业●拓展提高一、选择1、若22)6(-=a ,33)6(-=b ,则a+b 的所有可能值是( )A 、0B 、12-C 、0或12-D 、0或12或12- 2、若式子3112a a -+-有意义,则a 的取值围为( )A 、21≥aB 、1≤aC 、121≤≤a D 、以上均不对 二、填空3、64的立方根的平方根是4、若162=x ,则(—4+x )的立方根为三、解答题5、求下列各式中的x 的值(1)1253)2(-x =343 (2)64631)1(3-=-x6、已知:43=a ,且03)12(2=-++-c c b ,求333c b a ++的值●体验中考1、(09)实数8的立方根是2、(08市)已知0≠a ,a ,b 互为相反数,则下列各组数中,不是互为相反数的一组是( ) A 、3a 与3b B 、a +2与b +2 C 、2a 与2b - D 、3a 与3b 3、(08市)一个正方体的水晶砖,体积为100 cm 3,它的棱长大约在( ) A 、4~5cm 之间 B 、5~6cm 之间 C 、6~7 cm 之间D 、7~8cm 之间12.2实数与数轴◆随堂检测1、下列各数:23,722-,327-,414.1,3π-,12122.3,9-,••9641.3中,无理数有 个,有理数有 个,负数有 个,整数有 个. 2、33-的相反数是 ,|33-|=57-的相反数是 ,21-的绝对值=3、设3对应数轴上的点A ,5对应数轴上的点B ,则A 、B 间的距离为4、若实数a<b<0,则|a| |b|;大于17小于35的整数是 ; 比较大小:3 5 5、下列说法中,正确的是( )A .实数包括有理数,0和无理数B .无限小数是无理数C .有理数是有限小数D .数轴上的点表示实数.◆典例分析例: 设a 、b 是有理数,并且a 、b 满足等式2522-=++b b a ,求a+b 的平方根◆课下作业●拓展提高一、选择1、 如图,数轴上表示1,2的对应点分别为A 、B ,点B 关于点A 的对称点为C ,则点C 表示的实数为 ( )A .2-1B .1-2C .2-2D .2-22、设a 是实数,则|a|-a 的值( )A .可以是负数B .不可能是负数C .必是正数D .可以是整数也可以是负数二、填空3、写出一个3和4之间的无理数CAB4、下列实数1907,3π-,0,49-,21,31-,1.1010010001…(每两个1之间的0的个数逐次加1)中,设有m 个有理数,n 个无理数,则n m = 三、解答题5、比较下列实数的大小(1)|8-| 和3 (2)52- 和9.0- (3)215-和876、设m 是13的整数部分,n 是13的小数部分,求m-n 的值.● 体验中考2.(2011年二中模拟)如图,数轴上A B ,两点表示的数分别为1-, 点B 关于点A 的对称点为C ,则点C 所表示的数为( ) A.2- B.1-C.2-+D.1+3.(2011年)已知实数a在数轴上的位置如图所示,则化简|1|a -的结果为( )A .1B .1-C .12a -D .21a -3、(2011年)实数a b ,在数轴上对应点的位置如图所示, 则必有( )A .0a b +>B .0a b -<C .0ab >D .0ab< 4、(2011年省市模2)如图,数轴上点A 所表示的数的倒数是( )A. 2-B. 2C. 12D. 12-§13.1 幂的运算(第46题图)0 (第8题图)1. 同底数幂的乘法试一试(1) 23×24=( )×( )=2();(2) 53×54=5(); (3) a 3·a 4=a ().概 括:a m ·a n =( )( )= =a n m +.可得 a m ·a n =a n m +这就是说,同底数幂相乘, .例1计算:(1) 103×104; (2) a ·a 3; (3) a ·a 3·a 5.练习1. 判断下列计算是否正确,并简要说明理由.(1) a ·a2=a 2;(2) a +a 2=a 3;(3)a 3·a 3=a 9;(4)a 3+a 3=a 6.2. 计算:(1) 102×105; (2) a 3·a 7; (3) x ·x 5·x 7.3.填空:(1)ma 叫做a 的m 次幂,其中a 叫幂的________,m 叫幂的________;(2)写出一个以幂的形式表示的数,使它的底数为c ,指数为3,这个数为________; (3)4)2(-表示________,42-表示________;(4)根据乘方的意义,3a =________,4a =________,因此43a a⋅=)()()(+同底数幂的乘法练习题1.计算: (1)=⋅64a a(2)=⋅5b b(3)=⋅⋅32m m m (4)=⋅⋅⋅953c c c c(5)=⋅⋅p n ma a a (6)=-⋅12m t t (7)=⋅+q qn 1(8)=-+⋅⋅112p p n n n2.计算:(1)=-⋅23b b (2)=-⋅3)(a a(3)=--⋅32)()(y y (4)=--⋅43)()(a a(5)=-⋅2433 (6)=--⋅67)5()5((7)=--⋅32)()(q q n(8)=--⋅24)()(m m(9)=-32 (10)=--⋅54)2()2((11)=--⋅69)(b b(12)=--⋅)()(33a a3.下面的计算对不对?如果不对,应怎样改正?(1)523632=⨯; (2)633a a a =+;(3)nnny y y 22=⨯; (4)22m m m =⋅;(5)422)()(a a a =-⋅-; (6)1243a a a =⋅;(7)334)4(=-; (8)6327777=⨯⨯;(9)42-=-a ; (10)32n n n =+. 4.选择题: (1)22+m a可以写成( ).A .12+m aB .22a am+ C .22a a m ⋅ D .12+⋅m a a(2)下列式子正确的是( ).A .4334⨯= B .443)3(=- C .4433=- D .3443= (3)下列计算正确的是( ).A .44a a a =⋅ B .844a a a =+C .4442a a a =+D .1644a a a=⋅2. 幂的乘方根据乘方的意义及同底数幂的乘法填空:(1)(23)2=×=2();(2)(32)3=×=3();(3)(a3)4=×××=a().概括(a m)n=(n个)=(n个)=a mn可得(a m)n=a mn(m、n为正整数).这就是说,幂的乘方,.例2计算:(1)(103)5;(2)(b3)4.练习1. 判断下列计算是否正确,并简要说明理由.(1)(a3)5=a8;(2) a5·a5=a15;(3)(a2)3·a4=a9.2. 计算:(1)(22)2;(2)(y2)5;(3)(x4)3;( 4)(y3)2·(y2)3.3、计算:(1)x·(x2)3(2)(x m)n·(x n)m (3)(y4)5-(y5)4(4)(m3)4+m10m2+m·m3·m8 (5)[(a-b)n] 2 [(b-a)n-1] 2(6)[(a-b)n] 2 [(b-a)n-1] 2 (7)(m3)4+m10m2+m·m3·m8幂的乘方一、基础练习1、幂的乘方,底数_______,指数____.(a m)n= ___(其中m、n都是正整数)2、计算:(1)(23)2=_____;(2)(-22)3=______;(3)-(-a3)2=______;(4)(-x2)3=_______。
八年级数学梯形 同步练习2华师版 试题

梯形【学习目标】掌握梯形的概念,探索并了解等腰梯形的有关性质,并会运用分解梯形为平行四边形与三角形的方法解决一些简单的问题.【基础知识概述】 1.梯形的有关概念:(1)梯形的定义:一组对边平行而另一组对边不平行的四边形叫做梯形. 注意:定义需满足三个条件:①四边形;②一组对边平行;③一组对边不平行. (2)梯形的相关定义:①梯形的底:梯形中平行的两边叫做梯形的底.注意:通常把较短的底叫做上底,较长的底叫做下底,梯形的上下底则是以长短区分的,不是指位置定的. ②梯形的腰:梯形中不平行的两边叫做梯形的腰. ③梯形的高:梯形两底的距离叫做梯形的高. (3)特殊梯形的定义:①等腰梯形:两腰相等的梯形.②直角梯形:一腰垂直于底的梯形. 2.梯形的分类:⎪⎩⎪⎨⎧⎩⎨⎧等腰梯形直角三角形特殊梯形一般梯形梯形3.梯形的识别:(1)定义法判定,四边形中①一组对边平行;②另一组对边不平行. (2)有一组对边平行且不相等的四边形是梯形.注意:此识别方法可由梯形定义和一组对边平行且相等的四边形是平行四边形得出. 4.等腰梯形的特征:(1)等腰梯形两腰相等、两底平行. (2)等腰梯形在同一底上的两个角相等.(3)等腰梯形的对角线相等.(4)等腰梯形是轴对称图形,它只有一条对称轴,底的垂直平分线是它的对称轴.注意:等腰梯形在同一底上的两个角相等,不能说成:(1)等腰梯形两底上的角相等;(2)等腰梯形同一底上的两底角相等.这两种说法都是错误的.5.等腰梯形的识别:(1)两腰相等的梯形是等腰梯形.(2)在同一底上的两个角相等的梯形是等腰梯形. (3)对角线相等的梯形是等腰梯形. 6.等腰梯形特征及识别的作用:可以证明角、线段相等,直线平行及判定四边形为等腰梯形等. 7.解决梯形问题的基本思路:题三角形或平行四边形问分割、拼接转化 梯形问题−−−−−−→−.这种思路常通过平移或旋转来实现. 8.梯形的面积(如图12-3-1):DE )AB CD (21S ⋅+=梯.【例题精讲】例1 已知如图12-3-2,四边形ABCD 中,AB =DC ,AC =BD ,AD ≠BC ,试说明四边形ABCD 是等腰梯形.分析:由条件知只需证明四边形ABCD 为梯形,即证AD∥BC,可转证∠BAD+∠ABC=180°.解:∵AB=CD,BC=CB,AC=DB,∴△ABC与△DCB重合,∴∠ABC=∠DCB.同理可证∠BAD=∠CDA.∵∠ABC+∠DCB+∠BAD+∠CDA=360°,∴∠ABC+∠BAD=180°,∴AD∥BC.∵AD≠BC,AB=DC,∴四边形ABCD为等腰梯形.思考:如此题不给AD≠BC这个条件,这还是等腰梯形吗?(提示:不一定,它还可能为矩形)注意:所以证明四边形为梯形时,一定要考虑平行边是否相等(另一对边是否平行).例2如图12-3-3,在梯形ABCD中,AD∥BC,AD=AB=DC,BD⊥CD.求∠C的大小.分析:这是一个等腰梯形.所以∠ABC=∠C.其中又有△ABD是等腰三角形,所以有∠ABD=∠ADB.当平行线与等腰三角形在一起,常常能把角进行迁移,可以推得∠ADB=∠DBC=∠ABD,即∠C=∠ABC=2∠DBC,在Rt△BCD中便可容易地求得∠C=60°.解:因为在梯形ABCD中,AB=DC,所以∠ABC=∠C.又因为AD=AB,则∠ABD=∠ADB.又AD∥BC,所以∠ADB=∠DBC.因此∠C=∠ABC=2∠DBC.在Rt△BCD中,∠C+∠DBC=3∠DBC=90°,则∠DBC=30°,∠C=60°.例3 如图12-3-4,梯形ABCD中,AD∥BC,AD=8,BC=17,∠C=70°,∠B=55°,求DC的长.分析:要求DC的长,设法将DC放到一个三角形内去解决,这个三角形与已知条件AD=8,BC=17,∠C=70°,∠B=55°相联系,可过D作DE∥BA,在△DEC中求出DC.解:过D作DE∥AB交BC于E.∴∠1=∠B=55°.∵∠C=70°,∴∠2=55°,∴DC=EC=BC—BE.∵AD∥BC,DE∥AB,∴BE=AD=8.∵BC=17,∴DC=17—8=9.说明:作梯形一腰的平行线,把梯形分成一个平行四边形和一个三角形是常用的引辅助线的方法.例4如图12-3-5,在直角梯形ABCD中,AB∥CD,AD⊥CD,AB=BC,又AE⊥BC于E,试说明CD=CE.分析:题设中有AB=BC,AE⊥BC,故可联想连结AC,以构造等腰三角形,利用等腰三角形的性质证题.解: 连结AC , ∵AB =BC , ∴∠BAC =∠1. 又∵AB ∥CD , ∵∠BAC =∠2, ∴∠1=∠2.又AD ⊥CD ,AE ⊥BC , ∴∠D =∠AEC =90°, ∴△ADC 与△AEC 重合, ∴CD =CE .例5 如图12-3-6,已知等腰梯形ABCD 中,AD ∥BC ,AC ⊥BD ,AD +BC =10,DE ⊥BC 于E ,求DE 的长.分析:由等腰梯形知AC =BD ,又AC ⊥BD ,AD +BC =10,如过D 作DF ∥AC ,交BC 的延长线于F ,则△BDF 为等腰直角三角形,BF =BC +AD =2DE .解:过D 点作DF ∥AC ,交BC 的延长线于F ,则四边形ACFD 为平行四边形. ∴AC =DF ,AD =CF . ∵四边形ABCD 为等腰梯形, ∴AC =DB , ∴BD =FD . ∵DE ⊥BC , ∴51021)AD BC (21)CF BC (21BF 21EF BE =⨯=+=+===. ∵AC ∥DF ,BD ⊥AC ,∴BD ⊥DF . ∵BE =FE , ∴5BF 21EF BE DE ====.例6 已知如图12-3-7,在梯形ABCD 中,AD ∥BC ,AD<BC ,E 、F 分别为AD 、BC 的中点,且EF ⊥BC .试说明∠B =∠C .分析:要证∠B =∠C ,可把它们移到同一个三角形中,利用等腰三角形有关性质,证明这个问题. 解:过E 作EM ∥AB ,EN ∥CD ,交BC 于M 、N ,得.∴AE =BM ,AB 平行且等于EM ,DE =CN ,CD 平行且等于NE . ∵AE =DE , ∴BM =CN . 又∵BF =CF ,∴FM =FN . 又∵EF ⊥BC , ∴EM =EN , ∴∠1=∠2.∵AB ∥EM ,CD ∥EN , ∴∠1=∠B ,∠2=∠C , ∴∠B =∠C .例7 如图12-3-8,等腰梯形ABCD 中,AD ∥BC ,AB =CD ,对角线AC ⊥BD ,AD =4cm ,BC =10cm .求梯形的面积.解:过A 作AE ⊥BC 于E ,过D 作DF 上BC 于F , ∴32410CF BE =-==, ∴BF =7.∵AB =CD ,∠ABC =∠DCB , ∴△ABC 与△DCB 重合, ∴∠ACB =∠DBC . ∵AC ⊥BD ,∴∠ACB =∠DBC =45°, 在△DBF 中,DF =BF =7, ∴)cm (4972104S 2=⨯+=. 说明:梯形引辅助线的方法很多,本文只举几种,希望大家自己能认真理解、总结、完善自己的知识系统.【中考考点】①会利用梯形特征与识别方法解决相关问题. ②会把梯形问题转化为三角形和平行四边形问题.【命题方向】本节多以填空题、计算题出现,还常和三角形、平行四边形一起以综合证明题的形式出现.【常见错误分析】什么叫做梯形?错解:一组对边平行的四边形叫做梯形.分析:因为一组对边平行的四边形,当它的另一组对边还平行时,这样的四边形是平行四边形,因而上述梯形的定义犯了定义过宽的错误,这样定义的方法把平行四边形的概念也包括进去了,实际上梯形和平行四边形是两个并列的概念.正解:一组对边平行而另一组对边不平行的四边形叫梯形.【学习方法指导】(1)类似平行四边形的学法,把梯形的性质与识别用表格列出来,进行对比. (2)学会利用分割、拼补的办法解决梯形问题.【同步达纲练习】 一、填空题1.等腰梯形ABCD 的对角线相交于O 点,∠BOC =120°,∠BDC =80°,则∠DAB =________. 2.若等腰梯形的上底与一条腰长的和等于下底的长,则腰长与上底的夹角为________.3.一梯形是上底为4cm ,过上底的一顶点,作—直线平行于一腰,并与下底相交组成一个三角形,若三角形的周长为12cm ,则梯形的周长是________.4.等腰梯形ABCD 中,AD ∥BC ,∠A =120°,两底分别为15cm 和49cm ,则其腰长为________. 5.梯形ABCD 的面积是24,AD ∥BC ,且AD =5,BC =7,那么梯形的高是________. 6.在梯形ABCD 中,AD ∥BC ,∠B =50°,∠C =80°,BC =5,AC =3,则CD =________. 7.在梯形ABCD 中,AD ∥BC ,AD =3,AB =4,BC =5,那么腰CD 的取值范围是________. 8.在梯形ABCD 中,AD ∥BC ,∠B =90°,AD =1,△DBC 是等边三角形,则BC =________. 9.在等腰梯形ABCD 中,AD ∥BC ,∠B =60°,则∠D =________.二、选择题10.下列结论正确的是( ).A .四边形可以分成平行四边形和梯形两类B .梯形可分为直角梯形和等腰梯形两类C .平行四边形是梯形的特殊形式D .直角梯形和等腰梯形都是梯形的特殊形式11.四边形ABCD 中,若∠A ︰∠B ︰∠C ︰∠D =2︰2︰1︰3,那么这个四边形是( ). A .梯形 B .等腰梯形 C .直角梯形D .任意四边形12.一等腰梯形上底为9cm ,下底为17cm ,一底角为60°,则它的腰长为( ). A .8cm B .9cm C .cm 28D .8.5cm13.等腰梯形ABCD 中,对角线AC =BC +AD ,则∠DBC 的度数是( ). A .30° B .45° C .60° D .90°三、解答题14.如图12-3-11,已知△ABC 中,∠B =∠C ,点D 、E 分别在边AB 、AC 上,且AD =AE ,试说明四边形BCED 是等腰梯形.15.如图12-3-12,在梯形ABCD 中,AD ∥BC ,∠B =40°,∠C =70°,试说明AB +AD =BC .16.梯形ABCD 中,AB ∥CD ,AB>CD ,CE ∥DA ,交AB 于E ,且△BCE 的周长为7cm ,CD 为3cm ,求梯形ABCD 的周长.17.如图12-3-13所示,在梯形ABCD 中,上底AD =1 cm ,下底BC =4cm ,对角线BD ⊥AC ,且BD =3cm ,AC =4cm .求梯形ABCD 的面积.参考答案 【同步达纲练习】 一、1.110° 2.120° 3.20 cm 4.34 cm 5.4 6.2 7.2<CD<6 8.29.120° 二、10.D 11.C 12.A 13.C 14.略.15.过A 作AE ∥DC 交BC 于E , EC =AD ,AB =BE .BE +EC =BC ,所以AB +AD =BC . 16.周长为13cm .17.解:过点D 作DE ∥AC 交BC 的延长线于点E . 因为在梯形ABCD 中,AD ∥BC , 所以四边形ACED 是平行四边形, 则AC =DE ,AD =CE . 又因为AC ⊥BD . 所以BD ⊥DE ,即△BDE 是直角三角形. 因为△BDE 与梯形ABCD 同高,且梯形ABCD 中(AD +BC)=BC +CE =BE , 所以)cm (64321S S 2BDE ABCD =⨯⨯==∆梯形.。
八年级数学梯形 同步练习5华师版 试题

梯形(5)学习目标1.掌握梯形,等腰梯形,直角梯形的概念2.掌握等腰梯形的性质3.了解等腰梯形是轴对称图形,会画出它的对称轴.学法指导要弄清梯形的定义与平行四边形的定义的区别,要掌握梯形几种常见的辅助线的作法.基础知识讲解1.梯形的概念只有一组对边平行的四边形叫做梯形.如图所示:在梯形ABCD中,AB与DC不平行,其中AD,BC叫做梯形的上底和下底,AB,DC叫做梯形的腰.梯形的定义包含两个条件①四边形.②只有一组边平行两腰相等的梯形叫做等腰梯形;有一个角为直角的梯形叫做直角梯形.2.等腰梯形的性质(1)等腰梯形同一底边上的两个内角相等.(2)等腰梯形的两条对角线相等.(3)等腰梯形是轴对称图形,对称轴为上,下底中点的连线所在的直线.3.等腰梯形的识别(1)两腰相等的梯形是等腰梯形.(2)同一底边上的两个内角相等的梯形是等腰梯形.(3)对角线相等的梯形是等腰梯形.4.解决梯形问题的基本思路梯形问题三角形或平行四边形问题通常利用平移,旋转等,引辅助线来实现转化,常见的辅助线大致有十种之多,如图所示.重点难点重点:梯形、直角梯形、等腰梯形的概念,等腰梯形的性质.难点:1.等腰梯形的识别方法2.在梯形问题的转化过程中,添加辅助线的方法很多,选择方法,要根据条件和结论去选择添加辅助线.易错误区分析1.学习本节内容易犯概念不清的错误(1)下列命题中,正确的是()A.有一组对边平行,另一组对边相等的四边形是等腰梯形.B.有一组对边互补的梯形是等腰梯形C.有一组邻角相等的梯形是等腰梯形D.有两组角分别相等的四边形是等腰梯形错选:A正选:B错误分析:错在概念不清,等腰梯形是一组对边相等且不平行的梯形,这里只交待相等,没有交待它们不平行.2.判断①有一组对边平行的四边形是梯形()②一组对边平行且不相等的四边形是梯形()③一组对边平行,另一组对边不相等的四边形是梯形()错解:①正确 ②错误 ③错误 正解:①错误 ②正确 ③正确错误分析:没有认识到另一组对平行还是不平行.题目中交待一组对边平行,但没有说明这组对边是否相等,概念不清.3.已知:如图,梯形ABCD 中,∠B+∠C =90°,E 、F 分别为两底AD 、BC 的中点,连结EF.求证:EF=21(BC-AD ) 错证:延长BA 、CD 交于点G ,连结GE ∵∠B+∠C =90° ∴∠BGC =90°在Rt △BGC 中,∵F 是BC 的中点∴GF =21BC 在Rt △AGD 中,∵E 是AD 的中点∴GE =21AD∴EF =GF-GE=21BC-21AD =21(BC-AD )正证:延长BA 、CD 交于点G ,连结GE 、GF ,如图所示 ∵∠B+∠C =90° ∴∠BGC =90° 在Rt △BGC 中,∵F 是BC 的中点∴AE=GE=21AD ∴∠GAD=∠AGE ∴GF=BF=21BC ∴∠B=∠BGF在Rt △ADG 中,∵E 是AD 的中点∵AD ∥BC ∴∠B=∠GAD ∴∠BGF=∠AGE ∴线段GF 、GE 在同一条射线GF 上 ∴EF =GF-GE =21BC-21AD =21(BC-AD ). 错证分析:忽略了连结GF ,再证GE 、GF 在同一直线上才可用EF =GF-GE.点拨:本题还有几种证法:(1)过点E 作EMJAB 交BC 于M ,过点E 作EN ∥DC 交BC 于N ,证EF=21MN即可.(2)过点D作DK∥AB交BC于点K,取KC的中点L,连结DL,只要证四边形EFND是平行四边形即可.这两种方法同学们自己可以证一下.典型例题例1.如图所示,某加工车间现有一块梯形钢板废料.为响应厂里提出的节省开支计划,打算把它切割后焊接成一块三角形.使面积不变,请你设计一下切割方案.分析:任取一腰中点与上下的顶点连结进行切割.解:切割方案如图所示例2.如图所示,等腰梯形ABCD中AD∥CB,AD=3,AB=5,BC=8,求∠B的度.分析:过A作AE∥DC交BC于点E,则四边形AECD是平行四边形,故CE=AD,由此可得BE的长.解:过A作AE∥DC交BC于点E,则因为AD∥BC,AE∥CD,所以四边形AECD是平行四边形,故CE=AD.又AD=3,从而CE=3,故BE=BC-CE=8-3=5所以BE=AB,由于等腰梯形同一底上的两个内角相等,所以∠B=∠C,由AE∥CD,得∠AEB=∠C,故∠AEB=∠B所以AB=AE,所以AB=AE=BE.即△ABE是等边三角形,所∠B=60°例3.已知:如图,在梯形ABCD中,AD∥BC,AD=24cm,AB=8cm,BC=25cm.动点P从A开始沿AD 边向D以1cm/S的速度运动.动点Q从C点开始沿CB边向B以3cm/S的速度运动.P,Q分别从A,C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t秒,t分别为何值时,四边形PQCD为平行四边形?等腰梯形?分析:要使PQCD 为平行四边形,则只要PD=QC ,即24-t =3t ,要使PQCD 为等腰梯形,只要PQ=CD ,PD ≠QC 过P ,D 作BC 的垂线,垂足E ,F 则EF =PD ,QE =FC =2解:当PD =QC 时,四边形PQCD 为平行四边形. 即24-t =3t ,即t =6秒当PQ =CD ,且PD ≠QC 时,四边形PQCD 为等腰梯形过P ,D 分别作BC 的垂线段,垂足分别为E ,F 则EF =PD ,QE =FC =2即2=21[3t-(24-t)]即t=7秒 注意:由两点速度可知,自运动开始831秒内.两点均在运动中. 例4.已知:如图,在梯形ABCD 中,AD ∥BC ,∠B =40°,∠C =50°,M ,N 分别是BC ,AD 边的中点.BC >AD .求证:MN=21(BC-AD )分析:由于∠B+∠C =40°+50°=90°,因而想到作辅助线,构造直角三角形来求证,根据梯形的特点,可用不同的添线方法来构造直角三角形.证法一:分别延长BA ,CD 交于点O ,连结ON ,OM 因为∠B+∠C =90°,所以△AOD ,△BOC 为Rt △在Rt △AOD 中,ON=21AD=AN 在Rt △BOC 中,OM=21BC=BM因为∠B0M=∠B=∠OAN =∠AON 所以∠ANO =∠BMO所以∠ANM+∠ANO =∠ANM+∠BMO =180° 所以O ,N ,M 三点共线所以MN=OM-ON=21BC-21AD=21(BC-AD ) 证法二:分别过点N 作NG ∥AB 交BC 于G ,作NH ∥CD ,交BC 于H ,如图所示,由已知条件可知ABGN ,NHCD 都是平行四边形,则∠NHG =∠C ,AN =BG ,DN =CH ,△GNH 为直角三角形.在△GNH 中,证M 为CH 中点,所以NM=21GH=21(BC-CD ) 例5.如图,铁路基横断面为等腰梯形ABCD ,已知路基底顶AB =6m ,斜坡BC 与下底CD 的夹角为60°,路基高AE =23m ,求下底CD 的宽.分析:由上底的两个顶点,作下底的垂线段为BF ,AE .把等腰梯形分成两个全等的直角三角形和一个矩形.解:∵四边形ABCD 是等腰梯形∴AD =BC 又∵BF =AE ,BF ⊥CD ,AE ⊥CD ,∠C=∠D , ∴Rt △BCF ≌Rt △ADE ,∴CF=DE存Rt △BCF 中,∠C =60° ∴∠CBF =30° ∴CF=21BC ,即BC =2CF ∴BC 2=CF 2+BF 2即(2CF )2=CF 2+(23)2∴CF =2∴AB ∥CDBF ⊥CDAE ⊥CD ∴四边形ABEF 为矩形∴EF =AB =6(m ) ∴CD =DE+EF+CF =AB+2CF =6+2×2=10(m )6.如图,梯形ABCD 中,AD ∥BC ,AE 平分∠BAD ,BE 平分∠ABC ,且AE 、BE 交DC 于E 点,求证:AD =BA-BC分析:依题意得∠1+∠3=90°,加上∠1=∠2,可联想到证等腰三角形,看能否将底集中在一起,延长AE ,BC 就可以达到的证明:延长AE 交BC 的延长线于F∵AD ∥BC ,∴∠4=∠F ∴∠DAB+∠CBA=180° 又∵∠3=21∠DAB ,∴∠1=21∠CBA ∵∠1+3=90° ∴AE ⊥BC又∵∠1=∠2,BE 为公共边∴△ABE ≌△FBE ∴AB =BF =BC+CF =BC+AD ∴AE =EF在△AED 和△EFC 中∵AE =EF ,∠4=∠F ,∠DEA =∠FEC ∴△AED ≌△FEC ∴AD =CF ∴AD =AB-BC例7.已知:如图,在等腰梯形ABCD 中,AB ∥CD ,AB >CD ,AD=BC ,BD 平分∠ABC,∠A=60°,梯形周长是20cm ,求梯形的各边长.分析:由等腰梯形性质知:∠A =∠CBA=60°,又BD 平分∠ABC ,有∠1=∠2=30°,从而∠ADB=90°.则AD=21AB.又AB ∥CD ,知∠2=∠3=∠1,有BC=CD=AD .故由周长是20cm ,可求各边长.解:∵四边形ABCD 为等腰梯形,∴∠A =∠ABC =60° ∵BD 平分∠ABC , ∴∠1=∠2=30° ∴∠ADB=180°-∠A-∠2=180°-60°-30°=90°∴AD=21AB ∵AB ∥CD ,∴∠2=∠3,∴∠1=∠3 ∵BC=DC,∴AD=BC ∴AD=CD=BC=21AB∵AB+BC+CD+AD=20,∴AD=DC=BC=4,AB=8 答:梯形的各边长分别为4cm ,4cm ,4cm ,8cm. 创新思维例1.已知:四边形ABCD 中,AB =CD ,AC =BD ,AD ≠BC .求证:四边形ABCD是等腰梯形.分析:要证四边形ABCD是等腰梯形,因为AB=DC,所以只要证四边形ABCD是梯形即可,又因为AD≠BC,故只需证AD∥BC即可,要证AD∥BC现有图所示,四种作辅助线的方法,请任意选择其中两种图形,对原题进行证明.证明:方法一:在图(1)中作AE∥DC方法二:在题图(2)中,过A、D分别作BC的垂线交BC于E、F.注意用推出符号“ ”证题,这种证题方法,证明思路清晰,做题步骤清楚有条理.例2.要剪切如图(尺寸单位:mm)所示甲、乙两种直角梯形零件,且使两种零件的数量相等.有两种面积相等的矩形铝板,第一种长500mm,宽300mm,第二种长600mm,外宽250mm可供选用.(1)填空:为了充分利用材料,应选用第种铝板,这时一块铝板最多能剪甲、乙零件共个,剪下这些零件后,剩余的边角料的面积是。
八年级数学梯形 同步练习3华师版

梯形(3)【基础知识精讲】1.梯形的定义:一组对边平行而另一组对边不平行的四边形叫做梯形.2.梯形的元素:(1)梯形的底:梯形中平行的两边叫做梯形的底,通常把较短的底叫上底,较长的底叫下底.(2)梯形的腰:梯形中不平行的两边叫梯形的腰.(3)梯形的高:梯形两底的距离是梯形的高.3.特殊梯形的定义:(1)等腰梯形:两腰相等的梯形.(2)直角梯形:一腰垂直于底的梯形.4.梯形的判定(1)定义:略.(2)有一组对边平行且不相等的四边形是梯形.5.等腰梯形的判定(1)定义:略.(2)在同一底上的两个角相等的梯形是等腰梯形.(3)对角线相等的梯形是等腰梯形.【重点难点解析】解题中常用的是梯形的性质,特别是等腰梯形的如下性质:(1)两腰相等,两底平行;(2)在同一底上的两个角相等;(3)对角线相等;(4)是轴对称图形,底的垂直平分线是它的惟一对称轴.A.重点、难点提示1.掌握梯形的有关概念和性质;2.掌握等腰梯形的性质和判别条件;(这是重点,也是难点,要掌握好)3.掌握直角梯形的性质和判别条件.(有直角,就可以构造直角三角形,再利用直角三角形的性质处理直角梯形问题)B.考点指要梯形是重要的四边形之一,梯形的性质是中考的重要内容之一.一组对边平行而另一组对边不平行的四边形叫作梯形,平行的两边叫做梯形的底,不平行的两边叫做梯形的腰,夹在两底之间的垂线段叫作梯形的高.两条腰相等的梯形叫做等腰梯形.一条腰和底垂直的梯形叫做直角梯形.等腰梯形和直角梯形是两类特殊的梯形,它们的性质的考查频率较高.等腰梯形同一底上的两个内角相等,对角线相等.同一底上的两个内角相等的梯形是等腰梯形.(这些是常用方法,要掌握好)梯形问题常转化为三角形、平行四边形问题来解决,常用的转化方法有:【难题巧解点拨】例1:已知梯形ABCD 的面积是32,两底与高的和为16,如果其中一条对角线与两底垂直,则另一条对角线长为___________________.思路分析本题是几何中的计算问题.通过作对角线的平行线,可以将对角线与高,上底与下底和集中到同一个直角三角形中,这样就可以利用勾股定理求出对角线的长.解:如图4-50,梯形ABCD 中,AD ∥BC ,BD ⊥BC .设AD=x ,BC=y ,DB=z ,由题得:x+y+z=16,322z)y x (S ABCD =⋅+=梯形,(熟记梯形面积公式) 解得x+y=8,z=8,过D 作DE ∥AC 交BC 的延长线于E .∴四边形ADEC 是平行四边形,(注意这种辅助线的作法很常用) ∴DE=AC ,AD=CE .(将“上底+下底”转化到一条线段上) 在Rt △DBE 中,∠DBE=90°,BE=BC+CE=x+y=8,BD=8, 根据勾股定理得2888DB BE DE 2222=+=+=,∵AC=DE , 28AC =∴.点评:本题主要考查用“方程思想”解决几何中的计算问题.解题过程中作“对角线的平行线”,将对角线与高,上底与下底和集中到同一个直角三角形中,这样就可以通过解直角三角形计算出对角线长,体现了添加辅助线的目的是把“分散的条件得以集中,隐含条件加以显现”的作用.解梯形有关问题时,我们也常通过“作平行线将之转化为平行四边形的问题来解决”.例2:如图4-51,已知AB=BC ,AB ∥CD ,∠D=90°,AE ⊥BC .求证:CD=CE . 思路分析这是一个直角梯形,通过作CF ⊥AB ,可以将梯形分成矩形和三角形,结合直角梯形的性质,利用两次全等,达到证明CD=CE 的目的.证明:如图4-52,连结AC ,过C 作CF ⊥AB 于F .在△CFB 和△AEB 中, (这是直角梯形中常见的辅助线)⎪⎩⎪⎨⎧=∠=∠︒=∠=∠BC AB B B 90AEB CFB (构造三角形证明三角形全等)∴△CFB ≌△AEB (AAS ) ∴CF=AE .∵∠D=90°,CF ⊥AB 且AB ∥CD , ∴AD=CF , ∴AD=AE .在Rt △ADC 和Rt △AEC 中, ⎩⎨⎧==AC AC AEAD∴Rt △ADC ≌Rt △AEC (HL ) ∴CD=CE .点评:本题主要考查直角梯形、三角形全等的综合运用.在直角梯形中,通过作梯形一底的垂线,将梯形分成特殊的四边形(矩形)和三角形.将题中已知条件AB=BC 中的两条线段AB 和BC 分别放到两个三角形中,结合直角梯形的性质,利用两次全等,达到证明CD=CE 的目的.解决梯形问题时,除可作以上辅助线外,作一腰的平行线、连对角线、作对角线的平行线也是经常用到的.例3:如图4-53,梯形ABCD 中,AB ∥DC ,AD=BC ,延长AB 至E ,使BE=DC .求证:AC=CE . 思路分析本题主要考查等腰梯形的性质及证明两条线段相等的基本方法. 证法一:∵四边形ABCD 是等腰梯形,∴∠ADC=∠BCD (等腰梯形同一底上的两个角相等) 又∵AB ∥DC ,∴∠BCD=∠CBE ,(两直线平行,内错角相等) ∴∠ADC=∠CBE , 在△ADC 和△CBE 中,⎪⎩⎪⎨⎧=∠=∠=BE DC CBE ADC BCAD∴△ADC ≌△CBE (SAS ) ∴AC=CE .证法二:如图4-54,连结BD , ∵DC ∥BE ,DC=BE ,∴四边形DCEB 是平行四边形,(一组对边平行且相等的四边形是平行四边形) ∴DB=CE .又∵四边形ABCD 是等腰梯形, ∴AC=BD ,(等腰梯形对角线相等) ∴AC=CE .证法三:如图4-55,作CF ⊥AE 于F ,DM ⊥AE 于M . 在△AMD 和△BFC 中,⎪⎩⎪⎨⎧︒=∠=∠=∠=∠90CFB DMA BC AD CBF DAM∴△AMD ≌△BFC (AAS ) ∴AM=BF .又∵AB ∥DC ,MD ∥FC , ∴DC=MF . 又∵DC=BE , ∴AM+MF=BF+BE , ∴F 为AE 的中点, ∴CF 是AE 的垂直平分线, ∴AC=CE .证法四:如图4-54,连结BD . ∵DC ∥BE ,DC=BE ,∴四边形DCEB 是平行四边形,∴∠DBA=∠E ,(两直线平行,同位角相等) 又∵四边形ABCD 是等腰梯形, ∴AC=BD ,在△ABC 和△BAD 中,⎪⎩⎪⎨⎧===AB AB BC AD BDAC∴△ABC ≌△BAD (SSS ) ∴∠CAB=∠DBA , ∴∠CAB=∠E ,∴AC=CE .(等角对等边)(此种方法虽然较繁,但其思路很有价值,即通过证明“三线合一”说明是等腰三角形)点评:证法一证两三角形全等得两线段相等;证法二、四利用角相等证线段相等;证法三中通过梯形常加的辅助线,作梯形底边上的高,连结梯形的对角线,将梯形分割成两个直角三角形与一个矩形,连结对角线再作对角线的平行线,将梯形转化为一个平行四边形和一个三角形.例4:要剪切如图4-56(尺寸单位:mm )所示的甲、乙两种直角梯形零件,且使两种零件的数量相等.有两种面积相等的铝板,第一块长500mm ,宽300mm (如图4-57(1)),第二块长600mm ,宽250mm (如图4-57(2)),可供选用.(1)为了充分利用材料,应选用第_________种铝板,这时一块铝板最多能剪甲、乙两种零件共________个,剪完这些零件后,剩余的边角料面积是______________2mm . (2)从图4-57(1)、4-57(2)中选出你要的铝板示意图,在上面画出剪切线;并把边角余料用阴影表示出来.思路分析通过计算,两直角梯形零件面积分别为22mm 30000mm 40000和,而铝板的面积均为2mm 150000,最多能剪出两个甲、两个乙零件,即在两铝板中设计打样.设计时,为了充分利用材料,考虑到(1)中宽为300mm ,则一种方案作两个乙高,另一种方案为一个甲的下底,思路便打开,类似地,(2)也可以这样分割设计,做出尝试.解:(1)应选用第一块铝板,最多能剪出甲、乙两种零件共4个,由计算得第一块铝板面积为:)mm (150000300500S 2=⨯=, 而零件甲、乙的面积分别为)mm (40000200)300100(21S 2=⨯+⨯=甲, )mm (30000150)300100(21S 2=⨯+⨯=乙, ∴剩余的边角料的面积是2mm 10000; (2)如图4-58所示正确画出图形.(设计零件个数,从个数、数量上,结合图中数与数之间的关系考虑,往往是应用题的切入点,此外对图形的拼凑、计算、想象,可有利于思维向纵深发展.)【典型热点考题】例1 如图4-30,梯形ABCD 中,AD ∥BC ,DC ⊥BC ,E 为AB 的中点,求证:EC=ED .点悟:要证EC=ED,实际上只要证E点在CD的垂直平分线上,故过E点作EF⊥CD.又因为BC⊥CD,所以EF∥BC,由E为AB的中点,根据平行线等分线段定理的推论可证出F是CD的中点,EF是线段CD的中垂线,从而可证出EC=ED.解:过E作EF⊥CD,垂足为F.∵ BC⊥CD,∴ BC∥EF.∵ E为梯形ABCD腰AB的中点.∴ EF平分CD,∴ EF是CD的垂直平分线.∴ EC=ED.例2如图4-31,已知在四边形ABCD中,有AB=CD,∠B=∠C,AD<BC.求证:四边形ABCD为等腰梯形.点悟:由题意知,只需证AD∥BC即可.如延长BA、CD,由∠B=∠C可得等腰△EBC和△EAD,从而可得AD∥BC.解:延长BA、CD,它们交于点E,∵∠B=∠C,∴ EB=EC.又∵ AB=DC,∴ AE=ED.∴∠EAD=∠EDA∵∠E+∠EAD+∠EDA=180°,∠B+∠C+∠E=180°.∴∠EAD=∠B.∴ AD∥BC,又∵ AD<BC,∠B=∠C.∴四边形ABCD为等腰梯形.例3如图4-32,已知等腰梯形ABCD中,AD∥BC,AC⊥BD,AD+BC=10,DE⊥BC于E,求:DE的长.点悟:由等腰梯形知:AC=BD ,又AC ⊥BD ,AD +BC=10,如过D 作DF ∥CA ,交BC 的延长线于F ,则△BDF 为等腰直角三角形.BF=BC +AD=2DE .解:过D 作DF ∥AC ,交BC 的延长线于F ,则四边形ACFD 为平行四边形, ∴ AC=DF ,AD=CF∵ 四边形ABCD 为等腰梯形 ∴ AC=DB ,BD=FD . ∵ DE ⊥BC , ∴ 51021)(21)(2121=⨯=+=+===AD BC CF BC BF EF BE . ∵ AC ∥DF ,BD ⊥AC , ∴ BD ⊥DF . ∵ BE=EF ,∴ 521====BF EF BE DE 答:DE 的长为5.点拨:当对角线相等或垂直时,常作梯形对角线的平行线,构造成平行四边形,等腰三角形或直角三角形.例4 如图4-33,已知梯形ABCD 中,AD ∥BC ,E 、F 分别为AB 、CD 的中点,EF 分别交BD 、AC 于点G ,H ,求证:(1)EG=HF ,(2))(21AD BC GH -=点悟:由题知,EF 为梯形的中位线,所以EF ∥AD ∥BC ,则G 、H 也分别为BD 、AC 中点,故可应用三角形、梯形中位线定理解决问题.解:∵ E 、F 为梯形的两腰AB 、CD 的中点. ∴ AD ∥EF ∥BC ,且G 、H 分别为BD 、AC 的中点. ∴ AD EG 21=,AD FH 21=,BC EH 21=. ∴ EG=HF .∵ GH=EH -EG ∴ )(212121AD BC AD BC GH -=-=点拨:梯形中位线的性质是“梯形中位线平行于两底,并且等于两底和的一半”,如果从运动的观点来认识梯形、三角形、平行四边形,那便可以找到它们中位线之间的联系.如图4-33所示:当梯形上底AD 的点D 和点A 重合,即AD=0时梯形ABCD 便转化为三角形,由梯形中位线BC 21)BC AD (21EF =+=转化为三角形的中位线;当梯形的上底扩大,使AD=BC 时,梯形ABCD 就变成了平行四边形,这时ADFE 与EFCB 均是平行四边形,于是得BC=EF=AD . ∴ 平行四边形一组对边中线EF 表示为: )(21BC AD BC AD EF +=== 这样,梯形中位线的性质便与三角形中位线的性质以及平行四边形一组对边中点的连线统一起来了. 例5 如图4-34,已知四边形ABCD 为矩形,四边形ABDE 为等腰梯形,AE ∥BD .求证:△BED ≌△BCD .点悟:要证△BED ≌△BCD ,则考虑这两个三角形中的对应边,对应角的相等关系.而DE=AB=CD ,BD=BD ,且BE=AD=BC ,则问题得证,本题要证对应的角相等也不困难. 解:∵ 四边形ABCD 为矩形. ∴ DC=AB ,BC=AD ,∵ 四边形ABDE 为等腰梯形,且AD 、DE 为其对角线, ∴ DE=AB ,BE=AD .在△BED 和△BCD 中,DE=DC ,BE=BC , 又∵ BD=BD ,∴ △BED ≌△BCD .点拨:梯形有一组对边平行,而另一组对边不平行,在处理这类问题时,常把梯形问题转化为平行四边形的问题,或把直角梯形问题转化为矩形问题或直角三角形问题.例6 如图4-35,已知△ABC 中,D 为AB 的中点,E 为BC 的三等分点(BE >CE),AE 、CD 交于点F ,求证:F 为CD 的中点.点悟:我们知道,由平行线等分线段定理及推论可得到线段中点,故过D 作DN ∥AE ,构造平行线等分线段定理推论2的基本图形. 解:过D 作DN ∥AE 交BC 于N . ∵ D 为AB 中点,∴ BN=EN ,又∵ E 为BC 的三等分点,(BE>CE )∴ BN=NE=EC . ∵ DN ∥FE ,∴ F 是CD 的中点.点拨:从上述证明过程中看出,有效利用中点D 成为证明的关键,通常在已知有线段中点时,常过该点作平行线,构造平行线段等分线段定理及推论的基本图形,以达到有关证明的目的.例7 如图4-36,如果把矩形ABCD 纸对折,折痕为GH ,再把A 点叠在折痕线上,折痕为BE ,得到Rt △ABE ,BE 交折痕GH 于P ,延长EA ’交BC 于F ,求证△BEF 为等边三角形.点悟:由折叠过程和平行线等分线段定理的推论1知:P 、A ’分别为BE 、EF 中点,而 ∠EAB=90°,有PA ’=PE ,BA ’为EF 的垂直平分线,从而∠BEF=∠EA ’P=∠DEF=∠A ’EB= 60°,又BE=BF ,∴ △BEF 为等边三角形.解:∵ G 、H 分别为矩形ABCD 的边AB 、CD 的中点, ∴ 四边形AGHD ,GBCH 为矩形,AD ∥GH ∥BC .∴ P 、A ’分别为BE 、EF 的中点. ∵ Rt △A ’BE ≌Rt △ABE ,∴ ∠EA ’B=∠EAB=90°,∠AEB=∠BEF . ∴ ∠PA ’=PE=BE 21,BA ’为EF 的垂直平分线, ∴ ∠BEF=∠PA ’E ,BE=BF . ∵ GH ∥AD , ∴ ∠PA ’E=∠DEF , ∴ ∠A ’EB=∠BEF=∠DEF . ∵ ∠A ’EB +∠BEF +∠DEF=180°, ∴ ∠BEF=60°.∵ BE=BF , ∴ △BEF 为等边三角形.点拨:折叠问题是一种常见题型,解此类题的关键是:折叠后重叠部分是全等形,同时要注意折叠前后图形中有关元素的联系.例8 如图4-37,已知梯形ABCD 中,AD ∥BC ,AC 与BD 交于O ,且AC ⊥BD ,AC=4,BD=3.4,求梯形ABCD 的面积.点悟:梯形的面积常用(上底+下底)×高21⨯来计算,而此题上、下底和高都是未知的, 故不能用此公式.但⨯⨯=⋅=42121BD AC S ABCD 梯形 3.4=6.8故面积可求. 解:∵ AC ⊥BD ,∴ BD AO 21S ABD ⋅=∆, BD CO S BCD ⋅=∆21, ∴ BD CO AO BD CO BD AO S S S BCD ABD ABCD ⋅+=⋅+⋅=+=∆∆)(212121梯形,即 ⨯⨯=⋅=42121BD AC S ABCD 梯形 3.4=6.8答:梯形ABCD 的面积为6.8.点拨:当梯形(或任意四边形)对角线互相垂直时,它们的面积等于对角线乘积的一半.例9 如图4-38,已知在等腰梯形ABCD 中,AB ∥CD ,AB >CD ,AD=BC ,BD 平分∠ABC ,∠A=60°,梯形周长是20cm ,求梯形的各边长?点悟:由等腰梯形性质知:∠A=∠CBA=60°,又BD 平分∠ABC ,有∠1=∠2=30°,从而∠ADB=90°,则AB AD 21=又AB ∥CD ,知∠2=∠3=∠1,有BC=CD=AD .故由周长为20cm ,可求各边长. 解:∵ 四边形ABCD 为等腰梯形, ∴ ∠A=∠ABC=60°,∵ BD 平分∠ABC , ∴ ∠1=∠2=30°.∠A=60° ∴ ∠ADB=180°-∠A -∠2 =180°-60°-30° =90°. ∴ AB AD 21=. ∵ AB ∥CD , ∴ ∠2=∠3. ∴ ∠1=∠3, ∴ BC=DC . ∵ AD=BC , ∴ AB BC CD AD 21===.∵ AB +BC +CD +AD=20. ∴ AD=DC=BC=4, AB=8答:梯形的各边长分别为4cm ,4cm ,4cm ,8cm .【同步达纲练习一】 一、选择题1.下列命题中,真命题有 ( )①有两个角相等的梯形是等腰梯形; ②有两条边相等的梯形是等腰梯形; ③两条对角线相等的梯形是等腰梯形; ④等腰梯形上、下底中点连线,把梯形分成面积相等的两部分. (A)1个 (B)2个 (C)3个 (D)4个 2.以线段a=16,b=13,c=10,d=6为边作梯形,其中a 、c 作为梯形的两底,这样的梯形( )(A)只能作1个 (B)能作2个 (C)能作无数个 (D)不能作3.在直角梯形ABCD 中,AD ∥BC ,AB ⊥BC ,E 是CD 中点,则 ( ) (A)AE=BE (B)AE >BE(C)AE <BE (D)AE 、BE 大小不确定4.等腰梯形的两底长分别为a 、b ,且对角线互相垂直,它的一条对角线长是 ( ) (A))(22b a + (B)2 (a +b) (c))(21b a + (D)a +b二、填空题5.在梯形ABCD 中,AD ∥BC ,∠B=50°,∠C=80°,AD=a ,BC=b ,则∠D=________,CD=________. 6.直角梯形一底与一腰的夹角为30°,并且这腰长为6厘米,则另一腰长为_________.7.已知梯形ABCD 中,AD ∥BC ,AC <BC ,AC ⊥BD 于O ,AC=8,BD=6,则梯形ABCD 的面积为_________. 8.已知梯形上、下底长分别为6、8,一腰长为7,则另一腰a 的范围是 _______,若a 为奇数,则此梯形为_________梯形.9.梯形不在同一底上的两组角的比值分别为3∶6和4∶2,则四个角的度数分别为_________.三、解答题10.梯形ABCD 中,AD ∥BC ,BD ⊥DC ,若AB=AD=DC ,梯形ABCD 的周长为10,求梯形ABCD 的面积.11.已知梯形ABCD 中,AD ∥BC ,AD <BC ,且∠B +∠C=90°,E 为AD 中点,F 是BC 中点.求证:)(21AD BC EF -=【同步达纲练习二】1.有两个角相等的梯形是( )A.等腰梯形B.直角梯形C.一般梯形D.等腰梯形或直角梯形2.已知直角梯形的一腰长为10cm,这条腰与底所成的角为30°,那么另一腰的长为( )A.2.5cm B.5cm C.10cm D.15cm3.如图4-59,梯形ABCD中,AD∥BC,AB=CD,对角线AC与BD相交于点O,则图中全等三角形共有( )A.1对B.2对C.3对D.4对(平移对角线BD即可)4.如图4-60,AB∥CD,AE⊥DC,AE=12,BD=15,AC=20,则梯形ABCD的面积是( )A.130 B.140 C.150 D.1605.等腰梯形中,上底:腰:下底=1:2:3,则下底上的内角的度数是____________.6.已知梯形ABCD中,AD∥BC,AB=DC,若∠B=30°,AD=2cm,BC=6cm,那么梯形的周长为_____________.7.已知梯形的上底长为2,下底长为5,一腰长为4,则另一腰长的取值范围是_________________.89,则它的对角线长为8.已知:等腰梯形的两底分别为10cm和20cm,一腰长为cm_____________cm.9.如图4-61,已知等腰梯形ABCD,AD∥BC,E为梯形内一点且EA=ED.求证:EB=EC.10.如图4-62,四边形ABCD是矩形,四边形ABDE是等腰梯形,AE∥BD.求证:△BED≌△BCD.11.如图4-63,梯形ABCD 中,∠B+∠C=90°,E 、F 分别为上、下底的中点.求证:)AD BC (21EF -=.参考答案【同步达纲练习一】一、1.B ; 2.D ; 3.A ; 4.A . 二、5.100°,b-a ; 6.3; 7.24; 8.5<a<9,等腰梯形; 9.60°,60°,120°,120°. 三、10.∵AD=AB=DC . ∴ ∠1=∠2, ∵ AD ∥BC ,∴ ∠C=∠2+∠3,∠1=∠3. ∴ ∠2=∠3,∴ ∠C=2∠3. ∵ BD ⊥DC ,∴ ∠3=30°, ∴ BC CD 21=.设CD=x ,则x+x+x+2x=10, ∴ x=2.在Rt △BCD 中,BD=322422=-. 作DE ⊥BC ,垂足为E .则32221421⨯⨯=⨯⨯DE , ∴ 3=DE , ∴ 333)42(21S ABCD =⋅+=梯形. 11.过E 作EM//AB ,EN//CD 交BC 分别于M 、N ,则得、,有AE=BM ,EN=CD ,∠B=∠EMC ,∠C=∠ENB ,又∠B+∠C=90°,则∠EMC+∠ENB=90°,有∠MEN=90°。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
梯形(3)【基础知识精讲】1.梯形的定义:一组对边平行而另一组对边不平行的四边形叫做梯形.2.梯形的元素:(1)梯形的底:梯形中平行的两边叫做梯形的底,通常把较短的底叫上底,较长的底叫下底.(2)梯形的腰:梯形中不平行的两边叫梯形的腰.(3)梯形的高:梯形两底的距离是梯形的高.3.特殊梯形的定义:(1)等腰梯形:两腰相等的梯形.(2)直角梯形:一腰垂直于底的梯形.4.梯形的判定(1)定义:略.(2)有一组对边平行且不相等的四边形是梯形.5.等腰梯形的判定(1)定义:略.(2)在同一底上的两个角相等的梯形是等腰梯形.(3)对角线相等的梯形是等腰梯形.【重点难点解析】解题中常用的是梯形的性质,特别是等腰梯形的如下性质:(1)两腰相等,两底平行;(2)在同一底上的两个角相等;(3)对角线相等;(4)是轴对称图形,底的垂直平分线是它的惟一对称轴.A.重点、难点提示1.掌握梯形的有关概念和性质;2.掌握等腰梯形的性质和判别条件;(这是重点,也是难点,要掌握好)3.掌握直角梯形的性质和判别条件.(有直角,就可以构造直角三角形,再利用直角三角形的性质处理直角梯形问题)B.考点指要梯形是重要的四边形之一,梯形的性质是中考的重要内容之一.一组对边平行而另一组对边不平行的四边形叫作梯形,平行的两边叫做梯形的底,不平行的两边叫做梯形的腰,夹在两底之间的垂线段叫作梯形的高.两条腰相等的梯形叫做等腰梯形.一条腰和底垂直的梯形叫做直角梯形.等腰梯形和直角梯形是两类特殊的梯形,它们的性质的考查频率较高.等腰梯形同一底上的两个内角相等,对角线相等.同一底上的两个内角相等的梯形是等腰梯形.(这些是常用方法,要掌握好)梯形问题常转化为三角形、平行四边形问题来解决,常用的转化方法有:【难题巧解点拨】例1:已知梯形ABCD 的面积是32,两底与高的和为16,如果其中一条对角线与两底垂直,则另一条对角线长为___________________.思路分析本题是几何中的计算问题.通过作对角线的平行线,可以将对角线与高,上底与下底和集中到同一个直角三角形中,这样就可以利用勾股定理求出对角线的长.解:如图4-50,梯形ABCD 中,AD ∥BC ,BD ⊥BC .设AD=x ,BC=y ,DB=z ,由题得:x+y+z=16,322z)y x (S ABCD =⋅+=梯形,(熟记梯形面积公式) 解得x+y=8,z=8,过D 作DE ∥AC 交BC 的延长线于E .∴四边形ADEC 是平行四边形,(注意这种辅助线的作法很常用) ∴DE=AC ,AD=CE .(将“上底+下底”转化到一条线段上) 在Rt △DBE 中,∠DBE=90°,BE=BC+CE=x+y=8,BD=8, 根据勾股定理得2888DB B E DE 2222=+=+=,∵AC=DE , 28AC =∴.点评:本题主要考查用“方程思想”解决几何中的计算问题.解题过程中作“对角线的平行线”,将对角线与高,上底与下底和集中到同一个直角三角形中,这样就可以通过解直角三角形计算出对角线长,体现了添加辅助线的目的是把“分散的条件得以集中,隐含条件加以显现”的作用.解梯形有关问题时,我们也常通过“作平行线将之转化为平行四边形的问题来解决”.例2:如图4-51,已知AB=BC ,AB ∥CD ,∠D=90°,AE ⊥BC .求证:CD=CE . 思路分析这是一个直角梯形,通过作CF ⊥AB ,可以将梯形分成矩形和三角形,结合直角梯形的性质,利用两次全等,达到证明CD=CE 的目的.证明:如图4-52,连结AC ,过C 作CF ⊥AB 于F .在△CFB 和△AEB 中, (这是直角梯形中常见的辅助线)⎪⎩⎪⎨⎧=∠=∠︒=∠=∠BC AB B B 90AEB CFB (构造三角形证明三角形全等)∴△CFB ≌△AEB (AAS ) ∴CF=AE .∵∠D=90°,CF ⊥AB 且AB ∥CD , ∴AD=CF , ∴AD=AE .在Rt △ADC 和Rt △AEC 中, ⎩⎨⎧==AC AC AEAD∴Rt △ADC ≌Rt △AEC (HL ) ∴CD=CE .点评:本题主要考查直角梯形、三角形全等的综合运用.在直角梯形中,通过作梯形一底的垂线,将梯形分成特殊的四边形(矩形)和三角形.将题中已知条件AB=BC 中的两条线段AB 和BC 分别放到两个三角形中,结合直角梯形的性质,利用两次全等,达到证明CD=CE 的目的.解决梯形问题时,除可作以上辅助线外,作一腰的平行线、连对角线、作对角线的平行线也是经常用到的.例3:如图4-53,梯形ABCD 中,AB ∥DC ,AD=BC ,延长AB 至E ,使BE=DC .求证:AC=CE . 思路分析本题主要考查等腰梯形的性质及证明两条线段相等的基本方法. 证法一:∵四边形ABCD 是等腰梯形,∴∠ADC=∠BCD (等腰梯形同一底上的两个角相等) 又∵AB ∥DC ,∴∠BCD=∠CBE ,(两直线平行,内错角相等) ∴∠ADC=∠CBE , 在△ADC 和△CBE 中,⎪⎩⎪⎨⎧=∠=∠=BE DC CBE ADC BCAD∴△ADC ≌△CBE (SAS ) ∴AC=CE .证法二:如图4-54,连结BD , ∵DC ∥BE ,DC=BE ,∴四边形DCEB 是平行四边形,(一组对边平行且相等的四边形是平行四边形) ∴DB=CE .又∵四边形ABCD 是等腰梯形, ∴AC=BD ,(等腰梯形对角线相等) ∴AC=CE .证法三:如图4-55,作CF ⊥AE 于F ,DM ⊥AE 于M . 在△AMD 和△BFC 中,⎪⎩⎪⎨⎧︒=∠=∠=∠=∠90CFB DMA BC AD CBF DAM∴△AMD ≌△BFC (AAS ) ∴AM=BF .又∵AB ∥DC ,MD ∥FC , ∴DC=MF . 又∵DC=BE , ∴AM+MF=BF+BE , ∴F 为AE 的中点, ∴CF 是AE 的垂直平分线, ∴AC=CE .证法四:如图4-54,连结BD . ∵DC ∥BE ,DC=BE ,∴四边形DCEB 是平行四边形,∴∠DBA=∠E ,(两直线平行,同位角相等) 又∵四边形ABCD 是等腰梯形, ∴AC=BD ,在△ABC 和△BAD 中,⎪⎩⎪⎨⎧===AB AB BC AD BDAC∴△ABC ≌△BAD (SSS ) ∴∠CAB=∠DBA , ∴∠CAB=∠E ,∴AC=CE .(等角对等边)(此种方法虽然较繁,但其思路很有价值,即通过证明“三线合一”说明是等腰三角形)点评:证法一证两三角形全等得两线段相等;证法二、四利用角相等证线段相等;证法三中通过梯形常加的辅助线,作梯形底边上的高,连结梯形的对角线,将梯形分割成两个直角三角形与一个矩形,连结对角线再作对角线的平行线,将梯形转化为一个平行四边形和一个三角形.例4:要剪切如图4-56(尺寸单位:mm )所示的甲、乙两种直角梯形零件,且使两种零件的数量相等.有两种面积相等的铝板,第一块长500mm ,宽300mm (如图4-57(1)),第二块长600mm ,宽250mm (如图4-57(2)),可供选用.(1)为了充分利用材料,应选用第_________种铝板,这时一块铝板最多能剪甲、乙两种零件共________个,剪完这些零件后,剩余的边角料面积是______________2mm . (2)从图4-57(1)、4-57(2)中选出你要的铝板示意图,在上面画出剪切线;并把边角余料用阴影表示出来.思路分析通过计算,两直角梯形零件面积分别为22mm 30000mm 40000和,而铝板的面积均为2mm 150000,最多能剪出两个甲、两个乙零件,即在两铝板中设计打样.设计时,为了充分利用材料,考虑到(1)中宽为300mm ,则一种方案作两个乙高,另一种方案为一个甲的下底,思路便打开,类似地,(2)也可以这样分割设计,做出尝试.解:(1)应选用第一块铝板,最多能剪出甲、乙两种零件共4个,由计算得 第一块铝板面积为:)m m (150000300500S 2=⨯=, 而零件甲、乙的面积分别为)mm (40000200)300100(21S 2=⨯+⨯=甲, )mm (30000150)300100(21S 2=⨯+⨯=乙, ∴剩余的边角料的面积是2mm 10000;(2)如图4-58所示正确画出图形.(设计零件个数,从个数、数量上,结合图中数与数之间的关系考虑,往往是应用题的切入点,此外对图形的拼凑、计算、想象,可有利于思维向纵深发展.)【典型热点考题】例1 如图4-30,梯形ABCD 中,AD ∥BC ,DC ⊥BC ,E 为AB 的中点,求证:EC=ED .点悟:要证EC=ED,实际上只要证E点在CD的垂直平分线上,故过E点作EF⊥CD.又因为BC⊥CD,所以EF∥BC,由E为AB的中点,根据平行线等分线段定理的推论可证出F是CD的中点,EF是线段CD的中垂线,从而可证出EC=ED.解:过E作EF⊥CD,垂足为F.∵ BC⊥CD,∴ BC∥EF.∵ E为梯形ABCD腰AB的中点.∴ EF平分CD,∴ EF是CD的垂直平分线.∴ EC=ED.例2如图4-31,已知在四边形ABCD中,有AB=CD,∠B=∠C,AD<BC.求证:四边形ABCD为等腰梯形.点悟:由题意知,只需证AD∥BC即可.如延长BA、CD,由∠B=∠C可得等腰△EBC和△EAD,从而可得AD∥BC.解:延长BA、CD,它们交于点E,∵∠B=∠C,∴ EB=EC.又∵ AB=DC,∴ AE=ED.∴∠EAD=∠EDA∵∠E+∠EAD+∠EDA=180°,∠B+∠C+∠E=180°.∴∠EAD=∠B.∴ AD∥BC,又∵ AD<BC,∠B=∠C.∴四边形ABCD为等腰梯形.例3如图4-32,已知等腰梯形ABCD中,AD∥BC,AC⊥BD,AD+BC=10,DE⊥BC于E,求:DE的长.点悟:由等腰梯形知:AC=BD ,又AC ⊥BD ,AD +BC=10,如过D 作DF ∥CA ,交BC 的延长线于F ,则△BDF 为等腰直角三角形.BF=BC +AD=2DE .解:过D 作DF ∥AC ,交BC 的延长线于F ,则四边形ACFD 为平行四边形, ∴ AC=DF ,AD=CF∵ 四边形ABCD 为等腰梯形 ∴ AC=DB ,BD=FD . ∵ DE ⊥BC , ∴ 51021)(21)(2121=⨯=+=+===AD BC CF BC BF EF BE . ∵ AC ∥DF ,BD ⊥AC , ∴ BD ⊥DF . ∵ BE=EF ,∴ 521====BF EF BE DE 答:DE 的长为5.点拨:当对角线相等或垂直时,常作梯形对角线的平行线,构造成平行四边形,等腰三角形或直角三角形.例4 如图4-33,已知梯形ABCD 中,AD ∥BC ,E 、F 分别为AB 、CD 的中点,EF 分别交BD 、AC 于点G ,H ,求证:(1)EG=HF ,(2))(21AD BC GH -=点悟:由题知,EF 为梯形的中位线,所以EF ∥AD ∥BC ,则G 、H 也分别为BD 、AC 中点,故可应用三角形、梯形中位线定理解决问题.解:∵ E 、F 为梯形的两腰AB 、CD 的中点. ∴ AD ∥EF ∥BC ,且G 、H 分别为BD 、AC 的中点. ∴ AD EG 21=,AD FH 21=,BC EH 21=. ∴ EG=HF .∵ GH=EH -EG ∴ )(212121AD BC AD BC GH -=-=点拨:梯形中位线的性质是“梯形中位线平行于两底,并且等于两底和的一半”,如果从运动的观点来认识梯形、三角形、平行四边形,那便可以找到它们中位线之间的联系.如图4-33所示:当梯形上底AD 的点D 和点A 重合,即AD=0时梯形ABCD 便转化为三角形,由梯形中位线BC 21)BC AD (21EF =+=转化为三角形的中位线;当梯形的上底扩大,使AD=BC 时,梯形ABCD 就变成了平行四边形,这时ADFE 与EFCB 均是平行四边形,于是得BC=EF=AD . ∴ 平行四边形一组对边中线EF 表示为: )(21BC AD BC AD EF +=== 这样,梯形中位线的性质便与三角形中位线的性质以及平行四边形一组对边中点的连线统一起来了. 例5 如图4-34,已知四边形ABCD 为矩形,四边形ABDE 为等腰梯形,AE ∥BD .求证:△BED ≌△BCD .点悟:要证△BED ≌△BCD ,则考虑这两个三角形中的对应边,对应角的相等关系.而DE=AB=CD ,BD=BD ,且BE=AD=BC ,则问题得证,本题要证对应的角相等也不困难. 解:∵ 四边形ABCD 为矩形. ∴ DC=AB ,BC=AD ,∵ 四边形ABDE 为等腰梯形,且AD 、DE 为其对角线, ∴ DE=AB ,BE=AD .在△BED 和△BCD 中,DE=DC ,BE=BC , 又∵ BD=BD ,∴ △BED ≌△BCD .点拨:梯形有一组对边平行,而另一组对边不平行,在处理这类问题时,常把梯形问题转化为平行四边形的问题,或把直角梯形问题转化为矩形问题或直角三角形问题.例6 如图4-35,已知△ABC 中,D 为AB 的中点,E 为BC 的三等分点(BE >CE),AE 、CD 交于点F ,求证:F 为CD 的中点.点悟:我们知道,由平行线等分线段定理及推论可得到线段中点,故过D 作DN ∥AE ,构造平行线等分线段定理推论2的基本图形. 解:过D 作DN ∥AE 交BC 于N . ∵ D 为AB 中点,∴ BN=EN ,又∵ E 为BC 的三等分点,(BE>CE )∴ BN=NE=EC . ∵ DN ∥FE ,∴ F 是CD 的中点.点拨:从上述证明过程中看出,有效利用中点D 成为证明的关键,通常在已知有线段中点时,常过该点作平行线,构造平行线段等分线段定理及推论的基本图形,以达到有关证明的目的.例7 如图4-36,如果把矩形ABCD 纸对折,折痕为GH ,再把A 点叠在折痕线上,折痕为BE ,得到Rt △ABE ,BE 交折痕GH 于P ,延长EA ’交BC 于F ,求证△BEF 为等边三角形.点悟:由折叠过程和平行线等分线段定理的推论1知:P 、A ’分别为BE 、EF 中点,而 ∠EAB=90°,有PA ’=PE ,BA ’为EF 的垂直平分线,从而∠BEF=∠EA ’P=∠DEF=∠A ’EB= 60°,又BE=BF ,∴ △BEF 为等边三角形.解:∵ G 、H 分别为矩形ABCD 的边AB 、CD 的中点, ∴ 四边形AGHD ,GBCH 为矩形,AD ∥GH ∥BC .∴ P 、A ’分别为BE 、EF 的中点. ∵ Rt △A ’BE ≌Rt △ABE ,∴ ∠EA ’B=∠EAB=90°,∠AEB=∠BEF . ∴ ∠PA ’=PE=BE 21,BA ’为EF 的垂直平分线, ∴ ∠BEF=∠PA ’E ,BE=BF . ∵ GH ∥AD , ∴ ∠PA ’E=∠DEF , ∴ ∠A ’EB=∠BEF=∠DEF . ∵ ∠A ’EB +∠BEF +∠DEF=180°, ∴ ∠BEF=60°.∵ BE=BF , ∴ △BEF 为等边三角形.点拨:折叠问题是一种常见题型,解此类题的关键是:折叠后重叠部分是全等形,同时要注意折叠前后图形中有关元素的联系.例8 如图4-37,已知梯形ABCD 中,AD ∥BC ,AC 与BD 交于O ,且AC ⊥BD ,AC=4,BD=3.4,求梯形ABCD 的面积.点悟:梯形的面积常用(上底+下底)×高21⨯来计算,而此题上、下底和高都是未知的, 故不能用此公式.但⨯⨯=⋅=42121BD AC S ABCD 梯形 3.4=6.8故面积可求. 解:∵ AC ⊥BD ,∴ BD AO 21S ABD ⋅=∆, BD CO S BCD ⋅=∆21, ∴ BD CO AO BD CO BD AO S S S BCD ABD ABCD ⋅+=⋅+⋅=+=∆∆)(212121梯形,即 ⨯⨯=⋅=42121BD AC S ABCD 梯形 3.4=6.8答:梯形ABCD 的面积为6.8.点拨:当梯形(或任意四边形)对角线互相垂直时,它们的面积等于对角线乘积的一半.例9 如图4-38,已知在等腰梯形ABCD 中,AB ∥CD ,AB >CD ,AD=BC ,BD 平分∠ABC ,∠A=60°,梯形周长是20cm ,求梯形的各边长?点悟:由等腰梯形性质知:∠A=∠CBA=60°,又BD 平分∠ABC ,有∠1=∠2=30°,从而∠ADB=90°,则AB AD 21=又AB ∥CD ,知∠2=∠3=∠1,有BC=CD=AD .故由周长为20cm ,可求各边长. 解:∵ 四边形ABCD 为等腰梯形, ∴ ∠A=∠ABC=60°,∵ BD 平分∠ABC , ∴ ∠1=∠2=30°.∠A=60° ∴ ∠ADB=180°-∠A -∠2 =180°-60°-30° =90°. ∴ AB AD 21=. ∵ AB ∥CD , ∴ ∠2=∠3. ∴ ∠1=∠3, ∴ BC=DC . ∵ AD=BC , ∴ AB BC CD AD 21===.∵ AB +BC +CD +AD=20. ∴ AD=DC=BC=4, AB=8答:梯形的各边长分别为4cm ,4cm ,4cm ,8cm .【同步达纲练习一】 一、选择题1.下列命题中,真命题有 ( )①有两个角相等的梯形是等腰梯形; ②有两条边相等的梯形是等腰梯形; ③两条对角线相等的梯形是等腰梯形; ④等腰梯形上、下底中点连线,把梯形分成面积相等的两部分. (A)1个 (B)2个 (C)3个 (D)4个 2.以线段a=16,b=13,c=10,d=6为边作梯形,其中a 、c 作为梯形的两底,这样的梯形( )(A)只能作1个 (B)能作2个 (C)能作无数个 (D)不能作3.在直角梯形ABCD 中,AD ∥BC ,AB ⊥BC ,E 是CD 中点,则 ( ) (A)AE=BE (B)AE >BE(C)AE <BE (D)AE 、BE 大小不确定4.等腰梯形的两底长分别为a 、b ,且对角线互相垂直,它的一条对角线长是 ( ) (A))(22b a + (B)2 (a +b) (c))(21b a + (D)a +b二、填空题5.在梯形ABCD 中,AD ∥BC ,∠B=50°,∠C=80°,AD=a ,BC=b ,则∠D=________,CD=________. 6.直角梯形一底与一腰的夹角为30°,并且这腰长为6厘米,则另一腰长为_________.7.已知梯形ABCD 中,AD ∥BC ,AC <BC ,AC ⊥BD 于O ,AC=8,BD=6,则梯形ABCD 的面积为_________. 8.已知梯形上、下底长分别为6、8,一腰长为7,则另一腰a 的范围是 _______,若a 为奇数,则此梯形为_________梯形.9.梯形不在同一底上的两组角的比值分别为3∶6和4∶2,则四个角的度数分别为_________.三、解答题10.梯形ABCD 中,AD ∥BC ,BD ⊥DC ,若AB=AD=DC ,梯形ABCD 的周长为10,求梯形ABCD 的面积.11.已知梯形ABCD 中,AD ∥BC ,AD <BC ,且∠B +∠C=90°,E 为AD 中点,F 是BC 中点.求证:)(21AD BC EF -=【同步达纲练习二】1.有两个角相等的梯形是( )A.等腰梯形B.直角梯形C.一般梯形D.等腰梯形或直角梯形2.已知直角梯形的一腰长为10cm,这条腰与底所成的角为30°,那么另一腰的长为( )A.2.5cm B.5cm C.10cm D.15cm3.如图4-59,梯形ABCD中,AD∥BC,AB=CD,对角线AC与BD相交于点O,则图中全等三角形共有( )A.1对B.2对C.3对D.4对(平移对角线BD即可)4.如图4-60,AB∥CD,AE⊥DC,AE=12,BD=15,AC=20,则梯形ABCD的面积是( )A.130 B.140 C.150 D.1605.等腰梯形中,上底:腰:下底=1:2:3,则下底上的内角的度数是____________.6.已知梯形ABCD中,AD∥BC,AB=DC,若∠B=30°,AD=2cm,BC=6cm,那么梯形的周长为_____________.7.已知梯形的上底长为2,下底长为5,一腰长为4,则另一腰长的取值范围是_________________.89,则它的对角线长为8.已知:等腰梯形的两底分别为10cm和20cm,一腰长为cm_____________cm.9.如图4-61,已知等腰梯形ABCD,AD∥BC,E为梯形内一点且EA=ED.求证:EB=EC.10.如图4-62,四边形ABCD是矩形,四边形ABDE是等腰梯形,AE∥BD.求证:△BED≌△BCD.11.如图4-63,梯形ABCD 中,∠B+∠C=90°,E 、F 分别为上、下底的中点.求证:)AD BC (21EF -=.参考答案【同步达纲练习一】一、1.B ; 2.D ; 3.A ; 4.A . 二、5.100°,b-a ; 6.3; 7.24; 8.5<a<9,等腰梯形; 9.60°,60°,120°,120°. 三、10.∵AD=AB=DC . ∴ ∠1=∠2, ∵ AD ∥BC ,∴ ∠C=∠2+∠3,∠1=∠3. ∴ ∠2=∠3,∴ ∠C=2∠3. ∵ BD ⊥DC ,∴ ∠3=30°, ∴ BC CD 21=.设CD=x ,则x+x+x+2x=10, ∴ x=2.在Rt △BCD 中,BD=322422=-. 作DE ⊥BC ,垂足为E .则32221421⨯⨯=⨯⨯DE , ∴ 3=DE ,∴ 333)42(21S ABCD =⋅+=梯形. 11.过E 作EM//AB ,EN//CD 交BC 分别于M 、N ,则得、,有AE=BM ,EN=CD ,∠B=∠EMC ,∠C=∠ENB ,又∠B+∠C=90°,则∠EMC+∠ENB=90°,有∠MEN=90°。
