信号与系统 陆建华 05
清华大学《信号与系统》第二十四讲

2
陆建华
第十二章 系统的状态变量分析
§12.5 离散时间系统状态方程的求解
(一) 矢量差分方程的时域求解 离散系统状态方程
n
λ (n + 1) = Aλ (n) + Bx(n)
⎡ n −1 n −1−i ⎤ λ (n) = A λ (0)u (n) + ⎢ ∑ A Bx(i ) ⎥ u (n − 1) ⎣ i =0 ⎦ 零输入 零状态 y (n) = Cλ (n) + Dx(n) ⎡ n−1 ⎤ n = CA λ(0)u(n) + ⎢∑ CAn−1−i Bx(i)⎥ u(n −1) + Dx(n)u(n) ⎣ i =0 ⎦
= C( sI − A) −1 B + D
(三) A矩阵的对角化 A矩阵的对角化说明系统变换成并联结构。这种结构使 每一状态变量之间互不影响,可以独立研究系统参数对 状态变量的影响。对角元素即为特征值。
清华大学电子工程系
7
陆建华
§12.6 状态矢量的线性变换
例12-18 将图示系统的A矩阵对角化 解:系统状态方程为
1 p
r ( t ) = [1 1 0] ⎡ ⎣λ ( t )⎤ ⎦
T
−3
λ3 ( t )
λ2 (t ), λ3 (t ) 可控, B = [ 0 1 1] 中的0决定了λ1 (t ) 不可控
λ1 (t ), λ2 (t ) 可观, C = [1 1 0] 中的0决定了λ (t ) 不可观 3
清华大学电子工程系
15
清华大学电子工程系
陆建华
§12.7 系统的可控制性与可观测性
(三)可控性、可观性与H(s)的关系
H ( s ) = C ( sI − A )
清华导师简介,部分

清华导师简介,部分王京教授简介:1958年1月出生,男,清华大学教授,博士生导师。
现任清华信息科学与技术国家实验室副主任,清华大学信息技术研究院无线与移动通信技术研究中心主任、微波与数字通信国家重点实验室副主任兼无线传输与个人通信研究室主任。
中国第三代移动通信系统研究开发项目总体专家组专家,国家十五863计划FuTURE(B3G/4G)项目专家组专家,TD-SCDMA研究开发和产业化项目专家组专家,TD-SCDMA产业化联盟专家组专家。
目前已经培养博士生12名,硕士生30多名。
主讲《通信原理》、《数字微波通信》、《通信新技术讲座》等课程。
申请国家发明专利40余项,已获得批准的有16项;发表论文130余篇,其中SCI收录22篇,其中在IEEE Communications Magazine 上发表两篇论文。
曾承担过多项863项目和科技攻关项目,以及国防预研和型号项目。
承担的中国第三代移动通信系统研究开发项目获2003年国家科学技术进步二等奖,另获国防科学技术奖二等奖1项。
主要研究领域是无线移动通信和宽带无线传输技术,包括B3G/4G移动通信、WCDMA、TD-SCDMA系统研究,调制解调技术、纠错编译码技术、移动通信抗衰落技术、MIMO与时空联合数字信号处理技术、分布式无线通信系统等。
陆建华*陆建华:男,汉族,1963年7月生。
1986、1989年分别获清华大学电子工程系学士、硕士学位,之后留校任教,1995年由学校公派赴香港科技大学攻读博士学位,学成后于1998年返回学校。
现为清华大学教授、博士生导师,清华大学航空航天学院副院长、空天信息技术研究所所长。
长江学者特聘教授,系国家―863‖计划专家组专家,国家―973‖项目首席科学家,国家广电总局科技委特邀委员。
研究方向为宽带无线通信、多媒体信号处理等。
主持完成国家973课题、自然科学基金重点项目、863重点项目、教育部重大科研项目等多项研究任务,取得多项创新研究成果,部分技术被用于国家重要工程研究项目中,具有重要应用前景。
高效非均匀数字信道化及信号重建技术

图 1 2M 通道正交镜像滤波器组在 Z 域中的结构 Fig. 1 Structure of 2 M channel QMF in Z domain
样点序号, k 表示子信道序号 , 如果 i = 0, 则仅利用 l 综合滤波器组中 G 0 ( z ) , G 1 ( z ) , , GN u - N ( z ) 进行 i i 信号重建 ; 如果 G1( z ) , G2( z ) ,
u i l i i
H k( z ) =
H ( zWk2M ) ,
X
l=0
l ( zWM )
k=
i
H k+ N li- i ( zWM ) G k ( z ) ( 11)
l
47
www. teleonline. cn
电讯技术
2011 年
图 2 中原型滤波器长度设计为 2ML , 将原型滤 波器系数 h ( n) 进行多相分 解, 2M 为信道数, L 为 每个多相分支滤波器阶数。根据抽取和零值内插系 统的等效变换
第 51 卷 第 5 期 2011 年 5 月
电讯技术 Telecommunication Engineering
Vol. 51 No. 5 MayX( 2011) 05- 0046- 05
高效非均匀数字信道化及信号重建技术
王 芳,黄
1
振 , 陆建华
2
1, 2
Efficient Non uniform Digital Channelizer and Signal Reconstruction Technology
WANG Fang , H U ANG Zhen , L U Jian hua
1 2 1, 2
( 1. Department of Electronic Engineering, Tsinghua University, Beijing 100084, China; 2. School of Aerospace, Tsinghua University, Beijing 100084, China) Abstract: In view of the situation that the number of receiving signal in wideband receiver is large and signal spectrum distributes non uniformly, a method of eff icient non uniform digital channelizer based on polyphase fil ter banks and signal reconstruction is proposed in this paper. The digital channelizer is composed of both anal yser and synthesizer with a same coeff icient of prototype low pass filter, which is designed optimally to achieve high stopband attenuation, so that the parallel quadrature mirror filter banks can be used to reconstruct signal. Finally, the computational complexity of the proposed channelizer is compared with that of the parallel digital down conversion channelizer and mult i stage polyphase DFT( Discret Fourier Transform) filter banks, it can be seen that the proposed method is more efficient and feasible with a little signal distortion. Key words: wideband receiver; polyphase DFT; signal reconstruction; digital channelizer 带通滤波器带内相应频率分量完成下变频和抽取工
信号与系统课后答案(全)
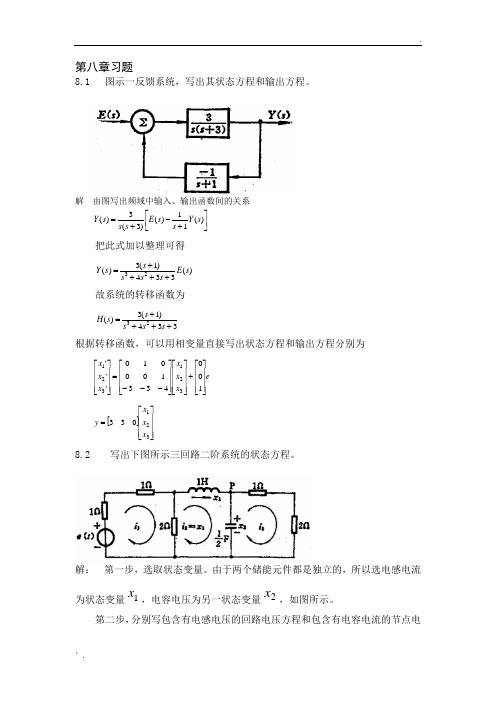
第八章习题8.1 图示一反馈系统,写出其状态方程和输出方程。
解由图写出频域中输入、输出函数间的关系⎥⎦⎤⎢⎣⎡+-+=)(11)()3(3)(sYssEsssY把此式加以整理可得)(334)1(3)(23sEsssssY++++=故系统的转移函数为334)1(3)(23++++=sssssH根据转移函数,可以用相变量直接写出状态方程和输出方程分别为exxxxxx⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡143311'''321321[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=32133xxxy8.2 写出下图所示三回路二阶系统的状态方程。
解:第一步,选取状态变量。
由于两个储能元件都是独立的,所以选电感电流为状态变量1x,电容电压为另一状态变量2x,如图所示。
第二步,分别写包含有电感电压的回路电压方程和包含有电容电流的节点电流方程。
根据第二个回路的回路方程,并代入元件参数,则有112122'ixxx+--=312'21ixx-=第三步,上两式中1i和3i不是状态变量,要把它们表为状态变量。
由第一个回路有1124xie-=,即112141xei+=由第三个回路有323ix=,即2331xi=把1i和3i分别代入第二步中两式,并经整理,最后得所求状态方程为exxx21'211+--=212322'xxx-=或记成矩阵形式8.3 图示一小信号谐振放大器的等效电路,这里的激励函数)(t e是一压控电流源,输出电压)(t y由耦合电路的电阻L R上取得。
要求写出此电路的状态方程和输出方程。
解:第一步,选状态变量。
因为电感电流和电容电压等三个变量都是独立的,所以选回路电感L中的电流1x、回路电容C上的电压2x、耦合电容c C上的电压3x为状态变量。
第二步,分别写回路方程或节点方程。
由RLC回路有211'xRxLx=+eixxCCx rc-=+++132''RL c i x C ='3第三步,消去非状态变量。
清华大学《信号与系统》第九讲

1 ⎛s⎞ L [ f (at )] = F ⎜ ⎟ a ⎝a⎠
( a > 0)
1 ⎛ω ⎞ 比较:F [ f ( at )] = F ⎜ ⎟ a ⎝a⎠
(七) s域微分
dF ( s ) = L [− tf (t )] ds
⇒思考题18:证明s域微分特性
23
清华大学电子工程系
陆建华
§4.3
L-变换的基本性质
L变换侧重于系统分析
3
清华大学电子工程系
陆建华
§4.1 引言
本章重点: L-变换在系统分析中应用,如系统函数的概念、系 统时域特性、系统频域特性、系统稳定性分析等。 本章思路: L-变换定义、性质→结合系统分析介绍L变换的应用
4
清华大学电子工程系
陆建华
第四章 拉普拉斯变换
§4.2 L-变换定义及其收敛性
清华大学电子工程系
[ ]
16
陆建华
§4.2 L-变换定义及其收敛性
1 n = 1 ,易得 L [t ] = 2 s 2 2 ⋅1 2 n = 2 , L [t ] = ⋅ L [t ] = 3 s s
┇ ⇒
L [t ] =
n
n! s n +1
⎡ e jω 0 t − e − jω 0 t ⎤ ② L [sin ω 0 t ] = L ⎢ ⎥ 2 j ⎣ ⎦
单边L-变换
(Unilateral or Single-sided) 本课程重点
下限取 − ∞ 称为双边L-变换(Bilateral or Double-Sided) F -变换与L-变换比较: F -变换
t → ω
L-变换
t → s s = σ + jω 复频域
信号与系统(第5版) 配套习题及答案详解

《信号与系统》(第5版)习题解答目录第1章习题解析 (2)第2章习题解析 (6)第3章习题解析 (16)第4章习题解析 (24)第5章习题解析 (32)第6章习题解析............................................................................ 错误!未定义书签。
第7章习题解析 (50)第1章习题解析1-1 题1-1图示信号中,哪些是连续信号?哪些是离散信号?哪些是周期信号?哪些是非周期信号?哪些是有始信号?(c) (d)题1-1图解 (a)、(c)、(d)为连续信号;(b)为离散信号;(d)为周期信号;其余为非周期信号;(a)、(b)、(c)为有始(因果)信号。
1-2 给定题1-2图示信号f ( t ),试画出下列信号的波形。
[提示:f ( 2t )表示将f ( t )波形压缩,f (2t )表示将f ( t )波形展宽。
] (a) 2 f ( t - 2 )(b) f ( 2t )(c) f ( 2t ) (d) f ( -t +1 )题1-2图解 以上各函数的波形如图p1-2所示。
图p1-21-3 如图1-3图示,R 、L 、C 元件可以看成以电流为输入,电压为响应的简单线性系统S R 、S L 、S C ,试写出各系统响应电压与激励电流函数关系的表达式。
题1-3图解 各系统响应与输入的关系可分别表示为)()(t i R t u R R ⋅= t ti L t u L L d )(d )(= ⎰∞-=t C C i Ct u ττd )(1)(1-4 如题1-4图示系统由加法器、积分器和放大量为-a 的放大器三个子系统组成,系统属于何种联接形式?试写出该系统的微分方程。
S R S L S C题1-4图解 系统为反馈联接形式。
设加法器的输出为x ( t ),由于)()()()(t y a t f t x -+=且)()(,d )()(t y t x t t x t y '==⎰故有 )()()(t ay t f t y -='即)()()(t f t ay t y =+'1-5 已知某系统的输入f ( t )与输出y ( t )的关系为y ( t ) = | f ( t )|,试判定该系统是否为线性时不变系统?解 设T 为系统的运算子,则可以表示为)()]([)(t f t f T t y ==不失一般性,设f ( t ) = f 1( t ) + f 2( t ),则)()()]([111t y t f t f T ==)()()]([222t y t f t f T ==故有)()()()]([21t y t f t f t f T =+=显然)()()()(2121t f t f t f t f +≠+即不满足可加性,故为非线性时不变系统。
信号与系统第5章习题答案

第5章连续时间信号的抽样与量化5.1试证明时域抽样定理。
证明:设抽样脉冲序列是一个周期性冲激序列,它可以表示为T(t)(tnT)sn由频域卷积定理得到抽样信号的频谱为:1F s ()F()T 2()1 T snFns式中F()为原信号f(t)的频谱,T ()为单位冲激序列T (t)的频谱。
可知抽样后信 号的频谱()F 由F()以s 为周期进行周期延拓后再与1T s 相乘而得到,这意味着如果 s s2,抽样后的信号f s (t)就包含了信号f(t)的全部信息。
如果s2m ,即抽样m 间隔 1 Tsf2m,则抽样后信号的频谱在相邻的周期内发生混叠,此时不可能无失真地重建 原信号。
因此必须要求满足1 Tsf2 m,f(t)才能由f s (t)完全恢复,这就证明了抽样定理。
5.2确定下列信号的最低抽样频率和奈奎斯特间隔:2t (1)Sa(50t)(2)Sa(100)2t (3)Sa(50t)Sa(100t)(4)(100)(60)SatSa解:抽样的最大间隔 T s 12f 称为奈奎斯特间隔,最低抽样速率f s 2f m 称为奈奎m斯特速率,最低采样频率s 2称为奈奎斯特频率。
m(1)Sa(t[u(50)u(50)],由此知m50rad/s ,则50)5025 f , m由抽样定理得:最低抽样频率50 f s 2f m ,奈奎斯特间隔1 T 。
sf50s2t(2))Sa(100)(1100200脉宽为400,由此可得radsm200/,则100f,由抽样定理得最低抽样频率m200f s2f m,奈奎斯特间隔1T。
sf200s(3)Sa[(50)(50)],该信号频谱的m50rad/s(50t)uu50Sa(100t)[u(100)u(100)],该信号频谱的m100rad/s10050Sa(50t)Sa(100t)信号频谱的m100rad/s,则f,由抽样定理得最低m抽样频率100f s2f m,奈奎斯特间隔1T。
清华大学信号与系统教学大纲

第一章绪论
1.1.信号与系统描述
1ቤተ መጻሕፍቲ ባይዱ2.阶跃信号、冲激信号
1.3.线性时不变系统
第二章连续时间系统
2.1.冲激响应和阶跃响应
2.2.卷积
第三章傅里叶变换
3.1.傅立叶级数、频谱
3.2.傅立叶变换
3.3.傅立叶变换的性质
3.4.周期信号和抽样信号的傅立叶变换,抽样定理
第四章拉普拉斯变换
4.1.拉普拉斯变换:拉普拉斯变换的性质,拉普拉斯逆变换
4.2.拉普拉斯变换的应用
4.3.系统函数,零点、极点
4.4.S-域分析,频响特性,反馈系统
第五章变换域分析方法的应用
5.1.傅立叶变换应用:理想滤波器,上升时间和带宽,调制,信号分析
8.4.DFT、FFT
第九章状态变量分析方法
9.1.信号流图
9.2.连续系统状态变量分析
9.3.离散系统状态变量分析,可观测性与可控制性
9.4.状态变量分析方法在控制系统中的应用
本科《信号与系统》课程教学大纲
一、课程基本情况
课程编号
开课单位
航天航空学院
课程名称
中文名称
信号与系统
英文名称
Signals and Systems
教学目的与重点
本课程教学目的是使学生掌握信号与系统理论的基本概念和基本分析方法。重点是确定性信号经线性、时不变系统传输与处理的基本理论和方法。
课程负责人
陆建华
课程类型
□文化素质课□公共基础课■学科基础课
□专业基础课□专业课□其它
教学方式
■讲授为主□实验/实践为主□专题讨论为主
信号和系统课后习题答案解析
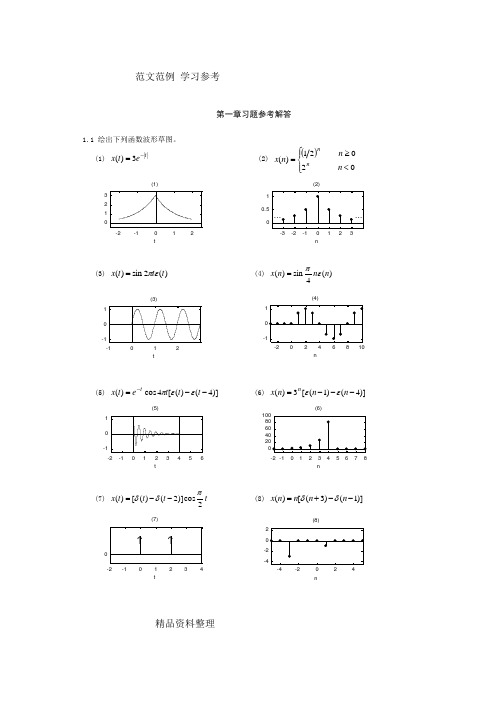
范文范例 学习参考精品资料整理第一章习题参考解答1.1 绘出下列函数波形草图。
(1) ||3)(t et x -=(2) ()⎪⎪⎨⎧<≥=02021)(n n n x n n(3) )(2sin )(t t t x επ=(4) )(4sin )(n n n x επ=(5) )]4()([4cos )(--=-t t t et x tεεπ(6) )]4()1([3)(---=n n n x nεε(7) t t t t x 2cos)]2()([)(πδδ--=(8) )]1()3([)(--+=n n n n x δδ范文范例 学习参考精品资料整理(9) )2()1(2)()(-+--=t t t t x εεε(10) )5(5)]5()([)(-+--=n n n n n x εεε(11) )]1()1([)(--+=t t dtdt x εε (12) )()5()(n n n x --+-=εε(13) ⎰∞--=td t x ττδ)1()((14) )()(n n n x --=ε1.2 确定下列信号的能量和功率,并指出是能量信号还是功率信号,或两者均不是。
(1) ||3)(t et x -=解 能量有限信号。
信号能量为:()⎰⎰⎰⎰∞-∞-∞∞--∞∞-+===02022||2993)(dt edt edt e dt t xE ttt ∞<=⋅-⋅+⋅⋅=∞-∞-9)21(92190202tte e(2) ()⎪⎩⎪⎨⎧<≥=02021)(n n n x n n解 能量有限信号。
信号能量为:()∞<=+=+==∑∑∑∑∑∞=--∞=∞=--∞=∞-∞=35)41(4])21[(2)(0102122n n n nn n n n n n xE(3) t t x π2sin )(=范文范例 学习参考精品资料整理 解 功率有限信号。
周期信号在(∞-∞,)区间上的平均功率等于在一个周期内的平均功率,t π2sin 的周期为1。
信号与系统的学习问题

信号与系统本人今年和同学一起考清华电子,本人没上,同学高分上榜,现转让我们一起搜集的资料,还有部分师兄传下来的,复试说明部分是我同学写的。
资料很多,你也可以看出来当初是下苦工夫收集的,我只卖给真心考清华电子的同学,关于信号的复习我觉得根本还是要吃透课本,自己理解透,资料只是起到辅助作用,不能买了资料就认为万事大吉,关于考清华其实还是不太难的,呵呵,自己没考上还这么说,只要自己有信心,认真复习,英语基础好一点还是很好考的,尤其现在一下扩招了这么多,所以大家要有信心,祝大家好运,其实考不上也没什么,都可以调剂到很好的地方。
主要资料有:信号与系统04/05年课堂讲义,老师:陆建华。
(现主要命题老师,07年以前是山老师出的,所以07年风格大变。
现在是教研组统一出题,陆是主要负责的)。
包括:讨论课,作业,习题课,期中期末考试大纲,实验辅导,专题讲座等。
信号与系统课堂讲义,老师:山秀明(07年以前命题老师,讲义中的精典,现在的考试题也部分延续了山老师的风格,山老师很注重数学理论在信号与系统的应用,看他的笔记对扎实基本功有很大的帮助)信号与系统课堂讲义,老师:任勇(命题老师之一)。
信号与系统课堂讲义,老师:乐正友(命题老师,有两种版本:电子版和课堂笔记,内容也不相同,我只看了课堂笔记)。
信号与系统课件,老师:叶大田(清华同学说已经退休,有时间可以看看,比较基础)清华大学00-09年信号与系统考研真题和部分答案(答案由于搜集的资料比较多,答案的版本也很多,我们后来做很多结果也不一样,用来参考吧)。
清华《信号与系统》课程课堂笔记,授课老师:山秀明;《信号与系统》郑君里课后答案。
第一版答案为郑老师亲自手写(其中很多为绘图题,对考试帮助很大),第二版答案为清华内部所留课后题答案,虽然只有部分,但十分宝贵,全部答案推荐市面上陕西师范出版社胡冰新所著。
清华大学《信号与系统》第六讲

冲激函数和阶跃函数之付立叶变换
F [δ (t )]
F [δ (t )] = ∫
∞ −∞
δ (t )e − jωt dt = 1
冲激函数之频谱覆盖所有频段,各种工业中产生的瞬间电 火花,其造成的干扰是全频段的。
F [1] = 2πδ (ω )
清华大学电子工程系
(利用付立叶逆变换)
23 陆建华
§3.6
§3.4 傅立叶变换
④傅立叶变换存在的条件:什么样的 f (t )可以取 F (ω ) ? 充分条件:
∫
∞
−∞
f (t ) dt < ∞ 类似于傅立叶级数的
Dirichlet条件,但不是必要条件。 借助奇异函数,周期信号、阶跃信号虽不满足以上条 件,但可以存在傅立叶变换。
8 清华大学电子工程系 陆建华
j ϕ (ω ) F (ω ) 一般为复函数,可以写作 F (ω ) = F (ω ) e
F (ω ) 为频谱函数的模,代表信号中各频率分量的相对大小;
ϕ (ω ) 为 F (ω ) 的相位函数,表示信号中各频率分量之间的
相位关系。
6 清华大学电子工程系 陆建华
§3.4 傅立叶变换
讨论: ① f (t )反映信号的时域特征,F (ω ) 反映信号的频域特征,
∞ ⎧ jnω 1 t = f ( t ) F ( n ω ) e ∑ 1 ⎪ n = −∞ ⎪ 由⎨ 演变 T1 ⎪F (nω ) = 1 2 f (t )e − jnω1t dt 1 T ∫ ⎪ − 1 T 1 2 ⎩
将 F (nω1 ) 除以 ω1 ⇒ 2π
F (nω1 )
ω1
定义为频谱密度(Spectrum Density)
3
清华大学电子系陆健华《信号与系统》电子课件推荐优秀PPT

如:通信信号设计满足传输要求 (如带宽限制)
清华大学电子工程系
5
陆建华
§1.1 信号与系统
本课程的范围及重点
讨论范围: 信号分析与系统分析
工程背景: 通信系统与控制系统 讲授重点: 基本概念(物理意义)、分析工具
(变换)、方法
本课程的性质与地位
专业基础课,其概念、方法为今后从事通信及控 制系统理论和工程技术研究之必备、之基石。
清华大学电子工程系
6
陆建华
§1.1 信号与系统
本课程的授课安排
教材:《信号与系统》郑君里等
参考:《Signals & Systems》 Oppenheim, 2nd Edition
《Circuits, Signals, and Systems》, Siebert, MIT
4 阶跃信号与冲激信号
举例:移动通信中的多径传播现象
变换域描述:正交变换、频谱分析
连续与离散: 2 信号的描述、分类和典型示例
系统设计:信号处理 (去噪增强、畸变恢复…)
有关细节(如波形、特征等)自学 P9
时间轴连续/离散 2 信号的描述、分类和典型示例
这一运算非常重要,在今后的章节(如第二、三、四章)中着重讲
信号与系统:
信号
系统
信号/行为
举例:
① 电流、电压作为电子线路中的时间之函数 信号
电路本身 系统 ② 汽车驾驶员踩油门发动机提速
清华大学电子工程系
发动机 系统
油门压力
信号
3
陆建华
§1.1 信号与系统
NOTE: ① 消息:信号的具体内容 ② 信息:抽象的、本质的内容,信号的内涵 ③ 信号与系统的概念广泛存在于许多领域,如:通信系
《信号与系统》清华期末复习习题课

∫ 输出为y(t)。计算如下所示的信号误差。 ∞ x(t) − y(t) 2 dt −∞
∫∞ x(t) − y(t) 2 dt = 13
−∞
4
14
十、 一离散LTI系统,单位样值响应h(n)如下右图所示:
其中k为整数,a,b,c均为实数,h(n)满足下列条件
1)H (e jω ) 为 h(n) 的傅立叶变换,H(ejω)ejω 为实偶函数;
1
λ2 (n)
E
2
y(n)
2
12
考研巴士论坛
(1)
λ
(
n
)
=
⎡ ⎢ ⎢ ⎢ ⎢ ⎢⎣
7 6
⋅
⎛ ⎜⎝ 2n−1
1 2
−
⎞n−1 ⎟⎠
1 6
⋅ ⎜⎝⎛
1 2
⎞n−1 ⎟⎠
⎤ ⎥ ⎥ ⎥ ⎥ ⎥⎦
u
(
n
−
1)
y
(n)
=
h(n)
=
2
⋅
⎛ ⎜⎝
1 2
⎞n ⎟⎠
−1
u
(n
K的取值范围
9
考研巴士论坛
1)系统函数H(z) 2)系统的极点为
H (z) = Y (z) =
z− 1 2
X (z) z2 + (K − 1)
4
p 1,2 = ±
1−K 4
K :0 →
1
4
K : 1 → +∞ 4
因果系统的稳定条件 0< K <
p 1 ,2 5 4
信号与系统习题课
教师:陆建华 助教:陶晓明
陈为刚
清华大学电子工程系 2005/6/10
健华《信号与系统》电子课件_习题课讲稿(期中考试_CV)

信号与系统习题课具有性质:一、判断其中由错。
是偶函数δ由于:3、设系统的输入为判断因果系统:现在的响应是否等于现在的激励+以前的激励判断线性系统:判断时不变系统:时移,再经系统是否等于先经系统,再时移4、已知系统微分方程为5、由于是判断题,所以只需检验特殊点。
针对此题,我们检验6错。
特别注意终值定理的应用条件:仅当sF时,终值定理才可应用。
而题中二、已知信号的表达式。
()x t该图为两个三角频谱相减而成,即另解:2−三、对图(e1) 求系统函数及冲激响应(t);∞∑四、系统用微分方式表示如下:1)试求输入输出间的传输函数第五题:非均匀抽样问题假设:i)ii)T+ mT+1m−(Hω1)设1(s t=jS−试求:T+T+1只在抽样的取值有意义(s tf2(s2)f⎛⎜⎝T+T+1(z2Y()s t f 3)试画出(Zω±所以,在故得到在频率范围图中黑实线的理想低通滤波器即可滤出没有混叠的原信号频谱,从而实现了信号的恢复。
[(22)3jω−↑−作业题:4-34(2)系统转移函数为:因此,完全响应为:E⎛⎜=⎜⎝这样,稳态响应为:若只考虑第一周期内的稳态响应,则有:故稳态响应为:∴取拉氏变换,得:列写电路微分方程,由于该电路对周期信号的稳态响应仍是一个周期信号,()1os V s s α=+因此,在第一个周期()((()( 0 0 0o o o V V V 1 对稳2 ∵又故,28补充题目一、计算1、直接法:利用31())('sin )(cos ')(sin x x x x x x δδδ+=2、间接法:sin ()0()0(sin ())'0sin '()0cos ()()x x x x x x x x x x δδδδδδ=⋅=∴=⇒=−=−∵f 二、频谱函数三、本例目的在于熟悉并正确应用傅里叶变换的对三、设1.证法一:F⎡∴⎣==eN−∑证法二:372、N =3时,请画出的大致波形(注明幅度及关键时间值)()f t3、f上课认真听讲,下课按时完成作业。
信号与系统-第十三讲_CV

清华大学 电子系/航院
陆建华
第五章 傅立叶变换应用于通信系统
§5.11 频分复用与时分复用
在同一个传输信道内,同时传输多路不同信号 多路复用:
频分复用(FDM)-正交频分复用(OFDM) 时分复用(TDM)-共享时隙、统计复用 码分复用(CDM)-码分、逻辑复用 波分复用(WDM)- 光载体
11
ωs
2
8
清华大学时间信号
一阶抽样保持:
ft
fs1(t)视为冲激序列 fs(t) 与
一三角单脉冲的卷积
⎧ t ⎪1 − h1 (t ) = ⎨ Ts ⎪0 ⎩ t < Ts t ≥ Ts
Ts
fs t
t
f s1 (t ) = f s (t ) ∗ h1 (t )
清华大学 电子系/航院
t
小波分析
4
陆建华
第五章 傅立叶变换应用于通信系统
§5.9 从抽样信号恢复连续时间信号 频域分析 抽样信号
1 Fs (ω ) = Ts
n = −∞
F S (ω )
1 TS
∑ F (ω − nω )
s
∞
− ω S − ωm ω m
ωS
ω
H (ω )
理想低通滤波
⎧T H (ω ) = ⎨ s ⎩0
H ( jω ) ≈ 1 + j (ω − 100) 1
1
H ( jω )
1 2
V2 ( jω ) = V1 ( jω ) ⋅ H ( jω ) ⋅ e jϕ (ω )
ϕ (ω ) 99 100 101 π 2
π 4
ω
v2 (t ) = F { 2 ( jω )} V
−1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
简记 Fn
周期矩形: Fn = (1) 谱线间隔
清华大学电子工程系
Eτ nω 1τ Sa T1 2
2π ω1 = T1
27
陆建华
第三章 傅里叶变换
(2) 包络线零点 (3) 带宽
m
2π
τ
2π
m 为整数
τ
BW =
下节课: 傅立叶变换—非周期信号的频谱分析 课后作业: 思考题: 参考书:
清华大学电子工程系
nω 1τ Eτ 2 = Eτ Sa nω 1τ = nω 1τ T1 T1 2 2
17
清华大学电子工程系
陆建华
§3.3 典型周期信号的傅里叶级数
偶对称: 三角函数形式展开,有 bn = 0
2 Eτ nω 1τ c n = a n = 2 Fn = Sa T1 2 Eτ c0 = a0 = T1
卷积定理 抽样定理
4
清华大学电子工程系
陆建华
第三章 傅里叶变换
§3.2 傅立叶级数
1822 Fourier 证明了将周期信号展开为正弦级数原理 傅立叶级数 (一) 三角函数形式级数展开(正交函数集 {cos nω1t , sin nω1t} ) 周期函数 f 当:
2π T1
(t ),周期为 T , 角频率为ω 1 =
Fn e jnω1t ∑
f (t )e jnω1t dt
∞
f (t ) =
1 Fn = T1
清华大学电子工程系
n = ∞
∫
t 0 +T1
t0
(同学可自行推导)
10
陆建华
§3.2 傅立叶级数
Fn与其它系数的关系:
F0 = a 0 = c 0
Fn = Fn e
j n
1 = (a n jbn ) , n 仍为 c n对应的 n 2
25
清华大学电子工程系
陆建华
§3.3 典型周期信号的傅里叶级数
(四) 周期三角脉冲信号 F 级数展开 (自行推导) (五) 周期半波余弦信号F 级数展开 (自行推导) (六) 周期全波信号
F 级数展开 (自行推导)
注意: 利用函数的对称性质
f (t ) = f ( t ) ,bn = 0 奇函数 f (t ) = f ( t ) , a n = 0
13
陆建华
§3.2 傅立叶级数
(2) 奇函数
f (t ) = f ( t )
f(t)
T 1 2
0
T1 2
t
a a0 = 0 , n = 0
c n = bn, n = π 2
(余弦分量)
Fn = F n
清华大学电子工程系
1 = jbn 2
14
陆建华
§3.2 傅立叶级数
T f (t ) = f t ± 1 (3) 奇谐函数 2
Fn = F n =
1 1 2 2 cn = a n + bn 2 2
利用下图矢量分解:
11
清华大学电子工程系
陆建华
§3.2 傅立叶级数
j bn 2
Fn
Fn =
an 2
cn
2
n
0
+ n
Fn
an
j
bn 2
须注意的两个现象:
(1) f(t)展开式中包含复数 (数学变换的结果) (2) 出现负频率分量 (原正频率分量的能量减半)
吉布斯现象
21
清华大学电子工程系
陆建华
§3.3 典型周期信号的傅里叶级数
(二)矩形对称方波周期信号:(特例)
f (t)
T1 2
T1 2
E/ 2
T1 = 2τ
E/ 2
τ τ
2 2
t
(1) 偶对称 b0 = 0 无正弦分量 (2) 正负交替,直流分量 (a 0 ) 为零 参照周期矩形脉冲频谱可得:
22
频谱图(Fn)
ω
18
2π
0
2π
4π
τ
ω1
τ
τ
陆建华
清华大学电子工程系
§3.3 典型周期信号的傅里叶级数
注意:
F 偶对称函数 bn = 0 ,n = 0, π, n 可由一图示出
一般情况:
Fn = Fn e j n
Fn 频谱幅度图, n 频谱相位图
以周期矩形脉冲为例说明周期信号谱特点(频谱分析要点) (1) 周期信号的频谱离散,谱线间隔
n =1
∞
1 其中: a 0 = T1
2 an = T1
∫
t 0 +T1
t0
t 0 +T1
f (t )dt
f (t ) cos nω 1 tdt
直流分量 余弦分量 正弦分量
∫
t0
2 bn = T1
∫
t 0 +T1
t0
f (t ) sin nω 1 tdt
6
清华大学电子工程系
陆建华
§3.2 傅立叶级数
清华大学电子工程系
陆建华
§3.3 典型周期信号的傅里叶级数
Fn
2ω1
2π
τ 3ω1
0
2π T1
4ω1
ω
偶次谐波=0!!
ω1
由 Fn 或 c n 公式(周期矩形脉冲信号)求基波及奇次谐波系数:
23
清华大学电子工程系
陆建华
§3.3 典型周期信号的傅里叶级数
2 Eτ nω 1τ cn = Sa T1 2
清华大学电子工程系
2π ω1 = T1
19
陆建华
§3.3 典型周期信号的傅里叶级数
T1 越大,谱线越密
T1 → ∞,非周期信号,频谱连续
一般信号 F 变换
nπτ nω 1τ (2) 幅度按 S a T 或 S a 2 变化 1 2mπ 当ω= ,谱线包络过零 τ
2π
0
偶函数 奇谐函数
清华大学电子工程系
f (t ) = f (t ±
T1 ) ,0 a 2
= 0 ,偶次谐波为0.
26
陆建华
第三章 傅里叶变换
本节课小结: 傅里叶级数(周期信号)
f (t ) =
n = ∞ ∞
∑
F (nω 1 )e jnω1t
1 F (nω 1 ) = T1
∫
T1
0
f ( t ) e jn ω 1 t dt
a n < 0 n = π
同样,还可以有另一种形式:
f (t ) = d 0 + ∑ d n sin (nω 1 t + θ n )
n =1 ∞
请同学们课后推导d0,dn 的表示式.
8
清华大学电子工程系
陆建华
§3.2 傅立叶级数
(二) 指数形式级数展开:(正交函数集 e jnω1t )
{
}
e jnω l t = cos nω 1t + j sin nω 1t 欧拉公式:
当 n =1
2 Eτ 1 ω 1τ Sa T1 2
(即 2 Fn )
2 Eτ = 2τ sin 2π 4 = 2E
π
π
n=3
n=5
1 = × π 3 2E 1 =+ × π 5
2E
2
2E 1 1 1 f (t ) = cos ω 1 t 3 cos 3ω 1 t + 5 cos 5ω 1 t 7 cos 7ω 1 t + π
12
清华大学电子工程系
陆建华
§3.2 傅立叶级数
负频率没有物理意义,不会在实际系统中出现, 其引入给信号分析带来便利.
(三) 函数的对称性与傅立叶系数的关系 (1) 偶函数
f (t ) = f ( t )
f(t)
T 1 2
0
T1 2
t
bn = 0
Fn = F n
清华大学电子工程系
(正弦分量) c n = a n , n = 0 1 = an 2
根据三角函数的性质,可将余弦分量和正弦分量合并:
f (t ) = c 0 + ∑ c n cos(nω 1 t + n )
n =1
∞
c0 = a0
(直流分量不变)
n
an
2 2 c n = a n + bn
n = tg
清华大学电子工程系
1
bn an
bn
cn
7
陆建华
§3.2 傅立叶级数
注意:
a 对于偶函数 bn = 0 , n > 0 n = 0 ;
§3.3 典型周期信号的傅里叶级数
f (t ) =
1 Fn = T1
E = T1
n = ∞
∑
∞
Fn e jnω1t
Ee
jnω 1 t
∫
T1 / 2
T1 / 2
1 dt = T1
τ /2
∫τ
τ /2
/2
Ee jnω 1t dt
1 jnω1t jnω e 1
sin
τ / 2
2 E e jnω1τ / 2 e jnω1τ / 2 = T1 nω 1 2j
ω1
2π
4π
ω
τ
τ
τ
(3) 周期信号含有无穷多条谱线,但根据其包络,能量主 2π ,即低频信号能量大. 要集中在第一个零点内 0 ~ τ
20
清华大学电子工程系
陆建华
§3.3 典型周期信号的傅里叶级数
定义 BW =
2π
τ
B 为信号带宽, W ∝
1
τ
信号带宽须与传输信道匹配 传输系统设计内容之一 采用信号带宽传输信号,去除高端频谱成份, 波形略有失真,但基本保持原形状.
