七年级数学线段的大小比较PPT优秀课件
合集下载
线段的大小比较PPT教学课件

韦伯
(1786-1826)
德国作曲家。他出生于一个戏剧之家,从小 随父母在各地旅行演出,对戏剧非常熟悉,对德 国民间音乐、风俗也有很深的体验。这对他以后 的音乐创作具有重要的意义。韦伯十岁学钢琴, 以后又学作曲,十二岁开始写作歌剧音乐。
1813年以后,他先后任布拉格剧院和德累斯顿交响乐团常任指挥, 对这两个演出团的成名起了重要的作用。 韦伯的代表作是歌剧《自由 射手》(即《魔弹射手》。它那浓郁的德国风格和浪漫气息,被认为 是德国第一部漫主义歌剧。此外,他还写了歌剧《奥伯龙》,以及少 序曲、协奏曲,奏鸣曲。其中,钢琴曲《邀舞》最为脍炙人口,人们 已将此改编成管弦乐曲和芭蕾舞演出。
平面上有四个点,过其中每两个点画直线,
可以画几条?
解:设平面内四点为A,B,C,D。
(1)当A、B、C、D四个点在同一条直线上时,
可以画出 一 条直线。
(2)当A、B、C、D四个点中有三个点在同一
条直线上时,可以画出 四 条直线。
(3)当A、B、C、D四个点中任意三个点都不在
同一条直线上时,可以画出 六 条直线。
线段的中点
中点的概念 :
把一条线段分成两条相等的线段的点, 叫做 这条线段的中点。(如图点C是线段AB的中点)
如果AB = 4 cm,那么
A
C
B
AC = BC
=
1 2
AB
=
2 cm
例:如图AB=6cm,点C是线段AB的中
点,点D是线段CB的中点,那么线段AD是
多长呢? A
CDB
解:∵C点是AB的中点
∴AC=CB= 1 AB = 3cm ∵ D点是BC的2中点 ∴ CD= 1 CB = 1.5cm
2
7.1线段的大小比较(公开课)ppt课件

拓展深化,发展思维
问:若要在西湖 风景区建造一个 消费场所,为了 方便游客,要求 是到图中四个红 色的旅游区的距 离之和最短,请 问应该建造在何 处?
F
C
D
EB
A
18
拓展深化,发展思维
我该怎么爬才能 B 最快吃到汉堡包
呢?
B
A
19拓展深化,发展思维源自我该怎么爬才 能最快吃到汉
堡包呢?
B
A’
A
c
20
12
适时归纳,内化小结
比较线段的大小的方法:
度量法和叠合法
尺规画线段的方法和步骤:
1、画射线
2、截线段(共端点)
3、写结论
13
活动二:他想尽快从教学楼到达活动室,
该选择哪条路,为什么?
联结两点的线段的长度叫做两点
活动 室
之间的距离(distance).
两点之间,线段最短.
③
② 教学 楼
① 14
巩固运用,内化新知
下列说法正确的是( D )
A、连结两点的线段叫做两点之间的距离. B、两点间的连线的长度,叫做两点之间的距离. C、连结两点的直线的长度,叫做两点之间的距离. D、连结两点的线段的长度,叫做两点之间的距离.
15
巩固运用,内化新知
有A、B、C三城市,已知A、B两市的距离为 50千米,B、C两市的距离是30千米,那么A、
已知线段AB,线段CD,如何比较 这两条线段的大小?
A
B
C
D
6
度量法
A
C
B
(3.8㎝)
D (4.1㎝)
因为量得AB=3.8cm,CD=4.1cm, 所以AB<CD
7
叠合法
6.3 线段的长短比较 教学课件 (共28张PPT)
讲授新课
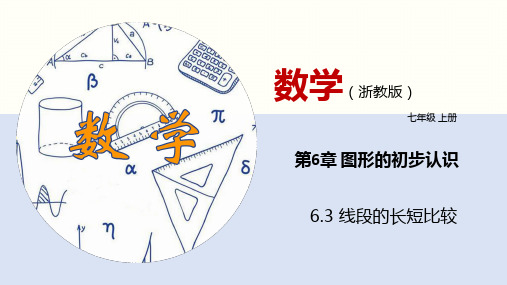
作一条线段等于已知线段 已知:线段 a,作一条线段 AB,使 AB=a. 第一步:用直尺画射线 AF; 第二步:用圆规在射线 AF 上截取 AB = a. 所以线段 AB 为所求线段.
a Aa B F
在数学中,我们常限定用无刻度的直尺和圆规作图,这就是尺规作图.
讲授新课
尺规作图的要点: 1.直尺只能用来画线,不能量距; 2.尺规作图要求作出图形,说明结果,并保留作图痕迹.
生活中我们常常会比较两个物体的长短。如图两支铅笔 谁长?
我们可以把两支铅笔看成两条线段,这样我们就把实际 问题转化为了几何问题.
讲授新课
思考:怎样比较两条线段的长短??
Aa B
(1)度量法 用刻度尺量出它们的 长度,再进行比较.
Cb
D
(2) 叠合法 将其中一条线段“移动”, 使其一端点与另一线段的 一端点重合,两线段的另 一端点均在同一射线上.
(2)连接两点的线段叫两点间的距离;
(3)两点之间所有连线中,线段最短;
(4)射个
C.3个
D.4个
当堂检测
2.某同学用剪刀沿直线将一片平整的银杏叶减掉一部分(如图),发现剩下的银
杏叶的周长比原银杏叶的周长要小,能正确解释这一现象的数学知识是(
)
A.两点之间线段最短 C.垂线段最短
解:作图步骤如下:
aa b
(1)作射线 AM;
A B1 B2
BM
(2)在 AM 上顺次截取 AB1=a,B1B2=a,
B2B=b,则线段 AB=2a+b.
讲授新课 知识点三 有关线段的基本事实
探究
我要去书店 怎么走呀?
商场
礼堂
书店
讲授新课
根据生活经验,容易发现: 两点之间的所有连线中,线段最短
《比较线段的长短》基本平面图形PPT优秀课件

记作AD= .
a
b
a-b a+b
a
b
A
a-b
D bB
C
巩固练习
1.如图,点B,C在线段 AD 上则AB+BC = ____; AD-CD = ___;ACBC= ___ -_A_C= __A_B- ___B.D
AC CD
A
B
C
D
2.如图,已知线段a,b,画一条线段AB,使AB=2a-b.
a
b
2a
b
a b (1)
三组图形中,线段 a与b的长度均相等
a
b
(2)
a
b (3)
很多时候,眼见未必为实. 准确比较线段的长短还需要更加严谨的办法.
探究新知
合作探究
做手工时,在没有刻度尺的条件下,若想从较长的木棍上截下一段 ,使截下的木棒等于另一根短木棒的长,我们常采用以上办法.
探究新知
思考画在黑板上的线段是无法移动的,在只有圆规和无刻度的直尺的情况下,请 大家想想办法,如何再画一条与它相等的线段?
个关于x的一元一次方程,解方程,得到x的值,即可得到所求各线段的长.
探究新知
AE B C
F
D
解:设AB=3x,BC=2x,CD=5x,
因为E,F分别是AB,CD的中点,
所以BE=
1 2
AB=
3 2
x,CF=
1 2
CD=52
x,
所以EF=BE+BC+CF=
3 2
x
+
2x
+
5 2
x
= 6x
因为EF=24,所以6x=24,解得x=4.
线段的中点
a
a
A
M
人教版线段的比较大小教学PPT课件

a
2、你能用直尺和圆规画出一条线段c,使它等于已知线段a的2倍。
尺规作图注意事项: 1、只要求作出图形,说明结果; 2、保留作图痕迹。
请说说你的画法
O
P
B
线段OB就是所求做的线段c
A
直尺只用来画线,不用来量距离;
已知:线段a,b(如图),用直尺和圆规画一条线段c,使得它的长度等于两条已知线段的长度的和。
=8-5=3cm
l
A
B
C
l
A
B
C
1、有A、B、C三个城市,已知A、B两城市的距离 为50千米,B、C两城市的距离为 30 千米,那么 A、C两城市的距离是( ) A、80千米 B、20千米 C、40千米 D、处于20千米到80千米间
数学小趣闻—尺规作图
①
②
③
A
B
B
A
A
B
C
D
E
F
M
N
AB>CD
AB=EF
AB<MN
比较线段长短的两种方法: 1、度量法——从“数值”的角度比较 2、叠合法——从“形”的角度比较
起点对齐,看终点
1) 用刻度尺量出图中的三角形 三条边的长: AC=__cm; BC=__cm; AB=__cm.
2) 用“=”、“<”或“>”号填入 下面的空格: AC___BC, AC___AB, AB___BC.
A
B
C
1.0
2.0
>
<
>
1.8
2、用圆规比较下列各组线段的长短。
>
<
=
1、已知线段a,用直尺和圆规画一条线段b,使它等于已知线段a。
线段的大小的比较ppt课件
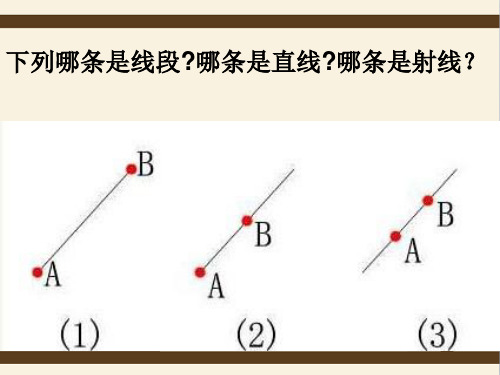
如图,已知线段a,画出线段AB ,使得AB=a.
a
解: 方法二: 1.画一条射线AC;
用直尺和圆
2.在射线AC上截取线段AB=a.
规
A
B
C
以点A为圆心,a
为半径画弧,交射
∴线段AB就是所要画的线段.
线AC于点B.
例题:先观察估计图中线段a,b的大小,然后用比较
线段大小的方法验证你的估计,并用“<”符号连结.
活动室
联结两点的线段的 长度叫做两点之间 的距离.
教学楼
两点之间,线段最短.
练习:下列叙述正确的是( D )
A.联结两点的直线叫做两点之间的距离. B.联结两点的线段叫做两点之间的距离. C.联结两点的直线的长度叫做两点之间的距离. D.联结两点的线段的长度叫做两点之间的距离.
线段是几何图形,两点 之间的距离是一个数量.
下列哪条是线段?哪条是直线?哪条是射线?
讨论:说一说直线、射线、线段之间的区别与联系.
名称
直线AB 射线AB 线段AB
图形 端点个数 延伸方向 能否度量
AB
AB
A
B
无 一个 两个
向两方无限 延伸
向一方无限 延伸
不向任何一 方延伸
不能 不能
能
线段和射线是直线的一部分.
线段的表示方式
(1)用表示端点的两个大写英文字母表示:
思考:如图为正方体和圆柱体实心木块,小老鼠从表面 爬过,走什么线路,吃到汉堡时爬过的路程最短?
A
自主小结:
1.线段的两种表示方法:
A 两个大写英文字母;
B 记作线段AB
一个小写英文字母.
a
记作线段a
2.线段大小的比较的一般方法:目测法;度量法;叠合法.
比较线段的大小PPT课件(精选)19页PPT

21、要知道对好事的称颂过于夸大,也会招来人们的反感轻蔑和嫉妒。——培根 22、业精于勤,荒于嬉;行成于思,毁于随。——韩愈
23、一切节省,归根到底都归结为时间的节省。——马克思 24、意志命运往往背道而驰,决心到最后会全部推倒。——莎士比亚
25、学习是劳动Байду номын сангаас是充满思想的劳动。——乌申斯基
谢谢!
比较线段的大小PPT课件(精选)
•
6、黄金时代是在我们的前面,而不在 我们的 后面。
•
7、心急吃不了热汤圆。
•
8、你可以很有个性,但某些时候请收 敛。
•
9、只为成功找方法,不为失败找借口 (蹩脚 的工人 总是说 工具不 好)。
•
10、只要下定决心克服恐惧,便几乎 能克服 任何恐 惧。因 为,请 记住, 除了在 脑海中 ,恐惧 无处藏 身。-- 戴尔. 卡耐基 。
数学七年级上册比较线段的大小课件_PPT公开课

• 如果一条线段上有两个点,将该线段分成相等的 三部分,那么这两个点就是该线段的三等分点。
• 如果一条线段上有三个点,将该线段分成相等的 四部分,那么这两个点就是该线段的四等分点。
• …… …… …… ……
(M-1) • 如果一条线段上有 个点,将该线段分成相等的 • M 部分,那么这两个点就是该线段的M等分点。
比较线段AB、线段CD的大小。
• 当然可以叠加!(使用尺规作图) 作出另一条线段与已知线段相等。
完成课本128页练习1。
a b 此时,AB=AC+CB=2a。
1、用有刻度的直尺,沿着直尺边缘画。
用好圆规即可。 作一条线段等于已知线段a。
a
b
如果一条线段上有两个点,将该线段分成相等的三部分,那么这两个点就是该线段的三等分点。
1、先用无刻度的直尺画一条直线(或射线),
A 1、先用无刻度的直尺画一条直线(或射线),
2、用没有刻度的直尺和圆规画。
C
B
• 记作: 1、直线、射线和线段有哪些特征?
限定只用无刻度的直尺和圆规作图。 4、得到结论:线段AB即为所求线段。
AB=AC+aCBb=a+b。 2、画图,需要哪些工具?
此时,AB=AC+CB=2a。 如何比较两条线段的长短?你有哪些方法?
作出另一条线段与已知线段相等。
画一条线段AB,使得AB=2a。
• 中几点何。语言: 后续会有更多尺规作图实例介绍。
此时,AB=AC+CB=2a。
此时,AB=AC+CB=2a。
• ∵C是AB中点,∴ AC=CB=½AB。
ቤተ መጻሕፍቲ ባይዱ
• 或∵C是AB中点,∴AB=2AC=2BC 16-11
• 如果一条线段上有三个点,将该线段分成相等的 四部分,那么这两个点就是该线段的四等分点。
• …… …… …… ……
(M-1) • 如果一条线段上有 个点,将该线段分成相等的 • M 部分,那么这两个点就是该线段的M等分点。
比较线段AB、线段CD的大小。
• 当然可以叠加!(使用尺规作图) 作出另一条线段与已知线段相等。
完成课本128页练习1。
a b 此时,AB=AC+CB=2a。
1、用有刻度的直尺,沿着直尺边缘画。
用好圆规即可。 作一条线段等于已知线段a。
a
b
如果一条线段上有两个点,将该线段分成相等的三部分,那么这两个点就是该线段的三等分点。
1、先用无刻度的直尺画一条直线(或射线),
A 1、先用无刻度的直尺画一条直线(或射线),
2、用没有刻度的直尺和圆规画。
C
B
• 记作: 1、直线、射线和线段有哪些特征?
限定只用无刻度的直尺和圆规作图。 4、得到结论:线段AB即为所求线段。
AB=AC+aCBb=a+b。 2、画图,需要哪些工具?
此时,AB=AC+CB=2a。 如何比较两条线段的长短?你有哪些方法?
作出另一条线段与已知线段相等。
画一条线段AB,使得AB=2a。
• 中几点何。语言: 后续会有更多尺规作图实例介绍。
此时,AB=AC+CB=2a。
此时,AB=AC+CB=2a。
• ∵C是AB中点,∴ AC=CB=½AB。
ቤተ መጻሕፍቲ ባይዱ
• 或∵C是AB中点,∴AB=2AC=2BC 16-11
人教版七年级上册比较线段的大小PPT

1、M是线段AB上的一点,其中不能判定点
M是线段AB中点的是( A )
A、AM+BM=AB C、AB=2BM
B、AM=BM D、AM= 1 AB
2
2、线段AB=6厘米,点C在直线AB上,
且BC=3厘米,则线段AC的长为( c)
A、3厘米
B、9厘米
C、3厘米或9厘米 D、无法确定
3、已知:线段AB=4cm,延长AB至点C, 使AC=12cm,点D是AB的中点,点E是BC AM = MN = NP = PB = AB
3、如图,点D是线段AB的中点,C 是线段AD的中点,若AB=4cm,求 线段AD与CD的长度。
A CD
B
解:∵点D是线段AB的中点,∴AD=BD= 1 AB, ∵AB=4cm, ∴AD= 1 ×4=2cm, 2
2
∵点C是线段AD的中点,
∴AC=CD=
1 2
AD
=
1 2
×2=1cm.
四、拓广延伸
解:
a
a
A
B
CP
AC=2a,则线段为所求作的图形.
点B把线段AC分成相等的两条线段AB与BC,点
B叫做线段AC的中点, 可知AB=BC= 1 AC,或者AC=2AB=2BC. 2
思 考 :什么叫做三等分点?四等分点呢?
三等分点:
A
M
N
B
AM = MN = NB = 1 AB 3
四等分点: A
M
N
——线段的大小比较与有关运算
一、情景活动
哪个高?
成成
明明
怎样比较他们的高矮呢?
二、学习新知
已知线段AB与线段CD, 如何比较这两条线段的长短(大小)?
人教版七年级上册 4.2 线段的大小比较(15张PPT)

例:如图,AB=12cm,-点D是线段CB的中点, 那么AD有多长呢?
解法一:
A
C DB
解: ∵点C是线段AB的中点
∴ AC=CB= 1 AB 6cm
2
CD 1 CB 3cm 2
AD AC CD 9cm
解法二: ∵点C是线段AB的中点
∴AC=CB= 1 AB 6c.AC=BD
B.AC<BD
C.AC>BD
D.不能确定
AB C D
4.如图,点C是线段AB的中点,点D是线段BC
的中点,下面等式正确的是( D )
A.CD=AD-BC
B.CD=AC-DB
C.CD= AB-BD
D.CD=AB-AD
A
CD B
5.如图,点M是线段AB的中点,点C、D把线 段AB三等分。已知线段CM=2.5cm,求线段AB 的长等于__1_5___.
2
BD 1 CB 3cm 2
AD AB BD 9cm
练习
1.观察下列三组图形,分别比较线段a、b的长短
a
b
(1)
b
(2)
a
(3)
b
a
答:三个小题中都是a=b.
练习 2.如图所示,从A村出发到B村,最近的路线
是( B )
A.A—C—D—B B.A—C—F—B C.A—C—E—F—B D.A—C—M—B
郝芳平 2019.12.9
情境引入 小红站在 石头上和小明比身高.你们能马上判 断出他们的高矮吗? 有什么方法来判断他们的高矮?
不能
他们站在同位 置上,再比较。
用刻度尺来测 量他们身高。
探究新知
比较两条线段的长短方法 1 度量法
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
平面上有四个点,过其中每两个点画直线,
可以画几条?
解设平面内四点为A,B,C,D。
(1)当A、B、C、D四个点在同一条直线上时,
可以画出 一 条直线。
(2)当A、B、C、D四个点中有三个点在同一
条直线上时,可以画出 四 条直线。
(3)当A、B、C、D四个点中任意三个点都不在
同一条直线上时,可以画出 六 条直线。
∴AC=CB= 1 AB = 3cm ∵ D点是BC的2中点 ∴ CD= 1 CB = 1.5cm
2
∴ AD= AC + CD= 3 + 1.5= 4.5cm
THANKS
FOR WATCHING
演讲人: XXX
PPT文档·教学课件
所以直线比射线长( );
3.如图,直线有 条,
分别是
;
线段有 条,
分别是
;
在直线EF上的射线有 条,
分别是
.
A
E BD C F
线段的长短比较
思考 :怎样比较两支铅笔的长短? 怎样比较两个同学的高矮?
比较两个同学高矮的方法:
① 让两个同学站在同一平地上,脚底平齐, 观看两人的头顶,直接比出高矮;
——重合法 ② 用卷尺分别度量出两个同学的身高,将
线段的中点
中点的概念 :
把一条线段分成两条相等的线段的点, 叫做 这条线段的中点。(如图点C是线段AB的中点)
如果AB = 4 cm,那么
A
C
B
AC = BC
=
1 2
AB
=
2 cm
例:如图AB=6cm,点C是线段AB的中
点,点D是线段CB的中点,那么线段AD是
多长呢? A
CDB
解:∵C点是AB的中点
想一想
凭你的直觉比一比下列三组图形中线段a、 b的长短
(1)
a
(2) a
b
b
(3)
a
b
用圆规作一条线段等于已知线段
做一做
用圆规作一条线段等于已知线段MN。
① 作射线AB; ② 用圆规量出已知线段MN的长度;
③ 在射线AB上以A为圆心, 截取AC = MN .
∴线段AC为 所求的线段。
MN AC
B
∴可以画出 一 或 四 或 六
条直线。
想一想
1、说出下列所示图形的名称及表示方法。
.
A
.
B
(线段AB)
.
.
A
B
.
.
A
B
(射线AB) (直线AB)
2.判断正误 ①延长直线AB到C( ); ②反向延长射线AB到C( ); ③延长线段AB到C( ); ④直线a、b相交于一点m( ); ⑤因为射线是直线的一半,
所得的数值进行比较。 ——度量法.
议 一 议 试比较线段AB、CD的长短。
.
.
.
.
A
B
C
D
(1) 度量法
用刻度尺量出线段AB长4cm,线段CD长
4.5cm,所以线段AB比线段CD短。(记作AB
<CD 或 CD >AB)
(2) 重合法 将一线段“移动”,使其一端点与
另一线段的一端点重合,两线段的另一 端点均在同一射线上。
可以画几条?
解设平面内四点为A,B,C,D。
(1)当A、B、C、D四个点在同一条直线上时,
可以画出 一 条直线。
(2)当A、B、C、D四个点中有三个点在同一
条直线上时,可以画出 四 条直线。
(3)当A、B、C、D四个点中任意三个点都不在
同一条直线上时,可以画出 六 条直线。
∴AC=CB= 1 AB = 3cm ∵ D点是BC的2中点 ∴ CD= 1 CB = 1.5cm
2
∴ AD= AC + CD= 3 + 1.5= 4.5cm
THANKS
FOR WATCHING
演讲人: XXX
PPT文档·教学课件
所以直线比射线长( );
3.如图,直线有 条,
分别是
;
线段有 条,
分别是
;
在直线EF上的射线有 条,
分别是
.
A
E BD C F
线段的长短比较
思考 :怎样比较两支铅笔的长短? 怎样比较两个同学的高矮?
比较两个同学高矮的方法:
① 让两个同学站在同一平地上,脚底平齐, 观看两人的头顶,直接比出高矮;
——重合法 ② 用卷尺分别度量出两个同学的身高,将
线段的中点
中点的概念 :
把一条线段分成两条相等的线段的点, 叫做 这条线段的中点。(如图点C是线段AB的中点)
如果AB = 4 cm,那么
A
C
B
AC = BC
=
1 2
AB
=
2 cm
例:如图AB=6cm,点C是线段AB的中
点,点D是线段CB的中点,那么线段AD是
多长呢? A
CDB
解:∵C点是AB的中点
想一想
凭你的直觉比一比下列三组图形中线段a、 b的长短
(1)
a
(2) a
b
b
(3)
a
b
用圆规作一条线段等于已知线段
做一做
用圆规作一条线段等于已知线段MN。
① 作射线AB; ② 用圆规量出已知线段MN的长度;
③ 在射线AB上以A为圆心, 截取AC = MN .
∴线段AC为 所求的线段。
MN AC
B
∴可以画出 一 或 四 或 六
条直线。
想一想
1、说出下列所示图形的名称及表示方法。
.
A
.
B
(线段AB)
.
.
A
B
.
.
A
B
(射线AB) (直线AB)
2.判断正误 ①延长直线AB到C( ); ②反向延长射线AB到C( ); ③延长线段AB到C( ); ④直线a、b相交于一点m( ); ⑤因为射线是直线的一半,
所得的数值进行比较。 ——度量法.
议 一 议 试比较线段AB、CD的长短。
.
.
.
.
A
B
C
D
(1) 度量法
用刻度尺量出线段AB长4cm,线段CD长
4.5cm,所以线段AB比线段CD短。(记作AB
<CD 或 CD >AB)
(2) 重合法 将一线段“移动”,使其一端点与
另一线段的一端点重合,两线段的另一 端点均在同一射线上。
