第一节向量组与矩阵的秩
向量组与矩阵的秩

1 2 0 8 6
0 0 0 9 8
1 2 0 1 2
1 2 0 1 2
r3 1 r2
0
2
3
2
0 0 0 0
1
r3
r4
0
2
3
2
0
0 0 0 9
1 8
B
0 0 0 9 8
0 0 0 0 0
R{1,2 , ,n} n ,则向量组 1,2 , ,n 线性无关。
如果向量组的秩小于向量组所含向量的个数,即
R{1,2 , ,n} n ,则向量组 1,2 , ,n 线性相关。
性质2.5 (1)若向量组A可由向量组B线性表示,则r(A)<=r(B). (2) 等价向量组的秩相同.
如果 A 为 mχ n 矩阵,则 R(A)≤ min (m,n)。
特别当 R(A)=m 时,称矩阵 A 为行满秩;当 R(A)=n 时,称矩
阵 A 为列满秩;当 R(A)=m=n 时,称矩阵 A 为满秩矩阵。
例 求矩阵的秩
2 1 0 3 2
B
0
3
1 2
5
0 0 0 4 3
1 1,2,0,1,2 0,1,0,1,3 1,3,0,2,4 1,2,1,1
解法1:构造矩阵
1 0 1 1
1 0 1 1
1 0 1 1
A
2
1
3
2
r2
2r1
0
1
1
0
r4
r2
0
矩阵的秩及向量组的极大无关组求法

7.1 矩阵的秩的概念
定义1 设A是m╳n矩阵,在A中任取k行k列(1≤k≤min{m,n}),
位于k行k列交叉位置上的k2个元素,按原有的次序组成的k阶行列
式,称为A的k阶子式. 如矩阵
1 A 1
1 1
0 2
2 1
0 0 3 2
第1,3行及第2,4列交叉位置上的元素组成的一个二阶子式为
4 2 , 1 ,4 , 7 ,5 5 , 8 ,1 ,2 .
解:以给定向量为列向量作成矩阵A,用初等行变换将A化为阶梯形矩阵
1 2 0 2 5
A
2 0 3
5 3 6
1 3 0
1 4 7
8
1 2
1 2 0 2 5
0 1 1 3 2
0 0
3 0
3 0
4 13
113
1 2 0 2 5 0 1 1 3 2
下页
11
求向量组的秩的方法
①把向量组的向量作为矩阵的列(或行)向量组成矩阵A; ②对矩阵A进行初等行变换化为阶梯形矩阵B; ③阶梯形B中非零行的个数即为所求向量组的秩.
例4. 求下列向量组 1=(1, 2, 3, 4),2 =( 2, 3, 4, 5),3 =(3, 4, 5, 6)的秩.
解2:以1,2,3为行向量作成矩阵A,用初等变换将A化为
阶梯形矩阵后可求.
1 2 3 r2 2 r1 1 2 3
2
3
3 4
4
5
r3 3 r1 r 4 4 r1
0
0
1
2
2 4
4 5 6
0 3 6
r3 2 r2 r4 3 r2
1 2 3
线性代数课件PPT第三章 线性方程组 S1 向量组与矩阵的秩

i
am1 am2 amn m
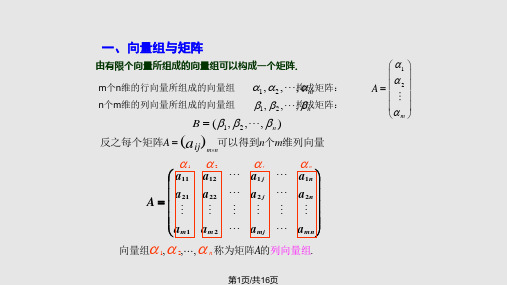
向量组 1 ,2 , ,m 称为矩阵A的行向量组.
11
反之,由有限个向量所组成的向量组可以构 成一个矩阵.
m个n维列向量所组成的向量组1, 2 ,, m ,
构成一个n m矩阵
A (1 , 2 ,, m )
m个n维行向量所组成
的向量组1, 2 , m ,构成
li hi 0, (i 1, 2, , s)
即 li hi , (i 1, 2, , s)
所以表示法唯一. 例5和例6的结论可作为定理使用
24
三、几个有关的结论
定理2 n阶行列式|A|=det(aij)=0 它的n个行(列) 向量线性相关.
25
推论 n阶行列式|A|≠0 它的n个行(列)向量线 性无关.
(a1 , a2 , , an ),
注意
b1
b2
bn
行向量和列向量都按照矩阵的运算法则进行运算.
9
§3.1.1.2向量组的线性相关性
一、向量、向量组与矩阵
若干个同维数的列向量(或行向量)所组成 的集合叫做向量组.
例如1 A
矩阵A
a11 a21
(a
2
a12
a22
ij)mn
但是,若A为可逆矩阵,则可以得到B=O.
| An | n | A |
注意: 矩阵与行列式线性运算的不同点,以及
(AB)T=BTAT
|AnBn| = |An| |Bn| = |Bn| |An|
2
3. 掌握逆矩阵及其性质、矩阵可逆的充要条 件,会用伴随矩阵求二阶矩阵逆矩阵. 如: |A|≠0时A可逆,或对于方阵A,若存在 方阵B,使 AB=E (AB=BA=E)则A可逆。 (AT)−1=(A−1)T, (AB)−1=B−1A−1, |A−1|=|A|−1 A−1=A* / |A|,注意A*中元素的排列顺 序 对任意方阵A,有 AA*=A*A=|A|E
3向量组与矩阵的秩

s
ki i
i 1
k1a1 p2
k2a2 p2
ksasp2
k1a1 pn k2a2 pn ksaspn
上两式只是各分量的排列顺序不同,因此
k11 k2 2 ks s 0
当且仅当 k11 k2 2 ks s 0
所以1,2 , s和1, 2 , s 有相同的线性相关性。
(8)1
(9)0 0
(10)k0 0
(11)如果k 0且 0,那么k 0
上页 下页
§2 线性相关与线性无关
矩阵与向量的关系:
通常把维数相同的一组向量简称为一个向量组,n维行
向量组 1,2 , s可以排列成一个s×n分块矩阵
1
2
s
其中 i为由A的第i行形成的子块, 1,2 , s称为A的行向量组。
上页 下页
定理5 在r维向量组1,2 , s 的各向量添上n-r个分 量变成n维向量组 1, 2 , s 。
(1)如果 1, 2 , s线性相关,
那么
1
,
2
,
也线性相关。
s
(2)如果1,2 , s线性无关,
那么1, 2 , s也线性无关。
证 对列向量来证明定理。
(1,2 , ,s ) A1
(1, 2,
当且仅当k1=k2=…=kn=0
因此 1 , 2 , n 线性无关。
1,2
,
称为基本单位向量。
n
上页
下页
例 设向量组 1,2 ,3线性无关,1 1 2 , 2 2 3 ,3 3 1,试证向量组 1, 2 , 3也
线性无关。
证 对任意的常数都有
k11 k22 k33 (k1 k3 )1 (k1 k2 )2 (k2 k3 )
向量组的秩与矩阵秩的关系

向量组1
a12
a22
a1n a2n
am1 am2 amn
A的列向量组为1,2 ,,n ; A的行向量组为 1T , 2T ,, mT.
➢ 称A的列向量组的秩为A的列秩;
➢ 称A的行向量组的秩为A的行秩.
向量组的秩与矩阵秩的关系
设矩阵A
1 0
1 1
1 2
,试确定矩阵的秩,行秩,列秩.
0 0 0
➢ 矩阵A的秩为 2;
➢ A的行向量组为:1T 1 1 1, 2T 0 1 2, 3T 0 0 0.
➢
1T
,
T 2
是
A 的行向量组的一个极大无关组,A 的行秩是2.
向量组的秩与矩阵秩的关系
1
1
1
A的列向量组为 1 0,2 1,3 2.
感谢观赏
小学教育专业群教学资源库
向量组的秩与矩阵秩的关系
Lorem Ipsum is simply dummy text of the printing and typesetting industry
01
向量组的秩与矩阵秩的关系
向量组的秩与矩阵秩的关系
含有限个向量的有序向量组与矩阵一一对应
Amn 1 2 n
向量组的秩与对应的矩阵的秩具有什么联系?
0
0
0
由于 1,2线性无关,3 22 1 ,故 1,2是A的列向量
组的一个极大无关组,因而A的列秩为2.
在本例中,我们发现矩阵的秩等于其行秩和列秩! 这一结论是否具有普遍意义呢?
向量组的秩与矩阵秩的关系
回顾
1 0
0 1
0 0
c11 c21
c1,nr c2,nr
A B 0 0 1 cr1 cr,nr
第四章-向量组的线性相关性与矩阵的秩

二、矩阵秩的性质
性质1 矩阵的秩等于其转置的秩,即 r(A)=r(AT).
利用行列式的性质1很容易证明此性质。
引理1 对于m×n 型矩阵 A , r(A)=n ÙA 的列向量组
线性无关。
所谓 a1, a2, …, as 线性无关,即如果 k1 a1 + k2 a2+ …+ks as = 0,
则必有 k1= k2= …= ks= 0.
例2 向量组 a1 = (1, 2, 0, 1)T, a2 = (1, 1, −1, 3) T, a3= (1, 3, 1, − 1)T
线性相关, 因为 2a1− a2 − a3 = 0.
x1 a1 + x2 a2+ …+xn an = b,
⇒
定理 1 对于方程组Ax=b, (1) Ax=b有解Ù向量b能由向量组a1, a2, …,an 线 性表示;
(2) Ax=b有唯一解Ù向量b能由向量组a1, a2, …,an 线性表,并且表示方法唯一.
齐次线性方程组Ax=0有非零解 Ù存在非零向量c,使得Ac=0。 设矩阵A为m×n阶矩阵,将A列分块为A=(a1,…, an)。
组的秩称为矩阵的列秩。
定义2 设 A 为 m × n 矩阵,在 A 中任取 k 行 k 列 ( 1 ≤ k
≤ min ( m, n) ), 由交叉处的 k2 个元素 ( 不改变它们 的相对位置 ) 所构成的方阵称为A的一个k 阶子阵,其 行列式称为 A 的一个 k 阶子式。
如:
⎡2 4 −1⎤
A = ⎢⎢1 0
充分性 <=
矩阵的秩与向量组的秩一致

矩阵的秩与向量组的秩一致矩阵和向量组是线性代数中非常重要的概念,秩也是矩阵和向量组中的一个重要性质。
矩阵的秩和向量组的秩之间有一个非常重要的关系,本文将对这个关系进行详细的探讨,希望能够帮助读者更好地理解这一概念。
一、矩阵的秩矩阵的秩是矩阵的一个重要属性,它可以反映出矩阵所包含的线性空间的维数。
在矩阵中,如果某些行或列之间有一定的线性关系,那么这些行或列就会被称为线性相关的行或列,相反,如果行或列之间没有任何线性关系,那么它们就被称为线性无关的行或列。
在进行矩阵的行变换或列变换时,矩阵的秩不会发生改变。
因此,我们可以通过这些变换来简化矩阵的计算,并最终得出矩阵的秩。
其中最常用的方法是高斯消元法和初等矩阵法。
从几何意义上讲,矩阵的秩可以表示为矩阵所包含的向量空间的维数。
在二维平面内的向量空间中,我们可以用一个二维矩阵来表示,这个矩阵的秩就等于所包含向量的个数;同样,在三维空间内,我们可以用一个三维矩阵来表示向量空间,其秩就代表该空间所包含的向量数。
二、向量组秩向量组秩是指一组向量的线性无关的个数,即向量组中最大的线性无关向量个数。
如果向量组中某些向量之间存在线性依赖关系,那么称这些向量是线性相关的。
因此,向量组的秩和矩阵的秩是有密切联系的。
从几何角度来看,向量组的秩可以理解为所构成的向量空间的维数。
当向量组的秩等于向量空间的维数时,这个向量组就可以作为向量空间的一组基,而向量空间中的任何向量都可以表示为这个向量组的线性组合。
矩阵的秩和向量组秩之间有一种非常重要的一致性,即矩阵的秩等于它所包含向量组的秩。
这个定理有以下两种不同的表述方式:1. 若矩阵A的秩为r,则矩阵A所包含的向量组的秩也为r。
这两种表述方式的本质是一样的,它们都说明了矩阵的秩与其所包含的向量组秩是完全一致的。
这个定理在线性代数的理论和实际应用中都发挥着非常重要的作用,因为它可以方便地将矩阵和向量组之间的关系进行转换和应用。
四、应用举例在实际应用中,矩阵的秩与向量组秩的一致性有很多不同的应用。
大学课程大一数学线性代数上册14.矩阵的秩课件

或
A
2
r1r2
B
1
2
,
s
s
则 A 的行向量组与 B 的行向量组等价, 由书上第127页推论
可知 A 的行向量组的秩与 B 的行向量组的秩相等.
(2) 用初等行变换化 A 为阶梯形矩阵 U;
(3) U 的行向量组的秩与 A 的行向量组的秩相同.
4
例1 求下列矩阵 A 行向量组的一个
1 2 1 0 1
(4) 阶梯形矩阵 U 的列向量组的极大无关组就是 U 中每个非
零行第一个非零元所在的列向量所组成的向量组.
3
向量组秩的求法之二
(1) 将向量组 1, 2, , s 按行排成矩阵,并作行初等变换,
例如 1
1
A
2
r2
B
2
,
0,
或
1
2
A
2
r1r2
B
1
,
s
s
s
s
1
1
其非零行的行数为 r(A), B 通过初等行变换化为阶梯形矩阵, 其非零行的行数为 r(B), 则
行 A0数为B0 r(A通)过+ 初r(B等),行故变r换 可A0以化B0 为 阶r梯(A形) 矩r阵(B,);其非零行的
9
(2) r(A+B) r(A) + r(B);
证法一 记 A = (1, 2 ,, n), B = (1, 2 , , n).
如果引入下列定义, 则可以把以上两个结论叙述的更简练.
定义1 矩阵 A = (aij)mn 中行向量组的秩称为行秩, 列向量组 的秩称为列秩.
定理1 初等变换不改变矩阵行秩和列秩.
3-3 矩阵的秩与向量组的秩

§3 矩阵的秩与向量组的秩定义 设在矩阵A 中有一个不等于零的r 阶子式D ,且所有1+r 阶子式(如果存在的话)全等于零,则称D 为矩阵A 的最高阶非零子式,数r 称为矩阵A 的秩,记作)(A R . 并规定零矩阵的秩等于0。
由行列式的性质可知,在A 中当所有1+r 阶子式全等于零时,所有高于1+r 阶的子式也全等于零,因此矩阵A 的秩)(A R 就是A 中不等于零的子式的最高阶数。
显然,A 的转置矩阵T A 的秩)()(A R A R T =.与矩阵的最高阶非零子式和矩阵的秩的定义相对应,可定义向量组的最大无关组和向量组的秩。
定义 设有向量组T ,如果(1)在T 中有r 个向量r ααα ,,,21线性无关;(2)T 中任意1+r 个向量(如果存在的话)都线性相关, 则称r ααα ,,,21是向量组T 的一个最大线性无关组,简称最大无关组,数r 称为向量组的秩。
并规定只含零向量的向量组的秩为0.矩阵的最高阶非零子式可能不止一个,向量组的最大无关组也可能不止一个。
例如,向量组A :)1,2,1(1-=α ,)1,3,2(2-=α ,)1,1,4(3-=α可构成三阶方阵⎪⎪⎪⎭⎫ ⎝⎛---=114132121A方阵A 只有一个3阶子式||A ,且0||=A ,而A 的9个2阶子式恰好都不等于零,因此A 中任何一个2阶子式都是A 的最高阶非零子式。
且21,αα 是向量组A 的一个最大无关组,而32,αα 或31,αα 也都是向量组A 的最大无关组。
例1 全体n 维向量构成的向量组记作n R ,求n R 的一个最大无关组及n R 的秩。
解 我们已经证明了n 维单位坐标向量组E :n εεε ,,,21是线性无关的,又由定理6的推论3可知,n R 中任意1+n 个向量都线性相关,因此向量组E 就是n R 的一个最大无关组,且n R 的秩等于n .显然,n R 的最大无关组很多,任何n 个线性无关的n 维向量都是n R 的最大无关组。
3.3向量组的秩与矩阵的秩

定义3.设A是一个矩阵,称A的行向量组的秩为 A的行秩;称A的列向量组的秩为A的列秩。
定理4.矩阵的初等变换不改变矩阵的行秩和列秩.
a1,1
证明:设AFra biblioteka2,1
M
a1,2 L a2,2 L ML
am
,1
am,2
L
a1,n
a2,n
M
am
,n
(1)首先证明矩阵的初等行变换不改变矩阵的行秩
类似可证:矩阵的初等列变换不改变矩阵的 列秩。
(2)证明矩阵的初等行变换也不改变矩阵的列秩
设A:1, 2, …, r, r+1, …, n是矩阵A的列向 量组,无妨说:1, 2, …, r是A的极大线性无关
组. P是一个m阶的初等方阵
B:P1, P2, …, Pr, Pr+1, …, Pn
依据定理3得知:
定义2. 设A是一组n维向量,1, 2, …, r是A的
一个极大线性无关组。称r为A向量组的秩, 记为R(A).
推论2:若向量组A和向量组B等价, 则R(A) = R(B)
证明:设1, 2, …, r是向量组A的一个极大线性 无关组;1, 2, …, s是向量组B的一个极大线性
无关组.
由于1, 2, …, r与A等价; A与B等价,同 时B与1, 2, …, s等价,所以1, 2, …, r与1, 2, …, s等价
组,简称极大无关组。
定理1.设有n维向量组A:a1, a2, …, as和B:b1, b2, …,bt .若A组向量线性无关,并且A组向 量可以被B组向量线性表出,则必然有 s t.
证明: (反证法)设不然,即s > t
a1 c1,1b1 c2,1b2 L ct,1bt 无妨说:a2 c1,2b1 c2,2b2 L ct,2bt
第3章 线性方程组解法 第1节 向量与矩阵基础

A = (α1 ,α2 ,L,αm )
m 个n维行向量所组成 的向量组 β 1 , β 2 ,L β m ,
T T T
构成一个 m × n矩阵
β1T T β2 B= M T β m
线性方程组的向量表示
a11 x1 + a12 x 2 + L + a1n x n = b1 , a 21 x1 + a 22 x 2 + L + a 2 n x n = b2 , LLLLLLLLLLLLLL a m 1 x1 + a m 2 x 2 + L + a mn x n = bm .
3 5 3 例3 : 设向量组 α 1 = 2 ,α 2 = 4 ,α 3 = 1 , 0 − 1 t 问t取何值时 ,向量组线性无关 ; t取何值时 , 向量组线性相关 .
3
解:因为
5 4
3
α1 α 2 α 3 = 2
Ch4 向量空间
第一节 向量组的线性相关 与线性无关
一、向量、向量组与矩 阵 向量、 二、线性相关性的概念 三、线性相关性的判定
四、向量组的线性相关 性质
五、线性表示、线性相 关以及 线性表示、 线性无关三者的关系
六、小节、思考题 小节、
一、向量、向量组与矩阵 向量、
n 维向量写成一行,称为行向量,也就是行 维向量写成一行,称为行向量 行向量, 矩阵, 等表示, 矩阵,通常用 aT , bT ,αT , β T 等表示,如:
b11 b12 L b1n b21 b22 L b2 n ( c1 , c2 , L , cn ) = α 1 ,α 2 ,L ,α s ) ( M M M b bs 2 L bsn s1
线性代数11-向量组的秩

1
1 1 1 8 0 4 6 2
因此这就是 A 的一个最高阶非零子式.
结论:矩阵的最高阶非零子式一般不是唯一的,但矩阵的秩
是唯一的.
2 1 1 1 r 1 1 1 0 A0 (a1 , a2 , a4 ) ~ 4 6 2 0 3 6 7 0
具体地说,就是:
若 a ∈ V, b ∈ V,则a + b ∈ V .(对加法封闭) 若 a ∈ V, l ∈ R,则 l a ∈ V .(对乘数封闭) 那么就称集合 V 为向量空间.
试讨论向量组 a1, a2, a3 及向量组a1, a2 的线性相关性.
解:
1 0 2 1 0 2 r 1 2 4 ~ 0 2 2 1 5 7 0 0 0
可见 r(a1, a2 ) = 2,故向量组 a1, a2 线性无关,
同时, r(a1, a2, a3 ) = 2,故向量组 a1, a2, a3 线性相关,
无关组及 Rn 的秩.
1 0 解: n 阶单位矩阵 I e1 , e2 , , en 0 0 0 1 0 的列向 0 1
量组是 Rn 的一个最大无关组,Rn 的秩等于n .
1 0 思考:上三角形矩阵 A 0 1 1 1 1 的列向量组是 Rn 的 0 1
从而 a1, a2 是向量组 a1, a2, a3 的一个最大无关组. 事实上, a1, a3 和 a2, a3 也是最大无关组.
最大无关组的等价定义
结论:向量组 A 和它自己的最大无关组 A0 是等价的. 定义:设有向量组 A ,如果在 A 中能选出 r 个向量a1, a2, …, ar,满足 ① 向量组 A0 :a1, a2, …, ar 线性无关; ② 向量组 A 中任意 r + 1个向量(如果 A 中有 r + 1个向量的 话)都线性相关; ② 向量组 A 中任意一个向量都能由向量组 A0 线性表示; 那么称向量组 A0 是向量组 A 的一个最大无关组.
《工程数学》教案9向量组的秩与矩阵的秩

《工程数学》教案9向量组的秩与矩阵的秩教学目标:1.了解向量组的秩的概念和性质;2.理解矩阵的秩的定义和特性;3.掌握计算向量组和矩阵的秩的方法;4.能够应用秩的概念解决实际问题。
教学重点:1.向量组的秩的概念和性质;2.矩阵的秩的定义和特性;3.计算向量组和矩阵的秩的方法。
教学难点:1.矩阵的秩和向量组的秩的关系;2.解决实际问题中秩的应用。
教学准备:1.教材:工程数学教材;2.手写板或投影仪;3.准备好习题和案例分析;4.PPT或其他教学辅助工具。
教学过程:一、导入(10分钟)1.通过一个实际例子引入向量组和矩阵的秩的概念;2.提问学生对向量组和矩阵的秩有什么了解。
二、向量组的秩(30分钟)1. 向量组的概念:向量组是由若干个向量组成的有限集合,记作{v1, v2, ..., vn};2.向量组的线性关系与线性方程组:引入向量组的线性关系的概念,并介绍线性方程组的解集;3.向量组的秩的定义:向量组的秩定义为向量组中能够线性表示的最大向量个数;4.向量组的扩展与收缩:引入向量组的扩展和收缩的概念,讨论向量组的秩是否受影响;5.向量组的秩的性质:介绍向量组的秩的性质,如秩的不等式性质等。
三、矩阵的秩(40分钟)1.矩阵的概念:引入矩阵的概念,讨论矩阵的基本运算和性质;2.线性方程组与矩阵:将线性方程组表示为矩阵形式,引入矩阵的秩的定义;3.矩阵等价与秩的概念:讨论矩阵的等价和秩的概念,引入等价矩阵和初等变换;4.计算矩阵的秩:介绍行列式、初等变换、阶梯形矩阵等方法计算矩阵的秩;5.矩阵秩与向量组秩的关系:讨论矩阵的秩和向量组的秩的关系,深化对秩的理解。
四、应用实例与习题训练(40分钟)1.案例分析:通过一个实际案例引导学生应用向量组和矩阵的秩解决问题;2.习题练习:布置一些习题,包括计算向量组和矩阵的秩,以及应用秩解决问题;3.解答疑问:针对学生的问题进行解答和讨论。
五、课堂总结(10分钟)1.总结向量组和矩阵的秩的概念和性质;2.强调向量组秩与矩阵秩的关系;3.评价学生对课堂内容的掌握情况和帮助学生解答疑惑;4.展望下一节课的主题。
向量组与矩阵的秩

一般,我们用小写的粗黑体字母,如 等来表示向量,(3.1)式称为一个行向量,(3.2)式称为一个列向量.数 称为这个向量的分量. 称为这个向量的第 个分量或坐标.分量都是实数的向量称为实向量;分量是复数的向量称为复向量.
实际上, 维行向量可以看成 矩阵, 维列向量也常看成 矩阵.
例1 设 , , ,求 .
解
例2 设 , , , 且 ,求 .
解 由 ,得
通常把维数相同的一组向量简称为一个向量组,n维行量组α1,α2,…,αs可以排列
成一个s×n分块矩阵
,
其中αi为由A的第i行形成的子块,α1,α2,…,αs称为A的行向量组.n维列向量组β1,β2,…,βs可以排成一个n×s矩阵B=(β1,β2,…,βs),其中βj为B的第j列形成的子块,β1,β2,…,βs称为B的列向量组.这样,矩阵 就与其列向量组或行向量组之间建立了一一对应关系.向量组之间的关系可用矩阵来研究;反过来,矩阵的问题也可用向量组来研究.
α=k1β1+k2β2+…+ktβt.
此时,也记 .
例6设α1=(1,1,1,1),α2=(1,1,-1,-1),α3=(1,-1,1,-1),α4=(1,-1,-1,1),
β=(1,2,1,1).试问β能否由α1,α2,α3,α4线性表出?若能,写出具体表达式.
解令
β=k1α1+k2α2+k3α3+k4α4
(4)α+(-α)=0;
(5)k(α+β)=kα+kβ;
(6)(k+l)α=kα+lα;
(7)k(lα)=(kl)α;
(8)1α=α;
(9)0α=0;
(10)k0=0.
向量组与矩阵
利用矩阵乘法,方程变形为
x1
1,
2
,,
m
x2
0
xm
这样由上一章线性方程组有解的条件可得如下结论:
第3页/共16页
定理 1 若列向量组 1,2 , ,所m 构造的矩阵A,则
行向量组 1,2 , ,线m 性相关的充要条件是 线性无关的充要条件是 r( A) m.
推论 m n时, m个n维向量总是线性相关的.
中对应
因此,我们不仅可以利用矩阵的初等行变换求出列向量的秩,还可以进一步确定 其中某个部分组的线性相关性,并求出出它的极大线性无关组。
第11页/共16页
例 4 求下面向量组的秩和一个极大无关组,并把不属于该极大无关 组的向量用该极大无关组线性表示:
T1 (1, 4,1, 0, 2) T2 (2,5, 1, 3,2)
a11 a21
a12 a22
a1n a2n
设矩阵 A
ai1
ai2
ain
am1 am 2 amn
则矩阵A可以看作由m个n维行向量或n个m维列向量构成,从而可以得到一个行 向量组和列向量组。矩阵A行向量组的秩称为A的行秩,列向量组的秩称为列 秩。
第10页/共16页
定理 5 矩阵的行秩等于列秩等于矩阵的秩。
例 3 基本向量组 1, 2 , 是n Rn 的极大无关组。
解 由上一节,基本向量组是线性无关的,且任何一个n维向量都可以由它线性表 示(即坐标表示)。
第7页/共16页
定理 4 如果向量组
能由向量组
线Байду номын сангаас
性表出,且向量组A线性无关,那么
。
证明 不妨设所给向量都是列向量,记矩阵
11向量组的秩与矩阵的秩

例1. 求向量组 1 2 1 0 2 2 4 2 6 6 α1 = ,α2 = ,α3 = ,α4 = ,α5 = 2 1 0 2 3 3 5 3 3 4 的极大线性无关组 1 2 1 0 2 1 2 1 0 解: 2 4 2 6 6 0 0 0 6 → 2 1 0 2 3 0 3 2 2 6 3 3 5 3 3 4 0 9
依据定理3得知: 依据定理 得知: 得知 Pβ1, Pβ2, …, Pβr线性无关,并且在 中任意 线性无关,并且在A中任意 向量组P 选取一个向量βj,向量组 β1, Pβ2, …, Pβr, Pβj皆 是线性相关的。 是线性相关的。 从而P 是向量组B的极大线性 从而 β1, Pβ2, …, Pβr是向量组 的极大线性 无关组. 无关组 也就是说:矩阵的初等行变换不改变矩阵 也就是说: 的列秩. 类似可证:矩阵的初等列变换也不改 的列秩 类似可证: 变矩阵的行秩. 变矩阵的行秩 综上所述, 综上所述,矩阵的初等变换不改变矩阵的 行秩和列秩. 行秩和列秩 证毕
等价; 与 等价 等价, 由于α1, α2, …, αr与A等价; A与B等价,同 等价 等价, 时B与β1, β2, …, βs等价,所以α1, α2, …, αr与β1, 与
β2, …, βs等价
故r = s,即R(A)=R(B) , 证毕
二.寻找极大线性无关组的方法 寻找极大线性无关组的方法
三. 初等变换与向量组的秩
定义3.设 是一个矩阵 是一个矩阵, 定义 设A是一个矩阵,称A的行向量组的秩为 的行向量组的秩为 A的行秩;称A的列向量组的秩为 的列秩。 的行秩; 的列向量组的秩为A的列秩 的行秩 的列向量组的秩为 的列秩。
定理4.矩阵的初等变换不改变矩阵的行秩和列秩 定理 矩阵的初等变换不改变矩阵的行秩和列秩. 矩阵的初等变换不改变矩阵的行秩和列秩 a1,1 a1,2 a1,n a a2,2 a2,n 2,1 证明: 证明: 设 A = am ,1 am ,2 am ,n (1)首先证明矩阵的初等行变换不改变矩阵的行秩 首先证明矩阵的初等行变换不改变矩阵的行秩 设A:α1, α2, …, αi, …, αj, …, αm是A的行向量组 : 的 B:α1, α2, …, αj, …, αi, …, αm : C:α1, α2, …, λαi, …, αj, …, αm,其中λ ≠ 0 : D:α1, α2, …, αi, …, αj + λαi, …, αm :
C3.向量组与矩阵的秩

所以 1 , 2 , 3 线性无关.
一般地,设
1 (a11 , a12 ,, a1n ), 2 (a21 , a22 ,, a2 n ),, s (as1 , as 2 ,, asn )
要判断这个向量组是否线性相关,只需考虑向量方程
x11 x2 2 xs s 0
§2 向量组的线性相关性
通常把维数相同的一组行(列)向量称为一个向量组. n 维 行向量组 1 , 2 ,, s可以排成一个s×n分块矩阵
1 2 A s
其中 i 为由A的第 i 行形成的子块,
1 , 2 , s 称为 A 的行向量组.
n 维列向量组1 , 2 ,, s 可以排成一个n×s矩阵
B ( 1 , 2 ,, s )
其中 j 为由B的第 j 列形成的子块, 1 , 2 ,, s 称为B的列 向量组.
定义5 向量组 1 , 2 , s 称为线性相关的, 如果 存在不全为零的数 k1,k2,…,ks,使
定义6 向量 称为向量组1,2,·,t 的一个线性组合, · · 或者说 可由向量组1,2,·,t 线性表示(出), 如果存 · · 在数 k1,k2,·,kt, 使 · ·
= k11+ k2 2+·· kt t . ·+ ·
上式也可记为
ki i
i 1 t
(3) 0 (4) ( ) 0 (5) k ( ) k k (6) (k l ) k l (7) (kl) k (l ) l (k ) (8) 1
(9) k 0 k 0 或 0
满足(1)-(8)的运算称为线性运算.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
矩阵的秩
(概念及求法) 概念及求法)
一、矩阵秩的概念
行阶梯形矩阵的特点:(1)、可 划出一条阶梯线,线的下方全为零; (2)、每个台阶 只有一行,台阶 数即是非零行的行数,阶梯线的竖 线后面的第一个元素为非零元,即 非零行的第一个非零元.
任何矩阵 Am × n , 总可经过有限次初等行 变换 梯形, 把它变为行阶 梯形,行阶 梯形矩阵中非零行的行 数是唯一确定的 .
R ( B ) = 3.
三、小结
1. 矩阵秩的概念 2. 求矩阵秩的方法 (1)利用定义 (1)利用定义 (即寻找矩阵中非零子式的最高阶数 (即寻找矩阵中非零子式的最高阶数); 即寻找矩阵中非零子式的最高阶数); (2)初等变换法 (2)初等变换法 (把矩阵用初等行变换变成为行阶梯形矩阵,行 把矩阵用初等行变换变成为行阶梯形矩阵, 把矩阵用初等行变换变成为行阶梯形矩阵 阶梯形矩阵中非零行的行数就是矩阵的秩). 阶梯形矩阵中非零行的行数就是矩阵的秩
a T = ( a 1 , a 2 ,L , a n )
n 维向量写成一列,称为列向量,也就是列 维向量写成一列,称为列向量 列向量, 矩阵, 等表示, 矩阵,通常用 a,b,α, β 等表示,如: a1 a2 a= M a n
注意 1.行向量和列向量总被看作是两个不同的 行向量和列向量总被看作是两个不同的 向量; 向量; 2.行向量和列向量都按照矩阵的运算法则 行向量和列向量都按照矩阵的运算法则 进行运算; 进行运算;
n
{
T
}
叫做 n 维向量空间. 维向量空间.
π = {x = ( x1 , x 2 ,L, x n ) a1 x1 + a 2 x 2 +L+ a n x n = b}
T
n维向量空间 Rn中的 n − 1 维超平面. 维超平面. 叫做
n 维向量的实际意义
确定飞机的状态, 确定飞机的状态,需 要以下6个参数 个参数: 要以下 个参数: 机身的仰角 机翼的转角 机身的水平转角
求矩阵 A 及矩阵 B = ( A b )的秩 .
~ ~ ~ 分析: 解 分析: B 的行阶梯形矩阵为 B = ( A, b ), 设 ~ 的行阶梯形矩阵, 则 A 就是 A 的行阶梯形矩阵, ~ ~ ~ 故从 B = ( A, b ) 中可同时看出 R( A) 及 R( B ).
1 2 B= −2 3
0 5 0 3 2 6 − 1 3 − 2 3 例4 设 A = , 求矩阵 A 的 2 0 1 5 −3 1 6 − 4 −1 4 秩,并求 A 的一个最高阶非零子式 .
解 对A作初等行变换,变成行 阶梯形矩阵: 作初等行变换, 阶梯形矩阵:
0 5 0 3 2 6 − 1 3 − 2 3 A= 2 0 1 5 − 3 1 6 − 4 −1 4
子式的最高阶数 .
对于 A , 显有 R( A ) = R( A).
T T
例1
1 2 3 求矩阵 A = 2 3 − 5 的秩 . 4 7 1
1 2 在 A 中, ≠ 0. 2 3
解
又 Q A的 3 阶子式只有一个 A, 且 A = 0,
∴ R ( A ) = 2.
显然,非零行的行数为 , 显然,非零行的行数为2,
∴ R ( A ) = 2.
此方法简单! 此方法简单!
二、矩阵秩的求法
因为对于任何矩阵Am×n ,总可经过有限次初 梯形. 等行变换把他变为行阶
问题:经过变换矩阵的秩变吗? 问题:经过变换矩阵的秩变吗?
定理1 若 A ~ B,则 R( A) = R( B).
: 向量空 的
{( x, y,z) ax+by+cz=d} {r =( x, y,z)
P( x, y, z)
T
ax+by+cz=d}
T
r = ( x, y, z)
n 维向量没有直观的几何形象. n > 3时, 维向量没有直观的几何形象.
R = x = ( x1 , x 2 ,L, x n ) x1 , x 2 ,L, x n∈ R
Q R ( B ) = 3,
故 A 中必有 3 阶非零子式.
计算 A 的前三行构成的子式
3 2 2 0 5
3 2
5
5 =2 0 5 3 − 2 6 6 0 11
2 5 = −2 = 16 ≠ 0. 6 11
的一个最高阶非零子式. 则这个子式便是A 的一个最高阶非零子式
设 n 阶可逆矩阵 A ,
Q
3 − 2 2 −1 0 3 1 −2 5 0 例2 求矩阵 B = 的秩 . 0 0 0 4 −3 0 0 0 0 0
解 Q B是一个行阶梯形矩阵, 其非零行有 3行, 是一个行阶梯形矩阵,
∴ B 的所有 4 阶子式全为零 .
2 −1 3 而 0 3 − 2 ≠ 0, 0 0 4
r1 ↔ r4 r2 − r4
r3 − 2r1 r4 − 3r1
6 4 −4 −1 1 3 1 −1 0 − 4 0 − 12 9 7 − 11 0 − 16 12 8 − 12
r3 − 3r2
r4 − 4r2
1 6 − 4 −1 1 0 − 4 3 0 0 0 4 0 0 0 4
经有限次初等行变换矩阵的秩不变. 经有限次初等行变换矩阵的秩不变.
设A经初等列变换变为 B,即有R( A) = R( B).
初等变换求矩阵秩的方法: 初等变换求矩阵秩的方法: 把矩阵用初等行变换变成为行阶梯形矩阵, 把矩阵用初等行变换变成为行阶梯形矩阵, 行阶梯形矩阵 行阶梯形矩阵中非零行的行数就是矩阵的秩. 零行的行数就是矩阵的秩 行阶梯形矩阵中非零行的行数就是矩阵的秩
A ≠ 0, ∴ A 的最高阶非零子式为 A ,
R( A ) = n, 故 A 的标准形为单位阵 E , A ~ E .
可逆矩阵的秩等于阶数 ,故称可逆矩阵 为满秩矩阵 . 奇异矩阵为降秩矩阵 .
1 2 例5 设 A = − 2 3
−2 −4
− 1 1 8 0 2 , b = 3 4 −2 3 4 − 6 0 − 6 2
例如
(1,2,3,L, n)
n维实向量 维实向量 n维复向量 维复向量
(1 + 2i ,2 + 3i ,L, n + ( n + 1)i )
第2个分量 个分量 第1个分量 个分量
第n个分量 个分量
二、n 维向量的表示方法
n 维向量写成一行,称为行向量,也就是行 维向量写成一行,称为行向量 行向量, 矩阵, 等表示, 矩阵,通常用 aT , bT ,αT , βT 等表示,如:
3 3 A 的 3 阶子式共有 C 4 • C 5 = 40 个 .
考察A的行阶梯形矩阵, 考察 的行阶梯形矩阵, 记A = ( a1 , a2 , a3 , a4 , a5 ), 则矩阵 B = (a1 , a2 , a4 )的行 阶梯形矩阵为
1 6 − 1 0 − 4 1 0 0 4 0 0 0
r4 + 3r2
1 − 2 0 0 0 0 0 0
1 − 2 0 0 0 0 0 0
2 −1 2 1 0 0 0 0
1 0 5 1
r3 ÷ 5
r4 − r3
2 − 1 1 2 1 0 0 0 1 0 0 0
∴ R ( A ) = 2,
ϕ ψ
(− ≤ ϕ ≤ ) 2 2 (−π < ψ ≤ π )
π
π
(0 ≤ θ < 2π ) 飞机重心在空间的位置参数P(x,y,z) 飞机重心在空间的位置参数
所以,确定飞机的状态,需用 维向量 所以,确定飞机的状态,需用6维向量 a = ( x, y, z,ϕ,ψ ,θ )
θ
课堂讨论
在日常工作、学习和生活中, 在日常工作、学习和生活中,有许多问题都 需要用向量来进行描述,请同学们举例说明. 需要用向量来进行描述,请同学们举例说明.
n维向量
(概念、表示方法、向量空间)
一、 n维向量的概念
定义1 定义1 n 个有次序的数 a1 , a2 ,L , an 所组成的数 维向量, 个分量, 组称为 n维向量,这 n个数称为该向量的 n个分量,
第i个数a i 称为第 i个分量 .
分量全为实数的向量称为实向量, 分量全为实数的向量称为实向量, 实向量 分量全为复数的向量称为复向量. 分量全为复数的向量称为复向量. 复向量
−2 −4
− 1 1 8 0 2 4 − 2 3 3 − 6 0 − 6 4 2
r2 − 2r1 1 − 2 2 − 1 r3 + 2r1 0 0 4 2 0 0 2 1 r4 − 3r1 0 0 − 6 − 3
1 0 5 1
r2 ÷ 2 r3 − r2
4 − 1 − 8 − 8
r4 − r3
1 6 − 4 −1 4 1 − 1 0 − 4 3 0 0 0 4 − 8 0 0 0 0 0
由阶梯形矩阵有三个非零行可知 R( A) = 3.
求 A 的一个最高阶子式 . Q R( A) = 3, 知 A 的最高阶非零子式为 3阶 . 阶
∴ R ( B ) = 3.
1 例3 已知 A = 0 − 2 1 3 = 2 ≠ 0, 解 Q 0 2
3 − 2 2 2 − 1 3 ,求该矩阵的秩. 求该矩阵的秩. 0 1 5
计算A的 阶子式 阶子式, 计算 的3阶子式,
3 −2 1 3 2 3 −2 2 1 −2 2 =0 , 0 2 − 1 = 00 2 3 = 2 , − 1 3 = 00 − 1 3 = 0, = , −2 0 1 −2 0 5 0 1 5 −2 1 5 1
