求曲线的交点
数学交点式的公式

数学交点式的公式在数学中,交点是指两条或多条曲线相交的点。
通过找到两条曲线的交点,可以解决许多数学和科学问题。
在本文中,我们将介绍数学交点的一些公式和方法。
数学交点的公式和方法主要与曲线的表示方式有关。
常见的曲线表示方法包括代数方程、参数方程和极坐标方程。
我们将分别介绍这些方法下的交点公式。
1.代数方程的交点公式:代数方程是指用变量的幂和系数构成的方程。
常见的代数方程包括线性方程、二次方程和高次方程等。
如果给定两个代数方程,我们可以通过联立方程求解交点。
具体步骤如下:a.将两个方程联立,得到一个方程组。
b.将方程组中的变量进行消元,使得方程组变成单变量方程。
c.求解单变量方程,得到变量的解。
d.将变量的解带入方程中,求解其他未知数的值。
例如,给定两个二次方程:y = ax^2 + bx + cy = dx^2 + ex + f我们将这两个方程联立,得到:ax^2 + bx + c = dx^2 + ex + f将方程进行变形,得到:(a-d)x^2+(b-e)x+(c-f)=0这是一个二次方程,我们可以使用求根公式或配方法求解交点。
2.参数方程的交点公式:参数方程是使用参数表示曲线坐标的方法。
一个参数方程可以表示一条曲线,通常由一个或多个参数组成。
给定两个参数方程,我们可以通过求解参数方程组得到交点。
具体步骤如下:a.将参数方程组中的参数相等,得到一个方程。
b.将方程进行变形,消去参数。
c.求解方程,得到变量的解。
d.将变量的解带入参数方程中,求解其他未知数的值。
例如,给定两个参数方程:x = a + bty = c + dt将参数方程组中的参数相等,得到:a + bt = c + dt将方程进行变形,得到:(b-d)t=c-a这是一个线性方程,我们可以求解t的值,然后将t的值代入参数方程中,求解其他未知数的值。
3.极坐标方程的交点公式:极坐标方程是一种使用极径和极角表示曲线坐标的方法。
给定两个极坐标方程,我们可以通过求解方程组得到交点。
高考数学中的参数方程解析技巧

高考数学中的参数方程解析技巧高中数学中,参数方程是一个比较重要的知识点,它在高考中也经常出现。
在考场上如何快速解析参数方程是一个必备的技巧。
本文将从以下几个方面探讨高考数学中的参数方程解析技巧。
一、掌握参数方程的基本概念和性质首先,我们需要掌握参数方程的基本概念和性质。
参数方程就是用一个或多个变量来表示一组解的方程,通常是用二元函数表示。
例如,设:x=f(t) , y=g(t) ,则称x,y是由参数t确定的一组函数或者向量。
又如,曲线的参数方程可以表示为:x=cos t, y=sin t。
同时,我们还需要了解参数方程的基本性质。
比如,当参数t取遍一个区间时,对应的点以一定的方式运动,从而构成一个曲线(或者说路径)。
因此,参数方程很适合用来表示一些曲线、轨迹等形状。
二、常见的参数方程解题方法1、画图法:画出参数曲线的关键点和性质,如切线斜率、弧长等,利用图形解决问题。
2、换元法:将复杂的参数方程化简成简单的形式,以便求解。
比如,将参数方程中的sin t,cos t换成tan t,以求得此函数的导数。
3、消元法:当问题中只需求出一种变量的值时,可以通过解方程组,消元得到所求的变量。
例如,已知x=f(t) , y=g(t),求y=f(x) 时,可以用消元法解得。
4、向量法:参数方程中的x,y一般可以看作是向量的i,j分量。
因此,我们可以构造出向量的形式,利用向量的性质解题。
三、解析参数方程的常见技巧1、化简参数方程:通过变形,将参数方程化为指数函数、三角函数等常见函数形式,以便于求导。
2、求导、求导数:通过求导,可以求出参数曲线的切线斜率、曲率等性质,以便于解析问题。
3、曲率半径:利用曲率半径和曲率公式,可以求出参数曲线上任意一点的曲率半径。
4、求交点、对称点:通过等式联立,求得参数方程下两曲线的交点坐标。
通过在参数方程下的对称关系求得参数曲线下的对称点。
四、例题分析1、设直线 L : y=x+k(k > 0),曲线 C 的参数方程为 x=cost ,y=sin(t+θ). 试确定θ的取值范围,并解决直线 L 在曲线 C 上的截距。
曲线相交

在作图过程中需要检查曲线相交的情况,本文从编程的角度对曲线相交的几种情况进行分析并提出检查方案。
曲线相交通常可以理解为曲线上的某两个线段相交,或交点位于其中一条或两条曲线的结点上,还有其中一段重合的情况。
1 交点不在任何结点上
2 交点在其中一条线的结点上
3 交点为两条线的结点
其中2,3情况只有当两条线相互交叉才算相交,只在一点相接或与交点相接的边重合的情况不算相交
自相交也需要遵循以上原则
对于第一种情况很好判断,问题主要在于2,3两种情况。
判断的方法主要是利用向量叉乘的性质,对于第2种情况,如果交点P在线A的边上及线段B的结点,则A的边向量叉乘以交点为起点的B上的两线段的向量,如果结果的符号相反,则认为在A和B在P点相交。
对于第三种情况,设交点为P,则以P为起点的A上的边向量必须分别在以P为起点的B上的两个边向量的同侧,如A的两个向量重合或B的两个向量方向一致,或A中一个向量与B的一个向量方向一致,则认为P 不是交点。
还有一种情况是有一段线段重叠,但是重叠的两端的走向不一致,如图。
12.1(1)曲线的交点
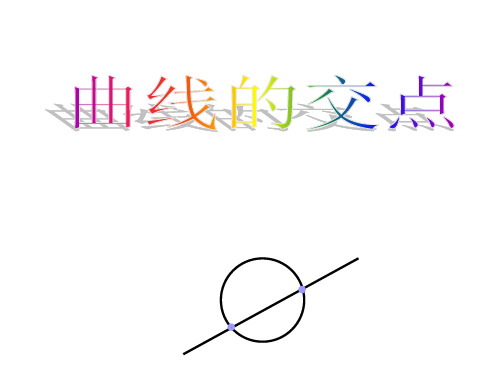
x2(y2)2(y2)2
因为曲线x在轴的上方,所y以 0.虽然原点 O的 坐标(0,0)是这个方程的解,属 但于 不已知曲线,
所以曲线的方程应 y 是1x2(x 0),它的图形 8
是关于y轴对称的抛物线,包 但括 不抛物线的顶点。
.
30
已知 AB的 C 两个A,顶 B的 点坐标分 (5,别 0),(5是 ,0),
y 解:如图,取直线l为x轴,
过点F且垂直于直线l的直线 为y轴,建立坐标系xOy. 设点M(x,y)是曲线上任意
F
M
OB
x
一点,作MB⊥x轴,垂足
为B,那么点M属于集合
P={M︱︱MF︱-︱MB︱=2}
.
29
由两点间的距离公式,点M适合的条件可表示为
x2(y2)2y2
移项后两边平方,得
化简得 y 1x2 8
C 与 y x
1
2
与 y1 x
3
C 与 y 4x2 2
.
22
例3 、证明圆心为坐标原点,半径等于5的圆的方程是
x2+ y2 =25,并判断点M1(3,-4)、M2( 2 5 ,2)是
否在这个圆上。
证明:
(1)设M(x0, y0)是圆上任意一点,因为点M到原点的距离等于5,
所以
x02 y02 5,
数解,因此直线与曲线C没有交点。
思考:这题除了用解方程组的方法外,还有其他方法解吗?
.
9
解题后的思考
例1,例2在解法上的相同之处是什么?
都是把直线方程与曲线方程联立成方程组, 通过消元变成一元二次方程,再通过解方程或 根的判别式来解决问题。
这两题在结果上有什么相同与不同吗?
双曲线的焦点坐标公式

双曲线的焦点坐标公式双曲线是一种二次曲线,具有特定的形状和性质。
在直角坐标系中,双曲线的方程可以表示为:x²/a²-y²/b²=1(水平双曲线)或者y²/a²-x²/b²=1(垂直双曲线)其中a和b是正常数,表示双曲线在x轴和y轴上的交点的距离。
在数学中,焦点是双曲线的一个重要属性。
双曲线有两个焦点,分别位于曲线的两条渐近线的中心。
双曲线的焦点坐标可以使用以下公式来计算:对于水平双曲线,焦点的坐标为(±c,0),其中c的计算公式为:c=√(a²+b²)对于垂直双曲线,焦点的坐标为(0,±c),其中c的计算公式也为:c=√(a²+b²)现在让我们更详细地解释这个公式。
双曲线的渐近线是根据双曲线的方程计算出来的,它们的方程为y=±(b/a)*x。
这意味着在渐近线上,y的绝对值除以x的绝对值的极限值将等于b/a。
换句话说,当x趋于正无穷或负无穷时,曲线将无限接近于渐近线。
一个重要的性质是,曲线和渐近线之间的距离被称为焦距,它等于c。
焦距是从焦点到曲线或渐近线的最短距离。
那么,如何计算焦点的坐标?首先,我们假设有一个水平双曲线,其方程为x²/a²-y²/b²=1、我们可以观察到,当x=c时,y=0。
这意味着曲线上的任何一个点(c,0)在x坐标轴上。
这个点到焦点的距离等于焦距c。
同样地,当x=-c时,y=0,曲线上的另一个点也在x坐标轴上,且到焦点的距离也等于焦距c。
所以,水平双曲线的焦点分别为(±c,0)。
对于垂直双曲线,我们可以得到类似的结论。
根据方程y²/a²-x²/b²=1,我们可以观察到,当y=c时,x=0。
这意味着曲线上的任何一个点(0,c)位于y坐标轴上,且到焦点的距离等于焦距c。
高中数学第2章2.6曲线与方程2.6.3曲线的交点讲义(含解析)苏教版选修2_1
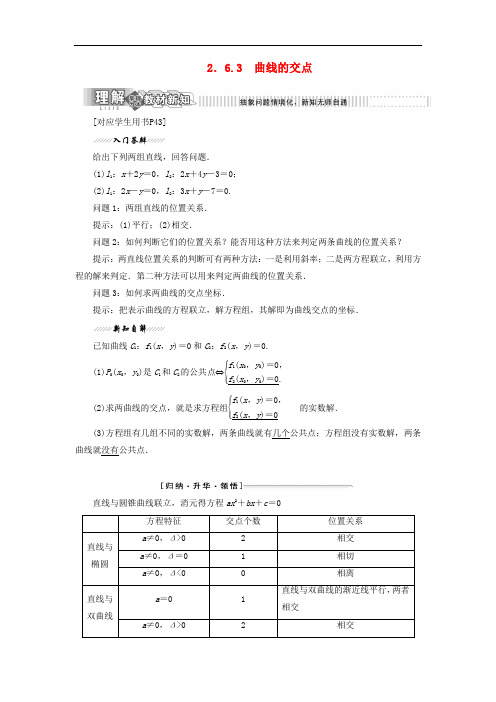
2.6.3曲线的交点[对应学生用书P43]给出下列两组直线,回答问题. (1)l 1:x +2y =0,l 2:2x +4y -3=0; (2)l 1:2x -y =0,l 2:3x +y -7=0. 问题1:两组直线的位置关系. 提示:(1)平行;(2)相交.问题2:如何判断它们的位置关系?能否用这种方法来判定两条曲线的位置关系? 提示:两直线位置关系的判断可有两种方法:一是利用斜率;二是两方程联立,利用方程的解来判定.第二种方法可以用来判定两曲线的位置关系.问题3:如何求两曲线的交点坐标.提示:把表示曲线的方程联立,解方程组,其解即为曲线交点的坐标.已知曲线C 1:f 1(x ,y )=0和C 2:f 2(x ,y )=0.(1)P 0(x 0,y 0)是C 1和C 2的公共点⇔⎩⎪⎨⎪⎧f 1(x 0,y 0)=0,f 2(x 0,y 0)=0.(2)求两曲线的交点,就是求方程组⎩⎪⎨⎪⎧f 1(x ,y )=0,f 2(x ,y )=0的实数解.(3)方程组有几组不同的实数解,两条曲线就有几个公共点;方程组没有实数解,两条曲线就没有公共点.直线与圆锥曲线联立,消元得方程ax 2+bx +c =0方程特征 交点个数位置关系 直线与椭圆a ≠0,Δ>0 2 相交 a ≠0,Δ=0 1 相切 a ≠0,Δ<0 0 相离直线与双曲线a =0 1 直线与双曲线的渐近线平行,两者相交a ≠0,Δ>02相交a≠0,Δ=0 1 相切a≠0,Δ<00 相离直线与抛物线a=0 1直线与抛物线的对称轴平行,两者相交a≠0,Δ>0 2 相交a≠0,Δ=0 1 相切a≠0,Δ<00 相离[对应学生用书P44]直线与圆锥曲线的位置关系[例1] 已知直线l:kx-y+2=0,双曲线C:x2-4y2=4,当k为何值时:(1)l与C无公共点;(2)l与C有惟一公共点;(3)l与C有两个不同的公共点.[思路点拨] 直线与圆锥曲线公共点的个数就是直线与圆锥曲线方程所组成的方程组解的个数,从而问题可转化为由方程组的解的个数来确定参数k的取值.[精解详析] 将直线与双曲线方程联立消去y,得(1-4k2)x2-16kx-20=0.①当1-4k2≠0时,有Δ=(-16k)2-4(1-4k2)·(-20)=16(5-4k2).(1)当1-4k2≠0且Δ<0,即k<-52或k>52时,l与C无公共点.(2)当1-4k2=0,即k=±12时,显然方程①只有一解.当1-4k2≠0,Δ=0,即k=±52时,方程①只有一解.故当k=±12或k=±52时,l与C有惟一公共点.(3)当1-4k2≠0,且Δ>0时,即-52<k<52,且k≠±12时,方程有两解,l与C有两个公共点.[一点通] 直线与圆锥曲线的位置关系,可以通过讨论直线方程与曲线方程组成的方程组的实数解的个数来确定,通常消去方程组中变量y (或x )得到关于变量x (或y )的一元二次方程,考虑该一元二次方程的判别式Δ,则有:Δ>0⇔直线与圆锥曲线相交于两个点; Δ=0⇔直线与圆锥曲线相交于一个点; Δ<0⇔直线与圆锥曲线无交点.1.对不同的实数值m ,讨论直线y =x +m 与椭圆x 24+y 2=1的位置关系.解:由⎩⎪⎨⎪⎧y =x +m ,x 24+y 2=1,消去y 得x 24+(x +m )2=1, 整理得5x 2+8mx +4m 2-4=0.Δ=(8m )2-4×5(4m 2-4)=16(5-m 2).当-5<m <5时,Δ>0, 直线与椭圆相交;当m =-5或m =5时,Δ=0, 直线与椭圆相切;当m <-5或m >5时,Δ<0, 直线与椭圆相离.2.已知抛物线的方程为y 2=4x ,直线l 过定点P (-2,1),斜率为k ,k 为何值时,直线l 与抛物线y 2=4x 只有一个公共点;有两个公共点;没有公共点?解:(1)当k =0时,直线l 与x 轴平行,易知与抛物线只有一个交点.(2)当k ≠0时,联立⎩⎪⎨⎪⎧y =k (x +2)+1,y 2=4x ,消去x ,得ky 2-4y +4(2k +1)=0,Δ=16-4k ×4(2k +1).①当Δ=0,即k =-1或12时,直线l 与抛物线相切,只有一个公共点;②当Δ>0,即-1<k <12且k ≠0时,直线l 与抛物线相交,有两个公共点;③当Δ<0,即k <-1或k >12时,直线l 与抛物线相离,没有公共点.综上:当k =-1或12或0时,直线l 与抛物线只有一个公共点;当-1<k <12,且k ≠0时,直线l 与抛物线有两个公共点;当k <-1或k >12时,直线l 与抛物线没有公共点.直线被圆锥曲线截得的弦长问题[例2] 已知斜率为2的直线经过椭圆x 25+y 24=1的右焦点F 1,与椭圆相交于A 、B 两点,求弦AB 的长.[思路点拨] 先求出直线与椭圆的两个交点,再利用两点间的距离公式,也可以从公式上考查A 、B 坐标间的联系,进行整体运算.[精解详析] 法一:∵直线l 过椭圆x 25+y 24=1的右焦点F 1(1,0),又直线的斜率为2.∴直线l 的方程为y =2(x -1),即2x -y -2=0. 由方程组⎩⎪⎨⎪⎧2x -y -2=0,x 25+y24=1,得交点A (0,-2),B ⎝ ⎛⎭⎪⎫53,43.则AB =(x A -x B )2+(y A -y B )2=(0-53)2+(-2-43)2=1259=553. 法二:设A (x 1,y 1),B (x 2,y 2),则A 、B 的坐标为方程组⎩⎪⎨⎪⎧2x -y -2=0,x 25+y24=1的公共解.对方程组消去y ,得3x 2-5x =0.则x 1+x 2=53,x 1·x 2=0.∴AB =(x 1-x 2)2+(y 1-y 2)2=(x 1-x 2)2(1+k 2AB )=(1+k 2AB )[(x 1+x 2)2-4x 1x 2] =(1+22)[(53)2-4×0]=553.法三:设A (x 1,y 1),B (x 2,y 2),联立⎩⎪⎨⎪⎧2x -y -2=0,x 25+y24=1,消去y ,得3x 2-5x =0,则x 1,x 2是方程3x 2-5x =0的两根. ∴x 1+x 2=53.由圆锥曲线的统一定义,得AF 1=15×(5-x 1),F 1B =15×(5-x 2),则AB =AF 1+F 1B =15×[10-(x 1+x 2)]=15×253=553.[一点通] 弦长的求法:(1)求出端点坐标,利用两点间的距离公式求解. (2)结合根与系数的关系,利用变形公式l =(1+k 2)[(x 1+x 2)2-4x 1x 2]或 l =(1+1k2)[(y 1+y 2)2-4y 1y 2]求解.(3)利用圆锥曲线的统一定义求解.3.过抛物线y 2=8x 的焦点作倾斜角为45°的直线,则被抛物线截得的弦长为________. 解析:由抛物线y 2=8x 的焦点为(2,0),得直线的方程为y =x -2,代入y 2=8x 得(x -2)2=8x ,即x 2-12x +4=0. ∴x 1+x 2=12,弦长=x 1+x 2+p =12+4=16. 答案:164.直线y =2x -3与双曲线x 22-y 2=1相交于两点A 、B ,则AB =________.解析:设直线y =2x -3与双曲线x 22-y 2=1两交点坐标分别为A (x 1,y 1),B (x 2,y 2).由⎩⎪⎨⎪⎧y =2x -3,x 22-y 2=1,得7x 2-24x +20=0,∴x 1+x 2=247,x 1x 2=207,∴|AB |=1+22|x 1-x 2|=5·(x 1+x 2)2-4x 1x 2=5·(247)2-4×207=457. 答案:4575.如图,椭圆x 216+y 29=1的左、右焦点分别为F 1,F 2,一条直线l经过F 1与椭圆交于A ,B 两点,若直线l 的倾斜角为45°,求△ABF 2的面积.解:由椭圆的方程x 216+y 29=1知,a =4,b =3,∴c =a 2-b 2=7.由c =7知F 1(-7,0),F 2(7,0), 又直线l 的斜率k =tan 45°=1, ∴直线l 的方程为x -y +7=0.设A (x 1,y 1),B (x 2,y 2),则由⎩⎪⎨⎪⎧x -y +7=0,x 216+y 29=1消去x ,整理得25y 2-187 y -81=0,∴y 1+y 2=18 725,y 1y 2=-8125.∴|y 1-y 2|= (y 1+y 2)2-4y 1y 2=⎝ ⎛⎭⎪⎫187252+4×8125=72225, ∴S △ABF 2=12|F 1F 2|·|y 1-y 2|=12×2 7×72 225=721425.两曲线相交的综合问题[例3] 已知椭圆x 216+y 24=1,过点P (2,1)作一弦,使弦在这点被平分,求此弦所在直线方程.[思路点拨] 设出直线的斜率,联立直线与椭圆方程,消去y ,得关于x 的方程,用根与系数的关系和弦中点坐标,得斜率的方程,求解即可,也可用“点差法”求解.[精解详析] 法一:设所求直线的方程为y -1=k (x -2),代入椭圆方程并整理,得(4k 2+1)x 2-8(2k 2-k )x +4(2k -1)2-16=0. 又设直线与椭圆的交点为A (x 1,y 1)、B (x 2,y 2), 则x 1,x 2是上面的方程的两个根, 所以x 1+x 2=8(2k 2-k )4k 2+1, 因为P 为弦AB 的中点,所以2=x 1+x 22=4(2k 2-k )4k 2+1, 解得k =-12,所以所求直线的方程为x +2y -4=0.法二:设直线与椭圆交点为A (x 1,y 1),B (x 2,y 2), 因为P 为弦AB 的中点,所以x 1+x 2=4,y 1+y 2=2, 又因为A ,B 在椭圆上, 所以x 21+4y 21=16,x 22+4y 22=16, 两式相减,得(x 21-x 22)+4(y 21-y 22)=0, 即(x 1+x 2)(x 1-x 2)+4(y 1+y 2)(y 1-y 2)=0, 所以y 1-y 2x 1-x 2=-(x 1+x 2)4(y 1+y 2)=-12,即k AB =-12. 所以所求直线的方程为y -1=-12(x -2),即x +2y -4=0.[一点通] 解决直线与圆锥曲线的位置关系时,一般采用“设而不求”的思想,将直线方程与圆锥曲线方程联成方程组,转化为一元二次方程,利用根与系数的关系,把已知条件转化为弦的端点坐标之间的关系求解,在涉及“中点弦”问题时,“点差法”是最常用的方法.6.已知过抛物线y 2=2px (p >0)的焦点F 的直线交抛物线于A (x 1,y 1),B (x 2,y 2)两点. 求证:(1)x 1x 2为定值;(2)1FA +1FB为定值.证明:(1)抛物线y 2=2px 的焦点为F ⎝ ⎛⎭⎪⎫p2,0,当AB 与x 轴不垂直时,设直线AB 的方程为y =k (x -p2)(k ≠0).由⎩⎪⎨⎪⎧y =k (x -p 2),y 2=2px消去y ,得k 2x 2-p (k 2+2)x +k 2p 24=0.由根与系数的关系,得x 1x 2=p 24(定值).当AB ⊥x 轴时,x 1=x 2=p 2,x 1x 2=p 24也成立.(2)由抛物线的定义知,FA =x 1+p 2,FB =x 2+p2.1FA +1FB =1x 1+p 2+1x 2+p2 =x 1+x 2+p p2(x 1+x 2)+x 1x 2+p 24=x 1+x 2+p p2(x 1+x 2)+p 22=x 1+x 2+pp 2(x 1+x 2+p )=2p (定值).7.设双曲线C :x 2a2-y 2=1(a >0)与直线l :x +y =1相交于两个不同点A ,B .(1)求双曲线C 的离心率e 的取值范围;(2)设直线l 与y 轴的交点为P ,若PA u u u r =512PB u u u r,求a 的值.解:(1)将y =-x +1代入双曲线x 2a2-y 2=1(a >0)中得(1-a 2).x 2+2a 2x -2a 2=0.所以⎩⎪⎨⎪⎧1-a 2≠0,4a 4+8a 2(1-a 2)>0,解得0<a <2,且a ≠1.又双曲线的离心率e =1+a2a=1a 2+1,所以e >62,且e ≠ 2. (2)设A (x 1,y 1),B (x 2,y 2),P (0,1),因为PA u u u r =512PB u u u r,所以(x 1,y 1-1)=512(x 2,y 2-1).由此得x 1=512x 2.由于x 1,x 2是方程(1-a 2)x 2+2a 2x -2a 2=0的两根,且1-a 2≠0,所以1712x 2=-2a21-a2,512x 22=-2a21-a2. 消去x 2,得-2a 21-a 2=28960.由a >0,解得a =1713. 8.(陕西高考)已知动圆过定点A (4,0),且在y 轴上截得弦MN 的长为8. (1)求动圆圆心的轨迹C 的方程;(2)已知点B (-1,0),设不垂直于x 轴的直线l 与轨迹C 交于不同的两点P ,Q ,若x 轴是∠PBQ 的角平分线,证明:直线l 过定点.解: (1)如图,设动圆圆心O 1(x ,y ),由题意得,O 1A =O 1M . 当O 1不在y 轴上时,过O 1作O 1H ⊥MN 交MN 于H ,则H 是MN 的中点, ∴O 1M = x 2+42, 又O 1A = (x -4)2+y 2, ∴(x -4)2+y 2= x 2+42, 化简得y 2=8x (x ≠0).当O 1在y 轴上时,O 1与O 重合,点O 1的坐标(0,0)也满足方程y 2=8x , ∴动圆圆心的轨迹C 的方程为y 2=8x .(2)证明:如图,由题意,设直线l 的方程为y =kx +b (k ≠0),P (x 1,y 1),Q (x 2,y 2),将y =kx +b 代入y 2=8x 中,得k 2x 2+(2bk -8)·x +b 2=0, 其中Δ=-32kb +64>0.由根与系数的关系得,x 1+x 2=8-2bkk2,① x 1x 2=b 2k2,②因为x 轴是∠PBQ 的角平分线,所以y 1x 1+1=-y 2x 2+1, 即y 1(x 2+1)+y 2(x 1+1)=0,(kx 1+b )(x 2+1)+(kx 2+b )(x 1+1)=0, 2kx 1x 2+(b +k )(x 1+x 2)+2b =0,③将①②代入③,得2kb 2+(k +b )(8-2bk )+2k 2b =0, ∴k =-b ,此时Δ>0, ∴直线l 的方程为y =k (x -1), ∴直线l 过定点(1,0).讨论直线与圆锥曲线的位置关系时,先联立方程,消去x 或y ,得出一个一元二次方程,通过研究判别式Δ的情况,研究位置关系,值得注意的是,若是直线与圆或椭圆时,无需讨论二次项系数是否为零(一定不为零),直接考察Δ的情况即可.若是直线与双曲线或抛物线时,则需讨论二次项系数等于零和不等于零两种情况.这是特别要注意的问题.同时还要注意直线斜率不存在时的情形.[对应课时跟踪训练(十七)]1.曲线x 2-xy -y 2-3x +4y -4=0与x 轴的交点坐标是________. 解析:当y =0时,得x 2-3x -4=0, 解得x 1=4或x 2=-1.所以交点坐标为(4,0)和(-1,0). 答案:(4,0),(-1,0)2.曲线x 2+y 2=4与曲线x 2+y 29=1的交点个数为________. 解析:由数形结合可知两曲线有4个交点. 答案:43.设抛物线y 2=8x 的准线与x 轴交于点Q ,若过点Q 的直线l 与抛物线有公共点,则直线l 的斜率的取值范围是________.解析:由y 2=8x ,得准线方程为x =-2. 则Q 点坐标为(-2,0). 设直线y =k (x +2).由⎩⎪⎨⎪⎧y =k (x +2),y 2=8x ,得k 2x 2+(4k 2-8)x +4k 2=0.若直线l 与y 2=8x 有公共点, 则Δ=(4k 2-8)2-16k 4≥0. 解得-1≤k ≤1. 答案:[-1,1]4.曲线y =x 2-x +2和y =x +m 有两个不同的公共点,则实数m 的范围是________.解析:由⎩⎪⎨⎪⎧y =x +m ,y =x 2-x +2,消去y ,得x 2-2x +2-m =0.若有两个不同的公共点,则Δ=4-4(2-m )>0, ∴m >1.答案:(1,+∞)5.如果椭圆x 236+y 29=1的一条弦被点(4,2)平分,那么这条弦所在直线的方程是 ________.解析:设直线与椭圆的交点为A (x 1,y 1),B (x 2,y 2). ∵P (4,2)为AB 中点,∴x 1+x 2=8,y 1+y 2=4. 又∵A ,B 在椭圆上,∴x 21+4y 21=36,x 22+4y 22=36. 两式相减得(x 21-x 22)+4(y 21-y 22)=0, 即(x 1+x 2)(x 1-x 2)+4(y 1+y 2)(y 1-y 2)=0, ∴y 1-y 2x 1-x 2=-(x 1+x 2)4(y 1+y 2)=-12. 即直线l 的斜率为-12.∴所求直线方程为x +2y -8=0. 答案:x +2y -8=06.已知椭圆的中心在原点,焦点在x 轴上,长轴长为42,离心率为64. (1)求椭圆的标准方程;(2)直线l 与该椭圆交于M 、N 两点,MN 的中点为A (2,-1),求直线l 的方程. 解:(1)由题意2a =42, ∴a =22,又e =c a =c 22=64,∴c = 3.∴b 2=a 2-c 2=8-3=5.故所求椭圆的标准方程为x 28+y 25=1.(2)∵点A 在椭圆内部,∴过A 点的直线必与椭圆有两交点.当直线斜率不存在时,A 点不可能为弦的中点,故可设直线方程为y +1=k (x -2),它与椭圆的交点分别为M (x 1,y 1),N (x 2,y 2),则⎩⎪⎨⎪⎧y +1=k (x -2),x 28+y25=1.消去y 得(8k 2+5)x 2-16k (2k +1)x +8[(2k +1)2-5]=0, ∴x 1+x 2=16k (2k +1)8k 2+5, 又∵A (2,-1)为弦MN 的中点, ∴x 1+x 2=4,即16k (2k +1)8k 2+5=4, ∴k =54,从而直线方程为5x -4y -14=0.7.已知椭圆C 1与抛物线C 2的焦点均在x 轴上,C 1的中心和C 2的顶点均为原点O ,从每条曲线上取两个点,将其坐标记录于下表中:(1)求C 1,C 2(2)请问是否存在直线l 满足条件:①过C 2的焦点F ;②与C 1交于不同两点M ,N 且满足OM u u u u r ⊥ON u u u r?若存在,求出直线l 的方程;若不存在,说明理由.解:(1)设抛物线C 2:y 2=2px (p ≠0),则有y 2x=2p (x ≠0),据此验证4个点知(3,-23),(4,-4)在抛物线上,易求C 2:y 2=4x .设C 1:x 2a 2+y 2b 2=1(a >b >0),把点(-2,0),⎝⎛⎭⎪⎫2,22代入得⎩⎪⎨⎪⎧4a 2=1,2a 2+12b 2=1,解得⎩⎪⎨⎪⎧a 2=4,b 2=1.∴C 1的方程为x 24+y 2=1.(2)容易验证直线l 的斜率不存在时,不满足题意;当直线l 的斜率存在时,假设存在直线l 过抛物线焦点F (1,0),设其方程为y =k (x -1),与C 1的交点坐标为M (x 1,y 1),N (x 2,y 2).由⎩⎪⎨⎪⎧x 24+y 2=1,y =k (x -1)消去y 得,(1+4k 2)x 2-8k 2x +4(k 2-1)=0,于是x 1+x 2=8k 21+4k 2,x 1x 2=4(k 2-1)1+4k 2. ①所以y 1y 2=k (x 1-1)·k (x 2-1) =k 2[x 1x 2-(x 1+x 2)+1]=k 2⎝ ⎛⎭⎪⎫4(k 2-1)1+4k 2-8k 21+4k 2+1=-3k 21+4k 2. ② 由OM u u u u r ⊥ON u u u r ,即OM u u u u r ·ON u u u r=0,得x 1x 2+y 1y 2=0. ③将①②代入③式得,4(k 2-1)1+4k 2-3k 21+4k 2=k 2-41+4k 2=0,解得k =±2.所以存在直线l 满足条件,且l 的方程为:y =2x -2或y =-2x +2.8.已知椭圆C 的中心在坐标原点,焦点在x 轴上,椭圆C 上的点到焦点的距离的最大值为3,最小值为1.(1)求椭圆C 的标准方程;(2)若直线l :y =kx +m 与椭圆C 相交于A ,B 两点(A ,B 不是左右顶点),且以AB 为直径的圆过椭圆C 的右顶点.求证:直线l 过定点,并求出该定点的坐标.解:(1)由题意设椭圆C 的标准方程为x 2a 2+y 2b2=1(a >b >0).由题意得a +c =3,a -c =1, ∴a =2,c =1,b 2=3. ∴椭圆的标准方程为x 24+y 23=1.(2)证明:设A (x 1,y 1),B (x 2,y 2),由⎩⎪⎨⎪⎧y =kx +m ,x 24+y23=1得,(3+4k 2)x 2+8mkx +4(m 2-3)=0, ∴Δ=64m 2k 2-16(3+4k 2)(m 2-3)>0, 即3+4k 2-m 2>0.∴x 1+x 2=-8mk 3+4k 2,x 1x 2=4(m 2-3)3+4k2.y 1y 2=(kx 1+m )·(kx 2+m )=k 2x 1x 2+mk (x 1+x 2)+m 2=3(m 2-4k 2)3+4k2. ∵以AB 为直径的圆过椭圆的右顶点D (2,0),k AD ·k BD =-1,∴y 1x 1-2·y 2x 2-2=-1,化简得 y 1y 2+x 1x 2-2(x 1+x 2)+4=0,即3(m 2-4k 2)3+4k 2+4(m 2-3)3+4k 2+16mk 3+4k 2+4=0,化简得7m 2+16mk +4k 2=0,解得m 1=-2k ,m 2=-2k 7,且满足3+4k 2-m 2>0.当m =-2k 时,l :y =k (x -2),直线过定点(2,0),与已知矛盾; 当m =-2k 7时,l :y =k ⎝ ⎛⎭⎪⎫x -27,直线过定点⎝ ⎛⎭⎪⎫27,0. 综上可知,直线l 过定点,定点坐标为⎝ ⎛⎭⎪⎫27,0.。
高中数学直线与曲线交点计算技巧

高中数学直线与曲线交点计算技巧在高中数学中,直线与曲线的交点计算是一个常见的题型。
这种题型考察了学生对直线和曲线的性质、方程的解法以及计算的技巧。
本文将通过具体的例题,详细解析这类题目的解题思路和方法,帮助高中学生和他们的父母更好地掌握这一知识点。
首先,我们来看一个简单的例子。
已知直线y = 2x + 1和曲线y = x^2 + 1,求它们的交点坐标。
解题思路:1. 将直线方程和曲线方程联立,得到一个二次方程。
2. 解二次方程,求出交点的横坐标。
3. 将横坐标代入直线方程或曲线方程,求出交点的纵坐标。
4. 得到交点的坐标。
具体步骤如下:1. 将直线方程和曲线方程联立,得到二次方程:x^2 + 1 = 2x + 1x^2 - 2x = 02. 解二次方程,求出交点的横坐标:x(x - 2) = 0解得 x = 0 或 x = 23. 将横坐标代入直线方程或曲线方程,求出交点的纵坐标:当 x = 0 时,直线方程变为 y = 1,曲线方程变为 y = 1,所以交点为 (0, 1)。
当 x = 2 时,直线方程变为 y = 5,曲线方程变为 y = 5,所以交点为 (2, 5)。
4. 得到交点的坐标:交点坐标为 (0, 1) 和 (2, 5)。
通过这个例子,我们可以看到求解直线与曲线交点的关键在于联立方程,并解方程得到交点的横坐标。
然后,将横坐标代入方程,求出交点的纵坐标。
这样,我们就能得到交点的坐标。
除了直接联立方程求解交点,还有一种更简便的方法,即利用图像求解。
下面我们来看一个例子。
已知直线y = 2x + 1和曲线y = x^2 + 1,求它们的交点坐标。
解题思路:1. 将直线方程和曲线方程绘制在同一坐标系中。
2. 观察图像,确定交点的大致位置。
3. 利用图像求解,求出交点的坐标。
具体步骤如下:1. 绘制直线y = 2x + 1和曲线y = x^2 + 1的图像。
注意,可以使用计算器或绘图软件辅助绘制。
直线与曲线的交点知识点总结

直线与曲线的交点知识点总结直线和曲线的交点问题是数学中的重要内容之一。
在解决这类问题时,我们需要了解一些相关的知识点。
本文将对直线与曲线的交点进行总结,帮助读者更好地理解和应用相关概念。
1. 直线与曲线的交点定义及求解方法直线与曲线的交点是指直线与曲线在平面上相交的点。
一般来说,我们常用代数的方法求解交点。
具体而言,可以使用以下方法:1.1 代数方法对于直线和曲线的交点问题,我们可以将直线和曲线的方程联立,将未知量表示为同一变量,通过求解方程组来确定交点的坐标。
1.2 图形方法通过绘制直线和曲线的图形,我们可以观察到交点的大致位置,并估计交点的坐标。
然后通过进一步的计算和分析,可以获得更精确的结果。
2. 直线与曲线的常见示例下面介绍一些常见的直线与曲线的交点问题。
2.1 直线与直线的交点当两条直线相交时,交点的坐标可以通过联立直线的方程求解得到。
如果两条直线平行或重合,则它们没有交点。
2.2 直线与圆的交点当一条直线与圆相交时,交点的坐标可以通过联立直线和圆的方程求解得到。
具体求解方法可根据情况选择直接代入或消元的方法。
2.3 直线与抛物线的交点直线与抛物线相交时,可将直线的方程代入抛物线的方程,通过解方程求解交点的坐标。
具体求解方法可根据方程的形式选择适当的方法,如二次方程求解法等。
2.4 直线与椭圆的交点直线与椭圆相交时,可以将直线的方程代入椭圆的方程,通过解方程求解交点的坐标。
同样,求解方法可根据方程的形式选择适当的方法。
3. 直线与曲线交点应用举例直线与曲线的交点问题在生活和工作中有许多应用,下面以几个简单的例子加以说明。
3.1 交通规划在城市的交通规划中,我们常常需要考虑不同道路的交叉口。
这其中就牵涉到直线与曲线的交点问题。
通过计算直线与曲线的交点坐标,可以确定交叉口的位置和道路的走向。
3.2 物体运动轨迹在物理学中,我们常常需要研究物体的运动轨迹。
当物体的运动由直线和曲线组成时,我们可以通过计算直线与曲线的交点来确定物体的位置和运动轨迹。
关于油藏的相渗曲线的以及含水饱和度曲线交点求法
关于油藏的相渗曲线的以及含水饱和度曲线交点求法小熊维尼在油藏的期末复习的时候,我就发现了这个问题,明明很正常的fw-Sw曲线,想当然的会以为直接对它求导,然后求得斜率相等的点就行了。
但是往往事与愿违,往往给出的是点的数据,就是测井数据。
那么我们怎么来精确地求得那个交点值呢,以下给出一种数值方法,希望对大家有用。
前期准备:你必须得有mathematical,matlab或者maple,当然如果你对自己的计算能力有信心,那也行的。
步骤:1,我们从Excel表格中读取数据(以下我以传姐的数据为例)2,对导入的数据进行插值(三次艾米尔特插值的精度就可以了),画出插值函数,即:这就是经过插值之后的fw-Sw曲线了,既然我们有了函数表达式,那么后面的步骤我相信很多人都明白了。
3,但是事情往往没这么简单,你可能会想:“对啊,我略懂mathematical或者matlab 我知道切点的斜率和切线的斜率相等,而且切线过(0.32,0)这个点,这个还不好求吗?不就是一个Solve命令嘛。
”如果你真要这么想,我只能表示呵呵了。
可以明确表示常规的解方程命令在这里都不起作用。
原因是你的曲线是插值分段函数,虽然你看起来就像一条完整的曲线一样。
4,穷则思变,我们采用的是牛顿切线法或者割线法,这是一种线性收敛的计算方法,但是对于这道题的要求够了。
在mathematical下命令是FindRoot,matlab我就不知道了(求教)。
本质上牛顿切线法是一种迭代方法,也就是说必须给出迭代初始点以上是mathematical下的FindRoot函数的调用格式,和普通解方程的格式一致,看看下面的例子就明白了5,通过这样的方法我们就可以得到交点的x数值了带入插值函数(就是上面的函数可以求得y值了。
这样就可以把切线完美的表达出来了(两个点了)。
如下图:以下是传姐同学的数据,大家可以先仿照做一遍,看看自己做对没有:。
曲线的交点

C2 : x y 1 0 C2 : x y 9
2 2
(4) C1 : 2x y b 0
x2 y2 9 解:解方程组 2 x y b 0 2 2 5 x 4bx b 9 0
C2 : x y 曲线没有交点.
例3 当a为何值时,曲线y a | x | 与方程 ( y - x )( y x a ) 0所表示的曲线有 三个公共点?
y xb 例4 当b为何值时,方程组 y x2 有且只有一组解?
小结:
1.通过解方程组,求两曲线交点坐标,将几 何问题转化为代数问题来解决; 2.反之,也可用两曲线交点的情况,即几何图 形的性质,说明代数方程组有无实数解. 3.本节课将几何和代数紧密结合,互相转化, 对数形结合的思想有了更加深刻的理解.
因此,求两曲线的交点,就是求这两个曲线方程所组成 的方程组的解.
例1 若直线l1 : 2 x y 0, l2 : x y 3 0, l3 : ax 3 y 4 0三线共点,则a ____ .
例2 判断下列各对曲线是否有交点. (1)C1 : y x 1 1 2 (2)C1 : x y 0 2 (3)C1 : 2 x y 8 0 2 C2 : y x
2
4 5(b 9) 4(b 45)
2 2
(1)当 0时,即 3 5 b 3 5 , 方程有两个不相等的实数根,
所以直线与曲线有两个不同的交点.
(2)当 0时,即b 3 5或b 3 5 ,方程有两个相等的实数根,
所以直线与曲线只有一个公共点.
(3)当 0时,即b 3 5或b 3 5 , 方程没有实数根,
直线与曲线的交点

直线与曲线的交点直线与曲线的交点是数学中的重要概念,在几何学和微积分中有广泛的应用。
当一条直线与一条曲线相交时,它们在某个点上有相同的坐标值,这个点就是它们的交点。
本文将探讨直线与曲线的交点的概念、求解方法和一些实际应用。
一、直线与曲线的交点概念直线与曲线的交点是指一条直线与一条曲线在平面上相交的点。
直线可以用一元一次方程表示,一般具有形式y = kx + b,其中k和b为常数。
曲线则可以用二元二次方程、三次方程等多项式方程或参数方程来表示。
曲线的形状和特征由方程的类型决定。
二、求解直线与曲线的交点的方法求解直线与曲线的交点可以通过代数或几何的方法进行。
下面将介绍两种常用的求解方法。
1. 代数方法:利用代数方法求解直线与曲线的交点时,需要将直线方程和曲线方程联立,然后解方程组。
对于一元一次方程和一元二次方程,可以通过联立方程组消元的方式求解;对于高次多项式方程或参数方程,一般需要借助数值计算或者计算机程序来求解。
2. 几何方法:几何方法通过画出直线和曲线的几何图形,确定它们的交点位置。
对于一元一次方程,可以在坐标平面上画出直线,然后观察它与曲线的交点个数和位置;对于一元二次方程,可以画出抛物线和直线的图像,通过图像的交点来确定实际的交点。
三、直线与曲线的交点的应用直线与曲线的交点在科学和工程中有广泛的应用。
下面列举几个例子。
1. 物理学中的运动学:在物理学中,运动学研究物体的运动状态和规律。
当一条直线表示物体的位移,曲线表示物体的轨迹时,它们的交点就表示物体在某个时刻的位置。
通过求解直线与曲线的交点可以确定物体的位置和速度。
2. 经济学中的需求曲线和供应曲线:在经济学中,需求曲线和供应曲线用于描述商品或服务的需求量和供应量之间的关系。
需求曲线一般为下降曲线,供应曲线一般为上升曲线。
当需求曲线和供应曲线相交时,它们的交点表示市场均衡的价格和数量。
3. 电路分析中的交流电路:在电路分析中,交流电路通常由电容、电感、电阻和电源等元件组成。
求两个二次曲线交点个数的解决策略

m(x -
2)与双曲线 M:
x2 3
-
y2 3
= 1 相交于四个点。求 m 的取值范围。
y2= m(x- 2) (4)
解:联立方程
x2 3
-
y2 3
=
1
(5)
消去 y 并化简得
x2- mx + 2m- 3= 0
(6)
判别式 = m2- 8m+ 12, x1+ x2= m, x1x2= 2m- 3
因为这个方程的根 x1, x2 必须代入(4)才能解出方程组
用判别式法讨论实数解的情况。这种转化是否等价, 是解答
正确与否的关键。
例1 已知抛物线 E: y= x 与圆 M: (x- 4)2+ y2= r2( r>
0)相交于 A、B、C、D 四个点, 求 r 的取值范围。
y= x 解:联立方程 (x - 4)2+ y2= r2 x2- 7x + 16- r2= 0 (3)
变化的对应规律, 交点个数与参数范围的关系则一目了然。
[责任编辑: 刘志军]
= (- 8)2- 12(8- 4r2)> 0 由此得 f (- 2)> 0
解得
6 3
<
r<
1
f (2)> 0
有些二次曲线的相交问题也可以用参数法。
例4 抛物线 E: y2= x 与圆 M: (x- m)2+ y2= 1 没有交 点,求 m 的取值范围。
解:圆 M: (x- m)2+ y2= 1 的参数方程为: x= m+ cos y= sin
中学生叛逆心理很强, 受各方面的影响, 在服饰穿着、语 言举止方面须强化礼仪观点。基于这一原则, 从人文角度来 处理, 应对服饰穿着进行正面的要求: ∃ 对于中学生来说现在 正是阳光灿烂, 激情飞扬的时刻, 应用色彩鲜明的运动服和简 洁大方的休闲服、校服来修饰自己。只有这样才可以迸发出 青春和朝气, 感染别人使其蓬勃向上。%对语言举止方面, 宜采 用对比方式进行教育。因为中学生现已具备分辨是非的能 力,把一些好的和坏的表达行为同时展现在学生面前, 让学生
掌握直线和曲线的交点计算方法

掌握直线和曲线的交点计算方法直线和曲线的交点计算方法在数学中,直线和曲线的交点计算是一个常见的问题。
通过掌握正确的计算方法,我们可以准确地确定直线和曲线的交点位置。
本文将介绍两种常见的计算方法:代数方法和几何方法。
一、代数方法使用代数方法计算直线和曲线的交点,我们需要了解直线和曲线的方程。
假设直线的方程为y=ax+b,曲线的方程为f(x),我们可以通过以下步骤求解交点的横纵坐标。
1. 将直线方程中的y用曲线方程中的x表示。
例如,将直线方程中的y=ax+b改写为x=a'y+b',其中a'为a的倒数,b'为b除以a。
2. 将直线方程和曲线方程相等,即a'y+b'=f(x)。
3. 求解上述方程的解,得到交点的横坐标x。
4. 将横坐标x代入直线方程或曲线方程,求解得到交点的纵坐标y。
举例说明,假设直线方程为y=2x+1,曲线方程为f(x)=x^2,我们可以按照以上步骤计算交点的坐标。
1. 将直线方程中的y用曲线方程中的x表示,得到x=1/2(y-1)。
2. 将直线方程和曲线方程相等,即1/2(y-1)=x^2。
3. 将方程1/2(y-1)=x^2转化为二次方程的标准形式,得到x^2-1/2(y-1)=0。
4. 求解上述二次方程,得到交点的横坐标x=±√[1/2(y-1)]。
5. 将横坐标x代入直线方程或曲线方程,求解得到交点的纵坐标y。
通过上述计算,我们可以得到直线和曲线的交点的坐标。
二、几何方法除了代数方法,我们还可以使用几何方法来计算直线和曲线的交点。
几何方法通过绘制图形,利用几何关系求解交点的位置。
1. 绘制直线和曲线的图形。
2. 在图中标注直线和曲线的方程。
3. 观察图形,找到直线和曲线的交点位置。
4. 使用尺规作图或其他几何方法,求解交点的坐标。
举例说明,假设直线方程为y=2x+1,曲线方程为f(x)=x^2,我们可以按照以上步骤计算交点的坐标。
直线与曲线的交点求解

直线与曲线的交点求解直线与曲线的交点求解是数学中一个重要的问题,它在几何学、物理学、工程学等领域都有广泛的应用。
本文将介绍两种常见的方法——代数法和几何法来求解直线与曲线的交点。
方法一:代数法代数法是通过解方程组来求解直线与曲线的交点。
设直线的方程为y = kx + b,曲线的方程为f(x) = 0。
我们可以将曲线的方程代入直线的方程中,得到一个关于x的方程:kx + b - f(x) = 0。
接下来,我们需要解这个方程。
这一步通常需要利用数值计算或者迭代法来求解。
在具体求解过程中,我们可以采用二分法、牛顿法等数值计算方法来逼近交点的解。
方法二:几何法几何法是通过图形的性质和几何关系来求解直线与曲线的交点。
它常用于解析几何中的问题。
下面我们以直线与抛物线的交点为例,介绍几何法的求解过程。
假设直线的方程为y = kx + b,抛物线的方程为y = ax^2 + bx + c。
我们可以将直线的方程代入抛物线的方程,得到一个关于x的二次方程:ax^2 + (b - k)x + (c - b) = 0。
接下来,我们需要解这个二次方程。
根据二次方程的求根公式,我们可以得到两个解x1和x2。
将这两个解分别代入直线的方程,得到对应的y1和y2。
这时候我们可以观察抛物线和直线的图像,通过图像的交点来验证我们的解。
总结:直线与曲线的交点求解是一个重要的数学问题。
本文介绍了两种常见的方法:代数法和几何法。
代数法通过解方程组来求解交点的坐标,而几何法则通过图形的性质来求解。
无论使用哪种方法,我们都需要利用数学工具,如数值计算或者图形分析,来得到准确的结果。
直线与曲线的交点求解在实际应用中有广泛的应用,比如刚体力学中的受力分析、电路中的电流分布等。
掌握这一求解方法对于理解和解决实际问题具有重要意义。
通过学习和应用直线与曲线的交点求解方法,我们可以更好地理解数学知识,并将其应用到实际问题中。
希望本文能对读者在解决相关问题时提供一些帮助。
曲线计算交点

43 43 43 43 43 43 43 43 43 43 43 43 43 0 25.70 25.70 25.70 25.70 25.70 25.70 25.70 25.70 25.70 25.70 25.70 25.70 25.70 25.70 25.70
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
3808083.8967 3808085.0675 3808086.2384 3808087.4092 3808088.5800 3804765.0521 3804770.8360 3804776.1399 3804782.5081 3804787.0521 3803456.6103 3803462.4644 3803471.8077 3803476.5144 3803480.1089 3803485.8811 3803491.7353 3803497.5895 3803499.9311 3803502.2728 3803503.4436 3803504.6145 3803509.2978 3803515.1520 3803521.1232 3803525.9864 3804636.3082 3804639.7342 3804653.0293 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000
一种快速求取空间任意两条曲线交点的算法

! 戴葵等译 R(美)/5FA01 SR 85251" 86T5F> PR +CUBA=" /5FV 8R PC5WC 著 R
X 焦李成 R 神经网络的应用与实现 R 西安:西安电子科技大学出版社, !**YR
’ 孙靖民 R 机械优化设计 R 北京:机械工业出版社,!**%R % 许崎,李永生,威学成 R 梯度法与 PQ 神经网络的结合在机械优化设
2在两条曲线存在交点的区间内计算两条曲线的最短距离在两条曲线存在交点可能的参数区间内利用控制顶点正算出所对应的曲线段求两条曲线的最短距离
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!"
《机械设计与制造》 ,GAR #&&’ -6R % /5G=01CFM +C@021 _ /51BD5GABFC
所对应的两条曲线没有交点,如图 0 + ; , 和图 0 + < , 所示。
上述判断原理的算法步骤为:
%=*&06 分别选取两条曲线控制多边形的其中一条边。
%=*&"6 计算 !0 和 !",如果 !0 与 !" 方向相反,计算 !! 与 !5,如果 !! 与 !5 方向相反,则所对应的两条曲线存在相交的可 能性,分别记录所对应的控制顶点 + !" $ 0/ !"/ !" 7 0/ !" 7 " , 、+ -$ $ 0/ -$/ -$ 7 0/ -$ 7 " , 及参数区间,以备下一步处理。如果 !! 与 !5 方向相 同,则所对应的两条曲线没有交点。如果 !0 与 !" 方向相同,则 所对应的两条曲线也没有交点。
求交点坐标的方法

求交点坐标的方法嘿,你问求交点坐标的方法啊?这事儿其实不难。
要是两个直线求交点坐标呢,那就先把两条直线的方程都摆出来。
比如说一条直线是 y = 2x + 1,另一条是 y = -x + 4。
然后让这两个式子相等,也就是 2x + 1 = -x + 4。
接着就来解这个方程呗。
把 x 都移到一边,数字移到另一边,就变成 2x + x = 4 - 1,那就是 3x = 3,一解就知道x = 1 啦。
再把 x = 1 代回到随便一个直线方程里,比如代到 y = 2x + 1 里,那 y 就等于2×1 + 1 = 3。
这样交点坐标就是(1,3)。
要是曲线和直线求交点坐标呢,也差不多这路子。
把曲线的方程和直线的方程放在一起,让它们相等,然后解方程。
比如说一个圆的方程是x² + y² = 9,一条直线是 y = x + 1。
那就把 y = x + 1 代到圆的方程里,变成x² + (x + 1)² = 9。
展开这个式子,x² + x² + 2x + 1 = 9,整理一下就是2x² + 2x - 8 = 0。
再用求根公式或者其他方法解这个方程,求出 x 的值。
再把 x 的值代回到直线方程里求出 y 的值,就得到交点坐标啦。
比如说有个同学在做数学作业,碰到一道题是求两条直线的交点坐标。
他就按照上面的方法,先把两条直线的方程摆出来,然后让它们相等,解出 x 的值,再代回去求出 y 的值。
最后找到了交点坐标,开心得不得了。
所以说啊,求交点坐标就是这么个事儿,只要掌握了方法,就不难啦。
咋样,现在知道怎么求交点坐标了吧?。
[经典]重要曲线交点桩号计算公式
![[经典]重要曲线交点桩号计算公式](https://img.taocdn.com/s3/m/ca14130ba66e58fafab069dc5022aaea988f4150.png)
缓和曲线计算方法(ZH~HY)中线000首先计算直线段坐标方位角(即ZH~JD坐标方位角),及ZH点坐标。
备用偏角公式:{30*L/(π*RLS)缓和曲线}000计算待求点偏角=((L/10)2 *(57296/(RLS ))/60。
其中L=待求点至ZH距离、R=圆曲线半径、LS =缓和曲线长。
000待求点方位角=直线方位角±待求点偏角。
(曲线左转-偏角,曲线右转+偏角)00 0待求点至ZH点弦长=L—L5 /(90*R2 *LS 2),其中L=待求点至ZH距离(里程)、R=圆曲线半径。
000待求点坐标:000X=ZH点X坐标+COS(待求点方位角)*弦长000Y= ZH点Y坐标+SIN(待求点方位角)*弦长000缓和曲线计算左右边线坐标(ZH~HY)000左侧方位角=(待求点方位角±2倍偏角=直线方位角±3倍偏角)—边线与中线夹角。
000右侧方位角=(待求点方位角±2倍偏角=直线方位角±3倍偏角)+边线与中线夹角。
000左侧边线坐标:000X=该点中线X坐标+COS(左侧方位角)*边线至中线距离000Y=该点中线Y坐标+SIN(左侧方位角)*边线至中线距离000右侧边线坐标:000X=该点中线X坐标+COS(右侧方位角)*边线至中线距离000Y=该点中线Y坐标+SIN(右侧方位角)*边线至中线距离000圆曲线计算方法(HY~YH)中线000注:(ZY-YZ)同理,方位角=用直线方位角-待求点偏角000首先计算直线段坐标方位角(即ZH~JD坐标方位角),及HY点坐标。
000求出缓圆点(HY)偏角=(LS*90)/(π* R)。
000求待求点偏角=(L*90)/(π* R)。
000其中:000L=待求点至HY距离(里程)、R=圆曲线半径、LS =缓和曲线长。
000待求点至HY点弦长=2* R*SIN(待求点偏角)。
000待求点方位角=直线方位角±HY点偏角±待求点偏角,(曲线左转-偏角,曲线右转+偏角)。
解析几何中的曲线与平面的交点

在解析几何中,曲线与平面的交点是重要的概念之一。
它们不仅是数学中的基础知识,还在科学和工程领域中有广泛的应用。
本文将以“解析几何中的曲线与平面的交点”为题,探讨曲线与平面的交点的性质和求解方法。
首先,我们来了解一下曲线与平面的基本概念。
曲线可以被看作是由一系列点组成的集合,而平面则是由无限多个点组成的集合。
当曲线与平面相交时,它们会有交点。
曲线可能与平面相切或相离,交点的个数也可能是有限的或无限的。
因此,曲线与平面的交点有多种情况,这取决于曲线和平面的性质。
接下来,我们将讨论求解曲线与平面交点的方法。
对于某些简单的曲线和平面,我们可以通过代数方法求解交点。
以一次函数和平面为例,设曲线为y=ax+b,平面为Ax+By+Cz+D=0。
要求曲线与平面的交点,我们可以将曲线方程代入平面方程,得到一个关于x和y的一次方程,然后求解这个方程组,即可找到交点的坐标。
当曲线和平面的方程复杂时,我们可以通过解析几何的方法进行求解。
以圆和平面为例,设圆的方程为(x-a)²+(y-b)²=r²,平面的方程为Ax+By+Cz+D=0。
要求圆与平面的交点,我们可以将圆方程代入平面方程,得到一个关于x、y和z的二次方程,然后将它化简为齐次二次方程组,进行分析和求解。
此外,曲线和平面的交点也可以通过几何方法求解。
例如,我们可以画出曲线和平面的图形,然后观察它们的位置关系,进而找到交点的坐标。
对于圆和平面的交点,我们可以利用圆和平面的几何性质,如圆心到平面的距离等,来求解交点的位置。
最后,我们需要了解曲线与平面交点的性质。
当曲线与平面相交时,交点的个数可能是有限的或无限的。
如果交点的个数为无限,则曲线和平面是共面的。
如果交点的个数为有限,交点可能是切点、交点或相离点。
通过分析曲线和平面的方程,我们可以推导出交点的性质,并用几何方式进行证明。
总之,解析几何中的曲线与平面的交点是重要的概念。
求解曲线与平面的交点可以通过代数、解析几何和几何方法进行。
