公路路线的交点曲线计算方法_secret
道路曲线高程计算公式

高速公路的一些线路坐标、高程计算公式(缓和曲线、竖曲线、圆曲线、匝道) 一、缓和曲线上的点坐标计算已知:①缓和曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当计算第二缓和曲线上的点坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反xZ,yZ为点HZ的坐标切线角计算公式:二、圆曲线上的点坐标计算已知:①圆曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当只知道HZ点的坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反xZ,yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明:l——任意点到起点的曲线长度(或缓曲上任意点到缓曲起点的长度)l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知:①第一坡度:i1(上坡为“+”,下坡为“-”)②第二坡度:i2(上坡为“+”,下坡为“-”)③变坡点桩号:SZ④变坡点高程:HZ⑤竖曲线的切线长度:T⑥待求点桩号:S计算过程:五、超高缓和过渡段的横坡计算已知:如图,第一横坡:i1第二横坡:i2过渡段长度:L待求处离第二横坡点(过渡段终点)的距离:x 求:待求处的横坡:i解:d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知:①待求点桩号:K②曲线起点桩号:K0③曲线终点桩号:K1④曲线起点坐标:x0,y0⑤曲线起点切线方位角:α0⑥曲线起点处曲率:P0(左转为“-”,右转为“+”)⑦曲线终点处曲率:P1(左转为“-”,右转为“+”)求:①线路匝道上点的坐标:x,y②待求点的切线方位角:αT计算过程:。
道路勘测设计交点要素计算

道路勘测设计交点要素计算篇一:道路勘测设计交点要素计算是道路勘测设计过程中非常重要的一步,它涉及到道路的几何形状、尺寸、交点位置等要素的确定。
下面将详细介绍交点要素计算的方法和应用。
一、交点要素计算的方法交点要素计算的方法主要包括以下几种:1. 几何要素计算法:根据道路的几何形状和尺寸,通过数学计算方式确定交点的位置和形状。
该方法需要使用专业的数学软件,如Excel、CAD等。
2. 测量要素计算法:通过测量道路的几何形状和尺寸,计算出交点的位置和形状。
该方法需要使用专业的测量工具,如GPS、激光扫描仪等。
3. 模拟要素计算法:通过计算机模拟道路的运行过程,计算出交点的位置和形状。
该方法需要使用专业的软件,如有限元分析软件、三维建模软件等。
二、交点要素计算的应用交点要素计算的应用非常广泛,主要包括以下几个方面:1. 道路勘测设计:交点要素计算是道路勘测设计的基础,它决定了道路的几何形状和尺寸,以及交点的位置和数量。
通过交点要素计算,可以确定道路的设计方案,为道路的建设提供重要的依据。
2. 道路养护管理:交点要素计算也是道路养护管理的基础,它决定了道路的磨损程度和维修方案。
通过交点要素计算,可以及时发现道路的异常情况,并及时采取措施。
3. 交通工程:交点要素计算也是交通工程的基础,它决定了道路的交通流量和拥堵程度。
通过交点要素计算,可以计算出道路的交点数量、交点位置和拥堵程度等信息,为交通工程的设计和管理提供重要的依据。
交点要素计算是道路勘测设计、道路养护管理和交通工程中非常重要的一环。
只有正确地计算交点要素,才能确保道路的正常使用和安全性。
篇二:道路勘测设计交点要素计算是道路勘测设计过程中非常重要的一步,它是为了保证道路的可行性和安全性所必需的。
交点要素计算包括计算道路各个相交部位的几何形状、尺寸、位置、交通流量等参数,以确保相交道路的通行能力和安全性。
以下是交点要素计算的一般步骤和注意事项:1. 几何形状计算:根据道路设计规范和地形图等资料,计算道路各个相交部位的几何形状和尺寸。
道路工程测量中平曲线要素相关公式计算

道路工程测量中平曲线要素计算一、路线转角、交点间距的计算(一)在地形图上量出路线起终点及各路线交点的坐标:()()()21Q 23810,27180JD 2399626977JD 2468426591D 、,、,、()3JD 24848025885,、()4JD 2535025204,、()ZD 2606225783,(二)计算公式及方法设起点坐标为()00,QD X Y ,第i 个交点坐标为(),,1,2,3,4,i i i JD X Y i =则坐标增量11,i i i i DX X X DY Y Y --=-=-交点间距D =象限角 arctanDYDXθ= 方位角A 是由象限角推算的:转角1i i i A A α-=- 1.1JD QD 与之间:坐标增量10=2396623810=1860DX X X =-->1026977271802030DY Y Y =-=-=-<交点间距275.33D m === 象限角 203arctanarctan 47.502186DY DX θ-=== 方位角036036047.502312.498A θ=-=-= 2.12JD JD 与之间:坐标增量21X =2468423966=6880DX X =-->21Y 26591269773860DY Y =-=-=-<交点间距788.89D m === 象限角 386arctanarctan 29.294688DY DX θ-=== 方位角136036029.294330.706A θ=-=-= 转角110=330.706312.49818.208A A α-=-= 3. 23JD JD 与之间:坐标增量32X =2484024684=1560DX X =-->32Y 25885265917060DY Y =-=-=-<交点间距723.03D m === 象限角 706arctanarctan 77.54156DY DX θ-=== 方位角236036077.54282.46A θ=-=-= 转角221=282.46330.70648.246A A α-=-=- 4. 34JD JD 与之间:坐标增量43X =2535024840=5100DX X =-->43Y 25204258856810DY Y =-=-=-<交点间距850.8D m === 象限角 510arctanarctan 53.171681DY DX θ===- 方位角336036053.171306.829A θ=-=-= 转角332=306.829282.4624.369A A α-=-= 5. 4ZD JD 与之间:坐标增量4X =2606225350=7120DX X =-->4Y 25783252045790DY Y =-=-=>交点间距917.706D m === 象限角 579arctanarctan 39.118712DY DX θ=== 方位角039.118A θ==转角443=39.118312.49892.289A A α-=-= 二、各平曲线要素的计算 (一)JD 1曲线要素计算取800m R =,设计速度为h km /60,JD 1桩号为K 0+275.33,转角18.208α= 1.缓和曲线长度S L ,则:33600.0360.0369.72(m)800S V L R ==⨯=)m (5036.36036.3=⨯=⨯≥V L S 800~~80088.89~800(m)99S R L R ===取整数,采用缓和曲线长120m (《公路工程技术标准》规定:=V h km 60时,最小缓和曲线长度为m 50).2.圆曲线内移值R ∆2424331201200.75(m)242688()248002688(800)S SL L R R R ∆=-=-=⨯⨯⨯3.总切线长h T先求332212012059.989(m)22402240800S S L L q R =-=-=⨯ 所以18.208()tan (8000.75)tan59.989188.31(m)22h T R R q α=+∆+=++= 4.曲线总长度h L=0.0752SL Rβ=(2)2+374.22(m)180180h S S L R L R L ππαβα=-+=∙=5.五个基本桩号1JD K 0+274.33 )- h T 188.311ZH K 0+087.02 )+ S L 120.00 1HY K 0+207.02 )+ )2(S h L L - 134.22 1YH K 0+341.24 )+ S L 120.001HZ K 0+461.24)- h 21L187.111QZ K 0+274.1318.208()sec(8000.75sec80010.97(m)22h E R R R α=+∆-=+-= 超距h 22188.31374.22 2.4(m)D T L =-=⨯-=。
公路路线的交点曲线计算法

公路路线的交点曲线计算法
随着时代的发展,科技的进步,交通运输的革新对加快国
家各项经济建设有着重大的意义。
路网规划是道路设计的基础,计算交点曲线有助于评估路网建设质量和探究不同道路特性。
首先,计算交点曲线时,需要确定公路路线上所有路口和
路段。
将所有节点定位信息、路段连接信息连接起来,形成路
段网络,实现路线图形化及数据化模拟,定位出路网的交叉点,形成的图中的顶点就是路段的交点。
其次,使用经过空间坐标定位的位置学方法可以很容易地
确定交点曲线的方位。
即,首先需要对路网的每一个节点进行
测量,对空间坐标进行变换,并根据相应的变形规律,根据实
际路网图和图形叠加,得到每个节点相应位置坐标,根据坐标
计算曲线上点到曲线外点的最短距离,确定曲线方位,可以在
规划道路时将交点曲线考虑进去。
最后,要改善公路的运行情况,计算交点曲线可以帮助信
息化管理系统比较有效地调节路口交通信号,以提高路口通行
效率。
另外,计算交点曲线还可以评价路口容量,实现进口规
划和车辆识别,还可以帮助规划路面布局,计算车辆行驶安全
距离,以提高路网安全性。
总之,计算交点曲线虽然是一个复杂的技术难点,但能够
帮助管理人员更加有效地规划公路路线,提升公路的安全性和
运行效率,也是未来发展的趋势。
道路曲线计算公式

高速公路线路(缓和曲线、竖曲线、圆曲线、匝道)坐标计算公式时间:2009-12-27 21:40:34 来源:本站作者:未知我要投稿我要收藏投稿指南高速公路的一些线路坐标、高程计算公式(缓和曲线、竖曲线、圆曲线、匝道)一、缓和曲线上的点坐标计算已知:①缓和曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:x Z,y Z计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当计算第二缓和曲线上的点坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反x Z,y Z为点HZ的坐标切线角计算公式:二、圆曲线上的点坐标计算已知:①圆曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:x Z,y Z计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当只知道HZ点的坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反x Z,y Z为点HZ的坐标三、曲线要素计算公式公式中各符号说明:l——任意点到起点的曲线长度(或缓曲上任意点到缓曲起点的长度)l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知:①第一坡度:i1(上坡为“+”,下坡为“-”)②第二坡度:i2(上坡为“+”,下坡为“-”)③变坡点桩号:S Z④变坡点高程:H Z⑤竖曲线的切线长度:T⑥待求点桩号:S计算过程:五、超高缓和过渡段的横坡计算已知:如图,第一横坡:i1第二横坡:i2过渡段长度:L待求处离第二横坡点(过渡段终点)的距离:x求:待求处的横坡:i解:d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知:①待求点桩号:K②曲线起点桩号:K0③曲线终点桩号:K1④曲线起点坐标:x0,y0⑤曲线起点切线方位角:α0⑥曲线起点处曲率:P0(左转为“-”,右转为“+”)⑦曲线终点处曲率:P1(左转为“-”,右转为“+”)求:①线路匝道上点的坐标:x,y②待求点的切线方位角:αT计算过程:注:sgn(x)函数是取符号函数,当x<0时sgn(x)=-1,当x>0时sgn(x)=1,当x=0时sgn(x)=0。
公路路线的交点曲线计算法

公路路线的交点曲线计算法摘要:本文介绍一种以曲线计算为内核的新的交点转角公路平曲线计算方法,适用于目前直曲线混合法定线时任意复杂线形的计算机辅助设计计算,并以标准的“直线、曲线及转角表”形式输出设计结果。
关键词:交点线元交点曲线计算法1.前言传统的公路平面敷设计算方法是以交点(JD)转角(α)为基础,以外距(E)为控制,通过求算切线长(T)来计算平曲线要素及各主点桩号的,与此相应的平面设计表达便是路线“直线、曲线及转角表”。
这种表达方式除了具有直观、方便的特点以外,更为重要的是它体现出公路路线设计的两个面,一是与之相适应直线加弯道的设计思路、定线方式、中线敷设和施工放样方法,另一个则是与汽车动力学相关的各项道路几何指标,因而应该说是十分经典并为大家所习惯采用的。
以后随着光电测距仪、全站仪等先进的测量仪器的出现,公路中线敷设及施工放线广泛采用极坐标法,从而摆脱了对特定计算方法的依赖,但对于较长距离的公路主线,传统的交点转角设计定线方法和“直线、曲线及转角表”的表达方式,却仍是其他方法和方式所不能取代的。
然而,当路线因为受到限制而不得不采用,诸如不对称曲线、卵形曲线、复曲线、凸曲线、双卵形曲线等复杂曲线,特别是需要曲线反算的情况下,采用传统的交点转角计算方法是很困难的。
对于复杂曲线的计算,大家一般采用了在传统方法的基础上,按曲线类型分别推导计算公式,并编写功能单一的计算程序进行计算的方法。
显然这种方法局限性大、程序功能单一,即使编写了针对不同类型曲线的许多模块,也不能涵盖任意的线形组合和曲线类型等情况。
笔者通过设计工作实践和纬地道路辅助设计系统的研究开发,在许多技术人员熟知的传统交点转角法布设平曲线的基础上,提出一种利用计算机进行平曲线计算的新交点转角法,该方法适用于任意复杂线形的设计计算。
2.交点曲线计算法该方法以适用于任意线元组合的复杂线形设计计算为目标,是以三种基本线元的统一参数模型为基础约定,以三线元捆绑式结构为通用的单交点曲线模型的交点可组合的计算方法,有别于传统的交点转角计算方法,暂称之为交点曲线计算法。
线路竖曲线计算公式

竖曲线计算公式
一、公路施工中经常见到线路竖向曲线计算标高的问题,采用近似计算方法以外耻距(E)变化量代替标高增减量计算,设和用于半径(R)大于5000m时,误差为0.2mm。
1、凸曲线:H计算=H起坡点+i×△L起坡点至计算点的距离-(1/conα-1)×R
2、凹面线:H计算=H起坡点- i×△L起坡点至计算点的距离+(1/conα-1)×R
二、公路施工中经常见到线路竖向曲线计算标高的问题,采用近似计算方法以外变高差(h)变化量代替标高增减量计算,适合用于半径(R)小于5000m时,误差为0.2mm。
1、凸曲线:H计算=H起坡点+ i×△L起坡点至计算点的距离-(△L起坡点至计算点的距离)2/2R
2、凹面线:H计算=H起坡点- i×△L起坡点至计算点的距离+(△L起坡点至计算点的距离)2/2R
三、计算时考虑是正方计算方向来确定公式变换,如果凹面曲线从坡度终点返算时:坡度值为正值采用2公式时就应为+(- i×△L)。
道路测量坐标计算系统交点法简介

⑴采用资源管理器界面类型进行设计,数据按照“工程、曲线、计算表”三级进行组织。
可以建立数个工程,每个工程包含数个曲线,每个曲线又包含若干计算表。
结构清晰,便于测量资料的计算、存储、管理。
⑵对于一个曲线,可以根据不同需要,计算不同的点位坐标(如中桩、边桩),产生一个相对独立的计算表,而不需重复输入曲线交点坐标、半径、缓和曲线长等资料。
⑶能够计算出中桩、边桩任意点的坐标。
软件提供中桩、中桩+左右边桩、中桩+左边桩、中桩+右边桩四种计算表类型,可以根据实际需要进行选择。
⑷能够计算法线方向及任意方向边桩的坐标。
⑸计算出中桩的切线方位角,便于您进行其他的计算。
⑹可以利用“坐标查询”窗口针对一个曲线或一项工程进行某一桩号的坐标查询,而不需建立计算表,灵活方便。
⑺已知一点的坐标,可以利用“桩号查询”窗口进行桩号查询。
利用此窗口可以计算出此点对应中桩的里程以及到中桩的距离,这样可以用于高边坡、挡土墙、隧道净空的检查。
⑻计算坐标时,桩号输入提供手动输入和自动输入两种方式。
自动输入方式能够自动产生整桩号以及固定距离的左右边桩;自动输入后还可以进入手动输入状态进行更改,以适合您的特殊需要。
⑼可以对桩号自动输入的起讫点进行设置。
⑽计算表产生后,可以输入置镜点、后视点坐标,能够计算出现场放样数据。
置镜点、后视点也可以从控制桩表中进行选择。
⑾每一项工程都有一个独立的控制桩表。
打开控制桩表后可以进行控制桩的添加、删除等操作。
⑿具有极强的纠错能力,能够对您输入的数据进行自动检查,对错误数据给出提示。
⒀计算结果可以导出,可以用Excel软件进行编辑或用于往测量仪器的传输;也可以自动生成精美报表,并能够进行打印预览或打印输出。
⑴软件采用Windows 界面风格进行设计,界面友好,易于理解。
软件提供下拉菜单、快捷键、工具栏三种操作方式,操作方便、快捷;⑵能够进行标准曲线、C型、S型、卵型曲线等任意复杂形式的线形坐标计算;⑶不仅能够计算任意点的平面坐标,而且还能够计算其标高;⑷通过设置可以自动计算全线任意区段的整桩号或固定间距的中桩及边桩坐标;⑸能够计算法线方向及任意方向边桩的坐标;⑹软件自动处理竖曲线及路面横坡,能够计算任一桩号的标高及路面横坡;⑺通过设置,可以计算出路基顶面、底基层、基层、路面等各施工层的标高,并能打印出标高计算表,可以直接用于路基、路面施工中的标高控制;⑻可以根据实测坐标反算出该点对应的桩号及与中桩的距离,也可以计算出该点的设计标高及实际与设计的高差,用于施工过程中的检查;⑼自动进行路面加宽数据的计算。
道路曲线高程计算公式

道路曲线高程计算公式集团标准化工作小组 [Q8QX9QT-X8QQB8Q8-NQ8QJ8-M8QMN]高速公路的一些线路坐标、高程计算公式(缓和曲线、竖曲线、圆曲线、匝道) 一、缓和曲线上的点坐标计算已知:①缓和曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当计算第二缓和曲线上的点坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反xZ,yZ为点HZ的坐标切线角计算公式:二、圆曲线上的点坐标计算已知:①圆曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当只知道HZ点的坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反xZ,yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明:l——任意点到起点的曲线长度(或缓曲上任意点到缓曲起点的长度)l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知:①第一坡度:i1(上坡为“+”,下坡为“-”)②第二坡度:i2(上坡为“+”,下坡为“-”)③变坡点桩号:SZ④变坡点高程:HZ⑤竖曲线的切线长度:T⑥待求点桩号:S计算过程:五、超高缓和过渡段的横坡计算已知:如图,第一横坡:i1第二横坡:i2过渡段长度:L待求处离第二横坡点(过渡段终点)的距离:x 求:待求处的横坡:i解:d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知:①待求点桩号:K②曲线起点桩号:K0③曲线终点桩号:K1④曲线起点坐标:x0,y0⑤曲线起点切线方位角:α0⑥曲线起点处曲率:P0(左转为“-”,右转为“+”)⑦曲线终点处曲率:P1(左转为“-”,右转为“+”)求:①线路匝道上点的坐标:x,y②待求点的切线方位角:αT计算过程:。
道路勘测设计交点要素计算

道路勘测设计交点要素计算道路勘测设计交点要素计算是指在道路勘测设计过程中,对交叉口要素进行计算,以确定交点的位置、形状和规模。
交点是道路交通中不同道路之间的交汇点,包括交叉口、环岛、立交桥等。
交点要素的准确计算是道路勘测设计的关键环节,对道路交通的安全、顺畅和效率均起到重要作用。
1.位置计算:根据道路规划和布局要求,在平面上确定交点的具体位置。
位置计算需要考虑到交点所在道路的交通流量、车辆转弯半径、视距要求等因素,并根据道路标准和规则进行合理的布局。
2.形状计算:交点的形状计算是指确定交点的形状和几何特征。
交点的形状计算需要根据道路类型(如城市道路、高速公路、乡村道路等)和交通流量进行分析和评估,确定最合适的交点形状,如直角交叉口、弯曲交叉口、环形交叉口等。
3.规模计算:交点的规模计算是指确定交点的尺寸和容量。
交点的规模计算需要考虑到交通流量、车辆速度和车辆类型等因素,合理确定交点的尺寸和容量,以确保交通的顺畅和安全。
4.设施计算:交点的设施计算是指确定交点所需的交通设施和交通标志。
交点的设施计算需要根据道路规划和交通要求,合理设置交通标志、交通信号灯、交通岛、人行横道等设施,确保交通的有序和安全。
在进行道路勘测设计交点要素计算时,需要使用各种测量仪器和软件工具,如全站仪、地质仪、土方计算软件等。
同时,还需要参考相关的道路标准和规范,如《城市道路交通设计规范》、《公路工程设计标准》等,确保计算结果的准确性和合理性。
总之,道路勘测设计交点要素计算是道路勘测设计的重要环节,通过准确计算交点要素,可以确保交通的安全、顺畅和高效,提高道路交通的运行效率。
公路平曲线坐标计算公式

O:缘和曲线起点里程
C:缘和曲线起点X坐标
Q:起始方位角(当J=-1时,方位角应+180。)
Z:偏角判定值(当J=1时,左偏为-1,右偏为1;当J=-1时,左偏为1,右偏为-1)
D:距中桩的距离
S:斜交角度
F:缘和曲线起点Y坐标
2、圆曲线
Lb10
{K,D}
①L=K-0
②X=C+R[sin(Q+L/R*180/π)-sinQ]+Dcos(Q+L/R*180/π+S)◢
③Y=F+LsinQ+Dsin(Q+S)◢
Goto 0
注:K:欲求点里程
O:直线起点里程
C:直线起点X坐标
Q:起始方位角
D:距中桩的距离
S:斜交角度
F:直线起点Y坐标
二、竖曲线计算公式
Lb1 0
①{K}
②L=K-(0-T)
③H=M-IT+LI-ZL2/2/R◢
Goto 0
注:K:欲求点里程
O:顶点里程
③Y=F-R[cos(Q+L/R*180/π)-cosQ]+Dsin(Q+L/R*180/π+S)◢
Goto 0
注:K:欲求点里程
O:圆曲线起点里程
C:圆曲线起点X坐标
R:圆曲线半径(左偏为负)
Q:起始方位角
D:距中桩的距离
S:斜交角度
F:圆曲线起点Y坐标
3、直线
Lb10
{K,D}
①L=K-0
②X=C+LcosQ+Dcos(Q+S)◢
一、公路平曲线坐标计算公式
1、缘和曲线:
公路路线的交点曲线计算法

基于如上的“ 缓圆缓” 结构模型 , 以及单一交点
责任编 辑: 王兴红
一
6 一 O
以 下这篇论文是通过应用 E g o t al p i 公路 e n 该方法以适用于任意线元组合的复杂线形的 表 1 基本线元统一参数模型 设计软件在埃塞俄比亚 国际招标工程 N M路的 设 计汁算为目标 , — 是以三种基本线元的统一参数模 实际没汁过程中的体会租 总结。 型为基础约定, 以三线元捆绑式结构为通用的单交 N M路工程简介: — 点曲线模型的交点可组合的计算方法 , 有别于传统 N M(  ̄oMe d) — N — ni 公路是埃塞俄比亚联邦民 的交 转角计算方法, 暂称之为交点曲线计算法。 主共和国公路局( uhry od ) A toi R as国际招标项 目的 t Z 1基本线元统—参数模型的建立 第二合同段。为 O E ( P C石油输出国家组织) 投资修 我们知道 , 公路线形的曲线分为直线、 圆曲线 建的由苏丹到埃塞俄比亚首都亚的斯阿贝巴的石 和缓和曲 回 线( 旋曲线 ) 三种线元 , 缓和曲线线元则 油运输干道的一部分 , 7 A m, 全长 3 k 工程造价 17 又分为完全缓和曲线( >。)( 一 64 R一 。 、 >R) 和部分缓 刀 元 , ∈ 相当于中国公路等级中的二级公路 。路线 和曲线( 一 R2。 R1 > )分析五种线元的特 陛及共 , 我 回旋曲 线参数 经过地区为山岭重丘区地 I 形较为复杂 , 路线线形以 们可将圆曲线视为起终点半径相等、 曲线为主。路面设计宽度 7 7m沥青混凝土面 A为 O m,c 的回旋曲线 , 而直线则同样视为半径为无穷 层,0 m水泥稳定碎石基层 ,0m红土粒料底基 大的圆曲线, 2c 2c 故我们可以用 s 线元长度 )A 线元 ( 、( 、 线元起 曲率半径 ) D( RO 、 线元 R 层; 最大挖方深度2 m, 7 最大填方高度 2 m, 4 土方挖 缓和曲线参数 ) ( 方量 1 0 2 万方,填方量 4 万方 ;全线共 5 2 m 终点曲率半径 ) 7 座 0 等四项参数建立一个统一的参数模 并根据各项参数的不同的定义域来分别描述直 3 跨简支梁桥。招标文件图纸为初步设计图, 施工 型, 力要完成路线的最后定线方案、 最终的虹 图设计 线 、 圆曲线和不同类型的缓和曲线, 统一的参数模 。 以及工程的全部施工任务。笔者在 N M项 目负责 型见表 1 — 道路路线的的平纵设计。 2 2交点曲线的捆绑式结构模型 l 概述 对于任意一种交点曲线类型 , 我们均可假定 传统的公路平面敷设计算方法是以交 点 J ) 为“ (D 缓圆缓” 三个线元昕构成的捆绑式的结构模型 , 个 I 前音 +R ( 转角( ) 为基础、 以外距( ) E为控制、 通过求算切线 即— 交 曲线由 A ( 暖 和曲线 ) c 中部 长() T 来计算平曲线要素及各主点桩号的, 与此相 圆曲线) 2后部缓和曲线 ) +A ( 组成。同时假设每相 应 的平面设计表达便是路线 “ 直线 、曲线及转角 邻两交点曲 线之间存在—段直线段( 但其长度可以 图 2 表”这种表达方式除了具有直观方便的特点以外 , 为 0。 。 ) 曲线的对称与非对称的{算 , { 当把两个相邻交点曲 更为重要的是它体现出公路路线设计的两个方面 , 显然, 缓圆缓” 当“ 结构中的两端缓和曲线长度 则可由两个单一交点的不同设置和不 为 时 该交点为单圆曲线 ; 当两端缓和曲线 的 线加以组合, 是与之相适应直线加弯道的设计思路 、 定线方 s 0 , 复曲线等其他复杂 式、 中线敷设和施工放样方法 , 另—个则是与汽车 参数取值相同时, 该交点为对称 曲 ; 线 当两端缓和 同搭接而任意组合为卵形曲线 、 曲线 , 并随之作出 相应的曲线计算。 曲线的参数取值不相同时, 该交点为不对称曲 ; 充 电 线 动力学相关的各项道路 , 1 侗指标 , 因而应该说是十 例如对于卵形曲线 , 可以把两个同向的交点 分经典并为大家所习惯采用的,随着光电测距仪、 如此等等。 曲线加以组合, 如图 2 所示, D 的后部缓和曲 当J 1 全站仪等先进的测量仪器的出现 , 公路中线敷设及 2  ̄-  ̄ 4 . t 3 曲线的 计算方法 1= , D 如图 1 所示, 对于一般单一交点曲线的计算 。 线的S 2 0 而 J 2的前部缓和曲线的曲率半径从 施工放线广泛采用坐标法, 从而摆瞬了对特定计算 ~R 如果两交 之间的直线段长度 L= , x 0 方法的依赖, 但对于较长距离的公路主线 , 传统的 我 们 可将 交 点 J 设 为 J 、 2J 等 三 个 虚 R1 > 2时, D假 D1J 、 D D3 D1 D 便组成 了典型的卵形曲线。 交 转角设计定线方法和“ 直线、 曲线及转角表” 的 拟交点 ,三个虚拟交点 的转角分别为 D1p 和 J 和J 2 、 其布设计算只需在 2 ' 3所述的单一交点曲线 和方 式所不 能取 代的 。 p2显然 : =pl : +p+p2 通常 , 缓圆缓 ” ’ 当“ 结构 D1 D s 已知时( 即两端的缓 计算方法的基础上,对 J 和 J 2分别进行单一 然而,当路线因为受到限制而不得不采用诸 中两端的缓和曲线的长度 () 之后通过调整 J 1 D 的有 D 和J 2 如不对称曲线、 卵形曲线 、 复曲线 、 凸曲线 、 双卵形 和曲线的 sA R 、 D等参数已知时 ) 、、OR ,则可相应 交 点曲线的计算 , 线参数 , 使得两交点曲 线间的直线段长度 L x 曲线等复杂曲线( 埃塞俄 比 N M路的路线设计 计算出前部缓和曲线 A1 亚 — 和后部缓和曲线 A 2的转 关 曲 , 形曲线的布设汁算。 当然, 这个 尤其突出) , 特别是需要曲线反算的情况下, 采用传 角值 p1 B 。另外 , 和 2 根据交点连线的方位可计 达到 O即可完成卵 统的交 转角计算方法是很困难的。 对于复杂曲 线 算出交 转角 d, 则有 p O p1 p , =t — 一 然后对于 调整的过程可以使用多 2
道路曲线要素计算公式
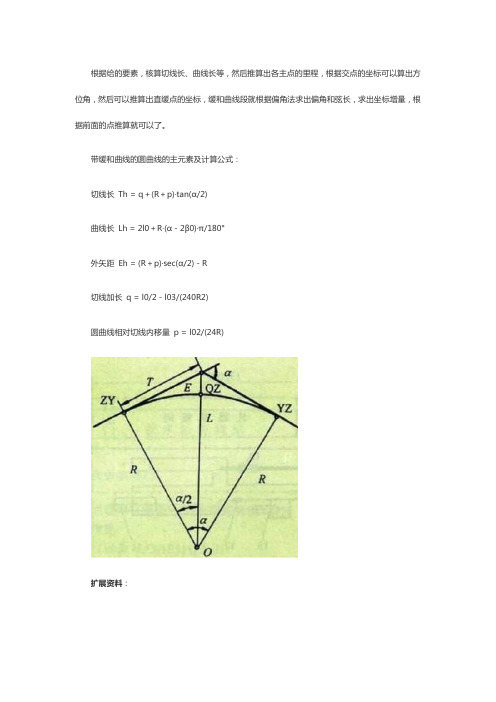
根据给的要素,核算切线长、曲线长等,然后推算出各主点的里程,根据交点的坐标可以算出方位角,然后可以推算出直缓点的坐标,缓和曲线段就根据偏角法求出偏角和弦长,求出坐标增量,根据前面的点推算就可以了。
带缓和曲线的圆曲线的主元素及计算公式:
切线长Th = q+(R+p)·tan(α/2)
曲线长Lh = 2l0+R·(α-2β0)·π/180°
外矢距Eh = (R+p)·sec(α/2)-R
切线加长q = l0/2-l03/(240R2)
圆曲线相对切线内移量p = l02/(24R)
扩展资料:
曲线要素,道路工程术语;是曲线的几个技术指标:如半径、缓和曲线、转角、圆曲线长、平曲线长、切线长、外距、切曲差、曲线的主点(变坡点)桩号。
曲线要素广泛应用于道路桥梁设计、施工测量中。
曲线要素又分为平曲线要素、竖曲线要素。
圆曲线各要素计算公式:
T=Rtan(A÷2)
L=π÷180(RA)
E0=R÷Cos(A÷2) -R
Q=2T-L。
道路曲线计算公式

高速公路线路(缓和曲线、竖曲线、圆曲线、匝道)坐标计算公式时间:2009-12-27 21:40:34 来源:本站作者:未知我要投稿我要收藏投稿指南高速公路的一些线路坐标、高程计算公式(缓和曲线、竖曲线、圆曲线、匝道)一、缓和曲线上的点坐标计算已知:①缓和曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:x Z,y Z计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当计算第二缓和曲线上的点坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反x Z,y Z为点HZ的坐标切线角计算公式:二、圆曲线上的点坐标计算已知:①圆曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:x Z,y Z计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当只知道HZ点的坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反x Z,y Z为点HZ的坐标三、曲线要素计算公式公式中各符号说明:l——任意点到起点的曲线长度(或缓曲上任意点到缓曲起点的长度)l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知:①第一坡度:i1(上坡为“+”,下坡为“-”)②第二坡度:i2(上坡为“+”,下坡为“-”)③变坡点桩号:S Z④变坡点高程:H Z⑤竖曲线的切线长度:T⑥待求点桩号:S计算过程:五、超高缓和过渡段的横坡计算已知:如图,第一横坡:i1第二横坡:i2过渡段长度:L待求处离第二横坡点(过渡段终点)的距离:x求:待求处的横坡:i解:d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知:①待求点桩号:K②曲线起点桩号:K0③曲线终点桩号:K1④曲线起点坐标:x0,y0⑤曲线起点切线方位角:α0⑥曲线起点处曲率:P0(左转为“-”,右转为“+”)⑦曲线终点处曲率:P1(左转为“-”,右转为“+”)求:①线路匝道上点的坐标:x,y②待求点的切线方位角:αT计算过程:注:sgn(x)函数是取符号函数,当x<0时sgn(x)=-1,当x>0时sgn(x)=1,当x=0时sgn(x)=0。
公路工程各点方位角及坐标计算公式

公路工程各点方位角及坐标计算公式(一)各点方位角计算:1、第一直线段(K0~ZH):F=arctgΔY/ΔX 注:直线方位角要考虑象限角才能定出正确线路走向2、第一缓和曲线段(KZH~KHY):δ1=(K0-KZH)2/(2RLh)×180/π3、圆曲线段(KHY~KYH):δ2=[2(K0-KZH)-Lh]/2R×180/πδ2=(KHY-KZH)/2R×180/π+(K0-KHY)/R×180/π无缓和曲线时:δ2=(K0-KHY)/R×180/π(即圆曲线圆心角)4、第二缓和曲线段(KYH~KHZ):δ3=(KHZ-K0)2/(2RLh)×180/π5、第二直线段(KHZ~KZH):F±α(左偏时F-α,右偏时F+α)注:K0——计算点的里程α——曲线交点偏角Lh——缓和曲线长(注意有时第一和第二缓和曲线长不一样)(二)各点坐标计算XZH=XJD-T?CosF XHZ=XJD+T?Cos(F±α)YZH=YJD-T?SinF YHZ=YJD+T?Sin(F±α)1、第一直线段:X=XZH+(K0-KZH)?CosF中桩Y=YZH+(K0-KZH)?SinFX边=X中±B?Cos(F-Δ)边桩Y边=Y中±B?Sin(F-Δ)注:B——中桩至所求点的距离(左幅时为+B,右幅时为-B,当设计轴线与线路不垂直时B取斜长,即B/SinΔ)设计轴线线路方向BΔ图S-12、第一缓和曲线段:XX=XZH-Y′?Sinθ+X′?Cosθ X X′ X′中桩′Y=YZH+Y′?Cosθ+X′?SinθYZH Y θ HZX边=X中±B?Cos(F+μδ1-Δ) HY YH边桩Y边=Y中±B?Sin(F+μδ1-Δ) JDY′注:(本公式只适用与图S-2线形)图S-2μ——曲线左转为-1,右转为+1θ——线路方位角与Y轴所夹的锐角,见图S-2Y′=L-L5/(40R2Lh2);X′=L3/(6RLh)-L7/(336R3Lh3);(R—圆曲线半径,L —缓和曲线上任一点至曲线起点长度)3、圆曲线段:X=XHY+2R?Sinφ?Cos(F+μ(ξ+φ))中桩Y=YHY+2R?Sinφ?Sin(F+μ(ξ+φ))X边=X中±B?Cos(F+μδ2-Δ)边桩Y边=Y中±B?Sin(F+μδ2-Δ)注:φ=(K0-KHY)/2R×180/π;ξ=(KHY-KZH)/2R×180/π4、第二缓和曲线段:X=XHZ-Y′?Sinθ+X′?Cosθ中桩Y=YHZ-Y′?Cosθ-X′?SinθX边=X中±B?Cos(F+μδ1-Δ)边桩Y边=Y中±B?Sin(F+μδ1-Δ)注:1、本公式只适用与图S-2线形,其他线形可根据本线形公式变换2、式中符号与第一缓和曲线意义相同3、注意有时第一缓和曲线长和第二缓和曲线长不一样4、第二直线段:X=XHZ+(K0-KHZ)?Cos(F±α)中桩Y=YHZ+(K0-KHZ)?Sin(F±α)X边=X中±B?Cos(F±α-Δ)边桩Y边=Y中±B?Sin(F±α-Δ)注:F——第一直线段的方位角(三)用CASIO fx-4500P计算已知坐标点在线路上的里程和距中线距离1、直线段(已知坐标X、Y)Pol(X-XHZ,Y-YHZ):K=V?Cos(F-W)+KHZ B=V?Sin(F-W)注:1、在fx-4500P中计算结果存入变量储存区V和W,要显示储存区内容时按RCL V 、 W 键。
两公路两缓和曲线相交交点坐标计算问题的探讨

两公路两缓和曲线相交交点坐标计算问题的探讨在道路设计中,交叉路口是必不可少的部分。
在大多数情况下,交叉路口是由两条道路交汇而成。
为了确保安全且高效地处理交通流量,设计师需要将两条道路连接起来并创建交叉路口。
在这篇论文中,我们将探讨如何计算两个公路的两个缓和曲线的交点坐标,并讨论计算方法和注意事项。
1.两个缓和曲线的概念在公路设计中,缓和曲线是用来连接两条直线道路的曲线,以便使车辆能够在道路上平滑转弯。
缓和曲线通常分为两种:圆弧曲线和直线缓和曲线。
圆弧曲线是以一个半径来描述曲线,使得曲线是连续和平滑的。
直线缓和曲线是以一系列的线性段描述的,这样可以在不同的曲率半径之间平滑地过渡。
2.如何计算缓和曲线的终点坐标在计算缓和曲线的终点坐标时,必须首先计算半径的长度。
这可以通过下面的公式计算:R = (V^2) / (127 * c) + f其中,V 表示车辆的速度,c 表示侧向加速度,f 表示道路横向坡度。
如果曲线是半圆弧,则曲线的长度可以通过以下公式计算:L = πR如果是直线缓和曲线,长度可以通过以下公式计算:L = Vt其中,t 表示直线段的长度。
一旦得出了曲线的长度,可以将起点坐标和曲线的长度用三角函数计算出终点坐标。
使用正弦函数可以计算曲线的末端y 坐标,使用余弦函数可以计算曲线的末端x 坐标。
3.计算两个公路的交点坐标如果有两条公路相交,可以通过计算两个公路的缓和曲线交点的坐标来确定交汇点的位置。
要做到这一点,必须首先计算两个道路的切点和切线方向。
然后可以通过数学运算计算两个道路的交点坐标。
要做到这一点,可以使用以下方程组:x1 + d1cos(θ1) = x2 + d2cos(θ2)y1 + d1sin(θ1) = y2 + d2sin(θ2)其中,x1 和y1 是第一个道路的起点坐标,d1 是第一个道路的长度,θ1 是第一个道路的走向角度,x2 和y2 是第二个道路的起点坐标,d2 是第二个道路的长度,θ2 是第二个道路的走向角度。
高速公路线路计算公式

高速公路的一些线路计算一、缓和曲线上的点坐标计算已知:①缓和曲线上任一点离ZH 点的长度:l②圆曲线的半径:R ③缓和曲线的长度:l 0 ④转向角系数:K(1或-1) ⑤过ZH 点的切线方位角:α ⑥点ZH 的坐标:x Z ,y Z 计算过程:y y ⑼y x x ⑻x αSsin y ⑺αScos x ⑹90ααα⑸y x ⑷S 180n x yarctg α⑶l 3456R l l 40R l l y ⑵)KR336l l 6Rl l (x ⑴Z1Z 11111012200004049202503307030+=+===-+=+=⋅+=+-=-=说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n 的取值如下:⎪⎩⎪⎨⎧=<<⎪⎩⎪⎨⎧=><⎪⎩⎪⎨⎧=<>⎪⎩⎪⎨⎧=>>1n 0y 0x 1n 0y 0x 2n 0y 0x 0n 0y 0x 00000000 当计算第二缓和曲线上的点坐标时,则: l 为到点HZ 的长度α为过点HZ 的切线方位角再加上180° K 值与计算第一缓和曲线时相反 x Z ,y Z 为点HZ 的坐标切线角计算公式:2Rl lβ02=二、圆曲线上的点坐标计算已知:①圆曲线上任一点离ZH 点的长度:l②圆曲线的半径:R ③缓和曲线的长度:l 0 ④转向角系数:K(1或-1) ⑤过ZH 点的切线方位角:α ⑥点ZH 的坐标:x Z ,y Z 计算过程:y y ⑿y x x ⑾x αSsin y ⑽αScos x ⑼90ααα⑻y x ⑺S 180n x y arctgα⑹m Rsin α'y ⑸p]K )cos α'[R(1x ⑷34560R l 240R l 2l ⑶m 2688R l 24R l ⑵p R π)l -90(2l ⑴α'Z1Z 11111012200000452300340200+=+===-+=+=⋅+=+=+-=+-=-==说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n 的取值如下:⎪⎩⎪⎨⎧=<<⎪⎩⎪⎨⎧=><⎪⎩⎪⎨⎧=<>⎪⎩⎪⎨⎧=>>1n 0y 0x 1n 0y 0x 2n 0y 0x 0n 0y 0x 00000000 当只知道HZ 点的坐标时,则: l 为到点HZ 的长度α为过点HZ 的切线方位角再加上180° K 值与知道ZH 点坐标时相反 x Z ,y Z 为点HZ 的坐标三、曲线要素计算公式β+∆=+=+=+-=++=++++-=++++-=-=-=+-=+-===+=+==D l l :βR R R2R P P 2β⒀曲线段长度:l )l l (21R αL ⑿圆曲线长度)l l (21R α⑾曲线全长度:L m 2α2R)tg p p (212α2tgp p T ⑽第二切线长:m 2α2R)tg p p (212α2tgp p T ⑼第一切线长:2688R l 24R l p ⑻第二曲线平移量:2688R l 24R l p ⑺第一曲线平移量:34560R l 240R l 2l m ⑹第二曲线顺移量:34560R l 240R l 2l m ⑸第一曲线顺移量:2Rl β:⑷第二缓曲段总转角值2R l β:⑶第一缓曲段总转角值)lP P (21l R R 2RR :β⑵曲线段任意点转角值2Rl l :β⑴缓曲段任意点转角值212121210212212121211213422223412114522322245123111221121212102的边缘曲线长度⒁偏离缓曲:D 公式中各符号说明:l ——任意点到起点的曲线长度(或缓曲上任意点到缓曲起点的长度) l 1——第一缓和曲线长度 l 2——第二缓和曲线长度 l 0——对应的缓和曲线长度 R ——圆曲线半径 R 1——曲线起点处的半径 R 2——曲线终点处的半径 P 1——曲线起点处的曲率 P 2——曲线终点处的曲率 α——曲线转角值四、竖曲线上高程计算已知:①第一坡度:i 1(上坡为“+”,下坡为“-”)②第二坡度:i 2(上坡为“+”,下坡为“-”) ③变坡点桩号:S Z ④变坡点高程:H Z ⑤竖曲线的切线长度:T ⑥待求点桩号:S计算过程:)i i T(412R T E ⑷i Ri 212R )i i R(21l H ⑶H i i 2T⑵R (带有符号)S S l ⑴122021212Z 12Z -==-⎥⎦⎤⎢⎣⎡+++=-=-=五、超高缓和过渡段的横坡计算已知:如图,第一横坡:i1第二横坡:i2过渡段长度:L待求处离第二横坡点(过渡段终点)的距离:x 求:待求处的横坡:i解:d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算 已知:①待求点桩号:K②曲线起点桩号:K 0 ③曲线终点桩号:K 1 ④曲线起点坐标:x 0,y 0 ⑤曲线起点切线方位角:α0⑥曲线起点处曲率:P 0(左转为“-”,右转为“+”) ⑦曲线终点处曲率:P 1(左转为“-”,右转为“+”) 求:①线路匝道上点的坐标:x,y②待求点的切线方位角:αT 计算过程:ααα Bcos NAsinT y y BsinT NAcosT x x 42240Cl l 336C l l 6C l l B 3456C l l 40C l l )l (l A /2C l N αT )/2/C l S(l α P P l C SN l l )P /(P P Nl l K K l )P SGN(P N 时:P P ⑶当αα )/P cos α(cos αy y )/P sin α(sin αx x αSP α 0时:P P ⑵当αα Ssin αy y Scos αx x 0时:P P ⑴当K -K S 10T 0051101137073034909250502000101S 0010S 001S 01101T 10101010011100T 0000100+=++=-+=-+---=-+---=-=+=-=+=-=-=-=≠=--=-+=+=≠==+=+====T。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
公路路线的交点曲线计算方法
1.前言
传统的公路平面敷设计算方法是以交点(JD)转角(α)为基础,以外距(E)为控制,通过求算切线长(T)来计算平曲线要素及各主点桩号的,与此相应的平面设计表达便是路线“直线、曲线及转角表”。
这种表达方式除了具有直观、方便的特点以外,更为重要的是它体现出公路路线设计的两个面,一是与之相适应直线加弯道的设计思路、定线方式、中线敷设和施工放样方法,另一个则是与汽车动力学相关的各项道路几何指标,因而应该说是十分经典并为大家所习惯采用的。
现在随着光电测距仪、全站仪、GPS等先进的测量仪器的出现,公路中线敷设及施工放线广泛采用极坐标法,从而摆脱了对特定计算方法的依赖,但对于较长距离的公路主线,传统的交点转角设计定线方法和“直线、曲线及转角表”的表达方式,却仍是其他方法和方式所不能取代的。
然而,当路线因为受到限制而不得不采用,诸如不对称曲线、卵形曲线、复曲线、凸曲线、双卵形曲线等复杂曲线,特别是需要曲线反算的情况下,采用传统的交点转角计算方法是很困难的。
对于复杂曲线的计算,一般采用了在传统方法的基础上,按曲线类型分别推导计算公式,并编写功能单一的计算程序进行计算的方法。
显然这种方法局限性大、程序功能单一,即使编写了针对不同类型曲线的许多模块,也不能涵盖任意的线形组合和曲线类型等情况。
笔者通过设计实践和纬地道路辅助设计系统的研究开发,在许多技术人员熟知的传统交点转角法布设平曲线的基础上,提出一种利用计算机进行平曲线计算的新交点转角法,该方法适用于任意复杂线形的设计计算。
2.交点曲线计算法
该方法以适用于任意线元组合的复杂线形设计计算为目标,是以三种基本线元的统一参数模型为基础约定,以三线元捆绑式结构为通用的单交点曲线模型的交点可组合的计算方法,有别于传统的交点转角计算方法,暂称之为交点曲线计算法。
2.a 基本线元统一参数模型的建立
我们知道,公路线形的曲线分为直线、圆曲线和缓和曲线(回旋曲线)三种线元,缓和曲线线元则又分为完全缓和曲线(R->∞)、(∞-> R)和部分缓和曲线(R1->R2)。
分析五种线元的特性及共性,我们可将圆曲线视为起终点半径相等、回旋曲线参数A为0的回旋曲线,而直线则同样视为半径为无穷大的圆曲线,故我们可以用S(线元长度)、A(线元缓和曲线参数)、RO(线元起点曲率半径)、RD(线元终点曲率半径)等四项参数建立一个统一的参数模型,并根据各项参数的不同定义域来分别描述直线、圆曲线和不同类型的缓和曲线,统一的参数模型见表1-1。
根据五种线元在统一参数模型中不同的定义域,我们可以相应编制出在已知S、A、RO、RD条件下的具体计算程序模块。
2.b 交点曲线的捆绑式结构模型
对于任意一种交点曲线类型,我们均可假定为“缓圆缓”三个线元所构成的捆绑式的结构模型,即一个交点曲线由A1(前部缓和曲线)+Rc(中部圆曲线)+A2(后部缓和曲线)组成。
同时假设每相邻两交点曲线之间存在一段直线段(但其长度可以为0)。
显然,当“缓圆缓”结构中的两端缓和曲线长度S为0时,该交点为单圆曲线;当两端缓和曲线的参数取值相同时,该交点为对称曲线;当两端缓和曲线的参数取值不相同时,该交点为不对称曲线;如此等等。
2.c 单一交点曲线的计算方法
如图1-2所示,对于一般单一交点曲线的计算,我们可将交点JD假设为JD1、JD2、JD3等三个虚拟交点,三个虚拟交点的转角分别为β1、β和β2。
显然:α=β1+β+β2。
通常,当“缓圆缓”结构中两端的缓和曲线长度(S)已知时(即两端的缓和曲线的S、A、RO、RD 等参数已知时),则可相应计算出前部缓和曲线A1和后部缓和曲线A2的转角值β1和β2。
另外,根据交点连线的方位可计算出交点转角α,则有β=α-β1-β2,然后对于中部圆曲线,在已知其半径R和其转角β的条件下,可确定出中间圆曲线的未知参数长度(S)。
这样“缓圆缓”结构中的三段线元的S、A、RO、RD等参数均已求得,下面只需利用2.a中所述的统一的线元计算模块分别对其进行计算,有关该交点的其他参数也就不难求出了,这里不再赘述。
显然,当A1=0和A2=0(单圆曲线)时,当A1=A2(对称曲线)时,当A1≠A2(不对称曲线)时或当A1和A2中某一个为0时,上述方法均可适用,并方便地完成单一交点曲线的计算问题。
图1-2
2.d 复杂曲线的交点组合计算方法
基于如上的“缓圆缓”结构模型,以及单一交点曲线的对称与非对称的计算,当把两个相邻交点曲线加以组合,则可由两个单一交点的不同设置和不同搭接而任意组合为卵形曲线、复曲线等其他复杂交点曲线,并随之做出相应的曲线计算。
例如,对于卵形曲线,可以把两个同向的交点曲线加以组合,如图1-3所示,当JD1的后部缓和曲线的S12=0,而JD2的前部缓和曲线的曲率半径从R1->R2时,如果两交点之间的直线段长度Lx=0,JD1和JD2便组成了典型的卵形曲线。
其布设计算只需在2.c所述的单一交点曲线计算方法的基础上,对JD1和JD2分别进行单一交点曲线的计算,之后通过调整JD1和JD2的有关曲线参数,使得两交点曲线间的直线段长度Lx达到0,即可完成卵形曲线的布设计算。
当然,这个调整的过程可以使用多种方法。
例如笔者在纬地道路辅助设计系统中就是采用先进的实时拖动技术,可以直观、快速的实现这一调整。
图1-3
依此类推,通过相邻交点曲线的组合,可以直接解决其他复杂线形的计算问题。
3. 结语
利用上述交点曲线的计算方法,可一下子解决任意交点曲线类型的计算问题。
这种方法的优点在于不需分门别类的推导出许多专用、复杂的计算公式来分别编制专门的计算程序模块,各种组合的复杂曲线的计算思路与方法基本统一、简便易行,最重要的是这种方法涵盖任意复杂类型的交点曲线形式。
