概率论第一章2011
合集下载
(完整版)概率论第一章随机事件与概率

P(A) = A中样本点的个数 / 样本点总数
解题思路
1、将事件定义为某个参数,如A,B,C; 2、确定总样本空间样本数与事件对应的样本数 技巧:可以采用概率的性质和事件的运算关系灵 活变换。
2. 样本点 ω—— 随机试验的每一个可能结果.
3. 样本空间(Ω) —— 随机试验的所有样本点构成的集合.
4. 两类样本空间: 离散样本空间 样本点的个数为有限个或可列个. 连续样本空间 样本点的个数为无限不可列个.
1.1.3 随机事件
1. 随机事件 —— 某些样本点组成的集合, Ω的子集,常用A、B、C…表示.
• 重复排列:nr
•
选排列: Pnr
n! n(n 1)......(n r 1) (n r)!
组合
•
组合:
Cnr
n r
n! r!(n r)!
Pnr r!
注意
求排列、组合时,要掌握和注意: 加法原则、乘法原则.
加法原理
完成某件事情有 n 类途径, 在第一类途径中有m1种方 法,在第二类途径中有m2种方法,依次类推,在第 n 类 途径中有mn种方法,则完成这件事共有 m1+m2+…+mn种 不同的方法.
§1.1 随机事件及其运算 §1.2 概率的定义及其确定方法 §1.3 概率的性质 §1.4 条件概率 §1.5 独立性
§1.1 随机事件及其运算
1.1.1 随机现象:自然界中的有两类现象 1. 必然现象
• 每天早晨太阳从东方升起; • 水在标准大气压下加温到100oC沸腾;
2. 随机现象
• 掷一枚硬币,正面朝上?反面朝上? • 一天内进入某超市的顾客数; • 某种型号电视机的寿命;
乘法原理
解题思路
1、将事件定义为某个参数,如A,B,C; 2、确定总样本空间样本数与事件对应的样本数 技巧:可以采用概率的性质和事件的运算关系灵 活变换。
2. 样本点 ω—— 随机试验的每一个可能结果.
3. 样本空间(Ω) —— 随机试验的所有样本点构成的集合.
4. 两类样本空间: 离散样本空间 样本点的个数为有限个或可列个. 连续样本空间 样本点的个数为无限不可列个.
1.1.3 随机事件
1. 随机事件 —— 某些样本点组成的集合, Ω的子集,常用A、B、C…表示.
• 重复排列:nr
•
选排列: Pnr
n! n(n 1)......(n r 1) (n r)!
组合
•
组合:
Cnr
n r
n! r!(n r)!
Pnr r!
注意
求排列、组合时,要掌握和注意: 加法原则、乘法原则.
加法原理
完成某件事情有 n 类途径, 在第一类途径中有m1种方 法,在第二类途径中有m2种方法,依次类推,在第 n 类 途径中有mn种方法,则完成这件事共有 m1+m2+…+mn种 不同的方法.
§1.1 随机事件及其运算 §1.2 概率的定义及其确定方法 §1.3 概率的性质 §1.4 条件概率 §1.5 独立性
§1.1 随机事件及其运算
1.1.1 随机现象:自然界中的有两类现象 1. 必然现象
• 每天早晨太阳从东方升起; • 水在标准大气压下加温到100oC沸腾;
2. 随机现象
• 掷一枚硬币,正面朝上?反面朝上? • 一天内进入某超市的顾客数; • 某种型号电视机的寿命;
乘法原理
概率第一章 概 率 论

第三节 概率的加法与乘法公式
由条件概率计算公式,可直接推得概率的乘法公式: 例6 讨论抓阄的公平性.设有10个阄中只有一个物阄,10个人不论 先后顺序抓阄,每人只能抓一次、一个阄,试讨论其结果与顺序 无关.
解 设Ai表示第i(i=1,2,…,10)个人抓到物阄,则第
6)是随机试验的6个基本事件,由于骰子的对称性,出现各个 基本事件的可能性相同,都为1/6,这个结果是可信的,没有人 会怀疑的.这种计算方法就叫做概率的古典概型方法. (1)有限性——样本空间的元素(基本事件)只有有限个,即Ω={ω 1,ω2,ω3,…,ωn}; (2)等可能性——每一个基本事件发生的可能性都相同,即 例2 先后抛掷两枚均匀的硬币,求出现一个正面一个背面的概率.
表格
例1 为实验炮弹在正常条件下的合格率,
第二节 随机事件的概率
对100000发炮弹中的100发炮弹进行发射试验,结果有90发炮弹正 常,合格的频率为90/100=0.9,因此,可以认为该批炮弹的 合格率基本在0.9左右,即任意从中抽取一发炮弹,能正常发射的 可能性为0.9. (1)0≤P(A)≤1; (2)P(Ω)=1; (3)P(⌀)=0; (4)若A⊂B,则P(A)≤P(B); (5)P(A)=1-P(). 二、概率的古典定义
事件组合而成的事件称为复合事件. 二、事件的关系与运算
在随机试验中有许多事件发生,而这些事件之间往往又有联 系.研究事件之间的各种关系与运算,可以帮助我们更深刻地认 识随机事件. 1.事件的包含与相等
第一节 随 机 事 件
2.事件的和(或并)
图 1-1
第一节 随 机 事 件
事件A与事件B至少有一个发生的事件,称为事件A与事件 B的和(或并)事件,记为A∪B(或A+B)(图1⁃2中的阴影 部分).因此,事件的和可以描述为:当且仅当事件A,B中至 少有一个发生时,事件A∪B发生.即A∪B={A,B至少有一 个发生}.
概率论-第一章_1

电子科技大学
概率论的基本概念
林家翘教授是国际公认的力学和应用数 学权威,尊称为应用数学大师.
2002年回国后他的第一个任务,是向学 生和公众厘清“应用数学”概念. 强调应 用数学是不同于纯数学的一门独立的基础 学科,应用数学的核心是用数学方法解决 实体科学问题,纯数学核心是逻辑构架, 在西方数学界,这已经是一个常识.
电子科技大学
概率论的基本概念
非确定性现象出现的原因:
受到微小变化因素的综合影响 在非确定性现象中有一类很重要的现象: 随机现象.
抛硬币试验
例如
新生婴儿性别比
炮弹发射试验
电子科技大学
概率论的基本概念
随机现象的各个结果出现的可能性大小 不依人们的主观意志转移. 进行大量重复观察时,可观察到出现各 种结果呈现某种规律. 称大量同类随机现象所呈现的固有规律为 随机现象的统计规律性.
— 数学是一种先进文化,是人类文 明的基础,在人类文明的进程中起着重 要推动作用.
从认识论的观点来看, 人们应该给数学 科学以无上的地位.
—— J.勒雷 《当代数学大师》
电子科技大学
概率论的基本概念
大师之忧: “我回国后发 现,‘应用数学’ 的薄弱对整个 科学的发展非 常不利,非常 不利。” ——林家翘
电子科技大学
概率论的基本概念
应用数学注重的是主动提出研究对象中 的科学问题,通过问题的解决加深对研究 对象的认识,或创造出新的知识,它所注 重的是用数学来解决科学问题.
传统数学课程特点: 细分科目,自成体系;
追求数学自身的严密性和完美性, 与其他学科的交叉与融合相对少.
电子科技大学
概率论的基本概念
过去: 四种基本数学素质与能力: 抽象思维能力、逻辑推理能力、 数学运算能力、空间想象能力.
概率论的基本概念
林家翘教授是国际公认的力学和应用数 学权威,尊称为应用数学大师.
2002年回国后他的第一个任务,是向学 生和公众厘清“应用数学”概念. 强调应 用数学是不同于纯数学的一门独立的基础 学科,应用数学的核心是用数学方法解决 实体科学问题,纯数学核心是逻辑构架, 在西方数学界,这已经是一个常识.
电子科技大学
概率论的基本概念
非确定性现象出现的原因:
受到微小变化因素的综合影响 在非确定性现象中有一类很重要的现象: 随机现象.
抛硬币试验
例如
新生婴儿性别比
炮弹发射试验
电子科技大学
概率论的基本概念
随机现象的各个结果出现的可能性大小 不依人们的主观意志转移. 进行大量重复观察时,可观察到出现各 种结果呈现某种规律. 称大量同类随机现象所呈现的固有规律为 随机现象的统计规律性.
— 数学是一种先进文化,是人类文 明的基础,在人类文明的进程中起着重 要推动作用.
从认识论的观点来看, 人们应该给数学 科学以无上的地位.
—— J.勒雷 《当代数学大师》
电子科技大学
概率论的基本概念
大师之忧: “我回国后发 现,‘应用数学’ 的薄弱对整个 科学的发展非 常不利,非常 不利。” ——林家翘
电子科技大学
概率论的基本概念
应用数学注重的是主动提出研究对象中 的科学问题,通过问题的解决加深对研究 对象的认识,或创造出新的知识,它所注 重的是用数学来解决科学问题.
传统数学课程特点: 细分科目,自成体系;
追求数学自身的严密性和完美性, 与其他学科的交叉与融合相对少.
电子科技大学
概率论的基本概念
过去: 四种基本数学素质与能力: 抽象思维能力、逻辑推理能力、 数学运算能力、空间想象能力.
概率论与数理统计教程(茆诗松)第1章

A = “针与平行线相交” 的充要条件是: x ≤ l/2 sin ϕ . 针是任意投掷的,所以这个问题可用几何方法 求解得
SA ∫0 P( A) = = SΩ
27 July 2011
π
l sinϕdϕ 2l 2 = d(π / 2) dπ
华东师范大学
第一章 随机事件与概率
第9页
§1.3 概率的性质
= (3/10)×(2/9)+(7/10)×(3/9) = 3/10
27 July 2011
华东师范大学
第一章 随机事件与概率
第24页 24页
1.4.4
贝叶斯公式
乘法公式是求“几个事件同时发生”的概率; 全概率公式是求“最后结果”的概率; 贝叶斯公式是已知“最后结果” ,求“原因” 的概率.
27 July 2011
第一章 随机事件与概率
第19页 19页
条件概率的三大公式
乘法公式; 全概率公式; 贝叶斯公式.
27 July 2011
华东师范大学
第一章 随机事件与概率
第20页 20页
1.4.2
性质1.4.2
乘法公式
(1) 若 P(B)>0,则 P(AB) = P(B)P(A|B); 若 P(A)>0,则 P(AB) = P(A)P(B|A). (2) 若 P(A1A2 ······An−1)>0,则 P(A1A2 ······An) = P(A1)P(A2|A1) ······ P(An|A1A2 ······An−1)
古典方法 设 Ω 为样本空间,若
① Ω只含有限个样本点; ② 每个样本点出现的可能性相等, 则事件A的概率为: P(A) = A中样本点的个数 / 样本点总数
SA ∫0 P( A) = = SΩ
27 July 2011
π
l sinϕdϕ 2l 2 = d(π / 2) dπ
华东师范大学
第一章 随机事件与概率
第9页
§1.3 概率的性质
= (3/10)×(2/9)+(7/10)×(3/9) = 3/10
27 July 2011
华东师范大学
第一章 随机事件与概率
第24页 24页
1.4.4
贝叶斯公式
乘法公式是求“几个事件同时发生”的概率; 全概率公式是求“最后结果”的概率; 贝叶斯公式是已知“最后结果” ,求“原因” 的概率.
27 July 2011
第一章 随机事件与概率
第19页 19页
条件概率的三大公式
乘法公式; 全概率公式; 贝叶斯公式.
27 July 2011
华东师范大学
第一章 随机事件与概率
第20页 20页
1.4.2
性质1.4.2
乘法公式
(1) 若 P(B)>0,则 P(AB) = P(B)P(A|B); 若 P(A)>0,则 P(AB) = P(A)P(B|A). (2) 若 P(A1A2 ······An−1)>0,则 P(A1A2 ······An) = P(A1)P(A2|A1) ······ P(An|A1A2 ······An−1)
古典方法 设 Ω 为样本空间,若
① Ω只含有限个样本点; ② 每个样本点出现的可能性相等, 则事件A的概率为: P(A) = A中样本点的个数 / 样本点总数
《概率论》第1章 事件与概率

第一章 事件与概率
25/27
5. 试用A、B、C 表示下列事件: ① A 出现; A ② 仅 A 出现;ABC ③ 恰有一个出现;ABC ABC ABC ④ 至少有一个出现;A B C ⑤ 至多有一个出现; ABC ABC ABC ABC ⑥ 都不出现; ABC ⑦ 不都出现; ABC A B C ⑧ 至少有两个出现; AC BC AB
第一章 事件与概率
3/27
在随后的200多年里,概率论不仅在理论上获得了一定 发展,而且在人口统计、保险业、误差理论、天文学等自 然科学中得到了应用.在这一时期,对概率论在理论和应用 方 面 作 出 重 要 贡 献 的 数 学 家 有 雅 格 布 · 努 利 (Jakob 伯 Bernoullii),丹尼尔· 伯努利(Daniel Bernoullii), 棣莫弗(De Moivre), 拉 普 拉 斯 (pace), 欧 拉 (L.Euler), 贝 叶 斯 (T.Bayes), 蒲 丰 (G.Buffon), 高 斯 (F.Gauss), 泊 松 (S.Poisson),布尼亚可夫斯基 (V.Bunjakovskii),切比雪夫 (Chebyshev), 马 尔 可 夫 (A.Markov), 李 雅 普 诺 夫 (A.Lyapunov)等. 尽管18,19世纪,概率论在理论和应用方面得到了很多 成果,但与其它数学分支比较,概率论的发展是缓慢的.甚 至直到20世纪以前概率论还未进入主流数学.其基本原因 是概率论缺乏严密的逻辑基础.
4/27
凯恩斯主张把任何命题都看作事件,例如“明天将下 雨”,“土星上有生命”等等都是事件,人们对这些事件的 可信程度就是概率,而与随机试验无关,通常称为 主观概 率. 米泽斯定义事件的概率为该事件出现的频率的极限, 而作为公理就必须把这一极限的存在作为第一条公理,通 常称为客观概率.
25/27
5. 试用A、B、C 表示下列事件: ① A 出现; A ② 仅 A 出现;ABC ③ 恰有一个出现;ABC ABC ABC ④ 至少有一个出现;A B C ⑤ 至多有一个出现; ABC ABC ABC ABC ⑥ 都不出现; ABC ⑦ 不都出现; ABC A B C ⑧ 至少有两个出现; AC BC AB
第一章 事件与概率
3/27
在随后的200多年里,概率论不仅在理论上获得了一定 发展,而且在人口统计、保险业、误差理论、天文学等自 然科学中得到了应用.在这一时期,对概率论在理论和应用 方 面 作 出 重 要 贡 献 的 数 学 家 有 雅 格 布 · 努 利 (Jakob 伯 Bernoullii),丹尼尔· 伯努利(Daniel Bernoullii), 棣莫弗(De Moivre), 拉 普 拉 斯 (pace), 欧 拉 (L.Euler), 贝 叶 斯 (T.Bayes), 蒲 丰 (G.Buffon), 高 斯 (F.Gauss), 泊 松 (S.Poisson),布尼亚可夫斯基 (V.Bunjakovskii),切比雪夫 (Chebyshev), 马 尔 可 夫 (A.Markov), 李 雅 普 诺 夫 (A.Lyapunov)等. 尽管18,19世纪,概率论在理论和应用方面得到了很多 成果,但与其它数学分支比较,概率论的发展是缓慢的.甚 至直到20世纪以前概率论还未进入主流数学.其基本原因 是概率论缺乏严密的逻辑基础.
4/27
凯恩斯主张把任何命题都看作事件,例如“明天将下 雨”,“土星上有生命”等等都是事件,人们对这些事件的 可信程度就是概率,而与随机试验无关,通常称为 主观概 率. 米泽斯定义事件的概率为该事件出现的频率的极限, 而作为公理就必须把这一极限的存在作为第一条公理,通 常称为客观概率.
概率论第一章

例如:在检查某些圆柱形产品时, 例如:在检查某些圆柱形产品时,如果规定只有它的长度及直径 都合格时才算产品合格,那么“产品合格” 直径合格” 都合格时才算产品合格,那么“产品合格”与“直径合格”、 长度合格”等事件有着密切联系。 “长度合格”等事件有着密切联系。
下面我们讨论事件之间的关系与运算
1、包含关系
⑶ 两个特殊事件
必然事件U ★ 必然事件U ★ 不可能事φ 不可能事φ
3、随机试验
如果一个试验可能的结果不止一个, 如果一个试验可能的结果不止一个,且事先不能肯定 会出现哪一个结果,这样的试验称为随机试验。 会出现哪一个结果,这样的试验称为随机试验。
例如, 掷硬币试验 例如, 寿命试验 测试在同一工艺条件下生产 掷骰子试验 掷一枚硬币,观察出正还是反. 掷一枚硬币,观察出正还是反 出的灯泡的寿命. 出的灯泡的寿命 掷一颗骰子, 掷一颗骰子,观察出现的点数
第一章 随机事件及其概率
随机事件及样本空间 频率与概率 条件概率及贝努利概型
§1 随机事件及样本空间
一、随机事件及其有关概念
1、随机事件的定义
试验中可能出现或可能不出现的情况叫“随机事件” 试验中可能出现或可能不出现的情况叫“随机事件”, 简称“事件” 记作A 简称“事件”。记作A、B、C等任何事件均可表示为样本空 间的某个子集。称事件A发生当且仅当试验的结果是子集A 间的某个子集。称事件A发生当且仅当试验的结果是子集A中 的元素。 的元素。
例如,一个袋子中装有10个大小、形状完全相同的球。 例如,一个袋子中装有10个大小、形状完全相同的球。 10个大小 将球编号为1 10。把球搅匀,蒙上眼睛,从中任取一球。 将球编号为1-10。把球搅匀,蒙上眼睛,从中任取一球。
因为抽取时这些球是完全平等的, 因为抽取时这些球是完全平等的, 我们没有理由认为10个球中的某一个会 我们没有理由认为10个球中的某一个会 10 比另一个更容易取得。也就是说,10个 比另一个更容易取得。也就是说,10个 球中的任一个被取出的机会是相等的, 球中的任一个被取出的机会是相等的, 均为1/10 1/10。 均为1/10。
下面我们讨论事件之间的关系与运算
1、包含关系
⑶ 两个特殊事件
必然事件U ★ 必然事件U ★ 不可能事φ 不可能事φ
3、随机试验
如果一个试验可能的结果不止一个, 如果一个试验可能的结果不止一个,且事先不能肯定 会出现哪一个结果,这样的试验称为随机试验。 会出现哪一个结果,这样的试验称为随机试验。
例如, 掷硬币试验 例如, 寿命试验 测试在同一工艺条件下生产 掷骰子试验 掷一枚硬币,观察出正还是反. 掷一枚硬币,观察出正还是反 出的灯泡的寿命. 出的灯泡的寿命 掷一颗骰子, 掷一颗骰子,观察出现的点数
第一章 随机事件及其概率
随机事件及样本空间 频率与概率 条件概率及贝努利概型
§1 随机事件及样本空间
一、随机事件及其有关概念
1、随机事件的定义
试验中可能出现或可能不出现的情况叫“随机事件” 试验中可能出现或可能不出现的情况叫“随机事件”, 简称“事件” 记作A 简称“事件”。记作A、B、C等任何事件均可表示为样本空 间的某个子集。称事件A发生当且仅当试验的结果是子集A 间的某个子集。称事件A发生当且仅当试验的结果是子集A中 的元素。 的元素。
例如,一个袋子中装有10个大小、形状完全相同的球。 例如,一个袋子中装有10个大小、形状完全相同的球。 10个大小 将球编号为1 10。把球搅匀,蒙上眼睛,从中任取一球。 将球编号为1-10。把球搅匀,蒙上眼睛,从中任取一球。
因为抽取时这些球是完全平等的, 因为抽取时这些球是完全平等的, 我们没有理由认为10个球中的某一个会 我们没有理由认为10个球中的某一个会 10 比另一个更容易取得。也就是说,10个 比另一个更容易取得。也就是说,10个 球中的任一个被取出的机会是相等的, 球中的任一个被取出的机会是相等的, 均为1/10 1/10。 均为1/10。
概率论第一章

k 1
k 1
频率是概率的近似值,概率P(A)也应有类似特征:
(1)0 P( A) 1;
( 2) P( ) 0, P( ) 1;
( 3) 若 A与 B 互 不 相 容 , 有 P( A B) P( A) P( B).
同
理
可
有
:
P
m
Ak
m
P( Ak).
k1 k1
定义2:在相同的条件下进行n次重复试验,当n趋于无
定义3:若对随机试验E所对应的样本空间中的每一事件 A,均赋予一实数P(A),集合函数P(A)满足条件:
(1) 非负性公理:P(A) ≥0;
(2) 规范性公理:P()=1 ,P()=0 ;
(3) 可列可加性公理:设A1,A2,…, 是一列两两互不相容 的事件,即AiAj=,(ij), i , j=1, 2, …, 有
AB= B
A
Ω 推广:n个事件A1, A2,…, An任意两个都互不相 容,则称n个事件两两互不相容。
n
若n个事件A1, A2,…, An 两两互不相容,且 Ai i 1
则称n个事件A1, A2,…, An 构成一个完备事件组。
6. 对立(逆)事件 AB= , 且AB=
记 作BA , 称 为 A的 对 立 事 件
P(AB)=P(A)-P(AB)=0.8-0.5=0.3
例1-7 设A与B互不相容, P(A)=0.5, P(B)=0.3, 求P(AB).
解 P(AB)=P( A B )=1-P(AB)=1-[P(A)+P(B)] =1-(0.5+0.3)=0.2
例 1-8
某地一年内发生
k
起交通事故的概率为
k
概率论第一章

统计概率的性质 非负性:0≤P(A)≤1 规范性:P(Ω)=1 有限可加性:若 A1,A2,…, An是一
组两两互不相容的事件,则有
n n P Ai P( Ai ) i 1 i 1
频率和概率有什么区别和联系? 频率决定于实验,而概率是先于实验而 客观存在的。 对于较大的n, n次试验中事件A的频率, 一般与事件A的概率P相差不大,试验次 数n越大,频率与概率有较大偏差的情形 就越少见.因此人们常取实验次数很大时 事件的频率或一系列频率的平均值作为 概率的估计值。
8 5 1 9 4 6 7 2 3 10
事件间的关系
1.事件的包含 2.事件的相等
A B A B A B A B
3.事件的积(交)
4.互不相容(互斥)事件
事件间的关系
5.事件的和(并)
A B
6.对立事件
若A B , 且A B , 则B为A的对立事件,记为A 。
组两两互不相容的事件,则有
n n P Ai P( Ai ) i 1 i 1
古典概率计算举例
例1. 从0,1,2, …,9共10个数字中任取1 个,假定每个数字都以1/10的概率被取 中,取后放回,先后取出4个数字,试 求下列各 事件的概率 。
A1 :“4个数字各不相同” A2 :“4个数字组成一个3位数” A3 :“4个数字组成一个4位偶数” A4 :“4个数字恰好有2个0”ΩBiblioteka ....A .
.
样本点ω
例子
掷骰子
样本点简记为: wi ={出现i点}, i = 1,2,…,6。 则样本空间可记为 Ω={w1,w2,… ,w6}
打靶直到击中靶心为止,记录其射击次数:
概率论第一章

2014-6-7
第二章 随机变量及其分布
‹#› / 19
注意
(1)随机变量与普通的函数不同
随机变量是一个函数,但它与普通的函数有着本质的差别 ,普通 函数是定义在实数轴上的,而随机变量是定义在样本空间上的 (样本 空间的元素不一定是实数).
(2)随机变量的取值具有一定的概率规律 随机变量随着试验的结果不同而取不同的值, 由于试验的各个 结果的出现具有一定的概率, 因此随机变量的取值也有一定的概率 规律. (3)随机变量与随机事件的关系 随机事件包容在随机变量这个范围更广的概念之内.或者说 : 随 机事件是从静态的观点来研究随机现象,而随机变量则是从动态的观 点来研究随机现象.
(2)单位时间内某电话交换台收到的呼叫次数用 X 表示 {收到不少于1次呼叫}
{ X 1}
{没有收到呼叫}
2014-6-7 第二章 随机变量及其分布
{X= 0}
‹#› / 19
例 在有两个孩子的家庭中,考虑 其性别 , 共有 4 个样本点:
e1 (男,男), e2 (男,女), e3 (女,男), e4 (女,女).
概率论与数理统计
2011-2012-2
第二章 随机变量及其分布
随机变量 离散型随机变量及其分布律 随机变量的分布函数 连续型随机变量及其概率密度 随机变量的函数的分布
2014-6-7
第二章 随机变量及其分布
‹#› 2 / 30 19
本章要点 关键词
随机变量、分布函数、概率密度、伯努利试
验、 (0-1)分布、二项分布、泊松分布、几何分 布、均匀分布、指数分布、正态分布
‹#› / 19
在一装有红球、白球的袋中任摸一个球,观 察摸出球的颜色.
概率论重要公式大全必看
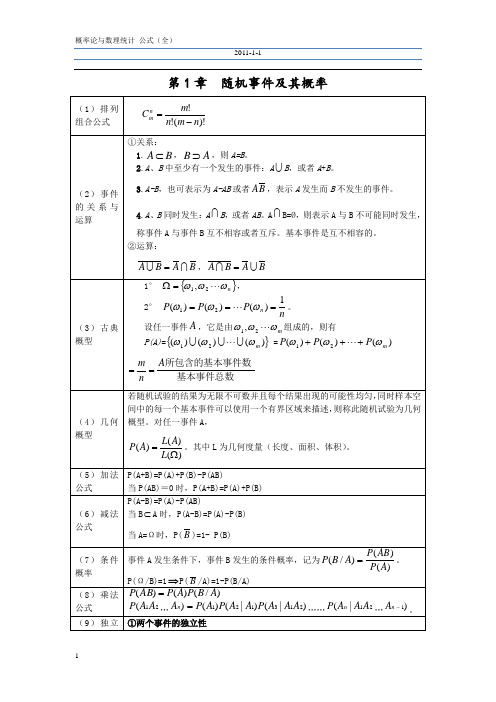
4.A、B 同时发生:A B,或者 AB。A B=Ø,则表示 A 与 B 不可能同时发生,
称事件 A 与事件 B 互不相容或者互斥。基本事件是互不相容的。 ②运算:
AB AB,AB AB
(3)古典 概型
1° 1, 2 n ,
2°
P(1 )
P( 2
)
P( n
)
1 n
。
设任一事件 A ,它是由1, 2 m 组成的,则有
F
1 (n2 , n1 )
第四章 随机变量的数字特征
(1) 一维 随机 变量 的数 字特 征
期望 期望就是平均值
函数的期望
离散型
n
E( X ) xk pk k 1
Y=g(X)
n
E(Y ) g(xk ) pk k 1
方差 D(X)=E[X-E(X)]2,
标准差 (X ) D(X ) , D( X ) [xk E( X )]2 pk k
Cii , 2
C
i2
2 i
i
i
若 X1, X2 Xn 相 互 独 立 , 其 分 布 函 数 分 别 为
Fx1 (x),Fx2 (x) Fxn (x) ,则 Z=max,min(X1,X2,…Xn)的分布
函数为:
Fmax(x) Fx1 (x) • Fx2 (x) Fxn (x)
Fmin (x) 1 [1 Fx1 (x)] • [1 Fx2 (x)][1 Fxn (x)]
否是互不影响的。
C Pn(k)
k n
pk qnk
,
k
0,1,2,, n
。
第二章 随机变量及其分布
(1)离散 型随机变 量的分布 律
(2)连续 型随机变 量的分布 密度 (3)分布 函数
称事件 A 与事件 B 互不相容或者互斥。基本事件是互不相容的。 ②运算:
AB AB,AB AB
(3)古典 概型
1° 1, 2 n ,
2°
P(1 )
P( 2
)
P( n
)
1 n
。
设任一事件 A ,它是由1, 2 m 组成的,则有
F
1 (n2 , n1 )
第四章 随机变量的数字特征
(1) 一维 随机 变量 的数 字特 征
期望 期望就是平均值
函数的期望
离散型
n
E( X ) xk pk k 1
Y=g(X)
n
E(Y ) g(xk ) pk k 1
方差 D(X)=E[X-E(X)]2,
标准差 (X ) D(X ) , D( X ) [xk E( X )]2 pk k
Cii , 2
C
i2
2 i
i
i
若 X1, X2 Xn 相 互 独 立 , 其 分 布 函 数 分 别 为
Fx1 (x),Fx2 (x) Fxn (x) ,则 Z=max,min(X1,X2,…Xn)的分布
函数为:
Fmax(x) Fx1 (x) • Fx2 (x) Fxn (x)
Fmin (x) 1 [1 Fx1 (x)] • [1 Fx2 (x)][1 Fxn (x)]
否是互不影响的。
C Pn(k)
k n
pk qnk
,
k
0,1,2,, n
。
第二章 随机变量及其分布
(1)离散 型随机变 量的分布 律
(2)连续 型随机变 量的分布 密度 (3)分布 函数
《概率论》第1章

有限可加性
若 A B, 则
P( ) P( B) P( A) P( B) P( A)
事件解释 为区域
S
B
A
第一章
概率解释为 区域面积
概率论的基本概念
§2 随机事件的概率
0 P( A) 1
P( A) 1 P( A) 由定义 A S B1 对任何事件 有 (加法公式) P( A) P( SA ) ,
随机事件
6/12
将一枚硬币连抛三次,观察正面 H、反面 T 的出现 则样本空间为
S { TTT , TTH , THT , HTT , THH , HTH , HHT , HHH}
记事件
A1 { 至少出现一次正面 }
A2 { 三次都是反面 } A3 { 第一次出现正面 }
A4 { 第一次出现反面 }
P( A1A2 ) P( A2 A3) P( A1A3) P( A1A2 A3 )
第一章 概率论的基本概念
§2 随机事件的概率 对于 n 个事件,有
P( A1 A2 An )
n
13/14
减二
P( Ai ) P( Ai A j ) i 1
1 i j n
1/13
第一章
概率论的基本概念
2/15
试验可以在相同的条件下重复进行 试验的结果可能不止一个,但试验前知道所 有可能的全部结果 在每次试验前无法确定会出现那个结果 具有上述特征的试验称为随机试验 ,简称试验
第一章
概率论的基本概念
§1
随机事件 样本空间 S 样本点 A S 中的子集
3/12
试验 E 的全部结果 基本结果 随机事件 事件 A发生
概率论第一章

若A B, 则有
P(B-A) = P(B)-P(A)
P(A) P(B)
特别地,对任何事件A,都有P(A) 1;
(5) 对任何两个事件A,B,都有
P ( A B) P ( A) P ( B) P ( AB )
一般地,对任何n个事件A1,A2,…,An,都有
P ( Ak ) P ( Ak )
A ( B C ) ( A B) ( A C )
(iv)对偶律:
A B A B, A B A B.
二.随机事件的概率及其性质
1.定义 设E是随机试验, S是它的样本空间, 对于E的每一事件 A赋予一个实数, 记为P(A), 称为事件A的概率, 如果集 合函数 P(.) 满足下列条件: (1)对于每一事件A, 有 P(A) 0; (2) P(S)=1. (3)设 A1 , A2 , 是两两互不相容的事件, 即 则有
5. 将6个球任意放入4个盒子中,每个盒子容
纳球的个数不限,求:
(1)恰有1个空盒的概率;
(2)恰有0个空盒的概率。 6.袋中有6只黑球,4只白球。从袋中取一 球,如果为黑球,则不放回;若是白球,
则将球放回。这样继续下去,问:
(1)第二次取到黑球的概率是多少?
(2)第三次取到黑球的概率是多少?
7.设随机事件A,B及其和事件 A B 的概率分 别是0.4,0.3和0.6, 求A和B至少有一个不发生的 概率.
设试验E的样本空间为S, A为E的事件, B1,B2,…,Bn 为S的一个划分, 且P(Bi)>0,i=1,2,…,n.则
P ( A)
P( B )P( A | B )
i 1 i i
n
概率论第一章知识点总结

概率论第一章知识点总结
概率论第一章主要介绍了以下几个知识点:
1. 随机试验:指具有以下三个特征的试验:可以进行多次独立重复;每次试验只有两个可能结果中的一个发生;每次试验发生的概率相同。
2. 样本空间:随机试验的所有可能结果构成的集合称为样本空间,通常用S表示。
3. 事件:样本空间的任意子集称为事件,通常用A、B等大写字母表示。
4. 概率:事件A发生的概率定义为P(A)=n(A)/n(S),其中n(A)表示事件A中元素的个数,n(S)表示样本空间中元素的个数。
5. 概率的性质:对于任意事件A和B,有以下性质:
(1) 0 ≤ P(A) ≤ 1
(2) P(S) = 1
(3) P(A∪B) = P(A) + P(B) - P(A∩B)
(4) 若A和B互不相容(即A∩B=),则P(A∪B) = P(A) + P(B) 6. 条件概率:事件B在事件A发生的条件下发生的概率称为条件概率,记为P(B|A),计算公式为P(B|A) = P(A∩B) / P(A)。
7. 乘法公式:对于任意事件A1,A2,…,An,有P(A1∩A2∩…∩An) = P(A1)P(A2|A1)P(A3|A1∩A2)…P(An|A1∩A2∩…∩An-1)。
8. 全概率公式和贝叶斯公式:全概率公式和贝叶斯公式是基于条件概率的重要公式,用于计算复杂事件的概率。
其中全概率公式为:
P(B) = Σi=1,2,…,nP(Ai)P(B|Ai),贝叶斯公式为:P(Aj|B) = P(Aj)P(B|Aj)/Σi=1,2,…,nP(Ai)P(B|Ai)。
概率论第一章基本概念

第一章 基本概念
绪言 §1.1 随机试验( Random experiment)
§1.2 随机事件( Random Events ) §1.3 事件的概率( Probability )
小结 课程要求 习题选讲 本章测验
上页
广 东 工 业 大 学
下页
返回
第一章 基本概念
本章主要讲述随机试验,样本空 间,随机事件,事件间的关系与运算, 频率,概率的统计定义,概率的性质, 古典概型。
E7:对目标进行射击,记录着弹点的位臵。
7 {( x, y ) | x, y D}
E8:掷两次骰子作为一次试验,观察两次试验结果。
第一次有6个可能的结果 第二次也有6个可能的结果
将两次试验结果排序, 则共有36种可能的结果:
8 {( x , y ) | x , y 1,2,3,4,5,6}
广 东 工 业 大 学
上页
下页
返回
具 体 例 子
1、进货问题 某商店某种商品销售的产品数量是不定的,该店需要在 月初进货,货多了有积压损失,货少了又有缺货损失,那么 每月进多少货合适? 2、服务台设臵问题
一个随机服务系统,每天到来的顾客及服务时间是不确 定的,那么需要设臵多少服务台的规模才能使顾客等候不太 久?服务台的工作人员有合适的忙闲程度? 3、保险问题
上页
广 东 工 业 大 学
下页
返回
何为随机现象?
人们通常将自然界或社会中出现的现象分成二类: 1、确定性的现象(必然现象)necessity, inevitability。 在一定条件下必然发生的现象称为确定性现象.
2、非确性的现象(偶然现象) randomly, chance。
在一定条件下可能出现也可能不出现的现象。 上抛一枚硬币,出现正面向上; 某商店某天某商品的销售量为50件; 测试某厂某元件的寿命为1000小时(或尺寸大小)。
绪言 §1.1 随机试验( Random experiment)
§1.2 随机事件( Random Events ) §1.3 事件的概率( Probability )
小结 课程要求 习题选讲 本章测验
上页
广 东 工 业 大 学
下页
返回
第一章 基本概念
本章主要讲述随机试验,样本空 间,随机事件,事件间的关系与运算, 频率,概率的统计定义,概率的性质, 古典概型。
E7:对目标进行射击,记录着弹点的位臵。
7 {( x, y ) | x, y D}
E8:掷两次骰子作为一次试验,观察两次试验结果。
第一次有6个可能的结果 第二次也有6个可能的结果
将两次试验结果排序, 则共有36种可能的结果:
8 {( x , y ) | x , y 1,2,3,4,5,6}
广 东 工 业 大 学
上页
下页
返回
具 体 例 子
1、进货问题 某商店某种商品销售的产品数量是不定的,该店需要在 月初进货,货多了有积压损失,货少了又有缺货损失,那么 每月进多少货合适? 2、服务台设臵问题
一个随机服务系统,每天到来的顾客及服务时间是不确 定的,那么需要设臵多少服务台的规模才能使顾客等候不太 久?服务台的工作人员有合适的忙闲程度? 3、保险问题
上页
广 东 工 业 大 学
下页
返回
何为随机现象?
人们通常将自然界或社会中出现的现象分成二类: 1、确定性的现象(必然现象)necessity, inevitability。 在一定条件下必然发生的现象称为确定性现象.
2、非确性的现象(偶然现象) randomly, chance。
在一定条件下可能出现也可能不出现的现象。 上抛一枚硬币,出现正面向上; 某商店某天某商品的销售量为50件; 测试某厂某元件的寿命为1000小时(或尺寸大小)。
概率论第一章

28
频率的性质:
1 0 ≤ fn ( A) ≤ 1
。
2 f n (S ) = 1
。
3 若A1 , A2 ,…,Ak 两两互不相容,
。
则 f n (U Ai ) = ∑ f n ( Ai )
i =1 i =1
29
k
k
例:抛硬币出现的正面的频率
试验 序号 1 2 3 4 5 6 7 8 9 10 n =5 nH fn(H) 0.4 2 0.6 3 0.2 1 1.0 5 0.2 1 0.4 2 0.8 4 0.4 2 0.6 3 0.6 3 n =50 nH fn(H) 0.44 22 0.50 25 0.42 21 0.50 25 0.48 24 0.42 21 0.36 18 0.48 24 0.54 27 0.62 31 n =500 nH fn(H) 251 0.502 249 0.498 256 0.512 253 0.506 251 0.502 246 0.492 244 0.488 258 0.516 262 0.524 247 0.494
21
“和”、“交”关系式
n n
IA =UA
i i =1
n
i
i =1
n
= A1 U A2 U L U An;
U A = I A=A A L A ;
i i 1 2 n i =1 i =1
22
例:设A={ 甲来听课 },B={ 乙来听 课 } ,则:
A I B = {甲、乙都来}
A U B = {甲、乙至少有一人来}
定义2:将概率视为测度,且满足:
1。 P( A) ≥ 0 2。 P( S ) = 1 3。 A1 , A2 ,...,Ak ,...,Ai Aj = ∅(i ≠ j) , ⇒ P(U Ai ) = ∑ P( Ai )
概率论(01章)课件。

出现正面的次数m 出现正面的频率m/n
1061 2048 6019 12012 14994
0.518 0.5069 0.5016 0.5005 0.4998
频率和概率
频率的稳定性 随机事件A在相同条件下重复多次时,事件A 随机事件 在相同条件下重复多次时,事件 发 在相同条件下重复多次时 生的频率在一个固定的数值p附近摆动, 生的频率在一个固定的数值 附近摆动,随试验次数 附近摆动 的增加更加明显 事件的概率 事件A的频率稳定在数值 ,说明了数值p可以用 事件 的频率稳定在数值p,说明了数值 可以用 的频率稳定在数值 来刻划事件A发生可能性大小,可以规定为事件 来刻划事件A发生可能性大小,可以规定为事件A 的概率
概率的统计定义
对任意事件A,在相同的条件下重复进行n 对任意事件A,在相同的条件下重复进行 A,在相同的条件下重复进行 次试验,事件A 次试验,事件A发 生的频率 m/n,随着试验次 , 数n的增大而稳定地在某个常数 附近摆动那么称 的增大而稳定地在某个常数 p为事件A的概率,记为 为事件A的概率, 为事件
随机试验: 随机试验:抛掷两颗骰子
Rolling two die 随机试验 抛掷两颗骰子, 抛掷两颗骰子,观察出现的点数 试验的样本点和基本事件
样本空间 ),(1, ) ( , ),( ),(1, ), ={(1,1),( ,2),(1,3),( ,4), , ),( ),(1, ), ,(6, ),( ),...,( ),(6, (1,5),( ,6), ,( ,1),( , , ),( 2), ,( ,6)}. ),...,( ), ,(6, )
样本空间 写出下列事件的样本空间
E1: 射手向以一目标射击,记录射击的次数 射手向以一目标射击,
1061 2048 6019 12012 14994
0.518 0.5069 0.5016 0.5005 0.4998
频率和概率
频率的稳定性 随机事件A在相同条件下重复多次时,事件A 随机事件 在相同条件下重复多次时,事件 发 在相同条件下重复多次时 生的频率在一个固定的数值p附近摆动, 生的频率在一个固定的数值 附近摆动,随试验次数 附近摆动 的增加更加明显 事件的概率 事件A的频率稳定在数值 ,说明了数值p可以用 事件 的频率稳定在数值p,说明了数值 可以用 的频率稳定在数值 来刻划事件A发生可能性大小,可以规定为事件 来刻划事件A发生可能性大小,可以规定为事件A 的概率
概率的统计定义
对任意事件A,在相同的条件下重复进行n 对任意事件A,在相同的条件下重复进行 A,在相同的条件下重复进行 次试验,事件A 次试验,事件A发 生的频率 m/n,随着试验次 , 数n的增大而稳定地在某个常数 附近摆动那么称 的增大而稳定地在某个常数 p为事件A的概率,记为 为事件A的概率, 为事件
随机试验: 随机试验:抛掷两颗骰子
Rolling two die 随机试验 抛掷两颗骰子, 抛掷两颗骰子,观察出现的点数 试验的样本点和基本事件
样本空间 ),(1, ) ( , ),( ),(1, ), ={(1,1),( ,2),(1,3),( ,4), , ),( ),(1, ), ,(6, ),( ),...,( ),(6, (1,5),( ,6), ,( ,1),( , , ),( 2), ,( ,6)}. ),...,( ), ,(6, )
样本空间 写出下列事件的样本空间
E1: 射手向以一目标射击,记录射击的次数 射手向以一目标射击,
概率论与数理统计-第一章 概率论的基本概念

j =1 j =1 n n
为条件பைடு நூலகம்率的全概率公式。
25
定理:接上面全概率公式的条件, 且P(A)>0,则
P( Bi | A) =
P ( Bi ) P ( A | Bi )
∑ P( B ) P( A | B )
j =1 j j
26
n
称此式为Bayes公式。
例:一单位有甲、乙两人,已知甲近期 出差的概率为70%,若甲出差,则乙出 差的概率为10%;若甲不出差,则乙出 差的概率为60%。 (1)求近期乙出差的概率; (2)若已知乙近期出差在外,求甲出差 的概率。
32
解:设A,B,C分别表示从第1,2,3箱取到次品,
P(C) = P( A)P(C | A) + P( A)P(C | A)
由条件概率全概率公式,
P (C A) = P ( B A) P (C | BA) + P( B A) P (C | BA)
3 3 4 2 17 = + = 7 6 7 6 42
A 表示事件“
至少有一个是女孩”,
A={ (男,女),女,男 ( ), (女,女) }
B = { (女,女) }
3
由于事件A已经发生,所以这时试 验的所有可能结果只有三种,而事 件B包含的基本事件只占其中的一 种, 所以有
1 P (B A) = 3
4
在这个例子中,若不知道事件A已经发生的信息,那 么事件发生的概率为
+ P( A1 ) ⋅ P( A2 | A1 )P( A3 | A1 A2 )
= 0.60+0.4 × 0.8 + 0.4 × 0.2 × 0.9 = 0.992
P( A2 | A1 ) = 1 − P( A2 | A1 ) = 1 − 0.8 = 0.2
为条件பைடு நூலகம்率的全概率公式。
25
定理:接上面全概率公式的条件, 且P(A)>0,则
P( Bi | A) =
P ( Bi ) P ( A | Bi )
∑ P( B ) P( A | B )
j =1 j j
26
n
称此式为Bayes公式。
例:一单位有甲、乙两人,已知甲近期 出差的概率为70%,若甲出差,则乙出 差的概率为10%;若甲不出差,则乙出 差的概率为60%。 (1)求近期乙出差的概率; (2)若已知乙近期出差在外,求甲出差 的概率。
32
解:设A,B,C分别表示从第1,2,3箱取到次品,
P(C) = P( A)P(C | A) + P( A)P(C | A)
由条件概率全概率公式,
P (C A) = P ( B A) P (C | BA) + P( B A) P (C | BA)
3 3 4 2 17 = + = 7 6 7 6 42
A 表示事件“
至少有一个是女孩”,
A={ (男,女),女,男 ( ), (女,女) }
B = { (女,女) }
3
由于事件A已经发生,所以这时试 验的所有可能结果只有三种,而事 件B包含的基本事件只占其中的一 种, 所以有
1 P (B A) = 3
4
在这个例子中,若不知道事件A已经发生的信息,那 么事件发生的概率为
+ P( A1 ) ⋅ P( A2 | A1 )P( A3 | A1 A2 )
= 0.60+0.4 × 0.8 + 0.4 × 0.2 × 0.9 = 0.992
P( A2 | A1 ) = 1 − P( A2 | A1 ) = 1 − 0.8 = 0.2
相关主题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
a.一红一黑的概率。 b.至少有一只黑球的概率。
第一章 随机事件及其概率
(超几何分布)一批产品共有N件,其中M 件是次品。现在从全部N件产品中随机的抽 取n件(n≤N),求恰好取到k(k≤M)件次品的 概率。
P ( A)
k nk CM C N M n CN
第一章 随机事件及其概率
例2. 有n (n ≤365)个人,设每个人的生日是任 一天的概率为1/365. 求这n 个人中至少有两个 人的生日相同的概率.
若他射击n发,中靶 m发,当n很大时,可 用频率m/n作为他中 靶概率的估计.
第一章 随机事件及其概率
医生在检查完病人的时候摇摇头,“你的病很 重,在十个得这种病的人中只有一个能救活. ” 当病人被这个消息吓得够呛时,医生继续说 “但你是幸运的.因为你找到了我,我已经看 过九个病人了,他们都死于此病.”
n P
22 0.476
23
24
30
40
50
57
60
0.507 0.538 0.706 0.891 0.970 0.990 0.994
第一章 随机事件及其概率
例3. 从0,1,2, …,9共10个数字中任取1个, 假定每个数字都以1/10的概率被取中,取后放 回,先后取出4个数字,试求下列各事件的概 率。 1. “4个数字各不相同” 2. “4个数字全相同” 3. “4个数字组成4位各不相同的4位数” 4. “4个数字组成一个3位数” 5. “4个数字组成一个4位偶数” 6. “4个数字恰好有2个0”
=m/n
m个 n个基本事件
第一章 随机事件及其概率
古典概率P(A)的性质?
非负性
0≤P(A)≤1
P(Ω)=1 P(φ)=0
规范性
有限可加性
若事件A1,A2,…,An两两互不相容,则有 P(A1+A2+…+An)=P(A1)+…+P(An)
第一章 随机事件及其概率
古典概率计算举例
例1. 袋中装有8只红球,2只黑球,从中任取两只。
8 5 1 9 4 6 7 2 3 10
第一章 随机事件及其概率
古典概型试验 1.试验有有限个基本事件 e1, e2, …,eN 2.每次试验中各基本事件出现的可能性均相同
第一章 随机事件及其概率
概率的古典定义 若试验中只有n个等可能的基本事件,而某 个事件A包含m个基本事件, 则m/n为事件A 的概率,即 事件A包含的基本事件数 P(A)= 所有可能的基本事件数
D的几何度量 P(A)= Ω的几何度量
其中“测度”即长度、面积或体积等。
第一章 随机事件及其概率
几何概率应用
1.设公共汽车每5分钟一班,求乘客在车站等 车不超过1分钟的概率。
2.甲、乙两人相约在 8时到9时 在某地会面. 先到 的人等候另一个人15分后即可离去.设每人在这1 小时内各时刻到达该地是等可能的 , 且两人到达 的时刻互不影响.求甲、乙两人能会面的概率.
第一章 随机事件及其概率
研究随机现象,不仅要关心试验中会 出现哪些事件,更重要的是要知道事件出 现的可能性大小。
第一章 随机事件及其概率
§1.2 概率的直观定义 古典概率 例如,一个袋子中装有 10个大小、形状完全相同 的球 ,其中六个红球,四 个黑球,把球搅匀,蒙上 眼睛,从中任取一球,求 取到红球的概率。
3.在圆周上任取三个点A,B,C,求三角形ABC 为锐角三角形的概率。
第一章 随机事件及其概率
补:蒲丰投针试验
1777年,法国科学家蒲丰(Buffon)提出了投针 试验问题.平面上画有等距离为a(>0)的一些平行直 线,现向此平面任意投掷一根长为b( <a )的针,试求 针与任一平行直线相交的概率.
在19世纪初,比利时的学者A.凯特勒率先 将概率应用到统计中,并将统计方法从自然科 学领域扩展到社会科学领域。他统计了欧洲大 部分国家的死亡、犯罪、结婚、自杀等社会现 象,得出一份调查报告,宣称他可以预知每年 的死亡、犯罪、结婚、自杀数量,此举轰动了 整个欧洲,为此他被冠以“近代统计学之父” 的称号。从此概率和统计在社会、经济、科学 等领域得到重大应用和发展。
1.频率取决于试验,而概率是先于试验而客观 存在的。 2.对于较大的n, n次试验中事件A的频率,一 般与事件A的概率P相差不大,试验次数n越大, 频率与概率有较大偏差的情形就越少见.因此 人们常取试验次数很大时事件的频率或一系列 频率的平均值作为概率的估计值。
第一章 随机事件及其概率
例如,若我们希望知道某射手中靶的概率,应 对这个射手在同样条件下大量射击情况进行观 察记录.
1. 2. 3. 4. 5.
3期中至少有1期中奖; 3期都中奖; 3期中恰好有1期中奖; 3期都不中奖; 3期中最多有1期中奖。
第一章 随机事件及其概率
例3:化简
( A B) B ( A B) B ( A B)( A B )
( A B)( A B )( A B)( A B ) ( AB) ( AB ) ( AB) ( AB )
第一章 随机事件及其概率
在掷骰子试验中,“点数小于7” 和“点数为8”是随机事件吗?
两个特殊的事件:
即在试验中必定发生的事件,记为Ω ;
即在试验中必定不发生的事件,记为φ 。
第一章 随机事件及其概率
用集合表示事件 样本空间,样本点 事件就是由样本点组成的某个集合. Ω
.
..
.A .
.
样本点ω
第一章 随机事件及其概率
1061
2048 4979 12012 14994
0.518
0.5069 0.4979 0.5005 0.4998
第一章 随机事件及其概率
频率稳定性
当各轮试验次数n1 ,n2 ,…,ns 充分大时,在各轮 试验中事件A出现的频率总在一个定值附近摆 动. 而且,试验次数越多,一般来说摆动越小.
m1 n1 m2 n2 ms ns
b a π 2
第一章 随机事件及其概率
作业
习题一:3、5 1. n双相异的鞋(共2n只)随机地分成n堆,每 堆2只 . 求“各堆都自成一双鞋” 的概率。 2. 某人将四封写好的信随机装入四个写好 地址的信封中(一个信封装一封信),问: a.四封信恰好都装对的概率? b.没有一封信装对地址的概率是多少? c.恰好有几封信装对的概率最大?
第一章 随机事件及其概率
统计概率
在n次重复试验中,事件A出现m次,则 n次试验中,事件A出现的频率 fn(A)=m/n
第一章 随机事件及其概率
抛硬币试验
实验者 抛掷次数 n 正面出现 次数m 正面出现 频率m/n
德摩尔根
蒲丰 弗勒 皮尔逊 维尼
2048
4040 10000 24000 30000
3.分配律 4.对偶原则
A ( B C ) ( A B) ( A C ) A ( B C ) ( A B) ( A C )
A B A B ; A B A B
第一章 随机事件及其概率
例2:某人连续买了3期彩票,设 Ai 表示事件 “第i期中奖”(i=1,2,3),试用 及对立事 Ai Ai 件 表示下列事件:
概率论起源
公元1651年法国著名数学家帕斯卡1623-1662 收到法国大贵族 德.美黑 的一封信,信中请教 了关于赌徒分赌金的问题:“两个赌徒规定谁 先赢3局就算赢了,如果一个人赢了2局,另一个 人赢了1局,此时赌博终止,应该怎样分配赌 本才算公平合理?” 帕斯卡将该问题和解答寄给法国数学家 费马1601-1665,费马也给出了新的解法,他们不 断探讨这类问题,擦出概率论最早的火花。
例1. 抛两颗骰子,观察点数。
样本空间
Ω={(x,y)|x,y=1,2,…,6}
A=“两颗点数相同” B=“两颗点数之和大于10” C=“两颗点数之和小于20” D=“两颗点数之和为10,点数之差为4”
第一章 随机事件及其概率
事件间的关系和运算 1.事件的包含 2.事件的相等
A B A B A B A B
频率
稳定在某个值 附近
第一章 随机事件及其概率
概率的统计定义 在相同条件下对试验E重复进行n次,其中事 件A出现m次。当试验次数n充分大时,事件 A出现的频率fn(A)=m/n的稳定值,称为事件 A的概率,记为P(A). P=P (A) ≈fn(A)=m/n
第一章 随机事件及其概率
频率和概率有什么区别 和联系?
第一章 随机事件及其概率
寿命试验 测试在同一工艺条件下生产出的 灯泡的寿命.
统计一天中进入某商店的顾客人数.
第一章 随机事件及其概率
随机事件 在随机试验中可能发生也可能不发生的事情称 为随机事件,简称事件.
基本事件 (试验中不 可再分解的事件)
事 件
(两个或一些基本事件并在一起, 复合事件 就 构成一个复合事件)
第一章 随机事件及其概率
几何概率 向该正方形随机投针,求针落在 红色区域A的概率
A
几何概型试验
r
1.样本空间是直线、平面或空间上的某个 有限区域,含有无限多个样本点; 2.各个样本点对应的基本事件的发生是 等可能的。
第一章 随机事件及其概率
几何概率定义
D
Ω
设随机试验E的每一个可能结果是等可能地落在 区域Ω上的一点M(称为随机点),且 D , 则点M落在区域D(事件A)上的概率为
a
M x
所关心的事件 A {针与任一平行直线相交 } 发生的充分必要条件为 中的点满足 b 0 x sin ,0 π 2来自第一章 随机事件及其概率
m(G ) G的面积 P ( A) m( ) 的面积
