平行线的判定与性质习题公开课一等奖

合集下载

(完整版)平行线的判定和性质练习题

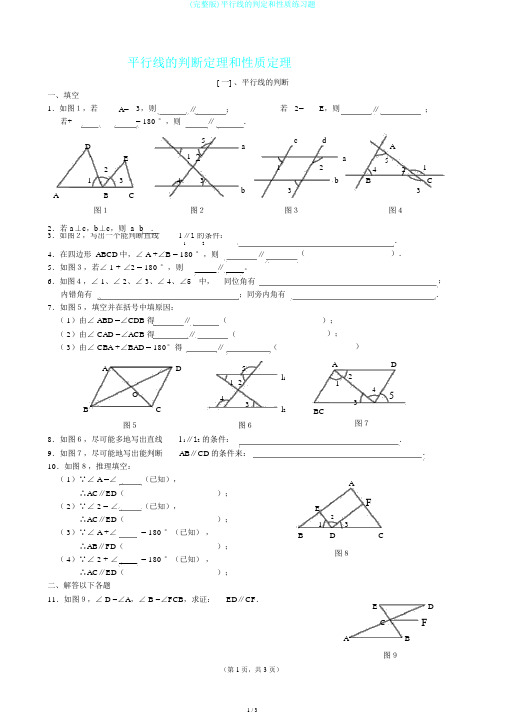
平行线的判断定理和性质定理[ 一] 、平行线的判断一、填空1．如图１，若A=3，则∥；若 2=E，则∥；若+= 180 °，则∥．D5ac dAE 1 212a51 2442133b3b B CA B C3图１图２图３图４2．若 a⊥c，b⊥c，则 a b ．3．如图２，写出一个能判断直线l ∥l的条件：124．在四边形 ABCD中，∠ A +∠B = 180 °，则∥5．如图３，若∠ 1 + ∠2 = 180 °，则∥。

6．如图４，∠ 1、∠ 2、∠ 3、∠ 4、∠5 中，同位角有内错角有；同旁内角有7．如图５，填空并在括号中填原因：（ 1）由∠ ABD =∠CDB 得∥（（ 2）由∠ CAD =∠ACB 得∥（（ 3）由∠ CBA +∠BAD = 180°得∥（A D5l112O43B l2C图５图６8．如图６，尽可能多地写出直线l 1∥l2的条件：9．如图７，尽可能地写出能判断AB∥CD的条件来：10．如图８，推理填空：（ 1）∵∠ A =∠（已知），∴AC∥ED（）；（ 2）∵∠ 2 = ∠（已知），∴AC∥ED（）；（ 3）∵∠ A +∠= 180 °（已知），∴AB∥FD（）；（ 4）∵∠ 2 + ∠= 180 °（已知），∴AC∥ED（）；二、解答以下各题11．如图９，∠ D =∠A，∠ B =∠FCB，求证：ED∥CF．．（）．；．）；）；）A D21435BC图７．．AEF213B D C图８E DC FA B图９（第 1页，共 3 页）12．如图 10，∠ 1∶∠ 2∶∠ 3 = 2 ∶3∶4， ∠AFE = 60 °，∠ BDE =120°，写出图中平行的直线，并说明原因．A1FE23BD C图 1013．如图 11，直线 AB 、 CD 被 EF 所截，∠ 1 = ∠2，∠ CNF =∠BME 。

平行线的判定1精选教学省公开课金奖全国赛课一等奖微课获奖课件

含着眼泪，带着多少担忧与牵挂永远离开了我。我唯一靠山倒了，不过母亲教会了我在逆境中学会坚强，勇敢地面对困难和失败，适应任何环境而求生存，这就是我母亲留给我无比宝贵财富和爱。
母亲即使走了，可她永远活在我心里，我永远思念她，她是我地唯一，无人取代，也是我最爱，更是难忘爱！我想不起小姨妈在母亲有病时候是怎样抱着我，还是背着我，我不知道，从小姨妈对那段往事回想中，我才知道他人对她冷眼，天寒地冷无奈…… 我才知道她棉衣前襟是明亮发光，而且经常是湿地；才知道烧无烟煤时熏黑了脸上那双有黑有大眼睛明亮。那时候小姨妈只有十六岁，一个失去父母关爱小女孩，能在姐姐病重时候撑起一个家，还带着一个不满周岁孩子，可想而知，这是多么不轻易事，每当小姨妈讲起那段往事，我就想起那苦难无助地童年，小姨妈无私爱，让我永远难忘。小姨妈人生很苦，极少有些人去关她，可是她却为我们这些没有母爱孩子现出了她青春和全部爱。我母亲逝世后小姨妈也经常照料我，关心我。她不但关爱我，还有我三姨家弟兄妹们。还在我母亲没有逝世时，我三姨妈因为有病逝世了，留下四个孩子，最小才两岁，她为了照料这四个孩子，就和我三姨父结婚，把他们养大成人，现在孩子们都有了自己家，可是小姨妈因为劳累过分，而病倒了，现在病在床上不能自理，当我今年回家看到小姨妈时，我很惭愧，她为我们付出太多了，可我们又给了她什么，她看到我时那含泪笑容，我才体会到母爱无私和伟大，可能她不求我们什么，能常回家看看足矣，可我们却做不到，当我们爱自己孩子时候，可曾想过，我们把爱孩子十分之一去爱母亲，她就足矣，往往这一点也做不到，说句心里话，我们欠母亲无法赔偿，更无法用语言表示。我有这两位母亲，即使我人生很不幸，但我有她们给我无私爱，我永远是幸福，她们对我爱我永存心里。在美国西雅图一所著名教堂里，有一位德高望重牧师――戴尔·泰勒。有一天，他向教会学校一个班学生们先讲了下面这个故事。那年冬天，猎人带着猎狗去打猎。猎人一枪击中了一只兔子后腿，受伤兔子拼命地逃生，猎狗在其后穷追不舍。可是追了一阵子，兔子跑得越来越远了。猎狗知道实在是追不上了，只好悻悻地回到猎人身边。猎人气急败坏地说：“你真没用，连一只受伤兔子都追不到！ ”

平行线的判定PPT比赛课市公开课一等奖省优质课获奖课件

几何语言表述：
∵∠1=∠2 (已知) ∴AB∥CD（同位角相等，两直线平行）
第6页
纸条，
第7页
1.如图,哪两个角相等能判定直线 AB∥CD?
2．已知∠1＝54°，
当
时，
AB∥CD？
第8页
3.假如∠∠123==∠∠2,54 能判定哪两条直线平行?
第9页
E
如图，直线AB、CD被EF A
所截，假如∠1=∠2，
1
3
A
∴ ∠2=∠3 （等量代换） ∴ DC∥AB （内错角相等，两直线平行）
C
2
B
第18页纸条，ຫໍສະໝຸດ 第19页本节课你有收获吗
教材p16 2、4题
第20页
文字叙述
图形表示
①________那么这两条直线也相互平行。
② 同位角相等两直线平行。
③___________两直线平行 ,
④___________两直线平行。
系是_____b_∥. c
A
D
E
F
B
第2题
C
第15页
4.如图1所表示,以下条件中,能判断AB∥CD是( )
A.∠BAD=∠BCD B.∠1=∠2; C.∠3=∠4 D.∠BAC=∠ACD
A
D
1
4
A
D
E
F
B
3
2
(1) C
B
C
(2)
5.如图2所表示,假如∠D=∠EFC,那么( )
A.AD∥BC B.EF∥BC C.AB∥DC
D.AD∥EF
第16页
6.如图3所表示,能判断AB∥CE条件是( )
A.∠A=∠ACE B.∠A=∠ECD C.∠B=∠BCA

平行线的判定华师大版七年级数学公开课一等奖优质课大赛微课获奖课件

能得出AB∥CD吗?
2
C5
D
F
解:∵ ∠4+∠2=180 °（已知） ∠4+∠3=180°（补角定义） ∴ ∠2=∠3（同角补角相等）
∴ AB∥CD（同位角相等, 两直线平行）
你尚有其它说理办法吗？
第9页
思考
E
如图, 假如
3
∠4+∠2=180°, A 1 4 B
能得出AB∥CD?
2
C5
D
F
解∵ ∠4+∠2=180 °（已知） ∠4+∠1=180°（补角定义） ∴ ∠2=∠1（同角补角相等）
∴ AB∥CD（内错角相等, 两直线平行）
第10页
A
E
B 推理形式
1
∵∠1+∠2 =1800
C
2
D ∴AB∥CD(同旁内角
F
互补,两直线平行)
两条直线被第三条直线所截, 假如同旁内角互补,那么这两条直线平行.
简朴地说:同旁内角互补,两直线平行.
第11页
A1 B2
D
若∠1＝∠2 则 ∥ 3 若__=__则AB ∥DC
（1）∠1＝∠2；（2） ∠3＝∠A；
（3） ∠A+∠2 +∠4＝180°.
D
C
1
A
243
B
第18页
火眼金睛 1.找出图中平行线
D B
A E C
假如∠ADE=∠ABC,则＿＿∥ ＿＿ F 假如∠ACD=∠F, 则＿＿∥ ＿＿假如∠DEC=∠BCF,则＿＿∥ ＿＿
注: 要拟定是哪两条直线被第三条直线所截得到同位角
第19页
2.如图,已知∠ABD=∠ACE，BF、CG分别是∠ABD.∠ACE平分线，请判断BF与CG 是否平行，并阐明理由。

七年级数学下册平行线的判定方法市公开课一等奖省优质课获奖课件

第10页
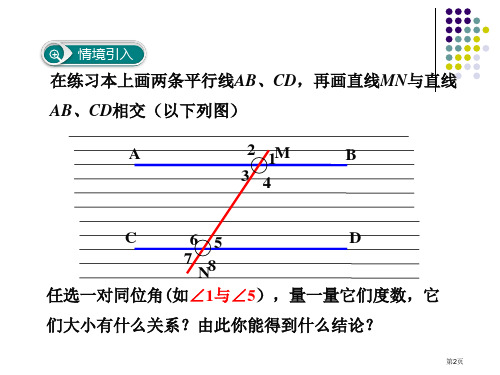
想一想
如图，∠1= ∠2 ，且∠1=∠3， AB和CD平行吗？
D
3C
A 12
B
第11页
பைடு நூலகம்
说一说
假如1+2=1800 能判定a//b吗? c
解:能, 因为1+2=180
1+3=180 所以 2=3 所以 a//b 数学转化思想
3
1
a
2 b
第12页
普通地,判断两直线平行有下面方法: 判定方法3 两条直线被第三条直线所截，假如同旁内角互补，那么这两条直线平行. 简单说成：同旁内角互补,两直线平行.
_∠__2_＝__1_5_0_或__∠__3_＝__3_0_°______，则a//b.
c a
3 2
1 b
第22页
7.直线ab被直线c所截，给出以下条件：
（1）∠1=∠2；（2）∠3=∠6；
（3）∠4=∠1；（4）∠6+∠7=180°.
其中能识别a//b条件序号是
5
(1)(2)(4.)
c
1
a
7
（A）∠2＝∠3 （B）∠1＝∠4
（C）∠1＝∠2
l1
l2
（D）∠1＝∠3
1
3 4
2
第17页
2. 如图,∠1＝∠2,则以下结论正确是（ C）
A. AD//BC B. AB//CD
A
D
1
E
C. AD//EF D. EF//BC
2
F
B
C
第18页
3.如图，哪些直线平行，哪些直线不平行？
l4
50o
120o
两直线平行
内错角相等
两直线平行

平行线的判定与性质习题公开课一等奖

∠A=∠F
理由如下：
证明：
又∵∠C＝∠D (已知)
∴ ∠D=∠ABD （两直线平行,内错角相等）
∴ BD∥CE(同位角相等，两直线平行)
变式：如图，已知∠A=∠F,∠C=∠D, 求证：BD//CE.
3
2
1
D
E
F
A
C
∴ ∠C=∠ABD(等量代换)
∵∠A=∠F(已知)
∴ DF∥AC(内错角相等，两直线平行)
E
F
B
抢答
A
B
C
D
E
F
1
2
3
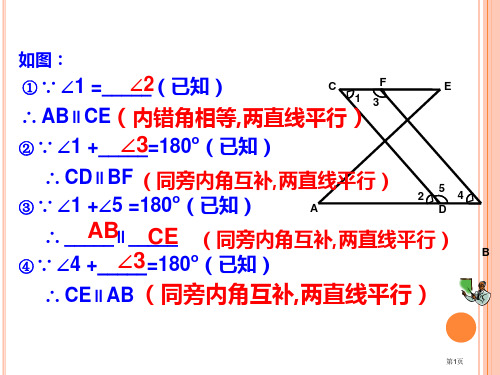
(1)、∵ ∠A=____, (已知） AC∥ED ,(_____________________)
(2)、 ∵AB ∥______, (已知） ∠2= ∠4，(______________________)
3
在例题变式的过程中，体会转化的数学思想，学会有条理表达自己，从而进一步增强分析、概括、表达能力。
教学目标
同位角相等
内错角相等
同旁内角互补
两直线平行
同位角相等
内错角相等
同旁内角互补
平行线的判定与性质的关系图
知识梳理
课前热身
如图所示，下列推理正确的是（） A．∵∠1=∠4，∴BC∥AD B．∵∠2=∠3，∴AB∥CD C．∵AD∥BC，∴∠BCD＋∠ADC=180° D．∵∠ABC＋∠C=180°，∴BC∥AD
5
(3)、 ___ ∥___, (已知） ∠B= ∠3. (___________ ___________)
1、如图，点B、E分别在AC、DF上，BD、CE均与AF相交，∠1=∠2，∠C=∠D，试问：∠A与∠F相等吗？请说出你的理由。

平行线的性质PPT市公开课一等奖省优质课获奖课件

c
d
a
1
2
3
b
第14页
3.已知： ∠ 1=130 °， ∠4=45 °， ∠3=50 °，求：∠2等于多少度？
ab 12 c
3
4d
第15页
平行线判定
平行线性质
同位角相等，两直线平行. 两直线平行，同位角相等. 内错角相等，两直线平行. 两直线平行，内错角相等. 同旁内角互补，两直线平行.两直线平行，同旁内角互补.
如图（2）：
ADE= B (已知）,
DE BC (同位角相等，两直线平行),
CED+C=180º( 两直线平行，同旁内角互补 ).
A
A
B
D
E
C
D
（1）
B
C
（2）
第18页
2.如图所表示, 已知AB//CD ,AD//BC, BF平分 ∠ABC ,DE平分∠ADC,
则 DE//FB,请说明理由.
D
F
C
A
E
B
第19页
3、如图1，已知AD∥BC，∠BAD=∠BCD。判断AB与CD 是否平行，并说明理由
4 、如图 2 ，已知 AB∥CD ， AE∥DF 。请说明 ∠BAE=∠CDF
D
C
A 图1
B
A
B
F
C
图2
E D
第20页
两条平行线被第三条直线所截，
同位角相等。
E
简单地说：两直线平行， A 同位角相等。
B 1
C
D
2
∵ AB∥CD（已知）
F
∴ ∠1=∠2（两直线平行,同位角相等）
第2页
如图，已知AG//CF，AB//CD，

平行线的判定华师大版七年级数学公开课一等奖优质课大赛微课获奖课件

2
C5
D
F
解:∵ ∠4+∠2=180 °（已知） ∠4+∠3=180°（补角定义） ∴ ∠2=∠3（同角补角相等）
∴ AB∥CD（同位角相等, 两直线平行）
你尚有其它说理办法吗？
第9页
思考
E
如图，假如
3
∠4+∠2=180°， A 1 4 B
能得出AB∥CD
2
C5
D
F
解∵ ∠4+∠2=180 °（已知） ∠4+∠1=180°（补角定义） ∴ ∠2=∠1（同角补角相等）
A F
1
B
D
2 C
G E
第20页
1 A
1.如图，AB⊥BC于B， 2
∠1=125°，∠2=35°， B
请阐明l1∥l2理由。
B
D
2.如图，∠B=40°， ∠DFC=140 ° ，
试判断AB与DE是否平行，
并阐明理由。
l1 C l2
A F
E C
第21页
你学到了什么？你认为尚有什么不懂？你有什么经验与收的
1.经历“平行线鉴定办法”发觉过程。
2.掌握平行线鉴定办法。 3. 会用它进行简朴推理和表述。
第2页
试一试猜一猜
如图，三根木条相交成 ∠1， ∠2，固定木条b、c，转动木条a , 观测∠1， ∠2满足什么条件时直线a与b平行.
当∠1＞∠2时
当∠1＝∠2时
当∠1＜∠2时
①直线a和b不平行 ②直线a∥b ③直线a和b不平第3页行
C
第12页
已知直线l1 ，l2被l3所截,如图，
∠1＝45°,∠2＝135°,试判断l1与l2是否平行.并阐明理由.

(完整版)平行线的判定和性质练习题

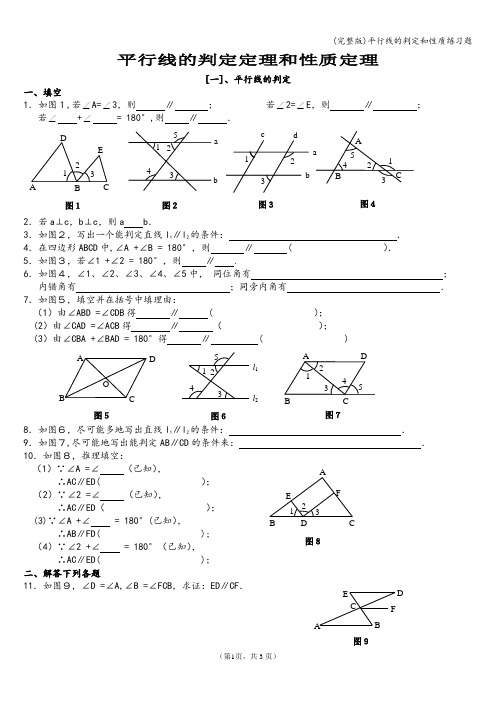
(完整版)平行线的判定和性质练习题平行线的判定定理和性质定理[一]、平行线的判定一、填空1．如图１,若∠A=∠3，则 ∥ ；若∠2=∠E ，则 ∥ ；若∠ +∠ = 180°,则 ∥ ．2．若a⊥c，b⊥c，则a b ．3．如图２，写出一个能判定直线l 1∥l 2的条件：． 4．在四边形ABCD 中,∠A +∠B = 180°，则 ∥ ( ）． 5．如图３，若∠1 +∠2 = 180°，则 ∥ .6．如图４，∠1、∠2、∠3、∠4、∠5中，同位角有；内错角有；同旁内角有． 7．如图５，填空并在括号中填理由：（1）由∠ABD =∠CDB 得 ∥ ( ）； (2）由∠CAD =∠ACB 得 ∥ （）； (3）由∠CBA +∠BAD = 180°得 ∥ ( )8．如图６，尽可能多地写出直线l 1∥l 2的条件：．9．如图７,尽可能地写出能判定AB∥CD 的条件来：． 10．如图８，推理填空：（1）∵∠A =∠ （已知）， ∴AC∥ED( ）；（2）∵∠2 =∠ （已知）， ∴AC∥ED（）； (3)∵∠A +∠ = 180°(已知）， ∴AB∥FD( );（4）∵∠2 +∠ = 180°（已知）， ∴AC∥ED( )；二、解答下列各题11．如图９，∠D =∠A,∠B =∠FCB，求证：ED∥CF．ACB41 23 5图４ab c d 123 图３A B C ED 1 2 3 图１图２43 2 1 5ab1 2 3A F C DB E图８EBAF D C图９ADCBO图５图６5 1 243 l 1 l 2图７54 32 1 A DC B12．如图10，∠1∶∠2∶∠3 = 2∶3∶4， ∠AFE = 60°，∠BDE =120°,写出图中平行的直线,并说明理由．13．如图11,直线AB 、CD 被EF 所截，∠1 =∠2，∠CNF =∠BME。

平行线的性质微课市公开课一等奖百校联赛获奖课件

3a
24
1
b
c
解：∵ a∥b(已知)
∴∠ 1= ∠ 2(两直线平行,内错角相等)
又∵∠ 1 = 50 ° (已知) ∴∠ 2= 50 ° (等量代换)
第14页
如图在四边形ABCD中,
D
已知AB∥CD,∠B = 60 ° ①求∠C度数;
A
②由已知条件能否求得
∠A度数?
B
C
解: ① ∵ AB∥CD(已知)
3、∵ a ∥ b (已知)
∴ ∠2+∠4=__1_8_0(° 两直线平行， ) 同旁内角互补
第11页
得出结论
平行线性质：
性质１：两直线平行，同位角相等．性质２：两直线平行，内错角相等．
性质３：两直线平行，同旁内角互补．
第12页
P178 练习第1、2题
看谁做得又快又好
完后请举起你手
第13页
如图，已知直线 a∥b，∠1 = 50 °, 求∠2度数.
∴∠3= 50 ° (等量代换)
∠4=180 °- 50 °=130 °（等式性质）
第17页
P178 练习第3、5题
第18页
已知∠3 =∠4， ∠1=47°,求∠2度 a 3
数？
b4
解：∵ ∠3 =∠4(已知)
d
∴a∥b(
∴ ∠1= ∠2（又∵∠ 1 = 47° ( 已知 ) ∴∠ 2= 47 °（等量代换）
简单地说：两直线平行，同旁内角互补。
1 4 2
c
几何语言表述:
∵ a ∥ b (已知)
∴ ∠2＋∠4=180 °( 两直线平行，
同旁内角互补)
第10页
书写方法
1、∵ a ∥ b (已知)

平行线的判定市公开课一等奖省优质课获奖课件

足是C.那么AC与直线 l1有什么位置关系？为何？
（3）在直线 l1上再任取一点B，经过点B作BD⊥ l2，
垂足是D。AC与BD有什么位置关系？为何？
（4）度量线段AC与线段BD长度，你发觉了什么？与
同学交流。
演示试验
假如两条直线平行，那么其中一条直线上每个点到另一条直线距离都相等。这个距离，叫做这两条平行线之间距离。
理数大小关系：假如 a﹥，b b﹥，c那么 a。﹥c
但有一些关系不含有传递性。比如直线垂直：
由直线，a⊥，b 不b⊥能c推出。 a⊥c
今后，我们还会碰到含有或不含有传递性例子。在过去学过知识中，你能举出一些含有传递性关系吗？
<<<返回
第17页
1.解：∠1=∠C或者∠2=∠B 或者由∠3+∠B=
N
又因为 ∠ DEC= ∠ B
所以 AB∥DE（同位角相等，两直线平行。）
所以DE∥MN（假如两条直线都和第三条直线
平行，那么这两条直线也相互平行。）
<<<返回
第21页
1.答：同位角相等，两直线平行。
M
N
（第1题）
P
Q
（第2题）
2.答：用点M和点N到直线PQ距离是否相等来判断MN是否平行于PQ，因为平行线之间距离处处相等。
第4页
1.如图，∠1=∠2， 2.如图，∠1与∠2互
直线a与直线b平行吗？补，直线a与直线b
为何？
平行吗？为何？
c
b
1
a
2
c
点
击
a
3
“
2
帮
b
1
助”
3 （第1题）

平行线的判定与性质习题公开课一等奖

(完整版)平行线的判定和性质练习题

平行线的判定1精选教学省公开课金奖全国赛课一等奖微课获奖课件

平行线的判定PPT比赛课市公开课一等奖省优质课获奖课件

平行线的判定华师大版七年级数学公开课一等奖优质课大赛微课获奖课件

七年级数学下册平行线的判定方法市公开课一等奖省优质课获奖课件

平行线的判定与性质习题公开课一等奖

平行线的性质PPT市公开课一等奖省优质课获奖课件

最新平行线的判定教学设计一等奖(通用8篇)

平行线的判定华师大版七年级数学公开课一等奖优质课大赛微课获奖课件

(完整版)平行线的判定和性质练习题

平行线的性质微课市公开课一等奖百校联赛获奖课件

平行线的判定市公开课一等奖省优质课获奖课件