前方交会计算
第12讲空间前方交会

S Z
Y
B
BX
a
Y X A S
Z Y
S
X
BZ
BY
a
Z
X
Y S
[二]空间前方交会公式
XYN NXYB BYX
NX NY
(5)
ZNZBZ NZ Z
Y
B
(c)
N
BX Z BZ X XZ ZX
S
BX
a
N
BX Z BZ X XZ ZX
Z
Y X A
A
Z Y
S
S BZ
X
BY
a
Z
X
Y
[二]空间前方交会公式
B
B
2 X
B
2 Y
B
2 Z
[三]模型点坐标和地面点坐标的计算过程 1、模型点坐标的计算 a. 连续像对相对定向之后,模型点坐标的计算过程
原始数据
确定角方位元素和基线分量
计算左右片在摄测坐标系中旋转 矩阵的方向余弦
a1 a2 a3
b1
b2
b3
E
c1 c2 c3
a1 a 2 a 3
b1
b 2
(X,Y,Z),(X,Y,Z)
计算投影系数 N和 N 计算模型点坐标( X,Y,Z)
X NX
Y
1 2
(NY
NY
BY
)
Z NZ
为什么Y 取中数?
X,Z?
[三]模型点坐标和地面点坐标的计算过程 1、模型点坐标的计算 a. 连续像对相对定向之后,模型点坐标的计算过程
Z Y
Z
XYNNXYBBYX
Z
BZ
N f
[二]空间前方交会公式
前方交会实验报告

前方交会实验报告1. 实验目的本实验的目的是通过前方交会方法测量两个点之间的距离和方位角,以及计算出测量误差,并分析误差来源。
2. 实验原理前方交会是一种基本的测量方法,用于确定两点之间的距离和方位角。
根据测量的原理,通过测量基线上A、B两个测站到待测点C的角度,再测量出A、B两个测站之间的方位角,即可计算出C点的坐标。
前方交会方法包括以下几个步骤:1.安装测量仪器:在点A和点B上,分别设置测站,安装全站仪或其他测量仪器。
2.观测角度:从点A观测点C的水平角和垂直角,从点B观测点C的水平角和垂直角。
3.计算方位角:根据测量仪器的读数和设定的测量参数,计算出A、B两个测站之间的方位角。
4.计算距离:根据测量仪器的读数和设定的测量参数,分别计算出A、B两个测站到点C的距离。
5.计算C点坐标:根据前面步骤得到的测量数据和计算结果,通过三角测量原理,计算出点C的坐标。
6.分析误差来源:根据实际测量和计算结果,分析误差的来源,并对测量结果进行评估和修正。
3. 实验步骤1.在实验区域内分别设置测站A和测站B,并确保两个测站之间有明显的目标点C供观测。
2.使用全站仪或其他测量仪器,分别观测点A和点B 到目标点C的水平角和垂直角,并记录测量数据。
3.根据测量数据,计算出测站A和测站B之间的方位角。
4.根据测量数据和方位角,计算出测站A到目标点C的距离,以及测站B到目标点C的距离。
5.使用三角测量原理,计算出目标点C的坐标。
6.分析误差的来源,评估测量结果的准确性,并进行相应的修正。
4. 实验数据和计算结果以下是实验中测量得到的数据和计算出的结果:•测站A到目标点C的水平角:30°•测站A到目标点C的垂直角:60°•测站B到目标点C的水平角:50°•测站B到目标点C的垂直角:40°•测站A和测站B之间的方位角:100°•测站A到目标点C的距离:50米•测站B到目标点C的距离:60米•目标点C的坐标:(100, 200)根据以上数据和计算结果,可以得出点C的坐标为(100, 200)。
空间后方—前方交会的原理

空间后方—前方交会的原理
以空间后方—前方交会的原理为题,我来为大家描述一下。
空间后方—前方交会是一种用于确定目标位置的方法,常用于航空、导航、测绘等领域。
它利用人眼的立体视觉和视差效应,通过观察目标在不同视角下的位置变化,来推断目标的实际位置。
这种方法可以较精确地确定目标的距离和方位,尤其适用于远距离观测。
在进行空间后方—前方交会时,我们首先需要选择两个观测点,它们之间的距离应足够远,以便产生明显的视差效应。
然后,我们分别在这两个观测点上观察目标,并记录下目标在两个观测点的位置。
接下来,我们需要测量观测点之间的距离,并确定观测点与目标之间的夹角。
这些数据将用于计算目标的实际位置。
通过对两个观测点的位置和距离进行几何分析,我们可以得到目标相对于观测点的位移向量。
然后,我们再将这个位移向量与观测点之间的夹角结合起来,就可以计算出目标相对于观测点的实际位置。
空间后方—前方交会的原理基于视差效应,即当我们观察远处的目标时,由于两只眼睛的视角不同,目标在两只眼睛中的位置也会有所不同。
通过比较这两个位置的差异,我们就可以推断出目标的实际位置。
总的来说,空间后方—前方交会是一种利用视差效应来确定目标位
置的方法。
它可以在远距离观测中提供较为准确的测量结果,具有广泛的应用前景。
角度前方交会法原理

角度前方交会法原理角度前方交会法是一种基本的测量方法,主要用于确定某一点的位置,特别是在野外测量和工程建设中。
该方法利用三角形相似性原理,将测量和计算过程分解为若干个简单的步骤,从而得到准确的测量结果。
本文将对角度前方交会法的原理、步骤和应用进行详细讲解。
角度前方交会法的原理角度前方交会法是基于三角形相似性原理的建立的。
三角形相似性原理指的是两个三角形的对应角度相等,对应边成比例关系。
在以下的图形中,三角形 ABC 和 DEF 相似,因为∠ABC =∠DEF,∠ACB =∠DFE和∠BAC =∠EDF。
与BC、AC、DC、EF、DF和DE相似的边成比例,即,BC/EF = AC/DF = DC/DE利用三角形相似性原理,可以得到角度前方交会法的基本原理:在已知两个点的位置和与这些点的连线所成夹角的情况下,可以测量出另外一个点的位置。
角度前方交会法的步骤角度前方交会法的测量可以分为以下步骤:第一步:在地面上确定两点的位置,并测量两点之间的距离。
这些点可以是明显的位置、桩点、或者标志物。
必须确认这些点的位置是精确的,以确保后续步骤的准确性。
第二步:测量这两点之间的夹角(或者方位角)。
这可以通过使用方位仪或者经纬仪测量得出。
如果使用经纬仪,则需要确定两点之间的经度和纬度,并计算方位角。
第三步:在第一点位置处测量与第一条线相交的第二条线的夹角(或者方位角),并测量与第二点位置的连线所成的夹角(或者方位角)。
记住将仪器调整到正确的方向上,确保夹角或者方位角的准确性。
第四步:从两个已知点的位置向前方测量出第三条线。
可以使用三角板或者望远镜或者其他测量仪器来测量这条线。
第五步:将第三条线的长度和与前两条线相交的夹角输入计算器。
计算器将使用三角形相似性原理来计算出第三条线相对于第一个点的位置。
确定了第三条线的位置之后,就可以测量和计算与该点相交的其他线。
角度前方交会法的应用角度前方交会法主要应用于建筑、土木工程和地理学中。
前方交会和侧方交会
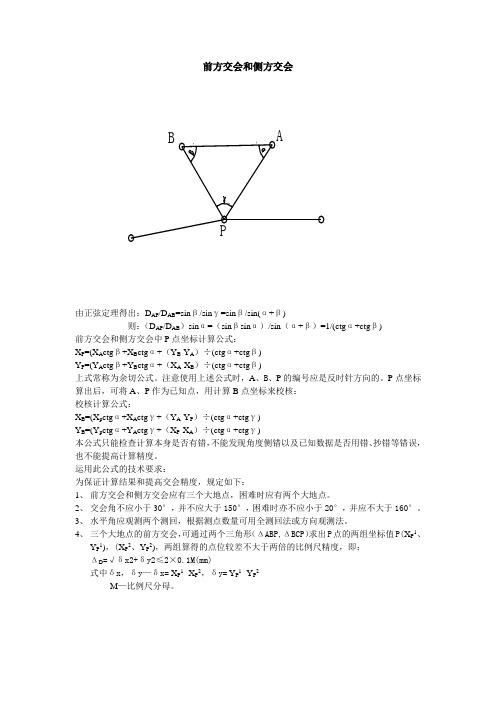
前方交会和侧方交会由正弦定理得出:D AP/D AB=sinβ/sinγ=sinβ/sin(α+β)则:(D AP/D AB)sinα=(sinβsinα)/sin(α+β)=1/(ctgα+ctgβ)前方交会和侧方交会中P点坐标计算公式:X P=(X A ctgβ+X B ctgα+(Y B-Y A)÷(ctgα+ctgβ)Y P=(Y A ctgβ+Y B ctgα+(X A-X B)÷(ctgα+ctgβ)上式常称为余切公式。
注意使用上述公式时,A、B、P的编号应是反时针方向的。
P点坐标算出后,可将A、P作为已知点,用计算B点坐标来校核:校核计算公式:X B=(X p ctgα+X A ctgγ+(Y A-Y P)÷(ctgα+ctgγ)Y B=(Y p ctgα+Y A ctgγ+(X P-X A)÷(ctgα+ctgγ)本公式只能检查计算本身是否有错,不能发现角度侧错以及已知数据是否用错、抄错等错误,也不能提高计算精度。
运用此公式的技术要求:为保证计算结果和提高交会精度,规定如下:1、前方交会和侧方交会应有三个大地点,困难时应有两个大地点。
2、交会角不应小于30°,并不应大于150°,困难时亦不应小于20°,并应不大于160°。
3、水平角应观测两个测回,根据测点数量可用全测回法或方向观测法。
4、三个大地点的前方交会,可通过两个三角形(ΔABP,ΔBCP)求出P点的两组坐标值P(X P1、Y P1),(X P2、Y P2),两组算得的点位较差不大于两倍的比例尺精度,即:ΔD=√δx2+δy2≤2×0.1M(mm)式中δx,δy—δx= X P1- X P2,δy= Y P1 -Y P2M—比例尺分母。
后方交会B如图所示,A、B、C是已知三角点,P点是导线点,将仪器安置在P点上,观测P至A、B、C各个方向之间的水平夹角α、β,然后根据已知三角点的坐标,可解算P点坐标。
前方交会的计算公式

前方交会的计算公式
前方交会是指在地球上从不同方向观察同一物体,利用三角测量原理计算出该物体在地球上的位置。
前方交会的计算公式由以下几部分组成:
1. 观测角度法
设物体在地球上的位置为A,观察者在地球上的位置为B,观察者在地球上另一点C处再次观测该物体,观测角度为α和β,则有以下公式:
tan α = (AB/AC) tan β = (AB/BC)
2. 向量法
设物体在地球上的位置为P,分别由两个观测者在地球上的位置A和B观测,得出向量AP和BP的方向角度分别为α和β,则设球半径为R,则有以下公式:
x = (Rsin α - Rsin β) / (cos α - cos β) y = (Rcos α(Rsin β - Rsin α) - Rcos β(cos α - cos β)) / (cos α - cos β)
3. 三边测量法
设物体在地球上的位置为P,分别由两个观测者在地球上的位置A和B观测,得出AP、BP和AB三条边的长度分别为a、b和c,则设球半径为R,则有以下公式:
cos A = (b^2 + c^2 - a^2) / (2bc) cos B = (a^2 + c^2 - b^2) / (2ac) cos C = (a^2 + b^2 - c^2) / (2ab)
其中,A、B、C分别为三个角度。
根据已知的A、B、C,可以使用三角函数计算出向量AP和BP的方向角度,进而求出物体在地球上的位置。
立体像对空间前方交会解算流程

立体像对空间前方交会解算流程下载温馨提示:该文档是我店铺精心编制而成,希望大家下载以后,能够帮助大家解决实际的问题。
文档下载后可定制随意修改,请根据实际需要进行相应的调整和使用,谢谢!并且,本店铺为大家提供各种各样类型的实用资料,如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等,如想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by the editor. I hope that after you download them, they can help yousolve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!In addition, our shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts,other materials and so on, want to know different data formats and writing methods, please pay attention!立体像对空间前方交会解算流程是一项重要的测量技术,用于测量和计算地球或宇宙空间中不同图像之间的空间位置和方向关系。
空间后方—前方交会的原理

空间后方—前方交会的原理空间后方—前方交会是一种导航技术,通过测量目标物体在不同观测点的角度,并利用三角测量原理计算目标物体的位置。
这种技术广泛应用于航空、航天、导航等领域,可以帮助人们准确地确定目标物体的位置和方向。
在空间后方—前方交会中,观测者需要站在不同的位置观测目标物体,并测量目标物体相对于观测点的角度。
观测者需要使用测角仪或其他测量工具来测量角度,并记录下相应的数据。
测量完所有观测点的角度后,观测者需要根据这些角度数据进行三角计算,以确定目标物体的位置。
三角计算是利用三角函数来计算角度和边长的关系,通过已知的角度和边长来计算未知的角度和边长。
观测者需要根据测量得到的角度数据和观测点之间的距离,使用三角函数计算目标物体的位置坐标。
空间后方—前方交会的原理简单明了,但在实际应用中需要考虑一些因素。
首先,观测者需要选择合适的观测点,观测点的位置应尽量避免遮挡物,以确保观测到目标物体的角度准确无误。
其次,观测者需要准确测量角度,并尽量避免误差的产生。
最后,观测者需要进行精确的三角计算,以确保计算出的目标物体位置准确无误。
空间后方—前方交会技术的应用非常广泛。
在航空领域,飞行员可以利用该技术确定飞机的位置和方向,以确保飞行安全。
在航天领域,航天员也可以利用该技术确定航天器的位置和方向,以实现精确的轨道控制。
此外,该技术还可以应用于导航系统中,帮助人们准确导航和定位。
空间后方—前方交会是一种通过测量目标物体在不同观测点的角度,并利用三角计算原理确定目标物体位置的导航技术。
该技术在航空、航天、导航等领域有着广泛的应用,可以帮助人们准确地确定目标物体的位置和方向。
通过合理的观测点选择、准确的角度测量和精确的三角计算,空间后方—前方交会技术可以为人们提供准确可靠的导航和定位服务。
前方后方交会计算方法

2.2.1两点后方交会解算原理图2.2.1.1 后方交会在图2.2.1.1中,已知M1(X1,Y1,Z1),M2(X2,Y2,Z2)是两个控制点,P(Xp ,Yp ,Zp)是待求点。
O1,O2是M1,M2通过P 点水平面的投影点。
在测站P 点上,观测得两个竖直角1β、2β和一个水平角γ,先要用已知点坐标以及这三个观测数据求出待定点P 的三维坐标(Xp ,Yp ,Zp)。
设h1=Z1-Zp=M1O1,h2=Z2-Zp=M2O2,h0=Z1-Z2=h1-h2,I 为仪器高,则经过计算整理得P 点坐标为Xp =X1+S 1Cos 1αYp=Y1+ S 1Sin 1αZp=Z1- S 1tg 1β-I式中,1α=12α + 1γ,12α是已知点间M 1M 2的方位角。
2.2.2 前方交会在已知控制点A 、B 上观测水平角α,β,根据已知点坐标和观测角值,计算待定点P 的坐标,称为前方交会(如图2.2.2.1)。
在前方交会图形中,由未知点至相邻两已知点间的夹角称为交会角。
当交会角过小(或过大) 时,待定点的精度较差,交会角一般应大于30度并且小于如图3所示,根据已知点A 、B 的坐标A (X A ,Y A )和B (X B ,Y B ),通过平面直角坐标系反算,可获得AB 边的坐标方位角AB α和边长S AB ,由坐标方位角 AB α和观测角α可推算出坐标方位角AP α,由正弦定理可AP 的边长S AP 。
由此,根据平面直角坐标系正算公式,即可求得待定点P 的坐标,即X P =X A +S AP*cos AP α,Y P =Y A +S AP*sin AP α当A 、B 、P 按逆时针编号时,AP α = AB α-α,将其代入上式,得X P = X A +S AP*cos(AB α-α) = X A +S AP (cos AB αcos α+sin AB αsin α)Y P = Y A +S AP*sin(AB α-α) = Y A +S AP (cos AB αcos α+sin AB αsin α)顾及X B -X A = S AB *cos AB α,Y B -Y A = S AB *sin AB α,则有 X P = X A +S AP *sin α[(X B -X A )*cot α+(Y B -Y A )]/S AB Y P = Y A +S AP *sin α[(Y B -Y A )*cot α+(X B -X A )]/S AB 由正弦定理并代入上式整理得X P = [X A *cot β+X B *cot β+(Y B -Y A )]/(cot α+cot β) Y P = [Y A *cot β+Y B *cot β+(X B -X A )]/(cot α+cot β)XY图2.2.2.1 前方交会。
交会法测量

"
"
/ D PC / D PC
0 . 15 M
三、后方交会
1.基本公式(仿权公式)
xP yP P A x A PB x B PC x C P A PB PC P A y a PB y B PC y C P A PB PC
0
α2 β1 α1 β2
P
辅 助 计 算
x 0 . 03
e 0 . 03 M 1000
e 容 2 0 . 1 M 200 mm 0 . 2 m
二、侧方交会法
在一个已知点A和未知点P上安置仪器,观测水平角α 和γ,并根据已知点A和B的坐标,计算P点坐标。
A
α
γ
P
ε
B C
37477.54 37327.20 37194.574 37327.20 37163.69 37194.54 37194.56 A
yA yB
yP′ yB yC yP″ yP
y
16307.24 16078.90 16226.42 16078.90 16046.65 16226.42 16226.42
C
1
A
1
2
B
e e 容 2 0 .1M
当两组坐标较差符合规定要求时,取其平均值作为 P点的最后坐标。
前方交会计算实例
点名 x 观测角
α1 40°41′57″
β1 75°19′02″ α2 58°11′35″ β2 69°06′23″
y
A B
P B C P 中数 略 图
xA xB
xP′ xB xC xP″ xP
立体像对的空间前方交会

内 容 安 排
一、空间前方交会(定义、公式、应用)
二、模型点、地面点坐标解算
第11讲 空间前方交会
一、空间前方交会(定义) 定义:由立体像对中两张像片的内、外方位元素 和像点坐标来确定相应地面点在物方空间坐标 (像空间辅助坐标系或地面测量坐标系)系中坐标的方法。
z1
S1 Z
结论:严格的、不受影像数量约束的空间前方交会解法
第11讲 空间前方交会
二、模型点、地面点坐标的解算 1、立体像对上模型点坐标解算(前方交会基本公式)
坐标系:左片的像空间辅助坐标系 S1-U1V1W1,右片的像空间辅助坐标 系S2-U2V2W2, 坐标系轴系相互平行 模型点A在S1-U1V1W1的坐标 (U1,V1,W1) 根据相对定向元素计算像 点的像空间辅助坐标
Ys1
X
第11讲 空间前方交会
一、空间前方交会(公式推导)
1、投影系数法 (重点)
地面点坐标计算公式
Y取平均值可消除相对定向后的残差影响
第11讲 空间前方交会
一、空间前方交会(公式推导)
1、投影系数法 (重点)
投影系数计算公式
第11讲 空间前方交会
2、利用共线方程的严密解法
x x0 f a1 ( X X s ) b1 (Y Ys ) c1 ( Z Z s ) a3 ( X X s ) b3 (Y Ys ) c3 ( Z Z s )
一、空间前方交会(公式推导)
1、投影系数法 (重点)
3个坐标系:物方坐标系M-XYZ,左片的像空间辅助坐标系S1-U1V1W1,右 片的像空间辅助坐标系S2-U2V2W2,3坐标系轴系相互平行 S1在M-XYZ的坐标坐标(Xs1,Ys1,Zs1)
交会测量(前方、后方、侧方交会测量)

前方交会法1.前方交会法定义自两已知坐标之三角点上,观测一欲测点之水平角,以推算其坐标位置,称之前方交会法。
图-1,前方交会法。
图-2,前方交会点。
图-1 前方交会法图-2 前方交会点2.前方交会点此种补点(前方交会点),通常为无法设置仪器之测点,如塔尖、避雷针、烟囱等等。
3.前方交会法适用场合:A.具两已知三角点。
B.三点(两已知点及欲测点)间可以通视。
C.两已知点可以架设仪器,但欲测点不方便架设仪器。
D.有数个欲测点待测定时。
图-3,为数个欲测点图-3 数个欲测点4.前方交会法施作步骤:A.经纬仪分别整置于A、B 两三角点上。
B.照准P 点,分别测得α、β两水平角。
C.以计算方法,求P 点坐标。
图-4,为量测角度。
图-4 量测角度5.已知、量测、计算之数据:A.已知:xA、yA、xB、yB。
B.量测:α、β。
C.计算:xP、yP。
图-5,为前方交会法相关角度位置图-5 前方交会法相关角度位置6.限制:α、β、γ三内角均必须介于30°~120°之间。
图-6 ,为角度限制。
图-6 为角度限制7.计算法前方交会法计算方法有三种:A.三角形法; B.角度法; C.方位角法8.三角形法19()()3891802890--++=---= βφφαφφABBP AB AP ()()()()()689cos sin cos 589sin cos sin 48922222---=-==---=-==---+-=∆+∆= ABAB AB AB AB AB A B AB A B A B y y AB ABy y x x AB ABx x y y x x AB y x AB φθφφθφ()()789sin sin sin sin sin sin --+===βαβγβγβAB AB AP ABAP γβαABP AB AB y y y -=∆ABNB.求方位角ψAP 、ψBP :C.求各邊邊長:①AB 邊長:有三種方法可求得②AP 邊長:()[](βαβαγγβα+=+-==++sin 180sin sin 180γβαsin sin sin AB AP BP ==20()()1289cos 1189sin --+=--+= BPB P BP B P BP y y BP x x φφ()()889sin sin sin sin sin sin --+===βααγαγαAB AB BP ABBP ()()1089cos 989sin --+=--+= APA P AP A P AP y y AP x x φφAPAP l φcos A Py yPBy y BPy y l y BP x x l x yy y x x x BP BP BP B P BP BP B P B P -=∆==-=∆=-=∆+=∆+=φφφφcos cos sin sin ③BP 邊長:D.求P 座標x P 、y P :①由A 點求P 點②由B 點求P 點9.角度法A.由上法直接代入:將(9-8-2)式與(9-8-7)式代入(9-8-9)式中,可得:yy y x x x A P A P ∆+=∆+=APy y l y AP x x l x AP AP AP AP AP AP -=∆=-=∆=φφcos sin21()()()1389sin sin sin sin ---++=+= αφβαβφAB A APA P AB x AP x x ()αφαφαφsin cos cos sin sin AB AB AB -=-()()()1489cos sin sin cos ---++=+= αφβαβφAB A APA P AB y AP y y ()αααφsin cos sin ABy y AB x x AB A B AB ---=-()()()()()1589sin sin sin sin sin cos --+--+-+= βαβαβαβαA B A B A P y y x x x x ()()()()()1789cot cot cot sin cos sin 1689tan tan tan sin cos sin 1cot cot 1tan tan sin cos sin cos cos sin sin cos sin --+=+--+=++=+=+=+ αβαβαβαββαβαβααββαβαβαβαβαβα或將(9-8-2)式與(9-8-7)式代入(9-8-9)式中,可得:B.化簡x P :由和差化積公式:將(9-8-5)式與(9-8-6)式代入,可得:再之代入(9-8-13)式中,可得:由和差化積公式:化簡下式,可得:()βαβαβαcos cos cos sin sin +=+22()2289cot cot cot cot --++-+=βααβBA B A P x x y y y ()()()()ABPB PA APBA BP A B A P APA B A P y y y y y y x x φφφφφφφcos sin cos sin tan ---+=-+=()()()()2089tan tan tan tan tan tan tan tan tan tan tan tan tan --+--+=+--+-+= βαβαβαβαβαβαβA B B A P A B A B A P y y x x x y y x x x x ()()()()()1989cot cot sin sin sin 1889tan tan tan tan sin sin sin tan 1tan 1sin sin sin cos cos sin sin sin sin --+=+--+=++=+=+ βαβαβαβαβαβαβααββαβαβαβαβα或()()()2189cot cot cot cot cot cot 1cot cot cot --+-++=+--+-+= βααββαβααBA B A P A B A B A P y y x x x y y x x x x 同理,化簡下式,可得:將(9-8-16)式與(9-8-18)式代入(9-8-15)式中,可得:或將(9-8-17)式與(9-8-19)式代入(9-8-15)式中,可得:C.化簡y P :(推演過程省略)D.角度法所得公式(9-18-21)式與(9-18-22)式,適於計算機使用,唯應注意:左A ,右B ;左α,右β。
前方交会投影系数法例题

前方交会投影系数法例题摘要:1.前方交会投影系数法简介2.例题介绍3.例题解答过程4.总结正文:一、前方交会投影系数法简介前方交会投影系数法是一种测量和计算工程中点、线、面等空间几何图形的方法。
该方法主要通过投影系数的计算,将空间几何图形投影到平面上,从而实现测量和计算的目的。
前方交会投影系数法的应用领域广泛,如土木工程、建筑工程、机械制造等。
二、例题介绍本例题为一个简单的前方交会投影系数法应用题,题目如下:已知空间几何体ABCD,其中A(0, 0, 0),B(2, 0, 0),C(2, 2, 0),D(0, 2,0)。
现要求在平面xoy 上投影该几何体,并求出投影后的图形。
三、例题解答过程1.计算各点在前方交会投影面上的投影系数以点A 为例,其在平面xoy 上的投影为A",由于A 在z 轴上,所以A"的坐标为(0, 0, 0)。
根据前方交会投影系数的计算公式,可得A 在平面xoy 上的投影系数为:K_A = (0 - 2) / (0 - 2) = -1同理,可计算出其他点在平面xoy 上的投影系数:K_B = (0 - 2) / (0 - 2) = -1K_C = (2 - 2) / (2 - 0) = 0K_D = (0 - 2) / (0 - 2) = -12.计算各点在平面xoy 上的投影根据投影系数和原点坐标,可以计算出各点在平面xoy 上的投影:A" = A * K_A = (0, 0, 0)B" = B * K_B = (0, 0, 0)C" = C * K_C = (2, 2, 0)D" = D * K_D = (0, -2, 0)3.连接投影后的点,得到投影后的图形将投影后的点A"、B"、C"、D"连接起来,得到投影后的四边形ABCD"。
四、总结本例题通过前方交会投影系数法,计算出了空间几何体在平面xoy 上的投影,并得到了投影后的图形。
前方交会投影系数法例题

前方交会投影系数法例题(最新版)目录一、前方交会投影系数法简介二、例题分析1.题目描述2.解题思路3.计算过程三、总结正文一、前方交会投影系数法简介前方交会投影系数法是一种测量和计算工程中点、线、面等空间几何形体的方法。
该方法主要通过测量物体在空间中的投影,然后根据投影数据计算空间几何形体的实际形状和尺寸。
前方交会投影系数法的应用范围广泛,例如在土木工程、建筑工程、机械制造等领域都有应用。
二、例题分析1.题目描述某工程项目需要测量一个长方体的尺寸,已知长方体的三个面的投影分别为长方形 A、B、C。
长方形 A 的长为 a,宽为 b;长方形 B 的长为 c,宽为 d;长方形 C 的长为 e,宽为 f。
要求计算长方体的长、宽、高。
2.解题思路根据前方交会投影系数法,我们可以通过测量物体在空间中的投影,然后根据投影数据计算空间几何形体的实际形状和尺寸。
对于这道题目,我们可以通过计算长方形 A、B、C 的投影系数,然后利用投影系数求出长方体的长、宽、高。
3.计算过程首先,我们需要计算长方形 A、B、C 的投影系数。
投影系数的计算公式为:投影系数 = 投影面积 / 物体面积长方形 A 的投影面积为 ab,物体面积为 ab,所以投影系数为:投影系数 A = ab / ab = 1同理,可以计算出长方形 B、C 的投影系数:投影系数 B = cd / cd = 1投影系数 C = ef / ef = 1然后,我们可以利用投影系数求出长方体的长、宽、高。
根据前方交会投影系数法的原理,长方体的长、宽、高分别等于投影面积除以投影系数。
所以,可以得到:长 = A 的投影面积 / A 的投影系数 = ab / 1 = ab宽 = B 的投影面积 / B 的投影系数 = cd / 1 = cd高 = C 的投影面积 / C 的投影系数 = ef / 1 = ef综上所述,长方体的长、宽、高分别为 ab、cd、ef。
三、总结本题通过前方交会投影系数法,利用物体在空间中的投影计算出长方体的长、宽、高。
全站仪前方交会原理

全站仪前方交会原理全站仪前方交会原理是全站仪测量中的一种方法。
前方交会是指利用两条或多条测线交叉的交会点位置,进而确定目标点的测量方法。
下面将详细介绍全站仪前方交会的原理和步骤。
全站仪前方交会原理是基于三角测量原理和地面平面坐标系的转换。
在进行测量之前,需要首先设置好全站仪的基准点,并将所有测线的起点和终点确定下来。
全站仪通过测量不同测线之间的水平角和垂直角,以及测线的长度,进而计算目标点的地面平面坐标。
首先,全站仪需要通过观测目标点和参考点之间的水平角和垂直角来确定两个测线之间的夹角。
全站仪有两个显示器,用于分别读取水平角和垂直角的值。
通过对测量方向的选择,可以得到正的或者负的夹角。
接下来,全站仪通过测量两个测线之间的水平距离和垂直距离,来计算目标点在地面平面上的坐标。
全站仪利用内置的测距仪来测量两个测线之间的斜距,而水平角和垂直角的数值则可通过仪器本身的测量系统进行读取。
通过将水平距离与斜距进行运算,可以得到目标点在地面平面上的坐标。
在进行全站仪前方交会测量时,需要注意几点。
首先,全站仪需要放置在一个稳定的支架上,以确保测量结果的准确性。
其次,需要避免测量过程中的人工误差,如手抖或读数不准确。
最后,测量之前需要校准全站仪,以确保仪器的精度和准确性。
总结起来,全站仪前方交会原理是通过测量目标点和参考点之间的水平角、垂直角以及斜距,来确定目标点在地面平面上的坐标。
该方法利用了三角测量原理和地面平面坐标系的转换,可以广泛应用于土木工程、测绘等领域。
在进行测量时,需要注意稳定的支架、准确的读数和仪器的校准,以确保测量结果的准确性和可靠性。
前方交会(计算塔尖)
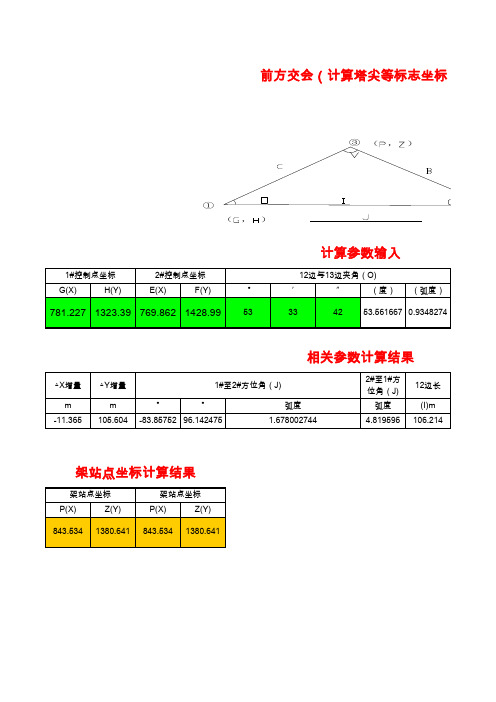
相关参数计算结果
△X增量 m -11.365 △Y增量 m 105.604 ° ° 1#至2#方位角(J) 弧度 1.678002744 -83.85752 96.142475 至1#方位角( 12边长 弧度 4.819595 (I)m 106.214
架站点坐标计算结果
架站点坐标 P(X) 843.534 Z(Y) 1380.641 架站点坐标 P(X) 843.534 Z(Y) 1380.641
前方交会计算塔尖等标志坐标计算参数输入弧度78122713233857698621428989533342535616667093482744503455505819444088282147相关参数计算结果弧度弧度113651056048385752489614247521678002743948195951062148461988120132394374架站点坐标计算结果架站点坐标架站点坐标843534138064184353413806411控制点坐标2控制点坐标12边与13边夹角o21边与23边夹角qx增量y增量1至2方位角j2至1方位角j12边长13边长23边长31边与32边夹角
标志坐标)
)
② ( , )
21边与23边夹角(Q) ° 50 ′ 34 ″ 55 (度) (弧度)
50.581944 0.8828215
13边长 (C)m 84.619
23边长 (B)m 88.120
31边与32边夹角 V(弧度) 1.3239437
前方交会(计算塔尖等标志坐标)
③(,)来自① ( , ) (,
计算参数输入
1#控制点坐标 G(X) H(Y) 2#控制点坐标 E(X) F(Y) ° 53 ′ 33 12边与13边夹角(O) ″ 42 (度) (弧度)
11-空间前方交会

-
a11 a 21
- a12 - a22
- a13 - a23
X Y Z
x y
-
x0
y0
当有两个(以上)同名像点时,就会有4个(以上)
误差方程式,可以解算三个未知数。由于各点是相
互独立的,因此,解算时可以采用逐点解算的方式。
影响前方交会结果的精度因素如下:
工业测量技术与数据处理
(空间前方交会)
内 [一]空间前方交会的定义
容 [二]空间前方交会的解算
安
排 [三]影响前方交会结果的精度
利用立体像对两张像片的同名像点坐标 和像对的相对方位元素(或外方位元素)解 算模型点坐标(或地面点坐标)的工作。
1、利用像对的相对方 位元素,计算模型点的 三维坐标; 2、利用像对的外方位 元素,计算相应像点的 地面坐标。
o1 a1
o2 a2
S1
S2
A
空间前方交会
单张像片像点坐标
地面点坐标
共
线
方 程
x2
x0
f
a1( X a3 ( X
X s2 ) b1(Y X s2 ) b3(Y
Ys2 ) c1(Z Zs2 ) Ys2 ) c3 (Z Zs2 )
y2
y0
各个像片之间的几何构型,包括像片的数量、摄站空间布 局及交会角度; 像点的成像质量,包含像点坐标测量本身的精度以及各项 系统误差的改正程度; 每张像片内方位元素、外方位元素以及附加参数的精度。
f
a2 ( X a3 ( X
X s2 ) b2 (Y X s2 ) b3(Y
前方交汇计算方法

前方交汇计算方法我折腾了好久前方交汇计算方法,总算找到点门道。
说实话,前方交汇计算这事儿,我一开始也是瞎摸索。
最开始我就只知道有这么个方法,但具体怎么操作完全没概念。
我就到处找书看,那时候觉得书上肯定都写得明明白白的。
可是啊,书上那些公式啊,术语啊,看得我真是一头雾水。
就像进入了一个迷宫,转来转去找不到出口。
比如说那个角度的测量,我当时就没太整明白到底是从哪个点开始测量到哪个点的。
我按照自己想当然的方法测了角度,然后套公式计算,结果那答案错得离谱。
这就是一个教训啊,千万不能想当然,每个步骤都得严格按照概念来。
后来我又试了另一种办法。
我找了个简单的场景,就像我们在操场上模拟那种交汇的情况。
我在操场的两边找了两个固定的点,然后从中间找一个目标点。
我就拿着那种简单的量角器去测量角度,这个时候我就比较仔细了,比着书上的图,确定好测量的起始边和终止边。
可又出新问题了,计算的时候我老是把数字搞得乱七八糟,公式是记住了,但是代入数字的时候就是容易出错,不是把角度值代错了位,就是在乘除法的时候算错。
然后我就想了个笨办法,每一步计算都写得清清楚楚的,计算之前再核对一遍数据,虽然这样速度很慢,但是准确率高了不少。
再后来我就开始考虑误差的问题了。
我发现很多时候测量角度的时候本身就存在一点小误差,设备不够精确啊什么的。
这时候我就会多测量几次取平均值,就像我们在量身高的时候多量几遍取中间数一样的道理。
关于前方交汇计算方法,到现在我也不敢说我完全掌握得透彻了。
像那种在很复杂的环境下,比如说有障碍物挡住视线或者角度特别刁钻的时候,怎样更精确地计算我还在摸索。
但我觉得吧,如果最开始和我一样对这个方法感到迷茫的话,可以先从简单的场景入手,像我在操场做的那样,把每一个步骤都搞清楚,然后再去处理复杂的情况。
还有就是计算一定要谨慎,别着急,一步一步来,有时间就多做几次来核对结果。
而且在测量角度的时候尽量多换几种测量工具或者方法,对比一下,这样可以减少误差。
