混凝土分离式箱梁桥荷载横向分配系数

合集下载

探讨横向分配系数计算方法

探讨横向分配系数计算方法桥梁荷载横向分配系数的计算主要有铰接板（梁）法、刚接板（梁）法、偏心压力法、修正偏压法、比拟正交异性板法（G-M法）、弹性支承连续梁法、考虑抗扭的弹性支承连续梁法等[1]。

如何正确选择适用方法是广大设计人员面对的一个重要问题。

1、荷载横向分配系数计算理论在荷载横向分配计算中，结构的横向连接刚度起着至关重要的作用。

横向连接刚度越大，荷载横向分布作用越显著，各主梁所分配的荷载也越趋均匀。

因此需要根据实际的横向结构拟定出较为合理的简化计算模型，从而确定相应的计算方法。

对于城市宽桥，需要用梁格法，通过有限元计算来得到桥梁的横向分配系数[2]。

梁格系理论是将桥梁上部结构用一个等效梁格来代替分析，等效梁格后再将其结果还原到结构中就可得到所需的计算结果。

此法易于理解，便于使用，而且比较精确。

一般说来等效梁格的网格越密，计算结果的精确度就越高。

梁格法主要应用简支梁桥挠度参数跟横向分配系数的关系来求得横向分配系数。

通过最不利荷载的布置求得各片主梁的挠度，再由在单片主梁上跨中加载所得的挠度，从而得出各片主梁的荷载横向分配系数[2]。

2、应用梁格法的实例橄榄河桥位于省道S214线上，原桥为5-15m双曲拱桥，由于该桥病害严重，相关单位对该桥进行了重建。

2014年重建桥梁为4跨预应力混凝土连续梁桥，主梁结构为4片预应力混凝土连续小箱梁。

桥跨布置为19.92m+20m+20m+19.92m。

梁格法采用Midas/civil结构分析软件进行计算，图1为计算模型。

全桥模型在横向最不利汽车荷载布置下各片梁所承受内力值与跨中各片梁内力值之和的比值即为该片梁的横向分配系数。

同时采用刚性梁法计算该桥在最不利汽车荷载作用下的横向分配系数。

主梁从左往右编号为1-4号见图2。

表1为两种方法计算出的1-4号梁的荷载横向分配系数。

3、结语采用刚接梁法及梁格法对一座4片小箱梁构成的主梁的横向分配系数进行了计算。

经过对计算结果比较，可以得到如下结论：1）因刚接梁法主要考虑箱梁翼缘及各片箱梁之间湿接缝的刚接，横隔板的刚度平均分配到梁的纵向，故其横向分配系数计算结果偏大。

桥梁荷载横向分布系数的各种计算方法综述.

桥梁荷载横向分布系数的各种计算方法综述姓名：XXX学号：50XXXXXXX3摘要：公路桥梁荷载横向分布有多种计算模型，其中比较实用的有：1）杠杆原理法；2）偏心压力法、修正偏心压力法；3）铰接板（梁）法；4）刚接板（梁）法等。

这些理论方法有各自的适用范围，应按具体情况选用适当的方法来运用。

关键词：混凝土简支梁桥；荷载横向分布系数；影响线；影响因素1引言随着国民经济的发展，对交通的需求日益提高，众多的高速公路及城市快速干道相继修建。

公路桥梁上行驶车辆的轴重加重、速度提高，车流密度也相应提高。

使之在设计过程中如何确保桥梁结构在使用寿命期限内的安全性，准确计算各片梁所需承担的最大活载弯矩就显得尤为重要。

特别是对于中小跨多片梁型的桥梁，当跨数较多时，用测试横向分布状态的方法对桥梁运营状态进行评价，具有简洁、实用、可靠等优点，具有较高的推广价值。

所谓荷载横向分布系数（Lateral Distribution Factor of Live Load）是指公路车辆荷载在桥梁横向各主梁间分配的百分数。

普通简支桥梁中它和各主梁间的联结方式（铰接或刚接），有无内横梁及其数目，断面的抗弯刚度和抗扭刚度，以及车辆荷载在桥上的位置等有关。

它是一个复杂的空间结构问题，在桥梁设计中常简化为平面问题而引用荷载横向分布系数。

[1]目前广泛采用的是利用主梁的纵向影响线和它的荷载横向分布影响线相结合的方法，荷载横向分布系数是在荷载横向分布影响线的基础上按荷载的最不利位置布载，并将荷载位置相应的影响线竖标值求和得到的最后数值结果。

对于混凝土简支梁桥，荷载横向分布系数的影响因素主要有桥粱跨度(Z)、主梁间距(S)、桥面板的厚度(t0)、主梁刚度(K0)、横隔梁(板)的数量及位置、车载类型及布栽位置、车辆间距、栏杆及横跨比等。

[2][3][4][9]2计算方法及其适用范围荷载横向分布理论在桥梁设计中占有重要地位。

目前桥梁荷载横向分布系数常用的计算方法主要有杠杆原理法、偏心压力法（修正偏心压力法）、铰接板（梁）法、刚接梁法和比拟正交异性板法（G-M法）等。

桥梁荷载横向分布系数的各种计算方法综述

桥梁荷载横向分布系数的各种计算方法综述姓名：XXX 学号：50XXXXXXX3摘要：公路桥梁荷载横向分布有多种计算模型，其中比较实用的有：1）杠杆原理法；2）偏心压力法、修正偏心压力法；3）铰接板（梁）法；4）刚接板（梁）法等。

这些理论方法有各自的适用范围，应按具体情况选用适当的方法来运用。

关键词：混凝土简支梁桥；荷载横向分布系数；影响线；影响因素1 引言随着国民经济的发展，对交通的需求日益提高，众多的高速公路及城市快速干道相继修建。

公路桥梁上行驶车辆的轴重加重、速度提高，车流密度也相应提高。

使之在设计过程中如何确保桥梁结构在使用寿命期限内的安全性，准确计算各片梁所需承担的最大活载弯矩就显得尤为重要。

所谓荷载横向分布系数（Lateral Distribution Factor of Live Load）是指公路车辆荷载在桥梁横向各主梁间分配的百分数。

普通简支桥梁中它和各主梁间的联结方式（铰接或刚接），有无内横梁及其数目，断面的抗弯刚度和抗扭刚度，以及车辆荷载在桥上的位置等有关。

它是一个复杂的空间结构问题，在桥梁设计中常简化为平面问题而引用荷载横向分布系数。

[2][3][4][9]2 计算方法及其适用范围荷载横向分布理论在桥梁设计中占有重要地位。

桥梁上部计算教程--横向力分布系数计算

桥梁上部计算教程--横向力分布系数计算(转)总的来说，横向力分布系数计算归结为两大类（对于新手能够遇到的）：1、预制梁（板梁、T梁、箱梁）这一类也可分为简支梁和简支转连续2、现浇梁（主要是箱梁）首先我们来讲一下现浇箱梁（上次lee_2007兄弟问了，所以先讲这个吧）在计算之前，请大家先看一下截面这是一个单箱三室跨径27+34+27米的连续梁，梁高1.55米，桥宽12.95米！！支点采用计算方法为为偏压法（刚性横梁法）mi=P/n±P×e×ai/(∑ai x ai)跨中采用计算方法为修正偏压法（大家注意两者的公式，只不过多了一个β）mi=P/n±P×e×ai×β/(∑ai x ai)β---抗扭修正系数β=1/(1+L^2×G×∑It/(12×E×∑ai^2 Ii)其中：∑It---全截面抗扭惯距Ii ---主梁抗弯惯距 Ii=K Ii` K为抗弯刚度修正系数，见后L---计算跨径G---剪切模量 G=0.4E 旧规范为0.43EP---外荷载之合力e---P对桥轴线的偏心距ai--主梁I至桥轴线的距离在计算β值的时候，用到了上次课程/thread-54712-1-1.html我们讲到的计算截面几何性质中的抗弯惯矩和抗扭惯矩，可以采用midas计算抗弯和抗扭，也可以采用桥博计算抗弯，或者采用简化截面计算界面的抗扭，下面就介绍一下这种大箱梁是如何简化截面的：简化后箱梁高度按边肋中线处截面高度(1.55m)计算，悬臂比拟为等厚度板。

①矩形部分(不计中肋):计算公式:It1=4×b^2×h1^2/(2×h/t+b/t1+b/t2)其中：t,t1,t2为各板厚度h,b为板沿中心线长度h为上下板中心线距离It1=4×((8.096+7.281)/2)^2×1.34^2/(2×1.401/0.603+8.097/0 .22+7.281/0.2)=5.454 m4②悬臂部分计算公式: It2=∑Cibiti3其中：ti,bi为单个矩形截面宽度、厚度Ci为矩形截面抗扭刚度系数,按下式计算:Ci=1/3×(1-0.63×ti/bi + 0.052×(ti/bi)^5)=1/3×(1-0.63×0.26/2.2+0.052×(0.26/2.2)^5)=0.309It2=2×0.309×2.2×0.26^3=0.0239 m4③截面总的抗扭惯距It= It1+ It2=5.454+0.0239=5.4779 m4大家可以用midas计算对比一下看看简化计算和实际能差多少？？先计算一下全截面的抗弯和中性轴，下面拆分主梁需要用的到采用<<桥梁博士>>V2.9版中的截面设计模块计算全截面抗弯惯距，输出结果如下：<<桥梁博士>>---截面设计系统输出文档文件: D: \27+34+27.sds文档描述: 桥梁博士截面设计调试任务标识: 组合截面几何特征任务类型: 截面几何特征计算------------------------------------------------------------截面高度: 1.55 m------------------------------------------------------------计算结果:基准材料: JTJ023-85: 50号混凝土基准弹性模量: 3.5e+04 MPa换算面积: 7.37 m2换算惯矩: 2.24 m4中性轴高度: 0.913 m沿截面高度方向 5 点换算静矩(自上而下):主截面:点号: 高度(m): 静矩(m××3):1 1.55 0.02 1.16 1.773 0.775 1.834 0.388 1.585 0.0 0.0------------------------------------------------------------计算成功完成结果：I全= 2.24 m4 中性轴高度H=0.913m下面来讲一下主梁拆分的原则：将截面划分为τ梁和I梁,保持将两截面中性轴与全截面中性轴位置一致。

桥宽12.5米单箱单室框架分析横向分布系数计算(1)

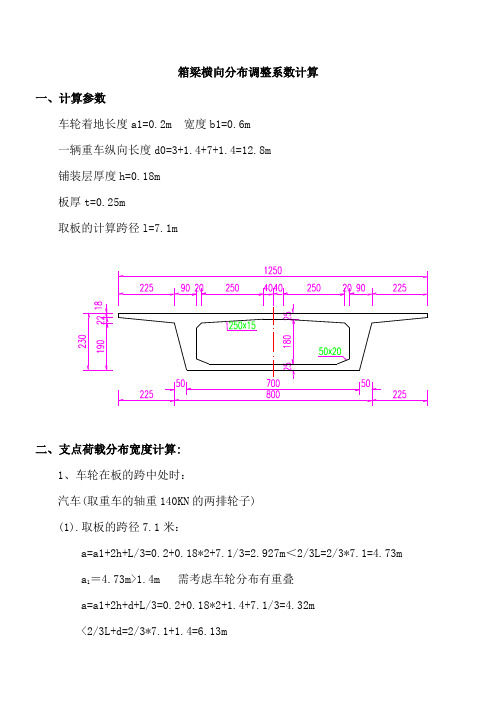
箱梁横向分布调整系数计算一、计算参数车轮着地长度a1=0.2m 宽度b1=0.6m一辆重车纵向长度d0=3+1.4+7+1.4=12.8m铺装层厚度h=0.18m板厚t=0.25m取板的计算跨径l=7.1m二、支点荷载分布宽度计算:1、车轮在板的跨中处时：汽车(取重车的轴重140KN的两排轮子)(1).取板的跨径7.1米：a=a1+2h+L/3=0.2+0.18*2+7.1/3=2.927m＜2/3L=2/3*7.1=4.73ma1＝4.73m>1.4m 需考虑车轮分布有重叠a=a1+2h+d+L/3=0.2+0.18*2+1.4+7.1/3=4.32m<2/3L+d=2/3*7.1+1.4=6.13m取a1＝6.13m2、车轮在顶板的支承处时：a=a1+2h+t=0.2+0.18*2+0.25=0.81m3、车轮在顶板的支承附近时，距支点的距离为x时a=a1+2h+t+2x=0.2+0.18*2+0.25+2x =(0.81+2x)m 4、车轮在悬臂板的支承附近时，当c值不大于2.5m时： a=a1+2h+2c=0.2+0.18*2+2*（0.18+x）=(0.92+2x)m 荷载分布宽度图示：三、折线横向分布系数计算：1、板跨中处（1）q11*a=P，则：q11=P/a=140*2/2/6.13=22.82、板跨中距支点x处（1）0.81+2x=2*7.1/3=4.73时，x=1.96q11*a=P，则：q11=P/a=140*2/2/6.13=22.83、板跨中距支点0.275m处，分布宽度开始重叠（0.81+2x=1.4时，x=0.295）q2*a=P，则：q2=P/a=140/2/1.4=504、板支承处q3*a=P，则：q3=P/a=140/2/0.81=86.425、悬臂板根部，q4*a=P，则：q4=P/a=140/2/0.92=76.16、悬臂板距支点0.24米处，分布宽度开始有重叠（0.92+2x=1.4时，x=0.24）q5*a=P，则：q5=P/a=140/2/1.4=507、悬臂板距支点的距离为1.25米处时a=a1+2h +2c=0.92+2*1.25 =3.42 ma＝3.42m>1.4m 需考虑车轮分布有重叠a＝3.42+1.4=4.82m则：q6=P/a=140*2/2/4.82=29.05汽车加载有效区域 1 11.5 分布系数。

桥梁荷载横向分布系数计算方法

桥梁荷载横向分布系数计算方法桥梁是交通系统中重要的基础设施，承载着大量的车辆和行人荷载。

桥梁荷载横向分布系数的计算对于桥梁设计和施工具有重要意义。

本文将详细介绍桥梁荷载横向分布系数的计算方法，包括计算原理、步骤和注意事项，并通过具体算例进行分析和说明。

桥梁荷载是指作用在桥梁上的各种力量，包括车辆荷载、人群荷载、风荷载等。

横向分布系数是用来描述桥梁荷载在桥面横向分布的系数，其大小与桥梁的形状、结构形式等因素有关。

桥梁荷载横向分布系数的计算是桥梁设计的重要环节，也是施工过程中的关键步骤。

计算桥梁荷载横向分布系数的方法可以分为理论计算和数值模拟两种。

理论计算方法包括集中力作用下的横向分布系数计算和均布力作用下的横向分布系数计算。

数值模拟方法则是利用计算机进行模拟分析，得到更精确的横向分布系数。

根据集中荷载作用下的弯矩和剪力，计算横向分布系数。

根据车道均布荷载的弯矩和剪力，计算横向分布系数。

数值模拟方法可以利用有限元软件进行模拟分析，得到更精确的横向分布系数。

具体步骤如下：通过对模型的应力、应变等进行分析，得出横向分布系数。

下面通过一个简单的算例来说明桥梁荷载横向分布系数的计算方法。

该桥梁为简支梁结构，跨度为20米，桥面宽度为10米。

车辆荷载为50吨的重车，速度为20公里/小时，作用在桥上长度为10米。

通过集中力作用下的横向分布系数计算方法，来计算该桥梁的横向分布系数。

计算桥梁单位长度的自重为5吨/米。

然后，确定车辆荷载的大小为50吨，位置为桥面中心线偏左1米处。

根据车辆荷载作用下的弯矩和剪力，可以得出横向分布系数为67。

根据横向分布系数的定义可知，该桥梁在车辆荷载作用下的横向分布系数为67。

桥梁荷载横向分布系数的计算是桥梁设计和施工中的重要环节，对于保证桥梁的安全性和正常使用具有重要意义。

本文详细介绍了桥梁荷载横向分布系数的计算方法，包括计算原理、步骤和注意事项，并通过具体算例进行了分析和说明。

随着计算机技术和数值模拟方法的发展，未来的研究方向将更加倾向于开发更加精确、便捷的计算方法和模型，以便更好地应用于实际工程中。

13桥梁荷载横向分布系数计算方法

１模态参数法
模态参数是指桥梁结构计算模态的同有频率、
振刑以及模态质量等参数。模态参数法与其他方法
不同之处在于荷载横向分布影响线是由这砦模态参数计算出来的。应用此方法时，首先通过模态参数
计算模态柔度∽］，此处模态柔度的物理意义为单他
荷载作用下，各片梁发乍的挠度；其次根据模态柔度，提取各片梁在跨中位置的变形值，根据变形值和
万方数据
第１期
刘华，等：桥梁荷载横向分布系数计算方法
６３
型的计算方法有刚（铰）接梁法、ＧＭ法、修正偏压法等，这些计算理论都有其独到之处和适用范围，同时，其（杠杆原理法除外）理论根据都是以主梁挠度横向分布规律来确定荷载横向分布。同样是依据于这一理沦根据，模态参数法的主要工作就是确定外荷载作用下横向各片梁之间挠度的比值关系，从而计算出荷载横向分布系数［１。２Ｊ。
式中：９ｉ为第ｉ个模态振型；ｃ。为模态系数，即第ｉ个模态振型对第Ｊ个柔度的贡献。
在时问ｔ时的位移向量也可以通过模态振型表示为Ｌ６’８１
Ｈ（ｆ）＝ｑｌ（￡）９１＋ｑｚ（ｆ）９２＋…＋ｑｐ（ｆ）妒。一面·Ｑ（￡）（６）式中：ｑ，（￡）为结构的广义坐标，即在时ｆｎＪｔ时第ｉ模
态对佗移的贡献系数；ＰＸＰ阶模态振型矩阵咖的
４００ＩＴＩＩＴＩ，桥面板厚度为６ｍｍ，丰梁肋尺寸１０ｍｍ× ４４ｍｍ，横梁肋尺寸为１０ｍｍ×３３ｍｍ，见【冬Ｉ３。有端横梁，中问分３种情况：无内横梁，仪有１根跨巾横梁，有３根内横梁在跨中央和四分点１１０Ｊ。
（ａ）荷载作用模式
旺二ＥＩ习习莎（ｂ）各梁的变形及荷载分配（ｃ）荷载横向分布影响线圈２跨中荷载横向影响线Ｆｉｇ．２Ｍｉｄｄｌｅｓｅｃｔｉｏｎ’ｓｉｎｆｌｕｅｎｃｉｎｇｌｉｎｅｏｆｔｒａｎｓｖｅｒｓａｌＩｏａｄｄｉｓｔｒｉｂｕｔｉｏｎ

桥梁上部计算教程--横向力分布系数计算

桥梁荷载横向分布系数

桥梁荷载横向分布系数
1.杠杆法；
2.梁格法，包括刚性横梁法(也称偏压法)以及修正刚性横梁法(修正偏压法)、弹性支承连续梁法；
3.梁系法，包括铰接板法、刚接板法、铰接梁法、刚接梁法；
4.板系法，如比拟正交异性板法(G-M法)；
5.增大系数法(弯矩增大15%，剪力增大5%)等。

不同截面类型、不同的横向连接方式、桥跨结构的不同位置通常具有不同的荷载横向分布系数计算方法。

梁格法、梁系法及板系法等都是建立在等截面简支体系结构上的荷载横向分布计算方法。

增大系数法一般用于箱形截面梁设计，其主导思想来自杆件弯扭相互独立理论，即认为杆件的中心荷载由梁的弯曲内力承担，而扭转荷载由杆件的自由与约束扭转内力承担，因截面翘曲约束正应力σw一般为纵向正应力σM的15%左右，故弯矩增大系数取1.15；而翘曲扭转剪应力τw约为弯曲剪应力τM的5%左右，故剪力增大系数取1.05；而实际上箱梁是弯扭共同作用，所以是不合理的，它与箱梁的综合抗扭刚度2H值有关，计算结果可能过安全也可能不安全，建议慎用！。

钢筋混凝土梁式桥的荷载横向分布影响线及横向分布系数.

荷载横向分布影响线及横向分布系数假设各构件处于弹性工作阶段，上部结构由若干个等截面构件组成，铰仅承受竖向剪力（图1）。

图1铰接板受力分析当单位荷载p=1作用在构件i 时，各构件（n i i i ,1,,,2,1+='）均受力，各构件实际受到的作用力称为单位荷载横向分布值。

如p=1作用在构件1时，构件1受到的作用力为，1111Q -=η，由静力平衡可知：5451434132312121Q Q Q Q Q Q Q Q -=-=-=-=ηηηη （1）式中 ηij —单位荷载作用于构件j 时，i 构件的单位荷载横向分布值； i —构件序号； j —荷载所在构件序号；Qi —构件i 与构件i+1间铰接处剪力;由于弹性变位与荷载大小成正比，按照弹性变位互等定理有：,2112ηη= ,3113ηη= 4114ηη=,5115ηη=,则上式又可写成：1111Q -=ηQ Q -=112η3213Q Q -=η (2)4314Q Q -=η 5415Q Q -=η式中的η11、η12、η13、η14、η15 即单位荷载作用于1、2、3、4、5构件时，1号构件在横向分配到的荷载。

如将η11、η12。

按比例画在各构件的基线中心，将各点连成直线，即为构件1的荷载横向分布影响线，如图2。

图2铰接板桥的荷载分布影响线欲求ηij 值需先求出铰接处的剪力Qi 。

Qi 与构件的抗弯刚度和抗扭刚度的比值γ有关。

比值 γ 可用下式表示：21)(8.5l b I I n =γ （ 3）式中 I ——构件截面抗弯惯性矩 In ――构件截面抗扭惯性矩 b1――构件的宽度 l ——构件的计算跨度对于矩形截面实心板，γ值按下式计：22107.2l b βγ=（4）式中 β――与截面形状有关的系数，可查表8-5。

表8-5 β系数表b /h 1.0 1.2 1.5 1.75 2.0 2.5 3.0 4.0 6.0 8.0 10.0 ≥10 β0.1410.1660.1960.2140.2290.2490.2630.2810.2990.3070.3120.333对于矩形截面空心板，常用的有箱形和开洞矩形截面（图3）。

荷载横向分布系数的计算

荷载横向分布影响线为三角形
适用情况 ①只有邻近两根主梁参与受力 ②虽为多主梁，但计算梁端支承处荷载 ③无中间横隔梁
2、荷载横向分布系数的计算方法
（1）杠杆分配法
作业1：画及出单3车、辆4荷号载梁作的用荷下载3横、向4分号布梁影荷响载线横，向
0.75m
分布系数 7m
0.75m
1
2 2m
3
4
（2）刚性横梁法（偏心受压法）假定 ①横梁是刚性的：宽跨比B/l≤0.5 ②忽略主梁抗扭刚度
▪ 计算假设： ①铰式键只传递竖
向剪力 gx ；
②桥上荷载近似作为一个沿桥连续分布的正弦荷载 P sin x，且作用于梁轴上。
l
求出各铰处gx，即可求出横向分布影响线
1号板 2号板 3号板 4号板 5号板
p11 1 g1
p21 p31
g1 g2
g2 g3
p41
g3
g4
p51 g4
(1 )g3 2(1 )g4 0
半波正弦荷载引起的变形
w pl4
4EI
pbl 2
2 2GIT
b
2
/w
b 2
pbl 2
2 2GIT
pl4
4
EI
2EI
4GIT
b l
2
5.8
I IT
b l
2
③ 刚结板（梁）法
▪ 在铰结板（梁）计算理论的基础上，在结合缝处补充引入冗余弯矩m，得到考虑板的横向刚性连接特点的变形协调方程，从而求解各梁荷载横向分布的方法。
P
ai Iie
n
ai2 Ii
i 1
P
P
Ii
n
Ii
i 1

横向分布系数计算(多种方法计算)

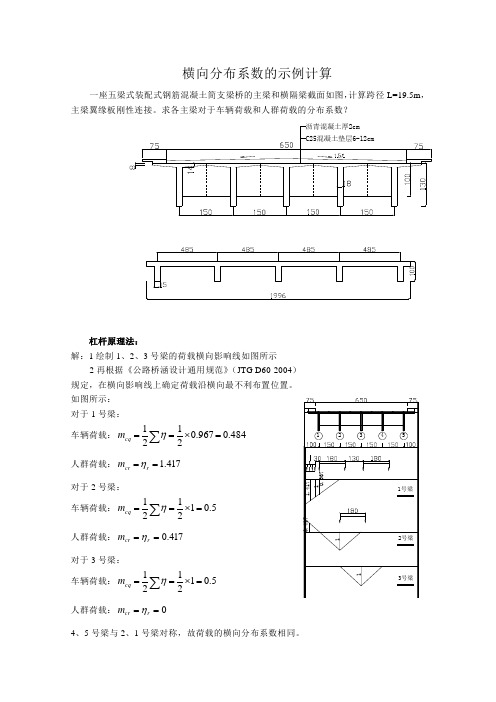
横向分布系数的示例计算一座五梁式装配式钢筋混凝土简支梁桥的主梁和横隔梁截面如图，计算跨径L=19.5m ，主梁翼缘板刚性连接。

求各主梁对于车辆荷载和人群荷载的分布系数？杠杆原理法：解：1绘制1、2、3号梁的荷载横向影响线如图所示2再根据《公路桥涵设计通用规范》（JTG D60-2004）规定，在横向影响线上确定荷载沿横向最不利布置位置。

如图所示：对于1号梁：车辆荷载：484.0967.02121=⨯==∑ηcq m 人群荷载：417.1==r cr m η 对于2号梁：车辆荷载：5.012121=⨯==∑ηcq m 人群荷载：417.0==r cr m η 对于3号梁：车辆荷载：5.012121=⨯==∑ηcq m 人群荷载：0==r cr m η4、5号梁与2、1号梁对称，故荷载的横向分布系数相同。

偏心压力法（一）假设：荷载位于1号梁 1长宽比为26.25.155.19>=⨯=b l ，故可按偏心压力法来绘制横向影响线并计算横向分布系数c m 。

本桥的各根主梁的横截面积均相等，梁数为5，梁的间距为1.5m ，则：5.220)5.11(2)5.12(2222524232221512=+⨯+⨯=++++=∑=a a a a a ai i2所以1号5号梁的影响线竖标值为：6.0122111=+=∑i a a n η 2.0122115-=-=∑i a a n η由11η和15η绘制荷载作用在1号梁上的影响线如上图所示，图中根据《公路桥涵设计通用规范》（JTG D60-2004）规定，在横向影响线上确定荷载沿横向最不利布置位置。

进而由11η和15η绘制的影响线计算0点得位置，设0点距离1号梁的距离为x ，则：4502.015046.0=⇒-⨯=x xx 0点已知，可求各类荷载相应于各个荷载位置的横向影响线竖标值3计算荷载的横向分布系数车辆荷载：()533.0060.0180.0353.0593.02121=-++⨯==∑ηcq m 人群荷载：683.0==r cr m η （二）当荷载位于2号梁时与荷载作用在1号梁的区别以下：4.0122112=+=∑i a a a n η0122552=-=∑ia a a n η 其他步骤同荷载作用在1号梁时的计算修正偏心压力法（一）假设：荷载位于1号梁 1计算I 和T I ：2.3813018)2814(150)18150()2814(1301821)(2122221=⨯++⨯-+++⨯⨯=+-++⨯=ch bd c b d ch y8.912.3813012=-=-=y y y[][]43333313132106543)112.38)(18150(2.381508.911831))((31cm d y c b by cy I ⨯=---⨯+⨯⨯=---+⨯=对于翼板1.0073.01501111<==b t ，对于梁肋151.01191822==b t 查下表得所以：311=c ，301.02=c 433331027518119301.01115031cm t b c I i i i T ⨯=⨯⨯+⨯⨯==∑2计算抗扭修正系数β 与主梁根数有关的系数ε则n=5，ε=1.042 G=0.425E875.055.15.1910654310275425.0042.111)(112332=⎪⎭⎫ ⎝⎛⨯⨯⨯⨯⨯+=+=E E B l EI GI T εβ 3计算荷载横向影响线竖标值11η和15η55.0122111=+=∑i a a n βη 15.0122115-=-=∑ia a n βη 由11η和15η绘制荷载作用在1号梁上的影响线如上图所示，图中根据《公路桥涵设计通用规范》（JTG D60-2004）规定，在横向影响线上确定荷载沿横向最不利布置位置。

刚性横梁法计算桥梁荷载横向分布系数

刚性横梁法计算桥梁横向分布系数
关于荷载横向分布系数的一些结论：
1.梁桥实用空间理论的计算,实际上是应用荷载横向分布,将空间问题转化为平面问题.
2.荷载横向分布,其实质是内力的横向分布. 3.严格地说,同一内力沿跨径方向在不同的截面横向分布系
数不同,不同内力在同一截面的横向分布系数也不同.在计算中,主梁各截面弯矩的横向分布系数均采用全跨一的跨中截面横向分布系数.但剪力必须考虑不同截面横向分布系数的变化. 4.试验证明,按挠度、弯矩及主梁反力求得的横向分布系数相差很小.报告结论中用实测挠度、应变求得的横向分布系数来验证理论计算值.
Ri RiRi
Ii
n
P
Iiai
n
P（ e10）
Ii
Iiai2
i1
i1
式10是在不等间距不等刚度的结构中推导出来的,但大多数的梁
桥还是做成等间距等刚度的,从式10中很容易得到这种梁桥的主
梁荷载分配表达式：
Ri RiRi
P n
Pe
n
a（ i 11）
ai2
i1
图2-4-25表示等间距b1布置的主梁,刚度相等,用刚性横梁连成整体.当P作用在左侧边梁,即e=2.5b1时,求分配给各片主梁的荷载.
从力矩的平衡条件可知：
n
n
Ri ai ai2Ii Pe(8)
i1
i1
从式7得出
R
i
a iI i
将β代入式8得：
n
ai2Ii
i1
aiIi
Ri
Pe得Ri
PneaiI（ i 9） aiIi
i1
3.偏心荷载P对各梁产生的总的作用力,即各片主梁所分配到的荷载,等于上述1和2两种情况的叠加,即：

11荷载横向分布计算Revised

三、刚性横梁法（偏心受压法） 1. 基本假定
将多梁式桥梁简化为由纵梁及横梁组成的梁格，计算各主梁在外荷载作用下分到的荷载
桥梁较窄时(B/L<0.5)横梁基本不变形。
2. 变形的分解
1）纯竖向位移 2）纯转动
3. 各主梁位移与内力的关系
1）与竖向位移的关系 2）与转角的关系
4. 内外力平衡 1）竖向位移时的平衡
• 对于弯矩计算一般取跨中的横向分配比例关系 • 跨中车轮占加载总和的75%以上 • 活载只占总荷载的30%左右
– 荷载横向分布等代内力横向分布的荷载条件半波正弦荷载可满足上述条件
7.常用计算方法
– 梁格法 Leonhardt-Homberg 刚性横梁法） – 板系法 (Guyon-Massonnet GM法) – 梁系法 (Hundry-Jarger 梁系法刚(铰)接梁(板)法)
荷载横向分布计算
一、桥面板与主梁分离式桥梁
横向分布系数——杠杆原理法 Nhomakorabea汽车人群
杠杆法(计算实例新版P118)
二、横向分布计算原理
1. 整体桥梁结构必须采用影响面加载计算最不利荷载
2. 为简化计算，采用近似影响面来加载近似影响面纵横方向分别相似
12 21
12
2 2
11 21
11
2 2
3.加载过程
将多梁式桥梁简化为数根并列而相互间横向铰接的狭长板（梁）
各主梁接缝间传递剪力、弯矩、水平压力、水平剪力
用半波正弦荷载作用在某一板上，计算各板（梁）间的力分配关系。
2. 铰接板法
假定各主梁接缝间仅传递剪力g，求得传递剪力后，即可计算各板分配到的荷载
传递剪力根据板缝间的变形协调计算

混凝土分离式箱梁桥荷载横向分配系数

混凝土分离式箱梁桥荷载横向分配系数城市桥梁一般桥面较宽，荷载空间作用效应明显。

荷载横向分配系数是设计时必须考虑的一个很重要的参数。

当桥梁工程师们进行桥梁设计时不可能对每一座桥梁都去进行空间分析，于是能不能只作平面计算就可以代替空间计算成了桥梁设计者们最关心的问题，基于这一目的，我们可以用活载的横向分配系数将二者联系起来。

参考美国AASHTO规范，可以这样定义荷载横向分配系数：通过空间有限元程序求出结构共同作用时每片主梁上的效应（包括正应力、负应力、剪力和挠度）除以理想化简支梁模型上的效应。

本文就针对城A级标准荷载对27座分离式简支箱梁桥通过跨度、分离式箱体的数目、车道数等几个参数的变化来进行数值模拟，对不同设计参数的桥梁进行仿真分析，得出结构的最不利内力和位移。

二、参数研究图1表示的是当分离式箱体个数为3时的横截面图，当分离式箱体个数为2或大于3时依此类推。

以往的研究表明，改变混凝土顶、底板及腹板厚度和桥梁高跨比对正应力、挠度和剪力的分配系数产生的影响很小。

因此，在本文中选取以下参数：车道数目、分离式箱体个数和跨度。

对于参数的研究，我们假设如下：（1）混凝土为匀质弹性，符合迭加原理；（2）在结构受弯矩作用区域的混凝土不开裂。

三、桥梁模型描述本文中所研究的27座分离式简支箱梁桥具有不同的截面尺寸。

在表1中列出了基本横截面的尺寸，所有截面的高跨比为1/20。

在表1桥梁模型一栏中出现的符号所代表的项目如下：L表示车道；数字20，25，30表示跨度，单位为米；b 表示分离式箱体的数目。

例如：4L－25－3b 表示的是有四个车道，跨度25米，分离式箱体的数目示3的简支箱梁桥。

表1中出现的横截面各种符号如图1所示。

在二车道桥梁中，分离式箱体数目为2，梁宽8.5米；三车道桥梁中，分离式箱体数目范围是2－3，梁宽13.2米；四车道桥梁中，分离式箱体数目范围是3－4，梁宽16.8米；六车道桥梁中，分离式箱体数目范围为3－5，梁宽为24m。

混凝土桥大作业—装配式混凝土简支梁桥荷载横向分布系数计算及主梁内力计算

混凝土桥大作业（一）——装配式混凝土简支梁桥荷载横向分布系数计算及主梁内力计算目录第一章大作业任务概述 (2)1.1 大作业目的 (2)1.2 设计规范 (3)1.3 大作业设计方案 (3);11.4 大作业计算基本流程 (5)第二章荷载横向分布系数的计算 (6)2.1.支座位置处荷载横向分布系数计算 (6)2.2.跨中位置处荷载横向分布系数计算 (6)第三章主梁内力计算 (8)3.1.恒载计算 (8)3.2.恒载内力 (9)3.3.活载计算 (10)第四章主梁内力组合 (18)4.1．按承载能力极限状态设计时作用效应的组合 (18)4.2.按正常使用极限状态设计时作用效应的组合 (19)4.3.作用长期效应的组合 (20)第一章大作业任务概述1.1 大作业目的通过大作业实际操作计算，掌握装配式简支梁桥的荷载横向分布系数的计算理论和方法；通过实际操作，掌握用结构分析的基本方法；掌握桥梁在承载能力极限状态和正常使用极限状态下的荷载组合方法;21.2 设计规范1、中华人民共和国行业标准《公路桥涵设计通用规范》JTG D60-2004，中华人民共和国交通部；2、中华人民共和国行业标准《公路钢筋混凝土及预应力混凝土桥涵设计规范》JTG D62-2004，中华人民共和国交通部。

1.3 大作业设计方案1.3.1方案概述大作业设计方案为公路装配式预应力混凝土简支T梁桥，T梁之间采用湿接缝连接。

横截面布置示意如图1-1所示,T梁的基本尺寸数据如图1-2所示。

T梁按全预应力混凝土或A类部分预应力混凝土设计。

图1-1单幅桥横截面尺寸 (单位:cm);3;4跨径(m) 梁长(m) 计算跨径(m)4140.9639.83注：尺寸单位cm图1-2T梁跨径及横截面尺寸1.3.2主要材料1、混凝土：T梁混凝土C50，湿接缝混凝土C50；2、预应力钢绞线：7 5钢绞线(f pk=1860MPa，单根面积140mm2)。

相关材料的材料参数查阅《公路钢筋混凝土及预应力混凝土桥涵设计规范》JTG D62-2004第3章(P10-13)。

桥梁工程荷载横向分布计算简介

桥梁工程荷载横向分布计算简介
分析：荷载横向分布影响线竖标值与刚度参数γ ，板块数n以及荷载作用位置有关。 5.8 I (b)2
IT l
抗弯I 惯 13矩 911 30cm 4 抗扭 IT 惯 2.3 7 矩 160 c4 m
桥梁工程荷载横向分布计算简介
采用查表法求荷载横向影响线竖标值（附录I）P404 (n=9, γ =0.0214)
公路－I级
桥梁工程荷载横向分布计算简介
七、横向分布系数沿桥纵向的变化
•对于弯矩
由于跨中截面车轮加载值占总荷载的绝大多数，近似认为其它截面的横向分布系数与跨中相同
•对于剪力
从影响线看跨中与支点均占较大比例从影响面看近似影响面与实际情况相差较大
桥梁工程荷载横向分布计算简介
荷载横向分布计算
桥梁工程荷载横向分布计算简介
一、概述
荷载：恒载：均布荷载（比重×截面积）活载：荷载横向分布
1、活载作用下，梁式桥内力计算特点：（1）单梁（平面问题）
S=P·η1（x）
P
x
L/4
1
桥梁工程荷载横向分布计算简介
（2）梁式板桥或由多片主梁组成的梁桥（空间问题）： S＝Ｐ·η（x，ｙ）实际中广泛使用方法：将空间问题转化成平面问题
先求翼板的有效作用宽度，由表2－5－4查得
c/l=235/(4x160)=0.368, λ/c=0.547 , λ=0.547x235=128cm
Iy＝3220x103cm4
主梁比拟单宽抗弯惯矩Jy＝Iy/a=3220x103cm4/485=6440 cm4/cm （3）主梁和横隔梁的抗扭惯矩
I`Tx= 208000cm4 ; I`Ty=88610cm4 因为主梁翼缘板刚性连接，所以按式（2－5－74）

关于新规范横向分布系数以及偏载系数的计算

关于新规范横向分布系数以及偏载系数的计算关于横向分布调整系数：一、进行桥梁的纵向计算时：a) 汽车荷载○1对于整体箱梁、整体板梁等整体结构其分布调整系数就是其所承受的汽车总列数，考虑纵横向折减、偏载后的修正值。

例如，对于一个跨度为230米的桥面4车道的整体箱梁验算时，其横向分布系数应为4 x 0.67（四车道的横向折减系数）x 1.15（经计算而得的偏载系数）x0.97（大跨径的纵向折减系数）= 2.990。

汽车的横向分布系数已经包含了汽车车道数的影响。

○2多片梁取一片梁计算时按桥工书中的几种算法计算即可，也可用程序自带的横向分布计算工具来算。

计算时中梁边梁分别建模计算，中梁取横向分布系数最大的那片中梁来建模计算。

b) 人群荷载○1对于整体箱梁、整体板梁等整体结构人群集度，人行道宽度，公路荷载填所建模型的人行道总宽度，横向分布系数填1 即可。

因为在桥博中人群效应= 人群集度x人行道宽度x人群横向分布调整系数。

城市荷载填所建模型的单侧人行道宽度，若为双侧人行道且宽度相等，横向分布系数填2，因为城市荷载的人群集度要根据人行道宽度计算。

○2多片梁取一片梁计算时人群集度按实际的填写，横向分布调整系数按求得的横向分布系数填写，一般算横向分布时，人行道宽度已经考虑了，所以人行道宽度填1。

c) 满人荷载○1对于整体箱梁、整体板梁等整体结构满人宽度填所建模型扣除所有护栏的宽度，横向分布调整系数填1。

与人群荷载不同，城市荷载不对满人的人群集度折减。

○2多片梁取一片梁计算时满人宽度填1，横向分布调整系数填求得的。

注：1、由于最终效应：人群效应= 人群集度x人行道宽度x人群横向分布调整系数。

满人效应= 人群集度x满人总宽度x满人横向分布调整系数。

所以，关于两项的一些参数，也并非一定按上述要求填写，只要保证几项参数乘积不变，也可按其他方式填写。

2 、新规范对满人、特载、特列没作要求。

所以程序对满人工况没做任何设计验算的处理，用户若需要对满人荷载进行验算的话，可以自定义组合。