3.2 平面直角坐标系课件(2)
八级数学上册 3.2 平面直角坐标系课件(2)北师大版

•最新精品中小学课件
•13
20.(13 分)先阅读下列一段文字,再回答后面的问题. 已知在平面内两点 P1(x1,y1),P2(x2,y2),这两点间的距离 P1P2= x2-x12+y2-y12,同时,当两点所在的直线在坐标轴或平行于坐标 轴或垂直于坐标轴时,两点间距离公式可简化为|x2-x1|或|y2-y1|. (1)已知 A(2,4),B(-3,-8),试求 A,B 两点间的距离; (2)已知 A,B 在平行于 y 轴的直线上,点 A 的纵坐标为 5,点 B 的 纵坐标为-1,试求 A,B 两点间的距离.
•最新精品中小学课件
•10
16.如图,在平面直角坐标系中,将线段AB绕点A按逆时针方向旋转
90°后,得到线段AB′,则点B′的坐标为________(4_,__2.)
17.下面四种说法:①如果一个点的横、纵坐标都为零,则这个点是
原点;
②若一个点在x轴上,那它一定不属于任何象限;
③纵轴上的点的横坐标均相等,且都等于零;
解:(1)图略 (2)在x轴上的点有(1,0)和(3,0),它们的纵
坐标都为0.在y轴上的点有(0,4),它的横坐
标为0
(3)有.线段上有三个点(0,4)(2,4)(4,4),它
们的纵坐标都为4
•最新精品中小学课件
•7
9.坐标平面内下列各点中,在坐标轴上的是( B)
A.(3,3)
B.(-3,0)
C.(-1,2)
•最新精品中小学课件
•2
1.(3分)若点A(-2,n)在x轴上,则点B(n-1,n+1)在( B )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
2.(3分)在平面直角坐标系中,点P(a2-1,a-1)是y轴上的点,则a的
北师大版初二数学上册3.2平面直角坐标系(第2课时)

第三章位置与坐标2 .平面直角坐标系(第2课时)兰州三十二中孔冠桥一、学生起点分析《平面直角坐标系》是八年级上册第三章《位置与坐标》第二节内容。
本章是“图形与坐标”的主体内容,不仅呈现了“确定位置的多种方法、平面直角坐标系”等内容,而且也从坐标的角度使学生进一步体会图形平移、轴对称的数学内涵,同时又是一次函数的重要基础。
《平面直角坐标系》反映平面直角坐标系与现实世界的密切联系,让学生认识数学与人类生活的密切联系和对人类历史发展的作用,提高学生参加数学学习活动的积极性和好奇心。
因此,教学过程中创设生动活泼、直观形象、且贴近他们生活的问题情境,会引起学生的极大关注,会有利于学生对内容的较深层次的理解;另一方面,学生已经具备了一定的学习能力,可多为学生创造自主学习、合作交流的机会,促使他们主动参与、积极探究。
二、教学任务分析【知识目标】1.知道在坐标轴上的点以及与坐标轴平行的直线上点的坐标的特征2.知道不同象限点的坐标的特征。
3.经历画坐标系、描点、连线、看图以及由点找坐标等过程,进一步体会平面直角坐标系中点与坐标之间的对应关系,发展数形结合意识。
【能力目标】.•经历画坐标系、描点、连线、看图以及由点找坐标等过程,发展学生的数形结合思想,培养学生的合作交流能力;2.通过由点确定坐标到根据坐标描点的转化过程,进一步培养学生的转化意识。
【情感目标】通过生动有趣的教学活动,发展学生的合情推理能力和丰富的情感、态度,提高学生学习数学的兴趣。
【教学重点、难点】体会平面直角坐标系中点与坐标之间的对应关系,发展数形结合意识。
三、教学过程设计第一环节导入新课.在上节课中我们学习了平面直角坐标系的定义,以及横轴、纵轴、点的坐标的定义,练习了在平面直角坐标系中由点找坐标,还探讨了横坐标或纵坐标相同的点的连线与坐标轴的关系,坐标轴上点的坐标有什么特点。
1•“平面直角坐标系”的定义:2•平面上的点与有序数对的关系:第二环节探索新知问题1•在直角坐标系中描出点D(-3,5) , E(-7,3),C(1,3),D(-3,5),并将各点用线段依次连接起来•观察所得的图形,根据图形回答问题:线段EC与x轴有什么位置关系?点E和点C的坐标有什么特点?线段EC 上其他点的坐标呢?问题2•在直角坐标系中描出点F(-6,3),G(-6,0),A(0,0) , B(0,3),并将各点用线段依次连接起点F、点G的坐标有什么共同特点,线段FG与Y轴有怎样的位置关系?[新知归纳]平行于x轴的直线上点的纵坐标相同平行于y轴的直线上点的横坐标相同问题3.观察所得的图形,你觉得它像什么?图中哪些点在坐标轴上?它们有什么特点?[议一议]在平面直角坐标系中,坐标轴上的点的坐标有什么特点? [新知归纳]x轴上的点纵坐标为0,一般记为(x,0).y轴上的点横坐标为0,—般记为(0, y).第三环节学有所用.1•已知点A(-3,2),点B (1,4 ),(1 )若CA平行于x轴,BC平行于y轴,则点C的坐标是;(2)若CA平行于y轴,BC平行于x轴,则点C的坐标是.2.若点P (m+5,m —2 )在x轴上,则m=;若点P (m+5,m —2 )在y轴上,则m=3•如图所示的笑脸中,⑴在“笑脸”上找出几个位于第一象限的点,指出它们的坐标,说说这些点的坐标有什么特点。
3.2 平面直角坐标系(课件)北师大版数学八年级上册

对称关系、平行关系、中点等 .
3.建立平面直角坐标系的方法是不唯一的,选择不同的
位置作为原点 ,其他位置的坐标是不同的 .
知4-练
例5 [母题 教材P60随堂练习]根据下面的条件画一幅示意图, 并在图中标出各个景点的位置和坐标. 菊花园:从中心广场向北走150 m,再向东走150 m. 湖心亭:从中心广场向西走150 m,再向北走100 m. 松风亭:从中心广场向西走100 m,再向南走50 m. 育德泉:从中心广场向北走200 m.
离为|b|,到 y 轴的距离为|a|,到原点的距离为 a2+b2 .
知2-练
例2 [母题 教材P59例1 ]如图3-2-2,写出点A,B,C,D, E,F,G,O的 坐标.
知2-练
解题秘方:紧扣点的坐标的定义,利用过点向两坐标 轴作垂线,用垂足表示的数求点的坐标.
解:A(3,4),B(-6,4),C(-5,-2),D(-5,2), E(0,3),F(2,0),G(-4,0),O(0,0).
知4-练
例6 [母题 教材P65例3]如图 3-2-6,已知正方形 ABCD 的
边长为4,建立适当的平面直角坐标系,写出各个顶点
的坐标.
(1)如果以点 C 为坐标原点,分别以 CB, CD 所在的直知线4-为练 x 轴、 y 轴建立平面直角坐标系,那么各个顶点的坐标分 别为 C(0,0), A _______, B_______ , D _______;
解:根据题意,可得点 A(2,2),点 B(2, -2), 点 C(-2, -2),点 D(-2,2) .
知4-练
6-1.如图,建立适当的直角坐标系,写出这个六角星 6 个 顶点 A, B, C,D, E, F 的坐标.
平面直角坐标系第2课时课件(14张)北师大版数学八年级上册

已知点A(a+3,a-2)与点B(b+1,b-1)是同一直角坐标系上不重合的两点. 问题2:若a=2,b=-1,则点A和点B分别在哪里? 解:(2) 若a=2,b=-1, 则点A坐标为(5,0),点B坐标为(0,-2), 点A在x轴上,点B在y轴上.
思考:根据上面的问题我们可以发现在x轴上的点和在y轴上的点有什么特点?
x轴上的点的纵坐标为0,y轴上的点的横坐标为0.
活动2:如图所示为一个在平面直角坐标系中从原点开始的回形 图,其中回形通道的宽和OA的长都是1.根据图形填写表格.
点 坐标
A (0,1) B (1,1) C (1,-1) D (-1,-1) E (-1,2) F (2,2)
所在象限或坐标轴 y轴
第一象限 第四象限 第三象限 第二象限 第一象限
解:(2)线段AB平行于x轴,
y
由题可知点A(6,4)、点B(0,4),
可发现点A、点B的纵坐标相等,
B
线段AB上其他点纵坐标也相同,均为4.
C
A Dx
(3)线段AD与y轴有什么位置关系?点A和点D的坐标有什么特点?线段AD上
的段AD平行于y轴,
由题可知点A(6,4)、点D(6,0),
A.(0,-2) B.(2,0) C.(4,0)
D.(0,-4)
3. 下列各点分别在坐标平面的什么位置上?
A (3,6) C (-7,-5) E (-3.6,5) G (0,0)
第一象限 第三象限 第二象限
原点
B (0,-8) D (-6,0) F (5,-6)
y轴上 x轴上 第四象限
针对本节课所学内容,你能说一说你都学到了哪些知识吗?
1.如图:正方形ABCD中点A和点C的坐标分别为(-2,3)和(3,-2),则点B 和点D的坐标分别为( B )
3.2平面直角坐标系(2)

归纳结论
“关于坐标轴对称的点”的坐标特征: (1) 关于x轴对称的点的坐标:横同纵反; (2) 关于y轴对称的点的坐标:横反纵同。
拓展提高三 如图,以矩形ABCD的中心为原点建立平面直角 坐标系: (1)点A与点C有什么位 y 置关系?点B与点D呢? A D (3, 5) 点A与点C关于原 (–3, 5) 点中心对称,点B与点 D关于原点中心对称; (2)关于原点中心对称的 O x 点的坐标有什么特征? 关于原点中心对称 C 的点横坐标互为相反数, B (3, –5) (–3, –5) 纵坐标互为相反数。
北师大版八年级(上)
3.2.2 平面直角坐标系
八年级数学备课组
主备人:倪印刚
学习目标:
1.在给定的直角坐标系下,会根 据点的坐标描出点的位置。 2.通过找点、连线、观察,确定 图像的大致形状。
复习旧知
1、“平面直角坐标系”的定义: 在平面内,两条互相垂直且有公共原点的数 轴组成平面直角坐标系。 2、“平面直角坐标系”的建立方法: (1)确立原点O; (2)过点O取向右为正方向,在水平位置建立数轴 叫x轴或横轴; (3)过点O取向上为正方向,在铅直位置建立数轴 叫y轴或纵轴。
2、 “四个象限、原点及两轴上点”的坐标特征:
课堂小结
3、“关于坐标轴对称的点”的坐标特征: (1) 关于x轴对称的点的坐标:横同纵反; (2) 关于y轴对称的点的坐标:横反纵同。 4、“关于原点对称的点”的坐标特征: 关于原点中心对称的点的坐标:横纵皆反。
达标检测
1、在直角坐标系中描出下列各组点,并将各组 内的点用线段依次连接起来。
观察所得的图形,你觉得它像什么?
自学检测
1、在如图的平面直角坐标系中描出下列各组点, 并将各组内的点用线段依次连接起来。
北师大版数学八上 3.2 平面直角坐标系 课件

A.第一象限 B.第二象限 C. 第三象限 D.第四象限
解析:如图,分别以AB、AC、BC为平行四边形的对角线画出平行四边形, 可知第四个顶点不可能在第三象限。
板书设计
平面直角坐标系
(-,+) (+,+) (-,-) (+,-)
大成殿: ; 中心广场: ; 碑林: 。
建入坐标
1)小红在旅游示意图上画上了方 格,标上数字,并用(0,0)表示 科技大学的位置,用(5,7)表示 中心广场的位置,那么钟楼的位 置如何表示? 【(3,8)】 (3,5)表示哪个地点的位置?
【大成殿】
12
11 10
9 8
7 6 5
4 3
2 1
0 1 2 3 4 5 6 7 8 9 1011
课 堂 练 习 【综合实践类作业】
7、 点P到x轴的距离是2,到y轴的距离是3,且在y轴的左侧, 则P点的坐标是 __________________
解∵P(x,y)到x轴的距离是2,到y轴的距离是3, ∴x=±3,y=±2; 又∵点P在y轴的左侧, ∴点P的横坐标x=-3, ∴点P的坐标为(-3,2)或(-3,-2).
A. 5
B. 11
C. 13
ห้องสมุดไป่ตู้D.2
布 置 作 业 【知识技能类作业 选做题】
6.已知点的坐标为(-5,-8),那么该点到y轴的距离为 5 。
7.若P(a+2,a-1)在y轴上,则点P的坐标是 (0,-3) 。
.
8.点P在第二象限,到x轴的距离是2,到y轴的距离是3,则P点的坐标
是 (-3,2)。 9.在平面直角坐标系中,点A是y轴上一点,若它的坐标为(a﹣1,a+1),
北师大版数学八上3.2 平面直角坐标系(第2课时)特殊点的横纵坐标关系 课件(共14张PPT)

1.已知点P(m+3,m+1)在平面直角坐标系X轴上, 则m=________.
2.已知线段MN平行于Y轴, 且M,N的坐标分别 为(3,-5) 和(x,2),那么x=_________.
3.平面直角坐标系中,已知点P(1-2a,a-2) 在第三象限角平分线上,求a的值和该点坐 标。
ห้องสมุดไป่ตู้
课后作业:
1.已知A(0,2m)和点B(-1,m+1),且直线AB//X 轴,则m=_________.
2.在直角坐标系XOY中,点P坐标为 (2,2),点Q 在Y轴上,Δ PQO是等腰三角形,则满足条件的Q点 有______个。
3.在直角坐标系XOY中,已知点A(0,8)和点B(6,8)。 ①尺规作图:求作一个点P,使点P到A、B两点的距离 相等,同时使P到两坐标轴的距离也相等。 ②写出点P的坐标。
1.若P(x,y)满足x+y<0,xy>0,则点P在第______象限; 若P(x,y)满足xy<0,则点P在第______象限; 若P(x,y)满足xy=0,则点P在_________位置.
2.直角坐标系中, (1)点M(a,b)在第二象限且点M到X轴和Y轴的距 离分别为3和5,则点M的坐标为_____________; (2)若点M到X轴和Y轴的距离分别为3和5, 则点M的坐标为_____________.
北师大版八年级数学上册第三章第二节
平面直角坐标系中特殊点的 横纵坐标关系
同学们,你们了解自己的 家乡吗?知道自己的学校是在 抚州的什么位置吗?
你还知道学校周边的景点 在哪儿吗?
人民公园
拟砚台
金巢实验学校
名人雕塑园
革命纪念馆
M
北师版八年级数学上册课件 第3章 第2课时 建立平面直角坐标系确定点的坐标

C
●
12 345 x
∴ S△ABC =
1 2
·BC·AD
=
1 2
×6×5=15.
新课讲解
【例2】如图,已知点A(2,-1),B(4,3),C(1,2),求△ABC
的面积.
解:如图,过点A作x轴的平行线,过点C 作y轴的平行线,两条平行线交于点E,过 点B分别作x轴、y轴的平行线,分别交EC 的延长线于点D,交EA的延长线于点F. ∵A(2,-1),B(4,3),C(1,2), ∴BD=3,CD=1,CE=3,AE=1,AF=2,BF=4, ∴S△ABC=S长方形BDEF-S△BDC-S△CEA-S△BFA
① (-6,5),(-10,3),(-9,3),(-3,3),(-2,3); ② (-9,3),(-9,0),(-3,0),(-3,3); ③ (3.5,9),(2,7),(3,7),(4,7),(5,7); ④ (3,7),(1,5),(2,5),(5,5),(6,5); ⑤ (2,5),(0,3),(3,3),(3,0),(4,0),(4,3),(7,3),(5,5).
B
4 x 的坐标分别为: A(0,0), B(4,0), C(4,4), D(0,4).
新课讲解
【想一想】还可以建立其他平
面直角坐标系,表示正方形的四
y
个顶点A,B,C,D的坐标吗?
D
C
A(0,--4,0), B(0,0),C(0,4), D(-4,4).
5
4
·(4,4)
3
2
·(3,2)
1
· -4
-3
-2
-1
O
-1
12345
x
-2
·(3,-2)
3.2 第2课时 平面直角坐标系中点的坐标特点

解:S△AOB=3×3-
1 2
×2×3-
1 ×2×1- 1 ×1×3= 7 .
2
2
2
例1 已知点A(m+1,-2),B(3,m-1). (1)若直线AB∥x轴,则m的值为 -1 ; (2)若直线AB∥y轴,则m的值为 2 .
分析:(1)因为直线AB∥x轴,所以A,B两点的纵坐标 相等,即m-1=-2;
(2)因为直线AB∥y轴,所以A,B两点的横坐标相等, 即m+1=3.
例2 若点(6-2x,x+6)到两坐标轴的距离相等,则该 点的坐标为 (6,6)或(-18,18) .
等的点
线上.
P,Q两点的 纵坐标 相等. P,Q两点的 横坐标 相等.
|x|=|y|,即x=y或 x= -y .
不规则图形面积的求法:补形法或割补法.
解题 策略
如图①,S△ABC=S长方形CDOE-S△ABO-S△ACD- S△BCE;如图②,S四边形OABC=S△COD+ S梯形ABCD.(如T5)
3.经过两点A(2,3),B(-4,3)作直线AB,则直线
AB( A )
A.平行于x轴
B.平行于y轴
C.经过原点
D.无法确定
4.已知点P的坐标为(2a+1,a-3).
(1)若点P在y轴上,则a=
1 2
;
(2)若点P到两坐标轴的距离相等,则a=
4或 2 3
.
5.在平面直角坐标系中,已知点A(2,3),B(3,1), O为坐标原点,求△AOB的面积.
分析:因为点到两坐标轴的距离相等,所以 |6-2x|=|x+6|,所以6-2x=x+6或6-2x=-(x+6), 所以x=0或12,即可求得该点的坐标.
1.若点P(m-3,m+1)在x轴上,则点P的坐标为 (C)
3.2平面直角坐标系(第二课时)平面直角坐标系 课件(共17张PPT) 北师大版八年级数学上册

课堂小结
1.坐标轴上点的坐标
坐标轴上的点的坐标中至少有一个是0,即横轴上的点的纵坐标为0,纵轴上 的点的横坐标为0.
2.各个象限内的点的坐标特征:
第一象限(+,+),第二象限(-,+), 第三象限(-,-),第四象限(+,-).
3.平行x轴的直线上的点的 纵坐标相同 ,平行于y轴的直线上的 点的 横坐标相同 .
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.如果点P(x,y)满足xy=0,那么点P必定在( D )
A.原点上 B.x轴上 C.y轴上 D.坐标轴上
4.点P(m+3,m+1)在直角坐标系的x轴上,则点P的坐标为( B )
A.(0,-2) B.(2,0) C.(4,0) D.(0,-4)
探究新知
任务二:利用平面直角坐标系内点的坐标确定字母的值
例3 已知在平面直角坐标系中,点P(m,m-2)在第一象限内,
则m的取值范围是__m__>___2_.
解析:根据第一象限内点的坐标的符号特征,横坐标为正,纵坐
标为正,可得关于m的一元一次不等式组
m 0, m 2 0,
解得m>2.
求点的坐标中字母的取值范围的方法:根据各个象限内点的坐标的符号 特征,列出关于字母的不等式或不等式组,解不等式或不等式组即可求 出相应字母的取值范围.
第三章 位置与坐标
3.2平面直角坐标系(第二课时)
学习目标
3. 进一步体会平面直角坐标系中点与坐标之间 的一一对应关系. 2. 能够分析某些特殊点(坐标轴上的点、与坐 标轴平行的直线上的点等)的特征. 1. 熟练地根据坐标确定点的位置以及写出给定 点的坐标.Fra bibliotek复习导入
1.什么是平面直角坐标系? 2.作平面直角坐标系 3.指出四个象限 4.写出 P 点坐标 P(3,4)
北师大版八年级数学上册课件:3.2 平面直角坐标系(共26张PPT)

2.对于边长为4的正三角形△ABC,建立适当的直角坐标系,
写出各个顶点的坐标.
y A 3
2
B
1
C
- –3–2– O 1 2 3 4 x
4
1–
–1
解:A(0,2 ), B(-2,0) ,C(2,0).
2–3
– 4
3.在一次“寻宝”游戏中,寻宝人已经找到了坐标为(3,2) 和(3,-2)的两个标志点,并且知道藏宝地点的坐标为(4, 4),如何确定直角坐标系找到“宝藏”?
y
5 4
·(4,4)
3 2
·(3,2)
·1
-4 -3 -2 -1-O1 1 -2
2
345 x
· (3,-2)
解:如图所示
-3
课堂 小结
坐标的特征
建立直角坐 标系
建立适当的 直角坐标系
第三章 位置与坐标 3.2 平面直角坐标系 建立平面直角坐标系确定点的坐标
学习目标
1.了解、掌握点的坐标及特殊位置上点的坐标特征;(重点) 2.能建立直角坐标系求点的坐标.(难点)
导入 1.你还记得什么是平面直角坐标系吗? 新课 2.两条坐标轴把平面分成了几部分?(不包括坐标轴)
3.给你平面上的一个点,如何确定它的坐标?
在直角坐标系中,对于平面上任意一点, 都有唯一的一个有序实数对(即点的坐标)与 它对应;
反过来,对于任意的一个有序实数对,都 有平面上唯一一点与之对应.
当堂 练习 1.在 y轴上的点的横坐标是( 0 ),在 x轴上的点的纵坐标是( )0.
2.点 A(2,- 3)关 于 x 轴 对 称 的 点 的 坐 标 是( ()2.,3)
当堂
练习 1. (南通·中考)在平面直角坐标系xOy中,已 知点P(2,2),点Q在y轴上,△PQO是等腰三角形, 则满足条件的点Q共有(B ) A.5个 B.4个 C.3个 D.2个
3.2 平面直角坐标系
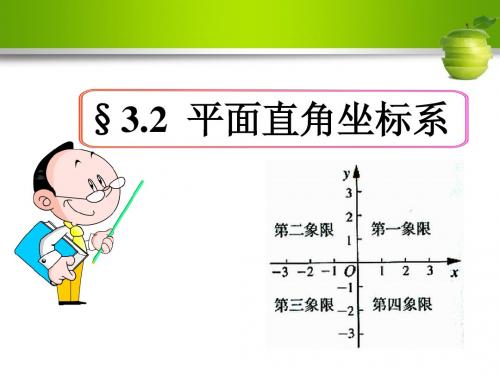
·
2
(+,+)
2 (-,+) ( -2,1 ) C 1
·
-4
-3
-2
-1
(-,-)-2
D ( -4,- 3 )
0 -1 -3 -4
1
3
· ·
4 5
B ( 4,2 )
F (5,0) x 横轴
·
· E
( 1,- 2 ) (+,-)
·G
(0,-4)
3-2 平面直角坐标系
想一想: 下列各点分别在平面坐标的什么位置上? A(3,2) B(0,-2) C(-3,-2) D(-3,0)E(-1.5,3) F(2,-3) 答:A点在第一象限; B点在y轴上; C点在第三象限; D点在x轴上; E点在第二象限; F点在第四象限。
3-2 平面直角坐标系
§3.2 平面直角坐标系
3-2 平面直角坐标系
温故而知新
1.请你画出一条数轴.你能说出数轴的 三要素吗?
规定了原点、正方向、单位长度的直线叫数轴. 2.如图,你能说出数轴上点A和点B的 坐标吗?
3-2 平面直角坐标系
温故而知新
3.已知数轴上点C的坐标是5,点D的坐标 是-2,你能在数轴上画出点C和点D吗?
例1(1)求出图形轮廓线 F F' 3-2 平面直角坐标系 上各转折点A,O,B,C,D, D' E' E D E,F的坐标 A(0,-2) A'(0,-2) C' B' C B 1 O(0,0) O'(0,0) B(3,2) B'(-3,2) -4 -3 -2 -1 O O' 2 3 4 1 -1 C(2,2) C'(-2,2) A A' D(2,3) D'(-2,3) E(1,3) E'(-1,3) F(0,5) F'(0,5) (2)利用坐标关系,求出它们关于y轴对称点的 坐标。 (3)在同一坐标系中,描点A′,O′,B′,C′, D′,E′,F′,并用线段依次将它们连接起来。
北师大版八年级数学上册3.2 平面直角坐标系 第2课时 平面直角坐标系中点的坐标特征

B.(-3,2)
C.(3,2)
D.(3,-2)
3. (中考·广安)点 M(x-1,-3)在第四象限,则 x 的 取值范围是 x>1 .
知识点 坐标轴上的点的坐标特征
4. 在平面直角坐标系中,点 A(-4,0)在( B )
A.x 轴正半轴上
B.x 轴负半轴上
C.y 轴正半轴上
D.y 轴负半轴上
5. 平面直角坐标系中,在 x 轴上的点是( B )
7. 过点 A(-3,2)和点 B(-3,5)作直线,则直线
AB( A ) A.平行于 y 轴
B.平行于 x 轴
C.与 y 轴相交
D.与 y 轴垂直
8. 如图,每个小正方 形的边长为单位长度 1.
(1) 写 出 多 边 形 ABCDEF 各个顶点的坐标;
(2)点 C 与 E,点 B 与 C 的坐标有什么关系?
与 y 轴垂直,则 l 也会通过下列哪
一点?( D )
A.A
B.B
C.C
D.D
19. (中考·阜新)如图,在平
面直角坐标系中,将△ABO 沿
x 轴向右滚动到△AB1C1 的位
置,再到△A1B1C2 的位置……
依次进行下去,若已知点 A(4,0),B(0,3),则点 C100
的坐标为( B )
A.(1200,12) 5
A.(3,-2)
B.(2,4)
C.(-3,2)
D.(-3,-4)
13. 如图,正方形 ABCD 在平面直角坐标系中,其 中三个顶点的坐标分别为 A(-2,3),B(-2,-2),C(3, -2),则第四个顶点 D 的坐标为 (3,3) .
14. (教材 P62 例 2 变式)在如图的平面直角坐标系中 描出下列各点,并将各点用线段顺次连接起来.
平面直角坐标系ppt课件

知识点2 坐标轴上点的坐标特征:
点在x轴上,纵坐标为0;点在y轴上,横坐标为0;点在原点,
横坐标和纵坐标都为0
【例2】(北师教材母题改编)在平面直角坐标系中,点(0,-4)
在( C )
A.x轴的正半轴
B.y轴的正半轴
C.y轴的负半轴
D.x轴的负半轴
【变式2】(北师教材母题改编)若点M(2x-1,x+3)在x轴上,则点
知识点2 根据坐标描出点的位置 【例2】在如图所示的平面直角坐标系中. (1)描出下面各点:A(0,3),B(1,-3), C(3,-5),D(-3,—5),E(5,3),F(-1, -3),并写出点A,B,C所在的象限; 解:(1)点A在y轴上,不在任何一个象限内; 点B在第四象限;点C在第四象限. (2)连接BC,FD,则线段BC,FD关于__y___轴对称.
(1)若点A在x轴上,求点A的坐标; 解:(1)依题意,得2a-6=0, 解得a=3. ∴点A(5,0). (2)点A 的纵坐标比横坐标大4,求点A 的坐标; 解:(2)依题意,得2a-6-2-a=4, 解得a=12. ∴点A(14,18).
5.(一题多设问)(北师教材母题改编)在平面直角坐标系中,点A的 坐标为(2+a,2a-6).
2.如图是象棋棋盘的一部分,若“帅”的坐标 为(1-2),“相”的坐标为(3,-2),则“炮”的坐标 为___(_-__2_,__1_) __.
3.如图,在长方形ABCD中,已知AB=6,AD= 4,在长方形ABCD外画△ABE,使AE=BE=5,请建立 适当的平面直角坐标系,并求出各顶点的坐标.
A.经过原点
B.平行于x轴
C.平行于y轴
D.无法确定
2.已知点A(-1,0),B(1,1),C(0,-3),D(-1,2),E(0,1),
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4. 与 x轴平行的直线上的点的纵坐标相同;与y轴平行
的直线上的点的橫坐标相同.
专题练习
专题一:利用点的坐标确定物体的位置(建立合理的直角坐标系) 类型一:各点坐标均未给出,如例一。 例一:请你在下图中建立适当的直角坐标系 , 并写出各地点的 坐标.
专题一:利用点的坐标确定物体的位置(建立合理的直角坐标系)
专题四:平面直角坐标系中坐标变化规律探究题
变式训练1:
如图,一个机器人从O点出发,向正东方向走3米到达A1点(3, 0),再向正北方向走南方向走 12米到达 A4 点,再向正东方向走 15 米到达
A5 点,按如此规律走下去,当机器人走到 A6 点时,则 A6 的坐标
2.在平面直角坐标系中,点A(-2,4),B(3,4),连接AB,若点
C为直线AB上的任何一点. (1)点C的纵坐标有什么特点? (2)如果一些点在平行于y轴的直线上,那么这些点的横坐标有什 么特点?
类型二:给出已知点坐标,如例二。
例二:如图所示的东莞地图,若在图中建立平面直角坐标系 ,
使 “ 虎 门 ” 的 坐 标 是 ( - 3 , - 2) , 则 “ 东 城 ” 的 坐 标 为 ___________.
专题二:点的坐标含参数问题
例三:若0<m<2,则点P(m-2,m) 在第____象限。
为?
变式训练2:详见导学全程练第28页第六题
思考题:在平面直角坐标系中 , 将线段 AB 绕点 A 按逆 时针方向旋转90°后,得到线段AB′,则点B′的坐标为 ___________.
作业(写在作业本上)
1.已知平面直角坐标系中有一点M(m-1,2m+3). (1)当m为何值时,点M到x轴的距离为1? (2)当m为何值时,点M到y轴的距离为2?
变式训练:已知点P(1 -2 m,m -1),则无论m取 何值,点P必不在第____象限。
专题三:写出满足条件的点的坐标
例四:在平面直角坐标系中,已知点A( 5 ,0 ),
B( 5 ,0 ),点C在坐标轴上,且AC+BC=6,写出满足条
件的所有点C的坐标。
变式训练: 已知在平面内两点 P1(x1,y1),P2(x2,y2),这两点间的距离 P1P2=
3.2 平面直角坐标系
第2课时 专题训练
梅外初二数学C班
上节内容复习
1. x轴上的点的坐标特点是:纵坐标为0. y轴上的点的 坐标特点是:橫坐标为0. 2.各象限内点的特点:第一象限(+,+);第二象限 (-,+);第三象限(-,-);第四象限(+,-). 3. 点P(a,b)到x轴的距离为|b|,到y轴的距离为|a|.
x2-x12+y2-y12,同时,当两点所在的直线在坐标轴
或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为|x2 -x1|或|y2-y1|. (1)已知 A(2,4),B(-3,-8),试求 A,B 两点间的距离; (2)已知 A,B 在平行于 y 轴的直线上,点 A 的纵坐标为 5, 点 B 的纵坐标为-1,试求 A,B 两点间的距离.
