第二章 X射线衍射方向
X射线衍射方向材料分析

X射线衍射⽅向材料分析第⼆章X射线衍射⽅向X射线照射晶体,电⼦受迫振动产⽣相⼲散射;同⼀原⼦内各电⼦散射波相互⼲涉形成原⼦散射波。
由于晶体内各原⼦呈周期排列,因此各原⼦散射波间也存在固定的位相关系⽽产⽣⼲涉作⽤,在某些⽅向上发⽣相长⼲涉,即形成了衍射波。
由此,可知衍射的本质是晶体中各原⼦相⼲散射波叠加(合成)的结果。
衍射波的两个基本特征—衍射线(束)在空间分布的⽅位(衍射⽅向)和强度,与晶体内原⼦分布规律(晶体结构)密切相关。
X射线衍射分析是以X射线在晶体中的衍射现象作为基础的。
衍射可归结为两⽅⾯的问题,即衍射⽅向及衍射强度。
布拉格⽅程是阐明衍射⽅向的基本理论,⽽倒易点阵与爱⽡尔德图解则是解决衍射⽅向的有⼒⼯具。
晶体⼏何结构是更为基础的知识,在讨论上述内容之前应该有所了解。
有关点阵、晶胞、晶系以及晶向指数、晶⾯指数等在某些课程中可能已涉及,为适应衍射分析的需要,⼤家课前应该有所准备,这⾥不在重复。
⼀、劳厄⽅程:波长为λ的⼀束X射线,以⼊射⾓α投射到晶体中原⼦间距为a的原⼦列上(图1)。
假设⼊射线和衍射线均为平⾯波,且晶胞中只有⼀个原⼦,原⼦的尺⼨忽略不计,原⼦中各电⼦产⽣的相⼲散射由原⼦中⼼点发出,那么由图1可知,相邻两原⼦的散射线光程差为:若各原⼦的散射波互相⼲涉加强,形成衍射,则光程差必须等于⼊射X射线波长λ德整数倍:式中:H为整数(0,1,2…),称为衍射级数。
⼊射X射线的⽅向S0确定后,则决定各级衍射⽅向α/⾓可由下式求得:由于只要α/⾓满⾜上式就能产⽣衍射,因此,衍射线将分布在以原⼦列为轴,以α/⾓为半顶⾓的⼀系列圆锥⾯上,每⼀个H值对应于⼀个圆锥。
在三维空间中,设⼊射X射线单位⽮量S0与三个晶轴a,b,c的交⾓分别为α,β,γ。
若产⽣衍射,则衍射⽅向的单位⽮量S 与三个晶轴的交⾓α/,β/,γ/必须满⾜:a(COSα/-COSα)= Hλb(COSβ/-COSβ)= Kλc (COSγ/-COSγ)= Lλ式中H,K,L均为整数,a,b,c分别为三个晶轴⽅向的晶体点阵常数。
第2章 X射线衍射方向

5. 点阵参数或晶格常数: 单胞大小和形状:用3个基矢
长度a、b、c及相应夹角α、β、 γ来表示。 a、b、c以及α、β、γ称为点阵 参数或晶格常数(lattice constant 或lattice parameter)。
有单晶、多晶、微晶、纳米晶等。 单晶体:整个晶体中原子按一定周期性重复排列的。
食盐(NaCl)的晶体结构
6
第一节 晶体几何学简介
多晶体:许多小单晶按不同取向聚集而成的晶体物质。 晶体并非局限于天然生成的固体,金属和合金在一般条件
下都是晶体,一些陶瓷材料是晶体,高聚物在某些条件下 也是晶体。 晶体的特点:长程有序,主要是周期性或准周期性。 不同的晶体,原子、离子或分子的排列方式各不相同,呈 现出各种不同的性质。
11
二、晶系
按照晶体点阵的对称性,划分为七种晶系。每个晶系最多
可包括 4 种点阵。
1848年,法国晶体学家布拉菲(Bravais.M.A)推导证实了七 种晶系中总共可有14种点阵,称此为“布拉菲点阵”。
晶系
立方(等轴) cubic
正方(四方) tetragonal
斜方(正交) orthorhombic
c
b a
简单单斜
c
b a
底心单斜
18
三、 7 种晶系、14种布拉菲点阵(7)
7. 三斜晶系:(triclinic)
a b c 900
c
a
b
简单三斜
19
三、 7 种晶系、14种布拉菲点阵
七个晶系及其所属的布拉菲点阵
晶 系 点阵常数 布拉菲点阵 点阵符号 阵点数
X射线衍射方向

14
2)当晶面间距一定,
2d n
2d
即只有当λ不大于2d,才发生衍射,
且λ较小时,较易发生衍射,衍射级数 较多。
但是波长过短会造成衍射角过小,使衍射 现象难以观察,也不宜使用。常用于X射 线衍射旳波长范围为:2.5—0.5埃。
15
第三节 倒易点阵与爱瓦尔德图解
倒易点阵对于解释X射线衍射方向及背面 旳电子衍射图像非常有用,对有些参数 旳计算也可大大简化,是个很有用旳工 具。
2d sinθ = nλ
这就是布拉格方程。
A
C
D
B
P′
hkl
Q′
dhkl
8
实际工作中所测旳角度不是角,而是 2 。2角是入射线和衍射线之间旳夹角, 习惯上称2角为衍射角,称为Bragg角, 或衍射半角。
9
布拉格定律:当X射线照射晶体时,只有 相邻面网散射线旳光程差为波长旳整数 倍时,才干形成干涉加强及衍射线,反 之不能。
λmin为短波极限, λmax为能够起作用旳最大波长)。 这时反射球已不是一种薄层而是具有一定厚度旳壳体,
从而倒易点落在这个壳体内者均与反射球相交,这么 也就增长了反射球与更多旳倒易点相交旳机会也即增 长了反射旳机会。 因为晶体不动,入射线和晶体作用后产生旳衍射束表 达了各晶面旳方向,所以此措施能够反应出晶体旳取 向和对称性。
旳晶面间距旳倒数。
证明:若用
R* HKL
表达从倒易原点到坐
标为(H,K,L)旳倒结点旳倒易矢量,
则有:
R* HKL
Ha
*
Kb *
Lc*
(HKL)为干涉面,即:
H=nh, K=nk, L=nl
故:R H* KL
nRh*kl
第二部分xrd衍射方向和强度

康普顿效应
1922年,康普顿在研究X射线被自由电子散射的时候, 发现一个奇怪的现象:散射出来的X射线分成两部分,一 部分和原来的入射线波长相同,而另一部分则比原来的波 长要长,具体的大小和散射角存在着函数关系。康普顿在 引入光量子的基础上推导出了波长变化和散射角的关系式, 和实验结果符合得非常好。
亨利.布拉格Henry Bragg 劳伦斯.布拉格Lawrence Bragg.
晶体结构的X射线分析
1917 物理 巴克拉Charles Glover Barkla
元素的特征X射线
1924 物理 卡尔.西格班Karl Manne Georg Siegbahn X射线光谱学
1937 物理
戴维森Clinton Joseph Davisson 汤姆孙George Paget Thomson
K系特征X射线 L系特征X射线 M系特征X射线
……
特征X射线产生示意图
特征X射线的频率和 波长决定于外层电 子与内层电子的能 量 差 ΔΕ=Ε 外 -Ε 内 即λ =hc/ ΔΕ
材料研究方法
特征X射线的成因
x 射线衍射分析
Kα1
L3 L2 L1
1s 2s 2p K Kα2
自由电子
材料研究方法
特征X射线的波长
d.Watson、
脱氧核糖核酸DNA测定
1964 化学 Dorothy Crowfoot Hodgkin
青霉素、B12生物晶体测定
1985 化学
霍普特曼Herbert Hauptman 卡尔Jerome Karle
直接法解析结构
鲁斯卡E.Ruska
第二章X射线衍射的方向和强度

X射线在晶体中的相干散射波必须满足条件:两束或两束 以上的波,其振动方向相同、频率相同、位相恒定,且须是 由同一个点光源发出的。但还需作以下的近似或假设: 1. X射线是平行光,且只有单一波长(单色); 2. 电子皆集中在原子中心(因为原子间距远大于核外电子 距离,所以这种近似是可行的); 3. 原子不作热振动,因为在讨论问题时,假设原子间距 没有任何变化。 X 射线在晶体上衍射的过程: X 射线照到晶体上、晶体作 为光栅产生衍射花样,衍射花样反映了光学显微镜所看不到 的晶体结构的特征;我们的目的就是利用衍射花样来推断晶 体中质点的排列规律。
六方晶系晶面夹角的公式为:
§2-3 衍射的概念与布拉格方程
一、两个同周期、同相位波之间的相互作用 二、衍射和反射的区别 三、X射线衍射
一、两个同周期、同用相位波之间的相互作用
下图的波波前为圆形,随传播距离增加,波前变成近似 垂直于传播方向的平面波。在A方向的两个波在出发点位相 相同,到达S处以后互相之间有ΔA的波程差。 即多走了 ΔA的距离。当 ΔA=nλ(n=0,1,2,3…) 时 , 两个波的位相完全一致, 在这个方向上两个波相互 加强:即两个波的合成振 幅等于两个波的原振幅的 叠加。
但在其它晶系中,晶面指数的数字绝对值相同的晶面就 不一定都属于同一晶面族。如:对正方晶系由于a=b≠c,因 此 {100} 被分成两组,其中 (100) 、 (010)、(ī00)、(0ī0)四个晶 面属于一族晶面,而(001)和(00ī)属于另一族晶面。
晶向指数的确定方法为:
1.在一族互相平行的结点直线中引出过坐标原点的结点直线 2.在该直线上选距原点最近的结点,量出它的结点坐标; 3.将三个坐标值用方括号括起,即为该族结点直线的晶向指数。 当泛指某晶向指数时,用[uvw] 表示。有对称关联的等同晶向 用<uvw>表示、如立方系的四 个体对角线:[111][1ī1][īī1][īll] 均用<111>表示。
第二章 X射线衍射方向

b ⊥ a,c平面
*
c × a ca sin β b = = V V
*
c ⊥ a, b 平面
*
*
cos β cos γ − cos α cos α = sin β sin γ
cos γ cos α − cos β cos β = sin λ sin α
*
a × b ab sin γ c = = V V
c
a
b
◆单位点阵 单胞 单位点阵(单胞 单位点阵 单胞):
1-7.swf
反映空间点阵中阵点周期性排列规律的最小 空间单元.空间点阵由单胞周期性堆砌而成 空间点阵由单胞周期性堆砌而成. 空间单元 空间点阵由单胞周期性堆砌而成 由三方向的基本矢量a、 、 及它们间夹 由三方向的基本矢量 、b、c及它们间夹 角α、β 、 γ描述.
■
布拉格方程的导出: 布拉格方程的导出:
2dSinθ = nλ
线 反 射 面 法
根据图示, 根据图示,干涉加强的条 件是: 件是:
式中:n为整数,称为反射 式中: 为整数, 为整数 数 θ为 射 反射 反射 的 ,称为 射 , 射 射 的 , 称为 射 , 2θ 称为 射 θ
θ θ
θ
布拉格方程的讨论 §2.2.1 布拉格方程的讨论
点阵与晶体结构:例子
c
b a
γ-Fe, fcc
Cu3Au, simple cubic
点阵与晶体结构:例子
c
b a
γ-Fe, fcc
CuAu, tetragonal
§2.1.4 晶体学指数
◆ 晶向和晶面指数
1.6.swf
◆ 晶面族
同一晶体点阵中,具相同的晶面间距,晶面上阵点 同一晶体点阵中,具相同的晶面间距, 分布规律相同的一级晶面,记着{hkl}. 分布规律相同的一级晶面,记着{hkl}.
XRAY2

例 已知两晶面(100)和(010),求二者决定的晶带。 1u+0v+0w=0 0u+1v+0w=0 u:v:w=(0×0-1 × 0):(0 × 0-0 × 1) :(1 × 1-0 × 0) =0:0:1 晶带为[001]
第二章 X射线衍射方向
二、晶体几何学基础 (四)晶带、晶面间距和晶面夹角 1、晶带与晶带定律 晶带定律的应用 2)已知两晶带[u1v1w1]和[u2v2w2],求交面(hkl)。 hu1+kv1+lw1=0 hu2+kv2+lw2=0 h:k:l=(v1w2-v2w1):(w1u2-w2u1):(u1v2-u2v1)
第二章 X射线衍射方向
二、晶体几何学基础 (四)晶带、晶面间距和晶面夹角 2、晶面间距的计算 若已知某个晶体的晶体常数a、b、c和α、β、γ,根 据解析几何原理,很容易推导出计算晶面间距的公式。
立方晶系
d hkl 2 2 a c
正方晶系
d hkl
第二章 X射线衍射方向
二、晶体几何学基础 (四)晶带、晶面间距和晶面夹角 2、晶面间距的计算 斜方晶系
d hkl 1 h2 k 2 l 2 2 2 2 a b c
其它晶系晶面间距计算公式可从结晶学的参考文 献中查得。对称程度越低,晶面间距的计算的公式越 复杂。 实际工作中这些晶面间距可以通过X射线的仪器 分析测得,并通过这些公式计算晶体的晶体常数。
劳厄的实验,于同一年推导了比
劳厄方程更为简单的衍射公式— —布拉格方程。它成为X射线分
析中最常用的公式。
2d’sinθ=nλ
在解释X射线衍射图谱时,有两个问题需要解决: • 这些衍射点的在空间上的分布规律,即衍射方向 • 衍射点的衍射强度
04-05 晶体几何学基础概述

晶体结构
萤石结构( CaF2 )
氯化钠结构(NaCl)
晶体结构
辉钼矿的化学成分:
MoS2,Mo 59.94%,S 40.06%;
辉钼矿的特征:
铅灰色,金属光泽, 硬度低,底面解理极 完全,比重大,光泽 强。
晶体结构
石墨的晶体结构
C60的晶体结构
金刚石的晶体结构
晶体结构X衍射图谱
石墨
金刚石
C60
b c c a * * a b (b c )(c a ) (c c )(b a ) V V cos * = * * = = abc2 sin a sin b | a b | bc sin a ca sin b V V cosa cos b cos = 同样可求 得α *, β *。 sin a sin b
a=bc, a=b==90
简单三角
四方 六角 立方
简单四方 体心四方
a=b, 六角 b==90, a=120 a=b=c, a=b==90 简单立方,体心立方 面心立方
七大晶系所要求最低的对称性
晶系 三斜 最低特征对称素 无对称素 晶胞形状 任意的平行六面体
单斜 正交 三角 四方 六角 立方
a = = d(200) 2 2 2 2 2 0 0
\ (200)
(110)
a
intersects with
a d(110) = 2 2 2 = 2 1 1 0
\ (110)
晶面间距
晶面间距(d)公式:
立方晶系:
1 d hkl
2
h k l = 2 a
2 2
2
h k l 四方晶系: = 2 2 2 a c d hkl 2 2 2 1 h k l 正交晶系: = 2 2 2 2 b c d hkl 1
第二章射线衍射原理
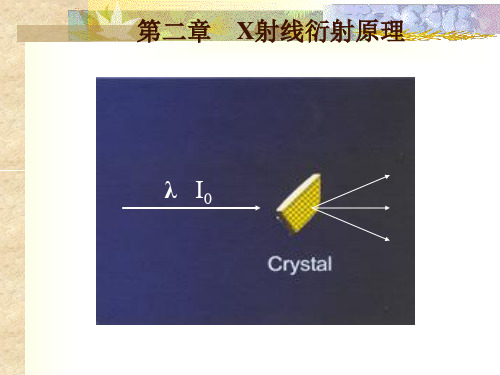
⑴干涉晶面和干涉指数
2dhklsinθ=nλ ↓
2(dhkl /n)sinθ=λ ↓ 令dHKL=dhkl /n
2dHKLsinθ=λ
(hkl)面的n级反射可以看成 是(HKL)面的一级反射, 对布拉格方程进行了简化。 (HKL)称为干涉晶面,H、 K、L称为干涉指数,其中:
H=nh, K=nk,L=nl 。
劳厄方程
1.一维劳厄 方程 —— 单一原子列衍射方向
a•(S S 0)H
a(cosβ1-cosα1)=H λ
S—衍射线单位方向矢量
S0—入射线线单位方向矢量
劳厄方程
当X射线照射到一列原子上时,各原子散射线之间相
干加强成衍射波,此时在空间形成一系列衍射圆锥。
劳厄方程
a 2、•(二S 维S 劳0)厄 方H 程→—a—(单co一sβ原1-c子os面α 1衍)射=H方λ向
⑵周转晶体法
——用单色X射线照射转动的单晶体的衍射方法。其衍 射原理如图示。单晶体转动相当于其对应倒易点阵绕 与入射线垂直轴线转动,使得原来与反射球不相交的 倒易点在转动过程中与反射球有一次或两次相交机会, 从而产生衍射。
周转晶体法
实验中,底片卷成圆筒状接受衍射线,衍射 花样为一系列斑点,其实质为衍射线与底片 的交点。分析这些斑点的分布可以得到晶体 结构信息。此方法常用于测定未知晶体结构。
可知,反射方向S的终点 必落在以O为中心,以 |S0|为半径的球上——厄 瓦尔德球或反射球。 OS方向即为相应晶面的
g2*
g1*
g3*
衍射线方向。
厄瓦尔德图解
厄瓦尔德图的构建——以1/λ为半径构建一个球,球 心位于试样O点,入射线与球交点O*为倒易原点,
则连接O*与S终点的矢量即为g*。在以O*为倒易原 点的倒易点阵中,只要阵点落在球面上,则该点对 应的晶面就可能产生衍射。S即为衍射方向。
02 X射线的方向和强度

ra x Ia <ZIe
即电子波合成有所损耗 定义
Aa Ia 1 2 f= =( ) Ae Ie
即为原子对X射线散射 大小atomic scattering factor,称散射因子
i
-i
i 2
= Ae i Ae -i=A 2
• 晶胞中N个原子1,2,3……的坐标为u1v1w1, u2v2w2,u3v3w3…… unvnwn • 散射因子为f1,f2,f3……位相差:φ1 ,φ 2,φ3 ……φn • 合成振幅 n
i1 i2 in A b=A ( f e + f e +......+ f e )=A e f je e 1 2 n j=1
e
0 0
温度因子=
加热振动IT f =e-2m或 =e-m 静止振动I f0
6n 2 ( x) 1 sin 2 m= [ ] 2 m a k x 4
( x)德拜函数 查表
x=/T -特征温度平均值
粉末法的衍射线强度
3 e2 2 V 2 -2M I=I0 ( ) P F ( ) A ( ) e 32 R mc2 Vc2 R为观察试样距离, Vc-晶胞体积 V被照射体积
=f[1 eLeabharlann i(h+k)]
h,k同性数(都是奇数或者偶数)时:F=2f F2=4f2 h,k异性数(一个奇数一个偶数)时:F=0 消光
3)体心立方
F=fe
2 i(0)
fe
h k l 2 i( + + ) 2 2 2
第2章X射线衍射原理
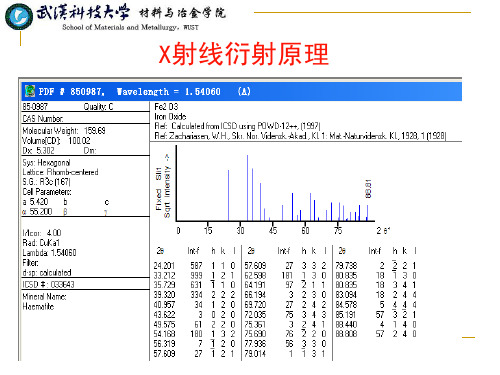
X射线晶体学中最基本的方程之一
据此,每当我们观测到一束衍射线,由衍射角θ便可依据布拉格方程计算出 这组晶面的 晶面 间距(X射线波长已知)
布拉格方程的讨论
2.2.3 布拉格方程的讨论 1).选择反射:
仅当d、、三者满足布拉格方程时才能产 生衍射,所以布拉格方程是X射线在晶体中产 生衍射必须满足的基本条件; 意义: 建立了衍射线方向(即空间分布,表征) 与晶体结构(d表征)之间的关系
衍射仪法
基本原理: 表面与测角仪中心轴严格重合的试样 绕测角仪中心轴旋转。改变其表面与入 射单色X射线的夹角,同时计数器按2 沿测角仪圆同向运动,从而使晶体中所 有晶面产生的衍射线均被探测、记录。 最终得到试样的X射线衍射谱图(I- 2)。
X射线衍射谱图(I-2)
140 120 100 80 60 40 20 0 15 25 35 45 55 65 75 85
n=1
n=1
d111
d333 d222
2d sinθ = λ
2.2.5 X射线衍射基本方法
(1)基本原理 基于布拉格方程: 通过连续改变 (使用白色 X 射线入 射),或者连续改变,以使被测晶体 中的各种晶面都有满足布拉格方程 (产生衍射的基本条件)的机会而产 生衍射线,从而使晶体特征均能在衍 射花样上得到反映。
2.2.4、布拉格方程的应用
1、已知入射x射线的波长,通过测量θ,求 晶面间距。并通过晶面间距,测定晶体结 构或进行物相分析。
2、已知晶体的d值。通过测量θ,求特征x 射线的λ,并通过λ判断产生特征x射线的元 素。这主要应用于x射线荧光光谱仪和电子 探针中元素分析。
练习题:
1、用CrKα辐射α-Fe多晶试样, 求最多可能得到几条衍射线? 解:查附录13和附录2:
材料现代分析技术-2X射线衍射方向

±1,±2共5个值。用Mo Kα 线(λ = 0.711Α) H 可取0, ±1, ±2, ±3, ±4, ±5共11个值。
劳埃第二方程
二维衍射 原子的二维排列称为原子网,可视为由一系 列周期为b的平行的原子列所组成。与一维衍 射时类同,这些原子列产生的衍射束要能加 强,也须满足以下条件:
x射线有强的穿透能力,在x射线作用下晶体的散射线来自若 干层原子面,除同一层原子面的散射线互相干涉外,各原子 面的散射线之间还要互相干涉。这里只讨论两相邻原子面的 散射波的干涉。过A点分别向入射线和反射线作垂线,则SA 之前和TA之后两束射线的光程相同,它们的光程差为:
d = QA′Q′ -PAP′=SA′+A′ T= 2dsinθ
首先作晶体的倒易点阵,O*为倒易原点。入射线沿OO*方向 入射,且令OO* =S0/λ=K0。 以0为球心,以1/λ为半径画 一 球 , 称 反 射 球 。 若 球 面 与 倒 易 点 G 相 交 , 连 OG 则 有 OGS0/λ =O*G,这里O*G为一倒易矢量。因OO* =OG=1/λ,故 △OO*G为等腰三角形,OG是一衍射线方向。由此可见,当x 射线沿OO*方向入射的情况下,所有能发生反射的晶面,其 倒易点都应落在以O为球心。以1/λ为半径的球面上,从球 心O指向倒易点的方向是相应晶面反射线的方向。以上求衍 射线方向的作图法称爱瓦尔德图解,它是解释各种衍射花样 的有力工具。
复杂点阵晶胞中含有n个相同或不同种类的原子,它们除占 据单胞的顶角外,还可能出现在体心、面心或其他位置。
复杂点阵单胞的散射波振幅应为单胞中各原子的散射振幅的 矢量合成。由于衍射线的相互干涉,某些方向的强度将会加 强,而某些方向的强度将会减弱甚至消失。这种规律称为系 统消光。
二章节X射线衍射方向-资料

干涉指数有公约数n,而晶面指数只能是互质的整数。当 干涉指数也互为质数时,它就代表一组真实的晶面,因此,
干涉指数为晶面指数的推广,是广义的晶面指数。
4、衍射线方向与晶体结构的关系
从
2dsin看出,波长选定之后,衍射线束的
方向(用 表示)是晶面间距d的函数。如将立方、正
方、斜方晶系的面间距公式代入布拉格公式,并进行平
a, b and c are the unit cell edge lengths.
α, β, and γare the angles
2.1.2 晶系
The 14 possible BRAVAIS LATTICES {note that spheres in this picture represent lattice points, not atoms!}
2.2.2、布拉格公式的推导
1、单一原子平面的散射
当一束平行的X射线以θ 角投射到原子平面上时,其中 任意两个原子的散射线在原子平面反射方向的光程差为:
A、B两 个b 原c 子 的a d 散 射a 波c 是s i 干n 涉 加a 强c 的s i 。n 0
由于A、B是任意的,所以可以认为此原子平面上所有原 子的散射波在该方向都是干涉加强的。
2.2.4、布拉格方程应用
布拉格方程是X射线衍射分布中最重要的基础公式, 从实验角度可归结为两方面的应用: 一方面是用已知波长的X射线去照射晶体,通过衍射角 的测量求得晶体中各晶面的面间距d,这就是结构分析 -- X射线衍射学; 另一方面是用一种已知面间距的晶体来反射从试样发 射出来的X射线,通过衍射角的测量求得X射线的波长, 这就是X射线光谱学。该法除可进行光谱结构的研究外, 从X射线的波长还可确定试样的组成元素。电子探针就 是按这原理设计的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
上一圆括号,即为晶面指数。
一般表示形式:(hkl) 。
晶面指数的确定
(二)晶面指数的确定
1.AGE面: 截距1,1,1; 倒数1,1,1 , 晶面指数(111)
2.PBEQ面: 截距是1/2,1,∞; 截距倒数是2,1,0; 化为最小整数后的晶 面指数(210)
晶面指数的确定
(二)晶面指数的确定
晶体结构与空间点阵的区别:
晶体结构:晶体中原子或分子的排列情况。 由空间点阵+结构基元而构成 晶体结构的形式是无限多的
空间点阵:把晶体结构中原子或分子等结构 基元抽象为周围环境相同的阵点之后,描述 晶体结构的周期性和对称性的图像。 空间点阵只有14种
14种布喇菲点阵
一、 基本概念
单位晶胞(Unit Cell):在三个方向上的重复周期矢量a、 b、c称为基本矢量。由基本矢量构成的平行六面体称为单 位晶胞。其在三个方向上重复即可建立整个空间点阵。
Your text in here
hu+kv+lw=0,
Your text in here
通常把这个关系式称为晶带定律。 晶带定律给出了晶面与晶向之间的关系,有了这个关系,我 们就可以根据已知的晶面或晶带来求得另外一些晶面或晶带。
三、晶带定律
晶带定律:hu+kv+lw=0 (1)已知某晶带中任意两个晶面(h1k1l1)和 Your text in here (h2k2l2),则可通过下式求出该晶带的晶带轴 方向[uvw]: h1u+k1v+l1w=0 h2u+k2v+l2w=0
u=k1l2—k2l1 v= l1h2—l2h1 w=h1k2—h2k1
三、晶带定律
晶带定律:hu+kv+lw=0 (2)已知某晶面同属于两个晶带[u1v1w1]和[u2v2w2], Your text in here 则可通过下式求出该晶面的晶面指数(hkl): hu1+kv1+lw1=0 hu2+kv2+lw2=0 h=v1w2—v2w1 k=w1u2—w2u1 l =u1v2—u2v1
布拉格方程的导出
这两束X射线到达NN2处的波程差为: δ=PM2+QM2 =dsinθ+dsinθ =2dsinθ 如果散射(入射)X射线的波长为λ,则在这个方向上散射线互相 加强的条件是: 2dsinθ=n λ
第二节 布拉格方程 干涉加强条件(布拉格方程)为:
2d sin n
式中:n —整数,“反射”级数(衍射级数) θ—布拉格角或掠射角(入射线与晶面) 半衍射角 2θ—衍射角(入射线与衍射线)
2.晶向指数
设晶向指数在三轴坐标系中为[UVW],四轴坐标系中为[uvtw] 在平 面上表示一个点只用两个坐标,则u+v+t=0,所以 t=-(u+v) (1)
三、晶带定理
1、晶带 在空间点阵中,所有平行于某一直线的一组晶面的组合称为 一个晶带。或者说交线相互平行的一组晶面的组合称为一个 Your text in here 晶带。 这一直线就称为晶带轴,它用晶向指数来表示。 已知一个晶面 (hkl) 和它所属的晶带轴指数[uvw],则由矢 量代数可以证明晶带轴[uvw]与该晶带的任一晶面(hkl)之间 均具有下列关系:
若各指数同乘以异于0的数n,则晶面位向不变,晶 向则或是同向(n>0)或是反向(n<0)。
(二)晶面指数的确定
在立方晶系中等同晶向和等同晶面的比较:
例1:写出立方晶系的<100>的等同晶向和{100}的 等同晶面。
<100>=[100]+[010]+[001]+[T00]+[0T0]+[00T]
{100}=(100)+(010)+(001)
例2:写出立方晶系的<111>的等同晶向和{111}的等 同晶面。
<111>=[111]+[T11]+[1T1]+[11T]+[TT1]+[1TT]+[T1 T]+[TTT] {111}=(111)+(T11)+(1T1)+(11T)
等价:数字相同,符号和排列次序不同。
(二)晶面指数的确定
晶面指数具有如下规律:
晶面指数,并非仅指一晶格中的某一个晶面,而 是泛指该晶格中所有那些与其相平行的位向相同 的晶面。 在一种晶格中,如果某些晶面,虽然 它们的位向 不同,但原子排列相同。如(100)、(010)及 (001)等,这时若不必要予以区别时,可把这些 晶面统用{100}表示。 即:(hkl)这类符号系指某一确定位向的晶面指 数;而{hkl}则可指所有那些位向不同而原子排列 相同的晶面指数。表示由等同晶面构成的晶面系 或晶面族。
(三)六方晶系的指数
1.晶面指数 从晶面指数上不能明确表示等同晶面,为了克服这一缺点, 采用a1、a2、a3及C四个晶轴,a1、a2、a3之间的夹角均为 120o,晶面指数以(hkil)表示。六个柱面的指数可确定为:
这六个晶 面可归并 为{ 11 00 } 晶面族。 根据立体 几何,在 三维空间 中独立的 坐标轴不 会超过三 个,可证 明 i=-(h+k) 或 h+k+i=0
LOGO
第二章
X射线衍射方向
第一节 晶体几何学基础
目录
第二节 布拉格方程
第三节 X射线衍射方法
第一节 晶体几何学基础
一、14 种布喇菲点阵
(一) 基本概念
晶体(crystal):由原子在三维 空间中规则排列而成。 空间点阵(Lattice):在研究 晶体结构时,一般只抽象出其重复 规律,这种抽象的图形。 空间点阵上的阵点不只限于原子, 也可以是离子、分子或原子集团。
晶向指数具有如下规律:
晶向指数表示着所有相互平行、方向一致的晶向。
若晶体中两晶向相互平行但方向相反,则晶向指数 中的数字相同,符号相反,例如[111]与[TTT]。
由于晶体的对称性,有些晶向上原子排列情况相同 ,因而性质也相同。晶体中原子排列情况相同的一组 晶向称为晶向族(family of lattice directions) ,用<uvw>表示。
正方晶系
立方晶系
d hkl
1 4 2 (h hk k 2 ) / a 2 l 2 / c 2 3
六方晶系
3、晶面夹角的计算
同理可以得到晶面夹角的计算公式。 立方晶系的晶面夹角的计算公式:
第二节 布拉格方程
(一)布拉格方程的推导
L
N1 N
L1
A
B
θ M1
θ
M θθ M2
N2 θ
A d B
3.DBEG面: 截距1,1,∞; 倒数 1,1,0, 晶面指数(110)
4.DCFG面: 截距1,∞,∞; 倒数1,0,0; 晶面指数(100)
晶面指数的确定
二、晶体学指数
(二)晶面指数的确定 注意:
当晶面交于晶轴的负端时,对应的指数就是负的, 并将负号标在数字的上面。
晶面指数中第一、二、三位分别代表与a、b、c轴 的关系,它们之间不能随意变换。 一个晶面指数实际上是代表某个方向上的一组晶 面,而不是一个面。 当晶面指数中某个位置上的指数为0时,表示该晶 面与对应的晶轴平行。如(100)( )(001)。
◆简单点阵的阵点坐标为[[000]]
(2)点阵类型 ◆底心点阵C 除八个顶点上有阵点外, 两个相对的面心上有阵点, 面心上的阵点为两个相邻 的平行六面体所共有。因 此,每个阵胞占有两个阵 点。阵点坐标为[[000]], [[1/2 1/2 0]]
(2)点阵类型 ◆体心点阵I
除8个顶点外,体心上 还有一个阵点,因此, 每个阵胞含有两个阵 点,[[000]],[[1/2 1/2 1/2]]
若晶体的三个基本矢量互相垂直,则有关系:
cos2α+cos2β+cos2γ=1
d2 d2 d2 1 (a / h) 2 (b / k ) 2 (c / l ) 2 1 则 :d hkl h2 / a 2 k 2 / b2 l 2 / c2
正交晶系的晶面间距公式。
2、晶面间距的计算 斜方(正交)晶系
(二比较:
晶向指数表示着所有相互平行、方向一致的晶向。 晶向族:晶体中原子排列情况相同的一组晶向(等 价晶向),用<uvw>表示。 晶面指数,指该晶格中所有那些与其相平行的位向 相同的晶面。 晶面系或晶面族:所有那些位向不同而原子排列相 同的一组晶面(等价晶面),用{hkl}表示。
2、晶面间距的计算 晶面间距:指相邻两个平行晶面之间的距离。
cosα=ON/OA=d/ma cosβ=ON/OB=d/nb cosγ=ON/OC=d/pc Z C (hkl) N O B A X Y
由于m、n、p与h、k、l具有倒数关系,故有:
cosα=d/(a/h) cosβ=d/(b/k) cosγ=d/(c/l)
例如立方晶系中[111],[T11],[1T1],[11T],[TT1], [1TT],[T1T],[TTT]八个晶向是立方体中四个体对角线的 方向,它们的原子排列完全相同,属于同一晶向族,用 <111>表示。
二、晶体学指数
(二)晶面指数的确定
⑴ 如图设晶格中,某一原子为原点,通过该点平行于晶胞的三棱边作 OX、OY、OZ三坐标轴,以晶格常数a、b、c分别作为相应的三个坐 标轴上的度量单位,求出所需确定的晶面在三坐标轴上的截距; ⑵ 将所得三截距之值变为倒数; ⑶ 再将这三个倒数按比例化为最小整数并加
选择依据: (1)晶胞应最能反映出点阵的对 称性; (2)基本失量长度a、b、c相等 的数目最多;三个方向的夹角应 尽可能是直角; (3)单胞体积最小。 根据这些条件选择出来的晶胞,其几何关 系、计算公式均最简单,称为布喇菲晶胞。
