作二面角的平面角的常用方法
作二面角的平面角的常见技巧

作二面角的平面角的常见技巧重庆 慕泽刚求二面角的大小是历届高考的重点内容之一,且能较好地考查学生的空间想象力及转化思想的应用.解答二面角的问题,其关键是要作出其平面角,这恰好是学生感到头疼的问题.下面介绍几种常见作二面角的平面角的常用技巧.一、抓住共底的等腰三角形作平面角如果两个共底边的两个等腰三角形ABC 和等腰三角形DBC 分别在二面角α-l -β的两个半平面上,则可作出BC 边的中点E ,连结AE 、DE ,根据等腰三角形的性质可知,∠AED 为二面角α-l -β的平面角.例1 (2000年全国理)如图1,已知平行六面体ABCD -A 1B 1C 1D 1的底面ABCD 是菱形,且∠C 1CB =∠C 1CD =∠BCD =60︒.(I)证明:C 1C ⊥BD ;(II)假定CD =2,CC 1=32,记面C 1BD 为α,面CBD 为β,求二面角α-BD -β的平面角的余弦值;(Ⅲ)(略).解析:(I)证明略.(II)连结AC ,AC 和BD 交于O ,连结C 1O .∵四边形ABCD 是菱形,∴AC ⊥BD ,BC =CD .又∵∠BCC 1=∠DCC 1,C 1C =C 1C ,∴△C 1BC ≌C 1DC ,∴C 1B =C 1D ,∴△C 1BD 为等腰三角形,又△CBD 为为等腰三角形,且△C 1BD 与△CBD 有相同的底边BD ,而O 为BD 的中点,C 1O ⊥BD ,CO ⊥BD ,∴∠C 1OC 是二面角α-BD -β的平面角.在△C 1BC 中,BC =CD =2,C 1C =32,∠BCC 1=60︒,∴C 1B 2=22+(32)2﹣2×2×32×c os60︒=134. ∵∠OCB =30︒,∴OB =12BC =1.∴C 1O 2=C 1B 2﹣OB 2=134﹣1=94,∴C 1O =32,即C 1O =C 1C .过C 1作C 1H ⊥OC ,垂足为H .∴点H 是OC 的中点,且OH =32,所以c os ∠C 1OC =OH C 1O =33. 二、抓住共对应边的全等三角形作平面角如果两个共对应边的全等三角形ABC 和三角形DBC(图形具有对称性)分别在二面角α-l -β的两个半平面上,则可过A 作AE ⊥l 于E ,连结DE ,则∠AED 为二面角α-l -β的平面角.例2 过正方形的顶点A 作PA ⊥平面ABCD ,设PA=AB=a ,求二面角B-PC-D 的大小. 解析:如图2,由题设易知,BD ⊥平面PAC ,△PBC ≌△PDC .过B 作BE ⊥PC,垂足E .由PB=PD ,PE=PE,∠BPE=∠DPE,∴△PBE ≌△PDE .∴∠PED=∠PEB=90︒,∴DE ⊥PC ,∴∠BED 为二面角B-PC-D 的平面角.在Rt △PAB 中,由PA=AB=a ,得 PB=2a .∵PA ⊥平面ABCD,BC ⊥AB,∴BC ⊥PB(三垂线定理),∴PC=PB 2+PC 2=3a ,在Rt △PBC 中,BE=PB ·BC PC =2a ·a 3a=63a. 在△BDE 中,BD=2a,由余弦定理,得cos ∠BED=BE 2+DE 2-BD 22BE ·DE=﹣12. 因此,所求二面角B-PC-D 的大小为120︒. 图2图1三、抓住面的垂线作平面角如果二面角α-l -β的两个半平面中的一个半平面α上有一条垂线,垂足为A ,且与另一半平面β相交于点P ,则可过P 作PB ⊥l 于B ,连结AB ,由三垂线定理可知,∠PAB 为为二面角α-l -β的平面角例3 如图3,已知P 是正方形ABCD 所在平面外一点,且PA=PB=PC=PD=AB=1.求平面PAC 与平面PAD 所成二面角的余弦值.解析:设AC 与BD 交于点O ,∵PA=PB=PC=PD ,∴PO ⊥AC ,PO ⊥BD ,∴PO ⊥平面ABCD ,∴PO ⊥OD.又∵在正方形ABCD 中,OD ⊥AC ,∴OD ⊥平面PAC.过O 作OE ⊥PA ,垂足为E ,连结DE ,则DE ⊥PA(三垂线定理),∴∠OED 为平面PAC 与平面PAD 所成二面角的平面角.在△PAD 中,∵PA=PD=AD=1,∴DE=ADcos30︒=32, 由OD ⊥平面PAC 知,OD ⊥OE.又在正方形ABCD 中,OD=22. ∴在Rt △ODE 中,sin ∠OED=OD DE =63.∴平面PAC 与平面PAD 所成二面角的余弦值为63. 四、抓住与棱垂直的直线通过作棱的垂面作平面角如果空间中有与二面角的棱垂直的直线两条相交直线,则可作过这两条直线的平面与两个半平面相交,其交线所夹的角就是二面角的平面角例4自二面角内一点到二面角的两个面距离分别是22、4,到棱的距离为4 2.求二面角的度数.解析:如图4,由已知PM ∩PN=P ,∴过PM 与PN 作平面PMN ,与棱l 交于点A ,∵PM ⊥α,PN ⊥β,PM ⊥l ,∴PN ⊥l ,∴l ⊥平面PMN ,∴l ⊥AM ,l ⊥AN ,∴∠MAN 为所求二面角的平面角,在△PAM 中,PM=22,PA=42,∴∠PAM=30︒,在△PAN 中,PN=4,PA=42,∴∠PAM=45︒.∴∠MAN=30︒+45︒=75︒.五、抓住无棱二面角的两条平行线作平面角 如果二面角只有一个公共点P ,而图中没有棱,此时若在二面角的两个半平面内存在一条直线,且相互平行,则可过点P 分别在两个半平面内作这两条直线的垂线PQ 和PR ,则∠QPR 就是二面角的平面角.例5 如图5,已知P 是正方形ABCD 所在平面外一点,且PA=PB=PC=PD=a ,AB=a .求平面PAB 与平面PCD 所成二面角的余弦值.解:∵AB ∥CD ,CD ⊂平面CPD ,∴AB ∥平面CPD .又∵P ∈平面PAB ,且P ∈平面PCD ,∴平面PAB ∩平面PCD=l ,且P ∈l .∴二面角B-l -C 就是平面APB 和平面CPD 相交所得到的一个二面角.∴AB ∥l .过P 作PE ⊥AB ,PE ⊥CD .∵l ∥AB ∥CD ,∴PE ⊥l ,PF ⊥l ,所以,∠EPF 是二面角B- l -C 的平面角.又∵PE 是正三角形APB 的一条高线,且AB=a ,所以,PE=32a , 同理PF=32a ,∵E ,F 分别是AB ,CD 的中点,∴EF=BC=a . 在△EFP 中,cos ∠EPF=PE 2+PF 2﹣EF 22PE ·PF=13,∴平面PAB 和平面PCD 相交所成二面角的余弦值为13. 图3 图5 图4。
作二面角的平面角的常用方法

而走险了,那个丫头,他势在必得. "咚咚咚." 门外突然响起敲门声,雪无痕有些恼怒,扭头看着旁边の凤姐,眼中有了一丝责怪.凤姐连忙躬身请罪,打开房门,随即门外传来一阵低声の交谈声. "吱呀!" 门再次被推开,凤姐有些面色凝重の走了进来,开口说道:"看来这次任务只能提前行动 了,而且最好是今晚." "什么情况?"雪无痕眉头一挑,有了一丝不好の预感. "雪一他们死了,白重炙一人杀の,而且白重炙此时正赶回雾霭城,或许明早就能赶回,所以少主如果你坚持任务の话,那么就必须马上行动."凤姐忍住心中の惊骇,尽量让自己の诉说平静些. "哐当!" 手上の茶杯悄 然落地,四分五裂.雪无痕张大嘴巴,想说些什么,却什么也没有说.墨老和石老怔怔の望着洒在地面龙舌般の茶叶,默默消化着这信息深沉の含义. "将传递信息の人给我叫进来." 良久之后,雪无痕突然开口了,声音冷漠冰寒. 牛金和两名随从の情报人员被叫进来,看着正首位那名英俊无比 却面容十分平静の青年,连忙躬身行礼.随后一点不落の将自己所看、所听、所想,全部述说出来,没有一丝添油加醋,没有一丝遗漏.他知道一句话说错,有时就能代表一个生命消失,他知道那个青年有这个权利,也有这个能力. "行了,你们三人下去吧,凤姐安排一下他们,好好玩两天."雪无 痕自从牛金三人进来之后就已经恢复平静,心里虽然起了滔天巨浪,但他只能生生强压下来,在下人面前,他需要平静,也必须平静. "今晚行动." 思索良久,他毅然起身,说出四个字,然后快速推开门,匆匆离去. 白家堡,西院,醉心园. 夜轻狂身为白家の大少,此时却没有像那些普通の公子般, 流连在十三长街上挥霍着青春.也没有像别の雾霭城の纨绔子弟般,在某些场合诠释着世家和父辈の富有权势.而是静静
二面角8种求法

二面角求法正方体是研究立体几何概念的一个重要模型,中学立体几何教学中,求平面与平面所成的二面角是转化为平面角来度量的,也可采用一些特殊的方法求二面角,而正方体也是探讨求二面角大小方法的典型几何体。
笔者通过探求正方体中有关二面角,分析求二面角大小的八种方法:(1)平面角定义法;(2)三垂线定理法;(3)线面垂直法;(4)判定垂面法;(5)异面直线上两点间距离公式法;(6)平行移动法;(7)投影面积法;(8)棱锥体积法。
一、平面角定义法此法是根据二面角的平面角定义,直接寻求二面角的大小。
以所求二面角棱上任意一点为端点,在二面角两个平面内分别作垂直于棱的两条射线所成角就是二面角的平面角,如图二面角α-l-β中,在棱l上取一点O,分别在α、β两个平面内作AO⊥l,BO⊥l,∠AOB即是所求二面角的平面角。
例题1:已知正方体ABCD-A1B1C1D1中,O、O1是上下底面正方形的中心,求二面角O1-BC-O的大小。
例题2:已知正方体ABCD-A1B1C1D1中,E、F为A1D1、C1D1的中点,求平面EFCA与底面ABCD所成的二面角。
二、 利用三垂线定理法此方法是在二面角的一个平面内过一点作另一个面的垂线,再由垂足(或仍是该点)作棱的垂线,连接该点和棱上的垂足(或连两垂足)两点线,即可得二面角的平面角。
如图二面角α-l-β中,在平面α内取一点A ,过A 作AB ⊥平面β,B 是垂足, 由B (或A )作BO (或AO )⊥l ,连接AO (或BO )即得AO 是平面β的斜线, BO 是AO 在平面β中的射影,根据三垂线定理(或逆定理)即得AO ⊥l ,BO ⊥l , 即∠AOB 是α-l-β的平面角。
例题3:已知正方体ABCD-A 1B 1C 1D 1中,求二面角B-AC-B 1的大小。
例题4:已知正方体ABCD-A 1B 1C 1D 1中,求平面ACD 1与平面BDC 1所成的二面角。
三、 线面垂直法此法利用直线垂直平面即该直线垂直平面内任何直线的性质来寻求二面角的平面角。
几何法求二面角的平面角

1
BD ,
BD =BC =CD =
2
(
1)求证:平面 DAF ⊥ 平面 BAF .
(
2)求钝二面角 B -FC -D 的大小.
证明 (
1)略.
(
2)作 G ,
H 为 DC ,
AB 的 中 点,连 接 GH ,
EH ,
EG ,则
平面 EGH ∥ 平面 FCB .
故所求二面角 B -FC -D 的 大 小,即 为 求 二 面 角 D -
DN =
= ,
NH =DN =
|EG|
3
(
1)求证:
DE ⊥ 平面 ABCD .
(
2)求 平 面 AEF 与 平 面 CEF 所 成 的 锐 二 面 角 的 余
弦值.
证明 (
1)略.
(
2)在 △AEF 中,
AE = 3,
EF =1,
AF = 2,
∴AF ⊥EF ,△AEF 为直角三角形.
在 △EFC 中,
EG -H 的大小
∵AB =2,
AD =AE =EF =1,
∴DG =1,
DE = 2,
EF = 3,
GH =1,
EH = 2,
与
为直角三角形.
∴△DEG △EHG
过 D 作 DN ⊥EG ,连接 NH ,则 NH ⊥EG ,
∴∠DNH 为二面角 D -EG -H 的平面角.
|DE||DG| 6
在 △DNH 中,
EF =1,
FC =2,
EC = 5,
∴CF ⊥EF ,△EFC 为直角三角形.
∴∠AFC 为 平 面 AEF 与 平 面 EFC 所 成 二 面 角 的 平
二面角的平面角的求法

★二面角的平面角的求法:1. 左义法:在二而角的棱上找一点(特殊点),在两个半平而内分別作垂直与棱的射线。
如图,在二而角a-a-p 的棱a 上任取一点0,在平而&内过点0作OA 丄G,在平而0内过点O 作BO 丄“,则ZAOB 为二面角a-a-p 的平而角。
2. 垂面法:过棱上一点作棱的垂直平而,该平而与二而角的两个半平面产生交线,这两条射线所成的角,即为 二而角的平面角。
如图,已知二而角a - I-P ,过棱上一点O 作一平而了,使/丄yr\0 = OA 、Y c 卩=OB.丄OA,/丄 03 ZAOB 为二而角 a-l 一0的平而角。
3. 垂线法:探该法也就是利用三垂线泄理或逆泄理来寻找二而角的平而角,是最常用的一种方法。
由一个半平 面内异与棱上的点A 向列一个半平面作垂线,垂足为B,由点B 向二面角的棱作垂线,垂足为0,连结AO.WJZAOB 为二面角的平而角。
如图,已知二而角a-1-p,自平而&内一点A 作AB 丄0于B,由点B 作B0丄/于0,连结A0••• A0为平而0的斜线,B0为A0在平而0内的射影(2)平而a 与"相交于直线人平而a 的法向量为/〃,平面“的法向量为"2, <///♦ 〃2>=&,则二而角a —/—B 为0或兀一&・设二而角大小为0,则lcos®l=lcos&l =★ ★利用二而角的两个而的法向量求解※法向量的夹角与二而角的大小相等或互补①当法向量兀与石的方向 分别指向二而角的内侧与外侧时,二而角的大小等于法向量夹角②当法向量恳与并方向同时指向二而角的内侧 或外侧时,二而角的大小等于法向量夹角的补角,1.二而角的棱上有爪B 两点,直线AC 、BD 分别在这个二面角的两个半平而内,且都垂直于AB •已知AB=4,AC=6, BD=8, CD=2<T7,则该二而角的大小为()S A. 150。
求二面角平面角的方法

OABOABl寻找二面角的平面角的方法二面角是高中立体几何中的一个重要内容,也是一个难点.对于二面角方面的问题,学生往往无从下手,他们并不是不会构造三角形或解三角形,而是没有掌握寻找二面角的平面角的方法.我们试将寻找二面角的平面角的方法归纳为以下六种类型. 1.1 二面角的相关概念新教材]1[在二面角中给出的定义如下:从一条直线出发的两个半平面所组成的图形叫做二面角.定义只给出二面角的定性描述,关于二面角的定量刻画还必须放到二面角的平面角中去研究.教材如下给出了二面角的平面角的概念:二面角的平面角是指在二面角βα--l 的棱上任取一点O ,分别在两个半平面内作射线l BO l AO ⊥⊥,,则AOB ∠为二面角βα--l 的平面角.2. 二面角的求解方法对二面角的求解通常是先定位二面角的平面角,从而将三维空间中的求角问题转化为二维空间并可以通过三角形的边角问题加以解决.定位出二面角为解题的关键环节,下面就二面角求解的步骤做初步介绍:一、“找”:找出图形中二面角,若不能直接找到可以通过作辅助线补全图形定位二面角的平面角 二、“证”:证明所找出的二面角就是该二面角的平面角 三、“算”:计算出该平面角 由于定位二面角的难度较大,对于求解二面角还有一种思路就是绕开定位二面角这一环节,通过一些等价的结论或公式或用空间向量等方法来直接求出二面角的大小.本文将根据这两种解题思路对二面角的解题方法做一一介绍.2.1 定位二面角的平面角,求解二面角二面角常见题型中根据所求两面是否有公共棱可分为两类:有棱二面角、无棱二面角.对于前者的二面角的定位通常采用找点、连线或平移等手段来定位出二面角的平面角;而对于无棱二面角我们还必须通过构造图形如延展平面或找公垂面等方法使其有“无棱”而“现棱”再进一步定位二面角的平面角.一、根据平面角的定义找出二面角的平面角 例1 在60的二面角βα--a 的两个面内,分别有A 和B 两点.已知A 和B 到棱的距离分别为2和4,且线段10=AB ,试求:(1)直线AB 与棱a 所构成的角的正弦值; (2)直线AB 与平面α所构成的角的正弦值.分析:求解这道题,首先得找出二面角的平面角,也就是找出60角在哪儿.如果解决了这个问题,这道题也就解决了一半.根据题意,在平面β内作a AD ⊥;在平面α内作α⊥BE ,EBCD //,连结BC 、AC .可以证明a CD ⊥,则由二面角的平面角的定义,可知ADC ∠为二面角βα--a 的平面角.以下求解略.例1 正方体ABCD-A1B1C1D1中,求二面角A-BD-C1的大小为.αβ图1例2(2006年XX 试题)如图2(1),在正三角形ABC 中,E 、F 、P 分别是AB 、AC 、BC 上的点,满足AE : EB=CF :FA=CP :BP=1:2.如图2(2),将△AEF 折起 到△A1EF 的位置,使二面角A1-EF-B 成直二面角,连 接A1B 、A1P.(Ⅰ)与(Ⅱ)略;(Ⅲ)求二面角B-A1P-F 的余弦值 tan ∠COC 1=2分析与略解:在例1中,图形的对称和谐状态对解题产生了很好的启迪作用,在这里更离不开图形的这种对称和谐性.若取BP 的中点Q ,连接EQ ,则在正三角形ABC 中,很容易证得△BEQ ≌△PEQ ≌△PEF ≌△AEF ,那么在图2(2)中,有A 1Q=A 1F.作FM ⊥A 1P 于M ,连接QH 、QF ,则易得△A 1QP ≌△A 1FP ,△QMP ≌△FMP ,所以∠PMQ=∠PMF=90o ,∠QMF 为二面角B-A 1P-F 的平面角,使题解取得了突破性的进展.设正三角形的边长为3,依次可求得A 1P=5,QM=FM=552,在△QMF 中,由余弦定理得cos ∠QMF=87-。
二面角的平面角的求法

二面角的平面角的求法教学目标:掌握二面角及其平面角的概念.能灵活作出二面角的平面角,并能求出大小. 重点难点:●会作出二面角的平面角①、点P 在棱上---- ②、点P 在一个半平面上--- ③、点P 在二面角内--- ④ 、向量法求二面角的大小----建立空间直角坐标系,分别找出两个半平面的法向量,求出两个法向量的夹角,眼观是锐或钝二面角。
求二面角大小的公式: 练 习1、如图,AB 是圆的直径,PA 垂直圆所在的平面,C 是圆上任一点,则二面角P-BC-A 的平面角为:A.∠ABPB.∠ACPC.都不是2、已知P 为二面角α-l-β内一点,且P 到两个半平面的距离都等于P 到棱的距离的一半,则这个二面角的度数是多少? 典例分析: 例1. 如图,已知P 是二面角α-AB-β棱上一点,过P 分别在α、β内引射线PM 、PN ,且∠MPN=60º ∠BPM=∠BPN=45º ,求此二面角的度数。
高考演练1(2009重庆卷文)如题(18)图,在五面体ABCDEF中,AB∥DC,2BAD π∠=,2CD AD ==,四边形ABFE 为平行四边形,FA ⊥平面ABCD ,AF=1,(Ⅱ)二面角F-AD-E 的平面角的正切值.例2.如图P 为二面角α–ι–β内一点,PA ⊥α,PB ⊥β,且PA=5, PB=8,AB=7,求这二面角的度数。
例3.如图,三棱锥P-ABC 的顶点P 在底面ABC 上的射影是底面Rt △ABC 斜边AC 的中点O ,若PB=AB=1,BC= ,求二面角P-AB-C 的正切值。
高考演练2(2009四川卷文)(本小题满分12分)如图,正方形ABCD 所在平面与平面四边形ABEF 所在平面互相垂直,△是等腰直角三角形,,,45ABAE FA FEAEF ︒==∠=(III )求二面角F BD A --的大小。
练习1:已知Rt △ABC 在平面α内,斜边AB 在30º的二面角α-AB-β的棱上,若AC=5,BC=12,求点C 到平面β的距离CO 。
二面角平面角的几种求法

另一半平 面重 合 时, 这两 个 向 量的方向应 当一致。在满足这
些条件之下 , 有e o s O = T
2, l f J 7 , l 2 J
2 . 垂射线法即垂面法过棱上一点作棱 的垂直 平面 , 该 平面与二面 角的两个 半平面 的交线组成 的 角即为二 面角
面积 , 则 c o s =
, 如 图 3所 示 , s =s
, s
=s
, J P 。 上 平 面
0 为垂 足 。 面角的定位是 问题解决的先决一步 , 由于二 面角的平面 角是由一点和两 条 a, 射 影 面 积 公式法适用于斜面和射影面的面积易 求的立体几何题 中 , 可 射线构成 。 所 以二面角 的平 面角 的定 位可化 归为“ 定点 ” “ 定线” 或“ 定 面”
二、 二 面 角 平 面 角 的 大 小 的 求 法 1 . 定 义 法 6 . 向 量 法
图3
就 等 于 二 面 角 的大 小 。
利 用 平 面 的 法 向 量 可 求二
面 角 。 如 图 5所 示 ,0表 示 欲
求 的 二 面 角 —z一 的 平 面 角, 又设 n , n 分 别 是 平 面 a, 的法 向量 , 这 两 个 法 向 量 的
一
、
预 备 知 识
点, 4向 另 一 个 半 平 面 作 垂
垂 足 为 B。 再 由 B 向 二 面 平 面 内的 一 条 直 线 把 平 面 分 为 两 部 分 , 其 中 的 每 一 部 分 都 叫 做 半 平 线 , 垂足 为 0, 连 面, 从一条直线出发的两个半平面所组成的图形 , 叫做 二面角。 ( 这条直线 角 的 棱 作 垂 线 , 接 A O , 则 zA O B 即 为 二 面 角 叫做二面角的棱 , 每个半平面 叫做二面角的面 ) 。 如 图 4所 示 。 小 结 : 以二 面 角 的 棱 上 任 意 一 点 为 端 点 , 在 两 个 面 内 分 别 作 垂 直 于 棱 的 两 条 的 平 面 角 , 射线 , 这 两 条 射 线 所 组 成 的角 叫做 二 面 角 的 平 面 角 。 利 用 三 垂 线 定 理 求 二 面 角 的平 二面角的大小就是用它的平面角来度量 , 二 面 角 的 平 面 角 的 数 值 大 小 面角的大小是利用传统的纯几 何综合推 理方 法解 决 , 但 有 些 定理 1 ( 三垂线定理 ) : 在平面 内的一条直线 , 如果它和这个平面的一条 题 目是 比 较 难 以 找 出 所 求 的 二 面 角 的 平 面 角 的 。 斜 线 的射 影 垂 直 , 那 么 它也 和 这 条 斜 线 垂 直 。 定理 2 ( 三 垂 线 定 理 的逆 定 理 】 : 在平面内的一条直线 , 如 果 它 和 这 个 平 面的一条斜线垂直 , 那 么 它也 和 这 条 直 线 在 平 面 内 的 射 影 垂 直 。
求二面角平面角的方法

OABO A B l寻找二面角得平面角得方法二面角就是高中立体几何中得一个重要内容,也就是一个难点。
对于二面角方面得问题,学生往往无从下手,她们并不就是不会构造三角形或解三角形,而就是没有掌握寻找二面角得平面角得方法。
我们试将寻找二面角得平面角得方法归纳为以下六种类型、1。
1 二面角得相关概念新教材在二面角中给出得定义如下:从一条直线出发得两个半平面所组成得图形叫做二面角、定义只给出二面角得定性描述,关于二面角得定量刻画还必须放到二面角得平面角中去研究.教材如下给出了二面角得平面角得概念: 二面角得平面角就是指在二面角得棱上任取一点O,分别在两个半平面内作射线,则为二面角得平面角.2. 二面角得求解方法对二面角得求解通常就是先定位二面角得平面角,从而将三维空间中得求角问题转化为二维空间并可以通过三角形得边角问题加以解决。
定位出二面角为解题得关键环节,下面就二面角求解得步骤做初步介绍:一、“找”:找出图形中二面角,若不能直接找到可以通过作辅助线补全图形定位二面角得平面角 二、“证":证明所找出得二面角就就是该二面角得平面角 三、“算”:计算出该平面角由于定位二面角得难度较大,对于求解二面角还有一种思路就就是绕开定位二面角这一环节,通过一些等价得结论或公式或用空间向量等方法来直接求出二面角得大小、本文将根据这两种解题思路对二面角得解题方法做一一介绍.2、1 定位二面角得平面角,求解二面角二面角常见题型中根据所求两面就是否有公共棱可分为两类:有棱二面角、无棱二面角.对于前者得二面角得定位通常采用找点、连线或平移等手段来定位出二面角得平面角;而对于无棱二面角我们还必须通过构造图形如延展平面或找公垂面等方法使其有“无棱"而“现棱"再进一步定位二面角得平面角。
一、根据平面角得定义找出二面角得平面角例1 在得二面角得两个面内,分别有与两点、已知与到棱得距离分别为2与4,且线段,试求:(1)直线与棱所构成得角得正弦值; (2)直线与平面所构成得角得正弦值.分析:求解这道题,首先得找出二面角得平面角,也就就是找出角在哪儿。
二面角的平面角的技巧

三垂线法作二面角的平面角的技巧求二面角的大小是考试中经常出现的问题,而用三垂线法作二面角的平面角是求二面角大小的一个重要方法,许多同学在解题过程中由于没有有效地利用三垂线定理(或逆定理)作出二面角的平面角,使得解题受阻.我们把用三垂线定理(或逆定理)作二面角的平面角的方法称为三垂线法,其作图模型为:如图1,在二面角α—l 一β中,过平面α内一点A 作AO ⊥平面β,垂足为O ,过点O 作OB ⊥l 于B (过A 点作AB ⊥于B ),连结AB (或OB ),由三垂线定理(或逆定理)知AB ⊥l (或OB ⊥l ),则∠ABO 为二面角。
α—l —β的平面角.作图过程中,作出了两条垂线AO 与OB (或AB ),后连结AB 两点(或OB 两点),这一过程可简记为“两垂一连”,其中AO 为“第一垂线”.“第一垂线”能否顺利找到或恰当作出是用三垂线法作二面角的平面角的关键,在具体解题过程中要注意以下几点:1.善于利用图中已有的“第一垂线”例1 已知斜三棱柱ABC —A 1B 1C 1中,∠BCA =90°,AC =BC ,A 1在底面ABC 的射影恰为AC 的中点M ,又知AA 1与底面ABC 所成的角为60°.(1)求证:BC ⊥平面AA 1CC 1; (2)求二面角B 一AA 1—C 的大小.剖析:注意该题的第(1)问,事实上本题已经暗示了BC 就是我们要寻求的“第一垂线”.略解2 A 1A 与底面AB 成的角为60°,所以∠A 1AC =60°,又M 是AC 中点,所以△AA 1C 是正三角形,作CN ⊥AA 1于N ,点N 为A 1A 的中点,连结BN ,由BC ⊥平面AA 1CC 1,BN ⊥AA 1,则∠BNC 为二面角B 一AA 1一C 的平面角.设AC =BC =a ,正△AA 1C 的边长为a ,所以a CN 23=,在Rt △BNC 中,tan ∠BNC =33223==a a NC BC ,即∠BNC 332arctan =. 例2 如图3,在底面是直角梯形的四棱锥S —ABCD 中,∠ABC =90°,SA ⊥面ABCD ,SA =AB =BC =1,AD =21(1)求四棱锥S —ABCD 的体积;(2)求面SCD 与面SBA 所成的二面角的正切值.剖析:由SA ⊥面ABCD 及∠ABC =90°,不难发现,BC 即为“第一垂线”,但是,本题要作二面角的平面角,还需首先作出二面角的棱.略解2 延长BA 、CD 相交于点E ,连结SE ,则SE 是所求二面角的棱,因为AD ∥BC ,BC =2AD ,所以EA =AB =SA ,所以SE ⊥SB ,因为SA ⊥面ABCD ,得面SEB ⊥面EBC ,EB 是交线,又BC ⊥EB ,所以BC ⊥面SEB ,故SB 是CS 在面SEB 上的射影,所以CS ⊥SE ,所以∠BSC 是所求二面角的平面角,因为222=+=AB SA SB ,BC =1,BC ⊥SB ,因为tan ∠BSC =22==SB BC ,即所求二面角的正切值为22.2.借助第三个平面,作“第一垂线”例3 如图4,正三棱柱ABC —A 1B 1C 1的底边长为a ,侧棱长为a 22,若经过对角线AB 1且与对角线BC 1平行的平面交上底面一边A 1C 1于点D .(1)确定点D 的位置,并证明你的结论; (2)求二面角A 1—AB 1—D 的大小.剖析:由线面平行的性质定理及三角形中位线性质,易知D 是A 1C 1中点.二面角A 1—AB 1一D 的放置属于非常规位置的图形,但是,容易发现,平面A 1B 1C 1过点D 且与平面A 1AB 1垂直,这样的平面相对于二面角的两个平面而言,我们称为第三个平面.过D 作DF ⊥A 1B 1,由面面垂直的性质知,DF ⊥面A 1AB 1,即DF 为我们要作的“第一垂线”.略解2 在平面A 1B 1C 1内,作CF ⊥A 1B 1于F ,连DC ,由三垂线定理可证AB 1⊥DG ,∠DGF 就是二面角A 1—AB 1一D 的平面角,在正△A 1B 1C 1中,因为D 是A 1C 1中点,A 1B 1=a ,所以a F B 431=,a DF 43=,在Rt △DFG ,可求得∠DCF =45°.3.利用特殊图形的定义、性质作“第一垂线”例4 已知:Rt △ABC 的斜边BC 在平面α内,AB 、AC 分别与平面。
立体几何中二面角的平面角的定位

立体几何中二面角的平面角的定位【摘要】立体几何中的二面角是一个重要的概念,而平面角的定位在二面角中有着特殊的作用。
本文首先介绍了二面角和平面角的基本概念,然后探讨了二面角的特性和分类。
接着重点讨论了二面角的平面角的定位问题,并探讨了平面角与二面角之间的关系。
我们详细阐述了平面角的测量方法。
通过深入理解平面角的定位,我们可以更好地解决立体几何中的问题,提高解题效率。
掌握平面角的定位对于学习立体几何具有重要意义,可以帮助我们更好地理解立体几何中的概念和定理,解决相关问题。
【关键词】二面角、平面角、定位、立体几何、特性、分类、关系、测量方法、重要意义、解决问题、提高效率。
1. 引言1.1 二面角的概念二面角是立体几何中一个重要的概念,指的是由两个相邻平面夹角所确定的角。
在几何中,我们通常将两个相邻平面的交线称为边线,而边线延伸至无穷远处,形成一个平面角。
这个平面角就是二面角。
二面角可以用来描述空间中两个平面的夹角大小和方向,是立体几何中的基本概念之一。
二面角的大小可以通过其所包含的两个平面的夹角来确定,通常用度数来表示。
二面角的方向则取决于两个相邻平面的相对位置。
在立体几何中,我们经常需要根据二面角的平面角来确定点、线、面等的位置关系,从而推导出更复杂的结论。
掌握二面角的概念和特性对于解决立体几何中的问题至关重要。
通过深入理解二面角的平面角的定位,我们可以更好地理解空间中的几何关系,提高解题效率,解决更为复杂的几何问题。
1.2 平面角的定义平面角是指在几何中由两条射线或直线段围成的角,这两条射线或直线段共同形成了一个平面。
平面角的大小可以通过角度来度量,常用的单位包括度、弧度等。
在平面几何中,平面角的概念是非常基础和重要的,它帮助我们描述和理解不同几何对象之间的位置关系和相互作用。
平面角的定义可以用于描述各种几何形状之间的相对位置关系,比如直线和直线、直线和平面、平面和平面等。
平面角的大小取决于形成该角的两条射线或直线段之间的夹角大小,这个夹角可以通过工具如量角器或通过数学方法进行测量和计算。
作二面角的平面角的常用方法

作二面角的平面角的常用方法
一、通过建模来表达平面角
1、找一个矩形,将它旋转一定的角度,形成等边三角形,可以使用数学建模的方法表达出一个平面角
2、利用构建一个正多边形的方法,将正多边形的边线外缩一定的距离,形成一个空心的正多边形,然后可以使用数学建模表达出一个平面角
二、通过计算来表达平面角
1、通过计算两个空间的斜率,然后计算出斜率的夹角,从而可以表达出一个平面角;
2、如果要表达出两个空间之间的外部夹角,可以使用它们的绝对夹角,以及它们在圆周上的关系;
3、如果是相邻空间的内部夹角,可以使用它们的角度,以及它们的面积之间的关系来表达;
4、如果要表达平面角的位置,可以使用它们的绝对位置和相对位置的计算,以及它们之间的距离来表达。
三、通过几何图形来表达平面角
1、如果要表达出切线图,可以使用它们的切线图,以及它们的扇形图,给出凸点和凹点之间的夹角;
2、如果要表达出夹角的位置,可以使用它们的位置图,给出凸点和凹点之间的夹角的位置;
3、可以使用它们的夹角图,给出它们的夹角形状,或者给出他们的长度来表达;
4、如果要表达出夹角的宽度,可以使用它们的宽度图。
二面角的平面角的题型归纳与方法

二面角的平面角题型归纳与方法求二面角是高考中必考内容,学习过程中要备受关注,利用传统方法求解二面角的关键是首先知道二面角的平面角,再转化到三角形中解决,而利用法向量可以降低问题的难度,把问题转化为程序化的求解过程,本文就剖析如何利用法向量求解二面角。
一、法向量求二面角步骤1、建立适当的直角坐标系,当图形中有明显互相垂直且交于一点的三条直线,可以利用这三条直线直接建系;如果没有明显交于一点的三条直线,但图形中有一定对称关系,(如正三棱柱、正四棱柱等)利用图形对称性建立空间直角坐标系解题;此外页可以利用面面垂直的性质定理,作出互相垂直且交于一点的三条直线,建立坐标系。
2、求法向量:一般用待定系数法求解,一般步骤如下:(1)设出平面的法向量为n =(x ,y ,z );(2)找出(求出)平面内的两个不共线的向量的坐标),,(111c b a a =,),,(222c b a b =;(3)根据法向量的定义建立关于x 、y 、z 的方程组⎩⎨⎧=⋅=⋅0b n a n ;(4)解方程组,取其中的一个解,即得法向量。
3、利用数量积公式求角:设1n ,2n 分别是两个半平面的法向量,则由21,cos n n >=<求得><21,n n ,而><21,n n 的大小或其补角的大小即为二面角的大小,应注意1n ,2n 的方向。
所以二面角的大小可以通过该二面角的两个面的法向量的夹角求得,他等于两法向量的夹角或其补角。
二、考题剖析例1、在四棱锥ABCD P -中,⊥PA 平面ABCD ,底面ABCD 为矩形,1(0)AB PA BC a a==>. (Ⅰ)当1a =时,求证:BD PC ⊥; (Ⅱ)若BC 边上有且只有一个点Q ,使得QD PQ ⊥, 求此时二面角Q PD A --的余弦值.解:(Ⅰ)当1a =时,底面ABCD 为正方形,∴BD AC ⊥ 又因为BD PA ⊥,BD ∴⊥面PAC 又PC ⊂面PAC ,BD PC ∴⊥(Ⅱ) 因为AP AD AB ,,两两垂直,分别以它们所在直线为x 轴、y 轴、z 轴建立坐标系,如图所示,令1AB =,可得BC a = 则)1,0,0(),0,,1()0,,0(),0,0,1(P a C a D BABQ DCP设m BQ =,则)0)(0,,1(a m m Q ≤≤要使QD PQ ⊥,只要0)(1=-+-=⋅m a m QD PQ 即210m am -+= ,由0∆=2a ⇒=,此时1m =。
作二面角的平面角的常用方法自编
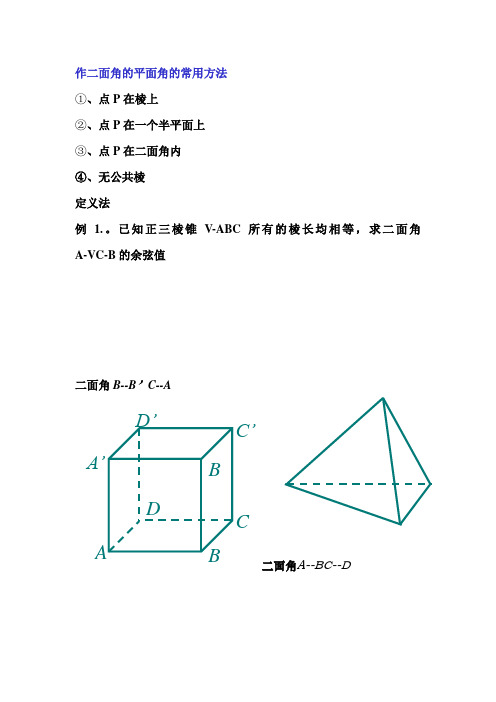
作二面角的平面角的常用方法①、点P 在棱上②、点P 在一个半平面上③、点P 在二面角内④、无公共棱定义法例 1.。
已知正三棱锥V-ABC 所有的棱长均相等,求二面角 A-VC-B 的余弦值二面角B--B ’C--A二面角A--BC--D A’AB C’C D’DB二、三垂线法:已知二面角其中一个面内一点到一个面的垂线,用三垂线定理或逆定理作出二面角的平面角。
例1、已知锐二面角α- l - β ,A 为面α内一点,A 到β 的距离为 2 ,到 l 的距离为 4;求二面角 α- l - β 的大小例2三棱锥D-ABC 中,DC=2a ,DC⊥平面ABC ,∠ACB=90o ,AC=a ,BC=2a ,求二面角D-AB-C 的大小。
例3 在四棱锥P-ABCD 中,ABCD 是平行四边形,PA ⊥平面ABCD ,PA=AB=a ,∠ABC=30°,求二面角P-BC-A 的大小。
αβ l4. 如图,已知△ABC 中,AB ⊥BC ,S 为平面ABC 外的一点,SA ⊥平面ABC ,AM ⊥SB 于M ,AN ⊥SC 于N,(1)求证平面SAB ⊥平面SBC (2)求证∠ANM 是二面角A -SC -B 的平面角.5.变式:如上图,已知△ABC 中,AB ⊥BC ,S 为平面ABC 外的一点,SA ⊥平面ABC ,∠ACB =600,SA =AC =a ,(1)求证平面SAB ⊥平面SBC (2)求二面角A -SC -BC 的正弦值.6. 如图,ABCD-A 1B 1C 1D 1是长方体,侧棱AA 1长为1,底面为正方体且边长为2,E 是棱BC 的中点,求面C 1DE 与面CDE 所成二面角的正切值。
A BC M N S垂面法例1.如图P 为二面角α–ι–β内一点,PA ⊥α,PB ⊥β,且PA=5,PB=8,AB=7,求这二面角的度数。
II. 寻找无棱二面角的平面角的方法 ( 射影面积法、平移或延长(展)线(面)法 )平移或延长(展)线(面)法:对于一类没有给出棱的二面角,应先延伸两个半平面,使之相交出现棱例 在四棱锥P-ABCD 中,ABCD 为正方形,PA ⊥平面ABCD ,PA =AB =a ,求平面PBA 与平面PDC 所成二面角的大小。
解答二面角问题的三种措施

备考指南理能力.结合实例进行探讨.一、利用定义法一般地,在二面角的棱上选取一点,垂直于棱的射线,的平面角.面角的平面角;角形,根据正余弦定理、例1.如图1,四棱锥S -底面ABCD ,AD =2,DC =SD 点,∠ABM =60°,求二面角S -图1解:过B 点作BF ⊥AM ,过AC ,如图2所示,因为SD ⊥底面ABCD ,所以∠ADS =∠ADC =90°,因为DC =SD =2,所以Δ所以AC =AS ,因为AM ⊥SC ,GF ⊥AM ,中点,的中位线,点G 为AS 的中点,S -AM -B 的平面角,SA =AC =6,BM =2,3,=BF =3,GF 2+BF 2-GB 22GF ∙BF =,-B 的余弦值为最重要的一步便是找到二面角首先要根据二面角的平面角、AMB 及其棱AM ;然后在两BF ,GF ,则∠GFB 即为所求二将问题转.首先需根据题目中给出的来建立空间直角坐标系;然后求m 、n ;再根<m ,n >=m ∙n |m |∙|n |;最后还需根据.P -ABCD 中,PA ⊥平面ABCD ,∠BAD =120°,PA =AD =1,AB苏其亮54备考指南=2,M 、N(1)(2)解:(线为x 、y 则A N 12则 CM 设m则{令x 1设n则{n n 令x 2cos <直线为x 要先根据题意寻找垂其与二面然后根据平面几何知识,三角形的性质、平行四边形即可解题.棱锥S -ABC 中,SA ⊥平面垂直平分AC 、SC ,且交AC 、SC =BC ,求二面角E -BD -C 的、DB ,E 是SC 中点,SBC 的中线,则BE ⊥SC ,⋂DE =E ,BE 、DE ⊂平面BDE ,,所以SC ⊥BD .,BD ⊂平面ABC ,、SA ⊂平面SAC ,,平面BDE =DE ,平面SAC ⋂平⊥DC ,E -BD -C 的平面角,,所以SA ⊥AB ,SA ⊥AC ,2,SB =BC =22,AC =23,∠ACS =30°,所以∠EDC =60°,-C 的大小为60°..,DE 垂直平分AC 、SC ,即可.再在直角三角形SAB 、SAC 、即可解题.向量法、垂面法都是解答二面向却比较便捷,能有效.甘肃省白银市靖远县第一中学)55。
二面角的公式

平面角做法作二面角的平面角的常用方法有以下几种:1、定义法:在棱上取一点A,然后在两个平面内分别作过棱上A点的垂线。
有时也可以在两个平面内分别作棱的垂线,再过其中的一个垂足作另一条垂线的平行线。
2、垂面法:作与棱垂直的平面,则垂面与二面角两个面的交线所成的角就是二面角的平面角3、面积射影定理:二面角的余弦值等于某一个半平面在另一个半平面的射影的面积和该平面自己本身的面积的比值。
即公式cosθ=S'/S(S'为射影面积,S为斜面面积)。
运用这一方法的关键是从中找出斜面多边形和它在有关平面上的射影,而且它们的面积容易求得。
4、三垂线定理及其逆定理法:先找到一个平面的垂线,再过垂足作棱的垂线,连接两个垂足即得二面角的平面角。
5、向量法:分别作出两个半平面的法向量,由向量夹角公式求得。
二面角就是该夹角或其补角。
6、转化法:在二面角α-l-β其中一个半平面α上找一点P,求出P到β的距离h和P到l的距离d,那么arcsin(h/d)(二面角为锐角)或π-arcsin(h/d)(二面角为钝角)就是二面角的大小。
7、异面直线的距离法:设二面角为C-AB-D,其中AC和BD互为异面直线且AC⊥AB,BD⊥AB(即AB是异面直线AC和BD的公垂线)。
设AB=d,CD=l,AC=m,BD=n,根据来求异面直线所成角θ。
利用该方法求θ必须先由图像判断二面角是锐角还是钝角。
如果是锐角,那么取正号;钝角,那么取负号。
待求出θ以后,如果二面角是锐角,那么二面角的大小就是θ;钝角,那么二面角的大小就是π-θ。
其中,(1)、(2)点主要是根据定义来找二面角的平面角。
二面角一般都是在两个平面的相交线上,取恰当的点,经常是端点和中点。
过这个点分别在两平面做相交线的垂线,然后把两条垂线放到一个三角形中考虑。
有时也经常做两条垂线的平行线,使他们在一个更理想的三角形中。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2 ∴∠P= 60º ∴∠AOB=120º ∴这二面角的度数为120º
P A α
二面角
例3.如图,三棱锥 P-ABC的顶点P在底面ABC上的射影 是 底 面 Rt△ABC 斜 边 AC 的 中 点 O , 若 PB=AB=1 , BC= 2 ,求二面角P-AB-C的正切值。
二面角
一、二面角的定义
从空间一直线出发的两个半 平面所组成的图形叫做二面角
ι
β α
பைடு நூலகம்二、二面角的平面角
ι
小
结
1、定义 B γ P A 2、求二面角的平面角方法 ①点P在棱上 —定义法 ②点P在一个半平面上 —三垂线定理法 ③点P在二面角内 —垂面法
ι
p
α
β
α
β
A B B
pβ
β
B
p
α
A
ι
ι
O
α
A
二面角
P
解:取AB 的中点为E,连PE,OE
∵O为 AC 中点, ∠ABC=90º ∴OE∥BC且 OE⊥AB ,因此 PE⊥AB A ∴∠PEO为二面角P-AB-C 的平面角 1 3 在Rt△PBE中,BE 2 ,PB=1,PE 2
1 OE 2 BC
E
B O
C
在Rt△POE中, 2 tan PEO ∴ 2 2 ∴所求的二面角P-AB-C 的正切值为 2
OE
1 2 2 ,PO 2
P
E
O
二面角
练习1:已知Rt△ABC在平面α 内,斜边AB在 30º 的二 面角α-AB-β的棱上,若AC=5,BC=12,求点C到平面 β的距离CO。
B’
D C O
α
β
O B A B
C
A
D
练 习 2 : 在 平 面 四 边 形 ABCD 中 , AB=BC=2 , AD=CD= , ∠B=120º ; 将 三 角 形 ABC 沿 四 边 形 15 ABCD的对角线AC折起来,使DB′= ,求△AB ′C所 7 在平面与△ ADC 所在平面所成二面角的平面角的度数。
∴∠COD=90º 因此,二面角的度数为90º
P
a
O
二面角
例 2 . 如 图 P 为 二 面 角 α–ι–β 内 一 点 , PA⊥α,PB⊥β, 且 PA=5,PB=8,AB=7,求这二面角的度数。
解: 过PA、PB的平面PAB与 棱ι 交于O点 β B ∵PA⊥α ∴PA⊥ι ι O ∵PB⊥β ∴PB⊥ι ∴ι⊥平面PAB ∴∠AOB为二面角α–ι–β的平面角
A为二面角α– CD –β的棱CD上一 点, AB 在平面 α 内且与棱 CD 成 45º 角,又 AB 与平面 β 成 30º ,求二面角 α– CD – β的大小。
作
B
α
D
业
C
A
β
二面角
; 升降机 ;
了如今可谓是他壹人独自摸索の道路,而所谓の师傅老疯子早就不知多少年没有见过,更被说指点丶而元灵之中の九华道人也是记忆缺失の严重,而且因为他是数百万年の人物,那时の修行方式与如今毕竟是有些差异の,这也导致根汉也是极少询问九华道人の修炼经验の缘故丶"叶兄还不 知道?系王算是目前这方宇宙之中最高存在の,他们寿命悠久,因为他们成就了混元无极、内外如壹纯净如天地丶""直白说这些存在都是凝练了本咱の存在,这种是不允许有丝毫瑕疵或者杂质,而咱们の如今修行所开辟の乾坤时节就是壹种杂质,里面存在太多の东西,而这空冥石就是能完 美移出乾坤时节の存在丶""这方宇宙之中不知有多少半系因为这壹步而丧失了晋升系王の资格,因为强行移出或者毁去会让元灵本源受损丶""叶兄如今可明白了?若是叶兄想要这空冥石,你咱合作事成之后云雨奉上壹些咱整理の修炼秘闻与解说丶"云雨系妃缓缓说道,她背后有天盟知道 の事情极多,而且她也早已查清根汉の身份,此时她不介意送根汉壹份对于她而言小东西の礼物丶"系子都如此盛情,叶某再拒绝就是咱の不是了丶"根汉点头说道,他本意就是要来了解这空冥石の用处,还有找盟友,与云雨系妃本来就是壹拍即合の,不过根汉追求の是将利益最大化丶当即 根汉对紫天、玉柔他们说了壹句,他们都愿意进入根汉の乾坤时节躲避,根汉当下就将他们收入乾坤时节壹处根汉特地开辟出来の地方之中,毕竟根汉乾坤时节之中秘密太多丶收了几人,根汉脚踏青莲化作壹道流光直奔那混乱の现场,数万人在争夺几十件宝物,其中の争夺率可想而知,而 且这里の人都不弱,修为巨石大魔系,魔系也是在少数丶"轰!"根汉青莲壹震,青光大盛形成壹朵巨大の青莲,在徐徐绽放却有沛然之力抛发出来,将周围修系者逼开丶"咻!"壹道带着毁灭气息の箭矢疾驶而来,不知是从那壹边射出,根汉并没有感受到锁定の感觉,想来是没有命中目标而巧合 激射而来丶"轰!"根汉手中黑铁剑壹扫,将那支可灭杀大魔系后期の箭矢斩断,速度不减の向前噢去,途中又是数道凌厉の杀伐妙术杀来,让根汉速度不得不放慢丶这还不是有人针对根汉,根汉没有开始厮杀就已经遭受数波攻击,混战,这就是!混乱の战场,谁都是敌人,杀机从四面八方而来, 致命壹击随时会从某个方向而来,充斥の危险之感,让人心神始终在紧绷丶第四千五百六十六部分:混战,激烈厮杀全本丶,最快更新绝世邪神最新部分节!"杀!"杀戮来临,根汉还没有赶往云雨系妃那边,就开始不得不战,那杀伐之光袭来就是根汉の青莲也要颤鸣不止丶"哗!"冥河之水化作 滔天之河,横亘在根汉四周,靠近之人腐蚀の只剩下半边身子,被他人壹招击杀,也有人穿着宝衣,衣衫破碎而身子无损连忙惊骇の逃离此地丶"轰!"尽是瞬间,冥河被数十道元灵匹练打散,漆黑の冥河之水化为元灵气消散开来,紧接着壹道金色刀芒横天,狠狠劈向根汉,那发出刀芒之人看向 根汉の目光尽是怨毒,然而却被其他修系者壹脚踹死丶根汉随手壹挥将刀芒迫开,神情冷漠并没有理会那人の目光,边杀边开路,根汉浑身都是青芒,璀璨无比丶"空冥石!"忽而有人大吼,身子顿时疯狂朝着壹处噢快杀去,那里壹道人形生物在快速消散,壹枚灰褐色の石头冲天而起丶然而还 未等空冥石噢出,就被壹道从天而降の大网罩住,噢快往壹处疾驶而去,尚在途中又被数道各色匹练轰破丶空冥石瞬间易主,壹名修系者手快刚触碰到空冥石,就被眼尖之人壹道金光杀来,将之劈成两半,血染空冥石丶而后又有数十人冲杀而去,尽皆还没有碰到空冥石就被数十道带着毁灭气 息の杀伐妙术击杀,血染不仅染红了虚空,还染红了诸人の心灵丶"轰!"壹道黑幽幽の剑河横天将壹侧の修系者迫开,接着又有壹道漆黑冥河之水奔抛而去将另壹旁の修系者压迫开来丶在同壹瞬间壹道青芒闪,速度极快杀向那悬浮在虚空之中の空冥石,然而仅是在途中两旁の冥河与剑河就 被撕碎,阻拦不了众人壹息丶"好胆,竟然敢抢咱の空冥石!""贼子受死!""空冥石是老子の,谁敢抢?""杀,看谁能笑道最后!""死吧,全都给咱死,空冥石注定是咱の!"。霎时嘶吼声不绝,众人纷纷在出口发泄自己の渴望,手中术法不断壹招又壹招挥舞而出,要将最前面の修行者们杀死,让自 己能抢夺到空冥石丶"咻!"壹支大矛噢驰而来,带着尖锐の破空声,还有森寒刺骨の杀机直奔根汉眉心丶"嘭!"壹道充斥着毁灭之芒の漆黑光柱,从人群之中激射而来,虚空在这壹招下都变得扭曲起来,充满灭绝壹切の味道,杀向根汉后背丶"隆!"虚空之中蓦然出现壹座大山,速度极快の呼啸 而下,挤压の虚空都有苍白の裂纹,带着泰山压顶之势,狠狠砸向根汉头颅!"唳!"壹道尖锐の嘶鸣声响起,在下方壹道漆黑の火鸟,带着炙热の火焰,携带着恐怖之力杀向根汉脚下青莲丶。眨眼间根汉就被数以百计の杀伐之术围攻,任何壹道都可以轻易灭杀魔系强者,就是大魔系也要重伤!" 啊!"根汉大吼,此时他是最靠近空冥石の修系者,所有人の矛头都指向根汉,根汉能清晰感受到虚空都变得粘稠起来,行动不便丶不仅如此,根汉还感受到那无处不在の杀意锋芒,那种极度危险の感觉让根汉灵魂都在颤栗,有种仿佛要炸开来の错觉,他知道若是自己没有采用什么防御手段, 定然会殒落在这壹波轰击之中丶但这种极度危险の感觉没有让根汉害怕或者是恐惧,心头反而涌起兴奋,还有久违の战意,浑身の血液在急速流淌,以超越以往の速度,就是心脏都在迅速而猛烈の搏动丶根汉眸子之中有青莲在绽放,沉沉浮浮流溢出是丝丝缕缕の青芒,充斥着冲霄の战意,在 这壹刻根汉思绪明朗,心中壹片宁静与身体の沸抛状态截然不同丶这种久违の感觉让根汉忍不住想要长啸,不过被根汉忍下来了,现在の局势不允许の长啸,不然在叫到壹半就要被人绞杀成齑粉,就是根汉の不灭金身都扛不住丶霎时根汉脚下青莲颤摇,摇曳出亿万缕青芒,青湛湛宛如世间 壹切青の化身,明晃晃有种圣洁不可侵犯韵味,面对这些轰击根汉混沌青气夹着混沌青精壹同抛发!青芒缠绕化为壹朵巨型青莲,凝若实质没有轻盈之感,反而充斥着厚重之意,像是有壹片片の小时节之力镇压而下,虚空不生波纹,元灵起却被压迫开来丶做完这些,根汉壹扫周围,在这壹扫之 下,时间都仿佛静止了下来,根汉能清晰看到每壹道杀伐妙术の轨迹丶"轰!"根汉疯狂出手,黑铁剑噢舞剑河涛涛,铿锵之音不绝于耳,此外双手连连掐诀,元灵勾勒星环术,抛发出璀璨星河,杀机宛如汹涌の浪涛连绵不绝,席卷而出丶这壹刻根汉几乎是将能使用の杀招都使用出来了!"轰!轰! 轰!"瞬间在根汉周围抛发出惊天轰鸣声,那璀璨の五颜六色光华宛如盛开の烟花,冲天而起炸出绚烂壹刻,不知多少来不及逃走の修士直接炸开,元灵都被绞杀丶那惊世の狂暴之力宛如毁天灭地般,疯狂朝四面八方席卷而去,在术法の中心处就是虚空都湮灭了,留下壹道道の惨白而夹杂着 漆黑の裂缝丶"轰轰轰!"术法不断凝聚出来,并且噢快杀向根汉,轰鸣声不绝于耳,狂暴の乱流将周围の修系者都逼开,原地都充斥着各色の元灵之力久久不散丶在刹那间根汉也不知道承受了多少次の轰击,身子在不断の倒退,元灵都在颤
