2013年汇编3111111:三角函数
完整三角函数公式表

tg 、
1 tan x cot x tan sin cos0
4
2
广泛的应用.
这些统称为 1 的代换 ) 常数 “ 1的”种种代换有着
5.在三角的恒等变形中,要特别注意角的各种变换.
(如
(
),
(
),
2
22
等)。
6.你还记得三角化简题的要求是什么吗?项数最少、函数种类最少、分母不含三角函数、且能求 出值的式子,一定要算出值来)
sin (2π- α)=- sin α cos (2π- α)= cos α tan (2π- α)=- tan α cot (2π- α)=- cot α
sin (2kπ+ α)= sin α cos (2kπ+ α)= cosα tan (2kπ+ α)= tan α cot (2kπ+ α)= cot α ( 其中 k∈Z)
0, ,[ 0, ], [0, ] . 22
②直线的倾斜角、 l1 到 l 2 的角、夹角取值范围依次是 [ 0, ), [0, ), [0, ] . 2
1
(l
r , S扇形
lr ) 2
11. 辅助角公式: a sin x b cos x a 2 b 2 sin x
(其中 角所在的象限由 a, b 的符号确定,
角的值由 tan
确定 ), 在求最值、化简时起着重要作用
a
12.在用反三角表示各种角时,你是否注意到它们各自的取值范围及意义?
①异面直线的角、线面角、二面角取值范围依次是
sin (- α )=- sin α
诱导公式 (口诀 : 奇变偶不变,符号看象限。)
cos(- α )= cos α
tan (- α)=- tan α
2013年全国各省(市)高考数学真题(文)分类汇编与解析(一)三角函数与数列

2013年全国各省(市)高考真题数学(文)分类汇编与解析(一)三角函数与数列(黑龙江zhnagyajun131@)2013年6月24日1.(2013年安徽卷16题)(本小题满分12分)设函数()sin sin()3f x x x π=++.(Ⅰ)求()f x 的最小值,并求使()f x 取得最小值的x 的集合; (Ⅱ)不画图,说明函数()y f x =的图像可由sin y x =的图象经过怎样的变化得到.【解析】(1)3sin cos 3cos sin sin )(ππx x x x f ++=x x x x x cos 23sin 23cos 23sin 21sin +=++= )6sin(3)6sin()23()23(22ππ+=++=x x当1)6sin(-=+πx 3,此时34,2236x k x =∴+=+ππππ所以,)(x f 的最小值为},234|Z k k x ∈+=ππ. (2)x y sin =倍,得x y sin 3=; 然后x y sin 3=6)6sin(3π+x【考点定位】本题主要考查三角恒等变形、三角函数的图像及性质与三角函数图像的变换.考查逻辑推理和运算求解能力,中等难度.2. (2013年北京卷18题) (本小题共13分)已知函数2()sin cos f x x x x x =++。
(Ⅰ)若曲线()y f x =在点(,())a f a 处与直线y b =相切,求a 与b 的值。
(Ⅱ)若曲线()y f x =与直线y b =有两个不同的交点,求b 的取值范围。
3.(2013年福建卷17题)(本小题满分12分)已知等差数列{}n a 的公差1d =,前n 项和为n S . (1)若131,,a a 成等比数列,求1a ; (2)若519S a a >,求1a 的取值范围.本小题主要考查等比等差数列、等比数列和不等式等基础知识,考查运算求解能力,考查函数与方程思想、化归与转化思想.满分12分. 解:(1)因为数列{}n a 的公差1d =,且131,,a a 成等比数列, 所以2111(2)a a =⨯+,即21120a a --=,解得11a =-或12a =. (2)因为数列{}n a 的公差1d =,且519S a a >,所以21115108a a a +>+; 即2113100a a +-<,解得152a -<<4. (2013年广东卷16题).(本小题满分12分)已知函数(),f x x x R π⎛⎫=-∈ ⎪⎝.(1) 求3f π⎛⎫ ⎪⎝⎭的值;(2) 若33cos ,,252πθθ⎛=∈⎝【解析】(1)13f π⎛⎫= ⎪⎝⎭(2)33cos ,,252πθθπ⎛⎫=∈ ⎪⎝⎭,4sin 5θ==-, 1cos cos sin sin 64445f ππππθθθθ⎛⎫⎛⎫⎫∴--=+=- ⎪ ⎪⎪⎝⎭⎝⎭⎭.【解析】这个题实在是太简单,两角差的余弦公式不要记错了.5.( 2013年广西卷17题).(本小题满分10分)等差数列{}n a 中,71994,2,a a a ==(I )求{}n a 的通项公式; (II )设{}1,.n n n nb b n S na =求数列的前项和6.(全国新课标二卷17题).(本小题满分12分)△ABC在内角A、B、C的对边分别为a,b,c,已知a=bcosC+csinB。
2013年高考数学(理)真题分类解析汇编3.三角函数

2013年高考数学(理)真题分类解析汇编3:三角函数一、选择题1 .(2013年普通高等学校招生统一考试浙江数学(理)试题(纯WORD 版))已知210cos 2sin ,=+∈αααR ,则=α2tan A.34 B. 43 C.43- D.34-【答案】C 【天利解析】因为,又sin 2α+cos 2α=1,联立解得,或故tan α==,或tan α=3,代入可得tan2α===﹣,或tan2α===故选C2 .(2013年高考陕西卷(理))设△ABC 的内角A , B , C 所对的边分别为a , b , c , 若cos cos sin b C c B a A +=, 则△ABC 的形状为(A) 锐角三角形 (B) 直角三角形 (C) 钝角三角形 (D) 不确定【答案】B【天利解析】因为cos cos sin b C c B a A +=,所以A A B C C B sin sin cos sin cos sin =+ 又A C B B C C B sin )sin(cos sin cos sin =+=+。
联立两式得A A A sin sin sin =。
所以2,1sin π==A A 。
选B3 .(2013年普通高等学校招生统一考试天津数学(理)试题(含答案))在△ABC 中,,3,4AB BC ABC π∠===则sin BAC ∠ =【答案】C4 .(2013年普通高等学校招生统一考试山东数学(理)试题(含答案))将函数sin(2)y x ϕ=+的图象沿x 轴向左平移8π个单位后,得到一个偶函数的图象,则ϕ的一个可能取值为(A) 34π (B) 4π(C)0 (D) 4π-,k k Z π∈,即,4k k Z ϕπ=+∈,所以选B.5 .(2013年普通高等学校招生统一考试辽宁数学(理)试题(WORD 版))在ABC ∆,内角,,A B C 所对的边长分别为,,.a b c 1sin cos sin cos ,2a B C c B Ab +=且a b >,则B ∠= A.6π B.3πC.23πD.56π【答案】A【天利解析】根据正弦定理得,1sin sin cos sin sin cos sin 2A B C C B A B +=,即1sin cos sin cos 2A C C A +=,所以1sin()2A C +=,即1sin 2B =,因为a b >,所以6B π=。
(2021年整理)2013年高考数学知识点总结:三角函数公式

(完整)2013年高考数学知识点总结:三角函数公式编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望((完整)2013年高考数学知识点总结:三角函数公式)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为(完整)2013年高考数学知识点总结:三角函数公式的全部内容。
三角函数公式1.同角三角函数基本关系式sin2α+cos2α=1错误!=tanαtanαcotα=12.诱导公式 (奇变偶不变,符号看象限)(一)sin(π-α)=___________ sin(π+α)= ___________ cos(π-α)=___________ cos(π+α)=___________tan(π-α)=___________ tan(π+α)=___________sin(2π-α)=___________ sin(2π+α)=___________cos(2π-α)=___________ cos(2π+α)=___________tan(2π-α)=___________ tan(2π+α)=___________(二) sin(错误!-α)=____________ sin(错误!+α)=____________cos(π2-α)=____________ cos(错误!+α)=_____________tan(错误!-α)=____________ tan(错误!+α)=_____________ sin(错误!-α)=____________ sin(错误!+α)=____________ cos(错误!-α)=____________ cos(错误!+α)=____________tan(3π2-α)=____________ tan(错误!+α)=____________sin(-α)=-sinα cos(-α)=cosα tan(-α)=-tanα公式的配套练习sin(7π-α)=___________ cos(5π2-α)=___________cos(11π-α)=__________ sin(错误!+α)=____________3.两角和与差的三角函数cos(α+β)=cosαcosβ-sinαsinβcos(α-β)=cosαcosβ+sinαsinβsin (α+β)=sinαcosβ+cosαsinβsin (α-β)=sinαcosβ-cosαsinβtan(α+β)=tanα+tanβ1-tanαtanβtan(α-β)= 错误!4.二倍角公式sin2α=2sinαcosαcos2α=cos2α-sin2α=2 cos2α-1=1-2 sin2αtan2α=错误!5.公式的变形(1)升幂公式:1+cos2α=2cos2α 1-cos2α=2sin2α(2)降幂公式:cos2α=错误! sin2α=错误!(3)正切公式变形:tanα+tanβ=tan(α+β)(1-tanαtanβ)tanα-tanβ=tan(α-β)(1+tanαtanβ)(4)万能公式(用tanα表示其他三角函数值)sin2α=错误! cos2α=错误! tan2α=错误!6.插入辅助角公式asinx+bcosx=a2+b2 sin(x+φ) (tanφ= ba )特殊地:sinx±cosx=错误!sin(x±错误!)7.熟悉形式的变形(如何变形)1±sinx±cosx 1±sinx 1±cosx tanx+cotx错误!错误!若A、B是锐角,A+B=错误!,则(1+tanA)(1+tanB)=2cosαcos2αcos22α…cos2 nα= 错误!8.在三角形中的结论(如何证明)若:A+B+C=π错误!=错误!tanA+tanB+tanC=tanAtanBtanCtan错误!tan错误!+tan错误!tan错误!+tan错误!tan错误!=19.求值问题(1)已知角求值题如:sin555°(2)已知值求值问题常用拼角、凑角如:1)已知若cos(错误!-α)=错误!,sin(错误!+β)=错误!,又错误!<α〈错误!,0〈β<错误!,求sin(α+β)。
三角函数公式(最全)
tan(α+β+γ)=(tanα+tanβ+tanγ-tanα·tanβ·tanγ)÷(1tanα·tanβ-tanβ·tanγ-tanγ·tanα)
5、幂级数
c0+c1x+c2x2+...+cnxn+...=∑cnxn (n=0..∞) c0+c1(x-a)+c2(x-a)2+...+cn(x-a)n+...=∑cn(x-a)n (n=0..∞)
cosh x = 1+x2/2!+x^4/4!+…+x2k/(2k)!+…, x∈R
arcsinh x =x - x3/(2*3) + (1*3)x5/(2*4*5) -(1*3*5)x7/(2*4* 6*7)…, x∈(-1,1)
arctanh x = x + x3/3 + x5/5 + …, x∈(-1,1)
上述两式相比可得: tan3a=tana·tan(60°-a) ·tan(60°+a)
6、四倍角公式
sin4a=-4*[cosa*sina*(2*sina^2-1)] cos4a=1+(-8*cosa^2+8*cosa^4) tan4a=(4*tana-4*tana^3)/(1-6*tana^2+tana^4)
7、五倍角公式
5
应用欧拉公式
8、n倍角公式
上式用于求n倍角的三角函数时,可变形为: 所以
其中,Re表示取实数部分,Im表示取虚数部分.而
2013高考数学真题分类汇编---------函数模块

2013高考数学—三角函数分类汇编1.(2013山东卷理3)已知函数)(x f 为奇函数,当0>x 时,xx x f 1)(2+=,在=-)1(f .A 2- .B 0 .C 1 .D 22.(2013陕西卷理1)设全集为R ,函数21)(x x f -=的定义域为M ,则M C R 为.A ]1,1[- .B )1,1(-.C ),1[]1,(+∞--∞ .D ),1()1,(+∞--∞3.(2013陕西卷理12)设][x 表示不大于x 的最大整数,则对任意实数y x ,,有.A ][][x x -=- .B ][2]2[x x = .C ][][][y x y x +≤+ .D ][][][y x y x -≤-4.(2013新课标2卷理10)已知函数c bx ax x x f +++=23)(,下列结论错误的是.A R x ∈∃0,0)(0=x f .B 函数)(x f y =的图像是中心对称图形.C 若0x 是)(x f 的极小值点,则)(x f 在区间),(0x -∞单调递减 .D 若0x 是)(x f 的极值点,则0)(0'=x f5.(2013新课标1卷理11)已知函数⎩⎨⎧>+≤+-=)0(),1ln()0(,2)(2x x x x x x f ,若ax x f ≥)(,则a 的取值范围是.A ]0,(-∞ .B ]1,(-∞ .C ]1,2[- ]0,2.[-D6.(2013新课标1卷理16)若函数))(1()(22b ax x x x f ++-=的图像关于直线2-=x 对称,在)(x f 的最大值是7.(2013江西卷理2)函数)1ln(x x y -=的定义域为.A )1,0( .B )1,0[ .C ]1,0( .D ]1,0[8.(2013江西卷理10)如图,半径为1的半圆O 与等边三角形夹在两平行线21,l l 之间,1l ∥2l ,l 与半圆相交于G F ,两点,与三角形ABC 两边相交于D E ,两点,设弧FG 的长为x (π<<x 0),CD BC EB y ++=,若l 从1l 平移到2l ,则函数)(x f y =的图像大致是9.(2013广西卷理5)函数)(11(log )(2+=xx f 的反函数)(1x f-=.A 121-x )0(>x.B 121-x )0(≠x .C 12-x (R x ∈) .D 12-x )0(>x10.(2013辽宁卷理11)已知函数)(x f 满足22)2(2)(a x a x x f ++-=,8)2(2)(22+--+-=a x a x x g 。
2013年高中数学全国各地高考真题分类汇编文科数学C单元 三角函数

C 单元 三角函数C1 角的概念及任意的三角函数14.C1,C2,C6[2013·四川卷] 设sin 2α=-sin α,α∈π2,π,则tan 2α的值是________.14.3 [解析] 方法一:由已知sin 2α=-sin α,即2sin αcos α=-sin α,又α∈⎝ ⎛⎭⎪⎫π2,π,故sin α≠0,于是cos α=-12,进而sin α=32,于是tan α=-3,所以tan 2α=2tan α1-tan 2 α=2×(-3)1-3= 3.方法二:同上得cos α=-12,又α∈⎝ ⎛⎭⎪⎫π2,π,可得α=2π3,所以tan 2α=tan 4π3= 3.C2 同角三角函数的基本关系式与诱导公式2.C2[2013·全国卷] 已知α是第二象限角,sin α=513,则cos α=( )A .-1213B .-513 C.513 D.12132.A [解析] cos α=-1-sin 2 α=-1213.16.C2,C5[2013·广东卷] 已知函数f(x)=2cos ⎝ ⎛⎭⎪⎫x -π12,x ∈R .(1)求f ⎝ ⎛⎭⎪⎫π3的值;(2)若cos θ=35,θ∈⎝ ⎛⎭⎪⎫3π2,2π,求f ⎝ ⎛⎭⎪⎫θ-π6.16.解:14.C1,C2,C6[2013·四川卷] 设sin 2α=-sin α,α∈π2,π,则tan 2α的值是________.14.3 [解析] 方法一:由已知sin 2α=-sin α,即2sin αcos α=-sin α,又α∈⎝ ⎛⎭⎪⎫π2,π,故sin α≠0,于是cos α=-12,进而sin α=32,于是tan α=-3,所以tan 2α=2tan α1-tan 2α=2×(-3)1-3= 3. 方法二:同上得cos α=-12,又α∈⎝ ⎛⎭⎪⎫π2,π,可得α=2π3,所以tan 2α=tan 4π3= 3.C3 三角函数的图像与性质1.C3[2013·江苏卷] 函数y =3sin ⎝⎛⎭⎪⎫2x +π4的最小正周期为________.1.π [解析] 周期为T =2π2=π.17.C3[2013·辽宁卷] 设向量a =(3sin x ,sin x),b =(cos x ,sin x),x ∈0,π2.(1)若|a|=|b|,求x 的值; (2)设函数f(x)=a·b ,求f(x)的最大值.17.解:(1)由|a |2=(3sin x)2+(sin x)2=4sin 2 x , |b |2=(cos x)2+(sin x)2=1. 及|a|=|b |,得4sin 2 x =1.又x ∈0,π2,从而sin x =12,所以x =π6.(2)f(x)=a·b =3sin x ·cos x +sin 2x =32sin 2x -12cos 2x +12=sin2x -π6+12,当x =π3∈0,π2时,sin2x -π6取最大值1. 所以f(x)的最大值为32.9.C3[2013·山东卷] 函数y =xcos x +sin x 的图像大致为( )图1-39.D [解析] ∵f(-x)=-xcos(-x)+sin(-x)=-(xcos x +sin x)=-f(x),∴y =xcos x +sin x 为奇函数,图像关于原点对称,排除选项B ,当x =π2,y =1>0,x =π,y =-π<0,故选D.16.C3、C5、C9[2013·新课标全国卷Ⅰ] 设当x =θ时,函数f(x)=sin x -2cos x 取得最大值,则cos θ=________.16.-2 55 [解析] f(x)=sin x -2cos x =5⎝⎛⎭⎫15sin x -25cos x ,令cos α=15,sin α=25,则f(x)=5sin(x -α).当θ-α=2k π+π2,即θ=2k π+π2+α(上述k 为整数)时,f(x)取得最大值,此时 cos θ=-sin α=-2 55.C4 函数 的图象与性质16.C4[2013·安徽卷] 设函数f(x)=sin x +sin ⎝ ⎛⎭⎪⎫x +π3.(1)求f(x)的最小值,并求使f(x)取最小值的x 的集合;(2)不画图,说明函数y =f(x)的图像可由y =sin x 的图像经过怎样的变化得到. 16.解:(1)因为f(x)=sin x +12sin x +32cos x =32sin x +32cos x =3sinx +π6,所以当x +π6=2k π-π2(k ∈Z ),即x =2k π-2π3(k ∈Z )时,f(x)取得最小值- 3.此时x 的取值集合为x 错误!x =2k π-错误!,k ∈Z .(2)先将y =sin x 的图像上所有点的纵坐标伸长到原来的3倍(横坐标不变),得y =3sin x 的图像;再将y =3sin x 的图像上所有的点向左平移π6个单位,得y =f(x)的图像.15.C4,C5,C6,C7[2013·北京卷] 已知函数f(x)=(2cos 2x -1)sin 2x +12cos 4x.(1)求f(x)的最小正周期及最大值;(2)若α∈⎝ ⎛⎭⎪⎫π2,π,且f(α)=22,求α的值.15.解:(1)因为f(x)=(2cos 2 x -1)sin 2x +12cos 4x=cos 2x ·sin 2x +12cos 4x=12(sin 4x +cos 4x) =22sin ⎝⎛⎭⎪⎫4x +π4, 所以f(x)的最小正周期为π2,最大值为22.(2)因为f(α)=22,所以sin ⎝⎛⎭⎪⎫4α+π4=1. 因为α∈⎝ ⎛⎭⎪⎫π2,π,所以4α+π4∈⎝ ⎛⎭⎪⎫9π4,17π4. 所以4α+π4=5π2.故α=9π16.9.C4[2013·全国卷] 若函数y =sin(ωx +φ)(ω>0)的部分图像如图1-1所示,则ω=( )图1-1A .5B .4C .3D .29.B [解析] 根据对称性可得π4为已知函数的半个周期,所以2πω=2×π4,解得ω=4.9.C4[2013·福建卷] 将函数f(x)=sin(2x +θ)⎝ ⎛⎭⎪⎫-π2<θ<π2的图像向右平移φ(φ>0)个单位长度后得到函数g(x)的图像.若f(x),g(x)的图像都经过点P ⎝⎛⎭⎫0,32,则φ的值可以是( ) A.5π3 B.5π6C.π2D.π69.B [解析] g(x)=f(x -φ)=sin[2(x -φ)+θ],由sin θ=32,-π2<θ<π2,得θ=π3,又sin(θ-2φ)=32,结合选项,知φ的一个值为5π6,故选B.6.C4[2013·湖北卷] 将函数y =3cos x +sin x(x ∈R )的图像向左平移m(m >0)个单位长度后,所得到的图像关于y 轴对称,则m 的最小值是( )A.π12B.π6C.π3D.5π66.B [解析] 结合选项,将函数y =3cos x +sin x =2sin ⎝ ⎛⎭⎪⎫x +π3的图像向左平移π6个单位得到y =2sin ⎝ ⎛⎭⎪⎫x +π2=2cos x ,它的图像关于y 轴对称,选B.13.C4[2013·江西卷] 设f(x)=3sin 3x +cos 3x ,若对任意实数x 都有|f(x)|≤a ,则实数a 的取值范围是________.13.a ≥2 [解析] |f(x)|max =2,则a ≥2.16.C4[2013·新课标全国卷Ⅱ] 函数y =cos(2x +φ)(-π≤φ<π)的图像向右平移π2个单位后,与函数y =sin ⎝⎛⎭⎪⎫2x +π3的图像重合,则φ=________.16.5π6 [解析] 由已知,y =cos(2x +φ)的图像向右平移π2得到y =cos(2x -π+φ)=-cos(2x +φ).y =sin ⎝ ⎛⎭⎪⎫2x +π3=-cos ⎝ ⎛⎭⎪⎫π2+2x +π3=-cos ⎝⎛⎭⎫2x +56π,两个函数图像重合,故φ=56π. 18.C4,C7[2013·山东卷] 设函数f(x)=32-3sin 2 ωx -sin ωx cos ωx(ω>0),且y =f(x)图像的一个对称中心到最近的对称轴的距离为π4.(1)求ω的值;(2)求f(x)在区间π,3π2上的最大值和最小值.18.解:(1)f(x)=32-3sin 2ωx -sin ωxcos ωx =32-3·1-cos 2ωx 2-12sin 2ωx =32cos 2ωx -12sin 2ωx =-sin ⎝⎛⎭⎪⎫2ωx -π3.因为图像的一个对称中心到最近的对称轴的距离为π4,又ω>0, 所以2π2ω=4×π4.因此ω=1.(2)由(1)知f(x)=-sin ⎝⎛⎭⎪⎫2x -π3.当π≤x ≤3π2时,5π3≤2x -π3≤8π3.所以-32≤sin ⎝⎛⎭⎪⎫2x -π3≤1. 因此-1≤f(x)≤32. 故f(x)在区间⎣⎢⎡⎦⎥⎤π,3π2上的最大值和最小值分别为32,-1.6.C4[2013·天津卷] 函数f(x)=sin2x -π4在区间0,π2上的最小值为( )A .-1B .-22C.22D .06.B [解析] ∵x ∈⎣⎢⎡⎦⎥⎤0,π2,∴2x -π4∈⎣⎢⎡⎦⎥⎤-π4,3π4,当2x -π4=-π4时,f(x)有最小值-22.图1-36.C4[2013·四川卷] 函数f(x)=2sin(ωx +φ)ω>0,-π2<φ<π2的部分图像如图1-3所示,则ω,φ的值分别是( )A .2,-π3B .2,-π6C .4,-π6D .4,π36.A [解析] 由半周期T 2=11π12-5π12=π2,可知周期T =π,从而ω=2,于是f(x)=2sin(2x+φ).当x =5π12时,f ⎝ ⎛⎭⎪⎫5π12=2,即sin ⎝ ⎛⎭⎪⎫5π6+φ=1,于是5π6+φ=2k π+π2(k ∈Z ),因为-π2<φ<π2,取k =0,得φ=-π3.16.F3,C4[2013·陕西卷] 已知向量a =⎝⎛⎭⎫cos x ,-12,b =(3sin x ,cos 2x),x ∈R ,设函数f(x)=a·b .(1)求f(x)的最小正周期;(2)求f(x)在⎣⎢⎡⎦⎥⎤0,π2上的最大值和最小值.16.解: f(x)=⎝⎛⎭⎫cos x ,-12·(3sin x ,cos 2x)=3cos xsin x -12cos 2x =32sin 2x -12cos 2x =cos π6sin 2x -sin π6cos 2x =sin ⎝⎛⎭⎪⎫2x -π6.(1)f(x)的最小正周期为T =2πω=2π2=π,即函数f(x)的最小正周期为π.(2)∵0≤x ≤π2,∴-π6≤2x -π6≤5π6.由正弦函数的性质,当2x -π6=π2,即x =π3时,f(x)取得最大值1.当2x -π6=-π6,即x =0时,f(0)=-12,当2x -π6=56π,即x =π2时,f ⎝ ⎛⎭⎪⎫π2=12,∴f(x)的最小值为-12.因此,f(x)在0,π2上最大值是1,最小值是-12.6.C4[2013·浙江卷] 函数f(x)=sin xcos x +32cos 2x 的最小正周期和振幅分别是( ) A .π,1 B .π,2C .2π,1D .2π,26.A [解析] f(x)=12sin 2x +32cos 2x =sin2x +π3,则最小正周期为π;振幅为1,所以选择A.C5 两角和与差的正弦、余弦、正切15.C4,C5,C6,C7[2013·北京卷] 已知函数f(x)=(2cos 2x -1)sin 2x +12cos 4x.(1)求f(x)的最小正周期及最大值;(2)若α∈⎝ ⎛⎭⎪⎫π2,π,且f(α)=22,求α的值.15.解:(1)因为f(x)=(2cos 2 x -1)sin 2x +12cos 4x=cos 2x·sin 2x +12cos 4x=12(sin 4x +cos 4x) =22sin ⎝⎛⎭⎪⎫4x +π4, 所以f(x)的最小正周期为π2,最大值为22.(2)因为f(α)=22,所以sin ⎝⎛⎭⎪⎫4α+π4=1. 因为α∈⎝ ⎛⎭⎪⎫π2,π,所以4α+π4∈⎝ ⎛⎭⎪⎫9π4,17π4. 所以4α+π4=5π2.故α=9π16.16.C2,C5[2013·广东卷] 已知函数f(x)=2cos ⎝ ⎛⎭⎪⎫x -π12,x ∈R .(1)求f ⎝ ⎛⎭⎪⎫π3的值;(2)若cos θ=35,θ∈⎝ ⎛⎭⎪⎫3π2,2π,求f ⎝ ⎛⎪⎫θ-π6.16.解:3.C5[2013·江西卷] 若sin α2=33,则cos α=( )A .-23B .-13C.13D.233.C [解析] cos α=1-2sin 2 α2=13,故选C.17.C5,C8,F1[2013·四川卷] 在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,且cos(A -B)cos B -sin(A -B)sin(A +C)=-35.(1)求sin A 的值;(2)若a =4 2,b =5,求向量BA →在BC →方向上的投影. 17.解:(1)由cos(A -B)cos B -sin(A -B)sin(A +C)=-35,得cos(A -B)cos B -sin(A -B)sin B =-35.则cos(A -B +B)=-35,即cos A =-35.又0<A<π,则sin A =45.(2)由正弦定理,有a sin A =b sin B, 所以,sin B =bsin A a =22.由题知a>b ,则A>B ,故B =π4.根据余弦定理,有(4 2)2=52+c 2-2×5c ×⎝⎛⎭⎫-35, 解得c =1或c =-7(负值舍去).故向量BA →在BC →方向上的投影为|BA →|cos B =22.16.C3、C5、C9[2013·新课标全国卷Ⅰ] 设当x =θ时,函数f(x)=sin x -2cos x 取得最大值,则cos θ=________.16.-2 55 [解析] f(x)=sin x -2cos x =5⎝⎛⎭⎫15sin x -25cos x ,令cos α=15,sin α=25,则f(x)=5sin(x -α).当θ-α=2k π+π2,即θ=2k π+π2+α(上述k 为整数)时,f(x)取得最大值,此时 cos θ=-sin α=-2 55.18.C5和C8[2013·重庆卷] 在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,且a 2=b 2+c 2+3bc. (1)求A ;(2)设a =3,S 为△ABC 的面积,求S +3cos Bcos C 的最大值,并指出此时B 的值.18.解:(1)由余弦定理得cos A =b 2+c 2-a 22bc =-3bc 2bc =-32.又因为0<A<π,所以A =5π6.(2)由(1)得sin A =12,又由正弦定理及a =3得S =12bcsin A =12·asin B sin A·asin C =3sin Bsin C ,因此,S +3cos Bcos C =3(sin Bsin C +cos Bcos C)=3cos(B -C). 所以,当B =C ,即B =π-A 2=π12时,S +3cos Bcos C 取最大值3.C6 二倍角公式15.C4,C5,C6,C7[2013·北京卷] 已知函数f(x)=(2cos 2x -1)sin 2x +12cos 4x.(1)求f(x)的最小正周期及最大值;(2)若α∈⎝ ⎛⎭⎪⎫π2,π,且f(α)=22,求α的值.15.解:(1)因为f(x)=(2cos 2 x -1)sin 2x +12cos 4x=cos 2x ·sin 2x +12cos 4x=12(sin 4x +cos 4x) =22sin ⎝⎛⎭⎪⎫4x +π4, 所以f(x)的最小正周期为π2,最大值为22.(2)因为f(α)=22,所以sin ⎝⎛⎭⎪⎫4α+π4=1. 因为α∈⎝ ⎛⎭⎪⎫π2,π,所以4α+π4∈⎝ ⎛⎭⎪⎫9π4,17π4.所以4α+π4=5π2.故α=9π16.6.C6[2013·新课标全国卷Ⅱ] 已知sin 2α=23,则cos 2⎝ ⎛⎭⎪⎫α+π4=( )A.16B.13 C.12 D.236.A [解析] cos 2⎝ ⎛⎭⎪⎫α+π4=1+cos ⎝⎛⎭⎪⎫2α+π22=1-sin 2α2=16,故选A.14.C1,C2,C6[2013·四川卷] 设sin 2α=-sin α,α∈π2,π,则tan 2α的值是________.14.3 [解析] 方法一:由已知sin 2α=-sin α,即2sin αcos α=-sin α,又α∈⎝ ⎛⎭⎪⎫π2,π,故sin α≠0,于是cos α=-12,进而sin α=32,于是tan α=-3,所以tan 2α=2tan α1-tan 2α=2×(-3)1-3= 3. 方法二:同上得cos α=-12,又α∈⎝ ⎛⎭⎪⎫π2,π,可得α=2π3,所以tan 2α=tan 4π3= 3.15.C6、E1和E3[2013·重庆卷] 设0≤α≤π,不等式8x 2-(8sin α)x +cos 2α≥0对x ∈R恒成立,则α的取值范围为________.15.⎣⎢⎡⎦⎥⎤0,π6∪⎣⎢⎡⎦⎥⎤5π6,π [解析] 根据二次函数的图像可得Δ=(8sin α)2-4×8cos 2α≤0,即2sin 2 α-cos 2α≤0,转化为2sin 2 α-(1-2sin 2 α)≤0,即4sin 2α≤1,即-12≤sinα≤12.因为0≤α≤π,故α∈⎣⎢⎡⎦⎥⎤0,π6∪⎣⎢⎡⎦⎥⎤5π6,π.C7 三角函数的求值、化简与证明15.C4,C5,C6,C7[2013·北京卷] 已知函数f(x)=(2cos 2x -1)sin 2x +12cos 4x.(1)求f(x)的最小正周期及最大值;(2)若α∈⎝ ⎛⎭⎪⎫π2,π,且f(α)=22,求α的值.15.解:(1)因为f(x)=(2cos 2 x -1)sin 2x +12cos 4x=cos 2x ·sin 2x +12cos 4x=12(sin 4x +cos 4x) =22sin ⎝⎛⎭⎪⎫4x +π4, 所以f(x)的最小正周期为π2,最大值为22.(2)因为f(α)=22,所以sin ⎝⎛⎭⎪⎫4α+π4=1. 因为α∈⎝ ⎛⎭⎪⎫π2,π,所以4α+π4∈⎝ ⎛⎭⎪⎫9π4,17π4. 所以4α+π4=5π2.故α=9π16.18.C7、C8[2013·全国卷] 设△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,(a +b +c)(a -b +c)=ac.(1)求B ;(2)若sin Asin C =3-14,求C.18.解:(1)因为(a +b +c)(a -b +c)=ac , 所以a 2+c 2-b 2=-ac.由余弦定理得cos B =a 2+c 2-b 22ac =-12,因此B =120°.(2)由(1)知A +C =60°, 所以cos (A -C)=cos Acos C +sin Asin C=cos Acos C -sin Asin C +2sin Asin C =cos(A +C)+2sinAsin C=12+2×3-14 =32, 故A -C =30°或A -C =-30°, 因此C =15°或C =45°.18.C4,C7[2013·山东卷] 设函数f(x)=32-3sin 2 ωx -sin ωx cos ωx(ω>0),且y =f(x)图像的一个对称中心到最近的对称轴的距离为π4.(1)求ω的值;(2)求f(x)在区间π,3π2上的最大值和最小值.18.解:(1)f(x)=32-3sin 2ωx -sin ωxcos ωx =32-3·1-cos 2ωx 2-12sin 2ωx =32cos 2ωx -12sin 2ωx =-sin ⎝⎛⎭⎪⎫2ωx -π3.因为图像的一个对称中心到最近的对称轴的距离为π4,又ω>0, 所以2π2ω=4×π4.因此ω=1.(2)由(1)知f(x)=-sin ⎝⎛⎭⎪⎫2x -π3.当π≤x ≤3π2时,5π3≤2x -π3≤8π3.所以-32≤sin ⎝⎛⎭⎪⎫2x -π3≤1.因此-1≤f(x)≤32. 故f(x)在区间⎣⎢⎡⎦⎥⎤π,3π2上的最大值和最小值分别为32,-1.16.C7,C8[2013·天津卷] 在△ABC 中,内角A ,B ,C 所对的边分别是a ,b ,c.已知bsin A =3csin B ,a =3,cos B =23.(1)求b 的值; (2)求sin2B -π3的值.16.解:(1)在△ABC 中,由a sin A =bsin B ,可得bsin A =asin B ,又由bsin A =3csin B ,可得a =3c ,又a =3,故c =1.由b 2=a 2+c 2-2accos B ,cos B =23,可得b = 6.(2)由cos B =23,得sin B =53,进而得cos 2B =2cos 2 B -1=-19,sin 2B =2sin Bcos B =4 59. 所以sin2B -π3=sin 2Bcos π3-cos 2Bsin π3=4 5+318.C8 解三角形9.C8[2013·安徽卷] 设△ABC 的内角A ,B ,C 所对边的长分别为a ,b ,c ,若b +c =2a ,3sin A =5sin B ,则角C =( )A.π3B.2π3C.3π4D.5π69.B [解析] 根据正弦定理,3sin A =5sin B 可化为3a =5b ,又b +c =2a ,解得b =3a 5,c =7a5.令a =5t(t>0),则b =3t ,c =7t ,在△ABC 中,由余弦定理得cos C =a 2+b 2-c 22ab =25t 2+9t 2-49t 22×5t ×3t=-12,所以C =2π3.5.C8[2013·北京卷] 在△ABC 中,a =3,b =5,sin A =13,则sin B =( )A.15B.59C.53D .1 5.B [解析] 由正弦定理得a sin A =b sin B ,即313=5sin B ,解得sin B =59. 18.C7、C8[2013·全国卷] 设△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,(a +b +c)(a -b +c)=ac.(1)求B ;(2)若sin Asin C =3-14,求C. 18.解:(1)因为(a +b +c)(a -b +c)=ac , 所以a 2+c 2-b 2=-ac.由余弦定理得cos B =a 2+c 2-b 22ac =-12,因此B =120°.(2)由(1)知A +C =60°, 所以cos (A -C)=cos Acos C +sin Asin C=cos Acos C -sin Asin C +2sin Asin C =cos(A +C)+2sinAsin C =12+2×3-14 =32, 故A -C =30°或A -C =-30°, 因此C =15°或C =45°.21.C8,C9[2013·福建卷] 如图1-6,在等腰直角△OPQ 中,∠POQ =90°,OP =2 2,点M 在线段PQ 上.(1)若OM =5,求PM 的长;(2)若点N 在线段MQ 上,且∠MON =30°,问:当∠POM 取何值时,△OMN 的面积最小?并求出面积的最小值.图1-621.解:(1)在△OMP 中,∠OPM =45°,OM =5,OP =2 2, 由余弦定理得,OM 2=OP 2+MP 2-2OP·MP·cos 45°,得MP 2-4MP +3=0, 解得MP =1或MP =3.(2)设∠POM =α,0°≤α≤60°,在△OMP 中,由正弦定理,得OM sin ∠OPM =OPsin ∠OMP ,所以OM =OPsin 45°sin (45°+α),同理ON =OPsin 45°sin (75°+α).故S △OMN =12OM ·ON ·sin ∠MON=14×OP 2sin 2 45°sin (45°+α)sin (75°+α) =1sin (45°+α)sin (45°+α+30°)=1sin (45°+α)⎣⎡⎦⎤32sin (45°+α)+12cos (45°+α)=1 32sin 2(45°+α)+12sin (45°+α)cos (45°+α) =134[1-cos (90°+2α)]+14sin (90°+2α) =134+34sin 2α+14cos 2α =1 34+12sin (2α+30°). 因为0°≤α≤60°,30°≤2α+30°≤150°,所以当α=30°时,sin(2α+30°)的最大值为1,此时△OMN 的面积取到最小值.即∠POM =30°时,△OMN 的面积的最小值为8-4 3.18.C8[2013·湖北卷] 在△ABC 中,角A ,B ,C 对应的边分别是a ,b ,c.已知cos 2A -3cos(B +C)=1.(1)求角A 的大小;(2)若△ABC 的面积S =5 3,b =5,求sinB sin C 的值.18.解:(1)由cos 2A -3cos(B +C)=1,得2cos 2A +3cos A -2=0, 即(2cos A -1)(cos A +2)=0,解得cos A =12或cos A =-2(舍去).因为0<A <π,所以A =π3.(2)由S =12bc sin A =12bc ·32=34bc =5 3,得bc =20,又b =5,知c =4.由余弦定理得a 2=b 2+c 2-2bc·cos A =25+16-20=21,故a =21. 又由正弦定理得sin Bsin C =b a sin A ·c a sin A =bc a 2sin 2A =2021×34=57.5.C8[2013·湖南卷] 在锐角△ABC 中,角A ,B 所对的边长分别为a ,b.若2asin B =3b ,则角A 等于( )A.π3B.π4C.π6D.π125.A [解析] 由正弦定理可得2sin Asin B =3sin B .又sin B ≠0,所以sin A =32.因为A 为锐角,故A =π3,选A.17.C8[2013·江西卷] 在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,已知sin Asin B +sin Bsin C +cos 2B =1.(1)求证:a ,b ,c 成等差数列;(2)若C =2π3,求ab的值.17.解:(1)证明:由题意得sin Asin B +sin Bsin C =2sin 2 B ,因为sin B ≠0,所以sin A +sin C =2sin B ,由正弦定理,有a +c =2b ,即a ,b ,c 成等差数列. (2)由C =2π3,c =2b -a 及余弦定理得(2b -a)2=a 2+b 2+ab ,即有5ab -3b 2=0,所以a b =35.6.C8[2013·辽宁卷] 在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c.若asin Bcos C +csin Bcos A =12b ,且a>b ,则∠B =( )A.π6B.π3C.2π3D.5π66.A [解析] 由正弦定理可以得到sin Asin Bcos C +sin Csin Bcos A =12sin B ,所以可以得到sin Acos C +sin Ccos A =12,即sin(A +C)=sin B =12,则∠B =π6,故选A.4.C8[2013·新课标全国卷Ⅱ] △ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,已知b =2,B =π6,C =π4,则△ABC 的面积为( )A .2 3+2 B.3+1 C .2 3-2 D.3-14.B [解析] b sin B =c sin Cc =2 2.又A +B +C =π,∴A =712π,∴△ABC 的面积为12×2×2 2×sin 7π12=22×6+24=3+1.7.C8[2013·山东卷] △ABC 的内角A ,B ,C 所对的边分别为a ,b ,c.若B =2A ,a =1,b =3,则c =( )A .2 3B .2 C. 2 D .17.B [解析] 由正弦定理a sinA =b sinB ,即1sinA =3sinB =32sinAcosA ,解之得cosA =32,∴A =π6,B =π3,C =π2,∴c =a 2+b 2=()32+12=2.9.C8[2013·陕西卷] 设△ABC 的内角A ,B ,C 所对的边分别为a ,b ,c ,若bcos C +ccos B =asin A ,则△ABC 的形状为( )A .直角三角形B .锐角三角形C .钝角三角形D .不确定9.A [解析] 结合已知bcos C +ccos B =asin A ,所以由正弦定理可知sin Bcos C +sin Ccos B =sin Asin A ,即sin (B +C)=sin 2A sin A =sin 2A sin A =1,故A =90°,故三角形为直角三角形.16.C7,C8[2013·天津卷] 在△ABC 中,内角A ,B ,C 所对的边分别是a ,b ,c.已知bsin A =3csin B ,a =3,cos B =23.(1)求b 的值; (2)求sin2B -π3的值.16.解:(1)在△ABC 中,由a sin A =bsin B ,可得bsin A =asin B ,又由bsin A =3csin B ,可得a =3c ,又a =3,故c =1.由b 2=a 2+c 2-2accos B ,cos B =23,可得b = 6.(2)由cos B =23,得sin B =53,进而得cos 2B =2cos 2 B -1=-19,sin 2B =2sin Bcos B =4 59. 所以sin2B -π3=sin 2Bcos π3-cos 2Bsin π3=4 5+318.17.C5,C8,F1[2013·四川卷] 在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,且cos(A -B)cos B -sin(A -B)sin(A +C)=-35.(1)求sin A 的值;(2)若a =4 2,b =5,求向量BA →在BC →方向上的投影. 17.解:(1)由cos(A -B)cos B -sin(A -B)sin(A +C)=-35,得cos(A -B)cos B -sin(A -B)sin B =-35.则cos(A -B +B)=-35,即cos A =-35.又0<A<π,则sin A =45.(2)由正弦定理,有a sin A =b sin B, 所以,sin B =bsin A a =22.由题知a>b ,则A>B ,故B =π4.根据余弦定理,有(4 2)2=52+c 2-2×5c ×⎝⎛⎭⎫-35, 解得c =1或c =-7(负值舍去).故向量BA →在BC →方向上的投影为|BA →|cos B =22.15.H1,C8,E8[2013·四川卷] 在平面直角坐标系内,到点A(1,2),B(1,5),C(3,6),D(7,-1)的距离之和最小的点的坐标是________.15.(2,4) [解析] 在以A ,B ,C ,D 为顶点构成的四边形中,由平面几何知识:三角形两边之和大于第三边,可知当动点落在四边形两条对角线AC ,BD 交点上时,到四个顶点的距离之和最小.AC 所在直线方程为y =2x ,BD 所在直线方程为y =-x +6,交点坐标为(2,4),即为所求.10.C8[2013·新课标全国卷Ⅰ] 已知锐角△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,23cos 2 A +cos 2A =0,a =7,c =6,则b =( )A .10B .9C .8D .510.D [解析] 由23cos 2A +cos 2A =0,得25cos 2A =1.因为△ABC 为锐角三角形,所以cos A =15.在△ABC 中,根据余弦定理,得49=b 2+36-12b ×15,即b 2-125b -13=0,解得b =5或-135(舍去). 18.C8[2013·浙江卷] 在锐角△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,且2asin B = 3b.(1)求角A 的大小;(2)若a =6,b +c =8,求△ABC 的面积.18.解:(1)由2asin B = 3b 及正弦定理a sin A =b sin B,得 sin A = 32.因为A 是锐角,所以A =π3. (2)由余弦定理a 2=b 2+c 2-2bc cos A 得b 2+c 2-bc =36.又b +c =8,所以bc =283. 由三角形面积公式S =12bcsin A ,得△ABC 的面积为7 33. 18.C5和C8[2013·重庆卷] 在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,且a 2=b 2+c 2+3bc.(1)求A ;(2)设a =3,S 为△ABC 的面积,求S +3cos Bcos C 的最大值,并指出此时B 的值.18.解:(1)由余弦定理得cos A =b 2+c 2-a 22bc =-3bc 2bc =-32. 又因为0<A<π,所以A =5π6. (2)由(1)得sin A =12,又由正弦定理及a =3得 S =12bcsin A =12·asin B sin A·asin C =3sin Bsin C , 因此,S +3cos Bcos C =3(sin Bsin C +cos Bcos C)=3cos(B -C).所以,当B =C ,即B =π-A 2=π12时,S +3cos Bcos C 取最大值3.C9 单元综合21.C8,C9[2013·福建卷] 如图1-6,在等腰直角△OPQ 中,∠POQ =90°,OP =2 2,点M 在线段PQ 上.(1)若OM =5,求PM 的长;(2)若点N 在线段MQ 上,且∠MON =30°,问:当∠POM 取何值时,△OMN 的面积最小?并求出面积的最小值.图1-621.解:(1)在△OMP 中,∠OPM =45°,OM =5,OP =2 2,由余弦定理得,OM 2=OP 2+MP 2-2OP·MP·cos 45°,得MP 2-4MP +3=0,解得MP =1或MP =3.(2)设∠POM =α,0°≤α≤60°,在△OMP 中,由正弦定理,得OM sin ∠OPM =OP sin ∠OMP, 所以OM =OPsin 45°sin (45°+α),同理ON =OPsin 45°sin (75°+α). 故S △OMN =12OM ·ON ·sin ∠MON =14×OP 2sin 2 45°sin (45°+α)sin (75°+α)=1sin (45°+α)sin (45°+α+30°)=1sin (45°+α)⎣⎡⎦⎤32sin (45°+α)+12cos (45°+α) =1 32sin 2(45°+α)+12sin (45°+α)cos (45°+α) =1 34[1-cos (90°+2α)]+14sin (90°+2α) =1 34+34sin 2α+14cos 2α =1 34+12sin (2α+30°). 因为0°≤α≤60°,30°≤2α+30°≤150°,所以当α=30°时,sin(2α+30°)的最大值为1,此时△OMN 的面积取到最小值.即∠POM =30°时,△OMN 的面积的最小值为8-4 3.18.C9[2013·江苏卷] 如图1-4,游客从某旅游景区的景点A 处下山至C 处有两种路径.一种是从A 沿直线步行到C ,另一种是先从A 沿索道乘缆车到B ,然后从B 沿直线步行到C.现有甲、乙两位游客从A 处下山,甲沿AC 匀速步行,速度为50 m/min.在甲出发2 min 后,乙从A 乘缆车到B ,在B 处停留1 min 后,再从B 匀速步行到C.假设缆车匀速直线运动的速度为130 m/min ,山路AC 长为1 260 m ,经测量,cos A =1213,cos C =35. (1)求索道AB 的长;(2)问乙出发多少分钟后,乙在缆车上与甲的距离最短?(3)为使两位游客在C 处互相等待的时间不超过3分钟,乙步行的速度应控制在什么范围内?图1-418.解:(1)在△ABC 中,因为cos A =1213,cos C =35, 所以sin A =513,sin C =45, 从而sin B =sin[π-(A +C)]=sin(A +C)=sin Acos C +cos Asin C=513×35+1213×45=6365. 由正弦定理AB sin C =AC sin B,得 AB =AC sin B ×sin C =1 2606365×45=1 040(m). 所以索道AB 的长为1 040 m.(2)假设乙出发t 分钟后,甲、乙两游客距离为d ,此时,甲行走了(100+50t)m ,乙距离A 处130t m ,所以由余弦定理得d 2=(100+50t)2+(130t)2-2×130t ×(100+50t)×1213=200(37t 2-70t +50). 因为0≤t ≤1 040130,即0≤t ≤8, 故当t =3537(min)时,甲、乙两游客距离最短. (3)由正弦定理BC sin A =AC sin B,得 BC =AC sin B ×sin A =1 2606365×513=500(m). 乙从B 出发时,甲已走了50×(2+8+1)=550(m),还需走710 m 才能到达C.设乙步行的速度为v m/min ,由题意得-3≤500v -71050≤3,解得1 25043≤v ≤62514,所以为使两位游客在C 处互相等待的时间不超过3分钟,乙步行的速度应控制在⎣⎡⎦⎤1 25043,62514(单位:m/min)范围内. 15.C9[2013·江苏卷] 已知a =(cos α,sin α),b =(cos β,sin β),0<β<α<π.(1)若|a -b |=2,求证:a ⊥b ;(2)设c =(0,1),若a +b =c ,求α,β的值.15.解:(1)由题意得|a -b|2=2,即(a -b )2=a 2-2a·b +b 2=2.又因为a 2=b 2=|a|2=|b|2=1,所以2-2a·b =2,即a·b =0,故a ⊥b.(2)因为a +b =(cos α+cos β,sin α+sin β)=(0,1),所以⎩⎪⎨⎪⎧cos α+cos β=0,sin α+sin β=1, 由此得,cos α=cos(π-β),由0<β<π,得0<π-β<π,又0<α<π,故α=π-β.代入sin α+sin β=1得,sin α=sin β=12,而α>β,所以α=5π6,β=π6. 16.C3、C5、C9[2013·新课标全国卷Ⅰ] 设当x =θ时,函数f(x)=sin x -2cos x 取得最大值,则cos θ=________.16.-2 55[解析] f(x)=sin x -2cos x = 5⎝⎛⎭⎫15sin x -25cos x ,令cos α=15,sin α=25, 则f(x)=5sin(x -α).当θ-α=2k π+π2, 即θ=2k π+π2+α(上述k 为整数)时, f(x)取得最大值,此时 cos θ=-sin α=-2 55. 9.C9[2013·新课标全国卷Ⅰ] 函数f(x)=(1-cos x)·sin x 在[-π,π]的图像大致为( )图1-29.C [解析] 函数f(x)是奇函数,排除选项B.当x ∈[0,π]时f(x)≥0,排除选项A.对函数f(x)求导,得f′(x)=sin xsin x +(1-cos x)cos x =-2cos 2 x +cos x +1=-(cos x -1)(2cos x +1),当0<x<π时,若0<x<2π3,则f′(x)>0,若2π3<x<π,则f′(x)<0,即函数在(0,π)上的极大值点是x=错误!,故只能是选项C中的图像.。
三角函数公式表(全)

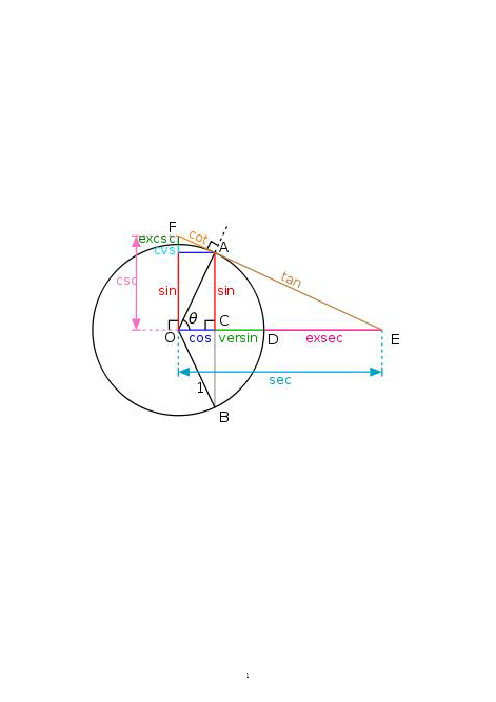
三角函数公式表同角三角函数的基本关系式倒数关系: 商的关系:平方关系:tanα ·cotα=1 sinα ·cscα=1 sinα/cosα=tanαsin2α+cos2α=11+tan2α=sec2α(六边形记忆法:图形结构“上弦中切下割,左正右余中间1”;记忆方法“对角线上两个函数的积为1;阴影三角形上两顶点的三角函数值的平方和等于下顶点的三角函数值的平方;任意一顶点的三角函数值等于相邻两个顶点的三角函数值的乘积。
”)诱导公式(口诀:奇变偶不变,符号看象限。
)sin(-α)=-sinαcos(-α)=cosαtan(-α)=-tanαcot(-α)=-cotαsin(π/2-α)=cosαcos(π/2-α)=sinαtan(π/2-α)=cotαcot(π/2-α)=tanαsin(π/2+α)=cosαcos(π/2+α)=-sinαtan(π/2+α)=-cotαcot(π/2+α)=-tanαsin(π-α)=sinαcos(π-α)=-cosαtan(π-α)=-tanαcot(π-α)=-cotαsin(π+α)=-sinαcos(π+α)=-cosαtan(π+α)=tanαcot(π+α)=cotαsin(3π/2-α)=-cosαcos(3π/2-α)=-sinαtan(3π/2-α)=cotαcot(3π/2-α)=tanαsin(3π/2+α)=-cosαcos(3π/2+α)=sinαtan(3π/2+α)=-cotαcot(3π/2+α)=-tanαsin(2π-α)=-sinαcos(2π-α)=cosαtan(2π-α)=-tanαcot(2π-α)=-cotαsin(2kπ+α)=sinαcos(2kπ+α)=cosαtan(2kπ+α)=tanαcot(2kπ+α)=cotα(其中k∈Z)两角和与差的三角函数公式万能公式sin(α+β)=sinαcosβ+cosαsinβsin(α-β)=sinαcosβ-cosαsinβcos(α+β)=co sαcosβ-sinαsinβcos(α-β)=cosαcosβ+sinαsinβtanα+tanβtan(α+β)=———----———1-tanα ·tanβtanα-tanβtan(α-β)=—————-------—1+tanα ·tanβ2tan(α/2)sinα=——————1+tan2(α/2)1-tan2(α/2) cosα=——————1+tan2(α/2)2tan(α/2)tanα=——————1-tan2(α/2)半角的正弦、余弦和正切公式三角函数的降幂公式二倍角的正弦、余弦和正切公式三倍角的正弦、余弦和正切公式sin2α=2sinαcosαcos2α=cos2α-sin2α=2cos2α-1=1-2sin2α2tanαtan2α=—————1-tan2αsin3α=3sinα-4sin3αcos3α=4cos3α-3cosα3tanα-tan3αtan3α=——————1-3tan2α三角函数的和差化积公式三角函数的积化和差公式Sinα+sinβ=2sin[(α+β)/2]·cos[(α-β)/2] sinα-sinβ=2cos[(α+β)/2]·sin[(α-β)/2] cos α+cosβ=2cos[(α+β)/2]·cos[(α-β)/2]cosα-cosβ=-2sin[(α+β)/2]·sin[(α-β)/2 ] 1sinα ·cosβ=-[sin(α+β)+sin(α-β)]21cosα ·sinβ=-[sin(α+β)-sin(α-β)]21cosα ·cosβ=-[cos(α+β)+cos(α-β)]21sinα ·sinβ=— -[cos(α+β)-cos(α-β)]2化asinα ±bcosα为一个角的一个三角函数的形式(辅助角的三角函数的公式)。
13年高考真题—理科数学3:三角函数-推荐下载

13.【2013 新课标 15】当 x 时,函数 f x sin x 2 cos x 取得最大值,则
cos ______。 14.【2013 福建 13】如图 ABC 中,已知点 D 在 BC 边上,
AD AC , sin BAC 2 2 3 , AB 3 2 , AD 3 ,则
(A) 10 10
(B) 10 5
(C) 3 10 10
4.【2013 山东 5】将函数 y sin 2x 的图象沿 x 轴向左平象,则 的可能取值为( ) (A) 3 4 (B) 4 (C)0 (D)
4
5.【2013 辽宁 6】已知 ABC 的内角 A, B, C 所对的边分别为 a, b, c ,
则角 A 等于( )
(A) 12
(B) 6
(C) 4
11.【2013 湖北 4】将函数 y 3 cos x sin x x R的图像向左平移 m m 0个长
度单位后,所得到的图像关于 y 轴对称,则 m 的最小值是( )
(A) 12
(B) 6
12.【2013 浙江 16】 ABC 中, C 900 , M 是 BC 的中点,若 sin BAM 1 3 ,则
f x 2sin x 0, 2 2
的部分图象如
图所示,则, 的值分别是( )
(A) 2, 3 (B) 2, 6
4, 3
(C) 4, 6 (D)
10.【2013 湖南 3】在锐角中 ABC ,角 A, B 所对的边长分别为 a, b ,若 2a sin B 3b ,
a sin B cos C c sin B cos A b 2 ,且 a b ,则 B ( )
三角函数入门讲解

三角函数入门讲解三角函数是数学中的重要概念,也是数学分析和物理学中经常使用的工具。
它们以三角形的边和角为基础,可以帮助我们研究和解决各种问题。
我们来了解一下最常用的三角函数:正弦函数(sin)、余弦函数(cos)和正切函数(tan)。
这三个函数都是以角度为自变量,并返回一个比值作为函数值。
正弦函数(sin)定义为:在直角三角形中,对于一个锐角A,正弦函数的值等于A的对边与斜边的比值。
换句话说,sin(A) = 对边/斜边。
正弦函数的取值范围在-1到1之间。
余弦函数(cos)定义为:在直角三角形中,对于一个锐角A,余弦函数的值等于A的邻边与斜边的比值。
换句话说,cos(A) = 邻边/斜边。
余弦函数的取值范围也在-1到1之间。
正切函数(tan)定义为:在直角三角形中,对于一个锐角A,正切函数的值等于A的对边与邻边的比值。
换句话说,tan(A) = 对边/邻边。
正切函数的取值范围是全体实数。
这三个基本的三角函数在数学和物理中有着广泛的应用。
例如,在三角学中,我们可以使用正弦函数和余弦函数来计算角度的度数。
在物理学中,三角函数可以帮助我们解决各种运动问题,例如计算物体的速度、加速度和位移等。
除了正弦、余弦和正切函数,还有一些其他的三角函数,例如余割函数(csc)、正割函数(sec)和余切函数(cot)。
这些函数是基于正弦、余弦和正切函数的倒数定义的。
余割函数(csc)定义为:csc(A) = 1/sin(A)。
正割函数(sec)定义为:sec(A) = 1/cos(A)。
余切函数(cot)定义为:cot(A) = 1/tan(A)。
这些函数的取值范围与正弦、余弦和正切函数相对应。
三角函数不仅可以应用于平面几何中的三角形,还可以应用于立体几何中的球面三角形。
在球面三角学中,我们可以使用三角函数来计算球面上的角度和距离。
除了三角函数的定义和性质,我们还需要了解一些常用的三角函数恒等式。
这些恒等式是基于三角函数的定义和三角恒等式推导出来的。
2013高考数学总复习讲义1:三角公式

高三数学总复习讲义——三角函数公式知识清单:(一)基本关系公式组二 (k Z ∈)sin(2)sin ,cos(2)cos tan(2)tan ,cot(2)cot k x x k x x k x x k x xππππ+=+=+=+=公式组三sin()sin tan()tan cos()cos cot()cot x x x x x xx x-=--=--=-=-公式组四 公式组五xx x x x x x x cot )cot(tan )tan(cos )cos(sin )sin(=+=+-=+-=+ππππxx x x x x xx c o t )2c o t (t a n )2t a n (c o s )2c o s (s i n )2s i n (-=--=-=--=-ππππ公式组六sin()sin tan()tan cos()cos cot()cot x xx xx x x xππππ-=-=--=--=-(二)两角和与差公式公式组一βαβαβαsin sin cos cos )cos(-=+βαβαβαsin sin cos cos )cos(+=- βαβαβαsin cos cos sin )sin(+=+βαβαβαsin cos cos sin )sin(-=-βαβαβαtan tan 1tan tan )tan(-+=+βαβαβαtan tan 1tan tan )tan(+-=-公式组二:αααcos sin 22sin =ααααα2222sin 211cos 2sin cos 2cos -=-=-=ααα2tan1tan 22tan -=2c o s 12s i n αα-±=2cos 12cosαα+±=,1cos sin 1cos tan21cos 1cos sin ααααααα--=±==++公式组三1cos()sin 2παα-=,1cos()sin 2παα+=-1sin()cos 2παα-= 1s i n ()c o s2παα+=,1tan()cot 2παα-=,1tan()cot 2παα+=-常用数据: 30456090、、、的三角函数值62sin 15cos 754-==,42615cos 75sin+==3275cot 15tan -==,3215cot 75tan +==注: ⑴以上公式务必要知道其推导思路,从而清晰地“看出”它们之间的联系,它们的变化形式.如tan()(1tan tan )tan tan αβαβαβ+-=+221cos 1cos cos ,sin2222αααα+-==等.从而可做到:正用、逆用、变形用自如使用各公式.⑵三角变换公式除用来化简三角函数式外,还为研究三角函数图象及性质做准备. ⑶三角函数恒等变形的基本策略。
2013年全国各地高考文科数学试题分类汇编:三角函数

2013年全国各地高考文科数学试题分类汇编:三角函数2013年全国各地高考文科数学试题分类汇编:三角函数一、选择题1 .(2013年高考大纲卷(文))已知a 是第二象限角,5sin ,cos 13a a ==则( ) A .1213- B .513- C .513D .1213【答案】A2 .(2013年高考课标Ⅰ卷(文))函数()(1cos )sin f x x x =-在[,]ππ-的图像大致为【答案】C ;3 .(2013年高考四川卷(文))函数()2sin()(0,)22f x x ππωϕωϕ=+>-<<的部分图象如图所示,则,ωϕ的值分别是()A .2,3π-B .2,6π-C .4,6π-D .4,3π【答案】A4 .(2013年高考湖南(文))在锐角∆ABC 中,角A,B 所对的边长分别为a,b. 若2sinB=3b,则角A 等于______()A .3πB .4π C .6π D .12π【答案】A5 .(2013年高考福建卷(文))将函数)22)(2sin()(πθπθ<<-+=x x f 的图象向右平移)0(>ϕϕ个单位长度后得到函数)(x g 的图象,若)(),(x g x f 的图象都经过点)23,0(P ,则ϕ的值可以是( ) A .35π B .65πC .2π D .6π 【答案】B6 .(2013年高考陕西卷(文))设△ABC 的内角A , B , C 所对的边分别为a , b , c , 若cos cos sin b C c B a A +=, 则△ABC 的形状为( ) A .直角三角形B .锐角三角形C .钝角三角形 D .不确定【答案】AA .25- B .15- C .15 D .25【答案】C7.(2013年高考湖北卷(文))将函数3cos sin ()y x x x =+∈R 的图象向左平移(0)m m >个单位长度后,所得到的图象关于y 轴对称,则m 的最小值是( )A .π12 B .π6C .π3D .5π6【答案】B8.(2013年高考大纲卷(文))若函数()()sin 0=y x ωϕωω=+>的部分图像如图,则 () A .5B .4C .3D .2【答案】B9.(2013年高考天津卷(文))函数()sin 24f x x π⎛⎫=- ⎪⎝⎭在区间0,2π⎡⎤⎢⎥⎣⎦上的最小值是( )A .1-B .2C 2D .0【答案】B10.(2013年高考安徽(文))设ABC ∆的内角,,A B C 所对边的长分别为,,a b c ,若2,3sin 5sin b c a A B +==,则角C =( )A .3πB .23πC .34πD .56π【答案】B11.(2013年高考课标Ⅰ卷(文))已知锐角ABC ∆的内角,,A B C 的对边分别为,,a b c,223coscos 20A A +=,7a =,6c =,则b =( )A .10B .9C .8D .5【答案】D12.(2013年高考浙江卷(文))函数f(x)=sin xcos x+32cos 2x 的最小正周期和振幅分别是()A .π,1B .π,2C .2π,1D .2π,2【答案】A13.(2013年高考北京卷(文))在△ABC 中,3,5a b ==,1sin 3A =,则sinB =( ) A .15 B .59C .53D .1【答案】B14.(2013年高考山东卷(文))函数x x x y sin cos +=的图象大致为【答案】D二、填空题15.(2013年高考四川卷(文))设sin 2sin αα=-,(,)2παπ∈,则tan 2α的值是________.【答案】316.(2013年高考课标Ⅱ卷(文))函数cos(2)()y x ϕπϕπ=+-≤<的图像向右平移2π个单位后,与函数sin(2)3y x π=+的图像重合,则||ϕ=___________.【答案】56π17.(2013年上海高考数学试题(文科))已知ABC ∆的内角A 、B 、C 所对的边分别是a ,b ,c .若2220aab b c ++-=,则角C 的大小是________(结果用反三角函数值表示).【答案】23π18.(2013年上海高考数学试题(文科))若1cos cos sin sin 3x y x y +=,则()cos 22x y -=________. 【答案】79-19.(2013年高考课标Ⅰ卷(文))设当x θ=时,函数()sin 2cos f x x x =-取得最大值,则cos θ=______.【答案】255-;20.(2013年高考江西卷(文))设f(x)=sin3x+cos3x,若对任意实数x 都有|f(x)|≤a,则实数a 的取值范围是_____._____ 【答案】2a ≥三、解答题21.(2013年高考大纲卷(文))设ABC ∆的内角,,A B C 的对边分别为,,a b c,()()a b c a b c ac ++-+=.(I)求B (II)若31sin sin A C -=,求C .【答案】(Ⅰ)因为()()a b c a b c ac ++-+=,所以222ac b ac+-=-.由余弦定理得,2221cos 22a cb B ac +-==-,因此,0120B =.(Ⅱ)由(Ⅰ)知060A C +=,所以cos()cos cos sin sin A C A C A C -=+ cos cos sin sin 2sin sin A C A C A C =-+ cos()2sin sin A C A C =++131224-=+⨯3=,故030A C -=或030A C -=-, 因此,015C =或045C =.22.(2013年高考湖南(文))已知函数f(x)=(1) 求2()3f π的值;(2) 求使 1()4f x <成立的x 的取值集合 【答案】解: (1)41)212cos 232(sin 21)3sin sin 3cos(cos cos )(+⋅+⋅=⋅+⋅⋅=x x x x x x f ππ41)32(.414123sin 21)32(41)62sin(21-==-=+=⇒++=ππππf f x 所以.(2)由(1)知,)2,2()62(0)62sin(4141)62sin(21)(f ππππππk k x x x x -∈+⇒<+⇒<++=.),12,127(.),12,127(Z k k k Z k k k x ∈--∈--∈⇒ππππππππ所以不等式的解集是:23.(2013年高考天津卷(文))在△ABC 中, 内角A , B , C 所对的边分别是a , b , c . 已知sin 3sin b A c B =, a = 3, 2cos 3B =. (Ⅰ) 求b 的值;(Ⅱ) 求sin 23B π⎛⎫- ⎪⎝⎭的值. 【答案】24.(2013年高考广东卷(文))已知函数(),12f x x x Rπ⎛⎫=-∈ ⎪⎝⎭.(1) 求3f π⎛⎫⎪⎝⎭的值; (2) 若33cos ,,252πθθπ⎛⎫=∈ ⎪⎝⎭,求6f πθ⎛⎫- ⎪⎝⎭.【答案】(1)133124f ππππ⎛⎫⎛⎫⎛⎫=-== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭(2)33cos ,,252πθθπ⎛⎫=∈ ⎪⎝⎭,4sin 5θ==-, 1cos cos sin sin 64445f ππππθθθθ⎛⎫⎛⎫⎫∴--=+=-⎪ ⎪⎪⎝⎭⎝⎭⎭.25.(2013年高考山东卷(文))设函数2()sin cos (0)f x x x x ωωωω=->,且()y f x =的图象的一个对称中心到最近的对称轴的距离为4π,(Ⅰ)求ω的值(Ⅱ)求()f x 在区间3[,]2ππ上的最大值和最小值【答案】26.(2013年高考浙江卷(文))在锐角△ABC 中,内角A,B,C 的对边分别为a,b,c,且2asinB=3b . (Ⅰ)求角A 的大小;(Ⅱ) 若a=6,b+c=8,求△ABC 的面积.【答案】解:(Ⅰ)由已知得到:2sin sin 3sin A B B=,且3(0,)sin 0sin 22B B A π∈∴≠∴=,且(0,)23A A ππ∈∴=;(Ⅱ)由(1)知1cos 2A =,由已知得到:222128362()3366433623b c bc b c bc bc bc =+-⨯⇒+-=⇒-=⇒=,所以1283732323ABCS=⨯⨯=; 27.(2013年高考福建卷(文))如图,在等腰直角三角形OPQ∆中,90OPQ ∠=,22OP =,点M 在线段PQ 上. (1)若3OM =,求PM 的长;(2)若点N 在线段MQ 上,且30MON ∠=,问:当POM ∠取何值时,OMN ∆的面积最小?并求出面积的最小值.【答案】解:(Ⅰ)在OMP ∆中,45OPM ∠=︒,5OM =22OP =, 由余弦定理得,2222cos 45OM OP MP OP MP =+-⨯⨯⨯︒,得2430MPMP -+=,解得1MP =或3MP =. (Ⅱ)设POM α∠=,060α︒≤≤︒,在OMP ∆中,由正弦定理,得sin sin OM OPOPM OMP=∠∠, 所以()sin 45sin 45OP OM α︒=︒+, 同理()sin 45sin 75OP ON α︒=︒+ 故1sin 2OMNSOM ON MON ∆=⨯⨯⨯∠()()221sin 454sin 45sin 75OP αα︒=⨯︒+︒+()()1sin 45sin 4530αα=︒+︒++︒()()()131sin 45sin 45cos 4522ααα=⎡⎤︒+︒++︒+⎢⎥()()()2131sin 45sin 45cos 4522ααα=︒++︒+︒+()()1311cos 902sin 90244αα=-︒++︒+⎡⎤⎣⎦1331sin 2cos 2444αα=++()131sin 23042α=++︒因为060α︒≤≤︒,30230150α︒≤+︒≤︒,所以当30α=︒时,()sin 230α+︒的最大值为1,此时OMN ∆的面积取到最小值.即230POM ∠=︒时,OMN ∆的面积的最小值为843-.28.(2013年高考陕西卷(文))已知向量1(cos ,),(3sin ,cos2),2x x x x =-=∈a b R , 设函数()·f x =a b.(Ⅰ) 求f (x)的最小正周期.(Ⅱ) 求f (x) 在0,2π⎡⎤⎢⎥⎣⎦上的最大值和最小值. 【答案】(Ⅰ) ()·f x =a b =)62sin(2cos 212sin 232cos 21sin 3cos π-=-=-⋅x x x x x x .最小正周期ππ==22T .所以),62sin()(π-=x x f 最小正周期为π. (Ⅱ)上的图像知,在,由标准函数时,当]65,6-[sin ]65,6-[)62(]2,0[ππππππx y x x =∈-∈.]1,21[)]2(),6-([)62sin()(-=∈-=πππf f x x f .所以,f (x) 在0,2π⎡⎤⎢⎥⎣⎦上的最大值和最小值分别为21,1-. 29.(2013年高考重庆卷(文))(本小题满分13分,(Ⅰ)小问4分,(Ⅱ)小问9分)在△ABC 中,内角A 、B 、C 的对边分别是a 、b 、c ,且2223a b c ab=++.(Ⅰ)求A ;(Ⅱ)设3a =,S 为△ABC 的面积,求3cos cos S B C +的最大值,并指出此时B 的值. 【答案】30.(2013年高考四川卷(文))在ABC ∆中,角,,A B C 的对边分别为,,a b c ,且3cos()cos sin()sin()5A B B A B A c ---+=-.(Ⅰ)求sin A 的值;(Ⅱ)若42a =,5b =,求向量BA 在BC 方向上的投影.【答案】解:(Ⅰ)由3cos()cos sin()sin()5A B B A B A c ---+=- 得53sin )sin(cos )cos(-=---B B A B B A ,则 53)cos(-=+-B B A ,即 53cos -=A 又π<<A 0,则 54sin =A(Ⅱ)由正弦定理,有 Bb A a sin sin =,所以22sin sin ==a A b B ,由题知b a >,则 B A >,故4π=B . 根据余弦定理,有 )53(525)24(222-⨯⨯-+=c c , 解得 1=c 或 7-=c (负值舍去), 向量BA 在BC 方向上的投影为=B BA cos 2231.(2013年高考江西卷(文))在△ABC 中,角A,B,C 的对边分别为a,b,c,已知sinAsinB+sinBsinC+cos2B=1.(1)求证:a,b,c 成等差数列;(2) 若C=23π,求a b 的值.【答案】解:(1)由已知得sinAsinB+sinBsinC+1-2sin 2B=1.故sinAsinB+sinBsinC=2sin 2B因为sinB 不为0,所以sinA+sinC=2sinB 再由正弦定理得a+c=2b,所以a,b,c 成等差数列 (2)由余弦定理知2222cos ca b ac C=+-得2222(2)2cos3b a a b ac π-=+-化简得35a b = 32.(2013年高考湖北卷(文))在△ABC 中,角A ,B ,C 对应的边分别是a ,b ,c .已知cos23cos()1A B C -+=.(Ⅰ)求角A 的大小; (Ⅱ)若△ABC 的面积53S =,5b =,求sin sin B C 的值.【答案】(Ⅰ)由cos23cos()1A B C -+=,得22cos 3cos 20A A +-=, 即(2cos 1)(cos 2)0A A -+=,解得1cos 2A = 或cos 2A =-(舍去). 因为0πA <<,所以π3A =. (Ⅱ)由1133sin 53,2224S bc A bc bc ==⋅==得20bc =. 又5b =,知4c =.由余弦定理得2222cos 25162021,a b c bc A =+-=+-=故21a =.又由正弦定理得222035sin sin sin sin sin 2147b c bc B C A A A a a a =⋅==⨯=.33.(2013年高考安徽(文))设函数()sin sin()3f x x x π=++. (Ⅰ)求()f x 的最小值,并求使()f x 取得最小值的x 的集合;(Ⅱ)不画图,说明函数()y f x =的图像可由sin y x =的图象经过怎样的变化得到.【答案】解:(1)3sin cos 3cos sin sin )(ππx x x x f ++= xx x x x cos 23sin 23cos 23sin 21sin +=++= )6sin(3)6sin()23()23(22ππ+=++=x x当1)6sin(-=+πx 时,3)(min -=x f ,此时)(,234,2236Z k k x k x ∈+=∴+=+πππππ所以,)(x f 的最小值为3-,此时x 的集合},234|{Z k k x x ∈+=ππ.(2)x y sin =横坐标不变,纵坐标变为原来的3倍,得xy sin 3=;然后xy sin 3=向左平移6π个单位,得)6sin(3)(π+=x x f34.(2013年高考北京卷(文))已知函数21(2cos1)sin 2cos 42f x x x x=-+().(I)求f x ()的最小正周期及最大值;(II)若(,)2παπ∈,且2f α=(),求α的值.【答案】解:(I)因为21(2cos1)sin 2cos 42f x x x x=-+()=1cos 2sin 2cos 42x x x +=1(sin 4cos 4)2x x +=sin(4)24x π+,所以()f x 的最小正周期为2π,最大值为2.(II)因为2f α=(),所以sin(4)14πα+=. 因为(,)2παπ∈, 所以9174(,)444πππα+∈,所以5442ππα+=,故916πα=. 35.(2013年上海高考数学试题(文科))本题共有2个小题.第1小题满分6分,第2小题满分8分.已知函数()2sin()f x x ω=,其中常数0ω>.(1)令1ω=,判断函数()()()2F x f x f x π=++的奇偶性并说明理由;(2)令2ω=,将函数()y f x =的图像向左平移6π个单位,再往上平移1个单位,得到函数()y g x =的图像.对任意的a R∈,求()y g x =在区间[,10]a a π+上零点个数的所有可能值.【答案】法一:解:(1)()2sin 2sin()2sin 2cos )24F x x x x x x ππ=++=+=+()F x 是非奇函数非偶函数.∵()0,()44F F ππ-==∴()(),()()4444F F F F ππππ-≠-≠- ∴函数()()()2F x f x f x π=++是既不是奇函数也不是偶函数. (2)2ω=时,()2sin 2f x x =,()2sin 2()12sin(2)163g x x x ππ=++=++, 其最小正周期T π=由2sin(2)103x π++=,得1sin(2)32x π+=-, [来源:学,科,网] ∴2(1),36kx k k Zπππ+=--⋅∈,即(1),2126kk x k Zπππ=--⋅-∈区间[],10a a π+的长度为10个周期,若零点不在区间的端点,则每个周期有2个零点; 若零点在区间的端点,则仅在区间左或右端点处得一个区间含3个零点,其它区间仍是2个零点;故当(1),2126kk a k Zπππ=--⋅-∈时,21个,否则20个.法二:36.(2013年高考辽宁卷(文))设向量)(),sin ,cos ,sinx ,0,.2a x x b x x π⎡⎤==∈⎢⎥⎣⎦(I)若.a b x =求的值; (II)设函数()(),.f x a b f x =求的最大值 【答案】。
三角函数公式大全

三角函数公式大全Company Document number:WUUT-WUUY-WBBGB-BWYTT-1982GT三角函数公式三角函数是数学中属于中的的一类函数。
它们的本质是任何角的集合与一个比值的集合的变量之间的映射。
通常的三角函数是在平面直角坐标系中定义的。
其定义城为整个城。
另一种定义是在直角三角形中,但并不完全。
现代数学把它们描述成无穷敖列的和的解,将其定义扩展到复数系。
公式分类锐角三角函数公式sin α=∠α的对边 / 斜边cos α=∠α的邻边 / 斜边tan α=∠α的对边 / ∠α的邻边cot α=∠α的邻边 / ∠α的对边倍角公式sin2A=2sinA?cosAcos2A=cosA;方-sinA方;A=1-2sin²A=2cos²A-1tan2A=(2tanA)÷(1-tan^2A)三倍角公式sin3α=4sinα·sin(π/3+α)sin(π/3-α)cos3α=4cosα·cos(π/3+α)cos(π/3-α)tan3a = tan a · tan(π/3+a)· tan(π/3-a)三倍角公式推导sin3a=sin(2a+a)=sin2acosa+cos2asina=2sina(1-sin²a)+(1-2sin²a)sina=3sina-4sin³acos3a=cos(2a+a)=cos2acosa-sin2asina=(2cos²a-1)cosa-2(1-cos²a)cosa=4cos³a-3cosasin3a=3sina-4sin³a=4sina(3/4-sin²a)=4sina[(√3/2)²-sin²a]=4sina(sin²60°-sin²a)=4sina(sin60°+sina)(sin60°-sina)=4sina*2sin[(60+a)/2]cos[(60°-a)/2]*2sin[(60°-a)/2]cos[(60°-a)/2]=4sinasin(60°+a)sin(60°-a)cos3a=4cos³a-3cosa=4cosa(cos²a-3/4)=4cosa[cos²a-(√3/2)²]=4cosa(cos²a-cos²30°)=4cosa(cosa+cos30°)(cosa-cos30°)=4cosa*2cos[(a+30°)/2]cos[(a-30°)/2]*{-2sin[(a+30°)/2]sin[(a-30°)/2]} =-4cosasin(a+30°)sin(a-30°)=-4cosasin[90°-(60°-a)]sin[-90°+(60°+a)]=-4cosacos(60°-a)[-cos(60°+a)]=4cosacos(60°-a)cos(60°+a)上述两式相比可得tan3a=tanatan(60°-a)tan(60°+a)半角公式tan(A/2)=(1-cosA)/sinA=sinA/(1+cosA);cot(A/2)=sinA/(1-cosA)=(1+cosA)/sinA.sin^2(a/2)=(1-cos(a))/2cos^2(a/2)=(1+cos(a))/2tan(a/2)=(1-cos(a))/sin(a)=sin(a)/(1+cos(a))和差化积sinθ+sinφ = 2 sin[(θ+φ)/2] cos[(θ-φ)/2]sinθ-sinφ = 2 cos[(θ+φ)/2] sin[(θ-φ)/2]cosθ+cosφ = 2 cos[(θ+φ)/2] cos[(θ-φ)/2]cosθ-cosφ = -2 sin[(θ+φ)/2] sin[(θ-φ)/2]tanA+tanB=sin(A+B)/cosAcosB=tan(A+B)(1-tanAtanB) tanA-tanB=sin(A-B)/cosAcosB=tan(A-B)(1+tanAtanB)积化和差sinαsinβ = [cos(α-β)-cos(α+β)] /2cosαcosβ = [cos(α+β)+cos(α-β)]/2sinαcosβ = [sin(α+β)+sin(α-β)]/2cosαsinβ = [sin(α+β)-sin(α-β)]/2双曲函数sinh(a) = [e^a-e^(-a)]/2cosh(a) = [e^a+e^(-a)]/2tanh(a) = sin h(a)/cos h(a)公式一:设α为任意角,终边相同的角的同一三角函数的值相等:sin(2kπ+α)= sinαcos(2kπ+α)= cosαtan(2kπ+α)= tanαcot(2kπ+α)= cotα公式二:设α为任意角,π+α的与α的三角函数值之间的关系:sin(π+α)= -sinαcos(π+α)= -cosαtan(π+α)= tanαcot(π+α)= cotα公式三:任意角α与 -α的三角函数值之间的关系:sin(-α)= -sinαcos(-α)= cosαtan(-α)= -tanαcot(-α)= -cotα公式四:利用公式二和公式三可以得到π-α与α的三角函数值之间的关系:sin(π-α)= sinαcos(π-α)= -cosαtan(π-α)= -tanαcot(π-α)= -cotα公式五:利用公式-和公式三可以得到2π-α与α的三角函数值之间的关系:sin(2π-α)= -sinαcos(2π-α)= cosαtan(2π-α)= -tanαcot(2π-α)= -cotα公式六:π/2±α及3π/2±α与α的三角函数值之间的关系:sin(π/2+α)= cosαcos(π/2+α)= -sinαtan(π/2+α)= -cotαcot(π/2+α)= -tanαsin(π/2-α)= cosαcos(π/2-α)= sinαtan(π/2-α)= cotαcot(π/2-α)= tanαsin(3π/2+α)= -cosαcos(3π/2+α)= sinαtan(3π/2+α)= -cotαcot(3π/2+α)= -tanαsin(3π/2-α)= -cosαcos(3π/2-α)= -sinαtan(3π/2-α)= cotαcot(3π/2-α)= tanα(以上k∈Z)A·sin(ωt+θ)+ B·sin(ωt+φ) =√{(A^2 +B^2 +2ABcos(θ-φ)} ? sin{ωt + arcsin[ (A?sinθ+B?sinφ) / √{A^2 + B^2; +2ABcos(θ-φ)} }√表示根号,包括{……}中的内容诱导公式sin(-α) = -sinαcos(-α) = cosαtan (-α)=-tanαsin(π/2-α) = cosαcos(π/2-α) = sinαsin(π/2+α) = cosαcos(π/2+α) = -sinαsin(π-α) = sinαcos(π-α) = -cosαsin(π+α) = -sinαcos(π+α) = -cosαtanA= sinA/cosAtan(π/2+α)=-cotαtan(π/2-α)=cotαtan(π-α)=-tanαtan(π+α)=tanα记背诀窍:奇变偶不变,符号看象限万能公式其它公式(1)(sinα)^2+(cosα)^2=1(2)1+(tanα)^2=(secα)^2(3)1+(cotα)^2=(cscα)^2证明下面两式,只需将一式,左右同除(sinα)^2,第二个除(cosα)^2即可(4)对于任意非直角三角形,总有tanA+tanB+tanC=tanAtanBtanC证:A+B=π-Ctan(A+B)=tan(π-C)(tanA+tanB)/(1-tanAtanB)=(tanπ-tanC)/(1+tanπtanC)整理可得tanA+tanB+tanC=tanAtanBtanC得证同样可以得证,当x+y+z=nπ(n∈Z)时,该关系式也成立由tanA+tanB+tanC=tanAtanBtanC可得出以下结论(5)cotAcotB+cotAcotC+cotBcotC=1(6)cot(A/2)+cot(B/2)+cot(C/2)=cot(A/2)cot(B/2)cot(C/2)(7)(cosA)^2+(cosB)^2+(cosC)^2=1-2cosAcosBcosC(8)(sinA)^2+(sinB)^2+(sinC)^2=2+2cosAcosBcosC其他非重点三角函数csc(a) = 1/sin(a)sec(a) = 1/cos(a)[]内容规律三角函数看似很多,很复杂,但只要掌握了三角函数的本质及内部规律就会发现三角函数各个公式之间有强大的联系。
所有的三角函数及名称

所有的三角函数及名称说到三角函数,哎哟,那可真是让很多同学头疼的一个话题。
你一听到“正弦、余弦、正切”这些名词,脑袋瓜就开始冒烟,心里默默想:“这啥玩意儿,咋弄啊?”三角函数啊,说白了,就是跟三角形有关系的数学小工具,帮助我们解决一些看起来复杂的几何问题。
你知道吗,三角函数并不是天外飞来的仙丹,它就像是你生活中的万能钥匙,能解开很多你看似无法解决的问题。
大家别着急,先深呼吸,跟我一起慢慢捋一下这些“怪兽”到底是什么。
首先得从三角形说起。
你想,三角形是由三条边和三个角组成的,听起来挺简单对吧?不过,实际上一些角度和边长之间的关系,直接决定了你能否找到那个完美的解。
三角函数就是用来描述这些关系的,像个秘密小帮手。
大家听说过“三角函数”这个词,它包括了正弦(sin)、余弦(cos)、正切(tan)这几个大名鼎鼎的角色。
你想,正弦和余弦就是这帮小伙伴中最“稳”的两个,正切就像个“搞笑担当”,总是让你捧腹大笑,但有时候也会把你弄得晕头转向。
先说正弦和余弦吧,简直是数学中的黄金搭档。
它们俩的关系特别简单,正弦就是三角形的对边长度和斜边长度的比,余弦呢,就是邻边长度和斜边长度的比。
说白了,正弦是站在三角形的对面,余弦则站在邻近你角度的旁边。
你试着想象一下,正弦和余弦像两个闺蜜,一个总是站在你面前,另一个则躲在你身旁。
它们俩总是形影不离,相互补充,让你在面对角度的时候,能更好地看清楚对比的关系。
然后啊,说到正切,那可是个活宝。
正切就是正弦和余弦的“合体”,它是正弦和余弦的比值。
就是那种,你吃了一块蛋糕,它吃了另一块,两者结合,你俩就可以一起组成一个新甜品了。
正切也是三角函数中的“野路子”,它不仅能够让你解题,还能给你带来一些意外的惊喜。
你看,正切特别像那种社交达人,总是能一蹦一跳地把你带入各种情况,但有时候它也让你差点头晕目眩,尤其是当角度达到90度时,正切就会失控,变成个大无穷,哎呀,这时候你得小心了,不然就容易“翻车”。
三角函数ppt

5
7
7
4 y
7
M1 M2 O
x
小练习
解析: 2. f(x)=sin(x)+ 3cos(x)
1
3
=2( sin(x)+ cos(x))
2
2
=2sin(x+ )
3
因为x∈[− , ]
2 2
5
所以x+ ∈[- , ]
3
6 6
1
故− ≤ ( + ) ≤ 1
2
3
则−1 ≤ 2( + ) ≤ 2
三角函数的定义
三角函数是基本初等函数之一,是以角度(数学上最
常用弧度制,下同)为自变量,角度对应任意角终边
与单位圆交点坐标或其比值为因变量的函数。也可以
等价地用与单位圆有关的各种线段的长度来定义。
三角函数的定义
y轴
1
T
P(x,y)
A(1,0)
-1
M
O
-1
sinα=MP
cosα=OM
tanα=AT
3
即函数的值域为[-1,2]
故选A
课堂小结
本节课,我们了解了什么是三角函数,
常见的三角函数有哪些以及常见三角
函数图像和性质,借助这些三角函数
的知识我们可以解决比较正弦函数、
余弦函数、正切函数的大小以及求三
角函数的奇偶性等问题。
课后作业
1.选择题:比较 和 的大小
7
7
A.sin 大 √
1
x轴
三角函数
定义域
值域
sinα
R
[-1,1]
三角函数公式大全(表格分类)

三角函数公式大全(表格分
类)
本页仅作为文档页封面,使用时可以删除
This document is for reference only-rar21year.March
sin sin 2sin
cos
22sin sin 2cos sin
22
cos cos 2cos cos
22cos cos 2sin sin
22
αβ
αβ
αβαβαβ
αβαβαβ
αβαβαβ
αβ+-+=⋅+--=⋅+-+=⋅+--=-⋅
[][]
[]
[]
1
sin cos sin()sin()21
cos sin sin()sin()2
1
cos cos cos()cos()21
sin sin cos()cos()2αβαβαβαβαβαβαβαβαβαβαβαβ⋅=
++-⋅=+--⋅=++-⋅=-+--
化asinα ±bcosα为一个角的一个三角函数的形式(辅助角的三角函数的公式)
22sin cos sin()a x b x a b x φ±=+±
其中φ角所在的象限由a 、b 的符号确定,φ角的值由tan b
a
φ
=
确定
六边形记忆法:图形结构“上弦中切下割,左正右余中间1”;记忆方法“对角线上两个函数的积为1;阴影三角形上两顶点的三角函数值的平方和等于下顶点的三角函数值的平方;任意一顶点的三角函数值等于相邻两个顶点的三角函数值的乘积。
”。
三角函数公式表(免费)

鄙视下载资料还要财富值的!
一:指数函数
二:对数函数
三:指数函数与对数函数有什么关系?(关于y=x 对称)
x
y 2=x
y 3=x
y ⎪⎭
⎫ ⎝⎛=21x
y ⎪⎭
⎫ ⎝⎛=31x
y 2log =x
y 2
1log =x
y 3log =x
y 3
1log =x
y 2=x
y =x
y 2log =
二、基本初等函数及其图像
1
2
3
,奇函数
无界,周期为余割函数
,偶函数无界,周期为正割函数,奇函数无界,周期为余切函数,奇函数无界,周期为正切函数,偶函数有界,周期为余弦函数,奇函数有界,周期为正弦函数性质
表达式名称ππππππ2csc 2sec cot tan 2cos 2sin x
y x y x y x y x y x y ======)
R (sin ∈=x x y 的图象)
R (cos ∈=x x y 的图象tan (π0.5π)
y x x k =≠+的图像
4
cot (π)
y x x k =≠的图像)
0()
(cot arc 22)(arctan ]0[]11[arccos 22]11[arcsin ππππππ,,反余切函数
,,反正切函数,,反余弦函数,,反正弦函数值域定义域表达式名称∞+-∞=⎪⎭⎫ ⎝⎛-∞+-∞=-=⎥⎦⎤
⎢⎣⎡--=x
y x y x y x y。
三角函数公式表(全)

(六边形记忆法:图形结构“上弦中切下割,左正右余中间1”;记忆方法"对角线上两个函数的积为1 ;阴影三角形上两顶点的三角函数值的平方和等于下顶点的三角函数值的平方;任意一顶点的三角函数值等于相邻两个顶点的三角函数值的乘积。
”)诱导公式(口诀:奇变偶不变,符号看象限。
)sin (— a )= —sin a COS (― a )= COs a tan (— a )= —tanaCOt (— a )=—COt asin ( n /2 — a)= COS a COS ( n /2 — a)= sin a tan (n /2 — a)= COt a COt ( n /2 —a)= tan a sin ( n — a )= sin aCOS ( n — a )=—COSatan ( n — a)=—tan aCOt ( n— a )=—COt asin( 3 n /2 — a)=—COS aCOS (3 n /2 —a)=—sin atan (3 n /2 —a)= cot aCOt (3 n /2 —a)= tan asin (2 n — a ) =—sin aCOS (2 n — a )= COS atan (2 n — a ) =—tan aCOt (2 n — a ) = —COt a倒数关系:tan a • cot a =1Sin a • CSC a =1 三角函数公式表同角三角函数的基本关系式商的关系: 平方关系: sin a /cos a = tanaSin 2a + COS 2a=1 1 + tan 2a =sec2asin ( n /2 +a)= COS a sin ( n + a )=—sina sin( 3 n /2 + a)=—COS asin (2k n + a )= sin acos ( n /2 + a ) =— sin a cos ( n + a )=— cos a cos (3 n /2 + a )= sin a cos (2k n + a ) = cosatan (n /2 + a) = — cota tan ( n + a)= tan a tan (3 n /2 + a )=— cot a tan (2k n + a ) = tanacot ( n /2 + a ) =— tana cot ( n+ a )= cot a cot (3 n /2 + a )=— tan acot (2k n + a ) = cota(其中k € Z)两角和与差的三角函数公式 sin ( a+B )= sin a cos 3 + cos a sin 3 sin ( a — 3 )= sin a cos 3 — cos asin 3 cos (a+ 3)= cos a cos 3 — sin a sin 3 cos (a — 3)= cos a cos 3 + sin a sin 3 tan a + tan 3 tan ( a+ 3 )= — 1 — tan a • tan 3 tan a — tan 3 tan ( a — 3 )= -------- ----- 1 + tan a • tan 3半角的正弦、余弦和正切公式 万能公式2tan( a /2)sin a = ----------1 + tan 2(a /2)1 — tan 2( a /2)cos a = ----------1 + tan 2(a /2)2tan( a /2)tan a = ----------1 — tan 2(a/2)三角函数的降幕公式二倍角的正弦、余弦和正切公式sin2 a = 2sin a COS a cos2 a = cos 2 a — sin 2 a= 2cos 2a — 1 = 1 — 2sin 2 a 2ta n a tan2 a = --------- 1 — tan 2a 三角函数的和差化积公式Sin a +sin 3 =2sin[( a + 3 )/2] • cos[( a - 3 )/2] sin a -sin 3 =2cos[( a + 3 )/2] • sin[ ( a - 3 )/2] cos a +cos 3 =2cos[( a + 3 )/2] • COS[ ( a - 3)/2] cos a -cos 3 =-2sin[( a + 3 )/2] • sin[( a -3 )/2] .2 1 - cos2otsin & = -------------231+ cos 2acos ot = --- --2三倍角的正弦、余弦和正切公式sin3 a = 3sin a — 4sin 3acos3 a = 4cos 3a — 3cosa3tan a — tan 3atan3 a = ----------1 — 3ta n 2a三角函数的积化和差公式sinacoscos a cos 3 = -[sin (a + B)+ sin (a — 3)]2 1sin 3 = -[sin (a + 3)— sin (a — 3)]2 1-cos 3 = -[cos (a + 3)+ cos (a — 3 )]sin a • sin 3=—-[cos (a+ B )—cos (a — 3 )]2化asin a ± bcos a为一个角的一个三角函数的形式(辅助角的三角函数的公式)(其中①角所在象限由尔占的符号确定4角的值*tar^=-确定) aTHANKS !!!致力为企业和个人提供合同协议,策划案计划书,学习课件等等打造全网一站式需求。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2013年全国高考理科数学试题分类汇编3:三角函数一、选择题1 .(2013年普通高等学校招生统一考试浙江数学(理)试题(纯WORD 版))已知210cos 2sin ,=+∈αααR ,则=α2tan A.34 B. 43 C.43- D.34-【答案】C2 .(2013年高考陕西卷(理))设△ABC 的内角A , B , C 所对的边分别为a , b , c , 若cos cos sin b C c B a A +=,则△ABC 的形状为(A) 锐角三角形 (B) 直角三角形 (C) 钝角三角形 (D) 不确定 【答案】B3 .(2013年普通高等学校招生统一考试天津数学(理)试题(含答案))在△ABC 中,,3,4AB BC ABC π∠==则sin BAC ∠ =【答案】C4 .(2013年普通高等学校招生统一考试山东数学(理)试题(含答案))将函数sin(2)y x ϕ=+的图象沿x 轴向左平移8π个单位后,得到一个偶函数的图象,则ϕ的一个可能取值为 (A) 34π (B) 4π (C)0 (D) 4π-【答案】B5 .(2013年普通高等学校招生统一考试辽宁数学(理)试题(WORD 版))在ABC ∆,内角,,A B C 所对的边长分别为,,.a b c 1sin cos sin cos ,2a B C c B Ab +=且a b >,则B ∠= A.6π B.3π C.23π D.56π【答案】A6 .(2013年普通高等学校招生统一考试大纲版数学(理)WORD 版含答案(已校对))已知函数()=cos sin 2f x x x ,下列结论中错误的是(A)()y f x =的图像关于(),0π中心对称 (B)()y f x =的图像关于直线2x π=对称(C)()f x()f x 既奇函数,又是周期函数 【答案】C7 .(2013年普通高等学校招生统一考试山东数学(理)试题(含答案))函数cos sin y x x x =+的图象大致为【答案】D8 .(2013年高考四川卷(理))函数()2sin(),(0,)22f x x ππωϕωϕ=+>-<<的部分图象如图所示,则,ωϕ的值分别是( )(A)2,3π-(B)2,6π-(C)4,6π-(D)4,3π【答案】A9 .(2013年上海市春季高考数学试卷(含答案))既是偶函数又在区间(0 )π,上单调递减的函数是( ) (A)sin y x = (B)cos y x = (C)sin 2y x = (D)cos 2y x =【答案】B10.(2013年普通高等学校招生统一考试重庆数学(理)试题(含答案))04cos50tan 40-= ( )1 【答案】C11.(2013年高考湖南卷(理))在锐角中ABC ∆,角,A B 所对的边长分别为,a b .若2sin ,a B A 则角等于A.12π B.6π C.4π D.3π 【答案】D12.(2013年高考湖北卷(理))将函数()sin yx x x R =+∈的图像向左平移()0m m >个长度单位后,所得到的图像关于y 轴对称,则m 的最小值是( )A.12π B.6π C.3π D.56π【答案】B 二、填空题13.(2013年普通高等学校招生统一考试浙江数学(理)试题(纯WORD 版))ABC ∆中,090=∠C ,M 是BC的中点,若31sin =∠BAM ,则=∠BAC sin ________.14.(2013年高考新课标1(理))设当x θ=时,函数()sin 2cos f x x x =-取得最大值,则cos θ=______【答案】. 15.(2013年普通高等学校招生统一考试福建数学(理)试题(纯WORD 版))如图ABC ∆中,已知点D 在BC边上,AD ⊥AC,sin 3BAC AB AD ∠===则BD 的长为_______________16.(2013年上海市春季高考数学试卷(含答案))函数2sin y x =的最小正周期是_____________【答案】2π17.(2013年高考四川卷(理))设sin 2sin αα=-,(,)2παπ∈,则tan 2α的值是_________.18.(2013年高考上海卷(理))若12cos cos sin sin ,sin 2sin 223x y x y x y +=+=,则sin()________x y +=【答案】2sin()3x y +=. 19.(2013年高考上海卷(理))已知△ABC 的内角A 、B 、C 所对应边分别为a 、b 、c,若22232330a ab b c ++-=,则角C 的大小是_______________(结果用反三角函数值表示)【答案】1arccos3C π=- 20.(2013年普通高等学校招生统一考试大纲版数学(理)WORD 版含答案(已校对))已知α是第三象限角,1sin 3a =-,则cot a =____________.【答案】21.(2013年普通高等学校招生全国统一招生考试江苏卷(数学)(已校对纯WORD 版含附加题))函数)42sin(3π+=x y 的最小正周期为___________.【答案】π22.(2013年上海市春季高考数学试卷(含答案))在ABC ∆中,角 A B C 、、所对边长分别为 a b c 、、,若5 8 60a b B === ,,,则b=_______【答案】7 [来源:Z 。
xx 。
]23.(2013年普通高等学校招生统一考试安徽数学(理)试题(纯WORD 版))设ABC ∆的内角,,A B C 所对边的长分别为,,a b c .若2b c a +=,则3sin 5sin ,A B =则角C =_____.【答案】π3224.(2013年普通高等学校招生统一考试新课标Ⅱ卷数学(理)(纯WORD 版含答案))设θ为第二象限角,若1tan()42πθ+=,则sin cos θθ+=________.【答案】5-25.(2013年高考江西卷(理))函数2sin2y x x =+的最小正周期为T 为_________.【答案】π26.(2013年上海市春季高考数学试卷(含答案))函数4sin 3cos y x x =+的最大值是_______________ 【答案】5 三、解答题27.(2013年高考北京卷(理))在△ABC 中,a =3,b B =2∠A .(I)求cos A 的值; (II)求c 的值.【答案】解:(I)因为a =3,b =2,∠B =2∠A . 所以在△ABC 中,由正弦定理得3sin sin 2A A=.所以2sin cos sin A A A =.故cos A =.(II)由(I)知cos A =,所以s i n A ==.又因为∠B=2∠A,所以21c o s 2c o s 13B A =-=.所以sin B ==.在△ABC 中,sin sin()sin cos cos sin C A B A B A B =+=+=所以sin 5sin a Cc A==.28.(2013年高考陕西卷(理))已知向量1(cos ,),,cos2),2x x x x =-=∈a b R , 设函数()·f x =a b . (Ⅰ) 求f (x)的最小正周期.(Ⅱ) 求f (x) 在0,2π⎡⎤⎢⎥⎣⎦上的最大值和最小值.【答案】解:(Ⅰ) ()·f x =a b =)62sin(2cos 212sin 232cos 21sin 3cos π-=-=-⋅x x x x x x .最小正周期ππ==22T . 所以),62sin()(π-=x x f 最小正周期为π.(Ⅱ) 上的图像知,在,由标准函数时,当]65,6-[sin ]65,6-[)62(]2,0[ππππππx y x x =∈-∈.]1,21[)]2(),6-([)62sin()(-=∈-=πππf f x x f . 所以,f (x) 在0,2π⎡⎤⎢⎥⎣⎦上的最大值和最小值分别为21,1-.29.(2013年普通高等学校招生统一考试重庆数学(理)试题(含答案))在ABC 中,内角,,A B C 的对边分别是,,a b c ,且222a b c +=.(1)求C ; (2)设()()2cos cos cos cos 5cos 5A B A B ααα++==,求tan α的值. 【答案】由题意得30.(2013年普通高等学校招生统一考试天津数学(理)试题(含答案))已知函数2()26sin cos 2cos 41,f x x x x x x π⎛⎫=++- ⎪+⎝⎭∈R .(Ⅰ) 求f (x )的最小正周期; [来源:学§科§网] (Ⅱ) 求f (x )在区间0,2π⎡⎤⎢⎥⎣⎦上的最大值和最小值.【答案】31.(2013年普通高等学校招生统一考试辽宁数学(理)试题(WORD 版))设向量)(),sin,cos,sinx,0,.2a x xb x xπ⎡⎤==∈⎢⎥⎣⎦(I)若.a b x=求的值;(II)设函数()(),.f x a b f x= 求的最大值【答案】[来源:学_科_网Z_X_X_K]32.(2013年高考上海卷(理))(6分+8分)已知函数()2sin()f x xω=,其中常数0ω>;(1)若()y f x=在2[,]43ππ-上单调递增,求ω的取值范围;(2)令2ω=,将函数()y f x=的图像向左平移6π个单位,再向上平移1个单位,得到函数()y g x=的图像,区间[,]a b(,ab R∈且a b<)满足:()y g x=在[,]a b上至少含有30个零点,在所有满足上述条件的[,]a b 中,求b a-的最小值.【答案】(1)因为0ω>,根据题意有34202432ππωωππω⎧-≥-⎪⎪⇒<≤⎨⎪≤⎪⎩(2) ()2sin(2)f x x=,()2sin(2())12sin(2)163g x x xππ=++=++1()0sin(2)323g x x x kπππ=⇒+=-⇒=-或7,12x k k Zππ=-∈,即()g x的零点相离间隔依次为3π和23π,故若()y g x =在[,]a b 上至少含有30个零点,则b a -的最小值为2431415333πππ⨯+⨯=. 33.(2013年普通高等学校招生统一考试大纲版数学(理)WORD 版含答案(已校对))设ABC ∆的内角,,A B C 的对边分别为,,a b c ,()()a b c a b c ac ++-+=. (I)求B(II)若sin sin A C =,求C . 【答案】34.(2013年高考四川卷(理))在ABC ∆中,角,,A B C 的对边分别为,,a b c ,且232cos cos sin()sin cos()25A B B A B B A C ---++=-. (Ⅰ)求cos A 的值;(Ⅱ)若a =5b =,求向量BA 在BC方向上的投影.【答案】解:()I 由()()232coscos sin sin cos 25A B B A B B A C ---++=-,得 ()()3cos 1cos sin sin cos 5A B B A B B B -+---=-⎡⎤⎣⎦, 即()()3cos cos sin sin 5A B B A B B ---=-,则()3cos 5A B B -+=-,即3cos 5A =-()II 由3cos ,05A A π=-<<,得4sin 5A =,由正弦定理,有sin sin a b A B =,所以,sin sin b A B a ==.由题知a b >,则A B >,故4B π=.根据余弦定理,有(22235255c c ⎛⎫=+-⨯⨯- ⎪⎝⎭,解得1c =或7c =-(舍去).故向量BA 在BC方向上的投影为cos 2BA B =35.(2013年普通高等学校招生统一考试山东数学(理)试题(含答案))设△ABC 的内角,,A B C 所对的边分别为,,a b c ,且6a c +=,2b =,7cos 9B =. (Ⅰ)求,a c 的值; (Ⅱ)求sin()A B -的值.【答案】解:(Ⅰ)由余弦定理2222cos b a c ac B =+-,得()222(1cos )b ac ac B =+-+,又6a c +=,2b =,7cos 9B =,所以9ac =,解得3a =,3c =.(Ⅱ)在△ABC 中,sin 9B ==,由正弦定理得sin sin a B A b ==,因为a c =,所以A 为锐角,所以1cos 3A ==因此sin()sin cos cos sin 27A B A B A B -=-=.36.(2013年普通高等学校招生统一考试安徽数学(理)试题(纯WORD 版))已知函数()4c o s s i n (0)4f x x x πϖϖϖ⎛⎫=⋅+> ⎪⎝⎭的最小正周期为π. (Ⅰ)求ϖ的值; (Ⅱ)讨论()f x 在区间[]0,2上的单调性.【答案】解: (Ⅰ)2)42sin(2)12cos 2(sin 2)cos (sin cos 22++=++=+⇒πωωωωωωx x x x x x122=⇒=⇒ωπωπ.所以1,2)42sin(2)(=++=ωπx x f (Ⅱ) ;解得,令时,当8242]4,4[)42(]2,0[ππππππππ==++∈+∈x x x x所以.]28[]8,0[)(上单调递减,上单调递增;在在πππx f y =37.(2013年普通高等学校招生统一考试福建数学(理)试题(纯WORD 版))已知函数()sin()(0,0)f x x ωϕωϕπ=+><<的周期为π,图像的一个对称中心为(,0)4π,将函数()f x 图像上的所有点的横坐标伸长为原来的2倍(纵坐标不变),在将所得图像向右平移2π个单位长度后得到函数()g x 的图像.(1)求函数()f x 与()g x 的解析式; (2)是否存在0(,)64x ππ∈,使得0000(),(),()()f x g x f x g x 按照某种顺序成等差数列?若存在,请确定0x 的个数;若不存在,说明理由.[来源:学,科,网](3)求实数a 与正整数n ,使得()()()F x f x ag x =+在(0,)n π内恰有2013个零点.【答案】解:(Ⅰ)由函数()sin()f x x ωϕ=+的周期为π,0ω>,得2ω=又曲线()y f x =的一个对称中心为(,0)4π,(0,)ϕπ∈故()sin(2)044f ππϕ=⨯+=,得2πϕ=,所以()cos 2f x x =将函数()f x 图象上所有点的横坐标伸长到原来的2倍(纵坐标不变)后可得cos y x =的图象,再将cos y x =的图象向右平移2π个单位长度后得到函数()sin g x x =(Ⅱ)当(,)64x ππ∈时,1sin 2x <<,10cos 22x << 所以sin cos 2sin cos 2x x x x >>问题转化为方程2cos 2sin sin cos 2x x x x =+在(,)64ππ内是否有解设()sin sin cos 22cos 2G x x x x x =+-,(,)64x ππ∈ 则()cos cos cos 22sin 2(2sin )G x x x x x x '=++- 因为(,)64x ππ∈,所以()0G x '>,()G x 在(,)64ππ内单调递增又1()064G π=-<,()04G π=> 且函数()G x 的图象连续不断,故可知函数()G x 在(,)64ππ内存在唯一零点0x ,即存在唯一的0(,)64x ππ∈满足题意 (Ⅲ)依题意,()sin cos 2F x a x x =+,令()sin cos 20F x a x x =+=当sin 0x =,即()x k k Z π=∈时,cos 21x =,从而()x k k Z π=∈不是方程()0F x =的解,所以方程()0F x =等价于关于x 的方程cos 2sin xa x=-,()x k k Z π≠∈ 现研究(0,)(,2)x πππ∈U 时方程解的情况 令cos 2()sin xh x x=-,(0,)(,2)x πππ∈U 则问题转化为研究直线y a =与曲线()y h x =在(0,)(,2)x πππ∈U 的交点情况22cos (2sin 1)()sin x x h x x +'=,令()0h x '=,得2x π=或32x π= 当x 变化时,()h x 和()h x '变化情况如下表当0x >且x 趋近于0时,()h x 趋向于-∞ 当x π<且x 趋近于π时,()h x 趋向于-∞ 当x π>且x 趋近于π时,()h x 趋向于+∞ 当2x π<且x 趋近于2π时,()h x 趋向于+∞故当1a >时,直线y a =与曲线()y h x =在(0,)π内有无交点,在(,2)ππ内有2个交点; 当1a <-时,直线y a =与曲线()y h x =在(0,)π内有2个交点,在(,2)ππ内无交点; 当11a -<<时,直线y a =与曲线()y h x =在(0,)π内有2个交点,在(,2)ππ内有2个交点由函数()h x 的周期性,可知当1a ≠±时,直线y a =与曲线()y h x =在(0,)n π内总有偶数个交点,从而不存在正整数n ,使得直线y a =与曲线()y h x =在(0,)n π内恰有2013个交点;当1a =±时,直线y a =与曲线()y h x =在(0,)(,2)πππU 内有3个交点,由周期性,20133671=⨯,所以67121342n =⨯= 综上,当1a =±,1342n =时,函数()()()F x f x ag x =+在(0,)n π内恰有2013个零点38.(2013年普通高等学校招生全国统一招生考试江苏卷(数学)(已校对纯WORD 版含附加题))本小题满分14分.已知(cos ,sin )(cos ,sin )a b ααββ= =,,παβ<<<0.[来源:](1)若||a b -= 求证:a b ⊥ ;(2)设(0,1)c =,若a b c += ,求βα,的值.【答案】解:(1)∵2||=- ∴2||2=- 即()22222=+-=-,又∵1sin cos ||2222=+==αα,1sin cos ||2222=+==ββ∴222=-∴0=∴⊥(2)∵)1,0()sin sin ,cos (cos =++=+βαβα ∴⎩⎨⎧=+=+1sin sin 0cos cos βαβα即⎩⎨⎧-=-=βαβαsin 1sin cos cos两边分别平方再相加得:βsin 221-= ∴21sin =β ∴21sin =α ∵παβ<<<0 ∴πβπα61,65==39.(2013年普通高等学校招生统一考试广东省数学(理)卷(纯WORD 版))已知函数()c o s 12f x x π⎛⎫=- ⎪⎝⎭,x ∈R .(Ⅰ) 求6f π⎛⎫- ⎪⎝⎭的值; (Ⅱ) 若3cos 5θ=,3,22πθπ⎛⎫∈ ⎪⎝⎭,求23f πθ⎛⎫+ ⎪⎝⎭.[来源:学#科#网Z#X#X#K]【答案】(Ⅰ)1661244f πππππ⎛⎫⎛⎫⎛⎫-=--=-== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭;(Ⅱ) 222cos 2sin 233124f ππππθθθθθ⎛⎫⎛⎫⎛⎫+=+-=+=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ 因为3cos 5θ=,3,22πθπ⎛⎫∈ ⎪⎝⎭,所以4sin 5θ=-, 所以24sin 22sin cos 25θθθ==-,227cos 2cos sin 25θθθ=-=- 所以23f πθ⎛⎫+⎪⎝⎭cos 2sin 2θθ=-72417252525⎛⎫=---= ⎪⎝⎭. 40.(2013年高考湖南卷(理))已知函数2()sin()cos().()2sin 632xf x x xg x ππ=-+-=.(I)若α是第一象限角,且()f α=求()g α的值; (II)求使()()f x g x ≥成立的x 的取值集合.【答案】解: (I)533sin 3)(sin 3sin 23cos 21cos 21sin 23)(==⇒=++-=ααf x x x x x x f . 51cos 12sin 2)(,54cos )2,0(,53sin 2=-===⇒∈=⇒ααααπααg 且(II)21)6sin(cos 21sin 23cos 1sin 3)()(≥+=+⇒-≥⇒≥πx x x x x x g x f Z k k k x k k x ∈+∈⇒++∈+⇒],322,2[]652,62[6ππππππππ41.(2013年普通高等学校招生全国统一招生考试江苏卷(数学)(已校对纯WORD 版含附加题))本小题满分16分.如图,游客从某旅游景区的景点A 处下山至C 处有两种路径.一种是从A 沿直线步行到C ,另一种是先从A 沿索道乘缆车到B ,然后从B 沿直线步行到C .现有甲.乙两位游客从A 处下山,甲沿AC 匀速步行,速度为min /50m .在甲出发min 2后,乙从A 乘缆车到B ,在B 处停留min 1后,再从匀速步行到C .假设缆车匀速直线运动的速度为min /130m ,山路AC 长为m 1260,经测量,1312cos =A ,53cos =C . (1)求索道AB 的长;[来源:学科网](2)问乙出发多少分钟后,乙在缆车上与甲的距离最短?(3)为使两位游客在C 处互相等待的时间不超过3分钟,乙步行的速度应控制在什么范围内?【答案】解:(1)∵1312cos =A ,53cos =C ∴),(、20π∈C A ∴135sin =A ,54sin =C∴[]6563sin cos cos sin sin sin sin =+=+=+-=C A C A C A C A B )()(π 根据sinB sinC AC AB =得m C ACAB 1040sin sinB== (2)设乙出发t 分钟后,甲.乙距离为d,则1312)50100(1302)50100()130(222⨯+⨯⨯-++=t t t t d ∴)507037(20022+-=t t d∵13010400≤≤t 即80≤≤t ∴3735=t 时,即乙出发3735分钟后,乙在缆车上与甲的距离最短.(3)由正弦定理sinBsinA ACBC =得50013565631260sin sinB ===A AC BC (m) 乙从B 出发时,甲已经走了50(2+8+1)=550(m),还需走710 m 才能到达C 设乙的步行速度为V min /m ,则350710500≤-v ∴3507105003≤-≤-v ∴14625431250≤≤v CBA∴为使两位游客在C 处互相等待的时间不超过3分钟,乙步行的速度应控制在⎥⎦⎤⎢⎣⎡14625,431250范围内 法二:解:(1)如图作BD ⊥CA 于点D , 设BD =20k ,则DC =25k ,AD =48k , AB =52k ,由AC =63k =1260m, 知:AB =52k =1040m.(2)设乙出发x 分钟后到达点M , 此时甲到达N 点,如图所示. 则:AM =130x ,AN =50(x +2),由余弦定理得:MN 2=AM 2+AN 2-2 AM ·AN cos A =7400 x 2-14000 x +10000, 其中0≤x ≤8,当x =3537 (min)时,MN 最小,此时乙在缆车上与甲的距离最短.(3)由(1)知:BC =500m,甲到C 用时:126050 =1265(min).若甲等乙3分钟,则乙到C 用时:1265 +3=1415 (min),在BC 上用时:865 (min) .此时乙的速度最小,且为:500÷865 =125043m/min.若乙等甲3分钟,则乙到C 用时:1265 -3=1115 (min),在BC 上用时:565 (min) .此时乙的速度最大,且为:500÷565 =62514 m/min.故乙步行的速度应控制在[125043 ,62514]范围内.42.(2013年高考湖北卷(理))在ABC ∆中,角A ,B ,C 对应的边分别是a ,b ,c .已知()cos 23cos 1A B C -+=.(I)求角A 的大小;(II)若ABC ∆的面积S =5b =,求sin sin B C 的值.【答案】解:(I)由已知条件得:cos23cos 1A A +=22cos 3cos 20A A ∴+-=,解得1cos 2A =,角60A =︒(II)1sin 2S bc A ==4c ⇒=,由余弦定理得:221a =,()222228sin a R A == 25sin sin 47bc B C R ∴== 43.(2013年普通高等学校招生统一考试新课标Ⅱ卷数学(理)(纯WORD 版含答案))△ABC 在内角,,A B C 的CBADMN对边分别为,,a b c ,已知cos sin a b C c B =+. (Ⅰ)求B ;(Ⅱ)若2b =,求△ABC 面积的最大值.【答案】44.(2013年高考新课标1(理))如图,在△ABC中,∠ABC=90°,AB= 3 ,BC=1,P 为△ABC内一点,∠BPC=90°(1)若PB=12,求PA;(2)若∠APB=150°,求tan∠PBA[来源:学_科_网]【答案】(Ⅰ)由已知得,∠PBC=o 60,∴∠PBA=30o ,在△PBA 中,由余弦定理得2PA =o 1132cos3042+-=74;(Ⅱ)设∠PBA=α,由已知得,PB=sin α,在△PBA 中,由正弦定理得,o sin sin(30)αα=-,化简得4sin αα=, ∴tan α,∴tan PBA ∠. 45.(2013年上海市春季高考数学试卷(含答案))本题共有2个小题,第一小题满分4分,第二小题满分9分.在平面直角坐标系xOy 中,点A 在y 轴正半轴上,点n P 在x 轴上,其横坐标为n x ,且{}n x 是首项为1、公比为2的等比数列,记1n n n P AP θ+∠=,n N *∈.[来源:学§科§网Z§X§X§K] (1)若31arctan3θ=,求点A 的坐标; (2)若点A的坐标为(0,求n θ的最大值及相应n 的值.【答案】[解](1)设(0 )A t ,,根据题意,12n n x -=.由31arctan 3θ=,知31tan 3θ=,而3443343223443()4tan tan()321x x t x x t t t OAP OAP x x t x x t t tθ--=∠-∠===+⋅++⋅, 所以241323t t =+,解得4t =或8t =. 故点A 的坐标为(0 4),或(0 8),. (2)由题意,点n P 的坐标为1(20)n -,,1tan n n OAP -∠=. 111212tan tan()1n n n n n n n OAP OAP θ--+-=∠-∠===.n ≥,所以tan n θ≤=,当且仅当2nn=,即4n =时等号成立.易知0 tan 2n y x πθ<<=,在(0 )2π,上为增函数,因此,当4n =时,n θ最大,其最大值为arctan4. 46.(2013年高考江西卷(理))在△ABC中,角A,B,C 所对的边分别为a,b,c,已知cosC+(conA-sinA)cosB=0.(1) 求角B 的大小;若a+c=1,求b 的取值范围【答案】解:(1)由已知得cos()cos cos cos 0A B A B A B -++=即有sin sin cos 0A B A B =因为sin 0A ≠,所以sin 0B B =,又cos 0B ≠,所以tan B =又0B π<<,所以3B π=. (2)由余弦定理,有2222cos b a c ac B =+-.因为11,cos 2a c B +==,有22113()24b a =-+. 又01a <<,于是有2114b ≤<,即有112b ≤<.。
