2019届江苏省启东中学高三上学期第一次月考数学试题(解析版)
2019-2020学年江苏省南通市启东中学高三(上)第一次月考数学试卷1 (含答案解析)

2019-2020学年江苏省南通市启东中学高三(上)第一次月考数学试卷1一、填空题(本大题共14小题,共70.0分)1. 设集合A ={x|x >2},B ={x|x <4},则A ∩B =______.2. 已知f(x)=ln(e 2x +1)+kx 是偶函数,则k =________.3. “x >1”是“x 2>x ”的__________条件.(选填“充分不必要”、“必要不充分”、“充要”、“既不充分又不必要”) 4. 幂函数f(x)=(m 2−3m +3)x m2−2m+1在区间(0,+∞)上是增函数,则m =______.5. 直线3x +√3y −6=0的倾斜角为_________6. 若命题“∃x 0∈R ,x 02+x 0+m <0”是假命题,则实数m 的范围是______.7. 若tanα+1tanα=103,α∈(π4,π2),则sin (2α+π4)+2cos π4cos 2α的值为 .8. 已知函数f(x)={x −1,x <0log 2x −3,x >0,则f(16)+f(−12)=______.9. 如果直线l :y =kx −1(k >0)与双曲线x 216−y 29=1的一条渐近线平行,那么k = ______ .10. 将函数f(x)=sin (ωx −π6)(ω>0)的图象向左平移π3个单位后,所得图象关于直线x =π对称,则ω的最小值为 .11. 已知函数f(x)={|x +1|,x ≤0|log 2x|,x >0,若方程f(x)=a(a ∈R)有四个不同的解x 1,x 2,x 3,x 4,且x 1<x 2<x 3<x 4,则(x 1+x 2)x 4的取值范围是______ . 12. 如图,已知抛物线y 2=2px(p >0)的焦点恰好是椭圆x 2a 2+y 2b 2=1(a >b >0)的右焦点F ,且两条曲线的交点连线也过焦点F ,则该椭圆的离心率为___________.13. 已知tanα+2tanα−1=2,则sinα+2cosαsinα−3cosα=______.14. 已知函数f (x )={e x ,x ≤01−x 2,x >0,若关于x 方程,f[f(x)]−1=m 有两个不同的根x 1,x 2,则x 1+x 2的取值范围是 .二、解答题(本大题共6小题,共90.0分)15. 已知p :函数f(x)=lg(ax 2−x +116a)的定义域为R ;q :a ≥1.如果命题“p ∨q 为真,p ∧q 为假”,求实数a 的取值范围.16.在△ABC中,a、b、c分别是角A、B、C的对边,设a+c=2b,A−C=π3,求sin B的值.17.椭圆C:x2a2+y2b2=1(a>b>0)的离心率为√22,两个焦点分别为F1(−1,0),F2(1,0).(1)求椭圆C的方程;(2)过点F2(1,0)的直线l交椭圆C于M,N两点,设点N关于x轴的对称点为Q(M、Q不重合),求证:直线MQ过x轴上一个定点.18.在水域上建一个演艺广场,演艺广场由看台Ⅰ,看台Ⅱ,三角形水域ABC,及矩形表演台BCDE四个部分构成(如图),看台Ⅰ,看台Ⅱ是分别以AB,AC为直径的两个半圆形区域,且看台Ⅰ的面积是看台Ⅱ的面积的3倍,矩形表演台BCDE中,CD=10米,三角形水域ABC的面积为400√3平方米,设∠BAC=θ.(1)求BC的长(用含θ的式子表示);(2)若表演台每平方米的造价为0.3万元,求表演台的最低造价.19.已知函数f(x)=x2+2x,g(x)=xe x.(1)求f(x)−g(x)的极值;(2)当x∈(−2,0)时,f(x)+1≥ag(x)恒成立,求实数a的取值范围.20.已知函数f(x)=(ax+b)e x−1的极值点为−1.(Ⅰ)讨论函数f(x)的单调性;(Ⅱ)若x≥0时,f(x)≥2x−1,求a的取值范围.-------- 答案与解析 --------1.答案:(2,4)解析:解:集合A={x|x>2}=(2,+∞);B={x|x<4}=(−∞,4);∴A∩B=(2,4).故答案为:(2,4).根据交集的定义进行求解即可.本题考查了交集的定义与运算问题,是基础题目.2.答案:−1解析:【分析】本题考查了函数的奇偶性问题,是一道基础题.根据函数的奇偶性的定义证明即可.【解答】解:f(−x)=ln(e−2x+1)−kx=ln (e2x+1)e2x−kx=ln(e2x+1)−lne2x−kx=ln(e2x+1)−2x−kx=ln(e2x+1)+(−k−2)x =ln(e2x+1)+kx,故−k−2=k,解得:k=−1,故答案为−1.3.答案:充分不必要解析:【分析】本题考查了充分条件与必要条件的判断,为基础题.此题还需解一元二次不等式.解:由x2>x得:x>1或x<0,∴“x>1”是“x2>x”的充分不必要条件.故答案为:充分不必要.4.答案:2解析:解:若幂函数f(x)=(m2−3m+3)x m2−2m+1在区间(0,+∞)上是增函数,则由m2−3m+3=1解得:m=2或m=1,m=2时,f(x)=x,是增函数,m=1时,f(x)=1,是常函数,故答案为:2.根据幂函数的定义求出m的值,判断即可.本题考查了幂函数的定义,考查函数的单调性问题,是一道基础题.5.答案:120∘解析:【分析】本题考查了直线的倾斜角与斜率之间的关系,属于基础题,利用直线的倾斜角与斜率之间的关系即可得出.【解答】解:解:设倾斜角为θ,∵直线3x+√3y−6=0,,θ=120∘,故答案为120∘.6.答案:解析:本题考查了特称命题与全称命题之间的关系,解题时应注意特称命题的否定是全称命题,全称命题的否定是特称命题,是基础题.写出该命题的否定命题,根据否定命题求出m的取值范围即可.【解答】解:命题“∃x0∈R,x02+x0+m<0”是假命题,它的否定命题是“∀x∈R,有x2+x+m≥0”,是真命题,即1−4m≤0;解得m≥14,∴m的取值范围是[14,+∞).故答案为[14,+∞).7.答案:0解析:【分析】本题考查同角三角函数关系,二倍角公式,考查和角的正弦公式,考查学生的计算能力,正确运用和角的正弦公式是关键,属基础题.【解答】解:∵tanα+1tanα=103,∴sinαcosα+cosαsinα=103,∴1sin2α=53,∴sin2α=35,∵α∈(π4,π2 ),∴cos2α=−45,=35×√22+(−45)×√22+√22(1−45)=0.故答案为0.8.答案:−1解析:本题考查函数值的求法以及分段函数,考查运算求解能力,属于基础题.推导出f(16)=log 216−3=1,f(−12)=(−12)−1=−2,由此能求出f(16)+f(−12)的值. 【解答】解:∵函数f(x)={x −1,x <0log 2x −3,x >0, ∴f(16)=log 216−3=1, f(−12)=(−12)−1=−2, ∴f(16)+f(−12)=1−2=−1. 故答案为−1.9.答案:34解析:解:双曲线x 216−y 29=1的渐近线方程为y =±34x ,由直线l :y =kx −1(k >0)与双曲线x 216−y 29=1的一条渐近线平行,可得k =34. 故答案为:34.求出双曲线的渐近线方程,由两直线平行的条件:斜率相等,即可得到所求k 的值.本题考查双曲线的方程和性质,主要是渐近线方程,考查两直线平行的条件:斜率相等,考查运算能力,属于基础题.10.答案:12解析: 【分析】本题考查三角函数的图象与性质,考查图象的平移,属于基础题. 依题意,的图象关于直线x =π对称,得ω=3k+24,k ∈Z ,从而求得结果.【解答】 解:的图象向左平移π3个单位后得,所以的图象关于直线x =π对称,所以ωπ+ωπ3−π6=kπ+π2,k ∈Z ,ω=3k+24,k ∈Z ,又ω>0,所以ω的最小值为12, 故答案为12.11.答案:[−4,−2)解析:解:由题意作函数f(x)={|x +1|,x ≤0|log 2x|,x >0与y =a 的图象如下,,结合图象可知,x 1+x 2=−2,0<log 2x 4≤1, 故x 1+x 2=−2,1<x 4≤2, 故−4≤(x 1+x 2)x 4<−2, 故答案为:[−4,−2).由题意作函数f(x)={|x +1|,x ≤0|log 2x|,x >0与y =a 的图象,从而可得x 1+x 2=−2,0<log 2x 4≤1,从而解得.本题考查了数形结合的思想应用及分段函数的应用.12.答案:√2−1解析: 【分析】本题考查抛物线与椭圆的综合问题.在研究圆锥曲线问题时,用定义来解题是比较常用的方法.先把对应图形画出来,求出对应焦点和点A 的坐标(都用p 写),利用椭圆定义求出2a 和2c 就可找到椭圆的离心率. 【解答】解:由题可得图,设椭圆另一焦点为E ,因为抛物线y2=4px(p>0)的焦点F(p,0)把x=p代入y2=4px解得y=±2p,所以A(p,2p)又E(−p,0).故|AE|=2√2p,|AF|=2p,|EF|=2p.所以2a=|AE|+|AF|=(2√2+2)p,2c=2p.椭圆的离心率e=ca=√2−1.故答案为√2−1.13.答案:6解析:解:由tanα+2tanα−1=2,得tanα=4.∴sinα+2cosαsinα−3cosα=tanα+2tanα−3=4+24−3=6.故答案为:6.由已知求得tanα,再由同角三角函数的基本关系式化弦为切求得sinα+2cosαsinα−3cosα的值.本题考查三角函数的化简求值,考查同角三角函数基本关系式的应用,是基础题.14.答案:[3ln2+1,+∞)解析:【分析】本题考查分段函数,复合函数的运用,再利用分类讨论的思想解题,属于难题.令t=f(x)−1则有t≤0,再分类讨论求出x1+x2的取值范围.【解答】解:f(x)的图象如图所示:令t=f(x)−1,则有t≤0(1)当−12≤t≤0时,x只有1个解,设此时的解为x0,则t=f(x0)−1,易知−ln2≤x0≤0,由图可知f(x)=x0只有一个解,故不成立;(2)当−1<t<−12时,x有2个解,不妨设此时的解为x3,x4,且x3<x4,则t=f(x3)−1,t=f(x4)−1,即f(x3)=f(x4),e x3=1−x42,推出x3=ln(1−x42),所以有x3<−ln2,0<x4<1,由图象可得,f(x)=x3有且仅有一个解,而f(x)=x4只有当12≤x4<1才满足只有一个解,此时满足题意,设x1<0,x2>0,则e x1=x4,1−x22=x3,所以x1=lnx4,x2=1−2x3,所以x1+x2=lnx4+1−2x3=lnx4−2ln(1−x4)+2ln2+1,且12≤x4<1,令g(x)=lnx−2ln(1−x)+2ln2+1,12≤x<1,易知g(x)在定义域上单调增,g(x)min=g(12)=3ln2+1,无最大值,所以g(x)∈[3ln2+1,+∞);(3)当t≤−1时,x只有1个解,设此时的解为x0,则t=f(x0)−1,易知x0≥1,由图可知f(x)=x0最多只有一个解,故不成立.综上所述,可知x1+x2的取值范围是[3ln2+1,+∞).故答案为[3ln2+1,+∞).15.答案:解:由p真,可知{a>0Δ=1−4a×116a<0,解得a>2,由p∨q为真,p∧q为假,可得:p和q中一个为真、一个为假.若p真q假时a不存在,若p假q真时1≤a≤2.综上,实数a的取值范围是1≤a≤2.解析:由p真,可知{a>0Δ=1−4a×116a<0,解得a,由p∨q为真,p∧q为假,可得:p和q中一个为真、一个为假.即可解出.本题考查了复合命题真假的判定方法、函数的性质、不等式的解法,考查了推理能力与计算能力,属于中档题.16.答案:解:△ABC中,由题意利用正弦定理可得sinA+sinC=2sinB,∴2sin A+C2cos A−C2=4sin B2cos B2,化简可得cos A−C2=2sin B2,即√32=2sin B2,解得sin B2=√34∴cos B2=√134.∴sinB=2sin B2cos B2=√398.解析:△ABC中,由题意利用正弦定理可得sinA+sinC=2sinB,故有2sin A+C2cos A−C2=4sin B2cos B2,化简可得sin B2=√34,故cos B2=√134.再根据sinB=2sin B2cos B2,计算求得结果.本题主要考查正弦定理的应用,两角和差的三角公式、诱导公式、二倍角公式的应用,属于中档题.17.答案:解:(1)∵依题意,{c=1ca=√22,∴c=1,a=√2,∴b=√a2−c2=1,∴椭圆的方程为x22+y2=1;(2)∵设M(x1,y1),N(x2,y2),Q(x2,−y2),l:y=k(x−1),代入x22+y2=1(y≠0),∴整理得(1+2k2)x2−4k2x+2k2−2=0,∵由韦达定理可得:x1+x2=4k21+2k2,x1x2=2k2−21+2k2,∴MQ的方程为y−y1=y1+y2x1−x2(x−x1),∵令y=0,∴得x=x1+y1(x2−x1)y1+y2=x1+k(x1−1)(x2−x1)k(x1+x2−2)=2x1x2−(x1+x2)x1+x2−2,代入x1+x2=4k21+2k2,x1x2=2k2−21+2k2,∴x=2x1x2−(x1+x2)x1+x2−2=2×2k2−21+2k2−4k21+2k24k21+2k2−2=2,即:x=2,∴直线过x轴上的一个定点,定点坐标为(2,0).解析:本题考查椭圆方程的求法,直线与椭圆的位置关系的应用,考查转化思想以及计算能力.(1)通过椭圆的离心率与焦距,求出a,c,得到b,即可求出椭圆C的方程;(2)依题意,设M(x1,y1),N(x2,y2),Q(x2,−y2),l:y=k(x−1),代入椭圆方程,利用韦达定理,结合MQ的方程为y−y1=y1+y2x1−x2(x−x1),令y=0,化简求解可得x=2,得到直线MQ过x轴上一个定点.18.答案:解:(1)∵看台Ⅰ的面积是看台Ⅱ的面积的3倍,∴12π(AB2)2=3×12π(AC2)2,∴AB=√3AC,∵S△ABC=12AB⋅AC⋅sinθ=√32AC2sinθ=400√3,∴AC2=800sinθ,∴AB2=2400sinθ,在△ABC中,由余弦定理得BC2=AB2+AC2−2AB⋅ACcosθ=3200−1600√3cosθsinθ,∴BC=40√2−√3cosθsinθ.(2)设表演台的造价为y万元,则y=120√2−√3cosθsinθ,设f(θ)=2−√3cosθsinθ(0<θ<π),则f′(θ)=√3−2cosθsin2θ,∴当0<θ<π6时,f′(θ)<0,当π6<θ<π时,f′(θ)>0,∴f(θ)在(0,π6)上单调递减,在(π6,π)上单调递增,∴当θ=π6时,f(θ)取得最小值f(π6)=1,∴y的最小值为120,即表演台的最小造价为120万元.解析:本题考查了解三角形,函数最值计算,余弦定理,属于中档题.(1)根据看台的面积比得出AB,AC的关系,代入三角形的面积公式求出AB,AC,再利用余弦定理计算BC;(2)根据(1)得出造价关于θ的函数,利用导数判断函数的单调性求出最小造价.19.答案:解:(1)令ℎ(x)=f(x)−g(x),则ℎ′(x)=(x+1)(2−e x),∴ℎ(x)极小值=ℎ(−1)=1e−1,∴ℎ(x)极大值=ℎ(ln2)=ln22;(2)由已知,当x∈(−2,0)时,x2+2x+1≥axe x恒成立即a≥x2+2x+1xe x =x+2+x−1e x恒成立,令t(x)=x+2+x−1e ,则t′(x)=−(x2+1)(x+1)x e,∴当x∈(−2,−1)时,t′(x)>0,t(x)单调递增,当x∈(−1,0)时,t′(x)<0,t(x)单调递减,故当x∈(−2,0)时,t(x)max=t(−1)=0,∴a≥0.解析:本题主要考查了利用导数研究函数的单调性等基础知识,考查恒成立问题的等价转化能力及计算能力,属于中档题.(1)令ℎ(x)=f(x)−g(x),求导数,确定函数的单调性,即可求f(x)−g(x)的极值;(2)当x∈(−2,0)时,x2+2x+1≥axe x恒成立,即a≥x2+2x+1xe x =x+2+x−1e x恒成立,求出右边的最大值,即可求实数a的取值范围.20.答案:解:(Ⅰ)函数f(x)的导数为f′(x)=(ax+b+a)⋅e x−1,由题意可得f′(−1)=0,即(−a+a+b)e−2=0,解得b=0;则f′(x)=ae x−1(x+1),当a=0时,函数f(x)=e x−1无极值,不符合题意.当a>0时,f(x)在(−1,+∞)上递增,在(−∞,−1)上递减;当a<0时,f(x)在(−1,+∞)上递减,在(−∞,−1)上递增;(Ⅱ)由(Ⅰ)可知f(x)=axe x−1,设g(x)=axe x−1−2x+1,若x≥0时,f(x)≥2x−1,必有g(1)=a−2+1≥0⇒a≥1,故a≥1是命题成立的一个必要条件.当a≥1,x≥0时,g′(x)=ae x−1(x+1)−2,令ℎ(x)=g′(x)ℎ′(x)=ae x−1(x+2)>0,故g′(x)在[0,+∞)单调递增,g′(x)min=g′(0)=ae−2.①当a≥2e时,g′(x)min≤0,g(x)在[0,+∞)单调递增,g(x)≥g(0)=1>0,②当1≤a<2e时,存在x0∈(0,1),使得g′(x0)=ae x0−1(x0+1)−2=0,且当x∈(0,x0)时,g′(x)<0,g(x)递减,x∈(x0,+∞)时,g′(x)>0,g(x)递增,∴g(x)≥g(x0)=ax0e x0−1−2x0+1=2x0x0+1−2x0+1=5−2(1x0+1+x0+1).∵x0∈(0,1),∴令t=x0+1,t∈(1,2).设函数m(t)=5−2t−2t,t∈(1,2),又m′(t)=2t2−2≤0,∴m(t)单调递减,∴m(t)>m(2)=0.∴g(x)≥g(x0)=ax0e x0−1−2x0+1=5−2(1+x0+1)>0,x0+1综上,a的取值范围为[1,+∞).解析:本题考查利用导数研究函数的单调性与极值,考查不等关系的求解,属于较难题.(Ⅰ)函数f(x)的导数为f′(x)=(ax+b+a)⋅e x−1,求出b的值,然后对a分类讨论,利用导数求出函数的单调性与极值即可;(Ⅱ)由(Ⅰ)可知f(x)=axe x−1,构造函数g(x)=axe x−1−2x+1,然后利用导数求出函数的单调性与最值,求出a的范围可得答案.。
江苏省启东中学高三上学期第一次月考数学(理)试题Word版含答案
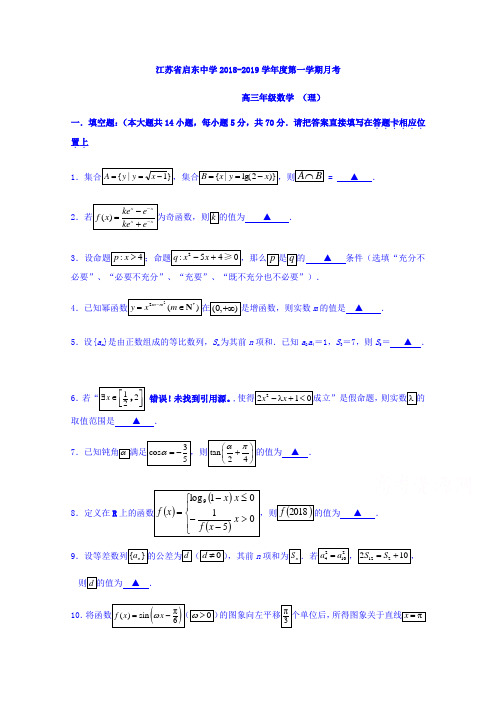
(1)求区域Ⅱ的总面积;
(2)若养殖区域Ⅰ、Ⅱ、Ⅲ的每平方千米的年收入分别是15万元、20万元、10万元,记年总收入为y万元. 试问当 为多少时,年总收入最大?
(3)若函数 存在极大值,且极大值点为1,证明: .
江苏省启东中学2018-2019学年度第一学期月考
高三年级数学答案
答题卷上只有第18题需要附图,其余按模式搞就行了
1. 2. 3.充分不必要4.1 5. 6. 7.
8. 9. 10. 11. 12. 13. 14.
15.解: 或
16.解:(1)在△ABC中,因为 , , ,
则 的值为▲.
10.将函数 ( )的图象向左平移 个单位后,所得图象关于直线
对称,则 的最小值为▲.
11.已知函数 , ,则 的解集是▲.
12.若向量 满足 , ,且对一切实数 , 恒成立,则向量 的夹角的大小为▲.
13.在斜三角形ABC中,若 ,则sinC的最大值为▲.
14.已知函数 , ( 为自然对数的底数),若函数
③若 ,则 时, ,
当 时, 的最小值为 ;
当 时, 的最小值为 .
因为 , ,所以 的最小值为 .14分
综上所述: ………………………………16分
20.解(1)当 ,函数 在 上单调递增;
当 ,函数 在 上单调递减,在 上单调递增;
当 ,函数 在 上单调递增,在 上单调递减.……………4分
(2) 若对任意 , 恒成立,求实数 的取值范围;
江苏省启东中学2019届高三上学期第一次月考数学(文)试题Word版含答案

江苏省启东中学2018-2019学年度第一学期月考高三年级数学 (文)一.填空题:(本大题共14小题,每小题5分,共70分.请把答案直接填写在答题卡相应位......置上..1.集合}1|{-==x y y A ,集合)}2lg(|{x y x B -==,则B A ⋂ = ▲ .2.若()x xx xke e f x ke e ---=+为奇函数,则k 的值为 ▲ . 3.设命题:4p x >;命题2:540q x x -+≥,那么p 是q 的 ▲ 条件(选填“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”).4.已知幂函数22*()m m y x m -=∈N 在(0,)+∞是增函数,则实数m 的值是 ▲ .5.直线0()x m m R +=∈的倾斜角为 ▲ .6.若“12x ⎡⎤∃∈⎢⎥⎣⎦, 错误!未找到引用源。
,使得2210x x -λ+<成立”是假命题,则实数λ的取值范围是 ▲ .7.已知钝角α满足3cos 5α=-,则tan 24απ⎛⎫+ ⎪⎝⎭的值为 ▲ . 8.定义在R 上的函数()()()⎪⎩⎪⎨⎧>--≤-=05101log 9x x f x x x f ,则()2018f 的值为 ▲ . 9.在平面直角坐标系xoy 中,双曲线222:1(0)4x y C a a -=>的一条渐近线与直线21y x =+平行,则实数a 的值是 ▲ .10.将函数()π()sin 6f x x ω=-(0ω>)的图象向左平移π3个单位后,所得图象关于直线πx = 对称,则ω的最小值为 ▲ .11.已知函数2()x f x +=,x ∈R ,则2(2)(2)f x x f x -<-的解集是 ▲ . 12.已知抛物线22(0)x py p =>的焦点F 是椭圆22221(0)y x a b a b +=>>的一个焦点,若P ,Q 是椭圆与抛物线的公共点,且直线PQ 经过焦点F ,则该椭圆的离心率为 ▲ .13.在斜三角形ABC 中,若 114tan tan tan A B C+=,则sinC 的最大值为 ▲ . 14.已知函数()22x x x f -=,()2+=x e x g x(e 为自然对数的底数),若函数()()[]k x g f x h -=有4个零点,则k 的取值范围为 ▲ .二.解答题:本大题共6小题,共90分.请在答题卡指定区域.......内作答. 解答时应写出文字 说明、证明过程或演算步骤.15. (本小题满分14分) 已知21>a 且1≠a ,条件p :函数()()x x f a 12log -=在其定义域上是减函数,条件q :函数()2--+=a x x x g 的定义域为R .如果“p 或q ”为真,试求a 的取值范围.16. (本小题满分14分)在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c .已知1a =,b =π6B A -=. (1)求sin A 的值;(2)求c 的值.。
江苏省启东中学2019届高三上学期第一次月考数学(理)试题(含答案)

江苏省启东中学2018-2019学年度第一学期月考高三年级数学 (理)一.填空题:(本大题共14小题,每小题5分,共70分.请把答案直接填写在答题卡相应位置上........ 1.集合}1|{-==x y y A ,集合)}2lg(|{x y x B -==,则B A ⋂ = ▲ .2.若()x x x xke e f x ke e ---=+为奇函数,则k 的值为 ▲ .3.设命题:4p x >;命题2:540q x x -+≥,那么p 是q 的 ▲ 条件(选填“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”).4.已知幂函数22*()m m y x m -=∈N 在(0,)+∞是增函数,则实数m 的值是 ▲ .5.设{a n }是由正数组成的等比数列,S n 为其前n 项和.已知a 2a 4=1,S 3=7,则S 5= ▲ .6.若“122x ⎡⎤∃∈⎢⎥⎣⎦, 错误!未找到引用源。
,使得2210x x -λ+<成立”是假命题,则实数λ的取值范围是 ▲ . 7.已知钝角α满足3cos 5α=-,则tan 24απ⎛⎫+ ⎪⎝⎭的值为 ▲ .8.定义在R 上的函数()()()⎪⎩⎪⎨⎧>--≤-=05101log 9x x f x x x f ,则()2018f 的值为 ▲ . 9.设等差数列{}n a 的公差为d (0≠d ),其前n 项和为n S .若22410a a =,122210S S =+,则d 的值为 ▲ .10.将函数()π()sin 6f x x ω=-(0ω>)的图象向左平移π3个单位后,所得图象关于直线πx =对称,则ω的最小值为 ▲ .11.已知函数2()||2x f x x +=+,x ∈R ,则2(2)(2)f x x f x -<-的解集是 ▲ . 12.若向量,a b →→满足a →=,1b →=,且对一切实数x ,a x b a b →→→→++≥恒成立,则向量,a b →→的夹角的大小为▲ .13.在斜三角形ABC 中,若114tan tan tan A B C+=,则sinC 的最大值为 ▲ . 14.已知函数()22x x x f -=,()2+=x e x g x(e 为自然对数的底数),若函数()()[]k x g f x h -=有4个零点,则k 的取值范围为 ▲ .二.解答题:本大题共6小题,共90分.请在答题卡指定区域.......内作答. 解答时应写出文字 说明、证明过程或演算步骤. 15. (本小题满分14分) 已知21>a 且1≠a ,条件p :函数()()x x f a 12log -=在其定义域上是减函数,条件q :函数()2--+=a x x x g 的定义域为R .如果“p 或q ”为真,试求a 的取值范围.16. (本小题满分14分)在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c .已知1a =,b =π6B A -=. (1)求sin A 的值; (2)求c 的值.17. (本小题满分14分)已知等比数列{}n a 的各项均为正数,且163221=+a a ,62234a a a =.(1) 求数列{}n a 的通项公式;(2) 设n n a a a b 22212log ...log log +++=,是否存在非零的实数λ,使得数列⎭⎬⎫⎩⎨⎧-λn b n 2为等差数列?若存在,求出λ的值;若不存在,说明理由.18.(本题满分16分)现有一个以OA 、OB 为半径的扇形池塘,在OA 、OB 上分别取点C 、D ,作DE ∥OA 、CF ∥OB 交弧AB 于点E 、F ,且BD = AC ,现用渔网沿着DE 、EO 、OF 、FC 将池塘分成如图所示的三种的养殖区域.若OA =1km ,π2AOB ∠=,π(0)2EOF θθ∠=<<.(1)求区域Ⅱ的总面积;(2)若养殖区域Ⅰ、Ⅱ、Ⅲ的每平方千米的年收入分别是15万元、20万元、10万元,记年总收入为y 万元. 试问当θ为多少时,年总收入最大?19. (本小题满分16分)已知函数()122++=ax x x f (a ∈R ) ,()x f '是()x f 的导函数.(1)若函数x e x f x ⋅'=)()(ϕ极小值为1-,求实数a 的值;(2)若[]1,2--∈x ,不等式()()x f x f '≤恒成立,求实数a 的取值范围;(3)设函数()()()()()()()⎩⎨⎧'<'≥'=x f x f x f x f x f x f x g ,,,求()x g 在[]4,2∈x 上的最小值.20.(本小题满分16分)已知函数()x ax x x f ln +=(∈a R ). (1)讨论函数()x f 的单调性;(2)若对任意),1[+∞∈x ,3)(x x f ≤恒成立,求实数a 的取值范围; (3)若函数()x f 存在极大值,且极大值点为1,证明:()21x ex f x+≤.江苏省启东中学2018-2019学年度第一学期月考高三年级数学答案答题卷上只有第18题需要附图,其余按模式搞就行了1.[)2,02.1±3.充分不必要4.15.314 6.(]22,∞- 7.3-8.21 9.10- 10.21 11.()2,0 12.43π 13.322 14.⎪⎭⎫⎝⎛-212,0e e15.解:121<<a 或2≥a16.解:(1)在△ABC 中,因为1a =,b =π6B A -=,由正弦定理得,1sin πsin 6A A =+…… 2分于是ππsin cos cos sin 66A A A =+,即cos A A =, …… 4分又22sin cos 1A A +=,所以7sin A . …… 6分(2)由(1)知,321cos A ,则33sin 22sin cos A A A =,213cos212sin 14A A =-=, …… 10分在△ABC 中,因为πA B C ++=,π6B A -=,所以5π26C A =-.则()5πsin sin 26C A =-5π5πsin cos2cos sin 266A A =-113214=⨯1114=. ……12分由正弦定理得,sin sin a C c A == …… 14分17. 解:(1)nn a 2=;(2)2-=λ18. 解:(1)因为BD AC OB OA ==,,所以OD OC =. 因为π2AOB ∠=,DE ∥OA ,CF ∥OB , 所以DE OB CF OA ⊥⊥,.又因为OE OF =,所以Rt ODE ∆≌Rt OCF ∆.所以1π()22DOE COF COF θ∠=∠∠=-,. ………………………………2分所以1πcos cos[()]22OC OF COF θ=⋅∠=-.所以11sin cos 24COF S OC OF COF θ∆=⋅⋅⋅∠=,所以II 1=cos 2S θ区域,π(0)2θ<<. …………………………………6分(2)因为I 12S θ=区域,所以III I II π11cos 422S S S S θθ=--=--总区域区域区域.所以11π111520cos 10(cos )22422y θθθθ=⨯+⨯+⨯--55ππ5cos (0)222θθθ=++<<,, …………………………………10分 所以5(12sin )2y θ'=-,令=0y ',则π=6θ. …………………………………12分当π6θ<<0时,0y '>,当ππ62θ<<时,0y '<. 故当π=6θ时,y 有最大值. 答:当θ为π6时,年总收入最大. …………………………………16 19. 解(1)12ln -…………………………………3分 (2)⎪⎭⎫⎢⎣⎡+∞,23 ………………………………… 7分 (3)因为()()()[]a x x x f x f 211)(---='-, ①若21-≥a ,则[]4,2∈x 时,()()x f x f '≥,所以()()a x x f x g 22+='=,从而()x g 的最小值为()422+=a g .………………………………9分②若23-<a ,则[]4,2∈x 时,()()x f x f '<,所以()()122++==ax x x f x g , 当232-<≤-a 时,()x g 的最小值为()542+=a g ;当24-<<-a 时,()x g 的最小值为()21a a g -=-;当4-≤a 时,()x g 的最小值为()1784+=a g ;………………………………12分③若2123-<≤-a ,则[]4,2∈x 时,()[)[]⎩⎨⎧-∈+-∈++=4,21,2221,2,122a x a x a x ax x x g ,当[]a x 21,2-∈时,()x g 的最小值为()542+=a g ; 当[]4,21a x -∈时,()x g 的最小值为()a a g 2221-=-. 因为2123-<≤-a ,()()0362254<+=--+a a a ,所以()x g 的最小值为54+a .14分综上所述:()⎪⎪⎪⎩⎪⎪⎪⎨⎧-≥+-<≤-+-<<---≤+=.21,42,212,54,24,1,4,1782mina a a a a a a a x g ………………………………16分20. 解(1)当0=a ,函数()x f 在()+∞,0上单调递增;当0>a ,函数()x f 在⎪⎪⎭⎫ ⎝⎛--a e 11,0上单调递减,在⎪⎪⎭⎫ ⎝⎛--a e 11上单调递增;当0<a ,函数()x f 在⎪⎪⎭⎫ ⎝⎛--a e 11,0上单调递增,在⎪⎪⎭⎫ ⎝⎛--a e 11上单调递减. ……………4分 (2)()x ax x x f ln +=若对任意),1[+∞∈x ,3)(x x f ≤恒成立,求实数a 的取值范围; 因为),1[+∞∈x ,所以3)(x x f ≤⇔0ln 12≥--x a x ,设),1[,ln 1)(2+∞∈--=x x a x x ϕ,则xa x x a x x -=-='222)(ϕ,所以 ……………6分① 当2≤a 时,0)(≥'x ϕ,)(x ϕ在),1[+∞上递增,所以0)1()(=≥ϕϕx ,所以2≤a 适合。
(全优试卷)江苏省启东中学高三上学期第一次月考数学(理)试题Word版含答案
江苏省启东中学2018-2019学年度第一学期月考高三年级数学 (理)一.填空题:(本大题共14小题,每小题5分,共70分.请把答案直接填写在答题卡相应位......置上..1= ▲ .2的值为 ▲ .3▲条件(选填“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”).4m 的值是 ▲ . 5.设{a n }是由正数组成的等比数列,S n 为其前n 项和.已知a 2a 4=1,S 3=7,则S 5= ▲ .6.错误!未找到引用源。
,取值范围是 ▲ .7的值为 ▲ .8.定义在R的值为 ▲ . 9,其前n的值为 ▲ .10.的最小值为▲.11的解集是▲.12的夹角的大小为▲ .13.在斜三角形ABC中,若则sinC的最大值为▲ .14,若函数4的取值范围为▲.二.解答题:本大题共6小题,共90分.请在答题卡指定区域.......内作答. 解答时应写出文字说明、证明过程或演算步骤.15. (本小题满分14分)R.16. (本小题满分14分)在△ABC B,C的对边分别为a,b,c(1(2)求c的值.17. (本小题满分14分)(1)(2)是否存在非零的实使得数列.18.(本题满分16分)现有一个以OA、OB为半径的扇形池塘,在OA、OB上分别取点C、D,作DE∥OA、CF∥OB交弧AB于点E、F,且BD = AC,现用渔网沿着DE、EO、OF、FC将池塘分成如图所示的三种的养殖区域.若OA=1km(1)求区域Ⅱ的总面积;(2)若养殖区域Ⅰ、Ⅱ、Ⅲ的每平方千米的年收入分别是15万元、20万元、10万元,记年总收入为y万元.19. (本小题满分16分) .(1(2(3.20.(本小题满分16分)).(1(2(31江苏省启东中学2018-2019学年度第一学期月考 高三年级数学答案答题卷上只有第18题需要附图,其余按模式搞就行了充分不必要 4.1 5.3146.15.16.解:(1)在△ABC…… 2分…… 4分…… 6分(2)由(1…… 10分在△ABC……12分…… 14分17. 解:(1(218. 解:(1DE∥OA,CF∥OB,………………………………2分…………………………………6分(2…………………………………10分…………………………………12分y有最大值. (16)19. 解(13分(2………………………………… 7分(3………………………………9分12分分16分20. 解(1. ……………4分(2……………6分①……………7分②……………9分注:分离变量、数形结合等方法得出正确结论的本小题给2分。
【配套K12】江苏省启东中学2019届高三数学上学期第一次月考试题 理

江苏省启东中学2018-2019学年度第一学期月考高三年级数学 (理)一.填空题:(本大题共14小题,每小题5分,共70分.请把答案直接填写在答题卡相应位......置上..1.集合}1|{-==x y y A ,集合)}2lg(|{x y x B -==,则B A ⋂ = ▲ .2.若()x x x xke e f x ke e---=+为奇函数,则k 的值为 ▲ . 3.设命题:4p x >;命题2:540q x x -+≥,那么p 是q 的 ▲ 条件(选填“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”).4.已知幂函数22*()m m y x m -=∈N 在(0,)+∞是增函数,则实数m 的值是 ▲ .5.设{a n }是由正数组成的等比数列,S n 为其前n 项和.已知a 2a 4=1,S 3=7,则S 5= ▲ .6.若“122x ⎡⎤∃∈⎢⎥⎣⎦,错误!未找到引用源。
,使得2210x x -λ+<成立”是假命题,则实数λ的取值范围是 ▲ .7.已知钝角α满足3cos 5α=-,则tan 24απ⎛⎫+ ⎪⎝⎭的值为 ▲ .8.定义在R 上的函数()()()⎪⎩⎪⎨⎧>--≤-=05101log 9x x f x x x f ,则()2018f 的值为 ▲ . 9.设等差数列{}n a 的公差为d (0≠d ),其前n 项和为n S .若22410a a =,122210S S =+,则d 的值为 ▲ .10.将函数()π()sin 6f x x ω=-(0ω>)的图象向左平移π3个单位后,所得图象关于直线πx =对称,则ω的最小值为 ▲ .11.已知函数2()||2x f x x +=+,x ∈R ,则2(2)(2)f x x f x -<-的解集是 ▲ . 12.若向量,a b →→满足a →=,1b →=,且对一切实数x ,a x b a b →→→→++≥恒成立,则向量,a b →→的夹角的大小为 ▲ . 13.在斜三角形ABC 中,若114tan tan tan A B C+=,则sinC 的最大值为 ▲ .14.已知函数()22x x x f -=,()2+=x e x g x(e 为自然对数的底数),若函数()()[]k x g f x h -=有4个零点,则k 的取值范围为 ▲ .二.解答题:本大题共6小题,共90分.请在答题卡指定.....区域..内作答. 解答时应写出文字 说明、证明过程或演算步骤. 15. (本小题满分14分) 已知21>a 且1≠a ,条件p :函数()()x x f a 12log -=在其定义域上是减函数,条件q :函数()2--+=a x x x g 的定义域为R .如果“p 或q ”为真,试求a 的取值范围.16. (本小题满分14分)在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c .已知1a =,b =,π6B A -=. (1)求sin A 的值; (2)求c 的值.17. (本小题满分14分)已知等比数列{}n a 的各项均为正数,且163221=+a a ,62234a a a =.(1) 求数列{}n a 的通项公式;(2) 设n n a a a b 22212log ...log log +++=,是否存在非零的实数λ,使得数列⎭⎬⎫⎩⎨⎧-λn b n 2为等差数列?若存在,求出λ的值;若不存在,说明理由.18.(本题满分16分)现有一个以OA 、OB 为半径的扇形池塘,在OA 、OB 上分别取点C 、D ,作DE ∥OA 、CF ∥OB 交弧AB 于点E 、F ,且BD = AC ,现用渔网沿着DE 、EO 、OF 、FC 将池塘分成如图所示的三种的养殖区域.若OA =1km ,π2AOB ∠=,π(0)2EOF θθ∠=<<.(1)求区域Ⅱ的总面积;(2)若养殖区域Ⅰ、Ⅱ、Ⅲ的每平方千米的年收入分别是15万元、20万元、10万元,记年总收入为y 万元. 试问当θ为多少时,年总收入最大?19. (本小题满分16分)已知函数()122++=ax x x f (a ∈R ) ,()x f '是()x f 的导函数.(1)若函数x e x f x ⋅'=)()(ϕ极小值为1-,求实数a 的值;(2)若[]1,2--∈x ,不等式()()x f x f '≤恒成立,求实数a 的取值范围;(3)设函数()()()()()()()⎩⎨⎧'<'≥'=x f x f x f x f x f x f x g ,,,求()x g 在[]4,2∈x 上的最小值.20.(本小题满分16分) (第18题)已知函数()x ax x x f ln +=(∈a R ). (1)讨论函数()x f 的单调性;(2)若对任意),1[+∞∈x ,3)(x x f ≤恒成立,求实数a 的取值范围; (3)若函数()x f 存在极大值,且极大值点为1,证明:()21x ex f x +≤.江苏省启东中学2018-2019学年度第一学期月考 高三年级数学答案答题卷上只有第18题需要附图,其余按模式搞就行了1.[)2,02.1±3.充分不必要4.15.314 6.(]22,∞- 7.3-8.21 9.10- 10.21 11.()2,0 12.43π13.32214.⎪⎭⎫ ⎝⎛-212,0e e 15.解:121<<a 或2≥a16.解:(1)在△ABC 中,因为1a =,b =π6B A -=,由正弦定理得,1sin πsin 6A A + …… 2分于是ππsin cos cos sin 66A A A =+,即cos A A =, …… 4分又22sin cos 1A A +=,所以sin A =. …… 6分(2)由(1)知,cos A =,则sin 22sin cos A A A =,213cos212sin 14A A =-=, …… 10分在△ABC 中,因为πA B C ++=,π6B A -=,所以5π26C A =-.则()5πsin sin 26C A =-5π5πsin cos2cos sin 266A A =-113214=⨯+1114=. ……12分由正弦定理得,sin sin a C c A == …… 14分17. 解:(1)nn a 2=;(2)2-=λ18. 解:(1)因为BD AC OB OA ==,,所以OD OC =. 因为π2AOB ∠=,DE ∥OA ,CF ∥OB , 所以DE OB CF OA ⊥⊥,.又因为OE OF =,所以Rt ODE ∆≌Rt OCF ∆.所以1π()22DOE COF COF θ∠=∠∠=-,. ………………………………2分所以1πcos cos[()]22OC OF COF θ=⋅∠=-.所以11sin cos 24COF S OC OF COF θ∆=⋅⋅⋅∠=,所以II 1=cos 2S θ区域,π(0)2θ<<. …………………………………6分(2)因为I 12S θ=区域,所以III I II π11cos 422S S S S θθ=--=--总区域区域区域.所以11π111520cos 10(cos )22422y θθθθ=⨯+⨯+⨯--55ππ5cos (0)222θθθ=++<<,, …………………………………10分 所以5(12sin )2y θ'=-,令=0y ',则π=6θ. …………………………………12分当π6θ<<0时,0y '>,当ππ62θ<<时,0y '<. 故当π=6θ时,y 有最大值. 答:当θ为π6时,年总收入最大. …………………………………16 19. 解(1)12ln -…………………………………3分 (2)⎪⎭⎫⎢⎣⎡+∞,23 ………………………………… 7分 (3)因为()()()[]a x x x f x f 211)(---='-, ①若21-≥a ,则[]4,2∈x 时,()()x f x f '≥,所以()()a x x f x g 22+='=,从而()x g 的最小值为()422+=a g .………………………………9分②若23-<a ,则[]4,2∈x 时,()()x f x f '<,所以()()122++==ax x x f x g , 当232-<≤-a 时,()x g 的最小值为()542+=a g ;当24-<<-a 时,()x g 的最小值为()21a a g -=-;当4-≤a 时,()x g 的最小值为()1784+=a g ;………………………………12分③若2123-<≤-a ,则[]4,2∈x 时,()[)[]⎩⎨⎧-∈+-∈++=4,21,2221,2,122a x a x a x ax x x g ,当[]a x 21,2-∈时,()x g 的最小值为()542+=a g ; 当[]4,21a x -∈时,()x g 的最小值为()a a g 2221-=-. 因为2123-<≤-a ,()()0362254<+=--+a a a ,所以()x g 的最小值为54+a .14分 综上所述:()⎪⎪⎪⎩⎪⎪⎪⎨⎧-≥+-<≤-+-<<---≤+=.21,42,212,54,24,1,4,1782mina a a a a a a a x g ………………………………16分20. 解(1)当0=a ,函数()x f 在()+∞,0上单调递增;当0>a ,函数()x f 在⎪⎪⎭⎫⎝⎛--a e 11,0上单调递减,在⎪⎪⎭⎫ ⎝⎛--a e 11上单调递增;当0<a ,函数()x f 在⎪⎪⎭⎫⎝⎛--a e 11,0上单调递增,在⎪⎪⎭⎫ ⎝⎛--a e 11上单调递减. ……………4分(2)()x ax x x f ln +=若对任意),1[+∞∈x ,3)(x x f ≤恒成立,求实数a 的取值范围; 因为),1[+∞∈x ,所以3)(x x f ≤⇔0ln 12≥--x a x ,设),1[,ln 1)(2+∞∈--=x x a x x ϕ,则xa x x a x x -=-='222)(ϕ,所以 ……………6分① 当2≤a 时,0)(≥'x ϕ,)(x ϕ在),1[+∞上递增,所以0)1()(=≥ϕϕx ,所以2≤a 适合。
(全优试卷)江苏省启东中学高三上学期第一次月考数学(文)试题Word版含答案

江苏省启东中学2018-2019学年度第一学期月考高三年级数学(文)一.填空题:(本大题共14小题,每小题5分,共70分.请把答案直接填写在答题卡相应位......置上..1= ▲ .2的值为▲.3的▲条件(选填“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”).4m的值是▲.5的倾斜角为▲ .6.错误!未找到引用源。
,取值范围是▲.7的值为▲ .8.定义在R的值为▲ .9.的值是▲ .10.的最小值为▲.11的解集是▲.12.,则该椭圆的离心率为▲.13.在斜三角形ABC中,若则sinC的最大值为▲ .14,若函数4的取值范围为▲.二.解答题:本大题共6小题,共90分.请在答题卡指定区域.......内作答. 解答时应写出文字说明、证明过程或演算步骤.15. (本小题满分14分)R.16. (本小题满分14分)在△ABC B,C的对边分别为a,b,c(1(2)求c的值.17. (本小题满分14分)已知椭圆C(1) 求椭圆C的方程;(2) 设点Q在椭圆C上,且PQ与x轴平行,过点P作两条直线分别交椭圆C于A(x1,y1),B(x2,y2)两点,若直线PQ平分∠APB,求证:直线AB的斜率是定值,并求出这个定值.18.(本题满分16分)现有一个以OA、OB为半径的扇形池塘,在OA、OB上分别取点C、D,作DE∥OA、CF∥OB交弧AB于点E、F,且BD = AC,现用渔网沿着DE、EO、OF、FC将池塘分成如图所示的三种的养殖区域.若OA=1km(1)求区域Ⅱ的总面积;(2)若养殖区域Ⅰ、Ⅱ、Ⅲ的每平方千米的年收入分别是15万元、20万元、10万元,记年总收入为y万元.19. (本小题满分16分) .(1(2(3.20.(本小题满分16分)).(1(2(31江苏省启东中学2018-2019学年度第一学期月考高三年级数学答案答题卷上只有第17、18题需要附图,其余按模式搞就行了充分不必要12. 2-115.16.解:(1)在△ABC…… 2分…… 4分…… 6分(2)由(1…… 10分在△ABC……12分…… 14分17. 解:(1) 由e =c a =32得a∶b∶c=2∶1∶3,椭圆C 的方程为x 24b 2+y2b 2=1.把P(2,-1)的坐标代入,得b 2=2,所以椭圆C 的方程是x 28+y22=1.(2) 解法一:由已知得PA ,PB 的斜率存在,且互为相反数. 设直线PA 的方程为y +1=k(x -2),其中k ≠0.由⎩⎪⎨⎪⎧y +1=k (x -2),x 2+4y 2=8,消去y 得x 2+4[kx -(2k +1)]2=8, 即(1+4k 2)x 2-8k(2k +1)x +4(2k +1)2-8=0. 因为该方程的两根为2,x A , 所以2x A =4(2k +1)2-81+4k 2, 即x A =8k 2+8k -21+4k 2. 从而y A =4k 2-4k -14k 2+1. 把k 换成-k ,得x B =8k 2-8k -21+4k 2,y B =4k 2+4k -14k 2+1. 计算,得k AB =y B -y A x B -x A =8k -16k =-12,是定值.解法二:由⎩⎪⎨⎪⎧y +1=k (x -2),x 2+4y 2=8得⎩⎪⎨⎪⎧y +1=k (x -2),4(y 2-1)=4-x 2,当(x ,y )≠(2,-1)时,可得⎩⎪⎨⎪⎧y +1=k (x -2),4k (y -1)=-x -2.解得⎩⎪⎨⎪⎧x A =8k 2+8k -24k 2+1,y A =4k 2-4k -14k 2+1. 以下同解法一.解法三:由A ,B 在椭圆C :x 2+4y 2=8上得(x 1+x 2)(x 1-x 2)+4(y 1+y 2)(y 1-y 2)=0,所以k AB =y 1-y 2x 1-x 2=-14·x 1+x 2y 1+y 2.同理k PA =y 1+1x 1-2=-14·x 1+2y 1-1,k PB =y 2+1x 2-2=-14·x 2+2y 2-1.由已知得k PA =-k PB ,所以y 1+1x 1-2=-y 2+1x 2-2,且x 1+2y 1-1=-x 2+2y 2-1,即x 1y 2+x 2y 1=2(y 1+y 2)-(x 1+x 2)+4,且x 1y 2+x 2y 1=(x 1+x 2)-2(y 1+y 2)+4. 从而可得x 1+x 2=2(y 1+y 2). 所以k AB =-14·x 1+x 2y 1+y 2=-12,是定值.18. 解:(1DE ∥OA ,CF ∥OB ,………………………………2分…………………………………6分(2…………………………………10分…………………………………12分y有最大值. (16)19. 解(13分(2………………………………… 7分(3………………………………9分;………………………………12分分16分20. 解(1. ……………4分(2……………6分①……………7分②……………9分注:分离变量、数形结合等方法得出正确结论的本小题给2分。
江苏省启东中学2019届高三数学上学期第一次月考试题文2018100901251

江苏省启东中学2018-2019学年度第一学期月考高三年级数学 (文)一.填空题:(本大题共14小题,每小题5分,共70分.请把答案直接填写在答题卡相应位置上1.集合,集合,则 = ▲ .}1|{-==x y y A )}2lg(|{x y x B -==B A ⋂2.若为奇函数,则的值为 ▲ . ()x xx xke e f x ke e---=+k 3.设命题;命题,那么是的 ▲ 条件(选填“充分不:4p x >2:540q x x -+≥p q 必要”、“必要不充分”、“充要”、“既不充分也不必要”).4.已知幂函数在是增函数,则实数m 的值是 ▲ . 22*()m m y x m -=∈N (0,)+∞5.直线的倾斜角为 ▲.0()x m m R ++=∈6.若“ 错误!未找到引用源。
,使得成立”是假命题,则实数的122x ⎡⎤∃∈⎢⎥⎣⎦,2210x x -λ+<λ取值范围是 ▲ .7.已知钝角满足,则的值为 ▲ .α3cos 5α=-tan 24απ⎛⎫+ ⎪⎝⎭8.定义在R 上的函数,则的值为 ▲ . ()()()⎪⎩⎪⎨⎧>--≤-=05101log 9x x f x x x f ()2018f 9.在平面直角坐标系中,双曲线的一条渐近线与直线平行,xoy 222:1(0)4x y C a a -=>21y x =+则实数的值是 ▲ .a 10.将函数()的图象向左平移个单位后,所得图象关于直线()π()sin 6f x x ω=-0ω>π3πx =对称,则的最小值为 ▲ .ω11.已知函数,,则的解集是 ▲ . 2()||2x f x x +=+x ∈R 2(2)(2)f x x f x -<-12.已知抛物线的焦点是椭圆的一个焦点,若,22(0)x py p =>F 22221(0)y x a b a b+=>>P Q是椭圆与抛物线的公共点,且直线经过焦点,则该椭圆的离心率为 ▲ . PQ F 13.在斜三角形ABC 中,若,则sinC 的最大值为 ▲ . 114tan tan tan A B C+=14.已知函数,(为自然对数的底数),若函数()22x x x f -=()2+=x e x g xe 有4个零点,则的取值范围为 ▲ .()()[]k x g f x h -=k 二.解答题:本大题共6小题,共90分.请在答题卡指定区域内作答. 解答时应写出文字说明、证明过程或演算步骤. 15. (本小题满分14分) 已知且,条件:函数在其定义域上是减函数,条件:函21>a 1≠a p ()()x x f a 12log -=q 数的定义域为R .如果“或”为真,试求的取值范围.()2--+=a x x x g p q a16. (本小题满分14分)在△ABC 中,角,B ,C 的对边分别为a ,b ,c .已知,,. A 1a =b =π6B A -=(1)求的值; sin A (2)求c 的值.17. (本小题满分14分)已知椭圆C :.22221(0)x y a b a b +=>>(2,1)P -(1) 求椭圆C 的方程;(2) 设点Q 在椭圆C 上,且PQ 与x 轴平行,过点P 作两条直线分别交椭圆C 于A(x 1,y 1),B(x 2,y 2)两点,若直线PQ 平分∠APB,求证:直线AB 的斜率是定值,并求出这个定值.18.(本题满分16分)现有一个以OA 、OB 为半径的扇形池塘,在OA 、OB 上分别取点C 、D ,作DE ∥OA 、CF ∥OB 交弧AB 于点E 、F ,且BD = AC ,现用渔网沿着DE 、EO 、OF 、FC 将池塘分成如图所示的三种的养殖区域.若OA =1km ,,.π2AOB ∠=π(0)2EOF θθ∠=<<(1)求区域Ⅱ的总面积;(2)若养殖区域Ⅰ、Ⅱ、Ⅲ的每平方千米的年收入分别是15万元、20万元、10万元,记年总收入为y 万元. 试问当为多少时,年总收入最大?θ19. (本小题满分16分)已知函数(R ) ,是的导函数.()122++=ax x x f a ∈()x f '()x f (1)若函数极小值为,求实数的值;x e x f x ⋅'=)()(ϕ1-a (2)若,不等式恒成立,求实数的取值范围; []1,2--∈x ()()x f x f '≤a (3)设函数,求在上的最小值.()()()()()()()⎩⎨⎧'<'≥'=x f x f x f x f x f x f x g ,,()x g []4,2∈x(第18题)OB D20.(本小题满分16分)已知函数(R ). ()x ax x x f ln +=∈a (1)讨论函数的单调性;()x f (2)若对任意,恒成立,求实数的取值范围; ),1[+∞∈x 3)(x x f ≤a (3)若函数存在极大值,且极大值点为1,证明:. ()x f ()21x ex f x +≤江苏省启东中学2018-2019学年度第一学期月考 高三年级数学答案答题卷上只有第17、18题需要附图,其余按模式搞就行了1. 2. 3.充分不必要 4.1 5. 6. 7.[)2,01±0150(]22,∞- 8.9. 1 10. 11. 12. -1 3-2121()2,0213.14. 322⎪⎭⎫⎝⎛-212,0ee 15.解:或 121<<a 2≥a16.解:(1)在△ABC 中,因为,,1a =b =π6B A -=由正弦定理得, …… 2分1sin A =于是,即, …… 4分ππsin cos cos sin 66A A A =+cos A A =又,所以. …… 6分22sin cos 1A A +=sin A =(2)由(1)知,,cos A =则,, …… 10分sin 22sin cos A A A =213cos212sin 14A A =-= 在△ABC 中,因为,,所以.πA B C ++=π6B A -=5π26C A =- 则()5πsin sin 26C A =-5π5πsin cos2cos sin 266A A =-. ……12分 113214=⨯1114=由正弦定理得,. …… 14分sin sin a C c A ==17. 解:(1) 由e ==得a∶b∶c=2∶1∶,椭圆C 的方程为+=1.c a 323x 24b 2y 2b2把P(2,-1)的坐标代入,得b 2=2,所以椭圆C 的方程是+=1.x 28y 22(2) 解法一:由已知得PA ,PB 的斜率存在,且互为相反数. 设直线PA 的方程为y +1=k(x -2),其中k ≠0. 由消去y 得x 2+4[kx -(2k +1)]2=8,{y +1=k (x -2),x 2+4y 2=8,)即(1+4k 2)x 2-8k(2k +1)x +4(2k +1)2-8=0. 因为该方程的两根为2,x A , 所以2x A =,4(2k +1)2-81+4k 2即x A =.8k 2+8k -21+4k 2从而y A =.4k 2-4k -14k 2+1把k 换成-k ,得x B =,y B =.8k 2-8k -21+4k 24k 2+4k -14k 2+1计算,得k AB ===-,是定值.y B -y A x B -x A 8k -16k 12解法二: 由得 {y +1=k (x -2),x 2+4y 2=8){y +1=k (x -2),4(y 2-1)=4-x 2,)当(x ,y)≠(2,-1)时, 可得{y +1=k (x -2),4k (y -1)=-x -2.)解得{x A =8k 2+8k -24k 2+1,y A =4k 2-4k -14k 2+1.)以下同解法一.解法三:由A ,B 在椭圆C :x 2+4y 2=8上得(x 1+x 2)(x 1-x 2)+4(y 1+y 2)(y 1-y 2)=0,所以k AB ==-·.y 1-y 2x 1-x 214x 1+x 2y 1+y 2同理k PA ==-·,y 1+1x 1-214x 1+2y 1-1k PB ==-·.y 2+1x 2-214x 2+2y 2-1由已知得k PA =-k PB ,所以=-,且=-,y 1+1x 1-2y 2+1x 2-2x 1+2y 1-1x 2+2y 2-1即x 1y 2+x 2y 1=2(y 1+y 2)-(x 1+x 2)+4,且x 1y 2+x 2y 1=(x 1+x 2)-2(y 1+y 2)+4. 从而可得x 1+x 2=2(y 1+y 2). 所以k AB =-·=-,是定值.14x 1+x 2y 1+y 21218. 解:(1)因为,所以. BD AC OB OA ==,OD OC =因为,DE ∥OA ,CF ∥OB , π2AOB ∠=所以.DE OB CF OA ⊥⊥,又因为,所以≌.OE OF =Rt ODE ∆Rt OCF ∆所以. ………………………………2分1π()22DOE COF COF θ∠=∠∠=-,所以.1πcos cos[()]22OC OF COF θ=⋅∠=-所以,11sin cos 24COF S OC OF COF θ∆=⋅⋅⋅∠=所以,. …………………………………6分II 1=cos 2S θ区域π(0)2θ<< (2)因为,所以.I 12S θ=区域III I II π11cos 422S S S S θθ=--=--总区域区域区域所以11π111520cos 10(cos )22422y θθθ=⨯+⨯+⨯--, …………………………………10分 55ππ5cos (0222θθθ=++<<,所以,令,则. …………………………………12分5(12sin )2y θ'=-=0y 'π=6θ当时,,当时,. π6θ<<00y '>ππ62θ<<0y '<故当时,y 有最大值. π=6θ答:当为时,年总收入最大. …………………………………16 θπ619. 解(1)…………………………………3分 12ln -(2) ………………………………… 7分 ⎪⎭⎫⎢⎣⎡+∞,23(3)因为, ()()()[]a x x x f x f 211)(---='-①若,则时,,所以,从而 21-≥a []4,2∈x ()()x f x f '≥()()a x x f x g 22+='=()x g 的最小值为.………………………………9分()422+=a g ②若,则时,,所以, 23-<a []4,2∈x ()()x f x f '<()()122++==ax x x f x g 当时,的最小值为;232-<≤-a ()x g ()542+=a g 当时,的最小值为;24-<<-a ()x g ()21a a g -=-当时,的最小值为;………………………………12分4-≤a ()x g ()1784+=a g ③若,则时,,2123-<≤-a []4,2∈x ()[)[]⎩⎨⎧-∈+-∈++=4,21,2221,2,122a x a x a x ax x x g 当时,的最小值为; []a x 21,2-∈()x g ()542+=a g 当时,的最小值为. []4,21a x -∈()x g ()a a g 2221-=-因为,,所以的最小值为.14分 2123-<≤-a ()()0362254<+=--+a a a ()x g 54+a 综上所述:………………………………16分()⎪⎪⎪⎩⎪⎪⎪⎨⎧-≥+-<≤-+-<<---≤+=.21,42,212,54,24,1,4,1782mina a a a a a a a x g 20. 解(1)当,函数在上单调递增;0=a ()x f ()+∞,0当,函数在上单调递减,在上单调递增;0>a ()x f ⎪⎪⎭⎫⎝⎛--a e 11,0⎪⎪⎭⎫ ⎝⎛--a e 11当,函数在上单调递增,在上单调递减. ……………4分0<a ()x f ⎪⎪⎭⎫⎝⎛--a e 11,0⎪⎪⎭⎫ ⎝⎛--a e 11(2)若对任意,恒成立,求实数的取值范围; ()x ax x x f ln +=),1[+∞∈x 3)(x x f ≤a 因为,所以,设,),1[+∞∈x 3)(x x f ≤⇔0ln 12≥--x a x ),1[,ln 1)(2+∞∈--=x x a x x ϕ则,所以 ……………6分xa x x a x x -=-='222)(ϕ① 当时,,在上递增,所以,2≤a 0)(≥'x ϕ)(x ϕ),1[+∞0)1()(=≥ϕϕx 所以适合。
【配套K12】江苏省启东中学2019届高三数学上学期第一次月考试题 文

江苏省启东中学2018-2019学年度第一学期月考高三年级数学 (文)一.填空题:(本大题共14小题,每小题5分,共70分.请把答案直接填写在答题卡相应位......置上..1.集合}1|{-==x y y A ,集合)}2lg(|{x y x B -==,则B A ⋂ = ▲ .2.若()x x x xke e f x ke e---=+为奇函数,则k 的值为 ▲ . 3.设命题:4p x >;命题2:540q x x -+≥,那么p 是q 的 ▲ 条件(选填“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”).4.已知幂函数22*()m m y x m -=∈N 在(0,)+∞是增函数,则实数m 的值是 ▲ . 5.直线0()x m m R +=∈的倾斜角为 ▲ .6.若“122x ⎡⎤∃∈⎢⎥⎣⎦, 错误!未找到引用源。
,使得2210x x -λ+<成立”是假命题,则实数λ的取值范围是 ▲ .7.已知钝角α满足3cos 5α=-,则tan 24απ⎛⎫+ ⎪⎝⎭的值为 ▲ .8.定义在R 上的函数()()()⎪⎩⎪⎨⎧>--≤-=05101log 9x x f x x x f ,则()2018f 的值为 ▲ . 9.在平面直角坐标系xoy 中,双曲线222:1(0)4x y C a a -=>的一条渐近线与直线21y x =+平行,则实数a 的值是 ▲ .10.将函数()π()sin 6f x x ω=-(0ω>)的图象向左平移π3个单位后,所得图象关于直线πx =对称,则ω的最小值为 ▲ .11.已知函数2()||2x f x x +=+,x ∈R ,则2(2)(2)f x x f x -<-的解集是 ▲ . 12.已知抛物线22(0)x py p =>的焦点F 是椭圆22221(0)y x a b a b+=>>的一个焦点,若P ,Q 是椭圆与抛物线的公共点,且直线PQ 经过焦点F ,则该椭圆的离心率为 ▲ . 13.在斜三角形ABC 中,若114tan tan tan A B C+=,则sinC 的最大值为 ▲ .14.已知函数()22x x x f -=,()2+=x e x g x(e 为自然对数的底数),若函数()()[]k x g f x h -=有4个零点,则k 的取值范围为 ▲ .二.解答题:本大题共6小题,共90分.请在答题卡指定区域.......内作答. 解答时应写出文字 说明、证明过程或演算步骤. 15. (本小题满分14分) 已知21>a 且1≠a ,条件p :函数()()x x f a 12log -=在其定义域上是减函数,条件q :函数()2--+=a x x x g 的定义域为R .如果“p 或q ”为真,试求a 的取值范围.16. (本小题满分14分)在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c .已知1a =,b =,π6B A -=. (1)求sin A 的值; (2)求c 的值.17. (本小题满分14分)已知椭圆C :22221(0)x y a b a b+=>>,且过点(2,1)P -.(1) 求椭圆C 的方程;(2) 设点Q 在椭圆C 上,且PQ 与x 轴平行,过点P 作两条直线分别交椭圆C 于A(x 1,y 1),B(x 2,y 2)两点,若直线PQ 平分∠APB,求证:直线AB 的斜率是定值,并求出这个定值.18.(本题满分16分)现有一个以OA 、OB 为半径的扇形池塘,在OA 、OB 上分别取点C 、D ,作DE ∥OA 、CF ∥OB 交弧AB 于点E 、F ,且BD = AC ,现用渔网沿着DE 、EO 、OF 、FC 将池塘分成如图所示的三种的养殖区域.若OA =1km ,π2AOB ∠=,π(0)2EOF θθ∠=<<.(1)求区域Ⅱ的总面积;(2)若养殖区域Ⅰ、Ⅱ、Ⅲ的每平方千米的年收入分别是15万元、20万元、10万元,记年总收入为y 万元. 试问当θ为多少时,年总收入最大?19. (本小题满分16分)已知函数()122++=ax x x f (a ∈R ) ,()x f '是()x f 的导函数.(1)若函数x e x f x ⋅'=)()(ϕ极小值为1-,求实数a 的值;(2)若[]1,2--∈x ,不等式()()x f x f '≤恒成立,求实数a 的取值范围; (3)设函数()()()()()()()⎩⎨⎧'<'≥'=x f x f x f x f x f x f x g ,,,求()x g 在[]4,2∈x 上的最小值.(第18题)20.(本小题满分16分)已知函数()x ax x x f ln +=(∈a R ). (1)讨论函数()x f 的单调性;(2)若对任意),1[+∞∈x ,3)(x x f ≤恒成立,求实数a 的取值范围; (3)若函数()x f 存在极大值,且极大值点为1,证明:()21x ex f x+≤.江苏省启东中学2018-2019学年度第一学期月考 高三年级数学答案答题卷上只有第17、18题需要附图,其余按模式搞就行了1.[)2,02.1±3.充分不必要4.15. 0150 6.(]22,∞-7.3- 8.21 9. 1 10.2111.()2,0 12. 2-1 13.322 14.⎪⎭⎫⎝⎛-212,0ee 15.解:121<<a 或2≥a16.解:(1)在△ABC 中,因为1a =,b =π6B A -=,由正弦定理得,1sin πsin 6A A + …… 2分于是ππsin cos cos sin 66A A A =+,即cos A A =, …… 4分又22sin cos 1A A +=,所以sin A =. …… 6分(2)由(1)知,cos A =,则sin 22sin cos A A A =,213cos212sin 14A A =-=, …… 10分在△ABC 中,因为πA B C ++=,π6B A -=,所以5π26C A =-.则()5πsin sin 26C A =-5π5πsin cos2cos sin 266A A =-113214=⨯+1114=. ……12分由正弦定理得,sin sin a C c A == …… 14分17. 解:(1) 由e =c a =32得a∶b∶c=2∶1∶3,椭圆C 的方程为x 24b 2+y2b 2=1.把P(2,-1)的坐标代入,得b 2=2,所以椭圆C 的方程是x 28+y22=1.(2) 解法一:由已知得PA ,PB 的斜率存在,且互为相反数. 设直线PA 的方程为y +1=k(x -2),其中k ≠0.由⎩⎪⎨⎪⎧y +1=k (x -2),x 2+4y 2=8,消去y 得x 2+4[kx -(2k +1)]2=8, 即(1+4k 2)x 2-8k(2k +1)x +4(2k +1)2-8=0. 因为该方程的两根为2,x A , 所以2x A =4(2k +1)2-81+4k 2, 即x A =8k 2+8k -21+4k 2. 从而y A =4k 2-4k -14k 2+1. 把k 换成-k ,得x B =8k 2-8k -21+4k 2,y B =4k 2+4k -14k 2+1. 计算,得k AB =y B -y A x B -x A =8k -16k =-12,是定值.解法二:由⎩⎪⎨⎪⎧y +1=k (x -2),x 2+4y 2=8得⎩⎪⎨⎪⎧y +1=k (x -2),4(y 2-1)=4-x 2, 当(x ,y )≠(2,-1)时,可得⎩⎪⎨⎪⎧y +1=k (x -2),4k (y -1)=-x -2.解得⎩⎪⎨⎪⎧x A =8k 2+8k -24k 2+1,y A =4k 2-4k -14k 2+1. 以下同解法一.解法三:由A ,B 在椭圆C :x 2+4y 2=8上得(x 1+x 2)(x 1-x 2)+4(y 1+y 2)(y 1-y 2)=0,所以k AB =y 1-y 2x 1-x 2=-14·x 1+x 2y 1+y 2.同理k PA =y 1+1x 1-2=-14·x 1+2y 1-1,k PB =y 2+1x 2-2=-14·x 2+2y 2-1.由已知得k PA =-k PB ,所以y 1+1x 1-2=-y 2+1x 2-2,且x 1+2y 1-1=-x 2+2y 2-1,即x 1y 2+x 2y 1=2(y 1+y 2)-(x 1+x 2)+4,且x 1y 2+x 2y 1=(x 1+x 2)-2(y 1+y 2)+4.从而可得x 1+x 2=2(y 1+y 2). 所以k AB =-14·x 1+x 2y 1+y 2=-12,是定值.18. 解:(1)因为BD AC OB OA ==,,所以OD OC =. 因为π2AOB ∠=,DE ∥OA ,CF ∥OB , 所以DE OB CF OA ⊥⊥,.又因为OE OF =,所以Rt ODE ∆≌Rt OCF ∆.所以1π()22DOE COF COF θ∠=∠∠=-,. ………………………………2分所以1πcos cos[()]22OC OF COF θ=⋅∠=-.所以11sin cos 24COF S OC OF COF θ∆=⋅⋅⋅∠=,所以II 1=cos 2S θ区域,π(0)2θ<<. …………………………………6分(2)因为I 12S θ=区域,所以III I II π11cos 422S S S S θθ=--=--总区域区域区域.所以11π111520cos 10(cos )22422y θθθθ=⨯+⨯+⨯--55ππ5cos (0)222θθθ=++<<,, …………………………………10分 所以5(12sin )2y θ'=-,令=0y ',则π=6θ. …………………………………12分当π6θ<<0时,0y '>,当ππ62θ<<时,0y '<. 故当π=6θ时,y 有最大值. 答:当θ为π6时,年总收入最大. …………………………………16 19. 解(1)12ln -…………………………………3分 (2)⎪⎭⎫⎢⎣⎡+∞,23 ………………………………… 7分 (3)因为()()()[]a x x x f x f 211)(---='-, ①若21-≥a ,则[]4,2∈x 时,()()x f x f '≥,所以()()a x x f x g 22+='=,从而()x g 的最小值为()422+=a g .………………………………9分②若23-<a ,则[]4,2∈x 时,()()x f x f '<,所以()()122++==ax x x f x g , 当232-<≤-a 时,()x g 的最小值为()542+=a g ;当24-<<-a 时,()x g 的最小值为()21a a g -=-;当4-≤a 时,()x g 的最小值为()1784+=a g ;………………………………12分③若2123-<≤-a ,则[]4,2∈x 时,()[)[]⎩⎨⎧-∈+-∈++=4,21,2221,2,122a x a x a x ax x x g ,当[]a x 21,2-∈时,()x g 的最小值为()542+=a g ; 当[]4,21a x -∈时,()x g 的最小值为()a a g 2221-=-. 因为2123-<≤-a ,()()0362254<+=--+a a a ,所以()x g 的最小值为54+a .14分 综上所述:()⎪⎪⎪⎩⎪⎪⎪⎨⎧-≥+-<≤-+-<<---≤+=.21,42,212,54,24,1,4,1782mina a a a a a a a x g ………………………………16分20. 解(1)当0=a ,函数()x f 在()+∞,0上单调递增;当0>a ,函数()x f 在⎪⎪⎭⎫⎝⎛--a e 11,0上单调递减,在⎪⎪⎭⎫ ⎝⎛--a e 11上单调递增;当0<a ,函数()x f 在⎪⎪⎭⎫⎝⎛--a e 11,0上单调递增,在⎪⎪⎭⎫ ⎝⎛--a e 11上单调递减. ……………4分(2)()x ax x x f ln +=若对任意),1[+∞∈x ,3)(x x f ≤恒成立,求实数a 的取值范围; 因为),1[+∞∈x ,所以3)(x x f ≤⇔0ln 12≥--x a x ,设),1[,ln 1)(2+∞∈--=x x a x x ϕ,则xa x x a x x -=-='222)(ϕ,所以 ……………6分① 当2≤a 时,0)(≥'x ϕ,)(x ϕ在),1[+∞上递增,所以0)1()(=≥ϕϕx ,所以2≤a 适合。
江苏省启东中学2019届高三上学期第一次月考数学(文)试题

江苏省启东中学2018-2019学年度第一学期月考高三年级数学 (文)一.填空题:(本大题共14小题,每小题5分,共70分.请把答案直接填写在答题卡相应位置上........ 1.集合}1|{-==x y y A ,集合)}2lg(|{x y x B -==,则B A ⋂ = ▲ .2.若()x x x xke e f x ke e ---=+为奇函数,则的值为 ▲ .3.设命题:4p x >;命题2:540q x x -+≥,那么是的 ▲ 条件(选填“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”).4.已知幂函数22*()m m y x m -=∈N 在(0,)+∞是增函数,则实数m 的值是 ▲ . 5.直线0()x m m R +=∈的倾斜角为 ▲ .6.若“122x ⎡⎤∃∈⎢⎥⎣⎦, 错误!未找到引用源。
,使得2210x x -λ+<成立”是假命题,则实数的取值范围是▲ .7.已知钝角满足3cos 5α=-,则tan 24απ⎛⎫+ ⎪⎝⎭的值为 ▲ .8.定义在R 上的函数()()()⎪⎩⎪⎨⎧>--≤-=05101log 9x x f x x x f ,则()2018f 的值为 ▲ . 9.在平面直角坐标系xoy 中,双曲线222:1(0)4x y C a a -=>的一条渐近线与直线21y x =+平行,则实数的值是 ▲ .10.将函数()π()sin 6f x x ω=-(0ω>)的图象向左平移π3个单位后,所得图象关于直线πx =对称,则的最小值为 ▲ .11.已知函数2()||2x f x x +=+,x ∈R ,则2(2)(2)f x x f x -<-的解集是 ▲ .12.已知抛物线22(0)x py p =>的焦点是椭圆22221(0)y x a b a b+=>>的一个焦点,若,Q 是椭圆与抛物线的公共点,且直线PQ 经过焦点,则该椭圆的离心率为 ▲ . 13.在斜三角形ABC 中,若114tan tan tan A B C+=,则sinC 的最大值为 ▲ . 14.已知函数()22x x x f -=,()2+=x e x g x(为自然对数的底数),若函数()()[]k x g f x h -=有4个零点,则k 的取值范围为 ▲ .二.解答题:本大题共6小题,共90分.请在答题卡指定区域.......内作答. 解答时应写出文字说明、证明过程或演算步骤. 15. (本小题满分14分) 已知21>a 且1≠a ,条件:函数()()x x f a 12log -=在其定义域上是减函数,条件:函数()2--+=a x x x g 的定义域为R.如果“或”为真,试求的取值范围.16. (本小题满分14分)在△ABC 中,角,B ,C 的对边分别为a ,b ,c .已知1a =,b =π6B A -=. (1)求sin A 的值; (2)求c 的值.17. (本小题满分14分)已知椭圆C :22221(0)x y a b a b+=>>,且过点(2,1)P -.(1) 求椭圆C 的方程;(2) 设点Q 在椭圆C 上,且PQ 与x 轴平行,过点P 作两条直线分别交椭圆C 于A(x 1,y 1),B(x 2,y 2)两点,若直线PQ 平分∠APB,求证:直线AB 的斜率是定值,并求出这个定值.18.(本题满分16分)现有一个以OA 、OB 为半径的扇形池塘,在OA 、OB 上分别取点C 、D ,作DE∥OA、CF∥OB 交弧AB 于点E 、F ,且BD = AC ,现用渔网沿着DE 、EO 、OF 、FC 将池塘分成如图所示的三种的养殖区域.若OA=1km ,π2AOB ∠=,π(0)EOF θθ∠=<<.(1)求区域Ⅱ的总面积;(2)若养殖区域Ⅰ、Ⅱ、Ⅲ的每平方千米的年收入分别是15万元、20万元、10万元,记年总收入为y万元. 试问当为多少时,年总收入最大?(第18题)19. (本小题满分16分)已知函数()122++=ax x x f (R) ,()x f '是()x f 的导函数. (1)若函数x e x f x ⋅'=)()(ϕ极小值为1-,求实数的值;(2)若[]1,2--∈x ,不等式()()x f x f '≤恒成立,求实数的取值范围;(3)设函数()()()()()()()⎩⎨⎧'<'≥'=x f x f x f x f x f x f x g ,,,求()x g 在[]4,2∈x 上的最小值.20.(本小题满分16分)已知函数()x ax x x f ln +=(∈a R ). (1)讨论函数()x f 的单调性;(2)若对任意),1[+∞∈x ,3)(x x f ≤恒成立,求实数的取值范围; (3)若函数()x f 存在极大值,且极大值点为1,证明:()21x ex f x +≤.江苏省启东中学2018-2019学年度第一学期月考高三年级数学答案答题卷上只有第17、18题需要附图,其余按模式搞就行了1.[)2,02.1±3.充分不必要4.15. 0150 6.(]22,∞- 7.3-8.21 9. 1 10.2111.()2,0 12. 2-1 13.322 14.⎪⎭⎫⎝⎛-212,0e e 15.解:121<<a 或2≥a16.解:(1)在△ABC 中,因为1a =,b =π6B A -=,由正弦定理得,1sin πsin 6A A +…… 2分于是ππsin cos cos sin 66A A A =+,即cos A A =, …… 4分又22sin cos 1A A +=,所以sin A . …… 6分(2)由(1)知,cos A ,则sin 22sin cos A A A ==,213cos212sin 14A A =-=, …… 10分在△ABC 中,因为πA B C ++=,π6B A -=,所以5π2C A =-.则()5πsin sin 2C A =-5π5πsin cos2cos sin 266A A =-113214=⨯1114=. ……12分由正弦定理得,sin sin a C c A = …… 14分 17. 解:(1) 由e =c a =32得a∶b∶c=2∶1∶3,椭圆C 的方程为x 24b 2+y2b 2=1.把P(2,-1)的坐标代入,得b 2=2,所以椭圆C 的方程是x 28+y22=1.(2) 解法一:由已知得PA ,PB 的斜率存在,且互为相反数. 设直线PA 的方程为y +1=k(x -2),其中k ≠0.由⎩⎪⎨⎪⎧y +1=k (x -2),x 2+4y 2=8,消去y 得x 2+4[kx -(2k +1)]2=8, 即(1+4k 2)x 2-8k(2k +1)x +4(2k +1)2-8=0. 因为该方程的两根为2,x A , 所以2x A =4(2k +1)2-81+4k 2, 即x A =8k 2+8k -21+4k 2. 从而y A =4k 2-4k -14k 2+1. 把k 换成-k ,得x B =8k 2-8k -21+4k 2,y B =4k 2+4k -14k 2+1. 计算,得k AB =y B -y A x B -x A =8k -16k =-12,是定值.解法二:由⎩⎪⎨⎪⎧y +1=k (x -2),x 2+4y 2=8得⎩⎪⎨⎪⎧y +1=k (x -2),4(y 2-1)=4-x 2, 当(x ,y )≠(2,-1)时,可得⎩⎪⎨⎪⎧y +1=k (x -2),4k (y -1)=-x -2.解得⎩⎪⎨⎪⎧x A =8k 2+8k -24k 2+1,y A =4k 2-4k -14k 2+1. 以下同解法一.解法三:由A ,B 在椭圆C :x 2+4y 2=8上得(x 1+x 2)(x 1-x 2)+4(y 1+y 2)(y 1-y 2)=0,所以k AB =y 1-y 2x 1-x 2=-14·x 1+x 2y 1+y 2.同理k PA =y 1+1x 1-2=-14·x 1+2y 1-1,k PB =y 2+1x 2-2=-14·x 2+2y 2-1.由已知得k PA =-k PB ,所以y 1+1x 1-2=-y 2+1x 2-2,且x 1+2y 1-1=-x 2+2y 2-1,即x 1y 2+x 2y 1=2(y 1+y 2)-(x 1+x 2)+4,且x 1y 2+x 2y 1=(x 1+x 2)-2(y 1+y 2)+4.从而可得x 1+x 2=2(y 1+y 2). 所以k AB =-14·x 1+x 2y 1+y 2=-12,是定值.18. 解:(1)因为BD AC OB OA ==,,所以OD OC =. 因为π2AOB ∠=,DE∥OA,CF∥OB, 所以DE OB CF OA ⊥⊥,.又因为OE OF =,所以Rt ODE ∆≌Rt OCF ∆.所以1π()22DOE COF COF θ∠=∠∠=-,. ………………………………2分所以1πcos cos[()]22OC OF COF θ=⋅∠=-.所以11sin cos 24COF S OC OF COF θ∆=⋅⋅⋅∠=,所以II 1=cos 2S θ区域,π(0)2θ<<. …………………………………6分(2)因为I 12S θ=区域,所以III I II π11cos 422S S S S θθ=--=--总区域区域区域.所以11π111520cos 10(cos )22422y θθθθ=⨯+⨯+⨯--55ππ5cos (0)222θθθ=++<<,, …………………………………10分 所以5(12sin )2y θ'=-,令=0y ',则π=6θ. …………………………………12分当π6θ<<0时,0y '>,当ππ62θ<<时,0y '<. 故当π=6θ时,y 有最大值. 答:当为π6时,年总收入最大. …………………………………16 19. 解(1)12ln -…………………………………3分 (2)⎪⎭⎫⎢⎣⎡+∞,23 ………………………………… 7分 (3)因为()()()[]a x x x f x f 211)(---='-, ①若21-≥a ,则[]4,2∈x 时,()()x f x f '≥,所以()()a x x f x g 22+='=,从而()x g 的最小值为()422+=a g .………………………………9分②若23-<a ,则[]4,2∈x 时,()()x f x f '<,所以()()122++==ax x x f x g , 当232-<≤-a 时,()x g 的最小值为()542+=a g ; 当24-<<-a 时,()x g 的最小值为()21a a g -=-;当4-≤a 时,()x g 的最小值为()1784+=a g ;………………………………12分③若2123-<≤-a ,则[]4,2∈x 时,()[)[]⎩⎨⎧-∈+-∈++=4,21,2221,2,122a x a x a x ax x x g ,当[]a x 21,2-∈时,()x g 的最小值为()542+=a g ; 当[]4,21a x -∈时,()x g 的最小值为()a a g 2221-=-. 因为2123-<≤-a ,()()0362254<+=--+a a a ,所以()x g 的最小值为54+a .14分 综上所述:()⎪⎪⎪⎩⎪⎪⎪⎨⎧-≥+-<≤-+-<<---≤+=.21,42,212,54,24,1,4,1782mina a a a a a a a x g ………………………………16分20. 解(1)当0=a ,函数()x f 在()+∞,0上单调递增;当0>a ,函数()x f 在⎪⎪⎭⎫⎝⎛--a e 11,0上单调递减,在⎪⎪⎭⎫ ⎝⎛--a e 11上单调递增;当0<a ,函数()x f 在⎪⎪⎭⎫⎝⎛--a e 11,0上单调递增,在⎪⎪⎭⎫ ⎝⎛--a e 11上单调递减. ……………4分(2)()x ax x x f ln +=若对任意),1[+∞∈x ,3)(x x f ≤恒成立,求实数的取值范围; 因为),1[+∞∈x ,所以3)(x x f ≤⇔0ln 12≥--x a x ,设),1[,ln 1)(2+∞∈--=x x a x x ϕ,则xa x x a x x -=-='222)(ϕ,所以 ……………6分① 当2≤a 时,0)(≥'x ϕ,)(x ϕ在),1[+∞上递增,所以0)1()(=≥ϕϕx ,所以2≤a 适合。
【高三数学试题精选】江苏启东中学2019届高三数学上学期第一次月考试题(文科含答案)

5
江苏省启东中学2019学年度第一学期月考
高三年级数学答案
答题卷上只有第17、18题需要附图,其余按模式搞就行了
1 2 3充分不必要41 5 6 7 8 9 1 10 11 12 2-1
13 14
15解或
16解(1)在△ABc中,因为,,,
解得xA=82+8-242+1,A=42-4-142+1
以下同解法一
解法三由A,B在椭圆cx2+42=8上得(x1+x2)(x1-x2)+4(1+2)(1-2)=0,所以AB=1-2x1-x2=-14 x1+x21+2
同理PA=1+1x1-2=-14 x1+21-1,பைடு நூலகம்
PB=2+1x2-2=-14 x2+22-1
②当时,令得(负值舍去),当时,,
在上递减,所以,这与在上恒成立矛盾。
所以不合。
综上可得,实数的取值范围是……………9分
注分离变量、数形结合等方法得出正确结论的本小题给2分。
(3)由(1)可知若函数存在极大值,且极大值点为1,则,且,解得,故……………10分
要证明,即证,设,
则,令,则,所以函数单调递增,又,,故在上存在唯一的零点,即所以当时,,当时,所以函数在上单调递减,在上单调递增,故,
所以只要证,…………………………………13分
由得
,所以,
又,所以只要证
若,则,,,所以
与矛盾。
故,得证。…………………………16分
5
因为,,所以的最小值为14分
综上所述………………………………16分
20解(1)当,函数在上单调递增;
当,函数在上单调递减,在上单调递增;
江苏省启东中学近年届高三数学上学期第一次月考试题文(2021年整理)

江苏省启东中学2019届高三数学上学期第一次月考试题文编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(江苏省启东中学2019届高三数学上学期第一次月考试题文)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为江苏省启东中学2019届高三数学上学期第一次月考试题文的全部内容。
江苏省启东中学2018—2019学年度第一学期月考高三年级数学 (文)一.填空题:(本大题共14小题,每小题5分,共70分.请把答案直接填写在答题卡相应位......置上..1.集合}1|{-==x y y A ,集合)}2lg(|{x y x B -==,则B A ⋂ = ▲ .2.若()x xx x ke e f x ke e---=+为奇函数,则k 的值为 ▲ .3.设命题:4p x >;命题2:540q x x -+≥,那么p 是q 的 ▲ 条件(选填“充分不必要”、“必要不充分”、“充要"、“既不充分也不必要”).4.已知幂函数22*()m m y x m -=∈N 在(0,)+∞是增函数,则实数m 的值是 ▲ . 5.直线0()x m m R ++=∈的倾斜角为 ▲ .6.若“122x ⎡⎤∃∈⎢⎥⎣⎦, 错误!未找到引用源。
,使得2210x x -λ+<成立”是假命题,则实数λ的取值范围是 ▲ .7.已知钝角α满足3cos 5α=-,则tan 24απ⎛⎫+ ⎪⎝⎭的值为 ▲ .8.定义在R 上的函数()()()⎪⎩⎪⎨⎧>--≤-=0511log 9x x f x x x f ,则()2018f 的值为 ▲ . 9.在平面直角坐标系xoy 中,双曲线222:1(0)4x y C a a -=>的一条渐近线与直线21y x =+平行,则实数a 的值是 ▲ .10.将函数()π()sin 6f x x ω=-(0ω>)的图象向左平移π3个单位后,所得图象关于直线πx =对称,则ω的最小值为 ▲ .11.已知函数2()||2x f x x +=+,x ∈R ,则2(2)(2)f x x f x -<-的解集是 ▲ .12.已知抛物线22(0)x py p =>的焦点F 是椭圆22221(0)y x a b a b+=>>的一个焦点,若P ,Q 是椭圆与抛物线的公共点,且直线PQ 经过焦点F ,则该椭圆的离心率为 ▲ .13.在斜三角形ABC 中,若114tan tan tan A B C+=,则sinC 的最大值为 ▲ . 14.已知函数()22x x x f -=,()2+=x e x g x(e 为自然对数的底数),若函数()()[]k x g f x h -=有4个零点,则k 的取值范围为 ▲ .二.解答题:本大题共6小题,共90分.请在答题卡指定区域.......内作答。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2016届江苏省启东中学高三上学期第一次月考数学试题及解析一、填空题1.已知集合{}1,2,4A =,{}|(1)(3)0B x x x =--≤,则A B = .【答案】{}1,2【解析】试题分析:由已知{|13}B x x =≤≤,所以{1,2}A B =.【考点】集合的运算.2.命题“[0,)x ∃∈+∞,23x >”的否定是 . 【答案】[0,)x ∀∈+∞,23x ≤【解析】试题分析:命题“[0,)x ∃∈+∞,23x >”的否定是“[0,)x ∀∈+∞,23x ≤” 【考点】命题的否定.3.在3和243中间插入3个实数1a ,2a ,3a ,使这5个数成等比数列,则2a = . 【答案】27【解析】试题分析:222324327a =⨯=,又2a 与2,243同号,所以227a =.【考点】等比数列的性质. 4.已知7sin cos 13αα+=-,π(,0)2α∈-,则tan α= . 【答案】125-【解析】试题分析:由7sin cos 13αα+=-得249(sin cos )169αα+=,所以60sin cos 169αα=-,因为(,0)2πα∈-,所以sin 0,cos 0αα<>,由7sin cos 1360sin cos 169αααα⎧+=-⎪⎪⎨⎪=-⎪⎩得12sin 135cos 13αα⎧=-⎪⎪⎨⎪=⎪⎩,所以sin 12tan cos 5ααα==-. 【考点】同角间的三角函数关系.5.函数()ln 23x f x x =+-在区间(1,2)上的零点个数为 . 【答案】1【解析】试题分析:函数()ln 23xf x x =+-是(0,)+∞上的增函数,又1(1)ln12310f =+-=-<,2(2)ln 223ln 210f =+-=+>,所以()f x 在(1,2)上有且只有一个零点. 【考点】函数的零点.6.已知定义在R 上的函数2()23f x ax x =++的值域为[2,)+∞,则()f x 的单调增区间为 .【答案】[1,)-+∞((1,)-+∞也对)【解析】试题分析:由已知012424a a a>⎧⎪-⎨=⎪⎩,解得1a =,22()23(1)2f x x x x =++=++,所以其增区间为[1,)-+∞. 【考点】二次函数的性质.7.函数3()812f x x x =+-在区间[33]-,上的最大值与最小值之和是 . 【答案】16【解析】试题分析:设在区间[3,3]-上()f x 的最大值为M ,最小值为m ,再设()()8g x f x =-,()g x 的最大值为8M -,最小值为8m -,又3()12g x x x =-是奇函数,所以在区间[3,3]-上max min ()()0g x g x +=,即(8)(8)0M m -+-=,16M m +=.【考点】函数的奇偶性.8.等差数列{}n a 的前m 项的和为30,前2m 项的和为100,求它的前3m 项的和为 .【答案】210【解析】试题分析:因为{}n a 是等差数列,所以232,,m m m m m S S S S S --也成等差数列,即2322()()m m m m m S S S S S -=+-,所以323()3(10030)210m m m S S S =-=⨯-=. 【考点】等差数列的性质. 9.若α、β均为锐角,且1cos 17α=,47cos()51αβ+=-,则cos β= . 【答案】13【解析】试题分析:由于αβ、都是锐角,所以αβ+∈(0,)π,又1cos 17α=,47cos()51αβ+=-,所以sin 17α=,sin()51αβ+=,cos cos[()]βαβα=+-cos()cos sin()sin αβααβα=+++4715117=-⨯+5117⨯13=. 【考点】两角和与差的余弦公式.【名师点睛】三角函数的给值求值,关键是把待求角用已知角表示: (1)已知角为两个时,待求角一般表示为已知角的和或差.(2)已知角为一个时,待求角一般与已知角成“倍”的关系或“互余互补”的关系. (3)在求值的过程中“拼凑角”对求值往往起到“峰回路转”的效果.通过适当地拆角、凑角来利用所给条件.常见的变角技巧有2αβ+=2βα⎛⎫-⎪⎝⎭-2αβ⎛⎫-⎪⎝⎭,α=(α-β)+β,4π+α=2π-4πα⎛⎫- ⎪⎝⎭,15°=45°-30°等. 10.函数()y f x =是R 上的奇函数,满足()()33f x f x +=-,当(0,3)x ∈时,()2x f x =,则(5)f -= .【答案】2-【解析】试题分析:由题意1(5)(32)(32)(1)22f f f f =+=-===,又()f x 是奇函数,所以(5)(5)2f f -=-=-.【考点】函数的奇偶性.11.如果若干个函数的图象经过平移后能够重合,则称这些函数为“互为生成”函数,给出下列函数:(1)1()sin cos f x x x =+;(2)2()f x x =;(3)3()cos )f x x x =+;(4)4()sin f x x =;(5)5()2cos (sin cos )222x x xf x =+,其中“互为生成”函数的有 .(请填写序号)【答案】(1)(2)(5)【解析】试题分析:1())4f x x π=+,3()2sin()4f x x π=+,5()sin cos 1)14f x x x x π=++=++,其中(1)(2)(5)都可以由y x =平移得到,它们是“互为生成”函数,(3)(4)不能由y x =平移得到,相互也不能平移得到,故填(1)(2)⑷. 【考点】函数图象的平移.12.已知ABC ∆是单位圆O 的内接三角形,AD 是圆的直径,若满足2AB AD AC AD BC ⋅+⋅=,则||BC = .【答案】2【解析】试题分析:因为AD 直径,所以2ABD ACD π∠=∠=,所以2AB AD AB ⋅=,2AC AD AC ⋅=,所以222AB AC BC +=,即2BAC π∠=,BC 直径,所以2BC =.【考点】向量的数量积. 13.已知直线l 与曲线1y x=-和曲线ln y x =均相切,则这样的直线l 的条数为 . 【答案】1【解析】试题分析:设1()ln f x x x =+,22111'()x f x x x x-=-=,当01x <<时,'()0f x <,()f x 单调递减,当1x >时,'()0f x >,()f x 单调递增,1x =时,()f x 取得极小值也是最小值(1)ln1110f =+=>,所以1ln 0x x +>恒成立,即1ln x x>-,因此设公直线l 与曲线1y x =-相切于点11(,)A x y ,与曲线ln y x =相切于点22(,)B x y ,必有10x <,1y x =-的导数为21'y x =,ln y x =的导数是1'y x=,由题意212212112111ln 1x x x x x x x ⎧=⎪⎪⎪⎨--⎪⎪=-⎪⎩,211221111ln 1x x x x x +⇒=-,1112ln()20x x x ⇒--+=,记()2ln()2g x x x x =--+,'()2ln()1g x x =-+,令'()0g x =,则12x e -=-,当12x e -<-时,'()0g x >,()g x 单调递增,当120ex --<<时,'()0g x <,()g x 单调递减,1122max ()()2(1)0g x g e e --=-=+>,又22()320g e e -=-+<,lim[2ln()2]20x x x x →---+=>,所以()0g x =只有一解,即1112ln()20x x x --+=只有一解,所以两曲线的切线只有一条.【考点】导数的几何意义,导数与函数的单调性.【名师点睛】1.求过点P 的曲线的切线方程的步骤为: 第一步,设出切点坐标P ′(x 1,f (x 1)); 第二步,写出过P ′(x 1,f (x 1))的切线方程为y -f (x 1)=f ′(x 1)(x -x 1); 第三步,将点P 的坐标(x 0,y 0)代入切线方程,求出x 1; 第四步,将x 1的值代入方程y -f (x 1)=f ′(x 1)(x -x 1),可得过点P (x 0,y 0)的切线方程.2.判断函数y =f (x )零点个数的常用方法:(1)直接法:令f (x )=0,则方程实根的个数就是函数零点的个数.(2)零点存在性定理法:判断函数在区间[a ,b]上是连续不断的曲线,且f (a )·f (b )<0,再结合函数的图象与性质(如单调性、奇偶性、周期性、对称性)可确定函数的零点个数.(3)数形结合法:转化为两个函数的图象的交点个数问题.画出两个函数的图象,其交点的个数就是函数零点的个数.在一个区间上单调的函数在该区间内至多只有一个零点,在确定函数零点的唯一性时往往要利用函数的单调性,确定函数零点所在区间主要利用函数零点存在定理,有时可结合函数的图象辅助解题. 14.已知数列{}n a 满足11a =,且111n n a a n +=++,*n ∈N ,则201420151()k k k aa =-=∑ .【答案】20291052【解析】试题分析:由已知1211111112n n n a a a n n nn--=+=++==+++-,2015111()()122015k k a a k k k -=+++++, 201420151()k k k a a =-=∑1111111()2()20142320153420152015+++++++++⨯ 11111(12)(123)(12)(122014)23412015k k =++⨯+++⨯+++++⨯+++++⨯+123201422222k =++++++20291052=. 【考点】数列求和.【名师点睛】 数列求和的方法:(1)一般的数列求和,应从通项入手,若无通项,先求通项,然后通过对通项变形,转化为与特殊数列有关或具备某种方法适用特点的形式,从而选择合适的方法求和. (2)解决非等差、等比数列的求和,主要有两种思路:①转化的思想,即将一般数列设法转化为等差或等比数列,这一思想方法往往通过通项分解或错位相减来完成.②不能转化为等差或等比数列的数列,往往通过裂项相消法、错位相减法、倒序相加法等来求和. 二、解答题15. 已知集合{}||21|3A x x =-<,{}2|(2)20B x x a x a =-++≤. (1)若1a =,求A B ;(2)若A B A =,求实数a 的取值范围. 【答案】(1)[1,2);(2)(,1]-∞.【解析】试题分析:先把集合,A B 化简,(1,2)A =-,(1)当1a =时,[1,2]B =,易得AB ;(2)题设条件A B A =说明A B ⊆,此时求集合B ,需分类讨论,分成2,2,2a a a <=>三类,分别求得a 的范围. 试题解析:由题意知,(1,2)A =-; (1)当1a =时,[1,2]B =, [1,2)A B ∴=; (2)A B A =,A B ∴⊆;①当2a =时,{}2B =,不符合题意;②当2a <时,[,2]B a =,由A B ⊆得:1a -≤; ③当2a >时,[2,]B a =,此时A B ⊄,不符合题意; 综上所述,实数a 的取值范围为(,1]-∞-. 【考点】集合的运算,集合的关系.16.已知ABC ∆中,角A 、B 、C 所对的边分别为a 、b 、c ,满足sin sin sin sin b a B Cc B A--=+. (1)求角A 的值;(2)若a ,c ,b 成等差数列,试判断ABC ∆的形状. 【答案】(1)3A π=;(2)等边三角形.【解析】试题分析:(1)题中已知条件sin sin sin sin b a B Cc B A--=+是边角关系,为了求角A ,我们应用正弦定理把它化为边的关系或者角的关系,本题化为边的关系后,可用余弦定理求得A 角;(2)判断三角形形状,由已知2c a b =+,再结合(1)222a b c bc =+-,消去a ,可得b c =,从而ABC ∆为等边三角形.试题解析:(1)由正弦定理,得:b a b cc b a --=+, 整理,得:222a b c bc =+-,由余弦定理,得:1cos 2A =,A 是ABC ∆的内角,π3A ∴=; (2)a ,c ,b 成等差数列,2c a b ∴=+,由(1)可知,222a b c bc =+-,222(2)c b b c bc ∴-=+-,整理,得:2330c bc -=,由0c >,得b c =,a b c ∴==, ∴ABC ∆是等边三角形.(注:本题第二小问可以用角的化简来处理)【考点】正弦定理,余弦定理,三角形形状的判断. 【名师点睛】判定三角形形状的两种常用途径:(1)通过正弦定理和余弦定理,化边为角,利用三角变换得出三角形内角之间的关系进行判断.(2)利用正弦定理、余弦定理,化角为边,通过代数恒等变换,求出边与边之间的关系进行判断.提醒:在判断三角形形状时一定要注意解是否唯一,并注重挖掘隐含条件.另外,在变形过程中要注意角A ,B ,C 的范围对三角函数值的影响.17.已知向量a ,b ,c 满足0a b c ++=,且a 与b 的夹角等于150︒,b 与c 的夹角等于120︒,||2c =,求||a ,||b . 【答案】||23a =,||4b =.【解析】试题分析:要求||a ,||b ,就要列出关于||a ,||b 的方程组,观察已知条件a 与b 的夹角等于150︒,b 与c 的夹角等于120︒,即为cos150a b a b ⋅=︒,cos120b c b c ⋅=︒,因此把0a b c ++=分别变发为a b c +=-,和b c a +=-,平方后可达到要求.试题解析:由0a b c ++=得:22222222a b c a b a b cb c a b c b c a ⎧⎧+=-++⋅=⎪⎪⇒⎨⎨+=-++⋅=⎪⎪⎩⎩, 2222||||2||||cos1504||422||cos120||a b a b b b a ︒︒⎧++=⎪∴⎨++⋅⋅=⎪⎩, 解之,得:||23a =,||4b =.(注:本题可先判断a c ⊥,或利用平行四边形法则或三角形法则来做)【考点】向量的数量积.18.设n S 是等比数列{}n a 的前n 项和,3S ,9S ,6S 成等差数列. (1)设此等比数列的公比为q ,求3q 的值;(2)问:数列中是否存在不同的三项m a ,n a ,p a 成等差数列?若存在,求出m ,n ,p 满足的条件;若不存在,请说明理由. 【答案】(1)312q =-;(2)存在不同的三项1a ,7a ,4a 成等差数列. 【解析】试题分析:(1)本题要求3q 值,已知是9362S S S ∴=+,我们借助n S 的最基本形态12n n S a a a =+++,有19123162()()()a a a a a a a ++=+++++,化简即得7894562()()0a a a a a a +++++=,而3789456()0a a a q a a a ++=++≠,由此可得3q ;(2)数列中的探索性命题,如果是肯定性结论,本题只要能找到三项,成等差数列即可,如果是否定性结论,则必须证明.具体找三项时,可写出数列{}n a 中连续一些项,从中观察寻找. 试题解析:(1)3S ,9S ,6S 成等差数列,9362S S S ∴=+,∴9693()()0S S S S -+-=,即789789456()()()0a a a a a a a a a ++++++++=,34564562()()0q a a a a a a ∴+++++=, 24564(1)0a a a a q q ++=++≠,312q ∴=-;(2)存在不同的三项1a ,7a ,4a 成等差数列. 671114a a q a ==,341112a a q a ==-,7142a a a ∴=+;一般地,当6n m =+,且3p m =+时,有m a ,n a ,p a 成等差数列.(注:若利用等比数列求和公式,则必须讨论公比q 是否等于1,不讨论者扣3分) 【考点】等比数列与等差数列的性质.19.已知各项均为正数的数列{}n a 的前n 项和为n S ,满足:2*11,2,n n n S ka ta n n -+=-∈N ≥(其中,k t 为常数). (1)若12k =,14t =,数列{}n a 是等差数列,求1a 的值; (2)若数列{}n a 是等比数列,求证:k t <.【答案】(1)11a =+;(2)证明见解析.【解析】试题分析:(1)已知条件是2111124n n n S a a -+=-,这种问题一般都是再写一次即21111124n n n S a a +++=-,两式相减变形后可得12n n a a +-=,注意这里有2n ≥,但由于数列{}n a 是等差数列,因此也有212a a -=,代入已知212211124a a a +=-可求得1a ;(2)与(1)相同方法得2211(2)n n n n n a ka ka ta ta n +++-=-≥,由数列{}n a 是等比数列,可设1n n a qa +=,代入化简得2(1)1(2)n t q a kq k n ∴-=-+≥,下面对此式分析,首先0q >,1q ≠,{}n a 不是常数列,这样此式对2n ≥恒成立,必有0t =,恒等式变为10kq k -+=,不能得出什么有用结论,回到已知条件,已知变为11n n S ka -∴+=-,此式中,10,0n n a S ->>,那么只能有0k <,命题得证. 试题解析:(1)由题意知,21111(*)24n n n S a a -+=-,21111124n n n S a a ++∴+=-, 两式相减,得:22111111(2)2244n n n n n a a a a a n +++-=-≥, 整理,得:11()(2)0(2)n n n n a a a a n +++--=≥, 0n a >,12(2)n n a a n +∴-=≥,数列{}n a 是等差数列,212a a ∴-=,由(*)得:212211124a a a +=-,11a ∴=10a >,11a =+;(2)由211n n n S ka ta -+=-得2111n n n S ka ta +++=-,两式相减,得:2211(2)n n n n n a ka ka ta ta n +++-=-≥,设等比数列{}n a 的公比为q ,∴222n n n n n a kqa ka tq a ta +-=-,2(1)1(2)n t q a kq k n ∴-=-+≥,由已知,可知0q >,∴1q ≠,{}n a 不是常数列,0t ∴=;11n n S ka -∴+=-,而0n a >且10n S ->,0k ∴<,k t ∴<.【考点】等差数列与等比数列的定义.20.已知函数()=e x f x (其中e 是自然对数的底数),2()1g x x ax =++,a ∈R .(1)记函数()()()F x f x g x =⋅,当0a >时,求()F x 的单调区间;(2)若对于任意的1x ,2[0,2]x ∈,12x x ≠,均有1212|()()||()()|f x f x g x g x ->-成立,求实数a 的取值范围. 【答案】(1)单调增区间为:(,1)a -∞--,(1,)-+∞,减区间为(1,1)a ---;(2)[1,22ln 2]--.【解析】试题分析:(1)求单调区间的方法是求出'()0F x =的解1,1a ---,确定'()0F x >(或'()0F x <)的取值区间,即函数的单调区间,此可用列表方法得出(同时可得出极值);(2)本小题不等式1212|()()||()()|f x f x g x g x ->-或有绝对值符号,有两个参数12,x x ,由于函数()f x 是增函数,因此设1202x x ≤<≤,则有12()()f x f x <,原问题等价于121221()()()()()()f x f x g x g x f x f x -<-<-恒成立,分两个问题,1212()()()()f x f x g x g x -<-恒成立和1221()()()()g x g x f x f x -<-恒成立,前面转化为1122()()()()f x g x f x g x -<-,可以考虑函数()()f x g x -在[0,2]上是单调递增的,后面一个转化为1122()()()()f x g x f x g x +<+,可以考虑函数()()f x g x +在[0,2]上是单调递增的.试题解析:(1)2()()()e (1)x F x f x g x x ax =⋅=++,()e (1)(+1)0x F x x x a '∴=++= , 得1x =-或1x a =--,()F x ∴的单调增区间为:(,1)a -∞--,(1,)-+∞,减区间为(1,1)a ---; (2)设12x x <,()e x f x =是单调增函数,12()()f x f x ∴<,2112121221()()|()()|()()()()()()f x f x g x g x f x f x g x g x f x f x ∴->-⇒-<-<-;①由1212()()()()f x f x g x g x -<-得:1122()()()()f x g x f x g x -<-, 即函数2()()e 1x y f x g x x ax =-=---在[0,2]上单调递增,()()e 20x y f x g x x a '''∴=-=--≥在[0,2]上恒成立, e 2x a x ∴-≤在[0,2]上恒成立;令()e 2x h x x =-,()e 20ln 2x h x x '∴=-=⇒=,∴[0,ln 2)x ∈时,()0h x '<;(ln 2,2]x ∈时,()0h x '>;ln 2min ()(ln 2)e 2ln 222ln 2h x h ∴==-=-, 22ln2a ∴-≤;②由1221()()()()g x g x f x f x -<-得:1122()()()()g x f x f x g x +<+, 即函数2()()e 1x y f x g x x ax =+=+++在[0,2]上单调递增,()()e 20x y f x g x x a '''∴=+=++≥在[0,2]上恒成立, e 2x a x ∴--≥在[0,2]上恒成立;函数e 2x y x =--在[0,2]上单调递减,∴当0x =时,0max e 201y =--⋅=-, 1a ∴≥-,综上所述,实数a 的取值范围为[1,22ln 2]--.【考点】导数与函数的单调性,不等式恒成立问题. 【名师点睛】1.用导数研究函数的单调性:(1)求函数f (x )单调区间的方法是,通过解不等式f ′(x )>0(或f ′(x )<0)直接得到单调递增(或递减)区间.(2)导数法证明函数f (x )在(a ,b )内的单调性的步骤: ①求f ′(x ).②确认f ′(x )在(a ,b )内的符号.③得出结论:f ′(x )>0时为增函数;f ′(x )<0时为减函数.2.不等式恒成立问题,一般通过转化与化归思想,转化为用导数求函数的最值,研究函数的单调性,这类问题比较复杂,考查学生的分析问题解决问题的能力,考查计算推理能力.。
