公式函数课堂实验二

wps表格2019使用公式与函数的实验报告

wps表格2019使用公式与函数的实验报告XX大学实验报告课程名称计算机导论项目名称电子表格处理学院专业指导教师报告人学号实验时间提交时间一、实验目的与要求1．掌握Excel的基本操作;2．掌握相对地址、绝对地址、混合地址以及公式和函数应用;3．掌握数据清单(排序、筛选、分类汇总和数据透视表)技术;4.．熟悉个人理财管理或贷款购房方案的设计与制作;5．学会自己提出问题，并得出解决问题的方法。

二、实验内容与方法1.了解并掌握关于Excel的基本操作，先学习大学计算机基础教程实验指导，再通过上机操作熟悉Excel的使用细节，最后掌握Excel的基本操作。

2．了解并掌握Excel中的相对地址、绝对地址、混合地址以及公式和函数应用，先学习大学计算机基础教程实验指导，再通过上机操作熟悉使用细节。

3.了解并掌握Excel中的数据清单(排序、筛选、分类汇总和数据透视表)技术，学习大学计算机基础教程实验指导，再通过上机操作熟悉使用细节。

4．进行个人理财管理或贷款购房方案的设计与制作，先学习大学计算机基础教程实验指导，再通过咨询老师或查阅图书馆有关书籍了解清楚设计制作的步骤，最后上机制作。

三、实验步骤与过程l。

Excel的基本操作1. Excel的启动及其窗口启动方式:执行“开始”菜单的“所有程序”→“Microsoft office”→"Microsoft office Excel2003”命令，或双击桌面上的Excel快捷图标。

Excel工作窗口组成:Excel的工作窗口由标题栏、工具栏、编辑栏、工作区、任务窗口、标签栏以及状态栏组成。

四、实验分析与体会通过这次实验我发现要熟练地运用好Excel这个软件，必须多多练习，在掌握好课本上的基本理论的基础上，多多上机实践，这样才能更好地运用它,同时在函数的输入过程中要注意绝对地址、相对地址和混合地址的不同应用场合。

这样会减少很多不必要的重复输入。

函数与公式实训报告1

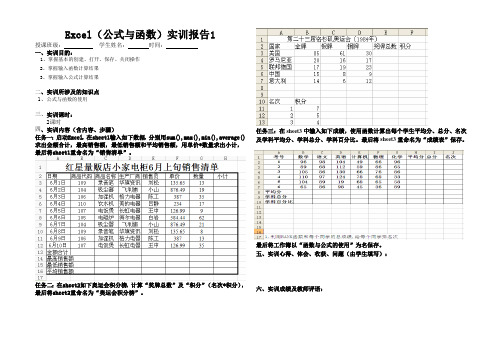
Excel（公式与函数）实训报告1
授课班级：学生姓名：时间：
一、实训目的：
1、掌握基本的创建、打开、保存、关闭操作
2、掌握输入函数计算结果
3、掌握输入公式计算结果
二、实训所涉及的知识点
1、公式与函数的使用
三、实训课时：
2课时
四、实训内容（含内容、步骤）
任务一：启动Excel，在sheet1输入如下数据，分别用
sum(),max(),min(),average()求出金额合计，最高销售额，最低销售额和平均销售额，用单价*数量求出小计，最后将sheet1
重命名为“销售清单”。

任务二：在sheet2如下奥运会积分榜，计算“奖牌总数”及“积分”（名次*积分），最后将sheet2重命名为“奥运会积分榜”。

任务三：在sheet3中输入如下成绩，使用函数计算出每个学生平均分、总分、名次及学科平均分、学科总分、学科百分比。

最后将sheet3重命名为“成绩表”保存。

最后将工作簿以“函数与公式的使用”为名保存。

五、实训心得、体会、收获、问题（由学生填写）：
六、实训成绩及教师评语：。

实验二函数逼近与曲线拟合

《数值分析》课程设计实验报告实验二函数逼近与曲线拟合一、问题提出从随机的数据中找出其规律性，给出其近似表达式的问题，在生产实践和科学实验中大量存在，通常利用数据的最小二乘法求得拟合曲线。

在某冶炼过程中，根据统计数据的含碳量与时间关系，试求含碳量与时间t 的拟合曲线。

二、实验步骤先写出线性最小二乘法的M文件function c=lspoly(x,y,m)% x是数据点的横坐标组成的向量，y是纵坐标组成的向量% m是要构成的多项式的次数，c是多项式由高到低次的系数所组成的向量n=length(x);b=zeros(1:m+1);f=zeros(n,m+1);for k=1:m+1f(:,k)=x.^(k-1);enda=f'*f;b=f'*y';c=a\b;c=flipud(c);方法一：近似解析表达式为：y（t）=a1t+a2t2+a3t3第二步在命令窗口输入：lspoly([0,5,10,15,20,25,30,35,40,45,50,55],[0,1.27,2.16,2.86,3.44 ,3.87,4.15,4.37,4.51,4.58,4.02,4.64],2)回车得到：ans =0.0000-0.00520.26340.0178即所求的拟合曲线为y=-0.0052t2+0.2634t+0.0178在编辑窗口输入如下命令：>>x=[0,5,10,15,20,25,30,35,40,45,50,55];y=[0,1.27,2.16,2.86,3.44, 3.87,4.15,4.37,4.51,4.58,4.02,4.64];>> t=0:0.1:55;>> z=-0.0052*t.^2+0.2634*t+0.0178;>> plot(x,y,'ro',t,z);grid命令执行得到如下图（图2-1）0102030405060拟合多项式与数据点的关系方法二：假设近似表达式为：y（t）=c0+c1t+c2t2第一步在命令窗口输入：>>lspoly([0,5,10,15,20,25,30,35,40,45,50,55],[0,1.27,2.16,2.86,3. 44,3.87,4.15,4.37,4.51,4.58,4.02,4.64],2)回车得到：ans =-0.00240.20370.2305即所求的拟合曲线为y=-0.0024t2+0.2037t+0.2305在编辑窗口输入如下命令：>>x=[0,5,10,15,20,25,30,35,40,45,50,55];y=[0,1.27,2.16,2.86,3.44,3.87,4.15,4.37,4.51,4.58,4.02,4.64];>> t=0:0.1:55;>> z=-0.0024*t.^2+0.2037*t+0.2305;>> plot(x,y,'ro',t,z);grid命令执行得到如下图（图2-2）拟合多项式与数据点的关系三、实验结论在利用数据的最小二乘法求拟合曲线时，选取合适的近似表达式很重要，应通过不断的试验找出较为合适的近似表达式，这样才能尽可能的提高拟合精度。

实验二-顺序结构程序设计

实验二顺序结构程序设计2.1实验要求与目的1．掌握程序设计的基本思想2．熟悉及掌握C语言基本数据类型（int，long，float，double）的说明3．掌握C语言程序设计中格式输入和输出函数的灵活应用4．算术表达式在实际问题中应用5．掌握算法：两数的交换、一个整数的拆数6．数学头文件的包含7．格式输入/输出函数scanf/printf的正确使用2.2 实验指导程序设计的学习过程也是算法积累的过程。

算法是在有限步内求解某一问题所使用的基本运算及规定的运算顺序所构成的完整的解题步骤。

也就是说是计算机解题的过程。

程序设计的基本思想：1）分析问题，理解题意、提出问题；2）建立模型，确立算法，寻找解决问题的有效算法或直接公式；4）编写程序，根据C语言程序结构编程；5）调试程序，若结果正确，结束。

否则检查程序，修改程序，重新调试程序，依次类推，直到调试结果正确为止。

初次自已动手编程，先要建立程序设计的基本思想，结构化程序设计的基本思想就是模块化。

即构成C语言程序的基本单位是函数，函数也是C程序中模块化程序程序设计的基础。

我们将程序设计比拟成“搭积木”，每个模块或每个算法都看成是一个形状及功能不同的“积木”，然后根据设计要求取材，搭建成完美的成品。

C语言是有且仅有一个主函数和若干个子函数组成。

从一个简单的程序设计开始学习，即先学习主函数（main）模块框架。

主函数（main）模块的基本框架设计。

#include <stdio.h>int main(){ 所有数据的数据类型定义说明;数据输入;算法或公式;数据输出;}首次编程，先来熟记2个编程时常用提示信息。

1）每条语句之后必须有分号“；”。

若程序语句的某一条漏写了分号，在编译时会报如下的错误：error C2146: syntax error : missing ';' before identifier 'scanf'含义： C2146错误:语法错误: 标识符 “scanf” 之前缺少“;”。

函数(二)实验报告

函数(二)实验报告
《函数(二)实验报告》
实验目的：通过本次实验，掌握函数的概念、性质和应用，加深对函数的理解，提高数学分析和解决问题的能力。

实验内容：
1. 函数的概念和性质：通过观察和分析不同函数的图像，探讨函数的定义域、
值域、单调性、奇偶性等性质。

2. 函数的应用：结合实际问题，利用函数的概念和性质进行建模和求解，探讨
函数在生活中的应用。

实验步骤：
1. 确定实验的函数范围和内容，选择适当的函数进行实验。

2. 绘制函数的图像，观察函数的变化规律，分析函数的性质。

3. 结合实际问题，利用函数建立数学模型，并求解相关问题。

实验结果：
1. 通过实验，我们深入理解了函数的定义和性质，掌握了函数的图像和变化规律。

2. 在实际问题中，我们成功利用函数的概念和性质建立了数学模型，并求解了
相关问题，验证了函数在生活中的应用价值。

实验结论：
通过本次实验，我们加深了对函数的理解，提高了数学分析和解决问题的能力。

函数是数学中的重要概念，具有广泛的应用价值，我们将继续深入学习和探索
函数的相关知识，不断提高自己的数学素养和解决问题的能力。

实验总结：
本次实验不仅加深了对函数的理解，还提高了我们的数学分析和解决问题的能力。

在今后的学习和工作中，我们将继续加强对函数的学习和应用，不断提升自己的数学素养和解决问题的能力。

三角函数的诱导公式2

三角函数的诱导公式（二）
SAN JIAO HAN SHU DE YOU DAO GONG SHI
三角函数的诱导公式
市实验一中高一数学组
三角函数的诱导公式（二）
忆一忆
公式一：
SAN JIAO HAN SHU DE YOU DAO GONG SHI
你还记得他们吗？
公式二：
sin( 2k ) sin
2
y

的终边
2
y=x
α 的终边
O
x
市实验一中高一数学组
三角函数的诱导公式（二）
y SAN JIAO HAN SHU DE YOU DAO GONG SHI 1P′(y,x)

-1

0 -1
P(x,y) 1 x
诱导公式（五）
sin(

2
) x cos
cos( ) y sin 2三角函数的诱导公式（二）
请你动手试一试？
SAN JIAO HAN SHU DE YOU DAO GONG SHI
请根据相关诱导公式推导:
3 3 3 3 sin( ) , cos( ) , sin( ) , cos( ) 2 2 2 2
分别等于什么？请你看看书：P26例3的答案，你做对了吗？
sin( ) sin cos( ) cos tan( ) tan
市实验一中高一数学组
函数名不变，符号看象限
三角函数的诱导公式（二）
探究
SAN JIAO HAN SHU DE YOU DAO GONG SHI
的终边与的终边什么关系 ?
sin( ) sin cos( 2k ) cos (k Z ) cos( ) cos tan( ) tan tan( 2k ) tan

大学IT课程Excel函数实验二

大学IT课程Excel函数实验一、实验要求打开“学生奖学金信息表.xlsx”，“学生基本信息”工作表内容如图1所示，“学院信息”工作表内容如图2所示。

图1 “学生基本信息”工作表内容图2“学院信息”工作表内容在上述数据的基础上，实现结果如图3所示。

图3 实现结果说明：1.学号的前四位表示年级，第5、6位表示学院代号，如：200601130007，2006表示年级，01表示文学院；身价证号的第17位表示性别，若为奇数表示“男”，若为偶数表示“女”，第7、8、9、10位表示出身年份。

2.奖学金等级分为两类：一等和二等，论文等级也分为两类：优秀和良好。

发放标准如下：奖学金等级为一等且论文为优秀的，奖学金额5000元，奖学金等级为一等且论文为良好的，奖学金额4000元，其他的为3000元。

二、实验操作过程1.为表格增加标题1)在行号为1的行号上右击，在快捷菜单中选择“插入”，插入一个空行，然后在A1单元格中输入“虚拟学校学生奖学金发放表”。

2）选中单元格区域A1：J1，单击“开始”选项卡中“对齐方式”组中的按钮，合并单元格区域A1：J1，并使标题居中显示。

3）在行号为1的行号上右击，在快捷菜单中选择“行高”，在出现的对话框中输入行高20，如图4所示。

图4设置行高更改标题字号为18并加粗显示，设置后的标题效果如图4-15所示。

2.填充“性别”列在D3单元格中输入公式：=IF(MOD(MID(C3,17,1),2)=0,"女","男")并回车，计算出当前单元格的性别，然后拖动填充柄至单元格D33，或双击填充柄，计算出所有人的性别。

3. 填充“学院”列在E3单元格中输入公式：=VLOOKUP(MID(A3,5,2),学院信息!$A$2:$B$16,2)，计算出当前单元格的学院，然后拖动填充柄至单元格E33，或双击填充柄，计算出所有人的学院信息。

4. 填充“年龄”列在F3单元格中输入公式：=YEAR(NOW())-(MID(C3,7,4))，计算出当前单元格的年龄，然后拖动填充柄至单元格F33，或双击填充柄，计算出所有人的年龄信息。

实验九Excel公式和函数的使用

姓名实验报告成绩评语：评分项目评分内容分值评分结果预习情况是否完成预习工作。

要求按实验指导书进行预习、并完成实验报告初稿、编写程序。

20实验方案实验方案是否可行。

要求目的、任务明确、原理清楚、步骤可操作、对实验过程数据有记录方案、对可能的错误有预备方案。

30实验过程与结果实验结果是否正确。

要求完成实验过程中的数据记录、记录要完整和准确、内容要详细，实验结果要与预期的正确结果一致。

35实验结论实验结论是否正确。

要求根据实验原理对实验过程中的数据、实验结果进行分析，得出实验结论。

15总分100指导教师（签名）年月日说明：指导教师评分后，实验报告交院（系）办公室保存。

实验九Excel公式和函数的使用一、实验目的1．掌握Excel公式的应用。

2．掌握Exc1e常用函数的应用。

3．掌握三大地址的区别与应用。

二、实验设备和软件（实验条件）1、硬件设备：Pentium Ⅳ以上微型计算机。

2、软件：Windows XP、Excel 2003或以上版本。

三、实验内容任务1：算术公式和逻辑函数的使用任务2：常用函数的使用任务3：三大地址的使用任务4：计算周岁任务5：混合地址计算任务6：计算九九乘法表任务7：学生成绩表绩点的计算和奖学金等级的判定四、实验方案和步骤任务一：①计算补贴。

②计算年龄。

③计算应发工资。

④计算所得税。

⑤计算实发工资。

任务二：①将Sheet4工作表改名为“公式与函数”。

②用函数统计出“工资表”工作表中职工的平均年龄、所得税总额和最高实发工资。

③实现函数运算。

④用日期公式填入有规律变化的日期数据。

⑤输入电话号码升位表。

任务三：①工作表重命名。

②混合地址计算。

任务四：①计算周岁。

任务五：①计算税后本息合计。

任务六：①计算九九乘法表。

②任务七：③计算总评成绩。

④计算各学生的课程“绩点”。

⑤计算各学生的“平均绩点”，并判断其应获得的“奖学金等级”。

五、实验过程与结果任务一：实验过程：①在H3单元格中输入公式：=IF(G3>2000,G3*12%,IF(G3>1500,G3*8%,95))。

Office高级应用实验指导 (实验二)

实验2 计算机等级考试报名表的设计与制作一、实验目的通过对计算机等级考试报名表的设计与制作，掌握Excel2010中常用的函数方法，利用函数能对表格数据进行简单推理和计算。

掌握数据查询表的制作和Excel中图表的使用和美化。

二、实验环境硬件：Pentium以上的计算机。

软件：Windows XP操作系统、Microsoft Office Excel2010软件。

三、实验指导请按照教程 2.4项目3教师档案管理表的设计与制作操作步骤上机进行验证，掌握操作方法。

四、实验内容按照下列给出的实验任务和要求完成任务，并在实验报告中写出主要操作步骤。

制作一张如图2-88所示的“计算机等级考试报名表”，要求如下：图2-88 计算等级考试报名表（1）给“准考证号”，“姓名”，“学号”，“身份证号码”等列输入10条记录内容。

（注意身份证号输入18位，其中7-14位出生日期，17位性别；准考证号9位，其中7-8位为所报考语种，11----一级OFFICE ，21---C语言，22---VFP语言，23---VB语言，24----JA V A语言，25---AOA。

（2）工作表美化，设置字体，颜色，边框，填充，列宽等。

（3）根据输入的身份证号码，利用公式计算出“性别”和“年龄”。

（4）根据准考证号，计算报考语种。

7、8位（5）“所属分院”数据使用有效性序列功能，分院为“工学院，文学院，理学院，医学院，教育学院”其中之一。

（6）分类汇总报考不同语种的男女考生人数。

（结果放sheet2---汇总）17位（7）制作考生信息查询表，通过输入准考证号码查看考生的相关信息。

(结果放sheet3----查询表)附录1丽水学院计算机实验报告附页：(共页，第页)丽水学院计算机实验报告一、实验目的通过对计算机等级考试报名表的设计与制作，掌握Excel2010中常用的函数方法，利用函数能对表格数据进行简单推理和计算。

掌握数据查询表的制作和Excel中图表的使用和美化。

Excel常用函数与公式应用实验报告

三．实验内容：《大学计算机应用基础实验指导与习题集》第7章实验2
四．实验设备与软件环境：
1、硬件： CPU:AMD Athlon（速龙） II P360 (双核)
主板:戴尔 0P89N9 (AMD RS880 + SB810/SB850)
内存:2 GBytes
显卡:ATI Mobility RADEON HD 5430/5450 [戴尔]
6．选择“N4”单元格，单击“公式”选项卡”函数库“组中的”插入函数“按钮，打开”插入函数“对话框，在”选择函数“中选定”IF“，单击”确定“按钮，打开”IF函数参数”对话框,在“Logical_test”文本框中输入”M4>=90”,在Value_if_true”文本框中输入“优秀”，单击“Value_if_false”文本框，再单击编辑栏最左边函数列表右侧的下拉箭头按钮，选定”IF“，打开第二层”IF函数参数“对话框，在”Logical_test”文本框中输入“M4>=60”,在”Value_if_true”文本框中输入“通过”，单击“Value_if_false”文本框，输入”未过“。单击”确定“完成。单击”N4“单元格，拖动填充柄至”N13“单元格。
2．选取“B4：D13”单元格区域。单击“数据”选项卡“数据工具”组的“数据有效性”按钮，打开“数据有效性”对话框，选“设置”选项卡。点击”允许“的下拉列表，选择”整数“，在”最小值“中输入”0“，在”最大值“中输入”20“。
3．选中“B4：D3”单元格区域，单击“数据“选项卡”数据工具“组的”数据有效性“按钮，打开”数据有效性“对话框，选”输入信息“选项卡。在”标题“下的空格里输入”必做题“，在”输入信息“下的空格里输入”满分20分“。选择”出错警告“选项卡，在”标题“下的空格里输入”无效“，在”错误信息“下的空格里输入”数据错误“。选中“E4：G13”单元格区域，单击“数据“选项卡”数据工具“组的”数据有效性“按钮，打开”数据有效性“对话框，选”设置“选项卡。点击“允许”右下方的下拉列表选择“整数”，“最小值“内输入”0“，”最大值“内输入”20“。选”输入信息“选项卡，在“标题”下的空格里输入“选做题”，在“输入信息”内输入“满分20分”。选“出错警告“选项卡，

2实验二!常用内置函数和math模块

实验二常用内置函数和math模块一、实验内容1.查看内置函数信息的函数；2.数值运算函数；3.数字类型转换函数；4.input()函数；5.eval()函数；6.print()函数；7.模块及其引用；8.math模块及其使用。

二、实验要求1.了解查看内置函数信息的函数；2.掌握数值运算函数；3.掌握数字类型转换函数；4.掌握input()函数；5.掌握eval()函数；6.掌握print()函数；7.掌握模块及其引用；8.掌握math模块及其使用。

三、实验过程1.查看内置函数信息>>> dir() #查看当前范围内的变量、方法和定义的类型列表>>> import sys>>> dir(sys) #查看sys模块的属性和方法>>> dir([]) #查看列表的方法2.数值运算函数>>> divmod(10,3) #输出商和余数(3, 1)>>> a,b=divmod(10,3) #求出商和余数，分别赋值给变量a和b>>> a3>>> b1>>> c=divmod(10,3) #求出商和余数，将商和余数放在元组c中>>> c[0],c[1](3, 1)>>> pow(4,3) #求幂函数，相当于4**364>>> round(3.1415) #只有一个参数，表示对这个参数四舍五入取整3>>> round(3.1415,3) #对第一个参数四舍五入保留3位小数3.142>>> max(1,4,6,2,9) #求最大值9>>> min(1,4,6,2,9) #求最小值13.数值类型转化函数>>> int(4.9) #将浮点型转换成整型4>>> type("10") #测试类型<class 'str'>>>> a=int("10") #将字符型转换成整型，赋值给变量a>>> type(a) #测试a的类型<class 'int'>>>> float(4) #将整数转换成浮点数4.0>>> float("4") #将字符串转换成浮点数4.0>>> complex(2,3) #生成一个复数(2+3j)4.input()函数：数据输入函数，输入的任何数据都是字符型的>>> x=input("请输入一个数据：")请输入一个数据：123>>> type(x)<class 'str'>>>> x=input("请输入一个数据：")请输入一个数据：abc>>> type(x)<class 'str'>5.eval()函数：将字符型转换成数值型，根据情况可能是整型，也可能是浮点型>>> a=15>>> eval("a+2") #将a+2转化成数值型并计算17>>> eval("pow(3,2)")9>>> eval("1.2+2.2")3.46.print()函数>>> s="hello" #将字符串赋值给变量s>>> s'hello'>>> print(s)hello>>> lb=[1,3,'a'] #将列表赋值给变量lb>>> print(lb)[1, 3, 'a']>>> t=(1,2,'a') #将元组赋值给变量t>>> print(t)(1, 2, 'a')>>> d={'a':1,'b':2} #将字典赋值给变量d>>> print(d){'a': 1, 'b': 2}>>> print(123,end='');print(456) # end=''表示不换行123456>>> print("我的名字是%s,年龄是%d"%("张三",20))我的名字是张三,年龄是20>>> x,y,z=1,2,3>>> print("%d%d%d"%(x,y,z))123>>> x,y,z=1.1,2.5,3.7>>> print("%5.2f%5.3f%6.7f"%(x,y,z))1.102.5003.7000000>>> x,y,z=1,2,3>>> print("%d%d%d"%(x,y,z))123>>> x,y,z=1.1,2.5,3.7>>> print("%5.2f%5.3f%6.7f"%(x,y,z))1.102.5003.70000007.已知x=1,y=3,计算并输出y/(2x)、2x/y、1/(x+y)8.编程实现对任意输入的一个三位自然数，计算并输出其各位上数字及其各位上数字的平方和。

计算方法实验二

《计算方法》实验报告实验二插值法二级学院：计算机学院专业：计算机科学与技术指导教师：爨莹班级学号：姓名：实验二插值法1、实验目的：1、掌握直接利用拉格郎日插值多项式计算函数在已知点的函数值；观察拉格郎日插值的龙格现象。

2、了解Hermite插值法、三次样条插值法原理，结合计算公式，确定函数值。

2、实验要求:1、认真分析题目的条件和要求，复习相关的理论知识，选择适当的解决方案和算法；2、编写上机实验程序，作好上机前的准备工作；3、上机调试程序，并试算各种方案，记录计算的结果（包括必要的中间结果）；4、分析和解释计算结果；5、按照要求书写实验报告；3、实验内容：1、用拉格郎日插值公式确定函数值；对函数f(x)进行拉格郎日插值，并对f(x)与插值多项式的曲线作比较。

2、已知函数表：（0.56160,0.82741）、（0.56280,0.82659）、（0.56401,0.82577）、（0.56521,0.82495）用三次拉格朗日插值多项式求x=0.5635时函数近似值。

3、P129,(12)4、题目：插值法5、原理：拉格朗日插值法是以法国十八世纪数学家约瑟夫·路易斯·拉格朗日命名的一种多项式插值方法。

许多实际问题中都用函数来表示某种内在联系或规律，而不少函数都只能通过实验和观测来了解。

如对实践中的某个物理量进行观测，在若干个不同的地方得到相应的观测值，拉格朗日插值法可以找到一个多项式，其恰好在各个观测的点取到观测到的值。

这样的多项式称为拉格朗日（插值）多项式。

数学上来说，拉格朗日插值法可以给出一个恰好穿过二维平面上若干个已知点的多项式函数。

6、设计思想：通过拉格朗日插值法找到拉格朗日多项式，计算某个x对应的y值。

7、对应程序：//Lagrange.cpp#include <stdio.h>#include <conio.h>#define N 4int checkvalid(double x[], int n);void printLag (double x[], double y[], double varx, int n);double Lagrange(double x[], double y[], double varx, int n);void main (){double x[N+1] = {0.56160, 0.56280, 0.56401, 0.56521};double y[N+1] = {0.82741, 0.82659, 0.82577, 0.82459};double varx = 0.5635;if (checkvalid(x, N) == 1){printf("\n\n插值结果: P(%f)=%f\n", varx, Lagrange(x, y, varx, N));}else{printf("结点必须互异");}getch();}int checkvalid (double x[], int n){int i,j;for (i = 0; i < n; i++){for (j = i + 1; j < n+1; j++){if (x[i] == x[j])//若出现两个相同的结点，返回-1{return -1;}}}return 1;}double Lagrange (double x[], double y[], double varx, int n){double fenmu;double fenzi;double result = 0;int i,j;printf("Ln(x) =\n");for (i = 0; i < n+1; i++){fenmu = 1;for (j = 0; j < n+1; j++){if (i != j){fenmu = fenmu * (x[i] - x[j]);}}printf("\t%f", y[i] / fenmu);fenzi = 1;for (j = 0; j < n+1; j++){if (i != j){printf("*(x-%f)", x[j]);fenzi = fenzi * (varx - x[j]);}}if (i != n){printf("+\n");}result += y[i] / fenmu * fenzi;}return result;}8、实验结果：9、实验体会：拉格朗日插值法能很好的解决生产和科研中的一些问题，计算机编程的实现有利于其更好的应用。

实验二斐波那契数列

功能：用 n 阶多项式拟合数据列(x,y)，使得在数据点处误差的平方和最小。说明：参数 x 和 y 都是数组，里面是数据列的横坐标和纵坐标；参数 n 是指定多项式的阶，在实验中参数 n 通过对数据列的分析而得到。例 1 对函数 y ln(1 x) 做 3 阶多项式拟合代码：x2 = 0:0.1:1; y2 = log(1+x2); p2 = polyfit(x2,y2,3) 运行结果：p2 = 0.1079 -0.3974 0.9825 0.0004。
Fn 2 Fn 1 Fn
有了这个递推公式，使用数学方法就能够得到这个数列的通项公式如下：
Fn {[(1 5) 2]n [(1 5) 2]n } 5
这个公式是法国数学家比内(Binet)早在 1843 年发现的，称为比内公式。有了这个公式后，第 n 个月后兔子的对数，就是计算 Fn 。
将这个文件保存为 fib3.m。在这个函数里，y 是因变量，用于将拟合结果传到函数外。
（1）选择 n=30，调用上述函数做拟合：代码：p1= fib3(30) 运行结果：p1 = 0.4799 -0.7768。
结论：取前 30 项做拟合，得到： log( Fn ) 0.7768+0.4799n （2）选择 n=50，调用上述函数做拟合：代码：p2= fib3(50) 运行结果：p2 = 0.4807 -0.7881。
图 2-1-9
n=30
图 2-1-10
n=50
（3）选择 n=500，调用上述函数画图：代码：fib2(500); legend('n = 500'); 运行结果：图 2-1-11。（4）选择 n=1000，调用上述函数画图：代码：fib2(1000); legend('n = 1000'); 运行结果：图 2-1-12。

Excel实验二

EXCEL实验二【实验目的】应用EXCEL的工作表函数进行计算。

【实验内容与步骤】打开“Y：”盘，将“Excel实验二”文件夹复制到“Z：”盘。

⒈数学函数打开“Z：\Excel实验二\FCT-EX.xlsx”，然后完成下列有关函数的操作。

将工作表sheet1命名为“数学”，然后在其中进行下列操作：①在A11单元中计算出区域A1:A10中的所有数值之和；②在区域C1：C10中用RANDBETWEEN函数产生10个介于10至99之间的随机整数；③保存文件。

⒉文本函数将工作表Sheet2命名为“文字”，然后在其中进行下列操作：在区域A1：A4中分别输入下面的数据：A1单元格：电子表格EXCEL2010A2单元格：=LEFT(A1,4)A3单元格：=MID(A1,5,5)A4单元格：=RIGHT(A1,4)⒊逻辑函数将工作表Sheet3命名为“逻辑”，然后在其中进入下列操作：①在B1中输入公式，当其左边单元格A1中的值大于等于60时，取值为“PASS”，否则取值为“FAIL”，把B1单元格的公式复制到B2~B10；（if函数）②在C1中输入公式，当其左边A1单元格中的值大于等于90、大于等于60小于90，小于60这三种情况分别取值为“优秀”、“及格”和“不及格”，把C1单元格的公式复制到C2~C10；（if函数）③在E1中输入公式，如果A1和D1两个单元格的分数都小于60，就显示“两门补考”，如果其中一个小于60，就显示“一门补考”，其他的显示“通过”，并把公式复制到E2：E10单元格中；④保存文件。

最后结果如下图所示：⒋统计函数在工作表“逻辑”之后插入一张工作表，并将其重命名为“统计”，然后在其中进行下列操作：①在区域A1：A6中依次输入NO、71、96、62、89、83；②在B1中计算区域A1：A6内数值的个数；（count函数）③在B2中计算区域A1：A6内大于80的数值的个数；（countif函数）④在B3中计算区域A2：A6内所有数的平均值；（average函数）⑤在B4中计算区域A2：A6内所有数的最大值；（max函数）⑥在B5中计算区域A2：A6内所有数的最小值；（min函数）⑦保存并关闭文件。

MATLAB实验二

h=
1 所以其解为 x=0.1342，y=0.9972，z=-0.0985，这三个方程的误差为 0.7690 10 8 ,
-0.0418 10 8 和-0.1054 10 8 ，且 h=1>0，这说明结果是可靠的
改进程序或思考：此题也可以用更便捷的 inline 函数或匿名函数方式求解
>> [x, f, h]=fsolve(fun,[0,0,0]) Optimization terminated: first-order optimality is less than options.TolFun.
x=
0.1342 0.9972 -0.0985
f=
1.0e-008 *
0.7690 -0.0418 -0.1054
程序（或命令）： % M 函数 eg4_4fun.m function f=fun(x) f(1)=9*x(1)^2+36*x(2)^2+4*x(3)^2-36; f(2)=x(1)^2-2*x(2)^2-20*x(3); f(3)=16*x(1)-x(1)^3-2*x(2)^2-16*x(3)^2;
>> [x ,f, h]=fsolve(@eg4_4fun ,[0,0,0]) Optimization terminated: first-order optimality is less than options. TolFun. x=
0.1342 0.9972 -0.0985
f=
1.0e-008 *
>> [x,f,h]=fsolve(@fun ,[0,0,0])得 Optimization terminated: first-order optimality is less than options.TolFun.

计算个数的函数公式

计算个数的函数公式计数函数也叫计算器，是一种统计分析的应用工具，用来指示和计算定量变量的取值。

计数函数是一种数学上运算结构，是由一个计算变量和一组参数组成的多项式，它可以基于一定的规律把定长变量转换成另一个定长变量，这样变量就可以从输入得到输出。

计数函数有很多种形式，可以用来描述不同的研究实验，如统计抽样、调查问卷设计、回归分析等。

可以用来了解某一实验的相关数据，也可以用来预测将来的数据情况。

用计数函数不仅可以帮助我们更好地理解实验，还可以对不确定性事件作出更准确的把握，从而降低实验失败或出错的可能性。

二、常用计数函数公式1、二项分布概率函数：P(X=x)=Cnx * px * (1-p)n-x其中，X表示实验成功的次数，n表示实验的次数，p表示每次实验成功的概率，Cnx表示从组合中取x个元素的方案数，即Cnx=n!/(x!*(n-x)!)。

2、泊松分布概率函数：P(X=x)=λx * e-λ/x!其中，X表示实验成功的次数，λ表示平均实验成功的概率，e 表示自然常数，x!表示x的阶乘。

3、卡方分布概率函数：P(X=x)=1/(2^(n/2)*Γ(n/2))*x^((n-2)/2)*e-x/2其中，X表示实验成功的次数，Γ表示背太沃尔函数，n表示方差分析的维度。

三、使用计数函数的方法1、对于二项分布函数，首先要确定试验次数n和成功概率p，然后计算实验成功次数X的概率值P(X=x)，也可以使用计算器查询得到结果。

2、对于泊松分布函数，首先要确定每次实验成功的概率λ，然后计算实验成功次数X的概率值P(X=x)，也可以使用计算器查询得到结果。

3、对于卡方分布函数，首先要确定实验的维度n，然后计算实验成功次数X的概率值P(X=x)，也可以使用计算器查询得到结果。

四、计数函数的优点1、计算简单，可以用很少的数学知识就能对实验结果及其敏感度进行快速分析。

2、可以快速地分析多个实验结果，从而进行深入研究。

3、可以用不同的计数函数找到不同的实验模式，从而更好地了解实验内容。

实验二：定积分的近似计算

并计算相对误差 1 dx
0 1 x2
解： a=0, b=1, n=100, f (x) = 1/( 1+x2 )
==> h =1/100=0.01, xi = i*h, yi = f (xi)
==>
1 dx 0 1 x2
h
y0 2
y1
yn1
yn 2
0.78539399673078
相对误差： 0.78539399673078 / 4 5.305 10-6 /4
>> quad('1./(1+x.^2)',0,1,10e-16)
函数表达式一定要用单引号括起来！涉及的运算一定要用数组运算！
2021/4/21
22
二重积分的计算
抛物线法计算二重积分： dblquad
dblquad(f,a,b,c,d,tol)
bd
a c f (x, y)dxdy
tol 为计算精度，若不指定，则缺省精度为 10-6
1
中点法：
0
1
dx x
2
n
h
i 1
f
(
xi1 2
xi
)
0.78540024673078
2021/4/21
6
矩形法举例
误差分析
理论值：
1 dx 0 1 x2
arctan x
1 0
π 4
左点法相对误差：0.78789399673078 / 4 0.003178 /4
右点法相对误差：0.78289399673078 / 4 0.003188 /4
i 1
x
2021/4/21
8
梯形法
曲边小梯形的面积可以由直边小梯形的面积来近似

二次函数顶点坐标公式及其应用

二次函数顶点坐标公式及其应用二次函数是指形如y=ax^2+bx+c的函数，其中a、b和c都是实数，且a≠0。

它的图像是抛物线。

顶点坐标公式：二次函数的顶点坐标可以用以下公式求得：x=-b/2ay=f(x)=a(x-h)^2+k其中，(h,k)表示顶点的坐标。

通过这个公式，我们可以很方便地求得二次函数的顶点坐标。

应用一：求解最优问题二次函数的顶点坐标在数学上具有重要的意义，它可以用来求解很多最优问题。

例如，我们想要在一个矩形内部，离一条边的距离最远，那么这个问题可以转化为求解顶点坐标的问题。

我们可以通过求解二次函数的极值来找到这个最优解。

应用二：描述物体运动的轨迹二次函数也可以用来描述物体的运动轨迹。

例如，一个物体从离地面一定高度开始自由下落，那么它的运动轨迹可以用二次函数来描述。

我们可以通过求解二次函数的顶点坐标，来确定物体的最高点、落地点和运动轨迹等信息。

应用三：经济学中的边际分析在经济学中，边际分析是一种重要的工具，而二次函数的顶点坐标可以用来分析边际效应。

边际效应是指增加或减少一个单位的其中一种输入所产生的效益变化。

通过求解二次函数的顶点坐标，我们可以找到产生边际效应最大或最小的输入水平，从而指导经济决策。

应用四：求解几何问题在几何学中，二次函数的顶点坐标也有广泛的应用。

例如，在平面几何中，已知一个抛物线和一条直线，我们想要找到抛物线上离直线最近和最远的点，就可以通过求解二次函数的顶点坐标来解决这个问题。

应用五：拟合实验数据二次函数的顶点坐标还可以用来拟合实验数据。

当我们通过实验或观察得到一些数据点时，可以通过求解二次函数的顶点坐标，来得到一个最佳的二次函数模型，以便与观察数据相拟合。

总结：二次函数的顶点坐标公式是一个简单且实用的工具，它在数学和应用领域都有着广泛的应用。

它可以用来解决最优问题、描述物体运动的轨迹、经济学中的边际分析、求解几何问题以及拟合实验数据等。

通过掌握二次函数的顶点坐标公式，我们可以更好地理解和应用这个函数模型。

数学实验教案

数学实验教案一、实验目的本实验旨在通过实际操作，帮助学生加深对数学概念的理解，提高数学实践能力，并培养学生的团队合作意识。

二、实验材料1. 教学软件（如Geogebra等）2. 白板、白板笔3. 直尺、量角器、铅笔、橡皮擦4. 实验纸及相应的写作工具三、实验内容和步骤实验一：探究三角函数的正弦定理步骤一：理论讲解1. 依据教材内容，讲解三角函数的概念和公式。

2. 引入正弦定理，解释其含义和应用场景。

步骤二：实验操作1. 将学生分组，并提供纸和写作工具。

2. 使用教学软件绘制不同形状的三角形，让学生观察并记录各边与角之间的关系。

3. 让学生通过实验纸和工具，测量各边和角的大小，并记录数据。

4. 鼓励学生在团队合作中，讨论和比较数据，试图找到三角形边与角之间的关联。

步骤三：实验总结1. 让学生根据实验结果，总结并描述出三角函数的正弦定理公式。

2. 鼓励学生思考公式的应用场景，以及如何通过公式解决实际问题。

实验二：验证平行线的性质步骤一：理论讲解1. 讲解平行线的定义和性质，引入相关的数学公式和推理过程。

2. 强调平行线性质在几何证明中的重要性，并鼓励学生对该性质的应用进行思考。

步骤二：实验操作1. 将学生分组，并要求每个小组准备一张纸、直尺和量角器。

2. 让学生在纸上绘制两条相交的直线，并在交点左右各绘制一条射线。

3. 引导学生观察和记录各个角度的大小，并找出相应的数学关系。

步骤三：实验总结1. 让学生根据实验结果，总结并描述平行线性质的相关定理和公式。

2. 引导学生思考如何利用这些定理和公式解决几何问题，并进一步拓展应用。

四、实验延伸1. 鼓励学生在校内或社区环境中，寻找和探究更多数学实践的机会。

2. 建议学生通过参与数学建模竞赛等活动，提高数学应用能力和创新思维。

五、实验小结通过本次数学实验，学生通过实际操作和观察，充分体验了数学的实践性和应用性。

实验中的团队合作和讨论，培养了学生的合作精神和思维能力。