2016年中考数学 微测试系列专题19 圆的有关计算及圆的综合(含解析)北师大版
(历年中考)北京市中考数学试题 含答案

2016年北京市高级中等学校招生考试数学试卷一、选择题(本题共30分,每小题3分)第1-10题均有四个选项,符合题意的选项只.有.一个。
1. 如图所示,用量角器度量∠AOB ,可以读出∠AOB 的度数为(A ) 45° (B ) 55° (C ) 125° (D ) 135° 答案:B考点:用量角器度量角。
解析:由生活知识可知这个角小于90度,排除C 、D ,又OB 边在50与60之间,所以,度数应为55°。
2. 神舟十号飞船是我国“神舟”系列飞船之一,每小时飞行约28 000公里。
将28 000用科学计数法表示应为(A ) (B ) 28(C )(D )答案:C考点:本题考查科学记数法。
解析:科学记数的表示形式为10n a ⨯形式,其中1||10a ≤<,n 为整数,28000=。
故选C 。
3. 实数a ,b 在数轴上的对应点的位置如图所示,则正确的结论是(A ) a (B )(C )(D )答案:D考点:数轴,由数轴比较数的大小。
解析:由数轴可知,-3<a <-2,故A 、B 错误;1<b <2, -2<-b <-1,即-b 在-2与-1之间,所以,。
4. 内角和为540的多边形是答案:c考点:多边形的内角和。
解析:多边形的内角和为(2)180n-⨯︒,当n=5时,内角和为540°,所以,选C。
5. 右图是某个几何体的三视图,该几何体是(A)圆锥(B)三棱锥(C)圆柱(D)三棱柱答案:D考点:三视图,由三视图还原几何体。
解析:该三视图的俯视为三角形,正视图和侧视图都是矩形,所以,这个几何体是三棱柱。
6. 如果,那么代数2()b aaa a b--的值是(A) 2 (B)-2 (C)(D)答案:A考点:分式的运算,平方差公式。
解析:2()b aaa a b--=22a b aa a b--=()()a b a b aa a b-+-=a b+=2。
中考数学 微测试系列专题19 圆的有关计算及圆的综合(含解析)

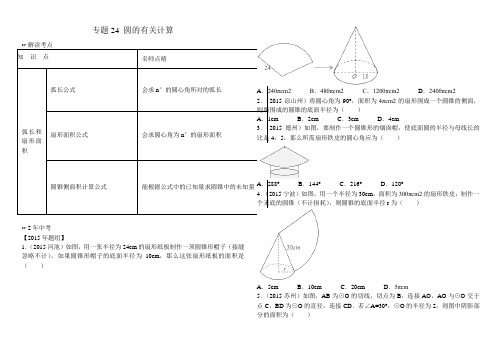
专题19 圆的有关计算及圆的综合学校:___________姓名:___________班级:___________1.【2015届湖北省黄石市6月中考模拟】圆锥底面圆的半径为3cm,其侧面展开图是半圆,则圆锥母线长为()A.3cm B.6cm C.9cm D.12cm【答案】B【解析】考点:圆锥的计算2.【辽宁葫芦岛2015年中考数学试卷】如图,⊙O是△ABC的外接圆,⊙O的半径为3,∠A=45°,则»BC的长是()A.34π B.32π C.452π D.94π【答案】B.【解析】试题分析:因为⊙O是△ABC的外接圆,⊙O的半径为3,∠A=45°,所以可得圆心角∠BOC=90°,所以»BC的长=903180π⨯=32π,故选B.考点:1.弧长的计算;2.圆周角定理.3.【辽宁盘锦2015年中考数学试卷】如图,从一块直径是8m的圆形铁皮上剪出一个圆心角为90°的扇形,将剪下的扇形围成一个圆锥,圆锥的高是()m.A.42 B.5 C.30 D.215【答案】C.【解析】考点:1.圆锥的计算;2.综合题.4.【2015届山东省日照市中考一模】如图,等腰直角△ABC中,AB=AC=8,以AB为直径的半圆O交斜边BC于D,则阴影部分面积为(结果保留π)()A.24-4πB.32-4πC.32-8πD.16【答案】A.【解析】考点:扇形面积的计算.5.【黑龙江哈尔滨2015年中考数学试题】一个扇形的半径为3cm,面积为π2cm,则此扇形的圆心角为 .【答案】40°.【解析】试题分析:根据扇形的面积计算公式可得:23360n p´=π,解得:n=40°,即圆心角的度数为40°.考点:扇形的面积计算.6.【黑龙江绥化2015年中考数学试题】如图,将一块含300角的直角三角版和半圆量角器按如图的方式摆放,使斜边与半圆相切。
中考数学圆的综合综合题汇编及详细答案

中考数学圆的综合综合题汇编及详细答案一、圆的综合1.如图,已知△ABC中,AC=BC,以BC为直径的⊙O交AB于E,过点E作EG⊥AC于G,交BC的延长线于F.(1)求证:AE=BE;(2)求证:FE是⊙O的切线;(3)若FE=4,FC=2,求⊙O的半径及CG的长.【答案】(1)详见解析;(2)详见解析;(3).【解析】(1)证明:连接CE,如图1所示:∵BC是直径,∴∠BEC=90°,∴CE⊥AB;又∵AC=BC,∴AE=BE.(2)证明:连接OE,如图2所示:∵BE=AE,OB=OC,∴OE是△ABC的中位线,∴OE∥AC,AC=2OE=6.又∵EG⊥AC,∴FE⊥OE,∴FE是⊙O的切线.(3)解:∵EF是⊙O的切线,∴FE2=FC•FB.设FC=x,则有2FB=16,∴FB=8,∴BC=FB﹣FC=8﹣2=6,∴OB=OC=3,即⊙O的半径为3;∴OE=3.∵OE∥AC,∴△FCG∽△FOE,∴,即,解得:CG=.点睛:本题利用了等腰三角形三线合一定理,三角形中位线的判定,切割线定理,以及勾股定理,还有平行线分线段成比例定理,切线的判定等知识.2.如图,AB为⊙O的直径,点D为AB下方⊙O上一点,点C为弧ABD的中点,连接CD,CA.(1)求证:∠ABD=2∠BDC;(2)过点C作CH⊥AB于H,交AD于E,求证:EA=EC;(3)在(2)的条件下,若OH=5,AD=24,求线段DE的长度.【答案】(1)证明见解析;(2)见解析;(3)92DE =. 【解析】 【分析】(1)连接AD ,如图1,设∠BDC =α,∠ADC =β,根据圆周角定理得到∠CAB =∠BDC =α,由AB 为⊙O 直径,得到∠ADB =90°,根据余角的性质即可得到结论;(2)根据已知条件得到∠ACE =∠ADC ,等量代换得到∠ACE =∠CAE ,于是得到结论; (3)如图2,连接OC ,根据圆周角定理得到∠COB =2∠CAB ,等量代换得到∠COB =∠ABD ,根据相似三角形的性质得到OH =5,根据勾股定理得到AB =22AD BD +=26,由相似三角形的性质即可得到结论.【详解】(1)连接AD .如图1,设∠BDC =α,∠ADC =β, 则∠CAB =∠BDC =α,∵点C 为弧ABD 中点,∴¶AC =¶CD,∴∠ADC =∠DAC =β,∴∠DAB =β﹣α, ∵AB 为⊙O 直径,∴∠ADB =90°,∴α+β=90°,∴β=90°﹣α,∴∠ABD =90°﹣∠DAB =90°﹣(β﹣α),∴∠ABD =2α,∴∠ABD =2∠BDC ;(2)∵CH ⊥AB ,∴∠ACE +∠CAB =∠ADC +∠BDC =90°, ∵∠CAB =∠CDB ,∴∠ACE =∠ADC , ∵∠CAE =∠ADC ,∴∠ACE =∠CAE ,∴AE =CE ; (3)如图2,连接OC ,∴∠COB =2∠CAB , ∵∠ABD =2∠BDC ,∠BDC =∠CAB ,∴∠COB =∠ABD , ∵∠OHC =∠ADB =90°,∴△OCH ∽△ABD ,∴12OH OC BD AB ==, ∵OH =5,∴BD =10,∴AB 22AD BD +,∴AO =13,∴AH =18,∵△AHE ∽△ADB ,∴AH AE AD AB =,即1824=26AE ,∴AE =392,∴DE =92.【点睛】本题考查了垂径定理,相似三角形的判定和性质,等腰三角形的判定和性质,正确的作出辅助线是解题的关键.3.不用圆规、三角板,只用没有刻度的直尺,用连线的方法在图1、2中分别过圆外一点A作出直径BC所在射线的垂线.【答案】画图见解析.【解析】【分析】根据直角所对的圆周角是直角,构造直角三角形,利用直角三角形性质可画出垂线;或结合圆的轴对称性质也可以求出垂线.【详解】解:画图如下:【点睛】本题考核知识点:作垂线.解题关键点:结合圆的性质和直角三角形性质求出垂线.4.如图,四边形ABCD内接于⊙O,对角线AC为⊙O的直径,过点C作AC的垂线交AD 的延长线于点E,点F为CE的中点,连接DB, DF.(1)求证:DF是⊙O的切线;(2)若DB平分∠ADC,AB=52AD,∶DE=4∶1,求DE的长.【答案】(1)见解析;(2)5【解析】分析:(1)直接利用直角三角形的性质得出DF=CF=EF,再求出∠FDO=∠FCO=90°,得出答案即可;(2)首先得出AB=BC即可得出它们的长,再利用△ADC~△ACE,得出AC2=AD•AE,进而得出答案.详解:(1)连接OD.∵OD=CD,∴∠ODC=∠OCD.∵AC为⊙O的直径,∴∠ADC=∠EDC=90°.∵点F为CE的中点,∴DF=CF=EF,∴∠FDC=∠FCD,∴∠FDO=∠FCO.又∵AC⊥CE,∴∠FDO=∠FCO=90°,∴DF是⊙O的切线.(2)∵AC为⊙O的直径,∴∠ADC=∠ABC=90°.∵DB平分∠ADC,∴∠ADB=∠CDB,∴¶AB=¶BC,∴BC=AB=52.在Rt△ABC中,AC2=AB2+BC2=100.又∵AC⊥CE,∴∠ACE=90°,∴△ADC~△ACE,∴ACAD =AEAC,∴AC2=AD•AE.设DE为x,由AD:DE=4:1,∴AD=4x,AE=5x,∴100=4x•5x,∴x=5,∴DE=5.点睛:本题主要考查了切线的判定以及相似三角形的判定与性质,正确得出AC2=AD•AE是解题的关键.5.如图AB是△ABC的外接圆⊙O的直径,过点C作⊙O的切线CM,延长BC到点D,使CD=BC,连接AD交CM于点E,若⊙OD半径为3,AE=5,(1)求证:CM⊥AD;(2)求线段CE的长.【答案】(1)见解析;(2)5【解析】分析:(1)连接OC,根据切线的性质和圆周角定理证得AC垂直平分BD,然后根据平行线的判定与性质证得结论;(2)根据相似三角形的判定与性质证明求解即可.详解:证明:(1)连接OC∵CM切⊙O于点C,∴∠OCE=90°,∵AB是⊙O的直径,∴∠ACB=90°,∵CD=BC,∴AC垂直平分BD,∴AB=AD,∴∠B=∠D∵∠B=∠OCB∴∠D=∠OCB∴OC∥AD∴∠CED=∠OCE=90°∴CM⊥AD.(2)∵OA=OB,BC=CD∴OC=1AD2∴AD=6∴DE=AD-AE=1易证△CDE ~△ACE∴CE DEAE CE = ∴CE 2=AE×DE∴CE=5点睛:此题主要考查了切线的性质和相似三角形的判定与性质的应用,灵活判断边角之间的关系是解题关键,是中档题.6.如图,已知⊙O 的半径为1,PQ 是⊙O 的直径,n 个相同的正三角形沿PQ 排成一列,所有正三角形都关于PQ 对称,其中第一个△A 1B 1C 1的顶点A 1与点P 重合,第二个△A 2B 2C 2的顶点A 2是B 1C 1与PQ 的交点,…,最后一个△A n B n C n 的顶点B n 、C n 在圆上.如图1,当n=1时,正三角形的边长a 1=_____;如图2,当n=2时,正三角形的边长a 2=_____;如图3,正三角形的边长a n =_____(用含n 的代数式表示).3831343n 【解析】分析:(1)设PQ 与11B C 交于点D ,连接1B O ,得出OD=1A D -O 1A ,用含1a 的代数式表示OD ,在△O 1B D 中,根据勾股定理求出正三角形的边长1a ;(2)设PQ 与2B 2C 交于点E ,连接2B O ,得出OE=1A E-O 1A ,用含2a 的代数式表示OE ,在△O 2B E 中,根据勾股定理求出正三角形的边长2a ;(3)设PQ 与n B n C 交于点F ,连接n B O ,得出OF=1A F-O 1A ,用含an 的代数式表示OF ,在△O n B F 中,根据勾股定理求出正三角形的边长an . 本题解析:(1)易知△A 1B 1C 1的高为323 ∴a 13.(2)设△A 1B 1C 1的高为h ,则A 2O =1-h ,连结B 2O ,设B 2C 2与PQ 交于点F ,则有OF =2h -1.∵B 2O 2=OF 2+B 2F 2,∴1=(2h -1)2+2212a ⎛⎫ ⎪⎝⎭.∵h=32a2,∴1=(3a2-1)2+14a22,解得a2=83.(3)同(2),连结B n O,设B n C n与PQ交于点F,则有B n O2=OF2+B n F2,即1=(nh-1)2+2 12na⎛⎫ ⎪⎝⎭.∵h=3a n,∴1=14a n2+2312nna⎛⎫-⎪⎪⎝⎭,解得a n=43n.7.如图,△ABC内接于⊙O,弦AD⊥BC垂足为H,∠ABC=2∠CAD.(1)如图1,求证:AB=BC;(2)如图2,过点B作BM⊥CD垂足为M,BM交⊙O于E,连接AE、HM,求证:AE∥HM;(3)如图3,在(2)的条件下,连接BD交AE于N,AE与BC交于点F,若NH=25,AD=11,求线段AB的长.【答案】(1)证明见解析;(2)证明见解析;(3)AB的长为10.【解析】分析:(1)根据题意,设∠CAD=a,然后根据直角三角形的两锐角互余的关系,推导出∠BAC=∠ACB,再根据等角对等边得证结论;(2)延长AD、BM交于点N,连接ED.根据圆周角定理得出∠N=∠DEN=∠BAN,进而根据等角对等边,得到DE=DN,BA=BN,再根据等腰三角形和直角三角形的性质,求得MH∥AE;(3)连接CE,根据(2)的结论,由三角形全等的判定与性质证得HF=HC,然后结合勾股定理求出AC2-AH2=CD2-DH2,解得CD=5,CH=4,AH=8,最后根据锐角三角函数的性质得到AB.详解:(1)证明:设∠CAD=a,则∠ABC=2a,∠C=90°-a,∠BAD=90°-2a,∴∠BAC=90°-2a+a=90°-a∴∠BAC=∠ACB.∴AB=BC(2)证明:延长AD 、BM 交于点N ,连接ED. ∵∠DEN=∠DAB,∠N=∠BCD,∠BCD=∠BAN∴∠N=∠DEN=∠BAN ∴DE=DN,BA=BN 又∵BH ⊥AN,DM ⊥EN ∴EM=NM,HN=HA,∴MH ∥AE (3)连接CE.∠BDA=∠BCA,∠BDM=∠BAC,由(1)知∠BCA=∠BAC ∴∠BDA=∠BDM,∴△BDM ≌△BDH, ∴DH=MH,∠MBD=∠HBD,∴BD ⊥MH 又∵MH ∥AE,∴BD ⊥EF,∴△FNB ≌△ENB, 同理可证△AFH ≌△ACH,∴HF=HC,又∵FN=NE∴NH ∥EC,EC=2NH,又∵NH=25∴EC=45∠EAC=2∠AEC=2a=∠ABC,可证弧AC=弧EC, ∴AC=EC=5 设HD=x ,AH=11-x ,∵∠ADC=2∠CAD,翻折△CHD 至△CHG,可证CG=CD=AG AH=CD+DH,CD=AH-DH=11-x-x=11-2x又∵AC 2-AH 2=CD 2-DH 2,∴(52-(11-x)2=(11-2x)2-x 2 ∴x 1=3,x 2=272(舍去)∴CD=5,CH=4,AH=8. 又∵tan2AH CHa BH DH==,∴BH=6 ∴22226810BM AH +=+= 点睛:此题主要考查了圆的综合,结合圆周角定理,勾股定理,全等三角形的判定与性质,解直角三角形的性质,综合性比较强,灵活添加辅助线,构造方程求解是解题关键.8.如图.在△ABC中,∠C=90°,AC=BC,AB=30cm,点P在AB上,AP=10cm,点E从点P 出发沿线段PA以2c m/s的速度向点A运动,同时点F从点P出发沿线段PB以1c m/s的速度向点B运动,点E到达点A后立刻以原速度沿线段AB向点B运动,在点E、F运动过程中,以EF为边作正方形EFGH,使它与△ABC在线段AB的同侧,设点E、F运动的时间为t (s)(0<t<20).(1)当点H落在AC边上时,求t的值;(2)设正方形EFGH与△ABC重叠部分的面积为S.①试求S关于t的函数表达式;②以点C为圆心,12t为半径作⊙C,当⊙C与GH所在的直线相切时,求此时S的值.【答案】(1)t=2s或10s;(2)①S=2229?(02)75050(210)240400?(1020)t tt t tt t t⎧<≤⎪⎪-+-<≤⎨⎪-+<<⎪⎩;②100cm2.【解析】试题分析:(1)如图1中,当0<t≤5时,由题意AE=EH=EF,即10﹣2t=3t,t=2;如图2中,当5<t<20时,AE=HE,2t﹣10=10﹣(2t﹣10)+t,t=10;(2)分四种切线讨论a、如图3中,当0<t≤2时,重叠部分是正方形EFGH,S=(3t)2=9t2.b、如图4中,当2<t≤5时,重叠部分是五边形EFGMN.c、如图5中,当5<t<10时,重叠部分是五边形EFGMN.d、如图6中,当10<t<20时,重叠部分是正方形EFGH.分别计算即可;②分两种情形分别列出方程即可解决问题.试题解析:解:(1)如图1中,当0<t≤5时,由题意得:AE=EH=EF,即10﹣2t=3t,t=2如图2中,当5<t<20时,AE=HE,2t﹣10=10﹣(2t﹣10)+t,t=10.综上所述:t=2s或10s时,点H落在AC边上.(2)①如图3中,当0<t≤2时,重叠部分是正方形EFGH,S=(3t)2=9t2如图4中,当2<t≤5时,重叠部分是五边形EFGMN,S=(3t)2﹣12(5t﹣10)2=﹣72t2+50t﹣50.如图5中,当5<t<10时,重叠部分是五边形EFGMN,S=(20﹣t)2﹣12(30﹣3t)2=﹣72t2+50t﹣50.如图6中,当10<t<20时,重叠部分是正方形EFGH,S=(20﹣t)2=t2﹣40t+400.综上所述:S=2229?(02)75050(210) 240400?(1020)t tt t tt t t⎧<≤⎪⎪-+-<≤⎨⎪-+<<⎪⎩.②如图7中,当0<t≤5时,12t+3t=15,解得:t=307,此时S=100cm2,当5<t<20时,12t+20﹣t=15,解得:t=10,此时S=100.综上所述:当⊙C与GH所在的直线相切时,求此时S的值为100cm2点睛:本题考查了圆综合题、正方形的性质、等腰直角三角形的性质、切线的性质等知识,解题的关键是灵活运用所学知识解决问题,学会用分类讨论的思想思考问题,注意不能漏解,属于中考压轴题.9.四边形ABCD内接于⊙O,点E为AD上一点,连接AC,CB,∠B=∠AEC.(1)如图1,求证:CE=CD;(2)如图2,若∠B+∠CAE=120°,∠ACD=2∠BAC,求∠BAD的度数;(3)如图3,在(2)的条件下,延长CE交⊙O于点G,若tan∠53,EG=2,求AE的长.【答案】(1)见解析;(2)60°;(3)7.【解析】试题分析:(1)利用圆的内接四边形定理得到∠CED=∠CDE.(2) 作CH⊥DE于H, 设∠ECH=α,由(1)CE=CD,用α表示∠CAE,∠BAC,而∠BAD=∠BAC+∠CAE.(3)连接AG,作GN⊥AC,AM⊥EG,先证明∠CAG=∠BAC,设NG=53m,可得AN=11m,利用直角n AGM,n AEM,勾股定理可以算出m的值并求出AE长.试题解析:(1)解:证明:∵四边形ABCD内接于⊙O.∴∠B+∠D=180°,∵∠B=∠AEC,∴∠AEC+∠D=180°,∵∠AEC+∠CED=180°,∴∠D=∠CED,∴CE=CD.(2)解:作CH⊥DE于H.设∠ECH=α,由(1)CE=CD,∴∠ECD=2α,∵∠B=∠AEC,∠B+∠CAE=120°,∴∠CAE+∠AEC=120°,∴∠ACE=180°﹣∠AEC﹣∠ACE=60°,∴∠CAE=90°﹣∠ACH=90°﹣(60°+α)=30°﹣α,∠ACD=∠ACH+∠HCD=60°+2α,∵∠ACD=2∠BAC,∴∠BAC=30°+α,∴∠BAD =∠BAC +∠CAE =30°+α+30°﹣α=60°.(3)解:连接AG ,作GN ⊥AC ,AM ⊥EG ,∵∠CED =∠AEG ,∠CDE =∠AGE ,∠CED =∠CDE ,∴∠AEG =∠AGE ,∴AE =AG ,∴EM=MG =12EG =1, ∴∠EAG =∠ECD =2α,∴∠CAG =∠CAD +∠DAG =30°﹣α+2α=∠BAC ,∵tan ∠BAC =53, ∴设NG=53m ,可得AN =11m ,AG =22AG AM -=14m , ∵∠ACG =60°,∴CN=5m ,AM =83m ,MG =22AG AM -=2m =1, ∴m =12, ∴CE=CD =CG ﹣EG =10m ﹣2=3, ∴AE =22AM EM +=221+43()=7.10.如图1,四边形ABCD 为⊙O 内接四边形,连接AC 、CO 、BO ,点C 为弧BD 的中点. (1)求证:∠DAC=∠ACO+∠ABO ;(2)如图2,点E 在OC 上,连接EB ,延长CO 交AB 于点F ,若∠DAB=∠OBA+∠EBA .求证:EF=EB ;(3)在(2)的条件下,如图3,若OE+EB=AB ,CE=2,AB=13,求AD 的长.【答案】(1)证明见解析;(2)证明见解析;(3)AD=7.【解析】试题分析:(1)如图1中,连接OA ,只要证明∠CAB=∠1+∠2=∠ACO+∠ABO ,由点C 是»BD中点,推出»»CD CB = ,推出∠BAC=∠DAC ,即可推出∠DAC=∠ACO+∠ABO ; (2)想办法证明∠EFB=∠EBF 即可;(3)如图3中,过点O 作OH ⊥AB ,垂足为H ,延长BE 交HO 的延长线于G ,作BN ⊥CF 于N ,作CK ⊥AD 于K ,连接OA .作CT ∠⊥AB 于T .首先证明△EFB 是等边三角形,再证明△ACK ≌△ACT ,Rt △DKC ≌Rt △BTC ,延长即可解决问题;试题解析:(1)如图1中,连接OA ,∵OA=OC ,∴∠1=∠ACO ,∵OA=OB ,∴∠2=∠ABO ,∴∠CAB=∠1+∠2=∠ACO+∠ABO ,∵点C 是BD u u u r 中点,∴CD CB =u u u r u u u r,∴∠BAC=∠DAC ,∴∠DAC=∠ACO+∠ABO .(2)如图2中,∵∠BAD=∠BAC+∠DAC=2∠CAB ,∠COB=2∠BAC ,∴∠BAD=∠BOC ,∵∠DAB=∠OBA+∠EBA ,∴∠BOC=∠OBA+∠EBA ,∴∠EFB=∠EBF ,∴EF=EB .(3)如图3中,过点O 作OH ⊥AB ,垂足为H ,延长BE 交HO 的延长线于G ,作BN ⊥CF 于N ,作CK ⊥AD 于K ,连接OA .作CT ∠⊥AB 于T .∵∠EBA+∠G=90°,∠CFB+∠HOF=90°,∵∠EFB=∠EBF ,∴∠G=∠HOF ,∵∠HOF=∠EOG ,∴∠G=∠EOG ,∴EG=EO ,∵OH ⊥AB ,∴AB=2HB ,∵OE+EB=AB ,∴GE+EB=2HB ,∴GB=2HB ,∴cos ∠GBA=12HB GB = ,∴∠GBA=60°, ∴△EFB 是等边三角形,设HF=a , ∵∠FOH=30°,∴OF=2FH=2a , ∵AB=13,∴EF=EB=FB=FH+BH=a+132, ∴OE=EF ﹣OF=FB ﹣OF=132﹣a ,OB=OC=OE+EC=132﹣a+2=172﹣a , ∵NE=12EF=12a+134, ∴ON=OE=EN=(132﹣a )﹣(12a+134)=134﹣32a , ∵BO 2﹣ON 2=EB 2﹣EN 2, ∴(172﹣a )2﹣(134﹣32a )2=(a+132)2﹣(12a+134)2, 解得a=32或﹣10(舍弃), ∴OE=5,EB=8,OB=7, ∵∠K=∠ATC=90°,∠KAC=∠TAC ,AC=AC ,∴△ACK ≌△ACT ,∴CK=CT ,AK=AT , ∵CD CB =u u u r u u u r ,∴DC=BC ,∴Rt △DKC ≌Rt △BTC ,∴DK=BT ,∵FT=12FC=5,∴DK=TB=FB ﹣FT=3,∴AK=AT=AB ﹣TB=10,∴AD=AK ﹣DK=10﹣3=7.11.如图,AC 是⊙O 的直径,OB 是⊙O 的半径,PA 切⊙O 于点A ,PB 与AC 的延长线交于点M ,∠COB =∠APB .(1)求证:PB 是⊙O 的切线;(2)当MB =4,MC =2时,求⊙O 的半径.【答案】(1)证明见解析;(2)3.【解析】【分析】(1)根据题意∠M +∠P =90°,而∠COB =∠APB ,所以有∠M +∠COB =90°,即可证明PB是⊙O 的切线.(2)设圆的半径为r ,则OM =r +2,BM=4,OB =r ,再根据勾股定理列方程便可求出r .【详解】证明:(1)∵AC 是⊙O 的直径,PA 切⊙O 于点A ,∴PA ⊥OA∴在Rt △MAP 中,∠M +∠P =90°,而∠COB =∠APB ,∴∠M +∠COB =90°,∴∠OBM =90°,即OB ⊥BP ,∴PB 是⊙O 的切线;(2)设⊙O 的半径为r ,2OM r ∴=+ ,OB r = ,4BM =OBM ∆Q 为直角三角形∴222OM OB BM =+ ,即222(2)+4r r +=解得:r =3,∴⊙O 的半径为3.【点睛】本题主要考查圆的切线问题,证明圆的切线有两种思路一种是证明连线是半径,另一种是证明半径垂直.12.如图,PA 切⊙O 于点A ,射线PC 交⊙O 于C 、B 两点,半径OD ⊥BC 于E ,连接BD 、DC 和OA ,DA 交BP 于点F ;(1)求证:∠ADC+∠CBD =12∠AOD ; (2)在不添加任何辅助线的情况下,请直接写出图中相等的线段.【答案】(1)详见解析;(2)详见解析;【解析】【分析】()1根据垂径定理得到BD CD =n n ,根据等腰三角形的性质得到()111809022ODA AOD AOD ∠=-∠=-∠o o ,即可得到结论; ()2根据垂径定理得到BE CE =,BD CD =n n ,根据等腰三角形的性质得到ADO OAD ∠=∠,根据切线的性质得到90PAO ∠=o ,求得90OAD DAP ∠+∠=o ,推出PAF PFA ∠=∠,根据等腰三角形的判定定理即可得到结论.【详解】()1证明:OD BC ⊥Q ,BD CD ∴=n n, CBD DCB ∴∠=∠,90DFE EDF ∠+∠=o Q ,90EDF DFE ∴∠=-∠o ,OD OA =Q ,()111809022ODA AOD AOD ∴∠=-∠=-∠o o , 190902DFE AOD ∴-∠=-∠o o , 12DEF AOD ∴∠=∠, DFE ADC DCB ADC CBD ∠=∠+∠=∠+∠Q ,12ADC CBD AOD ∴∠+∠=∠; ()2解:OD BC ⊥Q ,BE CE ∴=,BD CD =n n,BD CD ∴=,OA OD Q =,ADO OAD ∴∠=∠,PA Q 切O e 于点A ,90PAO ∴∠=o ,90OAD DAP ∴∠+∠=o , PFA DFE ∠=∠Q ,90PFA ADO ∴∠+∠=o ,PAF PFA ∴∠=∠,PA PF ∴=.【点睛】本题考查了切线的性质,等腰三角形的判定和性质,垂径定理,圆周角定理,正确的识别图形是解题的关键.13.如图1,AB 为半圆O 的直径,半径OP ⊥AB ,过劣弧AP 上一点D 作DC ⊥AB 于点C .连接DB ,交OP 于点E ,∠DBA =22.5°.⑴ 若OC =2,则AC 的长为 ;⑵ 试写出AC 与PE 之间的数量关系,并说明理由;⑶ 连接AD 并延长,交OP 的延长线于点G ,设DC =x ,GP =y ,请求出x 与y 之间的等量关系式. (请先补全图形,再解答)【答案】⑴ 222-;⑵ 见解析;⑶ y =2x【解析】【分析】(1)如图,连接OD ,则有∠AOD=45°,所以△DOC 为等腰直角三角形,又OC=2,所以DO=AO=22,故可求出AC 的长;(2)连接AD ,DP ,过点D 作DF ⊥OP ,垂足为点F . 证AC=PF 或AC=EF ,证DP=DE证PF=EF=12PE ,故可证出PE =2AC ; (3)首先求出22OD CD x ==,再求AB=22x ,再证△DGE ≌△DBA,得GE =AB =22x ,由PE=2AC 得PE =2(2)x x -,再根据GP =GE -PE 可求结论.【详解】(1)连接OD ,如图,∵∠B=22.5°,∴∠DOC=45°,∵DC ⊥AB∴△DOC 为等腰直角三角形,∵OC=2,∴2∴,∴AC=AO-OC=2.⑵连接AD,DP,过点D作DF⊥OP,垂足为点F.∵OP⊥AB,∴∠POD=∠DOC=45°,∴AD=PD,∵△DOC为等腰直角三角形,∴DC=CO,易证DF=CO,∴DC=DF,∴Rt△DAC≌Rt△DPF,∴PF=AC,∵DO=AO,∠DOA=45°∴∠DAC=67.5°∴∠DPE=67.5°,∵OD=OB,∠B=22.5°,∴∠ODE=22.5°∴∠DEP=22.5°+45°=67.5°∴∠DEP=∠DPE∴PF=EF=1PE2∴PE=2AC(3)如图2,由∠DCO=90°,∠DOC=45°得OD==∴AB=2OD=∵AB是直径,∴∠ADB=∠EDG=90°,由(2)得AD=ED,∠DEG=∠DAC∴△DGE≌△DBA∴GE=AB=∵PE=2AC∴PE=2)x--∴GP=GE-PE=-)x即:y=2x【点睛】本题是一道圆的综合题,涵盖的知识点较多,难度较大,主要考查了圆周角定理,等腰三角形的性质,三角形全等的判定与性质等知识,熟练掌握并运用这些知识是解题的关键. 14.如图1,D是⊙O的直径BC上的一点,过D作DE⊥BC交⊙O于E、N,F是⊙O上的一点,过F的直线分别与CB、DE的延长线相交于A、P,连结CF交PD于M,∠C=12∠P . (1)求证:PA 是⊙O 的切线;(2)若∠A =30°,⊙O 的半径为4,DM =1,求PM 的长;(3)如图2,在(2)的条件下,连结BF 、BM ;在线段DN 上有一点H ,并且以H 、D 、C 为顶点的三角形与△BFM 相似,求DH 的长度.【答案】(1)证明见解析;(2)PM =43﹣2;(3)满足条件的DH 的值为632- 或122311+. 【解析】【分析】(1)如图1中,作PH ⊥FM 于H .想办法证明∠PFH=∠PMH ,∠C=∠OFC ,再根据等角的余角相等即可解决问题;(2)解直角三角形求出AD ,PD 即可解决问题;(3)分两种情形①当△CDH ∽△BFM 时,DH CD FM BF =. ②当△CDH ∽△MFB 时,DH CD FB MF=,分别构建方程即可解决问题; 【详解】(1)证明:如图1中,作PH ⊥FM 于H .∵PD ⊥AC ,∴∠PHM =∠CDM =90°,∵∠PMH =∠DMC ,∴∠C =∠MPH ,∵∠C =12∠FPM ,∴∠HPF =∠HPM , ∵∠HFP+∠HPF =90°,∠HMP+∠HPM =90°,∴∠PFH =∠PMH ,∵OF =OC ,∴∠C =∠OFC ,∵∠C+∠CMD =∠C+∠PMF =∠C+∠PFH =90°,∴∠OFC+∠PFC =90°,∴∠OFP =90°,∴直线PA 是⊙O 的切线.(2)解:如图1中,∵∠A =30°,∠AFO =90°,∴∠AOF =60°,∵∠AOF =∠OFC+∠OCF ,∠OFC =∠OCF ,∴∠C =30°,∵⊙O 的半径为4,DM =1,∴OA =2OF =8,CD =3DM =3 ,∴OD =OC ﹣CD =4﹣3 ,∴AD =OA+OD =8+4﹣3 =12﹣3 ,在Rt △ADP 中,DP =AD•tan30°=(12﹣3 )×3 =43 ﹣1, ∴PM =PD ﹣DM =4 3﹣2.(3)如图2中,由(2)可知:BF =12BC =4,FM 3BF =3,CM =2DM =2,CD 3 , ∴FM =FC ﹣CM =3﹣2,①当△CDH ∽△BFM 时,DH CD FM BF = , ∴3432=- ,∴DH 63- ②当△CDH ∽△MFB 时,DH CD FB MF =,∴34432DH =- ,∴DH =1223+ , ∵DN =()22443833--=- ,∴DH <DN ,符合题意,综上所述,满足条件的DH 的值为63- 或1223+. 【点睛】本题考查圆综合题、切线的判定、解直角三角形、相似三角形的判定和性质等知识,解题的关键是熟练掌握基本知识,学会用分类讨论的思想思考问题.15.如图,是大半圆的直径,是小半圆的直径,点是大半圆上一点,与小半圆交于点,过点作于点. (1)求证:是小半圆的切线; (2)若,点在上运动(点不与两点重合),设,. ①求与之间的函数关系式,并写出自变量的取值范围;②当时,求两点之间的距离.【答案】(1)见解析;(2)①,,②两点之间的距离为或.【解析】【分析】 (1)连接CO 、CM ,只需证到CD ⊥CM .由于CD ⊥OP ,只需证到CM ∥OP ,只需证到CM 是△AOP 的中位线即可.(2)①易证△ODC ∽△CDP ,从而得到CD 2=DP•OD ,进而得到y 与x 之间的函数关系式.由于当点P 与点A 重合时x=0,当点P 与点B 重合时x=4,点P 在大半圆O 上运动(点P 不与A ,B 两点重合),因此自变量x 的取值范围为0<x <4.②当y=3时,得到-x 2+4x=3,求出x .根据x 的值可求出CD 、PD 的值,从而求出∠CPD ,运用勾股定理等知识就可求出P ,M 两点之间的距离.【详解】(1)连接,如图1所示∵是小半圆的直径,∴即∵∴∵∴∴,∵∴,∴∴.,即∵经过半径的外端,且∴直线是小半圆的切线.(2)①∵,,∴∴∴∽∴∴∵,,,∴当点与点重合时,;当点与点重合时,∵点在大半圆上运动(点不与两点重合),∴∴与之间的函数关系式为,自变量的取值范围是.②当时,解得,Ⅰ当时,如图2所示在中,∵,∴,∴∵,∴是等边三角形∵∴∴.Ⅱ当时,如图3所示,同理可得∵∴∴过点作,垂足为,连接,如图3所示∵,∴同理在中,∵,∴综上所述,当时,两点之间的距离为或.【点睛】考查了切线的判定、平行线的判定与性质、等边三角形的判定与性质、相似三角形的判定与性质、特殊角的三角函数值、勾股定理等知识,综合性比较强.。
中考数学总复习《圆的综合题》专项测试卷(附答案)

中考数学总复习《圆的综合题》专项测试卷(附答案)一、单选题(共12题;共24分)1.如图,在4×4的方格中(共有16个小方格),每个小方格都是边长为1的正方形,O,A,B分别是小正方形的顶点,则扇形OAB的面积等于()A.2πB.√2πC.2√2πD.√22π2.如图,已知A、B两点的坐标分别为(8,0)、(0,8),点C、F分别是直线x=−5和x轴上的动点,CF=10,点D是线段CF的中点,连接AD交y轴于点E,当△ABE面积取得最小值时,E点的坐标是()A.(0,103)B.(0,83)C.(0,2)D.(0,52)3.下列四边形中一定有外接圆的是()A.平行四边形B.菱形C.矩形D.梯形4.如图,⊙O是四边形ABCD的内切圆,下列结论一定正确的有()个:①AF=BG;②CG=CH;③AB+CD=AD+BC;④BG<CG.A.1B.2C.3D.45.如图,圆内接四边形ABCD中AB=AC,AC⊙BD,则⊙DAC是⊙BAC的()A.12B.13C.23D.256.如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为12,∠B=135°,则AC⌢的长为()A.6πB.12πC.2πD.3π7.如图,⊙ABC内接于⊙O,⊙B=65°,⊙C=70°.若BC=3 √2,则弧BC的长为()A.34πB.32πC.92πD.3 √2π8.如图,四边形ABCD内接于⊙O,F是CD̂上一点,且DF̂= BĈ,连接CF并延长交AD的延长线于点E,连接AC.若⊙ABC=105°,⊙BAC=30°,则⊙E的度数为()A.45°B.50°C.55°D.60°9.如图,A,B,C,D为⊙O的四等分点,动点P从圆心O出发,沿O﹣C﹣D﹣O路线作匀速运动,设运动时间为t(s).⊙APB=y(°),则下列图象中表示y与t之间函数关系最恰当的是()A.B.C.D.10.如图,将半径为2 cm的圆形纸片折叠后,圆弧恰好经过圆心O,则折痕AB的长为()A.2 cm B.√3cm C.2√3 cm D.2√5 cm11.如图的平面直角坐标系中有一个正六边形ABCDEF,其中C、D的坐标分别为(1,0)和(2,0).若在无滑动的情况下,将这个六边形沿着x轴向右滚动,则在滚动过程中这个六边形的顶点A,B,C,D,E,F中会过点(2017,2)的是()A.点A B.点C C.点E D.点F12.如图,AB 为⊙O 的直径,点C 是AB 上方半圆上的一点,点D 是AB 下方半圆的中点,连接AC,BC,AD,过点 D 作DE⊙AB 交CB 的延长线于点 E.若AD= 5 √2,则AC·CE的最大值为()A.50B.50 √2C.100D.75 √2二、填空题(共6题;共6分)13.如图,四边形内接于⊙O,若它的一个外角∠DCE=46°,则∠A的度数为.14.如图,AC与BD交于P,AD、BC延长交于点E,⊙AEC=37°,⊙CAE=31°,则⊙APB的度数为.15.如图,点A、B、C、D均在⊙O上,E为BC延长线上的一点,若∠A=110°,则∠DCE 的度数为°.16.如图,圆内接四边形ABCD的边AB过圆心O,过点C的切线与边AD所在直线垂直于点M,若⊙ABC=65°,则⊙ACD=°.17.如图,已知正⊙ABC的边长为9,⊙O是它的内切圆,则图中阴影部分的面积为.(结果保留π)18.如图,点A,点B,点C在⊙O上,分别连接AB,BC,OC.若AB=BC,⊙B=40°,则⊙OCB =.三、综合题(共6题;共56分)19.如图,AB为⊙O的直径,点C在⊙O上,连接AC,BC,过点O作OD⊥BC于点D,过点C作⊙O的切线交OD的延长线于点E.(1)求证:∠E=∠B;(2)连接AD.若CE=4√5,BC=8求AD的长.20.如图,AB是⊙O的直径,AE是⊙O的切线,点C为直线AE上一点,连接OC交⊙O于点D,连接BD并延长交线段AC于点E.(1)求证:∠CAD=∠CDE(2)若CD=6,tan∠BAD=√2求⊙O的半径.21.如图,在△ABC中AC=BC,以BC为直径作⊙O,交AC于点F,过C点作CD⊥AC交AB延长线于点D,E为CD上一点,且EB=ED.(1)求证:BE为⊙O的切线;(2)若AF=2,tanA=2求BE的长.22.如图,在Rt△ABC中∠C=90°,点O在AB上,以点O为圆心,OA长为半径的圆与AC、AB分别交于点D、E,且∠CBD=∠A.(1)求证:BD是⊙O的切线;(2)若AD:AE=5:6和BC=10求BD的长.23.如图1,在平面直角坐标系xOy中A,B两点的坐标分别为A(x1,y1),B(x2,y2),由勾股定理得AB2=|x2﹣x1|2+|y2﹣y1|2,所以A,B两点间的距离为:AB= √(x2−x1)2+(y2−y1)2我们知道,圆可以看成到圆心距离等于半径的点的集合,如图2,在平面直角坐标系xOy中A (x,y)为圆上任意一点,则A到原点的距离的平方为OA2=|x﹣0|2+|y﹣0|2,当⊙O的半径为r时,⊙O的方程可写为:x2+y2=r2.(1)问题拓展:如果圆心坐标为P(a,b),半径为r,那么⊙P的方程可以写为.(2)综合应用:如图3,⊙P与x轴相切于原点O,P点坐标为(0,6),A是⊙P上一点,连接OA,使⊙POA=30°,作PD⊙OA,垂足为D,延长PD交x轴于点B,连接AB.①证明:AB是⊙P的切线;②是否存在到四点O,P,A,B距离都相等的点Q?若存在,求Q点坐标,并写出以Q为圆心,以OQ为半径的⊙Q的方程;若不存在,说明理由.24.(1)解方程:x(x−4)=−2(x−4)(2)已知:如图,⊙O的直径AB与弦CD(不是直径)交于点F,若FB=2,CF=FD=4,设⊙O的半径为r,求AC的长.参考答案1.【答案】A2.【答案】A3.【答案】C4.【答案】B5.【答案】A6.【答案】A7.【答案】B8.【答案】A9.【答案】C10.【答案】C11.【答案】D12.【答案】C13.【答案】46°14.【答案】99°15.【答案】110°16.【答案】4017.【答案】27√3−9π418.【答案】20°19.【答案】(1)证明:连接OC如图:OD⊙CB∴OB=OC,⊙B=OCD又CE为圆O的切线∴OC⊙CE∴⊙ECD+⊙DCO=⊙ECD+⊙E=90°∴⊙E=⊙DCO=⊙B∴⊙E=⊙B(2)解:连接AD如图∵⊙EDC为Rt⊙∴DE=√EC2−DC2=√(4√5)2−42=8由(1)得⊙E=⊙B又AB为直径∴⊙BCA=90°在⊙CED和⊙ABC中∵{∠B=∠E∠EDC=∠BCAED=BC∴⊙CED⊙⊙ABC(AAS)∴AC=DC=12BC=420.【答案】(1)证明:∵AE是⊙O的切线,点A为切点∴∠OAE=90°,∴∠OAD+∠DAE=90°∵AB是⊙O的直径,∴∠ADB=90°∴∠B+∠OAD=90°,∴∠B=∠DAE∵OB=OD,∴∠B=∠ODB,∴∠ODB=∠DAE∵∠ODB=∠CDE,∴∠CDE=∠CAD;(2)解:∵∠BAD+∠DAE=90°,∠AEB+∠B=90°,∠BAD=∠B ∴∠BAD=∠AED∵tan∠BAD=√2∴tan∠AED =AB AE =AD DE =√2 ∵∠C =∠C ,∠CDE =∠CAD∴ΔCDE ∼ΔCAD∴CA CD =CD CE =AD DE∵CD =6,∴CA 6=6CE=√2 ∴CA =6√2,CE =3√2,∴AE =CA −CE =3√2 ∴AB 3√2=√2,∴AB =6 ∴OB =12AB =3,∴⊙O 的半径为3. 21.【答案】(1)证明:∵AC=BC ,EB=ED ∴⊙A=⊙ABC ,⊙D=⊙EBD∵CD⊙AC∴⊙A+⊙D=90°∴⊙ABC+⊙EBD=90°∴⊙CBE=90°∵BC 是⊙O 的直径.∴BE 是⊙O 的切线.(2)解:连接BF∵BC 是⊙O 的直径.∴⊙BFC=⊙BFA=90° 在Rt⊙ABF 中tanA=BF AF =BF 2=2 ∴BF=4设CF=x ,则AC=BC=x+2在Rt⊙BCF 中即(x +2)2=x 2+42∴x=3∴CF=3,BC=5∵⊙ACB=⊙AFB=90°∴BF⊙CD∴⊙1=⊙2又∵⊙CFB=⊙EBC=90°∴⊙CFB⊙⊙EBC∴FC BE =FB BC∴3BE =45∴BE=15422.【答案】(1)证明:连接OD∵点D 在⊙O 上∴OD =OA∴∠A =∠ADO∵∠C =90°∴∠CDB +∠CBD =90°∵∠CBD =∠A =∠ADO∴∠CDB +∠ADO =90°∴∠ODB =90°,即OD ⊥BD∵点D 在⊙O 上∴BD 是⊙O 的切线;(2)解:连接DE∵∠ADE =90°=∠C ,∠CBD =∠A∴△ADE ∽△BCD∴ADBC=AEBD,即ADAE=BCBD∵ADAE=56,BC=10∴BD=12.23.【答案】(1)(x﹣a)2+(y﹣b)2=r2(2)解:①∵PO=PA PD⊙OA∴⊙OPD=⊙APD在⊙POB和⊙PAB中{PO=PA ∠OPB=∠APB PB=PB∴⊙POB⊙⊙PAB∴⊙PAB=⊙POB=90°∴PA⊙AB∴AB是⊙P的切线②存在到四点O,P,A,B距离都相等的点Q 当点Q在线段BP中点时∵⊙POB=⊙PAB=90°∴QO=QP=QA=QB∴此时点Q到四点O,P,A,B距离都相等∵PB⊙OA,⊙POB=90°,⊙POA=30°∴⊙PBO=30°.∴在Rt⊙POB中OP=6∴OB= √3OP=6 √3,PB=2PO=12∴B点坐标为(6 √3,0)∵Q是PB中点,P(0,6),B(6 √3,0)∴Q点坐标为(3 √3,3)∴OQ= 12PB=6∴以Q为圆心,OQ为半径的⊙Q的方程为(x﹣3 √3)2+(y﹣3)2=36 24.【答案】(1)解:x(x−4)+2(x−4)=0,∴x2−2x−8=0∴(x+2)(x−4)=0解得:x1=−2,x2=4(2)解:连接OC,如图:∵AB是直径∴AB⊥CD∴42+(r−2)2=r2即r=5∴AF=2r−2=8∴由勾股定理得AC=√42+82=4√5.。
中考数学专题复习《圆的证明与计算》检测题(含答案)

专题二 圆的证明与计算类型一 圆基本性质的证明与计算1.如图,⊙O 的半径为5,点P 在⊙O 外,PB 交⊙O 于A 、B 两点,PC 交⊙O 于D 、C 两点. (1)求证:P A ·PB =PD ·PC ;(2)若P A =454,AB =194,PD =DC +2,求点O 到PC 的距离.第1题图2. 如图,△ABC 是⊙O 的内接三角形,AB =AC ,点P 是AB ︵的中点,连接P A ,PB ,PC .(1)如图①,若∠BPC =60°,求证:AC =3AP ; (2)如图②,若sin ∠BPC =2425,求tan ∠P AB 的值.第2题图3. 已知⊙O 中弦AB ⊥弦CD 于E ,tan ∠ACD =32. (1)如图①,若AB 为⊙O 的直径,BE =8,求AC 的长;(2)如图②,若AB 不为⊙O 的直径,BE =4,F 为BC ︵上一点,BF ︵=BD ︵,且CF =7,求AC 的长.第3题图4.如图,△ABC 中,AB =AC ,以AB 为直径作⊙O ,交BC 于点D ,交CA 的延长线于点E ,连接AD 、DE .(1)求证:D 是BC 的中点;(2)若 DE =3,BD -AD =2,求⊙O 的半径; (3)在(2)的条件下,求弦AE 的长.第4题图5.如图,⊙O 的半径为1,A ,P ,B ,C 是⊙O 上的四个点, ∠APC =∠CPB =60°.(1)判断△ABC 的形状:________;(2)试探究线段P A ,PB ,PC 之间的数量关系,并证明你的结论; (3)当点P 位于AB ︵的什么位置时,四边形APBC 的面积最大?求出最大面积.第5题图 备用图类型二与切线有关的证明与计算(一、与三角函数结合1.已知:如图,在△ABC中,AB=BC,D是AC中点,BE平分∠ABD 交AC于点E,点O是AB上一点,⊙O过B、E两点,交BD于点G,交AB于点F.(1)求证:AC与⊙O相切;(2)当BD=6,sin C=35时,求⊙O的半径.第1题图2.如图,AB为⊙O的直径,P是BA延长线上一点,PC切⊙O于点C,CG是⊙O的弦,CG⊥AB,垂足为D.(1)求证:∠PCA=∠ABC;(2)过点A作AE∥PC,交⊙O于点E,交CD于点F,连接BE.若sin ∠P =35,CF =5,求BE 的长.第2题图3. 如图①,在⊙O 中,直径AB ⊥CD 于点E ,点P 在BA 的延长线上,且满足∠PDA =∠ADC .(1)判断直线PD 与⊙O 的位置关系,并说明理由;(2)延长DO 交⊙O 于M (如图②),当M 恰为BC ︵的中点时,试求DE BE 的值;(3)若P A =2,tan ∠PDA =12,求⊙O 的半径.第3题图二、与相似三角形结合1.如图,在Rt △ABC 中,∠ACB =90°,E 是BC 的中点,以AC 为直径的⊙O 与AB 边交于点D ,连接DE . (1)求证:△ABC ∽△CBD ; (2)求证:直线DE 是⊙O 的切线.第1题图2. 如图,⊙O 的圆心在Rt △ABC 的直角边AC 上,⊙O 经过C 、D 两点,与斜边AB 交于点E ,连接BO 、ED ,有BO ∥ED ,作弦EF ⊥AC 于G ,连接DF .(1)求证:CO ·CD =DE ·BO ;(2)若⊙O 的半径为5,sin ∠DFE =35,求EF 的长.第2题图3. 如图,在△ABC 中,AB =AC ,以AB 为直径作半圆⊙O ,交BC 于点D ,连接AD ,过点D 作DE ⊥AC ,垂足为点E ,交AB 的延长线于点F .(1)求证:EF 是⊙O 的切线;(2)若⊙O 的半径为5,sin ∠ADE =45,求BF 的长.第3题图4.如图,在△ABC中,∠C=90°,以AB上一点O为圆心,OA长为半径的圆恰好与BC相切于点D,分别交AC、AB于点E、F.(1)若∠B=30°,求证:以A、O、D、E为顶点的四边形是菱形;(2)若AC=6,AB=10,连接AD,求⊙O的半径和AD的长.第4题图5.已知Rt△ABC中,AB是⊙O的弦,斜边AC交⊙O于点D,且AD =DC,延长CB交⊙O于点E.(1)图①的A、B、C、D、E五个点中,是否存在某两点间的距离等于线段CE的长?请说明理由;(2)如图②,过点E作⊙O的切线,交AC的延长线于点F.①若CF=CD时,求sin∠CAB的值;②若CF=aCD(a>0)时,试猜想sin∠CAB的值.(用含a的代数式表示,直接写出结果)第5题图6.已知:如图,AB是⊙O的直径,点C为⊙O上一点,OF⊥BC于点F,OF延长线交⊙O于点E,AE与BC交于点H,点D为OE的延长线上一点,且∠ODB=∠AEC.(1)求证:BD是⊙O的切线;(2)求证:CE2=EH·EA;(3)若⊙O 的半径为5,sin A =35,求BH 的长.第6题图7.如图①,△ABC 内接于⊙O ,∠BAC 的平分线交⊙O 于点D ,交BC 于点E (BE >EC ),且BD =2 3.过点D 作DF ∥BC ,交AB 的延长线于点F .(1)求证:DF 为⊙O 的切线;(2)若∠BAC =60°,DE =7,求图中阴影部分的面积;(3)若AB AC =43,DF +BF =8,如图②,求BF 的长.第7题图三、与全等三角形结合1.如图,已知PC 平分∠MPN ,点O 是PC 上任意一点,PM 与⊙O 相切于点E ,交PC 于A 、B 两点. (1)求证:PN 与⊙O 相切;(2)如果∠MPC =30°,PE =23,求劣弧BE ︵的长.第1题图2.如图,已知BC是⊙O的弦,A是⊙O外一点,△ABC为正三角形,D为BC的中点,M是⊙O上一点,并且∠BMC =60°.(1)求证:AB是⊙O的切线;(2)若E、F分别是边AB、AC上的两个动点,且∠EDF=120°,⊙O 的半径为2.试问BE+CF的值是否为定值,若是,求出这个定值;若不是,请说明理由.第2题图3. 已知:如图,AB是⊙O的直径,C是⊙O上一点,OD⊥AC于点D,过点C作⊙O的切线,交OD的延长线于点E,连接AE.(1)求证:AE与⊙O相切;(2)连接BD,若ED∶DO=3∶1,OA=9,求AE的长和tan B的值.第3题图4. 如图,PB为⊙O的切线,B为切点,直线PO交⊙O于点E、F,过点B作PO的垂线BA,垂足为点D,交⊙O于点A,延长AO与⊙O 交于点C,连接BC,AF.(1)求证:直线P A为⊙O的切线;(2)试探究线段EF、OD、OP之间的等量关系,并加以证明;(3)若BC=6,tan∠F=12,求cos∠ACB的值和线段PE的长.第4题图5. 如图,△ABC 内接于⊙O ,AB 为⊙O 的直径,∠ACB 的平分线CD 交⊙O 于点D ,过点D 作⊙O 的切线PD ,交CA 的延长线于点P ,过点A 作AE ⊥CD 于点E ,过点B 作BF ⊥CD 于点F . (1)求证:PD ∥AB ; (2)求证:DE =BF ;(3)若AC =6,tan ∠CAB =43,求线段PC 的长.第5题图6.如图,点P 是⊙O 外一点,P A 切⊙O 于点A ,AB 是⊙O 的直径,连接OP ,过点B 作BC ∥OP 交⊙O 于点C ,连接AC 交OP 于点D . (1)求证:PC 是⊙O 的切线;(2)若PD =163,AC =8,求图中阴影部分的面积;(3)在(2)的条件下,若点E 是AB ︵的中点,连接CE ,求CE 的长.第6题图7. 如图①,AB是⊙O的直径,OC⊥AB,弦CD与半径OB相交于点F,连接BD,过圆心O作OG∥BD,过点A作⊙O的切线,与OG 相交于点G,连接GD,并延长与AB的延长线交于点E.(1)求证:GD=GA;(2)求证:△DEF是等腰三角形;(3)如图②,连接BC,过点B作BH⊥GE,垂足为点H,若BH=9,⊙O的直径是25,求△CBF的周长.第7题图专题二圆的证明与计算类型一圆基本性质的证明与计算1. (1)证明:如解图,连接AD,BC,∵四边形ABCD内接于⊙O,∴∠P AD=∠PCB,∠PDA=∠PBC,∴△P AD ∽△PCB , ∴P A PD =PC PB , ∴P A ·PB =PD ·PC ;(2)解:如解图,连接OD ,过O 点作OE ⊥DC 于点E , ∵P A =454,AB =194,PD =DC +2,∴PB =P A +AB =16,PC =PD +DC =2DC +2, ∵P A ·PB =PD ·PC ,∴454×16=(DC +2)(2DC +2), 解得DC =8或DC =-11(舍去), ∴DE =12DC =4, ∵OD =5,∴在Rt △ODE 中,OE =OD 2-DE 2=3, 即点O 到PC 的距离为3.2. (1)证明:∵∠BAC 与∠BPC 是同弧所对的圆周角, ∴∠BAC =∠BPC =60°, 又∵AB =AC ,∴△ABC 为等边三角形, ∴∠ACB =60°, ∵点P 是AB ︵的中点, ∴P A ︵=PB ︵,∴∠ACP =∠BCP =12∠ACB =30°,而∠APC =∠ABC =60°, ∴△APC 为直角三角形, ∴tan ∠APC =AC AP , ∴AC =AP tan60°=3AP ;(2)解:连接AO 并延长交PC 于点E ,交BC 于点F ,过点E 作EG ⊥AC 于点G ,连接OC ,BO ,如解图,∵AB =AC , ∴AF ⊥BC , ∴BF =CF , ∵点P 是AB ︵中点, ∴∠ACP =∠PCB , ∴EG =EF .∵∠BPC =∠BAC =12∠BOC =∠FOC , ∴sin ∠FOC =sin ∠BPC =2425, 设FC =24a ,则OC =OA =25a ,∴OF =OC 2-FC 2=7a ,AF =25a +7a =32a , 在Rt △AFC 中,∵AC 2=AF 2+FC 2, ∴AC =(32a )2+(24a )2=40a , ∵∠EAG =∠CAF , ∴△AEG ∽△ACF , ∴EG CF =AE AC ,又∵EG =EF ,AE =AF -EF ,第2题解图∴EG 24a =32a -EG 40a , 解得EG =12a ,在Rt △CEF 中,tan ∠ECF =EF FC =12a 24a =12, ∵∠P AB =∠PCB ,∴tan ∠P AB =tan ∠PCB =tan ∠ECF =12. 3. 解:(1)如解图①,连接BD , ∵直径AB ⊥弦CD 于点E , ∴CE =DE ,∵∠ACD 与∠ABD 是同弧所对的圆周角, ∴∠ACD =∠ABD , ∴tan ∠ABD =tan ∠ACD =32, ∴ED EB =AE CE =32,即ED 8=32, ∴ED =12, ∴CE =ED =12, 又∵AE =32CE =18, ∴AC =AE 2+CE 2=613;(2)连接CB ,过B 作BG ⊥CF 于G ,如解图②, ∵BF ︵=BD ︵, ∴∠BCE =∠BCG , 在△CEB 和△CGB 中第3题解图①⎩⎪⎨⎪⎧∠BCE =∠BCG ∠BEC =∠BGC BC =BC, ∴△CEB ≌△CGB (AAS), ∴BE =BG =4,∵四边形ACFB 内接于⊙O , ∴∠A +∠CFB =180°, 又∵∠CFB +∠BFG =180°, ∴∠BFG =∠A , ∵∠FGB =∠AEC =90°, ∴△BFG ∽△CAE , ∴FG BG =AE CE =32, ∴FG =32BG =6, ∴CE =CG =13, ∴AE =32CE =392,∴AC =AE 2+CE 2=13213. 4. (1)证明:∵AB 是⊙O 的直径, ∴∠ADB =90°, 即AD ⊥BC , ∵AB =AC ,∴等腰△ABC ,AD 为BC 边上的垂线, ∴BD =DC , ∴D 是BC 的中点; (2)解:∵AB =AC ,∴∠ABC =∠C ,∵∠ABC 和∠AED 是同弧所对的圆周角, ∴∠ABC =∠AED , ∴∠AED =∠C , ∴CD =DE =3, ∴BD =CD =3, ∵BD -AD =2, ∴AD =1,在Rt △ABD 中,由勾股定理得AB 2=BD 2+AD 2=32+12=10, ∴AB =10,∴⊙O 的半径=12AB =102; (3)解:如解图,连接BE , ∵AB =10, ∴AC =10,∵∠ADC =∠BEA =90°,∠C =∠C , ∴△CDA ∽△CEB , ∴AC BC =CD CE ,由(2)知BC =2BD =6,CD =3, ∴106=3CE , ∴CE =9510,∴AE =CE -AC =9510-10=4510. 5. 解:(1)等边三角形.第4题解图【解法提示】∵∠APC =∠CPB =60°,又∵∠BAC 和∠CPB 是同弧所对的圆周角,∠ABC 和∠APC 是同弧所对的圆周角,∴∠BAC =∠CPB =60°,∠ABC =∠APC =60°, ∴∠BAC =∠ABC =60°, ∴AC =BC ,又∵有一个角是60°的等腰三角形是等边三角形, ∴△ABC 是等边三角形. (2)P A +PB =PC .证明如下:如解图①,在PC 上截取PD =P A ,连接AD , ∵∠APC =60°, ∴△P AD 是等边三角形, ∴P A =AD =PD ,∠P AD =60°, 又∵∠BAC =60°, ∴∠P AB =∠DAC , 在△P AB 和△DAC 中, ∵⎩⎪⎨⎪⎧AP =AD ∠P AB =∠DAC ,AB =AC ∴△P AB ≌△DAC (SAS), ∴PB =DC , ∵PD +DC =PC , ∴P A +PB =PC ,(3)当点P 为AB ︵的中点时,四边形APBC 的面积最大. 理由如下:如解图②,过点P 作PE ⊥AB ,垂足为E ,第5题解图①第5题解图②过点C 作CF ⊥AB ,垂足为F , ∵S △P AB =12AB ·PE ,S △ABC =12AB ·CF , ∴S 四边形APBC =12AB ·(PE +CF ).当点P 为AB ︵的中点时,PE +CF =PC ,PC 为⊙O 的直径, 此时四边形APBC 的面积最大, 又∵⊙O 的半径为1,∴其内接正三角形的边长AB = 3 , ∴四边形APBC 的最大面积为12×2×3= 3 . 类型二 与切线有关的证明与计算 一、与三角函数结合 针对演练1. (1)证明:连接OE ,如解图, ∵AB =BC 且D 是AC 中点, ∴BD ⊥AC , ∵BE 平分∠ABD , ∴∠ABE =∠DBE , ∵OB =OE , ∴∠OBE =∠OEB , ∴∠OEB =∠DBE , ∴OE ∥BD ,第1题解图∵BD ⊥AC , ∴OE ⊥AC , ∵OE 为⊙O 半径, ∴AC 与⊙O 相切;(2)解:∵BD =6,sin C =35,BD ⊥AC , ∴BC =BDsin C =10, ∴AB =BC =10.设⊙O 的半径为r ,则AO =10-r , ∵AB =BC , ∴∠C =∠A , ∴sin A =sin C =35, ∵AC 与⊙O 相切于点E , ∴OE ⊥AC ,∴sin A =OE OA =r 10-r =35,∴r =154, 即⊙O 的半径是154.2. (1)证明:连接OC ,如解图, ∵PC 切⊙O 于点C , ∴OC ⊥PC , ∴∠PCO =90°, ∴∠PCA +∠OCA =90°, ∵AB 为⊙O 的直径,第2题解图∴∠ACB =90°, ∴∠ABC +∠OAC =90°, ∵OC =OA , ∴∠OCA =∠OAC , ∴∠PCA =∠ABC ; (2)解:∵AE ∥PC , ∴∠PCA =∠CAF , ∵AB ⊥CG , ∴AC ︵=AG ︵, ∴∠ACF =∠ABC , ∵∠PCA =∠ABC , ∴∠ACF =∠CAF , ∴CF =AF , ∵CF =5, ∴AF =5, ∵AE ∥PC , ∴∠F AD =∠P , ∵sin ∠P =35, ∴sin ∠F AD =35,在Rt △AFD 中,AF =5,sin ∠F AD =35, ∴FD =3,AD =4, ∴CD =CF +FD =8, 在Rt △OCD 中,设OC =r , ∴r 2=(r -4)2+82,∴r =10, ∴AB =2r =20, ∵AB 为⊙O 的直径, ∴∠AEB =90°,在Rt △ABE 中,sin ∠EAD =35, ∴BE AB =35, ∵AB =20, ∴BE =12.3. 解:(1)直线PD 与⊙O 相切, 理由如下:如解图①,连接DO ,CO , ∵∠PDA =∠ADC , ∴∠PDC =2∠ADC , ∵∠AOC =2∠ADC , ∴∠PDC =∠AOC , ∵直径AB ⊥CD 于点E , ∴∠AOD =∠AOC , ∴∠PDC =∠AOD , ∵∠AOD +∠ODE =90°, ∴∠PDC +∠ODE =90°, ∴OD ⊥PD , ∵OD 是⊙O 的半径, ∴直线PD 与⊙O 相切; (2)如解图②,连接BD , ∵M 恰为BC ︵的中点,第3题解图①∴∠CDM =∠BDM , ∵OD =OB , ∴∠BDM =∠DBA , ∴∠CDM =∠DBA , ∵直线PD 与⊙O 相切, ∴∠PDA +∠ADO =90°, 又∵AB 是⊙O 的直径,∴∠ADB =90°,即∠ADO +∠BDM =90°, ∴∠PDA =∠BDM , ∴∠PDA =∠DBA =∠CDM , 又∵∠PDA =∠ADC , ∴∠PDM =3∠CDM =90°, ∴∠CDM =30°, ∴∠DBA =30°, ∴DE BE =tan30°=33; (3)如解图③,∵tan ∠PDA =12,∠PDA =∠ADC , ∴AE DE =12,即DE =2AE ,在Rt △DEO 中,设⊙O 的半径为r , DE 2+EO 2=DO 2, ∴(2AE )2+(r -AE )2=r 2, 解得r =52AE ,在Rt △PDE 中,DE 2+PE 2=PD 2,第3题解图②第3题解图③∴(2AE )2+(2+AE )2=PD 2, ∵直线PD 与⊙O 相切,连接BD , 由(2)知∠PDA =∠DBA ,∠P =∠P , ∴△P AD ∽△PDB , ∴PD PB =P A PD ,∴PD 2=P A ·PB ,即PD 2=2×(2+2r ), ∴(2AE )2+(2+AE )2=2×(2+2r ), 化简得5AE 2+4AE =4r , ∵r =52AE , 解得r =3. 即⊙O 的半径为3. 二、与相似三角形结合 针对演练1. 证明:(1)∵AC 为⊙O 的直径, ∴∠ADC =90°, ∴∠CDB =90°, 又∵∠ACB =90°, ∴∠ACB =∠CDB , 又∵∠B =∠B , ∴△ABC ∽△CBD ; (2)连接DO ,如解图,∵∠BDC =90°,E 为BC 的中点, ∴DE =CE =BE , ∴∠EDC =∠ECD ,第1题解图又∵OD =OC , ∴∠ODC =∠OCD ,而∠OCD +∠DCE =∠ACB =90°, ∴∠EDC +∠ODC =90°,即∠EDO =90°, ∴DE ⊥OD , ∵OD 为⊙O 的半径, ∴DE 与⊙O 相切.2. (1)证明:连接CE ,如解图, ∵CD 为⊙O 的直径, ∴∠CED =90°, ∵∠BCA =90°, ∴∠CED =∠BCO , ∵BO ∥DE , ∴∠BOC =∠CDE , ∴△CBO ∽△ECD , ∴CO DE =BO CD , ∴CO ·CD =DE ·BO ;(2)解:∵∠DFE =∠ECO ,CD =2·OC =10,∴在Rt △CDE 中,ED =CD ·sin ∠ECO =CD ·sin ∠DFE = 10×35=6,∴CE =CD 2-ED 2=102-62=8, 在Rt △CEG 中,EG CE =sin ∠ECG =35, ∴EG =35×8=245,第2题解图根据垂径定理得:EF =2EG =485. 3. (1)证明:如解图,连接OD , ∵AB 是⊙O 的直径, ∴∠ADB =90°, ∵AB =AC ,∴AD 垂直平分BC ,即DC =DB , ∴OD 为△BAC 的中位线, ∴OD ∥AC . 而DE ⊥AC , ∴OD ⊥DE , ∵OD 是⊙O 的半径, ∴EF 是⊙O 的切线;(2)解:∵∠DAC =∠DAB ,且∠AED =∠ADB =90°, ∴∠ADE =∠ABD ,在Rt △ADB 中,sin ∠ADE =sin ∠ABD =AD AB =45,而AB =10, ∴AD =8,在Rt △ADE 中,sin ∠ADE =AE AD =45, ∴AE =325, ∵OD ∥AE , ∴△FDO ∽△FEA ,∴OD AE =FO F A ,即5325=BF +5BF +10,第3题解图∴BF =907.4. (1)证明:如解图①,连接OD 、OE 、ED . ∵BC 与⊙O 相切于点D , ∴OD ⊥BC ,∴∠ODB =90°=∠C , ∴OD ∥AC , ∵∠B =30°, ∴∠A =60°, ∵OA =OE ,∴△AOE 是等边三角形, ∴AE =AO =OD ,∴四边形AODE 是平行四边行, ∵OA =OD ,∴平行四边形AODE 是菱形; (2)解:设⊙O 的半径为r . ∵OD ∥AC , ∴△OBD ∽△ABC ,∴OD AC =OBAB ,即10r =6(10-r ). 解得r =154, ∴⊙O 的半径为154.如解图②,连接OD 、DF 、AD . ∵OD ∥AC , ∴∠DAC =∠ADO ,第4题解图①∵OA =OD , ∴∠ADO =∠DAO , ∴∠DAC =∠DAO , ∵AF 是⊙O 的直径, ∴∠ADF =90°=∠C , ∴△ADC ∽△AFD , ∴AD AC =AF AD , ∴AD 2=AC ·AF ,∵AC =6,AF =154×2=152, ∴AD 2=152×6=45,∴AD =45=3 5.(9分) 5. 解:(1)存在,AE =CE . 理由如下:如解图①,连接AE ,ED , ∵AC 是△ABC 的斜边, ∴∠ABC =90°, ∴AE 为⊙O 的直径, ∴∠ADE =90°, 又∵D 是AC 的中点, ∴ED 为AC 的中垂线, ∴AE =CE ;(2)①如解图②,∵EF 是⊙O 的切线, ∴∠AEF =90°.第5题解图①由(1)可知∠ADE=90°,∴∠AED+∠EAD=90°,∵∠AED+∠DEF=90°,∴∠EAD=∠DEF.又∵∠ADE=∠EDF=90°∴△AED∽△EFD,∴ADED=EDFD,∴ED2=AD·FD.又∵AD=DC=CF,∴ED2=2AD·AD=2AD2,在Rt△AED中,∵AE2=AD2+ED2=3AD2,由(1)知∠AED=∠CED,又∵∠CED=∠CAB,∴∠AED=∠CAB,∴sin∠CAB=sin∠AED=ADAE=13=33.②sin∠CAB=a+2 a+2.【解法提示】由(2)中的①知ED2=AD·FD,∵CF=aCD(a>0),∴CF=aCD=aAD,∴ED2=AD·DF=AD(CD+CF)=AD(AD+aAD)=(a+1)AD2,在Rt△AED中,AE2=AD2+ED2=(a+2)AD2,∴sin ∠CAB =sin ∠AED =ADAE =1a +2=a +2a +2. 6. (1)证明:∵∠ODB =∠AEC ,∠AEC =∠ABC , ∴∠ODB =∠ABC , ∵OF ⊥BC , ∴∠BFD =90°,∴∠ODB +∠DBF =90°, ∴∠ABC +∠DBF =90°, 即∠OBD =90°, ∴BD ⊥OB , ∵OB 为⊙O 的半径, ∴BD 是⊙O 的切线;(2)证明:连接AC ,如解图①所示: ∵OF ⊥BC , ∴BE ︵=CE ︵, ∴∠ECH =∠CAE , ∵∠HEC =∠CEA , ∴△CEH ∽△AEC , ∴CE EH =EA CE , ∴CE 2=EH ·EA ;(3)解:连接BE ,如解图②所示: ∵AB 是⊙O 的直径, ∴∠AEB =90°,∵⊙O 的半径为5,sin ∠BAE =35,第6题解图①第6题解图②∴AB =10,BE =AB ·sin ∠BAE =10×35=6, 在Rt △AEB 中,EA =AB 2-BE 2=102-62=8, ∵BE ︵=CE ︵, ∴BE =CE =6, ∵CE 2=EH ·EA , ∴EH =CE 2EA =628=92,在Rt △BEH 中,BH =BE 2+EH 2=62+(92)2=152.7. (1)证明:连接OD ,如解图①, ∵AD 平分∠BAC 交⊙O 于D , ∴∠BAD =∠CAD , ∴BD ︵=CD ︵, ∴OD ⊥BC , ∵BC ∥DF , ∴OD ⊥DF , ∴DF 为⊙O 的切线;(2)解:连接OB ,连接OD 交BC 于P ,作BH ⊥DF 于H ,如解图①,∵∠BAC =60°,AD 平分∠BAC , ∴∠BAD =30°,∴∠BOD =2∠BAD =60°, 又∵OB =OD ,∴△OBD 为等边三角形, ∴∠ODB =60°,OB =BD =23,第7题解图①∴∠BDF =30°, ∵BC ∥DF , ∴∠DBP =30°,在Rt △DBP 中,PD =12BD =3,PB =3PD =3, 在Rt △DEP 中, ∵PD =3,DE =7,∴PE =(7)2-(3)2=2, ∵OP ⊥BC , ∴BP =CP =3,∴CE =CP -PE =3-2=1, 易证得△BDE ∽△ACE , ∴BE AE =DE CE ,即5AE =71, ∴AE =577. ∵BE ∥DF , ∴△ABE ∽△AFD ,∴BE DF =AE AD ,即5DF =5771277,解得DF =12,在Rt △BDH 中,BH =12BD =3, ∴S 阴影=S △BDF -S 弓形BD =S △BDF -(S 扇形BOD -S △BOD )=12·12·3-60·π·(23)2360+34·(23)2=93-2π;(7分)(3)解:连接CD ,如解图②,由AB AC =43可设AB =4x ,AC =3x ,BF =y , ∵BD ︵=CD ︵, ∴CD =BD =23, ∵DF ∥BC ,∴∠F =∠ABC =∠ADC , ∴∠FDB =∠DBC =∠DAC , ∴△BFD ∽△CDA , ∴BD AC =BF CD ,即233x =y 23,∴xy =4,∵∠FDB =∠DBC =∠DAC =∠F AD , 而∠DFB =∠AFD , ∴△FDB ∽△F AD , ∴DF AF =BF DF , ∵DF +BF =8, ∴DF =8-BF =8-y , ∴8-y y +4x =y 8-y , 整理得:16-4y =xy , ∴16-4y =4,解得y =3, 即BF 的长为3.(10分) 三、与全等三角形结合第7题解图②针对演练1. (1)证明:连接OE ,过点O 作OF ⊥PN ,如解图所示, ∵PM 与⊙O 相切, ∴OE ⊥PM ,∴∠OEP =∠OFP =90°, ∵PC 平分∠MPN , ∴∠EPO =∠FPO , 在△PEO 和△PFO 中, ⎩⎪⎨⎪⎧∠EPO =∠FPO ∠OEP =∠OFP OP =OP, ∴△PEO ≌△PFO (AAS), ∴OF =OE ,∴OF 为圆O 的半径且OF ⊥PN, 则PN 与⊙O 相切;(2)解:在Rt △EPO 中,∠MPC =30°,PE =23, ∴∠EOP =60°,OE =PE ·tan30°=2, ∴∠EOB =120°,则劣弧BE ︵的长为120π×2180=4π3.2. (1)证明:如解图①,连接BO 并延长交⊙O 于点N ,连接CN , ∵∠BMC =60°, ∴∠BNC =60°, ∵∠BNC +∠NBC =90°, ∴∠NBC =30°,又∵△ABC 为等边三角形,第1题解图∴∠BAC =∠ABC =∠ACB =60°, ∴∠ABN =30°+60°=90°, ∴AB ⊥BO ,即AB 为⊙O 的切线.(2)解:BE +CF =3,是定值. 理由如下:如解图②,连接D 与AC 的中点P , ∵D 为BC 中点, ∴AD ⊥BC , ∴PD =PC =12AC , 又∵∠ACB =60°,∴PD =PC =CD =BD =12AC , ∴∠DPF =∠PDC =60°, ∴∠PDF +∠FDC =60°, 又∵∠EDF =120°, ∴∠BDE +∠FDC =60°, ∴∠PDF =∠BDE , 在△BDE 和△PDF 中, ⎩⎪⎨⎪⎧∠EBD =∠DPF BD =PD∠BDE =∠PDF, ∴△BDE ≌△PDF (ASA), ∴BE =PF ,∴BE +CF =PF +CF =CP =BD , ∵OB ⊥AB ,∠ABC =60°,第2题解图②∴∠OBC =30°, 又∵OB =2,∴BD =OB ·cos30°=2×32=3, 即BE +CF = 3.3. (1)证明:连接OC ,如解图①, ∵OD ⊥AC ,OC =OA , ∴∠AOD =∠COD . 在△AOE 和△COE 中, ⎩⎪⎨⎪⎧OA =OC ∠AOE =∠COE OE =OE, ∴△AOE ≌△COE (SAS), ∴∠EAO =∠ECO . 又∵EC 是⊙O 的切线, ∴∠ECO =90°, ∴∠EAO =90°. ∴AE 与⊙O 相切;(2)解:设DO =t ,则DE =3t ,EO =4t , 在△EAO 和△ADO 中,⎩⎪⎨⎪⎧∠EOA =∠AOD ∠EAO =∠ADO, ∴△EAO ∽△ADO , ∴AO DO =EO AO ,即9t =4t 9, ∴t =92,即EO =18.第3题解图①∴AE =EO 2-AO 2=182-92=93;延长BD 交AE 于点F ,过O 作OG ∥AE 交BD 于点G , 如解图②, ∵OG ∥AE , ∴∠FED =∠GOD 又∵∠EDF =∠ODG , ∴△EFD ∽△OGD , ∴EF OG =ED OD =31,即EF =3GO . 又∵O 是AB 的中点, ∴AF =2GO ,∴AE =AF +FE =5GO , ∴5GO =93, ∴GO =935, ∴AF =1835, ∴tan B =AF AB =35.4. (1)证明:如解图,连接OB , ∵PB 是⊙O 的切线, ∴∠PBO =90°,∵OA =OB ,BA ⊥PO 于点D , ∴AD =BD ,∠POA =∠POB , 又∵PO =PO ,∴△P AO ≌△PBO (SAS), ∴∠P AO =∠PBO =90°,第3题解图②第4题解图∴OA ⊥P A ,∴直线P A 为⊙O 的切线;(2)解:线段EF 、OD 、OP 之间的等量关系为EF 2=4OD ·OP . 证明:∵∠P AO =∠PDA =90°,∴∠OAD +∠AOD =90°,∠OP A +∠AOP =90°,∴∠OAD =∠OP A ,∴△OAD ∽△OP A ,∴ OD OA =OA OP ,即OA 2=OD ·OP ,又∵EF =2OA ,∴EF 2=4OD ·OP ;(3)解:∵OA =OC ,AD =BD ,BC =6,∴OD =12BC =3,设AD =x ,∵tan ∠F =12,∴FD =2x ,OA =OF =FD -OD =2x -3,在Rt △AOD 中,由勾股定理,得(2x -3)2=x 2+32,解之得,x 1=4,x 2=0(不合题意,舍去),∴AD =4,OA =2x -3=5,∵AC 是⊙O 直径,∴∠ABC =90°,又∵AC =2OA =10,BC =6,∴ cos ∠ACB =610=35.∵OA 2=OD ·OP ,∴3(PE +5)=25,∴PE =103.5. (1)证明:连接OD ,如解图,∵AB 为⊙O 的直径,∴∠ACB =90°,∵∠ACB 的平分线交⊙O 于点D ,∴∠ACD =∠BCD =45°,∴∠DAB =∠ABD =45°,∴△DAB 为等腰直角三角形,∴DO ⊥AB ,∵PD 为⊙O 的切线,∴OD ⊥PD ,∴PD ∥AB ;(2)证明:∵AE ⊥CD 于点E ,BF ⊥CD 于点F ,∴AE ∥BF ,∴∠FBO =∠EAO ,∵△DAB 为等腰直角三角形,∴∠EDA +∠FDB =90°,∵∠FBD +∠FDB =90°,∴∠FBD =∠EDA ,在△FBD 和△EDA 中,⎩⎪⎨⎪⎧∠BFD =∠DEA ∠FBD =∠EDA BD =DA, ∴△FBD ≌△EDA (AAS),∴DE =BF ;第5题解图(3)解:在Rt △ACB 中,∵AC =6,tan ∠CAB =43,∴BC =6×43=8,∴AB =AC 2+BC 2=62+82=10,∵△DAB 为等腰直角三角形,∴AD =AB 2=52, ∵AE ⊥CD ,∴△ACE 为等腰直角三角形,∴AE =CE =AC 2=62=32, 在Rt △AED 中,DE =AD 2-AE 2=(52)2-(32)2=42,∴CD =CE +DE =32+42=72,∵AB ∥PD ,∴∠PDA =∠DAB =45°,∴∠PDA =∠PCD ,又∵∠DP A =∠CPD ,∴△PDA ∽△PCD ,∴PD PC =P A PD =AD DC =5272=57, ∴P A =57PD ,PC =75PD ,又∵PC =P A +AC ,∴57PD +6=75PD ,解得PD =354,∴PC =57PD +6=57×354+6=254+6=494.6. (1)证明:如解图①,连接OC ,∵P A 切⊙O 于点A ,∴∠P AO =90°,∵BC ∥OP ,∴∠AOP =∠OBC ,∠COP =∠OCB ,∵OC =OB ,∴∠OBC =∠OCB ,∴∠AOP =∠COP ,在△P AO 和△PCO 中,⎩⎪⎨⎪⎧OA =OC ∠AOP =∠COP OP =OP, ∴△P AO ≌△PCO (SAS),∴∠PCO =∠P AO =90°,∴OC ⊥PC ,∵OC 为⊙O 的半径,∴PC 是⊙O 的切线;(2)解:由(1)得P A ,PC 都为圆的切线,∴P A =PC ,OP 平分∠APC ,∠ADO =∠P AO =90°, ∴∠P AD +∠DAO =∠DAO +∠AOD ,又∵∠ADP =∠ADO ,∴∠P AD =∠AOD ,∴△ADP ∽△ODA ,∴AD PD =DO AD ,第6题解图①∴AD 2=PD ·DO ,∵AC =8,PD =163, ∴AD =12AC =4,OD =3,在Rt △ADO 中,AO =AD 2+OD 2=5,由题意知OD 为△ABC 的中位线,∴BC =6,AB =BC 2+AC 2=10.∴S 阴影=12S ⊙O -S △ABC =12·π·52-12×6×8=25π2-24;(3)解:如解图②,连接AE 、BE ,作BM ⊥CE 于点M , ∴∠CMB =∠EMB =∠AEB =90°,∵点E 是AB ︵的中点,∴AE =BE ,∠EAB =∠EBA =45°,∴∠ECB =∠CBM =∠ABE =45°,CM =MB =BC ·sin45°=32,BE =AB ·cos45°=52,∴EM =BE 2-BM 2=42,则CE =CM +EM =7 2.7. (1)证明:连接OD ,如解图①所示,∵OB =OD ,∴∠ODB =∠OBD .∵OG ∥BD ,∴∠AOG =∠OBD ,∠GOD =∠ODB ,∴∠DOG =∠AOG ,在△DOG 和△AOG 中,第6题解图②第7题解图①⎩⎪⎨⎪⎧OD =OA ∠DOG =∠AOG OG =OG, ∴△DOG ≌△AOG (SAS),∴GD =GA ;(2)证明:∵AG 切⊙O 于点A ,∴AG ⊥OA ,∴∠OAG =90°,∵△DOG ≌△AOG ,∴∠OAG =∠ODG =90°,∴∠ODE =180°-∠ODG =90°,∴∠ODC +∠FDE =90°,∵OC ⊥AB ,∴∠COB =90°,∴∠OCD +∠OFC =90°,∵OC =OD ,∴∠ODC =∠OCD ,∴∠FDE =∠OFC ,∵∠OFC =∠EFD ,∴∠EFD =∠EDF ,∴EF =ED ,∴△DEF 是等腰三角形;(3)解:过点B 作BK ⊥OD 于点K ,如解图②所示: 则∠OKB =∠BKD =∠ODE =90°,∴BK ∥DE ,∴∠OBK =∠E ,∵BH ⊥GE ,∴∠BHD =∠BHE =90°, ∴四边形KDHB 为矩形, ∴KD =BH =9,∴OK =OD -KD =72,在Rt △OKB 中,∵OK 2+KB 2=OB 2,OB =252, ∴KB =12,∴tan ∠E =tan ∠OBK =OK KB =724,sin ∠E =sin ∠OBK =OK OB =725,∵tan ∠E =OD DE =724,∴DE =3007,∴EF =3007,∵sin ∠E =BH BE =725,∴BE =2257,∴BF =EF -BE =757,∴OF =OB -BF =2514,在Rt △COF 中,∠COB =90°, ∴OC 2+OF 2=FC 2,∴FC =125214,在Rt △COB 中,∵OC 2+OB 2=BC 2,OC =OB =252, ∴BC =2522,∴BC +CF +BF =1502+757, ∴△CBF 的周长=1502+757.。
2016年中考数学复习专题学生版:圆的有关计算(含14.15中考真题解析)
专题24 圆的有关计算☞解读考点☞2年中考【2015年题组】1.(2015河池)如图,用一张半径为24cm的扇形纸板制作一顶圆锥形帽子(接缝忽略不计),如果圆锥形帽子的底面半径为10cm,那么这张扇形纸板的面积是()B.480πcm2 C.1200πcm2 D.2400πcm2 2015凉山州)将圆心角为90°,面积为4πcm2的扇形围成一个圆锥的侧面,)B.2cm C.3cm D.4cm2015德州)如图,要制作一个圆锥形的烟囱帽,使底面圆的半径与母线长的比是4:5,那么所需扇形铁皮的圆心角应为()A.288°B.144°C.216°D.120°2015宁波)如图,用一个半径为30cm,面积为300πcm2的扇形铁皮,制作一个无底的圆锥(不计损耗),则圆锥的底面半径r为()A.5cm B.10cm C.20cm D.5πcm5.(2015苏州)如图,AB为⊙O的切线,切点为B,连接AO,AO与⊙O交于点C,BD为⊙O的直径,连接CD.若∠A=30°,⊙O的半径为2,则图中阴影部分的面积为()A.43π B.43π- C.π D.23π-6.(2015成都)如图,正六边形ABCDEF 内接于⊙O ,半径为4,则这个正六边形的边心距OM 和BC 弧线的长分别为( )A .2,3πB.π C23π D.43π7.(2015甘孜州)如图,已知扇形AOB 的半径为2,圆心角为90°,连接AB ,则图中阴影部分的面积是( )A .π﹣2B .π﹣4C .4π﹣2D .4π﹣4 8.(2015攀枝花)如图,已知⊙O 的一条直径AB 与弦CD 相交于点E ,且AC=2,CE=1,则图中阴影部分的面积为( )ABC .29πD .49π9.(2015自贡)如图,AB 是⊙O 的直径,弦CD ⊥AB ,∠CDB =30°,CD =32,则阴影部分的面积为( )A .2πB .πC .3πD .32π10.(2015达州)如图,直径AB 为12的半圆,绕A 点逆时针旋转60°,此时点B 旋转到点B′,则图中阴影部分的面积是( )A .12πB .24πC .6πD .36π【答案】B .11.(2015德阳)如图,已知⊙O 的周长为4π,AB 的长为π,则图中阴影部分的面积为( )A .2π- B.π C .π D .212.(2015梧州)如图,在边长为6的正方形ABCD 中,E 是AB 的中点,以E 为圆心,ED 为半径作半圆,交A 、B 所在的直线于M 、N 两点,分别以直径MD 、ND 为直径作半圆,则阴影部分面积为( )A. B. C. D.13.(2015咸宁)如图,在△ABC 中,CA=CB ,∠ACB=90°,以AB 的中点D 为圆心,作圆心角为90°的扇形DEF ,点C 恰在EF 上,设∠BDF=α(0°<α<90°),当α由小到大变化时,图中阴影部分的面积( )A .由小到大B .由大到小C .不变D .先由小到大,后由大到小 14.(2015常德)若两个扇形满足弧长的比等于它们半径的比,则这称这两个扇形相似.如图,如果扇形AOB 与扇形A1O1B1是相似扇形,且半径OA :O 1A 1=k (k 为不等于0的常数).那么下面四个结论:①∠AOB=∠A 1O 1B 1;②△AOB ∽△A1O1B1;③11ABk A B =;④扇形AOB 与扇形A 1O 1B 1的面积之比为2k .成立的个数为( )A .1个B .2个C .3个D .4个 15.(2015邵阳)如图,在矩形ABCD 中,已知AB=4,BC=3,矩形在直线l 上绕其右下角的顶点B 向右旋转90°至图①位置,再绕右下角的顶点继续向右旋转90°至图②位置,…,以此类推,这样连续旋转2015次后,顶点A 在整个旋转过程中所经过的路程之和是( )A.2015π B.3019.5π C.3018π D.3024π16.(2015北海)用一个圆心角为120°,半径为6的扇形作一个圆锥的侧面,这个圆锥的底面圆的半径是.17.(2015贵港)如图,已知圆锥的底面⊙O的直径BC=6,高OA=4,则该圆锥的侧面展开图的面积为.18.(2015庆阳)如图,Rt△ABC中,∠ACB=90°,AC=BC=若把Rt△ABC 绕边AB所在直线旋转一周,则所得几何体的表面积为(结果保留π).19.(2015贺州)如图,在矩形ABCD中,AB=3,AD=4,将矩形ABCD绕点D 顺时针旋转90°得到矩形A′B′C′D′,则点B经过的路径与BA,AC′,C′B′所围成封闭图形的面积是(结果保留π).20.(2015天水)如图,△ABC是正三角形,曲线CDEF叫做正三角形的渐开线,其中弧CD、弧DE、弧EF的圆心依次是A、B、C,如果AB=1,那么曲线CDEF 的长是.21.(2015河南省)如图,在扇形AOB中,∠AOB=90°,点C为OA的中点,CE⊥OA交AB于点E,以点O为圆心,OC的长为半径作CD交OB于点D.若OA=2,则阴影部分的面积为.22.(2015烟台)如图,将弧长为6π,圆心角为120°的圆形纸片AOB围成圆锥形纸帽,使扇形的两条半径OA与OB重合(粘连部分忽略不计)则圆锥形纸帽的高是.23.(2015乐山)如图,已知A(2)、B(1),将△AOB绕着点O逆时针旋转,使点A旋转到点A′(﹣2,为.24.(2015镇江)图①是我们常见的地砖上的图案,其中包含了一种特殊的平面图形﹣正八边形.(1)如图②,AE是⊙O的直径,用直尺和圆规作⊙O的内接正八边形ABCDEFGH (不写作法,保留作图痕迹);(2)在(1)的前提下,连接OD,已知OA=5,若扇形OAD(∠AOD<180°)是一个圆锥的侧面,则这个圆锥底面圆的半径等于.26.(2015玉林防城港)如图,在⊙O中,AB是直径,点D是⊙O上一点且∠BOD=60°,过点D作⊙O的切线CD交AB的延长线于点C,E为AD的中点,连接DE,EB.(1)求证:四边形BCDE是平行四边形;(2)已知图中阴影部分面积为6π,求⊙O的半径r.27.(2015扬州)如图,已知⊙O的直径AB=12cm,AC是⊙O的弦,过点C作⊙O 的切线交BA的延长线于点P,连接BC.(1)求证:∠PCA=∠B;(2)已知∠P=40°,点Q在优弧ABC上,从点A开始逆时针运动到点C停止(点Q与点C不重合),当△ABQ与△ABC的面积相等时,求动点Q所经过的弧长.【2014年题组】1.(2014·扬州)如图,已知正方形边长为1,若圆与正方形的四条边都相切,则阴影部分的面积与下列各数最接近的是()A.1.0B.2.0 C.3.0 D.4.02.(2014·金华)一张圆心角为45°的扇形纸板和圆形纸板按如图方式剪得一个正方形,边长都为1,则扇形纸板和圆形纸板的面积比是()A.5:4B.5:2C2D3.(2014·辽宁省本溪市)底面半径为4,高为3的圆锥的侧面积是()A.12πB.15πC.20πD.36π4.(2014·山东省莱芜市)一个圆锥的侧面展开图是半径为R的半圆,则该圆锥的高是()5.(2014·贵州安顺市)已知圆锥的母线长为6cm,底面圆的半径为3cm,则此圆锥侧面展开图的圆心角是()A. 30°B. 60°C. 90°D. 180°6.(湖南衡阳市)圆心角为120 ,弧长为12π的扇形半径为()A.6B.9C.18D.367.(2014南京)如图,沿一条母线将圆锥侧面剪开并展开,得到一个扇形,若圆锥底面圆半径r=2cm,扇形圆心角120θ=︒,则该圆锥母线长l为cm.8.(2014·呼和浩特)一个底面直径是80cm,母线长为90cm的圆锥的侧面展开图的圆心角的度数为.9.(2014·潍坊)如图,两个半径均为3的⊙O1与⊙O2相交于A、B两点,且每个圆都经过另一个圆的圆心,则图中阴影部分的面积为.(结果保留π)10.(2014·重庆A)如图,△OAB中,OA=OB=4,∠A=30°,AB与⊙O相切于点C,则图中阴影部分的面积为.(结果保留π)【例1】在半径为2的圆中,弦AB的长为2,则AB的长等于()A.3πB.2πC.23πD.32π【例2】如图,将长为8cm的铁丝AB首尾相接围成半径为2cm的扇形,则S扇形= cm²【例3】一个圆锥的高为4cm,底面圆的半径为3cm,则这个圆锥的侧面积为()A. 12πcm2 B.15πcm2 C.20πcm2 D.30πcm2归纳4:阴影部分面积基本方法归纳:求阴影面积常用的方法:①直接用公式法;②和差法;③割补法.注意问题归纳:求阴影面积的主要思路是将不规则图形面积转化为规则图形的面积.【例4】如图,扇形OAB中,∠AOB=60°,扇形半径为4,点C在 AB上,CD⊥OA,垂足为点D,当△OCD的面积最大时,图中阴影部分的面积为.1.(2015届湖北省宜昌市兴山县校级模拟)劳技课上,小颖将一顶自制的圆锥形纸帽戴在头上,已知纸帽底面圆半径为10cm,母线长50cm,则这顶纸帽的侧面积为()cm2.A.250π B.500π C.750π D.1000π2.(2015届湖北省广水市校级模拟)如图,圆锥体的高h=2cm,底面半径r=2cm,则圆锥体的全面积为()cm2.A.4π B.8π C.12π D.(4+4)π3.(2015届山东省高密市模拟考试)如果圆锥的母线长为5cm,底面半径为2cm,那么这个圆锥的侧面积是()A.210cm B.210cmπC.220cm D.220cmπ4.(2015届山东省新泰市模拟考试)如图,Rt ABC△中,90ACB∠= ,30CAB∠= ,2BC=,O H,分别为边AB AC,的中点,将ABC△绕点B顺时针旋转120 到11A BC△的位置,则整个旋转过程中线段OH所扫过部分的面积(即阴影部分面积)为()A.7π3-B.4π3+C.πD.4π3+5.(2015届江苏省兴化顾庄等三校校级模拟)若粮仓顶部是圆锥形,且这个圆锥的高为2m,母线长为2.5m,为防雨需在粮仓顶部铺上油毡,则这块油毡的面积是m2.6.(2015届河南省三门峡市模拟考试)如图,在Rt△ABC中,∠ABC=90°,AB =8,BC=6,分别以A、C为圆心,以2AC的长为半径作圆,将Rt△ABC截去两个扇形,则剩余(阴影)部分的面积为.7.(2015届湖北省武汉市校级模拟)如图,在边长为1的正方形组成的网格中,△ABC的顶点均在格点上,点A、B、C的坐标分别是A(-2,3)、B(-1,2)、C (-3,1),△ABC绕点O顺时针旋转90°后得到△A1B1C1.(1)在正方形网格中作出△A1B1C1;(2)求点A经过的路径弧AA1的长度;(结果保留π)(3)在y轴上找一点D,使DB+DB1的值最小,并直接写出D点坐标.8.(2015届广东省中山市校级模拟)如图,AB 是的直径,点D 在上,∠DAB =45°,BC∥AD,CD∥AB.(1)、判断直线CD 与的位置关系,并说明理由;(2)、若的半径为1,求图中阴影部分的面积(结果保留π).9.(2015届山东省博兴县校级模拟)如图,点B、C、D都在半径为6的⊙O上,过点C作AC∥BD交OB延长线于点A,连接CD,且∠CDB=∠OBD=30°.(1)求证:AC是⊙O的切线;(2)求弦BD的长;(3)求图中阴影部分的面积.10.(2015届山东省高密市模拟考试)如图,BE是⊙O的直径,点A在EB的延长线上,弦PD⊥BE,垂足为C,连接OD,∠AOD=∠APC.(1)求证:AP是⊙O的切线.(2)若⊙O的半径是4,。
中考数学圆的综合(大题培优 易错 难题)及详细答案

中考数学圆的综合(大题培优易错难题)及详细答案一、圆的综合1.如图,⊙O是△ABC的外接圆,点E为△ABC内切圆的圆心,连接AE的延长线交BC于点F,交⊙O于点D;连接BD,过点D作直线DM,使∠BDM=∠DAC.(1)求证:直线DM是⊙O的切线;(2)若DF=2,且AF=4,求BD和DE的长.【答案】(1)证明见解析(2)23【解析】【分析】(1)根据垂径定理的推论即可得到OD⊥BC,再根据∠BDM=∠DBC,即可判定BC∥DM,进而得到OD⊥DM,据此可得直线DM是⊙O的切线;(2)根据三角形内心的定义以及圆周角定理,得到∠BED=∠EBD,即可得出DB=DE,再判定△DBF∽△DAB,即可得到DB2=DF•DA,据此解答即可.【详解】(1)如图所示,连接OD.∵点E是△ABC的内心,∴∠BAD=∠CAD,∴BD CD=,∴OD⊥BC.又∵∠BDM=∠DAC,∠DAC=∠DBC,∴∠BDM=∠DBC,∴BC∥DM,∴OD⊥DM.又∵OD为⊙O半径,∴直线DM是⊙O的切线.(2)连接BE.∵E为内心,∴∠ABE=∠CBE.∵∠BAD=∠CAD,∠DBC=∠CAD,∴∠BAD=∠DBC,∴∠BAE+∠ABE=∠CBE+∠DBC,即∠BED=∠DBE,∴BD=DE.又∵∠BDF=∠ADB(公共角),∴△DBF∽△DAB,∴DF DBDB DA=,即DB2=DF•DA.∵DF=2,AF=4,∴DA=DF+AF=6,∴DB2=DF•DA=12,∴DB=DE=23.【点睛】本题主要考查了三角形的内心与外心,圆周角定理以及垂径定理的综合应用,解题时注意:平分弦所对一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧;三角形的内心到三角形三边的距离相等;三角形的内心与三角形顶点的连线平分这个内角.2.如图1,将长为10的线段OA绕点O旋转90°得到OB,点A的运动轨迹为AB,P是半径OB上一动点,Q是AB上的一动点,连接PQ.发现:∠POQ=________时,PQ有最大值,最大值为________;思考:(1)如图2,若P是OB中点,且QP⊥OB于点P,求BQ的长;(2)如图3,将扇形AOB沿折痕AP折叠,使点B的对应点B′恰好落在OA的延长线上,求阴影部分面积;探究:如图4,将扇形OAB沿PQ折叠,使折叠后的弧QB′恰好与半径OA相切,切点为C,若OP=6,求点O到折痕PQ的距离.【答案】发现: 90°,102;思考:(1)103π=;(2)25π−1002+100;(3)点O到折痕PQ的距离为30.【解析】分析:发现:先判断出当PQ取最大时,点Q与点A重合,点P与点B重合,即可得出结论;思考:(1)先判断出∠POQ=60°,最后用弧长用弧长公式即可得出结论;(2)先在Rt△B'OP中,OP2+(102−10)2=(10-OP)2,解得OP=102−10,最后用面积的和差即可得出结论.探究:先找点O关于PQ的对称点O′,连接OO′、O′B、O′C、O′P,证明四边形OCO′B是矩形,由勾股定理求O′B,从而求出OO′的长,则OM=12OO′=30.详解:发现:∵P是半径OB上一动点,Q是AB上的一动点,∴当PQ取最大时,点Q与点A重合,点P与点B重合,此时,∠POQ=90°,PQ=22OA OB+=102;思考:(1)如图,连接OQ,∵点P 是OB 的中点,∴OP=12OB=12OQ . ∵QP ⊥OB ,∴∠OPQ=90° 在Rt △OPQ 中,cos ∠QOP=12OP OQ =, ∴∠QOP=60°,∴l BQ =6010101803ππ⨯=; (2)由折叠的性质可得,BP =B ′P ,AB ′=AB =102,在Rt △B'OP 中,OP 2+(102−10)2=(10-OP )2解得OP=102−10,S 阴影=S 扇形AOB -2S △AOP =290101210(10210)3602π⨯-⨯⨯⨯- =25π−1002+100;探究:如图2,找点O 关于PQ 的对称点O′,连接OO′、O′B 、O′C 、O′P ,则OM=O′M ,OO′⊥PQ ,O′P=OP=3,点O′是B Q '所在圆的圆心,∴O′C=OB=10,∵折叠后的弧QB′恰好与半径OA 相切于C 点,∴O′C ⊥AO ,∴O′C ∥OB ,∴四边形OCO′B 是矩形,在Rt △O′BP 中,226425-=在Rt △OBO′K ,2210(25)=230-,∴OM=12OO ′=12×23030 即O 到折痕PQ 30点睛:本题考查了折叠问题和圆的切线的性质、矩形的性质和判定,熟练掌握弧长公式l=180n R π(n 为圆心角度数,R 为圆半径),明确过圆的切线垂直于过切点的半径,这是常考的性质;对称点的连线被对称轴垂直平分.3.如图,已知在△ABC中,AB=15,AC=20,tanA=12,点P在AB边上,⊙P的半径为定长.当点P与点B重合时,⊙P恰好与AC边相切;当点P与点B不重合时,⊙P与AC边相交于点M和点N.(1)求⊙P的半径;(2)当AP=65时,试探究△APM与△PCN是否相似,并说明理由.【答案】(1)半径为35;(2)相似,理由见解析.【解析】【分析】(1)如图,作BD⊥AC,垂足为点D,⊙P与边AC相切,则BD就是⊙P的半径,利用解直角三角形得出BD与AD的关系,再利用勾股定理可求得BD的长;(2)如图,过点P作PH⊥AC于点H,作BD⊥AC,垂足为点D,根据垂径定理得出MN=2MH,PM=PN,再利用勾股定理求出PH、AH、MH、MN的长,从而求出AM、NC的长,然后求出AMMP、PNNC的值,得出AMMP=PNNC,利用两边对应成比例且夹角相等的两三角形相似即可证明.【详解】(1)如图,作BD⊥AC,垂足为点D,∵⊙P与边AC相切,∴BD就是⊙P的半径,在Rt△ABD中,tanA= 1BD2AD ,设BD=x,则AD=2x,∴x2+(2x)2=152,解得:5∴半径为5(2)相似,理由见解析,如图,过点P 作PH ⊥AC 于点H ,作BD ⊥AC ,垂足为点D ,∴PH 垂直平分MN ,∴PM=PN ,在Rt △AHP 中,tanA=12PH AH =, 设PH=y ,AH=2y ,y 2+(2y )2=(65)2解得:y=6(取正数),∴PH=6,AH=12,在Rt △MPH 中,MH=()22356-=3,∴MN=2MH=6,∴AM=AH-MH=12-3=9,NC=AC-MN-AM=20-6-9=5,∴935535AM MP ==,355PN NC =, ∴AM MP =PN NC, 又∵PM=PN ,∴∠PMN=∠PNM ,∴∠AMP=∠PNC ,∴△AMP ∽△PNC.【点睛】本题考查了解直角三角形、垂径定理、相似三角形的判定与性质等,综合性较强,有一定的难度,正确添加辅助线、灵活应用相关的性质与定理是解题的关键.4.如图,CD 为⊙O 的直径,点B 在⊙O 上,连接BC 、BD ,过点B 的切线AE 与CD 的延长线交于点A ,AEO C =∠∠,OE 交BC 于点F .(1)求证:OE ∥BD ;(2)当⊙O 的半径为5,2sin 5DBA ∠=时,求EF 的长.【答案】(1)证明见解析;(2)EF 的长为212 【解析】 试题分析:(1)连接OB ,利用已知条件和切线的性质证明;(2)根据锐角三角函数和相似三角形的性质,直接求解即可.试题解析:(1)连接OB , ∵CD 为⊙O 的直径 , ∴ 90CBD CBO OBD ∠=∠+∠=︒. ∵AE 是⊙O 的切线,∴ 90ABO ABD OBD ∠=∠+∠=︒. ∴ ABD CBO ∠=∠. ∵OB 、OC 是⊙O 的半径,∴OB=OC . ∴C CBO ∠=∠. ∴C ABD ∠=∠.∵E C ∠=∠,∴E ABD ∠=∠. ∴ OE ∥BD .(2)由(1)可得sin ∠C = ∠DBA= 25,在Rt △OBE 中, sin ∠C =25BD CD =,OC =5, 4BD =∴90CBD EBO ∠=∠=︒∵E C ∠=∠,∴△CBD ∽△EBO .∴BD CD BO EO= ∴252EO =. ∵OE ∥BD ,CO =OD ,∴CF =FB .∴122OF BD ==. ∴212EF OE OF =-=5.如图,AB 是⊙O 的直径,PA 是⊙O 的切线,点C 在⊙O 上,CB ∥PO .(1)判断PC 与⊙O 的位置关系,并说明理由;(2)若AB=6,CB=4,求PC 的长.【答案】(1)PC是⊙O的切线,理由见解析;(2)35 2【解析】试题分析:(1)要证PC是⊙O的切线,只要连接OC,再证∠PCO=90°即可.(2)可以连接AC,根据已知先证明△ACB∽△PCO,再根据勾股定理和相似三角形的性质求出PC的长.试题解析:(1)结论:PC是⊙O的切线.证明:连接OC∵CB∥PO∴∠POA=∠B,∠POC=∠OCB∵OC=OB∴∠OCB=∠B∴∠POA=∠POC又∵OA=OC,OP=OP∴△APO≌△CPO∴∠OAP=∠OCP∵PA是⊙O的切线∴∠OAP=90°∴∠OCP=90°∴PC是⊙O的切线.(2)连接AC∵AB是⊙O的直径∴∠ACB=90°(6分)由(1)知∠PCO=90°,∠B=∠OCB=∠POC∵∠ACB=∠PCO∴△ACB∽△PCO∴∴.点睛:本题考查了切线的判定.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.同时考查了勾股定理和相似三角形的性质.6.如图,AB是⊙O的直径,点C,D是半圆O的三等分点,过点C作⊙O的切线交AD的延长线于点E,过点D作DF⊥AB于点F,交⊙O于点H,连接DC,AC.(1)求证:∠AEC=90°;(2)试判断以点A,O,C,D为顶点的四边形的形状,并说明理由;(3)若DC=2,求DH的长.【答案】(1)证明见解析;(2)四边形AOCD为菱形;(3)DH=2.【解析】试题分析:(1)连接OC,根据EC与⊙O切点C,则∠OCE=90°,由题意得,∠DAC=∠CAB,即可证明AE∥OC,则∠AEC+∠OCE=180°,从而得出∠AEC=90°;(2)四边形AOCD为菱形.由(1)得,则∠DCA=∠CAB可证明四边形AOCD是平行四边形,再由OA=OC,即可证明平行四边形AOCD是菱形(一组邻边相等的平行四边形是菱形);(3)连接OD.根据四边形AOCD为菱形,得△OAD是等边三角形,则∠AOD=60°,再由DH⊥AB于点F,AB为直径,在Rt△OFD中,根据sin∠AOD=,求得DH的长.试题解析:(1)连接OC,∵EC与⊙O切点C,∴OC⊥EC,∴∠OCE=90°,∵点CD是半圆O的三等分点,∴,∴∠DAC=∠CAB,∵OA=OC,∴∠CAB=∠OCA,∴∠DAC=∠OCA,∴AE∥OC(内错角相等,两直线平行)∴∠AEC+∠OCE=180°,∴∠AEC=90°;(2)四边形AOCD为菱形.理由是:∵,∴∠DCA=∠CAB,∴CD∥OA,又∵AE∥OC,∴四边形AOCD是平行四边形,∵OA=OC,∴平行四边形AOCD是菱形(一组邻边相等的平行四边形是菱形);(3)连接OD.∵四边形AOCD为菱形,∴OA=AD=DC=2,∵OA=OD,∴OA=OD=AD=2,∴△OAD是等边三角形,∴∠AOD=60°,∵DH⊥AB于点F,AB为直径,∴DH=2DF,在Rt△OFD中,sin∠AOD=,∴DF=ODsin∠AOD=2sin60°=,∴DH=2DF=2.考点:1.切线的性质2.等边三角形的判定与性质3.菱形的判定与性质4.解直角三角形.7.如图,AB是圆O的直径,射线AM⊥AB,点D在AM上,连接OD交圆O于点E,过点D作DC=DA交圆O于点C(A、C不重合),连接O C、BC、CE.(1)求证:CD是⊙O的切线;(2)若圆O的直径等于2,填空:①当AD=时,四边形OADC是正方形;②当AD=时,四边形OECB是菱形.【答案】(1)见解析;(2)①1;②3.【解析】试题分析:(1)依据SSS证明△OAD≌△OCD,从而得到∠OCD=∠OAD=90°;(2)①依据正方形的四条边都相等可知AD=OA;②依据菱形的性质得到OE=CE,则△EOC为等边三角形,则∠CEO=60°,依据平行线的性质可知∠DOA=60°,利用特殊锐角三角函数可求得AD的长.试题解析:解:∵AM⊥AB,∴∠OAD=90°.∵OA=OC,OD=OD,AD=DC,∴△OAD≌△OCD,∴∠OCD=∠OAD=90°.∴OC⊥CD,∴CD是⊙O的切线.(2)①∵当四边形OADC是正方形,∴AO=AD=1.故答案为:1.②∵四边形OECB是菱形,∴OE=CE.又∵OC=OE,∴OC=OE=CE.∴∠CEO=60°.∵CE∥AB,∴∠AOD=60°.在Rt△OAD中,∠AOD=60°,AO=1,∴AD=.故答案为:.点睛:本题主要考查的是切线的性质和判定、全等三角形的性质和判定、菱形的性质、等边三角形的性质和判定,特殊锐角三角函数值的应用,熟练掌握相关知识是解题的关键.8.四边形ABCD内接于⊙O,点E为AD上一点,连接AC,CB,∠B=∠AEC.(1)如图1,求证:CE=CD;(2)如图2,若∠B+∠CAE=120°,∠ACD=2∠BAC,求∠BAD的度数;(3)如图3,在(2)的条件下,延长CE交⊙O于点G,若tan∠BAC= 5311,EG=2,求AE的长.【答案】(1)见解析;(2)60°;(3)7.【解析】试题分析:(1)利用圆的内接四边形定理得到∠CED=∠CDE.(2) 作CH⊥DE于H, 设∠ECH=α,由(1)CE=CD,用α表示∠CAE,∠BAC,而∠BAD=∠BAC+∠CAE.(3)连接AG,作GN⊥AC,AM⊥EG,先证明∠CAG=∠BAC,设NG=3m,可得AN=11m,利用直角AGM,AEM,勾股定理可以算出m的值并求出AE长.试题解析:(1)解:证明:∵四边形ABCD内接于⊙O.∴∠B+∠D=180°,∵∠B=∠AEC,∴∠AEC+∠D=180°,∵∠AEC+∠CED=180°,∴∠D=∠CED,∴CE=CD.(2)解:作CH⊥DE于H.设∠ECH=α,由(1)CE=CD,∴∠ECD=2α,∵∠B=∠AEC,∠B+∠CAE=120°,∴∠CAE+∠AEC=120°,∴∠ACE=180°﹣∠AEC﹣∠ACE=60°,∴∠CAE=90°﹣∠ACH=90°﹣(60°+α)=30°﹣α,∠ACD=∠ACH+∠HCD=60°+2α,∵∠ACD=2∠BAC,∴∠BAC=30°+α,∴∠BAD=∠BAC+∠CAE=30°+α+30°﹣α=60°.(3)解:连接AG,作GN⊥AC,AM⊥EG,∵∠CED=∠AEG,∠CDE=∠AGE,∠CED=∠CDE,∴∠AEG=∠AGE,∴AE=AG,∴EM=MG=1EG=1,2∴∠EAG=∠ECD=2α,∴∠CAG=∠CAD+∠DAG=30°﹣α+2α=∠BAC,∵tan∠BAC53,∴设NG=3,可得AN=11m,AG22-14m,AG AM∵∠ACG=60°,∴CN=5m,AM3,MG22-m=1,AG AM∴m =12, ∴CE=CD =CG ﹣EG =10m ﹣2=3, ∴AE =22AM EM +=221+43()=7.9.问题发现.(1)如图①,Rt △ABC 中,∠C =90°,AC =3,BC =4,点D 是AB 边上任意一点,则CD 的最小值为______.(2)如图②,矩形ABCD 中,AB =3,BC =4,点M 、点N 分别在BD 、BC 上,求CM+MN 的最小值.(3)如图③,矩形ABCD 中,AB =3,BC =4,点E 是AB 边上一点,且AE =2,点F 是BC 边上的任意一点,把△BEF 沿EF 翻折,点B 的对应点为G ,连接AG 、CG ,四边形AGCD 的面积是否存在最小值,若存在,求这个最小值及此时BF 的长度.若不存在,请说明理由.【答案】(1) 125CD =;(2) CM MN +的最小值为9625.(3) 152【解析】试题分析:(1)根据两种不同方法求面积公式求解;(2)作C 关于BD 的对称点C ',过C '作BC 的垂线,垂足为N ,求C N '的长即可;(3) 连接AC ,则ADCACGAGCD S SS=+四,321GB EB AB AE ==-=-=,则点G 的轨迹为以E 为圆心,1为半径的一段弧.过E 作AC 的垂线,与⊙E 交于点G ,垂足为M ,由AEM ACB ∽求得GM 的值,再由ACDACGAGCD S SS=+四边形 求解即可.试题解析:(1)从C 到AB 距离最小即为过C 作AB 的垂线,垂足为D ,22ABCCD AB AC BCS ⋅⋅==,∴341255AC BC CD AB ⋅⨯===,(2)作C 关于BD 的对称点C ',过C '作BC 的垂线,垂足为N ,且与BD 交于M ,则CM MN +的最小值为C N '的长, 设CC '与BD 交于H ,则CH BD ⊥, ∴BMC BCD ∽,且125CH =, ∴C CB BDC ∠=∠',245CC '=, ∴C NC BCD '∽,∴244965525CC BC C N BD ⨯⋅==='', 即CM MN +的最小值为9625.(3)连接AC ,则ADCACGAGCD S SS=+四,321GB EB AB AE ==-=-=,∴点G 的轨迹为以E 为圆心,1为半径的一段弧. 过E 作AC 的垂线,与⊙E 交于点G ,垂足为M , ∵AEM ACB ∽, ∴EM AEBC AC=, ∴24855AE BC EM AC ⋅⨯===, ∴83155GM EM EG =-=-=,∴ACDACGAGCD S SS=+四边形,113345225=⨯⨯+⨯⨯,152=. 【点睛】本题考查圆的综合题、最短问题、勾股定理、面积法、两点之间线段最短等知识,解题的关键是利用轴对称解决最值问题,灵活运用两点之间线段最短解决问题.10.如图1,等边△ABC 的边长为3,分别以顶点B 、A 、C 为圆心,BA 长为半径作AC 、CB 、BA ,我们把这三条弧所组成的图形称作莱洛三角形,显然莱洛三角形仍然是轴对称图形,设点l 为对称轴的交点.(1)如图2,将这个图形的顶点A 与线段MN 作无滑动的滚动,当它滚动一周后点A 与端点N 重合,则线段MN 的长为 ;(2)如图3,将这个图形的顶点A 与等边△DEF 的顶点D 重合,且AB ⊥DE ,DE =2π,将它沿等边△DEF 的边作无滑动的滚动当它第一次回到起始位置时,求这个图形在运动过程中所扫过的区域的面积;(3)如图4,将这个图形的顶点B 与⊙O 的圆心O 重合,⊙O 的半径为3,将它沿⊙O 的圆周作无滑动的滚动,当它第n 次回到起始位置时,点I 所经过的路径长为 (请用含n 的式子表示)【答案】(1)3π;(2)27π;(3)3. 【解析】试题分析:(1)先求出AC 的弧长,继而得出莱洛三角形的周长为3π,即可得出结论; (2)先判断出莱洛三角形等边△DEF 绕一周扫过的面积如图所示,利用矩形的面积和扇形的面积之和即可;(3)先判断出莱洛三角形的一个顶点和O 重合旋转一周点I 的路径,再用圆的周长公式即可得出.试题解析:解:(1)∵等边△ABC 的边长为3,∴∠ABC =∠ACB =∠BAC =60°,AC BC AB ==,∴AC BC l l ==AB l =603180π⨯=π,∴线段MN 的长为AC BC AB l l l ++=3π.故答案为3π;(2)如图1.∵等边△DEF 的边长为2π,等边△ABC 的边长为3,∴S 矩形AGHF =2π×3=6π,由题意知,AB⊥DE,AG⊥AF,∴∠BAG=120°,∴S扇形BAG=21203360π⨯=3π,∴图形在运动过程中所扫过的区域的面积为3(S矩形AGHF+S扇形BAG)=3(6π+3π)=27π;(3)如图2,连接BI并延长交AC于D.∵I是△ABC的重心也是内心,∴∠DAI=30°,AD=12AC=32,∴OI=AI=3230ADcos DAI cos∠=︒=3,∴当它第1次回到起始位置时,点I所经过的路径是以O为圆心,OI为半径的圆周,∴当它第n次回到起始位置时,点I所经过的路径长为n•2π•3=23nπ.故答案为23nπ.点睛:本题是圆的综合题,主要考查了弧长公式,莱洛三角形的周长,矩形,扇形面积公式,解(1)的关键是求出AC的弧长,解(2)的关键是判断出莱洛三角形绕等边△DEF 扫过的图形,解(3)的关键是得出点I第一次回到起点时,I的路径,是一道中等难度的题目.11.如图,AB是圆O的直径,O为圆心,AD、BD是半圆的弦,且∠PDA=∠PBD.延长PD 交圆的切线BE于点E(1)判断直线PD是否为⊙O的切线,并说明理由;(2)如果∠BED=60°,PD=3,求PA的长;(3)将线段PD以直线AD为对称轴作对称线段DF,点F正好在圆O上,如图2,求证:四边形DFBE为菱形.【答案】(1)证明见解析;(2)1;(3)证明见解析.【解析】【分析】(1)连接OD,由AB是圆O的直径可得∠ADB=90°,进而求得∠ADO+∠PDA=90°,即可得出直线PD为⊙O的切线;(2)根据BE是⊙O的切线,则∠EBA=90°,即可求得∠P=30°,再由PD为⊙O的切线,得∠PDO=90°,根据三角函数的定义求得OD,由勾股定理得OP,即可得出PA;(3)根据题意可证得∠ADF=∠PDA=∠PBD=∠ABF,由AB是圆O的直径,得∠ADB=90°,设∠PBD=x°,则可表示出∠DAF=∠PAD=90°+x°,∠DBF=2x°,由圆内接四边形的性质得出x 的值,可得出△BDE是等边三角形.进而证出四边形DFBE为菱形.【详解】(1)直线PD为⊙O的切线,理由如下:如图1,连接OD,∵AB是圆O的直径,∴∠ADB=90°,∴∠ADO+∠BDO=90°,又∵DO=BO,∴∠BDO=∠PBD,∵∠PDA=∠PBD,∴∠BDO=∠PDA,∴∠ADO+∠PDA=90°,即PD⊥OD,∵点D在⊙O上,∴直线PD为⊙O的切线;(2)∵BE是⊙O的切线,∴∠EBA=90°,∵∠BED=60°,∴∠P=30°,∵PD为⊙O的切线,∴∠PDO=90°,在Rt△PDO中,∠P=30°,3∴0 tan30ODPD=,解得OD=1,∴22PO PD OD+,∴PA=PO﹣AO=2﹣1=1;(3)如图2,依题意得:∠ADF=∠PDA,∠PAD=∠DAF,∵∠PDA=∠PBD∠ADF=∠ABF,∴∠ADF=∠PDA=∠PBD=∠ABF,∵AB是圆O的直径,∴∠ADB=90°,设∠PBD=x°,则∠DAF=∠PAD=90°+x°,∠DBF=2x°,∵四边形AFBD内接于⊙O,∴∠DAF+∠DBF=180°,即90°+x+2x=180°,解得x=30°,∴∠ADF=∠PDA=∠PBD=∠ABF=30°,∵BE、ED是⊙O的切线,∴DE=BE,∠EBA=90°,∴∠DBE=60°,∴△BDE是等边三角形,∴BD=DE=BE,又∵∠FDB=∠ADB﹣∠ADF=90°﹣30°=60°∠DBF=2x°=60°,∴△BDF是等边三角形,∴BD=DF=BF,∴DE=BE=DF=BF,∴四边形DFBE为菱形.【点睛】本题是一道综合性的题目,考查了切线的判定和性质,圆周角定理和菱形的性质,是中档题,难度较大.12.如图,PA切⊙O于点A,射线PC交⊙O于C、B两点,半径OD⊥BC于E,连接BD、DC和OA,DA交BP于点F;(1)求证:∠ADC+∠CBD=12∠AOD;(2)在不添加任何辅助线的情况下,请直接写出图中相等的线段.【答案】(1)详见解析;(2)详见解析; 【解析】 【分析】()1根据垂径定理得到BD CD =,根据等腰三角形的性质得到()111809022ODA AOD AOD ∠=-∠=-∠,即可得到结论; ()2根据垂径定理得到BE CE =,BD CD =,根据等腰三角形的性质得到ADO OAD ∠=∠,根据切线的性质得到90PAO ∠=,求得90OAD DAP ∠+∠=,推出PAF PFA ∠=∠,根据等腰三角形的判定定理即可得到结论. 【详解】()1证明:OD BC ⊥,BD CD ∴=,CBD DCB ∴∠=∠,90DFE EDF ∠+∠=, 90EDF DFE ∴∠=-∠,OD OA =, ()111809022ODA AOD AOD ∴∠=-∠=-∠,190902DFE AOD ∴-∠=-∠,12DEF AOD ∴∠=∠,DFE ADC DCB ADC CBD ∠=∠+∠=∠+∠,12ADC CBD AOD ∴∠+∠=∠;()2解:OD BC ⊥,BE CE ∴=,BD CD =,BD CD ∴=, OA OD =,ADO OAD ∴∠=∠, PA 切O 于点A ,90PAO ∴∠=,90OAD DAP ∴∠+∠=,PFA DFE ∠=∠, 90PFA ADO ∴∠+∠=,PAF PFA ∴∠=∠, PA PF ∴=. 【点睛】本题考查了切线的性质,等腰三角形的判定和性质,垂径定理,圆周角定理,正确的识别图形是解题的关键.13.如图,四边形为菱形,且,以为直径作,与交于点.请仅用无刻度的直尺按下列要求画图.(保留作图痕迹)(1)在如图中,过点作边上的高. (2)在如图中,过点作的切线,与交于点.【答案】(1)如图1所示.(答案不唯一),见解析;(2)如图2所示.(答案不唯一),见解析. 【解析】 【分析】(1)连接AC 交圆于一点F ,连接PF 交AB 于点E,连接CE 即为所求. (2)连接OF 交BC 于Q ,连接PQ 即为所求. 【详解】(1)如图1所示.(答案不唯一)(2)如图2所示.(答案不唯一)【点睛】本题考查作图-复杂作图,菱形和圆的性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.14.如图,在中,,以为直径作,交边于点,交边于点,过点作的切线,交的延长线于点,交于点.(1)求证:;(2)若,,求的半径.【答案】(1)证明见解析;(2)4.【解析】试题分析:(1)连接AD,根据等腰三角形三线合一即可证明.(2)设⊙O的半径为R,则FO=4+R,FA=4+2R,OD=R,连接OD,由△FOD∽△FAE,得列出方程即可解决问题.试题解析:(1)连接AD,∵AB是直径,∴∠ADB=90°,∵AB=AC,AD⊥BC,∴BD=DC.(2)设⊙O的半径为R,则FO=4+R,FA=4+2R,OD=R,连接OD、∵AB=AC,∴∠ABC=∠C,∵OB=OD,∴∠ABC=∠ODB,∴∠ODB=∠C,∴OD∥AC,∴△FOD∽△FAE,∴,∴,整理得R2﹣R﹣12=0,∴R=4或(﹣3舍弃).∴⊙O的半径为4.考点:切线的性质、等腰三角形的性质等知识.15.结果如此巧合!下面是小颖对一道题目的解答.题目:如图,Rt△ABC的内切圆与斜边AB相切于点D,AD=3,BD=4,求△ABC的面积.解:设△ABC的内切圆分别与AC、BC相切于点E、F,CE的长为x.根据切线长定理,得AE=AD=3,BF=BD=4,CF=CE=x.根据勾股定理,得(x+3)2+(x+4)2=(3+4)2.整理,得x2+7x=12.所以S△ABC=12 AC•BC=12(x+3)(x+4)=12(x2+7x+12)=12×(12+12)=12.小颖发现12恰好就是3×4,即△ABC的面积等于AD与BD的积.这仅仅是巧合吗?请你帮她完成下面的探索.已知:△ABC的内切圆与AB相切于点D,AD=m,BD=n.可以一般化吗?(1)若∠C=90°,求证:△ABC的面积等于mn.倒过来思考呢?(2)若AC•BC=2mn,求证∠C=90°.改变一下条件……(3)若∠C=60°,用m、n表示△ABC的面积.【答案】(1)证明见解析;(2)证明见解析;(3)S△ABC=3mn;【解析】【分析】(1)设△ABC的内切圆分别与AC、BC相切于点E、F,CE的长为x,仿照例题利用勾股定理得(x+m)2+(x+n)2=(m+n)2,再根据S△ABC=AC×BC,即可证明S△ABC=mn.(2)由AC•BC=2mn,得x2+(m+n)x=mn,因此AC2+BC2=(x+m)2+(x+n)2=AB2,利用勾股定理逆定理可得∠C=90°.(3)过点A作AG⊥BC于点G,在Rt△ACG中,根据条件求出AG、CG,又根据BG=BC-CG得到BG .在Rt△ABG中,根据勾股定理可得x2+(m+n)x=3mn,由此S△ABC=BC•AG=mn.【详解】设△ABC的内切圆分别与AC、BC相切于点E、F,CE的长为x,根据切线长定理,得:AE=AD=m、BF=BD=n、CF=CE=x,(1)如图1,在Rt△ABC中,根据勾股定理,得:(x+m)2+(x+n)2=(m+n)2,整理,得:x2+(m+n)x=mn,所以S△ABC=AC•BC=(x+m)(x+n)=[x2+(m+n)x+mn]=(mn+mn)=mn;(2)由AC•BC=2mn,得:(x+m)(x+n)=2mn,整理,得:x2+(m+n)x=mn,∴AC2+BC2=(x+m)2+(x+n)2=2[x2+(m+n)x]+m2+n2=2mn+m2+n2=(m+n)2=AB2,根据勾股定理逆定理可得∠C=90°;(3)如图2,过点A作AG⊥BC于点G,在Rt△ACG中,AG=AC•sin60°=(x+m),CG=AC•cos60°=(x+m),∴BG=BC﹣CG=(x+n)﹣(x+m),在Rt△ABG中,根据勾股定理可得:[(x+m)]2+[(x+n)﹣(x+m)]2=(m+n)2,整理,得:x2+(m+n)x=3mn,∴S△ABC=BC•AG=×(x+n)•(x+m)=3x2+(m+n)x+mn]=3(3mn+mn)3.【点睛】本题考查了圆中的计算问题、与圆有关的位置关系以及直角三角形,注意掌握方程思想与数形结合思想的应用.。
中考数学《圆的综合》专题训练(含有答案)
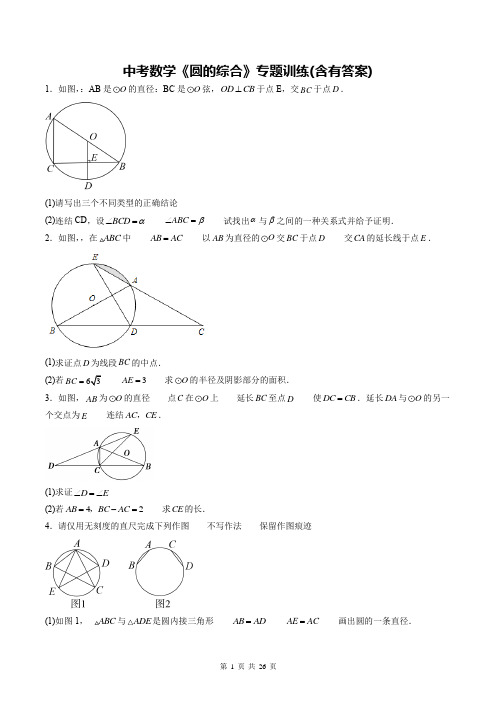
中考数学《圆的综合》专题训练(含有答案)1.如图,:AB 是O 的直径:BC 是O 弦,OD CB ⊥于点E ,交BC 于点D .(1)请写出三个不同类型的正确结论(2)连结CD ,设BCD α∠= ABC β∠= 试找出α与β之间的一种关系式并给予证明.2.如图,,在ABC 中 AB AC = 以AB 为直径的O 交BC 于点D 交CA 的延长线于点E .(1)求证点D 为线段BC 的中点.(2)若63BC = 3AE = 求O 的半径及阴影部分的面积.3.如图,AB 为O 的直径 点C 在O 上 延长BC 至点D 使DC CB =.延长DA 与O 的另一个交点为E 连结AC CE ,.(1)求证D E ∠=∠(2)若42AB BC AC =-=, 求CE 的长.4.请仅用无刻度的直尺完成下列作图 不写作法 保留作图痕迹(1)如图1, ABC 与ADE 是圆内接三角形 AB AD = AE AC = 画出圆的一条直径.(2)如图2 , AB CD 是圆的两条弦 AB CD =且不相互平行 画出圆的一条直径. 5.如图,AB 是O 的直径 点D 在AB 的延长线上 点C 在O 上 ,30CA CD CDA =∠=︒.(1)求证CD 是O 的切线(2)若O 的半径为6 求点A 到CD 所在直线的距离.6.如图, 点C 在以AB 为直径的O 上 过C 作O 的切线交AB 的延长线于E AD CE ⊥于D 连接AC .(1)求证ACD ABC ∠=∠(2)若3tan 4CAD ∠= 8AD = 求O 直径AB 的长.7.如图, 已知以Rt ABC 的直角边AC 为直径作O 交斜边AB 于点E 连接EO 并延长交BC 的延长线于点D 连接AD 点F 为BC 的中点 连接EF .(1)求证EF 是O 的切线(2)若O 的半径为6 8CD = 求AB 的长.8.如图, AB 是半圆O 的直径 D 为半圆O 上的点(不与A B 重合) 连接AD 点C 为BD 的中点 过点C 作CF AD ⊥ 交AD 的延长线于点F 连接BF AC 交于点E .(1)求证FC 是半圆O 的切线(2)若3AF = 23AC = 求半圆O 的半径及AE 的长.9.如图, AB 为O 的直径 C 为BA 延长线上一点 CD 是O 的切线 D 为切点 OF AD ⊥于点E 交CD 于点F .(1)求证ADC AOF ∠=∠ (2)若53OC OB = 24BD = 求EF 的长. 10.如图,所示 AB 是O 的直径 点D 在AB 上 点C 在O 上 AD AC =CD 的延长线交O 于点E .(1)在CD 的延长线上取一点F 使BF BC = 求证BF 是O 的切线 (2)若2AB = 2CE 求图中阴影部分的面积.11.如图, ABC 内接于O AB 为O 的直径 D 为BA 延长线上一点 连接CD 过O 作OF BC ∥交AC 于点E 交CD 于点F ACD AOF ∠=∠.(1)求证CD 为圆O 的切线 (2)若1sin 4D =10BC = 求EF 的长. 12.如图, 四边形ABCD 是O 的内接四边形 AD CD = 70BAC ∠=︒ 50∠=°ACB .(1)求ABD ∠的度数 (2)求BAD ∠的度数.13.如图, 四边形ABCD 是O 的内接四边形 且对角线BD 为O 的直径 过点A 作AE CD ⊥ 与CD 的延长线交于点E 且DA 平分BDE ∠.(1)求证AE 是O 的切线(2)若O 的半径为5 6CD = 求DA 的长.14.如图, 在正方形ABCD 中有一点P 连接AP BP 旋转APB △到CEB 的位置.(1)若正方形的边长是8 4BP =.求阴影部分面积 (2)若4BP = 7AP = 135APB ∠=︒ 求PC 的长.15.如图, AB 是O 的直径 OD 垂直于弦AC 于点E 且交O 于点D F 是BA 延长线上一点 若CDB BFD ∠=∠.(1)求证 FD 是O 的一条切线(2)若15AB = 9BC = 求DF 的长. 16.如图,O 是ABC ∆的外接圆 AE 切O 于点A AE 与直径BD 的延长线相交于点E .(1)如图,① 若70C ∠=︒ 求E ∠的大小 (2)如图,① 若AE AB = 求E ∠的大小.17.已知 如图, 直线MN 交O 于A B 两点 AC 是直径 AD 平分CAM ∠交O 于D 过D 作DE MN ⊥于E .(1)求证DE 是O 的切线(2)若8cm DE = 4cm AE = 求O 的半径.18.已知四边形ABCD 内接于O C 是DBA 的中点 FC AC ⊥于C 与O 及AD 的延长线分别交于点,E F 且DE BC =.(1)求证~CBA FDC(2)如果9,4AC AB == 求tan ACB ∠的值.参考答案与解析1.(1)见解析(2)关系式为2=90αβ+︒ 证明见解析【分析】(1)AB 是O 的直径 BC 是弦 OD BC ⊥于E 本题满足垂径定理. (2)连接,CD DB 根据四边形ACDB 为圆内接四边形 可以得到290αβ+=︒. 【解析】(1)解不同类型的正确结论有 ①BE CE = ①BD CD = ①90BED ∠=︒ ①BOD A ∠=∠ ①AC OD ∥ ①AC BC ⊥ ①222OE BE OB += ①ABC S BC OE =⋅△ ①BOD 是等腰三角形 ①BOE BAC △∽△等等. (2)如图, 连接,CD DBα与β之间的关系式为290αβ+=︒证明AB 为圆O 的直径90A ABC ∴∠+∠=︒①又四边形ACDB 为圆内接四边形180A CDB ∠∠∴+=︒①∴①-①得90CDB ABC ∠∠-=︒①18021802CDB BCD α∠=︒-∠=︒- 即180290αβ︒--=︒ ①2=90αβ+︒.【点评】本题考查了圆的一些基本性质 且有一定的开放性 垂径定理 圆内接四边形的性质掌握圆的相关知识. 2.(1)见解析 (2)半径为3 39π324S =阴【分析】(1)连结AD 可得90ADB ∠=︒ 已知AB AC = 根据等腰三角形三线合一的性质即可得证点D 为线段BC 的中点(2)根据已知条件可证ABC DEC ∽△△ 得到ED ECAB BC= 22BD AB EC =⋅ 且EDC △是等腰三角形 进而得到ED DC BD == 设AB x = 则(()22333x x =+ 解方程即可求得O 的半径连接OE 可证AOE △是等边三角形 再根据AOEAOE S S S =-阴扇形即可求出阴影部分的面积【解析】(1)连结AD①AB 为O 的直径 ①90ADB ∠=︒ ①AB AC = ①BD CD =即点D 为线段BC 的中点. (2)①B E ∠=∠ C C ∠=∠ ①ABC DEC ∽△△ ①ED ECAB BC= ①AB AC = ①B C ∠=∠ ①C E ∠=∠ ①ED DC BD == ①22BD AB EC =⋅ 设AB x = 则 (()22333x x =+解得19x =-(舍去) 26x = ①O 的半径为3 连接OE ①60AOE =︒∠ ①AOE △是等边三角形 ①AE 33①AOEAOE S S S=-阴扇形260313333602π⨯⨯=-⨯ 39π324=【点评】本题主要考查等腰三角形的性质 相似三角形的判定和性质 不规则图形面积的计算 熟练掌握相关知识点是解题的关键. 3.(1)见解析 (2)CE 的长为17【分析】(1)由AB 为O 的直径得90ACB ∠=︒ 通过证明()ACD ACB ≌SAS 得到D B ∠=∠ 又由B E ∠=∠ 从而得到D E ∠=∠(2)设BC x = 则2AC x =- 在Rt ABC 中 由勾股定理可得222AC BC AB += 即()22224x x -+= 解一元二次方程得到BC 的长 由(1)知D E ∠=∠ 从而得到CD CE = 又由DC CB = 得到17CE CB ==【解析】(1)证明AB 为O 的直径90ACB ∴∠=︒180ACD ACB ∠+∠=︒90ACD ∴∠=︒在ACD 和ACB △中AC AC ACD ACB DC BC =⎧⎪∠=∠⎨⎪=⎩()ACD ACB ∴≌SASD B ∴∠=∠ BE ∠=∠D E ∴∠=∠(2)解设BC x =2BC AC -=∴2AC x =-在Rt ABC 中 由勾股定理可得222AC BC AB += 即()22224x x -+=解得117x = 217x = 17BC ∴=由(1)得D E ∠=∠ CD CE ∴= DC CB =17CE CB ∴==∴ CE 的长为17【点评】本题主要考查了圆周角定理 三角形全等的判定与性质 等腰三角形的性质 勾股定理解直角三角形 熟练掌握圆周角定理 三角形全等的判定与性质 等腰三角形的性质是解题的关键. 4.(1)见解析 (2)见解析【分析】(1)设BC DE 交于点G 连接AG 交圆于点F 即可作答(2)连接BC AD 交于点F 延长BA DC 两线交于点E 作直线EF 交圆于点M N 即可作答.【解析】(1)如图, 设BC DE 交于点G 连接AG 并延长 交圆于点F线段AF 即为所求证明如图, BC AE 交于点Q DE AC 交于点P 连接DB 交AF 于点H①AB AD = AE AC = ①C E ∠=∠ ADE ABC =∠∠ ①DAE BAC ∠=∠①DAE BAC ≌ ①BC DE = ①DAE BAC ∠=∠ ①BAE DAC ∠=∠①AB AD = ADE ABC =∠∠ ①DAP BAQ ≌ ①AQ AP = ①AE AC = ①QE PC =①QGE PGC ∠=∠ C E ∠=∠ ①QGE PGC ≌ ①QG PG =①AG AG = AQ AP = ①QAG PAG ≌ ①QAG PAG ∠=∠ ①BAE DAC ∠=∠ ①BAG DAG ∠=∠ ①AH AH = AB AD = ①BAH DAH ≌①BH DH = 90AHB AHD ∠=∠=° ①AF 垂直平分弦DB ①AF 是圆的直径(2)如图, 连接BC AD 交于点F 延长BA DC 两线交于点E 作直线EF 交圆于点M N线段MN 即为所求. 证明方法同(1).【点评】本题主要考查了垂径定理 圆周角定理以及全等三角形的判定与性质等知识 掌握圆周角定理以及垂径定理是解答本题的关键. 5.(1)见解析 (2)9【分析】(1)已知点C 在O 上 先连接OC 由已知CA CD = 30CDA ∠=︒ 得30CAO ∠=︒ 30ACO ∠=︒ 所以得到60COD ∠=︒ 根据三角形内角和定理得90DCO ∠=︒ 即能判断直线CD 与O 的位置关系.(2)要求点A 到CD 所在直线的距离 先作AE CD ⊥ 垂足为E 由30CDA ∠=︒ 得12AE AD = 在Rt OCD △中 半径6OD = 所以212OD OC == 18AD OA OD =+= 从而求出AE .【解析】(1)①ACD 是等腰三角形 30D ∠=︒①30CAD CDA ∠=∠=︒.连接OC①AO CO =①AOC 是等腰三角形①30CAO ACO ∠=∠=︒①60COD ∠=︒在COD △中 又①30CDO ∠=︒①90DCO ∠=︒①CD 是O 的切线 即直线CD 与O 相切.(2)过点A 作AE CD ⊥ 垂足为E .在Rt OCD △中 ①30CDO ∠=︒①212OD OC ==61218AD AO OD =+=+=在Rt ADE △中①30EDA ∠=︒①点A 到CD 边的距离为92AD AE ==. 【点评】此题考查的知识点是切线的判定与性质 解题的关键是运用直角三角形的性质及30°角所对直角边的性质.6.(1)见解析 (2)252AB =.【分析】(1)连接OC 由DE 为O 的切线 得到OC DE ⊥ 再由AD CE ⊥ 得到AD OC ∥ 得到OCA CAD ∠=∠ 根据OA OC = 利用等边对等角得到OCA CAB ∠=∠ 等量代换得到CAD CAB ∠=∠ 由AB 为O 的直径 可知90ACB ∠=︒ 最后根据等角的余角相等可得结论 (2)在Rt CAD △中 利用锐角三角函数定义求出CD 的长 根据勾股定理求出AD 的长 由(1)易证ADC ACB 得到AD AC AC AB= 即可求出AB 的长. 【解析】(1)解连接OC由题意可知DE 与O 的相切于COC DE ∴⊥AD CE ⊥AD OC ∴∥OCA CAD ∴∠=∠OA OC =OCA CAB ∴∠=∠CAD CAB ∴∠=∠ AB 为O 的直径90ACB ∴∠=︒90CAD ACD CAB ABC ∴∠+∠=∠+∠=︒ACD ABC ∴∠=∠(2)在Rt CAD △中3tan 4CDCAD AD ∠== 8AD =364CD AD ∴==22226810AC CD AD ∴+=+=由(1)可知CAD CAB ∠=∠90D ACB ∠=∠=︒ADC ACB ∴ADACAC AB ∴=81010AB∴= 252AB ∴=【点评】此题考查了切线的性质 以及解直角三角形 熟练掌握切线的判定与性质是解本题的关键. 7.(1)证明见解析 (2)125AB =【分析】(1)连接FO 可根据三角形中位线的性质可判断OF AB ∥ 然后根据直径所对的圆周角是直角 可得CE AE ⊥ 进而知OF CE ⊥ 然后根据垂径定理可得FEC FCE ∠=∠OEC OCE ∠=∠ 再通过Rt ABC 可知90OEC FEC ∠+∠=︒ 因此可证EF 为O 的切线(2)根据题意可先在Rt OCD △中求出OD 然后在Rt EFD 中求出FC 最终在Rt ABC 中求解AB 即可.【解析】(1)证连接FO 则由题意OF 为Rt ABC 的中位线①OF AB ∥①AC 是O 的直径①CE AE ⊥①OF AB ∥①OF CE ⊥①由垂径定理知 OF 所在直线垂直平分CE①FC FE = OE OC =①FEC FCE ∠=∠ OEC OCE ∠=∠①90ACB ∠=︒即90OCE FCE ∠+∠=︒①90OEC FEC ∠+∠=︒即90FEO ∠=︒①EF 是O 的切线(2)解①O 的半径为6 8CD = 90ACB ∠=︒①OCD 为直角三角形 6OC OE == 8CD = ①2210OD OC CD += 10616ED OD OE =+=+=由(1)知 EFD △为直角三角形 且FC FE =①设FC FE x == 则8FD FC CD x =+=+①由勾股定理 222EF ED FD +=即()222168x x +=+ 解得12x =即12FC FE ==①点F 为BC 的中点①224BC FC ==①212AC OC ==①在Rt ABC 中 22125AB BC AC +①125AB =【点评】本题考查切线的证明 圆的基本性质 以及勾股定理解三角形等 掌握切线的证明方法 熟练运用圆中的基本性质是解题关键.8.(1)见解析(2)半径为2 123AE =【分析】(1)根据点C 为弧BD 的中点 得出FAC CAB ∠∠= 然后得出FAC ACO ∠∠= 根据平行线的性质得出CF OC ⊥ 进而即可求解(2)连接BC 设OC 与BF 相交于点P 证明AFC ACB ∽ 得出4AB = 证明BOP BAF ∽得出1322OP AF == 进而证明ECP EAF ∽ 根据相似三角形的性质列出比例式 进而即可求解. 【解析】(1)证明连接OC 如图,点C 为弧BD 的中点∴CD CB =FAC CAB ∠∠∴=又OA OC =CAB ACO ∠∠∴=FAC ACO ∠∠∴=∴OC AF ∥又CF AD ⊥CF OC ∴⊥FC ∴是半圆O 的切线.(2)解连接BC 如图,AB 是半圆O 的直径90ACB ∠∴=︒90AFC ACB ∠∠∴==︒又FAC CAB ∠∠=AFC ACB ∴∽ ∴AFACAC AB = 23234AB ∴=∴半圆O 的半径为2.设OC 与BF 相交于点POC AF ∥BOP BAF ∴∽ ∴12OPOB AF AB == ∴1322OP AF == ∴12PC OC OP =-=OC AF ∥ECP EAF ∴∽ ∴EC PCAE AF = 即123AC AEAE -= 2316AE-=∴123AE = 【点评】本题考查了切线的性质与判定 相似三角形的性质与判定 掌握切线的判定以及相似三角形的性质与判定是解题的关键.9.(1)见解析(2)3【分析】(1)连接DO 根据CD 是O 的切线 OF AD ⊥ 证明ADC DOF ∠∠= 利用等腰三角形三线合一性质 证明ADC AOF ∠∠=.(2) 利用平行线分线段成比例定理 计算OE 证明CFO CDB △∽△ 计算OF两线段作差即可求解.【解析】(1)如图, 连接DO CD 是O 的切线OD DF ∴⊥90ADC ADO ∠∠∴+=︒OF AD ⊥ OA OD =90DOF ADO ∠∠∴+=︒ DOF AOF ∠∠=ADC DOF ∠∠∴=ADC AOF ∠∠∴=.(2)如图, 连接DO CD 是O 的切线OD DF ∴⊥90CDO ∠∴=︒53OC OB =设5(0)CO k k => 则3DO OB AO k ===4CD k ∴=538CB CO OB k k k ∴=+=+= AB 是O 的直径 24BD =AD DB ∴⊥OF AD ⊥∴OF BD ∥ ∴AO AE OB ED = CFO CDB △∽△ ∴OF CO BD CB= AE ED ∴=5524538OF k k k ==+ ∴1122OE BD == 15OF = 3EF OF OE ∴=-=.【点评】本题考查了切线的性质 等腰三角形的三线合一性质 平行线分线段成比例定理 相似三角形的性质与判定 熟练掌握切线的性质 相似三角形的性质与判定是解题的关键.10.(1)证明过程见解析 (2)142π-【分析】(1)AB 是O 的直径 AC AD = BF BC = 可求出90FBD ∠=︒ AB BF ⊥ 由此即可求证(2)如图,所示(见解析)连接,CO EO 可得1OC OE == 可证222CO O CE += 90COE ∠=︒ 根据扇形面积的计算方法即可求解.【解析】(1)证明①AB 是O 的直径①90ACB ∠=︒①90ACD BCD ∠+∠=︒①AC AD =①ACD ADC ∠=∠①ADC BDF ∠=∠①ACD BDF ∠=∠①BC BF =①BCD F ∠=∠①90BDF F ∠+∠=︒①180()90FBD FDB F ∠=︒-∠+∠=︒①AB BF ⊥ 且OB 是O 的半径①BF 是O 的切线.(2)解如图,所示 连接,CO EO①2AB =①1OC OE == ①2CE ①222CO EO += 2222CE == ①222CO O CE +=①90COE ∠=︒ ①29011111360242ππS ⨯=-⨯⨯=-阴影 ①图中阴影部分的面积为142π-. 【点评】本题主要考查圆的基础知识 掌握圆的切线的证明方法 扇形面积的计算方法是解题的关键.11.(1)见解析(2)3【分析】(1)连接CO 根据OF BC ∥可得B AOF ∠=∠ 根据直径所对的圆周角为直角可得90B CAB ∠+∠=︒ 再根据AO CO =得出CAB ACO ∠=∠ 最后证明90ACD ACO ∠+∠=︒即可 (2)根据中位线定理得出152OE BC == 证明DBC DOF ∽ 根据相似三角形对应边成比例 即可求解.【解析】(1)证明连接CO①OF BC ∥①B AOF ∠=∠①AB 为O 的直径①90ACB ∠=︒ 则90B CAB ∠+∠=︒①90AOF CAB ∠+∠=︒①AO CO =①CAB ACO ∠=∠①ACD AOF ∠=∠①90ACD ACO ∠+∠=︒ 即OC CD ⊥①CD 为圆O 的切线(2)①AB 为O 的直径①点O 为AB 中点①OF BC ∥①OE 为ABC 中位线 ①152OE BC == ①1sin 4D = OC CD ⊥ ①4OD OC = 则5BD OD OB OC =+=①OF BC ∥①DBC DOF ∽ ①OF OF BC BD = 即4510OC OF OC = 解得8OF =①853EF OF OE =-=-=.【点评】本题主要考查了切线的判定和性质 圆周角定理 相似三角形的判定和性质以及解直角三角形 解题的关键是掌握切线的判定和性质以及相似三角形的判定和性质.12.(1)30︒(2)100︒【分析】(1)根据三角形内角和定理可得60ABC ∠=︒ 再由AD CD = 可得ABD CBD ∠=∠ 即可求解(2)根据圆周角定理可得30ABD ACD ∠∠==︒ 从而得到80BCD ∠=︒ 再由圆内接四边形的性质 即可求解.【解析】(1)解①70,50BAC ACB ∠=︒∠=︒①18060ABC BAC ACB ∠=︒-∠-∠=︒①AD CD = ①1302ABD CBD ABC ∠=∠=∠=︒ (2)解由圆周角定理得30ABD ACD ∠∠==︒①80BCD ACB ACD ∠=∠+∠=︒①四边形ABCD 是O 的内接四边形①180100BAD BCD ∠=︒-∠=︒.【点评】本题主要考查了圆内接四边形的性质 圆周角定理等知识 熟练掌握圆内接四边形的性质 圆周角定理是解题的关键.13.(1)见解析(2)AD 的长是25【分析】(1)连接OA 根据已知条件证明OA AE ⊥即可解决问题(2)作OF CD ⊥ 则四边形OAEF 是矩形 且132DF CD ==由此可求得DE 的长 在Rt OFD △中 勾股定理求出OF 即AE 的长 在Rt AED △中利用勾股定理求DA . 【解析】(1)证明如图, 连接OA①AE CD ⊥①90DAE ADE ∠+∠=︒.①DA 平分BDE ∠①ADE ADO ∠=∠又①OA OD =①OAD ADO ∠=∠①90DAE OAD ∠+∠=︒①OA AE ⊥①AE 是O 的切线(2)解过点O 作OF CD ⊥于F .①90OAE AEF OFE ∠︒=∠=∠=①四边形OAEF 是矩形①5EF OA AE OF ===,.①OF CD ⊥ ①132DF FC CD ===①532DE EF DF =-=-=在Rt OFD △中 2222534OF OD DF --=①4AE OF ==在Rt AED △中 22224225AD AE DE ++=①AD 的长是25【点评】本题考查了切线的判定与性质 垂径定理 圆周角定理 勾股定理 解决本题的关键是掌握切线的判定与性质.14.(1)12π(2)9【分析】(1) 根据题意 CEB APB ABC PBE S S S S S =+--阴影扇形扇形 根据公式计算即可.(2) 连接PE 根据题意 45,135,90PEB CEP PEC ∠=︒∠=︒∠=︒ 根据勾股定理计算即可.【解析】(1)如图, ①正方形ABCD 旋转APB △到CEB 的位置①APB CEB ≌ 90ABC PBE ∠=∠=︒ =CEB APB S S ①CEB APB ABC PBE S S S S S =+--阴影扇形扇形①ABC PBE S S S =-阴影扇形扇形①48BP AB ==, ①9064901612360360S πππ︒⨯⨯︒⨯⨯=-=︒︒阴影. (2)连接PE根据题意 45,135PEB APB CEP ∠=︒∠=∠=︒ AP CE =①90PEC ∠=︒①4BP = 7AP =①2227,4432CE PE ==+=①222273281PC CE PE =+=+=解得9PC =.【点评】本题考查了正方形的性质 旋转的性质 阴影面积的计算 扇形面积公式 勾股定理 熟练掌握旋转的性质 阴影面积的计算 扇形面积公式 勾股定理是解题的关键.15.(1)证明见解析(2)10DF =【分析】(1)因为CDB CAB ∠=∠ CDB BFD ∠=∠ 所以CAB BFD ∠=∠ 即可得出FD ①AC 可得得出OD FD ⊥ 进而得出结论(2)利用勾股定理先求解AC 再利用垂径定理得出AE 的长 可得OE 的长 证明AEO FDO ∽ 再利用相似三角形的判定与性质得出DF 的长.【解析】(1)①CDB CAB ∠=∠ CDB BFD ∠=∠①CAB BFD ∠=∠①FD AC ∥①OD 垂直于弦AC 于点E①OD FD ⊥①FD 是O 的一条切线(2)①AB 为O 的直径①90ACB ∠=︒①15AB = 9BC = ①2215912AC -= 7.5AO OB OD ===①DO AC ⊥①6AE CE == ①227.56 4.5OE -①AC FD ∥①AEO FDO ∽ ①AE EO FD DO = ①4.567.5FD= 解得10DF =.经检验符合题意.【点评】本题主要考查了相似三角形的判定与性质 垂径定理 圆周角定理 切线的判定 以及平行线的判定 掌握相似三角形的判定与性质 垂径定理 圆周角定理以及平行线的判定是解题的关键.16.(1)50︒(2)30︒【分析】(1)连接OA 先由切线的性质得OAE ∠的度数 求出2142AOB C ∠=∠=︒ 进而得AOE ∠ 则可求出答案(2)连接OA 根据等腰三角形的性质及切线的性质列方程求解即可.【解析】(1)连接OA .如图,①AE 切O 于点AOA AE ∴⊥90OAE ∴∠=︒70C ∠=︒2270140AOB C ∴∠=∠=⨯︒=︒又180AOB AOE ∠+∠=︒40AOE ∴∠=︒90AOE E ∠+∠=︒904050E ∴∠=︒-︒=︒.(2)连接OA 如图,①设E x ∠=.AB AE =ABE E x ∴∠=∠=OA OB =OAB ABO x ∴∠=∠=2AOE ABO BAO x ∴∠=∠+∠=. AE 是O 的切线OA AE ∴⊥ 即90OAE ∠=︒在OAE ∆中 90AOE E ∠+∠=︒即290x x +=︒解得30x =︒30E ∴∠=︒.【点评】本题主要考查了切线的性质 等腰三角形的性质 圆周角的性质 三角形内角和的性质 用方程思想解决几何问题 关键是熟悉掌握这些性质.17.(1)见解析(2)10cm【分析】(1)连接OD 根据平行线的判定与性质可得90ODE DEM ∠=∠=︒ 又点D 在O 上 即可证得DE 是O 的切线(2)首先根据勾股定理可得AD 的长 再由ACD ADE ∽ 根据相似三角形的性质列出比例式 代入数据即可求得圆的半径.【解析】(1)证明如图,连接ODOA OD =OAD ODA ∠=∠∴ AD 平分CAM ∠OAD DAE ∴∠=∠ODA DAE ∴∠=∠DO MN ∴∥DE MN ⊥90ODE DEM ∴∠=∠=︒ 即OD DE ⊥ 又点D 在O 上 OD 为O 的半径DE ∴是O 的切线(2)解90AED ∠=︒ 8cm DE = 4cm AE =22228445AD DE AE ∴++如图,连接CDAC 是直径90ADC AED ∴∠=∠=︒CAD DAE ∠=∠ACD ADE ∴△∽△AD AC AE AD ∴= 4545=解得20AC =O ∴的半径为10cm .【点评】本题考查圆了切线的判定;等边对等角 平行线的判定与性质 圆周角定理 勾股定理 相似三角形的判定和性质等知识 在圆中学会正确添加辅助线是解决问题的关键.18.(1)见解析 (2)49【分析】(1)欲证~CBA FDC ,只要证明两个角对应相等就可以.可以转化为证明DE BC =就可以 (2)由~CBA FDC 可得814CF = ACB F ∠=∠ 进而即可得到答案. 【解析】(1)证明①四边形ABCD 内接于O①CBA CDF ∠=∠.①DE BC =①BCA DCE ∠=∠.①~CBA FDC(2)解①C 是DBA 的中点①9CD AC ==①~CBA FDC 4AB = ①AB AC CD CF = 即499CF= ①814CF = ①~CBA FDC ①94tan tan 8194AC ACB F CF ∠=∠===.【点评】本题考查的是圆的综合题;涉及弧、弦的关系;等腰三角形的性质;相似三角形的判定与性质;锐角三角函数;掌握相似三角形的判定和性质是解答此题的关键.。
初三数学 圆的综合的专项 培优 易错 难题练习题含详细答案

初三数学 圆的综合的专项 培优 易错 难题练习题含详细答案一、圆的综合1.(1)如图1,在矩形ABCD 中,点O 在边AB 上,∠AOC =∠BOD ,求证:AO =OB ; (2)如图2,AB 是⊙O 的直径,PA 与⊙O 相切于点A ,OP 与⊙O 相交于点C ,连接CB ,∠OPA =40°,求∠ABC 的度数.【答案】(1)证明见解析;(2)25°.【解析】试题分析: (1)根据等量代换可求得∠AOD=∠BOC ,根据矩形的对边相等,每个角都是直角,可知∠A=∠B=90°,AD=BC ,根据三角形全等的判定AAS 证得△AOD ≌△BOC ,从而得证结论.(2)利用切线的性质和直角三角形的两个锐角互余的性质得到圆心角∠POA 的度数,然后利用圆周角定理来求∠ABC 的度数.试题解析:(1)∵∠AOC=∠BOD∴∠AOC -∠COD=∠BOD-∠COD即∠AOD=∠BOC∵四边形ABCD 是矩形∴∠A=∠B=90°,AD=BC∴AOD BOC ∆≅∆∴AO=OB(2)解:∵AB 是O 的直径,PA 与O 相切于点A , ∴PA ⊥AB ,∴∠A=90°.又∵∠OPA=40°,∴∠AOP=50°,∵OB=OC ,∴∠B=∠OCB.又∵∠AOP=∠B+∠OCB , ∴1252B OCB AOP ∠=∠=∠=︒.2.如图,在△ABC 中,AB =AC ,以AB 为直径作⊙O ,⊙O 交BC 于点D ,交CA 的延长线于点E .过点D 作DF ⊥AC ,垂足为F .(1)求证:DF为⊙O的切线;(2)若AB=4,∠C=30°,求劣弧BE的长.【答案】(1)证明见解析(2)4 3π【解析】分析:(1)连接AD、OD,根据直径所对的圆周角为直角,可得∠ADB=90°,然后根据等腰三角形的性质求出BD=CD,再根据中位线的性质求出OD⊥DF,进而根据切线的判定证明即可;(2)连接OE,根据三角形的外角求出∠BAE的度数,然后根据圆周角定理求出∠BOE的度数,根据弧长公式求解即可.详解:(1)连接AD、OD.∵AB是直径,∴∠ADB=90°.∵AB=AC,∴BD=CD,又∵OA=OB,∴OD是△ABC的中位线,∴OD∥AC,∵DF⊥AC,∴OD⊥DF即∠ODF=90°.∴DF为⊙O的切线;(2)连接OE.∵AB=AC,∴∠B=∠C=30°,∴∠BAE=60°,∵∠BOE=2∠BAE,∴∠BOE=120°,∴=·4π=π.点睛:本题是圆的综合题,考查了等腰三角形的性质和判定、切线的性质和判定、三角形的中位线、圆周角定理,灵活添加辅助线是解题关键.3.已知AB,CD都是O的直径,连接DB,过点C的切线交DB的延长线于点E.()1如图1,求证:AOD2E180∠∠+=;()2如图2,过点A作AF EC⊥交EC的延长线于点F,过点D作DG AB⊥,垂足为点G ,求证:DG CF =;()3如图3,在()2的条件下,当DG 3CE 4=时,在O 外取一点H ,连接CH 、DH 分别交O 于点M 、N ,且HDE HCE ∠∠=,点P 在HD 的延长线上,连接PO 并延长交CM 于点Q ,若PD 11=,DN 14=,MQ OB =,求线段HM 的长.【答案】(1)证明见解析(2)证明见解析(3)837+【解析】【分析】(1)由∠D +∠E =90°,可得2∠D +2∠E =180°,只要证明∠AOD =2∠D 即可;(2)如图2中,作OR ⊥AF 于R .只要证明△AOR ≌△ODG 即可;(3)如图3中,连接BC 、OM 、ON 、CN ,作BT ⊥CL 于T ,作NK ⊥CH 于K ,设CH 交DE 于W .解直角三角形分别求出KM ,KH 即可;【详解】()1证明:如图1中,O 与CE 相切于点C ,OC CE ∴⊥,OCE 90∠∴=,D E 90∠∠∴+=,2D 2E 180∠∠∴+=,AOD COB ∠∠=,BOC 2D ∠∠=,AOD 2D ∠∠=,AOD 2E 180∠∠∴+=.()2证明:如图2中,作OR AF ⊥于R .OCF F ORF 90∠∠∠===,∴四边形OCFR 是矩形,AF//CD ∴,CF OR =,A AOD ∠∠∴=,在AOR 和ODG 中,A AOD ∠∠=,ARO OGD 90∠∠==,OA DO =,AOR ∴≌ODG ,OR DG ∴=,DG CF ∴=,()3解:如图3中,连接BC 、OM 、ON 、CN ,作BT CL ⊥于T ,作NK CH ⊥于K ,设CH 交DE 于W .设DG 3m =,则CF 3m =,CE 4m =,OCF F BTE 90∠∠∠===,AF//OC//BT ∴,OA OB =,CT CF 3m ∴==,ET m ∴=, CD 为直径,CBD CND 90CBE ∠∠∠∴===,E 90EBT CBT ∠∠∠∴=-=,tan E tan CBT ∠∠∴=,BT CT ET BT∴=,BT 3m m BT∴=,BT ∴=负根已经舍弃),tan E ∠∴== E 60∠∴=,CWD HDE H ∠∠∠=+,HDE HCE ∠∠=,H E 60∠∠∴==,MON 2HCN 60∠∠∴==,OM ON =,OMN ∴是等边三角形,MN ON ∴=,QM OB OM ==,MOQ MQO ∠∠∴=,MOQ PON 180MON 120∠∠∠+=-=,MQO P 180H 120∠∠∠+=-=, PON P ∠∠∴=,ON NP 141125∴==+=,CD 2ON 50∴==,MN ON 25==,在Rt CDN 中,CN 48==,在Rt CHN 中,CN 48tan H HN HN∠===HN ∴=在Rt KNH 中,1KH HN 2==NK 24==,在Rt NMK 中,MK 7===,HM HK MK 7∴=+=.【点睛】本题考查圆综合题、全等三角形的判定和性质、平行线的性质、勾股定理、等边三角形的判定和性质、锐角三角函数等知识,添加常用辅助线,构造全等三角形或直角三角形解题的关键.4.不用圆规、三角板,只用没有刻度的直尺,用连线的方法在图1、2中分别过圆外一点A 作出直径BC 所在射线的垂线.【答案】画图见解析.【解析】【分析】根据直角所对的圆周角是直角,构造直角三角形,利用直角三角形性质可画出垂线;或结合圆的轴对称性质也可以求出垂线.【详解】解:画图如下:【点睛】本题考核知识点:作垂线.解题关键点:结合圆的性质和直角三角形性质求出垂线.5.如图,已知⊙O 的半径为1,PQ 是⊙O 的直径,n 个相同的正三角形沿PQ 排成一列,所有正三角形都关于PQ 对称,其中第一个△A 1B 1C 1的顶点A 1与点P 重合,第二个△A 2B 2C 2的顶点A 2是B 1C 1与PQ 的交点,…,最后一个△A n B n C n 的顶点B n 、C n 在圆上.如图1,当n=1时,正三角形的边长a 1=_____;如图2,当n=2时,正三角形的边长a 2=_____;如图3,正三角形的边长a n =_____(用含n 的代数式表示).38313 24313n【解析】 分析:(1)设PQ 与11B C 交于点D ,连接1B O ,得出OD=1A D -O 1A ,用含1a 的代数式表示OD ,在△O 1B D 中,根据勾股定理求出正三角形的边长1a ;(2)设PQ 与2B 2C 交于点E ,连接2B O ,得出OE=1A E-O 1A ,用含2a 的代数式表示OE ,在△O 2B E 中,根据勾股定理求出正三角形的边长2a ;(3)设PQ 与n B n C 交于点F ,连接n B O ,得出OF=1A F-O 1A ,用含an 的代数式表示OF ,在△O n B F 中,根据勾股定理求出正三角形的边长an . 本题解析:(1)易知△A 1B 1C 1的高为32 ∴a1.(2)设△A 1B 1C 1的高为h ,则A 2O =1-h ,连结B 2O ,设B 2C 2与PQ 交于点F ,则有OF =2h -1. ∵B 2O 2=OF 2+B 2F 2,∴1=(2h -1)2+2212a ⎛⎫ ⎪⎝⎭ .∵h2,∴1=2-1)2+14a 22,解得a 2=13. (3)同(2),连结B n O ,设B n C n 与PQ 交于点F ,则有B n O 2=OF 2+B n F 2, 即1=(nh -1)2+212n a ⎛⎫ ⎪⎝⎭.∵h a n ,∴1=14a n 2+212n ⎛⎫- ⎪ ⎪⎝⎭,解得a n6.如图,△ABC 内接于⊙O ,弦AD ⊥BC 垂足为H ,∠ABC =2∠CAD .(1)如图1,求证:AB =BC ;(2)如图2,过点B 作BM ⊥CD 垂足为M ,BM 交⊙O 于E,连接AE 、HM ,求证:AE ∥HM;(3)如图3,在(2)的条件下,连接BD 交AE 于N ,AE 与BC 交于点F ,若NH =AD =11,求线段AB 的长.【答案】(1)证明见解析;(2)证明见解析;(3)AB的长为10.【解析】分析:(1)根据题意,设∠CAD=a,然后根据直角三角形的两锐角互余的关系,推导出∠BAC=∠ACB,再根据等角对等边得证结论;(2)延长AD、BM交于点N,连接ED.根据圆周角定理得出∠N=∠DEN=∠BAN,进而根据等角对等边,得到DE=DN,BA=BN,再根据等腰三角形和直角三角形的性质,求得MH∥AE;(3)连接CE,根据(2)的结论,由三角形全等的判定与性质证得HF=HC,然后结合勾股定理求出AC2-AH2=CD2-DH2,解得CD=5,CH=4,AH=8,最后根据锐角三角函数的性质得到AB.详解:(1)证明:设∠CAD=a,则∠ABC=2a,∠C=90°-a,∠BAD=90°-2a,∴∠BAC=90°-2a+a=90°-a∴∠BAC=∠ACB.∴AB=BC(2)证明:延长AD、BM交于点N,连接ED.∵∠DEN=∠DAB,∠N=∠BCD,∠BCD=∠BAN∴∠N=∠DEN=∠BAN∴DE=DN,BA=BN又∵BH⊥AN,DM⊥EN∴EM=NM,HN=HA,∴MH∥AE(3)连接CE.∠BDA=∠BCA,∠BDM=∠BAC,由(1)知∠BCA=∠BAC∴∠BDA=∠BDM,∴△BDM≌△BDH,∴DH=MH,∠MBD=∠HBD,∴BD⊥MH又∵MH∥AE,∴BD⊥EF,∴△FNB≌△ENB,同理可证△AFH ≌△ACH,∴HF=HC,又∵FN=NE∴NH ∥EC,EC=2NH,又∵NH=25,∴EC=45∠EAC=2∠AEC=2a=∠ABC,可证弧AC=弧EC,∴AC=EC=45设HD=x ,AH=11-x ,∵∠ADC=2∠CAD,翻折△CHD 至△CHG,可证CG=CD=AGAH=CD+DH,CD=AH-DH=11-x-x=11-2x又∵AC 2-AH 2=CD 2-DH 2,∴(45)2-(11-x)2=(11-2x)2-x 2∴x 1=3,x 2=272(舍去)∴CD=5,CH=4,AH=8. 又∵tan2AH CH a BH DH==,∴BH=6 ∴AB=22226810BM AH +=+= 点睛:此题主要考查了圆的综合,结合圆周角定理,勾股定理,全等三角形的判定与性质,解直角三角形的性质,综合性比较强,灵活添加辅助线,构造方程求解是解题关键.7.如图,在RtΔABC 中,∠ABC=90°,AB=CB ,以AB 为直径的⊙O 交AC 于点D ,点E 是AB 边上一点(点E 不与点A 、B 重合),DE 的延长线交⊙O 于点G ,DF ⊥DG ,且交BC 于点F.(1)求证:AE=BF ;(2)连接EF ,求证:∠FEB=∠GDA ;(3)连接GF,若AE=2,EB=4,求ΔGFD 的面积.【答案】(1)(2)见解析;(3)9【解析】分析:(1)连接BD,由三角形ABC为等腰直角三角形,求出∠A与∠C的度数,根据AB 为圆的直径,利用圆周角定理得到∠ADB为直角,即BD垂直于AC,利用直角三角形斜边上的中线等于斜边的一半,得到AD=DC=BD=12AC,进而确定出∠A=∠FBD,再利用同角的余角相等得到一对角相等,利用ASA得到三角形AED与三角形BFD全等,利用全等三角形对应边相等即可得证;(2)连接EF,BG,由三角形AED与三角形BFD全等,得到ED=FD,进而得到三角形DEF为等腰直角三角形,利用圆周角定理及等腰直角三角形性质得到一对同位角相等,利用同位角相等两直线平行,再根据平行线的性质和同弧所对的圆周角相等,即可得出结论;(3)由全等三角形对应边相等得到AE=BF=1,在直角三角形BEF中,利用勾股定理求出EF的长,利用锐角三角形函数定义求出DE的长,利用两对角相等的三角形相似得到三角形AED与三角形GEB相似,由相似得比例,求出GE的长,由GE+ED求出GD的长,根据三角形的面积公式计算即可.详解:(1)连接BD.在Rt△ABC中,∠ABC=90°,AB=BC,∴∠A=∠C=45°.∵AB为圆O的直径,∴∠ADB=90°,即BD⊥AC,∴AD=DC=BD=12AC,∠CBD=∠C=45°,∴∠A=∠FBD.∵DF⊥DG,∴∠FDG=90°,∴∠FDB+∠BDG=90°.∵∠EDA+∠BDG=90°,∴∠EDA=∠FDB.在△AED和△BFD中,A FBDAD BDEDA FDB∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△AED≌△BFD(ASA),∴AE=BF;(2)连接EF,BG.∵△AED≌△BFD,∴DE=DF.∵∠EDF=90°,∴△EDF是等腰直角三角形,∴∠DEF=45°.∵∠G=∠A=45°,∴∠G=∠DEF,∴GB∥EF,∴∠FEB=∠GBA.∵∠GBA=∠GDA,∴∠FEB=∠GDA;(3)∵AE=BF,AE=2,∴BF=2.在Rt△EBF中,∠EBF=90°,∴根据勾股定理得:EF2=EB2+BF2.∵EB=4,BF=2,∴EF∵△DEF为等腰直角三角形,∠EDF=90°,∴cos∠DEF=DE EF.∵EF=∴DE=2.∵∠G=∠A,∠GEB=∠AED,∴△GEB∽△AED,∴GEAE=EBED,即GE•ED=AE•EB,∴10•GE =8,即GE =4105,则GD =GE +ED =9105. ∴1191011092252S GD DF GD DE =⨯⨯=⨯⨯=⨯⨯=.点睛:本题属于圆综合题,涉及的知识有:全等三角形的判定与性质,相似三角形的判定与性质,勾股定理,圆周角定理,以及平行线的判定与性质,熟练掌握判定与性质是解答本题的关键.8.解决问题:() 1如图①,半径为4的O 外有一点P ,且7PO =,点A 在O 上,则PA 的最大值和最小值分别是______和______.()2如图②,扇形AOB 的半径为4,45AOB ∠=,P 为弧AB 上一点,分别在OA 边找点E ,在OB 边上找一点F ,使得PEF 周长的最小,请在图②中确定点E 、F 的位置并直接写出PEF 周长的最小值;拓展应用()3如图③,正方形ABCD 的边长为42;E 是CD 上一点(不与D 、C 重合),CF BE ⊥于F ,P 在BE 上,且PF CF =,M 、N 分别是AB 、AC 上动点,求PMN 周长的最小值.【答案】(1)11,3;(2)图见解析,PEF 周长最小值为423)41042.【解析】【分析】()1根据圆外一点P 到这个圆上所有点的距离中,最远是和最近的点是过圆心和该点的直线与圆的交点,容易求出最大值与最小值分别为11和3;()2作点P 关于直线OA 的对称点1P ,作点P 关于直线OB 的对称点2P ,连接1P 、2P ,与OA 、OB 分别交于点E 、F ,点E 、F 即为所求,此时PEF 周长最小,然后根据等腰直角三角形求解即可;()3类似()2题作对称点,PMN 周长最小12PP =,然后由三角形相似和勾股定理求解. 【详解】解:()1如图①,圆外一点P 到这个圆上所有点的距离中,最大距离是和最小距离都在过圆心的直线OP 上,此直线与圆有两个交点,圆外一点与这两个交点的距离个分别最大距离和最小距离. PA ∴的最大值227411PA PO OA ==+=+=,PA 的最小值11743PA PO OA ==-=-=,故答案为11和3;()2如图②,以O 为圆心,OA 为半径,画弧AB 和弧BD ,作点P 关于直线OA 的对称点1P ,作点P 关于直线OB 的对称点2P ,连接1P 、2P ,与OA 、OB 分别交于点E 、F ,点E 、F 即为所求.连接1OP 、2OP 、OP 、PE 、PF ,由对称知识可知,1AOP AOP ∠∠=,2BOP BOP ∠∠=,1PE PE =,2PF P F = ∴1245AOP BOP AOP BOP AOB ∠∠∠∠∠+=+==,12454590POP ∠=+=,12POP ∴为等腰直角三角形,121PP ∴==PEF 周长1212PE PF EF PE P F EF PP =++=++=,此时PEF 周长最小.故答案为;()3作点P 关于直线AB 的对称1P ,连接1AP 、1BP ,作点P 关于直线AC 的对称2P , 连接1P 、2P ,与AB 、AC 分别交于点M 、N .如图③由对称知识可知,1PM PM =,2PN P N =,PMN 周长1212PM PN MN PM P N MN PP =++=++=,此时,PMN 周长最小12PP =.由对称性可知,1BAP BAP ∠∠=,2EAP EAP ∠∠=,12APAP AP ==, ∴1245BAP EAP BAP EAP BAC ∠∠∠∠∠+=+==12454590P AP ∠=+=,12P AP ∴为等腰直角三角形,PMN ∴周长最小值12PP =,当AP 最短时,周长最小.连接DF .CF BE ⊥,且PF CF =,45PCF ∠∴=,2PC CF = 45ACD ∠=, PCF ACD ∠∠∴=,PCA FCD ∠∠=,又2AC CD=, ∴在APC 与DFC 中,AC PC CD CF=,PCA FCD ∠∠= C AP ∴∽DFC ,2AP AC DF CD∴==, ∴2AP DF =90BFC ∠=,取AB 中点O .∴点F 在以BC 为直径的圆上运动,当D 、F 、O 三点在同一直线上时,DF 最短. 2222(22)(42)2221022DF DO FO OC CD OC =-=+-=+-=-, AP ∴最小值为2AP DF =∴此时,PMN 周长最小值()12222222102241042PP AP DF ==⋅=⋅-=-.【点睛】本题考查圆以及正方形的性质,运用圆的对称性和正方形的对称性是解答本题的关键.9.在平面直角坐标系中,已知点A (2,0),点B (0,),点O (0,0).△AOB 绕着O 顺时针旋转,得△A'OB',点A 、B 旋转后的对应点为A',B',记旋转角为α.(Ⅰ)如图1,A'B'恰好经过点A时,求此时旋转角α的度数,并求出点B'的坐标;(Ⅱ)如图2,若0°<α<90°,设直线AA'和直线BB'交于点P,求证:AA'⊥BB';(Ⅲ)若0°<α<360°,求(Ⅱ)中的点P纵坐标的最小值(直接写出结果即可).【答案】(Ⅰ)α=60°,B'(3,);(Ⅱ)见解析;(Ⅲ)点P纵坐标的最小值为﹣2.【解析】【分析】(Ⅰ)作辅助线,先根据点A(2,0),点B(0,),确定∠ABO=30°,证明△AOA'是等边三角形,得旋转角α=60°,证明△COB'是30°的直角三角形,可得B'的坐标;(Ⅱ)依据旋转的性质可得∠BOB'=∠AOA'=α,OB=OB',OA=OA',即可得出∠OBB'=∠OA'A =(180°﹣α),再根据∠BOA'=90°+α,四边形OBPA'的内角和为360°,即可得到∠BPA'=90°,即AA'⊥BB';(Ⅲ)作AB的中点M(1,),连接MP,依据点P的轨迹为以点M为圆心,以MP=AB=2为半径的圆,即可得到当PM∥y轴时,点P纵坐标的最小值为﹣2.【详解】解:(Ⅰ)如图1,过B'作B'C⊥x轴于C,∵OA=2,OB=2,∠AOB=90°,∴∠ABO=30°,∠BAO=60°,由旋转得:OA=OA',∠A'=∠BAO=60°,∴△OAA'是等边三角形,∴α=∠AOA'=60°,∵OB=OB'=2,∠COB'=90°﹣60°=30°,∴B'C=OB’=,∴OC=3,∴B'(3,),(Ⅱ)证明:如图2,∵∠BOB'=∠AOA'=α,OB=OB',OA=OA',∴∠OBB'=∠OA'A=(180°﹣α),∵∠BOA'=90°+α,四边形OBPA'的内角和为360°,∴∠BPA'=360°﹣(180°﹣α)﹣(90°+α)=90°,即AA'⊥BB';(Ⅲ)点P纵坐标的最小值为-2.理由是:如图,作AB的中点M(1,),连接MP,∵∠APB=90°,∴点P的轨迹为以点M为圆心,以MP=AB=2为半径的圆,除去点(2,2),∴当PM⊥x轴时,点P纵坐标的最小值为﹣2.【点睛】本题属于几何变换综合题,主要考查了旋转的性质,含30°角的直角三角形的性质,四边形内角和以及圆周角定理的综合运用,解决问题的关键是判断点P的轨迹为以点M为圆心,以MP 为半径的圆.10.如图,AB是圆O的直径,O为圆心,AD、BD是半圆的弦,且∠PDA=∠PBD.延长PD 交圆的切线BE于点E(1)判断直线PD是否为⊙O的切线,并说明理由;(2)如果∠BED=60°,PD=3,求PA的长;(3)将线段PD以直线AD为对称轴作对称线段DF,点F正好在圆O上,如图2,求证:四边形DFBE为菱形.【答案】(1)证明见解析;(2)1;(3)证明见解析.【解析】【分析】(1)连接OD,由AB是圆O的直径可得∠ADB=90°,进而求得∠ADO+∠PDA=90°,即可得出直线PD为⊙O的切线;(2)根据BE是⊙O的切线,则∠EBA=90°,即可求得∠P=30°,再由PD为⊙O的切线,得∠PDO=90°,根据三角函数的定义求得OD,由勾股定理得OP,即可得出PA;(3)根据题意可证得∠ADF=∠PDA=∠PBD=∠ABF,由AB是圆O的直径,得∠ADB=90°,设∠PBD=x°,则可表示出∠DAF=∠PAD=90°+x°,∠DBF=2x°,由圆内接四边形的性质得出x 的值,可得出△BDE是等边三角形.进而证出四边形DFBE为菱形.【详解】(1)直线PD为⊙O的切线,理由如下:如图1,连接OD,∵AB是圆O的直径,∴∠ADB=90°,∴∠ADO+∠BDO=90°,又∵DO=BO,∴∠BDO=∠PBD,∵∠PDA=∠PBD,∴∠BDO=∠PDA,∴∠ADO+∠PDA=90°,即PD⊥OD,∵点D在⊙O上,∴直线PD为⊙O的切线;(2)∵BE是⊙O的切线,∴∠EBA=90°,∵∠BED=60°,∴∠P=30°,∵PD为⊙O的切线,∴∠PDO=90°,在Rt△PDO中,∠P=30°,∴0 tan30ODPD=,解得OD=1,∴PO,∴PA=PO﹣AO=2﹣1=1;(3)如图2,依题意得:∠ADF=∠PDA,∠PAD=∠DAF,∵∠PDA=∠PBD∠ADF=∠ABF,∴∠ADF=∠PDA=∠PBD=∠ABF,∵AB是圆O的直径,∴∠ADB=90°,设∠PBD=x°,则∠DAF=∠PAD=90°+x°,∠DBF=2x°,∵四边形AFBD内接于⊙O,∴∠DAF+∠DBF=180°,即90°+x+2x=180°,解得x=30°,∴∠ADF=∠PDA=∠PBD=∠ABF=30°,∵BE、ED是⊙O的切线,∴DE=BE,∠EBA=90°,∴∠DBE=60°,∴△BDE是等边三角形,∴BD=DE=BE,又∵∠FDB=∠ADB﹣∠ADF=90°﹣30°=60°∠DBF=2x°=60°,∴△BDF是等边三角形,∴BD=DF=BF,∴DE=BE=DF=BF,∴四边形DFBE为菱形.【点睛】本题是一道综合性的题目,考查了切线的判定和性质,圆周角定理和菱形的性质,是中档题,难度较大.11.如图1,四边形ABCD是正方形,点E是边BC上一点,点F在射线CM上,∠AEF=90°,AE=EF,过点F作射线BC的垂线,垂足为H,连接AC.(1) 试判断BE与FH的数量关系,并说明理由;(2) 求证:∠ACF=90°;(3) 连接AF,过A,E,F三点作圆,如图2. 若EC=4,∠CEF=15°,求的长.图1 图2【答案】(1)BE="FH" ;理由见解析(2)证明见解析(3)=2π【解析】试题分析:(1)由△ABE≌△EHF(SAS)即可得到BE=FH(2)由(1)可知AB=EH,而BC=AB,FH=EB,从而可知△FHC是等腰直角三角形,∠FCH 为45°,而∠ACB也为45°,从而可证明(3)由已知可知∠EAC=30°,AF是直径,设圆心为O,连接EO,过点E作EN⊥AC于点N,则可得△ECN为等腰直角三角形,从而可得EN的长,进而可得AE的长,得到半径,得到所对圆心角的度数,从而求得弧长试题解析:(1)BE=FH.理由如下:∵四边形ABCD是正方形∴∠B=90°,∵FH⊥BC ∴∠FHE=90°又∵∠AEF=90°∴∠AEB+∠HEF="90°" 且∠BAE+∠AEB=90°∴∠HEF=∠BAE ∴∠AEB=∠EFH 又∵AE=EF∴△ABE≌△EHF(SAS)∴BE=FH(2)∵△ABE≌△EHF∴BC=EH,BE=FH 又∵BE+EC=EC+CH ∴BE="CH"∴CH=FH∴∠FCH=45°,∴∠FCM=45°∵AC是正方形对角线,∴∠ACD=45°∴∠ACF=∠FCM +∠ACD =90°(3)∵AE=EF,∴△AEF是等腰直角三角形△AEF外接圆的圆心在斜边AF的中点上.设该中点为O.连结EO得∠AOE=90°过E作EN⊥AC于点NRt△ENC中,EC=4,∠ECA=45°,∴EN=NC=Rt△ENA中,EN =又∵∠EAF=45°∠CAF=∠CEF=15°(等弧对等角)∴∠EAC=30°∴AE=Rt△AFE中,AE== EF,∴AF=8AE所在的圆O半径为4,其所对的圆心角为∠AOE=90°=2π·4·(90°÷360°)=2π考点:1、正方形;2、等腰直角三角形;3、圆周角定理;4、三角函数BC ,∠B=45°,点D在边BC上,联结AD,以点A 12.如图,已知△ABC,AB=2,3为圆心,AD为半径画圆,与边AC交于点E,点F在圆A上,且AF⊥AD.(1)设BD为x,点D、F之间的距离为y,求y关于x的函数解析式,并写出定义域;BD CD的值;(2)如果E是DF的中点,求:(3)联结CF,如果四边形ADCF是梯形,求BD的长.【答案】(1) 2442y x x (0≤x≤3); (2) 45; (3) BD 的长是1或1+52. 【解析】【分析】 (1)过点A 作AH ⊥BC ,垂足为点H .构造直角三角形,利用解直角三角形和勾股定理求得AD 的长度.联结DF ,点D 、F 之间的距离y 即为DF 的长度,在Rt △ADF 中,利用锐角三角形函数的定义求得DF 的长度,易得函数关系式.(2)由勾股定理求得:AC=22AH DH +.设DF 与AE 相交于点Q ,通过解Rt △DCQ 和Rt △AHC 推知12DQ CQ =.故设DQ=k ,CQ=2k ,AQ=DQ=k ,所以再次利用勾股定理推知DC 的长度,结合图形求得线段BD 的长度,易得答案.(3)如果四边形ADCF 是梯形,则需要分类讨论:①当AF ∥DC 、②当AD ∥FC .根据相似三角形的判定与性质,结合图形解答.【详解】(1)过点A 作AH ⊥BC ,垂足为点H .∵∠B =45°,AB 2∴·cos 1BH AH AB B ===.∵BD 为x ,∴1DH x =-.在Rt △ADH 中,90AHD ∠=︒,∴22222AD AH DH x x =+=-+. 联结DF ,点D 、F 之间的距离y 即为DF 的长度.∵点F 在圆A 上,且AF ⊥AD ,∴AD AF =,45ADF ∠=︒.在Rt △ADF 中,90DAF ∠=︒,∴2442cos AD DF x x ADF ==-+∠ ∴2442y x x =-+.()03x ≤≤ ;(2)∵E 是DF 的中点,∴AE DF ⊥,AE 平分DF .∵BC=3,∴312HC =-=.∴225AC AH HC +=.设DF 与AE 相交于点Q ,在Rt △DCQ 中,90DQC ∠=︒,tan DQ DCQ CQ ∠=. 在Rt △AHC 中,90AHC ∠=︒,1tan 2AH ACH HC ∠==.∵DCQ ACH ∠=∠,∴12DQ CQ =. 设,2DQ k CQ k ==,AQ DQ k ==,∵3k =k =,∴53DC ==. ∵43BD BC DC =-=,∴4:5BD CD =. (3)如果四边形ADCF 是梯形 则①当AF ∥DC 时,45AFD FDC ∠=∠=︒.∵45ADF ∠=︒,∴AD BC ⊥,即点D 与点H 重合. ∴1BD =.②当AD ∥FC 时,45ADF CFD ∠=∠=︒.∵45B ∠=︒,∴B CFD ∠=∠.∵B BAD ADF FDC ∠+∠=∠+∠,∴BAD FDC ∠=∠.∴ABD ∆∽DFC ∆.∴AB AD DF DC =. ∵DF =,DC BC BD =-.∴2AD BC BD =-.即23x =-,整理得 210x x --=,解得 12x ±=(负数舍去).综上所述,如果四边形ADCF 是梯形,BD 的长是1 【点睛】此题属于圆的综合题,涉及了平行四边形的性质、相似三角形的判定与性质、三角函数值以及勾股定理等知识,综合性较强,解答本题需要我们熟练各部分的内容,对学生的综合能力要求较高,一定要注意将所学知识贯穿起来.13.如图,AB 是O 的直径,DF 切O 于点D ,BF DF ⊥于F ,过点A 作AC //BF 交BD 的延长线于点C .(1)求证:ABC C ∠∠=;(2)设CA 的延长线交O 于E BF ,交O 于G ,若DG 的度数等于60,试简要说明点D 和点E 关于直线AB 对称的理由.【答案】(1)见解析;(2)见解析.【解析】【分析】(1)作辅助线,连接OD,由DF为⊙O的切线,可得OD⊥DF,又BF⊥DF,AC∥BF,所以OD∥AC,∠ODB=∠C,由OB=OD得∠ABD=∠ODB,从而可证∠ABC=∠C;(2)连接OG,OD,AD,由BF∥OD,GD=60°,可求证BG=GD AD==60°,由平行线的性质及三角形的内角和定理可求出∠OHD=90°,由垂径定理便可得出结论.【详解】(1)连接OD,∵DF为⊙O的切线,∴OD⊥DF.∵BF⊥DF,AC∥BF,∴OD∥AC∥BF.∴∠ODB=∠C.∵OB=OD,∴∠ABD=∠ODB.∴∠ABC=∠C.(2)连接OG,OD,AD,DE,DE交AB于H,∵BF∥OD,∴∠OBG=∠AOD,∠OGB=∠DOG,∴GD AD==BG.∵GD=60°,∴BG=GD AD==60°,∴∠ABC=∠C=∠E=30°,∵OD//CE∴∠ODE=∠E=30°.在△ODH中,∠ODE=30°,∠AOD=60°,∴∠OHD=90°,∴AB⊥DE.∴点D和点E关于直线AB对称.【点睛】本题考查的是切线的性质、圆周角定理及垂径定理,解答此题的关键是作出辅助线,利用数形结合解答.14.如图,在△ABC中,以AC为直径作⊙O交BC于点D,交AB于点G,且D是BC中点,DE⊥AB,垂足为E,交AC的延长线于点F.(1)求证:直线EF是⊙O的切线;(2)若CF=3,cosA=25,求出⊙O的半径和BE的长;(3)连接CG,在(2)的条件下,求CGEF的值.【答案】(1)见解析;(2)2,65(3)CG:EF=4:7【解析】试题分析:(1)连结OD.先证明OD是△ABC的中位线,根据中位线的性质得到OD∥AB,再由DE⊥AB,得出OD⊥EF,根据切线的判定即可得出直线EF是⊙O的切线;(2)先由OD∥AB,得出∠COD=∠A,再解Rt△DOF,根据余弦函数的定义得到cos∠FOD==,设⊙O的半径为R,解方程=,求出R=,那么AB=2OD=,解Rt△AEF,根据余弦函数的定义得到cosA==,求出AE=,然后由BE=AB﹣AE即可求解.试题解析:(1)证明:如图,连结OD.∵CD=DB,CO=OA,∴OD是△ABC的中位线,∴OD∥AB,AB=2OD,∵DE⊥AB,∴DE⊥OD,即OD⊥EF,∴直线EF是⊙O的切线;(2)解:∵OD∥AB,∴∠COD=∠A.在Rt△DOF中,∵∠ODF=90°,∴cos∠FOD==,设⊙O的半径为R,则=,解得R=,∴AB=2OD=.在Rt△AEF中,∵∠AEF=90°,∴cosA===,∴AE=,∴BE=AB﹣AE=﹣=2.【点睛】本题考查了切线的判定,解直角三角形,三角形中位线的性质知识点.要证某线是圆的切线,已知此线过圆上某点,连结圆心与这点(即为半径),再证垂直即可.15.如图,已知AB是⊙O的直径,点C、D在⊙O上,∠D=60°且AB=6,过O点作OE⊥AC,垂足为E.(1)求OE的长;(2)若OE的延长线交⊙O于点F,求弦AF、AC和弧CF围成的图形(阴影部分)的面积.(结果保留π)【答案】(1)OE的长为32;(2)阴影部分的面积为3 2π【解析】(1)OE=32(2)S=32π。
北师大版九年级数学圆测试题及答案(K12教育文档)

(完整word版)北师大版九年级数学圆测试题及答案(word版可编辑修改) 编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望((完整word版)北师大版九年级数学圆测试题及答案(word版可编辑修改))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为(完整word版)北师大版九年级数学圆测试题及答案(word版可编辑修改)的全部内容。
九年级数学圆测试题一、选择题1.若⊙O 所在平面内一点P 到⊙O 上的点的最大距离为a ,最小距离为b (a 〉b ),则此圆的半径为( )A .2ba + B .2ba - C.22b a b a-+或D .b ab a -+或2.如图24—A —1,⊙O 的直径为10,圆心O 到弦AB 的距离OM 的长为3,则弦AB 的长是( )A .4B .6C .7D .83.已知点O 为△ABC 的外心,若∠A=80°,则∠BOC 的度数为( ) A .40° B .80° C .160° D .120°4.如图24—A —2,△ABC 内接于⊙O,若∠A=40°,则∠OBC 的度数为( ) A .20° B .40° C .50° D .70°5.如图24—A-3,小明同学设计了一个测量圆直径的工具,标有刻度的尺子OA 、OB 在O 点钉在一起,并使它们保持垂直,在测直径时,把O 点靠在圆周上,读得刻度OE=8个单位,OF=6个单位,则圆的直径为( ) A .12个单位 B .10个单位 C .1个单位 D .15个单位6.如图24-A-4,AB 为⊙O 的直径,点C 在⊙O 上,若∠B=60°,则∠A 等于( )图24—A —5图24—A —1图24—A —2 图24—A —3 图24—A —4A .80°B .50°C .40°D .30°7.如图24—A-5,P 为⊙O 外一点,PA 、PB 分别切⊙O 于A 、B ,CD 切⊙O 于点E ,分别交PA 、PB 于点C 、D ,若PA=5,则△PCD 的周长为( ) A .5 B .7 C .8 D .108.若粮仓顶部是圆锥形,且这个圆锥的底面直径为4m ,母线长为3m ,为防雨需在粮仓顶部铺上油毡,则这块油毡的面积是( ) A .26m B .26m π C .212m D .212m π 9.如图24—A —6,两个同心圆,大圆的弦AB 与小圆相切于点P ,大圆的弦CD 经过点P,且CD=13,PC=4,则两圆组成的圆环的面积是( )A .16πB .36πC .52πD .81π10.已知在△ABC 中,AB=AC=13,BC=10,那么△ABC 的内切圆的半径为( ) A .310 B .512C . 2D .3 11.如图24—A —7,两个半径都是4cm 的圆外切于点C ,一只蚂蚁由点A 开始依A 、B 、C 、D 、E 、F 、C 、G 、A 的顺序沿着圆周上的8段长度相等的路径绕行,蚂蚁在这8段路径上不断爬行,直到行走2006πcm 后才停下来,则蚂蚁停的那一个点为( )A .D 点B .E 点C .F 点D .G 点二、填空题12.如图24-A-8,在⊙O 中,弦AB 等于⊙O 的半径,OC ⊥AB 交⊙O 于点C,则∠AOC= 。
2020年中考数学 微测试系列专题19 圆的有关计算及圆的综合(含解析)北师大版

2020年中考数学 专题19 圆的有关计算及圆的综合学校:___________姓名:___________班级:___________一、选择题:(共4个小题)1.【2015成都】如图,正六边形A BCDEF 内接于⊙O ,半径为4,则这个正六边形的边心距OM 和BC 弧线的长分别为( )A .2,3πB .πC 23πD .43π【答案】D .【解析】【考点定位】1.正多边形和圆;2.弧长的计算.2.【2015攀枝花】如图,已知⊙O 的一条直径AB 与弦CD 相交于点E ,且AC =2,AE ,CE =1,则图中阴影部分的面积为( )A C .29π D .49π【答案】D.【解析】【考点定位】1.扇形面积的计算;2.勾股定理的逆定理;3.圆周角定理;4.解直角三角形.3.【2015凉山州】将圆心角为90°,面积为4πcm2的扇形围成一个圆锥的侧面,则所围成的圆锥的底面半径为()A.1cm B.2cm C.3cm D.4cm【答案】A.【解析】试题分析:设扇形的半径为R,根据题意得2904360rππ=,解得R=4,设圆锥的底面圆的半径为r,则12•2π•r•4=4π,解得r=1,即所围成的圆锥的底面半径为1cm.故选A.【考点定位】圆锥的计算.4.【2015河池】我们将在直角坐标系中圆心坐标和半径均为整数的圆称为“整圆”.如图,直线l:y kx=+与x轴、y轴分别交于A、B,∠OAB=30°,点P在x轴上,⊙P与l相切,当P在线段OA上运动时,使得⊙P成为整圆的点P个数是()A.6 B.8 C.10 D.12【答案】A.【解析】【考点定位】1.切线的性质;2.一次函数图象上点的坐标特征;3.新定义;4.动点型;5.综合题.二、填空题:(共4个小题)5.【2015贵阳】小明把半径为1的光盘、直尺和三角尺形状的纸片按如图所示放置于桌面上,此时,光盘与AB,CD分别相切于点N,M.现从如图所示的位置开始,将光盘在直尺边上沿着CD向右滚动到再次与AB 相切时,光盘的圆心经过的距离是..【答案】3【解析】试题分析:如图,当圆心O移动到点P的位置时,光盘在直尺边上沿着CD向右滚动到再次与AB相切,切,点为Q,∵ON⊥AB,PQ⊥AB,∴ON∥PQ,∵ON=PQ,∴OH=PH,在Rt△PHQ中,∠P=∠B=60°,PQ=1,∴PH=3则OP.【考点定位】1.切线的性质;2.轨迹;3.应用题;4.综合题.6.【2015自贡】如图,已知AB 是⊙O 的一条直径,延长AB 至C 点,使AC =3BC ,CD 与⊙O 相切于D 点.若CD =3,则劣弧AD 的长为 .【答案】 32. 【解析】【考点定位】1.切线的性质;2.弧长的计算.7.【2015莱芜】如图,在扇形OAB 中,∠AOB =60°,扇形半径为r ,点C 在AB 上,CD ⊥OA ,垂足为D ,当△OCD 的面积最大时,AC 的长为 .【答案】14r π.【解析】【考点定位】1.垂径定理;2.弧长的计算;3.解直角三角形;4.最值问题;5.二次函数的最值;6.圆的综合题.8.【2015成都】如图,在半径为5的⊙O 中,弦AB =8,P 是弦AB 所对的优弧上的动点,连接AP ,过点A 作AP 的垂线交射线PB 于点C .当△PAB 是等腰三角形时,线段BC 的长为________.【答案】8BC =或5615或3. 【解析】试题分析:(1)当AB =AP 时,如图(1),作OH ⊥AB 于点H ,延长AO 交PB 于点G ;∵AB =AP ,∴AP AB =,∵AO 过圆心,∴AG ⊥PB ,∴PG =BG ,∠OAH =∠PAG ,∵OH ⊥AB ,∴∠AOH =∠BOH ,AH =BH =4,∵∠AOB =2∠P ,∴∠AOH =∠P ,∵OA =5,AH =4,∴OH =3,∵∠OAH =∠PAG ,∴sin ∠OAH =sin ∠PAG ,∴358PG =,∴PG =245,∵∠AOH =∠P ,∴cos ∠AOH =cos ∠P ,AP OH PC AO =,∴54033PC AP ==,∴BC =PC -2PG =4048563515-=;(3)当BA =BP 时,如图(3),∵BA =BP ,∴∠P =∠BAP ,∵∠P +∠C =90°,∠CAB +∠BAP =90°,∴∠C =∠CAB ,∴BC =AB =8.故答案为:8BC =或5615或3.【考点定位】1.等腰三角形的性质;2.解直角三角形;3.分类讨论;4.综合题.三、解答题:(共2个小题)9.【2015广安】如图,PB 为⊙O 的切线,B 为切点,过B 作OP 的垂线BA ,垂足为C ,交⊙O 于点A ,连接PA 、AO ,并延长AO 交⊙O 于点E ,与PB 的延长线交于点D .(1)求证:PA 是⊙O 的切线;(2)若23OC AC =,且OC =4,求PA 的长和tanD 的值.【答案】(1)证明见试题解析;(2)512.【解析】(2)连接BE,根据已知23OCAC=,且OC=4,可求AC,OA的值,然后由射影定理可求PC的值,从而可求OP的值,然后由勾股定理可求AP的值;由AC=BC,AO=OE,得到OC是△ABE的中位线,进而可得BE∥OP,BE=2OC=8,进而可证△DBE∽△DPO,进而可得:BD BEPD OP=,从而求出BD的值,进而即可求出tanD的值.试题解析:(1)连接OB,则OA=OB,∵OP⊥AB,∴AC=BC,∴OP是AB的垂直平分线,∴PA=PB,在△PAO 和△PBO中,∵PA=PB,PO=PO,OA=OB,∴△PAO≌△PBO(SSS),∴∠PBO=∠PAO,PB=PA,∵PB为⊙O的切线,B为切点,∴∠PBO=90°,∴∠PAO=90°,即PA⊥OA,∴PA是⊙O的切线;(2)连接BE,∵23OCAC=,且OC=4,∴AC=6,∴AB=12,在Rt△ACO中,由勾股定理得:AO∴AE=2OA=OB=OA=在Rt△APO中,∵AC⊥OP,∴2AC OC PC=⋅,解得:PC=9,∴OP=PC+OC=13,在Rt△APO中,由勾股定理得:AP,∴PB=PA=∵AC=BC,OA=OE,∴OC=12BE,OC∥BE,∴BE=2OC=8,BE∥OP,∴△DBE∽△DPO,∴BD BEPD OP=,即813=,解得:BD=5,在Rt△OBD中,tanD=5OBBD==512.【考点定位】1.切线的判定与性质;2.相似三角形的判定与性质;3.解直角三角形.10.【2015南宁】如图,AB 是⊙O 的直径,C ,G 是⊙O 上两点,且AC =CG ,过点C 的直线CD ⊥BG 于点D ,交BA 的延长线于点E ,连接BC ,交OD 于点F .(1)求证:CD 是⊙O 的切线.(2)若32=FD OF ,求∠E 的度数. (3)连接AD ,在(2)的条件下,若CD =3,求AD 的长.【答案】(1)证明见试题解析;(2)30°;(3【解析】(2)由OC ∥BD ,得到△OCF ∽△BDF ,△EOC ∽△EBD ,得到23OC OF BD DF ==,23OC OE BD BE ==,根据直角三角形的性质即可得到结论; (3)如图2,过A 作AH ⊥DE 于H ,解直角三角形得到BD ,DE ,BE ,在R t △DAH 中,用勾股定理即可得到AD 的长.(3)如图2,过A 作AH ⊥DE 于H ,∵∠E =30°,∴∠EBD =60°,∴∠CBD =12∠EBD =30°,∵CD ∴BD =3,DE =,BE =6,∴AE =13BE =2,∴AH =1,∴EH =,∴DH =,在R t △DAH 中,AD【考点定位】1.圆的综合题;2.切线的判定与性质;3.相似三角形的判定与性质;4.压轴题.。
中考数学圆的综合(大题培优 易错 难题)含详细答案

中考数学圆的综合(大题培优易错难题)含详细答案一、圆的综合1.在平面直角坐标中,边长为2的正方形OABC的两顶点A、C分别在y轴、x轴的正半轴上,点O在原点.现将正方形OABC绕O点顺时针旋转,当A点一次落在直线y x=上时停止旋转,旋转过程中,AB边交直线y x=于点M,BC边交x轴于点N(如图).(1)求边OA在旋转过程中所扫过的面积;(2)旋转过程中,当MN和AC平行时,求正方形OABC旋转的度数;(3)设MBN∆的周长为p,在旋转正方形OABC的过程中,p值是否有变化?请证明你的结论.【答案】(1)π/2(2)22.5°(3)周长不会变化,证明见解析【解析】试题分析:(1)根据扇形的面积公式来求得边OA在旋转过程中所扫过的面积;(2)解决本题需利用全等,根据正方形一个内角的度数求出∠AOM的度数;(3)利用全等把△MBN的各边整理到成与正方形的边长有关的式子.试题解析:(1)∵A点第一次落在直线y=x上时停止旋转,直线y=x与y轴的夹角是45°,∴OA旋转了45°.∴OA在旋转过程中所扫过的面积为24523602ππ⨯=.(2)∵MN∥AC,∴∠BMN=∠BAC=45°,∠BNM=∠BCA=45°.∴∠BMN=∠BNM.∴BM=BN.又∵BA=BC,∴AM=CN.又∵OA=OC,∠OAM=∠OCN,∴△OAM≌△OCN.∴∠AOM=∠CON=12(∠AOC-∠MON)=12(90°-45°)=22.5°.∴旋转过程中,当MN和AC平行时,正方形OABC旋转的度数为45°-22.5°=22.5°.(3)在旋转正方形OABC的过程中,p值无变化.证明:延长BA交y轴于E点,则∠AOE=45°-∠AOM,∠CON=90°-45°-∠AOM=45°-∠AOM,∴∠AOE=∠CON.又∵OA=OC,∠OAE=180°-90°=90°=∠OCN.∴△OAE≌△OCN.∴OE=ON,AE=CN.又∵∠MOE=∠MON=45°,OM=OM,∴△OME≌△OMN.∴MN=ME=AM+AE.∴MN=AM+CN,∴p=MN+BN+BM=AM+CN+BN+BM=AB+BC=4.∴在旋转正方形OABC的过程中,p值无变化.考点:旋转的性质.2.如图,A、B两点的坐标分别为(0,6),(0,3),点P为x轴正半轴上一动点,过点A作AP的垂线,过点B作BP的垂线,两垂线交于点Q,连接PQ,M为线段PQ的中点.(1)求证:A、B、P、Q四点在以M为圆心的同一个圆上;(2)当⊙M与x轴相切时,求点Q的坐标;(3)当点P从点(2,0)运动到点(3,0)时,请直接写出线段QM扫过图形的面积.【答案】(1)见解析;(2) Q的坐标为(32,9);(3)63 8.【解析】(1)解:连接AM、BM,∵AQ⊥AP,BQ⊥BP∵△APQ和△BPQ都是直角三角形,M是斜边PQ的中点∴AM=BM=PM=QM= 12 PQ,∴A、B、P、Q四点在以M为圆心的同一个圆上。
北师大9年初三圆中考练习题及答案

圆命题点 1 圆周角定理及其推论1. (2016 兰州 )如图,在⊙ O 中,点 C 是AB的中点,∠ A = 50°,则∠ BOC= ()A. 40°B.45 °C.50 °D. 60°第1题图2. (2016 济宁 )如图,在⊙ O 中,AB AC=,∠ AOB = 40°,则∠ ADC 的度数是 () 第2题图A. 40°B. 30 °C. 20°D. 15°3. (2016 永州 )如图,在⊙ O 中, A ,B 是圆上的两点,已知∠AOB = 40°,直径CD∥ AB ,连结 AC ,则∠ BAC =________度.第3题图4. (2016 青岛 )如图, AB 是⊙ O 的直径, C, D 是⊙ O 上的两点,若∠ BCD = 28°,则∠ ABD = ________°.第4题图命题点 2垂径定理及其推论5.(2016 黄石 )以下图,⊙ O 的半径为 13,弦 AB 的长度是 24, ON ⊥ AB ,垂足为N,则ON= ( )A. 5B. 7C. 9D. 116.(2016 眉山 )如图, A 、D 是⊙ O 上的两个点, BC 是直径,若∠ D = 32°,则∠ OAC 等于()第6题图A. 64°B. 58°C. 72°D. 55 °7.(2016 安顺 )如图, AB 是⊙ O 的直径,弦 CD⊥ AB 于点 E,若 AB = 8,CD= 6,则BE =________.第7题图命题点 3与圆有关的地点关系8. (2016 湘西 )在 Rt△ABC 中,∠ C= 90°, BC= 3 cm, AC= 4 cm,以点 C 为圆心,以2.5 cm 为半径画圆,则⊙ C 与直线 AB 的地点关系是 ()A. 订交B. 相切C. 相离D. 不可以确立9. (2016 上海 ) 如图,在Rt△ABC 中,∠ C= 90°, AC = 4, BC = 7,点 D 在边 BC上,CD= 3,⊙ A 的半径长为3,⊙ D 与⊙ A 订交,且点 B 在⊙ D 外,那么⊙ D 的半径长r第9题图的取值范围是()A.1< r< 4B.2< r< 4C.1< r< 8D.2< r< 8命题点 4与切线有关的证明与计算10. (2016 泉州 )如图, AB 和⊙ O 相切于点B,∠ AOB = 60°,则∠ A 的大小为 ()A. 15°B. 30°C. 45°D. 60°11.(2016 湖州 ) 如图,圆 O 是 Rt△ ABC 的外接圆,∠ ACB = 90°,∠ A = 25 C 作圆 O 的切线,交AB 的延伸线于点 D ,则∠ D 的度数是 ()第11题图A. 25 °B. 40 °C. 50 °D. 65 °12.(2016 呼和浩特 )在周长为 26π的⊙ O 中, CD 是⊙ O 的一条弦, AB 是⊙ O 的切线,且AB ∥ CD ,若 AB 和 CD 之间的距离为 18,则弦 CD 的长为 ________.13.(2015 宁波 )如图,在矩形 ABCD 中, AB = 8, AD =12,过 A , D 两点的⊙ O 与 BC 边相切于点 E.则⊙ O 的半径为 ________.第 13题图14. (2016 大连 10 分 )如图, AB 是⊙ O 的直径,点C、 D 在⊙ O 上,∠ A = 2∠BCD ,点 E 在 AB 的延伸线上,∠ AED =∠ ABC.(1)求证: DE 与⊙ O 相切;(2)若 BF = 2, DF=10,求⊙ O 的半径.第14题图命题点 5扇形的有关计算15. (2016 包头 )120 °的圆心角所对的弧长是6π,则此弧所在圆的半径是()16. (2016 宜宾 )半径为 6,圆心角为120 °的扇形的面积是()A. 3πB. 6πC. 9πD. 12π17.(2016 湘潭 )如图,一个扇形的圆心角为90°,半径为2,则该扇形的弧长是________.(结果保存π)命题点 6 圆锥的有关计算18. (2016 乌鲁木齐 )将圆心角为 90°,面积为 4π cm 2 的扇形围成一个圆锥的侧面,则此圆锥的底面圆的半径为 ()A. 1 cmB. 2 cmC. 3 cmD . 4 cm 19. (2016 孝感 )若一个圆锥的底面圆半径为3 cm ,其侧面睁开图的圆心角为120 °,则圆锥的母线长是________cm.20. (2016 淮安 )若一个圆锥的底面圆的半径为2,母线长为6,则该圆锥侧面睁开图的圆心角是 ________°.命题点 7暗影部分面积的计算21. (2016 重庆 A 卷)如图,以 AB 为直径,点O 为圆心的半圆经过点C ,若AC =BC =2,则图中暗影部分的面积是 ()πA. 41B. 2+ π4πC. 21 π+2第21题图22. (2016 资阳 )如图,在 Rt △ ABC 中,∠ ACB =90°, AC = 2 3,以点 B 为圆心, BC 的长为半径作弧,交 AB 于点 D ,若点 D 为 AB 的中点,则暗影部分的面积是 ( )第22题图2242A. 2 3- 3πB. 4 3- 3πC. 2 3-3πD. 3π23. (2016 重庆 B 卷 )如图,在边长为 6 的菱形 ABCD 中,∠ DAB =60°,以点 D 为圆心, 菱形的高 DF 为半径画弧,交 AD 于点 E ,交 CD 于点 G ,则图中暗影部分的面积是 ( )9πA. 18 3- 9πB. 18-3πC. 9 3-2D . 18 3- 3π第23题图24. (2016 常德 )如图,△分的面积是 ________.ABC是⊙ O 的内接正三角形,⊙O 的半径为3,则图中暗影部25.(2016 咸宁 8 分 )如图,在△ ABC 中,∠ C=90°,∠ BAC 的均分线交 BC 于点 D ,点 O 在 AB 上,以点 O 为圆心, OA 为半径的圆恰巧经过点 D ,分别交 AC ,AB 于点E、 F.(1)试判断直线BC 与⊙ O 的地点关系,并说明原因;(2)若 BD = 2 3,BF = 2,求暗影部分的面积(结果保存π).第25题图命题点 8 圆与正多边形的有关计算26. (2015 贵阳 )如图,四边形 ABCD 是⊙ O 的内接正方形,若正方形的面积等于4,则⊙O 的面积等于 ________.27. (2016 盐城 )如图,正六边形第26题图ABCDEF 内接于半径为 4 的圆,则B、E 两点间的距离为________.第27题图中考冲刺集训(时间:60 分钟满分:70分)一、选择题 (共 8 题,每题 3 分,共 24 分)1.(2016 无锡 )如图, AB 是⊙ O 的直径, AC 切⊙ O 于 A ,BC 交⊙ O 于点 D,若∠ C= 70°,则∠ AOD 的度数为( )A. 70°B. 35 °C. 20° D. 40°第1题图2.(2016 德阳 )如图, AP 为⊙ O 的切线, P 为切点,若∠ A = 20°,C、 D 为圆周上两点,且∠ PDC=60°,则∠ OBC 等于 ()第2题图A. 55°B. 65°C. 70°D. 75°3.(2016 衢州 )如图, AB 是⊙ O 的直径, C 是⊙ O 上的点,过点 C 作⊙ O 的切线交 AB 的延伸线于点E,若∠ A= 30°,则 sin∠ E 的值为 ()第3题图1 2 3 3A. 2B.2C.2D.34.(2016 山西 )如图,在 ?ABCD 中, AB 为⊙ O 的直径,⊙ O 与 DC 相切于点 E,与 AD订交于点 F,已知 AB = 12,∠ C= 60°,则FE的长为()ππA. 3B.2C.π D. 2π第4题图5. (2016 聊城 )如图,四边形ABCD 内接于⊙ O, F 是CD DF BC上一点,且=,连结 CF 并延伸交 AD 的延伸线于点E,连结 AC,若∠ ABC = 105°,∠ BAC =25°,则∠ E 的度数为 ()第5题图A. 45°B. 50 °C. 55°D. 60°3,则 S6. (2016 广安 ) 如图, AB 是圆 O 的直径,弦 CD⊥AB ,∠ BCD = 30°, CD=4暗影=()第6题图843A. 2πB. 3πC. 3π D . 8π7. (2016 陕西 )如图,⊙ O 的半径为 4,△ ABC若∠ BAC 与∠ BOC 互补,则弦 BC 的长为 ()3 3 3 3是⊙ O的内接三角形,连结OB 、OC ,第7题图的高是 8. (2016 南通 ) 以下图的扇形纸片半径为4 cm ,则该圆锥的底面周长是( )5 cm ,用它围成一个圆锥的侧面,该圆锥第8题图A. 3π cmB. 4π cmC. 5 π cm D . 6π cm 二、填空题 (共 4 题,每题 4 分,共 16 分)9. (2016 广州 ) 如图,以点 O 为圆心的两个齐心圆中,大圆的弦AB 是小圆的切线,点P 为切点, AB = 12 3,OP =6,则劣弧AB的长为 ________. (结果保存 π)第9题图10. (2016 徐州 )如图,⊙ O 是△ ABC 的内切圆,若∠ ABC = 70°,∠ ACB = 40°,则∠ BOC =________°.第10题图11. (2016 枣庄 )如图,在半径为 3 的⊙ O 中,直径 AB 与弦 CD 订交于点 E ,连结AC , BD ,若 AC = 2,则 tanD = ________.第11题图12. (2016 义乌 )如图①,小敏利用课余时间制作了一个脸盆架,图②是它的截面图,垂直搁置的脸盆与架子的交点为A ,B , AB = 40cm ,脸盆的最低点 C 到 AB 的距离为 10cm,则该脸盆的半径为________cm.第12题图三、解答题 (共 4 题,第13 题 6 分,第 14~16 题每题 8 分,共 30 分 )13.(2016 株洲 )已知 AB 是半径为 1 的圆 O 直径, C 是圆上一点, D 是 BC 延伸线上一点,过 D 点的直线交 AC 于 E 点,交 AB 于 F 点,且△ AEF 为等边三角形.(1)求证:△ DFB 是等腰三角形;(2)若 DA =7AF ,求证 CF⊥ AB.第13题图14.(2016 泰州 ) 如图,△ ABC 中,∠ ACB =90°, D 为 AB 上一点,以 CD 为直径的⊙O 交 BC 于点 E,连结 AE 交 CD 于点 P,交⊙ O 于点 F,连结 DF,∠ CAE =∠ ADF.(1)判断 AB 与⊙ O 的地点关系,并说明原因;(2)若 PF∶PC=1∶ 2, AF=5,求 CP 的长.第14题图15.(2016 沈阳 8 分 )如图,在△ ABC 中,以 AB 为直径的⊙ O 分别与 BC,AC 订交于点D ,E, BD =CD ,过点 D 作⊙ O 的切线交边 AC 于点 F.(1)求证: DF ⊥AC ;(2)若⊙ O 的半径为5,∠ CDF = 30°,求BD的长. (结果保存π)第15题图16.(2016 宿迁 )如图①,在△ ABC 中,点 D 在边 BC 上,∠ ABC∶∠ ACB ∶∠ ADB = 1∶ 2∶ 3,⊙ O 是△ ABD 的外接圆.(1)求证: AC 是⊙ O 的切线;(2)当 BD 是⊙ O 的直径时 (如图② ),求∠ CAD 的度数.第16题图1.A【分析】∵ OA=OB,∠ A=50°,∴∠ B=50°,∴∠ AOB=180°-∠ A-∠ B=180°- 50°- 50°= 80°,∵点 C 是AB的中点,1∴∠ BOC=∠ AOC= 2∠ AOB= 40°,应选 A.第 2题解图AB AC2.C【分析】如解图,连结CO,∵=,∴∠ AOC=∠ AOB=40°,1 1∴∠ ADC= 2∠ AOC= 2× 40°= 20 C.3.35 【分析】∵ OA = OB= OC,∴∠ OAB =∠ B ,∠ C=∠ OAC ,∵∠ AOB = 40°,1∴∠ B=∠ OAB = 70°,∵ CD∥ AB ,∴∠ BAC =∠ C,∴∠ OAC =∠ BAC =2∠OAB =35°.4. 62 【分析】依据直径所对的圆周角等于 90°及∠ BCD = 28°,可得∠ACD =∠ ACB -∠ BCD = 90°- 28°= 62°,再依据同弧所对圆周角相等有∠ABD =∠ ACD = 62°.命题点 2垂径定理及其推论【命题规律】1.考察形式:① 已知半径、弦长、弦心距中的两个量求另一个量;②联合垂径定理计算角度或线段长 .2.利用垂径定理求线段长考察许多,题型多为选择题和填空题.【命题展望】垂径定理及其推论是圆上当算线段长的重要工具,是命题的要点,需对这部分知 识做到熟 练掌握.AB5.A 【分析】 ∵ ON ⊥ AB , AB = 24,∴ AN = 2=12,∴在 Rt △ AON 中, ON =OA 2-AN2= 132-122= 5.6. B【分析】 ∵∠ D 与∠ AOC 同对弧 AC ,∴∠ AOC =2∠ D = 2× 32°= 64°,∵OA = OC ,∴∠ OAC =∠ OCA ,在△ OAC 中,依据三角形内角和为 180°,可得∠ OAC =1 12(180 °-∠ AOC)= 2× (180 °- 64°)=58°.第 7题解图7.4- 7【分析】 如解图,连结 OC ,∵ AB 是⊙ O 的直径, CD ⊥ AB , AB =8, CD = 6,∴ CE = DE = 3, OC = OB =4. 在 Rt △OCE 中,OE = 42- 32= 7,∴ BE = OB - OE =4- 7.命题点 3与圆有关的地点关系【命题规律】 考察内容:直线与圆的地点关系;一般考 查依据其地点关系, 计算某一量的取 值范围或已知 圆心和半径,求 圆与另向来 线的地点关系.【命题展望】 与圆有关的地点关系是 圆中命题点之一,常需判断直 线圆 的地点关系, 值得注意.8. A【分析】 如解图,在 Rt △ ABC 中, AC = 4, BC =3,由勾股定理得 AB =5.过 C1 1作 CD ⊥ AB 于 D ,则 S △ABC =2AC · BC = 2AB · CD ,解得 CD =,∴直线 AB 与⊙ C 订交.第 8题解图第9题解图9. B【分析】 连结 AD ,则 AD =AC 2+CD 2=42+32= 5,∵⊙ A 与⊙ D 订交,∴ 3- r <5<3+ r ,解得 2< r < 8,又∵点 B 在⊙ D 外,∴ r<BD ,即 r <4.∴ 2<r <4,应选 B.命题点 4 与切线有关的证明与计算【命题规律】 1.主要考 查:① 利用切 线性质求角度或 线段长;②判断一条 线是圆的切 线 .2.此类问题 一般在三大 题型中均有波及,此中小 题中常考 查利用切 线性质求角度或 计算线段长 问题 ,解答题中以两 问设题 居多,考察切线的判断和运用切 线性质进行有关 计算.【命题展望】 切线性质与判断作 为圆的重要知 识,愈来愈授命 题人的重 视,是全国命题主流.10. B 【分析】 ∵ AB 和⊙ O 相切于点 B ,∴ OB ⊥ AB ,∴∠ ABO = 90°,∵∠ AOB =60°,∴∠ A = 90°-∠ AOB = 90°- 60°= 30°.第 11 题解图11.B 【分析】 ∵∠ A = 25°,∠ ACB = 90°,∴∠ ABC = 65°如.解图,连结OC.∵ OB = OC ,∴∠ ABC =∠ BCO =65°∵.CD 是⊙的切线,∴ OC ⊥ CD ,∴∠ OCD = 90°, ∴∠ BCD = 90°-∠ BCO = 25°,∴∠ D =∠ ABC -∠ BCD = 65°- 25° = 40°.12. 24 【分析】 设 AB 切⊙ O 于点 E ,如解图,连结 EO 并延伸交 CD 于点 M ,∵ C ⊙O =26π= 2πr ,∴ r = 13,∵ AB ∥ CD ,且 AB 与 CD 之间的距离为18,∴ OM = 18-r = 5,∵ AB 为⊙ O 的切线,∴∠ CMO =∠ AEO =90°,∴在 Rt △CMO 中,CM = OC2- OM 2= 12,∴ CD = 2CM = 24.第 12 题解图第 13 题解图2513.4【分析】 如解图,连结 EO 并延伸交 AD 于点 F ,连结 OD 、OA ,则 OD = OA. ∵BC 与⊙ O 相切于点 E ,∴ OE ⊥ BC ,∵四边形 ABCD 是矩形,1 ∴AD ∥ BC ,∴ EF ⊥ AD ,∴ DF = AF =2AD = 6,在 Rt △ ODF 中,设 OD = r ,则 OF =EF - OE =AB - OE = 8-r ,在 Rt △ ODF 中,由勾股定理得 DF 2+ OF 2=OD 2,即25 2562+(8- r) 2= r 2,解得 r = 4.∴⊙ O 的半径为 4 .14. (1)证明: 如解图,连结 DO ,∴∠ BOD =2∠BCD =∠ A ,(2 分)第 14 题解图又∵∠ DEA =∠ CBA ,∴∠ DEA +∠ DOE =∠ CAB +∠ CBA , 又∵∠ ACB = 90°,∴∠ ODE =∠ ACB =90°,(5 分 ) ∴ OD ⊥ DE ,又∵ OD 是⊙ O 的半径, ∴ DE 与⊙ O 相切. (7 分) (2)解:如解图,连结BD ,可得△ FBD ∽△ DBO ,BD DF BF∴ BO =OD = BD ,(8 分 )∴ BD =DF = 10, ∴ OB =5, (10 分 ) 即⊙ O 的半径为 5. 命题点 5扇形的有关计算【命题规律】 1.考察内容:① 弧长的计算 (含圆的周 长 );② 扇形的面 积计 算;③ 求弧所在圆的半径 .2.考察形式:① 已知扇形 圆心角和半径求弧 长;② 已知扇形 圆心角和半径求面 积;③已知扇形 圆心角和弧 长求半径.【命题展望】 扇形的有关 计算是全国命 题趋向 之一..π r120π· rn15. C 【分析】 由扇形的弧长公式 l =180可得: 6π= 180 ,解得 r = 9.120 × π × 6216. D 【分析】 由扇形的面积公式可得: S =360=12π . n πr 90 × π × 217. π 【分析】 由扇形弧长公式 l = 180 可得: l =180=π.命题点 6 圆锥的有关计算【命题规律】 考察内容与形式:联合圆和扇形的知 识求圆锥 的底面 圆周长、半径以及 圆锥的母 线长或圆心角.【命题展望】 圆锥的有关 计算的考 查结 合圆和扇形的性 质,可以考察学生的 实践操作能力,在这方面更 切近新课标 的要求.90· π ·R 218. A【分析】 设扇形的半径为 R ,依据题意得360= 4π,解得R = 4,设90· π·4圆锥的底面圆的半径为r ,则2π r =180,解得r = 1,即所围成的圆锥的底面圆的半径为 1 cm.360r360 ×319. 9 【分析】 由 n = l得 120=l,解得 l =9.20. 120 【分析】 圆锥的侧面睁开图是扇形,扇形的弧长等于圆锥底面圆的周长,扇n π·6形的半径等于圆锥的母线长.设扇形的圆心角为命题点 7 暗影部分面积的计算n °,则2π× 2=180 ,解得n = 120.【命题规律】 暗影部分面 积的计算常通 过两种方法求解: ① 经过等积变换 ,把不规则 的图形变换 成规则图 形的面 积计算;② 和差法,把暗影部分面 积转 化为几个规则图 形面积和或差的形式 计算,这是做暗影部分面 积计 算题的一般思路.【命题展望】 暗影部分面 积的计算综合知 识较 多,考察学生识图 能力、剖析能力和理解能力,是全国命 题趋向 之一.21.A 【分析】 ∵ AB 为直径,∴∠ ACB = 90°,∵ AC = BC = 2,∴ AB = 2,则半径OA = OB = 1,∵△ AOC ≌△ BOC ,∴△ AOC 的面积与△ BOC 的面积相等,∴暗影部分的1π面积恰巧是四分之一圆的面积,即为4π× 12= 4 .22. A 【分析】 设 BC =x ,∵ D 为 AB 的中点,∴ AB = 2BC =2x, ∴在 Rt △ ABC 中,BC 1 2 23 2 AB 2由勾股定理有 (2x)= , ∴∠ A = 30°,∠ B = 60°,- x = (2 ) ,解得 x = 2,又∵ sinA = 1 60 × π × 222 ∴S 暗影 =S △ABC -S 扇形 BCD =2×2× 2 3-360 = 2 3- 3π.23. A 【分析】 ∵∠ DAB =60°, DF ⊥ AB , AD = 6,∴ DF = AD · sin60° = 3 3,∠ ADC = 120°,∴ S 暗影 = S 菱形 ABCD - S扇形 120π × (3 3)2EDG = 6×3 3-360 =18 3- 9π .24. 3π 【分析】 ∵△ ABC 是⊙ O 的内接正三角形,∴∠ AOB = 2∠ C = 2× 60°= 120 °120 × π × 32 ,∵⊙ O 的半径为 3,∴暗影部分的面积 S 扇形 OAB =360= 3π.25. (1)解:BC 与⊙ O 相切.原因以下:第 25 题解图如解图,连结 OD ,∵ AD 均分∠ BAC , ∴∠ CAD =∠ OAD. 又∵∠ OAD =∠ ODA , ∴∠ CAD =∠ ODA. ∴ OD ∥ AC ,(2 分) ∴∠ BDO =∠ C =90°, 又∵ OD 是⊙ O 的半径, ∴ BC 与⊙ O 相切. (4 分)(2)解: 设⊙ O 的半径为 r ,则 OD = r , OB =r +2, 由 (1)知∠ BDO = 90°,∴在 Rt △ BOD 中, OD 2+ BD 2= OB 2 ,即 r 2+(2 3)2= (r + 2)2. 解得 r =2.(5 分 )BD 23OD23= , ∵ tan ∠ BOD = =∴∠ BOD =60°.(7分)1 60πr22∴ S 暗影 = S △OBD -S 扇形 ODF =2· OD · BD -360 = 2 3- 3π.(8 分)命题点 8 圆与正多边形的有关计算【命题规律】 考察内容:① 圆内接正多 边形的性 质;②圆内接正多 边形与圆的面 积结合.【命题展望】 圆与多 边形联合类题目的考 查形式比 较固定,将圆的面 积与多边形的有关性 质结 合起来 进行考察,这个知识点将成 为一种常 态的命 题形式.26. 2π 【分析】 由题意得,正方形的边长AB = 2,则⊙ O 的半径为22× 2 = 2,∴⊙ O 的面积是 (2)2π= 2π.27.8 【分析】 ∵六边形 ABCDEF 为正六边形,∴AB BC EF ED AF CD = ====,∴BE的长是圆周长的一半,则BE 是圆的直径,∴ BE = 2× 4= 8.中考冲刺集训1. D 【分析】 ∵ AB 是⊙ O 的直径, AC 切⊙ O 于点 A ,∴∠ BAC =90°,∵∠ C = 70°, ∴∠ B =20°,∴∠ AOD =∠ B +∠ BDO = 2∠B = 2×20° = 40°.第 2题解图2. B 【分析】 连结 OP ,如解图,则 OP ⊥AP.∵∠ D = 60°,∴∠ COP = 120 °, ∵∠ A =20°,∠ APO =90°,∴∠ AOP = 70°,∴∠ AOC = 50°,∵ OB = OC ,∴∠ OBC =180° - 50°2 =65°.3. A【分析】 如解图,连结 OC ,∵ EC 切⊙ O 于 C ,∴∠ OCE = 90°,∵ OA =OC ,第 3题解图∴∠ ACO =∠ A = 30°,∴∠ COE =∠ ACO +∠ A= 30°+ 30°= 60°,∴∠ E =180°1-∠ OCE -∠ COE = 180°- 90°- 60°=30°,∴在 Rt △ COE 中, sin ∠E = sin30° = 2.第 4题解图4.C 【分析】 如解图,连结 OE 、 OF ,∵ AB 为⊙ O 的直径, AB =12,∴ AO =OB = 6,∵⊙ O 与 DC 相切于点 E ,∴∠ OEC = 90°,∵在 ?ABCD 中, ∠ C = 60°,AB ∥DC ,∴∠ A =∠ C = 60°,∠ AOE =∠ OEC = 90°,∵在△ AOF 中, ∠ A = 60°,AO = FO ,∴△ AOF 是等边三角形,即∠ AOF =∠ A = 60°,30π × 6∴∠ EOF =∠ AOE -∠ AOF = 90°-60°= 30°,弧 EF 的长=180 =π .5.B 【分析】 ∵四边形 ABCD 是圆内接四边形,∠ ABC = 105 °,∴∠ ADC = 75°, ∵ D F ⌒= BC ⌒,∴∠ BAC =∠ DCF =25°,∴∠ E =∠ ADC -∠ DCF = 50°.第 6题解图6. B 【分析】 如解图,连结 OC ,设 CD 与 OB 交于点 E ,∵在⊙ O 中,弦CD ⊥ AB ,∴ CE = DE =2 3,∵∠ BCD = 30°,∴∠ BOD =2∠ BCD = 60°,在 Rt △EOD 中, DEOE =tan60°= 2,∴ OD = 4,∴ BE =OB - OE = 4-2= 2,在△ DOE 和△ CBE中,CE =DE ,∠ CEB =∠ DEO , OE = BE ,∴△ DOE ≌△ CBE ,∴ S 暗影 = S 扇形 OBD= 60 × π × 42 8360= 3π .第 7题解图7.∠BOC =2∠ BACB 【分析】 如解图,延伸 CO 交⊙ O 于点 A ′,连结 A ′B.设∠ BAC = α,则= 2α,∵∠ BAC +∠ BOC = 180°,∴ α + 2α= 180°,∴ α =60°.∴∠ BA ′C =∠ BAC = 60°,∵ CA ′为直径,∴∠ A ′BC = 90°,则在 Rt △ A ′BC 中,3BC =A ′C · sin ∠BA ′C = 2× 4×2=4 3.8. D 【分析】 如解图,由题意可知, OA = 4 cm , AB = 5 cm ,在 Rt △ AOB 中,利用勾股定理可求得 OB =3 cm ,∴该圆锥的底面周长是6π cm.第8题解图第9题解图19. 8π 【分析】 ∵ AB 是小圆的切线,∴ OP ⊥AB ,∴ AP = 2AB = 6 3.如解图,连结 OA , OB ,∵ OA = OB ,∴∠ AOB = 2∠ AOP. 在 Rt △ AOP 中,AP 6 3 OP2+ AP2 OP 63 OA ==12, tan ∠ AOP == ,∴∠ AOP = 60°∴∠. AOB =120 °,∴劣=120π·12 弧 AB 的长为180 = 8π.10. 125【分析】 ∵⊙ O 是△ ABC 的内切圆,∴ OB 、 OC 分别是∠ ABC 、∠ ACB 的11 均分线,∴∠ OBC +∠ OCB = 2(∠ ABC +∠ ACB) = 2(70 °+ 40°)=55°∴∠. BOC = 180°- (∠ OBC +∠ OCB) =180°- 55°= 125°.11. 22【分析】 如解图,连结 BC ,∵ AB 是⊙ O 的直径,∴∠ ACB = 90°,∵AB = 3× 2= 6, AC =2,∴ BC = AB2- AC 2= 62-22= 4 2,∵∠ D =∠ A ,∴ tanD= ta BC 42nA =AC= 2 = 2 2.第 11 题解图第 12 题解图12. 25 【分析】 如解图,取圆心为 O ,连结 OA 、 OC , OC 交 OC ⊥ AB. 设⊙ O 的半径为 r ,则AB 于点 D ,则OA = OC = r ,又∵ CD = 10,∴ OD = r - 10,∵ AB = 40, OC ⊥ AB ,∴ AD =20.在 Rt △ ADO 中,由勾股定理得: r 2= 202+ (r - 10)2,解得 r =25,即脸盆的半径为 25 cm.13. (1)证明:∵ AB 为直径, ∴∠ ACB = 90°,∵△ AEF 是等边三角形, ∴∠ EAF =∠ EFA = 60°,∴∠ ABC = 30°,∴∠ FDB =∠ EFA -∠ B = 60°- 30°= 30°, (2 分) ∴∠ ABC =∠ FDB , ∴ FB = FD ,∴△ BDF 是等腰三角形. (3 分 )(2)解:设 AF =a ,则 AD = 7a ,第 13 题解图如解图,连结 OC ,则△ AOC 是等边三角形, 由 (1)得, BF = 2- a = DF ,∴ DE =DF -EF =2- a - a = 2- 2a , CE = AC -AE = 1- a ,在 Rt △ADC 中, DC = ( 7a )2-1= 7a2- 1,CE1- a3在 Rt △DCE 中, tan30° = DC = 7a2- 1=3 , 1解得 a =- 2(舍去 )或 a = 2, (5 分 )1∴ AF =2,在△ CAF 和△ BAC 中, CA BAAF = AC = 2,且∠ CAF =∠ BAC =60°, ∴△ CAF ∽△ BAC , ∴∠ CFA =∠ ACB = 90°, 即 CF ⊥ AB.(6 分)14. 解: (1)AB 与⊙ O 相切.原因以下:∵∠ ACB = 90°,∴∠ CAE +∠ AEC = 90°,又∵∠ AEC =∠ CDF ,∠ CAE =∠ ADF , ∴∠ CDF +∠ ADF = 90°, ∴∠ ADC =90°, 又∵ CD 为⊙ O 的直径,∴ AB 与⊙ O 相切. (3 分)(2)如解图,连结 CF ,第 14 题解图∵ CD 为⊙ O 的直径,∴∠ CDF+∠ DCF = 90°,又∵∠ CDF +∠ ADF = 90°,∴∠ DCF=∠ ADF ,又∵∠ CAE =∠ ADF ,∴∠ CAE =∠ DCF ,又∵∠ CPA =∠ FPC,∴△ PCF∽△ PAC ,PC PF∴PA=PC, (6 分 )又∵ PF∶ PC= 1∶ 2, AF = 5,故设 PF = a,则 PC= 2a,2a a∴a+5= 2a,5解得 a= 3,510∴PC= 2a=2× 3= 3 .(8 分 )15. (1)证明:如解图,连结OD, (1 分 )∵ DF 是⊙ O 的切线, D 为切点,第 15 题解图∴OD⊥ DF,∴∠ ODF= 90°, (2 分)∵BD =CD , OA = OB,∴OD 是△ ABC 的中位线, (3 分 )∴OD∥ AC ,∴∠ CFD=∠ ODF = 90°,∴DF⊥ AC.(4 分)(2)解:∵∠ CDF = 30°,由 (1)得∠ ODF = 90°,∴∠ ODB =180°-∠ CDF -∠ ODF =60°,∵OB=OD ,∴△ OBD 是等边三角形,(7 分 )∴∠ BOD =60°,nπR 60π× 5 5BD∴ l = 180 =180 = 3π.(8 分 )16.(1)证明:如解图,连结 OA , OD. 设∠ ABC =x,∵∠ ABC ∶∠ ACB ∶∠ ADB = 1∶ 2∶3,∴∠ ADB =3x ,∠ ACB = 2x ,第16 题解图∴ ∠DAC =x,∠AOD = 2∠ABC =2x ,180° -2x∴∠ OAD =2=90°-x,(2分)∴∠ OAC =90°-x+ x= 90°,∴OA⊥ AC ,又∵ OA 为⊙ O 的半径,∴AC 是⊙ O 的切线. (4 分)(2)解:∵ BD 是⊙ O 的直径,∴∠ BAD =90°,∵∠ ABC ∶∠ ACB ∶∠ ADB = 1∶ 2∶3,∠ABC +∠ ADB = 90°,∴∠ ABC + 3∠ ABC = 90°, (6 分 )解得∠ ABC = 22.5 °,∴∠ ADB =67.5 °,∠ ACB = 45°,∴∠ CAD =∠ ADB -∠ ACB = 22.5 °.(8分 )。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题19 圆的有关计算及圆的综合
学校:___________姓名:___________班级:___________
一、选择题:(共4个小题)
1.【2015成都】如图,正六边形A BCDEF 内接于⊙O ,半径为4,则这个正六边形的边心距
OM 和BC 弧线的长分别为( )
A .2,
3
π
B .π
C 23π
D .
【答案】D . 【解析】
【考点定位】1.正多边形和圆;2.弧长的计算.
2.【2015攀枝花】如图,已知⊙O 的一条直径AB 与弦CD 相交于点E ,且AC =2,AE CE =1,则图中阴影部分的面积为( )
C.29π D.49π
【解析】
【考点定位】1.扇形面积的计算;2.勾股定理的逆定理;3.圆周角定理;4.解直角三角形.
32
的圆锥的底面半径为(
A.1cm B.2cm
【答案】A.
【解析】
试题分析:设扇形的半径为=4,设圆锥的底面圆的半径为,解得r=1,即所围成的圆锥的底面半径为1cm.故选A.
4
轴、y轴分别交于A、B,∠OAB=30°,点P在x轴上,⊙P与l相切,当P在线段OA上运动时,使得⊙P成为整圆的点P个数是()
A.6 B.8 C.10 D.12
【解析】
【考点定位】1.切线的性质;2.一次函数图象上点的坐标特征;3.新定义;4.动点型;5.综合题.
二、填空题:(共4个小题)
5.【2015贵阳】小明把半径为1的光盘、直尺和三角尺形状的纸片按如图所示放置于桌面上,此时,光盘与AB,CD分别相切于点N,M.现从如图所示的位置开始,将光盘在直尺边上沿着CD向右滚动到再次与AB相切时,光盘的圆心经过的距离是.
.
【答案】
3
【解析】
试题分析:如图,当圆心O 移动到点P 的位置时,光盘在直尺边上沿着CD 向右滚动到再次与A
B 相切,切点为Q ,∵ON ⊥AB ,PQ ⊥AB ,∴ON ∥PQ ,∵ON =PQ ,∴OH =PH ,在Rt △PHQ 中,∠P =
∠B =60°,PQ =1,∴PH =
3,则OP =3,故答案为:3
.
【考点定位】1.切线的性质;2.轨迹;3.应用题;4.综合题.
6.【2015自贡】如图,已知AB 是⊙O 的一条直径,延长AB 至C 点,使AC =3BC ,CD 与⊙O 相切于D 点.若CD =3,则劣弧AD 的长为 .
【答案】
3
2
. 【解析】
【考点定位】1.切线的性质;2.弧长的计算.
7.【2015莱芜】如图,在扇形OAB 中,∠AOB =60°,扇形半径为r ,点C 在AB 上,CD ⊥OA ,垂足为D ,当△OCD 的面积最大时,AC 的长为 .
【答案】14
r π. 【解析】
【考点定位】1.垂径定理;2.弧长的计算;3.解直角三角形;4.最值问题;5.二次函数的最值;6.圆的综合题.
8.【2015成都】如图,在半径为5的⊙O 中,弦AB =8,P 是弦AB 所对的优弧上的动点,连接AP ,过点A 作AP 的垂线交射线PB 于点C .当△PAB 是等腰三角形时,线段BC 的长为________.
【答案】8BC =或5615. 【解析】
试题分析:(1)当AB =AP 时,如图(1),作OH ⊥AB 于点H ,延长AO 交PB 于点G ;∵AB =AP ,∴AP AB =,∵AO 过圆心,∴AG ⊥PB ,∴PG =BG ,∠OAH =∠PAG ,∵OH ⊥AB ,∴∠AOH =∠BOH ,
AH =BH =4,∵∠AOB =2∠P ,∴∠AOH =∠P ,∵OA =5,AH =4,∴OH =3,∵∠OAH =∠PAG ,
∴sin ∠OAH =sin ∠PAG ,∴
358PG =,∴PG =245
,∵∠AOH =∠P ,∴cos ∠AOH =cos ∠P ,AP OH PC AO =,∴54033PC AP ==,∴BC =PC -2PG =404856
3515
-=;
(3)当BA =BP 时,如图(3),∵BA =BP ,∴∠P =∠BAP ,∵∠P +∠C =90°,∠CAB +∠BAP =90°,∴∠C =∠CAB ,∴BC =AB =8.
故答案为:8BC =或
56153
.
【考点定位】1.等腰三角形的性质;2.解直角三角形;3.分类讨论;4.综合题. 三、解答题:(共2个小题)
9.【2015广安】如图,PB 为⊙O 的切线,B 为切点,过B 作OP 的垂线BA ,垂足为C ,交⊙O 于点A ,连接PA 、AO ,并延长AO 交⊙O 于点E ,与PB 的延长线交于点D . (1)求证:PA 是⊙O 的切线; (2)若
2
3
OC AC =,且OC =4,求PA 的长和tanD 的值.
【答案】(1)证明见试题解析;(2)
5 12
.
【解析】
(2)连接BE,根据已知
2
3
OC
AC
=,且OC=4,可求AC,OA的值,然后由射影定理可求PC的
值,从而可求OP的值,然后由勾股定理可求AP的值;由AC=BC,AO=OE,得到OC是△ABE的中
位线,进而可得BE∥OP,BE=2OC=8,进而可证△DBE∽△DPO,进而可得:BD BE
PD OP
=,从
而求出BD的值,进而即可求出tanD的值.
试题解析:(1)连接OB,则OA=OB,∵OP⊥AB,∴AC=BC,∴OP是AB的垂直平分线,∴PA= PB,在△PAO和△PBO中,∵PA=PB,PO=PO,OA=OB,∴△PAO≌△PBO(SSS),∴∠PBO=∠P AO,PB=PA,∵PB为⊙O的切线,B为切点,∴∠PBO=90°,∴∠PAO=90°,即PA⊥OA,∴PA 是⊙O的切线;
(2)连接BE,∵
2
3
OC
AC
=,且OC=4,∴AC=6,∴AB=12,在Rt△ACO中,由勾股定理得:A
O==AE=2OA=OB=OA=Rt△APO中,∵AC⊥OP,∴2
AC OC PC
=⋅,解得:PC=9,∴OP=PC+OC=13,在Rt△APO中,由勾股定理得:AP=
=,∴PB =PA
=AC =BC ,OA =OE ,∴OC =
1
2
BE ,OC ∥BE ,∴BE =2O C =8,BE ∥OP ,∴△DBE ∽△DPO ,∴
BD BE PD OP =
,即813
=,解得:BD
=,在Rt △OBD 中,tanD
=
OB BD =
=512
.
【考点定位】1.切线的判定与性质;2.相似三角形的判定与性质;3.解直角三角形. 10.【2015南宁】如图,AB 是⊙O 的直径,C ,G 是⊙O 上两点,且AC =CG ,过点C 的直线C D ⊥
BG 于点D ,交BA 的延长线于点E ,连接BC ,交OD 于点F .
(1)求证:CD 是⊙O 的切线. (2)若
3
2
=FD OF ,求∠E 的度数. (3)连接AD ,在(2)的条件下,若CD =3,求AD 的长.
. 【解析】
(2)由OC ∥BD ,得到△OCF ∽△BDF ,△EOC ∽△EBD ,得到
2
3
OC OF BD DF ==,
2
3
OC OE BD BE ==,根据直角三角形的性质即可得到结论; (3)如图2,过A 作AH ⊥DE 于H ,解直角三角形得到BD ,DE ,BE ,在R t △DAH 中,用勾股定理即可得到AD 的长.
CBD =
1
2
∠EBD =30°,∵
CD =DH =R t △DAH 中,AD
【考点定位】1.圆的综合题;2.切线的判定与性质;3.相似三角形的判定与性质;4.压轴题.。
