高考第一轮复习数学:三角函数(附答案) 精品推荐
2025年高考数学一轮复习课时作业-三角函数【含解析】

2025年高考数学一轮复习课时作业-三角函数【原卷版】(时间:45分钟分值:80分)【基础落实练】1.(5分)下列函数中,是周期函数的为()A.y=sin|x|B.y=cos|x|C.y=tan|x|D.y=(x-1)02.(5分)函数f(x)=ln(cos x)的定义域为()A.{x|kπ-π2<x<kπ+π2,k∈Z}B.{x|kπ<x<kπ+π,k∈Z}C.{x|2kπ-π2<x<2kπ+π2,k∈Z}D.{x|2kπ<x<2kπ+π,k∈Z}3.(5分)函数f(x)=sin(2x-π4)在区间[0,π2]上的最小值为()A.-1B.-22C.22D.04.(5分)函数f(x)=sin + cos + 2在[-π,π]上的图象大致为()5.(5分)(2024·哈尔滨模拟)方程2sin(2x+π3)-1=0在区间[0,4π)上的解的个数为()A.2B.4C.6D.8【6.(5分)(多选题)(2023·长沙模拟)已知函数f(x)=4cos2x,则下列说法中正确的是()A.f(x)为奇函数B.f(x)的最小正周期为πC.f(x)的图象关于直线x=π4对称D.f(x)的值域为[0,4]7.(5分)写出一个最小正周期为3的偶函数为f(x)=.8.(5分)已知函数y=sin(ωx+φ)(ω>0)的图象与直线y=12,距离最近的两点间的距离为π3,那么此函数的最小正周期是.9.(5分)已知f(x)=sin[π3(x+1)]-3cos[π3(x+1)],则f(x)的最小正周期为, f(1)+f(2)+…+f(2025)=.10.(5分)函数f(x)=cos x-cos2x,则f(x)是()A.奇函数,最大值为2B.偶函数,最大值为2C.奇函数,最大值为98D.偶函数,最大值为9811.(10分)已知函数f(x)=sin(2x-π3)+32.(1)求函数f(x)的最小正周期及其图象的对称中心;(2)若f(x0)≤3,求x0的取值范围.即x0的取值范围为[-π2+kπ,π3+kπ](k∈Z).【能力提升练】12.(5分)(多选题)对于函数f(x)=|sin x|+cos2x,下列结论正确的是()A.f(x)的值域为[0,98]B.f(x)在[0,π2]上单调递增C.f(x)的图象关于直线x=π4对称D.f(x)的最小正周期为π13.(5分)已知函数f(x)=2sin(ωx+φ)(ω>0,0<φ<π2)的图象的相邻两条对称轴间的距离为π2,且f(π12)=2,则f(π8)=.14.(10分)(2023·北京高考)设函数f(x)=sinωx cosφ+cosωx sinφ(ω>0,|φ|<π2).(1)若f(0)=-32,求φ的值.(2)已知f(x)在区间[-π3,2π3]上单调递增,f(2π3)=1,再从条件①、条件②、条件③这三个条件中选择一个作为已知条件,使函数f(x)存在,求ω,φ的值.条件①:f(π3)=2;条件②:f(-π3)=-1;条件③:f(x)在区间[-π2,-π3]上单调递减.2025年高考数学一轮复习课时作业-三角函数【解析版】(时间:45分钟分值:80分)【基础落实练】1.(5分)下列函数中,是周期函数的为()A.y=sin|x|B.y=cos|x|C.y=tan|x|D.y=(x-1)0【解析】选B.因为cos|x|=cos x,所以y=cos|x|是周期函数.其余函数均不是周期函数.2.(5分)函数f (x )=ln(cos x )的定义域为()A .{x |k π-π2<x <k π+π2,k ∈Z }B .{x |k π<x <k π+π,k ∈Z }C .{x |2k π-π2<x <2k π+π2,k ∈Z }D .{x |2k π<x <2k π+π,k ∈Z }【解析】选C .由cos x >0,解得2k π-π2<x <2k π+π2,k ∈Z .所以函数f (x )=ln(cos x )的定义域为{x |2k π-π2<x <2k π+π2,k ∈Z }.3.(5分)函数f (x )=sin(2x -π4)在区间[0,π2]上的最小值为()A .-1B .-22C .22D .0【解析】选B .由已知x ∈[0,π2],得2x -π4∈[-π4,3π4],所以sin(2x -π4)∈[-22,1],故函数f (x )=sin(2x -π4)在区间[0,π2]上的最小值为-22.4.(5分)函数f (x )=sin + cos + 2在[-π,π]上的图象大致为()【解析】选D .由f (-x )=sin (- )+(- )cos (- )+(- )2=-sin -cos + 2=-f (x ),得f (x )是奇函数,其图象关于原点对称,排除A;又f (π2)=1+π2(π2)2=4+2ππ2>1,f (π)=π-1+π2>0,排除B,C .5.(5分)(2024·哈尔滨模拟)方程2sin(2x +π3)-1=0在区间[0,4π)上的解的个数为()A .2B .4C .6D .8【解析】选D .由2sin(2x +π3)-1=0得sin(2x +π3)=12,x ∈[0,4π),分别画出y 1=sin(2x +π3)和y 2=12在x ∈0,4π上的图象,如图:两函数图象有8个交点,故方程2sin(2x +π3)-1=0在区间0,4π上的解的个数为8.6.(5分)(多选题)(2023·长沙模拟)已知函数f (x )=4cos 2x ,则下列说法中正确的是()A .f (x )为奇函数B .f (x )的最小正周期为πC .f (x )的图象关于直线x =π4对称D .f (x )的值域为[0,4]【解析】选BD .f (x )=4cos 2x =2cos 2x +2,该函数的定义域为R .因为f (-x )=2cos(-2x )+2=2cos 2x +2=f (x ),所以函数f (x )为偶函数,A 错误;函数f (x )的最小正周期为T =2π2=π,B 正确;因为f (π4)=2cos(2×π4)+2=2,所以f (π4)既不是函数f (x )的最大值,也不是该函数的最小值,C 错误;因为-1≤cos 2x ≤1,所以f (x )=2cos 2x +2∈[0,4],D 正确.7.(5分)写出一个最小正周期为3的偶函数为f (x )=.【解析】f (x )=cos(2π3x )为偶函数,且T =2π2π3=3.答案:cos(2π3x)(答案不唯一)8.(5分)已知函数y=sin(ωx+φ)(ω>0)的图象与直线y=12,距离最近的两点间的距离为π3,那么此函数的最小正周期是.【解析】根据正弦型函数的周期性,当sin(ωx+φ)=12时,若ωx1+φ=π6,则最近的另一个值为ωx2+φ=5π6,所以ω(x2-x1)=2π3,而x2-x1=π3,可得ω=2.故此函数的最小正周期是2π =π.答案:π9.(5分)已知f(x)=sin[π3(x+1)]-3cos[π3(x+1)],则f(x)的最小正周期为, f(1)+f(2)+…+f(2025)=.【解析】依题意可得f(x)=sin[π3(x+1)]-3cos[π3(x+1)]=2sinπ3x,其最小正周期T=6,且f(1)+f(2)+…+f(6)=0,故f(1)+f(2)+…+f(2025)=f(1)+f(2)+f(3)=3+3+0=23.答案:62310.(5分)函数f(x)=cos x-cos2x,则f(x)是()A.奇函数,最大值为2B.偶函数,最大值为2C.奇函数,最大值为98D.偶函数,最大值为98【解析】选D.由题意,f(-x)=cos(-x)-cos(-2x)=cos x-cos2x=f(x),所以该函数为偶函数,又f(x)=cos x-cos2x=-2cos2x+cos x+1=-2(cos x-14)2+98,所以当cos x=14时,f(x)取最大值98.11.(10分)已知函数f(x)=sin(2x-π3)+32.(1)求函数f(x)的最小正周期及其图象的对称中心;【解析】(1)f(x)的最小正周期T=π.由2x-π3=kπ,k∈Z得x=π6+ π2,k∈Z,故f(x)图象的对称中心为(π6+ π2,32)(k∈Z).(2)若f(x0)≤3,求x0的取值范围.【解析】(2)因为f(x0)≤3,所以sin(2x0-π3)+32≤3,即sin(2x0-π3)≤32,所以-4π3+2kπ≤2x0-π3≤π3+2kπ,k∈Z,即-π2+kπ≤x0≤π3+kπ,k∈Z.即x0的取值范围为[-π2+kπ,π3+kπ](k∈Z).【能力提升练】12.(5分)(多选题)对于函数f(x)=|sin x|+cos2x,下列结论正确的是()A.f(x)的值域为[0,98]B.f(x)在[0,π2]上单调递增C.f(x)的图象关于直线x=π4对称D.f(x)的最小正周期为π【解析】选AD.f(x)=|sin x|+cos2x=-2|sin x|2+|sin x|+1=-2(|sin x|-14)2+98[0,98],故A正确;当x∈[0,π2]时,|sin x|∈[0,1],|sin x|=sin x在[0,π2]上单调递增,f(x)=-2(|sin x|-14)2+98,故f(x)在[0,π2]上先增后减,故B错误;f(0)=|sin0|+cos(2×0)=1,f(π2)=|sin π2|+cos(2×π2)=0,f(0)≠f(π2),故C错误;易知y=|sin x|和y=cos2x的最小正周期均为π,故f(x)的最小正周期为π,故D正确.13.(5分)已知函数f(x)=2sin(ωx+φ)(ω>0,0<φ<π2)的图象的相邻两条对称轴间的距离为π2,且f(π12)=2,则f(π8)=.【解析】因为函数f(x)图象的相邻两条对称轴的距离为π2,所以 2=π2,得T=π,即2π =π,得ω=2,即f(x)=2sin(2x+φ),因为f(π12)=2,所以f(π12)=2=2sin(π6+φ),即sinπ6+φ)=1,因为0<φ<π2,所以π6+φ=π2,得φ=π2-π6=π3,则f(x)=2sin(2x+π3),则f(π8)=2sin(2×π8+π3)=2sin(π4+π3)=2(sinπ4cosπ3+cosπ4sinπ3)=2(22×12+22×32)=2+62.答案:2+6214.(10分)(2023·北京高考)设函数f(x)=sinωx cosφ+cosωx sinφ(ω>0,|φ|<π2). (1)若f(0)=-32,求φ的值.【解析】(1)因为f(x)=sinωx cosφ+cosωx sinφ(ω>0,|φ|<π2)所以f(0)=sin0cosφ+cos0sinφ=sinφ=-32,因为|φ|<π2,所以φ=-π3.(2)已知f(x)在区间[-π3,2π3]上单调递增,f(2π3)=1,再从条件①、条件②、条件③这三个条件中选择一个作为已知条件,使函数f(x)存在,求ω,φ的值.条件①:f(π3)=2;条件②:f(-π3)=-1;条件③:f(x)在区间[-π2,-π3]上单调递减.【解析】(2)因为f(x)=sinωx cosφ+cosωx sinφ(ω>0,|φ|<π2)所以f(x)=sin(ωx+φ)(ω>0,|φ|<π2),所以f(x)的最大值为1,最小值为-1.若选条件①:因为f(x)=sin(ωx+φ)的最大值为1,最小值为-1,所以f(π3)=2无解,故条件①不能使函数f(x)存在;若选条件②:因为f(x)在[-π3,2π3]上单调递增,且f(2π3)=1,f(-π3)=-1,所以 2=2π3-(-π3)=π,所以T=2π,ω=2π =1,所以f(x)=sin(x+φ),又因为f(-π3)=-1,所以sin(-π3+φ)=-1,所以-π3+φ=-π2+2kπ,k∈Z,所以φ=-π6+2kπ,k∈Z,因为|φ|<π2,所以ω=1,φ=-π6;若选条件③:因为f(x)在[-π3,2π3]上单调递增,在[-π2,-π3]上单调递减,所以f(x)在x=-π3处取得最小值-1,即f(-π3)=-1.以下与条件②相同.。
高考数学一轮复习《三角函数》复习练习题(含答案)

高考数学一轮复习《三角函数》复习练习题(含答案)一、单选题 1.函数tan2x y =是 A .周期为2π的奇函数 B .周期为2π的奇函数 C .周期为π的偶函数D .周期为2π的偶函数2.有一块矩形花圃ABCD 如图所示,其中10AB cm =,6BC cm =,现引进了新品种需将其扩大成矩形区域EFGH ,点A ,B ,C ,D 均落在矩形EFGH 的边上(不包括顶点),则扩大后的花圃的最大面积为( )A .2100mB .2128mC .2144mD .2196m3.已知函数()sin()(0,0,)f x A x A ωϕωϕπ=+>><,其部分图象如图所示,则()f x 的解析式为( )A .1()3sin 26f x x π⎛⎫=+ ⎪⎝⎭B .1()3sin 26f x x π⎛⎫=- ⎪⎝⎭C .15()3sin 26f x x π⎛⎫=+ ⎪⎝⎭D .1()3sin 26f x x π⎛⎫=- ⎪⎝⎭或15()3sin 26f x x π⎛⎫=+ ⎪⎝⎭ 4.若α是第四象限角,则π-α是第( )象限角.A .一B .二C .三D .四5.若一个底面半径为1的圆锥侧面展开图是一个顶角为23π的扇形,则该圆锥的体积为( )A .353π B .223πC .35πD .22π 6.已知函数()()sin 0,2f x x A πωϕϕ⎛⎫=+>< ⎪⎝⎭的图象如图所示,则tan ϕ=( )A 3B .1C 3D .37.下列函数中最小值为4的是( ) A .224y x x =++ B .4sin sin y x x=+ C .222x x y -=+D .4ln ln y x x=+8.已知函数()sin (0)6f x x πωω⎛⎫=+> ⎪⎝⎭的最小正周期为π,若()f x m =在[0,)π上有两个实根a ,b ,且||3a b π->,则实数m 的取值范围是( ) A .1,02⎛⎫- ⎪⎝⎭B .10,2⎛⎫ ⎪⎝⎭C .1,12⎛⎫ ⎪⎝⎭D .11,22⎛⎫- ⎪⎝⎭二、多选题9.设0θπ<<,非零向量()sin 2,cos a θθ=,()cos ,1b θ=,则( ) A .若1tan 2θ=,则//a b B .若34πθ=,则a b ⊥ C .存在θ,使2a b =D .若//a b ,则1tan 2θ=10.关于函数()cos 23cos f x x x x =+,下列结论正确的有( ) A .函数()f x 有最小值2-B .存在12,x x 有12x x π-=时,()()12f x f x =成立C .函数()f x 在区间,36ππ⎡⎤-⎢⎥⎣⎦上单调递增D .函数()f x 的图象关于点,06π⎛⎫⎪⎝⎭成中心对称11.若ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,则下列结论中正确的是( )A .若AB >,则sin sin A B >B .若cos cos a B b A c -=,则ABC 为直角三角形 C .若cos cos a A b B =,则ABC 为等腰三角形D .若2cos 22A c b c+=,则ABC 为直角三角形 12.已知函数()2sin (0)4f x x πωω⎛⎫=+> ⎪⎝⎭,则下列说法正确的是( )A .若函数()f x 的最小正周期为π,则其图象关于直线8x π=对称B .若函数()f x 的最小正周期为π,则其图象关于点,08π⎛⎫⎪⎝⎭对称C .若函数()f x 在区间0,8π⎛⎫⎪⎝⎭上单调递增,则ω的最大值为2D .若函数()f x 在[]0,2π有且仅有5个零点,则ω的取值范围是192388ω≤< 三、填空题13.已知tan 312πα⎛⎫-=- ⎪⎝⎭,则tan 6πα⎛⎫+= ⎪⎝⎭______.14.如图,某湖有一半径为1km 的半圆形岸边,现决定在圆心O 处设立一个水文监测中心(大小忽略不计),在其正东方向相距2km 的点A 处安装一套监测设备.为了监测数据更加准确,在半圆弧上的点B 以及湖中的点C 处,再分别安装一套监测设备,且90BAC ∠=︒,AB AC =.定义:四边形OACB 及其内部区域为“直接监测覆盖区域”,设AOB θ∠=.则“直接监测覆盖区域”面积的最大值为________.15.若1tan 3α=-,则3sin 2cos 2sin cos αααα+=-_______. 16.已知函数()sin 0,02y x πωϕωϕ⎛⎫=+><≤ ⎪⎝⎭的部分图像如图所示,则点(,)P ωϕ的坐标为___.四、解答题17.已知函数()sin 3cos 33x x f x ππ⎛⎫⎛⎫=-+- ⎪ ⎪⎝⎭⎝⎭.(1)求函数()1y f x =-的单调递增区间; (2)设函数()()()1sin g x x f x =+,求()g x 的值域.18.已知函数()sin()f x A x ωϕ=+,其中0A >,0>ω,22ππϕ-<<,x ∈R 其部分图象如图所示.(1)求函数()y f x =的解析式; (2)若23()f α=(0,)3πα∈,求cos2α的值.19.计算: (1)sin15︒;(2)sin cos cos sin 33ππαααα⎛⎫⎛⎫+-+ ⎪ ⎪⎝⎭⎝⎭;(3)sin13sin73cos13sin17︒︒+︒︒.20.已知函数()222sin 4cos 1f x x x =-+.(1)求()f x 的最小正周期;(2)求()f x 在区间0,3π⎡⎤⎢⎥⎣⎦上的最大值与最小值.21.在ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,且()3sin cos a bC C =+.(1)求B ;(2)已知23BC =,D 为边AB 上的一点,若1BD =,2ACD π∠=,求AC 的长.22.2020年一场突如其来的疫情让亿万中华儿女的心再一次凝结在一起,为控制疫情,让广大发热患者得到及时有效的治疗,武汉市某社区决定临时修建一个医院.医院设计平面图如图所示:矩形ABCD 中,400AB =米,300BC =米,图中DMN 区域为诊断区(M 、N 分别在BC 和AB 边上),ADN △、CDM 及BMN △区域为治疗区.受诊断区医疗设备的实际尺寸影响,要求MDN ∠的大小为4π.(1)若按照200AN CM ==米的方案修建医院,问诊断区是否符合要求?(2)按照疫情现状,病人仍在不断增加,因此需要治疗区的面积尽可能的大,以便于增加床位,请给出具体的修建方案使得治疗区面积S 最大,并求出最大值.23.已知向量,a b 满足2sin ,4a x x π⎛⎫⎛⎫=-+ ⎪ ⎪⎝⎭⎝⎭(cos ,cos sin )b x x x =-,函数()()f x a b x R =⋅∈.(1)求函数()f x 的单调区间;(2)在ABC 中,角A 、B 、C 所对的边分别为a 、b 、c ,且()222242cos a ac B a b c -=+-,求()f B参考答案1.A2.B3.B4.C5.B6.C7.C8.D 9.ABD10.ABC11.ABD12.ACD 13.12-14252km15.35 16.2,3π⎛⎫ ⎪⎝⎭17.(1)()2,2,22k k k Z ππππ⎡⎤-++∈⎢⎥⎣⎦(2)1,42⎡⎤-⎢⎥⎣⎦18.(1)()2sin()6f x x π=+(2)cos 2α=19.(1(2);(3)12.20.(1)π;(2)最小值是-3,最大值是32.21.(1)6B π=(2)AC =22.(1)不符合要求(2)按照tan 18ADN ADN π⎛⎫∠∠= ⎪⎝⎭修建,治疗区面积最大,最大值为240000-(平方米)23.(1)单调增区间为7,,1212k k ππππ⎡⎤--⎢⎥⎣⎦k Z ∈;单调减区间为5,,1212k kππππ⎡⎤-+⎢⎥⎣⎦k Z∈;(2)。
2022届新高考高三数学一轮复习考点讲义第7讲:三角函数【含答案】

三角函数一、知识点 (一)角的概念的推广1、角:一条射线绕着端点从一个位置旋转到另一个位置所成的图形。
其中顶点,始边,终边称为角的三要素。
角可以是任意大小的。
(1)角按其旋转方向可分为:正角,零角,负角。
①正角:习惯上规定,按照逆时针方向旋转而成的角叫做正角; ②负角:按照顺时针方向旋转而成的角叫做负角;③零角:当射线没有旋转时,我们也把它看成一个角,叫做零角。
(2)在直角坐标系中讨论角:①角的顶点在原点,始边在x 轴的非负半轴上,角的终边在第几象限,就说这个角是第几象限角。
②若角的终边在坐标轴上,就说这个角不属于任何象限,它叫轴线角。
(3)终边相同的角的集合:设α表示任意角,所有与α终边相同的角,包括α本身构成一个集合,这个集合可记为},360|{Z n n S ∈⋅+α=ββ= 。
集合S 的每一个元素都与α的终边相同,当0=k 时,对应元素为α。
2、弧度制和弧度制与角度制的换算(1)角度制:把圆周360等分,其中1份所对的圆心角是1度,用度作单位来度量角的制度叫做角度制。
(2)1弧度的角:长度等于半径长的圆弧所对的圆心角叫做1弧度的角。
规定:正角的弧度数为正数,负角的弧度数为负数,零角的弧度数为零。
任一已知角α的弧度数的绝对值rl =α||,这种以“弧度”作为单位来度量角的制度叫做弧度制。
(3)角度制与弧度制的互化:π=2360,π=180;815730.571801'≈≈π= rad ; rad 01745.01801≈π= 。
3、特殊角的三角函数值0 3045 60 90 120 135 150 1800 6π4π 3π 2π 32π 43π 65ππ sin 0 2122 23 1 232221 0 cos 1 232221 0 21- 22- 23- 1- tan 0 331 3 ⨯3- 1- 33- 0210 225 240 270 300 315 330 36067π 45π 34π 23π 35π 47π 611ππ2sin21- 22- 23- 1- 23- 22- 21- 04、平面直角坐标系中特殊线表示的角的集合:其中:Z n ∈,Z k ∈;x 轴正半轴 360⋅nπk 2 第一象限角平分线36045⋅+nπ+πk 24 x 轴负半轴 360180⋅+n π+πk 2 第二象限角平分线 360135⋅+nπ+πk 243 x 轴 180⋅n πk 第三象限角平分线 360225⋅+nπ+πk 245 y 轴正半轴 36090⋅+n π+πk 22第四象限角平分线 360315⋅+nπ+πk 247 y 轴负半轴 360270⋅+n π+πk 223 第一、三象限角平分线 18045⋅+n π+πk 4y 轴 18090⋅+nπ+πk 2 第二、四象限角平分线 180135⋅+n π+πk 43 坐标轴 90⋅n 2πk 象限角平分线 9045⋅+n 24π+πk 5、弧长及扇形面积公式:弧长公式:r l ⋅α=||扇形弧长,扇形面积公式:lr r S 21||212=⋅α=扇形,α是圆心角且为弧度制,r 是扇形半径。
高考一轮复习专题三角函数(全)

高考一轮复习专题——三角函数第1讲 任意角、弧度制及任意角的三角函数基础梳理1.任意角 (1)角的概念的推广①按旋转方向不同分为正角、负角、零角. ②按终边位置不同分为象限角和轴线角. (2)终边相同的角终边与角α相同的角可写成α+k ·360°(k ∈Z ). (3)弧度制①1弧度的角:把长度等于半径长的弧所对的圆心角叫做1弧度的角. ②规定:正角的弧度数为正数,负角的弧度数为负数,零角的弧度数为零, |α|=l r,l 是以角α作为圆心角时所对圆弧的长,r 为半径.③用“弧度”做单位来度量角的制度叫做弧度制,比值lr 与所取的r 的大小无关,仅与角的大小有关.④弧度与角度的换算:360°=2π弧度;180°=π弧度. ⑤弧长公式:l =|α|r ,扇形面积公式:S 扇形=12lr =12|α|r 2.2.任意角的三角函数定义设α是一个任意角,角α的终边上任意一点P (x ,y ),它与原点的距离为r (r >0),那么角α的正弦、余弦、正切分别是:sin α=yr ,cos α=x r,tan α=y x,它们都是以角为自变量,以比值为函数值的函数. 3.三角函数线设角α的顶点在坐标原点,始边与x 轴非负半轴重合,终边与单位圆相交于点P ,过P 作PM 垂直于x 轴于M ,则点M 是点P 在x 轴上的正射影.由三角函数的定义知,点P 的坐标为(cos_α,sin_α),即P (cos_α,sin_α),其中cos α=OM ,sin α=MP ,单位圆与x 轴的正半轴交于点A ,单位圆在A 点的切线与α的终边或其反向延长线相交于点T ,则tan α=AT .我们把有向线段OM 、MP 、AT 叫做α的余弦线、正弦线、正切线.三角函数线有向线段MP 为正弦线有向线段OM 为余弦线有向线段AT为正切线一条规律三角函数值在各象限的符号规律概括为:一全正、二正弦、三正切、四余弦. (2)终边落在x 轴上的角的集合{β|β=kπ,k ∈Z };终边落在y 轴上的角的集合⎭⎬⎫⎩⎨⎧∈+=Z k k ,2ππββ;终边落在坐标轴上的角的集合可以表示为⎭⎬⎫⎩⎨⎧∈=Z k k ,2πββ. 两个技巧(1)在利用三角函数定义时,点P 可取终边上任一点,如有可能则取终边与单位圆的交点,|OP |=r 一定是正值.(2)在解简单的三角不等式时,利用单位圆及三角函数线是一个小技巧. 三个注意(1)注意易混概念的区别:第一象限角、锐角、小于90°的角是概念不同的三类角,第一类是象限角,第二类、第三类是区间角.(2)角度制与弧度制可利用180°=π rad 进行互化,在同一个式子中,采用的度量制度必须一致,不可混用.(3)注意熟记0°~360°间特殊角的弧度表示,以方便解题.双基自测1.(人教A版教材习题改编)下列与9π4的终边相同的角的表达式是( ).A.2kπ+45°(k∈Z) B.k·360°+94π(k∈Z)C.k·360°-315°(k∈Z) D.kπ+5π4(k∈Z)2.若α=k·180°+45°(k∈Z),则α在( ).A.第一或第三象限B.第一或第二象限C.第二或第四象限D.第三或第四象限3.若sin α<0且tan α>0,则α是( ).A.第一象限角B.第二象限角C.第三象限角D.第四象限角4.已知角α的终边过点(-1,2),则cos α的值为( ).A.-55B.255C.-255D.-125.(2011·江西)已知角θ的顶点为坐标原点,始边为x轴非负半轴,若P(4,y)是角θ终边上一点,且sin θ=-255,则y=________.考向一角的集合表示及象限角的判定【例1】►(1)写出终边在直线y=3x上的角的集合;(2)若角θ的终边与6π7角的终边相同,求在[0,2π)内终边与θ3角的终边相同的角;(3)已知角α是第二象限角,试确定2α、α2所在的象限.【训练1】角α与角β的终边互为反向延长线,则( ).A.α=-βB.α=180°+βC.α=k·360°+β(k∈Z)D .α=k ·360°±180°+β(k ∈Z )考向二 三角函数的定义【例2】►已知角θ的终边经过点P (-3,m )(m ≠0)且sin θ=24m ,试判断角θ所在的象限,并求cos θ和tan θ的值.【训练2】(2011·课标全国)已知角θ的顶点与原点重合,始边与x 轴的非负半轴重合,终边在直线y =2x 上,则cos 2θ=( ). A .-45 B .-35 C.35 D.45考向三 弧度制的应用【例3】►已知半径为10的圆O 中,弦AB 的长为10. (1)求弦AB 所对的圆心角α的大小;(2)求α所在的扇形的弧长l 及弧所在的弓形的面积S .【训练3】已知扇形周长为40,当它的半径和圆心角取何值时,才使扇形面积最大?考向四 三角函数线及其应用【例4】►在单位圆中画出适合下列条件的角α的终边的范围.并由此写出角α的集合: (1)sin α≥32; (2)cos α≤-12.【训练4】求下列函数的定义域:(1)y =2cos x -1; (2)y =lg(3-4sin 2x ). 解 (1)∵2cos x -1≥0,∴cos x ≥12.重点突破——如何利用三角函数的定义求三角函数值【问题研究】三角函数的定义:设α是任意角,其终边上任一点P (不与原点重合)的坐标为(x ,y ),它到原点的距离是r (r =x 2+y 2>0),则sin α=yr、cosα=x r 、tan α=yx 分别是α的正弦、余弦、正切,它们都是以角为自变量,以比值为函数值的函数,这样的函数称为三角函数,这里x ,y 的符号由α终边所在象限确定,r 的符号始终为正,应用定义法解题时,要注意符号,防止出现错误.三角函数的定义在解决问题中应用广泛,并且有时可以简化解题过程.【解决方案】利用三角函数的定义求三角函数值时,首先要根据定义正确地求得x ,y ,r 的值;然后对于含参数问题要注意分类讨论.【示例】►(本题满分12分)(2011·龙岩月考)已知角α终边经过点P (x ,-2)(x ≠0),且cos α=36x ,求sin α、tan α的值.【试一试】已知角α的终边在直线3x +4y =0上,求sin α+cos α+45tan α.第2讲 同角三角函数的基本关系与诱导公式基础梳理1.同角三角函数的基本关系 (1)平方关系:sin 2α+cos 2α=1; (2)商数关系:sin αcos α=tan α.2.诱导公式公式一:sin(α+2k π)=sin α,cos(α+2k π)=cos α,其中k ∈Z .公式二:sin(π+α)=-sin α,cos(π+α)=-cos α, tan(π+α)=tan α.公式三:sin(-α)=-sin α,cos(-α)=cos α. 公式四:sin(π-α)=sin α,cos(π-α)=-cos α. 公式五:sin )2(απ-=cos α,cos )2(απ-=sin α.公式六:sin )2(απ+=cos α,cos )2(απ+=-sin α. 诱导公式可概括为k ·π2±α的各三角函数值的化简公式.记忆规律是:奇变偶不变,符号看象限.其中的奇、偶是指π2的奇数倍和偶数倍,变与不变是指函数名称的变化.若是奇数倍,则函数名称变为相应的余名函数;若是偶数倍,则函数名称不变,符号看象限是指把α看成锐角时原函数值的符号作为结果的符号.一个口诀诱导公式的记忆口诀为:奇变偶不变,符号看象限.三种方法在求值与化简时,常用方法有: (1)弦切互化法:主要利用公式tan α=sin αcos α化成正、余弦.(2)和积转换法:利用(sin θ±cos θ)2=1±2sin θcos θ的关系进行变形、转化.(3)巧用“1”的变换:1=sin 2θ+cos 2θ=cos 2θ(1+tan 2θ)=tan π4=…. 三个防范(1)利用诱导公式进行化简求值时,先利用公式化任意角的三角函数为锐角三角函数,其步骤:去负-脱周-化锐. 特别注意函数名称和符号的确定.(2)在利用同角三角函数的平方关系时,若开方,要特别注意判断符号. (3)注意求值与化简后的结果一般要尽可能有理化、整式化.双基自测1.(人教A 版教材习题改编)已知sin(π+α)=12,则cos α的值为( ).A .±12 B.12 C.32 D .±322.(2012·杭州调研)点A (sin 2 011°,cos 2 011°)在直角坐标平面上位于( ). A .第一象限 B .第二象限 C .第三象限D .第四象限3.已知cos α=45,α∈(0,π),则tan α的值等于( ).A.43B.34 C .±43 D .±344.cos )417(π--sin )417(π-的值是( ). A. 2 B .- 2 C .0 D.225.已知α是第二象限角,tan α=-12,则cos α=________.考向一 利用诱导公式化简、求值【例1】►已知)tan()2sin()2cos()sin()(απαπαπαπα++--=f ,求【训练1】已知角α终边上一点P (-4,3),则的值为________.考向二 同角三角函数关系的应用)3(πf )29sin()211cos()sin()2cos(απαπαπαπ+---+【例2】►(2011·长沙调研)已知tan α=2. 求:(1)2sin α-3cos α4sin α-9cos α;(2)4sin 2α-3sin αcos α-5cos 2α.【训练2】已知sin α+3cos α3cos α-sin α=5.则sin 2α-sin αcos α=________.考向三 三角形中的诱导公式【例3】►在△ABC 中,sin A +cos A =2,3cos A =-2cos(π-B ),求△ABC 的三个内角.【训练3】若将例3的已知条件“sin A +cos A =2”改为“sin(2π-A )=-2sin(π-B )”其余条件不变,求△ABC 的三个内角.重点突破——忽视题设的隐含条件致误【问题诊断】涉及到角的终边、函数符号和同角函数关系问题时,应深挖隐含条件,处理好开方、平方关系,避免出现增解与漏解的错误.,【防范措施】一要考虑题设中的角的范围;二要考虑题设中的隐含条件 【示例】►若sin θ,cos θ是关于x 的方程5x 2-x +a =0(a 是常数)的两根,θ∈(0,π),求cos 2θ的值.【试一试】已知sin θ+cos θ=713,θ∈(0,π),求tan θ.第3讲 三角函数的图象与性质基础梳理1.“五点法”描图(1)y =sin x 的图象在[0,2π]上的五个关键点的坐标为(0,0),)1,2(π,(π,0),)1,23(-π,(2π,0).(2)y =cos x 的图象在[0,2π]上的五个关键点的坐标为(0,1),)0,2(π,(π,-1),)0,23(π,(2π,1).2.三角函数的图象和性质定义域R R {x|x≠kπ+π2,k∈Z}图象值域[-1,1][-1,1]R对称性对称轴:x=kπ+π2(k∈Z)对称中心:(kπ,0)(k∈Z)对称轴:x=kπ(k∈Z)对称中心:错误!无对称轴对称中心:)0,2(πk(k∈Z)周期2π2ππ单调性单调增区间⎥⎦⎤⎢⎣⎡+-22,22ππππkk(k∈Z);单调减区间⎥⎦⎤⎢⎣⎡++ππππ232,22kk(k∈Z)单调增区间[2kπ-π,2kπ](k∈Z);单调减区间[2kπ,2kπ+π](k∈Z)单调增区间)2,2(ππππ+-kk(k∈Z)奇偶性奇偶奇两条性质(1)周期性函数y=A sin(ωx+φ)和y=A cos(ωx+φ)的最小正周期为2π|ω|,y=tan(ωx+φ)的最小正周期为π|ω|.(2)奇偶性三角函数中奇函数一般可化为y =A sin ωx 或y =A tan ωx ,而偶函数一般可化为y =A cos ωx +b 的形式.三种方法求三角函数值域(最值)的方法: (1)利用sin x 、cos x 的有界性;(2)形式复杂的函数应化为y =A sin(ωx +φ)+k 的形式逐步分析ωx +φ的范围,根据正弦函数单调性写出函数的值域;(3)换元法:把sin x 或cos x 看作一个整体,可化为求函数在区间上的值域(最值)问题.双基自测1.(人教A 版教材习题改编)函数y =cos )3(π+x ,x ∈R ( ).A .是奇函数B .是偶函数C .既不是奇函数也不是偶函数D .既是奇函数又是偶函数2.函数y =tan )4(x -π的定义域为( ).A.⎭⎬⎫⎩⎨⎧∈-≠Z k k x x ,4ππB.⎭⎬⎫⎩⎨⎧∈-≠Z k k x x ,42ππC.⎭⎬⎫⎩⎨⎧∈+≠Z k k x x ,4ππD.⎭⎬⎫⎩⎨⎧∈+≠Z k k x x ,42ππ3.(2011·全国新课标)设函数f (x )=sin(ωx +φ)+cos(ωx +φ)(20πϕω<,>)的最小正周期为π,且f (-x )=f (x ),则( ). A .f (x )在)2,0(π单调递减B .f (x )在)43,4(ππ单调递减C .f (x )在)2,0(π单调递增D .f (x )在)43,4(ππ单调递增4.y =sin )4(π-x 的图象的一个对称中心是( ).A .(-π,0) B.)0,43(π-C.)0,23(π D.)0,2(π5.(2011·合肥三模)函数f (x )=cos )62(π+x 的最小正周期为________.考向一 三角函数的定义域与值域【例1】►(1)求函数y =lg sin 2x +9-x 2的定义域. (2)求函数y =cos 2x +sin x (4π≤x )的最大值与最小值.【训练1】(1)求函数y =sin x -cos x 的定义域.(2)已知函数f (x )=cos )32(π-x +2sin )4(π-x ·sin )4(π+x ,求函数f (x )在区间⎥⎦⎤⎢⎣⎡-2,12ππ上的最大值与最小值.考向二 三角函数的奇偶性与周期性【例2】►(2011·大同模拟)函数y =2cos 2)4(π-x -1是( ).A .最小正周期为π的奇函数B .最小正周期为π的偶函数C .最小正周期为π2的奇函数D .最小正周期为π2的偶函数 【训练2】已知函数f (x )=(sin x -cos x )sin x ,x ∈R ,则f (x )的最小正周期是________.考向三 三角函数的单调性【例3】►已知f (x )=sin x +sin )2(x -π,x ∈[0,π],求f (x )的单调递增区间.【训练3】函数f (x )=sin )32(π+-x 的单调减区间为______.考向四 三角函数的对称性【例4】►(1)函数y =cos )32(π+x 图象的对称轴方程可能是( ).A .x =-π6B .x =-π12C .x =π6D .x =π12【训练4】(1)函数y =2sin(3x +φ)(2πϕ<)的一条对称轴为x =π12,则φ=________.(2)函数y =cos(3x +φ)的图象关于原点成中心对称图形.则φ=________.重点突破——利用三角函数的性质求解参数问题含有参数的三角函数问题,一般属于逆向型思维问题,难度相对较大一些.正确利用三角函数的性质解答此类问题,是以熟练掌握三角函数的各条性质为前提的,解答时通常将方程的思想与待定系数法相结合.下面就利用三角函数性质求解参数问题进行策略性的分类解析. 一、根据三角函数的单调性求解参数【示例】►(2011·镇江三校模拟)已知函数f (x )=sin )3(πω+x (ω>0)的单调递增区间为⎥⎦⎤⎢⎣⎡+-12,125ππππk k (k ∈Z ),单调递减区间为⎥⎦⎤⎢⎣⎡++127,12ππππk k (k ∈Z ),则ω的值为________.二、根据三角函数的奇偶性求解参数【示例】► (2011·泉州模拟)已知f (x )=cos(3x +φ)-3sin(3x +φ)为偶函数,则φ可以取的一个值为( ). A.π6 B.π3 C .-π6 D .-π3▲根据三角函数的周期性求解参数【示例】► (2011·合肥模拟)若函数y =sin ωx ·sin )2(πω+x (ω>0)的最小正周期为π7,则ω=________.▲根据三角函数的最值求参数【示例】► (2011·洛阳模拟)若函数f(x)=a sin x-b cos x在x=π3处有最小值-2,则常数a、b的值是( ).A.a=-1,b= 3 B.a=1,b=- 3C.a=3,b=-1 D.a=-3,b=1第4讲正弦型函数y=A sin(ωx+φ)的图象及应用基础梳理1.用五点法画y=A sin(ωx+φ)一个周期内的简图时,要找五个特征点如下表所示x 0-φωπ2-φωπ-φω3π2-φω2π-φωωx+φ0π2π3π22πy=A sin(ωx+φ)0 A 0-A 0 2.函数y=sin x的图象变换得到y=A sin(ωx+φ)的图象的步骤3.图象的对称性函数y =A sin(ωx +φ)(A >0,ω>0)的图象是轴对称也是中心对称图形,具体如下:(1)函数y =A sin(ωx +φ)的图象关于直线x =x k (其中 ωx k +φ=k π+π2,k∈Z )成轴对称图形.(2)函数y =A sin(ωx +φ)的图象关于点(x k,0)(其中ωx k +φ=k π,k ∈Z )成中心对称图形. 一种方法在由图象求三角函数解析式时,若最大值为M ,最小值为m ,则A =M -m 2,k =M +m 2,ω由周期T 确定,即由2πω=T 求出,φ由特殊点确定.一个区别由y =sin x 的图象变换到y =A sin (ωx +φ)的图象,两种变换的区别:先相位变换再周期变换(伸缩变换),平移的量是|φ|个单位;而先周期变换(伸缩变换)再相位变换,平移的量是|φ|ω(ω>0)个单位.原因在于相位变换和周期变换都是针对x 而言,即x 本身加减多少值,而不是依赖于ωx 加减多少值. 两个注意作正弦型函数y =A sin(ωx +φ)的图象时应注意: (1)首先要确定函数的定义域;(2)对于具有周期性的函数,应先求出周期,作图象时只要作出一个周期的图象,就可根据周期性作出整个函数的图象.双基自测1.(人教A 版教材习题改编)y =2sin )42(π-x 的振幅、频率和初相分别为( ). A .2,1π,-π4 B .2,12π,-π4 C .2,1π,-π8D .2,12π,-π82.已知简谐运动f (x )=A sin(ωx +φ)(2πϕ<)的部分图象如图所示,则该简谐运动的最小正周期T 和初相φ分别为( ). A .T =6π,φ=π6B .T =6π,φ=π3C .T =6,φ=π6D .T =6,φ=π33.函数y =cos x (x ∈R )的图象向左平移π2个单位后,得到函数y =g (x )的图象,则g (x )的解析式应为( ).A .-sin xB .sin xC .-cos xD .cos x4.设ω>0,函数y =sin )3(πω+x +2的图象向右平移4π3个单位后与原图象重合,则ω的最小值是( ). A.23 B.43 C.32D .35.(2011·重庆六校联考)已知函数f (x )=sin(ωx +φ)(ω>0)的图象如图所示,则ω=________.考向一 作函数y =A sin(ωx +φ)的图象【例1】►设函数f (x )=cos(ωx +φ)(02-0<<,>ϕπω)的最小正周期为π,且)4(πf =32.(1)求ω和φ的值;(2)在给定坐标系中作出函数f (x )在[0,π]上的图象.【训练1】已知函数f (x )=3sin )421(π-x ,x ∈R .(1)画出函数f (x )在长度为一个周期的闭区间上的简图; (2)将函数y =sin x 的图象作怎样的变换可得到f (x )的图象?考向二 求函数y =A sin(ωx +φ)的解析式【例2】►(2011·江苏)函数f (x )=A sin(ωx +φ)(A ,ω,φ为常数,A >0,ω>0)的部分图象如图所示,则f (0)的值是________.【训练2】已知函数y =A sin(ωx +φ)(A >0,|φ|<π2,ω>0)的图象的一部分如图所示. (1)求f (x )的表达式; (2)试写出f (x )的对称轴方程.考向三 函数y =A sin(ωx +φ)的图象与性质的综合应用【例3】►(2012·西安模拟)已知函数f (x )=A sin(ωx +φ),x ∈R (其中A >0,ω>0,0<φ<π2)的图象与x 轴的交点中,相邻两个交点之间的距离为π2,且图象上的一个最低点为M )2,32(-π. (1)求f (x )的解析式;(2)当x ∈⎥⎦⎤⎢⎣⎡2,12ππ时,求f (x )的值域.【训练3】(2011·南京模拟)已知函数y =A sin(ωx +φ)(A >0,ω>0)的图象过点P )0,12(π,图象上与点P 最近的一个最高点是Q )5,3(π.(1)求函数的解析式; (2)求函数f (x )的递增区间.重点突破——怎样求解三角函数的最值问题【问题研究】(1)求三角函数的最值是高考的一个热点.在求解中,一定要注意其定义域,否则容易产生错误.(2)主要题型:①求已知三角函数的值域(或最值);②根据三角函数的值域(或最值)求相关的参数;③三角函数的值域(或最值)作为工具解决其他与范围相关的问题.【解决方案】①形如y =a sin x +b cos x +c 的三角函数,可通过引入辅助角Φ(2222sin ,cos b a b b a a +=+=φφ),将原式化为y =a 2+b 2·sin(x +φ)+c的形式后,再求值域(或最值);②形如y =a sin 2x +b sin x +c 的三角函数,可先设t =sin x ,将原式化为二次函数y =at 2+bt +c 的形式,进而在t ∈[-1,1]上求值域(或最值);③形如y =a sin x cos x +b (sin x ±cos x )+c 的三角函数,可先设t =sin x ±cos x ,将原式化为二次函数y =±12a (t 2-1)+bt +c 的形式,进而在闭区间t ∈[-2,2]上求最值.【示例】►(本题满分12分)(2011·北京)已知函数f (x )=4cos x sin )6(π+x -1.(1)求f (x )的最小正周期;(2)求f (x )在区间⎥⎦⎤⎢⎣⎡-4,6ππ上的最大值和最小值.【试一试】是否存在实数a ,使得函数y =sin 2x +a cos x +58a -32在闭区间⎥⎦⎤⎢⎣⎡2,0π上的最大值是1?若存在,求出对应的a 值?若不存在,试说明理由.第5讲 两角和与差的正弦、余弦和正切基础梳理1.两角和与差的正弦、余弦、正切公式(1)C (α-β):cos(α-β)=cos αcos β+sin αsin β; (2)C (α+β):cos(α+β)=cos αcos β-sin αsin β; (3)S (α+β):sin(α+β)=sin αcos β+cos_αsin β; (4)S (α-β):sin(α-β)=sin αcos β-cos αsin β; (5)T (α+β):tan(α+β)=tan α+tan β1-tan αtan β;(6)T (α-β):tan(α-β)=tan α-tan β1+tan αtan β.2.二倍角的正弦、余弦、正切公式 (1)S 2α:sin 2α=2sin_αcos_α;(2)C 2α:cos 2α=cos 2α-sin 2α=2cos 2α-1=1-2sin 2α; (3)T 2α:tan 2α=2tan α1-tan 2α.3.有关公式的逆用、变形等(1)tan α±tan β=tan(α±β)(1∓tan_αtan_β); (2)cos 2α=1+cos 2α2,sin 2α=1-cos 2α2; (3)1+sin 2α=(sin α+cos α)2,1-sin 2α=(sin α-cos α)2, sin α±cos α=2sin )4(πα±.4.函数f (α)=a cos α+b sin α(a ,b 为常数),可以化为f (α)=a 2+b 2sin(α+φ)或f (α)=a 2+b 2cos(α-φ),其中φ可由a ,b 的值唯一确定.两个技巧(1)拆角、拼角技巧:2α=(α+β)+(α-β);α=(α+β)-β;β=α+β2-α-β2;α-β2=)2(βα+-)2(βα+.(2)化简技巧:切化弦、“1”的代换等.三个变化(1)变角:目的是沟通题设条件与结论中所涉及的角,其手法通常是“配凑”. (2)变名:通过变换函数名称达到减少函数种类的目的,其手法通常有“切化弦”、“升幂与降幂”等.(3)变式:根据式子的结构特征进行变形,使其更贴近某个公式或某个期待的目标,其手法通常有:“常值代换”、“逆用变用公式”、“通分约分”、“分解与组合”、“配方与平方”等.双基自测1.(人教A 版教材习题改编)下列各式的值为14的是( ).A .2cos 2 π12-1 B .1-2sin 275° C.2tan 22.5°1-tan 222.5°D .sin 15°cos 15° 2.(2011·福建)若tan α=3,则sin 2αcos 2α的值等于( ).A .2B .3C .4D .6 3.已知sin α=23,则cos(π-2α)等于( ).A .-53 B .-19 C.19 D.534.(2011·辽宁)设sin )4(θπ+=13,则sin 2θ=( ).A .-79B .-19 C.19 D.795.tan 20°+tan 40°+3tan 20° tan 40°=________.考向一 三角函数式的化简【例1】►化简)4(sin )4tan(221cos 2cos 2224x x x x +-+-ππ.【训练1】化简:ααααα2sin )1cos )(sin 1cos (sin +--+.考向二 三角函数式的求值【例2】►已知0<β<π2<α<π,且cos )2(βα-=-19,sin )2(βα-=23,求cos(α+β)的值.【训练2】已知α,β∈)2,0(π,sin α=45,tan(α-β)=-13,求cos β的值.考向三 三角函数的求角问题【例3】►已知cos α=17,cos(α-β)=1314,且0<β<α<π2,求β.【训练3】已知α,β∈)2,2(ππ-,且tan α,tan β是方程x 2+33x +4=0的两个根,求α+β的值.考向四 三角函数的综合应用【例4】►(2010·北京)已知函数f (x )=2cos 2x +sin 2x .(1)求f )3(π的值;(2)求f (x )的最大值和最小值.【训练4】已知函数f (x )=2sin(π-x )cos x . (1)求f (x )的最小正周期;(2)求f (x )在区间⎥⎦⎤⎢⎣⎡-2,6ππ上的最大值和最小值.重点突破——三角函数求值、求角问题策略面对有关三角函数的求值、化简和证明,许多考生一筹莫展,而三角恒等变换更是三角函数的求值、求角问题中的难点和重点,其难点在于:其一,如何牢固记忆众多公式,其二,如何根据三角函数的形式去选择合适的求值、求角方法. 一、给值求值一般是给出某些角的三角函数式的值,求另外一些角的三角函数值,解题的关键在于“变角”,如α=(α+β)-β,2α=(α+β)+(α-β)等,把所求角用含已知角的式子表示,求解时要注意角的范围的讨论.【示例】► (2011·江苏)已知tan )4(π+x =2,则tan x tan 2x 的值为________.二、给值求角“给值求角”:实质上也转化为“给值求值”,关键也是变角,把所求角用含已知角的式子表示,由所得的函数值结合该函数的单调区间求得角.【示例】► (2011·南昌月考)已知tan(α-β)=12,tan β=-17,且α,β∈(0,π),求2α-β的值.▲三角恒等变换与向量的综合问题两角和与差的正弦、余弦、正切公式作为解题工具,是每年高考的必考内容,常在选择题中以条件求值的形式考查.近几年该部分内容与向量的综合问题常出现在解答题中,并且成为高考的一个新考查方向.【示例】► (2011·温州一模)已知向量a =(sin θ,-2)与b =(1,cos θ)互相垂直,其中θ∈)2,0(π.(1)求sin θ和cos θ的值;(2)若5cos(θ-φ)=35cos φ,0<φ<π2,求cos φ的值.第6讲正弦定理和余弦定理基础梳理1.正弦定理:asin A =bsin B=csin C=2R,其中R是三角形外接圆的半径.由正弦定理可以变形为:(1)a∶b∶c=sin A∶sin B∶sin C;(2)a=2R sin_A,b=2R sin_B,c=2R sin_C;(3)sin A=a2R,sin B=b2R,sin C=c2R等形式,以解决不同的三角形问题.2.余弦定理:a2=b2+c2-2bc cos A,b2=a2+c2-2ac cos B,c2=a2+b2-2ab cos C.余弦定理可以变形为:cos A=b2+c2-a22bc,cos B=a2+c2-b22ac,cos C=a2+b2-c22ab.3.S△ABC=12ab sin C=12bc sin A=12ac sin B=abc4R=12(a+b+c)·r(R是三角形外接圆半径,r是三角形内切圆的半径),并可由此计算R,r.4.已知两边和其中一边的对角,解三角形时,注意解的情况.如已知a,b,A,则A为锐角A为钝角或直角图形关系式a<b sin A a=b sin Ab sin A<a<ba≥b a>b a≤b解的个数无解一解两解一解一解无解一条规律在三角形中,大角对大边,大边对大角;大角的正弦值也较大,正弦值较大的角也较大,即在△ABC中,A>B⇔a>b⇔sin A>sin B.两类问题在解三角形时,正弦定理可解决两类问题:(1)已知两角及任一边,求其它边或角;(2)已知两边及一边的对角,求其它边或角.情况(2)中结果可能有一解、两解、无解,应注意区分.余弦定理可解决两类问题:(1)已知两边及夹角求第三边和其他两角;(2)已知三边,求各角.两种途径根据所给条件确定三角形的形状,主要有两种途径:(1)化边为角;(2)化角为边,并常用正弦(余弦)定理实施边、角转换.双基自测1.(人教A版教材习题改编)在△ABC中,A=60°,B=75°,a=10,则c等于( ).A.5 2 B.10 2C.1063D.5 62.在△ABC中,若sin Aa=cos Bb,则B的值为( ).A.30° B.45° C.60° D.90°3.(2011·郑州联考)在△ABC中,a=3,b=1,c=2,则A等于( ). A.30° B.45° C.60° D.75°4.在△ABC中,a=32,b=23,cos C=13,则△ABC的面积为( ).A.3 3 B.2 3 C.4 3 D. 35.已知△ABC三边满足a2+b2=c2-3ab,则此三角形的最大内角为________.考向一利用正弦定理解三角形【例1】►在△ABC中,a=3,b=2,B=45°.求角A,C和边c.【训练1】(2011·北京)在△ABC中,若b=5,∠B=π4,tan A=2,则sin A=________;a=________.考向二利用余弦定理解三角形【例2】►在△ABC中,a、b、c分别是角A、B、C的对边,且cos Bcos C=-b2a+c.(1)求角B的大小;(2)若b=13,a+c=4,求△ABC的面积.【训练2】(2011·桂林模拟)已知A,B,C为△ABC的三个内角,其所对的边分别为a,b,c,且2cos2A2+cos A=0.(1)求角A的值;(2)若a=23,b+c=4,求△ABC的面积.考向三 利用正、余弦定理判断三角形形状【例3】►在△ABC 中,若(a 2+b 2)sin(A -B )=(a 2-b 2)sin C ,试判断△ABC 的形状.【训练3】在△ABC 中,若a cos A =b cos B =c cos C ;则△ABC 是( ). A .直角三角形B .等边三角形C .钝角三角形D .等腰直角三角形考向四 正、余弦定理的综合应用【例3】►在△ABC 中,内角A ,B ,C 对边的边长分别是a ,b ,c ,已知c =2,C =π3. (1)若△ABC 的面积等于3,求a ,b ;(2)若sin C +sin(B -A )=2sin 2A ,求△ABC 的面积.【训练4】(2011·北京西城一模)设△ABC 的内角A ,B ,C 所对的边长分别为a ,b,c,且cos B=45,b=2.(1)当A=30°时,求a的值;(2)当△ABC的面积为3时,求a+c的值.重点突破——忽视三角形中的边角条件致错【问题诊断】考查解三角形的题在高考中一般难度不大,但稍不注意,会出现“会而不对,对而不全”的情况,其主要原因就是忽视三角形中的边角条件., 【防范措施】解三角函数的求值问题时,估算是一个重要步骤,估算时应考虑三角形中的边角条件.【示例】►(2011·安徽)在△ABC中,a,b,c分别为内角A,B,C所对的边长,a=3,b=2,1+2cos(B+C)=0,求边BC上的高.【试一试】(2011·辽宁)△ABC的三个内角A,B,C所对的边分别为a,b,c,a sin A sin B+b cos2A=2a.(1)求b a ;(2)若c2=b2+3a2,求B.第7讲正弦定理、余弦定理应用举例基础梳理1.用正弦定理和余弦定理解三角形的常见题型测量距离问题、高度问题、角度问题、计算面积问题、航海问题、物理问题等.2.实际问题中的常用角(1)仰角和俯角在视线和水平线所成的角中,视线在水平线上方的角叫仰角,在水平线下方的角叫俯角(如图(1)).(2)方位角指从正北方向顺时针转到目标方向线的水平角,如B点的方位角为α(如图(2)).(3)方向角:相对于某正方向的水平角,如南偏东30°,北偏西45°,西偏东60°等.(4)坡度:坡面与水平面所成的二面角的度数.一个步骤解三角形应用题的一般步骤:(1)阅读理解题意,弄清问题的实际背景,明确已知与未知,理清量与量之间的关系.(2)根据题意画出示意图,将实际问题抽象成解三角形问题的模型.(3)根据题意选择正弦定理或余弦定理求解.(4)将三角形问题还原为实际问题,注意实际问题中的有关单位问题、近似计算的要求等.两种情形解三角形应用题常有以下两种情形(1)实际问题经抽象概括后,已知量与未知量全部集中在一个三角形中,可用正弦定理或余弦定理求解.(2)实际问题经抽象概括后,已知量与未知量涉及到两个或两个以上的三角形,这时需作出这些三角形,先解够条件的三角形,然后逐步求解其他三角形,有时需设出未知量,从几个三角形中列出方程(组),解方程(组)得出所要求的解.双基自测1.(人教A版教材习题改编)如图,设A,B两点在河的两岸,一测量者在A所在的同侧河岸边选定一点C,测出AC的距离为50 m,∠ACB=45°,∠CAB=105°后,就可以计算出A,B两点的距离为( ).A.50 2 m B.50 3 m C.25 2 m D.2522m2.从A处望B处的仰角为α,从B处望A处的俯角为β,则α,β的关系为( ). A.α>β B.α=βC.α+β=90° D.α+β=180°3.若点A在点C的北偏东30°,点B在点C的南偏东60°,且AC=BC,则点A 在点B的( ).A.北偏东15° B.北偏西15°C.北偏东10°D.北偏西10°4.一船向正北航行,看见正西方向相距10海里的两个灯塔恰好与它在一条直线上,继续航行半小时后,看见一灯塔在船的南偏西60°,另一灯塔在船的南偏西75°,则这艘船的速度是每小时( ).A.5海里B.53海里C.10海里D.103海里5.海上有A,B,C三个小岛,测得A,B两岛相距10海里,∠BAC=60°,∠ABC =75°,则B,C间的距离是________海里.考向一测量距离问题【例1】►如图所示,为了测量河对岸A,B两点间的距离,在这岸定一基线CD,现已测出CD=a和∠ACD=60°,∠BCD=30°,∠BDC=105°,∠ADC=60°,试求AB的长.【训练1】如图,A,B,C,D都在同一个与水平面垂直的平面内,B、D为两岛上的两座灯塔的塔顶,测量船于水面A处测得B点和D点的仰角分别为75°,30°,于水面C处测得B点和D点的仰角均为60°,AC=0.1 km.试探究图中B、D间距离与另外哪两点间距离相等,然后求B,D的距离.考向二测量高度问题【例2】►如图,山脚下有一小塔AB,在塔底B测得山顶C的仰角为60°,在山顶C测得塔顶A的俯角为45°,已知塔高AB=20 m,求山高CD.【训练2】如图所示,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与D,现测得∠BCD=α,∠BDC=β,CD=s,并在点C测得塔顶A的仰角为θ,求塔高AB.考向三正、余弦定理在平面几何中的综合应用【例3】►如图所示,在梯形ABCD中,AD∥BC,AB=5,AC=9,∠BCA=30°,∠ADB=45°,求BD的长.【训练3】如图,在△ABC中,已知∠B=45°,D是BC边上的一点,AD=10,AC=14,DC=6,求AB的长.重点突破——如何运用解三角形知识解决实际问【问题研究】1.解三角形实际应用问题的一般步骤是:审题——建模准确地画出图形——求解——检验作答;2.三角形应用题常见的类型:①实际问题经抽象概括后,已知量与未知量全部集中在一个三角形中,可用正弦定理或余弦定理解之;②实际问题经抽象概括后,已知量与未知量涉及两个三角形,这时需按顺序逐步在两个三角形中求出问题的解;③实际问题经抽象概括后,涉及的三角形只有一个,但由题目已知条件解此三角形需连续使用正弦定理或余弦定理.【解决方案】航海、测量问题利用的就是目标在不同时刻的位置数据,这些数据反映在坐标系中就构成了一些三角形,根据这些三角形就可以确定目标在一定的时间内的运动距离,因此解题的关键就是通过这些三角形中的已知数据把测量目标归入到一个可解三角形中.【示例】►(本题满分12分)如图,甲船以每小时302海里的速度向正北方航行,乙船按固定方向匀速直线航行.当甲船位于A1处时,乙船位于甲船的北偏西105°方向的B1处,此时两船相距20海里,当甲船航行20分钟到达A2处时,乙船航行到甲船的北偏西120°方向的B2处,此时两船相距102海里.问:乙船每小时航行多少海里?【试一试】如图所示,位于A处的信息中心获悉:在其正东方向相距40海里的B处有一艘渔船遇险,在原地等待营救.信息中心立即把消息告知在其南偏西30°、相距20海里的C处的乙船,现乙船朝北偏东θ的方向即沿直线CB前往B处救援,求cos θ.。
(完整版)高三一轮复习三角函数专题及答案解析.doc

弘知教育内部资料中小学课外辅导专家三角函数典型习题1 .设锐角ABC 的内角 A, B, C 的对边分别为a,b, c , a 2bsin A .(Ⅰ)求B的大小 ;(Ⅱ )求cos A sin C的取值范围 .A B C在中 ,角A, B,C所对的边分别为,, 2 .ABC c , sin sin2 . 2 2(I)试判断△ABC的形状 ;(I I)若△ABC的周长为 16,求面积的最大值 .3 .已知在ABC 中, A且与tan B是方程 x2 5 x 6 0 的两个根.B , tan A(Ⅰ )求tan( A B) 的值;(Ⅱ )若 AB 5 ,求BC的长.4.在ABC 中,角A.B.C所对的边分别是a,b,c,且a2 c 2 b 2 1 ac.A C 2(1)求sin2 cos 2B 的值;2(2)若 b=2,求△ABC面积的最大值 .5.已知函数f ( x) 2sin 2 π3 cos2x , xπ π.x4,4 2(1)求f ( x)的最大值和最小值;(2)f ( x) m 2 在 x π π上恒成立,求实数m 的取值范围.,4 26.在锐角△ABC 中,角..的对边分别为a、b、已知(b2 c 2 a 2) tanA bcA B C c, 3 .(I)求角 A;(II)若 a=2,求△ ABC面积 S 的最大值 ?7.已知函数f ( x) (sin x cos x)2 +cos2 x .(Ⅰ )求函数f x 的最小正周期 ;(Ⅱ )当x 0,2时 ,求函数f x 的最大值 ,并写出 x 相应的取值 .8 .在ABC中,已知内角 A . B . C 所对的边分别为 a 、 b 、 c, 向量r2sin B, rcos2B, 2cos2 B1r rm 3 , n 2 ,且m / / n ?(I)求锐角 B 的大小 ;(II)如果b 2 ,求ABC 的面积S ABC的最大值?答案解析11【解析】 :(Ⅰ )由 a2b sin A ,根据正弦定理得 sin A2sin B sin A ,所以 sin B ,2π由ABC 为锐角三角形得B.6(Ⅱ ) cos A sin C cos A sinAcos A sin6Acos A13 sin Acos A223 sin A .32【解析】 :I. sinC sin C cos C sin C 2 sin( C)C2 22 2 2 4即 C ,所以此三角形为直角三角形 .2422II. 16 a b22ab2ab , ab64(22) 2a b 时取等ab2 当且仅当 号,此时面积的最大值为326 4 2 .3【解析】 :(Ⅰ )由所给条件 ,方程 x 2 5 x 6 0 的两根 tan A 3, tan B2 .∴ tan( A B)tan A tan B2 311 tan A tan B 12 3(Ⅱ)∵ A B C 180 ,∴ C180 (A B) .由(Ⅰ )知 , tanCtan( A B)1,∵ C 为三角形的内角 ,∴ sin C22∵ tan A3 , A 为三角形的内角 ,∴ sin A3 ,10由正弦定理得 :AB BC5 3 ∴ BC 3 5 .21028【解析】 :(1)r r2sinB(2cos 2 B m / / n-1)=- 3cos2B22sinBcosB=- 3cos2Btan2B=- 32ππ ∵ 0<2B< π,∴ 2B= 3 ,∴ 锐角 B=3(2)由 tan2B=- 3π 5πB= 或63π① 当B= 时 ,已知 b=2,由余弦定理 ,得 :34=a 2+c 2 -ac ≥ 2ac-ac=ac(当且仅当 a=c=2 时等号成立 )1 3∵△ ABC 的面积 S △ABC =2 acsinB= 4 ac ≤ 3∴△ ABC 的面积最大值为 35π ② 当 B= 6 时 ,已知 b=2,由余弦定理 ,得 :4=a 2+c 2 + 3ac ≥2ac+ 3ac=(2+ 3)ac(当且仅当 a=c= 6- 2时等号成立 )∴ac ≤ 4(2-3)1 1∵△ ABC 的面积 S △ABC =2 acsinB=4ac ≤2- 3 ∴△ ABC 的面积最大值为 2- 314【解析】 :(1) 由余弦定理 :cosB=4sin 2A C+cos2B=124(2)由 cos B1,得 sin B15. ∵ b=2,44a218 115 2+ c =2ac+4≥2ac,得 ac ≤ ,S △ABC =2acsinB ≤(a=c 时取等号 )33故 S △ABC 的最大值为 1535 【解析】∵f ( x) 1 π3 cos2 x 1 sin 2x 3cos2 x( Ⅰ )cos2x21 2sin 2xπ.3又∵ xπ ππ 2xπ 2π, , ∴≤≤,4 2633即2≤12sin 2xπ≤ 3,3∴ f ( x) max 3, f ( x) min 2 .(Ⅱ ) ∵ f ( x)m 2f (x) 2 mf (x) 2 , xπ π ,4,2∴ mf ( x)max 2 且 m f ( x) min 2 ,∴1 m 4 ,即 m 的取值范围是 (14), .6【解析】 :(I)由已知得b 2c 2a 2 sin A3 32bccos A sin A22又在锐角 △ABC 中,所以 A=60°,[不说明是锐角 △ABC 中,扣 1 分 ](II)因为 a=2,A=60 所°以 b2c2bc 4, S1bc sin A3bc24而b 2c 22bc4 2bcbc4bc又 S1bc sin A3bc3 4 3244所以 △ ABC 面积 S 的最大值等于37【解析】 :(Ⅰ )因为 f ( x) (sin xcos x)2 +cos2 xsin 2 x 2sin x cos x cos 2 x cos2 x1 sin2 x cos2x ( ) =1+ 2 sin(2 x)4所以 2,即函数 f (x) 的最小正周期为, T2(Ⅱ )因为 0 x,得4 2x45,所以有2 sin(2 x) 1242 4 12 sin(2 x) 2,即0 12 sin(2 x)1244所以 ,函数 f x的最大值为 1 2此时 ,因为2 x5,所以 , 2 x,即 x844442。
高考数学一轮复习《三角函数》复习练习题(含答案)

高考数学一轮复习《三角函数》复习练习题(含答案)一、单选题1.已知(0,)θπ∈且满足cos 2cos θθ=,则tan θ=A .B .CD 2.在△ABC 中,7,5a c ==,则sin :sin A C 的值是( )A .75B .57C .712D .5123.已知曲线C 1:y =cos x ,C 2:y =sin (2x +2π3),则下面结论正确的是 A .把C 1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移π6个单位长度,得到曲线C 2B .把C 1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移π12个单位长度,得到曲线C 2C .把C 1上各点的横坐标缩短到原来的12倍,纵坐标不变,再把得到的曲线向右平移π6个单位长度,得到曲线C 2D .把C 1上各点的横坐标缩短到原来的12倍,纵坐标不变,再把得到的曲线向左平移π12个单位长度,得到曲线C 24.函数()3sin 6f x x π⎛⎫=+ ⎪⎝⎭在下列区间内递减的是( ) A .,22ππ⎡⎤-⎢⎥⎣⎦B .[],0π-C .22,33ππ⎡⎤-⎢⎥⎣⎦D .232,ππ⎡⎤⎢⎥⎣⎦5.已知a =116116tan tan +︒-,b =⎝⎭,c a 、b 、c 的大小关系为( ) A .c a b >> B .c b a >>C .a c b >>D .b a c >> 6.函数f (x )=3sin(2x -6π)在区间[0,2π]上的值域为 A .[32-,32] B .[32-,3]C .[D .[,3] 7.将函数cos 2y x =的图象向左平移4π个单位长度,所得函数的解析式是( )A .cos 24y x π⎛⎫=+ ⎪⎝⎭B .cos 24y x π⎛⎫=- ⎪⎝⎭C .sin 2y x =-D .sin 2y x = 8.函数tan y x =周期为( )A .2πB .2πC .πD .3π9.在ABC 中,60A =︒,43a =,42b =,则B 等于( )A .45︒B .135︒C .45︒或135︒D .3010.函数()sin()f x A x b ωϕ=++的图象如下:则()f x 的解析式和(0)(1)(2)(2006)S f f f f =+++⋯+的值分别为A .1()sin 122f x x π=+,2006S = B .1()sin 122f x x π=+,120062S = C .1()sin 122f x x π=+,120072S = D .1()sin 122f x x π=+,2007S = 11.设函数f (x )=2sin(2πx +5x ).若对任意x ∈R ,都有f (x 1)≤f (x )≤f (x 2)成立,则|x 1-x 2|的最小值为( )A .4B .2C .1D .12 12.如图所示,在ABC 中,D 是边AC 上的点,且AB AD =,23AB BD =,2BC BD =,若2BD =,则sin C 的值为( )A .33B .23C .223D .66二、填空题13.函数()()sin 0,0,y A x A ωϕωϕπ=+>><的图象如图所示,则该函数的解析式为y =______.14.在ABC ∆中,如果lg lg lgsin 2a c B -==-,且B 为锐角,则三角形的形状是__________.15.已知()2cos 3f x x π⎛⎫= ⎪⎝⎭,则(1)(2)(2022)f f f +++的值为________.16.sin 73cos13sin167cos 73︒︒-︒︒=________.17.已知△ABC 中,3cot 4A =-,则cos A =______. 18.252525sin cos tan 634πππ⎛⎫++-= ⎪⎝⎭______. 19.已知扇形的半径为3cm ,圆心角为60︒,则扇形的面积为 2cm .20.若sin 41cos 5γγ=+,则1cos 2sin γγ-=______.三、解答题21.求下列各式的值(1)2log 342233log 9log 2log 3log 432-++⋅; (2)()()()sin 1071sin99sin 171sin 261-︒︒+-︒-︒.22.已知一扇形的面积S 为定值,求当扇形的圆心角为多大时,它的周长最小?最小值是多少?23.在ABC 中,a 、b 、c 分别是内角A 、B 、C 的对边,()cos sin cos cos A A a C c A =+; (1)求角A 的大小;(2)若a =ABC 14b c +的最小值.24.△ABC 的内角A ,B ,C 的对边分别为a ,b ,c .已知2a =,b =2B A =. (1)求sin A ;(2)求△ABC 的面积.25.(1)已知tan()22βα-=,tan()32αβ-=-,求)tan(βα+的值; (2)化简:21tan 9sin (12sin 99)︒︒-︒-.26.已知在ABC ∆中,角,,A B C 的对边分别是,,a b c ,且有2cos (cos cos )C a B b A c +=. (1)求C ;(2)若3c =,求ABC ∆面积的最大值.27.已知函数()4cos sin()16f x x x π=+-. (1)求()f x 的最大值及此时的x 的集合;(2)求()f x 的单调增区间;(3)若1()2f α=,求sin(4)6πα-. 28.已知矩形纸片ABCD 中,AB=6,AD=12,将矩形纸片右下角折起,使该角的顶点B 落在矩形的边AD 上,且折痕的两端点M 、N 分别位于边AB ,BC 上,此时的点B 记为点P ,设MNB θ∠=,MN y =.(1)当15MNB ∠=时,判断N 的位置;(2)试将y 表示成θ的函数并求y 的最小值。
高考数学一轮复习《三角函数》复习练习题(含答案)1.docx

高考数学一轮复习《三角函数》复习练习题(含答案)一、单选题2TC1.已知cos。
= 一,0 < a < 勿,贝!jtan( -------- a)=( )3 4A.--B. -7C. -4A/5 - 9D. 4右-92.设函数f(x) = x3,若0<6><yHt, 恒成立,则实数扪的取值范围是A. (-8,1)B. [一°°,;]C.(YO,0)D. (0,1)3.如图,为了测量山坡上灯塔CD的高度,某人从高为人=40的楼/W的底部《处和楼顶B处分别测得仰角6=60。
,a=30。
,若山坡高为a=35,则灯塔的高度是( )A. 20B. 25C. 20^/2D. 30TT4.已知函数/(x) = A sin — x, g (x) = - 2), fc > 0. & 知A = 1 时,函数/z(x) = y(x)-g(x)的所有零点之和为6,贝。
当A = 2时,函数h(x) = f(x)-g(x)的所有零点之和为A. 6B. 8C. 10D. 125.下列说法中正确的是A.若数列{%}为常数列,贝州%}既是等差数列也是等比数列;B.若函数六了)为奇函数,贝0/(0) = 0;C.在AABC中,A>B是sinA>sinB的充要条件;D.若两个变量X,,的相关系数为「,贝越大,x与 > 之间的相关性越强.6.要得到函数y = 4sin]4x-f|的图像,只需要将函数y = 4sin4x的图像( )A.向左平移尚个单位B.向右平移%个单位C.向左平移:个单位D.向右平移:个单位7. 将函数f (x) = cos(2x-g)向左平移中(9>0)个单位长度,所得图像的对应函数为g(x),则“9 =;‘是“g(x)为奇函数"的( )取值范围是( )变横坐标压缩为原来的?,得到函数顼:的图象,则使球为增函数的一个区间是12.时钟的分针在1点到3点20分这段时间里转过的弧度为二、填空题13. A>4BC 的内角 4、B 、C 的对边分别为 a, b, c,已知 c+b (sinA - cosA) =0, c= ^2 , a =1,则人=.14. 在 AABC 中,若Z? = 2asinB,则 A 等于15. 甲船在岛A 处南偏西50。
高考数学一轮复习三角函数与解三角形多选题(讲义及答案)含答案

高考数学一轮复习三角函数与解三角形多选题(讲义及答案)含答案一、三角函数与解三角形多选题1.知函数()()sin 04f x x πωω⎛⎫=+> ⎪⎝⎭,则下述结论中正确的是( )A .若()f x 在[]0,2π有且仅有4个零点,则()f x 在[]0,2π有且仅有2个极小值点B .若()f x 在[]0,2π有且仅有4个零点,则()f x 在20,15π⎛⎫⎪⎝⎭上单调递增 C .若()f x 在[]0,2π有且仅有4个零点,则ω的范是1519,88⎡⎫⎪⎢⎣⎭D .若()f x 的图象关于4x π=对称,且在5,1836ππ⎛⎫⎪⎝⎭单调,则ω的最大值为9 【答案】ACD 【分析】 令4t x πω=+,由[]0,2x π∈,可得出,244t ππωπ⎡⎤∈+⎢⎥⎣⎦,作出函数sin y t =在区间,244ππωπ⎡⎤+⎢⎥⎣⎦上的图象,可判断A 选项正误;根据已知条件求出ω的取值范围,可判断C 选项正误;利用正弦型函数的单调性可判断B 选项的正误;利用正弦型函数的对称性与单调性可判断D 选项的正误. 【详解】 令4t x πω=+,由[]0,2x π∈,可得出,244t ππωπ⎡⎤∈+⎢⎥⎣⎦, 作出函数sin y t =在区间,244ππωπ⎡⎤+⎢⎥⎣⎦上的图象,如下图所示:对于A 选项,若()f x 在[]0,2π有且仅有4个零点,则()f x 在[]0,2π有且仅有2个极小值点,A 选项正确;对于C 选项,若()f x 在[]0,2π有且仅有4个零点,则4254ππωππ≤+<,解得151988ω<≤,C 选项正确; 对于B 选项,若151988ω<≤,则2192154604πππππω≤+<+,所以,函数()f x 在区间20,15π⎛⎫⎪⎝⎭上不单调,B 选项错误; 对于D 选项,若()f x 的图象关于4x π=对称,则()442k k Z ωππππ+=+∈,()14k k Z ω∴=+∈.52361812T ππππω∴=≥-=,12ω∴≤,()41k k Z ω=+∈,max 9ω∴=. 当9ω=时,()sin 94f x x π⎛⎫=+ ⎪⎝⎭,当5,1836x ππ⎛⎫∈⎪⎝⎭时,339442x πππ<+<, 此时,函数()f x 在区间5,1836ππ⎛⎫⎪⎝⎭上单调递减,合乎题意,D 选项正确. 故选:ACD. 【点睛】方法点睛:求较为复杂的三角函数的单调区间时,首先化简成()sin y A ωx φ=+形式,再求()sin y A ωx φ=+的单调区间,只需把x ωϕ+看作一个整体代入sin y x =的相应单调区间内即可,注意要先把ω化为正数.2.在ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,且::4:5:6a b c =,则下列结论正确的是( )A .sin :sin :sin 4:5:6ABC = B .ABC 是钝角三角形C .ABC 的最大内角是最小内角的2倍D .若6c =,则ABC 【答案】ACD 【分析】由正弦定理可判断A ;由余弦定理可判断B ;由余弦定理和二倍角公式可判断C ;由正弦定理可判断D. 【详解】解:由::4:5:6a b c =,可设4a x =,5b x =,6c x =,()0x >, 根据正弦定理可知sin :sin :sin 4:5:6A B C =,选项A 描述准确;由c 为最大边,可得2222221625361cos 022458a b c x x x C ab x x +-+-===>⋅⋅,即C 为锐角,选项B 描述不准确;2222222536163cos 22564b c a x x x A bc x x +-+-===⋅⋅,291cos 22cos 121cos 168A A C =-=⨯-==,由2A ,C ()0,π∈,可得2A C =,选项C 描述准确;若6c =,可得2sin 7cR C===,ABC外接圆半径为7,选项D 描述准确. 故选:ACD. 【点睛】本题考查三角形的正弦定理和余弦定理,二倍角公式,考查化简运算能力,属于中档题.3.(多选题)已知22tan 2tan 10x y --=,则下列式子成立的是( ) A .22sin 2sin 1y x =+ B .22sin 2sin 1y x =-- C .22sin 2sin 1y x =-D .22sin 12cos y x =-【答案】CD 【分析】对原式进行切化弦,整理可得:222222sin cos 2sin cos cos cos x y y x y x ⋅-⋅=⋅,结合因式分解代数式变形可得选项. 【详解】∵22tan 2tan 10x y --=,2222sin sin 210cos cos x yx y-⋅-=, 整理得222222sin cos 2sin cos cos cos x y y x y x ⋅-⋅=⋅,∴()()()22222221cos 1sin sin cos cos sin cos x x y x y y x ---⋅=+, 即22222221cos sin sin cos sin cos cos x y y x y x x --+⋅-⋅=, 即222sin 12cos 2sin 1y x x =-=-,∴C 、D 正确. 故选:CD 【点睛】此题考查三角函数的化简变形,根据弦切关系因式分解,结合平方关系变形.4.已知函数()f x 的定义域为D ,若对于任意()()()a b c D f a f b f c ∈,,,,,分别为某个三角形的边长,则称()f x 为“三角形函数”,其中为“三角形函数”的函数是( ) A .()4sin f x x =- B .()22sin 10cos 13f x x x =-++C .()tan 2xf x = D .()sin 20,34f x x x ππ⎛⎫⎡⎤=++∈ ⎪⎢⎥⎝⎭⎣⎦【答案】AD【分析】结合三角形的性质有:两边之差小于第三边,得若()f x 为 “三角形函数”则()()()max min min f x f x f x <-恒成立,即()()max min 2f x f x <恒成立即可,根据条件求出函数的最大值和最小值,进行判断即可. 【详解】解:①()4sin f x x =-,则()max 415f x =+=,()min 413f x =-= 则()()max min 2f x f x <恒成立,则A 满足条件②()22532cos 10cos 112cos 22f x x x x ⎛⎫=++=+= ⎪⎝⎭ 当0,2x π⎡⎤∈⎢⎥⎣⎦时,0cos 1x ≤≤∴当cos 0x =时,函数()f x 取得最小值()min 11f x =,当cos 1x =时,函数()f x 取得最大值,()max 23f x =则()()max min 2f x f x <不恒成立,则B 不满足条件 ③()()()tan ,00,2xf x =∈-∞⋃+∞,则不满足条件()()max min 2f x f x <恒成立,故C 不是④()sin 23f x x π⎛⎫=++ ⎪⎝⎭0,4x π⎡⎤∈⎢⎥⎣⎦,52,336x πππ⎡⎤∴+∈⎢⎥⎣⎦,则()max sin12f x π=+=+()min 51sin62f x π=+=+则()min 21f x =+,则()()max min 2f x f x <恒成立,故D 满足条件 故选AD 【点睛】本题考查了三角形的性质及“三角形函数”的概念,根据条件转化为()()max min 2f x f x <恒成立是解决本题的关键,综合性较强,有一定的难度.5.已知函数()2sin()05,||2f x x πωϕωϕ⎛⎫=+<<< ⎪⎝⎭,且对任意x ∈R ,()12f x f π⎛⎫≤ ⎪⎝⎭恒成立,3y f x π⎛⎫=+⎪⎝⎭为奇函数,则下列说法正确的是( ) A .函数()f x 的图象关于原点对称 B .函数()f x 的最小正周期为πC .函数()f x 的图象关于直线2x π=对称D .函数()f x 的单调递增区间为5,()1212k k k ππππ⎡⎤-+∈⎢⎥⎣⎦Z 【答案】BD 【分析】由()12f x f π⎛⎫≤ ⎪⎝⎭恒成立可得212f π⎛⎫=± ⎪⎝⎭,即()122k k ωππϕπ+=+∈Z ,由3y f x π⎛⎫=+ ⎪⎝⎭为奇函数可得()3k k ωπϕπ''+=∈Z ,即可求出2n 2)3(si f x x π⎛⎫=+⎪⎝⎭,再根据正弦函数的性质分别判断即可. 【详解】因为对任意x ∈R ,()12f x f π⎛⎫≤ ⎪⎝⎭恒成立,所以2sin 21212f πωπϕ⎛⎫⎛⎫=+=± ⎪⎪⎝⎭⎝⎭, 即sin 112ωπϕ⎛⎫+=±⎪⎝⎭,得()122k k ωππϕπ+=+∈Z ①. 2sin 2sin 333f x x x ππωπωϕωϕ⎡⎤⎛⎫⎛⎫⎛⎫+=++=++ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦,因为3y f x π⎛⎫=+ ⎪⎝⎭为奇函数,所以()3k k ωπϕπ''+=∈Z ②.由①②可得()(),3122k k k k ωπωπππ''-=--∈Z ,即()(42,)k k k k ω''=--∈Z .又05ω<<,所以1k k '-=,2ω=, 则(2,)33k k k k ππϕππ=+=-'∈'Z ,得3πϕ=,所以2n 2)3(si f x x π⎛⎫=+⎪⎝⎭,由于(0)0f =≠,故()f x 的图象不关于原点对称,所以A 不正确; ()f x 的最小正周期22T ππ==,所以B 正确;2sin 22sin 2sin 222333f ππππππ⎛⎫⎛⎫⎛⎫=⨯+=+=-=± ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,所以C 不正确;令222232k x k πππππ-≤+≤+,k ∈Z ,得51212k x k ππππ-≤≤+,k ∈Z , 故函数() f x 的单调递增区间为5,()1212k k k ππππ⎡⎤-+∈⎢⎥⎣⎦Z ,所以D 正确. 故选:BD. 【点睛】关键点睛:本题考查正弦型函数的性质,解题的关键是:(1)根据“对任意x ∈R ,()12f x f π⎛⎫≤ ⎪⎝⎭恒成立”得到“212f π⎛⎫=± ⎪⎝⎭”;(2)得到“2sin 33f x x πωπωϕ⎛⎫⎛⎫+=++ ⎪ ⎪⎝⎭⎝⎭”后,能根据“3y f x π⎛⎫=+⎪⎝⎭为奇函数”得到“()3k k ωπϕπ''+=∈Z ”.6.已知函数()cos f x x x =-,则下列说法正确的是( ) A .()f x 的图象关于点,06π⎛⎫⎪⎝⎭中心对称B .()f x 在区间,2ππ⎡⎤⎢⎥⎣⎦上单调递减 C .()f x 在()0,2π上有且仅有1个最小值点 D .()f x 的值域为[]1,2- 【答案】BC 【分析】利用特殊值法可判断A 选项的正误;化简函数()f x 在区间,2ππ⎡⎤⎢⎥⎣⎦上的解析式,利用正弦型函数的单调性可判断B 选项的正误;由()()f x f x π+=可得()f x 的周期为π,再在[]0,π上讨论函数()f x 的单调性、最值,可判断CD 选项的正误.【详解】对于A 选项,因为06f π⎛⎫-= ⎪⎝⎭,2f π⎛⎫= ⎪⎝⎭62f f ππ⎛⎫⎛⎫-≠- ⎪ ⎪⎝⎭⎝⎭, 所以()f x 的图象不关于点,06π⎛⎫⎪⎝⎭中心对称,故A 错误;对于B 选项,当,2x ππ⎡⎤∈⎢⎥⎣⎦时,()cos 2sin 6f x x x x π⎛⎫=+=+ ⎪⎝⎭,27,636x πππ⎡⎤+∈⎢⎥⎣⎦,所以,函数()f x 在区间,2ππ⎡⎤⎢⎥⎣⎦上单调递减,B 选项正确; 对于C 选项,()()()cos sin cos f x x x x x πππ+=+-+=--()cos x x f x =-=,所以π为函数()f x 的周期.当0,2x π⎡⎤∈⎢⎥⎣⎦时,()cos 2sin 6f x x x x π⎛⎫=-=- ⎪⎝⎭,,663x πππ⎡⎤-∈-⎢⎥⎣⎦,所以()f x 在区间0,2π⎡⎤⎢⎥⎣⎦上单调递增,()()min 01f x f ==-,()max 2f x f π⎛⎫== ⎪⎝⎭由B 选项可知,函数()f x 在区间,2ππ⎡⎤⎢⎥⎣⎦上单调递减,当,2x ππ⎡⎤∈⎢⎥⎣⎦时,()max 2f x f π⎛⎫== ⎪⎝⎭()()min1f x f π==-.所以,函数()f x 在()0,2π上有且只有1个最小值点,C 选项正确;对于D 选项,由C 选项可知,函数()f x 的值域为⎡-⎣,D 选项错误.故选:BC. 【点睛】方法点睛:求函数()()sin f x A x =+ωϕ在区间[],a b 上值域的一般步骤: 第一步:三角函数式的化简,一般化成形如()sin y A x k ωϕ=++的形式或()cos y A x k ωϕ=++的形式;第二步:由x 的取值范围确定x ωϕ+的取值范围,再确定()sin x ωϕ+(或()cos x ωϕ+)的取值范围;第三步:求出所求函数的值域(或最值).7.设函数()sin()(0)4f x x πωω=+>,已知()f x 在[]02π,有且仅有5个零点,则下列结论成立的有( )A .()1y f x =+在()02π,有且仅有2个零点 B .()f x 在023π⎛⎫⎪⎝⎭,单调递增C .ω的取值范围是192388⎡⎫⎪⎢⎣⎭,D .将()f x 的图象先右移4π个单位,再纵坐标不变,横坐标扩大为原来的2倍,得到函数1()sin()2g x x ω=【答案】BC 【分析】首先利用图象直接判断A 选项;再利用函数()f x 在[]02π,有且仅有5个零点,求得ω的范围,并利用整体代入的方法判断B 选项;最后利用图象的变换规律,求得变换之后的解析式,判断D. 【详解】A.如图,[]0,2π上函数仅有5个零点,但有3个最小值点,这3个最小值点就是()1y f x =+在()0,2π上的3个零点;B.[]0,2x π∈时,,2444t x πππωωπ⎡⎤=+∈⋅+⎢⎥⎣⎦ 若函数()f x 在[]02π,有且仅有5个零点,则5264ππωππ≤⋅+<,得192388ω≤<,当023x π⎛⎫∈ ⎪⎝⎭,时,,448t x πππω⎛⎫=+∈ ⎪⎝⎭,此时函数单调递增,故BC 正确; D. 函数()f x 的图象先右移4π个单位后得到sin sin 4444y x x ππωππωω⎡⎤⎛⎫⎛⎫=-+=-+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦,再将横坐标扩大为原来的2倍,得到()1sin 244g x x ωππω⎛⎫=-+ ⎪⎝⎭,故D 不正确;故选:BC 【点睛】关键点点睛:本题的关键是求出ω的取值范围,首先根据函数在区间[]0,2π有5个零点,首先求4t x πω=+的范围,再分析sin y t =的图象,求得ω的范围.8.将函数cos 2y x =的图象上所有点向左平移6π个单位长度,再向下平移1个单位长度,得到函数()y f x =的图象,则( ) A .()f x 的图象的对称轴方程为()62k x k Z ππ=-+∈ B .()f x 的图象的对称中心坐标为(),0212k k Z ππ⎛⎫+∈⎪⎝⎭ C .()f x 的单调递增区间为()2,36k k k Z ππππ⎡⎫-+-+∈⎪⎢⎣⎭ D .()f x 的单调递减区间为()2,63k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦【答案】AC 【分析】首先根据图象平移求函数()y f x =的解析式,再根据整体代入的方法判断函数的对称性和单调区间. 【详解】cos 2y x =的图象上所有点向左平移π6个单位长度,得到cos 26y x π⎛⎫=+ ⎪⎝⎭,再向下平移1个单位长度后得到()cos 213y f x x π⎛⎫==+- ⎪⎝⎭, 对于A ,令23x k ππ+=,解得,62k x k Z ππ=-+∈,函数的对称轴是,62k x k Z ππ=-+∈,故A 正确; 对于B ,令232x k πππ+=+,解得:,122k x k Z ππ=+∈,所以函数的对称中心,1,122k k Z ππ⎛⎫+-∈ ⎪⎝⎭,故B 不正确; 对于C ,令2223k x k ππππ-+≤+≤,解得:236k x k ππ-+π≤≤-+π,所以函数的单调递增区间是2,,36k k k Z ππππ⎡⎤-+-+∈⎢⎥⎣⎦,由于单点不具有单调性,所以()f x 的单调递增区间为()2,36k k k Z ππππ⎡⎫-+-+∈⎪⎢⎣⎭也正确,故C 正确;对于D ,令2223k x k ππππ≤+≤+,解得:63k x k ππππ-+≤≤+,所以函数单调递减区间是,63k k ππππ⎡⎤-++⎢⎥⎣⎦,k Z ∈,故D 不正确. 故选:AC 【点睛】方法点睛:本题考查函数的图象变换,以及()sin y A ωx φ=+的性质,属于中档题型,()sin y A x ϕ=+的横坐标伸长(或缩短)到原来的1ω倍,得到函数的解析式是()sin y A ωx φ=+,若sin y A x ω=向右(或左)平移ϕ(0ϕ>)个单位,得到函数的解析式是()sin y A x ωϕ=-⎡⎤⎣⎦或()sin y A x ωϕ=+⎡⎤⎣⎦.9.设函数()()1sin 022f x x x πωωω⎛⎫=++> ⎪⎝⎭,已知()f x 在[]0,π有且仅有3个零点,则( )A .在()0,π上存在1x 、2x ,满足()()122f x f x -=B .()f x 在()0,π有且仅有1个最小值点C .()f x 在0,2π⎛⎫⎪⎝⎭上单调递增 D .ω的取值范围是1723,66⎡⎫⎪⎢⎣⎭【答案】AD 【分析】化简函数()f x 的解析式为()sin 6f x x πω⎛⎫=+ ⎪⎝⎭,令6t x πω=+,由[]0,x π∈可求得,66t ππωπ⎡⎤∈+⎢⎥⎣⎦,作出函数sin ,066y t t ππωπω⎛⎫=≤≤+> ⎪⎝⎭的图象,可判断AB 选项的正误;由图象得出346ππωππ≤+<可判断D 选项的正误;取3ω=,利用正弦型函数的单调性可判断C 选项的正误. 【详解】()3131sin sin sin cos sin 2226f x x x x x x ππωωωωω⎛⎫⎛⎫=++=+=+ ⎪ ⎪⎝⎭⎝⎭, 当[]0,x π∈时,,666x πππωωπ⎡⎤+∈+⎢⎥⎣⎦,令6t x πω=+,则,66t ππωπ⎡⎤∈+⎢⎥⎣⎦,作出函数sin ,066y t t ππωπω⎛⎫=≤≤+>⎪⎝⎭的图象如下图所示:对于A 选项,由图象可知,max 1y =,min 1y =-,所以,在()0,π上存在1x 、2x ,满足()()122f x f x -=,A 选项正确; 对于B 选项,()f x 在()0,π上有1个或2个最小值点,B 选项错误; 对于D 选项,由于函数()f x 在[]0,π有且仅有3个零点,则346ππωππ≤+<,解得172366ω≤<,D 选项正确;对于C 选项,由于172366ω≤<,取3ω=,当0,2x π⎛⎫∈ ⎪⎝⎭时,53663x πππ<+<, 此时,函数()f x 在区间0,2π⎛⎫ ⎪⎝⎭上不单调,C 选项错误. 故选:AD.【点睛】关键点点睛:本题考查利用正弦型函数在区间上的零点个数判断正弦型函数的基本性质,解本题的关键在于换元6t x πω=+,将问题转化为函数sin y t =在区间,66ππωπ⎡⎤+⎢⎥⎣⎦上的零点个数问题,数形结合来求解.10.已知函数()()tan (0)6ωωπ=->f x x ,则下列说法正确的是( ) A .若()f x 的最小正周期是2π,则12ω= B .当1ω=时,()f x 的对称中心的坐标为()π0()6π+∈Z k k , C .当2ω=时,π2π()()125-<f f D .若()f x 在区间()π3π,上单调递增,则203ω<≤ 【答案】AD【分析】根据正切函数的性质,采用整体换元法依次讨论各选项即可得答案.【详解】解:对于A 选项,当()f x 的最小正周期是2π,即:2T ππω==,则12ω=,故A 选项正确;对于B 选项,当1ω=时,()()tan 6f x x π=-,所以令,62k x k Z ππ-=∈,解得:,62k x k Z ππ=+∈,所以函数的对称中心的坐标为()0()62k k ππ+∈Z ,,故B 选项错误; 对于C 选项,当2ω=时,()()tan 26f x x π=-,()()()()ππ10tan 2tan tan 12126330f πππ⎡⎤-=⨯--=-=-⎢⎥⎣⎦,()()()2π2π1911tan 2tan tan 5563030f πππ=⨯-==-,由于tan y x =在,02π⎛⎫- ⎪⎝⎭单调递增,故()()π2π125f f ->,故C 选项错误;对于D 选项,令,262k x k k Z ππππωπ-+<-<+∈,解得:233k k x ππππωωωω-+<<+ 所以函数的单调递增区间为:2,,33k k k Z ππππωωωω⎛⎫-++∈ ⎪⎝⎭,因为()f x 在区间()π3π,上单调递增,所以33,23k k Z k πππωωπππωω⎧-+≤⎪⎪∈⎨⎪+≥⎪⎩,解得:213,3k k k Z ω-+≤≤+∈,另一方面,233T ππππω=≥-=,32ω≤,所以2332k +≤,即56k ≤,又因为0>ω,所以0k =,故203ω<≤,故D 选项正确. 故选:AD【点睛】 本题考查正切函数的性质,解题的关键在于整体换元法的灵活应用,考查运算求解能力,是中档题.其中D 选项的解决先需根据正切函数单调性得213,3k k k Z ω-+≤≤+∈,再结合233T ππππω=≥-=和0>ω得0k =,进而得答案.。
1334_高考数学习题:一轮复习作业 三角函数的图象与性质(含解析).doc_0

三角函数的图象与性质一、选择题1.函数y =2cos 2x +1的定义域是()D[由题意知2cos 2x +1≥0,即cos 2x ≥-12.∴2k π-23π≤2x ≤2k π+23π,k ∈Z ,∴k π-π3≤x ≤k π+π3,k ∈Z ,故选D.]2.(2019·全国卷Ⅱ)若x 1=π4,x 2=3π4是函数f (x )=sin ωx (ω>0)的两个相邻的极值点,则ω=()A.2B.32C.1D.12A[由题意及函数y =sin ωx 的图象与性质可知,12T =3π4-π4,∴T =π,∴2πω=π,∴ω=2.故选A.])A.f (x )=|sin 2x |B.f (x )=tan|x |C.f (x )=-cos 2x D.f (x )=cos|2x |C[函数f (x )=tan|x |不是周期函数,因此排除B.函数f (x )=|sin 2x A.函数f (x )=cos|2x D,综上知选C.]4.(2021·陕西西安市高三一模)已知函数f (x )=sin(2x +φ)其中φ∈(0,2π),若f (x )≤f x ∈R 恒成立,则f (x )的单调递增区间是()A.k π,k π+π2(k ∈Z )B.k π-π3,k π+π6(k ∈Z )C.k π+π6,k π+2π3(k ∈Z )D.k π-π2,k π(k ∈Z )B[因为对任意x ∈R ,f (x )≤f 所以则φ=π6+2k π,又因为φ∈(0,2π),所以φ=π6,所以f (x x 令2k π-π2≤2x +π6≤2k π+π2(k ∈Z ),解得k π-π3≤x ≤k π+π6(k ∈Z ),所以f (x )的单调递增区间是k π-π3,k π+π6(k ∈Z );故选B.]5.函数f (x x )A.y =f (x )的一个周期为-πB.y =f (x C.y =f (x )图象关于直线x =-π6对称D.y =f x =π6C[A 中,因为周期T =2k π2=k π,k ∈Z ,所以-π是周期,A 正确;B 中,令2k π+π2≤2x +π3≤2k π+3π2,k ∈Z ,得k π+π12≤x ≤k π+7π12,k ∈Z ,令k =0得π12≤x ≤7π12,所以f (x )在π12,7π12上单调递减,故y =f (x 递减正确,B 正确;C 中,因为=sin 2+π3=0,故直线x =-π6不是对称轴,故C 错误;D 中,因为=sin 2+π3=0,所以y =f x =π6正确,故选C.]6.(2021·四川泸州市高三三模)已知f (x )=2sin(ωx )(ω>0)满足=0,则ω的取值不可能是()A.4B.6C.8D.12B[因为是函数f (x )=2sin(ωx )的对称中心,所以ω=4k (k ∈N *),ω≠6.]二、填空题7.(2021·山东日照市高三模拟)写出一个满足f (x )=f (2-x )的奇函数f (x )=.sin π2x (答案不唯一)[取f (x )=sinπ2x ,下面为证明过程:显然,其定义域为R ;由f (-x -π2x f (x ),故f (x )=sin π2x 为奇函数;又f (2-x )=sin π22-x=sinπ-π2x =sin π2x =f (x ).故答案为:sinπ2x (答案不唯一).]8.(2021·三明高三一模)函数y =cos 2x +sin 的最小值为.-98[y =cos 2x 2x +cos x x -98,当cos x =-14时,取得最小值为-98.]9.函数f (x )=3cos(3x -θ)-sin(3x -θ)是奇函数,则tan θ等于.-3[f (x )=3cos(3x -θ)-sin(3x -θ)=2sin x +=-x -π3-因为函数f (x )为奇函数,则有-π3-θ=k π,k ∈Z ,即θ=-k π-π3,k ∈Z ,故tan θk =-3.]三、解答题10.已知f (x )=A sin(ωx +φ)(A >0,ω>0)的最小正周期为2,且当x =13时,f (x )的最大值为2.(1)求f (x )的解析式;(2)在闭区间214,234上是否存在f (x )的对称轴?如果存在求出其对称轴.若不存在,请说明理由.[解](1)由T =2知2πω=2得ω=π.又当x =13时f (x )max =2,知A =2.且π3+φ=2k π+π2(k ∈Z ),故φ=2k π+π6(k ∈Z ).∴f (x x +2k x (2)存在.令πx +π6=k π+π2(k ∈Z ),得x =k +13(k ∈Z ).由214≤k +13≤234.得5912≤k ≤6512,又k ∈Z ,∴k =5.故在214,234上存在f (x )的对称轴,其方程为x =163.11.已知a =(sin x ,3cos x ),b =(cos x ,-cos x ),函数f (x )=a·b +32.(1)求函数y =f (x )图象的对称轴方程;(2)若方程f (x )=13在(0,π)上的解为x 1,x 2,求cos(x 1-x 2)的值.[解](1)f (x )=a·b +32=(sin x ,3cos x )·(cos x ,-cos x )+32=sin x ·cos x -3cos 2x +32=12sin 2x -32cos 2x x 令2x -π3=k π+π2(k ∈Z ),得x =5π12+k 2π(k ∈Z ),即函数y =f (x )图象的对称轴方程为x =5π12+k2π(k ∈Z ).(2)由(1)及已知条件可知(x 1,f (x 1))与(x 2,f (x 2))关于x =5π12对称,则x 1+x 2=5π6,∴cos(x 1-x 2)=cos x 1x 1x 1-π2x 1f (x 1)=13.1.(2021·天津高三二模)已知函数f (x )=3cos 2x -sin 2x ,则下列四个结论中:①f (x )的周期为π;②x =π3是f (x )图象的一条对称轴;③-7π12,-π12是f (x )的一个单调递增区间;④f (x )在区间0,7π12上的最大值为2,所有正确结论的序号是()A.①②B.①③C.①②④D.①③④B[由题可知:f (x )=3cos 2x -sin 2x x T =2π|ω|=2π2=π,故①正确,当x =π3时,2·π3+=-3,并没有取到最值,所以②错误,当x ∈-7π12,-π12时,2x +π6∈[-π,0],又函数y =cos x 在[-π,0]单调递增,所以-7π12,-π12是f (x )的一个单调递增区间,故③正确,当x ∈0,7π12时,2x +π6∈π6,4π3,所以f (x )max =2cos π6=3,故④错误.]2.已知函数f (x x )A.函数f (x B.函数f (x )的图象关于直线x =-π8对称C.函数f (x )在区间(-π,π)内有4个零点D.函数f (x )在区间-π2,0上单调递增C[对于函数f (x x x =5π12,求得f (x )=32,故函数f (x )的图象不A;令x =-π8,求得f (x f (x )的图象不关于直线x =-π8对称,故排除B;在区间(-π,π)上,2x -π6∈-13π6,2x -π6=-2π,-π,0,π时,f (x )=0,故函数f (x )在区间(-π,π)内有4个零点,故C 正确;在区间-π2,0上,2x -π6∈-7π6,-π6,f (x )没有单调性,故D 错误,故选C.]3.已知函数f (x )=sin(ωx +φ)(0<ω<1,0≤φ≤π)是R 上的偶函数,其图象关于点M (1)求φ,ω的值;(2)求f (x )的单调递增区间;(3)x ∈-3π4,π2,求f (x )的最大值与最小值.[解](1)因为f (x )=sin(ωx +φ)是R 上的偶函数,所以φ=π2+k π,k ∈Z ,且0≤φ≤π,则φ=π2,即f (x )=cos ωx .因为图象关于点M 所以ω×3π4=π2+k π,k ∈Z ,且0<ω<1,所以ω=23.(2)由(1)得f (x )=cos 23x ,由-π+2k π≤23x ≤2k π且k ∈Z 得,3k π-3π2≤x ≤3k π,k ∈Z ,所以函数f (x )的递增区间是3k π-3π2,3k π,k ∈Z .(3)因为x ∈-3π4,π2,所以23x ∈-π2,π3,当23x =0时,即x =0,函数f (x )的最大值为1,当23x =-π2时,即x =-3π4,函数f (x )的最小值为0.1.已知函数f (x )=sin x +3cos x 在x =θ时取得最大值,则θ)A.-2+64B.-12C.2-64D.32C [法一:∵f (x )=sin x +3cos x f (x )在x =θ时取得最大值,∴θ+π3=π2+2k π(k ∈Z ),即θ=π6+2k π(k ∈Z ),于是cos θ=+π4+4k =12×22-32×22=2-64,故选C.法二:∵f (x )=sin x +3cos x ,∴f ′(x )=cos x -3sin x .又f (x )在x =θ时取得最大值,∴f ′(θ)=cos θ-3sin θ=0,即tan θ=33,则θ=22(cos 2θ-sin 2θ)=22×1-tan 2θ-2tan θ1+tan 2θ=2-64,故选C.]2.已知函数f (x )=2x2+sin b .(1)若a =-1,求函数f (x )的单调增区间;(2)当x ∈[0,π]时,函数f (x )的值域是[5,8],求a ,b 的值.[解]f (x )=a (1+cos x +sin x )+b=2a a +b .(1)当a =-1时,f (x )=-2sin b -1,由2k π+π2≤x +π4≤2k π+3π2(k ∈Z ),得2k π+π4≤x ≤2k π+5π4(k ∈Z ),∴f (x )的单调增区间为2k π+π4,2k π+5π4(k ∈Z ).(2)∵0≤x ≤π,∴π4≤x +π4≤5π4,∴-22≤sina ≠0,①当a >0+a +b =8,∴a =32-3,b =5;②当a <0+a +b =5,∴a =3-32,b =8.综上所述,a =32-3,b =5或a =3-32,b =8.。
(完整版)高三一轮复习三角函数专题及答案解析

三角函数典型习题1 •设锐角ABC的内角A B, C的对边分别为a, b, c,a 2bsi nA.(I )求B的大小;(n)求cosA sin C的取值范围• A B C 厂2 •在ABC中角A,B,C所对的边分别为a, b, c,sin sin— 2 .2 2(1)试判断△ ABC的形状;(II)若厶ABC的周长为16,求面积的最大值•23 •已知在ABC中,A B,且tan A与tan B是方程x 5x 6 0的两个根•(I )求tan (A B)的值;(n )若AB 5 ,求BC的长•2 2 2 14. 在ABC中,角A. B. C所对的边分别是a,b,c,且a c b ac.22A C(1) 求sin cos2B 的值;2(2) 若b=2,求厶ABC面积的最大值.5. 已知函数f(x) 2s in2 n x 3cos2x, xn,-n•4 4 2(1 )求f (x)的最大值和最小值;(2)f(x) m 2在x n,n上恒成立,求实数m的取值范围.4 26. 在锐角△ ABC 中,角A. B. C 的对边分别为a、b、c,已知(b2 c2 a2)ta nA 3bc.(I) 求角A;(II) 若a=2,求厶ABC面积S的最大值?7. 已知函数f (x) (sin x cosx) +cos2 x .(I )求函数f x的最小正周期;(n )当x o,?时,求函数f x的最大值拼写出x相应的取值•8 .在ABC中,已知内角A . B . C所对的边分别为a、b、c,向量r r 2 B r r m 2sin B, 、3 ,n cos2B, 2cos 1,且m//n?2(I) 求锐角B的大小;(II) 如果b 2,求ABC的面积S ABC的最大值?答案解析11【解析】:(I )由a 2bsi nA ,根据正弦定理得si nA 2si n Bsin A ,所以sin B -,2 由ABC 为锐角三角形得B n .6(n )cosA sin C cos A sinAcos A sin -A61 3cos A cos Asin A22、、3sinA -.32【解析】 :I. sinC . sin CC cos .C sin2sin('—222 224C C 即C,所以此三角形为直角三角形2 422••• tanA 3, A 为三角形的内角,二sin A由正弦定理得:-A 艮 -BCsin C sin A-2 2b a b 2 abII.16 号,此时面积的最大值为 32 6 42 .-2ab ,—2ab 64(2 -.2)当且仅当a b 时取等3【解析】:(I )由所给条件 方程x 2 5x 6 ••• tan (A B) tan A tan B1 tan Atan BB C 180 ,• C180 (A 0 的两根 tan A 3, tan B 2 . 1B).由(I )知,tanCtan(A B)1,•/ C 为三角形的内角,• sinC_2 23 10弘知教育内部资料 中小学课外辅导专家2 3••• BC 1 —汇 3.5. 近 y/10 2r r 2B 厂8【解析】:(1) m//n2sinB(2cos ;-1)=-,3cos2B 2sinBcosB=- 3cos2Btan2B=- 32兀 心宀 n••• 0<2B< n,2B=y,A 锐角 B=3① 当B=n^,已知b=2,由余弦定理,得: 4=a 2+c ?-ac > 2aac=ac(当且仅当a=c=2时等号成立)■/ △ ABC 的面积 S ABC =3acsinBh^ac w 3ABC 的面积最大值为.3② 当B=6n 时,已知b=2,由余弦定理,得:4=a 2+c 2+ 3ac 县ac+ . 3ac=(2+ 3)ac(当且仅当 a=c= , 6- . 2时等号成立) •,ac < 4(23)1 1•••△ ABC 的面积 S AABC =2 acsinB^ac <2- , 3 ,△ ABC 的面积最大值为 2- 314【解析】:(1)由余弦定理:cosB=4sid +cos2B=1 24⑵由cos B4 得sinB.15 •/ b=2,4n1 2sin 2x —;=;ac+4 > 2c,得 acw —,c 233 2sin(2x -)2 ,即 0 1 -2sin(2x -) 12 44(2)由 tan2B=- .3n [、. 5nB=3或石 1 V15S\ ABc =~acsi nBw(a=c 时取等号)3故S A ABC 的最大值为5【解析】(I ) T f(x).n _1 cos 2x3cos2x 1 sin2x 3cos2x弘知教育内部资料 中小学课外辅导专家n nn n又••• x —< 2x -<4 2 613 又 S besin A be24所以△ ABC 面积S 的最大值等于32 27【解析】:(I )因为 f (x) (sin x eosx) +eos2 x sin1 sin2x eos2x ( ) =1+.2si n(2x )42所以,T —,即函数f(x)的最小正周期为2(n )因为 0 x ,得 2x L,所以有-sin(2x) 12 4 4 4 24所以,函数f x 的最大值为1 2此时,因为一2x —丄,所以,2x ,即x -4 4 4428即 2 < 1 2sinn2x -3 • f(x) maxf (X)min(n) •/ f (x)f(x)f(x)•- m f (X)maxf ( X) min••• 1 m 4,即m 的取值范围是(1,4).6【解析】:(1)由已知得b 1 2 * 4e 2 a 2 si nA ,32bccos A又在锐角△ ABC 中,所以A=60,[不说明是锐角 △ ABC 中,扣 1 分](II)因为 a=2,A=60 所以 b e be 4,S1 3besin Abe2而 b 2 e 2 2be be 42bcbe 4 ,3x 2sin xeosx eos 2 x eos2x。
2021年高考数学一轮复习《三角函数》精选练习(含答案)

2021年高考数学一轮复习《三角函数》精选练习一、选择题1.若函数f(x)=ax +b 的零点是2,那么函数g(x)=bx 2-ax 的零点是( )A .0,2B .0,0.5C .0,-0.5D .2,-0.52.若函数f(x)=ax +1在区间(-1,1)上存在一个零点,则实数a 的取值范围是( )A .(1,+∞)B .(-∞,1)C .(-∞,-1)∪(1,+∞)D .(-1,1) 3.函数f(x)=3x+x 2-2的零点个数为( )A .0B .1C .2D .3 4.函数f(x)=e x +2x-3的零点所在的一个区间为( )A .(-1,0)B .0,0.5 C.0.5,1 D .1,1.5 5.函数f(x)=3x |ln x|-1的零点个数为( )A .1B .2C .3D .4 6.下列函数中,在(-1,1)内有零点且单调递增的是( )A .y=log 0.5xB .y=2x-1 C .y=x 2-0.5 D .y=-x 37.一个扇形的弧长与面积的数值都是6,则这个扇形的圆心角的弧度数是( )A .1B .2C .3D .4 8.点P(cos 2 019°,sin 2 019°)所在的象限是( )A .第一象限B .第二象限C .第三象限D .第四象限 9.-510°是( )A.第一象限B.第二象限C.第三象限D.第四象限10.某扇形的面积为1cm 2,它的周长为4cm ,那么该扇形圆心角的度数为( )A.2°B.2C.4°D.4 11.如果弓形的弧所对的圆心角为3π,弓形的弦长为4 cm ,则弓形的面积是( ) A.(344-9π)cm 2 B.(344-3π)cm 2 C.(348-3π)cm 2 D.(328-3π)cm 212.已知角θ的始边与x 轴的非负半轴重合,终边过点M(-3,4),则cos 2θ-sin 2θ+tanθ的值为( )A .-12175 B.12175 C .-7975 D.797513.已知角α终边上一点P 的坐标是(2sin 2,-2cos 2),则sin α等于( )A .sin 2B .-sin 2C .cos 2D .-cos 214.已知tan(α-π)=0.75,且α∈[23,2ππ],则sin(2πα+)=( ) A.0.8 B.-0.8 C.0.6 D.-0.6 15.计算:0190sin 160sin 2350cos --=( )16.若(),2,53cos παππα<≤=+则()πα2sin --的值是( ) A.3/5 B.-3/5 C.4/5 D.-4/517.在平面直角坐标系xOy 中,角α的顶点为坐标原点,始边在x 轴的非负半轴上,终边经过点P(3,4),则sin ⎝⎛⎭⎪⎫α-2 019π2=( ) A .-45 B .-35 C.35 D.4518.已知倾斜角为α的直线l 与直线x +2y -3=0垂直,则)222017cos(απ-的值为( ) A.0.8 B.-0.8 C.2 D.-0.5 19.)2cos()2sin(21++-ππ等于( )A.sin2-cos2B.cos2-sin2C.±(sin2-cos2)D.sin2+cos220.已知函数f(x)=asin(πx+α)+bcos(πx+β),且f(4)=3,则f(2018)的值为( )A .-1B .1C .3D .-3 21.已知sin ⎝ ⎛⎭⎪⎫α-π12=13,则cos ⎝⎛⎭⎪⎫α+17π12等于( ) A.13 B.223 C .-13 D .-223 22.log 2⎝⎛⎭⎪⎫cos 7π4的值为( )A .-1B .-12 C.12 D.2223.将函数f(x)=sin 2x 图象上的所有点向右平移π4个单位长度后得到函数g(x)的图象.若g(x)在区间[0,a]上单调递增,则a 的最大值为( ) A.π8 B.π4 C.π6 D.π224.关于函数y=tan ⎝⎛⎭⎪⎫2x -π3,下列说法正确的是( ) A .是奇函数 B .在区间⎝⎛⎭⎪⎫0,π3上单调递减C.⎝⎛⎭⎪⎫π6,0为其图象的一个对称中心 D .最小正周期为π25.若函数y=3cos(2x +φ)的图象关于点⎝⎛⎭⎪⎫4π3,0对称,则|φ|的最小值为( )A.π6 B .π4 C.π3 D .π226.已知函数f(x)=cos ⎝⎛⎭⎪⎫2x +π3-cos 2x ,其中x∈R,给出下列四个结论:①函数f(x)是最小正周期为π的奇函数; ②函数f(x)图象的一条对称轴是直线x=2π3;③函数f(x)图象的一个对称中心为⎝⎛⎭⎪⎫5π12,0;④函数f(x)的递增区间为⎣⎢⎡⎦⎥⎤kx +π6,k π+2π3,k ∈Z.则正确结论的个数是( ) A .1 B .2 C .3 D .4 27.函数y=sin x +cos x 的最小值和最小正周期分别是( )A.-2,2πB.-2,2πC.-2,πD.-2,π 28.y=|cos x|的一个单调递增区间是( )A.⎣⎢⎡⎦⎥⎤-π2,π2 B .[0,π] C.⎣⎢⎡⎦⎥⎤π,3π2 D.⎣⎢⎡⎦⎥⎤3π2,2π29.设函数f(x)=3sin ωx+cos ωx(ω>0),其图象的一条对称轴在区间⎝ ⎛⎭⎪⎫π6,π3内,且f(x)的最小正周期大于π,则ω的取值范围为( )A.⎝ ⎛⎭⎪⎫12,1 B .(0,2) C .(1,2) D .[1,2) 30.已知函数f(x)=2cos ⎝⎛⎭⎪⎫2x +π4,则以下判断中正确的是( ) A .函数f(x)的图象可由函数y=2cos 2x 的图象向左平移π8个单位长度得到B .函数f(x)的图象可由函数y=2cos 2x 的图象向左平移π4个单位长度得到C .函数f(x)的图象可由函数y=2sin 2x 的图象向右平移3π8个单位长度得到D .函数f(x)的图象可由函数y=2sin 2x 的图象向左平移3π4个单位长度得到31.已知函数f(x)=Asin(ωx+φ)( ω>0,-π2<φ<π2)的部分图象如图所示,则φ的值为( )A .-π3 B.π3 C .-π6 D.π632.将函数y=f(x)=2sin ⎝⎛⎭⎪⎫2x +π6的图象向左平移π12个单位长度,再把所有点的横坐标缩短到原来的12,纵坐标不变,得到函数y=g(x)的图象,则下面对函数y=g(x)的叙述正确的是( )A .函数g(x)=2sin ⎝⎛⎭⎪⎫x +π3B .函数g(x)的周期为πC .函数g(x)的一个对称中心为点⎝ ⎛⎭⎪⎫-π12,0D .函数g(x)在区间⎣⎢⎡⎦⎥⎤π6,π3上单调递增33.已知函数f(x)=2sin(ωx+φ)( ω>0,φ∈⎣⎢⎡⎦⎥⎤π2,π )的部分图象如图所示,其中f(0)=1,|MN|=52,将f(x)的图象向右平移1个单位长度,得到函数g(x)的图象,则g(x)的解析式是( )A .g(x)=2cos π3xB .g(x)=2sin ⎝ ⎛⎭⎪⎫π3x +2π3C .g(x)=2sin ⎝ ⎛⎭⎪⎫2π3x +π3 D .g(x)=-2cos π3x34.已知函数f(x)=2sin ⎝ ⎛⎭⎪⎫ωx+π3(ω>0)图象的最高点与相邻最低点的距离是17,若将y=f(x)的图象向右平移16个单位长度得到y=g(x)的图象,则函数y=g(x)图象的一条对称轴方程是( )A .x=56B .x=13C .x=12 D .x=0二、填空题35.函数f(x)=3x -7+ln x 的零点位于区间(n ,n +1)(n∈N)内,则n=________. 36.已知α是第二象限角,则α3是第________象限角.37.已知()()()()29cos sin 4cos sin 3=+---++απαααπ,则αtan = . 38.已知向量a=(sin θ,-2)与b=(1,cos θ)互相垂直,其中θ∈(20π,),则cos θ=________.39.已知θ是第三象限角,且sinθ-2cosθ=-25,则sinθ+cosθ=________.40.已知函数f(x)=sin(ωx+φ)⎝⎛⎭⎪⎫ω>0,-π2≤φ≤π2的图象上的一个最高点和与它相邻的一个最低点的距离为22,且图象过点⎝ ⎛⎭⎪⎫2,-12,则函数f(x)=____________.答案解析41.答案为:C ; 42.答案为:C ;解析:由题意知,f(-1)f(1)<0,即(1-a)(1+a)<0,解得a<-1或a>1. 43.答案为:C ;解析:函数f(x)=3x+x 2-2的零点个数即为函数y=3x与函数y=2-x 2的图象的交点个数, 由图象易知交点个数为2,则f(x)=3x+x 2-2的零点个数为2,故选C. 44.答案为:C ; 45.答案为:B ;解析:选B.函数f(x)=3x|ln x|-1的零点即3x|ln x|-1=0的解,即|ln x|=⎝ ⎛⎭⎪⎫13x的解, 作出函数g(x)=|ln x|和函数h(x)=⎝ ⎛⎭⎪⎫13x的图象,由图象可知,两函数图象有两个公共点, 故函数f(x)=3x|ln x|-1有2个零点.46.答案为:B ;解析:选B.函数y=log 12x 在定义域上单调递减,y=x 2-12在(-1,1)上不是单调函数,y=-x 3在定义域上单调递减,均不符合要求.对于y=2x-1, 当x=0∈(-1,1)时,y=0且y=2x-1在R 上单调递增.故选B. 47.答案为:C ; 48.答案为:C ;49.[答案] C [解析] -510°=-720°+210°,∴-510°角与210°角终边相同,故选C. 50.B 51.C 52.答案为:A解析:由已知得|OM|=5,因而cosθ=-35,sinθ=45,tanθ=-43,则cos 2θ-sin 2θ+tanθ=925-1625-43=-12175.故选A.53.答案为:D ; 54.B. 55.D. 56.C57.答案为:C ;解析:∵角α的终边经过点P(3,4),∴sin α=45,cos α=35.∴sin ⎝ ⎛⎭⎪⎫α-2 019π2=sin ( α-2 020π2+π2 )=sin ( α+π2 )=cos α=35.故选C. 58.A . 59.A60.答案为:C ;解析:∵f(4)=asin(4π+α)+bcos(4π+β)=asinα+bcosβ=3,∴f(2018)=asin(2018π+α)+bcos(2018π+β)=asinα+bcosβ=3.故选C. 61.答案为:A ;解析:cos ⎝ ⎛⎭⎪⎫α+17π12=cos ⎣⎢⎡⎦⎥⎤3π2+⎝ ⎛⎭⎪⎫α-π12=sin ⎝ ⎛⎭⎪⎫α-π12=13.故选A. 62.答案为:B ;解析:log 2⎝ ⎛⎭⎪⎫cos 7π4=log 2⎝ ⎛⎭⎪⎫cos π4=log 222=-12.故选B.63.答案为:D ;f(x)的图象向右平移π4个单位长度得到g(x)=sin [ 2⎝ ⎛⎭⎪⎫x -π4 ]=-cos 2x 的图象.根据余弦函数的图象可知,当0≤2x≤π,即0≤x≤π2时,g(x)单调递增,故a 的最大值为π2. 64.答案为:C ;函数y=tan ⎝ ⎛⎭⎪⎫2x -π3是非奇非偶函数,A 错;函数y=tan ⎝ ⎛⎭⎪⎫2x -π3在区间⎝ ⎛⎭⎪⎫0,π3上单调递增,B 错;最小正周期为π2,D 错;由2x -π3=kπ2,k ∈Z ,得x=kπ4+π6,k ∈Z.当k=0时,x=π6,所以它的图象关于⎝ ⎛⎭⎪⎫π6,0对称.65.答案为:A.解析:由题意得3cos ⎝ ⎛⎭⎪⎫2×4π3+φ=3cos(2π3+φ+2π)=3cos ⎝ ⎛⎭⎪⎫2π3+φ=0,∴2π3+φ=kπ+π2,k ∈Z ,∴φ=k π-π6,k ∈Z. 取k=0,得|φ|的最小值为π6. 66.答案为:C.解析:f(x)=cos ⎝ ⎛⎭⎪⎫2x +π3-cos 2x=cos 2xcos π3-sin 2xsin π3-cos 2x=-sin ⎝ ⎛⎭⎪⎫2x +π6,不是奇函数,故①错误;当x=2π3时f ⎝ ⎛⎭⎪⎫2π3=-sin ⎝ ⎛⎭⎪⎫4π3+π6=1,故②正确;当x=5π12时f ⎝ ⎛⎭⎪⎫5π12=-sin π=0,故③正确;令2k π+π2≤2x +π6≤2k π+3π2,k ∈Z ,得k π+π6≤x ≤k π+2π3,k ∈Z ,故④正确.综上,正确的结论个数为3. 67.A68.答案为:D ;将y=cos x 的图象位于x 轴下方的部分关于x 轴对称向上翻折,x 轴上方(或x 轴上)的图象不变,即得y=|cos x|的图象(如图).故选D.69.答案为:C ;由题意f(x)=3sin ωx+cos ωx=2sin ⎝ ⎛⎭⎪⎫ωx+π6(ω>0).令ωx+π6=π2+kπ,k ∈Z , 得x=π3ω+kπω,k ∈Z.∵函数图象的一条对称轴在区间⎝ ⎛⎭⎪⎫π6,π3内,∴π6<π3ω+kπω<π3,k ∈Z ,∴3k +1<ω<6k+2,k ∈Z. 又∵f(x)的最小正周期大于π,∴2πω>π,解得0<ω<2.∴ω的取值范围为(1,2).故选C.70.答案为:A;解析:因为f(x)=2cos ⎝⎛⎭⎪⎫2x +π4,所以函数f(x)的图象可由函数y=2cos 2x 的图象向左平移π8个单位长度得到,故选A.71.答案为:B;解析:由题意,得T 2=π3-⎝ ⎛⎭⎪⎫-π6=π2,所以T=π,由T=2πω,得ω=2,由图可知A=1,所以f(x)=sin(2x +φ).又因为f ⎝ ⎛⎭⎪⎫π3=sin ⎝ ⎛⎭⎪⎫2π3+φ=0,-π2<φ<π2,所以φ=π3.72.答案为:C.解析:将函数f(x)=2sin ⎝ ⎛⎭⎪⎫2x +π6的图象向左平移π12个单位,可得函数y=2sin ⎣⎢⎡⎦⎥⎤2⎝ ⎛⎭⎪⎫x +π12+π6=2sin ⎝ ⎛⎭⎪⎫2x +π3的图象;再把所有点的横坐标缩短到原来的12,纵坐标不变,得到函数y=g(x)=2sin ⎝ ⎛⎭⎪⎫4x +π3的图象,故g(x)的周期为2π4=π2,排除A ,B.令x=-π12,求得g(x)=0,可得g(x)的一个对称中心为⎝ ⎛⎭⎪⎫-π12,0,故C 满足条件. 在区间⎣⎢⎡⎦⎥⎤π6,π3上,4x +π3∈⎣⎢⎡⎦⎥⎤π,5π3,函数g(x)没有单调性,故排除D.73.答案为:A ;解析:设函数f(x)的最小正周期为T.由题图及|MN|=52,得T 4=32,则T=6,ω=π3.又由f(0)=1,φ∈⎣⎢⎡⎦⎥⎤π2,π得sin φ=12,φ=5π6.所以f(x)=2sin ( π3x +5π6 ).则g(x)=2sin ⎣⎢⎡⎦⎥⎤π3x -1+5π6=2cos π3x.故选A.74.答案为:B ;解析:函数f(x)=2sin ⎝ ⎛⎭⎪⎫ωx+π3的最大值为2,由172-42=1可得函数f(x)的周期T=2×1=2,所以ω=π,因此f(x)=2sin ⎝⎛⎭⎪⎫πx+π3.将y=f(x)的图象向右平移16个单位长度得到的图象对应的函数解析式为g(x)=2sin ⎣⎢⎡⎦⎥⎤π⎝ ⎛⎭⎪⎫x -16+π3=2sin ⎝ ⎛⎭⎪⎫πx+π6,当x=13时,g ⎝ ⎛⎭⎪⎫13=2sin ⎝ ⎛⎭⎪⎫π3+π6=2, 为函数的最大值,故直线x=13为函数y=g(x)图象的一条对称轴.故选B.75.答案为:2;解析:因为f(x)在(0,+∞)上单调递增,且f(2)=-1+ln 2<0,f(3)=2+ln 3>0,所以函数f(x)的零点位于区间(2,3)内,故n=2.76.[答案] 一或第二或第四 [解析] 将平面直角坐标系中的每一个象限进行三等分,从x 轴右上方开始在每一等份中依次标数字1、2、3、4,如图所示.∵α第二象限角,∴图中标有数字2的位置即为α3角的终边所在位置,故α3是第一或第二或四象限角. 77.答案为:0.2; 78.答案:55. 79.答案为:-3125;解析:观察得sinθ=45,cosθ=35满足方程,但此时θ是第一象限角,不合题意.由⎩⎪⎨⎪⎧sinθ-2cosθ=-25,sin 2θ+cos 2θ=1,得5cos 2θ-85cosθ-2125=0,解得cosθ=35或-725.因为θ是第三象限角,所以cosθ=-725,从而sinθ=-2425,所以si nθ+cosθ=-3125.80.答案为:sin ⎝⎛⎭⎪⎫π2x +π6; 解析:依题意得22+⎝ ⎛⎭⎪⎫πω2=22,ω>0,所以ω=π2,所以f(x)=sin ⎝ ⎛⎭⎪⎫π2x +φ.因为该函数图象过点⎝ ⎛⎭⎪⎫2,-12,所以sin(π+φ)=-12,即sin φ=12. 因为-π2≤φ≤π2,所以φ=π6,所以f(x)=sin ⎝ ⎛⎭⎪⎫π2x +π6.。
高考数学一轮复习精选试题: 三角函数(解答题) Word版含答案

三角函数02解答题(本大题共6个小题,共70分,解答应写出文字说明,证明过程或演算步骤)1.已知角的终边经过点.(1) 求的值;(2)求的值.【答案】由角的终边过点知:, ,, (1) =, (2)=…11分 =。
2.已知函数. (Ⅰ)求函数的值域;α(3,4)P -sin()cos()tan()πααπα-+-+α(3,4)P -224sin 5(3)4α==-+223cos 5(3)4α==--+44tan 33α==--sin()cos()sin cos tan()tan πααααπαα-+-+=+4343()/()55320--=-))cos(2)23(cos()2sin(πααπαπ--+⋅+)cos 2(sin cos ααα+24336()2()55525⨯-+⨯-=2()23cos 2sin 333x x x f x =-()f x(Ⅱ)在△中,角所对的边分别为,若,且,求的值【答案】(1) ∵,∴ ∴ ∴函数的值域为(2), ∴,而, ∴. 在中,,,∴, 得 解得 ∵, ∴.3.如图所示,甲船在A 处,乙船在A 处的南偏东45°方向,距A 有9n mile 并以20n mile/h 的速度沿南偏西15°方向航行,若甲船以28n mile/h 的速度航行,应沿什么方向,用多少h 能尽快追上乙船?ABC ,,A B C ,,a b c ()1f C =2b ac =sinA 22()cos 133x x f x =+-22sin()136x π=+-x R ∈21sin()136x π-≤+≤232sin()1136x π-≤+-≤()f x [3,1]-2()2sin()1136C f C π=+-=2sin()136C π+=(0,)C π∈2C π=Rt ABC ∆2b ac =222c a b =+22c a ac =+2()10aa c c+-=a c =0sin 1A <<1sin 2a A c -==【答案】设用t 小时,甲船能追上乙船,且在C 处相遇.在△ABC 中,AC=28t ,BC=20t ,AB=9,∠ABC=1200,根据余弦定理得,AC 2=AB 2+BC 2-2AB ·Bccos ∠ABC即(28t)2=(20t)2+(20t)2-2×9×20tcos1200,整理得,128 t 2-60t -27=0,(4t -3)(32t+9)=0,解得或(舍). 所以AC=21,BC=15, 在△ABC 中,, 所以∠BAC=380,所以甲船应沿南偏西70方向行驶.答:甲船应沿南偏西70方向,用0.75h 能尽快追上乙船.4.已知向量,函数. (Ⅰ)求函数的最小正周期;(Ⅱ)已知、、分别为内角、、的对边, 其中为锐角,,且,求和的面积.【答案】(Ⅰ)3t 4=9t 32=-015BC sin1202sin BAC 0.6186AC21⋅∠===≈1(sin ,1),(3cos ,)2a xb x =-=-()()2f x a b a =+⋅-()f xT a b c ABC ∆A B C A 4a c ==()1f A =,A b ABC ∆S 2()()22f x a b a aa b =+⋅-=+⋅-21sin 1cos 22x x x =++-因为,所以5.化简:【答案】原式=6.已知函数(I )化简函数f (x )的解析式,并求函数f (x )的最小正周期;(Ⅱ)在锐角△ABC 中,若,求△AB C 的面积.【答案】(1) (2) 1cos 21sin 2222x x -=+-12cos 222x x =-sin(2)6x π=-2ω=22T ππ==)()(()(αππααπααπ+++323tan --cos )(cos )-cos sin αααααααα333323cos tan sin tan cos )cos (cos )sin (==-⋅⋅-2()2sin cos f x x x x x R =+-∈()1,2f A AB AC =⋅=)32sin(2)(π+=x x f ππ==22T 22=s。
新高考一轮复习特训-三角函数-(含答案)高中数学-高考专区-一轮复习

2025届新高考一轮复习特训 三角函数一、选择题1.函数()sin 2f x =到()g x 的图象,则()g x =( )A.cos 4xB.cos x- C.cos 4x- D.sin x-2.已知()1sin ,tan 5tan 2αβαβ+==,则()sin αβ-=( )3.已知函数π()sin (0)3f x x ωω⎛⎫=+> ⎪⎝⎭,若()f x 在2π0,3⎡⎤⎢⎥⎣⎦上有两个零点,则ω的取值范围是( )A.5,42⎡⎫⎪⎢⎣⎭B.5,2⎡⎫+∞⎪⎢⎣⎭C.511,22⎡⎫⎪⎢⎣⎭D.5,42⎡⎤⎢⎥⎣⎦4.已知角α的始边与x 轴非负半轴重合,终边过点()1,2P -,则cos 2α=( )355.与1990-︒终边相同的最小正角是( )A.80︒B.150︒C.170︒D.290︒6.已知tan α==( )7.下列区间中,函数π()7sin 6f x x ⎛⎫=- ⎪⎝⎭单调递增的区间是( )A.π0,2⎛⎫⎪⎝⎭B.π,π2⎛⎫ ⎪⎝⎭C.3ππ,2⎛⎫ ⎪⎝⎭D.3π,2π2⎛⎫ ⎪⎝⎭8.记函数π()sin (0)4f x x b ωω⎛⎫=++> ⎪⎝⎭πT <<,且()y f x =的图象关于点3π,22⎛⎫⎪⎝⎭中心对称,则π2f ⎛⎫= ⎪⎝⎭( )D.3二、多项选择题9.设x ∈R ,用[]x 表示不超过x 的最大整数,则函数[]y x =被称为高斯函数;例如[]2.13-=-,[]2.12=,已知()sin sin f x x =+()()x f x =⎡⎤⎣⎦,则下列说法正确的是( )A.函数()g x 是偶函数B.函数()g x 是周期函数C.函数()g x 的图像关于直线x =()g x x =只有1个实数根10.已知()π23f x x ⎛⎫=+ ⎪⎝⎭,则( )A.()()πf x f x += B.()f x 的图象关于直线x =C.()f x 的图象关于点π,06⎛⎫⎪⎝⎭对称D.()f x 在5ππ,1212⎛⎫-⎪⎝⎭单调递增11.已知函数ππ()sin(3)22f x x ϕϕ⎛⎫=+-<< ⎪⎝⎭的图象关于直线x =A.函数π12f x ⎛⎫+ ⎪⎝⎭为奇函数B.函数()f x 在ππ,123⎡⎤⎢⎥⎣⎦上单调递增)()12x f x -=-D.函数()f x 的图象关于5π,012⎛⎫ ⎪⎝⎭中心对称三、填空题12.若tan θ==____________.13.如图是古希腊数学家希波克拉底研究的几何图形,此图由三个半圆构成,直径分别是直角三角形ABC 的斜边AB ,直角边AC ,BC ,点E 在以AC 为直径的半圆上,延长AE ,BC 交于点D .若5AB =,sin CAB ∠=DCE ∠=ABE 的面积是______.14.如图所示,终边落在阴影部分(含边界)的角的集合是__________.四、解答题15.如图,弹簧挂着的小球做上下振动,它在t (单位:s )时相对于平衡位置(静止时的位置)的高度h (单位:cm )由关系式πsin 4h A t ω⎛⎫=+ ⎪⎝⎭确定,其中0A >,0ω>,[0,)t ∈+∞.在一次振动中,小球从最高点运动至最低点所用时间为1s ,且最高点与最低点间的距离为10cm .(1)求小球相对于平衡位置的高度h (单位:cm )和时间t (单位:s )之间的函数关系式;(2)小球在0t s 内经过最高点的次数恰为50次,求0t 的取值范围.16.已知α=(1)写出与角α终边相同的角的集合;(2)写出在()4π,2π-内与角α终边相同的角.17.已知函数()sin()f x A x ωϕ=+(0A >,0ω>,||πϕ<)图象的最高点为π,16⎛⎫⎪⎝⎭,距离该最高点最近的一个对称中心为5π,012⎛⎫⎪⎝⎭.(1)求()f x 的解析式及单调递减区间;(2)若函数()(0)2a g x f x a ⎛⎫=>⎪⎝⎭,()g x 的图象关于直线x =()g x 在π0,15⎡⎤⎢⎥⎣⎦上单调递增,求实数a 的值.18.已知函数(1)化简;(2)若的值.19.如图,锐角α和钝角β的终边分别与单位圆交于A ,B 两点,且OA OB ⊥.cos αβ的值.()f x =()f x ()0f x =00π2π2cos(2)63x x ⎛⎫-+- ⎪⎝⎭参考答案1.答案:A解析:()sin 2f x=ππsin 2sin 2cos 242y x x x ⎛⎫⎛⎫=+=+= ⎪ ⎪⎝⎭⎝⎭的图象,再把横坐标缩短为原来的一半,得到()cos 4g x x =的图象故选:A.2.答案:A解析:因为()sin sincos +cos sin αβαβαβ+===cos 5cos sin αβαβ=,所以11sin cos cos sin 6cos sin ,cos sin ,sin cos 212αβαβαβαβαβ+====所以()5141sin sin cos cos sin .1212123αβαβαβ-=-=-==故选:A.3.答案:A解析:因为2π0,3x ⎡⎤∈⎢⎥⎣⎦,0ω>,所以ππ2ππ,3333x ωω⎡+∈+⎢⎣π[2π,3π)3+∈,所以5,42ω⎡⎫∈⎪⎢⎣⎭.4.答案:D解析:因为角α的始边与x 轴非负半轴重合,终边过点()1,2P -,所以cos α==所以2cos 22cos 1αα=-=故选:D.5.答案:C解析:因为199********-=-⨯-︒︒︒,199********-=-⨯+︒︒︒,所以与1990-︒终边相同的最小正角是170︒.故选C.6.答案:B,故选:B.7.答案:A解析:方法一:令πππ2π2π262k x k -+-≤+≤,k ∈Z ,得π2π2π2π33k x k -+≤≤+,k ∈Z .取0k =,则π3x -≤≤ππ2π0,,233⎫⎡⎤-⎪⎢⎥⎭⎣⎦Ü,所以区间π0,2⎛⎫⎪⎝⎭是函数()f x 的单调递增区间.方法二:当π02x <<时,,所以在π0,2⎛⎫⎪⎝⎭上单调递增,故A 正πx <<π6x <-<()f x 在π,π2⎛⎫⎪⎝⎭上不单调,故B 错误;当πx <<π6x <-<()f x 在3ππ,2⎛⎫ ⎪⎝⎭上单调递减,故C 错误;当3π2π2x <<π6x <-<()f x 在3π,2π2⎛⎫⎪⎝⎭上不单调,故D 错误.8.答案:A T <<2ππω<<,解得23ω<<.因为()y f x =的图象关于点3π,22⎛⎫ ⎪⎝⎭中心对称,所以2b =,且,即,所以,又π4π4+=,解得ω=5π()sin 224f x x ⎛⎫=++ ⎪⎝⎭,所以π5ππ3πsin 2sin 2122242f ⎛⎫⎛⎫=⨯++=+= ⎪ ⎪⎝⎭⎝⎭.故选A.9.答案:AD解析:选项A ,函数()f x 的定义域为R ,2tan 313tan 2αα+==-πππ663x -<-<()f x 3ππsin 224b ω⎛⎫++= ⎪⎝⎭3ππsin 024ω⎛⎫+= ⎪⎝⎭3πππ()24k k ω+=∈Z 2ω<<3ππ24ω<+<因为()()()sin sin sin sin f x x x x x f x -=-+-=+=,所以()f x 为偶函数,当0πx <≤时,()sin sin 2sin f x x x x =+=,当π2πx <≤时,()sin sin 0f x x x =-=,当2π3πx <≤时,()sin sin 2sin f x x x x =+=,…因为()f x 为偶函数,所以函数()f x 的图象如下图所示由()()g x f x =⎡⎤⎣⎦可知,在0x ≥内,当2πx k =+∈Z 时,()2g x =,当π2π2π6k x k +≤≤+2πx k ≠+∈Z 时,()1g x =,当2π2πk x k ≤<5ππ2π2π6k x k +<≤+,k ∈Z 时,()0g x =,因为()()()()g x f x f x g x -=-==⎡⎤⎡⎤⎣⎦⎣⎦,所以()g x 为偶函数,则函数()g x 的图象如下图所示显然()g x 不是周期函数,故选项A 正确,B 错误,C 错误;()g x x =,当()0g x =时,0x =方程有一个实数根,当()1g x =时,x =π212⎛⎫=≠ ⎪⎝⎭,方程没有实数根,当()2g x =时,πx =,此时()π02g =≠,方程没有实数根,()g x x =只有1个实数根,故D 正确;故选:AD.10.答案:AD解析:对于A,函数()π23f x x ⎛⎫=+ ⎪⎝⎭的最小正周期2ππ2T ==,()()πf x f x +=,A正确;对于B,由πππ2π3266332f ⎛⎫⎛⎫=⨯+==≠ ⎪ ⎪⎝⎭⎝⎭()f x 的图象不关于直线x =对于C,由πππ2π32066332f ⎛⎫⎛⎫=⨯+==≠ ⎪ ⎪⎝⎭⎝⎭,得函数()f x 的图象不关于点π,06⎛⎫⎪⎝⎭对称,C 错误;对于D,当5ππ,1212x ⎛⎫∈- ⎪⎝⎭时,πππ2,322x ⎛⎫+∈- ⎪⎝⎭,而正弦函数sin y x =在ππ,22⎡⎤-⎢⎥⎣⎦上单调递增,因此函数()f x 在区间5ππ,1212⎛⎫- ⎪⎝⎭上单调递增,D 正确.故选:AD.11.答案:ACD解析: 函数ππ()sin(3)22f x x ϕϕ⎛⎫=+-<< ⎪⎝⎭的图象关于直线x =ππ3π42k ϕ∴⨯+=+,k ∈Z ,ππ4k ϕ∴=-+,k ∈Z因为ππ22ϕ-<<,所以ϕ=π()sin(3)4f x x =-.函数πππ()sin 3sin 312124f x x x ⎡⎤⎛⎫+=+-= ⎪⎢⎥⎝⎭⎣⎦为奇函数,故A 正确;当[,123ππx ∈,π3π0,434x ⎡-∈⎤⎢⎥⎣⎦,函数()f x 没有单调性,故B 错误;若12|()()|2f x f x -=,因为[]()1,1f x ∈-,所以()()1211f x f x =⎧⎪⎨=-⎪⎩或()()1211f x f x =-⎧⎪⎨=⎪⎩,则12|x x -2π3=5π5ππsin 3sin 012124f π⎛⎫⎛⎫=⨯-== ⎪ ⎪⎝⎭⎝⎭,所以函数()f x 图象关于5π,012⎛⎫⎪⎝⎭中心对称,故D 正确故选:ACD ..解析:由题意得:DCE ACE ∠+∠=π2CAE ACE +∠=所以DCE CAE ∠=∠,故sin sin DCE CAE ∠=∠=cos CAE ∠==因为sin CAB ∠=45CAB ∠=故()sin sin sin cos cos sin EAB CAE CAB CAE CAB CAE CAB∠=∠+∠=∠∠+∠∠343455=⨯=因为5AB =,ACB ∠=CAB ∠=3BC =,4AC =又因为AEC ∠=CAE ∠=,所以cos 4AE AC CAE =∠==的cos 11cos sin cos tan 131cos cos θθθθθθθ====+++所以ABE △的面积是11sin 522S AB AE EAB =⋅⋅∠=⨯=14.答案:36045360120{,|}k k k αα⋅︒-︒≤≤⋅︒+︒∈Z 解析:终边落在阴影部分第二象限最左边的角为360120k ⋅︒+︒,k ∈Z ,终边落在阴影部分第四象限最左边的角为,k ∈Z .所以终边落在阴影部分(含边界)的角的集合是.故答案为:36045360120{,|}k k k αα⋅︒-︒≤≤⋅︒+︒∈Z .15.答案:(1)π5sin π([0,))4h t t ⎛⎫=+∈+∞ ⎪⎝⎭(2)1198,10044⎡⎫⎪⎢⎣⎭解析:(1)由题意得1052A ==.因为在一次振动中,小球从最高点运动至最低点所用时间为1s ,所以最小正周期为2s ,即2T ==π=,所以π5sin π([0,))4h t t ⎛⎫=+∈+∞ ⎪⎝⎭.(2)由(1)知,当t =最高点.因为小球在0s t 0149504T tT +≤<+.因为2T =,所以01984t ≤<所以0t 的取值范围为1198,10044⎡⎫⎪⎢⎣⎭.16.答案:(1)π2π,3k k θθ⎧⎫=+∈⎨⎬⎩⎭Z (2)36045k ⋅︒-︒36045360120{,|}k k k αα⋅︒-︒≤≤⋅︒+︒∈Z解析:(1)与角α终边相同的角的集合为π2π,3k k θθ⎧⎫=+∈⎨⎬⎩⎭Z .(2)令π4π2π2π3k -<+<,得136k -<<又k ∈Z ,2k ∴=-,-1,0,∴在()4π,2π-内与角α终边相同的角是17.答案:(1)π()sin 26f x x ⎛⎫=+ ⎪⎝⎭;单调递减区间为π2π[π,π]()63k k k ++∈Z(2)a =5=解析:(1)由题意解题思路知A =5ππ126=-=所以πT =,2π2πω==,所以()sin(2)f x x ϕ=+.将π,16⎛⎫ ⎪⎝⎭代入()sin(2)f x x ϕ=+,得πsin 13ϕ⎛⎫+= ⎪⎝⎭,π2π2k ϕ+=+,k ∈Z ,即π2π6k ϕ=+,k ∈Z ,又||πϕ<,所以ϕ=π()sin 26f x x ⎛⎫=+ ⎪⎝⎭.π3π2π22π62k x k +≤+≤+,k ∈Z 2πππ3k x k +≤≤+,k ∈Z ,即()f x 的单调递减区间为π2π[π,π]()63k k k ++∈Z .(2)由(1)可得π()sin (0)6g x ax a ⎛⎫=+> ⎪⎝⎭,由()g x 的图象关于直线x =πππ62k =+,k ∈Z ,即51544a k =+,k ∈Z ,当π0,15x ⎡⎤∈⎢⎥⎣⎦时,ππππ,66156a ax ⎡⎤+∈+⎢⎥⎣⎦,由()g x 在[π0,15ππ62+≤,即5a ≤.又0a >且51544a k =+,k ∈Z ,所以a =5=.18.答案:(1)π()cos 23f x x ⎛⎫=+ ⎪⎝⎭(2)35-解析:(1)ππππcos 2cos 2π2tan 22333()ππtan 2πsin π233x x x f x x x ⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫-+-++ ⎪ ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦=⎡⎤⎛⎫⎛⎫-++++ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦πππsin 2cos 2tan 2π333cos 2ππ3tan 2sin 233x x x x x x ⎛⎫⎛⎫⎛⎫+++ ⎪ ⎪ ⎪⎛⎫⎝⎭⎝⎭⎝⎭==+ ⎪⎛⎫⎛⎫⎝⎭++ ⎪ ⎪⎝⎭⎝⎭.(2)因为()00πcos 23f x x ⎛⎫=+= ⎪⎝⎭所以000ππππsin 2sin 2cos(2)6323x x x ⎡⎤⎛⎫⎛⎫-=+-=-+= ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦0002πππcos 2cos 2πcos 2333x x x ⎡⎤⎛⎫⎛⎫⎛⎫-=+-=-+= ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦故00π2π33sin 2cos 2631010x x ⎛⎫⎛⎫-+-=--=⎪ ⎪⎝⎭⎝⎭19.答案:(1)1-(2)3225-解析:(1)由题意得π2βα=+sin sin cos cos αβαβ=πsin sin sin cos 21πcos sin cos cos 2αααααααα⎛⎫+⎪⎝⎭==-=-⎛⎫+ ⎪⎝⎭.35α=,sin α=则πcos cos sin 2βαα⎛⎫=+=-= ⎪⎝⎭所以442sin cos 255αβ⎛⎫=⨯⨯-= ⎪⎝⎭。
2025届高考数学一轮复习人教A版多选题专题练:第五章 三角函数(含解析)

6
63
6 3 23
2
不符合条件.
当 7 时, f (x) sin(7 x π ) ,当 x [π, 2π] 时, 7 x π [3π , 8π ] , f (x) [1,1] ,
6
63
6 3 23
不符合条件.
综上,当 1 时, f (x) sin(x π ) ,符合条件,故 B 错误;
6
2
(纵坐标不变),得到函数 g x 的图象,则下列关于函数 g x 的说法中正确的是( )
A.在
π 6
,
5π 12
上单调递增
B.当
x
π 2
,
π
时,函数
g
x
的值域是
2,1
C.其图象关于直线 x 5π 对称 6
D.直线 y 2 3x 1为曲线 y g x 的切线
10.已知函数
f
x
sin
y
sin
2x
π 4
的图象的是(
)
A.先将 y cos x 的图象上各点的横坐标缩小为原来的 1 ,再向右平移 3π 个单位长度
2
8
B.先将 y sin x 的图象上各点的横坐标缩小为原来的 1 ,再向右平移 π 个单位长度
2
8
C.先将 y sin x 的图象向右平移 π 个单位长度,再将各点的横坐标缩小为原来的 1
与单位圆
O
交于点
P
2 10
,
y
,则(
)
A. sin 7 2 10
B. tan 5
C. cos 2 24 25
D.
sin
2
π 4
17 2 50
1.答案:AD
高三一轮复习-三角函数、三角恒等变换、解三角形讲义(带答案)
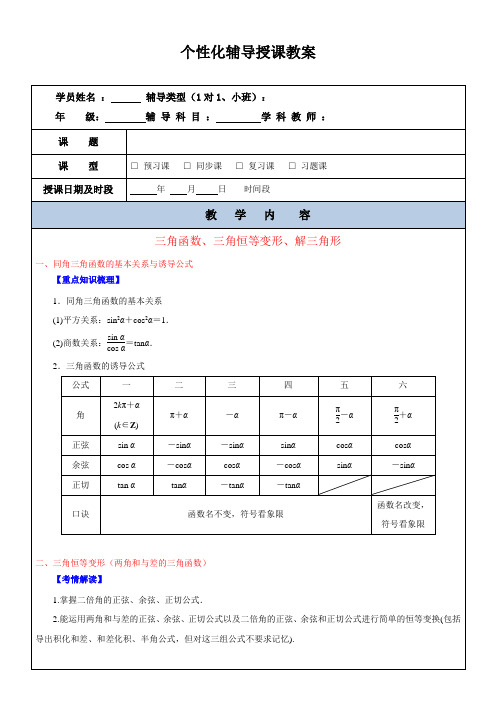
个性化辅导授课教案【重点知识梳理】1.两角和与差的正弦、余弦和正切公式 sin(α±β)=sin αcos β±cos αsin β. cos(α∓β)=cos αcos β±sin αsin β. tan(α±β)=tan α±tan β1∓tan αtan β.2.二倍角的正弦、余弦、正切公式 sin 2α=2sin αcos α.cos 2α=cos 2α-sin 2α=2cos 2α-1=1-2sin 2α. tan 2α=2tan α1-tan 2α. 3.有关公式的逆用、变形等(1)tan α±tan β=tan(α±β)(1∓tan αtan β). (2)cos 2α=1+cos 2α2,sin 2α=1-cos 2α2.(3)1+sin 2α=(sin α+cos α)2, 1-sin 2α=(sin α-cos α)2, sin α±cos α=2sin ⎝⎛⎭⎪⎫α±π4.4.函数f (α)=a sin α+b cos α(a ,b 为常数),可以化为f (α)=a 2+b 2sin(α+φ)⎝⎛⎭⎪⎫其中tan φ=b a或f (α)=a 2+b 2·cos(α-φ)⎝⎛⎭⎪⎫其中tan φ=a b . 【高频考点突破】考点一 三角函数式的化简与给角求值 【例1】 (1)已知α∈(0,π),化简: (1+sin α+cos α)·(cos α2-sin α2)2+2cos α=________.(2)[2sin 50°+sin 10°(1+3tan 10°)]·2sin 280°=______.【答案】(1)cos α (2) 6 【规律方法】(1)三角函数式的化简要遵循“三看”原则:①一看角之间的差别与联系,把角进行合理的拆分,正确使用公式;②二看函数名称之间的差异,确定使用的公式,常见的有“切化弦”;③三看结构特征,找到变形的方向,常见的有“遇到分式要通分”,“遇到根式一般要升幂”等.(2)对于给角求值问题,一般给定的角是非特殊角,这时要善于将非特殊角转化为特殊角.另外此类问题也常通过代数变形(比如:正负项相消、分子分母相约等)的方式来求值.【变式探究】 (1)4cos 50°-tan 40°=( ) A. 2 B.2+32C. 3 D .22-1(2)化简:sin 2αsin 2β+cos 2αcos 2β-12cos 2αcos 2β=________.【解析】(1)原式=4sin 40°-sin 40°cos 40°=4cos 40°sin 40°-sin 40°cos 40°=2sin 80°-sin 40°cos 40°=2sin (120°-40°)-sin 40°cos 40°=3cos 40°+sin 40°-sin 40°cos 40°=3cos 40°cos 40°=3,故选C.法三 (从“幂”入手,利用降幂公式先降次)原式=1-cos 2α2·1-cos 2β2+1+cos 2α2·1+cos 2β2-12cos 2α·cos 2β=14(1+cos 2α·cos 2β-cos 2α-cos 2β)+14(1+cos 2α·cos 2β+cos 2α+cos 2β)-12cos 2α·cos 2β=14+14=12.【答案】(1)C (2)12考点二 三角函数的给值求值、给值求角【例2】 (1)已知0<β<π2<α<π,且cos ⎝ ⎛⎭⎪⎫α-β2=-19,sin ⎝ ⎛⎭⎪⎫α2-β=23,求cos(α+β)的值;(2)已知α,β∈(0,π),且tan(α-β)=12,tan β=-17,求2α-β的值.(2)∵tan α=tan[(α-β)+β]=tan (α-β)+tan β1-tan (α-β)tan β=12-171+12×17=13>0,又α∈(0,π).∴0<α<π2,又∵tan 2α=2tan α1-tan 2α=2×131-⎝ ⎛⎭⎪⎫132=34>0, ∴0<2α<π2,∴tan(2α-β)=tan 2α-tan β1+tan 2αtan β=34+171-34×17=1.∵tan β=-17<0,∴π2<β<π,-π<2α-β<0,∴2α-β=-3π4.【规律方法】(1)解题中注意变角,如本题中α+β2=⎝ ⎛⎭⎪⎫α-β2-⎝ ⎛⎭⎪⎫α2-β;(2)通过求角的某种三角函数值来求角,在选取函数时,遵照以下原则:①已知正切函数值,选正切函数;②已知正、余弦函数值,选正弦或余弦函数;若角的范围是⎝ ⎛⎭⎪⎫0,π2,选正、余弦皆可;若角的范围是(0,π),选余弦较好;若角的范围为⎝ ⎛⎭⎪⎫-π2,π2,选正弦较好.【变式探究】 已知cos α=17,cos(α-β)=1314,且0<β<α<π2,(1)求tan 2α的值; (2)求β.【解析】(1)∵cos α=17,0<α<π2,∴sin α=437,∴tan α=43,∴tan 2α=2tan α1-tan 2α=2×431-48=-8347. (2)∵0<β<α<π2,∴0<α-β<π2,∴sin(α-β)=3314,∴cos β=cos[α-(α-β)]=cos αcos(α-β)+sin αsin(α-β) =17×1314+437×3314=12. ∴β=π3.考点三 三角变换的简单应用【例3】 (2014·广东卷)已知函数f (x )=A sin ⎝ ⎛⎭⎪⎫x +π4,x ∈R ,且f ⎝ ⎛⎭⎪⎫5π12=32.(1)求A 的值;(2)若f (θ)-f (-θ)=32,θ∈⎝ ⎛⎭⎪⎫0,π2,求f ⎝ ⎛⎭⎪⎫3π4-θ.【规律方法】解三角函数问题的基本思想是“变换”,通过适当的变换达到由此及彼的目的,变换的基本方向有两个,一个是变换函数的名称,一个是变换角的形式.变换函数名称可以使用诱导公式、同角三角函数关系、二倍角的余弦公式等;变换角的形式,可以使用两角和与差的三角函数公式、倍角公式等.【变式探究】 已知函数f (x )=sin ⎝ ⎛⎭⎪⎫3x +π4. (1)求f (x )的单调递增区间;(2)若α是第二象限角,f ⎝ ⎛⎭⎪⎫α3=45cos ⎝ ⎛⎭⎪⎫α+π4cos 2α,求cos α-sin α的值.【解析】(1)因为函数y =sin x 的单调递增区间为⎣⎢⎡⎦⎥⎤-π2+2k π,π2+2k π,k ∈Z ,由-π2+2k π≤3x +π4≤π2+2k π,k ∈Z ,得-π4+2k π3≤x ≤π12+2k π3,k ∈Z .所以函数f (x )的单调递增区间为⎣⎢⎡⎦⎥⎤-π4+2k π3,π12+2k π3,k ∈Z .【随堂练习】考点一 已知三角函数值求值例1、已知角A 、B 、C 为△ABC 的三个内角,OM →=(sin B +cos B ,cos C ),ON →=(sin C ,sin B -cos B ),OM →·ON →=-15.(1)求tan2A 的值;(2)求22cos 3sin 122sin()4AA A π--+ 的值.【解析】 (1)∵OM →·ON →=(sin B +cos B )sin C +cos C (sin B -cos B )=sin(B +C )-cos(B +C )=-15.∴sin A +cos A =-15,①两边平方并整理得:2sin A cos A =-2425,∵-2425<0,∴A ∈(π2,π),∴sin A -cos A =1-2sin A cos A =75.②联立①②得:sin A =35,cos A =-45,∴tan A =-34,∴tan2A =2tan A 1-tan 2A=-321-916=-247. (2)∵tan A =-34,∴22cos 3sin 122sin()4AA A π--+=cos A -3sin A cos A +sin A =1-3tan A 1+tan A=3134314⎛⎫-⨯- ⎪⎝⎭⎛⎫+- ⎪⎝⎭=13. 【方法技巧】对于条件求值问题,即由给出的某些角的三角函数值,求另外一些角的三角函数值,关键在于“变角”即使“目标角”变换成“已知角”.若角所在象限没有确定,则应分情况讨论,应注意公式的正用、逆用、变形运用,掌握其结构特征,还要注意拆角、拼角等技巧的运用.【变式探究】已知α∈(π2,π),且sin α2+cos α2=62.(1)求cos α的值;(2)若sin(α-β)=-35,β∈(π2,π),求cos β的值.考点二 已知三角函数值求角例2、如图,在平面直角坐标系xOy 中,以Ox 轴为始边做两个锐角α、β,它们的终边分别与单位圆相交于A、B两点,已知A、B两点的横坐标分别为210,255.(1)求tan(α+β)的值;(2)求α+2β的值.【方法技巧】(1)已知某些相关条件,求角的解题步骤:①求出该角的范围;②结合该角的范围求出该角的三角函数值.(2)根据角的函数值求角时,选取的函数在这个范围内应是单调的. 【变式探究】已知向量a =(sin θ,-2)与b =(1,cos θ)互相垂直,其中θ∈(0,π2).(1)求sin θ和cos θ的值; (2)若sin(θ-φ)=1010,0<φ<π2,求φ的值.三、三角函数的图像与性质【考情解读】1.能画出y =sin x ,y =cos x ,y =tan x 的图象,了解三角函数的周期性;2.理解正弦函数、余弦函数在区间[0,2π]上的性质(如单调性、最大值和最小值以及与x 轴的交点等),理解正切函数在区间⎝⎛⎭⎫-π2,π2内的单调性. 【重点知识梳理】1.用五点法作正弦函数和余弦函数的简图(1)正弦函数y =sin x ,x ∈[0,2π]的图象中,五个关键点是:(0,0),⎝⎛⎭⎫π2,1,(π,0),⎝⎛⎭⎫3π2,-1,(2π,0).(2)余弦函数y =cos x ,x ∈[0,2π]的图象中,五个关键点是:(0,1),⎝⎛⎭⎫π2,0,(π,-1),⎝⎛⎭⎫3π2,0,(2π,1). 2.正弦、余弦、正切函数的图象与性质(下表中k ∈Z )函数 y =sin xy =cos xy =tan x图象定义域RR{x |x ∈R ,且x ≠⎭⎬⎫k π+π2,k ∈Z值域 [-1,1] [-1,1] R 周期性 2π 2π π 奇偶性 奇函数偶函数 奇函数递增 区间 ⎣⎡⎦⎤2k π-π2,2k π+π2[2k π-π,2k π]⎝⎛⎭⎫k π-π2,k π+π2递减 区间 ⎣⎡⎦⎤2k π+π2,2k π+3π2 [2k π,2k π+π]无对称中心 (k π,0)⎝⎛⎭⎫k π+π2,0⎝⎛⎭⎫k π2,0对称轴 方程x =k π+π2x =k π无【高频考点突破】考点一 三角函数的定义域、值域【例1】 (1)函数y =1tan x -1的定义域为____________.(2)函数y =2sin ⎝⎛⎭⎫πx 6-π3(0≤x ≤9)的最大值与最小值之和为( ) A .2- 3 B .0 C .-1 D .-1- 3【答案】(1){x |x ≠π4+k π且x ≠π2+k π,k ∈Z } (2)A【规律方法】(1)求三角函数的定义域实际上是解简单的三角不等式,常借助三角函数线或三角函数图象来求解. (2)求解三角函数的值域(最值)常见到以下几种类型:①形如y =a sin x +b cos x +c 的三角函数化为y =A sin(ωx +φ)+k 的形式,再求最值(值域);②形如y =a sin 2x +b sin x +c 的三角函数,可先设sin x =t ,化为关于t 的二次函数求值域(最值);③形如y =a sin x cos x +b (sin x ±cos x )+c 的三角函数,可先设t =sin x ±cos x ,化为关于t 的二次函数求值域(最值).【变式探究】 (1)函数y =sin x -cos x 的定义域为________. (2)函数y =sin x -cos x +sin x cos x 的值域为________.【解析】(1)法一 要使函数有意义,必须使sin x -cos x ≥0.利用图象,在同一坐标系中画出[0,2π]上y =sin x 和y =cos x 的图象,如图所示.在[0,2π]内,满足sin x =cos x 的x 为π4,5π4,再结合正弦、余弦函数的周期是2π,所以原函数的定义域为⎩⎨⎧⎭⎬⎫x ⎪⎪2k π+π4≤x ≤2k π+5π4,k ∈Z . 法二 利用三角函数线,画出满足条件的终边范围(如图阴影部分所示).∴定义域为⎩⎨⎧⎭⎬⎫x ⎪⎪2k π+π4≤x ≤2k π+5π4,k ∈Z .【答案】(1)⎩⎨⎧⎭⎬⎫x ⎪⎪2k π+π4≤x ≤2k π+5π4,k ∈Z (2)⎣⎡⎦⎤-12-2,1 考点二 三角函数的奇偶性、周期性、对称性【例2】 (1)已知ω>0,0<φ<π,直线x =π4和x =5π4是函数f (x )=sin(ωx +φ)的图象的两条相邻的对称轴,则φ=( )A.π4B.π3 C.π2 D.3π4(2)函数y =2cos 2⎝⎛⎭⎫x -π4-1是( ) A .最小正周期为π的奇函数 B .最小正周期为π的偶函数 C .最小正周期为π2的奇函数D .最小正周期为π2的偶函数【答案】(1)A (2)A 【规律方法】(1)求f (x )=A sin(ωx +φ)(ω≠0)的对称轴,只需令ωx +φ=π2+k π(k ∈Z ),求x ;求f (x )的对称中心的横坐标,只需令ωx +φ=k π(k ∈Z )即可.(2)求最小正周期时可先把所给三角函数式化为y =A sin(ωx +φ)或y =A cos( ωx +φ)的形式,则最小正周期为T =2π|ω|;奇偶性的判断关键是解析式是否为y =A sin ωx 或y =A cos ωx +b 的形式.【变式探究】 (1)如果函数y =3cos(2x +φ)的图象关于点⎝⎛⎭⎫4π3,0中心对称,那么|φ|的最小值为( ) A.π6 B.π4 C.π3 D.π2 (2)若函数f (x )=sinx +φ3(φ∈[0,2π])是偶函数,则φ=( ) A.π2 B.2π3 C.3π2 D.5π3【答案】(1)A (2)C 考点三 三角函数的单调性【例3】 (1)已知f (x )=2sin ⎝⎛⎭⎫x +π4,x ∈[0,π],则f (x )的单调递增区间为________. (2)已知ω>0,函数f (x )=sin ⎝⎛⎭⎫ωx +π4在⎝⎛⎭⎫π2,π上单调递减,则ω的取值范围是( )A.⎣⎡⎦⎤12,54B.⎣⎡⎦⎤12,34C.⎝⎛⎦⎤0,12 D .(0,2]【答案】(1)⎣⎡⎦⎤0,π4 (2)A 【规律方法】(1)求较为复杂的三角函数的单调区间时,首先化简成y =A sin(ωx +φ)形式,再求y =A sin(ωx +φ)的单调区间,只需把ωx +φ看作一个整体代入y =sin x 的相应单调区间内即可,注意要先把ω化为正数.(2)对于已知函数的单调区间的某一部分确定参数ω的范围的问题,首先,明确已知的单调区间应为函数的单调区间的子集,其次,要确定已知函数的单调区间,从而利用它们之间的关系可求解,另外,若是选择题利用特值验证排除法求解更为简捷.【变式探究】 (1)若函数f (x )=sin ωx (ω>0)在区间⎣⎡⎦⎤0,π3上单调递增,在区间⎣⎡⎦⎤π3,π2上单调递减,则ω等于( )A.23B.32C .2D .3 (2)函数f (x )=sin ⎝⎛⎭⎫-2x +π3的单调减区间为______.【答案】(1)B (2)⎣⎡⎦⎤k π-π12,k π+5π12(k ∈Z )四、函数)sin(ϕ+=wx A y 的图像【考情解读】1. 了解函数y =A sin(ωx +φ)的物理意义;能画出y =A sin(ωx +φ)的图象,了解参数A ,ω,φ对函数图象变化的影响;2.了解三角函数是描述周期变化现象的重要函数模型,会用三角函数解决一些简单实际问题. 【重点知识梳理】1.“五点法”作函数y =A sin(ωx +φ)(A >0,ω>0)的简图“五点法”作图的五点是在一个周期内的最高点、最低点及与x 轴相交的三个点,作图时的一般步骤为: (1)定点:如下表所示.X-φωπ2-φωπ-φω3π2-φω2π-φωωx +φ 0 π2π 3π2 2π y =A sin(ωx +φ)A-A(2)作图:在坐标系中描出这五个关键点,用平滑的曲线顺次连接得到y =A sin(ωx +φ)在一个周期内的图象.(3)扩展:将所得图象,按周期向两侧扩展可得y =A sin(ωx +φ)在R 上的图象.2.函数y =sin x 的图象经变换得到y =A sin(ωx +φ)的图象的两种途径3.函数y =A sin(ωx +φ)的物理意义当函数y =A sin(ωx +φ)(A >0,ω>0),x ∈[0,+∞)表示一个振动量时,A 叫做振幅,T =2πω叫做周期,f=1T叫做频率,ωx +φ叫做相位,φ叫做初相.【高频考点突破】考点一 函数y =A sin(ωx +φ)的图象及变换【例1】 设函数f (x )=sin ωx +3cos ωx (ω>0)的周期为π. (1)求它的振幅、初相;(2)用五点法作出它在长度为一个周期的闭区间上的图象;(3)说明函数f (x )的图象可由y =sin x 的图象经过怎样的变换而得到. 【解析】(1)f (x )=sin ωx +3cos ωx =2⎝ ⎛⎭⎪⎫12sin ωx +32cos ωx =2sin ⎝ ⎛⎭⎪⎫ωx +π3, 又∵T =π,∴2πω=π,即ω=2.∴f (x )=2sin ⎝ ⎛⎭⎪⎫2x +π3.∴函数f (x )=sin ωx +3cos ωx 的振幅为2,初相为π3.(3)法一 把y =sin x 的图象上所有的点向左平移π3个单位,得到y =sin ⎝ ⎛⎭⎪⎫x +π3的图象;再把y =sin ⎝ ⎛⎭⎪⎫x +π3的图象上的点的横坐标缩短到原来的12倍(纵坐标不变),得到y =sin ⎝ ⎛⎭⎪⎫2x +π3的图象;最后把y =sin ⎝ ⎛⎭⎪⎫2x +π3上所有点的纵坐标伸长到原来的2倍(横坐标不变),即可得到y =2sin ⎝⎛⎭⎪⎫2x +π3的图象. 法二 将y =sin x 的图象上每一点的横坐标x 缩短为原来的12倍,纵坐标不变,得到y =sin 2x 的图象;再将y =sin 2x 的图象向左平移π6个单位,得到y =sin 2⎝ ⎛⎭⎪⎫x +π6=sin ⎝ ⎛⎭⎪⎫2x +π3的图象;再将y =sin ⎝ ⎛⎭⎪⎫2x +π3的图象上每一点的横坐标保持不变,纵坐标伸长到原来的2倍,得到y =2sin ⎝⎛⎭⎪⎫2x +π3的图象.【规律方法】作函数y =A sin(ωx +φ)(A >0,ω>0)的图象常用如下两种方法:(1)五点法作图法,用“五点法”作y =A sin(ωx +φ)的简图,主要是通过变量代换,设z =ωx +φ,由z 取0,π2,π,32π,2π来求出相应的x ,通过列表,计算得出五点坐标,描点后得出图象;(2)图象的变换法,由函数y =sin x 的图象通过变换得到y =A sin(ωx +φ)的图象有两种途径:“先平移后伸缩”与“先伸缩后平移”.【变式探究】 设函数f (x )=cos(ωx +φ)⎝ ⎛⎭⎪⎫ω>0,-π2<φ<0的最小正周期为π,且f ⎝ ⎛⎭⎪⎫π4=32.(1)求ω和φ的值;(2)在给定坐标系中作出函数f (x )在[0,π]上的图象.【解析】(1)∵T =2πω=π,ω=2,又f ⎝ ⎛⎭⎪⎫π4=cos ⎝ ⎛⎭⎪⎫2×π4+φ=32,∴sin φ=-32,又-π2<φ<0,∴φ=-π3.(2)由(1)得f (x )=cos ⎝⎛⎭⎪⎫2x -π3,列表: 2x -π3-π30 π2 π 32π 53π x 0 π6 512π 23π 1112π π f (x )121-112图象如图.考点二 利用三角函数图象求其解析式【例2】 (1)已知函数f (x )=A cos(ωx +φ)的图象如图所示,f ⎝ ⎛⎭⎪⎫π2=-23,则f (0)=( )A .-23B .-12 C.23 D.12(2)函数f (x )=A sin(ωx +φ)(A >0,ω>0,|φ|<π)的部分图象如图所示,则函数f (x )的解析式为________.【解析】(1)由三角函数图象得T 2=11π12-7π12=π3,即T =2π3,所以ω=2πT=3.又x =7π12是函数单调增区间中的一个零点,所以3×7π12+φ=3π2+2k π,解得φ=-π4+2k π,k ∈Z ,所以f (x )=A cos ⎝ ⎛⎭⎪⎫3x -π4. 由f ⎝ ⎛⎭⎪⎫π2=-23,得A =223,所以f (x )=223cos ⎝ ⎛⎭⎪⎫3x -π4,所以f (0)=223·cos ⎝ ⎛⎭⎪⎫-π4=23.【答案】(1)C (2)f (x )=2sin ⎝⎛⎭⎪⎫2x +π3 【规律方法】已知f (x )=A sin(ωx +φ)(A >0,ω>0)的部分图象求其解析式时,A 比较容易得出,困难的是求待定系数ω和φ,常用如下两种方法:(1)五点法,由ω=2πT即可求出ω;确定φ时,若能求出离原点最近的右侧图象上升(或下降)的“零点”横坐标x 0,则令ωx 0+φ=0(或ωx 0+φ=π),即可求出φ;(2)代入法,利用一些已知点(最高点、最低点或“零点”)坐标代入解析式,再结合图形解出ω和φ,若对A ,ω的符号或对φ的范围有要求,则可用诱导公式变换使其符合要求.【训练2】 (1)已知函数f (x )=A cos(ωx +φ)(A >0,ω>0,0<φ<π)为奇函数,该函数的部分图象如图所示,△EFG 是边长为2的等边三角形,则f (1)的值为( )A .-32 B .-62C. 3 D .- 3 (2)函数f (x )=A sin(ωx +φ)(A ,ω,φ为常数,A >0,ω>0,0<φ<π)的图象如图所示,则f ⎝ ⎛⎭⎪⎫π3的值为______.(2)由三角函数图象可得A =2,34T =11π12-π6=34π,所以周期T =π=2πω,解得ω=2.又函数图象过点⎝ ⎛⎭⎪⎫π6,2所以f ⎝ ⎛⎭⎪⎫π6=2sin ⎝ ⎛⎭⎪⎫2×π6+φ=2,0<φ<π,解得φ=π6,所以f (x )=2sin ⎝ ⎛⎭⎪⎫2x +π6,f ⎝ ⎛⎭⎪⎫π3=2sin ⎝ ⎛⎭⎪⎫2π3+π6=1.【答案】(1)D (2)1考点三 函数y =A sin(ωx +φ)的性质应用【例3】 (2014·山东卷)已知向量a =(m ,cos 2x ),b =(sin 2x ,n ),函数f (x )=a·b ,且y =f (x )的图象过点⎝⎛⎭⎪⎫π12,3和点⎝ ⎛⎭⎪⎫2π3,-2.(1)求m ,n 的值;(2)将y =f (x )的图象向左平移φ(0<φ<π)个单位后得到函数y =g (x )的图象,若y =g (x )图象上各最高点到点(0,3)的距离的最小值为1,求y =g (x )的单调递增区间.所以函数y =g (x )的单调递增区间为⎣⎢⎡⎦⎥⎤k π-π2,k π,k ∈Z . 【规律方法】解决三角函数图象与性质综合问题的方法:先将y =f (x )化为y =a sin x +b cos x 的形式,然后用辅助角公式化为y =A sin(ωx +φ)+b 的形式,再借助y =A sin(ωx +φ)的性质(如周期性、对称性、单调性等)解决相关问题.【变式探究】 已知函数f (x )=3sin(ωx +φ)-cos(ωx +φ)(0<φ<π,ω>0)为偶函数,且函数y =f (x )图象的两相邻对称轴间的距离为π2.(1)求f ⎝ ⎛⎭⎪⎫π8的值; (2)求函数y =f (x )+f ⎝⎛⎭⎪⎫x +π4的最大值及对应的x 的值.五、解三角形(正弦定理和余弦定理)【考情解读】1.掌握正弦定理、余弦定理,并能解决一些简单的三角形度量问题;【重点知识梳理】1.正、余弦定理在△ABC中,若角A,B,C所对的边分别是a,b,c,R为△ABC外接圆半径,则定理正弦定理余弦定理内容asin A=bsin B=csin C=2Ra2=b2+c22bc cos__A;b2=c2+a22ca cos__B;c2=a2+b2-2ab cos__C常见变形(1)a=2R sin A,b=2R sin__B,c=2R sin_C;(2)sin A=a2R,sin B=b2R,sin C=c2R;(3)a∶b∶c=sin__A∶sin__B∶sin__C;cos A=b2+c2-a22bc;cos B=c2+a2-b22ac;(4)a sin B =b sin A ,b sin C =c sin B ,a sin C =c sin A cos C =a 2+b 2-c 22ab2.S △ABC =12ab sin C =12bc sin A =12ac sin B =abc 4R =12(a +b +c )·r (r 是三角形内切圆的半径),并可由此计算R ,r .【高频考点突破】考点一 利用正、余弦定理解三角形例1、(1)在△ABC 中,∠ABC =π4,AB =2,BC =3,则sin ∠BAC =( )A.1010 B.105C.31010D.55(2)如图,在△ABC 中,已知点D 在BC 边上,AD ⊥AC ,sin ∠BAC =223,AB =32,AD =3,则BD 的长为________.【解析】(1)由余弦定理可得AC 2=9+2-2×3×2×22=5,所以AC = 5.再由正弦定理得AC sin B =BCsin A ,所以sin A =BC ·sin BAC =3×225=31010.【答案】 (1)C (2) 3【提分秘籍】利用正、余弦定理解三角形的关键是合理地选择正弦或余弦定理进行边角互化,解题过程中注意隐含条件的挖掘以确定解的个数.【变式探究】在△ABC 中,已知内角A ,B ,C 的对边分别为a ,b ,c ,且满足2a sin ⎝⎛⎭⎫B +π4=c . (1)求角A 的大小;(2)若△ABC 为锐角三角形,求sin B sin C 的取值范围.考点二 三角形形状的判断例2、设△ABC 的内角A ,B ,C 所对的边分别为a ,b ,c ,若b cos C +c cos B =a sin A ,则△ABC 的形状为( )A .锐角三角形B .直角三角形C .钝角三角形D .不确定【解析】依据题设条件的特点,由正弦定理,得sin B cos C +cos B sin C =sin 2A ,有sin(B +C )=sin 2A ,从而sin(B +C )=sin A =sin 2A ,解得sin A =1,∴A =π2,故选B.【答案】B 【提分秘籍】依据已知条件中的边角关系判断三角形的形状时,主要有如下两种方法(1)利用正、余弦定理把已知条件转化为边边关系,通过因式分解、配方等得出边的相应关系,从而判断三角形的形状;(2)利用正、余弦定理把已知条件转化为内角的三角函数间的关系,通过三角函数恒等变形,得出内角的关系,从而判断出三角形的形状,此时要注意应用A +B +C =π这个结论.注意:在上述两种方法的等式变形中,一般两边不要约去公因式,应移项提取公因式,以免漏解. 【变式探究】在△ABC 中,角A 、B 、C 所对的边分别为a ,b ,c ,且b 2+c 2=a 2+bc . (1)求角A 的大小;(2)若sin B ·sin C =sin 2A ,试判断△ABC 的形状.考点三 三角形的面积问题例3、在△ABC 中,角A ,B ,C 对应的边分别是a ,b ,c .已知cos 2A -3cos(B +C )=1. (1)求角A 的大小;(2)若△ABC 的面积S =53,b =5,求sin B sin C 的值.【解析】(1)由cos 2A -3cos(B +C )=1,得2cos 2A +3cos A -2=0, 即(2cos A -1)(cos A +2)=0,解得cos A =12或cos A =-2(舍去).因为0<A <π,所以A =π3.(2)由S =12bc sin A =12bc ·32=34bc =53,得bc =20.又b =5,知c =4.由余弦定理得a 2=b 2+c 2-2bc cos A=25+16-20=21,故a = 21.又由正弦定理得sin B sin C =b a sin A ·c a sin A =bc a 2sin 2A =2021×34=57.【方法技巧】三角形的面积求法最常用的是利用公式S =12ab sin C =12ac sin B =12bc sin A 去求.计算时注意整体运算及正、余弦定理的应用.【变式探究】在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,若a cos 2C 2+c cos 2A 2=32b .(1)求证:a ,b ,c 成等差数列;(2)若∠B =60°,b =4,求△ABC 的面积.考点四 解三角形例4、在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,且2cos 2A -B2cos B -sin(A -B )sin B +cos(A +C )=-35. (1)求cos A 的值;(2)若a =42,b =5,求向量BA →在BC →方向上的投影.【解析】(1)由2cos 2A -B 2cos B -sin(A -B )sin B +cos(A +C )=-35,得[cos(A -B )+1]cos B -sin(A -B )sin B -cos B =-35,2分即cos(A -B )cos B -sin(A -B )sin B =-35.4分则cos(A -B +B )=-35,即cos A =-35.6分【提分秘籍】正弦定理、余弦定理及其在现实生活中的应用是高考的热点,主要利用正弦定理、余弦定理解决一些简单的三角形的度量问题以及几何计算的实际问题,常与三角变换、三角函数的性质交汇命题、多以解答题形式出现. 【随堂练习】考点三 正、余弦定理的应用例3、在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c .已知cos A -2cos C cos B =2c -ab .(1)求sin Csin A的值; (2)若cos B =14,b =2,求△ABC 的面积S .【解析】 (1)由正弦定理,设a sin A =b sin B =csin C =k ,则2c -a b =2k sin C -k sin A k sin B =2sin C -sin Asin B, 所以cos A -2cos C cos B =2sin C -sin A sin B.即(cos A -2cos C )sin B =(2sin C -sin A )cos B , 化简可得sin(A +B )=2sin(B +C ). 又A +B +C =π, 所以sin C =2sin A . 因此sin Csin A=2.【方法技巧】(1)利用正弦定理,实施角的正弦化为边时只能是用a 替换sin A ,用b 替换sin B ,用c 替换sin C . sin A ,sin B ,sin C 的次数要相等,各项要同时替换,反之,用角的正弦替换边时也要这样,不能只替换一部分;(2)以三角形为背景的题目,要注意三角形的内角和定理的使用.像本例中B +C =60°;(3)在求角的大小一定要有两个条件才能完成:①角的范围;②角的某一三角函数值.在由三角函数值来判断角的大小时,一定要注意角的范围及三角函数的单调性.【变式探究】在锐角△ABC 中,a 、b 、c 分别为A 、B 、C 所对的边,且3a =2c sin A .(1)确定角C 的大小;(2)若c =7,且△ABC 的面积为332,求a +b 的值. 【解析】(1)由3a =2c sin A ,根据正弦定理,sin C =c sin A a =32, 又0<C <π2,则C =π3. (2)由已知条件⎩⎨⎧ 12ab sin C =332a 2+b 2-c 22ab =cos C ,即⎩⎪⎨⎪⎧ab =6a 2+b 2-7=ab , (a +b )2=a 2+b 2+2ab =3ab +7=25,∴a +b =5.。
高考第一轮复习数学:三角函数(附答案) 推荐

一、选择题(每小题6分,共60分)1.(2004年辽宁,1)若cos θ>0,且sin2θ<0,则角θ的终边所在象限是 A.第一象限 B.第二象限 C.第三象限 D.第四象限解析:由sin2θ<0得2sin θcos θ<0.又cos θ>0,∴sin θ<0.∴角θ的终边在第四象限. 答案:D2.要得到函数y =sin2x 的图象可由函数y =cos2x 的图象A.向左平移2π个单位 B.向右平移2π个单位 C.向左平移4π个单位 D.向右平移4π个单位 解析:y =sin2x =cos (2π-2x )=cos [2(x -4π)]. 答案:D3.已知函数y =A sin (ωx +ϕ)在同一周期内,当x =9π时,取得最大值21,当x =9π4时,取得最小值-21,则该函数的解析式为A.y =2sin (3x -6π) B.y =21sin (3x +6π) C.y =21sin (3x -6π) D.y =21sin (3x -6π) 解析:A =21,2T =3π,ω=T π2=3,易知第一个零点为(-18π,0),则y =21sin [3(x +18π)],即y =21sin (3x +6π).答案:B4.设集合M ={y |y =sin x },N ={y |y =cos x tan x },则M 、N 的关系是 A.N M B.M N C.M =N D.M ∩N =∅ 解析:M ={y |-1≤y ≤1},N ={y |-1<y <1},选A. 答案:A5.y =xxcos 2sin 3-的值域是A.[-1,1]B.[-3,3]C.[-3,1]D.[-1,3]解析:原式可化为3sin x +y cos x =2y ,23y +sin (x +ϕ)=2y (tan ϕ=3y ),sin (x +ϕ)=232yy +∈[-1,1],解得y ∈[-1,1].答案:A6.在△ABC 中,tan A ·tan B >1,则△ABC 为 A.直角三角形 B.锐角三角形 C.钝角三角形 D.等腰三角形解析:tan (A +B )=-tan C ,得BA BA tan tan 1tan tan ⋅-+=-tan C .∵tan A ·tanB >1,∴tan A >0,tan B >0.1-tan A ·tan B <0,∴-tan C <0.tan C >0,∴△ABC 为锐角三角形.故选B.答案:B7.方程cos x =lg x 的实根个数为 A.1个 B.2个 C.3个 D.无数个解析:当x =10时,lg x =1,在同一坐标系中画出y =cos x 和y =lg x 的图象,可知有3个交点,选C.答案:C 8.)()(3arctan 21arccos 23arcsin--+的值是 A.-3 B.2 C.-3πD.3π 解析:原式=-3,选A. 答案:A9.已知f (sin x )=sin3x ,则f (cos x )等于 A.-cos3x B.cos3x C.sin3x D.-sin3x解析:f (cos x )=f [sin (2π-x )]=sin3(2π-x )=-cos3x ,选A. 答案:A10.函数f (x )=sin2x +5sin (4π+x )+3的最小值是 A.-3B.-6C.89D.-1解析:f (x )=2sin x cos x +225(sin x +cos x )+3.令t =sin x +cos x ,t ∈[-2,2],则y =(t +425)2-89.则当t =-2时,y min =-1,选D.答案:D二、填空题(每小题4分,共16分)11.已知角α的终边上一点P (3,-1),则sec 2α+csc 2α+cot 2α=_________. 解析:sec α=32,csc α=-2,cot α=-3,代入得325. 答案:32512.(2005年春季上海,11)函数y =sin x +arcsin x 的值域是____________. 解析:该函数的定义域为[-1,1].∵y =sin x 与y =arcsin x 都是[-1,1]上的增函数, ∴当x =-1时,y min =sin (-1)+arcsin (-1)=-2π-sin1, 当x =1时,y max =sin1+arcsin1=2π+sin1, ∴值域为[-2π-sin1,2π+sin1]. 答案:[-2π-sin1,2π+sin1]13.△ABC 中,若sin A =53,cos B =135,则cos C =_______. 解析:由cos B =135,得sin B =1312>53=sin A .A 是锐角,cos A =54,cos C =cos (π-A -B )=6516. 答案:651614.若f (x )=a sin 3x +b tan x +1且f (3)=5,则f (-3)=_______. 解析:令g (x )=a sin 3x +b tan x ,则g (-x )=-g (x ). f (3)=g (3)+1=5,g (3)=4.f (-3)=g (-3)+1=-g (3)+1=-4+1=-3. 答案:-3三、解答题(本大题共6小题,共74分) 15.(12分)(2005年黄冈市调研题)已知sin 2α-cos2α=510,α∈(2π,π),tan (π-β)=21,求tan (α-2β)的值.解:∵sin2α-cos2α=510, ∴1-sin α=52.∴sin α=53.又∵α∈(2π,π),∴cos α=-α2sin 1-=-54. ∴tan α=-43. 由条件知tan β=-21, ∴tan2β=ββ2tan tan 2-1=-34.∴tan (α-2β)=βαβα2tan tan 2tan tan ⋅+1-=247.16.(12分)已知2cos2α-cos2β=1,求21sin 22α+sin 2β+2cos 4α的值.解:由2cos2α-cos2β=1,即2cos2α=1+cos2β,得cos2α=cos 2β.因此21sin 22α+sin 2β+2cos 4α=21sin 22α+sin 2β+2·(2+α2c o s 1)2=1+cos2α+sin 2β=1+cos 2β+sin 2β=2. 17.(12分)(2004年浙江,理17)在△ABC 中,角A 、B 、C 所对的边分别为a 、b 、c ,且cos A =31. (1)求sin 22C B ++cos2A 的值;(2)若a =3,求bc 的最大值.解:(1)sin 22C B ++cos2A =21[1-cos (B +C )]+(2cos 2A -1)=21(1+cos A )+(2cos 2A -1)=21(1+31)+(92-1)=-91.(2)∵bc a c b 2222-+=cos A =31,∴32bc =b 2+c 2-a 2≥2bc -a 2. ∴bc ≤43a 2.又∵a =3,∴bc ≤49.当且仅当b =c =23时,bc =49.故bc 的最大值是49. 18.(12分)已知a 1=xtan 1,a n +1=a n cos x -sin nx ,求a 2、a 3、a 4,推测a n 并证明. 解:a 2=a 1cos x -sin x =x x x sin sin cos 22-=x x sin 2cos ,a 3=a 2cos x -sin2x =x x sin 3cos ,a 4=xxsin 4cos .可推测a n =xnxsin cos ,数学归纳法可证之.(读者自己完成)19.(12分)设A 、B 、C 是三角形的内角,且lgsin A =0,又sin B 、sin C 是关于x 的方程4x 2-2(3+1)x +k =0的两个根,求实数k 的值.解:由lgsin A =0,得sin A =1,A =2π,B +C =2π,sin C =cos B . 又⎪⎪⎩⎪⎪⎨⎧=+=+,,4sin sin 213sin sin k C B C B∴⎪⎪⎩⎪⎪⎨⎧=+=+.4cos sin 213cos sin k B B B B , 由sin B cos B =21[(sin B +cos B )2-1],得4k =21[(213+)2-1],解得k =3. 20.(14分)已知F (θ)=cos 2θ+cos 2(θ+α)+cos 2(θ+β),问是否存在满足0≤α<β≤π的α、β,使得F (θ)的值不随θ的变化而变化?如果存在,求出α、β的值;如果不存在,请说明理由.解:F (θ)=23+21[cos2θ+cos (2θ+2α)+cos (2θ+2β)]=23+21(1+cos2α+cos2β)cos2θ-21(sin2α+sin2β)sin2θ.F (θ)的值不随θ变化的充要条件是⎩⎨⎧=+=++,,02sin 2sin 02cos 2cos 1βαβα 得(cos2α+1)2+sin 22α=1, cos2α=-21.同理,cos2β=-21. 又0≤α<β≤π,故存在α、β满足条件,其值分别为α=3π,β=3π2.。
高考数学一轮复习三角函数与解三角形多选题知识点-+典型题含答案

高考数学一轮复习三角函数与解三角形多选题知识点-+典型题含答案一、三角函数与解三角形多选题1.在ABC 中,角,,A B C 所对的边分别为,,a b c ,下列命题正确的是( )A .若::4:5:6a b c =,ABC 的最大内角是最小内角的2倍B .若cos cos a B b A c -=,则ABC 一定为直角三角形 C .若4,5,6a b c ===,则ABCD .若()()()cos cos cos 1A B B C C A ---=,则ABC 一定是等边三角形 【答案】ABD 【分析】对于A 选项,求得2A C =,由此确定选项正确.对于B 选项,求得2A π=,由此确定选项正确.对于C 选项,利用正弦定理求得ABC 外接圆半径,由此确定选项错误.对于D 选项,证得()()()cos cos cos 1A B B C C A -=-=-=,得到A B C ==,确定选项正确. 【详解】对于A 选项,A 角最小,C 角最大.由余弦定理得253616453cos 0256604A +-===>⨯⨯,16253651cos 0245408C +-===>⨯⨯,2231cos 22cos 12148A A ⎛⎫=-=⨯-= ⎪⎝⎭,cos2cos A C =.0,022A C ππ<<<<,则02A π<<,所以2A C =,所以A 选项正确.对于B 选项,cos cos a B b A c -=,由正弦定理得sin cos sin cos sin A B B A C -=,()sin cos cos sin sin sin cos cos sin A B A B A B A B A B -=+=+,cos sin 0=A B ,由于0,0A B ππ<<<<,所以2A π=,故B 选项正确.对于C 选项,16253651cos 245408C +-===⨯⨯,0C π<<,sin C ==, 设三角形ABC 外接圆半径为R,则2sin 2sin c cR R C C=⇒===,故C 选项错误.对于D 选项,0,0,A B A B ππππ<<-<-<-<-<,故()1cos 1A B -<-≤,同理可得()()1cos 1,1cos 1B C C A -<-≤-<-≤, 要使()()()cos cos cos 1A B B C C A ---=, 则需()()()cos cos cos 1A B B C C A -=-=-=,所以0,0,0A B B C C A -=-=-=,所以A B C ==,所以D 选项正确. 故选:ABD 【点睛】利用正弦定理可求得三角形外接圆的半径R ,要注意公式是2sin aR A=,而不是sin aR A =.2.如图,ABC 的内角A ,B ,C 所对的边分别为a ,b ,c .若a b =,且()3cos cos 2sin a C c A b B +=,D 是ABC 外一点,1DC =,3DA =,则下列说法正确的是( )A .ABC 是等边三角形B .若23AC =A ,B ,C ,D 四点共圆 C .四边形ABCD 533 D .四边形ABCD 533 【答案】AC 【分析】利用三角函数恒等变换化简已知等式可求sin B ,再利用a b =,可知ABC 为等边三角形,从而判断A ;利用四点A ,B ,C ,D 共圆,四边形对角互补,从而判断B ;设AC x =,0x >,在ADC 中,由余弦定理可得2106cos x D =-,利用三角形的面积公式,三角函数恒等变换的,可求ABCD S 四边形,利用正弦函数的性质,求出最值,判断CD .【详解】由正弦定理2sin ,2sin ,2sin a R A b R B c R C ===, 3(sin cos sin cos )2sin sin A C C A B B +=⋅,332sin ,sin B B =∴=, a b =,B 是等腰ABC 的底角,(0,)2B π∴∈,,3B ABC π∴=∴△是等边三角形,A 正确;B 不正确:若,,,A BCD 四点共圆,则四边形对角互补, 由A 正确知21,cos 32D D π∠==-,但由于1,3,DC DA AC ===22211cos 232DC DA AC D DA DC +-===-≠-⋅⋅,∴B 不正确. C 正确,D 不正确:设D θ∠=,则2222cos 106cos AC DC DA DC DA θθ=+-⋅⋅=-,(106cos )ABC S θθ∴=-=△, 3sin 2ADC S θ=△,3sin cos 222ABCADCABCD S S Sθθ∴=+=-+四边形,13(sin cos 2θθ=⋅-+,3sin()3πθ=-+(0,),sin()(3πθπθ∈∴-∈,3ABCD S <≤+四边形,∴C 正确,D 不正确; 故选:AC.. 【点睛】本题主要考查正弦定理,余弦定理,三角函数恒等变换,正弦函数的图象和性质在解三角形中的综合应用,考查计算能力和转化思想,属于中档题.3.已知函数()f x 的定义域为D ,若对于任意()()()a b c D f a f b f c ∈,,,,,分别为某个三角形的边长,则称()f x 为“三角形函数”,其中为“三角形函数”的函数是( ) A .()4sin f x x =- B .()22sin 10cos 13f x x x =-++C .()tan 2x f x = D .()sin 20,34f x x x ππ⎛⎫⎡⎤=++∈ ⎪⎢⎥⎝⎭⎣⎦【答案】AD 【分析】结合三角形的性质有:两边之差小于第三边,得若()f x 为 “三角形函数”则()()()max min min f x f x f x <-恒成立,即()()max min 2f x f x <恒成立即可,根据条件求出函数的最大值和最小值,进行判断即可. 【详解】解:①()4sin f x x =-,则()max 415f x =+=,()min 413f x =-= 则()()max min 2f x f x <恒成立,则A 满足条件②()22532cos 10cos 112cos 22f x x x x ⎛⎫=++=+= ⎪⎝⎭ 当0,2x π⎡⎤∈⎢⎥⎣⎦时,0cos 1x ≤≤∴当cos 0x =时,函数()f x 取得最小值()min 11f x =,当cos 1x =时,函数()f x 取得最大值,()max 23f x =则()()max min 2f x f x <不恒成立,则B 不满足条件 ③()()()tan ,00,2xf x =∈-∞⋃+∞,则不满足条件()()max min 2f x f x <恒成立,故C 不是④()sin 23f x x π⎛⎫=++ ⎪⎝⎭0,4x π⎡⎤∈⎢⎥⎣⎦,52,336x πππ⎡⎤∴+∈⎢⎥⎣⎦,则()max sin12f x π=+=+()min 51sin62f x π=+=+则()min 21f x =+,则()()max min 2f x f x <恒成立,故D 满足条件 故选AD 【点睛】本题考查了三角形的性质及“三角形函数”的概念,根据条件转化为()()max min 2f x f x <恒成立是解决本题的关键,综合性较强,有一定的难度.4.对于函数()sin cos 2sin cos f x x x x x =++,下列结论正确的是( ) A .把函数f (x )的图象上的各点的横坐标变为原来的12倍,纵坐标不变,得到函数g (x )的图象,则π是函数y =g (x )的一个周期 B .对123,,2x x ππ⎛⎫∀∈ ⎪⎝⎭,若12x x <,则()()12f x f x < C .对,44x f x f x ππ⎛⎫⎛⎫∀∈-=+ ⎪ ⎪⎝⎭⎝⎭R 成立D .当且仅当,4x k k Z ππ=+∈时,f (x )1【答案】AC 【分析】根据三角函数的变换规则化简即可判断A ;令sin cos 4t x x x π⎛⎫=+=+ ⎪⎝⎭,()21f t t t =+-,判断函数的单调性,即可判断B ;代入直接利用诱导公式化简即可;首先求出()f t 的最大值,从而得到x 的取值; 【详解】解:因为()2()sin cos 2sin cos sin cos sin cos 1f x x x x x x x x x =++=+++-,令sin cos 4t x x x π⎛⎫=+=+ ⎪⎝⎭,所以t ⎡∈⎣,所以()21f t t t =+-, 对于A :将()sin cos 2sin cos f x x x x x =++图象上的各点的横坐标变为原来的12倍,则()sin 2cos 22sin 2cos 2g x x x x x =++,所以()()()()()sin 2cos22sin 2cos2g x x x x x πππππ+=++++++()sin 2cos22sin 2cos2x x x x g x =++=,所以π是函数y =g (x )的一个周期,故A 正确;对于B :因为3,2x ππ⎛⎫∈ ⎪⎝⎭,所以57,444x πππ⎛⎫+∈ ⎪⎝⎭,则)14t x π⎛⎫⎡=+∈- ⎪⎣⎝⎭在5,4ππ⎛⎫ ⎪⎝⎭上单调递减,在53,42ππ⎛⎫⎪⎝⎭上单调递增, 又()2215124f t t t t ⎛⎫=+-=+- ⎪⎝⎭,对称轴为12t =-,开口向上,函数()21f t t t =+-在)1⎡-⎣上单调递减, 所以函数()f x 在5,4ππ⎛⎫ ⎪⎝⎭上单调递增,在53,42ππ⎛⎫⎪⎝⎭上单调递减, 故B 错误; 对于C :sin c 4os 2sin cos 4444f x x x x x πππππ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫-=----⎪ ⎪ ⎪ ⎪ ⎪⎝+⎝⎭⎝⎭⎭⎝⎭+⎝⎭sin c 4os 2sin cos 4444f x x x x x πππππ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫+=++++ ⎪ ⎪ ⎪ ⎪ ⎪⎝+⎝⎭⎝⎭⎭⎝⎭+⎝⎭c 2424242sin os 2sin cos 4x x x x ππππππππ⎥++⎡⎤⎡⎤⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=-------- ⎪ ⎪ ⎪ ⎪⎢⎥⎢⎥⎢⎥⎢⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦⎣⎦⎣⎦4444sin cos 2sin cos 4x x x x f x πππππ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫----=- ⎪ ⎪ ⎪ ⎪ ⎪=⎝⎭⎝⎭⎝⎭⎝⎭⎝+⎭+,故C 正确;因为()2215124f t t t t ⎛⎫=+-=+- ⎪⎝⎭,t ⎡∈⎣,当t =时()f t 取得最大值()max 1f t =,令4t x π⎛⎫=+= ⎪⎝⎭sin 14x π⎛⎫+= ⎪⎝⎭,所以2,42x k k Z πππ+=+∈,解得2,4x k k Z ππ=+∈,即当2,4x k k Z ππ=+∈时,函数()f x1,故D 错误;故选:AC 【点睛】本题考查三角函数的综合应用,解答的关键是换元令sin cos t x x =+,将函数转化为二次函数;5.已知函数()()3sin 222f x x ππϕϕ⎛⎫=+-<< ⎪⎝⎭的图象关于直线3x π=对称,则( )A .函数12f x π⎛⎫+⎪⎝⎭为奇函数 B .函数()f x 在,32ππ⎡⎤⎢⎥⎣⎦上单调递增 C .函数()f x 的图象向右平移()0a a >个单位长度得到的函数的图象关于6x π=对称,则a 的最小值是3π D .若方程()f x a =在2,63ππ⎡⎤⎢⎥⎣⎦上有2个不同实根1x ,2x ,则12x x -的最大值为3π【答案】ACD 【分析】 由条件可得13f π⎛⎫=±⎪⎝⎭,可得6πϕ=-从而得出()f x 的解析式, 选项A 先得出12f x π⎛⎫+ ⎪⎝⎭的表达式,可判断;选项B 求出函数的单调区间,可判断;选项C 根据图象平移变换得出解析式,可得答案;选项D 作出函数的图像,根据图象可判断. 【详解】 根据条件可得23sin 333f ππϕ⎛⎫⎛⎫=+=± ⎪ ⎪⎝⎭⎝⎭,所以2,32k k Z ππϕπ+=+∈ 则,6k k Z πϕπ=-∈,由22ππϕ-<<,所以6πϕ=-所以()3sin 26f x x π⎛⎫=- ⎪⎝⎭选项A. 3sin 212f x x π⎛⎫+= ⎪⎝⎭为奇函数,故A 正确. 选项B. 由3222262k x k k Z πππππ+≤-≤+∈, 2522233k x k k Z ππππ+≤≤+∈, 536k x k k Z ππππ+≤≤+∈, 当0k =时,536x ππ≤≤,所以函数()f x 在,32ππ⎡⎤⎢⎥⎣⎦上单调递减,故选项B 不正确.选项C. 函数()f x 的图象向右平移()0a a >个单位长度得到, ()3sin 23sin 2266y x a x a ππ⎡⎤⎛⎫=--=-- ⎪⎢⎥⎣⎦⎝⎭根据条件可得当6x π=时,3sin 23sin 23366a a πππ⎛⎫⎛⎫--=-=±⎪ ⎪⎝⎭⎝⎭所以2,62a k k Z πππ-=+∈,则1,26a k k Z ππ=--∈ 由0a >,则当1k =-时,a 有的最小值是3π,故C 正确. 选项D. 作出()3sin 26f x x π⎛⎫=- ⎪⎝⎭的图象,如图当2,63x ππ⎡⎤∈⎢⎥⎣⎦时,由()3f x =,可得3x π= 由33sin 662f ππ⎛⎫==⎪⎝⎭,当2,63x ππ⎡⎤∈⎢⎥⎣⎦时,由()32f x =,可得2x π= 当332a ≤<时,方程()f x a =在2,63ππ⎡⎤⎢⎥⎣⎦上有2个不同实根1x ,2x ,则1x +223x π= 设1x <2x ,则1211122233x x x x x ππ⎛⎫-=--=- ⎪⎝⎭,162x ππ⎡⎫∈⎪⎢⎣⎭,如图当32a =时,1x ,2x 分别为6π,2π时,12x x -最大,最大值为3π,故D 正确.故选:ACD【点睛】关键点睛:本题考查三角函数()sin y A x ωϕ=+的图像性质,考查三角函数的图象变换,解答本题的关键是根据正弦型函数的对称性求出ϕ的值,根据三角函数的对称性得到1211122233x x x x x ππ⎛⎫-=--=- ⎪⎝⎭,162x ππ⎡⎫∈⎪⎢⎣⎭,,属于中档题.6.已知函数()()()2sin 0,0f x x ωϕωϕπ=+><<的部分图象如图所示,则下列说法正确的是( )A .23ϕπ=B .()f x 的最小正周期为πC .()f x 的图象关于直线12x π=对称D .()f x 的图象关于点5,06π⎛⎫⎪⎝⎭对称 【答案】BCD 【分析】利用图象,把(3代入求ϕ,利用周期求出2ω=,从而2n 2)3(si f x x π⎛⎫=+⎪⎝⎭,研究对称轴和对称中心. 【详解】由图可知2sin ϕ=sin 2ϕ=,根据图象可知0x =在()f x 的单调递增区间上,又0ϕπ<<,所以3πϕ=,A 项错误;因为()2sin 3f x x πω⎛⎫=+ ⎪⎝⎭,所以结合图像,由五点法得33ωπππ+=,解得2ω=,则()f x 的最小正周期2T ππω==,B 项正确;将12x π=代入2n 2)3(si f x x π⎛⎫=+ ⎪⎝⎭,得2sin 21263f πππ⎛⎫⎛⎫=+= ⎪ ⎪⎝⎭⎝⎭,所以()f x 的图象关于直线12x π=对称,C 项正确﹔将56x π=代入可得552sin 0633f πππ⎛⎫⎛⎫=+= ⎪ ⎪⎝⎭⎝⎭,所以点5,06π⎛⎫ ⎪⎝⎭是()f x 图象的一个对称中心,D 项正确. 故选:BCD. 【点睛】求三角函数解析式的方法: (1)求A 通常用最大值或最小值; (2)求ω通常用周期;()求φ通常利用函数上的点带入即可求解.7.在ABC 中,下列说法正确的是( ) A .若A B >,则sin sin A B > B .若2C π>,则222sin sin sin C A B >+C .若sin cos A B <,则ABC 为钝角三角形D .存在ABC 满足cos cos 0A B +≤ 【答案】ABC 【分析】根据大角对大边,以及正弦定理,判断选项A ;利用余弦定理和正弦定理边角互化,判断选项B ;结合诱导公式,以及三角函数的单调性判断CD. 【详解】 A.A B >,a b ∴>,根据正弦定理sin sin a bA B=,可知sin sin A B >,故A 正确; B.2C π>,222cos 02a b c C ab +-∴=<,即222a b c +<,由正弦定理边角互化可知222sin sin sin C A B >+,故B 正确;C.当02A π<<时,sin cos cos cos 2A B A B π⎛⎫<⇔-< ⎪⎝⎭,即22A B A B ππ->⇒+<,即2C π>,则ABC 为钝角三角形,若2A π>,sin cos cos cos 2A B A B π⎛⎫<⇔-< ⎪⎝⎭,即22A B A B ππ->⇒>+成立,A 是钝角,当2A π=是,sin cos A B >,所以综上可知:若sin cos A B <,则ABC 为钝角三角形,故C 正确;D.A B A B ππ+<⇒<-,0,0A B πππ<<<-<,()cos cos cos A B B π∴>-=-,即cos cos 0A B +>,故D 不正确. 故选:ABC 【点睛】关键点点睛:本题考查判断三角形的形状,关键知识点是正弦定理和余弦定理,判断三角形形状,以及诱导公式和三角函数的单调性.8.已知函数()sin()(0,0,0)f x A x A ωϕωϕπ=+>><<的部分图象如图所示,则下列正确的是( )A .2()2sin 23f x x π⎛⎫=+⎪⎝⎭B .(2021)1f π=C .函数|()|y f x =为偶函数D .,066x f x f x ππ⎛⎫⎛⎫∀∈++-=⎪ ⎪⎝⎭⎝⎭R 【答案】AD 【分析】先利用图象得到2A =,T π=,求得2ω=,再结合12x π=-时取得最大值求得ϕ,得到解析式,再利用解析式,结合奇偶性、对称性对选项逐一判断即可. 【详解】由图象可知,2A =,5212122T πππ=+=,即2T ππω==,2ω=, 由12x π=-时,()2sin 2212f x =πϕ⎡⎤⎛⎫=⨯-+ ⎪⎢⎥⎝⎭⎣⎦,得22,122=k k Z ππϕπ⎛⎫⨯-++∈ ⎪⎝⎭, 即22,3=k k Z πϕπ+∈,而0ϕπ<<,故2=3πϕ,故2()2sin 23f x x π⎛⎫=+ ⎪⎝⎭,A 正确;22(2021)2sin 22021=2sin 33f ππππ⎛⎫=⨯+ ⎪⎝⎭B 错误; 由2()2sin 23y f x x π⎛⎫==+⎪⎝⎭知,222sin 2=2sin 233x x ππ⎛⎫⎛⎫-++⎪ ⎪⎝⎭⎝⎭不是恒成立,故函数|()|y f x =不是偶函数,故C 错误; 由6x π=时,22sin 22sin 0663f =ππππ⎛⎫⎛⎫=⨯+=⎪ ⎪⎝⎭⎝⎭,故06π⎛⎫⎪⎝⎭,是2()2sin 23f x x π⎛⎫=+ ⎪⎝⎭的对称中心,故,066x f x f x ππ⎛⎫⎛⎫∀∈++-= ⎪ ⎪⎝⎭⎝⎭R ,故D 正确. 故选:AD. 【点睛】 方法点睛:三角函数模型()sin()f x A x b ωϕ=++求解析式时,先通过图象看最值求A ,b ,再利用特殊点(对称点、对称轴等)得到周期,求ω,最后利用五点特殊点求初相ϕ即可.二、数列多选题9.已知数列{}n a 中,11a =,1111n n a a n n +⎛⎫-=+ ⎪⎝⎭,*n N ∈.若对于任意的[]1,2t ∈,不等式()22212na t a t a a n<--++-+恒成立,则实数a 可能为( ) A .-4 B .-2C .0D .2【答案】AB 【分析】由题意可得11111n n a a n n n n +-=-++,利用裂项相相消法求和求出122n a n n=-<,只需()222122t a t a a --++-+≥对于任意的[]1,2t ∈恒成立,转化为()()210t a t a --+≤⎡⎤⎣⎦对于任意的[]1,2t ∈恒成立,然后将选项逐一验证即可求解.【详解】111n n n a a n n++-=,11111(1)1n n a a n n n n n n +∴-==-+++,则11111n n a a n n n n --=---,12111221n n a a n n n n ---=-----,,2111122a a -=-, 上述式子累加可得:111n a a n n -=-,122n a n n∴=-<,()222122t a t a a ∴--++-+≥对于任意的[]1,2t ∈恒成立,整理得()()210t a t a --+≤⎡⎤⎣⎦对于任意的[]1,2t ∈恒成立,对A ,当4a =-时,不等式()()2540t t +-≤,解集5,42⎡⎤-⎢⎥⎣⎦,包含[]1,2,故A 正确;对B ,当2a =-时,不等式()()2320t t +-≤,解集3,22⎡⎤-⎢⎥⎣⎦,包含[]1,2,故B 正确;对C ,当0a =时,不等式()210t t +≤,解集1,02⎡⎤-⎢⎥⎣⎦,不包含[]1,2,故C 错误;对D ,当2a =时,不等式()()2120t t -+≤,解集12,2⎡⎤-⎢⎥⎣⎦,不包含[]1,2,故D 错误,故选:AB. 【点睛】本题考查了裂项相消法、由递推关系式求通项公式、一元二次不等式在某区间上恒成立,考查了转化与划归的思想,属于中档题.10.如图,已知点E 是ABCD 的边AB 的中点,()*n F n ∈N 为边BC 上的一列点,连接n AF 交BD 于n G ,点()*n G n ∈N满足()1223nn n n n G D aG A a G E +=⋅-+⋅,其中数列{}n a 是首项为1的正项数列,n S 是数列{}n a 的前n 项和,则下列结论正确的是( )A .313a =B .数列{}3n a +是等比数列C .43n a n =-D .122n n S n +=--【答案】AB 【分析】化简得到()()12323n n n n n n G D a a G A a G B +=--⋅-+⋅,根据共线得到1230n n a a +--=,即()1323n n a a ++=+,计算123n n a +=-,依次判断每个选项得到答案.【详解】()()112232n n n n n n G D a G A a G A G B +=⋅-+⋅+, 故()()12323n n n n n n G D a a G A a G B +=--⋅-+⋅,,n n G D G B 共线,故1230n n a a +--=,即()1323n n a a ++=+,11a =,故1342n n a -+=⨯,故123n n a +=-.432313a =-=,A 正确;数列{}3n a +是等比数列,B 正确;123n n a +=-,C 错误;2124323412nn n S n n +-=-=---,故D 错误.故选:AB . 【点睛】本题考查了向量运算,数列的通项公式,数列求和,意在考查学生的计算能力,转化能力和综合应用能力.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、选择题(每小题6分,共60分)1.(2018年辽宁,1)若cos θ>0,且sin2θ<0,则角θ的终边所在象限是 A.第一象限 B.第二象限 C.第三象限 D.第四象限解析:由sin2θ<0得2sin θcos θ<0.又cos θ>0,∴sin θ<0.∴角θ的终边在第四象限. 答案:D2.要得到函数y =sin2x 的图象可由函数y =cos2x 的图象A.向左平移2π个单位 B.向右平移2π个单位 C.向左平移4π个单位 D.向右平移4π个单位 解析:y =sin2x =cos (2π-2x )=cos [2(x -4π)]. 答案:D3.已知函数y =A sin (ωx +ϕ)在同一周期内,当x =9π时,取得最大值21,当x =9π4时,取得最小值-21,则该函数的解析式为A.y =2sin (3x -6π) B.y =21sin (3x +6π) C.y =21sin (3x -6π)D.y =21sin (3x -6π) 解析:A =21,2T =3π,ω=T π2=3,易知第一个零点为(-18π,0),则y =21sin [3(x +18π)],即y =21sin (3x +6π).答案:B4.设集合M ={y |y =sin x },N ={y |y =cos x tan x },则M 、N 的关系是 A.N M B.M N C.M =N D.M ∩N =∅ 解析:M ={y |-1≤y ≤1},N ={y |-1<y <1},选A. 答案:A5.y =xxcos 2sin 3-的值域是A.[-1,1]B.[-3,3]C.[-3,1]D.[-1,3]解析:原式可化为3sin x +y cos x =2y ,23y +sin (x +ϕ)=2y (tan ϕ=3y ),sin (x +ϕ)=232yy +∈[-1,1],解得y ∈[-1,1].答案:A6.在△ABC 中,tan A ·tan B >1,则△ABC 为 A.直角三角形 B.锐角三角形 C.钝角三角形 D.等腰三角形解析:tan (A +B )=-tan C ,得BA BA tan tan 1tan tan ⋅-+=-tan C .∵tan A ·tanB >1,∴tan A >0,tan B >0.1-tan A ·tan B <0,∴-tan C <0.tan C >0,∴△ABC 为锐角三角形.故选B.答案:B7.方程cos x =lg x 的实根个数为 A.1个 B.2个 C.3个 D.无数个解析:当x =18时,lg x =1,在同一坐标系中画出y =cos x 和y =lg x 的图象,可知有3个交点,选C.答案:C 8.)()(3arctan 21arccos 23arcsin--+的值是 A.-3 B.2 C.-3πD.3π 解析:原式=-3,选A. 答案:A9.已知f (sin x )=sin3x ,则f (cos x )等于 A.-cos3x B.cos3x C.sin3x D.-sin3x解析:f (cos x )=f [sin (2π-x )]=sin3(2π-x )=-cos3x ,选A. 答案:A18.函数f (x )=sin2x +5sin (4π+x )+3的最小值是 A.-3B.-6C.89D.-1解析:f (x )=2sin x cos x +225(sin x +cos x )+3.令t =sin x +cos x ,t ∈[-2,2],则y =(t +425)2-89.则当t =-2时,y min =-1,选D.答案:D二、填空题(每小题4分,共18分)18.已知角α的终边上一点P (3,-1),则sec 2α+csc 2α+cot 2α=_________. 解析:sec α=32,csc α=-2,cot α=-3,代入得325. 答案:32518.(2018年春季上海,18)函数y =sin x +arcsin x 的值域是____________. 解析:该函数的定义域为[-1,1].∵y =sin x 与y =arcsin x 都是[-1,1]上的增函数, ∴当x =-1时,y min =sin (-1)+arcsin (-1)=-2π-sin1, 当x =1时,y max =sin1+arcsin1=2π+sin1, ∴值域为[-2π-sin1,2π+sin1]. 答案:[-2π-sin1,2π+sin1]18.△ABC 中,若sin A =53,cos B =135,则cos C =_______. 解析:由cos B =135,得sin B =1312>53=sin A .A 是锐角,cos A =54,cos C =cos (π-A -B )=6516. 答案:651618.若f (x )=a sin 3x +b tan x +1且f (3)=5,则f (-3)=_______. 解析:令g (x )=a sin 3x +b tan x ,则g (-x )=-g (x ). f (3)=g (3)+1=5,g (3)=4.f (-3)=g (-3)+1=-g (3)+1=-4+1=-3. 答案:-3三、解答题(本大题共6小题,共74分) 18.(18分)(2018年黄冈市调研题)已知sin 2α-cos2α=510,α∈(2π,π),tan (π-β)=21,求tan (α-2β)的值.解:∵sin2α-cos2α=510, ∴1-sin α=52.∴sin α=53.又∵α∈(2π,π),∴cos α=-α2sin 1-=-54. ∴tan α=-43. 由条件知tan β=-21, ∴tan2β=ββ2tan tan 2-1=-34.∴tan (α-2β)=βαβα2tan tan 2tan tan ⋅+1-=247.18.(18分)已知2cos2α-cos2β=1,求21sin 22α+sin 2β+2cos 4α的值.解:由2cos2α-cos2β=1,即2cos2α=1+cos2β,得cos2α=cos 2β.因此21sin 22α+sin 2β+2cos 4α=21sin 22α+sin 2β+2·(2+α2c o s 1)2=1+cos2α+sin 2β=1+cos 2β+sin 2β=2. 18.(18分)(2018年浙江,理18)在△ABC 中,角A 、B 、C 所对的边分别为a 、b 、c ,且cos A =31. (1)求sin 22C B ++cos2A 的值;(2)若a =3,求bc 的最大值.解:(1)sin 22C B ++cos2A =21[1-cos (B +C )]+(2cos 2A -1)=21(1+cos A )+(2cos 2A -1)=21(1+31)+(92-1)=-91.(2)∵bc a c b 2222-+=cos A =31,∴32bc =b 2+c 2-a 2≥2bc -a 2. ∴bc ≤43a 2.又∵a =3,∴bc ≤49.当且仅当b =c =23时,bc =49.故bc 的最大值是49. 18.(18分)已知a 1=xtan 1,a n +1=a n cos x -sin nx ,求a 2、a 3、a 4,推测a n 并证明. 解:a 2=a 1cos x -sin x =x x x sin sin cos 22-=x x sin 2cos ,a 3=a 2cos x -sin2x =x x sin 3cos ,a 4=xxsin 4cos .可推测a n =xnxsin cos ,数学归纳法可证之.(读者自己完成)19.(18分)设A 、B 、C 是三角形的内角,且lgsin A =0,又sin B 、sin C 是关于x 的方程4x 2-2(3+1)x +k =0的两个根,求实数k 的值.解:由lgsin A =0,得sin A =1,A =2π,B +C =2π,sin C =cos B . 又⎪⎪⎩⎪⎪⎨⎧=+=+,,4sin sin 213sin sin k C B C B∴⎪⎪⎩⎪⎪⎨⎧=+=+.4cos sin 213cos sin k B B B B , 由sin B cos B =21[(sin B +cos B )2-1],得4k =21[(213+)2-1],解得k =3. 20.(18分)已知F (θ)=cos 2θ+cos 2(θ+α)+cos 2(θ+β),问是否存在满足0≤α<β≤π的α、β,使得F (θ)的值不随θ的变化而变化?如果存在,求出α、β的值;如果不存在,请说明理由.解:F (θ)=23+21[cos2θ+cos (2θ+2α)+cos (2θ+2β)]=23+21(1+cos2α+cos2β)cos2θ-21(sin2α+sin2β)sin2θ.F (θ)的值不随θ变化的充要条件是⎩⎨⎧=+=++,,02sin 2sin 02cos 2cos 1βαβα 得(cos2α+1)2+sin 22α=1, cos2α=-21.同理,cos2β=-21. 又0≤α<β≤π,故存在α、β满足条件,其值分别为α=3π,β=3π2.。
