中考数学一次函数专题
中考数学复习《一次函数》专项提升训练题-附带答案

中考数学复习《一次函数》专项提升训练题-附带答案学校:班级:姓名:考号:一、选择题1.下列各点在直线y=−2x+6上的是()A.(−1,4)B.(2,10)C.(3,0)D.(−3,0)2.将一次函数y=2x−1的图象沿y轴向上平移4个单位长度,所得直线的解析式为()A.y=2x−5B.y=2x−3C.y=2x+3D.y=2x+43.关于y是x的一次函数y=kx+b2+1(其中k<0,b为任意实数)的图象可能是()A.B.C.D.4.已知一次函数y=−2x+4,那么下列结论正确的是()A.y的值随x的值增大而增大B.图象经过第一、二、三象限C.图象必经过点(1,2)D.当x<2时5.若点A(x1,−1),B(x2,−2),C(x3,3)在一次函数y=−2x+m(m是常数)的图象上,则x1,x2,x3的大小关系是()A.x1>x2>x3B.x2>x1>x3C.x1>x3>x2D.x3>x2>x16.如图,函数y=mx和y=kx+b的图象相交于点P(1,m),则不等式−b≤kx−b≤mx的解集为()A.0≤x≤1B.−1≤x≤0C.−1≤x≤1D.−m≤x≤m7.已知一次函数y=32x+m和y=−12x+n的图象都经过点A(−2,0),且与y轴分别交于B、C两点,那么△ABC的面积是()A .2B .3C .4D .68.小明从家出发到公园晨练,在公园锻炼一段时间后按原路返回,同时小明爸爸从公园按小明的路线返回家中.如图是两人离家的距离y (米)与小明出发的时间x (分)之间的函数图象.下列结论中不正确的是( )A .公园离小明家1600米B .小明出发253分钟后与爸爸第一次相遇C .小明与爸爸第二次相遇时,离家的距离是960米D .小明在公园停留的时间为5分钟二、填空题9.若函数y =(m −1)x |m|−5是一次函数,则m 的值为 .10.一次函数y=(2m ﹣6)x+4中,y 随x 的增大而减小,则m 的取值范围是 .11.弹簧的自然长度为5cm ,在弹簧的弹性限度内,所挂的物体的质量x 每增加1kg ,弹簧的长度y 增加0.5cm ,则y 与x 之间的函数关系式是 .12.如图所示,直线y =kx +b 经过点(−2,0),则关于x 的不等式kx +b >0的解集为 .13.函数y =ax +b 和y =−x +2的图像如图所示,两图像交于点P(−1,m),则二元一次方程组:{y −ax =b y +x =2的解是 .三、解答题14.已知一次函数y=k(x+2)(k≠0).(1)求证:点(−2,0)在该函数图象上;(2)若该函数图象向上平移2个单位后过点(1,−2),求k的值;(3)若该函数图象与y轴的交点在x轴和直线y=−2之间,求k的取值范围.15.为丰富学生的业余生活,学校准备购进甲、乙两种畅销图书.经调查,甲种图书的总费用y(元)与购进本数x之间的函数关系如图所示,乙种图书每本20元.(1)直接写出当0≤x≤100和x>100时,y与x的函数关系式;(2)现学校准备购买300本图书,且两种图书均不少于80本,该如何购买,才能使总费用最少?最少的总费用为多少元?x+m的图象交于点P(n,−2).16.如图,函数y=−2x+3与y=−12(1)求出m,n的值;x+m≤−2x+3的解集;(2)观察图象,写出−12.(3)设△BOC和△ABP的面积分别为S1、S2,求S1S217.A、B两个码头之间航程为24千米,甲、乙两轮船同时出发,甲轮船从A码头顺流匀速航行到B码头后,立即逆流匀速航行返回到A码头,乙轮船从B码头逆流匀速航行到A码头后停止,两轮船在静水中速度均为10千米/时,水流速度不变,两轮船距A码头的航程y(千米)与各自的航行时间x(时)之间的函数图象如图所示.(顺流速度=静水速度+水流速度:逆流速度=静水速度-水流速度)(1)水流速度为千米/时;a值为;(2)求甲轮船从B码头向A码头返回过程中y与x之间的函数关系式;(3)当乙轮船到达A码头时,求甲轮船距A码头的航程.x−6的图象与坐标轴交于点A,B,BC平分∠OBA交x轴与点C,CD⊥AB垂足为18.如图1,一次函数y=34D.(1)求点A,B的坐标;(2)求CD所在直线的解析式;(3)如图2,点E是线段OB上的一点,点F是线段BC上的一点,求EF+OF的最小值.参考答案1.【答案】C2.【答案】C3.【答案】A4.【答案】C5.【答案】B6.【答案】B7.【答案】C8.【答案】C9.【答案】-110.【答案】m <311.【答案】y=5+0.5x12.【答案】x >−213.【答案】{x =−1y =314.【答案】(1)证明:当x =−2时y =k(x +2)=k(−2+2)=0 ∴点(−2,0)在y =k(x +2)图象上.(2)解:一次函数y =k(x +2)图象向上平移2个单位得y =k(x +2)+2.将(1,−2)代入得:−2=k(1+2)+2解得k =−43.(3)解:由题意得:该函数图象与y 轴的交点为(0,2k)∵该交点在x 轴和直线y =−2之间∴−2<2k <0∴−1<k <0.15.【答案】(1)解:由图可知:y ={25x(0≤x ≤100)19x +600(x >100)(2)解:设总费用为w 元.根据题意,得80≤x ≤220.当80≤x ≤100时w =25x +20(300−x)=5x +6000.∵k =5>0,w 随x 的增大而增大,∴当x =80时,总费用最少w 最小=5×80+6000=6400元.当100<x ≤220时w =19x +600+20(300−x)=−x +6600.∵k =−1<0,w 随x 的增大而减小,∴当x =220时,总费用最少w 最小=−220+6600=6380元<6400元.∴此时乙种图书为300−220=80本.∴应购买甲种图书220本,乙种图书80本,才能使总费用最少,最少总费用为6380元.16.【答案】(1)解:将点P(n ,−2)代入函数y =−2x +3得:−2n +3=−2 解得n =52∴P(52,−2) 将点P(52,−2)代入函数y =−12x +m 得:−12×52+m =−2解得m =−34.(2)解:不等式−12x +m ≤−2x +3表示的是函数y =−12x +m 的图象位于函数y =−2x +3的图象下方(含交点)则由函数图象可知,−12x +m ≤−2x +3的解集为x ≤52. .(3)解:对于函数y =−12x −34当x =0时y =−34,则OB =34当y =0时−12x −34=0,解得x =−32,则OC =32∴S 1=12×34×32=916 对于函数y =−2x +3当x =0时y =3,则OA =3∴AB =OA +OB =154 ∵P(52,−2) ∴S 2=12×154×52=7516 ∴S 1S 2=9167516=325.17.【答案】(1)2;2(2)解:设甲轮船从B 码头向A 码头返回过程中y 与x 之间的函数关系式为y =kx +b 由图象可得,甲轮船从B 码头向A 码头返回需要3小时∴点(2,24),(5,0)在该函数图象上∴{2k +b =245k +b =0,解得{k =−8b =40即甲轮船从B 码头向A 码头返回过程中y 与x 之间的函数关系式为y =−8x +40;(3)解:由(2)知,当x =3时即当乙轮船到达A 码头时,甲轮船距A 码头的航程为16千米.18.【答案】(1)解:由一次函数y=34x−6的图象与坐标轴交于点A,B 另y=0,则x=8,即A(8,0);另x=0,则y=-6,即B(0,-6).(2)解:根据题意,如图,延长DC交y轴于点G,设CD=m∵BC平分∠OBA,OC⊥OB,CD⊥BD∴OC=CD=m∵OA=8,OB=6∴AB=√62+82=10∴12AB•CD=12AC•OB∵AC=8−m∴12×10m=12×(8−m)×6∴m=3∴点C的坐标为(3,0);∵CD⊥AB∴∠BDG=∠AOB=∠90°又∵OB=BD,∠ABO=∠GBD∴△AOB≌△GBD(ASA)∴BG=AB=10,OG=BG-OB=4即G(0,4)∴设直线CD的解析式为y=kx+4把点C(3,0)代入,则k=−43∴直线CD的解析式为y=−43x+4;(3)解:根据题意,作点E关于直线BC的对称点E′,则EF=FE′,如图:∵BC是角平分线∴点E′恰好落在直线AB上∴EF+OF=E′F+OF≥OE′∴EF+OF的最小值就是OE′的最小值当OE′⊥AB时,OE′为最小值;∵12AB•OE′=12OA•OB∴12×10×OE′=12×8×6∴OE′=245∴EF+OF的最小值为245.。
中考数学复习《一次函数》专项提升训练题-附答案

中考数学复习《一次函数》专项提升训练题-附答案学校:班级:姓名:考号:一、选择题1.把一次函数的图象向上平移4个单位长度,得到图象表达式是()A.B.C.D.2.小红骑自行车到离家为千米书店买书,行驶了分钟后,遇到一个同学因说话停留分钟,继续骑了分钟到书店.图中的哪一个图象能大致描述她去书店过程中离书店的距离千米与所用时间分之间的关系()A.B.C.D.3.已知直线与x轴的交点在,之间(包括A,B两点),则a的取值范围是()A.B.C.D.4.已知一次函数的图像经过点,且当时,则该函数图象所经过的象限为()A.一、二、三B.二、三、四C.一、三、四D.一、二、四5.已知正比例函数的图象上两点、且,则下列不等式中一定成立的是()A.B.C.D.6.已知一次函数的图象与的图象交于点.则对于不等式,下列说法正确的是()A.当时B.当时C.当且时D.当且时7.如图,已知直线与轴、轴分别交于点和点,是线段上一点,若将沿折叠,点恰好落在x轴上的点处,则直线所对应的函数表达式是()A. B. C. D.8.如图,正方形、正方形、正方形的顶点、与和、与、分别在一次函数的图像和轴上,若正比例函数则过点,则的值是()A.B.C.D.二、填空题9.与直线垂直且过点的直线解析式是.10.已知一次函数的图象经过点,则不等式的解是. 11.已知为整数,且一次函数的图像不经过第二象限,则= .12.某家庭电话月租费为10元,若市内通话费平均每次为0.2元,则该家庭一个月的话费y(元)与通话次数x(次)之间的关系式是.13.如图,矩形OABC的边OA、OC分别在x轴、y轴的正半轴上,顶点B的坐标为(4,3),点D为对角线OB上一点.若OA=OD,则点D到x轴的距离为.三、解答题14.已知是一次函数.(1)求m的值;(2)若,求对应y的取值范围.15.某花农培育甲种樱花 3 株,乙种樱花 2 株,共需要成本 1700 元,乙种樱花 2 株,共需成本 1500 元.(1)求甲、乙两种樱花每株成本分别为多少元?(2)据市场调研,1 株甲种樱花售价为 160 元,1 株乙种樱花售价为 840 元.该花农决定在成本不超过 29000 元的前提下培育甲、乙两种樱花,那么要使总利润不少于 5000 元,花农有哪几种具体的培育方案?(3)求出选何种方案成本最少?16.如图,一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.根据图象解决下列问题:(1)求慢车和快车的速度;(2)求线段所表示的y与x之间的函数关系式,并写出自变量x的取值范围.17.为提升学生的文学素养,培养学生的阅读兴趣,某校准备购进A,B两种图书.经调查,购进A 种图书费用y元与购进A种图书本数x之间的函数关系如图所示,B种图书每本20元.(1)当和时,求y与x之间的函数关系式;(2)现学校准备购进300本图书,其中购进A种图书x本,设购进两种图书的总费用为w元.①当时,求出w与x间的函数表达式;②若购进A种图书不少于60本,且不超过B种图书本数的2倍,那么应该怎样分配购买A,B两种图书才能使总费用最少?最少总费用多少元?18.如图,在平面直角坐标系中,直线与轴交于点,直线与轴、轴分别交于点和点,且与直线交于点.(1)求直线的解析式;(2)若点为线段BC上一个动点,过点作轴,垂足为,且与直线交于点,当时,求点的坐标;(3)若在平面上存在点,使得以点A,C,D,H为顶点的四边形是平行四边形,请直接写出点的坐标.参考答案:1.A2.D3.D4.D5.C6.D7.B8.B9.10.11.-3或-212.13.14.(1)解:因为是一次函数,所以且,解得(2)解:由(1)可知,该一次函数的表达式为,因为,所以随的增大而减小.当时;当时,所以当时,.15.(1)解:设甲、乙两种樱花每株成本分别为 x则:解得:故甲种樱花每株成本为 100 元,乙种樱花每株成本为 700元。
中考数学常考考点专题之一次函数测试卷
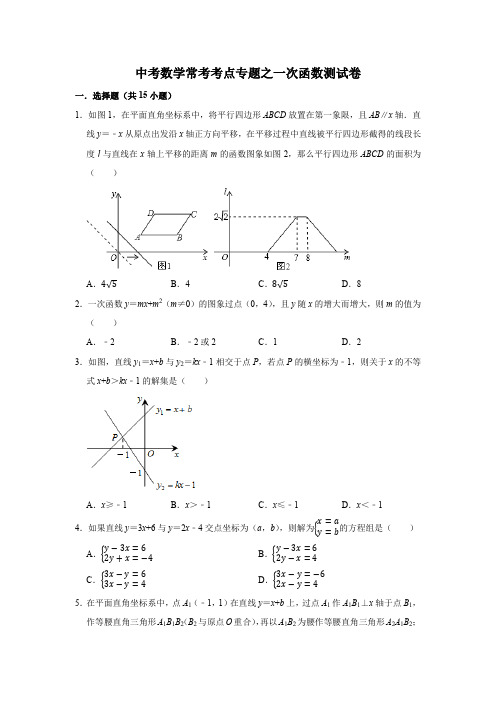
中考数学常考考点专题之一次函数测试卷一.选择题(共15小题)1.如图1,在平面直角坐标系中,将平行四边形ABCD 放置在第一象限,且AB ∥x 轴.直线y =﹣x 从原点出发沿x 轴正方向平移,在平移过程中直线被平行四边形截得的线段长度l 与直线在x 轴上平移的距离m 的函数图象如图2,那么平行四边形ABCD 的面积为( )A .4√5B .4C .8√5D .82.一次函数y =mx +m 2(m ≠0)的图象过点(0,4),且y 随x 的增大而增大,则m 的值为( )A .﹣2B .﹣2或2C .1D .23.如图,直线y 1=x +b 与y 2=kx ﹣1相交于点P ,若点P 的横坐标为﹣1,则关于x 的不等式x +b >kx ﹣1的解集是( )A .x ≥﹣1B .x >﹣1C .x ≤﹣1D .x <﹣14.如果直线y =3x +6与y =2x ﹣4交点坐标为(a ,b ),则解为{x =a y =b 的方程组是( )A .{y −3x =62y +x =−4B .{y −3x =62y −x =4C .{3x −y =63x −y =4D .{3x −y =−62x −y =45.在平面直角坐标系中,点A 1(﹣1,1)在直线y =x +b 上,过点A 1作A 1B 1⊥x 轴于点B 1,作等腰直角三角形A 1B 1B 2(B 2与原点O 重合),再以A 1B 2为腰作等腰直角三角形A 2A 1B 2;以A2B2为腰作等腰直角三角形A2B2B3;按照这样的规律进行下去,那么A2019的坐标为()A.(22018﹣1,22018)B.(22018﹣2,22018)C.(22019﹣1,22019)D.(22019﹣2,22019))6.已知一次函数y=kx+b的图象如图所示,则k,b的取值范围是()A.k>0,b>0B.k>0,b<0C.k<0,b>0D.k<0,b<0 7.关于x的一次函数y=﹣4x+8的图象,下列说法不正确的是()A.直线不经过第三象限B.直线经过点(1,4)C.直线与x轴交于点(2,0)D.y随x的增大而增大8.甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.则下列结论:①A,B两城相距300千米;②乙车比甲车晚出发1小时,却早到1小时;③乙车出发后2.5小时追上甲车;④当甲、乙两车相距50千米时,t=54或154.其中正确的结论有()A.1个B.2个C.3个D.4个9.已知A、B两地相距4千米.上午8:00,甲从A地出发步行到B的,8:20乙从B地出发骑自行车到A地,甲乙两人离A地的距离(千米)与甲所用的时间(分)之间的关系如图所示.由图中的信息可知,乙到达A地的时间为()A.8:30B.8:35C.8:40D.8:410.“漏壶”是古代一种计时器,在它内部盛一定量的水,不考虑水量变化对压力的影响,水从壶底小孔均匀漏出,壶内壁有刻度.人们根据壶中水面的位置计算时间.在漏壶漏完水之前,漏壶内水的深度与对应的漏水时间满足的函数关系式()A.正比例函数关系B.一次函数关系C.反比例函数关系D.二次函数关系11.将直线y=2x+1向右平移2个单位后所得图象对应的函数表达式为()A.y=2x+5B.y=2x+3C.y=2x﹣2D.y=2x﹣3 12.对于某个一次函数y=kx+b(k≠0),根据两位同学的对话得出的结论,错误的是()A.k>0B.kb<0C.k+b>0D.k=−1 2b13.已知正比例函数y=kx(k≠0)的函数值y随x的增大而减小,则一次函数y=x+k的图象大致是()A.B.C.D.14.若直线BC和直线y=x+3平行,其中点B的坐标为B(﹣2,3),将直线BC向右平移1个单位后为()A.y=﹣x+2B.y=﹣x+4C.y=x+6D.y=x+415.如图,甲从A村匀速骑自行车到B村,乙从B村匀速骑摩托车到A村,两人同时出发,到达目的地后,立即停止运动,甲、乙两人离A村的距离y(km)与他自骑车的时间x (h)之间的函数关系如图所示,则下列说法错误的是()A.A、B两村的距离为120km B.甲的速度为20kmhC.乙的速度为40km/h D.乙运动3.5h到达目的地二.填空题(共5小题)16.我国古代数学经典著作《九章算术》记载:“今有善行者行一百步,不善行者行六十步,今不善行者先行一百步,善行者追之.问几何步及之?”如图是善行者与不善行者行走路程s(单位:步)关于善行者的行走时间t的函数图象,则两图象交点P的纵坐标是.17.若一元二次方程x2﹣2x﹣m=0无实数根,则一次函数y=(m+1)x+m﹣1的图象不经过第象限.18.学校提倡“低碳环保,绿色出行”,小明和小亮分别选择步行和骑自行车上学,两人各自从家同时同向出发,沿同一条路匀速前进.如图所示,l1和l2分别表示两人到小亮家的距离s(km)和时间t(h)的关系,则出发h后两人相遇.19.若函数y=|2x﹣3|﹣2a始终大于y=|x+a|,则a的取值范围为.20.根据图象,可得关于x的不等式kx>﹣x+3的解集是.三.解答题(共5小题)21.在襄阳市创建“经济品牌特色品牌”政策的影响下.每到傍晚,市内某网红烧烤店就食客如云,这家烧烤店的海鲜串和肉串非常畅销,店主从食品加工厂批发以上两种产品进行加工销售,其中海鲜串的成本为m元/支,肉串的成本为n元/支;两次购进并加工海鲜串和肉串的数量与成本如下表所示(成本包括进价和其他费用):次数数量(支)总成本(元)海鲜串肉串第一次3000400017000第二次4000300018000针对团以消费,店主决定每次消费海鲜串不超过200支时,每支售价5元;超过200支时、不超过200支的部分按原价,超过200支的部分打八折.每支肉串的售价为3.5元.(1)求m、n的值;(2)五一当天,一个旅游团去此店吃烧烤,一次性消费海鲜串和肉串共1000支,且海鲜串不超过400支.在本次消费中,设该旅游团消费海鲜串x支,店主获得海鲜串的总利润为y元,求y与x的函数关系式,并写出自变量x的取值范围;(3)在(2)的条件下,该旅游团消费的海鲜串超过了200支,店主决定给该旅游团更多优惠,对每支肉串降价a(0<a<1)元,但要确保本次消费获得肉串的总利润始终不低于海鲜串的总利润,求a的最大值.22.在平面直角坐标系中,点B、E的坐标分别为B(﹣2,√3),E(4,0),过点E作直线l⊥x轴,设直线l上的动点A的坐标为(4,m),连接AB,将线段BA绕点B顺时针方向旋转30°得到线段BA′,在射线BA′上取点C,构造Rt△ABC,使得∠BAC=90°.(1)当m=−√3时,求直线AB的函数表达式.(2)当点C落在坐标轴上时,求△ABC的面积.(3)已知点B关于原点O的对称点是点D,在点A的运动过程中,是否存在某一位置,使以A,C,D为顶点的三角形与△ABC相似?若存在,求出点A的坐标;若不存在,请说明理由.23.在平面直角坐标系中,已知一次函数y1=3x﹣5与y2=2x﹣4.(1)求这两个函数图象的交点坐标;(2)求一次函数y2=2x﹣4的图象与坐标轴所围成三角形的面积.24.在平面直角坐标系xOy中,对于第一象限的P,Q两点,给出如下定义:若y轴正半轴上存在点P',x轴正半轴上存在点Q',使PP'∥QQ',且∠1=∠2=α(如图1),则称点P 与点Q为α﹣关联点.(1)在点Q1(3,1),Q2(5,2)中,与(1,3)为45°﹣关联点的是;(2)如图2,M(6,4),N(8,4),P(m,8)(m>1).若线段MN上存在点Q,使点P与点Q为45°﹣关联点,结合图象,求m的取值范围;(3)已知点A(1,8),B(n,6)(n>1).若线段AB上至少存在一对30°﹣关联点,直接写出n的取值范围.25.近年,净月潭公园将环潭公路改造为东北三省最长的人车分离彩色环保公路,平坦宽敞的路面分橙、黑两色,拓宽了原有的人行步道,成为市民健身的好去处.小明和爸爸参加了此公园举办的“亲子健身赛”,两人的行程y(千米)随时间x(时)变化的图象(全程)如图所示.(1)两人出发后小时相遇,此次“亲子健身赛”的全程是千米.(2)求出AB所在直线的函数关系式.(3)若小明想和爸爸一起到达终点,则需在两人出发 1.5小时后,将速度调整为千米/时.。
中考数学《一次函数》专题练习含答案解析

一次函数一、选择题1.在一次800米的长跑比赛中,甲、乙两人所跑的路程s(米)与各自所用时间t(秒)之间的函数图象分别为线段OA和折线OBCD,则下列说法正确的是()A.甲的速度随时间的增加而增大B.乙的平均速度比甲的平均速度大C.在起跑后第180秒时,两人相遇D.在起跑后第50秒时,乙在甲的前面2.在20km越野赛中,甲乙两选手的行程y(单位:km)随时间x(单位:h)变化的图象如图所示,根据图中提供的信息,有下列说法:①两人相遇前,甲的速度小于乙的速度;②出发后1小时,两人行程均为10km;③出发后1.5小时,甲的行程比乙多3km;④甲比乙先到达终点.其中正确的有()A.1个 B.2个 C.3个 D.4个3.今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.设他从山脚出发后所用时间为t(分钟),所走的路程为s(米),s与t之间的函数关系如图所示.下列说法错误的是()A.小明中途休息用了20分钟B.小明休息前爬山的平均速度为每分钟70米C.小明在上述过程中所走的路程为6600米D.小明休息前爬山的平均速度大于休息后爬山的平均速度4.如图是本地区一种产品30天的销售图象,图①是产品日销售量y(单位:件)与时间t(单位;天)的函数关系,图②是一件产品的销售利润z(单位:元)与时间t(单位:天)的函数关系,已知日销售利润=日销售量×一件产品的销售利润,下列结论错误的是()A.第24天的销售量为200件B.第10天销售一件产品的利润是15元C.第12天与第30天这两天的日销售利润相等D.第30天的日销售利润是750元二、填空题5.一食堂需要购买盒子存放食物,盒子有A,B两种型号,单个盒子的容量和价格如表.现有15升食物需要存放且要求每个盒子要装满,由于A型号盒子正做促销活动:购买三个及三个以上可一次性返还现金4元,则一次性购买盒子所需要最少费用为元.型号A B单个盒子容量(升)23单价(元)566.如图1,在某个盛水容器内,有一个小水杯,小水杯内有部分水,现在匀速持续地向小水杯内注水,注满小水杯后,继续注水,小水杯内水的高度y(cm)和注水时间x(s)之间的关系满足如图2中的图象,则至少需要s能把小水杯注满.7.如图所示,购买一种苹果,所付款金额y(元)与购买量x(千克)之间的函数图象由线段OA和射线AB组成,则一次购买3千克这种苹果比分三次每次购买1千克这种苹果可节省元.三、解答题8.“六一”期间,小张购进100只两种型号的文具进行销售,其进价和售价之间的关系如下表:型号进价(元/只)售价(元/只)A型1012B型1523(1)小张如何进货,使进货款恰好为1300元?(2)要使销售文具所获利润最大,且所获利润不超过进货价格的40%,请你帮小张设计一个进货方案,并求出其所获利润的最大值.9.已知某市的光明中学、市图书馆和光明电影院在同一直线上,它们之间的距离如图所示.小张星期天上午带了75元现金先从光明中学乘出租车去了市图书馆,付费9元;中午再从市图书馆乘出租车去了光明电影院,付费12.6元.若该市出租车的收费标准是:不超过3公里计费为m元,3公里后按n元/公里计费.(1)求m,n的值,并直接写出车费y(元)与路程x(公里)(x>3)之间的函数关系式;(2)如果小张这天外出的消费还包括:中午吃饭花费15元,在光明电影院看电影花费25元.问小张剩下的现金够不够乘出租车从光明电影院返回光明中学?为什么?10.某物流公司承接A、B两种货物运输业务,已知5月份A货物运费单价为50元/吨,B货物运费单价为30元/吨,共收取运费9500元;6月份由于油价上涨,运费单价上涨为:A货物70元/吨,B货物40元/吨;该物流公司6月承接的A种货物和B种数量与5月份相同,6月份共收取运费13000元.(1)该物流公司月运输两种货物各多少吨?(2)该物流公司预计7月份运输这两种货物330吨,且A货物的数量不大于B货物的2倍,在运费单价与6月份相同的情况下,该物流公司7月份最多将收到多少运输费?11.联通公司手机话费收费有A套餐(月租费15元,通话费每分钟0.1元)和B套餐(月租费0元,通话费每分钟0.15元)两种.设A套餐每月话费为y1(元),B套餐每月话费为y2(元),月通话时间为x分钟.(1)分别表示出y1与x,y2与x的函数关系式.(2)月通话时间为多长时,A、B两种套餐收费一样?(3)什么情况下A套餐更省钱?12.某工厂现有甲种原料360千克,乙种原料290千克,计划用这两种原料全部生产A、B两种产品共50件,生产A、B两种产品与所需原料情况如下表所示:甲种原料(千克)乙种原料(千克)原料型号A产品(每件)93B产品(每件)410(1)该工厂生产A、B两种产品有哪几种方案?(2)若生成一件A产品可获利80元,生产一件B产品可获利120元,怎样安排生产可获得最大利润?一次函数参考答案与试题解析一、选择题1.在一次800米的长跑比赛中,甲、乙两人所跑的路程s(米)与各自所用时间t(秒)之间的函数图象分别为线段OA和折线OBCD,则下列说法正确的是()A.甲的速度随时间的增加而增大B.乙的平均速度比甲的平均速度大C.在起跑后第180秒时,两人相遇D.在起跑后第50秒时,乙在甲的前面【考点】一次函数的应用.【分析】A、由于线段OA表示甲所跑的路程S(米)与所用时间t(秒)之间的函数图象,由此可以确定甲的速度是没有变化的;B、甲比乙先到,由此可以确定甲的平均速度比乙的平均速度快;C、根据图象可以知道起跑后180秒时,两人的路程确定是否相遇;D、根据图象知道起跑后50秒时OB在OA的上面,由此可以确定乙是否在甲的前面.【解答】解:A、∵线段OA表示甲所跑的路程S(米)与所用时间t(秒)之间的函数图象,∴甲的速度是没有变化的,故选项错误;B、∵甲比乙先到,∴乙的平均速度比甲的平均速度慢,故选项错误;C、∵起跑后180秒时,两人的路程不相等,∴他们没有相遇,故选项错误;D、∵起跑后50秒时OB在OA的上面,∴乙是在甲的前面,故选项正确.故选D.【点评】本题考查利用函数的图象解决实际问题,正确理解函数图象横纵坐标表示的意义,理解问题的过程,就能够通过图象得到函数问题的相应解决.2.在20km越野赛中,甲乙两选手的行程y(单位:km)随时间x(单位:h)变化的图象如图所示,根据图中提供的信息,有下列说法:①两人相遇前,甲的速度小于乙的速度;②出发后1小时,两人行程均为10km;③出发后1.5小时,甲的行程比乙多3km;④甲比乙先到达终点.其中正确的有()A.1个 B.2个 C.3个 D.4个【考点】一次函数的应用.【分析】根据题目所给的图示可得,两人在1小时时相遇,行程均为10km,出发0.5小时之内,甲的速度大于乙的速度,0.5至1小时之间,乙的速度大于甲的速度,出发1.5小时之后,乙的路程为15千米,甲的路程为12千米,再利用函数图象横坐标,得出甲先到达终点.【解答】解:在两人出发后0.5小时之前,甲的速度小于乙的速度,0.5小时到1小时之间,甲的速度大于乙的速度,故①错误;由图可得,两人在1小时时相遇,行程均为10km,故②正确;甲的图象的解析式为y=10x,乙AB段图象的解析式为y=4x+6,因此出发1.5小时后,甲的路程为15千米,乙的路程为12千米,甲的行程比乙多3千米,故③正确;甲到达终点所用的时间较少,因此甲比乙先到达终点,故④正确.故选C.【点评】本题考查了一次函数的应用,行程问题的数量关系速度=路程后÷时间的运用,解答时理解函数的图象的含义是关键.3.今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.设他从山脚出发后所用时间为t(分钟),所走的路程为s(米),s与t之间的函数关系如图所示.下列说法错误的是()A.小明中途休息用了20分钟B.小明休息前爬山的平均速度为每分钟70米C.小明在上述过程中所走的路程为6600米D.小明休息前爬山的平均速度大于休息后爬山的平均速度【考点】一次函数的应用.【分析】根据函数图象可知,小明40分钟爬山2800米,40~60分钟休息,60~100分钟爬山(3800﹣2800)米,爬山的总路程为3800米,根据路程、速度、时间的关系进行解答即可.【解答】解:A、根据图象可知,在40~60分钟,路程没有发生变化,所以小明中途休息的时间为:60﹣40=20分钟,故正确;B、根据图象可知,当t=40时,s=2800,所以小明休息前爬山的平均速度为:2800÷40=70(米/分钟),故B正确;C、根据图象可知,小明在上述过程中所走的路程为3800米,故错误;D、小明休息后的爬山的平均速度为:(3800﹣2800)÷(100﹣60)=25(米/分),小明休息前爬山的平均速度为:2800÷40=70(米/分钟),70>25,所以小明休息前爬山的平均速度大于休息后爬山的平均速度,故正确;故选:C.【点评】本题考查了函数图象,解决本题的关键是读懂函数图象,获取信息,进行解决问题.4.如图是本地区一种产品30天的销售图象,图①是产品日销售量y(单位:件)与时间t(单位;天)的函数关系,图②是一件产品的销售利润z(单位:元)与时间t(单位:天)的函数关系,已知日销售利润=日销售量×一件产品的销售利润,下列结论错误的是()A.第24天的销售量为200件B.第10天销售一件产品的利润是15元C.第12天与第30天这两天的日销售利润相等D.第30天的日销售利润是750元【考点】一次函数的应用.【专题】压轴题.【分析】根据函数图象分别求出设当0≤t≤20,一件产品的销售利润z(单位:元)与时间t(单位:天)的函数关系为z=﹣x+25,当0≤t≤24时,设产品日销售量y(单位:件)与时间t(单位;天)的函数关系为y=,根据日销售利润=日销售量×一件产品的销售利润,即可进行判断.【解答】解:A、根据图①可得第24天的销售量为200件,故正确;B、设当0≤t≤20,一件产品的销售利润z(单位:元)与时间t(单位:天)的函数关系为z=kx+b,把(0,25),(20,5)代入得:,解得:,∴z=﹣x+25,当x=10时,y=﹣10+25=15,故正确;C、当0≤t≤24时,设产品日销售量y(单位:件)与时间t(单位;天)的函数关系为y=k1t+b1,把(0,100),(24,200)代入得:,解得:,∴y=,当t=12时,y=150,z=﹣12+25=13,∴第12天的日销售利润为;150×13=1950(元),第30天的日销售利润为;150×5=750(元),750≠1950,故C错误;D、第30天的日销售利润为;150×5=750(元),故正确.故选:C【点评】本题考查了一次函数的应用,解决本题的关键是利用待定系数法求函数解析式.二、填空题5.一食堂需要购买盒子存放食物,盒子有A,B两种型号,单个盒子的容量和价格如表.现有15升食物需要存放且要求每个盒子要装满,由于A型号盒子正做促销活动:购买三个及三个以上可一次性返还现金4元,则一次性购买盒子所需要最少费用为29元.型号A B单个盒子容量(升)23单价(元)56【考点】一次函数的应用.【分析】设购买A种型号盒子x个,购买盒子所需要费用为y元,则购买B种盒子的个数为个,分两种情况讨论:①当0≤x<3时;②当3≤x时,利用一次函数的性质即可解答.【解答】解:设购买A种型号盒子x个,购买盒子所需要费用为y元,则购买B种盒子的个数为个,①当0≤x<3时,y=5x+=x+30,∵k=1>0,∴y随x的增大而增大,∴当x=0时,y有最小值,最小值为30元;②当3≤x时,y=5x+﹣4=26+x,∵k=1>0,∴y随x的增大而增大,∴当x=3时,y有最小值,最小值为29元;综合①②可得,购买盒子所需要最少费用为29元.故答案为:29.【点评】本题考查了一次函数的应用,解决本题的关键是根据题意列出函数解析式,利用一次函数的性质解决最小值的问题,注意分类讨论思想的应用.6.如图1,在某个盛水容器内,有一个小水杯,小水杯内有部分水,现在匀速持续地向小水杯内注水,注满小水杯后,继续注水,小水杯内水的高度y(cm)和注水时间x(s)之间的关系满足如图2中的图象,则至少需要5s能把小水杯注满.【考点】一次函数的应用.【分析】一次函数的首先设解析式为:y=kx+b,然后利用待定系数法即可求得其解析式,再由y=11,即可求得答案.【解答】解:设一次函数的首先设解析式为:y=kx+b,将(0,1),(2,5)代入得:,解得:,∴解析式为:y=2x+1,当y=11时,2x+1=11,解得:x=5,∴至少需要5s能把小水杯注满.故答案为:5.【点评】此题考查了一次函数的实际应用问题.注意求得一次函数的解析式是关键.7.如图所示,购买一种苹果,所付款金额y(元)与购买量x(千克)之间的函数图象由线段OA和射线AB组成,则一次购买3千克这种苹果比分三次每次购买1千克这种苹果可节省2元.【考点】一次函数的应用.【分析】根据函数图象,分别求出线段OA和射线AB的函数解析式,即可解答.【解答】解:由线段OA的图象可知,当0<x<2时,y=10x,1千克苹果的价钱为:y=10,设射线AB的解析式为y=kx+b(x≥2),把(2,20),(4,36)代入得:,解得:,∴y=8x+4,当x=3时,y=8×3+4=28.当购买3千克这种苹果分三次分别购买1千克时,所花钱为:10×3=30(元),30﹣28=2(元).则一次购买3千克这种苹果比分三次每次购买1千克这种苹果可节省2元.【点评】本题考查了一次函数的应用,解决本题的关键是分别求出线段OA和射线AB 的函数解析式.三、解答题8.“六一”期间,小张购进100只两种型号的文具进行销售,其进价和售价之间的关系如下表:型号进价(元/只)售价(元/只)A型1012B型1523(1)小张如何进货,使进货款恰好为1300元?(2)要使销售文具所获利润最大,且所获利润不超过进货价格的40%,请你帮小张设计一个进货方案,并求出其所获利润的最大值.【考点】一次函数的应用;一元一次方程的应用;一元一次不等式的应用.【分析】(1)设A文具为x只,则B文具为(100﹣x)只,根据题意列出方程解答即可;(2)设A文具为x只,则B文具为(100﹣x)只,根据题意列出函数解答即可.【解答】解:(1)设A文具为x只,则B文具为(100﹣x)只,可得:10x+15(100﹣x)=1300,解得:x=40.答:A文具为40只,则B文具为100﹣40=60只;(2)设A文具为x只,则B文具为(100﹣x)只,可得(12﹣10)x+(23﹣15)(100﹣x)≤40%[10x+15(100﹣x)],解得:x≥50,设利润为y,则可得:y=(12﹣10)x+(23﹣15)(100﹣x)=2x+800﹣8x=﹣6x+800,因为是减函数,所以当x=50时,利润最大,即最大利润=﹣50×6+800=500元.【点评】此题考查一次函数的应用,关键是根据题意列出方程和不等式,根据函数是减函数进行解答.9.已知某市的光明中学、市图书馆和光明电影院在同一直线上,它们之间的距离如图所示.小张星期天上午带了75元现金先从光明中学乘出租车去了市图书馆,付费9元;中午再从市图书馆乘出租车去了光明电影院,付费12.6元.若该市出租车的收费标准是:不超过3公里计费为m元,3公里后按n元/公里计费.(1)求m,n的值,并直接写出车费y(元)与路程x(公里)(x>3)之间的函数关系式;(2)如果小张这天外出的消费还包括:中午吃饭花费15元,在光明电影院看电影花费25元.问小张剩下的现金够不够乘出租车从光明电影院返回光明中学?为什么?【考点】一次函数的应用.【分析】(1)根据题意,不超过3公里计费为m元,由图示可知光明中学和市图书馆相距2公里,可由此得出m,由出租车的收费标准是:不超过3公里计费为m元,3公里后按n元/公里计费.当x>3时,由收费与路程之间的关系就可以求出结论;(2)分别计算小张所剩钱数和返程所需钱数,即可得出结论.【解答】解:(1)∵由图示可知光明中学和市图书馆相距2公里,付费9元,∴m=9,∵从市图书馆乘出租车去光明电影院,路程5公里,付费12.6元,∴(5﹣3)n+9=12.6,解得:n=1.8.∴车费y(元)与路程x(公里)(x>3)之间的函数关系式为:y=1.8(x﹣3)+9=1.8x+3.6(x>3).(2)小张剩下坐车的钱数为:75﹣15﹣25﹣9﹣12.6=13.4(元),乘出租车从光明电影院返回光明中学的费用:1.8×7+3.6=16.2(元)∵13.4<16.2,故小张剩下的现金不够乘出租车从光明电影院返回光明中学.【点评】本题考查了分段函数,一次函数的解析式,由一次函数的解析式求自变量和函数值,解答时求出函数的解析式是关键10.某物流公司承接A、B两种货物运输业务,已知5月份A货物运费单价为50元/吨,B货物运费单价为30元/吨,共收取运费9500元;6月份由于油价上涨,运费单价上涨为:A货物70元/吨,B货物40元/吨;该物流公司6月承接的A种货物和B种数量与5月份相同,6月份共收取运费13000元.(1)该物流公司月运输两种货物各多少吨?(2)该物流公司预计7月份运输这两种货物330吨,且A货物的数量不大于B货物的2倍,在运费单价与6月份相同的情况下,该物流公司7月份最多将收到多少运输费?【考点】二元一次方程组的应用;一元一次不等式的应用.【分析】(1)设A种货物运输了x吨,设B种货物运输了y吨,根据题意可得到一个关于x的不等式组,解方程组求解即可;(2)运费可以表示为x的函数,根据函数的性质,即可求解.【解答】解:(1)设A种货物运输了x吨,设B种货物运输了y吨,依题意得:,解之得:.答:物流公司月运输A种货物100吨,B种货物150吨.(2)设A种货物为a吨,则B种货物为(330﹣a)吨,依题意得:a≤(330﹣a)×2,解得:a≤220,设获得的利润为W元,则W=70a+40(330﹣a)=30a+13200,根据一次函数的性质,可知W随着a的增大而增大当W取最大值时a=220,即W=19800元.所以该物流公司7月份最多将收到19800元运输费.【点评】本题考查二元一次方程组的应用和一元一次不等式组以及一次函数性质的应用,将现实生活中的事件与数学思想联系起来,读懂题意列出方程组和不等式即可求解.11.联通公司手机话费收费有A套餐(月租费15元,通话费每分钟0.1元)和B套餐(月租费0元,通话费每分钟0.15元)两种.设A套餐每月话费为y1(元),B套餐每月话费为y2(元),月通话时间为x分钟.(1)分别表示出y1与x,y2与x的函数关系式.(2)月通话时间为多长时,A、B两种套餐收费一样?(3)什么情况下A套餐更省钱?【考点】一次函数的应用.【分析】(1)根据A套餐的收费为月租加上话费,B套餐的收费为话费列式即可;(2)根据两种收费相同列出方程,求解即可;(3)根据(2)的计算结果,小于收费相同时的时间选择B套餐,大于收费相同的时间选择A套餐解答.【解答】解:(1)A套餐的收费方式:y1=0.1x+15;B套餐的收费方式:y2=0.15x;(2)由0.1x+15=0.15x,得到x=300,答:当月通话时间是300分钟时,A、B两种套餐收费一样;(3)由0.1x+15<0.15x,得到x>300,当月通话时间多于300分钟时,A套餐更省钱.【点评】本题考查了一次函数的应用,是典型的电话收费问题,求出两种收费相同的时间是确定选择不同的缴费方式的关键.12.某工厂现有甲种原料360千克,乙种原料290千克,计划用这两种原料全部生产A、B两种产品共50件,生产A、B两种产品与所需原料情况如下表所示:原料甲种原料(千克)乙种原料(千克)型号A产品(每件)93B产品(每件)410(1)该工厂生产A、B两种产品有哪几种方案?(2)若生成一件A产品可获利80元,生产一件B产品可获利120元,怎样安排生产可获得最大利润?【考点】一次函数的应用;一元一次不等式组的应用.【分析】(1)设工厂可安排生产x件A产品,则生产(50﹣x)件B产品,根据不能多于原料的做为不等量关系可列不等式组求解;(2)可以分别求出三种方案比较即可.【解答】解:(1)设工厂可安排生产x件A产品,则生产(50﹣x)件B产品由题意得:,解得:30≤x≤32的整数.∴有三种生产方案:①A30件,B20件;②A31件,B19件;③A32件,B18件;(2)方法一:方案(一)A,30件,B,20件时,20×120+30×80=4800(元).方案(二)A,31件,B,19件时,19×120+31×80=4760(元).方案(三)A,32件,B,18件时,18×120+32×80=4720(元).故方案(一)A,30件,B,20件利润最大.【点评】本题考查理解题意的能力,关键是根据有甲种原料360千克,乙种原料290千克,做为限制列出不等式组求解,然后判断B生产的越多,A少的时候获得利润最大,从而求得解.。
2024年中考数学总复习:一次函数(附答案解析)
②每分钟出水3.75L;
③容器中水为25L的时间是8min或 min;
④第2或 min时容器内的水恰为10升;
错误的有( )
A.0个B.1个C.2个D.3个
25.甲、乙两人同时从家里出发,沿同一条笔直的公路向公园进行跑步训练,乙的家比甲的家离公园近100米,5分钟后甲追上乙.此时乙将速度提高到原来的速度的2倍,又经过15分钟后,乙先到达公园并立即返回,但因体力不支,乙返回时的速度又降低到原来的速度,甲跑到公园后也立即掉头回家,整个过程中,甲的速度始终保持不变,甲、乙两人相距的路程y(米)与甲出发的时间x(分钟)之间的部分函数关系如图所示,则当乙回到家时,甲离自己的家还有( )
A.30元B.20元C.15元D.10元
19.把y=2x+1的图象沿y轴向下平移5个单位后所得图象的关系式是( )
A.y=2x+5B.y=2x+6C.y=2x﹣4D.y=2x+4
20.正比例函数y=kx(k≠0)的函数值y随x的增大而增大,则一次函数y=﹣x﹣k的图象是( )
A. B.
C. D.
21.已知函数y=kx+b的图象如图所示,则函数y=﹣bx+k的图象大致是( )
A.±2B.﹣2C.2D.3
6.已知一次函数y=kx﹣2,若y随x的增大而减小,则它的图象经过( )
A.第一、二、三象限B.第一、二、四象限
C.第二、三、四象限D.第一、三、四象限
7.A,B两地相距30km,甲乙两人沿同一条路线从A地到B地.如图,反映的是两人行进路程y(km)与行进时间t(h)之间的关系,①甲始终是匀速行进,乙的行进不是匀速的;②乙用了4.5个小时到达目的地;③乙比甲迟出发0.5小时;④甲在出发5小时后被乙追上,以上说法正确的个数有( )
中考数学复习《一次函数》专项练习题-附带有答案

中考数学复习《一次函数》专项练习题-附带有答案一、单选题1.在函数y=√9−3x中,自变量x的取值范围是()A.x≤3B.x<3C.x≥3D.x>32.已知一次函数y=kx−3(k≠0),若y随x的增大而减小,则它的图象经过()A.第一、二、三象限B.第一、二、四象限C.第二、三、四象限D.第一、三、四象限3.实数k、b满足kb﹥0,不等式kx<b的解集是x>bk那么函数y=kx+b的图象可能是()A.B.C.D.4.如图,函数y=2x和y=ax+4的图象相交于点A(m,3),则不等式2x≥ax+4的解集为()A.x≥32B.x≤3 C.x≤32D.x≥35.如图,在平面直角坐标系中,直线y=- 32x+3与矩形OABC的边AB、BC分别交于点E、F,若点B的坐标为(m,2),则m的值可能为()A.12B.32C.52D.726.如图,等边△ABC 的顶点A 在y 轴上,顶点B 、C 在x 轴上,直线y =−√3x +√3经过点A 、C ,则等边△ABC 的面积是( )A .4B .2√3C .√5D .√37. 如图,在平面直角坐标系中,一次函数y =kx +b 的图象经过正方形OABC 的顶点A 和C ,已知点A 的坐标为(1,−2),则k 的值为( )A .1B .2C .3D .48.市自来水公司为鼓励居民节约用水,采取月用水量分段收费办法,某户居民应交水费y(元)与用水量x(吨)的函数关系如图,若该用户本月用水21吨,则应交水费( )A .52.5元B .48方C .45元D .42元二、填空题9.函数y= 32 x+m 与y=﹣ 12 x+n 均经过点A (﹣2,0),且与y 轴交于B 、C ,则S △ABC = . 10.已知一次函数y =kx +b (k ≠0)经过(2,-1),(-3,4)两点,则其图象不经过第 象限. 11.现有一小树苗高100cm ,以后平均每年长高50cm .x 年后树苗的总高度y (cm )与年份x (年)的关系式是 .12.如图,函数y =2x +b 与函数y =kx −1的图象交于点P ,关于x 的不等式kx −1<2x +b 的解集是 .13.甲、乙两车从A城出发匀速行驶至B城,在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与行驶时间x(小时)之间的函数关系如图所示,已知甲对应的函数关系式为y=60x,根据图象提供的信息可知从乙出发后追上甲车需要小时.三、解答题14.已知实数a满足a+b﹣4<0,b=√(−3)2,当2≤x≤4时,一次函数y=ax+1(a≠0)的最大值与最小值之差是6,求a的值.15.已知两直线l1,l2的位置关系如图所示,请求出以点A的坐标为解的二元一次方程组.16.某商店以40元/千克的单价新进一批茶叶,经调查发现,在一段时间内,销售量y(千克)与销售单价x(元/千克)之间的函数关系如图所示。
中考数学专题复习8一次函数(解析版)

一次函数考点1:一次函数图象与性质1.(2021·辽宁丹东市·中考真题)若实数k 、b 是一元二次方程(3)(1)0x x +-=的两个根.且k b <.则一次函数y kx b =+的图象不经过( ) A .第一象限 B .第二象限C .第三象限D .第四象限【答案】C 【分析】根据一元二次方程的解法求出k 、b 的值.由一次函数的图像即可求得. 【详解】∵实数k 、b 是一元二次方程(3)(1)0x x +-=的两个根.且k b <. ∵3,1k b =-=,∵一次函数表达式为31y x =-+.有图像可知.一次函数不经过第三象限. 故选:C .2.(2021·黑龙江大庆市·中考真题)已知反比例函数ky x=.当0x <时.y 随x 的增大而减小.那么一次的数y kx k =-+的图像经过第( ) A .一.二.三象限 B .一.二.四象限 C .一.三.四象限 D .二.三.四象限【答案】B 【分析】根据反比例函数的增减性得到0k >.再利用一次函数的图象与性质即可求解.解:∵反比例函数ky x=.当0x <时.y 随x 的增大而减小. ∵0k >.∵y kx k =-+的图像经过第一.二.四象限. 故选:B .3.(2021·湖北中考真题)下列说法正确的是( ) A .函数2y x =的图象是过原点的射线 B .直线2y x =-+经过第一、二、三象限C .函数()20y x x=-<.y 随x 增大而增大 D .函数23y x =-.y 随x 增大而减小 【答案】C 【分析】根据一次函数的图象与性质、反比例函数的图象与性质逐项判断即可得. 【详解】A 、函数2y x =的图象是过原点的直线.则此项说法错误.不符题意;B 、直线2y x =-+经过第一、二、四象限.则此项说法错误.不符题意;C 、函数()20y x x=-<.y 随x 增大而增大.则此项说法正确.符合题意; D 、函数23y x =-.y 随x 增大而增大.则此项说法错误.不符题意; 故选:C .4.(2020•成都)一次函数y =(2m ﹣1)x +2的值随x 值的增大而增大.则常数m 的取值范围为 .【分析】先根据一次函数的性质得出关于m 的不等式2m ﹣1>0.再解不等式即可求出m 的取值范围.【解析】∵一次函数y =(2m ﹣1)x +2中.函数值y 随自变量x 的增大而增大.∵2m ﹣1>0.解得m >12.故答案为:m >12.考点2:一次函数解析式的确定5.(2021·甘肃武威市·中考真题)将直线5y x =向下平移2个单位长度.所得直线的表达式为( ) A .52y x =- B .52y x =+C .()52y x =+D .()52y x =-【答案】A只向下平移.让比例系数不变.常数项减去平移的单位即可. 【详解】解:直线5y x =向下平移2个单位后所得直线的解析式为5-2y x = 故选:A6.(2021·安徽)某品牌鞋子的长度y cm 与鞋子的“码”数x 之间满足一次函数关系.若22码鞋子的长度为16cm.44码鞋子的长度为27cm.则38码鞋子的长度为( ) A .23cm B .24cmC .25cmD .26cm【答案】B 【分析】设y kx b =+.分别将()22,16和()44,27代入求出一次函数解析式.把38x =代入即可求解. 【详解】解:设y kx b =+.分别将()22,16和()44,27代入可得:16222744k bk b =+⎧⎨=+⎩. 解得125k b ⎧=⎪⎨⎪=⎩ .∵152y x =+. 当38x =时.1385242y cm =⨯+=.故选:B .7.(2021·陕西中考真题)在平面直角坐标系中.若将一次函数21y x m =+-的图象向左平移3个单位后.得到个正比例函数的图象.则m 的值为( ) A .-5 B .5C .-6D .6【答案】A 【分析】根据函数图像平移的性质求出平移以后的解析式即可求得m 的值. 【详解】解:将一次函数21y x m =+-的图象向左平移3个单位后 得到的解析式为:2(3)1y x m =++-. 化简得:25y x m =++.∵平移后得到的是正比例函数的图像.∵50m+=.解得:5m=-.故选:A.8.(2021·山东中考真题)甲、乙、丙三名同学观察完某个一次函数的图象.各叙述如下:甲:函数的图象经过点(0.1);乙:y随x的增大而减小;丙:函数的图象不经过第三象限.根据他们的叙述.写出满足上述性质的一个函数表达式为_______.【答案】y=-x+1(答案不唯一).【分析】设一次函数解析式为y=kx+b.根据函数的性质得出b=1.k<0.从而确定一次函数解析式.本题答案不唯一.【详解】解:设一次函数解析式为y=kx+b.∵函数的图象经过点(0.1).∵b=1.∵y随x的增大而减小.∵k<0.取k=-1.∵y=-x+1.此函数图象不经过第三象限.∵满足题意的一次函数解析式为:y=-x+1(答案不唯一).9.(2021·四川泸州市·中考真题)一次函数y=kx+b(k≠0)的图像与反比例函数m yx =的图象相交于A(2.3).B(6.n)两点(1)求一次函数的解析式(2)将直线AB沿y轴向下平移8个单位后得到直线l.l与两坐标轴分别相交于M.N.与反比例函数的图象相交于点P.Q.求PQMN的值【答案】(1)一次函数y=142x-+.(2)12PQMN=.【分析】(1)利用点A(2.3).求出反比例函数6yx=.求出B(6.1).利用待定系数法求一次函数解析式;(2)利用平移求出y=142x--.联立1426y xyx⎧=--⎪⎪⎨⎪=⎪⎩.求出P(-6,-1),Q(-2,-3),在Rt∵MON中.由勾股定理MN=45PQ=5【详解】解:(1)∵反比例函数myx=的图象过A(2.3).∵m=6,∵6n=6.∵n=1.∵B(6,1)一次函数y=kx+b(k≠0)的图像与反比例函数6yx=的图象相交于A(2.3).B(6.1)两点.∵61 23 k bk b+=⎧⎨+=⎩.解得124kb⎧=-⎪⎨⎪=⎩.一次函数y=14 2x-+.(2)直线AB沿y轴向下平移8个单位后得到直线l.得y=14 2x--.当y=0时.1402x.8x=-.当x=0时.y=-4.∵M(-8.0).N(0.-4).1426y x y x ⎧=--⎪⎪⎨⎪=⎪⎩. 消去y 得28120x x ++=. 解得122,6x x =-=-. 解得1123x y =-⎧⎨=-⎩.2261x y =-⎧⎨=-⎩.∵P (-6,-1),Q (-2,-3), 在Rt ∵MON 中.∵MN 2245OM ON +=, ∵PQ ()()22261325-++-+=∵251245PQ MN ==.考点3:一次函数与方程、不等式的关系10.(2021·内蒙古赤峰市·中考真题)点(),P a b 在函数43y x =+的图象上.则代数式821a b -+的值等于( )A .5B .-5C .7D .-6【答案】B 【分析】把点P 的坐标代入一次函数解析式可以求得a 、b 间的数量关系.所以易求代数式8a -2b +1的值. 【详解】解:∵点P (a .b )在一次函数43y x =+的图象上. ∵b =4a +3.8a -2b +1=8a -2(4a +3)+1=-5.即代数式821a b -+的值等于-5. 故选:B .11.(2020•乐山)直线y =kx +b 在平面直角坐标系中的位置如图所示.则不等式kx +b ≤2的解集是( )A .x ≤﹣2B .x ≤﹣4C .x ≥﹣2D .x ≥﹣4【分析】根据待定系数法求得直线的解析式.然后求得函数y =2时的自变量的值.根据图象即可求得.【解析】∵直线y =kx +b 与x 轴交于点(2.0).与y 轴交于点(0.1). ∵{2k +b =0b =1.解得{k =−12b =1 ∵直线为y =−12x +1.当y =2时.2=−12x +1.解得x =﹣2.由图象可知:不等式kx +b ≤2的解集是x ≥﹣2. 故选:C .12.(2020•济宁)数形结合是解决数学问题常用的思想方法.如图.直线y =x +5和直线y =ax +b 相交于点P .根据图象可知.方程x +5=ax +b 的解是( )A .x =20B .x =5C .x =25D .x =15【分析】两直线的交点坐标为两直线解析式所组成的方程组的解. 【解析】∵直线y =x +5和直线y =ax +b 相交于点P (20.25) ∵直线y =x +5和直线y =ax +b 相交于点P 为x =20.故选:A .考点4:一次函数的实际应用13.(2021·甘肃武威市·中考真题)如图1.小刚家.学校、图书馆在同一条直线上.小刚骑自行车匀速从学校到图书馆.到达图书馆还完书后.再以相同的速度原路返回家中(上、下车时间忽略不计).小刚离家的距离()m y 与他所用的时间()min x 的函数关系如图2所示.(1)小刚家与学校的距离为___________m .小刚骑自行车的速度为________m/min ; (2)求小刚从图书馆返回家的过程中.y 与x 的函数表达式; (3)小刚出发35分钟时.他离家有多远?【答案】(1)3000.200;(2)()20090002045y x x =-+≤≤;(3)2000m 【分析】(1)从起点处为学校出发去处为图书馆.可求小刚家与学校的距离为3000m.小刚骑自行车匀速行驶10分钟.从3000m 走到5000m 可求骑自行车的速度即可; (2)求出从图书馆出发时的时间与路程和回到家是的时间与路程.利用待定系数法求解析式即可;(3)小刚出发35分钟.在返回家的时间内.利用函数解析式求出当35x =时.函数值即可. 【详解】解:(1)小刚骑自行车匀速从学校到图书馆.从起点3000m 处为学校出发去5000m 处为图书馆.∵小刚家与学校的距离为3000m.小刚骑自行车匀速行驶10分钟.从3000m 走到5000m. 行驶的路程为5000-3000=2000m. 骑自行车的速度为2000÷10=200m/min. 故答案为:3000.200;(2)小刚从图书馆返回家的时间:()500020025min ÷=.总时间:()252045min +=. 设返回时y 与x 的函数表达式为y kx b =+. 把()()20,5000,45,0代入得:205000450k b k b +=⎧⎨+=⎩.解得.2009000k b =-⎧⎨=⎩.()20090002045y x x ∴=-+≤≤.(3)小刚出发35分钟.即当35x =时.2003590002000y =-⨯+=.答:此时他离家2000m .14.(2021·贵州毕节市·中考真题)某中学计划暑假期间安排2名老师带领部分学生参加红色旅游.甲、乙两家旅行社的服务质量相同,且报价都是每人1000元,经协商,甲旅行社的优惠条件是:老师、学生都按八折收费:乙旅行社的优惠条件是:两位老师全额收费,学生都按七五折收费,(1)设参加这次红色旅游的老师学生共有x 名,y 甲,y 乙(单位:元)分别表示选择甲、乙两家旅行社所需的费用,求y 甲,y 乙关于x 的函数解析式; (2)该校选择哪家旅行社支付的旅游费用较少?【答案】(1)甲800y x = ,乙750500y x =+ (2)当学生人数超过10人时,选择乙旅行社支付的旅游费最少;当学生人数少于10人时,选择甲旅行社支付的旅游费最少;学生人数等于10人时,选择甲、乙旅行社支付费用相等. 【分析】(1)根据旅行社的收费=老师的费用+学生的费用,再由总价=单价×数量就可以得出y 甲 、y 乙与x 的函数关系式;(2)根据(1)的解析式,若y y =甲乙,y y >甲乙,y y <甲乙,分别求出相应x 的取值范围,即可判断哪家旅行社支付的旅游费用较少. 【详解】 (1)由题意,得甲10000.8800y x x =⨯⨯=,乙1000210000.75(2)750500y x x =⨯+⨯-=+,答:y 甲 、y 乙 与x 的函数关系式分别是: 甲800y x = ,乙750500y x =+(2)当y y =甲乙时,800750500x x =+,解得10x = , 当y y >甲乙时,800750500x x =+,解得10x >, 当y y <甲乙时,800750500x x =+,解得10x <,答:当学生人数超过10人时,选择乙旅行社支付的旅游费最少;当学生人数少于10人时,选择甲旅行社支付的旅游费最少;学生人数等于10人时,选择甲、乙旅行社支付费用相等.15.(2021·辽宁大连市·中考真题)如图.四边形ABCD 为矩形.3AB =.4BC =.P 、Q 均从点B 出发.点P 以2个单位每秒的速度沿BA AC -的方向运动.点Q 以1个单位每秒的速度沿BC CD -运动.设运动时间为t 秒. (1)求AC 的长; (2)若BPQSS =.求S 关于t 的解析式.【答案】(1)5AC =;(2)223,023123,455228,4t t S t t t t t ⎧≤≤⎪⎪⎪=-+<≤⎨⎪->⎪⎪⎩【分析】(1)由题意易得90B ∠=︒.然后根据勾股定理可求解; (2)由题意易得∵当点P 在AB 上时.即302t ≤≤.则2,BP t BQ t ==.∵当点P 在AC 上.点Q 在BC 上时.即342t <≤.过点P 作PE ∵BC 于点E .然后可得()382,825PC t PE t =-=-.∵当点P 与点C 重合.点Q 在CD 上时.即4t >.则有4,7BP CQ t ==-.进而根据面积计算公式可求解.【详解】解:(1)∵四边形ABCD 是矩形.∵90B ∠=︒.∵3AB =.4BC =. ∵225AC AB +BC ;(2)由题意得当点P 到达点C 时.点Q 恰好到达点C .则有:当点P 在AB 上时.即302t ≤≤.如图所示:∵2,BP t BQ t ==. ∵211222S BP BQ t t t =⋅=⨯⨯=; 当点P 在AC 上.点Q 在BC 上时.即342t <≤.过点P 作PE ∵BC 于点E .如图所示:∵82PC t =-.由(1)可得3sin 5PCE ∠=. ∵()3sin 825PE CP PCE t =⋅∠=-. ∵()21133128222555S BQ PE t t t t =⋅=⨯⨯-⨯=-+; 当点P 与点C 重合.点Q 在CD 上时.即4t >.如图所示:∵4,4BP CQ t ==-. ∵()11442822S BP PQ t t =⋅=⨯⨯-=-; 综上所述:S 关于t 的解析式为223,023123,455228,4t t S t t t t t ⎧≤≤⎪⎪⎪=-+<≤⎨⎪->⎪⎪⎩. 16.(2021·黑龙江绥化市·中考真题)小刚和小亮两人沿着直线跑道都从甲地出发.沿着同一方向到达乙地.甲乙两地之间的距离是720米.先到乙地的人原地休息.已知小刚先从甲地出发4秒后.小亮从甲地出发.两人均保持匀速前行.第一次相遇后.保持原速跑一段时间.小刚突然加速.速度比原来增加了2米/秒.并保持这一速度跑到乙地(小刚加速过程忽略不计).小刚与小亮两人的距离S (米)与小亮出发时间t (秒)之间的函数图象.如图所示.根据所给信息解决以下问题.(1)m =_______.n =______;(2)求CD 和EF 所在直线的解析式;(3)直接写出t 为何值时.两人相距30米.【答案】(1)160163,;(2)80(4880)CD S t t =-+≤≤;40057201443EF S t t ⎛⎫-+≤≤ ⎝=⎪⎭;(3)t 为46 .50.110.138时.两人相距30米.【分析】(1)依次分析A 、B 、C 、D 、E 、F 各点坐标的实际意义:A 点是小刚先走了4秒.B 点小亮追上小刚.相遇.C 点是小刚开始加速.D 点是小刚追上小亮.E 点是小刚到达乙地.F 点是小亮到达乙地.则根据A 点的意义.可以求出m 的值.根据E 点的意义可以求出n 的值;(2)根据题意分别求得C 、D 、E 、F 各点坐标.代入直线解析式.用待定系数法求得解析式;(3)根据题意分别求出写出,,,BC CD DE EF 四 条直线的解析式.令S=30.即可求解.【详解】(1)∵小刚原来的速度1644=÷=米/秒.小亮的速度7201445=÷=米/秒B 点小亮追上小刚.相遇4165m m ∴⨯+=⨯=16m ∴E 点是小刚到达乙地720805160[(80)80](65)423-⨯∴+-⨯-=+ 1603n ∴=. (2)由题意可知点C 横坐标为801616482-+= ∵小刚原来的速度1644=÷=米/秒.小亮的速度7201445=÷=米/秒∵纵坐标为()()54481632-⨯-=()48,32C ∴设11(48,32)(80,0)CD S k t b C D =+,,11114832800k b k b +=⎧⎨+=⎩ 解得:11180k b =-⎧⎨=⎩ 80(4880)CD S t t ∴=-+≤≤E 的横坐标为7208054008063-⨯+= E 的纵坐标为40016080(65)33⎛⎫--= ⎪⎝⎭400160(,)33E ∴ (144,0)F 设22EF S k t b =+代入可得2222400160331440k b k b ⎧+=⎪⎨⎪+=⎩ 解得:225720k b =-=40057201443EF S t t =⎛⎫∴-+≤≤ ⎪⎝⎭. (3)(16,0)B ,()48,32C .(80,0)D .400160(,)33E .(144,0)F 设33(48,32)(16,0)BC S k t b C B =+,, 33334832160k b k b +=⎧⎨+=⎩ 解得:33=16k b -=1, ()161648BC S t t ∴<≤=- 设44400160(80,0),(,)33DE S k t b D E =+, 444440016033800k b k b ⎧+=⎪⎨⎪+=⎩ 解得:441,80k b ==-40083008DE S t t ⎛⎫∴<≤ ⎪⎝=⎭- 当S=30时 1630,46BC S t t =-==. 8030,50CD S t t =-+==. 80=30,110DE S t t =-=. 5720=30,138EF S t t -+== ∴t 为46 .50.110.138时.两人相距30米.。
中考数学《一次函数》专题训练(附带答案)

中考数学《一次函数》专题训练(附带答案)一、单选题1.已知一次函数y =(1﹣a )x+2a+1的图象经过第二象限,则a 的值可以是( )A .﹣2B .﹣1C .0D .12.如图,直线y =k 1x +b 1和直线y =k 2x +b 2相交于点M(23,−2),则关于x ,y 的方程组{y =k 1x +b 1y =k 2x +b 2,的解为( )A .{x =23,y =−2 B .{x =−2,y =23C .{x =23,y =2D .{x =−2,y =−233.若一次函数y=(3-k )x -k 的图象经过第二、三、四象限,则k 的取值范围是 ( )A .k >3B .0<k≤3C .0≤k <3D .0<k <34.如图,一直线与两坐标轴的正半轴分别交于A ,B 两点,P 是线段AB 上任意一点(不包括端点),过P 分别作两坐标轴的垂线与两坐标轴围成的矩形的周长为10,则该直线的函数表达式是( )A .y=x+5B .y=x+10C .y=﹣x+5D .y=﹣x+105.设min{x ,y}表示x ,y 两个数中的最小值,例如min{0,2}=0,min{12,8}=8,则关于x 的函数y=min{2x ,x+2}可以表示为( ) A .y={2x(x <2)x +2(x ≥2)B .y={x +2(x <2)2x(x ≥2)C .y=2xD .y=x+26.已知一次函数y=kx ﹣1,若y 随x 的增大而增大,则该函数的图象不经过( )A.第一象限B.第二象限C.第三象限D.第四象限7.已知k≠0,在同一坐标系中,函数y=k(x+1)与y= k x的图象大致为如图所示中的()A.B.C.D.8.下列函数中,当x>0时,y随x的增大而增大的是()A.y=-x+1B.y=x2-1C.y=1x D.y=-x2+19.下列y关于x的函数中,是正比例函数的为()A.y=x2B.y=2x C.y=x2D.y=x+1210.如图,在平面直角坐标系中,O为坐标原点,直线y=−x+4√2与x轴交于B点,与y轴交于A点,点C,D在线段AB上,且CD=2AC=2BD,若点P在坐标轴上,则满足PC+PD=7的点P的个数是()A.4B.3C.2D.111.已知在一次函数y=﹣1.5x+3的图象上,有三点(﹣3,y1)、(﹣1,y2)、(2,y3),则y1,y2,y3的大小关系为()A.y1>y2>y3B.y1>y3>y2C.y2>y1>y3D.无法确定12.一次函数y=(k-3)x|k|-2+2的图象不经过()A.第一象限B.第二象限C.第三象限D.第四象限二、填空题13.已知一次函数 y =(k +1)x −b ,若y 随x 的增大而减小,则k 的取值范围是 . 14.如图,一次函数与反比例函数的图象分别是直线 AB 和双曲线.直线 AB 与双曲线的一个交点为点 C ,CD ⊥x 轴于点 D ,OD =2OB =4OA =4 ,则此反比例函数的解析式为 .15.一次函数 y 1=k 1x +b 1 与 y 2=k 2x +b 2 的图象如图,则不等式组 {k 1x +b 1≤0k 2x +b 2>0 的解为 .16.若点 (m,n) 若在直线 y =3x −2 上,则代数式2n -6m+1的值是 .17.已知一次函数y =﹣x ﹣(a ﹣2)中,当a 时,该函数的图象与y 轴的交点坐标在x 轴的下方.18.已知一次函数 y =ax +|a −1| 的图象经过点(0,3),且函数y 的值随x 的增大而减小,则a 的值为 .三、综合题19.甲、乙两车分别从相距480千米的 A 、 B 两地相向而行,乙车比甲车先出发1小时,并以各自的速度匀速行驶,途经 C 地,甲车到达 C 地停留1小时,因有事按原路原速返回 A 地.乙车从 B 地直达 A 地,两车同时到达 A 地.甲、乙两车距各自出发地的路程 y (千米)与甲车出发后所用的时间 x (时)的函数图象如图所示.(1)求t的值;(2)求甲车距它出发地的路程y与x之间的函数关系式;(3)求两车相距120千米时乙车行驶的时间.20.根据对某市相关的市场物价调研,预计进入夏季后的某一段时间,某批发市场内的甲种蔬菜的销售利润y1(千元)与进货量x(吨)之间的函数y1=kx的图象如图①所示,乙种蔬菜的销售利润y2(千元)与进货量x(吨)之间的函数y2=ax2+bx的图象如图②所示.(1)分别求出y1、y2与x之间的函数关系式;(2)如果该市场准备进甲、乙两种蔬菜共10吨,设乙种蔬菜的进货量为t吨.①写出这两种蔬菜所获得的销售利润之和W(千元)与t(吨)之间的函数关系式.并求当这两种蔬菜各进多少吨时获得的销售利润之和最大,最大利润是多少元?②为了获得两种蔬菜的利润之和不少于8400元,则乙种蔬菜进货量应在什么范围内合适?21.已知一次函数y=-2x-2.(1)画出函数的图象;(2)求图象与x轴,y轴的交点A,B的坐标;(3)求A,B两点之间的距离;(4)求△AOB的面积;(5)当x为何值时,y≥0(利用图象解答)?22.在平面直角坐标系中,一次函数y=x+3的图象与x轴交于点A,二次函数y=x2+mx+n的图象经过点A.(1)当m=4时,求n的值;(2)设m=﹣2,当﹣3≤x≤0时,求二次函数y=x2+mx+n的最小值;(3)当﹣3≤x≤0时,若二次函数﹣3≤x≤0时的最小值为﹣4,求m、n的值.23.同时点燃甲乙两根蜡烛,蜡烛燃烧剩下的长度y(cm)与燃烧时间x(min)的关系如图所示.(1)求点P的坐标,并说明其实际意义;(2)求点燃多长时间,甲蜡烛剩下长度是乙蜡烛剩下长度的1.1倍.24.冰墩墩是2022年北京冬季奥运会的吉样物.冬奥会来临之际,冰墩墩玩偶非常畅销.小张在某网店选中A,B两款冰墩墩玩偶,决定用900元(全部用完)从该网店进货并销售.两款玩偶的进货价和销售价如下表:A款玩偶B款玩偶进货价(元/个)2520销售价(元/个)3325(1)求y与x之间的函数表达式;(2)如果小张购进A款玩偶20个,那么这次进货全部售完,能盈利多少元?参考答案1.【答案】C 2.【答案】A 3.【答案】A 4.【答案】C 5.【答案】A 6.【答案】B 7.【答案】D 8.【答案】B 9.【答案】C 10.【答案】A 11.【答案】A 12.【答案】C 13.【答案】k <−1 14.【答案】y =−4x15.【答案】x≤-4 16.【答案】-3 17.【答案】>2 18.【答案】-219.【答案】(1)由函数图象得:乙车的速度为:60÷1=60(千米/小时),甲车从A 地出发至返回A 地的时间为:(480−60)÷60=420÷60=7(小时) ∴t =(7−1)÷2=3 即t 的值是3;(2)当0≤x≤3时,设y 与x 的函数关系式为y =kx , 则360=3k ,解得k =120∴当0≤x≤3时,y 与x 的函数关系式为:y =120x 当3<x≤4时,y =360当4<x≤7,设y 与x 的函数关系式为:y =ax +b 则 {4a +b =3607a +b =0 解得: {a =−120b =840∴当4<x≤7,y与x的函数关系式为:y=−120x+840由上可得,y与x的函数关系式为:y={120x(0≤x≤3) 360(3<x≤4)−120x+840(4<x≤7)(3)设乙车行驶的时间为m小时时,两车相距120千米,乙车的速度为60千米/小时,甲车的速度为360÷3=120(千米/小时)甲乙第一次相遇前,60+(60+120)×(m−1)+120=480,得m=8 3甲乙第一次相遇之后,60+(60+120)×(m−1)=480+120,得m=4甲车返回A地的过程中,当m=5时,两车相距5×60-(480-360)=180(千米)∴(120−60)×(m−5)=180−120得m=6答:两车相距120千米时乙车行驶的时间是83小时、4小时或6小时.20.【答案】(1)解:由题意得,设y1=kx5k=3∴k=0.6∴y1=0.6x根据题意得,设y2=ax2+bx+c,由图知,抛物线经过点(0,0)、(1,2)、(5,6),代入得{c=0a+b+c=2 25a+5b+c=6∴{a=−0.2b=2.2c=0∴y2=−0.2x2+2.2x;(2)解:①设乙种蔬菜的进货量为t吨,w=y1+y2=0.6(10−t)+(−0.2t2+2.2t)=−0.2t2+1.6t+6=−0.2(t−4)2+9.2当t=4,利润之和最大W最大=9200(元)答:当乙种蔬菜进货4吨,甲种蔬菜进货6吨,利润之和最大,最大9200元.②w=y1+y2=−0.2t2+1.6t+6当w≥8.4时,即−0.2t2+1.6t+6≥8.4∴−0.2t2+1.6t−2.4≥0令−0.2t2+1.6t−2.4=0t2−8t−12=0(t−2)(t−6)=0解得t1=2,t2=6因为抛物线开口向下,所以2≤t≤6答:乙种蔬菜进货量为2吨到6吨范围内.21.【答案】(1)解:列表:x……-10……y……0-2……(2)解:由(1)可得该图象与x轴,y轴的交点坐标分别为A(-1,0),B(0,-2).(3)解:A,B两点之间的距离为√OA2+OB2=√12+22=√5(4)解:S△AOB= 12OA·OB=12×1×2= 1(5)解:由(1)中图象可得,当x≤-1时,y≥0.22.【答案】(1)解:当y=x+3=0时,x=﹣3∴点A 的坐标为(﹣3,0).∵二次函数y=x 2+mx+n 的图象经过点A ∴0=9﹣3m+n ,即n=3m ﹣9 ∴当m=4时,n=3m ﹣9=3.(2)解:抛物线的对称轴为直线x=﹣ m 2当m=﹣2时,对称轴为x=1,n=3m ﹣9=﹣15 ∴当﹣3≤x≤0时,y 随x 的增大而减小∴当x=0时,二次函数y=x 2+mx+n 的最小值为﹣15.(3)解:①当对称轴﹣ m2 ≤﹣3,即m≥6时,如图1所示.在﹣3≤x≤0中,y=x 2+mx+n 的最小值为0,∴此情况不合题意;②当﹣3<﹣ m2 <0,即0<m <6时,如图2,有 {4n−m 24=49−3m +n =0解得: {m =2n =−3 或 {m =10n =21(舍去)∴m=2、n=﹣3;③当﹣ m2 ≥0,即m≤0时,如图3有 {n =−49−3m +n =0 ,解得: {m =53n =−4(舍去).综上所述:m=2,n=﹣3. 23.【答案】(1)解:设乙蜡烛剩下的长度y 与燃烧时间x 的函数表达式为y=kx+b ,得:{b =4050k +b =0 ,解得: {k =−0.8b =40,即乙蜡烛剩下的长度y 与燃烧时间x 的函数表达式为y=﹣0.8x+40,将x=20代入得y=24,故P (20,24)该点表示的实际意义是点燃20分钟后,两支蜡烛剩下的长度都是24cm ; (2)解:设甲蜡烛剩下的长度y 甲与x 之间的函数表达式为y 甲=mx+n ,得: {48=n 24=20m +n,解得: {m =−1.2n =48 ,∴y 甲与x 之间的函数表达式为y 甲=﹣1.2x+48.∵甲蜡烛剩下长度是乙蜡烛剩下长度的1.1倍,∴﹣1.2x+48=1.1(﹣0.8x+40),解得:x=12.5. 答:点燃12.5分钟,甲蜡烛剩下长度是乙蜡烛剩下长度的1.1倍24.【答案】(1)解:由题意,得25x +20y =900∴y =−54x +45;(2)解:当x =20时,则y =−54×20+45=20∴这次进货全部售完,能盈利=20(33−25)+20(25−20)=260(元) 答:这次进货全部售完,能盈利260元.。
函数的基本性质-- 一次函数(解析版)-中考数学重难点题型专题汇总

函数的基本性质-中考数学重难点题型一次函数(专题训练)1.一次函数(21)2y m x =-+的值随x 的增大而增大,则点(,)P m m -所在象限为()A .第一象限B .第二象限C .第三象限D .第四象限【答案】B【分析】根据一次函数的性质求出m 的范围,再根据每个象限点的坐标特征判断P 点所处的象限即可.【详解】∵一次函数(21)2y m x =-+的值随x 的增大而增大,∴210m ->解得:12m >∴(,)P m m -在第二象限故选:B 【点睛】本题考查了一次函数的性质和各个象限坐标特点,能熟记一次函数的性质是解此题的关键.2.已知点)Am ,3,2B n ⎛⎫ ⎪⎝⎭在一次函数21y x =+的图像上,则m 与n 的大小关系是()A .m n>B .m n =C .m n <D .无法确定【答案】C【分析】根据一次函数的增减性加以判断即可.【详解】解:在一次函数y=2x+1中,∵k=2>0,∴y 随x 的增大而增大.∵2<94,32<.∴m<n .故选:C【点睛】本题考查了一次函数的性质、实数的大小比较等知识点,熟知一次函数的性质是解题的关键3.已知一次函数y =kx+3的图象经过点A ,且y 随x 的增大而减小,则点A 的坐标可以是()A .(﹣1,2)B .(1,﹣2)C .(2,3)D .(3,4)【分析】由点A 的坐标,利用一次函数图象上点的坐标特征求出k 值,结合y 随x 的增大而减小即可确定结论.【解析】A 、当点A 的坐标为(﹣1,2)时,﹣k+3=3,解得:k =1>0,∴y 随x 的增大而增大,选项A 不符合题意;B 、当点A 的坐标为(1,﹣2)时,k+3=﹣2,解得:k =﹣5<0,∴y 随x 的增大而减小,选项B 符合题意;C 、当点A 的坐标为(2,3)时,2k+3=3,解得:k =0,选项C 不符合题意;D 、当点A 的坐标为(3,4)时,3k+3=4,解得:k =13>0,∴y 随x 的增大而增大,选项D 不符合题意.故选:B .4.在平面直角坐标系中,一次函数51y x =+的图象与y 轴的交点的坐标为()A .()0,1-B .1,05⎛⎫- ⎪⎝⎭C .1,05⎛⎫ ⎪⎝⎭D .()0,1【答案】D【分析】令x=0,求出函数值,即可求解.【详解】解:令x=0,1y =,∴一次函数51y x =+的图象与y 轴的交点的坐标为()0,1.故选:D【点睛】本题主要考查了一次函数的图象和性质,熟练掌握一次函数的图象和性质是解题的关键.5.在平面直角坐标系中,若将一次函数21y x m =+-的图象向左平移3个单位后,得到个正比例函数的图象,则m 的值为()A .-5B .5C .-6D .6【答案】A【分析】根据函数图像平移的性质求出平移以后的解析式即可求得m 的值.【详解】解:将一次函数21y x m =+-的图象向左平移3个单位后得到的解析式为:2(3)1y x m =++-,化简得:25y x m =++,∵平移后得到的是正比例函数的图像,∴50m +=,解得:5m =-,故选:A .【点睛】本题主要考查一次函数图像的性质,根据“左加右减,上加下减”求出平移后的函数解析式是解决本题的关键.6.已知在平面直角坐标系xOy 中,直线y =2x+2和直线y =23x+2分别交x 轴于点A 和点B .则下列直线中,与x 轴的交点不在线段AB 上的直线是()A .y =x+2B .y =2x+2C .y =4x+2D .y =【分析】求得A 、B 的坐标,然后分别求得各个直线与x 的交点,进行比较即可得出结论.【解析】∵直线y =2x+2和直线y =23x+2分别交x 轴于点A 和点B .∴A (﹣1,0),B (﹣3,0)A 、y =x+2与x 轴的交点为(﹣2,0);故直线y =x+2与x 轴的交点在线段AB 上;B 、y =2x+2与x 轴的交点为(−2,0);故直线y =2x+2与x 轴的交点在线段AB 上;C 、y =4x+2与x 轴的交点为(−12,0);故直线y =4x+2与x 轴的交点不在线段AB 上;D 、y =与x 轴的交点为(−3,0);故直线y =与x 轴的交点在线段AB 上;故选:C .7.在直角坐标系中,已知点3,2A m ⎛⎫ ⎪⎝⎭,点,2B n ⎫⎪⎪⎝⎭是直线()0y kx b k =+<上的两点,则m ,n 的大小关系是()A .m n<B .m n >C .m n ≥D .m n≤【答案】A 【分析】因为直线()0y kx b k =+<,所以随着自变量的增大,函数值会减小,根据这点即可得到问题解答.【详解】解:∵因为直线()0y kx b k =+<,∴y 随着x 的增大而减小,∵32>2,∴322>∴m<n ,故选:A .【点睛】此题考查了一次函数的图象和性质,解题的关键是正确判断一次函数的增减性并灵活运用.8.如图,已知直线1:24l y x =-+与坐标轴分别交于A 、B 两点,那么过原点O 且将AOB 的面积平分的直线2l 的解析式为()A .12y x =B .y x =C .32y x =D .2y x=【答案】D【分析】根据已知解析式求出点A 、B 的坐标,根据过原点O 且将AOB 的面积平分列式计算即可;【详解】如图所示,当0y =时,240x -+=,解得:2x =,∴()2,0A ,当0x =时,4y =,∴()0,4B ,∵C 在直线AB 上,设(),24C m m -+,∴12OBC C S OB x =⨯⨯△,12OCA C S OA y =⨯⨯△,∵2l 且将AOB 的面积平分,∴OBC OCA S S =△△,∴y C C OB x OA ⨯=⨯,∴()4224m m =⨯-+,解得1m =,∴()1,2C ,设直线2l 的解析式为y kx =,则2k =,∴2y x =;故答案选D.【点睛】本题主要考查了一次函数的应用,准确计算是解题的关键.9.如图,一次函数y x=的图像与x轴、y轴分别交于点A、B,把直线AB绕点B顺时针旋转30°交x轴于点C,则线段AC长为()A B.C.2D【答案】A【分析】根据一次函数表达式求出点A和点B坐标,得到△OAB为等腰直角三角形和AB的长,过点C作CD⊥AB,垂足为D,证明△ACD为等腰直角三角形,设CD=AD=x,结合旋转的度数,用两种方法表示出BD,得到关于x的方程,解之即可.【详解】=+的图像与x轴、y轴分别交于点A、B,解:∵一次函数y x令x=0,则,令y=0,则x=,则A(,0),B(0),则△OAB为等腰直角三角形,∠ABO=45°,∴,过点C作CD⊥AB,垂足为D,∵∠CAD=∠OAB=45°,∴△ACD为等腰直角三角形,设CD=AD=x,∴x,∵旋转,∴∠ABC=30°,∴BC=2CD=2x ,∴x ,又BD=AB+AD=2+x ,∴2+x=,解得:+1,∴x=+1)故选A .【点睛】本题考查了一次函数与坐标轴的交点问题,等腰直角三角形的判定和性质,直角三角形的性质,勾股定理,二次根式的混合运算,知识点较多,解题的关键是作出辅助线,构造特殊三角形.10.已知112233()()()x y x y x y ,,,,,为直线23y x =-+上的三个点,且123x x x <<,则以下判断正确的是().A .若120x x >,则130y y >B .若130x x <,则120y y >C .若230x x >,则130y y >D .若230x x <,则120y y >【答案】D【分析】根据一次函数的性质和各个选项中的条件,可以判断是否正确,从而可以解答本题.【详解】解:∵直线y=−2x+3∴y 随x 增大而减小,当y=0时,x=1.5∵(x 1,y 1),(x 2,y 2),(x 3,y 3)为直线y=−2x+3上的三个点,且x 1<x 2<x 3∴若x 1x 2>0,则x 1,x 2同号,但不能确定y 1y 3的正负,故选项A 不符合题意;若x 1x 3<0,则x 1,x 3异号,但不能确定y 1y 2的正负,故选项B 不符合题意;若x 2x 3>0,则x 2,x 3同号,但不能确定y 1y 3的正负,故选项C 不符合题意;若x 2x 3<0,则x 2,x 3异号,则x 1,x 2同时为负,故y 1,y 2同时为正,故y 1y 2>0,故选项D 符合题意.故选:D .【点睛】本题考查一次函数图象上点的坐标特征,解题的关键是明确题意,利用一次函数的性质解答.11.一次函数()232y a x =++的值随x 值的增大而减少,则常数a 的取值范围是______.【答案】32a <-【分析】由题意,先根据一次函数的性质得出关于a 的不等式230a +<,再解不等式即可.【详解】解: 一次函数()232y a x =++的值随x 值的增大而减少,230a ∴+<,解得:32a <-,故答案是:32a <-.【点睛】本题考查了一次函数的图象与系数的关系,解题的关键是:熟知一次函数的增减性.12.若21x y +=,且01y <<,则x 的取值范围为______.【答案】102x <<【分析】根据21x y +=可得y =﹣2x+1,k =﹣2<0进而得出,当y =0时,x 取得最大值,当y =1时,x 取得最小值,将y =0和y =1代入解析式,可得答案.【详解】解:根据21x y +=可得y =﹣2x+1,∴k =﹣2<0∵01y <<,∴当y =0时,x 取得最大值,且最大值为12,当y =1时,x 取得最小值,且最小值为0,∴102x <<故答案为:102x <<.【点睛】此题考查了一次函数的性质,熟练掌握一次函数的性质是解题的关键.13.当自变量13x -≤≤时,函数y x k =-(k 为常数)的最小值为3k +,则满足条件的k 的值为_________.【答案】2-【分析】分1k <-时,13k -≤≤时,3k >时三种情况讨论,即可求解.【详解】解:①若1k <-时,则当13x -≤≤时,有x k >,故y x k x k =-=-,故当1x =-时,y 有最小值,此时函数1y k =--,由题意,1 3k k --=+,解得:2k =-,满足1k <-,符合题意;②若13k -≤≤,则当13x -≤≤时,0y x k =-≥,故当x k =时,y 有最小值,此时函数0y =,由题意,0 3k =+,解得:3k =-,不满足13k -≤≤,不符合题意;③若3k >时,则当13x -≤≤时,有x k <,故y x k k x =-=-,故当3x =时,y 有最小值,此时函数3y k =-,由题意,3 3k k -=+,方程无解,此情况不存在,综上,满足条件的k 的值为2-.故答案为:2-.【点睛】本题考查了一次函数的性质,绝对值的性质,分类讨论是解题的关键.14.如图,是一个“函数求值机”的示意图,其中y 是x 的函数.下面表格中,是通过该“函数求值机”得到的几组x 与y 的对应值.输人x…6-4-2-02…输出y …6-2-2616…根据以上信息,解答下列问题:(1)当输入的x 值为1时,输出的y 值为__________;(2)求k ,b 的值;(3)当输出的y 值为0时,求输入的x 值.【答案】(1)8(2)26k b =⎧⎨=⎩(3)3-【分析】对于(1),将x=1代入y=8x ,求出答案即可;对于(2),将(-2,2),(0,6)代入y=kx+b 得二元一次方程组,解方程组得出答案;对于(3),将y=0分别代入两个关系式,再求解判断即可.(1)当x=1时,y=8×1=8;故答案为:8;(2)将(-2,2),(0,6)代入y kx b =+,得226k b b -+=⎧⎨=⎩,解得26k b =⎧⎨=⎩;(3)令0y =,由8y x =,得08x =,∴01x =<.(舍去)由26y x =+,得026x =+,∴31x =-<.∴输出的y 值为0时,输入的x 值为3-.【点睛】本题主要考查了待定系数法求一次函数关系式,理解“函数求值机”的计算过程是解题的关键.15.在平面直角坐标系xOy 中,一次函数y =kx+b (k≠0)的图象由函数y =x 的图象平移得到,且经过点(1,2).(1)求这个一次函数的解析式;(2)当x >1时,对于x 的每一个值,函数y =mx (m≠0)的值大于一次函数y =kx+b 的值,直接写出m 的取值范围.【分析】(1)先根据直线平移时k 的值不变得出k =1,再将点A (1,2)代入y =x+b ,求出b 的值,即可得到一次函数的解析式;(2)根据点(1,2)结合图象即可求得.【解析】(1)∵一次函数y =kx+b (k≠0)的图象由直线y =x 平移得到,∴k =1,将点(1,2)代入y =x+b ,得1+b =2,解得b =1,∴一次函数的解析式为y =x+1;(2)把点(1,2)代入y =mx 求得m =2,∵当x >1时,对于x 的每一个值,函数y =mx (m≠0)的值大于一次函数y =x+1的值,∴m≥2.16.表格中的两组对应值满足一次函数y=kx+b,现画出了它的图象为直线1,如图.而某同学为观察k,b对图象的影响,将上面函数中的k与b交换位置后得另一个一次函数,设其图象为直线l'.x﹣10y﹣21(1)求直线1的解析式;(2)请在图上画出直线l'(不要求列表计算),并求直线l'被直线l和y轴所截线段的长;(3)设直线y=a与直线1,l′及y轴有三个不同的交点,且其中两点关于第三点对称,直接写出a的值.【分析】(1)根据待定系数法求得即可;(2)画出直线l,求得两直线的交点,根据勾股定理即可求得直线l'被直线l和y轴所截线段的长;(3)求得两条直线与直线y=a的交点横坐标,分三种情况讨论求得即可.【解析】(1)∵直线l′:y=bx+k中,当x=﹣1时,y=﹣2;当x=0时,y=1,∴−b+k=−2k=1,解得k=1b=3,∴直线1′的解析式为y=3x+1;∴直线1的解析式为y=x+3;(2)如图,解y=x+3y=3x+1得x=1y=4,∴两直线的交点为(1,4),∵直线1′:y=3x+1与y轴的交点为(0,1),∴直线l'被直线l和y轴所截线段的长为:12+(4−1)2=10;(3)把y=a代入y=3x+1得,a=3x+1,解得x=a−13;把y=a代入y=x+3得,a=x+3,解得x=a﹣3;当a﹣3+a−13=0时,a=52,当12(a﹣3+0)=a−13时,a=7,当12(a−13+0)=a﹣3时,a=175,∴直线y=a与直线1,l′及y轴有三个不同的交点,且其中两点关于第三点对称,则a的值为52或7或175.17.如图,在平面直角坐标系中,直线y=−12x﹣1与直线y=﹣2x+2相交于点P,并分别与x 轴相交于点A、B.(1)求交点P的坐标;(2)求△PAB的面积;(3)请把图象中直线y=﹣2x+2在直线y=−12x﹣1上方的部分描黑加粗,并写出此时自变量x的取值范围.【分析】(1)解析式联立,解方程组即可求得交点P 的坐标;(2)求得A 、B 的坐标,然后根据三角形面积公式求得即可;(3)根据图象求得即可.【解析】(1)由y =−12x −1y =−2x +2解得x =2y =−2,∴P (2,﹣2);(2)直线y =−12x ﹣1与直线y =﹣2x+2中,令y =0,则−12x ﹣1=0与﹣2x+2=0,解得x =﹣2与x =1,∴A (﹣2,0),B (1,0),∴AB =3,∴S △PAB =12AB ⋅|y P |=12×3×2=;(3)如图所示:自变量x 的取值范围是x <2.18.已知一次函数12y kx =+(k 为常数,k≠0)和23y x =-.(1)当k=﹣2时,若1y >2y ,求x 的取值范围;(2)当x<1时,1y >2y .结合图象,直接写出k 的取值范围.【解析】(1)当2k =-时,122y x =-+,根据题意,得223x x -+>-,解得53x <.(2)当x=1时,y=x−3=−2,把(1,−2)代入y 1=kx+2得k+2=−2,解得k=−4,当−4≤k<0时,y 1>y 2;当0<k≤1时,y 1>y 2.∴k 的取值范围是:41k -≤≤且0k ≠.19.如图,已知过点B (1,0)的直线l 1与直线l 2:y=2x+4相交于点P (-1,a ).(1)求直线l 1的解析式;(2)求四边形PAOC 的面积.【解析】(1)∵点P (-1,a )在直线l 2:y=2x+4上,∴2×(-1)+4=a ,即a=2,则P 的坐标为(-1,2),设直线l 1的解析式为:y=kx+b (k≠0),那么02k b k b +=⎧⎨-+=⎩,解得11k b =-⎧⎨=⎩.∴l 1的解析式为:y=-x+1.(2)∵直线l 1与y 轴相交于点C ,∴C 的坐标为(0,1),又∵直线l 2与x 轴相交于点A ,∴A 点的坐标为(-2,0),则AB=3,而S 四边形PAOC =S △PAB -S △BOC ,∴S 四边形PAOC =1153211222⨯⨯-⨯⨯=.20.在平面直角坐标系xOy 中,直线l :y=kx+1(k≠0)与直线x=k ,直线y=-k 分别交于点A ,B ,直线x=k 与直线y=-k 交于点C .(1)求直线l 与y 轴的交点坐标;(2)横、纵坐标都是整数的点叫做整点,记线段AB ,BC ,CA 围成的区域(不含边界)为W .①当k=2时,结合函数图象,求区域W 内的整点个数;②若区域W 内没有整点,直接写出k 的取值范围.【解析】(1)令x=0,y=1,∴直线l 与y 轴的交点坐标(0,1).(2)由题意,A (k ,k 2+1),B (1k k--,-k ),C (k ,-k ),①当k=2时,A (2,5),B (-32,-2),C (2,-2),在W 区域内有6个整数点:(0,0),(0,-1),(1,0),(1,-1),(1,1),(1,2);②直线AB 的解析式为y=kx+1,当x=k+1时,y=-k+1,则有k 2+2k=0,∴k=-2,当0>k≥-1时,W 内没有整数点,∴当0>k≥-1或k=-2时W 内没有整数点.。
中考数学总复习《一次函数图像与坐标轴的问题》专题测试卷带答案

中考数学总复习《一次函数图像与坐标轴的问题》专题测试卷带答案班级:___________姓名:___________考号:___________一、单选题(共12题;共24分)1.一次函数y=x﹣3的图象与y轴的交点坐标是()A.(0,﹣3)B.(0,3)C.(3,0)D.(﹣3,0)2.如图,直线y=−x+4与坐标轴交于A、B两点,点C为坐标平面内一点BC=1,点M为线段AC的中点,连接OM,则线段OM的最小值是()A.2√2+12B.2√2−12C.1D.2√23.如图在平面直角坐标系中,直线l1对应的函数表达式为y=2x,直线l2与x,y轴分别交于A、B,且l1∥ l2,OA=2,则线段OB的长为()A.3B.4C.2√2D.2√34.背面图案、形状大小都相同的四张卡片的正面分别记录着有关函数y=2x−4的四个结论,现将卡片背面朝上,随机抽取一张,抽到卡片上的结论正确的概率是()A.14B.12C.34D.15.已知一次函数的图象与y=2x+3平行,且过点(4,2),则该一次函数与坐标轴围成图形的面积为()A.6B.9C.12D.186.如图,已知直线y=−13x+√10与与双曲线y=kx(x>0)交于A、B两点,连接OA,若OA⊥AB,则k的值为()A.B.C.D.7.对于一次函数y=−x−2,下列说法错误的是()A.图象不经过第一象限B.图象与y轴的交点坐标为(0,−2)C.图象可由直线y=−x向下平移2个单位长度得到D.若点(−1,y1),(4,y2)在一次函数y=−x−2的图象上,则y1<y28.若一次函数y=ax+b的图象如图所示,则方程ax+b=0的解为()A.x=3B.x=0C.x=﹣2D.x=﹣39.我们将在直角坐标系中圆心坐标和半径均为整数的圆称为“整圆”.如图,直线l:y=kx+4 √3与x轴、y轴分别交于A,B,∥OAB=30°,点P在x轴上,∥P与l相切,当P在线段OA上运动时,使得∥P成为整圆的点P个数是()A.6B.8C.10D.1210.一次函数y=ax+b交x轴于点(-5,0),则关于x的方程ax+b=0的解是() A.x=5B.x=-5C.x=0D.无法求解11.下列四个选项中,不符合直线y=x﹣2的性质特征的选项是()A.经过第一、三、四象限B.y随x的增大而增大C.与x轴交于(﹣2,0)D.与y轴交于(0,-2)12.下列图形中,阴影部分的面积为2的有()个A.4个B.3个C.2个D.1个二、填空题(共6题;共7分)13.在直角坐标系xOy中,若直线y=x+4a-12与y轴的交点在x轴上方,则a的取值范围.14.函数y=m2x2+(2m+1)x+1与x轴有交点,则m的取值范围.15.如图,一次函数y=x+2的图像与坐标轴分别交于A,B两点,点P,C分别是线段AB,OB 上的点,且∥OPC=45°,PC=PO,则点P的坐标为.16.如果一次函数y=kx+4与两坐标轴围成的三角形面积为4,则k=.17.如图,在平面直角坐标系xOy中,直线y=−34x+3与x轴交于点A,与y轴交于点B,将∥AOB沿过点A的直线折叠,使点B落在x轴负半轴上,记作点C,折痕与y轴交点交于点D,则点C的坐标为,点D的坐标为.18.如图示直线y=√3x+√3与x轴、y轴分别交于点A、B,当直线绕着点A按顺时针方向旋转到与x轴首次重合时,点B运动到点B1,线段BB1长度为.三、综合题(共6题;共54分)19.如图,直线y=2x+1与x轴交于点A,与y轴交于点B.(1)求A、B两点的坐标;(2)过B点作直线BP与x轴交于点P,且使OP=2OA,求直线BP的函数关系式.20.如图,在直角坐标系中放入一个矩形纸片ABCO,将纸片翻折后,点B恰好落在x轴上,记为B′折痕为CE.直线CE的关系式是y=−12x+8,与x轴相交于点F,且AE=3.(1)OC=,OF=;(2)求点B′的坐标;(3)求矩形ABCO的面积.21.已知一次函数y=kx+b的图象经过点(0,1)和(1,-2)。
初中数学中考专项练习《一次函数》100道计算题包含与解析(中考冲刺)

初中数学中考专项练习《一次函数》100道计算题包含与解析(中考冲刺)(时间:60分钟满分:100分)班级:_________ 姓名:_________ 分数:_________一、计算题(共100题)1、如图所示的折线ABC•表示从甲地向乙地打长途电话所需的电话费y(元)与通话时间t(分钟)之间的函数关系的图象.(1)写出y与t•之间的函数关系式.(2)通话2分钟应付通话费多少元?(3)通话7分钟呢?2、如图所示的折线ABC•表示从甲地向乙地打长途电话所需的电话费y(元)与通话时间t(分钟)之间的函数关系的图象.(1)写出y与t•之间的函数关系式.(2)通话2分钟应付通话费多少元?(3)通话7分钟呢?3、如图,直线l是一次函数y=kx+b的图象,求l与两坐标轴所围成的三角形的面积.4、如图所示的折线ABC•表示从甲地向乙地打长途电话所需的电话费y(元)与通话时间t(分钟)之间的函数关系的图象.(1)写出y与t•之间的函数关系式.(2)通话2分钟应付通话费多少元?(3)通话7分钟呢?5、已知,与成正比例,与成正比例,且时,;时,,求y与x的解析式.6、一个正比例函数的图象经过点A(﹣2,3),B(a,﹣3),求a的值.7、设一次函数y=kx+b(k≠0)的图象经过A(1,3),B(0,-2)两点,试求k,b的值.8、如图,直线l是一次函数y=kx+b的图象,求l与两坐标轴所围成的三角形的面积.9、在中,当时,,当时,,求和的值.10、一个正比例函数的图象经过点A(﹣2,3),B(a,﹣3),求a的值.11、一次函数y =kx+b()的图象经过点,,求一次函数的表达式.12、在中,当时,,当时,,求和的值.13、已知,当时,;当时,. 求出k,b 的值;14、一次函数y =kx+b()的图象经过点,,求一次函数的表达式.15、已知y是x的一次函数,当x=3时,y=1;当x=﹣2时,y=﹣4,求这个一次函数的解析式.16、已知,与成正比例,与成正比例,且时,;时,,求y与x的解析式.17、如图,直线l是一次函数y=kx+b的图象,求l与两坐标轴所围成的三角形的面积.18、如图,直线l是一次函数y=kx+b的图象,求l与两坐标轴所围成的三角形的面积.19、已知y是x的一次函数,当x=3时,y=1;当x=﹣2时,y=﹣4,求这个一次函数的解析式.20、已知函数y=(2m+1)x+m-3(1)若函数图象经过原点,求m的值;(2)若这个函数是一次函数,且y随着x的增大而减小,求m的取值范围;(3)若这个函数是一次函数,且图象不经过第四象限, 求的取值范围.21、函数y=(k﹣1)x2|k|﹣3是正比例函数,且y随x增大而减小,求(k+3)2018的值.22、设一次函数y=kx+b(k≠0)的图象经过A(1,3),B(0,-2)两点,试求k,b的值.23、已知y=(k-3)x+k2-9是关于x的正比例函数,求当x=-4时,y的值.24、如图所示的折线ABC•表示从甲地向乙地打长途电话所需的电话费y(元)与通话时间t(分钟)之间的函数关系的图象.(1)写出y与t•之间的函数关系式.(2)通话2分钟应付通话费多少元?(3)通话7分钟呢?25、已知,与成正比例,与成正比例,且时,;时,,求y与x的解析式.26、在y=kx+b中,当x=1时y=4,当x=2时y=10.求k,b的值.27、已知函数y=(2m+1)x+m-3(1)若函数图象经过原点,求m的值;(2)若这个函数是一次函数,且y随着x的增大而减小,求m的取值范围;(3)若这个函数是一次函数,且图象不经过第四象限, 求的取值范围.28、如图所示的折线ABC•表示从甲地向乙地打长途电话所需的电话费y(元)与通话时间t(分钟)之间的函数关系的图象.(1)写出y与t•之间的函数关系式.(2)通话2分钟应付通话费多少元?(3)通话7分钟呢?29、已知,与成正比例,与成正比例,且时,;时,,求y与x的解析式.30、在y=kx+b中,当x=1时y=4,当x=2时y=10.求k,b的值.31、已知,与成正比例,与成正比例,且时,;时,,求y与x的解析式.32、在平面直角坐标系中,直线y=kx+3经过(2,7),求不等式kx﹣6≤0的解集.33、函数y=(k﹣1)x2|k|﹣3是正比例函数,且y随x增大而减小,求(k+3)2018的值.34、在中,当时,,当时,,求和的值.35、已知函数y=(2m+1)x+m-3(1)若函数图象经过原点,求m的值;(2)若这个函数是一次函数,且y随着x的增大而减小,求m的取值范围;(3)若这个函数是一次函数,且图象不经过第四象限, 求的取值范围.36、已知,当时,;当时,. 求出k,b 的值;37、一个正比例函数的图象经过点A(﹣2,3),B(a,﹣3),求a的值.38、函数y=(k﹣1)x2|k|﹣3是正比例函数,且y随x增大而减小,求(k+3)2018的值.39、在中,当时,,当时,,求和的值.40、已知y是x的一次函数,当x=3时,y=1;当x=﹣2时,y=﹣4,求这个一次函数的解析式.41、在平面直角坐标系中,直线y=kx+3经过(2,7),求不等式kx﹣6≤0的解集.42、设一次函数y=kx+b(k≠0)的图象经过A(1,3),B(0,-2)两点,试求k,b的值.43、如图,直线AB交x轴于点B,交y轴于点A(0,4),直线DM⊥x轴正半轴于点M,交线段AB于点C,DM=6,连接DA,∠DAC=90°,AD:AB=1:2.(1)求点D的坐标;(2)求经过O、D、B三点的抛物线的函数关系式.44、函数y=(k﹣1)x2|k|﹣3是正比例函数,且y随x增大而减小,求(k+3)2018的值.45、已知函数y=(2m+1)x+m-3(1)若函数图象经过原点,求m的值;(2)若这个函数是一次函数,且y随着x的增大而减小,求m的取值范围;(3)若这个函数是一次函数,且图象不经过第四象限, 求的取值范围.46、一个正比例函数的图象经过点A(﹣2,3),B(a,﹣3),求a的值.47、在平面直角坐标系中,直线y=kx+3经过(2,7),求不等式kx﹣6≤0的解集.48、函数y=(k﹣1)x2|k|﹣3是正比例函数,且y随x增大而减小,求(k+3)2018的值.49、已知y是x的一次函数,当x=3时,y=1;当x=﹣2时,y=﹣4,求这个一次函数的解析式.50、如图所示的折线ABC•表示从甲地向乙地打长途电话所需的电话费y(元)与通话时间t(分钟)之间的函数关系的图象.(1)写出y与t•之间的函数关系式.(2)通话2分钟应付通话费多少元?(3)通话7分钟呢?51、已知函数y=(2m+1)x+m-3(1)若函数图象经过原点,求m的值;(2)若这个函数是一次函数,且y随着x的增大而减小,求m的取值范围;(3)若这个函数是一次函数,且图象不经过第四象限, 求的取值范围.52、已知函数y=(2m+1)x+m-3(1)若函数图象经过原点,求m的值;(2)若这个函数是一次函数,且y随着x的增大而减小,求m的取值范围;(3)若这个函数是一次函数,且图象不经过第四象限, 求的取值范围.53、在直角坐标系中,用线段顺次连结点(-2,0),(0,3),(3,3),(0,4),(-2,0)。
2023年中考数学考点总结+题型专训专题15 一次函数的应用与综合篇(原卷版)

知识回顾专题15一次函数的应用与综合1. 一次函数的图像与性质:一次函数与x 轴的交点坐标公式为:⎪⎭⎫ ⎝⎛-0 ,k;与y轴的交点坐标公式为:()b ,0。
2. 一次函数的平移:①左右平移,自变量上进行加减。
左加右减。
即若()0≠+=k b kx y 向左移动了m 个单位,则平移后的函数解析式为:()()0≠++=k b m x k y ;若()0≠+=k b kx y 向右移动了m 个单位,则平移后的函数解析式为:()()0≠+-=k b m x k y 。
②上下平移,解析式整体后面进行加减。
上加下减。
k 的取值 b 的取值 所在象限y 随x 的变化情况大致图像0>k0>b (图像交于y 轴正半轴)一二三象限y 随x 增大而增大0<b (图像交于y 轴负半轴)一三四象限0<k0>b (图像交于y 轴正半轴)一二四象限y 随x 减小而减小0<b (图像交于y 轴负半轴)二三四象限即若()0≠+=k b kx y 向上移动了m 个单位,则平移后的函数解析式为:()0≠++=k m b kx y ;若()0≠+=k b kx y 向下移动了m 个单位,则平移后的函数解析式为:()0≠-+=k m b kx y 。
3. 一次函数的对称变换:①若一次函数关于x 轴对称,则自变量不变,函数值变为相反数。
即()0≠+=k b kx y 关于x 轴的函数解析式为:()0≠+=-k b kx y ,即()0≠--=k b kx y 。
②若一次函数关于y 轴对称,则函数值不变,自变量变成相反数。
即()0≠+=k b kx y 关于y 轴的函数解析式为:()()0≠+-=k b x k y ,即()0≠+-=k b kx y 。
③若一次函数关于原点对称,则自变量与函数值均变成相反数。
即()0≠+=k b kx y 关于原点的函数解析式为:()()0≠+-=-k b x k y ,即()0≠-=k b kx y 。
一次函数综合题(解析版)--2024年中考数学压轴题专项训练

一次函数综合题通用的解题思路:(1)一次函数与几何图形的面积问题首先要根据题意画出草图,结合图形分析其中的几何图形,再求出面积.(2)一次函数的优化问题通常一次函数的最值问题首先由不等式找到x 的取值范围,进而利用一次函数的增减性在前面范围内的前提下求出最值.(3)用函数图象解决实际问题从已知函数图象中获取信息,求出函数值、函数表达式,并解答相应的问题.1(2024•鼓楼区一模)如图,直线y =-3x +6与⊙O 相切,切点为P ,与x 轴y 轴分别交于A 、B 两点.⊙O 与x 轴负半轴交于点C .(1)求⊙O 的半径;(2)求图中阴影部分的面积.【分析】(1)由OP =OA ⋅sin60°,即可求解;(2)由图中阴影部分的面积=S 扇形COP -S ΔPOC ,即可求解.【解答】解:(1)对于直线y =-3x +6,令y =-3x +6=0,则x =23,即OA =23,由一次函数的表达式知,OB =6,则tan ∠BAC =OB AO =623=3,则∠BAC =60°连接OP ,则OP ⊥AB ,则OP =OA ⋅sin60°=23×32=3;(2)过点P 作PH ⊥AC 于点H ,∵∠POH =30°,则∠POC =150°,PH =12OP =32,则图中阴影部分的面积=S 扇形COP -S ΔPOC =150°360°×π×32-12×3×32=15π-94.【点评】本题考查了一次函数和圆的综合运用,涉及到圆切线的和一次函数的性质,解直角三角形,面积的计算等,综合性强,难度适中.2(2023•宿豫区三模)如图①,在平面直角坐标系中,直线l 1:y =x +1与直线l 2:x =-2相交于点D ,点A 是直线l 2上的动点,过点A 作AB ⊥l 1于点B ,点C 的坐标为(0,3),连接AC ,BC .设点A 的纵坐标为t ,ΔABC 的面积为s .(1)当t =2时,求点B 的坐标;(2)s 关于t 的函数解析式为s =14t 2+bt -54t -1或t 5 a t +1 t -5 (-1<t <5),其图象如图②所示,结合图①、②的信息,求出a 与b 的值;(3)在直线l 2上是否存在点A ,使得∠ACB =90°,若存在,请求出此时点A 的坐标;若不存在,请说明理由.【分析】(1)解法一:先根据t =2可得点A (-2,2),因为B 在直线l 1上,所以设B (x ,x +1),利用y =0代入y =x +1可得G 点的坐标,在Rt ΔABG 中,利用勾股定理列方程可得点B 的坐标;解法二:根据可以使用y =x +1与x 轴正半轴夹角为45度来解答;(2)先把(7,4)代入s =14t 2+bt -54中计算得b 的值,计算在-1<t <5范围内图象上一个点的坐标值:当t =2时,根据(1)中的数据可计算此时s =94,可得坐标2,94,代入s =a (t +1)(t -5)中可得a 的值;(3)存在,设B (x ,x +1),如图5和图6,分别根据两点的距离公式和勾股定理列方程可解答.【解答】解:(1)解法一:如图1,连接AG ,当t =2时,A (-2,2),设B (x ,x +1),在y =x +1中,当x =0时,y =1,∴G (0,1),∵AB ⊥l 1,∴∠ABG =90°,∴AB 2+BG 2=AG 2,即(x +2)2+(x +1-2)2+x 2+(x +1-1)2=(-2)2+(2-1)2,解得:x 1=0(舍),x 2=-12,∴B -12,12;解法二:如图1-1,过点B 作BE ⊥x 轴于E ,过点A 作AH ⊥BE 于H ,当x =0时,y =1,当y =0时,x +1=0,则x =-1,∴OF =OG =1,∵∠GOF =90°,∴∠OGF =∠OFG =45°,∴BE =EF ,∵∠ABD =90°,∴∠ABH =∠BAH =45°,∴ΔABH 是等腰直角三角形,∴AH =BH ,当t =2时,A (-2,2),设B (x ,x +1),∴x +2=2-(x +1),∴x =-12,∴B -12,12 ;(2)如图2可知:当t =7时,s =4,把(7,4)代入s =14t 2+bt -54中得:494+7b -54=4,解得:b =-1,如图3,过B 作BH ⎳y 轴,交AC 于H ,由(1)知:当t =2时,A (-2,2),B -12,12 ,∵C (0,3),设AC 的解析式为:y =kx +n ,则-2k +n =2n =3 ,解得k =12n =3 ,∴AC 的解析式为:y =12x +3,∴H -12,114,∴BH =114-12=94,∴s=12BH⋅|x C-x A|=12×94×2=94,把2,9 4代入s=a(t+1)(t-5)得:a(2+1)(2-5)=94,解得:a=-1 4;(3)存在,设B(x,x+1),当∠ACB=90°时,如图5,∵∠ABD=90°,∠ADB=45°,∴ΔABD是等腰直角三角形,∴AB=BD,∵A(-2,t),D(-2,-1),∴(x+2)2+(x+1-t)2=(x+2)2+(x+1+1)2,(x+1-t)2=(x+2)2,x+1-t=x+2或x+1-t=-x-2,解得:t=-1(舍)或t=2x+3,RtΔACB中,AC2+BC2=AB2,即(-2)2+(t-3)2+x2+(x+1-3)2=(x+2)2+(x+1-t)2,把t=2x+3代入得:x2-3x=0,解得:x=0或3,当x=3时,如图5,则t=2×3+3=9,∴A(-2,9);当x=0时,如图6,此时,A(-2,3),综上,点A的坐标为:(-2,9)或(-2,3).【点评】本题考查二次函数综合题、一次函数的性质、等腰直角三角形的判定和性质、三角形的面积、两点间距离公式等知识,解题的关键是灵活运用所学知识解决问题.3(2023•溧阳市一模)如图1,将矩形AOBC放在平面直角坐标系中,点O是原点,点A坐标为(0,4),点B坐标为(5,0),点P是x轴正半轴上的动点,连接AP,ΔAQP是由ΔAOP沿AP翻折所得到的图形.(1)当点Q落在对角线OC上时,OP= 165 ;(2)当直线PQ经过点C时,求PQ所在的直线函数表达式;(3)如图2,点M是BC的中点,连接MP、MQ.①MQ的最小值为;②当ΔPMQ是以PM为腰的等腰三角形时,请直接写出点P的坐标.【分析】(1)通过Q 点在OC 上,可以通过∠BOC 的三角函数和∠OAP 的三角函数来导出对应的边的关系,求得结果;(2)通过直角ΔAQC 中,得到QC 的长度,然后通过OP =PQ =x ,可以在Rt ΔBCP 中,得到对应的x 值然后求出结果;(3)通过QA =OA =4,可得出Q 点的运动轨迹,是以A 点为圆心,4为半径长度的圆弧,从而可知,MA 的连线上的Q 点为最短的MQ 长度,通过分类讨论,PM =PQ ,PM =QM ,PQ =QM 来求得对应的P 的坐标.【解答】解:(1)如图1,∵∠OAP +∠AOE =90°,∠BOC +∠AOE =90°,∴∠OAP =∠BOC ,又∵∠AOP =∠OBC =90°,∴ΔOAP ∽ΔBOC ,∴OP BC =OA OB ,即OP 4=45,∴OP =165,故答案为:165;(2)如图,∵AQ ⊥PQ ,∴∠AQC =90°,∴QC =AC 2-AQ 2=52-42=3,∵AQ =AO =4,设OP =PQ =x ,则CP =3+x ,PB =5-x ,∴CP 2=BP 2+BC 2,(3+x )2=(5-x )2+42,x =2,∴P 点的坐标为(2,0),将P (2,0)和C (5,4)代入y =kx +b 中,0=2k +b 4=5k +b ,解得:k =43b =-83,∴PQ 所在直线的表达式为:y =43x -83;(3)如图,①∵AQ =AO =4,∴Q 点的运动轨迹,是以A 为圆心,4为半径的圆弧,∴MQ 的最小值在AM 的连线上,如图,MQ ′即为所求,∵M 是BC 中点,CM =12BC =2,∴AM =52+22=29,MQ ′=MA -AQ ′=29-4,故答案为:29-4;②如图,设OP =PQ =x ,BP =5-x ,∴PM 2=(5-x )2+22=x 2-10x +29,当PM =PQ 时,PM 2=PQ 2,∴x 2-10x +29=x 2,x =2910,∴P 2910,0,当MP =MQ 时,如图,若点Q 在AC 上,则AQ =OA =4,∵MP =MQ ,MB =MC ,∠PBM =∠QCM ,∴ΔPMB ≅ΔQMC (HL ),∴PB =QC ,QC =AC -AQ =5-4=1,∴PB =1,∴OP =BO -PB =5-1=4,∴P (4,0);若点Q 在AC 上方时,由对称性可知OM =MQ ,∵MQ =MQ ,∴MO =MP ,∴P (10,0);当MQ =PQ 时,不符合题意,不成立,故P 点坐标为P 2910,0或P (4,0)或(10,0).【点评】本题考查一次函数的图象及应用,通过一次函数坐标图象的性质,三角函数的性质,全等三角形的性质和勾股定理,来求得对应的解.4(2022•启东市模拟)我们知道一次函数y =mx +n 与y =-mx +n (m ≠0)的图象关于y 轴对称,所以我们定义:函数y =mx +n 与y =-mx +n (m ≠0)互为“M ”函数.(1)请直接写出函数y =2x +5的“M ”函数;(2)如果一对“M ”函数y =mx +n 与y =-mx +n (m ≠0)的图象交于点A ,且与x 轴交于B ,C 两点,如图所示,若∠BAC =90°,且ΔABC 的面积是8,求这对“M ”函数的解析式;(3)在(2)的条件下,若点D 是y 轴上的一个动点,当ΔABD 为等腰三角形时,请求出点D 的坐标.【分析】(1)根据互为“M ”函数的定义,直接写出函数y =2x +5的“M ”函数;(2)现根据已知条件判断ΔABC 为等腰直角三角形,再根据互为“M ”函数的图象关于y 轴对称,得出OA =OB =OC ,再根据函数解析式求出点A 、B 、C 的坐标,再根据ΔABC 的面积是8求出m 、n 的值,从而求出函数解析式;(3)ΔABD 为等腰三角形,分以A 为顶点,以B 为顶点,以D 为顶点三种情况讨论即可.【解答】(1)解:根据互为“M ”函数的定义,∴函数y =2x +5的“M ”函数为y =-2x +5;(2)解:根据题意,y =mx +n 和y =-mx +n 为一对“M 函数”.∴AB =AC ,又∵∠BAC =90°,∴ΔABC 为等腰直角三角形,∴∠ABC =∠ACB =45°,∵OB =OC ,∴∠BAO =∠CAO =45°,∴OA =OB =OC ,又∵S ΔABC =12×BC ×AO =8且BC =2AO ,∴AO =22,∵A 、B 、C 是一次函数y =mx +n 与y =-mx +n (m ≠0)的图象于坐标轴的交点,∴A (0,n ),B -n m ,0 ,C n m ,0,∵OA =OB =n ,∴n m=22,∴m =1,∴y =x +22和y =-x +22;(3)解:根据等腰三角形的性质,分情况,∵AO =BO =22,∴AB =4,由(2)知,A (0,22),B (-22,0),C (22,0),∴①以A 为顶点,则AB =AD ,当点D 在点A 上方时,AD =22+4,当点D 在点A 下方时,AD =22-4,∴D 1(0,22+4),D 2(0,22-4),②以B 为顶点,则BA =BD ,此时点D 在y 轴负半轴,∴D 3(0,-22),③以D 为顶点,则DA =DB ,此时D 为坐标原点,∴D 4(0,0).∴D 点坐标为D 1(0,22+4),D 2(0,22-4),D 3(0,-22),∴D 4(0,0).【点评】本题考查一次函数的综合应用,以及新定义、等腰三角形的性质等知识,关键是理解新定义,用新定义解题.5(2024•新北区校级模拟)如图①,动点P 从矩形ABCD 的顶点A 出发,以v 1的速度沿折线A -B -C 向终点C 运动;同时,一动点Q 从点D 出发,以v 2的速度沿DC 向终点C 运动,当一个点到达终点时,另一个点也停止运动.点E 为CD 的中点,连接PE ,PQ ,记ΔEPQ 的面积为S ,点P 运动的时间为t ,其函数图象为折线MN -NF 和曲线FG (图②),已知,ON =4,NH =1,点G 的坐标为(8,0).(1)点P 与点Q 的速度之比v 1v 2的值为 85 ;AB AD的值为;(2)如果OM =15.①求线段NF 所在直线的函数表达式;②求FG 所在曲线的函数表达式;③是否存在某个时刻t ,使得S ≥154?若存在,求出t 的取值范围:若不存在,请说明理由.【分析】(1)由函数图象可知t =3时,Q 与E 重合,t =4时,P 与B 重合,t =6时,P 与C 重合,则Q 的速度v 2=DE 4,P 的速度v 1=AB 4,从而得出答案;(2)①当t =0时,P 与A 重合,Q 与D 重合,此时S ΔADE =2,可得AD =BC =DE =15,AB =CD =53AD =10,从而得出点P 与Q 的速度,即可得出点F 的坐标,利用待定系数法可得答案;②设FG 所在的曲线的数解析式为S =a (t -6)2+k (a ≠0),把F 5,154,G (8,0)代入解析式求得a ,k 值即可求解答;③利用待定系数法求出直线MN 的函数解析式,当S =154时,可得t 的值,根据图象可得答案.【解答】解:(1)∵ON =4,NH =1,G (8,0),∴N (4,0),H (5,0),由图象可知:t =4时,Q 与E 重合,t =5时,P 与B 重合,t =8时,P 与C 重合,∴Q 的速度v 2=DE 4,P 的速度v 1=AB 5,∵四边形ABCD 是矩形,∴AB =CD ,AD =BC ,∵E 为CD 的中点,∴DE =12CD =12AB ,∴v 1v 2=AB5DE 4=AB 5⋅4DE =85,∵P 从A 到B 用了5秒,从B 到C 用了3秒,∴AB =5v 1,BC =3v 1,∴AB =53BC ,∴AB :AD 的值为53,故答案为:85,53;(2)①∵OM =15,∴M (0,15),由题知,t =0时,P 与A 重合,Q 与D 重合,∴S ΔEPQ =12AD ⋅DE =15,∵AB :AD =53,DE =12AB ,∴DE =56AD ,∴12AD ⋅56AD =15,∴AD =BC =6(舍去负值),∴AB =CD =53AD =10,∴v 2=DE 4=54,当t =5时,DQ =v 2t =54×5=254,∴QE =DQ -DE =254-5=54,此时P 与B重合,∴S ΔEPQ =12EQ ⋅BC =12×54×6=154,∴F 5,154 ,设直线NF 的解析式为S =kt +b (k ≠0),将N (4,0)与F 5,154 代入得:4k +b =05k +b =154,∴k =154b =-15 ,∴线段NF 所在直线的函数表达式为S =154t -15(4<t ≤5);②设FG所在的曲线的数解析式为S=1254t-5(16-2t)=-54t2+15t-40,∴FG所在的曲线的函数解析式为S=-54t2+15t-40(5≤t≤8);③存在,分情况讨论如下:当Q在DE上,P在AB上时,∵直线MN经过点M(0,15),N(4,0),可求得直线MN的解析式为S=-54t+15(0≤t≤4),当s=154时,-154t+15=154,∴x=3,∵s随x的增大而减小,∴当0≤x≤3时,S≥154,当Q在CE上,P在BC上时,直线NF的解析式为S=154t-15(4<t≤5);由F5,15 4知:当t=5时,S=154,当S=154时,-54t2+15t-40=154,∴t=7或5,由图象知:当5≤x≤7,x的取值范围为0≤t≤3或5≤t≤7.【点评】本题是一次函数综合题,主要考查了待定系数法求函数解析式,三角形的面积,矩形的性质等知识,理解函数图象中每一个拐点的意义是解题的关键.6(2024•梁溪区校级模拟)在平面直角坐标系xOy 中,二次函数y =-ax 2+3ax +4a 的图象与x 轴交于A 、B 两点(点A 在点B 的左侧),与y 轴正半轴交于点C ,直线y =12x 交于第一象限内的D 点,且ΔABC 的面积为10.(1)求二次函数的表达式;(2)点E 为x 轴上一点,过点E 作y 轴的平行线交线段OD 于点F ,交抛物线于点G ,当GF =5OF 时,求点G 的坐标;(3)已知点P (n ,0)是x 轴上的点,若点P 关于直线OD 的对称点Q 恰好落在二次函数的图象上,求n 的值.【分析】(1)在y =-ax 2+3ax +4a 中,令y =0得A (-1,0),B (4,0),根据ΔABC 的面积为10,即得OC =4,C (0,4),用待定系数法即得二次函数的表达式为y =-x 2+3x +4;(2)设E (m ,0),则F m ,12m ,G (m ,-m 2+3m +4),由GF =5OF ,可得-m 2+52m +4=5×52m ,即可解得G (2,6);(3)连接PQ 交直线OD 于K ,过Q 作QT ⊥x 轴于T ,设Q (r ,s ),可得K n +r 2,s 2 ,即得s 2=12×n +r 2,n +r =2s ①,又r 2+s 2=n 2,(n +r )(n -r )=s 2②,可解得r =35n ,s =45n ,故Q 35n ,45n ,代入y =-x 2+3x +4得45n =-35n 2+3×35n +4,解得n =5或n =-209.【解答】解:(1)如图:在y =-ax 2+3ax +4a 中,令y =0得-ax 2+3ax +4a =0,解得x =4或x =-1,∴A (-1,0),B (4,0),∴AB =5,∵ΔABC 的面积为10,∴12AB ⋅OC =10,即12×5⋅OC =10,∴OC =4,∴C (0,4),把C (0,4)代入y =-ax 2+3ax +4a 得:4a =4,∴a =1,∴二次函数的表达式为y =-x 2+3x +4;(2)如图:设E (m ,0),则F m ,12m ,G (m ,-m 2+3m +4),∴OF =m 2+12m 2=52m ,GF =-m 2+3m +4-12m =-m 2+52m +4,∵GF =5OF ,∴-m 2+52m +4=5×52m ,解得m =2或m =-2(舍去),∴G (2,6);(3)连接PQ 交直线OD 于K ,过Q 作QT ⊥x 轴于T ,如图:∵P (n ,0)关于直线对称点为Q ,∴OQ =OP =|n |,K 是PQ 中点,设Q (r ,s ),∴K n +r 2,s 2,∵K 在直线y =12x 上,∴s 2=12×n +r 2,整理得:n +r =2s ①,∵OT 2+QT 2=OQ 2,∴r 2+s 2=n 2,变形得:(n +r )(n -r )=s 2②,把①代入②得:2s (n -r )=s 2,∵s ≠0,∴n -r =s2③,由①③可得r =35n ,s =45n ,∴Q 35n ,45n ,∵Q 在抛物线y =-x 2+3x +4上,∴45n =-35n 2+3×35n +4,解得n =5或n =-209,答:n 的值为5或-209.【点评】本题考查一次函数、二次函数综合应用,涉及待定系数法,三角形面积,对称变换等知识,解题的关键是用含n 的代数式表示Q 的坐标.7(2023•邗江区校级一模)如图1,在平面直角坐标系中,直线l :y =-33x +43分别与x 轴、y 轴交于点A 点和B 点,过O 点作OD ⊥AB 于D 点,以OD 为边构造等边ΔEDF (F 点在x 轴的正半轴上).(1)求A 、B 点的坐标,以及OD 的长;(2)将等边ΔEDF ,从图1的位置沿x 轴的正方向以每秒1个单位的长度平移,移动的时间为t (s ),同时点P 从E 出发,以每秒2个单位的速度沿着折线ED -DF 运动(如图2所示),当P 点到F 点停止,ΔDEF 也随之停止.①t =3或6(s )时,直线l 恰好经过等边ΔEDF 其中一条边的中点;②当点P 在线段DE 上运动,若DM =2PM ,求t 的值;③当点P 在线段DF 上运动时,若ΔPMN 的面积为3,求出t 的值.【分析】(1)把x =0,y =0分别代入y =-33x +43,即可求出点A 、B 的坐标,求出∠BAO =30°,根据直角三角形的性质,即可得出OD =12OA =6;(2)①当直线l 分别过DE 、DF 、EF 的中点,分三种情况进行讨论,得出t 的值,并注意点P 运动的最长时间;②分点P 在直线l 的下方和直线l 上方两种情况进行讨论,求出t 的值即可;③分点P 在DN 之间和点P 在NF 之间两种情况进行讨论,求出t 的值即可.【解答】解:(1)令x =0,则y =43,∴点B 的坐标为(0,43),令y =0,则-33x +43=0,解得x =12,∴点A 的坐标为(12,0),∵tan ∠BAO =OB OA=4312=33,∴∠BAO =30°,∵OD ⊥AB ,∴∠ODA =90°,∴ΔODA 为直角三角形,∴OD =12OA =6;(2)①当直线l 过DF 的中点G 时,∵ΔDEF 为等边三角形,∴∠DFE =60°,∵∠BAO =30°,∴∠FGA =60°-30°=30°,∴∠FGA =∠BAO ,∴FA =FG =12DF =3,∴OF =OA -FA =9,∴OE =OF -EF =9-6=3,∴t =3;当l 过DE 的中点时,∵DE ⊥l ,DG =EG ,∴直线l 为DE 的垂直平分线,∵ΔDEF 为等边三角形,∴此时点F 与点A 重合,∴t =12-61=6;当直线l 过EF 的中点时,运动时间为t =12-31=9;∵点P 从运动到停止用的时间为:6+62=6,∴此时不符合题意;综上所述,当t =3s 或6s 时,直线l 恰好经过等边ΔEDF 其中一条边的中点,故答案为:3或6;②∵OE =t ,AE =12-t ,∠BAO =30°,∴ME =6-t2,∴DM =DE -EM =t2,∵EP =2t ,∴PD =6-2t ,当P 在直线l 的下方时,∵DM =23DP ,∴t 2=23(6-2t ),解得:t =2411;当P 在直线l 的上方时,∵DM =2DP ,∴t2=2(6-2t ),解得t =83;综上所述:t 的值为2411或83;③当3<t ≤6时,∵∠D =60°,∠DMN =90°,DM =t2,∴∠DNM =90°-60°=30°,∴MN =DM ×tan60°=32t ,DN =2DM =2×t2=t ,∵DP =2t -6,∴PN =DN -DP =t -(2t -6)=6-t ,∵∠DNM =30°,∴边MN 的高h =12PN =3-12t ,∵ΔPMN 的面积为3,∴12×32t 3-12t =3,整理得:t 2-6t +8=0,解得t =2(舍)或t =4当点P 在NF 之间时,∵∠D =60°,∠DMN =90°,DM =t2,∴∠DNM =90°-60°=30°,∴MN =DM ×tan60°=32t ,DN =2DM =2×t2=t ,∵DP =2t -6,∴PN =DP -DN =2t -6-t =t -6,∵∠DNM =30°,∴∠FNA =∠DNM =30°,∴边MN 的高h =12PN =12t -3,∵ΔPMN 的面积为3,∴12×32t 12t -3 =3,解得t =3+17(舍)或t =3-17(舍),综上所述,t 的值为4s .【点评】本题主要考查了一次函数的性质、等边三角形的性质、直角三角形的性质、利用三角函数解直角三角形,熟练掌握含30°的直角三角形的性质并注意进行分类讨论是解题的关键.8(2023•武进区校级模拟)在平面直角坐标系xOy 中,对于任意两点P 1(x 1,y 1)与P 2(x 2,y 2)的“非常距离”,给出如下定义:若|x 1-x 2|≥|y 1-y 2|,则点P 1与点P 2的“非常距离”为|x 1-x 2|;若|x 1-x 2|<|y 1-y 2|,则点P 1与点P 2的“非常距离”为|y 1-y 2|.例如:点P 1(1,2),点P 2(3,5),因为|1-3|<|2-5|,所以点P 1与点P 2的“非常距离”为|2-5|=3,也就是图1中线段P 1Q 与线段P 2Q 长度的较大值(点Q 为垂直于y 轴的直线P 1Q 与垂直于x 轴的直线P 2Q 交点).(1)已知点A -12,0,B 为y 轴上的一个动点,①若点A 与点B 的“非常距离”为2,写出一个满足条件的点B 的坐标;②直接写出点A 与点B 的“非常距离”的最小值;(2)已知C 是直线y =34x +3上的一个动点,①如图2,点D 的坐标是(0,1),求点C 与点D 的“非常距离”的最小值及相应的点C 的坐标;②如图3,E 是以原点O 为圆心,1为半径的圆上的一个动点,求点C 与点E 的“非常距离”的最小值及相应的点E 与点C 的坐标.【分析】(1)①根据点B 位于y 轴上,可以设点B 的坐标为(0,y ).由“非常距离”的定义可以确定|0-y |=2,据此可以求得y 的值;②设点B 的坐标为(0,y ).因为-12-0 ≥|0-y |,所以点A 与点B 的“非常距离”最小值为-12-0 =12;(2)①设点C 的坐标为x 0,34x 0+3 .根据材料“若|x 1-x 2|≥|y 1-y 2|,则点P 1与点P 2的“非常距离”为|x 1-x 2|”知,C 、D 两点的“非常距离”的最小值为-x 0=34x 0+2,据此可以求得点C 的坐标;②根据“非常距离”的定义,点E 在过原点且与直线y =34x +3垂直的直线上,且C 与E 的横纵坐标差相等时,点C 与点E 的“非常距离”取最小值,据此求出C 与E 的坐标及“非常距离”的最小值.【解答】解:(1)①∵B 为y 轴上的一个动点,∴设点B 的坐标为(0,y ).∵-12-0 =12≠2,∴|0-y |=2,解得,y =2或y =-2;∴点B 的坐标是(0,2)或(0,-2);②点A 与点B 的“非常距离”的最小值为12.(2)①如图2,当点C 与点D 的“非常距离”取最小值时,需要根据运算定义“若|x 1-x 2|≥|y 1-y 2|,则点P 1与点P 2的“非常距离”为|x 1-x 2|”解答,此时|x 1-x 2|=|y 1-y 2|.即AC =AD ,∵C 是直线y =34x +3上的一个动点,点D 的坐标是(0,1),∴设点C 的坐标为x 0,34x 0+3 ,∴-x 0=34x 0+2,此时,x 0=-87,∴点C 与点D 的“非常距离”的最小值为:|x 0|=87,此时C -87,157;②如图3,当点E 在过原点且与直线y =34x +3垂直的直线上,且CF =EF 时,点C 与点E 的“非常距离”最小,设E (x ,y )(点E 位于第二象限).则y x=-43x 2+y 2=1 ,解得x =-35y =45,故E -35,45.设点C 的坐标为x 0,34x 0+3 ,-35-x 0=34x 0+3-45,解得x0=-8 5,则点C的坐标为-8 5,95,点C与点E的“非常距离”的最小值为1.【点评】本题考查了一次函数综合题.对于信息给予题,一定要弄清楚题干中的已知条件.本题中的“非常距离”的定义是正确解题的关键.9(2023•海安市一模)对于平面直角坐标系xOy中的图形W和点P,给出如下定义:F为图形W上任意一点,将P,F两点间距离的最小值记为m,最大值记为M,称M与m的差为点P到图形W的“差距离”,记作d(P,W),即d(P,W)=M-m,已知点A(2,1),B(-2,1)(1)求d(O,AB);(2)点C为直线y=-1上的一个动点,当d(C,AB)=1时,点C的横坐标是 (2-5)或(5-2,) ;(3)点D为函数y=x+b(-2≤x≤2)图象上的任意一点,当d(D,AB)≤2时,直接写出b的取值范围.【分析】(1)画出图形,根据点P到图形W的“差距离”的定义即可解决问题.(2)如图2中,设C(m,-1).由此构建方程即可解决问题.(3)如图3中,取特殊位置当b=6时,当b=-4时,分别求解即可解决问题.【解答】解:(1)如图1中,∵A(2,1),B(-2,1),∴AB⎳x轴,∴点O到线段AB的最小距离为1,最大距离为5,∴d(O,AB)=5-1.(2)如图2中,设C(m,-1).当点C在y轴的左侧时,由题意AC-2=1,∴AC=3,∴(2-m)2+22=9,∴m=2-5或2+5(舍弃),∴C(2-5,-1),当点C在y轴的右侧时,同法可得C(5-2,-1),综上所述,满足条件的点C的坐标为(2-5,-1)或(5-2,-1).故答案为:(2-5,-1)或(5-2,-1).(3)如图3中,当b=6时,线段EF:y=x+6(-2≤x≤2)上任意一点D,满足d(D,AB)≤2,当b=-4时,线段E′F′:y=x-4(-2≤x≤2)上任意一点D′,满足d(D′,AB)≤2,观察图象可知:当b≥6或b≤-4时,函数y=x+b(-2≤x≤2)图象上的任意一点,满足d(D,AB)≤2.【点评】本题属于一次函数综合题,考查了一次函数的性质,点P到图形W的“差距离”的定义等知识,解题的关键是理解题意,学会利用参数解决问题,学会寻找特殊位置解决问题,属于中考创新题型.10(2022•姑苏区校级模拟)平面直角坐标系xOy中,对于任意的三个点A、B、C,给出如下定义:若矩形的任何一条边均与某条坐标轴平行,且A,B,C三点都在矩形的内部或边界上,则称该矩形为点A,B,C的“三点矩形”.在点A,B,C的所有“三点矩形”中,若存在面积最小的矩形,则称该矩形为点A,B,C的“最佳三点矩形”.如图1,矩形DEFG,矩形IJCH都是点A,B,C的“三点矩形”,矩形IJCH是点A,B,C的“最佳三点矩形”.如图2,已知M(4,1),N(-2,3),点P(m,n).(1)①若m=2,n=4,则点M,N,P的“最佳三点矩形”的周长为18,面积为;②若m=2,点M,N,P的“最佳三点矩形”的面积为24,求n的值;(2)若点P在直线y=-2x+5上.①求点M,N,P的“最佳三点矩形”面积的最小值及此时m的取值范围;②当点M,N,P的“最佳三点矩形”为正方形时,求点P的坐标;(3)若点P(m,n)在抛物线y=ax2+bx+c上,当且仅当点M,N,P的“最佳三点矩形”面积为12时,-2≤m≤-1或1≤m≤3,直接写出抛物线的解析式.【分析】(1)①利用“最佳三点矩形”的定义求解即可,②利用“最佳三点矩形”的定义求解即可;(2)①利用“最佳三点矩形”的定义求得面积的最小值为12,②由“最佳三点矩形”的定义求得正方形的边长为6,分别将y=7,y=-3代入y=-2x+5,可得x分别为-1,5,点P的坐标为(-1,7)或(4,-3);(3)利用“最佳三点矩形”的定义画出图形,可分别求得解析式.【解答】解:(1)①如图,画出点M,N,P的“最佳三点矩形”,可知矩形的周长为6+6+3+3=18,面积为3×6=18;故答案为:18,18.②∵M(4,1),N(-2,3),∴|x M-x N|=6,|y M-y N|=2.又∵m=2,点M,N,P的“最佳三点矩形”的面积为24.∴此矩形的邻边长分别为6,4.∴n=-1或5.(2)如图,①由图象可得,点M,N,P的“最佳三点矩形”面积的最小值为12;分别将y=3,y=1代入y=-2x+5,可得x分别为1,2;结合图象可知:1≤m≤2;②当点M,N,P的“最佳三点矩形”为正方形时,边长为6,分别将y=7,y=-3代入y=-2x+5,可得x分别为-1,4;∴点P的坐标为(-1,7)或(4,-3);(3)设抛物线的解析式为y=ax2+bx+c,经过点(-1,1),(1,1),(3,3),∴a -b +c =1a +b +c =19a +3b +c =3,a =14b =0c =34,∴y =14x 2+34,同理抛物线经过点(-1,3),(1,3),(3,1),可求得抛物线的解析式为y =-14x 2+134,∴抛物线的解析式y =14x 2+34或y =-14x 2+134.【点评】本题主要考查了一次函数的综合题,涉及点的坐标,正方形及矩形的面积及待定系数法求函数解析式等知识,解题的关键是理解运用好“最佳三点矩形”的定义.11(2022•太仓市模拟)如图①,动点P 从矩形ABCD 的顶点A 出发,以v 1的速度沿折线A -B -C 向终点C 运动;同时,一动点Q 从点D 出发,以v 2的速度沿DC 向终点C 运动,当一个点到达终点时,另一个点也停止运动.点E 为CD 的中点,连接PE ,PQ ,记ΔEPQ 的面积为S ,点P 运动的时间为t ,其函数图象为折线MN -NF 和曲线FG (图②),已知,ON =3,NH =1,点G 的坐标为(6,0).(1)点P 与点Q 的速度之比v 1v 2的值为 32 ;AB :AD 的值为;(2)如果OM =2.①求线段NF 所在直线的函数表达式;②是否存在某个时刻t ,使得S ≥23?若存在,求出t 的取值范围;若不存在,请说明理由.【分析】(1)由函数图象可知t =3时,Q 与E 重合,t =4时,P 与B 重合,t =6时,P 与C 重合,则Q 的速度v 2=DE 3,P 的速度v 1=AB4,从而得出答案;(2)①当t =0时,P 与A 重合,Q 与D 重合,此时S ΔADE =2,可得AD =BC =DE =2,AB =CD =2AD =4,从而得出点P 与Q 的速度,即可得出点F 的坐标,利用待定系数法可得答案;②利用待定系数法求出直线MN 的函数解析式,当S =23时,可得t 的值,根据图象可得答案.【解答】解:(1)∵ON =3,NH =1,G (6,0),∴N (3,0),H (4,0),由图象可知:t =3时,Q 与E 重合,t =4时,P 与B 重合,t =6时,P 与C 重合,∴Q 的速度v 2=DE 3,P 的速度v 1=AB4,∵四边形ABCD 是矩形,∴AB =CD ,AD =BC ,∵E 为CD 的中点,∴DE =12CD =12AB ,∴v 1v 2=AB4DE 3=AB 4⋅3DE =AB 4⋅312AB =32,∵P 从A 到B 用了4秒,从B 到C 用了2秒,∴AB =4v 1,BC =2v 1,∴AB =2BC ,∴AB :AD 的值为2,故答案为:32,2;(2)①∵OM =2,∴M (0,2),由题知,t =0时,P 与A 重合,Q 与D 重合,∴S ΔEPQ =12AD ⋅DE =2,∵AB :AD =2,∴AD =DE =12AB ,∴12AD 2=2,∴AD =BC =DE =2,AB =CD =2AD =4,∴v 2=DE 3=23,当t =4时,DQ =v 2t =23×4=83,∴QE =DQ -DE =83-2=23,此时P 与B 重合,∴S ΔEPQ =12EQ ⋅BC =12×23×2=33,∴F 4,23,设直线NF 的解析式为S =kx +b (k ≠0),将N (3,0)与F 4,23 代入得:3k +b =04k +b =23 ,∴k =23b =-2,∴线段NF 所在直线的函数表达式为S =23x -2(3<x ≤4);②存在,分情况讨论如下:当Q 在DE 上,P 在AB 上时,∵直线MN 经过点M (0,2),N (3,0),同理求得直线MN 的解析式为S =-23x +2(0≤x ≤3),当s =23时,-23x +2=2,∴x =2,∵s随x的增大而减小,∴当0≤x≤2时,S≥23,当Q在CE上,P在AB上时,直线NF的解析式为S=23x-2(3<x≤4),由F4,2 3知:当x=4时,S=23,当Q在CE上,P在BC上时,SΔEPQ=12EQ⋅CP,∵DQ=v2t=23t,∴EQ=DQ-DE=23t-2,∵v1=AB4=44=1,∴AB+BP=v1t=t,∵AB+BC=4+2=6,∴CP=6-t,∴S=1223t-2(6-t)=-13t2+3t-6(4<x≤6),当S=23时,-13t2+3t-6=23,∴t=4或5,由图象知:当4<x≤5时,S≥2 3,综上,S≥23时,x的取值范围为0≤x≤2或4≤x≤5.【点评】本题是一次函数综合题,主要考查了待定系数法求函数解析式,三角形的面积,矩形的性质等知识,理解函数图象中每一个拐点的意义是解题的关键.12(2022•邗江区校级一模)在平面直角坐标系xOy中,对于点P和线段ST,我们定义点P关于线段ST的线段比k=PSST(PS<PT)PTST(PS≥PT) .(1)已知点A(0,1),B(1,0).①点Q(2,0)关于线段AB的线段比k= 22 ;②点C(0,c)关于线段AB的线段比k=2,求c的值.(2)已知点M(m,0),点N(m+2,0),直线y=x+2与坐标轴分别交于E,F两点,若线段EF上存在点使得这一点关于线段MN的线段比k≤14,直接写出m的取值范围.【分析】(1)①求出QA、QB、AB,根据线段比定义即可得到答案;②方法同①,分c>0和c≤0讨论;(2)分两种情况,画出图象,根据线段比定义,分别在M(N)为“临界点”时列出不等式,即可得到答案.【解答】解:(1)①∵A(0,1),B(1,0),Q(2,0),∴AB=2,QA=5,QB=1,根据线段比定义点Q(2,0)关于线段AB的线段比k=QBAB=22;故答案为:22;②∵A (0,1),B (1,0),C (0,c ),∴AB =2,AC =|1-c |,BC =1+c 2,AC 2=1+c 2-2c ,BC 2=1+c 2,当c >0时,AC 2<BC 2,即AC <BC ,由C (0,c )关于线段AB 的线段比k =2可得:|1-c |2=2,解得c =3或c =-1(舍去),∴c =3,当c ≤0时,AC 2≥BC 2,即AC ≥BC ,由C (0,c )关于线段AB 的线段比k =2可得:1+c 22=2,解得c =3(舍去)或c =-3,∴c =-3,综上所述,点C (0,c )关于线段AB 的线段比k =2,c =3或c =-3;(2)∵直线y =x +2与坐标轴分别交于E ,F 两点,∴E (-2,0),F (0,2),∵点M (m ,0),点N (m +2,0),∴MN =2,N 在M 右边2个单位,当线段EF 上的点到N 距离较小时,分两种情况:①当M 、N 在点E 左侧时,如图:线段EF 上存在点使得这一点关于线段MN 的线段比k ≤14,∴NE MN≤14,即-2-(m +2)2≤14,解得:m ≥-92,②当N 在E 右侧,M 在E 左侧时,过M 作MG ⊥EF 于G ,如图:线段EF 上存在点使得这一点关于线段MN 的线段比k ≤14,∴GM MN ≤14,即GM 2≤14,∴GM ≤12,而E (-2,0),F (0,2),∴∠FEO =45°,∴ΔHEM 时等腰直角三角形,∴GM =22EM ,∴22EM ≤12,即22[(m +2)-(-2)]≤12,解得m ≤-4+22,∴线段EF 上存在点使得这一点关于线段MN 的线段比k ≤14,线段EF 上的点到N 距离较小时,-92≤m ≤-4+22,当线段EF 上的点到M 距离较小时,也分两种情况:①当N 在E 右侧,M 在E 左侧时,如图:线段EF 上存在点使得这一点关于线段MN 的线段比k ≤14,∴ME MN≤14,即-2-m 2≤14,解得m ≥-52,②当M 、N 在点E 右侧时,过M 作MH ⊥EF 于H ,如图:线段EF 上存在点使得这一点关于线段MN 的线段比k ≤14,∴HM MN ≤14,即HM 2≤14,∴HM ≤12,而E (-2,0),F (0,2),∴∠FEO =45°,∴ΔHEM 时等腰直角三角形,∴HM =22EM ,∴22EM ≤12,即22[m -(-2)]≤12,解得:m ≤-2+22,∴线段EF 上存在点使得这一点关于线段MN 的线段比k ≤14,线段EF 上的点到M 距离较小时,-52≤m ≤-2+22,综上所述,线段EF 上存在点使得这一点关于线段MN 的线段比k ≤14,则-92≤m ≤-4+22或-52≤m ≤-2+22.【点评】本题考查一次函数应用,解题的关键是读懂线段比的定义,找出“临界点”列不等式.13(2022•泰州)定义:对于一次函数y 1=ax +b 、y 2=cx +d ,我们称函数y =m (ax +b )+n (cx +d )(ma +nc ≠0)为函数y 1、y 2的“组合函数”.(1)若m =3,n =1,试判断函数y =5x +2是否为函数y 1=x +1、y 2=2x -1的“组合函数”,并说明理由;(2)设函数y 1=x -p -2与y 2=-x +3p 的图像相交于点P .①若m +n >1,点P 在函数y 1、y 2的“组合函数”图像的上方,求p 的取值范围;②若p ≠1,函数y 1、y 2的“组合函数”图像经过点P .是否存在大小确定的m 值,对于不等于1的任意实数p ,都有“组合函数”图像与x 轴交点Q 的位置不变?若存在,请求出m 的值及此时点Q 的坐标;若不存在,请说明理由.【分析】(1)由y =5x +2=3(x +1)+(2x -1),可知函数y =5x +2是函数y 1=x +1、y 2=2x -1的“组合函数”;(2)①由y =x -p -2y =-x +3p得P (2p +1,p -1),当x =2p +1时,y =m (2p +1-p -2)+n (-2p -1+3p )=(p-1)(m +n ),根据点P 在函数y 1、y 2的“组合函数”图象的上方,有p -1>(p -1)(m +n ),而m +n >1,可得p <1;②由函数y 1、y 2的“组合函数” y =m (x -p -2)+n (-x +3p )图象经过点P ,知p -1=m (2p +1-p -2)+n (-2p -1+3p ),即(p -1)(1-m -n )=0,而p ≠1,即得n =1-m ,可得y =(2m -1)x +3p -(4p +2)m ,令y =0得(2m -1)x +3p -(4p +2)m =0,即(3-4m )p +(2m -1)x -2m =0,即可得m =34时,“组合函数”图象与x 轴交点Q 的位置不变,Q (3,0).【解答】解:(1)函数y =5x +2是函数y 1=x +1、y 2=2x -1的“组合函数”,理由如下:∵3(x +1)+(2x -1)=3x +3+2x -1=5x +2,∴y =5x +2=3(x +1)+(2x -1),∴函数y =5x +2是函数y 1=x +1、y 2=2x -1的“组合函数”;(2)①由y =x -p -2y =-x +3p得x =2p +1y =p -1 ,∴P (2p +1,p -1),∵y 1、y 2的“组合函数”为y =m (x -p -2)+n (-x +3p ),∴x =2p +1时,y =m (2p +1-p -2)+n (-2p -1+3p )=(p -1)(m +n ),∵点P 在函数y 1、y 2的“组合函数”图象的上方,∴p -1>(p -1)(m +n ),∴(p -1)(1-m -n )>0,∵m +n >1,∴1-m -n <0,∴p -1<0,∴p <1;②存在m =34时,对于不等于1的任意实数p ,都有“组合函数”图象与x 轴交点Q 的位置不变,Q (3,0),理由如下:由①知,P (2p +1,p -1),∵函数y 1、y 2的“组合函数”y =m (x -p -2)+n (-x +3p )图象经过点P ,∴p -1=m (2p +1-p -2)+n (-2p -1+3p ),∴(p -1)(1-m -n )=0,∵p ≠1,∴1-m -n =0,有n =1-m ,∴y =m (x -p -2)+n (-x +3p )=m (x -p -2)+(1-m )(-x +3p )=(2m -1)x +3p -(4p +2)m ,令y =0得(2m -1)x +3p -(4p +2)m =0,变形整理得:(3-4m )p +(2m -1)x -2m =0,∴当3-4m =0,即m =34时,12x -32=0,∴x =3,∴m =34时,“组合函数”图象与x 轴交点Q 的位置不变,Q (3,0).【点评】本题考查一次函数综合应用,涉及新定义,函数图象上点坐标的特征,一次函数与一次方程的关系等,解题的关键是读懂“组合函数“的定义.14(2024•钟楼区校级模拟)在同一平面内,具有一条公共边且不完全重合的两个全等三角形,我们称这两个三角形叫做“共边全等”.(1)下列图形中两个三角形不是“共边全等”是③;AB,点E、F分别在AC、BC边(2)如图1,在边长为6的等边三角形ABC中,点D在AB边上,且AD=13上,满足ΔBDF和ΔEDF为“共边全等”,求CF的长;(3)如图2,在平面直角坐标系中,直线y=-3x+12分别与直线y=x、x轴相交于A、B两点,点C是OB 的中点,P、Q在ΔAOB的边上,当以P、B、Q为顶点的三角形与ΔPCB“共边全等”时,请直接写出点Q 的坐标.【分析】(1)由于第③个图不符合共边要求,所以图③即为答案;(2)DF为两个全等三角形的公共边,由于F点在BC边上,E在AC边上,两个三角形的位置可以如图②,在公共边异侧,构成一个轴对称图形,也可以构成一个平行四边形(将图③的两条最长边重合形成),分两类讨论,画出图形,按照图②构图,会得到一个一线三等角模型,利用相似,列出方程来解决,按照平行四边形构图,直接得到ΔADE为等边三角形,计算边长即可求得;(3)由题目要求,可以知道两个全等三角形的公共边为PB边,由于要构成ΔPCB,所以P点只能在OA和OB边上,当P在OA边上,两个三角形可以在PB同侧,也可以在PB异侧,当在PB异侧构图时,可以得到图3和图4,在图3中,当在PB同侧构图时,可以得到图6,当P在OB边上时,Q只能落在OA上,得到图7,利用已知条件,解三角形,即可求出Q点坐标.【解答】解:(1)①②均符合共边全等的特点,只有③,没有公共边,所以③不符合条件,∴答案是③;(2)①如图1,当ΔBDF≅ΔEFD,且是共边全等时,∠BFD=∠EDF,∴DE⎳BC,∵ΔABC是等边三角形,∴ΔADE是等边三角形,AB=2,∵AD=13∴DE=AE=BF=2,∴CF=BC-BF=4,②如图2,当ΔBDF≅ΔEDF,且是共边全等时,BD=DE=6-AD=4,∠DEF=∠B=60°,EF=BF,∴∠AED+∠FEC=120°,又∠AED+∠EDA=120°,。
中考数学复习备考之一次函数(精选40题)

中考数学复习备考之一次函数(精选40题)1.当我们将一条倾斜的直线进行上下平移时,直线的左右位置也发生着变化.下面是关于“一次函数图象平移的性质”的探究过程,请补充完整.(1)如图1,将一次函数y=x+2的图象向下平移1个单位长度,相当于将它向右平移了个单位长度;(2)将一次函数y=﹣2x+4的图象向下平移1个单位长度,相当于将它向(填“左”或“右”)平移了个单位长度;(3)综上,对于一次函数y=kx+b(k≠0)的图象而言,将它向下平移m(m>0)个单位长度,相当于将它向(填“左”或“右”)(k>0时)或将它向(填“左”或“右”)(k<0时)平移了n(n>0)个单位长度,且m,n,k满足等式.2.在平面直角坐标系xOy中,函数y=kx+b(k≠0)的图象过点(4,3),(﹣2,0),且与y轴交于点A.(1)求该函数的解析式及点A的坐标;(2)当x>0时,对于x的每一个值,函数y=x+n的值大于函数y=kx+b(k≠0)的值,直接写出n的取值范围.3.如图,直线y=x+1与x轴交于点A,点A关于y轴的对称点为A′,经过点A′和y 轴上的点B(0,2)的直线设为y=kx+b.(1)求点A′的坐标;(2)确定直线A′B对应的函数表达式.4.探究函数性质时,我们经历了列表、描点、连线画出函数图象,观察分析图象特征,概括函数性质的过程.结合已有经验,请画出函数y=﹣|x|的图象,并探究该函数性质.(1)绘制函数图象①列表:下列是x与y的几组对应值,其中a=.x……﹣5﹣4﹣3﹣2﹣112345……y……﹣3.8﹣2.5﹣1155a﹣1﹣2.5﹣3.8……②描点:根据表中的数值描点(x,y),请补充描出点(2,a);③连线:请用平滑的曲线顺次连接各点,画出函数图象;(2)探究函数性质请写出函数y=﹣|x|的一条性质:;(3)运用函数图象及性质①写出方程﹣|x|=5的解;②写出不等式﹣|x|≤1的解集.5.某校组织学生从学校出发,乘坐大巴前往基地进行研学活动.大巴出发1小时后,学校因事派人乘坐轿车沿相同路线追赶.已知大巴行驶的速度是40千米/小时,轿车行驶的速度是60千米/小时.(1)求轿车出发后多少小时追上大巴?此时,两车与学校相距多少千米?(2)如图,图中OB,AB分别表示大巴、轿车离开学校的路程s(千米)与大巴行驶的时间t(小时)的函数关系的图象.试求点B的坐标和AB所在直线的解析式;(3)假设大巴出发a小时后轿车出发追赶,轿车行驶了1.5小时追上大巴,求a的值.6.随着“公园城市”建设的不断推进,成都绕城绿道化身成为这座城市的一个超大型“体育场”,绿道骑行成为市民的一种低碳生活新风尚.甲、乙两人相约同时从绿道某地出发同向骑行,甲骑行的速度是18km/h,乙骑行的路程s(km)与骑行的时间t(h)之间的关系如图所示.(1)直接写出当0≤t≤0.2和t>0.2时,s与t之间的函数表达式;(2)何时乙骑行在甲的前面?7.为满足顾客的购物需求,某水果店计划购进甲、乙两种水果进行销售.经了解,甲水果的进价比乙水果的进价低20%,水果店用1000元购进甲种水果比用1200元购进乙种水果的重量多10千克,已知甲,乙两种水果的售价分别为6元/千克和8元/千克.(1)求甲、乙两种水果的进价分别是多少?(2)若水果店购进这两种水果共150千克,其中甲种水果的重量不低于乙种水果重量的2倍,则水果店应如何进货才能获得最大利润,最大利润是多少?8.为了振兴乡村经济,我市某镇鼓励广大农户种植山药,并精加工成甲、乙两种产品、某经销商购进甲、乙两种产品,甲种产品进价为8元/kg;乙种产品的进货总金额y(单位:元)与乙种产品进货量x(单位:kg)之间的关系如图所示.已知甲、乙两种产品的售价分别为12元/kg和18元/kg.(1)求出0≤x≤2000和x>2000时,y与x之间的函数关系式;(2)若该经销商购进甲、乙两种产品共6000kg,并能全部售出.其中乙种产品的进货量不低于1600kg,且不高于4000kg,设销售完甲、乙两种产品所获总利润为w元(利润=销售额﹣成本),请求出w(单位:元)与乙种产品进货量x(单位:kg)之间的函数关系式,并为该经销商设计出获得最大利润的进货方案;(3)为回馈广大客户,该经销商决定对两种产品进行让利销售.在(2)中获得最大利润的进货方案下,甲、乙两种产品售价分别降低a元/kg和2a元/kg,全部售出后所获总利润不低于15000元,求a的最大值.9.(3分)(2022•深圳)某学校打算购买甲乙两种不同类型的笔记本.已知甲种类型的笔记本的单价比乙种类型的要便宜1元,且用110元购买的甲种类型的数量与用120元购买的乙种类型的数量一样.(1)求甲乙两种类型笔记本的单价.(2)该学校打算购买甲乙两种类型笔记本共100件,且购买的乙的数量不超过甲的3倍,则购买的最低费用是多少.10.(3分)(2022•黔西南州)某乡镇新打造的“田园风光”景区今年计划改造一片绿化地,种植A、B两种花卉,已知3盆A种花卉和4盆B种花卉的种植费用为330元,4盆A 种花卉和3盆B种花卉的种植费用为300元.(1)每盆A种花卉和每盆B种花卉的种植费用各是多少元?(2)若该景区今年计划种植A、B两种花卉共400盆,相关资料表明:A、B两种花卉的成活率分别为70%和90%,景区明年要将枯死的花卉补上相同的新花卉,但这两种花卉在明年共补的盆数不多于80盆,应如何安排这两种花卉的种植数量,才能使今年该项的种植费用最低?并求出最低费用.11.(3分)(2022•南通)某水果店购进甲、乙两种苹果的进价分别为8元/kg、12元/kg,这两种苹果的销售额y(单位:元)与销售量x(单位:kg)之间的关系如图所示.(1)写出图中点B表示的实际意义;(2)分别求甲、乙两种苹果销售额y(单位:元)与销售量x(单位:kg)之间的函数解析式,并写出x的取值范围;(3)若不计损耗等因素,当甲、乙两种苹果的销售量均为akg时,它们的利润和为1500元,求a的值.12.(3分)(2022•济宁)某运输公司安排甲、乙两种货车24辆恰好一次性将328吨的物资运往A,B两地,两种货车载重量及到A,B两地的运输成本如表:货车类型载重量(吨/辆)运往A地的成本(元/辆)运往B地的成本(元/辆)甲种161200900乙种121000750(1)求甲、乙两种货车各用了多少辆;(2)如果前往A地的甲、乙两种货车共12辆,所运物资不少于160吨,其余货车将剩余物资运往B地.设甲、乙两种货车到A,B两地的总运输成本为w元,前往A地的甲种货车为t辆.①写出w与t之间的函数解析式;②当t为何值时,w最小?最小值是多少?13.(3分)(2022•长春)已知A、B两地之间有一条长440千米的高速公路.甲、乙两车分别从A、B两地同时出发,沿此公路相向而行,甲车先以100千米/时的速度匀速行驶200千米后与乙车相遇,再以另一速度继续匀速行驶4小时到达B地;乙车匀速行驶至A地,两车到达各自的目的地后停止,两车距A地的路程y(千米)与各自的行驶时间x(时)之间的函数关系如图所示.(1)m=,n=;(2)求两车相遇后,甲车距A地的路程y与x之间的函数关系式;(3)当乙车到达A地时,求甲车距A地的路程.14.(3分)(2022•通辽)为落实“双减”政策,丰富课后服务的内容,某学校计划到甲、乙两个体育专卖店购买一批新的体育用品,两个商店的优惠活动如下:甲:所有商品按原价8.5折出售;乙:一次购买商品总额不超过300元的按原价付费,超过300元的部分打7折.设需要购买体育用品的原价总额为x元,去甲商店购买实付y甲元,去乙商店购买实付y元,其函数图象如图所示.乙(1)分别求y甲,y乙关于x的函数关系式;(2)两图象交于点A,求点A坐标;(3)请根据函数图象,直接写出选择去哪个体育专卖店购买体育用品更合算.15.(3分)(2022•广安)某企业下属A、B两厂向甲乙两地运送水泥共520吨,A厂比B厂少运送20吨,从A厂运往甲乙两地的运费分别为40元/吨和35元/吨,从B厂运往甲乙两地的运费分别为28元/吨和25元/吨.(1)求A、B两厂各运送多少吨水泥;(2)现甲地需要水泥240吨,乙地需要水泥280吨.受条件限制,B厂运往甲地的水泥最多150吨.设从A厂运往甲地a吨水泥,A、B两厂运往甲乙两地的总运费为w元.求w与a之间的函数关系式,请你为该企业设计一种总运费最低的运输方案,并说明理由.16.(3分)(2022•恩施州)某校计划租用甲、乙两种客车送180名师生去研学基地开展综合实践活动.已知租用一辆甲型客车和一辆乙型客车共需500元,租用2辆甲型客车和3辆乙型客车共需1300元.甲型客车每辆可坐15名师生,乙型客车每辆可坐25名师生.(1)租用甲、乙两种客车每辆各多少元?(2)若学校计划租用8辆客车,怎样租车可使总费用最少?17.(3分)(2022•包头)由于精准扶贫的措施科学得当,贫困户小颖家今年种植的草莓喜获丰收,采摘上市16天全部销售完.小颖对销售情况进行统计后发现,在该草莓上市第x天(x取整数)时,日销售量y(单位:千克)与x之间的函数关系式为y=,草莓价格m(单位:元/千克)与x之间的函数关系如图所示.(1)求第14天小颖家草莓的日销售量;(2)求当4≤x≤12时,草莓价格m与x之间的函数关系式;(3)试比较第8天与第10天的销售金额哪天多?18.(3分)(2022•天津)在“看图说故事”活动中,某学习小组结合图象设计了一个问题情境.已知学生公寓、阅览室、超市依次在同一条直线上,阅览室离学生公寓1.2km,超市离学生公寓2km.小琪从学生公寓出发,匀速步行了12min到阅览室;在阅览室停留70min 后,匀速步行了10min到超市;在超市停留20min后,匀速骑行了8min返回学生公寓.给出的图象反映了这个过程中小琪离学生公寓的距离ykm与离开学生公寓的时间xmin之间的对应关系.请根据相关信息,解答下列问题:(Ⅰ)填表:离开学生公寓的时间/min585087112离学生公寓的距离/km0.5 1.6(Ⅱ)填空:①阅览室到超市的距离为km;②小琪从超市返回学生公寓的速度为km/min;③当小琪离学生公寓的距离为1km时,他离开学生公寓的时间为min.(Ⅲ)当0≤x≤92时,请直接写出y关于x的函数解析式.19.(3分)(2022•内蒙古)某商店决定购进A、B两种北京冬奥会纪念品.若购进A种纪念品10件,B种纪念品5件,需要1000元;若购进A种纪念品5件,B种纪念品3件,需要550元.(1)求购进A、B两种纪念品的单价;(2)若该商店决定拿出1万元全部用来购进这两种纪念品,考虑市场需求,要求购进A 种纪念品的数量不少于B种纪念品数量的6倍,且购进B种纪念品数量不少于20件,那么该商店共有几种进货方案?(3)若销售每件A种纪念品可获利润20元,每件B种纪念品可获利润30元,在第(2)问的各种进货方案中,哪一种方案获利最大?求出最大利润.20.(3分)(2022•遵义)遵义市开展信息技术与教学深度融合的“精准化教学”,某实验学校计划购买A,B两种型号教学设备,已知A型设备价格比B型设备价格每台高20%,用30000元购买A型设备的数量比用15000元购买B型设备的数量多4台.(1)求A,B型设备单价分别是多少元;(2)该校计划购买两种设备共50台,要求A型设备数量不少于B型设备数量的.设购买a台A型设备,购买总费用为w元,求w与a的函数关系式,并求出最少购买费用.21.(3分)(2022•黑龙江)为抗击疫情,支援B市,A市某蔬菜公司紧急调运两车蔬菜运往B市.甲、乙两辆货车从A市出发前往B市,乙车行驶途中发生故障原地维修,此时甲车刚好到达B市.甲车卸载蔬菜后立即原路原速返回接应乙车,把乙车的蔬菜装上甲车后立即原路原速又运往B市.乙车维修完毕后立即返回A市.两车离A市的距离y(km)与乙车所用时间x(h)之间的函数图象如图所示.(1)甲车速度是km/h,乙车出发时速度是km/h;(2)求乙车返回过程中,乙车离A市的距离y(km)与乙车所用时间x(h)的函数解析式(不要求写出自变量的取值范围);(3)乙车出发多少小时,两车之间的距离是120km?请直接写出答案.22.(3分)(2022•吉林)李强用甲、乙两种具有恒温功能的热水壶同时加热相同质量的水,甲壶比乙壶加热速度快.在一段时间内,水温y(℃)与加热时间x(s)之间近似满足一次函数关系,根据记录的数据,画函数图象如下:(1)加热前水温是℃.(2)求乙壶中水温y关于加热时间x的函数解析式.(3)当甲壶中水温刚达到80℃时,乙壶中水温是℃.23.(3分)(2022•苏州)某水果店经销甲、乙两种水果,两次购进水果的情况如表所示:进货批次甲种水果质量(单位:千克)乙种水果质量(单位:千克)总费用(单位:元)第一次60401520第二次30501360(1)求甲、乙两种水果的进价;(2)销售完前两次购进的水果后,该水果店决定回馈顾客,开展促销活动.第三次购进甲、乙两种水果共200千克,且投入的资金不超过3360元.将其中的m千克甲种水果和3m千克乙种水果按进价销售,剩余的甲种水果以每千克17元、乙种水果以每千克30元的价格销售.若第三次购进的200千克水果全部售出后,获得的最大利润不低于800元,求正整数m的最大值.24.(3分)(2022•衡阳)冰墩墩(BingDwenDwen)、雪容融(ShueyRhonRhon)分别是2022年北京冬奥会、冬残奥会的吉祥物.冬奥会来临之际,冰墩墩、雪容融玩偶畅销全国.小雅在某网店选中两种玩偶.决定从该网店进货并销售.第一次小雅用1400元购进了冰墩墩玩偶15个和雪容融玩偶5个,已知购进1个冰墩墩玩偶和1个雪容融玩偶共需136元,销售时每个冰墩墩玩偶可获利28元,每个雪容融玩偶可获利20元.(1)求两种玩偶的进货价分别是多少?(2)第二次小雅进货时,网店规定冰墩墩玩偶进货数量不得超过雪容融玩偶进货数量的1.5倍.小雅计划购进两种玩偶共40个,应如何设计进货方案才能获得最大利润,最大利润是多少元?25.(3分)(2022•绍兴)一个深为6米的水池积存着少量水,现在打开水阀进水,下表记录了2小时内5个时刻的水位高度,其中x表示进水用时(单位:小时),y表示水位高度(单位:米).x00.51 1.52y1 1.52 2.53为了描述水池水位高度与进水用时的关系,现有以下三种函数模型供选择:y=kx+b(k ≠0),y=ax2+bx+c(a≠0),y=(k≠0).(1)在平面直角坐标系中描出表中数据对应的点,再选出最符合实际的函数模型,求出相应的函数表达式,并画出这个函数的图象.(2)当水位高度达到5米时,求进水用时x.26.(3分)(2022•云南)某学校要购买甲、乙两种消毒液,用于预防新型冠状病毒.若购买9桶甲消毒液和6桶乙消毒液,则一共需要615元;若购买8桶甲消毒液和12桶乙消毒液,则一共需要780元.(1)每桶甲消毒液、每桶乙消毒液的价格分别是多少元?(2)若该校计划购买甲、乙两种消毒液共30桶,其中购买甲消毒液a桶,且甲消毒液的数量至少比乙消毒液的数量多5桶,又不超过乙消毒液的数量的2倍.怎样购买,才能使总费用W最少?并求出最少费用.27.(3分)(2022•凉山州)为全面贯彻党的教育方针,严格落实教育部对中小学生“五项管理”的相关要求和《关于进一步加强中小学生体质健康管理工作的通知》精神,保障学生每天在校1小时体育活动时间,某班计划采购A、B两种类型的羽毛球拍.已知购买3副A型羽毛球拍和4副B型羽毛球拍共需248元;购买5副A型羽毛球拍和2副B型羽毛球拍共需264元.(1)求A、B两种类型羽毛球拍的单价.(2)该班准备采购A、B两种类型的羽毛球拍共30副,且A型羽毛球拍的数量不少于B 型羽毛球拍数量的2倍,请给出最省钱的购买方案,求出最少费用,并说明理由.28.(3分)(2022•丽水)因疫情防控需要,一辆货车先从甲地出发运送防疫物资到乙地,稍后一辆轿车从甲地急送防疫专家到乙地.已知甲、乙两地的路程是330km,货车行驶时的速度是60km/h.两车离甲地的路程s(km)与时间t(h)的函数图象如图.(1)求出a的值;(2)求轿车离甲地的路程s(km)与时间t(h)的函数表达式;(3)问轿车比货车早多少时间到达乙地?29.(3分)(2022•德阳)习近平总书记对实施乡村振兴战略作出重要指示强调:实施乡村振兴战略,是党的十九大作出的重大决策部署,是新时代做好“三农”工作的总抓手.为了发展特色产业,红旗村花费4000元集中采购了A种树苗500株,B种树苗400株,已知B种树苗单价是A种树苗单价的1.25倍.(1)求A、B两种树苗的单价分别是多少元?(2)红旗村决定再购买同样的树苗100株用于补充栽种,其中A种树苗不多于25株,在单价不变,总费用不超过480元的情况下,共有几种购买方案?哪种方案费用最低?最低费用是多少元?30.(3分)(2022•牡丹江)在一条平坦笔直的道路上依次有A,B,C三地,甲从B地骑电瓶车到C地,同时乙从B地骑摩托车到A地,到达A地后因故停留1分钟,然后立即掉头(掉头时间忽略不计)按原路原速前往C地,结果乙比甲早2分钟到达C地,两人均匀速运动,如图是两人距B地路程y(米)与时间x(分钟)之间的函数图象.请解答下列问题:(1)填空:甲的速度为米/分钟,乙的速度为米/分钟;(2)求图象中线段FG所在直线表示的y(米)与时间x(分钟)之间的函数解析式,并写出自变量x的取值范围;(3)出发多少分钟后,甲乙两人之间的路程相距600米?请直接写出答案.31.(3分)(2022•梧州)梧州市地处亚热带,盛产龙眼.新鲜龙眼的保质期短,若加工成龙眼干(又叫带壳圆肉)则有利于较长时间保存.已知3kg的新鲜龙眼在无损耗的情况下可以加工成1kg的龙眼干.(1)若新鲜龙眼售价为12元/kg.在无损耗的情况下加工成龙眼干,使龙眼干的销售收益不低于新鲜龙眼的销售收益,则龙眼干的售价应不低于多少元/kg?(2)在实践中,小苏发现当地在加工龙眼干的过程中新鲜龙眼有6%的损耗,为确保果农的利益,龙眼干的销售收益应不低于新鲜龙眼的销售收益,此时龙眼干的定价取最低整数价格.市场调查还发现,新鲜龙眼以12元/kg最多能卖出100kg,超出部分平均售价是5元/kg,可售完.果农们都以这种方式出售新鲜龙眼.设某果农有akg新鲜龙眼,他全部加工成龙眼干销售获得的收益与全部以新鲜龙眼销售获得的收益之差为w元,请写出w与a的函数关系式.32.(3分)(2022•十堰)某商户购进一批童装,40天销售完毕.根据所记录的数据发现,日销售量y(件)与销售时间x(天)之间的关系式是y=,销售单价p(元/件)与销售时间x(天)之间的函数关系如图所示.(1)第15天的日销售量为件;(2)0<x≤30时,求日销售额的最大值;(3)在销售过程中,若日销售量不低于48件的时间段为“火热销售期”,则“火热销售期”共有多少天?33.(3分)(2022•齐齐哈尔)在一条笔直的公路上有A、B两地,甲、乙二人同时出发,甲从A地步行匀速前往B地,到达B地后,立刻以原速度沿原路返回A地.乙从B地步行匀速前往A地(甲、乙二人到达A地后均停止运动),甲、乙二人之间的距离y(米)与出发时间x(分钟)之间的函数关系如图所示,请结合图象解答下列问题:(1)A、B两地之间的距离是米,乙的步行速度是米/分;(2)图中a=,b=,c=;(3)求线段MN的函数解析式;(4)在乙运动的过程中,何时两人相距80米?(直接写出答案即可)34.(3分)(2022•黑龙江)为了迎接“十•一”小长假的购物高峰.某运动品牌专卖店准备购进甲、乙两种运动鞋.其中甲、乙两种运动鞋的进价和售价如下表:运动鞋价格甲 乙进价(元/双)m m ﹣20 售价(元/双) 240 160 已知:用3000元购进甲种运动鞋的数量与用2400元购进乙种运动鞋的数量相同.(1)求m 的值;(2)要使购进的甲、乙两种运动鞋共200双的总利润(利润=售价﹣进价)不少于21700元,且不超过22300元,问该专卖店有几种进货方案?(3)在(2)的条件下,专卖店准备对甲种运动鞋进行优惠促销活动,决定对甲种运动鞋每双优惠a (50<a <70)元出售,乙种运动鞋价格不变.那么该专卖店要获得最大利润应如何进货?35.(3分)(2022•兰州)在平面直角坐标系中,P (a ,b )是第一象限内一点,给出如下定义:k 1=和k 2=两个值中的最大值叫做点P 的“倾斜系数”k .(1)求点P (6,2)的“倾斜系数”k 的值;(2)①若点P (a ,b )的“倾斜系数”k =2,请写出a 和b 的数量关系,并说明理由; ②若点P (a ,b )的“倾斜系数”k =2,且a +b =3,求OP 的长;(3)如图,边长为2的正方形ABCD 沿直线AC :y =x 运动,P (a ,b )是正方形ABCD 上任意一点,且点P 的“倾斜系数”k <,请直接写出a 的取值范围.36.(3分)(2022•河北)如图,平面直角坐标系中,线段AB 的端点为A (﹣8,19),B (6,5).(1)求AB所在直线的解析式;(2)某同学设计了一个动画:在函数y=mx+n(m≠0,y≥0)中,分别输入m和n的值,使得到射线CD,其中C(c,0).当c=2时,会从C处弹出一个光点P,并沿CD飞行;当c≠2时,只发出射线而无光点弹出.①若有光点P弹出,试推算m,n应满足的数量关系;②当有光点P弹出,并击中线段AB上的整点(横、纵坐标都是整数)时,线段AB就会发光.求此时整数m的个数.37.(3分)(2022•攀枝花)如图,直线y=x+6分别与x轴、y轴交于点A、B,点C为线段AB上一动点(不与A、B重合),以C为顶点作∠OCD=∠OAB,射线CD交线段OB于点D,将射线OC绕点O顺时针旋转90°交射线CD于点E,连结BE.(1)证明:=;(用图1)(2)当△BDE为直角三角形时,求DE的长度;(用图2)(3)点A关于射线OC的对称点为F,求BF的最小值.(用图3)38.(3分)(2022•沈阳)如图,在平面直角坐标系中,一次函数y=kx+b的图象与x轴交于点A,与y轴交于点B(0,9),与直线OC交于点C(8,3).(1)求直线AB的函数表达式;(2)过点C作CD⊥x轴于点D,将△ACD沿射线CB平移得到的三角形记为△A′C′D′,点A,C,D的对应点分别为A′,C′,D′,若△A′C′D′与△BOC重叠部分的面积为S,平移的距离CC′=m,当点A′与点B重合时停止运动.①若直线C′D′交直线OC于点E,则线段C′E的长为(用含有m的代数式表示);②当0<m<时,S与m的关系式为;③当S=时,m的值为.39.(3分)(2022•泰州)定义:对于一次函数y1=ax+b、y2=cx+d,我们称函数y=m(ax+b)+n(cx+d)(ma+nc≠0)为函数y1、y2的“组合函数”.(1)若m=3,n=1,试判断函数y=5x+2是否为函数y1=x+1、y2=2x﹣1的“组合函数”,并说明理由;(2)设函数y1=x﹣p﹣2与y2=﹣x+3p的图象相交于点P.①若m+n>1,点P在函数y1、y2的“组合函数”图象的上方,求p的取值范围;②若p≠1,函数y1、y2的“组合函数”图象经过点P.是否存在大小确定的m值,对于不等于1的任意实数p,都有“组合函数”图象与x轴交点Q的位置不变?若存在,请求出m的值及此时点Q的坐标;若不存在,请说明理由.40.(3分)(2022•黑龙江)如图,直线MN与x轴,y轴分别相交于A,C两点,分别过A,C两点作x轴,y轴的垂线相交于B点,且OA,OC(OA>OC)的长分别是一元二次方程x2﹣14x+48=0的两个实数根.(1)求C点坐标;(2)求直线MN的解析式;(3)在直线MN上存在点P,使以点P,B,C三点为顶点的三角形是等腰三角形,请直接写出P点的坐标.。
中考数学复习----《一次函数之定义、图像与性质》知识点总结与专项练习题(含答案解析)

中考数学复习----《一次函数之定义、图像与性质》知识点总结与专项练习题(含答案解析)知识点总结1. 一次函数的定义:一般地,形如()0≠+=k b k b kx y 是常数且,的函数叫做一次函数。
2. 一次函数的图像:是不经过原点的一条直线。
3. 一次函数的图像与性质:一次函数与x 轴的交点坐标公式为:⎪⎭⎫ ⎝⎛−0 ,k b;与y 轴的交点坐标公式为:()b ,0。
专项练习题1.(2022•沈阳)在平面直角坐标系中,一次函数y =﹣x +1的图像是( )A .B .C .D .【分析】依据一次函数y =x +1的图像经过点(0,1)和(1,0),即可得到一次函数y =﹣x +1的图像经过一、二、四象限.【解答】解:一次函数y =﹣x +1中,令x =0,则y =1;令y =0,则x =1, ∴一次函数y =﹣x +1的图像经过点(0,1)和(1,0), ∴一次函数y =﹣x +1的图像经过一、二、四象限, 故选:C .2.(2022•安徽)在同一平面直角坐标系中,一次函数y =ax +a 2与y =a 2x +a 的图像可能是( )A .B .C .D .【分析】利用一次函数的性质进行判断.【解答】解:∵y=ax+a2与y=a2x+a,∴x=1时,两函数的值都是a2+a,∴两直线的交点的横坐标为1,若a>0,则一次函数y=ax+a2与y=a2x+a都是增函数,且都交y轴的正半轴,图像都经过第一、二、三象限;若a<0,则一次函数y=ax+a2经过第一、二、四象限,y=a2x+a经过第一、三、四象限,且两直线的交点的横坐标为1;故选:D.3.(2022•辽宁)如图,在同一平面直角坐标系中,一次函数y=k1x+b1与y=k2x+b2的图像分别为直线l1和直线l2,下列结论正确的是()A.k1•k2<0B.k1+k2<0C.b1﹣b2<0D.b1•b2<0【分析】根据一次函数y=k1x+b1与y=k2x+b2的图像位置,可得k1>0,b1>0,k2>0,b2<0,然后逐一判断即可解答.【解答】解:∵一次函数y=k1x+b1的图像过一、二、三象限,∴k1>0,b1>0,∵一次函数y=k2x+b2的图像过一、三、四象限,∴k2>0,b2<0,∴A、k1•k2>0,故A不符合题意;B、k1+k2>0,故B不符合题意;C、b1﹣b2>0,故C不符合题意;D、b1•b2<0,故D符合题意;故选:D.4.(2022•六盘水)如图是一次函数y=kx+b的图像,下列说法正确的是()A.y随x增大而增大B.图像经过第三象限C.当x≥0时,y≤b D.当x<0时,y<0【分析】根据一次函数的图像和性质进行判断即可.【解答】解:由图像得:图像过一、二、四象限,则k<0,b>0,当k<0时,y随x的增大而减小,故A、B错误,由图像得:与y轴的交点为(0,b),所以当x≥0时,从图像看,y≤b,故C正确,符合题意;当x<0时,y>b>0,故D错误.故选:C.5.(2022•兰州)若一次函数y=2x+1的图像经过点(﹣3,y1),(4,y2),则y1与y2的大小关系是()A.y1<y2B.y1>y2C.y1≤y2D.y1≥y2【分析】先根据一次函数的解析式判断出函数的增减性,再根据﹣3<4即可得出结论.【解答】解:∵一次函数y=2x+1中,k=2>0,∴y随着x的增大而增大.∵点(﹣3,y1)和(4,y2)是一次函数y=2x+1图像上的两个点,﹣3<4,∴y1<y2.故选:A.6.(2022•凉山州)一次函数y=3x+b(b≥0)的图像一定不经过()A.第一象限B.第二象限C.第三象限D.第四象限【分析】根据一次函数的图像与系数的关系即可得出结论.【解答】解:∵函数y=3x+b(b≥0)中,k=3>0,b≥0,∴当b=0时,此函数的图像经过一、三象限,不经过第四象限;当b>0时,此函数的图像经过一、二、三象限,不经过第四象限.则一定不经过第四象限.故选:D.7.(2022•济宁)已知直线y1=x﹣1与y2=kx+b相交于点(2,1).请写出一个b值(写出一个即可),使x>2时,y1>y2.【分析】由题意可知,当b>﹣1时满足题意,故b可以取0.【解答】解:直线y1=x﹣1与y2=kx+b相交于点(2,1).∵x>2时,y1>y2.∴b>﹣1,故b可以取0,故答案为:0(答案不唯一).8.(2022•上海)已知直线y=kx+b过第一象限且函数值随着x的增大而减小,请列举出来这样的一条直线:.【分析】根据一次函数的性质,写出符合条件的函数关系式即可.【解答】解:∵直线y=kx+b过第一象限且函数值随着x的增大而减小,∴k<0,b>0,∴符合条件的函数关系式可以为:y=﹣x+1(答案不唯一).故答案为:y=﹣x+1(答案不唯一).9.(2022•无锡)请写出一个函数的表达式,使其图像分别与x轴的负半轴、y轴的正半轴相交:.【分析】设函数的解析式为y=kx+b(k≠0),再根据一次函数的图像分别与x轴的负半轴、y轴的正半轴相交可知k>0,b>0,写出符合此条件的函数解析式即可.【解答】解:设一次函数的解析式为y=kx+b(k≠0),∵一次函数的图像分别与x轴的负半轴、y轴的正半轴相交,∴k>0,b>0,∴符合条件的函数解析式可以为:y=x+1(答案不唯一).故答案为:y=x+1(答案不唯一).10.(2022•湘潭)请写出一个y随x增大而增大的一次函数表达式.【分析】根据y随着x的增大而增大时,比例系数k>0即可确定一次函数的表达式.【解答】解:在y=kx+b中,若k>0,则y随x增大而增大,∴只需写出一个k>0的一次函数表达式即可,比如:y=x﹣2,故答案为:y=x﹣2(答案不唯一).11.(2022•宿迁)甲、乙两位同学各给出某函数的一个特征,甲:“函数值y随自变量x增大而减小”;乙:“函数图像经过点(0,2)”,请你写出一个同时满足这两个特征的函数,其表达式是.【分析】根据甲、乙两位同学给出的函数特征可判断出该函数为一次函数,再利用一次函数的性质,可得出k<0,b=2,取k=﹣1即可得出结论.【解答】解:∵函数值y随自变量x增大而减小,且该函数图像经过点(0,2),∴该函数为一次函数.设一次函数的表达式为y=kx+b(k≠0),则k<0,b=2.取k=﹣1,此时一次函数的表达式为y=﹣x+2.故答案为:y=﹣x+2(答案不唯一).12.(2022•甘肃)若一次函数y=kx﹣2的函数值y随着自变量x值的增大而增大,则k=(写出一个满足条件的值).【分析】根据函数值y随着自变量x值的增大而增大得到k>0,写出一个正数即可.【解答】解:∵函数值y随着自变量x值的增大而增大,∴k>0,∴k=2(答案不唯一).故答案为:2(答案不唯一).13.(2022•柳州)如图,直线y1=x+3分别与x轴、y轴交于点A和点C,直线y2=﹣x+3分别与x轴、y轴交于点B和点C,点P(m,2)是△ABC内部(包括边上)的一点,则m的最大值与最小值之差为()A.1B.2C.4D.6【分析】由于P的纵坐标为2,故点P在直线y=2上,要求符合题意的m值,则P点为直线y=2与题目中两直线的交点,此时m存在最大值与最小值,故可求得.【解答】解:∵点P(m,2)是△ABC内部(包括边上)的一点,∴点P 在直线y =2上,如图所示,当P 为直线y =2与直线y 2的交点时,m 取最大值, 当P 为直线y =2与直线y 1的交点时,m 取最小值, ∵y 2=﹣x +3中令y =2,则x =1, y 1=x +3中令y =2,则x =﹣1, ∴m 的最大值为1,m 的最小值为﹣1.则m 的最大值与最小值之差为:1﹣(﹣1)=2. 故选:B .14.(2022•遵义)若一次函数y =(k +3)x ﹣1的函数值y 随x 的增大而减小,则k 值可能是( ) A .2B .23C .﹣21 D .﹣4【分析】根据一次项系数小于0时,一次函数的函数值y 随x 的增大而减小列出不等式求解即可.【解答】解:∵一次函数y =(k +3)x ﹣1的函数值y 随着x 的增大而减小, ∴k +3<0, 解得k <﹣3.所以k 的值可以是﹣4, 故选:D .15.(2022•包头)在一次函数y =﹣5ax +b (a ≠0)中,y 的值随x 值的增大而增大,且ab >0,则点A (a ,b )在( ) A .第四象限B .第三象限C .第二象限D .第一象限【分析】根据一次函数的增减性,确定自变量x 的系数﹣5a 的符号,再根据ab >0,确定b 的符号,从而确定点A (a ,b )所在的象限.【解答】解:∵在一次函数y =﹣5ax +b 中,y 随x 的增大而增大, ∴﹣5a >0,∴a <0. ∵ab >0, ∴a ,b 同号, ∴b <0.∴点A (a ,b )在第三象限. 故选:B .16.(2022•眉山)一次函数y =(2m ﹣1)x +2的值随x 的增大而增大,则点P (﹣m ,m )所在象限为( ) A .第一象限B .第二象限C .第三象限D .第四象限【分析】根据一次函数的性质求出m 的范围,再根据每个象限点的坐标特征判断P 点所处的象限即可.【解答】解:∵一次函数y =(2m ﹣1)x +2的值随x 的增大而增大, ∴2m ﹣1>0, 解得:m >,∴P (﹣m ,m )在第二象限, 故选:B .17.(2022•天津)若一次函数y =x +b (b 是常数)的图像经过第一、二、三象限,则b 的值可以是 (写出一个即可).【分析】根据一次函数的图像可知b >0即可.【解答】解:∵一次函数y =x +b (b 是常数)的图像经过第一、二、三象限, ∴b >0, 可取b =1,故答案为:1.(答案不唯一,满足b >0即可) 18.(2022•邵阳)在直角坐标系中,已知点A (23,m ),点B (27,n )是直线y =kx +b(k <0)上的两点,则m ,n 的大小关系是( ) A .m <nB .m >nC .m ≥nD .m ≤n【分析】根据k <0可知函数y 随着x 增大而减小,再根>即可比较m 和n 的大小.【解答】解:点A (,m ),点B (,n )是直线y =kx +b 上的两点,且k <0,∴一次函数y 随着x 增大而减小, ∵>,∴m <n , 故选:A .19.(2022•株洲)在平面直角坐标系中,一次函数y =5x +1的图像与y 轴的交点的坐标为( ) A .(0,﹣1)B .(﹣51,0) C .(51,0) D .(0,1)【分析】一次函数的图像与y 轴的交点的横坐标是0,当x =0时,y =1,从而得出答案. 【解答】解:∵当x =0时,y =1,∴一次函数y =5x +1的图像与y 轴的交点的坐标为(0,1), 故选:D .20.(2022•绍兴)已知(x 1,y 1),(x 2,y 2),(x 3,y 3)为直线y =﹣2x +3上的三个点,且x 1<x 2<x 3,则以下判断正确的是( ) A .若x 1x 2>0,则y 1y 3>0 B .若x 1x 3<0,则y 1y 2>0C .若x 2x 3>0,则y 1y 3>0D .若x 2x 3<0,则y 1y 2>0【分析】根据一次函数的性质和各个选项中的条件,可以判断是否正确,从而可以解答本题.【解答】解:∵直线y =﹣2x +3,∴y 随x 的增大而减小,当y =0时,x =1.5,∵(x 1,y 1),(x 2,y 2),(x 3,y 3)为直线y =﹣2x +3上的三个点,且x 1<x 2<x 3, ∴若x 1x 2>0,则x 1,x 2同号,但不能确定y 1y 3的正负,故选项A 不符合题意; 若x 1x 3<0,则x 1,x 3异号,但不能确定y 1y 2的正负,故选项B 不符合题意; 若x 2x 3>0,则x 2,x 3同号,但不能确定y 1y 3的正负,故选项C 不符合题意;若x 2x 3<0,则x 2,x 3异号,则x 1,x 2同时为负,故y 1,y 2同时为正,故y 1y 2>0,故选项D 符合题意; 故选:D .21.(2022•盘锦)点A (x 1,y 1),B (x 2,y 2)在一次函数y =(a ﹣2)x +1的图像上,当x 1>x 2时,y 1<y 2,则a 的取值范围是 . 【分析】根据一次函数的性质,建立不等式计算即可.【解答】解:∵当x1>x2时,y1<y2,∴a﹣2<0,∴a<2,故答案为:a<2.22.(2022•永州)已知一次函数y=x+1的图像经过点(m,2),则m=.【分析】由一次函数y=x+1的图像经过点(m,2),利用一次函数图像上点的坐标特征可得出2=m+1,解之即可求出m的值.【解答】解:∵一次函数y=x+1的图像经过点(m,2),∴2=m+1,∴m=1.故答案为:1.。
中考数学专题《一次函数》复习课件(共20张PPT)

2D
S△COD=
1 2
OC
OD
C
x
O1
122 2 23 3
考点二:确定一次函数解析式及其相关问题
例2:已知:一次函数图象经过A(1,5), B(-2,-4)两点, 图象与x轴交于点C,与 y轴交于点D.
(5)若直线l:y= x-4与此一次函数图象相交 于点P,试求点P的坐标
【解析】:(5)由题意可得:
例1:已知直线解析式为y=(3m-2)x+(1-2m) ,其中m为常数:
(2)当m为何值时,y随x的增大而减小?
【解析】:
∵y随x的增大而减小
2
∴3m-2<0
∴m<
本题考查一次函数的性质,即:在y3=kx+b(k≠0)中,
当k>0时,y随x的增大而增大;
当k<0时,y随x的增大而减小;
考点一:一次函数定义、图象、性质的相关知识
例1:已知直线解析式为y=(3m-2)x+(1-2m) , 其中m为常数:
(3)当m为何值时,图象经过第二、三、四象 限?
【解析】:∵图象经过第二、、四象限∴ 3m 2 0 1 2m 0
∴ 1m 2
2
3
本题考查一次函数的图象及其性质
例题分析
考点一:一次函数定义、图象、性质的相关知识 例1:已知直线解析式为y=(3m-2)x+(1-2m) ,其中m为
④直线AB上有一点C,
y
且点C的横坐标为1, 求点C的坐标及S△BOC的面积
B
C
解:在y=-2x+4中,
当x=1时,y=2
∴C:(1,2)
S△BOC= 1 OB×|1|=2
2
中考数学高频考点《一次函数》专项测试卷-附答案

中考数学高频考点《一次函数》专项测试卷-附答案学校:___________班级:___________姓名:___________考号:___________1.(10分)某健身器材专卖店推出两种优惠活动,并规定购物时只能选择其中一种.活动一:所购商品按原价打八折;活动二:所购商品按原价每满300元减80元.(如:所购商品原价为300元,可减80元,需付款220元;所购商品原价为770元,可减160元,需付款610元)(1)购买一件原价为450元的健身器材时,选择哪种活动更合算?请说明理由;(2)购买一件原价在500元以下的健身器材时,若选择活动一和选择活动二的付款金额相等,求一件这种健身器材的原价;(3)购买一件原价在900元以下的健身器材时,原价在什么范围内,选择活动二比选择活动一更合算?设一件这种健身器材的原价为a元,请直接写出a的取值范围.2.(9分)近日,教育部印发《义务教育课程方案》和课程标准(2022年版),将劳动从原来的综合实践活动课程中独立出来.某中学为了让学生体验农耕劳动,开辟了一处耕种园,需要采购一批菜苗开展种植活动.据了解,市场上每捆A种菜苗的价格是菜苗基地的倍,用300元在市场上购买的A种菜苗比在菜苗基地购买的少3捆.(1)求菜苗基地每捆A种菜苗的价格.(2)菜苗基地每捆B种菜苗的价格是30元.学校决定在菜苗基地购买A,B两种菜苗共100捆,且A 种菜苗的捆数不超过B种菜苗的捆数.菜苗基地为支持该校活动,对A,B两种菜苗均提供九折优惠.求本次购买最少花费多少钱.3.(9分)猕猴嬉戏是王屋山景区的一大特色,猕猴玩偶非常畅销.小李在某网店选中A,B两款猕猴玩偶,决定从该网店进货并销售.两款玩偶的进货价和销售价如下表:A款玩偶B款玩偶类别价格进货价(元/个)4030销售价(元/个)5645(1)第一次小李用1100元购进了A,B两款玩偶共30个,求两款玩偶各购进多少个.(2)第二次小李进货时,网店规定A款玩偶进货数量不得超过B款玩偶进货数量的一半.小李计划购进两款玩偶共30个,应如何设计进货方案才能获得最大利润,最大利润是多少?(3)小李第二次进货时采取了(2)中设计的方案,并且两次购进的玩偶全部售出,请从利润率的角度分析,对于小李来说哪一次更合算?(注:利润率=×100%)4.(9分)暑期将至,某健身俱乐部面向学生推出暑期优惠活动,活动方案如下.方案一:购买一张学生暑期专享卡,每次健身费用按六折优惠;方案二:不购买学生暑期专享卡,每次健身费用按八折优惠.设某学生暑期健身x(次),按照方案一所需费用为y1(元),且y1=k1x+b;按照方案二所需费用为y2(元),且y2=k2x.其函数图象如图所示.(1)求k1和b的值,并说明它们的实际意义;(2)求打折前的每次健身费用和k2的值;(3)八年级学生小华计划暑期前往该俱乐部健身8次,应选择哪种方案所需费用更少?说明理由.5.(9分)学校计划为“我和我的祖国”演讲比赛购买奖品.已知购买3个A奖品和2个B奖品共需120元;购买5个A奖品和4个B奖品共需210元.(1)求A,B两种奖品的单价;(2)学校准备购买A,B两种奖品共30个,且A奖品的数量不少于B奖品数量的.请设计出最省钱的购买方案,并说明理由.6.(9分)某公司推出一款产品,经市场调查发现,该产品的日销售量y(个)与销售单价x(元)之间满足一次函数关系关于销售单价,日销售量,日销售利润的几组对应值如表:销售单价x(元)8595105115日销售量y(个)17512575m87518751875875日销售利润w(元)(注:日销售利润=日销售量×(销售单价﹣成本单价))(1)求y关于x的函数解析式(不要求写出x的取值范围)及m的值;(2)根据以上信息,填空:该产品的成本单价是元,当销售单价x=元时,日销售利润w最大,最大值是元;(3)公司计划开展科技创新,以降低该产品的成本,预计在今后的销售中,日销售量与销售单价仍存在(1)中的关系.若想实现销售单价为90元时,日销售利润不低于3750元的销售目标,该产品的成本单价应不超过多少元?7.(9分)学校“百变魔方”社团准备购买A,B两种魔方,已知购买2个A种魔方和6个B种魔方共需130元,购买3个A种魔方和4个B种魔方所需款数相同.(1)求这两种魔方的单价;(2)结合社员们的需求,社团决定购买A,B两种魔方共100个(其中A种魔方不超过50个).某商店有两种优惠活动,如图所示.请根据以上信息,说明选择哪种优惠活动购买魔方更实惠.按买3个A种魔方和买4个B种魔方钱数相同解答8.(9分)学校准备购进一批节能灯,已知1只A型节能灯和3只B型节能灯共需26元;3只A型节能灯和2只B型节能灯共需29元.(1)求一只A型节能灯和一只B型节能灯的售价各是多少元?(2)学校准备购进这两种型号的节能灯共50只,并且A型节能灯的数量不多于B型节能灯数量的3倍,请设计出最省钱的购买方案,并说明理由.9.(9分)某游泳馆普通票价20元/张,暑假为了促销,新推出两种优惠卡:①金卡售价600元/张,每次凭卡不再收费.②银卡售价150元/张,每次凭卡另收10元.暑假普通票正常出售,两种优惠卡仅限暑假使用,不限次数.设游泳x次时,所需总费用为y元(1)分别写出选择银卡、普通票消费时,y与x之间的函数关系式;(2)在同一坐标系中,若三种消费方式对应的函数图象如图所示,请求出点A、B、C的坐标;(3)请根据函数图象,直接写出选择哪种消费方式更合算.10.(9分)某商店销售10台A型和20台B型电脑的利润为4000元,销售20台A型和10台B型电脑的利润为3500元.(1)求每台A型电脑和B型电脑的销售利润;(2)该商店计划一次购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元.①求y关于x的函数关系式;②该商店购进A型、B型电脑各多少台,才能使销售总利润最大?(3)实际进货时,厂家对A型电脑出厂价下调m(0<m<100)元,且限定商店最多购进A型电脑70台,若商店保持同种电脑的售价不变,请你根据以上信息及(2)中条件,设计出使这100台电脑销售总利润最大的进货方案.11.(9分)某文具商店销售功能相同的A、B两种品牌的计算器,购买2个A品牌和3个B品牌的计算器共需156元;购买3个A品牌和1个B品牌的计算器共需122元.(1)求这两种品牌计算器的单价;(2)学校开学前夕,该商店对这两种计算器开展了促销活动,具体办法如下:A品牌计算器按原价的八折销售,B品牌计算器5个以上超出部分按原价的七折销售,设购买x个A品牌的计算器需要y1元,购买x个B品牌的计算器需要y2元,分别求出y1、y2关于x的函数关系式;(3)小明准备联系一部分同学集体购买同一品牌的计算器,若购买计算器的数量超过5个,购买哪种品牌的计算器更合算?请说明理由.12.(9分)某旅行社拟在暑假期间面向学生推出“林州红旗渠一日游”活动,收费标准如下:人数m0<m≤100100<m≤200m>200收费标准(元/人)908575甲、乙两所学校计划组织本校学生自愿参加此项活动.已知甲校报名参加的学生人数多于100人,乙校报名参加的学生人数少于100人.经核算,若两校分别组团共需花费20800元,若两校联合组团只需花费18000元.(1)两所学校报名参加旅游的学生人数之和超过200人吗?为什么?(2)两所学校报名参加旅游的学生各有多少人?13.(9分)为响应“全民植树增绿,共建美丽中国”的号召,学校组织学生到郊外参加义务植树活动,并准备了A,B两种食品作为午餐.这两种食品每包质量均为50g,营养成分表如下.(1)若要从这两种食品中摄入4600kJ热量和70g蛋白质,应选用A,B两种食品各多少包?(2)运动量大的人或青少年对蛋白质的摄入量应更多.若每份午餐选用这两种食品共7包,要使每份午餐中的蛋白质含量不低于90g,且热量最低,应如何选用这两种食品?参考答案1.【答案】解:(1)选择活动一更合算.理由如下:选择活动一需付款:450×0.8=360(元)选择活动二需付款:450﹣80=370(元)∵360<370∴选择活动一更合算;(2)设一件这种健身器材的原价为x元当0<x<300时,则活动一按原价打八折,活动二按原价,此时付款金额不可能相等;当300≤x<500时,由题意,得∴0.8x=x﹣80解得x=400答:一件这种健身器材的原价是400元;当300≤a<600时,a﹣80<0.8a解得a<400;∴300≤a<400;当600≤a<900时,a﹣160<0.8a解得a<800;∴600≤a<800;综上所述,300≤a<400或600≤a<800.2.【答案】解:(1)设菜苗基地每捆A种菜苗的价格是x元根据题意得:=+3解得x=20经检验,x=20是原方程的解,且符合题意.答:菜苗基地每捆A种菜苗的价格是20元;设购买A种菜苗m捆,则购买B种菜苗(100﹣m)捆∵A种菜苗的捆数不超过B种菜苗的捆数∴m≤100﹣m解得m≤50设本次购买花费w元∴w=20×0.9m+30×0.9(100﹣m)=﹣9m+2700∵﹣9<0∴w随m的增大而减小∴m=50时,w取最小值w最小=-9×50+2700=2250(元)答:本次购买最少花费2250元.3.【答案】解:(1)设A款玩偶购进x个,B款玩偶购进(30﹣x)个由题意,得40x+30(30﹣x)=1100解得:x=20.30﹣20=10(个).答:A款玩偶购进20个,B款玩偶购进10个;(2)设A款玩偶购进a个,B款玩偶购进(30﹣a)个,获利y元∵A款玩偶进货数量不得超过B款玩偶进货数量的一半.∴a≤(30﹣a)解得a≤10由题意,得y=(56﹣40)a+(45﹣30)(30﹣a)=a+450.∵k=1>0∴y随a的增大而增大.∴当a=10时,y最大=460元.∴此时B款玩偶为:30﹣10=20(个).答:按照A款玩偶购进10个、B款玩偶购进20个的方案进货才能获得最大利润,最大利润是460元;(3)第一次的利润率=×100%≈42.7%第二次的利润率=×100%=46%∵46%>42.7%∴对于小李来说第二次的进货方案更合算.4.【答案】解:(1)∵y1=k1x+b的图象过点(0,30)与(10,180)∴,解得k1=15表示的实际意义是:购买一张学生暑期专享卡后每次健身费用为15元(2)b=30表示的实际意义是:购买一张学生暑期专享卡的费用为30元;(3)由题意可得,打折前的每次健身费用为15÷0.6=25(元)则k2=25×0.8=20;(3)选择方案一所需费用更少.理由如下:由题意可知,y1=15x+30,y2=20x.当健身8次时选择方案一所需费用:y1=15×8+30=150(元)选择方案二所需费用:y2=20×8=160(元)∵150<160∴选择方案一所需费用更少.5.【答案】解:(1)设A的单价为x元,B的单价为y元根据题意,得,解得答:A的单价30元,B的单价15元;(2)设购买A奖品m个,则购买B奖品为(30﹣m)个,购买奖品的花费为W元由题意可知,m≥(30﹣m)∴m≥,且m为正整数.∴W=30m+15(30﹣m)=15m+450∵15>0∴当m=8时,W有最小值答:购买A奖品8个,购买B奖品22个,花费最少.6.【答案】解:(1)设y关于x的函数解析式为y=kx+b,得即y关于x的函数解析式是y=﹣5x+600当x=115时,y=﹣5×115+600=25即m的值是25;(2)设成本为a元/个当x=85时,875=175×(85﹣a),得a=80w=(﹣5x+600)(x﹣80)=﹣5x2+1000x﹣48000=﹣5(x﹣100)2+2000∴当x=100时,w取得最大值,此时w=2000(3)设科技创新后成本为b元当x=90时,(﹣5×90+600)(90﹣b)≥3750解得b≤65答:该产品的成本单价应不超过65元.7.【答案】解:(1)设A种魔方的单价为x元/个,B种魔方的单价为y元/个根据题意得:,解得:.答:A种魔方的单价为20元/个,B种魔方的单价为15元/个.(2)设购进A种魔方m个(0<m≤50),总价格为w元,则购进B种魔方(100﹣m)个根据题意得:活动一w=20m×0.8+15(100﹣m)×0.4=10m+600;活动二w=20m+15(100﹣m﹣m)=-10m+1500.当w活动一<w活动二时,有10m+600<﹣10m+1500解得:m<45;当w活动一=w活动二时,有10m+600=﹣10m+1500解得:m=45;当w活动一>w活动二时,有10m+600>﹣10m+1500解得:45<m≤50.综上所述:当0<m<45时,选择活动一购买魔方更实惠;当m=45时,选择两种活动费用相同;当m>45时,选择活动二购买魔方更实惠.(按购买3个A种魔方和4个B种魔方需要130元解答)解:(1)设A种魔方的单价为x元/个,B种魔方的单价为y元/个根据题意得:,解得:.答:A种魔方的单价为26元/个,B种魔方的单价为13元/个.(2)设购进A种魔方m个(0<m≤50),总价格为w元,则购进B种魔方(100﹣m)个根据题意得:w活动一=26m×0.8+13(100﹣m)×0.4=15.6m+520;w活动二=26m+13(100﹣m﹣m)=1300.当w活动一<w活动二时,有15.6m+520<1300解得:m<50;当w活动一=w活动二时,有15.6m+520=1300解得:m=50;当w活动一>w活动二时,有15.6m+520>1300不等式无解.综上所述:当0<m<50时,选择活动一购买魔方更实惠;当m=50时,选择两种活动费用相同.8.【答案】解:(1)设一只A型节能灯的售价是x元,一只B型节能灯的售价是y元根据题意,得:,解得:答:一只A型节能灯的售价是5元,一只B型节能灯的售价是7元;(2)设购进A型节能灯m只,总费用为W元由题意m≤3(50-m)解得:m≤37.5,且m为正整数根据题意,得:W=5m+7(50-m)=-2m+350∵﹣2<0∴W随m的增大而减小∴当m=37时,W最小=﹣2×37+350=276此时50﹣37=13答:当购买A型灯37只,B型灯13只时,最省钱.9.【答案】解:(1)由题意可得:银卡消费:y=10x+150,普通消费:y=20x;(2)由题意可得:当10x+150=20x解得:x=15,则y=300∴B(15,300)当y=10x+150,x=0时,y=150∴A(0,150)当y=10x+150=600解得:x=45,则y=600∴C(45,600);(3)如图所示:由A,B,C的坐标可得:当0<x<15时,普通消费更划算;当x=15时,银卡、普通票的总费用相同,均比金卡合算;当15<x<45时,银卡消费更划算;当x=45时,金卡、银卡的总费用相同,均比普通票合算;当x>45时,金卡消费更划算.10.【答案】解:(1)设每台A型电脑销售利润为a元,每台B型电脑的销售利润为b元;根据题意得解得答:每台A型电脑销售利润为100元,每台B型电脑的销售利润为150元.(2)①据题意得,y=100x+150(100﹣x),即y=-50x+15000②据题意得,100﹣x≤2x解得x≥33,且x为正整数.∵-50<0∴y随x的增大而减小∵x为正整数∴当x=34时,y取最大值,则100﹣x=66即商店购进34台A型电脑和66台B型电脑的销售利润最大.(3)据题意得,y=(100+m)x+150(100﹣x),=(m﹣50)x+15000(33≤x≤70且x为正整数)①当0<m<50时m﹣50<0,y随x的增大而减小∴当x=34时,y取最大值即商店购进34台A型电脑和66台B型电脑的销售利润最大.②m=50时,m﹣50=0,y=15000即商店购进A型电脑数量满足33≤x≤70的整数时,均获得最大利润;③当50<m<100时m﹣50>0,y随x的增大而增大∴当x=70时,y取得最大值.即商店购进70台A型电脑和30台B型电脑的销售利润最大.11.【答案】解:(1)设A、B两种品牌的计算器的单价分别为a元、b元根据题意得,,解得:答:A种品牌计算器30元/个,B种品牌计算器32元/个;(2)A品牌:y1=30x•0.8=24x;B品牌:①当0≤x≤5时,y2=32x②当x>5时,y2=5×32+32×(x﹣5)×0.7=22.4x+48综上所述:y1=24xy2=;(3)当y1=y2时,24x=22.4x+48,解得x=30,即购买30个计算器时,两种品牌都一样;当y1>y2时,24x>22.4x+48,解得x>30,即购买超过30个计算器时,B品牌更合算;当y1<y2时,24x<22.4x+48,解得x<30,即购买不足30个且大于5个计算器时,A品牌更合算.12.【答案】解:(1)这两所学校报名参加旅游的学生人数之和超过200人,理由为:设两校人数之和为a若a>200,则a=18000÷75=240;若100<a≤200,则a=18000÷85=211>200,不合题意则这两所学校报名参加旅游的学生人数之和等于240人,超过200人.(2)设甲学校报名参加旅游的学生有x人,乙学校报名参加旅游的学生有y人,则①当100<x≤200时,得解得(6分)---------------------------②当x>200时,得解得不合题意,舍去.答:甲学校报名参加旅游的学生有160人,乙学校报名参加旅游的学生有80人.13.解:(1)设选用A 种食品x 包,B 种食品y 包根据题意得:7009004600101570x y x y +=⎧⎨+=⎩解得:42x y =⎧⎨=⎩. 答:应选用A 种食品4包,B 种食品2包;(2)设选用A 种食品m 包,则选用B 种食品(7)m -包根据题意得:1015(7)90m m +-解得:3m .设每份午餐的总热量为w kJ ,则700900(7)w m m =+-即2006300w m =-+2000-<w ∴随m 的增大而减小∴当3m =时,w 取得最小值,此时7734m -=-=.答:应选用A 种食品3包,B 种食品4包.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一次函数知识点汇总● 知识点一 一次函数的定义一般地,形如y kx b =+(k ,b 是常数,0k ≠)的函数,叫做一次函数,当0b =时,即y kx =,这时即是前一节所学过的正比例函数.⑴一次函数的解析式的形式是y kx b =+,要判断一个函数是否是一次函数,就是判断是否能化成以上形式.⑵当0b =,0k ≠时,y kx =仍是一次函数.⑶当0b =,0k =时,它不是一次函数.⑷正比例函数是一次函数的特例,一次函数包括正比例函数. ● 知识点二 一次函数的图象及其画法⑴一次函数y kx b =+(0k ≠,k ,b 为常数)的图象是一条直线.⑵由于两点确定一条直线,所以在平面直角坐标系内画一次函数的图象时,只要先描出两个点,再连成直线即可.①如果这个函数是正比例函数,通常取()00,,()1k ,两点;②如果这个函数是一般的一次函数(0b ≠),通常取()0b ,,0b k⎛⎫- ⎪⎝⎭,,即直线与两坐标轴的交点.⑶由函数图象的意义知,满足函数关系式y kx b =+的点()x y ,在其对应的图象上,这个图象就是一条直线l ,反之,直线l 上的点的坐标()x y ,满足y kx b =+,也就是说,直线l 与y kx b =+是一一对应的,所以通常把一次函数y kx b =+的图象叫做直线l :y kx b =+,有时直接称为直线y kx b =+. ● 知识点三 一次函数的性质⑴当0k >时,一次函数y kx b =+的图象从左到右上升,y 随x 的增大而增大; ⑵当0k <时,一次函数y kx b =+的图象从左到右下降,y 随x 的增大而减小. ●知识点四 一次函数y kx b =+的图象、性质与k 、b 的符号⑵一次函数y kx b =+中,当0k >时,其图象一定经过一、三象限;当0k <时,其图象一定经过二、四象限.当0b >时,图象与y 轴交点在x 轴上方,所以其图象一定经过一、二象限;当0b <时,图象与y 轴交点在x 轴下方,所以其图象一定经过三、四象限.反之,由一次函数y kx b =+的图象的位置也可以确定其系数k 、b 的符号.知识点五 用待定系数法求一次函数的解析式⑴定义:先设出函数解析式,再根据条件确定解析式中未知的系数,从而具体写出这个式子的方法,叫做待字系数法.⑵用待定系数法求函数解析式的一般步骤: ①根据已知条件写出含有待定系数的解析式; ②将x y ,的几对值,或图象上的几个点的坐标代入上述的解析式中,得到以待定系数为未知数的方程或方程组;③解方程(组),得到待定系数的值;④将求出的待定系数代回所求的函数解析式中,得到所求的函数解析式. 考查一:点的坐标方法: x 轴上的点纵坐标为0,y 轴上的点横坐标为0;若两个点关于x 轴对称,则他们的横坐标相同,纵坐标互为相反数; 若两个点关于y 轴对称,则它们的纵坐标相同,横坐标互为相反数;若两个点关于原点对称,则它们的横坐标互为相反数,纵坐标也互为相反数;例1:若点M (1-x,1-y )在第二象限,那么点N (1-x,y-1)关于原点的对称点在第______象限。
举一反三:【变式1】若点A (m,n )在第二象限,则点(|m|,-n )在第____象限;【变式2】若点P (2a-1,2-3b )是第二象限的点,则a,b 的范围为______________________。
考查二:关于点的距离的问题 方法:点到x 轴的距离用纵坐标的绝对值表示,点到y 轴的距离用横坐标的绝对值表示;任意两点(,),(,)A A B B A x y B x y若AB ∥x 轴,则(,0),(,0)A B A x B x 的距离为A B x x -; 若AB ∥y 轴,则(0,),(0,)A B A y B y 的距离为A B y y -;点(,)A A A x y例:两点(3,-4)、(5,a )间的距离是2,则a 的值为__________;举一反三:【变式1】已知点A(0,2)、B(-3,-2)、C(a,b),若C点在x轴上,且∠ACB=90°,则C点坐标为___________.【变式2】点D(a,b)到x轴的距离是_________;到y轴的距离是____________;到原点的距离是____________;考查三:正比例函数与一次函数定义方法:若y=kx+b(k,b是常数,k≠0),那么y叫做x的一次函数,特别的,当b=0时,一次函数就成为y=kx(k是常数,k≠0),这时,y叫做x的正比例函数,当k=0时,一次函数就成为若y=b,这时,y叫做常函数。
☆A与B成正比例 A=kB(k≠0)例:如果函数是正比例函数,那么().A.m=2或m=0 B.m=2 C.m=0 D.m=1举一反三:【变式1】已知y-3与x成正比例,且x=2时,y=7.(1)写出y与x之间的函数关系式;(2)当x=4时,求y的值;(3)当y=4时,求x的值.【变式2】已知一次函数(1)当m取何值时,y随x的增大而减小?(2)当m取何值时,函数的图象过原点?考查四:待定系数法求函数解析式方法:依据两个独立的条件确定k,b的值,即可求解出一次函数y=kx+b(k≠0)的解析式。
☆已知是直线或一次函数可以设y=kx+b(k≠0);☆若点在直线上,则可以将点的坐标代入解析式构建方程。
例:判断三点A(3,1),B(0,-2),C(4,2)是否在同一条直线上.举一反三:【变式1】已知弹簧的长度y(cm)在一定的弹性限度内是所挂重物的质量x(kg)的一次函数,现已测得不挂重物时,弹簧的长度为6cm,挂4kg的重物时,弹簧的长度是7.2cm,求这个一次函数的表达式.【变式2】已知直线y=2x+1.(1)求已知直线与y轴交点M的坐标;(2)若直线y=kx+b与已知直线关于y轴对称,求k,b的值.k(称为斜率)表示直线y=kx+b(k≠0)的倾斜程度;b(称为截距)表示直线y=kx+b(k≠0)与y轴交点的,也表示直线在y轴上的。
☆同一平面内,不重合的两直线 y=k1x+b1(k1≠0)与 y=k2x+b2(k2≠0)的位置关系:当时,两直线平行。
当时,两直线垂直。
当时,两直线相交。
当时,两直线交于y轴上同一点。
☆特殊直线方程:X轴 : 直线 Y轴 : 直线与X轴平行的直线与Y轴平行的直线一、三象限角平分线二、四象限角平分线例1:(模拟卷二.21)为了促进节能减排,倡导节约用电,某市将实行居民生活用电阶梯电价方案,图中折线反映了每户每月用电电费y(元)与用电量x(度)间的函数关系式.(1)小明家某月用电120度,需交电费元;(2)求第二档每月电费y(元)与用电量x(度)之间的函数关系式;(3)在每月用电量超过230度时,每多用1度电要比第二档多付电费m元,小刚家某月用电290度,交电费153元,求m的值.举一反三:【变式1】图中,射线l甲、l乙分别表示甲、乙两运动员在自行车比赛中所走的路程s与时间t的函数关系,求它们行进的速度关系。
【变式2】(2011四川内江)小高从家骑自行车去学校上学,先走上坡路到达点A,再走下坡路到达点B,最后走平路到达学校,所用的时间与路程的关系如图所示。
放学后,如果他沿原路返回,且走平路、上坡路、下坡路的速度分别保持和去上学时一致,那么他从学校到家需要的时间是( )A.14分钟B.17分钟C.18分钟D.20分钟【变式3】某种洗衣机在洗涤衣服时,经历了进水、清洗、排水、脱水四个连续的过程,其中进水、清洗、排水时洗衣机中的水量y(升)与时间x(分钟)之间的关系如图所示:根据图象解答下列问题:(1)洗衣机的进水时间是多少分钟?清洗时洗衣机中的水量是多少升?(2)已知洗衣机的排水速度为每分钟19升.①求排水时y与x之间的关系式;②如果排水时间为 2分钟,求排水结束时洗衣机中剩下的水量.考查六:一次函数的性质方法:⑴当0=+的图象从左到右上升,y随x的增大而增大;k>时,一次函数y kx b⑵当0=+的图象从左到右下降,y随x的增大而减小k<时,一次函数y kx b例1:(模拟卷四.6)若实数a、b、c满足a+b+c=0,且a<b<c,则函数y=ax+c的图象可能是()B DA举一反三:【变式1】已知关于x的一次函数.(1)m为何值时,函数的图象经过原点?(2)m为何值时,函数的图象经过点(0,-2)?(3)m为何值时,函数的图象和直线y=-x平行?(4)m为何值时,y随x的增大而减小?【变式2】函数在直角坐标系中的图象可能是().【变式3】一次函数 y=(6-3m)x+(2n-4)不经过第三象限,则m、n的范围是__________。
考查七:平移方法:直线y=kx+b与y轴交点为(0,b),直线平移则直线上的点(0,b)也会同样的平移,平移不改变斜率k,则将平移后的点代入解析式求出b即可。
直线y=kx+b向左平移2向上平移3 <=> y=k(x+2)+b+3;(“左加右减,上加下减”)。
例:把函数y=3x+1的图像向右平移2个单位再向上平移3个单位,可得到的图像表示的函数是____________。
举一反三:【变式1】过点(2,-3)且平行于直线y=-3x+1的直线是___________.【变式2】直线m:y=2x+2是直线n向右平移2个单位再向下平移5个单位得到的,而(2a,7)在直线n上,则a=____________;考查八:交点问题及直线围成的面积问题方法:两直线交点坐标必满足两直线解析式,求交点就是联立两直线解析式求方程组的解;复杂图形“外补内割”即:往外补成规则图形,或分割成规则图形(三角形);例:(模拟卷八)轴、y 轴分别交于点A 和点B ,点C 在直线AB 上,且点C xky =的图象上,CD 平行于y 轴,25=∆OCD S ,则k 的值为________.举一反三:【变式1】如图,A 、B 分别是x 轴上位于原点左右两侧的点,点P (2,p )在第一象限,直线PA 交y 轴于点C (0,2),直线PB 交y 轴于点D ,△AOP 的面积为6; (1) 求△COP 的面积;(2) 求点A 的坐标及p 的值;(3) 若△BOP 与△DOP 的面积相等,求直线BD 的函数解析式。
【变式2】已知:经过点(-3,-2),它与x 轴,y 轴分别交于点B 、A ,直线经过点(2,-2),且与y 轴交于点C (0,-3),它与x 轴交于点D(1)求直线的解析式; (2)若直线与交于点P ,求的值。
【变式3】如图,已知点A (2,4),B (-2,2),C (4,0),求△ABC 的面积。
考查九:一次函数综合例:已知一个正比例函数与一个一次函数的图象交于点A (3,4),且OA=OB (1) 求两个函数的解析式;(2)求△AOB 的面积;举一反三:【变式1】在长方形ABCD中,AB=3cm,BC=4cm,点P沿边按A→B→C→D的方向向点D 运动(但不与A,D两点重合)。
