重庆市万州区甘宁初级中学八年级数学上册 14.1.1-14.1.2阶段性复习 华东师大版
重庆市万州区甘宁初级中学八年级数学上册 13.1 幂的运算阶段性练习(无答案) 华东师大版

幂的运算一、内容回顾2.幂的乘方,底数________,指数________.即(a m)n=a( )(m,n都是正整数).4.同底数幂相除,底数_______,指数_______.即a m÷a n=a( )(a≠0,m,n都是______且_______).这样可以简化某些运算.二、巩固训练1.下列各式中,计算过程正确的是().A.3个 B.2个 C.1个 D.0个3.下列4个算式:①63+63②(2×62)(3×63)③(22×32)3④(22)3×(33)2其中,计算结果等于66的是().A.①②③ B.②③④ C.②③ D.③④4.下列各题计算正确的是().C.(x2)3=x2+3=x5 D.x3÷x2=x3-2=x5.已知│x│=1,│y│=12,则(x2y)3-x3y3等于().A.14B.0 C.-14D.-14或0或146.计算(23)2007×1.52008×(-1)2008的结果是().A.23B.32C.-23D.-327.计算-88×0.1258的结果是().A.-1 B.1 C.-2 D.28.计算:(12)2007×22007=_______.()200820078125_______.-⨯-=10、(12a 2b )4=________,(-2ab )3=________. 11、(-x )8÷(-x )3=______,a 10÷a 6=_______.()()3212________n n a a a a --⋅+⋅-=;()()()()312__________.m m b a a b a b b a +-⋅-+-⋅-=15、填上指数或底数()()()()()352201.a a a a a a ⋅=⋅== ()()()10923122.555⋅=⋅=16、计算下列各题:(9)(0.5×323)2006×(-2×311)2007 (10)0.12520×420×22017、已知a m =2,a n =3,求a2m+3n 的值.19.(1)比较大小:1625______275,450______950.1810101823______23⨯⨯(2)比较2200与3150大小.(3)()()()991003412,4,3,,2a b c a b c ⎛⎫=-⨯=-=- ⎪⎝⎭比较的大小。
重庆市万州区甘宁初级中学八年级数学上册 第13章《整式的乘除》单项式与单项式相乘,单项式与多项式相乘

单项式与单项式相乘,单项式与多项式相乘◆回顾归纳1.单项式乘以单项式,把它们的_____,_____分别相乘,•对于只在一个单项式里含有字母,则________作为积的一个因式.2.单项式与多项式相乘,就是用单项式去乘________,再把所得的积相加.•计算时注意多项式中的每一项包括它前面的________.◆课堂测控测试点1 单项式与单项式相乘1.计算:13a2b·2ab2=_____;(-6a2b)·2ab=_______.2.计算x3y2·(-xy3)2的结果是()A.x5y10 B.x5y8 C.-x5y8 D.x6y123.(经典题)如果单项式-3x4a-b y2与13x3y a+b是同类项,那么这两个单项式的积是()A.x6y4 B.-x3y2 C.-83x3y2 D.-x6y44.(变式题)计算:-4x2y·(-12y2)3.测试点2 单项式与多项式相乘5.a(2a2-3a+1)=_______.6.在下列各式中,计算正确的是()A.(a-3b+1)(-6a)=-6a2+18ab+6a B.(-13x2y)(-9xy+1)=3x3y2+1C.6mn·(2m+3n-1)=12m2n+18mn2-6mn D.-ab(a2-a-b)=-a3b-a2b-ab27.解方程2x(x2+x-1)-x2(2x+1)-x2=-6.8.(体验探究题)按下列程序计算,把答案填写在表格内,然后看看有什么规律,•想想为什么会有这个规律?x→平方→+x→÷x→-x→答案(1)填写表内空格:输入x 3 2 -2 13…输出答案 1 1 …(2)发现的规律是___________.(3)用简要的过程证明你发现的规律.dcba◆课后测控1.一个长方形的长为2xcm,宽比长少4cm,若将长方形的长和宽都扩大3cm,•则面积增大了_____;若x=2,则增大的面积为______cm2.2.如图,表示这个图形面积的代数式是()A.ab+bc B.c(b-d)+d(a-c)C.ad+cb-cd D.ad-cb3.若(x+t)(x+6)的积中不含x的一次项,则t的值为()A.0 B.6 C.-6 D.-6或64.若x(3x-4)+2x(x+7)=5x(x-7)+90,则x等于()A.-2 B.2 C.-12D.125.如果ax(3x-4x2y-by2)=6x2-8x3y+6xy2成立,则a,b的值为()A.a=3,b=2 B.a=2,b=-3 C.a=-3,b=2 D.a=-2,b=36.小李家住房的结构如图13.2-2所示,小李打算在卧室和客厅铺上地板,请你帮助他算一算,他至少需买木板的面积为()A.12xy B.10xy C.8xy D.6xy7.计算:(1)(-2xy2)·3x2y;(2)x2y3·(-516xyz2);(3)(-4m2n)·(-m2n2)·(12n3);(4)(3x2y n)·(-19xy n+3).8.若“三角”表示3abc,“方框”表示(x m+y n),试求=_______.9.一块长方形铁皮长为(6a2+4b2)米,宽为5a4米,•在它的四个角上各剪去一个边长为2a3米的小正方形,然后折成一个无盖的盒子,问这个盒子的表面积是多少?10.求图中阴影部分的面积.11.(变式题)计算:t3-2t[t2-2(t-3)].12.计算:3xy[6xy-3(xy-12x2y)].13.计算:5x(x2-2x+4)+x2(x-1).14.计算:-2a2·(12ab+b2)-5a·(a2b-ab2).◆拓展创新已知一列数:3,6,9,12,15,18,…(1)若将这列数的第一个数记为a1,第二个数记为a2,…,第n个数记为a n,•那么有a1=3,a2=3+(2-1)×3,a 3=3+(3-1)×3,…根据上述等式反映的规律,请写出第4个等式a 4=______,第n 个等式a n =______.(2)一般地,如果一列数a 1,a 2,a 3,…,a n 满足a 2-a 1=a 3-a 2=…=a n -a n -1=d ,•那么我们把这列数叫做等差数列,请用a 1,n ,d 表示这个等差数列的第n 个数a n =_______. (3)已知(2)中等差数列的前n 个数的和S n =1()2n n a a +,利用这个公式证明:S n =na 1+(1)2n n -d . 答案: 回顾归纳1.系数 相同字母 连同它的指数 2.多项式的每一项 符号 课堂测控1.23a 3b 3 -12a 3b 22.B 3.D 4.解:原式=-4x 2y ·(-18)y 6=12x 2y 7.5.2a 3-3a 2+a 6.C7.解:2x (x 2+x -1)-x 2(2x+1)-x 2=-6. 去括号,得2x 3+2x 2-2x -2x 3-x 2-x 2=-6. 合并同类项,得-2x=-6. 系数化为1,得x=3. 8.(1)1 1(2)输入一个非零数结果是1(3)设输入的数为x (x ≠0),则2x xx+-x=x+1-x=1课后测控1.12x -3 212.C (点拨:把图排成一个长方形,或进行分割) 3.C (点拨:原式=x 2+(6+t )x+6t ,∴6+t=0,t=-6) 4.B 5.B 6.A7.(1)-6x 3y 3; (2)-18x 3y 4z 2; (3)2m 4n 6; (4)-13x 3y 2n+3 8.原式=3·2mn (n 2+m 5)=6mn 3+6m 6n . 9.由题意,得(6a 2+4b 2)×5a 4-4×(2a 3)2=30a 6+20a 4b 2-4×4a 6=14a 6+20a 4b 2.答:这个盒子的表面积为(14a 6+20a 4b 2)平方米.10.(a+2a+a+2a+a )×(2.5a+1.5a )-2a ×2.5a ×2=7a ·4a -10a 2=18a 2. 11.原式=t 3-2t 3+4t (t -3)=t 3-2t 3+4t 2-12t=-t 3+4t 2-12t . 12.原式=18x 2y 2-9xy (xy -12x 2y )=18x 2y 2-9x 2y 2+92x 3y 2=9x 2y 2+92x 3y 2. 13.原式=5x 3-10x 2+20x+x 3-x 2=6x 3-11x 2+20x . 14.原式=-a 3b -2a 2b 2-5a 3b+5a 2b 2=-6a 3b+3a 2b 2. 拓展创新(1)3+(4-1)×3 3+(n -1)×3 (2)a 1+(n -1)d (3)证明:S n =1111[(1)]2(1)(1)222n a a n d na n n d n n dna ++-+--==+。
重庆市万州区甘宁初级中学八年级数学上学期第一次阶段

1 重庆市万州区甘宁初级中学2014-2015学年八年级数学上学期第一次阶段性检测试题(本卷共三个大题,满分150分,考试时间:120分钟)一、选择题(本大题共10个小题,每小题4分,共40分)每小题只有一个正确答案,请将正确答案的代号填写在答题卷对应的位置. 1.下列运算正确的是( )A.1055x x x =+B.623x x x =⋅C. 22(2)2a a =D. 23a a a +=2.如果21x =,那么3x 的值为( )A.1B.-1C.±1D. 无意义3.下列说法正确的个数有( )①0是最小实数;②数轴上所有的点都表示实数;③无理数都是带根号的数; ④18-的立方根是12±;⑤14的平方根是12±A.1个B.2个C.3个D. 4个4.下列各式从左到右的的变形中,是因式分解的是( )A.))((2224x x x x x x -+=-B.()a x y ax ay -=-C. 21055(21)x x x x +=+D. 244(4)4x x x x -+=-+5.马大哈同学完成了如下的计算题:其中结果正确的是( )①,2323x x x =,②,44x x x =,③,)(1535x x =④,6)3(1226x x =A . ①B . ②④C . ③D . ④6.计算22(1)(1)a a --+的结果是( )A.2-B. 4-C. 4a -D. 222a +7.已知)(则,5,3--===+n m n m a a aA . 243B . 125C . 15D . 88.(4分)计算:)(的结果是)2()2(20092008---+-20092009200820082,2,2,2D C B A --9.若022222=++-+b a b a ,则b a +的值为( )A.2-B.0C.2D. 310.已知)51)((++x q x 的乘积中不含x 项,则q 的值为( )2A .51-B .5-C .51D .5二、填空题(本大题共6个小题,每小题4分,共24分)请将正确答案填写在答题卷对应的位置.11.81的平方根是 _________ .12.比较大小5 _________ 7.2;1416.3- _________ π-. 13.计算:=÷34a aa _________ ;=-232)(x x _________ .14.的相反数是 _________ ,绝对值是 _________ .15.若249x ax -+是完全平方式,则=a _________ .八年级第一次阶段性测试答题卷一、(40分)题号 1 2 3 4 5 6 7 8 9 103二、(24分) 11. ,12. ,13. , 14. ,15. ,16. 。
重庆市万州区甘宁初级中学八年级数学上册 13.1.2 幂的乘方练习 华东师大版

13.1.2 幂的乘方【知能点分类训练】知能点1 幂的乘方的意义及法则1.计算(102)3=_______,(103)2=________.2.计算(-x5)2=_______,(-x2)5=________,[(-x)2] 5=______.3.下列运算正确的是().A.(x3)3=x3·x3; B.(x2)6=(x4)4; C.(x3)4=(x2)6; D.(x4)8=(x6)2 4.下列计算错误的是().A.(a5)5=a25; B.(x4)m=(x2m)2; C.x2m=(-x m)2; D.a2m=(-a2)m5.计算下列各题:(1)(a5)3(2)(a n-2)3(3)(43)3(4)(-x3)5(5)[(-x)2] 3(6)[(x-y)3] 4知能点2 法则的逆用及混合运算6.x3·(x n)5=x13,则n=_______.7.(x3)4+(x4)3=______,(a3)2·(a2)3=_________.8.下列各题中,运算正确的是().A.a4+a5=a9 B.a·a3·a7=a10C.(a3)2·(-a4)3=-a18 D.(-a3)2=-a69.计算a·(-a3)·(a2)5的结果是().A.a14 B.-a14 C.a11 D.-a1110.(1)已知a m=3,a n=2,求a m+2n的值;(2)已知a2n+1=5,求a6n+3的值.11.已知a=3555,b=4444,c=5333,试比较a,b,c的大小.【综合应用提高】12.当n为奇数时,(-a2)n·(-a n)2=_________.13.已知164=28m,则m=________.14.-{-[(-a2)3] 4}2=_________.15.1010可以写成().A.102×105 B.102+105 C.(102)5 D.(105)516.比较(27)4与(34)3的大小,可以得到().A.(27)4=(34)3 B.(27)4>(34)23C.(27)4<(34)3 D.无法判断17.已知n为正整数,且x2n=3,求9(x3n)2的值.18.若│a-2b│+(b-2)2=0,求a5b10的值.19.已知3x+4y-5=0,求8x×16y的值.【开放探索创新】20.若n为自然数,试确定34n-1的末位数字.【中考真题实战】21.(黑龙江)(x2)8·(x4)3等于().A.x18 B.x24 C.x28 D.x3222.(广西)当m为偶数时,(a-b)m·(b-a)n与(a-b)m+n的关系是().A.相等 B.互为相反数 C.大于 D.无法确定答案:1.106 1062.x10-x10 x10提示:利用乘方的意义.3.C 提示:(x3)4=x3×4=x12,(x2)6=x2×6=x12.4.D 提示:m为奇数时,(-a2)m=-a2m,m为偶数时,(-a2)m=a2m.5.(1)a15(2)a3n-6(3)49(4)-x15(5)x6(6)(x-y)126.2 提示:x3·(x n)5=x3·x5n=x3+5n=x13,∴3+5n=13,n=2.7.2x12 a12提示:(x3)4+(x4)3=x12+x12=2x12,(a3)2·(a2)3=a6·a6=a6+6=a12. 8.C 提示:原式=a6·(-a12)=-a6·a12=-a6+12=-a18.9.B 提示:原式=a·(-a3)·a10=-a1+3+10=-a14.10.(1)∵a m=3,a n=2.∴a m+2n=a m·a2n=a m·(a n)2=3×22=12.(2)∵a2n+1=5,∴a6n+3=a3(2n+1)=(a2n+1)3=53=125.11.∵a=3555=35×111=(35)111=243111,b=4444=44×111=(44)111=256111.c=5333=53×111=(53)111=125111,又∵256>243>125,∴256111>243111>125111.即b>a>c.12.-a4n提示:原式=(-a2n)·a2n=-a2n·a2n=-a4n.13.2 提示:∵164=(24)4=216=28m,∴8m=16,m=2.14.-a48提示:原式=-{-[-(-a6)] 4}2=-{-[-a6] 4}2=-{-a24}2=-a48.15.C 提示:A中102×105=107,B中102与105不能合并,D中(105)5=105×5=1025. 16.A 提示:(27)4=(33)4=33×4=312=(34)3.17.∵x2n=3,∴9(x3n)2=9x6n=9·(x2n)3=9×33=32×33=35=243.18.∵│a-2b│≥0,(b-2)2≥0,且│a-2b│+(b-2)2=0.∴│a-2b│=0,(b-2)2=0,∴20,4,20, 2.a b ab b-==⎧⎧∴⎨⎨-==⎩⎩∴a5b10=45×210=(22)5×210=210×210=220.19.∵3x+4y-5=0,∴3x+4y=5,∴8x·16y=(23)x×(24)y=23x×24y=23x+4y=25=32.20.先探索3的幂的末位数规律:31=3,32=9,33=27,34=81,35=243,36=729,37=2 187,38=6 561,…显示34n的末位数字为1,∴34n-1的末位数字为0.21.C ()22.D 提示:可能相等,可能互为相反数,与n值也有关.。
重庆市万州区甘宁初级中学八年级数学上册 13.2 整式的

整式的乘法一、填空题:(每题2分,共28分) 1.a 2b 5·a 2b 5=_________________.2.5(a + b )3·(a + b )4=________..;.__________3==+++++43421ΛΛ44443444421ΛΛnnaa aaa a a a a a.._________________42222=4484476ΛΛn a a a a5.-a (-a )2(-a )3(-a )4(-a )5=__________________.6.(-a -2b )(a +2b )=____________.(-a -2b )(-a +2b )=___________.7. 分解因式 a 4b -a 2b 5=____________8.(2 a +3b -c )2=___________________________.9.若(x +t )(x +6)的积中不含有的一次项,则t 的值是__________. 10.( )(-4x -3y )=16x 2-9y 2. 11.( _____-2)(3x ____ )=4-9x 2.12.分解因式 a 2b +2 a b + b =_______________; 13. 若3xm +2ny ·(-2xy 3m +4)=-6x 5y 6,则m =_______,n = ___.14.分解因式mx -my+ (3x -3y )=_______________. 二、选择题(每题3分,共24分)15.下列各式中,正确的是 ( ).(A )(a -b )2=a 2-2ab -b 2(B )(-b + a )( b + a )= b 2- a 2(C)(a +b )2=a 2+b 2(D )(a +b )2=a 2+2ab +b 216.把x 2-x -6分解因式的结果是 ( ).(A )(x +3)(x +2) (B)(x -3)(x -2) (C )(x +3)(x -2) (D) (x -3)(x +2) 17.下列分解因式正确的是( ).(A)15a 2-5a =5a (3a +1) (B)-x 2-y 2=-(x -y )(x +y ) (C )k (x +y )+x +y=(k +1)(x -y ) (D )a 2-ab +ac -bc =(a -b )(a +c ) 18.如果x +3是多项式x 2-2x -a 的一个因式,则a 等于( ). (A )6 (B )15 (C )-6 (D )-15 19.已知 a +b =5,ab = -2 ,那么a 2+ b 2的值为 ( ).(A )25 (B )29 (C )33 (D )不确定 20.下列四个式子中与多项式2x 2-3x 相等的是( ).16943)(16943)(89432)(89432)(2222+⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛-x D x C x B x A 21.一个矩形的周长为4a +4b ,若矩形的一边长用a 表示,则此矩形的面积为( ). (A ) a 2+ a 2b 2(B)4 a 2+4 a b (C) a 2+ 2b 2(D) a 2+ 2 a b 22.故事书每本m 元,漫画书每本n 元,买m 本故事书和n 本漫画书共需( )元. (A )m 2+n 2(B)(m +n )2(C)2mn (D)2m+2n 三、计算题(各小题3分,共18分)..323)2(4123⎥⎦⎤⎢⎣⎡-x x ..3324)101()2(2124x xy y x -⋅-⋅..2)76(37252332y x y x y x --⋅ ..)72)(5(26+-x x27.(3x +4y )2+(3x -4y )2-(3x -4y ) (3x +4y ).28. 化简求值 2(x -2y )2-4(x +3 y )(x -3 y )-2(x -y )(y +x )-5(-x -1)2,其中x =4, y =-1.四、分解因式(各小题4分,共16分)29.2a 3-4a 2b +2ab 2. 30.5(x +y )2-125m 2.31.4x2+3(4xy+3y2) 32.( x3-xy2)-x+y.五、解答题(各小题6分,共24分)33. 把2x2+3x-6表示成A(x-1)2+B(x+1)+C的形式.34. 有一块直径为2a+ b的图形木板,挖去直径分别为2a和 b的两个圆,问剩下的木板的面积是多少?35.为了保证长方形水闸闸门开启时最大过水面积不少于a2+4ab +3b2平方米,闸门开启时最大高度为a + b米, 闸门宽度至少多少米?36.请你试一试,说明连续四个整数的积加上1是一个整数的平方.13.1~13.3 整式的乘法测试(B卷)一、填空题:(每题2分,共28分)1.(-a2)5·(-a5)2 =_________________.2. a n b n +1·(a n bn -1)=____________.3.(x +2)(x -5)=_____________.4.(3m +7n )( 3m -7n )=___________ .5.( a +b +c )(a -b -c )=[a +( )][a -( )]=_______________.6._________·a 2= a 5...22)41(__________217-=+-x x x ..___________)31(_____82++=-xy y 9. 分解因式 ab 3+10 a b 2+25 a b =_______________10. 若9x 2+mxy +16y 2可以分解成(a -b )2的形式,则m =___________. 11. 若(x 2+mx+1)(x 2-x +2)的积中不含x 2项,则m 的值是__________. 12. 分解因式ax 3-121 a 3x =______________________..._____________)(45)(3)(81323=-⋅-⋅--x y x y y x14.已知m +n =7,mn =-0.5,则m 2+n 2=_______________. 二.选择题(每题3分,共24分)15.下列因式分解正确的是 ( ).(A )(a -b )2=a 2-2ab + b 2(B )a 4-b 4=(a 2-b 2)(a 2+b 2) (C)x 2-y 2+x +y =(x +y )(x -y +1) (D )x 2-x -6=(x -2)(x +3)16. 下列各式计算正确的是 ( ).(A )-4 x (2x 2+3x -1)=-8 x 3-12 x 2-4 x (B)(x + y )(x 2+ y 2)= x 3+ y 3(C )(-4x -1)(4x -1)=1-16 x 2(D) (x -2 y )2= x 2-2x y +4 y 217.已知x m=a , x n=b ,那么x3m +2n的值等于 ( ).(A )3a +2b (B )a 3+b 2(C )a 3b 2(D )a 3m b2n18.m 、n 满足|m +2|+(n -4)2=0,分解因式(x 2+ y 2)-(m x y+n )= ( ). (A )(x + y +2)2(B )(x -y +2) (x - y -2) (C )(x - y+2)2 (D )(x + y +2) (x +y -2) 19. 计算(a +b )3的结果为 ( ).(A )a 3+b 3(B )a 3+ab (a +b )+b 3(C )a 3+3a 2b +3ab 2+b 3(D )(a +b )2(a +b ) 20. a 3-b 3分解因式的结果为( ).(A )(a -b ) (a 2+b 2) (B )(a -b ) (a 2+2ab +b 2) (C )(a -b ) (a 2+ab +b 2) (D )(a -b ) (a 2-ab +b 2) ).(的值,则. )()(213521221n m b a b a b a m n n m +=⋅-++(A )1 (B)2 (C)3 (D)-3 22.学校要建一个无盖的长方形水箱,水箱的长为a 米,宽为b 米,高为c 米,现用一个半径为r 的圆形砂轮打磨内壁和箱底,则砂轮磨不到的部分的面积为( ).(A )12πr 2(B)3πr 2(C)3(4-π)r 2(D)4 r 2-πr 2三、计算题(各小题3分,共18分)..3222)32()3(2123x xy y x -⋅-⋅ ..)64(21)1(2422+-+-a a a a..22)5()5(25y x y x +-- 26.(a +b +c )2-(a -b -c )2 ..(.)812()41()41272222y x y x y x -⎥⎦⎤⎢⎣⎡-++的解.是方程其中,.化简求值 )21(22)1()2()4)(2)(2(2)2(2822222-=----++-+-+x x x x x x x x x x四、分解因式(各小题4分,共16分)..-42923x x x -+ 30. (ab +1)2-(a -2b )2.31.a (1-a )-(a -1)2. 32. (m +n )2- 8(m +n -2)五. 解答题(各小题6分,共24分)33. 如图1,在边长为a的正方形中挖掉一个边长为b的小正方形(a>b),把余下的部分剪成一个矩形(如图2),通过计算两个图形(阴影部分)的面积,验证了一个等式,你通过分析能找出来吗?根据以上所提供的方法,你能设计出一个图形说明(a+2b)(2a-b)=2a2+3ab-2b2吗?并配文字加以说明.34. 一个长方形的纸片,长5m+4n,宽4m+3n,在它的四个角处剪去一个边长为m+n的小正方形,然后折成一个无盖的盒子.你知道这无盖盒子的表面积多少吗?如果要做一个盖子至少需要面积多大的纸片?35. 说明对于任意正整数n,式子n(n+5)-(n-3)(n+2)的值都能被6整除.36. a、b、c是正整数,a<b,且a2-ab-ac+bc=7,求a-c的值.。
重庆市万州区甘宁初级中学八年级数学上学期综合测试题(八) 华东师大版

八年级(上)数学检测题一、选择题:(每小题3分,共30分) 1、4=( )A 、2±B 、2C 、2-D 、22、下列说法中,正确的是( )A 、4-有平方根;B 、1的立方根是1±;C 、5-的立方根是35-;D 、136的立方根是16; 3、对于实数5,说法正确的是( )A 、456<<B 、5是有理数C 、5是5的平方根D 、以上说法均不正确4、有以下四个式子:○1222358a a a +=;○22222m m m ⋅=;○33412x x x ⋅=; ○442(3)(3)36-⋅-=-;其中,正确的有( )个A 、1B 、2C 、3D 、45、已知1,2abx x ==,则22a bx+=( )A 、3B 、7C 、0D 、46、下列式子从左到右的变形中,属于因式分解的是 ( )A 、2(1)(1)1x x x +-=-B 、221(2)1x x x x -+=-+C 、22()()a b a b a b -=+- D 、()()mx my nx ny m x y n x y +++=+++ 7、分解因式2322610xy x y xy -+-时,合理地提取的公因式应为( )A 、2xy -B 、2xyC 、22xy -D 、22x y8、下列数据是三角形的三边长,其中能组成直角三角形的是( )A 、1 , 2 , 3B 、6 , 7 , 8C 、12 ,13 , 14D 、0.3 , 0.4 , 0.59、已知直角三角形三边中的两边长为8 , 17,那么第三边长为( )A 、15B 、353C 、3D 、15或35310、如图,正方形网格中,每个小方格的边长均是1,则网格上的ABC ∆中,边长为无理数的边数有 ( )条 A 、1B 、2C 、3D 、4二、填空题:(每题3分,共15分)1、108a a = ; 23()()xy xy = ; 32[()]x - ;2、一个正方体的体积是37m ,则这个正方体的边长是 ; 3、如图,有圆柱,其高为12cm ,底面半径为3cm ,在圆柱下底面A 点处有一只蚂蚁,它想得到上底面B 处的食物,则蚂蚁经过的最短离为 ;4、分解因式:232xy x y -+= ;52|3|0x y -+=,则2009()x y += ; 三、解答题:1、(每小题3分,共12分)计算:(1)223a a ⋅;(2)43a a a ⋅÷(3)4334(2)4x x y x y +⨯(4)3223(46)2x y x y xy xy +-÷2、(每小题3分,共12分)因式分解: (1)225x x -;(2) 22324x y y z -;(3)22mx mx m -+;(4)()()x x y y x y +-+;3、(3254、(每小题4分,共8分)已知3,12a b ab +==-,求下列各式的值: (1)22a b +;(2)22a ab b -+;5、(4分)如图,ABC ∆中,90,C AC BC ∠==o,若4AB =,求AC 和ABC ∆的面积;6、(5分)请说明任意奇数的平方被4除,余数是1;7、(5分)如图,一个蚂蚁要在在一个长、宽、高分别为2、3、1的长方体的表面从A点爬到B点,那么最短的路径是多少?(结果请保留根号)8、(6分)小溪边长着两棵树,恰好隔岩岸相望。
重庆市万州区甘宁初级中学八年级数学上学期期末复习试

八年级(上)数学期末复习测试题一、填空题:(每题2分,共20分)1.计算:x 3·(x 2)3÷x 6=________.2.计算:(9x 3-12x 2+3x )÷3x=________.3.直角三角形的两边长分别为3和4,则第三边长为________.4.Rt△ABC 中,∠C=90°,AB=13cm ,AC=12cm ,则AB 上的高CD=________. 5.已知A ,B ,O 三点不在同一直线上,A ,A′关于点O 对称,B ,B′关于点O 对称,那么AB 与A′B′的关系是________. 6.如图,△ABC 是等腰直角三角形,AD⊥BD 于D ,△A BD 可以看做由△ACD 旋转得到的,旋转的角度是________. 7.YABCD 的周长为30cm ,对角线交于O 点,△AOB 的周长比△BOC 的周长多4cm ,则AB=_________,BC=_________. 8.正方形ABCD 中,对角线AC 上一点E 到AB 的距离为3,则E 到AD 的距离是_____.9.梯形ABCD 的面积是48,AD∥BC,且AD=10,BC=2,那么梯形的高是_______.10.已知等腰梯形ABCD 中,AB∥CD,AD=BC ,对角线BD 平分∠ABC,•这个梯形的周长为18cm ,AB=3cm ,则CD=_________.二、选择题(每题3分,共24分) 11.下列说法不正确的是( ).A .164的立方根是14 B .8的立方根是±2 C .-14是的平方根116D .-0.027的立方根是-0.312.若x 2-kxy+y 2是一个完全平方式,则k 的值为( ).A .2B .±2 C.4 D .±413.一个三角形的三边比为1:3:2,则这个三角形是( ).A .锐角三角形B .直角三角形C .钝角三角形D .以上均不对 14.如图所示,不是中心对称,也不是轴对称图形的是( ).A B C D 15.平行四边形不一定具备的性质是( ).A .对角互补B .邻角互补C .对角相等D .内角和为360° 16.在梯形ABCD 中,AD∥BC,则∠A:∠B:∠C:∠D 的可能值为( ).A .3:5:4:6B .3:4:5:6C .5:4:6:3D .6:5:4:3C DA B17.在下列图形中,是中心对称图形的是().A.梯形 B.三角形 C.正方形 D.直角梯形18.已知菱形的周长是52cm,两对角线长度之比为5:12,•则这两条对角线的长度为(). A.10cm,24cm B.5cm,12cm C.20cm,48cm D.8cm,6cm三、解答题(共56分)19.(6分)分解因式:①3x2-12 ②(x+y)2-4xy20.(6分)计算:(1)(x+12)(x-13); (2)(x+2)(x-2)(x2+4).21.(7分)先化简再求值:(3x+2y)2-2(9x2-4y2)+(3x-2y)2,其中x=2008,y=2.22.(6分)如图所示,经过平移,小船上的点A移到了点B,作出平移后的小船.23.(7分)已知│x-12│+13z 和y2-10y+25互为相反数,试判断以x,y,z•为边的三角形形状是怎样的.24.(7分)(1)如图所示,菱形ABCD的周长为8,两邻角之比为1:2,求菱形的面积.(2)如图是由16个边长为1的正方形拼成的,任意连结这些小正方形的两个顶点,得到一些线段,请分别画出一条长度是有理数的线段和一条长度是无理数的线段,并求出这两条线段。
重庆市万州区甘宁初级中学八年级数学上册 13.5 因式分解阶段性复习 华东师大版

13.5 因式分解阶段性复习 一、阶段性内容回顾 1.把多项式化成几个整式_______的形式叫做因式分解,也叫________.2.多项式中每一项都含有_________的因式叫公因式.3.把一个多项式中各项的________提出来进行因式分解的方法叫提公因式法.4.运用多项式的_________进行因式分解的方法叫做公式法.5.a 2-b 2=_______,•即两个数的平方差等于这两个数的________•乘以这两个数的_______.6.a 2±2ab+b 2=________,即两个数的平方和加上(或减去)这两个数的积的2•倍等于这两个数的________.7.分解因式的一般步骤:如果多项式各项有_______,则先把_______提出来,•然后再考虑用________,最后_________.二、阶段性巩固训练1.(福州)分解因式:x 3-4x=_____________.2.(贵阳)分解因式:2x 2-20x+50=____________.3.下列变形属于因式分解的是( ).A .(x+1)(x -1)=x 2-1B .a 2-22112()a a b b b=-+ C .x 2+x+14=(x+12)2 D .3x 2-6x+4=3x 2(x -2x )+4 4.下列多项式加上4x 2后,可以成为完全平方式的是( ).A .a 2+2axB .-a 2+2axC .-2x+1D .x 4+45.①4xy ;②12xy 2;③-2y 2;④4y .其中可以作为多项式-28x 2y+12xy 2-24y 3的因式的是( ).A .④B .②④C .①③D .③④6.用因式分解的方法计算42.72+14.6×42.7+7.32的值为( ).A .5 730B .2 500C .250 000D .100 0007.分解下列多项式:(1)5ax 2-10axy+5ay 2 (2)4x 2-3y (4x -3y )(3)(x 2-1)2+6(1-x 2)+9 (4)1-x 2+6xy -9y2(5)(a 2-12a )2+(a 2-a )+1168.如果x 2+mxy+9y 2是完全平方式,求代数式m 2+4m+4的值.9.计算(1-22221111)(1)(1)(1)23410---g g g .10.如果m ,n 满足│m+2│+(n -4)2=0,那么你能将代数式(x 2+y 2)-(mxy+n )•分解因式吗?11.已知a 2+b 2+c 2=20,ab+bc+ac=10,试求出(a+b+c )2的值.12.已知a ,b ,c 为△ABC 的三边,且满足条件a 2-c 2+ab -bc=0,试说明△ABC•为等腰三角形.13.观察下列各式:32-12=4×2,42-22=4×3,52-32=4×4,…(1)猜想(n+2)2-n 2的结果.(2)请验证你的猜想.14.已知a+b=23,ab=12,求a 3b+2a 2b 2+ab 3的值.15.(1)如果x 2+2x+2y+y 2+2=0,求x 2007+y 2008的值.(2)已知m+n=34,m-n=14,求m2-2mn+3m+3n+n2的值.答案:阶段性内容回顾1.乘积分解因式 2.相同 3.公因式 4.乘法公式5.(a+b)(a-b)和差 6.(a±b)2和(或差)的平方7.公因式公因式公式检查分解是否彻底阶段性巩固训练1.x(x+2)(x-2) 2.2(x-5)23.C 提示:根据定义.4.D 提示:x4+4+4x2=(x2+2)2.5.A 提示:原式=-4y(7x2-3xy+6y2).6.B 提示:原式=(42.7+7.3)2=502=2 500.7.(1)原式=5a(x2-2xy+y2)=5a(x-y)2.(2)原式=4x2-12xy+9y2=(2x-3y)2.(3)原式=(x2-1)2-6(x2-1)+9=(x2-1-3)2=(x2-4)2=[(x+2)(x-2)] 2=(x+2)2(x-2)2.(4)原式=1-(x2-6xy+9y2)=1-(x-3)2=(1+x-3)[1-(x-3)]=(x-2)(1-x+3)=(x-2)(4-x).(5)原式=(a2-a+14)2=[(a-12)2] 2=(a-12)4.8.∵x2+mxy+9y2是完全平方式,∴有(x±3y)2=x2+mxy+9y2,∴mxy=±6xy,∴m=±6.∴m2+4m+4=(m+2)2=(±6+2)2=64或16.9.原式=(1+12)(1-12)(1+13)(1-13)(1-14)(1-14) (1)110)(1-110)=32×12×43×23×54×34×…×11911111101021020⨯=⨯=.10.∵│m+2│+(n-4)2=0,而│m+2│≥0,(n-4)2≥0.∴m+2=0,n-4=0,∴m=-2,n=4,∴(x2+y2)-(mxy+n)=(x2+y2)-(-2xy+4)=x2+y2+2xy-4=(x+y)2-4=(x+y+2)(x+y-2).11.∵a2+b2+c2=20,ab+bc+ac=10,∴2ab+2bc+2ac=20.(a+b+c)2=[(a+b)+c] 2=(a+b)2+2c(a+b)+c2=a2+2ab+b2+2ac+2bc+c2 =a2+b2+c2+2ab+2ac+2bc=20+20=40.或∵a2+b2+c2=20,ab+b c+ac=10,∴2ab+2bc+2ac=20,∴a2+b2+c2+2ab+2bc+2ac=40,即(a+b)2+2c(a+b)+c2=40,∴(a+b+c)2=40.12.∵a2-c2+ab-bc=0,∴(a2-c2)+(ab-bc)=0,∴(a+c)(a-c)+b(a-c)=0,∴(a-c)(a+c+b)=0,∵a,b,c为△ABC的三边,∴a+b+c>0,∴a-c=0,∴a=c,∴△ABC为等腰三角形.13.(1)4(n+1)(2)原式=(n+2+n)(n+2-n)=(2n+2)·2=4(n+1).14.∵a+b=23,ab=12,∴原式=ab(a2+2ab+b2)=ab(a+b)2=12×(23)2=12×49=29.15.(1)∵x2+2x+2y+y2+2=0,∴(x2+2x+1)+(y2+2y+1)=0,∴(x+1)2+(y+1)2=0,∴x+1=0,y+1=0.即x=-1,y=-1,∴x2007+y2008=(-1)2007+(-1)2008=-1+1=0.(2)∵m+n=34,m-n=14,∴原式=(m2-2mn+n2)+(3m+3n)=(m-n)2+3(m+n)=(14)2+3×34=116+94=3716.。
重庆市万州区甘宁初级中学2014-2015学年八年级上学期期中考试数学试题(无答案)

一.选择题:(本大题共12小题,每小题4分,共48分)每个小题都给出了代号为A 、B 、C 、D 的四个答案,其中只有一个是正确的,请将正确答案的代号填入答题卷对应的表格中。
1.在﹣2,0,36 ) A .﹣2 B .0 C .3 D. 62.下列计算正确的是 ( )A. 853b b b =+B.44443a a a a =⋅⋅C.10641243a a a =⨯ D.752)(b b -=- .3.下列六个数:144,-722,3π,9.0,327,0. 32 , 0..6.1,0.2020020002……(每两个2之间多一个0),其中无理数的个数有( ) A . 5个 B . 4个 C . 3个 D . 2个4. 如图,已知ND MB =,NDC MBA ∠=∠,下列条件中不能 判定△ABM ≌△CDN 的是( )A.N M ∠=∠B.CD AB = AM =D.AM ∥CN5. 若236a =,38b =, 则 b a +的值是 ( )A .8或4-B .8+或8-C .8-或4-D .4+或4-6.实数a b ,在数轴上对应点的位置如图所示, 则必有( )A .0a b +>B .0a b -<C .0ab >D .0a b< 7.等腰三角形的周长是18cm ,其中一边长为4cm ,其它两边长分别为( )0 第6题图A BDCMN第4题图A.4cm,10cm B.7cm,7cmC.4cm,10cm或7cm,7cm D.无法确定8. 在实数范围内,下列判断正确的是()A.若m=n,则nm=B.若22ba>, 则ba>C.若2a=2)(b,则ba=D.若3a=3b,则ba=10.等腰三角形一腰上的高与另一腰的夹角为30︒,则顶角的度数为( )A.60︒B.120︒C.60︒或150︒D.60︒或120︒11.如图,H是△ABC的高AD,BE的交点,且DH=DC,有下列结论:①△ABD为等腰直角三角形;②BC=AC;③BH=AC;④CE=CD。
重庆市万州区丁阳中学八年级数学上册《第14章:一次函

重庆市万州区丁阳中学八年级数学上册《第14章:一次函数》复习学案人教新课标版一、【使用说明】本节为复习第十三章而设计,见学习目标。
二、【学习目标】①结合具体情境体会一次函数的意义,根据条件确定一次函数表达式。
②会画一次函数的图象,根据一次函数的图象和解析表达式y=kx+b(k≠0)探索并理解其性质(h>0或b<0时,图象的变化情况)。
③理解正比例函数。
④能根据一次函数的图象求二元一次方程组的近似解。
⑤能用一次函数解决实际问题。
【学法指导】自主探究法三、【自主学习】1 已知一次函数y=-2x-6。
(1)当x=-4时,则y= ,当y=-2时,则x= ;(2)画出函数图象;(3)不等式-2x-6>0解集是_____,不等式-2x-6<0解集是_____;(4)函数图像与坐标轴围成的三角形的面积为;(5)若直线y=3x+4和直线y=-2x-6交于点A,则点A的坐标______;(6)如果y 的取值范围-4≤y≤2,则x的取值范围__________;(7)如果x的取值范围-3≤x≤3,则y的最大值是________,最小值是_______.2 。
已知一次函数y=32x+m和y=-12x+n的图象交于点A(-2,0)且与y轴的交点分别为B、C两点,求△ABC的面积.四、【合作探究】1、已知:一次函数的图象经过点(2,1)和点(-1,-3).(1)求此一次函数的解析式;(2)求此一次函数与x轴、y•轴的交点坐标以及该函数图象与两坐标轴所围成的三角形的面积;(3)若一条直线与此一次函数图象相交于(-2,a)点,且与y轴交点的纵坐标是5,•求这条直线的解析式;(4)求这两条直线与x轴所围成的三角形面积.2.已知一次函数的图像交x轴于点A(-6,0),交正比例函数于点B,若B点的横坐标是-2,△AOB的面积是6,求:一次函数与正比例函数的解析式。
3.某单位要印刷产品说明书,甲印刷厂提出:每份说明书收1元印刷费,另收1500元制版费;乙印刷厂提出:每份说明书收2.5元印刷费,不收制版费。
重庆市万州区甘宁初级中学八年级数学上册 14.2 勾股定

14.2 勾股定理的应用◆回顾归纳1.多边形的面积计算,一般把多边形分割成若干个规则的图形,包括_______,矩形等特殊四边形.2.航海问题:(1)画出物体的变化前后的位置.(2)构建_______,再运用勾股定理求解.3.实践中的有关线段或路程求解,•要运用题目条件创建直角三角形模型,•运用_______或_______来综合解答.◆课堂测控测试点1 简单的几何图形与勾股定理1.等腰△ABC的面积为12cm2,底边上的高AD=3cm,则它的周长为_____cm.2.已知直角三角形两直角边为6、8,则斜边的高为______.3.如图1,图中所有三角形是直角三角形,所有四边形是正方形,•S1=9,•S4=169,S3=144,则S2=_______.图1 图2 图34.在图2所示的图形中,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,则正方形A,B,C,•D•的面积之和是_______.5.如图3所示,在Rt△ABC中,∠ACB=90°,CD⊥AB,CD=2,•BD=1.(1)求BC;(2)求AD.测试点2 勾股定理与实际应用6.如果梯子底端离建筑物7•米,•那么25•米长的梯子可达到建筑物的高度是_______.7.如图4,一艘船从港口出发,先向正北航行30海里,再向正东航行15海里,到达一小岛,小岛到港口的距离为_______.图4 图5 图68.如图5,A、B两个村子在河CD的同侧,A、B两村到河的距离分别为AC=1km,BD=3km,且CD=3km,现要在河边建一水厂向A、B两村输送自来水,铺设水管的费用为2万元/千米,请你在CD上选择水厂位置O,使铺设水管的费用最低,并求出总费用.解题方案:(1)作点A关于直线CD的________点A′.(2)连结A′B交CD于点______,点O为______的位置.(3)由图形可知A′E=DC=3km,BE=BD+DE=3+_____=_____,在______中,•由勾股定理得A′B2=32+42=25,故A′B=_____km,总费用为2×5=10(万元).◆课后测控1.•测得一块三角形稻田的三边长分别为14m,•48m,•50m,•则这块稻田的面积为_______m2.2.如图6,在四边形ABCD中,∠B=∠D=90°,若CD=2,AB=5,∠A=60°,•则AD=_______,BC=_______.3.如图,在把易拉罐中的水倒入一个圆水杯的过程中,若水杯中的水在点P与易拉罐刚好接触,则此时水杯中的水深为()A.2cm B.4cm C.6cm D.8c m4.下列命题中,其中正确命题的个数为()(1)Rt△ABC中,已知两边长分别为3和4,则第三边长为5;(2)•有一个内角等于其他两个内角和的三角形是直角三角形;(3)三角形的三边分别为a,b,c,若a2+c2=b2,则∠C=90°;(4)在△ABC中,∠A:∠B:∠C=1:5:6,则△ABC是直角三角形.A.1个 B.2个 C.3个 D.4个5.如图,有一个小朋友拿着一根竹竿要通过一个长方形的门,如果把竹竿竖放就比门高出1尺,斜放就恰好等于门的对角线长,已知门宽4尺,求竹竿长与门高.6.一只蜘蛛在一底面半径为2m高为4m的水桶下边缘A处,发现水桶的上边缘B•处有一只蚊子,便决定捕捉它,为了不引起蚊子的注意,它故意不走直线,而是绕着水桶爬行(如图),沿一条螺旋路线从背后对蚊子进行突袭,结果,偷袭成功,蜘蛛获得了一顿丰盛的美餐.请问蜘蛛至少要爬行多少路程才能捕到蚊子?( 取3.14,结果保留1位小数)◆拓展创新如图,台风是一种自然灾害,•它以台风中心为圆心在周围数千米范围内形成气候风暴,有极强的破坏力,据气象观测距沿海某城市A的正南方向220km的B•处有一台风中心,其中心最大风力为12级,每远离台风中心20km风力就会减弱一级,•该台风中心现正在以15km/h的速度沿北偏东30°方向往C处移动,且台风中心风力不变,若城市所受风力达到或超过四级,则称受台风影响.(1)该城市是否会受到这次台风的影响?请说明理由.(2)若会受到台风影响,那么台风影响该城市的持续时间有多长?(3)该城市受到台风影响的最大风力为几级?答案:回顾归纳1.直角三角形 2.直角三角形 3.勾股定理直角三角形的识别课堂测控1.18 2.4.83.16(点拨:S1+S2=9+16=S4-S3)4.49(点拨:S A+S B=x2,S C+S D=y2,而x2+y2=72=49)5.(1)5(2)4 6.24米 7.15海里8.(1)对称(2)O 建水厂(3)1 4 Rt△A′BE 5课后测控1.3362.10-23 5-43(点拨:延长AD,BC交于点E,构建Rt△ABE,Rt△CDE,运用勾股定理求解)3.C 4.B5.设门高x尺,竹竿长为(x+1)尺,由勾股定理得x2+42=(x+1)2,x=7.5,门高7.5尺,竹竿长8.5尺.6.将水桶沿AB剪开,最短路线为矩形对角线,长约13.2m.拓展创新(1)过A作AD⊥BC,垂足为D.在Rt△ABD中,∠B=30°,AB=220km.所以AD=12×AB=12×220=110(km).因为110<20×(12-4)=160,所以A市受台风影响.(2)在BC上取点E,F,使AE=AF=160.则当台风中心在EF上运动时,城市受到影响.在Rt△ADE中,因为AD=110km,AE=160km.所以=km).,h).(3)台风中心到D处时,风力最强.因为11020=5.5级,台风从A到D减弱了5.5级.12-5.5=6.5(级),A市受到台风最大风力是6.5级.。
重庆市八年级数学上册第十四章《整式的乘法与因式分解》经典复习题(含答案解析)

一、选择题1.计算下列各式,结果为5x 的是( )A .()32xB .102x x ÷C .23x x ⋅D .6x x - 2.从边长为 2a +的正方形纸片中剪去一个边长为1a -的正方形纸片()1a >,则剩余部分的面积是( )A .41a +B .43a +C .63a +D .2+1a3.下列运算正确的是( ) A .()23636a = B .()()22356a a a a --=-+C .842x x x ÷=D .326326x x x ⋅=4.若3a b +=-,10ab =-,则-a b 的值是( )A .0或7B .0或13-C .7-或7D .13-或13 5.当代数式2()2020x y ++的值取到最小..时,代数式222||2||x y x y -+-=……( ) A .0 B .2- C .0或2- D .以上答案都不对 6.已知A 为多项式,且2221241A x y x y =--+++,则A 有( )A .最大值23B .最小值23C .最大值23-D .最小值23- 7.2a =1,b 是2的相反数,则a+b 的值是( ) A .1 B .-3 C .-1或-3D .1或-3 8.设, a b 是实数,定义一种新运算:()2*a b a b =-.下面有四个推断:①**a b b a =;②()222**a b a b =;③()()**a b a b -=-;④()**a b c a b a c +=+*.其中所有正确推断的序号是( )A .①②③④B .①③④C .①②D .①③ 9.已知5a b +=,2ab =-,则a 2+b 2的值为( ) A .21B .23C .25D .29 10.下列计算正确的是( ) A .()222x y x y +=+B .()32626m m =C .()2224x x -=-D .()()2111x x x +-=-11.已知1x =,1y =,则代数式222x xy y ++的值为( ).A .20B .10C .D .12.计算()()202020213232 -⨯的结果是( ) A .32- B .23- C .23 D .3213.下列各式中,正确的是( )A .2222x y yx x y -+=B .22445a a a +=C .()2424m m --=-+D .33a b ab += 14.若|m ﹣3n ﹣2019|=1,则(2020﹣m +3n )2的值为( ) A .1B .0C .1或2D .0或4 15.若|a |=13,b|=7,且a +b>0,则a -b 的值是( ).A .6或20B .20 或-20C .6或-6D .-6或20 二、填空题16.若2,3x y a a ==,则22x y a +=_______________________.17.观察下列各式:2(1)(1)1x x x -+=-;()23(1)11x x x x -++=-; ()324(1)11x xx x x -+++=-; …… (1)()432(1)1x x x x x -++++=___;(2)根据规律可得:()1(1)1n x x x --+++=_____(其中n 为正整数);(3)计算:()5049482(31)333331-++++++; 18.若2a x =,3b x =,则32a b x -=___________.19.若()230x -=,则x y -=______.20.如果关于x 的多项式24x bx ++是一个完全平方式,那么b =________. 21.计算:()()299990.045⎡⎤⨯-⎣⎦的结果是______. 22.因式分解:24ay a -=_______.23.因式分解()2228ac bc abc -+=______.24.分解因式:2221218ax axy ay -+=_________.25.若方程22(1)8m x mx x --+=是关于x 的一元一次方程,则代数式2008|1|m m --的值为________.26.若9m =4,27n =2,则32m ﹣3n =__. 三、解答题27.如图1是1个直角三角形和2个小正方形,直角三角形的三条边长分别是a 、b 、c ,其中a 、b 是直角边,两个小正方形的边长分别是a 、b .(1)将4个完全一样的直角三角形和2个小正方形构成一个大正方形(如图2).用两种不同的方法列代数式表示图2中的大正方形面积:方法一:________________;方法二:________________;(直接把答案填写在答题卡的横线上)(2)观察图2,试写出()2a b +,2a ,2ab ,2b 这四个代数式之间的等量关系:________________.(直接把答案填写在答题卡的横线上)(3)请利用(2)中等量关系解决问题:若图1中一个三角形面积是6,图2的大正方形面积是64,求22a b +的值.28.如图1是一个长为4a 、宽为b 的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成一个“回形”正方形(如图2)(1)观察图2请你写出2()a b +、2()a b -、ab 之间的等量关系是________; (2)根据(1)中的结论,若95,4x y x y ⋅+==,则x y -=________; (3)拓展应用:若22(2019)(2020)7m m -+-=,求(2019)m -(2020)m -的值.29.计算:(1)2(1)(1)(2)x x x +--+ (2)(34)(34)x y x y -++- 30.已知x 、y 为有理数,现规定一种新运算,满足1x y xy *=+.(1)求24*的值;(2)求(14)(2)*-的值;(3)探索()a b c *+与a b a c *+*的关系,并用等式把它们表达出来.。
重庆市万州区甘宁初级中学八年级数学上册 14.1.2 直角三角形的判定练习 华东师大版

14.1.2 直角三角形的判定◆回顾归纳如果三角形的三边长a、b、c有关系:a2+b2=_______,•那么这个三角形是_______三角形,这就是直角三角形的判定方法,也是勾股定理的_______.◆课堂测控测试点直角三角形的判定1.(1)3a,4a,5a(a>0);(2)5k,12k,13k;(3)3a,4b,5c,•以上各组数能组成直角三角形的是__________(填序号).2.一个三角形的最大边是5,另一边是4,要使三角形为直角三角形,•则第三边长为_______.3.三角形三边分别为x,2,x+1,且x+1是斜边,则x=____,三边长为______.4.在△ABC中,AB=17,BC=30,BC上的中线AD=8,则△ABC为()A.直角三角形 B.等腰三角形 C.等边三角形 D.等腰直角三角形5.以1,2,3为三边构建三角形是_________三角形(填“直角”、“锐角”或“钝角”).6.若一个三角形三边长分别为7,24,25,则三角形最短边上的高为________,•最大边所对的角为_______.7.设a,b,c为直角三角形的三边,则a:b:c不可能是()A.3:5:4 B.5:12:13 C.2:3:4 D.8:15:178.下列各组正数为边长,能组成直角三角形的是()A.a-1,2a,a+1 B.a-1,a a+1C.a-12a a+1 D.a-12a,a+19.三角形的三边长分别为n2-1,2n,n2+1(n>1),则此三角形的形状为()A.等腰三角形 B.直角三角形 C.等腰直角三角形 D.无法判断◆课后测控1.△ABC中,a=9,b=12,①当c2=______时,∠C是直角,②当c2=______时,∠B是直角.2.以a+b,a-b,2ab三边构成的三角形是_______三角形,最大边是______(ab≠0,a>b>0).3.已知一个三角形的三边分别为3m,•4m,•5m(•m•为自然数)•,则这个三角形为_______,理由是___________.4.如图,已知S1=81,S2=225,S3=144,则△ABC是______,∠ACB=______.5.正方形的对角线长为1,则正方形的边长为()A.2 B.22C.22 D.246.下列说法错误的是()A.△ABC中,若∠C=∠A-∠B,则△ABC为直角三角形B.△ABC中,若∠A:∠B:∠C=5:2:3,则△ABC为直角三角形 C.△ABC中,若a:b:c=2:2:3,则△ABC为直角三角形D.△ABC中,若a=35c,b=45c,则△ABC为直角三角形7.如图,AD⊥CD,AB=13,BC=12,CD=3,AD=4,试求四边形CDAB•的面积.8.如图,四边形ABCD为正方形,点E为AB中点,点F在AD边上,且AF=14AD.试探究图中有多少个直角三角形?并说明理由.解题方案:图中有4个直角三角形.(1)设正方形边长为1个单位,则AE=BE=12,AF=14,DF=34.(2)在R t△AEF中,EF2=AE2+AF2=(12)2+(14)2=516.在Rt△CDF中,FC2=CD2+DF2=12+(34)2=______.在Rt△BCE中,EC2=CB2+BE2=12+(12)2=______.(3)EF,FC,EC满足关系式EF2+EC2=_____.而FC2=_______.所以EF2+EC2______FC2.即∠FEC=_______.(4)所以图中有4个直角三角形.9.如图,已知四边形ABCD中,AB=20,BC=15,CD=7,AD=•24,∠B=90°,试说明∠A+∠C=180°.◆ 拓展创新(1)给出一组式子:32+42=52,82+62=102,82+152=172,242+102=262,则352+_____=372.(2)给出一组式子:32+42=52,62+82=102,92+______=152,…,一般规律是(3k)2+(4k)2=•_______.(3)给出一组式子:(22-1)2+42=(22+1)2,(32-1)2+62=(32+1)2,(42-1)2+82=(42+1)2,…,(52-1)2•+______=(52+1)2,一般规律是(n2-1)2+_____=(n2+1)2.答案:回顾归纳c 直角逆定理课堂测控1.(1) 2.3 3.3232,2,524.B 5.直角 6.24 90°7.C(点拨:利用勾股定理的逆定理.)8.B 9.B课后测控1.225 63 2.直角 a+b 3.直角三角形(3m)2+(4m)2=(5m)2 4.直角三角形90° 5.B 6.C7.S四边形CDAB=S△ABC+S△ACD=12×12×5+12×4×3=30+6=36.8.(2)255555202525(3)164164161616++=== 90°9.如图答-1所示,连结AC,因为∠B=90°,AB=20,BC=15,所以AC2=AB2+BC2=202+152=625,又因为AD2+DC2=242+72=576+49=625,所以AD2+DC2=AC2,所以∠D=90°,所以∠DAB+ ∠DCB=360°-∠B-∠D=360°-90°-90°=180°.拓展创新(1)122(2)122(5k)2(3)102(2n)2。
重庆市万州区甘宁初级中学八年级数学上册 13.1.4 同底

同底数幂的除法◆回顾归纳设m、n为正整数,m>n,a≠0,•则有a m÷a n=•_______.这就是说,•同底数幂相除,_________不变,__________相减.◆课堂测控测试点1 同底数幂相除1.下列计算正确的是()A.a6÷a3=a2 B.z5÷z4=zC.a3÷a=a3 D.(-c)4÷(-c)2=-c22.下列运算正确的是()A.x2+x2=x4 B.x·x4=x4 C.x6÷x2=x4 D.(ab)2=ab23.x6÷x2=_______.4.(易错题)(-a3)2÷(-a2)3=_________.5.(体验过程题)请阅读下面的解题过程,有错误的,请指出原因并改正.(1)a10÷a2=a10÷2=a5;(2)(x-y)6÷(y-x)3=(x-y)3;(3)(-a)8÷(-a2)=(-a)8-2=(-a)6=a6;(4)a3÷a2·1a=a3÷a=a3-1=a2.测试点2 同底数幂除法法则的逆用6.已知:a m=4,a n=8,求a3m-2n的值. 7.已知3m=6,9n=2,求32m-4n+1的值.◆课后测控1.下列计算正确的是()A.x3÷x3=0 B.x2m+3÷x2m-3=x0C.(-a)5÷(-a)3·(-a2)=1 D.x n·x÷x n·x=x22.在算式a m+n÷()=a m-2中,括号内的代数式应当是()A.a m+n+2 B.a n-2 C.a m+n+3 D.a n+23.下面的计算中正确的是()A.a10÷a5=a2 B.108÷108=10C.x3÷x=x3 D.(-m)4÷(-m)2=m24.若n为正整数,则(-5)n+1÷[5(-5)n]=()A.5n+1 B.0 C.-5n+1 D.-15.若x2m+n y n÷(xy)2=x5y,则m,n的值分别为()A.m=3,n=2 B.m=2,n=2 C.m=2,n=3 D.m=3,n=16.若x m+2n÷x m=x6,则n-2=_______.7.人们以分贝为单位来表示声音的强弱.通常说话的声音是50分贝,它表示声音的强度是105,摩托车发出的声音是110分贝,它表示声音的强度是1011.摩托车的声音强度是说话声音强度的_______倍.8.若5x-3y-2=0,则105x÷103y=_________.9.计算:(1)x6÷x2;(2)a n+4÷a n+1;(3)(a+1)3÷(a+1)2;(4)(-a)5÷(-a)2;(5)(-a)8÷(-a5);(6)(x3)2÷x2+x3·(-x)2.10.计算:(1)(ax)5÷(ax)3;(2)x2n+2÷x2n-1;(3)a m÷(a n÷a s);(4)(x-y)7÷(y-x)6.11.一种液体,每升含有3×1012个有害细菌.为了试验某种杀菌剂的效果,•科学家们进行了实验,发现1滴杀菌剂可以杀死1010个此种细菌.要将1升液体中的有害细菌全部杀死,需要这种杀菌剂多少滴?你是怎样计算的?12.如果1kg煤的全部能量都释放出来,则有9.04×104kJ热量,而实际上完全燃烧1kg煤却只能释放3.35×104kJ的热量,那么1kg•煤的全部能量是完全燃烧释放的热量的多少倍?(保留三个有效数字)13.(变式题)计算:(12a)7÷(12a)4.◆拓展创新已知2a=3,4b=6,8c=12,求a,b,c的关系.答案:回顾归纳a m-n底数指数课堂测控1.B 2.C 3.x4 4.-15.(1)错,应为a10-2=a8;(2)错,应为(x-y)6÷[-(x-y)3]=-(x-y)3;(3)错,应为a8÷(-a)2=-a8-2=-a6;(4)错,应为a3-2·1a=a·1a=1.6.a3m-2n=a3m÷a2n=(a m)3÷(a n)2=43÷82=1.7.27(点拨:本题可逆用幂的有关性质,•将结论中的代数式转化为含有已知条件的代数式进行求解,即要求32m-4n+1的值,要把已知条件转化为以3为底的幂的形式,如9n=(32)n=32n,值为27)课后测控1.D(点拨:x n·x÷x n·x=x n+1-n+1=x2.)2.D 3.D 4.D5.C(点拨:x2m+n y n÷x2y2=x2m+n-2y n-2=x5y.∴2252,213m n mn n+-==⎧⎧∴⎨⎨-==⎩⎩)6.1 7.106 8.1009.(1)原式=x6-2=x4;(2)原式=a4+n-(n+1)=a3;(3)原式=(a+1)3-2=a+1;(4)原式=(-a)5-2=-a3;(5)原式=-a8-5=-a3;(6)原式=x6÷x2+x3·x2=x6-2+x3+2=x4+x5.10.(1)原式=(ax)5-3=(ax)2=a2x2;(2)原式=x2n+2-(2n-1)=x3;(3)原式=a m÷a n-s=a m-(n-s)=a m-n+s;(4)原式=(x-y)7÷[-(x-y)] 6=(x-y)7-6=x-y. 11.3×1012÷1010=3×102=300(滴).12.2.70倍13.原式=(12a)7-4=(12a)3=18a3.拓展创新因为2a=3,4b=22b=6,8c=23c=12.所以2·2a=22b,a+1=2b;2·22b=23c,2b+1=3c.4·2a=23c,a+2=3c.所以2b-a=3c-2b,所以a-4b+3c=0.。
重庆市万州区甘宁初级中学八年级数学上册 14 勾股定理单元综合测试2 华东师大版
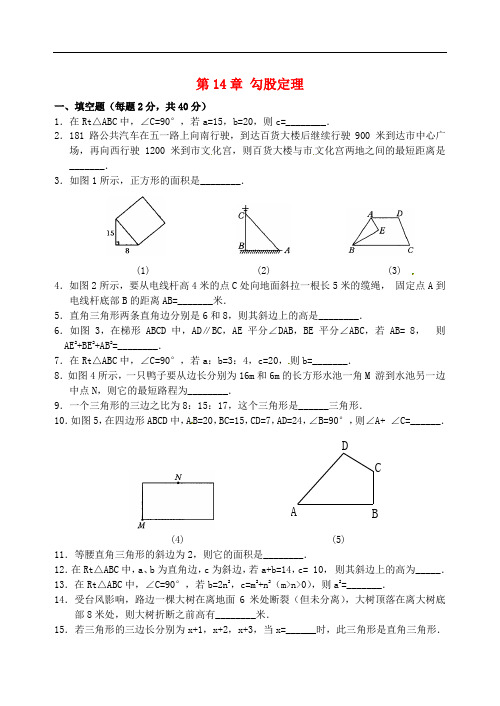
第14章勾股定理一、填空题(每题2分,共40分)1.在Rt△ABC中,∠C=90°,若a=15,b=20,则c=________.2.181路公共汽车在五一路上向南行驶,到达百货大楼后继续行驶900•米到达市中心广场,再向西行驶1200米到市文化宫,则百货大楼与市文化宫两地之间的最短距离是_______.3.如图1所示,正方形的面积是________.(1) (2) (3)4.如图2所示,要从电线杆高4米的点C处向地面斜拉一根长5米的缆绳,•固定点A到电线杆底部B的距离AB=_______米.5.直角三角形两条直角边分别是6和8,则其斜边上的高是________.6.如图3,在梯形ABCD中,AD∥BC,AE平分∠DAB,BE平分∠ABC,若AB=•8,• 则AE2+BE2+AB2=________.7.在Rt△ABC中,∠C=90°,若a:b=3:4,c=20,则b=_______.8.如图4所示,一只鸭子要从边长分别为16m和6m的长方形水池一角M•游到水池另一边中点N,则它的最短路程为________.9.一个三角形的三边之比为8:15:17,这个三角形是______三角形.10.如图5,在四边形ABCD中,A B=20,BC=15,CD=7,AD=24,∠B=90°,则∠A+•∠C=______.DCBA(4) (5)11.等腰直角三角形的斜边为2,则它的面积是________.12.在Rt△ABC中,a、b为直角边,c为斜边,若a+b=14,c=•10,•则其斜边上的高为_____.13.在Rt△ABC中,∠C=90°,若b=2n2,c=m2+n2(m>n>0),则a2=_______.14.受台风影响,路边一棵大树在离地面6米处断裂(但未分离),大树顶落在离大树底部8米处,则大树折断之前高有________米.15.若三角形的三边长分别为x+1,x+2,x+3,当x=______时,此三角形是直角三角形.16.在Rt △ABC 中,AB=n 2+1,BC=n 2-1,AC=2n ,那么∠A+∠B=______.17.李红从家到学校时,先向正南走了150m ,接着向正东方向走了200m ,则李红家离学校的最短距离为_______m .18.如图6所示,有一圆柱,其高为12cm ,底面半径为3cm ,在圆柱下底A•点有一只小虫,它想得到上底面B 处的食物,则蚂蚁经过的最短距离为_______cm ( 取3).M N CBA(6) (7) (8)19.已知│x-12│+(y-13)2=0和z 2-10z+25=0互为相反数,则以x 、y 、z 为三边的三角形是________三角形.20.直角三角形的两边为3,4,其第三边的平方为_______. 二、选择题(每题3分,共21分)21.满足下列条件中的△ABC ,不是直角三角形的是( ).A .a 2=b 2-c 2B .∠A-∠B=∠CC .∠A :∠B :∠C=3:4:5D .a :b :c=7:24:2522.斜边长为25,一条直角边长为7的直角三角形面积为( ). A .81 B .82 C .83 D .8423.直角三角形斜边的平方等于两直角边乘积的2倍,这个三角形有一个锐角是( ). A .15° B .30° C .60° D .45°24.已知如图7所示,△AB=AC=10,BD 是AC 边上的高线,CD=2,则BD 等于( ). A .8 B .6 C .5 D .425.如图8所示,在△ABC 中,∠ACB=90°,AC=12,BC=5,AN=AC ,BM=BC ,则MN 的长是( ).A .2B .3C .4D .526.直角三角形的周长为24,斜边长为10,则其面积为( ). A .96 B .49 C .24 D .48 27.三角形的三边是①1,2,5;②13,14,15;③32,42,52;④0.3,0.4,0.5;⑤2n+1,2n ,2n 2+2n+1(n 为正整数),能构成直角三角形的有( ). A .2个 B .3个 C .4个 D .5个三、解答题(第28题9分,其余各题10分,共39分)28.一艘轮船以20千米/时的速度离开港口向东北方向航行,•另一艘轮船同时离开港口以15千米/时的速度向东南方向航行,它们离开港口2小时后相距多少千米?29.一块四边形的绿地ABCD,AB=3,BC=4,CD=12,AD=13,∠B=90°,•求此绿地的面积.30.从旗杆的顶端系一条绳子,垂到地面还多2米,小丁拉起绳子下端绷紧,•刚好接触地面,发现绳子下端距旗杆底部8米,小丁马上计算出旗杆的高度,你知道他是如何解的吗?31.如图所示,△ABC中,AB=AC=20,BC=32,D是BC上一点,且AD⊥AC,求BD长.附加题(10分)1.学校科技小组研制了一套信号发射、接收系统,在对系统进行测试中(如图14-4-10所示),小明从路口A处出发,沿东南方向笔直公路行进,并发射信号,•小华同时从A 处出发,沿西南方向笔直公路行进,并接收信号,若小明步行速度为39米/分,小华步行速度为52米/分,恰好在出发后30分时信号开始不清楚.(1)你能求出他们的研制的信号收发系统的信号传递半径吗?(•以信号清晰为界限)(2)通过计算,你能找到题中数据与勾股数3,4,5的联系吗?试从中寻找求解决问题的简便算法.2.如图所示,公路MN和公路PQ在P处交汇,且∠QPN=30°,在A处在一所中学,AP=160米,假设拖拉机行驶时周围100米以内会受到噪声的影响,那么拖拉机在公路MN上沿PN方向行驶时,学校是否受到噪声影响?请你说明你的想法.[提示:作AQ⊥MN于Q]答案:一、1.25或7.1500 3.289 4.3米 5.4.8 6.128 7.16 8.109.•直角 10.180° 11.2 12.4.8 13.m2-n2 14.16米 15.2 16.90°17.250 18.15 •19.直角 20.7或25二、21.C 22.D 23.D 24.B 25.C 26.C 27.A三、•28.50km 29.略 30.15m 31.应用勾股定理附加题:1.(1)1950米(2)5×13•×30=1950米 2.会影响.。
重庆市万州区甘宁初级中学八年级数学上册 13.1.4 同底

13.1.4 同底数幂的除法【知能点分类训练】知能点1 同底数幂的除法法则1.(-x)8÷(-x)3=______,a10÷a6=_______.2.85÷82÷8=________,(m2-n2)4÷(m2-n2)=________.3.下列计算正确的是().A.a8÷a4=a2 B.x5÷x4=xC.x7÷x=x7 D.(-n)7÷(-n)5=-n24.计算(xy)4÷(xy)2的结果是().A.xy B.xy2 C.x2y D.x2y25.计算:(1)x6÷x3(2)a3b3÷a2b(3)-x9÷(-x)3÷x2(4)(-12)5÷(-12)4(5)(x+y)6÷(x+y)2(6)(x-y)8÷(y-x)4÷(x-y)3知能点2 逆用法则及综合运用6.已知2m=3,2n=4,则23m-2n等于().A.27927..1688B C D.17.在式子x m+n÷()=x m-2中,括号内的代数式应为(). A.x n+2 B.x m+n+3 C.x m-2+n D.x m-n 8.若10x=7,10y=49,则10y-x=().A.7 B.14 C.17D.1499.计算x20÷[(-x2)3] 2-x2·(-x)3÷(-x2)2.10.计算:(1)98×272÷(-3)18(2)162m÷82n÷4m×43m-3n+1【综合应用提高】11.请用不同的方法计算(-a)6÷(-a)3.12.已知3m=6,9n=2,求32m-4n-1的值.13.已知642x÷82x÷4=16,求x的值.14.已知x2m+2=3,y=5+9m,请你用含x的代数式表示y.15.某城市高科技园区超级计算机中心内,被称为“神州1•”的计算机运算速度为每秒1012次运算,要作1014运算需要多少秒?说说你运用了哪些知识.16.已知2x-5y-3=0,求4x÷32y的值.【中考真题实战】17.(山东)下列运算正确的是().A.a3+a3=2a3 B.a3-a2=a C.a3·a3=2a6 D.a6÷a2=a318.(西宁)下列运算中,计算结果正确的是().A.a4·a3=a12 B.a6÷a3=a2 C.a5+a5=2a10 D.(a3)2=a619.(荆门)下列计算正确的是().A.a3·b3=b6 B.(-a2)3=a5C.(ab)3=ab2 D.(-a)6÷(-a)3=-a320.(乌鲁木齐)下列运算正确的是().A.x3·x4=x12 B.(x3)4=x12 C.x6÷x2=x3 D.x3+x4=x7答案:1.-x5 a42.82或64 (m2-n2)3提示:85÷82÷8=85-2-1=82=64.3.B 提示:利用公式a m÷a n=a m-n.4.D 提示:原式=(xy)4-2=(xy)2=x2y2.5.(1)x3(2)ab2提示:原式=(a3÷a2)·(b3÷b)=a·b2.(3)原式=x9÷x3÷x2=x9-3-2=x4.(4)原式=-12.(5)(x+y)4.(6)原式=(x-y)8÷(x-y)4÷(x-y)3=(x-y)8-4-3=x-y. 6.A 提示:∵2m=3,2n=4.∴23m -2n =23m ÷22n =(2m )3÷(2n )2=33÷42=27÷16=2716. 7.A 提示:x m+n ÷x m -2=x m+n -(m -2)=x n+2.8.A 提示:10y -x =10y ÷10x =49÷7=7.9.原式=x 20÷x 12-x 2·(-x 3)÷x 4=x 20-12+x 5÷x 4=x 8+x .10.(1)原式=(32)8×(33)2÷(-3)18=316×36÷318=316+6-18=34=81.(2)原式=(24)2m ÷(23)2n ÷(22)m ×(22)3m -3n+1 =28m ÷26n ÷22m ×26m -6n+2=28m -6n -2m+6m -6n+2=212m -12n+2.11.①(-a )6÷(-a )3=(-a )6-3=(-a )3=-a 3.②(-a )6÷(-a )3=63333()()()()()a a a a a ---=--g =(-a )3=-a 3. 12.∵3m =6,9n =2,∴32m -4n -1=32m ÷34n ÷3=(3m )2÷(32n )2÷3=(3m )2÷[(32)n ] 2÷3=(3m )2÷(9n )2÷3=62÷22÷3=36÷4÷3=3. 13.642x ÷82x ÷4=(26)2x ÷(23)2x ÷22=212x ÷26x ÷22=26x -2=16=24,∴6x -2=4,∴x=1.14.∵x=32m+2=32m ×32=9×(32)m =9×9m ,∴9m =9x , ∴y=5+9m =5+.15.1014÷1012=102=(100)s ,用到了同底数幂除法.16.∵2x -5y -3=0,∴2x -5y=3,∴4x ÷32y =(22)x ÷(25)y =22x ÷25y =22x -5y =23=8.17.A 18.D 19.D 20.B.。
八年级数学上册第十四章整式的乘法与因式分解14.1整式的乘法14.1.2幂的乘方训练新人教版(20

八年级数学上册第十四章整式的乘法与因式分解14.1 整式的乘法14.1.2 幂的乘方同步训练(新版)新人教版编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(八年级数学上册第十四章整式的乘法与因式分解14.1 整式的乘法14.1.2 幂的乘方同步训练(新版)新人教版)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为八年级数学上册第十四章整式的乘法与因式分解14.1 整式的乘法14.1.2 幂的乘方同步训练(新版)新人教版的全部内容。
14.1.2 幂的乘方[学生用书P69]1.[2016·台州]下列计算正确的是()A.x2+x2=x4 B.2x2-x2=x2C.x2·x3=x6 D.(x2)3=x52.[2016·孝感]下列运算正确的是( )A.a2+a2=a4 B.a5-a3=a2C.a2·a2=2a2 D.错误!错误!=a103. 下列算式中:①a4·a2;②(a2)3;③a12+a2;④a2·a3。
计算结果为a6的算式的个数是( )A.1个 B.2个 C.3个 D.4个4.有下列运算:①(-x2)3=-x5;②3xy-3yx=0;③3100×(-3)100=0;④m·m5·m7=m12;⑤3a4+a4=3a8;⑥(x2)4=x16。
其中正确的有()A.1个 B.2个C.3个 D.4个5.化简(-a2)5+(-a5)2的结果是()A.-2a7 B.0C.a10 D.-2a106.计算下列各式,并用幂的形式表示结果:(1)(25)3=__ __;(2)(q6)5=____;(3)[(-5)4]3=_ __;(4)-3×(32)3=__ __.7.计算:(1)x n-2·x n+2(n是大于2的整数);(2)-(x3)5;(3)[(-2)2]3;(4)[(-a)3]2;(5)(a-b)·(b-a)2·(-a+b)4。
重庆市万州区甘宁初级中学八年级数学上册 13.1.1 同底数幂的乘法练习 华东师大版

13.1.1同底数幂的乘法【知能点分类训练】知能点1 同底数幂的乘法法则1.-103×104=________,a5·a10=_________.2.(-1)5×(-1)3=_______,-y·(-y)6·y3=________.3.下列各式中的两个幂,其中是同底数幂的是().A.-a2与(-a)3; B.(-a)m与a n; C.-a3与a2; D.105与5104.(荆门)计算a5·a5的结果是().A.a10 B.a25 C.2a5 D.2a105.(河北)化简(-x)3(-x)2的结果正确的是().A.-x6 B.x6 C.x5 D.-x56.计算:(1)-x3·x4; (2)(-a)6·(-a)9;(3)a2·a3·a5 ;(4)(-a)2·a3·(-a4)知能点2 底数是多项式的同底数幂的乘法7.(x-y)2·(y-x)3·(y-x)3=________.8.(a-b+2c)4·(-a+b-2c)5=________.9.下列各选项中不能用同底数幂的乘法法则化简的是().A.(a+b)2(a+b) B.(a+b)2(a-b)C.-(b-a)2(a-b) D.(a+b)(a+b)3(a+b)410.计算(x-y)2(y-x)2正确的是().A.(x-y)2(y-x)2=(x-y)2+2=(x-y)4B.(x-y)2(y-x)22(x-y)2×2=2(x-y)4C.(x-y)2(y-x)2=-(y-x)2·(y-x)2=-(y-x)2+2=-(x-y)4D.(x-y)2(y-x)2=2(x-y)211.计算:(1)(2a+b)m·(2a+b)2m; (2)(a-2b)2·(2b-a)3·(2b-a)4(3)(x-2y)2(2y-x)5; (4)(b-a)3·(a-b)n+(a-b)n+1·(b-a)2知能点3 逆用法则及混合运算12.(1)已知2m=3,2n=4,求2m+n的值; (2)已知a x·a x+1·a3=a6,求x的值.13.已知(x+y)a(x+y)2b=(x+y)5,(x-y)3a(x-y)4b=(x-y)11,试求:①a+b,②a2007·b3的值.14.计算:(1)x3·x5+x·x3·x4; (2)(b-a)5·(a-b)6+(a-b)7·(b-a)4【综合应用提高】15.(1)1 000×10n-3=________;(2)若a n+2·a2n=a8,那么n=________.(3)若22n+2=64,那么n=________.(4)若(m-n)2=4,(m-n)3=-8,则(m-n)5=_________.(5)x n-1·______=x m+n.16.(1)在等式x·x2·()=x10中,括号里面的代数式应为().A.x5 B.x6 C.x7 D.x8(2)若a,b均为正整数,且2a×2b=32,则a,b的值有().A.1对 B.2对 C.3对 D.4对(3)a9可以写成().A.(-a)2(-a)7 B.(-a2)·a7C.(-a)5·(-a4) D.(-a)(-a)8(4)32007×(-3)2007的计算结果是().A.0 B.34014 C.-34014 D.32008(5)算式22+22+22+22可化为().A.24 B.82 C.28 D.21617.(1)已知2a=3,2b=6,2c=12,求a,b,c的关系.(2)如果10a=4,10b=5,10c=9,试用10的幂(含a,b,c)的形式表示180.18.举世瞩目的“神舟”五号载人飞船于2003年10月15日上午9时发射升空.•中国航天第一人杨利伟乘坐的飞船实施变轨后进入椭圆轨道,飞船以每秒7.9×103m的速度飞行,历时21h 23min (约7.7×104s),那么,•杨利伟巡天之旅绕地球约行了多少米?(结果保留两个有效数字,并用科学记数法表示).【开放探索创新】19.已知a·b=735,试写出两个符合条件的a,b的值.【中考真题实战】20.(南京)计算x3·x2的结果是().A.x9 B.x8 C.x6 D.x521.(绵阳)下列式子中,与a4·a4运算结果相同的是().A.a2·a8 B.(a2)4 C.(a4)4 D.a8÷a222.(江西)下列运算,正确的是().A.a6·a3=a18 B.(-a)6·(-a)3=-a9C.a6÷a3=a2 D.(-a)6·(-a)3=a答案:1.-107 a15提示:-103×104=-(103×104)=-103+4=-107.2.1 -y10提示:(-1)5×(-1)3=(-1)5+3=(-1)8=1,-y·(-y)6·y3=-y·y6·y3=-y1+6+3=-y10.3.C 提示:底数均为a.4.A5.D 提示:原式=(-x)5=-x5.6.(1)-x7(2)-a15(3)a10(4)原式=a2·a3·(-a4)=-a2·a3·a4=-a97.(x-y)2·(y-x)3·(y-x)2=(y-x)2·(y-x)3·(y-x)2=(y-x)2+3+2=(y-x)78.(a-b+2c)4·(-a+b-2c)5=(a-b+2c)4·[-(a-b+2c)] 5=-(a-b+2c)4·(a-b+2c)5=-(a-b+2c)99.B 提示:底数经变化也不同.10.A 提示:(x-y)2(y-x)2=(x-y)2(x-y)2=(x-y)4.11.(1)原式=(2a+b)m+2m=(2a+b)3m.(2)原式=(2b-a)·2(2b-a)3·(2b-a)4=(2b-a)9.(3)原式=(2y-x)2(2y-x)5=(2y-x)7.(4)原式=-(a-b)3(a-b)n+(a-b)n+1·(a-b)2=-(a-b)n+3+(a-b)n+3=0.12.(1)∵2m=3,2n=4,∴2m+n=2m×2n=3×4=12.提示:逆用同底数幂乘法法则.(2)∵a x·a x+1·a3=a x+x+1+3=a2x+4=a6,∴2x+4=6,∴x=1.13.∵(x+y)a·(x+y)2b=(x+y)a+2b=(x+y)5,(x-y)3a·(x-y)4b=(x-y)3a+4b=(x-y)11,∴25,1, 34112, a b aa b b+==⎧⎧∴⎨⎨+==⎩⎩∴a+b=1+2=3(或用②-①直接可求得a+b),∴a2007·b3=12007×23=1×8=8.14.(1)原式=x8+x8=2x8.(2)原式=-(a-b)5(a-b)6+(a-b)7·(a-b)4=-(a-b)11+(a-b)11=0. 15.(1)10 提示:原式=103×10n-3=10n.(2)2 提示:a n+2·a2n=a3n+2=a8,∴3n+2=8,n=2.(3)2 提示:64=26=22n+2,∴2n+2=6,n=2.(4)-32 提示:(m-n)5=(m-n)2·(m-n)3=4×(-8)=-32.(5)x m+1提示:利用指数的关系.16.(1)C 提示:x·x2=x3,而x3·x7=x10.(2)D 提示:2a+b=25,a+b=5,讨论a,b的正整数解.(3)C 提示:原式=-a5·(-a4)=a5·a4=a9.(4)C 提示:原式=-32007×32007=-32007+2007=-34014.(5)A 提示:原式=4×22=22×22=24.17.(1)∵12=3×22=6×2,∴2c=12=3×22=2a×22=2a+2,2c=12=6×2=2b×2=2b+1.∴c=a+2,c=b+1,∴2c=a+b+3.提示:答案不唯一.(2)∵10a=4,10b=5,10c=9,∴180=4×5×9=10a×10b×10c=10a+b+c.提示:把180分解成4×5×9,然后再用10a,10b,10c找换.18.7.9×103×7.7×104=60.83×107≈6.1×108.答:略.19.答案不唯一,如75×730=735,故a=75,b=730等等.20.D 21.B 22.B。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
14.1.1-14.1.2 阶段性复习
阶段性内容回顾
1.如果直角三角形的两条直角边长分别是a,b,斜边长为c,那么______,•即直角三角形中两直角边的平方和等于________.
2.如果三角形的三边长a,b,c满足______,那么这个三角形是直角三角形.
3.若a,b,c是三个正整数,且满足a2+b2=c2,则称a,b,c为一组________.
阶段性巩固训练
1.一个长方形的长是15cm,对角线长为17cm,那么它的宽为_______.
2.若一个三角形的三边之比为5:12:13,且周长为60cm,则它的面积是____cm2.3.受台风影响,马路边一棵大树在离地面3m•处折断,•大树顶端落在离大树根部4m处,则大树折断之前高________m.
4.在△ABC中,如果a2+b2<c2,那么△ABC是().
A.锐角三角形 B.直角三角形
C.钝角三角形 D.不能确定
5.如果线段a,b,c能组成直角三角形,则它们的比可以是().
A.1:2:4 B.1:3:5 C.3:4:7 D.5:12:13
6.三角形的三边长分别为a,b,c,且满足(a-b)(a2+b2-c2)=0,则该三角形的形状为().
A.任意等腰三角形 B.任意直角三角形
C.等腰三角形或直角三角形 D.等腰直角三角形
7.有一只小鸟从高3m的小树上飞至距离该树24m远且高13m的另一棵大树顶上,•那么小鸟飞行了多少米?如果小鸟的飞行速度为5m/s,那么它飞行了多长时间?
8.如图,凸四边形ABCD的边AB,BC,CD和DA的长分别是3,4,12和13,且∠ABC=90°,则四边形ABCD的面积是多少?
9.若△ABC满足a=(m+n)2-1,b=2m+2n,c=(m+n)2+1,试判断△ABC的形状.
10.如图,在△ABC中,AB=AC=10cm,BC=12cm,求△ABC的面积S.
11.如图,在△ABC中,CD是AB边上的高,AC=4,BC=3,DB=9
5
.
(1)求AD的长;(2)△ABC是直角三角形吗?
12.一直角三角形的周长为12,斜边长为5,求这个三角形的面积.答案:
阶段性内容回顾
1.a 2+b 2=c 2
斜边的平方
2.a 2+b 2=c 2
3.勾股数
阶段性巩固训练
1.8 .
2.120 提示:三边分别为10,24,26.
3.8 提示:画图,树高为. 4.C 5.D 6.C
7(m ),26÷5=5.2(s ),答略. 提示:画出图形.
8.连接AC .∵AB=3,BC=4,∠ABC=90°,∴AC=5. ∵CD=12,AD=13,
∴52+122=132,即AC 2+CD 2=AD 2
. ∴∠ACD=90°,∴S 四ABCD =S △ABC +S △ACD =
12×3×4+1
2
×5×12=36. 9.直角三角形. 提示:计算a 2
,b 2
,c 2
.
10.48cm 2
提示:作高AD ,利用勾股定理及等腰三角形性质求出AD . 11.(1)∵BC=3,DB=
9
5
,CD ⊥AB ,
∴125
==. 又∵AC=4,
∴16
5
==.
(2)是.由(1)得AB=AD+DB=
165+9
5
=5, 而AC=4,BC=3,∴AC 2
+BC 2
=AB 2
,
∴△ABC 是直角三角形 12.设直角边分别为a ,b ,则
222512,
5,
a b a b ++=⎧⎨+=⎩
由①得a+b=7,(a+b)2=49,∴a2+2ab+b2=49,将②代入,∴2ab=49-25=24,
∴ab=12,∴S=1
2
ab=6.。
