重庆市万州区甘宁初级中学2014-2015学年八年级数学上学期综合测试题(三)(无答案) 华东师大版

合集下载

重庆万州第三中学2014-2015学年八年级上学期期中考试数学试题(含答案)

2014年秋季八年级期中考试数学试题考试时间120分钟总分150分第I 卷（选择题48分）一、选择题（每小题4分，共48分）1.、161的平方根是（） A 、41 B 、41- C 、41± D 、4± 2.下列命题中，真命题是（）A.、相等的角是直角B.、不相交的两条线段平行C.、两直线平行，同位角互补 D 、.经过两点有且只有一条直线3、如图，某同学把一块三角形的玻璃打碎成了三块，现在要到玻璃店去配一块完全一样的玻璃，那么最省事的办法是根据三角形的全等判定（）A 、SAS 带③B 、SSS 带③C 、ASA 带③D 、AAS 带③4. 在实数020.20200200843.143073，，，，，，，π－…中，无理数的个数是（）A 、1B 、2C 、3D 、45.在△ABC 和△A B C '''中,AB =A B '',∠B =∠B ',补充条件后仍不一定能保证△ABC ≌△A B C ''',则补充的这个条件是( )A ．BC =BC '' B ．∠A =∠A ' C ．AC =A C ''D ．∠C =∠C '6.下列运算中，正确的是（） A. B. C. D.7.已知实数x ，y 满足，则以x ，y 的值为两边长的等腰三角形的周长是（）A ． 20或16B ． 20C ． 16D ．以上答案均不对8.．下列从左边到右边的变形，属于因式分解的是（）A 、 1)1)(1(2-=-+x x xB 、1)2(122+-=+-x x x xC 、)4)(4(422y x y x y x -+=-D 、)3)(2(62-+=--x x x x9.设一个正方形的边长为错误！未找到引用源。

，若边长增加3cm ，则新正方形的面积增加了（）A.错误！未找到引用源。

重庆市万州区甘宁初级中学八年级数学上册 14 勾股定理单元综合测试2 华东师大版

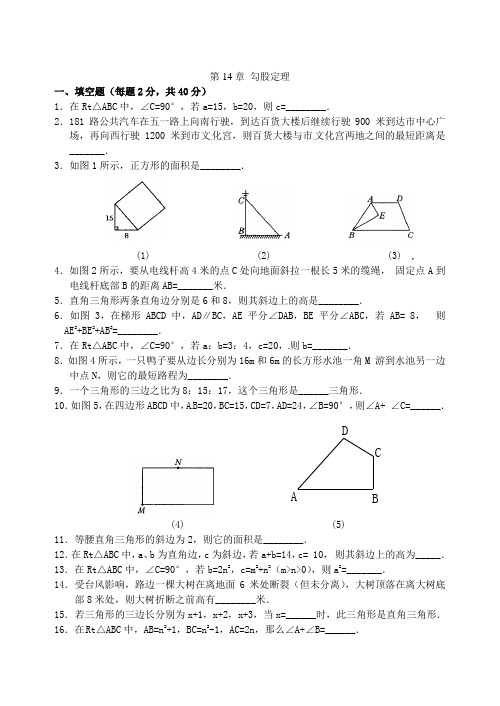
第14章勾股定理一、填空题（每题2分，共40分）1．在Rt△ABC中，∠C=90°，若a=15，b=20，则c=________．2．181路公共汽车在五一路上向南行驶，到达百货大楼后继续行驶900•米到达市中心广场，再向西行驶1200米到市文化宫，则百货大楼与市文化宫两地之间的最短距离是_______．3．如图1所示，正方形的面积是________．(1) (2) (3)4．如图2所示，要从电线杆高4米的点C处向地面斜拉一根长5米的缆绳，•固定点A到电线杆底部B的距离AB=_______米．5．直角三角形两条直角边分别是6和8，则其斜边上的高是________．6．如图3，在梯形ABCD中，AD∥BC，AE平分∠DAB，BE平分∠ABC，若AB=•8，• 则AE2+BE2+AB2=________．7．在Rt△ABC中，∠C=90°，若a：b=3：4，c=20，则b=_______．8．如图4所示，一只鸭子要从边长分别为16m和6m的长方形水池一角M•游到水池另一边中点N，则它的最短路程为________．9．一个三角形的三边之比为8：15：17，这个三角形是______三角形．10．如图5，在四边形ABCD中，A B=20，BC=15，CD=7，AD=24，∠B=90°，则∠A+•∠C=______．DCAB(4) (5)11．等腰直角三角形的斜边为2，则它的面积是________．12．在Rt△ABC中，a、b为直角边，c为斜边，若a+b=14，c=•10，•则其斜边上的高为_____．13．在Rt△ABC中，∠C=90°，若b=2n2，c=m2+n2（m>n>0），则a2=_______．14．受台风影响，路边一棵大树在离地面6米处断裂（但未分离），大树顶落在离大树底部8米处，则大树折断之前高有________米．15．若三角形的三边长分别为x+1，x+2，x+3，当x=______时，此三角形是直角三角形．16．在Rt△ABC中，AB=n2+1，BC=n2-1，AC=2n，那么∠A+∠B=______．17．李红从家到学校时，先向正南走了150m ，接着向正东方向走了200m ，则李红家离学校的最短距离为_______m ．18．如图6所示，有一圆柱，其高为12cm ，底面半径为3cm ，在圆柱下底A•点有一只小虫，它想得到上底面B 处的食物，则蚂蚁经过的最短距离为_______cm （取3）．M N CBA(6) (7) (8)19．已知│x-12│+（y-13）2=0和z 2-10z+25=0互为相反数，则以x 、y 、z 为三边的三角形是________三角形．20．直角三角形的两边为3，4，其第三边的平方为_______．二、选择题（每题3分，共21分）21．满足下列条件中的△ABC ，不是直角三角形的是（）．A ．a 2=b 2-c 2B ．∠A-∠B=∠CC ．∠A ：∠B ：∠C=3：4：5D ．a ：b ：c=7：24：2522．斜边长为25，一条直角边长为7的直角三角形面积为（）． A ．81 B ．82 C ．83 D ．8423．直角三角形斜边的平方等于两直角边乘积的2倍，这个三角形有一个锐角是（）． A ．15° B ．30° C ．60° D ．45°24．已知如图7所示，△AB=AC=10，BD 是AC 边上的高线，CD=2，则BD 等于（）． A ．8 B ．6 C ．5 D ．425．如图8所示，在△ABC 中，∠ACB=90°，AC=12，BC=5，AN=AC ，BM=BC ，则MN 的长是（）．A ．2B ．3C ．4D ．526．直角三角形的周长为24，斜边长为10，则其面积为（）． A ．96 B ．49 C ．24 D ．48 27．三角形的三边是①1，2，5；②13，14，15；③32，42，52；④0.3，0.4，0.5；⑤2n+1，2n ，2n 2+2n+1（n 为正整数），能构成直角三角形的有（）． A ．2个 B ．3个 C ．4个 D ．5个三、解答题（第28题9分，其余各题10分，共39分）29．一块四边形的绿地ABCD，AB=3，BC=4，CD=12，AD=13，∠B=90°，•求此绿地的面积．31．如图所示，△ABC中，AB=AC=20，BC=32，D是BC上一点，且AD⊥AC，求BD长．附加题（10分）1．学校科技小组研制了一套信号发射、接收系统，在对系统进行测试中（如图14-4-10所示），小明从路口A处出发，沿东南方向笔直公路行进，并发射信号，•小华同时从A 处出发，沿西南方向笔直公路行进，并接收信号，若小明步行速度为39米/分，小华步行速度为52米/分，恰好在出发后30分时信号开始不清楚．[提示：作AQ⊥MN于Q]答案:一、1．25或57 2．1500 3．289 4．3米 5．4.8 6．128 7．16 8．109．•直角 10．180° 11．2 12．4．8 13．m2-n2 14．16米 15．2 16．90°17．250 18．15 •19．直角 20．7或25二、21．C 22．D 23．D 24．B 25．C 26．C 27．A三、•28．50km 29．略 30．15m 31．应用勾股定理附加题：1．（1）1950米（2）5×13•×30=1950米 2．会影响．。

重庆市万州区甘宁初级中学八年级数学上学期第一次阶段

1 重庆市万州区甘宁初级中学2014-2015学年八年级数学上学期第一次阶段性检测试题（本卷共三个大题，满分150分，考试时间：120分钟）一、选择题（本大题共10个小题，每小题4分，共40分）每小题只有一个正确答案，请将正确答案的代号填写在答题卷对应的位置. 1.下列运算正确的是（）A.1055x x x =+B.623x x x =⋅C. 22(2)2a a =D. 23a a a +=2.如果21x =，那么3x 的值为（）A.1B.-1C.±1D. 无意义3.下列说法正确的个数有（）①0是最小实数；②数轴上所有的点都表示实数；③无理数都是带根号的数； ④18-的立方根是12±；⑤14的平方根是12±A.1个B.2个C.3个D. 4个4.下列各式从左到右的的变形中，是因式分解的是（）A.))((2224x x x x x x -+=-B.()a x y ax ay -=-C. 21055(21)x x x x +=+D. 244(4)4x x x x -+=-+5．马大哈同学完成了如下的计算题：其中结果正确的是（）①，2323x x x =，②，44x x x =，③，）（1535x x =④，6）3（1226x x =A ． ①B ． ②④C ． ③D ． ④6.计算22(1)(1)a a --+的结果是（）A.2-B. 4-C. 4a -D. 222a +7．已知)(则,5,3--===+n m n m a a aA ． 243B ． 125C ． 15D ． 88．（4分）计算：)(的结果是)2()2(20092008---+-20092009200820082,2,2,2D C B A --9.若022222=++-+b a b a ，则b a +的值为( )A.2-B.0C.2D. 310.已知)51)((++x q x 的乘积中不含x 项，则q 的值为（）2A ．51-B ．5-C ．51D ．5二、填空题（本大题共6个小题，每小题4分，共24分）请将正确答案填写在答题卷对应的位置.11.81的平方根是 _________ .12.比较大小5 _________ 7.2；1416.3- _________ π-. 13．计算：=÷34a aa _________ ；=-232)(x x _________ ．14．的相反数是 _________ ，绝对值是 _________ ．15.若249x ax -+是完全平方式，则=a _________ .八年级第一次阶段性测试答题卷一、(40分)题号 1 2 3 4 5 6 7 8 9 103二、(24分) 11. ，12. ，13. ， 14. ，15. ，16. 。

重庆市万州区甘宁初级中学2014_2015学年八年级数学上学期寒假作业二无答案华东师大版

abaDC BADEC BA2014～2015学年度第一学期八年级寒假作业班级姓名学号成绩____一、填空题：1、分解因式：=+-2232ab b a a ． 2、4的算术平方根是，－27的立方根是．3、如果分式392--x x 的值为0，那么x = ．4、已知在平行四边形ABCD 中周长等于24厘米，AB 比BC 长4厘米，则AB 和BC 分别为厘米和厘米．5、若实数a 、b 满足0132=+-b a ，则ba = ．6.在菱形ABCD 中，对角线AC 和BD 分别等于５厘米和６厘米，则菱形ABCD 面积等于7、小明与小亮从学校出发去邮局，小明每小时行a km ，小亮每小时比小明快b km ，若学校距邮局Skm ，则小亮比小明早到小时．8、如图，边长为a 、b 的矩形，它的周长为14，面积为10，则=+22ab b a 9、如图，AD A D ''，分别是锐角三角形ABC 和锐角三角形A B C '''中,BC B C ''边上的高，且AB A B AD A D ''''==，．若使ABC A B C '''△≌△，请你补充条件_____．(填写一个你认为适当的条件即可) 10、如图5，AD ＝AE ，∠1＝∠2，BD ＝CE ，则有△ABD ≌ ，理由是 . 11、菱形的两条对角线长分别为6cm 和8cm,则菱形的面积是________.12.如图,在平行四边形ABCD 中,AE ⊥BC 于E,AF ⊥CD 于E, BE=3厘米,AB=6厘米,DF=5厘米, 则 ABCD 的周长为______厘米. 13、如图：在梯形ABCD 中，BC AD //，对角线BD AC ⊥，且cm AC 8=，cm BD 6=，则此梯形的高为 cm ；14、如图：ABC ∆、ACD ∆、ADE ∆是三个全等的正三角形，那么ABC ∆绕着顶点A 沿逆时针方向至少旋转度才能与ADE ∆完全重合。

重庆市万州区甘宁初级中学八年级数学上册第13章整式的乘除周练试题(无答案) 华东师大版

第十三章整式的乘除周练试题班级姓名座号成绩一、填空题：（每小题2分，共34分）1、计算：①24x x = ②32()()x x -÷-= ③222(1)x x x ---= ④(27)(31)x x -+=2、计算：①()()x y x y -+--= ②2()x y -=③228_____(____)x x x -+=- ④222()x y x y +=++3、计算：①2226(3)xy x y -= ②23273a b ab -÷= ③75(4.510)(810)⨯⨯= ④522()()a b a b +÷+=4、若2172327(3)m m -=，则m =5、计算：①2(1)(1)(1)x x x +-+= ②2(1)(1)(1)x x x +--=6、如果224x x k -+恰好是另一个整式的平方，则常数k = .7、观察下列各式：22041-=⨯，224243-=⨯，226445-=⨯，228647-=⨯……请写出反映这种规律的一般结论二、选择题：（每题3分，共15分）8、下列各式正确的是（）A ．5210a a a =B ．5225()a a =C ．527a a a a =D ．5211()a a a = 9、若24(13)19M x x -=-，则M 等于（）A ．213x -B ．22(13)x -C ．213x +D ．22(13)x + 10、下列多项式相乘，可以应用平方差公式的是（）A ．()()x y x y --+B ．()()x y x y ---C ．()()x y y x --D ．()()x y z y z x --+-11、适合2(1)(25)12x x x x ---=的x 的值为（）A ．－4B ．4C ．1D ．012、如果281x kx ++是两个数的和的平方形式，那么k 的值是（）A ．±9B ．18C ．±18D ．－18三、解答题：13、计算题：（每题5分，共30分） ①211()32x y -②322(2793)(3)x y x y xy xy -+÷-③23322()()()x x x x -+-- ④202131()(1)43--⑤(2)(2)a b a b -+- ⑥2(2)(2)(2)x y x y x y +--+14、（5分）解方程：2(21)9x +=15、（5分）已知：5,6x y xy +==，求222,()x y x y +-的值.16、（5分）已知：－5x 与一个整式的积是234251520x x y x +-，求：这个整式.17、（6分）先化简，再求值.2(2)(2)(2)2(2)(2)a b a b a b a a b a ⎡⎤-+-+--÷-⎣⎦，其中a b ==附加题：（每小题5分，共20分） 1、1013008(0.5)= 2、22221111(1)(1)(1)(1)23499----= 3、已知：2221510,x x x x -+=+=求 4、23,26,212,a b c ===求:2b-a-c=。

重庆市万州区甘宁初级中学八年级数学上册 14.1.2 直角三角形的判定练习华东师大版

14.1.2 直角三角形的判定◆回顾归纳如果三角形的三边长a、b、c有关系：a2+b2=_______，•那么这个三角形是_______三角形，这就是直角三角形的判定方法，也是勾股定理的_______．◆课堂测控测试点直角三角形的判定1．（1）3a，4a，5a（a>0）；（2）5k，12k，13k；（3）3a，4b，5c，•以上各组数能组成直角三角形的是__________（填序号）．2．一个三角形的最大边是5，另一边是4，要使三角形为直角三角形，•则第三边长为_______．3．三角形三边分别为x，2，x+1，且x+1是斜边，则x=____，三边长为______．4．在△ABC中，AB=17，BC=30，BC上的中线AD=8，则△ABC为（）A．直角三角形 B．等腰三角形 C．等边三角形 D．等腰直角三角形5．以1，2_________三角形（填“直角”、“锐角”或“钝角”）．6．若一个三角形三边长分别为7，24，25，则三角形最短边上的高为________，•最大边所对的角为_______．7．设a，b， c为直角三角形的三边，则a：b：c不可能是（）A．3：5：4 B．5：12：13 C．2：3：4 D．8：15：178．下列各组正数为边长，能组成直角三角形的是（）A．a－1，2a，a+1 B．a－1，a+1C．a－1a+1 D．a－1，a+19．三角形的三边长分别为n2－1，2n，n2+1（n>1），则此三角形的形状为（）A．等腰三角形 B．直角三角形 C．等腰直角三角形 D．无法判断◆课后测控1．△ABC 中，a=9，b=12，①当c 2=______时，∠C 是直角，②当c 2=______时，∠B 是直角．2．以a+b ，a －b ，_______三角形，最大边是______（ab≠0，a>b>0）．3．已知一个三角形的三边分别为3m ，•4m ，•5m （•m•为自然数）•，则这个三角形为_______，理由是___________．4．如图，已知S 1=81，S 2=225，S 3=144，则△ABC 是______，∠ACB=______．5．正方形的对角线长为1，则正方形的边长为（）A ．2 C ．．46．下列说法错误的是（）A ．△ABC 中，若∠C=∠A－∠B，则△ABC 为直角三角形B ．△ABC 中，若∠A：∠B：∠C=5：2：3，则△ABC 为直角三角形C ．△ABC 中，若a ：b ：c=2：2：3，则△ABC 为直角三角形D ．△ABC 中，若a=35c ，b=45c ，则△ABC 为直角三角形 7．如图，AD⊥CD，AB=13，BC=12，CD=3，AD=4，试求四边形CDAB•的面积．8．如图，四边形ABCD 为正方形，点E 为AB 中点，点F 在AD 边上，且AF=14AD ．试探究图中有多少个直角三角形？并说明理由．解题方案：图中有4个直角三角形．（1）设正方形边长为1个单位，则AE=BE=12，AF=14，DF=34．（2）在Rt△AEF 中，EF 2=AE 2+AF 2=（12）2+（14）2=516．在Rt△CDF 中，FC 2=CD 2+DF 2=12+（34）2=______．在Rt△BCE 中，EC 2=CB 2+BE 2=12+（12）2=______．（3）EF ，FC ，EC 满足关系式EF 2+EC 2=_____．而FC 2=_______．所以EF 2+EC 2______FC 2．即∠FEC=_______．（4）所以图中有4个直角三角形．9．如图，已知四边形ABCD 中，AB=20，BC=15，CD=7，AD=•24，∠B=90°，试说明∠A+∠C=180°．◆ 拓展创新（1）给出一组式子：32+42=52，82+62=102，82+152=172，242+102=262，则352+_____=372．（2）给出一组式子：32+42=52，62+82=102，92+______=152，…，一般规律是（3k）2+（4k）2=•_______．（3）给出一组式子：（22－1）2+42=（22+1）2，（32－1）2+62=（32+1）2，（42－1）2+82=（42+1）2，…，（52－1）2•+______=（52+1）2，一般规律是（n2－1）2+_____=（n2+1）2．答案:回顾归纳c 直角逆定理课堂测控1．（1） 2．3 3．3232，2，524．B 5．直角 6．24 90°7．C（点拨：利用勾股定理的逆定理．）8．B 9．B课后测控1．225 63 2．直角 a+b 3．直角三角形（3m）2+（4m）2=（5m）2 4．直角三角形90° 5．B 6．C7．S四边形CDAB=S△ABC+S△ACD=12×12×5+12×4×3=30+6=36．8．（2）255555202525(3)164164161616++=== 90°9．如图答－1所示，连结AC，因为∠B=90°，AB=20，BC=15，所以AC2=AB2+BC2=202+152=625，又因为AD2+DC2=242+72=576+49=625，所以AD2+DC2=AC2，所以∠D=90°，所以∠DAB+ ∠DCB=360°－∠B－∠D=360°－90°－90°=180°．（1）122（2）122（5k）2（3）102（2n）2。

重庆市万州区甘宁初级中学八年级数学上学期质量检测试

2014-2015年八年级数学科质量检测班级：姓名：总分：一、填空题（每空1分，共17分）1. 25的平方根记作，结果是 .2. 361的平方根是，64的算术平方根是。

3.（-4）2的算术平方根是。

4. 9是数a 的一个平方根，数a 是。

5.求下列各式的值：⑴16-= ;(2)2(13)±- = .6.求下列各式中的x: ⑴若x 2=49,则x= ;(2)x ，则x= .7. 125的立方根是 ;64的立方根是 . 3127-的倒数是 ;39的相反数 . 364的平方根是___________.10. a 3 • a 5＝ ; (y 2)5 = .二、选择题(每题3分,共24分)1、8的立方根是（）.A.-2B.2C.2或-6D.02.一个数的平方根与这个数的立方根之和为0，则这个数是（）.A.-1 B .±1 C.不存在 D.03、有下列四个说法：①1的算术平方根是1;②81的立方根是±21;③-27没有立方根;④互为相反数的两数的立方根互为相反数，其中正确的是（）.A .①②B .①③C .①④D .②④4、下列各计算中，正确的是（）（A ） 5552b b b =•; （B ） 1055x x x =+;（C ） 532m m m =• （D ） 222b a b a =• 5、（x －y ）与（y －x ）的乘积是（）（A ）22y x - （B ）22x y - （C ）22y x -- （D ）222y xy x -+-6、1999200013 3•计算：（－）（－）＝（）（A ）31（B ）3 （C ）31- （D ）-37、下列多项式计算中，利用乘法公式正确的是（）（A ）（x －3y ）（x ＋5y ）＝x 2＋2xy －15y 2（B ）（xy 3）2＝xy 6；（C ）（－2x ）3＝－2x 3(D)（－2a 2）• （3ab 2－5ab 3）＝－6a 3b 2 －10a 3b 38、一个正方形的边长增加了cm 2，面积相应增加了232cm ，则这个正方形的边长为（）(A)6cm ；（B ）5cm ；（C ）8cm ；（D ）7cm 。

重庆市万州区甘宁初级中学八年级数学上册第13章整式

第13章整式的乘除一、填空题（每题2分，共20分）1．（－a5）·（－a2）3·（－a3）2=________．2．（－3xy2）2÷（－2x2y）=________．3．计算：（－8）2006×（－0.125）2007=________．4．若x n=5，y n=3，则（xy）2n=________．5．若A=3x－2，B=1－2x，C=－5x，则A·B+A·C=________．6．a2－9与a2－3a的公因式是________．7．（x+1）（x－1）（x2+1）=_________．8．4x2_________+36y2=（_______）2．9．若（x－2）2+（y+3）2=0，则（x+y）2=________．10．若4x2+kxy+y2是完全平方式，则k=________．二、选择题（每题3分，共24分）11．下列计算中，正确的是（）．A．2a+3b=5ab B．a·a3=a3 C．a6÷a2=a3 D．（－ab）2=a2b212．计算x3y2·（－xy3）2的结果是（）．A．x5y10 B．x5y8 C．－x5y8 D．x6y1213．若5x=3，5y=4，则25x+y的结果为（）．A．144 B．24 C．25 D．4914．999×1 001可利用的公式是（）．A．单项式乘以单项式 B．平方差C．完全平方 D．单项式乘以多项式15．x（x－y）2－y（y－x）2可化为（）．A．（x－y）2 B．（x－y）3 C．（y－x）2 D．（y－x）216．下面的计算结果为3x2+13x－10的是（）．A．（3x+2）（x+5） B．（3x－2）（x－5）C．（3x－2）（x+5） D．（x－2）（3x+5）17．已知（x－3）（x2+mx+n）的乘积项中不含x2和x项，则m，n的值分别为（）． A．m=3，n=9 B．m=3，n=6 C．m=－3，n=－9 D．m=－3，n=918．不论m，n为何有理数，m2+n2－2m－4n+8的值总是（）．A．负数 B．0 C．正数 D．非负数三、计算（每题4分，共20分）19．[（xy2）2] 3+[（－xy2）2] 3; 20．（x－y+9）（x+y－9）21．（－12a2b）（23b2－13a+14）; 22．991011251247⨯+-.23．（3x－2y）2－（3x+2y）2四、化简并求值（每题6分，共12分）24．6a2－（2a－1）（3a－2）+（a+2）（a－2），其中a=13．25．已知23,3 1.x yx y+=⎧⎨-=⎩，求7y（x－3y）2－2（3y－x）3的值．五、解答题（每题7分，共14分）26．如图，大正方形的面积为16，小正方形的面积为4，求阴影部分的面积．27．若（x+y）2=36，（x－y）2=16，求xy与x2+y2的值．六、作图题（10分）28．用如图所示的纸片，取其两片，可以拼合成几种不同形状的长方形？画出示意图，并写出所拼的长方形的面积．答案:1．a17提示：原式=（－a5）·（－a6）·a6=a5+6+6=a17．2．－92y3提示：原式=9x2y4÷（－2x2y）=－92y3．3．－1 8提示：原式=（－8）2006×（－18）2007=（－8）2006×（－18）2006×（－18）=－18．4．225 提示：原式=（x n·y n）2=（5×3）2=152=225．5．－21x2+17x－2 提示：原式=A（B+C）．6．a－3 提示：a2－9=（a+3）（a－3），a2－3a=a（a－3）．7．x4－1 8．±24xy 2x±6y9．1 提示：x=2，y=－3．10．±4 提示：4x2+kxy+y2=（2x±y）2．11．D 12．B13．A 提示：25x+y=25x×25y=（5x）2×（5y）2=32×42=144．14．B 提示：999×1 001=（1 000－1）（1 000+1）．15．B 提示：原式=x（x－y）2－y（x－y）2=（x－y）2（x－y）=（x－y）3． 16．C17．A 提示：原式=x3+（m－3）x2+（n－3m）x－3n．18．C 提示：原式=（m2－2m+1）+（n2－4n+4）+3=（m－1）2+（n－2）2+3>0． 19．原式=（xy2）6+（－xy2）6=x6y12+x6y12=2x6y12．20．原式=[x－（y－9）][x+（y－9）]=x2－（y－9）2=x2－（y2－18y+81）=x2－y2+18y－81．21．原式=（－12a2b）·23b2+（－12a2b）（－13a）+（－12a2b）·14=－13a2b3+16a3b－18a2b．22．原式=22 (1001)(1001)110011100444-++-+===2 500．23．原式=[（3x－2y）+（3x+2y）][（3x－2y）－（3x+2y）] =（3x－2y+3x+2y）（3x－2y－3x－2y）=6x·（－4y）=－24xy．24．原式=6a2－（6a2－4a－3a+2）+a2－4=6a2－6a2+7a－2+a2－4=a2+7a－6，当a=13时，原式=（13）2+7×13－6=－329．25．∵23,3 1.x yx y+=⎧⎨-=⎩∴原式=7y（x－3y）2+2（x－3y）3=（x－3y）2 [7y+2（x－3y）] =（x－3y）2（2x+y）=3×1=3．26．∵大正方形面积为16，小正方形面积为4．∴大正方形的边长为4，小正方形的边长为2．∴S阴=6×4－16－4=4．27．∵（x+y）2=36，（x－y）2=16，∴x2+2xy+y2=36，①x2－2xy+y2=16，②①－②得4xy=20，∴xy=5，①+②得2（x2+y2）=52，∴x2+y2=26．28．①+③ a（a+b）=a2+ab，如图（1）所示．②+③ b（a+b）=b2+ab，如图（2）所示．。

重庆市万州区甘宁初级中学八年级数学上学期寒假作业(

2014～2015学年度第一学期八年级寒假作业（一）班级姓名学号 (满分：100分考试时间：l00分钟) 一、填空(每小题2分，共24分)1、16的算术平方根是2、计算：=-÷-35)()(a a3、分解因式：=-92a4、在括号内填上合适的项：22y x +( )+41=2)21(+γx 5、如图1，直角三角形的两直角边长分别是2cm 、3cm ，则带阴影的正方形面积是 2cm 6、己知平行四边形ABCD 中，︒=∠30A ，则=∠C 度7、如图2，DEF ABC ∆≅∆，若︒=∠40A ，︒=∠20BCA ，则=∠E 度8、光速约为8103⨯米／秒，太阳光射到地球上的时间约为2105⨯秒，则地球与太阳的距离约为米9、如图3，DEF ∆是由ABC ∆平移得到的，若BC=6cm ，E 是BC 的中点，则平移的距离是 cm10、如图4，矩形ABCD 中，对角线AC 、BD 交于点O ，︒=∠64AOB ，则=∠ACB 度．11、如图5，在等腰梯形ABCD 中，A D ∥BC ，AD=5，BC=9，︒=∠60B ，则AB=12、如图6，正方形ABCD 的边长为8，M 在DC 上，且DM=2，N 是AC 上一动点，则DN+MN 的最小值为 .二、选择题：(每小题3分，共1 8分．下列各小题均有四个选项，其中只有一个是正确的．)13、下列计算正确的是( )A 、632x x x =⋅B 、532x x x =⋅C 、923)(x x =D 、5325)3)(2(x x x = 14、在实数3，4，π，3.0&，711，0.313113lll3…中，无理数的个数是( ) A 、3个 B 、4个 C 、5个 D 、6个15、如图7，平行四边形ABCD 中，对角线AC 、BD 相交于点0，则图中相等的线段共有( )A 、2对B 、3对C 、4对D 、5对16、矩形具有而平行四边形不具有的性质是( )A 、对角线互相平分B 、对角线互相垂直C 、对角线相等D 、四边相等17、下列各图中，是中心对称图形的是( )D AB C N M图618、如图8，ABC ∆中，︒=∠90B ，两直角边AB=7，BC=24，三角形内有一点P 到各边的距离都相等，则这个距离是( )A ，1 8，3 C ，4 D 、5 三、解答题：(共58分)19、(4分)计算：x x x ⋅-+-322)3()6(20、(4分)计算：2)1()25)(52(-+-+x x x21、(4分)分解因式：32244b ab b a +--22、(4分)先化简后求值：2a(a+1)-(2a+1)(2a-3)，其中2-=a .23、(5分)请画出图9中的ABC ∆绕点O 顺时针旋转︒90后的图形C B A '''∆24、(5分)如图l0，从电线杆离地面lom 处向地面拉一条长l 8m 的缆绳，这条缆绳在地面的固定点距离电线杆底部有多远?(精确到0.lm)25、(8分)如图l3，在平行四边形ABCD中，AE平分∠DAB，交DC于E.(1)试说明：AD=DE;∆的形状，并说明理由．(2)若E恰为DC的中点，试判断AEB26、(8分) 已知：如图，在梯形ABCD中，AD∥BC，AB=DC，点E、F、G•分别在边AB、BC、CD上，AE=GF=GC．（1）求证：四边形AEFG是平行四边形．（2）当∠FGC=2∠EFB时，求证：四边形AEFG是矩形．27、(8分)在Rt △ABC 中，∠B=90°,∠A=60°,点E 、F 分别在AB 、AC 上，沿EF 对折，使点A 落在BC 上的点D 处，且FD ⊥BC.①求证：四边形AEDF 是菱形； ②请你确定点F 在AC 上的位置，并简要说明理由.28、(8分)、在一张长10cm ，宽6cm 的矩形纸片上，要折出一个菱形，使菱形的顶点都在矩形的边上．小明同学沿矩形的对角线AC 折出∠CAE=∠DAC ，∠ACF=∠ACB 得到菱形AECF(如图l4)，(1)求菱形AECF 的边长；(2)若沿AE 把AEB ∆剪下，这时用．AEB ∆和四边形AECD 还可以拼成一些四边形．请你试一试，把所有拼好的四边形画出来．(3)用这张矩形的纸，你还能用与小明不同的方法折出一个菱形吗?试一试，若能折出来，请画出示意图(或说明你的折法，不必说明理由)AE B D C F。

重庆市万州区甘宁初级中学八年级数学上学期综合测试题

八年级数学（上）数学试卷姓名：班级：学号：分数：（本试卷共小题，满分100分，时间90分钟）一．选择题（本题共7小题，每题2分，共14分）1．下列计算正确的是（）A、236a a a⋅=； B、235a a a+=； C、3273--=； D、33(2)6x x-=-；2．计算2(1)(1)a a a-+-的结果为（）A、1；B、1-； C、221a+； D、221a-；3．下列说法中，正确的个数是（）①实数包括有理数、无理数和零；②三角形的三边之比为1:1:2，则三角形为等腰直角三角形；③幂的乘方，底数不变，指数相加；④平方根与立方根都等于它本身的数为0和1；A、4个；B、3个；C、2个；D、1个；4．已知，如图1，Rt ABC∆中，1AB AC==，若BCD∆为等边三角形，则四边形ABDC的周长为（）A、232+； B、222+； C、132+； D、122+；5．下列从左到右的变形，是分解因式的是（）A、222()2x y x xy y-+=-+； B、22()()4a b a b ab-=+-；C、229(3)(3)a b a b a b-+=-+-； D、2243(2)1x x x-+=--；6．下列图形，既是轴对称图形，又是中心对称图形的是（）A、B、C、 D、7．已知，如图2，ABC∆绕点A逆时针旋转055到''AB C∆的位置，则'BAB∠=（）A、055；B、045； C、090； D、060；二．填空题（本题共5小题，每题3分，共15分）8．64的平方根是，立方根是；9．已知，如图3，网格中每个小正方形的边长为1，则四边形ABCD的面积为；10．计算：2(93)(3)x x x-+÷-=；11．若22(3)0x y++-=，则y x xy-=；12、如图4：△ABC经过平移得△A1B1C1，则点A的对应点是，∠B= ，A1C1= ，AB∥，平移的方向是（在图上表示出来），平移的距离是（精确到mm），线段AB的中点M平移到（请在图上标出来）。

重庆市万州区甘宁初级中学八年级数学上学期竞赛练习题华东师大版

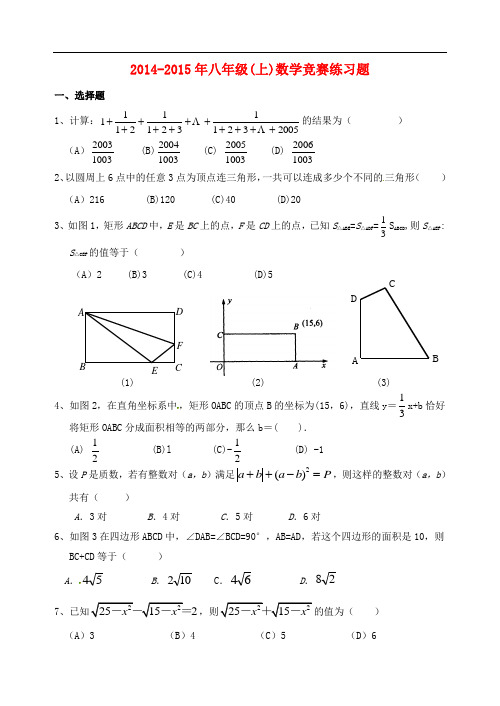
C A BD FECDAB2014-2015年八年级(上)数学竞赛练习题一、选择题 1、计算：2005321132112111+++++++++++ΛΛ的结果为（）（A ）10032003 (B)10032004 (C) 10032005 (D) 100320062、以圆周上6点中的任意3点为顶点连三角形，一共可以连成多少个不同的三角形（）（A ）216 (B)120 (C)40 (D)203、如图1，矩形ABCD 中，E 是BC 上的点，F 是CD 上的点，已知S △ABE =S △ADF =31S ABCD ,则S △AEF : S △CEF 的值等于（）（A ）2 (B)3 (C)4 (D)5(1) (2) (3) 4、如图2，在直角坐标系中，矩形OABC 的顶点B 的坐标为(15，6)，直线y ＝31x+b 恰好将矩形OABC 分成面积相等的两部分，那么b ＝( )． (A)21 (B)l (C)-21(D) -1 5、设P 是质数，若有整数对（a ，b ）满足P b a b a =-++2)(，则这样的整数对（a ，b ）共有（）A ．3对B ．4对C ．5对D ．6对6、如图3在四边形ABCD 中，∠DAB=∠BCD=90°，AB=AD ，若这个四边形的面积是10，则BC+CD 等于（）A ．54B ．102C ．64D ．2872225152x x －－－＝222515x x －＋－）（A ）3（B ）4（C ）5（D ）68、设323x a a =-，则x 的值为（）A 、正数B 、负数C 、非负数D 、零二、填空题：1、所谓机器洗牌，是将一副扑克牌按一定次序重新排列，即将第一张牌放到第k 1张牌的位置，将第二张牌放到第k 2张牌的位置，将第三张牌放到第k 3张牌的位置，……，等等。

设按原先点数的顺序排列的13张红心同色纸牌(正面朝上)：A ，2，3，4,5，6，7，8，9，1 0，J ，Q ，K 经一次洗牌后，牌的顺序变为 3，8，K ，A ，4，10，Q ，J ，5，7，6，2，9则再经过两次同样方式的洗牌后，牌的顺序应该是．2、方程1132=+++--y x y x 的整数解的个数是_______________.3、已知点A （1，1）在平面直角三角形系中,在坐标轴上确定点P,使△AOP 为等腰三角形,则符合条件的点P 共有________________个.4、在钟表面上，OA 是秒针，OB 是分针，现在是12：00，当三角形AOB 的面积第一次达到最大时，时间经过了秒。

初中数学重庆市万州区万州中学八年级数学上学期期中考模拟试题考试卷及答案新部编版.docx

xx学校xx学年xx学期xx试卷姓名:_____________ 年级:____________ 学号:______________题型选择题填空题简答题xx题xx题xx题总分得分一、xx题评卷人得分（每空xx 分，共xx分）试题1:与数轴上的点一一对应的是（）A、有理数B、整数C、无理数D、实数试题2:的平方根是（）A．9 B．C．D．3试题3:下列各题的计算,正确的是（）A. B.C. D.试题4:如图：若△ABE≌△ACF，且AB=5，AE=2，则EC的长为（）A.2B.3C.5D.2.5试题5:在，，，，，－0.2020020002…，中，无理数有（）个A.2B.3C.4D.5试题6:如果，那么p、q的值是（）A. B. C. D.试题7:在△ABC和△A′B′C′中，①AB=A′B′；②B C=B′C′；③AC=A′C′；④∠A=∠A′；⑤∠B=∠B′；⑥∠C=∠C′，则下列哪组条件不能保证△ABC≌△A′B′C′（）A. ①②③B. ①②⑤C. ①⑤⑥D.①②④试题8:若正数a的算术平方根比它本身大，则（）A. 0<a<1B. a>0C.a<1 D. a>1试题9:下列分解因式正确的是（）A．B．C．D ．试题10:若，则的值为（）A. B.－2 C. D.试题11:在边长为的正方形中挖去一个边长为的小正方形（）（如图甲），把余下的部分拼成一个矩形（如图乙），根据两个图形中阴影部分的面积相等，可以验证（）A．B．C．D．试题12:如图,在不等边△ABC中，PM⊥AB于点M，PN⊥AC于点N，且PM=PN，Q在AC上，PQ=QA，MP＝3,△AMP的面积是6，下列结论：① AM＜PQ+QN，②QP∥AM，③△BMP≌△PQC，④∠QPC＋∠MPB＝90°，⑤△PQN的周长是7，其中正确的有（）个A.1B.2C.3D.4试题13:若＝1，则_________.试题14:_______________. 试题15:分解因式：．试题16:若b为常数，且是完全平方式，那么b＝.试题17:如图所示，把△ABC绕点C顺时针旋转35°，得到△A′B′C,A′B′交AC于点D，若∠A′DC=90°，则∠A= .试题18:已知，则____________．试题19:试题20:试题21:试题22:试题23:解方程：试题24:因式分解：试题25:化简求值：，其中.试题26:如图, 已知：AB⊥BC , DC∥AB , DE⊥AC于点F , AB＝EC．求证：AC＝DE．试题27:已知，求的立方根.试题28:某家装公司的员工在安装玻璃时，不小心将一块三角形玻璃打碎. 要求他只带其中一块碎片到玻璃店去，就能配一块与原来一样的回来. 请根据图形回答问题：（1）碎片如图1，他应该带去，原因是.（2）碎片如图2，他应该带去，原因是.（图1）（图2）试题29:探索题：先填空，再解答，解答需要写出恰当的过程.……①运用以上方法求：的值；②运用以上方法求：的个位数字是多少？试题30:已知：如图，点E在△ABC的边AC上，且∠AEB=∠ABC.(1) 求证：∠ABE=∠C；(2) 若∠BAE的平分线AF交BE于F，FD∥BC交AC于D，设AB=6，AC=10，求DC的长；(3) 若BE平分∠ABC，AF平分∠BAC，且FD∥BC交AC于点D，连接FC，则△DFC是什么三角形？为什么？试题1答案:DC试题3答案: C试题4答案: B试题5答案:B试题6答案: C试题7答案:D试题8答案: A试题9答案:C试题10答案:A试题11答案:C试题12答案: C试题13答案:，，试题15答案:，试题16答案:，试题17答案: 55°，试题18答案:或试题19答案:试题20答案:试题21答案: 9200试题22答案:试题23答案:，试题25答案:化简得：，因为所以，所以原式试题26答案:证明：∵ AB⊥BC，∴∠ABC＝90°，，∵ DC∥AB ,∴∠ABC＋∠ECD＝180°,∴∠ECD＝90°,∴∠ABC＝∠ECD,∠BCA＋∠FCD＝90°,∵ DE⊥AC于点F ,∴∠DFC＝90°,∴∠CDE＋∠FCD＝90°,∴∠BCA＝∠CDE,∵ AB＝EC,∴△ABC≌△ECD（AAS）,∴ AC＝DE.试题27答案:解：化为，又∵，，，∴，，，∴，，，∴，试题28答案:（1）带 B 去，原因是两角及其夹边对应相等的两个三角形全等（ASA）.（2）带 A 去，原因是两边及其夹角对应相等的两个三角形全等（SAS）.试题29答案:探索题：先填空，再解答，解答需要写出恰当的过程.解：……①；②∵，，，，，，，…∴的各位数字按照规律：2，4，8，6；2，4，8，6循环出现，∴的个位数字是7.试题30答案:（1）证明：∵∠AEB=∠ABC，且∠AEB=∠EBC＋∠C，∠ABC=∠EBC＋∠ABE，∴∠EBC＋∠C＝∠EBC＋∠ABE，∴∠ABE＝∠C；（2）解：∵∠BAE的平分线AF交BE于F，∴∠BAF＝∠DAF，∵ FD∥BC交AC于D，∴∠ADF＝∠C，∵∠ABE＝∠C，∴∠ADF＝∠ABE，即∠ADF＝∠ABF，∵ AF＝AF，∴△BAF≌△DAF，∴ AD＝AB＝6,∴ DC＝AC－AD＝10－6＝4.（3）解：△DFC是等腰三角形.理由是：过点F分别作FH⊥AB，FN⊥BC，FM⊥AC，易证：△AFH≌△AFM（AAS），从而知FH＝FM，△BFH≌△BFM（AAS），从而知FH＝FN，∴FM＝FN，又FC＝FC，可证Rt△CFM≌Rt△CFN（HL）∴∠MCF＝∠NCF，∵FD∥BC，∴∠DFC＝∠BCF，∴∠DFC＝∠MCF，∴DF＝DC，∴△DFC是等腰三角形.。

重庆市万州区万州中学八年级数学上学期期中试题新人教版

重庆市万州区万州中学2014-2015学年八年级数学上学期期中试题（满分：150分，时间：120分钟）一、选择题（每小题4分，共48分） 1. 与数轴上的点一一对应的是（）A 、有理数B 、整数C 、无理数D 、实数 2．81的平方根是（）A ．9B ． 9±C ．3±D ．3 3. 下列各题的计算,正确的是（）A. 523)(a a = B. ()63293a a-=-C. ()()54a a a -=-•- D. 6332a a a =+4．如图：若△ABE ≌△ACF ，且AB=5，AE=2，则EC 的长为（） A.2 B.3 C.5 D.2.5 5．在33，1-，4，722，π，－0.2020020002…，3216-中，无理数有（）个 A.2 B.3 C.4 D.5 6．如果q px x x x -+=+-2)3)(2(，那么p 、q 的值是（）A. 6,1-==q pB. 6,5==q pC.6,1==q pD. 6,5-==q p7. 在△ABC 和△A′B′C′中，①AB=A′B′；②B C=B′C′；③AC=A′C′；④∠A=∠A′；⑤∠B=∠B′；⑥∠C=∠C′，则下列哪组条件不能保证△ABC≌△A′B′C′（） A. ①②③ B. ①②⑤ C. ①⑤⑥ D. ①②④ 8．若正数a 的算术平方根比它本身大，则（）A. 0<a<1B. a>0C. a<1D. a>1 9．下列分解因式正确的是（）A ．)1(222--=--y x x x xy x B ．)32(322---=-+-x xy y y xy xy C ．2)()()(y x y x y y x x -=--- D ． 3)1(32--=--x x x x 10．若54,32==yx，则y x 22-的值为（）A.53 B.－2 C. 553 D.5611．在边长为a 的正方形中挖去一个边长为b 的小正方形（a b >）（如图甲），把余下的部分拼成一个矩（第2题）FECBA第4题形（如图乙），根据两个图形中阴影部分的面积相等，可以验证（）A ．222()2a b a ab b +=++B ．222()2a b a ab b -=-+C ．22()()a b a b a b -=+-D ．22(2)()2a b a b a ab b +-=+-12．如图,在不等边△ABC 中，PM ⊥AB 于点M ，PN ⊥AC 于点N ，且PM=PN ，Q 在AC 上，PQ=QA ，MP ＝3,△AMP 的面积是6，下列结论：① AM ＜PQ+QN ，②QP ∥AM ，③△BMP ≌△PQC ，④∠QPC ＋∠MPB ＝90°，⑤△PQN 的周长是7，其中正确的有（）个A.1B.2C.3D.4二、填空题（每小题4分，共24分）13. 若2x ＝1，则=x _____ ____.14. 32)(2mx mx -•_______________.15. 分解因式：=-a ax 42．16. 若b 为常数，且1412+-bx x 是完全平方式，那么b ＝ .17. 如图所示，把△ABC 绕点C 顺时针旋转35°，得到△A ′B ′C,A ′B ′交AC 于点D ，若∠A ′DC=90°，则∠A= .18. 已知2122=+aa ，则=++-1122a a a ____________．三、解答题(每小题4分，共24分) 19. 计算：⑴ 3238)3(27-+- ⑵ ()()222332ca bc b a -÷-•⑶ 23991012322⨯-⨯ ⑷)2)(2(y x x y ---第11题A BCA ′B ′D第17题20.按要求解答： (1) 解方程：02)3(212=-+x (2) 因式分解：)12(422+--b b a四、解答题（每小题8分，共32分）21. 化简求值：22))(()32(y y x y x x --+--，其中0142=--x x .22. 如图, 已知：AB ⊥BC , DC ∥AB , DE ⊥AC 于点F , AB ＝EC ．求证：AC ＝DE ．23. 已知 0441|2|2=+-+++-y y z x ，求4-xyz 的立方根.24．某家装公司的员工在安装玻璃时，不小心将一块三角形玻璃打碎. 要求他只带其中一块碎片到玻璃A B CDE F店去，就能配一块与原来一样的回来. 请根据图形回答问题：（1）碎片如图1，他应该带去，原因是 . （图1）（2）碎片如图2，他应该带去，原因是 . （图2）五、解答题（共22分）25．（10分）探索题：先填空，再解答，解答需要写出恰当的过程.___;__________1)(1(=+-）xx____;__________)1)(1(2=++-xxx____;__________)1)(1(23=+++-xxxx……____;__________)1)(1(21=++⋯+++---xxxxx nnn①运用以上方法求：122222223456++++++的值；②运用以上方法求：1222222201220132014+++⋯+++的个位数字是多少？26.（12分）已知：如图，点E在△ABC的边AC上，且∠AEB=∠ABC.(1)求证：∠ABE=∠C；(2)若∠BAE的平分线AF交BE于F，FD∥BC交AC于D，设AB=6，AC=10，求DC的长；(3)若BE平分∠ABC，AF平分∠BAC，且FD∥BC交AC于点D，连接FC，则△DFC是什么三角形？为什么？AB万州中学初2016级八年级（上）中期考试数学试题（参考答案）一、选择题：（每小题4分，共48分） 1—12： D C C B B C D A C A C C 二、填空题: （每小题4分，共24分）13、1±， 14、542x m - ， 15、)2)(2(-+x x a ， 16、1±， 17、55°， 18、21或23三、解答题：(每小题4分，共24分) 19、（1）2- （2）c ab 36 （3）9200 （4）224y x -20、（1）5,121-=-=x x ，（2）)12(12(+--+b a b a 四、解答题：（每小题8分，共32分）21、化简得：9123))(()32(222+-=--+--x x y y x y x x ，因为0142=--x x 所以142=-x x ，所以原式129139)4(32=+⨯=+-=x x22. 证明：∵ AB ⊥BC ， 23. 解： 0441|2|2=+-+++-y y z x ，∴ ∠ABC ＝90°，化为，0)2(1|2|2=-+++-y z x ，∵ DC ∥AB , 又∵0|2|≥-x ，01≥+z ，0)2(2≥-y ，∴ ∠ABC ＋∠ECD ＝180°, ∴02=-x ，01=+z ，02=-y ， ∴ ∠ECD ＝90°, ∴2=x ，1-=z ，2=y ， ∴ ∠ABC ＝∠ECD, ∴334)1(224--⨯⨯=-xyz ， ∠BCA ＋∠FCD ＝90°, 38-=∵ DE ⊥AC 于点F , 2-= ∴ ∠DFC ＝90°, ∴ ∠CDE ＋∠FCD ＝90°, ∴ ∠BCA ＝∠CDE, ∵ AB ＝EC,∴ △ABC ≌△ECD （AAS ）, ∴ AC ＝DE.24.（1）带 B 去，原因是两角及其夹边对应相等的两个三角形全等（ASA ）. （2）带 A 去，原因是两边及其夹角对应相等的两个三角形全等（SAS ）.五、解答题（共22分）25．（10分）探索题：先填空，再解答，解答需要写出恰当的过程. 解：);1(1)(1(2-=+-x x x ） ;)1()1)(1(32-=++-x x x x;)1()1)(1(423-=+++-x x x x x ……;)1()1)(1(121-=++⋯+++-+--n n n n x x x x x x①12712)1222222)(12(122222272345623456=-=++++++-=++++++；②∵221=，422=，823=，1624=，3225=，6426=，12827=，,25628=…∴是整数）n n n ,,3,2,1(2⋯⋯=的各位数字按照规律：2，4，8，6；2，4，8，6循环出现， ∴1212222220152201220132014-=+++⋯+++的个位数字是7.26. （12分）（1）证明：∵ ∠AEB=∠ABC ，且∠AEB=∠EBC ＋∠C ，∠ABC=∠EBC ＋∠ABE ， ∴ ∠EBC ＋∠C ＝∠EBC ＋∠ABE ， ∴ ∠ABE ＝∠C ；（2）解： ∵ ∠BAE 的平分线AF 交BE 于F ，∴ ∠BAF ＝∠DAF ， ∵ FD ∥BC 交AC 于D ， ∴ ∠ADF ＝∠C ， ∵ ∠ABE ＝∠C ，∴ ∠ADF ＝∠ABE ，即∠ADF ＝∠ABF ，∵ AF ＝AF ，∴ △BAF ≌△DAF ， ∴ AD ＝AB ＝6,∴ DC ＝AC －AD ＝10－6＝4. （3）解： △DFC 是等腰三角形.理由是：过点F 分别作FH ⊥AB ，FN ⊥BC ，FM ⊥AC ，易证：△AFH ≌△AFM （AAS ），从而知FH ＝FM ， △BFH ≌△BFM （AAS ），从而知FH ＝FN ，∴FM ＝FN ，又FC ＝FC ，可证Rt △CFM ≌Rt △CFN （HL ） ∴∠MCF ＝∠NCF ， ∵FD ∥BC ，∴∠DFC ＝∠BCF ， ∴∠DFC ＝∠MCF ， ∴DF ＝DC ，∴△DFC 是等腰三角形.HMN。

重庆市万州区甘宁初级中学八年级数学上学期期中试题(无答案) 新人教版

1重庆市万州区甘宁初级中学2014-2015学年八年级数学上学期期中试题一．选择题：（本大题共12小题，每小题4分，共48分）每个小题都给出了代号为A 、B 、C 、D 的四个答案，其中只有一个是正确的，请将正确答案的代号填入答题卷对应的表格中。

1.在﹣2，0，3，6这四个数中，最大的数是（） A ．﹣2 B ．0 C ．3 D. 62.下列计算正确的是（）A. 853b b b =+B.44443a a a a =⋅⋅C.10641243a a a =⨯ D.752)(b b -=- .3.下列六个数：144，-722，3π，9.0，327，0.32 ， 0..6.1，0.2020020002……（每两个2之间多一个0），其中无理数的个数有（）A ． 5个B ． 4个C ． 3个D ． 2个4. 如图，已知ND MB =，NDC MBA ∠=∠，下列条件中不能判定△ABM ≌△CDN 的是（）A.N M ∠=∠B.CD AB = AM =D.AM ∥CN5. 若236a =，38b =, 则 b a +的值是 ( )A ．8或4-B ．8+或8-C ．8-或4-D ．4+或4-6.实数a b ，在数轴上对应点的位置如图所示，则必有（）A ．0a b +>B ．0a b -<C ．0ab >D ．0ab<7.等腰三角形的周长是18cm ，其中一边长为4cm ，其它两边长分别为（）A ．4cm ，10cmB ．7cm ，7cmC ．4cm ，10cm 或7cm ，7cmD ．无法确定8. 在实数范围内，下列判断正确的是（）A ．若m =n ，则n m =B ．若22b a >, 则b a > C ．若2a =2)(b ，则b a =D ．若3a =3b ，则b a =0 a 1 1-0b 第6题图A BDCMN第4题图210.等腰三角形一腰上的高与另一腰的夹角为30︒，则顶角的度数为 ( ) A ．60︒ B ．120︒ C ．60︒或150︒ D ．60︒或120︒11．如图，H 是△ABC 的高AD ，BE 的交点，且DH ＝DC 三角形；② BC ＝AC ；③ BH ＝AC ；④ CE ＝CD 。

重庆市万州区甘宁初级中学八年级数学上册 15.3 中心对称练习3 华东师大版

15.3 中心对称【知能点分类训练】知能点1 中心对称图形1．线段是中心对称图形，它的对称中心是_______；线段又是轴对称图形，它的对称轴是________．2．如图，下列图形是中心对称图形的是（）．3．如图，是几个国际通用的交通标志，其中不是中心对称图形的是（）．4．下列图形中既是中心对称图形，又是轴对称图形的是（）．5．下图中，既是轴对称图形又是中心对称图形的有（）．A．4个 B．3个 C．2个 D．1个6．26个大写英文字母中，既是轴对称图形，又是中心对称图形的有（）．A．1个 B．2个 C．3个 D．4个知能点2 中心对称及性质7．将△ABC绕其边BC的中点O旋转180°，得到△BCD，则△ABC和△BCD的位置关系是________．8．如图，△ABC和△A′B′C′关于点O成中心对称，那么线段AA′，BB′，CC•′都经过点_______，且_____=_______，______=______，______=________．9．如图，画出半圆O以直径上一点M为对称中心的中心对称图形．10．如图，已知四边形ABCD和点O，画四边形A′B′C′D′，使四边形A′B′C•′D′和四边形ABCD关于O点成中心对称．11．如图，△ABC与△BDE是成中心对称的两个三角形，试探索：（1）对称中心是哪一点？（2）点B，D，E的对应点分别是哪些点？（3）线段AC，AB，BC的对应线段是什么？AC与DE的关系是怎样的？【综合应用提高】12．写出两个你知道的中心对称图形：_______，_________．13．中心对称图形是旋转角为_______的特殊的旋转对称图形．14．关于中心对称的两个图形对应线段的关系是（）．A．相等 B．平行 C．平行且相等 D．平行（或线段）且相等15．香港于1997年7月1日成为中华人民共和国的一个特别行政区，它的区徽图案（紫荆花）如图，这个图形（）．A．是轴对称图形B．是中心对称图形C．既是轴对称图形又是中心对称图形;D．既不是轴对称图形，又不是中心对称图形16．下列说法：①图形的平移和旋转不会改变图形的形状和大小；②图形的平移和旋转一定会改变图形的位置；③旋转对称图形一定是中心对称图形；④中心对称图形一定是旋转对称图形；⑤轴对称图形一定是中心对称图形；⑥中心对称图形一定是轴对称图形；⑦一个旋转对称图形围绕旋转中心旋转180•°后形成的图形与原来的图形整体构成一个中心对称图形．其中正确的有（）．A．3个 B．4个 C．5个 D．617．找出下列各图的对称中心．18．分别从五个图形中选出一个独特的图形．（1）选（），原因：______________．（2）选（），原因：______________．19．按要求画图形：所画图形中同时要有正方形和圆（正方形和圆的个数不限），并且这个图形既是轴对称图形，又是中心对称图形，请按要求设计出两个图形，并给命上名字．【开放探索创新】20．有一块长方形土地ABCD，其中有一口井（如图）．现将此土地分给甲、•乙两户承包种植蔬菜，若使两家公平合理，你想怎么帮他们分呢？简要说明你的分法（假设土地都一样好）．【中考真题实战】21．（鸡西）在下列四个图案中，既是轴对称图形，又是中心对称图形的是（）．22．（江西）下列图案都是由字母“m”经过变形、组合而成的，其中不是中心对称图形的是（）．答案:1．中点线段垂直平分线2．B 提示：其余是旋转对称图形3．D 提示：D是轴对称图形．4．A5．B 提示：除第1个外，其余都是．6．D 提示：H，I，O，X．7．关于O点中心对称．8．O AO=A′O BO=B′O CO=C′O9．10．11．（1）B （2）B→B，D→C，E→A．（3）AC→ED，AB→EB，BC→BD；AC=DE且AC∥DE．12．答案不唯一，略．13．180° 14．D 15．D16．A 提示：①④⑦正确．17．提示：找对应点连线，交点即是．18．（1）D 旋转后不与其他图形重合;（2）D 不是旋转对称图形19．符合要求即可．20．图中实线L即为所求．根据中心对称图形的性质：过对称中心的任意一条直线能将其面积两等分．因此，由两个中心对称图形组合而成的复合图形，经过两个对称中心画一条直线，必将整个面积两等分．21．C 22．B.。

万州八年级上册数学测试卷

一、选择题（每题3分，共30分）1. 下列各数中，绝对值最小的是（）A. -3B. 0C. 3D. -52. 若a > b，则下列不等式中正确的是（）A. a + 1 > b + 1B. a - 1 > b - 1C. a + 1 < b + 1D. a - 1 < b - 13. 在△ABC中，∠A = 60°，∠B = 45°，则∠C的度数是（）A. 75°B. 120°C. 135°D. 150°4. 下列哪个图形是轴对称图形？（）A. 矩形B. 正方形C. 三角形D. 圆5. 若方程2x - 3 = 0的解为x，则方程3x + 6 = 0的解为（）A. xB. 2xC. 3xD. -2x6. 下列哪个数是有理数？（）A. √2B. πC. 0.1010010001...D. 1/37. 在平面直角坐标系中，点P（-2，3）关于y轴的对称点是（）A. （2，3）B. （-2，-3）C. （-2，6）D. （2，-3）8. 若a、b、c是三角形的三边，且a + b = c，则这个三角形是（）A. 直角三角形B. 等腰三角形C. 等边三角形D. 梯形9. 下列哪个函数是单调递增函数？（）A. y = x^2B. y = 2x + 1C. y = -xD. y = x^310. 若|a| = 5，|b| = 3，则|a + b|的最大值是（）A. 8B. 10C. 12D. 15二、填空题（每题3分，共30分）11. 若x - 2 = 5，则x = _______。

12. 在△ABC中，∠A = 45°，∠B = 90°，则∠C的度数是 _______。

13. 若方程3x - 4 = 0的解为x，则方程6x - 8 = 0的解为 _______。

14. 下列哪个数是无理数？（）A. √2B. πC. 0.1010010001...D. 1/315. 在平面直角坐标系中，点P（3，-2）关于x轴的对称点是 _______。