11.进制与编码
进制及编码练习

进制1、有一种利用打孔透光原理设计的简易身份识别卡:每张卡在规定位置上有一排顶打孔位,读卡器根据透光检测判断哪些孔位已打孔,哪些未打孔,从而识别出卡的编码。
如果要设计一种供1000人使用的身份卡,则卡上的预打孔位至少需要()A、5个B、7个C、9个D、10个2、某一数字显示器由7段发光二极管组成,通过各二极管的亮灭来显示数字。
若用“1”表示亮,“0”表示灭,按第2题图1所示的字母先后顺序对各二极管的亮灭状态编码,按此编码方法,第2题图2中数字“9”所对应的编码是第2题--1图第2题--2图A.1111011 B.1110011 C.1111100 D.11111103.算式1011B + 10D的运算结果是()(A)11101B (B)51H (C)15H (D)20D4.算式1010B*4D的值是()(A)100100B (B) 44D (C) 101001B (D) 28H5.当你升入高中后,学校会给每个学生一个固定的学号,比如:09071233,你觉得学号的的确定应该属于()(A)信息的采样(B)信息的编码(C)信息的处理(D)信息的加工内码6.小明用UltraEdit软件观察“SMTP协议”,显示的十六进制内码如第6题图所示,从中可以推断出字符“S”存储在计算机内部的编码是………………………………………()第6题图A.53H B.1010011B C.01010011B D.83D7.字符“A”比“a”的ASCII码值小32(十进制),已知字符“G”的二进制ASCII码值为1000111,则字符“g”的二进制ASCII码值是( )A.1001111 B.101011 C.1011111 D.11001118、用UltraEdit软件观察“Book”这几个字符的内码,如图所示,则“Look ”这几个字符的编码是A.42 6F 6F 6BB.4B 6F 6F 6BC.4C 6F 6F 6BD.4A 6F 6F 6B9.小孙用UltraEdit 软件观察“211人才网”这几个字,显示的十六进制内码如下图所示。
计算机中的数值和编码

计算机中的数制和编码一、数制的概念:数制是用一组固定的数字和一套统一的规则来表示数目的科学方法。
按照进位方式计算的数制叫做进位数制。
例如:逢十进一即为十进制,逢二进一为二进制,逢八进一为八进制,逢十六进一为十六进制。
进位计数制有两个要素:基数和权值。
1、基数:它是指各种进位计数制中允许选用基本数码的个数。
例如:十进制的数码有0、1、2、3、4、5、6、7、8、9十个数码,所以十进制的基数为10;二进制的数码有0、1两个数码,所以二进制的基数为2;八进制的数码有0、1、2、3、4、5、6、7八个数码,所以八进制的基数为8;十六进制的数码有0、1、2、3、4、5、6、7、8、9、A、B、C、D、E、F十六个数码,所以十六进制的基数为16。
2、权值:每个数码所表示的数值等于该数码乘以一个与数码所在位置相关的常数,这个常数叫权值。
其大小是以基数为底,数码所在位置的序号为指数的整数次幂。
例如:十进制数356.4=3×100+5×10+6×1+0.4=3×102+5×101+6×100+4×10-1(3在百位上,所以3×100=3×102;5是在十位上,所以5×10=5×101;6是在个位上,所以6×1=6×100;0.4为小数,所以0.4=4×10-1)。
二、十进制(D ecimal notation)及其特点:1、两个特点:①、十个数码:0、1、2、3、4、5、6、7、8、9;②、进位方法:逢十进一,借一当十。
(满了10个就得进一位)2、基数:103、按权展开式:任意一个a位整数和b位小数的十进制数D可以表示为:D=D a-1×10a-1+D a-2×10a-2+…+D0×100+D-1×10-1+D-2×10-2+…+D-b×10-b4、十进制在书写中的三种表达方式:128或者128D或(128)10三、二进制(B inary notation)及其特点:1、两个特点:①、两个数码:0、1;②、进位方法:逢二进一,借一当二。
1进制的转换与信息的编码知识点

1进制的转换与信息的编码知识点一、信息及其特征信息的载体和形态1.信息本身不是实体,必须通过载体才能体现,但不随载体的物理形式而变化。
2.语言、文字、声音、图像和视频等是信息的载体,也是信息的常见表现形态。
3.纸张可以承载文字和图像,磁带可以承载声音,电视可以承载语言、文字、声音、图像和视频,所以也把纸张、磁带、广播、电视、光盘、磁盘等称为信息的载体。
4.相同的信息,可以用多种不同的载体来表示和传播。
5.不存在没有载体的信息。
信息的五个特征1.载体依附性:信息的表示、传播、储存必须依附于某种载体,载体就是承载信息的事物。
2.可加工处理性:信息是可以加工和处理的。
信息也可以从一种形态转换成另一种形态。
3.传递性:信息可以脱离它所反映的事物被存储和保留和传播。
4.共享性:信息是可以传递和共享的。
信息可以被重复使用而不会像物质和能源那样产生损耗。
5.时效性二、信息的编码计算机只能识别和处理由“0”、“1”两个符号组成的数字代码。
或称计算机只能识别机器语言。
1.进位制的转换二进制:0、1进位规则:逢2进1二进制标识:B十进制:0、1、2、3、4、5、6、7、8、9进位规则:逢10进1十进制标识:D十六进制:0、1、2、3、4、5、6、7、8、9、A、B、C、D、E、F“逢十六进一”。
不同的是用A、B、C、D、E和F分别表示10、11、12、13、14和15六个数字符号。
十六进制标识:H传递、表达信息的规则:使用1个二进制位(比特)可以表示2种信息0使用2个二进制位(比特)可以表示4种信息00011011使用3个二进制位(比特)可以表示8种信息000100第1页001101010110011111用n个二进制位最多可以表示2种不同的信息例题:下列关于信息编码的说法,正确的是()。
A.4位二进制编码可以表示15种状态B.5位二进制编码可以表示31种状态C.6位二进制编码可以表示63种状态D.7位二进制编码可以表示128种状态解:因为4位二进制编码可以表示2=16种状态5位二进制编码可以表示2=32种状态6位二进制编码可以表示26=64种状态7位二进制编码可以表示2=128种状态所以,选D。
信息论与编码第三版 第3章

(2)增强通信的可靠性: 综上所述,提高抗干扰能力往往是以降低信息传输效率为代价
信息论与编码
信源编码的概念:对信源的原始符号按一定的数学规则进行变换的一种
代码。
信源编码包括两个功能:
(1)将信源符号变换成适合信道传输的符号; {b1, b2,…, bD}是适合 编码输出码字cm = cm1 cm2 … {a1, a2, …, (2)压缩信源冗余度,提高传输效率。 ak}为信 信道传输的D个符号, cmn, c mk∈{b1, b2,…, bD}, 源符号集,序列中 用作信源编码器的 k = 1, 2 , …, n ,n表示码字 每一个符号uml都取 信源编码模型: 编码符号。 长度,简称码长。 自信源符号集。
1 1 1 n 2 2 2 3 4 4 2.75 (码元/符号) 4 8 16
RD
H X n
2.75 1 (比特/码元时间) 2.75
信息论与编码
§3.2 等长码及等长编码定理
一.等长编码定理
考虑对一简单信源S进行等长编码,信源符号集有K个符号,码符号集 含D个符号,码字长度记为n。对信源作等长无差错编码,要得到惟一可译 码,必须满足下式:
扩展信源
信源编码器
信道符号(码符号)集{b1,b2,...bD}
信源符号集{a1,a2,...ak}
原码的N次扩展码是将信源作N次扩展得到的新信源符号序列u(N) =u1 …uN = (u11 u12 … u1L) … (uN1 uN2 … uNL),对应码符号序列c(N) =c1 …cN = (c11 c12 … c1n) … (cN1 cN2 … cNn) ,记集合C (N) = {c1(N), c2(N), …},C (N) 即原码C的N次扩展码。
数据编码的基本方式

28
机内码
文档仅供参考,如有不当之处,请联系改正。
GB2312-80统一要求了中文旳基本编码原则,但是 要存储在计算机中与西文编码在计算机中旳表达
)8= ( )16=
文档仅供参考,如有不当之处,请联系改正。
编码
计算机是美国人发明旳,所以计算机旳字 符集中自然包括了英文旳26个字母。
计算机要在全世界通用,必须采用公认旳 原则格式对字符、符号进行编码。
常用旳字符编码有ASCII码、BCD码、西文 字符编码和EBCDIC码。
21
文档仅供参考,如有不当之处,请联系改正。
文档仅供参考,如有不当之处,请联系改正。
二进制数转换为十六进制数
整数部分从低位向高位方向每4位用一种等值旳十六 进制数来替代,即四位并为一位,最终不足4位时在 高位处补0,补够4位;小数部分从高位向低位方向 每4位用一种等值旳十六进制数来替,最终不足4位 时在低位处补0,补够4位。 (1110 0101 1010 . 1011 1001)2 =(E5A.B9)16
78~7E
位 区 1~15
16~55
56~87
88~94
21 22 23 24 25 26 …………7C 7D 7E
7F
1 2 3 4 5 6 ………………91 92 93 94
非中文图形符号(常用符号、数字序号、俄文、 英文、法文、希腊字母、日文平、片假名等)
啊阿埃
一级中文
(3755个)
二级中文(3008个)
23
文档仅供参考,如有不当之处,请联系改正。
西文字符处理起来比较简朴,而中文信息 处理起来就复杂了。中文是图形文字,常 用中文就有3000~6000个,形状和笔画差 别很大。这就决定了中文字符旳编码方案 必须完全不同于西文旳编码方案。
信息论与编码试卷及答案

一、(11’)填空题(1)1948年,美国数学家香农发表了题为“通信的数学理论”的长篇论文,从而创立了信息论。
(2)必然事件的自信息是0 。
(3)离散平稳无记忆信源X的N次扩展信源的熵等于离散信源X的熵的N倍。
(4)对于离散无记忆信源,当信源熵有最大值时,满足条件为__信源符号等概分布_。
(5)若一离散无记忆信源的信源熵H(X)等于2.5,对信源进行等长的无失真二进制编码,则编码长度至少为3 。
(6)对于香农编码、费诺编码和霍夫曼编码,编码方法惟一的是香农编码。
(7)已知某线性分组码的最小汉明距离为3,那么这组码最多能检测出_2_______个码元错误,最多能纠正___1__个码元错误。
(8)设有一离散无记忆平稳信道,其信道容量为C,只要待传送的信息传输率R__小于___C(大于、小于或者等于),则存在一种编码,当输入序列长度n足够大,使译码错误概率任意小。
(9)平均错误概率不仅与信道本身的统计特性有关,还与___译码规则____________和___编码方法___有关二、(9?)判断题(1)信息就是一种消息。
(?)(2)信息论研究的主要问题是在通信系统设计中如何实现信息传输、存储和处理的有效性和可靠性。
(?)(3)概率大的事件自信息量大。
(?)(4)互信息量可正、可负亦可为零。
(?)(5)信源剩余度用来衡量信源的相关性程度,信源剩余度大说明信源符号间的依赖关系较小。
(?)(6)对于固定的信源分布,平均互信息量是信道传递概率的下凸函数。
(?)(7)非奇异码一定是唯一可译码,唯一可译码不一定是非奇异码。
(?)(8)信源变长编码的核心问题是寻找紧致码(或最佳码),霍夫曼编码方法构造的是最佳码。
(?)(9)信息率失真函数R(D)是关于平均失真度D 的上凸函数. ( ? )三、(5?)居住在某地区的女孩中有25%是大学生,在女大学生中有75%是身高1.6米以上的,而女孩中身高1.6米以上的占总数的一半。
计算机中的数制和码制

1-2-n≥N≥-(1-2-n)
符号位
数值位
↑小数点
31
定点数和浮点数
方法二:规定小数点固定在最低数值位之后,机器中所能表示的 数都是整数。n位数值部分所能表示的数N的范围是 2n-1≥N≥-(2n-1)
符号位 数 值 位
↑小数点 由于实际问题中很少有纯粹的整数或者小数,所以定点 法要求程序员为了调整所要表示的数值范围,而选择比例因 子。所有原始数据都要用比例因子化成小数或整数,计算结 果又要用比例因子恢复。对于复杂的计算,计算中间需要多 次调整比例因子。
32
定点数和浮点数
浮点法
任意一个二进制数N总可以写成下面的形式: N=±d·2±p
其中:d称为尾数,是二进制纯小数,指明数据的全部有效数字。 前面的符号称作数符,表示数的符号。P称为阶数,它前面的符 号称为阶符,由此可知,将尾数d的小数点向右(对+p)或向左(对 -p)移动p位,即得数值N。所以阶符和阶码指定小数点的位置, 小数点随着p的符号和大小而浮动,所以这种数称为浮点数。
21
原码表示法(2)
原码表示简单易懂,易于形成。但是,两个异号数相 加或两个同号数相减,就要做减法操作
22
反码表示法(1)
正数的反码表示与原码相同,最高位为符号位,用 “0”表示正,其余位为数值位
例如:
[+4]反=0000 0100
负数的反码,表示为该数对应的正数按位取反(包括
符号位)
例如:
对于8位二进制补码: 0的表示是唯一的:
[+0]补=[-0]补=0000 0000 所能表示的数值范围:-128~ +127
[+127]补 =0111 1111 [-128]补 =1000 0000
数据编码——进制及其转换 课件 2022—2023学年粤教版(2019)高中信息技术必修1

进
制
转
二
进
制
10 1
( 75 )8=( 111101)2
4、二进制与十六进制之间的转换:
必修 1 数据与计算
• 二进制转十六进制:与二进制转八进制方法近似,八进制是取三 合一,十六进制是取四合一。
• 十六进制转二进制:十六进制数通过除2取余法,得到二进制数, 对每个十六进制为4个二进制,不足时在最左边补零。
练习
5.现有二进制数10010。下列选项中,与此二进制大小相等的是 C
A.18H B.90H C.18D D.36D
第一章 数据与信息
练习
6.十进制数17转换成二进制数是(D )
必修 11 数据与计算
A.10010
B.10110
C.11001
D.10001
第一章 数据与信息
必修 11 数据与计算
2、二进制
必修 1 数据与计算
二进制计算法的特点: ① 二进制数只有“0”和“1”两个数码,基数是2,最大的数字是1; ② 采用逢二进一的原则。 ③ 二进制的位权一般表示为:2n-1.各位的权为以2为底的幂。例如,
(01101010)各位的权自至在依次为27、26、25、24、23、22、21、20。
练习
7.十进制数1000对应二进制数为__②____,对应十六进制数为__③____。
A:①1111101010 ②1111101000 ③1111101100 ④1111101110 B:①3C8 ②3D8 ③3E8 ④3F8
第一章 数据与信息
练习
8.二进制的1000001相当十进制的__④____。
第一章 数据与信息
练习
3.与二进制数(101010)等值的十进制数是:( C )
1数制与编码

二进制数的特点:
• 只有两个数码, 很容易用物理器件来实现。
• 运算规则简单。
• 可使用逻辑代数这一数学工具。
• 节省设备
例:如需表示数字0~999,共有1000个信息量。
十进制:用3位,每位10个数字,共需30个数字设备。
二进制:用10位,每位2个数字,共需20个数字设备。
⒈真值:在数值前加“+”号表示正数; 在数值前加“-”号表示负数。 ⒉机器数:把符号数值化的表示方法称~。 用“0”表示正数,用“1”表示负数。 例: 真值 机器数 +9 +1001 01001 -9 -1001 11001
符号位
常用的机器数有:原码、反码、补码 其符号位规则相同,数值部分的表示形式有差异。
几种常用数制的 表示方法(P5)
R=10 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
二进制 0 1 10 11 100 101 110 111 1000 1001 1010 1011 1100 1101 1110 1111 10000
八进制 0 1 2 3 4 5 6 7 10 11 12 13 14 15 16 17 20
X ⑷数值范围 [X]反= n 1 (2 1) X ;0 X 2n ;-2n X 0
00000 [0]反= 11111
⒉ 特点(续)
⑸两数和的反码等于两数反码之和; ⑹符号位参与运算,有进位时循环相加。
循环相 加
例:已知 X1=1100 X2=1010 求 Y1= X1- X2 ; Y2= X2- X1
⑴等精度转换
设α进制有 i位小数,转换后β进制有 j位小数。 (0.0…01)α= (1×α-i)10 i位 (0.01)2= (1×2-2)10 (0.0…01)β = (1×β-j)10 j位 (0.1)4= (1×4-1)10
信息编码(ASSCII码表)

非文本文件又有文档文件(如汉字文件)、可执行程序 (如在DOS系统中扩展名为EXE、COM的可执行文件)等, 不能以一般的方式在屏幕上显示其内容,因为文件中的不 可显示字符被视为控制代码,可能会使屏幕显示出错(出 现乱码),有时会扰乱系统的显示功能。如果是文档文件, 应该用相应的字处理软件进行显示或处理。一般来说,一 个字处理软件生成的文档,只能在该字处理软体中才能正 确地显示,除非字处理软件具有识别或转换其它字处理软 件生成的文档的能力,如 Word97/2000/2003/XP/2007/2010就能显示和处理其它常 用字处理软件生成的文档。
对照ASSCII字符编码表,可知阿拉伯数字0的二进制编码 为011 0000 ,转化为十六进制数为30H,故数字0的十六进制 编码为30H(在往年的考试中,均以十六进制数的形式表示), 以此类推:编码为011 0001(31H),2的编码为011 0010(32H), 3的编码为011 0011(33H),4的编码为011 0100(34H), 5的编码为011 0101(35H), 6的编码为011 0110(36H), 7的编码为011 0111(37H), 8的编码为011 1000(38H), 9的编码为011 1001(39H)
• 9 13 16 20 27 25 10
计算机的存储
• 位bit:存储信息的最小单位 binary digit • 字节Byte(简称B):存储信息的基本单位 • 1Byte=8bit • 1KB=210B=1024B • 1MB=210KB=1024KB • 1GB=210MB=1024MB • 1TB=210GB=1024GB
1.1.7.2字形编码
计算机显示的字符是从ASCII码转化为字符点阵 来实现的。常用的字符输出有两种手段:屏幕显示 和打印输出。例如,如果要输出字符H,则不应输 出其编码72或对应的二进制数、十六进制数,而 应输出字形H。这种用于输出的、表示字符字形的 数据,称为字形编码。屏幕显示时,字形编码为1 的点则亮,为0的点则不亮;打印机输出时,计算 机控制打印机的打印针,有的打下去,有的不打, 便打出所需的符号和文字。
信息论与编码技术第五章课后习题答案

码,并求出其编码效率。
解:
信源符号 概率 编码
码字 码长
X1
3/8 0
0
1
X2
1/6 1
0
10 2
X3
1/8
1
11 2
X4
1/8 2
0
20 2
X5
1/8
1
21 2
X6
1/12
2
22 2
H(X)=-((3/8)*log(3/8)+(1/6)*log(1/6)+(1/8)*log(1/8)+(1/8)*log(1/8)+(1/8)*log(1/8)+(1/12)*log(1/12))
=2.3852 (三进制单位/信源符号)
H3(X)= H(X)/ 1.5850=2.3852/1.5850= 1.5049(三进制单位/信源符号)
L =(3/8)*1+ (1/6)*2+ (1/8)*2+ (1/8)*2+ (1/8)*2+ (1/12)*2=1.625(码符号/信源符号)
η= H3(X)/ L =1.5049/1.625= 92.61 %
5.8 已知符号集合 {x1, x2 , x3,"} 为无限离散消息集合,它们出现的概率分别为 p(x1) = 1/ 2 , p(x2 ) = 1/ 4 , p(x3 ) = 1/ 8 , p(xi ) = 1/ 2i ,……。
(1) 用香农编码方法写出各个符号消息的码字。 (2) 计算码字的平均信息传输速率。
L =4*(1/4)*1=1(码符号/信源符号)
Rt= H(X)/(t* L )=1/(1*10*10-2)=10(比特/秒)
微型计算机中数的编码与字符的表示

3.汉字的编码
计算机要处理汉字信息,就必须首先解决汉字的 表示问题。同英文字符一样,汉字的表示也只能采 用二进制编码形式,目前使用比较普遍的是我国制 定的汉字编码标准GB2312-80,该标准共包含一、 二级汉字6763个,其他符号682个,每个符号都是 用14位(两个7位)二进制数进行编码,通常叫做国 标码。
所以在二\ 十六之间互相转换时,原则为: 二 到 十六, 以小数点为分界线,向左每4位一个组合转
换成一位十六进制数,不够的左边补0,而右边每4位 一个组合转换成16进制,不够的右边补0。 11011•101 0001 1011 1010
1 B ·A
1 数的表示与转换方法
十六 到 二 将每个十六进制位转为4位二进制数即可。
* 十六进制数 可认为是对二进制数的简化表现形式,它与二进制数有 明显的对应关系。 包含0、1…9、A、B、C、D、E、F 16个符号,逢十六 进一
1 数的表示与转换方法
(2) 不同进位位数值的转换 二\ 十六制 由于一个十六进制位正好由4位二进制数字构成: 0000 0001 0010…1001 1010 1011… 1110 1111 0 12 9AB E F 0 1 2 9 10 11 14 15
2.字符的编码
在计算机中除了数值之外,还有一类非常重要 的数据,那就是字符,如英文的大小写字母(A,B, C,…,a,b,c,…),数字符号(0,1,2,…, 9)以及其他常用符号(如:?、=、%、+等)。 在计算机中,这些符号都是用二进制编码的形式表 示。
目前,一般都是采用美国标准信息交换码,它使 用七位二进制编码来表示一个符号,通常把它称为 ASCII码。由于用七位码来表示一个符号,故该编码 方案中共有128个符号(27=128)。
编码基础(自学)

0.3203
十进制小数并不是都能够用有限位的其他进制数精确 地表示,这时应根据精度要求转换到一定的位数为止 ,作为其近似值; ∵23.32≈10
∴每3.32个二进制有效位对应1个十进制有效位 如果一个十进制数既有整数部分,又有小数部分,则
应将整数部分和小数部分分别进行转换; 二进制最低有效位之后的数据处理:0舍1入或舍去法
1010 0001 . 1001 1100 B ∴ A1.9CH = 1010 0001 . 1001 1100 B
计算机中的二进制
1、电子数字计算机内部均采用二进制数据; * 物理上容易实现二值化信息表示; * 运算规则简单,4条加法、 4条乘法; * 可以用逻辑代数、逻辑电路设计实现。
2、一切信息都需要转化为二进制(0与1)的 形式方可提交给计算机存储及处理;
3、在计算机内部表达同一类信息往往用固定 的长度(位数)——定长;
4、n位二进制数的码域为 n个“0”至n个“1”, 共有2 n个码,无符号值域为 0至(2 n-1 )
位权值:2n-1 ·······
5、常用的2的 n次方值
2 4 = 16 2 8 = 256 2 10 = 1024 = 1K 2 11 = 2048 = 2K 2 12 = 4096 = 4K
常用逻辑部件—编码器和译码器
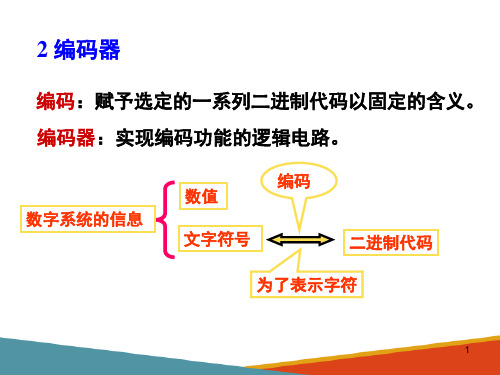
编码:赋予选定的一系列二进制代码以固定的含义。 编码器:实现编码功能的逻辑电路。
数字系统的信息
数值
编码
文字符号
二进制代码
为了表示字符
1
1. 二进制编码器 将一系列信号状态编制成二进制代码。
n个二进制代码(n位二进制数)有2n种不同的 组合,可以表示2n个信号。
输入: 输出:
N个信号 n位二进制代码
Y2 Y1 Y0 YEX Y0
0
0 1 11 111 1
11 1 01
0
0 11 111 1
11 0 01
0
01 111 1
10 1 01
0
0 111 1
10 0 01
0
0 1 1 1
01 1 01
0
0 1 1
01 0 01
0
0 1
00 1 01
0
0
00 0 01
Y8 Y9 Y10 Y11 Y12 Y13 Y14 Y15
20
译码输出
2. 显示译码器
在数字系统中,常常需要将运算结果用人们习 惯的十进制显示出来,这就要用到显示译码器。
二-十进 制编码
显示译 码器
显示器件
显示器件: 常用的是七段显示器件 a
f gb
e
c
21
d
接法:
共阴极:
“1”亮,“0”不亮
ab c d e f g
十-四线编码器
10
编码表
输入
Y3
Y2
Y1
Y0
I0
0
0
0
0
I1
0
0
0
1
I2
0
数字技术1.1数值和编码

例如,一个三位八进制数625,可以表示成
(625)O=6×82+2×81+5×80 4.十六进制数
十六进制数是以16为基数的计数体制,它用0,1, 2,…,9,A,B,C,D,E,F这16个数码表示,采用 “逢十六进一”的计数规律。四位二进制码可用一位 十六进制码表示。任意一个十六进制数(N)H可以写成 按权展开式
=
Ki 10i
(8—1)
i0
式中,Ki代表第i位的系数,可取0~9这10个数码中的任
一个;10i为第i位的权;n为原数的位数。本书只讲整数
的数制。关于小数数制,请阅读其它资料。
2. 二进制数
二进制数是以2为基数的计数体制。它只有0和1两 个数码,采用“逢二进一”的计数规律。任意一个二
进(制N)数B=(KNnin)-0B11都×K可2i n以-12+i写K成n-2按×权2 n展-2+开…+式K1×21+K0×20
(N)H=K n-1×16 n-1+K n-2×16 n-2+…+K1×161+K0×160
=
n1
Ki 16i
i0
例如,一个多位十六进制数4A8C,可以表示成 (4A8C)H=4×163+10×162+8×161+12×160 表8.1为几种计数体制对照表。
1.1.2 数制转换 1.二进制、八进制、十六进制数转换为十进制数 将一个二进制、八进制或十六进制数转换成十进 制数,只要写出该进制数的按权展开式,然后按十进 制数的计数规律相加,就可得到所求的十进制数。
(785)D=7×102+8×101+5×100
括号加下标“D”表示十进制数。等式右边中的102,
单片机数与编码

§计算机中数的表示方法与编码一、进位计数制在计算机系统中,采用的是二进制计数,而在日常生活中,我们熟知的是十进制计数,我们首先介绍进位计数的有关概念。
⒈十进制计数大约公元400年,印度人发明了十进制计数,这可能与我们的手指有关。
公元800年,阿拉伯人开始使用十进制计数,后来又传入欧洲,十进制计数有以下特点:①.有十个相互独立的数字:0,1,2,3,4,5,6,7,8,9;②.逢十进一;③.权为10n任一十进制数:N=αn-1αn-2┅α1α0.α-1α-2┅α-mN=αn-1·10n-1+αn-2·10n-2+ ┅ +α1·101+α0·100+α-1·10-1+α-2·10-2+ ┅ +α-m·10-m⒉二进制计数(用B表示)计算机中普遍采用二机制计数,其特点为:①.有两个独立的数字:0 和 1 ;②.逢二进一;③.权为2n;任一二进制数: N=αn-1αn-2 …α1α0.α-1α-2 …α-mN=αn-1·2n-1+αn-2·2n-2+ … +α1·21+α0·20+α-1·2-1+α-2·2-2+ … +α-m·2-m如:.1=1·27+1·26+1·25+1·24+1·23+1·22+1·21+1·20+1·2-1=128+64+32+16+8+4+2+1+=⒊十六进制计数(用H表示)特点: 十六个独立的数字:0 1 2 3 4 5 6 7 8 9 A B C D E F;逢十六进一;权为十六;任一十六进制数: N=αn-1αn-2 …α1α0.α-1α-2 …α-mN=αn-1·16n-1+αn-2·16n-2+ … +α1·161+α0·160+α-1·16-1+α-2·16-2+ … +α-m·16-m 如:3E8H=3·162+14·16 + 8 = 1000十六进制数本质上可以说与二进制数相同,将二进制数按四位划分,有:二进制数十六进制数十进制数0000 0 00001 1 10010 2 20011 3 30100 4 40101 5 50110 6 60111 7 71000 8 81001 9 91010 A 101011 B 111100 C 121101 D 131110 E 141111 F 15因此,同一个数有多种表示方法,一定要注明采用什么数制,否则,容易引起误解,如:11十进制数为:11二进制数为:3 表示为:11B十六进制为:3二、数制之间的转换主要是二进制和十进制之间的转换,因为十六进制可以很方便地转化成二进制。
信息论与编码填空题新

1. 在无失真的信源中,信源输出由 HX 来度量;在有失真的信源中,信源输出由 RD 来度量; 2. 要使通信系统做到传输信息有效、可靠和保密,必须首先 信源 编码,然后_加密_编码,再_信道编码,最后送入信道;3. 带限AWGN 波形信道在平均功率受限条件下信道容量的基本公式,也就是有名的香农公式是log(1)C W SNR =+;当归一化信道容量C/W 趋近于零时,也即信道完全丧失了通信能力,此时E b /N 0为 dB,我们将它称作香农限,是一切编码方式所能达到的理论极限;4. 保密系统的密钥量越小,密钥熵HK 就越 小 ,其密文中含有的关于明文的信息量IM ;C 就越 大 ;5. 已知n =7的循环码42()1g x x x x =+++,则信息位长度k 为 3 ,校验多项式hx = 31x x ++ ;6. 设输入符号表为X ={0,1},输出符号表为Y ={0,1};输入信号的概率分布为p =1/2,1/2,失真函数为d 0,0 = d 1,1 = 0,d 0,1 =2,d 1,0 = 1,则D min = 0 ,RD min = 1bit/symbol ,相应的编码器转移概率矩阵py/x =1001⎡⎤⎢⎥⎣⎦;D max = ,RD max = 0 ,相应的编码器转移概率矩阵py/x =1010⎡⎤⎢⎥⎣⎦; 7. 已知用户A 的RSA 公开密钥e,n =3,55,5,11p q ==,则()φn = 40 ,他的秘密密钥d,n =27,55 ;若用户B 向用户A 发送m =2的加密消息,则该加密后的消息为 8 ;1.设X的取值受限于有限区间a,b,则X 服从 均匀 分布时,其熵达到最大;如X 的均值为μ,方差受限为2σ,则X 服从 高斯 分布时,其熵达到最大;2.信息论不等式:对于任意实数0>z ,有1ln -≤z z ,当且仅当1=z 时等式成立;3.设信源为X={0,1},P0=1/8,则信源的熵为 )8/7(log 8/78log 8/122+比特/符号,如信源发出由m 个“0”和100-m 个“1”构成的序列,序列的自信息量为)8/7(log )100(8log 22m m -+比特/符号;4.离散对称信道输入等概率时,输出为 等概 分布;5.根据码字所含的码元的个数,编码可分为 定长 编码和 变长 编码; 6.设DMS 为⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡03.007.010.018.025.037.0.654321u u u u u u P U U ,用二元符号表}1,0{21===x x X 对其进行定长编码,若所编的码为{000,001,010,011,100,101},则编码器输出码元的一维概率=)(1x P , =)(2x P ;1. 在现代通信系统中,信源编码主要用于解决信息传输中的 有效性 ,信道编码主要用于解决信息传输中的 可靠性 ,加密编码主要用于解决信息传输中的 安全性 ;2. 离散信源⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡8/18/14/12/1)(4321x x x x x p X ,则信源的熵为 符号 ; 3. 对称DMC 信道的输入符号数为n,输出符号数为m,信道转移概率矩阵为p ij ,则该信道的容量为ij mj ij p p m C log log 1∑=+=;4. 采用m 进制编码的码字长度为K i ,码字个数为n,则克劳夫特不等式为11≤∑=-n i K i m , 它是判断 唯一可译码存在 的充要条件;5. 差错控制的基本方式大致可以分为 前向纠错 、 反馈重发 和 混合纠错 ;6. 如果所有码字都配置在二进制码树的叶节点,则该码字为 唯一可译码 ;7. 齐次马尔可夫信源的一步转移概率矩阵为P ,稳态分布为W ,则W 和P 满足的方程为 W=WP ;8. 设某信道输入端的熵为HX,输出端的熵为HY,该信道为无噪有损信道,则该信道的容量为 MAX HY ;9. 某离散无记忆信源X,其符号个数为n,则当信源符号呈 等概_____分布情况下,信源熵取最大值_logn ;10. 在信息处理中,随着处理级数的增加,输入消息和输出消息之间的平均互信息量趋于减少 ;12.信息论不等式:对于任意实数0>z ,有1ln -≤z z ,当且仅当1=z 时等式成立;3.设信源为X={0,1},P0=1/8,则信源的熵为 )8/7(log 8/78log 8/122+比特/符号,如信源发出由m 个“0”和100-m 个“1”构成的序列,序列的自信息量为)8/7(log )100(8log 22m m -+比特/符号;4.离散对称信道输入等概率时,输出为 等概 分布;5.根据码字所含的码元的个数,编码可分为 定长 编码和 变长 编码;6.设DMS 为⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡03.007.010.018.025.037.0.654321u u u u u u P U U ,用二元符号表}1,0{21===x x X 对其进行定长编码,若所编的码为{000,001,010,011,100,101},1. 信息的基本概念在于它的 不确定性 ;2. 按照信源发出的消息在时间和幅度上的分布情况,可将信源分成 离散 信源和 连续 信源两大类;3. 一个随机事件的 自信息量 定义为其出现概率对数的负值;4. 按树图法构成的码一定满足 即时码 的定义;5. 有扰离散信道编码定理 称为香农第二极限定理;6. 纠错码的检、纠错能力是指 检测、纠正错误码元的数目 ;7.信道一般指传输信息的物理媒介,分为有线信道和无线信道;8.信源编码的主要目的是提高通信系统的有效性;1.设信源X包含4个不同离散消息,当且仅当X中各个消息出现的概率为___1/4___时,信、、源熵达到最大值,为__2__,此时各个消息的自信息量为__2 __;2.如某线性分组码的最小汉明距dmin=4,则该码最多能检测出___3____个随机错,最多能纠正__1____个随机错;3.克劳夫特不等式是唯一可译码___存在___的充要条件;4.平均互信息量IX;Y与信源熵和条件熵之间的关系是___X;Y=HX-HX/Y___;5._信源___提高通信的有效性,_信道____目的是提高通信的可靠性,_加密__编码的目的是保证通信的安全性;6.信源编码的目的是提高通信的有效性 ,信道编码的目的是提高通信的可靠性 ,加密编码的目的是保证通信的安全性 ;7.设信源X包含8个不同离散消息,当且仅当X中各个消息出现的概率为__1/8__时,信源熵达到最大值,为___3____;8.自信息量表征信源中各个符号的不确定度,信源符号的概率越大,其自信息量越_小___;9.信源的冗余度来自两个方面,一是信源符号之间的__相关性__,二是信源符号分布的__不均匀性__;10.最大后验概率译码指的是译码器要在已知r的条件下找出可能性最大的发码作为译码估值 ,即令=maxP |r_ __;11.常用的检纠错方法有__前向纠错___、反馈重发和混合纠错三种;1.给定x i条件下随机事件y j所包含的不确定度和条件自信息量py j /x i,DA.数量上不等,单位不同B.数量上不等,单位相同C.数量上相等,单位不同D.数量上相等,单位相同2.条件熵和无条件熵的关系是:CA.HY/X<HY B.HY/X>HYC.HY/X≤HY D.HY/X≥HY3.根据树图法构成规则, DA.在树根上安排码字B.在树枝上安排码字C.在中间节点上安排码字D.在终端节点上安排码字4.下列说法正确的是:CA.奇异码是唯一可译码B.非奇异码是唯一可译码C.非奇异码不一定是唯一可译码D.非奇异码不是唯一可译码5.下面哪一项不属于熵的性质:BA.非负性B.完备性C.对称性D.确定性1.下面表达式中正确的是A ;A.∑=j i j x y p 1)/( B.∑=i i j x y p 1)/( C.∑=j j j iy y x p )(),(ω D.∑=ii j i x q y x p )(),( 2.彩色电视显像管的屏幕上有5×105 个像元,设每个像元有64种彩色度,每种彩度又有16种不同的亮度层次,如果所有的彩色品种和亮度层次的组合均以等概率出现,并且各个组合之间相互独立;每秒传送25帧图像所需要的信道容量C ;A. 50106B. 75106C. 125106D. 2501063.已知某无记忆三符号信源a,b,c 等概分布,接收端为二符号集,其失真矩阵为d=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡1 21 12 1,则信源的最大平均失真度max D 为 D ;A. 1/3B. 2/3C. 3/3D. 4/34.线性分组码不具有的性质是 C ;A.任意多个码字的线性组合仍是码字B.最小汉明距离等于最小非0重量C.最小汉明距离为3D.任一码字和其校验矩阵的乘积c m H T=05.率失真函数的下限为 B ;A .HU U; V D.没有下限6.纠错编码中,下列哪种措施不能减小差错概率 D ;A. 增大信道容量B. 增大码长C. 减小码率D. 减小带宽7.一珍珠养殖场收获240颗外观及重量完全相同的特大珍珠,但不幸被人用外观相同但重量仅有微小差异的假珠换掉1颗;一人随手取出3颗,经测量恰好找出了假珠,不巧假珠又滑落进去,那人找了许久却未找到,但另一人说他用天平最多6次能找出,结果确是如此,这一事件给出的信息量A ;A. 0bitB. log6bitC. 6bitD. log240bit8.下列陈述中,不正确的是 D ;A.离散无记忆信道中,HY 是输入概率向量的凸函数B.满足格拉夫特不等式的码字为惟一可译码C.一般地说,线性码的最小距离越大,意味着任意码字间的差别越大,则码的检错、纠错能力越强D.满足格拉夫特不等式的信源是惟一可译码9.一个随即变量x 的概率密度函数Px= x /2,V 20≤≤x ,则信源的相对熵为 C ;A . B. C. 1bit D.10.下列离散信源,熵最大的是 D ;A. H1/3,1/3,1/3;B. H1/2,1/2;C. H,;D. H1/2,1/4,1/8,1/811.下列不属于消息的是 B ;A.文字B.信号C.图像D.语言12.为提高通信系统传输消息有效性,信源编码采用的方法是 A ;A.压缩信源的冗余度B.在信息比特中适当加入冗余比特C.研究码的生成矩阵D.对多组信息进行交织处理13.最大似然译码等价于最大后验概率译码的条件是 D ;A.离散无记忆信道B.无错编码C.无扰信道D.消息先验等概14.下列说法正确的是 C ;A.等重码是线性码B.码的生成矩阵唯一C.码的最小汉明距离等于码的最小非0重量D.线性分组码中包含一个全0码字15.二进制通信系统使用符号0和1,由于存在失真,传输时会产生误码,用符号表示下列事件,u0:一个0发出 u1:一个1发出 v0 :一个0收到 v1:一个1收到则已知收到的符号,被告知发出的符号能得到的信息量是 A ;A. HU/VB. HV/UC. HU,VD. HUV16. 同时扔两个正常的骰子,即各面呈现的概率都是1/6,若点数之和为12,则得到的自信息为B ;A. -log36bitB. log36bitC. -log 11/36bitD. log 11/36bit17.下列组合中不属于即时码的是 A ;A. { 0,01,011}B. {0,10,110}C. {00,10,11}D. {1,01,00}18.已知某6,3线性分组码的生成矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=011101110001111010G ,则不用计算就可判断出下列码中不是该码集里的码是 D ;A. 000000B. 110001C. 011101D. 11111119.一个随即变量x 的概率密度函数Px= x /2,V 20≤≤x ,则信源的相对熵为 C ;A. 符号B. 符号C. 1bit/符号D. 符号20.设有一个无记忆信源发出符号A 和B,已知4341)(,)(==B p A p ,发出二重符号序列消息的信源,无记忆信源熵)(2X H 为 A ; 6、只要,当N 足够长时,一定存在一种无失真编码;7、当R <C 时,只要码长足够长,一定能找到一种编码方法和译码规则,使译码错误概率无穷小;8、在认识论层次上研究信息的时候,必须同时考虑到 形式、含义和效用 三个方面的因素; 9、1948年,美国数学家 香农 发表了题为“通信的数学理论”的长篇论文,从而创立了信息论;按照信息的性质,可以把信息分成 语法信息、语义信息和语用信息 ;按照信息的地位,可以把信息分成 客观信息和主观信息 ;人们研究信息论的目的是为了 高效、可靠、安全 地交换和利用各种各样的信息;信息的 可度量性 是建立信息论的基础;统计度量 是信息度量最常用的方法;熵 是香农信息论最基本最重要的概念;事物的不确定度是用时间统计发生 概率的对数 来描述的;10、单符号离散信源一般用随机变量描述,而多符号离散信源一般用随机矢量描述;11、一个随机事件发生某一结果后所带来的信息量称为自信息量,定义为其发生概率对数的负值 ;12、自信息量的单位一般有 比特、奈特和哈特 ;13、必然事件的自信息是 0 ;14、不可能事件的自信息量是 ∞ ;15、两个相互独立的随机变量的联合自信息量等于 两个自信息量之和 ;16、数据处理定理:当消息经过多级处理后,随着处理器数目的增多,输入消息与输出消息之间的平均互信息量 趋于变小 ;17、离散平稳无记忆信源X 的N 次扩展信源的熵等于离散信源X 的熵的 N 倍 ;18、离散平稳有记忆信源的极限熵,=∞H )/(lim 121-∞→N N N X X X X H ;19、对于n 元m 阶马尔可夫信源,其状态空间共有 nm 个不同的状态;20、一维连续随即变量X 在a,b 区间内均匀分布时,其信源熵为 log2b-a ;21、平均功率为P 的高斯分布的连续信源,其信源熵,HcX=eP π2log 212;22、对于限峰值功率的N 维连续信源,当概率密度 均匀分布 时连续信源熵具有最大值;23、对于限平均功率的一维连续信源,当概率密度 高斯分布 时,信源熵有最大值;24、对于均值为0,平均功率受限的连续信源,信源的冗余度决定于平均功率的限定值P 和信源的熵功率P 之比 ;25、若一离散无记忆信源的信源熵HX等于,对信源进行等长的无失真二进制编码,则编码长度至少为 3 ;26、m元长度为ki,i=1,2,···n的异前置码存在的充要条件是:∑=-≤nik im11;27、若把掷骰子的结果作为一离散信源,则其信源熵为 log26 ;28、同时掷两个正常的骰子,各面呈现的概率都为1/6,则“3和5同时出现”这件事的自信息量是 log2181+2 log23;29、若一维随即变量X的取值区间是0,∞,其概率密度函数为mxemxp-=1)(,其中:0≥x,m是X的数学期望,则X的信源熵=)(XHCme2log;30、一副充分洗乱的扑克牌52张,从中任意抽取1张,然后放回,若把这一过程看作离散无记忆信源,则其信源熵为52log2 ;31、根据输入输出信号的特点,可将信道分成离散信道、连续信道、半离散或半连续信道;32、信道的输出仅与信道当前输入有关,而与过去输入无关的信道称为无记忆信道;33、具有一一对应关系的无噪信道的信道容量C= log2n ;34、强对称信道的信道容量C= log2n-Hni ;35、对称信道的信道容量C= log2m-Hmi ;36、对于离散无记忆信道和信源的N次扩展,其信道容量CN= NC ;37、对于N个对立并联信道,其信道容量 CN = ∑=NkkC1 ;38、多用户信道的信道容量用多维空间的一个区域的界限来表示;39、多用户信道可以分成几种最基本的类型:多址接入信道、广播信道和相关信源信道;40、广播信道是只有一个输入端和多个输出端的信道;41、当信道的噪声对输入的干扰作用表现为噪声和输入的线性叠加时,此信道称为加性连续信道 ;42、高斯加性信道的信道容量C=)1(log212NXPP+;43、信道编码定理是一个理想编码的存在性定理,即:信道无失真传递信息的条件是信息率小于信道容量 ;44、信道矩阵⎥⎦⎤⎢⎣⎡12/12/1代表的信道的信道容量C= 1 ;45、信道矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡111代表的信道的信道容量C= 1 ;46、高斯加性噪声信道中,信道带宽3kHz,信噪比为7,则该信道的最大信息传输速率Ct= 9 kHz ;47、对于具有归并性能的无燥信道,达到信道容量的条件是 pyj=1/m ;48、信道矩阵⎥⎦⎤⎢⎣⎡1001代表的信道,若每分钟可以传递6105个符号,则该信道的最大信息传输速率Ct= 10kHz ;49、信息率失真理论是量化、数模转换、频带压缩和 数据压缩 的理论基础;50、求解率失真函数的问题,即:在给定失真度的情况下,求信息率的 极小值 ;51、信源的消息通过信道传输后的误差或失真越大,信宿收到消息后对信源存在的不确定性就 越大 ,获得的信息量就越小;52、信源的消息通过信道传输后的误差或失真越大道传输消息所需的信息率 也越小 ;53、单符号的失真度或失真函数dxi,yj 表示信源发出一个符号xi,信宿再现yj 所引起的 误差或失真 ;54、汉明失真函数 dxi,yj=⎩⎨⎧≠=j i j i 10 ; 55、平方误差失真函数dxi,yj=yj- xi2;56、平均失真度定义为失真函数的数学期望,即dxi,yj 在X 和Y 的 联合概率空间PXY 中 的统计平均值;57、如果信源和失真度一定,则平均失真度是 信道统计特性 的函数;58、如果规定平均失真度D 不能超过某一限定的值D,即:D D ≤;我们把D D ≤称为 保真度准则 ;59、离散无记忆N 次扩展信源通过离散无记忆N 次扩展信道的平均失真度是单符号信源通过单符号信道的平均失真度的 N 倍;60、试验信道的集合用PD 来表示,则PD= {}m j n i D D x y p i j ,,2,1,,,2,1;:)/( ==≤ ;61、信息率失真函数,简称为率失真函数,即:试验信道中的平均互信息量的 最小值 ;62、平均失真度的下限取0的条件是失真矩阵的 每一行至少有一个零元素 ;63、平均失真度的上限Dmax 取{Dj :j=1,2,···,m}中的 最小值 ;64、率失真函数对允许的平均失真度是 单调递减和连续的 ;65、对于离散无记忆信源的率失真函数的最大值是 log2n ;66、当失真度大于平均失真度的上限时Dmax 时,率失真函数RD= 0 ;67、连续信源X 的率失真函数RD= );()/(Y X I P x y p Inf D ∈ ;68、当2σ≤D 时,高斯信源在均方差失真度下的信息率失真函数为 =)(D R D 22log 21σ ; 69、保真度准则下的信源编码定理的条件是 信源的信息率R 大于率失真函数RD ;70、某二元信源⎭⎬⎫⎩⎨⎧=⎥⎦⎤⎢⎣⎡2/12/110)(X P X 其失真矩阵D=⎥⎦⎤⎢⎣⎡00a a ,则该信源的Dmax= a/2 ; 71、某二元信源⎭⎬⎫⎩⎨⎧=⎥⎦⎤⎢⎣⎡2/12/110)(X P X 其失真矩阵D=⎥⎦⎤⎢⎣⎡00a a ,则该信源的Dmin= 0 ; 72、某二元信源⎭⎬⎫⎩⎨⎧=⎥⎦⎤⎢⎣⎡2/12/110)(X P X 其失真矩阵D=⎥⎦⎤⎢⎣⎡00a a ,则该信源的RD= 1-HD/a ;73、按照不同的编码目的,编码可以分为三类:分别是 信源编码、信道编码和安全编码 ;74、信源编码的目的是: 提高通信的有效性 ;75、一般情况下,信源编码可以分为 离散信源编码、连续信源编码和相关信源编码 ;76、连续信源或模拟信号的信源编码的理论基础是 限失真信源编码定理 ;77、在香农编码中,第i 个码字的长度ki 和pxi 之间有)(log 1)(log 22i i i x p k x p -<≤- 关系; 78、对信源⎭⎬⎫⎩⎨⎧=⎥⎦⎤⎢⎣⎡16/116/116/116/18/18/14/14/1(87654321x x x x x x x x X P X )进行二进制费诺编码,其编码效率为 1 ;79、对具有8个消息的单符号离散无记忆信源进行4进制哈夫曼编码时,为使平均码长最短,应增加 2 个概率为0的消息;80、对于香农编码、费诺编码和哈夫曼编码,编码方法惟一的是 香农编码 ;82、设无记忆二元序列中,“0”和“1”的概率分别是p0和p1,则“0”游程长度L0的概率为 11)0(0)]0([p p L p L -= ;83、游程序列的熵 等于 原二元序列的熵;84、若“0”游程的哈夫吗编码效率为η0,“1”游程的哈夫吗编码效率为η1,且η0>η1对应的二元序列的编码效率为η,则三者的关系是 η0>η>η1 ;85、在实际的游程编码过程中,对长码一般采取 截断 处理的方法;86、“0”游程和“1”游程可以分别进行哈夫曼编码,两个码表中的码字可以重复,但 C 码 必须不同;87、在多符号的消息序列中,大量的重复出现的,只起占时作用的符号称为 冗余位 ;88、“冗余变换”即:将一个冗余序列转换成一个二元序列和一个 缩短了的多元序列 ;89、L-D 编码是一种 分帧传送冗余位序列 的方法;90、L-D 编码适合于冗余位 较多或较少 的情况;91、信道编码的最终目的是 提高信号传输的可靠性 ;92、狭义的信道编码即:检、纠错编码 ;93、BSC 信道即:无记忆二进制对称信道 ;94、n 位重复码的编码效率是 1/n ;95、等重码可以检验 全部的奇数位错和部分的偶数位错 ;96、任意两个码字之间的最小汉明距离有称为码的最小距dmin,则dmin=)',(min 'c c d c c ≠;97、若纠错码的最小距离为dmin,则可以纠正任意小于等于t= ⎥⎦⎥⎢⎣⎢-21min d 个差错; 98、若检错码的最小距离为dmin,则可以检测出任意小于等于l= dmin-1 个差错;99、线性分组码是同时具有 分组特性和线性特性 的纠错码;100、循环码即是采用 循环移位特性界定 的一类线性分组码;。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
为什么要用二进制而不使用十进制?
二进制的优点在于:
(1)物理上容易实现,可靠性强;
(2)运算简单;
(3)便于进行逻辑运算。
128瓦
64瓦
32瓦
16瓦
8瓦
4瓦
2瓦
1瓦
1
1
1
0
1
0
10Leabharlann 二进制运算0+0=0
二进制有 0 、1 二个数字 加法式只有 4 个 用电子元件实现起来比较容易 十进制有 0 ~ 9 十个数字 加法式共有 100 个 比二进制复杂了很多很多
二进制中, 5 表示为 00000101
-3 表示为 10000011
二数相加,得 10001000 结果为 -8
最高位为符号位
而非正确答案 2
5 的补码 00000101 -3 的补码 11111101
正数不变 负数取反后加 1 减法变加法,结果正确
二数相加,得 00000010
结果为 +2
采用补码运算具有如下两个特征:
0
0 0 0 0 0 0 0
0
0 0 1 0 0 0 1
0
0 0 0 0 0 0 0
0
0 0 0 0 0 0 0
0
0 0 1 0 0 0 1
0
0 0 0 0 0 0 0
int 数据 18
int 数据 -18
int 最大是 31 个 1 ,相当于 2^31 - 1 = 2147483647 由于负数采用补码表示,故 int 最小 -2147483648
结果为
-8
而非正确答案 2
为解决这个问题,采用 原码、反码、补码 这种方法
正数的原码:
+5
的原码 00000101
反码:
补码: 负数的原码: 反码: 补码:
+5
+5
的反码 00000101
的补码 00000101 的原码 10000101 的反码 11111010 的补码 11111011
三者相同
运算规则为:
0 ·0=0
0 ·1=0 1 ·0=0 1 ·1=1
读作 0“与”0 等于 0
读作 0“与”1 等于 0 读作 1“与”0 等于 0 读作 1“与”1 等于 1 10101011 ∧11000010 1 0 0 0 0 0 1 0
例:
异或运算
异或运算表示为 0⊕ 0=0
⊕ 、xor
一、进位计数制 二进制
( 100101 ) 2
= 1× 25 + 0× 24 + 0× 23 + 1× 22 + 0× 21 + 1× 20
= 32 + = 37
二进制共有 0 、1 共二个数字
0
+
0
+
4
+
0
+
1
( 100101 ) 2 = ( 37 ) 10
每个位置带“权”,这个“权”是 2 的幂次
数据 25 的存储形态
布尔型数据长度是一个字节
0 0 0 0 0 0 0 0
false 值
0
0
0
0
0
0
0
1
ture 值
实际上,只有 0 是 false , 其它值(非 0)都是 true 。
int 整型数由四个字节32位构成,最高位为符号位
0
0 0 0 1 0 0 0
0
0 0 0 0 0 0 0
-5 -5 -5
符号不变,其余取反 反码加 1
[+0]原=00000000 [+0]反=00000000 [-0]原=10000000 [-0]反=11111111
[+0]补=00000000 [-0]补=00000000
+0 -0 补码的表示是相同的
数学中,减法 5 – 3 = 2
可以做成加法 5 + (-3) = 2
示例: 0.8125 ╳ 2 1.625 ╳ 2 1.25 ╳ 2 0.5 ╳ 2 1.0
( 0.8125 ) 10 = ( 0.1101 ) 2
整数 = 1 整数 = 1 ( 0.1101 ) 2 = 1 x 2-1 + 1 x 2-2 + 0 x 2-3 + 1 x 2-4 = 0.5 + 0.25 + 0 + 0.625 = 0.8125 直到小数值为 0 或要求的精度
二进制、八进制、十六进制数之间的相互转换
( D 5 9 . C 8 )16
( 110101011001.11001000 )2
通过二进制
( 110101011001.11001000 )2
( 6 5 3 1 . 6 2 )8
进行转换
字节 byte 一个字节由 8 个二进制位 bit 构成
0 0 0 1 1 0 0 1
2
3 4 5 6 7 10 11 12 13 14
2
3 4 5 6 7 8 9 A B C
13
14 15
1101
1110 1111
15
16 17
D
E F
[例] ( 7155.625 )10 = ( ? )16
解: 16 16 16 16 7155 447 27 1 0 则 ( 7155 )10 = ( 1BF3 )16 余数 3 余数 15 (F) 余数 11 (B) 余数 1 0.625 × 16 10.000 整数部分 10 (A)
0
0 0
0
0 0
0
1 0
0
0 0
0
0 0 0 0 0 0
0
0 0 0 0 0 0
0
0 0 0 0 0 0
0
0 0 0 0 0 1
0
0 0 0 0 0 0
0
0 0 0 0 0 0
0
0 0 0 0 0 1
0
0 0 0 0 0 0
long long 数据 -18
二进制数的原码、反码和补码
数学中,减法 5 – 3 = 2 可以做成加法 5 + (-3) = 2 二进制中, 5 表示为 00000101 -3 表示为 10000011 二数相加,得 10001000 最高位为符号位
2)加法运算比减法运算更易于实现。使减法运算转换为 加法运算,进一步简化计算机中运算器的线路设计。
实数的浮点数表示法
1000011000010010 2 -6 X +0.18
- 23
类似于科学计数法 + 0.6289347953 X 10
或 运 算
或运算也叫逻辑加法、逻辑和。
符号表示为 + 、∨ 、∪ 、or
则 ( 0.625 )10 = ( 0.A )16
( 7155.625 )10 = ( 1BF3.A )16
二进制、八进制、十六进制数之间的相互转换 ( 110101001011.110010 )2 = ( ? )8
( 6 5 1 3 . 6 2 )8
( 110101001011.110010 )2
运算规则为:
0+0=0
0+1=1 1+0=1 1+1=1
读作 0“或”0 等于 0
读作 0“或”1 等于 1 读作 1“或”0 等于 1 读作 1“或”1 等于 1 10101011 ∨11000010 1 1 1 0 1 0 1 1
例:
与 运 算
与运算也叫逻辑乘法、逻辑积
符号表示为 · 、 ∧ 、 ∩ 、and
一、进位计数制 十进制
( 3059.62 ) 10 = 3× 103 + 0× 102 + 5× 101 + 9× 100 + 6× 10-1 + 2× 10-2 = 3000 + 0 + 50 + 9 + 0.6 + 0.02
= 3059.62
十进制共有 0 、1 、2 、… 、9 共十个数字 每个位置带“权”,这个“权”是 10 的幂次
= ( 11.5 ) 10
十进制整数转换成二进制整数
除以 2 倒取余数法
例: ( 37 ) 10 = (
?
)2
2 2 2
37 18 9 2 4 2 2
1 0 1 0 0
所以: ( 37 ) 10 = ( 100101 ) 2
2 1
1
0
十进制小数转换成二进制小数
进位法:用十进制小数乘基数,当积为 0 或达到所要求 的精度时,取其整数部分由上而下排列。
0+1=1
1+0=1 1+1=10
逢二进一
+ 01001001 + 00101011 = 01110100
二进制整数转换成十进制整数
按 “ 权 ” 展开计算 二进制数 ( 1011.1 ) 2 转化为十进制数 ( 1011.1 ) 2 = 1×23 + 0×22 + 1×21 + 1 ×20 + 1 × 2-1 = 8 + 0 + 2 + 1 + 0.5
long long 整型数由八个字节构成, 共有 64 个二进制位,最高位为符号位
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0
0 0 0
0
0 0 0
0
0 0 0
0
0 0 0
0
0 0 0
0
0 0 0
0
0 0 0
0
0 0 0
long long 数据 18
0
0 1
0
0 0
