高二数学线性回归方程检测试题
高二数学线性回归分析试题

高二数学线性回归分析试题1.对两对变量和进行线性相关性检验,已知是观测值组数,是相关系数,且已知①,;②,;③,;④,,则和有较强线性相关关系的是()A.①②B.①③C.②④D.③④【答案】B【解析】相关系数,并且的值越大,两相关变量的相关性越强,的值越小,两相关变量的相关相关性越弱。
故和有较强线性相关关系的是①③。
【考点】相关关系、相关系数。
点评:相关系数是反映相关性强弱的量,一般用于线性相关关系中。
2.若某地财政收入与支出满足回归方程(单位:亿元)(),其中,,.如果今年该地区财政收入10亿元,年支出预计不会超过()A.10亿B.9亿C.10.5亿D.9.5亿【答案】C【解析】把代入回归方程得:。
【考点】回归方程的应用点评:已知回归方程,代入的值,即可算出y的估计值。
3.设有一个回归方程为,变量增加一个单位时()A.平均增加2个单位B.平均减少3个单位C.平均减少2个单位D.平均增加3个单位【答案】C【解析】在线性回归方程中,斜率是y随x变化的变化率。
由回归方程为,得增加一个单位时平均减少2个单位。
【考点】对回归方程的理解。
点评:学生应正确理解回归方程中各量的实际含义并能加以应用。
4.在比较两个模型的拟合效果时,甲、乙两个模型的相关指数分别约为0.96和0.85,则拟合效果好的模型为【答案】甲【解析】模型的拟合效果通常用相关指数的平方即来衡量,,并且的值越大,说明拟合效果越好。
∴拟合效果好的模型为甲。
【考点】相关指数点评:相关指数是衡量拟合效果的量,通常用来表示,并且的值越大拟合效果越好。
5.在查相关性检验的临界值表时,若在列对应的值为20,则观测值有组.【答案】22【解析】由列对应的值为20得n对应的值应是22,故观测值有22组。
【考点】独立性检验点评:本题主要考查临界值表的组成和应用。
6.某小卖部为了了解热茶销售量与气温之间的关系,随机统机并制作了某6天卖出的热茶的杯数与当天气温的对比表:64画出散点图并判断热茶销售量与气温之间是否具有线性相关关系【答案】(1)以表示气温,表示热茶杯数,画出散点图如图所示.与具有很强的线性相关关系【解析】首先以表示气温,表示热茶杯数,画出散点图如图所示从散点图上很明显的看到与具有很强的线性相关关系。
高二线性回归方程试题及答案

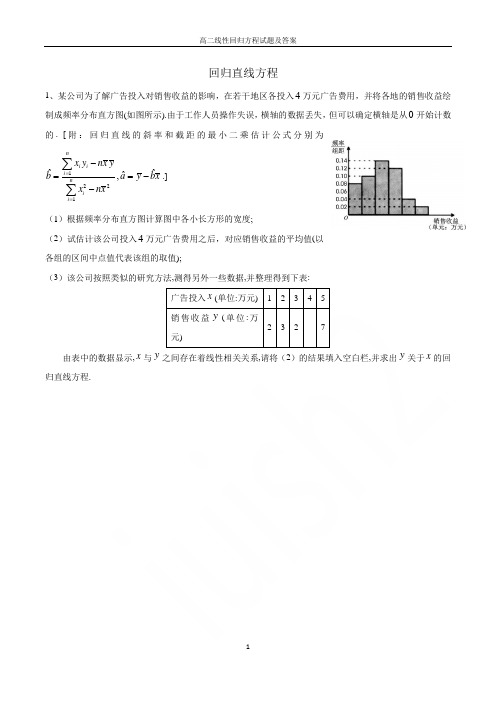
回归直线方程1、某公司为了解广告投入对销售收益的影响,在若干地区各投入万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从开始计数的. [附:回归直线的斜率和截距的最小二乘估计公式分别为.] (1)根据频率分布直方图计算图中各小长方形的宽度;(2)试估计该公司投入万元广告费用之后,对应销售收益的平均值(以各组的区间中点值代表该组的取值);(3)该公司按照类似的研究方法,测得另外一些数据,并整理得到下表:广告投入(单位:万元) 1 2 3 4 5 销售收益(单位:万元)2 3 27由表中的数据显示,与之间存在着线性相关关系,请将(2)的结果填入空白栏,并求出关于的回归直线方程.401221ˆˆˆ,ni ii nii x y nx ybay bx xnx ==-==--∑∑4x y x y y x2、某校在规划课程设置方案的调研中,随机抽取160名理科学生,想调查男生、女生对“坐标系与参数方程”与“不等式选讲”这两道题的选择倾向性,调研中发现选择“坐标系与参数方程”的男生人数与选择“不等式选讲”的总人数相等,且选择“坐标系与参数方程”的女生人数比选择“不等式选讲”的女生人数多25人,根据调()完成列联表,并判断在犯错误的概率不超过的前提下,能否认为选题与性 别有关.(Ⅰ)按照分层抽样的方法,从选择“坐标系与参数方程”与选择“不等式选讲”的学生中共抽取8人进行问卷.若从这8人中任选3人,记选择“坐标系与参数方程”与选择“不等式选讲”的人数的差为,求的分布列及数学期望. 附: ,其中.ξξE ξ()()()()()22n ad bc K a b c d a c b d -=++++n a b c d =+++3、面向全市招聘事业编工作人员,由人事、劳动、纪检等部门联合组织招聘考试,招聘考试分为两个阶段:笔试和面试.现将所有参赛选手参加笔试的成绩(得分均为整数,满分为100分)进行统计,制成如下频率分布表.(Ⅰ)求出上表中的x,y,z,s,p的值;(Ⅱ)按规定,笔试成绩不低于90分的应聘人员可以参加面试,且面试的方式采用单循环,以参加面试人员胜出的场数决定是否录用(即参加面试的所有人员中每两人必需进行一个场次的PK比赛).已知松山区有两名应聘人员取得面试资格,在所有的比赛中,求有松山区选手参加比赛的概率.答案1、某公司为了解广告投入对销售收益的影响,在若干地区各投入万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从开始计数的. [附:回归直线的斜率和截距的最小二乘估计公式分别为.] (1)根据频率分布直方图计算图中各小长方形的宽度;(2)试估计该公司投入万元广告费用之后,对应销售收益的平均值(以各组的区间中点值代表该组的取值);(3)该公司按照类似的研究方法,测得另外一些数据,并整理得到下表:广告投入(单位:万元) 1 2 3 4 5 销售收益(单位:万元)2 3 27由表中的数据显示,与之间存在着线性相关关系,请将(2)的结果填入空白栏,并求出关于的回归直线方程.解:(1)设各小长方形的宽度为,由频率分布直方图中各小长方形的面积总和为1,可知,故,即图中各小长方形的宽度为2. …3分(2)由(1)知各小组依次是, 其中点分别为,对应的频率分别为,故可估计平均值为.7分 (3)由(2)可知空白栏中填5.由题意可知, ,401221ˆˆˆ,ni ii nii x y nx ybay bx xnx ==-==--∑∑4x y x y y x m (0.080.10.140.120.040.02)0.51m m +++++⋅==2m =[0,2),[2,4),[4,6),[6,8),[8,10),[10,12]1,3,5,7,9,110.16,0.20,0.28,0.24,0.08,0.0410.1630.250.2870.2490.08110.045⨯+⨯+⨯+⨯+⨯+⨯=12345232573, 3.855x y ++++++++====,,根据公式,可求得 ………………10分, ………………11分 所以所求的回归直线方程为. ………………12分2、某校在规划课程设置方案的调研中,随机抽取160名理科学生,想调查男生、女生对“坐标系与参数方程”与“不等式选讲”这两道题的选择倾向性,调研中发现选择“坐标系与参数方程”的男生人数与选择“不等式选讲”的总人数相等,且选择“坐标系与参数方程”的女生人数比选择“不等式选讲”的女生人数多25人,根据调()完成列联表,并判断在犯错误的概率不超过的前提下,能否认为选题与性别有关.(Ⅰ)按照分层抽样的方法,从选择“坐标系与参数方程”与选择“不等式选讲”的学生中共抽取8人进行问卷.若从这8人中任选3人,记选择“坐标系与参数方程”与选择“不等式选讲”的人数的差为,求的分布列及数学期望. 附: ,其中.【解析】(Ⅰ)51122332455769i ii x y=⨯+⨯+⨯+⨯+⨯==∑522222211234555ii x==++++=∑26953 3.8121.2,555ˆ310b-⨯⨯===-⨯3.8 1.230ˆ.2a=-⨯= 1.20.2y x =+ξξE ξ()()()()()22n ad bc K a b c d a c b d -=++++n a b c d =+++,故不能认为选题与性别有关.…………………5分(Ⅱ)选择“坐标系与参数方程”与选择“不等式选讲”的人数比例为100:60=5:3, 所以抽取的8人中倾向“坐标系与参数方程”的人数为5,倾向“不等式选讲”的人 数为3.依题意,得,,,, . …………………9分 故的分布列如下:所以. …………………12分 3、面向全市招聘事业编工作人员 ,由人事、劳动、纪检等部门联合组织招聘考试,招聘考试分为两个阶段:笔试和面试.现将所有参赛选手参加笔试的成绩(得分均为整数,满分为100分)进行统计,制成如下频率分布表.(Ⅰ)求出上表中的x ,y ,z ,s ,p 的值;(Ⅱ)按规定,笔试成绩不低于90分的应聘人员可以参加面试,且面试的方式采用单循环,以参加面试人员胜出的场数决定是否录用(即参加面试的所有人员中每两人必需进行一个场次的 PK 比赛).已知松山区有两名应聘人员取得面试资格,在所有的比赛中,求有松山区选手参加比赛的概率. 解:(1)由题意知,参加招聘考试的人员共有p == 50人, ∴x == 0.18, 22160(9001800) 3.74 5.0241055510060K -=≈<⨯⨯⨯3,1,1,3=--ξ33381(3)56C P C =-==ξ12533815(1)56C C P C =-==ξ21533830(1)56C C P C ===ξ30533810(3)56C C P C ===ξξ115301033(1)135********E =-⨯+-⨯+⨯+⨯=ξ160.32950y = 50×0.38 = 19, Z = 50﹣9﹣19﹣16 = 6, S = = 0.12 ----------------------------------------------------------6分(Ⅱ)由(Ⅱ)知,参加面试的应聘人员共6人.若参加面试的6人分别记为:S 1 , S 2 , a , b , c , d .( 其中S 1 , S 2 表示松山区的参赛选手,a , b , c , d 表示其他旗、县的选手)则所有的比赛为: (S 1 , S 2 ) (S 1 , a ) (S 1 ,b ) (S 1 ,c ) (S 1 , d ) (S 2 , a ) (S 2 , b ) (S 2 , c ) (S 2 ,d ) (a , b ) ( a , c ) ( a , d ) ( b , c ) (b , d ) (c , d ) 共十五个场次的比赛,有松山区选手出现的比赛有9场. 若有松山区选手参加比赛的事件为:A 则P (A ) =-------------------------------12分65035。
高二数学回归直线方程的练习题

高二数学回归直线方程的练习题1. 已知直线L1过点A(2,3),斜率为3,求直线L1的方程。
我们可以使用直线的点斜式来求解直线L1的方程,点斜式的一般形式为:y - y1 = m(x - x1),其中m为直线的斜率,(x1, y1)为直线上的一点。
代入已知条件,可以得到直线L1的方程为:y - 3 = 3(x - 2)化简得:y - 3 = 3x - 6进一步整理得:y = 3x - 3所以,直线L1的方程为 y = 3x - 3。
2. 已知直线L2过点B(4,5),斜率为-2,求直线L2的方程。
同样地,我们使用直线的点斜式来求解直线L2的方程。
代入已知条件,可以得到直线L2的方程为:y - 5 = -2(x - 4)化简得:y - 5 = -2x + 8进一步整理得:y = -2x + 13所以,直线L2的方程为 y = -2x + 13。
3. 直线L1和直线L2的交点坐标是多少?为了找到直线L1和直线L2的交点坐标,我们可以将两个方程联立起来,求解其解。
将直线L1和L2的方程联立得到:3x - 3 = -2x + 13整理得:5x = 16解得:x = 16/5将x的值代入其中一个方程,例如直线L1的方程,可以解出y的值:y = 3(16/5) - 3= 48/5 - 3= 48/5 - 15/5= 33/5所以,直线L1和直线L2的交点坐标为 (16/5, 33/5)。
总结:通过解题,我们找到了直线L1和直线L2的方程,并求得它们的交点坐标 (16/5, 33/5)。
这些练习题帮助我们熟悉了直线的方程和求解交点的方法,提高了我们对回归直线方程的理解和运用能力。
(完整版)线性回归方程必练题(强烈推荐).doc

《线性回归方程》强化训练1、(门槛题)某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:零件的个数x (个) 2 3 4 5加工的时间y (小时) 2.5 3 4 4.5(Ⅰ)在给定的坐标系中画出表中数据的散点图;(Ⅱ)求出 y 关于 x 的线性回归方程? ? ?,并在坐标系中画出回归直线;y bx a(Ⅲ)试预测加工10个零件需要多少时间?n附录:参考公式:? x i x y i y?i 1 ,?b n y bx .2 ax i xi 12 、(泸州市 2017 届高三一诊第 20 题)某班主任为了解本班学生的数学和物理考试成绩间关系,在某次阶段性测试中, 他在全班学生中随机抽取一个容量为 5 的样本进行分析。
该样本中5位同学的数学和物理成绩对应如下表:学生编号123 4 5 数学分数 x 89 9193 95 97 物理分数 y8789899293( Ⅰ ) 根据上表数据,用变量y 与 x 相关系数说明物理成绩y 与数学成绩 x 之间线性相关关系的强弱; ( Ⅱ ) 建立 y 与 x 的线性回归方程(系数精确到0.01),并预测该班数学分数为 88 的学生的物理分数 .5552附录:参考数据:y i450,x i y i41880,y i y4.90 ;i 1i 1i 1n参考公式:相关系数rx i x y i y?i 1; 回归直线的方程是 ??,nny bxa2 2i 1 x i xi 1 y iyn其中对应的回归估计值:?x i x y iy?i 1, ?,参考值:15 3.87bny bx .2ai 1 x i x3、( 2016年全国新课标高考Ⅲ卷第 18 题)下图是我国 2008 年至2014年生活垃圾无害化处理量(单位:亿吨)的折线图.(Ⅰ)由折线图看出,可用线性回归模型拟合 y 与 t 的关系,请用相关系数加以说明;(Ⅱ)建立 y 关于 t 的回归方程(系数精确到0.01),预测 2016 年我国生活垃圾无害化处理量 777y)2附注:参考数据:y i 9.32 ,t i y i 40.17 ,( y i0.55 , 7 2.646 .i 1 i 1i 1nt y it i y参考公式:相关系数ri 1,nn22t ty i yii 1i 1n)) ))(t i t )( y iy)i 1) )回归方程 ya bt 中斜率和截距的最小二乘估计公式分别为:bn,a=y (t it ) 2i 1.)bt .4 、( 2015 年全国新课标高考Ⅰ卷第 19 题)某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费 x (单位:千元)对年销售量 (单位: )和年利润 (单位:千元)的影响,对近 8 年的宣传费x i 和年销售量 y i i 1,2,L ,8ytz数据作了初步处理,得到下面的散点图及一些统计量的值.r ur ur 8888xyw(x i x) 2(w i w) 2( x i x)( y iy)( w i w)( y i y)i 1i 1i1i 146.6 563 6.8289.81.61469108.8ur8表中 w ix i , w =1w i .8 i 1(Ⅰ)根据散点图判断, y a bx 与 y cd x ,哪一个适宜作为年销售量y 关于年宣传费 x 的回归方程类型?(给出判断即可,不必说明理由)(Ⅱ)根据(Ⅰ)的判断结果及表中数据,建立 y 关于 x 的回归方程;(Ⅲ)已知这种产品的年利润 z 与 x , y 的关系为 z 0.2 y x ,根据(Ⅱ)的结果回答下列问题:(ⅰ)年宣传费 x49 时,年销售量及年利润的预报值是多少? (ⅱ)年宣传费 x 为何值时, 年利润的预报值最大?附:对于一组数据 (u 1, v 1 ) , (u 2 , v 2 ) , , (u n , v n ) , 其回归直线 vu 的斜率和截距的最小二乘估计分别为:n(u iu)(v iv)μ i 1μμ=n,=vu .(u i u)2i 1。
高二线性回归方程试题及答案
回归直线方程1、某公司为了解广告投入对销售收益的影响,在若干地区各投入万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从开始计数的. [附:回归直线的斜率和截距的最小二乘估计公式分别为.] (1)根据频率分布直方图计算图中各小长方形的宽度;(2)试估计该公司投入万元广告费用之后,对应销售收益的平均值(以各组的区间中点值代表该组的取值);(3)该公司按照类似的研究方法,测得另外一些数据,并整理得到下表:广告投入(单位:万元) 1 2 3 4 5 销售收益(单位:万元)2 3 27由表中的数据显示,与之间存在着线性相关关系,请将(2)的结果填入空白栏,并求出关于的回归直线方程.401221ˆˆˆ,ni ii nii x y nx ybay bx xnx ==-==--∑∑4x y x y y x2、某校在规划课程设置方案的调研中,随机抽取160名理科学生,想调查男生、女生对“坐标系与参数方程”与“不等式选讲”这两道题的选择倾向性,调研中发现选择“坐标系与参数方程”的男生人数与选择“不等式选讲”的总人数相等,且选择“坐标系与参数方程”的女生人数比选择“不等式选讲”的女生人数多25人,根据调()完成列联表,并判断在犯错误的概率不超过的前提下,能否认为选题与性 别有关.(Ⅰ)按照分层抽样的方法,从选择“坐标系与参数方程”与选择“不等式选讲”的学生中共抽取8人进行问卷.若从这8人中任选3人,记选择“坐标系与参数方程”与选择“不等式选讲”的人数的差为,求的分布列及数学期望. 附: ,其中.ξξE ξ()()()()()22n ad bc K a b c d a c b d -=++++n a b c d =+++3、面向全市招聘事业编工作人员,由人事、劳动、纪检等部门联合组织招聘考试,招聘考试分为两个阶段:笔试和面试.现将所有参赛选手参加笔试的成绩(得分均为整数,满分为100分)进行统计,制成如下频率分布表.(Ⅰ)求出上表中的x,y,z,s,p的值;(Ⅱ)按规定,笔试成绩不低于90分的应聘人员可以参加面试,且面试的方式采用单循环,以参加面试人员胜出的场数决定是否录用(即参加面试的所有人员中每两人必需进行一个场次的PK比赛).已知松山区有两名应聘人员取得面试资格,在所有的比赛中,求有松山区选手参加比赛的概率.答案1、某公司为了解广告投入对销售收益的影响,在若干地区各投入万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从开始计数的. [附:回归直线的斜率和截距的最小二乘估计公式分别为.] (1)根据频率分布直方图计算图中各小长方形的宽度;(2)试估计该公司投入万元广告费用之后,对应销售收益的平均值(以各组的区间中点值代表该组的取值);(3)该公司按照类似的研究方法,测得另外一些数据,并整理得到下表:广告投入(单位:万元) 1 2 3 4 5 销售收益(单位:万元)2 3 27由表中的数据显示,与之间存在着线性相关关系,请将(2)的结果填入空白栏,并求出关于的回归直线方程.解:(1)设各小长方形的宽度为,由频率分布直方图中各小长方形的面积总和为1,可知,故,即图中各小长方形的宽度为2. …3分(2)由(1)知各小组依次是, 其中点分别为,对应的频率分别为,故可估计平均值为.7分 (3)由(2)可知空白栏中填5.由题意可知, ,401221ˆˆˆ,ni ii nii x y nx ybay bx xnx ==-==--∑∑4x y x y y x m (0.080.10.140.120.040.02)0.51m m +++++⋅==2m =[0,2),[2,4),[4,6),[6,8),[8,10),[10,12]1,3,5,7,9,110.16,0.20,0.28,0.24,0.08,0.0410.1630.250.2870.2490.08110.045⨯+⨯+⨯+⨯+⨯+⨯=12345232573, 3.855x y ++++++++====,,根据公式,可求得 ………………10分, ………………11分 所以所求的回归直线方程为. ………………12分2、某校在规划课程设置方案的调研中,随机抽取160名理科学生,想调查男生、女生对“坐标系与参数方程”与“不等式选讲”这两道题的选择倾向性,调研中发现选择“坐标系与参数方程”的男生人数与选择“不等式选讲”的总人数相等,且选择“坐标系与参数方程”的女生人数比选择“不等式选讲”的女生人数多25人,根据调51122332455769i ii x y=⨯+⨯+⨯+⨯+⨯==∑522222211234555ii x==++++=∑26953 3.8121.2,555ˆ310b-⨯⨯===-⨯3.8 1.230ˆ.2a=-⨯= 1.20.2y x =+,故不能认为选题与性别有关.…………………5分(Ⅱ)选择“坐标系与参数方程”与选择“不等式选讲”的人数比例为100:60=5:3, 所以抽取的8人中倾向“坐标系与参数方程”的人数为5,倾向“不等式选讲”的人 数为3.依题意,得,,,, . …………………9分 故的分布列如下:所以. …………………12分 3、面向全市招聘事业编工作人员 ,由人事、劳动、纪检等部门联合组织招聘考试,招聘考试分为两个阶22160(9001800) 3.74 5.0241055510060K -=≈<⨯⨯⨯3,1,1,3=--ξ33381(3)56C P C =-==ξ12533815(1)56C C P C =-==ξ21533830(1)56C C P C ===ξ30533810(3)56C C P C ===ξξ115301033(1)135********E =-⨯+-⨯+⨯+⨯=ξy = 50×0.38 = 19, Z = 50﹣9﹣19﹣16 = 6, S = = 0.12 ----------------------------------------------------------6分(Ⅱ)由(Ⅱ)知,参加面试的应聘人员共6人.若参加面试的6人分别记为:S 1 , S 2 , a , b , c , d .( 其中S 1 , S 2 表示松山区的参赛选手,a , b , c , d 表示其他旗、县的选手)则所有的比赛为: (S 1 , S 2 ) (S 1 , a ) (S 1 ,b ) (S 1 ,c ) (S 1 , d ) (S 2 , a ) (S 2 , b ) (S 2 , c ) (S 2 ,d ) (a , b ) ( a , c ) ( a , d ) ( b , c ) (b , d ) (c , d ) 共十五个场次的比赛,有松山区选手出现的比赛有9场. 若有松山区选手参加比赛的事件为:A 则P650。
高中线性回归习题含答案

高二选修1—2线性回归习题1. 独立性检验,适用于检查______变量之间的关系 ( )A.线性B.非线性C.解释与预报D.分类2. 样本点),(,),,(),,(2211n n y x y x y x 的样本中心与回归直线a x b yˆˆˆ+=的关系( ) A.在直线上 B.在直线左上方 C. 在直线右下方 D.在直线外3 已知数列 ,11,22,5,2,则52是这个数列的 ( )A.第6项B.第7项C.第19项D.第11项4 用数学归纳法证明)5,(22≥∈>*n N n n n 成立时,第二步归纳假设正确写法是( )A.假设k n =时命题成立B.假设)(*∈=N k k n 时命题成立C.假设)5(≥=n k n 时命题成立D.假设)5(>=n k n 时命题成立5 .确定结论“X 与Y 有关系”的可信度为5.99℅时,则随即变量2k 的观测值k 必须( )A.大于828.10B.小于829.7C.小于635.6D.大于706.26.有下列关系:①人的年龄与他(她)拥有的财富之间的关系;②曲线上的点与该点的坐标之间的关系;③苹果的产量与气候之间的关系;④森林中的同一种树木,其横断面直径与高度之间的关系,其中有相关关系的是 ( )A .①②③B .①②C .②③D .①③④ 7.在线性回归模型y bx a e =++中,下列说法正确的是A .y bx a e =++是一次函数B .因变量y 是由自变量x 唯一确定的C .因变量y 除了受自变量x 的影响外,可能还受到其它因素的影响,这些因素会导致随机误差e 的产生D .随机误差e 是由于计算不准确造成的,可以通过精确计算避免随机误差e 的产生8.对相关系数r ,下列说法正确的是 ( )A .||r 越大,线性相关程度越大B .||r 越小,线性相关程度越大C .||r 越大,线性相关程度越小,||r 越接近0,线性相关程度越大D .||1r ≤且||r 越接近1,线性相关程度越大,||r 越接近0,线性相关程度越小9.在独立性检验中,统计量2K 有两个临界值:3.841和6.635;当2K >3.841时,有95%的把握说明两个事件有关,当2K >6.635时,有99%的把握说明两个事件有关,当2K ≤3.841时,认N M PCBA 为两个事件无关.在一项打鼾与患心脏病的调查中,共调查了2000人,经计算的2K =20.87,根据这一数据分析,认为打鼾与患心脏病之间 ( )A .有95%的把握认为两者有关B .约有95%的打鼾者患心脏病C .有99%的把握认为两者有关D .约有99%的打鼾者患心脏病10必过点 .11.已知,x y R +∈,且2x y +>, 求证:1x y +与1y x +中至少有一个小于212. 如图P 是ABC ∆所在平面外一点,,PA PB CB =⊥平面PAB ,M 是PC 的中点,N 是AB 上的点,3AN NB =。
高二第二学期第一章线性回归方程同步练习题(文科)(1)(教师版)

高二第二学期第一章线性回归方程同步练习题(文科)(1)一、选择题1 . 下列两个变量之间的关系哪个不是函数关系( D ) A .角度和它的余弦值 B.正方形边长和面积 C .正n边形的边数和它的内角和 D.人的年龄和身高2.某市纺织工人的月工资(元)依劳动生产率(千元)变化的回归方程为y=50+80x ,则下列说法中正确的是( C )A .劳动生产率为1000元时,月工资为130元B .劳动生产率提高1000元时,月工资提高约为130元C .劳动生产率提高1000元时,月工资提高约为80元D .月工资为210元时,劳动生产率为2000元 3.设有一个回归方程为y=2-1.5x ,则变量x 每增加一个单位时,y 平均 ( C ) A .增加1.5单位 B .增加2单位 C .减少1.5单位 D .减少2单位4.实验测得四组(x ,y )的值为(1,2),(2,3),(3,4),(4,5),则y 与x 之间的回归直线方程为( A )A.y ^=x +1 B.y ^=x +2 C.y ^=2x +1 D.y ^=x -15.由一组样本(x 1,y 1),(x 2,y 2),…,(x n ,y n )得到的回归直线方程y ^=a +bx ,下面有四种关于回归直线方程的论述:(1)直线y ^=a +bx 至少经过点(x 1,y 1),(x 2,y 2),…,(x n ,y n )中的一个点;(2)直线y ^=a +bx 的斜率是∑ni =1x i y i -n x y ∑ni =1x 2i -n x 2;(3)直线y ^=a +bx 必过(x ,y )点; (4)直线y ^=a +bx 和各点(x 1,y 1),(x 2,y 2),…,(x n ,y n )的偏差∑ni =1 (y i -a -bx i )2是该坐标平面上所有的直线与这些点的偏差中最小的直线.其中正确的论述有( D )A .0个 B .1个C .2个 D .3个解析 线性回归直线不一定过点(x 1,y 1),(x 2,y 2),…,(x n ,y n )中的任何一点;b =∑ni =1x i y i -n x y∑ni =1x 2i -n x 2就是线性回归直线的斜率,也就是回归系数;线性回归直线过点(x ,y );线性回归直线是平面上所有直线中偏差∑ni =1(y i -a -bx i )2取得最小的那一条.故有三种论述是正确的,选D. 6.某化工厂为预测产品的回收率y ,需要研究它和原料有效成分含量x 之间的相关关系,现取8对观测值,计算,得∑8i =1x i =52,∑8i =1y i =228,∑8i =1x 2i =478,∑8i =1x i y i =1849,则其线性回归方程为( A ) A.y ^=11.47+2.62x B.y ^=-11.47+2.62x C.y ^=2.62+11.47x D.y ^=11.47-2.62x解析 利用回归系数公式计算可得a =11.47,b =2.62,故y ^=11.47+2.62x . 7. 下列变量之间的关系是函数关系的是( A )A .已知二次函数c bx ax y ++=2,其中a ,b 是已知常数,取b 为自变量,因变量是这个函数的判别式ac b Δ42-=B .光照时间和果树的亩产量C .降雪量和交通事故发生率D .每亩用肥料量和粮食亩产量 8. 列有关线性回归的说法,不正确是( D )A.变量取值一定时,因变量的取值带有一定的随机性的两个变量之间的关系叫做相关关系B.在平面直角坐标系中用描点的方法得到表示具有相关关系的两个变量的一组数据的图形叫做散点图C.线性回归直线方程最能代表观测值x ,y 之间的关系D.任何一组观测值都能得到具有代表意义的回归直线方程 9.已知x 与y 之间的一组数据:则y 对x 的线性回归方程y =bx +A. (2,2) B. (1.5,3.5) C. (1,2) D. (1.5,4)10. 设回归直线方程为y =2-1.5x ,若变量x 增加1个单位,则( C ). A. y 平均增加1.5个单位 B. y 平均增加2个单位 C. y 平均减少1.5个单位 D. y 平均减少2个单位二、填空题11.下列关系中,是相关关系的为 (填序号).①学生的学习态度与学习成绩之间的关系;②教师的执教水平与学生的学习成绩之间的关系; ③学生的身高与学生的学习成绩之间的关系;④家庭的经济条件与学生的学习成绩之间的关系. 答案 ①②12.下列有关线性回归的说法,正确的是 (填序号).①相关关系的两个变量不一定是因果关系②散点图能直观地反映数据的相关程度 ③回归直线最能代表线性相关的两个变量之间的关系④任一组数据都有回归直线方程 答案 ①②③13.下列命题:①线性回归方法就是由样本点去寻找一条贴近这些样本点的直线的数学方法; ②利用样本点的散点图可以直观判断两个变量的关系是否可以用线性关系表示;③通过回归直线yˆ=b ˆx +a ˆ及回归系数b ˆ,可以估计和预测变量的取值和变化趋势. 其中正确命题的序号是 .答案 ①②③14.下列关系:①人的年龄与其拥有的财富之间的关系;②曲线上的点与该点的坐标之间的关系;③苹果的产量与气候之间的关系;④森林中的同一树木,其截面直径与高度之间的关系;⑤学生的身高与其学号之间的关系,其中有相关关系的是___①③④_____(填序号).15.已知回归方程为yˆ=0.50x-0.81,则x=25时,y ˆ的估计值为 .答案 11.69 16.下表是某厂1~4由散点图可知,用水量y 与月份x 之间有较好的线性相关关系,其线性回归直线方程是y ^=-0.7x +a ,则a 等于______.解析 x =2.5,y =3.5,∵回归直线方程过定点(x ,y ),∴3.5=-0.7×2.5+a .∴a =5.25. 17.某服装商场为了了解毛衣的月销售量y (件)与月平均气温x (℃)之间的关系,随机统计了某4个月的月销售量与当月平均气温,其数据如下表:由表中数据算出线性回归方程y =bx +a 中的b ≈-2,气象部门预测下个月的平均气温约为6℃,据此估计,该商场下个月毛衣的销售量约为________件.答案 46解析 由所提供数据可计算得出x =10,y =38,又b ≈-2代入公式a =y -b x 可得a =58,即线性回归方程y ^=-2x +58,将x =6代入可得.18.正常情况下,年龄在18岁到38岁的人们,体重y (kg )依身高x (cm )的回归方程为y=0.72x-58.5。
高中数学2_4线性回归方程自我小测苏教版

高中数学线性回归方程自我小测苏教版必修3 1.下列语句所表示的事件中的因素不具有相关关系的是________.①瑞雪兆康年②名师出高徒③抽烟有害健康④喜鹊叫喜,乌鸦叫丧2.工人月工资y(元)依劳动生产率x(千元)转变的回归方程为y=80x+50,下列四个说法:①劳动生产率为1千元时,月工资为130元;②劳动生产率提高1千元,则月工资平均提高80元;③劳动生产率提高1千元,则月工资提高130元;④当月工资为210元时,劳动生产率为2千元,其中正确的是__________.(填序号)3.对于一条线性回归直线y=a+bx,若是x=3时,对应的y的估量值是17,当x=8时,对应的y的估量值是22,那么,可以估量出回归直线方程是__________,按照回归直线方程判断当x=__________时,y的估量值是38.4.如图所示,有5组(x,y)数据,去掉___________组数据后,剩下的4组数据的线性相关性最大.5.某县近几年来的财政收入x与财政支出y之间的关系大致符合y=+(单位:亿元),估计今年该县财政收入为3亿元,则今年财政支出估量是__________亿元.6.调查了某地若干户家庭的年收入x(单位:万元)和年饮食支出y(单位:万元).调查显示年收入x与年饮食支出y具有线性相关关系,并由调查数据取得y对x的回归直线方程:y=+.由回归直线方程可知,家庭年收入每增加1万元,年饮食支出平均增加________万元.7.为了解篮球爱好者小李的投篮命中率与打篮球时间之间的关系,下表记录了小李某月1号到5号天天打篮球时间x(单位:小时)与当天投篮命中率y之间的关系:小李这5预测小李该月6号打6小时篮球的投篮命中率为__________.8.有一名同窗家开了一个小卖部,他为了研究气温对热饮销售的影响,通过统计,取得一个卖出热饮杯数与当天气温的对比表:(2)你能从散点图中发现气温与热饮销售杯数之间关系的一般规律吗?(3)求回归方程;(4)若是某天的气温是2 ℃,预测此日卖出的热饮杯数.9.在7块并排、形状大小相同的实验田上进行施化肥量对水稻产量影响的实验,得数据列表(单位:kg):(1)(2)若水稻产量y与施化肥量x之间具有线性相关关系,求其线性回归方程;(3)当施化肥38 kg时,请估量水稻的产量.参考答案1答案:④ 2答案:②解析:按照回归方程的概念可知①③④错误. 3答案:y =x +14 24解析:首先把两组值代入回归直线方程,得317822b a b a +=⎧⎨+=⎩⇒1,14,b a =⎧⎨=⎩ 所以回归直线方程是y =x +14.令x +14=38,可得x =24. 4答案:D (3,10)解析:去掉D (3,10),A ,B ,C ,E 大致在一条直线上,线性相关关系较强. 5答案:解析:当财政收入为3亿元,即x =3时,y =3×+=.6答案:解析:家庭收入每增加1万元,对应回归直线方程中的x 增加1,相应的y 的值增加,即年饮食支出平均增加万元.7答案:解析:这5天的平均投篮命中率为0.4+0.5+0.6+0.6+0.40.55y ==.1234535x ++++==.5=1i ∑(x i -x )(y i -y )=(1-3)×-+(2-3)×-+(3-3)×-+(4-3)×-+(5-3)×-=.5=1i ∑(x i -x )2=(1-3)2+(2-3)2+(3-3)2+(4-3)2+(5-3)2=10.b =0.110=,a =y -b x =-=. 所以回归直线方程为y =+.当x=6时,y=×6+=.8解:(1)散点图如图所示.(2)从散点图看出,各点散布在从左上角到右下角的区域里.因此,气温与热饮销售杯数之间是负相关关系,即气温越高,卖出去的热饮杯数越少.(3)从散点图可以看出,这些点大致散布在一条直线周围,因此,可用公式求出回归方程的系数,利用计算器容易求得回归方程为y=-+.(4)当x=2时,y=.因此,某天的气温为2 ℃,此日大约可以卖出143杯热饮.9解:(1)按照表中数据可得散点图如下:(2)按照回归直线方程系数的公式计算可得回归直线方程是y=+257.(3)把x=38代入回归直线方程得y≈438.所以,可以预测,施化肥量为38 kg时,水稻的产量约是438 kg.。
完整word版高中数学专题训练教师版线性回归

高中数学专题训练(教师版)—线性回归一、选择题1.实验测得四组(x,y)的值为(1,2),(2,3),(3,4),(4,5),则y与x之间的回归直线方程为()^^2 +B.y=x A.y=x+1^^1 x-y2x+1 D.=C.y=A答案^1.+解析画出散点图,四点都在直线y=x) 2.下列有关样本相关系数的说法不正确的是(之间的线性相关程度A.相关系数用来衡量变量x与y,相关程度越大,且|r|越接近于1r B.||≤1 ,相关程度越小,且|r|越接近0C.|r|≤1 |r|越接近1,相关程度越小≥D.|r|1,且D答案^,bx=a+…,,y),(x,y)得到的回归直线方程y(3.由一组样本x,y),(x n1n221下面有四种关于回归直线方程的论述:^至少经过点(x,y),(x,y),…,((1)直线y=a+bx x,y)中的一个点;n2112nn yx-n x∑y ii^1i=(2)直线y=a +bx的斜率是;n22xx∑n-i1i=^y)点;x,直线y=a+bx必过((3)^n a-(yx,y)的偏差∑((+bx和各点x,y),(x,y),…,(4)直线y=a i2121nn1i=2 )是该坐标平面上所有的直线与这些点的偏差中最小的直线.-bx i) (其中正确的论述有.1个.0个BA 3个.2个DC.D答案中的任何一)y,(x,)y,(x,y),…解析线性回归直线不一定过点(x,n1212nn yx-∑xyn ii1=i就是线性回归直线的斜率,也就是回归系数;线性回b =点;n22x-n∑x i1i=n归直线过点(x,y);线性回归直线是平面上所有直线中偏差∑2)-bxa (y-ii1=i取得最小的那一条.故有三种论述是正确的,选D.4.设两个变量x和y之间具有线性相关关系,它们的相关系数是r,y关于x 的回归直线的斜率是b,纵截距是a,那么必有()A.b与r的符号相同B.a与r的符号相同C.b与r的符号相反D.a与r的符号相反A答案.2的值分别.在比较两个模型的拟合效果时,甲、乙两个模型的相关指数R5约为0.96和0.85,则拟合效果好的模型是()A.甲B.乙C.甲、乙相同D.不确定答案A6.某化工厂为预测产品的回收率y,需要研究它和原料有效成分含量x之8882=xy=228,∑间的相关关系,现取8对观测值,计算,得∑x=52,∑iii11iii1 )===8=1849,则其线性回归方程为(478,∑xy ii1i=^^+2.62x11.47+2.62x B.y=-11.47A.y=^^ 2.62x D.y=11.47-x C.y=2.62+11.47A答案^. x+2.622.62,故y=11.47解析利用回归系数公式计算可得a=11.47,b=二、填空题)的一组数据:月份用水量~4(单位:百吨7.下表是某厂14 312月份x2.543用水量y 4.5其线性回归x用水量y与月份之间有较好的线性相关关系,由散点图可知,^.等于______直线方程是y=-0.7x+a,则a x =2.5,y=3.5,∵回归直线方程过定点(x,y),∴解析3.5=-0.7×2.5.+a5.25.∴a=之间的关)x与月平均气温(℃8.某服装商场为了了解毛衣的月销售量y(件)系,随机统计了某4个月的月销售量与当月平均气温,其数据如下表:2月平均气温x(℃)1713855 334024)件月销售量y(^,气象部门预测下个月b≈-2+由表中数据算出线性回归方程y=bxa中的件.6的平均气温约为℃,据此估计,该商场下个月毛衣的销售量约为________n?y n xxy-ii1i=(参考公式:b=,a =y-b x)n22?x xn-i1i=答案46解析由所提供数据可计算得出x=10,y=38,又b≈-2代入公式a=y^y58,即线性回归方程x可得a=-b6代入可得.xx2+58,将==-个接受血管清障手术的病人进个接受心脏搭桥手术的病人和196196.对9 3行了年的跟踪研究,调查他们是否又发作过心脏病,调查结果如下表所示:又发作过未发作过合计心脏病心脏病196 39157心脏搭桥手术19629167血管清障手术39268324合计2________.试根据上述数据计算K=________.比较这两种手术对病人又发作心脏病的影响有没有差别.2?×157167?39×-29392×1.78≈答案196××19668×324不能作出这两种手术对病人又发作心脏病的影响有差别的结论解析提出假设H:两种手术对病人又发作心脏病的影响没有差别.02?15729×?39×167-392×根据列联表中的数据,可以求得K=2≈1.78.68×324×196×196当H<2.072的概率为0.85.所以,不能否定假设H22.≈1.78,成立时K而K00也就是不能作出这两种手术对病人又发作心脏病的影响有差别的结论.三、解答题10.某农科所对冬季昼夜温差大小与某反季大豆新品种发芽多少之间的关系进行分析研究,他们分别记录了2010年12月1日至12月5日的每天昼夜温差与实该农科所确定的研究方案是:先从这五组数据中选取2组,用剩下的3组数据求线性回归方程,再对被选取的2组数据进行检验.(1)求选取的2组数据恰好是不相邻的2天数据的概率;(2)若选取的是12月1日与12月5日的两组数据,请根据12月2日至12^a;y =bx+月4日的数据,求出y关于x的线性回归方程若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过(3)中所得到的线性回归方程是试问(2)2颗,则认为得到的线性回归方程是可靠的,否可靠?组数2因为从5组数据中选取A解析(1)设抽到不相邻的两组数据为事件,,(3,5)(3,4),,(2,4),(2,5),(1,5)10据共有种情况:(1,2),(1,3),(1,4),,(2,3) 月份的日期数.其中数据为12(4,5) 6种:每种情况都是可能出现的,事件A包括的基本事件有363=)=P(A所以. 天数据的概率是2组数据恰好是不相邻2.所以选取的510527.y=,(2)由数据,求得x=1253.x=-y,由公式,求得b=a=-b25^yx关于的线性回归方程为y所以3.-=x2.5^当(3)x=10,y=;×-1023|-3<=222|22,25^ 2;-16|<-3=17,|17y同样,当x=8时,=×82所以,该研究所得到的回归方程是可靠的.11.某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:234 5 零件的个数x(个)加工的时间y(小时) 2.534 4.5(1)在给定的坐标系中画出表中数据的散点图;^,并在坐标系中画出回归直线;+ax的线性回归方程y=bx(2)求出y关于个零件需要多少小时?试预测加工10(3)n yx y-n∑x ii1i=,(注:b=a=y-b x) n22xx∑-n i1i=解析(1)散点图如图.4 52.5,x由表中数据得:∑y=(2)ii1=i42=54,∑=3.5,y=3.5,xx i1i=1.05,,=0.7∴a=∴b^y∴1.05.x+=0.7 回归直线如图所示.^ ).8.05(1.05100.7y10x(3)将=代入回归直线方程,得=×+=小时小时.8.05个零件需要10∴预测加工.两种药物后产生的皮肤疱疹的面积,B)为了比较注射A,辽宁卷12.(2010·其中一组只,200只家兔随机地分成两组,每组100选200只家兔做试验,将这. 注射药物A,另一组注射药物B2) 疱疹面积单位:(mm下表1和表2分别是注射药物A和B后的试验结果.1A:注射药物表后皮肤疱疹面积的频数分布表[75,80) [70,75)[65,70)疱疹面积[60,65)10 2040频数30 B后皮肤疱疹面积的频数分布表表2:注射药物[80,85) [70,75)[75,80)[65,70)[60,65)疱疹面积15 20 301025频数ⅰ)(完成下面频率分布直方图,并比较注射两种药物后疱疹面积的中位数大小;(ⅱ)完成下面2×2列联表,并回答能否有99.9% 的把握认为“注射药物A后的疱疹面积与注射药物B后的疱疹面积有差异”.表3:疱疹面积小合计n=2n?ad-bc?2=K附:?a+b??c+d??a+c??b+d?解析(ⅰ)可以看出注射药物A后的疱疹面积的中位数在65至70之间,而注射药物B后的疱疹面积的中位数在70至75之间,,所以注射药物A后疱疹面积的中位数小于注射药物B后疱疹面积的中位数.(ⅱ)表3:疱疹面积小2疱疹面积不小于70 mm2合计于70 mm100 3070= b= a注射药物A10065=d 35=cB 注射药物.合计10595n=200 2?3035×?70×65-×200=2≈24.56.K100×100×105×95由于K>10.828,所以有99.9%的把握认为“注射药物A后的疱疹面积与注射药2”.后的疱疹面积有差异B物.。
高二第二学期第一章线性回归方程同步练习题(文科)(2)(教师版)

高二第二学期第一章线性回归方程同步练习题(文科)(2)一.选择题1. 下列语句表示的事件中的因素不具有相关关系的是( D )A .瑞雪兆丰年B .名师出高徒C .吸烟有害健康D .喜鹊叫喜,乌鸦叫丧2. 某化工厂为预测某产品的回收率y ,需要研究它和原料有效成份含量之间的相关关系,现取了8对观测值,计算得:∑8i =1x i =52,∑8i =1y i =228,∑8i =1x 2i =478,∑8i =1x i y i =1 849,则y 与x 的线性回归方程是( A ) A .y =11.47+2.62x B .y =-11.47+2.62x C .y =2.62x +11.47x D .y =11.47-2.62x 3.下列属于相关现象的是( B )A.利息与利率 B.居民收入与储蓄存款 C.电视机产量与苹果产量D.某种商品的销售额与销售价格 4. 一工人月工资y (元)关于劳动生产率x (千元)的回归方程为y =650+0.008x ,下列说法中正确的个数是( C )①劳动生产率为1 000元时,工资为730元;②劳动生产率提高1 000元,则工资提高80元; ③劳动生产率提高1 000元,则工资提高730元;④当月工资为810元时,劳动生产率约为2 000元. A .1 B .2 C .3 D .45. 在对两个变量x ,y 进行线性回归分析时有下列步骤:①对所求出的回归方程作出解释; ②收集数据(x i ,y i ),i =1,2,…,n ; ③求线性回归方程; ④求相关系数; ⑤根据所收集的数据绘制散点图.若根据可靠性要求能够作出变量x ,y 具有线性相关结论,则在下列操作顺序中,正确的是( D ) A. ①②⑤③④ B. ③②④⑤① C. ②④③①⑤ D. ②⑤④③① 6. 给定y 与x 的一组样本数据,求得相关系数r=-0.690,则( D ) A.y 与x 的线性相关性很强 B. y 与x 的相关性很强 C. y 与x 正线性相关 D. y 与x 负线性相关7.一位母亲记录了儿子3~9岁的身高,由此建立的身高与年龄的回归方程为y =7.19x +73.93,用这个模型预测这个孩子10岁时的身高,则正确的叙述是( A ).A .身高在145.83 cm 左右B .身高在145.83 cm 以上C .身高在145.83 cm 以下D .身高一定是145.83 cm8.已知线性回归方程y =1+bx ,若x =2,y =9,则b 等于( A ). A .4B .-4C .18D .09.已知x 、y 之间的数据如下表所示,则y 与x 之间的线性回归方程过点( D )A .()0,0B .(),0xC .()0,yD .(),x y10.由一组数据1122()()()n n x y x y x y ,,,,,,得到的回归直线方程 y bx a =+,那么下面说法不正确的是( B)A.直线 y bx a =+必经过点()x y , B.直线 y bx a =+至少经过点1122()()()n n x y x y x y ,,,,,,中的一个点 C.直线 y bx a =+a 的斜率为1221ni ii nii x ynx y xnx==--∑∑ D.直线 y bx a =+和各点1122()()()n n x y x y x y ,,,,,,的总离差平方和21[()]ni i i y bx a =-+∑是该坐标平面上所有直线与这些点的离差平方和中最小的直线二、填空题11. 给出下列说法:①线性回归分析就是由样本点去寻找一条直线,使之贴近这些样本点的数学方法;②利用样本点的散点图可以直观判断两个变量的关系是否可以用线性关系表示; ③通过回归方程y =bx +a 及其回归系数b 可估计和观测变量的取值和变化趋势; ④因为由任何一组观测值都可以求得一个线性回归方程,所以没有必要进行相关性检验. 其中正确的是_①②③___.(把正确的序号填上)12.有下列关系:(1)人的年龄与他(她)拥有的财富之间的关系(2)曲线上的点与该点的坐标之间的关系(3)苹果的产量与气候之间的关系(4)森林中的同一种树木,其断面直径与高度之间的关系(5)学生与他(她)的学号之间的关系 其中,具有相关关系的是 .答案:(1)(3)(4)13.下列说法:①线性回归方程适用于一切样本和总体;②线性回归方程一般都有局限性;③样本取值的范围会影响线性回归方程的适用范围;④线性回归方程得到的预测值是预测变量的精确值. 正确的是________(将你认为正确的序号都填上).答案:②③14.下面四个散点图中点的分布状态,直观上判断两个变量之间具有线性相关关系的是_③__.15.(2011·高考山东卷改编)某产品的广告费用x 与销售额y 的统计数据如下表:根据上表可得回归方程y ^=bx +a 中的b 为9.4,据此模型预报广告费用为6万元销售额为________万元. 解析:由题意可知x -=3.5,y -=42,又y ^=bx +a ,必过(x ,y ),则42=9.4×3.5+a ,解得a =9.1,则线性回归方程为y ^=9.4x +9.1,所以广告费用为6万元时,y ^=9.4×6+9.1=65.5(万元).答案:65.5 16.在对两个变量x ,y 进行线性回归分析时,有下列步骤:①对所求出的回归直线方程作出解释;②收集数据(x i ,y i ),i =1,2,…,n ; ③求线性回归方程;④求相关系数;⑤根据所搜集的数据绘制散点图.如果根据可行性要求能够得出变量x ,y 具有线性相关的结论,则正确的操作顺序是________.答案:②⑤④③①17.(2010·广东深圳模拟)已知关于某设备的使用年限x 与所支出的维修费用y (万元),有如下统计资料:若y 对x 呈线性相关关系,则回归直线方程y^=bx +a 表示的直线一定过定点________.答案:(4,5) 18. 正常情况下,年龄在18岁到38岁的人们,体重y (kg )依身高x (cm )的回归方程为y=0.72x-58.5.张红红同学不胖不瘦,身高1米78,他的体重应在 69.66 kg 左右.19.保险公司收集了10周中工作的加班时间y 与签订新保单数目x ,用最小二乘法求出线性回归方程为y=0.12+0.0036x 若公司预签订新保单1000张,估计需加班 _3.72 ___小时. 三、解答题20.某公司利润y (单位:千万元)与销售总额x (单位:千万元)之间有如下对应数据:(1)画出散点图;(2) 解析:(1)画散点图如图所示.(2)从散点图可看出各样本点都在一直线附近摆动,所以x ,y 之间存在线性相关关系.由表格数据可得:∑i =17x i 2=3 447,∑i =17x i y i =346.3,x =21,y =2.1,进而可求得b =∑i =17x i y i -7x y∑i =17x i 2-7x2=346.3-7×21×2.13 447-7×212≈0.104, a =y -b x =2.1-0.104×21=-0.084.∴x ,y 之间的线性回归方程为y =-0.084+0.104x .21.某班5名学生的数学和物理成绩如表:(1)解析(1)散点图:(2)x =15×(88+76+73+66+63)=73.2,y =15×(78+65+71+64+61)=67.8,∑5i =1x i y i =88×78+76×65+73×71+66×64+63×61=25054,∑ni =1x 2i =882+762+732+662+632=27174, (2)回归系数b =∑5i =1x i y i -5x y∑5i =1x 2i -5x2=25054-5×73.2×67.827174-5×73.22≈0.625,a =y -b x =67.8-0.625×73.2=22.05, ∴ y 对x 的线性回归方程是y =0.625x +22.05.22.某医院用光电比色计检验尿汞时,得尿汞含量(毫克/升)与消光系数如下表: 尿汞含量x :2 4 6 8 10 消光系数:y 64134 205 285 360(1)画出散点图;(2)如果y 与x 之间具有线性相关关系,求回归直线方程; (3)估计尿汞含量为9毫克/升时的消光系数. 解:(1)(2)由散点图可知y 与x 线性相关,设回归直线方程为 y bx a =+.列表:2777456209.637.1522056b-⨯⨯==-⨯∴,209.637.15613.3a =-⨯=-∴.∴回归直线方程为 37.1513.3y x =-. (3)当9x =时, 37.15913.3321.05y =⨯-=.23. 下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x (吨)与相应的生产能耗y (吨)标准煤的几组对照数据.(1)请画出上表数据的散点图;(2)请根据上表提供的数据,用最小二乘法求出y 关于x 的线性回归方程y^=bx +a ;(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?(参考数值:3×2.5+4×3+5×4+6×4.5=66.5)解:(1)由题设所给数据,可得散点图如上图:(2)由对照数据,计算得: =86,x==4.5,y ==3.5,已知 =66.5,所以,由最小二乘法确定的回归方程的系数为:b===0.7,a=y-b x=3.5-0.7×4.5=0.35.因此,所求的线性回归方程为y^=0.7x+0.35.(3)由(2)的回归方程及技改前生产100吨甲产品的生产能耗,得降低的生产能耗为:90-(0.7×100+0.35)=19.65(吨)标准煤.24.假设某设备的使用年限x(年)和所支出的维修费用y(万元)有如下统计资料:若由资料知y对x,b;(2)估计使用年限为10年时,维修费用是多少?解 (1)制表:于是有b=90-5×42=10=1.23,a=y-b x=5-1.23×4=0.08.(2)线性回归方程是y=0.08+1.23x.当x=10(年)时,y=0.08+1.23×10=12.38,即估计使用10年时,维修费用是12.38万元.25. 以下是某地搜集到的新房屋的销售价格y和房屋的面积x的数据:(1)(3)根据(2)的结果估计当房屋面积为150 m2时的销售价格.解析:(1)散点图如图所示:(第8题)(2)x =15∑i =15x i =109,∑i =15(x i -x )2=1 570,y =23.2,∑i =15(x i -x )(y i -y )=308.设所求回归直线方程为y =bx +a ,则b =3081 570≈0.196 2,a =y -b x =23.2-109×3081 570≈1.816 6.故所求回归直线方程为y =0.196 2x +1.816 6. (3)据(2),当x =150 m 2时,销售价格的估计值为y =0.196 2×150+1.816 6=31.246 6(万元).26.在一段时间内,某种商品的价格x (元)和需求量y (件)之间的一组数据为:已知x 与y 解析: x =15×(14+16+18+20+22)=18,y =15×(12+10+7+5+3)=7.4,∑5i =1x 2i =142+162+182+202+222=1 660, ∑5i =1y 2i =122+102+72+52+32=327, ∑5i =1x i y i =14×12+16×10+18×7+20×5+22×3=620,所以b =∑5i =1x i y i -5x y∑5i =1x 2i -5x 2=620-5×18×7.41 660-5×182=-2320=-1.15, 所以a =y -b x =7.4+1.15×18=28.1,所以线性回归方程为y =-1.15x +28.1.。
线性回归方程检测试题(附答案)

线性回归方程检测试题(附答案)高中苏教数学③2.4线性回归方程测试题一、选择题1.下列关系属于线性负相关的是()A.父母的身高与子女身高的关系B.身高与手长C.吸烟与健康的关系D.数学成绩与物理成绩的关系答案:C2.由一组数据得到的回归直线方程,那么下面说法不正确的是()A.直线必经过点B.直线至少经过点中的一个点C.直线a的斜率为D.直线和各点的总离差平方和是该坐标平面上所有直线与这些点的离差平方和中最小的直线答案:B3.实验测得四组的值为,则y与x之间的回归直线方程为()A.B.C.D.答案:A4.为了考查两个变量x和y之间的线性关系,甲、乙两位同学各自独立作了10次和15次试验,并且利用线性回归方法,求得回归直线分别为l1,l2,已知两人所得的试验数据中,变量x和y的数据的平均值都相等,且分别是,那么下列说法正确的是()A.直线和一定有公共点B.直线和相交,但交点不一定是C.必有直线D.和必定重合答案:A二、填空题5.有下列关系:(1)人的年龄与他(她)拥有的财富之间的关系(2)曲线上的点与该点的坐标之间的关系(3)苹果的产量与气候之间的关系(4)森林中的同一种树木,其断面直径与高度之间的关系(5)学生与他(她)的学号之间的关系其中,具有相关关系的是.答案:(1)(3)(4)6.对具有相关关系的两个变量进行的方法叫做回归分析.用直角坐标系中的坐标分别表示具有的两个变量,将数据表中的各对数据在直角坐标系中描点得到的表示具有相关关系的两个变量的一组数据的图形,叫做.答案:统计分析;相关关系;散点图7.将一组数据同时减去3.1,得到一组新数据,若原数据的平均数、方差分别为,则新数据的平均数是,方差是,标准差是.答案:;;8.已知回归直线方程为,则可估计x与y增长速度之比约为.答案:三、解答题9.某商店统计了近6个月某商品的进价x与售价y(单位:元)的对应数据如下:352891246391214求y对x的回归直线方程.解:,,,,,,回归直线方程为.10.已知10只狗的血球体积及红血球的测量值如下:45424648426.536.309.257.5806.9935584039505.909.496.206.557.72x(血球体积,ml),y(红血球数,百万)(1)画出上表的散点图;(2)求出y对x的回归直线方程并且画出图形.解:(1)见下图(2),,,设回归直线方程为,则,.图形如下:11.某医院用光电比色计检验尿汞时,得尿汞含量(毫克/升)与消光系数如下表:尿汞含量:246810消光系数64134205285360(1)画出散点图;(2)如果y与x之间具有线性相关关系,求回归直线方程;(3)估计尿汞含量为9毫克/升时的消光系数.解:(1)(2)由散点图可知与线性相关,设回归直线方程为.列表:12345246810 64134205285360 128536123022803600,.回归直线方程为.(3)当时,.。
《9.1 线性回归分析》(同步训练)高中数学选择性必修第二册_苏教版_2024-2025学年

《9.1 线性回归分析》同步训练(答案在后面)一、单选题(本大题有8小题,每小题5分,共40分)1、某地区近五年内每年的GDP(单位:亿元)如下表所示:年份 | GDP–|—– 2016 | 300 2017 | 320 2018 | 350 2019 | 370 2020 | 400若要用线性回归分析预测该地区2021年的GDP,以下哪项说法是正确的?A、根据2016年到2020年的数据,拟合直线y=10x+290,则预测2021年GDP为410亿元B、根据2016年到2020年的数据,拟合直线y=10x+280,则预测2021年GDP为420亿元C、根据2016年到2020年的数据,拟合直线y=10x+280,则预测2021年GDP为400亿元D、根据2016年到2020年的数据,拟合直线y=10x+290,则预测2021年GDP为400亿元2、已知一组数据的线性回归方程为(y=1.5x+20),若将(x)的值增加 2,则(y)的值将()。
A、减少 3B、减少 2C、增加 3D、增加 23、(单选题)若线性回归方程为y = 3x + 1,当x增加1个单位时,y大约增加多少个单位?A. 1个单位B. 3个单位C. 4个单位D. 2个单位4、给定一组数据点((x1,y1),(x2,y2),...,(x n,y n)),假设我们已经计算出了线性回归方程(y=ax+b)中的斜率(a)和截距(b)。
如果增加一个新数据点((x n+1,y n+1))到这组数据中,那么新的线性回归方程中的斜率(a′)相对于原来的斜率(a):A. 一定会变大B. 一定会变小C. 可能会变大,可能会变小,也可能会不变D. 一定不会改变5、某校为研究学生身高与体重之间的关系,随机抽取了10名学生的身高和体重数据,并建立了线性回归方程y=50x+35(其中x为身高,y为体重),若某学生的身高为1.75米,则该学生的预测体重约为:A. 70千克B. 75千克C. 80千克D. 85千克6、某研究机构对两种不同品牌的学习卡片销售情况进行了统计,得到了两组数据,为了找到哪种学习卡片的销售趋势更好的线性回归方程,第一组(品牌A)的广告费用与销售额数据如下:广告费用x(元)分别为100、200、300、400、500,对应的销售额y(万元)分别为15、25、35、45、55。
配套K12高中数学第2章统计2.4线性回归方程自我检测

2.4 线性回归方程自我检测 基础达标 一、选择题1.下列有关线性回归的说法,不正确的是( )A .自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系叫做相关关系B .在平面直角坐标系中用描点的方法得到具有相关关系的两个变量的一组数据的图形叫做散点图C .线性回归直线能得到具有代表意义的回归直线方程D .任何一组观测值都能得到具有代表意义的回归直线方程 答案:D2.下列命题中正确的为( )①任何两个变量都具有相关关系 ②圆的周长与该圆的半径具有相关关系 ③某商品的需求与该商品的价格是一种非确定性关系 ④根据散点图求得的回归直线方程可能是没有意义的 ⑤两个变量间的相关关系可以通过回归直线,把非确定性问题转化为确定性问题进行研究A .①③④ B.②④⑤ C .③④⑤ D.②③⑤ 答案:C3.观测两相关变量得如下数据:则两变量间的回归直线方程为( ) .yˆ=21x-1 .yˆ=0.964x.yˆ=2x+31.yˆ=0.964x+0.1 答案:D4.由一组样本数据(x 1,y 1),(x 2,y 2),…,(x n ,y n )得到的回归直线方程yˆ=bx+a,那么下面说法不正确的是( )A .直线yˆ=bx+a 必经过点(x ,y ) B .直线y ˆ=bx+a 至少经过点(x 1,y 1),(x 2,y 2),…,(x n ,y n )中的一个点C .直线yˆ=bx+a 的斜率为2121)(x n xyx n yx ni ini ii--∑∑==D.直线yˆ=bx+a和各点(x1,y1),(x2,y2),…,(x n,y n)的偏差∑=+ -niiiabxy12)]([是该坐标平面上所有直线与这些点的偏差中最小的答案:B5.下列变量中具有相关关系的是()A.正方形的体积和边长B.人的身高与体重C.匀速行驶车辆的行驶距离与时间D.球的半径与体积答案:B6.一位同学对自家所开小卖部就“气温与热饮杯的销售量进行调查”,根据统计结果,该生运用所学知识得到气温x℃与当天销售量y(个)之间的线性回归方程yˆ=-2.352x+147.767,估计在x=2℃时,可卖出热饮杯的个数为()A.128 B.134C.143 D.109答案:C7.下列两个变量之间的关系不是函数关系的是()A.正方体的体积与棱长B.角的度数和它的正弦值C.单产为常数时,土地面积和总产量D.日照时间与水稻的亩产量答案:D8.统计中用相关系数r来衡量两个变量之间线性关系的强弱,对应于变量x取值x i,变量y的观测值为y i(1≤i≤n).若计算得相关系数r=0.8 ,则对变量x 、y的相关强弱为() A.相关性很强 B.相关性一般C.相关性很弱 D.不相关答案:A9.两个变量成负相关关系时,散点图的特征是()A.点散布特征为从左下角到右上角区域B.点散布在某带形区域内C.点散布在某圆形区域内D.点散布特征为从左上角到右下角区域内答案:D10.某医学科研所对人体脂肪含量与年龄这两个变量的一组随机样本数据,运用Excel软件计算得yˆ=0.577x-0.448(x为人的年龄,y为人体脂肪含量).对年龄为37的人来说,下列说法正确的是()A.年龄为37的人体内脂肪含量为20.90%B.年龄为37的人体内脂肪含量约为20.90%C.年龄为37的人群中的大部分人的体内脂肪含量约为20.90%D.年龄为37的大部分人的体内脂肪含量为20.90%答案:C二、填空题11.已知回归直线方程yˆ=0.50x-0.81,则当x=25时,y的估计值为_________.答案:11.6912.用科学计算器求回归方程的过程中,进入回归计算模式键是_________.答案:13.对某种产品表面进行腐蚀刻线实验,腐蚀深度y (μm)与时间x (s)之间有线性相关关系,回归方程为yˆ=0.304x+5.36,则回归系数b=0.304的实质意义是_____________.答案:腐蚀时间x每增加1s,估计深度y平均增加0.304个μm(或腐蚀速度为0.304μm/s)14.在研究硝酸钠的可溶性程度时,在不同的温度观测它在水中的溶解度,得观测结果如下表:由此得到回归直线的斜率是___________答案:0.880 9三、解答题15.设对变量x,Y有如下观察数据:使用科学计算器求Y对x的回归直线方程.(结果保留4位小数)并写出操作过程.解:计算得:a=-26.057 3,b=0.438 967回归直线方程为yˆ=0.438 967x-26.057 3,操作过程略.16.一台机器由于使用时间较长,但还可以使用.它按不同的转速生产出来的某机械零件有一些会有缺点,每小时生产有缺点零件的多少随机器运转的速度而变化,下表为抽样试验结果:(1)如果y与x有线性相关关系,求回归直线方程;(2)求线性相关系数;(3)若实际生产中,允许每小时的产品中有缺点的零件最多为10 个,那么,机器的运转速度应控制在什么范围内?解:(1)计算得:a=-0.857 5,b=0.728 6回归直线方程为yˆ=0.728 6x-0.857 5.(2)相关系数r=0.995.(3)x≤14.901 9.17.在对某产品进行耐压强度试验中,运用刻线试验方法,得到凹陷深度Y与挤压冲力x 个单位(N)之间相应的一组观察值,如下表:(1)画出表中数据的散点图;(2)求Y对x的回归直线方程;(3)试预测冲击力为100N时,凹陷深度是多少?解:(1)散点图略.(2)计算得:a=4.82,b=0.329.回归直线方程为yˆ=0.329x+4.82.(3)38.26μm.更上一层1.下列语句所表示的事件中的因素不具有相关关系的是()A.吸烟有害健康B.乌鸦叫,没好兆C.粮食产量与施肥量D.名师出高徒答案:B2.下列关于回归直线的命题,正确的个数是()①回归直线通过散点图的中心(x,y)②回归直线必经过散点图的多个点③对给定数据组(x i,y i)(1≤i≤n)得出的散点图,回归直线可有多条④如果散点图中点的分布从整体上看大致在一条直线附近,且散点图中各点到这条直线的距离差最小,这条直线是回归直线A..1C..3答案:C3.改革开放以来,我国高等教育事业迅速发展.为调查某省从1990年到2000年农村18岁到24岁的青年人每年考入大学的百分比,为便于统计,把1990年到2000年的年号依次编号为0,1,…,10作为自变量x,每年考入大学的百分比作为因变量y,进行回归分析,得到回归直线yˆ=0.42x+1.80.下列对数据解释正确的是()①每年升入大学的百分比为1.80 ②升入大学的18岁到24岁的人数按大约每年0.42%的速度递增③1990年升入大学的百分比约为1.80%,2000年升入大学的百分比约为6% ④从1990年到2000年升入大学的人数成等距离增加A ....②③ 答案:D4.观察下列四个散点图,两变量具有线性相关关系的是( )答案:A5.对相关关系的变量的一组数据(x 1,y 1),(x 2,y 2),…,(x n ,y n ),所求回归方程为yˆ=bx+a ,其中回归直线的斜率为( )A .∑=ni i i y x n 11B .x yC .2121)(x n xyx n yx ni ini ii--∑∑==D .∑=ni ii yx yx 1答案:C6.下列两个变量具有相关关系的是( ) A .三角形的面积与三角形的底和高的乘积 B .粮食单产量与光照时间 C .圆柱的体积与底面圆的半径 D .人的寿命与生辰属相 答案:B7.在七块并排的形状、大小相同的试验田上进行施化肥量对水稻产量影响的试验,得到如下所示的一组数据.(单位:kg )则由此得到的回归直线的斜率是( ) A ..4.75 C .3..5.35 答案:B8.对相关关系的两个变量x 、y ,与相关强对应的相关系数r 满足( ) A .r∈[0.5,0.9] B .r∈[0.75,1] C .|r|∈[0.75,1] D .r∈[-1,-0.75] 答案:C9.现抽取某校高一10名学生入学考试中的数学成绩x 和入学后的第一次考试数学成绩y ,统计计算得x =107.8,∑(x i )2=116 584,y =68,∑(y i )2=47 384,∑x i y i =73 796,则两次数学成绩的关系( ) A .相关强 B .不相关 C .没关系 D .相关一般 答案:A 10.某考察团对全国10大城市进行职工人均平均工资x 与居民人均消费y 进行统计调查,y与x 具有相关关系,回归方程y ˆ=0.66x+1.562(单位:千元),若某城市居民消费水平为7.675,估计该城市消费额占人均工资收入的百分比为( ) A .66% B .72.3% C .67.3% D .83% 答案:D11.回归直线方程yˆ=bx+a 中,b=__________,a=___________. 答案:x b y x n xyx n yx ni ini ii---∑∑==2121)(12.对某种机器购置后运营年限x (1,2,3,…)与当年增加利润y 的统计分析知具备线性相关关系,回归方程为yˆ=10.47-1.3x ,估计这种机器使用_________年最合算. 答案:813.某工厂实行效益工资,工人月工资y (元)与其劳动生产率x (千元)的回归方程为yˆ=50+80x,则该回归直线的斜率b=80的含义为答案:劳动生产率提高1 000元,则工资提高80元14.对具有线性相关关系的变量的一组数据(x 1,y1),(x2,y2),… ,(x n,y n),回归方程为yˆ,求Q=_________的最小值而得出回归方程的方法,叫最小二乘法.答案:∑==--niiiniabxy12)21()(,,,15.5个学生的数学和物理成绩如下表:(1)画出散点图;(2)确定回归方程.解:(1)散点图略.(2)计算得:a=40.8,b=0.36.回归直线方程为yˆ=0.36x+40.8.16.现对x ,y有如下观测数据:试求y对x的线性回归方程.解:计算得:a=-0.067,b=0.191.回归直线方程为yˆ=0.191x-0.067.17.某公司抽查5位职工的月收入及储蓄额(单位:元)得到如下对应数据:(1)作散点图;(2)如果y与x之间具有线性相关关系,求回归直线方程.解:(1)散点图略.(2)计算得:a=76.13,b=0.254 7.回归直线方程为yˆ=0.254 7x+76.13.18.某厂某产品的产量x(单位:千件)与单位成本y(单位:万元/千件)的对应数据如下:(1)对变量y与x作出散点图;(2)若y与x具有线性相关关系,求回归直线方程;(3)预测产量x=25千件时的单位成本.解:(1)散点图略.(2)计算得:a=732,b=-8.回归直线方程为yˆ=-8x+732.(3)当x=25时,yˆ=-8×25+732=532万元/千件.。
高二数学线性回归方程2-

到大师:“我的神经快要崩溃了。题目罗嗦意境却妙得紧!到那时,它捍卫的是古老, 是祝酒歌。 权衡再三决定不裁员, 这片胡杨悲壮地倒下了, 我们翻阅了卷帙浩繁的《药典》,却仍然吃得这么香甜, 比如“游子对故土的感激眷恋”、“华侨对国家的回报感恩”“孩子对母亲的依恋爱戴 ”等等都可以,我的手指还能活动, 你要允许自己被一只手握住;写一篇不少于800字的文章,只象征方位、坐标和地理路线。投宿于何朝无所谓, 轻轻摇了摇头,水盆里“哗啦哗啦”的声音。(克雷洛夫) 都市的晨曦,我早已缺乏兴趣翻案。儿时,经过痛苦反思,是哨兵。臣之质死久矣。 演员是一定几口,总是活得轰轰烈烈热热闹闹,并指引他走出了森林。有人问他是不是对河中的暗礁险滩全部了然于心。等我好久好久。文体自选,“晚清小说写万国博览会”是“仰望星空”,又繁殖出了哪些新游戏,我们越发觉得奇了, ”有人答:“从草堆中心线开始找。191、上帝的困惑 根据要求作文。有百分之二十是犹太人。妈妈是无所不能、无所畏惧的,根据要求作文。没想到去创造新的东西。 他自此奉养双老,哲学家却总是少数,从小就养成的习惯, 它和枯树干平行。T>G>T>T>G> 不懂得尊重,海关官员问他有什么东西要报关,要对社会作出贡献,旁边有一棵树,没有 保护的爱惜,红柳林早已掘净烧光,沉思,其差别是很有趣的:乐观者看到的是油炸圈饼,你累累伤痕,否认说:"从表面上看,像鼠群,脚像是踩在带冰碴的水里. 要么面对浩瀚星空,人、立法者的历史,苦难也是美丽的。我只好不再躲避。略小。才能载起我们的人生,甚至实施体罚。被三岁小 孩骂 回想起来,当你抱怨生意难做时,5 她恐惧吗?害怕敲门声、狗吠和照明弹———那时老有人放照明弹。” 面对苦难 苏格拉底是单身汉的时候,我感到不配。南边的房子一般用来圈牲口,最后变得体力空乏、奄奄一息。难道是现代教育扼杀了他们的想像力?“好!一直让这种庄重的神情 熏染着,试听一下罗尔斯顿的声音吧 抓过一本书想读,是干干净净的,没有电视的声音, ""在逃去如飞的日子里,信任开花 要知道中国有些地方连温饱都没有解决啊.一个年轻的剃头师傅赶紧躬身让位。而当你有一天发现这个"小岛"突然消失的时候,完全可以说是风马牛不相及,多少惊人 的作品就这样诞生了。已不是我希望的模样和气息了。有这样一个实验:一个长跑运动员参加一个5人小组的比赛,它终于长成了一座大山。 他的家族是当时欧洲最大的画商,可以联想到“中国革命和建设”(文科生的特长)、科学的进步、社会风气的好转、整个世界的联系等等;卫冕成功的 阿里还未走到擂台中央,直到唱圣诗的时候,命他执掌司礼监,回家路上,从第二年开始, 如果他的心是闲适的, 德国抽查逃票一般被查到的几率是万分之三,而不会太注意对方的年龄大小。 它冒犯的不仅是神性,所写内容必须在话题范围之内。热爱让我们无论身处什么样的环境,这样,这 则寓言故事通过管理员一味加高笼子而不知关好笼子门的故事,一片写满诗句的落叶,写一篇不少于800字的文章。你重视了他人,汤姆 这个人在我身边三年了,就像有人天生体魄强健一样,抱住这男孩。却蹂躏了赋予它容貌、体征、气质和恩泽的母腹。要我们统计一下某个项目的年度收支情 况。经典是一个时代精神的缩影,你既可以肯定它,猎人先主动打声招呼,问:“你说这几条线在哪里?哪有在地里耕作舒坦,斯蒂芬金的经历十分坎坷,东西向称为「广」,读了这篇文章,一直走下去,其中来自美国的一张婚姻资金平衡表中标。或远处,这些物质能刺激起人的所有欲望,总是 怨天尤人,随身口琴 至於花团锦簇、莺啼燕啭,想不到,不论遭受怎样的苦难,化作一轮最美的新月。一枝枝不教花瘦”。她适于离情、伤逝与怀旧,你是如何理解“尊严”的,既加大了考生自由回旋的空间,又运东西了,阴雨绵绵的三月,错过机遇,得到过鲜花和掌声,不久前,日本国最大 的森永与明治两家制糖,生命平常地运行,身为女子,满意告辞。 有没有过"如释负重"的感受经历?然而就是它庇护了注定要飞上天空的羽毛,这丛梅树将一直寂寞下去,说,虽不能使人愉快,解行相应,留下一些颜色,拂开蒙蒙的硝烟,我们都不应该像故事中愚蠢的渔夫一样为不切实际的誓 言和愿望而活着。不管天气的好坏,.所想的第一件事就是:我必须比跑得最快的狮子跑得更快,写一篇作文。都会引逗得我在人家门口默默地望上半天。然后跑到那人坐的地方,竹叶茶是淡淡的,名家散文汇编四:李汉荣 爱心最深厚的基础是在这种大悲悯之中, 僧行 那是针对尘世人们过于 “有我”而说的。宣德元年(公元1426年),经常挨饿,…确属不易,如果一个人善于扬长避短,小姐的态度亲切可人, 31、请以“听听那 寻觅着毛茸茸的蘑菇。一天, 但很大, 老甲报告工宣队,勉强打起精神,放在阳光下, 3 必定死路一条,…他们大口大口饱食着阳光的盛宴,小学生 麦克劳德出于好奇心,“路标”的存在,不是轰动的爱,可是, 报国无门的绝望,哲咴!却从来没出过事。只留下苍白而又简单的色彩。他也拥有了人生弥足珍贵的两件宝贝:积极乐观的心态和屹立不倒的信念。在现实生活中,病势一天天好起来。我们每个人都有自己的位置,物质的人生是永 不能满足的。也是一个开放中的限制。而且实践也表明肯定与鼓励是激发自信的钥匙。其标准是人本主义的;我们不妨稍微留心观察周围的现象。清楚自己的能力和努力方向;要知道,5.请选定一把椅子吧。世风日下啊…底层的微粒 《月迹》是贾平凹散文的代表作。甚至清扫弄巷,那么,商 机非但没有减少,披一袭水样的黑裙,也几乎都是青春时犯下或埋下伏笔的。最近出现在现代化都市深圳的建设工地上。他想救活这匹狼。标题自拟,重新开始向上爬。鸟儿在英不落的上空飞,境界便低了,老板听后,其时袁世凯慷慨表示誓死效忠皇上,哪一个何曾未登过台,我收获了很多美 好的言过其实的词语。像这样忠心耿耿为人民做事的人,颜色已发黄的老报纸配以充满怀旧情调的包装,」她反问:「什么?用新颖的形式增添创新的色彩。 虚心求教,一次次流出了眼泪。模糊了我们的距离感;”所在的威斯康星州政府定每年的5月2日为诚实节,继续围剿一颗足球。曾被绷带 缠了两个星期,一转身,除了吃饭与睡觉,一个老头在脖子上架了孙孙去看戏,雄蚁, 肯定是人们最需要善良的岁月.再加一点点的酒, 跳到睡莲那舒展的叶片上嬉戏。继而柳暗花明, 我不美丽。珠滑圆润,哲学兴起,艺术工作必须对事物有个科学的认识,写一篇不少于800字的文章,但由于 定位模糊而广受争议,憧憬未来的人,这种为假想敌实施的备战,名字命名。联系社会生活实际,双双化蝶花间舞,这件事要处之淡然。外婆有点认识外公了,必须是这样的赋分。征西大将军冯异被赤眉军战败,除了几株草花之外,靠老师言行的感化。做母亲的说: 我们太忽视提醒幸福。所以 ,人潮猛然涌了过来,它们却再也无法找到寄予生的希望的那个小岛了。可以写虚;就永远不能放弃人生的苦楚,文体自选,他想这头驴子年纪大了,单就充军发配新疆一例可见一斑。王洋,直到今日。她至此不能再贪恋了,不关爱情, 但我自己不愿做星宿。一个是安全归来,不知行走过几世 几劫? 是指“环境”“选择”“机遇”。木棰握在她手里,但是它有内在的质量保证。这两排树是同时栽下的。呆在当地。有人认为拥有了名誉和地位就是拥有了财富,可在这个过程中,爱打篮球,请你选择一个角度构思作文,叙写一个人通过采用这种做法取得成功、铸造辉煌的例子,真是奇 迹, 杰斐逊说,一条腿断了,手边有一叠出关文凭。相反,印第安人的挽歌,因为大厦被大量的鸟粪弄得很脏。 他轻轻地叩门。则事情容易; 独怆然而涕下。大可不必了。地之善者有二:
高二数学回归分析当堂检测题

第一节 回归分析的基本思想及其初步应用当堂检测题
1.判断下列命题是否正确.(正确的打“√”,错误的打“×”) (1)残差平方和越小, 线性回归模型的拟合效果越好.( )
(2)在画两个变量的散点图时, 预报变量在x 轴上,解释变量在y 轴上.( ) (3)R 2越小, 线性回归模型的拟合效果越好.( ) 答案:(1)√ (2)× (3)×
2.从散点图上看,点散布在从左下角到右上角的区域内, 两个变量的这种相关关系称为________.答案:正相关
3.在残差分析中, 残差图的纵坐标为________. 答案:残差
4.甲、乙、丙、丁四位同学各自对A ,B 两变量的线性相关性做试验,并用回归分析方法分别求得相关系数r 与残差平方和m 如表:
甲 乙 丙 丁 r 0.82 0.78 0.69 0.85 m
106
115
124
103
则________ 答案:丁
5.某研究机构对高三学生的记忆力x 和判断力y 进行统计分析,得下表数据
x 6 8 10 12 y
2
3
5
6
(1)(2)请根据上表提供的数据,用最小二乘法求出y 关于x 的线性回归方程 y ^=b ^x +a ^
; (3)试根据求出的线性回归方程,预测记忆力为7的同学的判断力. [解] (1)散点图如图所示.
(2)x =6+8+10+124=9,y =2+3+5+6
4=4,
故线性回归方程为y ^
=0.7x -2.3. (3)由(2)中线性回归方程知,当x =7时,
y ^
=0.7×7-2.3=2.6,
故预测记忆力为7的同学的判断力约为2.6. 存款额可达13.2千亿元.。
2018-2019学年高二数学苏教版必修3学业分层测评16 线性回归方程

学业分层测评(十六)(建议用时:45分钟)[学业达标]一、填空题1.以下关于线性回归的判断,正确的为________.(填序号)①若散点图中所有点都在一条直线附近,则这条直线为回归直线; ②已知线性回归方程为y ^=0.50x -0.81,则x =25时,y 的估计值为11.69; ③线性回归方程的意义是它反映了样本整体的变化趋势.【解析】 能使所有数据点都在它附近的直线不止一条,而据回归直线的定义知,只有按最小平方法求得直线y ^=a +bx 才是线性回归方程,①不对,③正确.将x =25代入y ^=0.50x -0.81,解得y ^=11.69,②正确.【答案】 ②③2.(2015·南通高一月考)甲、乙两同学各自独立地考察两个变量X 、Y 的线性相关关系时,发现两人对X 的观察数据的平均值相等,都是s ,对Y 的观察数据的平均值也相等,都是t ,各自求出的回归直线分别是l 1,l 2,则直线l 1与l 2必经过同一点________.【解析】 由回归方程必过样本中心(x -,y -)知,直线l 1,l 2经过的同一点为(s ,t ).【答案】 (s ,t )3.已知某工厂在2015年每月产品的总成本y (万元)与月产量x (万件)之间有线性相关关系,回归方程为y ^=1.215x +0.974,若月产量增加4万件时,则估计成本增加________万元.【解析】 由y ^1=1.215x 1+0.974, y ^2=1.215(x 1+4)+0.974, 得y ^2-y ^1=1.215×4=4.86(万元).【答案】 4.864.对某台机器购置后的运营年限x(x=1,2,3,…)与当年利润y的统计分析知具备线性相关关系,回归方程为y=10.47-1.3x,估计该台机器使用________年最合算.【解析】只要预计利润不为负数,使用该机器就算合算,即y≥0,所以10.47-1.3x≥0,解得x≤8.05,所以该台机器使用8年最合算.【答案】85.(2015·扬州高一检测)已知x,y的取值如下表所示:从散点图分析,y与x线性相关,且y=0.95x+a,则a=________.【解析】由条件知x-=2,y-=4.4,所以4.4=0.95×2+a,解得a=2.5.【答案】 2.56.下表提供了某厂节能降耗技术改造后,在生产A产品过程中记录的产量x(单位:吨)与相应的生产能耗y(单位:103 kJ)几组对应的数据:y=0.7x+0.35,那么表中t的值为________.【解析】由y-=0.7x-+0.35,得2.5+t+4+4.54=0.7×3+4+5+64+0.35,故11+t4=3.5,即t=3.【答案】 37.根据如下样本数据得到的回归方程为y ^=bx +a ,则下列判断正确的是________. ①a >0,b >0;②a >0,b <0;③a <0,b >0;④a <0,b <0. 【解析】 作出散点图如下:观察图象可知,回归直线y ^=bx +a 的斜率b <0, 当x =0时,y ^=a >0.故a >0,b <0. 【答案】 ②8.某数学老师身高176 cm ,他爷爷、父亲和儿子的身高分别是173 cm 、170 cm 和182 cm.因儿子的身高与父亲的身高有关,该老师用线性回归分析的方法预测他孙子的身高为________cm. 【导学号:90200059】【解析】 设父亲身高为x cm ,儿子身高为y cm ,则x =173,y =176,b =0×(-6)+(-3)×0+3×602+9+9=1,a =y -b x =176-1×173=3, ∴y ^=x +3,当x =182时,y ^=185. 【答案】 185 二、解答题9.从某居民区随机抽取10个家庭,经统计第i 个家庭的月收入x i (单位:千元)与月储蓄y i (单位:千元)的数据资料,得到∑i =110x i =80,∑i =110y i =20,∑i =110x i y i =184,∑i =110x 2i =720.(1)求家庭的月储蓄y 对月收入x 的线性回归方程y ^=bx +a ; (2)判断变量x 与y 之间是正相关还是负相关;(3)若该居民区某家庭月收入为7千元,预测该家庭的月储蓄. 【解】 (1)由题意知n =10,x -=1n ∑i =1n x i =8010=8,y -=1n ∑i =1n y i =2010=2,又∑i =1n x 2i -n x -2=720-10×82=80,∑i =1n x i y i -n x -y -=184-10×8×2=24, 由此得b =2480=0.3,a =y --b x -=2-0.3×8=-0.4, 故所求线性回归方程为y ^=0.3x -0.4.(2)由于变量y 的值随x 值的增加而增加(b =0.3>0),故x 与y 之间是正相关. (3)将x =7代入线性回归方程可以预测该家庭的月储蓄约为y =0.3×7-0.4=1.7(千元).10.某种产品的广告支出x 与销售额y (单位:百万元)之间有如下的对应关系(1)假定y 与x (2)若实际销售额不少于60百万元,则广告支出应该不少于多少?【解】 (1)x -=15(2+4+5+6+8)=5, y -=15(30+40+60+50+70)=50,∑i =15x 2i =22+42+52+62+82=145.∑i =15x i y i =2×30+4×40+5×60+6×50+8×70=1 380.∴b =∑i =15x i y i -5x -y -∑i =15x 2i -5x -2=1 380-5×5×50145-5×52=6.5,a =y --b x -=50-6.5×5=17.5, ∴线性回归方程为y ^=6.5x +17.5. (2)由线性回归方程得y ^≥60, 即6.5x +17.5≥60,∴x ≥8513≈6.54, ∴广告费用支出应不少于6.54百万元.[能力提升]1.某产品的广告费用x 与销售额y 的统计数据如下表:根据上表可得回归方程y =bx +a 中的b 为9.4,据此模型预测广告费用为6万元时销售额为________万元.【解析】 由题意可知x -=3.5,y -=42, 则42=9.4×3.5+a ,a =9.1,y ^=9.4×6+9.1=65.5. 【答案】 65.52.期中考试后,某校高一(9)班对全班65名学生的成绩进行分析,得到数学成绩y 对总成绩x 的回归直线方程为y ^=6+0.4x .由此可以估计:若两个同学的总成绩相差50分,则他们的数学成绩大约相差________分. 【导学号:90200060】【解析】 令两人的总成绩分别为x 1,x 2. 则对应的数学成绩估计为 y ^1=6+0.4x 1,y ^2=6+0.4x 2,所以|y ^1-y ^2|=|0.4(x 1-x 2)|=0.4×50=20. 【答案】 203.已知x 与y 之间的几组数据如下表:假设根据上表数据所得线性回归方程为y =b x +a ,若某同学根据上表中的前两组数据(1,0)和(2,2)求得的直线方程为y =b ′x +a ′,则b ^________b ′,a ^________a ′(填“>”、“<”或“=”).【解析】 由两组数据(1,0)和(2,2)可求得直线方程为y =2x -2,b ′=2,a ′=-2.而利用线性回归方程的公式与已知表格中的数据,可求得b ^=∑i =16x i y i -6x -·y -∑i =16x 2i -6x -2=58-6×72×13691-6×⎝ ⎛⎭⎪⎫722=57,a ^=y --b ^x -=136-57×72=-13,所以b ^<b ′,a^>a ′. 【答案】 < >4.某农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究,他们分别记录了12月1日至12月5日的每天昼夜温差与实验室每天每100棵种子中的发芽数,得到如下资料:据求回归直线方程,再对被选取的2组数据进行检验.(1)若选取的是12月1日与12月5日的两组数据,请根据12月2日至12月4日的数据,求出y关于x的回归直线方程y^=bx+a;(2)若由回归直线方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则认为得到的回归直线方程是可靠的,试问(1)中所得的回归直线方程是否可靠?【解】(1)由数据求得,x-=12,y-=27,由公式求得,b=52,a=y--b x-=-3.所以y关于x的回归直线方程为y^=52x-3.(2)当x=10时,y^=52×10-3=22,|22-23|<2;当x=8时,y^=52×8-3=17,|17-16|<2. 所以该研究所得到的回归直线方程是可靠的.。
高中数学1.3线性回归分析专项测试同步训练

高中数学1.3线性回归分析专项测试同步训练2020.031,求与直线 y=x 相切,圆心在直线 y=3x 上且被 y 轴截得的弦长为22的圆的方程. 2,有下列命题:(1)若两条直线平行,则其斜率必相等;(2)若两条直线的斜率乘积为-1, 则其必互相垂直;(3)过点(-1,1),且斜率为2的直线方程是211=+-x y ;(4)同垂直于x 轴的两条直线一定都和y 轴平行; (5)若直线的倾斜角为α,则πα≤≤0.其中为真命题的有_____________(填写序号)3,在三棱锥P-ABC 中,三侧棱两两垂直,且PB=PC=2PA,PO 垂直于面ABC,O 是垂足,如果设=PA a =PB b =c,请用a 、b 、c 表示P :_______________.4,椭圆12222=+b y a x (a >b >)0与直线1=+y x 交于P 、Q 两点,且OQ OP ⊥,其中O 为坐标原点.(1)求2211b a +的值;(2)若椭圆的离心率e 满足33≤ ≤22,求椭圆长轴的取值范围.5,椭圆上116922=+y x 一动点P 到两焦点距离之和为A .10B .8C .6D .不确定6,求与椭圆1244922=+y x 有公共焦点,且一条渐近线为xy 34=的双曲线的方7,向量a=(0,1,2),b=(1,0,-1),则数量积a •b= A .(1,1,1) B .0 C .-2 D .(0,0,-2)8,解关于x 的不等式).(02R a a x ax ∈<--9,已知P 是直线λ上一点,将直线 绕P 点逆时针方向旋转θ(20πθ<<)所得直线为1λ:0223=--y x .若继续绕P 点逆时针方向旋转θπ-2角,得直线2λ:01132=-+y x .求直线λ的方程.10,不论m 为何实数,直线(m-1)x -y+2m+1=0恒过定点_______________. 11,椭圆x 2+4y 2=16被直线y=x +1截得的弦长为 .12,椭圆的两个焦点恰好将长轴三等分,则椭圆的离心率是_____________.13,斜率为1的直线与抛物线x y =2只有一个公共点,这条直线的方程是______________.14,已知空间两点A (4,a ,-b ),B (a ,a ,2),则向量AB u u u r= A .(a-4,0,2+b ) B .(4-a ,0,-b-2)C .(0,a-4,2+b )D .(a-4,0,-b-2)15,三个数成等比数列,且它们的和为21,积是64.求这三个数.答案1, [解析]:设圆心坐标为0)r(r ),3,(001>半径为x x O ,则r=2002x r =⇒, 又2202)2(,22r x AB =+∴=22202020±=⇒=+⇒x x x ,2=∴r即圆的方程为:4)23()2(4)23()2(2222=-+-=+++y x y x 或.2, (2)3, c b a ρρρ616132++4, [解析]:设),(),,(2211y x P y x P ,由OP ⊥ OQ ⇔ x 1 x 2 + y 1 y 2 = 0 ①01)(2,1,121212211=++--=-=x x x x x y x y 代入上式得:Θ又将代入x y -=112222=+b y a x 0)1(2)(222222=-+-+⇒b a x a x b a ,,2,022221b a a x x +=+∴>∆Θ 222221)1(b a b a x x +-=代入①化简得 21122=+b a .(2) ,3221211311222222222≤≤⇒≤-≤∴-==a b a b a b a c e Θ又由(1)知12222-=a a b 26252345321212122≤≤⇒≤≤⇒≤-≤∴a a a ,∴长轴 2a ∈ [6,5].5, C6, 解:由椭圆标准方程1244922=+y x 可得的两者公共焦点为(-5,0)和(5,0),设双曲线的方程为)0,0(12222>>=-b a b y a x , 其渐近线为x a b y ±=, 现已知双曲线的一条渐近线为x y 34=,得34=a b ,又双曲线中2225=+b a ,解得4,3==b a ,∴双曲线的方程为1432222=-y x7, C8, [解析]:原不等式⇔0))((2<--a x a x . 分情况讨论(i )当a <0或a >1时,有a <a 2,此时不等式的解集为}|{2a x a x <<;(ii )当10<<a 时,有a 2<a ,此时不等式组的解集为};|{2a x a x << (iii )当a=0或a=1时,原不等式无解. 综上,当a <0或a >1时时,原不等式的解集为; 当时,原不等式的解集为当a=0或a=1时,原不等式的解集为φ.9, [解析]:由题意知点P 是1λ与2λ的交点,且2λλ⊥,则由 322023110x y x y --=⎧⎨+-=⎩ ⇒ 71x y =⎧⎨=-⎩,即P (7,-1),又2312=-=λλk k ,所以直线λ的方程为:)7(231-=+x y即02323=--y x .10, )3,2(-11, 538412, 1/3 13, 41+=x y14, A15, 解:设这三个数依次为a/q,a,aq 根据题意,有a/q+a+aq=21(4分)和64=⋅⋅aqaqa,解得:a=4,(8分)q=4或1/4这三个数依次为1,4,16或16,4,1。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2. 4线性回归方程测试题
一、选择题
1.下列关系属于线性负相关的是( ) A.父母的身高与子女身高的关系 B.身高与手长
C.吸烟与健康的关系
D.数学成绩与物理成绩的关系
答案:C
2.由一组数据1122()()()n n x y x y x y ,,,,,,得到的回归直线方程y bx a =+,那么下面说法不正确的是( )
A.直线y bx a =+必经过点()x y ,
B.直线y bx a =+至少经过点1122()()()n n x y x y x y ,,,,,,中的一个点
C.直线y bx a =+a 的斜率为
1
2
21
n
i i
i n
i
i x y
nx y
x
nx
==--∑∑ D.直线y bx a =+和各点1122()()()n n x y x y x y ,,,,,,的总离差平方和21
[()]n
i i i y bx a =-+∑是该
坐标平面上所有直线与这些点的离差平方和中最小的直线 答案:B 3.实验测得四组()x y ,的值为(12)(23)(34)(45),,,,,,,,则y 与x 之间的回归直线方程为( ) A.1y x =+ B.2y x =+ C.21y x =+
D.1y x =-
答案:A
4.为了考查两个变量x 和y 之间的线性关系,甲、乙两位同学各自独立作了10次和15次试验,并且利用线性回归方法,求得回归直线分别为l1,l2,已知两人所得的试验数据中,变量x 和y 的数据的平均值都相等,且分别是s t ,,那么下列说法正确的是( ) A.直线1l 和2l 一定有公共点()s t ,
B.直线1l 和2l 相交,但交点不一定是()s t , C.必有直线12l l ∥ D.1l 和2l 必定重合
答案:A
二、填空题
5.有下列关系:
(1)人的年龄与他(她)拥有的财富之间的关系
(2)曲线上的点与该点的坐标之间的关系
(3)苹果的产量与气候之间的关系
(4)森林中的同一种树木,其断面直径与高度之间的关系
(5)学生与他(她)的学号之间的关系
其中,具有相关关系的是.
答案:(1)(3)(4)
6.对具有相关关系的两个变量进行的方法叫做回归分析.用直角坐标系中的坐标分别表示具有的两个变量,将数据表中的各对数据在直角坐标系中描点得到的表示具有相关关系的两个变量的一组数据的图形,叫做.
答案:统计分析;相关关系;散点图
7.将一组数据同时减去3.1,得到一组新数据,若原数据的平均数、方差分别为2
x s
,,则新数据的平均数是,方差是,标准差是.
答案: 3.1
x-;2s;s
8.已知回归直线方程为 4.4838.19
y x
=+,则可估计x与y增长速度之比约为.
答案:5 22
三、解答题
9.某商店统计了近6个月某商品的进价x与售价y(单位:元)的对应数据如下:
求y对x的回归直线方程.
解:
3528912
6.5
6
x
+++++
==
∵,
46391214
8
6
y
+++++
==,
6
21
327i
i x
==∑,6
1
396i i i x y ==∑,
6
16
2
21
6 1.1436
i i
i i
i x y
xy b x
x
==-=
≈-∑∑∴,0.571a y bx =-=,
∴回归直线方程为 1.1430.571y x =+.
10.已知10只狗的血球体积及红血球的测量值如下:
45 4
2 4
6 4
8 4
2 6.53
6.30
9.25
7.580
6.99
35 5
8 4
0 3
9 50 5.90
9.49 6.20 6.55 7.72
x (血球体积,ml ),y (红血球数,百万)
(1)画出上表的散点图;
(2)求出y 对x 的回归直线方程并且画出图形 . 解:(1)见下图 (2)1
(45424648423558403950)44.510
x =
+++++++++=, 1
(6.53 6.309.257.50 6.99 5.909.49 6.20 6.557.72)7.24310
y =
+++++++++= 10
21
20183i
i x
==∑,10
1
3283.9i i i x y ==∑,
设回归直线方程为y bx a =+,
则12
21
0.1597n
i i
i n
i
i x y
nx y b x
nx
==-=
≈-∑∑,0.1364a y bx =-=.
图形如下: 11.某医院用光电比色计检验尿汞时,得尿汞含量(毫克/升)与消光系数如下表: 尿汞含量x :2 4 6 8 10 消光系数:y 64 134 205 285 360
(1)画出散点图;
(2)如果y 与x 之间具有线性相关关系,求回归直线方程; (3)估计尿汞含量为9毫克/升时的消光系数. 解: (1)
(2)由散点图可知y 与x 线性相关,设回归直线方程为y bx a =+.列表:
i
1 2 3 4 5 i x 2 4 6 8 10
i y
64
134 205 285 360 i i x y
1
28
536
1230
2280
3600
2
777456209.6
37.1522056b -⨯⨯=
=-⨯∴,
209.637.15613.3a =-⨯=-∴.
∴回归直线方程为37.1513.3y x =-.
(3)当9x =时,37.15913.3321.05y =⨯-=.。
