三角形的面积 练习题及答案 (2)
【小升初数学专项练习】《二、图形与几何6.三角形的周长与面积--基础(附答案)

小升初数学专项练习一线名师严选内容,逐一攻克☆基本概念、基本原理、基础技能一网打尽☆点拨策略思路,侧重策略指导,拓宽眼界思路☆6.三角形的周长与面积【小升初考点归纳】三角形的周长等于三边长度之和.三角形面积=底×高÷2.【经典例题】一.选择正确的答案,把序号填在括弧中(共9小题)1.(2019春•镇康县期中)把一根铁丝围成一个等腰三角形,它的两条邻边分别长16cm、6cm;如果把这根铁丝围成一个正方形,边长是()cm.A.7B.9.5C.7或9.5【解析】解:(16+16+6)÷4=38÷4=9.5(厘米)答:边长是9.5厘米.故选:B.2.(2018秋•黄冈期末)一个等腰直角三角形一条直角边的长是4厘米,它的面积是()平方厘米.A.16B.8C.4【解析】解:4×4÷2=16÷2=8(平方厘米)答:它的面积是8平方厘米,故选:B.3.(2018秋•龙泉驿区期末)把一个等腰梯形分成两个三角形,这两个三角形的()完全相同.A.面积B.周长C.形状D.前面三个都不正确【解析】解:把一个等腰梯形分成两个三角形,如右图:A:这两个三角形等高,但是底不相等,它们的面积不相等;B:一个三角形的周长是梯形的上底+梯形的腰长+对角线的长度;另一个三角形的周长是梯形的下底+梯形的腰长+对角线的长度;上底和下底不相等,所以它们的周长也不相同;C:一个是钝角三角形一个锐角三角形,它们的形状不同;故选:D.4.(2018秋•荔湾区期末)一个直角三角形如图(单位:cm),a是()cm.A.1.2B.2.4C.4.8D.6【解析】解::3×4÷2=6(cm2)6×2÷5=2.4(cm)答:a是2.4cm.故选:B.5.(2018秋•成都期末)一个直角三角形的两条直角边分别是3m和5m,它的面积是()A.18m2B.8m2C.7.5m2D.无法计算【解析】解:3×5÷2=15÷2=7.5(m2)答:它的面积是7.5m2.故选:C.6.(2018秋•西山区期末)一个三角形的底和高都扩大到原来的3倍,它的面积就扩大到原来的()倍.A.3B.6C.9D.27【解析】解:3×3=9答:它的面积就扩大到原来的9倍.故选:C.7.(2018秋•崂山区期末)一个三角形和一个平行四边形底相等,面积也相等,如果平行四边形的高是6厘米,那么三角形的高是()厘米.A.6B.3C.12D.18【解析】解:设三角形的高为H,平行四边形的高为h,三角形的面积=底×H×,平行四边形的面积=底×h;底×H×=底×h;则H=h,所以三角形的高=6×2=12(厘米);答:三角形的高是12厘米.故选:C.8.(2018秋•崂山区期末)图中平行四边形的面积是64cm2,涂有阴影的三角形面积是()cm2.A.16B.32C.128【解析】解:64÷2=32(平方厘米);答:涂有阴影的三角形面积是32cm2.故选:B.9.(2018秋•盘龙区期末)一个等腰直角三角形的一条直角边是5cm,它的面积是()A.25cm2B.12.5cm2C.50cm2D.无法确定【解析】解:5×5÷2,=25÷2,=12.5(平方厘米),答:它的面积是12.5平方厘米,故选:B.二.将正确答案填写在横线上(共11小题)10.(2019春•庆云县期中)等腰三角形的两条边长分别是3cm和6cm,则它的周长是15cm.【解析】解:因为3+3=6,所以3不能是等腰三角形等腰,只能是底边,所以这个等腰三角形的腰是6厘米,底是3厘米,6+6+3=12+3=15(cm)答:则它的周长是15cm.故答案为:15cm.11.(2018秋•黄冈期末)一个三角形的面积是130平方厘米,与它等底等高的平行四边形的面积是260平方厘米.【解析】解:130×2=260(平方厘米)答:与它等底等高的平行四边形的面积是260平方厘米.故答案为:260.12.(2018秋•黄冈期末)一个三角形的面积是30平方分米,底是7.5分米,它的高是8分米.【解析】解:30×2÷7.5=60÷7.5=8(分米)答:它的高是8分米.故答案为:8.13.(2018秋•中山市期末)一个直角三角形两条直角边分别是7厘米和9厘米,这个三角形斜边上对应的高是6.3厘米,它的斜边长为10厘米.【解析】解:设它的斜边长为x厘米,6.3x÷2=7×9÷26.3x=63x=10答:它的斜边长为10厘米.故答案为:10.14.(2018秋•黄埔区期末)一个三角形的面积是16cm2,其中一个底是8cm,这个底上的高是4cm,用两个这样的三角形拼成的平行四边形的面积是32cm2.【解析】解:16×2÷8=32÷8=4(厘米)16×2=32(平方厘米)答:这个底上的高是4cm,用两个这样的三角形拼成的平行四边形的面积是32cm2.故答案为:4,32.15.(2019•福田区)一个三角形的底是16厘米,高是10厘米,三角形的面积是80厘米2;与它等底等高的平行四边形的面积是160厘米2.【解析】解:三角形的面积:16×10÷2=160÷2=80(厘米2)平行四边形的面积:80×2=160(厘米2)答:三角形的面积是80厘米2,与它等底等高的平行四边形的面积是160厘米2.故答案为:80;160.16.(2018秋•南通期末)一个三角形的面积是200平方米,高是20米,底是20米,与它等底等高的平行四边形面积是400平方米.【解析】解:(1)200×2÷20=400÷20=20(米)答:底是20米.(2)200×2=400(平方米)答:与它等底等高的平行四边形的面积是400平方米.故答案为:20,400.17.(2018秋•龙泉驿区期末)三角形的底是1.25分米,这条底对应的高是1.6分米,与这个三角形等底等高的平行四边形的面积是2平方分米.【解析】解:1.25×1.6=2(平方分米)答:与这个三角形等底等高的平行四边形的面积是2平方分米.故答案为:2.18.(2018秋•成都期末)一个等腰三角形的两条直角边的长度和是20cm,它的面积是50 cm2.【解析】解:20÷2=10(cm)10×10÷2=100÷2=50(cm2)答:它的面积是50cm2.故答案为:50.19.(2018秋•台安县期末)一块三角形草坪面积是96平方米,底是16米,高是12米.【解析】解:96×2÷16=192÷16=12答:高是12米.故答案为:12.20.(2018秋•成华区期末)读图可知:三角形通过割补转化成了平行四边形.原三角形的高是平行四边形高的2倍,平行四边形与三角形的底相等.【解析】解:读图可知:三角形通过割补转化成了平行四边形.原三角形的高是平行四边形高的2倍,平行四边形与三角形的底相等.故答案为:2倍,相等.三.解析题(共5小题)21.(2019•虹口区模拟)一块三角形的交通标志牌(如右图),它的面积大约是28平方分米,底是8分米,高大约是7分米.【解析】解:28×2÷8,=56÷8,=7(分米);故答案为:7.22.(2018•杭州模拟)我们都知道,三角形面积的计算公式是“底×高÷2”.那么,为什么要“÷2”呢?请写一写或画一画的方式,把你的想法表达出来.【解析】解:用两个完全相同的三角形拼成一个平行四边形,因为平行四边形的面积=底×高,而平行四边形的一半为三角形,所以要“÷2“.23.(2017秋•宁都县期末)图中三角形的面积是12平方厘米,(1)求出它的高;(2)把它分成甲乙两个小三角形,使甲三角形的面积是乙三角形的2倍.【解析】解:12×2÷6=24÷6=4(厘米)6×=4(厘米)6﹣4=2(厘米)如图所示:24.(2018春•南开区期末)在图中,BC∥DE,∠1=63.5°,AE=EC.(1)∠2+∠3=116.5°.(2)∠1+∠3+∠4+∠5=243.5°.(3)若梯形BCED的面积是3.6cm2,则三角形ABC的面积是 4.8cm2.【解析】解:(1)因为BC∥DE,所以∠3=∠CDE,∠2+∠3=∠2+∠CDE=∠ADC,又因为∠1=63.5°,所以,∠ADC=180°﹣63.5°=116.5°.即:∠2+∠3=116.5°(2)∠1+∠3+∠4+∠5=∠1+∠CDE+∠4+∠5,因为∠CDE+∠4+∠5正好是三角形DCE的内角和=180°,所以:∠1+∠3+∠4+∠5=63.5°+180°=243.5°(3)因为E为AC的中点,BC∥DE,所以:D是AB的中点,三角形ADE的面积=三角形DCE的面积,三角形ADC的面积=三角形BDC的面积,设三角形DEC的面积为x平方厘米,则:三角形BDC的面积=三角形ADC的面积=2x=3.6﹣x,所以:x=1.2,三角形ABC的面积=(1.2+1.2)×2=4.8(平方厘米)故答案为:(1)116.5°,(2)243.5°,(3)4.825.(2018春•长沙期中)一根长6分米的铁丝.围绕如图一周够吗?【解析】解:17+23+17=40+17=57(厘米)6分米=60厘米,60厘米>57厘米,所以6分米围绕图形一周够.答:围绕如图一周够.。
中考数学复习专题-【三角形的面积】填空题考点专练(二)(解析版)

2021年中考数学复习专题-【三角形的面积】填空题考点专练(二)1.如图,△ABC中,D是AB的中点,且AE:CE=3:1,S△CEP=1,则S△BPC=.2.如图,EM=6,EF=4,EN=10,且F为MN边上的中点,则△EMN的面积为.3.一个三角形的面积为平方米,一条边长为米,则这条边上的高为米.4.如图,在△ABC中,点D、E分别是BC、AD边的中点,且S△ABC=8cm2,则S△ABE =cm2.5.如图,点D是△ABC的边BC上任意一点,点E、F分别是线段AD、CE的中点,且△ABC的面积为36cm2,则△BEF的面积=.6.如图,△ABC两边的中线BE,CF相交于点G,若S△ABC=10,则图中阴影部分面积是.7.若D、E分别是BC、AD的中点,且S△ABC=10,则S△AEC=.8.如图,D、E分别是△ABC的AC,AB边上的点,BD,CE相交于点O,若S△OCD=1,S△OBE=2,S△OBC=3,那么S四边形ADOE=.9.一块三角形的菜地,一边为米,三角形面积是16平方米,则这条边上的高是米.10.在平面直角坐标系中,A(﹣2,0),B(﹣1,2),C(1,0),连接AB,点D为AB的中点,连接OB交CD于点E,则四边形DAOE的面积为.11.如图,在△ABC中,CD是中线.若S△ACD=5,则S△ABC的值是.12.如图,四边形ABCD中,E、F、G、H依次是各边的中点,O是四边形ABCD内一点,若四边形AEOH、四边形BFOE、四边形CGOF的面积分别为10、12、14,则四边形DHOG的面积=.13.如图,已知点D、E、F分别是BC、AD、BE的中点,S△ABC=4,则S△EFC=.14.已知点A(﹣1,0),点B(2,0),在y轴上存在一点C,使三角形ABC面积为6,则C点坐标为.15.如图,在4×4的正方形网格中,每个小正方形的边长都是1,A、B两点在格点上,点C也是该网格中的格点,那么使△ABC的面积为1的点C的个数有个.16.如图,在△ABC中,点E是AC边上的点,且AE=EC,点D是BC边上的点,且BD=CD,AD与BE相交于点F,若四边形CDFE的面积是15,则△ABC的面积为.17.如图,每个小正方形边长均为1,则下列图中的三角形(阴影部分)与图中△ABC面积相等的是.18.平面直角坐标系中,已知点A(2,5)和点B(3,0),点C在x轴上,若△ABC的面积等于10,则点C的坐标为.19.如图,在四边形ABCD中,连接AC和BD,若AC=BC,BD=2AD,∠DAC=∠DBC=45°,△ADC的面积为30,则BD=.20.如图所示,将△ABC沿BC方向平移得到△DEF,若BC=a,且△ABC面积是四边形ABFD面积的.则平移的距离为.(用含a的代数式表示)参考答案1.解:连接PA,∵D是AB的中点,∴S△ADC=S△BCD,S△PAD=S△PBD,∴S△BPC=S△APC,∵AE:CE=3:1,S△CEP=1,∴S△AEP=3S△CEP=3,∴S△APC=4,∴S△BPC=4,故答案为4.2.解:延长EF至A,使AF=EF=4,连接AN,如图所示:则AE=AF+EF=8,∵F为MN边上的中点,∴FN=FM,在△ANF和△EMF中,,∴△ANF≌△EMF(SAS),∴∠A=∠MEF,AN=EM=6,∵AN=6,AE=8,EN=10,∴AN2+AE2=EN2,∴△AEN是直角三角形,∠A=90°,∴∠MEF=90°,∴△EMN的面积=EM×EF=×6×4=12,故答案为:12.3.解:这条边上的高为,故答案为:.4.解:∵点D、E分别是BC、AD边的中点,∴S△ABD=S△ABC,S△ABE=S△ABD,∴S△ABE=S△ABC,∵S△ABC=8cm2,∴S△ABE=8×=2(cm2),故答案为:2.5.解:∵AE=DE,∴S△BDE=S△ABE,S△CDE=S△ACE,∴S△BDE=S△ABD,S△CDE=S△ACD,∴S△BCE=S△ABC=×36=18(cm2);∵EF=CF,∴S△BEF=S△BCF,∴S△BEF=S△BCE=×18=9(cm2),即△BEF的面积是9cm2,故答案为:9cm2.6.解:连接AG并延长交BC于D,则AD为△ABC的中线,∵△ABC的三条中线AD、BE,CF交于点G,∴S△CGE=S△AGE=S△ACF,S△BGF=S△BGD=S△BCF,∵S△ACF=S△BCF=S△ABC=×10=5,∴S△CGE=S△ACF=×5=,S△BGF=S△BCF==,∴S阴影=S△CGE+S△BGF=.故答案为:.7.解:∵AD是△ABC的BC边上的中线,∴S△ADC=S△BDC=S△ABC=5,∵CE是△ADC的AD边上的中线,∴S△AEC=S△ADC=2.5,故答案为2.5.8.解:连接DE,因为=,=,将已知数据代入可得S△DOE=,设S△ADE=x,则由==,==,得方程=,解得:x=,所以四边形ADOE的面积=x+=.故四边形ADOE的面积是.故答案为:.9.解:这条边上的高为=112米,故答案为:112.10.解:如图,∵A(﹣2,0),B(﹣1,2),D是AB中点,∴D(﹣,1),∵C(1,0),∴直线CD的解析式为y=﹣x+,直线OB的解析式为y=﹣2x,由,解得,∴E(﹣,),∴S四边形DAOE=S△ADC﹣S△EOC=×3×1﹣×1×=,故答案为.11.解:∵CD是中线,∴AD=BD,∴S△ACD=S△BDC=5,∴S△ABC=S△ACD+S△BDC=5+5=10,故答案为10.12.解:连接OC,OB,OA,OD,∵E、F、G、H依次是各边中点,∴△AOE和△BOE等底等高,所以S△OAE=S△OBE,同理可证,S△OBF=S△OCF,S△ODG=S△OCG,S△ODH=S△OAH,∴S四边形AEOH+S四边形CGOF=S四边形DHOG+S四边形BFOE,∵S四边形AEOH=10,S四边形BFOE=12,S四边形CGOF=14,∴10+14=12+S四边形DHOG,解得,S四边形DHOG=12.故答案为:12.13.解:∵点D是BC的中点,∴S△ABD=S△ACD=S△ABC,∵点E是AD的中点,∴S△BDE=S△CDE=S△ACD,∴S△BCE=S△BDE+S△CDE=(S△ABD+S△ACD)=S△ABC,∵点F是BE的中点,∴S△EFC=S△BCE=×S△ABC=×4=1.故答案为1.14.解:设点C的坐标是(0,y).∵点A(﹣1,0),点B(2,0),∴AB=3,又∵三角形ABC面积为6,∴6=AB•|y|=×3•|y|,解得,y=±4,∴点C的坐标是(0,±4).故答案是:(0,±4).15.解:如图,使△ABC的面积为1的点C共有4个.故答案为:4.16.解:作DH∥BE交AC于H.∵BD=CD,DH∥BE,∴EH=CH,∵AE=EC,∴AE:EH:HC=1:1:2,AH=HC,设S△DHC=2m,则S△ADH=2m,∵EF∥DH,AE=EH=AH,∴△AFE∽△ADH,∴=,∴S△AEF=m,S四边形EFDC=2m﹣m+2m=m=15,∴m=,∴S△ADC=4m=,∵BD=CD,∴S△ABD=,∴S△ABC=S△ABD+S△ADC=,故答案为.17.解:△ABC面积是:=1.A、该三角形的面积是:=1,与图中△ABC面积相等.B、该三角形的面积是:=,与图中△ABC面积不相等.C、该三角形的面积是:=,与图中△ABC面积不相等.D、该三角形的面积是:=2,与图中△ABC面积不相等.故答案是:A.18.解:∵A(2,5)、B(3,0),△ABC的面积等于10,则△ABC的面积=BC•y A=BC×5=10,解得BC=4,所以点C的坐标为(7,0)或(﹣1,0).故答案为:(7,0)或(﹣1,0).19.解:过D作DE⊥AC于E,DF⊥BC于F,∵∠DAC=∠DBC=45°,∴△ADE与△BDF是等腰直角三角形,∴△ADE∽△BDF,∴==,∵∠DAC=∠DBC=45°,∴A,B,C,D四点共圆,∴∠ABD=∠ACD,∠BAC=∠BDC,∵AC=BC,∴∠CAB=∠CBA,∴∠CBA=∠BDC,∵∠ABD=∠ABC﹣45°,∠CDF=∠BDC﹣45°,∴∠ABD=∠CDF,∴∠CDF=∠DCE,∵∠DEC=∠CFD=90°,CD=DC,∴△CDE≌△DCF(AAS),∴DF=CE,∴CE=DF=2DE,设AE=DE=x,则CE=DF=2x,∴AC=3x,∵△ADC的面积为30,∴AC•DE=×3x•x=30,∴x=2,∴DF=2x=4,∴BD=DF=4.故答案为:4.20.解:△ABC沿BC方向平移得到△DEF,得四边形ABED是平行四边形、四边形ABFD是梯形,△ABC与梯形ABFD等高.设平移距离是x,△ABC的BC边上的高为h,∴AD=BE=x,BC=EF=a由题意,得S△ABC=S梯形ABFD,即ah=×(x+a+x)•h∴a=(2x+a)解得x=a.故答案为a.。
苏教版五年级数学上册第二单元2-3《三角形面积的计算练习课》说课稿

苏教版五年级数学上册第二单元2-3《三角形面积的计算练习课》说课稿一. 教材分析苏教版五年级数学上册第二单元2-3《三角形面积的计算练习课》这一节课,是在学生已经掌握了三角形面积的计算公式的基础上进行的一节练习课。
目的是让学生通过练习,加深对三角形面积计算公式的理解,提高计算能力,培养学生的逻辑思维能力和解决问题的能力。
教材中安排了多个不同类型的练习题,包括填空题、选择题、计算题和应用题,涵盖了三角形面积计算公式的各个方面。
这些练习题既有基础知识的巩固,也有对学生解决问题能力的培养。
二. 学情分析五年级的学生已经学习过三角形面积的计算公式,对本节课的内容有一定的了解。
但学生在运用公式解决实际问题时,可能会因为对公式的理解不深,而导致计算错误。
因此,在教学过程中,我需要引导学生深化对公式的理解,提高计算的准确性。
三. 说教学目标1.知识与技能目标:让学生掌握三角形面积的计算方法,能够准确计算三角形的面积。
2.过程与方法目标:通过练习,培养学生的逻辑思维能力和解决问题的能力。
3.情感态度与价值观目标:激发学生学习数学的兴趣,培养学生的自主学习能力。
四. 说教学重难点1.教学重点:三角形面积的计算方法。
2.教学难点:对三角形面积计算公式的理解,以及运用公式解决实际问题。
五. 说教学方法与手段在本节课的教学中,我将采用引导发现法、练习法、小组合作学习法等教学方法。
通过引导学生自主探究、合作交流,发现三角形面积的计算方法,提高学生的逻辑思维能力和解决问题的能力。
同时,运用多媒体教学手段,为学生提供丰富的学习资源,提高教学效果。
六. 说教学过程1.复习导入:通过复习三角形面积的计算公式,为学生进入本节课的学习做好铺垫。
2.自主探究:让学生独立完成教材中的练习题,巩固对三角形面积计算公式的理解。
3.合作交流:学生分组讨论,分享解题心得,互相学习,提高解决问题的能力。
4.教师讲解:针对学生练习中出现的问题,进行讲解,引导学生深化对公式的理解。
小学数学冀教版第九册多边形的面积三角形的面积-章节测试习题(2)

6×1÷2=a×1,
6÷2=a
a=3.
平行四边形的底是3厘米。
3.【答题】图中两个阴影部分的面积相比a()b.
A.大于B.小于C.等于
【答案】C
【分析】根据三角形的面积公式,知道等底等高的两个三角形面积相等,据此解答.
【解答】两个三角形的面积等底等高,所以它们的面积相等.选C.
【答案】B
【分析】根据三角形的面积=底×高÷2可知:等底等高的三角形面积相等;据此解答.
【解答】因为三角形的面积=底×高÷2,如果两个三角形等底等高,那么这两个三角形面积相等.选B.
7.【题文】求阴影部分面积(单位:厘米).
【答案】48平方厘米
【分析】阴影的部分的面积等于平行四边形的面积减去空白三角形的面积,根据平行四边形的面积=底×高,三角形的面积=底×高÷2,把数据代入公式求出它们的面积差即可.
【解答】解:(1)如图所示:
红色垂线段即为平行四边形A点到BC边上的高;
(2)以高为一条直角边,AD为另一条直角边画出的三角形最大,因为平行四边形和三角形是等底等高的;所以三角形面积= ah,平行四边形面积=ah,则这个三角形的面积是这个平行四边形面积的 。
15.【答题】一个三角形面积是30平方厘米,高是5厘米,底是()厘米.
【答案】30
【分析】根据三角形的面积是与它等底等高的平行四边形的面积的一半,所以三角形的面积就是比平行四边形的面积少的那部分,所以三角形的面积为30平方厘米.
【解答】根据分析可知,这个三角形的面积是30平方厘米.故此题的答案是30.
20.【答题】图中平行四边形的面积是64cm2,那么涂有阴影三角形的面积是()cm2.
【解答】图见答案,
小学数学《三角形的等积变形》练习题(含答案)

内容概述
我们已经知道三角形面积的计算公式:三角形面积=底×高÷2
从这个公式我们可以发现:三角形面积的大小,取决于三角形底和高的乘积.
如果三角形的底不变,高越大(小),三角形面积也就越大(小);
如果三角形的高不变,底越大(小),三角形面积也就越大(小);
这说明当三角形的面积变化时,它的底和高之中至少有一个要发生变化.但是,当三角形的底和高同时发生变化时,三角形的面积不一定变化.比如当高变为原来的3倍,底变为原来的1/3,则三角形面积与原来的一样。这就是说:一个三角形的面积变化与否取决于它的高和底的乘积,而不仅仅取决于高或底的变化.同时也告诉我们:一个三角形在面积不改变的情况下,可以有无数多个不同的形状.
于是:三角形ABD的面积=12×高÷2=6×高
三角形ABC的面积=(12+4)×高÷2=8×高
三角形ADC的面积=4×高÷2=2×高
所以,三角形ABC的面积是三角形ABD面积的4/3倍;三角形ABD的面积是三角形ADC面积的3倍。
巩固理解结论:两个三角形等高时,面积的倍数=底的倍数
【例2】如右图,E在AD上,AD垂直BC,AD=12厘米,DE=3厘米。
【例6】如右图所示,在平行四边形ABCD中,E为AB的中点,AF=2CF,三角形AFE(图中阴影部分)的面积为8平方厘米.平行四边形的面积是多少平方厘米?
【例7】图中△AOB的面积为15cm2,线段OB的长度为OD的3倍,求梯形ABCD的面积.
【例8】(北京市第一届“迎春杯”刊赛)如右图.将三角形ABC的BA边延长1倍到D,CB边延长2倍到E,AC边延长3倍到F.如果三角形ABC的面积等于l,那么三角形DEF的面积是?
例题精讲
五年级数学上册第二单元:三角形面积的实际应用专项练习(解析版)苏教版

2022-2023学年五年级数学上册典型例题系列之第二单元:三角形面积的实际应用专项练习(解析版)1.一个三角形的面积是15平方米,它的底是10米,则它的高是多少米?【答案】3米【分析】三角形的面积=底×高÷2,据此用三角形的面积乘2,再除以底即可求出高。
【详解】15×2÷10=30÷10=3(米)答:它的高是3米。
【点睛】本题考查三角形的面积。
牢记并灵活运用三角形的面积公式是解题的关键。
2.一块三角形地的底是10米,高是6米,一共收蔬菜960千克。
这块地平均每平方米收蔬菜多少千克?【答案】32千克【分析】根据三角形的面积公式:底×高÷2,把数代入公式即可求出三角形地的面积,由于一共收蔬菜960千克,用收蔬菜的质量除以三角形地的面积即可求解。
【详解】10×6÷2=60÷2=30(平方米)960÷30=32(千克)答:这块地平均每平方米收蔬菜32千克。
【点睛】本题主要考查三角形的面积公式,熟练掌握三角形的面积公式并灵活运用。
3.三角形的面积是216平方厘米,底是24厘米。
底边上的高是多少厘米?【答案】18厘米【分析】根据三角形面积公式:三角形面积=底×高÷2;高=三角形面积×2÷底,代入数据,即可解答。
【详解】216×2÷24=432÷24=18(厘米)答:底边上的高是18厘米。
【点睛】本题考查三角形面积公式的应用,关键是熟记公式,灵活运用。
4.一块三角形麦田,底长80米,高60米,如果每公顷收小麦5吨,这块地能收小麦多少吨?【答案】1.2吨【分析】根据三角形面积公式:底×高÷2,求出这块三角形麦田的面积;1公顷=10000平方米,把平方米化成公顷,再乘5,就是这块地能收小麦的吨数。
【详解】80×60÷2=4800÷2=2400(平方米)2400平方米=0.24公顷0.24×5=1.2(吨)答:这块地能收小麦1.2吨。
五年级上册数学试题-6、2 三角形的面积练习卷及答案-人教版
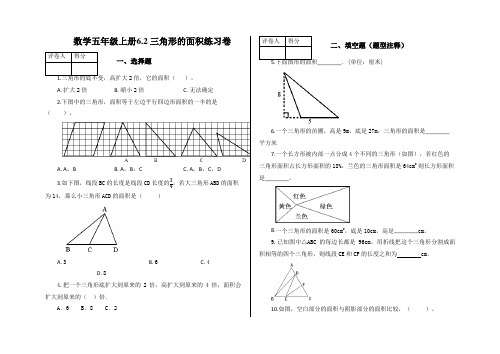
数学五年级上册6.2 三角形的面积练习卷一、选择题2倍,它的面积( )。
A. 扩大2倍B. 缩小2倍C. 无法确定2.下图中的三角形,面积等于左边平行四边形面积的一半的是( )。
A. A ,BB. A ,B ,CC. A ,B ,C ,D3.如下图,线段BC 的长度是线段CD 长度的34,若大三角形ABD 的面积为14,那么小三角形ACD 的面积是( )A. 3B. 6C. 4D. 84.把一个三角形底扩大到原来的2倍,高扩大到原来的4倍,面积会扩大到原来的( )倍.A .6B .8C .2二、填空题(题型注释)________.(单位:厘米)6.一个三角形的苗圃,高是9m ,底是27m ,三角形的面积是________平方米7.一个长方形被内部一点分成4个不同的三角形(如图),若红色的三角形面积占长方形面积的18%,兰色的三角形面积是64cm 2 则长方形面积是________。
8.一个三角形的面积是60cm 2,底是10cm,高是________cm。
9.已知图中△ABC 的每边长都是96cm ,用折线把这个三角形分割成面积相等的四个三角形,则线段CE 和CF 的长度之和为 cm .10.如图,空白部分的面积与阴影部分的面积比较,( )。
A. 空白部分面积大B. 阴影部分面积大C. 空白部分和阴影部分面积相等D. 无法确定三、解答题(题型注释)120m,160m,200m,一共产小麦6720kg,这块麦田平均每平方米产小麦多少千克?12.如下图,在三角形ABC中,DC=2BD,CE=3AE,阴影部分的面积是20平方厘米,求三角形ABC的面积。
13.有一块三角形菜地的面积是24平方米,底是120分米,高是多少米?14.先测量下面各图形的底和高,再分别算出它们的面积。
(精确到毫米。
)(1)底________高________面积________(2)底________高________面积________15.一个三角形(如图)(1)量出∠A的度数.∠A=________°(2)过A点画出底边BC上的高,在测量并标出底和高的长度.(取整厘米数)(3)与这个三角形底边等高的平行四边形的面积是________平方厘米.四、判断题等.(_____)17.图中的长方形中的甲与乙两个三角形比较,甲比乙大.(____)18.如下图的周长是4厘米.(____)19.三角形面积是与它等底等高的平行四边形面积的一半。
五年级上册数学试题-一课一练-第6单元第2课时《三角形的面积》(含答案及解析)|人教新课标

第6单元第2课时《三角形的面积》同步练习一、精挑细选。
1、一个三角形的底是4分米,高是2分米,它的面积是().A.2平方分米B.4平方分米C.1平方分米D.4分米2、在如图两条平行线间,三角形ABC、三角形DBC和三角形EBC的面积()A.相等B.不相等 C.无法确定3、两个同底等高的三角形,它们的()一定相等.A.形状B.面积C.周长4、一个三角形的高是6分米,面积是30平方分米,底是().A.6分米 B.12分米C.10分米D.5分米5、一个直角三角形的三条边分别是3厘米、4厘米、5厘米,这个直角三角形的面积是().A.10平方厘米B.7.5平方厘米C.12平方厘米 D.6平方厘米6、如图有甲乙丙三个面积相等的平行四边形,它们阴影部分的面积相比较().A.甲大B.乙大C.丙大D.相等7、一个三角形的底不变,如果高扩大4倍,那么它的面积().A.扩大4倍 B.扩大2倍 C.无法确定8、一个平行四边形的面积比与它等底等高的三角形面积大28平方厘米,则三角形的面积是()平方厘米.A.28 B.14 C.42 D.569、三角形斜边上的高是()厘米.A.20 B.24 C.2810、如图,梯形ABCD中共有8个三角形,其中面积相等的三角形有().A.1对 B.2对 C.3对 D.4对二、填一填、我最棒。
1、三角形的底是5分米,高是4分米.和它等底等高的平行四边形的面积是 .2、一个三角形与一个平行四边形的底和面积分别相等,已知三角形的高是6厘米.平行四边形的高是厘米.3、一个三角形,它的面积是24平方厘米,底是8厘米,高是厘米.4、把三角形的底和高都扩大到原来的3倍,则三角形的面积扩大到原来的倍.5、一个等边三角形的周长是12厘米,高是3.46厘米,它的面积是厘米².三、计算下面三角形的面积。
(1)(2)(3)四、解答题。
1、如图平行四边形的面积是36平方米,求阴影部分的面积.(单位:米)2、求阴影部分的面积(单位:cm)五、应用题。
新初中数学三角形基础测试题含答案解析(2)

新初中数学三角形基础测试题含答案解析(2)一、选择题1.如图,赵爽弦图是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形两条直角边长分别为a和b.若8ab ,大正方形的边长为5,则小正方形的边长为()A.1 B.2 C.3 D.4【答案】C【解析】【分析】由题意可知:中间小正方形的边长为a﹣b,根据勾股定理以及题目给出的已知数据即可求出小正方形的边长.【详解】解:由题意可知:中间小正方形的边长为:a﹣b,∵每一个直角三角形的面积为:12ab=12×8=4,∴根据4×12ab+(a﹣b)2=52=25,得4×4+(a﹣b)2=25,∴(a﹣b)2=25﹣16=9,∴a﹣b=3(舍负),故选:C.【点睛】本题考查勾股定理,解题的关键是熟练运用勾股定理以及完全平方公式,本题属于基础题型.2.如图,已知△ABC是等腰直角三角形,∠A=90°,BD是∠ABC的平分线,DE⊥BC于E,若BC=10cm,则△DEC的周长为()A.8cm B.10cm C.12cm D.14cm【答案】B【分析】根据“AAS”证明ΔABD≌ΔEBD .得到AD=DE,AB=BE,根据等腰直角三角形的边的关系,求其周长.【详解】∵BD是∠ABC的平分线,∴∠ABD=∠EBD.又∵∠A=∠DEB=90°,BD是公共边,∴△ABD≌△EBD (AAS),∴AD=ED,AB=BE,∴△DEC的周长是DE+EC+DC=AD+DC+EC=AC+EC=AB+EC=BE+EC=BC=10 cm.故选B.【点睛】本题考查了等腰直角三角形的性质,角平分线的定义,全等三角形的判定与性质. 掌握全等三角形的判定方法(即SSS、SAS、ASA、AAS和HL)和全等三角形的性质(即全等三角形的对应边相等、对应角相等)是解题的关键.3.如图,在▱ABCD中,E为边AD上的一点,将△DEC沿CE折叠至△D′EC处,若∠B=48°,∠ECD=25°,则∠D′EA的度数为()A.33°B.34°C.35°D.36°【答案】B【解析】【分析】由平行四边形的性质可得∠D=∠B,由折叠的性质可得∠D'=∠D,根据三角形的内角和定理可得∠DEC,即为∠D'EC,而∠AEC易求,进而可得∠D'EA的度数.【详解】解:∵四边形ABCD是平行四边形,∴∠D=∠B=48°,由折叠的性质得:∠D'=∠D=48°,∠D'EC=∠DEC=180°﹣∠D﹣∠ECD=107°,∴∠AEC=180°﹣∠DEC=180°﹣107°=73°,∴∠D'EA=∠D'EC﹣∠AEC=107°﹣73°=34°.【点睛】本题考查了平行四边形的性质、折叠的性质、三角形的内角和定理等知识,属于常考题型,熟练掌握上述基本知识是解题关键.4.如图,已知AB∥CD,直线AB,CD被BC所截,E点在BC上,若∠1=45°,∠2=35°,则∠3=()A.65°B.70°C.75°D.80°【答案】D【解析】【分析】由平行线的性质可求得∠C,在△CDE中利用三角形外的性质可求得∠3.【详解】解:∵AB∥CD,∴∠C=∠1=45°,∵∠3是△CDE的一个外角,∴∠3=∠C+∠2=45°+35°=80°,故选:D.【点睛】本题主要考查平行线的性质,掌握平行线的性质和判定是解题的关键,即①两直线平行⇔同位角相等,②两直线平行⇔内错角相等,③两直线平行⇔同旁内角互补,④a∥b,b ∥c⇒a∥c.5.如图,在菱形ABCD中,AB=10,两条对角线相交于点O,若OB=6,则菱形面积是()A.60 B.48 C.24 D.96【答案】D【解析】【分析】由菱形的性质可得AC⊥BD,AO=CO,BO=DO=6,由勾股定理可求AO的长,即可求解.【详解】解:∵四边形ABCD是菱形,∴AC⊥BD,AO=CO,BO=DO=6,∴AO=22100368AB OB-=-=,∴AC=16,BD=12,∴菱形面积=12162⨯=96,故选:D.【点睛】本题考查了菱形的性质,勾股定理,掌握菱形的对角线互相垂直平分是本题的关键.6.五根小木棒,其长度分别为7,15,20,24,25,现将它们摆成两个直角三角形,如图,其中正确的是()A.B.C.D.【答案】C【解析】【分析】欲求证是否为直角三角形,这里给出三边的长,只要验证两小边的平方和等于最长边的平方即可.【详解】A、72+242=252,152+202≠242,(7+15)2+202≠252,故A不正确;B、72+242=252,152+202≠242,故B不正确;C、72+242=252,152+202=252,故C正确;D、72+202≠252,242+152≠252,故D不正确,故选C.【点睛】本题考查勾股定理的逆定理的应用.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.勾股定理的逆定理:若三角形三边满足a2+b2=c2,那么这个三角形是直角三角形.7.如图,在ABC ∆中,AB 的垂直平分线交BC 于D ,AC 的中垂线交BC 于E ,20DAE ∠=o ,则BAC ∠的度数为( )A .70oB .80oC .90oD .100o【答案】D【解析】【分析】 根据线段垂直平分线的性质得到DA=DB,EA=EC,在由等边对等角,根据三角形内角和定理求解.【详解】如图所示:∵DM 是线段AB 的垂直平分线,∴DA=DB,B DAB ∠=∠ ,同理可得:C EAC ∠=∠ ,∵ 20DAE ∠=o ,180B DAB C EAC DAE ︒∠+∠+∠+∠+∠=,∴80DAB EAC ︒∠+∠=∴100BAC ︒∠=故选:D【点睛】本题考查了线段的垂直平分线和三角形的内角和定理,解题的关键是掌握线段垂直平分线上的点到线段两端的距离相等.8.如图,在Rt ABC ∆中,90BCA ∠=︒,CD 是高,BE 平分∠ABC 交CD 于点E ,EF ∥AC 交AB 于点F ,交BC 于点G .在结论:(1) EFD ∠=BCD ∠;(2) AD CD =;(3)CG EG =;(4) BF BC =中,一定成立的有( )A .1个B .2个C .3个D .4个【答案】B【解析】【分析】 根据两直线平行,同旁内角互补求出∠CGE=∠BCA=90°,然后根据等角的余角相等即可求出∠EFD=∠BCD ;只有△ABC 是等腰直角三角形时AD=CD ,CG=EG ;利用“角角边”证明△BCE 和△BFE 全等,然后根据全等三角形对应边相等可得BF=BC .【详解】∵EF ∥AC ,∠BCA=90°,∴∠CGE=∠BCA=90°,∴∠BCD+∠CEG=90°,又∵CD 是高,∴∠EFD+∠FED=90°,∵∠CEG=∠FED (对顶角相等),∴∠EFD=∠BCD ,故(1)正确;只有∠A=45°,即△ABC 是等腰直角三角形时,AD=CD ,CG=EG 而立,故(2)(3)不一定成立,错误;∵BE 平分∠ABC ,∴∠EBC=∠EBF ,在△BCE 和△BFE 中,EFD BCD EBC EBF BE BE ∠∠∠∠⎧⎪⎨⎪⎩===,∴△BCE ≌△BFE (AAS ),∴BF=BC ,故(4)正确,综上所述,正确的有(1)(4)共2个.故选:B .【点睛】本题主要考查了角平分线的性质,全等三角形的判定与性质,直角三角形的性质,等腰直角三角形的性质,综合题,但难度不大,熟记性质是解题的关键.9.把一副三角板如图(1)放置,其中∠ACB =∠DEC =90°,∠A =45°,∠D =30°,斜边AB =4,CD =5.把三角板DCE 绕着点C 顺时针旋转15°得到△D 1CE 1(如图2),此时AB 与CD 1交于点O ,则线段AD 1的长度为( )A .13B .5C .22D .4【答案】A【解析】 试题分析:由题意易知:∠CAB=45°,∠ACD=30°.若旋转角度为15°,则∠ACO=30°+15°=45°.∴∠AOC=180°-∠ACO-∠CAO=90°.在等腰Rt △ABC 中,AB=4,则AO=OC=2.在Rt △AOD 1中,OD 1=CD 1-OC=3,由勾股定理得:AD 1=13.故选A.考点: 1.旋转;2.勾股定理.10.如图,直线a b ∥,点A 、B 分别在直线a 、b 上,145∠︒=,若点C 在直线b 上,105BAC ∠︒=,且直线a 和b 的距离为3,则线段AC 的长度为( )A .32B .33C .3D .6【答案】D【解析】【分析】 过C 作CD ⊥直线a ,根据30°角所对直角边等于斜边的一半即可得到结论.【详解】过C 作CD ⊥直线a ,∴∠ADC =90°.∵∠1=45°,∠BAC =105°,∴∠DAC =30°.∵CD =3,∴AC =2CD =6.故选D .【点睛】本题考查了平行线间的距离,含30°角的直角三角形的性质,正确的理解题意是解题的关键.11.如图,在ABC V 中,分别以点A 和点B 为圆心,以相同的长(大于12AB )为半径作弧,两弧相交于点M 和点N ,作直线MN 交AB 于点D ,交AC 于点E ,连接CD .已知CDE △的面积比CDB △的面积小4,则ADE V 的面积为( )A .4B .3C .2D .1【答案】A【解析】【分析】 由作图步骤可知直线MN 为线段AB 的垂直平分线,根据三角形中线的性质可得S △CDA =S △CDB ,根据△CDE 的面积比△CDB 的面积小4即可得答案.【详解】由作图步骤可知直线MN 为线段AB 的垂直平分线,∴CD 为AB 边中线,∴S △CDA =S △CDB ,∵△CDE 的面积比△CDB 的面积小4,∴S △ADE =S △CDA -S △CDE =S △CDB -S △CDE =4.故选:A .【点睛】本题考查尺规作图——垂直平分线的画法及三角形中线的性质,三角形的中线,把三角形分成两个面积相等的三角形;熟练掌握三角形中线的性质是解题关键.12.如图,△ABC 的角平分线CD 、BE 相交于F ,∠A =90°,EG ∥BC ,且CG ⊥EG 于G ,下列结论:①∠CEG =2∠DCB ;②∠ADC =∠GCD ;③CA 平分∠BCG ;④∠DFB =12∠CGE.其中正确的结论是( )A.②③B.①②④C.①③④D.①②③④【答案】B【解析】【分析】根据平行线的性质、角平分线的定义、垂直的性质及三角形内角和定理依次判断即可得出答案.【详解】①∵EG∥BC,∴∠CEG=∠ACB,又∵CD是△ABC的角平分线,∴∠CEG=∠ACB=2∠DCB,故正确;②∵∠A=90°,∴∠ADC+∠ACD=90°,∵CD平分∠ACB,∴∠ACD=∠BCD,∴∠ADC+∠BCD=90°.∵EG∥BC,且CG⊥EG,∴∠GCB=90°,即∠GCD+∠BCD=90°,∴∠ADC=∠GCD,故正确;③条件不足,无法证明CA平分∠BCG,故错误;④∵∠EBC+∠ACB=∠AEB,∠DCB+∠ABC=∠ADC,∴∠AEB+∠ADC=90°+12(∠ABC+∠ACB)=135°,∴∠DFE=360°-135°-90°=135°,∴∠DFB=45°=12∠CGE,,正确.故选B.【点睛】本题主要考查了角平分线的定义,平行线的性质,三角形内角和定理及多边形内角和,三角形外角的性质,熟知直角三角形的两锐角互余是解答此题的关键.13.如图,在△ABC中,AC=BC,∠ACB=90°,点D在BC上,BD=3,DC=1,点P是AB上的动点,则PC+PD的最小值为()A .4B .5C .6D .7【答案】B【解析】 试题解析:过点C 作CO ⊥AB 于O ,延长CO 到C ′,使OC ′=OC ,连接DC ′,交AB 于P ,连接CP .此时DP +CP =DP +PC ′=DC ′的值最小.∵DC =1,BC =4,∴BD =3,连接BC ′,由对称性可知∠C ′BE =∠CBE =45°,∴∠CBC ′=90°,∴BC ′⊥BC ,∠BCC ′=∠BC ′C =45°,∴BC =BC ′=4,根据勾股定理可得DC ′=22'BC BD +=2234+=5.故选B .14.如图,在菱形ABCD 中,60BCD ∠=︒,BC 的垂直平分线交对角线AC 于点F ,垂足为E ,连接BF 、DF ,则DFC ∠的度数是( )A .130︒B .120︒C .110︒D .100︒【答案】A【解析】【分析】 首先求出∠CFB=130°,再根据对称性可知∠CFD=∠CFB 即可解决问题;【详解】∵四边形ABCD 是菱形,∴∠ACD =∠ACB =12∠BCD=25°, ∵EF 垂直平分线段BC ,∴FB=FC ,∴∠FBC=∠FCB=25°,∴∠CFB=180°-25°-25°=130°,根据对称性可知:∠CFD=∠CFB=130°,故选:A .【点睛】此题考查菱形的性质、线段的垂直平分线的性质,解题的关键是熟练掌握基本知识,属于中考常考题型.15.如图,在ABC ∆中,AB AC =,分别是以点A ,点B 为圆心,以大于12AB 长为半径画弧,两弧交点的连线交AC 于点D ,交AB 于点E ,连接BD ,若40A ∠=︒,则DBC ∠=( )A .40︒B .30︒C .20︒D .10︒【答案】B【解析】【分析】 根据题意,DE 是AB 的垂直平分线,则AD=BD ,40ABD A ==︒∠∠,又AB=AC ,则∠ABC=70°,即可求出DBC ∠.【详解】解:根据题意可知,DE 是线段AB 的垂直平分线,∴AD=BD ,∴40ABD A ==︒∠∠,∵AB AC =,∴1(18040)702ABC ∠=⨯︒-︒=︒, ∴704030DBC ∠=︒-︒=︒;故选:B.【点睛】 本题考查了垂直平分线的性质,等腰三角形的性质,以及三角形的内角和,解题的关键是熟练掌握所学的性质,正确求出DBC ∠的度数.16.如图,ABC V 中,5AB AC ==,AE 平分BAC ∠交BC 于点E ,点D 为AB 的中点,连接DE ,则DE 的长为( )A .2B .2.5C .3D 5【答案】B【解析】【分析】 根据等腰三角形三线合一可得AE ⊥BC ,再根据直角三角形斜边上的中线是斜边的一半即可求得DE 的长度.【详解】解:∵5AB AC ==,AE 平分BAC ∠,∴AE ⊥BC ,又∵点D 为AB 的中点, ∴1 2.52DE AB ==, 故选:B .【点睛】 本题考查等腰三角形三线合一和直角三角形斜边上的中线.熟练掌握相关定理,并能正确识图,得出线段之间的关系是解题关键.17.如图,经过直线AB 外一点C 作这条直线的垂线,作法如下:(1)任意取一点K ,使点K 和点C 在AB 的两旁.(2)以点C 为圆心,CK 长为半径作弧,交AB 于点D 和E .(3)分别以点D 和点E 为圆心,大于12DE 的长为半径作弧,两弧相交于点F . (4)作直线CF .则直线CF 就是所求作的垂线.根据以上尺规作图过程,若将这些点作为三角形的顶点,其中不一定...是等腰三角形的为( )A.△CDF B.△CDK C.△CDE D.△DEF【答案】A【解析】【分析】根据作图过程和等腰三角形的定义进行分析即可.【详解】由作图过程可得:CD=CD,DF=EF,CD=CK所以,是等腰三角形的有△CDK,△CDE,△DEF;△CDF不一定是等腰三角形.故选:A【点睛】考核知识点:等腰三角形.理解等腰三角形的定义是关键.18.△ABC中,AB=AC,∠A=36°,∠ABC和∠ACB的平分线BE、CD交于点F,则共有等腰三角形( )A.7个B.8个C.9个D.10个【答案】B【解析】∵等腰三角形有两个角相等,∴只要能判断出有两个角相等就行了,将原图各角标上后显示如左下:因此,所有三角形都是等腰三角形,只要判断出有哪几个三角形就可以了.如右上图,三角形有如下几个:①,②,③;①+②,③+②,①+④,③+④;①+②+③+④;共计8个. 故选:B.点睛:本题考查了等腰三角形的判定与性质、三角形内角和定理以及三角形外角的性质,此题难度不大,解题的关键是求得各角的度数,掌握等角对等边与等边对等角定理的应用.19.两组邻边分别相等的四边形叫做“筝形”,如图,四边形ABCD 是一个筝形,其中AD=CD ,AB=CB ,詹姆斯在探究筝形的性质时,得到如下结论:①AC ⊥BD ;②AO=CO=12AC ;③△ABD ≌△CBD , 其中正确的结论有( )A .0个B .1个C .2个D .3个【答案】D【解析】 试题解析:在△ABD 与△CBD 中,{AD CDAB BC DB DB===,∴△ABD ≌△CBD (SSS ),故③正确;∴∠ADB=∠CDB ,在△AOD 与△COD 中,{AD CDADB CDB OD OD=∠=∠=,∴△AOD ≌△COD (SAS ),∴∠AOD=∠COD=90°,AO=OC ,∴AC ⊥DB ,故①②③正确;故选D .考点:全等三角形的判定与性质.20.(11·十堰)如图所示为一个污水净化塔内部,污水从上方入口进入后流经形如等腰直角三角形的净化材料表面,流向如图中箭头所示,每一次水流流经三角形两腰的机会相同,经过四层净化后流入底部的5个出口中的一个。
小学奥数竞赛专题:五年级奥数中等难度练习题二

பைடு நூலகம்
三角形面积:: (中等难度)
右图是由大、小两个正方形组成的,小正方形的边长是
4 厘米,求三角形 ABC的面积. [来源:学科网]
三角形面积答案::
这道题似乎缺少大正方形的边长这个条件, 实际上本题的结果与大正方形的边长没关系.连接
AD(见
右上图),可以看出,三角形 ABD与三角形 ACD的底都等于小正方形的边长,高都等于大正方形的边长,
年龄:: (中等难度) 现在哥哥的年龄恰好是弟弟年龄的 2 倍。 而 9 年前哥哥的年龄是弟弟年龄的 5 倍,则哥哥现在的年龄
是__________岁。
年龄答案:: [ 来源 :学学科科网网 ZXXK] 把弟弟 9 年前的年龄看作是 1 份,那么哥哥 9 年前的年龄是 5 份,年龄之差为 4 份。现在弟弟的年 龄为 "1 份加上 9 岁" ,哥哥的年龄是弟弟年龄的 2 倍,所以年龄之差为 " 份加上 9 岁" ,所以 1 份的年龄 为 9÷( 4-1 )=3 岁,哥哥现在的年龄为 3×5+9=24 岁。
7.3 米,分别所用的时间是 6,7,8 分
钟,所以三只蚂蚁的速度之比为: 28:24:21 ,注意题目中有一个条件,就是第一次出发的时候,他们是同
所以二等奖有 13 名。
【小结】根据题意列出方程组,解不定方程需要尝试未知数的值。
圆形跑道问题::(中等难度)
有甲、乙、丙三人,甲每分钟行走 120 米,乙每分钟行走 100 米,丙每分钟行走 70 米。如果三人同
时同向从同地出发,沿周长是 300 米的圆形跑道行走,那么分钟之后,三个人又可以相聚。
数论问题:: (中等难度)
2021年中考数学九年级复习小专题专项课时练:三角形的面积(二)

2021年中考数学九年级复习小专题专项课时练:三角形的面积(二)1.三角形的下列线段中能将三角形的面积分成相等两部分的是()A.中线B.角平分线C.高D.中位线2.如图,△ABC中,D,E两点分别在AB,BC上,若AD:DB=CE:EB=2:3,则△DBE与△ADC的面积比为()A.3:5 B.4:5 C.9:10 D.15:163.如图,△ABC的面积为16,点D是BC边上一点,且BD=BC,点G是AB上一点,点H在△ABC内部,且四边形BDHG是平行四边形,则图中阴影部分的面积是()A.3 B.4 C.5 D.64.如图,两个三角形的面积分别是9,6,对应阴影部分的面积分别是m,n,则m﹣n 等于()A.2 B.3 C.4 D.无法确定5.如图,在四边形ABCD中,∠ABC=90°,AB=BC=2,E、F分别是AD、CD 的中点,连接BE、BF、EF.若四边形ABCD的面积为6,则△BEF的面积为()A.2 B.C.D.36.在平面直角坐标系xOy中,若A点坐标为(﹣3,3),B点坐标为(2,0),则△ABO 的面积为()A.15 B.7.5 C.6 D.37.如图中,∠ACB=90°,AC>BC,分别以△ABC的边AB、BC、CA为一边向△ABC 外作正方形ABDE、BCMN、CAFG,连接EF、GM、ND,设△AEF、△CGM、△BND的面积分别为S、S2、S3,则下列结论正确的是()1A.S1=S2=S3B.S1=S2<S3C.S1=S3<S2D.S2=S3<S18.如图,在长方形网格中,每个小长方形的长为2,宽为1,A、B两点在网格格点上,若点C也在网格格点上,以A、B、C为顶点的三角形面积为2,则满足条件的点C个数是()A.2 B.3 C.4 D.59.如图,在△ABC中E是BC上的一点,EC=2BE,点D是AC的中点,设△ABC,△ADF,△BEF的面积分别为S△ABC,S△ADF,S△BEF,且S△ABC=12,则S△ADF﹣S△=()BEFA.1 B.2 C.3 D.410.能把一个三角形分成面积相等的两部分的是该三角形的一条()A.中线B.角平分线C.高线D.边的垂直平分线11.如图将四个全等的矩形分别等分成四个全等的小矩形,其中阴影部分面积相等的是()A.只有①和②相等B.只有③和④相等C.只有①和④相等D.①和②,③和④分别相等12.在如图的方格纸中,每个小方格都是边长为1的正方形,点A、B是方格纸中的两个格点(即正方形的顶点),在这个5×5的方格纸中,找出格点C使△ABC的面积为2个平方单位,则满足条件的格点C的个数是()A.5 B.4 C.3 D.213.如图,要判断△ABC的面积是△DBC的面积的几倍,只有一把仅有刻度的直尺,需要度量的次数最少是()A.3次以上B.3次C.2次D.1次14.已知:如图△ABC中,点D、E、F分别在三边上,E是AC的中点,AD,BE,CF 交于一点G,BD=2DC,S△BGD=8,S△AGE=3,则△ABC的面积是()A.25 B.30 C.35 D.4015.一定能把三角形分成面积相等的两个三角形的线段是这个三角形的()A.角平分线B.中线C.高线D.中位线16.如图,D为△ABC内部一点,E、F两点分别在AB、BC上,且四边形DEBF为矩形,直线CD交AB于G点.若CF=6,BF=9,AG=8,则△ADC的面积为何?()A.16 B.24 C.36 D.5417.已知在正方形网格中,每个小方格都是边长为1的正方形,A,B两点在小方格的顶点上,位置如图所示,点C也在小方格的顶点上,且以A,B,C为顶点的三角形面积为1,则点C的个数为()A.3个B.4个C.5个D.6个18.已知四边形ABCD的对角线AC与BD相交于点O,若S△AOB=4,S△COD=9,则四边形ABCD的面积S四边形ABCD的最小值为()A.21 B.25 C.26 D.3619.10个全等的小正方形拼成如图所示的图形,点P、X、Y是小正方形的顶点,Q是边XY一点.若线段PQ恰好将这个图形分成面积相等的两个部分,则的值为()A.B.C.D.20.如图,D,E分别是△ABC的边AB,AC的中点,H,G是边BC上的点,且HG=BC,S=24,则图中阴影部分的面积为()△ABCA.4 B.6 C.8 D.12参考答案1.解:∵三角形的中线把三角形分成两个等底同高的三角形,∴三角形的中线将三角形的面积分成相等两部分.故选:A.2.解:∵AD:DB=CE:EB=2:3,∴S△BDC:S△ADC=3:2,S△BDE:S△DCE=3:2,∴设S△BDC=3x,则S△ADC=2x,S△BED=1.8x,S△DCE=1.2x,故△DBE与△ADC的面积比为:1.8x:2x=9:10.故选:C.3.解:设△ABC底边BC上的高为h,△AGH底边GH上的高为h1,△CGH底边GH 上的高为h2,则有h=h1+h2.S=BC•h=16,△ABCS=S△AGH+S△CGH=GH•h1+GH•h2=GH•(h1+h2)=GH•h.阴影∵四边形BDHG是平行四边形,且BD=BC,∴GH=BD=BC,∴S阴影=×(BC•h)=S△ABC=4.故选:B.4.解:设空白出图形的面积为x,根据题意得:m+x=9,n+x=6,则m﹣n=9﹣6=3.故选:B.5.解:连接AC,过B作EF的垂线交AC于点G,交EF于点H,∵∠ABC=90°,AB=BC=2,∴AC===4,∵△ABC为等腰三角形,BH⊥AC,∴△ABG,△BCG为等腰直角三角形,∴AG=BG=2∵S△ABC=•AB•BC=×2×2=4,∴S△ADC=2,∵=2,∵△DEF∽△DAC,∴GH=BG=,∴BH=,又∵EF=AC=2,∴S△BEF=•EF•BH=×2×=,故选C.方法二:S△BEF=S四边形ABCD﹣S△ABE﹣S△BCF﹣S△FED,易知S△ABE+S△BCF=S四边形ABCD=3,S△EDF=,∴S△BEF=S四边形ABCD﹣S△ABE﹣S△BCF﹣S△FED=6﹣3﹣=.故选:C.6.解:如图,根据题意得,△ABO的底长OB为2,高为3,∴S△ABO=×2×3=3.故选:D.7.解:作ER⊥FA交FA的延长线于R,作DH⊥NB交NB的延长线于H,作NT⊥DB 交DB的延长线于T,设△ABC的三边长分别为a、b、c,∵分别以△ABC的边AB、BC、CA为一边向△ABC外作正方形ABDE、BCMN、CAFG,∵AE=AB,∠ARE=∠ACB,∠EAR=∠CAB,∴△AER≌△ABC,∴ER=BC=a,FA=b,∴S1=ab,S=ab,2同理可得HD=AR=AC,∴S1=S2=S3=.故选:A.8.解:C点所有的情况如图所示:故选:C.9.解:∵S△ABC=12,EC=2BE,点D是AC的中点,∴S△ABE==4,S==6,△ABD∴S△ABD﹣S△ABE,=S△ADF﹣S△BEF,=6﹣4,=2.故选:B.10.解:把三角形的面积分成相等的两部分的是三角形的中线.此时两个三角形等底同高.故选:A.11.解:小矩形的长为a,宽为b,则①中的阴影部分为两个底边长为a,高为b的三角形,∴S=×a•b×2=ab;②中的阴影部分为一个底边长为a,高为2b的三角形,∴S=×a•2b=ab;③中的阴影部分为一个底边长为a,高为b的三角形,∴S=×a•b=ab;④中的阴影部分为一个底边长为a,高为b的三角形,∴S=×a•b=ab.∴①和②,③和④分别相等.故选:D.12.解:满足条件的C点有5个,如图平行于AB的直线上,与网格的所有交点就是.故选:A.13.解:连接AD并延长交BC于M,作DF∥BC交AP于点F.测量AM以及AD即可,由=,即可求出△ABC的面积是△DBC的面积的几倍.所以只量2次.故选:C.14.解:三角形BDG和CDG中,BD=2DC.根据这两个三角形在BC边上的高相等,那么S△BDG=2S△GDC,因此S△GDC=4,同理S△AGE=S△GEC=3,S△BEC=S△BGC+S△GEC=8+4+3=15,∴三角形ABC的面积=2S△BEC=30.故选:B.15.解:三角形的中线把三角形分成两个等底等高的三角形,面积相等.故选:B.16.解:S△ADC=S△AGC﹣S△ADG=×AG×BC﹣×AG×BF=×8×(6+9)﹣×8×9=60﹣36=24.故选:B.17.解:C点所有的情况如图所示:故选:D.18.解:设点A到边BD的距离为h.如图,任意四边形ABCD中,S△AOB=4,S△COD=9;∵S△AOD=OD•h,S△AOB=OB•h=4,∴S△AOD=OD•=4×,S△BOC=OB•=9×;设=x,则S△AOD=4x,S△BOC=;∴S 四边形ABCD=4x++13≥2•+13=12+13=25;故四边形ABCD的最小面积为25.故选:B.19.解:设QY=x,根据题意得到PQ下面的部分的面积为:S△+S正方形=×5×(1+x)+1=5,解得x=,∴XQ=1﹣=,∴==,故选:B.20.解:连接DE,作AF⊥BC于F,设DE和AF相交于点I,DG和EH相交于点O,如图所示,∵D,E分别是AB,AC的中点,∴DE=BC,DE∥BC,AI=FI,∴△ADE∽△ABC,AI⊥DE,∴△ADE的面积=24×=6,∴四边形DBCE的面积=24﹣6=18,∵HG=BC,∴DE=HG,∴△DOE的面积+△HOG的面积=2×DE×FI=△ADE的面积=6,∴图中阴影部分的面积=18﹣6=12,故选:D.。
2022年人教版小学《三角形的面积2》精品教案(推荐)

第二课时教学内容三角形的面积的练习(二)。
(教材第93~94页)教学目标1.稳固学生对三角形面积计算公式的理解和掌握,使其熟练应用三角形面积计算公式解决问题。
2.进一步培养学生灵活应用公式解题的能力。
3.培养学生仔细观察,积极思考的学习习惯。
重点难点重点:理解和掌握三角形面积计算公式。
难点:灵活运用三角形的面积计算公式解题。
教具学具实物投影。
教学过程一复习提问:三角形的面积怎样计算三角形的面积计算公式是怎样推导出来的二教学实施1.指导学生完成教材第94页第7题。
提问:三角形的面积和高,怎样求底(学生口答方法)教师提醒学生注意,不要忘记三角形的面积要先乘2,再除以高,才能得到三角形的底。
2.指导学生完成教材第93页第4题。
(学生先独立完成,再指名板演)请学生表达解题思路:求种这片草坪需要多少钱,首先要求出这片草坪的面积,再用每平方米草坪的价格乘面积。
3.指导学生完成教材第93页第5题。
(思路与第4题相同,学生独立完成,集体订正)4.指导学生完成教材第94页第8题。
学生先讨论:在图中你能找出几个三角形哪两个三角形的面积相等为什么再根据等底等高的三角形面积相等的道理,画出其他三角形。
小结:三角形面积相等的根本条件是等底等高,应用这个知识我们可以解答这个问题。
5.指导学生完成教材第94页第9*题。
学生先独立思考,然后同桌同学互相交流思路,再解答。
请学生板演计算过程,并说出解题思路。
(三角形的面积和高,可以分别求出它们的底,也就是平行四边形的两条边长。
再根据平行四边形的对边相等,即可求出平行四边形的周长)6.指导学生完成教材第94页第10*题。
学生先独立完成,再分小组讨论后解答,汇报自己的思考过程。
(平行四边形的对角线把平行四边形分成两个相等的三角形,每个三角形的面积是平行四边形面积的一半;A点是其中一个三角形底边的中点。
根据等底等高的三角形面积相等,涂色的三角形的面积就是这个三角形面积的一半,也就是平行四边形面积的1/4)三课堂作业新设计1.填表。
解三角形专题练习【附答案】

解三角形专题(高考题)练习【附答案】1、在ABC ∆中,已知内角3A π=,边BC =.设内角B x =,面积为y .(1)求函数()y f x =的解析式和定义域; (2)求y 的最大值.8、△ABC 中,a ,b ,c 分别是角A ,B ,C 的对边,且有sin2C+3cos (A+B )=0,.当13,4==c a ,求△ABC 的面积。
2、已知ABC ∆中,1||=AC ,0120=∠ABC ,θ=∠BAC ,…记→→•=BC AB f )(θ,(1)求)(θf 关于θ的表达式; (2)(2)求)(θf 的值域;3、在△ABC 中,角A 、B 、C 所对的边分别是a ,b ,c ,且.21222ac b c a =-+ (1)求B CA 2cos 2sin 2++的值; (2)若b =2,求△ABC 面积的最大值. 4、在ABC ∆中,已知内角A 、B 、C 所对的边分别为a 、b 、c ,向量(2sin ,m B =,2cos 2,2cos 12B n B ⎛⎫=- ⎪⎝⎭,且//m n 。
(I )求锐角B 的大小; (II )如果2b =,求ABC ∆的面积ABC S ∆的最大值。
5、在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,且.cos cos 3cos B c B a C b -= (I )求cos B 的值; (II )若2=⋅,且22=b ,求c a 和b 的值. 6、在ABC ∆中,cos A =cos 10B =. —(Ⅰ)求角C ; (Ⅱ)设AB =,求ABC ∆的面积.7、在△ABC 中,A 、B 、C 所对边的长分别为a 、b 、c ,已知向量(1,2sin )m A =,A B C120°θ(sin ,1cos ),//,3.n A A m n b c a =++=满足 (I )求A 的大小;(II )求)sin(6π+B 的值.8、△ABC 中,a ,b ,c 分别是角A ,B ,C 的对边,且有sin2C+3cos (A+B )=0,.当13,4==c a ,求△ABC 的面积。
2022年五年级上册数学同步练习 5 2三角形的面积 西师大版(含答案) (1)

五年级上册数学一课一练三角形的面积一、单项选择题1.三角形的面积是〔〕A. 3.84B. 34.8C. 384D. 38.42.比拟以下图长方形内阴影局部面积的大小,甲〔〕乙。
A. >B. <C. =3.下面图形(单位:厘米)的面积是〔〕A. 99.15平方厘米B. 432平方厘米C. 112平方厘米D. 15.99平方厘米4.三角形的面积等于〔〕的一半.A. 两个三角形所拼成的平行四边形面积B. 两个等底等高的三角形所拼成的四边形面积C. 两个完全一样的三角形所拼成的平行四边形面积D. 和这个三角形完全一样的两个三角形所拼成的平行四边形面积二、判断题5.等底等高的两个三角形面积相等。
6.两个面积相等的三角形可以拼成一个平行四边形7.两个三角形的面积相等,那么这两个三角形一定等底等高.8.图中的长方形中的甲与乙两个三角形比拟,甲比乙大.三、填空题9.学校花园里有一块三角形草地(见以下图),这块草地的面积是________平方米10.填表.(从左到右填写)11.一个长方形被内部一点分成4个不同的三角形〔如图〕,假设红色的三角形面积占长方形面积的18%,兰色的三角形面积是64cm2 那么长方形面积是________。
12.在以下图三角形中,BC=4cm,AD=2cm,CE=3cm,那么AB=________cm.四、解答题13.我们都知道,三角形面积的计算公式是“底×高÷2〞。
那么,为什么要“÷2〞呢?请写一写或画一画的方式,把你的想法表达出来。
五、应用题14.一块三角形的果园,底是280米,高是26米,共栽了910棵果树,平均每棵果树占地多少平方米?15.计算下面图形阴影局部的面积.(单位:米)参考答案一、单项选择题1.【答案】D【解析】【解答】平方厘米【分析】用三角形面积公式S=ah÷2直接计算即可。
2.【答案】C【解析】【解答】在三角形中,等底等高的两个三角形的面积相等,由此可得三角形1面积=三角形2面积,三角形3面积=三角形4面积,即可得面积甲=面积乙.故答案为:C.【分析】根据图意,空白局部和阴影局部组成一个大三角形,两个大三角形的面积相等,然后依据等底等高的两个三角形的面积相等,由此可得三角形1面积=三角形2面积,三角形3面积=三角形4面积,即可得面积甲=面积乙,据此解答.3.【答案】D【解析】【解答】7.8×4.1÷2=31.98÷2〔平方厘米〕【分析】这道题考查的是求三角形的面积的知识,解答此题要运用三角形面积=底×高÷2的公式,然后代入数据计算即可。
五年级数学上册平行四边形和三角形的面积练习题

4、两个面积相等的三角形一定可以拼成一个平行四边形()
5、三角形的面积就是平行四边形面积的一半()
6、周长相等的两个三角形面积一定相等()
7、两个面积相等的三角形,它们的底和高一定相等()
8、一个三角形的底和高都是5厘米,它的面积是25平方厘米。()
9、两个同底等高的三角形,形状相同,面积相等。()
0.15m
0.2m
(1)4.5平方米=()平方分米2400平方厘米=()平方分米
3平方米=()平方厘米1.7公顷=()平方米
(2)一个平行四边形的底是9分米,高是底的2倍,它的面积是()平方分米。
(3)一个平行四边形的底是12厘米,面积是156平方厘米,高是()厘米。
(4)一块平行四边形钢板,底是1.5米,高是1.2米,如果每平方米钢板重23.5千克,这块钢板重()千克
不要忘记:平行四边形面积=底×高三角形的面积=底×高÷2。
一、填空(24分)
1、两个完全一样的三角形能拼()所以三角形的面积等于()。用字母表示是()。
2、一个三角形底是5cm,高是7cm,面积是()。
3、一个三角形的面积是4.8m2,与它等底等高的平行四边形的面积是()。
4、1.25公顷=()平方米5600平方分米=()平方米
二、判断题。
1、平行四边形的面积等于长方形面积。()
2、一个平行四边形的底是5分米,高是20厘米,面积是100平方分米。()
3、一个平行四边形面积是42平方米,高是6米,底是7米。()
4、等底等高的两个平行四边形面积也相等。()
三、选择题。
1、平行四边形的底扩大6倍,高缩小3倍,它的面积()。
苏教版五年级上册数学第二单元知识点+练习题带答案

第二单元知识点1. 平行四边形面积的计算平行四边形的面积=底×高,用字母表示为S=a×h。
2. 三角形面积的计算三角形的面积=底×高÷2,用字母表示为S=a×h÷2。
等底等高的三角形面积相等。
3. 梯形面积的计算梯形的面积=(上底+下底)×高÷2,用字母表示为S=(a+b)×h÷2。
4. 公顷测量或计量土地面积,常用公顷作单位。
公顷可以写成hm25. 公顷和平方米之间的进率1公顷=10000平方米6.把高级单位改写成低级单位要乘进率,把低级单位改写成高级单位要除以进率。
7.平方千米测量或计量大面积的土地,通常用平方千米作单位,平方千米可以写成km2。
平方千米是比公顷大的面积单位。
8. 平方千米、平方米和公顷之间的换算1平方千米=1000000平方米=100公顷9. 组合图形面积的计算在计算组合图形的面积时,通常先把组合图形分割成已学过的简单图形,分别计算出各个简单图形的面积,再把它们加起来,也可以把组合图形补成一个简单的图形,再用补成的简单图形的面积减去补上的简单图形的面积。
10. 不规则图形面积的计算方法一:数方格法。
求不规则图形的面积,可以用数方格法进行估计。
估计时,先数整格的,再数不满整格的,不满整格的按半格计算。
注意:估计不规则图形的面积时,也可以先数整格的和超过半格的,把超过半格的也当作整格数,不足半格的不计。
方法二:转化法。
可以把不规则图形近似的看作由一个或几个简单的规则图形组成。
求出简单的规则图形的面积来估计出不规则图形的面积。
苏教版五年级上册第二单元测试题及答案一.填空。
(每空2分,共10分)1.一个平行四边形,底是12厘米,高是6厘米,则它的面积是()平方厘米。
2.一个三角形,底是8米,高是6米,这个三角形的面积是()平方米。
3.一个梯形,上底是3厘米,下底是7厘米,高是5厘米,这个梯形的面积是()平方厘米。
五年级奥数学习讲义 第19讲 组合图形的面积(二) 练习及答案

第19讲组合图形的面积(二)一、知识要点在组合图形中,三角形的面积出现的机会很多,解题时我们还可以记住下面三点:1.两个三角形等底、等高,其面积相等;2.两个三角形底相等,高成倍数关系,面积也成倍数关系;3.两个三角形高相等,底成倍数关系,面积也成倍数关系。
二、精讲精练【例题1】如图,ABCD是直角梯形,求阴影部分的面积和。
(单位:厘米)练习1:1.求下图中阴影部分的面积。
2.求图中阴影部分的面积。
(单位:厘米)3.下图的长方形是一块草坪,中间有两条宽1米的走道,求植草的面积。
【例题2】下图中,边长为10和15的两个正方体并放在一起,求三角形ABC (阴影部分)的面积。
练习2:1.下图中,三角形ABC的面积是36平方厘米,三角形ABE与三角形AEC的面积相等,如果AB=9厘米,FB=FE,求三角形AFE的面积。
2.图中两个正方形的边长分别是10厘米和6厘米,求阴影部分的面积。
3.图中三角形ABC的面积是36平方厘米,AC长8厘米,DE长3厘米,求阴影部分的面积(ADFC不是正方形)。
【例题3】两条对角线把梯形ABCD分割成四个三角形。
已知两个三角形的面积(如图所示),求另两个三角形的面积各是多少?(单位:平方厘米)练习3:1.如下图,图中BO=2DO,阴影部分的面积是4平方厘米,求梯形ABCD的面积是多少平方厘米?2.下图的梯形ABCD中,下底是上底的2倍,E是AB的中点。
那么梯形ABCD的面积是三角形BDE面积的多少倍?3.下图梯形ABCD中,AD=7厘米,BC=12厘米,梯形高8厘米,求三角形BOC的面积比三角形AOD的面积大多少平方厘米?【例题4】在三角形ABC中,DC=2BD,CE=3AE,阴影部分的面积是20平方厘米,求三角形ABC的面积。
练习4:1.把下图三角形的底边BC四等分,在下面括号里填上“>”、“<”或“=”。
甲的面积()乙的面积。
2.如图,在三角形ABC中,D是BC的中点,E、F是AC的三等分点。
