初中数学基础知识1第七单元图形的变化第26课时《图形的平移与旋转》
平移与旋转PPT课件

旋转是将图形绕某一点转动一定的角度,其实质是点的旋转。旋转不改
变图形中各点之间的相对位置关系,但改变其角度。
03
平移与旋转的联系
平移和旋转都是图形在平面内的运动,它们都可以改变图形的位置,但
不改变其形状和大小。在实际应用中,平移和旋转常常结合使用,以实
现图平移
在实际应用中,物体往往同时进行平 移和旋转运动,这种运动称为复合运 动。
旋转运动
旋转运动是围绕一个固定点进行的运 动,物体在平面内以该点为中心进行 旋转,其轨迹是一个圆或一个圆弧。
计算机图形学
计算机图形学是研究计算机生成 和操作图形的科学,它广泛应用 于游戏开发、电影制作、建筑设
计等领域。
平移与旋转是计算机图形学中基 本变换之一,通过这些变换可以
三维平移
总结词
三维平移是指空间内的移动,可以沿 三个方向进行。
详细描述
在三维空间中,三维平移可以表示为在 x轴、y轴和z轴上的三个单位向量的组 合,例如[1,0,0]、[0,1,0]和[0,0,1]。三 维平移会改变物体的位置和方向。
03 旋转的数学表示
一维旋转
总结词
一维旋转是指绕着一条直线进行的旋转。
都有广泛的应用。
THANKS FOR WATCHING
感谢您的观看
总结词
一维平移是指沿一个方向进行的移动。
详细描述
在数学中,一维平移通常表示为在坐标轴上的一个单位向量,例如在x轴上,可 以表示为[1,0,0]。一维平移不改变物体的方向,只改变位置。
二维平移
总结词
二维平移是指平面内的移动,可以沿两个方向进行。
详细描述
在二维坐标系中,二维平移可以表示为在x轴和y轴上的两个单位向量的组合, 例如[1,0]和[0,1]。二维平移会改变物体的位置,但不改变方向。
(完整版)图形的平移与旋转知识点

第三章图形的平移与旋转复习要点专点一:图形的平移1.平移的定义:在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移。
平移是由移动的方向和距离决定的。
2.平移的性质:(1)平移不改变图形的形状和大小:即平移前后的线段相等,平移前后的三角形或多边形全等。
(2)平移后的图形与原来图形的对应线段平行且相等,对应角相等。
(3)平移后两图形的对应点所连的线段平行且相等。
专点二:图形的旋转1.旋转的定义:在平面内,将一个图形绕着一个定点沿着某个方向(顺时针或逆时针)旋转一定的角度,这样的图形运动成为旋转,这个定点称为旋转中心,旋转的角度称为旋转角。
2.旋转的性质:(1)旋转不改变图形的形状和大小:即旋转前后的图形是一组全等形。
(2)旋转后的图形与原来的图形的对应线段相等,对应角相等。
(3)经过旋转,图形上的每一点都绕着旋转中心沿相同的方向转动了相同的角度。
(4)任意一对对应点与旋转中心的距离相等。
考点三、中心对称1、定义把一个图形绕着某一个点旋转180°,如果旋转后的图形能够和原来的图形互相重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心。
2、性质(1)关于中心对称的两个图形是全等形。
(2)关于中心对称的两个图形,对称点连线都经过对称中心,并且被对称中心平分。
(3)关于中心对称的两个图形,对应线段平行(或在同一直线上)且相等。
3、判定如果两个图形的对应点连线都经过某一点,并且被这一点平分,那么这两个图形关于这一点对称。
4、中心对称图形把一个图形绕某一个点旋转180°,如果旋转后的图形能够和原来的图形互相重合,那么这个图形叫做中心对称图形,这个店就是它的对称中心。
考点四、坐标系中对称点的特征1、关于原点对称的点的特征:两个点关于原点对称时,它们的坐标的符号相反,即点P(x,y)关于原点的对称点为P’(-x,-y)2、关于x轴对称的点的特征:两个点关于x轴对称时,它们的坐标中,x相等,y的符号相反,即点P(x,y)关于x轴的对称点为P’(x,-y)3、关于y轴对称的点的特征:两个点关于y轴对称时,它们的坐标中,y相等,x的符号相反,即点P(x,y)关于y轴的对称点为P’(-x,y)专点五:利用轴对称、旋转和平移作图1.平移作图的一般步骤:(1)确定平移的方向和距离;(2)确定构成图形的关键点(线段两个端点,三角形三个顶点,n边形n 个顶点);(3)按照平移的方向和距离平移各个关键点;(4)顺次连接各个关键点的对应点,所得的图形就是平移后的图形。
初中数学图形的平移与旋转知识点归纳

初中数学图形的平移与旋转知识点归纳在初中数学中,图形的平移和旋转是涉及到几何图形的基本操作。
通过平移和旋转,我们可以改变图形的位置和朝向,从而建立几何图形之间的联系和性质。
本文将对初中数学中与图形的平移和旋转相关的知识点进行归纳和总结。
一、图形的平移平移是指将一个图形沿着指定的方向和距离移动,而不改变该图形的大小、形状和方向。
图形的平移可以通过向左、向右、向上或向下平移来完成。
以下是与图形的平移相关的知识点:1. 平移向量:平移向量表示平移的方向和距离,可以用箭头表示。
平移向量的长度表示平移的距离,箭头的方向表示平移的方向。
2. 平行平移:平行平移是指图形沿着平行于给定方向的线段移动。
在平行平移过程中,图形的各个点保持相对位置不变。
3. 坐标平移:坐标平移是指根据给定的平移向量,将图形上每个点的坐标分别增加或减少相应的数值。
例如,对于二维平面上的点A(x, y),进行平移向量为(3, 4)的平移,那么新的点A'(x+3, y+4)就是平移后的坐标。
二、图形的旋转旋转是指将一个图形按照一定的角度围绕某个固定点旋转,使得图形绕着该点旋转后,图形上的各个点的位置发生相应的变化。
以下是与图形的旋转相关的知识点:1. 旋转中心:旋转中心是围绕其进行旋转的点,也称为旋转的原点。
2. 旋转角度:旋转角度是指旋转的角度大小,可以是正数、负数或零。
正数表示顺时针旋转,负数表示逆时针旋转。
3. 旋转方向:旋转方向可以根据旋转角度的正负来确定,正数表示顺时针旋转,负数表示逆时针旋转。
4. 中心旋转:中心旋转是指图形围绕一个给定的点旋转。
在中心旋转中,图形上的各个点以旋转中心为中心点,按照给定的旋转角度进行旋转。
5. 角度旋转:角度旋转是指图形围绕一个给定的角度进行旋转。
在角度旋转中,旋转中心通常是坐标原点,图形上的各个点按给定的旋转角度进行旋转。
三、图形的平移与旋转的性质和应用图形的平移和旋转不仅是数学中的重要概念,也在实际生活中广泛应用。
《平移和旋转》图形的运动平移和旋转课件

垂直平移
图形在垂直方向上移动,也称为上 下平移。
对角线平移
图形沿着对角线方向移动,也称为 对角平移。
平移运动的实现方法
手动平移
通过手动操作,将图形从一个位置移动到另一个位置。
计算机辅助平移
利用计算机图形软件,通过鼠标或键盘操作,将图形从一个位置移动到另一个位置。
03
旋转运动的基本概念与分类
旋转运动的基本概念
为(x+dx, y+dy, z+dz)。
旋转还可以用于实现游戏中的视角变换 、物体翻转、飞行控制等行为,例如摄 像机跟随角色旋转以展示角色的周围环
境。
平移和旋转结合在游戏开发中的应用
平移和旋转结合可以实现更加复杂的 运动效果,例如物体在空中翻滚、飘 动、跳跃等。
平移和旋转结合可以通过同时改变物 体的位置和朝向实现,例如在2D平面 上,可以将物体的初始位置设为(x1, y1),目标位置设为(x2, y2),同时将 物体的初始朝向设为(a1, b1),目标 朝向设为(a2, b2),通过计算出物体 移动的增量(dx, dy)和物体旋转的角 度(da, db),然后将物体的位置更新 为(x1+dx, y1+dy),将物体的旋转更 新为(a1+da, b1+db)。
THANK S感谢观看
平移的性质
平移不改变图形的形状、大小和方向,只改变图形的位置。平移后,图形的对 应线段平行(或共线)且相等,对应角相等,对应点所连接的线段平行(或共 线)且相等。
旋转的定义与性质
旋转的定义
旋转是一种图形变换,将图形绕某一点旋转一定的角度,而图形的形状和大小保 持不变。
旋转的性质
旋转不改变图形的形状、大小和方向,只改变图形的位置。旋转后,图形的对应 线段相等,对应角相等,对应点所连接的线段相等且平行(或共线)。
《图形平移旋转》课件

图形平移的实例演示
04
平面图形的平移
特点:形状和大小不变,只是位置发生了变化
规律:平移前后的图形是全等的,对应点所连接的线段平行且相等
定义:平面图形在平面内沿某一方向移动一定的距离
实例:矩形、三角形、梯形的应用
立体图形平移的规律
立体图形平移的实例演示
立体图形平移的概念
旋转的应用场景
* 通过旋转,可以方便地构造复杂的几何图形
* 旋转可以用于创建动画、游戏和虚拟现实中的三维场景
旋转在计算机图形学中的应用 * 旋转可以用于创建动画、游戏和虚拟现实中的三维场景
* 旋转可以描述物体的运动状态,如旋转的陀螺和旋转的星球
* 旋转可以用于机械设计和制造,如旋转的齿轮和涡轮机
平移的应用场景
日常生活中的应用:如电梯上下移动、传送带上的物品移动等
工业生产中的应用:如流水线上的产品移动、自动化设备中的部件移动等
图形设计中的应用:如平移变换在图形设计中的应用,如平移对称图案等
数学教育中的应用:如平移变换在数学中的运用,如平移函数图像等
图形旋转的实例演示
05
平面图形的旋转
题目:一个正方形在平面直角坐标系中,以原点为中心,按顺时针方向旋转90度,得到新的正方形,求新的正方形各顶点的坐标。
题目:一个三角形在平面直角坐标系中,以原点为中心,按顺时针方向旋转90度,得到新的三角形,求新的三角形各顶点的坐标。
题目:一个圆形在平面直角坐标系中,以原点为中心,按顺时针方向旋转90度,得到新的圆形,求新的圆形各顶点的坐标。
旋转的定义与性质
旋转的度数:旋转的角度可以用度数来表示
旋转的定义:旋转是围绕一个点旋转的运动
旋转的性质:旋转前后的图形形状和大小不变,只是位置发生了变化
七年级数学图形的平移和旋转知识点

七年级数学图形的平移和旋转知识点
关于七年级数学图形的平移和旋转知识点
平移:①在平面内,将一个图形沿着某个方向移动一定的距离,这样的图形运动叫做平移。
②经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等。
旋转:①在平面内,将一个图形绕一个定点沿某个方向转动一个角度,这样的图形运动叫做旋转。
②经过旋转,图形商店每一个点都绕旋转中心沿相同方向转动了相同的角度,任意一对对应点与旋转中心的.连线所成的角都是旋转角,对应点到旋转中心的距离相等。
【关于七年级数学图形的平移和旋转知识点】。
平移旋转知识点总结

平移旋转知识点总结一、平移的基本概念1、平移的定义平移是指图形沿着一条直线方向移动,移动的距离和方向保持一致。
在平移过程中,图形的大小和形状都不发生变化,只是位置发生了改变。
可以将平移看作是图形的每个点都按照同一个方向和距离进行移动,从而得到了一个新的位置。
2、平移的表示平移可以用向量来表示,假设有一个向量V(u,v),其中u和v表示平移的水平和垂直方向上的距离。
对于一个点P(x,y),通过向量表示的平移操作可以表示为P'=(x+u, y+v)。
这表示点P经过向量V的平移操作后得到了新的点P'(x+u, y+v)。
3、平移的性质平移具有以下几个重要的性质:(1)平移是保形变换,即平移前后的图形形状相同;(2)平移不改变图形的大小;(3)平移不改变图形的角度;(4)平移保持了图形内的任意两点间的距离关系。
二、旋转的基本概念1、旋转的定义旋转是指图形以一个固定的点为中心,按照一定的角度转动。
在旋转过程中,图形的大小和形状都不发生变化,只是方向发生了改变。
可以将旋转看作是图形的每个点都按照同一个中心和角度进行转动,从而得到了一个新的方向。
2、旋转的表示旋转可以用矩阵来表示,假设有一个点P(x,y),以原点为中心,顺时针旋转角度为θ的旋转操作可以表示为P'=(x*cosθ-y*sinθ, x*sinθ+y*cosθ)。
这表示点P经过矩阵表示的旋转操作后得到了新的点P'(x',y')。
3、旋转的性质旋转具有以下几个重要的性质:(1)旋转是保形变换,旋转前后的图形形状相同;(2)旋转不改变图形的大小;(3)旋转保持了图形内的任意两点间的距禿;(4)旋转不改变图形的中心;(5)对任意两个点A和B,它们的连线在旋转前后的夹角不变。
三、平移和旋转的混合变换在实际问题中,往往需要对图形进行平移和旋转的组合变换。
对于平移和旋转的组合变换,其实际操作可以分为两步:首先进行平移,然后进行旋转。
湖南省2017中考数学 第一部分 教材知识梳理 第七单元 图形的变化 第26课时 图形的平移、对称与旋转讲义

第26课时图形的平移、对称 与旋转
中考考点清单
图形 的平 移、 对称 与旋 转
考点1:图形的平移 考点2:图形的对称 考点3:图形的旋转(高频) 考点4:网格作图
考点 1 图形的平移
1. 定义:把图形上所有的点都按同一方向移动相同的
距离叫做平移.
2. 性质:
(1)平移前后,对应线段平行(或在一条直线上)且相等,
每一个点与定点的连线绕定点O旋转角α),
得到图形F′,图形的这种变换就叫做旋转,
这个定点O叫做旋转中心,角α叫做旋转角.
ห้องสมุดไป่ตู้
2. 旋转的三大要素:⑤_旋__转__中___、旋转方向和旋转角.
3. 旋转的性质:
心
(1)对应点到旋转中心的距离相等; (2)对应点与旋转中心所连线段的夹角⑥_等_____旋转角;
对应角相等;
(2)对应点所连线段平行(或在一条直线上)且①_相_____;
(3)平移前、后的图形全等.
等
考点 2 图形的对称
1. 轴对称图形与轴对称
轴对称图形
轴对称
图 示
如果一个平面图形沿一条 如果一个图形关于某一条
直线折叠后,直线两侧的 直线作轴对称变换后,能
定 部分能够互相重合,那么 够与另一个图形重合,那
【温馨提示】轴对称与轴对称图形两个概念的主要区别 是:轴对称是对两个图形而言;轴对称图形是对一个 图形而言.
2. 中心对称图形与中心对称
中心对称图形
中心对称
图 示
把一个图形绕着某个点旋转 把一个图形绕着某一点 ③_1_8_0_°_,如果旋转后的图 旋转④_1_8_0_°_,它能够 定 形能与原来的图形完全重合 与另一个图形重合,那
人教版初中数学总复习第七章图形与变换第26课时图形的平移和旋转课件

2.旋转作图的步骤
(1)找出旋转中心与旋转角;
(2)找出构成图形的关键点;
(3)作出这些关键点旋转后的对应点;
(4)顺次连接各对应点.
规律方法探究
命题点1
平移
【例1】 如图,把图①中的☉A经过平移得到☉O(如图②),如果图①中☉A
上一点P的坐标为(m,n),那么平移后在图②中的对应点P'的坐标为(
又∠BEQ=∠BEP+∠DEF,
∴∠BEP=∠CQE,∴△BPE∽△CEQ,
∴
=
.
又 BE=CE,∴BE
92
=BP·CQ= 2 ,
2
3 2
∴BE=
,∴BC=3
2
2a.
∴在 Rt△ABC 中,AB=AC=3a,
9
3
∴AQ=QC-AC=2a-3a=2a,
AP=AB-BP=3a-a=2a.
(3)对应线段平行(或共线)且相等;
(4)对应角相等.
考点二 图形的旋转
1.定义
在平面内,把一个平面图形绕着一个定点沿着某个方向旋转一定的角度,图
形的这种变换叫做旋转变换.这个定点叫做旋转中心,这个角度叫做旋转角.
图形的旋转由旋转中心、旋转方向和旋转角所决定.
2.性质
(1)图形上的每一点都绕着旋转中心沿着相同的方向旋转了同样大小的角
(m+2,n-1).
答案:D
命题点2
旋转
【例2】 如图,在Rt△ABC中,∠ACB=90°,∠B=30°,BC=6.Rt△ABC绕直角顶
点C逆时针旋转,当点A的对应点A'落在AB边的起始位置上时即停止转动,
图形的运动一平移和旋转教学ppt

xx年xx月xx日
图形的运动一平移和旋转教学ppt
contents
目录
平移和旋转的定义平移和旋转的应用平移和旋转的数学模型平移和旋转的实例平移和旋转的练习题及解答
平移和旋转的定义
01
平移是在平面内,将一个图形沿某个方向移动一定的距离,这种移动称为平移变换,简称平移。
平移定义
平移不改变图形的形状、大小和方向,平移前后的两个图形是全等图形。
平移性质
平移的定义与性质
旋转定义
旋转是指将一个图形绕某一点转动一定的角度,这种变换称为旋转变换,简称旋转。
旋转性质
旋转不改变图形的形状、大小和方向,旋转前后的两个图形是全等图形。在旋转过程中,对应线段相等且平行,对应角相等且邻边成比例。
旋转的定义与性质
平移和旋转的应用
02
平移的应用
平移不改变图形的形状和大小,只改变图形的位置。
练习题1
将一个三角形绕其重心逆时针旋转90度,作出旋转后的图形。
解答
按照旋转的定义和性质,将长方形的每一个顶点绕其左上角顺时针旋转60度,连接各个顶点即可得到旋转后的长方形。
旋转的练习题及解答
THANKS
谢谢您的观看
解答
按照旋转的定义和性质,将三角形的每一个顶点绕其重心逆时针旋转90度,连接各个顶点即可得到旋转后的三角形。
详细描述
旋转的定义是图形绕某一点按顺时针或逆时针方向转动一定的角度;旋转的性质是图形旋转前后的形状和大小不变,只是位置发生改变
练习题2
将一个长方形绕其左上角顺时针旋转60度,作出旋转后的图形。
当门打开或关闭时,它围绕一个轴线做旋转运动。
车轮的转动
当车轮向前滚动时,它围绕车轴做旋转运动。
初二上册数学期末复习要点归纳:图形的平移与旋转

初二上册数学期末复习要点归纳:图形的平移与旋转
初二上册数学期末复习要点归纳:图形的平移与旋转
定义:在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移。
平移不改变图形的形状和大小。
经过平移,对应点所连的线段平行也相等;对应线段平行
且相等,对应角相等。
任意一对对应点与旋转中心的.连线所成的角都是旋转角,对应点到旋转中心的距离相等。
s();
【初二上册数学期末复习要点归纳:图形的平移与旋转】。
初中数学《图形的平移与旋转》课件
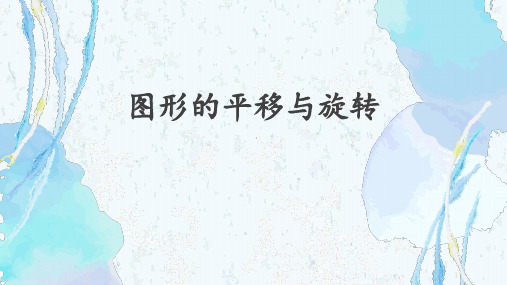
7.如图,在三角形ABC中,AC=4cm,BC=3cm,△ABC沿AB方向平 移至△DEF,若AE=8cm,BD=2cm. 求:(1)△ABC沿AB方向平移的距离;
(2)四边形AEFC的周长.
C
F
A
D
B
E
8.如图,在平面直角坐标系中,点A、B、C的坐标分别为(0,3) 、(-2,0)、(1,0),直线经过点A,B.设点D与点A、B、C构成 平行四边形,直接写出所有符合条件的点D的坐标.
旋转角
变换 条件
对称轴
平移方向和平移距离
旋转中心、旋转方向和 旋转角
联系
1.都是在平面内进行的图形变换; 2.都只改变图形的位置,不改变图形的大小和形状,即变换前后的两个图形 是全等图形; 3.都是把一个图形变换后得到另一个图形。
第二部分
平移专练
1.下列现象中,属于平移的是( )
①小朋友在荡秋千;②打气筒打气时,活塞的运动;③钟摆的
第三部分
旋转专练
1.如图,在△ABC中,∠CAB =75°,在同一平面内,将△ABC
绕点A旋转到△AB'C'的位置,使得CC'∥AB,则∠BAB'=( )
A.30°
B.35° C.40° D.45°
C`
C
B`
A
B
2.如图,ΔABC经过一次旋转得到ΔA'B'C',请找出这一旋转 的旋转中心.
A
B'
△ABC沿CB方向向右平移得到△DEF.若四边形ABED的面积为8,
则平移距离为 ( )
A.2
B.4
C.8
D.16
A
D
C
F
B
图形的旋转和平移变换

图形的旋转和平移变换在我们的日常生活和数学学习中,图形的变换是一个非常有趣且重要的概念。
其中,图形的旋转和平移变换更是常见且实用。
先来说说平移变换。
简单来说,平移就是把一个图形沿着某个方向移动一段距离。
就好像你把一本书从桌子的一端推到另一端,书的形状、大小都没有改变,只是位置发生了变化。
在数学中,平移的特点是图形上所有的点都沿着相同的方向移动相同的距离。
比如说,一个三角形在平面上向左平移 5 个单位,那么这个三角形的每个顶点都向左移动了 5 个单位。
平移在生活中的应用比比皆是。
比如,电梯的上下运动,就是一个垂直方向的平移;在工厂的生产线上,物品的传送也是平移;还有我们在电脑上移动文件或图标,这也是一种平移操作。
再谈谈旋转变换。
旋转就像是我们转动一个风车,图形围绕着一个固定的点按照一定的方向和角度转动。
这个固定的点叫做旋转中心,而转动的角度就是旋转角。
比如,一个时钟的指针围绕着时钟的中心旋转,就是典型的旋转现象。
旋转在实际生活中也有很多例子。
像游乐场里的摩天轮,就是围绕着中心轴不停地旋转;还有风扇的扇叶转动,也是一种旋转。
无论是平移还是旋转,它们都有一些共同的性质。
首先,图形在变换前后的形状和大小都不会改变,这被称为图形的全等性。
也就是说,经过平移或旋转后的图形和原来的图形是一模一样的。
其次,在变换过程中,对应点之间的距离或者对应线段的长度是相等的。
在数学中,我们经常会遇到需要利用图形的旋转和平移来解决的问题。
比如说,通过平移和旋转可以把一个复杂的图形变得更简单,从而方便我们计算它的面积、周长等。
举个例子,假设有一个不规则的多边形,我们可以通过适当的平移和旋转,把它变成一个我们熟悉的规则图形,比如长方形或者正方形,然后利用我们已知的公式来计算它的面积或周长。
又比如,在几何证明题中,有时候通过对图形进行旋转或平移,可以让原本分散的条件集中起来,从而找到解题的关键。
学习图形的旋转和平移变换,不仅能够帮助我们更好地理解数学知识,还能培养我们的空间想象力和逻辑思维能力。
