河北省石家庄市届高中毕业班第一次模拟考试理科数学试题
石家庄市一模理科数学试题及答案

届石家庄市高中毕业班第一次模拟考试试卷数学(理科)B 卷 第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.已知集合{}|05A x x =≤≤,{}*|12B x N x =∈-≤,则A B =I ( ) A .{}|13x x ≤≤ B .{}|03x x ≤≤ C .{}0,1,2,3D .{}1,2,32.若z 是复数,121iz i-=+,则z z ⋅=( )A .2 B .2C .1D .523.下列说法错误的是( ) A .回归直线过样本点的中心(,)x yB .两个随机变量的线性相关性越强,则相关系数的绝对值就越接近于1C .对分类变量X 与Y ,随机变量2K 的观测值k 越大,则判断“X 与Y 有关系”的把握程度越小 D .在回归直线方程$0.20.8y x =+中,当解释变量x 每增加1个单位时,预报变量$y 平均增加个单位 4.函数()31xf x e x =--(e 为自然对数的底数)的图象大致是( )5.函数()sin()f x A x ωϕ=+(0A >,0ω>)的最小正周期为π,其图象关于直线3x π=对称,则||ϕ的最小值为( )A .12π B .6π C .56π D .512π6.已知三个向量a r ,b r ,c r 共面,且均为单位向量,0a b ⋅=r r ,则||a b c +-r r r的取值范围是( )A .1⎤⎦B .⎡⎣C .D .1,1⎤⎦7.某几何体的三视图如图所示(在如图的网格线中,每个小正方形的边长为1),则该几何体的表面积为( ) A .48B .54C .64D .608.已知函数()f x 在(1,)-+∞上单调,且函数(2)y f x =-的图象关于1x =对称,若数列{}n a 是公差不为0的等差数列,且5051()()f a f a =,则{}n a 的前100项的和为( ) A .200-B .100-C .0D .50-9.祖暅是南北朝时代的伟大科学家,5世纪末提出体积计算原理,即祖暅原理:“幂势既同,则积不容异”.意思是:夹在两个平行平面之间的两个几何体,被平行于这两个平面的任何一个平面所截,如果截面面积都相等,那么这两个几何体的体积一定相等.现有以下四个几何体:图①是从圆柱中挖出一个圆锥所得的几何体;图②、图③、图④分别是圆锥、圆台和半球,则满足祖暅原理的两个几何体为( ) A .①②B .①③C .②④D .①④10.已知x ,y 满足约束条件20,220,220,x y x y x y +-≤⎧⎪--≤⎨⎪-+≥⎩若20x y k ++≥恒成立,则直线20x y k ++=被圆22(1)(2)25x y -+-=截得的弦长的最大值为( )A .10B.C.D.11.已知过抛物线22(0)y px p =>的焦点F 的直线与抛物线交于A ,B 两点,且3AF FB =u u u r u u u r,抛物线的准线l 与x 轴交于点C ,1AA l ⊥于点1A ,若四边形1AA CF的面积为则准线l 的方程为( ) A.x =B.x =-C .2x =-D .1x =-12.已知函数()ln f x ax e x =+与2()ln x g x x e x=-的图象有三个不同的公共点,其中e 为自然对数的底数,则实数a 的取值范围为( ) A .a e <-B .1a >C .a e >D .3a <-或1a >第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上) 13.已知命题p :n N ∀∈,22nn <,则p ⌝为 .14.程序框图如图所示,若输入0s =,10n =,0i =,则输出的s 为 .15.已知1F 、2F 分别为双曲线22221x y a b-=(0a >,0b >)的左、右焦点,点P 为双曲线右支上一点,M 为12PF F ∆的内心,满足1212MPF MPF MF F S S S λ∆∆∆=+,若该双曲线的离心率为3,则λ= (注:1MPF S ∆、2MPF S ∆、12MF F S ∆分别为1MPF ∆、2MPF ∆、12MF F ∆的面积).16.已知数列{}n a 中,1a a =,1386n n a a n +=++,若{}n a 为递增数列,则实数a 的取值范围为 . 三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.) 17.在ABC ∆中,内角A ,B ,C 的对边分别是a ,b ,c ,且sin sin sin C a bA B a c+=--.(Ⅰ)求角B 的大小;(Ⅱ)点D 满足2BD BC =u u u r u u u r,且线段3AD =,求2a c +的最大值.18.在四棱锥S ABCD -中,底面ABCD 为平行四边形,60DBA ∠=︒,30SAD ∠=︒,AD SD ==,4BA BS ==.(Ⅰ)证明:BD ⊥平面SAD ; (Ⅱ)求二面角A SB C --的余弦值.19.人耳的听力情况可以用电子测听器检测,正常人听力的等级为0-25db (分贝),并规定测试值在区间(0,5]为非常优秀,测试值在区间(5,10]为优秀.某班50名同学都进行了听力测试,所得测试值制成频率分布直方图:(Ⅰ)现从听力等级为(0,10]的同学中任意抽取出4人,记听力非常优秀的同学人数为X ,求X 的分布列与数学期望; (Ⅱ)在(Ⅰ)中抽出的4人中任选一人参加一个更高级别的听力测试,测试规则如下:四个音叉的发生情况不同,由强到弱的次序分别为1,2,3,4.测试前将音叉随机排列,被测试的同学依次听完后给四个音叉按发音的强弱标出一组序号1a ,2a ,3a ,4a (其中1a ,2a ,3a ,4a 为1,2,3,4的一个排列).若Y 为两次排序偏离程度的一种描述,1234|1||2||3||4|Y a a a a =-+-+-+-,求2Y ≤的概率.20.已知椭圆C :2212x y +=的左顶点为A ,右焦点为F ,O 为原点,M ,N 是y 轴上的两个动点,且MF NF ⊥,直线AM 和AN 分别与椭圆C 交于E ,D 两点.(Ⅰ)求MFN ∆的面积的最小值; (Ⅱ)证明:E ,O ,D 三点共线.21.已知函数2()1ln(1)f x x a x =-+-,a R ∈.(Ⅰ)若函数()f x 为定义域上的单调函数,求实数a 的取值范围; (Ⅱ)若函数()f x 存在两个极值点1x ,2x ,且12x x <,证明:1221()()f x f x x x >. 请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分. 22.选修4-4:坐标系与参数方程在平面直角坐标系,将曲线1C 上的每一个点的横坐标保持不变,纵坐标缩短为原来的12,得到曲线2C ,以坐标原点O 为极点,x 轴的正半轴为极轴,建立极坐标系,1C 的极坐标方程为2ρ=. (Ⅰ)求曲线2C 的参数方程;(Ⅱ)过原点O 且关于y 轴对称的两条直线1l 与2l 分别交曲线2C 于A 、C 和B 、D ,且点A 在第一象限,当四边形ABCD 的周长最大时,求直线1l 的普通方程.23.选修4-5:不等式选讲已知函数()|24|||f x x x a =++-.(Ⅰ)当2a <-时,()f x 的最小值为1,求实数a 的值; (Ⅱ)当()|4|f x x a =++时,求x 的取值范围.2017届石家庄市高中毕业班第一次模拟考试试卷数学(理科)B 卷答案一、选择题1-5:DDCDB 6-10:ADBDB 11、12:AB 二、填空题13.0n N ∃∈,0202nn ≥ 15.1316.7a >- 三、解答题 17.解:(Ⅰ)∵sin sin sin C a b A B a c +=--,由正弦定理得c a ba b a c+=--, ∴()()()c a c a b a b -=+-, 即222a cb ac +-=,又∵2222cos a c b ac B +-=, ∴1cos 2B =, ∵(0,)B π∈,∴3B π=.(Ⅱ)在ABC ∆中由余弦定理知:222(2)22cos 603c a a c +-⋅⋅⋅︒=, ∴2(2)932a c ac +-=⋅,∵ 222()2a c ac +≤, ∴223(2)9(2)4a c a c +-≤+,即2(2)36a c +≤,当且仅当2a c =,即32a =,3c =时取等号,所以2a c +的最大值为6. 18.(Ⅰ)证明:在ABD ∆中,sin sin AB ADADB DBA=∠∠,由已知60DBA ∠=︒,AD =4BA =, 解得sin 1ADB ∠=,所以90ADB ∠=︒,即AD BD ⊥,可求得2BD =. 在SBD ∆中,∵SD =4BS =,2BD =, ∴222DB SD BS +=,∴SD BD ⊥,∵BD ⊄平面SAD ,SD AD D =I ,∴BD ⊥平面SAD .(Ⅱ)过D 作直线l 垂直于AD ,以D 为坐标原点,以DA 为x 轴,以DB 为y 轴,以l 为z 轴,建立空间直角坐标系. ∵由(Ⅰ)可知,平面SAD ⊥平面ABCD ,∴S 在平面ABCD 上的投影一定在AD 上,过S 作SE AD ⊥于E,则DE =3SE =,则(S ,易求A ,(0,2,0)B,(2,0)C -,则2,3)SB =-u u r,3)SA =-u u r,(2,3)SC =-u u u r,设平面SBC 的法向量1(,,)n x y z =u r,230,230,y z y z +-=+-=⎪⎩解得1(0,3,2)n =--u r .同理可求得平面SAB的法向量2(1n =u u r,∴1212cos ||||n n n n θ⋅===⋅u r u u r u r u u r19.解:(Ⅰ)X 的可能取值为:0,1,2,3,4.4641015(0)210C P X C ===,134641080(1)210C C P X C ===,224641090(2)210C C P X C ===,314641024(3)210C C P X C ===, 444101(4)210C P X C ===, X 的分布列为:X 01234P15210 80210 90210 242101210158090241()01234 1.621021**********E X =⨯+⨯+⨯+⨯+⨯=.(Ⅱ)序号1a ,2a ,3a ,4a 的排列总数为4424A =种,当0Y =时,11a =,22a =,33a =,44a =.当1234|1||2||3||4|2Y a a a a =-+-+-+-=时,1a ,2a ,3a ,4a 的取值为11a =,22a =,34a =,43a =;11a =,23a =,32a =,44a =;12a =,21a =,33a =,44a =.故41(2)246P Y ≤==. 20.解:(Ⅰ)设(0,)M m ,(0,)N n ,∵MF NF ⊥,可得1mn =-,11||||||22AMFN S AF MN MN ==, ∵222||||||2||||MN MF NF MF NF =+≥⋅,当且仅当||||MF NF =时等号成立. ∴min ||2MN =, ∴min 1()||12MFN S MN ==, ∴四边形AMFN 的面积的最小值为1.(Ⅱ)∵(A ,(0,)M m ,∴直线AM的方程为y x m =+,由22,22,y x m x y ⎧=+⎪⎨⎪+=⎩得2222(1)2(1)0m x x m +++-=,由222(1)1E m x m -=+,得E x =,①同理可得D x =,∵1m n ⋅=-,∵221()11()1D m x m⎤-⎥⎣⎦=+=② 故由①②可知:E D x x =-,代入椭圆方程可得22E D y y =∵MF NF ⊥,故M ,N 分别在x 轴两侧,E D y y =-, ∴E DE Dy y x x =,∴E ,O ,D 三点共线.21.解:(Ⅰ)函数()f x 的定义域为(,1)-∞,由题意222'()2,111a x x a f x x x x x -+-=-=<--, 224(2)()48a a ∆=---=-.①若480a ∆=-≤,即12a ≥,则2220x x a -+-≤恒成立, 则()f x 在(,1)-∞上为单调减函数;②若480a ∆=->,即12a <,方程2220x x a -+-=的两根为112x =,212x +=,当1(,)x x ∈-∞时,'()0f x <,所以函数()f x 单调递减,当11(,)2x x ∈时,'()0f x >,所以函数()f x 单调递增,不符合题意. 综上,若函数()f x 为定义域上的单调函数,则实数a 的取值范围为1(,)2+∞. (Ⅱ)因为函数()f x 有两个极值点,所以'()0f x =在1x <上有两个不等的实根, 即2220x x a -+-=在1x <有两个不等的实根1x ,2x ,于是102a <<,12121,,2x x a x x +=⎧⎪⎨=⎪⎩且满足11(0,)2x ∈,21(,1)2x ∈, 211111*********()1ln(1)(1)(1)2ln(1)(1)2ln(1)f x x a x x x x x x x x x x x x -+--++-===-++-, 同理可得22221()(1)2ln(1)f x x x x x =-++-. 122111222222221()()2ln(1)2ln(1)212(1)ln 2ln(1)f x f x x x x x x x x x x x x x x -=-+---=-+---, 令()212(1)ln 2ln(1)g x x x x x x =-+---,1(,1)2x ∈.[]22'()2ln (1)1x g x x x x x =--++-,1(,1)2x ∈, ∵1(1)4x x -<,∴[]2ln (1)0x x -->, 又1(,1)2x ∈时,201x x x 2+>-,∴'()0g x >,则()g x 在1(,1)2x ∈上单调递增, 所以1()()02g x g >=,即1221()()0f x f x x x ->,得证. 22.解:(Ⅰ)2214x y +=,2cos sin x y θθ=⎧⎨=⎩(θ为参数). (Ⅱ)设四边形ABCD 的周长为l ,设点(2cos ,sin )A q q ,8cos 4sin l θθ=+))θθθϕ==+,且cos ϕ=,sin ϕ= 所以,当22k πθϕπ+=+(k Z ∈)时,l 取最大值,此时22k πθπϕ=+-,所以,2cos 2sin θϕ==sin cos θϕ==此时,A ,1l 的普通方程为14y x =.23.解:(Ⅰ)当2a <-时,函数34,,()|24|||4,2,34, 2.x a x a f x x x a x a a x x a x -+-<⎧⎪=++-=---≤≤-⎨⎪-+>-⎩可知,当2x =-时,()f x 的最小值为(2)21f a -=--=,解得3a =-. (Ⅱ)因为()|24||||(24)()||4|f x x x a x x a x a =++-≥+--=++, 当且仅当(24)()0x x a +-≤时,()|4|f x x a =++成立, 所以,当2a <-时,x 的取值范围是{}|2x a x ≤≤-; 当2a =-时,x 的取值范围是{}2-;当2a >-时,x 的取值范围是{}|2x x a -≤≤.。
石家庄市高中第一次模拟考试数学试题

石家庄市高中第一次模拟考试数学试题Company Document number:WTUT-WT88Y-W8BBGB-BWYTT-19998石家庄市高中第一次模拟考试 数 学 试 题说明:本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分.考试时间120分钟.以下公式供参考:(1)台体体积:V =)(312211S S S S h +⋅+(其中h 是台体的高,S 1,S 2分别是台体上、下底的面积); (2)12+22+32+……+n 2=)(6)12)(1(N n n n n ∈++ 第Ⅰ卷 (选择题 共60分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知集合M ={-1,1,2,4},N ={0,1,2},给出下列四个对应法则:(1)y =x 2,(2)y =x +1,(3)y =2x ,(4)y =log 2|x |,其中能构成从M 到N 的函数的是A.(1)B.(2)C.(3)D.(4)2.当0<a <1时,函数①y =a |x |与函数②y =log a |x |在区间(-∞,0)上的单调性为A.都是增函数B.都是减函数C.①是增函数,②是减函数D.①是减函数,②是增函数3.若a ,b 是两条异面直线,则存在惟一..确定的平面β,满足 A. a βββ⊂βa ⊥β且b ⊥β β⊂且b ⊥β4.某单位职工工资经过六年翻了三番,则每年比上一年平均增长的百分数(下列数据仅供参考: )38.16,44.13,73.13,41.1263====为% % % %5.在一半径为1,高为定值的圆锥内有一底面半径为x 的内接圆柱,圆柱的侧面积S 是x 的函数,则函数s =f (x )的大致图象是6.将(x +y +z )10展开后,则展开式中含x 5y 3z 2项的系数为A.210310510C C C ⋅⋅B. 2235510C C C ⋅⋅C.31025C C ⋅D.24510C C ⋅,32t x +=7.(理)已知直线l : (t 为参数)与直线2x +y +1=0相交于点P ,则点P 与点y =-1-4t .A (2,-1)的距离为A.25B. 52 (文)点P (2,1)到线段:x -y +2=0(-2≤x ≤-1)上的点的最近距离是A.223B.-3C.17D.22 8.(理)函数y =a sin x +b cos x (R x ∈)的最大值为5,则a +b 的最小值是A.52B.-52C.10D.-10 (文)y =sin x +3cos x ⎥⎦⎤⎢⎣⎡∈2,0πx ,则y 的最小值为 A.-2 B.-1 D.39.△ABC 的内角A 满足tg A -sin A <0,sin A +cos A >0,则角A 的取值范围为A.(0,4π) B.(2,4ππ) C. (43,2ππ) D. (ππ,43) 10.椭圆13422=+y x 上有n 个不同的点: P 1、P 2、…P n ,椭圆的右焦点为F .数列{|P n F |}是公差大于1001的等差数列,则n 的最大值为,b 为不相等的正实数,且a ,x ,y ,b 成等差数列,a ,m ,n ,b 成等比数列,则下列关系成立的是+y >m +n +y =m +n+y <m +n +y 与m +n 的大小关系不能确定12.定义:函数y =f (x ),x ∈D ,若存在常数c ,对于任意x 1∈D ,存在惟一的x 2∈D ,使c x f x f =+2)()(21,则称函数f (x )在D 上的均值为c .已知f (x ) =lg x ,x ∈[10,100],则函数f (x ) =lg x 在[10,100]上的均值为A.43B.23C.101 第Ⅱ卷(非选择题 共90分)二、填空题(本大题共4小题,每小题4分,共16分.把答案填在题中横线上)13.已知f (x )=________)(,2)(,222=-=--a f a f xx 则. 14.有一密码为的手提保险箱,现显示的号码为要打开箱子,至少需要经过旋(每一个旋钮上显示的数字可为0,1,2,3,4,5,6,7,8,9的任意一个,只要一个旋钮上转出一个新数字就为一步,逆转、顺转都可以)________步.15.(理)抛物线y =b (a x )2,x 轴及直线AB :x =a 围成了如图(1)的阴影部分,AB 与x 轴交于A ,把线段OA 分成n 等分,作以na 为底的内接矩形如图(2),阴影部分的面积S 等于这些内接矩形面积之和,当n →∞时的极限值.则S =__________.6 3 1 2 0 8 0 8 0 1 2 7(文)已知数列{a n }的通项a n =n (n +1),S n 是前n 项和,则3lim n S n n ∞→= ________. 16.有六根细木棒,其中较长的两根木棒长分别为a 3、a 2,其余四根长均为a ,请你用它们搭成三棱锥.则其中两条较长的棱所在的直线所成角的余弦值为__________.三、解答题(本大题共6个小题,共74分.解答应写出文字说明、证明过程或演算步骤)17.(本小题满分11分)已知复数ω=ii i i -+++1)31)(21)(1( (1)求|ω|及arg ω;(2)设复数z =cos θ+i sin θ,求使得|z -ω|取得最大值时,复数z 的值.18.(本小题满分12分)已知△ABC 中,三个内角A 、B 、C 对应的三边分别为a 、b 、c .(1)求证△ABC 的面积为S =;sin 21C ab (2)求证:Cc B b A a sin sin sin ==; (3)若A 、B 、C 成等差数列,且a =10,b =9.求sin C 的值.19.(本小题满分12分)如图,三棱台ABC -A 1B 1C 1中,平面AC 1⊥平面ABC ,平面BC 1⊥平面ABC ,∠ACB =120°,AC =a ,BC =2a ,C 1B 1=a ,异面直线AB 1与CC 1所成的角为60°.(1)求证CC 1⊥平面ABC ;(2)求二面角B 1-AC -B 的大小(文科只求正切值);(3)求多面体AA 1C 1CB 1的体积.20.(本小题满分12分)为了治理“沙尘暴”,西部某地区政府经过多年努力,到1998年底,将当地沙漠绿化了40%,从1999年开始,每年将出现这种现象: 原有沙漠面积的12%被绿化,即改造为绿洲(被绿化的部分叫绿洲),同时原有绿洲面积的8%又被侵蚀为沙漠.问至少经过几年的绿化,才能使该地区的绿洲面积超过50%(可参考数据lg2=,最后结果精确到整数.)21.(本小题满分13分)(理)已知函数f (x ) =x 2-1(x ≥1)的图象是C 1,函数y =g (x )的图象C 2与C 1关于直线 y =x 对称.(1)求函数y =g(x )的解析式及定义域M ;(2)对于函数y =h (x ),如果存在一个正的常数a ,使得定义域A 内的任意两个不等的值x 1,x 2都有|h (x 1)-h (x 2)|≤a | x 1-x 2|成立,则称函数y =h (x )为A 上的利普希茨1类函数.试证明:y =g (x )是M 上的利普希茨1类函数.(3)设A ,B 是曲线C 2上任意不同两点,证明:直线AB 与直线y =x 必相交.(文)已知函数g (x )=-x 1的图象关于点A (21,21-)的对称图象为函数y = f (x )的图象. (1)求y = f (x );(2)用函数单调性定义证明函数y = f (x )在区间(-1,+∞)上为单调递增函数;(3)若a >b >0,c =b b a )(1-,试比较f (a +c )与43的大小. 22.(本小题满分14分)已知⊙F 过定点A (a ,0)(a >0),圆心F 在抛物线C :y 2=2ax 上运动,MN 为⊙F 在y 轴上截得的弦.(1)试判断MN 的长是否随圆心F 的运动而变化并证明你的结论;(2)当|OA |是|OM |与|ON |的等差中项时,抛物线C 的准线与⊙F 有怎样的位置关系并说明理由.湖北省黄冈市高三模拟考试 数 学 试 题 说明:本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分.考试时间120分钟. 第Ⅰ卷(选择题 共60分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.设I 为全集,A 为非空集合,且A ⊂B ⊂I,则下列集合为空集的是A.BA B.B A C. B A D.B A2.函数y =4sin(x +4π)sin )4(x -π是A.周期为π2的偶函数B.周期为π2的奇函数C.周期为π的偶函数D.周期为π的奇函数 3.如图,点P 在正方形ABCD 所在平面外,P A ⊥平面ABCD ,P A =AB ,则PB 与AC 所成的角是 A ︒90 B.︒60 C.︒45 D.︒30 4.对于函数f (x )=ax 2+bx +c (a ≠0)作代换x =g (t ),则不改变函数f (x )的值域的代换是 (t )=2' B. g (t )=|t | C. g (t )=sin t D. g (t )=log 2t5.已知点P (sin αααtg ,cos -)在第一象限,且∈α[0,π2],则α的取值范围是A.()45,()2,4ππππ B.)23,45()43,2(ππππ C.),43()2,4(ππππ D. )45,()43,2(ππππ 6.(理)原点与极点重合,x 轴正半轴与极轴重合时,圆ρ=10cos(6πθ+)的中心的直角坐标是 A.25,325(--) B.)25,325(- C.)25,325( D. )25,325(- 6.(文)圆x 2+y 2-ax +2y +1=0关于直线x -y =1对称的圆的方程是x 2+y 2=1,则实数a 的值是A.±2个身高均不相同的学生排成一排合影留念,高个子站中间,从中间到左边一个比一个矮,从中间到右边也一个比一个矮,则这样的排法有种 种 种 种8.已知函数f (x )满足f (x 2-3)=lg 226xx -,则y =f (x )在定义域内 A.是奇函数且是增函数B.是奇函数且是减函数C.是偶函数D.是增函数,但既非奇函数又非偶函数9.(理)若曲线y =42-x 与直线y =k (x -2)+3有两个不同的公共点,则实数k 的取值范围是≤k ≤1 ≤k ≤43 C. -1<k ≤43 D.-1<k ≤0 (文)如果直线l 将曲线x 2+2y 2-2x -8y =0的周长分成长度相等的两段,且不经过第四象限,则直线l 的斜率k 的取值范围是A.[0,21]B.(0,1)C.[0,2]D.[0,1] 10.一个半径为5cm,圆心角为216°的扇形,卷成一个圆锥的侧面,则此圆锥的高是53 54 11.若将离心率为43的椭圆12222=+b y a x (a >b >0)绕着它的左焦点按逆时针方向旋转2π后,所得新椭圆的一条准线方程是3y +14=0,则新椭圆的另一条准线方程是A. 3y -14=0B. 3y -23=0-32=0 -50=012.某大学的信息中心A 与大学各部门、各院系B ,C ,D ,E ,F ,G ,H ,I 之间拟建立信息联网工程,实际测算的费用如图所示(单位:万元).请观察图形可以不建部分网线,而使得中心与各部门、各院系都能连通(直接或中转).则最小的建网费用(万元)是第Ⅱ卷(非选择题 共90分)二、填空题(本大题共4小题,每小题4分,共16分.把答案填在题中横线上)13.已知二条直线m ,n ,三个平面α,β,γ,给出下列命题:①若α⊥β, α β=m ,n ⊥m ,则n ⊥α或n ⊥β;②若αα ααα ⊄α⊄α其中正确命题的序号是______________.(x )的图象是如图两条线段,它的定义域是[-1,0]( 0,1],则不等式f (x )-f (-x )>-1的解集是__________.15.已知抛物线y 2=2px (p >0)的焦点在直线y =x -2上,现将抛物线平移,当抛物线的焦点沿直线y =x -2移到点(2a ,4a +2)时,所得抛物线的方程为_______________.16.数列满足条件:①任意连续二项的和大于零;②任意连续三项的和小于零;则这样的数列最多有____________项.三、解答题(本大题共6个小题,共74分.解答应写出文字说明、证明过程或演算步骤)17.(本小题满分12分)(理)已知方程x 2+2px +1=0(p ∈R )的两虚根为α,β,且在复平面上α,β,1所对应的点是一个正三角形的三个顶点,求p 的值.(文)已知复数ω对应点在第一象限,|ω|=4,且原点和ω,ω的对应点是正三角形的三个顶点,若ω=,1)1(3iz i -+,求复数z 的辐角主值.18.(本小题满分12分)(理)设a ,b ,c 分别为△ABC 的边BC ,CA ,AB 的长,且a 2+b 2-mc 2=0(m 为常数).若(ctg A +ctg B )tg C =1,求m 的值. (文)在△ABC 中,若(a +b +c )(a -b +c )=3ac ,且tg A +tg C =3+3,求三内角.19.(本小题满分12分)直三棱柱ABC -A 1B 1C 1中,底面△ABC 是直角三角形,∠ABC =90°,且2AB =BC =BB 1=a ,设A 1C 与AC 1交于D ,BC 1与B 1C交于E ,连DE . (1)求证:DE ⊥平面BB 1C 1C ;(2)求二面角D -BB 1-E 的大小;(3)求三棱锥A 1-BDE 的体积.20.(本小题满分12分)某企业开发了一种新产品,现准备投入适当的广告费,对产品进行促销.在一年内,预计年销量Q (万件)与广告费x (万元)之间的函数关系为:Q =).0(23>-x xx 已知生产此产品的年固定投入为3万元,每生产1万件此产品仍需再投入32万元.若年销售额为“年生产成本的150%”与“年广告费的50%”之和,当年产销量相等.(1)试将年利润P 万元表示为年广告费x 万元的函数;(2)当年广告费投入多少万元时,企业年利润最大21. (本小题满分12分) 已知双曲线的12222=-by a x 离心率332=e ,过A (a ,0),B (0,-b )的直线到原点的距离是23. (1)求双曲线的方程;(2)已知直线y =kx +5(k ≠0)交双曲线于不同的两点C 、D ,且C 、D 都在以B 为圆心的圆上,求k 的值.22.(本小题满分14分)设数列{a n }的首项a 1=1,前n 项和S n 满足关系3tS n -(2t +3)S n -1=3t (t >0,n =2,3,4,…)(1)求证:数列{a n }是等比数列;(2)设数列{a n }的公比是f (t ),作数列b n ,使b 1=1,b n =)1(1-n b f (n =2,3,4…),求b n 及nn n b a lg lim ∞→; (3)求和:B n =b 1b 2-b 2b 3+b 3b 4-…+(-1)n -1b n b n +1.。
河北省石家庄市高三数学一模考试(理科)试题 Word版含答案

2017届石家庄市高中毕业班第一次模拟考试试卷数学(理科)B 卷 第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}|05A x x =≤≤,{}*|12B x N x =∈-≤,则A B =( )A .{}|13x x ≤≤B .{}|03x x ≤≤C .{}0,1,2,3D .{}1,2,32.若z 是复数,121iz i-=+,则z z ⋅=( )A B C .1 D .523.下列说法错误的是( ) A .回归直线过样本点的中心(,)x yB .两个随机变量的线性相关性越强,则相关系数的绝对值就越接近于1C .对分类变量X 与Y ,随机变量2K 的观测值k 越大,则判断“X 与Y 有关系”的把握程度越小D .在回归直线方程0.20.8y x =+中,当解释变量x 每增加1个单位时,预报变量y 平均增加0.2个单位4.函数()31xf x e x =--(e 为自然对数的底数)的图象大致是( )5.函数()sin()f x A x ωϕ=+(0A >,0ω>)的最小正周期为π,其图象关于直线3x π=对称,则||ϕ的最小值为( ) A .12π B .6π C .56π D .512π6.已知三个向量a ,b ,c 共面,且均为单位向量,0a b ⋅=,则||a b c +-的取值范围是( )A .1⎤⎦B .⎡⎣C .D .1,1⎤⎦7.某几何体的三视图如图所示(在如图的网格线中,每个小正方形的边长为1),则该几何体的表面积为( )A .48B .54C .64D .608.已知函数()f x 在(1,)-+∞上单调,且函数(2)y f x =-的图象关于1x =对称,若数列{}n a 是公差不为0的等差数列,且5051()()f a f a =,则{}n a 的前100项的和为( )A .200-B .100-C .0D .50-9.祖暅是南北朝时代的伟大科学家,5世纪末提出体积计算原理,即祖暅原理:“幂势既同,则积不容异”.意思是:夹在两个平行平面之间的两个几何体,被平行于这两个平面的任何一个平面所截,如果截面面积都相等,那么这两个几何体的体积一定相等.现有以下四个几何体:图①是从圆柱中挖出一个圆锥所得的几何体;图②、图③、图④分别是圆锥、圆台和半球,则满足祖暅原理的两个几何体为( )A .①②B .①③C .②④D .①④10.已知x ,y 满足约束条件20,220,220,x y x y x y +-≤⎧⎪--≤⎨⎪-+≥⎩若20x y k ++≥恒成立,则直线20x y k ++=被圆22(1)(2)25x y -+-=截得的弦长的最大值为( )A .10B.C.D.11.已知过抛物线22(0)y px p =>的焦点F 的直线与抛物线交于A ,B 两点,且3AF FB =,抛物线的准线l 与x 轴交于点C ,1AA l ⊥于点1A ,若四边形1AA CF的面积为则准线l 的方程为( )A.x =B.x =-C .2x =-D .1x =-12.已知函数()ln f x ax e x =+与2()ln x g x x e x=-的图象有三个不同的公共点,其中e 为自然对数的底数,则实数a 的取值范围为( ) A .a e <-B .1a >C .a e >D .3a <-或1a >第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上) 13.已知命题p :n N ∀∈,22n n <,则p ⌝为 .14.程序框图如图所示,若输入0s =,10n =,0i =,则输出的s 为 .15.已知1F 、2F 分别为双曲线22221x y a b-=(0a >,0b >)的左、右焦点,点P 为双曲线右支上一点,M 为12PF F ∆的内心,满足1212MPF MPF MF F S S S λ∆∆∆=+,若该双曲线的离心率为3,则λ= (注:1MPF S ∆、2MPF S ∆、12MF F S ∆分别为1MPF ∆、2MPF ∆、12MF F ∆的面积).16.已知数列{}n a 中,1a a =,1386n n a a n +=++,若{}n a 为递增数列,则实数a 的取值范围为 .三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.) 17.在ABC ∆中,内角A ,B ,C 的对边分别是a ,b ,c ,且sin sin sin C a bA B a c+=--. (Ⅰ)求角B 的大小;(Ⅱ)点D 满足2BD BC =,且线段3AD =,求2a c +的最大值.18.在四棱锥S ABCD -中,底面ABCD 为平行四边形,60DBA ∠=︒,30SAD ∠=︒,AD SD ==,4BA BS ==.(Ⅰ)证明:BD ⊥平面SAD ; (Ⅱ)求二面角A SB C --的余弦值.19.人耳的听力情况可以用电子测听器检测,正常人听力的等级为0-25db (分贝),并规定测试值在区间(0,5]为非常优秀,测试值在区间(5,10]为优秀.某班50名同学都进行了听力测试,所得测试值制成频率分布直方图:(Ⅰ)现从听力等级为(0,10]的同学中任意抽取出4人,记听力非常优秀的同学人数为X ,求X 的分布列与数学期望;(Ⅱ)在(Ⅰ)中抽出的4人中任选一人参加一个更高级别的听力测试,测试规则如下:四个音叉的发生情况不同,由强到弱的次序分别为1,2,3,4.测试前将音叉随机排列,被测试的同学依次听完后给四个音叉按发音的强弱标出一组序号1a ,2a ,3a ,4a (其中1a ,2a ,3a ,4a 为1,2,3,4的一个排列).若Y 为两次排序偏离程度的一种描述,1234|1||2||3||4|Y a a a a =-+-+-+-,求2Y ≤的概率.20.已知椭圆C :2212x y +=的左顶点为A ,右焦点为F ,O 为原点,M ,N 是y 轴上的两个动点,且MF NF ⊥,直线AM 和AN 分别与椭圆C 交于E ,D 两点.(Ⅰ)求MFN ∆的面积的最小值; (Ⅱ)证明:E ,O ,D 三点共线.21.已知函数2()1ln(1)f x x a x =-+-,a R ∈.(Ⅰ)若函数()f x 为定义域上的单调函数,求实数a 的取值范围; (Ⅱ)若函数()f x 存在两个极值点1x ,2x ,且12x x <,证明:1221()()f x f x x x >.请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分. 22.选修4-4:坐标系与参数方程在平面直角坐标系,将曲线1C 上的每一个点的横坐标保持不变,纵坐标缩短为原来的12,得到曲线2C ,以坐标原点O 为极点,x 轴的正半轴为极轴,建立极坐标系,1C 的极坐标方程为2ρ=.(Ⅰ)求曲线2C 的参数方程;(Ⅱ)过原点O 且关于y 轴对称的两条直线1l 与2l 分别交曲线2C 于A 、C 和B 、D ,且点A 在第一象限,当四边形ABCD 的周长最大时,求直线1l 的普通方程. 23.选修4-5:不等式选讲已知函数()|24|||f x x x a =++-.(Ⅰ)当2a <-时,()f x 的最小值为1,求实数a 的值; (Ⅱ)当()|4|f x x a =++时,求x 的取值范围.2017届石家庄市高中毕业班第一次模拟考试试卷数学(理科)B 卷答案一、选择题1-5:DDCDB 6-10:ADBDB 11、12:AB 二、填空题13.0n N ∃∈,0202nn ≥ 14.1024 15.1316.7a >- 三、解答题 17.解:(Ⅰ)∵sin sin sin C a b A B a c +=--,由正弦定理得c a ba b a c+=--, ∴()()()c a c a b a b -=+-, 即222a c b ac +-=,又∵2222cos a c b ac B +-=, ∴1cos 2B =, ∵(0,)B π∈,∴3B π=.(Ⅱ)在ABC ∆中由余弦定理知:222(2)22cos 603c a a c +-⋅⋅⋅︒=, ∴2(2)932a c ac +-=⋅,∵ 222()2a c ac +≤, ∴223(2)9(2)4a c a c +-≤+,即2(2)36a c +≤,当且仅当2a c =,即32a =,3c =时取等号,所以2a c +的最大值为6.18.(Ⅰ)证明:在ABD ∆中,sin sin AB ADADB DBA=∠∠,由已知60DBA ∠=︒,AD =4BA =,解得sin 1ADB ∠=,所以90ADB ∠=︒,即AD BD ⊥,可求得2BD =. 在SBD ∆中,∵SD =4BS =,2BD =, ∴222DB SD BS +=,∴SD BD ⊥, ∵BD ⊄平面SAD ,SDAD D =,∴BD ⊥平面SAD .(Ⅱ)过D 作直线l 垂直于AD ,以D 为坐标原点,以DA 为x 轴,以DB 为y 轴,以l 为z 轴,建立空间直角坐标系.∵由(Ⅰ)可知,平面SAD ⊥平面ABCD ,∴S 在平面ABCD 上的投影一定在AD 上,过S 作SE AD ⊥于E,则DE =3SE =,则(S ,易求A ,(0,2,0)B,(2,0)C -,则(3,2,3)SB =-,(33,0,3)SA =-,(2,3)SC =-,设平面SBC 的法向量1(,,)n x y z=,230,230,y z y z +-=+-=⎪⎩解得1(0,3,2)n =--.同理可求得平面SAB的法向量2(1n =,∴1212cos 91||||13n n n n θ⋅===-⋅.19.解:(Ⅰ)X 的可能取值为:0,1,2,3,4.4641015(0)210C P X C ===,134641080(1)210C C P X C ===,224641090(2)210C C P X C ===,314641024(3)210C C P X C ===, 444101(4)210C P X C ===, X 的分布列为:X 01234P15210 80210 90210 242101210158090241()01234 1.621021**********E X =⨯+⨯+⨯+⨯+⨯=.(Ⅱ)序号1a ,2a ,3a ,4a 的排列总数为4424A =种,当0Y =时,11a =,22a =,33a =,44a =.当1234|1||2||3||4|2Y a a a a =-+-+-+-=时,1a ,2a ,3a ,4a 的取值为11a =,22a =,34a =,43a =;11a =,23a =,32a =,44a =;12a =,21a =,33a =,44a =.故41(2)246P Y ≤==. 20.解:(Ⅰ)设(0,)M m ,(0,)N n ,∵MF NF ⊥,可得1mn =-,11||||||22AMFN S AF MN MN ==, ∵222||||||2||||MN MF NF MF NF =+≥⋅,当且仅当||||MF NF =时等号成立. ∴min ||2MN =, ∴min 1()||12MFN S MN ==, ∴四边形AMFN 的面积的最小值为1.(Ⅱ)∵(A ,(0,)M m ,∴直线AM的方程为y x m =+,由22,22,y x m x y ⎧=+⎪⎨⎪+=⎩得2222(1)2(1)0m x x m +++-=,由222(1)1E m x m -=+,得E x =,①同理可得221)1D n x n -=+,∵1m n ⋅=-,∵221()11()1D m x m⎤-⎥⎣⎦=+22),1m m -=+② 故由①②可知:E D x x =-,代入椭圆方程可得22E D y y =∵MF NF ⊥,故M ,N 分别在x 轴两侧,E D y y =-, ∴E DE Dy y x x =,∴E ,O ,D 三点共线.21.解:(Ⅰ)函数()f x 的定义域为(,1)-∞,由题意222'()2,111a x x af x x x x x -+-=-=<--, 224(2)()48a a ∆=---=-.①若480a ∆=-≤,即12a ≥,则2220x x a -+-≤恒成立, 则()f x 在(,1)-∞上为单调减函数;②若480a ∆=->,即12a <,方程2220x x a -+-=的两根为1x =,2x =,当1(,)x x ∈-∞时,'()0f x <,所以函数()f x 单调递减,当11(,)2x x ∈时,'()0f x >,所以函数()f x 单调递增,不符合题意.综上,若函数()f x 为定义域上的单调函数,则实数a 的取值范围为1(,)2+∞. (Ⅱ)因为函数()f x 有两个极值点,所以'()0f x =在1x <上有两个不等的实根, 即2220x x a -+-=在1x <有两个不等的实根1x ,2x ,于是102a <<,12121,,2x x a x x +=⎧⎪⎨=⎪⎩且满足11(0,)2x ∈,21(,1)2x ∈, 211111*********()1ln(1)(1)(1)2ln(1)(1)2ln(1)f x x a x x x x x x x x x x x x -+--++-===-++-,同理可得22221()(1)2ln(1)f x x x x x =-++-. 122111222222221()()2ln(1)2ln(1)212(1)ln 2ln(1)f x f x x x x x x x x x x x x x x -=-+---=-+---,令()212(1)ln 2ln(1)g x x x x x x =-+---,1(,1)2x ∈.[]22'()2ln (1)1x g x x x x x =--++-,1(,1)2x ∈, ∵1(1)4x x -<,∴[]2ln (1)0x x -->, 又1(,1)2x ∈时,201x x x 2+>-,∴'()0g x >,则()g x 在1(,1)2x ∈上单调递增,所以1()()02g x g >=,即1221()()0f x f x x x ->,得证. 22.解:(Ⅰ)2214x y +=,2cos sin x y θθ=⎧⎨=⎩(θ为参数). (Ⅱ)设四边形ABCD 的周长为l ,设点(2cos ,sin )A q q ,8cos 4sin l θθ=+))θθθϕ==+,且cos ϕ=,sin ϕ=, 所以,当22k πθϕπ+=+(k Z ∈)时,l 取最大值,此时22k πθπϕ=+-,所以,2cos 2sin θϕ==sin cos θϕ==此时,A ,1l 的普通方程为14y x =.23.解:(Ⅰ)当2a <-时,函数34,,()|24|||4,2,34, 2.x a x a f x x x a x a a x x a x -+-<⎧⎪=++-=---≤≤-⎨⎪-+>-⎩可知,当2x =-时,()f x 的最小值为(2)21f a -=--=,解得3a =-. (Ⅱ)因为()|24||||(24)()||4|f x x x a x x a x a =++-≥+--=++, 当且仅当(24)()0x x a +-≤时,()|4|f x x a =++成立, 所以,当2a <-时,x 的取值范围是{}|2x a x ≤≤-; 当2a =-时,x 的取值范围是{}2-;当2a >-时,x 的取值范围是{}|2x x a -≤≤.。
河北省石家庄市2020届高中毕业班第一次模拟考试理科数学试题

河北省石家庄市2019届高中毕业班第一次模拟考试理科数学试题(时间120分钟,满分150分)注意事项:1. 本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分,答卷前,考生务必将自己的 姓名、准考证号填写在答题卡上.2. 回答第I 卷时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如 需改动,用橡皮擦干净后,再选涂其他答案标号.写在本试卷上无效.3. 回答第II 卷时,将答案写在答题卡上,写在本试卷上无效.4. 考试结束后,将本试卷和答题卡一并交回.第I 卷(选择题,共60分)一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目 要求的.A.第一象限B.第二象限C.第三象限D.第四象限 2. 若集合}822|{2≤<∈=+x Z x A ,}02|{2>-∈=x x R x B ,则)(B C A R 所含的元素个数为A. OB. 1C. 2D. 33. 设随机变量ξ服从正态分布),1(2σN .若P(ξ<2)=0.8,则p(0<ξ<1)的值为A. 0.2B. 0.3C.0.4D. 0.64 已知双曲线的一个焦点与抛物线x 2=20y 的焦点重合,且其渐近线的方程为3x ±4y=0,则 该双曲线的标准方程为5. 执行右面的程序框图,输出的S值为A. 1B. 9C. 17D. 20A. π2B. 4C. πD.-9π7. 现釆用随机模拟的方法估计该运动员射击4次,至少击中3次的概率:先由计算器给出 0到9之间取整数值的随机数,指定0、1表示没有击中目标,2、3、4、5、6、7、8、9表示击中目标,以4个随机数为一组,代表射击4次的结果,经随机模拟产生了 20组随机数:7527 0293 7140 9857 0347 4373 8636 6947 1417 46980371 6233 2616 8045 6011 3661 9597 7424 7610 4281根据以上数据估计该射击运动员射击4次至少击中3次的概率为A. 0.852B. 0.8192 C O.8 D. 0.758.巳知点(x,y)在ΔABC所包围的阴影区域内(包含边界),若B(3,A.f(x-2)—定是奇函数B.f(x+1)—定是偶函数C. f(x+3)一定是偶函数D, f(x-3)一定是奇函数10. 已知正三棱锥P-ABC的主视图和俯视图如图所示,则此三棱锥的外接球的表面积为A 4πB, 12πA. a>b>c B, a>c>b C. c>b>a D. b>a>c第II 卷(非选择题,共90分)本卷包括必考题和选考题两部分,第13题~第21题为必考题,每个试题考生都必须作答.第22题~第24题为选考题,考生根据要求作答.二、填空題,本大通共4小题,每小题5分,共20分.13.过点(2,3)与圆(x-1)2+y 2=1相切的直线方程为_____.14. 如图,正方形ABCD 中,EF//AB,若沿EF 将正方形折成一个二面角15.为举办校园文化节,某班推荐2名男生3名女生参加文艺技能培训,培训项目及人数分 别为:乐器1人,舞蹈2人,演唱2人,每人只参加一个项目,并且舞蹈和演唱项目必须 有女生参加,則不同的推荐方案的种数为_______.(用数字作答)16.在ΔABC 中,B ∠=600,O 为ΔABC 的外心,P 为劣弧AC 上一动点,且OC y OA x OP += (x,y∈R),则x+y 的取值范围为 ____ _____三、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤. 17. (本小题满分12分)如图,有两座建筑物AB 和CD 都在河的对岸(不知 道它们的高度,且不能到达对岸),某人想测量两 座建筑物尖顶A 、C 之间的距离,但只有卷尺和测 角仪两种工具.若此人在地面上选一条基线EF ,用 卷尺测得EF 的长度为a ,并用测角仪测量了一些角度:a AEF =∠,β=∠AFE ,θ=∠CEF ,ϕ=∠CFE ,γ=∠AEC 请你用文字和公式写出计算A 、C 之间距离的步骤和结果.18.(本小题满分12分)为了调査某大学学生在某天上网的时间,随机对lOO 名男生和100名女生进行了不记名的问卷调查.得到了如下的统计结果:表l:男生上网时间与频数分布表表2:女生上网时间与频数分布表(I)从这100名男生中任意选出3人,其中恰有1人上网时间少于60分钟的概率;(II)完成下面的2X2列联表,并回答能否有90%的把握认为“大学生上网时间与性别有关”?表3:•附:19. (本小题满分i2分)如图,在四棱锥P-ABCD中,PA丄平面ABCD, 0120=∠BAD,AD=AB=1,AC 和 BD 交于O点.ABC,090∠ADC∠==(I)求证:平面PBD丄平面PAC(II)当点A在平面PBD内的射影G恰好是ΔPBD的重心时,求二面角B-PD-G的余弦值.20. (本小题满分12分)直线l 交椭圆于A,B 两点.(I)若ΔABF 2为正三角形,求椭圆的离心率;21 (本小题满分12分) 设函数f(x )=x 2+aln(x+1)(I)若函数y=f(x)在区间[1,+∞)上是单调递增函数,求实数a 的取值范围;请考生在22〜24三题中任选一题做答,如果多做,则按所做的第一题记分. 22. (本小题满分10分)选修4-l:几何证明选讲如图,过圆O 外一点P 作该圆的两条割线PAB 和PCD,分别交圆 O 于点A,B,C,D 弦AD 和BC 交于Q 点,割线PEF 经过Q 点交圆 O 于点E 、F ,点M 在EF 上,且BMF BAD ∠=∠:(I)求证:PA·PB=PM·PQ (II)求证:BOD BMD ∠=∠23. (本小题满分10分)选修4-4:坐标系与参数方程在平面直角坐标系.x0y 中,以原点O 为极点,x 轴的正半轴为极轴建立极坐标系,已知曲线 C 的极坐标方程为: θθρcos sin 2=(I)求曲线l的直角坐标方程;的值24. (本小题满分10分)选修4-5:不等式选讲 巳知函数f(x)=|x-2|+2|x-a|(a∈R). (I)当a=1时,解不等式f(x)>3;(II)不等式1)(≥x f 在区间(-∞,+∞)上恒成立,求实数a 的取值范围2019年高中毕业班第一次模拟考试数学理科答案一、选择题A 卷答案1-5 DCBCC 6-10 ADADD 11-12 ADB 卷答案1-5 DBCBB 6-10 ADADD 11-12 AD 二、填空题13 . 4310x y -+=或2x = 14 .4515 . 24 16 . []1,2三、解答题:(阅卷老师,可根据学生的答题情况,酌情给分)17.解:第一步:在AEF ∆中,利用正弦定理,sin sin(180)AE EFβαβ︒=--, 解得sin sin()a AE βαβ=+;……………4分第二步:在CEF ∆中,同理可得sin sin()a CE ϕθϕ=+;……………8分第三步:在ACE ∆中,利用余弦定理,AC ==…………12分 (代入角的测量值即可,不要求整理,但如果学生没有代入,扣2分) 18.解:(Ⅰ)由男生上网时间频数分布表可知100名男生中,上网时间少于60分钟的有60人,不少于60分钟的有40人,………………2分故从其中任选3人,恰有1人上网的时间少于60分钟的概率为 1260403100C C C ……………4分 156539=………………6分 (Ⅱ) (822)200(18002800)200 2.201001001307091K ⨯-==≈⨯⨯⨯,………………10分∵2 2.20 2.706K ≈<∴没有90%的把握认为“大学生上网时间与性别有关”.………………12分 19. 解:(Ⅰ)依题意Rt ABC Rt ADC ∆≅∆,BAC DAC ∠=∠,ABO ADO ∆≅∆,所以AC BD ⊥,……2分而PA ⊥面ABCD ,PA BD ⊥,又PA AC A =,∴BD ⊥面PAC , 又BD ⊂面PBD ,∴平面PAC ⊥平面PBD …………4分(Ⅱ)过A 作AD 的垂线为x 轴,AD 为y 轴,AP 为z 轴,建立如图所示坐标系,则1,0)2B -,(0,1,0)D,0)C ,设(0,0,)P λ,所以1,)63G λ, 31(,)2PB λ=--,由AG PB ⊥,得311(,)(,,)066322AG PB λλ⋅=⋅--= 解得212λ=,λ=.………………6分 ∴P 点的坐标为(0,;面PBD的一个法向量为6(3,1,AG ==m ,……………8分设面PCD 的一个法向量为(,,)x y z =n,(CD=,(0,1,PD = 00PDCD ⎧⋅=⎪⎨⋅=⎪⎩n n 即00z -==⎪⎩,∴=n ………………10分cos ,||||⋅<>===n m n m n m , 所以二面角B PD A --.……………12分 20. 解:(Ⅰ)由椭圆的定义知1212||||||||AF AF BF BF +=+,又22||||AF BF =,∴11||||AF BF =,即12F F 为边AB 上的中线,∴12F F AB⊥,……………………2分 在12Rt AFF △中,2cos30,43c a ︒=则c a =,.…………………4,没有过程扣3分) (Ⅱ)设11(,)A x y ,22(,)B x y 因为0e <<,1c =,所以a >…………6分 ①当直线AB x 与轴垂直时,22211y a b +=,422b y a=,4121221b OA OB x x y y a ⋅=+=-,42231a a a -+-=22235()24a a --+, 因为2532+>a ,所以0OA OB ⋅<, AOB ∴∠恒为钝角,∴222OA OB AB +<.………………………8分②当直线AB 不与x 轴垂直时,设直线AB 的方程为:(1)y k x =+,代入22221x y a b+=,整理得:2222222222()20b a k x k a x a k a b +++-=,22122222a k x x b a k -+=+,222212222a k ab x x b a k -=+ 1212OA OB x x y y ⋅=+212121212(1)(1)x x y y x x k x x +=+++ 2221212(1)()x x k k x x k =++++22222242222222()(1)2()a k ab k a k k b a k b a k -+-++=+ 2222222222()k a b a b a b b a k +--=+ 24222222(31)k a a a b b a k -+--=+………………10分 令42()31m a a a =-+-, 由 ①可知 ()0m a <,AOB ∴∠恒为钝角.,所以恒有222OA OB AB +<.………………12分21. 解:(Ⅰ)0122)(2/≥+++=x ax x x f 在区间),1[+∞上恒成立, 即x x a 222--≥区间),1[+∞上恒成立, …………………1分4-≥a .………………3分经检验, 当a =- 4时, 1)1)(2(21422)(2/+-+=+-+=x x x x x x x f ,),1[+∞∈x 时,0)(/>x f ,所以满足题意的a 的取值范围为[4,)-+∞.………………4分(Ⅱ)函数的定义域),1(+∞-,0122)(2/=+++=x ax x x f ,依题意方程0222=++a x x 在区间),1(+∞-有两个不等的实根,记a x x x g ++=22)(2,则有⎪⎪⎩⎪⎪⎨⎧->->->∆1210)1(0g ,得210<<a .……………………6分,121-=+x x 022222=++a x x ,221212a x -+-=,0212<<-x ,2222222121)1ln()22()(x x x x x x x f --++-=,令)0,21(,1)1ln()22()(22-∈--++-=x x x x x x x k ……………………8分)1ln(21)(2+++-=x x x x x k ,)1ln(2)1()(22/+++=x x x x k , 32//)1(262)(+++=x x x x k , 因为2)0(,1)1(////=-=-k k ,存在)0,1(0-∈x ,使得0)(0//=x k , 0)0(/=k ,02ln 21)2(/<-=-k ,0)(/<∴x k ,所以函数)(x k 在)0,2(-为减函数,…………………10分)21()()0(-<<k x k k 即2ln 21)(012+-<<x x f ……………………12分 法二:6分段后面还有如下证法,可以参照酌情给分.【证法2】2x 为方程2220x x a ++=的解,所以22222x x a --=,∵102a <<, 120x x <<,212x =-,∴2102x -<<, 先证21()0f x x >,即证2()0f x <(120x x <<),在区间12(,)x x 内,()0f x '<,2(,0)x 内()0f x '>,所以2()f x 为极小值,2()(0)0f x f <=,即2()0f x <,∴21()0f x x >成立;…………………8分再证21()1ln 22f x x <-+,即证22211()(ln 2)(1)(ln 2)(1)22f x x x >-+--=-+,222222211(22)ln(1)(ln 2)ln 222x x x x x -++-->-,令221()(22)ln(1)(ln 2)2g x x x x x x =-++--, 1(,0)2x ∈-…………………10分2(1)1()2(42)ln(1)(ln 2)12x x g x x x x x +'=-++---+,12(21)ln(1)(ln 2)2x x =-++--,ln(1)0x +<,210x +>,1ln 202-<,∴()0g x '>,()g x 在1(,0)2-为增函数.111111()()(21)ln (ln 2)244222g x g >-=-⨯-+-111111ln ln 2ln 2422422=++-=-. 综上可得21()10ln 22f x x <<-+成立.………………………12分22.证明:(Ⅰ)∵∠BAD =∠BMF ,所以A,Q,M,B 四点共圆,……………3分所以PA PB PM PQ ⋅=⋅.………………5分(Ⅱ)∵PA PB PC PD ⋅=⋅ ,∴PC PD PM PQ ⋅=⋅ ,又 CPQ MPD ∠=∠ , 所以~CPQ MPD ∆∆,……………7分 ∴PMD PCQ ∠=∠ ,则DCB FMD ∠=∠,………………8分 ∵BAD BCD ∠=∠,∴2BMD BMF DMF BAD ∠=∠+∠=∠,2BOD BAD ∠=∠,所以BMD BOD ∠=∠.…………………10分23.解:(Ⅰ)依题意22sin cos ρθρθ=………………3分得:x y =2∴曲线1C 直角坐标方程为:x y =2.…………………5分(Ⅱ)把⎪⎪⎩⎪⎪⎨⎧=-=ty tx 22222代入x y =2整理得:0422=-+t t ………………7分0>∆总成立,221-=+t t ,421-=t t23)4(4)2(221=-⨯--=-=t t AB ………………10分 另解:(Ⅱ)直线l 的直角坐标方程为x y -=2,把x y -=2代入x y =2得:0452=+-x x ………………7分0>∆总成立,521=+x x ,421=x x 23)445(212212=⨯-=-+=x x k AB …………………10分 24. 解:(Ⅰ)⎩⎨⎧>-+-≥32222x x x 解得37>x ⎩⎨⎧>-+-<<322221x x x 解得φ∈x ⎩⎨⎧>-+-≤32221x x x 解得13x <…………………3分 不等式的解集为17(,)(,)33-∞+∞………………5分 (Ⅱ)时,2>a ⎪⎩⎪⎨⎧≥--<<-+-≤++-=a x a x a x a x x a x x f ,2232,222,223)(; 时,2=a 36,2()36,2x x f x x x -+≤⎧=⎨->⎩; 时,2<a ⎪⎩⎪⎨⎧≥--<<+-≤++-=2,2232,22,223)(x a x x a a x a x a x x f ; ∴)(x f 的最小值为)()2(a f f 或;………………8分 则⎩⎨⎧≥≥1)2(1)(f a f ,解得1≤a 或3≥a .………………10分。
【2020年数学高考】石家庄市2020届高中毕业班模拟考试(一)理科数学.doc

石家庄市2020届高中毕业班模拟考试(一)理科数学(A卷)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知集合,,则()A. B. C. D.【答案】A【解析】故选A.2. 已知为虚数单位,,其中,则()A. B. C. 2 D. 4【答案】A【解析】,其中,解得,,故选3. 函数,其值域为,在区间上随机取一个数,则的概率是()A. B. C. D.【答案】B【解析】函数的值域为,即,则在区间上随机取一个数的概率.故选B.4. 点是以线段为直径的圆上的一点,其中,则()A. 1B. 2C. 3D. 4【答案】D【解析】故选5. ,满足约束条件:,则的最大值为()A. -3B.C. 3D. 4【答案】C【解析】依题意可画出可行域如下:联立,可得交点(2,-1),如图所示,当经过点(2,-1)时,z最大为3.故选C.点睛:线性规划的实质是把代数问题几何化,即数形结合的思想.需要注意的是:一、准确无误地作出可行域;二、画标准函数所对应的直线时,要注意与约束条件中的直线的斜率进行比较,避免出错;三、一般情况下,目标函数的最大或最小会在可行域的端点或边界上取得.6. 程序框图如图所示,该程序运行的结果为,则判断框中可填写的关于的条件是()A. B. C. D.【答案】C【解析】第一次运行,第二次运行,第三次运行,第四次运行,第五次运行,此时,输出25,故选C7. 南宋数学家秦九韶早在《数书九章》中就独立创造了已知三角形三边求其面积的公式:“以小斜幂并大斜幂,减中斜幂,余半之,自乘于上,以小斜幂乘大斜幂减之,以四约之,为实,一为从隅,开方得积.”(即:,),并举例“问沙田一段,有三斜(边),其小斜一十三里,中斜一十四里,大斜一十五里,欲知为田几何?”则该三角形田面积为()A. 82平方里B. 83平方里C. 84平方里D. 85平方里【答案】C【解析】由题意可得:代入:则该三角形田面积为平方里故选8. 如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体的表面积为()A. B. C. D.【答案】D【解析】由图可知,几何体为半圆柱挖去半球体几何体的表面积为故选9. 已知是定义在上的偶函数,且在上为增函数,则的解集为()A. B. C. D.【答案】B【解析】是定义在上的偶函数,,即,则函数的定义域为函数在上为增函数,故两边同时平方解得,故选10. 在中,,,则的最大值为()A. B. C. D.【答案】D【解析】有正弦定理可得,故当时,的最大值为.故选D.11. 过抛物线焦点的直线交抛物线于,两点,点在直线上,若为正三角形,则其边长为()A. 11B. 12C. 13D. 14【答案】B【解析】如图:设,则:,取中点,分别作垂直于直线,连接则有,相减可得:即故设则,解得故,解得故选12. 设,为两个平面直角坐标系,它们具有相同的原点,正方向到正方向的角度为,那么对于任意的点,在下的坐标为,那么它在坐标系下的坐标可以表示为:,.根据以上知识求得椭圆的离心率为()A. B. C. D.【答案】A【解析】则故可化为方程表示为椭圆化简得:代入方程得:,,,故故选点睛:本题主要考查了三角函数的计算问题,以平面直角坐标系为载体,新定义坐标系,建立两坐标之间的关系,代入化简,由题意中的椭圆求出的值,再次代入求出结果,计算量比较大,有一定的难度。
石家庄市2019届高中毕业班第一次模拟测试数学(理科)试卷含答案

C M y
B
CB n x2 3 y2 0 则 CF n x2 3z2 0
解得 x2
3 , y2 1 , z2 1 即 n ( 3, 1, 1) „„„„10 分
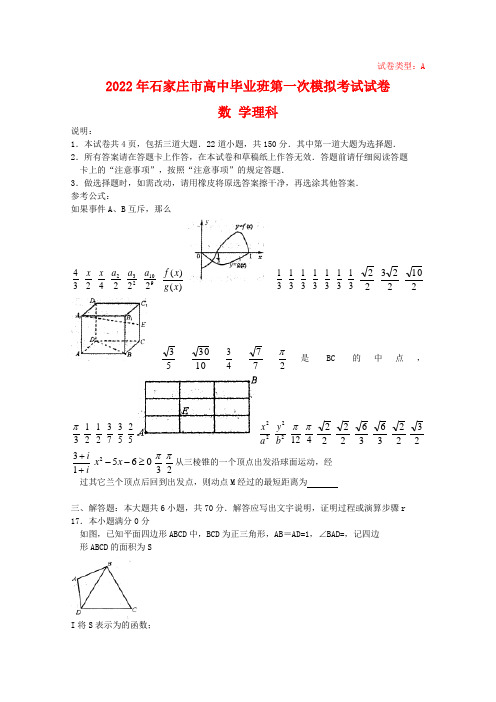
mn 3 1 0 2 5 2 2 m n 2 3 1 1 5
∴ BD 3 ,即 BD 长的最小值为 3. „„12 分
18. 解: (1)证明:在 PBC 中, PBC 60 , BC 2 , PB 4 ,由余弦定理可得 PC 2 3 ,
o
PC 2 BC 2 PB2 , PC BC ,„„„„2 分
又 PC AB, AB BC B ,
2
三、解答题 17. 解: (1) ∵△ABC 三内角 A、B、C 依次成等差数列,∴B=60° 设 A、B、C 所对的边分别为 a 、 b 、 c ,由 S 3 3 =
1 ac sin B 可得 ac 12 .„„2 分 2
„„4 分
∵ sin C 3sin A ,由正弦定理知 c 3a ,∴ a 2, c 6 . △ABC 中,由余弦定理可得 b2 a 2 c 2 2ac cos B 28 ,∴b= 2 7 . 即 AC 的长为 2 7 (2)∵BD 是 AC 边上的中线,∴ BD
2019届河北省石家庄市高三毕业班模拟考试_理科数学(解析版)

4
tan tan 4
1 tan tan
2 1
1 21
3 .
4
4.下列说法中正确的是( )
A. 若数列{an} 为常数列,则{an} 既是等差数列也是等比数列;
B. 若函数 f (x) 为奇函数,则 f (0) 0 ;
C. 在△ABC 中, A B 是 sin A sin B 的充要条件; D. 若两个变量 x, y 的相关系数为 r ,则 r 越大, x 与 y 之间的相关性越强.
c 2 ,e
2
.
a2
10.已知函数
f (x) 2cos(x )
0,
2
的部分函数图像如图所示,点
A(0,
3),
B
6
,
0
,
则函数
f (x) 图像的一条对称轴方程为(
)
A. x
3
10.答案:D
B. x
12
C. x
18
D. x
24
解析:
6
,
4 ,
f
(x)
1
C.
4
答案:D
2
2
2i
i1
2.解析: z z z
= 1 i
1i 2 2 .
1
D.
2
3.已知 cos
2 cos(
)
,则 tan
(
)
2
4
A. 3
3.答案:A
B.3
1 C.
3
1
D.
3
sin
解析:由题意结合诱导公式可得: sin 2cos , tan
2,
cos
据此有:
2020届石家庄一模理科数学 05-29

5
.
………………………12 分
2
18.解:(Ⅰ)证明:如图 1,取线段 DF 的中点 H,连接 HG, G 是线段 CF 的中点, 1
则 HG∥CD 且 HG= CD. …………2 分 2
在菱形 ABCD 中 E 为线段 AB 中点, 则 BE∥CD 且 BE= 1 CD.
2 则 HG∥BE 且 HG=BE, 故四边形 BEHG 为平行四边形, 所以 BG∥EH. …………………………………………………4 分 又因为 BG 平面 DEF,EH 平面 DEF, 所以 BG∥平面 DEF . ………………………………………5 分
………………………………… 12 分
20.解:(Ⅰ)设 A x1, y1 , B x2, y2 ,
方式一:
由题 x12 2 py1, x22 2 py2 ,
由 x1 x2 4 ,则直线 l 斜率为
………………………1 分
………………………2 分
整理得 3sin B cos C 2 sin B 0 .
因为 sin B
0 ,所以 cos C
2 3
.
…………………………………4 分
解法 2:由 3c cos B 3a 2b 得 3ac cos B 3a2 2ab ,
由余弦定理得: 3 a2 c2 b2 6a2 4ab …………………………2 分
故点 M 在直线 x 上, f x x ,
过 P 作 f x 的切线,设切点坐标为 A x, y x ,
则有
f
x
f x
x
,即 x
x ,解得 x
,
此时切线斜率 k
,切线方程为
y
x
.
河北省石家庄市高中毕业班第一次模拟考试 数学理科

2009石家庄市高三第一次模拟考试数学理科答案一、A卷选择题:本大题共12小题,每小题5分,共60分.1.A2. B3. A4. B5.D6.A7. B8.A9. C 10. D 11.B 12.C 一、B卷选择题:本大题共12小题,每小题5分,共60分.1. B2. A3. B4.D5.A6. B7.A8. C9. D 10.B 11.C 12.A 二、填空题:本大题共4小题,每小题5分,共20分 13.13a = 14.12315. 1 16.③ ,④三、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤. 17.(本题10分)解:(Ⅰ)该天平均每人的课外阅读时间为0.520110 1.515251.0550⨯+⨯+⨯+⨯=(小时)答:这一天平均每人的课外阅读时间为1.05小时.………………………4分 (Ⅱ) 记这2名学生该天阅读时间量互不相同为事件A ,222220151052502()7C C C C P A C +++==,………………………7分 25()1()177P A P A =-=-=.…………………………………9分 答: 这2名学生该天阅读时间量互不相同的概率为57.…………………10分18.(本题12分)解: (Ⅰ)由余弦定理知:2cos 2A ==………2分cos 1)12AB AC AB AC A ∴⋅=⋅=⋅=.……………5分 (Ⅱ)由AC mAO nAB =+,知,. AB AC mAB AO nAB AB AC AC mAC AO nAC AB ⎧⋅=⋅+⋅⎪⎨⋅=⋅+⋅⎪⎩∴2 1(31), 2(31).mAB AO nmAC AO n=⋅+=⋅+⎪⎩…………………………………7分O为ABC∆的外心,2112cos(1)2ABAB AO AB AO BAO AB AOAO∴⋅=⋅∠=⋅⋅=.同理1AC AO∴⋅=.………………………………10分即22111)1),221).m nm n=+⎪=+⎩,解得:1,mn⎧=⎪⎨=⎪⎩……12分19.(本题12分)(Ⅰ)取BC的中点M,连结PM,AM.四边形ABCD为菱形,0120BAD∠=,则,,BC AM BC PM⊥⊥……………2分BC APM∴⊥平面,BC PA⊥从而.同理DC PA⊥故PA ABCD⊥平面.……………………4分(或用同一法可证)(Ⅱ)先求二面角E AC B--的大小取AB的中点H,过H作HN AC⊥于点N,连结EN.则EH ABCD⊥平面,ENH∠是二面角E AC B--的平面角,……6分可求得ENH∠=,又PAC ABCD⊥平面平面,所以二面角E AC P--的大小为arctan2π-……………………8分BCDEPA HN法二: 过A 作AM AB ⊥交CD 于M , 以A 为坐标原点,直线AM 、AB 、AP 分别为x y 、、z 轴, 建立空间直角坐标系A xyz -. 则A (0,0,0),,0)C ,P (0,0,2),(0,1,1)E .(0,0,2)AP ∴=,(3,1,0),AC =(0,1,1)AE =.…………………6分设平面PAC 的法向量为1111(,,)x y z =n , 则110,0.AP AC ⎧⋅=⎪⎨⋅=⎪⎩n n11120,0.z y =⎧⎪+=即取1x =1,-则1(1=-n . 设平面AEC 的法向量为2222(,,)x y z =n ,则220,0.AC AE ⎧⋅=⎪⎨⋅=⎪⎩n n22220,0.y y z +=+=⎪⎩即取21y =,则2(1)=-n . cos <1n ,2n >=1212⋅=⋅n n n n ,∴二面角E AC P --的大小为arccos7……………………8分 (Ⅲ)先求点B 到平面PAF 的最大距离.PA ABCD PAF ABCD PAFABCD AF ⊥∴⊥=平面,平面平面,平面平面,∴点B 到直线AF 的距离即为点B 到平面PAF 的距离. ……10分过B 作直线AF 的垂线段,在所有的垂线段中长度最大为2AB =. E 为PB 的中点,故点E 到平面PAF 的最大距离为1. ……………………12分 20.(本题12分)解:(Ⅰ)2()2,xf x e a '=-(ⅰ)当0a ≤时, ()0,f x '>∴()f x 的单调递增区间是(,-∞+∞).……………………2分(ⅱ) 当0a >时,令()0,f x '=得1ln .22a x =当1ln 22ax <时,()0,f x '< 当1ln 22ax >时,()0.f x '>()f x ∴的单调递减区间是(1,ln 22a-∞),()f x 的单调递增区间是 (1ln ,22a+∞).……………………5分(Ⅱ)()f x a <,∴2,x e ax a -<2(1),x a x e +>(1,1]x ∈-,10x +>.∴2,1x e a x >+设2(),1xe g x x =+ 若存在实数(1,1]x ∈-,使得()f x a <成立, 则a >min ().g x ……………………8分22(21)(),(1)x e x g x x +'=+解得()0,g x '=得12x =-, ∴当112x -<<-时, ()0,g x '<当112x -<≤时, ()0,g x '>∴()g x 在1(1,)2--上是减函数,在1(,1]2-上是增函数. …………………10分∴1min12()(),1212e g x g e-=-==-a 的取值范围是(2,e+∞).…………………………………………………12分21.(本题12分)(I )由2OP OM ON =+,得P 是MN 的中点. …………2分 设),(),,(),,(2211mx x N mx x M y x P -依题意得:121222212122,2,()()2.x x x mx mx y x x mx mx ⎧+=⎪-=⎨⎪-++=⎩ 消去21,x x ,整理得112222=+m y m x . 当1>m 时,方程表示焦点在y 轴上的椭圆;当10<<m 时,方程表示焦点在x 轴上的椭圆;当1=m 时,方程表示圆. ……………………………5分 (II )由1m >,焦点在y 轴上的椭圆,直线l 与曲线C 恒有两交点, 直线斜率不存在时不符合题意;可设直线l 的方程为1y kx =+,直线与椭圆交点1122(,),(,)A x y B x y .224222221()21011y kx x y m k x kx m m m =+⎧⎪⎪⇒+++-=⎨+=⎪⎪⎩ 21212424221,k m x x x x m k m k -+=-=++22212124242(1)2(1)(1)1k m k y y kx kx m k m k--=++=++++.………………7分 要使AOB ∠为锐角,只需0OA OB ⋅>422121242(1)10m k m x x y y m k -++∴+=>+.………………9分即422(1)10m k m -++>, 可得22211m k m+>+,对于任意1m >恒成立. 而2212m m+>,21211,.k k ∴+≤-≤≤所以k 的取值范围是[1,1]-.………………12分 22(本题12分) 解:(Ⅰ)21231n n n a a n n --=+⋅-,………………1分 2211122323232(13)1313n nn n a n---=++⋅+⋅++⋅-=+=-,即13n n a n -=⋅(n ∈*N ).………………3分 (II )1()n b n n =∈*N ,111111,12,2234+>+++> 1111111132345678+++++++<.猜想当3n ≥时,2n S n <.………………4分 下面用数学归纳法证明:①当3n =时,由上可知323S <成立; ②假设(3)n k k =≥时,上式成立,即1111232k k ++++<. 当1n k =+时,11111111232212112122121k k k k k kk k k k ++=++++++++<++++<+<++左边所以当1n k =+时成立.由①②可知当3n ≥()n ∈*N 时,2n S n <. ………………7分 综上所述当1n =时, 121S >;当2n =时, 222S >;当3n ≥()n ∈*N 时,2n S n <. ………………8分(III )131n n n a c n +==+ 当2n ≥时,121123232311(31)(31)(33)(31)(31)3131n n n n n n n n n n---⨯⨯⨯≤==--------.所以22222233232331111()()2(31)(31)22313131n n n T ⨯⨯=+++≤+-+------ +1111()22313131n n n -+-=-<---.………………12分。
河北省石家庄市高三第一次模拟考试——数学理数学(理)

河北省石家庄市 2017届高三第一次模拟考试数学(理)试题第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合,{}*|12B x N x =∈-≤,则 ( ) A . B .C .D .2.若是复数, ,则 ( ) A . B .C .1D .3.下列说法错误的是( ) A .回归直线过样本点的中心B .两个随机变量的线性相关性越强,则相关系数的绝对值就越接近于1C .对分类变量与,随机变量的观测值越大,则判断“与有关系”的把握程度越小D .在回归直线方程中,当解释变量每增加1个单位时,预报变量平均增加0.2个单位 4.函数 (为自然对数的底数)的图象大致是( )5.函数 (,)的最小正周期为,其图象关于直线对称,则的最小值为( ) A . B .C .D .6.已知三个向量,,共面,且均为单位向量,,则的取值范围是( ) A . B .C .D .7.某几何体的三视图如图所示(在如图的网格线中,每个小正方形的边长为1),则该几何体的表面积为( )A.48 B.54 C.64 D.608.已知函数在上单调,且函数的图象关于对称,若数列是公差不为0的等差数列,且,则的前100项的和为( )A. B.C.D.9.祖暅是南北朝时代的伟大科学家,5世纪末提出体积计算原理,即祖暅原理:“幂势既同,则积不容异”.意思是:夹在两个平行平面之间的两个几何体,被平行于这两个平面的任何一个平面所截,如果截面面积都相等,那么这两个几何体的体积一定相等.现有以下四个几何体:图①是从圆柱中挖出一个圆锥所得的几何体;图②、图③、图④分别是圆锥、圆台和半球,则满足祖暅原理的两个几何体为()A.①②B.①③C.②④D.①④10.已知,满足约束条件20,220,220,x yx yx y+-≤⎧⎪--≤⎨⎪-+≥⎩若恒成立,则直线被圆22(1)(2)25x y-+-=截得的弦长的最大值为( )A. B.C.D.11.已知过抛物线的焦点的直线与抛物线交于,两点,且,抛物线的准线与轴交于点,于点,若四边形的面积为,则准线的方程为( )A. B.C.D.12.已知函数与的图象有三个不同的公共点,其中为自然对数的底数,则实数的取值范围为( )A .B .C .D .或 第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上) 13.已知命题:,,则为 .14.程序框图如图所示,若输入, , ,则输出的为 .15.已知、分别为双曲线(,)的左、右焦点,点为双曲线右支上一点,为的内心,满足1212MPF MPF MF F S S S λ∆∆∆=+,若该双曲线的离心率为3,则 (注:、、分别为、、的面积).16.已知数列中, , ,若为递增数列,则实数的取值范围为 .三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.) 17.在中,内角,,的对边分别是,,,且. (Ⅰ)求角的大小;(Ⅱ)点满足,且线段,求的最大值. 18.在四棱锥中,底面为平行四边形,,,,.(Ⅰ)证明:平面; (Ⅱ)求二面角的余弦值.19.人耳的听力情况可以用电子测听器检测,正常人听力的等级为0-25(分贝),并规定测试值在区间为非常优秀,测试值在区间为优秀.某班50名同学都进行了听力测试,所得测试值制成频率分布直方图:(Ⅰ)现从听力等级为的同学中任意抽取出4人,记听力非常优秀的同学人数为,求的分布列与数学期望;(Ⅱ)在(Ⅰ)中抽出的4人中任选一人参加一个更高级别的听力测试,测试规则如下:四个音叉的发生情况不同,由强到弱的次序分别为1,2,3,4.测试前将音叉随机排列,被测试的同学依次听完后给四个音叉按发音的强弱标出一组序号,,,(其中,,,为1,2,3,4的一个排列).若为两次排序偏离程度的一种描述,1234|1||2||3||4|Y a a a a =-+-+-+-,求的概率.20.已知椭圆:的左顶点为,右焦点为,为原点,,是轴上的两个动点,且,直线和分别与椭圆交于,两点.(Ⅰ)求的面积的最小值; (Ⅱ)证明:,,三点共线.21.已知函数2()1ln(1)f x x a x =-+-,.(Ⅰ)若函数为定义域上的单调函数,求实数的取值范围; (Ⅱ)若函数存在两个极值点,,且,证明:.请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分. 22.选修4-4:坐标系与参数方程在平面直角坐标系,将曲线上的每一个点的横坐标保持不变,纵坐标缩短为原来的,得到曲线,以坐标原点为极点,轴的正半轴为极轴,建立极坐标系,的极坐标方程为. (Ⅰ)求曲线的参数方程;(Ⅱ)过原点且关于轴对称的两条直线与分别交曲线于、和、,且点在第一象限,当四边形的周长最大时,求直线的普通方程. 23.选修4-5:不等式选讲已知函数()|24|||f x x x a =++-. (Ⅰ)当时,的最小值为1,求实数的值; (Ⅱ)当时,求的取值范围.参考答案一、选择题1-5: 6-10: 11、12: 二、填空题13., 14.1024 15. 16. 三、解答题17.解:(Ⅰ)∵,由正弦定理得, ∴()()()c a c a b a b -=+-, 即,又∵2222cos a c b ac B +-=, ∴, ∵,∴.(Ⅱ)在中由余弦定理知:222(2)22cos 603c a a c +-⋅⋅⋅︒=, ∴, ∵ ,∴223(2)9(2)4a c a c +-≤+,即,当且仅当,即,时取等号, 所以的最大值为6. 18.(Ⅰ)证明:在中,sin sin AB ADADB DBA=∠∠,由已知,,, 解得,所以,即,可求得. 在中, ∵, , , ∴,∴,∵平面, ,∴平面.(Ⅱ)过作直线垂直于,以为坐标原点,以为轴,以为轴,以为轴,建立空间直角坐标系. ∵由(Ⅰ)可知,平面平面,∴在平面上的投影一定在上,过作于,则,,则, 易求,,, 则,,,设平面的法向量,230,230,y z y z +-=+-=⎪⎩解得.同理可求得平面的法向量,∴1212cos ||||13n n n n θ⋅===⋅19.解:(Ⅰ)的可能取值为:0,1,2,3,4.4641015(0)210C P X C ===,134641080(1)210C C P X C ===,224641090(2)210C C P X C ===,314641024(3)210C C P X C ===, 444101(4)210C P X C ===, 的分布列为:0 1 2 3 4158090241()01234 1.621021**********E X =⨯+⨯+⨯+⨯+⨯=. (Ⅱ)序号,,,的排列总数为种, 当时,,,,.当1234|1||2||3||4|2Y a a a a =-+-+-+-=时,,,,的取值为,,,;,,,;,,,. 故.20.解:(Ⅰ)设,,∵,可得,11||||||22AMFN S AF MN MN ==, ∵222||||||2||||MN MF NF MF NF =+≥⋅,当且仅当时等号成立. ∴,∴min 1()||12MFN S MN ==, ∴四边形的面积的最小值为1. (Ⅱ)∵,,∴直线的方程为,由22,22,y x m x y ⎧=+⎪⎨⎪+=⎩得2222(1)2(1)0m x x m +++-=, 由,得,① 同理可得,∵,∵221()11()1D m x m⎤-⎥⎣⎦=+②故由①②可知:, 代入椭圆方程可得 ∵,故,分别在轴两侧,, ∴,∴,,三点共线.21.解:(Ⅰ)函数的定义域为,由题意222'()2,111a x x af x x x x x-+-=-=<--,224(2)()48a a ∆=---=-.①若,即,则恒成立, 则在上为单调减函数;②若,即,方程的两根为,,当时,,所以函数单调递减,当时,,所以函数单调递增,不符合题意. 综上,若函数为定义域上的单调函数,则实数的取值范围为. (Ⅱ)因为函数有两个极值点,所以在上有两个不等的实根, 即在有两个不等的实根,,于是,12121,,2x x a x x +=⎧⎪⎨=⎪⎩且满足,, 211111*********()1ln(1)(1)(1)2ln(1)(1)2ln(1)f x x a x x x x x x x x x x x x -+--++-===-++-, 同理可得22221()(1)2ln(1)f x x x x x =-++-. 122111222222221()()2ln(1)2ln(1)212(1)ln 2ln(1)f x f x x x x x x x x x x x x x x -=-+---=-+---, 令()212(1)ln 2ln(1)g x x x x x x =-+---,.[]22'()2ln (1)1xg x x x x x=--++-,, ∵,∴,又时,,∴,则在上单调递增, 所以,即,得证. 22.解:(Ⅰ),(为参数). (Ⅱ)设四边形的周长为,设点,))θθθϕ=+=+, 且,,所以,当()时,取最大值, 此时,所以,2cos 2sin θϕ==,此时,,的普通方程为.23.解:(Ⅰ)当时,函数34,,()|24|||4,2,34, 2.x a x a f x x x a x a a x x a x -+-<⎧⎪=++-=---≤≤-⎨⎪-+>-⎩可知,当时,的最小值为,解得.(Ⅱ)因为()|24||||(24)()||4|f x x x a x x a x a =++-≥+--=++, 当且仅当时,成立, 所以,当时,的取值范围是; 当时,的取值范围是; 当时,的取值范围是.。
石家庄市高中毕业班第一次模拟考试试卷.docx

2016届石家庄市高中毕业班第一次模拟考试试卷数学(理科)A 卷第Ⅰ卷(选择题,共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.若复数i i z -=12(i是虚数单位),则=z ( )A .i +-1B .i --1C .i +1D .i -12.已知集合}065|{2<--=x x x A ,}33|{<<-=x x B ,则=B A I ( )A .)3,3(-B .)6,3(-C .)3,1(-D .)1,3(-3.设变量y ,满足约束条件⎪⎩⎪⎨⎧≤--≥-+≥+02202201y x y x x ,则目标函数y x z 43+=的最小值为( )A .1B .3C .526D .19-4.函数)0,0)(sin()(>>+=ωϕωA x A x f 的部分图像如右图所示,则)2411(πf 的值为( )A .26- B .23- C .22- D .1-5.程序框图如图,当输入x 为2016时,输出的y 的值为( )A .81B .1C .2D .46.为比较甲乙两地某月11时的气温情况,随机选取该月中的5天中11时的气温数据(单位:℃)制成如图所示的茎叶图,考虑以下结论:甲 乙 9 8 2 6 8 92 10 3 1 1 ①甲地该月11时的平均气温低于乙地该月11时的平均气温②甲地该月11时的平均气温高于乙地该月11时的平均气温③甲地该月11时的气温的标准差小于乙地该月11时的气温的标准差④甲地该月11时的气温的标准差大于乙地该月11时的气温的标准差其中根据茎叶图能得到的正确结论的编号为( )A .①③B .①④C .②③D .②④7.过点)1,0(A 作直线,与双曲线1922=-y x 有且只有一个公共点,则符合条件的直线的条数为( ) A .0 B .2 C .4 D .无数8.如图所示的数阵中,用),(n m A 表示第m 行的第n 个数,则依此规律)2,15(A 为( )A .4229B .107C .2417 D .102739.已知函数)2(+=x f y 的图象关于直线2-=x 对称,且当),0(+∞∈x 时,|log |)(2x x f =,若)3(-=f a ,)41(f b =,)2(f c =,则c b a ,,的大小关系是( ) A .c b a >> B .c a b >> C .b a c >> D .b c a >>10.某几何体的三视图如图所示,图中网格小正方形边长为1,则该几何体的体积是( )A .4B .316C .320 D .1211.C B A ,,是圆O 上不同的三点,线段CO 与线段AB 交于D ,若OB OA OC μλ+=(R R ∈∈μλ,),则μλ+的取值范围是( ) A .)1,0( B .),1(+∞ C .]2,1( D .)0,1(-12.如图所示,一个圆柱形乒乓球筒,高为20厘米,底面半径为2厘米.球筒的上底和下底分别粘有一个乒乓球,乒乓球与球筒底面及侧面均相切(球筒和乒乓球厚度忽略不计).一个平面与两乒乓球均相切,且此平面截球筒边缘所得的图形为一个椭圆,则该椭圆的离心率为( )A .415B .51C .562D .41第Ⅱ卷(非选择题,共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上) 13.6)41(x x -的展开式中常数项为. 14.已知函数⎪⎩⎪⎨⎧<<+≤<-=10),1(log 01,2sin )(2x x x x x f π,且21)(-=x f ,则x 的值为 . 15.已知ABC ∆中,BC AD BAC BC AC ⊥=∠==,60,72,4ο于D ,则CD BD 的值为 . 16.若函数),()(23R b a bx ax x x f ∈++=的图象与x 轴相切于一点)0)(0,(≠m m A ,且)(x f 的极大值为21,则m 的值为 . 三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.(本小题满分12分)18.(本小题满分12分)在平面四边形ACBD (图①)中,ABC ∆与ABD ∆均为直角三角形且有公共斜边AB ,设2=AB ,ο30=∠BAD ,ο45=∠BAC ,将ABC ∆沿AB 折起,构成如图②所示的三棱锥ABC C -',且使2'=D C . (Ⅰ)求证:平面⊥AB C '平面DAB ;(Ⅱ)求二面角B D C A --'的余弦值.19.(本小题满分12分)某篮球队对篮球运动员的篮球技能进行统计研究,针对篮球运动员在投篮命中时,运动员在篮筐中心的水平距离这项指标,对某运动员进行了若干场次的统计,依据统计结果绘制如下频率分布直方图:(Ⅰ)依据频率分布直方图估算该运动员投篮命中时,他到篮筐中心的水平距离的中位数;(Ⅱ)在某场比赛中,考察他前4次投篮命中到篮筐中心的水平距离的情况,并且规定:运动员投篮命中时,他到篮筐中心的水平距离不少于4米的记1分,否则扣掉1分.用随机变量X 表示第4次投篮后的总分,将频率视为概率,求X 的分布列和数学期望.20. (本小题满分12分)已知抛物线C :)0(22>=p px y 过点)2,(m M ,其焦点为F ,且2||=MF .(Ⅰ)求抛物线C 的方程;(Ⅱ)设E 为y 轴上异于原点的任意一点,过点E 作不经过原点的两条直线分别与抛物线C 和圆F :1)1(22=+-y x 相切,切点分别为B A ,,求证:直线AB 过定点.21. (本小题满分12分)已知b x ax e x f x +--=2)(2(e 为自然对数的底数,R b a ∈,).(Ⅰ)设)('x f 为)(x f 的导函数,证明:当0>a 时,)('x f 的最小值小于0;(Ⅱ)若0)(,0>>x f a 恒成立,求符合条件的最小整数b . AD CB ① D 'CB A ②请考生在22、23、24三题中任选一题作答,如果多做,则按所做的第一题记分.22. (本小题满分10分)选修4-1:几何证明选讲如图所示,过点P 分别做圆O 的切线PA 、PB 和割线PCD ,弦BE 交CD 于F ,满足P 、B 、F 、A 四点共圆.(Ⅰ)证明:CD AE //;(Ⅱ)若圆O 的半径为5,且3===FD CF PC ,求四边形PBFA 的外接圆的半径.23.(本小题满分10分)选修4-4:坐标系与参数方程在极坐标系中,已知曲线1C :θρcos 2=和曲线2C :3cos =θρ,以极点O 为坐标原点,极轴为x 轴非负半轴建立平面直角坐标系.(Ⅰ)求曲线1C 和曲线2C 的直角坐标方程;(Ⅱ)若点P 是曲线1C 上一动点,过点P 作线段OP 的垂线交曲线2C 于点Q ,求线段PQ 长度的最小值.24.(本小题满分10分)选修4-5:不等式选讲已知函数|1|||)(-+=x x x f .(Ⅰ)若|1|)(-≥m x f 恒成立,求实数m 的最大值M ;(Ⅱ)在(Ⅰ)成立的条件下,正实数b a ,满足M b a =+22,证明:ab b a 2≥+.2016届高三数学一模理科答案一.选择题:A 卷答案:1-5 BCBDA 6-10 CCCBB 11-12 BAB 卷答案:1-5 ACADB 6-10 CCCAA 11-12 AB二.填空题: 13.. 516- 14. 13-15. 6 16.32 三、解答题: 17. 解:(I )由已知得2351112=4+8=2010910+=10+45=1002a a a a d a d a d ++⎧⎪⎨⨯⎪⎩, -------------------------------2分 解得112a d =⎧⎨=⎩,-------------------------------4分 所以{}n a 的通项公式为52(3)21n a n n =+-=-,--------------------------------5分(II )由(I )可知21(21)2n n n a b n -⋅=-⨯,所以1352321123252(23)2(21)2n n n S n n --=⨯+⨯+⨯+⋅⋅⋅+-⨯+-⨯,① 35721214123252(23)2(21)2n n n S n n -+=⨯+⨯+⨯+⋅⋅⋅+-⨯+-⨯,②---------------------7分①-②得:352121322(222)(21)2n n n S n -+-=+⨯++⋅⋅⋅+--⨯ 35212122(222)(21)23n n n n S -++⨯++⋅⋅⋅+--⨯∴=-………………9分 1218(14)22()(21)2143n n n -+-+⨯--⨯-=- 121628(14)(63)29n n n -+-+⨯-+-⨯=---------------------11分 2110(65)29n n ++-⨯=--------------------------12分 18. 解:(1)取AB 的中点O ,连,C O DO ',在,RT ACB RT ADB ∆∆,2AB =,则1C O DO '==,又2C D '=Q ,∴222C O DO C D ''+=,即C O OD '⊥,…………2分又C O AB '⊥Q ,AB OD O =I ,,AB OD ⊂平面ABDC O '∴⊥平面ABD ,…………………4分又C O '⊂Q 平面ABC '∴平面C AB '⊥平面DAB…………5分(2)以O 为原点,AB ,OC '所在的直线分别为,y z 轴,建立如图空间直角坐标系,则31(0,1,0),(0,1,0),(0,0,1),(,,0)22A B C D '-, 31(0,1,1),(0,1,1),(,,1)22AC BC C D '''∴==-=-u u u u r u u u u r u u u u r …………6分 设平面AC D '的法向量为1111(,,)n x y z =u u r ,则11n AC n C D ⎧'⊥⎪⎨'⊥⎪⎩u u r u u u u r u u r u u u u r ,即1100n AC n C D ⎧'⋅=⎪⎨'⋅=⎪⎩u u r u u u u r u u r u u u u r , 11111031022y z x y z +=⎧⎪⎨+-=⎪⎩,令11z =,则11y =-,13x =, 1(3,1,1)n ∴=-u u r …………8分设平面BC D '的法向量为2222(,,)n x y z =u u r ,则22n BC n C D ⎧'⊥⎪⎨'⊥⎪⎩u u r u u u u r u u r u u u u r ,即2200n BC n C D ⎧'⋅=⎪⎨'⋅=⎪⎩u u r u u u u r u u r u u u u r , 22222031022y z x y z -+=⎧⎪⎨+-=⎪⎩,令21z =,则21y =,233x =, 23(,1,1)3n ∴=u u r ………………10分 1233(1)11111053cos ,351731111533n n ⨯+-⨯+⨯∴===++⋅++⋅u u r u u r ,二面角A C D B '--的余弦值为35105-.……………12分 19.解:(I ) 设该运动员到篮筐的水平距离的中位数为x , ∵5.020.010.0205.0<++⨯,且5.06.01)20.040.0(>=⨯+,∴]5,4[∈x …………………2分随机变量ξ的所有可能取值为-4,-2,0,2,4; …………………………………8分()421645625P X ⎛⎫=-== ⎪⎝⎭,625216)53()52()2(3134===C X P 62596)53()52()2(314==-=C X P 625216)53()52()0(2224===C X P ; 625216)53()52()2(3134===C X P ()438145625P X ⎛⎫=== ⎪⎝⎭ X-4 -2 0 2 4 P 16625 96625 216625 216625 81625 …………………10分…………………12分 20.解:(1)抛物线C 的准线方程为:2p x =-, ||22p MF m ∴=+=,又42pm =Q ,即42(2)2p p =---------------------2分 2440,2p p p ∴-+=∴=()1696216216814420246256256256256255EX ()=-⨯+-⨯+⨯+⨯+⨯=抛物线C 的方程为24y x =. -------------------4分(2)设点E (0,)(0)t t ≠,由已知切线不为y 轴,设:EA y kx t =+ 联立24y kx ty x =+⎧⎨=⎩,消去y ,可得222(24)0k x kt x t +-+= Q 直线EA 与抛物线C 相切,222(24)40kt k t ∴∆=--=,即1kt = 代入222120x x t t-+=,2x t ∴=,即2(,2)A t t --------------------------------------6分 设切点00(,)B x y ,则由几何性质可以判断点,O B 关于直线:EF y tx t =-+对称,则0000010122y t x y x t t -⎧⨯=-⎪-⎪⎨⎪=-⋅+⎪⎩,解得:202022121t x t t y t ⎧=⎪⎪+⎨⎪=⎪+⎩,即22222(,)11t t B t t ++-------------------------------8分 思路1:直线AB 的斜率为22(1)1AB t k t t =≠±- 直线AB 的方程为222()21t y x t t t =-+-,--------------------------------------10分 整理22(1)1t y x t =-- ∴直线AB 过定点恒过定点(1,0)F --------------------------------------11分当1t =±时,(1,2),(1,1)A B ±±,此时直线AB 为1x =,过点(1,0)F .综上,直线AB 过定点恒过定点(1,0)F --------------------------------------12分思路2:直线AF 的斜率为22(1)1AF t k t t =≠±-, 直线BF 的斜率为22222021(1)2111BF t t t k t t t t -+==≠±--+, AF BF k k ∴=,即,,A B F 三点共线--------------------------------------10分当1t =±时,(1,2),(1,1)A B ±±,此时,,A B F 共线. --------------------------------------11分 ∴直线AB 过定点F .--------------------------------------12分21. 解:(Ⅰ)证明:令()()22x g x f x e ax '==--,则()2xg x e a '=-因为0a >,令0()0g x '=,0ln 2x a =所以当(,ln 2)x a ∈-∞时,()0g x '<,()g x 单调递减;当(ln 2,)x a ∈+∞时,()0g x '>,()g x 单调递增--------------------2分则ln 2min min ()()(ln 2)2ln 22=22ln 22a f x g x g a ea a a a a '===------------------------3分 令()ln 2G x x x x =--,(0)x >()1(ln 1)ln G x x x '=-+=-当(0,1)x ∈时,()0G x '>,()G x 单调递增当(1,)x ∈+∞时,()0G x '<,()G x 单调递减所以max ()(1)10G x G ==-<,所以min ()0f x '<成立. --------------------5分(Ⅱ)证明:()0f x >恒成立,等价于min ()0f x >恒成立令()()22x g x f x e ax '==--,则()2xg x e a '=-因为0a <,所以()0g x '>,所以()g x 单调递增,又(0)10g =-<,022)1(g >--=a e ,所以存在0(0,1)x ∈,使得0()0g x =---------------------6分则0(,)x x ∈-∞时,()()0,g x f x '=<()f x 单调递减; 0(,)x x ∈+∞时,()()0,g x f x '=>()f x 单调递增;所以02min 000()()20x f x f x e ax x b ==--+>恒成立 (1)且00220x e ax --= (2)由(1)(2),000020000002(1)2(1)22x x x x x e b e ax x e x x e x >-++=-+-+=-+即可-----------------8分 又由(2)00202x e a x -=<,所以0(0,ln 2)x ∈---------------------9分 令()(1),(0,ln 2)2x xm x e x x =-+∈()n x =1()(1)12x m x x e '=-+ 1()02x n x xe '=>, 所以021)0()(>=>n x n ,所以()m x 单调递增, 1)1()0()(0-=-=>e m x m , 22ln 22ln )122ln ()2(ln )(2ln -=+-=<e m x m ---------------------11分所以1b >-,所以符合条件的=0b ---------------------12分法2:令0,(0)10,1x f b b ==+>>-,故符合条件的最小整数0b =.-------------------6分现证明0b =时,()0f x > 求2()2x f x e ax x =--的最小值即可令()()22x g x f x e ax '==--,则()2xg x e a '=-因为0a <,所以()0g x '>,所以()g x 单调递增,又(0)10g =-<,(1)220g e a =-->,所以存在0(0,1)x ∈,使得0()0g x =则0(,)x x ∈-∞时,()()0,g x f x '=<()f x 单调递减; 0(,)x x ∈+∞时,()()0,g x f x '=>()f x 单调递增;所以02min 000()()2x f x f x e ax x ==-- .(1) 且00220x e ax --= (2)00000min 000()()(2)2(1)22x x x x x f x f x e e x e x ==---=-----------------8分 又由(2)00202x e a x -=<,所以0(0,ln 2)x ∈---------------9分 现在求函数()(1),(0,ln 2)2x xp x e x x =--∈的范围 0()q x =1()(1)12x p x x e '=--,01()02x q x xe '=-<, 所以021)0()(<-=<q x q ,所以()p x 单调递减, 1)1()0()(0=-=<e p x p02ln 22ln )22ln 1()2(ln )(2ln >-=--=>e p x p -------------11分所以=0b 是符合条件的. -------------12分选做题:22.解:(I )连接AB,Q P 、B 、F 、A 四点共圆,PAB PFB ∴∠=∠. .................2分 又Q PA 与圆O 切于点A, PAB AEB ∴∠=∠,.............4分 PFB AEB ∴∠=∠//AE CD ∴..............5分 (II )因为PA 、PB 是圆O 的切线,所以P 、B 、O 、A 四点共圆, 由PAB ∆外接圆的唯一性可得P 、B 、F 、A 、O 共圆,四边形PBFA 的外接圆就是四边形PBOA 的外接圆,∴OP 是该外接圆的直径. .............7分由切割线定理可得23927PA PC PD =⋅=⨯=.............9分 222725213OP PA OA ∴=+=+=.∴四边形PBFA 的外接圆的半径为13. ............10分 23解:(I )1C 的直角坐标方程为()2211x y -+=, ............2分 2C 的直角坐标方程为3x =;............4分(II )设曲线1C 与x 轴异于原点的交点为A,PQ OP ⊥Q ,PQ ∴过点A (2,0),设直线PQ 的参数方程为()2cos sin x t t y t θθ=+⎧⎨=⎩为参数, 代入1C 可得22cos 0,t t θ+=解得1202cos t t θ==-或,可知2|||||2cos |AP t θ==............6分代入2C 可得2cos 3,t θ+=解得/1cos t θ=, 可知/1||||||cos AQ t θ==............8分所以PQ=1 |||||2cos|||22,cosAP AQθθ+=+≥当且仅当1|2cos|||cosθθ=时取等号,所以线段PQ长度的最小值为22.............10分24.解:(I)由已知可得12,0()1, 0121,1x xf x xx x-<⎧⎪=≤<⎨⎪-≥⎩,所以min()1f x=,............3分所以只需|1|1m-≤,解得111m-≤-≤,02m∴≤≤,所以实数m的最大值2M=. ............5分(II)法一:综合法222a b ab+≥Q1ab∴≤1ab∴≤,当且仅当a b=时取等号,①............7分又2a bab+≤Q21≤+∴baab2abbaab≤+∴,当且仅当a b=时取等号,②............9分由①②得,21≤+∴baab,所以2a b ab+≥.............10分法二:分析法因为0,0a b>>,所以要证2a b ab +≥,只需证222()4a b a b +≥,即证222224a b ab a b ++≥,22a b M +=Q ,所以只要证22224ab a b +≥,............7分 即证22()10ab ab --≤,即证(21)(1)0ab ab +-≤,因为210ab +>,所以只需证1ab ≤, 下证1ab ≤,因为ab b a 2222≥+=,所以1ab ≤成立,所以2a b ab +≥............10分。
河北省石家庄市高中毕业班第一次模拟考试 数学理科

2009石家庄市高三第一次模拟考试数学理科答案一、A卷选择题:本大题共12小题,每小题5分,共60分.1.A2. B3. A4. B5.D6.A7. B8.A9. C 10. D 11.B 12.C 一、B卷选择题:本大题共12小题,每小题5分,共60分.1. B2. A3. B4.D5.A6. B7.A8. C9. D 10.B 11.C 12.A 二、填空题:本大题共4小题,每小题5分,共20分 13.13a = 141cos 315. 1 16.③ ,④三、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤. 17.(本题10分)解:(Ⅰ)该天平均每人的课外阅读时间为0.520110 1.515251.0550⨯+⨯+⨯+⨯=(小时)答:这一天平均每人的课外阅读时间为1.05小时.………………………4分 (Ⅱ) 记这2名学生该天阅读时间量互不相同为事件A ,222220151052502()7C C C C P A C +++==,………………………7分 25()1()177P A P A =-=-=.…………………………………9分 答: 这2名学生该天阅读时间量互不相同的概率为57.…………………10分18.(本题12分)解: (Ⅰ)由余弦定理知:2cos 2A ==,………2分cos 1)1AB AC AB AC A ∴⋅=⋅==.……………5分 (Ⅱ)由AC mAO nAB =+,知,. AB AC mAB AO nAB AB AC AC mAC AO nAC AB ⎧⋅=⋅+⋅⎪⎨⋅=⋅+⋅⎪⎩∴21(31),2(31).mAB AO nmAC AO n=⋅+=⋅+⎪⎩…………………………………7分O为ABC∆的外心,2112cos(1)2ABAB AO AB AO BAO AB AOAO∴⋅=⋅∠=⋅⋅=.同理1AC AO∴⋅=.………………………………10分即22111)1),221).m nm n=+⎪=+⎩,解得:1,mn⎧=⎪⎨=⎪⎩……12分19.(本题12分)(Ⅰ)取BC的中点M,连结PM,AM.四边形ABCD为菱形,0120BAD∠=,则,,BC AM BC PM⊥⊥……………2分BC APM∴⊥平面,BC PA⊥从而.同理DC PA⊥故PA ABCD⊥平面.……………………4分(或用同一法可证)(Ⅱ)先求二面角E AC B--的大小取AB的中点H,过H作HN AC⊥于点N,连结EN.则EH ABCD⊥平面,ENH∠是二面角E AC B--的平面角,……6分可求得arctan3ENH∠=,又PAC ABCD⊥平面平面,所以二面角E AC P--的大小为arctan23π-……………………8分BCDEPA HN法二: 过A 作AM AB ⊥交CD 于M , 以A 为坐标原点,直线AM 、AB 、AP 分别为x y 、、z 轴, 建立空间直角坐标系A xyz -. 则A (0,0,0),C ,P (0,0,2),(0,1,1)E .(0,0,2)AP ∴=,(3,1,0),AC =(0,1,1)AE =.…………………6分设平面PAC 的法向量为1111(,,)x y z =n ,则110,0.AP AC ⎧⋅=⎪⎨⋅=⎪⎩n n11120,0.z y =⎧⎪+=即取1x =1,-则1(1=-n . 设平面AEC 的法向量为2222(,,)x y z =n ,则220,0.AC AE ⎧⋅=⎪⎨⋅=⎪⎩n n22220,0.y y z +=+=⎪⎩即取21y =,则2(,1,1)3=--n . cos <1n ,2n >=1212⋅=⋅n n n n∴二面角E AC P --的大小为arc ……………………8分 (Ⅲ)先求点B 到平面PAF 的最大距离.PA ABCD PAF ABCD PAFABCD AF ⊥∴⊥=平面,平面平面,平面平面,∴点B 到直线AF 的距离即为点B 到平面PAF 的距离. ……10分 过B 作直线AF 的垂线段,在所有的垂线段中长度最大为2AB =. E 为PB 的中点,故点E 到平面PAF 的最大距离为1. ……………………12分20.(本题12分)解:(Ⅰ)2()2,xf x e a '=-(ⅰ)当0a ≤时, ()0,f x '>∴()f x 的单调递增区间是(,-∞+∞).……………………2分(ⅱ) 当0a >时,令()0,f x '=得1ln .22a x =当1ln 22ax <时,()0,f x '< 当1ln 22ax >时,()0.f x '>()f x ∴的单调递减区间是(1,ln 22a-∞),()f x 的单调递增区间是 (1ln ,22a+∞).……………………5分(Ⅱ)()f x a <,∴2,x e ax a -<2(1),x a x e +>(1,1]x ∈-,10x +>.∴2,1x e a x >+设2(),1xe g x x =+ 若存在实数(1,1]x ∈-,使得()f x a <成立, 则a >min ().g x ……………………8分22(21)(),(1)x e x g x x +'=+ 解得()0,g x '=得12x =-, ∴当112x -<<-时, ()0,g x '<当112x -<≤时, ()0,g x '>∴()g x 在1(1,)2--上是减函数,在1(,1]2-上是增函数. …………………10分∴1min12()(),1212e g x g e-=-==-a 的取值范围是(2,e+∞).…………………………………………………12分21.(本题12分)(I )由2OP OM ON =+,得P 是MN 的中点. …………2分 设),(),,(),,(2211mx x N mx x M y x P -依题意得:121222212122,2,()()2.x x x mx mx y x x mx mx ⎧+=⎪-=⎨⎪-++=⎩ 消去21,x x ,整理得112222=+m y m x . 当1>m 时,方程表示焦点在y 轴上的椭圆;当10<<m 时,方程表示焦点在x 轴上的椭圆;当1=m 时,方程表示圆. ……………………………5分 (II )由1m >,焦点在y 轴上的椭圆,直线l 与曲线C 恒有两交点, 直线斜率不存在时不符合题意;可设直线l 的方程为1y kx =+,直线与椭圆交点1122(,),(,)A x y B x y .224222221()21011y kx x y m k x kx m m m =+⎧⎪⎪⇒+++-=⎨+=⎪⎪⎩ 21212424221,k m x x x x m k m k -+=-=++22212124242(1)2(1)(1)1k m k y y kx kx m k m k--=++=++++.………………7分 要使AOB ∠为锐角,只需0OA OB ⋅>422121242(1)10m k m x x y y m k -++∴+=>+.………………9分即422(1)10m k m -++>, 可得22211m k m+>+,对于任意1m >恒成立. 而2212m m+>,21211,.k k ∴+≤-≤≤所以k 的取值范围是[1,1]-.………………12分 22(本题12分) 解:(Ⅰ)21231n n n a a n n --=+⋅-,………………1分 2211122323232(13)1313n nn n a n---=++⋅+⋅++⋅-=+=-,即13n n a n -=⋅(n ∈*N ).………………3分(II )1()n b n n =∈*N ,111111,12,2234+>+++> 1111111132345678+++++++<.猜想当3n ≥时,2n S n <.………………4分 下面用数学归纳法证明:①当3n =时,由上可知323S <成立; ②假设(3)n k k =≥时,上式成立,即1111232kk ++++<. 当1n k =+时,11111111232212112122121k k k k k kk k k k ++=++++++++<++++<+<++左边所以当1n k =+时成立.由①②可知当3n ≥()n ∈*N 时,2n S n <. ………………7分综上所述当1n =时, 121S >;当2n =时, 222S >;当3n ≥()n ∈*N 时,2n S n <. ………………8分(III )131n n n a c n +==+ 当2n ≥时,121123232311(31)(31)(33)(31)(31)3131n n n nn n n n n n---⨯⨯⨯≤==--------.所以22222233232331111()()2(31)(31)22313131n n n T ⨯⨯=+++≤+-+------ +1111()22313131n n n -+-=-<---.………………12分。
河北省石家庄市高中毕业班第一次模拟考试理科数学试题

河北省石家庄市2021届高中毕业班第|一次模拟考试理科数学试题(时间120分钟 ,总分值150分 )考前须知:1. 本试卷分第I 卷 (选择题 )和第II 卷 (非选择题 )两局部 ,答卷前 ,考生务必将自己的 姓名、准考证号填写在答题卡上.2. 答复第I 卷时,选出每题答案后 ,用铅笔把答题卡上对应题目的答案标号涂黑.如 需改动 ,用橡皮擦干净后 ,再选涂其他答案标号.写在本试卷上无效.3. 答复第II 卷时 ,将答案写在答题卡上,写在本试卷上无效.4. 考试结束后 ,将本试卷和答题卡一并交回.第I 卷(选择题,共60分 )一、选择题:本大题共12小题 ,每题5分 ,在每题给出的四个选项中 ,只有一项为哪一项符合题目 要求的.1.复数z =1 -i,那么z z+1对应的点所在的象限为 A.第|一象限 B.第二象限 C.第三象限 D.第四象限2. 假设集合}822|{2≤<∈=+x Z x A ,}02|{2>-∈=x x R x B ,那么)(B C A R 所含的元素个数为A. OB. 1C. 2D. 33. 设随机变量ξ服从正态分布),1(2σN .假设P(ξ ,那么p(0<ξ<1)的值为 A. B C.0.4 D.4 双曲线的一个焦点与抛物线x 2=20y 的焦点重合 ,且其渐近线的方程为3x ±4y =0,那么 该双曲线的标准方程为A. 116922=-y xB. 191622=-y xC. 116922=-x yD. 191622=-x y5. 执行右面的程序框图 ,输出的S 值为 A. 1B. 9C. 17D. 206. 等比数列{a n } ,且dx x a a ⎰-=+22644 ,那么a 6(a 3 +2a 6 +a 10))的值为A. π2B. 4C. πD. -9π7. 现釆用随机模拟的方法估计该运发动射击4次 ,至|少击中3次的概率:先由计算器给出 0到9之间取整数值的随机数 ,指定0、1表示没有击中目标,2、3、4、5、6、7、8、9表示击中目标,以4个随机数为一组,代表射击4次的结果,经随机模拟产生了 20组随机数:7527 0293 7140 9857 0347 4373 8636 6947 1417 4698 0371 6233 2616 8045 6011 3661 9597 7424 7610 4281 根据以上数据估计该射击运发动射击4次至|少击中3次的概率为A. 0.852B. 0.8192C O.8D.8. 巳知点(x,y)在ΔABC 所包围的阴影区域内(包含边界),假设B(3,25)是 使得z =ax -y 取得最|大值的最|优解,那么实数a 的取值范围为A. 21-≥a B. 0≥a C. 21-≤a D. 021≤≤-a 9. 假设函数)0)(2sin()(>+=A x A x f ϕπ满足f(1) =0,那么A.f(x -2) -定是奇函数B.f(x +1) -定是偶函数C. f(x +3)一定是偶函数D, f(x -3)一定是奇函数10. 正三棱锥P -ABC 的主视图和俯视图如图所 示,那么此三棱锥的外接球的外表积为A 4π B, 12πC.316π D. 364π 11. 数列{a n },41,32,23,14,31,22,13,21,12,11… ,依它的10项的规律 ,那么a 99 +a 100 的值为A 2437B 67. C. 1511 D. 157 -12. 定义域为R 的奇函数f(x)的导函数为)(x f ' ,当0≠x 时 ,0)()(>+'xx f x f ,假设)2(ln 21ln ),2(2),21(21f c f b f a =--==,那么以下关于a,b,c 的大小关系正确的选项是 A. a>b>c B, a>c>bC. c>b>aD. b>a>c第II 卷(非选择题,共90分 )本卷包括必考题和选考题两局部,第13题~第21题为必考题,每个试题考生都必须作答.第22题~第24题为选考题,考生根据要求作答.二、填空題,本大通共4小题,每题5分,共20分.13.过点(2,3)与圆(x -1)2+y 2=1相切的直线方程为_____.14. 如图,正方形ABCD 中,EF//AB,假设沿EF 将正方形折成一个二面角后,AE:ED:AD =1:1:2,那么AF 与CE 所成的角的余弦值为______.15.为举办校园文化节,某班推荐2名男生3名女生参加文艺技能培训 ,培训工程及人数分 别为:乐器1人,舞蹈2人,演唱2人,每人只参加一个工程 ,并且舞蹈和演唱工程必须 有女生参加,則不同的推荐方案的种数为_______.(用数字作答 )16.在ΔABC 中 ,B ∠ =600 ,O 为ΔA BC 的外心 ,P 为劣弧AC 上一动点 ,且OC y OA x OP += (x,y ∈R) ,那么x +y 的取值范围为 __ _____三、解答题:本大题共6小题 ,共70分.解容许写出文字说明 ,证明过程或演算步骤. 17. (本小题总分值12分 )如图 ,有两座建筑物AB 和CD 都在河的对岸 (不知 道它们的高度 ,且不能到达对岸 ) ,某人想测量两 座建筑物尖顶A 、C 之间的距离 ,但只有卷尺和测 角仪两种工具.假设此人在地面上选一条基线EF ,用 卷尺测得EF 的长度为 a ,并用测角仪测量了一些角度:a AEF =∠,β=∠AFE ,θ=∠CEF ,ϕ=∠CFE ,γ=∠AEC 请你用文字和公式写出计算A 、C 之间距离的步骤和结果.18.(本小题总分值12分 )为了调査某大学学生在某天上网的时间 ,随机对lOO 名男生和100名女生进行了不记名的问卷调查.得到了如下的统计结果:表l:男生上网时间与频数分布表表2:女生上网时间与频数分布表(I)从这100名男生中任意选出3人 ,其中恰有1人上网时间少于60分钟的概率;(II)完成下面的2X2列联表 ,并答复能否有90%的把握认为 "大学生上网时间与性别有关〞 ?表3:•附:19. (本小题总分值i2分 )如图 ,在四棱锥P -ABCD 中 ,PA 丄平面ABCD, 090=∠=∠ADC ABC ,0120=∠BAD ,AD =AB =1,AC 和 BD 交于O 点.(I)求证:平面PBD 丄平面PAC(II)当点A在平面PBD 内的射影G 恰好是ΔPBD 的重心时 ,求二面角B -PD -G 的余弦值.20. (本小题总分值12分 )椭圆)0(12222>>=+b a by a x 的左、右焦点分别为F 1( -1 ,0) ,F 2(1,0) ,过F 1作与x 轴不重合的直线l 交椭圆于A,B 两点.(I)假设ΔABF 2为正三角形 ,求椭圆的离心率; (II)假设椭圆的离心率满足2150-<<e ,0为坐标原点 ,求证:OA 2 +OB 2<AB 221 (本小题总分值12分 ) 设函数f(x ) =x 2 +aln(x +1)(I)假设函数y =f(x)在区间[1, +∞ )上是单调递增函数 ,求实数a 的取值范围; (II)假设函数y =f(x)有两个极值点x 1,x 2且x 1<x 2求证: 2ln 21)(012+-<<x x f请考生在22〜24三题中任选一题做答 ,如果多做 ,那么按所做的第|一题记分.22. (本小题总分值10分)选修4 -l:几何证明选讲如图,过圆O 外一点P 作该圆的两条割线PAB 和PCD,分别交圆 O 于点A,B,C,D 弦AD 和BC 交于Q 点 ,割线PEF 经过Q 点交圆 O 于点E 、F ,点M 在EF 上 ,且BMF BAD ∠=∠:(I)求证:PA·PB =PM·PQ (II)求证:BOD BMD ∠=∠23. (本小题总分值10分 )选修4 -4:坐标系与参数方程在平面直角坐标系.x0y 中 ,以原点O 为极点,x 轴的正半轴为极轴建立极坐标系 ,曲线 C 的极坐标方程为: θθρcos sin 2=(I)求曲线l的直角坐标方程;|AB|的值24. (本小题总分值10分)选修4 -5:不等式选讲 巳知函数f(x) =|x -2| +2|x -a|(a∈R). (I)当a =1时 ,解不等式f(x)>3;(II)不等式1)(≥x f 在区间 ( -∞ , +∞)上恒成立 ,求实数a 的取值范围高中毕业班第|一次模拟考试数学理科答案一、选择题 A 卷答案1 -5 DCBCC 6 -10 ADADD 11 -12 AD B 卷答案1 -5 DBCBB 6 -10 ADADD 11 -12 AD 二、填空题13 . 4310x y -+=或2x = 14 .4515 . 24 16 . []1,2三、解答题:(阅卷老师,可根据学生的答题情况,酌情给分)17.解:第|一步:在AEF ∆中 ,利用正弦定理 ,sin sin(180)AE EFβαβ︒=-- , 解得sin sin()a AE βαβ=+;……………4分第二步:在CEF ∆中 ,同理可得sin sin()a CE ϕθϕ=+;……………8分第三步:在ACE ∆中 ,利用余弦定理,AC…………12分 (代入角的测量值即可 ,不要求整理 ,但如果学生没有代入 ,扣2分 )18.解: (Ⅰ )由男生上网时间频数分布表可知100名男生中 ,上网时间少于60分钟的有60人 ,不少于60分钟的有40人 ,………………2分故从其中任选3人 ,恰有1人上网的时间少于60分钟的概率为 1260403100C C C ……………4分 156539=………………6分 (Ⅱ ) (8)22200(18002800)200 2.201001001307091K ⨯-==≈⨯⨯⨯ ,………………10分∵2 2.20 2.706K ≈<∴没有90%的把握认为 "大学生上网时间与性别有关〞.………………12分 19. 解: (Ⅰ )依题意Rt ABC Rt ADC ∆≅∆ ,BAC DAC ∠=∠ ,ABO ADO ∆≅∆ ,所以AC BD ⊥ ,……2分而PA ⊥面ABCD ,PA BD ⊥ ,又PA AC A = ,∴BD ⊥面PAC , 又BD ⊂面PBD ,∴平面PAC ⊥平面PBD …………4分 (Ⅱ ) 过A 作AD 的垂线为x 轴 ,AD 为y 轴 ,AP 为z 轴 ,建立如下图坐标系 ,那么1,0)2B - ,(0,1,0)D,0)C ,设(0,0,)P λ ,所以1,)63G λ , 31(,)22PB λ=-- ,由AG PB ⊥,得311(,),)066322AG PB λλ⋅=⋅--= 解得212λ=,λ=.………………6分 ∴P 点的坐标为(0,;面PBD 的一个法向量为6(3,1AG ==m ,……………8分设面PCD 的一个法向量为(,,)x y z =n,(CD =- ,(0,1,PD = 00PDCD ⎧⋅=⎪⎨⋅=⎪⎩n n 即0z -==⎪⎩ ,∴=n ………………10分cos ,||||⋅<>==n m n m n m ,所以二面角B PD A --.……………12分 20. 解: (Ⅰ )由椭圆的定义知1212||||||||AF AF BF BF +=+ ,又22||||AF BF = ,∴11||||AF BF = ,即12F F 为边AB 上的中线 ,∴12F FAB ⊥,……………………2分 在12Rt AF F △中,2cos30,43ca ︒=那么c a = ,…………………4分 (注: ,没有过程扣3分) (Ⅱ )设11(,)A x y ,22(,)B x y 因为0e <<1c = ,所以12a +>…………6分 ①当直线AB x 与轴垂直时 ,22211y a b += ,422b y a= ,4121221b OA OB x x y y a ⋅=+=-,42231a a a -+- =22235()24a a --+, 因为2532+>a ,所以0OA OB ⋅< , AOB ∴∠恒为钝角 ,∴222OA OB AB +<.………………………8分②当直线AB 不与x 轴垂直时 ,设直线AB 的方程为:(1)y k x =+ ,代入22221x y a b+= ,整理得:2222222222()20b a k x k a x a k a b +++-= ,22122222a k x x b a k -+=+ ,222212222a k ab x x b a k -=+ 1212OA OB x x y y ⋅=+212121212(1)(1)x x y y x x k x x +=+++2221212(1)()x x k k x x k =++++22222242222222()(1)2()a k ab k a k k b a k b a k-+-++=+ 2222222222()k a b a b a b b a k +--=+ 24222222(31)k a a a b b a k -+--=+………………10分 令42()31m a a a =-+- , 由 ①可知 ()0m a < ,AOB ∴∠恒为钝角. ,所以恒有222OA OB AB +<.………………12分21. 解: (Ⅰ )0122)(2/≥+++=x ax x x f 在区间),1[+∞上恒成立 , 即x x a 222--≥区间),1[+∞上恒成立 , …………………1分4-≥a .………………3分经检验 , 当a = - 4时 , 1)1)(2(21422)(2/+-+=+-+=x x x x x x x f ,),1[+∞∈x 时 ,0)(/>x f ,所以满足题意的a 的取值范围为[4,)-+∞.………………4分(Ⅱ )函数的定义域),1(+∞- ,0122)(2/=+++=x ax x x f ,依题意方程0222=++a x x 在区间),1(+∞-有两个不等的实根 ,记a x x x g ++=22)(2 ,那么有⎪⎪⎩⎪⎪⎨⎧->->->∆1210)1(0g ,得210<<a .……………………6分 ,121-=+x x 022222=++a x x ,221212a x -+-= ,0212<<-x , 2222222121)1ln()22()(x x x x x x x f --++-=,令)0,21(,1)1ln()22()(22-∈--++-=x x x x x x x k ……………………8分)1ln(21)(2+++-=x x x x x k ,)1ln(2)1()(22/+++=x x x x k , 32//)1(262)(+++=x x x x k , 因为2)0(,1)1(////=-=-k k ,存在)0,1(0-∈x ,使得0)(0//=x k , 0)0(/=k ,02ln 21)2(/<-=-k ,0)(/<∴x k ,所以函数)(x k 在)0,2(-为减函数 ,…………………10分)21()()0(-<<k x k k 即2ln 21)(012+-<<x x f ……………………12分法二:6分段后面还有如下证法 ,可以参照酌情给分.【证法2】2x 为方程2220x x a ++=的解 ,所以22222x x a --=,∵102a <<, 120x x << ,212x =- ,∴2102x -<<,先证21()0f x x > ,即证2()0f x < (120x x << ), 在区间12(,)x x 内 ,()0f x '< ,2(,0)x 内()0f x '> ,所以2()f x 为极小值 ,2()(0)0f x f <=, 即2()0f x < ,∴21()0f x x >成立;…………………8分 再证21()1ln 22f x x <-+ ,即证22211()(ln 2)(1)(ln 2)(1)22f x x x >-+--=-+, 222222211(22)ln(1)(ln 2)ln 222x x x x x -++-->-,令221()(22)ln(1)(ln 2)2g x x x x x x =-++-- , 1(,0)2x ∈-…………………10分2(1)1()2(42)ln(1)(ln 2)12x x g x x x x x +'=-++---+,12(21)ln(1)(ln 2)2x x =-++--,ln(1)0x +< ,210x +> ,1ln 202-<,∴()0g x '> ,()g x 在1(,0)2-为增函数.111111()()(21)ln (ln 2)244222g x g >-=-⨯-+-111111ln ln 2ln 2422422=++-=-.综上可得21()10ln 22f x x <<-+成立.………………………12分22.证明: (Ⅰ )∵∠BAD =∠BMF ,所以A,Q,M,B 四点共圆 ,……………3分所以PA PB PM PQ ⋅=⋅.………………5分(Ⅱ)∵PA PB PC PD ⋅=⋅ ,∴PC PD PM PQ ⋅=⋅ ,又 CPQ MPD ∠=∠ , 所以~CPQ MPD ∆∆ ,……………7分 ∴PMD PCQ ∠=∠ ,那么DCB FMD ∠=∠,………………8分 ∵BAD BCD ∠=∠ ,∴2BMD BMF DMF BAD ∠=∠+∠=∠,2BOD BAD ∠=∠,所以BMD BOD ∠=∠.…………………10分23.解:(Ⅰ)依题意22sin cos ρθρθ=………………3分得:x y =2∴曲线1C 直角坐标方程为:x y =2.…………………5分(Ⅱ)把⎪⎪⎩⎪⎪⎨⎧=-=ty tx 22222代入x y =2整理得:0422=-+t t ………………7分0>∆总成立 ,221-=+t t ,421-=t t23)4(4)2(221=-⨯--=-=t t AB ………………10分 另解:(Ⅱ)直线l 的直角坐标方程为x y -=2 ,把x y -=2代入x y =2得: 0452=+-x x ………………7分0>∆总成立 ,521=+x x ,421=x x23)445(212212=⨯-=-+=x x k AB …………………10分 24. 解:(Ⅰ)⎩⎨⎧>-+-≥32222x x x 解得37>x ⎩⎨⎧>-+-<<322221x x x 解得φ∈x⎩⎨⎧>-+-≤32221x x x 解得13x <…………………3分 不等式的解集为17(,)(,)33-∞+∞………………5分 (Ⅱ)时,2>a ⎪⎩⎪⎨⎧≥--<<-+-≤++-=a x a x a x a x x a x x f ,2232,222,223)(; 时,2=a 36,2()36,2x x f x x x -+≤⎧=⎨->⎩; 时,2<a ⎪⎩⎪⎨⎧≥--<<+-≤++-=2,2232,22,223)(x a x x a a x a x a x x f ; ∴)(x f 的最|小值为)()2(a f f 或;………………8分那么⎩⎨⎧≥≥1)2(1)(f a f ,解得1≤a 或3≥a .………………10分。
河北省石家庄市2012届高中毕业班第一次模拟考试(数学理)()

2012年石家庄市高中毕业班第一次模拟考试高三数学(理科)注意事项:1. 本试卷分第I卷(选择题)和第II卷(非选择题)两部分,答卷前,考生务必将自己的姓名、准考证号填写在答题卡上.2.回答第I卷时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
写在本试卷上无效.3. 回答第II卷时,将答案写在答题卡上,写在本试卷上无效.4. 考试结束后,将本试卷和答题卡一并交回。
第I卷(选择题60分)一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1。
复数=A。
i B. –i C . 1-i D。
1+i2。
下面四个条件中,使a〉b成立的充要条件是A。
a > b + 1 B。
a >b—1 C. a2〉b2 D. a3 > b33。
已知向量,且,则点P的坐标为A. (2,—4)B. (—)C。
(-) D. (-2,4)4. 函数为常数,)的部分图象如右图所示,则f(0)的值为A。
B。
C. 0 D.5。
已知.,若,则f(-a)的值为A. -3B. —2 C。
—1 D。
06。
已知实数x,y满足则的最大值为A。
9 B. 17 C. 5 D. 157。
已知等差数列{a n}的前n项和为,则使S n取得最小值时n的值为A。
4 B. 5 C。
6 D. 78. 已知程序框图如右图所示,当输入2与—2时,输出的值均为10,则输入1时输出的值为A. 2 B。
4 C. 6 D。
89。
已知A、B、C是球O的球面上三点,三棱锥O—ABC的高为且,AB=2,BC=4,则球O的表面积为A。
B. C. D.10. 设F1,F2分别为双曲线的左、右焦点,点P在双曲线的右支上,且,F2到直线PF1的距离等于双曲线的实轴长,则该双曲线的离心率为A.B。
C。
D。
11. 已知点P在曲线y=e x(e自然对数的底数)上,点Q在曲线y=lnx 上,则丨PQ丨的最小值是A. B.2E C.D。
河北省石家庄市高三数学第一次模拟考试 理(扫描版)

2010-2011年度石家庄市第一次模拟考试理科数学答案一、选择题:本大题共12个小题,每小题5分,共60分.(A 卷答案):1-5 ADCDA 6-10 BDDAB 11-12 CD(B 卷答案):1-5 BDCDB 6-10 ADDBA 11-12 CD二、填空题: 本大题共4个小题,每小题5分,共20分13.1或2 14. 15. ( 16. 0 三、解答题:本大题共6小题,共70分.解答应写文字说明,证明过程或演算步骤.17.(本小题满分10分)解:(I )解法一:∵0cos )2(cos =++B c a C b ,由正弦定理得:B A BC C B cos sin 2cos sin cos sin -=+,即B A C B cos sin 2)sin(-=+.………………2分在ABC △中,A C B -=+π,∴B A A cos sin 2sin -=,0sin ≠A ………………3分 ∴21cos -=B ,∴3π2=B .………………5分 解法二: 因为0cos )2(cos =++B c a C b ,由余弦定理222222(2)022a b c a c b b a c ab ac+-+-++=, 化简得222a ac c b ++=,……………2分又余弦定理2222cos a c ac B b +-=,……………3分 所以1cos 2B =-,又(0,)B ∈π,有23B =π.……………5分 (II )解法一: ∵2222cos b a c ac B =+-,∴224a c ac =++,……………6分 23ac ac ac ≥+=. ∴43ac ≤,………………8分∴114sin 223ABC S ac B ∆=≤⨯=9分当且仅当a c ==10分解法二: 由正弦定理知:Bb Cc sin sin =, )3πsin(3343π2sin )3πsin(2sin sin A A B C b c -=-⋅==.………………6分 ∴ABC S △==A bc sin 21)3π0(sin )3πsin(334<<-A A A , A A A sin )sin 21cos 23(334-=A A A 2sin 332cos sin 2-= )2cos 1(332sin A A --=332cos 332sin -+=A A 33)6π2sin(332-+=A ,………………8分 ∵3π0<<A ,∴6π56π26π<+<A , ∴12πsin )6π2sin(=≤+A ,………………9分 ∴3333)6π2sin(332≤-+A , 即ABC △的面积ABC S △的最大值是33.………………10分 18.(本小题满分12分)解:方法一:(Ⅰ)取AB 中点M ,连结CM 、EM ,由ABC ∆为正三角形,得CM AB ⊥,又AE A B C ⊥面,则AE CM ⊥,可知C M A B E ⊥面,所以MEC ∠为CE 与平面ABE 所成角.……………2分tan CM EM α==,………………4分因为[,]64αππ∈,得tan [,1]3α∈,得2k ≤≤.……………6分 (Ⅱ)延长AC ED 、交于点S,连BS ,可知平面BDE 平面ABC =BS .………………………7分由//CD AE ,且12C D A E =,又因为AC CS BC ===1,从而AB BS ⊥,…………………8分又AE ⊥面ABC ,由三垂线定理可知BE BS ⊥,即EBA ∠为平面BDE 与平面ABC 所成的角;……………………10分则tan AE EBA AB∠== 从而平面BDE 与面ABC所成的角的大小为arc .………………12分方法二:解:(Ⅰ)如图以C 为坐标原点,CA 、CD 为y 、z 轴,垂直于CA 、CD 的直线CT 为x 轴,建立空间直角坐标系(如图),则设(0,1,0)A ,(0,0,)2kD ,(0,1,)E k,1,0)2B .……………2分 取AB 的中点M,则3,0)4M , 易知,ABE 的一个法向量为33(,0)4CM =,由题意3sin ||||CE CM CE CM α⋅===⋅.………………4分由[,]64αππ∈,则12sin 2α≤=≤,得2k ≤≤…………………6分 (Ⅱ)由(Ⅰ)知k 最大值为,则当k =时,设平面BDE 法向量为x,y,z )n =(,则0,230.2DE y z yBE z ⎧⋅=+=⎪⎪⎨⎪⋅=++=⎪⎩n n 取n=, (8)分 又平面ABC 法向量为m =(0,0,1),……………………10分所以cos(,)n m=, 所以平面BDE 与平面ABC 所成角大小……………………12分 19.(本小题满分12分)解:(Ⅰ)()f x 的定义域为(0,)+∞.…………………1分21()f x x a x '=+-=221x ax x-+(0x >), 设2()21g x x ax =-+,只需讨论()g x 在(0,)+∞上的符号.…………………2分(1)若04a ≤,即0a ≤,由()g x 过定点(0,1),知()g x 在(0,)+∞上恒正,故()0f x '>,()f x 在(0,+∞)上为增函数.…………………3分 (2)若04a >,当280a -≤时,即0a <≤()0g x ≥(当2x =时,取“=”),故()0f x '≥,()f x 在(0,+∞)上为增函数;……………………4分当280a ->时,由2210,x ax -+=得x = 当0x <<或x>()0g x '>,即()0f x '>, x<<时,()0g x '<,即()0f x '<. 则()f x 在(44a a +上为减函数,在(0,)4a -,()4a +∞上为增函数.………………5分综上可得:当a ≤(f x )的单调增区间(0,+∞);当a >(f x )的单调增区间为(0,4a ,()4a ++∞;函数(f x )的单调减区间为(44a a -+.…………………6分 (Ⅱ)由条件可得2ln 00)x x ax x --≤>(,则当0x >时,ln x a x x≥-恒成立,………………8分 令ln ()(0)x h x x x x =->,则21ln (),x x h x x--'=…………………9分 方法一:令2()1ln (0)k x x x x =-->,则当0x >时,1()20k x x x '=--<,所以()k x 在(0,+∞)上为减函数. 又(1)0h '=,所以在(0,1)上,()0h x '>;在(1,+∞)上,()0h x '<.………10分 所以()h x 在(0,1)上为增函数;在(1,+∞)上为减函数.所以max ()(1)1h x h ==-,所以 1.a ≥-……………12分方法二:当01x <<时,210,ln 0,x x ->->()0h x '>;当1x >时,210,ln 0,x x -<-<()0h x '<.……………10分所以()h x 在(0,1)上为增函数;在(1,+∞)上为减函数.所以max ()(1)1h x h ==-,所以 1.a ≥-………………12分20.(本小题满分12分)解:(Ⅰ)记总分得50分为事件D ,记A ,B 答对,C 答错为事件D 1,记A ,B 答错,C 答对为事件D 2,则D =D 1+D 2,且D 1,D 2互斥.……………1分 又81)411(3121)(1=-⨯⨯=D P ,………………3分36141)311(21)(33222=⨯⨯-⨯=A A D P .…………………5分 所以12121111()()()()83672P D P D D P D P D =+=+=+=. 所以此选手可自由选择答题顺序,必答题总分为50分的概率为1172.……………6分 (Ⅱ)ξ可能的取值是0,30,50,70,80100,.……………7分100=ξ表示A ,B ,C 三题均答对, 则241413121)100(=⨯⨯==ξP ,……………8分 同理,2414131)211()80(=⨯⨯-==ξP , 12141)311(21)70(=⨯-⨯==ξP , 81)411(3121)50(=-⨯⨯==ξP , 81)411(31)211()30(=-⨯⨯-==ξP , 127)311()211()411()311(21)0(=-⨯-+-⨯-⨯==ξP , 所以,ξ的分布列为所以ξ的数学期望111117010080705030242412883E ξ=⨯+⨯+⨯+⨯+⨯=.……………12分 21.(本小题满分12分)解:(Ⅰ)方法一:设直线M A 1与N A 2的交点为),(y x P ,∵21A A ,是椭圆1322=+y x 的上、下顶点, ∴12(0A A ,,…………………1分111yA M y xx-=:,121yA N y xx++=-:,两式相乘得22121233xxyy--=-.………………………3分而),(11yxM在椭圆1322=+yx(1x≠)上,所以132121=+yx,即332121=--xy,所以2233xy=-.……………4分又当0x=时,不合题意,去掉顶点.∴直线MA1与NA2的交点的轨迹C的方程是221(0)3yx x-=≠;……………5分方法二:设直线MA1与NA2的交点为),(yxP,∵21AA,是椭圆1322=+yx的上、下顶点,∴12(0A A,,…………………1分∵PMA、、1共线,PNA、、2共线,∴xyxy3311-=-…………①xyxy3311+=-+…………②…………………3分①⨯②得22212133xyxy-=--,又∵132121=+yx即332121=--xy,∴3322=-xy,即221(0)3yx x-=≠,∴直线MA1与NA2的交点的轨迹C的方程是1322=-xy;(0x≠)……………5分(Ⅱ)假设存在满足条件的直线,由已知,其斜率一定存在,设其斜率为k,设)(11y x A ,,)(22y x B ,,)0(0y E , , 由2221.3y kx y x =+⎧⎪⎨-=⎪⎩,得)3(014)3(222≠=++-k kx x k , 3134221221-=--=+k x x k k x x ,.…………………6分 11(2)AF x y =--,,22(2)FB x y =-,,∵AF FB λ=,∴21x x λ=-,∵02≠x ,∴21x x -=λ, ∵(02)OF =,,110()EA x y y =-,,220()EB x y y =-,,121020()EA EB x x y y y y λλλλ-=---+,,, 又∵()OF EA EB λ⊥-,∴()0OF EA EB λ⋅-=,∴0)2(0020121=+--⨯+-⨯y y y y x x λλλ(),即00201=+--y y y y λλ.………………………8分将211+=kx y ,222+=kx y ,21x x -=λ代入上式并整理得0212121)()(22y x x x x x kx +=++,…………………9分当021≠+x x 时,232332222221210=+--=++=k k kx x x kx y , 当021=+x x 时,0=k ,0212121)()(22y x x x x x kx +=++恒成立,…………………11分所以,在y 轴上存在定点E ,使得()OF EA EB λ⊥-,点E 的坐标为)230(,.………12分22.(本小题满分12分)(I )证明:方法一:∵011>=a ,由12131)11(-+++=n n n a n a 得02>a ,于是易得0>n a .………………2分 又*12110()3n n n n a a a n n +--=+>∈N ,即*1()n n a a n +>∈N 又∵32=a ,∴32=≥a a n (2≥n ).…………………4分 方法二:数学归纳法(1)当2=n 时,332≥==a a n ,命题成立.………………1分(2)假设当k n =(2≥n )时命题成立,即3≥k a , 当1+=k n 时, 12131)11(-+++=k k k a k a 33112≥>++=-k k k k a k a a ∴1+=k n 时命题成立.………………3分由(1)(2)可知,当2≥n 时,3≥n a .…………………4分 (II )证明:由(I )知12131)11(-+++=n n n a n a 2121111(1)(1)33n n n n n a a a n n --≤++=++,……………5分 两边取自然对数得:)3111ln(ln ln 121-++++≤n n n n a a .………………6分 令)0()1ln()(≥-+=x x x x f , 则当0x >时,01111)(<+-=-+='xx x x f 恒成立, ∴)(x f 为)0[∞+,上的减函数,∴0)0()(=≤f x f ∴x x <+)1ln(在0>x 时恒成立,………………7分 12111111ln ln ln (1)33n n n n n a a a n n n +--<++<++-131111ln -+--+=n n n n a 即<-+n n a a ln ln 1131111-+--n n n (2≥n ),………………9分 故,21311121ln ln --+---<-n n n n n a a , 321312131ln ln ---+---<-n n n n n a a , ……………………………31211ln ln 23+-<-a a ,以上各式相加得:2211[1()]11333ln ln 11112213n n a a n ---<-+<+=--,(3≥n )…………10分 又∵32=a ,∴33ln 23ln <+<n a ,∴3e <n a (3≥n ),………………11分 又∵<=11a 3e ,<=32a 3e , ∴3e <n a (*n ∈N ).…………………12分。
河北省石家庄市2022年高三数学高中毕业班第一次高考模拟考试(理)人教版
试卷类型:A2022年石家庄市高中毕业班第一次模拟考试试卷数 学理科说明:1.本试卷共4页,包括三道大题.22道小题,共150分.其中第一道大题为选择题. 2.所有答案请在答题卡上作答,在本试卷和草稿纸上作答无效.答题前请仔细阅读答题 卡上的“注意事项”,按照“注意事项”的规定答题.3.做选择题时,如需改动,请用橡皮将原选答案擦干净,再选涂其他答案. 参考公式:如果事件A 、B 互斥,那么342x 4x 22a 232a 9102a )()(x g x f 313131313131312222321053103043772π是BC 的中点,3π212173535222a x 22b y 12π4π222236362223i i ++130652≥--x x 3π2π从三棱锥的一个顶点出发沿球面运动,经 过其它兰个顶点后回到出发点,则动点M 经过的最短距离为三、解答题:本大题共6小题,共70分.解答应写出文宇说明,证明过程或演算步骤r 17.本小题满分0分如图,已知平面四边形ABCD 中,BCD 为正三角形,AB =AD=1,∠BAD=,记四边 形ABCD 的面积为SI 将S 表示为的函数;Ⅱ求S 的最大值及此时的大小. 18.《本小题满分12分已知公比q 为正数的等比数列{}的前n 项和为,且4245s s =. I 求q 的值;Ⅱ若()*-∈≥+=N n n S q b n n ,2,1且数列{}也为等比数列,求数列{2n 一1}的前n 项和.19本小题满分2分为提高某篮球运动员的投篮水平,教练对其平时训练的表现作以详细的数据记录:每 次投中记分,投不中记一1分,统计平时的数据得如图所示频率分布条形图.若在某场训练中,该运动员前n 次投篮所得总分司为,且每次投篮是否命中相互之间没有影响.I 若设3S =ξ,求的分布列及数学期望; Ⅱ求出现28=S 且()3,2,10=≥i S i 的概率。
20.本小题满分12分如图,平行六面体ABCD —1111D C B A 中,底面ABCD 是边长为2的菱形,∠BAD=3π 其中AC 与BD 交于点G ,点在面ABCD 上的射影0恰好为线段AD 的中点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高中毕业班第一次模拟考试理科数学试题(时间120分钟,满分150分)注意事项:1. 本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分,答卷前,考生务必将自己的 姓名、准考证号填写在答题卡上.2. 回答第I 卷时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如 需改动,用橡皮擦干净后,再选涂其他答案标号.写在本试卷上无效.3. 回答第II 卷时,将答案写在答题卡上,写在本试卷上无效.4. 考试结束后,将本试卷和答题卡一并交回.第I 卷(选择题,共60分)一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目 要求的.1.复数z=1-i,则z z+1对应的点所在的象限为 A.第一象限 B.第二象限 C.第三象限 D.第四象限 2. 若集合}822|{2≤<∈=+x Z x A ,}02|{2>-∈=x x R x B ,则)(B C A R 所含的元素个数为A. OB. 1C. 2D. 33. 设随机变量ξ服从正态分布),1(2σN .若P(ξ<2)=0.8,则p(0<ξ<1)的值为A. 0.2B. 0.3C.0.4D. 0.64 已知双曲线的一个焦点与抛物线x 2=20y 的焦点重合,且其渐近线的方程为3x ±4y=0,则 该双曲线的标准方程为A. 116922=-y xB. 191622=-y xC. 116922=-x yD. 191622=-x y5. 执行右面的程序框图,输出的S 值为 A. 1B. 9C. 17D. 206. 已知等比数列{a n },且dx x a a ⎰-=+22644,则a 6(a 3+2a 6+a 10))的值为A. π2B. 4C. πD.-9π7. 现釆用随机模拟的方法估计该运动员射击4次,至少击中3次的概率:先由计算器给出 0到9之间取整数值的随机数,指定0、1表示没有击中目标,2、3、4、5、6、7、8、9表示击中目标,以4个随机数为一组,代表射击4次的结果,经随机模拟产生了 20组随机数:7527 0293 7140 9857 0347 4373 8636 6947 1417 4698 0371 6233 2616 8045 6011 3661 9597 7424 7610 4281 根据以上数据估计该射击运动员射击4次至少击中3次的概率为 A. 0.852B. 0.8192C O.8D. 0.758.巳知点(x,y)在ΔABC 所包围的阴影区域内(包含边界),若B(3,25)是 使得z=ax-y 取得最大值的最优解,则实数a 的取值范围为 A. 21-≥a B. 0≥a C. 21-≤a D. 021≤≤-a9. 若函数)0)(2sin()(>+=A x A x f ϕπ满足f(1)=0,则A.f(x-2)—定是奇函数B.f(x+1)—定是偶函数C. f(x+3)一定是偶函数D, f(x-3)一定是奇函数10. 已知正三棱锥P-ABC 的主视图和俯视图如图所 示,则此三棱锥的外接球的表面积为A 4π B, 12πC.316π D. 364π 11. 已知数列{a n },41,32,23,14,31,22,13,21,12,11…,依它的10项的规律,则a 99+a 100 的值为A 2437B 67. C. 1511 D. 157- 12. 已知定义域为R 的奇函数f(x)的导函数为)(x f ',当0≠x 时,0)()(>+'xx f x f ,若)2(ln 21ln ),2(2),21(21f c f b f a =--==,则下列关于a,b,c 的大小关系正确的是A. a>b>c B, a>c>b C. c>b>a D. b>a>c第II 卷(非选择题,共90分)本卷包括必考题和选考题两部分,第13题~第21题为必考题,每个试题考生都必须作答.第22题~第24题为选考题,考生根据要求作答.二、填空題,本大通共4小题,每小题5分,共20分.13.过点(2,3)与圆(x-1)2+y 2=1相切的直线方程为_____.14. 如图,正方形ABCD 中,EF//AB,若沿EF 将正方形折成一个二面角后,AE:ED:AD=1:1:2,则AF 与CE 所成的角的余弦值为______.15.为举办校园文化节,某班推荐2名男生3名女生参加文艺技能培训,培训项目及人数分 别为:乐器1人,舞蹈2人,演唱2人,每人只参加一个项目,并且舞蹈和演唱项目必须 有女生参加,則不同的推荐方案的种数为_______.(用数字作答)16.在ΔABC 中,B ∠=600,O 为ΔABC 的外心,P 为劣弧AC 上一动点,且OC y OA x OP += (x,y ∈R),则x+y 的取值范围为 ____ _____三、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤. 17. (本小题满分12分)如图,有两座建筑物AB 和CD 都在河的对岸(不知 道它们的高度,且不能到达对岸),某人想测量两 座建筑物尖顶A 、C 之间的距离,但只有卷尺和测 角仪两种工具.若此人在地面上选一条基线EF ,用 卷尺测得EF 的长度为a ,并用测角仪测量了一些角度:a AEF =∠,β=∠AFE ,θ=∠CEF ,ϕ=∠CFE ,γ=∠AEC 请你用文字和公式写出计算A 、C 之间距离的步骤和结果.18.(本小题满分12分)为了调査某大学学生在某天上网的时间,随机对lOO 名男生和100名女生进行了不记名的问卷调查.得到了如下的统计结果:表l:男生上网时间与频数分布表表2:女生上网时间与频数分布表(I)从这100名男生中任意选出3人,其中恰有1人上网时间少于60分钟的概率;(II)完成下面的2X2列联表,并回答能否有90%的把握认为“大学生上网时间与性别有关”?表3:•附:19. (本小题满分i2分) 如图,在四棱锥P-ABCD中,PA丄平面ABCD, 090=∠=∠ADC ABC ,0120=∠BAD ,AD=AB=1,AC 和 BD 交于O 点.(I)求证:平面PBD 丄平面PAC(II)当点A 在平面PBD 内的射影G 恰好是ΔPBD 的重心时,求二面角B-PD-G 的余弦值.20. (本小题满分12分)椭圆)0(12222>>=+b a by a x 的左、右焦点分别为F 1(-1,0),F 2(1,0),过F 1作与x 轴不重合的直线l 交椭圆于A,B 两点.(I)若ΔABF 2为正三角形,求椭圆的离心率; (II)若椭圆的离心率满足2150-<<e ,0为坐标原点,求证:OA 2+OB 2<AB 221 (本小题满分12分) 设函数f(x )=x 2+aln(x+1)(I)若函数y=f(x)在区间[1,+∞)上是单调递增函数,求实数a 的取值范围; (II)若函数y=f(x)有两个极值点x 1,x 2且x 1<x 2求证: 2ln 21)(012+-<<x x f请考生在22〜24三题中任选一题做答,如果多做,则按所做的第一题记分. 22. (本小题满分10分)选修4-l:几何证明选讲如图,过圆O 外一点P 作该圆的两条割线PAB 和PCD,分别交圆 O 于点A,B,C,D 弦AD 和BC 交于Q 点,割线PEF 经过Q 点交圆 O 于点E 、F ,点M 在EF 上,且BMF BAD ∠=∠:(I)求证:PA ·PB=PM ·PQ(II)求证:BOD BMD ∠=∠23. (本小题满分10分)选修4-4:坐标系与参数方程在平面直角坐标系.x0y 中,以原点O 为极点,x 轴的正半轴为极轴建立极坐标系,已知曲线 C 的极坐标方程为: θθρcos sin 2=(I)求曲线l 的直角坐标方程;(II)若直线l 的参数方程为⎪⎪⎩⎪⎪⎨⎧===t y t x 22222(t 为参数),直线l 与曲线C 相交于A 、B 两点求|AB|的值24. (本小题满分10分)选修4-5:不等式选讲 巳知函数f(x)=|x-2|+2|x-a|(a ∈R). (I)当a=1时,解不等式f(x)>3;(II)不等式1)(≥x f 在区间(-∞,+∞)上恒成立,求实数a 的取值范围2013年高中毕业班第一次模拟考试数学理科答案一、选择题A 卷答案1-5 DCBCC 6-10 ADADD 11-12 AD B 卷答案1-5 DBCBB 6-10 ADADD 11-12 AD 二、填空题13 . 4310x y -+=或2x = 14 .4515 . 24 16 . []1,2三、解答题:(阅卷老师,可根据学生的答题情况,酌情给分)17.解:第一步:在AEF ∆中,利用正弦定理,sin sin(180)AE EFβαβ︒=--, 解得sin sin()a AE βαβ=+;……………4分第二步:在CEF ∆中,同理可得sin sin()a CE ϕθϕ=+;……………8分第三步:在ACE ∆中,利用余弦定理,222cos AC AE CE AE CE γ=+-⋅ 2222222sin sin sin sin cos 2sin ()sin ()sin()sin()a a a βϕβϕγαβθϕαβθϕ=+-++++…………12分 (代入角的测量值即可,不要求整理,但如果学生没有代入,扣2分) 18.解:(Ⅰ)由男生上网时间频数分布表可知100名男生中,上网时间少于60分钟的有60人,不少于60分钟的有40人,………………2分故从其中任选3人,恰有1人上网的时间少于60分钟的概率为 1260403100C C C ……………4分 156539=………………6分 (Ⅱ)上网时间少于60分 上网时间不少于60分 合计 男生 60 40 100 女生 70 30 100 合计13070200……………8分22200(18002800)200 2.201001001307091K ⨯-==≈⨯⨯⨯,………………10分∵2 2.20 2.706K ≈<∴没有90%的把握认为“大学生上网时间与性别有关”.………………12分 19. 解:(Ⅰ)依题意Rt ABC Rt ADC ∆≅∆,BAC DAC ∠=∠,ABO ADO ∆≅∆,所以AC BD ⊥,……2分而PA ⊥面ABCD ,PA BD ⊥,又PA AC A =,∴BD ⊥面PAC ,又BD ⊂面PBD ,∴平面PAC ⊥平面PBD …………4分 (Ⅱ)过A 作AD 的垂线为x 轴,AD 为y 轴,AP 为z 轴,建立如图所示坐标系,则 31(,,0)22B -,(0,1,0)D ,(3,1,0)C ,设(0,0,)P λ, 所以31(,,)663G λ, 31(,,)22PB λ=--,由AG PB ⊥,得3131(,,)(,,)066322AG PB λλ⋅=⋅--= 解得212λ=,22λ=.………………6分 ∴P 点的坐标为2(0,0,)2;面PBD 的一个法向量为6(3,1,2)AG ==m ,……………8分设面PCD 的一个法向量为(,,)x y z =n ,(3,0,0)CD =-,2(0,1,)2PD =-00PD CD ⎧⋅=⎪⎨⋅=⎪⎩n n 即2030y z x ⎧-=⎪⎨-=⎪⎩,∴(0,1,2)=n ………………10分 (0,1,2)(3,1,2)2cos ,||||236⋅⋅<>===⋅n m n m n m , 所以二面角B PD A --的余弦值为22.……………12分 20. 解:(Ⅰ)由椭圆的定义知1212||||||||AF AF BF BF +=+,又22||||AF BF =,∴11||||AF BF =,即12F F 为边AB 上的中线,∴12F F AB ⊥,……………………2分 在12Rt AF F △中,2cos30,43c a ︒=则33c a =, ∴椭圆的离心率33.…………………4分(注:若学生只写椭圆的离心率33,没有过程扣3分) (Ⅱ)设11(,)A x y ,22(,)B x y 因为5102e -<<,1c =,所以15.2a +>…………6分 ①当直线AB x 与轴垂直时,22211y a b +=,422b y a=,4121221b OA OB x x y y a ⋅=+=-,42231a a a -+-=22235()24a a --+, 因为2532+>a ,所以0OA OB ⋅<, AOB ∴∠恒为钝角,∴222OA OB AB +<.………………………8分②当直线AB 不与x 轴垂直时,设直线AB 的方程为:(1)y k x =+,代入22221x y a b+=,整理得:2222222222()20b a k x k a x a k a b +++-=,PBACDz xy22122222a k x x b a k -+=+,222212222a k a bx x b a k -=+ 1212OA OB x x y y ⋅=+ 212121212(1)(1)x x y y x x k x x +=+++ 2221212(1)()x x k k x x k =++++22222242222222()(1)2()a k ab k a k k b a k b a k -+-++=+ 2222222222()k a b a b a b b a k +--=+ 24222222(31)k a a a b b a k -+--=+………………10分 令42()31m a a a =-+-, 由 ①可知 ()0m a <,AOB ∴∠恒为钝角.,所以恒有222OA OB AB +<.………………12分21. 解:(Ⅰ)0122)(2/≥+++=x ax x x f 在区间),1[+∞上恒成立, 即x x a 222--≥区间),1[+∞上恒成立, …………………1分4-≥a .………………3分经检验, 当a =- 4时, 1)1)(2(21422)(2/+-+=+-+=x x x x x x x f ,),1[+∞∈x 时,0)(/>x f ,所以满足题意的a 的取值范围为[4,)-+∞.………………4分(Ⅱ)函数的定义域),1(+∞-,0122)(2/=+++=x ax x x f ,依题意方程0222=++a x x 在区间),1(+∞-有两个不等的实根,记a x x x g ++=22)(2,则有⎪⎪⎩⎪⎪⎨⎧->->->∆1210)1(0g ,得210<<a .……………………6分,121-=+x x 022222=++a x x ,221212a x -+-=,0212<<-x ,2222222121)1ln()22()(x x x x x x x f --++-=,令)0,21(,1)1ln()22()(22-∈--++-=x x x x x x x k ……………………8分)1ln(21)(2+++-=x x x x x k ,)1ln(2)1()(22/+++=x x x x k , 32//)1(262)(+++=x x x x k , 因为2)0(,21)21(////=-=-k k ,存在)0,21(0-∈x ,使得0)(0//=x k , x),21(0x -0x )0,(0x)(//x k-+0)0(/=k ,02ln 21)21(/<-=-k ,0)(/<∴x k ,所以函数)(x k 在)0,21(-为减函数,…………………10分)21()()0(-<<k x k k 即2ln 21)(012+-<<x x f ……………………12分 法二:6分段后面还有如下证法,可以参照酌情给分.【证法2】2x 为方程2220x x a ++=的解,所以22222x x a --=,∵102a <<, 120x x <<,211222ax -=-+,∴2102x -<<, 先证21()0f x x >,即证2()0f x <(120x x <<),在区间12(,)x x 内,()0f x '<,2(,0)x 内()0f x '>,所以2()f x 为极小值,2()(0)0f x f <=,即2()0f x <,∴21()0f x x >成立;…………………8分再证21()1ln 22f x x <-+,即证22211()(ln 2)(1)(ln 2)(1)22f x x x >-+--=-+,222222211(22)ln(1)(ln 2)ln 222x x x x x -++-->-,令221()(22)ln(1)(ln 2)2g x x x x x x =-++--, 1(,0)2x ∈-…………………10分2(1)1()2(42)ln(1)(ln 2)12x x g x x x x x +'=-++---+,12(21)ln(1)(ln 2)2x x =-++--,ln(1)0x +<,210x +>,1ln 202-<,∴()0g x '>,()g x 在1(,0)2-为增函数.111111()()(21)ln (ln 2)244222g x g >-=-⨯-+-111111ln ln 2ln 2422422=++-=-. 综上可得21()10ln 22f x x <<-+成立.………………………12分22.证明:(Ⅰ)∵∠BAD =∠BMF ,所以A,Q,M,B 四点共圆,……………3分所以PA PB PM PQ ⋅=⋅.………………5分(Ⅱ)∵PA PB PC PD ⋅=⋅ ,∴PC PD PM PQ ⋅=⋅ ,又 CPQ MPD ∠=∠ , 所以~CPQ MPD ∆∆,……………7分 ∴PMD PCQ ∠=∠ ,则DCB FMD ∠=∠,………………8分 ∵BAD BCD ∠=∠,∴2BMD BMF DMF BAD ∠=∠+∠=∠,2BOD BAD ∠=∠,所以BMD BOD ∠=∠.…………………10分23.解:(Ⅰ)依题意22sin cos ρθρθ=………………3分得:x y =2∴曲线1C 直角坐标方程为:x y =2.…………………5分(Ⅱ)把⎪⎪⎩⎪⎪⎨⎧=-=ty tx 22222代入x y =2整理得:0422=-+t t ………………7分0>∆总成立,221-=+t t ,421-=t t23)4(4)2(221=-⨯--=-=t t AB ………………10分 另解:(Ⅱ)直线l 的直角坐标方程为x y -=2,把x y -=2代入x y =2得:0452=+-x x ………………7分0>∆总成立,521=+x x ,421=x x 23)445(212212=⨯-=-+=x x k AB …………………10分24. 解:(Ⅰ)⎩⎨⎧>-+-≥32222x x x 解得37>x⎩⎨⎧>-+-<<322221x x x 解得φ∈x⎩⎨⎧>-+-≤32221x x x 解得13x <…………………3分 不等式的解集为17(,)(,)33-∞+∞………………5分(Ⅱ)时,2>a ⎪⎩⎪⎨⎧≥--<<-+-≤++-=ax a x a x a x x a x x f ,2232,222,223)(;时,2=a 36,2()36,2x x f x x x -+≤⎧=⎨->⎩;时,2<a ⎪⎩⎪⎨⎧≥--<<+-≤++-=2,2232,22,223)(x a x x a a x ax a x x f ;∴)(x f 的最小值为)()2(a f f 或;………………8分 则⎩⎨⎧≥≥1)2(1)(fa f ,解得1≤a 或3≥a .………………10分。
