2018届高三数学二轮复习课件 第7讲三角恒等变换与解三角形
第七讲 解三角形

第7讲│ 命题立意追溯
命题立意追溯
应用意识——通过解三角形进行数学建模 示例 某城市有一块不规则的绿地如图2-7-2所示,城建 部门欲在该地上建造一个底座为三角形的环境标志,
图2-7-2
第7讲│ 命题立意追溯
小李、小王设计的底座形状分别为△ABC、△ABD, 经测量AD=BD=14,BC=10,AC=16,∠C=∠D. (1)求AB的长度; (2)若建造环境标志的费用与用地面积成正比,不考虑 其他因素,小李、小王谁的设计使建造费用最低,请说明 理由.
第7讲 │ 二轮复习建议
预计2013年对该部分的考查会延续前几年的命题方向, 并有适度的创新,如把平面向量、三角恒等变换等结合起来 进行考查. 复习建议:该部分的知识点不多,但可以与三角函数、 平面向量、实际应用题等问题相互交汇,具有较为广阔的命 题背景.从五年来课程标准卷的考查情况看,该部分出现过 一个实际应用题、一个解三角形与三角变换交汇的解答题, 出现过两个难度为C级的解三角形的试题,因此复习该部分 时要重在引导学生提高使用正弦定理、余弦定理解一般的斜 三角形的能力(实际应用题也是解一般的斜三角形).
第7讲│ 要点热点探究
[思考流程] (1)(分析)欲求cosC只要求出cos2B ⇨ (推理)只 需求出cosB ⇨ (结论)在8b=5c,C=2B下使用正弦定理即得. (2)(分析)欲求cosC的最小值,建立cosC关于边a,b,c的 关系式 ⇨ (推理)代入a2+b2=2c2消去c得关于a,b的关系式 ⇨ (结论)使用基本不等式a2+b2≥2ab即得.
第7讲 │ 主干知识整合
3.面积公式 1 abc 1 S= absinC.导出公式:S= (R为外接圆半径),S= (a 2 4R 2 +b+c)r(r为内切圆半径). 4.常用技巧 (1)利用正弦定理实现边角互化; π (2)若三角形ABC为锐角三角形,则A+B> ,sinA>cosB, 2 cosA<sinB,a2+b2>c2.类比三角形ABC为钝角三角形可得相 应结论.
2018届高三数学理高考二轮复习书讲解课件第一部分 专题二 第二讲 三角恒等变换与解三角形 精品

由已知及余弦定理得 a2+b2-2abcos C=7,
故 a2+b2=13,从而(a+b)2=25.
所以△ABC 的周长为 5+ 7.
考点三 三角恒等变换与解三角形的综合问题
试题 解析
考点一 考点二 考点三
5.(2016·高考山东卷)在△ABC 中,角 A,B,C 的对边分别为 a, b,c.已知 2(tan A+tan B)=tcaons BA+tcaons AB. (1)证明:a+b=2c; (2)求 cos C 的最小值.
试题 解析
(1)证明:根据正弦定理,可设sina A=sinb B=sinc C=k(k>0). 则 a=ksin A,b=ksin B,c=ksin C, 代入coas A+cobs B=sinc C中,有kcsoisnAA+kcsoisnBB=kssiinnCC,变形可得 sin Asin B=sin Acos B+cos Asin B=sin(A+B). 在△ABC 中,由 A+B+C=π, 有 sin(A+B)=sin(π-C)=sin C, 所以 sin Asin B=sin C.
试题 解析
考点三
考点一 考点二 考点三
根据上面所做题目,请填写诊断评价
错因(在相应错因中画√)
考点 错题题号
诊
知识性 方法性 运算性 审题性
断 考点一
评 价 考点二
考点三
※ 用自己的方式诊断记录 减少失误从此不再出错
考点一 三角恒等变换
考点一 考点二 考点三
[经典结论·全通关] 三角函数恒等变换“四大策略” (1)常值代换:特别是“1”的代换,1=sin2θ+cos2θ=tan 45° 等; (2)项的分拆与角的配凑:如 sin2α+2cos2α=(sin2α+cos2α)+cos2α, α=(α-β)+β 等; (3)降次与升次:正用二倍角公式升次,逆用二倍角公式降次; (4)弦、切互化:一般是切化弦.
三角恒等变换与解三角形课件-2023届高三数学二轮专题复习

.
解析:由题意得 S△ABC= acsin B= ac=
,则 ac=4,所以 a2+c2=3ac=3×4=12,
所以 b2=a2+c2-2accos B=12-2×4× =8,则 b=2
答案:2
,B=60°,
.
5. △ABC 的内角 A,B,C 的对边分别为 a,b,c.已知 B=150°.
=
( cos α- sin α)=
cos(α+ )=
sin( -α)=
得 sin( -α)= .
所以 sin(α+
答案:-
)=-sin[2π-(α+
)]=-sin( -α)=- .
,
(1)三角恒等变换的基本思路:统一名称,统一角度.一个流程:一角、二名、
三结构,即一看角的变化(已知角和所求角之间的联系),二看函数名称的变化,
D.473
解析:如图所示,根据题意过 C 作 CE∥C′B′,交 BB′于 E,过 B 作 BD∥A′B′,交 AA′于 D,
则 BE=100,C′B′=CE=
°
.
′′× °
在△A′C′B′中,∠C′A′B′=75°,则 BD=A′B′=
角为 45°,所以 AD=BD=
,
结合 A= 知 bc=12.
又 b+c=4
,
所以由余弦定理得 a2=b2+c2-2bccos A=(b+c)2-2bc-2bccos =(4
所以 a=2
.故选 A.
)2-3bc=48-3×12=12,
高考数学二轮复习 第二篇 专题通关攻略 专题2 三角函数及解三角形 专题能力提升练七 2.2.2 三

专题能力提升练七三角恒等变换与解三角形(45分钟80分)一、选择题(每小题5分,共30分)1.cos15°-4sin215°cos15°=()A. B. C.1D.【解析】选D.cos 15°-4sin215°cos 15°=cos 15°-2sin 15°×2sin 15°cos 15°=cos 15°-2sin 15°sin 30°=cos 15°-sin 15°=2cos(15°+30°)=.2.(2018·永州二模)已知△ABC的内角A,B,C的对边分别是a,b,c,若+=2a,则△ABC是()A.等边三角形B.锐角三角形C.等腰直角三角形D.钝角三角形【解析】选 C.因为+=2a,所以由正弦定理可得,+=2sinA≥2=2,所以sin A=1,当=时,“=”成立,所以A=,b=c,所以△ABC是等腰直角三角形.3.(2018·全国卷Ⅱ)在△ABC中,cos=,BC=1,AC=5,则AB= ( )A.4B.C.D.2【解析】选A.cos C=2cos2-1=2×-1=-,在△ABC中,由余弦定理AB2=CA2+CB2-2CA·CB·cos C,得AB2=25+1-2×1×5×=32,所以AB=4.4.若向量a=,向量b=(1,sin22.5°),则a·b=( )A.2B.-2C.D.-【解析】选A.由题得a·b=tan67.5°+=tan 67.5°+=tan 67.5°-tan 22.5°=tan 67.5°-==2×=2×=2.【加固训练】(2018·会宁一中一模)已知x为锐角,=,则a的取值X围为( ) A.[-2,2] B.(1,)C.(1,2]D.(1,2)【解析】选C.由=,可得:a=sin x+cos x=2sin,又x∈,所以x+∈,所以a的取值X围为(1,2].5.在锐角△ABC中,A=2B,则的取值X围是( )A.(-1,3)B.(1,3)C.(,)D.(1,2)【解析】选D.====3-4sin2B.因为△ABC是锐角三角形,所以得<B<⇒sin2B∈.所以=3-4sin2B∈(1,2).6.(2018·全国卷Ⅲ)△ABC的内角A,B,C的对边分别为a,b,c.若△ABC的面积为,则C= ()A. B. C. D.【解析】选C.由题意S△ABC=absin C=,即sin C=,由余弦定理可知sin C=cos C,即tan C=1,又C∈(0,π),所以C=.【加固训练】(2018·某某一模) 已知△ABC中,sinA,sinB,sinC成等比数列,则的取值X围是( )A. B.C.(-1,]D.【解析】选 B.由已知可知sin2B=sin A·sin C,即b2=ac,cos B==≥=,即0<B≤,sin B+cos B=sin∈(1,],原式==,设t=sin B+cos B,即原式==t-(1<t≤),函数是增函数,当t=1时,函数等于0,当t=时,函数等于,所以原式的取值X围是.二、填空题(每小题5分,共10分)7.(2018·全国卷Ⅱ)已知tan=,则tanα=________.【解析】因为tan=tan=,所以=,解得tan α=.答案:【加固训练】(2018·某某市一模) 已知cos=,则sin2α=________.【解析】sin 2α=sin=-cos2=1-2cos2=1-2×=-.答案:-8.为了竖起一块广告牌,要制造三角形支架,如图,要求∠ACB=60°,BC的长度大于1米,且AC 比AB长0.5米,为了稳定广告牌,要求AC越短越好,则AC最短为________.【解题指南】首先根据余弦定理找出边BC与AC之间的关系,用边BC表示出边AC,结合函数知识即可求解.【解析】由题意设BC=x(x>1)米,AC=t(t>0)米,依题设AB=AC-0.5=(t-0.5)米,在△ABC中,由余弦定理得:AB2=AC2+BC2-2AC·BCcos 60°,即(t-0.5)2=t2+x2-tx,化简并整理得:t=(x>1),即t=x-1++2,因为x>1,故t=x-1++2≥2+,当且仅当x=1+时取等号,此时取最小值2+. 答案:2+三、解答题(每小题10分,共40分)9.(2018·全国卷Ⅰ)在平面四边形ABCD中,∠ADC=90°,∠A=45°,AB=2,BD=5.(1)求cos∠ADB.(2)若DC=2,求BC.【解析】(1)在△ABD中,由正弦定理得=.由题设知,=,所以sin∠ADB=.由题意知,∠ADB<90°,所以cos∠ADB==.(2)由题意及(1)知,cos∠BDC=sin∠ADB=.在△BCD中,由余弦定理得BC2=BD2+DC2-2·BD·DC·cos∠BDC=25+8-2×5×2×=25. 所以BC=5.10.如图,在△ABC中,AB=2,cosB=,点D在线段BC上.(1)若∠ADC=,求AD的长.(2)若BD=2DC,△ACD的面积为,求的值.【解题指南】(1)首先利用同角三角函数间的基本关系求得sin B的值,然后利用正弦定理即可求得AD的长.(2)首先利用三角形面积间的关系求得S△ABC,然后利用三角形面积公式结合余弦定理即可求得的值.【解析】(1)在三角形中,因为cos B=,所以sin B=,在△ABD中,由正弦定理得=,又AB=2,∠ADB=,sin B=.所以AD=.(2)因为BD=2DC,所以S△ABD=2S△ADC,S△ABC=3S△ADC,又S△ADC=,所以S△ABC=4,因为S△ABC=AB·BCsin∠ABC,所以BC=6,因为S△ABD=AB·ADsin∠BAD,S△ADC=AC·ADsin∠CAD,S△ABD=2S△ADC,所以=2·,在△ABC中,由余弦定理得AC2=AB2+BC2-2AB·BCcos∠ABC.所以AC=4,所以=2·=4.11.已知函数f(x)=2sinxcosx+2cos2x-1(x∈R).(1)求函数f(x)的最小正周期及在区间上的最大值和最小值.(2)若f(x0)=,x0∈,求cos2x0的值.【解析】(1)f(x)=2sin xcos x+2cos2x-1=(2sin xcos x)+(2cos2x-1)=sin 2x+cos 2x=2sin,所以函数f(x)的最小正周期为π;因为x∈,所以2x+∈,sin∈,所以函数f(x)=2sin在区间上的最大值为2,最小值为-1.(2)由(1)可知f(x0)=2sin,又因为f(x0)=,所以sin=,由x0∈,得2x0+∈,从而cos=-=-,所以cos 2x0=cos=cos cos +sin sin =12.在△ABC中,D是边BC上的点,AB=AD=,cos∠BAD=.(1)求sinB.(2)若AC=4,求△ADC的面积.【解题指南】(1)直接利用余弦定理和正弦定理求出结果.(2)利用(1)的结论和余弦定理求出三角形的面积.【解析】(1)在△ABD中,BD2=AB2+AD2-2AB·AD·cos∠BAD=7+7-2×××=12,得BD=2.由cos∠BAD=,得sin∠BAD=,在△ABD中,由正弦定理得=,所以sin B=×=.(2)因为sin B=,B是锐角,所以cos B=,设BC=x,在△ABC中,AB2+BC2-2AB·BC·cos B=AC2,即7+x2-2·x··=16,化简得:x2-2x-9=0,解得x=3或x=-(舍去),则CD=BC-BD=3-2=,由∠ADC和∠ADB互补,得sin∠ADC=sin∠ADB=sin B=,所以△ADC的面积S=·AD·DC·sin∠ADC=×××=.【加固训练】(2018·某某二模)△ABC的内角A,B,C的对边分别为a,b,c,已知△ABC的面积为acsin2B.(1)求sinB的值.(2)若c=5,3sin2C=5sin2B·sin2A,且BC的中点为D,求△ABD的周长.【解析】(1)由S△ABC=acsinB=acsin2B,得sin B=2sin B·cos B,因为0<B<π,所以sin B>0,故cos B=,又sin2B+cos2B=1,所以sin B=.(2)由(1)和3sin2C=5sin2B·sin2A得16sin2C=25sin2A,由正弦定理得16c2=25a2,因为c=5,所以a=4,BD=a=2,在△ABD中,由余弦定理得:AD2=c2+BD2-2c·BD·cos B=52+22-2×5×2×=24,所以AD=2.所以△ABD的周长为c+BD+AD=7+2.(建议用时:50分钟)1.(2018·某某一模)南宋数学家秦九韶早在《数书九章》中就独立创造了已知三角形三边求其面积的公式:“以小斜幂并大斜幂,减中斜幂,余半之,自乘于上,以小斜幂乘大斜幂减之,以四约之,为实,一为从隅,开方得积.”(即:S=,c>b>a),并举例“问沙田一段,有三斜(边),其小斜一十三里,中斜一十四里,大斜一十五里,欲知为田几何?”则该三角形田面积为( )A.82平方里B.83平方里C.84平方里D.85平方里【解析】选C.由题意可得:a=13,b=14,c=15代入:S===84,则该三角形田面积为84平方里.2.已知△ABC的三个内角A,B,C的对边分别为a,b,c,若2sin=1,且a=2,则△ABC 的面积的最大值为( )A. B. C. D.2【解析】选B.sin=,-=,A=,由于a=2为定值,由余弦定理得4=b2+c2-2bccos ,即4=b2+c2+bc.根据基本不等式得4=b2+c2+bc≥2bc+bc=3bc,即bc≤,当且仅当b=c时,等号成立.S△=bcsin A≤··=.3.在△ABC中,a,b,c分别是内角A,B,C的对边,sinAcosB-(c-cosA)·sinB=0,则边b=________.【解析】由sin Acos B-(c-cos A)·sin B=0,得sin Acos B+cos Asin B=csin B,所以sin C=csin B,即=sin B,由正弦定理=,故b==1.答案:14.在△ABC中,角A,B,C的对边分别为a,b,c,设△ABC的面积为S,若3a2=2b2+c2,则的最大值为________.【解析】因为3a2=2b2+c2,所以3a2=3b2-b2+3c2-2c2,所以b2+2c2=3(b2+c2-a2)=6bccos A,所以==tan A.由题得a2=,所以 cos A===≥=,所以tan A=≤=,当且仅当b=c时取等号.所以的最大值为.答案:【加固训练】(2018·某某中学模拟)在锐角△ABC中,角A,B,C的对边分别为a,b,c,已知a=,(b2+c2-3)tanA=bc,2cos2=(-1)cosC,则△ABC的面积等于________.【解析】条件(b2+c2-3)tan A=bc即为(b2+c2-a2)tan A=bc,由余弦定理得2bccos Atan A=bc,所以得sin A=,又A为锐角,所以A=.又2cos2=1+cos(A+B)=1-cos C=(-1)cos C,所以cos C=,得C=,故B=.在△ABC中,由正弦定理得=,所以c===.故△ABC的面积S=acsin B=×××sin =.答案:5.△ABC的内角A,B,C的对边分别为a,b,c,已知(b-c)2=a2-bc.(1)求sinA.(2)若a=2,且sinB,sinA,sinC成等差数列,求△ABC的面积.【解析】(1)由(b-c)2=a2-bc,得b2+c2-a2=bc,即=,由余弦定理得cos A=,因为0<A<π,所以sin A=.(2)由sin B,sin A,sin C成等差数列,得sin B+sin C=2sin A,由正弦定理得b+c=2a=4,所以16=(b+c)2,所以16=b2+c2+2bc.由(1)得16=a2+bc,所以16=4+bc,解得bc=,所以S△ABC=bcsin A=××=.6.(2018·某某一模)△ABC的内角为A,B,C的对边分别为a,b,c,已知=+.(1)求sin(A+B)+sinAcosA+cos(A-B)的最大值.(2)若b=,当△ABC的面积最大时,求△ABC的周长.【解题指南】(1)先根据正弦定理将边角关系转化为角的关系,再根据三角公式转化为二次函数求解.(2)根据余弦定理利用基本不等式求解.【解析】(1)由=+得:=,a=bcos C+csin B,即sin A=sin Bcos C+sin Csin B,所以cos B=sin B,B=;由sin(A+B)+sin Acos A+cos(A-B)=(sin A+cos A)+sin Acos A,令t=sin A+cos A,原式=t2+t-,当且仅当A=时,上式取最大值,最大值为.(2)S=acsin B=ac,b2=a2+c2-2accos B,即2=a2+c2-ac≥(2-)ac,ac≤2+,当且仅当a=c=等号成立;S max=,周长L=a+b+c=2+.7.(2018·某某二模) 如图,在平面四边形ABCD中,AB=2,AC=2,∠ADC= ∠CAB=90°,设∠DAC=θ.(1)若θ=60°,求BD 的长度;(2)若∠ADB=30°,求tanθ.【解题指南】(1)在△ABD中,利用余弦定理直接求出BD.(2)在△ABD中,写出正弦定理再化简即得解.【解析】(1)由题意可知,AD=1.在△ABD中,∠DAB=150°,AB=2,AD=1,由余弦定理可知,BD2=(2)2+12-2×2×1×=19,BD=.(2)由题意可知,AD=2cos θ,∠ABD=60°-θ,在△ABD中,由正弦定理可知,=,所以=4,所以tan θ=.。
2018年高考数学二轮复习课件 专题3 第2讲三角恒等变换与解三角形(58张)

• • • • • • • •
[解析] 等式右边=sin Acos C+(sin Acos C+cos Asin C) =sin Acos C+sin(A+C) =sin Acos C+sin B, 等式左边=sin B+2sin Bcos C, ∴sin B+2sin Bcos C=sin Acos C+sin B. 由cos C>0,得sin A=2sin B. 根据正弦定理,得a=2b. 故选A.
• (3)tan 2α=______________.
1-cos 2α • 5.降幂公式 2 1+cos 2α 2 (1)sin2α=_____________ ;
1-tan2α
•
• (2)cos2α=_____________.
6.正弦定理
b a c sin B sin A=__________=sin C=2R(2R 为△ABC 外接圆的直径).
1 bcsin A 1 1 2 S△ABC=____________=2acsin B=2absin C.
• 1.同角关系应用错误:利用同角三角函数的平方关系开 方时,忽略判断角所在的象限或判断出错,导致三角函数 符号错误. • 2.诱导公式的应用错误:利用诱导公式时,三角函数名 变换出错或三角函数值的符号出错.
2 2 2 2 a + b sin( α + φ ) = a + b cos(α+θ) . (4)辅助角公式:asin α+bcos α=____________________________________
• 4.二倍角的正弦、余弦、正切公式 2sin αcos α • (1)sin 2α=_____________ ; cos2α-sin2α 2α-1=1-2sin2α; • (2)cos 2α=_______________ = 2cos 2tan α
2018届高考数学二轮复习专题五三角恒等变换与解三角形课件文
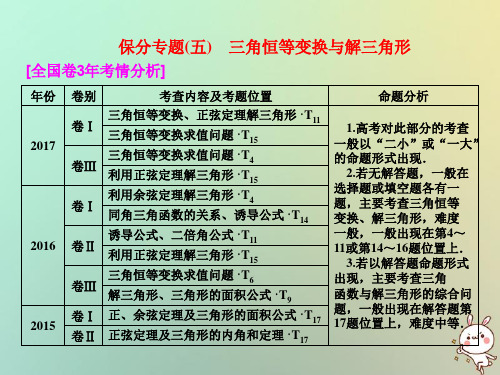
解析:由于tan 20°+msin 20°=
3,所以m=
3-tan 20° sin 20°
=
3scions2200°°c-oss2in0°20°=2
3 2 cos
20°-12sin
1
20°
2sin 40°
=4sinsi6n0°4-0°20°=4.
答案:4
正、余弦定理解三角形及其应用
[师生共研·悟通] 1.正弦定理及其变形 在△ABC中,sina A=sinb B=sinc C=2R(R为△ABC的外接圆 半径). 变形:a=2Rsin A,sin A=2aR,a∶b∶c=sin A∶sin B∶ sin C等. 2.余弦定理及其变形 在△ABC中,a2=b2+c2-2bccos A. 变形:b2+c2-a2=2bccos A,cos A=b2+2cb2c-a2.
[典例] (1)(2017·全国卷Ⅱ)△ABC 的内角 A,B,C 的对 边分别为 a,b,c,若 2bcos B=acos C+ccos A,则 B=________.
[解析] 法一:由2bcos B=acos C+ccos A及正弦定 理,得
2sin Bcos B=sin Acos C+sin Ccos A =sin(A+C)=sin B>0, 因此cos B=12. 又0<B<π,所以B=π3.
3.如图,为了估测某塔的高度,在同一水 平面的A,B两点处进行测量,在点A处 测得塔顶C在西偏北20°的方向上,仰角 为60°;在点B处测得塔顶C在东偏北40° 的方向上,仰角为30°.若A,B两点相距130 m,则塔的高 度CD=________m.
解析:设CD=h,则AD= h3,BD= 3h, 在△ADB中,∠ADB=180°-20°-40°=120°, ∴由余弦定理AB2=BD2+AD2-2BD·AD·cos 120°, 可得1302=3h2+h32-2· 3h·h3·-12, 解得h=10 39,故塔的高度为10 39 m. 答案:10 39
高三数学二轮复习 2-8三角恒等变换、解三角形

3.(2017·北京高考)在平面直角坐标系 xOy 中,角 α 与角 β 均以 Ox 为
始边,它们的终边关于 y 轴对称。若 sinα=13,则 sinβ=________。
答案
1 3
解析 解法一:当角 α 的终边在第一象限时,取角 α 终边上一点 P1(2 2, 1),其关于 y 轴的对称点(-2 2,1)在角 β 的终边上,此时 sinβ=13;当角 α 的
解法二:求△BDC 的面积同解法一。先在△BDC 中,由余弦定理,得 CD2 =BC2+BD2-2BC·BD·cos∠DBC=22+22-2×2×2×-14=10,所以 CD=
第7页
赢在微点 无微不至
考前顶层设计·数学文·二轮教案
2.(2017·江苏高考)若 tanα-π4=16,则 tanα=________。
答案
7 5
解析 tanα=tanα-π4+4π =1t-antaαn-α4π-+π4ttaannπ4π4=161+ -116=75。
第8页
赢在微点 无微不至
考前顶层设计·数学文·二轮教案
第15页
赢在微点 无微不至
考前顶层设计·数学文·二轮教案
■方向 3 三角形的实际应用 【例 4】 某观测站 C 在目标 A 的南偏西 25°方向,从 A 出发有一条 南偏东 35°走向的公路,在 C 处测得与 C 相距 31 km 的公路 B 处有一个人 正沿着此公路向 A 走去,走 20 km 到达 D,此时测得 CD 距离为 21 km, 若此人必须在 20 分钟内从 D 处到达 A 处,则此人的最小速度为( )
15 4
= 215。在△BDC 中,因为 BD=BC,所以∠BDC=∠BCD,所以∠BDC=
第21页
高三数学二轮复习课件课标专题第讲三角恒等变换与三角函数-精品文档

三角函数、平面向量
Evaluation only. 第6讲 解三角形 ed with Aspose.Slides for .NET 3.5 Client Profile 5.2 第7讲 平面向量 Copyright 2019-2019 Aspose Pty Ltd.
第5讲 三角恒等变换与三角函数
ed with Aspose.Slides for .NET 3.5 Client Profile 5.2
专题二 │ 考情分析预测
Evaluation only. ed with Aspose.Slides for .NET 3.5 Client Profile 5.2 Copyright 2019-2019 Aspose Pty Ltd.
专题二 │ 考情分析预测
考情分析预测
考向预测
该专题是高考重点考查的部分,从最近几年考查的情况看,主要考查三角函数 的图象和性质、三角函数式的化简与求值、正余弦定理解三角形、三角形中的三角 恒等变换、平面向量的线性运算、平面向量的数量积、平面向量的平行与垂直,以 及三角函数、解三角形和平面向量在立体几何、解析几何等问题中的应用.该部分 在试卷中一般是 2~3 个选择题或者填空题,一个解答题,选择题在于有针对性地 考查本专题的重要知识点(如三角函数性质、平面向量的数量积等),解答题一般有 三个命题方向,一是以考查三角函数的图象和性质为主,二是把解三角形与三角函 数的性质、三角恒等变换交汇,三是考查解三角形或者解三角形在实际问题中的应 用.由于该专题是高中数学的基础知识和工具性知识,在试题的难度上不大,一般 都是中等难度或者较为容易的试题.基于这个实际情况以及高考试题的相对稳定 性,我们预测在 2012 年的高考中该部分的可能考查情况如下:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
-2热点考题诠释 高考方向解读
1.(2017山东,理9)在△ABC中,角A,B,C的对边分别为a,b,c,若△ABC 为锐角三角形,且满足sin B(1+2cos C)=2sin Acos C+cos Asin C,则 下列等式成立的是( ) A.a=2b B.b=2a C.A=2B D.B=2A
=
3 13 . 13
故 b 的值为 13,sin A 的值为
=
7 2 . 26
-6热点考题诠释 高考方向解读
4.(2017 全国 1,理 17)△ABC 的内角 A,B,C 的对边分别为 a,b,c.已知 △ABC
������2 的面积为3sin������.
(1)求 sin Bsin C; (2)若 6cos Bcos C=1,a=3,求△ABC 的周长.
3 13 . 13 2 13 (2)由(1)及 a<c,得 cos A= 13 , 12 所以 sin 2A=2sin Acos A= , 13 5 cos 2A=1-2sin2A=- . 13 π π π 故 sin 2������ + 4 =sin 2Acos4+cos 2Asin4 ������sin������ A= ������
-9热点考题诠释 高考方向解读
解: (1)由题设及 A+B+C=π,得 sin B=8sin , 故 sin B=4(1-cos B). 上式两边平方,整理得 17cos2B-32cos B+15=0,
15 解得 cos B=1(舍去),cos B= . 17 15 8 (2)由 cos B= ,得 sin B= , 17 17 1 4 故 S△ABC=2acsin B=17ac. 17 又 S△ABC=2,则 ac= 2 . 2Βιβλιοθήκη -7热点考题诠释 高考方向解读
1 ������2 1 解: (1)由题设得2acsin B=3sin������,即2csin 1 sin������ 由正弦定理得 sin Csin B= . 2 3sin������ 2 故 sin Bsin C=3.
������ B=3sin������.
(2)由题设及(1)得 cos Bcos C-sin Bsin 以 B+C= 3 ,故 A=3.
又△ABC为锐角三角形, ∴2sin B=sin A, 由正弦定理 ,得a=2b.故选A. A
解析
关闭
关闭
答案
-3热点考题诠释 高考方向解读
2.(2017浙江,14)已知△ABC,AB=AC=4,BC=2.点D为AB延长线上一 关闭 点,BD=2,连接CD,则△BDC的面积 如图,取 BC 中点 E,DC 中点 F,由题意知 AE⊥BC,BF⊥CD. 是 ,cos∠BDC= . ������������ 1 在 Rt△ABE 中,cos∠ABE= = ,
������������ 4
∴cos∠DBC=-4,sin∠DBC= 1- 16 = ∴S△BCD=2×BD×BC×sin∠DBC=
1 1 15 . 2
1
1
15 . 4
∵cos∠DBC=1-2sin2∠DBF=-4,且∠DBF 为锐角, ∴sin∠DBF=
10 . 4
在 Rt△BDF 中,cos∠BDF=sin∠DBF=
π 2������ + 4 3 5
的值.
-5热点考题诠释 高考方向解读
解: (1)在△ABC 中,因为 a>b, 故由 sin B=5,可得 cos B=5.
������ ������ 3 4
由已知及余弦定理,有 b2=a2+c2-2accos B=13, 所以 b= 13. 由正弦定理sin������ = sin������, 得 sin
2π π 1 由题设得2bcsin ������2 A=3sin������,即
1 C=-2,即
1 cos(B+C)=-2.所
bc=8.
由余弦定理得 b2+c2-bc=9,即(b+c)2-3bc=9,得 b+c= 33. 故△ABC 的周长为 3+ 33.
-8热点考题诠释 高考方向解读
5.(2017全国2,理17)△ABC的内角A,B,C的对边分别为a,b,c.已知 sin(A+C)=8sin2 ������ . 2 (1)求cos B; (2)若a+c=6,△ABC的面积为2,求b.
15 10 综上 2 ,可得 4 △BCD
的面积是
15 10 ,cos ∠ BDC= . 2 4
10 . 4
关闭
解析
答案
-4热点考题诠释 高考方向解读
3.(2017 天津,理 15)在△ABC 中,内角 A,B,C 所对的边分别为 a,b,c,已 知 a>b,a=5,c=6,sin B= . (1)求 b 和 sin A 的值; (2)求 sin
2������
由余弦定理及 a+c=6 得 b2=a2+c2-2accos B=(a+c)2-2ac(1+cos B) 17 15 =36-2× 2 × 1 + 17 =4. 所以 b=2.
-10热点考题诠释 高考方向解读
本部分主要考查三角函数的基本公式、三角恒等变换及解三角 形等基本知识.三角函数与解三角形相结合或三角函数与平面向量 相结合是考向的主要趋势,试题难度为中低档.三角恒等变换是高考 的热点内容,主要考查利用各种三角函数进行求值与化简,其中降幂 公式、辅助角公式是考查的重点,切化弦、角的变换是常考的三角 变换思想.正弦定理、余弦定理以及解三角形问题是高考的必考内 容,主要考查:①边和角的计算;②三角形形状的判断;③面积的计算; ④有关的范围问题. 考向预测:三角恒等变换和解三角形综合的问题是浙江高考主要 考查方式,以考查三角恒等变换公式、正余弦定理公式和面积公式 为主.这部分内容是解答题常考题型,但从2017年高考和样卷角度来 看目前这部分内容以填空题形式出现,2018年很可能延续这种风格.
∵sin B(1+2cos C)=2sin Acos C+cos Asin C, ∴sin B+2sin Bcos C=(sin Acos C+cos Asin C)+sin Acos C, ∴sin B+2sin Bcos C=sin B+sin Acos C, ∴2sin Bcos C=sin Acos C,
