河北南宫中学2016届高三5月第三次模拟考试(石家庄二模)数学(理)试题(图片版)
河北省南宫中学2016届高三语文5月第三次模拟考试(石家庄二模)试题不分版本

河北省南宫中学2016届高三语文5月第三次模拟考试(石家庄二模)试题不分版本石家庄市2016届高中毕业班第二次模拟考试语文试卷考前须知:1.本试卷分第一卷〔阅读题〕和第II卷〔表达题〕两局部。
答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.作答时请认真阅读答题卡上的考前须知,将答案写在答题卡上。
写在试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
第一卷阅读题甲必考题一、现代文阅读〔9分,每题3分〕阅读下面的文字,完成1-3题。
罗马是一个世界性的城市,这并非仅仅因为它是一个庞大帝国的首邑。
埃及与阿非利加省的小麦养育了它。
小亚细亚、叙利亚和希腊的石料构筑了它的城市。
帝国领土的富饶物产使它蜚声东方。
更重要的是,它拥有非凡的罗马人——他们来自远至美索不达米亚和不列颠的广阔疆域。
在“四海一家〞的时代精神之下,他们将自己的神祇带到“万神殿〞,共同成就了罗马。
这并不仅仅完全是罗马文明的特质。
在“丝绸之路〞的东端,有河西走廊上的敦煌。
汉代,这块处沙漠边缘的小绿洲向东可到达中原长安和洛阳;向西,那么开始了“丝绸之路〞的行旅。
敦煌东部61公里处有悬泉置遗址,这是一个驿站兼接待站。
这里出土的西汉昭帝〔公元前87~前74年〕以后的简牍说明,敦煌曾是接待过来往于汉王朝和西域之间的安息、大月氏、康居、大宛〔今乌兹别克共和国境内〕、龟兹、于阗、等29国使节。
敦煌是一座伟大城市的前哨。
公元前202年,汉朝利用秦朝在渭河南岸留下的宫殿,开始兴建长安城;汉高祖刘邦始在渭河以南、秦兴乐宫的根底上重修宫殿,命名为长乐宫,后又命萧何建造了未央宫;汉惠帝起修筑城墙并建成;汉武帝继位后,对长安城进行了大规模扩建,兴建北宫、桂宫和明光宫,在城南开太学,在城西扩充了秦朝的上林苑,开凿昆明池,建章宫等。
与罗马一样,长安是东方的奇观。
它有宏伟的城墙——全部用黄土夯砌而成,高12米,基宽12~16米,全城周长2.57万米,有城门12座。
河北省邢台市南宫一中高考数学三模试卷(理科).docx

高中数学学习材料鼎尚图文*整理制作2016年河北省邢台市南宫一中高考数学三模试卷(理科)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知复数z=1+i,则等于()A.2i B.﹣2i C.2 D.﹣22.若集合A={0,1},B={﹣1,a2},则“A∩B={1}”是“a=1”的()A.充分非必要条件B.必要非充分条件C.充要条件 D.既不充分也不必要条件3.下列命题中正确命题的个数是()(1)对分类变量X与Y的随机变量K2的观测值k来说,k越小,判断“X与Y有关系”的把握越大;(2)若将一组样本数据中的每个数据都加上同一个常数后,则样本的方差不变;(3)若a>0,b>0且+=1,则a+b≥4;(4)设随机变量ξ服从正态分布N(0,1),若P(ξ>1)=p,则P(﹣1<ξ<0)=﹣p.A.4 B.3 C.2 D.14.某程序框图如图所示,则该程序运行后输出的k值是()A.5 B.6 C.7 D.85.设x∈R,记不超过x的最大整数为[x],令{x}=x﹣[x],则{},[],()A.是等差数列但不是等比数列B.是等比数列但不是等差数列C.既是等差数列又是等比数列D.既不是等差数列也不是等比数列6.某由圆柱切割获得的几何体的三视图如图所示,其中俯视图是中心角为60°的扇形,则该几何体的体积为()A.2πB.πC. D.7.设a=(sinx﹣1+2cos2)dx,则(a﹣)6•(x2+2)的展开式中常数项是()A.332 B.﹣332 C.320 D.﹣3208.若函数f(x)=在区间(,)上单调递增,则实数a的取值范围是()A.[2,+∞)B.(2,+∞)C.[,+∞)D.(﹣,+∞)9.已知棱锥S﹣ABC中,SA=BC=,SB=AC=,SC=AB=,则该三棱锥的外接球表面积为()A.64πB.16πC.14πD.4π10.已知定义在区间[0,]上的函数y=f(x)的图象关于直线x=对称,当x时,f(x)=cosx,如果关于x的方程f(x)=a有解,记所有解的和为S,则S不可能为()A.B. C. D.3π11.如图,已知双曲线﹣=1(a>0,b>0)的左右焦点分别为F1,F2,|F1F2|=4,P是双曲线右支上的一点,F2P与y轴交于点A,△APF1的内切圆在边PF1上的切点为Q,若|PQ|=1,则双曲线的离心率是()A.3 B.2 C.D.12.已知f(x)是定义在(0,+∞)上的单调函数,且对任意的x∈(0,+∞),都有f[f(x)﹣log2x]=3,则方程f(x)﹣f′(x)=2的解所在的区间是()A.(0,)B.(,1)C.(1,2)D.(2,3)二、填空题(每题5分,满分20分,将答案填在答题纸上)13.从某地高中男生中随机抽取100名同学,将他们的体重(单位:kg)数据绘制成频率分布直方图(如图).若要从身高在[60,70),[70,80),[80,90]三组内的男生中,用分层抽样的方法选取6人参加一项活动,再从这6人选两人当正负队长,则这两人体重不在同一组内的概率为______.14.过平面区域内一点P作圆O:x2+y2=1的两条切线,切点分别为A,B,记∠APB=α,当α最小时,此时点P坐标为______.15.设S n是数列{a n}的前n项和,且a1=﹣1,=S n.则数列{a n}的通项公式a n=______.16.设非空集合A,若对A中任意两个元素a,b,通过某个法则“•”,使A中有唯一确定的元素c与之对应,则称法则“•”为集合A上的一个代数运算.若A上的代数运算“•”还满足:(1)对∀a,b,c∈A,都有(a•b)•c=a•(b•c);(2)对∀a∈A,∃e,b∈A,使得e•a=a•e=a,a•b=b•a=e.称A关于法则“•”构成一个群.给出下列命题:①实数的除法是实数集上的一个代数运算;②自然数集关于自然数的加法不能构成一个群;③非零有理数集关于有理数的乘法构成一个群;④正整数集关于法则a°b=a b构成一个群.其中正确命题的序号是______.(填上所有正确命题的序号).三、解答题(本大题共5小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.如图,在海岛A上有一座海拔1千米的山,山顶设有一个观察站P,上午11时,测得一轮船在岛北偏东30°,俯角为30°的B处,到11时10分又测得该船在岛北偏西60°,俯角为60°的C处.(1)求船的航行速度是每小时多少千米?(2)又经过一段时间后,船到达海岛的正西方向的D、处,问此时船距岛A有多远?18.某商场销售某种品牌的空调器,每周周初购进一定数量的空调器,商场每销售一台空调器可获利500元,若供大于求,则每台多余的空调器需交保管费100元;若供不应求,则可从其他商店调剂供应,此时每台空调器仅获利润200元.(Ⅰ)若该商场周初购进20台空调器,求当周的利润(单位:元)关于当周需求量n(单位:台,n∈N)的函数解析式f(n);(Ⅱ)该商场记录了去年夏天(共10周)空调器需求量n(单位:台),整理得表:周需求量n 18 19 20 21 22频数 1 2 3 3 1以10周记录的各需求量的频率作为各需求量发生的概率,若商场周初购进20台空调器,X 表示当周的利润(单位:元),求X的分布列及数学期望.19.已知四边形ABCD满足AD∥BC,BA=AD=DC=BC=a,E是BC的中点,将△BAE沿AE翻折成△B1AE,使面B1AE⊥面AECD,F为B1D的中点.(1)求四棱锥B1﹣AECD的体积;(2)证明:B1E∥面ACF;(3)求面ADB1与面ECB1所成锐二面角的余弦值.20.已知椭圆E:的一个交点为,而且过点.(Ⅰ)求椭圆E的方程;(Ⅱ)设椭圆E的上下顶点分别为A1,A2,P是椭圆上异于A1,A2的任一点,直线PA1,PA2分别交x轴于点N,M,若直线OT与过点M,N的圆G相切,切点为T.证明:线段OT的长为定值,并求出该定值.21.已知函数f(x)=lnx﹣x(1)求函数g(x)=f(x)﹣x﹣2的图象在x=1处的切线方程(2)证明:(3)设m>n>0,比较与的大小,并说明理由.请考生在22、23、24三题中任选一题作答,如果多做,则按所做的第一题记分.[选修4-1:几何证明选讲]22.如图,EP交圆于E,C两点,PD切圆于D,G为CE上一点且PG=PD,连接DG并延长交圆于点A,作弦AB垂直EP,垂足为F.(Ⅰ)求证:AB为圆的直径;(Ⅱ)若AC=BD,求证:AB=ED.[选修4-4:坐标系与参数方程]23.已知直线l的参数方程:(t为参数),曲线C的参数方程:(α为参数),且直线交曲线C于A,B两点.(Ⅰ)将曲线C的参数方程化为普通方程,并求θ=时,|AB|的长度;(Ⅱ)已知点P:(1,0),求当直线倾斜角θ变化时,|PA|•|PB|的范围.[选修4-5:不等式选讲]24.已知a>0,b>0,且a2+b2=,若a+b≤m恒成立,(Ⅰ)求m的最小值;(Ⅱ)若2|x﹣1|+|x|≥a+b对任意的a,b恒成立,求实数x的取值范围.2016年河北省邢台市南宫一中高考数学三模试卷(理科)参考答案与试题解析一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知复数z=1+i,则等于()A.2i B.﹣2i C.2 D.﹣2【考点】复数代数形式的混合运算.【分析】复数代入表达式,利用复数乘除运算化简复数为a+bi的形式即可.【解答】解:因为复数z=1+i,所以===﹣=2i.故选A.2.若集合A={0,1},B={﹣1,a2},则“A∩B={1}”是“a=1”的()A.充分非必要条件B.必要非充分条件C.充要条件 D.既不充分也不必要条件【考点】必要条件、充分条件与充要条件的判断.【分析】根据充分必要条件的定义,分别判断其充分性和必要性,从而得到答案.【解答】解:若A∩B={1},则a=±1,不是充分条件,若a=1,则A∩B={1},是必要条件,故选:B.3.下列命题中正确命题的个数是()(1)对分类变量X与Y的随机变量K2的观测值k来说,k越小,判断“X与Y有关系”的把握越大;(2)若将一组样本数据中的每个数据都加上同一个常数后,则样本的方差不变;(3)若a>0,b>0且+=1,则a+b≥4;(4)设随机变量ξ服从正态分布N(0,1),若P(ξ>1)=p,则P(﹣1<ξ<0)=﹣p.A.4 B.3 C.2 D.1【考点】命题的真假判断与应用.【分析】根据独立性检验的方法步骤,可判断①的正误.根据方差的意义,可判断②的正误;运用均值不等式,化简a+b=(a+b)(+)进行计算即可判断③的正误.根据正态分布的对称性,求出P(﹣1<ξ<0),可判断④的正误;【解答】解:①对分类变量x与y的随机变量k2的观测值k来说,k越大,判断“x与y有关系”的把握越大,故③错误.②若将一组样本数据中的每个数据都加上同一个常数后,数据的离散程度不变,则样本的方差不变,故②正确;③a>0,b>0且+=1,则a+b=(a+b)(+)=2+1++≥3+2,所以③不正确.④设随机变量ξ服从正态分布N(0,1),若P(ξ>1)=p,则P(ξ<﹣1)=p,则P(﹣1<ξ<1)=1﹣2p,则P(﹣1<ξ<0)=﹣p,故④正确;故正确的命题的个数为2个,故选:C.4.某程序框图如图所示,则该程序运行后输出的k值是()A.5 B.6 C.7 D.8【考点】程序框图.【分析】执行程序框图,写出每次循环得到的S,k的值,当S=126,K=7时不满足条件S <100,输出K的值为7.【解答】解:执行程序框图,有k=1,S=0满足条件S<100,S=2,K=2;满足条件S<100,S=6,K=3;满足条件S<100,S=14,K=4;满足条件S<100,S=30,K=5;满足条件S<100,S=62,K=6;满足条件S<100,S=126,K=7;不满足条件S<100,输出K的值为7.故选:C.5.设x∈R,记不超过x的最大整数为[x],令{x}=x﹣[x],则{},[],()A.是等差数列但不是等比数列B.是等比数列但不是等差数列C.既是等差数列又是等比数列D.既不是等差数列也不是等比数列【考点】等差关系的确定;等比关系的确定.【分析】可分别求得,.则等比数列性质易得三者构成等比数列.【解答】解:根据题意可得,.∵×=12, +≠2∴{},[],为等比数列,不是等差数列故选B.6.某由圆柱切割获得的几何体的三视图如图所示,其中俯视图是中心角为60°的扇形,则该几何体的体积为()A.2πB.πC. D.【考点】由三视图求面积、体积.【分析】由三视图知几何体为圆柱的一部分,且圆柱的高为3,底面圆的半径为2,根据正视图与俯视图可判断底面扇形的中心角为60°,求出圆柱的体积乘以可得答案.【解答】解:由三视图知几何体为圆柱的一部分,且圆柱的高为3,底面圆的半径为2,由正视图与俯视图判断底面扇形的中心角为60°,∴几何体的体积V=×π×22×3=2π,故选:A.7.设a=(sinx﹣1+2cos2)dx,则(a﹣)6•(x2+2)的展开式中常数项是()A.332 B.﹣332 C.320 D.﹣320【考点】定积分.【分析】根据微积分基本定理求得a的值,求出二项式展开式的通项公式,分类讨论,当k=3时,当k=5时,即可求得展开式中的常数项的值.【解答】解:a=(sinx﹣1+2cos2)dx=(sinx+cosx)dx=(﹣cosx+sinx)|=﹣cosπ﹣(﹣cos0)=1+1=2,(a﹣)6•(x2+2)=(2﹣)6•(x2+2),其中(2﹣)6的通项公式C6k26﹣k(﹣1)k x3﹣k,当3﹣k=0,即k=3时,为常数项,为C6323(﹣1)3=﹣160,当3﹣k=﹣2时,即k=5时,为C6526﹣5(﹣1)5x3﹣5=﹣12x﹣2,故(a﹣)6•(x2+2)的展开式中常数项是﹣160×2﹣12=﹣332,故选:B.8.若函数f(x)=在区间(,)上单调递增,则实数a的取值范围是()A.[2,+∞)B.(2,+∞)C.[,+∞)D.(﹣,+∞)【考点】函数单调性的判断与证明.【分析】可求导数得到,而根据f(x)在区间上单调递增即可得出在上恒成立,而可求出sinx在上的范围,从而便可得出实数a的取值范围.【解答】解:;∵f(x)在区间上单调递增;∴f′(x)≥0在上恒成立;即asinx﹣1≥0在上恒成立;即在上恒成立;∵,∴;∴;∴a≥2;∴实数a的取值范围是[2,+∞).故选A.9.已知棱锥S﹣ABC中,SA=BC=,SB=AC=,SC=AB=,则该三棱锥的外接球表面积为()A.64πB.16πC.14πD.4π【考点】球的体积和表面积.【分析】构造长方体,使得面上的对角线长分别为,,,则长方体的对角线长等于三棱锥S﹣ABC外接球的直径,即可求出三棱锥S﹣ABC外接球的表面积.【解答】解:∵三棱锥S﹣ABC中,SA=BC=,SB=AC=,SC=AB=,∴构造长方体,使得面上的对角线长分别为,,,则长方体的对角线长等于三棱锥S﹣ABC外接球的直径.设长方体的棱长分别为x,y,z,则x2+y2=13,y2+z2=10,x2+z2=5,∴x2+y2+z2=14∴三棱锥S﹣ABC外接球的直径为,∴三棱锥S﹣ABC外接球的表面积为=14π.故选:C.10.已知定义在区间[0,]上的函数y=f(x)的图象关于直线x=对称,当x时,f(x)=cosx,如果关于x的方程f(x)=a有解,记所有解的和为S,则S不可能为()A.B. C. D.3π【考点】余弦函数的图象;函数的图象.【分析】作函数f(x)的图象,分析函数的图象得到函数的性质,分类讨论后,结合方程在a取某一确定值时所求得的所有解的和记为S,即可得到答案【解答】解:依题意作出在区间[0,]上的简图,当直线y=a与函数y=f(x)的图象有交点时,则可得﹣1≤a≤0①当<a≤0,f(x)=a有2个解,此时S=②当时,f(x)=a有3个解,此时S==③当﹣1<a时,f(x)=a有4个交点,此时S==3π④a=﹣1时,f(x)=a有2个交点,此时S==故选A11.如图,已知双曲线﹣=1(a>0,b>0)的左右焦点分别为F1,F2,|F1F2|=4,P是双曲线右支上的一点,F2P与y轴交于点A,△APF1的内切圆在边PF1上的切点为Q,若|PQ|=1,则双曲线的离心率是()A.3 B.2 C.D.【考点】双曲线的简单性质.【分析】由|PQ|=1,△APF1的内切圆在边PF1上的切点为Q,根据切线长定理,可得|PF1|﹣|PF2|=2,结合|F1F2|=4,即可得出结论.【解答】解:由题意,∵|PQ|=1,△APF1的内切圆在边PF1上的切点为Q,∴根据切线长定理可得AM=AN,F1M=F1Q,PN=PQ,∵|AF1|=|AF2|,∴AM+F1M=AN+PN+NF2,∴F1M=PN+NF2=PQ+PF2∴|PF1|﹣|PF2|=F1Q+PQ﹣PF2=F1M+PQ﹣PF2=PQ+PF2+PQ﹣PF2=2PQ=2,∵|F1F2|=4,∴双曲线的离心率是e==2.故选:B.12.已知f(x)是定义在(0,+∞)上的单调函数,且对任意的x∈(0,+∞),都有f[f(x)﹣log2x]=3,则方程f(x)﹣f′(x)=2的解所在的区间是()A.(0,)B.(,1)C.(1,2)D.(2,3)【考点】根的存在性及根的个数判断;对数函数图象与性质的综合应用.【分析】根据题意,由单调函数的性质,可得f(x)﹣log2x为定值,可以设t=f(x)﹣log2x,则f(x)=log2x+t,又由f(t)=3,即log2t+t=3,解可得t的值,可得f(x)的解析式,对其求导可得f′(x);将f(x)与f′(x)代入f(x)﹣f′(x)=2,变形化简可得log2x﹣=0,令h(x)=log2x﹣,由二分法分析可得h(x)的零点所在的区间为(1,2),结合函数的零点与方程的根的关系,即可得答案.【解答】解:根据题意,对任意的x∈(0,+∞),都有f[f(x)﹣log2x]=3,又由f(x)是定义在(0,+∞)上的单调函数,则f(x)﹣log2x为定值,设t=f(x)﹣log2x,则f(x)=log2x+t,又由f(t)=3,即log2t+t=3,解可得,t=2;则f(x)=log2x+2,f′(x)=,将f(x)=log2x+2,f′(x)=代入f(x)﹣f′(x)=2,可得log2x+2﹣=2,即log2x﹣=0,令h(x)=log2x﹣,分析易得h(1)=﹣<0,h(2)=1﹣>0,则h(x)=log2x﹣的零点在(1,2)之间,则方程log2x﹣=0,即f(x)﹣f′(x)=2的根在(1,2)上,故选C.二、填空题(每题5分,满分20分,将答案填在答题纸上)13.从某地高中男生中随机抽取100名同学,将他们的体重(单位:kg)数据绘制成频率分布直方图(如图).若要从身高在[60,70),[70,80),[80,90]三组内的男生中,用分层抽样的方法选取6人参加一项活动,再从这6人选两人当正负队长,则这两人体重不在同一组内的概率为.【考点】频率分布直方图.【分析】由题意,可先计算出体重在[60,70),[70,80),[80,90]三组的频率,计算出6人中各组应抽取的人数,再计算出概率即可.【解答】解:由图知,体重在[60,70),[70,80),[80,90]三组的频率分别为0.3,0.2,0.1,故各组的人数分别为30,20,10,用分层抽样的方法从三组中抽取6人,每组被抽取的人数分别为3,2,1,从这6人选两人当正负队长,总的抽取方法是6×5=30种这两人这两人体重不在同一组内的抽取方法是3×2+3×1+2×1=11种,故这两人这两人体重不在同一组内的概率,故答案为:.14.过平面区域内一点P作圆O:x2+y2=1的两条切线,切点分别为A,B,记∠APB=α,当α最小时,此时点P坐标为(﹣4,﹣2).【考点】简单线性规划;直线与圆的位置关系.【分析】先依据不等式组,结合二元一次不等式(组)与平面区域的关系画出其表示的平面区域,再利用圆的方程画出图形,确定α最小时点P的位置即可.【解答】解:如图阴影部分表示,确定的平面区域,当P离圆O最远时,α最小,此时点P坐标为:(﹣4,﹣2),故答案为::(﹣4,﹣2).15.设S n是数列{a n}的前n项和,且a1=﹣1,=S n.则数列{a n}的通项公式a n=.【考点】数列的求和.【分析】由已知推导出{}是首项为﹣1,公差为﹣1的等差数列,从而求出S n=﹣,由此能求出数列{a n}的通项公式.【解答】解:S n是数列{a n}的前n项和,且a1=﹣1,=S n,∴S n+1﹣S n=S n+1S n,∴=﹣1,=﹣1,∴{}是首项为﹣1,公差为﹣1的等差数列,∴=﹣1+(n﹣1)×(﹣1)=﹣n.∴S n=﹣,n=1时,a1=S1=﹣1,=﹣+=.n≥2时,a n=S n﹣S n﹣1∴a n=.故答案为:.16.设非空集合A,若对A中任意两个元素a,b,通过某个法则“•”,使A中有唯一确定的元素c与之对应,则称法则“•”为集合A上的一个代数运算.若A上的代数运算“•”还满足:(1)对∀a,b,c∈A,都有(a•b)•c=a•(b•c);(2)对∀a∈A,∃e,b∈A,使得e•a=a•e=a,a•b=b•a=e.称A关于法则“•”构成一个群.给出下列命题:①实数的除法是实数集上的一个代数运算;②自然数集关于自然数的加法不能构成一个群;③非零有理数集关于有理数的乘法构成一个群;④正整数集关于法则a°b=a b构成一个群.其中正确命题的序号是②③.(填上所有正确命题的序号).【考点】命题的真假判断与应用.【分析】利用代数运算“•”的定义,对①②③④四个选项逐一分析即可.【解答】解:①因为a÷0没有意义,故命题错误;②自然数的加法是一个代数运算,加法满足结合律(1)、(2)有单位元0、但不满足使a+b=0,故命题正确;③有理数集的乘法是一个代数运算,满足(1)、(2),有单位元1、存在逆元使,故命题正确;④是代数运算,运算不满足(1).如(2°1)°2=21°2=4,2°(1°2)=2°12=2,故命题错误.故答案为:②③.三、解答题(本大题共5小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.如图,在海岛A上有一座海拔1千米的山,山顶设有一个观察站P,上午11时,测得一轮船在岛北偏东30°,俯角为30°的B处,到11时10分又测得该船在岛北偏西60°,俯角为60°的C处.(1)求船的航行速度是每小时多少千米?(2)又经过一段时间后,船到达海岛的正西方向的D、处,问此时船距岛A有多远?【考点】解三角形的实际应用.【分析】(1)先Rt△PAB、Rt△PAC中确定AB、AC的长,进而求得,∠CAB=30°+60°=90°,最后利用勾股定理求得BC,用里程除以时间即为船的速度.(2)利用sin∠DCA=sin=sin∠ACB求得sin∠DCA的值,利用sin∠CDA=sin(∠ACB﹣30°)=sin∠ACB•cos30°﹣cos∠ACB•sin30°求得sin∠CDA的值,进而利用正弦定理求得AD.【解答】解:(1)在Rt△PAB中,∠APB=60°,PA=1,∴AB=.在Rt△PAC中,∠APC=30°,∴AC=.在△ACB中,∠CAB=30°+60°=90°,∴BC===.则船的航行速度为÷=2(千米/时).(2)在△ACD、中,∠DAC=90°﹣60°=30°,sin∠DCA=sin=sin∠ACB===,sin∠CDA=sin(∠ACB﹣30°)=sin∠ACB•cos30°﹣cos∠ACB•sin30°=•﹣=.由正弦定理得=.∴AD===.故此时船距岛A有千米.18.某商场销售某种品牌的空调器,每周周初购进一定数量的空调器,商场每销售一台空调器可获利500元,若供大于求,则每台多余的空调器需交保管费100元;若供不应求,则可从其他商店调剂供应,此时每台空调器仅获利润200元.(Ⅰ)若该商场周初购进20台空调器,求当周的利润(单位:元)关于当周需求量n(单位:台,n∈N)的函数解析式f(n);(Ⅱ)该商场记录了去年夏天(共10周)空调器需求量n(单位:台),整理得表:周需求量n 18 19 20 21 22频数 1 2 3 3 1以10周记录的各需求量的频率作为各需求量发生的概率,若商场周初购进20台空调器,X 表示当周的利润(单位:元),求X的分布列及数学期望.【考点】离散型随机变量的期望与方差;离散型随机变量及其分布列.【分析】(I)对n分类讨论,利用利润与周需求量的关系即可得出.(II)利用频率估计概率,利用随机变量的分布列即可得出.【解答】解:(I)当n≥20时,f(n)=500×20+200×(n﹣20)=200n+6000,当n≤19时,f(n)=500×n﹣100×(20﹣n)=600n﹣2000,∴.(II)由(1)得f(18)=8800,f(19)=9400,f(20)=10000,f(21)=10200,f(22)=10400,∴P(X=8800)=0.1,P(X=9400)=0.2,P(X=10000)=0.3,P(X=10200)=0.3,P(X=10400)=0.1,X的分布列为X 8800 9400 10000 10200 10400P 0.1 0.2 0.3 0.3 0.1∴EX=8800×0.1+9400×0.2+10000×0.3+10200×0.3+10400×0.1=9860.19.已知四边形ABCD满足AD∥BC,BA=AD=DC=BC=a,E是BC的中点,将△BAE沿AE翻折成△B1AE,使面B1AE⊥面AECD,F为B1D的中点.(1)求四棱锥B1﹣AECD的体积;(2)证明:B1E∥面ACF;(3)求面ADB1与面ECB1所成锐二面角的余弦值.【考点】用空间向量求平面间的夹角;棱柱、棱锥、棱台的体积;直线与平面平行的判定.【分析】(Ⅰ)取AE的中点M,连接B1M,证明B1M⊥面AECD,从而可求四棱B1﹣AECD 的体积;(Ⅱ)证明B1E∥面ACF,利用线面平行的判定定理,证明FO∥B1E即可;(Ⅲ)连接MD,分别以ME,MD,MB1为x,y,z轴建立空间直角坐标系,用坐标表示点与向量,求出面ECB1与面ADB1的法向量,利用向量的夹角公式,即可求得二面角的余弦值.【解答】(Ⅰ)解:取AE的中点M,连接B1M,因为,E是BC的中点,所以△ABE为等边三角形,所以,又因为面B1AE⊥面AECD,所以B1M⊥面AECD,…所以…(Ⅱ)证明:连接ED交AC于O,连接OF,因为AECD为菱形,OE=OD,又F为B1D的中点,所以FO∥B1E,因为FO⊂面ACF所以B1E∥面ACF…(Ⅲ)解:连接MD,分别以ME,MD,MB1为x,y,z轴,建立空间直角坐标系.则…设面ECB1的法向量,则,令x'=1,则设面ADB1的法向量为,则,令x=1,则…则,所以二面角的余弦值为…20.已知椭圆E:的一个交点为,而且过点.(Ⅰ)求椭圆E的方程;(Ⅱ)设椭圆E的上下顶点分别为A1,A2,P是椭圆上异于A1,A2的任一点,直线PA1,PA2分别交x轴于点N,M,若直线OT与过点M,N的圆G相切,切点为T.证明:线段OT的长为定值,并求出该定值.【考点】圆与圆锥曲线的综合;椭圆的定义;椭圆的标准方程.【分析】(Ⅰ)解法一:根据椭圆E:的一个交点为,过点,可得a2﹣b2=3,,联立即可求得椭圆E的方程;解法二:椭圆的两个焦点分别为,利用椭圆的定义,可求椭圆E的方程;(Ⅱ)解法一:由(Ⅰ)可知A1(0,1),A2(0,﹣1),设P(x0,y0),求出,同设圆G的圆心为,利用,即可得到线段OT的长度;解法二:由(Ⅰ)可知A1(0,1),A2(0,﹣1),设P(x0,y0),求出,,可得,由切割线定理可得线段OT的长度.【解答】(Ⅰ)解法一:由题意,∵椭圆E:的一个交点为,∴a2﹣b2=3,①∵椭圆过点.∴,②①②解得a2=4,b2=1,所以椭圆E的方程为.…解法二:椭圆的两个焦点分别为,由椭圆的定义可得,所以a=2,b2=1,所以椭圆E的方程为.…(Ⅱ)解法一:由(Ⅰ)可知A1(0,1),A2(0,﹣1),设P(x0,y0),直线PA1:,令y=0,得;直线PA2:,令y=0,得;设圆G的圆心为,则r2=,而,所以,所以,所以|OT|=2,即线段OT的长度为定值2.…解法二:由(Ⅰ)可知A1(0,1),A2(0,﹣1),设P(x0,y0),直线PA1:,令y=0,得;直线PA2:,令y=0,得;则,而,所以,所以,由切割线定理得OT2=|OM|•|ON|=4所以|OT|=2,即线段OT的长度为定值2.…21.已知函数f(x)=lnx﹣x(1)求函数g(x)=f(x)﹣x﹣2的图象在x=1处的切线方程(2)证明:(3)设m>n>0,比较与的大小,并说明理由.【考点】利用导数研究曲线上某点切线方程;利用导数研究函数的单调性;利用导数求闭区间上函数的最值.【分析】(1)求导数,确定切线斜率,切点坐标,即可求函数g(x)=f(x)﹣x﹣2的图象在x=1处的切线方程;(2)确定f(x)max=f(1)=ln1﹣1=﹣1,|f(x)|min=1,设G(x)=,则,故G(x)在(0,e)上是增加的,在(e,+∞)上是减少的,故,G(x)max<|f(x)|min,即可证明结论;(3),,m>n>0,可得,故只需比较ln﹣与O的大小.【解答】(1)解:因为g(x)=lnx﹣2(x+1)所以,g'(1)=﹣1…又因g(1)=﹣4,所以切点为(1,﹣4)…故所求的切线方程为:y+4=﹣(x﹣1),即y+x+3=0…(2)证明:因为,所以f(x)在(0,1)上是增加的,在(1,+∞)上是减少的,所以f(x)max=f(1)=ln1﹣1=﹣1,|f(x)|min=1…设G(x)=,则,故G(x)在(0,e)上是增加的,在(e,+∞)上是减少的,故,G(x)max<|f(x)|min所以对任意x∈(0,+∞)恒成立…(3)解:,∵m>n>0,∴,故只需比较ln﹣与O的大小…令=t,设G(t)=lnt﹣…因为t>1,所以G'(t)>0,所以函数G(t)在(1,+∞)上是增加的,故G(t)>G(1)=0…所以G(t)>0对任意t>1恒成立…即,从而有>…请考生在22、23、24三题中任选一题作答,如果多做,则按所做的第一题记分.[选修4-1:几何证明选讲]22.如图,EP交圆于E,C两点,PD切圆于D,G为CE上一点且PG=PD,连接DG并延长交圆于点A,作弦AB垂直EP,垂足为F.(Ⅰ)求证:AB为圆的直径;(Ⅱ)若AC=BD,求证:AB=ED.【考点】圆周角定理;与圆有关的比例线段.【分析】(Ⅰ)证明AB为圆的直径,只需证明∠BDA=90°;(Ⅱ)证明Rt△BDA≌Rt△ACB,再证明∠DCE为直角,即可证明AB=ED.【解答】证明:(Ⅰ)∵PG=PD,∴∠PDG=∠PGD,∵PD为切线,∴∠PDA=∠DBA,∵∠PGD=∠EGA,∴∠DBA=∠EGA,∴∠DBA+∠BAD=∠EGA+∠BAD,∴∠BDA=∠PFA,∵AF⊥EP,∴∠PFA=90°.∴∠BDA=90°,∴AB为圆的直径;(Ⅱ)连接BC,DC,则∵AB为圆的直径,∴∠BDA=∠ACB=90°,在Rt△BDA与Rt△ACB中,AB=BA,AC=BD,∴Rt△BDA≌Rt△ACB,∴∠DAB=∠CBA,∵∠DCB=∠DAB,∴∠DCB=∠CBA,∴DC∥AB,∵AB⊥EP,∴DC⊥EP,∴∠DCE为直角,∴ED为圆的直径,∵AB为圆的直径,∴AB=ED.[选修4-4:坐标系与参数方程]23.已知直线l的参数方程:(t为参数),曲线C的参数方程:(α为参数),且直线交曲线C于A,B两点.(Ⅰ)将曲线C的参数方程化为普通方程,并求θ=时,|AB|的长度;(Ⅱ)已知点P:(1,0),求当直线倾斜角θ变化时,|PA|•|PB|的范围.【考点】参数方程化成普通方程.【分析】(Ⅰ)利用三角函数的平方关系式,将曲线C的参数方程化为普通方程,求出直线AB的方程,代入,可得3x2﹣4x=0,即可求出|AB|的长度;(Ⅱ)直线参数方程代入,A,B对应的参数为t1,t2,则|PA|•|PB|=﹣t1t2,即可求出|PA|•|PB|的范围.【解答】解:(Ⅰ)曲线C的参数方程:(α为参数),曲线C的普通方程为.当θ=时,直线AB的方程为,y=x﹣1,代入,可得3x2﹣4x=0,∴x=0或x=∴|AB|=•=;(Ⅱ)直线参数方程代入,得(cos2θ+2sin2θ)t2+2tcosθ﹣1=0.设A,B对应的参数为t1,t2,∴|PA|•|PB|=﹣t1t2==∈[,1].[选修4-5:不等式选讲]24.已知a>0,b>0,且a2+b2=,若a+b≤m恒成立,(Ⅰ)求m的最小值;(Ⅱ)若2|x﹣1|+|x|≥a+b对任意的a,b恒成立,求实数x的取值范围.【考点】绝对值不等式.【分析】(Ⅰ)变形已知表达式,利用柯西不等式,求出a +b 的最大值,即可求m 的最小值;(Ⅱ)通过2|x ﹣1|+|x |≥a +b 对任意的a ,b 恒成立,结合(Ⅰ)的结果,利用x 的范围分类讨论,求出实数x 的取值范围.【解答】解:(Ⅰ)∵a >0,b >0,且a 2+b 2=,∴9=(a 2+b 2)(12+12)≥(a +b )2,∴a +b ≤3,(当且仅当,即时取等号)又∵a +b ≤m 恒成立,∴m ≥3.故m 的最小值为3.…(II )要使2|x ﹣1|+|x |≥a +b 恒成立,须且只须2|x ﹣1|+|x |≥3.∴或或∴或.…2016年9月20日。
河北南宫一中2016届高三上学期期中模拟测试数学(理)试题(解析版)

南宫一中2016届高三上学期期中模拟测试数学(理)试题一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的1.已知全集U=R ,集合 {}{}2|02,|0A x x B x x x =≤≤=->,则图中的阴影部分表示的集合为A .(-∞,1]U(2,+∞)B .()(),01,2-∞C .[1,2)D .(1,2] 【答案】A【解析】图中的阴影部分表示的集合为()()(](),12,A B C A B =-∞+∞ , 故选 A . 2、复数122ii +-的共轭复数是( ) A .35i B .35i- C .i D .i -【答案】D 【解析】复数===i .所以复数的122ii+-的共轭复数是:﹣i .故选D 3、下列说法中正确的是 ( )A 、若命题:p x R ∀∈有20x >,则:p x R ⌝∀∈有20x ≤;B 、若命题1:01p x >-,则1:01p x ⌝≤-; C 、若p 是q 的充分不必要条件,则p ⌝是q ⌝的必要不充分条件;D 、方程20ax x a ++=有唯一解的充要条件是12a =±【答案】C【解析】A 选项,因为:p x R ⌝∃∈有20x ≤,所以错误;B 选项,因为则1:01p x ⌝≤-或x=1,所以错误;C 选项,若p q ⇒,其等价命题为q p ⌝⇒⌝,即p ⌝是q ⌝的必要不充分条件,所以正确;D 选项,当a=0时,也有唯一解,所以错误,综上知选C.4设,a b 是两个非零向量,则“0<⋅”是“,a b夹角为钝角”的 A.充分不必要条件 B.必要不充分条件 C.充分必要条件 D.既不充分也不必要条件 【答案】B【解析】因为0<⋅时,,a b 夹角为钝角或平角,而,a b夹角为钝角时,0<⋅成立,所以“0<⋅b a ”是“,a b夹角为钝角”的必要不充分条件.故选B.5.运行如图所示的程序框图,则输出的结果S 为( ) A .2014 B .2013 C .1008 D .1007【答案】D【解析】由程序框图可知12320131110061007S =-+-+=+⨯= ,所以选D.6.已知i 是虚数单位,则ii 31+= ( )A .i 4143- B .i 4143+ C .i 2123+ D .i 2123- 【答案】B【解析】114i i -===,所以选B. 7.已知1,3O A O ==,0,OA OB =点C 在AOB ∠内,且30AOC ∠=︒,设,O C m O A n OB =+ (),m n R ∈,则nm等于( ) A .31 B .3 C .33 D .3 【答案】B【解析】∵1,OA OB == 0,OA OB =∴OA OB ^ ,1||2OCOBOC ? ,1||OC OA OC ??,∴OC 在x 轴方向上的分量为1||2OC ,OC 在y|OC∵OC mOA nOB m j =++∴1||||2OC OC m =两式相比可得:3mn=.故选B.8.已知实数的取值范围是【答案】C【解析】由约束条件作可行域如图,联立,解得,∴A (2,﹣1),联立,解得,∴.令u=2x ﹣2y ﹣1,则,由图可知,当经过点A (2,﹣1)时,直线在y 轴上的截距最小,u 最大,最大值为u=2×2﹣2×(﹣1)﹣1=5; 当经过点时,直线在y 轴上的截距最大,u 最小,最小值为u=.∴,∴z=|u|∈[0,5).故选:C .9.已知A,B,C 三点是某球的一个截面的内接三角形的三个顶点,其中30,24,18===AC BC AB ,球心到这个截面的距离为球半径的一半,则该球的表面积为A.π1200B.π1400C.π1600D.π1800 【答案】A【解析】因为222AB BC AC +=,所以三角形ABC 外接圆圆心在AC 中点处,半径为15,设球半径为R ,由球的截面性质得222152R R ⎛⎫-= ⎪⎝⎭,得2300R =,所以该球的表面积为241200R ππ=,则选A.10.已知m ,n 是两条不同直线,α,β是两个不同的平面,且//m α,n ⊂β,则下列叙述正确的是(A )若//αβ,则//m n (B )若//m n ,则//αβ(C )若n α⊥,则m β⊥ (D )若m β⊥,则αβ⊥ 【答案】D【解析】A 中m ,n 可能异面;B 中α,β可能相交;C 中可能m β⊂或//m β,故选D. 11. 函数()2232xlog e lnx a f x x --+=的一个极值点在区间()12,内,则实数a 的取值范围是()A .()13,B .()12,C .()03,D .()02, 【答案】C【解析】因为()2'2xf x a x=--,若函数的一个极值点在区间()12,内,则()()'1'20f f <,即(-a)(3-a)<0,解得0<a <3,所以选C.12.已知F 是椭圆22221+=x y a b(0>>a b )的左焦点,A 为右顶点,P 是椭圆上一点,⊥PF x轴.若14=PF AF ,则该椭圆的离心率是( ) (A )14 (B )34 (C )12(D【答案】B【解析】Rt PFA 中,222|PF||FA ||PA |+=,||c FA a =+,2|PF |b a=, 又14=PF AF ,21(c)4b a a =+,得22430c ac a +-=,34c a ∴=,故选B.二、填空题:本大题共4小题,每小题5分..已知某几何体的三视图如图所示,则该几何体的表面积等于【答案】64+【解析】由三视图可知该几何体为直三棱柱截去一个三棱锥,因为SB AC ==则其表面积等于()()11114884484444642222⨯+⨯++⨯⨯++⨯⨯+⨯⨯=+.14.一个几何体的三视图如图所示,则该几何体的体积为【答案】10【解析】该几何体为直四棱柱,底面为直角梯形,S=(2+3)×2=5,h=2;故V=Sh=5×2=10.故答案为:10.15. 已知n S 和n T 分别为数列{}n a 与数列{}n b 的前n 项和,且41a e =,51n n S eS e +=-, nb n a e=(*n N ∈).则当n T 取得最大值时,n 的值为____________. 【答案】4或5【解析】S n 和T n 分别为数列{a n }与数列{b n }的前n 项和,S n =eS n+1﹣e 5,S n ﹣1=eS n ﹣e 5,n ≥2,相减得出:a n =ea n+1,=,n ≥2,∵a 1=e 4,S n =eS n+1﹣e 5,∴a 2=e 3,=.∴数列{a n }是等比数列.a n =e5﹣n,∵a n =e bn (n ∈N *).∴b n =lne5﹣n=5﹣n .∵b n+1﹣b n =﹣1.∴数列{b n }是等差数列.∴T n ==,对称轴n=根据函数的性质得出:n=5,n=4时最大值.故答案为:4或5. 16.已知偶函数y= f (x)对于任意的x [0,)2π∈满足f '(x)cosx +f(x)sinx>0(其中f ' (x)是函数f (x)的导函数),则下列不等式中成立的有【答案】 (2) (3) (4)【解析】∵偶函数y=f (x )对于任意的x ∈[0,)满足f ′(x )cosx+f (x )sinx >0∴g (x )=,g ′(x )=>0,∴x ∈[0,),g (x )=是单调递增,且是偶函数, ∴g (﹣)=g (),g (﹣)=g (),∵g ()<g (),∴,即f (>f (),(1)化简得出f (﹣)=f ()<f (),所以(1)不正确. (2)化简f (﹣)>f (﹣),得出f ()>f (),所以(2)正确.又根据g (x )单调性可知:g ()>g (0),∴>,∴f (0)<f (),∵偶函数y=f (x )∴即f (0)<f (﹣),所以(3)正确.∵根据g (x )单调性可知g ()>g (),∴,f ()>f ().所以(4)正确.故答案为:(2)(3)(4)三、解答题:解答应写出文字说明,证明过程或演算步骤. 17.(本小题满分12分)已知等差数列{n a }的各项均为正数,1a =1,且34115,,2a a a +成等比数列. (I )求n a 的通项公式,(II )设11n n n b a a +=,求数列{n b }的前n 项和T n . 【答案】 (Ⅰ) 213-=n a n ;(Ⅱ)232n n T n =+.【解析】(Ⅰ)设等差数列公差为d ,由题意知0>d , 因为1143,25,a a a +成等比数列,所以11324)25(a a a =+, )101)(21()327(2d d d ++=+∴,即,04536442=+-d d所以),2215(23舍去-==d d ……… 4分 所以213-=n a n . ……… 6分(Ⅱ))231131(34)23)(13(411+--=+-==+n n n n a a b n n n , ……… 8分所以41111112().32558313232n nT n n n =-+-++-=-++ . ……… 12分18、(本小题满分12分)某中学随机抽取部分高一学生调查其上学路上所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中上学路上所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100]. (Ⅰ)求直方图中x 的值;(Ⅱ)如果上学路上所需时间不少于1小时的学生可申请在学校住宿,若招生1200名,请估计新生中有多少名学生可以申请住宿;(Ⅲ)从学校的高一学生中任选4名学生,这4名学生中上学路上所需时间少于20分钟的人数记为X ,求X 的分布列和数学期望.(以直方图中的频率作为概率)【答案】(Ⅰ)0.0125x =;(Ⅱ)144名;(Ⅲ) E(X)=1 【解析】(Ⅰ)由直方图可得:200.025200.0065200.0032201x ⨯+⨯+⨯+⨯⨯=. 所以 0.0125x =.(Ⅱ)新生上学所需时间不少于1小时的频率为:0.0032200.12⨯⨯=, 因为12000.12144⨯=,所以1200名新生中有144名学生可以申请住宿.(Ⅲ)X 的可能取值为0,1,2,3,4. 由直方图可知,每位学生上学所需时间少于20分钟的概率为14,4381(0)4256P X ⎛⎫=== ⎪⎝⎭, 3141327(1)C 4464P X ⎛⎫⎛⎫=== ⎪⎪⎝⎭⎝⎭, 22241327(2)C 44128P X ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭,334133(3)C 4464P X ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭,411(4)4256P X ⎛⎫=== ⎪⎝⎭.0123412566412864256EX =⨯+⨯+⨯+⨯+⨯=.(或414EX =⨯=)所以X 的数学期望为1.19.如图,在四棱锥P D ABC -中,四边形ABCD 是边长为1的菱形,且60DAB ∠=,2P P D B A P ===,E F ,分别是BC PC ,的中点。
石家庄二模理综答案

石家庄二模理综答案文档编制序号:[KK8UY-LL9IO69-TTO6M3-MTOL89-FTT688]2016石家庄二模理综答案【篇一:2016年石家庄市数学二模理科试卷及答案】p> 一、选择题1-5 baacb 6-10cabba 11-12cc二、填空题13. 4 14. 240 515. -616. 1或9三、解答题abc2r可得: sinasinbsinca=3r2sbincco2rsin…………………1分abc 17.(i)由正弦定理sinasin(bc)=3sinbcosc,-------------------------3分即sinbcosccosbsinc=3sinbcosccosbsinc=2sinbcosc故cosbsicn=2 sinbcosctanc=2. -------------------------5分 tanb (ii)(法一)由abc,得tan(bc)tan(a)3, tanbtanc3tanb3, 将tanc2tanb 代入得:3,-------------------------7分 21tanbtanc12tanb1解得tanb1或tanb, 2tanb同正,根据tanc2tanb得tanc、所以tanb1,tanc2.…………………8分即则tana3,可得sinbsincsina,b10分所以sabc11absinc33.-------------------------12分 22(法二)由abc 得tan(bc)tan(a)3, tanbtanc3tanb3, 将tanc2tanb代入得:3,-------------------------7分 1tanbtanc12tan2b即【篇二:石家庄2016年二模化学答案】7.c 8.b 9.d 10.b 11.c 12.d 13.a 26.(13分)(1)cu+4hno3(浓)=cu(no3)2+2no2↑+2h2o (2分)(2)无水氯化钙(或硅胶或p2o5)(1分)防止e中水蒸气进入c中与na2o2反应(2分)(3)从左口通入一段时间n2 ,排尽空气后,关闭活塞k1和k2,打开k3 (2分)(4)①2no2+na2o2=2nano3 (2分)②若有o2生成,o2在通过装置e时会参与反应被吸收(2分)(1)2︰1︰1 (2分)(2)c(na)>c(rh)>c(h)>c(r2)>c(oh) (2分),<(1分)+-+--(3)5 h4c4o4+ 12 mno4-+ 36 h+ =12 mn2++ 20 co2↑+ 28 h2o (2分)(4)①2h2o+2e=h2↑+2oh或2h+ +2e=h2↑(2分)---②阳极室发生:2h2o-4e=o2↑+4h,原料室的r2穿过阴膜扩散至阳极室,与h-+-+反应生成酒石酸(2分)(5)①富集r2 (合理答案即可)(2分)②0.36 mol/l(2分)-28.(15分)---② a (1分),该反应为放热反应,升高温度平衡逆向移动,平衡常数减小。
【精品试卷】高考化学复习河北南宫中学高三5月第三次模拟考试(石家庄二模)理综化学试题(图片版)(复习

高中化学学习材料(灿若寒星**整理制作)河北南宫中学2016届高三5月第三次模拟考试(石家庄二模)理综化学试题(图片版)2016年5月高三二模化学试题参考答案及评分标准7.C 8.B 9.D 10.B 11.C 12.D 13.A26.(13分)(1)Cu+4HNO3(浓)=Cu(NO3)2+2NO2↑+2H2O (2分)(2)无水氯化钙(或硅胶或P2O5)(1分)防止E中水蒸气进入C中与Na2O2反应(2分)(3)从左口通入一段时间N2 ,排尽空气后,关闭活塞K1和K2,打开K3 (2分)(4)①2NO2+Na2O2=2NaNO3 (2分)②若有O2生成,O2在通过装置E时会参与反应被吸收(2分)③取反应后的C中固体,加水溶解,向所得溶液中滴加少量酸性KMnO4溶液,若溶液紫色褪去,则假设II正确;若溶液紫色不褪去,则假设I正确(2分, 用淀粉KI溶液不给分。
)27.(15分)(1)2︰1︰1(2分)(2)c(Na+)>c(RH-)>c(H+)>c(R2-)>c(OH-) (2分),<(1分)(3)5 H4C4O4+ 12 MnO4-+ 36 H+=12 Mn2++ 20 CO2↑+ 28 H2O(2分)(4)①2H2O+2e-=H2↑+2OH-或2H++2e-=H2↑(2分)②阳极室发生:2H2O-4e-=O2↑+4H+,原料室的R2-穿过阴膜扩散至阳极室,与H+反应生成酒石酸(2分)(5)①富集R2-(合理答案即可)(2分)②0.36 mol/L(2分)28.(15分)(1)-206.3 kJ ·mol -1 (2分)(2)增大 (1分) ,增大压强反应Ⅰ平衡正向移动,反应Ⅲ平衡不移动,总体上缩小容器体积CO 转化率增大 (2分,对反应I 和反应III 的影响各占1分。
) (3)①0.04 mol ·L -1·min -1 (2分)② a (1分),该反应为放热反应,升高温度平衡逆向移动,平衡常数减小 。
河北南宫中学2016届高三5月第三次模拟考试(石家庄二模

河北南宫中学2016届高三5月第三次模拟考试(石家庄二模)数学(文)试题本试卷分第I 卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试时间120分钟。
第I 卷(选择题 共60分)注意事项:1. 答第I 卷前,考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上。
2. 每题选出答案后,用2B 铅笔把答题卡对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,在改涂在其他答案标号。
一.选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设集合A={x|x<2},集合B={x|y=x -3},则B A =A.{x|x ≤2}B.{x|x<2}C.{x|x ≤3}D.{x|x<3} 2.设i 是虚数单位,复数iia +-1为纯虚数,则实数a 的值为 A.1 B. -1 C.21D.-23.设函数()x f =sinx-x ,则()x fA.既是奇函数又是减函数B.既是奇函数又是增函数C.是增函数且有零点D.是减函数且没有零点4. 4.命题p :xy y x 2≥+;命题q :在ABC ∆中,若sinA>sinB ,则A>B 。
下列命题为真命题的是A.pB.p ⌝C.q p ∨D. q p ∧ 5.已知()x f =()⎩⎨⎧>+-≤0,110,cos 2x x f x x π则⎪⎭⎫⎝⎛34f 的值为 A.-1 B. 1 C.23 D.25 6.已知等差数列{}n a 的前n 项和为n S ,若11=a ,公差d=2,1+n S -n S =32,则n 的值为A.5B.6C.7D.87.一个几何体的三视图如图所示,则该几何体的体积为A.41 B.31 C.32D.1 8.若实数x ,y 满足14||9||≤+y x ,则z=2x-y 的最小值为 A.-18 B.-4 C.4 D.-210 9.运行下面的程序框图()x f ,输出的结果是A.7B.6C.-5D.-410.已知数列{}n a 的前n 项和为n S ,且11=a ,11++-=n n n S S a ,则使2101nnS nS +取得最大值时n 的值为A. 2B. 5C.4D.311. 在正四棱锥V-ABCD 中(底面是正方形,侧棱均相等),AB=2,VA=6,且该四棱锥可绕着AB 任意旋转,旋转过程中CD//平面α,则正四棱锥V-ABCD 在平面α内的正投影的面积的取值范围是A. [2,4]B.(2,4]C.[6,4]D. [2,26]12. 已知实数p>0,直线4x+3y-2p=0,与抛物线)0(22>=p px y 和圆4)2(222p y p x =+-从上到下的交点依次是A,B,C,D ,则||||BD AC 的值为A.81 B.165 C.83 D.167 第II 卷(非选择题 共90分)注意事项:第II 卷所有题目的答案考生需用黑色签字笔答在“数学”答题卡指定的位置。
河北省石家庄市高三毕业班第二次模拟考试(图片)——数

2016-2017学年度石家庄市第二次模拟考试数学理科答案一、选择题1-5DDACA 6-10 DADBA 11-12AB二、填空题13. 14 .15. 16.三、解答题17.解:(1)当时, 1121212(1)222-1)(2)22n n n n a a na n a a n a n +-+++=-++++=-+①(②……………………2分 ①-②得1(1)2(2)22n n n n na n n n +=---=⋅所以,……………………3分当时,,所以,…………………………………………4分 (2)因为,22211111()log log (2)22n n n b a a n n n n +===-⋅++.……………………6分 因此 1111111111111112322423521122n T n n n n ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=-+-+-++-+- ⎪ ⎪ ⎪ ⎪ ⎪-++⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭. ………………………8分111112212n n ⎛⎫=+-- ⎪++⎝⎭…………………10分 3111342124n n ⎛⎫=-+< ⎪++⎝⎭ 所以,对任意,.…………………12分18.(1)证明:取AD 中点M ,连接EM ,AF =EF =DE =2,AD =4,可知EM =AD ,∴AE ⊥DE ,………………………………2分又AE ⊥EC , ∴AE ⊥平面CDE ,∴AE ⊥CD , 又CD ⊥AD ,,∴CD ⊥平面ADEF , 平面ABCD ,∴平面ABCD ⊥平面ADEF ;………………………………5分(2)如图,作EO ⊥AD ,则EO ⊥平面ABCD ,故以O 为原点,分别以的方向为x 轴、y 轴、z 轴的正方向建立空间平面直角坐标系,依题意可得,,, ,所以,,…………………………7分设为平面EAC 的法向量,则00n EA n AC ⎧=⎪⎨=⎪⎩即30440x x y ⎧=⎪⎨-+=⎪⎩ 不妨设x =1, 可得,…………………………9分所以cos ,70||||285CF n CF n CF n <>=== =, ………………………………11分直线CF 与平面EAC 所成角的正弦值为………………………………12分19.解:(1)四天均不降雨的概率,四天中恰有一天降雨的概率31243221655625P C ⎛⎫== ⎪⎝⎭, ……………………………………2分 所以四天中至少有两天降雨的概率128121632811625625625P P P =--=--= ………4分 (2)由题意可知1234535x ++++==, …………………………………………5分 50+85+115+140+160=1105y = …………………………………………………………6分 51521()()275==27.510()i ii ii x x y y b x x ==--=-∑∑,………………………………………………………8分所以,关于的回归方程为:. ……………………………………10分将降雨量代入回归方程得: ˆ27.5627.5192.5y=⨯+=. 所以预测当降雨量为6毫米时需要准备的快餐份数为193份. …………………………12分20.(Ⅰ)方法一:设M (x ,y ),由题意可知,A (1-r ,0),因为弦AM 的中点恰好落在轴上,所以x=r-1>0,即r=x+1, ………………2分所以,化简可得y 2=4x (x>0)所以,点M 的轨迹E 的方程为:y 2=4x (x>0)………………………4分方法二:设M (x ,y ),由题意可知,A (1-r ,0),AM 的中点,x>0,因为C (1,0),,.………………………2分在⊙C 中,因为CD ⊥DM ,所以,,所以.所以,y 2=4x (x>0)所以,点M 的轨迹E 的方程为:y 2=4x (x>0)………………………4分(Ⅱ) 设直线MN 的方程为,,,直线BN 的方程为 2214404x my y my y x=+⎧⇒--=⎨=⎩,可得12124,4y y m y y +==-,…………………6分 由(1)可知,,则点A ,所以直线AM 的方程为,22222222()44044y y k x y ky y y ky y x ⎧=-+⎪⇒-+-=⎨⎪=⎩,,可得, 直线BN 的方程为,………………………8分 联立11222,22,2y y x y y y x y ⎧=+⎪⎪⎨⎪=+⎪⎩可得21111441,222B B y my x y m y y -=-===, 所以点B (-1,2m )………………………10分,2d ==,与直线MN 相切………………………12分21.【解】(1).若,则,则函数是单调增函数,这与题设矛盾.所以,令,则.................................................................................. 2分当时,,是单调减函数;时,,是单调增函数;于是当时,取得极小值.因为函数()e ()x f x ax a a =-+∈R 的图象与轴交于两点, (x 1<x 2),所以,即................................................. 4分此时,存在;(或寻找f (0))存在33ln ln (3ln )3ln a a f a a a a a >=-+,,又由在及上的单调性及曲线在R 上不间断,可知为所求取值范围. ................................................................................................ 5分(2)因为两式相减得. ......................7分 记,则()121221212221e e e e 2(e e )22x x x x x x s s x x f s x x s ++-+-'⎡⎤=-=--⎣⎦-, …………………9分设,则,所以是单调减函数,则有,而,所以.又是单调增函数,且,所以。
河北省南宫中学高三理综5月第三次模拟考试(石家庄二模)试题(扫描版)

河北南宫中学2016届高三5月第三次模拟考试(石家庄二模)理综试题(图片版)2016届石家庄市高中毕业班第二次模拟考试试卷生物参考答案一.选择题1.B2. C3. D4.C5.A6.D二、简答题29. (9分,除标注外,每空1分)(1)氨基酸 (空间)结构改变(破坏) (2)降低活化能(3)纳豆激酶(NK) (2分) 直接 (2分) (4)释放组织纤溶酶原激活剂 (2分)30.(10分,每空2分)(1)赤霉素(2)能 0-10 抑制作用逐渐减弱(3)极性31.(12分,每空2分)(1)性状分离(2)第一组和第二组(3)a1a1、 a2a2(两种写全才得分) (4)杂交和自交(5)1/18 (6)(基因的)分离32.(8分,除标注外,每空1分)(1)捕食(2)数学 (负)反馈(3)种群密度 b (2分) d (2分)39.(15分,除标注外,每空2分)(1)萃取(1分)乙酸乙酯干燥水浴回流冷凝(冷凝回流或冷凝) 过滤(2)乳白无水硫酸钠40.(15分,除标注外,每空2分)Ⅰ.(1)农杆菌转化法 Ti质粒(2)苏云金(芽孢)杆菌无(3)蛋白质工程(4)环境安全Ⅱ.(1)物质循环再生(2)C(1分)2016年5月高三二模化学试题参考答案及评分标准7.C 8.B 9.D 10.B 11.C 12.D 13.A26.(13分)(1)Cu+4HNO3(浓)=Cu(NO3)2+2NO2↑+2H2O (2分)(2)无水氯化钙(或硅胶或P2O5)(1分)防止E中水蒸气进入C中与Na2O2反应(2分)(3)从左口通入一段时间N2 ,排尽空气后,关闭活塞K1和K2,打开K3 (2分)(4)①2NO2+Na2O2=2NaNO3 (2分)②若有O2生成,O2在通过装置E时会参与反应被吸收(2分)③取反应后的C中固体,加水溶解,向所得溶液中滴加少量酸性KMnO4溶液,若溶液紫色褪去,则假设II正确;若溶液紫色不褪去,则假设I正确(2分, 用淀粉KI溶液不给分。
河北省南宫中学2016届高三数学5月第三次模拟考试(石家庄二模)试题 理(扫描版)

某某南宫中学2016届高三5月第三次模拟考试(某某二模)数学(理)试题(图片版)2016年某某市第二次模拟考试试题答案(数学理科)一、选择题1-5 BAACB 6-10CABBA 11-12CC 二、填空题 13.5414. 240 15. -6 16. 1或9三、解答题 17.(I )由正弦定理2sin sin sin a b cR A B C===可得: 2sin =32sin cos R A R B C ⨯…………………1分A B C π++=sin sin()=3sin cos A B C B C ∴=+, -------------------------3分即sin cos cos sin =3sin cos B C B C B C +cos sin =2sin cos B C B C ∴cos sin =2sin cos B CB C∴故tan =2tan CB. -------------------------5分 (II )(法一)由A B C π++=,得tan()tan()3B C A π+=-=-, 即tan tan 31tan tan B C B C +=--⨯, 将tan 2tan C B =代入得:23tan 312tan BB=--,-------------------------7分 解得tan 1B =或1tan 2B =-, 根据tan 2tan C B =得tan tan C B 、同正,所以tan 1B =,tan 2C =. …………………8分 则tan 3A =,可得225310sin sin sin 2510B C A ===,,, 代入正弦定理可得3=3102102b ,∴5b =,………………10分 所以1125sin 353225ABC S ab C ∆==⨯⨯⨯=.-------------------------12分 (法二)由A B C π++=得tan()tan()3B C A π+=-=-,即tan tan 31tan tan B C B C +=--⨯, 将tan 2tan C B =代入得:23tan 312tan BB=--,-------------------------7分 解得tan 1B =或1tan 2B =-,根据tan 2tan C B =得tan tan C B 、同正, 所以tan 1B =,tan 2C =.………………8分 又因为3cos 3a b C ==,所以cos 1b C =,∴cos 3ab C =cos tan 6ab C C ∴=. -------------------------10分 11sin 6322ABC S ab C ∆∴==⨯=.-------------------------12分18.DABE CP解析:(1)在矩形ABCD 中,:2:1AB BC =,且E 是AB 的中点,∴tan ∠ADE =tan ∠2CAB =……………1分 ∴∠ADE =∠CAB ,∵∠CAB +∠DAC 90=,∴∠ADE +∠DAC 90=,即AC ⊥DE .…………3分 由题可知面PAC ⊥面ABCD ,且交线为AC ,∴DE ⊥面PAC .∴…………5分 (2) 解法一:令AC 与BD 交于点O ,∵PA PC =,且O 是AC 的中点,∴PO AC ⊥. ∵面PAC ⊥面ABCD ,∴PO ⊥面ABCD .取BC 中点F ,连接,OE OF ,因为底面ABCD 为矩形,所以OE OF ⊥. 建立如右图所示的空间直角坐标系:(1,(1,),(0,0,),A B D P a -(1,2,)AP a =-……………6分设PBD 面的法向量为111(,,)c x y z =,(2,DB =,(0,0,)OP a =由11102000c DB x az c OP ⎧⎧•=+=⎪⎪⇒⎨⎨=•=⎪⎪⎩⎩,111x y ==-令则∴PBD 面的法向量为(21,0)c =-,由61c AP a c AP•=⇒=…………8分 设平面PAD 的法向量为222(,,),(2,0,0)m x y z AD ==-,(AP =-由222220000x m AD xz m AP -=⎧⎧•=⎪⎪⇒⎨⎨-++=•=⎪⎪⎩⎩221,y z ==令则(0,1,m ∴=设平面PAB 的法向量为333(,,)n x y z =,(0,22,0),(1,AB AP ==-由3333333001,0, 1.00n AB x y z n AP x z ⎧⎧=•=⎪⎪⇒⇒===⎨⎨•=-+=⎪⎪⎩⎩令则(1,0,1)n ∴=……………………………10分23cos 332m n m nθ•-===-∴二面角D PA B --的余弦值为3-……………12分 解法二:令AC 与BD 交于点O ,过点A 作AH BD ⊥于点H ,连结PH , ∵PA PC =,且O 是AC 的中点,∴PO AC ⊥. ∵面PAC ⊥面ABCD ,∴PO ⊥面ABCD .DABECOPHF∴PO AH ⊥,∵AH BD ⊥,∴AH ⊥面PBD . ∴∠APH 为PA 与面PBD 所成的角. …………………7分 ∴sin ∠6AH APH PA ==,∵223AH =, ∴2PA PB PC PD ====.……………8分取PA 的中点F ,连结,FD FE .∵2PA AD PD ===,∴PA FD ⊥在AB △P 中,2PA PB ==,22AB =,∴222PA PB AB +=,即PA PB ⊥∵,E F 分别是,AB AP 的中点,∴EF ∥PB ,∴PA FE ⊥. 所以∠DFE 是二面角D PA B --的平面角. ……………10分 在DFE △中,∵3FD =,6ED =1FE =.∴cos ∠33DFE =-∴二面角D PA B --的余弦值为33-……………12分 19.解:(1)由茎叶图可知抽取的10户中用水量为一阶的有2户,二阶的有6户, 三阶的有2户。
2016石家庄第二中学高三联考第三期模拟仿真理数答案
石家庄二中第三期月考理数答案一.选择题 ADACB BABBC BC11.【解析】B.,为函数的一个极值点,所以有,设,若,则,有,,在两侧不变号,故一定不成立。
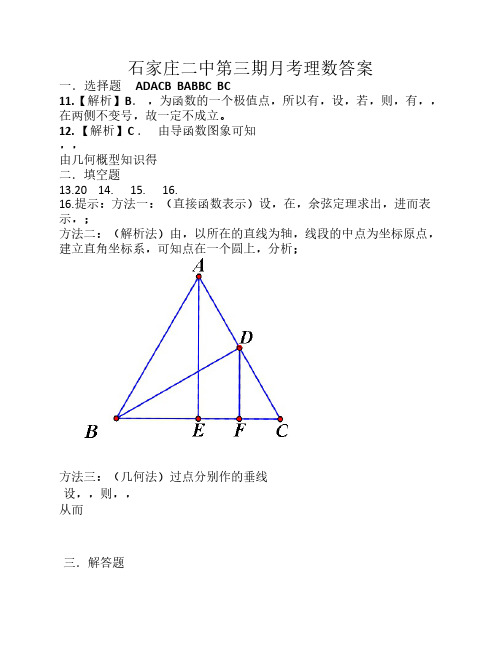
12. 【解析】C .由导函数图象可知,,由几何概型知识得二.填空题13.20 14. 15. 16.16.提示:方法一:(直接函数表示)设,在,余弦定理求出,进而表示,;方法二:(解析法)由,以所在的直线为轴,线段的中点为坐标原点,建立直角坐标系,可知点在一个圆上,分析;方法三:(几何法)过点分别作的垂线设,,则,,从而三.解答题课外体育不达标课外体育达标合计男 603090女9020110合计1505020017. (Ⅰ)由(Ⅱ)当为奇数时当为偶数时(或18 .解答:(Ⅰ)所以在犯错误的概率不超过的前提下不能判断 “课外体育达标”与性别有关.(Ⅱ)由表中数据可得,抽到“课外体育达标”学生的频率为0.25,将频率视为概率,.19.解:(I)证明:(II)如图以为原点,所在的直线为x轴,所在的直线为z轴,y轴∥,建立空间直角坐标系,则,的法向量;设平面的法向量为,则,不妨取,,平面与所成二面角为,20.(I)解:设点,的坐标分别为,设P点坐标为,由题意:可得:,又以的轨迹方程为;(II)设直线的斜率为,易得直线的斜率为,直线的方程:;的方程:,将代入直线中,可得,点作标,,所以直线垂直,所以过三点的圆是以的中点为圆心,为直径的圆,由对称性,若过定点,定点必在轴上,且定点与点关于对称,可得定点坐标为21.解:(1)记则,因为,则由得到(i)当,即时,在上是单调减函数,在上是单调增函数,所以(ii)当,即时,在上是单调减函数,在上是单调减函数,在上是单调增函数,且所以综上,(2) 证明如下:不防设由(1)可知,当时,,又,所以故,即,;又,由(1)知,在上也只有一个零点;故,即,可得所以,令,分析易得,即,由在上单减,可得:即。
(3)不防设,由(1)知,若,在上是单调增函数,不满足题意,故,因此,且,①当时,有:代入表达式可解得,所以,所以;②当时,有:代入表达式可解得,所以,所以;令,令,则,所以,所以,综上所述,得证。
【解析】河北南宫一中2016届高三理科实验班第三次周模拟测试数学试题 Word版含解析[ 高考]
![【解析】河北南宫一中2016届高三理科实验班第三次周模拟测试数学试题 Word版含解析[ 高考]](https://img.taocdn.com/s3/m/4daf452390c69ec3d5bb753c.png)
南宫一中2016届高三理科实验班第三次周模拟测试数学试题一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的1. 已知集合{}|12M x x =-<<,{}|N x x a =<,若M N ⊆,则实数a 的取值范围是( )A. ()2,+∞B. [2,)+∞C. (),1-∞-D. (,1]-∞- 【答案】B【解析】由题意得{}|20{|2}M x x x x =-<=<,因为M N ⊆,所以2a ≥故选B. 2. 已知i 是虚数单位,m 和n 都是实数,且(1)7m i ni +=+,则m nim ni+=-( )A .1-B .1C .i -D .i 【答案】D【解析】因为m 和n 都是实数,且(1)7m i ni +=+,所以可得:7m mi ni +=+,解得7,7m n ==,所以7777m ni ii m ni i++==--,故选D.3.已知数列的A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件【答案】A【解析】若a n ,a n+1,a n+2(n ∈N +)成等比数列,则a n+12=a n a n+2成立,当a n =a n+1=a n+2=0时,满足a n+12=a n a n+2成立,但a n ,a n+1,a n+2(n ∈N +)成等比数列不成立,‘ 故a n ,a n+1,a n+2(n ∈N +)成等比数列是“a n+12=a n a n+2”的充分不必要条件,故选:A 4.已知等差数列{}n a 且()()48231310753=++++a a a a a ,则数列{}n a 的前13项和为 A.24 B.39 C.52 D.104 【答案】C【解析】因为()()3571013410732661248a a a a a a a a ++++=+==,所以74a =,则1371352S a ==,所以选C. 5. 设z x y =+,其中实数,x y 满足2000x y x y y k +≥⎧⎪-≤⎨⎪≤≤⎩,若z 的最大为6,则z 的最小值为A.3-B.2-C.1-D.0 【答案】A【解析】作出不等式对应的平面区域,由z=x+y ,得y=﹣x+z ,平移直线y=﹣x+z ,由图象可知当直线y=﹣x+z 经过点A 时,直线y=﹣x+z 的截距最大, 此时z 最大为6.即x+y=6.经过点B 时,直线y=﹣x+z 的截距最小,此时z 最小. 由得,即A (3,3),∵直线y=k 过A ,∴k=3.由,解得,即B (﹣6,3).此时z 的最小值为z=﹣6+3=﹣3,故选:A .6 已知实数,x y 满足⎪⎩⎪⎨⎧≥++≥+-≤-010102y x y x y x ,则y x z +=2的最大值为A .2-B .1-C .0D .4【答案】D 【解析】由2010x y x y -=⎧⎨-+=⎩得(1,2)2010x y x y -=⎧⎨++=⎩得(-13,43)1010x y x y -+=⎧⎨++=⎩得(-1,0)由题意得最大值为2*1+2=47.如图, 一个四棱锥的底面为正方形,其三视图如图所示,则这个四棱锥的侧面积为A .2B .6 C. D.2++【答案】C2,与这条棱相对的另一条棱的长为,剩余两条侧棱长为,可求得这个四棱锥的侧面积为+,故选C.8()m M ,1()0>m 到其焦点的距离为5,双曲线,若双曲线的一条渐近线与直线AM 平行,则实数=aA.B. C . D. 【答案】A【解析】因为抛物线的准线为2p x =-,则有152p+=,得p=8,所以m=4,又双曲线的左顶点坐标为=,解得19a =,所以选A.9.设函数()f x 是定义在R 上的奇函数,当0x >时,()23,xf x x =+-则()f x 的零点个数为( )A .1B .2C .3D .4 【答案】C【解析】∵函数f (x )是定义域为R 的奇函数, ∴f (0)=0,所以0是函数f (x )的一个零点 当x >0时,令f (x )=e x +x-3=0,则e x =-x+3,分别画出函数y=e x ,和y=-x+3的图象,如图所示,有一个交点,所以函数f (x )有一个零点,又根据对称性知,当x<0时函数f(x)也有一个零点.综上所述,f(x)的零点个数为3个,故选C.10.2015年开春之际,六中食堂的伙食在百升老师的带领下进行了全面升级.某日5名同学去食堂就餐,有米饭,花卷,包子和面条四种主食.每种主食均至少有一名同学选择且每人只能选择其中一种.花卷数量不足仅够一人食用,甲同学因肠胃不好不能吃米饭,则不同的食物搭配方案种数为A. 96B. 120C. 132D.240【答案】C【解析】分类讨论:甲选花卷,则有2人选同一种主食,方法为=18,剩下2人选其余主食,方法为=2,共有方法18×2=36种;甲不选花卷,其余4人中1人选花卷,方法为4种,甲包子或面条,方法为2种,其余3人,若有1人选甲选的主食,剩下2人选其余主食,方法为3=6;若没有人选甲选的主食,方法为=6,共有4×2×(6+6)=96种,故共有36+96=132种,故选:C.11.如图,矩形ABCD中,AB=2AD,E为边AB的中点,将△ADE沿直线DE翻折成△A1DE.若M为线段A1C的中点,则在△ADE翻折过程中,下面四个命题中不正确的是A.|BM|是定值B.点M在某个球面上运动C.存在某个位置,使DE⊥A1 CD.存在某个位置,使MB//平面A1DE【答案】C【解析】取CD中点F,连接MF,BF,则MF∥DA1,BF∥DE,∴平面MBF∥平面A1DE,∴MB∥平面A1DE,故D正确由∠A1DE=∠MNB,MN=A1D=定值,NB=DE=定值,由余弦定理可得MB 2=MN 2+NB 2﹣2MN •NB •cos ∠MNB ,所以MB 是定值,故A 正确. ∵B 是定点,∴M 是在以B 为圆心,MB 为半径的圆上,故B 正确, ∵A 1C 在平面ABCD 中的射影为AC ,AC 与DE 不垂直, ∴存在某个位置,使DE ⊥A 1C 不正确.故选:C .12.设 ()ln f x x =,若函数 ()()g x f x ax =-在区间(0,4)上有三个零点,则实数a 的 取值范围是(A) 10,e ⎛⎫ ⎪⎝⎭ (B) ln 2,2e ⎛⎫ ⎪⎝⎭ ( C) ln 21,2e ⎛⎫⎪⎝⎭ (D) ln 20,2⎛⎫⎪⎝⎭【答案】C【解析】即方程ln x ax =区间(0,4)上有三个根,令()()1ln h x x h x x '=⇒=,由h(x)在()00,ln x x 处切线()0001ln y x x x x -=-过原点得0x e =,即曲线h(x)过原点得切线斜率为1e ,而点()4,ln 4与原点确定的直线的斜率为ln 22所以实数a 的 取值范围是ln 21,2e ⎛⎫⎪⎝⎭,故选 C. 二、填空题:本大题共4小题,每小题5分.13、已知函数()2cos ()1(0,0,0)2f x A wx A w πϕϕ=++>><<的最大值为3,()f x 的图象与y 轴的交点坐标为(0,2),其相邻两条对称轴间的距离为2,则()()()122015f f f +++=【答案】4030【解析】∵函数f (x )=Acos 2(ωx+φ)+1=A•+1=cos (2ωx+2φ)+1+ (A >0,ω>0,0<φ<)的最大值为3,∴+1+=3,∴A=2.根据函数图象相邻两条对称轴间的距离为2,可得函数的最小正周期为4,即=4,∴ω=.再根据f (x )的图象与y 轴的交点坐标为(0,2),可得 cos (2φ)+1+1=2,∴cos2φ=0,2φ=,∴φ=.故函数的解析式为 f (x )=cos (x+)+2=﹣sinx+2,∴f (1)+f (2)+…+f(2014)+f (2015)=﹣(sin +sin+sin+…+sin+sin)+2×2015=503×0﹣sin﹣sin﹣sin+4030=0+4030=4030,故答案为:4030.14、若双曲线()222210,0x y a b a b -=>>的一个焦点到一条渐近线的距离等于焦距的14,则该双曲线的离心率为 。
石家庄市高中毕业班第二次数学模拟考试答案.doc

参考答案一、选择题1.C2.D3.A4.A5.A6.B7.B8.A9.D 10.D二、填空题11.16π 12.92 13.2+1 14.625.(理)48(文)240 三、解答题16.(理)解:∵z1·z2=(a+bi)(cosA+icosB)=(acosA -bcosB)+i(bcosA+acosB),3分且z1·z2的对应点在复平面的虚轴上,∴分6 )2(,0cos cos )1(,0cos cos ⎩⎨⎧≠+=-B a A b B b A a 对①式利用余弦定理,得 a·,022222222=-+⋅--+acb c a b bc a c b (或用正弦定理均可以) 即(a2-b2)(c2-a2-b2)=0∴a=b或c2=a2+b2. 10分这两种情形都有A 、B ∈(0,2π),因而都满足②, ∴△ABC为等腰三角形或直角三角形.11分(文)解:∵z1·z2=(a+bi)(sinA+isinB)=(asinA- bsinB)+i(bsinA+asinB), 4分且z1·z2在复平面上对应的点恰好在虚轴上,∴分6 )2(,0cos cos )1(,0cos cos ⎩⎨⎧≠+=-B a A b B b A a 对①式利用正弦定理得a2-b2=0,即a=b.此时A 、B ∈(0,2π),满足②, ∴△ABC为等腰三角形.11分17.解:(Ⅰ)设P (x ,y )为C 2上任意一点,点P 关于点A 的对称点为M (x′,y′)则有⎪⎪⎩⎪⎪⎨⎧=+=+.12',22'y y x x 即(*).2',4'⎩⎨⎧-=-=x y x x 2分 ∵点M 在C1上,∴y′=x′+'1x . 将(*)代入上式,整理得y=x-2+41-x即g (x )=x -2+41-x .6分 (Ⅱ)原不等式为loga (x-2+41-x )<loga 29,当0<a<1时,上面不等式⎪⎪⎩⎪⎪⎨⎧-+--+-⇔(2) .29412(1) ,0412φφx x x x 2-⇔x +41-x 29φ04)29)((φ---⇔x x b x 解得4<x<29或x>6. 9分 当a>1时,不等式⇔⇔⎪⎪⎩⎪⎪⎨⎧-----⇔⎪⎪⎩⎪⎪⎨⎧-+--+-.04)29)(6(04)3(.29412,04122πφπφx x x x x x x x x .629.62944πππππφx x x x ⇔⎪⎩⎪⎨⎧或 综上,当0<a<1时不等式的解集为{x|4<x<29或x>6}; 当a>1时不等式的解集为{x|29<x<6}.12分 18.(Ⅰ)解:连结B 1C,∵四边形B1BCC1为平行四边形,∴F 为B 1C的中点,又E 是AB 1的中点,∴EF∥AC,∴EF∥平面ABC. 3分(Ⅱ)证明:∵AB=CC1,∴AB=BB1.又∵三棱柱ABC—A1B1C1为直三棱柱,∴四边形ABB 1A 1为正方形, 5分连结A1B,则AB1⊥A1B,又∵AB1⊥BC1,∴AB1⊥平面A1BC1, 6分∴AB1⊥A1C1.又∵A1C1⊥AA1,∴A1C1⊥平面A1ABB1,∴A1C1⊥AB.(Ⅲ)解:∵A1B1∥AB∴A1B1∥平面ABC1故A1到平面ABC1的距离即为B 1到平面ABC1的距离 9分由(Ⅰ)知A1B1⊥平面A A1C1C∴AB⊥平面AA1C1C∴平面ABC1⊥平面AA1C1C平面ABC1∩平面AA1C1C=AC1.过A 1作A1G⊥AC1于G ,则A1G⊥平面ABC 1,即A1G就是点B 1到平面ABC 1的距离. 在Rt△A1AC1中 AC1·AG=AA1·A1C1. ∴222a b a -+·A1G=a·22a b -∴A1G=ba b a 22- ∴B1到平面ABC的距离为ba b a 22- 12分 19.解:(Ⅰ)设C0=0.25克/米3,又C1=0.249875克/米3 2分则C 1·2×106=C0·2×106-q·C0解得:q=1000(米3) 4分(Ⅱ)依已知条件得: Cn +1=n C 66102)1000102(⨯-⨯ n 6分 ∴9995.0102)1000102(661=⨯-⨯=+n n C C ∴数列{C n }为等比数列,其首项C1=0.249875,公比为0.9995. 8分∴Cn =0.249875×(0.9995)n -1=0.25×(0.9995)n . 9分(Ⅲ)欲使水库中该种污染物浓度不超过0.05克/米3,当且仅当0.25×(0.9995)n ≤0.05,解得:n≥3495.即需要3495天可以达标. 12分20.(Ⅰ)解:由f (-1)=0得a -b +c =0,①令x=1有f (1)-1≥0和f(1)≤(211+)2, 所以f (1)=1. 3分(Ⅱ)解:由(Ⅰ)得a +b +c =1,②联立①、②可得b=a+c=21.③ 由题意知,对于任意实数x ,都有f(x)-x≥0,即ax2-21x+c≥0对任意实数x 恒成立. 于是a>0且Δ≤0,即ac≥161.④ 故c>0. 7分由③、④得a+c≥2ac ≥2×41=21,则a=c=41,故a=c=,41b=21. 9分 (Ⅲ)由(Ⅱ)得:g (x )=f (x )-mx =41x 2+(21-m)x+41=41[x2+(2-4m)x+1]. 12分又x∈[-1,1]时,函数g (x )是单调的, 所以|-242m -|≥1, 解得:m≤0或m≥1.故m 的取值范围是m≤0或m≥1. 14分21.解:(Ⅰ)抛物线y2=8(x+2)的焦点坐标为(0,0).准线方程为x=-4. 2分 设椭圆短轴的端点为B (x ,y ).则c =x ,b =|y |,∴a=22y x +,e=a c =22yx x +, 4分 由定义得:,42222y x xx y x +=++ 化简整理得:y2=4x(x>0).所以椭圆短轴端点B 的轨迹为一抛物线,但不包括其顶点,其方程为y2=4x(x>0) 7分(Ⅱ)设A ().,4(),,4(),,42222121y y M y y B y y 则kMA =,44412121y y y y y y +=-- =MB k ,44422222y y y y y y +=-- ∵MA⊥MB.∴kMA ·kMB =-1. ∴,14421-=+⋅+y y y y 化简得:y2+(y1+y2)y+y1y2+16=0① 10分又直线AB 方程为:y=3(x-1), 联立⎪⎩⎪⎨⎧=-=.4),1(32x y x y消去x得:034432=--y y.4,342121-==+∴y y y y 12分代入①式得y2+34y+12=0.∵Δ=(34)2-48<0.∴方程②无解.故不存在点M 满足题意. 14分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2016年石家庄市第二次模拟考试试题答案数学理科一、选择题1-5 BAACB 6-10CABBA 11-12CC 二、填空题 13.5414. 240 15. -616. 1或9三、解答题 17.(I )由正弦定理2sin sin sin a b cR A B C ===可得: 2s i n =32s i n c o R A R B C ⨯…………………1分A B C π++=sin sin()=3sin cos A B C B C ∴=+, -------------------------3分即sin cos cos sin =3sin cos B C B C B C +cos sin =2sin cos B C B C ∴ c o s s i n=2sin cos B C B C∴故tan =2tan CB. -------------------------5分 (II )(法一)由A B C π++=,得tan()tan()3B C A π+=-=-,即tan tan 31tan tan B C B C +=--⨯, 将tan 2tan C B =代入得:23tan 312tan BB=--,--------------------7分解得tan 1B =或1tan 2B =-,根据tan 2tan C B =得tan tan C B 、同正, 所以tan 1B =,tan 2C =. …………………8分则tan 3A =,可得sin sin sin 2510B C A ===,∴b =10分所以11sin 33225ABC S ab C ∆==⨯=.-------------------------12分 (法二)由A B C π++=得tan()tan()3B C A π+=-=-,即tan tan 31tan tan B C B C +=--⨯, 将tan 2tan C B =代入得:23tan 312tan BB=--,-------------------------7分解得tan 1B =或1tan 2B =-,根据tan 2tan C B =得tan tan C B 、同正, 所以tan 1B =,tan 2C =.………………8分 又因为3cos 3a b C ==,所以cos 1b C =, ∴cos 3ab C =cos tan 6ab C C ∴=. -------------------------10分11sin 6322ABC S ab C ∆∴==⨯=.-------------------------12分 18.DA BE CP解析:(1)在矩形ABCD中,:AB BC =,且E 是AB 的中点, ∴tan ∠ADE =tan∠CAB =……………1分 ∴∠ADE =∠CAB ,∵∠CAB +∠DAC 90= ,∴∠ADE +∠DAC 90=,即AC ⊥DE .…………3分由题可知面PAC ⊥面ABCD ,且交线为AC ,∴DE ⊥面PAC .∴…………5分 (2) 解法一:令AC 与BD 交于点O ,∵PA PC =,且O 是AC 的中点,∴PO AC ⊥. ∵面PAC ⊥面ABCD ,∴PO ⊥面ABCD .取BC 中点F ,连接,OE OF ,因为底面ABCD 为矩形,所以OE OF ⊥. 建立如右图所示的空间直角坐标系:(1,(1(1,),(0,0,),A B D P a -(1)AP a =-……………6分设PBD面的法向量为111(,,)c x y z = ,DB = ,(0,0,)OP a =由11102000c DB x az c OP ⎧⎧∙=+=⎪⎪⇒⎨⎨=∙=⎪⎪⎩⎩,111x y =-令则∴PBD 面的法向量为1,0)c =-由13c AP a c AP∙=⇒= …………8分 设平面PAD 的法向量为222(,,),(2,0,0)m x y z AD ==-,(1AP =-由222220000x m AD x z m AP -=⎧⎧∙=⎪⎪⇒⎨⎨-+=∙=⎪⎪⎩⎩221,y z ==令则(0,1,m ∴=设平面PAB 的法向量为333(,,)n x y z = ,(1AB AP ==-由3333333001,0, 1.00n AB x y z n AP x z ⎧⎧=∙=⎪⎪⇒⇒===⎨⎨∙=-++=⎪⎪⎩⎩ 令则 (1,0,1)n ∴=……………………………10分cos m n m nθ∙===∴二面角D PA B --的余弦值为 ……………12分 解法二:令AC 与BD 交于点O ,过点A 作AH BD ⊥于点H ,连结PH , ∵PA PC =,且O 是AC 的中点,∴PO AC ⊥. ∵面PAC ⊥面ABCD ,∴PO ⊥面ABCD .DABEOPHF∴PO AH ⊥,∵AH BD ⊥,∴AH ⊥面PBD . ∴∠APH 为PA 与面PBD 所成的角.…………………7分 ∴sin ∠3AH APH PA ==,∵AH = ∴2PA PB PC PD ====.……………8分取PA 的中点F ,连结,FD FE .∵2PA AD PD ===,∴PA FD ⊥在AB △P中,2PA PB ==,AB =222PA PB AB +=,即PA PB ⊥ ∵,E F 分别是,AB AP 的中点,∴EF ∥PB ,∴PA FE ⊥. 所以∠DFE 是二面角D PA B --的平面角. ……………10分 在DFE △中,∵FD ,ED =1FE =.∴cos ∠DFE =∴二面角D PA B --的余弦值为12分 19.解:(1)由茎叶图可知抽取的10户中用水量为一阶的有2户,二阶的有6户,三阶的有2户。
第二阶梯水量的户数X 的可能取值为0,1,2,3 ………………1分30463101(0)30C C P X C ⋅=== 21463103(1)10C C P X C ⋅=== 12463101(2)2C C P X C ⋅=== 03463101(3)6C C P X C ⋅===………………………5分 EX=13110123301026⨯+⨯+⨯+⨯95= ……………………………6分 (2)设Y 为从全市抽取的10户中用水量为二阶的家庭户数,依题意得Y ~B 3(10)5,, 所以101032()()()55kkkP Y k C -==,其中0,1,2,,10k =L ………………8分设101011111032()()()3(11)55(1)2()()55k k k k k k C P Y k k t P Y k k C ----=-====- …………………10分 若1t >,则 6.6k <,(1)()P Y k P Y k =-<=; 若1t <,则 6.6k >,(1)()P Y k P Y k =->=。
所以当6k =或7,()P Y k =可能最大,664107731032()()(6)755132(7)6()()55C P Y P Y C ===>= 所以n 的取值为6。
………………12分20.解析:(1)120000(,)(,)DF DF c x y c x y ∙=----- 22222220002c x c y x b c a=-+=+-,………2分因为2200x a ≤≤,所以当220x a =时,12DF DF ∙ 得最大值2b .………………………………3分 所以224a b =,故离心率2e =4分(2)由题意知1b =,可得椭圆方程为:2214x y +=, 设1122(,),(,),(,)B x y C x y H x y由2244y kx m x y =+⎧⎨+=⎩,得222(14)84(1)0k x kmx m +++-=, 122814kmx x x k -+=+,21224(1)14m x x k-=+ ……………………………6分 由0AB C ∙=A 得:1212(1)(1)0x x y y +--=即221212(1)(1)()(1)0k x x k m x x m ++-++-=,……………………………8分将韦达定理代入化简可得:35m =-……………………………10分 所以直线BC 的方程为:35y kx =-,即直线BC 恒过定点3(0,)5D -由AH ⊥DH 可知,点H 的轨迹为以AD 为直径的圆,圆心1(0,)5,半径为45故动点H 的轨迹方程为22116()(1)525x y y +-=≠……………………………12分 21. 解析:(Ⅰ)当1k =时,()(1)(1)xf x e x =--,(1)0f =,(1)1f e '=-所以在(1,(1))f 处的切线方程是(1)(1)y e x =--………………………2分 所证问题等价于(1)(1)(1)(1),(1)x e x e x x -->--≠…………………………3分 即()(1)0,(1)x e e x x -->≠当1x >时,0,10,()(1)0x x e e x e e x ->->--> 当1x <时0,10,()(1)0x x e e x e e x -<-<--> 命题得证!…………………………5分(Ⅱ)当2k =时,2()(1)(1)x f x e x =--,(2,)x ∈+∞2()(1)2(1)(1)(1)[(1)2]x x x f x e x e x x e x '=-+--=-+-……………………6分因为(2,)x ∈+∞(1)0,(1)2,()0xx e x f x '->+->> 即函数在(2,)x ∈+∞单调递增………………………8分 设3213322112),(),,(),,(x x x y x C y x B y x A <<<,且,∴123()()()f x f x f x <<.∵)),()(,()),()(,(23232121x f x f x x x f x f x x --=--= ∴))()())(()(())((23212321x f x f x f x f x x x x BC BA --+--=⋅. ··········· 10分∵,0)()(,0)()(,0,023212321>-<->-<-x f x f x f x f x x x x ∴B B ∠<∴<⋅,0cos ,0为钝角. 故△ABC 为钝角三角形.…………12分(注意:利用图象说明,需画图准确,说明充分,可给四分;只画图,不说明,给2分)选做题22.(I )证明: 在O 中,弦AC BF 、相交于E ,FE EB AE EC ∴⋅=⋅,又E 为AC 的中点,所以2FE EB AE ⋅=,-------------------------2分又因为OA AD ⊥,OE AE ⊥,根据射影定理可得2AE DE EO =⋅,-------------------------4分 ∴DE EO FE EB ⋅=⋅, ------------------------5分(II )因为AB 为直径,所以0=90C ∠,又因为o 45CBE ∠=,所以BCE ∆为等腰直角三角形. ………………6分 2AC BC ∴=,根据勾股定理得222580AC BC BC +==,解得4BC =,---------------------8分所以42AE OE ==,,由(I )得2AE DE EO =⋅所以8DE =,所以AD == ------------------------10分23解:(I)由2cos ρθθ,得22cos sin ρθθ,………………2分∴曲线1C的直角坐标方程为2x =, -----------------------------------4分(II )将=3πα代入22cos :2sin x C y αα=⎧⎨=⎩得(1P ,由题意可知切线AB 的倾斜角为56π, --------------------------6分 设切线AB的参数方程为112x y t ⎧=⎪⎪⎨⎪=⎪⎩(t 为参数),代入2x得:21(1))22t -=,即232042t --=, --------------------------8分设方程的两根为1t 和2t 可得:12t t +=所以12||||2t t MP +==分 24解:(I )()|||||()()|f x x a x b x a x b a b =--+≤--+=+,--------------------------2分所以()f x 的最大值为a b +,3a b ∴+=,--------------------------4分(II )当x a ≥时,()||||=()3f x x a x b x a x b a b =--+--+=--=-, --------------------------6分对于x a ∀≥,使得()()g x f x <等价于x a ∀≥,max ()3g x <-成立,()g x 的对称轴为2a x a =-<, ∴()g x 在[,)x a ∈+∞为减函数,()g x ∴的最大值为222()23g a a a b a a =---=-+-,--------------------------8分2233a a ∴-+-<-,即220a a ->,解得0a <或12a >, 又因为0,0,3a b a b >>+=,所以132a <<.--------------------------10分。
