一线三角与全等三角形B4
第7讲 一线三等角模型与全等三角形

第7讲一线三等角模型与全等三角形基本模型1如下图,AB=AC,BD⊥DE,AB⊥AC,CE⊥DE,则△ADB≡△CEA规律:含有等腰直角三角形的条件,通常可以构造一线三垂直,利用全等三角形进行边角的等量转化。
练习:如图,A(3,0),C(0,6),AC⊥BC,且AC=BC,求点B的坐标。
变式2如图,已知B(4,0),C(0,2),AC⊥BC,AC=BC,求点A的坐标变式3如图,△ABC中,AC=BC,∠ACB=90°,C在X轴上,BC交Y轴于M,BM=CM,C(-1,,0),点A的横坐标为-3,求点B的坐标练习(武汉第三寄宿中学10月月考14.)如图,点C在线段AB上,DA⊥AB,EB⊥AB,FC⊥AB,且DA=BC,EB=AC,FC=AB,∠AFB=49︒则∠DFE=____︒分析:构造三垂直:△ADB≌△CBF,∴DB=BF,DB⊥BF,∠DFB=45°∵BE=AC,FC=AB,∴△ACF≌△EBA,AE=AF,AE⊥AF,∠AFE=45°∴∠DFE=∠AFE+∠DFB-∠AFB=45°+45°-49°=41°基本模型2:如图1,∠D=∠BAC=∠E,AB=AC则△ADB≌△CEA.如图2,∠BAC=∠BDF=∠CEF,AB=AC,则△ADB≌ACEA.图1图2教材变式1如图,点D、A、E在一条直线上,AB=AC,∠ADB=∠AEC=∠BAC=60°,试探究BD、CE与DE之间的数量关系.解:DE=DB+CE,证△ADB≌△CEA;教材变式2如图,D、A、E三点都在一条直线上,且∠BDA=∠AEC=∠BAC,AB=AC.试探究BD,CE与DE之间的数量关系。
解:∠BDA=∠BAC=α,∠DBA+∠BAD=∠BAD+∠CAE=180°-α,∴∠DBA=∠CAE,∵∠BDA=∠AEC=α,AB=AC ,∴.△ADB ≌△CEA.∴AE=BD ,AD=CE,∴DE=AE+AD=BD+CE.教材变式3如图,AB=AC.∠BAC=60°,D 、E 为AD 上两点,∠ADB=∠AEC=120°.探究BD 、CE 与DE 之间的数量关系。
全等三角形——一线三等角模型

全等三角形——一线三等角模型一、一线三等角概念“一线三等角”指的是有三个等角的顶点在同一条直线,这个角可以是直角,也可以是锐角或钝角。
二、一线三等角的类型同侧:锐角 直角 钝角异侧:三、“一线三等角”的性质当∠1=∠2=∠3,且当等角所对的边相等时,则两个三角形全等. 如右图,若 CE=ED ,则△AEC ≌△BDE. 四、“一线三等角”的应用 1.适用于直角的情况例1:在ABC Rt ∆中,︒=∠90ACB ,BC AC =,直线l 经过点C ,且l AE ⊥于点E ,l BF ⊥于点F . (1)当直线l 绕点C 旋转到如图1的位置时,○1图中有几对相等的锐角? ○2求证:AEC ∆≌CFB ∆; ○3试探究AE 、BF 、EF 之间的数量关系,并说明理由; (2)当直线l 绕点C 旋转到如图2的位置时,试探究AE 、BF 、EF 之间的数量关系,并说明理由; (3)当直线l 绕点C 旋转到如图3的位置时,试探究AE 、BF 、EF 之间的数量关系,不必说明理由.图1 图2 图3lFE B ACl FEB AC lFEBAC DCC A BDDC DBADB CAAB2.适用于锐角或钝角的情况例2:如图,在△ABC 中,AB =AC ,BD =CF ,BE =CD , 若∠A =40°,则∠EDF 的度数为( )A. 75°B. 70°C. 65°D. 60°★演练题:(勾股定理)如图,在ABC Rt ∆中,︒=∠90ACB ,BC AC =,点D 为斜边AB 上一点,连接CD ,过点A 作CD AE ⊥于点E .若︒=∠45BED ,4=AE ,则=AB ___________.练习1.如图,ABC ∆是等腰三角形,DE 过直角顶点A ,︒=∠=∠90E D ,则下列结论正确的个数有( ) ○1AE CD =; ○221∠=∠; ○3︒=∠+∠9043; ○4BE AD =; ⑤DE=CD+BE. (A )1个 (B )2个 (C )3个 (D )4个2.(1)已知△ABC 是直角三角形,∠BAC =90°,AB =AC ,直线l 经过点A ,分别从点B 、C 向直线l 作垂线,垂足分别为D 、E .当点B ,C 位于直线l 的同侧时(如图1),易证△ABD ≌△CAE .如图2,若点BC 在直线l 的异侧,其它条件不变,△ABD ≌△CAE 是否依然成立?若成立,请写出证明过程;若不成立,请说明理由.(2)变式一:如图3,△ABC 中,AB =AC ,直线l 经过点A ,点D 、E 分别在直线l 上,点B 、C 位于l 的同一侧,如果∠CEA =∠ADB =∠BAC ,求证:△ABD ≌△CAE .(3)变式二:如图4,△ABC 中,依然有AB =AC ,若点B ,C 位于l 的两侧,如果∠BDA+∠BAC =180°,∠BDA =∠AEC ,求证:BD =CE+DE .4321EB DC AEC DA。
专题十:“一线三等角”模型下的全等三角形问题解析(有答案)
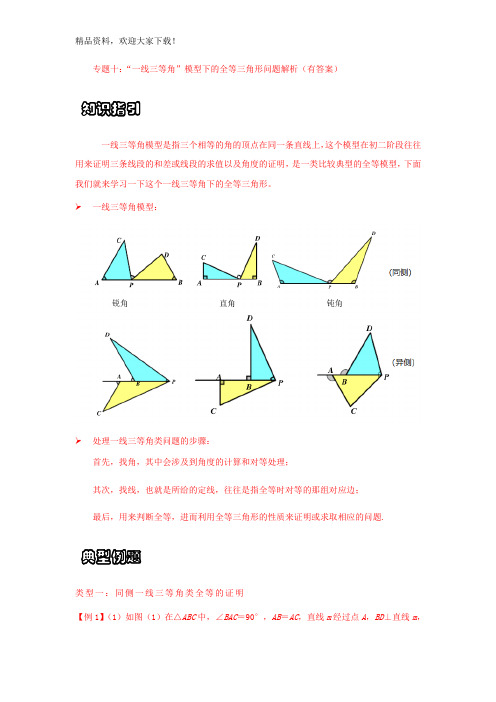
专题十:“一线三等角”模型下的全等三角形问题解析(有答案)一线三等角模型是指三个相等的角的顶点在同一条直线上,这个模型在初二阶段往往用来证明三条线段的和差或线段的求值以及角度的证明,是一类比较典型的全等模型,下面我们就来学习一下这个一线三等角下的全等三角形。
➢ 一线三等角模型:➢ 处理一线三等角类问题的步骤:首先,找角,其中会涉及到角度的计算和对等处理;其次,找线,也就是所给的定线,往往是指全等时对等的那组对应边;最后,用来判断全等,进而利用全等三角形的性质来证明或求取相应的问题.类型一:同侧一线三等角类全等的证明【例1】(1)如图(1)在△ABC 中,∠BAC =90°,AB =AC ,直线m 经过点A ,BD ⊥直线m,知识指引 典型例题CE ⊥直线m ,垂足分别为点D 、E .求证:DE =BD +CE ;(2)如图(2)将(1)中的条件改为:在△ABC 中,AB =AC ,D 、A 、E 三点都在直线m 上,并且有∠BDA =∠AEC =∠BAC =α,其中α为任意锐角或钝角.请问结论DE =BD +CE 是否成立?如成立,请给出证明;若不成立,请说明理由.【分析】(1)根据AAS 证明△ADB ≌△CEA ,得到AE =BD ,AD =CE ,即可证明;(2)同理证明△ADB ≌△CEA ,得到AE =BD ,AD =CE ,即可证明;【详解】(1)∵BD ⊥直线m ,CE ⊥直线m ,∴∠BDA =∠CEA =90°,∵∠BAC =90°,∴∠BAD +∠CAE =90°,∵∠BAD +∠ABD =90°,∴∠CAE =∠ABD ,∵在△ADB 和△CEA 中,{∠ABD =∠CAE ,∠BDA =∠CEA ,AB =AC ,∴△ADB ≌△CEA (AAS ),∴AE =BD ,AD =CE ,∴DE =AE +AD =BD +CE ;(2)∵∠BDA =∠BAC =α,∴∠DBA +∠BAD =∠BAD +∠CAE =180°﹣α,∴∠CAE =∠ABD ,在△ADB 和△CEA 中,{∠ABD =∠CAE ,∠BDA =∠CEA ,AB =AC ,∴△ADB ≌△CEA (AAS ),∴AE =BD ,AD =CE ,∴DE =AE +AD =BD +CE .类型二:异侧一线三等角类全等的证明【例2】如图,在Rt△ABC 中,AB=AC ,∠BAC=90°,直线l 为经过点A 的任一直线,BD⊥l 于D ,CE⊥AE,若BD >CE ,试问:(1)AD 与CE 的大小关系如何?请说明理由;(2)线段BD ,DE ,CE 之间的数量之间关系如何?并说明理由.【分析】(1)由已知可得AB=AC ,∠BDA=∠AEC=90°,∠BAD=∠ACE ;两角及其一角的对边对应相等的两个三角形全等,利用△ABD ≌△CAE 即可得到AD=CE ;(2)据△ABD ≌△CAE ,可得BD=AE ,AD=EC ,又AE=AD+DE ,故可得BD=DE+CE .【解答】(1)AD 与CE 的大小关系为AD=CE ,理由是:∵CE⊥l 于E ,∴∠ACE+∠EAC=90°,又∵∠BAD+∠EAC=∠BAC=90°,∴∠BAD=∠ACE;∵BD⊥l 于D ,CE⊥l 于E ,∴∠BDA=∠AEC=90°;又∵AB=AC;∴△ABD≌△CAE(AAS ),∴AD=CE.(2)线段BD ,DE ,CE 之间的数量之间关系为:BD=DE+CE ,理由如下:∵△ABD≌△CAE,∴BD=AE,AD=CE ,又∵AE=DE+AD,∴BD=DE+CE.1.如图,△ABC 中,AB ⊥BC ,AD ⊥BD ,CE ⊥BD ,AB=BC ,若CE=6,AD=2,求DE 的长.解:∵AB⊥BC,AD⊥BD,CE⊥BD,∴∠D=∠CEB=∠ABC=90°,∴∠BCE+∠CBE=90°,∠CBE+∠ABD=90°,∴∠BCE=∠ABD ,在△ADB 和△BEC 中,{∠CEB =∠D ,∠ABD =∠BCE ,AB =BC ,∴△BCE ≌△ABD (AAS ),强化练习∴BD=CE=6,BE=AD=2,∴DE=BD-BE=6-2=4,答:DE的长是4.2.已知∠ACB=90°,AC=BC,AD⊥CM,BE⊥CM,垂足分别为D,E,(1)如图1,①线段CD和BE的数量关系是;②请写出线段AD,BE,DE之间的数量关系并证明.(2)如图2,上述结论②还成立吗?如果不成立,请直接写出线段AD,BE,DE之间的数量关系.【详解】(1)①CD=BE,理由:∵AD⊥CM,BE⊥CM,∴∠ACB=∠BEC=∠ADC=90°,∴∠ACD+∠BCE=90°,∠BCE+∠CBE=90°,∴∠ACD=∠B,在△ACD和△CBE中,{∠ADC=∠BEC,∠ACD=∠B,AC=CB,∴△ACD≌△CBE,∴CD=BE.②AD=BE+DE.理由:∵△ACD≌△CBE,∴AD=CE,CD=BE,∵CE=CD+DE=BE+DE,∴AD=BE+DE.(2)②中的结论不成立. DE=AD+BE.理由:∵AD⊥CM,BE⊥CM,∴∠ACB=∠BEC=∠ADC=90°,∴∠ACD+∠BCE=90°,∠BCE+∠CBE=90°,∴∠ACD=∠B,在△ACD和△CBE中,{∠ADC=∠BEC,∠ACD=∠B,AC=CB,∴△ACD≌△CBE,∴AD=CE,CD=BE,∵DE=CD+CE=BE+AD,∴DE=AD+BE.3.如图1,AB⊥BD于B,ED⊥BD于D,点C在直线BD上且与F重合,AB=FD,BC=DE (1)请说明△ABC≌△FDE,并判断AC是否垂直FE?(2)若将△ABC 沿BD方向平移至如图2的位置时,且其余条件不变,则AC是否垂直FE?请说明为什么? 【解答】(1)AC ⊥EF ,理由:∵AB ⊥BD 于B ,ED ⊥BD ,∴∠B=∠D=90°,在△ABC 和△FDE 中,{AB =DF ,∠B =∠D ,BC =DE ,∴△ABC ≌△FDE ,∴∠A=∠EFD ,∵∠B=90°,∴∠A+∠ACB=90°,∴∠ACB+∠ECD=90°,∴∠ACE=180°-90°=90°,∴AC ⊥CE ,即AC ⊥FE .(2)AC 垂直FE ,理由是∵∠A=∠F (已证),∠ABC=∠ABF=90°,∠AMN=∠FMB ,∴∠F+∠FMB=90°,∴∠A+∠AMN=90°,∴∠ANM=180°-90°=90°,∴AC ⊥FE .4.如图,在△ABC 中,∠ACB=90°,AC=BC ,直线l 过点C ,BD⊥l,AE⊥l,垂足分别为D 、E .(1)当直线l 不与底边AB 相交时,求证:ED=AE+BD ;(2)如图2,将直线l 绕点C 顺时针旋转,使l 与底边AB 相交时,请你探究ED ,AE ,BD 三者之间的数量关系.【解析】(1)∵直线l 过点C ,BD⊥l,AE⊥l,∴∠AEC=∠BDC=90°,∵∠ACB=90°,∴∠EAC+∠ACE=90°,∠BCD+∠ACE=90°,∴∠EAC=∠BCD,在△AEC 和△CDB 中,{∠EAC =∠BCD ,∠AEC =∠BDC ,AC =BC ,∴△AEC≌△CDB(AAS ),∴CE=BD,AE=CD ,∵ED=C E+CD ,∴ED=AE+BD;(2)ED=BD ﹣AE , 理由是:∵直线l 过点C ,BD⊥l,AE⊥l,∴∠AEC=∠BDC=90°,∵∠ACB=90°,∴∠EAC+∠ACE=90°,∠BCD+∠ACE=90°,∴∠EAC=∠BCD,在△AEC 和△CDB 中,{∠EAC =∠BCD ,∠AEC =∠BDC ,AC =BC ,∴△AEC≌△CDB (AAS ),∴CE=BD,AE=CD ,∵ED=CE ﹣CD ,∴ED=BD﹣AE .5.如图,∠BCA=90°,AC=BC ,BE⊥CF 于点E ,AF⊥CF 于点F ,其中0°<∠ACF <45°.(1)求证:△BEC ≌△CFA ;(2)若AF=5,EF=8,求BE 的长;(3)连接A B ,取AB 的中点为Q ,连接QE ,QF ,判断△QEF 的形状,并说明理由..【解答】(1)∵∠BCA=∠BEC=∠F=90°,∴∠BCE+∠B=90°,∠BCE+∠ACF=90°,∴∠B=∠ACF ,在△BEC 和△CFA 中,{∠B =∠ACF ,∠BEC =∠F ,BC =A ,∴△BEC ≌△CFA .6.在△ABC 中,∠ACB =90°,AC =BC ,直线,MN 经过点C ,且AD ⊥MN 于点D ,BE ⊥MN 于点E 。
第12章全等三角形重难点专题3:一线三角模型(课件)八年级数学上册(人教版)

∴AD=CE,BD=AE∴DE=AE-AD=BD-CE
已知:在△ABC中,AB=AC,∠BAC=90° ,过点A作直线l,过B,C
分别作BD⊥l于点D,CE⊥l于点E.
(3)当直线l在△ABC的内部如图3所示时,直接写出DE, BD,CE
DE=CE-BD
三者之间的数量关系式为____________.
(1)如图1,当直线l在△ABC的外部时,求证:DE= BD+CE;
(2)当直线l在△ABC的内部如图2所示时,求证:DE=BD-CE;
(3)当直线l在△ABC的内部如图3所示时,直接写出DE, BD,CE
三者之间的数量关系式为____________.
已知:在△ABC中,AB=AC,∠BAC=90° ,过点A作直线l,过B,C
解:(1)∵BD⊥l于点D,CE⊥l于点E.
∴∠BDA=∠CEA=90°
∴∠BAD+∠ABD=180°-∠BDA=90°
∵∠BAC=90°
∴∠BAD+∠CAE=180°-∠BAC=90°
则∠ABD=∠CAE
在△BDA和△AEC中
∠ = ∠ = 90°
∵
∠ = ∠
=
“一线三等角”在初中几何中出现得比较多,是一种常见的全
等或相似模型,指的是有三个等角的顶点在同一条直线上构成全
等或相似图形.这三个等角可以是直角也可以是锐角或钝角,可
以是在直线的同侧,也可以是在直线的异侧.
已知:在△ABC中,AB=AC,∠BAC=90° ,过点A作直线l,过B,C
初中数学经典几何模型03-一线三垂直模型构造全等三角形(含答案)

初中数学经典几何模型专题03 一线三垂直模型构造全等三角形【专题说明】一线三垂直问题,通常问题中有一线段绕某一点旋转900,或者问题中有矩形或正方形的情况下考虑,作辅助线,构造全等三角形形或相似三角形,建立数量关系使问题得到解决。
【知识总结】过等腰直角三角形的直角顶点或者正方形直角顶点的一条直线。
过等腰直角三角形的另外两个顶点作该直线的垂线段,会有两个三角形全等(AAS)常见的两种图形:图1 图21、如图,在直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=3,设∠BCD=α,以D为旋转中心,将腰DC绕点D逆时针旋转90°至DE.当α=45°时,求△EAD的面积.当α=30°时,求△EAD的面积当0°<α<90°,猜想△EAD的面积与α大小有无关系,若有关,写出△EAD的面积S与α的关系式,若无关,请证明结论.2、如图,向△ABC的外侧作正方形ABDE,正方形ACFG,过A作AH⊥BC于H,AH的反向延长线与EG 交于点P,求证:BC=2AP3、已知:在△ABC中,∠BAC=90°,AB=AC,AE是多点A的一条直线,且BD⊥AE于D,CE⊥AE于点E.当直线AE处于如图1的位置时,有BD=DE+CE,请说明理由.当直线AE处于如图2的位置时,则BD、DE、CE的关系如何?请说明理由.4、如图,在△ABC中,∠ABC=45°,点F是△ABC的高AD、BE的交点,已知CD=4,AF=2,则线段BC 的长为()5、如图所示,直线α经过正方形ABCD的顶点A,分别过顶点B,D作DE⊥α于点F,若DE=4,BF=3,则EF的长为()6、如图,矩形ABCD中,E在AD上,且EF⊥EC,EF=EC,DE=2,矩形的周长为16,则AE的长是()7、如图,在△ABC中,∠A=90°,AB=AC,∠ABC的平分线BD交AC于D,CE⊥BD的延长线于点E,求BD证:CE=12【基础训练】1、如图,在平面直角坐标系中,等腰R t△ABC有两个顶点在坐标轴上,求第三个顶点的坐标.2、已知点P为∠EAF平分线上一点,PB⊥AE于点B,PC⊥AF于C,点M、N分别是射线AE、AF上的点.如图1,当点M在线段AB上,点N在线段AC的延长线上,且PM=PN,求证BM=CN.在(1)的条件下,直接写出线段AM、CN与AC的数量关系_______3、如图,在△ABC中,AB=AC=2,∠B=∠C=40°,点D在线段BC上运动(D不与B,C重合),连接AD,作∠ADE=40°,DE交线段AC于点E.当DC等于多少是,△ABD≌△DCE?请证明你的结论.4、如图,在△ABC中,AB=AC,∠A=90°,点D在线段BC上,∠BDE=1∠C,BE⊥DE,垂足为E,DE与AB2DF.交于点F,求证:BE=125、已知:在等腰直角△ABC中,∠BAC=90°,AB=AC,E是AC边上的点,AF⊥BE交BC于点D,如果AE=CD 证明:BF平分∠ABC证明:AB+AE=BC【巩固提升】1、如图,AB⊥BD于点B,CD⊥BD于点D,P是BD上一点,且AP=PC,AP⊥PC,求证:△ABP≌△PDC2、如图,二次函数y=x2+bx+c的图象与x轴交于点A(-1,0)和点B(3,0),与y轴交于点N,以AB 为边在x轴上作正方形ABCD,点P是x轴上一动点,连接CP,过点P作CP的垂线与y轴交于点E。
第12章:一线三等角与全等三角形

第12章:一线三等角与全等三角形-CAL-FENGHAI.-(YICAI)-Company One12一线三等角与全等三角形一、一线三等角概念“一线三等角”指的是有三个等角的顶点在同一条直线,这个角可以是直角,也可以是锐角或钝角。
二、一线三等角的类型同侧:锐角 直角 钝角异侧:三、“一线三等角”的性质当∠1=∠2=∠3,且当等角所对的边相等时,则两个三角形全等. 如右图,若 CE=ED ,则△AEC ≌△BDE. 四、“一线三等角”的应用 1.适用于直角的情况例1:在ABC Rt ∆中,︒=∠90ACB ,BC AC =,直线l 经过点C ,且l AE ⊥于点E ,l BF ⊥于点F .(1)当直线l 绕点C 旋转到如图1的位置时,○1图中有几对相等的锐角 ○2求证:AEC ∆≌CFB ∆; ○3试探究AE 、BF 、EF 之间的数量关系,并说明理由; (2)当直线l 绕点C 旋转到如图2的位置时,试探究AE 、BF 、EF 之间的数量关系,并说明理由; (3)当直线l 绕点C 旋转到如图3的位置时,试探究AE 、BF 、EF 之间的数量关系,不必说明理由.图1 图2 图3lFE BACl FEBAC lFEBAC DCCDC D BADB CAAB3巩固提高1:1.如图,ABC ∆是等腰三角形,DE 过直角顶点A ,︒=∠=∠90E D ,则下列结论正确的个数有( )○1AE CD =; ○221∠=∠; ○3︒=∠+∠9043; ○4BE AD =. (A )1个 (B )2个 (C )3个 (D )4个2.适用于锐角或钝角的情况例2:如图,在△ABC 中,AB =AC ,BD =CF ,BE =CD ,若∠A =40°,则∠EDF 的度数为( )A.75°B.70°C.65°D.60° ?演练题:1.如图,在ABC Rt ∆中,︒=∠90ACB ,BC AC =,直线l 经过点C ,且l AE ⊥于点E ,l BF ⊥于点F .若25=AB ,4=AE ,则=EF __________.2.如图,在ABC Rt ∆中,︒=∠90ACB ,BC AC =,点D 为斜边AB 上一点,且CD AE ⊥于点E ,CD BF ⊥交CD 的延长线于点F .若2:1:=AE BF ,4=AE ,则=AB _________.3.如图,在ABC Rt ∆中,︒=∠90ACB ,BC AC =,点D 为斜边AB 上一点,连接CD ,过点A 作CD AE ⊥于点E .若︒=∠45BED ,4=AE ,则=AB ___________.4321EB DC Al F EBACEC DBAEC DAB4.(1)已知△ABC是直角三角形,∠BAC=90°,AB=AC,直线l经过点A,分别从点B、C向直线l作垂线,垂足分别为D、E.当点B,C位于直线l的同侧时(如图1),易证△ABD≌△CAE.如图2,若点BC在直线l的异侧,其它条件不变,△ABD≌△CAE是否依然成立若成立,请写出证明过程;若不成立,请说明理由.(2)变式一:如图3,△ABC中,AB=AC,直线l经过点A,点D、E分别在直线l上,点B、C 位于l的同一侧,如果∠CEA=∠ADB=∠BAC,求证:△ABD≌△CAE.(3)变式二:如图4,△ABC中,依然有AB=AC,若点B,C位于l的两侧,如果∠BDA+∠BAC =180°,∠BDA=∠AEC,求证:BD=CE+DE.5.如图(1),AB=4cm,AC⊥AB,BD⊥AB,AC=BD=3cm.点P在线段AB上以1cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动.它们运动的时间为t(s).(1)若点Q的运动速度与点P的运动速度相等,当t=1时,△ACP与△BPQ是否全等,请说明理由,并判断此时线段PC和线段PQ的位置关系;4。
建构数学模型 深化解题策略——以“一线三等角全等”模型为例

技法点拨互成60°角的大小相等的两个水平恒力F 作用下,经过一段时间,物体获得的速度为v ,在力的方向上获得的速度分别为v 1、v 2,总位移为s 。
W 合=3Fs =12mv 2v 1=v2W 分=Fs cos30°=14mv 2≠12mv 12=16mv 2可见本题中对力所在的方向使用动能定理是错误的,能量依旧不能分解。
这是不是说明例题1的做法只是个例、巧合,完全没有可取之处呢?也不尽然,经典统计力学的“能量均分定理”告诉我们分子在每个自由度上都具有相同的平均动能。
由此可见,能量在某些情况下是可以分解的。
对比例题1、例题2以及能量均分定理可以发现,例题1和能量均分定理中都是在直角坐标系中进行分解,而例题2可以看做是在一个斜坐标系中分解。
似乎动能能否分方向使用是由分解坐标系的选取决定的,以下我们就直接证明直角坐标系和斜坐标系中是否能够使用。
1.直角坐标W 合=Fs =12mv 2W x =F x s x =Fs cos 2θ=12mv x 2=12mv 02cos 2θW y =F y s y =Fs sin 2θ=12mv y 2=12mv 02sin 2θ由于v 02cos 2θ+v 02sin 2θ=v 02,可以得到W 合=W x +W y ,同理空间直角坐标系中也可以得到同样的结论,所以在直角坐标系中动能定理是可以分方向使用的。
2.斜坐标系W 合=Fs =12mv 2W x =F x s x =Fs cos 2θ=12mv x 2=12mv 02cos 2θW y =F y s y =Fs cos 2α=12mv y 2=12mv 02cos 2α此时v 02cos 2θ+v 02cos 2α≠v 02,W 合≠W x +W y ,同理在空间斜坐标系可以得到一样的结论。
所以,在斜坐标系中动能定理不能分方向使用。
根据上面的证明,我们会发现只有在直角坐标系中动能定理分方向使用才成立,而且这只是在直角坐标系中数学计算恰好和动能定理计算相同,不能证明能量可以分解。
第12章全等三角形模型一:一线三等角讲义2022—2023学年人教版数学八年级上册
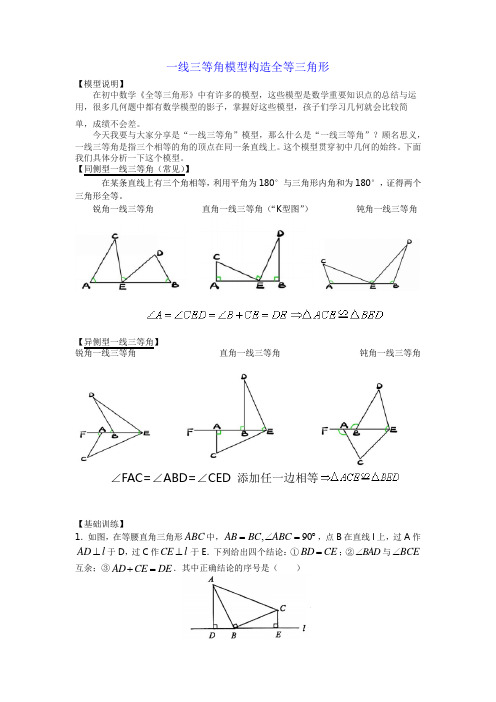
一线三等角模型构造全等三角形【模型说明】在初中数学《全等三角形》中有许多的模型,这些模型是数学重要知识点的总结与运用,很多几何题中都有数学模型的影子,掌握好这些模型,孩子们学习几何就会比较简单,成绩不会差。
今天我要与大家分享是“一线三等角”模型,那么什么是“一线三等角”?顾名思义,一线三等角是指三个相等的角的顶点在同一条直线上。
这个模型贯穿初中几何的始终。
下面我们具体分析一下这个模型。
【同侧型一线三等角(常见)】 在某条直线上有三个角相等,利用平角为180°与三角形内角和为180°,证得两个三角形全等。
锐角一线三等角 直角一线三等角(“K 型图”) 钝角一线三等角直角一线三等角 钝角一线三等角∠FAC=∠ABD=∠CED 添加任一边相等【基础训练】1.如图,在等腰直角三角形ABC 中,,90AB BC ABC =∠=︒,点B 在直线l 上,过A 作AD l ⊥于D ,过C 作CE l ⊥于E .下列给出四个结论:①BD CE =;②BAD ∠与BCE∠互余;③AD CE DE +=.其中正确结论的序号是( )A.①②B.①③C.②③D.①②③2.如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别为D,E,AD=2.5cm,BE=1cm,求DE的长.3.如图1,在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE ⊥直线m,垂足分别为D,E.(1)求证:△ABD≌△CAE;(2)若BD=2cm,CE=4cm,DE=cm.4.如图,在△ABC中,AC=BC,D、E分别为AB、BC上一点,∠CDE=∠A.若BC=BD,求证:CD=DE.5.在△ABC中,AB=AC,D,A,E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC,求证:DE=BD+CE.6.如图,点P,M,N分别在等边△ABC的各边上,MP⊥AB于点P,MN⊥BC于点M,PN⊥AC于点N.(1)求证:△PMN是等边三角形;(2)若BP=2cm,求等边△ABC的边长.7.如图①,点B 、C 在∠MAN 的边AM 、AN 上,点E ,F 在∠MAN 内部的射线AD 上,∠1、∠2分别是△ABE 、△CAF 的外角.已知AB =AC ,∠1=∠2=∠BAC .求证:△ABE ≌△CAF .8.如图,已知∠DCE =90°,∠DAC =90°,BE ⊥AC 于B ,且DC =EC ,能否在△BCE 中找到与AB+AD 相等的线段,并说明理由.9、如图,在等腰△ABC 中,AB =AC ,点D 、E 、F 分别在AB 、BC 、AC 边上,且BE =CF ,BD =CE .(1)求证:△DEF 是等腰三角形; (2)当∠A =36°时,求∠DEF 的度数.10.如图,在ABC ∆中,2==AC AB ,︒=∠36B ,点D 在线段BC 上运动(点D 不与点B 、C 重合),连接AD ,作︒=∠36ADE ,DE 交线段AC 于点E.线段DC 的长度为何值时,DCEABD∆≅∆请说明理由;【提升训练】1.在△ABO中,∠AOB=90°,AO=BO,直线MN经过点O,且AC⊥MN于C,BD ⊥MN于D(1)当直线MN绕点O旋转到图①的位置时,求证:CD=AC+BD;(2)当直线MN绕点O旋转到图②的位置时,求证:CD=AC﹣BD;(3)当直线MN绕点O旋转到图③的位置时,试问:CD、AC、BD有怎样的等量关系?请写出这个等量关系,并加以证明.2.(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD ⊥直线m,CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.(3)拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状并说明理由.ADEB C3.如图,CD是经过∠BCA顶点C的一条直线,CA=CB,E、F分别是直线CD上两点,且∠BEC=∠CFA=α.(1)若直线CD经过∠BCA的内部,且E、F在射线CD上.①如图1,若∠BCA=90°,α=90°,则BE CF;②如图2,若0°<∠BCA<180°,请添加一个关于α与∠BCA关系的条件,使①中的结论仍然成立,并说明理由;(2)如图3,若线CD经过∠BCA的外部,α=∠BCA,请提出关于EF,BE,AF三条线段数量关系的合理猜想,并简述理由.4.(1)如图1,直线m经过等腰直角△ABC的顶点A,过点B、C分别作BD⊥m,CE⊥m,垂足分别为D、E,求证:BD+CE=DE;(2)如图2,直线m经过△ABC的顶点A,AB=AC,在直线m上取两点D,E,使∠ADB=∠AEC=α,补充∠BAC=(用α表示),线段BD,CE与DE之间满足BD+CE=DE,补充条件后并证明;(3)在(2)的条件中,将直线m绕着点A逆时针方向旋转一个角度到如图3的位置,并改变条件∠ADB=∠AEC=(用α表示).通过观察或测量,猜想线段BD,CE与DE之间满足的数量关系,并予以证明.5.如图1,已知∠ACB=90°,AC=BC,BD⊥DE,AE⊥DE,垂足分别为D、E.(这几何模型具备“一线三直角”)如下图1:(1)①请你证明:△ACE≌△CBD;②若AE=3,BD=5,求DE的长;(2)迁移:如图2:在等腰Rt△ABC中,且∠C=90°,CD=2,BD=3,D、E分别是边BC,AC上的点,将DE绕点D顺时针旋转90°,点E刚好落在边AB上的点F 处,则CE=.(不要求写过程)6.通过对下面数学模型的研究学习,解决下列问题:【模型呈现】(1)如图1,∠BAD=90°,AB=AD,过点B作BC⊥AC于点C,过点D作DE⊥AC 于点E.由∠1+∠2=∠2+∠D=90°,得∠1=∠D.又∠ACB=∠AED=90°,可以推理得到△ABC≌△DAE.进而得到AC=,BC=.我们把这个数学模型称为“K字”模型或“一线三等角”模型;【模型应用】(2)如图2,∠BAD=∠CAE=90°,AB=AD,AC=AE,连接BC,DE,且BC⊥AH 于点H,DE与直线AH交于点G.求证:点G是DE的中点;7.如图所示,在△ABC中,AB=AC=24cm,BC=18cm,∠B=∠C,D为AB的中点,点P在线段BC上由点B出发向点C运动,同时点Q在线段CA上由点C出发向点A 运动,设运动时间为t(s).(1)若点P与点Q的速度都是3cm/s,则经过多长时间△BPD与△CQP全等?请说明理由.(2)若点P的速度比点Q的速度慢3cm/s,则经过多长时间△BPD与△CQP全等?请求出此时两点的速度.(3)若点P、点Q分别以(2)中的速度同时从点B,C出发,都按逆时针方向沿△ABC 三边运动,则经过多长时间点P与点Q第一次相遇?相遇点在△ABC的哪条边上?请求出相遇点到点B的距离.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一线三角与全等三角形
探究:
在ABC Rt ∆中,︒=∠90ACB ,BC AC =,直线l 经过点C ,且l AE ⊥于点E ,l BF ⊥于点F .
(1)当直线l 绕点C 旋转到如图1的位置时, ○
1图中有几对相等的锐角? ○
2求证:AEC ∆≌CFB ∆; ○
3试探究AE 、BF 、EF 之间的数量关系,并说明理由; (2)当直线l 绕点C 旋转到如图2的位置时,试探究AE 、BF 、EF 之间的数量关系,并说明理由;
、
巩固提高:
1.如图,ABC ∆是等腰三角形,
DE 过直角顶点A ,︒=∠=∠90E D ,则下列结论正确的个数有( ) ○1AE CD =;○2
21∠=∠;○
3︒=∠+∠9043;○4BE AD =.
(A )1个 (B )2个 (C )
3个 (D )4个
(第1题图)
(第2题图)
2.如图,在ABC Rt ∆中,︒=∠90ACB ,BC AC
=,直线l 经过点C ,且l AE ⊥于点E ,
l BF ⊥于点F .若25=AB ,4=AE ,则=EF _______________.
3.如图,在ABC Rt ∆中,︒=∠90ACB ,BC AC =,点D 为斜边AB 上一点,且CD AE ⊥于
点E ,CD BF ⊥交CD 的延长线于点F .若2:1:=AE BF ,4=AE ,则=AB _______________.
4.如图,在ABC Rt ∆中,︒=∠90ACB ,BC AC =,点D 为斜边AB 上一点,连接CD ,过点A 作CD AE ⊥于点E .若︒=∠45BED ,4=AE ,则=AB _______________.
(第3题图) (第4题图)
5.在ABC Rt ∆中,︒=∠90ACB ,BC AC =,直线l 经过点C ,且l AE ⊥于点E ,l BF ⊥于点F .若25=AB ,4=AE ,则=EF _______________.
6.在ABC Rt ∆中,︒=∠90ACB ,25==BC AC ,直线l 经过斜边AB 的中点D ,且l AE ⊥于点E ,l CF ⊥于点F .若4=AE ,则=EF _______________.
(第6题图)
7.如图,在等边ABC ∆中,点D 为边AB 上一点,连接CD ,点E 在CD 上,连接AE ,
︒=∠60AED ,过点B 作BF ∥AE 交CD 的延长线于点F . 求证:EF AE =.
(第7题图)
F。
