高三一轮复习资料-算法初步.doc

合集下载

高三数学一轮复习精练算法初步

I=1 While I<8 S=2I+3高三数学一轮复习精练：算法初步一、选择题1.某程序框图如图所示，该程序运行后输出的k 的值是 ( ) A ．4 B ．5 C ．6 D ．72.某程序框图如上（右）图所示，该程序运行后输出的k 的值是（）A ．4B ．5C ．6D ．7 3. 下图的程序语句输出的结果S 为（）A ．17B ．19C ．21D ．234. 上边（右）是一个算法的程序框图，当输入的x 值为3时，输出y 的结果恰好是31，则？处的关系式是（）. A ．3x y = B ．xy -=3C ．xy 3= D ．31x y =5.某店一个月的收入和支出总共记录了 N 个数据1a ，2a ，。

N a ，其中收入记为正数，支出记为负数。

该店用右边的程序框图计算月总收入S 和月净盈利V ，那么在图中空开始输入a b c ，，x a =b x >x b =x c =输出x结束是是否否白的判断框和处理框中，应分别填入下列四个选项中的（A ）A ＞0,V ＝S －T (B) A ＜0,V ＝S －T (C) A ＞0, V ＝S ＋T （D ）A ＜0, V ＝S ＋T6.上边右面的程序框图，如果输入三个实数a ，b ，c ，要求输出这三个数中最大的数，那么在空白的判断框中，应该填入下面四个选项中的（） A ．c x > B ．x c > C ．c b > D ．b c >7. 如图，下边（左）程序框图所进行的求和运算是（） A ． 12 + 14 + 16 + … + 120 B ．1 + 13 + 15 + … + 119C ． 1 + 12 + 14 + … + 118D ． 12 + 12 2 + 12 3 + … + 12 10开始 s = 0,nn < 是否s = s +n = n输出结束开1i =n整是输入m n ，结束 a m i=⨯ 输出a i ， 1i i =+否 8. 根据上边（右）程序框图，若输出y 的值是4，则输入的实数x 的值为 (A)1 (B)2- (C)1或2 (D) 1或2-二、填空题9.执行下边的程序框图1，若p ＝0.8，则输出的n ＝4.10. 阅读上边（右）的程序框图，若输入4m =，6n =，则输出a = ，i = （注：框图中的赋值符号“=”也可以写成“←”或“:=”）11.某篮球队6名主力队员在最近三场比赛中投进的三分球个数如下表所示：队员i 123456三分球个数1a 2a 3a 4a 5a 6a下图（右）是统计该6名队员在最近三场比赛中投进的三分球总数的程序框图，则图中判断框应填，输出的s= (注：框图中的赋值符号“=”也可以写成“←”或“：=”)是S=S+1k(k+2)S ＝0k ＝1k=k+2k>2010？输出S 结束否开始12.随机抽取某产品n 件，测得其长度分别为12,,,n a a a ，则图3所示的程序框图输出的s = ，s 表示的样本的数字特征是．（注：框图上（右）中的赋值符号“=”也可以写成“←”“：=”）13.某地区为了解70~80岁老人的日平均睡眠时间（单位：h 随机选择了50位老人进行调查。

高考数学一轮复习讲义第70课时算法初步理

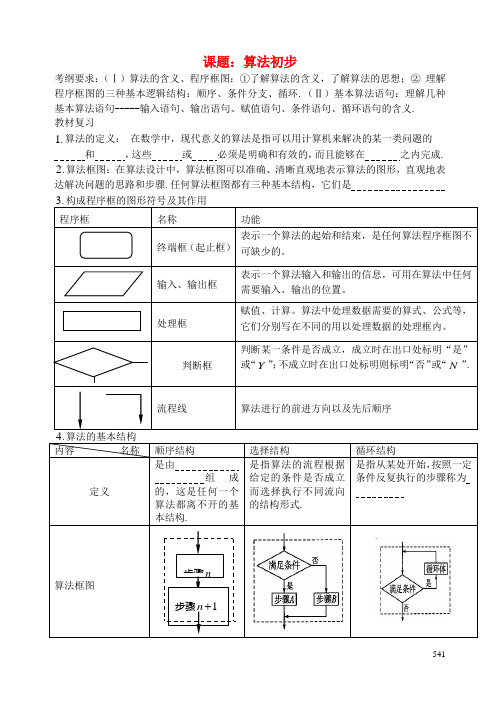
课题：算法初步考纲要求：（Ⅰ）算法的含义、程序框图：①了解算法的含义，了解算法的思想；②理解程序框图的三种基本逻辑结构：顺序、条件分支、循环.（Ⅱ）基本算法语句：理解几种基本算法语句-----输入语句、输出语句、赋值语句、条件语句、循环语句的含义.教材复习1.算法的定义：在数学中，现代意义的算法是指可以用计算机来解决的某一类问题的和，这些或必须是明确和有效的，而且能够在之内完成.2.算法框图：在算法设计中，算法框图可以准确、清晰直观地表示算法的图形，直观地表达解决问题的思路和步骤.任何算法框图都有三种基本结构，它们是541542基本知识方法：1.区分循环结构，搞清循环结构中循环体是什么，以及循环执行的次数是解决循环的核心2.For 循环语句用于预先知道循环次数的循环结构.Do Loop 循环结构，在满足Loop While 后面的条件时，将跳出循环.典例分析：考点一算法概念问题1：1.下列说法正确的是.A 算法就是某个问题的解题过程；.B 算法执行后可以产生不同的结果；.C 解决某一个具体问题算法不同结果不同；.D 算法执行步骤的次数不可以为很大，否则无法实施。

2.下列说法不正确的是.A 任何一种算法一定含有顺序结构；.B 任何一种算法都可能由顺序结构、条件结构、循环结构构成；.C 循环结构中一定含有条件结构；.D 条件结构中一定含有循环结构.考点二算法的基本结构问题2：()1(2013全国新课标Ⅰ)运行如右程序框图，如果输入的[]1,3t ∈-，则输出s 属于.A [3,4]- .B [5,2]- .C [4,3]- .D [2,5]-()2(2013江西) 阅读如下程序框图，如果输出5i =，那么在空白矩形框中应填入的语句为.A 2*2S i =- .B 2*1S i =- .C 2*S i = .D 2*4S i =+考点三算法框图的综合性问题问题3：（2012陕西）右图是用模拟方法估计圆周率π的程序框图，P 表示估计结果，则图中空白框内应填入.A 1000N P = .B 41000NP =.C 1000M P = .D 41000MP =考点四基本算法语句问题4：()1 (2013陕西)根据下列算法语句, 当输入x 为60时，输出y 的值为.A 25 .B 30 .C 31 .D 61()2执行如图所示的算法语句，输入N 的值为2013，则输出S 的值是.A 2011 .B 2012 .C 2010 .D 2009544()3执行下列用For 语句写出的算法，输出的结果为走向高考：1.（07海南）如果执行下面的程序框图，那么输出的S = .A 2450 .B 2500 .C 2550 .D 26522.（08广东）阅读的程序框图，若输入4m =，6n =，则输出a = ，i =3.（08海南）右面的程序框图，如果输入三个实数,,a b c ，要求输出这三个数中最大的数，那么在空白的判断框中，应该填入下面四个选项中的 .A c x > .B x c >.C c b >.D b c >结束a i ，第3题第1题5454.（09天津文）阅读右面的程序框图，则输出的S =.A 14 .B 20.C 30.D 555.（09浙江文）某程序框图如图所示，该程序运行后输出的k 的值是.A 4 .B 5 .C 6 .D 76.（2013江西文）阅读如下程序框图，如果输出4i =，那么空白的判断框中应填入的条件是.A 8S < .B 9S < .C 10S < .D 11S <7.（2013重庆）执行如图所示的程序框图，如果输出3s =，那么判断框内应填入的条件是 .A 6k ≤ .B 7k ≤ .C 8k ≤ .D 9k ≤5468.（2013天津）阅读右边的程序框图，运行相应的程序，若输入x 的值为1，则输出S 的值为.A 64 .B 73 .C 512 .D 5859.（2013浙江）某程序框图如图所示，若该程序运行后输出的值是59，则 .A 4=a .B 5=a .C 6=a .D .7=a。

【含五套高考卷】高考一轮复习教案：10.1 算法初步 word版含答案

第一节算法初步程序框图与算法语句1．算法的含义、程序框图(1)了解算法的含义，了解算法的思想．(2)理解程序框图的三种基本逻辑结构：顺序结构、条件结构、循环结构． 2．基本算法语句理解几种基本算法语句——输入语句、输出语句、赋值语句、条件语句、循环语句的含义．知识点一算法与程序框图 1．算法(1)算法通常是指按照一定规则解决某一类问题的明确和有限的步骤． (2)应用：算法通常可以编成计算机程序，让计算机执行并解决问题． 2．程序框图定义：程序框图又称流程图，是一种用程序框、流程线及文字说明来表示算法的图形．易误提醒易混淆处理框与输入框，处理框主要是赋值、计算，而输入框只是表示一个算法输入的信息．[自测练习]1.如果执行右边的程序框图，输入x ＝－12，那么其输出的结果是( )A ．9B ．3 C. 3 D.19解析：依题意得，执行完第1次循环后，x ＝－12＋3＝－9≤0；执行完第2次循环后，x ＝－9＋3＝－6≤0；执行完第3次循环后，x ＝－6＋3＝－3≤0；执行完第4次循环后，x ＝－3＋3＝0≤0；执行完第5次循环后，x ＝0＋3＝3>0，程序结束．结合题中的程序框图可知，最后输出的结果是 3.答案：C2．如图，按如下程序框图，若输出结果为170，则判断框内应补充的条件为()C．i>10? D．i>11?解析：∵21＋23＋25＋27＝170，∴判断框内应补充的条件为i>7或i≥9，故选A.答案：A知识点二三种基本逻辑结构及相应语句易误提醒易忽视循环结构中必有选择结构，其作用是控制循环进程，避免进入“死循环”，是循环结构必不可少的一部分．易混淆当型循环与直到型循环．直到型循环是“先循环，后判断，条件满足时终止循环”；而当型循环则是“先判断，后循环，条件满足时执行循环”；两者的判断框内的条件表述在解决同一问题时是不同的，它们恰好相反．[自测练习]3．如图是一个程序框图，则输出的n的值是________．解析：该程序框图共运行5次，各次2n的值分别是2,4,8,16,32，所以输出的n的值是5.答案：54．当a＝1，b＝3时，执行完下面一段过程后x的值是________．4.答案：4考点一算法的基本结构|1．(2015·高考天津卷)阅读如图所示的程序框图，运行相应的程序，则输出的S的值为( )A．－10B．6C．14D．18解析：执行程序框图可知，i＝2，S＝18；i＝4，S＝14；i＝8，S＝6.故输出S的值为6.答案：B2．(2016·威海一模)根据给出的程序框图，计算f(－1)＋f(2)＝( )A ．0B ．1C ．2D ．4解析：输入－1，满足x≤0，所以f(－1)＝4×(－1)＝－4；输入2，不满足x≤0，所以f(2)＝22＝4，即f(－1)＋f(2)＝0.故选A. 答案：A3．(2015·高考重庆卷)执行如图所示的程序框图，若输出k 的值为8，则判断框内可填入的条件是( )A ．s≤34B ．s≤56C ．s≤1112D ．s≤2524解析：第一次循环，得k ＝2，s ＝12；第二次循环，得k ＝4，s ＝12＋14＝34；第三次循环，得k ＝6，s＝34＋16＝1112；第四次循环，得k ＝8，s ＝1112＋18＝2524，此时退出循环，输出k ＝8，所以判断框内可填入的条件是s≤1112，故选C.答案：C1．解决程序框图问题要注意几个常用变量：(1)计数变量：用来记录某个事件发生的次数，如i ＝i ＋1. (2)累加变量：用来计算数据之和，如S ＝S ＋i. (3)累乘变量：用来计算数据之积，如p ＝p×i.2．处理循环结构的框图问题，关键是理解并认清终止循环结构的条件及循环次数．考点二算法的交汇性问题|算法是高考热点内容之一，算法的交汇性问题是新课标高考的一大亮点，归纳起来常见的探究角度有： 1．与统计的交汇问题． 2．与函数的交汇问题． 3．与不等式的交汇问题． 4．与数列求和的交汇问题．探究一与统计的交汇问题1．如图是某县参加2016年高考的学生身高条形统计图，从左到右的各条形表示的学生人数依次记为A 1，A 2，…，A 10(如A 2表示身高(单位：cm)在[150,155)内的学生人数)．图(2)是统计图(1)中身高在一定范围内学生人数的一个程序框图．现要统计身高在160～180 cm(含160 cm ，不含180 cm)的学生人数，则在流程图中的判断框内应填写( )A ．i<6？B ．i<7?C ．i<8?D ．i<9?解析：统计身高在160～180 cm 的学生人数，即求A 4＋A 5＋A 6＋A 7的值．当4≤i≤7时，符合要求．答案：C探究二与函数的交汇问题2．(2015·高考山东卷)执行如图所示的程序框图，输出的T 的值为________．1＋12x 2| 10＝解析：开始n ＝1，T ＝1，因为1<3，所以T ＝1＋⎠⎛01x 1dx ＝1＋12×12＝32，n ＝1＋1＝2；因为2<3，所以T ＝32＋⎠⎛01x 2dx ＝32＋13x 3| 10＝32＋13×13＝116，n ＝2＋1＝3.因为3<3不成立，所以输出T ，即输出的T 的值为116. 答案：116探究三与不等式的交汇问题3．关于函数f(x)＝⎩⎪⎨⎪⎧－x ，1<x≤4，cos x ，－1≤x≤1的程序框图如图所示，现输入区间[a ，b]，则输出的区间是________．解析：由程序框图的第一个判断条件为f(x)>0，当f(x)＝cos x ，x∈[－1,1]时满足．然后进入第二个判断框，需要解不等式f′(x)＝－sin x≤0，即0≤x≤1.故输出区间为[0,1]．答案：[0,1]第3题图第4题图探究四与数列求和的交汇问题4．(2015·高考湖南卷)执行如图所示的程序框图，如果输入n ＝3，则输出的S ＝( ) A.67 B.37 C.89D.49解析：第一次循环，S ＝11×3，此时i ＝2，不满足条件，继续第二次循环，S ＝11×3＋13×5，此时i ＝3，不满足条件，继续第三次循环，S ＝11×3＋13×5＋15×7＝12⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫1－13＋⎝ ⎛⎭⎪⎫13－15＋⎝ ⎛⎭⎪⎫15－17＝37，此时i ＝4>3，退出循环，输出S 的值为37，选B.答案：B解决算法交汇问题的三个关键点(1)读懂程序框图，明确交汇知识； (2)根据给出问题与程序框图处理问题； (3)注意框图中结构的判断．考点三算法基本语句|按照如图程序运行，则输出K 的值是________．X ＝3 K ＝0 DO X ＝2] [解析] 第一次循环，X ＝7，K ＝1；第二次循环，X ＝15，K ＝2；第三次循环，X ＝31，K ＝3；终止循环，输出K 的值是3. [答案] 3算法语句应用的关注点(1)输入语句、输出语句和赋值语句基本对应于算法的顺序结构．(2)在循环语句中也可以嵌套条件语句，甚至是循环语句，此时需要注意嵌套格式，这些语句需要保证算法的完整性，否则就会造成程序无法执行．(2015·高考江苏卷)根据如图所示的伪代码，可知输出的结果S 为________． S←1I←1While I<8 S←S＋2 I←I＋3End While Print S解析：该伪代码运行3次，故输出的S 为7. 答案：725.变量的含义理解不准致误【典例】 (2015·高考全国卷Ⅰ)执行如图所示的程序框图，如果输入的t ＝0.01，则输出的n ＝( )A ．5B ．6C ．7D ．8[易错点析] (1)读不懂程序框图，把执行循环体的次数n 误认为是变量S 的值，没有注意到n 的初始值为0.(2)对循环结构：①判断条件把握不准；②循环次数搞不清楚；③初始条件容易代错． [解析] 由程序框图可知，S ＝1－12＝12，m ＝14，n ＝1，12>0.01；S ＝12－14＝14，m ＝18，n ＝2，14>0.01； S ＝14－18＝18，m ＝116，n ＝3，18>0.01； S ＝18－116＝116，m ＝132，n ＝4，116>0.01； S ＝116－132＝132，m ＝164，n ＝5，132>0.01； S ＝132－164＝164，m ＝1128，n ＝6，164>0.01； S ＝164－1128＝1128，m ＝1256，n ＝7，1128<0.01，输出n ＝7，故选C. [答案] C[方法点评] (1)要分清是当型循环结构还是直到型循环结构；要理解循环结构中各变量的具体含义以及变化规律．(2)在处理含有循环结构的算法问题时，关键是确定循环的次数，循环中有哪些变量，且每一次循环之后的变量S 、n 值都要被新的S 、n 值所替换．[跟踪练习] 执行如图所示的程序框图，则输出S 的值为( )A ．3B ．－6C ．10D ．－15解析：第一次执行程序，得到S ＝0－12＝－1，i ＝2；第二次执行程序，得到S ＝－1＋22＝3，i ＝3；第三次执行程序，得到S ＝3－32＝－6，i ＝4；第四次执行程序，得到S ＝－6＋42＝10，i ＝5；第五次执行程序，得到S ＝10－52＝－15，i ＝6，到此结束循环，输出的S ＝－15. 答案：DA 组考点能力演练1．定义运算a ⊗b 为执行如图所示的程序框图输出的S 值，则⎝⎛⎭⎪⎫2cos5π3⊗⎝ ⎛⎭⎪⎫2tan 5π4的值为( )A ．4B ．3C ．2D ．－1 解析：由程序框图可知，S ＝⎩⎪⎨⎪⎧－，a≥b，＋，a<b ，2cos 5π3＝1,2tan 5π4＝2,1<2，所以⎝⎛⎭⎪⎫2cos5π3⊗⎝ ⎛⎭⎪⎫2tan 5π4＝2(1＋1)＝4.答案：A2．(2016·贵州模拟)阅读如图所示的程序框图，运行相应的程序，输出s 的值等于( )A ．－3B ．－10C ．0D ．－2解析：第一次循环k ＝0＋1＝1，s ＝2×1－1＝1，满足k<4；第二次循环k ＝1＋1＝2，s ＝2×1－2＝0，满足k<4；第三次循环k ＝2＋1＝3，s ＝2×0－3＝－3，满足k<4；第四次循环k ＝3＋1＝4，不满足k<4，输出的s ＝－3，故选A.答案：A3．(2016·长春模拟)阅读如图所示的程序框图，运行相应的程序．若输出的S 为1112，则判断框中填写的内容可以是( )A ．n ＝6?B ．n<6?C ．n≤6?D ．n≤8?解析：∵12＋14＋16＝1112，∴n ＝6时满足条件，而n ＝8时不满足条件，∴n≤6，故选C.答案：C4.某程序框图如图所示，若输出的S ＝120，则判断框内为( )A ．k>4?B ．k>5?C ．k>6?D ．k>7?解析：依题意，进行第一次循环时，k ＝1＋1＝2，S ＝2×1＋2＝4；进行第二次循环时，k ＝2＋1＝3，S ＝2×4＋3＝11；进行第三次循环时，k ＝3＋1＝4，S ＝2×11＋4＝26；进行第四次循环时，k ＝4＋1＝5，S ＝2×26＋5＝57；进行第五次循环时，k ＝5＋1＝6，S ＝2×57＋6＝120，此时结束循环，因此判断框内应为“k>5？”，选B.答案：B5.某流程图如图所示，现输入如下四个函数，则可以输出的函数是( )A ．f(x)＝x 2B ．f(x)＝|x|xC ．f(x)＝e x－e－xe x ＋e－xD ．f(x)＝1＋sin x ＋cos x1＋sin x －cos x解析：由框图可知输出函数为奇函数且存在零点，依次判断各选项，A 为偶函数，B 不存在零点，不符合，对于C ，由于f(－x)＝e －x－exe －x ＋e x ＝－f(x)，即函数为奇函数，且存在零点为x ＝0，对于D ，由于其定义域不关于原点对称，故其为非奇非偶函数，故选C.答案：C6．(2016·南京模拟)根据如图所示的伪代码，最后输出的S 的值为________． S ＝0For I From 1 To 10S ＝S ＋I End For Print S解析：这是一个1＋2＋3＋…＋10的求和，所以输出的S 的值为55. 答案：557．执行如图所示的程序框图，输出的S 的值为______．解析：S ＝sin1×π3＋sin 2×π3＋sin 3×π3＋sin 4×π3＋sin 5×π3＋sin 6×π3＋…＋sin 2 013×π3＝⎝⎛sin1×π3＋sin 2×π3＋sin 3×π3＋sin 4×π3＋⎭⎪⎫sin 5×π3＋sin 6×π3×335＋sin 1×π3＋sin 2×π3＋sin 3×π3＝ 3.答案： 38．(2016·黄冈模拟)随机抽取某中学甲、乙两个班各10名同学，测量它们的身高获得身高数据的茎叶图如左下图，在样本的20人中，记身高在[150,160)，[160,170)，[170,180)，[180,190)的人数依次为A1，A2，A3，A4.右下图是统计样本中身高在一定范围内的人数的算法框图．若图中输出的S＝18，则判断框应填________．解析：本题考查程序框图与统计交汇问题．由于i从2开始，也就是统计大于或等于160的所有人数，于是就要计算A2＋A3＋A4，因此，判断框应填i<5或i≤4.答案：i<5或i≤49．给出以下10个数：5,9,80,43,95,73,28,17,60,36.要求把大于40的数找出来并输出．试画出该问题的算法程序框图．解：程序框图如下：10．某篮球队6名主力队员在最近三场比赛中投进的三分球个数如表格所示：统计该6名队员在最近三场比赛中投进的三分球总数的程序框图如上图所示． (1)试在判断框内填上条件； (2)求输出的s 的值．解：(1)依题意，程序框图是统计6名队员投进的三分球的总数． ∴判断框内应填条件“i≤6？”．(2)6名队员投进的三分球数分别为a 1，a 2，a 3，a 4，a 5，a 6.故输出的s ＝a 1＋a 2＋…＋a 6.B 组高考题型专练1．(2014·高考江西卷)阅读如下程序框图，运行相应的程序，则程序运行后输出的结果为( )A ．7B ．9C ．10D ．11解析：执行程序框图，第一次循环：i ＝1，S ＝lg 13>－1，否；执行第二次循环：i ＝3，S ＝lg 13＋lg 35＝lg 15>－1，否；执行第三次循环：i ＝5，S ＝lg 15＋lg 57＝lg 17>－1，否；执行第四次循环：i ＝7，S ＝lg 17＋lg 79＝lg 19>－1，否；执行第五次循环：i ＝9，S ＝lg 19＋lg 911＝lg 111<－1，是，结束循环，输出i 为9，故选B.答案：B2．(2014·高考新课标全国卷Ⅰ)执行下面的程序框图，若输入的a ，b ，k 分别为1,2,3，则输出的M ＝( )A.203 B.72 C.165D.158解析：第一次循环，M ＝32，a ＝2，b ＝32，n ＝2；第二次循环，M ＝83，a ＝32，b ＝83，n ＝3；第三次循环，M ＝158，a ＝83，b ＝158，n ＝4，退出循环，输出M 为158，故选D. 答案：D3．(2015·高考全国卷Ⅱ)程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”．执行该程序框图，若输入的a，b分别为14,18，则输出的a＝( )A．0 B．2C．4 D．14解析：第一次执行，输入a＝14，b＝18，因为a<b，所以b＝18－14＝4；第二次执行，因为a＝14，b＝4，a>b，所以a＝14－4＝10；第三次执行，因为a＝10，b＝4，a>b，所以a＝10－4＝6；第四次执行，因为a＝6，b＝4，a>b，所以a＝6－4＝2；第五次执行，因为a＝2，b＝4，a<b，所以b＝4－2＝2，此时a＝b＝2，故选B.答案：B4.根据框图，当输入x为2 016时，输出的y＝( )A．2 B．4C．10 D．28解析：由题意可得，x依次为2 016，2 014，2 012，…，0，－2，执行y＝3－(－2)＋1＝10，故输出的y＝10，选C.答案：C数学高考模拟试卷（理科）注意事项：1. 答题前，考生先将自己的姓名、准考证号填写清楚，将条形码准确粘贴在考生信息条形码粘贴区。

2020高三数学一轮复习(人教版文)：算法初步

第九章算法初步、统计、统计案例第一节算法初步2019考纲考题考情「基础微械理一知识必备哂椒基JICHUWE1SHUL.I1. 三种基本逻辑结构\^称内补y顺序结构条件结构循环结构定义由若F个依次执行的步骤组成的，这是任何一个算法都离不开的基本结构算法的流程根据条件是否成从某处开始，按照一定的条件反复执行某些步骤的情况，反复执行的步骤称为循环体宴有不同的流向裏条件结构就是处理这种过程的结构考纲要求考鈕举创考向标諾L i■昴H辻约比亶」■辭篦适的黠轮二用钳輕1?杠闪的三呻临宮時詰为r吨序蒂枸*殆件塔耐.漪炜帖恂XTM几种甚杰舞祂谄旬一ffiAifitj.iffi J：识＜r, Kffi m 4i梟”谍冒圖评1,",旬的201 fi・全個淮||・［；〔判IM第悴｝201 i •无坤届唐* T,C^；hiA)::1 ■- g満号* 1 •亦；閘1如林•愛国曲1・T屮如押川书*件＞JO1?・全国軽U・T显输川犁累〉20)7・全M$nj・1?崔竹战蜡果)曲販币度「1.法的苓事箱钳瓷挥屹怖主忙性闻■ 轉心H岸；抽亍盘損敦材I“I扣垄础白別2•算法的特征概括性、逻辑性、有穷性、不唯一性、普遍性。

语句一般格式功能输人语句INPUT"提示内容J变量输入信息输出语句PRINT提示内容S表达式输出常量、变量的值和系统信息赋值语句变量=表达式将表达式的值赋给变量4•条件语句(1) 算法中的条件结构与条件语句相对应。

(2) 条件语句的格式及框图。

①IF —THEN格式：5.循环语句(1)算法中的循环结构与循环语句相对应。

⑵循环语句的格式及框图。

①UNTIL语句：IX)循环体UN I IL 条件②WHILE语句:1.赋值号左边只能是变量（不能是表达式）,在一个赋值语句中只能给一个变量赋值。

2. 直到型循环是“先循环，后判断，条件满足时终止循环”；当型循环则是“先判断，后循环，条件满足时执行循环”；两者的判断框内的条件表述在解决同一问题时是不同的，它们恰好相题纠徴谢身-TIZl WEIRESHEN一、走进教材1.（必修3P25例5改编）如图为计算y= |x|函数值的程序框图，则此程序框图中的判断框内应填___________ 。

高三理科数学一轮总复习第十一章算法初步

第十一章算法初步高考导航种基本逻辑结构：的一些基本语句结构.知识网络11.1 算法的含义与程序框图典例精析题型一算法的含义【例1】已知球的表面积是16π，要求球的体积，写出解决该问题的一个算法. 【解析】算法如下：第一步，s ＝16π. 第二步，计算R ＝s 4π. 第三步，计算V ＝4πR 33.第四步，输出V .【点拨】给出一个问题，设计算法应该注意：(1)认真分析问题，联系解决此问题的一般数学方法，此问题涉及到的各种情况； (2)将此问题分成若干个步骤； (3)用简练的语句将各步表述出来.【变式训练1】设计一个计算1×3×5×7×9×11×13的算法.图中给出程序的一部分，则在横线①上不能填入的数是( )A.13B.13.5C.14D.14.5【解析】当I ＜13成立时，只能运算 1×3×5×7×9×11.故选A.题型二程序框图【例2】图一是某县参加2010年高考的学生身高条形统计图，从左到右的各条形表示的学生人数依次记为A 1，A 2，…，A 10(如A 2表示身高(单位：cm)在[150,155)内的学生人数).图二是统计图一中身高在一定范围内学生人数的一个算法流程图.现要统计身高在160～180 cm(含160 cm ，不含180 cm)的学生人数，那么在流程图中的判断框内应填写的条件是( )A.i ＜6？B.i ＜7？C.i ＜8？D.i ＜9？图一【解析】根据题意可知，i 的初始值为4，输出结果应该是A 4＋A 5＋A 6＋A 7，因此判断框中应填写i ＜8？，选C.【点拨】本题的命题角度较为新颖，信息量较大，以条形统计图为知识点进行铺垫，介绍了算法流程图中各个数据的引入来源，其考查点集中于循环结构的终止条件的判断，考查了学生合理地进行推理与迅速作出判断的解题能力，解本题的过程中不少考生误选A ，实质上本题中的数据并不大，考生完全可以直接从头开始限次按流程图循环观察，依次写出每次循环后的变量的赋值，即可得解.【变式训练2】(2009辽宁)某店一个月的收入和支出，总共记录了N 个数据a 1，a 2，…，a N .其中收入记为正数，支出记为负数，该店用如图所示的程序框图计算月总收入S 和月净盈利V ，那么在图中空白的判断框和处理框中，应分别填入下列四个选项中的( )A.A ＞0？，V ＝S －TB.A ＜0？，V ＝S －TC.A ＞0？，V ＝S ＋TD.A ＜0？，V ＝S ＋T 【解析】选C.题型三算法的条件结构【例3】某快递公司规定甲、乙两地之间物品的托运费用根据下列方法计算： f ＝⎩⎨⎧⨯-+⨯).50＞(85.0)50(53.050),50≤＜0(53.0ωωωω其中f (单位：元)为托运费，ω为托运物品的重量(单位：千克)，试写出一个计算费用f 的算法，并画出相应的程序框图.【解析】算法如下：第一步，输入物品重量ω.第二步，如果ω≤50，那么f＝0.53ω，否则，f＝50×0.53＋(ω－50)×0.85.第三步，输出托运费f.程序框图如图所示.【点拨】求分段函数值的算法应用到条件结构，因此在程序框图的画法中需要引入判断框，要根据题目的要求引入判断框的个数，而判断框内的条件不同，对应的框图中的内容或操作就相应地进行变化.【变式训练3】(2010天津)阅读如图的程序框图，若输出s的值为－7，则判断框内可填写()A.i＜3？B.i＜4？C.i＜5？D.i＜6？【解析】i＝1，s＝2－1＝1；i＝3，s＝1－3＝－2；i＝5，s＝－2－5＝－7.所以选D.题型四算法的循环结构【例4】设计一个计算10个数的平均数的算法，并画出程序框图.【解析】算法步骤如下：第一步，令S＝0.第二步，令I＝1.第三步，输入一个数G.第四步，令S＝S＋G.第五步，令I＝I＋1.第六步，若I＞10，转到第七步，若I≤10，转到第三步.第七步，令A＝S/10.第八步，输出A.据上述算法步骤，程序框图如图.【点拨】(1)引入变量S作为累加变量，引入I为计数变量，对于这种多个数据的处理问题，可通过循环结构来达到；(2)计数变量用于记录循环次数，同时它的取值还用于判断循环是否终止，累加变量用于输出结果.【变式训练4】设计一个求1×2×3×…×10的程序框图.【解析】程序框图如下面的图一或图二.图一图二总结提高1.给出一个问题，设计算法时应注意：(1)认真分析问题，联系解决此问题的一般数学方法；(2)综合考虑此类问题中可能涉及的各种情况；(3)借助有关的变量或参数对算法加以表述；(4)将解决问题的过程划分为若干个步骤；(5)用简练的语言将各个步骤表示出来.2.循环结构有两种形式，即当型和直到型，这两种形式的循环结构在执行流程上有所不同，当型循环是当条件满足时执行循环体，不满足时退出循环体；而直到型循环则是当条件不满足时执行循环体，满足时退出循环体.所以判断框内的条件，是由两种循环语句确定的，不得随便更改.3.条件结构主要用在一些需要依据条件进行判断的算法中.如分段函数的求值，数据的大小关系等问题的算法设计.11.2 基本算法语句典例精析题型一输入、输出与赋值语句的应用【例1】阅读程序框图(如下图)，若输入m ＝4，n ＝6，则输出a ＝，i ＝ .【解析】a ＝12，i ＝3.【点拨】赋值语句是一种重要的基本语句，也是程序必不可少的重要组成部分，使用赋值语句，要注意其格式要求.【变式训练1】(2010陕西)如图是求样本x 1，x 2，…，x 10的平均数x 的程序框图，则图中空白框中应填入的内容为( )A.S ＝S ＋x nB.S ＝S ＋x nnC.S ＝S ＋nD.S ＝S ＋1n【解析】因为此步为求和，显然为S ＝S ＋x n ，故选A. 题型二循环语句的应用【例2】设计算法求11×2＋12×3＋13×4＋…＋199×100的值.要求画出程序框图，写出用基本语句编写的程序.【解析】这是一个累加求和问题，共99项相加，可设计一个计数变量，一个累加变量，用循环结构实现这一算法.程序框图如下图所示：程序如下：语句编写程序解决问题时，一定要注意格式和条件的表述方法，WHILE语句是当条件满足时执行循环体，UNTIL语句是当条件不满足时执行循环体.(2)在解决一些需要反复执行的运算任务，如累加求和、累乘求积等问题中应注意考虑利用循环语句来实现.(3)在循环语句中，也可以嵌套条件语句，甚至是循环语句，此时需要注意嵌套的这些语句，保证语句的完整性，否则就会造成程序无法执行.【变式训练2】下图是输出某个有限数列各项的程序框图，则该框图所输出的最后一个数据是 .【解析】由程序框图可知，当N ＝1时，A ＝1；N ＝2时，A ＝13；N ＝3时，A ＝15，…，即输出各个A值的分母是以1为首项以2为公差的等差数列，故当N ＝50时，A ＝11＋(50－1)×2＝199，即为框图最后输出的一个数据.故填199.题型三算法语句的实际应用【例3】某电信部门规定：拨打市内电话时，如果通话时间3分钟以内，收取通话费0.2元，如果通话时间超过3分钟，则超过部分以每分钟0.1元收取通话费(通话不足1分钟时按1分钟计算).试设计一个计算通话费用的算法，要求写出算法，编写程序.【解析】我们用c (单位：元)表示通话费，t (单位：分钟)表示通话时间，则依题意有⎩⎨⎧⨯+=,3＞2],[0.10.23,≤＜0,2.0t t-t c算法步骤如下：第一步，输入通话时间t .第二步，如果t ≤3，那么c ＝0.2；否则c ＝0.2＋0.1×[t －2]. 第三步，输出通话费用c . 程序如下：IF 【点拨】法步骤，画出程序框图，最后准确地编写出程序，同时要注意结合题意加深对算法的理解.【变式训练3】(2010江苏)下图是一个算法流程图，则输出S 的值是 .【解析】n＝1时，S＝3；n＝2时，S＝3＋4＝7；n＝3时，S＝7＋8＝15；n＝4时，S＝15＋24＝31；n ＝5时，S＝31＋25＝63.因为63≥33，所以输出的S值为63.总结提高1.输入、输出语句可以设计提示信息，加引号表示出来，与变量之间用分号隔开.2.赋值语句的赋值号左边只能是变量而不能是表达式；赋值号左右两边不能对换，不能利用赋值语句进行代数式计算，利用赋值语句可以实现两个变量值的互换，方法是引进第三个变量，用三个赋值语句完成.3.在某些算法中，根据需要，在条件语句的THEN分支或ELSE分支中又可以包含条件语句.遇到这样的问题，要分清内外条件结构，保证结构的完整性.4.分清WHILE语句和UNTIL语句的格式，在解决一些需要反复执行的运算任务，如累加求和，累乘求积等问题中应主要考虑利用循环语句来实现，但也要结合其他语句如条件语句.5.编程的一般步骤：(1)算法分析；(2)画出程序框图；(3)写出程序.11.3 算法案例典例精析题型一求最大公约数【例1】(1)用辗转相除法求840与1 764的最大公约数；(2)用更相减损术求440与556的最大公约数.【解析】(1)用辗转相除法求840与1 764的最大公约数：1 764＝840×2＋84，840＝84×10＋0.所以840与1 764的最大公约数是84.(2)用更相减损术求440与556的最大公约数：556－440＝116，440－116＝324，324－116＝208，208－116＝92，116－92＝24，92－24＝68，68－24＝44，44－24＝20，24－20＝4，20－4＝16，16－4＝12，12－4＝8，8－4＝4.所以440与556的最大公约数是4.【点拨】(1)辗转相除法与更相减损术是求两个正整数的最大公约数的方法，辗转相除法用较大的数除以较小的数，直到大数被小数除尽结束运算，较小的数就是最大公约数；更相减损术是用两数中较大的数减去较小的数，直到所得的差和较小数相等为止，这个较小数就是这两个数的最大公约数.一般情况下，辗转相除法步骤较少，而更相减损术步骤较多，但运算简易，解题时要灵活运用.(2)两个以上的数求最大公约数，先求其中两个数的最大公约数，再用所得的公约数与其他各数求最大公约数即可.【变式训练1】求147,343,133的最大公约数.【解析】先求147与343的最大公约数.343－147＝196，196－147＝49，147－49＝98，98－49＝49，所以147与343的最大公约数为49.再求49与133的最大公约数.133－49＝84，84－49＝35，49－35＝14，35－14＝21，21－14＝7，14－7＝7.所以147,343,133的最大公约数为7.题型二秦九韶算法的应用【例2】用秦九韶算法写出求多项式f(x)＝1＋x＋0.5x2＋0.016 67x3＋0.041 67x4＋0.008 33x5在x＝－0.2时的值的过程.【解析】先把函数整理成f(x)＝((((0.008 33x＋0.041 67)x＋0.166 67)x＋0.5)x＋1)x＋1，按照从内向外的顺序依次进行.x＝－0.2，a5＝0.008 33，v0＝a5＝0.008 33；a4＝0.041 67，v1＝v0x＋a4＝0.04；a3＝0.016 67，v2＝v1x＋a3＝0.008 67；a2＝0.5，v3＝v2x＋a2＝0.498 27；a1＝1，v4＝v3x＋a1＝0.900 35；a0＝1，v5＝v4x＋a0＝0.819 93；所以f(－0.2)＝0.819 93.【点拨】秦九韶算法是多项式求值的最优算法，特点是：(1)将高次多项式的求值化为一次多项式求值；(2)减少运算次数，提高效率；(3)步骤重复实施，能用计算机操作.【变式训练2】用秦九韶算法求多项式f(x)＝8x7＋5x6＋3x4＋2x＋1当x＝2时的值为.【解析】1 397.题型三进位制之间的转换【例3】(1)将101 111 011(2)转化为十进制的数；(2)将53(8)转化为二进制的数.【解析】(1)101 111 011(2)＝1×28＋0×27＋1×26＋1×25＋1×24＋1×23＋0×22＋1×21＋1＝379.(2)53(8)＝5×81＋3＝43.所以53(8)＝101 011(2).【点拨】将k进制数转换为十进制数，关键是先写成幂的积的形式再求和，将十进制数转换为k进制数，用“除k取余法”，余数的书写是由下往上，顺序不能颠倒，k进制化为m进制(k，m≠10)，可以用十进制过渡.【变式训练3】把十进制数89化为三进制数.【解析】具体的计算方法如下：89＝3×29＋2，29＝3×9＋2，9＝3×3＋0，3＝3×1＋0，1＝3×0＋1，所以89(10)＝10 022(3).总结提高1.辗转相除法和更相减损术都是用来求两个数的最大公约数的方法.其算法不同，但二者的原理却是相似的，主要区别是一个是除法运算，一个是减法运算，实质都是一个递推的过程.用秦九韶算法计算多项式的值，关键是正确的将多项式改写，然后由内向外，依次计算求解.2.将k进制数转化为十进制数的算法和将十进制数转化为k进制数的算法操作性很强，要掌握算法步骤，并熟练转化；要熟练应用“除基数，倒取余，一直除到商为0”.。

高三一轮复习精品算法初步

x－3y＋z＝2 3x＋y－z＝1 2x＋3y－2z＝3
① ② ③
，写出解方程组的算法．
课堂互动讲练
解：第一步：①＋②得4x－2y＝3④ 第二步：②×2－③得4x－y＝－1⑤ 第三步：④－⑤得y＝－4； 5 第四步：将 y＝－4 代入④，解得 x＝－； 4 5 第五步：将 y＝－4，x＝－代入①，解得 z 4 35 ＝－ . 4
三基能力强化
课堂互动讲练
考点一算法设计
算法不同于求解一个具体问题的方法，它要满足以下条件： (1)写出的算法要适用于一类问题，并且再遇到类似问题时能够重复使用； (2)算法过程要做到能一步一步地执行，每一步执行的操作必须是明确有效的，不能含糊不清； (3)所确定的算法必须在有限步后得到问题的结果，决不能无限地进行下去．
复习课
第一单元算法初步
导航
考纲解读
1.算法与程序框图 (1)了解算法的含义、了解算法的思想． (2)理解程序框图的三种基本逻辑结构：顺序、条件、循环．
高考导航
考纲解读
2．基本算法语句及算法案例理解几种基本算法语句——输入语句、输出语句、赋值语句、条件语句、循环语句的含义.
高考导航
命题探究
基础知识梳理
三种基本逻辑结构的共同点是什么？【思考·提示】三种逻辑结构的共同点即只有一个入口和一个出口，每一个基本逻辑结构的每一部分都有机会被执行到，而且结构内不存在死循环．
三基能力强化
1．任何一个算法都必须有的基本结构是( ) A．顺序结构 B．条件结构 C．循环结构 D．三个都是答案：A
三基能力强化
4．指出下列程序框图的运行结果．若输入－4，则输出结果________．答案：是负数

高考一轮总复习数学第9章第4讲算法初步

B．7,4 D．9,5
解析第一次，i＝1 时，i＝1＋1＝2，S＝2×2－1＝3，i＝2＋2＝4.第二次，i＝4＋1＝5，S＝2×5－1 ＝9，i＝5＋2＝7，第三次条件不成立，输出 S＝9，i＝7，选 C.
3．[2015·天津高考]阅读下边的程序框图，运行相应的程序，则输出 i 的值为( )
A．2 C．4
A．[－3,4]
B．[－5,2]
C．[－4,3]
D．[－2,5]
[解析] 由程序框图可知，s 与 t 可用分段函数 3t，－1≤t<1，
表示为 s＝4t－t2，1≤t≤3，则 s∈[－3,4]．
命题角度 2 与数列求和的交汇问题例 3 [2015·湖南高考]执行如图所示的程序框图，如果输入 n＝3，则输出的 S＝( )
DO S＝S＋x i＝i＋1
LOOP UNTIL a＝S/20
PRINT a END
A．i<＝20
B．i<20
C．i>＝20
D．i>20
[解析] 由于是求 20 个数的平均数，所以应是“直到 i>20”时，退出循环，故选 D.
[易错指导] 解答循环语句时，区分当型循环与直到型循环的主要方法是：当型循环先判断后循环，而直到型循环是先循环后判断，最重要也是最易搞错的地方是终止循环的条件，对于本例(1)易错选 A.
命题角度 3 与统计的交汇问题例 4 某班有 24 名男生和 26 名女生，数据 a1，a2，…，a50 是该班 50 名学生在一次数学学业水平模拟考试中的成绩(成绩不为 0)，如图所示的程序用来同时统计全班成绩的平均分：A，男生平均分：M，女生平均分：W，为了便于区别性别，输入时，男生的成绩用正数，女生的成绩用其成绩的相反数，那么在图中空白的判断框和处理框中，应分别填入( )

第九章第4讲算法初步

高三一轮复习学案课题第九章第4讲算法初步年级高三年级学科数学组编人核定人审核人日期学习目标：1.了解算法的含义，了解算法的思想．2.理解算法框图的三种基本结构.3.了解几种基本算法语句的含义.高考要求：1. 算法的基本结构2. 程序框图的识别与应用3. 基本算法语句一、知识导学：1. 算法的框图及结构(1)算法算法通常是指按照一定________解决某一类问题的____________的步骤．这些程序或步骤必须是________和________的，而且能够在有限步之内完成．(2)程序框图程序框图又称________，是一种用________、________及________来表示算法的图形．通常，程序框图由程序框和流程线组成，一个或几个程序框的组合表示算法中的一个步骤；________带有方向箭头，按照算法进行的顺序将________连接起来．2．算法语句的格式及框图(1)输入语句、输出语句、赋值语句的格式与功能(2)条件语句的格式及框图①IF－THEN格式②IF－THEN－ELSE格式(3)循环语句的格式及框图①UNTIL语句②WHILE语句二、要点突破：1条重要规律顺序结构是每个算法结构都含有的，而对于循环结构有重复性，条件结构具有选择性没有重复性，并且循环结构中必定包含一个条件结构，用于确定何时终止循环体．循环结构和条件结构都含有顺序结构2点必记注意1. 循环语句有两种格式：WHILE循环和UNTIL循环，WHILE循环语句尤其适合于解决一些事先不确定循环次数的问题，WHILE循环语句中的表达式的结果为真时，执行循环体，为假时跳出循环体．2. 赋值号左右不能对换，赋值语句是将赋值号右边的表达式的值赋给赋值号左边的变量，例如Y＝x, 表示用x的值替代变量Y的原先的取值，不能改写为x＝Y.因为后者表示用Y的值替代变量x的值．3项必须防范1. 利用循环结构表示算法，一定要先确定是用当型循环结构，还是用直到型循环结构；当型循环结构的特点是先判断再循环，直到型循环结构的特点是先执行一次循环体，再判断．2. 框图内的内容包括累加(积)变量初始值，计算变量初始值，累加值，前后两个变量的差值都要仔细斟酌，不能有丝毫差错．3. 判断框内内容的填写，有时大于等于，有时大于，有时小于，有时还是小于等于，它们的含义是各不相同的，要根据所选循环结构的类型，正确地进行选择.三、考点解析：考点一算法的基本结构例1①[2012·辽宁]执行如图所示的程序框图，则输出的S值是()A. －1B.23 C.32 D. 4②[2012·天津]阅读下面的程序框图，运行相应的程序，当输入x的值为－25时，输出x的值为_______【听课记录】考点二程序框图的识别与应用例2 ①[2012·江西]下图为某算法的程序框图，则程序运行后输出的结果是________．②[2013·合肥联考]如果执行如图所示的程序框图，输入N＝5，那么输出的S＝________.【听课记录】考点三基本算法语句例3[2013·福建模]运行以下程序时，输出的值共有( )A. 5个B. 4个C. 3个D. 9个【听课记录】四、练习提升：1. [2012·北京]执行如图所示的程序框图，输出的S值为()A. 2B. 4C. 8D. 162. [2013·银川模拟]下面程序运行结果为()A. 7B. 6C. 5D. 43. [2013·宁德模拟]某程序框图如右图所示，若输出的S>80，则m的最小值是()A. 7B. 6C. 5D. 44. 已知程序如图所示，则输出结果S＝________.5. [2012·湖北]阅读如图所示的程序框图，运行相应的程序，输出的结果s＝________.【课后反思】。

数学高考一轮复习算法初步知识点

数学高考一轮复习算法初步知识点
算法是由基本运算及规定的运算顺序所构成的完整的解题步骤。

下面是查字典数学网整理的算法初步知识点，请考生认真学习。

(1)算法的含义、程序框图①通过对解决具体问题过程与步骤的分析(如，二元一次方程组求解等问题)，体会算法的思想，了解算法的含义。

②通过模仿、操作、探索，经历通过设计程序框图表达解决问题的过程。

在具体问题的解决过程中(如，三元一次方程组求解等问题)，理解程序框图的三种基本逻辑结构：顺序、条件分支、循环。

(2)基本算法语句经历将具体问题的程序框图转化为程序语句的过程，理解几种基本算法语句--输入语句、输出语句、赋值语句、条件语句、循环语句，进一步体会算法的基本思想。

(3)通过阅读中国古代数学中的算法案例，体会中国古代数学对世界数学发展的贡献。

算法初步知识点的全部内容就是这些，查字典数学网预祝广大考生可以时时有进步。

第 1 页共 1 页。

高三一轮复习资料第3节算法初步

第3节算法初步基础打磨1.(2020届河北衡水模拟)阅读如图所示的程序框图,若输入x的值为3,则输出y的值为().A.24B.25C.30D.40第1题图第2题图2.(2020届天津红桥区二模)执行如图所示的程序框图,则输出s的值为().A.2B.13C.-12D.-33.(2020届天津部分区一模)执行如图所示的程序框图,则输出a的值为().A.3B.2C.23D.-12第3题图第4题图4.(2020届河南省一诊)根据如图所示的程序框图,对大于2的整数N,输出的数列的通项公式是().A.a n=2nB.a n=2(n-1)C.a n=2nD.a n=2n-15.(2020届河南省信阳市二模)执行如图所示的程序框图,若输出的y的值为5,则判断框中可以填入的条件是().A.i<6?B.i<5?C.i<4?D.i<3?第5题图第6题图6.(2020届辽宁大连市二模)执行如图所示的程序框图,若输出y的值为1,则可输入的实数x的个数为().A.1B.2C.3D.47.(2020届安徽模拟)《九章算术》中有如下问题:“今有牛、羊、马食人苗,苗主责之粟五斗,羊主曰:‘我羊食半马.’马主曰:‘我马食半牛.’今欲衰偿之,问各出几何?”翻译为:现有牛、马、羊吃了别人的禾苗,禾苗主人要求赔偿5斗粟.羊主人说:“我的羊所吃的禾苗只有马的一半.”马主人说:“我的马吃的禾苗只有牛的一半.”打算按此比例偿还.问:牛、马、羊的主人各应赔偿多少粟?已知1斗=10升,针对这一问题,设计程序框图如图所示,若输出k的值为2,则m=().A.503B.507C.103D.10078.(2020届湖南长沙模拟)执行如图所示的程序框图,若输入m=351,n=143,则输出n的值为().A.2B.9C.11D.139.(2020届广东省茂名市二模)执行如图所示的程序框图,已知集合A={x|框图中输出的x值},集合B={y|框图中输出的y值},全集U=Z,Z为整数集,则当x=-1时,(U A)∩B= .第9题图第10题图能力拔高10.(2020届哈尔滨二模)我国古代名著《庄子·天下篇》中有一句名言“一尺之棰,日取其半,万世不竭”,其意思为:一尺的木棍,每天截取一半,永远都截不完.现将该木棍依此规律截取,如图所示的程序框图的功能就是计算截取20天后所剩木棍的长度(单位:尺),则①②③处可分别填入的是().,i=2iA.i<20?,S=S-1iB.i≤20?,S=S-1,i=2ii,i=i+1C.i<20?,S=S2D.i≤20?,S=S,i=i+1211.(2020届广东汕头二模)执行如图所示的程序框图,若输出的S=1022,则判断框内应填入的条件是().A.n>7?B.n>8?C.n>9?D.n>10?第11题图第12题图12.(2020届湖北模拟)我国南宋时期的数学家秦九韶在他的著作《数书九章》中提出了多项式求值的秦九韶算法.如图所示的框图给出了利用秦九韶算法求多项式的一个实例.若输入的n=5,υ=1,x=2,则输出的υ的值为().A.15B.31C.63D.12713.(2020届广东省佛山市一模)执行如图所示的程序框图,输出的S的值是().B.-1A.√22C.-1-√2D.02思维拓展14.(2020届新疆月考)定义某种运算 ,a b的运算原理如图所示,设f(x)=(0 x)x,则f(x)在区间[-2,2]上的最小值为.15.(2020届山东青岛高三联考)如图,一块黄铜板上插着三根宝石针,在其中一根针上从下到上穿好由大到小的若干金片.若按照下面的法则移动这些金片:每次只能移动一片金片;每次移动的金片必须套在某根针上;大片不能叠在小片上面.设移完n片金片总共需要的次数为a n,可推得a1=1,a n+1=2a n+1.如图是求移动次数在1000次以上的最小片数的程序框图模型,则输出的i的值是().A.8B.9C.10D.11。

高三第一轮复习算法初步、框图

算法初步、框图【提纲挈领】主干知识归纳1．算法的概念：算法通常是指按一定规则解决某一类问题的明确和有限的步骤．2.程序框图又称流程图，是一种用程序框、流程线及文字说明来表示算法的图形.3.程序框图的三种基本逻辑结构是顺序结构、条件结构、循环结构．4.算法的描述方式有：自然语言、程序框图、程序语言．5.算法的基本特征：①明确性：算法的每一步执行什么是明确的；②顺序性：算法的“前一步”是“后一步”的前提，“后一步”是“前一步”的继续；③有限性：算法必须在有限步内完成任务，不能无限制的持续进行；④通用性：算法应能解决某一类问题.方法规律总结⒈三种逻辑结构的主要作用顺序结构是最简单的算法结构，它是任何一个算法都离不开的一种基本算法结构，条件分支结构主要用在一些需要依据条件进行判断的算法中，如分段函数的求值、数据的大小比较等问题。

循环结构主要用在一些有规律的重复计算的算法中，如累加求和、累乘求积等问题。

⒉循环结构的程序框图的运用①循环结构的循环过程是由两个变量控制，一个是计数变量，一个是累加变量。

②循环的结束由判断条件决定。

因此，解决带有循环结构的程序框图时要注意三看：一看开始时设定的变量；二看变量的变化规律；三看循环终止的条件。

⒊输入、输出和赋值语句是任何一个算法中必不可少的语句，一个语句可以输出多个表达式。

在赋值语句中，一定要注意其格式的要求，如“ ”的右侧必须是表达式，左侧必须是变量；一个语句只能给一个变量赋值；变量的值始终等于最近一次赋给它的值，先前的值将被替换；条件语句的主要功能是实现算法中的条件结构，解决像“判断一个数的正负”“比较两个数的大小”“对一组数进行排序”“求分段函数的函数值”等问题，计算时就需要用到条件语句。

【指点迷津】【类型一】基本逻辑结构【例1】： (1)(2013·浙江卷)某程序框图如图所示，若该程序运行后输出的值是95，则( )．A．a＝4 B．a＝5 C．a＝6 D．a＝7(2)．执行下面的程序框图，若输入的ε的值为0.25，则输出的n的值为________．【解析】：(1)依框图知：当k ＞a 时，S ＝1＋11×2＋12×3＋…＋1k k ＋1＝1＋⎝⎛⎭⎫11－12＋⎝⎛⎭⎫12－13＋…＋⎝⎛⎭⎫1k －1k ＋1＝1＋1－12＋12－13＋…＋1k －1k ＋1＝2－1k ＋1.当S ＝95时，k ＝4，故由程序框图可知k ＝4＞a 不成立，k ＝5＞a 成立，所以a ＝4. (2)由程序框图可知：第一次运行：F 1＝1＋2＝3，F 0＝3－1＝2，n ＝1＋1＝2，1F 1＝13＞ε，不满足要求，继续运行；第二次运行：F 1＝2＋3＝5，F 0＝5－2＝3，n ＝2＋1＝3，1F 1＝15＝0.2＜ε，满足条件．结束运行，输出n ＝3. 【答案】： (1)A (2)3规律方法：此类问题的一般解法是严格按照程序框图设计的计算步骤逐步计算，逐次判断是否满足判断框内的条件，决定循环是否结束．要注意初始值的变化，分清计数变量与累加(乘)变量，掌握循环体等关键环节．【例2】：阅读下边的程序框图，运行相应的程序，则输出n 的值为( ).A ．7B ．6C ．5D ．4【解析】：第1次，S ＝－1，不满足判断框内的条件；第2次，n ＝2，S ＝1，不满足判断框内的条件；第3次，n ＝3，S ＝－2，不满足判断框内的条件；第4次，n ＝4，S ＝2，满足判断框内的条件，结束循环，所以输出的n ＝4. 【答案】： D【类型二】程序框图的识别与应用问题【例1】：(1)(2013·新课标全国Ⅱ卷)执行如图1的程序框图，如果输入的N ＝4，那么输出的S ＝( )．图1 图2A ．1＋12＋13＋14B ．1＋12＋13×2＋14×3×2C ．1＋12＋13＋14＋15D ．1＋12＋13×2＋14×3×2＋15×4×3×2(2)．执行如图2所示的程序框图，如果输出s ＝3，那么判断框内应填入的条件是( )． A ．k ≤6? B ．k ≤7? C ．k ≤8? D ．k ≤9?【解析】：(1)由框图知循环情况为：T ＝1，S ＝1，k ＝2；T ＝12，S ＝1＋12，k ＝3；T ＝12×3，S ＝1＋12＋12×3，k ＝4；T ＝12×3×4，S ＝1＋12＋12×3＋12×3×4，k ＝5＞4，故输出S .(2)首次进入循环体，s ＝1×log 23，k ＝3；第二次进入循环体，s ＝lg 3lg 2×lg 4lg 3＝2，k ＝4；依次循环，第六次进入循环体，s ＝3，k ＝8，此时终止循环，则判断框内填k ≤7？. 【答案】： (1)B (2)B规律方法：识别、运行程序框图和完善程序框图的思路 (1)要明确程序框图的顺序结构、条件结构和循环结构． (2)要识别、运行程序框图，理解框图所解决的实际问题． (3)按照题目的要求完成解答并验证．【例2】：阅读如图所示的程序框图，若输入的k ＝10，则该算法的功能是( )． A ．计算数列{2n －1}的前10项和 B ．计算数列{2n －1}的前9项和 C ．计算数列{2n －1}的前10项和 D ．计算数列{2n－1}的前9项和【解析】：由程序框图可知：输出S ＝1＋2＋22＋…＋29，所以该算法的功能是计算数列{2n －1}的前10项的和．【答案】： A【类型三】基本算法语句【例１】： (1)(2013·陕西卷)根据图1算法语句，当输入x 为60时，输出y 的值为( )．图1 图2A ．25B ．30C ．31D ．61(2)．根据图2的程序写出相应的算法功能为________．【解析】：(1)通过阅读理解知，算法语句是一个分段函数y ＝f (x )＝⎩⎨⎧0.5x ，x ≤50，25＋0.6x －50x ＞50，∴y ＝f (60)＝25＋0.6×(60－50)＝31.(2)该程序是计算1～999中连续奇数的平方和．【答案】： (1)C (2)求和：12＋32＋52＋…＋9992【例２】： (1)请写出图1运算输出的结果为________．图1(2)为了在运行图2的程序之后得到结果y ＝16，则键盘输入的x 应该是________．图2【解析】：(1)语句c ＝a ＋b 是将a ，b 的和赋值给c ，故c ＝2＋3＝5；语句b ＝a ＋c －b 是将a ＋c －b 的值赋值给b .故b ＝2＋5－3＝4.输出的结果为：2,4,5. (2)∵算法语句一个分段函数f (x )＝⎩⎨⎧x ＋12，x ＜0，x －12，x ≥0.∴当x ＜0时，令(x ＋1)2＝16，∴x ＝－5；当x ≥0时，令(x －1)2＝16，∴x ＝5，∴x ＝±5.【答案】： (1)2,4,5 (2)±5【同步训练】【一级目标】基础巩固组一、选择题1.阅读如图所示的程序框图，运行相应的程序，当输入x 的值为－25时，输出x 的值为 ( )A ．－1B ．1C ．3D ．9【解析】：当x ＝－25时，|x |>1，所以x ＝25－1＝4>1，x ＝4－1＝1>1不成立，所以输出x ＝2×1＋1＝3.【答案】：C2.阅读如图所示的程序框图，运行相应的程序，输出的结果i ＝________.解析：从题中程序框图知，a ＝10，i ＝1；a ＝5，i ＝2；a ＝16，i ＝3；a ＝8，i ＝4；a ＝4，i ＝5.故输出i ＝5.【答案】：53.(2013·课标全国)执行下面的程序框图，如果输入的t ∈[－1,3]，则输出的s 属于（）A ．[－3,4]B ．[－5,2]C ．[－4,3]D ．[－2,5]【解析】：由题中框图知s 是关于t 的分段函数：s ＝⎩⎨⎧3t ，－1≤t <1，4t －t 2，1≤t ≤3，当t ∈[－1,1)时，s ∈[－3,3)；当t ∈[1,3]时，s ＝4t －t 2＝4－(t －2)2∈[3,4]，故s ∈[－3,4]，故选A. 【答案】：A4.阅读下边的程序框图，运行相应的程序，则输出n 的值为（） A ．7 B ．6 C ．5 D ．4【解析】：由题中程序框图知，该框图的功能是输出满足S ＝－1＋2－3＋…＋(－1)n·n ≥2的n 的值．因为S ＝－1＋2－3＝－2<2，S ＝－1＋2－3＋4≥2，所以n ＝4，故输出n 的值为4.选D.【答案】：D5.阅读如下程序框图，如果输出i ＝4，那么空白的判断框中应填入的条件是（）A ．S <8B ．S <9C ．S <10D ．S <11【解析】：由框图及输出i ＝4可知循环应为：i ＝2，S ＝5；i ＝3，S ＝8；i ＝4，S ＝9，输出i ＝4，所以应填入的条件是S <9，故选B. 【答案】：B 二、填空题6.某算法的程序框图如图所示，则输出量y 与输入实数x 满足的关系式是________．【解析】：由题意知，程序框图表达的是一个分段函数 y ＝⎩⎨⎧2x，x ≤1x －2，x >1.【答案】：y ＝⎩⎨⎧2x，x ≤1x －2，x >17．(2013·湖北)阅读如图所示的程序框图，运行相应的程序，输出的结果i ＝________.【解析】：从题中程序框图知，a ＝10，i ＝1；a ＝5，i ＝2；a ＝16，i ＝3；a ＝8，i ＝4；a ＝4，i ＝5.故输出i ＝5.【答案】：58．若某程序框图如图所示，则该程序运行后输出的值等于________．【解析】：第一步，S ＝1＋12＝32，k ＝2；第二步，S ＝32＋12×3＝53，k ＝3；第三步，S ＝53＋13×4＝74，k ＝4；第四步，S ＝74＋14×5＝95，k ＝5，结束循环．输出S ＝95.【答案】：95三、解答题9.画出计算S ＝1·22＋2·23＋3·24＋…＋10·211的值的程序框图．【解析】：如图所示：10.到银行办理个人异地汇款(不超过100万元)，银行收取一定的手续费，汇款额不超过100元，收取1元手续费；超过100元但不超过5 000元，按汇款额的1%收取；超过5 000元，一律收取50元手续费，设计一个描述汇款额x 元，银行收取手续费y 元的算法．试画出程序框图．【解析】：由题意可知，y ＝⎩⎪⎨⎪⎧1，0＜x ≤100，0.01x ，100＜x ≤5 000，50，5 000＜x ≤1 000 000.算法如下：第一步：输入x .第二步：若0＜x ≤100，则y ＝1；否则执行第三步．第三步：若x ≤5 000，则y ＝0.01；否则y ＝50. 第四步：输出y . 程序框图如下：【二级目标】能力提升题组一、选择题1.依据小区管理条例，小区编制了如图所示的住户每月应缴纳卫生管理费的程序框图，并编写了相应的程序．已知小张家共有4口人，则他家每个月应缴纳的卫生管理费(单位：元)是( )．A．3.6 B．5.2 C．6.2 D．7.2【解析】：当n＝4时，S＝5＋1.2×(4－3)＝6.2.【答案】 C2.(2013·重庆)执行如图所示的程序框图，如果输出s＝3，那么判断框内应填入的条件是（）A．k≤6 B．k≤7 C．k≤8 D．k≤9【解析】：第一步，s＝s·log k(k＋1)＝log23，k＝2＋1＝3；第二步，s＝s·log k(k＋1)＝log23·log34＝log24，k＝3＋1＝4；第三步，s＝s·log k(k＋1)＝log24·log45＝log25，k＝5；…；第n步，s＝log2(n＋1)·log(n＋1)(n＋2)＝log2(n＋2)，k＝n＋2，若输出s＝3，则log2(n＋2)＝3，n＋2＝8，n＝6，k＝n＋2＝8，说明k＝8时结束，故应填k≤7.选B.【答案】：B二、填空题3.执行下面的程序框图，若输入的ε的值为0.25，则输出的n的值为________．【解析】：输入ε＝0.25后，程序执行如下：①⎩⎪⎨⎪⎧ε＝0.25，F 0＝1，F 1＝2，n ＝1，②⎩⎪⎨⎪⎧F 1＝F 0＋F 1＝3，F 0＝F 1－F 0＝2，n ＝2，1F 1＝13>0.25，③⎩⎪⎨⎪⎧F 1＝F 0＋F 1＝5，F 0＝F 1－F 0＝3，n ＝3，1F 1＝15≤0.25，此时输出的n 的值为3.【答案】：3三、解答题4.(2011·汕头模拟)已知数列{a n }的各项均为正数，观察程序框图，若k ＝5，k ＝10时，分别有S ＝511和S＝1021. (1)试求数列{a n }的通项；(2)令b n ＝2a n ，求b 1＋b 2＋…＋b m 的值．【解析】：由题中框图可知S ＝1a 1a 2＋1a 2a 3＋…＋1a k a k ＋1，∵数列{a n }是等差数列，设公差为d ，则有1a k a k ＋1＝1d (1a k －1a k ＋1)，∴S ＝1d (1a 1－1a 2＋1a 2－1a 3＋…＋1a k －1a k ＋1)＝1d (1a 1－1a k ＋1)．(4分) (1)由题意可知，k ＝5时，S ＝511；k ＝10时，S ＝1021.∴⎩⎨⎧1d 1a 1－1a 6511，1d1a 1－1a 111021，解得⎩⎨⎧ a 1＝1，d ＝2或⎩⎨⎧a 1＝－1，d ＝－2(舍去)．故a n ＝a 1＋(n －1)d ＝2n －1.(8分)(2)由(1)可得b n ＝2a n ＝22n －1，∴b 1＋b 2＋…＋b m＝21＋23＋…＋22m －1＝21－4m1－4＝23(4m －1)．【答案】：（1）1d (1a 1－1a k ＋1)；（2）23(4m－1)。

届高三数学第一轮复习算法初步

i=13 算法初步§1.1-2 算法的含义、程序框图重难点：通过实例体会算法的思想，了解算法的含义，了解算法的主要特点（有限性和确定性）；能用流程图表示顺序、选择、循环这三种基本结构，能识别简单的流程图所描述的算法．考纲要求：①了解算法的含义、了解算法的思想．②理解程序框图的三种基本逻辑结构：顺序、条件分支、循环．经典例题：阅读下列伪代码，并指出当3,5a b ==-时的计算结果：⑴read a, b (2) read a, b (3) read a, b X ←a+b a ←a+b a ←a+b y ←a-b b ←a-b b ←a-b a ←(x+y)/2 a ←(a+b)/2 a ←(a-b)/2 b ←(x-y)/2 b ←(a-b)/2 b ←(a+b)/2 Print a, b Print a, b Print a, b a= ，b= a= ，b= a= ，b= 当堂练习：1．算法的有穷性是指（）A ．算法必须包含输出B ．算法中每个操作步骤都是可执行的C ．算法的步骤必须有限D ．以上说法均不正确2用电水壶烧一壶开水，壶中还有一点儿水，若规定盖上水壶盖是最后一步，则插上电源是（）A ．第二步B ．第三步C ．最后第二步D ．最后第三步 3．下列哪个不是算法的特征（）A ．抽象性B ．精确性C ．有穷性D ．惟一性 4．以下给出的各数中不可能是八进制数的是（）A ．312B ．10 110C ．82D ．7 457 5．下面对算法描述正确的一项是（）A ．算法只能用自然语言来描述B ．算法只能用图形方式来表示C ．同一问题可以有不同的算法D ．同一问题的算法不同，结果必然不同 6．下列各数中最小的数是（）A ．(9)85 B ．(6)210 C ．(4)1000 D ．(2)1111117．算法共有三种逻辑结构，即顺序结构，条件结构和循环结构，下列说法正确的是（）A ．一个算法只能含有一种逻辑结构B ．一个算法最多可以包含两种逻辑结构C ．一个算法必须含有上述三种逻辑结构D ．一个算法可以含有上述三种逻辑结构的任意组合 8．运行以下程序时,WHILE 循环体内语句的执行次数是（）n=0while n<100 n=n+1 n=n*n wend print n end（第8题）A ．5B ．4C ．3D ．9 9．计算机执行下面的程序段后，输出的结果是（）A ．1，3B ．4，1C ．0，0D ．6，0 10．当2x =时，下面的程序段结果是（）A ．3B ．7C ．15D ．1711．在一个算法中，算法的流程根据条件可以有几种不同的流向（） A ．1 B ．2 C ．3 D ．多于3个 12．对赋值语句的描述正确的是（）①可以给变量提供初值 ②将表达式的值赋给变量 ③可以给一个变量重复赋值 ④不能给同一变量重复赋值A ．①②③B ．①②C ．②③④D ．①②④ 13．给出以下四个问题,①x , 输出它的相反数. ②求面积为6的正方形的周长.③求三个数a,b,c 中输入一个数的最大数. ④求函数f(x)=0.10.2{≥-<+x x x x 的函数值. 其中不需要用条件语句来描述其算法的有（）A ．1个B ．2个C ．3个D ．4个 14．用秦九韶算法计算当x=5时多项式 f (x)=55x +44x +33x +22x +x+1的值．15．一堆形状大小完全相同的珠子，其中只有一粒重量比其他的轻，某同学利用科学的算法，两次利用天平找出了这棵最轻的珠子，则这堆珠子至多有粒． 16．用冒泡排序法从小到大排列数据{ 13，5，9 ，10，7，4 }，需要经过趟排序才能完成．17．循环结构描述算法，在画出算法流程图之前需要确定三件事：(1)确定循环变量和；(2)确定；(3)确定． 18．某电信部门规定：拨打市内电话时，如果通话时间不超过3分钟，则收取通话费0.2元，如果通话时间超过3分钟，则超过部分以每分钟0.1元收取通话费（通话不足1分钟时按1分钟计），试设计一个计算通话费用的算法.要求写出算法． 19．画出方程20(0)ax bx c a ++=≠的根的流程图．20．设计算法求111112233499100+++⋅⋅⋅+⨯⨯⨯⨯的值.要求画出程序框图．21．已知函数21,1||1,113,1x x y x x x -<=+-≤≤>⎧⎪⎨, 编写一程序求函数值．Z=Z+1 第2第1章算法初步§1.3 算法基本语句重难点：经历将具体问题的流程图转化为伪代码的过程；理解用伪代码表示的基本语句――输入语句、输出语句、赋值语句、条件语句、循环语句，进一步体会算法的基本思想．考纲要求：①理解几种基本算法语句――输入语句、输出语句、赋值语句、条件语句、循环语句的含义．经典例题：意大利数学家菲波拉契,在1202年出版的一书里提出了这样的一个问题:一对兔子饲养到第二个月进入成年,第三个月生一对小兔,以后每个月生一对小兔,所生小兔能全部存活并且也是第二个月成年,第三个月生一对小兔,以后每月生一对小兔.问这样下去到年底应有多少对兔子? 试画出解决此问题的程序框图,并编写相应的程序．当堂练习：1．下边程序运行后的输出结果为（）A ．17B ．19C ．212A 3A 5 6 7 C ． 6 7 8 D ． 6 7 8 9 4右图给出的是计算111124620+++⋅⋅⋅+的值的一个程序框图，其中判断框内应填入的条件是（） A ．i>10 B ．i<10 C ．i>20 D ．i<20 5．算法: S1 输入n ；S2 判断n 是否是2，若n=2，则n 满足条件，若n>2，则执行S3；s3 依次从2到n 一1检验能不能整除n ，若不能整除n, 则输出n ．则输出n 是（）A ．质数B ．奇数C ．偶数 D.约数 6．读程序甲：INPUT i=1 乙：INPUT I=1000 S=0 S=0 WHILE i≤1000 DOS=S+i S=S+i i=i+l I=i 一1 WEND Loop UNTIL i<1 PRINT S PRINT SEND END对甲乙两程序和输出结果判断正确的是（）A ．程序不同结果不同B ．程序不同，结果相同C ．程序相同结果不同D ．程序相同，结果相同 7．阅读下列程序：输入x ；if x ＜0， then y ：＝32x π+；else if x ＞0， then y ：＝52x π-+；else y ：＝0；如果输入x＝－2，则输出结果y为（）A．3＋π B．3－πC．π－5 D．－π－5 8．x=5y=6PRINT xy=11END上面程序运行时输出的结果是（）A．xy≠11 B．11 C．xy=11 D．出错信息9．下面的问题中必须用条件结构才能实现的个数是（）（1）已知三角形三边长，求三角形的面积；（2）求方程ax+b=0(a,b为常数)的根；（3）求三个实数a,b,c中的最大者；（4）求1+2+3+…+100的值。

2019年高考数学一轮复习：算法初步

2019年高考数学一轮复习：算法初步算法初步1．算法的概念及特点(1)算法的概念在数学中，算法通常是指按照一定______解决某一类问题的________和________的步骤．(2)算法的特点之一是具有______性，即算法中的每一步都应该是确定的，并能有效地执行，且得到确定的结果，而不应是模棱两可的；其二是具有______性，即算法步骤明确，前一步是后一步的前提，只有执行完前一步才能进行后一步，并且每一步都准确无误才能解决问题；其三是具有______性，即一个算法应该在有限步操作后停止，而不能是无限的；另外，算法还具有不唯一性和普遍性，即对某一个问题的解决不一定是唯一的，可以有不同的解法，一个好的算法应解决的是一类问题而不是一两个问题．2．程序框图(1)程序框图的概念程序框图又称流程图，是一种用、及来表示算法的图形．(2)构成程序框图的图形符号、名称及其功能3.算法的基本逻辑结构(1)顺序结构顺序结构是最简单的算法结构，语句与语句之间，框与框之间是按__________的顺序进行的．它是由若干个__________的步骤组成的，它是任何一个算法都离不开的基本结构．顺序结构可用程序框图表示为如图所示的形式．(2)条件结构在一个算法中，经常会遇到一些条件的判断，算法的流程根据条件是否成立有不同的流向．常见的条件结构可以用程序框图表示为如图所示的两种形式．(3)循环结构在一些算法中，经常会出现从某处开始，按照一定的条件反复执行某些步骤的情况，这就是．反复执行的步骤称为．循环结构有如下两种形式：①如图1，这个循环结构有如下特征：在执行了一次循环体后，对条件进行判断，如果条件不满足，就继续执行循环体，直到条件满足时终止循环．因此，这种循环结构称为____________．②如图2表示的也是常见的循环结构，它有如下特征：在每次执行循环体前，对条件进行判断，当条件满足时，执行循环体，否则终止循环．因此，这种循环结构称为____________．4．输入(INPUT)语句输入语句的一般格式：.要求：(1)输入语句要求输入的值是具体的常量；(2)提示内容提示用户输入的是什么信息，必须加双引号，“提示内容”原原本本地在计算机屏幕上显示，提示内容与变量之间要用分号隔开；(3)一个输入语句可以给多个变量赋值，中间用“，”分隔．5．输出(PRINT)语句输出语句的一般格式：.功能：实现算法输出信息(表达式)．要求：(1)表达式是指算法和程序要求输出的信息；(2)提示内容提示用户要输出的是什么信息，提示内容必须加双引号，提示内容要用分号和表达式分开；(3)如同输入语句一样，输出语句可以一次完成输出多个表达式的功能，不同的表达式之间可用“，”分隔．6．赋值语句赋值语句的一般格式：.赋值语句中的“＝”叫做赋值号，它和数学中的等号不完全一样．作用：赋值语句的作用是将表达式所代表的值赋给变量．要求：(1)赋值语句左边只能是变量，而不是表达式，右边表达式可以是一个常量、变量或含变量的运算式．如：2＝x是错误的．(2)赋值号的左右两边不能对换．赋值语句是将赋值号右边的表达式的值赋给赋值号左边的变量．如“A＝B”“B＝A”的含义和运行结果是不同的，如x＝5是对的，5＝x是错的，A＋B＝C是错的，C＝A＋B是对的．(3)不能利用赋值语句进行代数式的演算(如化简、因式分解、解方程等)．7．条件语句(1)“IF—THEN”语句格式：____________________．说明：当计算机执行“IF—THEN”语句时，首先对IF后的条件进行判断，如果(IF)条件符合，那么(THEN)执行语句体，否则执行END IF之后的语句．(2)“IF—THEN—ELSE”语句格式：____________________．说明：当计算机执行“IF—THEN—ELSE”语句时，首先对IF后的条件进行判断，如果(IF)条件符合，那么(THEN)执行语句体1，否则(ELSE)执行语句体2.8．循环语句(1)直到型循环语句直到型(UNTIL型)语句的一般格式为：______________．(2)当型循环语句当型(WHILE型)语句的一般格式为：________________．自查自纠1．(1)规则明确有限(2)确定有序有穷2．(1)程序框流程线文字说明 (2)①终端框(起止框) ②输入、输出框③处理框(执行框) ④判断框 ⑤流程线 ⑥连接点 3．(1)从上到下依次执行 (3)循环结构循环体 ①直到型循环结构 ②当型循环结构 4．INPUT “提示内容”；变量 5．PRINT “提示内容”；表达式 6．变量＝表达式7．(1)IF 条件 THEN语句体END IF(2)8. (1)DO 循环体LOOP UNTIL 条件 (2)WHILE 条件循环体WEND下列各式中的S 值不可以用算法求解的是( ) A ．S ＝1＋2＋3＋4B ．S ＝12＋22＋32＋…＋1002C ．S ＝1＋12＋13＋…＋110 000D ．S ＝1＋2＋3＋4＋…解：由算法的有限性知，D 不正确，而A ，B ，C 都可以通过有限步骤操作，输出确定结果，故选D .下面程序运行后输出结果是3，则输入的x 值一定是( )INPUT x IF x>0 THEN y ＝x ELSE y ＝－xEND IFPRINT yENDA．3 B．－3 C．3或－3 D．0解：该程序语句是求函数y＝|x|的函数值，因为y＝3，所以x＝±3.故选C.(2016·北京)执行如图所示的程序框图，输出的s的值为()A．8 B．9 C．27 D．36解：初始值k＝0，s＝0.第一次循环得s＝0，k＝1；第二次循环得s＝1，k＝2；第三次循环得s＝9，k＝3>2，退出循环，输出的s值为9.故选B.下面程序运行后输出的结果为________．N＝5S＝0WHILE S<15S＝S＋NN＝N－1WENDPRINT NEND解：执行第一次后，S＝5，N＝4；执行第二次后，S＝9，N＝3；执行第三次后，S＝12，N＝2；执行第四次后，S＝14，N＝1；执行第五次后，S＝15，N＝0；跳出循环结构，输出N的值，N＝0，故填0.(2016·山东)执行如图所示的程序框图，若输入的a，b的值分别为0和9，则输出的i的值为____________．解：输入a ＝0，b ＝9，第一次循环：a ＝0＋1＝1，b ＝9－1＝8，i ＝1＋1＝2；第二次循环：a ＝1＋2＝3，b ＝8－2＝6，i ＝2＋1＝3；第三次循环：a ＝3＋3＝6，b ＝6－3＝3，a >b 成立，故输出i 的值为3.故填3.类型一算法的概念下列语句是算法的个数为( )①从济南到巴黎：先从济南坐火车到北京，再坐飞机到巴黎； ②统筹法中“烧水泡茶”的故事； ③测量某棵树的高度，判断其是否为大树；④已知三角形的两边及夹角，利用三角形的面积公式求出该三角形的面积． A ．1 B ．2 C ．3 D ．4解：①中勾画了从济南到巴黎的行程安排，完成了任务；②中节约时间，烧水泡茶完成了任务；③中对“树的大小”没有明确的标准，无法完成任务，不是有效的算法构造；④是纯数学问题，利用三角形的面积公式求出三角形的面积．故选C .【点拨】算法过程要做到一步一步地执行，每一步执行的操作必须确切，不能含糊不清，且在有限步后必须得到问题的结果．能设计算法计算下列各式中S 的值的是( )①S ＝12＋14＋18＋…＋12100②S ＝12＋14＋18＋…＋12100＋…③S ＝12－14＋18－…－122 018＋122 019A ．①②B ．①③C ．②③D ．①②③解：因为算法的步骤是有限的，所以②不能设计算法求解，故选B .类型二顺序结构已知直角三角形两直角边长为a，b，求斜边长c的一个算法分下列三步：①计算c＝a2＋b2；②输入直角三角形两直角边长a，b的值；③输出斜边长c的值；其中正确的顺序是()A．①②③B．②③①C．①③②D．②①③解：第一步：输入直角三角形两直角边长a，b的值，第二步：计算c＝a2＋b2，第三步：输出斜边长c的值．故选D.【点拨】顺序结构是一种最简单、最基本的结构，可严格按照传统的解题思路写出算法步骤，画出程序框图．注意语句与语句之间，框与框之间是按从上到下的顺序进行的．阅读如图所示的程序框图，若输入的a，b，c的值分别是21，32，75，则输出的a，b，c分别是()A．75，21，32 B．21，32，75C．32，21，75 D．75，32，21解：该程序框图的执行过程是：输入21，32，75；x＝21；a＝75；c＝32；b＝21；输出75，21，32.故选A.类型三条件结构下面的程序框图能判断任意输入的整数x是奇数还是偶数．其中判断框内的条件是()A．m＝0? B．m＝1?C．x＝0? D．x＝1?解：由程序框图所体现的算法可知判断一个整数是奇数还是偶数，看这个数除以2的余数是1还是0.由图可知应该填m＝1？.故选B.【点拨】条件结构的运用与数学的分类讨论有关．设计算法时，哪一步要分类讨论，哪一步就需要用条件结构．＝()A．0 B．2 C．4 D．14解：执行该程序，输入a，b的值依次为a＝14，b＝18；a＝14，b＝4；a＝10，b＝4；a＝6，b＝4；a＝2，b＝4；a＝b＝2，此时退出循环，输出的a＝2.故选B.类型四循环结构(2017·全国卷Ⅱ)执行下面的程序框图，如果输入的a＝－1，则输出的S＝()A ．2B ．3C ．4D ．5 解：S ＝0－1＋2－3＋4－5＋6＝3，故选B .【点拨】解决此类型问题时要注意：①要明确是当型循环结构，还是直到型循环结构，根据各自的特点执行循环体；②要明确图中的累计变量，明确每一次执行循环体前和执行循环体后，变量的值发生的变化；③要明确循环体终止的条件是什么，会判断什么时候终止循环体．(2016·全国卷Ⅰ)执行如图的程序框图，如果输入的x ＝0，y ＝1，n ＝1，则输出x ，y 的值满足( )A ．y ＝2xB ．y ＝3xC ．y ＝4xD ．y ＝5x解：当x ＝0，y ＝1，n ＝1时，x ＝0＋1－12＝0，y ＝1×1＝1，不满足x 2＋y 2≥36；n ＝2，x ＝0＋2－12＝12，y ＝2×1＝2，不满足x 2＋y 2≥36；n ＝3，x ＝12＋3－12＝32，y ＝3×2＝6，满足x 2＋y 2≥36，输出x ＝32，y ＝6，则输出的x ，y 的值满足y ＝4x .故选C .类型五输入、输出和赋值语句下列程序语句的算法功能是()INPUT a，b，cIF a<b THENa＝bEND IFIF a<c THENa＝cEND IFPRINT aENDA．输出a，b，c三个数中的最大数B．输出a，b，c三个数中的最小数C．将a，b，c从小到大排列D．将a，b，c从大到小排列解：由程序语句可知，当比较a，b的大小后，选择较大的数赋给a；当比较a，c的大小后，选择较大的数赋给a，最后输出a，所以此程序的作用是输出a，b，c中最大的数．故选A.【点拨】①将一个变量的值赋给另一个变量，前一个变量的值保持不变；②可先后给一个变量赋多个不同的值，但变量的取值总是最后被赋予的值．下列程序段执行后，变量a，b的值分别为()a＝15b＝20a＝a＋bb＝a－ba＝a－bPRINT a，bA．20，15 B．35，35C．5，5 D．－5，－5解：a＝15，b＝20，把a＋b赋给a，因此得出a＝35，再把a－b赋给b，即b＝35－20＝15.再把a－b赋给a，此时a＝35－15＝20，因此最后输出的a，b的值分别为20，15.故选A .类型六条件语句已知函数y ＝⎩⎪⎨⎪⎧x 2－1，x ≥0，2x 2－5，x <0，编写一个程序，对每输入的一个x 值，都得到相应的函数值．解：程序如下：INPUT “x ＝”；x IF x>＝0 THEN y ＝x^2－1 ELSEy ＝2*x^2－5 END IFPRINT “y ＝”；y END【点拨】条件语句：“IFTHEN ”及“IFTHENELSE ”的用法在“考点梳理”栏有说明，需要注意的是，若是三段或三段以上的分段函数，通常需用条件语句的嵌套结构．下列程序语句是求函数y ＝|x －4|＋1的函数值，则①处为( )INPUT “x ＝”；x IF x>＝4 THEN y ＝x －3 ELSE ① END IF PRINT y ENDA ．y ＝3－xB ．y ＝x －5C ．y ＝5－xD ．y ＝x ＋5 解：y ＝|x －4|＋1＝⎩⎪⎨⎪⎧x －3，x ≥4，5－x ，x <4，故选C .类型七循环语句运行下面的程序，执行后输出的s 的值是( )i ＝1 WHILE i<6 i ＝i ＋2 s ＝2*i ＋1 WEND PRINT s ENDA ．11B ．15C ．17D ．19解：当i ＝3时，s ＝7，当i ＝5时，s ＝11，当i ＝7时，s ＝15，此时不满足“i <6”，所以输出s ＝15，故选B .【点拨】计算机执行此程序时，遇到WHILE 语句，先判断条件是否成立，如果成立，则执行WHILE 和WEND 之间的循环体，然后返回到WHILE 语句再判断上述条件是否成立，直至返回到WHILE 语句判断上述条件不成立为止，这时不再执行循环体，而执行WEND 后面的语句，这是当型循环．计算12＋22＋32＋…＋1002的值，分别用WHILE 型语句和UNTIL 型语句编写程序．解：WHILE 型：UNTIL 型： i ＝1 S ＝0WHILE i<＝100 S ＝S ＋i^2 i ＝i ＋1 WEND PRINT S ENDi ＝1 S ＝0 DO S ＝S ＋i^2 i ＝i ＋1LOOP UNTIL i>100 PRINT S END1．设计算法时，要根据题目进行选择，以简单、程序短、易于在计算机上执行为原则． 2．画程序框图首先要进行结构选择，套用格式．若求只含有一个关系式的函数的函数值时，只用顺序结构就能够解决；若是分段函数或执行时需要先判断才能执行后继步骤的，就必须引入条件结构；如果问题涉及的运算进行了许多重复的步骤，有规律，就可引入变量，应用循环结构．当然，应用循环结构一定要用到顺序结构与条件结构．3．循环结构的循环控制通过累加变量记录循环次数，通过判断框决定循环终止与否．用循环结构来描述算法，在画出算法程序框图之前，需要确定的三件事是：(1)确定循环变量与初始条件；(2)确定循环体；(3)确定终止条件．注意直到型循环与当型循环的区别，二者判断框内的条件表述在解决同一问题时恰好相反．解决循环结构框图问题，当循环次数比较少时，可依次列出；当循环次数较多时，可先循环几次，找出规律．要特别注意最后输出的是什么，不要出现多一次或少一次循环的错误．4．在具体绘制程序框图时，要注意以下几点：(1)流程线上要标有执行顺序的箭头．(2)判断框后边的流程线应根据情况标注“是(Y)”或“否(N)”．(3)框图内的内容包括累加(积)变量初始值，计数变量初始值，累加值，前后两个变量的差值都要仔细斟酌，不能有丝毫差错．(4)判断框内条件常用“>”“≥”“<”“≤”“＝”等符号，它们的含义是各不相同的，要根据所选循环结构的类型，正确地进行选择．5．当型循环与直到型循环的区别(1)WHILE型是先判断条件，后执行循环体，而UNTIL型则是先执行循环体，后判断条件；(2)WHILE型是当条件满足时执行循环体，不满足时结束循环，而UNTIL型则是条件不满足时执行循环体，条件满足时结束循环；(3)UNTIL型至少执行一次循环体，而WHILE型执行循环体的次数可能为0.1．下列叙述能称为算法的个数为()①植树需要运苗、挖坑、栽苗、浇水这些步骤；②顺序进行下列运算：1＋1＝2，2＋1＝3，3＋1＝4，…，99＋1＝100；③从宜昌乘火车到武汉，从武汉乘飞机到北京；④3x>x＋1；⑤求所有能被3整除的正数，即3，6，9，12，….A．2 B．3 C．4 D．5解：①②③可称为算法，④⑤不是，故选B.2．结合下面的算法：第一步：输入x.第二步：判断x是否小于0，若是，则输出x＋2，否则执行第三步．第三步：输出x－1.当输入的x的值为－1，0，1时，输出的结果分别为()A．－1，0，1 B．－1，1，0C．1，－1，0 D．0，－1，1解：根据x值与0的关系，选择执行不同的步骤，当x的值为－1，0，1时，输出的结果分别为1，－1，0，故选C.3．如图是一个算法的程序框图，已知a1＝1，输出的b＝3，则输入的a2等于() A．3 B．5 C．7 D．9解：由题意知该算法是计算a1＋a22的值，则1＋a22＝3，解得a2＝5.故选B.4．(教材练习改编)阅读下面的程序：INPUT xIF9<x ANDx<100THENa＝x\10b＝x MOD10x＝10*b＋aPRINT xEND IFEND如果上述程序输入的值是51，则运行结果是()A．51 B．15 C．105 D．501解：因为51÷10＝5……1，所以a＝5，b＝1，x＝10×1＋5＝15.故选B. 5．(2016·天津)阅读如图所示的程序框图，运行相应的程序，则输出S的值为()A ．2B ．4C ．6D ．8解：第一次循环，S ＝8，n ＝2；第二次循环，S ＝2，n ＝3；第三次循环，S ＝4，n ＝4，故输出S 的值为4.故选B .6．(2017·全国卷Ⅲ)执行如图所示的程序框图，为使输出S 的值小于91，则输入的正整数N 的最小值为( )A ．5B ．4C ．3D ．2解：当输入的正整数N 是所给选项中最小的正整数2时，t ＝1，M ＝100，S ＝0，则第一次循环，S ＝0＋100＝100，M ＝－10010＝－10，t ＝2；第二次循环，S ＝100－10＝90，M ＝－－1010＝1，t ＝3，此时t ≤2不成立，输出S ＝90<91.故选D . 7．给出下面一个程序：A ＝5B ＝8 X ＝A A ＝B B ＝X ＋A PRINT B END此程序运行的结果是________．解：X ＝5，A ＝8，B ＝5＋8＝13.故填13.8．(2015·安徽)执行如图所示的程序框图(算法流程图)，输出的n 为________．解：由题意，程序框图循环如下：a ＝1，n ＝1；a ＝1＋11＋1＝32，n ＝2；a ＝1＋132＋1＝75，n ＝3；a ＝1＋175＋1＝1712，n ＝4，此时⎪⎪⎪⎪1712－1.414≈0.003<0.005，所以输出n ＝4，故填4. 9．(2016·四川改编)秦九韶是我国南宋时期的数学家，普州(现四川省安岳县)人，他在所著的《数书九章》中提出的多项式求值的秦九韶算法，至今仍是比较先进的算法．如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例，若输入n ，x 的值分别为3，2，求输出v 的值．解：该程序框图的执行过程如下：v ＝1，i ＝2；v ＝1×2＋2＝4，i ＝1；v ＝4×2＋1＝9，i ＝0；v ＝9×2＋0＝18，i ＝－1，此时输出v ＝18.10．如果以下程序运行后输出的结果是132，求程序中UNTIL 后面的条件中a 的取值范围．i ＝12 S ＝1 DO S ＝S*i i ＝i －1LOOP UNTIL i<aPRINT S END解：程序的功能是计算S ＝12×11×10×…，输出结果为132，即循环体只执行了两次，即i ＝10时，就结束了循环，所以a 满足10<a ≤11.故a 的取值范围为(10，11]．11．某篮球队6名主力队员在最近三场比赛中投进的三分球个数如表格所示：队员i 1 2 3 4 5 6 三分球个数a 1a 2a 3a 4a 5a 6统计该6名队员在最近三场比赛中投进的三分球总数的程序框图如图所示．(1)试在判断框内填上条件； (2)求输出的s 的值．解：(1)依题意，程序框图是统计6名队员投进的三分球的总数，所以判断框内应填条件“i ≤6？”．(2)6名队员投进的三分球个数分别为a 1，a 2，a 3，a 4，a 5，a 6，故输出的s ＝a 1＋a 2＋…＋a 6.(2015·全国卷Ⅰ)执行如图所示的程序框图，如果输入的t ＝0.01，则输出的n ＝( )A ．5B ．6C ．7D ．8解法一：执行程序，S ＝12，m ＝14，n ＝1；S ＝14，m ＝18，n ＝2；S ＝18，m ＝116，n ＝3；S＝116，m ＝132，n ＝4；S ＝132，m ＝164，n ＝5；S ＝164，m ＝1128，n ＝6；S ＝1128<t ＝0.01，m＝1256，n＝7，循环结束，输出n＝7.解法二：记第n次循环后S的值为a n()n＝0，1，2，…，其中a0＝1，则a n＝a n－1－⎝⎛⎭⎫12n，递推可得an ＝a0－⎝⎛⎫12＋122＋…＋12n＝1－12⎣⎡⎦⎤1－⎝⎛⎭⎫12n1－12＝12n≤t＝0.01.显然n>6，故n＝7.故选C.。