宁波大学3801弹性力学考博真题试题2018年
宁波大学理论力学2017--2020年考博初试真题

宁波大学 2020 年博士研究生招生考试初试试题(A 卷)
(答案必须写在考点提供的答题纸上)
(A) 0 (C) (vA - vB)/2
(B) (vA + vB)/2 (D) (vB - vA)/2
4. 点的加速度合成定理 aa=ae+ar 的适应条件是( )。
(A) 牵连运动只能是平移 (B) 各种牵连运动都适用 (C) 牵连运动只能是转动 (D) 牵连运动为零
5. 均质圆盘 O 的质量为 2m,半径为 r,物体 A、B 的质量为 m。如果绳与
(B) J z2 J z1 m a2 b2 (C) J z2 J z1 m b2 a2
z1
z
z2
a
b
C
(D) J z2 J z1 m a2 b2
5. 平面运动刚体的动能,等于它以( )速度作平动时的动能加上绕(
的动能。
(A) 初始,质心
(B) 质心,重心
(C) 质心,质心
B
A
θ
D
第2页共2页
宁波大学 2017 年博士研究生招生考试初试试题(B 卷)
(答案必须写在考点提供的答题纸上)
科目代码 : 2613 科目名称:
理论力学
一、 单项选择题:本大题共 5 小题,每小题 4 分,共 20 分。
1. 力学上把约束加在物体上的作用力称为约束反力,约束反力是( 的。如果没有任何( )存在,约束反力也就不存在了。
2. 质量为 100kg、半径为 1m 的均质圆轮,以转速 n=120r/min 绕 O 轴转 动,如左图所示。有一常力 F 作用于闸杆,轮经 10s 后停止转动。已 知摩擦因数 f=0.1,求力 F 的大小。(14 分)
宁波大学流体力学2019--2020年考博初试真题

(答案必须写在考点提供的答题纸上)(答案必须写在考点提供的答题纸上)如图所示,有一具有水平底面的水池,水深为h,水池的一个侧面为矩形ABCD(垂直于纸面方向)记为b,该侧面相对于底面的倾角记为θ。
已知水的密度为)请确定水对侧面ABCD所施加的压力p的分布情况(5分);(2)计算其合力出合力的大小,方向和作用点)(13分)。
(答案必须写在考点提供的答题纸上)第1页共3页科目代码:3802总分值:100科目名称:流体力学一.单项选择题:(共12分,每小题1分)1.流体按照是否考虑其粘性,可将流体分为:()(A)牛顿流体及非牛顿流体;(B)可压缩流体与不可压缩流体;(C)均质流体与非均质流体;(D)理想流体与真实流体。
2.动力粘性系数的量纲是()。
(A)FL -2T ;(B)FL -1T -1;(C )FLT -2;(D)FLT 2。
3.圆管层流,管轴心处的流速为1.8m/s ,则该断面的平均流速为()。
(A)2.4m/s ;(B)1.8m/s ;(C)1.35m/s ;(D)0.9m/s.4.流体力学中,用无量纲数Re 来判别真实流体的两种流态—层流和湍流,其临界值大约是()。
(A )2300;(B)1200;(C)3600;(D)这些都不是。
5.并联管路的总阻力损失等于()。
(A )各管段阻力损失之和的2倍;(B)各管段的阻力损失之和;(C )任一支管的阻力损失。
(D )不确定。
6.层流断面流速分布规律符合()。
(A )对数分布;(B )直线分布;(C)抛物线分布;(D )椭圆分布。
7.对于层流边界层,()将加速边界层的分离。
(A )减少逆压梯度和减少运动粘滞系数;(B)增加逆压梯度和减少运动粘滞系数;(C )减少逆压梯度和增加运动粘滞系数;(D )增加逆压梯度和增加运动粘滞系数。
8.流体有势的充分必要条件是()。
(A )流动是无旋的;(B)必须是平面流动;(C )必须是无旋的平面流动;(D )流线是直线的流动;9.船舶在水中航行时,船体对水的作用相当于连续分布的压力点在水面上运动,每一压力点均产生波浪,但兴波作用最强的是在()。
弹性力学试题及答案

《弹性力学》试题参考答案(答题时间:100分钟)一、填空题(每小题4分)1.最小势能原理等价于弹性力学基本方程中:平衡微分方程, 应力边界条件。
2.一组可能的应力分量应满足:平衡微分方程,相容方程(变形协调条件) 。
3.等截面直杆扭转问题中,的物理意义是杆端截面上剪应力对转轴的矩等于杆截面内的扭矩M.4.平面问题的应力函数解法中,Airy应力函数在边界上值的物理意义为边界上某一点(基准点)到任一点外力的矩。
5.弹性力学平衡微分方程、几何方程的张量表示为:,。
二、简述题(每小题6分)1.试简述力学中的圣维南原理,并说明它在弹性力学分析中的作用。
圣维南原理:如果物体的一小部分边界上的面力变换为分布不同但静力等效的面力(主矢与主矩相同),则近处的应力分布将有显著的改变,但远处的应力所受影响可以忽略不计。
作用:(1)将次要边界上复杂的面力(集中力、集中力偶等)作分布的面力代替。
(2)将次要的位移边界条件转化为应力边界条件处理。
2.图示两楔形体,试分别用直角坐标和极坐标写出其应力函数的分离变量形式。
题二(2)图(a)(b)3.图示矩形弹性薄板,沿对角线方向作用一对拉力P,板的几何尺寸如图,材料的弹性模量E、泊松比 已知.试求薄板面积的改变量.题二(3)图设当各边界受均布压力q时,两力作用点的相对位移为。
由得,设板在力P作用下的面积改变为,由功的互等定理有:将代入得:显然,与板的形状无关,仅与E、、l有关。
4.图示曲杆,在边界上作用有均布拉应力q,在自由端作用有水平集中力P.试写出其边界条件(除固定端外)。
题二(4)图(1);(2)(3)5.试简述拉甫(Love)位移函数法、伽辽金(Galerkin)位移函数法求解空间弹性力学问题的基本思想,并指出各自的适用性Love、Galerkin位移函数法求解空间弹性力学问题的基本思想:(1)变求多个位移函数或为求一些特殊函数,如调和函数、重调和函数。
(2)变求多个函数为求单个函数(特殊函数)。
2018年宁波大学考博试题3801弹性力学(A卷)

三、计算题(每题 20 分,共 60 分)
1. 已知下列的应变分量是物体变形时产生的,试求系数之间应满足的关系式。 ������������ = ������0 + ������1 (������ 2 + ������ 2 ) + ������ 4 + ������ 4 ������������ = ������0 + ������1 (������ 2 + ������ 2 ) + ������ 4 + ������ 4 ������������������ = ������0 + ������1 ������������(������ 2 + ������ 2 + ������2 ) ������������ = ������������������ = ������������������ =0 2. 如图所示三角形悬壁梁只受重力作用, 材料的密度为������, 试用纯三次式的应力函数求应力分量。
宁波大学 2018 年博士研究生招生考试初试试题(A 卷)
(答案必须写在考点提供的答题纸上)
科目代码:
3801
科共 2 页
3. 试 用 虚 位 移 原 理 求 如 图 所 示 梁 的 挠 度 曲 线 , 并 求 出 当 ������ = ������/2 处 的 挠 度 值 , 设 ������ = ∑
∞ ������=1
������������ sin
������������������ ������
。
第 1 页 共 2 页
宁波大学 2018 年博士研究生招生考试初试试题(A 卷)
(答案必须写在考点提供的答题纸上)
科目代码:
宁波大学弹性力学2012,2014,2015,2018,2019年考博真题

sin
������������������。
������
第1页共2页
宁波大学 2018 年博士研究生招生考试初试试题(A 卷)
(答案必须写在考点提供的答题纸上)
科目代码: 3801 科目名称:
弹性力学
第2页共2页
宁波大学 2019 年博士研究生招生考试初试试题(A 卷)
(答案必须写在考点提供的答题纸上)
(1) 经过此点且方程为
斜面上的全应力、正应力和剪应力的大小。
(2) 该点的三个主应力大小及第一个主应力相应的方向余弦。 5.(25 分)悬臂梁一端受集中力作用,梁高为 h,跨度为 L,如下图所示,若不考虑体积力,使用
应力函数 dxy3 bxy ,求该问题的应力和位移。
题5图
第1页共2页
宁波大学 2019 年博士研究生招生考试初试试题(A 卷)
科目代码: 3801 总分值: 100 科目名称:
弹性力学
1.(10 分)什么是平面应变问题?写出应变和位移基本特点。 2.(15 分)导出体应变公式和体应变的虎克定律。
3.(15 分)试推导应力状态特征方程,并写出应力张量不变量的表达式。
4.(15 分)已知物体内某点的 6 个应力分量为
,
,
,
,试求:
4.(35 分) 写出弹性体的虚(可能)功原理并从它导出弹性力学的基本方程。
第 1 页共 1 页
考试科目: 适用专业:
宁波大学 2014 年攻读博士学位研究生
入 学 考 试 试 题(B 卷) (答案必须写在答题纸上)
弹性力学 工程力学
科目代码: 3801
1. (35 分)已知下图所示问题的非零应力解为
且假设为小变形,试求:1)过点 0,2, − 1 的应变张量������������������ 和转动张量������������������ ;2) 该点的主应变。
宁波大学2020年《3813抽象代数》考博专业课真题试卷

(答案必须写在考点提供的答题纸上)
科目代码: 3813 总分值: 100 科目名称:
抽象代数
本试卷共四道大题,每道大题 25 分,总分 100 分。
一、设 A Rnn , b Rn 。定义 Rn 上的线性变换 T( A,b) 为 T(A,b) ( ) A b, Rn。
证明:
(1)当 A 的行列式不为 0 时, T( A,b) 既是单射又是满射。
(2) G T(A,b) |A| 0 关于映射的乘法构成群。 (3) K T(A,0) A 0 是 G 的子群,且与 Rn 上所有可逆矩阵组成的线性群 GL(n, R) 同构。
二、设
R
ab 23a Nhomakorabea b Z, a b 为偶数 ,证明 R 在数的加法和乘法下构成一个整环(无零因子的交
换幺环)。并求出 R 的单位群U ,即所有可逆元素的集合。
三、证明: x 是多项式整环 Zx的素理想,但不是极大理想。
四、设 : Qx Q 3 2 为 f x f 3 2 。证明:
(1) 是环同态。
(2) ker x3 2 。
(3) Q x
是域,且与域Q 3 2 同构。
x3 2
第1页共1页
宁波大学信息功能材料2013,2015--2020年考博初试真题

二、判断题:本大题共 10 小题,每小题 2 分,共 20 分,对的打√,错的打。
1. 电子和空穴的移动都能形成电流。( ) 2. 金属与半导体导电机制的区别在于:金属由自由电子导电,半导体由非平衡载流子导电。( ) 3. 费米能级物理意义是指:该能级上的一个状态被电子占据的几率是 1/2。( ) 4. 四能级固体激光器比三能级或准三能级激光器容易产生振荡发射。( ) 5. 掺铒碲化物光纤放大器具有超宽的增益带宽特性,其增益带宽可达 80nm,特别适合于 DWDM
三、简答计算题:共 50 分,第 1 题 15 分,第 2 题 20 分,第 3 题 15 分。
1. 平衡 p-n 结的空间电荷区示意图如下,画出空间电荷区中载流子漂移运动和扩散运动的方向(在下图 右侧直线上添加箭头),并说明扩散电流和漂移电流之间的关系。
2. 光纤按照制作材料、折射率分布形式以及光波模式的不同来划分,各分为哪些类型? 一阶跃光纤 n1 =1.5,n2=1.498,工作波长 1.32m,试求: (1)单模传输时光纤的纤芯半径是多少? (2)此光纤的数值孔径是多大?
(A)辐射跃迁;(B)非辐射跃迁;(C)受激辐射;(D)自发辐射
2. 在绝对零度下,可以被电子填满的最高能带为( ) (A)导带;(B)价带;(C)禁带;(D)带隙
3. 激光晶体 YAG 是指( )。 (A)蓝宝石;(B)钇铝石榴石;(C)钇镓石榴石;(D)钆镓石榴石
4. 目前,通信用光纤的纤芯和包层构成的材料绝大多数是( )。 (A)多成分玻璃;(B)石英和塑料;(C)石英;(D)塑料
(D)灵敏度比致冷型高很多
弹性力学试题及答案讲解

弹性力学与有限元分析复习题及其答案一、填空题1、弹性力学研究弹性体由于受外力作用、边界约束或温度改变等原因而发生的应力、形变和位移。
_2、在弹性力学中规定,线应变以伸长时为正,缩短时为负,与正应力的正负号规定相适应。
3、在弹性力学中规定,切应变以直角变小时为正,变大时为负,与切应力的正负号规定相适应。
4、物体受外力以后,其内部将发生内力,它的集度称为应力。
与物体的形变和材料强度直接有关的,是应力在其作用截面的法线方向和切线方向的分量, 也就是正应力和切应力。
应力及其分量的量纲是L-1MT-2。
5、弹性力学的基本假定为连续性、完全弹性、均匀性、各向同性_________6、平面问题分为平面应力问题和平面应变问题。
7、已知一点处的应力分量匚x =100 MPa,二y =50 MPa,X^1O 50 MPa,则主应力G = 150MPa,35 16 。
~2 = 0MPa,-冷=&已知一点处的应力分量,二x=200 MPa,二y=0MPa ,“*400 MPa,则主应力G = 512 MPa,二2 =-312 MPa,: 1 = -37° 57'。
9、已知一点处的应力分量,;「x=:-2000MPa,匚y =1000 MPa, xy*400 MPa,则主应力匚尸1052MPa,匚2二-2052 MPa ,:计-82° 32'。
10、在弹性力学里分析问题,要考虑静力学、几何学和物理学三方面条件,分别建立三套方程。
11、表示应力分量与体力分量之间关系的方程为平衡微分方程。
12、边界条件表示边界上位移与约束,或应力与面力之间的关系式。
分为位移边界条件、应力边界________________条件和混合边界条件。
13、按应力求解平面问题时常采用逆解法和半逆解法。
14、有限单元法首先将连续体变换成为离散化结构,然后再用结构力学位移法讲行求解。
其具体步骤分为单元分析和整体分析两部分。
宁波大学材料科学基础2013,2016,2018年考博初试专业课真题

力包括:
、
、
。
3. 纺丝方法可分为:
、
。
4. 在晶体结构中,空间点阵只能有
种形式。n 次对称轴的基本旋转操作为旋
转
,因此,晶体能在外形和宏观中反映出来的轴对称性也只限于这些轴次。5ຫໍສະໝຸດ 分子筛按骨架元素可以分为、
、
。按照孔道大小分
为
、
、
。
6. 分子筛的修饰与改性主要依靠分子筛的
,以达到无法用直接一次合成得到的结
果
7. 传统的金属有机框架材料的合成方法有:
、
、
。
8. 按合金的结构和相图,合金一般可以分为三类
、
与
。
9. 在离子晶体中,如正负离子半径比在 0.732 与 0.414 之间,则为配位数为
。
第2页共3页
宁波大学 2018 年博士研究生招生考试初试试题(B 卷)
(答案必须写在考点提供的答题纸上)
科目代码 : 2609 科目名称:
C、晶体具有自发地形成封闭几何多面体的特性
D、 晶体对称性不仅表现在外部形态上,而且其内部构造也同样是对称的
6. 下列不属于描述晶体宏观对称性时常用的对称元素与其相应的对称操作是: (
)
A、 对称轴和旋转操作
B、 反轴和旋转倒反
C、 反映面和反映操作
D、 旋转轴和旋转操作
7. 以下为可制备为高硅铝比分子筛结构的为: (
)。
A、 结构单元是原子组成与单体相同的单元 B、结构单元总是与单体对应
C、 尼龙-66 中有两种结构单元 D、结构单元数描述聚合物的分子量
3. 以下哪种过程需要最高的跨膜压力?(
)
A、微滤膜
B、超滤膜
《弹性力学》历年考博真题10-17

x、 y、 xy yx 三个应力分量。
(2)平面应变问题 : 很长的柱形体,在柱面上受有平行于横截面并且不沿长度变化的面力,而且体力 也平行于横截面且不沿长度变化。这一类问题可以简化为平面应变问题。例如挡土墙和重力坝的受力分析。
该种问题
xz zx 0; yz zy 0而一般 z并不等于零。
平面问题的几何方程: 揭示的是形变分量与位移分量间的相互关系。应注意当物体的位移分量完全确 定时,形变量即完全确定。反之,当形变分量完全确定时,位移分量却不能完全确定。
平面问题中的物理方程:揭示的是形变分量与应力分量间的相互关系。应注意平面应力问题和平面应 变问题物理方程的转换关系。
2.按照边界条件的不同,弹塑性力学问题分为那几类边界问题?试作简要说明。
2.什么是圣维南原理?其在弹塑性力学的问题求解中有什么实际意义?
圣维南原理可表述为: 如果把物体的一小部分边界上的面力变换为分布不同但静力等效的面力(主矢量相同,对于同一点的主 矩也相同),那麽近处的应力分布将有显著的改变,但远处所受的影响可以不计. 弹塑性力学的问题求解中可利用圣维南原理将面力分布不明确的情况转化为静力等效但分布表达明确 的情况而将问题解决。还可解决边界条件不完全满足的问题的求解。
3.什么是平面应力问题?其受力特点如何,试举例予以说明。
答:平面应力问题 是指很薄的等厚度板,只在板边上受有平行于板面并且不沿厚度变化的面力,这 一类问题可以简化为平面应力问题。例如深梁在横向力作用下的受力分析问题。在该种问题中只存在
x、 y、 xy yx 三个应力分量。
4
2014 年北京工业大学攻读博士研究生入学考试试题 《弹塑性力学》
1
答:按照边界条件的不同,弹塑性力学问题分为位移边界问题、应力边界问题和 混合边界问题。
宁波大学3803结构力学2009--2019年考博初试专业课真题

结构力学 工程力学
科目代码: 3803
一、多跨梁受荷载作用如图一所示。求 1)判定该多跨梁是静定梁还是超静定梁? 2)试绘制图示多跨梁的弯矩图(20 分)。
2kN
2kN
N
1kN/m
A
BC D E
F
G
2m 2m 2m 2m 2m 4m 4m
4m
H 4m
题一图 二、试作图示体系的几何构造(组成)分析。(20 分)
题四图
第2页共3页
考试科目: 适用专业:
宁波大学 2015 年攻读博士学位研究生 入 学 考 试 试 题(A 卷) (答案必须写在答题纸上)
结构力学 工程力学
科目代码: 3803
五、平面超静定结构受荷载作用如图五所示,抗弯刚度 EI 为常数。求:1)判断该 结构的超静定次数;2)采用力法绘弯矩图。(20 分)
a
2ql 4 3EI
,b
ql 4 6EI
。(20 分)
题五图 六、求图示静定梁 A 截面弯矩影响线和 B 支座的反力影响线。(15 分)
Fp=1 A
B
C
3aaFra bibliotek题六图
第3页共3页
考试科目: 适用专业:
宁波大学 2015 年攻读博士学位研究生 入 学 考 试 试 题(A 卷) (答案必须写在答题纸上)
梁中稳态的振幅为 2mm,求共振时的振幅 A。
图2 3.(20 分)一总质量为 m 的刚性梁两端由弹簧支撑,梁的质量均匀分布,两弹簧的刚度分别为 k 和 2k。定义的两个自由度 u1 和 u2 如图 3 所示,建立结构体系的运动方程,并求出自振频率和主 振型。
图3
第2页共3页
宁波大学 2019 年博士研究生招生考试初试试题(B 卷)
宁波大学理论力学(甲)2018—2020年考研真题试题

图二
3、(30 分)均质箱体 A 的宽度 b=1m,高 h=2m,重 P=200kN,放在倾角 20 的斜面上,如图三所 示。箱体与斜面之间的静摩擦系数为 fs 0.2 。在 C 点作用一斜向上力 F,且 F 0 。C 点与斜面之间
的距离 BC=a=1.8m。求:(1)使箱子不翻到又不滑动的 F 最小值是多少?(2)使箱子不翻到又不滑 动的 F 最大值是多少?
所受的力;(3)求支座 A 处的约束力。
图一
2、(30 分)图二所示结构位于铅直平面内,由杆 AB,CD 及斜 T 型杆 BCE 所组成,不计各杆的自重。
已知载荷 F1, F2,M 及尺寸 a,且 M F1 a ,F2 作用于销钉 B 上。(1)求 D 支座的约束力;(2)
求 T 型杆受到销钉 B 的作用力。(3)求固定端 A 的约束力和力偶;
题三图
四. 图示机构中,半径为 r 的轮 O 绕其形心轴 O 以角速度 2 rad/s 转动,杆 AB 与轮铰连
接于 A 点。已知:r=30cm,OC=130cm,BC=30cm,图示瞬时, OA 垂直于 OB, BC 处于水平 位置。 求:(1)图示瞬时 BC 杆的角速度;(2)图示瞬时 BC 杆的角加速度。 (25 分)
图三
第1页共2页
宁波大学 2020 年硕士研究生招生考试初试试题(A 卷)
(答案必须写在考点提供的答题纸上)
科目代码: 891 总分值: 150 科目名称:
理论力学(甲)
4、(30 分)如图四所示的三角板在滑动的过程中,其顶点 A 和 B 始终分别与铅垂墙面及水平地面相接 触。已知: AB BC AC b , vB v0 为已知常数。在图示位置 AC 水平。求:(1)此时顶点 C 的速度大 小和方向;(2)此时顶点 C 的加速度大小和方向。
2018年宁波大学考博试题3809智能系统(B卷)

科目代码: 3809 科目名称:智能系统
1. 机器学习通常可分为指导性学习和非指导性学习,学习模型则可分为生成模型和
判别模型二类。
假定现在要完成以下的任务:
(a)函数拟合与插值;(b)聚类分析;(c)模式识别,
请简要解释以下学习模型各自属于生成模型还是判别模型,可以胜任哪种任务:(1)深度学习网络,(2)RBF网络,(3)Boltzmann机,(4)SOM网络。
(10%) 2. 如果将异或(XOR)问题推广为3输入的parity问题,要求输入和输出实现如下
真值表:
输入1 输入2 输入3 输出
0 0 0 0
0 0 1 1
0 1 0 1
0 1 1 0
1 0 0 1
1 0 1 0
1 1 0 0
1 1 1 1
请设计一个多层网络实现3-parity,并给出相应的学习算法。
(12%)
3. Hopfield网络是全相连的反馈型网络,可以用于实现“吸引子”联想记忆,如果
要使一个Hopfield网络同时记住“A”、“I”、“Y”三个字母(3x4点阵),试为其设计一个合理的结构,并给出学习算法和具体的网络权值。
(12%)
科目代码: 3809 科目名称:智能系统
科目代码: 3809 科目名称:智能系统
;
同时生成模型则以产生出能够“愚弄”判别模型使其以为真的数据为目标,即极。
2018年宁波大学3810数字集成电路设计基础博士研究生初试试卷(A卷)
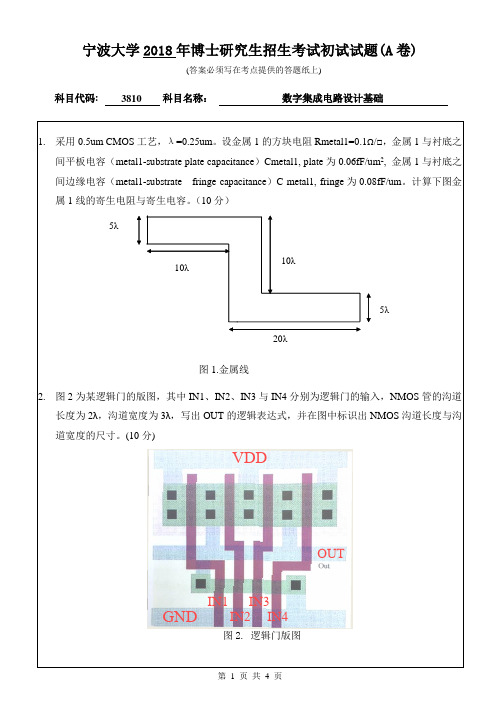
科目代码: 3810 科目名称:数字集成电路设计基础VDDGND IN1IN2IN3IN4OUT科目代码: 3810 科目名称:数字集成电路设计基础科目代码: 3810 科目名称:数字集成电路设计基础5.说明如图5所示的静态CMOS反相器的总功耗由哪几部分组成,并列出每一项功耗的具体表达式。
(10分)pmosnmosVDDC L图5. 静态CMOS反相器6.分析图6所示的电路,在不同时钟CLK输入下Q0、Q1、Q2与Q3的输出状态,并将状态量填入表1。
假设各个D触发器的初始输出状态皆为Q=0。
(10分)图6.D触发器构成的时序逻辑电路表1.电路输出状态表CLK的顺序输入D1 Q0Q1Q2Q30 0 0 0 0 01 12 03 14 15 0科目代码: 3810 科目名称:数字集成电路设计基础7.试用差分串联电压开关逻辑(DCVSL)与互补传输管逻辑(CPL)实现二输入的XOR/NXOR逻辑门,要求画出其晶体管级电路图。
(10分)8.在图7所示电路中,已知CMOS集成施密特触发器的电源电压V DD=15V, V T+=10V,V T-=5V,R=100KΩ, C=10μF。
试画出u c和u0的波形,并求出u0的频率以及占空比。
(10分)图7. 施密特触发器电路9.叙述图8所示的单管动态CMOS存储单元读与写的工作原理与工作过程。
(8分)T C1C2图8. 单管动态CMOS存储单元10.试回答下列问题:(1)在标准CMOS工艺中,NMOS衬底(阱)通常与电路中最低电位相接,若NMOS衬底(阱)与最高电位相接,会产生什么害处? (4分)(2)MOS管有三种主要漏电流(4分)(3)试分别说明: 在65nm以下工艺,哪两种漏电流起主要作用?(4分)。
宁波大学2020年《3801弹性力学》考博专业课真题试卷

(答案必须写在考点提供的答题纸上)
科目代码: 3801 总分值: 100 科目名称:
一、简答题(20 分)
1. (10 分)何谓逆解法和半逆解法?
弹性力学
2. (10 分)常体力情况下,按应力求解平面问题可进一步简化为按应力函数求解。应力函数必须满 足哪些条件?
二、证明题(15 分)
设某一物体发生如下的位移:
u a0 a1x a2 y a3z, v b0 b1x b2 y b3z, w c0 c1x c2 y c3z, 试证明:各个应变分量在物体内为常量,在变形以后,物体内的平面保持为平面,直线保持为直线。
三、计算题(65 分)
1.
ห้องสมุดไป่ตู้
能表达式。
第2页共2页
(20 分)物体中一点 P 处的应力状态为 σ xxy
yx y
zx zy
1 0
0 4
3
0
,
xz yz z 4 0 5
试求:(1)过
P
点法向为
n
1 2
,
1 2
,
1 2
的斜面上的应力矢量
p
。
(2)求应力矢量 p 的大小、 p 与 n 之间的夹角。
(3)求该斜面上的正应力 n 和切应力 n 。
2. (20 分)设有矩形截面的竖柱,其密度为 ,在一边侧面上受均布剪力 q ,如下图所示,试求应力 分量。
第1页共2页
宁波大学 2020 年博士研究生招生考试初试试题(A 卷)
(答案必须写在考点提供的答题纸上)
科目代码: 3801 总分值: 100 科目名称:
弹性力学
3. (25 分)试根据弹性力学中应变能的表达式,导出材料力学中拉伸和弯曲问题用位移表示的应变
