结构力学公式大全e
结构力学常用公式

结构力学常用公式
1.应力公式:σ=F/A,其中 F 为作用力,A 为作用面积,σ为应力。
2. 应变公式:ε = ΔL/L0,其中ΔL 为变形量,L0 为原始长度,ε为应变。
3. 弹性模量公式:E = σ/ε,其中 E 为弹性模量。
4. 餘弦定理:c = a + b - 2abcosC,其中 a,b 为两边的长度,
C 为两边之间的夹角,c 为斜边的长度。
5. 正弦定理:a/sinA = b/sinB = c/sinC,其中 a,b,c 为三角形三条边的长度,A,B,C 为三角形对应的内角。
6. 面积公式:A = 1/2bh,其中 b 为底边的长度,h 为高度。
7. 矩形截面抵消矩阵算式:I = bh/12,其中 I 为矩形截面的抵消矩阵,b 为宽度,h 为高度。
8. 圆形截面抵消矩阵算式:I = πr/4,其中 I 为圆形截面的抵消矩阵,r 为半径。
9. 计算杆件最大承受力公式:Fmax = σmaxA,其中 Fmax 为杆件最大承受力,σmax 为材料的最大允许应力,A 为杆件横截面积。
10. 悬索线的张力公式:T = (Wl)/(8d),其中 T 为悬索线的张力,W 为悬挂物的重量,l 为悬挂物的长度,d 为悬索线的跨度。
- 1 -。
结构力学公式大全

结构力学公式大全Last revision on 21 December 2020结构力学公式大全1、常用截面几何与力学特征表注:1.I称为截面对主轴(形心轴)的截面惯性矩(mm4)。
基本计算公式如下:2.W称为截面抵抗矩(mm3),它表示截面抵抗弯曲变形能力的大小,基本计算公式如下:3.i称截面回转半径(mm),其基本计算公式如下:4.上列各式中,A为截面面积(mm2),y为截面边缘到主轴(形心轴)的距离(mm),I为对主轴(形心轴)的惯性矩。
5.上列各项几何及力学特征,主要用于验算构件截面的承载力和刚度。
2、单跨梁的内力及变形表简支梁的反力、剪力、弯矩、挠度悬臂梁的反力、剪力、弯矩和挠度一端简支另一端固定梁的反力、剪力、弯矩和挠度两端固定梁的反力、剪力、弯矩和挠度外伸梁的反力、剪力、弯矩和挠度3.等截面连续梁的内力及变形表二跨等跨梁的内力和挠度系数注:1.在均布荷载作用下:M=表中系数×ql2;V=表中系数×ql;。
2.在集中荷载作用下:M=表中系数×Fl;V=表中系数×F;。
[例1] 已知二跨等跨梁l=5m,均布荷载q=m,每跨各有一集中荷载F=,求中间支座的最大弯矩和剪力。
[解] MB支=(-××52)+(-××5)=(-)+()=-·mVB左=(-××5)+(-×)=(-)+(-)=-[例2] 已知三跨等跨梁l=6m,均布荷载q=m,求边跨最大跨中弯矩。
[解] M1=××62=·m。
三跨等跨梁的内力和挠度系数注:1.在均布荷载作用下:M=表中系数×ql2;V=表中系数×ql;。
2.在集中荷载作用下:M=表中系数×Fl;V=表中系数×F;。
四跨等跨连续梁内力和挠度系数注:同三跨等跨连续梁。
五跨等跨连续梁内力和挠度系数注:同三跨等跨连续梁。
结构力学公式大全

结构力学公式大全结构力学公式大全1、常用截面几何与力学特征表注:1.I称为截面对主轴(形心轴)的截面惯性矩(mm4)。
基本计算公式如下:2.W称为截面抵抗矩(mm3),它表示截面抵抗弯曲变形能力的大小,基本计算公式如下:3.i称截面回转半径(mm),其基本计算公式如下:4.上列各式中,A为截面面积(mm2),y为截面边缘到主轴(形心轴)的距离(mm),I为对主轴(形心轴)的惯性矩。
5.上列各项几何及力学特征,主要用于验算构件截面的承载力和刚度。
2、单跨梁的内力及变形表2.1 简支梁的反力、剪力、弯矩、挠度2.2 悬臂梁的反力、剪力、弯矩和挠度2.3 一端简支另一端固定梁的反力、剪力、弯矩和挠度2.4 两端固定梁的反力、剪力、弯矩和挠度2.5 外伸梁的反力、剪力、弯矩和挠度3.等截面连续梁的内力及变形表3.1 二跨等跨梁的内力和挠度系数注:1.在均布荷载作用下:M=表中系数×ql2;V=表中系数×ql;。
2.在集中荷载作用下:M=表中系数×Fl;V=表中系数×F;。
[例1] 已知二跨等跨梁l=5m,均布荷载q=11.76kN/m,每跨各有一集中荷载F=29.4kN,求中间支座的最大弯矩和剪力。
[解] MB支=(-0.125×11.76×52)+(-0.188×29.4×5)=(-36.75)+(-27.64)=-64.39kN·mVB左=(-0.625×11.76×5)+(-0.688×29.4)=(-36.75)+(-20.23)=-56.98kN[例2] 已知三跨等跨梁l=6m,均布荷载q=11.76kN/m,求边跨最大跨中弯矩。
[解] M1=0.080×11.76×62=33.87kN·m。
3.2 三跨等跨梁的内力和挠度系数注:1.在均布荷载作用下:M=表中系数×ql2;V=表中系数×ql;。
结构力学公式大全

结构力学公式大全之高陈檩檀创作1、经常使用截面几何与力学特征表注:1.I称为截面对主轴(形心轴)的截面惯性矩(mm4)。
基本计算公式如下:2.W称为截面抵抗矩(mm3),它暗示截面抵抗弯曲变形能力的大小,基本计算公式如下:3.i称截面回转半径(mm),其基本计算公式如下:4.上列各式中,A为截面面积(mm2),y为截面边沿到主轴(形心轴)的距离(mm),I为对主轴(形心轴)的惯性矩。
5.上列各项几何及力学特征,主要用于验算构件截面的承载力和刚度。
2、单跨梁的内力及变形表2.1 简支梁的反力、剪力、弯矩、挠度2.2 悬臂梁的反力、剪力、弯矩和挠度2.3 一端简支另一端固定梁的反力、剪力、弯矩和挠度2.4 两端固定梁的反力、剪力、弯矩和挠度2.5 外伸梁的反力、剪力、弯矩和挠度3.等截面连续梁的内力及变形表3.1 二跨等跨梁的内力和挠度系数注:1.在均布荷载作用下:M=表中系数×ql2;V=表中系数×ql;。
2.在集中荷载作用下:M=表中系数×Fl;V=表中系数×F;。
[例1] 已知二跨等跨梁l=5m,均布荷载q=11.76kN/m,每跨各有一集中荷载F=29.4kN,求中间支座的最大弯矩和剪力。
[解] MB支=(-0.125×11.76×52)+(-0.188×29.4×5)=(-36.75)+(-27.64)=-64.39kN·mVB左=(-0.625×11.76×5)+(-0.688×29.4)[例2] 已知三跨等跨梁l=6m,均布荷载q=11.76kN/m,求边跨最大跨中弯矩。
[解] M1=0.080×11.76×62=33.87kN·m。
3.2 三跨等跨梁的内力和挠度系数注:1.在均布荷载作用下:M=表中系数×ql2;V=表中系数×ql;。
结构力学公式大全(完整资料).doc
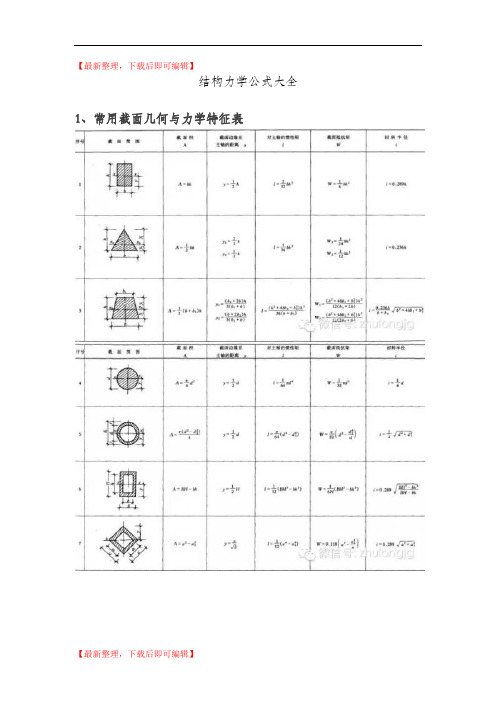
【最新整理,下载后即可编辑】结构力学公式大全1、常用截面几何与力学特征表注:1.I称为截面对主轴(形心轴)的截面惯性矩(mm4)。
基本计算公式如下:2.W称为截面抵抗矩(mm3),它表示截面抵抗弯曲变形能力的大小,基本计算公式如下:3.i称截面回转半径(mm),其基本计算公式如下:4.上列各式中,A为截面面积(mm2),y为截面边缘到主轴(形心轴)的距离(mm),I为对主轴(形心轴)的惯性矩。
5.上列各项几何及力学特征,主要用于验算构件截面的承载力和刚度。
2、单跨梁的内力及变形表2.1 简支梁的反力、剪力、弯矩、挠度2.2 悬臂梁的反力、剪力、弯矩和挠度2.3 一端简支另一端固定梁的反力、剪力、弯矩和挠度2.4 两端固定梁的反力、剪力、弯矩和挠度2.5 外伸梁的反力、剪力、弯矩和挠度3.等截面连续梁的内力及变形表3.1 二跨等跨梁的内力和挠度系数注:1.在均布荷载作用下:M=表中系数×ql2;V=表中系数×ql;。
2.在集中荷载作用下:M=表中系数×Fl;V=表中系数×F;。
[例1] 已知二跨等跨梁l=5m,均布荷载q=11.76kN/m,每跨各有一集中荷载F=29.4kN,求中间支座的最大弯矩和剪力。
[解] MB支=(-0.125×11.76×52)+(-0.188×29.4×5)=(-36.75)+(-27.64)=-64.39kN·mVB左=(-0.625×11.76×5)+(-0.688×29.4)=(-36.75)+(-20.23)=-56.98kN[例2] 已知三跨等跨梁l=6m,均布荷载q=11.76kN/m,求边跨最大跨中弯矩。
[解] M1=0.080×11.76×62=33.87kN·m。
3.2 三跨等跨梁的内力和挠度系数注:1.在均布荷载作用下:M=表中系数×ql2;V=表中系数×ql;。
结构力学公式大全
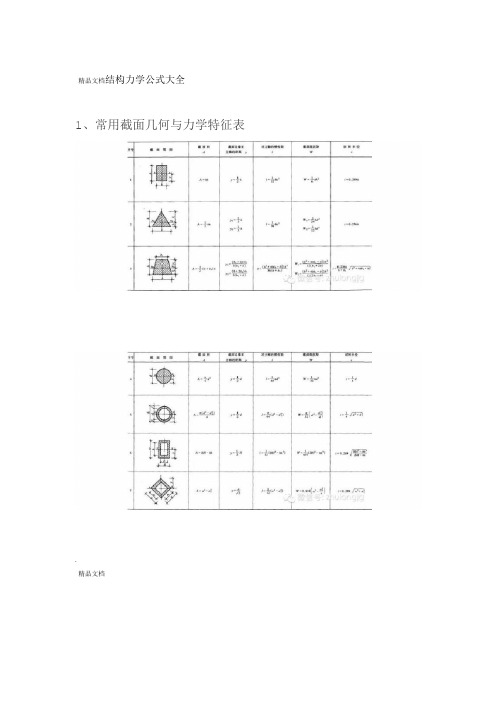
精品文档结构力学公式大全1、常用截面几何与力学特征表.精品文档.精品文档.精品文档)。
基本计算公式如mm4.I称为截面对主轴(形心轴)的截面惯性矩(1注:下:),它表示截面抵抗弯曲变形能力的大小,基本mm3W称为截面抵抗矩(2.计算公式如下:mm),其基本计算公式如下:3.i称截面回转半径(为截面边缘到主轴(形心轴)的距y为截面面积(mm2),.上列各式中,4A I为对主轴(形心轴)的惯性矩。
mm离(),.上列各项几何及力学特征,主要用于验算构件截面的承载力和刚度。
52、单跨梁的内力及变形表简支梁的反力、剪力、弯矩、挠度2.1 .精品文档.精品文档.精品文档2.2 悬臂梁的反力、剪力、弯矩和挠度.精品文档.精品文档2.3 一端简支另一端固定梁的反力、剪力、弯矩和挠度.精品文档.精品文档2.4 两端固定梁的反力、剪力、弯矩和挠度.精品文档.精品文档2.5 外伸梁的反力、剪力、弯矩和挠度.精品文档.精品文档.精品文档.等截面连续梁的内力及变形表3 3.1 二跨等跨梁的内力和挠度系数.精品文档;。
qlql2;V=表中系数×注:1.在均布荷载作用下:M=表中系数×;。
;V =表中系数×F 2.在集中荷载作用下:M=表中系数×Fl,每跨各有一集11.76kN/m,均布荷载q=例1] 已知二跨等跨梁l=5m [ =29.4kN,求中间支座的最大弯矩和剪力。
中荷载F 5))+(-0.188×29.4××解[] MB 支=(-0.125×11.7652m64.39kN·36.75)+(-27.64)=-=(-29.40.688×)0.625 VB左=(-×11.76×5)+(-56.98kN)+(-20.23)=-=(-36.75,求边跨最大跨中11.76kN/m6m,均布荷载q==2] [例已知三跨等跨梁l 弯矩。
结构力学公式大全
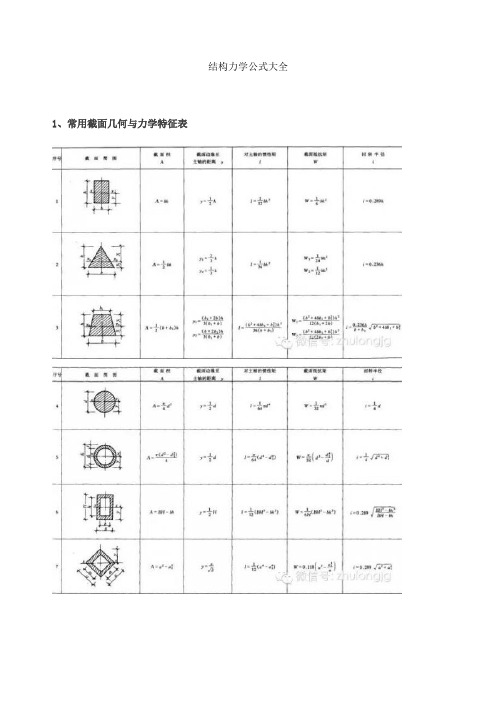
结构力学公式大全1、常用截面几何与力学特征表注:1.I称为截面对主轴(形心轴)的截面惯性矩(mm4)。
基本计算公式如下:2.W称为截面抵抗矩(mm3),它表示截面抵抗弯曲变形能力的大小,基本计算公式如下:3.i称截面回转半径(mm),其基本计算公式如下:4.上列各式中,A为截面面积(mm2),y为截面边缘到主轴(形心轴)的距离(mm),I 为对主轴(形心轴)的惯性矩。
5.上列各项几何及力学特征,主要用于验算构件截面的承载力和刚度。
2、单跨梁的内力及变形表简支梁的反力、剪力、弯矩、挠度悬臂梁的反力、剪力、弯矩和挠度一端简支另一端固定梁的反力、剪力、弯矩和挠度两端固定梁的反力、剪力、弯矩和挠度外伸梁的反力、剪力、弯矩和挠度3.等截面连续梁的内力及变形表二跨等跨梁的内力和挠度系数注:1.在均布荷载作用下:M=表中系数×ql2;V=表中系数×ql;。
? ? ? 2.在集中荷载作用下:M=表中系数×Fl;V=表中系数×F;。
? ? ?[例1] ?已知二跨等跨梁l=5m,均布荷载q=m,每跨各有一集中荷载F=,求中间支座的最大弯矩和剪力。
? [解] ? MB支=(-××52)+(-××5)=(-)+()=-·m? ? ? ? ?VB左=(-××5)+(-×)=(-)+(-)=-? ?[例2] ?已知三跨等跨梁l=6m,均布荷载q=m,求边跨最大跨中弯矩。
? [解] ?M1=××62=·m。
三跨等跨梁的内力和挠度系数注:1.在均布荷载作用下:M=表中系数×ql2;V=表中系数×ql;。
2.在集中荷载作用下:M=表中系数×Fl;V=表中系数×F;。
四跨等跨连续梁内力和挠度系数注:同三跨等跨连续梁。
五跨等跨连续梁内力和挠度系数注:同三跨等跨连续梁。
结构力学公式大全

结构力学公式大全1、常用截面几何与力学特征表注:1.I称为截面对主轴(形心轴)的截面惯性矩(mm4)。
基本计算公式如下:2.W称为截面抵抗矩(mm3),它表示截面抵抗弯曲变形能力的大小,基本计算公式如下:3.i称截面回转半径(mm),其基本计算公式如下:4.上列各式中,A为截面面积(mm2),y为截面边缘到主轴(形心轴)的距离(mm),I为对主轴(形心轴)的惯性矩。
5.上列各项几何及力学特征,主要用于验算构件截面的承载力和刚度。
2、单跨梁的内力及变形表2.1 简支梁的反力、剪力、弯矩、挠度2.2 悬臂梁的反力、剪力、弯矩和挠度2.3 一端简支另一端固定梁的反力、剪力、弯矩和挠度2.4 两端固定梁的反力、剪力、弯矩和挠度2.5 外伸梁的反力、剪力、弯矩和挠度3.等截面连续梁的内力及变形表3.1 二跨等跨梁的内力和挠度系数注:1.在均布荷载作用下:M=表中系数×ql2;V=表中系数×ql;。
2.在集中荷载作用下:M=表中系数×Fl;V=表中系数×F;。
[例1] 已知二跨等跨梁l=5m,均布荷载q=11.76kN/m,每跨各有一集中荷载F=29.4kN,求中间支座的最大弯矩和剪力。
[解] MB支=(-0.125×11.76×52)+(-0.188×29.4×5)=(-36.75)+(-27.64)=-64.39kN·mVB左=(-0.625×11.76×5)+(-0.688×29.4)=(-36.75)+(-20.23)=-56.98kN[例2] 已知三跨等跨梁l=6m,均布荷载q=11.76kN/m,求边跨最大跨中弯矩。
[解] M1=0.080×11.76×62=33.87kN·m。
3.2 三跨等跨梁的内力和挠度系数注:1.在均布荷载作用下:M=表中系数×ql2;V=表中系数×ql;。
结构力学公式大全

结构力学公式大全之欧侯瑞魂创作1、经常使用截面几何与力学特征表注:1.I称为截面对主轴(形心轴)的截面惯性矩(mm4)。
基本计算公式如下:2.W称为截面抵抗矩(mm3),它暗示截面抵抗弯曲变形能力的大小,基本计算公式如下:3.i称截面回转半径(mm),其基本计算公式如下:4.上列各式中,A为截面面积(mm2),y为截面边沿到主轴(形心轴)的距离(mm),I为对主轴(形心轴)的惯性矩。
5.上列各项几何及力学特征,主要用于验算构件截面的承载力和刚度。
2、单跨梁的内力及变形表2.1 简支梁的反力、剪力、弯矩、挠度2.2 悬臂梁的反力、剪力、弯矩和挠度2.3 一端简支另一端固定梁的反力、剪力、弯矩和挠度2.4 两端固定梁的反力、剪力、弯矩和挠度2.5 外伸梁的反力、剪力、弯矩和挠度3.等截面连续梁的内力及变形表3.1 二跨等跨梁的内力和挠度系数注:1.在均布荷载作用下:M=表中系数×ql2;V=表中系数×ql;。
2.在集中荷载作用下:M=表中系数×Fl;V=表中系数×F;。
[例1] 已知二跨等跨梁l=5m,均布荷载q=11.76kN/m,每跨各有一集中荷载F=29.4kN,求中间支座的最大弯矩和剪力。
[解] MB支=(-0.125×11.76×52)+(-0.188×29.4×5)=(-36.75)+(-27.64)=-64.39kN·mVB左=(-0.625×11.76×5)+(-0.688×29.4)=(-36.75)+(-20.23)=-56.98kN[例2] 已知三跨等跨梁l=6m,均布荷载q=11.76kN/m,求边跨最大跨中弯矩。
[解] M1=0.080×11.76×62=33.87kN·m。
3.2 三跨等跨梁的内力和挠度系数注:1.在均布荷载作用下:M=表中系数×ql2;V=表中系数×ql;。
结构力学公式大全
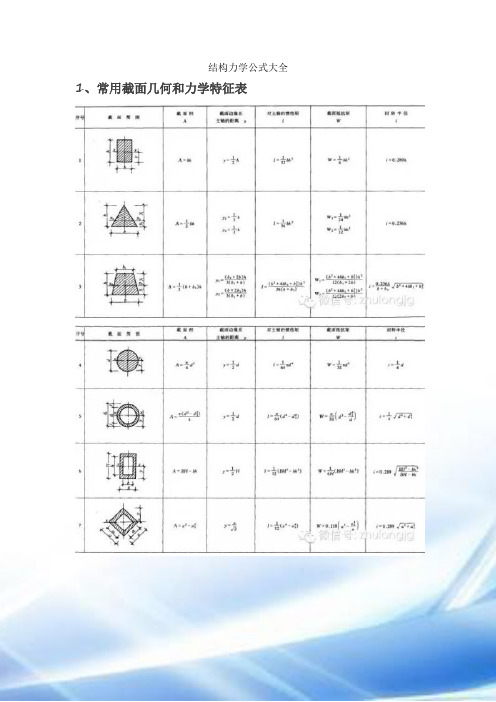
结构力学公式大全1、常用截面几何和力学特征表注:1.I称为截面对主轴(形心轴)的截面惯性矩(mm4)。
基本计算公式如下:2.W称为截面抵抗矩(mm3),它表示截面抵抗弯曲变形能力的大小,基本计算公式如下:3.i称截面回转半径(mm),其基本计算公式如下:4.上列各式中,A为截面面积(mm2),y为截面边缘到主轴(形心轴)的距离(mm),I为对主轴(形心轴)的惯性矩。
5.上列各项几何及力学特征,主要用于验算构件截面的承载力和刚度。
2、单跨梁的内力及变形表2.1 简支梁的反力、剪力、弯矩、挠度2.2 悬臂梁的反力、剪力、弯矩和挠度2.3 一端简支另一端固定梁的反力、剪力、弯矩和挠度2.4 两端固定梁的反力、剪力、弯矩和挠度2.5 外伸梁的反力、剪力、弯矩和挠度3.等截面连续梁的内力及变形表3.1 二跨等跨梁的内力和挠度系数注:1.在均布荷载作用下:M=表中系数×ql2;V=表中系数×ql;。
2.在集中荷载作用下:M=表中系数×Fl;V=表中系数×F;。
[例1] 已知二跨等跨梁l=5m,均布荷载q=11.76kN/m,每跨各有一集中荷载F=29.4kN,求中间支座的最大弯矩和剪力。
[解] MB支=(-0.125×11.76×52)+(-0.188×29.4×5)=(-36.75)+(-27.64)=-64.39kN·mVB左=(-0.625×11.76×5)+(-0.688×29.4)=(-36.75)+(-20.23)=-56.98kN[例2] 已知三跨等跨梁l=6m,均布荷载q=11.76kN/m,求边跨最大跨中弯矩。
[解] M1=0.080×11.76×62=33.87kN·m。
3.2 三跨等跨梁的内力和挠度系数注:1.在均布荷载作用下:M=表中系数×ql2;V=表中系数×ql;。
结构力学公式大全

结构力学公式大全1、常用截面几何与力学特征表注:1.I称为截面对主轴(形心轴)的截面惯性矩(mm4)。
基本计算公式如下:2.W称为截面抵抗矩(mm3),它表示截面抵抗弯曲变形能力的大小,基本计算公式如下:3.i称截面回转半径(mm),其基本计算公式如下:4.上列各式中,A为截面面积(mm2),y为截面边缘到主轴(形心轴)的距离(mm),I为对主轴(形心轴)的惯性矩。
5.上列各项几何及力学特征,主要用于验算构件截面的承载力和刚度。
2、单跨梁的内力及变形表2.1 简支梁的反力、剪力、弯矩、挠度2.2 悬臂梁的反力、剪力、弯矩和挠度2.3 一端简支另一端固定梁的反力、剪力、弯矩和挠度2.4 两端固定梁的反力、剪力、弯矩和挠度2.5 外伸梁的反力、剪力、弯矩和挠度3.等截面连续梁的内力及变形表3.1 二跨等跨梁的内力和挠度系数注:1.在均布荷载作用下:M=表中系数×ql2;V=表中系数×ql;。
2.在集中荷载作用下:M=表中系数×Fl;V=表中系数×F;。
[例1] 已知二跨等跨梁l=5m,均布荷载q=11.76kN/m,每跨各有一集中荷载F=29.4kN,求中间支座的最大弯矩和剪力。
[解] MB支=(-0.125×11.76×52)+(-0.188×29.4×5)=(-36.75)+(-27.64)=-64.39kN·mVB左=(-0.625×11.76×5)+(-0.688×29.4)=(-36.75)+(-20.23)=-56.98kN[例2] 已知三跨等跨梁l=6m,均布荷载q=11.76kN/m,求边跨最大跨中弯矩。
[解] M1=0.080×11.76×62=33.87kN·m。
3.2 三跨等跨梁的内力和挠度系数注:1.在均布荷载作用下:M=表中系数×ql2;V=表中系数×ql;。
结构力学公式大全

结构力学公式大全之南宫帮珍创作1、经常使用截面几何与力学特征表注:1.I称为截面对主轴(形心轴)的截面惯性矩(mm4)。
基本计算公式如下:2.W称为截面抵抗矩(mm3),它暗示截面抵抗弯曲变形能力的大小,基本计算公式如下:3.i称截面回转半径(mm),其基本计算公式如下:4.上列各式中,A为截面面积(mm2),y为截面边沿到主轴(形心轴)的距离(mm),I为对主轴(形心轴)的惯性矩。
5.上列各项几何及力学特征,主要用于验算构件截面的承载力和刚度。
2、单跨梁的内力及变形表2.1 简支梁的反力、剪力、弯矩、挠度2.2 悬臂梁的反力、剪力、弯矩和挠度2.3 一端简支另一端固定梁的反力、剪力、弯矩和挠度2.4 两端固定梁的反力、剪力、弯矩和挠度2.5 外伸梁的反力、剪力、弯矩和挠度3.等截面连续梁的内力及变形表3.1 二跨等跨梁的内力和挠度系数注:1.在均布荷载作用下:M=表中系数×ql2;V=表中系数×ql;。
2.在集中荷载作用下:M=表中系数×Fl;V=表中系数×F;。
[例1] 已知二跨等跨梁l=5m,均布荷载q=11.76kN/m,每跨各有一集中荷载F=29.4kN,求中间支座的最大弯矩和剪力。
[解] MB支=(-0.125×11.76×52)+(-0.188×29.4×5)=(-36.75)+(-27.64)=-64.39kN·mVB左=(-0.625×11.76×5)+(-0.688×29.4)=(-36.75)+(-20.23)=-56.98kN[例2] 已知三跨等跨梁l=6m,均布荷载q=11.76kN/m,求边跨最大跨中弯矩。
[解] M1=0.080×11.76×62=33.87kN·m。
3.2 三跨等跨梁的内力和挠度系数注:1.在均布荷载作用下:M=表中系数×ql2;V=表中系数×ql;。
结构力学公式大全

结构力学公式年夜全之迟辟智美创作1、经常使用截面几何与力学特征表注:1.I称为截面对主轴(形心轴)的截面惯性矩(mm4).基本计算公式如下:2.W称为截面抵当矩(mm3),它暗示截面抵当弯曲变形能力的年夜小,基本计算公式如下:3.i称截面回转半径(mm),其基本计算公式如下:4.上列各式中,A为截面面积(mm2),y为截面边缘到主轴(形心轴)的距离(mm),I为对主轴(形心轴)的惯性矩.5.上列各项几何及力学特征,主要用于验算构件截面的承载力和刚度.2、单跨梁的内力及变形表2.1 简支梁的反力、剪力、弯矩、挠度2.2 悬臂梁的反力、剪力、弯矩和挠度2.3 一端简支另一端固定梁的反力、剪力、弯矩和挠度2.4 两端固定梁的反力、剪力、弯矩和挠度2.5 外伸梁的反力、剪力、弯矩和挠度3.等截面连续梁的内力及变形表3.1 二跨等跨梁的内力和挠度系数注:1.在均布荷载作用下:M=表中系数×ql2;V=表中系数×ql;.2.在集中荷载作用下:M=表中系数×Fl;V=表中系数×F;.[例1] 已知二跨等跨梁l=5m,均布荷载q=11.76kN/m,每跨各有一集中荷载F=29.4kN,求中间支座的最年夜弯矩和剪力.[解] MB支=(-0.125×11.76×52)+(-0.188×29.4×5)=(-36.75)+(-27.64)=-64.39kN·mVB左=(-0.625×11.76×5)+(-0.688×29.4)[例2] 已知三跨等跨梁l=6m,均布荷载q=11.76kN/m,求边跨最年夜跨中弯矩.[解] M1=0.080×11.76×62=33.87kN·m.3.2 三跨等跨梁的内力和挠度系数注:1.在均布荷载作用下:M=表中系数×ql2;V=表中系数×ql;.2.在集中荷载作用下:M=表中系数×Fl;V=表中系数×F;.3.3 四跨等跨连续梁内力和挠度系数注:同三跨等跨连续梁.3.4 五跨等跨连续梁内力和挠度系数注:同三跨等跨连续梁.3.5 二不等跨梁的内力系数注:1.M=表中系数×ql21;V=表中系数×ql1;2.(Mmax)、(Vmax)暗示它为相应跨内的最年夜内力.3.6 三不等跨梁内力系数注:1.M=表中系数×ql21;V=表中系数×ql1;2.(Mmax)、(Vmax)为荷载在最晦气安插时的最年夜内力.4.双向板在均布荷载作用下的内力及变形系数表符号说明如下:刚度式中 E——弹性模量;h——板厚;ν——泊松比;ω、ωmax——分别为板中心点的挠度和最年夜挠度;Mx——为平行于lx方向板中心点的弯矩;My——为平行于ly方向板中心点的弯矩;Mx0——固定边中点沿lx方向的弯矩;My0——固定边中点沿ly方向的弯矩.正负号的规定:弯矩——使板的受荷面受压者为正;挠度——变位方向与荷载方向相同者为正.4.1 四边简支4.2 三边简支,一边固定4.3 两边简支,两边固定4.4 一边简支,三边固定4.4 四边固定4.5 两边简支,两边固定5.拱的内力计算表注:表中的K为轴向力变形影响的修正系数.(1)无拉杆双铰拱1)在竖向荷载作用下的轴向力变形修正系数式中 Ic——拱顶截面惯性矩;Ac——拱顶截面面积;A——拱上任意点截面面积.当为矩形等宽度实腹式变截面拱时,公式I=Ic/cosθ所代表的截面惯性矩变动规律相当于下列的截面面积变动公式:此时,上式中的n可表告竣如下形式:下表中列出了矩形等宽度实腹式变截面拱的n值.2)在水平荷载作用下的轴向力变形修正系数,近似取K=1(2)带拉杆双铰拱1)在竖向荷载作用下的轴向力变形修正系数式中 E——拱圈资料的弹性模量;E1——拉杆资料的弹性模量;A1——拉杆的截面积.2)在水平荷载作用下的轴向力变形修正系数(略去拱圈轴向力变形影响)式中 f——为矢高;l——为拱的跨度.6.刚架内力计算表内力的正负号规定如下:V——向上者为正;H——向内者为正;M——刚架中虚线的一面受拉为正.6.1 “┌┐”形刚架内力计算表(一)6.2“┌┐”形刚架内力计算表(二)6.3“”形刚架的内力计算表。
最新结构力学重点公式

(3)优惠多荷载频率θ=2πn/60
阻尼比ζ=(1/20π)*ln
动力系数β=1/
最大弯矩 Mmax=(G*βFp)*l*0.25
最大正应力σmax=(G+βFp)*l/4Wz
标题:大学生究竟难在哪?—创业要迈五道坎2004年3月23日最大竖向位移Ymax=(G+βFp)δ
=-
Beadwrks公司还组织各国的“芝自制饰品店”定期进行作品交流,体现东方女性聪慧的作品曾在其他国家大受欢迎;同样,自各国作品也曾无数次启发过中国姑娘们的灵感,这里更是创作的源泉。W= =
400-500元1326%Y2max=y02+( )2
V0=w*
(五)DIY手工艺品的“价格弹性化”柔度系数б=L3/48EI
据统计,上海国民经济持续快速增长。03全年就实现国内生产总值(GDP)6250.81亿元,按可比价格计算,比上年增长11.8%。第三产业的增速受非典影响而有所减缓,全年实现增加值3027.11亿元,增长8%,增幅比上年下降2个百分点。=(б11m1- )(22m2- )-б12m2б21m1=0
主振型 =-
主振型 =-
=-
W= =
Y2max=y02+( )2
V0=w*
柔度系数б=L3/48EI
自振频率w=
荷载频率θ=2πn/60
阻尼比ζ=(1/20π)*ln
动力系数β=1/
最大弯矩 Mmax=(G*βFp)*l*0.25
结构力学公式大全

结构力学公式年夜全之马矢奏春创作1、经常使用截面几何与力学特征表注:1.I称为截面对主轴(形心轴)的截面惯性矩(mm4).基本计算公式如下:2.W称为截面抵当矩(mm3),它暗示截面抵当弯曲变形能力的年夜小,基本计算公式如下:3.i称截面回转半径(mm),其基本计算公式如下:4.上列各式中,A为截面面积(mm2),y为截面边缘到主轴(形心轴)的距离(mm),I为对主轴(形心轴)的惯性矩.5.上列各项几何及力学特征,主要用于验算构件截面的承载力和刚度.2、单跨梁的内力及变形表2.1 简支梁的反力、剪力、弯矩、挠度2.2 悬臂梁的反力、剪力、弯矩和挠度2.3 一端简支另一端固定梁的反力、剪力、弯矩和挠度2.4 两端固定梁的反力、剪力、弯矩和挠度2.5 外伸梁的反力、剪力、弯矩和挠度3.等截面连续梁的内力及变形表3.1 二跨等跨梁的内力和挠度系数注:1.在均布荷载作用下:M=表中系数×ql2;V=表中系数×ql;.2.在集中荷载作用下:M=表中系数×Fl;V=表中系数×F;.[例1] 已知二跨等跨梁l=5m,均布荷载q=11.76kN/m,每跨各有一集中荷载F=29.4kN,求中间支座的最年夜弯矩和剪力. [解] MB支=(-0.125×11.76×52)+(-0.188×29.4×5)=(-36.75)+(-27.64)=-64.39kN·mVB左=(-0.625×11.76×5)+(-0.688×29.4)=(-36.75)+(-20.23)=-56.98kN[例2] 已知三跨等跨梁l=6m,均布荷载q=11.76kN/m,求边跨最年夜跨中弯矩.[解] M1=0.080×11.76×62=33.87kN·m.3.2 三跨等跨梁的内力和挠度系数注:1.在均布荷载作用下:M=表中系数×ql2;V=表中系数×ql;. 2.在集中荷载作用下:M=表中系数×Fl;V=表中系数×F;. 3.3 四跨等跨连续梁内力和挠度系数注:同三跨等跨连续梁.3.4 五跨等跨连续梁内力和挠度系数注:同三跨等跨连续梁.3.5 二不等跨梁的内力系数注:1.M=表中系数×ql21;V=表中系数×ql1;2.(Mmax)、(Vmax)暗示它为相应跨内的最年夜内力.3.6 三不等跨梁内力系数注:1.M=表中系数×ql21;V=表中系数×ql1;2.(Mmax)、(Vmax)为荷载在最晦气安插时的最年夜内力. 4.双向板在均布荷载作用下的内力及变形系数表符号说明如下:刚度式中E——弹性模量;h——板厚;ν——泊松比;ω、ωmax——分别为板中心点的挠度和最年夜挠度;Mx——为平行于lx方向板中心点的弯矩;My——为平行于ly方向板中心点的弯矩;Mx0——固定边中点沿lx方向的弯矩;My0——固定边中点沿ly方向的弯矩.正负号的规定:弯矩——使板的受荷面受压者为正;挠度——变位方向与荷载方向相同者为正.4.1 四边简支4.2 三边简支,一边固定4.3 两边简支,两边固定4.4 一边简支,三边固定4.4 四边固定4.5 两边简支,两边固定5.拱的内力计算表5.1各种荷载作用下双铰抛物线拱计算公式注:表中的K为轴向力变形影响的修正系数.(1)无拉杆双铰拱1)在竖向荷载作用下的轴向力变形修正系数式中Ic——拱顶截面惯性矩;Ac——拱顶截面面积;A——拱上任意点截面面积.当为矩形等宽度实腹式变截面拱时,公式I=Ic/cosθ所代表的截面惯性矩变动规律相当于下列的截面面积变动公式:此时,上式中的n可表告竣如下形式:下表中列出了矩形等宽度实腹式变截面拱的n值.2)在水平荷载作用下的轴向力变形修正系数,近似取K=1(2)带拉杆双铰拱1)在竖向荷载作用下的轴向力变形修正系数式中E——拱圈资料的弹性模量;E1——拉杆资料的弹性模量;A1——拉杆的截面积.2)在水平荷载作用下的轴向力变形修正系数(略去拱圈轴向力变形影响)式中f——为矢高;l——为拱的跨度.6.刚架内力计算表内力的正负号规定如下:V——向上者为正;H——向内者为正;M——刚架中虚线的一面受拉为正.6.1 “┌┐”形刚架内力计算表(一)6.2“┌┐”形刚架内力计算表(二)6.3“”形刚架的内力计算表。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
结构力学公式大全1、常用截面几何与力学特征表
注:1.I称为截面对主轴〔形心轴〕的截面惯性矩〔mm4〕。
根本计算公式如下:
2.W称为截面抵抗矩〔mm3〕,它表示截面抵抗弯曲变形能力的大小,根本计算公式如下:
3.i称截面回转半径〔mm〕,其根本计算公式如下:
4.上列各式中,A为截面面积〔mm2〕,y为截面边缘到主轴〔形心轴〕的距离〔mm〕,I为对主轴〔形心轴〕的惯性矩。
5.上列各项几何及力学特征,主要用于验算构件截面的承载力和刚度。
2、单跨梁的内力及变形表
2.1 简支梁的反力、剪力、弯矩、挠度
2.2 悬臂梁的反力、剪力、弯矩和挠度
2.3 一端简支另一端固定梁的反力、剪力、弯矩和挠度
2.4 两端固定梁的反力、剪力、弯矩和挠度
2.5 外伸梁的反力、剪力、弯矩和挠度
3.等截面连续梁的内力及变形表3.1 二跨等跨梁的内力和挠度系数
注:1.在均布荷载作用下:M=表中系数×ql2;V=表中系数×ql;。
2.在集中荷载作用下:M=表中系数×Fl;V=表中系数×F;。
[例1] 二跨等跨梁l=5m,均布荷载q=11.76kN/m,每跨各有一集中荷载F=29.4kN,求中间支座的最大弯矩和剪力。
[解] MB支=〔-0.125×11.76×52〕+〔-0.188×29.4×5〕
=〔-36.75〕+〔-27.64〕=-64.39kN·m
VB左=〔-0.625×11.76×5〕+〔-0.688×29.4〕
[例2] 三跨等跨梁l=6m,均布荷载q=11.76kN/m,求边跨最大跨中弯矩。
[解] M1=0.080×11.76×62=33.87kN·m。
3.2 三跨等跨梁的内力和挠度系数
注:1.在均布荷载作用下:M=表中系数×ql2;V=表中系数×ql;。
2.在集中荷载作用下:M=表中系数×Fl;V=表中系数×F;。
3.3 四跨等跨连续梁内力和挠度系数
注:同三跨等跨连续梁。
3.4 五跨等跨连续梁内力和挠度系数注:同三跨等跨连续梁。
3.5 二不等跨梁的内力系数
注:1.M=表中系数×ql21;V=表中系数×ql1;2.〔Mmax〕、〔Vmax〕表示它为相应跨内的最大内力。
3.6 三不等跨梁内力系数
注:1.M=表中系数×ql21;V=表中系数×ql1;2.〔Mmax〕、〔Vmax〕为荷载在最不利布置时的最大内力。
4.双向板在均布荷载作用下的内力及变形系数表符号说明如下:
刚度
式中 E——弹性模量;
h——板厚;
ν——泊松比;
ω、ωmax——分别为板中心点的挠度和最大挠度;Mx——为平行于lx方向板中心点的弯矩;
My——为平行于ly方向板中心点的弯矩;
Mx0——固定边中点沿lx方向的弯矩;
My0——固定边中点沿ly方向的弯矩。
正负号的规定:
弯矩——使板的受荷面受压者为正;
挠度——变位方向与荷载方向相同者为正。
4.1 四边简支
4.2 三边简支,一边固定
4.3 两边简支,两边固定4.4 一边简支,三边固定
4.4 四边固定
4.5 两边简支,两边固定5.拱的内力计算表
注:表中的K为轴向力变形影响的修正系数。
〔1〕无拉杆双铰拱
1〕在竖向荷载作用下的轴向力变形修正系数
式中 Ic——拱顶截面惯性矩;
Ac——拱顶截面面积;
A——拱上任意点截面面积。
当为矩形等宽度实腹式变截面拱时,公式I=Ic/cosθ所代表的截面惯性矩变化规律相当于以下的截面面积变化公式:
此时,上式中的n可表达成如下形式:
下表中列出了矩形等宽度实腹式变截面拱的n值。
2〕在水平荷载作用下的轴向力变形修正系数,近似取
K=1
〔2〕带拉杆双铰拱
1〕在竖向荷载作用下的轴向力变形修正系数
式中 E——拱圈材料的弹性模量;
E1——拉杆材料的弹性模量;
A1——拉杆的截面积。
2〕在水平荷载作用下的轴向力变形修正系数〔略去拱圈轴向力变形影响〕
式中 f——为矢高;
l——为拱的跨度。
6.刚架内力计算表
内力的正负号规定如下:
V——向上者为正;
H——向内者为正;
M——刚架中虚线的一面受拉为正。
6.1 “┌┐〞形刚架内力计算表〔一〕
6.2“┌┐〞形刚架内力计算表〔二〕
6.3“
〞形刚架的内力计算表。
