解直三角形应用 新 参赛 优质文档
《解直角三角形》数学教学PPT课件(3篇)

获取新知
B
对边 a C
c 斜边
b 邻边 A
定义:一般地,直角三角形中,除直角外 还有五个元素,即三条边和两个锐角.由直角三 角形中的已知元素,求出其余未知元素的过程 叫做解直角三角形.
直角三角形中,未知的5个元素之间的关系
B
①三边之间的关系
a
c
a2 b2 c2
C
A
b
已知任意两边可求出第
直角三角形中,未知的5个元素之间的关系
解:过点 A作 AD⊥BC于D.
在△ACD中,∠C=45°,AC=2,
∴CD=AD=sinC·AC=2sin45°= 2 .
在△ABD中,∠B=30°, ∴BD= AD 2 6
tan B 3
∴BC=CD+BD=3 2 + 6
A
D B
归纳总结
C
┐
AD
BB
A D
CE
┐
提 求解非直角三角形的边角问题,常通过添加适 示
解:∵△ABD是等边三角形,∴∠B=60°.
在Rt△ABC中,AB=2,∠B=60°,
BC
AB cosB
2 1
4,AC
AB
tanB
2
3.
2
△ABC的周长为2+ 2 3 +4=6+ 2 3 .
3.在Rt△ABC中,∠C=90°,tanA= 12 ,△ABC 5
的周长为45cm,CD是斜边AB上的高,求CD的长.(精 确到0.1 cm)
例5 在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分
别为a,b,c,且c=100,∠A=26°44′.求这个三角形
的其他元素.(长度精确到0.01)
2.4.1 解直角三角形课件-2024-2025学年九上教材配套教学课件+同步练习(青岛版)

例3.在Rt△ABC 中,已知∠C=90°,c = 28,∠ B=60°.
解这个直角三角形。
解:在Rt△ ABC中
B 60
A 30
a
a
1
sin A
c 28 2
a 14
b b
3
cos A
c 28
2
b 14 3
结论:若已知一边一角,能解直角三角形.
b
tan B , b 30,
a
b
30
∴a
64.
tan B tan 25
b
30
c
25°
B
也可以利用勾股定
理求出第三条边.
a
C
观察下面的三组等式,你发现在直角三角形中,除直角以外,至少
知道几个元素就可以求出其他的未知元素?
B
除直角以外,如果再知道直角三角
形的两个元素(至少一个是边),
∴ = .
5
=
=
,
15
B
探究二:已知一边和一个锐角解直角三角形
想一想:在Rt△ABC中,如果已知一边和一个锐角,你能求出这个三角
形的其他元素吗?
A
如图,在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的
边分别为a, b, c,且b=30,∠B=25°,求这个直角三角形的
其他元素(边长精确到1).
90 A ;________.
已知和解法
已知条件
三角形类型
解法步骤
A;a b______
_______
tan A;
锐角,邻边 B 90
初中九年级数学 解直角三角形及其应用

0.1m)?
B
A
D
C
3海里内有暗礁,一艘客轮以每小
时9海里的速度由西向东航行,行
至A处测得灯塔P在它的北偏东60°,
继续行驶20分钟后,到达B处,又
测得灯塔P在它的北偏东45°,问客
轮不改变方向,继续前进有无触礁
解:过P的点作危P险D垂?直于AB,交AB的延
P
长∵线∠于1=D60∠2=45°∴
在R°t△BDP∠PBD∠=P4AD=30°,∠PBD=45°
例l3.一铁路路基的l 横断面是等腰梯 形,路基顶部的宽为9.8米,路基高为 5.8米,斜坡与地面所成的角A为60 度.求路基低部的宽(精确到0.1米)
❖ 练习:热气球的探测器显示,从热 气球看一栋高楼顶部的仰角为30°, 看这栋高楼底部的俯角为60°,热 气球与高楼的水平距离为120m,这 栋高楼有多高?(结果精确到
3 山坡与地面成300的倾斜角,某人上坡走 60米,则他
(目标3) 上升 米,坡度是
D
C
4 如图已知堤坝的横断面为梯形,AD坡面
的水平宽度为
A
B
3√3米,DC=4米,B=600,则
(1)斜坡AD 的铅直高度是
(2)斜坡AD 的长是 (3)坡角A的
(目标3) 6 如图从山 顶A望地面的C、D 两点,俯角分别时 A
α
练习: 如图,某飞机于空中A 处探测到目标C,此时飞行高 度AC=1200米,从飞机上看低 平面控制点B的俯角α=16031/,
练习 某人在A处测得大厦的仰角∠BAC
为300 ,沿AC方向行20米至D处,测得仰角 ∠BDC 为450,求此大厦的高度BC.
B
A 300
450
D
初三数学教案-解直三角形应用 精品

解直三角形应用(一)知识目标使学生会把实际问题转化为解直角三角形问题,从而会把实际问题转化为数学问题来解决. (二)能力目标:逐步培养学生分析问题、解决问题的能力.(三)情感目标:渗透数学来源于实践又反过来作用于实践的观点,培养学生用数学的意识. 二、教学重点、难点1.重点:要求学生善于将某些实际问题中的数量关系,归结为直角三角形元素之间的关系,从而利用所学知识把实际问题解决.2.难点:要求学生善于将某些实际问题中的数量关系,归结为直角三角形中元素之间的关系,从而利用所学知识把实际问题解决. 三、教学过程 1.导入新课上节课我们解决的实际问题是应用正弦及余弦解直角三角形,在实际问题中有时还经常应用正切和余切来解直角三角形,从而 使问题得到解决. 2.例题分析例1.如图6-21,厂房屋顶人字架(等腰三角形)的跨度为10米, ∠A =26°,求中柱BC(C 为底边中点)和上弦AB 的长(精确到0.01米).分析:上图是本题的示意图,同学们对照图形,根据题意思考 题目中的每句话对应图中的哪个角或边,本题已知什么,求什么?由题意知,△ABC 为直角三角形,∠ACB=90°,∠A=26°, AC=5米,可利用解Rt △ABC 的方法求出BC 和AB .学生在把实际问题转化为数学问题后,大部分学生可自行完成。
例题小结:求出中柱BC 的长为2.44米后,我们也可以利用正弦 计算上弦AB 的长。
如果在引导学生讨论后小结,效果会更好,不仅使学生掌握选何 关系式,更重要的是知道为什么选这个关系式,以培养学生分析 问题、解决问题的能力及计算能力,形成良好的学习习惯. 另外,本题是把解等腰三角形的问题转化为直角三角形的问题, 渗透了转化的数学思想.例2.如图,一艘海轮位于灯塔P 的北偏东650方向,距离灯塔 80海里的A 处,它沿正南方向航行一段时间后,到达位于灯塔P 的南偏东340方向上的B 处。
解直角三角形教案最新

28.2.1 解直角三角形教学目标:知识与技能:1、使学生理解直角三角形中五个元素的关系,会运用勾股定理,直角三角形的两个锐角互余及锐角三角函数解直角三角形.2、通过综合运用勾股定理,直角三角形的两个锐角互余及锐角三角函数解直角三角形,逐步培养学生分析问题、解决问题的能力.3、渗透数形结合的数学思想,培养学生良好的学习习惯.过程与方法:通过综合运用勾股定理,直角三角形的两个锐角互余及锐角三角函数解直角三角形,逐步培养学生分析问题、解决问题的能力.情感态度与价值观:渗透数形结合的数学思想,培养学生良好的学习习惯.重难点、关键:1.重点:直角三角形的解法.2.难点:三角函数在解直角三角形中的灵活运用.教学过程:一、复习旧知、引入新课【引入】我们一起来解决关于比萨斜塔问题见课本在Rt△ABC中,∠C=90°,BC=5.2m,AB=54.5m.sin=5.254.5BCAB≈0.0954.所以∠A≈5°28′.二、探索新知、分类应用【活动一】理解直角三角形的元素【提问】1.在三角形中共有几个元素?什么叫解直角三角形?总结:一般地,直角三角形中,除直角外,共有5个元素,即3条边和2个锐角,由直角三角形中除直角外的已知元素,求出其余未知元素的过程,叫做解直角三角形。
【活动二】直角三角形的边角关系直角三角形ABC 中,∠C=90°,a 、b 、c 、∠A 、∠B 这五个元素间有哪些等量关系呢?(1)边角之间关系a b A b a A c b A c a A ====cot ;tan ;cos ;sin如果用α∠表示直角三角形的一个锐角,那上述式子就可以写成.的对边的邻边;的邻边的对边;斜边的邻边;斜边的对边αααααααααα∠∠=∠∠=∠=∠=cot tan cos sin(2)三边之间关系a 2 +b 2 =c 2 (勾股定理)(3)锐角之间关系∠A+∠B=90°.以上三点正是解直角三角形的依据,通过复习,使学生便于应用.【活动三】解直角三角形例1:在△ABC 中,∠C 为直角,∠A 、∠B 、∠C 所对的边分别为a 、b 、c ,且2a=6解直角三角形的方法很多,灵活多样,学生完全可以自己解决,但例题具有示范作用.因此,此题在处理时,首先,应让学生独立完成,培养其分析问题、解决问题能力,同时渗透数形结合的思想.其次,教师组织学生比较各种方法中哪些较好,选一种板演.例2:在Rt△ABC中,∠B =35°,b=20,解这个三角形(结果保留小数点后一位.引导学生思考分析完成后,让学生独立完成。
解直角三角形应用题(方位角、仰角与俯角、坡度)分类汇编

:i h l=hlα基础知识2解直角三角形的应用举例1.仰角与俯角:仰角:视线在水平线上方的角;俯角:视线在水平线下方的角。
2.坡度与坡角:坡面的铅直高度h 和水平宽度l 的比叫做坡度(坡比)。
用字母i 表示,即hi l=。
坡度一般写成1:m 的形式,如1:5i =等. 把坡面与水平面的夹角记作α(叫做坡角),那么tan hi lα== 3.方位角:指北或指南方向线与目标方向线所成的小于90°的水平角,叫做方位角.如图,OA 、OB 、OC 、OD 的方向角分别是:北偏东30°(东北方向),南偏东45°(东南方向),南偏西60°(西南方向),北偏西60°(西北方向).【题型1】仰角与俯角如图,两幢建筑物AB 和CD ,AB ⊥BD ,CD ⊥BD ,AB =15m ,CD =20m ,AB 和CD 之间有一观景池,小南在A 点测得池中喷泉处E 点的俯角为42°,在C 点测得E 点的俯角为45°(点B 、E 、D 在同一直线上),求两幢建筑物之间的距离BD (结果精确到0.1m ).(参考数据:sin 42°≈0.67,cos 42°≈0.74,tan 42°≈0.90)【变式训练】1.如图,宁宁在家里楼顶上的点A处,测量建在与自家楼房同一水平线上相邻的电梯楼的高,在点A处看电梯楼顶部点B处的仰角为60°,在点A处看这栋电梯楼底部点C处的俯角为45°,两栋楼之间的距离为30m,则电梯楼的高BC为多少米(精确到0.1).2.如图,大楼AB右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同一水平直线上),已知AB=80m,DE=10m,求障碍物B,C两点间的距离(结果精确到0.1m).(参考数据:≈1.414,≈1.732)3.如图,热气球的探测器显示,从热气球A看一栋大楼顶部B的俯角为30°,看这栋大楼底部C的俯角为60°,热气球A的高度为240米,求这栋大楼的高度.4.如图,曦曦在M处用高1米(DM=1米)的测角仪测得旗杆AB的顶端B的仰角为30°,再向旗杆方向前进10米到F处,又测得旗杆顶端B的仰角为60°,请求出旗杆AB的高度.【题型2】坡度与坡角如图,某水库堤坝横断面迎水坡AB的坡比是1,堤坝高BC=50m,则应水坡面AB的长度是多少?【变式训练】1.如图,在坡度为1∶2的山坡上种树,要求株距(相邻两树间的水平距离)是6米,斜坡上相邻两树间的坡面距离是多少米?2.如图,为了缓解交通拥堵,方便行人,在某街道计划修建一座横断面为梯形ABCD的过街天桥,若天桥斜坡AB的坡角∠BAD为35°,斜坡CD的坡度为i=1∶1.2(垂直高度CE与水平宽度DE的比),上底BC=10 m,天桥高度CE=5 m,求天桥下底AD的长度.(结果精确到0.1 m,参考数据:sin35°≈ 0.57,cos35°≈ 0.82,tan35°≈ 0.70)3.如图,一楼房AB后有一假山,其坡度为i=1∶3,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=25米,与亭子距离CE=20米,小丽从楼房顶测得E点的俯角为45°,求楼房AB的高.(注:坡度i是指坡面的铅直高度与水平宽度的比).4.如图,曦曦在山坡坡脚A 处测得电视塔尖点C 的仰角为60° ,沿山坡向上走到P 处再测得点C 的仰角为45° ,已知OA=100米,山坡坡度为i=1:2, 且O 、A 、B 在同一条直线上。
4.3--解直角三角形

4. 如图,根据图中已知数据,求△ABC其余各边的长, 各角的度数和△ABC的面积.
解: AC 4 2,BC 2( 2 6), BAC 1050 SΔABC 4 4 3
B
A
4 450
300
C
课堂小结
说说解直角三角形时,有哪些注意点? 在遇到解直角三形的问题时,最好先画一个直角三角 形的草图,按题意标明哪些元素是已知的,哪些元素 是未知的,以得于分析解决问题.
结论
在直角三角形中,除直角外的5个元素(3条边和2个 锐角),只要知道其中的2个元素(至少有一个是边),利 用上述关系式,就可以求出其余的3个未知元素,把在直 角三角形中利用已知元素求其余未知元素的过程叫作解 直角三角形.
结论
解直角三角形的依据
(1)三边之间的关系: a2+b2=c2(勾股定理);
如图4-23,在直角三角形ABC中,∠C=90°, ∠A,∠B,∠C的对边分别记作a,b,c .
图4-23
问题1 直角三角形的三边之间有什么关系?
a2+b2=c2(勾股定理)
图4-23
问题2 直角三角形的锐角之间有什么关系?
∠A+∠B=90°.
图4-23
问题3 直角三角形的边和锐角之间有什么关系?
c a2 b2 sin A a ;求A c B 90 A
B
c a
A
b
C
小结:解直角三角形,只有上面两种情况:
一共有四种小的情况。
15
练习
1. 在Rt△ABC中, C 90, B 45 ,b=3cm, 求∠A,a,c (精确到0.01cm).
答: A = 45 , a = 3 cm , c = 4.24cm.
2.5解直角三角形的应用+课件 +2024—2025学年青岛版数学九年级上册

C,E 在同一直线上,那么开挖点E 离点D 的距离是
(
A )m.
A. 500sin44°
C. 500tan44°
B. 500cos44°
D.
°
感悟新知
知1-练
2-2.[模拟·武汉] 如图, 沿AB 方向架桥修路,为加快施工
∴ QH=BC,BH=CQ.
由题意可得AP=80 米,∠ PAH=60 °,∠ PCQ=30 °,
AB=70 米,∴ PH=AP·sin60°=80× =40 (米),
感悟新知
知2-练
AH=AP·cos6
0°=80× =4
0(米).
∴CQ=BH=70-40 =30(米). ∴PQ=CQ·tan30°=10 米.
学习目标
第2章 解直角三角形
2.5 解直角三角形的应用
感悟新知
知识点 1
解直角三角形在实际中的应用
知1-讲
1. 利用解直角三角形解决实际问题的一般步骤
(1)画出平面图形,将实际问题抽象为数学问题,转化为解
直角三角形的问题.
(2)根据已知条件的特点,灵活选用锐角三角比等知识解直
角三角形.
(3)得到数学问题的答案.(4)得到实际问题的答案.
感悟新知
知1-练
例 1 京杭大运河是世界文化遗产.综合实践活动小组为
了测出某段运河的河宽(岸沿是平行的),如图2.5-1
所示,在岸边分别选定了点A,B 和点C,D,先用卷
尺量得AB=160 m,CD=40 m,再
用测角仪测得∠ CAB=30 °,∠
DBA=60 °,求该段运河的河宽
[初中数学]解直角三角形的应用教案 人教版
![[初中数学]解直角三角形的应用教案 人教版](https://img.taocdn.com/s3/m/6ae7bfc19b89680203d825a0.png)
《解直三角形的应用》教案一.教学三维目标(一)、知识目标使学生了解仰角、俯角的概念,使学生根据直角三角形的知识解决实际问题.(二)、能力目标逐步培养分析问题、解决问题的能力.二、教学重点、难点和疑点1.重点:要求学生善于将某些实际问题中的数量关系,归结为直角三角形中元素之间的关系,从而解决问题.2.难点:要求学生善于将某些实际问题中的数量关系,归结为直角三角形中元素之间的关系,从而解决问题.三、教学过程(一)回忆知识1.解直角三角形指什么?2.解直角三角形主要依据什么?(1)勾股定理:a 2+b 2=c 2(2)锐角之间的关系:∠A+∠B=90°(3)边角之间的关系:tanA=的邻边的对边A A ∠∠斜边的邻边A A ∠=cos 斜边的对边A A ∠=sin(二)新授概念1.仰角、俯角当我们进行测量时,在视线与水平线所成的角中,视线在水平线上方的角叫做仰角,在水平线下方的角叫做俯角.教学时,可以让学生仰视灯或俯视桌面以体会仰角与俯角的意义.2.例1如图(6-16),某飞机于空中A 处探测到目标C ,此时飞行高度AC=1200米,从飞机上看地平面控制点B 的俯角α=16°31′,求飞机A 到控制点B 距离(精确到1米) 解:在Rt △ABC 中sinB=AB ACAB=B AC sin =2843.01200=4221(米)答:飞机A 到控制点B 的距离约为4221米.例2.2003年10月15日“神州”5号载人航天飞船发射成功。
当飞船完成变轨后,就在离地形表面350km 的圆形轨道上运行。
如图,当飞船运行到地球表面上P 点的正上方时,从飞船上能直接看到地球上最远的点在什么位置?这样的最远点与P 点的距离是多少?(地球半径约为6400km ,结果精确到0.1km )分析:从飞船上能看到的地球上最远的点,应是视线与地球相切时的切点。
将问题放到直角三角形FOQ 中解决。
F.解决此问题的关键是在于把它转化为数学问题,利用解直角三角形知识来解决,在此之前,学生曾经接触到通过把实际问题转化为数学问题后,用数学方法来解决问题的方法,但不太熟练.因此,解决此题的关键是转化实际问题为数学问题,转化过程中着重请学生画几何图形,并说出题目中每句话对应图中哪个角或边(包括已知什么和求什么),会利用平行线的内错角相等的性质由已知的俯角α得出Rt △ABC 中的∠ABC ,进而利用解直角三角形的知识就可以解此题了.例1小结:本章引言中的例子和例1正好属于应用同一关系式 sinA=斜边的对边A ∠ 来解决的两个实际问题即已知α∠和斜边,求∠α的对边;以及已知∠α和对边,求斜边.(三).巩固练习1.热气球的探测器显示,从热气球看一栋高楼顶部的仰角为,看这栋楼底部的俯角为600,热气球与高楼的水平距离为120m ,这栋高楼有多高(结果精确到0.1`m )2.如图6-17,某海岛上的观察所A 发现海上某船只B 并测得其俯角α=80°14′.已知观察所A 的标高(当水位为0m 时的高度)为43.74m ,当时水位为+2.63m ,求观察所A 到船只B 的水平距离BC(精确到1m)教师在学生充分地思考后,应引导学生分析:(1).谁能将实物图形抽象为几何图形?请一名同学上黑板画出来.(2).请学生结合图形独立完成。
第2讲 解直角三角形

A的邻边 b
A的对边 a
这三个关系式中,每个关系式都包含三个元素,知其中两个元素就可以求出第三个元 素。(1)已知两边求第一边;(2)已知一锐角求另一角;(3)已知两边求锐角,已知一边一角求 另一边。
这些关系式是解直角三角形的依据,已知其中两个元素(至少有一个是边)就可 以求出其余的三个未知元素。
【例 5】 如图所示,在△ABC 中,∠B=45°,AC=5,BC=3。求:sinA 和 AB。 A
D
B
C
【例 6】某校数学兴趣小组在测量一座池塘边上 A,B 两点间的距离时用了以下三种测量方 法,如下图所示.图中 a,b,c 表示长度,β表示角度.请你求出 AB 的长度(用含有 a, b,c,β字母的式子表示).
形。
【例 4】在△ABC 中,∠C=90°,b=35,c=45,(cos39°=0.7778),解直角三角形。 由以上所述,归纳总结出解直角三角形题目分为四种类型:
已知条件(两个)
解
法
( 1) ∠ B 90o ∠ A
一条直角边和一个锐角 ( a, ∠ A)
( 2) sin A a c a
)
A. 3
B. 4
4
3
C. 3 5
D. 5 3
2. 在△ABC 中,∠A=105°,∠B=45°,tanC 的值是(
)
A. 1 2
B. 3 3
C. 1
D.
3.
)
2
A. 锐角三角形
B. 直角三角形 C. 钝角三角形
D. 等腰三角形
【例 7】已知:如图,在平行四边形 ABCD 中,E 是 AD 的中点,连接 BE、CE,∠BEC=90°. (1)求证:BE 平分∠ABC;
解直角三角形的应用

i
B
C l
AB 2 BC 2 3.22 0.42 3.1749(米).
BC 0.4 1: 7.938. AC 3.1749 BC 0.4 tan A 0.12599, AC 3.1749 ' A 7 1.
' 答:残疾人通道的坡度约为1:7.938,坡角约为 7 1.
解直角三角形的
应用
1.解直角三角形
在直角三角形中,除直角外,由已知两元素 (必有一边) 求其余未知元素的过程叫解直角三角形.
2.解直角三角形的依据
(1)三边之间的关系:a2+b2=c2(勾股定理);c (2)两锐角之间的关系: (3)边角之间的关系: a sinA= c b cosA= c a tanA= b
α
在每小段上,我们都构造出直角三角形,利用上面的方法分别算 出各段山坡的高度h1,h2,…,hn,然后我们再“积零为整”,把 h1,h2,…,hn相加,于是得到山高h. 以上解决问题中所用的“化整为零,积零为整”“化曲为直,以直代曲” 的做法,就是高等数学中微积分的基本思想,它在数学中有重要地位,在 今后的学习中,你会更多地了解这方面的内容.
我们在生活中会见到 很多斜坡,有的斜坡比较 陡,有的比较平缓. 这只是我们的直观认识, 我们怎么来定量的表示坡 的陡缓程度呢?
如右图,坡面的铅垂高度 h 和水平宽度l 的比叫做坡
h 面的坡度(或坡比), 记作i, 即i . l 坡度通常写成1: m的形式, 如i 1:1.5.
坡面与水平面的夹角叫做坡角,记作 . 坡度i与坡角 之间的关系从右图可以得出 : h i tan . l
例题7 如图,一段铁路路基的横断面为等腰梯形 ABCD,路基顶宽BC为2.8米,路基高为1.2米,斜坡AB的 坡度为i=1:1.6 . (1)计算路基的下底宽(精确到0.1米). (2)求坡角 (精确到1°).
4.4解直角三角形的应用课件九年级数学上册

感悟新知
水平方向飞行 200m 到达点 Q,测得奇楼底端 B 的俯 角为 45° ,求奇楼 AB 的高度.(结果精确到 1m,参 考数据: sin 1 5 ° ≈ 0 . 26,cos 15 ° ≈ 0 . 97, tan15° ≈ 0.27) 解:如图,延长BA交PQ的 延长线于点C,则∠ACQ=90°. 由题意得,BC=225 m,PQ=200 m,
课堂新授
2. 解决实Βιβλιοθήκη 问题时,常见的基本图形及相应的关系式如下 表所示:
图形
关系式
图形
关系式
AC=BC·tanα, AG=AC+BE
BC=DC-BD= AD·(tanα -tanβ )
课堂新授
续表
图形
关系式
AB=DE= AE·tanβ, CD=CE+DE =AE·(tanα+
tanβ)
图形
关系式
感悟新知
(1) 求登山缆车上升的高度 DE; (2)若步行速度为 30m/min,登山缆车的速度为60m/min,
求 从山底 A 处到达山顶 D 处大约需要多少分钟 .(结果 精确到 0.1min,参考数据: sin53° ≈ 0.80, cos53° ≈ 0.60,tan53° ≈ 1.33)
感悟新知
课堂新授
例2
课堂新授
解题秘方:在建立的非直角三角形模型中,用 “化斜为直法”解含公共直角边的 直角三角形.
课堂新授
课堂新授
计算结果必须根据 题目要求进行保留.
课堂新授
方法点拨 解直角三角形的实际应用问题的求解方法: 1. 根据题目中的已知条件,将实际问题抽象为解直角三角
形的数学问题, 画出平面几何图形,弄清已知条件中 各量之间的关系; 2. 若条件中有直角三角形,则直接选择合适的三角函数关 系求解即可;若条件中没有直角三角形,一般需添加辅 助线构造直角三角形,再选用合适的三角函数关系求解.
人教版九年级数学下册第二十八章《28.2解直角三角形-应用举例》公开课 课件(共13张PPT)

A
设DF= x , AD=2x 则在Rt△ADF中,根据勾股定理
60°
AF = AD2 DF 2 = 2x2 x2 = 3x
B
DF
在Rt△ABF中,
30°
AF tan ABF =
tan 30 =
3x
BF
12 + x
解得x=6
AF = 6x = 6 3 10.4
10.4 > 8没有触礁危险
2. 如图,拦水坝的横断面为梯形ABCD(图中i=1:3是指坡面的铅直高 度DE与水平宽度CE的比),根据图中数据求:
解直角三角形—应用举例
例题
例3: 2012年6月18日,“神舟”九号载人航天飞船与“天宫”一号目标飞 行器成功实现交会对接. ,“神舟”九号与“天宫”一号的组合体在离地球表 面343km的圆形轨道上运行.如图,当组合体运行到地球表面上P点的正上 方时,从中能直接看到地球表面最远的点在什么位置?最远点与P点的距离 是多少?(地球半径约为6 400km,π取3.142,结果取整数)
• 17、儿童是中心,教育的措施便围绕他们而组织起来。2021/7/272021/7/272021/7/272021/7/27
• 2、Our destiny offers not only the cup of despair, but the chalice of opportunity. (Richard Nixon, American President )命运给予我们的不是失望之酒,而是机会之杯。二〇二一年六月十七日2021年6月17日星期四 • 3、Patience is bitter, but its fruit is sweet. (Jean Jacques Rousseau , French thinker)忍耐是痛苦的,但它的果实是甜蜜的。10:516.17.202110:516.17.202110:5110:51:196.17.202110:516.17.2021 • 4、All that you do, do with your might; things done by halves are never done right. ----R.H. Stoddard, American poet做一切事都应尽力而为,半途而废永远不行6.17.20216.17.202110:5110:5110:51:1910:51:19 • 5、You have to believe in yourself. That's the secret of success. ----Charles Chaplin人必须相信自己,这是成功的秘诀。-Thursday, June 17, 2021June 21Thursday, June 17, 20216/17/2021
解直角三角形

解直角三角形一、目标与策略明确学习目标及主要的学习方法是提高学习效率的首要条件,要做到心中有数!学习目标:●了解解直角三角形的含义,会综合运用平面几何中有关直角三角形的知识和锐角三角函数的定义解直角三角形;●会运用有关解直角三角形的知识解决实际生活中存在的解直角三角形问题.重点难点:●重点:掌握解直角三角形的一般方法和步骤,在以后的学习和实际生活、生产中经常运用.●难点:把实际生活、生产中存在的和平面图形计算的有关问题转化为解直角三角形问题.学习策略:●本节课的主要内容是解直角三角形的概念及应用解直角三角形的知识去解决实际问题.学习本节知识主要把握好三个关系——边边关系、边角关系、锐角之间的关系,把锐角三角函数、勾股定理同实际问题有机结合起来,核心是找到可解的直角三角形.●解直角三角形的口诀:有斜(斜边)用弦(正弦、余弦),无斜边用切(正切),宁乘勿除,取原(原始数据)避中(中间数据).二、学习与应用“凡事预则立,不预则废”。
科学地预习才能使我们上课听讲更有目的性和针对知识回顾——复习学习新知识之前,看看你的知识贮备过关了吗?(一)锐角三角函数的概念在Rt△ABC中,∠C=90°,∠A所对的直角边称为∠A的对边,另一条直角边称为∠A的邻边.锐角A的与的比叫做∠A的正弦,记作;锐角A的与的比叫做∠A的余弦,记作;锐角A的与的比叫做∠A的正切,记作.(二)特殊角的三角函数值锐角αsinαcosαtanα30°45°60°(三)锐角三角函数之间的关系如图所示,在Rt△ABC中,∠C=90°.(1)互余关系:..........................sin cos(90)cosA=-=o,..........................cos sin(90)sinA=-=o;(2)平方关系:22.............sin cosA A+=;(3)倒数关系:.............tan tan(90)1A-=og或.............1tantanA=;(4)相除关系:..........................sintancosA=.知识点一:解直角三角形在直角三角形中,由已知元素(直角除外)求未知元素的过程,叫做解直角三角形.在直角三角形中,除直角外,一共有5个元素,即三条边和两个锐角.设在Rt△ABC中,∠C=90°,∠A、∠B、∠C所对的边分别为a、b、c,则有:(1)边之间的关系: (勾股定理).(2)锐角之间的关系: + =90°.(3)边角之间的关系:知识要点——预习和课堂学习认真阅读、理解教材,尝试把下列知识要点内容补充完整,带着自己预习的疑惑认真听课学习。
(7)28.2解直三角形应用(三)----坡度问题
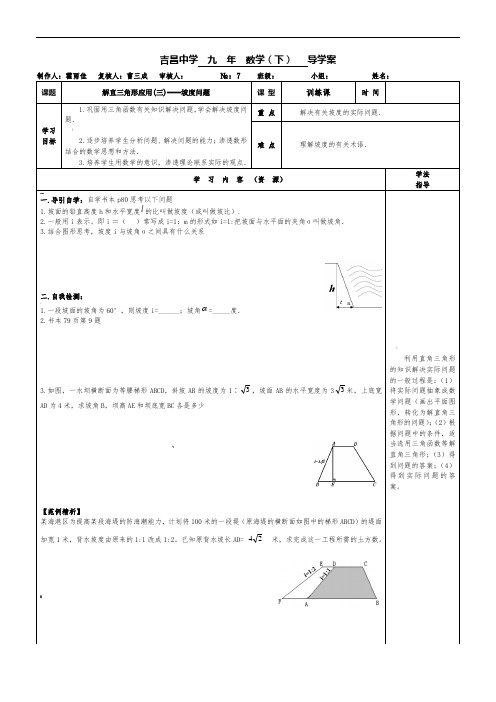
吉昌中学九年数学(下)导学案课题解直三角形应用(三)----坡度问题课型训练课时间学习目标1.巩固用三角函数有关知识解决问题,学会解决坡度问题.!2.逐步培养学生分析问题、解决问题的能力;渗透数形结合的数学思想和方法.3.培养学生用数学的意识,渗透理论联系实际的观点.重点解决有关坡度的实际问题.难点理解坡度的有关术语.学习内容(资源)学法指导…一.导引自学:自学书本p80思考以下问题1.坡面的铅直高度h和水平宽度l的比叫做坡度(或叫做坡比).2.一般用i表示。
即i=()常写成i=1:m的形式如i=1:把坡面与水平面的夹角α叫做坡角.3.结合图形思考,坡度i与坡角α之间具有什么关系二.自我检测::1.一段坡面的坡角为60°,则坡度i=______;坡角 =_____度.2.书本79页第9题3.如图,一水坝横断面为等腰梯形ABCD,斜坡AB的坡度为1∶3,坡面AB的水平宽度为33米,上底宽AD为4米,求坡角B,坝高AE和坝底宽BC各是多少~【范例精析】某海港区为提高某段海堤的防海潮能力,计划将100米的一段堤(原海堤的横断面如图中的梯形ABCD)的堤面加宽1米,背水坡度由原来的1:1改成1:2。
已知原背水坡长AD= 24米,求完成这一工程所需的土方数。
])利用直角三角形的知识解决实际问题的一般过程是:(1)将实际问题抽象成数学问题(画出平面图形,转化为解直角三角形的问题);(2)根据问题中的条件,适当选用三角函数等解直角三角形;(3)得到问题的答案;(4)得到实际问题的答案。
【达标测评】1、如图,沿江堤坝的横断面是梯形ABCD,坝顶AD=4m,坝高AE=6 m,斜坡AB的坡比2:1=i,∠C=60°,求斜坡AB、CD的长。
¥2、同学们,如果你是修建三峡大坝的工程师,现在有这样一个问题请你解决:如图水库大坝的横断面是梯形,坝顶宽6m,坝高23m,斜坡AB的坡度i=1∶3,斜坡CD的坡度i=1∶,求斜坡AB的坡面角α,坝底宽AD和斜坡AB的长(精确到->方法总结:课后反思A DCBE2:1=i。
解三角形在现实生活中的应用——正,余弦定理

解三角形正,余弦定理在现实生活中的应用解三角形的正弦定理和余弦定理在现实生活中有广泛的应用。
例如,测量距离、测量高度、航海模型、物理问题等都与这些定理有关。
以下是一些例子:
1. 测量距离
利用正弦定理和余弦定理可以测量出无法直接测量的距离。
假设你想知道两个建筑物之间的距离,但你不能直接测量它们之间的直线距离。
你可以站在其中一个建筑物旁边,用一个工具测量你与另一个建筑物之间的角度和高度差,然后使用正弦定理或余弦定理计算出两个建筑物之间的直线距离。
2. 测量高度
同样可以利用正弦定理和余弦定理测量出无法直接测量的高度。
假设你想知道一个树的高度,但你只能在地面附近测量树的影子长度。
你可以使用正弦定理或余弦定理计算出树的高度。
3. 航海模型
在航海中,可以利用正弦定理和余弦定理计算船只的位置。
假设你知道船只在某个时间点的位置和朝向,以及它的速度和方向,你可以使用正弦定理和余弦定理计算出船只在任何其他时间点的位置和朝向。
这对于导航非常重要。
4. 物理问题
在物理学中,正弦定理和余弦定理也有很多应用,例如在振
动、波动等问题中。
例如,当一个弹簧上放置一个小球时,小球会以一定的频率来回摆动。
通过测量小球的振幅、周期等参数,可以使用正弦定理和余弦定理计算出小球的运动轨迹和速度。
直角三角形的应用问题解决

直角三角形的应用问题解决直角三角形是我们学习数学中最基本的图形之一,它的一些特性在实际生活中有着广泛的应用。
本文将从实际问题的角度出发,探讨直角三角形的一些应用问题并给出解决方法。
一、测量不可直接测量的距离直角三角形的应用之一是测量不可直接测量的距离。
例如,一个湖泊中有一个小岛,我们需要测量从湖岸到小岛的距离,但由于湖面的水位不断变化,无法直接测量。
这时我们可以利用直角三角形的性质来解决这个问题。
我们可以选择一个湖岸上的标志物作为视觉参考点,然后选择一个角度,在湖岸上测量出与视线方向垂直的距离,再测量出与视线方向平行的距离。
通过三角形的性质,我们可以得到从视觉参考点到小岛的距离。
二、航海中的导航问题直角三角形的应用问题还可以在航海中进行导航。
航海中的导航问题需要考虑航线、航速、航向等因素,而其中涉及到的距离也是利用直角三角形的性质来解决的。
假设我们需要航行从A点到B点,但在海上船只难以直接航行,我们可以选择一个C点作为中转点。
通过测量从A点到C点的距离、从B点到C点的距离以及A点到C点与B点到C点之间的夹角,利用三角函数的计算,我们可以计算出从A点到B点的距离和方向。
三、建筑物的高度测量直角三角形的应用问题还可以用于测量建筑物的高度。
在现实生活中,我们经常需要测量高楼大厦的高度,但由于无法直接测量,我们可以利用直角三角形的性质来解决这个问题。
在建筑物底部选择一个适当的位置,站立并掌握一个简单的仪器使其水平,并向上朝建筑物顶部看。
这时我们可以选择一个固定距离,移动到该距离上并记录下此时的观测角度。
通过测量观测角度和已知的水平距离,我们可以通过三角函数计算出建筑物的高度。
四、地震定位问题在地震研究中,直角三角形的应用可以用于地震定位问题。
当地震发生时,地震波会在不同的地点以不同的速度传播,我们可以利用这个原理来定位地震的位置。
我们选取至少三个地震站作为观测点,并测量地震波从震源到达各个地震站的时间差。
28.23坡度

第3课时解直三角形应用一、(一)知识教学点巩固用三角函数有关知识解决问题,学会解决坡度问题.(二)能力目标逐步培养学生分析问题、解决问题的能力;渗透数形结合的数学思想和方法.(三)德育目标培养学生用数学的意识,渗透理论联系实际的观点.二、教学重点、难点和疑点1.重点:解决有关坡度的实际问题.2.难点:理解坡度的有关术语.3.疑点:对于坡度i表示成1∶m的形式学生易疏忽,教学中应着重强调,引起学生的重视.三、教学过程1.创设情境,导入新课.例同学们,如果你是修建三峡大坝的工程师,现在有这样一个问题请你解决:如图6-33水库大坝的横断面是梯形,坝顶宽6m,坝高23m,斜坡AB的坡度i=1∶3,斜坡CD的坡度i=1∶2.5,求斜坡AB的坡面角α,坝底宽AD和斜坡AB的长(精确到0.1m).通过前面例题的教学,学生已基本了解解实际应用题的方法,会将实际问题抽象为几何问题加以解决.但此题中提到的坡度与坡角的概念对学生来说比较生疏,同时这两个概念在实际生产、生活中又有十分重要的应用,因此本节课关键是使学生理解坡度与坡角的意义.介绍概念坡度与坡角结合图6-34,教师讲述坡度概念,并板书:坡面的铅直高度h 和水平宽度l 的比叫做坡度(或叫做坡比),一般用i 表示。
即i=l h,把坡面与水平面的夹角α叫做坡角.引导学生结合图形思考,坡度i 与坡角α之间具有什么关系?答:i =l h=tan α这一关系在实际问题中经常用到,教师不妨设置练习,加以巩固.练习(1)一段坡面的坡角为60°,则坡度i=______;______,坡角α______度.为了加深对坡度与坡角的理解,培养学生空间想象力,教师还可以提问:(1)坡面铅直高度一定,其坡角、坡度和坡面水平宽度有什么关系?举例说明.(2)坡面水平宽度一定,铅直高度与坡度有何关系,举例说明.答:(1)如图,铅直高度AB 一定,水平宽度BC 增加,α将变小,坡度减小,因为 tan α=BC AB,AB 不变,tan α随BC 增大而减小(2)与(1)相反,水平宽度BC 不变,α将随铅直高度增大而增大,tan α也随之增大,因为tan α=BC AB不变时,tan α随AB 的增大而增大2.讲授新课引导学生分析例题,图中ABCD 是梯形,若BE ⊥AD ,CF ⊥AD ,梯形就被分割成Rt △ABE ,矩形BEFC 和Rt △CFD ,AD=AE+EF+FD ,AE 、DF 可在△ABE 和△CDF 中通过坡度求出,EF=BC=6m ,从而求出AD .以上分析最好在学生充分思考后由学生完成,以培养学生逻辑思维能力及良好的学习习惯.坡度问题计算过程很繁琐,因此教师一定要做好示范,并严格要求学生,选择最简练、准确的方法计算,以培养学生运算能力.解:作BE ⊥AD ,CF ⊥AD ,在Rt △ABE 和Rt △CDF 中,∴AE=3BE=3×23=69(m).FD=2.5CF=2.5×23=57.5(m).∴AD=AE+EF+FD=69+6+57.5=132.5(m).因为斜坡AB 的坡度i =tan =31≈0.3333,查表得α≈18°26′答:斜坡AB 的坡角α约为18°26′,坝底宽AD 为132.5米,斜坡AB 的长约为72.7米.3.巩固练习引导学生回忆前述例题,进行总结,以培养学生的概括能力.1.弄清坡度、坡角、等概念的意义,明确各术语与示意图中的什么元素对应,只有明确这些概念,才能恰当地把实际问题转化为数学问题2.认真分析题意、画图并找出要求的直角三角形,或通过添加辅助线构造直角三角形来解决问题.3.选择合适的边角关系式,使计算尽可能简单,且不易出错.4.按照题中的精确度进行计算,并按照题目中要求的精确度确定答案以及注明单位.四、布置作业1.看教材,培养看书习惯,作本章小结.2.课本习题P96第5,8题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解直角三角形应用 参赛教学设计
一.教学三维目标
(一)知识目标
使学生理解直角三角形中五个元素的关系,会运用勾股定理,直角三角形的两个锐角互余及锐角三角函数解直角三角形.
(二)能力训练点
通过综合运用勾股定理,直角三角形的两个锐角互余及锐角三角函数解直角三角形,逐步培养学生分析问题、解决问题的能力.
(三)情感目标
渗透数形结合的数学思想,培养学生良好的学习习惯.
二、教学重点、难点和疑点
1.重点:直角三角形的解法.
2.难点:三角函数在解直角三角形中的灵活运用.
3.疑点:学生可能不理解在已知的两个元素中,为什么至少有一个是边.
三、教学过程
(一)知识回顾
1.在三角形中共有几个元素?
2.直角三角形ABC 中,∠C=90°,a 、b 、c 、∠A 、∠B 这五个元素间有哪些等量关系呢?
(1)边角之间关系 sinA=
c a cosA=c b tanA=b a (2)三边之间关系
a 2 +
b 2 =
c 2 (勾股定理)
(3)锐角之间关系∠A+∠B=90°.
以上三点正是解直角三角形的依据,通过复习,使学生便于应用.
(二) 探究活动
1.我们已掌握Rt △ABC 的边角关系、三边关系、角角关系,利用这些关系,在知道其中的两个元素(至少有一个是边)后,就可求出其余的元素.这样的导语既可以使学生大概了解解直角三角形的概念,同时又陷入思考,为什么两个已知元素中必有一条边呢?激发了学生的学习热情.
2.教师在学生思考后,继续引导“为什么两个已知元素中至少有一条边?”让全体学生的思维目标一致,在作出准确回答后,教师请学生概括什么是解直角三角形?(由直角三角形中除直角外的两个已知元素,求出所有未知元素的过程,叫做解直角三角形).
3.例题评析
例 1在△ABC 中,∠C 为直角,∠A 、∠B 、∠C 所对的边分别为a 、b 、c ,且b= 2
a=6,解这个三角形.
∠=350,例2在△ABC中,∠C为直角,∠A、∠B、∠C所对的边分别为a、b、c,且b= 20 B
解这个三角形(精确到0.1).
解直角三角形的方法很多,灵活多样,学生完全可以自己解决,但例题具有示范作用.因此,此题在处理时,首先,应让学生独立完成,培养其分析问题、解决问题能力,同时渗透数形结合的思想.其次,教师组织学生比较各种方法中哪些较好,选一种板演.
完成之后引导学生小结“已知一边一角,如何解直角三角形?”
答:先求另外一角,然后选取恰当的函数关系式求另两边.计算时,利用所求的量如不比原始数据简便的话,最好用题中原始数据计算,这样误差小些,也比较可靠,防止第一步错导致一错到底.
例3在Rt△ABC中,a=104.0,b=20.49,解这个三角形.
(三) 巩固练习
∠的平分线AD=43,解此直角三角形。
在△ABC中,∠C为直角,AC=6,BAC
解直角三角形是解实际应用题的基础,因此必须使学生熟练掌握.为此,教材配备了练习针对各种条件,使学生熟练解直角三角形,并培养学生运算能力.
(四)总结与扩展
请学生小结:1在直角三角形中,除直角外还有五个元素,知道两个元素(至少有一个是边),就可以求出另三个元素.2解决问题要结合图形。
四、布置作业
.p96 第1,2题
解直三角形应用(二)
一.教学三维目标
(一)、知识目标
使学生了解仰角、俯角的概念,使学生根据直角三角形的知识解决实际问题.
(二)、能力目标。
