4.2解一元一次方程(3)
解一元一次方程(4个课时+7个知识点+10个题型)学案苏科版七年级数学上册

4.2 解一元一次方程【学习目标】1.了解方程的解与解方程的概念,会根据等式的基本性质解方程。
2.掌握解一元一次方程的方法,了解解一元一次方程的一般步骤,并能灵活运用,能判别解的合理性。
3.经历和体会解一元一次方程中“转化”的思想方法。
【学习内容】1.用等式的基本性质解一元一次方程方程的解与解方程等式的基本性质利用等式的基本性质解简单的一元一次方程2.用移项法解一元一次方程·1·移项的概念·2·用移项的方法解一元一次方程3.用去括号法解方程·1·解含有一个括号的一元一次方程·2·解含有两个(或以上)括号的一元一次方程4.用去分母法解方程·1·解分母为整数的一元一次方程·2·解分母含小数的一元一次方程4.2.1 用等式的基本性质解一元一次方程【基础知识】·知识点01 方程的解与解方程1.方程的解:能使方程两边的值相等的未知数的值叫做方程的解。
使方程左右两边的值相等的未知数的值可以不止一个,即方程的解可以有注意多个。
2.解方程:求方程的解的过程叫做解方程。
★细节剖析:(1)检验一个数是否为方程的解的步骤③比较方程左右两边的值,则此数值是方程的解;若左边的值≠右边的值,则此数值不是方程的解。
·例1·检验下列各数是不是方程4x-2=6x-3的解。
1(1)x=-2;(2)x=2·练习·1.下列方程中,解为x=-1的是()A.2x=-1+x B.3-x=2C.x-4=3D.-2x-2=42.已知关于x的方程2x-a-5=0的解是x=-2,则a的值为()A.1B.-1C.9D.-93.已知x=4是方程ax-2=a+10的解,则a的值为()A.2B.-3C.4D.-45.小强在解方程时,不小心把一个数字用墨水污染成了一2x +=3x ,他翻阅了答案知道这个方程的解为x =-1,于是他判断的值应为___________。
4.2解一元一次方程3

解:2x+6-5+5x=3x-3
解:2x+3-5-5x=3x-3 2x-5x-3x= -3+5-3 -6x= -1
2x+5x-3x= -3+5-6
4x= -4 x= -1
1 x=6
次 程 解 一元 一 方
例6 解方程2(2x+1)=1-5(x-2)
注:去括号时要注意符号
例5.解方程: -3(x+1)=9 方程两边同除以-3,得: X+1=-3 移项,得:X=-3-1 即: X=- 4
ቤተ መጻሕፍቲ ባይዱ
次 程 解 一元 一 方 议一议:观察上述两种解法,说出它们的区别
此方程可以先去括号,也可以当做为(X+1)的 一元一次方程进行求解.
找一找
解方程
次 程 解 一元 一 方
下列方程的解对不对?如果不对,应怎样改正?
x+2(30-x)=50
2.合作质疑,探索新知
次 程 解 一元 一 方
例5.解方程: -3(x+1)=9 去括号,得: -3x-3=9 移项,得: -3x=9+3 化简,得: -3x=12 方程两边同除以-3,得: x=-4
2.合作质疑,探索新知
问题三:
次 程 解 一元 一 方
你还有其他方法去掉方程中的括号吗?
3 .合作探究
次 程 解 一元 一 方
解下列方程:
(1) 5(x+2)=2(2x+7) (2) 3(2y+1)=2(1+y)-3(y+3)
从
4.课堂小结,感悟收获
问
题
到
方
程
苏科版七年级上册数学4.2《解一元一次方程》课件 (共20张PPT)

移项、合并同类项,得 5x=10
系数化为1,得 x=2
讲授新课
如何解方程 x 2 x 1 3? 0.2 0.5
解:去分母,得 5(x-2)-2(x+1)=3 去括号,得 5x-10-2x-2=3 移项、合并同类项,得 3x=15 系数化为1,得 x=5
讲授新课
解一元一次方程有哪些步骤? 一般步骤:去分母;去括号;移项;合并同类项; 未知数系数化为1.
讲授新课 例3、解方程:2x=5x-21 思考:方程2x=5x-21变形为2x-5x=-21 解:两边都减去5x,得 从形式上发生了什么变化? 2x-5x=-21 合并同类项,得 -3x=-21 两边都除以-3,得 x=7 方程中的某些项改变符号后,可以从方程的一边移到另一 边,这样的变形叫做移项 .
讲授新课
例4、解方程:x-3=4- 1 x
解:移项,得
1 x+
2 x=4+3
合并同类项,得3 2 x=7
两边都除以
3,得2
14 x=
2
3
方 乘程2 ,32 都x=能7的把两未边知都数除的以系32数或化 3
为1.
注意:(1)移项时,通常把含有未知数的项移到等号的左边,
把常数项移到等号的右边.
(2)移项要改变符号.
5x=15 系数化为1,得 x=3
(2) x 1 x 3 2
解:去分母,得 x-1=2(x+3) 去括号,得 x-1=2x+6 移项、合并同类项,得 -x=7 系数化为1,得 x=-7
移项,得 -4x=7-3-3
合并同类项,得 -4x=1
两边除以-4,得
1 x=-
4
(2)x-3 =2(x+1) 解:去括号,得 x-3=2x+2 移项,得 x-2x=2+3 合并同类项,得 -x=5 两边除以-1,得 x=-5
4.2解一元一次方程(第3课时)课件(苏科版七上)

系数化为1
2、移项,合并同类项,系数为化1, 要注意什么? ①移项要变号。 ②合并同类项时,只是把同类项的 系数相加作为所得项的系数,字母 部分不变。
③系数化为1,要方程两边同时除以
未知数前面的系数。
小明用45元钱买了面值为2 元和3元的邮票 共20张。问他买 了多少张面值为2元的邮票?
移项得:
x=15 ⑵括号前是“-”号,把括号和它前面的“-” 号去掉,括号里各项都改变符号 答:小明买了15张面值为2元的邮票。
系数化为1得:
• 思考: • 通过解上面的方程,你对解一元 一次方程有什么新的认识吗?
现在我们解方程的步骤有 变化吗?
解一元一次方程的步骤: 去括号
移项
合并同类项
系数化为1
《评价手册》P70 第三课时
分析:若设小明买了x张面值为2元的邮票, (20-x) 张 则面值为3元的邮票共有 2元的共用去 元, 2x 3元的共用去 3(20-x) 元
因为一共用去了45元, 所以,可列方程 2x+ 3(20-x)=45
。
小明用45元钱买了面值为2 元和3元的邮票 共20张。问他买 了多少张面值为2元的邮票?
解:设小明买了x张面值为2元的邮票, 则他买了3元的邮票为 (20-x)ቤተ መጻሕፍቲ ባይዱ, 根据题意列方程得:
2x+ 3(20-x)=45 去括号得: 去括号法则: 2x+60-3x=45
方程中有 2x-3x=45-60 括号怎么 ⑴括号前是“ +”号,把括号和它前面的“ +” 合并同类项得: -x=-15 号去掉,括号里各项都不变符号。 解呀?
3x-7x+2x=3-6-7
4.2 用配方法解一元一次方程

归 纳:
上面,我们把方程 -4x+3=0变形为 =1,它的左边 是一个含有未知数的完全平方式,右边是一个非负常数.这样,就能应用直接开平方的方法求解.这种解一元二次方程的方法叫做配方法.
注意到第一步在方程两边同时加上了一个数后 ,左边可以用完全平方公式从而转化为用直接开平方法求解。
那么,在方程两边同时加上的这个数有什么规律 呢 ?
(3) (4)
布置作业:课后习题1
教学反思:
年级科目
九年级数学
课题
4.2用配方法解一元一次方程
主备人
审核人
总课时数
教学
目标
1.会用开平方法解形如(x+m)2=n(n ≥0)的方程;
2.经历用配方法求解一元二次方程的探究过程,体会转化的数学思想。
重点
难点
重点:利用配方法解一元二次方程
难点:把一元二次方程通过配方转化为(x+m)2=n(n≥0)的形式
试一试:对下列各式进行配方:
(1) ;
(2) ;
(3) ;
通过练习,使学生探讨配方的关键是
活 动三:运用新知解决问题
用配方法解下列方程:
(1) -6x-7=0;(2) +3x+1=0.
三归纳总结,பைடு நூலகம்力提升
用配方法解二次项系数为1的一元二次方程的步骤:
(1)、移项:把常数项移到方程的右边;
(2)、配方:方程两边都加上一次项系数一半的平方;
+2x=5; (2) -4x+3=0.
三、自主学习,合作探究
活动一:自主探究,合作交流
试一试:
解下列方程: +2x=5;(2) -4x+3=0.
思考 :能否经过适当变形,将它们转化为
4.2解一元一次方程数学教案

4.2解一元一次方程数学教案标题:以4.2解一元一次方程为主题的数学教案一、教学目标:1. 学生能够掌握一元一次方程的基本概念。
2. 学生能够熟练运用加法、减法、乘法、除法四种基本运算来求解一元一次方程。
3. 培养学生的逻辑思维能力和解决问题的能力。
二、教学内容:1. 一元一次方程的基本概念2. 解一元一次方程的基本方法(加法、减法、乘法、除法)三、教学过程:(一) 导入新课通过复习以前学过的知识,引导学生进入新的学习内容。
例如,让学生回忆一下什么是等式,以及等式的性质是什么。
(二) 新课讲解1. 介绍一元一次方程的概念:只含有一个未知数,并且未知数的最高次数是1的方程叫做一元一次方程。
2. 讲解解一元一次方程的基本方法:- 加法消元:在等式的两边同时加上同一个数,等式的值不变。
- 减法消元:在等式的两边同时减去同一个数,等式的值不变。
- 乘法消元:在等式的两边同时乘以同一个不为零的数,等式的值不变。
- 除法消元:在等式的两边同时除以同一个不为零的数,等式的值不变。
(三) 实践操作设计一些一元一次方程的题目,让学生尝试用刚学到的方法进行解答。
在学生解答的过程中,教师要进行指导和纠正。
(四) 总结回顾总结本节课的主要内容,强调一元一次方程的概念和解一元一次方程的基本方法。
并鼓励学生在课后多做练习,提高自己的解题能力。
四、作业布置布置一些一元一次方程的习题,要求学生独立完成。
五、教学反思在教学结束后,教师应对自己的教学进行反思,看看哪些地方做得好,哪些地方需要改进,以便于下次更好地进行教学。
初中数学苏科版七年级上册第四章 一元一次方程4.2 解一元一次方程-章节测试习题(3)

章节测试题1.【答题】若代数式3a4b2x与0.2b3x﹣1a4能合并成一项,则x的值是()A. B. 1 C. D. 0【答案】B【分析】根据题意列方程,解出方程即可判断.【解答】∵代数式3a4b2x与0.2b3x﹣1a4能合并成一项,∴代数式3a4b2x与0.2b3x﹣1a4是同类项,∴,解得:.选B.2.【答题】已知:|m﹣2|+(n﹣1)2=0,则方程2m+x=n的解为()A. x=﹣4B. x=﹣3C. x=﹣2D. x=﹣1 【答案】B【分析】根据非负数的性质求出m,n,代入方程求出x的值即可.【解答】∵|m﹣2|+(n﹣1)2=0,∴,∴,∴方程可化为:,解得.3.【答题】方程的解是()A. B. C. D.【答案】B【分析】根据移项、合并同类项法则解方程即可判断.【解答】1-3x=0,-3x=-1,∴.选B.4.【答题】关于的方程的解与方程的解相同,则的值是()A. B. C. D.【答案】A【分析】根据方程的解相同,可得关于a的方程,解方程即可得答案.【解答】解:解方程,得把代入得,,解得5.【答题】若代数式x﹣3的值为2,则x等于()A. 1B. ﹣1C. 5D. ﹣5【答案】C【分析】根据题意列出方程,解方程即可.【解答】根据题意得:x﹣3=2,解得:x=5,选C.6.【答题】如果x=-2是关于x的方程3a-2x=7的解,那么a的值是()A. B. a=1 C. D.【答案】B【分析】先将x的值代入方程,再根据移项、合并同类项法则求出a的值即可. 【解答】由题意把代入方程得:,解得:. 选B.7.【答题】方程x﹣3=2x﹣4的解为()A. 1B. ﹣1C. 7D. ﹣7【答案】A【分析】根据移项、去括号、系数化为一解方程判断.【解答】移项,得x﹣2x=﹣4+3,合并同类项,得﹣x=﹣1,系数化成1,得x=1选A.8.【答题】解方程4x-2=3-x,正确的步骤是()①合并同类项,得5x=5;②移项,得4x+x=3+2;③系数化为1,得x=1.A. ①②③B. ③②①C. ②①③D.③①②【答案】C【分析】根据移项、去括号、系数化为一解方程判断.【解答】解方程4x-2=3-x,第一步先移项,可得4x+x=3+2;第二步合并同类项,得5x=5;最后系数化为1,得x=1.所以正确的步骤为②①③,选C.9.【答题】下列方程中,移项正确的是( )A. 由x-3=4得x=4-3B. 由2=3+x得2-3=xC. 由3-2x=5+6得2x-3=5+6D. 由-4x+7=5x+2得5x-4x=7+2【答案】B【分析】根据移项法则即可判断.【解答】把方程的某一项改变符号后从方程的一边移到另一边叫做移项.根据移项的定义,四个选项中只有选项B符合移项的要求,选B.10.【答题】方程5x=1+4x的解是()A. x=-5B. x=-1C. x=1D. x=2【答案】C【分析】根据移项、去括号、系数化为一解方程判断即可.【解答】移项得,5x-4x=1;合并同类项得,x=1,选C.11.【答题】解方程2x-3=1时,移项正确的是()A. 2x=1-3B. 2x=1+3C. 2x=-1-3D. 2x=-1+3【答案】B【分析】根据移项法则即可判断.【解答】把方程的某一项改变符号后从方程的一边移到另一边叫做移项.根据移项的定义,把方程2x-3=1移项,即可得 2x=1+3,选B.方法总结:本题主要考察移项法则,“移项”是指将方程的某一项从等号的左边移到右边或从右边移到左边,移项时要先变号后移项.12.【答题】下列各式中的变形属于移项的是()A. 由3y-7-2x得2x-7-3yB. 由3x-6=2x+4得3x-6=4+2xC. 由5x=4x+8得5x-4x=8D. 由x+6=3x-2得3x-2=x+6【答案】C【分析】根据移项法则即可判断.【解答】把方程的某一项改变符号后从方程的一边移到另一边叫做移项.根据移项的定义可得,只有选项C符合移项的要求,选C.13.【答题】方程-2x+3=0的解是()A. x=B. x=-C. x=D. x=-【答案】C【分析】根据移项、去括号、系数化为一解方程判断即可.【解答】解:移项得:-2x=-3,系数化为1得:.选C.14.【答题】若代数式与的值相等,则x的值是()A. 1B. 2D. 5【答案】A【分析】【解答】根据题意得:3x-4=-2x+1,移项合并得:5x=5,解得:x=1,选A.15.【答题】若代数式3x-4与-2x+1的值相等,则x的值是()A. 1B. 2C. 3D. 5 【答案】A【分析】先列出方程,再根据移项、去括号、系数化为一解方程判断即可.【解答】根据题意得:3x-4=-2x+1,移项合并得:5x=5,解得:x=1,选A.16.【答题】方程2x=0的解是()A. x=﹣2C. x=-D. x=【答案】B【分析】根据移项、去括号、系数化为一解方程判断即可.【解答】解:化系数为1得:x=0,选B.17.【答题】下列各组方程中,解相同的是()A. x=3与4x+12=0B. x+1=2与2(x+1)=2xC. 7x-6=25与D. x=9与x+9=0【答案】C【分析】根据移项、去括号、系数化为一解方程判断即可.【解答】解:A、方程4x+12=0的解为x=-3,因而两个方程的解不相同;B、方程x+1=2的解为x=1,方程2(x+1)=2x无解,因而两个方程的解不相同;C、这两个方程的解都是x=,因而两个方程的解相同;D、方程x+9=0解为x=-9,因而两个方程的解不相同;选C.18.【答题】对任意四个有理数a,b,c,d定义新运算:,已知,则x=()A. ﹣1B. 2C. 3D. 4【答案】C【分析】本题考查了新定义公式,解答本题的关键是明确新定义运算的算理,由可知,可转化为2x+4x=18,从而求出x的值.【解答】解:∵,∴2x+4x=18,即:x=3,选C.19.【答题】已知ax2+2x+14=2x2﹣2x+3a是关于x的一元一次方程,则其解是()A. x=﹣2B. x=C. x=﹣D. x=2【答案】A【分析】根据题意整理,得出a的值,再代入求出x的值即可.【解答】解:方程整理得:(a﹣2)x2+4x+14﹣3a=0,由方程为一元一次方程,得到a﹣2=0,即a=2,方程为4x+14﹣6=0,解得:x=﹣2故选A.20.【答题】a※b是新规定的这样一种运算法则:a※b=a+2b,例如3※(﹣2)=3+2×(﹣2)=﹣1。
4.2 解一元一次方程(3)(移项)

情境创设
1、
2、
例1:……
……
……
例2:……
……
……
习题……
……
……
作业布置
P102
课后随笔
1、学生从利用逆运算解方程到用移项法则解方程要有个过程,不宜操之过急.在移项时,学生常犯的错误是忘记变号,这主要是学生不熟悉移项法则,要对照等式的性质逐渐来理解.
2、解例题时要不拘泥于课本上的解法,追求解题策略的多样化.另外,注意解题格式的规范化和检验的必要性.
教学过程
教学内容
教师活动
学生活动
解方程(写出解答过程中的第一步):
(1)x+2=7→;(2)3+2x=1+x→;
(3)-x+3=-2→;(4)2x-3=1→;
(5)-2x+9=-5→;(6)3+4x=1-2x→.
结合上面问题与课本
例2解方程4x-15=9
例3解方程2x=5x-21
牢记:从等式左边移到等式右边的项要变号;从等式右边移到等式左边的项也要变号.“叛变”了嘛!
7x=5x-4
5x+2=7x-8
2x+5=25-8x
8xቤተ መጻሕፍቲ ባይዱ2=7x-2
2x+3=11-6x
3x-4+2x=4x-3
10y+7=12-5-3y
学生尝试解答,讨论辨析
先让学生自主探求,学生自主总结出移项法则——移项要变号.
认真听讲,注意格式
进一步认识到解方程的基本变形,感悟了解方程过程中的转化思想,求方程的解就是将方程变形为x=a的形式
能否直接把等式左边的-15改变符号移到等式右边?方程4x-15=9与4x=9+15的差别在哪儿?
解方程2x=5 x-21时,能否直接把等式右边的5 x改变符号移到等式左边?为什么?
4.2 解一元一次方程(3)

随堂练习 1、解下列方程:
2x 1 x 2 (1) 1 3 4 1 1 (2) ( x 1) 2 ( x 2); 2 5
解方程的步骤归纳:
步骤
去分 母
具体做法
依据
注意事项
在方程两边都乘以各 等式 分母的最小公倍数 性质2 不要漏乘不含分母的项
去括 一般先去小括号,再去 分配率 去括号 不要漏乘括号中的每一项 号 中括号,最后去大括号 法则 移项 把含有未知数的项移 1)移动的项一定要变号, 到方程一边,其它项 移项 不移的项不变号 都移到方程另一边, 法则 2)注意项较多时不要漏项 注意移项要变号 合并 把方程变为ax=b 合并同类 1)把系数相加 同类 (a≠0 ) 的最简形式 项法则 2)字母和字母的指数不变 项 系数 将方程两边都除以未知 等式 解的分子,分母位置 数系数a,得解x=b/a 性质2 化1 不要颠倒
移项,得 -0.4x-0.2x=-3+2
合并同类项,得 0.2 x 5
两边同除以-0.2得 x 25
合并同类项,得 -0.6x=-1
∴
x 5 3
已知2x+1与-12x+5 的值是相反数,求x的值。
解下列方程:
3 x x4 (1) ; 2 3 1 1 (2) ( x 1) ; 3 7 x2 x (3) ; 5 4 1 1 (4) ( x 1) ( x 1)。 4 3
(2)
x
得 2x-5(3-2x)=10x。 解得x=
15 。 2
想一想:解一元一次方程有哪些步骤?
解一元一次方程的步骤是: (1)去分母。 (2)去括号。 (3)移项。
(4)合并同类项
(5)等式两边除以未知数前面的系数。
2024年苏科版七年级数学上册 4.2 一元一次方程及其解法(课件)

知1-练
解:(1)3x-2=7, 两边同时加2,得3x-2+2=7+2 , 等式的性质1
即3x=9, 两边同时除以3,得x=3 .
等式的性质2
(2)12x+3=23x-1, 两边同时减3,得12x+3-3=23x-1-3 ,
知1-练
等式的性质1
即12x=23x-4, 两边同时减23x,得12x-23x= 23x-4-23x,
知1-练
例 2 若(m+2)x|m|-1=4是关于x的一元一次方程,求m的值. 解题秘方:由一元一次方程的概念可知未知数的次 数为1,系数不为0,据此求待定字母的值. 解:根据题意,可得|m|-1=1,且m+2 ≠ 0 . 由|m|-1=1,得|m|=2,所以m=± 2 . 由m+2 ≠ 0,得m ≠-2 .所以m=2 .
系数化为1,得x=12.
(2)15x-1=65x,
15x-65x=3+1 , -x=4, x=-4 .
移项 合并同类项 系数化为1
知2-练
知2-练
方法提醒 移项一般将含未知数的项放在等号的左边,常数项放
在等号的右边,若移项时为计算简便不是这样放置的,在 合并同类项时可直接交换过来,不需要变号,因为等式具 有对称性.
知2-练
例 4 解方程: (1)8-3x=x+6; (2)15x-1=3+65x. 解题秘方:利用移项解一元一次方程的步骤:移项 →合并同类项→系数化为1 .
解:(1)8-3x=x+6, -3x-x=6-8, -4x=-2 ,
移项 合并同类项
知2-练
x=12.
系数化为1
也 可 移 项 , 得 8 - 6=x + 3x. 合 并 同 类 项 , 得 4x = 2.
1 7
x=19这样等号两边都是整式,
4.2解一元一次方程(3)

【探索活动】
x 2(30 x) 50
如何去掉方程中的括号?依据是什么?
例1.解方程
x+2(30-x)=50
解:去括号,得 x+60-2x=50 . 移项,得 x-2x=50-60 . 合并同类项,得 -x=-10 . 系数化为1,得 x=10 .
做一做
h 4 ,求 a . 9,
5.m=2x+1,n=x-1,并且m-3n=0,
求X的值以及m+n的值。 6已知关于x的方程kx=9-2x的解为
正整数,求k所能取的整数值
5. 在绿化校园的活动中,某班共植树 130棵,有5位学生每人种了2棵,其 做一做 余学生每人种了3棵.这个班共有 多少学生?
解方程 -3(x-1)=15 解: 去括号,得 -3x+3=15 . 移项,得 -3x=15-3 . 合并同类项,得 -3x=12 . 系数化为1,得 x=-4 .
还有其他解 法吗?
做一做
解方程 -3(x-1)=15 解:两边都除以(-3),得 x-1=-5. 还有其他去 移项,得 括号的方法吗? x=-5+1. 合并同类项,得 x=-4 .
例2.解方程 3(x-1)-5(3-2x)= 8(x-8)+6
解:去括号,得 3x-3-15 +10x= 8x-64+6. 移项,得 3x+10x-8x=-64+6+3+15 合并同类项,得 5x=-40. 系数化为1,得 x=-8.
试一试
括号内都要乘 不能忘记变号
【例题讲解】
例2、解方程:
2(2 x 1) 1 5( x 2)
(7)4x-3(20-x)=6x-7(x+2)
解一元一次方程(第三课时 去括号与去分母)(课件)七年级数学上册(苏教版)

D、将方程3( + 1) − (2 − 3) = 12去括号,得3 + 3 − 2 + 3 = 12,故此项错误
故选:B.
利用去括号法解一元一次方程(提高)
4.若方程2x+1=﹣3的解是关于x的方程7﹣2(x﹣a)=3的解,则a的值为( )
移项,得30-10+8=-20+20-5-4
合并同类项,得28x=-9
系数化成1,得x=-
9
28
利用去分母求解一元一次方程
2x 1 x 2
1 下列去分母的过程正确的是( )
1.解一元一次方程: 3 6 ,
A.2(2x-1)-x+2=1 B.(2x-1)-(x+2)=1
C.2(2x-1)-x+2=6 D.2(2x-1)-(x+2)=6
已知合计为33
分析:
(1)设这个数为x.
(2)它的三分之二为
1
x
2
(3)它的一半为
2
x
3
;
;
1
(4)它的七分之一为 7x ;
等式中含有分数,如何求得方程的解呢?
2
1
1
x+ x+ x+x=33
3
2
7
(5)根据题意可列方程为________________________
探索与思考
如何求方程 x+ x+ x+x=33的解?
D.将方程3( + 1) − (2 − 3) = 12去括号,得3 + 1 − 2 + 3 = 12
七年级数学上册 第四章 一元一次方程 4.2 解一元一次方程 解一元一次方程的一般步骤素材 苏科版 精
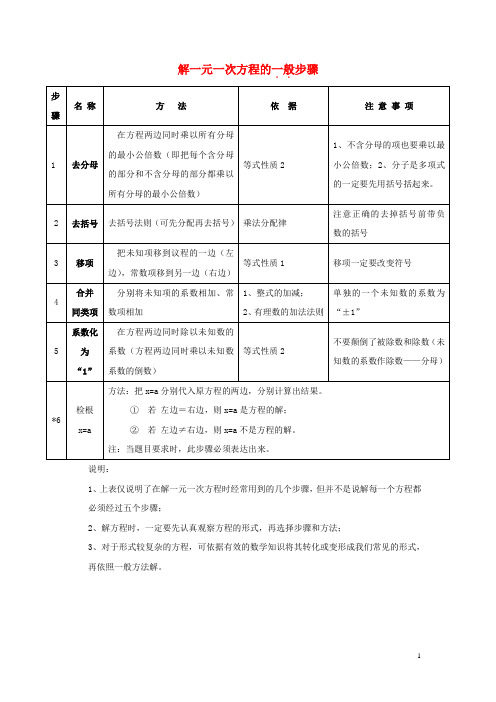
3
移项
把未知项移到议程的一边(左边),常数项移到另一边(右边)
等式性质1
移项一定要改变符号
4
合并同类项
分别将未知项的系数相加、常数项相加
1、整式的加减;
2、有理数的加法法则
单独的一个未知数的系数为“±1”
5
系数化为“1”
在方程两边同时除以未知数的系数(方程两边同时乘以未知数系数的倒数)
等式性质2
不要颠倒了被除数和除数(未知数的系数作除数——分母)
*6
检根
x=a
方法:把x=a分别代入原方程的两边,分别计算出结果。
① 若左边=右边,则x=a是方程的解;
②若左边≠右边,则x=出来。
说明:
1、上表仅说明了在解一元一次方程时经常用到的几个步骤,但并不是说解每一个方程都必须经过五个步骤;
2、解方程时,一定要先认真观察方程的形式,再选择步骤和方法;
解一元一次方程的
步骤
名称
方法
依据
注意事项
1
去分母
在方程两边同时乘以所有分母的最小公倍数(即把每个含分母的部分和不含分母的部分都乘以所有分母的最小公倍数)
等式性质2
1、不含分母的项也要乘以最小公倍数;2、分子是多项式的一定要先用括号括起来。
2
去括号
去括号法则(可先分配再去括号)
乘法分配律
注意正确的去掉括号前带负数的括号
七年级(上)数学 4.2 解一元一次方程(3)学案

七年级(上)数学 4.2 解一元一次方程(3)学案学习目标:1、掌握含有括号的一元一次方程的解法。
2、初步了解解一元一次方程一般步骤。
3、进一步体会“转化”的思想方法。
学习过程:一、情境创设校团委要举办知识竞赛,共30道题。
规则规定:答对一题得5分,答错一题扣2分,不答不得分。
初一(8)班代表队回答了所有问题共得122分。
问该班代表队答对了几道题?解:设该班代表队答对了x道题则由题意可得方程____________________二、探索活动问题:1、如何去掉方程中的括号?依据是什么?2、上面列的方程你会解吗?三、例题教学例1、解方程:-3(x+1)=9思考:你还有其他方法去掉方程中的括号吗?例2、解方程2(2x+1)=1―5(x―2)拓展:解方程3x-2(3x+1)+7x=6x―4(4―3x)例3、当x取何值时,代数式3(2-x)和2(3+x)的值相等?四、巩固练习1、解下列方程:⑴5(x+1)=3(3x+1) ⑵2(x―2)=3(4x―1)+92、某班在绿化校园的活动中共植树130棵,有5位学生每人种了2棵,其余学生每人种了3棵,这个班共有多少名学生?五、小结思考:解含有括号的一元一次方程的一般步骤是什么?六、当堂检测:1、解下列方程:⑴2(x+1)=6 ⑵4(x-1)=1-x⑶3-(1+2x)=2x ⑷3(2x―1)―2(1―x)=92、y为何值时,2(3y+4)的值比5(2y-7)的值大3?3、若y=1是方程3―2(m―2y)=5y的解,求方程m(x+2)=1―2(x―m)的解。
选做:解方程3{2x―1―[3(2x―1)+3]}=5。
鲁教版(五四制)六年级数学上册:4.2 解一元一次方程 教案

解一元一次方程【课时安排】3课时【第一课时】【教学目标】1.要求学生学会使用移项的方法解一元一次方程;2.要求学生理解移项的含义及注意事项;3.培养学生由算术解法过渡到代数解法的解方程的基本能力,渗透化未知为已知的重要数学思想。
【教学重难点】1.重点是正确掌握移项的方法求方程的解。
2.难点是采用移项方法解一元一次方程的步骤。
【教学过程】(一)复习旧知利用等式性质解下列方程(两名学生上台板演,其余学生在座位上做)。
(1)3x=2x+7(2)5x-2=8解完后,请学生观察:3x-2x=2x+7-2x;5x-2+2=8+2;3x-2x=7。
5x=8+2。
思考:上述演变过程中,你发现了什么?(分组讨论)若学生思考一阵后,还不会作答,可作如下提示:从原方程3x=2x+7演变为3x-2x=7,等号两边的项是否发生变化?若有变化,是如何变化的?方程(2)也有类似的结论吗?请将你发现的结论说出来与大家交流。
(二)感受新知。
1.根据学生回答,老师指出:像这样把方程中的项改变符号后从方程的一边移到另一边的变形过程,被称之为“移项”,板书如下:能对具体情境中的等量关系做出合理的推断,并能用方程来刻画其中的相互关系。
【教学过程】(一)情境引入,初步理解。
(可用幻灯机打出字幕)小明家来客人了,爸爸给了小明20元钱,让他买1听果奶和4听可乐,从商店回来后,小明交给爸爸3元钱。
如果我们知道1听可乐比1听果奶多0.5元,能不能求出1听果奶是多少钱呢?1.小组讨论:(1)小明买东西共用去多少元?(20元-3元=17元)(2)如何用未知数x表示1听果奶或者1听可乐的价钱?(若设1听果奶为x元时,则1听可乐为(x+0.5)元;若设1听可乐为x元时,则1听果奶为(x-0.5)元。
)(3)这个问题中有怎样的等量关系?(如,买可乐的钱+买果奶的钱=用去的钱。
也可列成其他形式,只要合理即可。
)2.小组汇报,教师板书。
注意:(1)小组讨论时,教师应给学生充分思考、交流的时间。
2022-2023学年苏科版七年级数学上册《4-2解一元一次方程》解方程能力达标测评(附答案)

2022-2023学年苏科版七年级数学上册《4.2解一元一次方程》解方程能力达标测评(附答案)(共20小题,每小题6分,满分120分)1.解方程:2x﹣3=4x+5.2.解方程:(1)4x﹣1=3;(2)5x﹣200=2x+100.3.解方程:x+3=﹣x﹣2.4.化简:(1)4x+2=10;(2)5+=.5.解方程:+=5.6.求未知数x:(1)3x+20=65;(2)x=2.75.7.解方程:(1)9x﹣7=2(3x+4);(2)=.8.解方程:.9.解下列方程:(1)2(3x﹣2)=14;(2)x﹣.10.解方程:=﹣3.11.解方程:;.12.解下列方程:(1)5(x+2)﹣3(2x﹣1)=7;(2)﹣=1.13.解下列方程:(1)4﹣(x+3)=2(x﹣1);(2).14.解方程:﹣=﹣1.15.(1)3x+7=32﹣2x;(2).16.解下列方程(1)10x+7=14x﹣5;(2).17.解方程.(1)3x﹣2=4(2)=1+18.解下列方程:(1)3x﹣1=2x+1;(2).19.解方程(1)3x﹣2=5x﹣4;(2)8y﹣3(3y+2)=6;(3);(4).20.解方程:(1)4x﹣3=7﹣x;(2)=1.(3).参考答案1.解:移项,得2x﹣4x=5+3,合并同类项,得﹣2x=8,系数化成1,得x=﹣4.2.解:(1)4x﹣1=3,4x=1+3,4x=4,x=1;(2)5x﹣200=2x+100,5x﹣2x=200+100,3x=300,x=100.3.解:3x+18=﹣2x﹣12,3x+2x=﹣12﹣18,5x=﹣30,x=﹣6.4.解:(1)4x+2=10,移项,得4x=10﹣2,合并同类项,得4x=8,系数化成1,得x=2;(2)5+=,去分母,得30+2x=3(5﹣x),去括号,得30+2x=15﹣3x,移项,得2x+3x=15﹣30,合并同类项,得5x=﹣15,系数化成1,得x=﹣3.5.解:去分母,得12m﹣2(5m﹣1)+3(7﹣m)=30,去括号,得12m﹣10m+2+21﹣3m=30,移项,得12m﹣10m﹣3m=30﹣2﹣21,合并同类项,得﹣m=7,系数化为1,得m=﹣7.6.解:(1)移项得:3x=65﹣20,合并得:3x=45,解得:x=15;(2)去分母得:6x﹣x=22,合并得:5x=22,解得:x=.7.解:(1)9x﹣7=2(3x+4),9x﹣7=6x+8,9x﹣6x=8+7,3x=15,x=5;(2)=,3(3x﹣1)=2(5x﹣7),9x﹣3=10x﹣14,9x﹣10x=﹣14+3,﹣x=﹣11,x=11.8.解:去分母,得3x﹣(x﹣1)=2﹣6x,去括号,得3x﹣x+1=2﹣6x,移项、合并同类项,得8x=1,方程两边同除以8,得x=.9.解:(1)2(3x﹣2)=14,6x﹣4=14,6x=14+4,6x=18,x=3;(2)x﹣,15x﹣5(x﹣1)=105﹣3(x+3),15x﹣5x+5=105﹣3x﹣9,15x﹣5x+3x=105﹣9﹣5,13x=91,x=7.10.解:去分母得:2(1﹣2x)=3(x﹣1)﹣18,去括号得:2﹣4x=3x﹣3﹣18,移项得:﹣4x﹣3x=﹣3﹣18﹣2,合并得:﹣7x=﹣23,系数化为1得:x=.11.解:(1)去括号得:2﹣3x=﹣x,移项得:3x﹣x=2﹣,合并得:2x=,解得:x=;(2)去分母得:3(x+2)﹣12=2(3﹣2x),去括号得:3x+6﹣12=6﹣4x,移项得:3x+4x=12,合并得:7x=12,解得:x=.12.解:(1)5(x+2)﹣3(2x﹣1)=7,5x+10﹣6x+3=7,5x﹣6x=7﹣10﹣3,﹣x=﹣6,x=6;(2)﹣=1,3(x+1)﹣2(2﹣3x)=6,3x+3﹣4+6x=6,3x+6x=6﹣3+4,9x=7,x=.13.解:(1)4﹣(x+3)=2(x﹣1),4﹣x﹣3=2x﹣2,﹣x﹣2x=﹣2﹣4+3,﹣3x=﹣3,x=1;(2),21﹣7(2x+5)=3(4﹣3x),21﹣14x﹣35=12﹣9x,﹣14x+9x=12﹣21+35,﹣5x=26,x=﹣.14.解:﹣=﹣1,3(3x+1)﹣(2x﹣5)=﹣6,9x+3﹣2x+5=﹣6,9x﹣2x=﹣6﹣3﹣5,7x=﹣14,x=﹣2.15.解:(1)移项得,3x+2x=32﹣7,合并同类项得,5x=25,两边都除以5得,x=5;(2)两边都乘以6得,2(2x+1)﹣(10x﹣1)=6,去括号得,4x+2﹣10x+1=6,移项得,4x﹣10x=6﹣2﹣1,合并同类项得,﹣6x=3,两边都除以﹣6得,x=﹣0.5.16.解:(1)移项得:10x﹣14x=﹣5﹣7,合并得:﹣4x=﹣12,系数化为1得:x=3;(2)去分母得:4(2x﹣1)﹣2(10x﹣1)=3(2x+1)﹣12,去括号得:8x﹣4﹣20x+2=6x+3﹣12,移项得:8x﹣20x﹣6x=3﹣12+4﹣2,合并得:﹣18x=﹣7,系数化为1得:x=.17.解:(1)移项,可得:3x=4+2,合并同类项,可得:3x=6,系数化为1,可得:x=2.(2)去分母,可得:4(2x﹣1)=24+3(4x﹣1),去括号,可得:8x﹣4=24+12x﹣3,移项,可得:8x﹣12x=24﹣3+4,合并同类项,可得:﹣4x=25,系数化为1,可得:x=﹣.18.解:(1)移项,可得:3x﹣2x=1+1,合并同类项,可得:x=2.(2)去分母,可得:2(2x﹣1)﹣(x﹣2)=6,去括号,可得:4x﹣2﹣x+2=6,移项,可得:4x﹣x=6+2﹣2,合并同类项,可得:3x=6,系数化为1,可得:x=2.19.解:(1)3x﹣2=5x﹣4,移项,得3x﹣5x=2﹣4,合并同类项,得﹣2x=﹣2,系数化为1,得x=1;(2)8y﹣3(3y+2)=6,去括号,得8y﹣9y﹣6=6,移项,得8y﹣9y=6+6,合并同类项,得﹣y=12,系数化为1,得y=﹣12;(3),去分母,得2(x+1)﹣4=8+(2﹣x),去括号,得2x+2﹣4=8+2﹣x,移项,得2x+x=8+4+2﹣2,合并同类项,得3x=12,系数化为1,得x=4;(4),去分母,得2(2x+1)﹣(10x+1)=6,去括号,得4x+2﹣10x﹣1=6,移项,得4x﹣10x=6+1﹣2,合并同类项,得﹣6x=5,系数化为1,得x=﹣.20.解:(1)4x﹣3=7﹣x,4x+x=7+3,5x=10,x=2.(2)=1,2(2x+1)﹣(10x+1)=6,4x+2﹣10x﹣1=6,﹣6x+1=6,﹣6x=5,x=.(3),﹣=,3(6x+5)﹣(3x+20)=2(x﹣9),18x+15﹣3x﹣20=2x﹣18,15x﹣5=2x﹣18,15x﹣2x=5﹣18,13x=﹣13,x=﹣1.。
练习53 4.2 解一元一次方程(3)

学校班级姓名考号________________考试时间 ______________装订线内不要答题 ◆◆◆◆◆◆◆◆◆◆◆◆◆装◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆订◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆线◆◆◆◆◆◆◆◆ 2014-2015学年度七年级数学练习五十三 4.2 解一元一次方程(3) 本试卷共印6个班:初一9、10、11、12、14、15, 命题人:朱学范 时间:2014-11-19 一、选择题. 1.在解方程:632213=+--)()(x x 时,去括号正确的是( ) (A )63413=+--x x (B )66433=---x x (C )63413=--+x x (D )66413=-+-x x 2.解方程6(1-31x -)=1,去括号得( ) A.6226=+-x B.1226=+-x C.1316=--x D.126=--x 3.解方程12131=--x ,去分母正确的是( ) A. 1-(x-1)=1; B. 2-3(x-1)=6 C. 2-3(x-1)=1; D. 3-2(x-1)=6 4.方程2-342-x =-67-x 去分母得( ) A.2-2 (2x -4)= -(x -7) B .12-2 (2x -4)= -x -7 C .12-2 (2x -4)= -(x -7) D .12-(2x -4)= -(x -7) 5.下列方程中解是x=0的方程为( ) A. 0.3x-4=5.7x+1 B. 1-{3x-[(4x+2)-3]}=0 C. 0314213=--+x x D. x x 211011-=+ 6.若关于x 的方程)23()12(3+-=++a x a x 的解是0,则a 的值是( ) A.51 B. 53 C. 51- D. 53- 7.当x=2时,代数式ax-2的值是4,那么当x=-2时,代数式的值是( )A. –4B. –8C. 8D. 2 二、填空题. 8.42-m -3m =1去分母得______________________. 9.当m=________时,代数式354-m 的值是5.10.方程432-=+x m x 与方程6)16(21-=-x 的解相同,则m 的值为______. 11.已知4-=x ,4=y ,且0322=-px y ,则=p _________.三、解答题.12.解下列方程:(1)6)13(21=--x (2) 3)20(34=--x x(3) )()(1161232+-=-+x x x (4) )11(76)20(34y y y y --=--(5)09)3()52(3)13(=++----x x x (6) 32)]4(212[+=--+x x x(7)612141+=--x x (8)710x -32017x -=1(9) 1122(1)(1)223x x x x ⎡⎤---=-⎢⎥⎣⎦ (10) )1(21)1(2)1(31)1(3+--=--+x x x x13.若3a 4b n+2与5a m-1b2n+3是同类项,求(m+n)(m-n)的值;14.代数式231y +-2y 的值与1互为相反数,试求y 的值.15.已知代数式416+x 与代数式)21(3-x 的值互为相反数,求x 的值.16.若6=x 是关于x 的方程16)(32-=-ax a x 的解,求代数式122++a a 的值.17.当3=x 时,代数式)4(5a x +的值比)(4a x -的值的2倍多1,求a 的值.18.已知2ax=(a+1)x+6,求当a为何整数时,方程的解是正整数.19. 已知关于x的方程3(x-2)=2x+a的解比x+a=2x-a的解小2,求a的值.20. 已知关于x的方程1x2=-2的解比关于x的方程5x-2a=0的解小2,试解关于y的方程y-15a=0更上一层楼(10分)1.解方程:|x-|3x+2||=4.(6分)2.已知方程111+5x-=420052(),求代数式3+201x-2005()的值.(4分)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4.2 解一元一次方程(3)
感受·理解
1.在解方程:632213=+--)()(x x 时,去括号正确的是( )
(A )63413=+--x x (B )66433=---x x
(C )63413=--+x x (D )66413=-+-x x
2.解方程6(1-
3
1x -)=1,去括号得( ) A.6226=+-x B.1226=+-x C.1316=--x D.126=--x 3.若关于x 的方程)23()12(3+-=++a x a x 的解是0,则a 的值是( ) A.51 B. 53 C. 51- D. 5
3- 4.解下列方程:
(1)6)13(21=--x (2) 3)20(34=--x x
(3) )()(1161232+-=-+x x x (4) )11(76)20(34y y y y --=--
(5)09)3()52(3)13(=++----x x x (6) 32)]4(2
12[+=--+x x x
(7) 1122(1)(1)223x x x x ⎡⎤---=-⎢⎥⎣⎦
(8) )1(21)1(2)1(31)1(3+--=--+x x x x
思考·运用
5.已知代数式416+
x 与代数式)2
1(3-x 的值互为相反数,求x 的值.
6.若6=x 是关于x 的方程16
)(32-=-ax a x 的解,求代数式122++a a 的值.
7.学校食堂4个月共用煤19.1t ,已知后面3个月的平均用煤量比第一个月少0.3t ,求第一个月的用煤量.
8.小明买了4听可乐和一瓶酸奶,已知1听可乐比1瓶酸奶贵0.5元,小明付给营业员20元,找回3 元,求1听酸奶的价格.
探究·拓展
9.当3=x 时,代数式)4(5a x +的值比)(4a x -的值的2倍多1,求a 的值.
10.已知方程)2(3)1(2+=-x x 的解是5=m ,求关于x 的方程[])2(3)1(4)(32-=+--m x m x。
