3.2.2平面的法向量与平面的向量表示
平面向量与平面的关系

平面向量与平面的关系平面向量是向量的一种形式,它的组成部分是一个起点和一个终点,可以用箭头来表示。
平面是二维的,由二维点的集合构成,其上的点可以用二维坐标表示。
本文将探讨平面向量与平面之间的关系及相关的性质。
一、平面向量的定义与性质平面向量可以表示为两个点之间的差向量。
设点A(x1, y1)和点B(x2, y2)是平面上的两个点,其联结的平面向量可以表示为AB = (x2 -x1, y2 - y1)。
平面向量具有以下性质:1. 平面向量的模:平面向量AB的模可以通过勾股定理求得,即|AB| = √[(x2 - x1)^2 + (y2 - y1)^2]。
2. 平面向量的加法:两个平面向量的加法可以通过将它们的对应分量相加得到。
设平面向量A(x1, y1)和平面向量B(x2, y2),它们的和为A +B = (x1 + x2, y1 + y2)。
3. 平面向量的数量积:两个平面向量的数量积定义为它们对应分量的乘积的和。
设平面向量A(x1, y1)和平面向量B(x2, y2),它们的数量积为A · B = x1x2 + y1y2。
4. 平面向量的夹角:设平面向量A和平面向量B不同时为零向量,它们的夹角θ可以由余弦定理求得,即cosθ = (A · B) / (|A| |B|),从而可以计算出夹角的大小。
二、平面向量与平面之间的关系平面向量和平面之间有着密切的关系,我们将讨论以下几个方面:1. 平面上的平行向量:若两个平面向量的方向相同或相反,它们为平行向量。
若平面向量A(a, b)与平面向量B(x, y)平行,则存在实数k,使得a = kx,b = ky。
2. 平面上的法向量:设平面向量A(a, b)与平面向量B(x, y)垂直,则A为平面的法向量。
当且仅当a = -ky,b = kx时,平面向量A与平面向量B垂直。
3. 平面与平面之间的夹角:设平面P1的法向量为A(a1, b1),平面P2的法向量为B(a2, b2),则两个平面之间的夹角θ可以由以下公式计算得到:cosθ = (a1a2 + b1b2) / (|A| |B|)。
高二数学选修课件:3-2-2平面的法向量与平面的向量表示

人 教 B 版 数 学
第三章
空间向量与立体几何
[例 1]
如图, ABCD 是直角梯形, ∠ABC=90° SA⊥ ,
人 教 B 版 数 学
1 平面 ABCD,SA=AB=BC=1,AD=2,求平面 SCD 与平 面 SAB 的法向量.
第三章
空间向量与立体几何
[分析] 解答本题可先建立空间直角坐标系,写出每
个平面内两个不共线向量的坐标,再利用待定系数法求出 平面的法向量.
人 教 B 版 数 学
[解析]
∵AD、AB、AS 是三条两两垂直的线段,
→ → → ∴以 A 为原点,以AD、AB、AS的方向为 x 轴,y 轴, 1 z 轴的正方向建立坐标系, A(0,0,0), 2, 则 D( 0,0), C(1,1,0), → =(1,0,0),是平面 SAB 的法向量, S(0,0,1),AD 2 设平面 SCD 的法向量 n=(1,λ,μ),
第三章
空间向量与立体几何
人 教 B 版 数 学
第三章
空间向量与立体几何
人 教 B 版 数 学
第三章
空间向量与立体几何
1.知识与技能
掌握平面的法向量的概念及性质. 理解平面的向量表示. 2.过程与方法 用向量的观点认识平面、利用平面的法向量证明平行人ຫໍສະໝຸດ 教 B 版 数 学或垂直问题.
3.情感态度与价值观 培养学生转化的数学思想,增强应用意识.
第三章
空间向量与立体几何
人 教 B 版 数 学
第三章
空间向量与立体几何
重点:平面法向量的概念及性质. 难点:利用法向量法解决几何问题.
人 教 B 版 数 学
第三章
空间向量与立体几何
人 教 B 版 数 学
3.2.2平面的法向量与平面的向量表示
A' A'
B
二、概念形成
概念5.用法向量证明“三垂线定理”
三垂线定理: 如果在平面内的一条直线与平面的一条斜线在这个平面内 的射影垂直,则它也和这条斜线垂直。
的斜线, A' B 是 l 在平面 直线 a 且 a A ' B l 求证: a l A
已知 l 是平面
已知 l 是平面 直线
向量。那么 n DA y 0 n DB1 ,0),B 1(1,0,1)
z A1 B1 A B x
y 0 x z 0
A B C
D
令z=1,得 n (1,0,1)
n a 0, n b 0 n m 0 即 nm 所以 n m
因为 n 垂直于平面 内任意一条直 线,所以 n
因为 a , b ,由共面向量定理可知,存在唯一的数对(x,y),使
n
n
b
b
a
m a b m
设平面AMN的一个法向量为 n1 ( x1 , y1 , z1 ) A
D B
C
x
向量解法
A
利用法向量证明两个平面平行的基本思路是证明两个平面
的法向量平行(或共线)。
三、应用举例
例2.已知正方体ABCD-A1B1C1D1,求证: (1)AD1//平面BDC1 ; (2)AC1⊥平面BDC1 。
→ =OM → +OA → =(9,1,1).故选 B. ∴OB
2→ → 2.已知 A(3,-2,4),B(0,5,-1),若OC=3AB,则 C 的坐标是 14 10 A.(2,- 3 , 3 ) 14 10 C.(2,- ,- ) 3 3 ( )
(人教课标版)普通高中课程标准实验教科书《数学》目录(B版)

(人教课标版)普通高中课程标准实验教科书《数学》目录(B版)(人教课标版)普通高中课程标准实验教科书《数学》目录(B版)必修一第一章集合1.1集合与集合的表示方法1.1.1集合的概念1.1.2集合的表示方法1.2集合之间的关系与运算1.2.1集合之间的关系1.2.2集合的运算本章小结阅读与欣赏聪明在于学习,天才由于积累第二章函数2.1函数2.1.1函数2.1.2函数的表示方法2.1.3函数的单调性2.1.4函数的奇偶性2.1.5用计算机作函数的图象(选学)2.2一次函数和二次函数2.2.1一次函数的性质与图象2.2.3待定系数法2.3函数的应用(Ⅰ)2.4函数与方程2.4.1函数的零点2.4.2求函数零点近似解的一种计算方法——二分法本章小结阅读与欣赏函数概念的形成与发展第三章基本初等函数(Ⅰ)3.1指数与指数函数3.1.1实数指数幂及其运算3.1.2指数函数3.2对数与对数函数3.2.1对数及其运算3.2.2对数函数3.2.3指数函数与对数函数的关系3.3幂函数3.4函数的应用(Ⅱ)本章小结阅读与欣赏对数的发明必修二第一章立体几何初步1.1空间几何体1.1.1构成空间几何体的基本元素1.1.2棱柱、棱锥和棱台的结构特征1.1.3圆柱、圆锥、圆台和球1.1.4投影与直观图1.1.5三视图1.1.6棱柱、棱锥、棱台和球的表面积1.1.7柱、锥、台和球的体积实习作业1.2点、线、面之间的位置关系1.2.1平面的基本性质与推论1.2.2空间中的平行关系1.2.3空间中的垂直关系本章小结阅读与欣赏散发着数学芳香的碑文第二章平面解析几何初步2.1平面直角坐标系中的基本公式2.1.1数轴上的基本公式2.1.2平面直角坐标系中的基本公式2.2直线的方程2.2.1直线方程的概念与直线的斜率2.2.2直线方程的几种形式2.2.3两条直线的位置关系2.2.4点到直线的距离2.3圆的方程2.3.1圆的标准方程2.3.2圆的一般方程2.3.3直线与圆的位置关系2.3.4圆与圆的位置关系2.4空间直角坐标系2.4.1空间直角坐标系2.4.2空间两点的距离公式本章小结阅读与欣赏笛卡儿必修三第一章算法初步1.1算法与程序框图1.1.1算法的概念1.1.2程序框图1.1.3算法的三种基本逻辑结构和框图表示1.2基本算法语句1.2.1赋值、输入和输出语句1.2.2条件语句1.2.3循环语句1.3中国古代数学中的算法案例本章小结阅读与欣赏我国古代数学家秦九韶附录1解三元一次方程组的算法、框图和程序附录2Scilab部分函数指令表第二章统计2.1随机抽样2.1.2系统抽样2.1.4数据的收集2.2用样本估计总体2.2.1用样本的频率分布估计总体的分布2.2.2用样本的数字特征估计总体的数字特征2.3变量的相关性2.3.1变量间的相关关系2.3.2两个变量的线性相关本章小结阅读与欣赏蚂蚁和大象谁的力气更大附录随机数表第三章概率3.1事件与概率3.1.1随机现象3.1.2事件与基本事件空间3.1.3频率与概率3.1.4概率的加法公式3.2古典概型3.2.1古典概型3.2.2概率的一般加法公式(选学)3.3随机数的含义与应用3.3.1几何概型3.3.2随机数的含义与应用3.4概率的应用本章小结阅读与欣赏概率论的起源必修四第一章基本初等函数(Ⅱ)1.1任意角的概念与弧度制1.1.1角的概念的推广1.1.2弧度制和弧度制与角度制的换算1.2任意角的三角函数1.2.1三角函数的定义1.2.2单位圆与三角函数线1.2.3同角三角函数的基本关系式1.2.4诱导公式1.3三角函数的图象与性质1.3.1正弦函数的图象与性质1.3.2余弦函数、正切函数的图象与性质1.3.3已知三角函数值求角教学建模活动本章小结阅读与欣赏三角学的发展第二章平面向量2.1向量的线性运算2.1.1向量的概念2.1.2向量的加法2.1.3向量的减法2.1.4数乘向量2.1.5向量共线的条件与轴上向量坐标运算2.2向量的分解与向量的坐标运算2.2.1平面向量基本定理2.2.2向量的正交分解与向量的直角坐标运算2.2.3用平面向量坐标表示向量共线条件2.3平面向量的数量积2.3.1向量数量积的物理背景与定义2.3.2向量数量积的运算律2.3.3向量数量积的坐标运算与度量公式2.4向量的应用2.4.1向量在几何中的应用2.4.2向量在物理中的应用本章小结阅读与欣赏向量概念的推广与应用第三章三角恒等变换3.1和角公式3.1.1两角和与差的余弦3.1.2两角和与差的正弦3.1.3两角和与差的正切3.2倍角公式和半角公式3.2.1倍角公式3.2.2半角的正弦、余弦和正切3.3三角函数的积化和差与和差化积本章小结阅读与欣赏和角公式与旋转对称必修五第一章解三角形1.1正弦定理和余弦定理1.1.1正弦定理1.1.2余弦定理1.2应用举例本章小结阅读与欣赏亚历山大时期的三角测量第二章数列2.1数列2.1.1数列2.1.2数列的递推公式(选学)2.2等差数列2.2.1等差数列2.2.2等差数列的前n项和2.3等比数列2.3.1等比数列2.3.2等比数列的前n项和本章小结阅读与欣赏级数趣题无穷与悖论第三章不等式3.1不等关系与不等式3.1.1不等关系与不等式3.1.2不等式的性质3.2均值不等式3.3一元二次不等式及其解法3.4不等式的实际应用3.5二元一次不等式(组)与简单的线性规划问题3.5.1二元一次不等式(组)所表示的平面区域3.5.2简单线性规划本章小结选修1-1第一章常用逻辑用语1.1命题与量词1.1.1命题1.1.2量词1.2基本逻辑联结词1.2.1“且”与“或”1.2.2“非”(否定)1.3充分条件、必要条件与命题的四种形式1.3.1推出与充分条件、必要条件1.3.2命题的四种形式本章小结阅读与欣赏什么是数理逻辑第二章圆锥曲线与方程2.1椭圆2.1.1椭圆及其标准方程2.1.2椭圆的几何性质2.2双曲线2.2.1双曲线及其标准方程2.2.2双曲线的几何性质2.3抛物线2.3.1抛物线级其标准方程2.3.2抛物线的几何性质本章小结阅读与欣赏圆锥面与圆锥曲线第三章导数及其应用3.1导数3.1.1函数的平均变化率3.1.2瞬时速度与导数3.1.3导数的几何意义3.2导数的运算3.2.1常数与幂函数的导数3.2.2导数公式表3.2.3导数的四则运算法则3.3导数的应用3.3.1利用导数判断函数的单调性3.3.2利用导数研究函数的极值3.3.3导数的实际应用本章小结阅读与欣赏微积分与极限思想选修1-2第一章统计案例1.1独立性检验1.2回归分析本章小结“回归”一词的由来附表相关性检验的临界值表第二章推理与证明2.1合情推理与演绎推理2.1.1合情推理2.1.2演绎推理2.2直接证明与间接证明2.2.1综合法与分析法2.2.2反证法本章小结阅读与欣赏《原本》与公理化思想数学证明的机械化——机器证明第三章数系的扩充与复数的引入3.1数系的扩充与复数的引入3.1.1实数系3.1.2复数的引入3.2复数的运算3.2.1复数的加法和减法3.2.2复数的乘法和除法本章小结复平面与高斯第四章框图4.1流程图4.2结构图本章小结阅读与欣赏冯·诺伊曼选修2-1第一章常用逻辑用语1.1命题与量词1.1.1命题1.1.2量词1.2基本逻辑联结词1.2.1“且”与“或”1.2.2“非”(否定)1.3充分条件、必要条件与命题的四种形式1.3.1推出与充分条件、必要条件本章小结阅读与欣赏什么是数理逻辑第二章圆锥曲线与方程2.1曲线与方程2.1.1曲线与方程的概念2.1.2由曲线求它的方程、由方程研究曲线的性质2.2椭圆2.2.1椭圆的标准方程2.2.2椭圆的几何性质2.3双曲线2.3.1双曲线的标准方程2.3.2双曲线的几何性质2.4抛物线2.4.1抛物线的标准方程2.4.2抛物线的几何性质2.5直线与圆锥曲线本章小结阅读与欣赏圆锥面与圆锥曲线第三章空间向量与立体几何3.1空间向量及其运算3.1.1空间向量的线性运算3.1.2空间向量的基本定理3.1.3两个向量的数量积3.1.4空间向量的直角坐标运算3.2空间向量在立体几何中的应用3.2.1直线的方向向量与直线的向量方程3.2.2平面的法向量与平面的向量表示3.2.3直线与平面的夹角3.2.4二面角及其度量3.2.5距离(选学)本章小结阅读与欣赏向量的叉积及其性质选修2-2第一章导数及其应用1.1导数1.1.1函数的平均变化率1.1.2瞬时速度与导数1.1.3导数的几何意义1.2导数的运算1.2.1常数函数与冥函数的导数1.2.2导数公式表及数学软件的应用1.2.3导数的四则运算法则1.3导数的应用1.3.1利用导数判断函数的单调性1.3.2利用导数研究函数的极值1.3.3导数的实际应用1.4定积分与微积分基本定理1.4.1曲边梯形面积与定积分1.4.2微积分基本定理本章小结阅读与欣赏微积分与极限思想第二章推理与证明2.1合情推理与演绎推理2.1.1合情推理2.1.2演绎推理2.2直接证明与间接证明2.2.1综合法与分析法2.2.2反证法2.3数学归纳法2.3.1数学归纳法2.3.2数学归纳法应用举例本意小结阅读与欣赏《原本》与公理化思想第三章数系的扩充与复数3.1数系的扩充与复数的概念3.1.1实数系3.1.2复数的概念3.1.3复数的几何意义3.2复数的运算3.2.1复数的加法与减法3.2.2复数的乘法3.2.3复数的除法本章小节阅读与欣赏复平面与高斯选修2-3第一章计数原理1.1基本计数原理1.2排列与组合1.2.1排列1.2.2组合1.3二项式定理1.3二项式定理1.3.2杨辉三角本章小结第二章概率2.1离散型随机变量及其分布列2.1.1离散型随机变量2.1.2离散型随机变量的分布列2.1.3超几何分布2.2条件概率与事件的独立性2.2.1条件概率2.2.2事件的独立性2.2.3独立重复试验与二项分布2.3随机变量的数字特征2.3.1离散型随机变量的数学期望2.3.2离散型随机变量的方差2.4正态分布本章小结阅读与欣赏关于“玛丽莲问题”的争论第三章统计案例3.1独立性检验3.2回归分析本章小结阅读与欣赏“回归”一词的由来附表选修3-1第一讲早期的算术与几何一古埃及的数学二两河流域的数学三丰富多彩的记数制度第二讲古希腊数学一希腊数学的先行者二毕达哥拉斯学派三欧几里得与《原本》四数学之神──阿基米德第三讲中国古代数学瑰宝一《周髀算经》与赵爽弦图二《九章算术》三大衍求一术四中国古代数学家第四讲平面解析几何的产生一坐标思想的早期萌芽二笛卡儿坐标系三费马的解析几何思想四解析几何的进一步发展第五讲微积分的诞生一微积分产生的历史背景二科学巨人牛顿的工作三莱布尼茨的“微积分”第六讲近代数学两巨星一分析的化身──欧拉二数学王子──高斯第七讲千古谜题一三次、四次方程求根公式的发现二高次方程可解性问题的解决三伽罗瓦与群论四古希腊三大几何问题的解决第八讲对无穷的深入思考一古代的无穷观念二无穷集合论的创立三集合论的进一步发展与完善第九讲中国现代数学的开拓与发展一中国现代数学发展概观二人民的数学家──华罗庚三当代几何大师──陈省身选修3-2暂缺选修3-3第一讲从欧氏几何看球面一平面与球面的位置关系二直线与球面的位置关系和球幂定理三球面的对称性第二讲球面上的距离和角一球面上的距离二球面上的角第三讲球面上的基本图形一极与赤道二球面二角形三球面三角形1.球面三角形2.三面角3.对顶三角形4.球极三角形第四讲球面三角形一球面三角形三边之间的关系二、球面“等腰”三角形三球面三角形的周长四球面三角形的内角和第五讲球面三角形的全等1.“边边边”(s.s.s)判定定理2.“边角边”(s.a.s.)判定定理3.“角边角”(a.s.a.)判定定理4.“角角角”(a.a.a.)判定定理第六讲球面多边形与欧拉公式一球面多边形及其内角和公式二简单多面体的欧拉公式三用球面多边形的内角和公式证明欧拉公式第七讲球面三角形的边角关系一球面上的正弦定理和余弦定理二用向量方法证明球面上的余弦定理1.向量的向量积2.球面上余弦定理的向量证明三从球面上的正弦定理看球面与平面四球面上余弦定理的应用──求地球上两城市间的距离第八讲欧氏几何与非欧几何一平面几何与球面几何的比较二欧氏平行公理与非欧几何模型──庞加莱模型三欧氏几何与非欧几何的意义阅读与思考非欧几何简史选修3-4第一讲平面图形的对称群一平面刚体运动1.平面刚体运动的定义2.平面刚体运动的性质二对称变换1.对称变换的定义2.正多边形的对称变换3.对称变换的合成4.对称变换的性质5.对称变换的逆变换三平面图形的对称群第二讲代数学中的对称与抽象群的概念一n元对称群Sn二多项式的对称变换三抽象群的概念1.群的一般概念2.直积第三讲对称与群的故事一带饰和面饰二化学分子的对称群三晶体的分类四伽罗瓦理论选修4-1第一讲相似三角形的判定及有关性质一平行线等分线段定理二平行线分线段成比例定理三相似三角形的判定及性质1.相似三角形的判定2.相似三角形的性质四直角三角形的射影定理第二讲直线与圆的位置关系一圆周角定理二圆内接四边形的性质与判定定理三圆的切线的性质及判定定理四弦切角的性质五与圆有关的比例线段第三讲圆锥曲线性质的探讨一平行摄影二平面与圆柱面的截线三平面与圆锥面的截线选修4-2引言第一讲线性变换与二阶矩阵一线性变换与二阶矩阵(一)几类特殊线性变换及其二阶矩阵1.旋转变换2.反射变换3.伸缩变换4.投影变换5.切变变换(二)变换、矩阵的相等二二阶矩阵与平面向量的乘法(二)一些重要线性变换对单位正方形区域的作用第二讲变换的复合与二阶矩阵的乘法一复合变换与二阶矩阵的乘法二矩阵乘法的性质第三讲逆变换与逆矩阵一逆变换与逆矩阵1.逆变换与逆矩阵2.逆矩阵的性质二二阶行列式与逆矩阵三逆矩阵与二元一次方程组1.二元一次方程组的矩阵形式2.逆矩阵与二元一次方程组第四讲变换的不变量与矩阵的特征向量一变换的不变量——矩阵的特征向量1.特征值与特征向量2.特征值与特征向量的计算二特征向量的应用1.Aa的简单表示2.特征向量在实际问题中的应用选修4-5第一章不等式的基本性质和证明的基本方法1.1 不等式的基本性质和一元二次不等式的解法1.2基本不等式1.3绝对值不等式的解法1.4绝对值的三角不等式1.5不等式证明的基本方法本章小结第二章柯西不等式与排序不等式及其应用2.1 柯西不等式2.2排序不等式2.3平均值不等式(选学)2.4最大值与最小值问题,优化的数学模型本章小结阅读与欣赏第三章数学归纳法与贝努利不等式3.1数学归纳法原理3.2用数学归纳法证明不等式,贝努利不等式本章小结阅读与欣赏附录部分中英文词汇对照表后记选修4-6引言第一讲整数的整除一整除1.整除的概念和性质2.带余除法3.素数及其判别法二最大公因数与最小公倍数1.最大公因数2.最小公倍数三算术基本定理第二讲同余与同余方程一同余1.同余的概念2.同余的性质二剩余类及其运算三费马小定理和欧拉定理四一次同余方程五拉格朗日插值法和孙子定理六弃九验算法第三讲一次不定方程一二元一次不定方程二二元一次不定方程的特解三多元一次不定方程第四讲数伦在密码中的应用一信息的加密与去密二大数分解和公开密钥学习总结报告附录一剩余系和欧拉函数附录二多项式的整除性选修4-7引言第一讲优选法一什么叫优选法二单峰函数三黄金分割法——0.618法1.黄金分割常数2.黄金分割法——0.618法阅读与思考黄金分割研究简史四分数法1.分数法阅读与思考斐波那契数列和黄金分割2.分数法的最优性五其他几种常用的优越法1.对分法2.盲人爬山法3.分批试验法4.多峰的情形六多因素方法1.纵横对折法和从好点出发法2.平行线法3.双因素盲人爬山法第二讲试验设计初步一正交试验设计法1.正交表2.正交试验设计3.试验结果的分析4.正交表的特性二正交试验的应用选修4-9引言第一讲风险与决策的基本概念一风险与决策的关系二风险与决策的基本概念1.风险(平均损失)2.平均收益3.损益矩阵4.风险型决策探究与发现风险相差不大时该如何决策第二讲决策树方法第三讲风险型决策的敏感性分析第四讲马尔可夫型决策简介一马尔可夫链简介1.马尔可夫性与马尔可夫链2.转移概率与转移概率矩阵二马尔可夫型决策简介三长期准则下的马尔可夫型决策理论1.马尔可夫链的平稳分布2.平稳分布与马尔可夫型决策的长期准则3.平稳准则的应用案例说明:A版适用于文件生使用,B版适用于理科生使用,B 版比A版略难。
平面的法向量

g = xm + yn , l g = xl m + yl n , l
∵ l m = 0, l n = 0 , ∴ l g = 0, 即l ⊥ g .
g l m
m
n
n g
l ∴ l ⊥ g , 即 l 垂 直 于 平 面 α内 任 一 直 线 . ⊥ α .
6.有关平面的斜线概念, 6.有关平面的斜线概念, 有关平面的斜线概念 三垂线定理及其逆定理 P104
答:a⊥PO
为什么呢? 为什么呢?
三垂线定理
三垂线定理:在平面内的一条直线, 三垂线定理:在平面内的一条直线,如果和这个平面的 一条斜线的射影垂直,那么它也和这条斜线垂直。 一条斜线的射影垂直,那么它也和这条斜线垂直。
PA⊥α a α
P
PA⊥a ② a⊥平面PAO
AO⊥a PO 平面PAO
①
③
a⊥PO
a α A o
数式板书
三垂线定理
对三垂线定理的说明: 对三垂线定理的说明: 1、三垂线定理描述的是PO(斜线)、AO(射 三垂线定理描述的是PO(斜线) AO(射 PO(斜线 影)、a(直线)之间的垂直关系。 a(直线 之间的垂直关系。 直线) 2、a与PO可以相交,也可以异面。 PO可以相交,也可以异面。 可以相交 3、三垂线定理的实质是平面的一条斜线和 平面内的一条直线垂直的判定定理。 平面内的一条直线垂直的判定定理。 4、三垂线定理的图形是由“四线一面”五 三垂线定理的图形是由“四线一面” 个部件组成——垂线 斜线、射影、面内一线、 垂线、 个部件组成——垂线、斜线、射影、面内一线、 平面
高中数学选修2 高中数学选修2-1
3.2.2平面的法向量与 3.2.2平面的法向量与 平面的向量表示
法向量与平面的向量表示
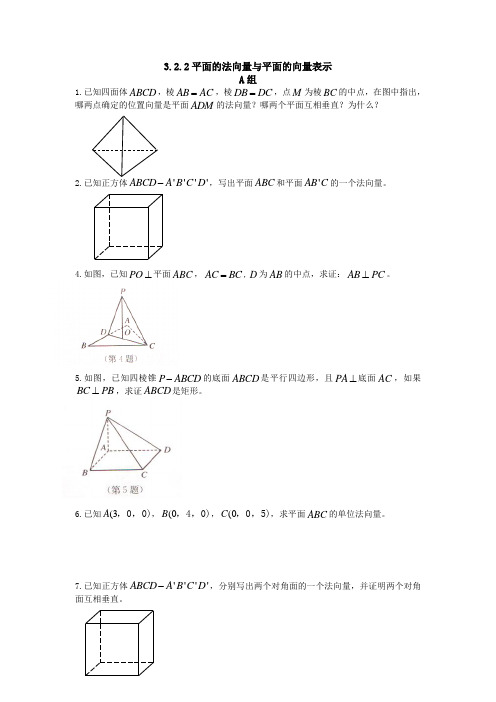
3.2.2平面的法向量与平面的向量表示
A 组
1.已知四面体ABCD ,棱AB AC =,棱DB DC =,点M 为棱BC 的中点,在图中指出,哪两点确定的位置向量是平面ADM 的法向量?哪两个平面互相垂直?为什么?
2.已知正方体''''ABCD A B C D -,写出平面ABC 和平面'AB C 的一个法向量。
4.如图,已知PO ⊥平面ABC ,AC BC =,D 为AB 的中点,求证:AB PC ⊥。
5.如图,已知四棱锥P ABCD -的底面ABCD 是平行四边形,且PA ⊥底面AC ,如果BC PB ⊥,求证ABCD 是矩形。
6.已知(3A ,0,0),(0B ,4,0),(0C ,0,5),求平面ABC 的单位法向量。
7.已知正方体''''ABCD A B C D -,分别写出两个对角面的一个法向量,并证明两个对角面互相垂直。
8.已知四面体ABCD 的棱AB CD ⊥,AC BD ⊥,求证:AD BC ⊥。
B 组
9.直四棱柱1111ABCD A BC D -中,底面ABCD 是矩形,121 3.AB AD AA ===,, M 是BC 的中点.在1DD 上是否存在一点N ,使1MN DC ⊥?。
3.2.2平面的法向量与平面的向量表示

3.2.2 平面的法向量与平面的向量表示峡山中学 高二数学组 2010-12-23【课标点击】(一)学习目标:1、掌握平面的法向量;2、利用平面的法向量判定平面的位置关系;3、平面的向量表示;4、线面垂直的判定定理;5、三垂线定理.(二)教学重、难点:平面的向量表示、线面垂直的判定,面面垂直的判定【课前准备】(一)知识连接:1、 空间直线的向量参数方程:a t OA OP +=或OB t OA t OP +-=)1(2、 设P 为AB 之中点则)(21OB OA OP +=3、 直线1l 与2l 的方向向量为1v 和2v ,则2121////v v l l ⇔,212121v v v v l l ⋅⇔⊥⇔⊥=04、 两直线成的角,与两直线的方向向量成角的关系5、 p 与a ,b 共面(a ,b 不共线)⇔R y x ∈∃,使b y a x p +=6、 点A 、B 、C 不共线,则点A 、B 、C 、P 共面⇔∃x 、y R ∈使AC y AB x AP += (二)问题导引:如何证明线面平行、线面垂直、面面平行、面面垂直?【学习探究】(一)自学引导:自主学习课本102页至103页部分. 1、平面的法向量2、直线与平面垂直的判定定理:如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直于这个平面(用向量方法证明)3、平面的向量表示:4、设1n 、2n分别是平面α、β的法向量,那么:α//β或α与β重合⇔ 21//n n αβ⊥⇔21n n ⊥5、三垂线定理 在平面内的一条直线,如果它和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直已知:,PO PA 分别是平面α的垂线和斜线,O A 是P A 在平面α内的射影,a α⊂,且a O A ⊥求证:a P A ⊥;证明:∵P O α⊥ ∴PO a ⊥,又∵,a OA PO OA O ⊥=∴a ⊥平面P O A ,∴a P A ⊥. 说明:(1)定理的实质是判定平面内的一条直线和平面的一条斜线的垂直关系;(2)推理模式:,,PO O PA A a PA a a O A αααα⊥∈⎫⎪=⇒⊥⎬⎪⊂⊥⎭6条斜线的射影垂直证明思路: ,,PO O PA A a AO a a AP αααα⊥∈⎫⎪=⇒⊥⎬⎪⊂⊥⎭.(二)思考与讨论:⑴三垂线指: (PA ,PO ,AO 都垂直α内的直线a )2)其实质是: ( 斜线和平面内一条直线垂直的判定和性质定理)注意:要考虑a 的位置,并注意两定理交替使用(三)典型例题:例1.在正方体111ABCD A B C D -中,求证:1D B是平面1AC D 的法向量.例2:已知正方体''''ABC D A B C D -.求证:平面''//A B D 平面'B D C .例3.如图,底面A B C D 是正方形,SA ⊥底面A B C D ,且SA AB =,E 是S C 中点. 求证:平面BD E ⊥平面A B C D .说明:一.证明垂直关系,可通过向量的数量积等于0来实现;二.要善于转化,即挖掘已知的垂直关系,将未知向已知转化(四)变式拓展:已知正方体1111ABC D A B C D -中,,E F 分别为1,BB C D 的中点, 求证:1D F ⊥平面A D E 。
3.2.2学案

3.2.2平面的法向量与平面的向量表示班级___姓名:__________时间2012.2.10 一、【教材知识梳理】1.已知平面α,如果向量n 的基线与平面α垂直,则向量n叫做____________________。
2.平面α的一个法向量垂直于与平面α共面的所有向量,同时,一个平面的所有法向量____________。
3.如果一条直线和平面内的两条___________直线垂直,那么这条直线_______于这个平面。
4.设12n n 、分别是平面αβ、的法向量,则容易得到:α∥β或(αβ、重合)⇔_________,12n n αβ⊥⇔⊥⇔_______________。
5.已知平面α和一点A ,过点A 作α的垂线l 与α相交于点'A ,则'A 就是点A 在平面α内的________,简称_________________。
6.如果一条直线AB 和平面α相交于点B ,但不和α垂直,那么直线AB 叫做这个平面的____________,斜线和平面的交点B 叫做____________,斜线上一点A 与斜足B 之间的线段叫做_____________。
7.如果在平面内的一条直线与平面的一条斜线在这个平面的____________重直,则它也和这条_________垂直。
8.如果________________的一条直线和这个平面的一条斜线垂直,则它也和这条斜线在平面内的______垂直。
二、【课前检测】1.若平面αβ、的法向量分别为1n =(1,2,-2),2n =(-3,-6,6),则( ) A.α∥β B.αβ⊥ C.αβ,相交但不垂直 D.以上说法都不对2.已知==AB AC(2,2,1),(4,5,3),则平面ABC 的一个单位法向量为( )A.122333(-,-,-) B.122333(-,,-) C.122333(-,,) D. 122333(,,)3.设平面α的法向量为(1,2,-2),平面β的法向量为k (-2,-4,),若α∥β,则k =__________;若αβ⊥,则k =________________。
课件1:3.2.2平面的法向量与平面的向量表示

令 z1=1,得 x1=a-1, ∴n1=(a-1,0,1). 设平面 C1DE 的一个法向量为 n2=(x2,y2,z2),
三垂线定理及其逆定理
求平面的法向量
如图 3-2-10,ABCD 是直角梯形,∠ABC=90°, SA⊥平面 ABCD,SA=AB=BC=1,AD=12,求平面 SCD 的法 向量.
【思路探究】 先确定平面 SCD 内的两个不共线向量,比 如D→C,S→C,再设出平面的法向量为 n=(x,y,z),构造方程组 求解.
∵P→D=0,2 3 3,-1,显然P→D=
3 3 n.
∴P→D∥n,∴P→D⊥平面 ABE,
即 PD⊥平面 ABE.
利用空间向量解决探索性问题 (12 分)在正方体 ABCD-A1B1C1D1 中,E 是棱 BC 的中点,试在棱 CC1 上求一点 P,使得平面 A1B1P⊥平面 C1DE.
图 3-2-13
D→A=(2,0,0),A→E=(0,2,1).
(1)设 n1=(x1,y1,z1)是平面 ADE 的法向量,
则 n1⊥D→A,n1⊥A→E,
即 n1·D→A=2x1=0, n1·A→E=2y1+z1=0,
得xz11==-0,2y1,
令 z1=2,则 y1=-1, 所以 n1=(0,-1,2).
因为F→C1·n1=-2+2=0,所以F→C1⊥n1. 又因为 FC1⊄平面 ADE,所以 FC1∥平面 ADE.
的中点,N 为 BC 的中点.
证明:直线 MN∥平面 OCD. 【思路探究】 只需建系证明M→N·n
高中数学平面的法向量与平面的向量表示知识点解析

第三章 §3.2 直线的方向向量与直线的向量方程
3.2.2 平面的法向量与平面的向量表示
学习目标
XUEXIMUBIAO
1.理解平面的法向量的概念,会求平面的法向量. 2.会用平面的法向量证明平面与平面平行、垂直. 3.了解三垂线定理及其逆定理.
内容索引
NEIRONGSUOYIN
自主学习 题型探究 达标检测
12345
课堂小结
KETANGXIAOJIE
1.用法向量来解决平面与平面的关系问题,思路清楚,不必考虑图形的位置 关系,只需通过向量运算,就可得到要证明的结果. 2.利用三垂线定理证明线线垂直,需先找到平面的一条垂线,有了垂线,才 能作出斜线的射影,同时要注意定理中的“平面内的一条直线”这一条件, 忽视这一条件,就会产生错误结果.
置;若不存在,请说明理由.
题型三 利用空间向量证明垂直问题
例3 三棱锥被平行于底面ABC的平面所截得的几何体如图所示,截面为 A1B1C1,∠BAC=90°,A1A⊥平面ABC,A1A= 3,AB=AC=2A1C1=2,D为 BC的中点.证明:平面A1AD⊥平面BCC1B1.
反思感悟 利用空间向量证明面面垂直通常可以有两个途径,一是利用两 个平面垂直的判定定理将面面垂直问题转化为线面垂直进而转化为线线垂 直;二是直接求解两个平面的法向量,证明两个法向量垂直,从而得到两 个平面垂直.
1 自主学习
PART ONE
知识点一 平面的法向量 已知平面α,如果 向量n的基线与平面α垂直 ,则向量n叫做平面α的法向量或 说向量n与平面α正交. 知识点二 平面的向量表示 设A是空间任一点,n为空间内任一非零向量,则适合条件 A→M·n=0 的点M的 集合构成的图形是过空间内一点A并且与n垂直的平面.这个式子称为一个平面 的向量表示式.
高中数学 3.2.2平面的法向量与平面的向量表示配套课件 新人教B版选修21

3.2.2 平面的法向量与平面的向量表示
【学习要求】 1.理解平面的法向量的概念,会求平面的法向量. 2.会用平面的法向量证明平面与平面平行、垂直. 3.理解并会应用三垂线定理及其逆定理,证明有关垂直问题. 【学法指导】
在证明过程中,体会向量法与几何法证明的不同之处.从不同 的角度阐明数学证明的原理,培养我们善于探索、独立思考、 集体交流的好习惯.
第十二页,共28页。
研一研·问题探究、课堂(kètáng)
3.2.2
更高效
跟踪训练 2 已知正方体 ABCD—A1B1C1D1 的棱长为 2,E、
F 分别是 BB1、DD1 的中点,求证:
(1)FC1∥平面 ADE;
(2)平面 ADE∥平面 B1C1F.
证明 (1)建立如图所示空间直角坐标系
Dxyz,
研一研·问题(wèntí)探究、课堂
3.2.2
更高效
例2 在四面体 ABCD 中,AB⊥平面 BCD,BC=CD,∠BCD
=90°,∠ADB=30°,E、F 分别是 AC、AD 的中点,求
证:平面 BEF⊥平面 ABC.
证明 建系如图,设 A(0,0,a),
则易得 B(0,0,0),C
23a,
23a,0,
练一练·当堂检测(jiǎn cè)、目标达成 落实处
3.2.2
3.已知 l∥α,且 l 的方向向量为(2,m,1),平面 α 的法向量 为1,12,2,则 m=________. 解析 ∵(2,m,1)·1,12,2=2+12m+2=0. ∴m=-8.
答案 -8
第二十五页,共28页。
练一练·当堂检测(jiǎn cè)、目标达成
3.2.2
问题 2 根据下列条件,判断相应的直线与平面、平面与平 面的位置关系. (1)直线 l 的方向向量、平面 α 的法向量分别是 a=(3,2,1), n=(-1,2,-1); (2)平面 α、β 的法向量分别是 n1=(1,3,0),n2=(-3,-9,0); (3)平面 α、β 的法向量分别是 n1=(1,-3,-1),n2=(8,2,2). 解 (1)∵a=(3,2,1),n=(-1,2,-1), ∴a·n=-3+4-1=0,∴a⊥n,∴l⊂α 或 l∥α.
高二数学(人教B版)选修2-1全册同步练习:3-2-2平面的法向量与平面的向量表示

3.2.2平面的法向量与平面的向量表示一、选择题1.下列命题中正确的是( )A .如果一条直线与平面的一条斜线在这个平面内的射影垂直,则它也和这条斜线垂直B .如果一条直线与平面的一条斜线垂直,则它与斜线在平面上的射影垂直C .如果一向量和斜线在平面内的射影垂直,则它垂直于这条斜线D .如果一非零向量和一平面平行,且和一条斜线垂直,则它垂直于斜线在平面内的射影[答案] D[解析] 由三垂线定理知D 成立.2.在正方体ABCD —A 1B 1C 1D 1中,平面ACB 1的一个法向量为( )A.BD 1→B.DB →C.BA 1→D.BB 1→ [答案] A3.点A (a,0,0),B (0,b,0),C (0,0,c ),则平面ABC 的一个法向量为( )A .(bc ,ac ,ab )B .(ac ,ab ,bc )C .(bc ,ab ,ac )D .(ab ,ac ,bc ) [答案] A[解析] 设法向量为n =(x ,y ,z ),则AB ·n =0,AC →·n =0,则⎩⎪⎨⎪⎧-ax +by =0-ax +cz =0∴n =(bc ,ac ,ab ). 故选A. 4.在正方体ABCD -A 1B 1C 1D 1中,若E 为A 1C 1的中点,则直线CE 垂直于( ) A .ACB .BDC .A 1DD .A 1A[答案] B[解析] 直线CE 在平面AC 内的射影为AC ,又AC ⊥BD ,∴BD ⊥CE ,故选B.5.正方体AC 1中,E ,F 分别是AB ,CD 的中点,则下列直线中不互相垂直的是( )A .B 1C 与C 1D 1B .D 1B 与B 1C C .D 1B 与EFD .A 1B 与B 1C 1 [答案] C[解析]D1B与EF所成角等于∠D1BC,其余弦值为33,故选C.6.若平面α、β的法向量分别为u=(-2,3,-5),v=(3,-1,4),则()A.α∥βB.α⊥βC.α、β相交但不垂直D.以上均不正确[答案] C[解析]∵u=(-2,3,-5),v=(3,-1,4),∴u与v不平行且u与v不垂直,故选C.7.平面α的一个法向量为v1=(1,2,1),平面β的一个法向量v2=-(2,4,2),则平面α与平面β()A.平行B.垂直C.相交D.不能确定[答案] A[解析]由v1∥v2故可判定α∥β.8.设平面α的法向量为(1,2,-2),平面β的法向量(-2,-4,k),若α∥β,则k=() A.2B.-4C.4D.-2[答案] C[解析]∵α∥β,∴1-2=2-4=-2k,∴k=4,故选C.9.若直线l的方向向量为a=(-1,0,-2),平面α的法向量为u=(4,0,8),则() A.l∥αB.l⊥αC.l⊂αD.l与α斜交[答案] B[解析]∵u=-4a,∴u∥a,∴a⊥α,∴l⊥α.故选B.10.在正方体ABCD—A1B1C1D1中,E、F分别是BB1、CD的中点,则()A.面AED∥面A1FD1B.面AED⊥面A1FD1C.面AED与面A1FD相交但不垂直D.以上都不对[答案] B[解析] 以D 为原点,DA →、DC →,DD 1→分别为x ,y ,z 建立空间直角坐标系求面AED 的法向量n 1与面A 1FD 1的法向量n 2.∵n 1·n 2=0,∴n 1⊥n 2,∴平面AED ⊥平面A 1FD 1.二、填空题11.若直线l 与β的法向量分别是a =(1,0,-2),b =(-1,0,2),则直线l 与β的位置关系是________.[答案] l ⊥β[解析] ∵a ∥b ,∴l ⊥β.12.已知l ∥α,且l 的方向向量为(2,m,1),平面α的法向量为⎝⎛⎭⎫1,12,2,则m =________.[答案] -8[解析] 设a =(2,m,1),b =(1,12,2). ∵l ∥α,∴a ⊥b ,∴2+12m +2=0,∴m =-8. 13.已知正四棱锥(如图所示),在向量PA →-PB →+PC →-PD →,PA→+PC →,PB →+PD →,PA →+PB →+PC →+PD →中,不能作为底面ABCD 的法向量的向量是________.[答案] PA →-PB →+PC →-PD →[解析] ∵PA →-PB →+PC →-PD →=BA →+DC →=0,不能作为这个平面的法向量,对其它三个化简后可知均与PO →共线.而PO ⊥平面ABCD ,它们可作为这个平面的法向量.14.如图所示,已知矩形ABCD ,AB =1,BC =a ,P A ⊥平面ABCD ,若在BC 上只有一个点Q 满足PQ ⊥QD ,则a 的值等于________.[答案] 2[解析] 以A 为原点,建立如图所示坐标系,则A (0,0,0),B (1,0,0),D (0,a,0),C (1,a,0),设Q (1,x,0),P (0,0,z ),PQ →=(1,x ,-z ),QD→=(-1,a -x,0).由PQ →·QD →=0,得-1+x (a -x )=0,即x 2-ax +1=0.当Δ=a 2-4=0,即a =2时,Q 只有一个.三、解答题15.已知△ABC 的三个顶点坐标分别为A (0,0,2),B (4,2,0),C (2,4,0),求平面ABC 的单位法向量.[解析] AB →=(4,2,-2),AC →=(2,4,-2)设n =(x ,y ,z )是平面ABC 的单位法向量,则有⎩⎪⎨⎪⎧ |n |2=1,n ·AB →=0,n ·AC →=0,⇒⎩⎪⎨⎪⎧ x 2+y 2+z 2=1,2x +y -z =0,x +2y -z =0. 取z >0,得x =y =111,z =311 . ∴n =111(1,1,3).16.如图所示,M 、N 、P 分别是正方体ABCD —A 1B 1C 1D 1中的棱CC 1、BC 、CD 的中点.求证:A 1P ⊥平面DMN .[证明] 建立如图所示的空间直角坐标系,设正方体棱长为2,则D (0,0,0),A 1(2,0,2),P (0,1,0),M (0,2,1),N (1,2,0).∴向量A 1P →=(0,1,0)-(2,0,2)=(-2,1,-2),DM →=(0,2,1)-(0,0,0)=(0,2,1),DN →=(1,2,0).∴A 1P →·DM →=(-2,1,-2)·(0,2,1)=(-2)×0+1×2+(-2)×1=0.A 1P →·DN →=(-2,1,-2)·(1,2,0)=(-2)×1+1×2+(-2)×0=0.∴A 1P →⊥DM →,A 1P →⊥DN →,即A 1P ⊥DM ,A 1P ⊥DN ,又DM ∩DN =D ,∴A 1P ⊥平面DMN .17.棱长为a 的正方体ABCD —A 1B 1C 1D 1中,在棱DD 1上是否存在点P 使B 1D ⊥面P AC?[解析] 以D 为原点建立如图所示的坐标系,设存在点P (0,0,z ),AP →=(-a,0,z ),AC →=(-a ,a,0),DB 1→=(a ,a ,a ),∴B 1D ⊥面PAC ,∴DB 1→·AP →=0,DB 1→·AC →=0.∴-a 2+az =0.∴z =a ,即点P 与D 1重合.∴点P 与D 1重合时,DB 1⊥面P AC .18.如图所示,ABCD 为矩形,PA ⊥平面ABCD ,PA =AD ,M 、N 、Q 分别是PC 、AB 、CD 的中点,(1)求证:MN ∥PAD ;(2)求证:平面QMN ∥平面PAD ;(3)求证:MN ⊥平面PCD .[解析] (1)如图以A 为原点,以AB ,AD ,AP 所在直线为坐标轴建立空间直角坐标系,设B (b,0,0),D (0,d,0),P (0,0,d ),则C (b ,d,0)∵M ,N ,Q 分别是PC ,AB ,CD 的中点,∴M ⎝⎛⎭⎫b 2,d 2,d 2,N ⎝⎛⎭⎫b 2,0,0,Q ⎝⎛⎭⎫b 2,d ,0 ∴MN →=⎝⎛⎭⎫0,-d 2,-d 2, ∵面PAD 的一个法向量为m =(1,0,0)∴MN →·m =0,即MN →⊥m ,∴MN 不在面P AD 内,∴MN ∥面PAD ,(2)QN →=(0,-d,0),QN →⊥m ,又QN 不在面P AD 内,又QN ∥面PAD .又∵MN ∩QN =N ,∴面MNQ ∥平面P AD .(3)PD →=(0,d ,-d ),DC →=(b,0,0), ∴MN →·PD →=⎝⎛⎭⎫-d 2d +⎝⎛⎭⎫-d 2(-d )=0, MN →·DC →=0,∴MN →⊥PD →,MN →⊥DC ,又PD ∩DC =D , ∴MN →⊥平面PCD .。
【精品课件】第三章3.2.2《平面法向量与平面的向量表示》

C
B
练习:三棱柱 ABC-A1B1C1 是各棱长均为 a 的 正三棱柱,D 是棱 CC1 的中点,求证: 平面 AB1 D 平面ABB1 A1
例3:如图, 直三棱柱ABC A1 B1C1中, ACB 90 ,
0
AC 1, CB 2, 侧棱AA1 1, 侧面AA1 B1 B的 两条对角线交点为D, B1C1的中点为M . 求证:CD 平面BDM
课堂小结
1、平面法向量的定义及性质 2、平面的向量表示式 3、平面法向量的应用 4、平面法向量的求法
A D
A1
C
B
B1
C1
M
长方体ABCD A1 B1C1 D1,高为 ,底面 1 例 4. 为正方形边长为 . E为BC的中点, 2 求证:BD1 平面C1 DE .
D1 A1
C1
D
A
B1
C
B
E
例 5. 在三棱锥P ABC中,三条侧棱两两垂
直,G为PAB的重心,E、F分别为BC、 PB上的点且BE : EC PF : FB 1 : 2. (1)求证:平面 GEF 平面PBC; (2)求证:EG是PG与BC的公垂线.
3、平面法向量的应用
设
n
1
n , 2 分别是平面 , 的法向量,
//或 重合 与 n n n 0 1 n 2 1 2
n1 n2 n 1 // n 2
总结:
1)总结利用向量证明两平面平行的方法。 • 一个平面的一组基底与另一个平面共面 两平面至少有 一个非公共点 • 两平面的法向量互相平行 2)证明两平面垂直即证两平面的法向量互相垂直 3)如何利用平面的法向量证明直线与平面垂直? 设 是平面 的法向量, 是直线 l 的方向向量
平面的法向量与平面的向量表示_图文

D1
C1
A1
B1
E
D
F
C
A B
利用法向量证明两个平面垂直的基本思路是证明两个平面
的法向量互相垂直。
二、概念形成
概念5.用法向量证明“三垂线定理”
预备知识: 射影:已知平面 于点 ,则 称射影。
和一点A,过点A作 的垂线 与 交 就是点A在平面 内的正射影,也可简
斜线在平面上的正射影:设直
斜线在平面上的正射影:在直
三垂线定理
三垂线定理:在平面内的一条直线,如果和这个平面的
一条斜线的射影垂直,那么它也和这条斜线垂直。
PA⊥α aα
①
PA⊥a AO⊥a
② a⊥平面PAO PO 平面PAO
③
a⊥PO
P
a Ao α
数式板书
[例1] 已知点A(1,0,0)、B(0,2,0)、C(0,0,3), 求平面ABC的一个法向量.
A
D
B
C
一个平面的法向量不只一个,但它们都是平行(或共线)的 ,我们借助于待定系数法可求出平面的一个法向量。
待定系数法
例题ห้องสมุดไป่ตู้
例1:已知点
,
,
求平面 的一个法向量。
,其中
有何 关系?
二、概念形成
概念3.平面的向量表示
空间直线可以用向量来表示,对于空间的平面也可以用向 量来刻画。
设A是空间任意一点, 为空间任意一个非零向量,适合条
小结
1.直线与平面垂直的定义 2. 平面的法向量: 3. 平面的向量表示: 4. 两平面平行或重合、垂直的充要条件
6.有关平面的斜线概念, 三垂线定理及其逆定理
再见
例. 在空间直角坐标系内,设平面 经过
人教版【高中数学】选修2-1第三章平面的法向量与平面的向量表示讲义

案例(二)----精析精练课堂 合作 探究重点难点突破知识点一 平面的法向量1.平面法向量的定义(1)定义:已知平面a 如果向量n 的基线与平面a 垂直,则向量n 叫做平面a 的法向量或说向量n 与平面a 正交.(2)平面法向量的性质:①平面a 的一个法向量垂直于与平面a 共面的所有向量;②一个平面的法向量有无数个,一个平面的所有法向量互相平行.2.平面的法向量的求法方法一:找到一条与已知平面垂直的直线,则该直线的任意方向向量都是该平面的法向量方法二:待定系数法,即若要求出一个平面的法向量的坐标,一般要建立空间直角坐标系,然后用待定系数法求解,一般步骤如下:①设出平面的法向量为n=(x,y,x);②找出(求出)平面内的两个不共线的向量的坐标a=(x 1,y 1,z 1),b=(x 2,y 2,z 2);③根据法向量的定义,建立关于x,y,z 的方程组⎩⎨⎧=∙=∙;0,0b n a n ④解方程组,取其中的一个解,即得法向量.这里需要说明的是:①方法二必须建立空间直角坐标系,而方法一却不一定要建立空间直角坐标系,视具体情况而定;②在求平面的法向量时,要先找有没有和平面垂直的直线,若没有则用待定系数法;③在利用方法二求解平面的法向量时,方程组⎩⎨⎧=∙=∙;0,0b n a n 有无数多个解,只需给x,y,之中的一个变量赋予一个特值,即可确定平面的一个法向量.赋予的值不同,所求平面的法向量就不同,但它们是共线向量.3.平面法向量的作用详解:设n 1,m 2分别是平面a,β的法向量,m 是直线l 的方向向量,则有:①l ∥a 或l ⊂a ⇔m ⊥n 1⇔m ·n 1=0;②l ⊥a ⇔m ∥n 1;③a ∥β或a 与β重合⇔n 1∥n 2;④a ⊥β⇔=n 1⊥n 2⇔n 1·n 2=0.知识点二 三垂线定理及其逆定理.三垂线定理及逆定理实际上反映的是斜线和射影的关系.①三垂线定理的符号描述如右图,PO 、PA 分别是平面a 的垂线、斜线,OA 是PA 在a 内的射影,a ⊂a,且a ⊥OA,则a ⊥PA.②三垂线定理的逆定理的符号描述如上图,PO 、PA 分别是平面a 的垂线、斜线,OA 是PA 在a 内的射影,a ⊂a,且a ⊥PA,则a ⊥OA.关于定理的应用,首先是找出平面的垂线,至于射影则是由垂足,斜足来确定的,因而是第二位的,由此,我们可以得出三垂线定理证明a ⊥b 的一个程序:一垂、二射、三证,即:第一:找平面及平面的垂线;第二:找射影线(或斜线),这时a,b 便成为平面内的一条直线及一条斜线(或射影);第三:证明射影(或斜线)与直线a 垂直,从而得出a,b 垂直.典型例题分析题型1 求平面的法向量【例1】已知平面a 经过三点A(1,2,3),B(2,0,-1),C(3,-2,0),试求平面a 的一个法向量.解析 用待定系数法求解平面a 的法向量.答案 因为A(1,2,3),B(2,0,-1),C(3,-2,0),所以=(1,-2,-4),=(2,-4,-3).设平面a 的法向量为n=(x,y,z),依题意,应有n ·=0,n ·=0,即有⎩⎨⎧=--=--,0342,042z y x z y x 解得⎩⎨⎧==.0,2z y x 令y=1,则x=2,所以平面a 的一个法向量为n=(2,1,0 方法指导 用待定系数法求解平面的法向量,关键是在平面内找两个不共线的向量,然后列出方程组,方程组有无数解取其中的一个解即可,但要注意在取方程组的一组解时,不能都取零,否则得到零向量,而零向量的方向不能确定,不能作为法向量.【变式训练1】 已知点A(3,0,0),B(0,4,0),C(0,0,5),求平面ABC 的一个单位法向量 答案 因为A(3,0,0),B(0,4,0),C(0,0,5),所以=(-3,4,0),=(-3,0,5).设平面ABC 的法向量为n=(x,y,z)依题意,应有n ·=0,n ·=0,即有⎩⎨⎧=+-=+-,053,043z x y x 解得⎪⎪⎩⎪⎪⎨⎧==,53,43x z x y ,即平面A 的法向量为n(x ,43x,53x),所以平面ABC 的单位向量为n 0=n n =(76920,76915,76912)或n 0=-n n =(-76920,-76915,-76912). 【例2】 在棱长为1的正方体ABCD-A 1B 1C 1D 1中,求平面ACD 1的法向量n 和单位法向量n 0.解析 首先建立空间直角坐标系,再用待定系数法求解平面的法向量.答案 建立空间直角坐标系,如图,则A(1,0,0),C(0,1,0).设平面ACD1的法向量n=(x,y,1).得AC =(-1,1,0),AD =(-1,0,1).又n ⊥面ACD,得n ⊥,n ⊥,所以有⎩⎨⎧=-∙=-∙,0)1,0,1()1,,(,0)0,1,1()1,,(y x y x 得⎩⎨⎧==,1,1y x ∴n=(1,1,1), n 0=n n =111)1,1,1(++=⎪⎪⎭⎫ ⎝⎛33,33,33. 方法指导 用待定系数法求解平面的法向量,应该说是个基本方法,它具有操作简单的特点,应切实掌握其实,对于本题来说,却未必是一个好的方法,这是因为我们可以利用三垂线定理得出直线DB 1⊥AD 1,DB 1⊥CD 1,从而DB 1⊥平面ACD 1,所以1DB 就是平面ACD 1的一个法向量.【变式训练2】 已知正方体ABCD-A 1B 1C 1D 1的棱长为1,在BC,DD 1上是否存在点E,F,使B 1是平面ABF 的法向量?若存在,请证明你的结论,并求出点E,F 满足的条件;若不存在,请说明理由.答案 建立如图所示的空间直角坐标系,则A(1,0,1),B(1,1,1),B 1(1,1,0).设F(0,0,h),E(m,1,1),则=(0,1,0),B 1=(m-1,0,1),=(1,0,1-h).∵·E B 1=0,∴AB ⊥B 1E. 若F B 1是平面ABF 的法向量,则F B 1·=m-1+1-h=m-h=0,∴h=m 即E,F 满足D 1F=CE 时,F B 1是平面ABF 的法向量.所以存在,且E,F 满足D 1F=CE.题型2 三垂线定理及其逆定理的应用【例3】 如下图,下列5个正方体图形中,线段l 是正方体的条对角线,点M 、N 、P 分别为其所在棱的中点,能得出l ⊥面MNP 的图形的序号是 .(写出所有符合要求的图形序号)① ② ③④ ⑤ 解析 本题以正方体为依托,主要考查直线与平面垂直的判定,比较深刻地考查了空间想象能力.为了得到本题答案,必须对5个图形逐一进行判别.对于给定的正方体,l 位置固定,截面MNP 变动,l 与面MNP 是否垂直,可以从正、反两方面进行判断,MN 、NP 、MP 三条线中,若有一条不垂直l ,则可断定l 与面MNP 不垂直;若有两条相交直线与l 都垂直,则可断定l ⊥ 面MNP.答案 解法一:如果记正方体对角线l 所在的对角线截面为a,各图可讨论如下:在图①中,MN 、NP 在平面a 上的射影为同一直线,且与l 垂直故l ⊥面MNP.事实上,还可这样考虑:l 在上底面的射影是MP 的垂线,故l ⊥MP ;在左侧的射影是MN 的垂线,故l ⊥MN,从而l ⊥面MNP.在图②中,由MP ⊥面a,可证明MN 在平面a 上的射影不是l 的垂线,故l 不垂直于MN.从而l不垂直于面MNP.在图③中,点M在a上的射影是l的中点,点P在a上的射影是上底面的中点,知MP在a 上的射影不是l的垂线,得l不垂直于面MNP.在图④中,平面a平分线段MN,故l⊥MN,又l在左侧面的射影(即侧面正方形的一条对角线)与MP垂直,从而l⊥MP,故l⊥平面MNP.在图⑤中,点N在平面a上的射影是对角线l的中点,故M、P在平面a上的射影分别是下、下底面对角线的4等分点,三个射影在同一条直线上,且l与这一直线垂直从而l⊥面MNP.至此,得①④⑤为本题答案.解法二:建立空间直角坐标系O-xyz,设正方体的棱长为2,则对角线l的方向向量可取为l=(2,2,-2).对图①,有=(0,1,0)-(1,0,0)=(-1,1,0),=(0,0,-1)-(1,0,0)=(-1,0,-1),由l·MP=0,l·=0,得l⊥面MNP.对图②,有MN=(2,2,-1)-(1,0,-2)=(1,2,1),由l·≠0知l与面MNP不垂直.对图③,有=(0,1,0)-(2,0,-1)=(-2,1,1),由l·MP≠0知与面MNP不垂直.对图④,有MP=(1,0,-2)-(2,0,-1)=(-1,0,-1),=(0,2,-1)-(2,0,-1)=(-2,2,0),由l·=0,l·=0,得l⊥面MNP.对图⑤,有MP=(2,1,0)-(1,0,-2)=(1,1,2),MN=(0,2,-1)-(1,0,-2)=(-1,2,1),由l·=0,l·=0,得l⊥面MNP综合得本题答案为①④⑤.方法指导从解法二可以看到:应用向量法讨论两直线是否垂直十分方便,操作也比较简单,无须多动脑筋,只需要计算正确即可.【变式训练3】已知正方体ABCD-A1B1C1D1中,E、F、G分别是棱AB、BC、BB1上的点,且BE=BF=BG,求证:BD1⊥平面EFG.答案如下图所示,因为四边形ABCD是正方形,BE=BF,所以EF∥AC,又因为AC⊥BD,所以EF ⊥BD.因为BD 为BD 1在平面AB 上的射影,所以BD 1⊥EF(三垂线定理).同理BD 1⊥EG,故BD 1⊥平面EFG.【例4】 如右图,P 是△ABC 所在平M 面外一点,且PA ⊥平面ABC,若O,Q 分别是△ABC 和△PBC 的垂心,求证:OQ ⊥平面PBC.解析 欲证线面垂直,只须证明OQ 垂直于面PBC中的两条相交线,据重心,结合PA ⊥面ABC,利用三垂线定理其逆定理及求解答案PAE BC PE BC PBC Q AE BC ABC O 平面的垂心是的垂心是⊥⇒⎭⎬⎫⊥⇒∆⊥⇒∆. 因为OQ ⊂平面PAE,所以OQ ⊥BC,因为PA ⊥平面ABC,BFC 平面ABC 所以BF ⊥PA,又因为O 是△ABC 的垂心,所以BF ⊥AC,所以BF ⊥平面PAC,则FM 是BM 在平面PAC 上的射影. 因为BM ⊥PC,根据三垂线定理的逆定理,可得FM ⊥PC,从而PC ⊥平面BFM,又OQ ⊂平面BFM,所以OQ ⊥PC,又PC ∩BC=C,所以OQ ⊥平面PBC.方法指导 三垂线定理及其逆定理是证明线线垂直,特别是异面直线垂直的常用工具. 利用三垂线定理及其逆定理证明线线垂直的问题时,解决问题的关键是找准“一面三线”.【变式训练4】如下左图,在正三棱柱ABC=A 1B 1C 1中,AB 1⊥BC 1,求证:A 1C ⊥BC 1.答案 如上右图,取BC 、B 1C 1的中点分别为D 、D 1,由正三棱柱的性质知AD ⊥面BCC 1B 1,A 1D 1⊥面BCC 1B 1,所以B 1D 、CD 1分别为AB 1、A 1C 在面BCC 1B 1上的射影.因为AB 1⊥BC 1,所以B 1D ⊥BC 1(三垂线定理的逆定理)又D 、D 1分别为BC 、B 1C 1的中点,所以B 1D ∥CD 1,所以CD 1⊥BC 1,所以BC 1⊥A 1C(三垂线定理).题型3 利用法向量证明平行与垂直【例5】已知正方体OABC-O 1A 1B 1C 1的棱长为1,E 是C 1O 1上的点,且C 1E=21EO 1,F 是CC 1上的点,且C 1F=21FC. (1)求平面A 1BC 1的一个法向量;(2)证明EF ∥平面A1BC1.解析 一建立恰当的空间直角坐标系,用待定系教法求出平面A 1BC 1的一个法向量n,然后证明EF ⊥n.答案 建立如右图所示的空间直角坐标系,则B(1,1,0),A 1(1,0,1),C 1(0,1,1).(1)设n=(x,y,z)是平面A 1BC 1的一个法向量,则n ⊥1,n ⊥1BC ,从而n ·1=0,n ·1BC =0 ∵1=(0,-1,1),1BC =(-1,0,1),∴⎩⎨⎧=+-=+-,0,0z x z y x=z=y.取x=y=z=1,则n=(1,1,1)为平面A 1BC 1的一个法向量.(2) 要证明EF ∥平面A 1BC 1只要证明⊥n.∵E(0,32,1)F(0,1,32),=(0,31,-31).∵n ·EF =31-31=0,∴n ⊥EF ,∴E ∥平面A 1BC 1. 又EF 不在平面A 1BC 1内,∴EF ∥平面A 1BC 1.方法指导 由于有了第(1)小题,所以产生了上面第(2)小题的证明方法对于第(2)小题的证明也可以由EF =F C 1-E C 1=31(C C 1-11O C )=31(B B 1-11A B )=31B A 1,得∥B A 1,∴∥平面A 1BC 1,又EF ⊄平面A 1BC 1,故EF ∥平面A 1BC 1.或由=(0,31,-31),B A 1=(0,1,-1)=3EF 来证明.【变式训练5】 已知正方体ABCD-A 1B 1C 1D 1的棱长为2,E 、F 分别是BB 1、DD 1的中点,求证:(1)FC 1∥平面ADE ;(2)平面ADE ∥平面B 1C 1F.答案 如下图,建立空间直角坐标系D-xyz,则有D(0,0,0)、A(2,0,0)、C(0,2,0)、C 1(0,2,2)、E(2,2,1)、F(0,0,1),所以1FC =(0,2,1)、=(2,0,0)、=(0,2,1). 设n 1=(x 1,y 1,z 1),n 2=(x 2,y 2,z 2)分别是平面ADE 、平面B 1C 1F 的法向量,则n 1⊥,n 1⊥AE ,∴⎪⎩⎪⎨⎧=+=∙==∙,02,0211z y n x n∴⎩⎨⎧-==,2,0y z x 取y=1.则n 1=(0,1,-2).同理可求n 2=(0,1,-2).(1) ∵n1·1FC =(0,1,-2)·(0,2,1)=0,∴n 1⊥1FC ,又FC 1¢平面ADE,FC 1∥平面ADE.(2) n 1∥n 2,∴平面ADE ∥平面B 1C 1F.【例6】 在正方体ABCD 一A 1B 1C 1D 1中,E 是棱BC 的中点,试在棱CC 1上求一点P,使得平面A 1B 1P ⊥平面C 1DE.解析 若要在棱CC 1上求一点P,使得平面A 1B 1P ⊥平面C 1DE,需建立恰当的空间直角坐标系,并设出点P 的坐标,求出平面A 1B 1P 与平面C 1DE 的法向量,建立方程求出点P 的坐标,确定点P 的位置.答案 如右图,以D 为原点,建立如图所示的空间直角坐标系,设正方体的棱长为1,则P(0,1,a),A 1(1,0,1),B 1(1,1,1)E(21,1,0), C 1(0,1,1)∴11B A =(0,1,0,A 1=(-1,1,a-1) ,DE =(21,1,0)1DC =(0,1,1). 设平面A 1B 1P 的一个法向量为n 1=(x,y,z),则⎪⎩⎪⎨⎧=∙=∙,0,011111A n B A n ⇒⎩⎨⎧=-++-=.0)1(,0z a y x y 令z=1,则得x=a-1,所以平面A1BD 的一个法向量为n1=(a-1,0,1).设平面C1DE 的一个法向量为n2=(x,y,z), 则⎪⎩⎪⎨⎧=∙=∙,0,0122DC n n ⇒⎪⎩⎪⎨⎧=+=+.0,021z y y x 令y=1,则得x=-2,z=-1,所以平面CB 1D 1的一个法向量为n 2=(-2,1,-1).因为平面A 1B 1P ⊥平面C 1DE,所以n 1·n 2=0,⇒-2(a-1)-1=0,解得a=21,所以当P 为CC 1的中点时,平面A 1B 1P ⊥平面C 1DE.规律总结 此题是确定点P 的位置,但考查的是两个平面垂直的充要条件,解决本题的关键是建立恰当的空间直角坐标系,求出两个平面的法向量.这里法向量的坐标一个都不能求错,否则将得到错误答案.【变式训练6】 如下图,△ABC 是一个正三角形,EC ⊥平面ABC,BD ∥CE,且CE=CA=2BD,M 是EA 的中点.求证:平面DEA ⊥平面ECA.答案 不妨设CA=2,则CE=2,BD=1,C(0,0,0),A(3,1,0),B(0,2,0),E(0,0,2),D(0,2,1),EA =(3,1,-2),CE =(0,0,2),ED =(0,2,-1),设面CEA 与面DEA 的法向量是n 1=(x 1,y 1,z 1)、n 2=(x 2,y 2,z 3),所以得⎩⎨⎧==-+,02,0231111z z y x ⇒⎩⎨⎧=-=,0,3111z x y ⎩⎨⎧=-=-+,02,02322222z y z y x ⇒⎩⎨⎧==,2,32222y z y x 不妨取n 1=(1,-3,0),n 2=(3,1,2)从而计算得n 1·n 2=0,所以两个法向量相互垂直,两个平面就相互垂直.规律 方法 总结(1)求平面法向量的方法:求一个平面的法向量的坐标的方法步骤:①建立空间直角坐标系,设出平面的法向量为n=(x,y,z)②找出(求出)平面内的两个不共线的向量的坐标a=(a0,b1,c1),b=(a2,b2,c2).③根据法向量的定义建立关于x 、y 、x 的方程组⎩⎨⎧=∙=∙.0,0b n a n ④解方程组,取其中的一个解,即得法向量.由于一个平面的法向量有无数个,故可在代入方程组的解中取一个最简单的作为平面的法向量.(2)用空间向量证明平行问题,主要是运用直线的方向向量和平面的法向量,借助空间中已有的一些关于平行的定理,再通过向量运算来解决.(3)用空间向量证明垂直问题,主要是运用直线的方向向量和平面的法向量,借助空间中已有的一些关于垂直的定理,再通过向量运算来解决.定时巩固检测基础训练1. 下列说法中不正确的是()A.平面a的法向量垂直于与平面a共面的所有向量B一个平面的所有法向量互相平行C.如果两个平面的法向量垂直,那么这两个平面也垂直D.如果a,b与平面a共面,且n⊥a,n⊥b,那么n就是平面a的一个法向量【答案】 D(点拨:a与b所在直线必须为相交直线时,n才是平面a的一个法向量,否则不是.)2. 给定下列命题:①若n1,n2分别是平面a,β的法向量,则n1∥n2⇔a∥β;②若n1,n2分别是平面a,β的法向量,则a∥β⇔n1·n2=0;③若n是平面a的法向量,且向量a与平面a 共面,则a·n=0;④若两个平面的法向量不垂直,则这两个平面定不垂直其中正确命题的个数是()A.1B.2C.3D.4【答案】 C(点拔:①③④正确,②中a∥p=mn∥m,)3. 给定下列命题:①若a是平面a的斜线,直线b垂直于a在平面a内的射影,则a⊥b;②若a是平面a的斜线,平面β内的条直线b垂直于a在平面a内的射影,则a⊥b;③若a是平面a的斜线,直线b⊂a,且b垂直于a在平面β内的射影,则a⊥b;④若a是平面a的斜线,直线b⊂a,且b垂直于a在平面a内的射影,则a⊥b.其中,正确命题的个数是()A.1B.2C.3D.3【答案】 B(点拨:根据三垂线定理及其逆定理判断只有④正确.)4. Rt△ABC的斜边BCC平面a,顶点A∉a,则△ABC的两条直角边在平面a内的射影与斜边所成的图形只能是 ( )A.一条线段或一个直角三角形B一条线段或一个锐角三角形C.一条线段或一个锐角三角形D.一个锐角三角形或一个直角三角形【答案】 C(点拨:当平面ABC ⊥平面a 时,Rt △ABC 在平面内的射影是一条线段.当平面ABC 与平面a 斜交时,如右图所示,过A 作AO ⊥a,连接BO,CO,在△BOC 中,AB 2一AO 2=BO 2,在Rt △AOC 中,AC 2-AO 2=CO 2,②在Rt △ABC 中,AB2+AC2=BC2,③在Rt △ABC 中,cos ∠BOC=COBO BC CO BQ ∙∙-+2222,④ 将①②③代入④,得cos ∠BOC=COBO AO ∙∙-22<0,所以∠BOC 是钝角,所以△BOC 是钝角三角形.)5. 设A 是空间任意一点,n 为空间任一非零向量,则适合条件·n=0的点M 的轨迹是 .【答案】 过点A 且与向量n 垂直的平面(点拨:AM ·n=0称为一个平面的向量表示式,这里考察的是基本概念.)能力提升6. 已知=(2,2,1),=(4,5,3),则平面ABC 的单位向量是 .【答案】 ±(31,-32,32)(点拨:设单位法向量n=(x,y,z), 则⎪⎩⎪⎨⎧=++=++=++,0354,022,1222z y x z y x z y x 解得⎪⎪⎪⎩⎪⎪⎪⎨⎧=-==32,32,31z y x 或⎪⎪⎪⎩⎪⎪⎪⎨⎧-==-=.32,32,31z y x ) 7. 如下图,PA 垂直于⊙O 所在的平面,AB 是⊙O 的直径,C 是⊙O 上的一点,E 、F 分别是点A 在PB 、PC 上的射影,给出下列结论:①AF ⊥PB ;②EF ⊥PB ;③AF ⊥BC ;④AE ⊥平面PBC.其中真命题的序号是 .【答案】①②③(点拨:利用三垂线定理及其逆定理判断即可.)8. 如右图所示,在四棱锥P一ABCD中,PA⊥底面ABCD,底面各边都相等,M是PC上的一动点,当点M满足时,平面MBD⊥平面PCD.(注:只要填写一个你认为正确的条件即可)【答案】 DM⊥PC(点拨:由三垂线定理可知BD⊥PC,当DM⊥PC(或BM⊥PC)时,即有PC⊥平面BMD.所以平面MBD⊥平面PCD.)9. 如右图,△ADB和△ADC都是以D为直角顶点的直角三角形,且AD=BD=CD,∠BAC=60°. (1)求证:BD⊥平面ADC; (2)若H为△ABC的垂心,求证:H是D在平面ABC内的射影【答案】 (1)因为AD=BD=CD,∠ADB=∠ADC=90°,所以△ADB≌△ADC,AB=AC,∠BAC=60°,所以△ABC为正三角形,所以AB=BC,所以△ABD≌△CBD,所以△BDC为直角三角形,∠BDC=90°,BD⊥CD.又BD⊥AD,所以BD⊥平面ADC.(2)如右图所示,设D在△ABC内的射影为H′,连接CH′并延长交AB于E,因为CD⊥AD,且CD⊥DB,所以CD⊥面ADB,所以CD⊥AB,由三垂线定理的逆定理得CE⊥AB.同理,连接BH′并延长交AC于F,可得BF⊥AC,所以H′为△ABC的垂心,即D在平面ABC内的射影为△ABC的垂心,所以H′与H重合,即H是D在平面ABC内的射影.。
课件4:3.2.2平面的法向量与平面的向量表示

①证明两直线的
方向向量的数量
积为0.
②证明两直线所
成角为直角.
线面垂直
①证明直线的
方向向量与平
面的法向量是
平行向量.
②证明直线与
平面内的相交
直线互相垂直.
面面垂直
①证明两个平
面的法向量垂
直.
②证明二面角
的平面角为直
角.
例题解析
例1
已知点A(a,0,0),B(0,b,0),C(0,0,c),其中
间的平行、垂直问题.(重点、难点)
自学导引
1.平面的法向量
已知平面α,如果向量n的基线与平面α垂直,则
法向量 或 说 向 量 n 与 平 面
向 量 n 叫 做 平 面 α 的 _______
正交
α_____.
自学导引
1.平面的法向量
平面法向量的性质:
(1)平面α的一个法向量垂直于平面α内的所有向量.
(2)条件m⊂α并非可有可无.把m⊂α,改为m∥α,
其他条件不变,三垂线定理仍然成立.
(3) 三 垂 线 定 理 是 证 明 空 间 两 条 直 线 垂 直 的 依
据.应用定理的关键是:要证线线垂直,转化为
证明m与l在α内的射影l′垂直.
2.三垂线定理及逆定理的理解
(4)三垂线定理及其逆定理合起来可表述为:设l是
求证:l⊥AC.
证明:取向量v∥l,则v∥ α,且v ⊥ .
因为AB⊥ α ,l ⊂ α,所以
v⊥.
又因为·v=( + )·v= ·v + ·v=0.
因此v⊥,得⊥AC.
本例证明所得的结论,通常称为三垂线定理.
线面平 ②根据线面平行判定定理在平面内找一个向量与已知直线的方向向
3.2.2 平面的法向量与平面的向量表示

直线与平面垂直的判定定理 如果一条直线和平面的两条相交直线垂 直,那么这条直线垂直于这个平面。 那么这条直线垂直于这个平面。 已知: 、 是平面 是平面α内 已知 a、b是平面 内 的两条相交直线, 的两条相交直线,且 直线n⊥ , ⊥ , 直线 ⊥a,n⊥b, 求证: ⊥ 求证:n⊥α.
α
n b c a
例3.已知点 .已知点A(a,0,0),B(0,b,0), , , , , , , C(0,0,c),其中abc≠0,如图,求平面 , , ,其中 ,如图, ABC的一个法向量。 的一个法向量。 的一个法向量
z C n
r , , n =(bc,ac,ab)
O B x
y
分别是平面α的垂线 例4.已知:AB,AC分别是平面 的垂线 .已知: , 分别是平面 和斜线, 是 在 内的射影 内的射影, α且 和斜线,BC是AC在α内的射影,l ⊂ 且 l⊥BC,求证:l⊥AC. ⊥ ,求证: ⊥ 三垂线定理
4. 如图,在长方体 ABCD-A1B1C1D1 中,AB 如图, - =BC=2,AA1=1,则 BC1 与平面 BB1D1D 所 = , , 成角的正弦值为( 成角的正弦值为 D ) 6 2 5 15 10 A. B. C. D. 3 5的向量表示
r 已知平面α, 的基线与平面α 已知平面 ,如果向量 n的基线与平面 r 垂直,则向量 叫做平面α的法向量或说 垂直, 叫做平面 的法向量或说 n r 向量 与平面α正交。 与平面 正交。 正交 n
由平面法向量的定义可知,平面 的一个 由平面法向量的定义可知,平面α的一个 法向量垂直于与平面共面的所有向量。 法向量垂直于与平面共面的所有向量。 由于同时垂直于同一平面的两条直线平 可以推知, 行,可以推知,一个平面的所有法向量互 相平行。 相平行。 由平面法向量的性质, 由平面法向量的性质,很容易通过向量 运算证明直线与平面垂直的判定定理。 运算证明直线与平面垂直的判定定理。 直线与平面垂直的判定定理
人B版数学选修2-1:第3章 3.2.2 平面的法向量与平面的向量表示

学业分层测评(建议用时:45分钟)[学业达标]一、选择题1.已知平面α的法向量为a =(1,2,-2),平面β的法向量为b =(-2,-4,k ),若α⊥β,则k =( )A .4B .-4C .5D .-5【解析】 ∵α⊥β,∴a ⊥b ,∴a ·b =-2-8-2k =0.∴k =-5.【答案】 D2.已知平面α的一个法向量是(2,-1,1),α∥β,则下列向量可作为平面β的一个法向量的是( )A .(4,2,-2)B .(2,0,4)C .(2,-1,-5)D .(4,-2,2)【解析】 ∵α∥β,∴β的法向量与α的法向量平行,又∵(4,-2,2)=2(2,-1,1),故应选D.【答案】 D3.已知AB→=(1,5,-2),BC →=(3,1,z ),若AB →⊥BC →,BP →=(x -1,y ,-3),且BP ⊥平面ABC ,则实数x ,y ,z 分别为( )A.337,-157,4 B .407,-157,4 C.407,-2,4 D .4,407,-15【解析】 ∵AB →⊥BC →,∴AB →·BC→=0,即3+5-2z =0,得z =4, 又BP ⊥平面ABC ,∴BP→⊥AB →,BP →⊥BC →,则⎩⎪⎨⎪⎧ (x -1)+5y +6=0,3(x -1)+y -12=0,解得⎩⎪⎨⎪⎧ x =407,y =-157.【答案】 B4.已知平面α内有一个点A (2,-1,2),α的一个法向量为n =(3,1,2),则下列点P 中,在平面α内的是( )A .(1,-1,1)B .⎝ ⎛⎭⎪⎫1,3,32 C.⎝ ⎛⎭⎪⎫1,-3,32 D .⎝ ⎛⎭⎪⎫-1,3,-32 【解析】 对于B ,AP →=⎝ ⎛⎭⎪⎫-1,4,-12, 则n ·AP →=(3,1,2)·⎝ ⎛⎭⎪⎫-1,4,-12=0, ∴n ⊥AP →,则点P ⎝ ⎛⎭⎪⎫1,3,32在平面α内. 【答案】 B5.设A 是空间一定点,n 为空间内任一非零向量,满足条件AM →·n =0的点M 构成的图形是( )A .圆B .直线C .平面D .线段【解析】 M 构成的图形经过点A ,且是以n 为法向量的平面.【答案】 C二、填空题6.已知直线l 与平面α垂直,直线l 的一个方向向量u =(1,-3,z ),向量v =(3,-2,1)与平面α平行,则z =________.【解析】 由题意知u ⊥v ,∴u ·v =3+6+z =0,∴z =-9.【答案】 -97.已知a =(x,2,-4),b =(-1,y,3),c =(1,-2,z ),且a ,b ,c 两两垂直,则(x ,y ,z )=________.。
高二数学高效课堂资料平面的法向量(用)

证明:因为OA BC OA (OC OB)
O OA OC OA OB
| OA | | OC | cos | OA | | OB | cos
| OA | | OB | cos | OA | | OB | cos
D
AD 、D C 、DD的中点,
P
求证:⑴平面PQR∥平面EFG。 A R
⑵ BD⊥平面EFG
D
A
E
B
Q
C
B
G C
F B
例. 在空间直角坐标系内,设平面 经过 点 P(x0 , y0 , z0 ) ,平面 的法向量为 e ( A, B, C), M (x, y, z) 为平面 内任意一点,求 x, y, z
例1、设平面α的法向量为(1, 2, -2),平面β 的法向量为(-2, -4, k),
若α//β,则k=
4;
若α⊥β, 则 k= -5 。
练习 1、已知l//α,且l的方向向量为(2, m, 1), 平面α的法向量为(1, 1 , 2), 则m= -8 .
2
2、已知l⊥α,且l的方向向量为(2, 1, m), 平面α的法向量为(1, 1 , 2), 则m= 4 .
关于三垂线定的应用:关键是找出平面(基准面)
及垂线。至于射影则是由垂足、斜足来确定的,因而是第 二位的。
第一、定平面(基准面) 第二、找平面垂线(电线杆)
第三、看斜线,射影可见
第四、证明直线a垂直于射影线,从而得出a与b垂直。
强调:1°四线是相对同一个平面而言。
2°定理的关键是找“基准面”和“电线
P
a PA a (PO OA)
a PO a OA
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
因为 a , b ,由共面向量定理可知,存在唯一的数对(x,y),使
n
a
n
b
因为 n 垂直于平面 内任意一条直 线,所以 n
m m
b
a b
向量证法
a
三、概念形成
概念3.平面的向量表示
空间直线可以用向量来表示,对于空间的平面也可以用向 量来刻画。 设A是空间任意一点, n 为空间任意一个非零向量,适合条 件 A M n 0 的点 M 的集合构成什么样的图形? 我们可以通过空间一点和一个 非零向量确定唯一的一个与该
AB OB OA (a,b 0 , ) AC OC OA (a,0 c) ,
O z C
n
设平面 (y ABC n ,, 的一个法向量 z x ) B
y
AB ,yz b ) n x , ) ( a , ax ( , 0 by 0 则 AC ,yz 0 ) n x , ) ( a , ax ( , c cz0
n
M1
向量垂直的平面。 AM n 0
称此为平面的向量表达式。
M
A
M2
三、概念形成
概念4.用法向量证明平面与平面平行及垂直
设 n1 , n 2 分别是平面 , 的法向量,则有 // 或 与 重 合 n1 // n 2
解得 y a b x z , a c x
A x
bc ,ab 令 , y ac x bc, 则 z ab n( ,ac )
a a 令 , x 1则y ,z b c
a a n (1, , ) b c
有何 关系?
三、概念形成
概念2.直线与平面垂直的判定定理的向量证明
直线与平面垂直的判定定理: 如果一条直线和平面内的两条相交直线垂直,那么这条直 线垂直于这个平面。 已知:a , b 是平面 内的两条相交的直线,且 n a , n b 求证: n n
一、复习引入
1.直线与平面垂直的定义、判定和性质
定义:如果一条直线垂直于一个平面内的任意一条直线, 那么称这条直线和这个平面垂直。 判定:如果一条直线垂直于一个平面内的两条相交直线, 则这条直线与这个平面垂直。 性质: (1)垂直于同一个平面的两条直 线平行。 (2)垂直于同一条直线的两个平 面平行。
( x 1 , y 1 , z 1 ) ( 2, 0, 0 ) 0 ( x 1 , y 1 , z 1 ) ( 2, 2,1) 0 x1 0 A1 2 y1 z1 0
中点。求证:平面DEA⊥平面A1FD1 。
C1 B1 F E C
A1
a n
A'
B
向量证法
A'
B
一、选择题 → → 1.设 M(5,-1,2),A(4,2,-1),若OM=AB,则点 B 应为 ( )
A.(-1,3,-3) C.(1,-3,3)
B.(9,1,1) D.(-9,-1,-1)
[答案] B
[解析] → → → → ∵OM=AB=OB-OA,
→ → → ∴OB=OM+OA=(9,1,1).故选 B.
由平面的法向量的定义可知,平面 的法向量有无穷多个, 法向量一定垂直于与平面 共面的所有向量。 由于垂直于同一平面的两条直线
概念1.平面的法向量
平行,所以,一个平面的所有法 向量都是平行的。 模为1的法向量,叫做单位法向量, 记作 n 0 显然
n n0 |n|
D A x
D A
向量证法
B 利用法向量证明两个平面垂直的基本思路是证明两个平面 的法向量互相垂直。
四、应用举例
例1.在正方体 A B C D A1 B 1 C 1 D 1 中,M,N,E,F分别是棱 A1B1,A1D1,B1C1,C1D1的中点, C1 F 求证:平面AMN//平面EFDB。 D1 N E M B1 A1
已知:a , b 是平面 内的两条相交的直线,且 n a , n b 求证: n 证明:设 m 是 内任意一条直线。在 n , a , b , m 上分别取非 零向量 n , a , b , m 。
m xa yb n m n ( xa yb) x n a yn b n a 0, n b 0 nm 0 即 nm 所以 n m
→ =2AB,则 2.已知 A(3,-2,4),B(0,5,-1),若OC 3 → C 的坐标是 14 10 A.(2,- 3 , 3 ) 14 10 C.(2,- ,- ) 3 3 ( )
三、概念形成
概念5.用法向量证明“三垂线定理”
预备知识: 射影:已知平面 和一点A,过点A作 的垂线 l 与 交 于点 A ' ,则 A ' 就是点A在平面 内的正射影,也可简 称射影。 斜线在平面上的正射影:在直 斜线在平面上的正射影:设直 线 l 与平面 交于点B,但不 上任取一点A,作A点在平 面 和 垂直,那么直线 l 叫做 内的射影 A ' ,则平面内 直线 A ' B 叫做斜线 l 在该平 这个平面的斜线。斜线和平面 面内的射影。 的交点B叫做斜足。
AB n ( AA ' A 'B) n AA ' n A 'B n 0 因此 n A B a l
A
l
A
a
l
n
l'
m A
二、提出问题
1.如何用向量来表示空间直线与平面的垂直? 2.直线的向量表示为 A P t a 平面怎样用向量来表达呢?
三、概念形成
已知平面 ,如果向量 n 的基线与平面 垂直,则 n 叫做平面 的法向量或说向量 n 与平面 正交。
l
A
A
A'
A'
B
三、概念形成
概念5.用法向量证明“三垂线定理”
三垂线定理: 如果在平面内的一条直线与平面的一条斜线在这个平面内 的射影垂直,则它也和这条斜线垂直。 已知 l 是平面 的斜线, A ' B 是 l 在平面 内的射影, 直线 a 且 a A ' B l 求证: a l
1 A D 1 ( 1, 0,1), A1 C ( 1,1, 1) A1 D B (1,1, 0 ), D C 1 (0 ,1,1) 设 n ( x , y , z ) 为平面BDC1的法向量, n D B ( x , y , z ) (1,1, 0 ) 0 n D C 1 ( x , y , z ) (0 ,1,1) 0
n b a
mm c
三、概念形成
概念1.平面的法向量
例子:正方体AC1棱长为1,求平面ADB1的一个法向量。
A1
正方体AC1棱长为1,求平面ADB1的一个法向量。 解:建立如图所示的坐标系A-xyz,则
D A (0 , 1, 0 ), D B 1 (1, 1,1) 设 n ( x , y , z ) 是平面ADB1的法
1 n1 A M 2 y 1 z 1 0 n AN 1 x z 0 1 1 1 2
D A B
y x
向量解法
A
利用法向量证明两个平面平行的基本思路是证明两个平面
的法向量平行(或共线)。
四、应用举例
例2.已知正方体ABCD-A1B1C1D1,求证: (1)AD1//平面BDC1 ; (2)AC1⊥平面BDC1 。
例2.已知正方体ABCD-A1B1C1D1,求证:(1)AD1//平面BDC1 ; (2)AC1⊥平面BDC1 。 证明:以D为坐标原点建立如图所示坐标系Dxyz, 设正方体棱长为1,则D(0,0,0),A(1,0,0),D1(0,0,1),A1(1,0,1)
D1
C1
A1
C1
B1
D C
C(0,1,0),B(1,1,0),C (0,1,1)。
z
D1 B1
D B
C
yABiblioteka x y 0 y z 0
令x=1,得 n (1, 1,1)
x
向量解法
B A 利用法向量证明直线与平面的平行的基本思路是证明法向 量与直线平行(或共线)的向量垂直;证明直线与平面垂直 只要证明法向量与该直线共线的向量平行即可。
D
令z=1,得 n ( 1, 0,1)
向量证法
一个平面的法向量不只一个,但它们都是平行(或共线)的, 我们借助于待定系数法可求出平面的一个法向量。
例题
例1:已知点 A(a,0,0) , (0, b,0) , (0,0, c),其中 abc 0 B C 求平面 ABC 的一个法向量。
解:由已知得
A B C D A1 B 1 C 1 D 1
例1.在正方体
中,M,N,E,F分别是棱
A1 B1 ,A1 D1 ,B1 C1 ,C1 D1 的中点, 求证:平面AMN//平面EFDB。 解:以D为原点,分别以DA,DC,DD1为x轴,y轴,z轴建立空间 直角坐标系,则 z C1 F D(0,0,0),A(1,0,0),B(1,1,0), D
已知 l 是平面 的斜线, A ' B 是 l 在平面 内的射影, 求证: a l 直线 a 且 a A ' B 证明:取向量 n // a,则 n // ,且 n A ' B A A ' , a , n A A ' 又 AB AA ' A 'B
