初二数学几何试题.

合集下载

初二数学几何图形练习题

初二数学几何图形练习题1. 设△ABC 为等腰直角三角形，其中∠BAC = 90°，∠ABC =∠ACB。

已知 AB = 5cm。

(a) 求 BC 的长度。

(b) 求△ABC 的面积。

2. 在△ABC 中，AD 是边 BC 的中线，且 AB = 3cm，BC = 4cm。

连接 BD，BD 的延长线交 AC 于 E 点。

(a) 求 BD 和 DE 的长度。

(b) 求△ADE 的面积。

3. 在△ABC 中，D、E 两点分别在边 AB、AC 上。

若DE ║ BC，则证明：AD/BD + AE/CE = 1。

4. 已知△ABC 中，∠BAC = 40°，∠ABC = 70°，点 D 在边 BC 上，且满足 BD = AC。

(a) 求∠BDC 的度数。

(b) 求∠ADB 的度数。

5. 在△ABC 中，D、F 分别是边 AB、AC 上的两个点，连接 BF、CD。

已知 AF = 6cm，BF = 4cm，CF = 3cm，FD = 1.5cm。

(a) 求△BFD 的面积。

(b) 求△ABC 的面积。

6. △ABC 的三个内角分别为 60°、75°、45°。

(a) 将△ABC 分别绕着顶点 A，边 BC，边 AC 旋转 90°，分别得到△A'B'C'、△AB'C'、△A'BC。

求△A'B'C'、△AB'C'、△A'BC 的内角。

(b) 证明△A'B'C' 是等腰三角形。

7. 在平面直角坐标系中，点 A(3, 4)、B(-1, -2)、C(-2, 6) 是顶点坐标。

连接 AB、AC，垂直平分 AC 的线段交 AB 的延长线于点 D。

求点 D 的坐标。

8. 已知△ABC 中，点 D、E 分别是边 AB、BC 上的两个点，且 DE ║ AC。

初二几何经典难题集锦(含答案)

初二几何经典训练题1、如图,在直角梯形ABCD中,AB∥DC,∠ABC=90°,AB=2DC,对角线AC⊥BD,垂足为F,过点F作EF∥AB,交AD于点E,CF=4cm.⑴求证：四边形ABFE是等腰梯形;⑵求AE的长.2、如图，矩形ABCD的对角线AC、BD相交于点O，E、F分别是OA、OB的中点．（1）求证：△ADE≌△BCF；（2）若AD=4cm，AB=8cm，求CF和OF的长。

3、如图，已知直角梯形ABCD中，AD∥BC，∠B=90°，AB=12cm，BC=8cm，DC=13cm，动点P沿A→D→C线路以2cm/秒的速度向C运动，动点Q沿B→C线路以1cm/秒的速度向C运动．P、Q两点分别从A、B同时出发，当其中一点到达C点时，另一点也随之停止．设运动时间为t秒，△PQB的面积为ycm2．（1）求A D的长及t的取值范围；（2）当1.5≤t≤t0（t0为（1）中t的最大值）时，求y关于t的函数关系式；（3）请具体描述：在动点P、Q的运动过程中，△PQB的面积随着t的变化而变化的规律。

4、如图,AB与CD相交于E,AE=EB,CE=ED,D为线段FB的中点,GF与AB相交于点G,若CF=15cm,求GF 之长。

5、如图所示，在平行四边形ABCD中，过点B作BE⊥CD，垂足为E，连接AE，F为AE上的一点，且∠BFE =∠C。

（1）求证：△ABF∽△EAD；（2）若AB=4，∠BAE=30°，求AE的长；（3）在（1）、（2）的条件下，若AD=3，求BF的长（计算结果可含根号）。

6、如图是一个常见铁夹的侧面示意图，OA，OB表示铁夹的两个面，C是轴，CD⊥OA于点D，已知DA ＝15mm，DO＝24mm，DC＝10mm，我们知道铁夹的侧面是轴对称图形，请求出A、B两点间的距离。

7、如图，用三个全等的菱形ABGH、BCFG、CDEF拼成平行四边形ADEH，连接AE与BG、CF分别交于P、Q，（1）若AB=6，求线段BP的长；（2）观察图形，是否有三角形与△ACQ全等？并证明你的结论．8、如图已知点E、F在△ABC的边AB所在的直线上，且AE=BF，FH∥FG∥AC，FH、EG分别交边BC所在的直线于点H、G。

初二数学几何题50道,要带答案带过程

初二数学几何题50道,要带答案带过程选择题：1. 若两角互为补角，则它们的差是（）。

A.0°B.45°C.60°D.90°2. 在图中，如点S、T分别在边AB的延长线上，且∠ASP=60°，∠BAT=20°，则∠AST为（）。

A.40°B.50°C.80°D.110°3. 已知正方形ABCD的边长为5cm，点E、F分别在边AD、AB上，且AE=BF，则三角形CEF的面积为（）。

A.(5/8) cm²B.(9/8) cm²C.(13/8) cm²D.(15/8) cm²4. 如果一个圆心角的度数为30°，则它所对的弧度数是（）。

A.π/6B.π/3C.π/4D.π/2填空题：1.如图，已知BC平分∠ABD，设∠BAC=a°，∠BCA=b°，则∠CBD=\_\_\_\_°。

2.如图，点A、B、C在同一条直线上，则对于ΔABC来说，以下说法正确的是：①AB＝AC；②\angleBAC是钝角；③\angleABC＋\angleACB ＝180^\circ，所以\angleABC＝\_\_\_\_°，\angleACB＝\_\_\_\_°。

3. 已知直角三角形ABC，其中\angleC=90°，BC＝3，AC＝4，则AB=\_\_\_\_。

4.如图，长方形ABCD中，点E、F分别为BC、CD上的点，若∠BAE=∠EFD，AB=10cm，则DF=\_\_\_\_cm。

解答题：1.如图，在\triangleABC中，垂足分别为D、E、F。

若AC＝6，BD＝8，DE＝5，EF＝9，则BC＝（）。

2.如图，已知\angleBAC=60°，AD平分\angleBAC，且BD=AD，点E为AD的延长线上的点，且\angleBEC=140°，则\angleACD=\_\_\_\_\_\_°。

初二数学几何难题训练题及答案

初二数学几何难题训练题及答案1.已知⊙O的直径AB=10cm，点C、D、E、F分别在弧AB 上，若AC=3cm，BE=2cm，CF=4cm，求DE+FA的长度。

解：∠ABC=90°，∠AOC=180°，所以∠AFC=90°。

同理，∠ADE=90°。

又因为△ABC与△AED相似，所以$\frac{DE}{AC}=\frac{AB}{BC} \RightarrowDE=\frac{AB\times AC}{BC}$同理，因为△ABE与△AFC相似，所以$\frac{FA}{BE}=\frac{AB}{BC} \RightarrowFA=\frac{AB\times BE}{BC}$代入已知数据得到$DE=\frac{10\times 3}{7},FA=\frac{10\times 2}{7}$ 所以 DE+FA=4cm。

答案：4cm。

2.在△ABC中，D、E分别在AB、AC上，DE//BC，已知AB=6cm，AC=9cm，BD:DA=1:2，CE:EA=2:3，求BC的长。

解：因为DE//BC，所以$\frac{BD}{DA}=\frac{CE}{EA}=\frac{DB+BC}{DA+AC}$ 代入已知数据得到$\frac{1}{2}=\frac{2P+BC}{3P+9} \RightarrowBC=\frac{9}{2}$所以BC的长为4.5cm。

答案：4.5cm。

3.在四棱锥ABCD-P中，AB=BC=CD=l，PA=2l，PB=3l，PC=4l，且四棱锥的底面ABCD是个正方形，求四棱锥的体积V。

解：设△PAB与底面平行，交底面为E，△PAD与底面平行，交底面为F。

则有$PE=2l,PF=3l$由于ABCD是个正方形，所以$AE=BF=CF=DF=l$又因为連接PC与數直BD平行，所以$\frac{BD}{PC}=\frac{AE}{AF}$带入已知数据得到$\frac{BD}{4l}=\frac{l}{PF} \RightarrowBD=\frac{l^2}{PF}\times 4l=\frac{16l^3}{9}$所以四棱锥的高为$h=\sqrt{(PA-BD/3)^2-PF^2}=\sqrt{(2l-\frac{16l^3}{3\times 9l^2})^2-9l^2}=(8\sqrt{3}-9)l$ 最后利用公式$V=\frac{1}{3}S\times h$求出四棱锥的体积V，其中S为底面积，S=AB×BC=l²。

初中数学几何证明经典试题(含答案)

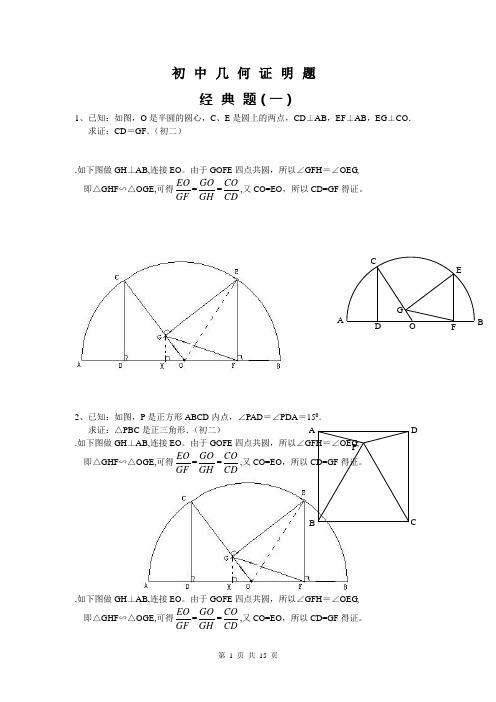
初中几何证明题经典题（一）1、已知：如图，O是半圆的圆心，C、E是圆上的两点，CD⊥AB，EF⊥AB，EG⊥CO．求证：CD＝GF．（初二）.如下图做GH⊥AB,连接EO。

由于GOFE四点共圆，所以∠GFH＝∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO，所以CD=GF得证。

2、已知：如图，P是正方形ABCD内点，∠PAD＝∠PDA＝150．求证：△PBC是正三角形．（初二）.如下图做GH⊥AB,连接EO。

由于GOFE四点共圆，所以∠GFH＝∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO，所以CD=GF得证。

.如下图做GH⊥AB,连接EO。

由于GOFE四点共圆，所以∠GFH＝∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO，所以CD=GF得证。

APCDBAFGCEBOD3、如图，已知四边形ABCD 、A 1B 1C 1D 1都是正方形，A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点．求证：四边形A 2B 2C 2D 2是正方形．（初二）4、已知：如图，在四边形ABCD 中，AD ＝BC ，M 、N 分别是AB 、CD 的中点，AD 、BC的延长线交MN 于E 、F ．求证：∠DEN ＝∠F ．经典题（二）1、已知：△ABC 中，H 为垂心（各边高线的交点），O 为外心，且OM ⊥BC 于M ．（1）求证：AH ＝2OM ；（2）若∠BAC ＝600，求证：AH ＝AO ．（初二）D 2 C 2B 2 A 2D 1 C 1 B 1 C B DA A 1 A N FE CDMB · A HEOF2、设MN 是圆O 外一直线，过O 作OA ⊥MN 于A ，自A 引圆的两条直线，交圆于B 、C 及D 、E ，直线EB 及CD 分别交MN 于P 、Q ．求证：AP ＝AQ ．（初二）3、如果上题把直线MN 由圆外平移至圆内，则由此可得以下命题：设MN 是圆O 的弦，过MN 的中点A 任作两弦BC 、DE ，设CD 、EB 分别交MN 于P 、Q ．求证：AP ＝AQ ．（初二）4、如图，分别以△ABC 的AC 和BC 为一边，在△ABC 的外侧作正方形ACDE 和正方形CBFG ，点P 是EF 的中点．求证：点P 到边AB 的距离等于AB 的一半．经典题（三）1、如图，四边形ABCD 为正方形，DE ∥AC ，AE ＝AC ，AE 与CD 相交于F ．求证：CE ＝CF ．（初二）2、如图，四边形ABCD 为正方形，DE ∥AC ，且CE ＝CA ，直线EC 交DA 延长线于F ．求证：AE ＝AF ．（初二）3、设P 是正方形ABCD 一边求证：PA ＝PF ．（初二）4、如图，PC 切圆O 于C ，AC 为圆的直径，PEFB 、D ．求证：AB ＝DC ，BC ＝AD．（初三）经典1、已知：△ABC 是正三角形，P 是三角形内一点，PA ＝3，PB ＝4，求：∠APB 的度数．（初二）2、设P 是平行四边形ABCD 内部的一点，且∠PBA ＝∠PDA ．求证：∠PAB ＝∠PCB ．（初二）3、设ABCD 为圆内接凸四边形，求证：AB ·CD ＋AD ·BC ＝AC ·BD ．（初三）4、平行四边形ABCD 中，设E 、F 分别是BC 、AB 上的一点，AE 与CF 相交于P ，且 AE ＝CF ．求证：∠DPA ＝∠DPC ．（初二）经典难题（五）1、设P 是边长为1的正△ABC 内任一点，L ＝PA ＋PB ＋PC ，求证：≤L ＜2．2、已知：P 是边长为1的正方形ABCD 内的一点，求PA ＋PB ＋PC 的最小值．3、P 为正方形ABCD 内的一点，并且PA ＝a ，PB ＝2a ，PC ＝3a ，求正方形的边长．C BD A F PD E CB A APCBACPDA CBPD4、如图，△ABC中，∠ABC＝∠ACB＝800，D、E分别是AB、AC上的点，∠DCA＝300，∠EBA＝200，求∠BED的度数．经典题（一）1.如下图做GH⊥AB,连接EO。

初二几何试题及答案

初二几何试题及答案1. 已知三角形ABC中，AB=AC，D是BC边上的中点。

求证：AD垂直于BC。

答案：因为AB=AC，所以三角形ABC是等腰三角形。

根据等腰三角形的性质，底边的中线、高线和角平分线重合。

因此，AD既是BC边上的中线，也是高线，所以AD垂直于BC。

2. 一个矩形的长是宽的两倍，且对角线长为10cm。

求矩形的长和宽。

答案：设矩形的宽为x cm，则长为2x cm。

根据勾股定理，对角线的长度满足方程x^2 + (2x)^2 = 10^2。

解得x^2 + 4x^2 = 100，即5x^2 = 100，所以x^2 = 20，x = √20。

因此，矩形的宽为√20 cm，长为2√20 cm。

3. 一个圆的直径是10cm，求这个圆的面积。

答案：圆的面积公式为A = πr^2，其中r是圆的半径。

因为直径是10cm，所以半径r = 10/2 = 5cm。

代入公式得A = π * 5^2 = 25π cm^2。

4. 一个梯形的上底是8cm，下底是12cm，高是5cm。

求梯形的面积。

答案：梯形的面积公式为A = (a + b) * h / 2，其中a和b分别是上底和下底的长度，h是高。

代入数据得A = (8 + 12) * 5 / 2 = 20 * 5 / 2 = 50 cm^2。

5. 已知一个直角三角形的两条直角边分别是6cm和8cm，求斜边的长度。

答案：根据勾股定理，斜边的长度c满足方程c^2 = a^2 + b^2，其中a和b分别是两条直角边的长度。

代入数据得c^2 = 6^2 + 8^2 = 36+ 64 = 100，所以c = √100 = 10cm。

6. 一个正六边形的边长是4cm，求它的面积。

答案：正六边形可以被分成6个等边三角形，每个等边三角形的边长都是4cm。

等边三角形的面积公式为A = (√3 / 4) * a^2，其中a是边长。

因此，正六边形的面积为6 * (√3 / 4) * 4^2 = 6 * √3 * 4 = 24√3 cm^2。

上海数学初二几何试题及答案

上海数学初二几何试题及答案一、选择题（每题3分，共15分）1. 下列几何图形中，属于二次图形的是：A. 圆B. 正方形C. 三角形D. 直线答案：A2. 在直角三角形中，如果一个锐角为30°，那么另一个锐角为：A. 45°B. 60°C. 30°D. 90°答案：B3. 已知一个矩形的长为6cm，宽为4cm，其面积为：A. 20cm²B. 24cm²C. 18cm²D. 12cm²答案：B4. 一个正六边形的内角和为：A. 720°B. 360°C. 540°D. 900°答案：A5. 一个圆的半径为3cm，那么它的周长为：A. 6π cmB. 12π cmC. 18π cmD. 24π cm答案：B二、填空题（每题2分，共10分）1. 在直角三角形中，如果两条直角边分别为3cm和4cm，那么斜边的长度为_______cm。

答案：52. 一个正五边形的外接圆半径为r，则其边长为_______cm。

答案：r√5/23. 如果一个平行四边形的对角线互相平分，那么这个平行四边形是______。

答案：矩形4. 已知一个圆的直径为10cm，那么它的面积为_______cm²。

答案：25π5. 一个三角形的三边长分别为3cm，4cm，5cm，这是一个______三角形。

答案：直角三、解答题（共75分）1. （15分）已知一个等腰三角形的底边长为6cm，两腰边长为5cm，求这个三角形的面积。

解：设等腰三角形的底边为AB，两腰边为AC和BC。

根据勾股定理，我们可以求出高CD的长度：CD² = AC² - AD² = 5² - (6/2)² = 25 - 9 = 16 CD = √16 = 4cm三角形ABC的面积= (1/2) × AB × CD = (1/2) × 6 × 4 =12cm²2. （15分）在一个正方形内，画一个最大的圆，已知正方形的边长为10cm，求这个圆的面积。

初二数学几何试题及答案

初二数学几何试题及答案一、选择题（每题2分，共10分）1. 下列哪个选项不是三角形的内角和？A. 180°B. 360°C. 540°D. 720°2. 如果一个三角形的两条边长分别为3和4，第三边的长度可能为：A. 1B. 5C. 7D. 93. 一个圆的半径为5厘米，那么它的周长是：A. 10π cmB. 20π cmC. 30π cmD. 40π cm4. 一个正方形的对角线长度为10厘米，那么它的边长是：A. 5 cmB. 7.07 cmC. 10 cmD. 14.14 cm5. 一个长方形的长和宽分别是8厘米和6厘米，那么它的面积是：A. 48 cm²B. 36 cm²C. 24 cm²D. 12 cm²二、填空题（每题2分，共10分）6. 一个等腰三角形的底角是45°，那么它的顶角是________度。

7. 如果一个正多边形的每个内角都是120°，那么它是________边形。

8. 一个圆的直径是14厘米，那么它的半径是________厘米。

9. 一个直角三角形的两条直角边分别是3厘米和4厘米，那么它的斜边长是________厘米。

10. 如果一个平行四边形的对角线互相平分，那么它是一个________。

三、计算题（每题10分，共20分）11. 一个正六边形的边长为2厘米，求它的周长和面积。

12. 已知一个圆的半径为7厘米，求它的面积和周长。

四、解答题（每题15分，共30分）13. 在一个等边三角形ABC中，点D是边AB上的一点，且AD=2，BD=1。

求∠ADC的度数。

14. 一个圆的半径为10厘米，圆心到一个点P的距离为8厘米，求点P到圆上任意一点的距离的最大值和最小值。

答案：一、选择题1. B2. B3. B4. B5. A二、填空题6. 907. 68. 79. 510. 矩形三、计算题11. 周长：2×6=12厘米；面积：(3√3)×2²=12√3平方厘米。

初二数学几何证明题（5篇可选）

初二数学几何证明题（5篇可选）第一篇：初二数学几何证明题1.在△ABC中，AB=AC，D在AB上，E在AC的延长线上，且BD=CE，线段DE交BC于点F，说明：DF=EF。

2.已知：在正方形ABCD中，M是AB的中点，E是AB延长线上的一点，MN垂直DM于点M，且交∠CBE的平分线于点N.（1）求证：MD＝MN.（2）若将上述条件中的“M是AB的中点”改为“M 是AB上任意一点”其余条件不变，则（1）的结论还成立吗？如果成立，请证明，如果不成立，请说明理由。

3.。

如图，点E,F分别是菱形ABCD的边CD和CB延长线上的点，且DE=BF，求证∠E=∠F。

4，如图，在△ABC中，D,E,F,分别为边AB,BC,CA,的中点，求证四边形DECF为平行四边形。

5.如图，在菱形ABCD中，∠DAB=60度，过点C作CE垂直AC 且与AB的延长线交与点E，求证四边形AECD是等腰梯形？6.如图，已知平行四边形ABCD中，对角线AC,BD，相交与点0，E是BD延长线上的点，且三角形ACE是等边三角形。

1.求证四边形ABCD是菱形。

2.若∠AED=2∠EAD，求证四边形ABCD是正方形。

7.已知正方形ABCD中，角EAF=45度，F点在CD边上，E点在BC边上。

求证：EF=BE+DF第二篇：初二几何证明题1如图，在△ABC中，D是BC边上的一点，E是AD的中点，过点A作BC的平行线交BE的延长线于F，且AF=DCCF．（1）求证：D是BC的中点；（2）如果AB=ACADCF的形状，并证明你的结论AEB第三篇：初二几何证明题初二几何证明题1.已知：如图，在△ABC中，AD⊥BC，垂足为D，BE⊥AC，垂足为E。

M为AB中点，联结ME,MD、ED求证：角EMD=2角DAC证明：∵M为AB边的中点，AD⊥BC，BE⊥AC，∴MD=ME=MA=MB(斜边上的中线=斜边的一半)∴△MED为等腰三角形∵ME=MA∴∠MAE=∠MEA∴∠BME=2∠MAE∵MD=MA∴∠MAD=∠MDA,∴∠BMD=2∠MAD,∵∠EMD=∠BME-∠BMD=2∠MAE-2∠MAD=2∠DAC2.如图，已知四边形ABCD中，AD=BC,E、F分别是AB、CD中点，AD、BC的延长线与EF的延长线交于点H、D求证：∠AHE=∠BGE证明：连接AC，作EM‖AD交AC于M，连接MF.如下图：∵E是CD的中点，且EM‖AD，∴EM=1/2AD，M是AC的中点，又因为F是AB的中点∴MF‖BC，且MF=1/2BC.∵AD=BC，∴EM=MF，三角形MEF为等腰三角形，即∠MEF=∠MFE.∵EM‖AH，∴∠MEF=∠AHF ∵FM‖BG，∴∠MFE=∠BGF∴∠AHF=∠BGF.3.写出“等腰三角形两底角的平分线相等”的逆命题，并证明它是一个真命题这是经典问题,证明方法有很多种,对于初二而言,下面的反证法应该可以接受如图,已知BD平分∠ABC,CE平分∠ACB,BD=CE,求证:AB=AC证明:BD平分∠ABC==>BE/AE=BC/AC==>BE/AB=BC/(BC+AC)==>BE=AB*BC/(BC+AC)同理:CD=AC*BC/(BC+AB)假设AB≠AC,不妨设AB>AC.....(*)AB>AC==>BC+ACAC*BC==>AB*AB/(BC+AC)>AC*BC/(BC+AB)==>BE>CDAB>AC==>∠ACB>∠ABC∠BEC=∠A+∠ACB/2,∠BDC=∠A+∠ABC/2==>∠BEC>∠BDC过B作CE平行线,过C作AB平行线,交于F,连DF则BECF为平行四边形==>∠BFC=∠BEC>∠BDC (1)BF=CE=BD==>∠BDF=∠BFDCF=BE>CD==>∠CDF>∠CFD==>∠BDF+∠CDF>∠BFD+∠CFD==>∠BDC>∠BFC (2)(1)(2)矛盾,从而假设(*)不成立所以AB=AC。

几何题目初二数学3篇

几何题目初二数学题目1：求扇形的面积扇形是一个常见的几何图形，它由一个圆心和两条半径组成，圆心角的度数决定了扇形的大小。

我们可以通过以下公式来求解一个扇形的面积：S = (θ / 360) × πr^2其中，θ代表圆心角的度数，r代表扇形的半径，π是一个常数，约等于3.14。

举个例子，如果一个扇形的半径为5cm，圆心角的度数为60°，那么它的面积应该为：S = (60 / 360) × 3.14 × 5^2 ≈ 13.09(cm^2)注意：在使用这个公式时，需要将度数换算成弧度，即用角度×π/180来计算角度的弧度值。

例如60°的弧度值应该是60×π/180=π/3。

题目2：求直角三角形的斜边长度直角三角形是一个有一条直角边的三角形，我们可以利用勾股定理来求解它的斜边长度。

勾股定理指出：在一个直角三角形中，直角边的两个平方和等于斜边的平方，即a^2+b^2=c^2。

（其中a和b分别为直角边，c为斜边）例如，如果一个直角三角形的直角边长度分别为3cm和4cm，那么它的斜边长度应该为：c = √(3^2 + 4^2) ≈ 5(cm)注意：在使用勾股定理时，必须要保证直角边的长度已知，且只能求解斜边长度，不能求解其他两个角或两个边的长度。

题目3：求圆柱的表面积和体积圆柱是一个由一个圆形底面和一个长方形侧面组成的几何体，我们可以通过以下公式来求解一个圆柱的表面积和体积：表面积S = 2πr^2 + 2πrh体积V = πr^2h其中，r代表圆柱的半径，h代表圆柱的高，π是一个常数，约等于3.14。

举个例子，如果一个圆柱的半径为3cm，高为5cm，那么它的表面积应该为：S = 2π×3^2 + 2π×3×5 ≈ 113.1(cm^2)它的体积应该为：V = π×3^2×5 ≈ 141.3(cm^3)注意：在使用这些公式时，需要将所有的长度单位统一转换成同一单位，例如上述例子中，半径和高都是用厘米表示，因此得到的表面积和体积单位也是厘米的平方和立方。

(完整版)八年级数学几何经典题【含答案】

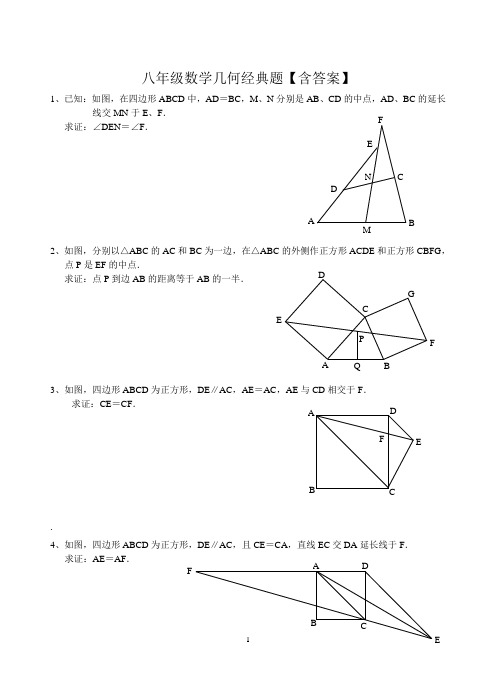
F八年级数学几何经典题【含答案】1、已知：如图，在四边形ABCD 中，AD ＝BC ，M 、N 分别是AB 、CD 的中点，AD 、BC 的延长线交MN 于E 、F ．求证：∠DEN ＝∠F ．2、如图，分别以△ABC 的AC 和BC 为一边，在△ABC 的外侧作正方形ACDE 和正方形CBFG ，点P 是EF 的中点．求证：点P 到边AB 的距离等于AB 的一半．3、如图，四边形ABCD 为正方形，DE ∥AC ，AE ＝AC ，AE 与CD 相交于F ．求证：CE ＝CF ．.4、如图，四边形ABCD 为正方形，DE ∥AC ，且CE ＝CA ，直线EC 交DA 延长线于F ．求证：AE ＝AF ．B5、设P 是正方形ABCD 一边BC 上的任一点，PF ⊥AP ，CF 平分∠DCE ．求证：PA ＝PF ．6、平行四边形ABCD 中，设E 、F 分别是BC 、AB 上的一点，与CF 相交于P ，且 AE ＝CF ．求证：∠DPA ＝∠DPC ．7如图，△ABC 中，∠C 为直角，∠A=30°，分别以AB 、AC 为边在△ABC 的外侧作正△ABE 与正△ACD ，DE 与AB 交于F 。

求证：EF=FD 。

8如图，正方形ABCD 中，E 、F 分别为AB 、BC 的中点，EC 和DF 相交于G ，连接AG ，求证：AG=AD 。

9、已知在三角形ABC 中,AD 是BC 边上的中线,E 是AD 上的一点,且BE=AC,延长BE 交AC 与F,求证AF=EFD FEP CB AFPDE CBA，九年级数学【答案】1.如下图连接AC 并取其中点Q ，连接QN 和QM ，所以可得∠QMF=∠F ，∠QNM=∠DEN 和∠QMN=∠QNM ，从而得出∠DEN ＝∠F 。

2.过E,C,F 点分别作AB 所在直线的高EG ，CI ，FH 。

可得PQ=2EGFH。

由△EGA ≌△AIC ，可得EG=AI ，由△BFH ≌△CBI ，可得FH=BI 。

初二数学几何试题及答案

初二数学几何试题及答案一、选择题（每题3分，共30分）1. 下列哪个选项是直角三角形的判定条件？A. 两角之和为90°B. 两边之和大于第三边C. 斜边的平方等于两直角边的平方和D. 任意两边之和大于第三边2. 一个圆的半径是5厘米，那么它的直径是：A. 10厘米B. 15厘米C. 20厘米D. 25厘米3. 如果一个三角形的三个内角分别为40°、60°和80°，那么这个三角形是：A. 直角三角形B. 钝角三角形C. 锐角三角形D. 不能确定4. 一个矩形的长是10厘米，宽是6厘米，那么它的面积是：A. 60平方厘米B. 100平方厘米C. 120平方厘米D. 150平方厘米5. 一个等腰三角形的底边长为8厘米，腰长为5厘米，那么它的高是：A. 3厘米B. 4厘米C. 6厘米D. 8厘米6. 一个正方形的对角线长度为10厘米，那么它的边长是：A. 5厘米B. 7.07厘米C. 8厘米D. 10厘米7. 一个梯形的上底是4厘米，下底是8厘米，高是6厘米，那么它的面积是：A. 12平方厘米B. 24平方厘米C. 30平方厘米D. 40平方厘米8. 一个平行四边形的对角线互相垂直，那么这个平行四边形是：A. 矩形B. 菱形C. 正方形D. 梯形9. 一个正五边形的内角和是：A. 540°B. 720°C. 900°D. 1080°10. 一个圆的周长是62.8厘米，那么它的半径是：A. 10厘米B. 11厘米C. 12厘米D. 13厘米二、填空题（每题4分，共20分）1. 如果一个三角形的两个内角分别为30°和60°，那么第三个内角是______°。

2. 一个圆的周长是31.4厘米，那么它的直径是______厘米。

3. 一个直角三角形的两条直角边长分别为3厘米和4厘米，那么它的斜边长是______厘米。

八年级数学几何题目

八年级数学几何题目一、三角形相关（1 - 10题）题1：在△ABC中，∠A = 50°，∠B = 60°，求∠C的度数。

解析：根据三角形内角和为180°，所以∠C=180° - ∠A - ∠B = 180°- 50° - 60° = 70°。

题2：已知等腰三角形的一个底角为40°，求这个等腰三角形的顶角的度数。

解析：等腰三角形两底角相等，所以另一个底角也是40°。

根据三角形内角和为180°，顶角的度数为180° - 40°×2 = 180° - 80° = 100°。

题3：三角形三边分别为3，4，x。

若该三角形是直角三角形，求x的值。

解析：当x为斜边时，根据勾股定理x=√(3^2)+ 4^{2}=√(9 + 16)=√(25) = 5；当4为斜边时，x=√(4^2)-3^{2}=√(16 - 9)=√(7)。

所以x的值为5或√(7)。

题4：在△ABC中，AB = AC，AD是BC边上的中线，若AB = 10，BC = 12，求AD的长。

因为AB = AC，AD是中线，所以AD⊥BC，BD = BC÷2 = 12÷2 = 6。

在直角三角形ABD中，根据勾股定理AD=√(A B^2)-BD^{2}=√(10^2)-6^{2}=√(100 - 36)=√(64) = 8。

题5：一个三角形的三条高的交点恰是三角形的一个顶点，则这个三角形是（）A. 锐角三角形。

B. 直角三角形。

C. 钝角三角形。

D. 以上都有可能。

解析：直角三角形的三条高的交点是直角顶点，锐角三角形三条高的交点在三角形内部，钝角三角形三条高所在直线的交点在三角形外部。

所以答案是B。

题6：如图，在△ABC中，∠ACB = 90°，CD是高，∠A = 30°，AB = 4，求BD的长。

初二上册数学几何试题(附答案)

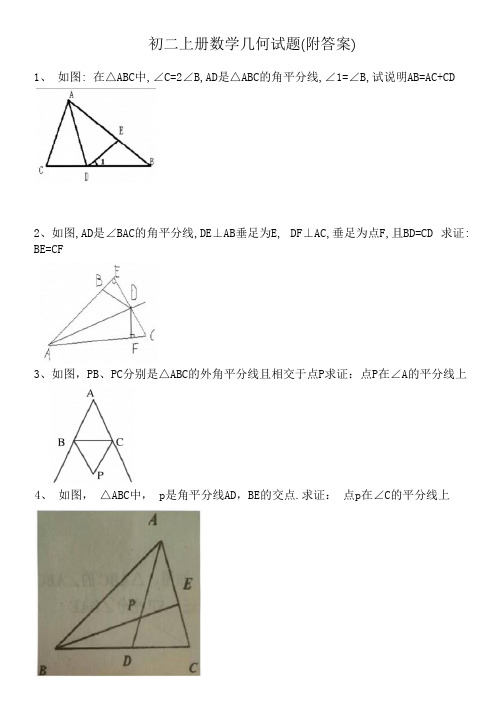
初二上册数学几何试题(附答案)1、如图: 在△ABC中,∠C=2∠B,AD是△ABC的角平分线,∠1=∠B,试说明AB=AC+CD2、如图,AD是∠BAC的角平分线,DE⊥AB垂足为E, DF⊥AC,垂足为点F,且BD=CD 求证: BE=CF3、如图，PB、PC分别是△ABC的外角平分线且相交于点P求证：点P在∠A的平分线上4、如图，△ABC中， p是角平分线AD，BE的交点.求证：点p在∠C的平分线上5、下列说法中，错误的是( )A. 三角形任意两个角的平分线的交点在三角形的内部B. 三角形两个角的平分线的交点到三边的距离相等C. 三角形两个角的平分线的交点在第三个角的平分线上D. 三角形任意两个角的平分线的交点到三个顶点的距离相等6、如图在三角形ABC 中BM=MC∠ABM=∠ACM 求证 AM平分∠BAC7、如图, AP、CP分别是△ABC外角∠MAC与∠NCA的平分线, 它们相交于点P, PD⊥BM 于点D, PF⊥BN于点F. 求证: BP为∠MBN的平分线。

8、如图,在∠AOB的两边OA, OB上分别取 OM=ON, OD=OE, DN 和EM 相交于点C. 求证: 点C在∠AOB的平分线上.9、如图, ∠B=∠C=90° , M是BC的中点, DM平分∠ADC.(1)若连接AM，则AM是否平分∠BAD?请你证明你的结论；(2)线段 DM与AM有怎样的位置关系?请说明理由.参考答案：1、因为∠1=∠B所以∠DEA=2∠B=∠C因为 AD是△ABC的角平分线所以∠CAD=∠EAD 因为 AD=AD所以△ADC 全等于△ADE 所以 AC=AE CD=DE 因为∠1=∠B 所以△EDB 为等腰三角形所以 EB=DE 因为 AB=AE+EB AC=AE CD=DE EB=DE所以 AB=AC+CD2、因为 ad是∠bac的角平分线, ,DE⊥AB, DF⊥AC, 所以DE=DF三角形DEB和三角形DFC均为直角三角形,又因为 BD=CD 所以BE=CF3、作PF⊥AD, PH⊥BC, PG⊥AE∵PB 平分∠DBC, PC平分∠ECB, PF⊥AD, PH⊥BC, PG⊥AE∴PF=PH，PG=PH(角平分线上的点到这个角的两边的距离相等)∴PF=PG∵PF⊥AD, PG⊥AE, PF=PG∴PA平分∠BAC(在一个角的内部，且到角的两边距离相等的点，在这个角的平分线上)4、作PG⊥BC,PH⊥AC,PQ⊥AB,垂足分别为G、H、Q,AD为∠A的平分线,PH=PQ;BE为∠B 的平分线, PQ=PG;所以PG=PH,又CP为RT△CGP和RT△CEP的公共斜边,所以△CGP≌△CHP,所以∠GCP=∠ECP,CP为∠的平分线，P点在∠C的平分线上5、 A6、∵BM=MC, ∴∠MBC=∠MCB, ∵∠ABM=∠ACM, ∴∠ABM+∠MBC=∠ACM+∠MCB, 即∠ABC=∠ACB,∴AB=AC, 在△AMB与△AMC中, AB=AC, ∠ABM=∠ACM, MB=MC, ∴△AMB≌△AMC(SAS),∴ ∠MAB=∠MAC, 即AM平分∠BAC。

初中数学经典几何题(难)及答案分析

经典难题（一）1、已知：如图，O 是半圆的圆心，C 、E 是圆上的两点，CD ⊥AB ，EF ⊥AB ，EG ⊥CO ．求证：CD ＝GF ．（初二）2、已知：如图，P 是正方形ABCD 内点，∠PAD ＝∠PDA ＝150．求证：△PBC 是正三角形．（初二）3、如图，已知四边形ABCD 、A 1B 1C 1D 1都是正方形，A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点．求证：四边形A 2B 2C 2D 2是正方形．（初二）4、已知：如图，在四边形ABCD 中，AD ＝BC ，M 、N 分别是AB 、CD 的中点，AD 、BC的延长线交MN 于E 、F ．求证：∠DEN ＝∠F ．A P C DB A FG CE BO D D 2 C 2B 2 A 2D 1 C 1 B 1C B DA A 1 BF1、已知：△ABC 中，H 为垂心（各边高线的交点），O（1）求证：AH ＝2OM ；（2）若∠BAC ＝600，求证：AH ＝AO ．（初二）2、设MN 是圆O 外一直线，过O 作OA ⊥MN 于A ，自A 及D 、E ，直线EB及CD 分别交MN 于P 、Q ．求证：AP ＝AQ ．（初二）3、如果上题把直线MN 由圆外平移至圆内，则由此可得以下命题：设MN 是圆O 的弦，过MN 的中点A 任作两弦BC 、DE 于P 、Q ．求证：AP ＝AQ ．（初二）4、如图，分别以△ABC 的AC 和BC 为一边，在△ABC 的外侧作正方形ACDE 和正方形CBFG ，点P 是EF 的中点．求证：点P 到边AB 的距离等于AB 的一半．1、如图，四边形ABCD 为正方形，DE ∥AC ，AE ＝AC ，AE 与CD 相交于F ．求证：CE ＝CF ．（初二）2、如图，四边形ABCD 为正方形，DE ∥AC ，且CE ＝CA ，直线EC 交DA 延长线于F ．求证：AE ＝AF ．（初二）3、设P 是正方形ABCD 一边BC 上的任一点，PF ⊥AP ，CF 平分∠DCE ．求证：PA ＝PF ．（初二）4、如图，PC 切圆O 于C ，AC 为圆的直径，PEF 为圆的割线，AE 、AF 与直线PO 相交于B 、D ．求证：AB ＝DC ，BC ＝AD ．（初三）1、已知：△ABC 是正三角形，P 是三角形内一点，PA ＝3，PB ＝4，PC ＝5．求：∠APB 的度数．（初二）2、设P 是平行四边形ABCD 内部的一点，且∠PBA ＝∠PDA ．求证：∠PAB ＝∠PCB ．（初二）3、设ABCD 为圆内接凸四边形，求证：AB ·CD ＋AD ·BC ＝AC ·BD ．（初三）4、平行四边形ABCD 中，设E 、F 分别是BC 、AB 上的一点，AE 与CF 相交于P ，且 AE ＝CF ．求证：∠DPA ＝∠DPC ．（初二）1、设P 是边长为1的正△ABC 内任一点，L ＝PA ＋PB ＋PC ，求证：≤L ＜2．2、已知：P 是边长为1的正方形ABCD 内的一点，求PA ＋PB ＋PC 的最小值．3、P 为正方形ABCD 内的一点，并且PA ＝a ，PB ＝2a ，PC ＝3a ，求正方形的边长．4、如图，△ABC 中，∠ABC ＝∠ACB ＝800，D 、E 分别是AB 、AC 上的点，∠DCA ＝300，∠EBA ＝200，求∠BED 的度数．AP CB ACBPDEDCB A A CBPD1.如下图做GH⊥AB,连接EO。

2024年数学八年级上册几何基础练习题(含答案)

2024年数学八年级上册几何基础练习题（含答案）试题部分一、选择题1. 在一个等腰三角形中，如果底边长为10cm，腰长为13cm，那么这个三角形的周长是多少？A. 26cmB. 36cmC. 46cmD. 56cm2. 一个直角三角形的两个锐角分别是30度和60度，如果斜边长为20cm，那么直角边长是多少？A. 10cmB. 10√3 cmC. 20cmD. 20√3 cm3. 一个圆的半径为5cm，那么它的直径是多少？A. 2.5cmB. 5cmC. 10cmD. 20cm4. 一个正方形的对角线长为10cm，那么它的边长是多少？B. 10cmC. 10√2 cmD. 20cm5. 一个等边三角形的边长为6cm，那么它的高是多少？A. 3cmB. 3√3 cmC. 6cmD. 6√3 cm6. 一个长方形的长是宽的两倍，如果长方形的周长是30cm，那么长和宽分别是多少？A. 长为15cm，宽为7.5cmB. 长为10cm，宽为5cmC. 长为20cm，宽为10cmD. 长为12cm，宽为6cm7. 一个圆的周长是31.4cm，那么它的半径是多少？A. 5cmB. 10cmC. 15cmD. 20cm8. 一个正方形的面积是36cm²，那么它的边长是多少？A. 6cmB. 9cmC. 12cm9. 一个等腰三角形的底边长为8cm，腰长为10cm，那么这个三角形的周长是多少？A. 16cmB. 20cmC. 24cmD. 28cm10. 一个直角三角形的两个锐角分别是45度和45度，如果斜边长为10cm，那么直角边长是多少？A. 5cmB. 5√2 cmC. 10cmD. 10√2 cm二、判断题1. 一个圆的半径是直径的一半。

（）2. 一个等腰三角形的底边和腰的长度相等。

（）3. 一个直角三角形的两个锐角之和是90度。

（）4. 一个正方形的对角线长等于边长的两倍。

（）5. 一个等边三角形的高等于边长的根号3倍。

初二上册数学几何题

初二上册数学几何题【例一】如图，△ABC中，∠C为直角，∠A=30°，分别以AB、AC为边在△ABC 的外侧作正△ABE与正△ACD，DE与AB交于F。

求证：EF=FD。

证明：过D作D G//A B交E A的延长线于G，可得∠D A G=30°∵∠B A D=30°＋60°=90°∴∠A D G=90°∵∠D A G=30°=∠C A B，A D=A C∴R t△A GD≌R t△A B C∴A G=A B，∴A G=A E∵D G//A B∴E F//F D【例二】如图，正方形A B C D中，E、F分别为A B、B C的中点，E C和D F相交于G，连接A G，求证：A G=A D。

证明：作D A、C E的延长线交于H∵A B C D是正方形，E是A B的中点∴A E=B E，∠A E H=∠B E C,∠B E C=∠E A H=90°∴△A E H≌△B E C（A SA）∴A H=B C，A D=A H又∵F是B C的中点∴R t△D F C≌R t△C E B∴∠D F C=∠C E B∴∠G C F＋∠GF C=∠E C B＋∠C E B=90°∴∠C GF=90°∴∠D GH=∠C G F=90°∴△D G H是R t△∵A D=A H∴A G=1/2D H=A D【例三】已知在三角形A B C中,A D是B C边上的中线,E是A D上的一点,且B E=A C,延长B E交A C与F,求证A F=E F证明：如图连接E C,取E C的中点G,A E的中点H，连接D G,H G则：G H=D G∴角1=∠2，而∠1=∠4，∠2=∠3=∠5∴∠4=∠5，∴A F=E F.【例四】如图，四边形A B C D为正方形，D E∥A C，A E＝A C，A E 与C D相交于F．求证：C E＝C F．顺时针旋转△A D E，到△A B G，连接C G.由于∠A B G=∠A D E=90°+45°=13°从而可得B，G，D在一条直线上，可得△A G B≌△C GB推出A E=A G=A C=G C，可得△A G C为等边三角形。

初二数学上几何试题及答案

初二数学上几何试题及答案一、选择题（每题2分，共10分）1. 下列哪个选项不是正多边形的内角和的计算公式？A. $ (n-2) \times 180^\circ $B. $ n \times 180^\circ $C. $ 360^\circ $D. $ 720^\circ $答案：C2. 在一个正三角形中，每个内角的度数是多少？A. $ 30^\circ $B. $ 60^\circ $C. $ 90^\circ $D. $ 120^\circ $答案：B3. 一个圆的半径是5厘米，那么它的直径是多少厘米？A. 10厘米B. 15厘米C. 20厘米D. 25厘米答案：A4. 一个正方形的周长是16厘米，那么它的边长是多少厘米？A. 4厘米B. 8厘米C. 16厘米D. 32厘米答案：A5. 如果一个圆的面积是28.26平方厘米，那么它的半径是多少厘米？A. 3厘米B. 4厘米C. 5厘米D. 6厘米答案：B二、填空题（每题2分，共10分）6. 一个正六边形的内角和是________。

答案：720°7. 一个圆的周长是其直径的________倍。

答案：π8. 如果一个矩形的长是8厘米，宽是5厘米，那么它的面积是________平方厘米。

答案：409. 直角三角形的两个锐角的和是________度。

答案：90°10. 一个等边三角形的每个内角都是________度。

答案：60°三、解答题（每题10分，共30分）11. 已知一个圆的半径是7厘米，求它的周长和面积。

答案：周长 = $ 2 \times 7 \times \pi = 14\pi $ 厘米，面积 = $ \pi \times 7^2 = 49\pi $ 平方厘米。

12. 一个矩形的长是15厘米，宽是10厘米，求它的对角线长度。

答案：对角线长度 = $ \sqrt{15^2 + 10^2} = \sqrt{225 + 100} = \sqrt{325} $ 厘米。

初二数学经典几何题型及答案

F初二数学经典几何题型1．已知：如图，P 是正方形ABCD 内点，∠PAD＝∠PDA＝150．求证：△PBC 是正三角形．证明如下。

首先，PA=PD ，∠PAD=∠PDA=（180°-150°）÷2=15°，∠PAB=90°-15°=75°。

在正方形ABCD 之外以AD 为底边作正三角形ADQ ，连接PQ ，则∠PDQ=60°+15°=75°，同样∠PAQ=75°，又AQ=DQ,，PA=PD ，所以△PAQ≌△PDQ，那么∠PQA=∠PQD=60°÷2=30°，在△PQA 中，∠APQ=180°-30°-75°=75°=∠PAQ=∠PAB，于是PQ=AQ=AB ，显然△PAQ≌△PAB，得∠PBA=∠PQA=30°，PB=PQ=AB=BC ，∠PBC=90°-30°=60°，所以△PBC 是正三角形。

2.已知：如图，在四边形ABCD 中，AD ＝BC ，M 、N 分别是AB 、CD 的中点，AD 、BC 的延长线交MN 于E 、F ．求证：∠DEN＝∠F．证明:连接AC,并取AC 的中点G,连接GF,GM.又点N 为CD 的中点,则GN=AD/2;GN∥AD,∠GNM=∠DEM;(1)同理:GM=BC/2;GM∥BC,∠GMN=∠CFN;(2)又AD=BC,则:GN=GM,∠GNM=∠GMN.故:∠DEM=∠CFN.3、如图，分别以△ABC 的AC 和BC 为一边，在△ABC 的外侧作正方形ACDE 和正方形CBFG ，点P 是EF 的中点．求证：点P 到边AB 的距离等于AB 的一半．证明：分别过E 、C 、F 作直线AB 的垂线，垂足分别为M 、O 、N ，在梯形MEFN 中，WE 平行NF因为P 为EF 中点，PQ 平行于两底所以PQ 为梯形MEFN 中位线，所以PQ ＝（ME ＋NF ）/2又因为，角0CB ＋角OBC ＝90°＝角NBF ＋角CBO 所以角OCB=角NBF而角C0B ＝角Rt ＝角BNF CB=BF所以△OCB全等于△NBF△MEA全等于△OAC（同理）所以EM＝AO，0B＝NF所以PQ=AB/2.4、设P是平行四边形ABCD内部的一点，且∠PBA＝∠PDA．求证：∠PAB＝∠PCB．过点P作DA的平行线，过点A作DP的平行线，两者相交于点E；连接BE因为DP//AE，AD//PE所以，四边形AEPD为平行四边形所以，∠PDA=∠AEP已知，∠PDA=∠PBA所以，∠PBA=∠AEP所以，A、E、B、P四点共圆所以，∠PAB=∠PEB因为四边形AEPD为平行四边形，所以：PE//AD，且PE=AD而，四边形ABCD为平行四边形，所以：AD//BC，且AD=BC所以，PE//BC，且PE=BC即，四边形EBCP也是平行四边形所以，∠PEB=∠PCB所以，∠PAB=∠PCB5.P为正方形ABCD内的一点，并且PA＝a，PB＝2a，PC=3a正方形的边长．解：将△BAP绕B点旋转90°使BA与BC重合，P点旋转后到Q点，连接PQ因为△BAP≌△BCQ所以AP＝CQ，BP＝BQ，∠ABP＝∠CBQ，∠BPA＝∠BQC因为四边形DCBA是正方形所以∠CBA＝90°，所以∠ABP＋∠CBP＝90°，所以∠CBQ＋∠CBP＝90°即∠PBQ＝90°，所以△BPQ是等腰直角三角形所以PQ＝√2*BP，∠BQP＝45因为PA=a，PB=2a，PC=3a所以PQ＝2√2a，CQ＝a，所以CP^2＝9a^2，PQ^2＋CQ^2＝8a^2＋a^2＝9a^2所以CP^2＝PQ^2＋CQ^2，所以△CPQ是直角三角形且∠CQA＝90°所以∠BQC＝90°＋45°＝135°，所以∠BPA＝∠BQC＝135°作BM⊥PQ则△BPM是等腰直角三角形所以PM＝BM＝PB/√2＝2a/√2＝√2a所以根据勾股定理得：AB^2＝AM^2＋BM^2＝(√2a＋a)^2＋(√2a)^2＝[5＋2√2]a^2所以AB＝[√(5＋2√2)]a6.一个圆柱形容器的容积为V 立方米，开始用一根小水管向容器内注水，水面高度达到容器高度一半后，改用一根口径为小水管２倍的大水管注水。

初二数学上册：几何问题专项训练

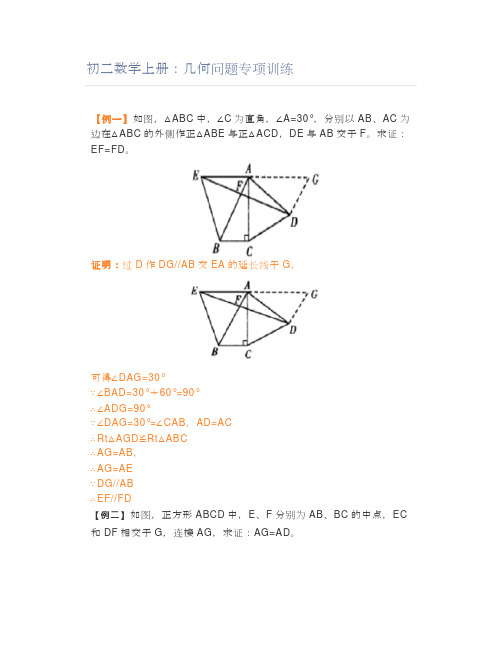
初二数学上册：几何问题专项训练【例一】如图，△ABC中，∠C为直角，∠A=30°，分别以AB、AC为边在△ABC的外侧作正△ABE与正△ACD，DE与AB交于F。

求证：EF=FD。

证明：过D作DG//AB交EA的延长线于G，可得∠DAG=30°∵∠BAD=30°＋60°=90°∴∠ADG=90°∵∠DAG=30°=∠CAB，AD=AC∴Rt△AGD≌Rt△ABC∴AG=AB，∴AG=AE∵DG//AB∴EF//FD【例二】如图，正方形ABCD中，E、F分别为AB、BC的中点，EC 和DF相交于G，连接AG，求证：AG=AD。

证明：作DA、CE的延长线交于H∵ABCD是正方形，E是AB的中点∴AE=BE，∠AEH=∠BEC,∠BEC=∠EAH=90°∴△AEH≌△BEC（ASA）∴AH=BC，AD=AH又∵F是BC的中点∴Rt△DFC≌Rt△CEB∴∠DFC=∠CEB∴∠GCF＋∠GFC=∠ECB＋∠CEB=90°∴∠CGF=90°∴∠DGH=∠CGF=90°∴△DGH是Rt△∵AD=AH∴AG=1/2DH=AD【例三】已知在三角形ABC中,AD是BC边上的中线,E是AD上的一点,且BE=AC,延长BE交AC与F,求证AF=EF证明：如图连接EC,取EC的中点G,AE的中点H，连接DG,HG则：GH=DG∴角1=∠2，而∠1=∠4，∠2=∠3=∠5∴∠4=∠5，∴AF=EF.【例四】如图，四边形ABCD为正方形，DE∥AC，AE＝AC，AE与CD相交于F．求证：CE＝CF．顺时针旋转△ADE，到△ABG，连接CG.由于∠ABG=∠ADE=90°+45°=13°从而可得B，G，D在一条直线上，可得△AGB≌△CGB推出AE=AG=AC=GC，可得△AGC为等边三角形。