理论力学计算题复习
理论力学复习题及答案(计算题部分)
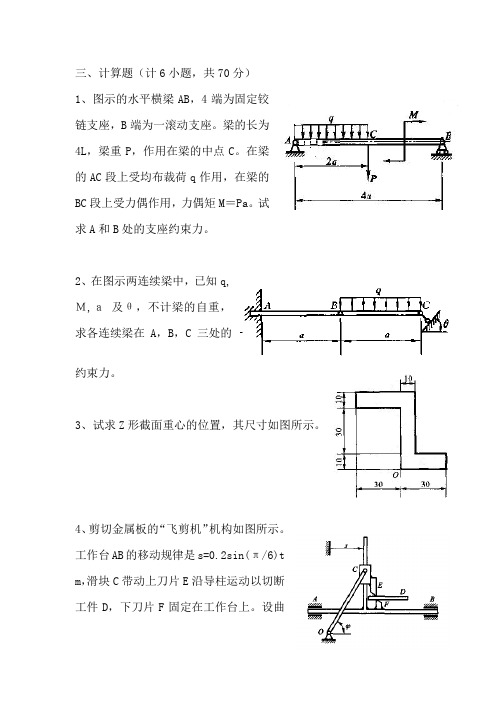
三、计算题(计6小题,共70分)1、图示的水平横梁AB,4端为固定铰链支座,B端为一滚动支座。
梁的长为4L,梁重P,作用在梁的中点C。
在梁的AC段上受均布裁荷q作用,在梁的BC段上受力偶作用,力偶矩M=Pa。
试求A和B处的支座约束力。
2、在图示两连续梁中,已知q,M,a及θ,不计梁的自重,求各连续梁在A,B,C三处的约束力。
3、试求Z形截面重心的位置,其尺寸如图所示。
4、剪切金属板的“飞剪机”机构如图所示。
工作台AB的移动规律是s=0.2sin(π/6)tm,滑块C带动上刀片E沿导柱运动以切断工件D,下刀片F固定在工作台上。
设曲柄OC=0.6m,t=1 s时,φ=60 º。
求该瞬时刀片E相对于工作台运动的速度和加速度,并求曲柄OC转动的角速度及角加速度。
5、如图所示,在筛动机构中,筛子的摆动是由曲柄连杆机构所带动。
已知曲柄OA的转速n OA=40 r/min,OA=0.3 m。
当筛子BC运动到与点O在同一水平线上时,∠BAO=90 º。
求此瞬时筛子BC的速度。
6、在图示曲柄滑杆机构中,曲柄以等角速度ω绕 O 轴转动。
开始时,曲柄OA水平向右。
已知:曲柄的质量为m1,沿块4的质量为m2,滑杆的质量为m3,曲柄的质心在OA的中点,OA=l;滑杆的质心在点C。
求:(1)机构质量中心的运动方程;(2)作用在轴O的最大水平约束力。
7、无重水平粱的支承和载荷如题图所示。
已知力F、力偶矩为M的力偶和强度为q的均布载荷。
求支座A和B处的约束力。
8、在图所示两连续梁中,已知M 及a,不计梁的自重,求各连续梁在A ,B ,C 三处的约束力。
9、工宇钢截面尺寸如图所示。
求此截面的几何中心。
10、如图所示,半径为R 的半圆形凸轮D 以等速v 0沿水平线向右运动,带动从动杆AB 沿铅直方向上升,求φ=30º时杆AB 相对于凸轮的速度和加速度。
11、图示机构中,已知: ,OA=BD=DE=0.1m ,曲柄OA 的角速度ω=4rad/s 。
理论力学复习题及答案
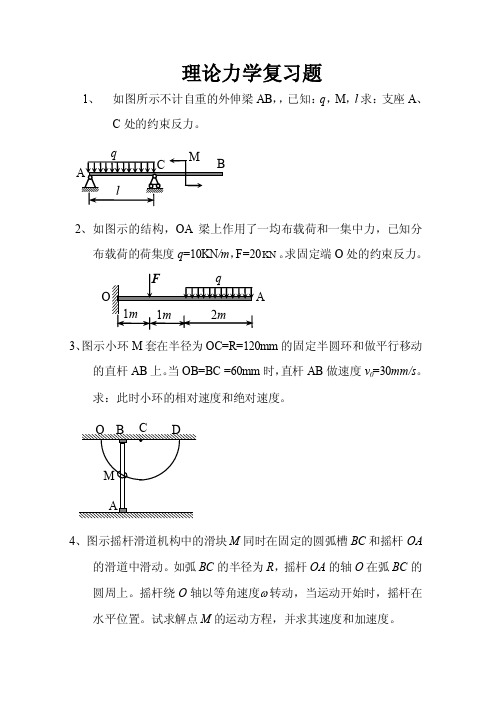
理论力学复习题1、 如图所示不计自重的外伸梁AB ,,已知:q ,M ,l 求:支座A 、C 处的约束反力。
2、如图示的结构,OA 梁上作用了一均布载荷和一集中力,已知分布载荷的荷集度q =10KN /m ,F=20KN 。
求固定端O 处的约束反力。
A3、图示小环M 套在半径为OC=R=120mm 的固定半圆环和做平行移动的直杆AB 上。
当OB=BC =60mm 时,直杆AB 做速度v 0=30mm/s 。
求:此时小环的相对速度和绝对速度。
4、图示摇杆滑道机构中的滑块M 同时在固定的圆弧槽BC 和摇杆OA的滑道中滑动。
如弧BC 的半径为R ,摇杆OA 的轴O 在弧BC 的圆周上。
摇杆绕O 轴以等角速度 转动,当运动开始时,摇杆在水平位置。
试求解点M 的运动方程,并求其速度和加速度。
5、半径为R 的偏心轮绕O 轴以匀角速度ω转动,推动导板沿铅直轨道运动,如图所示。
导板顶部放有一质量为m 的物块A ,设偏心距e OC =,开始时OC沿水平线。
求:(1)物块对导板的最大压力;(2)使物块不离开导板的ω最大值。
6、图示曲柄连杆机构与滑块B 连接。
曲柄OA 和绕O 轴转动。
并且曲柄OA 以等角速度0ω转动。
已知机构的尺寸为:l OA =l AB 3=,系统的每个构件均匀质,且质量都为m ,求:当曲柄OA 处于竖直向上时,系统的动能。
7、半径为R 的半圆形凸轮C 以匀速0v 沿水平面向右运动,带动从动杆AB 沿铅垂上运动,如图所示。
求θ=30o 时,AB 杆的速度。
8、如图所示的曲柄连杆滚轮机构,滚轮B 在水平面上滚而不滑,并且滚轮的轮心B 和OA 杆的转轴O 处于同一水平线上。
已知:OA 杆以匀角速度ω=π rad/s 绕O 转动,OA=0.1m ;滚轮B 的半径为R=0.05m ,当机构运动到图示瞬间θ=600,AB 杆垂直OA 杆。
求:此时AB 杆的角速度ωAB 及滚轮B 的角加速度αB 。
(18分)9、图示机构由长为l 质量为m 的OA 杆和半径为R 质量为2m 圆盘A 焊接而成。
理论力学(上)复习题计算题

一. 计算题1.平面力系向O 点简化,得到主矢N F R 10'=,主矩cm N M o ⋅=10方向如图所示,现将该力系向A 点简化,求主矢和主矩。
2某平面力系向A 、B 两点简化的结果均为一个力和一个力偶,若已知该力系向B点简化的主矢为'B F 、主矩为B M ,且与AB 连线的夹角为︒60,AB=a ,如图所示,求该力系向A 点简化的主矢和主矩。
3已知图示正方体边长为a, 在侧面作用已知力F ,求力系对x 、y 轴的力矩。
4已知A 重100kN ,B 重25kN ,A 物与地面间摩擦系数为0.2。
端铰处摩擦不计。
求物体A 与地面间的摩擦力的大小。
5.五根等长的细直杆铰接成图示杆系结构,各杆重量不计;若A P =C P =P ,且垂直BD 。
求杆BD 的内力。
6.直角刚杆AO = 2m ,BO = 3m ,已知某瞬时A 点的速度 A v = 6m/s ;而B 点的加速度与BO 成α= 60°角。
求该瞬时刚杆的角速度和角加速度。
7平面机构如图所示。
已知AB 平行于21O O ,且AB =21O O =L ,r BO AO ==21,ABCD是矩形板,AD=BC=b ,1AO 杆以匀角速度ω绕1O 轴转动,求矩形板重心1C 点的速度和加速度的大小(在图上标出它们的方向)8.直角曲杆AB O 1以匀角速度1ω绕1O 轴转动,求在图示位置(1AO 垂直21O O )时,摇杆C O 2的角速度。
9.如图所示, P 60kM ,T F =20kN ,A , B 间的静摩擦因数s f =0.5,动摩擦因数f =0.4,求物块A 所受的摩擦力。
10.如图所示,边长为a 2的正方形薄板,截去四分之一后悬挂在A 点,今若使BC 边保持水平,求点A 距右端的距离x11. 图示一正方体,边长为a ,力F 沿AB 作用于A 点,求该力对x 、y 轴之矩。
12. 图示平面桁架结构,求杆1、2的内力。
理论力学复习试题和答案(哈工大版)

C :作用于质点系的约束反力主矢恒等于零; D:作用于质点系的主动力主矢恒等于零;
..
..
6、 若作用在 A 点的两个大小不等的力 F 1 和 F 2,沿同一直
反。则其合力可以表示为
③
。
① F 1- F 2; ② F 2- F 1; ③ F 1+ F 2;
7、 作用在一个刚体上的两个力 F A、 F B,满足 F A=- F B 的条件,则该二力可能是②
( √) (× )
14、 已知质点的质量和作用于质点的力,质点的运动规律就完全确定。
(× )
15、 质点系中各质点都处于静止时,质点系的动量为零。于是可知如果质点
系的动量为零,则质点系中各质点必都静止。
(×)
16、 作 用 在 一 个 物 体 上 有 三 个 力 , 当 这 三 个 力 的 作 用 线 汇 交 于 一 点 时 , 则 此 力 系 必 然 平 衡 。
..
..
..
..
2、图示平面结构,自重不计。 求支座 A 的约束反力。
B 处为铰链联接。已知: P = 100 kN , M = 200 kN · m, L1 = 2m , L2 = 3m 。试
3、 一 水平 简支梁 结 构, 约 束和载 荷如 图 所示 , 求支座
q A
D
M B
E
P C
A和
B 的约束反力。
一、 是非题
1、 力 有 两 种 作 用 效 果 , 即 力 可 以 使 物 体 的 运 动 状 态 发 生 变 化 , 也 可 以 使 物 体 发 生 变 形 。
( √)
2、 在理论力学中只研究力的外效应。
( √)
3、 两端用光滑铰链连接的构件是二力构件。
理论力学计算练习题复习复习.doc

精品 文 档习题1-1 图中设AB=l ,在A 点受四个大小均等于F 的力1F r 、2F r 、3F r 和4F r作用。
试分别计算每个力对B 点之矩。
【解答】:112()sin 452B M F F l F l =-⋅⋅︒=-⋅r22()B M F F l F l =-⋅=-⋅r332()sin 452B M F F l F l =-⋅⋅︒=-⋅r4()0B M F =r。
习题1-2 如图所示正平行六面体ABCD ,重为P F =100N ,边长AB=60cm ,AD=80cm 。
今将其斜放使它的底面与水平面成30ϕ=︒角,试求其重力对棱A 的力矩。
又问当ϕ等于多大时,该力矩等于零。
【解法1——直接计算法】:设AC 与BD 的交点为O ,∠BAO=α,则:cos()cos cos sin sin 33410.11965252αϕαϕαϕ+=-=⨯-⨯= 221806050cm=0.5m 2AO =+=()cos()1000.50.1196 5.98N mA P P P M F F d F AO αϕ=⋅=⨯⨯+=⨯⨯=⋅r当()0A P M F =r 时,重力P F r的作用线必通过A 点,即90αβ+=︒,所以: 令cos()cos cos sin sin 0αϕαϕαϕ+=-=→34cos sin 055ϕϕ⨯-⨯=,得: 3tan 4ϕ=→3652ϕ'=︒。
【解法2——利用合力矩定理】:将重力P F r 分解为两个正交分力1P F r 和2P F r , 其中:1P F AD r P ,2P F AB rP ,则:1cos P P F F ϕ=⨯,2sin P P F F ϕ=⨯根据合力矩定理:1212()()()22cos 0.3sin 0.411000.31000.4 5.98N m 2A P A P A P P P P P AB AD M F M F M F F F F F ϕϕ=+=⨯-⨯=⨯⨯-⨯⨯=-⨯⨯=⋅r r r 确定ϕ等于多大时,()0A P M F =r令()0A P M F =r,即:cos 0.3sin 0.40P P F F ϕϕ⨯⨯-⨯⨯=→100cos 0.3100sin 0.40ϕϕ⨯⨯-⨯⨯=→3tan 4ϕ=→3652ϕ'=︒。
理论力学复习题

表0.2 示(
)。
2、a、b、c三种材料的应力——应变曲线如图所
示。其中强度最高的材料是( ),弹性模量最
小的材料是( ),塑性最好的材料是( )。
第九页,共九十二页。
1、表示塑性应变(yìngbiàn)等于
0.2%时的应力值。
2、a, c, c
• 3、一轴向拉杆(lāgān),横截面为a b的矩形,受
);为使
MC=0,则m=( );为使全梁不出现正弯矩,
则m ( )。
第三十六页,共九十二页。
ql 2 m 82 ql 2 4 ql 2 2
• 试作(shìzuò)图示外伸梁的剪力图和弯矩图,并给 出最大弯矩和最大剪力。
qa 2
q
2a
a
a
第三十七页,共九十二页。
• 选择题:
1、在推导弯曲正应力公式时,由于作了“纵向纤维互 不挤压”假设,从而有以下四种答案,正确的是
综合 复 (zōnghé)
习
第一页,共九十二页。
选择题:
1、关于确定截面(jiémiàn)内力的截面(jiémiàn)法的适 用范围有下列说法:正确D的是( ):
A、适用于等截面杆
B、适用于直杆承受基本变形 C、适用于不论基本变形还是组合变形,但限于直 杆的横截面 D、适用于不论等截面或变截面、直杆或曲杆、基 本变形或组合变形、横截面或任意截面的普遍情 况
( B)。
A、保证法向内力系的合力为零。
第二十五页,共九十二页。
答案(dá àn): C
• 4、材料不同的两根 受扭圆轴,其直径和 长度均相同 , (xiānɡ tónɡ) 在扭矩相同 的 (xiānɡ tónɡ) 情况下,他们的最大 切应力之间和扭转角 之间的关系正确的是 ( )。
理论力学复习题(答案)

理论力学复习题一、填空题1、力对物体的作用效果一般分为力的外效应和力的内效应。
2、作用在刚体上的力可沿其作用线任意移动,而不改变该力对刚体的作用效果。
3、质点动力学的三个基本定律:惯性定律、力与加速度之间的关系定律、作用力与反作用力定律4、质点系动能定理建立了质点系动能的改变量和作用力的功之间的关系。
5、一对等值、反向、不共线的平行力组成的特殊力系,称为力偶6、两个或两个以上力偶的组合称为力偶系。
7、力矩与矩心的位置有关,力偶矩与矩心的位置无关。
8、物体质量的改变与发生这种改变所用合外力的比值叫做加速度。
9、力的三要素为大小、方向和作用点。
10、物体相对于地球静止或作匀速直线运动称为平衡状态。
11、作用在一个物体上的两个力使物体平衡,这两个力一定是大小相等、方向相反、作用在同一条直线上。
12、平面运动的速度分析法有三种方法基点法、速度瞬心法和速度投影法。
13、在刚体的平面运动中,刚体的平移和转动是两种最基本运动。
14、动力学的三个基本定律:动量定理、动量矩定理、动能定理。
15、空间力系分为空间汇交力系和空间力偶。
16、带传动中,带所产生的约束力属于柔性约束,带只能承受拉约束。
17、质点动力学的三个基本定律:惯性定律、力与加速度之间的关系定律、作用力与反作用力定律18、质点系动能定理建立了质点系动能的改变量和作用力的功之间的关系。
19、当力为零或力的作用线过矩心时,力矩为零,物体不产生效果。
二、判断题1实际位移和虚位移是位移的两种叫法(×)2.作用力和反作用力等值、反向、共线、异体、且同时存在。
(√)3.力偶无合力。
(×)4.运动物体的加速度大,它的速度也一定大。
(×)5.平面任意力系的合力对作用面内任一点之矩等于力系中各分力对于同一点之矩的代数和。
(√)6.若力偶有使物体顺时针旋转的趋势,力偶矩取正号;反之,取负号。
(×)7.既不完全平行,也不完全相交的力系称为平面一般力系(√)8.二力构件是指两端用铰链连接并且只受两个力作用的构件。
理论力学复习题(含答案)

理论⼒学复习题(含答案)《理论⼒学》复习题A⼀、填空题1、⼆⼒平衡和作⽤反作⽤定律中的两个⼒,都是等值、反向、共线的,所不同的是⼆⼒平衡是作⽤在⼀个物体上,作⽤效果能抵消、作⽤⼒与反作⽤⼒是作⽤在两个物体上,作⽤效果不能抵消。
2、平⾯汇交⼒系平衡的⼏何条件是;平衡的解析条件是。
静滑动摩擦系数与摩擦⾓之间的关系为tanφ=fs。
点的切向加速度与其速度的变化率⽆关,⽽点的法向加速度与其速度的变化率⽆关。
的条件,则点作牵连运动。
6、动点相对于的运动称为动点的绝对运动;相对于系的运动称为动点的相对运动;⽽相对于的运动称为牵连运动。
转动题7图题8图8、图⽰均质圆盘,质量为,半径为R,则其对O轴的动量矩为。
9、在惯性参考系中,不论初始条件如何变化,只要质点不受⼒的作⽤,则该质点应保持静⽌或等速直线⼼.在下述公理、规则、原理和定律中,适⽤的有D)。
A.⼆⼒平衡公理⼒的平⾏四边形规则加减平衡⼒系原理⼒的可传性分析图中画出的5个共⾯⼒偶,与图(a)所⽰的⼒偶等效的⼒偶是()。
图(b)图(c)图(d)图(e)题2图3.平⾯⼒系向点1简化时,主⽮,主矩,如将该⼒系向另⼀点2简化,则(D)。
B.C.D.4.将⼤⼩为100N的⼒F沿x、y⽅向分解,若F在x轴上的投影为86.6?N,⽽沿x⽅向的分⼒的⼤⼩为115.47?N,则F在y轴上的投影为(B)。
A.?0;B.?50N;C.?70.7N;D.?86.6N;题4图题5图5.如图所⽰,当左右两⽊板所受的压⼒均为F时,物体A夹在⽊板中间静⽌不动。
若两端⽊板所受压⼒各为2F,则物体A所受到的摩擦⼒为(A)。
与原来相等是原来的两倍是原来的四倍点作曲线运动时,“匀变速运动”指的是(B)。
=常⽮量=常量=常⽮量=常量刚体作平动时,刚体内各点的轨迹(C)。
⼀定是直线⼀定是曲线可以是直线,也可以是曲线可以是直线,也可以是不同半径的圆⼀对外啮合或内啮合的定轴传动齿轮,若啮合处不打滑,则任⼀瞬时两轮啮合点处的速度和加速度所满⾜的关系为()。
理论力学复习考试题(12土木)答案2

理论力学复习题1答案三、计算题1、两根铅直杆AB、CD与梁BC铰接,B、C、D均为光滑铰链,A为固定端约束,各梁的长度均为L=2m,受力情况如图。
已知:P=6kN,M=4kN·m,qO=3kN/m,试求固定端A及铰链C的约束反力。
2、求指定杆1、2、3的内力。
3、一均质杆AB 重为400N ,长为l ,其两端悬挂在两条平行等长的绳上处于水平位置,如图所示。
今其中一根绳子突然被剪断,求另一根绳AE 此时的张力。
解:运动分析绳子突然被剪断,杆AB 绕A 作定轴转动。
假设角加速度为α,AB 杆的质心为C ,由于A 点的 绝对速度为零,以瞬心A 为基点,因此有:e CC a a α =la C α21= 方向如图所示 受力分析:AB 杆承受重力、绳子拉力、惯性力和惯性力矩 利用动静法,对质心C 建立力矩方程:由 0=∑CM有 021=⨯-*l T M C即 0211212=-Tl ml α (1)由0=∑Y有=-+*mg F T C即 021=-+mg lm T α (2)联立(1)(2)两式,解得:ACe ca α α2/l 2/lABCα*CF *CM mgT2/l 2/lABEDl g 23=α N T 100=【注】本题利用质心运动定理和绕质心转动的动量矩定理也可求解4、边长b =100mm 的正方形均质板重400N ,由三根绳拉住,如图所示。
求:1、当FG 绳被剪断的瞬时,AD 和BE 两绳的张力;2、当AD 和BE 两绳运动到铅垂位置时,两绳的张力。
A D E B60ºFG5、图中,均质梁BC质量为4m、长4R,均质圆盘质量为2m、半径为R,其上作用转矩M,通过柔绳提升质量为m的重物A。
已知重物上升的加速度为a=0.4g,求固定端B处约束反力。
6、均质杆AB长为L=2.5m,质量为50kg,位于铅直平面内,A端与光滑水平面接触,B端由不计质量的细绳系于距地面h高的O点,如图所示。
理论力学期末复习

讨论三种可能发生
FD f D FND 0.4 300N 120N, 的运动情况 FE f E FNE 0.2 643N 128.6N
Fx 0, FT1 FD FE 0
FT1 FD FE 248.6N
线圈架沿AB梁滚动而无滑动
FD f D FND , FE f E FNE =128.6 N
解:解除约束,画整体受力图
列平衡方程
M A F 0
•
FNB AB FT AD r FT DE r 0
FNB FT AD DE 120 2 1.5 kN 105 kN AB 4
FAy FNB FT 0
•
Fy 0
2-4-2 物系平衡问题解法
受力分析
① 首先从二力构件入手,可使受力图比较简单,易于求解。
② 解除约束时,要严格地按照约束的性质,画出相应的约 束力,切忌凭主观想象。对于一个销钉连接三个或三个以上物 体时,要明确所选对象中是否包括该销钉?解除了哪些约束? 然后正确画出相应的约束力。
③ 画受力图时,关键在于正确画出铰链约束力,除二力构
d FR
MO FR
FR 0 M O 0
FR 0
MO 0
合力 力螺旋
FR 0 M O 0 FR // MO
FR 0 M O 0 ( FR , MO )= 力螺旋
1-3-3 力系的最简形式
1.图示力系沿正方体棱边作用,F1=F2=F3=F,
三 点的复合运动
3-1 运动学基础(填空题) 3-2 点的复合运动概念 3-3 点的运动合成定理(注意科氏加速度) 3-4 点的复合运动问题(计算题2)
理论力学练习题理论力学_运动学_复习及经典例题解答

◇速度投影法的缺点:不能求刚体角速度。
8
3) 速度瞬心法 以速度瞬心为基点求任一点速度的方法
B vB A
P
ω
已知:vP= 0, ω
vA vB = BP ⋅ω vA = AP ⋅ω
关键是正确到找瞬心
9
刚体平面运动加速度分析
求a的一种方法 --- 基点法 A——基点
arB = arA + arBτA + arBnA aτBA = AB ⋅α aBnA = AB ⋅ω 2
例1图示曲柄连杆机构中,已知曲柄OA长0.2 m,连杆AB长1m,
OA以匀角速度ω =10 rad/s绕O轴转动。求图示位置滑块B的速度、
加速度和AB杆的角加速度。
P
【解】1、求ωAB 、vB
OA : vA = OA⋅ω = 0.2×10 = 2m/s
AB : 瞬心P vA = AP ⋅ωAB
ω AB
=
vA AP
=
2rad/s
vA
ω
A
O
45º
vB = BP ⋅ωAB = 2.828m/s
ωAB
45º
vB
B
15
2、求αΑΒ、aB
aA = aAn = OA ⋅ω2 = 20 m s2
以A点为基点
avB = avA + avBnA + avBt A
aBnA
=
AB
⋅
ω
2 AB
= 4m
s2
η
aA A
O 45º
ω1
=
vC CD
=
0.25rad/s
100 100
P
ωBC
vC
C
45º
理论力学复习题及参考答案
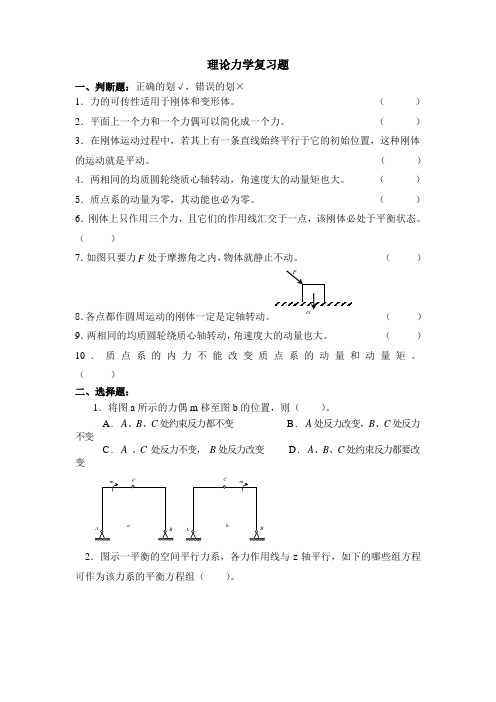
理论力学复习题一、判断题:正确的划√,错误的划×1.力的可传性适用于刚体和变形体。
()2.平面上一个力和一个力偶可以简化成一个力。
()3.在刚体运动过程中,若其上有一条直线始终平行于它的初始位置,这种刚体的运动就是平动。
()4.两相同的均质圆轮绕质心轴转动,角速度大的动量矩也大。
()5.质点系的动量为零,其动能也必为零。
()6.刚体上只作用三个力,且它们的作用线汇交于一点,该刚体必处于平衡状态。
()7.如图只要力F处于摩擦角之内,物体就静止不动。
()8.各点都作圆周运动的刚体一定是定轴转动。
()9.两相同的均质圆轮绕质心轴转动,角速度大的动量也大。
()10.质点系的内力不能改变质点系的动量和动量矩。
()二、选择题:1.将图a所示的力偶m移至图b的位置,则()。
A . A、B、C处约束反力都不变B . A处反力改变,B、C处反力不变C . A 、C处反力不变,B处反力改变D . A、B、C处约束反力都要改变2.图示一平衡的空间平行力系,各力作用线与z轴平行,如下的哪些组方程可作为该力系的平衡方程组()。
3.如图所示,质量为m ,长为L 的匀质杆OA ,以匀角速度ω绕O 轴转动,图示位置时,杆的动量、对O 轴的动量矩的大小分别为( )。
A .12/2/12ωωmL L mL p O ==B .12/02ωmL L p O ==C .L mL L mL p O )21(212/1ωω== D .3/2/12ωωmL L mL p O ==4.点M 沿半径为R 的圆周运动,其速度为 是有量纲的常数。
则点M 的全加速度为( )。
A .B .C .D .5. 动点沿其轨迹运动时( )。
A .若0,0≠≡n a a τ,则点作变速曲线运动 B .若0,0≠≡n a a τ,则点作匀速率曲线运动 C .若0,0≡≠n a a τ,则点作变速曲线运动 D .若0,0≡≠n a a τ,则点作匀速率曲线运动6.一刚体上只有两个力偶M A 、M B 作用,且M A + M B = 0,则此刚体( )。
理论力学计算题

理论⼒学计算题理论⼒学复习题(计算题)⼀、分析⼒学部分半经为r 的光滑半球形碗,固定在⽔平⾯上,⼀均质棒斜靠在碗缘,⼀端在碗内,⼀端在碗外,在碗内的长度为c ,试⽤虚功原理证明棒的全长为:()cr c l 2224-=解:建坐标如图⽰,棒受主动⼒为重⼒,作⽤点在质⼼c 上,⽅向竖直向下,即j mg P -=由虚功原理得 ()()0=-=+?-=∑y mg j y i x j mg A F δδδδ由图可知θsin 2??? ?--=l c y⼜由⼏何关系知r c r 24sin 22-=θ所以r c r l c y 24222-??? ?--=对c 求变分得()()()()[]cl c c c r rc r c c c r r l c c r c r y δδδδ-----=??--??? ??-+--=-2424424212122422221212222代⼊虚功原理得()()[]0242442222=----?c l c c c r rc r mg δ由于0≠c δ故()()024222=---l c c cr整理得()cr c l 2224-=六.五根长度相同的匀质杆,各重为P ⽤铰连接,与固定边AB 成正六边形,设在⽔平杆的中点施⼒F 以维持平衡,⽤虚功原理求⼒F 之⼤⼩?解:设六边形边长为a ,建坐标系如图,取⾓θ为⼴义坐标由虚功原理得:∑=-++=0223321y F y P y P y p AFδδδδδ由⼏何关系知θθθθθcos 2,cos 23cos 2cos ,cos 2321a y a a a y a y ==+== 变分δθθδ?-=sin 21a y ,δθθδ?-=sin 232ay ,δθθδ?-=sin 22a y代⼊虚功原理()()()0sin 26sin 2sin 6sin 2sin 2sin 232sin 22=+-=+-=---+??-+? -θδθθδθθδθθδθθδθθδθθδθa F P Fa Pa a F a P a P a P 由于θ的任意性,0,0sin ≠≠δθθ所以 P F 3=等边六⾓形连杆铅直放置,各杆间⽤光滑铰链连接,底边固定不动,C 、D 点⽤绳拉紧,连杆AB 中点受⼒Q 作⽤,已知平衡时∠ACD=α,试⽤虚功原理求平衡时Q 与绳内张⼒T 之间的关系?解:设六边形边长为a ,建坐标系如图,取⾓α为⼴义坐标由虚功原理得:∑=-+-=01D C Fx T x T y Q Aδδδδ由⼏何关系知αααcos 2),cos 2(,sin 21a ax a a x a y D C +=+-==变分δααδδααδδααδ?-=?=?=sin ,sin ,cos 21a x a x a y D C 代⼊虚功原理2)sin cos (0sin sin cos 2=?+-=?+?+?-δαααδααδααδααa T Q Ta Ta a Q由于的α任意性,0≠δα所以αtan T Q =如图所⽰平⾯机构有五根长度相同的匀质杆与固定杆AB 组成⼀正六边形,杆AF 中点与杆BC 中点有⼀刚度系数为k 的⽔平弹簧相连,已知各杆长度⽤弹簧原长均为l ,其重量与各铰接处摩擦均不计,若在ED 中点作⽤⼀铅垂⼒F ,则此机构平衡时⾓φ的⼤⼩为多少。
理论力学期末复习题全套

理论力学期末复习题一一、单选题1、F= 100N 方向如图示,若将F 沿图示x ,y 方向分解,则x 向分力大小为( )。
A) 86.6 N ; B) 70.7 N ; C) 136.6 N ; D) 25.9 N 。
2、某平面任意力系F1 =4KN ,F2=3 KN ,如图所示,若向A 点简化,则得到( )A .F ’=3 KN ,M=0.2KNmB .F ’=4KN ,M=0.3KNmC .F ’=5 KN ,M=0.2KNmD .F ’=6 KN ,M=0.3 KNm第1题图 第2题图3、实验测定摩擦系数的方法,把物体放在斜面上,逐渐从零起增大斜面的倾角φ直到物体刚开始下滑为止,这时的φ就是对应的摩擦角φf ,求得摩擦系数为( )4、直角杆自重不计,其上作用一力偶矩为M 的力偶,图(a )与图(b )相比,B 点约束反力的关系为( )。
A 、大于B 、小于C 、相等D 、不能确定图(a ) 图(b )5、圆轮绕固定轴O 转动,某瞬时轮缘上一点的速度为v ,加速度为a ,如图所示。
试问哪些情况是不可能的?( )A 、(a)、(b)B 、(b)、(c)C 、(c)、(d)D 、(a)、(d)6、杆AB 的两端可分别沿水平、铅直滑道运动,已知B 端的速度为vB ,则图示瞬时B 点相对于A 点的速度为____________________。
A) B v sinθ; B) B v cosθ; C) B v ⁄ sinθ; D) B v ⁄ cosθ.第6题图 第7题图二、填空题7、图示物块重G=100N ,用水平力P 将它压在铅垂墙上,P=400N ,物块与墙间静摩擦系数fs=0.3,物块与墙间的摩擦力为F= 。
8、鼓轮半径R=0.5m ,物体的运动方程为x=52t (t 以s 计,x 以m 计),则鼓轮的角速度ω= ,角加速度α= 。
第8题图 第9题图 9、平面图形上任意两点的加速度A a 、B a 与A 、B 连线垂直,且A a ≠ B a ,则该瞬时,平面图形的角速度ω= 和角加速度α应为 。
理论力学复习题

理论⼒学复习题⼀、填空题1、试求下列各题A⽀座反⼒:(1)______________________________________________________________________;(2)_____________________________________________________________________ ;(3)_______________________________________________________________________。
并在图中画出反⼒的⽅向。
2、试求下列结构B⽀座反⼒:(1)_____________________________________(2)_____________________________________(3)_____________________________________3、不计质量的杆OA以匀⾓速度ω绕O轴转动,其A端⽤铰链与质量为m、半径为r的均质⼩圆盘相连,⼩圆盘在半径为R的固定圆盘的圆周表⾯作纯滚动,则系统对O点的动量矩的⼤⼩为__________________。
4、已知半径为R的圆盘平⾯与铅直轴成?30⾓,以匀⾓速度ω转动。
轮缘上有⼀点M,以相对于盘的速度rv沿圆盘边缘运动。
则M点经过⽔平直径AB的端点A时的科⽒加速度为________________(⽅向在图上表⽰)。
5、半径为R,质量为A m的均质圆盘A,与半径为2/R,质量为B m的均质圆盘B如图固结在⼀起,并置于⽔平光滑平⾯上,初始静⽌,受⼆平⾏⼒21FF,作⽤。
若FmmBA====21,,则系统质⼼位置在(按图⽰瞬时给定坐标)__________________,系统作何种运动______________________ 。
6、已知⼀匀质矩形薄板质量为m,尺⼨如图所⽰,质⼼为C,薄板对三根相互平⾏轴321,,zzz的转动惯量分别为321,,zzzJJJ,若2/7(maJz=,则对_______________轴的转动惯量最⼤,其值为_________________。
理论力学计算题复习

习题1-1 图中设AB=l ,在A 点受四个大小均等于F 的力1F 、2F 、3F 和4F 作用。
试分别计算每个力对B 点之矩。
【解答】:11()sin 452B M F F l F l =-⋅⋅︒=-⋅ 22()B M F F l F l =-⋅=-⋅33()sin 452B M F F l F l =-⋅⋅︒=-⋅ 4()0B M F =。
习题1-2 如图所示正平行六面体ABCD ,重为P F =100N ,边长AB=60cm ,AD=80cm 。
今将其斜放使它的底面与水平面成30ϕ=︒角,试求其重力对棱A 的力矩。
又问当ϕ等于多大时,该力矩等于零。
【解法1——直接计算法】:设AC 与BD 的交点为O ,∠BAO=α,则:cos()cos cos sin sin 3410.1196552αϕαϕαϕ+=-=⨯=150cm=0.5m 2AO == ()cos()1000.50.1196 5.98N m A P P P M F F d F AO αϕ=⋅=⨯⨯+=⨯⨯=⋅当()0A P M F =时,重力P F 的作用线必通过A 点,即90αβ+=︒,所以:令cos()cos cos sin sin 0αϕαϕαϕ+=-=→34cos sin 055ϕϕ⨯-⨯=,得: 3tan 4ϕ=→3652ϕ'=︒。
【解法2——利用合力矩定理】:将重力P F 分解为两个正交分力1P F 和2P F ,其中:1P F AD ,2P F AB ,则:1cos P P F F ϕ=⨯,2sin P P F F ϕ=⨯根据合力矩定理:1212()()()22cos 0.3sin 0.411000.31000.4 5.98N m 2A P A P A P P P P P AB AD M F M F M F F F F F ϕϕ=+=⨯-⨯=⨯⨯-⨯⨯=-⨯⨯=⋅ 确定ϕ等于多大时,()0A P M F =令()0A P M F =,即:cos 0.3sin 0.40P P F F ϕϕ⨯⨯-⨯⨯=→100cos 0.3100sin 0.40ϕϕ⨯⨯-⨯⨯=→3tan 4ϕ=→3652ϕ'=︒。
理论力学期末前复习题-计算题

(六)计算题[1101] 一圆轮以匀速V。
沿直线作纯滚动,如图所示,设初始时刻P点与坐标原点0重合,轮半径为r求轮缘上一点P的运动学方程以及P点的速度、加速度大小。
0,,求质[1201]质点沿x轴运动,加速度x = k2x.k为常数点的运动学方程。
【1202]质点作平面运动时,其速率v为常数C,位矢旋转的角速度&为常数°,设t = 01甘,厂=0和*0求质点的运动学方程和轨道方程。
[1301】某人以一定的功率划船,逆流而上,当船经过一桥时,船上的鱼竿不慎掉入河中。
两分钟后,此人才发觉,立即返棹追赶。
追到鱼竿之处是在桥的下游600米的地方,问河水的流速是多大[1302] 一人手持5cm成和两端开口的管子在雨中站立,管顶向北倾斜4ccm, 雨点直线穿过此管;如此人向南以s的速度行走,则管顶向北倾斜3cm就可以使雨点穿过,求雨点速度。
[1501] 一质点受力F = ——,此力指向坐标原点0,试求质点沿x轴从距原x点为/处由静止开始运动,达到原点所需要的时间。
[1502]有孔小珠穿在光滑的拋物线形钢丝上且能自由滑动,抛物线的正交弦为4a,其轴沿铅直方向而顶点位于下方,小珠从顶点开始运动时具有某一速率,这个速率使它恰能达到过焦点的水平面,试求小珠在顶点上方高为y «Q)时受到的约束力。
[1503】船在水中航行,停机时的速度为%,水的阻力为f = kmv2,问经过多少时间后航速减至土。
2[1504]质量为m的小球,在重力的作用下,在空气中竖直下落,其运动规律为s = —求空气阻力(以v的函数表示之)[1901]求质量为m的质点在反立方引力场中的运动轨道。
【1902]质点在有心力的作用下作双纽线r2 = a1 cos26>运动,试求有心力。
[2101]求半径为R 的均质半球体的质心。
[2701】总长度为a 的均质链条的一段b (0<b<a )挂在光滑桌而AB 边缘上,另 一端躺在桌面上。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
习题1-1 图中设AB=l ,在A 点受四个大小均等于F 的力1F 、2F 、3F 和4F 作用。
试分别计算每个力对B 点之矩。
【解答】:112()sin 452B M F F l F l =-⋅⋅︒=-⋅ 22()B M F F l F l =-⋅=-⋅332()sin 452B M F F l F l =-⋅⋅︒=-⋅ 4()0B M F =。
习题1-2 如图所示正平行六面体ABCD ,重为P F =100N ,边长AB=60cm ,AD=80cm 。
今将其斜放使它的底面与水平面成30ϕ=︒角,试求其重力对棱A 的力矩。
又问当ϕ等于多大时,该力矩等于零。
【解法1——直接计算法】:设AC 与BD 的交点为O ,∠BAO=α,则:cos()cos cos sin sin 33410.11965252αϕαϕαϕ+=-=⨯-⨯= 221806050cm=0.5m 2AO =+=()cos()1000.50.1196 5.98N mA P P P M F F d F AO αϕ=⋅=⨯⨯+=⨯⨯=⋅当()0A P M F =时,重力P F 的作用线必通过A 点,即90αβ+=︒,所以: 令cos()cos cos sin sin 0αϕαϕαϕ+=-=→34cos sin 055ϕϕ⨯-⨯=,得: 3tan 4ϕ=→3652ϕ'=︒。
【解法2——利用合力矩定理】:将重力P F 分解为两个正交分力1P F 和2P F , 其中:1P F AD ,2P F AB ,则:1cos P P F F ϕ=⨯,2sin P P F F ϕ=⨯根据合力矩定理:1212()()()22cos 0.3sin 0.411000.31000.4 5.98N m 2A P A P A P P P P P AB AD M F M F M F F F F F ϕϕ=+=⨯-⨯=⨯⨯-⨯⨯=-⨯⨯=⋅ 确定ϕ等于多大时,()0A P M F =令()0A P M F =,即:cos 0.3sin 0.40P P F F ϕϕ⨯⨯-⨯⨯= →100cos 0.3100sin 0.40ϕϕ⨯⨯-⨯⨯=→3tan 4ϕ=→3652ϕ'=︒。
习题1-11习题1-22R F 'O MRF 'M RF 'RF RF RF习题2-1 三力作用在正方形上,各力的大小、方向及位置如图所示,试求合力的大小、方向及位置。
分别以O 点和A 点为简化中心,讨论选不同的简化中心对结果是否有影响。
【解答】:(1)以O 点为简化中心,求主矢和主矩。
31024N 5=⨯-=∑xF 41044N 5=⨯-=∑y F因此,主矢大小为:2222()()4442N Rx y F F F '=+=+=∑∑ 主矢与x 轴夹角为:tan 454yxFarc rad Fπα===︒∑∑,如图中红色箭头所示。
xy主矩大小为:43()21010455O OM M F a a a a ==⨯+⨯⨯-⨯⨯=∑(逆时针,如图所示。
) (2)确定最终合成结果根据主矢和主矩均不为零,可知力系最终合成一个合力,合力大小和方向与主矢相同,即:R RF F '= 合力作用线方程由下式确定:Ry Rx O x F y F M ⋅-⋅=→444x y a -= 这说明合力作用线通过A 点,如上图所示。
(3)如果以A 点为简化中心,求得主矢为:2222()()4442N Rx y F F F '=+=+=∑∑ 主矩为:3()241005A AM M F a a a ==⨯+⨯-⨯⨯=∑ 此时合力等于主矢。
习题2-2 如图所示等边三角形ABC ,边长为l ,现在其三顶点沿三边作用三个大小相等的力F ,试求此力系的简化结果。
【解答】:力系的合成结果与简化中心的选择无关, 因此任选一点(例如A 点作简化中心),建立坐标系,计算主矢和主矩:(注意三角形ABC 为等边三角形)cos60cos600xF F F F =-⨯︒-⨯︒=∑ sin60sin600yFF F =⨯︒-⨯︒=∑因此主矢大小为:22()()0Rx y F F F '=+=∑∑3()sin 602A A M M F F l Fl ==⨯⨯︒=∑(逆时针) 由此判断力系的简化结果是一个逆时针转动的力偶,力偶矩等于主矩。
习题2-7 求如图所示平行力系合力的大小和方向,并求平行力系中心。
图中每格代表1m 。
【解答】:(1)根据题目示意图,合力大小为:1015203025kN R F F==+--=∑写出各力的作用点坐标:11x =,11y =,10z = 21x =,23y =,20z =32x =,32y =,30z = 43x =,15y =,10z =(2)根据平行力系中心坐标公式,求力系的中心:112233441011512023034.210152030C F x F x F x F x x F ⋅+⋅+⋅+⋅⨯+⨯-⨯-⨯===+--∑m11223344101153202305 5.410152030C F y F y F y F y x F ⋅+⋅+⋅+⋅⨯+⨯-⨯-⨯===+--∑0C z =习题3-1如图所示简易起重机用钢丝绳吊起重为2kN 的重物。
不计杆件自重、摩擦及滑轮尺寸,A 、B 、C 三处简化为铰链连接,试求杆AB 和AC 所受的力。
【解答】:(1)选择销钉A 为研究对象,画出其受力图 忽略滑轮的大小尺寸,则AC 杆、AB 杆以及绳子 作用在销钉上的力组成平面汇交力系而且 处于平衡状态。
根据定滑轮的性质可知:2kN T P F F ==(2)列平衡方程0xF =∑,sin 30cos30sin 750AC AB T F F F ⋅︒-⋅︒-⋅︒= 0yF=∑,cos30sin 30cos 750AC AB T P F F F F ⋅︒+⋅︒-⋅︒-=(3)解平衡方程,确定未知量求解上面的方程组,得到:0.4142kN AB F =, 3.146kN AC F =(书中答案有误,请更正)习题3-2 均质杆AB 重力为P F 、长为l ,两端置于相互垂直的两光滑斜面上,如图所示。
已知一斜面与水平成角α,求平衡时杆与水平所成的角ϕ及距离OA 。
【解答】:选择AB 杆为研究对象, 画出受力图。
根据三力平衡汇交定理,AB 杆 保持平衡必须满足以下条件:A F 、B F 、P F 的作用线汇交于一点(图中D 点)。
又因为AB 杆的重心C 必为其中点, 则在矩形OADB 中,AB 为一条对角线,DCO 连线也为对角线,所以重力P F 的作用线必通过O 点。
根据图中几何关系可知:ADO ABO DAB α∠=∠=∠=,得到如下结果:90αϕα++=︒→902ϕα=︒-,sin sin OA AB l αα=⋅=⋅。
习题3-3 构件的支承及载荷情况如图所示,求支座A 、B 的约束力。
【解答】:(1)选择构件AB 为研究对象,画出受力图B 端为活动铰支座,约束力B F 必须垂直于斜支承面,再结合力偶只能与力偶平衡的性质,可知A 端固定铰支座的约束力A F 必与B F 组成力偶(等值、反向、平行),才能与主动力偶(F ,F ')相平衡。
根据平面力偶系的平衡方程,得:0M =∑,sin 450AFl F a ⨯⨯︒-⨯=解方程,得:2A B FaF F ==习题3-8求如图所示物体在A 、B 处的支座约束力,图中长度单位为m 。
【解答】:此题示意图有一些问题,请按上图更正。
(1)画出水平杆的受力图(在题目示意图基础上加上A 、B 两处的约束力即可) (2)列平衡方程并求解:0xF=∑,0Ax F =;()0A M F =∑,1220.51(kN/m)3(kN)1(m)=02B F ⨯+⨯-⨯⨯⨯→ 1.510.25kN 2BF -== 0y F =∑,121302Ay BF F +--⨯⨯=→ 3.50.25 3.25kN Ay F =-=。
习题3-24 重力为P F 的矩形水平板由三根铅垂直杆吊挂,尺寸如图(a )所示,求各杆内力。
若在板的形心处(应改为在D 点处)放置一重物,则各杆内力又如何?(a ) (b ) (c ) 【解答】:(1)画出矩形板的受力图如图(b )所示,为空间平行力系的平衡问题。
(2)列出平衡方程:0F =∑,1230P F FF F ++-= (1)()0x M F =∑,302P a F a F ⨯-⨯=→312P F F = (2) ()0y M F =∑,102P b F b F ⨯-⨯=→112P F F = (3) 将(2)、(3)代入(1)得:20F =(3)当在D 点放一重物时,假设其重力大小为W F ,画出受力图如图(c )所示。
列平衡方程如下:0F =∑,1230P W F FF F F ++--= (4)()0x M F =∑,302P W a F a F F a ⨯-⨯-⨯=→312P W F F F =+ (5) ()0y M F =∑,102P W b F b F F b -⨯+⨯+⨯=→112P W F F F =+ (6) 将(5)、(6)代入(4)得:2W F F =-。
习题3-25 如图所示三圆盘A 、B 和C 的半径分别为15cm 、10cm 和5cm ,三轴OA 、OB 和OC 在同一平面内,∠AOB 为直角,在这三圆盘上分别作用力偶。
组成各力偶的力作用在轮缘上,它们的大小分别等于10N 、20N 和F 。
若这三圆盘所构成的物系是自由的,求能使此物系平衡的角度α力F 的大小。
【解答】:用矢量表示A 、B 、C 三个轮上作用的力偶矩,如图(b )所示。
各力偶矩大小分别为:11024N m A M r =⨯⨯=⋅ 22023N m B M r =⨯⨯=⋅A M 与B 的合力偶矩大小为:2222435N m R A B M M M =+=+=⋅ 4tan 3B AM M β==,53.13β=︒ 使此物系平衡的条件是,C M 与R M 等值、反向、共线,即:3220.055N m C M F r F =⨯⨯=⨯⨯=⋅,5N m50N 0.1mF ⋅==。
由图中关系得:180126.87γβ=︒-=︒90360αγ++︒=︒→36090126.87143.131438α'=︒-︒-︒=︒=︒。
习题4-1试求如图所示各桁架上标有数字的各杆的内力。
图(a )中各杆的长度相等。
【(a )解答】:(1)取整体画受力图,列平衡方程,求一端约束力()0EMF =∑,4 2.52 1.50I F a F a F a ⋅-⋅-⋅=解方程,得:118I F F =(2)用截面法截断1、2、3杆,取右半桁架 为研究对象,画受力图,列平衡方程, 求1、2、3杆的内力。
