数轴上的距离公式和中点公式
两点之间的距离公式及中点坐标公式

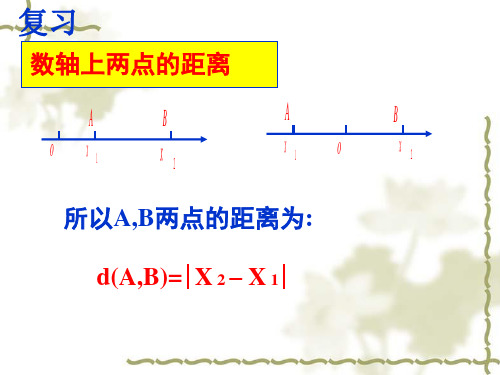
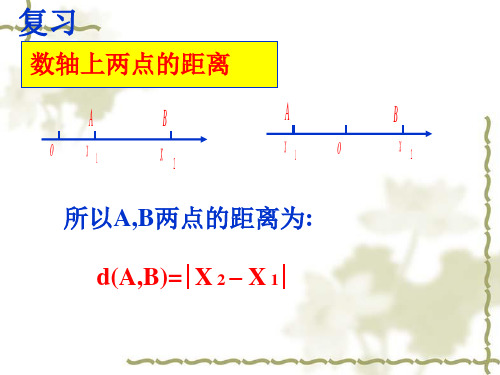
数轴上两点的距离
A
B
o x1
x2
A x1
o
B x2
所以A,B两点的距离为 两点的距离为: 所以 两点的距离为 d(A,B)= X 2 – X 1
2.1.2平面直角坐标系中的基本公式
1.两点的距离公式 两点的距离公式
如图:有序实数对 与点P对 如图:有序实数对( x,y)与点 对 与点 这时( 称为点P的坐标 应,这时 x,y)称为点 的坐标, 这时 称为点 的坐标, 并记为P(x,y),x叫做点 的横坐 叫做点P的横坐 并记为 叫做点 叫做点P的纵坐标 标,y叫做点 的纵坐标。 叫做点 的纵坐标。
O
AD = (b − a) + c ,
AC = b + c ,
2 2 2
A(0 A(0,0)
B(a,0 B(a,0)
BD = (b − 2a) + c
2 2
2
AC + BD = 4a + 2b + 2c − 4ab,
2 2 2 2 2
= 2(2a + b + c − 2ab), 2 2 2 2 2 AB + AD = 2a + b + c − 2ab, 所以 AC2 + BD2 = 2(AB2 + AD2 ).
证明:取A为坐标原点,AB所在直线为X 证明:取A为坐标原点,AB所在直线为X轴建 立平面直角坐标系 xOy ,依据平行四边形的 性质可设点A 性质可设点A,B,C,D的坐标为
(
)
A(0,0), B(a,0), C(b, c), D(b − a, c).
所以 AB
2
2
=a ,
2
初一动点问题的解题公式口诀

初一动点问题的解题公式口诀
1、数轴上两点之间的距离。
可用绝对值来表示,即两点所表示的数差的绝对值。
如,数轴上点A,B所表示的数是a,b,则AB=|a-b|或|b-a|。
2、数轴上一个动点用字母来表示。
用有理数的加法或减法即可解决,就是起点所表示的数加上或减去动点运动的距离,向正方向用加,负方向用减。
如,数轴上点A对应的数为-1,点P从A出发,以每秒2个单位长度的速度向右运动,设运动的时间是t,则点P所表示的数是-1+2t。
3、数轴上任意两点间的线段的中点。
两点所表示的数相加的和除以2,如数轴上的点所表示的数是a,b,则线段AB的中点所表示的数是(a+b)/2。
8.1.1数轴上的距离公式和中点公式--李晓玲

如,点 A 的坐标为 1 ,记作 A(1);
点 B 的坐标为-4,记作 B(-4) .
观察数轴,完成下列题目:
P
-4 -3
B
-2 -1
O
0 1 2
A
3 4 x
(1)点 P 与 -3.5 对应,则点 P 的坐标是 (2)点 A 的坐标是 (3)点 B 的坐标是 (4)点 O 的坐标是 ,记作 ,记作 ,记作 ; ; .
(2)设点 M(x) 是 A,B 两点的中点,则
x=
3 5 =1. 2
即 A,B 的中点坐标为 1 .
已知点 A(-6),B(-1), C(2),D(4.5),E(7)
求:(1)|AB|,|AC|,|BD|,|DE|; (2)A,B 的中点坐标;B,E
的中点坐标.
1.数轴上点的坐标. 2.数轴上两点间的距离公式.
x B 1 0 -1 A -2 -3 -4 2 4 3 4 3 2 1 0 -1 -2 -3 -4 B
A
试求两个图中点 A 与 B 之间的距离.
如图:
C
-4 -3 -2
A
-1 0 1
D
2 3 4 x
(1)点 A(-1),C(-3)的中点坐 标是多少?中点坐标与 A,C 两点的坐标有 怎样的关系? (2)点 A(-1),D(2)的中点坐标是
3.数轴上两点的中点公式.
1. 已知点 A(-5),B(-1),
C(3),D(4),E(8)
求:(1)|AB|,|AC|,|BD|,|DE|;
(2)A,B 的中点坐标;B,E 的中点坐标.
2.在数轴上标出坐标满足下列条 件的所有点: (1)x<2; (2) ∣x∣≥5;
(3)2<x<5;
数轴上的基本公式

一.直线坐标系定义
数轴: 一条给出了原点、度量单位和正方向的直线叫做 数轴,或说在这条直线上建立了直线坐标系。如图:
1、数轴上点的坐标
N P(x)
1
-3
-2
-1
0
2
M
3
x
若点P与实数x对应,则称点P的坐标为 x 记作
数轴上的一点M的坐标为3 记作:
x1
A M(x)
x2 B x
【变式】 :平行四边形的三个顶点坐标分别为
(- 3,0),(2,-2),(5,2).求:第四个顶点D的坐标。
y D (x,y)
M
C(5,2)
A(-3,0)
O
x B(2,-2)
课本:P71页,A组题目,B组1、2
例2. 已知点A(1,2),B(3, 4), C(5, 0),
求证:△ABC是等腰三角形
证明:
d(A,B)= 8
d(A,C)= 20
d(B,C)= 20 又A,B,C三点不共线, 所以△ABC是等腰三角形
【例3】已知 :平行四边形ABCD的三个顶点坐标
A(- 3,0),B(2,-2),C(5,2).求:顶点D的坐标。
2.数轴上两点间的距离公式:
用d(A,B)表示A、B两点间的距离,
则
d(A,B) = AB = |x2-x1|.
3.中点公式 已知平面直角坐标系中的两点 A(x1), B(x2),点 x1+x2 M(x)是线段 AB 的中点,则 x=_______ 2 ,
2.1.2 平面直角坐标系中的基本公式
1、已知平面上两点A (x1,y1),B (x2,y2),A 、B 两点间的距离:
d ( A, B ) AB
两点之间的距离公式及中点坐标公式
A(x1,y1) A2
o
A1
c
B1
x
d (A ,B ) |A B |(x 2 x 1 )2 (y 2 y 1 )2
显然,当AB平行于坐标轴或在坐标轴上时,公式 仍然成立。
❖ 给两点的坐标赋值:
x 1 ? ,y 1 ? ,x 2 ? ,y 2 ? ;
❖ 计算两个坐标的差,并赋值给另外两个量, 即
xx2x1 yy2y1
y D (b-a, c) C (b, c)
A2D ba2c2,
AC2 b2c2,
x
O A(0,0) B(a,0)
B2D b2a2c2
A2 C B2 D 4 a 2 2 b 2 2 c 2 4 a,b 2(2a2b2c22a)b,
A2 B A2D 2 a 2 b 2 c2 2 a,b
所以 A 2 C B 2 D 2 A 2 A B 2 .D
❖ 计算 d x2y2
❖ 给出两点的距离 d
题型分类举例与练习
【例1】已知A(2、-4)、B(-2,3). 求d(A,B)
解: x 1 2 ,x 2 2 ,y 1 4 ,y 2 3
x x 2 x 1 2 2 4 ,
y y 2 y 1 3 4 7
d(B A ), (42)72 65
A 2 C B 2 D 2 A 2 A B 2 .D
证明:取A为坐标原点,AB所在直线为X轴建 立平面直角坐标系 xOy ,依据平行四边形的 性质可设点A,B,C,D的坐标为
A 0 , 0 ,B a , 0 , C b , c ,D b a , c .
所以 AB2 a2,
【例2】已知:点A(1,2),B(3,4),C(5, 0)
求证:三角形ABC是等腰三角形。
数轴上的距离公式和中点公式

8.1.1 数轴上的距离公式和中点公式
发一张白纸,第一步画数轴;校正 第二步写两个数; 第三步同桌交换标点 A(3)
例1
1.数轴上点的坐标. 记作 P(x).
B(1)
O(0)
C(-2)
D(-3.5)
|OA|=3=xA B(x2) A(x1) 解:设P点的坐标为x,则 2.数轴上两点间的距离公式. |AO|=3=xA |AP|=|PB| |OA|=|x1| |OC|=2=|xB| |AB|=|x2-x1| =x2-x1 (X2>X1) |x-(-1)| =|x-2| |AB|= 2=xA -xB 3.数轴上两点的中点公式. |CA|= 5=xA -xC
例2
x=
x1 + x2
一般化
2
3. 数轴上的中点公式
x= x1 + x2
2
A(x1)
P(x)
-1 0 1
B(x2) 2
-4
-3
-2
3
4
x
观察数轴,完成下列题目:
D C -2 -1
O
0
B 1 2
A
-4
-3
3
4
x
(1) A,B 的中点坐标是
2
;
(2) B,C 的中点坐标是 -0.5 ;
(3)点 D 与 -3.5 对应, C,D 的中点坐标是 -2.75 .
例:已知点 A(-6),B(-1),C(2),
D(4.5),E(7),
求:(1)|AB|,|AC|,|BD|,|DE|;
(2)A,B 的中点坐标;B,E 的中点坐标.
1.数轴上点的坐标.
2.数轴上两点间的距离公式.
3.数轴上两点的中点公式.
数轴上的距离公式与中点公式

数轴上的距离公式与中点公式考点解析及例题讲解1. 数轴上点的坐标在数轴上,如果点P 与x 对应,则称点P 的坐标为x ,记作P (x ).练习一观察数轴,完成下列题目:(1)点P 与-3.5对应,则点P 的坐标是 ,记作 ;(2)点A 的坐标是 ,记作 ;(3)点B 的坐标是 ,记作 ;(4)点O 的坐标是 ,记作 .2. 数轴上的距离公式探究一如图,填空:(1)图中点A 的坐标是 ,B 的坐标是 ,C 的坐标是 ,点D 的坐标是 ;(2)点A 与B 之间的距离|AB |=,点C 与A 之间的距离|CA |=,点B 与C 之间的距离|BC |=;(3)你能找出数轴上两点间距离与两个点坐标之间的关系吗? 一般地,如果A (x 1),B (x 2),则这两点的距离公式为|AB |=|x 2-x 1|.探究二在以上例子中,我们遇到的数轴都是水平放置的,如果数轴不是水平放置的(如下图所示),数轴上的距离公式成立吗?x ● xP ● ● ● B A O ● x● ● C ● ● 1 2 4 12 34B试求两个图中点A 与B 之间的距离.3. 数轴上的中点公式探究三根据下图回答问题:(1)点A (-1),C (-3)的中点坐标是多少?中点坐标与A ,C 两点的坐标有怎样的关系?(2)点A (-1),D (1)的中点坐标是多少?中点坐标与A ,D 两点的坐标有怎样的关系?一般地,在数轴上,A (x 1),B (x 2)的中点坐标x 满足关系式x = x 1+x 22.4. 应用例 已知点A (-3),B (5),求:(1)|AB |;(2)A ,B 两点的中点坐标.解 (1)|AB |=|5-(-3)|=8;(2)设点M (x )是A ,B 两点的中点,则x = -3+52=1.即A ,B 的中点坐标为1.平面直角坐标系中的距离公式和中点公式1. 距离公式探究一如图,设A (x 1,y 1),B (x 2,y 2).y 轴作垂线AA 1,AA 2和BB 1,BB 2,垂足分别为A 1,A 2,B 1,B 2,其中直线BB 1和AA 2相交于点C .两点的距离公式|AB |=(x 2-x 1)2+(y 2-y 1)2.x● ● C A D ●探究二求两点之间的距离的计算步骤:S1 给两点的坐标赋值x 1=?,y 1=?,x 2=?,y 2=?S2 计算两个坐标的差,并赋值给另外两个变量,即d x =x 2-x 1,d y =y 2-y 1;S3 计算d =d 2x +d 2y ; S4 给出两点的距离d .例1 已知A (2,-4),B (-2,3),求|AB |.解 因为x 1=2,x 2=-2,y 1=-4,y 2=3,所以dx =x 2-x 1=-2-2=-4,d y =y 2-y 1=3-(-4)=7.因此|AB |=d 2x +d 2y =(-4)2+72 =65.练习一求两点之间的距离:(1)A (6,2),B (-2,5);(2)C (2,-4),D (7,2).2. 中点公式探究三如图所示,若已知A (x 1,y 1),B (x 2,y 2),那么怎么求它们的对称中心的坐标?设M (x ,y )是A ,B 的对称中心,即线段AB 的中点.过A ,B ,M 分别向x 轴,y 轴作垂线,AA 1,AA 2,BB 1,BB 2,MM 1,MM 2,垂足分别是A 1,A 2,B 1,B 2,M 1,M 2.在平面直角坐标系内,两点A (x 1,y 1),B (x 2,y 2)的中点M (x ,y )的坐标满足x =x 1+x 22,y =y 1+y 22.例2 求证:任意一点P (x ,y )与点P '(-x ,-y )关于坐标原点成中心对称. 证明 设P 与P '的对称中心为(x 0,y 0),则x 0=x +(-x )2=0,y 0=y +(-y )2=0.所以坐标原点为P 与P ′的对称中心.练习二求下列各点关于坐标原点的对称点:A (2,3),B (-3,5),C (-2,-4),D (3,-5).例3 已知坐标平面内的任意一点P (a ,b ),分别求它关于x 轴的对称点P ′,关于y 轴的对称点P ′′的坐标.练习三求下列点关于x 轴和y 轴的对称点坐标:A (2,3),B (-3,5),C (-2,-4),D (3,-5).例4 已知平行四边形ABCD 的三个顶点A (-3,0),B (2,-2),C (5,2),求顶点D 的坐标.解 因为平行四边形的两条对角线的中点相同,所以它们的坐标也相同.设点D 的坐标为(x ,y ),则⎩⎪⎨⎪⎧x +22=-3+52=1y -22=0+22=1解得⎩⎪⎨⎪⎧x =0y =4所以顶点D 的坐标为(0,4).。
七年级数学数轴上的动点问题

七年级数学数轴上的动点问题数轴上的线段与动点问题一、与数轴上的动点问题相关的基本概念数轴上的动点问题离不开数轴上两点之间的距离.主要涉及以下几个概念:1.数轴上两点间的距离,即为这两点所对应的坐标差的绝对值d=|a-b|,也即用右边的数减去左边的数的差.即数轴上两点间的距离=右边点表示的数—左边点表示的数.2.两点中点公式:线段AB中点坐标=(a+b)÷2.3.点在数轴上运动时,由于数轴向右的方向为正方向,因此向右运动的速度看作正速度,而向左运动的速度看作负速度.这样在起点的基础上加上点的运动路程就可以直接得到运动后点的坐标.即一个点表示的数为a,向左运动b个单位后表示的数为a—b;向右运动b个单位后所表示的数为a+b.4.数轴是数形结合的产物,分析数轴上点的运动要结合图形进行分析,点在数轴上运动形成的路径可看作数轴上线段的和差关系.二、数轴不动点问题求解的基本思路和方法:1.标明题目中动点的坐标(一般用含时间t的公式表示)。
2.根据两点间的距离公式,表示问题中相关线段的长度(一般用含时间t的公式表示)。
3.根据题中线段的等价关系(一般是和差关系)列出绝对值方程。
4、解绝对值方程并根据实际问题验算结果.注:数轴上线段的动点问题方法类似1.已知数轴上点a和b对应的数是-2和4,p是数轴上的动点,对应的数是x.A B-2-1 0 1 2 3 4(1)若P为AB线段的三等分点,求P对应的数;(2)数轴上是否存在P,使P到A点、B点距离和为10,若存在,求出x;若不存在,说明理由.(3)如果a点、b点和p点(p点在原点)同时向左移动,它们的速度分别为1、2和1。
个长度单位/分,则第几分钟时,P为AB的中点?2、已知:b是最小的正整数,且a、b、c满足(c-5)2+|a+b|=0,请回答问题(1)请直接写出a、b、c的值.a=________,b=________,c=________(2)a、b、c所对应的点分别为A、B、C,点P为一动点,其对应的数为x,点P在到2之间运动时(即0≤x≤2时),请化简式子:|x+1|-|x-1|+2|x+5|.(3)若点A、点C分别以每秒1个单位和2个单位长度的速度向左运动,请问几秒时,A,C之间的距离为1个单位长度?(4)点a、b、c开始在数轴上移动。
两点之间距离公式及中点坐标公式

一、概述在数学几何中,两点之间的距离以及中点的坐标是非常重要的概念。
这些公式不仅在数学中有着广泛的应用,也在物理学、工程学等领域中被广泛使用。
本文将就两点之间距离公式以及中点坐标公式进行详细的讲解,以帮助读者更好地理解和运用这些重要的数学概念。
二、两点之间的距离公式1. 欧几里得距离公式在数学中,两点之间的距离通常使用欧几里得距离公式来计算。
欧几里得距离是指在n维空间中,两点之间的直线距离。
在二维空间中,两点P1(x1, y1)和P2(x2, y2)之间的欧几里得距离公式为:D = √((x2−x1)² + (y2−y1)²)其中D表示两点之间的距离。
2. 三维空间中的距离公式在三维空间中,计算两点之间的距离公式稍有不同。
设两点P1(x1, y1, z1)和P2(x2, y2, z2),它们之间的距离可以用以下公式计算:D = √((x2−x1)² + (y2−y1)² + (z2−z1)²)这就是三维空间中两点之间距离的公式,它是欧几里得距离公式的推广。
3. 数轴上的距离在一维空间,即数轴上,两点之间的距离可以简化为:D = |x2 - x1|其中| |表示绝对值符号。
这个公式表明了在数轴上两点之间的距离就是它们的坐标差的绝对值。
三、中点坐标公式1. 二维空间中的中点坐标在二维空间中,两点P1(x1, y1)和P2(x2, y2)之间的中点坐标可以用以下公式计算:M = ((x1 + x2)/2, (y1 + y2)/2)其中M表示中点的坐标。
2. 三维空间中的中点坐标在三维空间中,两点P1(x1, y1, z1)和P2(x2, y2, z2)之间的中点坐标可以用以下公式计算:M = ((x1 + x2)/2, (y1 + y2)/2, (z1 + z2)/2)这个公式表示了三维空间中两点的中点坐标。
3. 数轴上的中点坐标在数轴上,两点之间的中点坐标可以简化为:M = (x1 + x2)/2这就是一维空间中两点的中点坐标公式,很简单但却非常有用。
两点之间的距离公式及中点坐标公式
所以它们的中点的坐标也相同.
设D 点的坐标为(x,y).
y D (x,y)
x2 35
则
2
2
M
C(5,2)
y2 02
O
A(-3,0)
x
2
2
B(2,-2)
解得 x=0 ∴D(0精,选4p)pt课件
18
y=4
〖课堂检测〗 1、求两点的距离: (1) A(6,2) , B(-2,5) (2) A (2 , -4) , B (7 , 2)
复习
数轴上两点的距离
A
B
o x1
x2
A
B
x1 o
x2
所以A,B两点的距离为:
d(A,B)= X 2 – X 1
2.1.2平面直角坐标系中的基本公式
1.两点的距离公式
精选ppt课件P对 应,这时( x,y)称为点P的坐标, 并记为P(x,y),x叫做点P的横坐 标,y叫做点P的纵坐标。
B1
(X2,0)
x
16
即: x x1 x2 2
y y1 y2 2
这就是线段中点坐标 的计算公式 ,简称
—— 中点公式
精选ppt课件
17
【例4】已知 :平行四边形ABCD的三个顶点坐标
A(- 3,0),B(2,-2),C(5,2).求:顶点D的坐标。
解:因为平行四边形的两条对角线中点相同,
2、已知A(a,0), B(0,10)两点 的距离等于17,求a的值。
3、已知 : AB的C三D 个顶点坐标分别是
A(- 1,-2),B(3,1),C(0,2).求:第D点的坐
标。
精选ppt课件
19
1.两点间的距离公式;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
X =
a b 2
35 =1. 2
即 A,B 的中点对应的数为 1 .
已知点 A(-6),B(-1),C(2),D(4.5), E(7),求: (1)|AB|,|AC|,|BD|,|DE|; (2)AB 的中点对应的数;BE 的中点对应的数.
1.数轴上两点间的距离公式.
|AB|=|a-b|= |b-a|
2.数轴上两点的中点公式.
A(a)
-4 -3 -2 -1 0 1
B(b)
2 3 4 x
一般地,在数轴上,如果 A对应的数为a,B
对应数为b,则这两点的距离公式为
|AB|=|a-b|= |b-a|
在以上例子中,我们遇到的数轴都是水平放置的,
如果数轴不是水平放置的 ( 如图所示 ) ,数轴上的距离 公式成立吗?
x B 2 1 0 -1 A -2 -3 -4 4 3 x 4 3 2 1 0 -1 -2 -3 -4
-4 -3 -2 -1 0 1
B(b)
2 3 4
x
一般地,在数轴上,A对应的数为a,B对应 的数为b,则AB中点对应的数x满足关系式
X =
a b 2
例
数轴上,已知点 A对应的数为-3,点B对应
的数为5,求:
(1)|AB|;(2)A,B 两点的中点对应的数. 解:(1)|AB|=|5-(-3)|=8; (2)设x是 A,B 两点的中点对应的数,则 x=
B
A
试求两个图中点 A 与 B 之间的距离.
如图:
C
-4 -3 -2
A
-1 0 1
D
2 3 4 x
(1)线段 AC的中点对应的数是多少?中点对
应的数与 A、C 两点对应的数有怎样的关系?
(2) 线段AD的中点对应的数是多少?中点对应 的数与 A、D 两点对应的数有怎样的关系?
数轴上的中点公式
A(a)
(1)图中点 A 对应的数是
,点 B对应的数是
,
点 C对应的数是
,点 D对应的数是
;
;点 C 与 A 之 .
(2)点 A 与 B 之间的距离 |AB|= 的距离 |CA|=
;点 B 与 C 之间的距离 |BC|=
(3)你能找出数轴上两点间距离与两个点对应 的数之间的关系吗?是怎样的?
距 离 公 式
数轴上的
距离公式和中点公式
直线
1.数轴
-4 -3
-2
-1
0
1
2
3
4
x
观察数轴,完成下列题目:
P
-4 -3
B
-2 -1
O
0 1 2
A
3 4 x
(1)点 P 对应的数记作 (2)点 A对应的数记作
; ;
(3)点 B对应的数记作
(4)点 O对应的数记作
;
.
C
-4 -3 -2
A
-1 0
D B
1 2 3 4 x
