【高考】圆锥曲线的极坐标方程、焦半径公式、焦点弦公式

高中数学-圆锥曲线有关焦点弦的几个公式及应用

圆锥曲线有关焦点弦的几个公式及应用如果圆锥曲线的一条弦所在的直线经过焦点，则称此弦为焦点弦。

圆锥曲线的焦点弦问题涉及到离心率、直线斜率（或倾斜角）、定比分点（向量）、焦半径和焦点弦长等有关知识。

焦点弦是圆锥曲线的“动脉神经”，集数学知识、思想方法和解题策略于一体，倍受命题人青睐，在近几年的高考中频频亮相，题型多为小题且位置靠后属客观题中的压轴题，也有作为大题进行考查的。

本文介绍圆锥曲线有关焦点弦问题的几个重要公式及应用，与大家交流。

定理1已知点是离心率为的圆锥曲线的焦点，过点的弦与的焦点所在的轴的夹角为，且。

（1）当焦点内分弦时，有；（2）当焦点外分弦时（此时曲线为双曲线），有。

证明设直线是焦点所对应的准线，点在直线上的射影分别为，点在直线上的射影为。

由圆锥曲线的统一定义得，，又，所以。

（1）当焦点内分弦时。

如图1，，所以。

图1（2）当焦点外分弦时（此时曲线为双曲线）。

如图2，，所以。

图2评注特别要注意焦点外分焦点弦（此时曲线为双曲线）和内分焦点弦时公式的不同，这一点很容易不加区别而出错。

例1（2009年高考全国卷Ⅱ理科题）已知双曲线的右焦点为，过且斜率为的直线交于两点。

若，则的离心率为（）解这里，所以，又，代入公式得，所以，故选。

例2（2010年高考全国卷Ⅱ理科第12题）已知椭圆的离心率为。

过右焦点且斜率为的直线于相交于两点，若，则（）解这里，，设直线的倾斜角为，代入公式得，所以，所以，故选。

例3 （08高考江西卷理科第15题）过抛物线的焦点作倾斜角为的直线，与抛物线交于两点（点在轴左侧），则有＿＿＿＿图3解如图3，由题意知直线与抛物线的地称轴的夹角，当点在轴左侧时，设，又，代入公式得，解得，所以。

例4（2010年高考全国卷Ⅰ理科第16题）已知是椭圆的一个焦点，是短轴的一个端点，线段的延长线交于点，且，则的离心率为＿＿＿解设直线与焦点所在的轴的夹角为，则，又，代入公式得，所以。

例5（自编题）已知双曲线的离心率为，过左焦点且斜率为的直线交的两支于两点。

圆锥曲线焦半径公式

圆锥曲线焦半径公式
圆锥曲线焦半径公式是一种比较复杂的数学运算公式，通过利用该公式，我们
可以求得圆锥曲线的焦半径。

一般来说，这个公式非常重要，因为它与圆锥曲线的属性有关，可以对圆锥曲线的平面投影或者轮廓作出准确的描述。

圆锥曲线焦半径公式可以用简洁的数学表示式来表示，如下：
R=c/2√2h
其中：R 为圆锥曲线焦半径，c 为圆锥曲线曲线圆心到曲线上任一点的距离，
h 为圆锥曲线曲线圆心到曲线外点的距离。

圆锥曲线的焦半径是由圆锥曲线的半角和曲率来决定的，它与曲率之间的关系
是正比的，这意味着，随着曲率的增加，圆锥曲线的焦半径也会相应增加。

圆锥曲线焦半径公式的应用非常广泛，它既可以用于求解圆锥曲线的几何特征，也可以用于计算圆锥曲线曲线与所需圆或椭圆的关系。

圆锥曲线的焦半径公式已经被广泛应用于室内景观设计、建筑设计、测量计算等领域。

总之，圆锥曲线焦半径公式是一个复杂但又非常有用的数学公式，它与圆锥曲
线的曲率有关，对于求解圆锥曲线属性和计算各类圆或椭圆的关系有着重要的作用，应用范围也十分广泛，值得我们加以重视。

圆锥曲线焦点弦长公式(极坐标全参数方程)

圆锥曲线焦点弦长公式（极坐标参数方程）圆锥曲线的焦点弦问题是高考命题的大热点，主要是在解答题中，全国文科一般为压轴题的第22题，理科和各省市一般为第21题或者第20题，几乎每一年都有考察。

由于题目的综合性很高的，运算量很大，属于高难度题目，考试的得分率极低。

本文介绍的焦点弦长公式是圆锥曲线（椭圆、双曲线和抛物线）的通用公式，它是解决这类问题的金钥匙，利用这个公式使得极其复杂的问题变得简单明了，中等学习程度的学生完全能够得心应手！?定理已知圆锥曲线（椭圆、双曲线或者抛物线）的对称轴为坐标轴(或平行于坐标轴)，焦点为F ，设倾斜角为α的直线l 经过F ，且与圆锥曲线交于A 、B 两点，记圆锥曲线的离心率为e ，通径长为H ，则（1）当焦点在x 轴上时，弦AB 的长|cos 1|||22αe HAB -=；（2）当焦点在y 轴上时，弦AB 的长|sin 1|||22αe HAB -=.推论：（1）焦点在x 轴上，当A 、B 在椭圆、抛物线或双曲线的一支上时，α22cos 1||e HAB -=；当A 、B 不在双曲线的一支上时，1cos ||22-=αe HAB ；当圆锥曲线是抛物线时，α2sin ||HAB =. （2）焦点在y 轴上，当A 、B 在椭圆、抛物线或双曲线的一支上时，α22sin 1||e HAB -=；当A 、B 不在双曲线的一支上时，1sin ||22-=αe HAB ；当圆锥曲线是抛物线时，α2cos ||HAB =.典题妙解下面以部分高考题为例说明上述结论在解题中的妙用.例1（06湖南文第21题）已知椭圆134221=+y x C ：，抛物线px m y 22=-）（（p ＞0），且1C 、2C 的公共弦AB 过椭圆1C 的右焦点.（Ⅰ）当x AB ⊥轴时，求p ，m 的值，并判断抛物线2C 的焦点是否在直线AB 上；（Ⅱ）若34=p 且抛物线2C 的焦点在直线AB 上，求m 的值及直线AB 的方程.2FOABxy例2（07全国Ⅰ文第22题）已知椭圆12322=+y x 的左、右焦点分别为1F 、2F ，过1F 的直线交椭圆于B 、D 两点，过2F 的直线交椭圆于A 、C 两点，且BD AC ⊥，垂足为P.（1）设P 点的坐标为），（00y x ，证明：232020yx +＜1. （2）求四边形ABCD 的面积的最小值.2FABCD Oxy 1F P例3（08全国Ⅰ理第21题文第22题）双曲线的中心为原点O ，焦点在x 上，两条渐近线分别为1l 、2l ，经过右焦点F 垂直于1l 的直线分别交1l 、2l 于A 、B 两点. 已知||OA 、||AB 、||OB 成等差数列，且BF 与FA 同向.（Ⅰ）求双曲线的离心率；（Ⅱ）设AB 被双曲线所截得的线段的长为4，求双曲线的方程.A ByO F x1l2lN M金指点睛1. 已知斜率为1的直线l 过椭圆1422=+x y 的上焦点F 交椭圆于A 、B 两点，则||AB =_________.2. 过双曲线1322=-y x 的左焦点F 作倾斜角为6π的直线l 交双曲线于A 、B 两点，则||AB =_________.3. 已知椭圆02222=-+y x ，过左焦点F 作直线l 交A 、B 两点，O 为坐标原点，求△AOB 的最大面积.B O xy AF4. 已知抛物线px y 42=（p ＞0），弦AB 过焦点F ，设m AB =||，△AOB 的面积为S ，求证：mS 2为定值.yO F x AB5.（05全国Ⅱ文第22题）P 、Q 、M 、N 四点都在椭圆1222=+y x 上，F 为椭圆在y 轴正半轴上的焦点. 已知PF 与FQ 共线，MF 与FN 共线，且0=⋅MF PF .求四边形PQMN 的面积的最大值和最小值.O xNPy MQF6. (07重庆文第22题)如图，倾斜角为α的直线经过抛物线x y 82=的焦点F ，且与抛物线交于A 、B 两点.（Ⅰ）求抛物线的焦点F 的坐标及准线l 的方程；（Ⅱ）若α为锐角，作线段AB 的垂直平分线m 交x 轴于点P ，证明α2cos ||||FP FP -为定值，并求此定值.yO F xA BDEC lαm P7. 点M 与点)2,0(F 的距离比它到直线03:=+y l 的距离小1.（1）求点M 的轨迹方程；（2）经过点F 且互相垂直的两条直线与轨迹相交于A 、B ；C 、D. 求四边形ACBD 的最小面积.FO xA BD C y8. 已知双曲线的左右焦点1F 、2F 与椭圆1522=+y x 的焦点相同，且以抛物线x y 22-=的准线为其中一条准线. （1）求双曲线的方程；（2）若经过焦点2F 且互相垂直的两条直线与双曲线相交于A 、B ；C 、D. 求四边形ACBD的面积的最小值.y2FAO x1l2l B CD参考答案：证明：设双曲线方程为12222=-by a x （a ＞0，b ＞0），通径a b H 22=，离心率a ce =，弦AB 所在的直线l 的方程为）（c x k y +=（其中αtan =k ，α为直线l 的倾斜角），其参数方程为为参数）（，t t y t c x ⎩⎨⎧=+-=.sin cos αα. 代入双曲线方程并整理得：0cos 2cos sin 4222222=-⋅+⋅-b t c b t b a ααα）（. 由t 的几何意义可得：|cos 1|2|cos 1|2|cos sin |2cos sin 4cos sin cos 24||||22222222222222222222222122121αααααααααe a b e a b b a ab b a b b a c b t t t t t t AB -=-=-=-----=-+=-=）（）（.|cos 1|22αe H-=例1.解：（Ⅰ）当x AB ⊥轴时，点A 、B 关于x 轴对称，0=∴m ，直线AB 的方程为1=x . 从而点A 的坐标为），（231或），（231-. 点A 在抛物线2C 上，.249p =∴即.89=p此时抛物线2C 的焦点坐标为），（0169，该焦点不在直线AB 上. （Ⅱ）设直线AB 的倾斜角为α，由（Ⅰ）知2πα≠.则直线AB 的方程为）（1tan -⋅=x y α.抛物线2C 的对称轴m y =平行于x 轴，焦点在AB 上，通径382==p H ，离心率1=e ，于是有又 AB 过椭圆1C 的右焦点，通径322==a b H ，离心率21=e . ∴.cos 412|cos 1|||222αα-=-=e H AB∴）（α2cos 138-.cos 4122α-= 解之得：6tan 71cos 2±==αα，.抛物线2C 的焦点），（m F 32在直线）（1tan -⋅=x y α上， ∴αtan 31-=m ，从而36±=m . 当36=m 时，直线AB 的方程为066=-+y x ；当36-=m 时，直线AB 的方程为066=--y x 例2.（1）证明：在12322=+y x 中，123===c b a ，，. ，︒=∠9021PF F O 是1F 2F 的中点，.1||21||21===∴c F F OP 得.12020=+y x ∴点P 在圆122=+y x 上.显然，圆122=+y x 在椭圆12322=+y x 的内部. 故232020yx +＜1.（2）解：如图，设直线BD 的倾斜角为α，由BD AC ⊥可知，直线AC 的倾斜角απ+2..cos 138sin ||22）（αα-==H AB 2FOABxy通径33422==a b H ，离心率33=e . 又 BD 、AC 分别过椭圆的左、右焦点1F 、2F ，于是.sin 3342cos 1||cos 334cos 1||222222ααπαα-=+-=-=-=）（，e H AC e H BD ∴四边形ABCD 的面积.2sin 2496sin 334cos 33421||||21222ααα+=-⋅-⋅=⋅=AC BD S [)]10[2sin 02，，，∈∴∈απα . ⎥⎦⎤⎢⎣⎡∈∴42596，S .故四边形ABCD 面积的最小值为2596. 例3，解：（Ⅰ）设双曲线的方程为12222=-by a x （a ＞0，b ＞0）.||OA 、||AB 、||OB 成等差数列，设m AB =||，公差为d ，则d m OA -=||，d m OB +=||，∴222)()(d m m d m +=+-. 即2222222d dm m m d dm m ++=++-. ∴4m d =. 从而43||m OA =，45||mOB =. 又设直线1l 的倾斜角为α，则α2=∠AOB . 1l 的方程为x aby =. ∴.tan ab=α 而.34||||tan 2tan ==∠=OA AB AOB α 2FABCD Oxy 1F P∴34)(12tan 1tan 222=-⨯=-ab a bαα. 解之得：.21=a b∴.25)(12=+=a b e （Ⅱ）设过焦点F 的直线AB 的倾斜角为θ, 则απθ+=2.∴αθsin cos -=. 而.51)21(1)21(tan 1tan sin 22222=+=+=ααα∴51cos 2=θ.通径b abb a b H =⨯==222. 又设直线AB 与双曲线的交点为M 、N. 于是有：4cos 1||22=-=θe HMN .即451)25(12=⨯-b .解得3=b ，从而6=a .∴所求的椭圆方程为193622=-y x .1. 解：3,1,2===c b a ，离心率23==a c e ，通径122==ab H ，直线l 的倾斜角4πα=.∴58)22()23(11sin 1||2222=⋅-=-=αe HAB . 2. 解：2,3,1===c b a ，离心率2==ace ，通径622==a b H ，直线的倾斜角6πα=. A ByO F x1l2lN M∴3|)23(21|6|cos 1|||2222=⋅-=-=αe HAB .3. 解：1222=+y x ，1,1,2===c b a ，左焦点)0,1(-F ，离心率22==a c e ，通径222==ab H .当直线l 的斜率不存在时，x l ⊥轴，这时22||2===ab H AB ，高1||==c OF ，△AOB 的面积221221=⨯⨯=S . 当直线l 的斜率存在时，设直线l 的倾斜角为α，则其方程为)1(tan +⋅=x y α，即tan tan =+-⋅ααy x ，原点O 到直线AB 的距离ααααααs i n|s e c ||t a n|1t a n |t a n 0ta n 0|2==++-⨯=d . αααα222222sin 122cos 222cos )22(12cos 1||+=-=⋅-=-=e HAB . ∴△AOB 的面积αα2sin 1sin 2||21+=⨯⨯=d AB S . 0＜α＜π，∴αsin ＞0. 从而ααsin 2sin 12≥+. ∴22sin 2sin 2=≤ααS .当且仅当1sin =α，即2πα=时，“=”号成立. 故△AOB 的最大面积为22. 4. 解：焦点为)0,(p F ，通径p H 4=.当直线AB 的斜率不存在时，x AB ⊥轴，这时p m AB 4||==，高p OF =||，△AOBBO xy AF的面积22||||21p OF AB S =⨯⨯=. ∴3442444p pp m p m S ===，是定值.当直线AB 的斜率存在时，设直线的倾斜角为α，则其方程为)(tan p x y -⋅=α，即tan tan =+-⋅ααp y x ，原点O 到直线AB 的距离αααααs i n |s e c ||t a n|1t a n |t a n |2p p p d ==+=. αα22sin 4sin ||pH AB ==. ∴△AOB 的面积αsin 2||212p d AB S =⨯⨯=.∴32242424sin sin 41sin 4p pp m p m S =⨯=⨯=ααα. ∴不论直线AB 在什么位置，均有32p m S =（3p 为定值）.5. 解：在椭圆1222=+y x 中，.112===c b a ，，由已知条件，MN 和PQ 是椭圆的两条弦，相交于焦点），（10F ，且PQ MN ⊥. 如图，设直线PQ 的倾斜角为α，则直线MN 的倾斜角απ+2.通径222==ab H ，离心率22=e .于是有.sin 222sin 1||cos 222)2(sin 1||222222ααααπ-=-=-=+-=e H PQ e HMN ，∴四边形PQMN 的面积O xNPy MQFyO F x AB.2sin 816sin 222cos 22221||||21222ααα+=-⋅-⋅=⋅=PQ MN S [)]10[2sin 02，，，∈∴∈απα . ⎥⎦⎤⎢⎣⎡∈∴2916，S .故四边形PQMN 面积的最小值和最大值分别为916和2. 6.（Ⅰ）解：4,82==p p ，∴抛物线的焦点F 的坐标为)2,0(，准线l 的方程为2-=x .（Ⅱ）证明：作l AC ⊥于C ，AC FD ⊥于D. 通径82==p H . 则ααααcos ||||,cos ||||,sin 8sin ||22AF AD FP EF H AB ====.∴4cos ||||||||+=+==αAF p AD AC AF .∴αcos 14||-=AF .∴αααα22sin cos 4sin 4cos 14||21||||||||=--=-=-=AB AF AE AF EF ，从而αα2sin 4cos ||||==EF FP . ∴8sin 2sin 4)2cos 1(||2cos ||||22=⋅=-=-ααααFP FP FP . 故α2cos ||||FP FP -为定值，此定值为8.7. 解：（1）根据题意，点M 与点)2,0(F 的距离与它到直线2:-=y l 的距离相等，∴点M 的轨迹是抛物线，点)2,0(F 是它的焦点，直线2:-=y l 是它的准线.从而22=p，∴4=p . ∴所求的点M 的轨迹方程是y x 82=.（2）两条互相垂直的直线与抛物线均有两个交点， ∴它们的斜率都存在. 如图，设直线AB 的倾斜角为α，则直线CD 的倾斜角为α+︒90.y O F xA BDEClαm P BDy抛物线的通径82==p H ，于是有：αααα2222sin 8)90(cos ||,cos 8cos ||=+︒===H CD H AB .∴四边形ACBD 的面积.2sin 128sin 8cos 821||||21222ααα=⋅⋅=⋅=CD AB S 当且仅当α2sin 2取得最大值1时，128min =S ，这时︒=︒=45,902αα.∴四边形ACBD 的最小面积为128.8. 解：（1）在椭圆1522=+y x 中，2,1,522=-===b a c b a ，∴其焦点为)0,2(1-F 、)0,2(2F .在抛物线x y 22-=中，1=p ，∴其准线方程为212==p x . 在双曲线中，21,22==c a c ，∴3,122=-==a c b a . ∴所求的双曲线的方程为1322=-y x .（2）两条互相垂直的直线与双曲线均有两个交点，∴它们的斜率都存在. 如图，设直线AB 的倾斜角为α，则直线CD 的倾斜角为α+︒90.双曲线的通径622==a b H ，离心率2==a ce . 于是有： αααα222222sin 416)90(cos 1||,cos 416cos 1||-=+︒-=-=-=e H CD e H AB .∴四边形ACBD 的面积.2sin 4318sin 416cos 41621||||21222ααα+-=-⋅-⋅=⋅=CD AB S =18 y2FAO x1l2l B CD当且仅当α2sin 2取得最大值1时，18min =S ，这时︒=︒=45,902αα.∴四边形ACBD 的最小面积为18.。

圆锥曲线焦点弦长公式

圆锥曲线焦点弦长公式
椭圆：
对于椭圆，其标准方程为 a2x2+b2y2=1（其中 a>b）。

焦点到椭圆上任意一点的距离之和为常数，等于椭圆的长轴长，即 2a。

焦点弦长的一般公式比较复杂，但如果是过焦点的直线与椭圆相交，且直线的斜率存在，设为 k，则弦长 L 可以用以下公式表示：
L=a2k2+b22b2
双曲线：
对于双曲线，其标准方程为 a2x2−b2y2=1。

焦点到双曲线上任意一点的距离之差为常数，等于双曲线的实轴长，即 2a。

对于双曲线的焦点弦长，情况与椭圆类似，但公式会有所不同。

如果过焦点的直线与双曲线相交，且直线的斜率存在，设为 k，则弦长 L 可以用以下公式表示：L=b2−a2k22b2
抛物线：
对于抛物线，其标准方程为 y2=4px（其中 p 是焦距）。

焦点到抛物线上任意一点的距离等于该点到准线的距离。

对于抛物线的焦点弦长，如果过焦点的直线与抛物线相交，且直线的斜率存在，设为 k，则弦长 L 可以用以下公式表示：
L=k22p。

圆锥曲线的焦半径公式及其应用

技法点拨圆锥曲线的焦半径公式及其应用■郭海先摘要：利用圆锥曲线的焦半径公式以及圆锥曲线的第二定义解答圆锥曲线类问题，能起到事半功倍之效果。

关键词：椭圆焦半径公式；双曲线的焦半径公式；抛物线的焦半径公式圆锥曲线上任意一点到焦点的距离叫作圆锥曲线关于该点的焦半径。

利用圆锥曲线的第二定义很容易得到圆锥曲线的焦半径公式。

一、椭圆的焦半径公式椭圆上的任意一点到焦点F 的长，称为此曲线上该点的焦半径。

根据椭圆的定义，很容易推导出椭圆的焦半径公式。

在涉及焦半径或焦点弦的一些问题时，用焦半径公式解题可以简化运算过程。

1.若P （x 0，y 0）为椭圆x 2a 2+y 2b2=1（a>b >0）上任意一点，F 1、F 2分别为椭圆的左、右焦点，则||PF 1=a+ex 0，||PF 2=a-e x 0.2.若P （x 0，y 0）为椭圆y 2a 2+x 2b2=1（a>b >0）上任意一点，F 2、F 1分别为椭圆的上、下焦点，则||PF 1=a+e y 0，||PF 2=a-e y 0.例1．椭圆x 225+y 29=1上三个不同的点A （x 1，y 1）、B （4，95）、C（x 2，y 2）到焦点F （4，0）的距离成等差数列，求x 1+x 2的值.解：在已知椭圆中，右准线方程为x =254，设A 、B 、C 到右准线的距离为d 1、d 2、d 3，则d 1=254-x 1、d 2=254-4、d 3=254-x 2.∵|AF |=d 1·e ，|BF |=d 2·e ，|CF |=d 3·e ，而|AF|、|BF|、|CF|成等差数列.∴2d 2=d 1+d 3，即2（254-4）=2×254-（x 1+x 2），x 1+x 2=8.评析：涉及椭圆上点到焦点的距离问题，一般采用焦半径公式求解，即利用焦半径公式可求出A 、B 、C 三点到焦点的距离，再利用等差数列的性质即可求出x 1+x 2的值。

高考圆锥曲线公式知识点总结

高考圆锥曲线公式学问点总结高考圆锥曲线公式学问点总结导语：人生，没有过不去的坎，你不行以坐在坎边等它消逝，你只能想方法穿过它。

下面是为大家整理，数学学问。

词更多相关信息请关注CNFLA相关栏目!圆锥曲线公式：椭圆1、中心在原点，焦点在x轴上的椭圆标准方程：其中x/a+y/b=1,其中ab0,c=a-b2、中心在原点，焦点在y轴上的椭圆标准方程：y/a+x/b=1,其中ab0,c=a-b参数方程：x=acos;y=bsin(为参数，02)圆锥曲线公式：双曲线1、中心在原点，焦点在x轴上的.双曲线标准方程：x/a-y/b=1,其中a0，b0，c=a+b.2、中心在原点，焦点在y轴上的双曲线标准方程：y/a-x/b=1,其中a0，b0，c=a+b.参数方程：x=asec;y=btan(为参数)圆锥曲线公式：抛物线参数方程:x=2pt;y=2pt(t为参数)t=1/tan(tan为曲线上点与坐标原点确定直线的斜率)特殊地，t可等于0 直角坐标:y=ax+bx+c(开口方向为y轴，a0)x=ay+by+c(开口方向为x轴，a0)离心率椭圆，双曲线，抛物线这些圆锥曲线有统一的定义：平面上，到定点的距离与到定直线的距离的比e是常数的点的轨迹叫做圆锥曲线。

且当01时为双曲线。

圆锥曲线公式学问点总结圆锥曲线椭圆双曲线抛物线标准方程x/a+y/b=1(ab0) x/a-y/b=1(a0,b0) y=2px(p0) 范围x[-a,a] x(-，-a][a,+) x[0,+)y[-b,b] yR yR对称性关于x轴，y轴，原点对称关于x轴，y轴，原点对称关于x轴对称顶点(a,0),(-a,0),(0,b),(0,-b) (a,0),(-a,0) (0,0)焦点(c,0),(-c,0) (c,0),(-c,0) (p/2,0)准线x=a/c x=a/c x=-p/2渐近线y=(b/a)x离心率e=c/a,e(0,1) e=c/a,e(1,+) e=1焦半径∣PF∣=a+ex ∣PF∣=∣ex+a∣∣PF∣=x+p/2∣PF∣=a-ex ∣PF∣=∣ex-a∣焦准距p=b/c p=b/c p通径2b/a 2b/a 2p参数方程x=acos x=asec x=2pty=bsin，为参数y=btan，为参数y=2pt,t为参数过圆锥曲线上一点x0x/a+y0y/b=1 x0x/a-y0y/b=1 y0y=p(x+x0)(x0,y0)的切线方程斜率为k的切线方程y=kx(ak+b) y=kx(ak-b)y=kx+p/2k。

圆锥曲线的极坐标方程、焦半径公式、焦点弦公式good

圆锥曲线的极坐标方程知识点精析椭圆、双曲线、抛物线可以统一定义为：与一个定点(焦点)的距离和一条定直线(准线)的距离的比等于常数e 的点的轨迹．以椭圆的左焦点(双曲线的右焦点、抛物线的焦点)为极点，过点F 作相应准线的垂线，垂足为K ，以FK 的反向延长线为极轴建立极坐标系．椭圆、双曲线、抛物线统一的极坐标方程为： θρcos 1e ep-=.其中p 是定点F 到定直线的距离，p ＞0 ．当0＜e ＜1时，方程表示椭圆；当e ＞1时，方程表示双曲线，若ρ＞0，方程只表示双曲线右支，若允许ρ＜0，方程就表示整个双曲线；当e=1时，方程表示开口向右的抛物线.引论（1）若 1+cos epe ρθ=则0＜e ＜1当时，方程表示极点在右焦点上的椭圆当e=1时时，方程表示开口向左的抛物线当e ＞1方程表示极点在左焦点上的双曲线（2 ）若1-sin epe ρθ=当 0＜e ＜1时，方程表示极点在下焦点的椭圆当e=1时，方程表示开口向上的抛物线当 e ＞1时!方程表示极点在上焦点的双曲线（3）1+sin epe ρθ=当 0＜e ＜1时，方程表示极点在上焦点的椭圆当e=1时，方程表示开口向下的抛物线当 e ＞1时!方程表示极点在下焦点的双曲线（2）圆锥曲线弦长问题若圆锥曲线的弦MN 经过焦点F ，1、椭圆中，cb c c a p 22=-=，θθπθ2222cos 2)cos(1cos 1c a ab e ep e ep MN -=--+-=.2、双曲线中，（注释：双曲线问题比较特殊，很多参考书上均有误解。

）若M 、N 在双曲线同一支上，θθπθ2222cos 2)cos(1cos 1c a ab e ep e ep MN -=--+-=；若M 、N 在双曲线不同支上，2222cos 2cos 1cos 1a c ab e ep e ep MN -=--+-=θθθ.3、抛物线中，θθπθ2sin 2)cos(1cos 1pp p MN =--+-=例1过双曲线22x y -145=的右焦点，引倾斜角为3π的直线，交双曲线与A 、B 两点，求AB ｜｜解：根据题意，建立以双曲线右焦点为极点的极坐标系即得所以又由得注释：求椭圆和抛物线过焦点的弦长时，无需对 v 加绝对值，但求双曲线的弦长时，一定要加绝对值，这是避免讨论做好的方法。

圆锥曲线焦点弦长公式(极坐标全参数方程)

圆锥曲线焦点弦长公式（极坐标参数方程）圆锥曲线的焦点弦问题是高考命题的大热点，主要是在解答题中，全国文科一般为压轴题的第22题，理科和各省市一般为第21题或者第20题，几乎每一年都有考察。

由于题目的综合性很高的，运算量很大，属于高难度题目，考试的得分率极低。

本文介绍的焦点弦长公式是圆锥曲线（椭圆、双曲线和抛物线）的通用公式，它是解决这类问题的金钥匙，利用这个公式使得极其复杂的问题变得简单明了，中等学习程度的学生完全能够得心应手！?定理已知圆锥曲线（椭圆、双曲线或者抛物线）的对称轴为坐标轴(或平行于坐标轴)，焦点为F ，设倾斜角为α的直线l 经过F ，且与圆锥曲线交于A 、B 两点，记圆锥曲线的离心率为e ，通径长为H ，则（1）当焦点在x 轴上时，弦AB 的长|cos 1|||22αe HAB -=；（2）当焦点在y 轴上时，弦AB 的长|sin 1|||22αe HAB -=.推论：（1）焦点在x 轴上，当A 、B 在椭圆、抛物线或双曲线的一支上时，α22cos 1||e HAB -=；当A 、B 不在双曲线的一支上时，1cos ||22-=αe HAB ；当圆锥曲线是抛物线时，α2sin ||HAB =. （2）焦点在y 轴上，当A 、B 在椭圆、抛物线或双曲线的一支上时，α22sin 1||e HAB -=；当A 、B 不在双曲线的一支上时，1sin ||22-=αe HAB ；当圆锥曲线是抛物线时，α2cos ||HAB =.典题妙解下面以部分高考题为例说明上述结论在解题中的妙用.例1（06湖南文第21题）已知椭圆134221=+y x C ：，抛物线px m y 22=-）（（p ＞0），且1C 、2C 的公共弦AB 过椭圆1C 的右焦点.（Ⅰ）当x AB ⊥轴时，求p ，m 的值，并判断抛物线2C 的焦点是否在直线AB 上；（Ⅱ）若34=p 且抛物线2C 的焦点在直线AB 上，求m 的值及直线AB 的方程.2FOABxy例2（07全国Ⅰ文第22题）已知椭圆12322=+y x 的左、右焦点分别为1F 、2F ，过1F 的直线交椭圆于B 、D 两点，过2F 的直线交椭圆于A 、C 两点，且BD AC ⊥，垂足为P.（1）设P 点的坐标为），（00y x ，证明：232020yx +＜1. （2）求四边形ABCD 的面积的最小值.2FABCD Oxy 1F P例3（08全国Ⅰ理第21题文第22题）双曲线的中心为原点O ，焦点在x 上，两条渐近线分别为1l 、2l ，经过右焦点F 垂直于1l 的直线分别交1l 、2l 于A 、B 两点. 已知||OA 、||AB 、||OB 成等差数列，且BF 与FA 同向.（Ⅰ）求双曲线的离心率；（Ⅱ）设AB 被双曲线所截得的线段的长为4，求双曲线的方程.A ByO F x1l2lN M金指点睛1. 已知斜率为1的直线l 过椭圆1422=+x y 的上焦点F 交椭圆于A 、B 两点，则||AB =_________.2. 过双曲线1322=-y x 的左焦点F 作倾斜角为6π的直线l 交双曲线于A 、B 两点，则||AB =_________.3. 已知椭圆02222=-+y x ，过左焦点F 作直线l 交A 、B 两点，O 为坐标原点，求△AOB 的最大面积.B O xy AF4. 已知抛物线px y 42=（p ＞0），弦AB 过焦点F ，设m AB =||，△AOB 的面积为S ，求证：mS 2为定值.yO F x AB5.（05全国Ⅱ文第22题）P 、Q 、M 、N 四点都在椭圆1222=+y x 上，F 为椭圆在y 轴正半轴上的焦点. 已知PF 与FQ 共线，MF 与FN 共线，且0=⋅MF PF .求四边形PQMN 的面积的最大值和最小值.O xNPy MQF6. (07重庆文第22题)如图，倾斜角为α的直线经过抛物线x y 82=的焦点F ，且与抛物线交于A 、B 两点.（Ⅰ）求抛物线的焦点F 的坐标及准线l 的方程；（Ⅱ）若α为锐角，作线段AB 的垂直平分线m 交x 轴于点P ，证明α2cos ||||FP FP -为定值，并求此定值.yO F xA BDEC lαm P7. 点M 与点)2,0(F 的距离比它到直线03:=+y l 的距离小1.（1）求点M 的轨迹方程；（2）经过点F 且互相垂直的两条直线与轨迹相交于A 、B ；C 、D. 求四边形ACBD 的最小面积.FO xA BD C y8. 已知双曲线的左右焦点1F 、2F 与椭圆1522=+y x 的焦点相同，且以抛物线x y 22-=的准线为其中一条准线. （1）求双曲线的方程；（2）若经过焦点2F 且互相垂直的两条直线与双曲线相交于A 、B ；C 、D. 求四边形ACBD的面积的最小值.y2FAO x1l2l B CD参考答案：证明：设双曲线方程为12222=-by a x （a ＞0，b ＞0），通径a b H 22=，离心率a ce =，弦AB 所在的直线l 的方程为）（c x k y +=（其中αtan =k ，α为直线l 的倾斜角），其参数方程为为参数）（，t t y t c x ⎩⎨⎧=+-=.sin cos αα. 代入双曲线方程并整理得：0cos 2cos sin 4222222=-⋅+⋅-b t c b t b a ααα）（. 由t 的几何意义可得：|cos 1|2|cos 1|2|cos sin |2cos sin 4cos sin cos 24||||22222222222222222222222122121αααααααααe a b e a b b a ab b a b b a c b t t t t t t AB -=-=-=-----=-+=-=）（）（.|cos 1|22αe H-=例1.解：（Ⅰ）当x AB ⊥轴时，点A 、B 关于x 轴对称，0=∴m ，直线AB 的方程为1=x . 从而点A 的坐标为），（231或），（231-. 点A 在抛物线2C 上，.249p =∴即.89=p此时抛物线2C 的焦点坐标为），（0169，该焦点不在直线AB 上. （Ⅱ）设直线AB 的倾斜角为α，由（Ⅰ）知2πα≠.则直线AB 的方程为）（1tan -⋅=x y α.抛物线2C 的对称轴m y =平行于x 轴，焦点在AB 上，通径382==p H ，离心率1=e ，于是有又 AB 过椭圆1C 的右焦点，通径322==a b H ，离心率21=e . ∴.cos 412|cos 1|||222αα-=-=e H AB∴）（α2cos 138-.cos 4122α-= 解之得：6tan 71cos 2±==αα，.抛物线2C 的焦点），（m F 32在直线）（1tan -⋅=x y α上， ∴αtan 31-=m ，从而36±=m . 当36=m 时，直线AB 的方程为066=-+y x ；当36-=m 时，直线AB 的方程为066=--y x 例2.（1）证明：在12322=+y x 中，123===c b a ，，. ，︒=∠9021PF F O 是1F 2F 的中点，.1||21||21===∴c F F OP 得.12020=+y x ∴点P 在圆122=+y x 上.显然，圆122=+y x 在椭圆12322=+y x 的内部. 故232020yx +＜1.（2）解：如图，设直线BD 的倾斜角为α，由BD AC ⊥可知，直线AC 的倾斜角απ+2..cos 138sin ||22）（αα-==H AB 2FOABxy通径33422==a b H ，离心率33=e . 又 BD 、AC 分别过椭圆的左、右焦点1F 、2F ，于是.sin 3342cos 1||cos 334cos 1||222222ααπαα-=+-=-=-=）（，e H AC e H BD ∴四边形ABCD 的面积.2sin 2496sin 334cos 33421||||21222ααα+=-⋅-⋅=⋅=AC BD S [)]10[2sin 02，，，∈∴∈απα . ⎥⎦⎤⎢⎣⎡∈∴42596，S .故四边形ABCD 面积的最小值为2596. 例3，解：（Ⅰ）设双曲线的方程为12222=-by a x （a ＞0，b ＞0）.||OA 、||AB 、||OB 成等差数列，设m AB =||，公差为d ，则d m OA -=||，d m OB +=||，∴222)()(d m m d m +=+-. 即2222222d dm m m d dm m ++=++-. ∴4m d =. 从而43||m OA =，45||mOB =. 又设直线1l 的倾斜角为α，则α2=∠AOB . 1l 的方程为x aby =. ∴.tan ab=α 而.34||||tan 2tan ==∠=OA AB AOB α 2FABCD Oxy 1F P∴34)(12tan 1tan 222=-⨯=-ab a bαα. 解之得：.21=a b∴.25)(12=+=a b e （Ⅱ）设过焦点F 的直线AB 的倾斜角为θ, 则απθ+=2.∴αθsin cos -=. 而.51)21(1)21(tan 1tan sin 22222=+=+=ααα∴51cos 2=θ.通径b abb a b H =⨯==222. 又设直线AB 与双曲线的交点为M 、N. 于是有：4cos 1||22=-=θe HMN .即451)25(12=⨯-b .解得3=b ，从而6=a .∴所求的椭圆方程为193622=-y x .1. 解：3,1,2===c b a ，离心率23==a c e ，通径122==ab H ，直线l 的倾斜角4πα=.∴58)22()23(11sin 1||2222=⋅-=-=αe HAB . 2. 解：2,3,1===c b a ，离心率2==ace ，通径622==a b H ，直线的倾斜角6πα=. A ByO F x1l2lN M∴3|)23(21|6|cos 1|||2222=⋅-=-=αe HAB .3. 解：1222=+y x ，1,1,2===c b a ，左焦点)0,1(-F ，离心率22==a c e ，通径222==ab H .当直线l 的斜率不存在时，x l ⊥轴，这时22||2===ab H AB ，高1||==c OF ，△AOB 的面积221221=⨯⨯=S . 当直线l 的斜率存在时，设直线l 的倾斜角为α，则其方程为)1(tan +⋅=x y α，即tan tan =+-⋅ααy x ，原点O 到直线AB 的距离ααααααs i n|s e c ||t a n|1t a n |t a n 0ta n 0|2==++-⨯=d . αααα222222sin 122cos 222cos )22(12cos 1||+=-=⋅-=-=e HAB . ∴△AOB 的面积αα2sin 1sin 2||21+=⨯⨯=d AB S . 0＜α＜π，∴αsin ＞0. 从而ααsin 2sin 12≥+. ∴22sin 2sin 2=≤ααS .当且仅当1sin =α，即2πα=时，“=”号成立. 故△AOB 的最大面积为22. 4. 解：焦点为)0,(p F ，通径p H 4=.当直线AB 的斜率不存在时，x AB ⊥轴，这时p m AB 4||==，高p OF =||，△AOBBO xy AF的面积22||||21p OF AB S =⨯⨯=. ∴3442444p pp m p m S ===，是定值.当直线AB 的斜率存在时，设直线的倾斜角为α，则其方程为)(tan p x y -⋅=α，即tan tan =+-⋅ααp y x ，原点O 到直线AB 的距离αααααs i n |s e c ||t a n|1t a n |t a n |2p p p d ==+=. αα22sin 4sin ||pH AB ==. ∴△AOB 的面积αsin 2||212p d AB S =⨯⨯=.∴32242424sin sin 41sin 4p pp m p m S =⨯=⨯=ααα. ∴不论直线AB 在什么位置，均有32p m S =（3p 为定值）.5. 解：在椭圆1222=+y x 中，.112===c b a ，，由已知条件，MN 和PQ 是椭圆的两条弦，相交于焦点），（10F ，且PQ MN ⊥. 如图，设直线PQ 的倾斜角为α，则直线MN 的倾斜角απ+2.通径222==ab H ，离心率22=e .于是有.sin 222sin 1||cos 222)2(sin 1||222222ααααπ-=-=-=+-=e H PQ e HMN ，∴四边形PQMN 的面积O xNPy MQFyO F x AB.2sin 816sin 222cos 22221||||21222ααα+=-⋅-⋅=⋅=PQ MN S [)]10[2sin 02，，，∈∴∈απα . ⎥⎦⎤⎢⎣⎡∈∴2916，S .故四边形PQMN 面积的最小值和最大值分别为916和2. 6.（Ⅰ）解：4,82==p p ，∴抛物线的焦点F 的坐标为)2,0(，准线l 的方程为2-=x .（Ⅱ）证明：作l AC ⊥于C ，AC FD ⊥于D. 通径82==p H . 则ααααcos ||||,cos ||||,sin 8sin ||22AF AD FP EF H AB ====.∴4cos ||||||||+=+==αAF p AD AC AF .∴αcos 14||-=AF .∴αααα22sin cos 4sin 4cos 14||21||||||||=--=-=-=AB AF AE AF EF ，从而αα2sin 4cos ||||==EF FP . ∴8sin 2sin 4)2cos 1(||2cos ||||22=⋅=-=-ααααFP FP FP . 故α2cos ||||FP FP -为定值，此定值为8.7. 解：（1）根据题意，点M 与点)2,0(F 的距离与它到直线2:-=y l 的距离相等，∴点M 的轨迹是抛物线，点)2,0(F 是它的焦点，直线2:-=y l 是它的准线.从而22=p，∴4=p . ∴所求的点M 的轨迹方程是y x 82=.（2）两条互相垂直的直线与抛物线均有两个交点， ∴它们的斜率都存在. 如图，设直线AB 的倾斜角为α，则直线CD 的倾斜角为α+︒90.y O F xA BDEClαm P BDy抛物线的通径82==p H ，于是有：αααα2222sin 8)90(cos ||,cos 8cos ||=+︒===H CD H AB .∴四边形ACBD 的面积.2sin 128sin 8cos 821||||21222ααα=⋅⋅=⋅=CD AB S 当且仅当α2sin 2取得最大值1时，128min =S ，这时︒=︒=45,902αα.∴四边形ACBD 的最小面积为128.8. 解：（1）在椭圆1522=+y x 中，2,1,522=-===b a c b a ，∴其焦点为)0,2(1-F 、)0,2(2F .在抛物线x y 22-=中，1=p ，∴其准线方程为212==p x . 在双曲线中，21,22==c a c ，∴3,122=-==a c b a . ∴所求的双曲线的方程为1322=-y x .（2）两条互相垂直的直线与双曲线均有两个交点，∴它们的斜率都存在. 如图，设直线AB 的倾斜角为α，则直线CD 的倾斜角为α+︒90.双曲线的通径622==a b H ，离心率2==a ce . 于是有： αααα222222sin 416)90(cos 1||,cos 416cos 1||-=+︒-=-=-=e H CD e H AB .∴四边形ACBD 的面积.2sin 4318sin 416cos 41621||||21222ααα+-=-⋅-⋅=⋅=CD AB S =18 y2FAO x1l2l B CD当且仅当α2sin 2取得最大值1时，18min =S ，这时︒=︒=45,902αα.∴四边形ACBD 的最小面积为18.。

圆锥曲线焦点弦公式

圆锥曲线焦点弦公式
圆锥曲线是指圆锥与平面相交而产生的曲线。

焦点弦是指通过
焦点，并且与曲线相交于两点的直线。

对于圆锥曲线的焦点弦公式，具体的形式取决于所讨论的具体曲线类型，比如椭圆、双曲线或抛
物线。

下面我将分别介绍这三种情况下的焦点弦公式。

对于椭圆而言，焦点弦的公式可以表示为，对于椭圆
$\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$，焦点弦的公式可以表示为$\frac{x^2}{a^2} \frac{y^2}{b^2} = 1$。

对于双曲线而言，焦点弦的公式可以表示为，对于双曲线
$\frac{x^2}{a^2} \frac{y^2}{b^2} = 1$，焦点弦的公式可以表示为$\frac{x^2}{a^2} \frac{y^2}{b^2} = -1$。

对于抛物线而言，焦点弦的公式可以表示为，对于抛物线$y^2
= 4ax$，焦点弦的公式可以表示为$y = mx + \frac{a}{m}$。

需要注意的是，以上给出的焦点弦公式是简化的形式，实际应
用中可能会根据具体问题的要求进行变形。

焦点弦在几何学和物理
学中有着重要的应用，比如在光学中的折射定律、天体运动中的轨
道分析等方面都有着重要的作用。

希望这些信息能够帮助到你理解焦点弦的公式。

圆锥曲线焦半径公式及其应用(学生版)

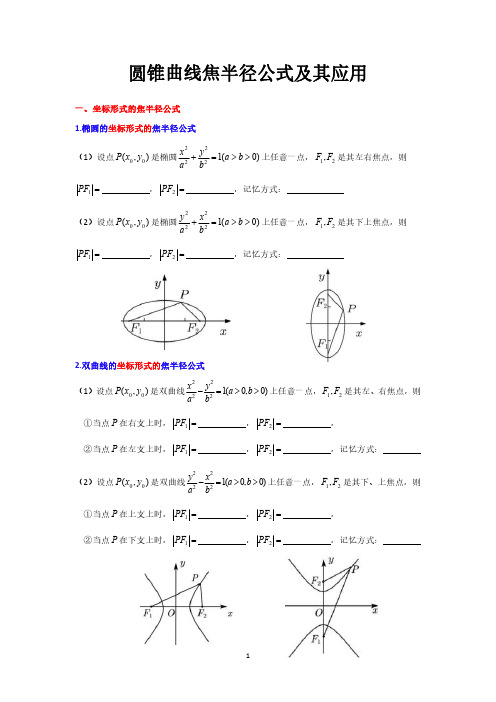
圆锥曲线焦半径公式及其应用一、坐标形式的焦半径公式1.椭圆的坐标形式的焦半径公式（1）设点),(00y x P 是椭圆)0(12222>>=+b a b y a x 上任意一点，21,F F 是其左右焦点，则=1PF ，=2PF ，记忆方式：（2）设点),(00y x P 是椭圆)0(12222>>=+b a b x a y 上任意一点，21,F F 是其下上焦点，则=1PF ，=2PF ，记忆方式：2.双曲线的坐标形式的焦半径公式（1）设点),(00y x P 是双曲线)0,0(12222>>=-b a by a x 上任意一点，21,F F 是其左、右焦点，则①当点P 在右支上时，=1PF ，=2PF ，②当点P 在左支上时，=1PF ，=2PF ，记忆方式：（2）设点),(00y x P 是双曲线)0,0(12222>>=-b a bx a y 上任意一点，21,F F 是其下、上焦点，则①当点P 在上支上时，=1PF ，=2PF ，②当点P 在下支上时，=1PF ，=2PF ，记忆方式：（3）若弦AB 过左焦点，则=AB ；若弦AB 过右焦点，则=AB 3.抛物线的坐标形式的焦半径公式（1）设),(00y x P 是抛物线)0(22>=p px y 上任意一点，F 为其焦点，则=PF （2）设),(00y x P 是抛物线)0(22>-=p px y 上任意一点，F 为其焦点，则=PF （3）设),(00y x P 是抛物线)0(22>=p py x 上任意一点，F 为其焦点，则=PF （4）设),(00y x P 是抛物线)0(22>-=p py x 上任意一点，F 为其焦点，则=PF 例1.（2021年新高考Ⅰ卷）已知21,F F 是椭圆C ：14922=+y x 的两个焦点，点M 在C 上，则21MF MF ⋅的最大值为（）A.13B.12C.9D.6例2.（2019年全国Ⅲ卷理）设21,F F 为椭圆C ：1203622=+y x 的两个焦点，M 为C 上一点且在第一象限，若21F MF ∆为等腰三角形，则点M 的坐标为例3.点),(00y x P 为双曲线C ：132422=-y x 的右支上一点，若点P 到右焦点的距离等于02x ，则=0x例4.双曲线116922=-y x 的两个焦点为21,F F ，点P 在双曲线上，若21PF PF ⊥，则点P 到x轴的距离为例5.（2011年辽宁卷）已知F 是抛物线x y =2的焦点，B A ,是该抛物线上两点，3=+BF AF ，则线段AB 的中点到y 轴的距离为A.43 B.1C.45 D.47例8.（2013年全国Ⅱ卷）设抛物线C ：)0(22>=p px y 的焦点为F ，点M 在C 上，5=MF ，若以MF 为直径的圆过点)2,0(，则C 的方程为（）A.x y 42=或x y 82= B.x y 22=或x y 82=C.x y 42=或xy 162= D.x y 22=或xy 162=注：以抛物线的焦半径为直径的圆与y 轴相切二、角度形式的焦半径公式1.椭圆的角度形式的焦半径公式（1）设过椭圆)0(12222>>=+b a b y a x 的焦点F 的弦AB 的倾斜角为θ，则=AF ；=BF ；焦点弦长=AB ；（2）设过椭圆)0(12222>>=+b a bx a y 的焦点F 的弦AB 的倾斜角为θ，则=AF ；=BF ；焦点弦长=AB ；2.双曲线的角度形式的焦半径公式设过双曲线)0,0(12222>>=-b a by a x 右焦点)0,(c F 的弦AB 的倾斜角为α，渐近线xa b y ±=的倾斜角为θ，则（1）当θπαθ-<<时，焦点弦AB 在右支上，=AF ；=BF ；=AB ，弦AB 在双曲线一支上时，焦点弦最短为（2）当θα<≤0或παθπ<<-焦点弦AB 在两支上，=AF ；=BF ；=AB ，弦AB 交双曲线两支上时，焦点弦最短为3.抛物线的角度形式的焦半径公式（1）设过焦点F 且倾斜角为θ的直线交抛物线)0(22>=p px y 于B A ,两点，则=AF ；=BF ；=AB （2）设过焦点F 且倾斜角为θ的直线交抛物线)0(22>=p py x 于B A ,两点，则=AF ；=BF ；=AB 例1.如图，设过椭圆13422=+y x 的右焦点F 的直线l 交椭圆于B A ,两点，线段AB 的垂直平分线交x 轴于点M ，则=ABMF例2.如图，过椭圆13422=+y x 的左焦点F 任作一直线交椭圆于B A ,两点，若=+BF AF BF AF λ，则=λ例2.已知椭圆12322=+y x 的左右焦点分别为21,F F ，过1F 的直线交椭圆于D B ,两点，过2F 的直线交椭圆于C A ,两点，且BD AC ⊥，则四边形ABCD 的面积的最小值为例3.过双曲线)0,0(12222>>=-b a by a x 的一个焦点F 作平行于渐近线的两直线，与双曲线分别交于B A ,两点，若a AB 2=，双曲线的离心率为e ，则[]=e 例4.已知双曲线191622=-y x 的左焦点弦交双曲线左支于B A ,两点，且772=AB ，求直线AB 的方程例5.已知F 为抛物线C ：x y 42=的焦点，过F 作两条互相垂直的直线21,l l ，直线1l 与C 交于B A ,两点，直线2l 与C 交于E D ,两点，则DE AB +的最小值为三、焦半径定比模型（1）设AB 为焦点在x 轴上的圆锥曲线的过焦点F 的弦，AB 的倾斜角为θ，斜率为k ，且FB AF λ=，则=θcos e ；=e （2）设AB 为焦点在y 轴上的圆锥曲线的过焦点F 的弦，AB 的倾斜角为θ，斜率为k ，且FB AF λ=，则=θsin e ；=e 例1.（2010年辽宁理科）设椭圆C ：)0(12222>>=+b a by a x 的左焦点为F ，过点F 的直线与椭圆C 相交于B A ,两点，直线l 的倾斜角为060，FB AF 2=，则椭圆的离心率为例2.（2010年全国Ⅰ卷）已知F 是椭圆C 的一个焦点，B 是短轴的一个端点，线段BF 的延长线交C 于D ，FD BF 2=，则C 的离心率为例3.（2010年全国Ⅱ卷）已知椭圆)0(12222>>=+b a by a x 的离心率为23，过右焦点F 且斜率为)0(>k k 的直线与C 相交于B A ,两点，若FB AF 3=，则=k （）A.1B.2C.3D.2例4.（2014年全国Ⅱ卷理）设21,F F 分别是椭圆)0(12222>>=+b a b y a x 的左右焦点，M 是C 上一点且2MF 与x 轴垂直，直线1MF 与C 的另一个交点为N ，若直线MN 在y 轴上的截距为2，且N F MN 15=，则椭圆C 的方程为。

圆锥曲线的极坐标方程与参数方程解析

圆锥曲线的极坐标方程与参数方程解析极坐标方程与参数方程是圆锥曲线的两种常用表示形式。

在研究圆锥曲线时，利用这两种方程形式可以更加直观地描述曲线的特征与性质。

本文将详细介绍圆锥曲线的极坐标方程和参数方程的解析过程，并通过具体的例子来进一步说明。

一、圆锥曲线的极坐标方程圆锥曲线的极坐标方程可以用极坐标系中的极径r和极角θ来表示。

对于圆锥曲线而言，其极坐标方程的一般形式如下：r = f(θ)其中，函数f(θ)代表了曲线的性质与形状，具体形式根据不同的圆锥曲线类型而异。

以下是几种常见的圆锥曲线的极坐标方程及其解析过程：（一）圆的极坐标方程圆是一种特殊的圆锥曲线，其极坐标方程可以表示为：r = a其中，a代表圆的半径。

（二）椭圆的极坐标方程椭圆的极坐标方程形式如下：r = a(1 - ε²) / (1 - εcosθ)其中，a代表椭圆的半长轴长度，ε代表椭圆的离心率。

（三）双曲线的极坐标方程双曲线的极坐标方程可以写为：r = a(1 + εcosθ) / (1 - εcosθ)其中，a代表双曲线的焦距，ε代表双曲线的离心率。

（四）抛物线的极坐标方程抛物线的极坐标方程可以表示为：r = a / (1 + cosθ)其中，a代表抛物线的焦点到准线的距离。

通过以上例子可以看出，圆锥曲线的极坐标方程形式多样，每一种形式代表了不同的曲线类型和特征。

研究圆锥曲线时，可以根据需要选择不同的极坐标方程进行分析。

二、圆锥曲线的参数方程除了极坐标方程外，参数方程也是描述圆锥曲线常用的一种形式。

在参数方程中，圆锥曲线的坐标可以通过参数t的取值得到。

一般来说，圆锥曲线的参数方程具有以下形式：x = f(t)y = g(t)其中，函数f(t)和g(t)分别表示曲线的x坐标与y坐标，具体形式根据不同的圆锥曲线类型而定。

以下是几种常见圆锥曲线的参数方程及其解析过程：（一）圆的参数方程圆的参数方程可以表示为：x = acos(t)y = asin(t)其中，a代表圆的半径，t取值范围通常为0到2π。

圆锥曲线的焦半径公式及其应用

圆锥曲线的焦半径公式及其应用圆锥曲线上任意一点到焦点的距离叫做圆锥曲线关于该点的焦半径。

利用圆锥曲线的第二定义很容易得到圆锥曲线的焦半径公式。

1.椭圆的焦半径公式(1)若P(x,y)为椭圆+=1(a>b>0)上任意一点，F、F分别为椭圆的左、右焦点，则=a+e x,=a-e x.(2) 若P(x,y)为椭圆+=1(a>b>0)上任意一点，F、F分别为椭圆的上、下焦点，则=a+e y,=a-e y.2.双曲线的焦半径公式(1)若P(x,y)为双曲线-=1(a>0，b>0)上任意一点，F、F分别为双曲线的左、右焦点，则①当点P在双曲线的左支上时，=-e x-a,= -e x+a.②当点P在双曲线的右支上时，=e x+a,= e x-a.(2)若P(x,y)为双曲线-=1(a>0，b>0)上任意一点， F、 F分别为双曲线的上、下焦点，则①当点P在双曲线的下支上时，=-e y-a,= -ey+a.②当点P在双曲线的上支上时，=ey+a,= ey-a.3.抛物线的焦半径公式(1)若P(x,y)为抛物线y=2px(p>0)上任意一点，则= x+(2) 若P(x,y)为抛物线y=-2px(p>0)上任意一点，则= -x+(3) 若P(x,y)为抛物线x=2py(p>0)上任意一点，则= y+(4)若P(x,y)为抛物线x=-2py(p>0)上任意一点，则= -y+下面举例说明上述各公式的应用例1．求椭圆+=1上一点M(2.4,4)与焦点F、F的距离.解：易知a=5,e=且椭圆的焦点在轴上，∴= a+ey=5+×4=,= a-e y=5-×4= 。

例2.试在椭圆+=1上求一点P，使它到左焦点的距离是它到右焦点的距离的两倍．解：由，得。

设P(x, y),则=a+ex,即5+x=，解之得x=，所以P(,).例3.在双曲线-=1上求一点M，使它到左、右两焦点的距离的比为3：2，并求M点到两准线的距离。

圆锥曲线的极坐标方程

圆锥曲线的极坐标方程
圆锥曲线的极坐标方程是一种用极坐标表示的曲线形式。

它是由一条椭圆和一条圆组成，它们之间有一个共同点，就是这一点处曲线可以分成左右两部分，而这一点也是圆锥曲线的焦点。

圆锥曲线的极坐标方程可以用如下的公式表示：
r = a*secθ
其中，a 为椭圆的长轴，θ 为极坐标里的角度，r 为曲线上每一点的半径。

圆锥曲线的极坐标方程的特点是，它的图形可以从椭圆和圆的并集看出来，它的性质可以从极坐标中的变量及其依赖关系看出来。

圆锥曲线的极坐标方程是数学中一类相对简单的曲线形式，它在计算中有着重要的作用，比如可以用它来表示二次抛物线、双曲线、等等。

圆锥曲线的极坐标方程是一种通用的曲线形式，它在计算中有着广泛的应用，比如在空间几何中，可以用它来表示某一个曲面，而在天文学中，则可以用它来表示某一个星系的形状等。

圆锥曲线的极坐标方程的优点是，它能够将一个数学问题转化成一种更加容易理解的形式，并且它的计算比较简单，从而大大简化了计算的过程。

总的来说，圆锥曲线的极坐标方程是一种比较常用的曲线形式，它在数学计算中有着重要的应用，而且因为它的简单性，所以比较容易理解和计算。

圆锥曲线焦半径公式推导过程

圆锥曲线焦半径公式推导过程
要推导圆锥曲线的焦半径公式，我们可以从圆锥曲线的定义和焦点的性质开始。

首先，圆锥曲线可以通过一个定点（焦点）和一个定直线（准线）的几何性质来定义。

根据焦点的性质，对于任意一点P到焦点F的距离与到准线的距离的比值始终是一个常数e，这个常数被称为离心率。

圆锥曲线有三种形式，椭圆、双曲线和抛物线，它们的焦半径公式略有不同。

首先，我们以椭圆为例进行推导。

椭圆的焦半径公式为r =
a(1 e^2) / (1 + e cosθ)，其中a为长半轴，e为离心率，θ为极角，r为极径。

我们可以通过极坐标系来推导这个公式。

首先，假设椭圆的极坐标方程为r = (l / (1 + e cosθ))，其中l为焦距。

我们知道焦距l与长半轴a的关系为l = a e。

接下来，我们可以利用焦点到极点的距离公式r = l / (1 + e
cosθ)来推导焦半径公式。

首先，我们可以利用勾股定理得到焦点到极点的距离的平方为r^2 = x^2 + y^2，其中x = l / (1 + e) cosθ，y = l / (1 + e) sinθ。

将x和y代入上式，经过一系列的化简和代换，最终可
以得到焦半径公式r = a(1 e^2) / (1 + e cosθ)。

对于双曲线和抛物线的焦半径公式推导过程，我们需要分别利用它们的极坐标方程进行推导，具体的推导过程与椭圆有所不同，但是基本的思路是类似的。

总的来说，圆锥曲线的焦半径公式是通过极坐标系和焦点的性质推导而来的，具体的推导过程需要利用数学知识和技巧进行推导和证明。

希望这个回答能够帮助你理解圆锥曲线焦半径公式的推导过程。

圆锥曲线的极坐标方程焦半径公式焦点弦公式

椭圆、曲线、抛物线统一的极坐标方程为
ρ = ep . 1 − e cosθ
其中 p 是定点 F 到定直线的距离，p＞0 ．
当 0 e 1 时，方程表示椭圆
当 e＞1 时，方程表示曲线，若ρ＞0，方程只表示曲线右支，若允
许ρ 0，方程就表示整个曲线
当 e=1 时，方程表示开口向右的抛物线.
二、圆锥曲线的焦半径公式
推论若圆锥曲线的弦 MN 过焦点 F，则有 1 + 1 = 2 . MF NF ep
、圆锥曲线的焦点弦长若圆锥曲线的弦 MN 过焦点 F，
1、椭圆中， p = a 2 − c = b2 ， MN = ep +
ep
= 2ab2 .
c
c
1− ecosθ 1− ecos(π −θ) a2 − c2 cos2 θ
圆锥曲线的极坐标方程、焦半径公式、焦点弦公式
湖北省天门中学薛德斌
一、圆锥曲线的极坐标方程
椭圆、曲线、抛物线可以统一定义为一个定点(焦点)的距离和一条定
直线(准线)的距离的比等于常数 e 的点的轨迹．
以椭圆的左焦点( 曲线的右焦点、抛物线的焦点)为极点，过点 F 作相
应准线的垂线，垂足为 K，以 FK 的向延长线为极轴建立极坐标系．
3、抛物线中， MN = p +
p
= 2p .
1 − cosθ 1 − cos(π − θ ) sin 2 θ
四、直角坐标系中的焦半径公式设 P x,y 是圆锥曲线的点，
1、若 F1、F2 分别是椭圆的左、右焦点，则 PF1 = a + ex ，、 F2 分别是曲线的左、右焦点，
设 F 为椭圆的左焦点( 曲线的右焦点、抛物线的焦点)，P 为椭圆( 曲线的右支、抛物线) 任一点，则

圆锥曲线的极坐标方程、焦半径公式、焦点弦公式

圆锥曲线的极坐标方程、焦半径公式、焦点弦公式湖北省天门中学薛德斌一、圆锥曲线的极坐标方程椭圆、曲线、抛物线可以统一定义为一个定点(焦点)的距离和一条定直线(准线)的距离的比等于常数e 的点的轨迹．以椭圆的左焦点( 曲线的右焦点、抛物线的焦点)为极点，过点F 作相应准线的垂线，垂足为K，以FK 的向延长线为极轴建立极坐标系．椭圆、曲线、抛物线统一的极坐标方程为 θρcos 1e ep −=. 其中p 是定点F 到定直线的距离，p＞0 ．当0 e 1时，方程表示椭圆当e＞1时，方程表示曲线，若ρ＞0，方程只表示曲线右支，若允许ρ 0，方程就表示整个曲线当e=1时，方程表示开口向右的抛物线.二、圆锥曲线的焦半径公式设F 为椭圆的左焦点( 曲线的右焦点、抛物线的焦点)，P 为椭圆( 曲线的右支、抛物线) 任一点，则 PQ e PF =， )cos (p PF e PF +=θ，其中FH p =，=θ x 轴，FP 焦半径θcos 1e ep PF −=．当P 在曲线的左支时，θcos 1e ep PF +−=. 推论若圆锥曲线的弦MN 过焦点F，则有epNF MF 211=+.、圆锥曲线的焦点弦长若圆锥曲线的弦MN 过焦点F， 1、椭圆中，cb c c a p 22=−=，θθπθ2222cos 2)cos(1cos 1c a ab e ep e ep MN −=−−+−=. 2、曲线中，若M、N 在曲线同一支，θθπθ2222cos 2)cos(1cos 1c a ab e ep e ep MN −=−−+−= 若M、N 在曲线同支，2222cos 2cos 1cos 1a c ab e ep e ep MN −=−−+−=θθθ. 3、抛物线中，θθπθ2sin 2)cos(1cos 1p p p MN =−−+−=. 四、直角坐标系中的焦半径公式设P x,y 是圆锥曲线的点，1、若1F 、2F 分别是椭圆的左、右焦点，则ex a PF +=1，ex a PF −=22、若1F 、2F 分别是曲线的左、右焦点，当点P 在曲线右支时，a ex PF +=1，a ex PF −=2 当点P 在曲线左支时，ex a PF −−=1，ex a PF −=23、若F 是抛物线的焦点，2p x PF +=.。

高考数学-圆锥曲线公式.doc

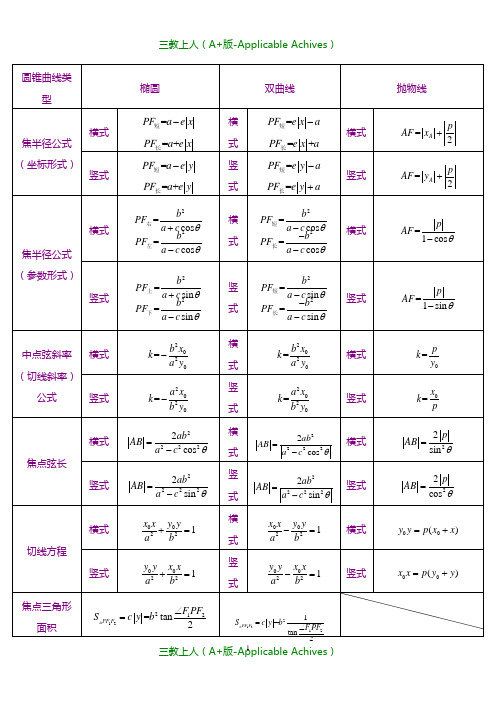
12PF F S=12PF F S=注：双曲线焦半径公式P 在右支则2=cos b PF a c θ-短,2=cos b PF a c θ--长,P 在左支则下面改为+,竖式cos 换sin抛物线中：若AB 为焦点弦，1122(,),(,)A x y B x y①以AB 为直径的圆与准线相切；以AF 和BF 为直径的圆与y 轴相切。

②2124p x x =,212y y p =-③1202AB x x p x p =++=+22sin p θ==21(1)2p k +⋅（0x 为AB 中点横坐标）④1cos P AF θ=-,1cos PBF θ=+；112AF BF P+=⑤22sin AOB P Sθ=⑥∠CFD ＝90°.（θ为焦点弦倾斜角）通用弦长公式：22212121212211+()41(y )4AB k x x x x y y y k =+-=++-（2121212()4x x x x x x A∆+-=-=）如图：若椭圆与双曲线共焦点12,F F ,P 是两曲线的一交点,令122F PF θ∠=,则2222sin cos +1e e θθ=双椭.AOBS（AB为焦点弦）横式2222sin =cos AOB ab c S a c θθ- 横式 2222sin =cos AOB ab c S a c θθ- 横式 2=2sin AOB p S θ竖式2222cos =sin AOB ab c S a c θθ-竖式2222cos =sin AOB ab c S a c θθ- 竖式2=2cos AOB p S θθ2θP F 2F 1二次曲线的“四种线”：设22(,)f x y Ax By Dx Ey F =++++,则二次曲线方程为(,)0f x y =,22000000(,)f x y Ax By Dx Ey F =++++,记0000+22x x y yH Ax x By y DE F +=++++ ①二次曲线在点00(,)x y 处的切线方程为0H =②过二次曲线外一点00(,)x y 作二次曲线两切线，则两切点连线方程为0H = ③二次曲线以点00(,)x y 为中点的弦所在直线方程为00(,)H f x y =④二次曲线过点00(,)x y 的动弦中点轨迹方程为(,)H f x y =，（需要加上定义域限制）圆锥曲线的焦点弦：直线l 过圆锥曲线的焦点F 与圆锥曲线交于,A B 两点，若AF BF λ= ,l 倾斜角为θ,则：1cos 1e λθλ-=+(等价形式为：22211+1e k λλ-⎛⎫= ⎪+⎝⎭,e 为圆锥曲线离心率，竖式cos 换sin ；若为抛物线则e =1）圆锥曲线焦点弦、焦半径：圆锥曲线的焦半径长通式：1cos pAF e θ=- （p 为通径一半）圆锥曲线焦点弦长通式：2221cos pAB e θ=- （p 为通径一半）圆锥曲线知识点：1．定义：⑴椭圆：|)|2(,2||||2121F F a a MF MF >=+；⑵双曲线：|)|2(,2||||||2121F F a a MF MF <=-；⑶抛物线：到定点距离与到定直线距离相等 2．结论 ⑴焦半径：①椭圆：0201,ex a PF ex a PF -=+=（e 为离心率）；（左“+”右“-”）； ②抛物线：20p x PF +==1cos pθ-(θ为将x 轴正向逆时针旋转与PF 重合的旋转角) ⑵弦长公式：]4))[(1(1212212122x x x x k x x k AB -++=-⋅+=]4)[()11(11212212122y y y y ky y k -+⋅+=-⋅+=；注：（Ⅰ）焦点弦长：①椭圆：)(2||21x x e a AB +±=；②抛物线：AB ＝x 1+x 2+p=α2sin 2p =212(1)p k + ；（Ⅱ）通径（最短弦）：①椭圆、双曲线：ab 22；②抛物线：2p 。

圆锥曲线极坐标

圆锥曲线极坐标1 介绍圆锥曲线极坐标（又称圆锥面坐标）是一种常用的曲线参数描述方法，它把曲线转换为极坐标的形式来表示，可以用来描述圆锥曲线的特性。

圆锥曲线极坐标是应用在几何、机械设计、机器人等广泛领域的坐标系统。

2 计算公式所谓圆锥曲线极坐标，它把常见的曲线表示为极坐标的形式。

圆锥曲线极坐标的计算公式很简单：x=rcosθ，y=rsinθ。

计算公式的意思是，x坐标的取值范围为-r<=x<=r，y坐标的取值范围为-r<=y<=r，以及坐标原点的取值为(0,0)。

ϴ取值范围为0<÷ϴ<2π。

因此，使用该公式可以表示任何接近圆锥曲线的曲线，例如圆心，半圆形等。

3 应用领域圆锥曲线极坐标在几何和机械设计领域有着广泛的应用。

它经常用于机器视觉，数据处理，机器人等应用中。

例如，在机器视觉、机器人和机械设计中，经常用圆锥曲线极坐标表示抓取机械关节的角度；在计算机辅助设计、机械设计和机器人程序中，经常用圆锥曲线极坐标表示物体的周围的形状；在精密3D打印中，也经常用圆锥曲线极坐标表示一些复杂的物体的形状。

4 参考文献[1] 吴庆江，刘勇，等. 基于圆锥曲线极坐标的自由抓取运动控制研究[J]. 清华大学学报（自然），2018，58（6）:499-504.[2] Gizem Bayik-Kutuk, Zenon Mulyar. Robot Manipulator Path Planning Based on the Polar Representation of Paths[J]. Robotics, 2017, 6(1):25.[3] 郭昌安，陈晓晴. 基于圆锥曲线极坐标的非球抛步态步态规划[J]. 自动化学报， 2019，45（3）: 430-438.。

【高考】圆锥曲线的极坐标方程、焦半径公式、焦点弦公式

高中数学-圆锥曲线有关焦点弦的几个公式及应用

圆锥曲线焦半径公式

圆锥曲线焦点弦长公式(极坐标全参数方程)

圆锥曲线焦点弦长公式

圆锥曲线的焦半径公式及其应用

高考圆锥曲线公式知识点总结

圆锥曲线的极坐标方程、焦半径公式、焦点弦公式good

圆锥曲线焦点弦长公式(极坐标全参数方程)

圆锥曲线焦点弦公式

圆锥曲线焦半径公式及其应用(学生版)

圆锥曲线的极坐标方程与参数方程解析

圆锥曲线的焦半径公式及其应用

圆锥曲线的极坐标方程

圆锥曲线焦半径公式推导过程

圆锥曲线的极坐标方程 焦半径公式 焦点弦公式

圆锥曲线的极坐标方程、焦半径公式、焦点弦公式

高考数学-圆锥曲线公式.doc

圆锥曲线极坐标

圆锥曲线的极坐标方程焦半径公式焦点弦公式