西电数字信号实验第二次上机实验报告

合集下载

西电DSP上机实验报告2

DSP实验报告及大作业学院：电子信息工程班级：学号：姓名：实验一 VISUAL DSP++的使用入门一、实验目的1、熟悉VISUAL DSP++的开发环境。

针对ADSP－21065L SHARC DSP，利用几个用C、C++和汇编语言写成的简单例子来描述VISUAL DSP＋十编程环境和调试器（debugger）的主要特征和功能。

2、对于运行在其它类型SHARC处理器的程序只需对其链接描述文件（．LDF）做一些小的变化，用于ADSP－21065L硬件仿真。

二、实验内容实验一：启动Visual DSP++，建立一个用C源代码的工程（Project），同时用调试器来评估用C 语言所编写代码的性能；实验二：创立一个新的工程，修改源码来调用一个汇编（asm）程序，重新编译工程，用调试器来评估用汇编语言所写程序的性能；实验三：利用调试器的绘图（plot）功能来图形显示一个卷积算法中的多个数据的波形；实验四：利用调试器的性能统计功能（Statistical profile来检查练习三中卷积算法的效率。

利用所收集到的性能统计数据就能看出算法中最耗时的地方。

三、实验步骤及结果练习一：1、进入 Visual DSP＋＋，显示Visual DSP++的集成开发和调试环境窗口。

选择菜单中的Session\New Session\SHARK\ADSP-21065L SHARK processing Simulator.此过程为将要编译运行的程序建立了一个Session.2、选择菜单File 中Open 打开Project\E:\float\unit_1\dot_product_c \dotprodc．dpj。

（注：练习中将float压缩包解压与E盘）3、在菜单 Project中选择 Build Project来对工程进行编译。

在本例子中，编译器会检测到一个未定义的错误，显示为：“．＼dotprod_main.c”，line 115：error ＃20：identifier“itn”is undefined itn i；双击该行文字，光标会自动定位出错行，再该行中将“itn”改为“int”,重新编译后没有错误。

数字信号处理实验报告(西电)

数字信号处理实验报告班级：****姓名：郭**学号：*****联系方式：*****西安电子科技大学电子工程学院绪论数字信号处理起源于十八世纪的数学，随着信息科学和计算机技术的迅速发展，数字信号处理的理论与应用得到迅速发展，形成一门极其重要的学科。

当今数字信号处理的理论和方法已经得到长足的发展，成为数字化时代的重要支撑，其在各个学科和技术领域中的应用具有悠久的历史，已经渗透到我们生活和工作的各个方面。

数字信号处理相对于模拟信号处理具有许多优点，比如灵活性好，数字信号处理系统的性能取决于系统参数，这些参数很容易修改，并且数字系统可以分时复用，用一套数字系统可以分是处理多路信号；高精度和高稳定性，数字系统的运算字符有足够高的精度，同时数字系统不会随使用环境的变化而变化，尤其使用了超大规模集成的DSP 芯片，简化了设备，更提高了系统稳定性和可靠性；便于开发和升级，由于软件可以方便传送，复制和升级，系统的性能可以得到不断地改善；功能强，数字信号处理不仅能够完成一维信号的处理，还可以试下安多维信号的处理；便于大规模集成，数字部件具有高度的规范性，对电路参数要求不严格，容易大规模集成和生产。

数字信号处理用途广泛，对其进行一系列学习与研究也是非常必要的。

本次通过对几个典型的数字信号实例分析来进一步学习和验证数字信号理论基础。

实验一主要是产生常见的信号序列和对数字信号进行简单处理，如三点滑动平均算法、调幅广播（AM ）调制高频正弦信号和线性卷积。

实验二则是通过编程算法来了解DFT 的运算原理以及了解快速傅里叶变换FFT 的方法。

实验三是应用IRR 和FIR 滤波器对实际音频信号进行处理。

实验一●实验目的加深对序列基本知识的掌握理解●实验原理与方法1.几种常见的典型序列：0()1,00,0(){()()(),()sin()j n n n n u n x n Aex n a u n a x n A n σωωϕ+≥<====+单位阶跃序列：复指数序列：实指数序列：为实数正弦序列：2.序列运算的应用：数字信号处理中经常需要将被加性噪声污染的信号中移除噪声，假定信号 s(n)被噪声d(n)所污染，得到了一个含噪声的信号()()()x n s n d n =+。

新版西电微机原理第二次上机实验报告-新版-精选.pdf

西电微机原理第二次上机实验报告学号：姓名：一、实验目的1.熟练掌握汇编语言程序设计的方法及上机步骤。

2.掌握算术运算中，十进制数调整指令的应用。

3.掌握子程序的设计方法。

4.掌握DOS功能的调用方法。

二、实验仪器586微机 1台三、实验内容编写求十进制数12678532与21736543之和的程序，并将和以十进制数的形式送屏幕显示。

编程要求与提示：[1] 两个加数均以压缩(组合)十进制数形式存放在ADD1和ADD2为首址的存贮器单元。

[2] 和以压缩十进制数的形式存入SUM以下单元。

[3] 将和送到屏幕显示部分功能的实现采用子程序的形式。

[4] 实验步骤如下：a. 用全屏幕编辑软件建立源程序。

b．用masm.exe汇编程序对源程序进行汇编，形成目标程序。

c. 用link.exe连接程序对目标程序进行连接形成可执行文件。

d. 用DEBUG对连接通过的可执行程序进行调试。

四、实验内容对应的源程序及流程源程序如下：STACK SEGMENT STACKDB 10H DUP(00)STACK ENDSDATA SEGMENTADD1 DB 12H,67H,85H,32HADD2 DB 21H,73H,65H,43HSUM DB 4H DUP(?)DATA ENDSCODE SEGMENTASSUME CS:CODE,DS:DATA,ES:DATA,SS:STACKSTART:MOV AX, DATAMOV DS, AXMOV AX, DATAMOV ES, AXMOV AX,STACKMOV SS,AXLEA SI, ADD1[3]LEA BX, ADD2[3]LEA DI,SUM[3]MOV CX,4CLCL1:MOV AL,[SI]ADC AL,[BX]DAAMOV [DI],ALDEC SIDEC BXDEC DILOOP L1CALL DISPAL; －－－－－－－－－－－－EXITPROC:MOV AH,4CH ;结束程序MOV AH,1INT 21H; －－－－－－－－－－－－DISPAL PROC NEARPUSH AXPUSH BXPUSH CXPUSH DXPUSH DILEA DI,SUMMOV CX,4DISPAL2:MOV AL,[DI]SHR AL,1SHR AL,1SHR AL,1SHR AL,1MOV AH,2MOV DL,ALADD DL,30HINT 21HMOV AL,[DI]AND AL,0FHMOV AH,2MOV DL,ALADD DL,30HINT 21HINC DILOOP DISPAL2POP DIPOP DXPOP CXPOP BXPOP AXRETDISPAL ENDPCODE ENDSEND START运行结果如下：五、问题讨论1．在以十进制数形式参加运算的程序设计中，应注意那些问题。

西电微机原理实验报告

微机系统实验报告班级：031214学号：*********名：***地点：E-II-312时间：第二批实验一汇编语言编程实验一、实验目的(1)掌握汇编语言的编程方法(2)掌握DOS功能调用的使用方法(3)掌握汇编语言程序的调试运行过程二、实验设备PC机一台。

三、实验内容（1）将指定数据区的字符串数据以ASCII码形式显示在屏幕上，并通过DOS功能调用完成必要提示信息的显示。

(2) 在屏幕上显示自己的学号姓名信息。

（3）循环从键盘读入字符并回显在屏幕上，然后显示出对应字符的ASCII码，直到输入“Q”或“q”时结束。

（4）自主设计输入显示信息，完成编程与调试，演示实验结果。

考核方式：完成实验内容（1）（2）（3）通过，完成实验内容（4）优秀。

实验中使用的DOS功能调用：INT 21H表3-1-1 显示实验中可使用DOS功能调用四、实验步骤(1)运行QTHPCI软件，根据实验内容编写程序，参考程序流程如图3-1-1所示。

(2)使用“项目”菜单中的“编译”或“编译连接”命令对实验程序进行编译、连接。

(3)“调试”菜单中的“进行调试”命令进入Debug调试，观察调试过程中数据传输指令执行后各寄存器及数据区的内容。

按F9连续运行。

(4)更改数据区的数据，考察程序的正确性。

五、实验程序DATA SEGMENTBUFFER DB '03121370konglingling:',0AH,0DH,'$'BUFFER2 DB 'aAbBcC','$'BUFFER3 DB 0AH,0DH,'$'DATA ENDSCODE SEGMENTASSUME CS:CODE,DS:DA TASTART:MOV AX,DA TAMOV DS,AXmov ah,09hmov DX,OFFSET BUFFERint 21hMOV SI,OFFSET BUFFER2lab1:cmp BYTE PTR [SI],'$'je lab2MOV AL,DS:[SI]AND AL,0F0H ;取高4位MOV CL,4SHR AL,CLCMP AL,0AH ;是否是A以上的数JB C2ADD AL,07HC2: ADD AL,30HMOV DL,AL ;show characterMOV AH,02HINT 21HMOV AL,DS:[SI]AND AL,0FH ;取低4位CMP AL,0AHJB C3ADD AL,07HC3: ADD AL,30HMOV DL,AL ;show characterMOV AH,02HINT 21Hadd SI,1jmp lab1lab2:mov ah,09hmov DX,OFFSET BUFFER3int 21hmov ah,01hint 21hcmp al,'q'je lab3mov B L,ALAND AL,0F0H ;取高4位MOV CL,4SHR AL,CLCMP AL,0AH ;是否是A以上的数JB C4ADD AL,07HC4: ADD AL,30HMOV DL,AL ;show characterMOV AH,02HINT 21HMOV AL,BLAND AL,0FH ;取低4位CMP AL,0AHJB C5ADD AL,07HC5: ADD AL,30HMOV DL,AL ;show characterMOV AH,02HINT 21Hjmp lab2lab3:mov ah,4chint 21hCODE ENDSend START六、实验结果实验二数码转换实验一、实验目的(1)掌握不同进制数及编码相互转换的程序设计方法。

西电数字电子技术实验报告2

数字电子技术实验报告学院班级：软件学院131213班学生学号：13121228学生姓名：黄雯同作者:实验日期：2014年5月11日实验题目：组合逻辑的研究二一、实验目的：1.了解译码器、数据选择器的工作原理及其功能;2.掌握用译码器、数据选择器实现组合逻辑电路的方法。

3.了解用SSI 器件实现简单组合逻辑电路的方法。

4.了解编码、译码与显示的工作原理二、实验环境：直流稳压电源数字电路实验板三、实验内容及实验原理（一）基本命题：1.用3-8译码器74LS138和门电路实现三变量多数表决器电路。

2.用3-8译码器实现函数：3.用8选1数据选择器74LS151实现函数：(二)实验原理： 1.三变量多数表决器：a.其真值表如表1.1所示，其卡诺图如图1.1所示，由3-8译码器组成的参考电路如图1.2所示：表1.1 三变量表决器表1.1∑∑==)7,6,5,4,2,1()6,4,1(21m F m F ∑=)14,13,12,8,5,4,0(),,,(1m D C B A F图1.1三变量表决器卡诺图由以上的真值表和卡诺图可得此电路的逻辑表达式为 F= AC BC ⋅⋅AB b.74LS138译码器（又称3-8译码器）其引脚图如1.3所示，其中4、5、6脚是控制脚，只有当6脚为高电平而4、5脚都为低电平时，74LS138才对1、2、3脚的输入进行译码，选择和从这三个管脚输入的三位二进制码相对应的某一个输出脚，输出低电平，否则所有的输出脚都是输出高电平。

FA BC 01图1.3 74LS138引脚图2.根据最小项表达式和译码器输出之间的关系：i i Y m =∑ 可以将F 1 和F 2的函数表达式化为其真值表2.1如下所示：1146203F Y Y Y F Y Y ==3.根据其真值表（表3.1）及8选1数据选择器74LS151功能特点，假设A B C 为地址变量得出：D 0 = D ，D 1 = 0 ，D 2= 1， D 3= 0， D 4= 0， D 5 = D ， D 6 = 0， D 7 = 1， D 8=D ，因此通过逻辑开关和74LS00S 实现D 。

西电电院数字信号处理上机实验报告六

实验六、FIR数字滤波器设计及其网络结构班级: 学号: 姓名: 成绩:1实验目得(1)熟悉线性相位FIR数字滤波器得时域特点、频域特点与零极点分布;(2)掌握线性相位FIR数字滤波器得窗函数设计法与频率采样设计法;(3)了解IIR数字滤波器与FIR数字滤波器得优缺点及其适用场合。

2 实验内容(1)设计计算机程序,根据滤波器得主要技术指标设计线性相位FIR数字低通、高通、带通与带阻滤波器;(2)绘制滤波器得幅频特性与相频特性曲线,验证滤波器得设计结果就是否达到设计指标要求;(3)画出线性相位FIR数字滤波器得网络结构信号流图。

3实验步骤(1)设计相应得四种滤波器得MATLAB程序;(2)画出幅频相频特性曲线;(3)画出信号流图。

4 程序设计%% FIR低通f=[0、2,0、35];m=[1,0];Rp=1;Rs=40;dat1=(10^(Rp/20)-1)/(10^(Rp/20)+1);dat2=10^(-Rs/20);rip=[dat1,dat2];[M,f0,m0,w]=remezord(f,m,rip);M=M+2;hn=remez(M,f0,m0,w);w=0:0、001:pixn=[0:length(hn)-1];H=hn*exp(-j*xn'*w);figuresubplot(2,1,1)plot(w/pi,20*log10(abs(H)));gridon;xlabel('\omega/\pi'),ylabel('|H(e^j^w)|/dB')subplot(2,1,2)plot(w/pi,angle(H)/pi);xlabel('\omega/\pi'),ylabel('\phi(\omega)/\pi') %% FIR高通f=[0、7,0、9];m=[0,1];Rp=1;Rs=60;dat1=(10^(Rp/20)-1)/(10^(Rp/20)+1);dat2=10^(-Rs/20);rip=[dat2,dat1];[M,f0,m0,w]=remezord(f,m,rip);hn=remez(M,f0,m0,w);w=0:0、001:pixn=[0:length(hn)-1];H=hn*exp(-j*xn'*w);figuresubplot(2,1,1)plot(w/pi,20*log10(abs(H)));gridon;xlabel('\omega/\pi'),ylabel('|H(e^j^w)|/dB')subplot(2,1,2)plot(w/pi,angle(H)/pi);xlabel('\omega/\pi'),ylabel('\phi(\omega)/\pi') %% FIR带通f=[0、2,0、35,0、65,0、8];m=[0,1,0];Rp=1;Rs=60;dat1=(10^(Rp/20)-1)/(10^(Rp/20)+1);dat2=10^(-Rs/20);rip=[dat2,dat1,dat2];[M,f0,m0,w]=remezord(f,m,rip);M=M+3hn=remez(M,f0,m0,w);w=0:0、001:pixn=[0:length(hn)-1];H=hn*exp(-j*xn'*w);figuresubplot(2,1,1)plot(w/pi,20*log10(abs(H)));gridon;xlabel('\omega/\pi'),ylabel('|H(e^j^w)|/dB')subplot(2,1,2)plot(w/pi,angle(H)/pi);xlabel('\omega/\pi'),ylabel('\phi(\omega)/\pi') %% FIR带阻f=[0、2,0、35,0、65,0、8];m=[1,0,1];Rp=1;Rs=60;dat1=(10^(Rp/20)-1)/(10^(Rp/20)+1);dat2=10^(-Rs/20);rip=[dat1,dat2,dat1];[M,f0,m0,w]=remezord(f,m,rip);hn=remez(M,f0,m0,w);w=0:0、001:pixn=[0:length(hn)-1];H=hn*exp(-j*xn'*w);figuresubplot(2,1,1)plot(w/pi,20*log10(abs(H)));gridon;xlabel('\omega/\pi'),ylabel('|H(e^j^w)|/dB')subplot(2,1,2)plot(w/pi,angle(H)/pi);xlabel('\omega/\pi'),ylabel('\phi(\omega)/\pi') 5实验结果及分析(1)FIR低通滤波器自动得到得M值不满足要求,故我们将M加上2 在w=0、2π时,H=-0、5dB;w=0、35π时,H=-41dB。

西安电子科技大学数字信号处理上机报告

数字信号处理大作业院系：电子工程学院学号：02115043姓名：邱道森实验一：信号、系统及系统响应一、实验目的(1) 熟悉连续信号经理想采样前后的频谱变化关系，加深对时域采样定理的理解。

(2) 熟悉时域离散系统的时域特性。

(3) 利用卷积方法观察分析系统的时域特性。

(4) 掌握序列傅里叶变换的计算机实现方法，利用序列的傅里叶变换对连续信号、离散信号及系统响应进行频域分析。

二、实验原理采样是连续信号数字处理的第一个关键环节。

对连续信号()a x t 进行理想采样的过程可用(1.1)式表示：()()()ˆa a xt x t p t =⋅ 其中()t xa ˆ为()a x t 的理想采样，()p t 为周期冲激脉冲，即 ()()n p t t nT δ∞=-∞=-∑()t xa ˆ的傅里叶变换()j a X Ω为 ()()s 1ˆj j j a a m X ΩX ΩkΩT ∞=-∞=-∑进行傅里叶变换，()()()j ˆj e d Ωt a a n X Ωx t t nT t δ∞∞--∞=-∞⎡⎤=-⎢⎥⎣⎦∑⎰ ()()j e d Ωtan x t t nT t δ∞∞--∞=-∞=-∑⎰()j e ΩnTan x nT ∞-=-∞=∑式中的()a x nT 就是采样后得到的序列()x n ，即()()a x n x nT =()x n 的傅里叶变换为()()j j e enn X x n ωω∞-=-∞=∑比较可知()()j ˆj e aΩTX ΩX ωω==为了在数字计算机上观察分析各种序列的频域特性，通常对()j e X ω在[]0,2π上进行M 点采样来观察分析。

对长度为N 的有限长序列()x n ，有()()1j j 0eekk N nn X x n ωω--==∑其中2π,0,1,,1k k k M Mω==⋅⋅⋅-一个时域离散线性时不变系统的输入/输出关系为()()()()()m y n x n h n x m h n m ∞=-∞=*=-∑上述卷积运算也可以转到频域实现()()()j j j e e e Y X H ωωω= (1.9)三、实验内容及步骤(1) 认真复习采样理论、离散信号与系统、线性卷积、序列的傅里叶变换及性质等有关内容，阅读本实验原理与方法。

西安邮电数字信号处理实验报告

西安邮电大学通信与信息工程学院实验报告（2016/2017学年第2学期）实验名称：数字信号处理实验学生姓名：石龙飞专业：通信工程学号：03151307指导教师：常虹2017年06月01日西安邮电大学通院《数字信号处理实验》独立设课实验过程考核表西安邮电大学通院《数字信号处理实验》独立设课实验成绩鉴定表1 熟悉MATLAB1.1 实验目的1、了解MATLAB 程序设计语言的基本特点，熟悉MATLAB 软件的运行环境。

2、掌握各种信号的建模方式。

3、掌握各种信号的托兴表示方法。

4、掌握变量等有关概念，具备初步的将一般数学模型转化为对应的计机模型并进行处理的能力。

1.2 实验原理1、图形保持hold on/off 命令控制是保持原有图形还是刷新原有图形，不带参数的hold 命令在两种状态之间进行切换。

2、绘图修饰命令 title(图形名称) xlabel(x 轴说明) ylabel(y 轴说明) text(x,y,图形说明) legend1.3 实验内容以及步骤单位采样序列代码：单位阶跃序列代码：矩形序列代码：三角波代码：方波代码：锯齿波代码：Sinc函数代码：1.4 实验结果分析学习使用MATLAB7.0软件；学习信号的图形表示方法，掌握各种各种信号的的建模方式；实现单位采样序列、单位阶跃序列、举行序列、三角波、方波、锯齿波、Sinc函数。

1.5 实验总结以及体会构成经过本次试验，我对于用MATLAB来作出一些数字信号中的一些基本波形的图像有了深刻的认识，可以熟练而又准确地以MATLAB为工具做出诸如单位阶跃序列，矩形序列等多种序列的图形，不仅如此，在作图中，我对于MATLAB的一些作图的基本指令，以及需要作出的序列有了深刻的认识与见解；本节课做出这些图形并不是重点，重点是了解MATLAB程序设计语言的基本特点，掌握这一个重要的工具，并且可以将数学模型熟练地转化为计算机模型，并进行处理，这才是本次实验真正的作用与意义，也是作为当代大学生的我们所必须具备的基本能力。

西安电子科技大学数字电路实验报告

数字电路实验报告1. 组合逻辑研究（一）一实验目的1．了解用SSI器件实现简单组合逻辑电路的方法。

2．了解编码、译码与显示的工作原理。

3．掌握用MSI器件实现四位全加器的方法，并掌握全加器的应用。

4．熟悉四位数字比较器的原理，掌握四位数字比较器的应用。

二实验所用仪器、设备1. 万用表一块2. 直流稳压电源一台3. 数字电路实验板一块三实验说明组合逻辑电路是数字电路中最常见的逻辑电路之一，它是根据给定的逻辑功能，设计出实现这些功能的逻辑电路。

组合逻辑电路的特点，就是在任一时刻电路的输出仅取决于该时刻的输入信号，而与信号作用前电路所处的状态无关。

组合逻辑电路的设计一般可按以下步骤进行：（1）逻辑抽象。

将文字描述的逻辑命题转换成真值表。

（2）选择器件类型。

根据命题的要求和器件的功能决定采用哪种器件。

（3）根据真值表和选用逻辑器件的类型，写出相应的逻辑函数表达式。

当采用SSI集成门电路设计时，为了使电路最简，应将逻辑表达式化简，并变换成与门电路相对应的最简式；当采用MSI组合逻辑器件设计时，则不用将逻辑函数进行化简，只需将其变换成MSI器件所需要的函数形式。

（4）根据逻辑函数表达式及选用的逻辑器件画出逻辑电路图。

四实验内容（一）基本命题1.按照P104图4-1-3连接实验线路，输入加逻辑开关，输出加LED显示器，测试三变量多数表决器的功能，并记录真值表。

图4-1-3 用门电路实现的多数表决电路2.用四2输入异或门74LS86和四2输入与非门74LS00组成一位全加器电路，输入加逻辑开关，输出加LED 显示器，测试其功能,并记录真值表。

卡诺图 iABC Fi+1图5-1 一位全加器电路图5-1所示电路是由四2输入与非门74LS00和四2输入异或门74LS86组成的一位全加器电路。

此电路可以实现两个一位二进制数 A i 和B i 相加，并考虑来自低一位的进位 C i ，输出 S i 为本位和，C i-1为本位向高一位的进位。

数字信号处理上机实验

第十章上机实验数字信号处理是一门理论和实际密切结合的课程，为深入掌握课程内容，最好在学习理论的同时，做习题和上机实验。

上机实验不仅可以帮助读者深入的理解和消化基本理论，而且能锻炼初学者的独立解决问题的能力。

本章在第二版的基础上编写了六个实验，前五个实验属基础理论实验，第六个属应用综合实验。

实验一系统响应及系统稳定性。

实验二时域采样与频域采样。

实验三用FFT 对信号作频谱分析。

实验四 IIR 数字滤波器设计及软件实现。

实验五 FIR 数字滤波器设计与软件实现实验六应用实验——数字信号处理在双音多频拨号系统中的应用任课教师根据教学进度，安排学生上机进行实验。

建议自学的读者在学习完第一章后作实验一；在学习完第三、四章后作实验二和实验三；实验四IIR 数字滤波器设计及软件实现在。

学习完第六章进行；实验五在学习完第七章后进行。

实验六综合实验在学习完第七章或者再后些进行；实验六为综合实验，在学习完本课程后再进行。

10.1 实验一: 系统响应及系统稳定性1.实验目的（1）掌握求系统响应的方法。

（2）掌握时域离散系统的时域特性。

（3）分析、观察及检验系统的稳定性。

2.实验原理与方法在时域中，描写系统特性的方法是差分方程和单位脉冲响应，在频域可以用系统函数描述系统特性。

已知输入信号可以由差分方程、单位脉冲响应或系统函数求出系统对于该输入信号的响应，本实验仅在时域求解。

在计算机上适合用递推法求差分方程的解，最简单的方法是采用MA TLAB 语言的工具箱函数filter 函数。

也可以用MATLAB 语言的工具箱函数conv 函数计算输入信号和系统的单位脉冲响应的线性卷积，求出系统的响应。

系统的时域特性指的是系统的线性时不变性质、因果性和稳定性。

重点分析实验系统的稳定性，包括观察系统的暂态响应和稳定响应。

系统的稳定性是指对任意有界的输入信号，系统都能得到有界的系统响应。

或者系统的单位脉冲响应满足绝对可和的条件。

西电数字信号处理上机实验报告

数字信号处理上机实验报告14020710021 张吉凯第一次上机实验一：设给定模拟信号()1000t a x t e -=，t 的单位是ms 。

(1) 利用MATLAB 绘制出其时域波形和频谱图（傅里叶变换），估计其等效带宽（忽略谱分量降低到峰值的3%以下的频谱）。

(2) 用两个不同的采样频率对给定的()a x t 进行采样。

○1()()15000s a f x t x n =以样本秒采样得到。

()()11j x n X e ω画出及其频谱。

○2()()11000s a f x t x n =以样本秒采样得到。

()()11j x n X e ω画出及其频谱。

比较两种采样率下的信号频谱，并解释。

（1）MATLAB 程序：N=10; Fs=5; Ts=1/Fs;n=[-N:Ts:N];xn=exp(-abs(n)); w=-4*pi:0.01:4*pi;X=xn*exp(-j*(n'*w));subplot(211)plot(n,xn);title('x_a(t)时域波形');xlabel('t/ms');ylabel('x_a(t)');axis([-10, 10, 0, 1]);subplot(212);plot(w/pi,abs(X));title('x_a(t)频谱图');xlabel('\omega/\pi');ylabel('X_a(e^(j\omega))'); ind = find(X >=0.03*max(X))*0.01;eband = (max(ind) -min(ind));fprintf('等效带宽为%fKHZ\n',eband);运行结果：等效带宽为12.110000KHZ（2）MATLAB程序：N=10;omega=-3*pi:0.01:3*pi;%Fs=5000Fs=5;Ts=1/Fs;n=-N:Ts:N;xn=exp(-abs(n));X=xn*exp(-j*(n'*omega));subplot(2,2,1);stem(n,xn);grid on;axis([-10, 10, 0, 1.25]); title('时域波形(f_s=5000)');xlabel('n');ylabel('x_1(n)');subplot(2,2,2);plot(omega/pi,abs(X));title('频谱图(f_s=5000)');xlabel('\omega/\pi');ylabel('X_1(f)');grid on;%Fs=1000Fs=1;Ts=1/Fs;n=-N:Ts:N;xn=exp(-abs(n));X=xn*exp(-j*(n'*omega));subplot(2,2,3);stem(n,xn);grid on;axis([-10, 10, 0, 1.25]); title('时域波形(f_s=1000)');xlabel('n');ylabel('x_2(n)');grid on; subplot(2,2,4); plot(omega/pi,abs(X)); title('频谱图(f_s=1000)'); xlabel('\omega/\pi'); ylabel('X_2(f)'); grid on;运行结果：实验二：给定一指数型衰减信号()()0cos 2at x t e f t π-=，采样率1s f T=，T 为采样周期。

2017年西电电院数字信号处理上机实验报告六

实验六、FIR数字滤波器设计及其网络结构班级：学号：姓名：成绩：1实验目的（1）熟悉线性相位FIR数字滤波器的时域特点、频域特点和零极点分布；（2）掌握线性相位FIR数字滤波器的窗函数设计法和频率采样设计法；（3）了解IIR数字滤波器和FIR数字滤波器的优缺点及其适用场合。

2 实验内容（1）设计计算机程序.根据滤波器的主要技术指标设计线性相位FIR数字低通、高通、带通和带阻滤波器；（2）绘制滤波器的幅频特性和相频特性曲线.验证滤波器的设计结果是否达到设计指标要求；（3）画出线性相位FIR数字滤波器的网络结构信号流图。

3实验步骤（1）设计相应的四种滤波器的MATLAB程序；（2）画出幅频相频特性曲线；（3）画出信号流图。

4 程序设计%% FIR低通f=[0.2,0.35];m=[1,0];Rp=1;Rs=40;dat1=(10^(Rp/20)-1)/(10^(Rp/20)+1);dat2=10^(-Rs/20);rip=[dat1,dat2];[M,f0,m0,w]=remezord(f,m,rip);M=M+2;hn=remez(M,f0,m0,w);w=0:0.001:pixn=[0:length(hn)-1];H=hn*exp(-j*xn'*w);figuresubplot(2,1,1)plot(w/pi,20*log10(abs(H)));gridon;xlabel('\omega/\pi'),ylabel('|H(e^j^w)|/dB')subplot(2,1,2)plot(w/pi,angle(H)/pi);xlabel('\omega/\pi'),ylabel('\phi(\omega)/\pi')%% FIR高通f=[0.7,0.9];m=[0,1];Rp=1;Rs=60;dat1=(10^(Rp/20)-1)/(10^(Rp/20)+1);dat2=10^(-Rs/20);rip=[dat2,dat1];[M,f0,m0,w]=remezord(f,m,rip);hn=remez(M,f0,m0,w);w=0:0.001:pixn=[0:length(hn)-1];H=hn*exp(-j*xn'*w);figuresubplot(2,1,1)plot(w/pi,20*log10(abs(H)));gridon;xlabel('\omega/\pi'),ylabel('|H(e^j^w)|/dB')subplot(2,1,2)plot(w/pi,angle(H)/pi);xlabel('\omega/\pi'),ylabel('\phi(\omega)/\pi')%% FIR带通f=[0.2,0.35,0.65,0.8];m=[0,1,0];Rp=1;Rs=60;dat1=(10^(Rp/20)-1)/(10^(Rp/20)+1);dat2=10^(-Rs/20);rip=[dat2,dat1,dat2];[M,f0,m0,w]=remezord(f,m,rip);M=M+3hn=remez(M,f0,m0,w);w=0:0.001:pixn=[0:length(hn)-1];H=hn*exp(-j*xn'*w);figuresubplot(2,1,1)plot(w/pi,20*log10(abs(H)));gridon;xlabel('\omega/\pi'),ylabel('|H(e^j^w)|/dB')subplot(2,1,2)plot(w/pi,angle(H)/pi);xlabel('\omega/\pi'),ylabel('\phi(\omega)/\pi')%% FIR带阻f=[0.2,0.35,0.65,0.8];m=[1,0,1];Rp=1;Rs=60;dat1=(10^(Rp/20)-1)/(10^(Rp/20)+1);dat2=10^(-Rs/20);rip=[dat1,dat2,dat1];[M,f0,m0,w]=remezord(f,m,rip);hn=remez(M,f0,m0,w);w=0:0.001:pixn=[0:length(hn)-1];H=hn*exp(-j*xn'*w);figuresubplot(2,1,1)plot(w/pi,20*log10(abs(H)));gridon;xlabel('\omega/\pi'),ylabel('|H(e^j^w)|/dB')subplot(2,1,2)plot(w/pi,angle(H)/pi);xlabel('\omega/\pi'),ylabel('\phi(\omega)/\pi') 5实验结果及分析（1）FIR低通滤波器自动得到的M值不满足要求.故我们将M加上2 在w=0.2π时.H=-0.5dB；w=0.35π时.H=-41dB。

西电微机原理上机报告上机报告

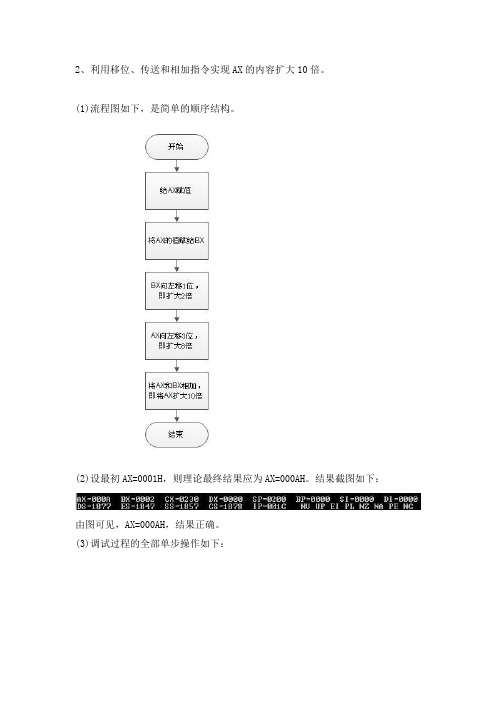
2、利用移位、传送和相加指令实现AX的内容扩大10倍。

(1)流程图如下，是简单的顺序结构。

(2)设最初AX=0001H，则理论最终结果应为AX=000AH。

结果截图如下：由图可见，AX=000AH，结果正确。

(3)调试过程的全部单步操作如下：(4)程序代码：DATAS SEGMENT DATAS ENDSSTACKS SEGMENT DW100H DUP(?)TOP LABEL WORD STACKS ENDSCODES SEGMENTASSUME CS:CODES,DS:DATAS,SS:STACKSSTART:MOV AX,DATASMOV DS,AXMOV AX,0003HMOV BX,AXSHL AX,1SHL BX,1SHL BX,1SHL BX,1ADD AX,BXMOV AH,4CHINT21HCODES ENDSEND START3、在缓冲区VAR中连续存放着3个16位的无符号数，编写程序实现将其按递增关系排列；如果VAR中保存的为有符号数，再编写程序实现将其按递减关系排列。

（1）流程图如下。

第一个为无符号数的递增排列；第二个为有符号数的递减排列。

三个数字进行递增或者递减排列，最终结果仅有6种情况。

因此采用多重分支结构，对三个数字进行排列。

(2)将三个无符号数：2500、1000、4500进行递增排列，结果输出为：最终输出AX=03E8H=1000；BX=09C4H=2500；CX=1194H=4500。

结果正确。

将三个有符号数：-2500、-1000、-4500进行递减排列，结果输出为：最终输出AX=03E8H= -1000；BX=09C4H= -2500；CX=1194H= -4500。

结果正确。

（3）调试过程中的全部单步操作如下：(4)程序代码：<1>三个无符号数的递增排列：STACK SEGMENT STACKSTACK ENDSDATA SEGMENTVAR DW2500,1000,4500DATA ENDSCODE SEGMENTASSUME CS:CODE,DS:DATA,SS:STACK START:MOV AX,DATAMOV DS,AXMOV AX,VARCMP AX,VAR+2JBE S1JMP T1S1:CMP AX,VAR+4JAE S2MOV BX,VAR+2CMP BX,VAR+4JAE S3JMP S4T1:MOV AX,VAR+2CMP AX,VAR+4JAE T2MOV BX,VARJAE T3 JMP T4S2:MOV AX,VAR+4 MOV BX,VAR MOV CX,VAR+2 JMP FINS3:MOV AX,VAR MOV BX,VAR+4 MOV CX,VAR+2 JMP FINS4:MOV AX,VAR MOV BX,VAR+2 MOV CX,VAR+4 JMP FINT2:MOV AX,VAR+4 MOV BX,VAR+2 MOV CX,VAR JMP FINT3:MOV AX,VAR+2 MOV BX,VAR+4 MOV CX,VAR JMP FINT4:MOV AX,VAR+2MOV CX,VAR+4JMP FINFIN:MOV AH,4CHINT21HCODE ENDSEND START<2>三个有符号数的递减排序：STACK SEGMENT STACKSTACK ENDSDATA SEGMENTVAR DW-2500,-1000,-4500DATA ENDSCODE SEGMENTASSUME CS:CODE,DS:DATA,SS:STACK START:MOV AX,DATAMOV DS,AXMOV AX,VARCMP AX,VAR+2JGE S1JMP T1S1:CMP AX,VAR+4JLE S2MOV BX,VAR+2CMP BX,VAR+4JLE S3 JMP S4T1:MOV AX,VAR+2 CMP AX,VAR+4 JLE T2 MOV BX,VAR CMP BX,VAR+4 JLE T3 JMP T4S2:MOV AX,VAR+4 MOV BX,VAR MOV CX,VAR+2 JMP FINS3:MOV AX,VAR MOV BX,VAR+4 MOV CX,VAR+2 JMP FINS4:MOV AX,VAR MOV BX,VAR+2 MOV CX,VAR+4 JMP FINT2:MOV AX,VAR+4 MOV BX,VAR+2 MOV CX,VAR JMP FINT3:MOV AX,VAR+2MOV BX,VAR+4MOV CX,VARJMP FINT4:MOV AX,VAR+2MOV BX,VARMOV CX,VAR+4JMP FINFIN:MOV AH,4CHINT21HCODE ENDSEND START5、在变量VAR1和VAR2中分别保存有两个字节型的正整数，编写完整的汇编语言程序实现：（1）当两数中有一个奇数时，将奇数存入VAR1，偶数存入VAR2；（2）当两数均为奇数时，两个变量的内容不变；（3）当两数均为偶数时，两数缩小一半后存入原处。

西电数字信号处理上机实验报告

数字信号处理上机实验报告14020710021 张吉凯第一次上机实验一：设给定模拟信号()1000t a x t e -=，t 的单位是ms 。

(1) 利用MATLAB 绘制出其时域波形和频谱图（傅里叶变换），估计其等效带宽（忽略谱分量降低到峰值的3%以下的频谱）。

(2) 用两个不同的采样频率对给定的()a x t 进行采样。

○1()()15000s a f x t x n =以样本秒采样得到。

()()11j x n X e ω画出及其频谱。

○2()()11000s a f x t x n =以样本秒采样得到。

()()11j x n X e ω画出及其频谱。

比较两种采样率下的信号频谱，并解释。

（1）MATLAB 程序：N=10; Fs=5; T s=1/Fs;n=[-N:T s:N];xn=exp(-abs(n)); w=-4*pi:0.01:4*pi; X=xn*exp(-j*(n'*w)); subplot(211) plot(n,xn);title('x_a(t)时域波形');xlabel('t/ms');ylabel('x_a(t)'); axis([-10, 10, 0, 1]); subplot(212);plot(w/pi,abs(X)); title('x_a(t)频谱图');xlabel('\omega/\pi');ylabel('X_a(e^(j\omega))');ind = find(X >=0.03*max(X))*0.01; eband = (max(ind) -min(ind)); fprintf('等效带宽为%fKHZ\n',eband); 运行结果：等效带宽为12.110000KHZ（2）MATLAB程序：N=10;omega=-3*pi:0.01:3*pi;%Fs=5000Fs=5;T s=1/Fs;n=-N:T s:N;xn=exp(-abs(n));X=xn*exp(-j*(n'*omega));subplot(2,2,1);stem(n,xn);grid on;axis([-10, 10, 0, 1.25]); title('时域波形(f_s=5000)');xlabel('n');ylabel('x_1(n)');subplot(2,2,2);plot(omega/pi,abs(X));title('频谱图(f_s=5000)');xlabel('\omega/\pi');ylabel('X_1(f)');grid on;%Fs=1000Fs=1;T s=1/Fs;n=-N:T s:N;xn=exp(-abs(n));X=xn*exp(-j*(n'*omega));subplot(2,2,3);stem(n,xn);grid on;axis([-10, 10, 0, 1.25]); title('时域波形(f_s=1000)');xlabel('n');ylabel('x_2(n)');grid on;subplot(2,2,4);plot(omega/pi,abs(X));title('频谱图(f_s=1000)');xlabel('\omega/\pi');ylabel('X_2(f)');grid on;运行结果：实验二：给定一指数型衰减信号()()0cos 2at x t e f t π-=，采样率1s f T=，T 为采样周期。

西工大数电实验第二次实验实验报告

数电实验2一．实验目的1.学习并掌握硬件描述语言（VHDL 或Verilog HDL）；熟悉门电路的逻辑功能，并用硬件描述语言实现门电路的设计。

2.熟悉中规模器件译码器的逻辑功能，用硬件描述语言实现其设计。

3.熟悉时序电路计数器的逻辑功能，用硬件描述语言实现其设计。

4.熟悉分频电路的逻辑功能，并用硬件描述语言实现其设计。

二.实验设备1.Quartus开发环境2.ED0开发板三.实验内容要求1：编写一个异或门逻辑电路，编译程序如下。

1）用QuartusII 波形仿真验证；2）下载到DE0 开发板验证。

要求2：编写一个将二进制码转换成0-F 的七段码译码器。

1）用QuartusII 波形仿真验证；2）下载到DE0 开发板，利用开发板上的数码管验证。

要求3：编写一个计数器。

1）用QuartusII 波形仿真验证；2）下载到DE0 开发板验证。

要求4：编写一个能实现占空比50%的5M 和50M 分频器即两个输出，输出信号频率分别为10Hz 和1Hz。

1）下载到DE0 开发板验证。

（提示：利用DE0 板上已有的50M 晶振作为输入信号，通过开发板上两个的LED 灯观察输出信号）。

2）电路框图如下：扩展内容：利用已经实现的VHDL 模块文件，采用原理图方法，实现0-F 计数自动循环显示，频率10Hz。

（提示：如何将VHDL 模块文件在逻辑原理图中应用，参考参考内容5）四.实验原理1.实验1实现异或门逻辑电路，VHDL源代码如下：LIBRARY IEEE;USE IEEE.STD_LOGIC_1164.ALL;ENTITY EXORGATE ISPORT(A,B:IN STD_LOGIC;C:OUT STD_LOGIC);END EXORGATE;ARCHITECTURE fwm OF EXORGATE ISBEGINC<=A XOR B;END;2.实验2实现一个将二进制码转换成0-F的七段译码器，VHDL源代码如下：LIBRARY IEEE;USE IEEE.STD_LOGIC_1164.ALL;ENTITY sevendecoder ISPORT (data_in:IN STD_LOGIC_VECTOR(3 DOWNTO 0);dis_out:OUT STD_LOGIC_VECTOR(6 DOWNTO 0));END sevendecoder;ARCHITECTURE fwm OF sevendecoder ISBEGINPROCESS(data_in)BEGINCASE data_in ISWHEN"0000"=>dis_out<="1000000";--显示0 WHEN"0001"=>dis_out<="1111001";--显示1 WHEN"0010"=>dis_out<="0100100";--显示2 WHEN"0011"=>dis_out<="0110000";--显示3 WHEN"0100"=>dis_out<="0011001";--显示4 WHEN"0101"=>dis_out<="0010010";--显示5 WHEN"0110"=>dis_out<="0000010";--显示6WHEN"0111"=>dis_out<="1111000";--显示7 WHEN"1000"=>dis_out<="0000000";--显示8 WHEN"1001"=>dis_out<="0010000";--显示9 WHEN"1010"=>dis_out<="0001000";--显示A WHEN"1011"=>dis_out<="0000011";--显示b WHEN"1100"=>dis_out<="1000110";--显示C WHEN"1101"=>dis_out<="0100001";--显示d WHEN"1110"=>dis_out<="0000110";--显示E WHEN"1111"=>dis_out<="0001110";--显示FWHEN OTHERS=> dis_out<="1111111";--灭灯，不显示END CASE;END PROCESS;END fwm;3.实验3完成一个计数器，VHDL源代码如下：LIBRARY IEEE;USE IEEE.STD_LOGIC_1164.ALL;USE IEEE.STD_LOGIC_UNSIGNED.ALL;ENTITY counter ISPORT ( clk,RST : IN STD_LOGIC;DOUT : OUT STD_LOGIC_VECTOR (3 DOWNTO 0); --四位计数COUT : OUT STD_LOGIC); --进位位END counter;ARCHITECTURE fwm OF counter ISSIGNAL Q1 : STD_LOGIC_VECTOR (3 DOWNTO 0);BEGINPROCESS(clk,RST)BEGINIF RST = '0' THEN Q1<=(OTHERS => '0'); COUT<= '0';ELSIF clk'EVENT AND clk='1' THENQ1<=Q1+1;COUT<= '0';IF Q1 >= "1001" THEN Q1<=(OTHERS => '0'); COUT<= '1';END IF;END IF;END PROCESS;DOUT<=Q1 ;END fwm;4.实验4编写一个能实现占空比50%的5M 和50M 分频器即两个输出，输出信号频率分别为10Hz 和1Hz，VHDL源代码如下：LIBRARY IEEE;USE IEEE.STD_LOGIC_1164.ALL;ENTITY fpq ISPORT(clk:IN STD_LOGIC;clk_out,clk_out1:OUT STD_LOGIC);END fpq;ARCHITECTURE fwm OF fpq ISCONSTANT m : INTEGER:= 25000000; --50M 分频到1Hz 时=25000000。

西电数字信号处理上机实验

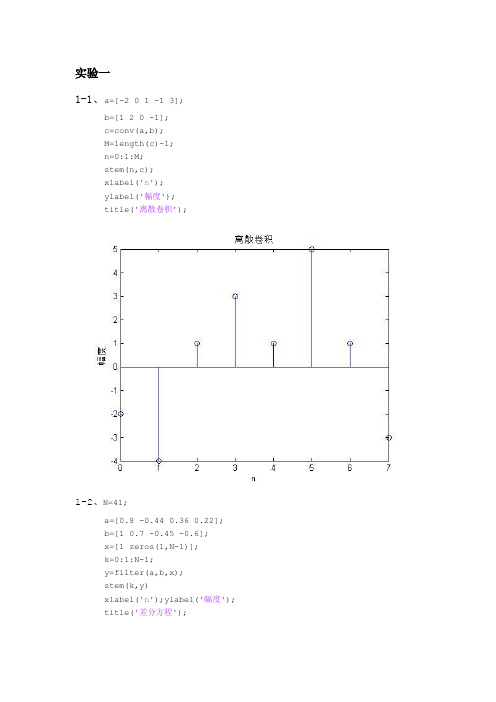
实验一1-1、a=[-2 0 1 -1 3];b=[1 2 0 -1];c=conv(a,b);M=length(c)-1;n=0:1:M;stem(n,c);xlabel('n');ylabel('幅度');title('离散卷积’);1-2、N=41;a=[0.8 -0.44 0.36 0.22]; b=[1 0.7 -0.45 -0.6];x=[1 zeros(1,N-1)];k=0:1:N-1;y=filter(a,b,x);stem(k,y)xlabel('n');ylabel('幅度'); title('差分方程');1-3、k=256;num=[0.8 -0.44 0.36 0.02];den=[1 0.7 -0.45 -0.6];w=0:pi/k:pi;h=freqz(num,den,w);subplot(2,2,1);plot(w/pi,real(h));gridtitle('实部');xlabel('\omega/\pi');ylabel('幅度'); subplot(2,2,2);plot(w/pi,imag(h));gridtitle('虚部');xlabel('\omega/\pi');ylabel('Amplitude'); subplot(2,2,3);plot(w/pi,abs(h));gridtitle('幅度谱');xlabel('\omega/\pi');ylabel('幅值'); subplot(2,2,4);plot(w/pi,angle(h));gridtitle('相位谱');xlabel('\omega/\pi');ylabel('弧度');实验二2-1、N=16;n=0:1:15;p=8;q=4;a=0.1;f=0.0625;xa=exp(-((n-p).^2)./q);figure(1)stem(n, xa,'.');title('xa(n)序列')xlabel('n')ylabel('xa(n)')grid on[H, w] = freqz(xa, 1, [], 'whole', 1); Hamplitude = abs(H);Hphase = angle(H);Hphase = unwrap(Hphase);figure(2)subplot(2, 1, 1)plot(w, Hamplitude)title('幅频响应')xlabel('w/(2*pi)')ylabel('|H(exp(jw))|') grid onsubplot(2, 1, 2)plot(w, Hphase)title('相频响应')xlabel('w/(2*pi)')ylabel('fai(H(exp(jw)))') grid on2-2、n=0:1:15;a=0.1;f1=0.0625;f2=0.04375;f3=0.05625;xb1=exp(-a*n).*sin(2*pi*f1*n);figuresubplot(3,2,1)stem(n, xb1,'.');title('f=0.0625的时域特性')xlabel('n')ylabel('xb1(n)')grid on[H, w] = freqz(xb1, 1, [], 'whole', 1); Hamplitude = abs(H);subplot(3,2,2)plot(w, Hamplitude)title('f=0.0625的幅频响应')xlabel('w/(2*pi)')ylabel('|H(exp(jw))|')grid onxb2=exp(-a*n).*sin(2*pi*f2*n);subplot(3,2,3)stem(n, xb2,'.');title('f=0.04375的时域特性')xlabel('n')ylabel('xb2(n)')grid on[H, w] = freqz(xb2, 1, [], 'whole', 1); Hamplitude = abs(H);subplot(3,2,4)plot(w, Hamplitude)title('f=0.04375的幅频响应')xlabel('w/(2*pi)')ylabel('|H(exp(jw))|')grid onxb3=exp(-a*n).*sin(2*pi*f3*n);subplot(3,2,5)stem(n, xb3,'.');title('f=0.05625的时域特性')xlabel('n')ylabel('xb3(n)')grid on[H, w] = freqz(xb3, 1, [], 'whole', 1); Hamplitude = abs(H);subplot(3,2,6)plot(w, Hamplitude)title('f=0.05625的幅频响应')xlabel('w/(2*pi)')ylabel('|H(exp(jw))|')grid on2-3、n1=0:1:3;xc1=n1+1;n2=4:7;xc2=8-n2;xc=[xc1,xc2];n =[n1,n2];figurestem(n,xc);xlabel('n'); ylabel('xc');title('三角序列');n1=0:1:3;xd1=4-n1;n2=4:7;xd2=n2-3;xd=[xd1,xd2];n =[n1,n2];figurestem(n,xd);xlabel('n'); ylabel('xd');title('反三角序列');N = 16;[H1,w1] = freqz(xc,1, 256, 'whole', 1); Hamplitude1 = abs(H1);figureplot(2*w1, Hamplitude1)title('xc幅频响应')xlabel('w/pi')ylabel('|H(exp(jw))|')grid on[H2,w2] = freqz(xd,1, 256, 'whole', 1); Hamplitude2 = abs(H2);figureplot(2*w2, Hamplitude2)title('xd幅频响应')xlabel('w/pi')ylabel('|H(exp(jw))|')grid on[H3, w3] = freqz(xc, 1, N, 'whole', 1); Hamplitude3 = abs(H3);figuresubplot(2, 1, 1)h3 = stem(2*w3, Hamplitude3, '*');title('xc幅频响应进行N点FFT’);xlabel('n')ylabel('|H(exp(jw))|')grid on[H4, w4] = freqz(xd, 1, N, 'whole', 1); Hamplitude4 = abs(H4);subplot(2, 1, 2)h4 = stem(2*w4, Hamplitude4, '*');title('xd幅频响应进行N点FFT');xlabel('n')ylabel('|H(exp(jw))|')grid on2-4、N = 128;f1 = 1/16;n = 0:N-1;xn = sin(2*pi*0.125.*n)+ cos(2*pi*(0.125+f1).*n); figurestem(n,xn);figuresubplot(2,1,1),plot(n,abs(fft(xn)));title('f =1/16 幅频响应');f2 = 1/64;xn = sin(2*pi*0.125.*n)+ cos(2*pi*(0.125+f2).*n); subplot(2,1,2),plot(n,abs(fft(xn)));title('f =1/64 幅频响应');2-5、N=16;n=0:1:15;p=8;q=2;a=0.1;f=0.0625;xa=exp(-((n-p).^2)./q);xb=exp(-a*n).*sin(2*pi*f*n);%线性卷积x=conv(xa,xb);XDft= fft(x, 32);XDftR = abs(XDft);XDftPhase = angle(XDft);XDftPhase = unwrap(XDftPhase);figure(1);stem(x,'.');title('x(n)序列');xlabel('n')ylabel('x(n)')grid onfigure(2)subplot(2, 1, 1)stem(XDftR, '.');title('X(k)的幅度’);xlabel('k')ylabel('|X(k)|')grid onsubplot(2, 1, 2)stem(XDftPhase, '.');title('X(k)的相角')xlabel('k')ylabel('fai((X(k)))')grid on%圆周卷积XDft161 = fft(xa, N);XDft16R1 = abs(XDft161);XDft16Phase1 = angle(XDft161);XDft16Phase1 = unwrap(XDft16Phase1); XDft162 = fft(xb, N);XDft16R2 = abs(XDft162);XDft16Phase2 = angle(XDft162);XDft16Phase2 = unwrap(XDft16Phase2); XDft16=XDft161.*XDft162;XDft16R=XDft16R1.*XDft16R2;XDft16Phase=XDft16Phase2 +XDft16Phase1 ; x = ifft(XDft16, N);figure(3)stem(x,'.')title('x(n)序列')xlabel('n')ylabel('x(n)')grid onfigure(4)subplot(2, 1, 1)t= 0 : 1 : N - 1;stem(t, XDft16R, '.');title('X(k)的幅度')xlabel('k')ylabel('|X(k)|')grid onsubplot(2, 1, 2)stem(t,XDft16Phase, '.');title('X(k)的相角')xlabel('k')ylabel('fai((X(k)))')grid on2-6、xe=rand(1,512);n1=0:1:3;xc1=n1+1;n2=4:7;xc2=8-n2;xc=[xc1,xc2];%重叠相加法yn=zeros(1,519);for j=0:7xj=xe(64*j+1:64*(j+1));xak=fft(xj,71);xck=fft(xc,71);yn1=ifft(xak.*xck);temp=zeros(1,519);temp(64*j+1:64*j+71)=yn1; yn=yn+temp;end;n=0:518;figure(1)subplot(2,1,1);plot(n,yn);xlabel('n');ylabel('y(n)');title('xc(n)与xe(n)的线性卷积的时域波形-重叠相加法'); subplot(2,1,2);plot(n,abs(fft(yn)));xlabel('k');ylabel('Y(k)');axis([0,600,0,300]);title('xc(n)Óëxe(n)的线性卷积的幅频特性-重叠相加法'); %重叠保留法k=1:7;xe1=k-k;xe_1=[xe1,xe];yn_1=zeros(1,519);for j=0:7xj_1=xe_1(64*j+1:64*j+71);xak_1=fft(xj_1);xck_1=fft(xc,71);yn1_1=ifft(xak_1.*xck_1);temp_1=zeros(1,519);temp_1(64*j+1:64*j+64)=yn1_1(8:71);yn_1=yn_1+temp_1;end;n=0:518;figure(2)subplot(2,1,1);plot(n,yn_1);xlabel('n');ylabel('y(n)');title(' xc(n)的线性卷积的时域波形-重叠保留法'); subplot(2,1,2);plot(n,abs(fft(yn_1)));xlabel('k');ylabel('Y(k)');axis([0,600,0,300]);title('xc(n)Óëxe(n)的线性卷积的幅频特性-重叠保留法');实验三3-1、Wp=0.3;Ws=0.2;Rp=0.8;Rs=20;[N,Wpo]=cheb1ord(Wp,Ws,Rp,Rs);[Bz,Az]=cheby1(N,Rp,Wpo,'high');w=0:0.1:pi;[H,w1]=freqz(Bz,Az,w);H=20*log10(abs(H));plot(w/pi,H),grid onxlabel('\omega/\pi');ylabel('|H(e^j^\omega)|/dB') title('Chebyshev高通滤波器');3-2、Wp=0.2;Ws=0.3;Rp=1;Rs=25;[N,Wc]=buttord(Wp,Ws,Rp,Rs);[Bs,As]=butter(N,Wc,'s');[Bz,Az]=impinvar(Bs,As);w=0:0.1:pi;[H,w1]=freqz(Bz,Az,w);H=20*log10(abs(H));subplot(211);plot(w/pi,H),grid onxlabel('\omega/\pi');ylabel('|H(e^j^\omega)|/dB') title('脉冲响应不变法')[N,Wc]=buttord(Wp,Ws,Rp,Rs);[Bz,Az]=butter(N,Wc);w=0:0.1:pi;[H,w1]=freqz(Bz,Az,w);H=20*log10(abs(H));subplot(212);plot(w/pi,H),grid onxlabel('\omega/\pi');ylabel('|H(e^j^\omega)|/dB') title('双线性变换法')3-3、Wp=1.2/8;Ws=2/8;Rp=0.5;Rs=40;[N,Wpo]=cheb1ord(Wp,Ws,Rp,Rs);[Bz,Az]=cheby1(N,Rp,Wpo);w=0:0.1:pi;[H,w1]=freqz(Bz,Az,w);H=20*log10(abs(H));subplot(311);plot(w/pi,H),grid onxlabel('\omega/\pi');ylabel('|H(e^j^\omega)|/dB') title('切比雪夫')[N,Wc]=buttord(Wp,Ws,Rp,Rs);[Bz,Az]=butter(N,Wc);w=0:0.1:pi;[H,w1]=freqz(Bz,Az,w);H=20*log10(abs(H));subplot(312);plot(w/pi,H),grid onxlabel('\omega/\pi');ylabel('|H(e^j^\omega)|/dB') title('巴特沃斯')[N,Wpo]=ellipord(Wp,Ws,Rp,Rs);[Bz,Az]=ellip(N,Rp,Rs,Wpo);w=0:0.1:pi;[H,w1]=freqz(Bz,Az,w);H=20*log10(abs(H));subplot(313);plot(w/pi,H),grid ontitle('椭圆')xlabel('\omega/\pi');ylabel('|H(e^j^\omega)|/dB')3-4、Wp1=2/15;Wpu=0.2;Ws1=0.1;Wsu=0.4;Rp=3;Rs=20;Wp=[Wp1,Wpu];Ws=[Ws1,Wsu];[N,Wc]=buttord(Wp,Ws,Rp,Rs);[Bz,Az]=butter(N,Wc);w=0:0.1:pi;[H,w1]=freqz(Bz,Az,w);H=20*log10(abs(H));plot(w/pi,H),grid onxlabel('\omega/\pi');ylabel('|H(e^j^\omega)|/dB') title('双线性变换法Butterworth型数字带通滤波器')。

数字信号处理第二次实验报告

2
% 设计Butterworth低通模拟滤波器 % 通带衰减小于1分贝、阻带（>0.6pi）衰减大于25分贝 % n: 阶数 % wn:低通模拟滤波器的3分贝通带截止频率 [B1,A1] = BUTTER(n,wn,'s'); % 设计Butterworth低通模拟滤波器 % B,A：模拟滤波器传递函数分子、分母多项式系数 [b1,a1]=impinvar(B1,A1,fs); % 用脉冲响应不变法将模拟低通滤波器转换为数字滤波器b,a：分子、分母多项式系数 % 双曲变换的预畸变 [B2,A2]=butter(n,2000*tan(pi/5),'s'); % 用双曲变换法将模拟低通滤波器转化为数字滤波器b,a:分子,分母多项式系数 [b2,a2]=bilinear(B2,A2,fs);
(3) 熟悉巴特沃思滤波器，切比雪夫滤波器和椭圆滤波器的频率特性。
二. 实验原理:
(1) 实验中有关变量的定义：fc 通带边界频率ห้องสมุดไป่ตู้fr 阻带边界频率，tao 通带波动，at 最小阻带衰减，fs 采样频率，t 采样周期。
(2) 设计一个数字滤波器一般包括以下两步： a.按照任务要求，确定滤波器性能指标 b.用一个因果稳定的离散时不变系统的系统函数去逼近这一性能要求
姓名:陈桐学号:04004316
实验日期:2006 年 11 月 14 日
一. 实验目的:
(1) 掌握双线形变换法及脉冲响应不变法设计 IIR 数字滤波器的具体设计方法及其原理，熟悉用双线形变换法及脉冲响应不变法设计低通，高通和带通 IIR 数字滤波器的计算机编程。
(2) 观察双线形变换法及脉冲响应不变法设计的滤波器的频域特性，了解双线形变换法及脉冲响应不变法的特点。

西安电子科技大学数字信号处理上机报告

程序代码如下：
xbn=[1]; xcn=ones(1,10); han=ones(1,10);
2
西安电子科技大学电子工程学院 02091478 陈步华
hbn=[1,2.5,2.5,1]; yn=conv(xbn,hbn); %计算信号 xb(n)通过系统 hb(n)的响应 y(n) n1=0:length(yn)-1; n2=0:length(hbn)-1; subplot(2,1,1);stem(n1,yn,'.') %绘制 y(n)的时域特性曲线 xlabel('n');ylabel('y(n)') title('y(n)的时域特性曲线') subplot(2,1,2);stem(n2,hbn,'.') %绘制 hb(n)的时域特性曲线 xlabel('n');ylabel('hb(n)') title('hb(n)的时域特性曲线')
subplot(2,1,2);
plot(w/pi,angle(Hb)); xlabel('\omega/π');ylabel('相位') title('DTFT[hb(n)]的相位');
zn=conv(xcn,han); %观察系统 ha(n)对信号 xc(n)的响应特性
figure(4)
n3=[0:length(zn)-1];
2、实验步骤
8ቤተ መጻሕፍቲ ባይዱ
西安电子科技大学电子工程学院 02091478 陈步华
(1) 复习 DFT 的定义、性质和用 DFT 作谱分析的有关内容。 (2) 复习 FFT 算法原理与编程思想，并对照 DIT-FFT 运算流图和程序框图，读懂本实验提供的 FFT 子程序。 (3) 编制信号产生子程序，产生以下典型信号供谱分析用：

2017年西电电院数字信号处理上机实验报告六

2 实验内容（1）设计计算机程序，根据滤波器的主要技术指标设计线性相位FIR数字低通、高通、带通和带阻滤波器；（2）绘制滤波器的幅频特性和相频特性曲线，验证滤波器的设计结果是否达到设计指标要求；（3）画出线性相位FIR数字滤波器的网络结构信号流图。

3实验步骤（1）设计相应的四种滤波器的MATLAB程序；（2）画出幅频相频特性曲线；（3）画出信号流图。

4 程序设计%% FIR低通f=[0.2,0.35];m=[1,0];Rp=1;Rs=40;dat1=(10^(Rp/20)-1)/(10^(Rp/20)+1);dat2=10^(-Rs/20);rip=[dat1,dat2];[M,f0,m0,w]=remezord(f,m,rip);M=M+2;hn=remez(M,f0,m0,w);w=0:0.001:pixn=[0:length(hn)-1];H=hn*exp(-j*xn'*w);figuresubplot(2,1,1)plot(w/pi,20*log10(abs(H)));gridon;xlabel('\omega/\pi'),ylabel('|H(e^j^w)|/dB')subplot(2,1,2)plot(w/pi,angle(H)/pi);xlabel('\omega/\pi'),ylabel('\phi(\omega)/\pi')%% FIR高通f=[0.7,0.9];m=[0,1];Rp=1;Rs=60;dat1=(10^(Rp/20)-1)/(10^(Rp/20)+1);dat2=10^(-Rs/20);rip=[dat2,dat1];[M,f0,m0,w]=remezord(f,m,rip);hn=remez(M,f0,m0,w);w=0:0.001:pixn=[0:length(hn)-1];H=hn*exp(-j*xn'*w);figuresubplot(2,1,1)plot(w/pi,20*log10(abs(H)));gridon;xlabel('\omega/\pi'),ylabel('|H(e^j^w)|/dB')subplot(2,1,2)plot(w/pi,angle(H)/pi);xlabel('\omega/\pi'),ylabel('\phi(\omega)/\pi')%% FIR带通f=[0.2,0.35,0.65,0.8];m=[0,1,0];Rp=1;Rs=60;dat1=(10^(Rp/20)-1)/(10^(Rp/20)+1);dat2=10^(-Rs/20);rip=[dat2,dat1,dat2];[M,f0,m0,w]=remezord(f,m,rip);M=M+3hn=remez(M,f0,m0,w);w=0:0.001:pixn=[0:length(hn)-1];H=hn*exp(-j*xn'*w);figuresubplot(2,1,1)plot(w/pi,20*log10(abs(H)));gridon;xlabel('\omega/\pi'),ylabel('|H(e^j^w)|/dB')subplot(2,1,2)plot(w/pi,angle(H)/pi);xlabel('\omega/\pi'),ylabel('\phi(\omega)/\pi')%% FIR带阻f=[0.2,0.35,0.65,0.8];m=[1,0,1];Rp=1;Rs=60;dat1=(10^(Rp/20)-1)/(10^(Rp/20)+1);dat2=10^(-Rs/20);rip=[dat1,dat2,dat1];[M,f0,m0,w]=remezord(f,m,rip);hn=remez(M,f0,m0,w);w=0:0.001:pixn=[0:length(hn)-1];H=hn*exp(-j*xn'*w);figuresubplot(2,1,1)plot(w/pi,20*log10(abs(H)));gridon;xlabel('\omega/\pi'),ylabel('|H(e^j^w)|/dB')subplot(2,1,2)plot(w/pi,angle(H)/pi);xlabel('\omega/\pi'),ylabel('\phi(\omega)/\pi') 5实验结果及分析（1）FIR低通滤波器自动得到的M值不满足要求，故我们将M加上2 在w=0.2π时，H=-0.5dB；w=0.35π时，H=-41dB。