第一章勾股定理评价试题

合集下载

第1章勾股定理北师大版八年级数学上册综合素质评价(含解析)

第一章综合素质评价一、选择题：本大题共10小题，每小题3分，共30分．1．【2023·佛山南海区期中】下列各组数为勾股数的是( )A ．2，3，5B ．0.3，0.4，0.5C ．5，12，13D ．7，8，92．【2023·深圳福田区期中】如图，已知正方形A 的面积为3，正方形B 的面积为4，则正方形C 的面积为( )A ．7B ．5C ．25D ．13．在Rt △ABC 中，∠C ＝90°，AC ＝5，BC ＝12，则点C 到AB 的距离是( )A ．1360B ．6013C ．13D ．5134．在Rt △ABC 中，AB 2＝10，AC 2＝6，则BC 2＝( )A ．8B ．16或64C ．4D ．4或165．【2022·佛山顺德区期末】如图所示的4个图中，能够验证勾股定理的有( )A ．4个B ．3个C ．2个D ．1个6．亮亮准备测量河水的深度，他把一根竹竿竖直插到离岸边1.2 m 远的水底，竹竿高出水面0.4 m ，把竹竿的顶端拉向岸边，竿顶和岸边的水面刚好相齐，则河水的深度为( )A ．1.6 mB ．2 mC ．2.5 mD ．3 m7．《九章算术》是古代东方数学代表作，书中记载：今有开门去阃(读kǔn ，门槛的意思)一尺，不合二寸，问门广几何？题目大意是：如图①，②(图②为图①的平面示意图)，推开双门，双门间隙CD的距离为2寸，点C 和点D 距离门槛AB 都为1尺(1尺＝10寸)，则AB 的长是( )A．50.5寸B．52寸C．101寸D．104寸8．如图，动点P从点A出发，沿着圆柱的侧面移动到BC的中点S处，若BC＝16，底面半径为2(π取3)，则点P移动的最短距离为( )A．8 B．10 C．15 D．209．如图，有一块直角三角形纸片，∠C＝90°，AC＝6 cm，BC＝8 cm.现将直角边AC 沿直线AD折叠，使它落在斜边AB上，且与AE重合，则CD的长为( ) A．2 cm B．3 cm C．4 cm D．5 cm10．如图，在Rt△ABC中，∠ACB＝90°，BC＝3，AB＝5，点E为射线BC上一点，若△ABE是等腰三角形，则△ABE的面积不可能是( )A．10 B．12 C．253D．256二、填空题：本大题共5小题，每小题3分，共15分．11．【2023·佛山禅城区月考】如图，一棵18 m高的树被风刮断了，树顶落在离树根12 m处，则折断处距地面的高度为________m.12．如图，在高为5 m，坡面长为13 m的楼梯表面铺地毯，地毯的长度至少需要________m.13．【2023·佛山南海区校级月考】如图，在Rt△ABC中，∠ACB＝90°.若AB＝13，BC＝12，在AB同侧分别以AB，BC，AC为直径作三个半圆，则阴影部分的面积为________．14．【2023·广州增城区期末】如图，供给船要给C岛运送物资，从海岸线上的港口A出发，向北偏东40°方向直线航行60海里到达C岛．测得海岸线上的港口B在C岛南偏东50°方向．若A，B两港口之间的距离为65海里，则C岛到港口B的距离是________海里．15．“绿水青山就是金山银山”这一科学论断成为树立生态文明观，引领中国走向绿色发展之路的理论之基．小张在数学活动课上用正方形纸片制作成图①的“七巧板”，设计拼成了图②的水杉树冠，如果已知图①中正方形纸片的边长为 2 cm，则图②中水杉树冠的高(即点A到线段BC的距离)是________cm.三、解答题(一)：本大题共3小题，每小题8分，共24分．16．【母题：教材P4习题T4】如图，在△ABC中，AD⊥BC，AD＝12，BD＝16，CD ＝5，求△ABC的周长．17．某市规定：小汽车在城市道路上的行驶速度不得超过70千米/时．如图，一辆小汽车在一条城市道路上直道行驶，某一时刻刚好行驶到车速检测仪A正前方60米的C处，过了4秒后行驶到B处，此时测得小汽车与车速检测仪间的距离为100米，请问这辆小汽车是否超速行驶？18．如图，某住宅小区在施工过程中留下了一块空地(四边形ABCD)，经测量，AB ＝3 m，BC＝4 m，CD＝12 m，DA＝13 m，∠B＝90°.小区为美化环境，欲在空地上铺草坪，已知草坪每平方米30元，铺满这块空地共需花费多少元？四、解答题(二)：本大题共3小题，每小题9分，共27分．19．如图，在笔直公路MN的一侧点A处有一村庄，村庄到公路MN的距离AB为600米，假设宣讲车周围1 000米以内能听到广播宣传，宣讲车在公路MN上由M向N行驶．(1)请问村庄能否听到广播宣传，说明理由；(2)已知宣讲车的速度是200米/分，如果能听到广播宣传，那么村庄总共能听到多长时间的广播宣传？20．如图，在△ABC中，AB＝AC，D在CB的延长线上．(1)试说明：AD2－AB2＝BD·CD.(2)若D在线段CB上，结论如何？试说明你的结论．21．(1)如图①，长方体的长为4 cm，宽为3 cm，高为12 cm.求该长方体中能放入木棒(木棒直径忽略不计)的最大长度；(2)如图②，透明圆柱形容器(容器厚度忽略不计)的高为12 cm，底面周长为10cm，在容器内壁离容器底部3 cm的点B处有一饭粒，此时一只壁虎正好在容器外壁且离容器上沿3 cm与饭粒相对的点A处．求壁虎吃到饭粒需要爬行的最短路程．五、解答题(三)：本大题共2小题，每小题12分，共24分．22．如图，在△ABC中，AB∶CB∶CA＝3∶4∶5，且周长为72 cm.点M以每秒2 cm 的速度从A向B运动，点N以每秒3 cm的速度从B向C运动．如果两点同时出发，经过4秒时，△BMN的面积为多少？23．如图，在Rt△ABC中，∠ACB＝90°，AB＝5 cm，AC＝3 cm，动点P从点B 出发沿射线BC以1 cm/s的速度移动，设运动的时间为t s.(1)求BC的长；(2)连接AP，当△ABP为直角三角形时，求t的值．答案一、1．C 点拨：22＋32＝13，52＝25，13≠25，故A 不符合题意；0.3，0.4，0.5都不是正整数，故B 不符合题意；52＋122＝169＝132，且5，12，13均为正整数，故C 符合题意；72＋82＝113≠92，故D 不符合题意．2．A 点拨：因为正方形A 的面积为3，正方形B 的面积为4，所以正方形C 的面积为3＋4＝7.3．B 点拨：如图，过点C 作CD ⊥AB 于点D .因为在Rt △ABC 中，∠ACB ＝90°，AC ＝5，BC ＝12，所以AB ＝13.因为12AC ·BC ＝12CD ·AB ，所以5×12＝13CD ，解得CD ＝6013.4．D 点拨：当∠C ＝90°时，BC 2＝AB 2－AC 2＝10－6＝4；当∠A ＝90°时，BC 2＝AB 2＋AC 2＝10＋6＝16.综上所述，BC 2＝4或16.5．A 点拨：第1个图：中间小正方形的面积为c 2＝(a ＋b )2－4×12ab ，化简得c 2＝a 2＋b 2；第2个图：中间小正方形的面积为(b －a )2＝c 2－4×12ab ，化简得a 2＋b 2＝c 2；第3个图：梯形的面积为12(a ＋b )(a ＋b )＝2×12ab ＋12c 2，化简得a 2＋b 2＝c 2；第4个图：易知割补前后的两个小直角三角形全等，则正方形的面积为(b －b －a 2)(a ＋b －a 2)＝12ab ＋12c ·12c ，化简得a 2＋b 2＝c 2.所以能够验证勾股定理的有4个．6．A 点拨：设河水的深度为x m ，则竹竿的长为(x ＋0.4)m.由题意得x 2＋1.22＝(x ＋0.4)2，解得x ＝1.6，所以河水的深度为1.6 m.7．C 点拨：如图所示．由题意可知，CD ∥AB ，OA ＝OB ＝AD ＝BC ，设OA ＝OB ＝AD ＝BC ＝r 寸，则AB ＝2r 寸，AE ＝12(AB －CD )＝12(2r －2)＝(r －1)(寸)．在Rt △ADE 中，由勾股定理得AE 2＋DE 2＝AD 2，所以(r －1)2＋102＝r 2，解得r ＝50.5，所以AB ＝101寸．8．B 点拨：将圆柱的侧面展开，如图所示，连接AS ，则AS 的长即为点P 移动的最短距离．因为BC ＝16，S 为BC 的中点，所以BS ＝8.因为圆柱的底面半径为2，所以AB ＝12×2×2×3＝6，在Rt △ABS 中，由勾股定理得AS 2＝AB 2＋BS 2，即AS 2＝62＋82，所以AS ＝10.9．B 点拨：在Rt △ABC 中，因为AC ＝6 cm ，BC ＝8 cm ，所以AB ＝10 cm.因为△ADE 是由△ADC 翻折得到的，所以CD ＝DE ，AC ＝AE ＝6 cm ，所以EB ＝AB －AE ＝10－6＝4(cm)．设CD ＝DE ＝x cm ，则DB ＝(8－x )cm.在Rt △DEB 中，由勾股定理得DE 2＋EB 2＝DB 2，所以x 2＋42＝(8－x )2，所以x ＝3，所以CD ＝3 cm.10．D 点拨：因为在Rt △ABC 中，∠ACB ＝90°，BC ＝3，AB ＝5，所以AC ＝4.由△ABE 是等腰三角形可分三种情况讨论：①当BE ＝AB ＝5时，S △ABE ＝12BE ·AC ＝12×5×4＝10；②当AE ＝AB 时，因为AC ⊥BE ，所以易得BC ＝CE ＝3，所以BE ＝6，所以S △ABE ＝12BE ·AC ＝12×6×4＝12；③当AE ＝BE 时，因为BE ＝BC ＋CE ＝3＋CE ，AE 2＝AC 2＋CE 2，所以(3＋CE )2＝42＋CE 2，解得CE ＝76，所以BE ＝3＋76＝256，所以S △ABE ＝12BE ·AC ＝12×256×4＝253.综上所述，△ABE 的面积是10或12或253.二、11．5　点拨：由题意得BC ＝12 m ，AC ＋AB ＝18 m ，∠ABC ＝90°.设AB＝x m，则AC＝(18－x)m.由勾股定理得AB2＋BC2＝AC2，即x2＋122＝(18－x)2，解得x＝5，所以AB＝5 m，即折断处距地面的高度为5 m. 12．17　点拨：由勾股定理得，楼梯的水平长度为12 m，所以地毯的长度至少需要12＋5＝17(m)．13．30　点拨：因为∠ACB＝90°，AB＝13，BC＝12，所以AC2＝AB2－BC2＝25，所以AC＝5，所以S△ABC＝12BC·AC＝12×12×5＝30.所以阴影部分的面积为12π×(12AC)2＋12π×(12BC)2＋S△ABC－12π×(12AB)2＝π8(AC2＋BC2－AB2)＋S△ABC＝S△ABC＝30.14．25　点拨：如图，过点A作AD垂直于南北方向的直线CD于点D，则∠ADC ＝90°.根据题意得∠CAD＝90°－40°＝50°，所以∠ACD＝90°－∠CAD＝40°，所以∠ACB＝40°＋50°＝90°.因为AC＝60海里，AB＝65海里，所以BC＝25海里．故C岛到港口B的距离是25海里．15．(2＋1)　点拨：如图，过A作AE⊥MN于E，∵MN＝BH＝2 cm，∴AE ＝12MN ＝1(cm)，HF ＝BF ＝22BH ＝2(cm)，∴水杉树冠的高为AE ＋HF ＝(2＋1)cm.三、16．解：在Rt △ABD 和Rt △ACD 中，根据勾股定理得AB 2＝AD 2＋BD 2，AC 2＝AD 2＋CD 2.因为AD ＝12，BD ＝16，CD ＝5，所以AB ＝20，AC ＝13，所以△ABC 的周长为AB ＋AC ＋BC ＝AB ＋AC ＋BD ＋DC ＝20＋13＋16＋5＝54.17．解：根据题意得AC ＝60 m ，AB ＝100 m ，∠C ＝90°.在Rt △ACB 中，根据勾股定理得BC 2＝AB 2－AC 2，所以BC ＝80米．由题意知小汽车4秒行驶80米，即小汽车的行驶速度为72千米/时．因为 72＞70，所以这辆小汽车超速行驶．18．解：如图，连接AC .因为在△ABC 中，AB ＝3 m ，BC ＝4 m ，∠B ＝90°，所以AC ＝5 m.因为在△ACD 中，AC ＝5 m ，CD ＝12 m ，DA ＝13m ，所以AC 2＋CD 2＝AD 2，所以△ACD 是直角三角形，所以S四边形ABCD＝S△ABC＋S△ACD＝12×3×4＋12×5×12＝6＋30＝36 (m2)．36×30＝1 080(元)．故铺满这块空地共需花费1 080元．四、19．解：(1)村庄能听到广播宣传．理由：因为村庄到公路MN的距离AB为600米，600<1 000，所以村庄能听到广播宣传．(2)如图，假设宣讲车行驶到P点村庄开始听到广播宣传，行驶到Q点村庄刚好听不到广播宣传，连接AP，AQ，则AP＝AQ＝1 000米，由勾股定理得BP＝BQ＝800米，所以PQ＝1 600米，1 600÷200＝8(分)．所以村庄总共能听到8分的广播宣传．20．解：过点A作AE⊥BC于点E.(1)因为AB＝AC，所以易得BE＝CE.在Rt△ADE中，AD2－AE2＝DE2，①在Rt△ACE中，AC2－AE2＝CE2，②①－②，得AD2－AC2＝DE2－CE2＝(DE－CE)(DE＋CE)＝(DE－BE)·CD＝BD·CD，即AD2－AB2＝BD·CD.(2)AB2－AD2＝BD·CD.说明如下：易知AD2－AE2＝DE2，AC2－AE2＝CE2.因为点D在线段CB上，所以AC＞AD，所以AC2－AD2＝CE2－DE2＝(CE－DE)(CE＋DE)＝(BE－DE)(CE＋DE)＝BD·CD，即AB2－AD2＝BD·CD.21．解：(1)连接AC，AG.在Rt△ABC中，由勾股定理得AC＝5 cm.在Rt△ACG中，由勾股定理得AG＝13 cm.故该长方体中能放入木棒的最大长度是13 cm.(2)如图，将容器部分侧面展开，作点A关于直线EF的对称点A′，连接A′B，与EF交于点C，连接AC，则A′B的长即为最短路程．过点A′作A′D⊥BF交BF的延长线于点D.易知A′D＝5 cm，BD＝12－3＋3＝12(cm)．所以A′B＝13 cm.故壁虎吃到饭粒需要爬行的最短路程为13 cm.五、22．解：设AB＝3x cm，则CB＝4x cm，CA＝5x cm，所以3x＋4x＋5x＝72.所以x＝6.所以AB＝18 cm，CB＝24 cm，CA＝30 cm.因为AB2＋CB2＝182＋242＝900，CA2＝302＝900，所以AB2＋CB2＝CA2.所以△ABC是直角三角形，且∠B＝90°.当经过4秒时，BM＝AB－AM＝18－2×4＝10(cm)，BN＝3×4＝12(cm)，所以S△BMN＝12BM·BN＝60(cm2)．故经过4秒时，△BMN的面积为60 cm2.23．解：(1)在Rt△ABC中，由勾股定理得AB2＝AC2＋BC2.因为AB＝5 cm，AC＝3 cm，所以BC＝4 cm.(2)由题意得BP＝t cm.由△ABP为直角三角形可知需分两种情况：①当∠APB＝90°时，如图①所示，点P与点C重合，所以BP＝BC＝4 cm，所以t＝4.②当∠BAP ＝90°时，如图②所示，则CP ＝(t －4)cm ，∠ACP ＝90°.在Rt △ACP 中，由勾股定理得AP 2＝AC 2＋CP 2，在Rt △ABP 中，由勾股定理得AP 2＝BP 2－AB 2，所以AC 2＋CP 2＝BP 2－AB 2，即32＋(t －4)2＝t 2－52，解得t ＝254.综上所述，当△ABP 为直角三角形时，t 的值为4或254.。

新北师大版八年级数学《勾股定理》单元测试卷

2017-2018北师大版八年级上册数学评价检测试卷第一章勾股定理班级姓名座号成绩一、选择题1．以下列各组数据为三角形三边，能构成直角三角形的是（）（A ）4cm ，8cm ，7cm （B ）2cm ，2cm ，2cm（C ）2cm ，2cm ，4cm （D ）13cm ，12cm ，5cm2．一个三角形的三边长分别为15cm ，20cm ，25cm ，则这个三角形最长边上的高为（）（A ）12cm （B ）10cm （C ）12.5cm （D ）10.5cm3．Rt ∆ABC 的两边长分别为3和4，若一个正方形的边长是∆ABC 的第三边，则这个正方形的面积是（）（A ）25 （B ）7 （C ）12 （D ）25或74．有长度为9cm ，12cm ，15cm ，36cm ，39cm 的五根木棒，可搭成（首尾连接）直角三角形的个数为（）（A ）1个（B ）2个（C ）3个（D ）4个5．将直角三角形的三边长扩大相同的倍数后，得到的三角形是（）（A ）直角三角形（B ）锐角三角形（C ）钝角三角形（D ）以上结论都不对6．在△ABC 中，AB =12cm ，AC =9cm ，BC =15cm ，下列关系成立的是（）（A ）B C A ∠+∠>∠（B ）B C A ∠+∠=∠（C ）B C A ∠+∠<∠（D ）以上都不对7．小刚准备测量河水的深度,他把一根竹竿插到离岸边1.5m 远的水底，竹竿高出水面0.5m ，把竹竿的顶端拉向岸边，竿顶和岸边的水平刚好相齐，河水的深度为（）（A ）2m （B ）2.5cm （C ）2.25m （D ）3m8．若一个三角形三边满足ab c b a 2)(22=-+，则这个三角形是（）（A ）直角三角形（B ）等腰直角三角形（C ）等腰三角形（D ）以上结论都不对9．一架250cm 的梯子斜靠在墙上，这时梯足与墙的终端距离为70cm ，如果梯子顶端沿墙下滑40cm ，那么梯足将向外滑动（）B （A ）150cm （B ）90cm（C ）80cm （D ）40cm 10．三角形三边长分别为12+n 、n n 222+、1222++n n （n 为自然数），则此三角形是（）（A ）直角三角形（B ）等腰直角三角形（C ）等腰三角形（D ）以上结论都不对二、填空题11．写四组勾股数组.______，______，______，______.12．若一个直角三角形的三边为三个连续的偶数，则它的周长为____________。

八年级上册数学第一章《勾股定理》检测题及答案解析

第2页共8页
三、解答题（共 46 分）
19.（ 6 分）若△ ABC 三边长满足下列条件，判断△
哪个角是直角 .
（ 1） BC 3 , AB 5 , AC 1 ;
4
4
ABC 是不是直角三角形，若是，请说明
（ 2 ） △ ABC 中， ∠ A, ∠ B, ∠ C 所对的边分别为 a ， b ， c ， a=n2 1，b=2n，
求：（ 1）这个三角形各内角的度数；（ 2）另外一条边长的平方 .
22.（ 7 分）如图，台风过后，一希望小学的旗杆在离地某处断裂，旗杆顶部落在离旗杆底部 8 m 处，已知旗杆原长 16 m ，你能求出旗杆在离底部多少米的位置断裂吗？ 23.（ 7 分）张老师在一次“探究性学习”课中，设计了如下数表：
）
A. 三内角之比为 1︰ 2︰ 3
B.三边长的平方之比为 1︰2︰ 3
C. 三边长之比为 3︰ 4︰ 5
D.三内角之比为 3︰ 4︰ 5
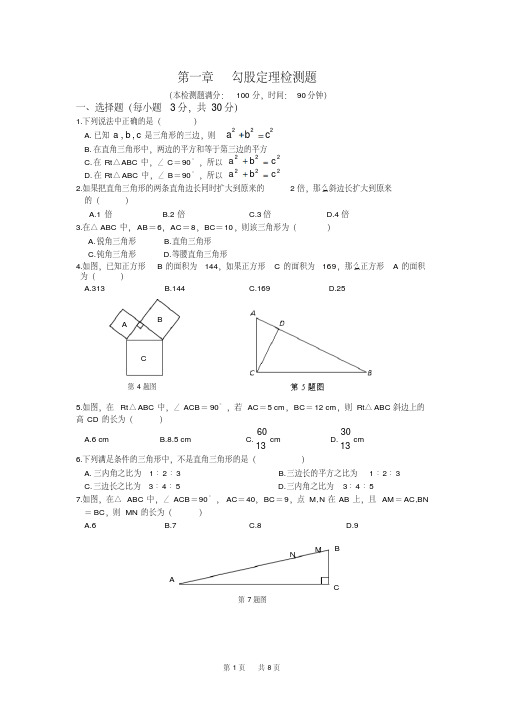
7.如图，在△ ABC 中，∠ ACB＝90°， AC＝ 40， BC＝ 9，点 M ,N 在 AB 上，且 AM＝ AC,BN
＝ BC，则 MN 的长为（
）
A.6
第一章勾股定理检测题
（本检测题满分： 100 分，时间： 90 分钟）
一、选择题（每小题 3 分，共 30 分）
1.下列说法中正确的是（
）
A. 已知 a , b , c 是三角形的三边，则 a2 b2 c2
B. 在直角三角形中，两边的平方和等于第三边的平方
C. 在 Rt△ABC 中，∠ C＝90°，所以 a 2 b 2 c 2 D. 在 Rt△ ABC 中，∠ B＝90°，所以 a 2 b 2 c 2

北师大版数学八年级上册第一章勾股定理综合测评 (含答案)

第一章勾股定理综合测评（本试卷满分100分）一、选择题（本大题共10小题，每小题3分，共30分）1.在直角三角形中，若勾长为3，股长为4，则弦长为（） A ．5 B ．6 C ．7 D ．82.在△ABC 中，∠B=90°，则（）A ．AC=AB+BCB ．AC 2=AB 2+BC 2 C ．AB 2=AC 2+BC 2D ．BC 2=AB 2+AC 2 3.下列各组数中是勾股数的是（）A.0.3，0.4，0.5B.5，12，13C.13 ，14 ，15D. 32，42，52 4.如图1，在Rt △ABC 中，∠ACB=90°，若AB=15 cm ，则正方形ADEC 和正方形BCFG 的面积和为（）A ．150 cm 2B ．200 cm 2C ．225 cm 2D ．无法计算图1 图25. 两个边长分别为a ，b ，c 的直角三角形和一个两条直角边长都是c 的直角三角形拼成图2所示的图形，用两种不同的计算方法计算这个图形的面积，则可得等式为（） A.（a +b ）2=c 2 B. （a -b ）2=c 2 C. a 2-b 2=c 2 D. a 2+b 2=c 26. 如图3，在Rt △ABC 中，∠ACB =90°，AC =8 cm ，BC =15 cm ，其斜边AB 上的高CD 为（） A. 17 cmB. 8.5 cmC.6017cm D.12017cm图3 图4 图5 7. △ABC 的三条边分别为a ，b ，c ，下列条件不能判断△ABC 是直角三角形的是（） A. ∠A ∶∠B ∶∠C=3∶4∶5 B. a =6，b =8，c =10 C. ∠A =∠B +∠C D. a 2+b 2=c 28. 如图4，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形的边长为7 cm ，则图中所有正方形的面积之和为（） A. 49 cm 2 B. 100 cm 2 C.147 cm 2 D. 149 cm 2 9.如图5，为了测算出学校旗杆的高度，小明将升旗的绳子拉到旗杆底端，并在与旗杆等长的地方打了一个结，然后将绳子底端拉到离旗杆底端5米的地面某处，发现此时绳子底端距离打结处约1米，则旗杆的高度是（）A. 24米B. 15米C. 13米D. 12米10.2002年8月在北京召开的国际数学家大会会标如图6所示，它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形.若大正方形的面积是13，小正方形的面积是1，直角三角形的较长直角边为a，较短直角边为b，则（a+b）2的值为（）A. 25B. 19C. 13D. 169图6二、填空题（本大题共6小题，每小题3分，共18分）11. 已知△ABC的三边长分别是AB=5，BC=4，AC=3，那么∠C=°.12. 已知直角三角形的两条边长分别为5，6，则第三边长的平方为.13.如图7，已知A，B两艘船同时从港口O出发，船A以20 km/h的速度向东航行，船B以15 km/h的速度向北航行，则A，B两船离开港口2 h后相距km.图7 图8 图9 图1014. 如图8，一只蚂蚁从实心长方体的顶点A出发，沿长方体的表面爬到对角顶点C1处（三条棱长如图所示），则最短路线长为.15. 如图9，在Rt△ABC中，∠ACB=90°，AC=3，BC=4，点D在AB边上，AD=AC，AE⊥CD，垂足为F，与BC交于点E，连接DE，则BE的长是.16.我国古代有这样一道数学问题：“枯木一根直立地上，高二丈，周三尺，有葛藤自根缠绕而上，五周而达其顶，问葛藤之长几何？”题意是：如图10所示，把枯木看作一个柱体，因一丈是十尺，则该圆柱的高为20尺，底面周长为3尺，有葛藤自点A处缠绕而上，绕五周后其末端恰好到达点B处，则葛藤的最短长度是尺.三、解答题（本大题共6个小题，满分52分）17.（6分）如图11，在△ABC中，AD⊥BC，AD=12，BD=16，CD=5．求△ABC的周长．图1118.（6分）如图12，在四边形ABCD 中，AB=13，BC=5，CD=15，AD=9，对角线AC ⊥BC ．（1）求AC 的长；（2）求∠CAD 的度数．图1219.（8分）如图13，有一架秋千，当它静止时，踏板离地的垂直高度DE =1 m ，将它往前推送6 m （水平距离BC =6 m ）时，秋千的踏板离地的垂直高度BF =3 m ，秋千的绳索始终拉得很直，求绳索AD 的长.图1320.（10分）在△ABC 中，AB =15，BC =14，AC =13，求△ABC 的面积.某学习小组经过合作交流，给出了下面的解题思路，请你按照他们的解题思路完成解答过程.图1421.（10分）如图15，在某地的一次抗洪救灾中，某受灾学校A 到直线公路BD 的距离AB 为3千米，且与该公路上一个车站D 相距5千米，为了便于运输救灾物资，现要在公路边上建一个救灾物资存储中心C ，使之与学校A 与车站D 的距离相等．根据勾股定理求出AD 的长，再计算三角形面积根据勾股定理，利用AD 作为“桥梁”，建立方程模型求出x如图14，作AD ⊥BC 于点D ，设BD =x ，用含x 的代数式表示CDAB D（1）用尺规作图的方法，找出存储中心C 的位置（不写作法，保留痕迹）．（2）求储存中心C 与车站D 的距离．图1522.（12分）课堂上学习了勾股定理后，知道“勾三、股四、弦五”.王老师给出一组数让学生观察：3，4，5；5，12，13；7，24，25；9，40，41；…；学生发现这些勾股数的勾都是奇数，且从3开始就没有间断过，于是王老师提出以下问题让学生解决.（1）请你根据上述规律写出下一组勾股数：11，，；（2）若第一个数用字母a （a 为奇数，且a ≥3）表示，那么后两个数用含a 的代数式分别如何表示？聪明的小明发现每组第二个数有这样的规律4=2312-，12=2512-，24=2712-，…，于是他很快表示了第二个数为212a -，则用含a 的代数式表示第三个数为；（3）用所学知识加以说明.附加题（共20分，不计入总分）1.（6分）如图1，正方形纸片ABCD 的边长为15，E ，F 分别是CD ，AD 边上的点，连接AE ，把正方形纸片沿BF 折叠，使点A 落在AE 上点G 处.若CE =7，则GE 的长为 .2.（14分）数学实验室：制作4张全等的直角三角形纸片（如图2-①），把这4张纸片拼成以弦长c为边长的正方形构成“弦图”（如图2-②），古代数学家利用“弦图”验证了勾股定理．图2 探索研究：（1）小明将“弦图”2-②中部分三角形进行了旋转，得到图2-③，请利用图2-③验证勾股定理；C A BD 数学思考：（2）小芳认为用其它的方法改变“弦图”中某些三角形的位置，也可以证明勾股定理．请你想一种方法支持她的观点（先在备用图中补全图形，再予以证明）．（广东刘明）第一章勾股定理综合测评一、1. A 2. B 3. B 4. C 5. D 6. D 7. A 8. C 9.D10. A 提示：因为a 2+b 2=13，（a-b ）2=a 2+b 2-2ab=1，所以2ab=12. 所以（a +b ）2=a 2+b 2+2ab=25. 二、11. 90 12. 11或61 13. 50 14.515. 2.5 提示：连接DE ，由勾股定理，得AB =5，BD =2.因为AD =AC ，AE ⊥CD ，所以CF =DF .所以CE =DE .可证△ACE ≌△ADE .所以△BDE 为直角三角形.设BE =x ，则CE =DE =4-x .所以22+（4-x ）2=x 2，解得x =2.5. 16. 25 提示：如图1，一条直角边（即枯木的高）长20尺，另一条直角边长5×3=15（尺），因此，葛藤长的平方为202+152=625=252，所以葛藤长为25尺．图1 三、17.解：在Rt △ABD 和Rt △ACD 中，根据勾股定理，得AB 2=AD 2+BD 2=400，AC 2=AD 2+CD 2=169，所以AB=20，AC=13.所以△ABC 的周长为AB+AC+BC=AB+AC+BD+DC=20+13+16+5=54． 18.解：（1）因为AB=13，BC=5，AC ⊥BC ，所以AC 2= AB 2−BC 2=132−52=144，所以AC=12.（2）因为AC=12，CD=15，AD=9，所以CD 2=AC 2+AD 2.所以△ADC 是直角三角形，∠CAD=90°. 19.解：设绳索AD 的长为x m ，则AB=x m ，AC=x+1-3=（x -2）m. 根据题意，得x 2=62+（x -2）2，解得x =10. 答：绳索AD 的长为10 m.20.解：设BD =x ，则CD =14﹣x .在Rt △ADB 和Rt △ADC 中，由勾股定理，得AD 2=AB 2-BD 2=152-x 2，AD 2=AC 2-CD 2=132-（14-x ）2，所以152-x 2=132-（14-x ）2，解得x =9.所以BD =9.所以AD =12.所以S △ABC =12BC ∙AD ＝12×14×12＝84. 21.解：（1）作出的点C 如图2所示；图2（2）由题意知，AD=5千米，AB=3千米，∠B=90°.在Rt △ABD 中，由勾股定理，得BD 2=AD 2-AB 2=16，所以BD=4千米. 设C ，D 之间的距离为x 千米，则AC=x 千米，BC=（4-x ）千米. 在Rt △ABC 中，222AB BC AD +=，即32+（4-x ）2=x 2，解得258. 即储存中心C 与车站D 的距离是258千米． 22.解：（1）60 61（2）212a +（3）因为a 2+2212a ⎛⎫- ⎪⎝⎭=42214a a ++，2212a ⎛⎫+ ⎪⎝⎭=42214a a ++，所以a 2+2212a ⎛⎫- ⎪⎝⎭=2212a ⎛⎫+ ⎪⎝⎭.因为a 为奇数，且a ≥3，所以由a ，212a -，212a +都是正整数.所以这三个数组成的数是勾股数.附加题 1.4917提示：设AG 与BF 交于点H . 因为CE =7，所以DE =15-7=8.由已知可得△ABF ≌△DAE ，所以AF =DE =8.所以BF =AE =17.所以AH =AB AF BF ⋅=12017. 由折叠，得AH =△GH .所以AG =2AH =24017.所以GE =AE -AG =4917. 2. 解：（1）如图1，连接AD.因为图形的面积可表示为12（a+b ）（a+b ）+12c 2，也可表示为c 2+2×12ab ，所以12（a+b ）（a+b ）+c 2+2×12ab.所以a 2+b 2=c 2，即直角三角形两直角边的平方和等于斜边的平方．（2）如图2所示，因为大正方形的面积可以表示为（a+b ）2，也可表示为c 2+4×12ab ，所以（a+b ）2=c 2+4×12ab.所以a 2+b 2=c 2，即直角三角形两直角边的平方和等于斜边的平方．。

第1章勾股定理北师大版数学八年级上册综合素质评价(含答案)

第一章　综合素质评价一、选择题(每题3分，共30分)1.如图，在Rt △ABC 中，∠C ＝90°，AC ＝4，BC ＝5，则AB 的平方为( )(第1题)A .9B .16C .25D .412.下列各组数中，是勾股数的是( )A .0.3，0.4，0.5B .35，45，1C .4，5，6D .7，24，253.在△ABC 中，∠B ＝35°，BC 2－AC 2＝AB 2，则∠C 的大小为( )A .35°B .55°C .65°D .90°4.如图，在Rt △ABC 中，∠ACB ＝90°，AC ＝3，BC ＝4，以点A 为圆心，AC 长为半径画弧，交AB 于点D ，则BD 的长度是( )(第4题)A .2B .3C .4D .55.[情境题生活应用]如图，在A 村与B 村之间有一座大山，原来从A 村到B 村，需沿道路A →C →B (∠C ＝90°)绕过村庄间的大山，打通A ，B 间的隧道后，就可直接从A 村到B 村.已知AC ＝9 km ，BC ＝12 km ，那么打通隧道后从A 村到B 村比原来减少的路程为( )(第5题)A.7kmB.6kmC.5kmD.2km6.如图，在Rt△ABC中，∠ACB＝90°，若AB＝15，则正方形ADEC 和正方形BCFG的面积和为( )(第6题)A.225B.200C.150D.无法计算7.[情境题生活应用母题教材P6习题T1]如图母题①，小霞将升旗的绳子拉到旗杆底端，并在绳子上打了一个结，然后将绳子拉到离旗杆底端12米处，发现此时绳子底端距离打结处约6米，如图②，则滑轮到地面的距离为( )(第7题)A.9米B.12米C.15米D.24米8.[2024岳阳月考]如图，长为6cm的橡皮筋AB固定两端A和B后把中点C向上竖直拉升4cm至D点，则橡皮筋被拉长了( )(第8题)A .2 cmB .3 cmC .4 cmD .5 cm9.如图，在△ABC 中，AB ＝2，AC ＝3，AD ⊥BC 于点D ，E 为AD 上任意一点，则CE 2－BE 2＝( )(第9题)A .1B .2C .4D .510.[新考向数学文化]意大利著名画家达·芬奇用下图所示的方法证明了勾股定理.若设图①中空白部分的面积为S 1，图③中空白部分的面积为S 2，则下列等式成立的是( )(第10题)A . S 1＝a 2＋b 2＋2abB . S 1＝a 2＋b 2＋abC . S 2＝c 2D . S 2＝c 2＋12ab 二、填空题(每题3分，共15分)11.[2024天津西青区期中]如图，阴影部分是一个正方形，则此正方形的面积为 cm 2.(第11题)12.已知三角形的三边长分别为5，12，13，则此三角形的最长边上的高等于 .13.如图，一座桥横跨一河，桥AB的长为40m，一艘小船自桥北头(A处)出发，向正南方驶去，因水流原因到达南岸(C处)后，发现已偏离桥南头(B处)9m，则小船实际行驶的路程为 m.(第13题)14.[母题教材P17复习题T5]如图，某港口P位于东西方向的海岸线上，甲、乙轮船同时离开港口，各自沿一固定方向航行，甲、乙轮船每小时分别航行12n mile和16n mile，1h后两轮船分别位于点A，B处，且相距20n mile.如果知道甲轮船沿北偏西40°方向航行，则乙轮船沿方向航行.15.[2024青岛期末]如图是某滑雪场U型池的示意图，该U型池可以看成是一个长方体去掉一个“半圆柱”而成，中间可供滑行部分的截面是半径为3m的半圆，其边缘AB＝CD＝16m，点E在CD上，CE＝4m.一名滑雪爱好者从A点滑到E点时，他滑行的最短路程约为 m.(π取3)三、解答题(16题10分，17～19题每题12分，20题14分，21题15分，共75分)16.如图，∠B＝90°，求x的值.17.如图，四边形ABCD中，∠ACB＝90°，AB＝15，BC＝9，AD＝5，DC＝13.试说明△ACD是直角三角形.18.[2024赣州期末]图①是放置在水平面上的可折叠式护眼灯，其中底座的高AB＝5cm，连杆BC＝30cm，灯罩CD＝20cm.如图②，转动BC，CD，使得∠BCD成平角，且灯罩端点D离桌面l的高度DH为45cm，求AH的距离.19.观察下列勾股数：①3，4，5，且32＝4＋5；②5，12，13，且52＝12＋13；③7，24，25，且72＝24＋25；④9，b，c，且92＝b＋c；…(1)请你根据上述规律，并结合相关知识求：b＝，c＝；(2)猜想第n组勾股数，并说明你的猜想正确.20.如图①，已知圆柱底面的周长为12，圆柱的高为8，在圆柱的侧面上，过点A，C嵌有一圈长度最短的金属丝.(1)现将圆柱侧面沿AB剪开，所得的圆柱侧面展开图是；A B C D(2)求该长度最短的金属丝的长；(3)如图②，若将金属丝从点B绕四圈到达点A，则所需金属丝的最短长度为m，则m2的值为 .21.“赵爽弦图”是四个全等的直角三角形与一个小正方形拼成的大正方形.赵爽利用几何图形的截、割、拼、补来证明代数式之间的恒等关系，验证勾股定理，为中国古代以形证数、形数统一，代数和几何紧密结合、互不可分的独特风格树立了一个典范.(1)如图①，是小琪制作的一个“赵爽弦图”纸板.①设AH＝a，BH＝b，AB＝c，请你利用图①验证a2＋b2＝c2；②若大正方形ABCD的边长为13，小正方形EFGH的边长为7，求直角三角形两直角边之和为多少.(2)如图②，小昊把四个全等的直角三角板紧密地拼接在一起，已知外围轮廓(实线)的周长为48，OB＝6，求这个图案的面积.答案详解详析一、1. D　2. D　3. B　4. A　5. B　6. A　7. A　8. C9. D【点拨】在Rt△ABD和Rt△ADC中，BD2＝AB2－AD2，CD2＝AC2－AD2，所以在Rt△BDE和Rt△CDE中，BE2＝BD2＋ED2＝AB2－AD2＋ED2，EC2＝CD2＋ED2＝AC2－AD2＋ED2，所以EC2－EB2＝（AC2－AD2＋ED2）－（AB2－AD2＋ED2）＝AC2－AB2＝32－22＝5.10. B　13.41二、11.64　12.601314.北偏东50°（或东偏北40°）【点拨】因为AP＝1×12＝12（nmile），PB＝1×16＝16（n mile），AB＝20n mile，所以AP2＋BP2＝400＝AB2，所以∠APB＝90°.因为∠APN＝40°，所以∠BPN＝50°.因为∠EPN＝90°，所以∠BPE＝40°.所以乙轮船沿北偏东50°（或东偏北40°）方向航行.15.15【点拨】如图是U型池的内侧面展开图，则AD≈3×3＝9（m），CD＝16m，CE＝4m.所以DE＝CD－CE ＝16－4＝12（m）.在Rt△ADE中，AE2＝AD2＋DE2≈92＋122＝152，所以AE≈15 m.故他滑行的最短路程约为15m.三、16.【解】由勾股定理，得62＋x2＝（x＋4）2，解得x＝2.5.故x的值为2.5.17.【解】因为AB ＝15，BC ＝9，∠ACB ＝90°，所以AC 2＝152－92＝144.因为52＋144＝132，所以AD 2＋AC 2＝CD 2，所以∠DAC ＝90°，所以△ACD 是直角三角形.18.【解】由题意，得BD ＝BC ＋CD ＝50 cm .如图，过点B 作BE ⊥DH 于点E ，易得EH ＝AB ＝5 cm ，BE ＝AH ，所以DE ＝DH －EH ＝40 cm ，所以BE 2＝BD 2－DE 2＝302.所以BE ＝30 cm ，所以AH ＝30 cm .19.【解】（1）40；41（2）猜想第n 组勾股数为2n ＋1，2n 2＋2n ，2n 2＋2n ＋1.因为（2n ＋1）2＋（2n 2＋2n ）2＝4n 4＋8n 3＋8n 2＋4n ＋1，（2n 2＋2n ＋1）2＝4n 4＋8n 3＋8n 2＋4n ＋1，所以（2n ＋1）2＋（2n 2＋2n ）2＝（2n 2＋2n ＋1）2.因为n 是正整数，所以2n ＋1，2n 2＋2n ，2n 2＋2n ＋1是一组勾股数.20.【解】（1）A（2）由（1）可知该长度最短的金属丝的长为2AC .因为圆柱底面的周长为12，所以BC ＝12×12＝6.因为圆柱的高AB ＝8，所以AC2＝62＋82＝100，所以AC＝10，所以该长度最短的金属丝的长为2AC＝2×10＝20.（3）2368【点拨】若将金属丝从点B绕四圈到达点A，则m2＝42×1222＝2368.21.【解】（1）①设题图①中大、小两个正方形的面积分别为S1和S2，则S2＝（b－a）2＝a2＋b2－2ab，S1＝S2＋4×12ab＝a2＋b2.又因为S1＝c2，所以a2＋b2＝c2.②因为AB＝13，EF＝7，所以大正方形的面积是169，小正方形的面积是49，所以四个直角三角形的面积和为169－49＝120，设AE为x，DE为y，则4×12xy＝2xy＝120，易知x2＋y2＝132＝169，所以（x＋y）2＝x2＋y2＋2xy＝169＋120＝289，所以x＋y＝17，所以直角三角形两直角边之和为17.（2）由题意，得AB＋BC＝48÷4＝12，OH＝OB＝6.设AH＝BC＝x，则AB＝12－x，OA＝6＋x，在Rt△AOB中，由勾股定理，得OB2＋OA2＝AB2，即62＋（6＋x）2＝（12－x）2，解得x＝2，所以OA＝OH＋AH＝6＋2＝8，所以该图形的面积为4×12OB·OA＝2OB·OA＝2×6×8＝96.。

北师大版八年级数学第一章《勾股定理》评估卷

第12题②第12题①八年级数学（上）素质评估卷第一单元评估卷评估内容：（第一章）勾股定理一、仔细选一选(每题4分,共24分)1、如果梯子的底端离建筑物 5米，13米长的梯子可以达到该建筑物的高度是（）A ．12米 B.13米 C.14米 D.15米2、下列各组数中，以a ，b ，c 为边的三角形不是直角三角形的是（） A. a=1.5，b=2, c=3 B. a=7,b=24,c=25C. a=6,b=8,c=10D. a=3,b=4,c=53、若线段a ，b ，c 是直角三角形的三边，则它们的比可以是（）A. 2∶3∶4B. 3∶4∶5C. 4∶5∶6D. 4∶6∶74、三角形的三边长满足（a+b ）2=c 2+2ab,则这个三角形是( )A. 等边三角形B. 钝角三角形C. 直角三角形D. 锐角三角形. 5、某市在旧城改造中，计划在市内一块如图所示的三角形空地上种植草皮以美化环境，已知这种草皮每平方米售价a 元，则购买这种草皮至少需要（） A. 450a 元 B.225a 元 C ． 150a 元 D.300a 元6、如图，有一块直角三角形纸片，两直角边AC=6cm,BC=8cm,现将直角边AC 沿直线AD 折叠，使它落在斜边AB 上，且与AE 重合，则CD 等于（）A. 2cmB. 3cmC. 4cmD. 5cm 二、细心填一填（每空3分，共21分） 7、在Rt △ABC 中，∠C=90°，①若a=5，b=12，则c=___________；②若a=15，c=25，则b=___________；③若a ∶b=3∶4，c=10则S Rt△ABC =________。

8、在长为50cm,宽为40cm 高为30cm 的木箱中,能否放下长为70cm 的木棍?答: 。

9、已知直角三角形两条直角边的长分别是5c m 和12c m,则斜边上的高的长是 c m 。

10、在平静的湖面上，有一支红莲，高出水面1米，阵风吹来，红莲被吹到一边，花朵齐及水面，已知红莲移动的水平距离为2米，问这里水深是________m 。

(典型题)初中数学八年级数学上册第一单元《勾股定理》检测卷(包含答案解析)

一、选择题1．如图，四个全等的直角三角形和中间的小正方形可以拼成一个大正方形，若直角三角形的较长直角边长为a ，较短直角边长为b ，大正方形面积为S 1，小正方形面积为S 2，则（a +b ）2可以表示为（）A ．S 1﹣S 2B ．S 1+S 2C ．2S 1﹣S 2D ．S 1+2S 2 2．学习勾股定理后，老师布置的课后作业为“利用绳子（绳子足够长）和卷尺，测量学校教学楼的高度”，某数学兴趣小组的做法如下：①将绳子上端固定在教学楼顶部，绳子自由下垂，再垂直向外拉到离教学楼底部3m 远处，在绳子与地面的交点处将绳子打结；②将绳子继续往外拉，使打结处离教学楼的距离为6m ，此时测得绳结离地面的高度为 1m ，则学校教学楼的高度为（）A ．11 mB ．13 mC ．14 mD ．15 m 3．如图，在Rt △ABC 中，∠BCA ＝90°，点D 是BC 上一点，AD ＝BD ，若AB ＝8，BD ＝5，则CD ＝（）A ．2.1B ．1.4C ．3.2D ．2.4 4．在下列四组数中，属于勾股数的是（） A ．0.3，0.4，0.5 B ．9，40，41 C ．2，3，4 D ．123 5．《九章算术》是我国古代的数学名著，其中“勾股”章有一题，大意是说：已知矩形门的高比宽多6尺，门的对角线长10尺，那么门的高和宽各是多少？如果设门的宽为x 尺，根据题意可列方程（）A ．222(6)10x x ++=B ．222(6)10x x -+=C ．222(6)10x x +-=D ．222610x +=6．在Rt ABC 中，90C ∠=︒，且4c =，若3a =，那么b 的值是（）A ．1B ．5C 7D 57．在△ABC 中，∠A 、∠B 、∠C 的对边分别为a 、b 、c ，下列条件不能判断△ABC 是直角三角形的是（）A ．∠B ＝∠C +∠A B ．a 2＝（b +c ）（b ﹣c ）C ．∠A ：∠B ：∠C ＝3：4：5D ．a ：b ：c ＝3：4：58．如图，已知ABC 中，45ABC ∠=︒，F 是高AD 和BE 的交点，5AC =，2BD =，则线段DF 的长度为（）A ．22B ．2C ．3D ．1 9．在Rt △ABC 中，∠ACB ＝90°，AC ＝BC ＝1.点Q 在直线BC 上，且AQ ＝2，则线段BQ 的长为（）A ．3B ．5C ．31+或31-D ．51+或51- 10．如图，在矩形OABC 中，点B 的坐标是(2,5)，则,A C 两点间的距离是（）A ．26B ．33C ．29D ．511．如图，在Rt ABC △中，6AB =，8BC =，AD 为BAC ∠的平分线，将ADC 沿直线AD 翻折得ADE ，则DE 的长为（）A ．4B ．5C ．6D ．712．如图，圆柱的底面周长是24，高是5，一只在A 点的蚂蚁想吃到B 点的食物，沿着侧面需要爬行的最短路径是（）A ．9B ．13C ．14D ．25二、填空题13．如图，已知圆柱的底面周长为10cm ，高AB 为12cm ，BC 是底面的直径，一只蚂蚁沿着圆柱侧面爬行觅食从点C 爬到点A ，则蚂蚁爬行的最短路线为________cm ．14．已知ABC 中，90C ∠=︒，2cm,6cm AB AC BC =+=，则ABC 的面积为_______． 15．如图是“赵爽弦图”，ABH ，BCG ，CDF 和DAE △是四个全等的直角三角形，四边形ABCD 和EFGH 都是正方形．如果10AB =，且:3:4AH AE =．那么AH 等于________．16．如图，在ABC 中，90C =∠，AB 的中垂线DE 交AB 于E ，交BC 于D ，若5AB =，3AC =，则ACD △的周长为__________．17．如图，在4×4方格中，小正方形格的边长为1，则图中阴影正方形的边长是____．18．如图，一架长2.5m 的梯子斜靠在垂直的墙AO 上，这时AO 为2m .如果梯子的顶端A 沿墙下滑0.5m ，那么梯子的底端B 向外移动_________m .19．若直角三角形的两直角边长为a 、b ，且满足21025a a -++|b ﹣12|＝0，则该直角三角形的斜边长为_____．20．如图，阴影部分是两个正方形，其它部分是两个直角三角形和一个正方形．若右边的直角三角形ABC 中，34AC =，30BC =，则阴影部分的面积是_________．三、解答题21．一种盛饮料的圆柱形杯，测得内部底面半径为2.5㎝，高为12㎝，吸管放进杯里，杯口外面至少要露出4.6㎝，问吸管要做多长？22．已知：如图，一块R t △ABC 的绿地，量得两直角边AC =8cm ，BC =6cm.现在要将这块绿地扩充成等腰△ABD ，且扩充部分（△ADC ）是以8cm 为直角边长的直角三角形，求扩充等腰△ABD 的周长.（1）在图1中，当AB =AD =10cm 时，△ABD 的周长为．（2）在图2中，当BA =BD =10cm 时，△ABD 的周长为．（3）在图3中，当DA =DB 时，求△ABD 的周长.23．如图，在△ABC 中，∠C ＝90°，将△ACE 沿着AE 折叠以后C 点正好落在AB 边上的点D 处．（1）当∠B ＝28°时，求∠CAE 的度数；（2）当AC ＝6，AB ＝10时，求线段DE 的长．24．定义：如果一个三角形中有两个内角α，β满足290αβ+=︒，那我们称这个三角形为“近直角三角形”．（1）若ABC 是“近直角三角形”，90B ∠>︒，50C ∠=︒，则A ∠=_____度；（2）如图，在Rt ABC △中，90BAC ∠=︒，3AB =，4AC =．若CD 是ACB ∠的平分线，①求证：BDC 是“近直角三角形”；②求BD 的长．（3）在（2）的基础上，边AC 上是否存在点E ，使得BCE 也是“近直角三角形”？若存在，直接写出．．．．CE 的长；若不存在，请说明理由．25．如图，已知AB=CD ，∠B=∠C ，AC 和BD 交于点O ，OE ⊥AD 于点E ．（1）△AOB 与△DOC 全等吗?请说明理由；（2）若OA=3，AD=4，求△AOD 的面积．26．我国著名的数学家赵爽，早在公元3世纪，就把一个矩形分成四个全等的直角三角形，用四个全等的直角三角形拼成了一个关的正方形（如图1），这个矩形称为赵爽弦图，验证了一个非常重要的结论：在直角三角形中两直角边a 、b 与斜边c 满足关系式222+=a b c ．称为勾股定理．（1）爱动脑筋的小明把这四个全等的直角三角形拼成了另一个大的正方形（如图2），也能验证这个结论，请你帮助小明完成验证的过程；（2）如图3所示，90ABC ACE ∠=∠=︒，请你添加适当的辅助线证明结论222+=a b c ．【参考答案】***试卷处理标记，请不要删除一、选择题1．C解析：C【分析】根据图形和勾股定理可知S 1＝c 2＝a 2+b 2，再由完全平方公式即可得到结果．【详解】解：如图所示：设直角三角形的斜边为c ，则S 1＝c 2＝a 2+b 2S 2＝（a ﹣b ）2＝a 2+b 2﹣2ab ，∴2ab ＝S 1﹣S 2，∴（a +b ）2＝a 2+2ab +b 2＝S 1+S 1﹣S 2＝2S 1﹣S 2，故选：C【点睛】本题考查勾股定理，解题的关键是熟练运用勾股定理以及完全平方公式．2．C解析：C【分析】根据题意画出示意图，设学校教学楼的高度为x ，可得AC AD x ==，()1AB x m =-，6BC m =，利用勾股定理可求出x ．【详解】解：如图，设学校教学楼的高度为x ，则AD x =，()1AB x m =-，6BC m =，左图，根据勾股定理得，绳长的平方223x =+，右图，根据勾股定理得，绳长的平方()2216x =-+，∴()2222316x x +=-+，解得：14x =．故选：C ．【点睛】本题考查了勾股定理的应用，解答本题的关键是构造直角三角形，构造直角三角形的一般方法就是作垂线．3．B解析：B【分析】设CD=x ，在Rt △ACD 和Rt △ABC 中，利用勾股定理列式表示出AC 2，然后解方程即可．【详解】解：设CD=x ，则BC=5+x ，在Rt △ACD 中，AC 2=AD 2-CD 2=25-x 2，在Rt △ABC 中，AC 2=AB 2-BC 2=64-（5+x ）2，所以，25-x 2=64-（5+x ）2，解得x=1.4，即CD=1.4．故答案为：B ．【点睛】本题考查了勾股定理，熟记定理并在两个三角形列出等式表示出AC 2，然后列出方程是解题的关键．4．B解析：B【分析】根据勾股数的定义：满足222+=a b c 的三个正整数，成为勾股数，据此可判断．【详解】A ．0.3、0.4、0.5，不是正整数，所以不是勾股数，选项错误；B ．9、40、41，是正整数，且满足22294041+=，是勾股数，选项正确；C ．2、3、4，是正整数，但222234+≠，所以不是勾股数，选项正确；D ．1故选：B ．【点睛】本题考查了勾股数的判定方法，解题关键是要看这组数是否为正整数，且满足最小两个数的平方和等于最大数的平法．5．A解析：A【分析】设门的宽为x 尺，则高为（x+6）尺，根据勾股定理解答．【详解】设门的宽为x 尺，则高为（x+6）尺，根据题意可列方程222(6)10x x ++=，故选：A ．【点睛】此题考查勾股定理计算，正确理解题意掌握勾股定理计算公式是解题的关键．6．C解析：C【分析】根据勾股定理计算，即可得到答案．【详解】在Rt △ABC 中，∠C ＝90°，由勾股定理得，b =故选：C ．【点睛】本题考查的是勾股定理，关键是掌握“如果直角三角形的两条直角边长分别是a ，b ，斜边长为c ，那么a 2＋b 2＝c 2”．7．C解析：C【分析】由三角形的内角和定理求解B 可判断,A 由勾股定理的逆定理可判断,B 由三角形的内角和定理求解 ,C ∠ 可判断,C 设()30,a k k =≠ 则4,5,b k c k == 利用勾股定理的逆定理可判断.D【详解】解：,180,B C A A B C ∠=∠+∠∠+∠+∠=︒2180B ∴∠=︒，90B ∴∠=︒，故A 不符合题意； ()()222,a b c b c b c =+-=-222,a c b ∴+=90B ∴∠=︒，故B 不符合题意； ::3:4:5,A B C ∠∠∠=51807512C ∴∠=⨯︒=︒， ABC ∴不是直角三角形，故C 符合题意，::3:4:5,a b c =设()30,a k k =≠ 则4,5,b k c k ==()()()222222234255,a b k k k k c ∴+=+===90C ∴∠=︒，故D 不符合题意，故选：.C【点睛】本题考查的是三角形的内角和定理，勾股定理的逆定理的应用，掌握以上知识是解题的关键．8．D解析：D【分析】先证明△BDF ≌△ADC ，得到BF=AC=5，再根据勾股定理即可求解．【详解】解：∵AD 和BE 是△ABC 的高线，∴∠ADB=∠ADC=∠BEC=90°，∴∠DBF+∠C=90°，∠CAD+∠C=90°，∴∠DBF=∠CAD ，∵45ABC ∠=︒，∴∠BAD=45°，∴BD=AD ，∴△BDF ≌△ADC ，∴BF=AC=5，在Rt △BDF 中，DF=()2222521BF BD -=-=．故选：D【点睛】本题考查了全等三角形的判定与性质，勾股定理等知识，证明△BDF ≌△ADC 是解题关键． 9．C解析：C【分析】分Q 在CB 延长线上和Q 在BC 延长线上两种情况分类讨论，求出CQ 长，根据线段的和差关系即可求解．【详解】解：如图1，当Q 在CB 延长线上时，在Rt △ACQ 中，2222213CQ AQ AC =-=-=，∴BQ=CQ-BC=31-；如图2，当Q 在BC 延长线上时，在Rt △ACQ 中，2222213CQ AQ AC =-=-=，∴BQ=CQ+BC=31+；∴BQ 3131．故选：C【点睛】本题考查了勾股定理，根据题意画出图形，分类讨论是解题关键．10．C解析：C【分析】根据矩形的性质可得OB ＝AC ，根据勾股定理即可求出答案．【详解】在矩形OABC 中，OB ＝AC ，∵B （2，5），∴222529OB =+=29AC OB ==故选：C ．【点睛】本题考查矩形的性质，解题的关键是熟练运用矩形的性质以及勾股定理．11．B解析：B【分析】由勾股定理求出AC ＝10，求出BE ＝4，设DE ＝x ，则BD ＝8−x ，得出（8−x ）2＋42＝x 2，解方程求出x 即可得解．【详解】∵AB ＝6，BC ＝8，∠ABC ＝90°，∴22226810AB BC +=＋，∵将△ADC沿直线AD翻折得△ADE，∴AC＝AE＝10，DC＝DE，∴BE＝AE−AB＝10−6＝4，在Rt△BDE中，设DE＝x，则BD＝8−x，∵BD2＋BE2＝DE2，∴（8−x）2＋42＝x2，解得：x＝5，∴DE＝5．故选B．【点睛】本题考主要查了勾股定理，直角三角形的性质，折叠的性质等知识，熟练掌握勾股定理是解题的关键．12．B解析：B【分析】画出该圆柱的侧面展开图，根据两点之间线段最短，可知沿着侧面需要爬行的最短路径即为AB，然后根据勾股定理求出AB即可求出结论．【详解】解：该圆柱的侧面展开图，如下图所示，根据两点之间线段最短，可知沿着侧面需要爬行的最短路径即为ABAB恰为一个矩形的对角线，该矩形的长为圆柱的底面周长的一半，即长为24÷2=12宽为5∴22=13512即沿着侧面需要爬行的最短路径长为13．故选：B．【点睛】此题考查的是勾股定理与最短路径问题，掌握勾股定理和两点之间线段最短是解题关键．二、填空题13．13【分析】把圆柱沿母线AB剪开后展开点C展开后的对应点为C′利用两点之间线段最短可判断蚂蚁爬行的最短路径为AC′然后利用勾股定理计算出AC′即可【详解】把圆柱沿母线AB剪开后展开点C展开后的对应点解析：13【分析】把圆柱沿母线AB 剪开后展开，点C 展开后的对应点为C′，利用两点之间线段最短可判断蚂蚁爬行的最短路径为AC′，然后利用勾股定理计算出AC′即可．【详解】把圆柱沿母线AB 剪开后展开，点C 展开后的对应点为C′，则蚂蚁爬行的最短路径为AC′，如图，∵AB ＝12， BC′＝5，在Rt △ABC′，AC′2251213+=∴蚂蚁爬行的最短路程为13cm ．故答案是：13【点睛】本题考查了平面展开−最短路径问题，先根据题意把立体图形展开成平面图形后，再确定两点之间的最短路径．一般情况是两点之间，线段最短．在平面图形上构造直角三角形解决问题．14．cm2【分析】设BC=acmAC=bcm 则a+b=即可得到根据勾股定理得到进而得到根据三角形面积公式即可求解【详解】解：设BC=acmAC=bcm 则a+b=∴即∵∠C=90°∴∴∴cm2故答案为：c 解析：12cm 2 【分析】设BC=acm ，AC=bcm ，则6，即可得到()26a b +=，根据勾股定理得到22=4a b +，进而得到22ab =，根据三角形面积公式即可求解．【详解】解：设BC=acm ，AC=bcm ，则6，∴()26a b +=，即2226a b ab ++=，∵∠C=90°，∴222=4a b AB +=,∴22ab =， ∴11=22ABC S ab =△cm 2．故答案为：12cm 2 【点睛】本题考查了完全平方公式，勾股定理等知识，准确掌握两个知识点并建立联系是解题关键．15．6【分析】根据题意设则可得即可得由勾股定理列方程求出x 的值即可得出结论【详解】解：∵∴设则和是四个全等的直角三角形在中解得：故答案为：6【点睛】此题主要考查了勾股定理的应用熟练运用勾股定理是解答此题解析：6【分析】根据题意设3AH x =，则可得4AE x =，HE x =，即可得4BH x =，由勾股定理列方程求出x 的值即可得出结论．【详解】解：∵:3:4AH AE =∴设3AH x =，则4AE x =，HE AE AH x =-=， ABH △，BCG ，CDF 和DAE △是四个全等的直角三角形，4BH AE x ∴==，在Rt ABH △中，222AB AH BH =+，22210(3)(4)x x ∴=+，解得：2x =．36AH x ∴==．故答案为：6．【点睛】此题主要考查了勾股定理的应用，熟练运用勾股定理是解答此题的关键．16．7【分析】先根据勾股定理求出BC 的长再由线段垂直平分线的性质得出AD=BD 即AD+CD=BC 再由AC=6即可求出答案【详解】解：∵△ABC 中∠C=90°AB=5AC=3∴BC==4∵DE 是线段AB 的解析：7【分析】先根据勾股定理求出BC 的长，再由线段垂直平分线的性质得出AD=BD ，即AD+CD=BC ，再由AC=6即可求出答案．【详解】解：∵△ABC 中，∠C=90°，AB=5，AC=3，∴=4，∵DE 是线段AB 的垂直平分线，∴AD=BD ，∴AD+CD=BD+CD ，即AD+CD=BC ，∴△ACD 的周长=AC+CD+AD=AC+BC=3+4=7．故答案为：7．【点睛】本题考查了勾股定理及线段垂直平分线的性质，能根据线段垂直平分线的性质求出AD+CD=BC是解题的关键．17．【分析】根据勾股定理即可得出结果【详解】解：正方形的边长=故答案为：【点睛】本题主要考查的是勾股定理掌握勾股定理的计算方法是解题的关键【分析】根据勾股定理即可得出结果．【详解】解：正方形的边长．【点睛】本题主要考查的是勾股定理，掌握勾股定理的计算方法是解题的关键．18．5【分析】由题意先根据勾股定理求出OB的长再根据梯子的长度不变求出OD的长根据BD=OD-OB即可得出结论【详解】解：∵Rt△OAB中AB=25mAO=2m∴；同理Rt△OCD中∵CD=25mOC=解析：5【分析】由题意先根据勾股定理求出OB的长，再根据梯子的长度不变求出OD的长，根据BD=OD-OB即可得出结论．【详解】解：∵Rt△OAB中，AB=2.5m，AO=2m，∴ 1.5OB m；同理，Rt△OCD中，∵CD=2.5m，OC=2-0.5=1.5m，∴2OD m，∴BD=OD-OB=2-1.5=0.5（m）．答：梯子底端B向外移了0.5米．故答案为：0.5．【点睛】本题考查的是勾股定理的应用，在应用勾股定理解决实际问题时勾股定理与方程的结合是解决实际问题常用的方法，解题的关键是从题中抽象出勾股定理这一数学模型，画出准确的示意图．19．13【分析】根据非负数的性质得到ab的值然后结合勾股定理求得斜边的长度即可【详解】解：∵∴∴|a﹣5|+|b﹣12|＝0∴a＝5b＝12∴该直角三角形的斜边长为：故答案是：13【点睛】本题考查了勾股解析：13【分析】根据非负数的性质得到a、b的值，然后结合勾股定理求得斜边的长度即可．【详解】解：∵21025|12|0-++-=，a a b∴()25|12|0-+-=a b∴|a﹣5|+|b﹣12|＝0，∴a＝5，b＝12，∴该直角三角形的斜边长为：22+=．51213故答案是：13．【点睛】本题考查了勾股定理，非负数的性质﹣绝对值、算术平方根．任意一个数的绝对值（二次根式）都是非负数，当几个数或式的绝对值相加和为0时，则其中的每一项都必须等于0．20．256【分析】两个阴影正方形的面积和等于直角三角形另一未知边的平方利用勾股定理即可求出【详解】解：两个阴影正方形的面积和为342-302=256故答案为：256【点睛】本题考查了直角三角形中勾股定理解析：256【分析】两个阴影正方形的面积和等于直角三角形另一未知边的平方．利用勾股定理即可求出．【详解】解：两个阴影正方形的面积和为342-302=256．故答案为：256．【点睛】本题考查了直角三角形中勾股定理的运用，考查了正方形面积的计算，本题中根据勾股定理求阴影部分的边长是解题的关键．三、解答题21．6【分析】在吸管（杯内部分）、杯底直径、杯高构成的直角三角形中，由勾股定理可求出杯内吸管部分的长度，再加上外露部分的长度即可求出吸管的总长．【详解】解：如图；杯内的吸管部分长为AC，杯高AB=12cm，杯底直径BC=5cm；Rt△ABC中，AB=12cm，BC=5cm；由勾股定理得：AC=13cm故吸管的长度最少要：13+4.6=17.6cm．22．（1）32m；（2）（5m；（3）80 3m【分析】（1）利用勾股定理得出DC的长，进而求出△ABD的周长；（2）利用勾股定理得出AD的长，进而求出△ABD的周长；（3）首先利用勾股定理得出DC、AB的长，进而求出△ABD的周长．【详解】：（1）如图1，∵AB=AD=10m，AC⊥BD，AC=8m，∴226()DC AD AC m=-=则△ABD的周长为：10+10+6+6=32（m）．故答案为32m；（2）如图2，当BA=BD=10m时，则DC=BD-BC=10-6=4（m），故2245(m)AD AC DC+=则△ABD的周长为：5（5m；故答案为（5m；（3）如图3，∵DA=DB，∴设DC=xm，则AD=（6+x）m，∴DC2+AC2=AD2，即x2+82=（6+x）2，解得；x=7 3∵AC=8m，BC=6m，∴AB=10m，故△ABD的周长为：AD+BD+AB=2780610() 33m ⎛⎫++=⎪⎝⎭【点睛】此题主要考查了勾股定理的应用，根据题意熟练应用勾股定理是解题关键．23．（1）31°；（2）3．【分析】（1）在Rt△ABC中，利用互余得到∠BAC＝62°，再根据折叠的性质得∠CAE＝12∠CAB＝31°，然后根据互余可计算出∠AEC ＝59°；（2）Rt △ABC 中，利用勾股定理即可得到BC 的长；设DE ＝x ，则EB ＝BC ﹣CE ＝8﹣x ，依据勾股定理可得，Rt △BDE 中DE 2+BD 2＝BE 2，再解方程即可得到DE 的长．【详解】解：（1）在Rt △ABC 中，∠ABC ＝90°，∠B ＝28°，∴∠BAC ＝90°﹣28°＝62°，∵△ACE 沿着AE 折叠以后C 点正好落在点D 处，∴∠CAE ＝12∠CAB ＝12×62°＝31°；（2）在Rt △ABC 中，AC ＝6，AB ＝10，∴BC 8，∵△ACE 沿着AE 折叠以后C 点正好落在点D 处，∴AD ＝AC ＝6，CE ＝DE ，∴BD ＝AB ﹣AD ＝4，设DE ＝x ，则EB ＝BC ﹣CE ＝8﹣x ，∵Rt △BDE 中，DE 2+BD 2＝BE 2，∴x 2+42＝（8﹣x ）2，解得x ＝3．即DE 的长为3．【点睛】本题考查了折叠问题，折叠是一种对称变换，它属于轴对称，解题时常设要求的线段长为x ，然后根据折叠和轴对称的性质用含x 的代数式表示其他线段的长度，选择适当的直角三角形，运用勾股定理列出方程求出答案．24．（1）20︒，（2）①见解析；②53BD =；（3）52CE =或74=CE ．【分析】（1）先判断出B 不可能是α或β，再根据条件计算即可；（2）①根据DC 平分ACB ∠，得到2ACB BCD ∠=∠，再根据90BAC ∠=︒，即可得到结果；②作DH BC ⊥交于点H ，根据勾股定理得到5AC =，证明ADC HDC △≌△，再根据勾股定理计算即可；（3）根据点E 存在的两种情况分类讨论即可；【详解】（1）B 不可能是α或β，当A α∠=时，50C β∠==︒，290αβ+=︒，不成立；故A β∠=，C α∠=，290αβ+=︒，则20β=︒，（2）①∵DC 平分ACB ∠，∴2ACB BCD ∠=∠，∵90BAC ∠=︒，∴90B ACB ∠+∠=︒，即290B BCD ∠+∠=︒．∴BCD △是“近直角三角形”．②作DH BC ⊥交于点H ，∵3AB =，4AC =，∴5AC =（勾股定理）．在ADC 和HDC △中，DAC DHC ∠=∠，ACD HCD ∠=∠，DC DC =，∴ADC HDC △≌△，∴DH DA =，4AC HC ==，∴1BH =．设BD x =，则3DH x =-，在Rt BDH △中，()22231x x =-+，得53x =，即53BD =．（3）52CE =或74=CE ．如图所示，点E 在ABC ∠的角平分线上，作EF BC ⊥，设EC x =，则4AE x =-，则4EF x =-，根据已知条件可得：3AB BF ==， ∴532FC =-=，在Rt △EFC 中， ()22242x x -+=， 52x =；在AC 上面找一点E ，连接BE ，使得ABE C ∠=∠，延长EA 至G ，使得AE=AG ，根据条件可得：△△ABG ABE ≅，∴GBA EBA C ∠=∠=∠，∵90GBA G ∠+∠=︒，∴90C G ∠+∠=︒，∴90CBG ∠=︒，设EC x =，则4AE AG x ==-， ∴()()222224385BG x x =-+=--，74x =； ∴97444CE AC AE =-=-=； ∴边AC 上存在点E ，使得BCE 也是“近直角三角形”，此时52CE =或74=CE ．【点睛】本题主要考查了勾股定理和全等三角形的判定与性质，准确计算是解题的关键． 25．（1）△AOB ≌△DOC ，理由见解析；（2）△AOD 的面积为5【分析】（1）根据全等三角形的判定定理即可得到结论；（2）根据全等三角形的性质得到AO=DO ，根据等腰三角形的性质得到AE=12AD=2，由勾股定理得到225OE AO AE =-=【详解】（1）证明：在△AOB 和△DOC 中， AOB COD B CAB CD ∠=∠⎧⎪∠=∠⎨⎪=⎩，所以△AOB ≌△DOC （AAS ）；（2）因为△AOB ≌△DOC ，所以AO ＝DO ，因为OE ⊥AD 于点E ．所以AE 12=AD ＝2，所以OE 225AO AE =-=，所以S △AOD 1452=⨯⨯=25．【点睛】本题考查了全等三角形的判定和性质，勾股定理，三角形的面积的计算，熟练掌握全等三角形的判定和性质是解题的关键．26．（1）见解析；（2）见解析【分析】（1）由图1可知：四个全等的直角三角形的面积+中间小正方形的面积=大正方形的面积，然后化简即可证明；（2）如图，过A 作AF AB ⊥交BC 线于D ，先证明ABC CED △≌△可得ED BC a ==，CD AB b ==，然后根据梯形EDBA 的面积列式化简即可证明．【详解】（1）证明：大正方形面积为：214()()2ab c a b a b ⨯⨯+=++ 整理得22222ab c a b ab +=++∴222+=a b c ；（2）过A 作AF AB ⊥交BC 线于D∵AC CE =，90B D ∠=∠=︒，90ECD ACB ∠+∠=︒，90ACB BAC ∠+∠=︒ ∴BAC ECD ∠=∠，∴ABC CED △≌△，∴ED BC a ==，CD AB b ==∴()2EDBA a b S a b +=⋅+梯形211222ab c =⨯+ ∴()22211222a b ab ab c ++=+ ∴222+=a b c ．【点睛】本题主要考查了运用几何图形来证明勾股定理，矩形和正方形的面积，三角形的面积，锻炼了同学们的数形结合的思想方法．。

《第一章勾股定理》单元检测(含答案)

单元评价检测（一）第一章勾股定理（45分钟 100分）一、选择题(每小题4分,共28分)1.（2010·长沙中考）下列每一组数据中的三个数值分别为三角形的三边长，不能构成直角三角形的是（）A．3、4、5 B．6、8、10C2D．5、12、13【解析】选A.∵72)3(22=+≠2)5(2三角形.2. (2010•铁岭中考)如图所示，一场暴雨过后，垂直于地面的一棵树在距地面1米处折断，树尖B 恰好碰到地面，经测量AB=2米，则树高为（）A.5米B.3米C. (5+1)米D. 3 米【解析】选C.在Rt⊿ABC中，根据勾股定理得，222ABACBC+=∴2BC＝2212+＝5∴BC＝5∴树高为（5+1）米.3. (2010·南宁中考)图中，每个小正方形的边长为1，ABC的三边a，b，c的大小关系是：（）（Ａ）a<c<b （Ｂ）a<b<c （Ｃ）c<a<b （Ｄ）c<b<a【解析】选C.如图根据勾股定理得：a ＝2241+＝17；b ＝2243+＝5；c ＝4.∴c ＜a ＜b. 4.如图,已知AD=4,CD=3,AD ⊥CD,AB=13,BC=12,则四边形ABCD 的面积为( )（A ）12（B ）24（C ）48（D ）25【解析】选B.如图,连接AC,因为AD ⊥CD,所以在Rt △ADC 中,AC 2=AD 2+CD 2=42+32=52,所以AC=5,又因为AC 2+BC 2=52+122=132,AB 2=132,所以AC 2+BC 2=AB 2,所以△ACB 是直角三角形，所以S 四边形ABCD =S △ABC -S △ACD = 12×12×5- 12×3×4=24.5. （2010·河池中考）如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案，已知大正方形面积为49，小正方形面积为4，若用x ，y 表示直角三角形的两直角边（x y >），下列四个说法：①2249x y +=，②2x y -=，③2449xy +=，④9x y +=.其中说法正确的是 …（）A ．①② B. ①②③ C. ①②④ D. ①②③④【解析】选B.∵大正方形面积为49，∴2249x y +=①；∵小正方形面积为4，∴2)(y x -=4，∴x-y=2;∴4222=+-y xy x ∴2xy=45,∴2xy ＋4＝49;由①得，2)(y x +- 2xy=49∴2)(y x +=94∴x+y=94；.6.下列说法不能得到△ABC 是直角三角形的是( )(A)a 2-c 2=b 2(B)(a-b)(a+b)+c2=0(C)∠A=∠B=∠C(D)∠A=2∠B=2∠C【解析】选C.A项可变形为a2=b2+c2,B项可变形为b2=a2+c2, 根据勾股定理逆定理可知△ABC为直角三角形,C项中∠A=∠B=∠C=180°×1=60°,不是直角三角形,D项中可求得∠A=90°,△ABC为直角三角3形.7.如图，有一块直角三角形纸片，两直角边AB=6，BC=8，将△ABC折叠，使AB落在斜边AC上，点B 落在B′位置，折痕为AD，则BD的长为( )(A)3 (B)4 (C)5 (D)6【解析】选A.在Rt△ABC中，由勾股定理可得AC=10，因为折叠，所以△AB′D≌△ABD,所以AB′=AB=6,B′D=BD,B′C=10-6=4,∠AB′D=90°,在Rt△CDB′中，设B′D=x,则BD=x，CD=8-x，由勾股定理，得（8-x）2=x2+42，解得x=3,即BD=3.二、填空题（每小题5分，共25分）8.如图所示,要在一个三角形的零件上钻两个圆孔,两个圆孔的水平距离AC是40cm,垂直距离BC是30cm,则两个圆孔之间的距离AB是___________cm.【解析】AB2=AC2+BC2=402+302=2500=502，故AB=50cm.答案：509. (2010•厦门中考)如图，以第①个等腰直角三角形的斜边长作为第②个等腰直角三角形的腰，以第②个等腰直角三角形的斜边长做为第③个等腰直角三角形的腰，依次类推，若第⑨个等腰直角三角形的斜边长为厘米，则第①个等腰直角三角形的斜边长为 _________厘米.【解析】设第①个等腰直角三角形的斜边长为x厘米，第②个等腰直角三角形的斜边长为2x厘米，第③个等腰直角三角形的斜边长为2x 厘米，第④个等腰直角三角形的斜边长为22x 厘米…第⑨个等腰直角三角形的斜边长为16x 厘米，∴16x＝∴x ＝3 答案：310.如图，一轮船以16海里/时的速度从港口A 出发向东北方向航行，另一轮船以12海里/时的速度同时从港口A 出发向东南方向航行，离开港口2小时后，两船相距_________海里.【解析】由题意知，两船行驶的方向互相垂直，一轮船向东北方向航行了16×2=32（海里），一轮船向东南方向航行了12×2=24（海里），由勾股定理得:322+242=1024+576=1600=402,所以两船相距40海里.答案：4011.如图，某宾馆在重新装修后，准备在大厅的主楼梯上铺设一种红色的地毯.如果主楼梯宽3.5米,购买每平方米50元的地毯,则购买地毯至少需要___________元.【解析】地毯的面积为(5+5.8)×3.5=37.8 m 2,37.8×50=1890元.答案：189012. (2010·泰安中考)如图，将矩形ABCD 纸片沿EF 折叠，使D 点与BC 边的中点D ′重合，若BC=8，CD=6，则CF=____________。

第1章勾股定理北师大版数学八年级上册综合素质评价卷(含答案)

第一章综合素质评价八年级数学上(BS版) 时间：90分钟　满分：120分一、选择题(每题3分，共30分)1．在△ABC中，∠C＝90°，∠A，∠B，∠C的对边分别为a，b，c.若a2＝5，b2＝12，则c2的值为( )A．13 B．17 C．7 D．1692. (2024重庆江津区期末) 已知△ABC的三边分别是a，b，c，下列条件中不能判断△ABC为直角三角形的是( )A．a2＋b2＝c2B．∠A∶∠B∶∠C＝3∶4∶5C．∠A＝∠C－∠B D．a＝8，b＝15，c＝173. （教材P7习题T2变式) 历史上对勾股定理的一种验证方法采用了如图所示的图形，其中两个全等直角三角形的边AE，EB在一条直线上，验证勾股定理用到的面积相等的关系式是( )A．S△EDA＝S△CEB B．S△EDA＋S△CEB＝S△CDEC．S四边形CDAE＝S四边形CDEB D．S△EDA＋S△CDE＋S△CEB＝S四边形ABCD4．如图，正方形ABCD的边长为4，点E在AB上且BE＝1，F为对角线AC上一动点，则△BFE周长的最小值为( )A．5 B．6 C．7 D．85. （2023日照) 已知直角三角形的三边a，b，c满足c＞a＞b，分别以a，b，c为边作三个正方形，把两个较小的正方形放置在最大正方形内，如图，设三个正方形无重叠部分的面积为S1，均重叠部分的面积为S2，则( )A．S1＞S2B．S1＜S2C．S1＝S2D．S1，S2大小无法确定6.（2023天津) 如图，在△ABC中，分别以点A和点C为圆心，大于12AC的长为半径作弧(弧所在圆的半径都相等)，两弧相交于M，N两点，直线MN分别与边BC，AC相交于点D，E，连接A D.若BD＝DC，AE＝4，AD＝5，则AB的长为( )A．9 B．8 C．7 D．67.（2023泸州) 《九章算术》是中国古代重要的数学著作，该著作中给出了勾股数a，b，c的计算公式：a＝12(m2－n2)，b＝mn，c＝12(m2＋n2)，其中m＞n＞0，m，n是互质的奇数．下列四组勾股数中，不能由该勾股数计算公式直接得出的是( )A．3，4，5 B．5，12，13 C．6，8，10 D．7，24，258. （新考向数学文化）《九章算术》中记载：今有户不知高、广，竿不知长、短．横之不出四尺，纵之不出二尺，斜之适出．问户高、广、斜各几何？译文是：今有门，不知其高、宽，有竿，不知其长、短．横放，竿比门宽长出4尺；竖放，竿比门高长出2尺；斜放，竿与门对角线恰好相等．问门高、宽、对角线长分别是多少？若设门对角线长为x尺，则可列方程为( )A．2x2＝(x－4)2＋(x－2)2B．x2＝(x－4)2＋(x－2)2C．x2＝(x－4)2＋22D．x2＝42＋(x－2)29．如图，某超市为了吸引顾客，在超市门口离地高4.5 m的墙上，装有一个由传感器控制的门铃A，人只要移至该门口4 m及4 m以内时，门铃就会自动发出语音“欢迎光临”．一个身高1.5 m的学生刚走到D处，门铃恰好自动响起，则该学生头顶C到门铃A的距离为( )(第9题)A．7 m B．6 m C．5 m D．4 m10．如图，在Rt△ABC中，∠ACB＝90°，AC＝3，BC＝4，点D在AB上，AD＝AC，AF⊥CD交CD于点E，交CB于点F，则CF的长是( )A．1.5 B．1.8 C．2 D．2.5二、填空题(每题3分，共24分)11．如图，AC⊥CE，AD＝BE＝13，BC＝5，DE＝7，那么AC＝________．12．已知a，b，c是△ABC的三边长，且满足关系式(a2－c2－b2)2＋|c－b|＝0，则△ABC的形状为____________________．13.（2023东营) 一艘船由A港沿北偏东60°方向航行30 km至B港，然后再沿北偏西30°方向航行40 km至C港，则A，C两港之间的距离为________km. 14.如图所示的象棋盘中，各个小正方形的边长均为1.“马”从图中的位置出发，不走重复路线，按照“马走日”的规则，走两步后的落点与出发点间的最短距离的平方为________．(第14题)15.如图，在Rt△ABC中，∠ACB＝90°，AB＝4，分别以AC，BC为直径向外作半圆，半圆形的面积分别记为S1，S2，则S1＋S2的值为________．(第15题) (第16题)16．如图，在长方形ABCD中，AB＝8，AD＝10，点E为BC上一点，将△ABE 沿AE折叠，点B恰好落在线段DE上的点F处，则BE的长为________．17.（新情境环境保护）如图，这是某路口处草坪的一角，当行走路线是A→C→B时，有人为了抄近道而避开路的拐角∠ACB(∠ACB＝90°)，于是在草坪内走出了一条捷径A B.某学习实践小组通过测量可知，AC的长为6米，BC的长为8米，为了提醒居民爱护草坪，他们想在A，B处设立“踏破青白可惜，多行数步无妨”的提示牌，则提示牌上的“多行数步”是指多行________米．(第17题)18.“勾股树”是以正方形一边为斜边向外作直角三角形，再以该直角三角形的两直角边为边分别向外作正方形，重复这一过程所画出来的图形，因为重复数次后的形状好似一棵树而得名．假设如图分别是第一代勾股树、第二代勾股树、第三代勾股树，按照勾股树的作图原理作图，则第六代勾股树中正方形的个数为________．三、解答题(每题11分，共66分)19.（2024合肥蜀山区期末) 如图所示，在每个小正方形的边长为单位1的网格中，△ABC是格点图形，求△ABC中AB边上的高．20．某消防部队进行消防演练．在模拟演练现场，有一建筑物发生了火灾，消防车到达后，发现离建筑物的水平距离最近为12 m，如图，即AD＝BC＝12 m，此时建筑物中距地面12.8 m高的P处有一被困人员需要救援．已知消防车的车身高AB是3.8 m，问此消防车的云梯至少应伸长多少米？21.（新视角新定义题）定义：如图，点M，N把线段AB分割成AM，MN，NB，若以AM，MN，NB为边的三角形是一个直角三角形，则称点M，N是线段AB的勾股分割点．(1)已知点M，N把线段AB分割成AM，MN，NB，若AM＝5，MN＝13，BN＝12，则点M，N是线段AB的勾股分割点吗？请说明理由．(2)已知点M，N是线段AB的勾股分割点，且AM为直角边，若AB＝12，AM＝5，求BN的长．22.（2024开封龙亭区期末) 如图，一工厂位于点C，河边原有两个取水点A，B，其中AB＝AC，由于某种原因从工厂C到取水点A的路受阻，为了取水更方便，工厂新建一个取水点H(点A，H，B在一条直线上)，并新修一条路CH，测得CB＝2.5 km，CH＝2 km，BH＝1.5 km.(1)CH是否为从工厂C到河边最近的一条路(即CH与AB是否垂直)？请说明理由．(2)求AC的长．23.（教材P15习题T4变式) 如图，长方体的底面(正方形)边长为3 cm，高为5cm.若一只蚂蚁从点A开始经过四个侧面爬行一圈到达点B，求蚂蚁爬行的最短路径有多长．24．如图，在长方形ABCD中，DC＝5 cm，在DC上存在一点E，沿直线AE把△AED折叠，使点D恰好落在BC边上，设落点为F.若△ABF的面积为30 cm2，求△ADE的面积．答案一、1.B 2.B 3.D4．B 点拨：如图，连接ED 交AC 于点F .因为四边形ABCD 是正方形，所以点B 与点D 关于AC 对称．所以BF ＝DF .所以△BFE 的周长＝BF ＋EF ＋BE ＝DE ＋BE ，此时△BFE 的周长最小．根据勾股定理易求得DE ＝5，所以△BFE 的周长最小为DE ＋BE ＝5＋1＝6.5．C 点拨：因为直角三角形的三边a ，b ，c 满足c ＞a ＞b ，所以该直角三角形的斜边为c ，所以c 2＝a 2＋b 2，即c 2－a 2－b 2＝0.所以S 1＝c 2－a 2－b 2＋b (a ＋b －c )＝ab ＋b 2－bc ，因为S 2＝b (a ＋b －c )＝ab ＋b 2－bc ，所以S 1＝S 2.6．D 点拨：由题意得MN 是AC 的垂直平分线，所以AC ＝2AE ＝8，DA ＝DC ，所以∠DAC ＝∠C .因为BD ＝CD ，所以BD ＝AD ，所以∠B ＝∠BAD ，因为∠B ＋∠BAD ＋∠C ＋∠DAC ＝180°，所以2∠BAD ＋2∠DAC ＝180°.所以∠BAD ＋∠DAC ＝90°，即∠BAC ＝90°.在Rt △ABC 中，BC ＝BD ＋CD ＝2AD ＝10，所以AB 2＝BC 2－AC 2＝102－82＝62，所以AB ＝6.7．C 点拨：因为当m ＝3，n ＝1时，a ＝12(m 2－n 2)＝12×(32－12)＝4，b ＝mn ＝3×1＝3，c ＝12(m 2＋n 2)＝12×(32＋12)＝5，所以选项A 不符合题意；因为当m ＝5，n ＝1时，a ＝12(m 2－n 2)＝12×(52－12)＝12，b ＝mn ＝5×1＝5，c ＝12(m 2＋n 2)＝12×(52＋12)＝13，所以选项B 不符合题意；因为当m ＝7，n ＝1时，a ＝12(m 2－n 2)＝12×(72－12)＝24，b ＝mn ＝7×1＝7，c ＝12(m 2＋n 2)＝12×(72＋12)＝25，所以选项D 不符合题意；因为没有符合条件的m ，n 使a ，b ，c 各为6，8，10，所以选项C 符合题意，故选C.8．B 9.C10．A 点拨：如图，连接DF ，在Rt △ABC 中，∠ACB ＝90°，AC ＝3，BC ＝4.所以AB 2＝AC 2＋BC 2＝32＋42＝52，所以AB ＝5.因为AD ＝AC ＝3，AF ⊥CD ，所以CE ＝DE ，BD ＝AB －AD ＝2，所以CF ＝DF .在△ADF 和△ACF 中， {AD ＝AC ，DF ＝CF ，AF ＝AF ，所以△ADF ≌△ACF (SSS )，所以∠ADF ＝∠ACF ＝90°，所以∠BDF ＝90°.设 CF ＝DF ＝x ，则 BF ＝4－x .在Rt △BDF 中，由勾股定理得DF 2＋BD 2＝BF 2，即 x 2＋22＝(4－x )2，解得x ＝1.5，所以CF ＝1.5.二、11.12　12.等腰直角三角形13．50　14.2　15.2π　16.4　17.418．127　点拨：因为第一代勾股树中正方形有1＋2＝3(个)，第二代勾股树中正方形有1＋2＋22＝7(个)，第三代勾股树中正方形有1＋2＋22＋23＝15(个)，……所以第六代勾股树中正方形有1＋2＋22＋23＋24＋25＋26＝127(个)．三、19.解：设AB 边上的高为h ，因为AB 2＝32＋42＝52，所以AB ＝5，所以12×5h ＝12×3×3，解得h ＝95，即AB 边上的高是95.20．解：由题意知PC ＝12.8 m ，CD ＝AB ＝3.8 m ，所以PD ＝PC －CD ＝12.8－3.8＝9(m)．在Rt △ADP 中，AP 2＝AD 2＋PD 2，所以AP 2＝122＋92.所以AP ＝15 m.故此消防车的云梯至少应伸长15 m.21．解：(1)是．理由如下：因为AM 2＋BN 2＝52＋122＝169，MN 2＝132＝169，所以AM 2＋BN 2＝MN 2.所以以AM ，MN ，NB 为边的三角形是一个直角三角形．故点M ，N 是线段AB 的勾股分割点．(2)设BN ＝x ，则MN ＝AB －AM －BN ＝7－x ，①当MN 为最长线段时，MN 2＝AM 2＋BN 2，即(7－x )2＝x 2＋25，解得x ＝127；②当BN 为最长线段时，BN 2＝AM 2＋MN 2，即x 2＝25＋(7－x )2，解得x ＝377.综上所述，BN 的长为127或377.22．解：(1)CH 是从工厂C 到河边最近的一条路．理由如下：在△CHB 中，因为CH 2＋BH 2＝22＋1.52＝6.25，BC 2＝2.52＝6.25，所以CH 2＋BH 2＝BC 2，所以△CHB 是直角三角形，且∠CHB ＝90°，所以CH 与AB 垂直，即CH 是从工厂C 到河边最近的一条路；(2)设AC ＝x km ，则AB ＝AC ＝x km.因为∠CHB ＝90°，所以∠CHA ＝90°.在Rt △ACH 中，AH ＝(x －1.5)km ，CH ＝2 km ，由勾股定理得AC 2＝AH 2＋CH 2，所以x 2＝(x －1.5)2＋22，解这个方程，得x ＝2512.所以AC 的长为2512 km.23．解：将长方体的侧面展开如图所示，连接AB ′.因为在Rt △AA ′B ′中，AA ′＝12 cm ，A ′B ′＝5 cm ，所以AB ′2＝AA ′2＋A ′B ′2＝169.　所以AB ′＝13 cm.所以蚂蚁爬行的最短路径长为13 cm.24．解：由折叠可知AD ＝AF ，DE ＝EF .由S △ABF ＝12BF ·AB ＝30 cm 2，AB ＝DC ＝5 cm ，得BF ＝12 cm.在Rt △ABF 中，由勾股定理得AF 2＝AB 2＋BF 2＝52＋122＝169，所以AF ＝13 cm.所以BC ＝AD ＝AF ＝13 cm.设DE ＝x cm ，则EC ＝(5－x )cm ，EF ＝x cm.在Rt △ECF 中，FC ＝13－12＝1(cm)，由勾股定理得EC 2＋FC 2＝EF 2，即(5－x )2＋12＝x 2，解得x ＝135.所以DE ＝135cm.所以△ADE 的面积为12AD ·DE ＝12×13×135＝16.9 (cm 2)．。

初中数学北师大版八年级上册第一章勾股定理单元测试(含答案)

第一章勾股定理一、选择题1. 若a，b，c为△ABC的三边长，则下列条件中不能判定△ABC是直角三角形的是( )A．a=1.5，b=2，c=2.5B．a:b:c=3:4:5C．∠A+∠B=∠C D．∠A:∠B:∠C=3:4:52. 在Rt△ABC中，若∠C=90∘，AC=3，BC=4，则点C到直线AB的距离为( )A．3B．4C．5D．2.43. 如图，四边形ABCD中，∠B=90∘，且AB=BC=2，CD=3，DA=1，则∠DAB的度数为( )A．90∘B．120∘C．135∘D．150∘4. 如图，在高为5 m，坡面长为13 m的楼梯表面铺地毯，地毯的长度至少需要( )A．17 m B．18 m C．25 m D．26 m5. 如图是一株美丽的勾股树，其中所有四边形都是正方形，所有的三角形都是直角三角形．若正方形A，B，C，D的面积分别为3，5，2，3，则最大正方形E的面积是( )A．47B．13C．11D．86. 如图，将一根长度为8 cm，自然伸直的弹性皮筋AB两端固定在水平的桌面上，然后把皮筋中点C竖直向上拉升3 cm到点D，则此时该弹性皮筋被拉长了( )A．6 cm B．5 cm C．4 cm D．2 cm7. 如图，为了测得湖两岸A点和B点之间的距离，一个观测者在C点设桩，使∠ABC=90∘，并测得BC长为16 m，若已知AC比AB长8 m，则A点和B点之间的距离为( )A．25 m B．12 m C．13 m D．43 m8. 如图，在三角形纸片ABC中，∠ACB=90∘，AC=4，BC=3，点D，E分别在AB，AC上，连接DE，将△ADE沿DE翻折，使点A的对应点F落在BC的延长线上．若FD平分∠EFB，则AD的长为( )A．259B．258C．157D．207二、填空题9. 在△ABC中，∠C=90∘．（1）已知a=10，b=24，那么c=．（2）已知b:c=4:5，a=9，那么b=，c=．10. 如图是“赵爽弦图”，△ABH，△BCG，△CDF和△DAE是四个全等的直角三角形，四边形ABCD和EFGH都是正方形，如果AH=6，EF=2，那么AB等于．11. 《九章算术》中的“折竹抵地”问题：今有竹高一丈，末折抵地，去根六尺．问折高者几何？意思是：一根竹子，原高一丈（一丈=10尺），一阵风将竹子折断，其竹梢恰好抵地，抵地处离竹子底部6尺远，问折断处离地面的高度是多少？设折断处离地面的高度为x尺，则可列方程为．12. 如图，一个长方体长4 cm，宽3 cm，高12 cm，则它上下两底面的对角线MN的长为cm．13. 已知a，b，c为△ABC的三边，且满足a2+b2+c2+338=10a+24b+26c，则可以判断△ABC的形状为．14. 如图所示的网格是正方形网格，则∠PAB+∠PBA=∘（点A，B，P是网格线的交点）．15. 对角线互相垂直的四边形叫做“垂美”四边形，现有如图所示的“垂美”四边形ABCD，对角线AC，BD交于点O．若AD=2，BC=4，则AB2+CD2=．三、解答题16. 在Rt△ABC中，∠C=90∘．(1) 已知a=8，c=17，求b．(2) 已知b=40，c=41，求a．17. 如图，在四边形ABCD中，∠DBC=90∘，AB=9，AD=12，BC=8，DC=17，求四边形ABCD的面积．18. 如图，滑竿在机械槽内运动，∠C=90∘，AB=2.5 m，BC=1.5 m，当底端B向右移动0.5 m时，顶端A下滑了多少米？19. 假期中，王强和同学到某海岛上去旅游．他们按照如图所示路线．在点A登陆后租借了自行车，骑车往东走8千米，又往北走2千米；遇到障碍后往西走3千米，再折向北走到6千米处往东拐，走了1千米到达景点B．登陆点A到景点B的直线距离是多少千米？20. 若正整数a，b，c（a<b<c）满足a2+b2=c2，则称（a，b，c）为一组“勾股数”．观察下列两类“勾股数”：第一类（a是奇数）：(3,4,5)，(5,12,13)，(7,24,25)，⋯⋯第二类（a是偶数）：(6,8,10)，(8,15,17)，(10,24,26)，⋯⋯(1) 请再写出两组勾股数，每类各写一组；(2) 分别就a为奇数、偶数两种情形，用a表示b和c，并选择其中一种情形证明(a,b,c)是“勾股数”．答案一、选择题1. D2. D3. C4. A5. B6. D7. B8. D二、填空题9. 26；12；1510. 1011. x2+62=(10−x)212. 1313. 直角三角形14. 4515. 20三、解答题16.(1) 15．(2) 9．17. ∵∠DBC=90∘，DC=17，BC=8，∴BD2=CD2−BC2=172−82=225=152，∴BD=15．∵AD2+AB2=122+92=144+81=225，BD 2=225， ∴AD 2+AB 2=BD 2，∴△ABD 是直角三角形，且 ∠A =90∘，∴ 四边形 ABCD 的面积 =△ABD 的面积 +∠CBD 的面积 =12×9×12+12×15×8=54+60=114．18. 依题意得 AB =DE =2.5 m ，BC =1.5 m ，∠C =90∘，∴AC 2+BC 2=AB 2，即 AC 2+1.52=2.52，解得 AC =2 m ． ∵BD =0.5 m ， ∴CD =2 m ．在 Rt △ECD 中，CE 2+CD 2=DE 2， ∴CE =1.5 m ， ∴AE =0.5 m ．答：顶端 A 下滑了 0.5 m ．19. 10 千米．20.(1) 第一组（a 是奇数）：9,40,41（答案不唯一）；第二组（a 是偶数）：12,35,37（答案不唯一）．(2) 当 a 为奇数时，b =a 2−12，c =a 2+12；当 a 为偶数时，b =a 24−1，c =a 24+1．证明：当 a 为奇数时，a 2+b 2=a 2+(a 2−12)2=(a 2+12)2=c 2，∴(a,b,c ) 是“勾股数”．当 a 为偶数时，a 2+b 2=a 2+(a 24−1)2=(a 24+1)2=c 2，∴(a,b,c ) 是“勾股数”．。

初中数学第一章勾股定理评估试卷(含答案)

C第一章勾股定理评估试卷一、选择题（每小题3分，共30分）1. 直角三角形一直角边长为12，另两条边长均为自然数，则其周长为( ). （A ）30 （B ）28 （C ）56 （D ）不能确定2. 直角三角形的斜边比一直角边长2 cm ，另一直角边长为6 cm ，则它的斜边长（A ）4 cm（B ）8 cm （C ）10 cm（D ）12 cm3. 已知一个Rt △的两边长分别为3和4，则第三边长的平方是（）（A ）25（B ）14（C ）7（D ）7或254. 等腰三角形的腰长为10,底长为12,则其底边上的高为( ) （A ）13 （B ）8 （C ）25 （D ）645. 五根小木棒，其长度分别为7，15，20，24，25，现将他们摆成两个直角三角形，其中正确的是（）6. 将直角三角形的三条边长同时扩大同一倍数, 得到的三角形是( )（A ）钝角三角形（B ）锐角三角形（C ）直角三角形（D ）等腰三角形. 7. 如图小方格都是边长为1的正方形,则四边形ABCD 的面积是 ( ) （A ） 25 （B ） 12.5 （C ） 9 （D ） 8.5 8. 三角形的三边长为,则这个三角形是( ) （A ）等边三角形（B ）钝角三角形（C ）直角三角形（D ）锐角三角形.9.△ABC 是某市在拆除违章建筑后的一块三角形空地.已知∠C=90°，AC=30米，AB=50米，如果要在这块空地上种植草皮，按每平方米草皮元计算，那么共需要资金（）. （A ）50元（B ）600元（C ）1200元（D ）1500元 10.如图，A B ⊥CD 于B ，△ABD 和△BCE 都是等腰直角三角形，如果CD=17，BE=5，那么AC 的长为（）.7152425207152024257252024257202415(A)(B)(C)(D)ab c b a 2)(22+=+a a a a a（A）12 （B）7 （C）5 （D）13（第10题）（第11题）（第14题）二、填空题（每小题3分，24分）11.如图为某楼梯,测得楼梯的长为5米,高3米,计划在楼梯表面铺地毯,地毯的长度至少需要____________米.12.在直角三角形中，斜边=2，则=______.13. 直角三角形的三边长为连续偶数，则其周长为.14.如图，在△ABC中，∠C=90°，BC=3，AC=4.以斜边AB为直径作半圆，则这个半圆的面积是____________.（第15题）（第16题）（第17题）15.如图，校园内有两棵树，相距12米，一棵树高13米，另一棵树高8米，一只小鸟从一棵树的顶端飞到另一棵树的顶端，小鸟至少要飞___________米.16. 如图，△ABC中，∠C=90°，AB垂直平分线交BC于D若BC=8，AD=5，则AC等于______________.17.如图，四边形是正方形，垂直于，且=3，=4，阴影部分的面积是______.18.如图，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形的边和长为7cm,则正方形A，B，C，D的面积之和为___________cm2.5米3米ABC AB222AB AC BC++ABCD AE BE AEBEEABCDABDCEABCD第18题图7cm三、解答题（每小题8分，共40分）19. 11世纪的一位阿拉伯数学家曾提出一个“鸟儿捉鱼”的问题：“小溪边长着两棵棕榈树，恰好隔岸相望.一棵树高是30肘尺（肘尺是古代的长度单位），另外一棵高20肘尺；两棵棕榈树的树干间的距离是50肘尺.每棵树的树顶上都停着一只鸟.忽然，两只鸟同时看见棕榈树间的水面上游出一条鱼，它们立刻飞去抓鱼，并且同时到达目标.问这条鱼出现的地方离开比较高的棕榈树的树跟有多远？20.如图，已知一等腰三角形的周长是16，底边上的高是4.求这个三角形各边的长.21.如图，A、B两个小集镇在河流CD的同侧，分别到河的距离为AC=10千米，BD=30千米，且CD=30千米，现在要在河边建一自来水厂，向A、B两镇供水，铺设水管的费用为每千米3万，请你在河流CD上选择水厂的位置M，使铺设水管的费用最节省，并求出总费用是多少？BALC D第21题图22. 如图所示的一块地，∠ADC=90°，AD=12m ，CD=9m ，AB=39m ，BC=36m ，求这块地的面积。

八年级数学(上)第一章《勾股定理》测试题及答案

八年级数学(上)第一章《勾股定理》测试题及答案选择题
1.一直角三角形的斜边长比一直角边长大2，另一直角边长为6，则斜边长为（）
A.4
B.8
C.10
D.12
2.小丰的妈妈买了一部29英寸(74m)的电视机,下列对29英寸的说法中正确的是()
A.小丰认为指的是屏幕的长度
B.小丰的妈妈认为指的是屏幕的宽度
C.小丰的爸爸认为指的是屏幕的周长
D.售货员认为指的是屏幕对角线的长度
3.将直角三角形的三条边长同时扩大同一倍数，得到的三角形是（）
A.钝角三角形
B.锐角三角形
C.直角三角形
D. 等腰三角形
4.一直角三角形的一条直角边长是 7cm，另一条直角边与斜边长的和是 49cm，则斜边的长()
A.18cm
B.20 cm
C.24 cm
D.25cm
填空题
1. 小华和小红都从同一点0出发，小华向北走了9米到 A 点，小红向东走了12米到了B点，则AB=_____米。

2.一个三角形三边满足(a+b)2-c2=2ab，则这个三角形是_____三角形。

3.木工做一个长方形桌面，量得桌面的长为 60cm，宽为
32cm，对角线为 68cm,这个桌面______(填“合格”或“不合格”)。

4.直角三角形一直角边为12cm，斜边长为13cm，则它的面积为_______。

参考答案：
选择题：CDCD
填空题：1.15；2.直角；3.合格；4.30。

第一章勾股定理综合素质评价

第一章勾股定理综合素质评价一、选择题(每题3分，共30分)1．如图，在Rt△ABC中，∠A＝90°，BC＝2.5 cm，AC＝1.5 cm，则AB的长为() A．3.5 cm B．2 cm C．3 cm D．4 cm(第1题)(第3题)(第4题)2．【教材P16复习题T2改编】下列长度的线段能构成直角三角形的一组是() A．30，40，50 B．7，12，13C．5，9，12 D．3，4，63．【教材P7习题T2改编】历史上对勾股定理的一种验证方法采用了如图所示的图形，其中两个全等直角三角形的边AE，EB在一条直线上，其中用到的面积相等的关系式是()A．S△EDA＝S△CEB B．S△EDA＋S△CEB＝S△CDEC．S四边形CDAE＝S四边形CDEB D．S△EDA＋S△CDE＋S△CEB＝S四边形ABCD 4．如图，在Rt△ABC中，∠ACB＝90°，若AB＝15 cm，则正方形ADEC和正方形BCFG的面积之和为()A．150 cm2B．200 cm2C．225 cm2D．无法计算5．【教材P14习题T1改编】如图，阴影部分是一个长方形，则长方形的面积是() A．3 cm2B．4 cm2C．5 cm2D．6 cm2(第5题)(第7题)6．满足下列条件的△ABC，不是．．直角三角形的为()A．∠A＝∠B－∠C B．∠A∶∠B∶∠C＝1∶1∶2C．b2＝a2－c2D．a∶b∶c＝2∶3∶47．如图，在△ABC中，AB＝AC＝13，BC＝10，点D为BC的中点，DE⊥AB，垂足为点E，则DE等于()A.1013 B.1513 C.6013 D.75138．【教材P15习题T5改编】【2021·襄阳】我国古代数学著作《九章算术》中记载了一个问题：“今有池方一丈，葭(j iā)生其中央，出水一尺，引葭赴岸，适与岸齐，问水深几何”．(丈、尺是长度单位，1丈＝10尺)其大意为：有一个水池，水面是一个边长为10尺的正方形，在水池正中央有一根芦苇，它高出水面1尺，如果把这根芦苇拉向水池一边的中点，它的顶端恰好到达池边的水面(如图，单位：尺)，水的深度是多少？则水深为()A．10尺B．11尺C．12尺D．13尺(第8题)(第9题)(第10题)9．【2020·恩施州】如图，正方形ABCD的边长为4，点E在AB上且BE＝1，F 为对角线AC上一动点，则△BFE周长的最小值为()A．5 B．6 C．7 D．810．如图，圆柱的底面直径为16π，BC＝12，动点P从A点出发，沿着圆柱的侧面移动到BC的中点S的最短距离为()A．10 B．12 C．20 D．14二、填空题(每题3分，共24分)11．请任意写出一组勾股数：__________．12．如图，某人从A点出发欲横渡一条河，由于水流的影响，实际上岸地点C 偏离欲到达地点B 300 m，结果他在水中实际游了500 m，则该河的宽度为__________．(第12题)(第13题)(第15题)(第16题)13．如图，在Rt△ABC中，∠B＝90°，AB＝3 cm，AC＝5 cm，将△ABC折叠，使点C与点A重合，得到折痕DE，则△ABE的周长等于__________．c－b＝0，14．已知a，b，c是△ABC的三边长，且满足关系式(a2－c2－b2)2＋||则△ABC的形状为____________________．15．【中考·邵阳】公元3世纪初，中国古代数学家赵爽注《周髀算经》时，创造了“赵爽弦图”．如图，设勾a＝6，弦c＝10，则小正方形ABCD的面积是________．16．【2021·玉林】如图，某港口P位于东西方向的海岸线上，甲、乙轮船同时离开港口，各自沿一固定方向航行，甲、乙轮船每小时分别航行12海里和16海里，1小时后两船分别位于点A，B处，且相距20海里，如果知道甲船沿北偏西40°方向航行，则乙船沿________方向航行．17．【中考·南京】无盖圆柱形杯子的展开图如图所示．将一根长为20 cm的细木筷斜放在该杯子内，木筷露在杯子外面的部分至少有________cm.(第17题)(第18题)18．【2020·雅安】对角线互相垂直的四边形叫做“垂美”四边形，现有如图所示的“垂美”四边形ABCD，对角线AC，BD交于点O.若AD＝2，BC＝4，则AB2＋CD2＝________．三、解答题(每题11分，共66分)19．如图，在锐角三角形ABC中，高AD＝12，边AC＝13，BC＝14，求AB的长．20．如图，在4×4的正方形网格中，每个小正方形的边长都是1.线段AB，AE分别是图中两个1×3的长方形的对角线，请你说明：AB⊥AE.21．【教材P14习题T3变式】某消防部队进行消防演练．在模拟演练现场，有一建筑物发生了火灾，消防车到达后，发现离建筑物的水平距离最近为12 m，如图，即AD＝BC＝12 m，此时建筑物中距地面12.8 m高的P处有一被困人员需要救援．已知消防车的车身高AB是3.8 m，问此消防车的云梯至少应伸长多少米？22．如图，在四边形ABCD中，AB＝AD＝2，BC＝3，CD＝1，∠A＝90°，求∠ADC的度数．23．【教材P15习题T4变式】如图，长方体的底面(正方形)边长为3 cm，高为5 cm.若一只蚂蚁从点A开始经过四个侧面爬行一圈到达点B，求蚂蚁爬行的最短路径有多长．24．如图，在长方形ABCD中，DC＝5 cm，在DC上存在一点E，沿直线AE把△AED折叠，使点D恰好落在BC边上，设落点为F. 若△ABF的面积为30cm2，求△ADE的面积．第一章勾股定理综合素质评价答案一、1.B 2.A 3.D 4.C 5.C 6.D7.C8．C9 .B点技巧：根据B，D两点关于AC对称，利用对称的性质将线段和的最小值转化为一条线段的长(可求解)．点拨：如图，连接ED交AC于点F，连接BF.因为四边形ABCD是正方形，所以点B与点D关于AC对称．所以BF＝DF.所以△BFE的周长＝BF＋EF＋BE＝DE＋BE，此时△BFE的周长最小．根据勾股定理易求DE＝5，所以△BFE的周长最小为DE＋BE＝5＋1＝6.10．A点拨：将圆柱的侧面沿DA展开，如图，连接BC，AS，则AB＝12×16π×π＝8，BS＝12BC＝6.在Rt△ABS中，由勾股定理得AS＝10，即动点P从点A沿着圆柱的侧面移动到点S的最短距离为10.二、11.3，4，5(答案不唯一)12.400 m13.7 cm14．等腰直角三角形15.416.北偏东50°17.518.20点思路：由勾股定理得AB2＋CD2＝AO2＋BO2＋CO2＋DO2，AD2＋BC2＝AO2＋DO2＋BO2＋CO2，所以AB2＋CD2＝AD2＋BC2＝22＋42＝20.三、19.解：在Rt△ADC中，AC＝13，AD＝12，由勾股定理得CD2＝AC2－AD2＝25，所以CD＝5.因为BC＝14，所以BD＝BC－CD＝9.在Rt△ABD中，由勾股定理得AB2＝AD2＋BD2＝225，所以AB＝15. 20．解：如图，连接BE.因为AE2＝12＋32＝10，AB2＝12＋32＝10，BE2＝22＋42＝20，所以AE2＋AB2＝BE2.所以△ABE是直角三角形，且∠BAE＝90°，即AB⊥AE.21．解：由题意知CD＝AB＝3.8 m，所以PD＝PC－CD＝12.8－3.8＝9(m)．在Rt△ADP中，AP2＝AD2＋PD2，所以AP2＝122＋92.所以AP＝15 m.答：此消防车的云梯至少应伸长15 m.22．解：连接BD.在Rt△BAD中，因为AB＝AD＝2，所以∠ADB＝45°，BD2＝AD2＋AB2＝22＋22＝8.在△BCD中，因为BD2＋CD2＝8＋1＝9＝BC2，所以△BCD是直角三角形，且∠BDC＝90°.所以∠ADC＝∠ADB＋∠BDC＝45°＋90°＝135°.23．解：将长方体的侧面展开如图所示，连接AB′.因为在Rt△AA′B′中，AA′＝12 cm，A′B′＝5 cm，所以AB′2＝AA′2＋A′B′2＝169.所以AB′＝13 cm.所以蚂蚁爬行的最短路径长为13 cm. 24．解：由折叠可知AD＝AF，DE＝EF.由S△ABF ＝12BF·AB＝30 cm2，AB＝DC＝5 cm，得BF＝12 cm.在Rt△ABF中，由勾股定理得AF2＝AB2＋BF2＝52＋122＝169，所以AF＝13 cm.所以BC＝AD＝AF＝13 cm.设DE＝x cm，则EC＝(5－x)cm，EF＝x cm.在Rt△ECF中，FC＝13－12＝1(cm)，由勾股定理得EC2＋FC2＝EF2，即(5－x)2＋12＝x2，解得x＝13 5.所以DE＝135cm.所以△ADE的面积为12AD·DE＝12×13×135＝16.9 (cm2)．。

第一章勾股定理评价

第一章勾股定理评价北师大版八年级上册第一章勾股定理评价试题及答案(时间：45 分钟满分：100 分)一、选择题(每小题4 分，共12 分)1.(1)9，12，15；(2)7，24，25；(3)32；42，52；(4)3a，4a，5a(a＞0) 四组数中可以构成直角三角形的边长的有()A.4 组B.3 组C.2 组D.1 组2.一架25 分米长的梯子，斜立在一竖直的墙上，这时梯足距离墙底端7 分米.如果梯子的顶端沿墙下滑4 分米，那幺梯足将滑动()A.9 分米B.15 分米C.5 分米D.8 分米3.如果一个三角形的三边a、b、c 满足a2+b2+c2+338=10a+24b+26c，则这个三角形一定是()A.锐角三角形B.直角三角形C.钝角三角形D.等腰三角形二、填空题(每小题4 分，共12 分)1.已知两条线段长分别为5cm、12cm，当第三条线段长为________时，这三条线段可以组成一个直角三角形，其面积是______.2.△ABC 中，AB=AC=17cm，BC=16cm，AD⊥BC 于D，则AD=_____.3.在三角形ABC 中，若三边长分别为9、12、15，则以两个这样的三角形拼成的矩形面积为__________.三、(每小题10 分，共40 分)1.如图，一艘船由岛A 正南30 海里的B 处向东以每小时20 海里的速度航行2 小时后到达C 处。

求AC 间的距离.2.如图，已知一等腰三角形的周长是16，底边上的高是4.求这个三角形各边的长.3.若三角形的三个内角的比是1:2:3，最短边长1cm，最长边长2cm. 求：(1)这个三角形各角的度数；(2)另外一边长的平方.4.如图，直角三角形三条边的比是3:4:5.求这个三角形三条边上的高的比.四、(每题12 分，共计36 分)1. 在△ABC 中，三条边的长分别为a、b、c，a=n2-1，b=2n，c=n2+1(n＞1，且n 为整数)，这个三角形是直角三角形吗？若是，哪个角是直角？与同伴一起研究.2.如图，折叠长方形一边AD，点D 落在BC 边的点F 处，BC=10cm，AB=8cm，求：(1)FC 的长；(2)EF 的长.3.如图，在△ABC 中，∠C=90°，BC=3，AC=4.以斜边AB 为直径作半圆，求这个半圆的面积.参考答案一、1.B 2.D 3.B二、1.cm 或13cm，30cm2 或cm2 2.15cm 3.108三、解1.由勾股定理，可以得到AB2+BC2=AC2因为AB=30，BC=20×2=40，所以302+202=AC2所以AC=50答：AC 间的距离为50 海里.2.设BD=x，则AB=8-x由勾股定理，可以得到AB2=BD2+AD2，也就是(8-x)2=x2+42.所以x=3，所以AB=AC=5，BC=63.(1)因为180÷(1+2+3)=30，30×2=60，30×3=90，所以各角的度数分别为30°、60°、90°(2)设另外一边长为x，则x2+12=22，也就是x2=34.由三角形面积公式，可得・AB ・CD=・BC ・AC.设BC=3k，AC=4k，AB=5k，则5k ・CD=2k ・4k.所以CD=k.所以AC:BC:CD=4k:3k: k=20:15:12.四、解1.因为a2=n4-2n2+1，b2=4n，c2=n4+2n2+1，a2+b2=c2所以△ABC 是直角三角形，∠C 为直角.2.(1)在Rt△ABC 中，由勾股定理可以得到AF2=AB2+BF2，也就是102=82+BF2.所以BF=6，FC=4(cm)(2)在Rt△ABC 中，由勾股定理，可以得到EF2=FC2+(8-EF)2.也就是EF2=42+(8-EF)2.所以EF=5(cm)3.在Rt△ABC 中，由勾股定理可以得到AB2=42+32=25，所以AB=5.所以半圆的面积S=()2=.。

北师大版八年级数学上册第一章勾股定理综合测评 (Word版含答案)

第一章勾股定理综合测评（本试卷满分100分）一、选择题（每小题3分，共30分）1.如图1，在△ABC中，∠C＝90°，则下列结论正确的是（）A．AB＝AC+BC B．AB＝AC•BCC．AB2＝AC2+BC2D．AC2＝AB2+BC2图1 图2 图3 图4 图52.下列各组数据中，不是勾股数的是（）A．3，4，5 B．7，24，25 C．8，15，17 D．5，7，93.如图2，分别标有“放”“鸡”“岛”的三个正方形围成一个直角三角形，标有“放”、“鸡”的正方形的面积分别为18，50，则图中标有“岛”字的正方形的面积是( )A.34B.32C.30D.284．已知△ABC中，a，b，c分别是∠A，∠B，∠C的对边，下列条件不能判断△ABC是直角三角形的是（）A．∠A＝∠C﹣∠B B．a：b：c＝2：3：4C．a2＝b2﹣c2D．a＝，b＝，c＝15.如图3，有一块长方形空地ABCD，如果AB=300米，AD=400米，要从A走到C，至少要走（）A．300米B．400米C．500米D．700米6.在Rt△ABC中，∠C＝90°，AC＝9，BC＝12，则点C到AB的距离是（）A．3 B．4 C．15 D．7.27.如图4，在Rt△ABC中，∠B=90°，以AC为直径的圆恰好过点B，AB=8，BC=6，则阴影部分的面积是（）A．100π-24 B．100π-48 C．25π-24 D．25π-488.如图5，已知蚂蚁从长、宽都是3，高是8的长方体纸箱的A点沿纸箱爬到B点，那么它所爬行的最短路线长是（）A.8B.10C.12D.169.如图6，梯子AB靠在墙上，梯子的底端A到墙根O的距离为7 m，梯子的顶端B到地面的距离为24 m，现将梯子的底端A向外移动到A′，使梯子的底端A′到墙根O的距离等于15 m．同时梯子的顶端B下降至B′，那么BB′等于（）A.3 m B．4 m C．5 m D．6 m图6 图710.如图7，在长方形纸片ABCD中，AB=12，AD=5，点E在AB上，将△DAE沿DE折叠，使点A落在对角线BD上的点F处，则BE的长为（）A.263B.9C.38D.37二、填空题（每小题3分，共18分）11.已知一直角三角形的两条直角边长分别是20，15，斜边长为x，则x=_____.12.有一组勾股数，如果其中的两个数分别是17和8，那么第三个数是_____.13.图8所示的“赵爽弦图”中，△ABH，△BCG，△CDF，△DAE是四个全等的直角三角形，四边形ABCD 和EFGH都是正方形，如果EF=4，AH=12，那么AB的长为_____.图814.在△ABC中，三边长a，b，c满足a:b:c=9:40:41，周长为90，则△ABC的面积为_____.15.《九章算术》卷九“勾股”中记载：今有立木，系索其末，委地三尺．引索却行，去本八尺而索尽，问索长几何？译文：今有一竖立着的木柱，在木柱的上端系有绳索，绳索从木柱上端顺木柱下垂后，堆在地面的部分尚有3尺．牵着绳索（绳索头与地面接触）退行，在距木柱根部8尺处时绳索用尽．问绳索长是多少？设绳索长为x尺，可列方程为．16. 勾股定理a2+b2=c2本身就是一个关于a，b，c的方程，满足这个方程的正整数解（a，b，c）通常叫做勾股数组．毕达哥拉斯学派提出了一个构造勾股数组的公式，根据该公式可以构造出如下勾股数组：（3，4，5），（5，12，13），（7，24，25），…．分析上面勾股数组可以发现，4=1×（3+1），12=2×（5+1），24=3×（7+1），…分析上面规律，第5个勾股数组为________________．三、解答题（共52分）17.（6分）如图9，在△ABC 中，AB=25，AC=17，边BC 上的高AD=15，求BC 的长．18.（6分）在△ABC 中，∠A ，∠B ，∠C 的对边分别是a ，b ，c ，如果a=215，b=225，c=10，这个三角形是直角三角形吗？请说明理由. 小康的解答如下：解：这个三角形不是直角三角形.理由如下：因为a 2+b 2=（215）2+（225）2=2425，c 2=100，所以a 2+b 2≠c 2. 所以△ABC 不是直角三角形.请问：小康的解答正确吗？若不正确，请给出正确的解答过程.19.（8分）如图10，甲、乙两船同时从港口A 出发，甲船以12海里/时的速度向北偏东35°的方向航行，乙船向南偏东55°的方向航行．2小时后，甲船到达C 岛，乙船到达B 岛，若C ，B 两船相距40海里，问：乙船的航行速度是每小时多少海里？20.(10分）某游乐场计划修建一个图11所示的游泳池供游客休闲娱乐，泳池底部如图所示.已知∠DAB=90°，AB 的长为40 m ，AD 的长为30 m ，BC 的长为120 m ，CD 的长为130 m.求该泳池的占地面积.21.（10分）图12是小明家的一块直角三角形绿地，量得两条直角边的长分别为BC=18米和AC=24米，现要将该直角三角形绿地扩充成一个等腰三角形，且扩充部分是以AC 为直角边的直角三角形，请你求出扩充后的等腰三角形绿地的面积.22.（12分）如图13，在△ABC中，已知AB=1，AC=2，CB＇⊥BC，且CB＇=CB，△A＇B＇C≌△ABC，连接AB＇，AA＇.（1）判断△ACA＇的形状，并说明理由；（2）若AB＇=3，求∠B＇A＇C的度数.附加题（20分，不计入总分）23.勾股定理神秘而美妙，它的证法多样，其巧妙各有不同，其中的“面积法”给了小东以灵感，他惊喜地发现，当两个全等的直角三角形如图15-①或图15-②摆放时，都可以用“面积法”来证明，下面是小东利用图14-①验证勾股定理的过程：将两个全等的直角三角形按图14-①所示摆放，其中∠DAB=90°，试说明：a2+b2=c2.解：连接DB，过点D作BC边上的高DF，则DF=EC=b-a．因为S四边形ADCB=S△ACD+S△ABC=12b2+12ab，又S四边形ADCB=S△ADB+S△DCB=12c2+12a（b-a），所以12b2+12ab=12c2+12a（b-a）.所以a2+b2=c2.解决问题：请参照上述方法，利用图15-②完成下面的验证：将两个全等的直角三角形按图15-②所示摆放，其中∠DAB=90°．试说明：a2+b2=c2．第一章勾股定理综合测评一、1.C 2.D 3.B 4.B 5.C 6.D 7.C 8.B 9.B10. A 提示：在Rt △ABD 中，由勾股定理求得BD=13.根据折叠的性质，得EF=AE ，∠DFE=∠A=90º，DF=DA=5.设AE=x ，则EF=x.在Rt △BEF 中，FB=13-5=8，BE=12-x ，根据勾股定理，得FE 2+FB 2=EB 2，即x 2+82=(12-x)2，解得x=310.所以BE=12-310=263. 二、11.25 12. 15 13.20 14.180 15.（x ﹣3）2+64＝x 2 16. （11，60，61）三、17.解：在Rt △ADC 中，由勾股定理，得DC 2=AC 2-AD 2=172-152=64，所以DC=8.在Rt △ABD 中，由勾股定理，得BD 2=AB 2-AD 2=252-152=400，所以BD=20.所以BC=BD+DC=20+8=28. 18.解：小康的解答不正确.正确的解答过程如下：这个三角形是直角三角形.理由：因为21510225>>，所以b 是这个三角形的最长边. 因为a 2+c 2=（215）2+102=4625，b 2=(4625)2252=，所以a 2+c 2=b 2.所以△ABC 是直角三角形.19. 解：由题意，得AC=12×2=24（海里）．因为∠EAC=35°，∠FAB=55°，所以∠CAB=90°．因为BC=40海里，AC=24海里，在Rt △ABC 中，AB 2=BC 2-AB 2=402-242=1024，所以AB=32海里．因为乙船也行驶了2小时，所以乙船的航行速度是32÷2=16（海里/时）． 20.解：连接BD.因为∠DAB=90°，AB=40 m ，AD=30 m ，所以BD=50 m.因为BC=120 m ，CD=130 m ，所以BD 2+BC 2=CD 2.所以△BCD 是直角三角形.所以∠DBC=90°. 所以S 四边形ABCD =S △DAB +S △BCD =12AB·AD+12BC·BD=12×40×30+12×120×50=3600（m 2）. 答：该泳池的占地面积为3600 m 2.21.解：在Rt △ABC 中，∠ACB=90º，AC=24米，BC=18米，由勾股定理可得AB=30米.应分以下三种情况：①如图2，当AB=BD=30米时，S △ABD =21AC·BD=21×24×30=360（平方米）.②如图3，当AD=AB 时，因为 AD=30米，AC=24米，由勾股定理可得DC=18米.因为AC ⊥BD ，所以BD=2DC=36米.所以S △ABD =21AC·BD=21×24×36=432（平方米）. ③如图4，当AD=BD 时，设AD=BD=x 米，则CD=(x-18)米.在Rt △ACD 中，DC 2+AC 2=AD 2，即 (x-18)2+242=x 2，解得x=25，所以S △ABD =21AC·BD=21×24×25=300（平方米）. 综上所述，扩充后的等腰三角形绿地的面积为360平方米或432平方米或300平方米. 22.解：（1）△ACA ＇是等腰直角三角形.理由：因为CB ＇⊥BC ，所以∠BCA+∠ACB ＇=90º.因为△A ＇B ＇C ≌△ABC ，所以∠BCA=∠B ＇CA ＇，AC=A ＇C.所以∠ACB ＇+∠B ＇CA ＇=90º，即∠ACA ＇=90º.所以△ACA ＇是等腰直角三角形.（2）因为△ACA ＇是等腰直角三角形，所以∠AA ＇C=45º.在Rt △ACA ＇中，根据勾股定理，得AA ＇2=AC 2+ A ＇C 2=22+22=8.因为A ＇B ＇=AB=1，所以AA ＇2+A ＇B ＇2=8+1=9，AB ＇2=9.所以AA ＇2+A ＇B ＇2= AB ＇2.所以△A ＇AB ＇是直角三角形，且∠AA ＇B ＇=90º.所以∠B ＇A ＇C=45º+90º=135º. 23.解：如图5，连接BD ，过点B 作DE 边上的高BF ，可得BF=b-a.因为S 五边形ACBED =S △ACB +S △ABE +S △ADE =12ab+12b 2+12ab ，又S 五边形ACBED =S △ACB +S △ABD +S △BDE =12ab+12c 2+12a （b-a ），所以12ab+12b 2+12ab=12ab+12c 2+12a （b-a ），整理，得a 2+b 2=c 2．。

北师大版八年级数学上册第一章《勾股定理》测试卷(含答案)

北师大版八年级数学上册第一章《勾股定理》测试卷（含答案）一、选择题（共8 小题，4*8=32）1. 在直角三角形中，若勾为3，股为4，则弦为( )A ．5B ．6C ．7D ．82. 在ΔABC 中，∠A，∠B，∠C 的对边分别是a，b，c，若∠A+∠C ＝90°,则下列等式中成立的是( )A ．a2＋b2 ＝2c2B ．b2＋c2 ＝a2C ．a2＋c2 ＝b2D ．c2－a2 ＝b23. 若ΔABC 的三边a ，b，c 满足(a－b)2＋|a2＋b2－c2 | ＝0，则ΔABC 是( )A ．等腰三角形B ．直角三角形C ．等腰直角三角形D ．等腰三角形或直角三角形4. 如图，在某次海上编队演习中，两艘航母护卫舰从同一港口O 同时出发，一号舰沿南偏西30°方向以12 海里/小时的速度航行，二号舰以16 海里/小时的速度航行，离开港口 1.5 小时后它们分别到达相距30 海里的A ，B 两点，则二号舰航行的方向是( )A ．南偏东30°B ．北偏东30°C ．南偏东60°D ．南偏西60°5. 一架250cm 的梯子斜靠在墙上，这时梯足与墙的终端距离为70cm，如果梯子顶端沿墙下滑40cm，那么梯足将向外滑动( )A. 150cmB. 90cmC. 80cmD. 40cm6. 如图，长为12 cm 的橡皮筋放置在直线l 上，固定两端A 和B ，把中点C 竖直向上拉升4.5 cm 至点D 处，则拉长后橡皮筋的长为( )A ．20 cmB ．18 cmC ．16 cmD ．15 cm67. 如图所示，圆柱高8 cm，底面圆的半径为π cm，一只蚂蚁从点A 爬到点B 处吃蜂蜜，则要爬行的最短路程是( )A ．20 cmB ．10 cmC ．14 cmD ．无法确定8. 有下面的判断：①△ABC 中，a2＋b2≠c2 ，则ΔABC 不是直角三角形。

北师大版八年级数学上册第1章勾股定理章节测试卷 (含解析)

第1章《勾股定理》章节测试卷一．选择题（共10小题，满分30分，每小题3分）1．在我国古代，人们将直角三角形中短的直角边叫做勾，长的直角边叫做股，斜边叫做弦．古希腊哲学家柏拉图研究了勾为偶数，弦与股相差为2的一类勾股数，如：6，8，10；8，15，17…若此类勾股数的勾为2m（m≥3，m为正整数），则其弦（结果用含m的式子表示）是（）A．4m2−1B．4m2+1C．m2−1D．m2+12．如图，五个正方形放在直线MN上，正方形A、C、E的面积依次为3、5、4，则正方形B、D 的面积之和为（）A．11B．14C．17D．203．观察下列各方格图中阴影部分所示的图形（每个方格的边长为1），如果将它们沿方格边线或对角线剪开后无缝拼接，不能拼成正方形的是（）A．B．C．D．4．如图，小巷左右两侧是竖直的墙，一架梯子斜靠在左墙时，梯子底端到左墙角的距离为0.7米，顶端距离地面2.4米，如果保持梯子底端位置不动，将梯子斜靠在右墙时，顶端距离地面2米，则小巷的宽度为( )A．2.2米B．2.3米C．2.4米D．2.5米5．如图，在Rt△ABC中，∠ABC=90°，AB=3，AC=5，AD为∠BAC的平分线，将△DAC沿AD向上翻折得到△DAE，使点E在射线AB上，则DE的长为（）A．2B．52C．5D．2546．如图，三角形纸片ABC中，点D是BC边上一点，连接AD，把△ABD沿着直线AD翻折，得到△AED，DE交AC于点G，连接BE交AD于点F．若DG＝EG，AF＝4，AB＝5，△AEG的面积为92，则BD2的值为（）A．13B．12C．11D．107．图中不能证明勾股定理的是（）A． B．C．D．8．如图，将有一边重合的两张直角三角形纸片放在数轴上，纸片上的点A表示的数是-2，AC=BC=BD=1，若以点A为圆心，AD的长为半径画弧，与数轴交于点E（点E位于点A右侧)，则点E表示的数为（）A．3B．−2+3C．−1+3D．−39．如图，一个底面周长为24cm，高为5cm的圆柱体，一只蚂蚁沿侧表面从点A到点B所经过的最短路线长为（）A．12cm B．13cm C．25cm D．26cm10．勾股定理是人类早期发现并证明的重要数学定理之一，是数形结合的重要纽带．数学家欧几里得利用下图验证了勾股定理．以直角三角形ABC的三条边为边长向外作正方形ACHI，正方形ABED，正方形BCGF，连接BI，CD，过点C作CJ⊥DE于点J，交AB于点K．设正方形ACHI 的面积为S1，正方形BCGF的面积为S2，矩形AKJD的面积为S3，矩形KJEB的面积为S4，下列结论中：①BI⊥CD；②S1∶S△ACD＝2∶1；③S1－S4＝S3－S2；④S1S4＝S3S2，正确的结论有（）A．1个B．2个C．3个D．4个二．填空题（共6小题，满分18分，每小题3分）11．小明将4个全等的直角三角形拼成如图所示的五边形，添加适当的辅助线后，用等面积法建立等式证明勾股定理．小明在证题中用两种方法表示五边形的面积，分别是S1= ，S2= ．12．勘测队按实际需要构建了平面直角坐标系，并标示了A，B，C三地的坐标，数据如图（单位：km）．笔直铁路经过A，B两地．（1）A，B间的距离 km；（2）计划修一条从C到铁路AB的最短公路l，并在l上建一个维修站D，使CD=13，则AD 的长为 km．13．如图，图1是第七届国际数学教育大会（ICME−7）会徽图案、它是由一串有公共顶点O的直角三角形（如图2）演化而成的．如果图2中的OA1=A1A2=A2A3=⋅⋅⋅=A7A8=1，若S1代表△A1OA2的面积，S2代表△A2OA3的面积，以此类推，则S10的值为．14．把由5个小正方形组成的十字形纸板（如图1）剪开，以下剪法中能够将剪成的若干块拼成一个大正方形的有（填写序号）．15．如图，在△ABC中，∠C=90°，BC=16cm，AC=12cm，点E是BC的中点，动点P从A 点出发以每秒1cm的速度沿A→C→B运动，设点P运动的时间是t秒，那么当t=，△APE的面积等于12．16．已知△ABC中，AC=8，AB=41，BC边上的高AG=5，D为线段AC上的动点，在BC上截取CE=AD，连接AE，BD，则AE+BD的最小值为．三．解答题（共7小题，满分52分）17．（6分）如图，在△ABC中，AD为BC边上的中线，AB=3，AC=5，AD=2，求证：AD⊥AB．18．（6分）如图，∠AOB＝90°，OA＝8m，OB＝3m，一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O，机器人立即从点B出发，沿直线匀速前进拦截小球，恰好在点C处截住了小球．如果小球滚动的路程与机器人行走的路程相等，那么机器人行走的路程BC是多少？19．（8分）以3，4，5为边长的三角形是直角三角形，称3，4，5为勾股数组，记为（3，4，5），类似地，还可得到下列勾股数组：（5，12，13），（7，24，25）等．(1)根据上述三组勾股数的规律，写出第四组勾股数组；(2)用含n（n为正整数）的数学等式描述上述勾股数组的规律，并证明．20．（8分）现有一个长、宽、高分别为5dm、4dm、3dm的无盖长方体木箱(如图,AB=5dm,BC=4dm,AE=3dm)．(1) 求线段BG的长；(2) 现在箱外的点A处有一只蜘蛛，箱内的点C处有一只小虫正在午睡，保持不动．请你为蜘蛛设计一种捕虫方案，使得蜘蛛能以最短的路程捕捉到小虫．(木板的厚度忽略不计)21．（8分）如图，在△ABC中，∠ACB=90°，AC=6，BC=8．(1)如图（1），把△ABC沿直线DE折叠，使点A与点B重合，求BE的长；(2)如图（2），把△ABC沿直线AF折叠，使点C落在AB边上G点处，请直接写出BF的长．22．（8分）如图1，纸上有五个边长为1的小正方形组成的图形纸，我们可以把它剪开拼成一个正方形如图2．（1）你能在3×3方格图（图3）中，连接四个格点（网格线的交点）组成面积为5的正方形吗？若能，请用虚线画出．（2）你能把十个小正方形组成的图形纸（图4），剪开并拼成正方形吗？若能，请仿照图2的形式把它重新拼成一个正方形．（3）如图，是由两个边长不等的正方形纸片组成的一个图形，要将其剪拼成一个既不重叠也无空隙的大正方形，则剪出的块数最少为________块．请你在图中画出裁剪线，并说明拼接方法．23．（8分）公元3世纪初，我国学家赵爽证明勾定理的图形称为“弦图”．1876年美国总统Garfeild用图1（点C、点B、点C′三点共线）进行了勾股定理的证明．△ACB与△BC′B′是一样的直角三角板，两直角边长为a，b，斜边是c．请用此图1证明勾股定理．拓展应用l：如图2，以△ABC的边AB和边AC为边长分别向外作正方形ABFH和正方形ACED，过点F、E分别作BC的垂线段FM、EN，则FM、EN、BC的数量关系是怎样？直接写出结论．拓展应用2：如图3，在两平行线m、n之间有一正方形ABCD，已知点A和点C分别在直线m、n 上，过点D作直线l∥n∥m，已知l、n之间距离为1，l、m之间距离为2．则正方形的面积是．答案解析一．选择题1．D【分析】根据题意得2m为偶数，设其股是a，则弦为a+2，根据勾股定理列方程即可得到结论．【详解】解：∵m为正整数，∴2m为偶数，设其股是a，则弦为a+2，根据勾股定理得，(2m)2+a2=(a+2)2，解得a=m2−1，∴弦是a+2=m2−1+2=m2+1，故选：D．2．C【分析】如图：由题意可得∠ABC=∠ACE=∠CDE=90°,S=AB2=3,S C=DE2=5,S B=AC2,AAC=CE，再根据全等三角形和勾股定理可得S B=S C+S A=5+3=8，同理可得S D=S C+ S E=5+4=9，最后求正方形B、D的面积之和即可．【详解】解：如图：由题意可得：∠ABC=∠ACE=∠CDE=90°,S=AB2=3,S C=DE2=5,S B=AC2,AC=CEA∴∠BAC+∠ACB=90°,∠DCE+∠ACB=90°,∴∠BAC=∠DCE，∴△ABC≅△CDE,∴DE=BC,∵∠ABC=90°，∴AC2=BC2+AB2，∴AC2=DE2+AB2,即S B=S C+S A=5+3=8,同理：S=S C+S E=5+4=9;D∴S+S B=8+9=17．D故选C．3．C【分析】根据网格的特点分别计算阴影部分的面积即可求得拼接后的正方形的边长，根据网格的特点能否找到构成边长的格点即可求解．【详解】解：A. 阴影部分面积为4，则正方形的边长为2，故能拼成正方形，不符合题意；B.阴影部分面积为10，则正方形的边长为10，∵12+32=10，故能拼成正方形，不符合题意；C.阴影部分面积为11，则正方形的边长为11，根据网格的特点不能构造出11的边，故不能拼成正方形，符合题意D. 阴影部分面积为13，则正方形的边长为13，∵22+32=13，故能拼成正方形，不符合题意；故选C．4．A【分析】将梯子斜靠在墙上时，形成的图形看做直角三角形，根据勾股定理，直角边的平方和等于斜边的平方，可以求出梯子的长度，再次利用勾股定理即可求出梯子底端到右墙的距离，从而得出答案.【详解】如图，在Rt△ACB中，∵∠ACB=90°，BC=0.7米，AC=2.4米，AB2=AC2+BC2∴AB2=0.72+ 2.42= 6.25在Rt△A‘BD中，∵∠A’BD=90°，A’D=2米，BD2+A'D2=A'B2∴BD2+22= 6.25∴BD2= 2.25∵BD>0，∴BD=1.5米，∴CD=BC+BD=0.7+1.5=2.2米即小巷的宽度为2.2米，故答案选A5．B【分析】根据勾股定理求得BC，进而根据折叠的性质可得AE=AC，可得BE=2，设DE=x，表示出BD,DE，进而在Rt△BDE中，勾股定理列出方程，解方程即可求解．【详解】解：∵在Rt△ABC中，∠ABC=90°，AB=3，AC=5，∴BC=AC2−A B2=52−32=4，∵将△DAC沿AD向上翻折得到△DAE，使点E在射线AB上，∴AE=AC，设DE=x，则DC=DE=x,BD=BC−CD=4−x，BE=AE−AB=5−3=2，在Rt△BDE中，BD2+BE2=DE2，即(4−x)2+22=x2，解得：x=52，即DE的长为52故选：B．6．A【分析】首先根据SAS证明△BAF≌△EAF可得AF⊥BE，根据三角形的面积公式求出AD，根据勾股定理求出BD即可．【详解】解：由折叠得，AB=AE，∠BAF=∠EAF，在△BAF和△EAF中，{AB=AE∠BAF=∠EAFAF=AF，∴△BAF≌△EAF(SAS)，∴BF=EF，∴AF⊥BE，又∵AF＝4，AB＝5，∴BF=AB2−A F2=3，在△ADE中，EF⊥AD，DG＝EG，设DE边上的高线长为h，∴S△ADE =12AD⋅EF=12DG⋅h+12EG⋅h，即S△ADG +S△AEG=12AD⋅EF，∵S△AEG =12⋅GE⋅h=92，S△ADG=S△AEG，∴S△ADG +S△AEG=92+92=9，∴9=12AD⋅3，∴AD=6，∴FD=AD−AF=6−4=2，在Rt△BDF中，BF=3，FD=2，∴BD2=BF2+FD2=32+22=13，故选：A．7．A【分析】根据各个图象，利用面积的不同表示方法，列式证明结论a2+b2=c2，找出不能证明的那个选项．【详解】解：A选项不能证明勾股定理；B选项，通过大正方形面积的不同表示方法，可以列式(a+b)2=4×12ab+c2，可得a2+b2 =c2；C选项，通过梯形的面积的不同表示方法，可以列式(a+b)22=2×12ab+12c2，可得a2+b2=c2；D选项，通过这个不规则图象的面积的不同表示方法，可以列式c2+2×12ab=a2+b2+2×12ab，可得a2+b2=c2．故选：A．8．B【详解】根据勾股定理得：AB=2，AD=3，∴AE=3，∴OE=2−3，∴点E表示的数为−2+3．故答案为：B．9．B【分析】先将圆柱圆的侧面沿着点A所在的棱线剪开，得到长方形，得到AC=5cm,BC=242=12 cm，由此即可以利用勾股定理求出蚂蚁爬行的最短路线AB的长.【详解】如图，沿着点A所在的棱线剪开，此时AC=5cm,BC=242=12cm，∴蚂蚁爬行的最短路线AB=AC2+BC2=52+122=13cm，故选：B.10．D【分析】利用正方形的性质证明△ABI≌△ADC，得出∠AIB=∠ACD，即可得出∠CNI=∠NAI，即可判断①，利用△ABI≌△ADC，即可求出△ABI的面积，即可判断②，由勾股定理和S3+S4=S▱ABED，即可判断③，由③S1-S4=S3-S2，两边平方，根据勾股定理可得AC2−B C2=AK2−B K2，然后计算S12+S42−(S22+S32)=0，即可判断④．【详解】解：∵四边形ACHI和四边形ABED为正方形，∴AI=AC，AD=AB，∠CAI=∠BAD=90°，∵∠BAI=∠BAC+∠CAI，∠DAC=∠BAC+∠BAD，∴∠BAI=∠DAC，∴△ABI≌△ADC（SAS），∴∠AIB=∠ACD，∵∠CNI=∠CAI=90°，∴BI⊥CD，故①正确；∵S△ACD=S△AIB=12×AI×AC，S正方形ACHI=S1=AI×AC，∴S1：S△ACD=2：1，故②正确；∵S1=AC2，S2=BC2，S3+S4=S正方形ADEB=AB2，AC2+BC2=AB2，∴S1+S2=S3+S4，∴S1-S4=S3-S2，故③正确；∵ S1-S4=S3-S2，∴S12+S42−2S1S4=S22+S32−2S2S3，∵S1=AC2，S2=BC2，S3=AK•KJ= AK•AB，S4=BK•KJ=BK•AB，∴S12+S42=AC4+AB2BK2，S22+S32=BC4+AK2AB2，∵AB2=AC2+ BC2，AC2=AK2+CK2,BC2=BK2+CK2，∴AC2−A K2=BC2−B K2，即AC2−B C2=AK2−B K2，∴S12+S42−(S22+S32)=AC4+AB2BK2−(BC4+AK2AB2)=AC4−B C4+AB2(BK2−A K2)=(AC2+BC2)(AC2−B C2)−A B2(AC2−B C2) =AB2(AC2−B C2)−AB2(AC2−B C2)=0，∴S1•S4=S2•S3，故④正确，二．填空题11．c2+ab a2+b2+ab【详解】解：如图所示：S1=c2+12ab×2=c2+ab，S2=a2+b2+12ab×2=a2+b2+ab．故答案为c2+ab，a2+b2+ab．12． 20 13【分析】（1）根据两点的纵坐标相同即可得出AB的长度；（2）过C作AB的垂线交AB于点E，连接AD，构造方程解出即可．【详解】（1）根据A、B两点的纵坐标相同，得AB=12−（−8）=20故答案为：20（2）如图：设AD=a，根据点A、B的纵坐标相同，则AE=12，CE=1−（−17）=18由ΔADE是直角三角形，得：（CE−CD）2+AE2=a2∴52+122=a2故答案为：13 13．102【分析】利用勾股定理依次计算出OA2=2，OA3=3，OA4=4=2，.. OA n=n，然后依据计算出前几个三角形的面积，然后依据规律解答求得S10即可．【详解】由题意得：OA2=OA12+A1A22=12+12=2，OA3=OA22+A2A32=12+(2)2=3，OA4=OA32+A3A42=12+(3)2=4=2,∴OAn=n，∴OA10=10，∴S10=12OA10⋅A10A11=12×10×1=102，故答案为：102．14．①③【分析】设小正方形的边长为1，则5个小正方形的面积为5，进而可知拼成的大正方形的边长为5，再根据所画虚线逐项进行拼接，看哪种剪法能拼成边长为5的正方形即可．【详解】解：按照①中剪法，在外围四个小正方形上分别剪一刀然后放到相邻的空处，可拼接成边长为5的正方形，符合题意；如下图所示，按照③中剪法，通过拼接也可以得到边长为5的正方形，符合题意；按照②中剪法，无法拼接成边长为5的正方形，不符合题意；故选①③．故答案为：①③．15．3或18或22【分析】分当点P在线段AB上运动时，当点P在线段BC上运动且在点E的右边时和当点P在线段BC上运动且在点E的左边时三种情况讨论，即可求出t的值．【详解】解：∵∠C=90°，BC＝16cm，AC＝12cm，∴AB=AC2+BC2=162+122=20，∵点E是BC的中点，∴CE＝BE=12BC＝8cm，S△ACE=S△ABE=12S△ABC=12×12×12×16=48cm2．当点P在线段AC上运动时，∵△APE的面积等于12，即S△APE =14S△ACE，∴AP=14AC=3，∴t=3÷1=3秒；当点P在线段BC运动时上且在点E的右边时，，如图2所示，同理可知BP=14BE=2cm，∴t=(12+8+2)÷1=22秒；当点P在线段BC上运动且在点E的左边时，如图3所示，同理可知CP=12CE=2cm，∴t=(12+8−2)÷1=18秒；故答案为∶3或18或22．16．13【分析】通过过点A 作GC 的平行线AN ，并在AN 上截取AH =AC ，构造全等三角形，得到当B ，D ，H 三点共线时，可求得AE +BD 的最小值；再作垂线构造矩形，利用勾股定理求解即可．【详解】如图，过点A 作GC 的平行线AF ，并在AF 上截取AH =AC ，连接DH ，BH ．则∠HAD =∠C ．在△ADH 和△CEA 中，{AD =CE ，∠HAD =∠C ，AH =CA ，∴△ADH≌△CEA(SAS)，∴DH =AE ，∴AE +BD =DH +BD ，∴当B ，D ，H 三点共线时，DH +BD 的值最小，即AE +BD 的值最小，为BH 的长．∵AG ⊥BG ，AB =41，AG =5，∴在Rt △ABG 中，由勾股定理，得BG =AB 2−A G 2=(41)2−52=4．如图，过点H 作HM ⊥GC ，交GC 的延长线于点M ，则四边形AGMH 为长方形，∴HM =AG =5，GM =AH =AC =8，∴在Rt △BMH 中，由勾股定理，得BH =BM 2+HM 2=(4+8)2+52=13．∴AE+BD的最小值为13．故答案为：13．三．解答题17．证明：如图，延长AD至点E，使得AD=DE，连接CE，∵AD为BC边上的中线，∴BD=DC，又∵AD=DE,∠ADB=∠EDC，∴△ABD≌△ECD，∴AB=EC=3，∠BAD=∠E，又∵AE=2AD=4,AC=5，∴AC2=AE2+CE2，∴∠E=90°∴∠BAD=∠E=90°∴AD⊥AB．18．解：∵小球滚动的速度与机器人行走的速度相等，∴BC=AC，设BC=AC=x m，则OC=（8-x）m，在Rt△BOC中，∵OB2+OC2=BC2，．∴32+（8-x）2=x2，解得x=7316∴机器人行走的路程BC为73m．1619．（1）解：第一组勾股数的第一个数为3=2×1+1，第二个数为4=2×1×(1+1)，第三个数为4=2×(1+1)+1，第二组勾股数的第一个数为5=2×2+1，第二个数为12=2×2×(2+1)，第三个数为12=2×2×(2+1)+1，第三组勾股数的第一个数为7=2×3+1，第二个数为24=2×3×(3+1)，第三个数为25=2×3×(3+1)+1，所以第四组勾股数组的第一个数为2×4+1=9，第二个数为2×4×(4+1)=40，第三个数为2×4×(4+1)+1=41，∴第四组勾股数组为(9,40,41)；（2）解：由（1）可知：第n组勾股数为(2n+1,2n2+2n,2n2+2n+1)，证明：∵(2n+1)2+(2n2+2n)2=4n2+4n+1+4n4+8n3+4n2=4n4+8n3+8n2+4n+1，(2n2+2n+1)2=(2n2+2n+1)(2n2+2n+1)=4n4+4n3+2n2+4n3+4n2+2n+2n2+2n+1=4n4+8n3+8n2+4n+1∴(2n+1)2+(2n2+2n)2=(2n2+2n+1)220．解：（1）如图，连接BG．在直角△BCG中，由勾股定理得到：BG＝BC2+GC2＝42+32＝5（dm），即线段BG的长度为5dm；（2）①把ADEH展开，如图此时总路程为(3+3+5)2+42＝137②把ABEF展开，如图此时的总路程为(3+3+4)2+52＝125＝55③如图所示，把BCFGF展开，此时的总路程为(3+3)2+(5+4)2＝117由于117＜125<137，所以第三种方案路程更短，最短路程为117．21．（1）解：∵直线DE是对称轴，∴AE=BE，∵AC=6,BC=8，设AE=BE=x，则CE=8−x在Rt△ACE中，∠C=90°，∴AC2+CE2=AE2，∴62+(8−x)2=x2，，解得x=254∴BE=254（2）解：∵直线AF是对称轴，∴AC=AG，CF=CG，∵AC=6,BC=8，设CF=CG=x，则BF=8−x，∴在Rt△ACB中，∠C=90°，AB=AC2+BC2=62+82=10，∴BG=AB−AG=4，在Rt△BGF中，∠BGF=90°，∴GF2+BG2=BF2，∴x2+42=(8−x)2，解得x=3，∴BF=8−3=5．22．解：（1）能，如图所示，正方形ABCD即为所求；（2）能，如图所示，正方形ABCD即为所求；（3）如图所示，在AB上截取AM＝BE，连接DM、MF，DM、FM即为裁剪线，将△DAM拼接△DCH处，使DA与DC重合，将△MEF拼接至△HGF处，使ME和HG重合，EF与FG 重合，得到正方形DMFH，∴剪出的块数最少为5块，故答案为：5．23．如图：∵点C、点B、点B′三点共线，∠C＝∠C′＝90°，∴四边形ACC′B′是直角梯形，∵△ACB与△BC′B′是一样的直角三角板，∴Rt△ACB≌Rt△BC′B′，∴∠CAB＝∠C′BB′，AB＝BB′，∴∠CBA+∠C′BB’＝90°∴△ABB′是等腰直角三角形，，所以S梯形ACC′B′＝（AC+B′C′）•CC′÷2＝(a+b)22S △ACB ＝12AC ⋅BC =12ab ，S △BC ′B ′＝12ab ，S △ABB ′＝12c 2，所以(a +b)22=12ab +12ab +12c 2，a 2+2ab+b 2＝ab+ab+c 2，∴a 2+b 2＝c 2；拓展1．过A 作AP ⊥BC 于点P ，如图2，则∠BMF ＝∠APB ＝90°，∵∠ABF ＝90°，∴∠BFM+∠MBF ＝∠MBF+∠ABP ，∴∠BFM ＝∠ABP ，在△BMF 和△ABP 中，{∠BFM =∠ABP ∠BMF =∠APB =900BF =AB，∴△BMF ≌△ABP （AAS ），∴FM ＝BP ，同理，EN ＝CP ，∴FM+EN ＝BP+CP ，即FM+EN ＝BC ，故答案为FM+EN ＝BC ；拓展2．过点D 作PQ ⊥m ，分别交m 于点P ，交n 于点Q ，如图3，则∠APD ＝∠ADC ＝∠CQD ＝90°，∴∠ADP+∠DAP ＝∠ADP+∠CDQ ＝90°，∴∠DAP ＝∠CDQ ，在△APD 和△DQC 中，{∠DAP =∠CDQ ∠APD =∠DQC AD =DC，∴△APD ≌△DQC （AAS ），∴AP ＝DQ ＝2，∵PD ＝1，∴AD 2＝22+12＝5，∴正方形的面积为 5，故答案为5．。

第一章 勾股定理评价试题

第1章 勾股定理 北师大版八年级数学上册综合素质评价(含解析)

新北师大版八年级数学《勾股定理》单元测试卷

八年级上册数学第一章《勾股定理》检测题及答案解析

北师大版数学八年级上册 第一章 勾股定理综合测评 (含答案)

第1章 勾股定理 北师大版数学八年级上册综合素质评价(含答案)