(5-2)泊松分布概率的计算—Book2
numpy 泊松分布计算概率

numpy 泊松分布计算概率摘要:1.引言2.泊松分布的概念和特点3.泊松分布的概率计算方法4.使用Python 的numpy 库计算泊松分布概率5.实例:计算30 分钟内到达顾客数的概率6.结论正文:1.引言在概率论和统计学中,泊松分布是一种离散型概率分布,用于描述在一定时间或空间内随机事件发生的次数。
在实际应用中,泊松分布被广泛应用于各种场景,如排队问题、生物统计学、保险数学、信号处理等领域。
本文将介绍如何使用Python 的numpy 库来计算泊松分布的概率。
2.泊松分布的概念和特点泊松分布是由法国数学家泊松(Siméon-Denis Poisson)在19 世纪初提出的。
泊松分布的概率质量函数(Probability Mass Function,PMF)表示在给定事件发生次数的情况下,事件发生的概率。
泊松分布的概率质量函数具有以下特点:- 当k=0 时,概率质量函数取最大值,表示事件不发生的概率;- 当k 增加时,概率质量函数逐渐减小,表示事件发生的概率逐渐降低;- 当k 趋近于无穷大时,概率质量函数趋近于0,表示事件发生的概率极低。
3.泊松分布的概率计算方法泊松分布的概率质量函数可以通过以下公式计算:P(X=k) = (e^(-λ) * λ^k) / k!其中,P(X=k) 表示事件发生k 次的概率,λ表示事件的平均发生率,e 表示自然对数的底数。
4.使用Python 的numpy 库计算泊松分布概率Python 的numpy 库提供了一种简单易用的方法来计算泊松分布的概率。
首先,需要导入numpy 库,并使用numpy.random.poisson 函数生成泊松分布的随机数。
然后,可以通过遍历随机数数组,统计各个事件发生次数的概率。
以下是一个简单的示例:```pythonimport numpy as np# 生成泊松分布的随机数lambda_value = 4 # 事件的平均发生率um_trials = 1000 # 试验次数x = np.random.poisson(lambda_value, num_trials)# 计算各个事件发生次数的概率probabilities = []for k in range(0, x.max() + 1):probabilities.append(np.sum(x == k) / num_trials)print(probabilities)```5.实例:计算30 分钟内到达顾客数的概率假设一家咖啡店在30 分钟内到达的顾客数服从泊松分布,平均每分钟到达4 位顾客。
泊松分布的概念及表和查表方法
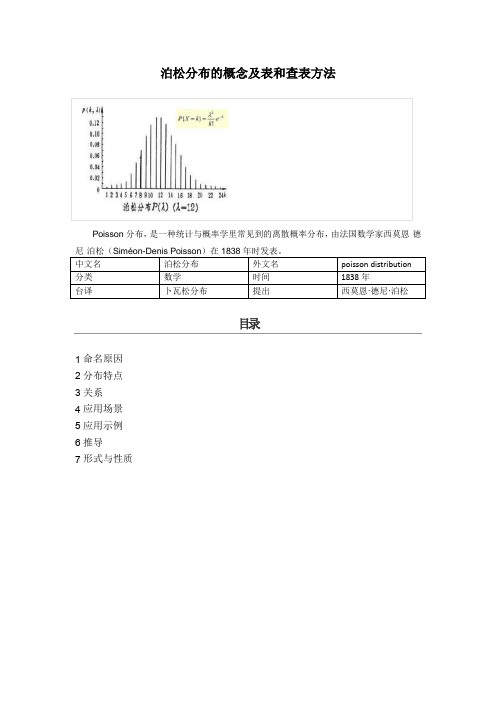
泊松分布的概念及表和查表方法目录1命名原因2分布特点3关系4应用场景5应用示例6推导7形式与性质命名原因泊松分布实例泊松分布(Poisson distribution),台译卜瓦松分布(法语:loi de Poisson,英语:Poisson distribution,译名有泊松分布、普阿松分布、卜瓦松分布、布瓦松分布、布阿松分布、波以松分布、卜氏分配等),是一种统计与概率学里常见到的离散机率分布(discrete probability distribution)。
泊松分布是以18~19 世纪的法国数学家西莫恩·德尼·泊松(Siméon-Denis Poisson)命名的,他在1838年时发表。
这个分布在更早些时候由贝努里家族的一个人描述过。
分布特点泊松分布的概率函数为:泊松分布的参数λ是单位时间(或单位面积)内随机事件的平均发生次数。
泊松分布适合于描述单位时间内随机事件发生的次数。
泊松分布的期望和方差均为特征函数为关系泊松分布与二项分布泊松分布当二项分布的n很大而p很小时,泊松分布可作为二项分布的近似,其中λ为np。
通常当n≧20,p≦0.05时,就可以用泊松公式近似得计算。
事实上,泊松分布正是由二项分布推导而来的,具体推导过程参见本词条相关部分。
应用场景在实际事例中,当一个随机事件,例如某电话交换台收到的呼叫、来到某公共汽车站的乘客、某放射性物质发射出的粒子、显微镜下某区域中的白血球等等,以固定的平均瞬时速率λ(或称密度)随机且独立地出现时,那么这个事件在单位时间(面积或体积)内出现的次数或个数就近似地服从泊松分布P(λ)。
因此,泊松分布在管理科学、运筹学以及自然科学的某些问题中都占有重要的地位(在早期学界认为人类行为是服从泊松分布,2005年在nature上发表的文章揭示了人类行为具有高度非均匀性)。
应用示例泊松分布适合于描述单位时间(或空间)内随机事件发生的次数。
泊松分布的数学公式

泊松分布的数学公式
泊松分布是一种常见的离散概率分布,它描述了在一定时间或空间内某事件发生的概率分布情况。
泊松分布的数学公式为:P(X=k) = (λ^k * e^(-λ)) / k!,其中,X表示事件发生的次数,k表示事件发生的次数,λ表示事件发生的平均次数。
泊松分布的应用非常广泛,例如,在工业生产中,可以用泊松分布来描述一定时间内机器出现故障的次数;在保险业中,可以用泊松分布来描述一定时间内发生的车祸数量;在交通运输领域,可以用泊松分布来描述一定时间内发生的交通事故数量等等。
泊松分布的特点是具有单峰、正偏、离散分布的特性。
在泊松分布中,当λ值越大,分布形状越趋向于对称,同时峰值也越高。
当λ值越小,分布形状越趋向于右偏,同时峰值也越低。
泊松分布有许多重要的性质,例如,泊松分布的期望值和方差均等于λ,即E(X) = λ,Var(X) = λ。
此外,泊松分布还具有无记忆性的特性,即已知前面发生了若干事件,对后续事件的发生概率没有影响。
在实际应用中,为了更好地描述事件发生的概率分布情况,我们可以采用泊松分布的参数估计方法来确定λ的值。
其中,最常用的方法是最大似然估计法,即选择使得样本数据出现概率最大的λ值作为估计值。
需要注意的是,泊松分布的适用条件是事件独立、稀疏、随机和均匀等,因此在实际应用中需要结合具体情况进行判断。
同时,在进行泊松分布的应用时,需要注意数据的选择、处理和分析,以充分发挥泊松分布的应用价值。
泊松分布课件

平稳性: 在任意时间区间内,事件发生k次(k≥0)的 概率只依赖于区间长度而与区间端点无关. 无后效性: 在不相重叠的时间段内,事件的发生是相 互独立的. 普通性: 如果时间区间充分小,事件出现两次或 两次以上的概率可忽略不计.
例如
一放射性源放射出的 粒子数; 某电话交换台收到的电话呼叫数;
解: 设该商品每月的销售数为X, 已知X服从参数λ=5的泊松分布. 设商店在月底应进某种商品m件, 求满足 P(X≤m)>0.95 的最小的m .
进货数
销售数
求满足 P(X≤m)>0.95 的最小的m. 也即 P(X>m) ≤ 0.05
e 5 0.05 或 k m 1 k!
查泊松分布表得
P ( X k ) e
k
k!
, k0,1,2,,
其中 λ >0 是常数, 则称 X 服从参数为λ 的 泊松分布, 记作X~P(λ ).
泊松分布的图形特点:X~P( λ)
二、二项分布与泊松分布 历史上,泊松分布是作为二项分布的近 似,于1837年由法国数学家泊松引入的. 近数十年来,泊松分布日益显示 其重要性, 成为概率论中最重要的几 个分布之一. 在实际中,许多随机现象服从或近 似服从泊松分布.
5 k
e 5 0.032, k 10 k!
于是得 m+1=10,
5 k
e 5 0.068 k! k 9
m=9件
5 k
这一讲,我们介绍了泊松分布
n重贝努里试验中稀有事件出现的次数近 似地服从泊松分布. 我们给出了泊松分布产生的一般条件
泊松分布在管理科学、运筹学以及自然 科学的某些问题中都占有重要的地位 .
泊松分布的概念及表和查表方法

泊松分布的概念及表和查表方法Poisson分布,是一种统计与概率学里常见到的离散概率分布,由法国数学家西莫恩·德尼·泊松〔Siméon-Denis Poisson〕在1838年时发表。
中文名泊松分布外文名poisson distribution 分类数学时间1838年台译卜瓦松分布提出西莫恩·德尼·泊松目录1命名原因2分布特点3关系4应用场景5应用例如6推导7形式与性质命名原因泊松分布实例泊松分布〔Poisson distribution〕,台译卜瓦松分布〔法语:loi de Poisson,英语:Poisson distribution,译名有泊松分布、普阿松分布、卜瓦松分布、布瓦松分布、布阿松分布、波以松分布、卜氏分配等〕,是一种统计与概率学里常见到的离散机率分布〔discrete probability distribution〕。
泊松分布是以18~19 世纪的法国数学家西莫恩·德尼·泊松〔Siméon-Denis Poisson〕命名的,他在1838年时发表。
这个分布在更早些时候由贝努里家族的一个人描述过。
分布特点泊松分布的概率函数为:泊松分布的参数λ是单位时间(或单位面积)内随机事件的平均发生次数。
泊松分布适合于描述单位时间内随机事件发生的次数。
泊松分布的期望和方差均为特征函数为关系泊松分布与二项分布泊松分布当二项分布的n很大而p很小时,泊松分布可作为二项分布的近似,其中λ为np。
通常当n≧20,p≦0.05时,就可以用泊松公式近似得计算。
事实上,泊松分布正是由二项分布推导而来的,具体推导过程参见本词条相关局部。
应用场景在实际事例中,当一个随机事件,例如某交换台收到的呼叫、来到某公共汽车站的乘客、某放射性物质发射出的粒子、显微镜下某区域中的白血球等等,以固定的平均瞬时速率λ〔或称密度〕随机且独立地出现时,那么这个事件在单位时间〔面积或体积〕内出现的次数或个数就近似地服从泊松分布P(λ)。
常用十个泊松展开公式

常用十个泊松展开公式1. 泊松公式$$e^{-\lambda} = \sum_{k=0}^{\infty} \frac{\lambda^k}{k!} $$2. 泊松分布的概率质量函数$$P(X=k) = \frac{e^{-\lambda} \lambda^k}{k!}$$3. 期望值泊松分布的期望值为 lambda。
$$E(X) = \lambda$$4. 方差泊松分布的方差也为 lambda。
$$Var(X) = \lambda$$5. 合并多个泊松分布如果有两个独立的泊松分布,其参数分别为 lambda1 和lambda2,那么合并后的泊松分布参数为 lambda = lambda1 + lambda2。
6. 次序统计量对于独立同分布的泊松随机变量 X1, X2, ..., Xn,它们的次序统计量满足以下公式:$$X_{(1)} \leq X_{(2)} \leq ... \leq X_{(n)}$$7. 泊松分布的中位数和众数泊松分布的中位数近似等于 lambda,众数近似等于floor(lambda) 或 ceil(lambda)。
8. 泊松分布的性质- 泊松分布是一种离散概率分布,用于描述单位时间内某事件发生次数的概率分布。
- 泊松分布的取值范围是非负整数。
- 泊松分布的参数 lambda 表示单位时间内事件的平均发生次数。
- 泊松分布是二项分布的一种特殊情况,当二项分布中的 n 很大但 p 很小时,可以用泊松分布来逼近。
9. 泊松分布的应用领域泊松分布在实际生活中的应用十分广泛,例如:- 电话接线员接到的电话数量。
- 网络服务器收到的请求数量。
- 单位时间内航班抵达某机场的次数。
- 某设备的故障次数。
10. 泊松展开公式的推导泊松展开公式是将多项式展开成指数级数的公式。
其推导过程比较复杂,可以在相关教材或数学论文中找到详细的推导方法。
以上是常用的十个泊松展开公式的介绍,希望对您有所帮助。
泊松分布的概念及表和查表方法

泊松分布的概念及表和查表方法Poisson分布,是一种统计与概率学里常见到的离散概率分布,由法国数学家西莫恩·德尼·泊松(Siméon-Denis Poisson)在1838年时发表。
中文名泊松分布外文名poisson distribution 分类数学时间1838年台译卜瓦松分布提出西莫恩·德尼·泊松目录1命名原因2分布特点3关系4应用场景5应用示例6推导7形式与性质命名原因泊松分布实例泊松分布(Poisson distribution),台译卜瓦松分布(法语:loi de Poisson,英语:Poisson distribution,译名有泊松分布、普阿松分布、卜瓦松分布、布瓦松分布、布阿松分布、波以松分布、卜氏分配等),是一种统计与概率学里常见到的离散机率分布(discrete probability distribution)。
泊松分布是以18~19 世纪的法国数学家西莫恩·德尼·泊松(Sim éon-Denis Poisson)命名的,他在1838年时发表。
这个分布在更早些时候由贝努里家族的一个人描述过。
分布特点泊松分布的概率函数为:泊松分布的参数λ是单位时间(或单位面积)内随机事件的平均发生次数。
泊松分布适合于描述单位时间内随机事件发生的次数。
泊松分布的期望和方差均为特征函数为关系泊松分布与二项分布泊松分布当二项分布的n很大而p很小时,泊松分布可作为二项分布的近似,其中λ为np。
通常当n≧20,p≦0.05时,就可以用泊松公式近似得计算。
事实上,泊松分布正是由二项分布推导而来的,具体推导过程参见本词条相关部分。
应用场景在实际事例中,当一个随机事件,例如某电话交换台收到的呼叫、来到某公共汽车站的乘客、某放射性物质发射出的粒子、显微镜下某区域中的白血球等等,以固定的平均瞬时速率λ(或称密度)随机且独立地出现时,那么这个事件在单位时间(面积或体积)内出现的次数或个数就近似地服从泊松分布P(λ)。
泊松分布的计算

泊松分布的计算
泊松分布是一种概率分布,用于描述在一段时间或空间内某事件发生的次数。
泊松分布的计算需要以下几个步骤:
1. 确定事件发生的平均次数λ。
泊松分布的参数λ表示单位时间或单位空间内事件的平均发生次数。
2. 根据泊松分布的公式,计算事件发生x次的概率。
泊松分布的概率密度函数为:
P(x) = (e^-λ* λ^x) / x!
其中,e是自然对数的底数,x是事件发生的次数。
3. 如果需要计算事件发生不超过x次的概率,可以使用累积分布函数。
泊松分布的累积分布函数为:
F(x) = ∑(i=0 to x) (e^-λ* λ^i) / i!
其中,i表示事件发生的次数。
4. 如果需要计算事件发生的期望值和方差,可以使用泊松分布的公式。
泊松分布的期望值和方差分别为:
E(x) = λ
Var(x) = λ
其中,E(x)表示事件发生的平均次数,Var(x)表示事件发生次数的方差。
总结起来,泊松分布的计算需要确定参数λ,使用概率密度函数或累积分布函数计算概率,使用期望值和方差计算分布的特征。
生成泊松分布的随机数

生成泊松分布的随机数随机数是计算机科学中的一个重要概念,它在模拟、加密、游戏等领域都扮演着重要的角色。
而生成随机数的方法也是多种多样的,其中包括泊松分布。
本文将介绍泊松分布的概念、性质以及如何生成泊松分布的随机数。
一、泊松分布的概念泊松分布是一种离散概率分布,它描述了在给定时间、空间或体积内某个事件发生的次数。
例如,某个工厂每小时生产的零件数量、某个公路上每小时通过的车辆数量等。
泊松分布的概率质量函数为:$P(x) = frac{lambda^x}{x!}e^{-lambda}$其中,$x$表示事件发生的次数,$lambda$表示单位时间、空间或体积内事件发生的平均次数。
二、泊松分布的性质泊松分布具有以下性质:1. 期望值:$mu = lambda$2. 方差:$sigma^2 = lambda$3. 无记忆性:即事件发生的概率与之前的事件发生情况无关。
三、生成泊松分布的随机数生成泊松分布的随机数有多种方法,下面介绍两种常见的方法。
1. 使用泊松分布的概率质量函数根据泊松分布的概率质量函数,可以使用以下方法生成泊松分布的随机数:Step 1:生成一个0到1之间的随机数$u$。
Step 2:令$x=0$,$p=e^{-lambda}$。
Step 3:重复执行以下步骤,直到$p<u$:- $x=x+1$- $p=p+frac{lambda^x}{x!}e^{-lambda}$Step 4:输出$x$。
2. 使用反函数变换法反函数变换法是一种常见的生成概率分布的随机数的方法。
对于泊松分布,其反函数为:$P(Xleq k) = sum_{i=0}^kfrac{lambda^i}{i!}e^{-lambda}$ 因此,可以使用以下方法生成泊松分布的随机数:Step 1:生成一个0到1之间的随机数$u$。
Step 2:令$k=0$,$p=0$。
Step 3:重复执行以下步骤,直到$p>u$:- $k=k+1$- $p=p+frac{lambda^{k-1}}{(k-1)!}e^{-lambda}$Step 4:输出$k-1$。
泊松分布的计算方法

泊松分布的计算方法泊松分布是统计学中的一种重要概率分布,广泛应用于各类随机事件的计数分析。
本文将详细介绍泊松分布的计算方法,帮助读者更好地理解和应用这一概念。
一、泊松分布的定义泊松分布描述了在固定时间或空间内,随机事件发生次数的概率分布。
其概率质量函数为:[ P(X=k) = frac{e^{-lambda} lambda^k}{k!} ]其中,( X ) 表示随机事件发生的次数,( k ) 为非负整数,( lambda ) 为事件在单位时间(或单位空间)内发生的平均次数,( e ) 为自然对数的底数。
二、泊松分布的计算方法1.确定参数( lambda )在实际应用中,首先需要确定事件在单位时间(或单位空间)内发生的平均次数( lambda )。
可以通过历史数据、实验观察等方法来估计( lambda ) 的值。
2.计算概率根据泊松分布的概率质量函数,可以计算出事件发生特定次数的概率。
例如,计算事件恰好发生( k ) 次的概率:[ P(X=k) = frac{e^{-lambda} lambda^k}{k!} ]3.计算累积概率有时候,我们需要计算事件发生次数小于等于某个值( k ) 的概率,即累积概率。
可以通过以下公式计算:[ P(X leq k) = sum_{i=0}^{k} frac{e^{-lambda} lambda^i}{i!} ]4.计算期望和方差泊松分布的期望和方差分别为:[ E(X) = lambda ][ Var(X) = lambda ]三、泊松分布的应用泊松分布广泛应用于以下领域:1.生物学:描述基因突变、病毒感染等随机事件的发生次数。
2.工程学:分析产品缺陷、故障等随机现象。
3.通信工程:计算信号传输过程中的错误码率。
4.保险业:评估保险事故发生的概率。
5.其他领域:如排队论、库存管理、质量控制等。
四、总结泊松分布是一种重要的概率分布,适用于描述随机事件发生次数的概率。
泊松分布联合分布律

泊松分布联合分布律泊松分布是离散随机变量的一种概率分布,可以用来描述单位时间(或空间)内随机事件发生的次数。
泊松分布的概率质量函数如下:P(X=k) = (e^(-λ) * λ^k) / k!其中,X表示随机变量的取值,k表示随机事件发生的次数,λ表示在单位时间(或空间)内平均发生的次数,e是自然对数的底数。
接下来我们考虑两个泊松分布随机变量X和Y,它们的参数分别为λX和λY。
我们可以求出它们的联合分布律。
首先,我们定义一个事件A,它表示随机变量X的取值为i (X=i),同时随机变量Y的取值为j(Y=j)。
我们可以表示事件A的概率为P(X=i, Y=j)。
然后,我们可以用X的概率质量函数和Y的概率质量函数来表示事件A的概率。
P(X=i, Y=j) = P(X=i) * P(Y=j)根据泊松分布的概率质量函数,我们可以将上式展开为:P(X=i, Y=j) = ((e^(-λX) * λX^i) / i!) * ((e^(-λY) * λY^j) / j!)接下来,我们可以用以上公式来计算任意的联合概率。
我们也可以计算出X和Y的边缘分布,即X和Y分别的概率分布。
对于X来说,它的边缘分布可以用如下公式表示:P(X=i) = Σ P(X=i, Y=j) = Σ ((e^(-λX) * λX^i) / i!) * ((e^(-λY) *λY^j) / j!)其中,Σ是求和符号,表示对所有可能的Y=j进行求和。
同样地,对于Y来说,它的边缘分布可以用如下公式表示:P(Y=j) = Σ P(X=i, Y=j) = Σ ((e^(-λX) * λX^i) / i!) * ((e^(-λY) *λY^j) / j!)其中,Σ是求和符号,表示对所有可能的X=i进行求和。
通过以上的联合分布律和边缘分布律,我们可以计算出泊松分布随机变量X和Y之间的一系列联合概率和边缘概率。
这些概率可以用来研究和分析随机事件发生的次数之间的相关性和依赖关系。
python二元泊松分布计算概率

一、Python概述Python是一种高级编程语言,具有清晰易读的语法和丰富的库。
它被广泛应用于数据分析、人工智能、网络开发等领域。
Python的简洁和强大使得它成为许多领域的首选编程语言之一。
二、泊松分布概念泊松分布是描述在一段固定时间或空间内事件发生次数的概率分布。
它适用于描述独立事件在连续或离散时间内的分布情况。
泊松分布的概率质量函数为:P(x) = (λ^x * e^(-λ)) / x!其中,λ是单位时间(或单位空间)内事件的平均发生率,x是事件发生的次数。
三、Python二元泊松分布计算概率使用Python可以方便地计算二元泊松分布的概率。
下面将介绍如何使用Python进行二元泊松分布的概率计算。
1. 导入库我们需要导入Python的一些数学计算库,例如numpy和scipy,以便进行计算。
```pythonimport numpy as npfrom scipy.stats import poisson```2. 输入参数接下来,我们需要输入二元泊松分布的参数,包括事件的平均发生率λ和事件发生的次数x。
```pythonlambda1 = 2lambda2 = 3x1 = 1x2 = 2```3. 计算概率我们利用scipy库中的泊松分布函数来计算概率。
```pythonP1 = poisson.pmf(x1, lambda1)P2 = poisson.pmf(x2, lambda2)print("事件发生次数为{}的概率为:{}".format(x1, P1))print("事件发生次数为{}的概率为:{}".format(x2, P2))```通过以上步骤,我们可以得到二元泊松分布中事件发生次数为x1和x2的概率。
四、示例代码下面是完整的示例代码:```pythonimport numpy as npfrom scipy.stats import poissonlambda1 = 2lambda2 = 3x1 = 1x2 = 2P1 = poisson.pmf(x1, lambda1)P2 = poisson.pmf(x2, lambda2)print("事件发生次数为{}的概率为:{}".format(x1, P1))print("事件发生次数为{}的概率为:{}".format(x2, P2))```五、总结本文介绍了如何使用Python进行二元泊松分布的概率计算。
numpy 泊松分布计算概率

numpy 泊松分布计算概率摘要:一、泊松分布简介1.泊松分布的定义2.泊松分布的概率计算公式3.泊松分布的适用场景二、使用numpy 计算泊松分布概率1.导入numpy 库2.设定事件发生的平均次数λ3.计算泊松分布的概率4.输出结果正文:泊松分布(Poisson Distribution)是一种离散型概率分布,用于描述在固定时间或空间内,事件发生的次数的概率分布。
在Python 中,可以使用numpy 库中的poisson 函数来计算泊松分布的概率。
一、泊松分布简介1.泊松分布的定义泊松分布是一种离散型概率分布,描述了在固定时间或空间内,事件发生的次数的概率分布。
其概率质量函数(Probability Mass Function,PMF)定义为:P(X=k) = (e^(-λ) * λ^k) / k!,其中λ表示事件发生的平均次数,k 表示实际发生的次数,e 表示自然对数的底数(约等于2.71828)。
2.泊松分布的概率计算公式泊松分布的概率计算公式为:P(X=k) = (e^(-λ) * λ^k) / k!,其中λ表示事件发生的平均次数,k 表示实际发生的次数,e 表示自然对数的底数(约等于2.71828)。
3.泊松分布的适用场景泊松分布适用于那些满足以下条件的场景:事件之间是独立的,且在固定时间或空间内,事件发生的概率是恒定的。
例如:在一定时间内,某个网站的访问次数、某个电话交换台的电话呼叫次数等。
二、使用numpy 计算泊松分布概率1.导入numpy 库在Python 中,我们可以使用numpy 库中的poisson 函数来计算泊松分布的概率。
首先,需要导入numpy 库:```pythonimport numpy as np```2.设定事件发生的平均次数λ假设我们想要计算在一定时间内,某个事件发生的概率。
我们可以先设定事件发生的平均次数λ:```pythonlambda_value = 5```3.计算泊松分布的概率接下来,我们可以使用numpy 的poisson 函数计算泊松分布的概率:```pythonpoisson_probability = np.poisson(lambda_value)```4.输出结果最后,我们将计算得到的泊松分布的概率输出到控制台:```pythonprint("泊松分布的概率:", poisson_probability)```在这个示例中,我们设定了事件发生的平均次数为5,然后使用numpy 的poisson 函数计算泊松分布的概率。
泊松公式、泊松分布与大数定律

====Word 行业资料分享--可编辑版本--双击可删====
源-于-网-络-收-集 7. 泊松公式、泊松分布与泊松大数定律
泊松(Possion )的名字对学概率论与数理统计的人来说,可谓耳熟能详。
原因主要在于泊松近似公式,以及更重要的,原于该近似公式的泊松分布,分布的重要性和知名度在离散型分布中仅次于二项分布。
泊松的另一个重要工作是把伯努利大数定律推广到每次试验中事件发生的概率可以不同的情况,现称泊松大数定律。
继狄莫佛给出二项概率近似计算公式(10)之后,丹尼尔和拉普拉斯也给出了二项概率近似计算公式,但这些公式在现今的教科书上已很少提及,只有泊松近似公式则不然,其形式为
,
!),,(lim k e k p N b k N λλ-∞→= (11) 其中Np N ∞→=lim λ,N k ,,2,1,0 =。
公式(11)在教科书上通称为泊松逼近公式、泊松近似公式
或泊松公式。
它是泊松在1838年于一本有关《概率在法律审判的应用》一书中所引进,此公式适用于p 很小,N 很大而Np 又不甚大时,这正好填补了狄莫佛公式(10)的不足,因后者只适用于p 不太接近于0和1的时候。
不过,从历史上看,狄莫佛早在1712年已实质上做出了这个结果。
泊松分布简单解释

泊松分布简单解释
嘿,朋友!你知道泊松分布吗?这玩意儿可有意思啦!咱就说,假如你在一个热闹的大街上,每分钟平均有 3 个人走过,那下一分钟正好走过 5 个人的概率是多少呢?这就是泊松分布要研究的呀!
比如说,一个面包店平均每小时卖出 10 个面包,那这一小时卖出 8 个面包的可能性有多大呢?这就好像抛硬币,你知道正面朝上的概率是二分之一,但泊松分布是在研究更复杂一些的情况呢!
泊松分布就像是一个神奇的工具,能帮我们理解和预测很多这种类似的随机事件。
它不是死板的,是很灵活的哦!好比天气预报,虽然不能百分百准确,但能给我们一个大概的情况。
再举个例子,一个图书馆平均每天有 50 个人来借书,那某天来 45 个人借书的概率是多少呢?这就是泊松分布能解答的问题呀!它不是高高在上、遥不可及的,而是和我们的生活息息相关的呢!
你想想看,生活中有多少事情是这种不确定的呀!泊松分布不就是在帮我们在这种不确定中找到一些规律嘛!这不就像在黑暗中找到一盏明灯吗?难道你不想了解一下这么神奇的东西吗?
我的观点就是泊松分布真的超级实用,它能让我们更好地理解和应对生活中的各种随机现象,就像是给我们配备了一副特殊的眼镜,能看到别人看不到的规律和可能性!。
讲解最清楚的泊松分布

讲解最清楚的泊松分布
一、泊松分布
日常生活中,大量事件是有固定频率的。
-某医院平均每小时出生3个婴儿
-某公司平均每10分钟接到1个电话
-某超市平均每天销售4包xx牌奶粉
-某网站平均每分钟有2次访问
它们的特点就是,我们可以预估这些事件的总数,但是没法知道具体的发生时间。
已知
平均每小时出生3个婴儿,请问下一个小时,会出生几个?
有可能一下子出生6个,也有可能一个都不出生。
这是我们没法知道的。
泊松分布就是描述某段时间内,事件具体的发生概率。
上面就是泊松分布的公式。
等号的左边,P表示概率,N表示某种函数关系,t表示时间,n表示数量,1小时内出生3个婴儿的概率,就表示为P(N(1) = 3)。
等号的右边,久表示事件的频率。
接下来两个小时,一个婴儿都不出生的概率是0.25%,基本不可能发生。
P 网2)=。
)"心2
0! 牝
0.0025
P(N(t) =n)= (Xt)n e~xt
nl
接下来一个小时,至少出生两个婴儿的概率是80%。
小都不太可能。
每小时出生3个婴儿,这是最可能的结果,出生得越多或越少,就越不可能。
泊松分布概率

泊松分布概率一、概述泊松分布是一种离散型概率分布,用于描述在一个固定时间内,某个事件发生的次数。
它的特点是:事件发生的概率相互独立,且在单位时间内发生的平均次数是已知的。
二、定义设随机变量X表示在一个固定时间内某个事件发生的次数,如果X服从参数为λ(λ>0)的泊松分布,则其概率函数为:P(X=k)=e^(-λ) * λ^k / k!其中k为非负整数。
三、性质1. 期望和方差泊松分布的期望和方差都等于λ。
2. 概率函数图像泊松分布的概率函数图像呈现出单峰形态,当λ越大时,峰值越靠近x=λ处。
3. 泊松定理当n很大,p很小时,二项分布可以近似地用泊松分布代替。
即当n→∞,p→0且np=λ时,P(X=k)=e^(-λ) * λ^k / k!近似地等于:P(X=k)=e^(-np) * (np)^k / k!四、应用场景1. 电话交换机中呼叫中心接待电话数量的统计分析。
2. 网络流量的统计分析。
3. 人口出生、死亡、移民等事件的统计分析。
4. 汽车交通事故发生的概率分析。
五、例题1. 在某个工厂,每小时平均有2件次品,求下列事件的概率:(1)这个小时不出现次品;(2)这个小时出现了4件次品。
解:设X表示一个小时内出现次品的件数,则X服从参数为λ=2的泊松分布。
根据公式可得:(1)P(X=0)=e^(-2) * 2^0 / 0!=0.1353;(2)P(X=4)=e^(-2) * 2^4 / 4!=0.0902。
因此,这个小时不出现次品的概率为0.1353,出现了4件次品的概率为0.0902。
2. 某网站每分钟平均接收到10个访问请求,求下列事件的概率:(1)这一分钟接收到了13个访问请求;(2)两分钟内接收到了20个访问请求以上的概率。
解:设X表示一分钟内接收到访问请求的数量,则X服从参数为λ=10的泊松分布。
根据公式可得:(1)P(X=13)=e^(-10) * 10^13 / 13!=0.0729;(2)P(X>20)=1-P(X≤20)=1-∑(k=0~20) e^(-10) * 10^k /k!=0.0006。
泊松分布定理

一、社会生活对服务的各种要求
某电话交换台在一段时间内收到的电话呼叫数; 一个售货员接待的顾客数; 公共汽车站在一段时间内来到的乘客数等等 都近似服从泊松分布。
二、物理学和生物学领域
一放射性源放射出的 粒子数; 放射性分裂落在某区域的质点数,热电子的发射 显微镜下落在某区域中的血球或微生物的数目
定理1(泊松Poisson定理)
设λ>0是一常数,n是正整数,若limnpn=λ,则 对任一固定的非负整数k,有
lim C p (1 pn )
n k n k n
nk
k
k!
e
一、泊松分布的定义及图形特点
设随机变量X所有可能取的值为0 , 1 , 2 , … , 且概率分布为:
P ( X k ) e
无后效性: 在不相重叠的时间段内,事件的发生是相 互独立的. 普通性:
如果时间区间充分小,事件出现两次或 两次以上的概率可忽略不计.
例如
一放射性源放射出的 粒子数; 某电话交换台收到的电话呼叫数; 到某机场降落的飞机数; 一个售货员接待的顾客数; 一台纺纱机的断头数; …
ห้องสมุดไป่ตู้
都可以看作泊松流.
对泊松流,在任意时间间隔(0,t)内,事件 (如交通事故)出现的次数服从参数为 λ t 的 泊松分布 . λ 称为泊松流的强度.
泊松分布产生的一般条件
在自然界和人们的现实生活中,经常要遇 到在随机时刻出现的某种事件.我们把在随机 时刻相继出现的事件所形成的序列,叫做随机 事件流. 若事件流具有平稳性、无后效性、普通性, 则称该事件流为泊松事件流(泊松流).
下面简要解释平稳性、无后效性、普通性.
平稳性:
