正交投影神经网络的BP和GS杂交学习算法

合集下载

BP神经网络详解-最好的版本课件(1)

月份 1
销量月份销量
2056 7
1873
2
2395 8
1478
3
2600 9
1900
4
2298 10
1500
5
1634 11
2046
6
1600 12
1556
BP神经网络学习算法的MATLAB实现
➢%以每三个月的销售量经归一化处理后作为输入
P=[0.5152
0.8173 1.0000 ;
0.8173
计算误差函数对输出层的各神经元的偏导
数
。 o ( k )
p
e e yio w ho y io w ho
(
yio(k) h who
whohoh(k)bo)
who
hoh(k)
e
yio
(12oq1(do(k)yoo(k)))2 yio
(do(k)yoo(k))yoo(k)
(do(k)yoo(k))f(yio(k)) o(k)
1.0000 0.7308;
1.0000
0.7308 0.1390;
0.7308
0.1390 0.1087;
0.1390
0.1087 0.3520;
0.1087
0.3520 0.0000;]';
➢%以第四个月的销售量归一化处理后作为目标向量
T=[0.7308 0.1390 0.1087 0.3520 0.0000 0.3761];
BP神经网络模型
三层BP网络
输入层 x1
x2
隐含层
输出层
-
y1
z1
1
T1
y2
z2
-
2

bp神经网络的原理

bp神经网络的原理BP神经网络（也称为反向传播神经网络）是一种基于多层前馈网络的强大机器学习模型。

它可以用于分类、回归和其他许多任务。

BP神经网络的原理基于反向传播算法，通过反向传播误差来调整神经网络的权重和偏差，从而使网络能够学习和适应输入数据。

BP神经网络的基本结构包括输入层、隐藏层和输出层。

每个层都由神经元组成，每个神经元都与上一层的所有神经元连接，并具有一个权重值。

神经元的输入是上一层的输出，通过加权和和激活函数后得到输出。

通过网络中的连接和权重，每层的输出被传递到下一层，最终得到输出层的结果。

BP神经网络的训练包括两个关键步骤：前向传播和反向传播。

前向传播是指通过网络将输入数据从输入层传递到输出层，计算网络的输出结果。

反向传播是基于网络输出结果与真实标签的误差，从输出层向输入层逆向传播误差，并根据误差调整权重和偏差。

在反向传播过程中，通过计算每个神经元的误差梯度，我们可以使用梯度下降算法更新网络中的权重和偏差。

误差梯度是指误差对权重和偏差的偏导数，衡量了误差对于权重和偏差的影响程度。

利用误差梯度，我们可以将误差从输出层反向传播到隐藏层和输入层，同时更新每层的权重和偏差，从而不断优化网络的性能。

通过多次迭代训练，BP神经网络可以逐渐减少误差，并提高对输入数据的泛化能力。

然而，BP神经网络也存在一些问题，如容易陷入局部最优解、过拟合等。

为了克服这些问题，可以采用一些技巧，如正则化、随机初始权重、早停等方法。

总结而言，BP神经网络的原理是通过前向传播和反向传播算法来训练网络，实现对输入数据的学习和预测。

通过调整权重和偏差，网络可以逐渐减少误差，提高准确性。

bp神经训练目标

BP（反向传播）神经网络的训练目标通常是通过最小化预测误差来优化网络的性能。

预测误差通常使用损失函数来衡量，损失函数描述了实际输出值与预测输出值之间的差异。

在BP神经网络中，常见的训练目标包括：
1. 均方误差（Mean Squared Error, MSE）：MSE是最常用的训练目标，它计算预测值与真实值之间的平均平方差。

MSE的计算公式为：
```
MSE = 1/N * Σ(y_pred - y_true)^2
```
其中，N为样本数量，y_pred为预测值，y_true为真实值。

2. 交叉熵损失（Cross-Entropy Loss）：交叉熵损失常用于多分类问题，它衡量预测概率分布与真实概率分布之间的差异。

交叉熵损失的计算公式为：
```
cross_entropy_loss = -Σ[y_true * log(y_pred)]
```
其中，y_true为真实概率分布，y_pred为预测概率分布。

3. 对数损失（Log Loss）：对数损失也是一种常见的训练目标，它适用于二分类问题，计算预测值与真实值之间的对数损失。

对数损失的计算公式为：
```
log_loss = -[y_true * log(1 - y_pred) + (1 - y_true) * log(y_pred)]
```
其中，y_true为真实值（0或1），y_pred为预测值（0或1）。

bp算法公式

bp算法公式
BP算法是一种常用的人工神经网络训练算法。

其全称为“反向传播算法”，其基本思想是利用链式求导法则，通过计算输出误差对每个权重的偏导数来更新网络中各层之间的连接权重，从而不断调整网络参数直到达到预定的训练目标。

BP算法的公式如下：
1. 前向传播
对于输入样本x，在神经网络中进行前向传播，计算出每个神经元的输出值，并将这些值作为输入传递到下一层神经元中，直至输出层。

2. 计算误差项
对于输出层每个神经元j，计算其误差项δj = yj - tj，其中yj为神经元j的输出值，tj为样本对应的真实标签值。

3. 反向传播
从输出层开始，计算每个神经元的误差项，然后根据误差项计算每个权重的偏导数，最后根据偏导数调整权重。

对于隐藏层每个神经元h，其误差项δh可由以下公式计算：
δh = f"(netH) * Σ(δj * wjh)
其中f"为h的激活函数的导数，netH表示神经元h的净输入，wjh为从神经元h到神经元j的权重，Σ表示对输出层每个神经元j 求和。

对于连接h->j的权重wjh，其偏导数可以使用以下公式计算： E/wjh = δj * ah
其中ah为连接h->j的输入值。

4. 更新权重
根据计算出来的各个权重的偏导数，利用梯度下降法更新权重。

具体地，对于权重wjh，更新方式为：
wjh = wjh - η * E/wjh
其中η为学习率，即权重的调整步长。

bp算法原理

bp算法原理BP算法原理BP算法是神经网络中应用最广泛的一种学习算法，它的全称是“反向传播算法”，用于训练多层前馈神经网络。

BP算法基于误差反向传播原理，即先通过前向传播计算网络输出值，再通过反向传播来调整各个神经元的权重，使误差函数最小化。

BP算法的步骤如下：1. 初始化：随机初始化网络每个神经元的权重，包括输入层、隐藏层和输出层的神经元的权重。

2. 前向传播：将训练样本输送到输入层，通过乘积和运算得到每个隐藏层神经元的输出，再通过激活函数得到隐藏层神经元的实际输出值。

然后，将隐藏层的输出值输送到输出层，按照同样的方法计算输出层神经元的输出值。

3. 反向传播：通过误差函数计算输出层神经元的误差值，然后反向传播计算隐藏层神经元的误差值。

4. 权值调整：按照梯度下降法，计算误差对每个神经元的权重的偏导数，根据偏导数的大小来调整各个神经元的权重，使误差逐渐减小。

5. 重复步骤2~4，直到误差小到一定程度或者训练次数达到预定值。

其中，误差函数可以选择MSE（Mean Squared Error）函数，也可以选择交叉熵函数等其他函数，不同的函数对应不同的优化目标。

BP算法原理的理解需要理解以下几个方面：1. 神经元的输入和输出：神经元的输入是由上一层神经元的输出和它们之间的权重乘积的和，加上神经元的偏置值（常数）。

神经元的输出是通过激活函数把输入值转化为输出值。

2. 前向传播和反向传播：前向传播是按照输入层到输出层的顺序计算神经元的输出值。

反向传播是一种误差反向传播的过程，它把误差从输出层往回传递，计算出每个神经元的误差，然后调整各个神经元的权重来使误差逐渐减小。

3. 梯度下降法：梯度下降法是一种优化算法，根据误差函数的梯度方向来寻找误差最小的点。

BP算法就是基于梯度下降法来优化误差函数的值，使神经网络的输出结果逼近实际值。

综上所述，BP算法是一种常用的神经网络学习算法，它利用前向传播和反向传播的过程来调整神经元的权重，不断优化误差函数的值，从而使神经网络的输出结果更加准确。

机器学习-BP(back propagation)神经网络介绍

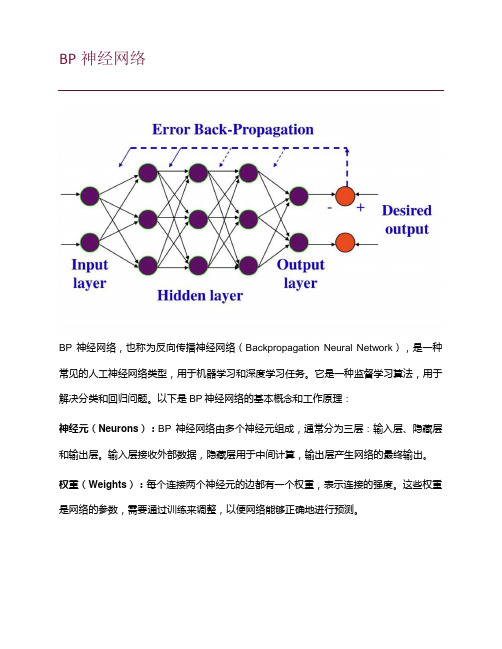
BP神经网络BP神经网络，也称为反向传播神经网络（Backpropagation Neural Network），是一种常见的人工神经网络类型，用于机器学习和深度学习任务。

它是一种监督学习算法，用于解决分类和回归问题。

以下是BP神经网络的基本概念和工作原理：神经元（Neurons）：BP神经网络由多个神经元组成，通常分为三层：输入层、隐藏层和输出层。

输入层接收外部数据，隐藏层用于中间计算，输出层产生网络的最终输出。

权重（Weights）：每个连接两个神经元的边都有一个权重，表示连接的强度。

这些权重是网络的参数，需要通过训练来调整，以便网络能够正确地进行预测。

激活函数（Activation Function）：每个神经元都有一个激活函数，用于计算神经元的输出。

常见的激活函数包括Sigmoid、ReLU（Rectified Linear Unit）和tanh（双曲正切）等。

前向传播（Forward Propagation）：在训练过程中，输入数据从输入层传递到输出层的过程称为前向传播。

数据经过一系列线性和非线性变换，最终产生网络的预测输出。

反向传播（Backpropagation）：反向传播是BP神经网络的核心。

它用于计算网络预测的误差，并根据误差调整网络中的权重。

这个过程分为以下几个步骤：1.计算预测输出与实际标签之间的误差。

2.将误差反向传播回隐藏层和输入层，计算它们的误差贡献。

3.根据误差贡献来更新权重，通常使用梯度下降法或其变种来进行权重更新。

训练（Training）：训练是通过多次迭代前向传播和反向传播来完成的过程。

目标是通过调整权重来减小网络的误差，使其能够正确地进行预测。

超参数（Hyperparameters）：BP神经网络中有一些需要人工设置的参数，如学习率、隐藏层的数量和神经元数量等。

这些参数的选择对网络的性能和训练速度具有重要影响。

BP神经网络在各种应用中都得到了广泛的使用，包括图像分类、语音识别、自然语言处理等领域。

BP算法的基本原理

BP算法的基本原理BP算法（反向传播算法）是一种神经网络训练算法，用于更新神经网络的权重和偏置，以使之能够适应所需任务的输入输出关系。

BP算法基于梯度下降优化方法，通过求解损失函数关于权重和偏置的偏导数来进行参数更新。

其基本原理涉及到神经网络的前向传播和反向传播两个过程。

以下将详细介绍BP算法的基本原理。

1.前向传播：在神经网络的前向传播过程中，输入数据通过网络的各个层，通过各个神经元的激活函数，最终得到网络的输出。

在前向传播过程中，每个神经元接收到上一层的信号，并通过权重和偏置进行加权求和，然后经过激活函数处理后输出。

具体而言，假设神经网络有L层，第l层的神经元为h(l)，输入为x，激活函数为f(l)，权重为w(l)，偏置为b(l)。

其中，输入层为第1层，隐藏层和输出层分别为第2层到第L层。

对于第l层的神经元h(l)，其输入信号为：z(l)=w(l)*h(l-1)+b(l)其中，h(l-1)表示第(l-1)层的神经元的输出。

然后，通过激活函数f(l)处理输入信号z(l)得到第l层的输出信号：h(l)=f(l)(z(l))。

依次类推，通过前向传播过程，神经网络可以将输入信号转化为输出信号。

2.反向传播：在神经网络的反向传播过程中，根据网络的输出和真实值之间的差异，通过链式法则来计算损失函数对于各层权重和偏置的偏导数，然后根据梯度下降法则对权重和偏置进行更新。

具体而言，假设网络的输出为y，损失函数为L，权重和偏置为w和b，求解L对w和b的偏导数的过程为反向传播。

首先，计算L对于网络输出y的偏导数：δ(L)/δy = dL(y)/dy。

然后，根据链式法则，计算L对于第L层的输入信号z(L)的偏导数：δ(L)/δz(L)=δ(L)/δy*δy/δz(L)。

接着，计算L对于第(L-1)层的输入信号z(L-1)的偏导数：δ(L)/δz(L-1) = δ(L)/δz(L) * dz(L)/dz(L-1)。

依次类推，通过链式法则得到L对于各层输入信号z(l)的偏导数。

BP算法的基本原理

BP算法的基本原理BP算法，全称为反向传播算法（Back Propagation），是一种用于训练人工神经网络的常用算法。

它基于梯度下降的思想，通过不断地调整网络中的权值和偏置来最小化预测值与实际值之间的误差。

在前向传播阶段，输入数据通过网络的各个层，产生输出结果。

首先，每个输入特征通过输入层的神经元传递，并在隐藏层中进行加权求和。

在隐藏层中，每个神经元根据激活函数的结果计算输出值，然后传递给下一层的神经元。

最后，输出层的神经元根据激活函数的结果计算输出结果，并与实际值进行比较。

在反向传播阶段，误差被反向传播回网络中的每个神经元，从而计算每个权值和偏置的梯度，以便调整它们的值。

首先，计算输出层误差，即预测值与实际值之间的差异。

然后，将输出层误差反向传播到隐藏层和输入层，计算每个神经元的误差。

最后，根据误差和激活函数的导数，计算每个权值和偏置的梯度。

通过计算梯度，可以根据梯度下降的思想，按照一定的学习率调整每个权值和偏置的值。

学习率决定了每次调整的幅度，通常设置为一个小的正数。

在调整过程中，权值和偏置会根据梯度的方向逐渐减小误差，直到达到最小化误差的目标。

总结起来，BP算法的基本原理可以归纳为以下几个步骤：1.初始化网络的权值和偏置。

2.前向传播：输入数据通过网络的各个层，产生输出结果。

3.计算输出层误差：根据预测值和实际值之间的差异，计算输出层的误差。

4.反向传播：将输出层误差反向传播到隐藏层和输入层，并计算每个神经元的误差。

5.计算梯度：根据误差和激活函数的导数，计算每个权值和偏置的梯度。

6.根据梯度下降的思想，按照一定的学习率调整每个权值和偏置的值。

7.重复步骤2~6，直到达到最小化误差的目标。

需要注意的是，BP算法可能会面临一些问题，例如局部极小值和过拟合等。

为了解决这些问题，可以采用一些改进的技术，例如随机梯度下降、正则化等方法。

总之，BP算法是一种通过调整权值和偏置来训练人工神经网络的常用算法。

BP神经网络算法步骤

BP神经网络算法步骤
1.初始化神经网络参数
-设置网络的输入层、隐藏层和输出层的神经元数目。

-初始化权重和偏置参数，通常使用随机小值进行初始化。

2.前向传播计算输出
-将输入样本数据传入输入层神经元。

-根据权重和偏置参数，计算隐藏层和输出层神经元的输出。

- 使用激活函数（如Sigmoid函数）将输出映射到0到1之间。

3.计算误差
4.反向传播更新权重和偏置
-根据误差函数的值，逆向计算梯度，并将梯度传播回网络中。

-使用链式法则计算隐藏层和输出层的梯度。

-根据梯度和学习率参数，更新权重和偏置值。

5.重复迭代训练
-重复执行2-4步，直到网络输出误差满足预定的停止条件。

-在每次迭代中，使用不同的训练样本对网络进行训练，以提高泛化性能。

-可以设置训练轮数和学习率等参数来控制训练过程。

6.测试和应用网络
-使用测试集或新样本对训练好的网络进行测试。

-将测试样本输入网络，获取网络的输出结果。

-根据输出结果进行分类、回归等任务，评估网络的性能。

7.对网络进行优化
-根据网络在训练和测试中的性能，调整网络的结构和参数。

-可以增加隐藏层的数目，改变激活函数，调整学习率等参数，以提高网络的性能。

以上是BP神经网络算法的基本步骤。

在实际应用中，还可以对算法进行改进和扩展，如引入正则化技术、批量更新权重等。

同时，数据的预处理和特征选择也对网络的性能有着重要的影响。

在使用BP神经网络算法时，需要根据实际问题对网络参数和训练策略进行适当调整，以获得更好的结果。

bp算法流程

bp算法流程BP算法流程。

BP（Back Propagation）算法是一种常用的神经网络训练算法，它通过不断地调整神经网络的权重和偏置来最小化神经网络的输出与实际值之间的误差，从而使神经网络能够更好地完成特定的任务。

下面将详细介绍BP算法的流程。

1. 初始化神经网络。

首先，我们需要初始化神经网络的结构，包括输入层、隐藏层和输出层的神经元数量，以及它们之间的连接权重和偏置。

通常情况下，这些参数可以随机初始化，然后通过BP算法来不断调整以适应具体的任务。

2. 前向传播。

在前向传播过程中，输入样本会经过输入层，通过隐藏层逐层传播至输出层，最终得到神经网络的输出结果。

在每一层中，神经元会根据输入和当前的权重、偏置计算出输出，并将输出传递给下一层的神经元。

整个过程可以用数学公式表示为：\[a^l = \sigma(w^la^{l-1} + b^l)\]其中，\(a^l\)表示第l层的输出，\(\sigma\)表示激活函数，\(w^l\)和\(b^l\)分别表示第l层的权重和偏置，\(a^{l-1}\)表示上一层的输出。

3. 计算误差。

在前向传播过程中，我们得到了神经网络的输出结果，接下来需要计算输出结果与实际值之间的误差。

通常情况下，我们会使用均方误差（MSE）来衡量输出结果与实际值之间的差异。

\[E = \frac{1}{2}\sum_{i=1}^{n}(y_i o_i)^2\]其中，\(E\)表示总误差，\(n\)表示样本数量，\(y_i\)表示第i个样本的实际值，\(o_i\)表示第i个样本的输出值。

4. 反向传播。

在反向传播过程中，我们需要根据误差来调整神经网络的权重和偏置，以减小误差。

这一过程可以通过梯度下降法来实现，即沿着误差下降最快的方向调整参数。

\[w^l \leftarrow w^l \eta\frac{\partial E}{\partialw^l}\]\[b^l \leftarrow b^l \eta\frac{\partial E}{\partialb^l}\]其中，\(\eta\)表示学习率，\(\frac{\partial E}{\partial w^l}\)和\(\frac{\partial E}{\partial b^l}\)分别表示误差对权重和偏置的偏导数。

BP神经网络算法实验报告

计算各层的输入和输出
es
计算输出层误差 E(q)
E(q)<ε
修正权值和阈值
结
束
图 2-2 BP 算法程序流程图
3、实验结果
任课教师：何勇强
日期： 2010 年 12 月 24 日
中国地质大学（北京）课程名称：数据仓库与数据挖掘班号：131081 学号：13108117 姓名：韩垚成绩：
任课教师：何勇强
（2-7）
wki
输出层阈值调整公式：
（2-8）
ak
任课教师：何勇强
E E netk E ok netk ak netk ak ok netk ak
（2-9）
日期： 2010 年 12 月 24 日
中国地质大学（北京）课程名称：数据仓库与数据挖掘隐含层权值调整公式：班号：131081 学号：13108117 姓名：韩垚成绩：
Ep
系统对 P 个训练样本的总误差准则函数为：
1 L (Tk ok ) 2 2 k 1
（2-5）
E
1 P L (Tkp okp )2 2 p 1 k 1
（2-6）
根据误差梯度下降法依次修正输出层权值的修正量 Δwki，输出层阈值的修正量 Δak，隐含层权值的修正量 Δwij，隐含层阈值的修正量
日期： 2010 年 12 月 24 日
隐含层第 i 个节点的输出 yi：
M
yi (neti ) ( wij x j i )
j 1
（2-2）
输出层第 k 个节点的输入 netk：
q q M j 1
netk wki yi ak wki ( wij x j i ) ak

BP算法程序实现

BP算法程序实现BP算法（Back Propagation Algorithm，即反向传播算法）是一种用于训练神经网络的常用算法。

它的基本思想是通过不断地调整神经元之间的连接权值，使得网络的输出接近于期望的输出。

在实现BP算法时，需要进行以下几个步骤：1.初始化参数：首先，需要初始化神经网络的权值和偏置，通常可以使用随机的小数来初始化。

同时，需要设置好网络的学习率和最大迭代次数。

2.前向传播：通过前向传播过程，将输入数据输入到神经网络中，并计算出每个神经元的输出。

具体来说，对于第一层的神经元，它们的输出即为输入数据。

对于后续的层，可以使用如下公式计算输出：a[i] = sigmoid(z[i])其中，a[i]表示第i层的输出，z[i]为第i层的输入加权和，sigmoid为激活函数。

3.计算误差：根据网络的输出和期望的输出，可以计算出网络的误差。

一般来说，可以使用均方差作为误差的度量指标。

loss = 1/(2 * n) * Σ(y - a)^2其中，n为训练样本的数量，y为期望输出，a为网络的实际输出。

4.反向传播：通过反向传播算法，将误差从输出层向输入层逐层传播，更新权值和偏置。

具体来说，需要计算每一层神经元的误差，并使用如下公式更新权值和偏置：delta[i] = delta[i+1] * W[i+1]' * sigmoid_derivative(z[i])W[i] = W[i] + learning_rate * delta[i] * a[i-1]'b[i] = b[i] + learning_rate * delta[i]其中，delta[i]为第i层的误差，W[i]为第i层与i+1层之间的权值，b[i]为第i层的偏置，learning_rate为学习率，sigmoid_derivative为sigmoid函数的导数。

5.迭代更新：根据步骤4中的更新公式，不断迭代调整权值和偏置，直到达到最大迭代次数或误差小于一些阈值。

BP神经网络算法步骤

BP神经网络算法步骤1.初始化网络参数：首先，需要确定网络的架构，包括输入层、输出层和隐藏层的数量和节点数。

然后，通过随机选取初始权重和阈值来初始化网络参数，这些参数将用于每个节点的计算。

2.前向传播计算：对于每个输入样本，将其输入到网络中，通过计算每个节点的输出来实现前向传播。

每个节点的输入是上一层节点的输出，通过加权求和并使用激活函数得到节点的输出。

3.计算误差：对于每个输出节点，将其输出与实际的目标值进行比较，得到误差。

通常使用均方误差函数来计算误差。

4.反向传播调整权重：根据误差大小来调整网络的权重和阈值。

先从输出层开始计算误差梯度，并根据梯度下降算法调整输出层的权重和阈值。

然后，逐层向前计算误差梯度并调整隐藏层的权重和阈值，直到达到输入层。

5.更新参数：根据反向传播计算得到的梯度更新网络的参数。

通常使用梯度下降法来更新权重和阈值。

梯度下降法根据每个参数的梯度进行参数更新，以使误差最小化。

6.重复迭代：通过多次重复迭代步骤2到步骤5，持续调整网络参数，使得网络能够逐渐学习和逼近目标函数。

每次迭代都会计算新的误差和梯度，并根据梯度下降法更新参数。

7.终止条件：迭代过程应设置一个终止条件，通常是达到一定的最大迭代次数或者误差的变化小到一定程度时停止。

8.测试网络性能：使用测试数据集对训练好的网络进行性能评估。

将测试数据输入网络中，通过前向传播计算输出结果，并与实际结果进行比较，计算准确率或其他性能指标。

以上就是BP神经网络算法的基本步骤。

这个算法能够通过不断的反向传播和参数更新，使得网络能够学习和逼近非线性函数，是一种非常常用的神经网络算法。

bp网络的基本原理

bp网络的基本原理bp网络是一种常用的人工神经网络模型，用于模拟和解决复杂问题。

它是一种前馈型神经网络，通过前向传播和反向传播的过程来实现信息的传递和参数的更新。

在bp网络中，首先需要定义输入层、隐藏层和输出层的神经元。

输入层接收外部输入的数据，隐藏层用于处理和提取数据的特征，输出层用于输出最终的结果。

每个神经元都有一个对应的权重和偏置，用于调节输入信号的强弱和偏移。

前向传播是bp网络中的第一步，它从输入层开始，将输入的数据通过每个神经元的加权和激活函数的运算，逐层传递到输出层。

加权和的计算公式为：S = Σ(w * x) + b其中，w是权重，x是输入，b是偏置。

激活函数则负责将加权和的结果转换为神经元的输出。

常用的激活函数有sigmoid 函数、ReLU函数等。

反向传播是bp网络的第二步，它通过比较输出层的输出与实际值之间的误差，反向计算每个神经元的误差，并根据误差调整权重和偏置。

反向传播的目标是不断减小误差，使神经网络的输出与实际值更加接近。

具体的反向传播算法是通过梯度下降法实现的，它通过计算每个神经元的误差梯度，按照梯度的方向更新权重和偏置。

误差梯度表示误差对权重和偏置的变化率，通过链式法则可以计算得到。

在更新权重和偏置时，一般使用学习率来调节更新的步长，避免权重和偏置的变化过大。

通过多次迭代的前向传播和反向传播过程，bp网络不断优化和调整参数，最终使得输出与实际值的误差达到最小。

这样的训练过程可以使bp网络逐渐学习到输入数据之间的关联性和规律性，从而达到对问题进行分类、回归等任务的目的。

总结起来，bp网络的基本原理是通过前向传播将输入的数据逐层传递并计算每个神经元的输出，然后通过反向传播根据实际输出与目标输出之间的误差来调整权重和偏置，最终达到训练和优化神经网络的目标。

BP神经网络的基本原理_一看就懂

BP神经网络的基本原理_一看就懂BP神经网络（Back propagation neural network）是一种常用的人工神经网络模型，也是一种有监督的学习算法。

它基于错误的反向传播来调整网络权重，以逐渐减小输出误差，从而实现对模型的训练和优化。

1.初始化网络参数首先，需要设置网络的结构和连接权重。

BP神经网络通常由输入层、隐藏层和输出层组成。

每个神经元与上下层之间的节点通过连接权重相互连接。

2.传递信号3.计算误差实际输出值与期望输出值之间存在误差。

BP神经网络通过计算误差来评估模型的性能。

常用的误差计算方法是均方误差（Mean Squared Error，MSE），即将输出误差的平方求和后取平均。

4.反向传播误差通过误差反向传播算法，将误差从输出层向隐藏层传播，并根据误差调整连接权重。

具体来说，根据误差对权重的偏导数进行计算，然后通过梯度下降法来更新权重值。

5.权重更新在反向传播过程中，通过梯度下降法来更新权重值，以最小化误差。

梯度下降法的基本思想是沿着误差曲面的负梯度方向逐步调整权重值，使误差不断减小。

6.迭代训练重复上述步骤，反复迭代更新权重值，直到达到一定的停止条件，如达到预设的训练轮数、误差小于一些阈值等。

迭代训练的目的是不断优化模型，使其能够更好地拟合训练数据。

7.模型应用经过训练后的BP神经网络可以应用于新数据的预测和分类。

将新的输入数据经过前向传播，可以得到相应的输出结果。

需要注意的是，BP神经网络对于大规模、复杂的问题，容易陷入局部最优解，并且容易出现过拟合的情况。

针对这些问题，可以采用各种改进的方法，如加入正则化项、使用更复杂的网络结构等。

综上所述，BP神经网络通过前向传播和反向传播的方式，不断调整权重值来最小化误差，实现对模型的训练和优化。

它是一种灵活、强大的机器学习算法，具有广泛的应用领域，包括图像识别、语音识别、自然语言处理等。

JAVA实现BP神经网络算法

JAVA实现BP神经网络算法BP神经网络是一种基于误差逆传播算法的人工神经网络模型，它可以用于解决分类、回归和模式识别等问题。

在本文中，将介绍BP神经网络的基本原理以及如何使用Java实现该算法。

首先，要了解BP神经网络的基本原理。

BP神经网络由输入层、隐藏层和输出层组成。

输入层负责接收输入数据，隐藏层用来处理输入数据并学习特征，输出层用来产生最终的输出结果。

BP神经网络的训练过程主要包括前向传播和反向传播两个阶段。

前向传播是指从输入层到输出层的过程，其中输入数据通过隐藏层传递到输出层，不断调整参数权重，直到产生最终的输出结果。

隐藏层中的每个神经元都会计算输入的加权和，并将其传递给激活函数进行激活，然后将结果传递给下一层。

反向传播是指从输出层到输入层的过程，其中通过比较输出结果和期望结果的差异来计算误差。

然后将误差沿着网络的方向向后传播，逐层调整权重和偏差，以减小误差。

反向传播使用梯度下降法来更新网络参数，直到达到一定的停止条件。

接下来，我们将介绍如何使用Java实现BP神经网络算法。

首先，我们需要定义一个神经元类，该类包含神经元的权重、偏差和激活函数。

```javapublic class Neuronprivate double[] weights; // 神经元的权重private double bias; // 神经元的偏差private Function<Double, Double> activationFunction; // 神经元的激活函数public Neuron(int inputSize, Function<Double, Double> activationFunction)this.weights = new double[inputSize];this.bias = 0;this.activationFunction = activationFunction;//初始化权重和偏差for (int i = 0; i < inputSize; i++)this.weights[i] = Math.random(;}this.bias = Math.random(;}//计算神经元的输出public double calculateOutput(double[] inputs)double sum = 0;for (int i = 0; i < inputs.length; i++)sum += inputs[i] * weights[i];sum += bias;return activationFunction.apply(sum);}```其次，我们需要定义一个神经网络类，该类包含多个神经元，以及前向传播和反向传播的方法。

cbow 和 skip-gram计算公式

cbow 和 skip-gram计算公式一、模型简介CBW（Convolutional Bottleneck）和Skip-Gram（Skip-Gramm）模型是深度学习领域中的两种常见隐含层生成模型，主要用于自然语言处理任务，如文本分类、情感分析、语言生成等。

这两种模型通过学习上下文信息之间的关系，进而预测当前词的标签。

二、计算公式1. CBW模型CBW模型的基本思想是在输入词的上下文中提取特征，并通过卷积神经网络（Convolutional Neural Network，CNN）进行特征提取。

其计算公式如下：y_t = σ(W_1*[x_t-1, x_t, x_t+1] + b_1)h_t = σ(W_2*y_t + b_2)其中，y_t表示当前词的预测值，x_t表示当前词的上下文特征，σ为激活函数，W_1和W_2为权重矩阵，b_1和b_2为偏置项。

通过这种方式，模型能够学习到上下文信息之间的关联，进而预测当前词的标签。

2. Skip-Gram模型Skip-Gram模型的基本思想是直接从上下文中预测当前词的标签。

其计算公式如下：y = σ(W*[x_t-1, x_t, x_t+1] + b)其中，y表示当前词的标签预测值，x_t表示当前词的上下文特征，W和b为权重矩阵和偏置项，σ为激活函数。

模型通过学习上下文特征与标签之间的映射关系，进而预测当前词的标签。

三、模型训练CBW和Skip-Gram模型可以通过反向传播算法进行训练。

具体来说，对于每个训练样本（输入词和对应的标签），模型会根据当前词的上下文特征进行预测，并根据预测值与实际标签之间的误差进行反向传播，更新权重矩阵和偏置项。

通过多次迭代训练，模型能够逐渐学习到上下文信息之间的关联，并提高预测的准确度。

四、总结CBW和Skip-Gram模型是深度学习领域中常用的隐含层生成模型，主要用于自然语言处理任务。

这两种模型通过学习上下文信息之间的关系，能够有效地预测当前词的标签。

BP算法推算过程

BP算法推算过程BP算法（Back Propagation，反向传播算法）是一种用于训练多层前馈神经网络（MLP）的监督学习算法。

它通过将误差从输出层向输入层进行传播来调整网络的权重，以最小化预测输出与实际输出之间的差异。

你所期望的1200字以上解释是无法在一个答案中完全涵盖的，因此我将会提供一个尽可能详细的解释，但依然有一些内容需要自行进一步学习。

首先，我们需要了解一些基本概念。

一个多层前馈神经网络由输入层、若干个隐藏层和输出层组成。

每一层都由许多神经元构成，这些神经元接受来自上一层的输入，并将它们通过一个非线性函数（如sigmoid函数）进行加权和激活。

网络中的每个连接都有一个权重，这些权重可以决定每个输入对应的重要性。

从直观上说，BP算法通过不断调整网络中的权重来使得预测输出与实际输出之间的差异最小化。

为了找到最优的权重，算法需要计算每一对权重的梯度值，然后使用梯度下降法来更新它们。

接下来，我们来看一下BP算法的具体步骤。

1.初始化权重：为网络中的每个连接随机分配一个初始权重值。

2.前向传播：从输入层开始，将输入向前传递到隐藏层和输出层，通过加权和激活函数得到每个神经元的输出。

3.计算误差：将网络的预测输出与实际输出进行比较，计算出每个输出神经元的误差。

4.反向传播：从输出层开始，将误差反向传播回隐藏层和输入层。

这一步骤可以通过计算每个神经元的误差梯度来实现。

5.更新权重：使用梯度下降法来更新每个连接的权重值。

新的权重值可以通过当前权重值加上一个学习速率与对应的梯度相乘得到。

6.重复步骤2-5，直到达到停止条件（例如达到指定的迭代次数或误差小于一些阈值）。

通过循环执行这些步骤，BP算法可以逐渐学习和调整网络中的权重，使得网络的预测输出与实际输出之间的差异越来越小。

最终，网络将会达到一个比较好的拟合效果，并可以用于对未知样本的预测。

值得注意的是，BP算法有一些局限性。

首先，它可能会收敛到一个局部最小值而不是全局最小值。

正交投影神经网络的BP和GS杂交学习算法

BP神经网络详解-最好的版本课件(1)

bp神经网络的原理

bp神经 训练目标

bp算法公式

bp算法原理

机器学习-BP(back propagation)神经网络介绍

BP算法的基本原理

BP算法的基本原理

BP神经网络算法步骤

bp算法流程

BP神经网络算法实验报告

BP算法程序实现

BP神经网络算法步骤

bp网络的基本原理

BP神经网络的基本原理_一看就懂

JAVA实现BP神经网络算法

cbow 和 skip-gram计算公式

BP算法推算过程

bp神经训练目标