七年级数学第二学期第一次阶段检测20150405
(完整版)人教版七年级数学下册第一章试题.doc

精心整理2014~ 2015年度第二学期黄流二中七年级数学第一次月考试题姓名:班级:座位号:一、选择题(每小题 3 分,共 30 分)1、如图所示, ∠1和 ∠2是对顶角的是( )A121C11B D222AD214B32、如图 AB ∥CD 可以得到( )(第 2题)CA 、∠1=∠2B 、∠2=∠3C 、∠1=∠4D 、 ∠3=∠43、直线 AB 、CD 、EF 相交于 O ,则 ∠1+∠2+∠3=( )A 、90°B 、120°C 、180° D、1401°24、如图所示,直线 a 、b 被直线 c 所截,现给出下列四种条 3件: (第三题)①∠2= ∠6 ②∠2=∠8 ③∠1+ ∠4=180° ④∠3= ∠8,其中能判断是 a ∥b 的条件的序号是( ) A 、①② B 、①③ C 、①④ D 、③④5、某人在广场上练习驾驶汽车,两次拐弯后,行驶方向与原2 c1 34b来相同,这两次拐弯的角度可能是( )A 、第一次左拐 30°,第二次右拐 30°65 7 8a(第4题)精心整理B、第一次右拐 50°,第二次左拐 130°C、第一次右拐 50°,第二次右拐 130°D、第一次向左拐50°,第二次向左拐130°6、下列哪个形是由左平移得到的()7、如,在一个有4×4个小正方形成的正方形网格中,阴影部分面与正方形ABCD面的比是()A、3:4B、5:8C、9:16D、1:28、下列象属于平移的是()① 打气筒活塞的复运,② 梯的上下运,③ 的,④ 的,⑤ 汽在一条笔直的路上行走A、③ B 、②③ C 、①②④ D 、①②⑤9、下列法正确的是() AA、有且只有一条直与已知直平行 EB、垂直于同一条直的两条直互相垂直C、从直外一点到条直的垂段,叫做点到C( 第10题)条直的距离。
七年级(下)数学第一次阶段测试试卷

七年级(下)数学第一次阶段测试试卷班级: 姓名: 得分一、选择题(每题3分,共27分)1..如图,下列条件中,不能判断直线1l ∥2l 的是( )A 、∠2+∠4=180°B 、∠4=∠5C 、∠2=∠3D 、∠1=∠32.如图,AB ∥CD ,直线EF 分别交AB 、CD 于E 、F 两点,若∠FEB=110°,则∠EFD 等于( )A .50° B.60°C.70°D.110°3.有四根木条的长度分别为6cm 、5 cm 、4 cm 、2 cm ,选其中三根木条使他们能构成一个三角形,则可有几种选择方法( )A 、4种B 、3种C 、2种D 、1种4.若两条直线被第三条直线所截,则一组同旁内角的平分线互相( )A 、垂直B 、平行C 、重合D 、相交5.如图,AB ∥CD ,下列结论中正确的是( )A 、∠1+∠2+∠3=180°B 、∠1+∠2+∠3=360°C 、∠1+∠3=2∠2D 、∠1+∠3=∠26.以下运算正确的是( )①()4a 4=a 8;②()[]222b =b 8;③()[]32y -=y 6;④623a a a =∙;⑤x 2+x 2=x 4;⑥933x x x =∙A 、①③B 、③⑥C 、④⑤⑥D 、②③7.若()159382b a b a n m m =+成立,则( )A 、m=3, n=2B 、m= n=3C 、m=6, n=2D 、m=3, n=58.将一副直角三角尺如图放置,已知AE ∥BC ,则∠AFD 的度数是( )A 、75°B 、59°C 、77°D 、103°9.将五边形纸片ABCDE 按如图方式折叠,折痕为AF ,点E 、D 分别落在。
已知∠AFC=76°,则∠ 等于( )A 、31°B 、28°C 、24°D 、22°二、 填空题(每空2分)10.五边形的内角和为 °;外角和为 °。
七年级数学下学期第一次质量检测试题 新人教版-新人教版初中七年级全册数学试题
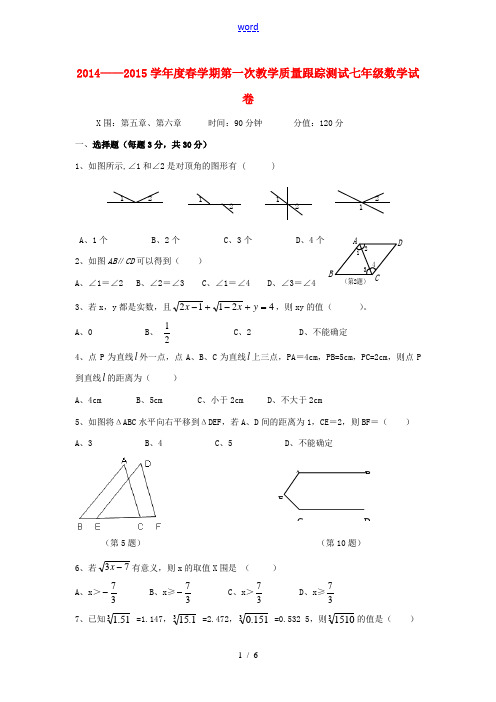
ABCD 1234(第2题)2014——2015学年度春学期第一次教学质量跟踪测试七年级数学试卷X 围:第五章、第六章 时间:90分钟 分值:120分 一、选择题(每题3分,共30分)1、如图所示,∠1和∠2是对顶角的图形有 ( )12121221A 、1个B 、2个C 、3个D 、4个 2、如图AB ∥CD 可以得到( )A 、∠1=∠2B 、∠2=∠3C 、∠1=∠4D 、∠3=∠43、若x ,y 都是实数,且42112=+-+-y x x ,则xy 的值( )。
A 、0 B 、21C 、2D 、不能确定 4、点P 为直线l 外一点,点A 、B 、C 为直线l 上三点,PA =4cm ,PB=5cm ,PC=2cm ,则点P 到直线l 的距离为( ) A 、4cm B 、5cmC 、小于2cmD 、不大于2cm5、如图将ΔABC 水平向右平移到ΔDEF ,若A 、D 间的距离为1,CE =2,则BF =( ) A 、3B 、4C 、5D 、不能确定(第5题)(第10题)6、若73-x 有意义,则x 的取值X 围是 ( ) A 、x >37-B 、x ≥37- C 、x >37 D 、x ≥377、已知351.1 =1.147,31.15 =2.472,3151.0 =0.532 5,则31510的值是( )A BCDEA 、24.72B 、53.25C 8、大于52-且小于23的整数有( )A 、9个B 、8个C 、7个D 、5个9、下列命题:①对顶角未必相等;②在同一平面内,如果b //a ,c //b ,那么c //a ;③在同一平面内,若b a ⊥,c b ⊥ 那么c a ⊥;④如果ac=bc ,那么a=b ;⑤互补的两个角相等; 其中正确的有( )A 、1个B 、2个C 、3个D 、4个 10、如图,AB ∥CD ,那么∠BAE+∠AEC+∠ECD =( ) A 、1800B 、2700C 、3600D 、5400二、填空题(每题3分,共30分)11、3-绝对值是,364 的平方根是 ,-343的立方根是。
2015学年第二学期七年级数学第1次质量监测答题卡

密封线内不要 答题考号学号姓名班级南江中学七年级数学第一次教学质量监测试卷第二部分 答题卡一、选择题:(每小题3分,共30分)二、填空题:11、 。
12、 º。
13、 º。
14、 。
15、 。
三、解答题:(要有必要的解题步骤.共55分)16. 计算:(每小题4分,共12分)(1)232(2)(2)x y xy -- (2) ()(2)x y x y -+;(3))2(])()[(22xy y x y x ÷--+.17.一个角的补角与这个角的余角的和比平角少10°,求这个角.(6分)4321FEDCB Ac ba 1218. (6分)如图,根据题意填空: (1)∵ =∠4(已知)∴CD ∥EF( ) (2)∵∠1= (已知)∴AB ∥EF ( ) (3)∵∠3+∠ =180°(已知)∴CD ∥EF ( ) 19. (6分)先化简,再求值:x x y x x 2)1()2(2++-+,其中231=x ,23-=y .20. (6分)如图,∠1=60°,∠2=120°,直线a 与b 平行吗?说明你的理由。
21.(6分) 在长为23+a ,宽为12-b 的长方形铁片上,挖去长为42+a ,宽为b 的小长方形铁片,求剩余部分面积。
(答案要求化简)22.(6分) (7分) 阅读理解题: (1)(x -1)(x +1)= x 2 -1, (x -1)(x 2 +x +1)= x 3 -1,(x -1)(x 3+x 2 +x +1)= , 猜想12(1)(1)nn x x xx x --+++++ = ,(2)根据以上结果,试写出下列式子的结果.49482(1)(1)x x x x x -+++++= ,(3)由以上情形,你能求出下面式子的结果吗?20(1)(1)x x -÷-=密封线内不要 答 题23.图1是由4块长为m 、宽为 n 的小长方形拼在一起形成的一个大长方形;图2是由4块相同的长为m 、宽为 n 的小长方形拼成一个正方形。
2015学年第二学期七年级阶段性教学质量检测(数学)试卷题
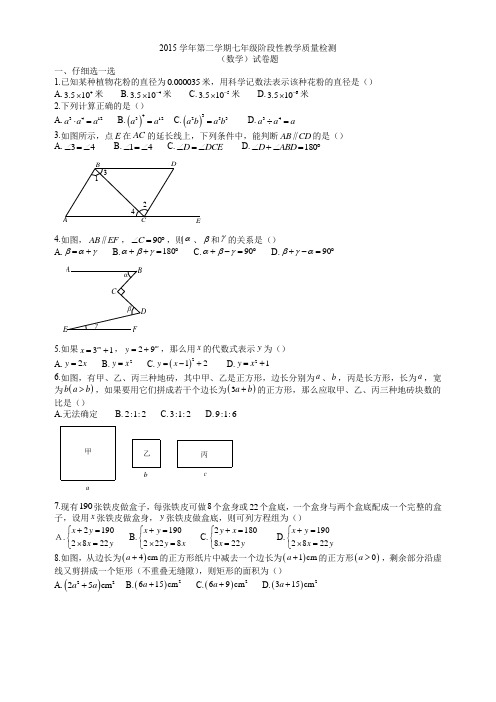
2015学年第二学期七年级阶段性教学质量检测(数学)试卷题一、仔细选一选1.已知某种植物花粉的直径为0.000035米,用科学记数法表示该种花粉的直径是() A.43.510⨯米 B.43.510-⨯米 C.53.510-⨯米 D.63.510-⨯米2.下列计算正确的是()A.3412a a a ⋅=B.()4312a a = C.()3253a b a b = D.34a a a ÷=3.如图所示,点E 在AC 的延长线上,下列条件中,能判断AB CD ∥的是() A.34∠=∠ B.14∠=∠ C.D DCE ∠=∠ D.180D ABD ∠+∠=︒4.如图,AB EF ∥,90C ∠=︒,则α、β和γ的关系是()A.βαγ=+B.180αβγ++=︒C.90αβγ+-=︒D.90βγα+-=︒5.如果31m x =+,29m y =+,那么用x 的代数式表示y 为() A.2y x = B.2y x = C.()212y x =-+ D.21y x =+6.如图,有甲、乙、丙三种地砖,其中甲、乙是正方形,边长分别为a 、b ,丙是长方形,长为a ,宽为()b a b >,如果要用它们拼成若干个边长为()3a b +的正方形,那么应取甲、乙、丙三种地砖块数的比是()A.无法确定B.2:1:2C.3:1:2D.9:1:67.现有190张铁皮做盒子,每张铁皮可做8个盒身或22个盒底,一个盒身与两个盒底配成一个完整的盒子,设用x 张铁皮做盒身,y 张铁皮做盒底,则可列方程组为() A.21902822x y x y +=⎧⎨⨯=⎩ B.1902228x y y x +=⎧⎨⨯=⎩ C.2180822y x x y +=⎧⎨=⎩ D.1902822x y x y+=⎧⎨⨯=⎩ 8.如图,从边长为()4cm a +的正方形纸片中减去一个边长为()1cm a +的正方形()0a >,剩余部分沿虚线又剪拼成一个矩形(不重叠无缝隙),则矩形的面积为() A.()2225cm a a + B.()2615cm a + C.()269cm a + D.()2315cm a +4321EDCB AγβαF EDCBA甲a乙b丙c9.已知m 为正整数,且关于x ,y 的二元一次方程组210320mx y x y +=⎧⎨-=⎩有整数解,则2m 的值为()A.4B.4,49C.1,4,49D.无法确定10.已知关于x ,y 的方程组3453x y ax y a +=-⎧⎨-=⎩,给出下列结论:①51x y =⎧⎨=-⎩是方程组的解;②无论a 取何值,x ,y 的值都不可能互为相反数; ③当1a =时,方程组的解也是方程4x y a +=-的解;④x ,y 都为自然数的解有4对. 其中正确的个数为()A.1个B.2个C.3个D.4个 二、认真填一填11.若34x =,97y =,则23x y -的值为_______.12.()()22015011π 3.142⎛⎫-+---= ⎪⎝⎭_______.13.已知32a -=,53b -=,用“<”来比较a 、b 的大小:________.14.若()()2125x x mx +++的计算结果中2x 项的系数为3-,则m =_______.15.若3723190x y x y y kx --=+-=-+=,则k 的值为_______. 16.图中与1∠构成同位角的个数有_______个.17.已知111222a x b y c a x b y c +=⎧⎨+=⎩的解是34x y =⎧⎨=⎩,则方程组()()()()11122231433143a x b y c a x b y c ⎧-++=⎪⎨-++=⎪⎩的解是______.18.两个角的两边互相平行,其中一个角比另一角的2倍少30︒,则这两个角度数分别是______. 19.已知a 、b 、m 均为整数,若()()217x mx x a x b +-=++,则整数m 的值有_______.20.已知关于x ,y 的二元一次方程()()12120m x m y m ++-+-=,无论实数m 取何值,此二元一次方程都有一个相同的解,则这个相同的解是______. 三、前面答一答21.(1)计算:()()()()233322222x y xy x y x ⋅-+-÷(2)()()222226633m n m n m m --÷-(3)先化简,再求值:()()()()222151131x x x x +-+-+-,其中112x -⎛⎫= ⎪⎝⎭22.下列方程:①257x y +=;②21x y=+;③21x y +=;1④()()28x y x y +--=;⑤210x x --=;⑥132x y x y-+=-; (1)请找出上面方程中,属于二元一次方程的是:________(只需填写序号); (2)请选择一个二元一次方程,求出它的正整数解;(3)任意选择两个二元一次方程组成二元一次方程组,并求出这个方程组的解. 23.将一张长为8,宽为6的长方形纸片沿对角线剪开(如图1),得到两张三角形纸片,然后将两张纸片如如图2所示位置摆放.(1)请在图2中画出EDC △沿DC 方向将点D 平移到AC 中点的图形'''E D C △; (2)设平移后''E D 与BC 交于点F ,直接写出图(2)中所有与A ∠度数相同的角. 24.按要求完成下列各题:(1)已知实数a 、b 满足()21a b +=,()29a b -=,求22a b ab +-的值.(2)已知()()201520162017a a --=,试求()()2220152016a a -+-的值.25.2016年20G 峰会将于9月45-日在杭州举行,“丝绸细节”助力杭州打动世界.某丝绸公司为20G 设计手工礼品,投入W 元钱,若以2条领带和1条丝巾为一份礼品,则刚好可制作600份礼品;若以1条领带和3条丝巾为一份礼品,则刚好可制作400份礼品. (1)若24W =万元,求领带及丝巾的制作成本是多少? (2)若用W 元钱全部用于制作领带,总共可以制作几条?(3)若用W 元钱恰好能制作300份其他的礼品,可以选择a 条领带和b 条丝巾作为一份礼品(两种都要有),请求出所有可能的a 、b 值.26.同一平面内的两条直线有相交和平行两种位置关系.(1)如图a ,若AB CD ∥,点P 在AB 、CD 外部,我们过点P 作AB 、CD 的平行线PE ,则有AB CD PE ∥∥,则BPD ∠,B ∠,D ∠之间的数量关系为_________.将点P 移到AB 、CD 内部,如图b ,以上结论是否成立?若成立,说明理由;若不成立,则BPD ∠、B ∠、D ∠之间有何数量关系?请证明你的结论.(2)迎“20G ”科技节上,小兰制作了一个“飞旋镖”,在图b 中,将直线AB 绕点B 逆时针方向旋转一定角度交直线CD 于点Q ,如图c ,他很想知道BPD ∠、ABP ∠、D ∠、BQD ∠之间的数量关系,请你直接写出它们之间的数量关系:__________.(3)设BF 交AC 于点P ,AE 交DF 于点Q ,已知126APB ∠=︒,100AQF ∠=︒,直接写出B E F ∠+∠+∠的度数为_______度,A ∠比F ∠大______度.图1BCDA图2EDCA图b图aABCPOP ED CBA图d图cPQF ABCEA'QABCDP。
人教版2014–2015学年第二学期第一次阶段性测试.docx

xxxxDCB A3333-1-1-1-12014–2015学年第二学期第一次阶段性测试七年级数学试卷(考试时间:100分钟 满分:100分)温馨提示:同学们,你们好!今天是展示你才能的时候了,只要你仔细审题、认真答题,把平常的水平发挥出来,你就会有出色的表现,放松一点,相信自己的实力!请把选择题和填空题的答案写在答题卷上一、选择题(每小题3分,满分30分)1.如图,已知AB ∥CD ,∠A =70°,则∠1的度数是( )A .70°B .100°C .110°D .130°2.如图,已知直线a 、b 被直线c 所截,那么∠1的同位角是( )A. ∠2B. ∠3C. ∠4D. ∠53.x 的2倍减3的差不大于1,列出不等式是( )A. 2x -3≤1B. 2x -3≥1C. 2x -3<1D. 2x -3>1 4.如图,在数轴上表示-1≤x <3正确的是( )5.下列命题中,是假命题的是( )A 、同旁内角互补B 、对顶角相等C 、直角的补角仍然是直角D 、两点之间,线段最短6.下列四个命题中,正确的有( )①若a <b ,则a +1<b +1;②若a <b ,则a -1<b -1;③若a <b ,则-2a >-2b ; ④若a <b ,则2a >2b.A. 1个B. 2个C. 3个D. 4个 7.如图,已知∠1=70°,要使AB ∥CD ,则须具备另一个条件( ) A. ∠2=70°B. ∠2=100°C. ∠2=110°D. ∠3=110°8.如图,点O 在直线AB 上且OC ⊥OD .若∠COA=36°,则∠DOB 的大小为( )A. 36°B. 54°C. 64°D. 72°考室座位号姓名 班级 准考证号(考场编号)密 封 装 订 线C BA 1D第1题 第2题 第7题 第8题9.将图形A 向右平移3个单位得到图形B ,再将图形B 向左平移5个单位得到图形C 。
2014---2015学年度第二学期阶段性学业水平检测七年级数学试题(第一次月考)

B AC O 5题图 1A B F D C E 22014---2015学年度第二学期阶段性学业水平检测七年级数学试题(第一次月考)姓名_________ 班级__________一、选择题:(每小题3分,满分36分)1、下列说法中正确的是( )A 、有且只有一条直线与已知直线垂直.B 、从直线外一点到这条直线的垂线段,叫做这点到这条直线的距离.C 、互相垂直的两条线段一定相交.D 、直线L 外一点A 与直线L 上各点连接而成的所有线段中最短的长是3厘米,则A 到L 的距离是3厘米。
2、下面四个图形中,∠1与∠2是对顶角的图形有( )A 、1个B 、2个C 、3个D 、4个3.判断两角相等,错误的是( )A 、对顶角相等B 、两条直线被第三条直线所截,内错角相等C 、两直线平行,同位角相等D 、∵∠1=∠2,∠2=∠3,∴∠1=∠34.下列说法中,正确的是( )A 、有公共端点的两条射线组成的图形叫做角;B 、两条射线组成的图形叫做角;C 、两条线段组成的图形叫做角;D 、一条射线从一个位置移到另一个位置所形成的图形叫做角。
5、如图:已知AB ∥CD ,∠B=1200,∠D=1500,则∠O 等于( ).(A )500 (B )600 (C )800 (D )9006.如上右图,若AB ∥CD ,CD ∥EF ,那么∠BCE =() A .∠1+∠2 B .∠2-∠1C .180°-∠1+∠2D .180°-∠2+∠17. 下列四个图形中,能同时用∠1,∠ABC ,∠B 三种方法表示同一个角的图形是()8、若∠1=5005' ∠2=50.50 则∠1与∠2的大小关系是( )A 、∠1=∠2B 、∠1>∠2C 、∠1<∠2D 、无法确定(D)(C)(B)(A)B A A9、已知:如图,AB CD ⊥,垂足为O , EF 为过点O 的一条直线,则1∠与2∠的关系一定成立的是( ) A .相等 B .互余C .互补D .互为对顶角10.下列说法正确的是( )A 、垂直于同一直线的两条直线互相垂直.B 、平行于同一条直线的两条直线互相平行.C 、平面内两个角相等,则他们的两边分别平行.D 、两条直线被第三条直线所截,那么有两对同位角相等.11、二元一次方程组2383212x y x y +=⎧⎨+=⎩的解满足x+y 等于( ) A 、3 B 、4 C 、5 D 、612、如图,AB ⊥BC ,∠ABD 的度数比∠DBC 的度数的两倍少15°,设∠ABD 和∠DBC 的度数分别为x 、y ,那么下面可以求出这两个角的度数的方程组是( )A 、B 、C 、D 、二:填空题(本题共5个小题,每小题3分,共15分.只要求填写最后结果)13、时钟的分针和时针在3时30分时,所成的角度是 度14、方程032233=+--+-n m n y x 是二元一次方程,则,m = n =15. 一个角的补角与这个角的余角的度数比为3:1,这个角 度.16、已知一条射线OA ,若从点O 处再引两条射线OB 和OC ,使∠AOB=60°,∠BOC=20°,则∠AOC=_______21世纪教育网版权所有BC 17、把一张长方形纸片ABCD 沿EF 折叠后ED 与的交点为G ,D 、C 分别在M 、N 的位置上,若∠EFG=55°, 则∠1=_______,∠2=_______.9015x y x y +=⎧⎨=-⎩90215x y x y +=⎧⎨=-⎩90152x y x y +=⎧⎨=-⎩290215x x y =⎧⎨=-⎩(17题图) B A C D E F G M N 1265D 1CB AFE432D 1C B A E 32三、解答题(本题共8个小题,共69分.解答应写出文字说明、证明过程或推演步骤)18、(7分) 如图,根据下列条件,可以判定哪两条直线平行?并说明判定的依据.(1)∠1=∠C ( ) ( )(2)∠2=∠4 ( ) ( )(3)∠2+∠5=180°( )( )19、(8分)计算: (1)131。
七年级数学下册 第一次阶段性检测卷(全解全析)

2022-2023学年下学期阶段性检测卷七年级数学·全解全析注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答第Ⅰ卷时,选出每小题答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
写在本试卷上无效。
3.回答第Ⅱ卷时,将答案写在答题卡上。
写在本试卷上无效。
4.测试范围:第7章、第8章。
5.考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一个选项是符合题目要求的)1.下列四组图形中,不能视为由一个基本图形通过平移得到的是()A .B .C .D .【详解】解:由图可知,A 、B 、D 可以由平移得到,C 由轴对称得到.故本题选:C .2.下列长度的三条线段首尾相接不能围成三角形的是()A .2,3,4B .8,7,15C .6,8,10D .13,12,20【详解】解:A 、234+>,能组成三角形,故此选项不合题意;B 、8715+=,不能组成三角形,故此选项符合题意;C 、6810+>,能组成三角形,故此选项不合题意;D 、131220+>,能组成三角形,故此选项不合题意.故本题选:B .3.下列运算正确的是()A .235()a a -=-B .3515a a a ⋅=C .23246()a b a b -=D .2232a a a-=【详解】解:A 项根据幂乘方的运算法则可知236()a a -=-,故不合题意;B 项根据同底数幂的乘方的运算法则可知358a a a ⋅=,故不合题意;C 项根据积的乘方的运算法则可知23246()a b a b -=,故符合题意;D 项根据合并同类项的运算法则可知22232a a a -=,故不合题意.故本题选:C .4.已知一个正n 边形的一个外角为40︒,则(n =)A .10B .9C .8D .7【详解】解: 正n 边形的一个外角为40︒,外角和是360︒,360409n ∴=÷=.故本题选:B .5.下列说法正确的是()A .三角形的三条高至少有一条在三角形内B .直角三角形只有一条高C .三角形的角平分线其实就是角的平分线D .三角形的角平分线、中线、高都在三角形的内部【详解】解:A 、三角形的三条高至少有一条在三角形内,正确;B 、直角三角形只有三条高,而题目中是只有一条高,错误;C 、三角形的角平分线是线段,而角的平分线是射线,错误;D 、锐角三角形的角平分线、中线、高都在三角形的内部,但钝角三角形的高有的在外部,错误.故本题选:A .6.503,404,305的大小关系为()A .504030345<<B .305040534<<C .304050543<<D .403050453<<【详解】解:50510103(3)243== ,40410104(4)256==,30310105(5)125==,305040534∴<<.故本题选:B .7.如图在Rt ABC ∆中,90B ∠=︒,60ACB ∠=︒,//EF GH ,若158∠=︒,则2∠的度数是()A .22︒B .26︒C .28︒D .32︒【详解】解:Rt ABC ∆ 中,90B ∠=︒,60ACB ∠=︒,30A ∴∠=︒,由三角形外角性质,可得128ADF A ∠=∠-∠=︒,又//EF GH ,228ADF ∴∠=∠=︒,故本题选:C .8.如图,已知80F FGD ∠+∠=︒(其中)F FGD ∠>∠,添加一个以下条件:①280FEB FGD ∠+∠=︒;②180F FGC ∠+∠=︒;③180F FEA ∠+∠=︒;④100FGC F ∠-∠=︒.能证明//AB CD 的个数是()A .0个B .1个C .2个D .3个【详解】解:①如图,过点F 作//FH CD ,则:HFG FGD ∠=∠,EFG EFH HFG ∠=∠+∠ ,80EFG FGD ∠+∠=︒,280EFH FGD ∴∠+∠=︒,280FEB FGD ∠+∠=︒ ,EFH FEB ∴∠=∠,//AB FH ∴,//AB CD ∴,故①符合题意;②180F FGC ∠+∠=︒ ,//CD FE ∴,故②不符合题意;180EFG FEA ∠+∠=︒ ,//AB FG ∴,故③不符合题意;④100FGC EFG ∠-∠=︒ ,80EFG FGD ∠+∠=︒,10080FGC EFG EFG FGD ∴∠-∠+∠+∠=︒+︒,180FGC FGD ∴∠+∠=︒,故④不符合题意.故本题选:B .9.如图,ABC ∆的角平分线CD 、BE 相交于F ,90A ∠=︒,//EG BC ,且CG EG ⊥于G ,下列结论:①2CEG DCB ∠=∠;②CA 平分BCG ∠;③ADC GCD ∠=∠;④12DFB CGE ∠=∠.其中正确的结论是()A .①③B .②④C .①③④D .①②③④【详解】解:①//EG BC ,CEG ACB ∴∠=∠,又CD 是ABC ∆的角平分线,2CEG ACB DCB ∴∠=∠=∠,故正确;②无法证明CA 平分BCG ∠,故错误;③90A ∠=︒ ,90ADC ACD ∴∠+∠=︒,CD 平分ACB ∠,ACD BCD ∴∠=∠,90ADC BCD ∴∠+∠=︒.//EG BC ,且CG EG ⊥,90GCB ∴∠=︒,即90GCD BCD ∠+∠=︒,ADC GCD ∴∠=∠,故正确;④EBC ACB AEB ∠+∠=∠ ,DCB ABC ADC ∠+∠=∠,190()1352AEB ADC ABC ACB ∴∠+∠=︒+∠+∠=︒,36013590135DFE ∴∠=︒-︒-︒=︒,1452DFB CGE ∴∠=︒=∠,故正确.故本题选:C .10.设ABC ∆的面积为a ,如图①将边BC 、AC 分别2等份,1BE 、1AD 相交于点O ,AOB∆的面积记为1S ;如图②将边BC 、AC 分别3等份,1BE 、1AD 相交于点O ,AOB ∆的面积记为2S ;⋯⋯,依此类推,若5311S =,则a 的值为()A .1B .2C.6D .3【详解】解:如图①,连接OC ,11AE CE = ,11BD CD =,∴11OAE OCE S S = ,11OBD OCD S S = ,111122ABE ABD ABC S S S a ∆=== , 11OAE ABE OAB S S S ∆=- ,11OBD ABD OAB S S S ∆=- ,∴11OAE OBD S S = ,∴1111OAE OCE OBD OCD S S S S === ,设1111OAE OCE OBD OCD S S S S x ==== ,则11124S x aS x a⎧+=⎪⎨⎪+=⎩,解得:113S a =;如图,连接2OE 、OC 、2OD ,则1113ABE ABD S S a == ,11221122OAE OE E OCE OBD OD D OCD S S S S S S ===== ,设11221122OAE OE E OCE OBD OD D OCD S S S S S S x ====== ,则23136S x aS x a⎧+=⎪⎨⎪+=⎩,解得:215S a =;如图③,连接2OE 、3OE 、OC 、2OD 、3OD ,则1114ABE ABD S S a ==,112233112233OAE OE E OE E OCE OBD OD D OD D OCD S S S S S S S S ======= ,设112233112233OAE OE E OE E OCE OBD OD D OD D OCD S S S S S S S S x ======== ,则33148S x aS x a ⎧+=⎪⎨⎪+=⎩,解得:317S a =,.....,121n S a n =+,5311S = ,∴1325111a =⨯+,解得:3a =.故本题选:D .第Ⅱ卷二、填空题(本大题共8小题,每小题3分,共24分)11.科学家发现一种病毒的直径为0.0043微米,则用科学记数法表示为微米.【详解】解:30.0043 4.310-=⨯.故本题答案为:34.310-⨯.12.一个n 边形内角和等于1620︒,则边数n 为.【详解】解:由题意得,180(2)1620n -=,解得:11n =.故本题答案为:11.13.计算:2022202353()(2)135⨯=.【详解】解:2022202353((2135⨯2022202251313()(1355=⨯⨯202251313(1355=⨯⨯1315=⨯135=.故本题答案为:135.14.等腰三角形一腰上的中线将这个三角形的周长分成了12和18两部分,这个三角形的底边长为.【详解】解:如图:在ABC ∆中,AB AC =,BD 是AC 边上的中线,12AD DC AC ∴==,分两种情况:①当1218AB AD BC CD +=⎧⎨+=⎩时,解得:814AB BC =⎧⎨=⎩,∴这个三角形的底边长为14;②当1812AB AD BC CD +=⎧⎨+=⎩时,解得:126AB BC =⎧⎨=⎩,∴这个三角形的底边长为6;综上,这个三角形的底边长为14或6.故本题答案为:14或6.15.如图,已知//AB EF ,90C ∠=︒,则α、β与γ的关系是.【详解】解:如图,过点C 作//CM AB ,过点D 作//DN AB ,//AB EF ,//////AB CM DN EF ∴,BCM α∴∠=,DCM CDN ∠=∠,EDN γ∠=,CDN EDN CDN βγ=∠+∠=∠+ ①,90BCD CDN α∠=+∠=︒②,由①②得:90αβγ+-=︒.故本题答案为:90αβγ+-=︒.16.如图,将ABC ∆纸片沿DE 折叠,使点A 落在点A '处,且BA '平分ABC ∠,CA '平分ACB ∠,若115BA C ∠'=︒,则12∠+∠的度数为.【详解】解:如图,连接AA ',A B ' 平分ABC ∠,A C '平分ACB ∠,12A BC ABC '∴∠=∠,12A CB ACB '∠=∠,115BAC '∠=︒ ,18011565A BC A CB ''∴∠+∠=︒-︒=︒,130ABC ACB ∴∠+∠=︒,18013050BAC ∴∠=︒-︒=︒, 沿DE 折叠,DAA DA A ''∴∠=∠,EAA EA A ''∠=∠,12DAA DA A DAA '''∠=∠+∠=∠ ,22EAA EA A EAA '''∠=∠+∠=∠,12222250100DAA EAA BAC ''∴∠+∠=∠+∠=∠=⨯︒=︒.故本题答案为:100︒.17.如图,在ABC ∆中,3BC =,将ABC ∆平移5个单位长度得到△111A B C ,点P 、Q 分别是AB 、11A C 的中点,PQ 的取值范围.【详解】解:如图,取AC 的中点M ,11A B 的中点N ,连接PM ,MQ ,NQ ,PN ,将ABC ∆平移5个单位长度得到△111A B C ,113B C BC ∴==,5PN =,点P 、Q 分别是AB 、11A C 的中点,111322NQ B C ∴==,335522PQ ∴-+,即71322PQ,PQ ∴的取值范围为71322PQ.故本题答案为:71322PQ.18.如图,在ABC ∆中,90C ∠=︒,8BC cm =,6AC cm =,点E 是BC 的中点,动点P 从A 点出发,先以每秒2cm 的速度沿A C →运动,然后以1/cm s 的速度沿CB →运动.若设点P 运动的时间是t 秒,那么当t =,APE ∆的面积等于8.【详解】解:①如图1,当点P 在AC 上,在ABC ∆中,90C ∠=︒,8BC cm =,6AC cm =,点E 是BC 的中点,4CE ∴=,2AP t =.APE ∆ 的面积等于8,114822APE S AP CE AP ∆∴==⨯= ,4AP = ,2t ∴=;②如图2,当点P 在BC 上,点E 是BC 的中点,4BE CE == .28BP t =- ,()628142PC t t =--=-,116822S EP AC EP ∴==⨯= ,83EP ∴=,8133433t ∴=+-=或8293433t =++=;综上,当2t =或133或293时APE ∆的面积会等于8.故本题答案为:2或133或293.三、解答题(本大题共8小题,满分66分)19.(8分)计算:(1)2019021118(2)()(2)4π----⨯-+⨯-;(2)2345()()a a a a ⋅-⋅-÷;(3)32333272()(3)(5)x x x x x ⋅-+⋅;(4)7632()()()()x y y x x y x y -÷-+--÷+.【详解】解:(1)原式118116(2=--⨯+⨯-188=---17=-;(2)原式2345a a a a =⋅⋅÷4a =;(3)原式6392722725x x x x x =⋅-+⋅99922725x x x =-+0=;(4)原式7632()()()()x y x y x y x y =-÷--+÷+()()x y x y =--+x y x y =---2y =-.20.(4分)先化简再求值33223(2)()()a b ab --⋅-+-,其中13a =-,2b =.【详解】解:33223(2)()()a b ab --⋅-+-3636(8)()a b a b =--⋅+-36368a b a b =-367a b =,当13a =-,2b =时,原式3614487()2327=⨯-⨯=-.21.(6分)求值:(1)已知23142x x -=,求x 的值.(2)已知23n a =,35m a =,求69n m a -的值.(3)已知132240x x +⋅+=,求x 的值.【详解】解:(1)23142x x -= ,43122x x -∴=,431x x ∴=-,1x ∴=-;(2)23n a = ,35m a =,69n m a -∴69n m a a =÷2333()()n m a a =÷3335=÷27125=;(3)132240x x +⋅+= ,322240x x ∴⋅+⋅=,5240x ∴⋅=,28x ∴=,3x ∴=.22.(8分)如图,在边长为1个单位的正方形网格中,ABC ∆经过平移后得到△A B C ''',图中标出了点B 的对应点B '.根据下列条件,利用网格点和无刻度的直尺画图并解答相关的问题(保留画图痕迹):(1)画出△A B C ''';(2)画出ABC ∆的高BD ;(3)连接AA '、CC ',那么AA '与CC '的关系是,线段AC 扫过的图形的面积为.【详解】解:(1)如图,△A B C'''即为所求;(2)如图,BD即为所求;(3)如图,AA'与CC'的关系是平行且相等,线段AC扫过的图形的面积为11 1022412611022⨯-⨯⨯⨯-⨯⨯⨯=,故本题答案为:平行且相等,10.23.(8分)如图,AF BC⊥于点E,BD BC⊥于点B,12∠=∠.(1)求证:BAF∠与AFD∠互补;(2)若AD平分BAF∠,40C∠=︒,求COD∠的度数.【详解】(1)证明:AF BC⊥于点E,BD BC⊥于点B,90CEF∴∠=︒,90CBD∠=︒,CEF CBD∴∠=∠,//AF BD∴,1BDC∴∠=∠,12∠=∠,2BDC∴∠=∠,//AB CD ∴,180BAF AFD ∴∠+∠=︒,即BAF ∠与AFD ∠互补;(2)解:在Rt CEF ∆中,40C ∠=︒,1180904050∴∠=︒-︒-︒=︒,//AB CD ,150BAF ∴∠=∠=︒,AD 平分BAF ∠,∴11502522DAF BAF ∠=∠=⨯︒=︒,90AEO CEF ∠=∠=︒ ,9025115COD AEO DAF ∴∠=∠+∠=︒+︒=︒.24.(10分)规定两数a ,b 之间的一种运算,记作(,)a b ;如果c a b =,那么(,)a b c =.例如:因为328=,所以(2,8)3=.(1)根据上述规定,填空:①(4,16)=,(3,81)-=;②若1(,)416x =-,则x =.(2)小明在研究这种运算时发现一个特征:(3n ,4)(3n =,4),小明给出了如下的证明:设(3n ,4)n x =,则(3)4n x n =,即(3)4x n n =,所以34x =,即(3,4)x =,所以(3n ,4)(3n =,4).试解决下列问题:.①计算(9,100)(81-,10000)②若(16,49)a =,(4,3)b =,(16,441)c =,请探索a ,b ,c 之间的数量关系.【详解】解:(1)①2416= ,(4,16)2∴=,4(3)81-= ,(3,81)4∴-=,故本题答案为:2,4;②由题意得:4116x -=,∴4411(2)x =±,2x ∴=±,故本题答案为:2±;(2)①(9,100)(81-,10000)2(3=,2410)(3-,410)(3=,10)(3-,10)0=;②(16,49)a = ,(16,441)c =,(4,7)a ∴=,(4,21)c =,47a ∴=,421c =,43b =,43744c a b =⨯=⨯ ,c a b ∴=+.25.(10分)(问题背景)90MON ∠=︒,点A 、B 分别在OM 、ON 上运动(不与点O 重合).(问题思考)(1)如图①,AE 、BE 分别是BAO ∠和ABO ∠的平分线,随着点A 、点B 的运动,AEB ∠=.(2)如图②,若BC 是ABN ∠的平分线,BC 的反向延长线与OAB ∠的平分线交于点D .①若70BAO ∠=︒,则D ∠=︒.②随着点A 、B 的运动,D ∠的大小会变吗?如果不会,求D ∠的度数;如果会,请说明理由;(问题拓展)(3)在图②的基础上,如果MON α∠=,其余条件不变,随着点A 、B 的运动(如图③),D ∠=.(用含α的代数式表示)【详解】解:(1)90MON ∠=︒ ,90OAB OBA ∴∠+∠=︒,AE 、BE 分别是BAO ∠和ABO ∠角的平分线,12BAE BAO ∴∠=∠,12ABE ABO ∠=∠,1()452BAE ABE BAO ABO ∴∠+∠=∠+∠=︒,135AEB ∴∠=︒;故本题答案为:135︒;(2)①90AOB ∠=︒ ,70BAO ∠=︒,20ABO ∴∠=︒,160ABN ∠=︒,BC 是ABN ∠的平分线,1160802OBD CBN ∴∠=∠=⨯︒=︒,AD 平分BAO ∠,35DAB ∴∠=︒,18018080352045D ABD BAD AOB ∴∠=︒-∠-∠-∠=︒-︒-︒-︒=︒,故本题答案为:45;②D ∠的度数不随A 、B 的移动而发生变化,设BAD x ∠=,AD 平分BAO ∠,2BAO x ∴∠=,90AOB ∠=︒ ,180902ABN ABO AOB BAO x ∴∠=︒-∠=∠+∠=+,BC 平分ABN ∠,45ABC x ∴∠=︒+,180ABC ABD D BAD ∠=︒-∠=∠+∠ ,4545D ABC BAD x x ∴∠=∠-∠=︒+-=︒;(3)设BAD x ∠=,AD 平分BAO ∠,2BAO x ∴∠=,AOB α∠= ,1802ABN ABO AOB BAO x α∴∠=︒-∠=∠+∠=+,BC 平分ABN ∠,12ABC x α∴∠=+,180ABC ABD D BAD ∠=︒-∠=∠+∠ ,1122D ABC BAD x x αα∴∠=∠-∠=+-=;故本题答案为:12α.26.(12分)如图1,直角三角形DEF 与直角三角形ABC 的斜边在同一直线上,30EDF ∠=︒,CD 平分ACB ∠,将DEF ∆绕点D 按逆时针方向旋转,记ADF ∠为(0180)αα︒<<︒,在旋转过程中:(1)如图2,40ABC ∠=︒,当α∠=时,//DE BC ,当α∠=时,DE BC ⊥;(2)如图3,40ABC ∠=︒,当顶点C 在DEF ∆内部时(不包含边界),边DF 、DE 分别交BC 、AC 的延长线于点M 、N ,①此时α∠的度数范围是.②BMD ∠与AND ∠度数的和是否变化?若不变,求出BMD ∠与AND ∠的度数和;若变化,请说明理由:.(3)如图4,将DEF ∆绕点D 按逆时针方向旋转过程中,边DE 与射线BC 有交点P ,边DF 与射线AC 有交点Q ,则BPD ∠与AQD ∠有什么关系.(4)如图5,将DEF ∆绕点D 按逆时针方向旋转过程中,边DE 与射线BC 有交点P ,边DF 与射线AC 有交点Q 、请在备用图中画出其他可能位置,并写出BPD ∠与AQD ∠的关系.【详解】解:(1)40B ∠=︒ ,∴当40EDA B ∠=∠=︒时,//DE BC ,30EDF ∠=︒ ,403010α∴=︒-︒=︒;当//DE AC 时,DE BC ⊥,180A EDA ∴∠+∠=︒,9050A B ∠=︒-∠=︒,180********EDA A ∴∠=︒-∠=︒-︒=︒,13030100α∴=︒-︒=︒,故本题答案为:10︒,100︒;(2)①40ABC ∠=︒ ,CD 平分ACB ∠,45ACD ∴∠=︒,50A ∠=︒,85CDA ∴∠=︒,当点C 在DE 边上时,3085α+︒=︒,解得:55α=︒,当点C 在DF 边上时,85α=︒,∴当顶点C 在DEF ∆内部时,5585α︒<<︒,故本题答案为:5585α︒<<︒;②1∠与2∠度数的和不变,理由如下:如图3,连接MN ,在CMN ∆中,180CNM CMN MCN ∠+∠+∠=︒ ,90CNM CMN ∴∠+∠=︒,在MND ∆中,180DNM DMN MDN ∠+∠+∠=︒ ,即180AND CNM CMN BMD MDN ∠+∠+∠+∠+∠=︒,180903060BMD AND ∴∠+∠=︒-︒-︒=︒;(3)180180AQD A ADQ A α∠=︒-∠-∠=︒-∠-∠ ,30(90)60BPD ADP B A A αα∠=∠-∠=+︒-︒-∠=+∠-︒,120AQD BPD ∴∠+∠=︒,故本题答案为:120AQD BPD ∠+∠=︒;(4)同(3)可得,120AQD BPD ∠+∠=︒,故本题答案为:120∠+∠=︒.AQD BPD。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
七年级第二学期数学阶段检测题2015.4.5
一、选择题(每小题3分,共30分)
1. 下列各题的计算,正确的是( )
A. 927)(a a =
B. 1427a a a =⋅
C. 522632a a a =+
D. 22)5.0(101100=⨯-
2. 如果单项式243y x b a --与b a y x +33
1是同类项,那么这两个单项式的积是( ). A.46y x B.23y x - C.2338y x - D.4
6y x -
3. 计算223)3(a a ÷-的结果是( ).
A.49a
B. 49a -
C.46a
D. 39a
4. 若,12,7==+mn n m 则22n mn m +-的值是( )
A. 11
B. 13
C. 37
D. 61
5.计算()()()-++2021
1
1
101010的结果是( ) A. 1 B. 201 C.1
101100 D. 1
100100
6.三个连续偶数中,中间一个为m ,则它们的积是( )
A.m m -288
B. m m -34
C. m m -382
D. m m -34
7.一个正方形的边长增加了2cm ,面积增加了24cm 2 ,则这个正方形的原边长是(
) A. 8 B. 7 C. 6 D. 5
8.计算()()-+-2014201533的结果是( )
A. -3
B. -2×20143
C.-1
D.-20143
9.已知三个非零度角之和是180°,那么这三个角中至少有一个角不大于( )
A. 30°
B. 45°
C. 60°
D. 90°
10.下列各式计算正确的是( ).
A.3)3)(3(2-=-+x x x
B.92)32)(32(2-=-+x x x
C.92)3)(32(2-=-+x x x
D.125)15)(15(22-=-+b a ab ab
二、填空题(每题2分,共12分)
11. ()-2510=
12. 532)(y y ÷=_______
13. 若194a a a y =⋅,则=y .
14.已知n y =1
3,n x =15,则()n xy =
15. 在同一平面内,已知∠AOB =60°,∠AOC =45°,则∠BOC = 。
16.表示成度:43°13′48″= 。
三、解答题
17. 计算题(每小题4分,共16分)
(1) ()ab -25
12
(2) ()()a a -∙-2332
233
(3)()()m m +-57
(4)()()m m m --+2132412
18. (6分)先化简,再求值:
)32(3)143(222--+-x x x x x ,其中3-=x .
19. (6分)如图有三种纸片若干.
A 如果用它们制成一个长为()m n +2,宽为()m n +2的大的纸片,则纸片I 需要 张,
纸片II 需要 张,纸片III 需要 张;
B 在右上方画出这个大的矩形纸片。
III II I
n
m
20.(6分)已知()()x
x x b -++2321中不含有x 2项,求b 的值。
21.(6分)已知a =1020,b =1105
,求()()a b -÷-55。
22. (6分)已知a m
=4,b m =5,c m =6求a b c m -+32的值。
23.(6分)解方程:()()()
m m m m
+--+= 21312310
24. (6分)在平面上有一点O,以O为顶点引出2条射线,可以组成1个角;引出3条射线,可以组成3个角;引出4条射线,可以组成几个角?引出5条呢?6条呢?如果引出射线n条呢?。
