1.2函数及其表示练习题
高中数学必修一1.2函数及其表示练习题及答案

高中数学必修一1.2函数及其表示练习题及答案一:单项选择题: (共10题,每小题5分,共50分)1. 函数()y f x =的图象与直线1x =的公共点数目是( )A 1B 0C 0或1D 1或22. 为了得到函数(2)y f x =-的图象,可以把函数(12)y f x =-的图象适当平移,这个平移是( )A 沿x 轴向右平移1个单位B 沿x 轴向右平移12个单位C 沿x 轴向左平移1个单位D 沿x 轴向左平移12个单位3. 已知集合{}{}421,2,3,,4,7,,3A k B a a a ==+,且*,,a N x A y B ∈∈∈使B 中元素31y x =+和A 中的元素x 对应,则,a k 的值分别为( )A 2,3 B 3,4 C 3,5 D 2,54. 判断下列各组中的两个函数是同一函数的为( ) ⑴3)5)(3(1+-+=x x x y ,52-=x y ;⑵111-+=x x y ,)1)(1(2-+=x x y ; ⑶x x f =)(,2)(x x g =;⑷()f x =()F x = ⑸21)52()(-=x x f ,52)(2-=x x fA ⑴、⑵B ⑵、⑶C ⑷D ⑶、⑸5. 设⎩⎨⎧<+≥-=)10()],6([)10(,2)(x x f f x x x f 则)5(f 的值为( )A 10 B 11 C 12 D 13 6. 函数f (x )=的定义域是( )A .-∞,0]B .[0,+∞C .(-∞,0)D .(-∞,+∞)7. 若函数f(x) = + 2x+ log 2x 的值域是 {3, -1, 5 + , 20},则其定义域是( ) (A) {0,1,2,4} (B) {,1,2,4} (C) {,2,4} (D) {,1,2,4,8}8.反函数是( ) A. B.C. D.9. 若任取x 1,x 2∈[a ,b ],且x 1≠x 2,都有成立,则称f (x ) 是[a ,b ]上的凸函数。
【高中数学】《1.2 函数及其表示(1)》测试题

【高中数学】《1.2 函数及其表示(1)》测试题【高中数学】《1.2函数及其表示(1)》测试题一、多项选择题1.(2021安徽理)下列函数中,不满足的是().a、不列颠哥伦比亚省。
考查目的:考查学生对函数符号的理解.回答:C解析:经验证,只有不满足.2.在以下函数中,与函数定义字段相同的是()a.b.c、 d。
考查目的:主要考查函数定义域的求法.回答:B解析:解不等式组得函数定义域为,故答案选b3.如果函数的定义字段为,则其值字段为()a.b.c.d.目的:主要考察功能价值范围的概念答案:a分析:代入并分别得到函数值,因此函数的取值范围为,答案为a二、填空题4.如果函数已知,则值集为考查目的:主要考查对分段函数的理解.答复:解析:函数,,则,解得;或,解得,∴取值的集合为.5.如果已知它是一个主函数,并且满足它,则考查目的:主要考查对函数符号的理解和利用待定系数法求函数解析式.答复:解析:设,则由得,即,∴,解得,∴.6.如果函数的定义字段为,则函数的定义字段为考查目的:对函数符号以及函数定义域概念的理解.答复:解析:由已知得,解得,∴函数的定义域为.三、回答问题7.函数对于任意实数满足条件,若,求.检查目的:主要检查对功能符号的理解答案:解析:∵, ∧, ∧,∴.8.城市居民自来水收费标准为:每户月用水量不超过4吨时,每吨1.80元;当用水量超过4吨时,超出部分为每吨3.00元。
一个月内,a户和B户共缴纳水费元。
据了解,a、B用户当月用水量分别为万吨⑴求关于的函数;?(2)如果a户和B户当月共缴纳水费26.4元,则分别计算a户和B户当月的用水量和水费考查目的:主要考查根据实际问题,列函数关系式,分段函数求值.分析:⑴ 甲方用水量不超过4吨,即乙方用水量不超过4吨,;当甲的用水量超过4吨,乙的用水量不超过4吨时,即且时,.乙方用水量超过4吨时,即:,,∴.(2)到那时,问题就可以解决了;当时,,解得;当时发现a户用水量为吨,支付4×1.8+3.5×3=17.70元;乙方用水量为(吨),费用为4×1.8+0.5×3=8.70元。
【高一数学试题精选】1.2函数及其表示训练试题(含答案和解释)

1.2函数及其表示训练试题(含答案和解释)
5 主动成长
夯基达标
1 下列各组函数是否表示同一个函数?
(1)f(x)=x,g(x)=(x)2;
(2)f1(x)=(x+2)2,f2(x)=|x+2|;
(3)f(x)=x2-2x-1,g(t)=t2-2t-1;
(4)=x,=
思路解析定义域和对应法则是确定函数的两个基本要素,两个函数是否相同取决于定义域和对应法则是否分别相同
答案(1)f(x)=x的定义域为R,g(x)=()2的定义域为{x|x≥0},两函数的定义域不同,所以不是同一个函数(2)f1(x)= =|x+2|,它与f2(x)=|x+2|的对应法则与定义域均相同,所以是同一个函数
(3)两函数的对应法则和定义域相同,而函数与表示函数的字母无关,所以表示同一函数
(4)两个函数,其中一个是分段函数,它的定义域为R,不管s >0,s<0,s=0都有=s,对应法则和=x相同因此这两个函数定义域和对应法则都相同,所以它们是相同的函数
2 已知函数f(x)=x2-2x-3的定义域为F,g(x)= 的定义域为G,那么集合F、G的关系是( )
A F=G
B F G
c G F
D F∪G=G
思路解析函数的定义域是使函数思路分析式有意义的自变量的值。
1.2函数及其表示练习题及答案1

1.2函数及其表示练习题一.选择题1 函数)23(,32)(-≠+=x x cx x f 满足,)]([x x f f =则常数c 等于( ) A 3 B 3- C 33-或 D 35-或2. 已知)0(1)]([,21)(22≠-=-=x xx x g f x x g ,那么)21(f 等于( ) A 15 B 1C 3D 303.函数2y =的值域是( )A [2,2]-B [1,2]C [0,2] D[]4 已知2211()11x x f x x--=++,则()f x 的解析式为( )A21x x + B 212x x+- C 212x x + D 21x x+-5.设()f x 是R 上的任意函数,则下列叙述正确的是 ( )(A)()()f x f x -是奇函数 (B)()()f x f x -是奇函数 (C) ()()f x f x --是偶函数 (D) ()()f x f x +-是偶函数6. 下列图中,画在同一坐标系中,函数bx ax y +=2与)0,0(≠≠+=b a b ax y 函数的图象只可能是 ( )7.已知二次函数)0()(2>++=a a x x x f ,若0)(<m f ,则)1(+m f 的值为( )A .正数B .负数C .0D .符号与a 有关 8. 已知)(x f 的定义域为)2,1[-,则|)(|x f 的定义域为 ( ) A .)2,1[-B .]1,1[-C .)2,2(-D .)2,2[-9. 已知在x 克%a 的盐水中,加入y 克%b 的盐水,浓度变为%c ,将y 表示成x 的函数关系式 ( )A .x bc ac y --=B .x c b a c y --=C .x a c b c y --=D .x ac cb y --= 10.已知f 满足f (ab )=f (a )+ f (b),且f (2)=p ,q f =)3(那么)72(f 等于 ( )A .q p +B .q p 23+C .q p 32+D .23q p +11. (2010陕西文数)某学校要招开学生代表大会,规定各班每10人推选一名代表,当各班人数除以10的余数大于..6.时再增选一名代表.那么,各班可推选代表人数y 与该班人数x 之间的函数关系用取整函数y =[x ]([x ]表示不大于x 的最大整数)可以表示为(A )y =[10x] (B )y =[310x +] (C )y =[410x +](D )y =[510x +]12.(2009海口模拟)已知函数()()2113,f x x x =+≤≤则A .()()12202f x x x -=+≤≤B .()()12124f x x x -=-+≤≤C .()()12202f x x x -=-≤≤D .()()12104f x x x -=-≤≤ 13.(2009江西理)函数ln 1x y +=的定义域为A .()4,1--B .4,1-C .()1,1-D .(1,1]-14.(2008山东)设函数()221, 1,2, 1,x x f x x x x ⎧-≤⎪=⎨+->⎪⎩则()12f f ⎛⎫⎪ ⎪⎝⎭的值为 A .1516B .2716-C .89 D.1815.(2008陕西) 定义在R 上的函数()f x 满足()()()()()2,,12f x y f x f y xy x y R f +=++∈=则()3f -等于( )A. 2B. 3C. 6 D .916.(2009福建)下列函数中与函数y =有相同定义域的是 ( ) A .()ln f x x = B 。
1.2 函数及其表示

1 0.5 -2 -1 O -1 -2
1
2
x
练习: (课本23页) 1. 如图, 把截面半径为 25 cm 的 圆形木头据成矩形木料, 如果矩形的 一边长为 x cm, 面积为 y cm2, 把 y 表示为 x 的函数. 解: 由勾股定理得矩形的宽为 502 - x 2 , 则矩形面积的函数为 y = x 502 - x 2 , (0<x<50)
5 公里的分段. 设里程为 x, 票价为 y, 则解析式为:
2, 0<x≤5, y= 3, 5<x≤10, 4, 10<x≤15, 5, 15<x≤20. 其图象为:
y 5 4 3 2 1 o
5
10 15 20
x
练习: (补充题) 画出下列函数的图象, 根据图象写出定义域和值域:
1 (0 x 1) ; (1) y = x x ( x 1)
笔记本数 x 钱数 y 1 5 2 10
y 25 20 15 10 5
3 15
4 20
(直接反 25 映函数值)
5
(3) 图象表示: 问: 三种表示 方法各有什么优点?
(直观反映 出定义域, 值域及大 O 1 2 3 4 5 x小关系)
· · · · ·
例4. 下表是某校高一 (1) 班三名同学在高一学 年度六次数学测试的成绩及班级平均分表.
1.2.2 函数的表示法
第一课时
函数的表示
返回目录
1. 函数有哪三种表示方法? 2. 函数的各种表示方法各自最能反映函数的 哪些特性? 3. 函数的各种表示方法怎样互相联系, 互相 转化?
问题1. 初中我们学了一次函数, 二次函数, 反 比例函数等, 这些函数可以用哪些方法进行表示? 函数的表示一般有三种方法: 解析法、图象法和 列表法. 解析法, 就是用数学表达式表示两个变量之间的 对应关系, 这个表达式又称解析式. 图象法, 就是用图象表示两个变量之间的对应关 系. 列表法, 就是列出表格来表示两个变量之间的对 应关系.
人教A版高中数学必修1《1.2 函数及其表示 习题1.2》_2

掌握函数的三种表示方法(列表法,解析法,图象法),及其互相转化;理解分段函数的概念。
列表法:
解析法:
图象法:
三、典例欣赏
例1.购买某种饮料x听,所需钱数为y元。
若每听2元,试分别用解析法、列表法、图象法将y表示为x(x∈{1,2,3,4})的函数,并指出函数的值域。
例2.某市出租汽车收费标准如下:在以内(含)路程按起步价7元收费,超过以外的路程按2.4元收费,试写出收费额关于路程的函数的解析式。
(1)概念:
(2)理解:
练习与思考:考虑例2中所求得的函数解析式,
回答下列问题:
(2)理解:
练习与思考:考虑例2中所求得的函数解析式,
回答下列问题:
(1)函数的定义域是_______________.
(2)若x = 8,则y =_______________;若y = 11.8,则x =_______________.
(3)画出函数的图像.
(4)函数的值域是_______________.
例3.(1)已知,求。
(2)已知函数,若。
例4.如图是边长为2的正三角形,这个三角形在直线左侧部分的面积为y,求函数的解析式,并画出的图象.。
人教A版高中数学必修1《1.2函数及其表示习题1.2》0

A
B,U为全集,则以下会合为空集的是
(
)
A.A∩B
B.A∩(?UB)
C.A∪(?UB)
D.(?UA)∩(?UB)
分析:选B.由Venn图可知.
4.设全集U={a,b,c,d},会合A={a,b},B={b,c,d},则(?UA)∪(?UB)=________.分析:∵(?UA)={c,d},(?UB)={a},∴(?UA)∪(?UB)={a,c,d}.答案:{a,c,d}5.若U={n|n是小于9的正整数},A={n∈U|n是奇数},B={n∈U|n是3的倍数},则?U(A∪B)=________.分析:U={1,2,3,4,5,6,7,8},则A={1,3,5,7},B={3,6},∴A∪B={1,3,5,6,7},?U(A∪B)={2,4,8}.答案:{2,4,8}1
a>0
要使B??R
,只要
1
A
a≤
2
∴0<a≤
1
2
1
综上,a≤2.
A.1
B.2
C.3
D.4
分析:选B.因为会合A={1,2},B={2,4},所以A∪B={1,2,4},所以?U(AB)={3,5}.4.已知全集U={0,1,2,3,4},会合A={1,2,3},B={2,4},则(?UA)∪B为________.分析:?UA={0,4},所以(?UA)∪B={0,2,4}.答案:{0,2,4}5.设会合A={x|1<x<4},B={x|-1≤x≤3},则A∩(?RB)=________.分析:?RB={x|x<-1或x>3}∴A∩?RB={x|3<x<4}答案:{x|3<x<4}6.已知全集U={x|x取不大于30的质数},A、B是U的两个子集,且A∩(?UB)={5,13,23},(?UA)∩B={11,19,29},(?UA)∩(?UB)={3,7},求会合A、B.
【创新设计】高中数学(人教版必修一)配套练习:1.2函数及其表示习题课(含答案解析)

§1.2 习题课
课时目标 1.加深对函数概念的理解,加深对映射概念的了解.2.在实际情境中,会根据不同的需要选择恰当的方法(如图象法、列表法、解析法)表示函数.3.通过具体实例,理解简单的分段函数,并能简单应用.
1.下列图形中,不可能作为函数y=f(x)图象的是()
2.已知函数f:A→B(A、B为非空数集),定义域为M,值域为N,则A、B、M、N 的关系是()
A.M=A,N=B B.M?A,N=B
C.M=A,N?B D.M?A,N? B
3.函数y=f(x)的图象与直线x=a的交点()
A.必有一个B.一个或两个
C.至多一个D.可能两个以上
4.已知函数,若f(a)=3,则a的值为()
A. 3 B.- 3
C.±3 D.以上均不对
5.若f(x)的定义域为[-1,4],则f(x2)的定义域为()
A.[-1,2] B.[-2,2]
C.[0,2] D.[-2,0]
6.函数y=
x
kx2+kx+1
的定义域为R,则实数k的取值范围为()
A.k<0或k>4 B.0≤k<4 C.0<k<4 D.k≥4或k≤0
一、选择题
1.函数f(x)=
x
x2+1
,则f(
1
x
)等于()。
高考数学 1.2 函数及其表示练习

【师说高中全程复习构想】(新课标)2015届高考数学 1.2 函数及其表示练习一、选择题1.(2014·嘉兴调研)设集合M={x|-2≤x≤2},N={y|0≤y≤2},给出下列四个图形,其中能表示以集合M为定义域,N为值域的函数关系的是( )A. B. C. D.解析:利用函数的定义,要求定义域内的任一变量都有唯一的函数值与之对应,A 中函数的定义域是[-2,0),C 中任一x ∈[-2,2)对应的值不唯一,D 中的值域不是N ,故选B. 答案:B2.已知f :x→-sinx 是集合A(A ⊆[0,2π])到集合B ={0,12}的一个映射,则集合A 中的元素个数最多有( )A .4个B .5个C .6个D .7个解析:由-sinx =0,得sinx =0.又x ∈[0,2π],故x =0或π或2π;由-sinx =12,得sinx =-12.又x ∈[0,2π],故x =7π6或11π6.选B. 答案:B3.已知f(x +1)=-f(x),且f(x)=⎩⎪⎨⎪⎧ 1-1<x <0,00≤x≤1,则f(3)=( )A .-1B .0C .1D .1或0解析:f(3)=-f(2)=f(1)=0,故选B.答案:B4.若f(x)对于任意实数x 恒有2f(x)-f(-x)=3x +1,则f(x)=( )A .x -1B .x +1C .2x +1D .3x +3解析:在2f(x)-f(-x)=3x +1①将①中x 换为-x ,则有2f(-x)-f(x)=-3x +1②①×2+②得3f(x)=3x +3,∴f(x)=x +1.答案:B5.图中的图象所表示的函数的解析式为( )A .y =32|x -1| (0≤x≤2) B .y =32-32|x -1| (0≤x≤2) C .y =32-|x -1| (0≤x≤2) D .y =1-|x -1| (0≤x≤2)解析:取x =1,则y =32,只有B 、C 满足.取x =0,则y =0,在B 、C 中只有B 满足,所以选B.答案:B6.某学校要召开学生代表大会,规定各班每10人推选一名代表,当各班人数除以10的余数大于6时再增选一名代表.那么,各班可推选代表人数y 与该班人数x 之间的函数关系用取整函数y =[x]([x]表示不大于x 的最大整数)可以表示为( )A .y =[x 10]B .y =[x +310] C .y =[x +410] D .y =[x +510] 解析:当各班人数除以10的余数大于6时再增选一名代表,可以看作先用该班人数除以10再用这个余数与3相加,若和大于等于10就增选一名代表,将二者合并便得到推选代表人数y 与该班人数x 之间的函数关系,用取整函数y =[x]([x]表示不大于x 的最大整数)可以表示为y =[x +310]. 答案:B二、填空题7.已知f ⎝ ⎛⎭⎪⎫x -1x =x2+1x2,则函数f(3)=________. 解析:∵f ⎝ ⎛⎭⎪⎫x -1x =x2+1x2=⎝ ⎛⎭⎪⎫x -1x 2+2, ∴f(x)=x2+2,∴f(3)=32+2=11.答案:118.(2014·荆州质检)设f(x)=⎩⎪⎨⎪⎧ lgx ,x >0,10x ,x≤0,则f[f(-2)]=__________. 解析:因为f(x)=⎩⎪⎨⎪⎧ lgx ,x >0,10x ,x≤0,又-2<0,∴f(-2)=10-2,10-2>0,f(10-2)=lg10-2=-2.答案:-29.设函数f(x)=⎩⎪⎨⎪⎧ x ,x≥0,⎝ ⎛⎭⎪⎫12x ,x <0,则f[f(-4)]=________.解析:f[f(-4)]=f(24)=24=4.答案:4三、解答题10.二次函数f(x)满足f(x +1)-f(x)=2x ,且f(0)=1.(1)求f(x)的解析式;(2)解不等式f(x)>2x +5.解析:(1)设二次函数f(x)=ax2+bx +c(a≠0).∵f(0)=1,∴c =1.把f(x)的表达式代入f(x +1)-f(x)=2x ,有a(x +1)2+b (x +1)+1-(ax2+bx +1)=2x.∴2ax +a +b =2x.∴a =1,b =-1.∴f(x )=x2-x +1.(2)由x2-x +1>2x +5,即x2-3x -4>0,解得x >4或x <-1.故原不等式解集为{x|x >4或x <-1}.11.函数f(x)对一切函数x 、y 均有f(x +y)-f(y)=x(x +2y +1)成立,且f(1)=0,(1)求f(0)的值;(2)试确定函数f(x)的解析式.解析:(1)令x =1,y =0,得f(1)-f(0)=2.又∵f(1)=0,∴f(0)=-2.(2)令y =0,则f(x)-f(0)=x(x +1),由(1)知,f(x)=x(x +1)+f(0)=x(x +1)-2=x2+x -2.12.已知函数f(x)=⎩⎪⎨⎪⎧ cx +1, 0<x <c2-x c2+1, c≤x<1)满足f(c2)=98.(1)求常数c 的值;(2)解不等式f(x)>28+1.解析:(1)因为0<c <1,所以c2<c ,由f(c2)=98,即c3+1=98,c =12.(2)由(1)得f(x)=⎩⎪⎨⎪⎧ 12x +1,0<x <122-4x +1,12≤x<1由f(x)>28+1得,当0<x <12时,解得24<x <12,当12≤x<1时,解得12≤x<58,所以f(x)>28+1的解集为{x|24<x <58}.。
1.2函数及其表示测试

1.2函数及其表示测试题一. 选择题1. 设集合A={ x ∣0≤x ≤2},B={ y ∣1≤y ≤2},下图中能表示从集合A 到集合B 的映射的是( )A. B. C. D.2. 若f(x)=,则方程f(4x)=x 的根为( ) xx 1-A. B. - C.2 D. -2 21213. 定义运算x ※y=,若(2-m )※(2m-1)=2-m ,则m 的取值范围为{)()(y x x y x y ≤>( ) A.(-∞,1) B.(-∞,1]C.(1,∞)D. [1,∞)4. 向高为H 的水瓶中注水,注满为止。
如果注水量V 与水深h 的函数关系的图象如右图所示,那么水瓶的形状是( )A. B. C. D.5. 已知f(x)=,则f(3)=( ){)6(4)6)(2(≥-<+x x x x f A.1 B.2 C.3 D.4二. 填空题 1. 函数f(x)= 的定义域为 。
xx 3+2. 已知a 、b 为常数,若f(x)=+4x+3,f(ax+b)=+10x+24,则x 2x 25a-b= 。
3. 已知函数f(x),g(x)分别由下表给出 x 1 2 3 g(x) 32 1 则f[g(1)]的值为 ;满足f[g(x)]>g[f(x)]的x 的值为 。
4. 已知函数f(x)对任意实数x 都满足条件f(x+1)=,若f(1)=-5,则)(1x f f(11)= 。
5. 设函数f(x)=,若f(a)>a ,则实数a 的取值范围是 。
{)1(!21)1(3≤+>+-x x x x 三. 解答题1. 据报道,我国目前已成为世界上受荒漠化危害最严重的国家之一,图(1)表示我国土地沙化总面积在上个世纪五六十年代、七八十年代、九十年代的变化情况。
由图中的相关信息,可将上述有关年代中,我国年平均土地沙化面积在图(2)中图示为:2. 《中华人民共和国个人所得税法》规定,公民全月工资、薪金所得不超过800x 1 23 f(x) 13 1元的部分不必纳税,超过800元的部分为全月应纳税所得额。
【高中数学必修一】1.2.2 函数的表示法-高一数学人教版(必修1)(解析版)

第一章 集合与函数概念1.2.2 函数的表示法一、选择题1.若()()20(0)x x f x x x ⎧≥=⎨-<⎩,,,则f [f (–2)]=A .2B .3C .4D .5【答案】C【解析】∵–2<0,∴f (–2)=–(–2)=2.又∵2>0,∴f [f (–2)]=f (2)=22=4,故选C .2.“龟兔赛跑”讲述了这样的故事:领先的兔子看着缓缓爬行的乌龟,骄傲起来,睡了一觉.当它醒来时,发现乌龟快到终点了,于是急忙追赶,但为时已晚,乌龟还是先到了终点.用S 1和S 2分别表示乌龟和兔子经过时间t 所行的路程,则下列图象中与故事情节相吻合的是A .B .C .D .【答案】D3.已知函数f (x +1)=3x +2,则f (x )的解析式是A.f(x)=3x+2 B.f(x)=3x+1C.f(x)=3x–1 D.f(x)=3x+4【答案】C【解析】设t=x+1,∵函数f(x+1)=3x+2=3(x+1)–1,∴函数f(t)=3t–1,即函数f(x)=3x–1,故选C.4.已知映射f:A→B,其中A={a,b},B={1,2},已知a的象为1,则b的象为A.1,2中的一个B.1,2 C.2 D.无法确定【答案】A【解析】映射f:A→B,其中A={a,b},B={1,2},已知a的象为1,可得b的象为1或2,故选A.5.若f(x)满足关系式f(x)+2f(1x)=3x,则f(2)的值为A.1 B.–1 C.–32D.32【答案】B【解析】∵f(x)满足关系式f(x)+2f(1x)=3x,分别令x=2,和x=12,得()()12262132222f ff f⎧⎛⎫+=⎪⎪⎪⎝⎭⎨⎛⎫⎪+=⎪⎪⎝⎭⎩①②,①–②×2得–3f(2)=3,∴f(2)=–1,故选B.6.甲、乙两人在一次赛跑中,路程s与时间t的函数关系如图所示,则下列说法正确的是A.甲比乙先出发B.乙比甲跑的路程多C.甲、乙两人的速度相同D.甲先到达终点【答案】D7.已知f(x–2)=x2–4x,那么f(x)=A .x 2–8x –4B .x 2–x –4C .x 2+8xD .x 2–4【答案】D【解析】由于f (x –2)=x 2–4x =(x 2–4x +4)–4=(x –2)2–4,从而f (x )=x 2–4.故选D . 8.国内某快递公司规定:重量在1000 g 以内的包裹快递邮资标准如下表:运送距离x (km ) 0<x ≤500 500<x ≤10001000<x ≤15001500<x ≤2000… 邮资y (元)5.006.007.008.00如果某人从北京快递900 g 的包裹到距北京1300 km 的某地,他应付的邮资是 A .5.00元B .6.00元C .7.00元D .8.00元【答案】C【解析】邮资y 与运送距离x 的函数关系式为 5.00(0500)6.00(5001000)7.00(10001500)8.00(15002000)x x y x x <≤⎧⎪<≤⎪=⎨<≤⎪⎪<≤⎩,∵1300∈(1000,1500],∴y =7.00,故选C .9.已知函数()()()32121x x f x x x x ⎧>⎪=⎨-+≤⎪⎩.若()54f a =-,则a 的值为A .12-或52B .12或52C .12-D .12【答案】C【解析】当a >1时,f (a )=3514a >≠-,此时a 不存在,当a ≤1,f (a )=–a 2+2a =–54,即4a 2–8a –5=0,解可得a =–12或a =52(舍),综上可得a =12-,故选C .10.已知函数f (x )=()20(0)x x x x ⎧≥⎨<⎩,,,则f (f (–2))的值是A .2B .–2C .4D .–4【答案】C【解析】∵已知函数()()20(0)x x f x x x ⎧≥=⎨<⎩,,,∴f (–2)=(–2)2,∴f (f (–2))=f (4)=4,故选C .二、填空题11.已知f+1)=x,则f (x )=__________.【答案】x 2–1,(x ≥1)【解析】∵()12fx x x +=+=x +2x +1–1=(x +1)2–1,∴则f (x )=x 2–1,(x ≥1).故答案为:x 2–1,(x ≥1).12.已知f (x +1)=2x 2+1,则f (x –1)=__________.【答案】2x 2–8x +9【解析】设x +1=t ,则x =t –1,f (t )=2(t –1)2+1=2t 2–4t +3,f (x –1)=2(x –1)2–4(x –1)+3=2x 2–4x +2–4x +4+3=2x 2–8x +9.故答案为:2x 2–8x +9. 13.已知f (x +1)=x 2,则f (x )=__________.【答案】(x –1)2【解析】由f (x +1)=x 2,得到f (x +1)=(x +1–1)2,故f (x )=(x –1)2.故答案为:(x –1)2. 14.已知函数f (x )=ax –b (a >0),f (f (x ))=4x –3,则f (2)=__________.【答案】3三、解答题15.()()()11032f x kx b f f =+==-,,,求f (4)的值. 【解析】∵()()()11032f x kx b f f =+==-,,,∴0132k b k b +=⎧⎪⎨+=-⎪⎩,解得k =–14,b =14, ∴f (x )=–14x +14,∴f (4)=–14×4+14=–34.16.二次函数f (x )满足f (x +1)–f (x )=2x 且f (0)=1.(1)求f (x )的解析式;(2)当x ∈[–1,1]时,不等式f (x )>2x +m 恒成立,求实数m 的取值范围. 【解析】(1)由题意,设f (x )=ax 2+bx +c , 则f (x +1)=a (x +1)2+b (x +1)+c .从而f (x +1)–f (x )=[a (x +1)2+b (x +1)+c ]–(ax 2+bx +c )=2ax +a +b , 又f (x +1)–f (x )=2x ,∴220a a b =⎧⎨+=⎩即11a b =⎧⎨=-⎩,又f (0)=c =1, ∴f (x )=x 2–x +1.17.已知函数f (x )=()()221(12)22x x x x x x ⎧+≤-⎪-<<⎨⎪≥⎩(1)在坐标系中作出函数的图象; (2)若f (a )=12,求a 的取值集合. 【解析】(1)函数f (x )=()()221(12)22x x x x x x ⎧+≤-⎪-<<⎨⎪≥⎩的图象如下图所示:(2)当a ≤–1时,f (a )=a +2=12,可得:a =32-;当–1<a <2时,f (a )=a 2=12,可得:a =22±;当a ≥2时,f(a )=2a =12,可得:a =14(舍去); 综上所述,a 的取值构成集合为{32-,22-,22}.18.(1)已知3311f x x x x ⎛⎫+=+ ⎪⎝⎭,求f (x ). (2)已知21f lgx x ⎛⎫+=⎪⎝⎭,求f (x ). (3)已知f (x )是一次函数,且满足3f (x +1)–2f (x –1)=2x +17,求f (x ). (4)已知f (x )满足()123f x f x x ⎛⎫+=⎪⎝⎭,求f (x ). 【解析】(1)∵3331111()3f x x x x x x x x ⎛⎫⎛⎫+=+=+-+ ⎪ ⎪⎝⎭⎝⎭, ∴f (x )=x 3–3x (x ≥2或x ≤–2).(2)令21t x +=(t >1), 则21x t =-,∴()21f t lg t =-,∴()()211f x lg x x =->.19.已知函数f (x )=1+2x x -(–2<x ≤2),用分段函数的形式表示该函数.【解析】f (x )=1+1021202x x x x x ≤≤-⎧=⎨--<<⎩,,.。
高一数学必修1《1.2函数及其表示》单元测试题(含答案)
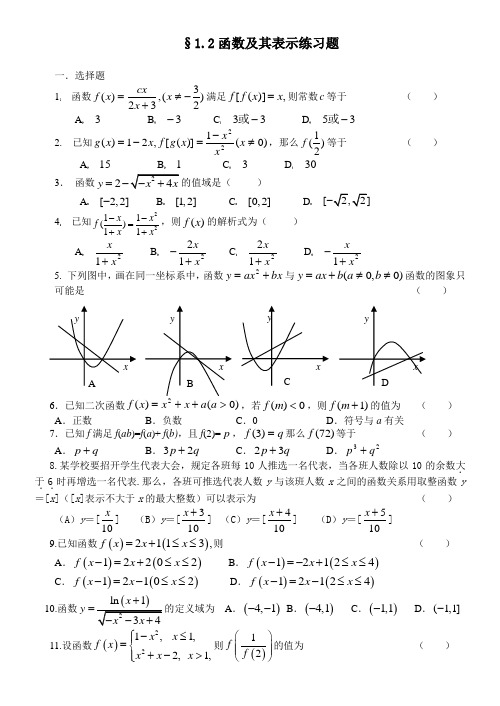
§1.2函数及其表示练习题一.选择题1 函数)23(,32)(-≠+=x x cx x f 满足,)]([x x f f =则常数c 等于 ( ) A 3 B 3- C 33-或 D 35-或2. 已知)0(1)]([,21)(22≠-=-=x x x x g f x x g ,那么)21(f 等于 ( ) A 15 B 1 C 3 D 303.函数2y =的值域是( )A [2,2]-B [1,2]C [0,2] D[]4 已知2211()11x x f x x--=++,则()f x 的解析式为( ) A21x x + B 212x x +- C 212x x + D 21x x+-5. 下列图中,画在同一坐标系中,函数bx ax y +=2与)0,0(≠≠+=b a b ax y 函数的图象只可能是( )6.已知二次函数)0()(>++=a ax x x f ,若0)(<m f ,则)1(+m f 的值为 ( ) A .正数 B .负数 C .0 D .符号与a 有关 7.已知f 满足f (ab )=f (a )+ f (b),且f (2)=p ,q f =)3(那么)72(f 等于 ( )A .q p +B .q p 23+C .q p 32+D .23q p +8.某学校要招开学生代表大会,规定各班每10人推选一名代表,当各班人数除以10的余数大.于.6.时再增选一名代表.那么,各班可推选代表人数y 与该班人数x 之间的函数关系用取整函数y =[x ]([x ]表示不大于x 的最大整数)可以表示为( )(A )y =[10x ] (B )y =[310x +] (C )y =[410x +] (D )y =[510x +] 9.已知函数()()2113,f x x x =+≤≤则 ( )A .()()12202f x x x -=+≤≤B .()()12124f x x x -=-+≤≤C .()()12102f x x x -=-≤≤D .()()12124f x x x -=-≤≤ 10.函数ln 1x y +=的定义域为 A .()4,1-- B .()4,1- C .()1,1- D .(1,1]-11.设函数()221, 1,2, 1,x x f x x x x ⎧-≤⎪=⎨+->⎪⎩则()12f f ⎛⎫⎪ ⎪⎝⎭的值为 ( )A .1516 B .2716- C .89D.18 12.已知A 、B 两地相距150千米,某人开汽车以60千米/小时的速度从A 地到达B 地,在B 地停留1小时后再以50千米/小时的速度返回A 地,把汽车离开A 地的距离S 表示为时间t (小时) 的函数表达式是 ( ) A .S=60t B .S=60t +50tC .S=⎩⎨⎧>-≤≤)5.3(,50150)5.20(,60t t t tD .S=⎪⎩⎪⎨⎧≤<--≤<≤≤)5.65.3(),5.3(50150)5.35.2(,150)5.20(,60t t t t t13.下列函数中与函数y =有相同定义域的是 ( ) A .()ln f x x = B. ()1f x x= C. ()f x x = D. ()x f x e =14.下列各组函数表示同一函数的是 ( ) A.2(),()f x g x == B .0()1,()f x g x x ==C .())()()t t g x x x x x f =⎩⎨⎧<-≥=,00D .21()1,()1x f x x g x x -=+=- 15 设⎩⎨⎧<+≥-=)10()],6([)10(,2)(x x f f x x x f 则)5(f 的值为 ( )A 10B 11C 12D 13 二.填空题1. 函数1(0)y x x x=+>的值域为 2. 设()x x x f -+=22lg ,则⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛x f x f 22的定义域为3.已知()234log 3233,x f x =+则()()()()82482f f f f ++++ 的值等于4.已知2211f x x x x ⎛⎫-=+ ⎪⎝⎭,则函数值()3f = 5. 设函数.)().0(1),0(121)(a a f x x x x x f >⎪⎪⎩⎪⎪⎨⎧<≥-=若则实数a 的取值范围是 6. 函数xx f -=11)(的定义域为M ,x x g +=1)(的定义域为N ,则=⋂N M ________7. 已知一次函数)(x f 满足关系式52)2(+=+x x f ,则=)(x f_____________ 8. 全集U ={1,2,3,4,5},A ={1,2},若{3}⊆B UA ,则集合B 可能是_____________§1.2函数及其表示练习题答题卡班级:______ 姓名:______ 成绩:________一、选择题1-5_____________ 6-10_____________ 11-15_____________二、填空题1、_________ 2、_________ 3、_________ 4、_________5、_________6、_________7、_________8、_________三、解答题1 设,αβ是方程24420,()x mx m x R -++=∈的两实根,当m 为何值时,22αβ+有最小值?求出这个最小值2 求下列函数的值域(1)x x y -+=43 (2)152222++++=x x x x y (3) 13y x x =-+-3. (1) 设,)1(2)()(x xf x f x f =-满足求)(x f(2) 已知:1)0(=f ,对于任意实数x 、y ,等式)12()()(+--=-y x y x f y x f 恒成立,求)(x f .4.动点P 从边长为1的正方形ABCD 的顶点A 出发顺次经过B 、C 、D 再回到A ;设x 表示P 点的行程,y 表示PA 的长,求y 关于x 的函数解析式.5 已知函数2()23(0)f x ax ax b a =-+->在[0,3]有最大值5和最小值2,求a 、b 的值6.动物园要建造一面靠墙的2间面积相同的矩形熊猫居室(如图),如果可供建造围墙的材料总长是30m ,那么宽x (单位:m )为多少才能使建造的熊猫居室面积最大?最大面积是多少?§1.2函数及其表示练习题答案BACCB ABBDC ADACB 1.()3,(),32()3223cf x x cxx f x c f x c x x ====-+-+得2. 令[]2211111(),12,,()()152242x g x x x f f g x x -=-===== 3224(2)44,02,20x x x -+=--+≤≤-≤≤022,02y ≤≤≤≤4. 令22211()1121,,()11111()1t x t t t t x f t t x t t t----+====-+++++则11. 解析:法一:特殊取值法,若x=56,y=5,排除C 、D ,若x=57,y=6,排除A ,所以选B 法二:设)90(10≤≤+=ααm x ,,时⎥⎦⎤⎢⎣⎡==⎥⎦⎤⎢⎣⎡++=⎥⎦⎤⎢⎣⎡+≤≤10103103,60x m m x αα19. [][](5)(11)(9)(15)(13)11f f f f f f f =====二.填空题答案1. 因为0>x ,于是2121=⋅≥+=xx x x y ,当且仅当x =1时取等号 所以1(0)y x x x=+>的值域为),2[+∞ 2. 由202x x +>-得,()f x 的定义域为22x -<<。
1.2函数及其表示精选练习题(可编辑修改word版)

1 1+ 1x⎩1.2 函数及其表示精选练习题(1)一、选择题⒈ 下列各组函数表示同一函数的是( )A. f (x ) = x 2 -1x -1与 g (x ) = x +1B. f (x ) =与 g (x ) = x ⋅C. f (x ) = x 与 g (x ) = (x )2D. f (x ) = x 2 - 2x -1与 g (t ) = t 2 - 2t -1⒉ 函 数 y =的定义域是 ()A.{x x > 0}B.{x x > 0或x ≤ -1}C.{x x > 0或x < -1}D.{x 0 < x < 1}⒊ 函数 y = x 2 - x (-1 ≤ x ≤ 4, x ∈ Z )的值域是()A.[0,12]B.⎡- 1 ,12⎤C. {0,2,6,12} D. {2,6,12}⎣⎢ 4 ⎥⎦4. 二次函数 y = x 2 - 2x + 2 的值域是( )A. RB.C.[0,+∞)D.[1,+∞)5. 若函数 y =f (x ) 的定义域为[-6,2], 则函数 y = f ( x ) 的定义域为()A.[-4,4]B.[-2,2]C.[0, 2]D.[0,4]6. 已知函数 f (x ) = x 2 +1, 则 f [ f (-1)] 的值等于()A. 2B. 3 C. 4D. 5二、填空题7. 已知 g (x ) = 1- 2x , f [g (x )] = 1- x 2x 2(x ≠ 0), 则 f (0) =.8. 已知 f (x ) = 11+ x, g (x ) = x 2 + 2, 则 f (2) =.f [g (2)] =.9. 函数 f (x ) =x + 4 的定义域为 .x + 2⎧x + 2(x ≥ 2), 10. 已知定义在[0,+∞) 上的函数 f (x ) = ⎨x 2 (0 ≤ x ≤ 2).若 f { f [ f (k )]} = 25, k = .4三、解答题- 2x 3 - 2x3⎨ ⎩⎨f [ f (x + 6)],(x < 10) 11.已知函数 f (x ) = x 2 + 2x - 3, 求 f (2), f (- 12.画出函数 f (x ) = 2x -1 的图像.2), f (a ) 的值.1.2 函数及其表示练习题(2)一、选择题1. 函数 y = f (x ) 的图象与直线 x = 1 的公共点数目是()A. 1B.C.0 或1 D. 1或2⎧x + 2(x ≤ -1) 2. 已知 f (x ) = ⎪x 2(-1 < x < 2) ,若 f (x ) = 3 ,则 x 的值是()⎪2x (x ≥ 2)A. 1B. 1或323. 为了得到函数 y = C. 1, 3或±D.2f (-2x ) 的图象,可以把函数 y =f (1- 2x ) 的图象适当平移,这个平移是()A. 沿 x 轴向右平移1个单位C. 沿 x 轴向左平移1个单位B. 沿D. 沿x 轴向右平移 12 x 轴向左平移 12个单位个单位4. 设 f (x ) = ⎧x - 2,(x ≥ 10)⎩则 f (5) 的值为( )A.10 B. 11 C. 12D.13二、填空题5. 函 数 y =x - 2 x 2 - 4的定义域 .6. 若二次函数 y = ax 2 + bx + c 的图象与 x 轴交于 A (-2, 0), B (4, 0) ,且函数的最大值为9 , 则这个二次函数的表达式是.(x -1)07. 函数 y = 的定义域是.x - x8. 函数 f (x ) = x 2 + x - 1的最小值是.三、解答题39. 求函数 f (x )= 的定义域.10. 求函数 y =的值域.11. 已知函数 f (x ) = ax 2 - 2ax + 3 - b (a > 0) 在[1, 3] 有最大值5 和最小值2 ,求 a 、b 的值.x +1x 2 + x + 1。
人教版高一必修一《3.1.2函数的表示》练习题

3.1.2 函数的表示法基础过关练题组一 函数的表示法及其应用1、已知函数()x f 由下表给出,则()11f =( )A 、2B 、3C 、4D 、5 2、观察下表:则()()()31g f f --=( )A 、-1B 、-3C 、3D 、53、如图,李老师早晨出门去锻炼,一段时间内沿半圆形路径M →A →C →B →M 匀速慢跑,那么李老师离出发点M 的距离y 与时间x 之间的函数关系的大致图象是( )题组二 函数解析式的求法4、已知()x f 是一次函数,且()531-=-x x f ,则()x f 的解析式为()x f =( ) A. 23-x B. 32+x C. 23+x D. 3-2x5、若函数()x x x f 2122-=+,则()3f =( )A 、-1B 、0C 、1D 、3 6、已知函数()xmx f -=x 的图像过点(5,4),则实数m 的值为 。
7题组三 分段函数问题的解法 10、已知()(){)6(4)6(3=≥-<+x x x x f x f ,则()2f 等于 ( )A 、2B 、3C 、5D 、4 11、已知函数(){01,110,12≤≤-+≤<+=x x x x x f ,则下列函数图像正确的是( )12、函数2,321,210,2{)(2≥<≤<≤=x x x x x f ,的值域是( )A 、RB 、[0,+∞)C 、[0,3]D 、[0,2]⋃{3}14、已知函数()4||1x x x f -+=. (1)用分段函数的形式表示函数f(x); (2)在平面直角坐标系中画出函数f(x)的图象;(3)在同一平面直角坐标系中,再画出函数g(x)=x1(x>0)的图象(不用列表),观察图象直接写出当x>0时,不等式f(x)>x1的解集.能力提升练题组一:函数的表示及其应用1、若函数()521-=-x x f ,且()612=-a f ,在a 等于 ( ) A 、411 B 、47 C 、34 D 、37 2、德国数学家狄利克在1837年时提出:“如果对于x 的每一个值,y 总有一个完全确定的值与之对应,则y 是x 的函数,”这个定义较清楚地说明了函数的内涵。
2021年高中数学 1.2函数及其表示习题 新人教A版必修1

2021年高中数学 1.2函数及其表示习题新人教A版必修1典例1:作出下列函数的图象.(1)y=2x+2.(2)y=(3)y=(4)y=|log2x-1|.分析:(1)(3)(4)可通过图象变换画出函数的图象,对于(2)可先化简解析式,分离常数,再用图象变换画图象.规范解答 (1)将y=2x的图象向左平移2个单位.图象如图.(2)因y= ,先作出y= 的图象,将其图象向右平移1个单位,再向上平移1个单位,即得y= 的图象,如图.(3)作出y= 的图象,保留y= 图象中x≥0的部分,加上y= 的图象中x>0部分关于y轴的对称部分,即得y=的图象,如图实线部分.(4)先作出y=log2x的图象,再将其图象向下平移一个单位,保留x轴上方的部分,将x轴下方的图象翻折到x轴上方,即得y=|log2x-1|的图象,如图.【易错警示】关注函数定义域本例在作函数图象时,有时会忽略定义域而致误,在作函数图象时要注意函数定义域.【规律方法】作函数图象的三个重要方法及适用类型(1)直接法:当函数表达式(或变形后的表达式)是熟悉的函数或解析几何中熟悉的曲线的局部(如圆、椭圆、双曲线、抛物线的一部分)时,就可根据这些函数的奇偶性、周期性、对称性或曲线的特征直接作出.(2)图象变换法:①若函数图象可由某个基本函数的图象经过平移、翻折、对称和伸缩得到,可利用图象变换作出,但要注意变换顺序;②对不能直接找到熟悉函数的,要先变形,同时注意平移变换与伸缩变换的顺序对变换单位及解析式的影响.(3)描点法:当上面两种方法都失效时,则可采用描点法.为了通过描少量点,就能得到比较准确的图象,常常需要结合函数的单调性、奇偶性等性质进行分析.提醒:当函数表达式是较复杂的高次、分式、指数、对数及三角函数式时,常借助于导数探究图象的变化趋势从而画出图象的大致形状.【变式训练】作出下列函数的图象.(1)y=e lnx. (2)y=|log2(x+1)|.(3)y= . (4)y=x2-2|x|-1.解析如下:(1)(2)(3)(4)典例2:(1)(xx·杭州模拟)已知函数f(x)是定义在R上的增函数,则函数y=f(|x-1|)-1的图象可能是( )(2)(xx·山东高考)函数y=xcosx+sinx的图象大致为( )分析:(1)根据函数f(x)的单调性及图象的平移、对称变换求解.(2)利用函数的奇偶性和函数值的变化规律求解.规范解答:(1)选 B.根据题意,由于函数f(x)是定义在R上的增函数,那么可知函数y=f(|x-1|)-1的图象先是保留在y轴右侧的图象不变为增函数,再作关于y轴对称的图象,再整体向右平移一个单位,再整体向下平移一个单位,那么可知为先减后增,同时关于直线x=1对称,故选B.(2)选D.函数y=xcosx+sinx为奇函数,所以图象关于原点对称,所以排除B,C.当x=π时,f(π)=-π<0,排除A,故选D.【互动探究】若本例题(1)中,函数f(x)是定义在R上的增函数改为“减函数”,则结果如何? 26928 6930 椰 26566 67C6 柆'32817 8031 耱 24780 60CC 惌@38706 9732 露22994 59D2 姒Y 99。
数学必修1 1.2.2《函数及其表示》同步讲练

高中数学必修一《函数及其表示》导学导练【范例析考点】考点一:函数及映射的概念 例1:判断下列对应是否为函数:(1);,,Z y R x x y y x ∈∈→的最大整数,为不大于其中 (2)2,,,x y y x x N y R →=∈∈;(3)x y x →=,{|06}x x x ∈≤≤,{|03}y y y ∈≤≤; (4)16x y x →=,{|06}x x x ∈≤≤,{|03}y y y ∈≤≤.【变式练习】1、判断下列对应:f A B →是否是从集合A 到集合B 的函数:(1){},0,:,:;A R B x R x f x x f A B ==∈>→→ (2)*,,:1,:.A N B N f x x f A B ==→-→ (3){}20,,:,:.A x R x B R f x x f A B =∈>=→→2、在映射中B A f →:,},|),{(R y x y x B A ∈==,且),(),(:y x y x y x f +-→,则与A 中的元素)2,1(-对应的B 中的元素为( ) A 、)1,3(-B 、)3,1(C 、)3,1(--D 、)1,3(3、设M ={x |-2≤x ≤2},N ={y |0≤y ≤2},函数f (x )的定义域为M ,值域为N ,则f (x )的图象可以是( )考点二:画函数图象 例2:画出下列函数的图象: (1)()1f x x =+;(2)2()(1)1,[1,3)f x x x =-+∈; (3)5y x =,{1,2,3,4}x ∈; (4)()f x【变式练习】1、画出下列函数的图象、 (1)y =x 2-2,x ∈Z 且|x |≤2; (2)y =-2x 2+3x ,x ∈(0,2]; (3)y =x |2-x |; (4)⎪⎩⎪⎨⎧≥≤.-,<--,<-=2322323x x x x y考点三:求函数的定义域 例3:求下列函数的定义域:(1);24)(++=x x x f (2)y=11---x x ;(3)1()2f x x=-.【变式练习】1、已知函数()11x f x x+=-的定义域为A ,函数()y f f x =⎡⎤⎣⎦的定义域为B ,则( ) A .AB B =B .A ≠⊂BC .A B =D .A B B =2、若)(x f 的定义域为[0,1],则)2(+x f 的定义域为( )A 、[0,1]B 、[2,3]C 、[-2,-1]D 、无法确定 3、函数xx x f -++=211)(的定义域为4、若函数()f x R ,则m 的取值范围是考点四:求函数的值域例4:已知函数2361y x x =-+,利用函数图象分别求它在下列区间上的值域:(1)[1,2]x ∈-; (2)[4,0]x ∈-; (3)[2,5]x ∈.例5:函数y =x +x 21-的值域是( )A.(-∞,1]B.(-∞,-1]C.RD.[1,+∞)例6:求函数125x y x -=+的值域。
1.2函数及其表示练习题

A. { x | x 1} B. { x | x 2} C. { x | x 1且 x 2} D. { x | x 1或 x 2} 3.定义域为 R的函数的值域为 [] ,则函数 ) 的值域为 ( )
A.[2 , C.[
B.[0, D.[
4.下列各组函数中,表示同一函数的是(
)
A . y | x |, y x2
(2) 所给函数可化简为 y=
图象是一条折
1-x (0<x<1),
线. (如图② )
1
图①
图②
12.解: (1)设 f(x)=ax+b(a≠0,)
则 3f(x+1)-2f(x-1)
= 3ax+3a+3b-2ax+2a-2b
= ax+b+5a=2x+17,
∴ a=2,b=7,∴ f(x)=2x+7.
(2)2f(x)+ f 1 =3x,①
x
1 把①中的 x 换成 x,得 2 f
1 x
3 +f( x)= x,②
3 ① ×2-②得 3f(x)=6x-x,
1 ∴ f( x) =2x-x
16.
4.A 解析: B、C、D 三个选项中的两个函数的定义域不相同 ,不 表示同一个函数, A 选项中的两个函数的定义域与对应关系都相 同,表示相同的函数 .故选 A.
5.D
解析;从 A地到 B 地用了 150 2.5 ( 时 ),因此当 0 t 2.5 时 ,
60
x 60t .
因为在 B 地停留 1 小时 ,所以当 2.5 t 3.5 时 , x 150 .
⒈D ⒍D ⒏3 ⒒3
2
⒉C
⒎D ⒐ 1;1
37
参考答案
⒊C
⒋A
⒑ x x 4且x 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
人教新课标数学必修Ⅰ1.2函数及其表示练习题(1)
一、选择题(5357'='⨯)
⒈下列各组函数表示同一函数的是()
A.1
1)(2--=x x x f 与1)(+=x x g B.32)(x x f -=与x x x g 2)(-⋅= C.x x f =)(与2)()(x x g =D.12)(2--=x x x f 与12)(2--=t t t g ⒉函数x y 1
11
+=的定义域是()
A.{}0>x x B.{}10-≤>x x x 或C.{}10-<>x x x 或D.{}10<<x x
⒊函数()Z x x x x y ∈≤≤--=,412的值域是()
A.[]12,0B.⎥⎦⎤⎢⎣⎡-12,41
C.{}12,6,2,0D.{}12,6,2 ⒋已知映射B A f →:,其中集合{},4,3,2,1,1,2,3---=A 集合B 中的元素都是A 中的元
素在映射B A f →:下的对应的元素.且对任意的,)(,a a f A a =∈则集合B 中的元素的个数是()
A.4B.5C.6D.3
5.二次函数222+-=x x y 的值域是()
A.R B.φC.),0[+∞D.),1[+∞
⒍若函数)(x f y =的定义域为],2,6[-则函数)(x f y =的定义域为() A.]4,4[-B.]2,2[-C.]2,0[D.]4,0[
⒎已知函数,1)(2+=x x f 则)]1([-f f 的值等于()
A.2B.3C.4D.5
二、 填空题(0254'='⨯) ⒏已知),0(1)]([,21)(22≠-=-=x x
x x g f x x g 则=)0(f ______________. ⒐已知,2)(,11)(2+=+=x x g x
x f 则=)2(f ______________.=)]2([g f __________. ⒑函数2
4)(++=x x x f 的定义域为______________. ⒒已知定义在),0[+∞上的函数⎩
⎨⎧≤≤≥+=).20(),2(2)(2x x x x x f 若,4
25)]}([{=k f f f =k _____. 三、 解答题(5495'='⨯)
⒓已知函数,32)(2-+=x x x f 求)(),2(),2(a f f f -的值.
⒔已知二次函数),(x f 当2=x 时有最大值,16它的图像截x 轴所得线段长为8,求).(x f ⒕画出函数12)(-=x x f 的图像.
⒖某山海拔7500,m 海平面温度为,25C o 气温是高度的函数,而且高度每升高,100m 温度
就下降.6.0C o 请你用解析式表示出气温T 随高度x 变化的函数关系,并指出函数的定义
域和值域.
参考答案
⒈D ⒉C ⒊C ⒋A ⒌D ⒍D ⒎D
⒏3⒐7
1
;31⒑{}24-≠-≥x x x 且
⒒
2
3
⒓3
2
,1
2
2
,52-
+
-
-a
a⒔12
4
)
(2+
+
-
=x
x
x
f⒕图略
15.x
x
T
500
3
25
)
(-
=定义域]
7500
,0[值域]
25
,
20
[-
1.2.1函数的概念1.2.2函数的表示法
建议用时实际用时满分实际得分45分钟100分
一、选择题(本大题共6小题,每小题6分,共
36分)
1.设集合,,则在下面四个图形中,能表示集合到集合的函数关系的
有()
A.①②③④B.①②③
C.②③D.②
2.已知函数()1
1
f x
x
=
+
,则函数()
()
f f x的定义域是()
A.}1
|
{-
≠
x
x
B.}2
|
{-
≠
x
x
C.}21|{-≠-≠x x x 且
D.}21|{-≠-≠x x x 或
3.定义域为R 的函数的值域为[],则函数)的值域为()
A.[2,
B.[0,
C.[
D.[
4.下列各组函数中,表示同一函数的是()
A .2|,|x y x y ==
B .
C .33,1x x y y ==
D .2)(|,|x y x y ==
5.已知A 、B 两地相距150千米,某人开汽车以 60千米/时的速度从地到达地,在地停留 1 小时后再以50千米/时的速度返回A 地,把汽车离开A 地的距离(千米)表示为时间(时)的函数表达式是()
A .
B .
C .
D . 6.下列对应关系:
①{1,4,9},{-3,-2,-1,1,2,3},→的算术平方根; ②,,的倒数;
③,,.
其中是A 到B 的函数的是( )
4 , 2 2 2 ? ? ? ? ? x y x x y ? ? ? ? ? ? ? ? ? ? )
5 . 3 ( 50 150 ) 5 . 2 0 ( 60 t t t t x ? ?
? ? ? ? ? ? ? ? ? ? ? ) 5 . 6 5 . 3 ( 50 325 ) 5 . 3 5 . 2 ( 150 ) 5 . 2 0 ( 60 t t t t t x
A .①③
B .②③
C .①②
D .①②
③
二、填空题(本大题共3小题,每小题6分,共 18分)
7.设函数()23,(2)()f x x g x f x =++=,则()g x .
8.已知函数则((6))f f
9.已知且=4,则的值
为.
三、解答题(本大题共3小题,共46分)
10.(14分)求下列函数的定义域:
(1)x x x y -+=
||)1(0; (2)x x x y 121
32+--
+=. 11.(16分)作出下列各函数的图象:
(1)∈Z ;
(20).
12.(16分)求下列函数解析式.
(1)已知f (x )是一次函数,且满足3f (x +1)-2f (x -1)=2x +17,求f (x );
(2)已知f (x )满足2f (x )+f ()=3x ,求f (x
一、选择题
1.C 解析:由函数的定义知①中的定义域不是,④中集合中有的元素在集合中对应两个函数值不符合函数定义,故不对,只有②③成立.故选C .
2.C 解析:由()1f x ≠-,即111
x ≠-+,得1x ≠-且2x ≠-.
3.C 解析:因为函数()f x 的定义域为R ,所以的取值范围也是R ,因此函数()()f x a f t +=的值域与函数()f x 的值域相同,是.
4.A 解析:B 、C 、D 三个选项中的两个函数的定义域不相同,不表示同一个函数,A 选项中的两个函数的定义域与对应关系都相同,表示相同的函数.故选A.
5.D 解析;从A地到B地用了150 2.560
=(时),因此当0 2.5t ≤≤时,t x 60=. 因为在B 地停留1小时,所以当2.5 3.5t <≤时,150x =.
经3.5小时开始返回,由B 地到A 地用了150350=(时),因此当
3.5 6.5t <≤时,
综上所述,
6.A 解析:根据函数的概念,对于集合A 中的每一个元素在集合B 中都有唯一的元素与它对应.
对于①,集合中的1,4,9在集合B 中都有唯一的元素与它对应,故是函数;
对于②,集合A 中的元素0在集合B 中没有元素对应;
对于③,集合A 中的元素x ∈在集合B 中都有唯一的元素x 22与它对应,故是函数.
故选A .
二、填空题
7.12-x 解析:()()()223221g x f x x x +==+=+-,所以()2 1.g x x =- 8.25-解析:((6))f f =()225
f -=-.
9.5解析:∵f (2x +1)=3x -2=(2x +1)-,
∴f (x )=x -.∵f (a )=4,∴a -=4,
∴a =5.
三、解答题
10.解:(1)由⎩
⎨⎧>-≠+,0||,01x x x 得⎩⎨⎧<-≠,0,1x x 故函数x x x y -+=||)1(0
的定义域是{x |x <0,且x ≠1-}.
(2)由⎪⎩⎪⎨⎧≠>-≥+,0,02,032x x x 得32,2,0.x x x ⎧-⎪<⎨⎪≠⎩
≥∴23-≤x <2,且x ≠0. 故函数的定义域是{x |2
3-≤<2,且x ≠0}.
11.解:(1)因为x ∈Z ,所以函数的图象是由一些点组成的,这些点都在直线y =1-x 上.(如图①)
(2)所给函数可化简为y =(x ≥1),,1-x (0<x <1),))图象是一条折线.(如图②)
12.解:(1)设f (x )=ax +b (a ≠0), 则3f (x +1)-2f (x -1)
=3ax +3a +3b -2ax +2a -2b
=ax +b +5a =2x +17,
∴a =2,b =7,∴f (x )=2x +7. (2)2f (x )+1f x
⎛⎫ ⎪⎝⎭=3x ,① 把①中的x 换成,得21f x
⎛⎫ ⎪⎝⎭+f (x )=,② ①×2-②得3f (x )=6x -,
∴f (x )=2x -
16. 图①图②
1。
