【数学】2017-2018年江苏省苏州市昆山市七年级上学期数学期中试卷和解析答案PDF

2017-2018学年度第一学期七年级期中联考数学科试卷和解析答案

2017-2018学年度第一学期七年级期中联考数学科试卷命题人：王红霞审题人：叶志考试时间：90分钟一、选择题（共12小题；共36分） 1. 下列用字母表示数的写法中，规范的是A.B. 315⨯⨯y xC.xy 35D.2. 有下列各数：，，，，)4(2--，其中属于非负整数的共有（） A. 个B. 个C. 个D. 个3. 在代数式，，，，中，整式共有个．A.B.C.D.4. 检验个工件，其中超过标准质量的克数记作正数，不足标准质量的克数记作负数，从轻重的角度看，最接近标准的工件是C.D.5. 火星和地球的距离约为34000000千米，用科学记数法表示34000000千米的结果是千米． A.B.C.D.6. 下列各组数中，互为相反数的是与B.与与与7. 用平面去截如图所示的三棱柱，截面形状不可能是A. 三角形B. 四边形C. 五边形D. 六边形8. 下列各式计算正确的是A. 12317315-=-- B.C.D.9. 下列说法中正确的是A. 不是单项式的系数是C.的次数是D.的系数是10. 如果点，，，所对应的数为，，，，则，，，的大小关系是A.B. c a d b <<<C. D.11. 某企业去年月份产值为万元，月份比月份减少，月份比月份增加了，则月份的产值是A.万元B. 万元C. %)15%10(+-a 万元D.万元12. 规定一种新的运算“”：对于任意实数，，满足．如，则A.B.C.D.二、填空题（共4小题；共12分） 13. 已知单项式与是同类项，则．14. 如图1，将一刻度尺放在数轴上（数轴的单位长度是”分别对应数轴上的和，那么的值为．15. 如图2，数，，在数轴上对应点的位置，化简得．16. 用棋子摆出下列一组三角形，三角形每边有枚棋子，每个三角形的棋子总数为，如图按此规律推断，当三角形的边上有枚棋子时，该三角形棋子总数（用含的式子表示）．三、解答题（共7小题；共52分） 17. （各5分，共10分）计算：（1；（2）．18. （6分）先化简，再求值：（其中）．19. （6分）某中学七年级A 班有人，某次活动中分为四组，第一组有人，第二组比第一组的一半多人，第三组的人数等于前两组人数的和．求：（1）第二组的人数是；（1分）图2图1（2）第三组的人数是；（1分）（3）第四组的人数是；（2分）（4）找一个你喜欢的数作为的值，求出此时第四组的人数．（2分）20. （6分）某食品厂从生产的袋装食品中抽出样品袋，检测每袋的质量是否符合标准，超过标准质量的部分用正数来表示，不足标准质量的部分用负数来表示，检测结果如下表：若每袋食品的标准质量为克，求抽样检测的袋食品的平均质量是多少克?21. （6分）如图是小强用八块相同的小立方体搭成的一个几何体，从正面、左面和上面观察这个几何体，请你在下面相应的位置分别画出你所看到的几何体的形状图（在答题卡上画完图后请用黑色签字笔描图）．22. （8分）张老师把某小组的小明等5名同学的成绩简记为：+10， —5 , 0 ， +8 ， —3，又知道小明同学实际考了90分，且在这 5名同学中排名第三，请写出来这 5名同学各考了多少分，并计算这5名同学的平均分．23. （10分）在解决数学问题的过程中，我们常用到“分类讨论”的数学思想，下面是运用分类讨论的数学思想解决问题的过程，请仔细阅读，并解答题目后提出的“探究”．【提出问题】三个有理数，，满足，求的值．【解决问题】解：由题意得：，，三个有理数都为正数或其中一个为正数，另两个为负数． ①当，，都是正数，即，，时，；（备注：一个非零数除以它本身等于1，如：3÷3=1，则1,(0)aa a=≠） ②当，，有一个为正数，另两个为负数时，设，，，的值为或（备注：一个非零数除以它的相反数等于-1，如：-3÷3= -1，则1,(0)bb b-=-≠）【探究】请根据上面的解题思路解答下面的问题：（1）三个有理数，，满足，求的值；（6分）（2）已知，且，求的值．（4分）。

2017-2018年七年级上册数学期中试卷及答案

1 在代数式 x2 + 5, - 1, x 2 -3 x + 2, π , 5 , x 2 +x + 1 中，整式有（位 … 姓… C 、 -5abc 2 的系数是 -5 D 、 2 a + b是一次单项式 …… … … … … … … 2017~2018 学年第一学期考试七年级数学试卷题号一二三四总分得分一、选择题（每小题 3 分，共 30 分）1xA 、3 个B 、4 个C 、5 个D 、6 个）… … 号 … 座装 … … … … … … … … 订 … … 名 … … … … … … 线 … … … … … 级 … 班… … …2、我国教育事业快速发展，去年普通高校招生人数达 540 万人，用科学记数法表示 540 万人为（）A 、5.4 ×102 人B 、0.54×104 人C 、5.4 ×106 人D 、5.4×107 人3、一潜水艇所在的海拔高度是-60 米，一条海豚在潜水艇上方 20 米，则海豚所在的高度是海拔（）A 、-60 米B 、-80 米C 、-40 米D 、40 米4、原产量 n 吨，增产 30%之后的产量应为（）A 、（1-30%）n 吨B 、（1+30%）n 吨C 、(n+30%)吨D 、30%n 吨5、下列说法正确的是( )①0 是绝对值最小的有理数 ②相反数大于本身的数是负数③数轴上原点两侧的数互为相反数 ④两个数比较，绝对值大的反而小A 、①②B 、①③C 、①②③D 、①②③④6、如果 0 < a < 1 ，那么 a 2 , a, 1 之间的大小关系是aA 、 a < a 2 < 1B 、 a 2 < a < 1C 、 1 < a < a 2D 、 1 < a 2 < aa a a a7、下列说法正确的是（）1A 、0.5ab 是二次单项式B 、 x 和 2x 是同类项( ) 9 38、已知：A和B都在同一条数轴上，点A表示-2，又知点B和点A相距5个单位长度，则点B表示的数一定是（）A、3B、-7C、7或-3D、-7或39、一个多项式与x2－2x＋1的和是3x－2，则这个多项式为（）A、x2－5x＋3B、－x2＋x－1C、－x2＋5x－3D、x2－5x－1310、观察下列算式：31＝3，32=9,33=27,34=81,35=243,36=729,…,通过观察，用你所发现的规律确定32016的个位数字是（）A、3B、9C、7D、1二、填空题（每题3分，共15分）11、单项式-2πxy2的系数是____________。

苏州市昆山吴江区2017-2018学年初一上期中数学试卷含解析

A． 0 【答案】C 【解析】由题意得，
B． 10
C． 25
D． 50
第 1 次操作后，笔尖在 1 处，第 2 次操作后，笔尖在 1 处，第 3 次操作后，笔尖在 2 处，第 4 次操作后，笔尖在 2 处，

第 n 次操作后，当 n 为奇数时，笔尖在
n 1 处， 2
n 当 n 为偶数时，笔尖在处， 2
B ． | 2 x 1|≥ 0 ，故 B 错；
C ． 2 x 2 1≥ 1 ，故 C 对；
D ． 2 x 2 1≥ 1 ，故 D 错．
故选 C ．
7．当 x 2 时，代数式 ax3 bx 2 的值为 3 ，那么当 x 2 时，代数式 ax3 bx 2 的值是（）． A． 3 【答案】B 【解析】当 x 2 时， 8a 2b 2 3 ， ∴ 8a 2a 1 ，当 x 2 时， 8a 2b 2
A． 2 个【答案】A
B． 3 个
C． 4 个
D． 5 个
【解析】①最大的负整数是 1 ，①对； ②平方后等于 9 的数是 3 ，故②错； ③ (3)3 32 27 ，故③对；
数数 , a 0 ④ a 0, a 0 ，故④错；⑤若 a 、 b 互为相反数，则 ab ≤ 0 ，故⑤错；数数期中教学质量调研测试初一数学
一、选择题（本大题共 10 小题，每小题 3 分，共 30 分） 1． 3 的相反数是（）． A． 3 【答案】A 【解析】 A ． 3 是 3 的相反数； B．
1 3
C．
1 3
D． 3
1 B ．是 3 的倒数； 3 1 C ．是 3 的负倒数； 3
B ． x 2 x 3x ，故 B 错；

2017-2018学年江苏省苏州市吴中区七年级(上)期中数学试卷(解析版)

2017-2018学年江苏省苏州市吴中区七年级（上）期中数学试卷一、选择题（本大题共10小题，每小题3分，共30分.每小题只有一个选项是正确的，把正确选项前的字母填涂在答题卷相应位置上.）1．（3分）下列各个运算中，结果为负数的是（）A．﹣（﹣4）B．|﹣4|C．﹣42 D．（﹣4）22．（3分）地球与月球的平均距离大约为384000km，则这个平均距离用科学记数法表示为（）A．384×103km B．3.84×104km C．3.84×105km D．3.84×106km3．（3分）下列各数：0，π，3.141，，其中有理数的个数是（）A．3个 B．4个 C．2个 D．1个4．（3分）下列方程中，是一元一次方程的是（）A．B．x﹣1=0 C．x2﹣x﹣1=0 D．2（x﹣1）=2x5．（3分）下列各组式子中为同类项的是（）A．5x2y与﹣2xy2B．4x与4x2C．﹣3x2y与yx2D．6x3y4与﹣6x3z46．（3分）已知5是关于x的方程3x﹣2a=7的解，则a的值是（）A．8 B．12 C．3.5 D．47．（3分）已知|x|=1，y=2，则x﹣y的值为（）A．﹣1或﹣3 B．±5 C．1或3 D．±38．（3分）一种商品每件进价为a元，按进价增加20%定出售价，后因库存积压降价，按售价的八折出售，每件亏损（）A．0.01a元 B．0.15a元 C．0.25a元 D．0.04a元9．（3分）下列方程变形错误的是（）A．由方程，得3x﹣2x+2=6B．由方程，得3（x﹣1）+2x=6C．由方程，得2x﹣1=3﹣6x+3D．由方程，得4x﹣x+1=410．（3分）如图所示，每个正方形由边长为1的小正方形组成：观察图形，在边长为n（n≥1，n为奇数）的正方形中，黑色小正方形的个数为（）A．n2B．2n﹣1 C．n2﹣2n+1 D．n2﹣2n二、填空题（本大题共8小题，每小题3分，共24分）11．（3分）﹣2的相反数是．12．（3分）比较大小，用“＜”“＞”或“=”连接：﹣﹣．13．（3分）数轴上与﹣3距离4个单位长度的点表示的正数是．14．（3分）“x的2倍与y的的和”用代数式表示为．15．（3分）若关于x的多项式3x2+（k﹣1）x﹣1中不含有x的一次项，则k=．16．（3分）3x5y6与﹣x n﹣1y6是同类项，则n=．17．（3分）已知代数式x+3y的值2，则代数式2x+6y+1值是．18．（3分）如图所示的运算程序中，若开始输入的x值为﹣5，我们发现第1次输出的数为﹣2，再将﹣2输入，第2次输出的数为﹣1，如此循环，则第2017次输出的结果为．三、解答题（本大题共l0小题，共76分.解答时应写出文字说明、证明过程或演算步骤.）19．（8分）计算或化简：（1）﹣7+3﹣5+12；（2）﹣23+（2﹣3）﹣2×（﹣1）2017．20．（8分）解下列方程：（1）2（x﹣1）=x+3；（2）．21．（5分）先化简，再求值：7x2y﹣[3xy﹣2（xy﹣x2y+1）+xy]，其中x=6，y=﹣．22．（5分）已知：A=3a2﹣4ab，B=a2+2ab．（1）求A﹣2B；（2）若|2a+1|+（2﹣b）2=0，求A﹣2B的值．23．（6分）当m是何值时，关于x的方程4x﹣2m=3x+1的解是方程2x﹣3=x的解的2倍．24．（7分）若“三角”表示运算：a﹣b+c，若“方框”，表示运算：x﹣y+z+w，求的值，列出算式并计算结果．25．（8分）已知a是方程3x﹣5=10的解，求代数式3a2﹣[a2﹣2（a﹣a2）+1]的值．26．（9分）苏州市出租车的计价标准为：行驶路程不超过3km收费10元，超过3km的部分按排每千米1.8元收费．（1）某出租车行程为xkm，若x＞3km，则该出租车驾驶员收到车费元（用含有x的代数式表示）；（2）某出租车驾驶员从公司出发，在东西向的宝带西路上连续接送4批客人，行驶路程记录如下（规定向东为正，向西为负，单位：km）．①送完第4批客人后，该出租车驾驶员在公司的边（填“东或西”），距离公司km的位置；②在这过程中该出租车驾驶员共收到车费多少元？27．（10分）在计算1+5+9+13+17+21时，我们发现，从第一个数开始，后面的每个数与它前面的一个数的差都是一个相等的常数，具有这种规律的一列数，除了直接相加外，我们可以用下列公式来求和S，S=（其中n表示这列数的个数，a1表示表示第一个数，a n表示第n个数），所以，1+5+9+13+17+21==66．用上面的知识解答下列问题：吴中区科学技术协会为了扶持高科技产业，准备投资两个符合条件的企业A、B，拟定分别对A、B两个企业投资方案如下：A企业：每年投资一次，第一年投资30万元、以后每年比前一年增加投资1万元；B企业：每半年投资一次，第一个半年投资6万元，以后每半年比前半年增加投资0.5万元．（1）如果投资期限为3年，则A企业共需投资万元，B企业共需投资万元；（2）如果投资期限为n年，则A企业共需投资万元，B企业共需投资万元；（用含有n的代数式表示）（3）吴中区科学技术协会决定对这两个企业累计投资12年，通过计算哪个企业获得的投资比较多？比另一个企业多多少万元？28．（10分）如图：在数轴上点A表示数a，点B表示数b，点C表示数c，a是多项式﹣2x2﹣4x+1的一次项系数，b是最小的正整数，单项式﹣的次数为c．（1）a=，b=，c=；（2）若将数轴在点B处折叠，则点A与点C重合（填“能”或“不能”）；（3）点A，B，C开始在数轴上运动，若点C以每秒1个单位长度的速度向右运动，同时，点A和点B分别以每秒3个单位长度和2个单位长度的速度向左运功，t分钟过后，若点A与点B之间的距离表示为AB，点B与点C之间的距离表示为BC，则AB=，BC=（用含t的代数式表示）；（4）请问：3AB﹣BC的值是否随着时间t的变化而改变？若变化，请说明理由；若不变，请求其值．2017-2018学年江苏省苏州市吴中区七年级（上）期中数学试卷参考答案与试题解析一、选择题（本大题共10小题，每小题3分，共30分.每小题只有一个选项是正确的，把正确选项前的字母填涂在答题卷相应位置上.）1．（3分）下列各个运算中，结果为负数的是（）A．﹣（﹣4）B．|﹣4|C．﹣42 D．（﹣4）2【解答】解：A、﹣（﹣4）=4，是正数；B、|﹣4|）=4，是正数；C、﹣42=﹣16，是负数；D、（﹣4）2=16，是正数，故选：C．2．（3分）地球与月球的平均距离大约为384000km，则这个平均距离用科学记数法表示为（）A．384×103km B．3.84×104km C．3.84×105km D．3.84×106km【解答】解：384000=3.84×105，故选：C．3．（3分）下列各数：0，π，3.141，，其中有理数的个数是（）A．3个 B．4个 C．2个 D．1个【解答】解：0，π，3.141，，其中是有理数的有0，3.141，这3个，故选：A．4．（3分）下列方程中，是一元一次方程的是（）A．B．x﹣1=0 C．x2﹣x﹣1=0 D．2（x﹣1）=2x【解答】解：A、不是一元一次方程，故此选项错误；B、是一元一次方程，故此选项正确；C、不是一元一次方程，故此选项错误；D、不是一元一次方程，故此选项错误；故选：B．5．（3分）下列各组式子中为同类项的是（）A．5x2y与﹣2xy2B．4x与4x2C．﹣3x2y与yx2D．6x3y4与﹣6x3z4【解答】解：A、5x2y与﹣2xy2，不是同类项，故本选项错误；B、4x与4x2，不是同类项，故本选项错误；C、﹣3x2y与yx2是同类项，故本选项正确；D、6x3y4与﹣6x3z4，不是同类项，故本选项错误．故选：C．6．（3分）已知5是关于x的方程3x﹣2a=7的解，则a的值是（）A．8 B．12 C．3.5 D．4【解答】解：把x=5代入方程，得15﹣2a=7，解得a=4，故选：D．7．（3分）已知|x|=1，y=2，则x﹣y的值为（）A．﹣1或﹣3 B．±5 C．1或3 D．±3【解答】解：∵|x|=1，∴x=±1，∴x﹣y=1﹣2=﹣1，或x﹣y=﹣1﹣2=﹣3．故选：A．8．（3分）一种商品每件进价为a元，按进价增加20%定出售价，后因库存积压降价，按售价的八折出售，每件亏损（）A．0.01a元 B．0.15a元 C．0.25a元 D．0.04a元【解答】解：由题意可得，每件亏损为：a﹣a（1+20%）×0.8=a﹣0.96a=0.04a元，故选：D．9．（3分）下列方程变形错误的是（）A．由方程，得3x﹣2x+2=6B．由方程，得3（x﹣1）+2x=6C．由方程，得2x﹣1=3﹣6x+3D．由方程，得4x﹣x+1=4【解答】解：A、由方程﹣=1，得3x﹣2x+2=6，正确；B、由方程（x﹣1）+=1，得3（x﹣1）+2x=6，正确；C、由方程=1﹣3（2x﹣1），得2x﹣1=3﹣18x+9，错误；D、由方程x﹣=1，得4x﹣x+1=4，正确，故选：C．10．（3分）如图所示，每个正方形由边长为1的小正方形组成：观察图形，在边长为n（n≥1，n为奇数）的正方形中，黑色小正方形的个数为（）A．n2B．2n﹣1 C．n2﹣2n+1 D．n2﹣2n【解答】解：当n=1时，黑色小正方形的个数为1，当n=3时，黑色小正方形的个数为5=2×3﹣1，当n=5时，黑色小正方形的个数为9=2×5﹣1，…∴在边长为n（n≥1，n为奇数）的正方形中，黑色小正方形的个数为2n﹣1，故选：B．二、填空题（本大题共8小题，每小题3分，共24分）11．（3分）﹣2的相反数是2．【解答】解：﹣2的相反数是：﹣（﹣2）=2，故答案为：2．12．（3分）比较大小，用“＜”“＞”或“=”连接：﹣＞﹣．【解答】解：∵|﹣|==，|﹣|==，＜，∴﹣＞﹣．故答案为：＞．13．（3分）数轴上与﹣3距离4个单位长度的点表示的正数是1．【解答】解：设该点表示的数为x，根据题意得：|﹣3﹣x|=4，解得：x=﹣7或x=1．数轴上与﹣3距离4个单位长度的点表示的正数是1，故答案为：1．14．（3分）“x的2倍与y的的和”用代数式表示为2x+y．【解答】解：“x的2倍与y的的和”用代数式表示为2x+y．故答案为：2x+y．15．（3分）若关于x的多项式3x2+（k﹣1）x﹣1中不含有x的一次项，则k=1．【解答】解：∵多项式3x2+（k﹣1）x﹣1中不含有x的一次项，∴k﹣1=0，∴k=1．故答案为1．16．（3分）3x5y6与﹣x n﹣1y6是同类项，则n=6．【解答】解：∵3x5y6与﹣x n﹣1y6是同类项，∴n﹣1=5．解得：n=6．故答案为：6．17．（3分）已知代数式x+3y的值2，则代数式2x+6y+1值是5．【解答】解：∵x+3y=2，∴2x+6y+1=2（x+3y）+1=4+1=5，故答案为5．18．（3分）如图所示的运算程序中，若开始输入的x值为﹣5，我们发现第1次输出的数为﹣2，再将﹣2输入，第2次输出的数为﹣1，如此循环，则第2017次输出的结果为1．【解答】解：若开始输入的x值为﹣5，我们发现第1次输出的数为﹣2，再将﹣2输入，第2次输出的数为﹣1，将﹣1输入，得到结果为2，将2输入得到结果为1，将1输入，得到结果为4，将4输入得到结果为2，依此类推，以1，4，2为循环节循环，∵（2017﹣3）÷3=671…1，∴第2017次输出的结果为1．故答案为：1．三、解答题（本大题共l0小题，共76分.解答时应写出文字说明、证明过程或演算步骤.）19．（8分）计算或化简：（1）﹣7+3﹣5+12；（2）﹣23+（2﹣3）﹣2×（﹣1）2017．【解答】解：（1）原式=﹣12+12+3=3；（2）原式=﹣8﹣1+2=﹣7．20．（8分）解下列方程：（1）2（x﹣1）=x+3；（2）．【解答】解：（1）2（x﹣1）=x+32x﹣2=x+3，则2x﹣x=3+2，解得：x=5；（2）=3（3x+5）=2（2x﹣1）9x+15=4x﹣2解得：x=﹣．21．（5分）先化简，再求值：7x2y﹣[3xy﹣2（xy﹣x2y+1）+xy]，其中x=6，y=﹣．【解答】解：7x2y﹣[3xy﹣2（xy﹣x2y+1）+xy]=7x2y﹣[3xy﹣2xy+7x2y﹣2+xy]=7x2y﹣3xy+2xy﹣7x2y+2﹣xy=﹣xy+2，当x=6，y=﹣时，原式=﹣×6×（﹣）+2=3.5．22．（5分）已知：A=3a2﹣4ab，B=a2+2ab．（1）求A﹣2B；（2）若|2a+1|+（2﹣b）2=0，求A﹣2B的值．【解答】解：（1）∵A=3a2﹣4ab，B=a2+2ab，∴A﹣2B=3a2﹣4ab﹣2a2﹣4ab=a2﹣8ab；（2）∵|2a+1|+（2﹣b）2=0，∴a=﹣，b=2，则原式=+8=8．23．（6分）当m是何值时，关于x的方程4x﹣2m=3x+1的解是方程2x﹣3=x的解的2倍．【解答】解：2x﹣3=x解得x=3，由关于x的方程4x﹣2m=3x+1的解是方程2x﹣3=x的解的2倍，得12﹣2m=9+1，解得m=1，当m=1时，关于x的方程4x﹣2m=3x+1的解是方程2x﹣3=x的解的2倍．24．（7分）若“三角”表示运算：a﹣b+c，若“方框”，表示运算：x﹣y+z+w，求的值，列出算式并计算结果．【解答】解：根据题意得：原式=（﹣+）×（﹣2﹣1.5+1.5﹣6）=（﹣）×（﹣8）=．25．（8分）已知a是方程3x﹣5=10的解，求代数式3a2﹣[a2﹣2（a﹣a2）+1]的值．【解答】解：3x﹣5=10，3x=15，x=5，∴a=5，3a2﹣[a2﹣2（a﹣a2）+1]，=3a2﹣（a2﹣2a+2a2+1），=3a2﹣a2+2a﹣2a2﹣1，=2a﹣1，当a=5时，原式=2×5﹣1=9．26．（9分）苏州市出租车的计价标准为：行驶路程不超过3km收费10元，超过3km的部分按排每千米1.8元收费．（1）某出租车行程为xkm，若x＞3km，则该出租车驾驶员收到车费（1.8a+4.6）元（用含有x的代数式表示）；（2）某出租车驾驶员从公司出发，在东西向的宝带西路上连续接送4批客人，行驶路程记录如下（规定向东为正，向西为负，单位：km）．①送完第4批客人后，该出租车驾驶员在公司的西边（填“东或西”），距离公司9km的位置；②在这过程中该出租车驾驶员共收到车费多少元？【解答】解：（1）由题意可得，该出租车驾驶员收到车费为：10+（a﹣3）×1.8=1.8a+4.6，故答案为：（1.8a+4.6）；（2）①由题意可得，5+2+（﹣4）+（﹣12）=﹣9，∴送完第4批客人后，该出租车驾驶员在公司的西边，距离公司9km，故答案为：西，9；②由题意可得，在这过程中该出租车驾驶员共收到车费为：1.8×5+4.6+10+1.8×4+4.6+1.8×12+4.6=61.6（元），答：在这过程中该出租车驾驶员共收到车费61.6元．27．（10分）在计算1+5+9+13+17+21时，我们发现，从第一个数开始，后面的每个数与它前面的一个数的差都是一个相等的常数，具有这种规律的一列数，除了直接相加外，我们可以用下列公式来求和S，S=（其中n表示这列数的个数，a1表示表示第一个数，a n表示第n个数），所以，1+5+9+13+17+21==66．用上面的知识解答下列问题：吴中区科学技术协会为了扶持高科技产业，准备投资两个符合条件的企业A、B，拟定分别对A、B两个企业投资方案如下：A企业：每年投资一次，第一年投资30万元、以后每年比前一年增加投资1万元；B企业：每半年投资一次，第一个半年投资6万元，以后每半年比前半年增加投资0.5万元．（1）如果投资期限为3年，则A企业共需投资93万元，B企业共需投资37.5万元；（2）如果投资期限为n年，则A企业共需投资万元，B企业共需投资n（2n+5）万元；（用含有n的代数式表示）（3）吴中区科学技术协会决定对这两个企业累计投资12年，通过计算哪个企业获得的投资比较多？比另一个企业多多少万元？【解答】解：（1）根据题意得：企业A：3年共需投资的总金额为30+（30+1）+（30+2）=93（万元）；企业B：3年共需投资的总金额为6+（6+0.5）+（6+1）+（6+1.5）+（6+2）+（6+2.5）=37.5（万元）；（2）根据题意得：企业A：n年共需投资的总金额为30n+（1+2+…+n﹣1）=（万元）；企业B：n年共需投资的总金额为6n+[0.5+1+…+0.5（2n﹣1）]=n（2n+5）万元；（3）企业A：当n=12时，=426万元，企业B：n（2n+5）=348万元，426﹣348=78（万元）故A企业获得的投资比较多，比另一个企业多78万元．故答案为：93，37.5；，n（2n+5）．28．（10分）如图：在数轴上点A表示数a，点B表示数b，点C表示数c，a是多项式﹣2x2﹣4x+1的一次项系数，b是最小的正整数，单项式﹣的次数为c．（1）a=﹣4，b=1，c=6；（2）若将数轴在点B处折叠，则点A与点C能重合（填“能”或“不能”）；（3）点A，B，C开始在数轴上运动，若点C以每秒1个单位长度的速度向右运动，同时，点A和点B分别以每秒3个单位长度和2个单位长度的速度向左运功，t分钟过后，若点A与点B之间的距离表示为AB，点B与点C之间的距离表示为BC，则AB=t+5，BC=3t+5（用含t的代数式表示）；（4）请问：3AB﹣BC的值是否随着时间t的变化而改变？若变化，请说明理由；若不变，请求其值．【解答】解：（1）由题意可知：a=﹣4，b=1，c=6，（2）能重合，由于﹣4与6的中点为1，故将数轴在点B处折叠，则点A与点C能重合；（3）由于点A和点B分别以每秒3个单位长度和2个单位长度的速度向左运功，∴t分钟后，AB=3t+1﹣（﹣4）﹣2t=t+5由于点C以每秒1个单位长度的速度向右运动，∴t分钟后，BC=2t+6﹣1+t=3t+5（4）3AB﹣BC=3（t+5）﹣3t﹣5=3t+15﹣3t﹣5=10∴3AB﹣BC的值不会随着时间t的变化而改变，故答案为：（1）﹣4，1，6；（2）能；（3）t+5，3t+5；。

苏科版2017—2018学年七年级上期中数学试卷及答案

江苏省高邮市三垛初中2017—2018七年级数学（考试时间为120分钟满分150分）卷首语：同学们，升入初中已经半学期了，经过半学期的学习，感受到初中数学的魅力了吧！祝贺你与新课程一起成长.完成这份试卷需要你的细心、自信和智慧，相信你一定行！一、选择题（每小题3分，共24分.每小题仅有一个答案正确，请把正确答案填入下表）1．若收入500 元记作500元，则支出237元应记作 A ．－500元B ．－237元C ．237元D ．500元2．我市去年某一天的的最高气温为2℃，最低气温为－8℃，则那天的气温最高比最低高出 A ．－10℃B ．－6℃C ．6℃D ． 10℃3．据统计数据显示，截止2012年5月21日，我国“NET ”域名注册量约为560000个．居世界第三位， 560000可用科学记数法表示为A ．0.56×106B ．5.6×104C ．5.6×105D ．56×104 4．下列各组中，不是同类项的是 A ．x 3y 4与x 3z 4 B ．3x 与－x C ．5ab 与－2ba D ．－3x 2y 与212yx 5．已知长方形周长为20cm ，若设长为x cm ，则宽为 A ．x -20 B ．220x- C ．x 220- D．x -10 6．5个数：2--，(2)--，2(2)-，3(2)-，22-中，负数的个数为A ．2个B ．3个C ．4个D ．5个7．下列说法：①－a 一定是负数；②|－a |一定是正数；③倒数等于它本身的数是±1；④绝对值等于它本身的数是0和1.其中正确的个数是.A ．1个B ．2个C ．3个D ．4个8．用同样大小的正方形纸片按下图的方式拼正方形，那么第（n +1）个图形比第n 个图形多A ．n 个B ．(n +1)个C ．(2n －1)个D ．(2n+1)个二、填空题（每小题3分，共30分.把答案填在下面的横线上）9. 10. 11. 12. 13.14. 15. 16. 17. 18.9．4的相反数是 ▲ ．10．计算222a a +的结果为 ▲ ．11．数轴上与原点相距3个单位长度的点所对应的数为 ▲ ． 12．一元一次方程3x －6=0的解是 ▲ ． 13．若ab<0，则bba a -的值是 ▲ ． 14．若x ＝－2是关于x 的方程mx －6=15＋m 的解，则m ＝ ▲ ． 15．比较大小： 71-▲ 61-．（填“＜”或“＞”） 16．已知3x －y ＝－2，则3－3x ＋y 的值是 ▲ ．17．七年级男生入住的一楼有x 间，如果每间住6人，恰好空出一间；如果每间住5人就有4人不得住．求一楼共有多少间？根据题意可列出关于x 的方程为 ▲ ． 18．定义：若a 是不为1的有理数，则11a -为a 的差倒数．．．．如：2的差倒数是1112=--；－1的差倒数是111(1)2=--．已知113a =-，2a 是1a 的差倒数，3a 是2a 的差倒数，4a 是3a 的差倒数，…，依此类推，a 2012的差倒数a 2013= ▲ ．三、解答题（本大题共10题，共96分.解答应写出必要的文字说明、证明过程或演算步骤）第1个图第2个图第3个图第4个图19．（本题满分8分）计算: （1）2125-+--（2）2332(3)()2--⨯-÷-20．（本题8分）画出数轴，在数轴上表示下列各数，并用“<”连接： +5，－3.5，12，－212，4，2.521．（本题10分）化简、计算：（1）3m 2＋2mn －5 m 2＋3mn（2）(x 2＋2x )－2( x 2－x ）22．（本题10分）解方程：（1）18(75)2(53)x x x --=+-（2）131225=--+x x23．（本题10分）先化简，再求值.(2a 2b+5ab 2) －[2a 2b －1－(3ab 2+2)]，其中a =2，b =－2．24．（本题满分10分）已知关于x 的方程mx +3=x 与方程5－2x =1的解相同，求m 的值．25．（本题10分）出租车一天下午以车站为出发地在东西方向的道路上运营，向东走为正，向西走为负，行车里程（单位：km ）依先后次序记录如下：+9，－3，－5，+4，－8，+6，－3，－6，－4，+10．（1）将最后一名乘客送到目的地，出租车离车站多远?在车站的什么方向?（2）如果当地出租车收费标准为：起步价5元（即3km 内的车费），超过3km 的部分每km 的价格为1.6元，那么这个司机一个下午的营业额是多少?26．（本题10分）马虎的李明在计算多项式M 加上237x x -+时，因错看成加上237x x ++，尽管计算过程没有错误，也只能得到一个错误的答案为2524x x +-．（1）求多项式M ；（2）求出本题的正确答案．27．（本题12分）阅读理解：在解形如4223+-=-x x 这一类含有绝对值的方程时，我们可以根据绝对值的意义分2x <和2x ≥两种情况讨论：①当2x <时，原方程可化为3(2)(2)4x x --=--+，解得：0x =，符合2x < ②当2x ≥时，原方程可化为3(2)(2)4x x -=-+，解得：4x =，符合2x ≥ ∴原方程的解为：0x =，4x =．解题回顾：本题中2为2x -的零点，它把数轴上的点所对应的数分成了2x <和2x ≥两部分，所以分2x <和2x ≥两种情况讨论．知识迁移：（1）运用整体思想先求3x -的值，再去绝对值符号的方法解方程：3833x x -+=-；知识应用：（2）运用分类讨论先去绝对值符号的方法解类似的方程：2319x x x --+=-．提示：本题中有两个零点，它们把数轴上的点所对应的数分成了几部分呢？28．（本题12分）”表示数据输入、输（根据条件决定执行两条路径中的某一条）（1）①如图1，当输入数x ＝-2时，输出数y ＝______；②如图2______； ______；（2）①如图3，当输入数x ＝1时，输出数y ＝______；②如图4，当输出．．的值y ＝26，则输入．．的值x ＝_________；（3）为鼓励节约用水,决定对用水实行“阶梯价”：当每月用水量不超过15吨时（含15吨），以2元/吨的价格收费；当每月用水量超过15吨时，超过部分以3元/吨的价格收费．请设计出一个“计算框图”，使得输入数为用水量x ，输出数为水费y ．图3图4图1图22012—2013七年级数学答案说明：本评分标准每题给出了一种或几种解法供参考，如果考生的解法与本解答不同，参照本评分标准的意思给分．一、选择题：（每题3分，共24分）二、填空题：（每题3分，共30分）9．－4 10．23a 11．±3 12．2x = 13．2或－2 14．－7 15．＞ 16．5 17．6(1)54x x -=+ 18． 4三、解答题：（本大题有10题，共96分．解答应写出文字说明、证明过程或演算步骤） 19．（1）解原式=－10－5 …………………2分=－15 …………………4分（2）解原式=－9－4 …………………7分 =－13 …………………8分20．解：图略 …………………4分－3.5＜112-＜0＜12＜2.5＜4＜+5 ………………8分21．（1）解原式=－2 m 2＋5m ……………………5分（2）解原式==－x 2+4x ……………………10分22．解（1）x=－1 ……………………5分解（2）x=11 ……………………10分23．解：原式=2a 2b+5ab 2－2a 2b +1+3ab 2+2 ……………………4分 = 8ab 2+3 ……………………6分当a =2，b =－2时，原式=8×2×(－2) ……………………8分=－32 ……………………10分2012.1124．解：5－2x =1 －2x =－2 x =2 ……………………3分将x =2代入方程mx +3=x 中得：2m +3=2 ……………………7分 m =－12 ……………………10分25．解：（1）+8－3－5+4－8+6－3－6－4+10=－1 …………………4分答：出租车离农工商出发点1km ，在农工商的西边. …………………5分（2）( 5+5×1.6)+5+( 5+2×1.6)+ ( 5+1×1.6)+ ( 5+5×1.6) + ( 5+3×1.6)+5+ ( 5+3×1.6) ( 5+1×1.6) + ( 5+7×1.6)=93.2 …………………9分答：这个司机下午的营业额是93.2元 …………………10分26．解：（1）M ＝2524x x +--(237x x ++) …………………4分＝2211x x -- …………………6分（2）正确答案为：2211x x --+（237x x -+） …………………8分＝2344x x -- …………………10分27．解：（1）0x =，4x = …………………6分（2）14x =- …………………12分28．解：（1）①y ＝ ﹣9 ； …………………2分”内，应填 ×5 ； …………………3分”内，应填 ﹣3 ； …………………4分（2）①y ＝ ﹣27 ； …………………6分②x ＝ 31或﹣5 ； …………………8分（3）…………………12分图5。

2017-2018学年度第一学期七年级期中联考数学科试卷和解析答案

2017-2018学年度第一学期七年级期中联考数学科试卷考试时间：90分钟一、选择题（共12小题；共36分） 1. 下列用字母表示数的写法中，规范的是A.B. 315⨯⨯y xC.xy 35D.2. 有下列各数：，，，，)4(2--，其中属于非负整数的共有（） A. 个B. 个C. 个D. 个3. 在代数式，，，，中，整式共有个．A.B.C.D.4. 检验个工件，其中超过标准质量的克数记作正数，不足标准质量的克数记作负数，从轻重的角度看，最接近标准的工件是C.D.5. 火星和地球的距离约为34000000千米，用科学记数法表示34000000千米的结果是千米． A.B.C.D.6. 下列各组数中，互为相反数的是与B.与与与7. 用平面去截如图所示的三棱柱，截面形状不可能是A. 三角形B. 四边形C. 五边形D. 六边形8. 下列各式计算正确的是A. 12317315-=-- B.C.D.9. 下列说法中正确的是A. 不是单项式的系数是C.的次数是D.的系数是10. 如果点，，，所对应的数为，，，，则，，，的大小关系是A.B. c a d b <<<C. D.11. 某企业去年月份产值为万元，月份比月份减少，月份比月份增加了，则月份的产值是A. 万元B. 万元C. %)15%10(+-a 万元D.万元12. 规定一种新的运算“”：对于任意实数，，满足．如，则A.B.C.D.二、填空题（共4小题；共12分） 13. 已知单项式与是同类项，则．14. 如图1，将一刻度尺放在数轴上（数轴的单位长度是”分别对应数轴上的和，那么的值为．15. 如图2，数，，在数轴上对应点的位置，化简得．16. 用棋子摆出下列一组三角形，三角形每边有枚棋子，每个三角形的棋子总数为，如图按此规律推断，当三角形的边上有枚棋子时，该三角形棋子总数（用含的式子表示）．三、解答题（共7小题；共52分） 17. （各5分，共10分）计算：（1；（2）．18. （6分）先化简，再求值：（其中19. （6分）某中学七年级A 班有人，某次活动中分为四组，第一组有人，第二组比第一组的一半多人，第三组的人数等于前两组人数的和．求：（1）第二组的人数是；（1分）（2）第三组的人数是；（1分）（3）第四组的人数是；（2分）图2图1（4）找一个你喜欢的数作为的值，求出此时第四组的人数．（2分）20. （6分）某食品厂从生产的袋装食品中抽出样品袋，检测每袋的质量是否符合标准，超过标准质量的部分用正数表示，不足标准质量的部分用负数表示，检测结果如下表：若每袋食品的标准质量为克，求抽样检测的袋食品的平均质量是多少克?21. （6分）如图是小强用八块相同的小立方体搭成的一个几何体，从正面、左面和上面观察这个几何体，请你在下面相应的位置分别画出你所看到的几何体的形状图（在答题卡上画完图后请用黑色签字笔描图）．22. （8分）张老师把某小组的小明等5名同学的成绩简记为：+10，—5 , 0 ，+8 ，—3，又知道小明同学实际考了90分，且在这 5名同学中排名第三，请写出这 5名同学各考了多少分，并计算这5名同学的平均分．23. （10分）在解决数学问题的过程中，我们常用到“分类讨论”的数学思想，下面是运用分类讨论的数学思想解决问题的过程，请仔细阅读，并解答题目后提出的“探究”．【提出问题】三个有理数，，满足，求的值．【解决问题】解：由题意得：，，三个有理数都为正数或其中一个为正数，另两个为负数． ①当，，都是正数，即，，时，；（备注：一个非零数除以它本身等于1，如：3÷3=1，则1,(0)aa a=≠） ②当，，有一个为正数，另两个为负数时，设，，，的值为或（备注：一个非零数除以它的相反数等于-1，如：-3÷3= -1，则1,(0)bb b-=-≠）【探究】请根据上面的解题思路解答下面的问题：（1）三个有理数，，满足，求的值；（6分）（2）已知，且，求的值．（4分）。

2017-2018学年苏科版七年级上期中统考数学试题含答案

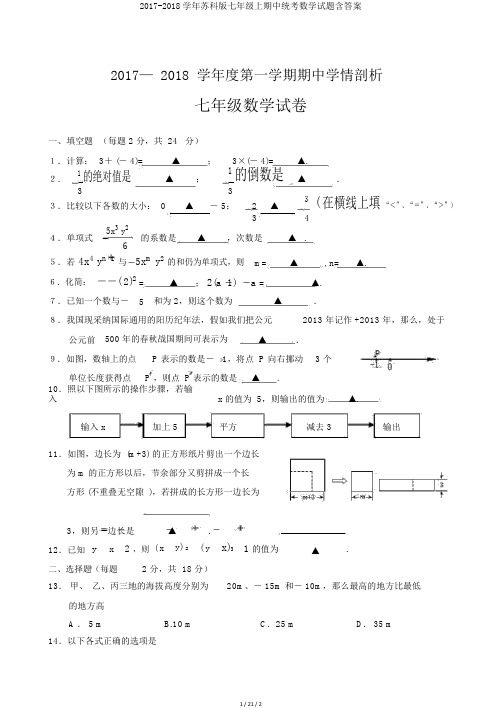
2017— 2018 学年度第一学期期中学情剖析七年级数学试卷一、填空题（每题 2 分，共 24 分）１．计算：3＋ (－ 4)= ▲；3×(－ 4)= ▲.２．1 的绝对值是▲； 1 的倒数是▲．3 3３．比较以下各数的大小： 0 ▲－ 5； 2 ▲3 （在横线上填“＜”、“＝”、“＞”）5x3 y2 3 4４．单项式的系数是▲，次数是▲ .6５．若 4x4 y n 1与5x m y2的和仍为单项式，则m= ▲, n= ▲.６．化简：－－( 2)2 = ▲； 2(a 1) a = ▲.７．已知一个数与－ 5 和为 2，则这个数为▲．８．我国现采纳国际通用的阳历纪年法，假如我们把公元2013 年记作 +2013 年，那么，处于公元前500 年的春秋战国期间可表示为▲．９．如图，数轴上的点P 表示的数是－1，将点 P 向右挪动 3 个单位长度获得点P ，则点 P 表示的数是▲．10．照以下图所示的操作步骤，若输入x 的值为 5，则输出的值为▲.输入 x 加上 5 平方减去 3 输出11．如图，边长为 (m+3) 的正方形纸片剪出一个边长为 m 的正方形以后，节余部分又剪拼成一个长方形 (不重叠无空隙 )，若拼成的长方形一边长为3，则另一边长是▲．12．已知y x 2 ，则( x y) 2 ( y x)3 1的值为▲.二、选择题（每题 2 分，共18 分）13．甲、乙、丙三地的海拔高度分别为20m、－ 15m 和－ 10m，那么最高的地方比最低的地方高A ． 5 m B.10 m C．25 m D． 35 m14．以下各式正确的选项是A. 6 a－5a=1B. a+2a2=3 a3C.－( a－ b)=－ a+bD.2(a+b)=2 a+b。

苏科版七年级上册数学《期中考试卷》附答案解析

苏科版数学七年级上学期期中测试卷一、选择题（每小题2分，共16分）1.0.5-的倒数是( )A. 0.5B. 2C. -2D. 12-2.下列各题中合并同类项，结果正确的是（） A 222347a a a += B. 222236a a a +=C. 532xy xy -=D. 336235a a a +=3.在下列五个数中：23，0，2π，1.3，－1.212212221…（两个1之间依次多一个2）有理数个数为（）A. 4B. 3C. 2D. 14.若代数式a 2+2b 的值为4，则代数式3a 2+6b-3的值为（） A. 3B. －9C. －3D. 95.我市某文具店进行促销活动，决定将单价为a 元的笔记本降价10%销售，降价后的销售价为（） A. 10%aB. a －10%C. （1－10%）aD. （1＋10%）a6.a ，b 是有理数，且|a |＝－a ，|b |＝b ，|a |＞|b |，用数轴上的点来表示a ，b ，正确的是( ) A.B.C.D.7.无论a 取什么值，下列哪个代数式的值一定是正的？（） A. 21a +B. 8a +C. 2(3)a +D. 3100a +8.一家商店以每包a 元的价格进了20包甲种茶叶，又以每包b 元的价格买进30包乙种茶叶（a <b ），如果以每包2a b+元的价格卖出这两种茶叶，则卖完后，这家商店（） A. 赚了B. 赔了C. 不赔不赚D. 不能确定赚或赔二、填空题（每小题2分，共20分）9.－12的相反数为_______，－12的绝对值等于_______． 10.据报道，春节期间微信红包收发高达3280000000次，数字3280000000用科学记数法表示为___________． 11.比较大小，用“＜”“＞”或“＝”连接：（1）－|23-| ___－（34-）；（2）－3.14___－|－π|．12.若312a x y -与223bx y -的和仍是单项式，则-a b ＝_________．13.袋装牛奶的标准质量为100克，现抽取5袋进行检测，超过标准的质量记为正数，不足的记为负数，结果如下表所示：（单位：克）代号 ① ② ③ ④ ⑤ 质量－2＋4－1＋5－6其中，质量最接近标准的是__________号（填写序号）．14.定义一种新的运算“*”，并且规定：a*b ＝a 2－2b ．则（－3）*（－1）＝_______． 15.如图，用代数式表示图中阴影部分的面积为___________________.16.已知x ＝5，y ＝4，且x ＞y ，则x －y ＝_________． 17.已知2a ＋b ＝23，a ＋2b ＝25，则代数式a ＋b ＝________．18.如图所示的运算程序中，若开始输入的x 值为64，我们发现第一次输出的结果为32，第二次输出的结果为16，……，则第2018次输出的结果为_________．三、计算题（每小题4分，共16分）19.（1）14―25＋12―17；（2）113()(60)234--+⨯-；（3）54(25)(32)45-÷⨯÷-；（4）22123(3)6⎡⎤--⨯--⎣⎦. 四、计算与化简（20题每小题5分，21题6分，共16分）20.化简下列各式：（1）324576x y x y -+---+；（2）4(32)3(52)x y y x ----.21.化简求值22225(3)4(3),2, 3.a b ab ab a b a b ---+=-=其中，五、解答题（共32分）22.列式计算：已知三角形的第一条边长为5a ＋3b ，第二条边比第一条边短2a －b ，第三条边比第二条边短a －b ．（1）求第二条边长；（2）求这个三角形的周长．23.用同样大小的两种不同颜色的正方形纸片，按下图方式拼正方形．…第（1）个图形中有1个正方形；第（2）个图形有1＋3＝4个小正方形；第（3）个图形有1＋3＋5＝9个小正方形；第（4）个图形有25小正方形； ……（1）根据上面发现我们可以猜想：1＋3＋5＋7＋...＋（2n －1）的结果（用含n 的代数式表示）；（2）请根据你的发现计算：① 1＋3＋5＋7＋...＋99； ② 101＋103＋105＋ (199)24.某市为鼓励居民节约用水，采用分段计费方法按月计算每户家庭的水费，月用水量不超过30立方米时，按2元/立方米计费；月用水量超过30立方米时，其中的30立方米仍按2元/立方米收费，超过部分按2.5元/立方米计费．设每户家庭月用水量为x 立方米．（1）当x不超过30时，应收多少水费（用x的代数式表示）；当x超过30时，应收多少水费（用x的代数式表示）；（2）小明家四月份用水20立方米，五月份用水36立方米，请帮小明计算一下他家这两个月一共应交多少元水费？25.阅读材料：如图（1），在数轴上A示的数为a，B点表示的数为b，则点A到点B的距离记为AB．线段AB的长可以用右边的数减去左边的数表示，即AB＝b－a．解决问题：如图（2），数轴上点A表示的数是－4，点B表示的数是2，点C表示的数是6．（1）若数轴上有一点D，且AD＝3，求点D表示的数；（2）点A、B、C开始在数轴上运动，若点A以每秒1个单位长度的速度向左运动，同时，点B和点C分别以每秒2个单位长度和3个单位长度的速度向右运动，假设t秒钟过后，若点A与点B之间的距离表示为AB，点A与点C之间的距离表示为AC，点B与点C之间的距离表示为BC．求点A表示的数（用含t的代数式表示），BC等于多少（用含t的代数式表示）．（3）请问：3BC－AB的值是否随着时间t的变化而改变？若变化，请说明理由；若不变，请求其值．答案与解析一、选择题（每小题2分，共16分）1.0.5-的倒数是( ) A. 0.5 B. 2C. -2D. 12-【答案】C 【解析】【分析】根据倒数的定义解答即可. 【详解】∵-0.5×（-2）=1， ∴0.5-的倒数是是-2. 故选C.【点睛】本题考查了倒数的定义，熟知乘积是1 的两个数互为倒数是解题的关键. 2.下列各题中合并同类项，结果正确的是（） A. 222347a a a += B. 222236a a a +=C. 532xy xy -=D. 336235a a a +=【答案】A 【解析】【分析】原式各项合并得到结果，即可做出判断．【详解】A 、3a 2+4a 2=7a 2，正确； B 、2a 2+3a 2=5a 2，错误； C 、5xy-3xy=2xy ，错误； D 、原式不能合并，错误，故选A ．【点睛】此题考查了合并同类项，熟练掌握合并同类项法则是解本题的关键． 3.在下列五个数中：23，0，2π，1.3，－1.212212221…（两个1之间依次多一个2）有理数个数为（）A. 4B. 3C. 2D. 1【答案】B 【解析】【分析】根据有理数的定义、无理数的定义进行判断即可得解．【详解】在23，0，2，1.3，－1.212212221…（两个1之间依次多一个2）中，有理数有23，0，1.3，有理数的个数是3个．故选B．【点睛】本题考查了实数，主要利用了有理数和无理数定义，熟记概念是解题的关键．4.若代数式a2+2b的值为4，则代数式3a2+6b-3的值为（）A. 3B. －9C. －3D. 9【答案】D【解析】【分析】3a2+6b可看为a2+2b的3倍．【详解】3a2+6b-3=3（a2+2b）-3=12-3=9．故选D【点睛】此题主要考查了代数式求值，将待求的式子前两项提取3整体出现a2+2b是解本题的关键．5.我市某文具店进行促销活动，决定将单价为a元的笔记本降价10%销售，降价后的销售价为（）A. 10%aB. a－10%C. （1－10%）aD. （1＋10%）a【答案】C【解析】【分析】根据题意可以求得降价后的销售价格，本题得以解决．【详解】由题意可得，降价后的销售价为：（1-10%）a，故选C．【点睛】本题考查列代数式，解题的关键是明确题意，列出相应的代数式．6.a，b是有理数，且|a|＝－a，|b|＝b，|a|＞|b|，用数轴上的点来表示a，b，正确的是( )A. B. C. D.【答案】A【解析】分析：根据绝对值的定义和数轴的定义解答此题即可．详解：|a|=-a ，|b|=b ，|a|＞|b|， ∴a≤0，b≥0，|a|＞|b|，故选A ．点睛：此题考查了数轴的知识，解答本题的关键是理解数轴上各点的大小关系，掌握原点左边的数小于0，原点右边的数大于0．7.无论a 取什么值，下列哪个代数式的值一定是正的？（） A. 21a + B. 8a +C. 2(3)a +D. 3100a +【答案】A 【解析】【分析】讨论每个选项后，作出判断．注意平方数和绝对值都可是非负数．【详解】A 、无论a 是何值，代数式a 2+1的值都是正数，符合题意； B 、当a=-8时，代数式8a +的值为0，0不是正数，不符合题意； C 、当a=-3时，代数式（a+3）2的值为0，0不是正数，不符合题意； D 、当x≤-10时，代数式3100a +的值小于等于0，，不符合题意. 故选A ．【点睛】注意0既不是正数，也不是负数．平方数和绝对值都可以为0，也可以为正数．8.一家商店以每包a 元的价格进了20包甲种茶叶，又以每包b 元的价格买进30包乙种茶叶（a <b ），如果以每包2a b+元的价格卖出这两种茶叶，则卖完后，这家商店（） A. 赚了 B. 赔了C. 不赔不赚D. 不能确定赚或赔【答案】B 【解析】【分析】根据题意知商店获得的利润为2a b+×（20+30）-20a-30b=5（a-b ），由a<b 知5（a-b ）<0，可得答案．【详解】该商店一共购进茶叶50包,若每包以2a b+元的价格卖出，则共收入50×2a b+=25(a +b )元；购进两种茶叶共花费：20a+30b；25(a+b)−(20a+30b)=25a+25b−20a−30b=5a−5b=5(a−b)∵a<b，即a−b<0，所以5(a−b)<0即卖完后，这家商店赔了.故选B.【点睛】本题主要考查列代数式的能力及整式的化简，理解题意列出商店获取利润的代数式是解题的关键．二、填空题（每小题2分，共20分）9.－12的相反数为_______，－12的绝对值等于_______．【答案】(1). 12(2).12【解析】【分析】分别根据相反数的概念及绝对值的性质进行解答即可．【详解】-12与12只有符号相反，∴-12的相反数等于12，∵-12＜0，∴|-12|=12．故答案为12；12．【点睛】本题考查的是相反数的概念及绝对值的性质，熟知以上知识是解答此题的关键．10.据报道，春节期间微信红包收发高达3280000000次，数字3280000000用科学记数法表示为___________．【答案】93.2810【解析】【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．【详解】将3280000000用科学记数法表示为3.28×109．故答案为3.28×109．【点睛】此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n 的形式，其中1≤|a|＜10，n 为整数，表示时关键要正确确定a 的值以及n 的值． 11.比较大小，用“＜”“＞”或“＝”连接：（1）－|23-| ___－（34-）；（2）－3.14___－|－π|．【答案】 (1). ＜ (2). ＞【解析】【分析】（1）先化简，然后根据正数大于负数即可判断；（2）先化简，然后再求绝对值，最后根据两个负数比较大小，绝对值大的反而小即可比较．【详解】（1）∵-|-23|=-23＜0，-（-34）=34＞0， ∴-|-23|＜-（-34）；（2）∵-|-π|=-π，|-3.14|=3.14，|-π|=π，且3.14＜π， ∴-314＞-|-π|，故答案为（1）＜；（2）＞．【点睛】本题考查的是有理数的大小比较，熟知两负数比较大小的法则是解答此题的关键．12.若312a x y -与223bx y -的和仍是单项式，则-a b ＝_________．【答案】-1 【解析】【分析】利用已知得出两个单项式是同类项，进而得出a ，b 的值即可得出答案．【详解】∵单项式312a x y -与223bx y -的和仍是单项式，∴a=2，b=3，则a b -=-1，故答案为-1．【点睛】此题主要考查了同类项，正确把握同类项的定义是解题关键．13.袋装牛奶的标准质量为100克，现抽取5袋进行检测，超过标准的质量记为正数，不足的记为负数，结果如下表所示：（单位：克）其中，质量最接近标准的是__________号（填写序号）．【答案】③【解析】【分析】根据表中数据求出每袋的质量，选出和100克比较接近的即可；也可以根据-2，+4，-1，+5，-6直接得出答案．【详解】∵①的质量是100-2=98（克），②的质量是100+4=104（克），③的质量是100-1=99（克），④的质量是100+5=105（克），⑤的质量是100-6=94（克），∴最接近100克的是③，故答案为③．【点睛】本题考查了正数和负数的应用，解此题的关键是理解题意．14.定义一种新的运算“*”，并且规定：a*b＝a2－2b．则（－3）*（－1）＝_______．【答案】11【解析】分析】根据题中的新定义运算的方法列出所求算式，计算即可得到结果．【详解】（-3）*（-1）=（-3）2-2×（-1）=9+2=11．故答案为11．【点睛】此题考查了有理数的混合运算，弄清题中的新定义运算的方法是解本题的关键．15.如图，用代数式表示图中阴影部分的面积为___________________.【答案】212ab b π-【解析】阴影部分的面积等于长方形的面积减去两个小扇形的面积差．长方形的面积是ab ,两个扇形的圆心角是90∘，∴这两个扇形是分别是半径为b 的圆面积的四分之一． ∴2211242ab b ab b ππ-⨯=- . 【点睛】本题考查了列代数式,由数和表示数的字母经有限次加、减、乘、除、乘方和开方等代数运算所得的式子，或含有字母的数学表达式称为代数式．理解图意得到阴影部分的面积长方形的面积-2个14圆的面积是解题的关键. 16.已知x ＝5，y ＝4，且x ＞y ，则x －y ＝_________．【答案】1或9【解析】【分析】根据绝对值的代数意义分别求出x 与y 的值，然后根据x ＞y 得到满足题意的x 与y 的值，代入所求的式子中计算即可．【详解】∵|x|=5，|y|=4，∴x=±5，y=±4，又∵x ＞y ，∴x=5，y=4或x=5，y=-4，则x-y=5-4=1，或x-y=5-（-4）=9．故答案1或9．【点睛】此题考查了有理数的减法，绝对值的代数意义，掌握绝对值的代数意义是解本题的关键，注意不要漏解．17.已知2a＋b＝23，a＋2b＝25，则代数式a＋b＝________．【答案】16【解析】【分析】把两式相加，得到3a+3b=48，即可求解.【详解】2a＋b＝23①，a＋2b＝25②，①+②，得3a+3b=48，即3(a+b)=48，得a+b=16，故答案为16【点睛】此题考查了代数式求值，把a+b看作一个整体是解题的关键.18.如图所示的运算程序中，若开始输入的x值为64，我们发现第一次输出的结果为32，第二次输出的结果为16，……，则第2018次输出的结果为_________．【答案】2【解析】【分析】把x=64代入程序中计算，以此类推得到一般性规律，即可确定出第2018次输出的结果．【详解】把x=64代入得：12×64=32，把x=32代入得：12×32=16，把x=16代入得：12×16=8，把x=8代入得：12×8=4，把x=4代入得：12×4=2，把x=2代入得：12×2=1，把x=1代入得：1+3=4，以此类推，∵（2018-3）÷3=671…2，∴第2018次输出的结果为2，故答案为：2．【点睛】此题考查了代数式求值，弄清题中的程序框图是解本题的关键．三、计算题（每小题4分，共16分）19.（1）14―25＋12―17；（2）113()(60)234--+⨯-；（3）54(25)(32)45-÷⨯÷-；（4）22123(3)6⎡⎤--⨯--⎣⎦. 【答案】（1）－16；（2）5；（3）12；（4）－3. 【解析】【分析】（1）把正数负数分别结合计算即可；（2）运用乘法分配律计算可得；（3）先把除法转化成乘法，再根据有理数的乘法法则计算即可．（4）先算乘方和括号里面的，再算乘法，最后算减法即可.【详解】（1）14―25＋12―17=14＋12―25―17=26―42=-16；（2）()11360234⎛⎫--+⨯- ⎪⎝⎭=()()()113 6060603020234⎛⎫-⨯--⨯-+⨯-=+ ⎪⎝⎭-45=5；（3）()()54253245-÷⨯÷-=()4414411 2525553255322⎛⎫-⨯⨯⨯-=⨯⨯⨯= ⎪⎝⎭；（4）()2212336⎡⎤--⨯--⎣⎦=-4-16⨯(3-9)= -4-16⨯(-6)=-4+1=-3 【点睛】此题主要考查了有理数的混合运算，要熟练掌握，注意明确有理数混合运算顺序：先算乘方，再算乘除，最后算加减；同级运算，应按从左到右的顺序进行计算；如果有括号，要先做括号内的运算．四、计算与化简（20题每小题5分，21题6分，共16分）20.化简下列各式：（1）324576x y x y -+---+；（2）4(32)3(52)x y y x ----.【答案】（1）-8x-5y+2；（2）-6x-7y.【解析】【分析】（1）直接合并同类项即可；（2）先去括号，然后合并同类项．【详解】（1）324576x y x y -+---+=()()()352746x x y y --+-+-+=-8x-5y+2；（2）()()432352x y y x ----=-12x+8y-15y+6x=(-12x+6x) +(8y-15y)=-6x-7y ．【点睛】本题考查了整式的加减，整式的加减的实质就是去括号、合并同类项．去括号时，要注意两个方面：一是括号外的数字因数要乘括号内的每一项；二是当括号外是“-”时，去括号后括号内的各项都要改变符号．21.化简求值22225(3)4(3),2, 3.a b ab ab a b a b ---+=-=其中，【答案】54．【解析】【分析】原式去括号合并得到最简结果，把a 与b 的值代入计算即可求出值．【详解】原式＝15a 2b ﹣5ab 2+4ab 2﹣12a 2b ＝3a 2b ﹣ab 2，当a ＝﹣2，b ＝3时，原式＝36+18＝54．【点睛】此题考查了整式的加减﹣化简求值，熟练掌握运算法则是解本题的关键．五、解答题（共32分）22.列式计算：已知三角形的第一条边长为5a ＋3b ，第二条边比第一条边短2a －b ，第三条边比第二条边短a －b ．（1）求第二条边长；（2）求这个三角形的周长．【答案】（1）3a ＋4b ；（2）10a ＋12b【解析】【分析】(1)根据题意即可列出第二条边的长度；(2)根据题意列出第三条边的长度，然后即可求出三角形的周长．【详解】（1） 5a＋3b －（2a－b）＝ 5a＋3b －2a＋b ＝ 3a＋4b；（2）5a＋3b＋（3a＋4b）＋（3a＋4b）－（a－b）＝5a＋3b＋3a＋4b＋3a＋4b－a＋b＝ 10a＋12b 【点睛】本题考查整式的加减，涉及列代数式，属于基础题型．23.用同样大小的两种不同颜色的正方形纸片，按下图方式拼正方形．…第（1）个图形中有1个正方形；第（2）个图形有1＋3＝4个小正方形；第（3）个图形有1＋3＋5＝9个小正方形；第（4）个图形有25小正方形；……（1）根据上面的发现我们可以猜想：1＋3＋5＋7＋...＋（2n－1）的结果（用含n的代数式表示）；（2）请根据你的发现计算：① 1＋3＋5＋7＋ (99)② 101＋103＋105＋ (199)【答案】（1）2n，①2500，②7500.【解析】【分析】（1）直接分别解各数据得出答案；（2）①利用（1）规律求出答案；②由以上规律可得原式可看作是1002-502.【详解】第（1）个图形中有1=12个正方形；第（2）个图形有1＋3＝4=22个小正方形；第（3）个图形有1＋3＋5＝9=32个小正方形；第（4）个图形有1+3+5+7=16=42小正方形；……第n个图形有1+3+5+…+(2n-1)=n2小正方形；（1）1+3+5+…+（2n-1）=n2；（2）① 1＋3＋5＋7＋…＋99=502=2500；②101＋103＋105＋…＋199=(1＋3＋5＋7＋…＋199)+( 1＋3＋5＋7＋…＋99)=1002-502=7500.【点睛】此题主要考查了图形的变化类，正确得出数字之间变化规律是解题关键．24.某市为鼓励居民节约用水，采用分段计费的方法按月计算每户家庭的水费，月用水量不超过30立方米时，按2元/立方米计费；月用水量超过30立方米时，其中的30立方米仍按2元/立方米收费，超过部分按2.5元/立方米计费．设每户家庭月用水量为x立方米．（1）当x不超过30时，应收多少水费（用x的代数式表示）；当x超过30时，应收多少水费（用x的代数式表示）；（2）小明家四月份用水20立方米，五月份用水36立方米，请帮小明计算一下他家这两个月一共应交多少元水费？【答案】（1）2x，60+2.5（x-30）或2.5x-15；（2）这两个月一共应交115元水费【解析】【分析】（1）因为月用水量不超过30m3时，按2元/m3计费，所以当0≤x≤30时，水费为是2x；因为月用水量超过30m3时，其中的30m3仍按2元/m3收费，超过部分按 2.5元/m3计费，所以当x＞30时，水费为：2×30+2.5（x-30）=2.5x-15；（2）由题意可得：因为四月份用水20立方米，所以用2x计算水费；五月份用水36立方米，所以用（2.5x-15）计算用水量．【详解】（1）月用水量不超过30立方米时水费为：2x元,月用水量超过30立方米时水费为：60+2.5（x-30）=2.5x-15；（2）当x＝20时，2x＝2×20＝40，x-=⨯-=当x＝36时，2.515 2.5361575答：这两个月一共应交115元水费【点睛】本题是贴近社会生活的应用题，赋予了生活气息，使学生真切地感受到“数学来源于生活”，体验到数学的“有用性”．这样设计体现了《新课程标准》的“问题情景-建立模型-解释、应用和拓展”的数学学习模式．25.阅读材料：如图（1），在数轴上A示的数为a，B点表示的数为b，则点A到点B的距离记为AB．线段AB的长可以用右边的数减去左边的数表示，即AB＝b－a．解决问题：如图（2），数轴上点A表示的数是－4，点B表示的数是2，点C表示的数是6．（1）若数轴上有一点D，且AD＝3，求点D表示的数；（2）点A、B、C开始在数轴上运动，若点A以每秒1个单位长度的速度向左运动，同时，点B和点C分别以每秒2个单位长度和3个单位长度的速度向右运动，假设t秒钟过后，若点A与点B之间的距离表示为AB，点A与点C之间的距离表示为AC，点B与点C之间的距离表示为BC．求点A表示的数（用含t的代数式表示），BC等于多少（用含t的代数式表示）．（3）请问：3BC－AB的值是否随着时间t的变化而改变？若变化，请说明理由；若不变，请求其值．【答案】（1）－7或－1，（2）－4－t t＋4 （3）不变，理由见解析.【解析】【分析】（1）设D表示的数为a，由绝对值的意义容易得出结果；（2）分别表示出t秒后A、B、C分别对应的数，再求AC即可；（3）表示出BC和AB，再相减即可得出结论．【详解】（1）设D表示的数为a，∵AD=3，∴|-4-a|=3，解得：a=-7或-1；（2）将点A向左移动t个单位长度，则移动后的点表示的数为-4-t；将点B和点C分别向右运动2t和3t个单位长度，则移动后的点表示的数分别为2+2t，6+3t；则BC=（6+3t）-（2+2t）=t+4；（3）AB=（2+2t）-（-4-t）=3t+6，3BC－AB=3（t+4）-（3t+6）=6，故3BC－AB的值不随时间t的变化而改变.【点睛】此题考查了数轴，掌握数轴上两点之间的距离求解方法是解决问题的关键．。

苏科版2017-2018学年度七年级上期中考试数学试卷及答案

锡山区东亭八校2017—2018学年度第一学期期中考试试卷七年级数学(考试时间为100分钟，本试卷满分100分)【卷首语】亲爱的同学，升入初中已半个学期，祝贺你与新课程一起成长，比以前变的更有智慧了。

现在就请走进数学世界，通过下面一些问题的解决来展示自己对数学的理解、亮出数学学习的风采吧。

只要你认真答题不马虎，相信成功必将属于你！一、精心选一选（本题为单选题，共10题，每题2分，共20分）1.32-的倒数是（）A ．23-B ．23C ．32D ．32-2.钓鱼岛是中国固有领土。

从今年4月至今，日本妄图通过“购岛”等伎俩等实施侵吞。

温总理掷地有声地说：日方此举严重伤害了13亿中国人的感情；中国政府和人民绝不会退让半步；中华民族任人欺凌的时代已经一去不复返了！其中的13亿用科学记数法可表示为（）A 、1.3×106B 、1.3×107C 、1.3×108D 、1.3×1093．有理数a 、b 在数轴上的位置如图所示，则下列判断错误的是（） A ． a ＞0 B ． b ＜0 C ．－a ＜0 D ．b ＋a ＞04．在下列各数－(＋3)、－22、(－2)2、(－1)2012、－|－4|中，负数有（）A ．2个B ．3 个C ．4 个D ．5个5.一只蚂蚁从数轴上的点A 出发爬了6个单位长度到了原点，则点A 所表示的数是（） A ．6 B ．-6 C ． ±6 D ．±96．马小虎做了6道题：① (-1)2013=-2013； ② 0-(-1)=1； ③ -21+31=-61； ④)21(21-÷=-1；⑤ 2×(-3)2=36； ⑥ -3÷21×2=-3.那么，他做对了几题呢？答：（）A 、1题B 、2题C 、3题D 、4题7．已知b a m 225-和n b a -347是同类项，则n m +的值是（） A 、2 B 、3 C 、4 D 、68．下列各式，成立的是（） A 、a-b+c=a-(b-c) B 、3a -a = 3 C 、8a -4 = 4a D 、-2(a-b)=-2a+b9．给出下列判断：① 2πa 2b 与ba 231是同类项； ②多项式5a+4b-1中，常数项是1；③y y 2+-x x 是二次三项式； ④4y x +，12+x，4a 都是整式.其中判断正确的是（）A ．①②③B ．①③C ．①③④D ．①②③④10．如下数表是由从1 开始的连续自然数组成。

苏州市吴中区2017～2018学年度第一学期初一数学期中试题(含答案)

2017-2018学年度第一学期学科教学质量情况调查初一数学 2017.11 注意事项:1.本试卷满分130分，考试时间120分钟;2.答卷前将密封线内的项目填写清楚，所有解答均须写在答题卷上，在本试卷上答题无效.一、选择题(本大题共10小题，每小题3分，共30分.每小题只有一个选项是正确的，把正确选项前的字母填涂在答题卷相应位置上.)1.下列各个运算中，结果为负数的是A.－(－4)B.4-C.－42D.(－4)22.地球与月球的平均距离人约为384000km ，则这个平均距离用科学记数法表示为A.384×103 kmB. 3.84×105kmC.0.384×106 kmD. 3.84×104 km3.下列各数:0, π， 3.141，237，其中有理数的个数是 A.3个 B.4个 C.2个 D.1个4.下列方程中，是一元一次方程的是 A. 110x-= B. 10x -=C. 210x x --=D. 2(1)2x x -=5.下列各组式子中为同类项的是A.25x y 与22xy - B .4x 与24xC.23x y -与213yx D .346x y 与346x z - 6.已知5是关于x 的方程327x a -=的解，则a 的值是A. 8B. 12C. 3.5D. 47.已知1,2x y ==，则x y -的值为A .－1或－3 B.±5 C.1或3 D.±318.如图所示的运算程序中，若开始输入的x 值为－5，我们发现第1次输出的数为－2，再将－2输入，第2次输出的数为－1，如此循环，则第2017次输出的结果为 .三、解答题(本大题共l0小题，共76分.解答时应写出文字说明、证明过程或演算步骤.)19.(每小题4分，共8分)计算或化简:(1)－7+3－5+12; (2)－23 +(2－3)－2×(－1)2017.20.(每小题4分，共8分)解下列方程:(1)2(1)3x x -=+; (2)0.30.5210.23x x +-=.21.(本题满分5分) 先化简，再求值：22717[32(1)]22x y xy xy x y xy ---++，其中16,6x y ==-.22.(本题满分5分)已知: 2234,2A a ab B a ab =-=+.(1)求:2A B -;(2)若221(2)0a b ++-=，求2A B -的值.23.(本题满分6分)当m 是何值时，关于x 的方程4231x m x -=+的解是方程23x x -=的解的2倍.24.(本题满分7分)若“三角” 表示运算，“方框” 表示运算x y z w -++. 求：的值.(列出算式并计算结果)25.(本题满分8分)已知a 是方程3510x -=的解，求代数式2223[2()1]a a a a ---+的值.26.(本题满分9分)苏州市出租车的计价标准为:行驶路程不超过3km 收费10元，超过3km 的部分按排每千米1.8元收费.(1)某出租车行程为x km,若x >3km ，则该出租车驾驶员收到车费元(用含有x 的代数式表示)；(2)某出租车驾驶员从公司出发，在东西向的宝带西路上连续接送4批客人，行驶路程记录如下(规定向东为正，向西为负，单位:km).①送完第4批客人后，该出租车驾驶员在公司的月边(填“东或西”),距离公司 km 的位置；②在这过程中该出租车驾驶员共收到车费多少元?27.(本题满分10分)在计算1+5+9+13+17+21时，我们发现，从第一个数开始，后面的每个数与它前面的一个数的差都是一个相等的常数，具有这种规律的一列数，除了直接相加外，我们可以用下列公式来求和1(),2n n a a S S +=(其中n 表示这列数的个数，1a 表示表示第一个数，n a 表示第n 个数), 所以，1+5+9+13+17+21=6(121)662⨯+=. 用上面的知识解答下列问题:吴中区科学技术协会为了扶持高科技产业，准备投资两个符合条件的企业A 、B ，拟定分别对A 、B 两个企业投资方案如下：A 企业:每年投资一次，第一年投资30万元、以后每年比前一年增加投资1万元;B 企业:每半年投资一次，第一个半年投资6万元，以后每半年比前半年增加投资0.5万元.(1)如果投资期限为3年，则A 企业共需投资万元，B 企业共需投资万元;(2)如果投资期限为n 年，则A 企业共需投资万元，B 企业共需投资万元； (用含有n 的代数式表示)(3)吴中区科学技术协会决定对这两个企业累计投资12年，通过计算哪个企业获得的投资比较多?比另一个企业多多少万元？28.(本题满分10分)如图:在数轴上点A 表示数a ，点B 表示数b ，点C 表示数c ，a 是多项式2241x x --+的一次项系数，b 是最小的正整数，单项式2412x y -的次数为c .(1) a = ，b = ，c = ;(2)若将数轴在点B 处折叠，则点A 与点C 重合( 填“能”或“不能”)；(3)点,,A B C 开始在数轴上运动，若点C 以每秒1个单位长度的速度向右运动，同时,点A 和点B 分别以每秒3个单位长度和2个单位长度的速度向左运功，t 分钟过后，若点A 与点B 之间的距离表示为AB ，点B 与点C 之间的距离表示为BC ，则AB = , BC = (用含t 的代数式表示);(4)请问：3AB BC -的值是否随着时间t 的变化而改变？若变化，请说明理由；若不变，请求其值.。

2017-2018学年江苏省苏州市吴中区七年级(上)期中数学试卷(解析版)

2017-2018学年江苏省苏州市吴中区七年级（上）期中数学试卷一、选择题（本大题共10小题，每小题3分，共30分.每小题只有一个选项是正确的，把正确选项前的字母填涂在答题卷相应位置上.）1．（3分）下列各个运算中，结果为负数的是（）A．﹣（﹣4）B．|﹣4|C．﹣42 D．（﹣4）22．（3分）地球与月球的平均距离大约为384000km，则这个平均距离用科学记数法表示为（）A．384×103km B．3.84×104km C．3.84×105km D．3.84×106km3．（3分）下列各数：0，π，3.141，，其中有理数的个数是（）A．3个 B．4个 C．2个 D．1个4．（3分）下列方程中，是一元一次方程的是（）A．B．x﹣1=0 C．x2﹣x﹣1=0 D．2（x﹣1）=2x5．（3分）下列各组式子中为同类项的是（）A．5x2y与﹣2xy2B．4x与4x2C．﹣3x2y与yx2D．6x3y4与﹣6x3z46．（3分）已知5是关于x的方程3x﹣2a=7的解，则a的值是（）A．8 B．12 C．3.5 D．47．（3分）已知|x|=1，y=2，则x﹣y的值为（）A．﹣1或﹣3 B．±5 C．1或3 D．±38．（3分）一种商品每件进价为a元，按进价增加20%定出售价，后因库存积压降价，按售价的八折出售，每件亏损（）A．0.01a元 B．0.15a元 C．0.25a元 D．0.04a元9．（3分）下列方程变形错误的是（）A．由方程，得3x﹣2x+2=6B．由方程，得3（x﹣1）+2x=6C．由方程，得2x﹣1=3﹣6x+3D．由方程，得4x﹣x+1=410．（3分）如图所示，每个正方形由边长为1的小正方形组成：观察图形，在边长为n（n≥1，n为奇数）的正方形中，黑色小正方形的个数为（）A．n2B．2n﹣1 C．n2﹣2n+1 D．n2﹣2n二、填空题（本大题共8小题，每小题3分，共24分）11．（3分）﹣2的相反数是．12．（3分）比较大小，用“＜”“＞”或“=”连接：﹣﹣．13．（3分）数轴上与﹣3距离4个单位长度的点表示的正数是．14．（3分）“x的2倍与y的的和”用代数式表示为．15．（3分）若关于x的多项式3x2+（k﹣1）x﹣1中不含有x的一次项，则k=．16．（3分）3x5y6与﹣x n﹣1y6是同类项，则n=．17．（3分）已知代数式x+3y的值2，则代数式2x+6y+1值是．18．（3分）如图所示的运算程序中，若开始输入的x值为﹣5，我们发现第1次输出的数为﹣2，再将﹣2输入，第2次输出的数为﹣1，如此循环，则第2017次输出的结果为．三、解答题（本大题共l0小题，共76分.解答时应写出文字说明、证明过程或演算步骤.）19．（8分）计算或化简：（1）﹣7+3﹣5+12；（2）﹣23+（2﹣3）﹣2×（﹣1）2017．20．（8分）解下列方程：（1）2（x﹣1）=x+3；（2）．21．（5分）先化简，再求值：7x2y﹣[3xy﹣2（xy﹣x2y+1）+xy]，其中x=6，y=﹣．22．（5分）已知：A=3a2﹣4ab，B=a2+2ab．（1）求A﹣2B；（2）若|2a+1|+（2﹣b）2=0，求A﹣2B的值．23．（6分）当m是何值时，关于x的方程4x﹣2m=3x+1的解是方程2x﹣3=x的解的2倍．24．（7分）若“三角”表示运算：a﹣b+c，若“方框”，表示运算：x﹣y+z+w，求的值，列出算式并计算结果．25．（8分）已知a是方程3x﹣5=10的解，求代数式3a2﹣[a2﹣2（a﹣a2）+1]的值．26．（9分）苏州市出租车的计价标准为：行驶路程不超过3km收费10元，超过3km的部分按排每千米1.8元收费．（1）某出租车行程为xkm，若x＞3km，则该出租车驾驶员收到车费元（用含有x的代数式表示）；（2）某出租车驾驶员从公司出发，在东西向的宝带西路上连续接送4批客人，行驶路程记录如下（规定向东为正，向西为负，单位：km）．①送完第4批客人后，该出租车驾驶员在公司的边（填“东或西”），距离公司km的位置；②在这过程中该出租车驾驶员共收到车费多少元？27．（10分）在计算1+5+9+13+17+21时，我们发现，从第一个数开始，后面的每个数与它前面的一个数的差都是一个相等的常数，具有这种规律的一列数，除了直接相加外，我们可以用下列公式来求和S，S=（其中n表示这列数的个数，a1表示表示第一个数，a n表示第n个数），所以，1+5+9+13+17+21==66．用上面的知识解答下列问题：吴中区科学技术协会为了扶持高科技产业，准备投资两个符合条件的企业A、B，拟定分别对A、B两个企业投资方案如下：A企业：每年投资一次，第一年投资30万元、以后每年比前一年增加投资1万元；B企业：每半年投资一次，第一个半年投资6万元，以后每半年比前半年增加投资0.5万元．（1）如果投资期限为3年，则A企业共需投资万元，B企业共需投资万元；（2）如果投资期限为n年，则A企业共需投资万元，B企业共需投资万元；（用含有n的代数式表示）（3）吴中区科学技术协会决定对这两个企业累计投资12年，通过计算哪个企业获得的投资比较多？比另一个企业多多少万元？28．（10分）如图：在数轴上点A表示数a，点B表示数b，点C表示数c，a是多项式﹣2x2﹣4x+1的一次项系数，b是最小的正整数，单项式﹣的次数为c．（1）a=，b=，c=；（2）若将数轴在点B处折叠，则点A与点C重合（填“能”或“不能”）；（3）点A，B，C开始在数轴上运动，若点C以每秒1个单位长度的速度向右运动，同时，点A和点B分别以每秒3个单位长度和2个单位长度的速度向左运功，t分钟过后，若点A与点B之间的距离表示为AB，点B与点C之间的距离表示为BC，则AB=，BC=（用含t的代数式表示）；（4）请问：3AB﹣BC的值是否随着时间t的变化而改变？若变化，请说明理由；若不变，请求其值．2017-2018学年江苏省苏州市吴中区七年级（上）期中数学试卷参考答案与试题解析一、选择题（本大题共10小题，每小题3分，共30分.每小题只有一个选项是正确的，把正确选项前的字母填涂在答题卷相应位置上.）1．（3分）下列各个运算中，结果为负数的是（）A．﹣（﹣4）B．|﹣4|C．﹣42 D．（﹣4）2【解答】解：A、﹣（﹣4）=4，是正数；B、|﹣4|）=4，是正数；C、﹣42=﹣16，是负数；D、（﹣4）2=16，是正数，故选：C．2．（3分）地球与月球的平均距离大约为384000km，则这个平均距离用科学记数法表示为（）A．384×103km B．3.84×104km C．3.84×105km D．3.84×106km【解答】解：384000=3.84×105，故选：C．3．（3分）下列各数：0，π，3.141，，其中有理数的个数是（）A．3个 B．4个 C．2个 D．1个【解答】解：0，π，3.141，，其中是有理数的有0，3.141，这3个，故选：A．4．（3分）下列方程中，是一元一次方程的是（）A．B．x﹣1=0 C．x2﹣x﹣1=0 D．2（x﹣1）=2x【解答】解：A、不是一元一次方程，故此选项错误；B、是一元一次方程，故此选项正确；C、不是一元一次方程，故此选项错误；D、不是一元一次方程，故此选项错误；故选：B．5．（3分）下列各组式子中为同类项的是（）A．5x2y与﹣2xy2B．4x与4x2C．﹣3x2y与yx2D．6x3y4与﹣6x3z4【解答】解：A、5x2y与﹣2xy2，不是同类项，故本选项错误；B、4x与4x2，不是同类项，故本选项错误；C、﹣3x2y与yx2是同类项，故本选项正确；D、6x3y4与﹣6x3z4，不是同类项，故本选项错误．故选：C．6．（3分）已知5是关于x的方程3x﹣2a=7的解，则a的值是（）A．8 B．12 C．3.5 D．4【解答】解：把x=5代入方程，得15﹣2a=7，解得a=4，故选：D．7．（3分）已知|x|=1，y=2，则x﹣y的值为（）A．﹣1或﹣3 B．±5 C．1或3 D．±3【解答】解：∵|x|=1，∴x=±1，∴x﹣y=1﹣2=﹣1，或x﹣y=﹣1﹣2=﹣3．故选：A．8．（3分）一种商品每件进价为a元，按进价增加20%定出售价，后因库存积压降价，按售价的八折出售，每件亏损（）A．0.01a元 B．0.15a元 C．0.25a元 D．0.04a元【解答】解：由题意可得，每件亏损为：a﹣a（1+20%）×0.8=a﹣0.96a=0.04a元，故选：D．9．（3分）下列方程变形错误的是（）A．由方程，得3x﹣2x+2=6B．由方程，得3（x﹣1）+2x=6C．由方程，得2x﹣1=3﹣6x+3D．由方程，得4x﹣x+1=4【解答】解：A、由方程﹣=1，得3x﹣2x+2=6，正确；B、由方程（x﹣1）+=1，得3（x﹣1）+2x=6，正确；C、由方程=1﹣3（2x﹣1），得2x﹣1=3﹣18x+9，错误；D、由方程x﹣=1，得4x﹣x+1=4，正确，故选：C．10．（3分）如图所示，每个正方形由边长为1的小正方形组成：观察图形，在边长为n（n≥1，n为奇数）的正方形中，黑色小正方形的个数为（）A．n2B．2n﹣1 C．n2﹣2n+1 D．n2﹣2n【解答】解：当n=1时，黑色小正方形的个数为1，当n=3时，黑色小正方形的个数为5=2×3﹣1，当n=5时，黑色小正方形的个数为9=2×5﹣1，…∴在边长为n（n≥1，n为奇数）的正方形中，黑色小正方形的个数为2n﹣1，故选：B．二、填空题（本大题共8小题，每小题3分，共24分）11．（3分）﹣2的相反数是2．【解答】解：﹣2的相反数是：﹣（﹣2）=2，故答案为：2．12．（3分）比较大小，用“＜”“＞”或“=”连接：﹣＞﹣．【解答】解：∵|﹣|==，|﹣|==，＜，∴﹣＞﹣．故答案为：＞．13．（3分）数轴上与﹣3距离4个单位长度的点表示的正数是1．【解答】解：设该点表示的数为x，根据题意得：|﹣3﹣x|=4，解得：x=﹣7或x=1．数轴上与﹣3距离4个单位长度的点表示的正数是1，故答案为：1．14．（3分）“x的2倍与y的的和”用代数式表示为2x+y．【解答】解：“x的2倍与y的的和”用代数式表示为2x+y．故答案为：2x+y．15．（3分）若关于x的多项式3x2+（k﹣1）x﹣1中不含有x的一次项，则k=1．【解答】解：∵多项式3x2+（k﹣1）x﹣1中不含有x的一次项，∴k﹣1=0，∴k=1．故答案为1．16．（3分）3x5y6与﹣x n﹣1y6是同类项，则n=6．【解答】解：∵3x5y6与﹣x n﹣1y6是同类项，∴n﹣1=5．解得：n=6．故答案为：6．17．（3分）已知代数式x+3y的值2，则代数式2x+6y+1值是5．【解答】解：∵x+3y=2，∴2x+6y+1=2（x+3y）+1=4+1=5，故答案为5．18．（3分）如图所示的运算程序中，若开始输入的x值为﹣5，我们发现第1次输出的数为﹣2，再将﹣2输入，第2次输出的数为﹣1，如此循环，则第2017次输出的结果为1．【解答】解：若开始输入的x值为﹣5，我们发现第1次输出的数为﹣2，再将﹣2输入，第2次输出的数为﹣1，将﹣1输入，得到结果为2，将2输入得到结果为1，将1输入，得到结果为4，将4输入得到结果为2，依此类推，以1，4，2为循环节循环，∵（2017﹣3）÷3=671…1，∴第2017次输出的结果为1．故答案为：1．三、解答题（本大题共l0小题，共76分.解答时应写出文字说明、证明过程或演算步骤.）19．（8分）计算或化简：（1）﹣7+3﹣5+12；（2）﹣23+（2﹣3）﹣2×（﹣1）2017．【解答】解：（1）原式=﹣12+12+3=3；（2）原式=﹣8﹣1+2=﹣7．20．（8分）解下列方程：（1）2（x﹣1）=x+3；（2）．【解答】解：（1）2（x﹣1）=x+32x﹣2=x+3，则2x﹣x=3+2，解得：x=5；（2）=3（3x+5）=2（2x﹣1）9x+15=4x﹣2解得：x=﹣．21．（5分）先化简，再求值：7x2y﹣[3xy﹣2（xy﹣x2y+1）+xy]，其中x=6，y=﹣．【解答】解：7x2y﹣[3xy﹣2（xy﹣x2y+1）+xy]=7x2y﹣[3xy﹣2xy+7x2y﹣2+xy]=7x2y﹣3xy+2xy﹣7x2y+2﹣xy=﹣xy+2，当x=6，y=﹣时，原式=﹣×6×（﹣）+2=3.5．22．（5分）已知：A=3a2﹣4ab，B=a2+2ab．（1）求A﹣2B；（2）若|2a+1|+（2﹣b）2=0，求A﹣2B的值．【解答】解：（1）∵A=3a2﹣4ab，B=a2+2ab，∴A﹣2B=3a2﹣4ab﹣2a2﹣4ab=a2﹣8ab；（2）∵|2a+1|+（2﹣b）2=0，∴a=﹣，b=2，则原式=+8=8．23．（6分）当m是何值时，关于x的方程4x﹣2m=3x+1的解是方程2x﹣3=x的解的2倍．【解答】解：2x﹣3=x解得x=3，由关于x的方程4x﹣2m=3x+1的解是方程2x﹣3=x的解的2倍，得12﹣2m=9+1，解得m=1，当m=1时，关于x的方程4x﹣2m=3x+1的解是方程2x﹣3=x的解的2倍．24．（7分）若“三角”表示运算：a﹣b+c，若“方框”，表示运算：x﹣y+z+w，求的值，列出算式并计算结果．【解答】解：根据题意得：原式=（﹣+）×（﹣2﹣1.5+1.5﹣6）=（﹣）×（﹣8）=．25．（8分）已知a是方程3x﹣5=10的解，求代数式3a2﹣[a2﹣2（a﹣a2）+1]的值．【解答】解：3x﹣5=10，3x=15，x=5，∴a=5，3a2﹣[a2﹣2（a﹣a2）+1]，=3a2﹣（a2﹣2a+2a2+1），=3a2﹣a2+2a﹣2a2﹣1，=2a﹣1，当a=5时，原式=2×5﹣1=9．26．（9分）苏州市出租车的计价标准为：行驶路程不超过3km收费10元，超过3km的部分按排每千米1.8元收费．（1）某出租车行程为xkm，若x＞3km，则该出租车驾驶员收到车费（1.8a+4.6）元（用含有x的代数式表示）；（2）某出租车驾驶员从公司出发，在东西向的宝带西路上连续接送4批客人，行驶路程记录如下（规定向东为正，向西为负，单位：km）．①送完第4批客人后，该出租车驾驶员在公司的西边（填“东或西”），距离公司9km的位置；②在这过程中该出租车驾驶员共收到车费多少元？【解答】解：（1）由题意可得，该出租车驾驶员收到车费为：10+（a﹣3）×1.8=1.8a+4.6，故答案为：（1.8a+4.6）；（2）①由题意可得，5+2+（﹣4）+（﹣12）=﹣9，∴送完第4批客人后，该出租车驾驶员在公司的西边，距离公司9km，故答案为：西，9；②由题意可得，在这过程中该出租车驾驶员共收到车费为：1.8×5+4.6+10+1.8×4+4.6+1.8×12+4.6=61.6（元），答：在这过程中该出租车驾驶员共收到车费61.6元．27．（10分）在计算1+5+9+13+17+21时，我们发现，从第一个数开始，后面的每个数与它前面的一个数的差都是一个相等的常数，具有这种规律的一列数，除了直接相加外，我们可以用下列公式来求和S，S=（其中n表示这列数的个数，a1表示表示第一个数，a n表示第n个数），所以，1+5+9+13+17+21==66．用上面的知识解答下列问题：吴中区科学技术协会为了扶持高科技产业，准备投资两个符合条件的企业A、B，拟定分别对A、B两个企业投资方案如下：A企业：每年投资一次，第一年投资30万元、以后每年比前一年增加投资1万元；B企业：每半年投资一次，第一个半年投资6万元，以后每半年比前半年增加投资0.5万元．（1）如果投资期限为3年，则A企业共需投资93万元，B企业共需投资37.5万元；（2）如果投资期限为n年，则A企业共需投资万元，B企业共需投资n（2n+5）万元；（用含有n的代数式表示）（3）吴中区科学技术协会决定对这两个企业累计投资12年，通过计算哪个企业获得的投资比较多？比另一个企业多多少万元？【解答】解：（1）根据题意得：企业A：3年共需投资的总金额为30+（30+1）+（30+2）=93（万元）；企业B：3年共需投资的总金额为6+（6+0.5）+（6+1）+（6+1.5）+（6+2）+（6+2.5）=37.5（万元）；（2）根据题意得：企业A：n年共需投资的总金额为30n+（1+2+…+n﹣1）=（万元）；企业B：n年共需投资的总金额为6n+[0.5+1+…+0.5（2n﹣1）]=n（2n+5）万元；（3）企业A：当n=12时，=426万元，企业B：n（2n+5）=348万元，426﹣348=78（万元）故A企业获得的投资比较多，比另一个企业多78万元．故答案为：93，37.5；，n（2n+5）．28．（10分）如图：在数轴上点A表示数a，点B表示数b，点C表示数c，a是多项式﹣2x2﹣4x+1的一次项系数，b是最小的正整数，单项式﹣的次数为c．（1）a=﹣4，b=1，c=6；（2）若将数轴在点B处折叠，则点A与点C能重合（填“能”或“不能”）；（3）点A，B，C开始在数轴上运动，若点C以每秒1个单位长度的速度向右运动，同时，点A和点B分别以每秒3个单位长度和2个单位长度的速度向左运功，t分钟过后，若点A与点B之间的距离表示为AB，点B与点C之间的距离表示为BC，则AB=t+5，BC=3t+5（用含t的代数式表示）；（4）请问：3AB﹣BC的值是否随着时间t的变化而改变？若变化，请说明理由；若不变，请求其值．【解答】解：（1）由题意可知：a=﹣4，b=1，c=6，（2）能重合，由于﹣4与6的中点为1，故将数轴在点B处折叠，则点A与点C能重合；（3）由于点A和点B分别以每秒3个单位长度和2个单位长度的速度向左运功，∴t分钟后，AB=3t+1﹣（﹣4）﹣2t=t+5由于点C以每秒1个单位长度的速度向右运动，∴t分钟后，BC=2t+6﹣1+t=3t+5（4）3AB﹣BC=3（t+5）﹣3t﹣5=3t+15﹣3t﹣5=10∴3AB﹣BC的值不会随着时间t的变化而改变，故答案为：（1）﹣4，1，6；（2）能；（3）t+5，3t+5；。

2017～2018学年度第一学期期中考试七年级数学参考答案

2017～2018学年度第一学期期中考试七年级数学参考答案一、选择题二、填空题11．1-； 12．1； 13．24或40；（若写出一个答案给3分） 14．4n三、（本大题共2小题，每小题8分，满分16分）15．计算．（1）解：原式=3212-+ ………………（2分） =20- ………………（4分）（2）解：原式=184-⨯………………（2分） =2- ………………（4分）16．计算．（1）解：原式b a )15()32(+-++= ………………（2分） b a 45-= ………………（4分）（2）解：原式b a ab ab b a 222212436+--= ………（2分）22718a b b a -= ………………（4分）四、（本大题共2小题，每小题8分，满分16分）17．数轴（略） ……………………………（6分）()2133201212<<--<<-<- ………………（8分）18．解：原式=2x 2+4 x －4－2x 2－2x +4 ………………（4分）=x 2 ………………（6分）当x =－3时，原式=()32-⨯=6- ………………（8分）五、（本大题共2小题，每小题10分，满分20分）19．解：由题意得：1，1，02===+m cd b a ……………（6分）原式=1+0-1……………………………………（8分）=0 …………………………………………（10分） 20．（1）0.5；85；……………………………………………（4分）（2）（85+0.5x ）；…………………………………………（6分）（3）当x =45-15=30时，85+0.5x =100cm ．…………（10分）六、（本大题满分12分）21．解：（1）4a +b ……………………………………………（4分）（2）≠ ………………………………………………………（6分）（3）∵a ⊙（-2b ）=4a -2b =4，∴2a -b =2 ………………（8分）（a -b ）⊙（2a +b ）=4（a -b ）+（2a +b ）=6a -3b =3（2a -b ）=3×2=6． ………………（12分）七、（本大题满分12分）22．解：（1）（+3，—2），A ；……………………………………………………（4分）（2）贝贝走过的路程A →B →C →D ，即5+2+2+1=10； ………………（6分）（3）如图所示：E 点即为所求．………………（8分）（4）贝贝走过的路程为2+2+2+1+2+3+1+2=15，共需消耗15×1.5=22.5焦耳的能量． ………………（12分）八、（本大题满分14分）23．（1）1…………………………………………………………………………（2分）（2）AB =6，P 点到A 、B 两点的距离和为10，所以P 点不可能在A 、B 两点之间．①当P 点在A 点的左边时，设P 点表示的数为x ，则有：2410x x --+-= 解得4x =-………………………………………………（5分）②当P 点在B 点的右边时，设P 点表示的数为x ，则有：4(2)10x x -+--= 解得6x =………………………………………………（8分）综上，P 表示的数为-4或6；（3）设运动x 分钟后，P 为AB 中点，由题意可得0.5(2)[4(0.5)]x ---=--- 解得3x = … ………………………（12分）0.531 3.5--⨯=-，所以P 点表示的数为 3.5-． ………………………（14分）【注：学生解答只要合理，均应酌情赋分】。

苏州市吴中区2017～2018学年度七年级上数学期中试题(含答案)

2017-2018 学年度第一学期学科教学质量情况调查初一数学2017.11注意事项:1.本试卷满分 130 分，考试时间 120 分钟;2.答卷前将密封线内的项目填写清楚，所有解答均须写在答题卷上，在本试卷上答题无效.一、选择题(本大题共 10 小题，每小题 3 分，共 30 分.每小题只有一个选项是正确的，把正确选项前的字母填涂在答题卷相应位置上.)1.下列各个运算中，结果为负数的是A.－(－4)B.C.－42D.(－4)24-2.地球与月球的平均距离人约为 384000km ，则这个平均距离用科学记数法表示为A.384×103 kmB. 3.84×105kmC.0.384×106 kmD. 3.84×104 km 3.下列各数:0, π， 3.141，，其中有理数的个数是237A.3 个 B.4 个C.2 个D.1 个4.下列方程中，是一元一次方程的是A. - 1 = 01xB. x - 1 = 0C. x 2 - x - 1 = 0D. 2( x -1) = 2 x5.下列各组式子中为同类项的是A. 5x 2 y 与 -2 x y 2 B . 4 x 与 4 x 2C. -3x 2 y 与yx 2 D . 6 x 3 y 4 与 -6 x 3 z 4136.已知 5 是关于 x 的方程 3x - 2a = 7 的解，则 a 的值是A. 8 B. 12 C. 3.5 D. 47.已知 = 1, y = 2 ，则 x - y 的值为x A .－1 或－3 B.±5 C.1 或 3 D.±38.一种商品每件进价为 a 元，按进价增加 20%定出售价，后因库存积压降价，按售价的八折出售，每件亏损A. 0.01a 元月B. 0.15a 元C. 0.25a 元D. 0.04a 元9.下列方程变形错误的是A.由方程，得 3x - 2 x + 2 = 6 .1123x x --=B.由方程( x -1) +，得 3( x -1) + 2 x = 6 .1213x =C.由方程，得 2 x - 1 = 3 - 6 x + 3 .2113(21)3x x -=--D.由方程x -，得 4 x - x + 1 = 4 .114x -=10.如图所示，耳个正方形由边长为 1 的小正方形组成:观察图形，在边长为 n (n 引，目.，?为奇数)的正方形中，黑色小正方形的个数为A. n 2B. 2n - 1C. n 2 - 2n + 1D. n 2 - 2n二、填空题(本大题共 8 小题，每小题 3 分，共 24 分.把答案填在答题卷相应位置上.)11.－2 的相反数是 .12.比较大小，用“<”“>”或“=”连接: - -566713.数轴上与－3 距离 4 个单位长度的点表示的正数是 .14.“ x 的 2 倍与 y 的的和”用代数式表示为 .1315.若关于 x 的多项式 3x 2 + (k -1) x -1 中不含有 x 的一次项，则 k = .16. 3x 5 y 6 与 - x n -1 y 6 是同类项，则 n = .1217.已知代数式 x + 3 y 的值是 2，则代数式 2 x + 6 y + 1 值是.18.如图所示的运算程序中，若开始输入的 x 值为－5，我们发现第 1 次输出的数为－2，再将－2 输入，第 2 次输出的数为－1，如此循环，则第 2017 次输出的结果为 .三、解答题(本大题共 l0 小题，共 76 分.解答时应写出文字说明、证明过程或演算步骤.)19.(每小题 4 分，共 8 分)计算或化简:(1)－7+3－5+12;(2)－23 +(2－3)－2×(－1)2017.20.(每小题 4 分，共 8 分)解下列方程:(1) 2( x -1) = x + 3 ;(2).0.30.5210.23x x +-=21.(本题满分 5 分)先化简，再求值：7 x 2y - [3xy - 2( x y - x 2 y +1) + xy ] ，其中 x = 6, y = - .72121622.(本题满分 5 分)已知A = 3a 2 - 4ab , B = a 2 + 2ab .(1)求: A - 2B ;(2)若+ (2 - b ) 2= 0 ，求 A - 2B 的值.21a +23.(本题满分6 分)当m 是何值时，关于x 的方程4x- 2m = 3x +1的解是方程2x- 3 =x 的解的2 倍.24.(本题满分7 分)若“三角” 表示运算，“方框” 表示运算x -y +z +w .求：的值.(列出算式并计算结果)25.(本题满分8 分)已知a 是方程3x - 5 =10 的解，求代数式3a2 -[a2 - 2(a -a2 ) +1] 的值.26.(本题满分9 分)苏州市出租车的计价标准为:行驶路程不超过3km 收费10 元，超过3km 的部分按排每千米1.8 元收费.(1)某出租车行程为x km,若x >3km，则该出租车驾驶员收到车费元(用含有x的代数式表示)；(2)某出租车驾驶员从公司出发，在东西向的宝带西路上连续接送4 批客人，行驶路程记录如下(规定向东为正，向西为负，单位:km).第 1 批第 2 批第 3 批第 4 批52－4－12①送完第 4 批客人后，该出租车驾驶员在公司的月边(填“东或西”),距离公司 km 的位置；②在这过程中该出租车驾驶员共收到车费多少元?27.(本题满分 10 分)在计算 1+5+9+13+17+21 时，我们发现，从第一个数开始，后面的每个数与它前面的一个数的差都是一个相等的常数，具有这种规律的一列数，除了直接相加外，我们可以用下列公式来求和 S , S =(其中 n 表示这列数的个数，a 1 表示表示第1()2n n a a +一个数， a n 表示第 n 个数), 所以，1+5+9+13+17+21== 66 .6(121)2⨯+用上面的知识解答下列问题:吴中区科学技术协会为了扶持高科技产业，准备投资两个符合条件的企业 A 、B ，拟定分别对 A 、B 两个企业投资方案如下：A 企业:每年投资一次，第一年投资 30 万元、以后每年比前一年增加投资 1 万元;B 企业:每半年投资一次，第一个半年投资 6 万元，以后每半年比前半年增加投资 0.5万元.(1)如果投资期限为 3 年，则 A 企业共需投资万元，B 企业共需投资万元; (2)如果投资期限为 n 年，则 A 企业共需投资万元，B 企业共需投资万元；(用含有 n 的代数式表示)(3)吴中区科学技术协会决定对这两个企业累计投资 12 年，通过计算哪个企业获得的投资比较多?比另一个企业多多少万元？28.(本题满分 10 分)如图:在数轴上点 A 表示数 a ，点 B 表示数 b ，点 C 表示数 c ，a 是多项式 -2 x 2 - 4 x + 1 的一次项系数， b 是最小的正整数，单项式 - x 2 y 4 的次数为 c .12(1) a = ， b = ， c = ;(2)若将数轴在点 B 处折叠，则点 A 与点 C重合( 填“能”或“不能”)；(3)点 A , B , C 开始在数轴上运动，若点 C 以每秒 1 个单位长度的速度向右运动，同时,点 A 和点 B 分别以每秒 3 个单位长度和 2 个单位长度的速度向左运功，t 分钟过后，若点 A 与点 B 之间的距离表示为 AB ，点B 与点C 之间的距离表示为 BC ，则 AB = , BC = (用含 t 的代数式表示);(4)请问： 3 A B - BC 的值是否随着时间 t 的变化而改变？若变化，请说明理由；若不变，请求其值.。

昆山吴江区2017-2018学年上学期期中七年级数学试卷及解析

2017-2018学年上学期期期中调研测试初一数学试卷（考时120分钟，满分130分）一、选择题（本大题共10小题，每小题3分，共30分） 1．3-的相反数是（）．A ．3B ．13-C ．13D ．3±2．下列各数：2(1)-，(3)--，12--，3(2)-，(2)(3)-⨯-其中负数有（）．A ．1个B ．2个C ．3个D ．4个3．下列各式，正确的是（）． A ．235a b ab +=B ．223x x x +=C ．2()2a b a b +=+D ．()m n m n --=-+C ．2()22a b a b +=+，故C 错；D ．()m n m n --=-+，故D 对．故选D ．4．若||0x x +=，则x 是（）．A ．正数B ．负数C ．0D ．负数或05．有理数a ，b ，c ，d 在数轴上的对应点的位置如图所示，这四个数中，绝对值最大的是（）．A ．aB ．bC ．cD ．d 6．无论x 取什么值，下列代数式中值一定是正数的是（）． A ．2(21)x +B ．|21|x +C ．221x +D ．221x -7．当2x =时，代数式32ax bx -+的值为3，那么当2x =-时，代数式32ax bx -+的值是（）．A ．3-B ．1C ．1-D ．28．下列说法中：①最大的负整数是1-；②平方后等于9的数是3；③33(3)3-=-；④a -是负数；⑤若a 、b 互为相反数，则0ab <；⑥2232xy x y -+-是关于x 、y 的二次三项式，其中正确的有（）．A ．2个B ．3个C ．4个D ．5个9．如图，数轴上A 、B 两点分别对应有理数a 、b ，则下列结论正确的是（）．A ．0ab >B ．0a b ->C ．0a b +>D ．||||0a b ->10．小明同学将2B 铅笔笔尖从原点O 开始沿数轴进行连续滑动，先将笔尖沿正方向滑动1个单位长度完成第一次操作，再沿负方向滑动2个单位长度完成第二次操作；又沿正方向滑动3个单位长度完成第三次操作；再沿负方向滑动4个单位长度完成第四次操作；L L ，以此规律继续操作，经过第50次操作后笔尖停留在点P 处，则点P 对应的数是（）．A ．0B ．10-C ．25-D ．50二、填空题（本大题共8小题，每小题3分，共24分） 11．3-的绝对值是__________．12．我国正在建设的港珠澳大桥，是连接香港、珠海、澳门的超大型跨海通道，建成后将成为世界最长的跨海大桥，全长55000米，用科学计数法表示55000为__________．13．数轴上某点到表示1-的点的距离为3，那么该点所表示的数是__________ 14．若30m <，|2|3m -=，则m =__________． 15．已知233a b -=-，则546a b -+的值为__________．16．一个多项式加上22x x -+-得到21x -，那么这个多项式是__________．17．已知0a <，0ab <，且||||a b >，那么a ，b ，a -，b -按照由小到大的顺序排列，并用“<”连接是__________． 18．将正整数按如图所示的规律排列下去，若用整数对(,)m n 表示第m 排，从左到右第n 个数，如(4,3)表示整数9，则(20,8)表示整数是__________．1第一排 23第二排 45 6第三排 7 89 10第四排三、解答题（本大题共10小题，共76分）19．计算：（本题共4小题，每小题4分，共16分）（1）20(18)(5)(9)---+++-．（2）3126(2)3⎛⎫-+÷-⨯- ⎪⎝⎭．（3）231115125462⎛⎫⎛⎫--⨯-⨯+- ⎪ ⎪⎝⎭⎝⎭．（4）222112[2(5)]162--⨯--+-．20．化简：（本题共2小题，每小题4分，共8分）（1）1232213ab a a ab --+-+．（2）12(23)(612)3m n n m +--．21．（本题6分）先化简，再求值：222214()232xy x y x xy y ⎡⎤⎛⎫---+- ⎪⎢⎥⎝⎭⎣⎦，其中x ，y 满足21(2)02x y ++-=．22．（本题6分）已知多项式||2322(3)2m m x y x y xy --+-是关于x ，y 的四次三项式．（1）求m 的值．（2）当32x =，1y =-时，求此多项式的值．23．解方程：（本题共2小题，每小题4分，共8分）（1）3(2)2x x -=-．（2）124123x x ---=．24．（本题6分）某电路检修小组在东西方向的一道路上检修用电线路，检修车辆从该道路P 处出发，如果规定检修车辆向东行驶为正，向西行驶为负，某一天施工过程中七次车辆行驶记录如下（单位：千米）：（1（2）在第__________次记录时距P 处最远．（3）若检修车辆每千米耗油0.2升，每升汽油需6.2元，问这一天检修车辆所需汽油费多少元？ 25．（本题6分）小丽同学完成一道题“已知两个多项式M 、N ，计算2M N -”，小丽将2M N -误抄写成2M N +，求得结果是P ．若222M a ab b =+-，25P a ab =+．请你帮助小丽求出2M N -的正确答案．26.（本题6分）如果关于x 、y 的代数式22(26)(2351)x ax y bx x y +-+--+-的值与字母x 所取的值无关，试求代数式“323212234a b a b ⎛⎫--- ⎪⎝⎭的值．27．（本题6分）观察下列等式：111122=-⨯，1112323=-⨯，1113434=-⨯LL 用你发现的规律解答下列问题：（1）猜想并写出：1(1)n n =-__________．（2）直接写出下列各式的计算结果：①111112233420102011++++=⨯⨯⨯⨯L __________． ②1111122334(1)n n ++++=⨯⨯⨯+L __________．（3）探究算式，直接写出计算结果：111124466820102012++++=⨯⨯⨯⨯L __________．28．（本题8分）已知点A 在数轴上对应数a ，点B 对应数b ，且2|4|(1)0a b ++-=，A 、B 之间的距离记作||AB ．（1）求线段AB 的长||AB ．（2）设点P 在数轴上对应的数为x ，当||||2PA PB -=时，求x 的值．（3）若点P 在点A 的左侧，M 、N 分别是PA 、PB 的中点，当点P 在A 的左侧移动时，下列两个结论：①||||PM PN +的值不变；②||||PN PM -的值不变，其中只有一个结论正确，则正确结论是__________（填写序号），其不变的值是__________．【解析卷】 2017-2018学年上学期期期中调研测试初一数学试卷一、选择题（本大题共10小题，每小题3分，共30分） 1．3-的相反数是（）．A ．3B ．13-C ．13D ．3±【答案】A【解析】A ．3是3-的相反数；B ．13-是3-的倒数；C ．13是3-的负倒数；D ．3±是3-的相反数与其本身的合并．故选A ． 2．下列各数：2(1)-，(3)--，12--，3(2)-，(2)(3)-⨯-其中负数有（）．A ．1个B ．2个C ．3个D ．4个【答案】B【解析】2(1)1-=，是正数；(3)3--=，是正数；1122--=-，是负数；3(2)8-=-，是负数； (2)(3)6-⨯-=，是正数，所以有2个负数，故选B ．3．下列各式，正确的是（）． A ．235a b ab += B ．223x x x +=C ．2()2a b a b +=+D ．()m n m n --=-+【答案】D【解析】A ．2323a b a b +=+，故A 错；B ．23x x x +=，故B 错；C ．2()22a b a b +=+，故C 错；D ．()m n m n --=-+，故D 对．故选D ． 4．若||0x x +=，则x 是（）．A ．正数B ．负数C ．0D ．负数或0【答案】D【解析】||0x x +=，故||x 与x 互为相反数，所以x 为负数或0x =．故选D ．5．有理数a ，b ，c ，d 在数轴上的对应点的位置如图所示，这四个数中，绝对值最大的是（）．A ．aB ．bC ．cD ．d【答案】A【解析】由图可知，43a -<<-，所以3||4a <<，21b -<<-，所以1||2b <<， 01c <<，所以0||1c <<，23d <<，所以2||3d <<，所以||a 是最大的．故选A ．6．无论x 取什么值，下列代数式中值一定是正数的是（）． A ．2(21)x +B ．|21|x +C ．221x +D ．221x -【答案】C【解析】A ．2(21)0x +≥，故A 错；B ．|21|0x +≥，故B 错；C ．2211x +≥，故C 对；D ．2211x --≥，故D 错．故选C ．7．当2x =时，代数式32ax bx -+的值为3，那么当2x =-时，代数式32ax bx -+的值是（）．A ．3-B ．1C ．1-D ．2【答案】B【解析】当2x =时，8223a b -+=，∴821a a -=，当2x =-时，822a b -++(82)2a b =--+12=-+1=．故选B ．8．下列说法中：①最大的负整数是1-；②平方后等于9的数是3；③33(3)3-=-；④a -是负数；⑤若a 、b 互为相反数，则0ab <；⑥2232xy x y -+-是关于x 、y 的二次三项式，其中正确的有（）．A ．2个B ．3个C ．4个D ．5个【答案】A【解析】①最大的负整数是1-，①对；②平方后等于9的数是3±，故②错；③32(3)327-=-=-，故③对；④,00,0,0a a a a >⎧⎪-==⎨⎪<⎩负数正数，故④错；⑤若a 、b 互为相反数，则0ab ≤，故⑤错；⑥2232xy x y -+-是关于x 、y 的三次三项式，故⑥错．故选A ．9．如图，数轴上A 、B 两点分别对应有理数a 、b ，则下列结论正确的是（）．A ．0ab >B ．0a b ->C ．0a b +>D ．||||0a b ->【答案】D【解析】由图可得1a <-，01b <<，A ．0ab <，故A 错；B ．0a b -<，故B 错；C ．0a b +<，故C 错；D ．||||(1)10a b a b -=-->---=．故选D ．10．小明同学将2B 铅笔笔尖从原点O 开始沿数轴进行连续滑动，先将笔尖沿正方向滑动1个单位长度完成第一次操作，再沿负方向滑动2个单位长度完成第二次操作；又沿正方向滑动3个单位长度完成第三次操作；再沿负方向滑动4个单位长度完成第四次操作；L L ，以此规律继续操作，经过第50次操作后笔尖停留在点P 处，则点P 对应的数是（）． A ．0B ．10-C ．25-D ．50【答案】C【解析】由题意得，第1次操作后，笔尖在1处，第2次操作后，笔尖在1-处，第3次操作后，笔尖在2处，第4次操作后，笔尖在2-处， L L第n 次操作后，当n 为奇数时，笔尖在12n +处，当n 为偶数时，笔尖在2n-处，故第50次操作后，笔尖在25-处．故选C ．二、填空题（本大题共8小题，每小题3分，共24分） 11．3-的绝对值是__________．【答案】3【解析】|3|3-=．12．我国正在建设的港珠澳大桥，是连接香港、珠海、澳门的超大型跨海通道，建成后将成为世界最长的跨海大桥，全长55000米，用科学计数法表示55000为__________．【答案】45.510⨯【解析】455000 5.510=⨯．13．数轴上某点到表示1-的点的距离为3，那么该点所表示的数是__________ 【答案】4-或2【解析】设该点为x ，则x 与1-之间的距离为|1|x --，则|1|3x --=， 13x --=或13x --=-，解得4x =-或2x =．14．若30m <，|2|3m -=，则m =__________．【答案】1-【解析】∵30m <，∴0m <，∵|2|3m -=，∴23m -=，∴1m =-．15．已知233a b -=-，则546a b -+的值为__________．【答案】11【解析】∵233a b -=-，∴546a b -+52(23)a b =--52(3)=-⨯-56=+11=． 16．一个多项式加上22x x -+-得到21x -，那么这个多项式是__________．【答案】221x x -+【解析】由题意得221(2)x x x ---+-2212x x x =-+-+221x x =-+．则这个多项式是221x x -+． 17．已知0a <，0ab <，且||||a b >，那么a ，b ，a -，b -按照由小到大的顺序排列，并用“<”连接是__________．【答案】a b b a <-<<-【解析】∵0a <，0ab <，∴0b >，0b -<，∵||||a b >，∴a b ->，∴a b <-，∴a b b a <-<<-． 18．将正整数按如图所示的规律排列下去，若用整数对(,)m n 表示第m 排，从左到右第n 个数，如(4,3)表示整数9，则(20,8)表示整数是__________．1 第一排 23第二排 45 6第三排 7 89 10第四排【答案】198【解析】由题意知，(20,8)是第20排第8个数，则偶数排从左到右依次增大， ∴到第19排共有12319190++++=L （个），故1908198+=．故(20,8)为198．三、解答题（本大题共10小题，共76分） 19．计算：（本题共4小题，每小题4分，共16分）（1）20(18)(5)(9)---+++-．（2）3126(2)3⎛⎫-+÷-⨯- ⎪⎝⎭．（3）231115125462⎛⎫⎛⎫--⨯-⨯+- ⎪ ⎪⎝⎭⎝⎭．（4）222112[2(5)]162--⨯--+-．【答案】见解析．【解析】（1）20(18)(5)(9)---+++-201859=-++-259=-+-39=-6=-．（2）3126(2)3⎛⎫-+÷-⨯- ⎪⎝⎭126(8)3⎛⎫=-+÷-⨯- ⎪⎝⎭112683⎛⎫⎛⎫=-+⨯-⨯- ⎪ ⎪⎝⎭⎝⎭124=-+314=-．（3）231115125462⎛⎫⎛⎫--⨯-⨯+- ⎪ ⎪⎝⎭⎝⎭9111512121225462=-⨯-⨯-⨯+⨯93265=---+45=-．（4）222112[2(5)]162--⨯--+-114[425]62=--⨯-+71422=-++0=．20．化简：（本题共2小题，每小题4分，共8分）（1）1232213ab a a ab --+-+．（2）12(23)(612)3m n n m +--．【答案】见解析．【解析】（1）1232213ab a a ab --+-+1(22)(23)13ab a =-+--+23a =-+．（2）12(23)(612)3m n n m +--4624m n n m =+-+84m n =+．21．（本题6分）先化简，再求值：222214()232xy x y x xy y ⎡⎤⎛⎫---+- ⎪⎢⎥⎝⎭⎣⎦，其中x ，y 满足21(2)02x y ++-=．【答案】见解析．【解析】222214()232xy x y x xy y ⎡⎤⎛⎫---+- ⎪⎢⎥⎝⎭⎣⎦22224[26]xy x y x xy y =----+24[6]xy x xy =---246xy x xy =++210x xy =+．∵21(2)02x y ++-=，2(2)0x +≥，102y -≥，∴2(2)0x +=，102y -=，∴2x =-，12y =，将2x =-，12y =代入得，原式21(2)10(2)2=-+⨯-⨯410=-6=-．22．（本题6分）已知多项式||2322(3)2m m x y x y xy --+-是关于x ，y 的四次三项式．（1）求m 的值．（2）当32x =，1y =-时，求此多项式的值．【答案】见解析．【解析】（1）∵||2322(3)2m m x y x y xy --+-是四次三项式，∴30||21m m -≠⎧⎨-=⎩，∴33m m ≠⎧⎨=±⎩，∴3m =-．（2）由（1）得32262xy x y xy -+-将32x =，1y =-代入得32262xy x y xy -+- 2323336(1)(1)2(1)222⎛⎫=-⨯⨯-+⨯--⨯⨯- ⎪⎝⎭9934=--154=．23．解方程：（本题共2小题，每小题4分，共8分）（1）3(2)2x x -=-．（2）124123x x ---=．【答案】见解析．【解析】（1）3(2)2x x -=-362x x -=-，326x x +=+，48x =，2x =．（2）124123x x ---=3(1)2(24)6x x ---=，33486x x --+=，34638x x -=+-，1x -=， 1x =-． 24．（本题6分）某电路检修小组在东西方向的一道路上检修用电线路，检修车辆从该道路P 处出发，如果规定检修车辆向东行驶为正，向西行驶为负，某一天施工过程中七次车辆行驶记录如下（单位：千米）：（1（2）在第__________次记录时距P 处最远．（3）若检修车辆每千米耗油0.2升，每升汽油需6.2元，问这一天检修车辆所需汽油费多少元？【答案】见解析．【解析】（1）由题意得389104622-+-++--=，答：检修小组在收工时在P 的正东方向，距P 处2千米．（2）第1次距离3千米，第2次距离835-=千米，第3次距离954-=千米，第4次距离1046-=千米，第5次距离6410+=千米，第6次距离1064-=千米，第7次距离422-=千米，故第5次距离P 点最远．（2）3891046242++++++=（千米）， 420.2 6.252.08⨯⨯=（元）．答：这一天检修车辆所需汽油费为52.08元． 25．（本题6分）小丽同学完成一道题“已知两个多项式M 、N ，计算2M N -”，小丽将2M N -误抄写成2M N +，求得结果是P ．若222M a ab b =+-，25P a ab =+．请你帮助小丽求出2M N -的正确答案．【答案】见解析．【解析】由题意得2P M N =+，∴222252(2)N P M a ab a ab b =-=+-+-2225422a ab a ab b =+--+222a ab b =-+∴222222(2)(2)M N a ab b a ab b -=+---+22224222a ab b a ab b =---+-2234a ab b =--．26.（本题6分）如果关于x 、y 的代数式22(26)(2351)x ax y bx x y +-+--+-的值与字母x 所取的值无关，试求代数式“323212234a b a b ⎛⎫--- ⎪⎝⎭的值．【答案】见解析．【解析】由题意得22(26)(2351)x ax y bx x y +-+--+-22262351x ax y bx x y =+-+-+-+2(22)(3)67b x a x y =-++-+，∵与x 取值无关，∴220b -=，30a +=，∴3a =-，1b =，∴323212234a b a b ⎛⎫--- ⎪⎝⎭32321262a b a b =--+32142a b =+．将3a =-，1b =代入得原式321(3)412=⨯-+⨯192=-．27．（本题6分）观察下列等式： 111122=-⨯，1112323=-⨯，1113434=-⨯LL 用你发现的规律解答下列问题：（1）猜想并写出：1(1)n n =-__________．（2）直接写出下列各式的计算结果：①111112233420102011++++=⨯⨯⨯⨯L __________． ②1111122334(1)n n ++++=⨯⨯⨯+L __________．（3）探究算式，直接写出计算结果：111124466820102012++++=⨯⨯⨯⨯L __________．【答案】见解析．【解析】（1）111(1)1n n n n=---．（2）①111112233420102011++++⨯⨯⨯⨯L 11111122320102011=-+-++-L 112011=-20102011=． ②1111122334(1)n n ++++⨯⨯⨯+L 11111111223341n n =-+-+-++-+L 111n =-+ 1nn =+．（3）111124466820102012++++⨯⨯⨯⨯L 111111111224466820102012⎛⎫=-+-+-++- ⎪⎝⎭L 111222012⎛⎫=- ⎪⎝⎭1100522012=⨯10054024=．28．（本题8分）已知点A 在数轴上对应数a ，点B 对应数b ，且2|4|(1)0a b ++-=，A 、B 之间的距离记作||AB ．昆山吴江区2017-2018学年上学期期中七年级数学试卷及解析11 （1）求线段AB 的长||AB ．（2）设点P 在数轴上对应的数为x ，当||||2PA PB -=时，求x 的值．（3）若点P 在点A 的左侧，M 、N 分别是PA 、PB 的中点，当点P 在A 的左侧移动时，下列两个结论：①||||PM PN +的值不变；②||||PN PM -的值不变，其中只有一个结论正确，则正确结论是__________（填写序号），其不变的值是__________．【答案】见解析．【解析】（1）∵2|4|(1)0a b ++-=，∴4a =-，1b =，∴|||||41|5AB a b =-=--=．（2）||||PA PB -|(4)||1|x x =----|4||1|x x =+--2=．①若4x -≤，则|4||1|x x +--41x x =--+-5=-．∵52-≠，∴4x -≤时，无P 点． ②若41x -<≤，则|4||1|x x +--41x x =++-23x =+．232x +=，21x =-，12x =-， ∵1412-<-≤，∴P 点为12-．③若1x >，则|4||1|x x +--41x x =+-+5=．∵52≠，∴1x >时，无P 点．综上，12x =-．（3）∵MN 分别是PA ，PB 中点，∴1||||2PM PA =，1||||2PN PB =， ①111||||||||(||||)222PM PN PA PB PA PB +=+=+，∴||||PM PN +将随着点P 的左移而增大．②11115||||||||(||||)||22222PN PM PB PA PB PA AB -=-=-==，∴||||PN PM -的值不变．综上，正确结论为②，其不变值为52．。

江苏省昆山市七年级上期中数学试卷有答案(精选)

第一学期期中教学质量调研试卷初一数学注意事项1．本试卷由填空题、选择题和解答题三大题组成，共28题，满分130分。

考试用时120分钟。

2. 答题前，考生务必将学校、姓名、考场号、座位号、考试号填写在答题卷相应的位置上.3. 答题必须用0.5mm 黑色墨水签字笔写在答题卷指定的位置上，不在答题区域内的答案一律无效，不得用其他笔答题.4. 考生答题必须在答题卷上，答在试卷和草稿纸上一律无效.一、选择题 (本大题共10小题，每小题3分，共30分．请将下列各题唯一正确的选项代号填涂在答题卡相应的位置上)1.用科学记数法表示217000是（）A.32.1710⨯B.42.1710⨯C.52.1710⨯D.321710⨯2.下列各数：318, 6.7,0,80,,(4),|3|,(2),3--------- 其中属于非负整数的有（）A ． 1个B ．2 个C ．3 个 D. 4 个3.下列各算式中，计算正确的是（）A ．2219910a b ab ab -=B ．336x y xy +=C ．221997y y -=D ．3454x x x x -+=4．某同学做了以下4道计算题：①0|1|1--=，②11()122÷-=-，③1(9)999-÷⨯=-，④2017(1)2017-=-，请你帮他检查一下，他一共做对了（）A ．1道B ．2道C ． 3道D ．4道5．如果a 与1互为相反数，则|2|a -等于（）A ．1B ．-1C ．-3D ．36．减去4x 等于的多项式2321x x --为（）A ．2361x x --B ．251x -C ．2321x x +-D ．2361x x +-7．若a 是有理数，则||a a +A ．可以是负数B ．不可能是负数C ．必是正数D ．可以是正数也可是负数8．,m n 都是正整数，多项式3m n m n x x x +++的次数是（）A ．22m n +B ．m 或nC ．m n +D ．,m n 中较大的数9．有理数,a b 在数轴上的位置如图所示，则下列各式中错误的是A ．b a <B ．||||b a >C ．0a b +>D ．0ab <10．观察下列算式：133= 239= 3327= 4381= 53243= 63729=……通过观察，用你所发现的规律得出20163的末位数是（）A ．1B ． 3C ． 7D ． 9二、填空题 (本大题共8小题，每小题3分，共24分) 11. 23-的倒数是_______. 12.大于 3.5-小于4.7的整数有______.13.比较大小：45____56--. 14.若2(2)|1|0m n ++-=，则m n +的值为______.15.多项式||(2)3m m x mx -+-是关于x 的二次三项式，则m =_______.16.已知75x y +=，则代数式6(2)2(2)x y x y +--的值为_______17.当1x =时，代数式35ax bx ++的值是6，那么当1x =-时，35ax bx ++的值是_____18.A 、B 两地相距s km ，某人计划t 小时到达，结果提前2小时到达，那么每小时需多走_______km三、解答题 (本大题共10小题，共76分，应写出必要的计算过程、推理步骤或文字说明)19.计算或化简：（每小题4分共8分） (1)112542(4)429-⨯+-⨯ (2) 2108(2)(4)(3)-+÷---⨯-(3) 157()(24)2612+-⨯- (4) 3212(10.5)[2(3)]3---⨯⨯--20.化简：（本题共2小题，每小题3分，共6分）（1）222121863234a a a a --+-+（2）2222(32)2(2)x xy y x xy y ---+-21.先化简后求职：（本题共2小题，每小题4分，满分8分）（1）2222332232x y xy xy x y +-+-，其中12,4x y ==-.（2）323111(3)(23)(233)326x y x y x x y -+--++，其中2,3x y ==.22．（本题满分6分）已知332y a b +-与24x a b 是同类项，求代数式：35533532(3)3(3)4(3)2x y y x x y x -+-+--的值.23.（本题满分6分）已知||7x =，||12y =，求代数式x y +的值.24.（本题满分6分）已知：234A a ab =-，22B a ab =+（1）求2A B -;（2）若2|21|(2)0a b ++-=，求2A B -的值.25．（本题满分8分）观察下列等式： 223181;-=⨯ 225382;-=⨯ 227583;-=⨯ 229784;-=⨯（1）根据上面规律，若2222985,1788,a b -=⨯-=⨯则_____,______;a b ==（2）用含有自然数n 的式子表示上述规律为______________.26.（本题满分8分）我们规定运算符号⊗的意义是：当a b >时，a b a b ⊗=-；当a b ≤时，a b ⊗a b +，其他运算符号意义不变，按上述规定，请计算：4431215[()()](34)(68)25-+⨯-⊗--⊗÷-.27．（本题满分8分）如图，在5×5的方格（每小格边长为1）内有4只甲虫A 、B 、C 、D ，它们爬行规律总是先左右，再上下．规定：向右与向上为正，向左与向下为负．从A 到B 的爬行路线记为：A →B （+1，+4），从B 到A 的爬行路线为：B →A （-1，-4），其中第一个数表示左右爬行信息，第二个数表示上下爬行信息，那么图中（1）A →C （______，______），B →D （______，______），C →______（+1，______）；（2）若甲虫A 的爬行路线为A →B →C →D ，请计算甲虫A 爬行的路程；（3）若甲虫A 的爬行路线依次为（+2，+2），（+1，-1），（-2，+3），（-1，-2），最终到达甲虫P 处，请在图中标出甲虫A 的爬行路线示意图及最终甲虫P 的位置．28.（本题满分8分）（1）若22a -≤≤，化简：|2||2|_________a a ++-=.（2）若2a ≥-，化简 |2||2|a a ++-（3）化简：|2||2|a a ++-参考答案一．选择题CDDAD CBCBA二．填空题 11. 32- 12.-3，-2，-1,0,1,2,3,4 13.> 14.-1 15.-2 16.10 17.4 18.2s t - 三．简答题 19. 11222- -20 -18 176- 20. 124a --2232x xy y -+ 21.(1)122xy + 74 (2) 2132x x y -- -4 22. 359x y - 1823.19 -19 5 -524. 28a ab - 18425.(1) 11 15 (2) 22(21)(21)8n n n +--= 26. 154-27. （1）A →C （+3，+4）；B →D （+3，-2）；C →D （+1，-2）故答案为：+3，+4；+3，-2；D ，-2；（2）据已知条件可知：A →B 表示为：（1，4），B →C 记为（2，0）C →D 记为（1，-2）；则该甲虫走过的路线长为1+4+2+0+1+2=10．答：甲虫A 爬行的路程为10；（3）甲虫A 爬行示意图与点P 的位置如图所示：28.(1) 4 (2) 当22a -≤≤时，原式=4；当2a >时，原式= 2a（3）当2a <-时，原式= 2a -；当22a -≤≤时，原式=4；当2a >时，原式= 2a。