八年级数学下册_分式的乘除_(1)_教学课件新人教版
数学2.2《分式的乘除法》课件(2)

Conversation 4 Anna: Mei Ling, can you come to my party on Saturday? Mei Ling: Sorry, but I’m not available. I must study for a math test. Anna: Ok. Good luck!
①把各分式中分子或分母里的多项式分解因式; ②在乘除过程中遇到整式则视其为分母为1; ③应用分式乘除法法则进行运算; ④结果为最简分式或整式.
随堂练习 1、计算 (1)
a b b a2
(2) (a2 a) a
a 1
1
解(1)原式= a
(2)原式= (a-1)2
2.计算 a2 b 1 a2 1 a2 正确吗?
A: Can you play basketball with us?
B: Sorry, I can’t. I …
prepare for an exam
A: Can you … ? B: Sorry, I can’t. I …
go to the doctor
meet my friend
A: Can you …?
to meet my friend on Saturday.
Conversation 2 Anna: Hello, Mary! Can you come
to my party on Saturday? Mary: I’d love to. Do I need to bring
anything? Anna: No, I’ll buy all the circle can or can’t.
1. Jeff can/ can’t go to the party. 2. Mary can/ can’t go to the party. 3. May can/ can’t go to the party. 4. Mei Ling can/ can’t go to the party. 5. Paul can/ can’t go to the party.
分式教案(2)

分式教案一、教学内容本节课的教学内容来自人教版初中数学八年级下册第22章《分式》。
本节课主要讲解分式的概念、分式的基本性质、分式的运算以及分式方程的解法。
二、教学目标1. 理解分式的概念,掌握分式的基本性质。
2. 学会分式的运算方法,提高运算能力。
3. 学会解分式方程,提高解决问题的能力。
三、教学难点与重点重点:分式的概念、分式的基本性质、分式的运算方法、分式方程的解法。
难点:分式方程的解法。
四、教具与学具准备教具:黑板、粉笔、多媒体教学设备。
学具:教材、练习本、铅笔、橡皮。
五、教学过程1. 实践情景引入:教师出示实际问题:“甲、乙两地相距100公里,甲地有一辆汽车以每小时40公里的速度向乙地行驶,同时乙地有一辆汽车以每小时60公里的速度向甲地行驶。
问两辆汽车相遇时,它们之间的距离是多少?”学生尝试解决实际问题,引出分式的概念。
2. 自主学习:学生自主阅读教材,理解分式的概念,并尝试解决教材中的例题。
3. 课堂讲解:教师讲解分式的概念,强调分式的分子、分母以及分式的值。
4. 课堂练习:教师出示练习题,学生独立完成,巩固分式的概念。
5. 分式的基本性质:教师讲解分式的基本性质,引导学生发现分式的基本性质。
6. 课堂练习:教师出示练习题,学生独立完成,巩固分式的基本性质。
7. 分式的运算:教师讲解分式的运算方法,引导学生发现分式的运算规律。
8. 课堂练习:教师出示练习题,学生独立完成,巩固分式的运算方法。
9. 分式方程的解法:教师讲解分式方程的解法,引导学生发现解分式方程的方法。
10. 课堂练习:教师出示练习题,学生独立完成,巩固解分式方程的方法。
六、板书设计板书设计如下:分式的概念:分子分母分式的值分式的基本性质:分式的分子、分母都乘(或除以)同一个不为零的数,分式的值不变。
分式的运算:加减法:通分后相加(减)乘除法:分子相乘(除),分母相乘(除)分式方程的解法:去分母求解七、作业设计1. 请解释分式的概念,并给出一个例子。
人教版初中数学试讲逐字稿《分式的乘除》

初中数学试讲稿《分式的乘除》【选自人教版数学八年级下册】各位评委老师好(鞠躬)我是应聘初中数学的3号考生,今天我抽到的课题是《分式的乘除》,下面开始我的试讲。
(所有的X,都是假装有数字或者公式,感谢各位配合)一、导入师:好,同学们上课师:大家小时候都见过大拖拉机和小拖拉机吧?见过它们耕地吗?生:(有的说有,有的说没有)师:有得见过有的没见过啊,没关系,那大家接着想一下假设大拖拉机m天耕地a公顷,小拖拉机n天耕地b公顷,那请问大拖拉机的工作效率是小拖拉机的多少倍呢?师:大家动笔算算师:有请中间那位穿红衣服的女生说一下你的计算结果生:XX倍师:大家说她说的对不?生:对师:也就是,先分别算出大、小拖拉机的工作效率,然后直接求倍数,是吧?生:点头师:那大家再想一下假设有个长方体容器,容积为V,底面长为a,宽为b,,当容器内的水占容积的X时,水面的高度为多少?师:好,班长很快举起手了,那就请班长回答一下生:长方体容器本来的高为X,以为水占容积的X,长宽不变,所以水面的高为XXX师:班长很清晰的给大家分析出了水面的高度,那就像上面的问题,讨论数量关系时,有时需要进行分式的乘除运算,那么分式的乘除法有哪些法则呢?二、新授师:大家都知道分式与分数有类似的形式,所以学习分式的乘除运算之前,先回顾一下分数的乘除法则,谁能说说分数的乘除法则呢?师:好,最后那位男生生:分数乘法法则是分数乘分数,用分子的积作为积的分子,分母的积作为积的分母;除法是先把除式的分数的分子、分母颠倒位置后,再按照乘法法则与被除的分数相乘师:大家说这位男生说的完整不?说的对不对呀?生:对师:恩,这位男生说的很对,那接下来请大家按照前后桌为一组,进行分组,然后试着类比刚才分数的乘除法则,总结分式的乘除法则,讨论完后,举手示意师:好,各小组很快举起了手,再等等还没想好的同学师:大家都边商量边写完了,有请最先举手的前排这个小组说一下你们的结果生:乘法法则:俩分式相乘,用分子的积作为积的分子,分母的积作为分母;除法法则是,先把除式的分式分子分母颠倒位置后,再与被除式相乘师:恩,其他小组有需要补充的嘛?生:摇头示意师:那大家都认可这个小组的回答了?恩,的确刚才这位同学说的很正确,那么大家可以用数学式子来表示吗?用咱们数学语言来描述上述法则吗?提醒一下,大家可以用a、b、c、d........字母来表示分式的分子分母,自己在练习本上试着写写师:刚才我在下面看看了大家写的,大部分同学呢,写的很好,有得同学呢,把除法写错了,在这里,老师再次强调一下,除法其实也是转化为乘法来运算的,但是必须得先把除式的分子分母颠倒位置,其他不变,再与被除式相乘。
人教版八年级数学第十五章《分式》全章教案[1]
![人教版八年级数学第十五章《分式》全章教案[1]](https://img.taocdn.com/s3/m/1916d946aaea998fcd220e2b.png)
人教版八年级数学第十五章《分式》全章教案[1]-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN第三章分式3.1 分式的基本性质(1)教学目标1.了解分式的基本性质,体会类比的思想方法.2.掌握分式的约分,了解最简分式的概念.教学重、难点分式的基本性质和分式的约分教学过程设计一、创设问题,激发兴趣问题1下列分数是否相等?追问这些分数相等的依据是什么?问题2你能叙述分数的基本性质吗?分数的基本性质:一个分数的分子、分母乘(或除以)同一个不为0的数,分数的值不变.问题3 你能用字母的形式表示分数的基本性质吗?问题4 类比分数的基本性质,你能想出分式有什么性质吗?分式的基本性质:分式的分子与分母乘(或除以)同一个不等于0的整式,分式的值不变.追问1 如何用式子表示分式的基本性质?二、知识应用,巩固提高追问2 应用分式的基本性质时需要注意什么?(1)分子、分母应同时做乘、除法中的同一种运算;(2)所乘(或除以)的必须是同一个整式;(3)所乘(或除以)的整式应该不等于零.例2 填空:问题5 观察上例中(1)中的两个分式在变形前后的分子、分母有什么变化类比分数的相应变形,你联想到什么像这样,根据分式的基本性质,把一个分式的分子与分母的公因式约去,叫做分式的约分.经过约分后的分式,其分子与分母没有公因式.像这样分子与分母没有公因式的式子,叫做最简分式.例3 约分:追问1 由上例你能归纳出在分式中,找分子和分母的公因式的方法是什么吗追问2 如果分式的分子或分母是多项式,那么该如何思考呢?三、应用提高、拓展创新教科书132页练习1四、归纳小结(1)本节课学习了哪些主要内容(2)运用分式的基本性质时应注意什么(3)分式约分的关键是什么如何找公因式(4)探究分式的基本性质和分式的约分的过程,你认为体现了哪些数学思想方法?五、布置作业:教科书习题15.1第4、6题.教后反思:3.1 分式的基本性质(2)教学目标1.了解最简公分母的概念,会确定最简公分母.2.通过类比分数的通分来探索分式的通分,能进行分式的通分,体会数式通性和类比的思想.教学重、难点准确确定分式的最简公分母教学过程设计一、创设问题,激发兴趣问题1 通分:追问1 分数通分的依据是什么?追问2 如何确定异分母分数的最小公分母?问题2 填空:像这样,根据分式的基本性质,把几个异分母的分式分别化成与原来的分式相等的同分母的分式,叫做分式的通分.追问1 你认为分式通分的关键是什么?分式通分的关键是找出分式各分母的公分母.追问2 上面问题中的两个分式的公分母是什么?为通分要先确定各分式的公分母,一般取各分母的所有因式的最高次幂的积作公分母,它叫做最简公分母.追问3 两个分式的最简公分母是如何确定的?最简公分母的确定方法:取各分母系数的最小公倍数与各字母因式的最高次幂的乘积.分母是多项式时,最简公分母的确定方法是:先因式分解,再将每一个因式看成一个整体,最后确定最简公分母.二、知识应用,巩固提高例通分:三、应用提高、拓展创新教科书132页练习1四、归纳小结(1)本节课学习了哪些主要内容(2)分式通分的关键是什么?(3)分式通分时,确定最简公分母的方法是什么?五、布置作业:教科书习题15.1第7题教后反思:3.3 分式的乘除(1)教学目标1.理解分式的乘除法法则,体会类比的思想.2.会根据分式的乘除法法则进行简单的运算,并理解其算理教学重、难点分式的乘除法法则的运用教学过程设计一、创设问题,激发兴趣问题1 一个水平放置的长方体容器,其容积为V,底面的长为a,宽为m时,水面的高度为多少?b,当容器内的水占容积的n(1)这个长方体容器的高怎么表示?(2)容器内水面的高与容器内的水所占容积间有何关系?容器内水面的高与容器高的比和容器内的水所占容积的比相等.问题2 大拖拉机m 天耕地a hm2,小拖拉机n天耕地b hm2,大拖拉机的工作效率是小拖拉机的工作效率的多少倍?(1)本题中出现的“工作效率”的含义是什么?(2)大拖拉机和小拖拉机的工作效率怎样表示?观察上述两个问题中所列出的式子中,其中涉及到分式的有哪些运算你能用学过的运算法则求出结果吗问题3 计算:在计算的过程中,你运用了分数的什么法则你能叙述这个法则吗如果将分数换成分式,那么你能类比分数的乘除法法则,说出分式的乘除法法则吗?怎样用字母来表示分式的乘除法法则呢?二、知识应用,巩固提高分式的乘除法法则如何用文字语言来描述?乘法法则:分式乘分式,用分子的积作为积的分子,分母的积为积的分母.除法法则:分式除以分式,把除式的分子、分母颠倒位置后,与被除式相乘.例1 计算:三、应用提高、拓展创新教科书138页练习2四、归纳小结(1)本节课学习了哪些主要内容?(2)分式的乘除法运算与分数的乘除法运算有什么区别和联系?五、布置作业:教材第144页第1题;第145页第10、11题.教后反思:3.3分式的乘除(2)教学目标1.能运用分式的乘除法法则进行复杂计算.2.能运用分式的乘除法解决一些简单的实际问题.教学重、难点用分式的乘除法法则进行计算,并解决一些实际问题.教学过程设计一、创设问题,激发兴趣问题1 约分:分子与分母分别是多项式的分式如何约分?问题2 计算:分子与分母都是单项式的两个分式如何乘除?二、知识应用,巩固提高例1 计算:分子或分母是多项式的两个分式如何乘除呢?解题策略:对于分子与分母都是单项式的两个分式乘除,可直接利用分式的乘除法法则,再根据分式的基本性质进行约分,将最后的结果化成最简分式.而对于分子或分母中含有多项式的两个分式相乘,为了使算式简洁,也便于找出分子与分母中的公因式,需要先将多项式因式分解,把多项式化成整式的积的形式,然后利用分式的乘除法法则进行运算,利用分式的基本性质进行约分,并把最后的结果化成最简分式.例2 “丰收1号”小麦的试验田是边长为a m(a>1)的正方形去掉一个边长为1 m的正方形蓄水池后余下的部分,“丰收2号”小麦的试验田是边长为(a-1)m的正方形,两块试验田的小麦都收获了500 kg.(1)哪种小麦的单位面积产量高?(2)高的单位面积产量是低的单位面积产量的多少倍?思考以下问题:①你能说出小麦的“单位产量”的含义吗?②如何表示这两块试验田的单位产量③怎样确定哪种小麦的单位产量高?④你能列式表示(2)的问题吗?归纳解题步骤:(1)先根据题意分别列出表示两个量的代数式;(2)再根据题意列出相应的算式;(3)最后通过计算解决问题.三、应用提高、拓展创新教科书138页练习3四、归纳小结运用分式的乘除法法则计算分子或分母含有多项式的分式主要步骤是什么?五、布置作业:教材第144页第2题.教后反思:3.3 分式的乘方(3)教学目标1.理解分式乘方的运算法则,能根据法则进行乘方运算,体会数式通性.2.能根据混合运算法则进行分式乘除、乘方混合运算.教学重、难点分式的乘方及分式乘除、乘方混合运算教学过程设计一、创设问题,激发兴趣例1 计算: 2235353259.-+-x xxx x ÷⋅练习1 计算:2222222222222551334216423282816--+----++++m n p q mnp q pq mnm n n m m n m m n m n a a a a a a a ⋅÷⋅÷÷⋅();()();()(). 思考 你能结合有理数乘方的概念和分式乘法的法则写出结果吗? 2310===a a a b b b ()? ()? ()?猜想:n 为正整数时=⎪⎭⎫ ⎝⎛n b a你能写出推导过程吗?试试看.你能用文字语言叙述得到的结论吗?分式的乘方法则:一般地,当n 是正整数时,这就是说,分式乘方要把分子、分母分别乘方.二、知识应用,巩固提高例2 计算:例3 计算:分式的乘除、乘方混合运算与分数的乘除、乘方混合运算有什么联系和区别吗?练习2 计算:三、应用提高、拓展创新教科书139页练习2四、归纳小结(1)本节课学习了哪些主要内容?(2)运用分式乘方法则计算的步骤是什么它与整式的乘方运算有什么区别和联系(3)分式的乘方与乘除混合运算的运算顺序是什么?五、布置作业:教科书习题15.2第3(3)(4)题.教后反思:3.5分式的加减教学目标1.理解分式的加减法法则,体会类比思想.2.会运用法则进行分式的加减运算,体会化归思想.教学重、难点分式的加减法法则教学过程设计一、创设问题,激发兴趣问题1 甲工程队完成一项工程需n 天,乙工程队要比甲队多用3天才能完成这项工程,两队共同工作一天完成这项工程的几分之几?(1)甲工程队一天完成这项工程的几分之几?(2)乙工程队一天完成这项工程的几分之几?(3)甲乙两队共同工作一天完成这项工程的几分之几?问题2 2009年、2010年、2011年某地的森林面积(单位:km2)分别是S1,S2,S3,2011年与2010年相比,森林面积增长率提高了多少?(1)什么是增长率?(2)2010年、2011年的森林面积增长率分别是多少(3)2011年与2010年相比,森林面积增长率提高了多少?分式的加减法与分数的加减法类似,它们实质相同.观察下列分数加减运算的式子,你能将它们推广,得出分式的加减法法则吗分式的加减法法则:同分母分式相加减,分母不变,把分子相加减;异分母分式相加减,先通分,变为同分母的分式,再加减.二、知识应用,巩固提高例 计算: 1122323++-p q p q ().三、应用提高、拓展创新课本141页 练习1、练习2练习:你能应用本节课所学知识解决“问题1”和“问题2”吗?四、归纳小结(1)本节课学习了哪些主要内容?(2)我们是怎么引出分式加减法法则的?(3)在进行分式的加减运算时要注意哪些问题?五、布置作业:教科书习题15.2第4、5题.教后反思:3.5分式的混合运算教学目标1.理解分式混合运算的顺序.2.会正确进行分式的混合运算.3.体会类比方法在研究分式混合运算过程中的重要价值.教学重、难点分式的混合运算.教学过程设计一、创设问题,激发兴趣问题数的混合运算的顺序是什么你能将它们推广,得出分式的混合运算顺序吗分式的混合运算顺序:“从高到低、从左到右、括号从小到大”.例1 计算:这道题的运算顺序是怎样的?通过对例1的解答,同学们有何收获?对于不带括号的分式混合运算:(1)运算顺序:先乘方,再乘除,然后加减;(2)计算结果要化为最简分式.二、知识应用,巩固提高例2 计算:2252412232142244-++--+-----+m m m m x x x x x x x x ⎛⎫⋅ ⎪⎝⎭⎛⎫÷ ⎪⎝⎭() ;() .通过对例2的解答,同学们有何收获?对于带括号的分式混合运算:(1)将各分式的分子、分母分解因式后,再进行计算;(2)注意处理好每一步运算中遇到的符号;(3)计算结果要化为最简分式.三、应用提高、拓展创新练习1 计算:四、归纳小结(1)本节课学习了哪些主要内容?(2)分式混合运算的顺序是什么我们是怎么得到它的(3)在进行分式混合运算时要注意哪些问题?五、布置作业:教科书习题15.2第6题.教后反思:3.7 分式方程(1)教学目标1.了解分式方程的概念.2.会用去分母的方法解可化为一元一次方程的简单的分式方程,体会化归思想和程序化思想.3.了解解分式方程根需要进行检验的原因.教学重、难点利用去分母的方法解分式方程教学过程设计一、创设问题,激发兴趣问题1 为了解决引言中的问题,我们得到了方程v v -=+30603090.仔细观察这个方程,未知数的位置有什么特点?追问1 方程13321;251051;32212++=+-=-+=x x x x x x x x 与上面的方程有什么共同特征?分母中含有未知数.分式方程的概念:分母中含有未知数的方程叫做分式方程.追问2 你能再写出几个分式方程吗?注意: 我们以前学习的方程都是整式方程,它们的未知数不在分母中. 问题2 你能试着解分式方程vv -=+30603090吗问题3 这些解法有什么共同特点?总结:这些解法的共同特点是先去分母,将分式方程转化为整式方程,再解整式方程.思考:(1)如何把分式方程转化为整式方程呢?(2)怎样去分母?(3)在方程两边乘以什么样的式子才能把每一个分母都约去呢?(4)这样做的依据是什么?总结:(1)分母中含有未知数的方程,通过去分母就化为整式方程了.(2)利用等式的性质2可以在方程两边都乘同一个式子——各分母的最简公分母.追问 你得到的解6=v 是分式方程vv -=+30603090的解吗二、知识应用,巩固提高问题4 解分式方程: 2110525=.--x x追问1 你得到的解5=x 是分式方程 2510512-=-x x 的解吗该如何验证呢5=x 是原分式方程变形后的整式方程的解,但不是原分式方程的解.追问2 上面两个分式方程的求解过程中,同样是去分母将分式方程化为整式方程,为什么整式方程90306030-=+v v ()()的解6=v 是分式方程v v -=+30603090的解,而整式方程510+=x 的解5=x 却不是分式方程2510512-=-x x 的解?原因:在去分母的过程中,对原分式方程进行了变形,而这种变形是否引起分式方程解的变化,主要取决于所乘的最简公分母是否为0.检验的方法主要有两种:(1)将整式方程的解代入原分式方程,看左右两边是否相等;(2)将整式方程的解代入最简公分母,看是否为0.显然,第2种方法比较简便!问题5你能概括出解分式方程的基本思 路和一般步骤吗解分式方程应该注意什么基本思路 将分式方程化为整式方程一般步骤:(1)去分母;(2)解整式方程;(3)检验.注意:由于去分母后解得的整式方程的解不一定是原分式方程的解,所以需要检验.三、应用提高、拓展创新例 解下列方程:四、归纳小结(1)本节课学习了哪些主要内容?(2)解分式方程的基本思路和一般步骤是什么解分式方程应该注意什么五、布置作业:教科书习题15.3第1(1)~(4)题.教后反思:3.7 分式方程(2)教学目标1.会解较复杂的分式方程和较简单的含有字母系数的分式方程.2.能够列分式方程解决简单的实际问题.3.通过学习分式方程的解法,体会转化的数学思想.教学重、难点分式方程的解法教学过程设计一、创设问题,激发兴趣例1 解方程31112-=.--+x x x x ()()解分式方程的步骤:(1)去分母,将分式方程转化为整式方程;(2)解这个整式方程;(3)检验.用框图的方式总结为:二、知识应用,巩固提高例2 解关于x 的方程11+=.-a b b x a ()例3 两个工程队共同参与一项筑路工程,甲队单独施工1个月完成总工程的三分之一,这时增加了乙队,两队又共同工作了半个月,总工程全部完成,哪个队的施工速度快?三、应用提高、拓展创新某车间有甲、乙两个小组,甲组的工作效率比乙组工作效率高25%,因此甲组加工2 000个零件所用的时间比乙组加工1 800个零件所用的时间少半小时,问甲、乙两组每小时各加工多少个零件?四、归纳小结(1)本节课学习了哪些主要内容?(2)解分式方程的一般步骤有哪些关键是什么解方程的过程中要注意的问题有哪些(3)列分式方程解应用题的步骤是什么与列整式方程解应用题的过程有什么区别和联系五、布置作业:教科书习题15.3第1(2)(4)(6)(8)、4、5题.教后反思:3.7 分式方程(3)教学目标列分式方程解决实际问题.教学重、难点列分式方程解实际问题.教学过程设计一、创设问题,激发兴趣例1 某进货员发现一种应季衬衫,预计能畅销,他用8 000元购进一批衬衫,很快销售一空.再进货时,他发现这种衬衫的单价比上一次贵了4 元/件,他用 17 600元购进2 倍于第一次进货量的这种衬衫.问第一次购进多少件衬衫?分析:二、知识应用,巩固提高例2 某次列车平均提速v km/h.用相同的时间,列车提速前行驶s km,提速后比提速前多行驶50 km,提速前列车的平均速度为多少?思考:(1)这个问题中的已知量有哪些未知量是什么(2)你想怎样解决这个问题关键是什么表达问题时,用字母不仅可以表示未知数(量),也可以表示已知数(量).上面例题中,出现了用一些字母表示已知数据的形式,这在分析问题寻找规律时经常出现.例2中列出的方程是以x 为未知数的分式方程,其中v,s 是已知常数,根据它们所表示的实际意义可知,它们是正数.三、应用提高、拓展创新练习1 商场用50 000元从外地采购回一批T恤衫,由于销路好,商场又紧急调拨18.6万元采购回比上一次多两倍的T恤衫,但第二次比第一次进价每件贵12元.求第一次购进多少件T恤衫.练习2 八年级学生去距学校s km的博物馆参观,一部分学生骑自行车先走,过了t min后,其余学生乘汽车出发,结果他们同时到达.已知汽车的速度是学生骑车速度的2倍,求学生骑车的速度.四、归纳小结(1)借助分式方程解决实际问题时,应把握哪些主要问题?(2)本节课的分式方程的应用方面应注意些什么?举例说明.五、布置作业:教科书习题15.3第6、7、8题.教后反思:。
八年级分式的乘除说课稿9篇

八年级分式的乘除说课稿9篇八年级分式的乘除说课稿(精选篇1)教学目标(一)教学知识点1.分式乘除法的运算法则,2.会进行分式的乘除法的运算。
(二)能力训练要求1.类比分数乘除法的运算法则。
探索分式乘除法的运算法则。
2.在分式乘除法运算过程中,体会因式分解在分式乘除法中的作用,发展有条理的思考和语言表达能力。
3.用分式的乘除法解决生活中的实际问题,提高“用数学”的意识。
(三)情感与价值观要求1.通过师生共同交流探讨,使学生在掌握知识的基础上,认识事物之间的内在联系,获得成就感。
2.培养学生的创新意识和应用数学的意识。
教学重点让学生掌握分式乘除法的法则及其应用。
教学难点分子分母是多项式的分式的乘除法的运算。
教学方法引导启发探求教具准备投影片四张第一张:探索交流,(记作§3.2 A);第二张:例1,(记作§3.2 B);第三张:例2,(记作§3.2 C);第四张:做一做,(记作§3.2 D)。
教学过程Ⅰ。
创设情境,引入新课[师]上节课,我们学习了分式的基本性质,我们可以发现它与分数的基本性质类似,那么分式的运算是否也和分数的运算类似呢?下面我们看投影片(§3.2 A)探索交流--观察下列算式:× = , × = ,÷ = × = , ÷ = × = .猜一猜× =? ÷ =?与同伴交流。
[生]观察上面运算,可知:两个分数相乘,把分子相乘的积作为积的分子,把分母相乘的积作为积的分母;两个分数相除,把除数的分子和分母颠倒位置后,再与被除数相乘。
即× = ;÷ = × = .这里字母a,b,c,d都是整数,但a,c,d不为零。
[师]如果让字母代表整式,那么就得到类似于分数的分式的乘除法。
Ⅱ。
讲授新课1.分式的乘除法法则[师生共析]分式的乘除法法则与分数的乘除法法则类似:两个分式相乘,把分子相乘的积作为积的分子,把分母相乘的积作为积的分母;两个分式相除,把除式的分子和分母颠倒位置后再与被除式相乘。
分式的乘除法教学课件

机械设计
在机械设计中,机器的效率和功率可以用分 式表示,通过分式的乘除法可以计算出机器 的效率和功率等参数。
分式乘除法的扩展与提高
05
分式的约分与通分
要点一
约分
将分式化简为最简形式的过程,通过约简分子和分母中的 公因式来实现。
要点二
通分
将两个或多个分式化为相同分母的过程,以便进行加法或 减法运算。
乘法法则的应用
总结词
掌握分式乘法法则的应用是解决复杂分式问题的关键。
详细描述
分式乘法法则的应用可以通过多种方式进行。例如,在解决物理、化学等实际问 题时,常常需要使用分式乘法法则来计算复杂分式的结果。此外,在数学竞赛和 数学研究中,分式乘法法则也是解决复杂数学问题的关键技巧之一。
分式除法法则
02
通分
对于分母不同的分式,可以进行通分, 将它们转化为同分母的分式,便于进 行乘除运算。
注意事项和常见错误
01
符号的处理
在进行分式的混合运算时,应注意符号的处理,特别是 加减法的转换和括号内的运算符号。
02
避免运算顺序混乱
在复杂的混合运算中,应遵循正确的运算顺序,避免因 顺序错误导致计算结果错误。
03
忽略约分的简化
在运算过程中,应注意约分的运用,避免因忽略约分导 致计算结果复杂化。
分式乘除法在日常生活中的应 用
04
物理问题中的应用
电路计算
在电路中,电流、电压和电阻之间的 关系可以用分式表示,通过分式的乘 除法可以计算出电路中的电流、电压 和功率等参数。
力学问题
在力学中,力、质量和加速度之间的 关系可以用分式表示,通过分式的乘 除法可以计算出物体的加速度、速度 和位移等参数。
人教版八年级数学分式的乘除分式的乘方课件

a c ac b d bd
2 4 2 5 25 (3) = = 3 5 3 4 3 4
a c ? b d
分式的除法法则:分式除以分式,把除式的分子、分母 颠倒位置后,与被除式相乘. 用符号语言表达:a c a d a d .
b d b c bc
【跟踪训练】
1.计算:
a 4a 4 a 1 2 . 2 a 2a 1 a 4
2
2
(a 2) a 1 解:原式 2 (a 1) (a 2)(a 2) (a 2) 2 (a 1) 2 (a 1) (a 2)(a 2) a2 . (a 1)(a 2)
a 1
4 5 4 4 4 4 4 45 1 024 ( ) 5 . 3 3 3 3 3 3 3 243
4 n 4 4 ( ) 3 3 3
4 44 3 33
n
4 4n n. 3 3
对于任意一个正整数n,有
f n f ( ) = n . g g
500 a2 1
500 , ∴“丰收2号”小麦的单位面积产量高. 2 (a 1)
500 500 500 a 2 1 a 1 (2) 2 , ቤተ መጻሕፍቲ ባይዱ 2 (a 1) a 1 (a 1) 500 a 1
∴“丰收2号”小麦的单位面积产量是“丰收1号”小 麦的单位面积产量的 a 1 倍.
【例题】
4x y 【例1】 计算: (1) . 3 3y 2x
ab3 5a 2 b 2 (2) 2 . 2c 4cd
4x y 4 xy 2 3= 3 2. 【解析】 (1) 3 y 2 x 6 x y 3x
八年级数学下册教案《分式的乘除》

16.2.1分式的乘除一、教学目标:理解分式乘除法的法则,会进行分式乘除运算. 二、重点、难点1.重点:会用分式乘除的法则进行运算. 2.难点:灵活运用分式乘除的法则进行运算 . 三、例、习题的意图分析1.P13本节的引入还是用问题1求容积的高,问题2求大拖拉机的工作效率是小拖拉机的工作效率的多少倍,这两个引例所得到的容积的高是nmab v ⋅,大拖拉机的工作效率是小拖拉机的工作效率的⎪⎭⎫⎝⎛÷n b m a 倍.引出了分式的乘除法的实际存在的意义,进一步引出P14[观察]从分数的乘除法引导学生类比出分式的乘除法的法则.但分析题意、列式子时,不易耽误太多时间.2.P14例1应用分式的乘除法法则进行计算,注意计算的结果如能约分,应化简到最简.3.P14例2是较复杂的分式乘除,分式的分子、分母是多项式,应先把多项式分解因式,再进行约分.4.P14例3是应用题,题意也比较容易理解,式子也比较容易列出来,但要注意根据问题的实际意义可知a>1,因此(a-1)2=a 2-2a+1<a 2-2+1,即(a-1)2<a 2-1.这一点要给学生讲清楚,才能分析清楚“丰收2号”单位面积产量高.(或用求差法比较两代数式的大小)四、课堂引入1.出示P13本节的引入的问题1求容积的高nmab v ⋅,问题2求大拖拉机的工作效率是小拖拉机的工作效率的⎪⎭⎫⎝⎛÷n b m a 倍.[引入]从上面的问题可知,有时需要分式运算的乘除.本节我们就讨论数量关系需要进行分式的乘除运算.我们先从分数的乘除入手,类比出分式的乘除法法则.1.P14[观察] 从上面的算式可以看到分式的乘除法法则.3.[提问] P14[思考]类比分数的乘除法法则,你能说出分式的乘除法法则? 类似分数的乘除法法则得到分式的乘除法法则的结论. 五、例题讲解P14例1.[分析]这道例题就是直接应用分式的乘除法法则进行运算.应该注意的是运算结果应约分到最简,还应注意在计算时跟整式运算一样,先判断运算符号,在计算结果.P15例2.[分析] 这道例题的分式的分子、分母是多项式,应先把多项式分解因式,再进行约分.结果的分母如果不是单一的多项式,而是多个多项式相乘是不必把它们展开.P15例.[分析]这道应用题有两问,第一问是:哪一种小麦的单位面积产量最高?先分别求出“丰收1号”、“丰收2号”小麦试验田的面积,再分别求出“丰收1号”、“丰收2号”小麦试验田的单位面积产量,分别是15002-a 、()21500-a ,还要判断出以上两个分式的值,哪一个值更大.要根据问题的实际意义可知a>1,因此(a-1)2=a 2-2a+1<a 2-2+1,即(a-1)2<a 2-1,可得出“丰收2号”单位面积产量高. 六、随堂练习计算(1)ab c 2c b a 22⋅ (2)322542n m m n ⋅- (3)⎪⎭⎫ ⎝⎛-÷x x y 27 (4)-8xy x y 52÷ (5)4411242222++-⋅+--a a a a a a (6))3(2962y y y y -÷++- 七、课后练习计算(1)⎪⎪⎭⎫ ⎝⎛-⋅y xy x 132 (2)⎪⎭⎫ ⎝⎛-÷a bc ac b 2110352(3)()yx a xy 28512-÷(4)ba ab ab b a 234222-⋅- (5))4(12x x x x -÷-- (6)3222)(35)(42x y x xy x --⋅-八、答案:六、(1)ab (2)nm 52- (3)14y -(4)-20x 2 (5))2)(1()2)(1(+--+a a a a (6)23+-y y七、(1)x 1- (2)227c b-(3)ax 103-(4)bb a 32+ (5)x x -1 (6)2)(5)(6y x y x x -+课后反思:。
《分式的乘除》人教版数学ppt课件1

45 35
1 024 . 243
2.对于任意一个正整数n,第n步得到的折线的总长度是多少?
(4)n 4 4 3 33
4 44 3 33
4 3
4n 3n
.
分
对于任意一个正整数n,有
式
的
( f )n g
=
fn gn
.
乘 方 法
分式乘方要把分子、分母分别乘方.
则
【例题】
例3 计算:
(1 )
(
x y2
1
(a-1)2 m2,单位面积产量是 5 0 0 kg/m2.
(a 1)2
∵0<(a-1)2< a 2-1,
∴ 500 a2 1
500 (a 1)
2
,∴“丰收2号”小麦的单位面积产量高.
( 2 ) (a 5 0 1 0 )2a 5 2 0 0 1(a 5 0 1 0 )2a 5 2 0 0 1a a 1 1 ,
n 航行的时间比是______.
面积产量是 kg/m2;
a b ∴“丰收2号”小麦的单位面积产量是“丰收1号”小麦的单位面积产量的 倍.
作效率的( )倍. 第二步,把上述折线中每一条线段重复第一步的做法,便得到由长度相等的线段组成的折线,总长度为
m n 【例2】“丰收1号”小麦的试验田是边长为a m的正方形去掉一个边长为1 m的正方形蓄水池后余下的部分,“丰收2号”小麦的试验
m m 7
课堂练习 计算
3a 16b
3ab 10xy
(1) 4b 9a 2 (2) 4x 2 y 21b
12xy (3)
8x 2 y
5a
2y 2 (4) 3xy
3x
太有趣了,我还想做
人教版《分式的乘除》初中数学-教学课件1

情景思考
(2)高的单位面积产量是低的单位面积产量的多少倍?
课堂测试
课堂测试
课堂测试
第十五章 分式
PPT模板:www. 1ppt.co m/ mob an/
PPT素材:/s ucai/
PPT背景:/beiji ng/
PPT图表:www.1ppt .co m/tu biao/
丰收一号
1
a-1
【分析】
丰收二号 a-1 1)丰收一号试验田面积_______㎡;单位
a
面积产量_______kg/㎡
a-1
2)丰收二号试验田面积_______㎡;单位
面积产量_______kg/㎡
分式及其运算(完整版)ppt课件

(1)x2
x 2x
(
x2
)
(分子分母都乘以 x)
(2)3x2 3xy xy
6x2
(
)
(分子分母都除以 3x)
例3(补充)判断下列变形是否正确.
(1)
a b
a2 b2
(
)
(2) b bc a ac
(c≠0)
(
)
(3) b b 1 ( )
a a 1
(4)
2x 2x 1
x x 1
(
)
(四)课堂练习
无意
-1 义 -1 0
思考:
1、第2个分式在什么情况下无意义? 2、 这三个分式在什么情况下有意义? 3、这三个分式在什么情况下值为零?
练习3:
A
1、归纳:对于分式 B
(1) 分式无意义的条件是 B=0 。
(2)分式有意义的条件是 B≠0
。
(3)分式的值为零的条件是 B≠0且A=0 。
2、当x ≠2 时,分式 x 有意义。 x2
5a2b2
4ab3cd
2bd .
10a2b2c2
5ac
课堂练习
练习1 计算:
( 1 ) b a ; ( 2 ) 2b; ( 3 ) n y m y. ac a2 a m x n x
课堂练习
练习2 计算:
(1)3a 4b
196ab2 ; (2)
3xy
2y2 3x
;
(3)12xy 8x2y;(4)x y y x.
解: 即2011年与2010年相比,森林面积增长率提 高了 S 1 S 3 - S 2 2 . S1S 2
八年级 上册
15.2 分式的运算
分式的乘方及分式乘除、乘方混合运算
15.2.1分式的乘除(第一课时)教案

课堂解决方案教学详案15.2.1分式的乘除(第1课时)【设计说明】本节课从生活中的问题引入,让学生感受到学习分式乘除运算是生产和生活的实际需要,从而激发学生的学习兴趣。
由于分式的乘除法法则与分数的乘除法法则类似,故以类比的方法得出分式的乘除法则,易于学生理解、接受。
利用表格给出分式的乘除法法则更利于学生的对比和理解;例题采取学生自主运用新知识代替单纯的教师讲授,这是教学方法的一大尝试。
本节课采取把自主权交给学生,遵循“教师为主导,学生为主体”原则。
体现了自主探索,合作学习的新理念,在实际问题解决的过程中培养了学生分析问题和解决问题的能力。
【教学目标】1、理解并掌握分式的乘除法法则,能进行简单的分式乘除法运算,能解决一些与分式乘除有关的实际问题。
2、经历从分数的乘除法运算到分式的乘除法运算的过程,培养学生类比的探究能力,加深从特殊到一般的数学思想认识。
3、教学中渗透类比转化的思想,培养学生主动探究,合作交流的能力,使学生在学知识的同时感受探索的乐趣和成功的体验。
【教学重点难点】重点:运用分式的乘除法法则进行运算。
难点:分子、分母为多项式的分式乘除运算。
【课前准备】课件、多媒体【教学过程】(-)导入新课一、提出问题,引入课题(出示多媒体)活动1:问题1 :一个水平放置的长方体容器器,其容积为V,底面的长为a,宽为b,当容器内的水占容积的时,水面的高度为多少?问题2:大拖拉机m天耕地ahm2,小拖拉机n天耕地b hm2,大拖拉机的工作效率是小拖拉机的工作效率的多少倍?师生活动:学生根据题意,分别列出问题1、问题2所求的数量关系式为:问题 1:求得容积的高:问题2:大拖拉机的工作效率是小拖拉机的倍教师引导学生观察分析以上两式的特点得出它们分别是分式的乘法和分式的除法。
从上面的问题可知,解决生活中的问题有时需要进行分式的乘除运算,那么分式的乘除是怎样运算的呢?这是我们本节课要学习的内容。
.教师板书课题。
(二)探究新知活动2 :类比联想,探究新知计算下式:类比分数的乘除法则猜想分式的乘除法则本环节的任务:让学生从分数的乘除法法则类比探究得出分式的乘除法法则。
人教版八年级数学上册15.分式的乘除法课件

n个
(a)n b
a b
•
a b
•
•
a b
a b
• •
a b
•• a • • b
an
bn
n个
n个
即:
分式乘方要把分子、分母分别乘方.
P139 例5 计算:
( 2a2b)2 (1) 3c ;
( a2b )3 2a ( c )2 (2) cd 3 d 3 2a .
P139 例5 计算:
(1) ( 2a2b )2 3c
解:
(2) 16 y2 y 4 x2 6x 9 x 3
解:原式=
2x2y3 12x4 y
y2 16 x 3 x2 6x 9 y 4
y4 x3
P138 例4
计算: 2x
5x
3
3 25x2
9
•
x 5x
。 3
解:原式
2x
25x2 9
•
•
x
5x 3 3 5x 3
2x • (5x 3)(5x 3) • x
2、计算 解:原式=
分母是什么?
可省略.
P138
( a )2 ? ( a )3 ? ( a )10 ?
b
b
b
根据乘方的意义和分式乘法法则,可得:
( a )2 a a a a a2
b b b bb b2
( a )10 a1 0
b
b10
一般地,当n是正整数时,
1.分式的乘法法则:分式乘分式, 用分子
的积作为积的分子, 分母的积作为积的分母.
2.分式的除法法则:分式除以分式, 把除
式的分子、分母颠倒位置后, 与被除式相乘.
八年级数学分式的乘除1

下列关于协方差和相关系数的说法中,不正确的是()。A、如果协方差大于0,则相关系数一定大于0B、相关系数为1时,表示一种证券报酬率的增长总是等于另一种证券报酬率的增长C、如果相关系数为0,则表示不相关,但并不表示组合不能分散任何风险D、证券与其自身的协方差就是其方差 互联网消费金融业务有负责监管。A.人民银行B.银监会C.证监会D.保监会 如果电流强度不随时间而变,这种电流就称为。A、直流B、交流C、感应电流D、涡流 芝加哥期货交易所于年开始实行保证金制度。A.1848B.1882C.1851D.1865 违反《医疗废物管理条例》规定,导致传染病传播或者发生环境污染事故,给他人造成损害的相关机构,依法 “治崩三法”指的是。A.止血、固脱、调经B.调经、固本、善后C.补肾、扶脾、调肝D.塞流、澄源、复旧E.塞流、固本、调经 深Ⅱ度烧伤创面处理不正确的是。A.1:2000氯己定清洗创面,去除异物B.去除水泡皮C.油质纱布包扎创面D.面部创面不包扎E.创面使用抗生素预防全身感染 对慢性阻塞性肺气肿诊断最有意义的检查是A.血气分析B.胸部X线检查C.心电图和心电向量检查D.肺功能检查E.肺动脉压测定 难通过血-脑屏障的药物特点为A.分子量大、极性高、脂溶性小B.分子量小、极性低、脂溶性小C.分子量大、极性低、脂溶性大D.分子量小、极性高、脂溶性大E.分子量小、极性低、脂溶性大 保列治(非那雄胺)治疗前列腺增生的机制是A.抑制α受体B.抑制5-α还原酶C.抑制H受体D.抑制β受体E.抑制雄性激素受体 撒漏的易燃固体,收集的残留物不能任意排放、抛弃,而应置于原包装内。A.正确B.错误 项目分析的内容包括、及三方面。 早期胃癌根治术后哪种情况不必辅助化疗()A.年龄>60岁B.癌灶面积>5cmC.年龄<40岁D.病理类型恶性程度高E.多发性癌灶 铸态管插口内重皮如何调整? 一般而言,电站(机组)受阻容量是指机组受技术因素制约所能发出的出力与之差的总称。A.额定出力B.保证出力C.平均出力D.最小出力 封面有两大基本功能,一是功能,一是功能。A.装饰B.保护C.宣传D.护水 工程师无正当理由不确认承包商提出的变更工程价款报告时,则变更工程价款报告自行生效的时间是自变更价款报告送达之日起天后。A.7B.10C.14D.28 房屋修缮是在基础上进行的。A.已有房屋B.新方案C.修缮意见D.用户要求 心在液为A.汗B.泪C.涕D.唾E.涎 以下不属于出版专业中级编辑的职责是。A.提出选题设想,进行组稿B.研究特殊书稿的设计方案C.做好图书宣传工作D.指导、培养助理编辑 1998年12月29日全国人大常委会通过的《关于惩治骗购外汇、逃汇和非法买卖外汇犯罪的决定》属于下列哪种刑事法律?()A.刑法立法解释B.单行刑法C.刑法修正案D.附属刑法 什么是秘密? 线性电阻的伏安特性曲线为通过的一条直线。A、X轴B、Y轴C、第Ⅰ象限D、原点 是最常见的一种险别。其原意是“对单独海损不赔”,即对部分损失不负责赔偿,只赔全部损失,它是海上运输货物保险中责任范围最小的一种险别。A、平安险B、水渍险C、一切险D、战争险 药物性卵巢切除导致暂时性闭经是指()A.达那唑B.孕三烯酮C.GnRH-aD.甲羟孕酮E.溴隐亭 下列现象与哪种非生物因素有关:沙丁鱼在水温降到8度时,就会向岸边聚集? 下列哪种膳食成分对非血红素铁的吸收有促进作用。A.大豆蛋白B.植酸盐C.钙D.多酚类物质E.肉类 [问答题,论述题]如何处理TJK2型减速器无制动缓解表示故障? 设,则(AB)-1=。ABCD 医院感染的主要研究对象是A.门诊和急诊患者B.住院和手术患者C.患者和探访人员D.住院患者和医护人员E.患者和患者家属 测定某有色溶液的吸光度,用lcm比色皿时吸光度为A,若用2cm比色皿,吸光度为。A、2AB、A/2C、AD、4A 关于强制对流说法正确的是。A、凡是受温度的影响而发生的对流都称为强制对流B、凡是受动能的影响而发生的对、流都称为强制对流C、凡是受外力的影响而发生的流体运动都称为强制对流D、凡是受做功的影响而发生的流体运动都称为强制对流 体现“培土生金”治法的方剂是A.参苓白术散B.四君子汤C.玉屏风散D.补中益气汤E.归脾汤 社区专职工作者的素质要求? 下列阴和阳的概念中,最确切的是A.阴和阳是中国古代的两点论B.阴和阳即是矛盾C.阴和阳代表对立的事物D.阴和阳代表相互对立又相互关联的事物属性E.阴和阳说明相互关联着的事物 财产权按照其各项权能的内容划分,包括:A.所有权B.占有权C.使用权D.收益及处置权 下列关于胃壁结构的描述正确的是A.分3层B.幽门瓣为纵行皱襞C.外膜为浆膜D.肌层分为内环、外纵2层E.幽门瓣突向胃 FIATA2006年年会在召开。A.上海B.纽约C.东京D.南非 采用热装法装配轴承时,将轴承放入机油槽中加热,温度不超过℃为宜A.200B.150C.100D.50 甲、乙订立买卖合同,约定甲于2011年3月1日向乙供货,乙在收到货物后1个月内一次性付清全部价款。甲依约供货后,乙未付款,若甲一直未向乙主张权利,则甲对乙的付款请求权诉讼时效期间届满日为。A.2012年4月1日B.2013年3月1日C.2012年3月1日D.2013年4月1日
八下数学21分式的乘除(基础)知识讲解

分式的乘除(基础)【学习目标】1.学会用类比的方法总结出分式的乘法、除法法则.2.会分式的乘法、除法运算.3.掌握乘方的意义,能根据乘方的法则,先乘方,再乘除进行分式运算. 【要点梳理】要点一、分式的乘除法1.分式的乘法法则:分式乘分式,用分子的积作为积的分子,分母的积作为积的分母.用字母表示为:a c acb d bd⋅=,其中a b c d 、、、是整式,0bd ≠. 2.分式的除法法则:分式除以分式,把除式的分子、分母颠倒位置后,与被除式相乘.用字母表示为:a c a d adb d bc bc÷=⋅=,其中a b c d 、、、是整式,0bcd ≠. 要点诠释:(1)分式的乘除法都能统一成乘法,然后约去公因式,化为最简分式或整式.(2)分式与分式相乘,若分子和分母是多项式,则先分解因式,看能否约分,然后再乘.(3)整式与分式相乘,可以直接把整式(整式可以看作分母是1的代数式)和分式的分子相乘作为分子,分母不变.当整式是多项式时,同样要先分解因式,便于约分.(4)分式的乘除法计算结果,要通过约分,化为最简分式或整式.要点二、分式的乘方分式的乘方运算法则:分式的乘方是把分子、分母分别乘方,用字母表示为:nn n a a b b⎛⎫= ⎪⎝⎭(n 为正整数). 要点诠释:(1)分式乘方时,一定要把分式加上括号.不要把nn n a a b b ⎛⎫= ⎪⎝⎭写成nn a a b b ⎛⎫= ⎪⎝⎭(2)分式乘方时,要首先确定乘方结果的符号,负数的偶次方为正,负数的奇次方为负.(3)在一个算式中同时含有分式的乘方、乘法、除法时,应先算乘方,再算乘除,有多项式时应先分解因式,再约分.(4)分式乘方时,应把分子、分母分别看作一个整体.如()222222a b a b a b b b b ---⎛⎫=≠ ⎪⎝⎭. 【典型例题】 类型一、分式的乘法1、计算:(1)422449158a b xx a b;(2)222441214a a a a a a -+--+-. 【思路点拨】(1)中分子、分母都是单项式,直接用分式乘法法则计算,结果要通过约分化简;(2)中分子、分母都是多项式,要先把可分解因式的分子、分母分解因式,然后用乘法法则化简计算. 【答案与解析】解:(1)422449158a b x x a b 422449315810a b x bx a b x==. (2)222441214a a a a a a -+--+-22(2)1(1)(2)(2)a a a a a --=-+-22(2)(1)(1)(2)(2)a a a a a --=-+-222(1)(2)2a a a a a a --==-++-. 【总结升华】分式的乘法运算的实质就是运用分式的基本性质把分式约分化简的过程,熟练之后也可先约分后运用乘法法则计算. 举一反三: 【变式】计算.(1)26283mx xm ;(2)22122x x x x+-+ 【答案】解:(1)原式22621283242m x mx xx m mx ===;(2)原式22112(2)2x x x x x x+==-+-;类型二、分式的除法2、 计算:(1)222324a b a bc cd-÷;(2)2222242222x y x y x xy y x xy -+÷+++. 【思路点拨】(1)先运用法则将分式的除法转化为乘法,然后约分化简;(2)先运用分式的除法法则将分式的除法转化为乘法,同时将分子、分母分解因式,然后约分化简. 【答案与解析】解:(1)222324a b a b c cd -÷22222244236a bcd a b cd c a b c a b ==--23dc=-. (2) 2222242222x y x y x xy y x xy-+÷+++2(2)(2)2()()2x y x y x x y x y x y+-+=++22(2)24x x y x xyx y x y --==++.【总结升华】分式的除法和实数的除法一样,均是转化为乘法来完成的. 举一反三:【变式】(•宝鸡校级模拟)化简:.【答案】 解:原式=•=.类型三、分式的乘方3、(秋•华龙区校级月考)下列计算正确的是( ) A.B.C. D.【思路点拨】把四个选项先利用分式的乘方法则,将分子分母分别乘方,然后利用积与幂的乘法法则,积的乘方的运算法则,积的乘方等于积中每一个因式分别乘方并把结果相乘,幂的乘方法则是底数不变,指数相乘,即可计算出结果,得到计算正确的选项.【答案】C . 【解析】解:A 、,本选项错误;B 、,本选项错误;C 、,本选项正确;D 、,本选项错误.所以计算结果正确的是C .【总结升华】此题考查了分式的乘方法则,考查了积的乘方及幂的乘方法则,完全平方公式的运用,是一道基础题.类型四、分式的乘除法、乘方的混合运算4、 计算:(1)(春•淅川县期中)(﹣2ab ﹣2c ﹣1)2÷×()3;(2)222223()a b ab a ab b b a ⎛⎫-⎛⎫÷+ ⎪ ⎪-⎝⎭⎝⎭.【思路点拨】先算乘方,再算乘、除. 【答案与解析】解:(1)(﹣2ab ﹣2c ﹣1)2÷×()3=﹣••=﹣.(2)222223()a b ab a ab b b a ⎛⎫-⎛⎫÷+ ⎪ ⎪-⎝⎭⎝⎭ 2222232()1()[()]()a b ab b a a b b a -=+-22222332()()1()()a b a b a b b a a b a b +-=+-211()a a b a ab==++.【总结升华】(1)题中有除法和乘方运算,应先算乘方,要特别注意符号的处理.(2)本题是乘除混合运算,首先把除法运算转化为乘法运算,再用乘法运算法则计算. 举一反三:【变式】计算:(1)332212b b a a ab ⎛⎫⎛⎫⎛⎫-÷-÷ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭;(2)2222()m n n m m nm n mn m --+⎛⎫÷ ⎪-⎝⎭. 【答案】解: (1)332212b b a a ab ⎛⎫⎛⎫⎛⎫-÷-÷ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭23263382633312212b b b a a b a b a a a ba b ⎛⎫⎛⎫=-÷-÷==⎪ ⎪⎝⎭⎝⎭. (2)2222()m n n m m n m n mn m --+⎛⎫÷ ⎪-⎝⎭22222()()()()m n m n m n m m nm n m n m n mn +---==-+.【巩固练习】 一.选择题 1.计算261053ab cc b 的结果是( ) A .24a c B .4a C .4a c D .1c2. (•迁安市一模)化简:(a ﹣2)•的结果是( )A .a ﹣2B .a +2C .D .3.(•蜀山区一模)化简的结果是( )A.12B.1a a +C.D.4.分式32)32(ba 的计算结果是( ) A .3632b aB .3596b aC .3598b aD .36278b a5.下列各式计算正确的是( ) A .yx y x =33B .326m m m =C .b a ba b a +=++22D .b a a b b a -=--23)()(6.22222nm m n m n ⋅÷-的结果是( )A .2n m -B .32nm -C .4mn -D .-n二.填空题7.1a c b c÷⨯_____; 2233y xy x -÷_____.8.389()22x y y x ⋅-=______;=+-÷-xyx x xy x 33322______. 9.(泰安模拟)化简的结果是 .10.如果两种灯泡的额定功率分别是21UPR=,225UPR=,那么第一只灯泡的额定功率是第二只灯泡额定功率的________倍.11.3322()abc=____________;=-522)23(zyx____________.12.222222.2ab b a ba ab b a ab+-=++-______.三.解答题13.(•黄石)先化简,再求值:÷•,其中a=2016.14.阅读下列解题过程,然后回答后面问题计算:2111a b c db c d÷⨯÷⨯÷⨯解:2111a b c db c d÷⨯÷⨯÷⨯=2a÷1÷1÷1①=2a.②请判断上述解题过程是否正确?若不正确,请指出在①、②中,错在何处,并给出正确的解题过程.15.小明在做一道化简求值题:22222().,x xy y x yxy x xyx-+--÷他不小心把条件x的值抄丢了,只抄了y=-5,你说他能算出这道题的正确结果吗?为什么?【答案与解析】 一.选择题 1.【答案】C ; 【解析】 ∵ 2261061045353ab c ab c ac b c b c==,∴ 选C 项. 2.【答案】B ;【解析】原式=(a ﹣2)•=a +2,故选B .3.【答案】B ; 【解析】解:原式=×=.故选B.4.【答案】D ;【答案】23663333228()3327a a a b b b==. 5.【答案】D ;【解析】3322()()()()a b a b a b b a a b --==---. 6.【答案】B ;【解析】222222222223n n m n m m m m n n m m n n-÷⋅=-⋅⋅=-.二.填空题7.【答案】2abc;292x y -;【解析】2111a a ac b c b c c bc÷⨯=⨯⨯=.22223933322y x x xy xy x y y -÷=-⨯=-. 8.【答案】218x-;-1; 【解析】328918()22x y y x x⋅-=-;22233()3133()x xy x y x x y x x x x x y --+-÷=⨯=---. 9.【答案】;【解析】解:原式=••=.10.【答案】5;【解析】222122555U U U RP P R R R U ÷=÷=⨯=. 11.【答案】9368a b c;1010524332x y z -;【解析】3399323636228()a a a bc b c b c==;25101052510510533243()2232x x x y z y z y z -=-=-. 12.【答案】ba; 【解析】()()()()()2222222.2b a b a b a b ab b a b ba ab b a ab a a b aa b ++-+-=⋅=++--+. 三.解答题 13.【解析】 解:原式=••=(a ﹣1)•=a +1当a=2016时,原式=2017. 14.【解析】解:第①步不正确,因为乘除运算为同级运算时,应从左到右依次计算.应为:22111111111a b c d a b c d b b c c d d ÷⨯÷⨯÷⨯=⨯⨯⨯⨯⨯⨯=2222a b c d.15.【解析】解:22222().x xy y x yxy x xy x-+--÷ =()()22xyx yx x y x x y ---⨯⨯- =5y -=这道题的结果与x 的值无关,所以他能算出正确结果是5.11。
八年级数学分式的乘除1(PPT)5-2

53法则125用式35125
ba1405dc
9 2
ac bd
53子表125示为53: 125ba
c32a 5d15b
d7c65ab225dc
类比分数的乘除法法则,你能想出分式
的乘除法法则吗?
乘法法则:分式乘分式,用分子的积作为积 的分子,分母的积作为积的分母.
除法法则:分式除以分式,把除式的分子、 分母颠倒位置后,与被除式相乘.
类的事物辨别异同或高下:这两块料子~起来,颜色是这块好,质地是那块好。②介用来比较性状和程度的差别:这项政策贯彻以后,农民的生产积极性~ 前一时期又有所提高。③副表示具有一定程度:这篇文章写得~好。 【比较价格】不变价格。 【比较文学】现代人文学科之一。主要运用比较方法,对不同 民族的文学现象进行综合分析,探讨彼此的相互影响及其与时代、社会、文化间的关系。 【比况】〈书〉动跟某事物相比较;比照。 【比来】〈书〉名近来。 【比例】名①表示两个比相等的式子,如∶=∶。②两个同类量之间的倍数关系:教师和学生的~已经达到要求。③比重?:在所销商品中,国货的~比较大。 【比例尺】名①绘制地图或机械制图时,图上距离与它所表示的实际距离的比。②指线段比例尺,附在图边的表示比例的数字或线段。③制图用的一种工具, 上面有几种不同比例的刻度。 【比例税制】-对同一征税对象不论数额多少,都按同一比例计征的税率制度。 【比量】?ɑ动①不用尺而用手、绳、棍等大概 地量一量:他用胳膊一~,那棵树有两围粗。②比试?:他拿起镰刀~了~,就要动手割麦子。 【比邻】①〈书〉名近邻;街坊:海内存知己,天涯若~。 ②动位置接近;邻近:~星(离太阳最近的一颗恒星)。 【比率】ǜ名比值。 【比美】动美好的程度不相上下,足以相比:乡镇企业的一些产品,已经可以 跟大工厂的产品~。 【比目鱼】名鲽、鳎、鲆、鳒等鱼的统称。这几种鱼身体扁平,成长中两眼逐渐移到头部的一侧,平卧存海底。也叫偏口鱼。 【比拟】 ①动
【新苏科版】八年级下册10.4分式的乘除(1)-教案设计
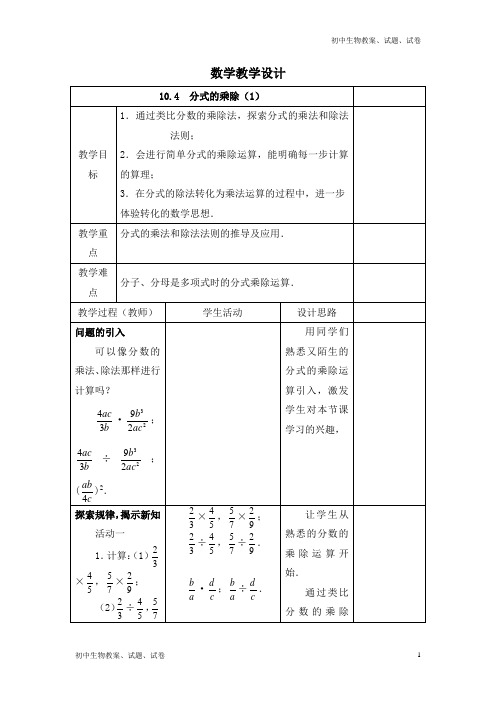
数学教学设计10.4 分式的乘除(1)教学目标1.通过类比分数的乘除法,探索分式的乘法和除法法则;2.会进行简单分式的乘除运算,能明确每一步计算的算理;3.在分式的除法转化为乘法运算的过程中,进一步体验转化的数学思想.教学重点 分式的乘法和除法法则的推导及应用.教学难点分子、分母是多项式时的分式乘除运算.教学过程(教师) 学生活动设计思路问题的引入可以像分数的乘法、除法那样进行计算吗?43ac b ·3292b ac ;43ac b÷3292b ac ;(4ab c)2.用同学们熟悉又陌生的分式的乘除运算引入,激发学生对本节课学习的兴趣,探索规律,揭示新知活动一1.计算:(1)23×45,57×29; (2)23÷45,5723×45,57×29; 23÷45,57÷29.b a ·dc ;b a ÷d c. 让学生从熟悉的分数的乘除运算开始.通过类比分数的乘除÷29.问题1:上面运算的根据是什么?问题2:你能回忆并说出分数的乘法和除法法则吗?2.问题3:你能“类比”分数的运算,计算完成下面的式子吗?b a ·dc;ba÷dc.3.问题4:再举几个这样的例子试一试.与同伴交流你的想法.问题5:请你“类比”分数的乘除法则,用语言描述出分式的乘除法则(小组内交流得出结论).分式的乘法法则:分式乘分式,用分子的积做积的分子,分母的积做积的分母.分式的除法法则:分式除以分式,把除式的分子、分母法,引导学生尝试去进行分式的乘除.让学生再举这样的例子,认识到一般规律,此时学生通过小组交流合作,通过不完全归纳探究总结分式的乘除法法则.颠倒位置后,与被除式相乘.用字母表示为:b a ·dc=bd ac ;b a ÷dc =b a ×cd =bc ad. 活动二 试一试: (1)43ac b ·3292b ac; (2)43acb÷3292bac. 注意:运用分式的乘除法运算法则进行分式的乘法和除法时,能约分的要约分.43acb·3292b ac =3322249366326⋅⋅==ac b ab c b b ac abc c;43acb÷3292b ac =43ac b ·2233428927=ac a c b b. 在学生探究出分式的乘除法法则后,通过两个简单问题的尝试,进一步熟悉运算法则.通过计算,认识到分式运算时,能约分的先约分,结果最后要化成最简.尝试反馈,领悟新知例 1 计算: (1)226cb a ·2243-ca b ; (2)(4ab c)2. 例 2 计算: (1)226xay÷例1 可由学生自己来完成,同学们互相改正错误.例2 由学生小组合作完成.在熟悉分式的乘除法法则后,例1的设计让学生尝试解决问题,巩固所学知识.例2的设计让学生应用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2x 6 x x6 2 (5) ( x 3) 2 4 4x x 3 x x2
2
熟练运用
x 2 2 xy y 2 x y 1.化简( xy x 2 ) 2 = -y xy x
2、 x 2004, y 2005时 当 x y yx 求 2 2 的值 2 2 x 2 xy y x y
4 4
先化简 再求值
原式= -(x+y)=-(2004+2005)=-4009
小结:
分式的乘除法法则是什么?
a 1
P13
练习1
3a 16b 2 4b 9a
计算
:
12 xy 2 8x y 5a
2
2y 3xy 3x
x y x y x y x y
练习2
计算
:
2 3
3a 3b 25a b 2 2 10ab a b
2 2
x 4y x 2y 2 2 2 x 2 xy y 2 x 2 xy
观察、思考:
3 15 3 15 a45 c a c 9 法则用式 2 b10 d 2 b d 5 2 5 3 15 3 2 c 2a d a 2d 6 子表示为: a 3 b d b c 5 2 5 15 5 15 75 b c 25 类比分数的乘除法法则,你能想出分式 的乘除法法则吗? 乘法法则:分式乘分式,用分子的积作为积 的分子,分母的积作为积的分母.
除法法则:分式除以分式,把除式的分子、 分母颠倒位置后,与被除式相乘.
例1 计算:
4x y 3 3y 2x ab 5a b 2 2c 4cd
3
4 xy 2 3 2 6 x y 3x
2 2
ab 4cd 2 2 2 2c 5a b 3 4ab cd 2 2 2 10a b c 2bd 5ac
2
例2 计算:
1 1 2 2 49 m m 7m 1 2 2 (m 7 m) m 49 m( m 7) ( m 7)(m 7) m m7
在分式有关的运算中,一般总是先把分子、
分母分解因式;
注意:过程中,分子、分母一般保持分解因
式的形式。
500 500 ∴ a 2 1 < (a 1) 2 “丰收2号”小麦的单位面积产量高。 500 500 500 a 2 1 a 1 (2) 2 2 2 (a 1) a 1 (a 1) 500 a 1
“丰收2号”小麦的单位面积产量是“丰收1号”小麦的单位 面积产量的 a 1 倍。
a b 1a 2b . ; b a . 1 ; 2
b
a b 1. 2 ; b a
2
a
ቤተ መጻሕፍቲ ባይዱ
x 1 a 1 1 x 2x 1x 1 y 2 yx 1 3.aa 1 a 2 .a y y y x 1 2 a 1 x 1x 1 y 2 yx 1 a 1 y x 1 a
2
课堂练习
计算
1 a2 (1)a 2 b 2 b b 3y y 3 (2) (4 x ) x 4x x 1 x2 x2 1 (3) 2 ( x 1) x2 x 4x 4 x 1
a2 4 a 3 a 2 (4) 2 2 2 a 4a 3 a 3a 2 a 1
3
例2 计算:
a 4a 4 a 1 2 2 a 2a 1 a 4 2 ( a 2) a 1 2 ( a 1) ( a 2)(a 2)
2
( a 2) ( a 1) 2 ( a 1) ( a 2)(a 2) a2 ( a 1)(a 2)
复习回顾
4a 2b (1) 2ab 2a (b a ) 2 a b ( 2) 2( a b ) 2 a2 b2 a b (3) 2 a a ab ( a b)(b c )(a c ) ( 4) 1 (b a )(c a )(c b)
课堂练习
下面的计算对吗?如果不对,应该怎样改正?
x 6b 3b 3 (1) 2 2b x x x
8 4x a 2 x ( 2) 3a 2 x 3 a 2 3
2
太有趣了,我还想做
课堂练习
a 212 a .a ; .a a 1 2 a a a 2 x 2 1 1 x 1 x a 2 2. a a 3. x . ; 3 . 2 yy y a 1 y
例3
“丰收1号”小麦的试验田是边长为a米的正方形减去 一个边长为1米的正方形蓄水池后余下的部分, “丰收2号” 小麦的试验田是边长为(a-1)米的正方形,两块试验田的 小麦都收获了500千克。 (1)哪种小麦的单位面积产量高? (2)高的单位面积产量是低的单位面积产量的多少倍? 解(1)∵ 0<(a-1)< a 2-1
