19.3选择方案1
19.3课题学习选择方案(1--4)

4 3 2 1
0
1
2
3
4
x/件
反馈检测
如图,l1、l2分别表示一种白炽灯和一种节能灯的费用y(费用= 灯的售价+电费,单位:元)与照明时间x的函数图象,假设两种灯 的使用寿命都是2000小时,照明效果一样。据图象解答下列问题: (1)一个白炽灯的售价为____元;一个节能灯的售价是____元; (2)分别求出 l1、l2的解析式; y(元) (3)当照明时间,两种灯的费用相等? L1(白) (4)小亮房间计划照明2500小节) 请你帮他设计最省钱的用灯方法。
即当照明时间小于2280小时,购买白炽灯较省钱.
从“形”上解 问题:(1)X取何值时,y1=y2?
(2)X取何值时,y1=y2?
(3)X取何值时,y1=y2? 探究二:你能利用函数的图象给出解答吗?
解法二:
解:设照明时间是x小时, 节能灯的费用y1元表示,白炽灯的费用y2 元表示,则有:y1 =0.005x +60, y2 =0.03x + 3 列表,画图,得
哪种灯更钱省
灯具店老板介绍说:
一种节能灯的功率是10瓦(即0.01千瓦),售价60元; 一种白炽灯的功率是60瓦(即0.06千瓦),售价为3元.两种 灯的照明效果是一样的,使用寿命也相同(3000小时以 上)。
父亲说:“买白炽灯可以省钱”.而小刚正好读八年级, 他在心里默算了一下说:“还是买节能灯吧”.父子二人 争执不下。咱们本地电费为0.5元/千瓦.时,请聪明的你 帮助他们选择哪一种灯可以省钱呢?
y1 =60+0.5×0.01x=0.005x+60;
y2 =3+0.5×0.06x =0.03x+3.
问题4:观察上述两个函数
(1)若使用两种灯的费用相等,它的含义是什么?y1= y2 (2)若使用节能灯省钱,它的含义是什么? y1< y2 (3)若使用白炽灯省钱,它的含义是什么? y1> y2
人教版八年级下册数学试题:19.3 课题学习 选择方案 习题(无答案) (1)

课题学习 选择方案 【问题探究】例1一种节能灯的功率为10瓦(即0。
01千瓦),售价为60元;一种白炽灯的功率为60瓦(即0。
06千瓦),售价为3元。
两种灯的照明效果一样,使用寿命也相同(3000小时以上)。
如果电费价格为0。
5元/(千瓦时),消费者选用哪种灯可以节省费用? 设照明时间为x 小时,则用节能灯的总费用为y 1=x 001.05.0⨯+60. ① 类似地可以写出作白炽灯的总费用为 y 2= . ②讨论:根据①②两个函数,考虑下列问题 : ⑴x 为何值时21y y =? ⑵x 为何值时21y y φ?⑶x 为何值时21y y π?,,。
解:例2 .学校计划在总费用2300元的限制内,租用汽车送234名学生和6名教师集体外出活动,每辆汽车上至少要有1名教师。
现有甲、乙两种大客车,它们的载客量(1) 共需要多少辆汽车? (2) 给出最节省费用的方案。
分析:(1)可以从乘车人数的角度考虑租多少辆汽车,即要注意到以下两点:①要保证 名学生有车坐;②要使每辆车上至少要有 名教师。
根据①可知,汽车总数不能少于 ; 根据②可知,汽车总数不能大于 。
综合起来可知汽车总数为 。
(2)租车费用与租车种数有关,可以看出,当汽车总数a 确定后,在满足各项要求的前提下,尽可能少地租用 种客车可以节省费用。
设租用x 辆甲种客车,,则租用乙种客车 , 租车总费用y (单位:元)是x 的函数,即y =400x +280(a - x ).将(1)中确定的a 值代入上式,化简得 y = 解:【课后巩固】1.某博物馆的门票每张10元,一次购买30张到99张门票按8折优惠,一次购买100张以上(含100张)按7折优惠。
甲班有56名学生,乙班有54名学生。
(1)若两班学生一起前往参观博物馆,请问购买门票最少共需花费多少元?(2)当两班实际前往该博物馆参观的总人数多于30人且不足100人时,至少要多少人,才能使得按7折优惠购买100张门票比实际人数按8折优惠购买门票更便宜?解:2.我市某镇组织20辆汽车装运完A 、B 、C 三种脐橙共100吨到外地销售。
零件工艺及夹具设计(铣槽20专用夹具)

┊┊┊┊┊┊┊┊┊┊┊┊┊装┊┊┊┊┊订┊┊┊┊┊线┊┊┊┊┊┊┊┊┊┊┊┊┊零件工艺及夹具设计摘要机械工业是一种基本工业形式,对于我们国家来说,它关系到国计民生的方方面面。
近年来机械工业领域向着高精度、高质量、高效率、低成本方向发展,数字化,自动化水平日益提高。
同时由于机械工业的发展,其他各工业部门也向着高深度迈进,机械工业的发展日趋重要。
机械加工工艺规程是规定零件机械加工工艺过程和操作方法的重要工艺文件。
它不仅是企业生产中重要的技术文件,也是机械制造过程中用于指导生产组织加工和管理工作的基本依据。
机械制造过程及检测,检验中,都要使用大量的夹具。
夹具是能够使产品按一定的技术要求准确定位和牢固夹紧的工艺装置,它的主要用于保证产品的加工质量、减轻劳动强度、辅助产品检测、展示、运输等。
关键词:零件工艺;铣床;槽;夹具┊┊┊┊┊┊┊┊┊┊┊┊┊装┊┊┊┊┊订┊┊┊┊┊线┊┊┊┊┊┊┊┊┊┊┊┊┊AbstractMachinery industry is a basic industry, for our country, it is related to aspects of beneficial to the people's livelihood. In recent years the field of machinery industry towards high precision, high quality, high efficiency, low-cost development, digitalization, automatization level is improved. At the same time as the development of machinery industry, other industries are also facing high depth forward, the development of mechanical industry is becoming more and more important.Machining process planning is to provide spare parts machining process and operation method of the important technological document. It is not only the production technology in the important file, is a mechanical manufacturing process used to guide the production of tissue processing and management based on.Mechanical manufacturing process and testing, inspection, will use a lot of fixture. The fixture is to be able to make products according to the technical requirements of accurate positioning and tight clamping technology device, it is mainly used to ensure the product processing quality, reduce labor intensity, auxiliary products detection, display, transportation etc..Key words: Component technology; milling machine; groove;fixture┊┊┊┊┊┊┊┊┊┊┊┊┊装┊┊┊┊┊订┊┊┊┊┊线┊┊┊┊┊┊┊┊┊┊┊┊┊目录第1章零件机械加工工艺规程的编制 (4)1.1中批量生产工艺特征 (4)1.2零件的分析 (4)1.3选择毛坯及毛坯制造方法 (5)1.4工艺规程设计 (5)1.4.1定位基面的选择 (5)1.4.2拟定工艺路线 (5)第2章铣槽夹具的设计 (8)2.1机床夹具设计的基本要求和设计原则 (8)2.1.1夹具概念 (8)2.1.2机床夹具的分类 (8)2.1.3铣床专用夹具的设计原则 (9)2.1.4对专用夹具的基本要求 (9)2.2 零件的铣床夹具设计 (9)2.2.1确定定位方案 (9)2.2.2夹紧方案设计 (10)2.2.3对刀方案设计 (10)2.2.4定位误差分析 (10)2.2.5定向键设计 (11)2.2.6夹具体设计 (11)2.2.7夹具装配图 (14)第3章总结 (14)答谢词 (15)参考文献 (16)┊┊┊┊┊┊┊┊┊┊┊┊┊装┊┊┊┊┊订┊┊┊┊┊线┊┊┊┊┊┊┊┊┊┊┊┊┊第1章零件机械加工工艺规程的编制1.1中批量生产工艺特征生产纲领的大小对生产组织和零件加工工艺过程起着重要的作用,它决定了各工序所需专业化和自动化的程度,以及所选用的工艺方法和工艺装备。
人教版八年级下册数学课时练《193 课题学习、选择方案》(1) 试题试卷 含答案解析
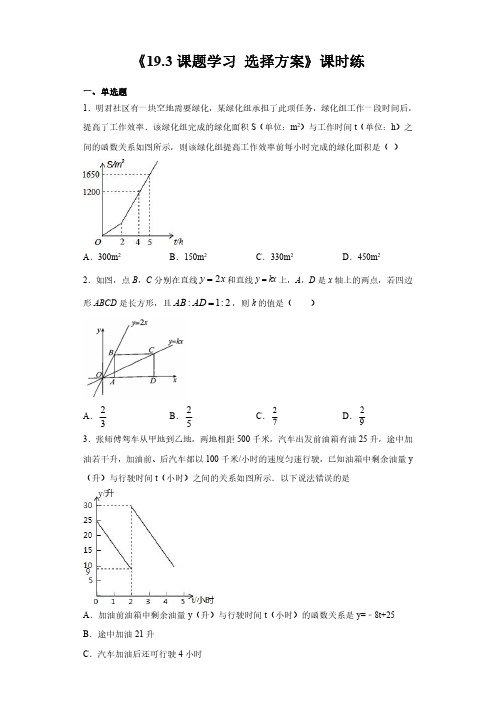
《19.3课题学习选择方案》课时练一、单选题1.明君社区有一块空地需要绿化,某绿化组承担了此项任务,绿化组工作一段时间后,提高了工作效率.该绿化组完成的绿化面积S (单位:m 2)与工作时间t (单位:h )之间的函数关系如图所示,则该绿化组提高工作效率前每小时完成的绿化面积是()A .300m 2B .150m 2C .330m 2D .450m 22.如图,点B ,C 分别在直线2y x =和直线y kx =上,A ,D 是x 轴上的两点,若四边形ABCD 是长方形,且:1:2AB AD =,则k 的值是()A .23B .25C .27D .293.张师傅驾车从甲地到乙地,两地相距500千米,汽车出发前油箱有油25升,途中加油若干升,加油前、后汽车都以100千米/小时的速度匀速行驶,已知油箱中剩余油量y (升)与行驶时间t (小时)之间的关系如图所示.以下说法错误的是A .加油前油箱中剩余油量y (升)与行驶时间t (小时)的函数关系是y=﹣8t+25B .途中加油21升C .汽车加油后还可行驶4小时D.汽车到达乙地时油箱中还余油6升4.某种品牌的同一种洗衣粉有A,B,C三种袋装包装,每袋分别装有400克、300克、200克的洗衣粉,售价分别为3.5元、2.8元、1.9元.A,B,C三种包装的洗衣粉,每袋的包装费用(含包装袋成本)分别为0.8元、0.6元、0.5元.厂家销售A,B,C三种包装的洗衣粉各1200千克,获得利润最大的是()A.A种包装的洗衣粉B.B种包装的洗衣粉C.C种包装的洗衣粉D.三种包装的都相同5.如图是邻居张大爷去公园锻炼及原路返回时离家的距离y(千米)与时间t(分钟)之间的函数图象,根据图象信息,下列说法不正确的是()A.张大爷去时所用的时间多于回家的时间.B.张大爷在公园锻炼了40分钟C.张大爷去是走上坡路,回家时走下坡路D.张大爷去时的速度比回家时的速度慢6.一个生产、装箱流水线,生产前没有积压产品,开始的3小时只生产,3小时后安排装箱(生产没有停止),8小时后生产停止只安排装箱,第13小时时生产流水线刚好没有积压产品,已知流水线的生产、装箱的速度保持不变,流水线上积压产品(没有装箱产品)y(吨)与流水线工作时间x(小时)之间的函数关系如图所示,则在整个过程中,积压产品最多为()A.9.5吨B.10吨C.11吨D.12吨7.快车从甲地驶往乙地,慢车从乙地驶往甲地,两车同时出发并且在同一条公路上匀速行驶.图中折线表示快、慢两车之间的路程(km)y 与它们的行驶时间(h)x 之间的函数关系.小欣同学结合图像得出如下结论:①快车途中停留了0.5h ;②快车速度比慢车速度多20km/h ;③图中340a =;④快车先到达目的地.其中正确的是()A .①③B .②③C .②④D .①④8.港口A 、B 、C 依次在同一条直线上,甲、乙两艘船同时分别从A 、B 两港出发,匀速驶向C 港,甲、乙两船与B 港的距离y (海里)与行驶时间x 时)之间的函数关系如图所示,则下列说法错误的是()A .甲船平均速度为60海里/时B .乙船平均速度为30海里/时C .甲、乙两船在途中相遇两次D .A 、C 两港之间的距离为120海里9.甲、乙两名运动员同时从A 地出发到B 地,在直线公路上进行骑自行车训练.如图,反映了甲、乙两名自行车运动员在公路上进行训练时的行驶路程S(千米)与行驶时间t(小时)之间的关系,下列四种说法:①甲的速度为40千米/小时;②乙的速度始终为50千米/小时;③行驶1小时时,乙在甲前10千米;④甲、乙两名运动员相距5千米时,t=0.5或t=2或t=5.其中正确的个数有()A.1个B.2个C.3个D.4个10.甲、乙两船沿直线航道AC匀速航行.甲船从起点A出发,同时乙船从航道AC中途的点B出发,向终点C航行.设t小时后甲、乙两船与B处的距离分别为d1,d2,则d1,d2与t的函数关系如图.下列说法:①乙船的速度是40千米/时;②甲船航行1小时到达B处;③甲、乙两船航行0.6小时相遇;④甲、乙两船的距离不小于10千米的时间段是0≤t≤2.5.其中正确的说法的是()A.①②B.①②③C.①②④D.①②③④二、填空题11.小明从家步行到学校,图中的折线OAB反映了小明从家步行到学校所走的路程s (米)与时间t(分钟)的函数关系,根据图像提供的信息,线段OA表示的函数解析式是_________.12.油箱中有油20升,油从管道中匀速流出,100分钟流完.匀速流出的过程,油箱中剩油量y(升)与流出的时间x(分钟)之间的函数关系式是_____(并写出自变量取值范围).13.在锅中倒入了一些油,用煤气灶均匀加热,每隔20秒测一次油温,得到下表:时间x(秒)0204060…油温y(℃)105090130…加热110秒时,油刚好沸腾了,估计这种油沸点的温度为_____℃.14.本年度某单位常有集体外出学习活动,因此准备与出租车公司签订租车协议.现有甲、乙两家出租车公司供选择.设每月行驶x千米,应付给甲公司1y元,应付给乙公司2y元,1y、2y分别与x之间的函数关系如图所示,若这个单位估计每月需要行驶的路程为3500千米,那么为了省钱,这个单位应租__________公司.15.我市认真落实国家“精准扶贫”政策,计划在对口帮扶的贫困县种植甲、乙两种火龙果共100亩,根据市场调查,甲、乙两种火龙果每亩的种植成本分别为0.9万元、1.1万元,每亩的销售额分别为2万元、2.5万元,如果要求种植成本不少于98万元,但不超过100万元,且所有火龙果能全部售出,则该县在此项目中获得的最大利润是_____万元.(利润=销售额﹣种植成本)三、解答题16.某景区售票处规定:非节假日的票价打a折售票;节假日根据团队人数x(人)实行分段售票;若x≤10,则按原展价购买;若x>10,则其中10人按原票价购买,超过部分的按原那价打b折购买.某旅行社带团到该景区游览,设在非节假日的购票款为y1元,在节假日的购票款为y2元,y1、y2与x之间的函数图象如图所示.(1)观察图象可知:a=_______,b=_______;(2)当x>10时,求y2与x之间的函数表达式;(3)该旅行社在今年5月1日带甲团与5月10日(非节假日)带乙团到该景区游览,两团合计50人,共付门票款3120元,求甲团人数与乙团人数.17.兰州市居民用电现有两种用电收费方式:智能分时电表普通电表峰时(8:00﹣22:00)谷时(22:00﹣次日8:00)电价0.51/千瓦时电价0.76元/千万时电价0.26元/千瓦时设某家庭某月用电总量为x千瓦时,其中谷时用电60千瓦时,则峰时用电(x﹣60)千瓦时,智能分时电表计价时的总价为为y1(元),普通电表计价时的总价为y2(元).请分别写出两种电表计价时的总价与用电总量之间的函数关系式.18.某水果店每天都会进一些草莓销售.在一周销售过程中他发现每天的销售量y(单位:千克)会随售价x(单位:元/千克)的变化而变化,部分数据记录如表:售价x(单位:元/千克)302520每天销售量y(单位:千克)54585如果已知草莓每天销量y与售价x(14<x<30.625)满足一次函数关系.(1)请根据表格中数据求出这个一次函数关系式;(2)如果进价为14元/千克,请判断售价分别定为20元/千克和25元/千克时,哪个的销售利润更高?参考答案1.B2.B3.C4.B5.B6.D7.B8.C9.B10.C11.120y x =.12.y =20﹣15x (0≤x ≤100)13.23014.甲15.12516.(1)6,8;(2)y 2=64x +160(x >10),(3)甲团有35人,乙团有15人.17.10.7630(60)y x x =-³,20.51(60)y x x =³.18.(1)y =﹣8x +245;(2)当售价为20元/千克时的销售利润更高。
人教版八年级数学下册:19.3 课题学习 选择方案(共20张PPT)

3. 某商店销售A型和B型两种电脑,其中A型电脑每台的利润为400元,B 型电脑每台的利润为500元.该商店计划再一次性购进两种型号的电脑共100 台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这 100台电脑的销售总利润为y元.
(1)求y关于x的函数关系式; (2)该商店购进A型、B型电脑各多少台,才能使销售总利润最大,最大 利润是多少? (3)实际进货时,厂家对A型电脑出厂价下调a(0<a<200)元,且限定商 店最多购进A型电脑60台,若商店保持同种电脑的售价不变,请你根据以上 信息,设计出使这100台电脑销售总利润最大的进货方案.
其中正确结论的个数是( )
பைடு நூலகம்A.0 B.1
D
C.2 D.3
2. 某学校期末考试要给学生印制复习资料若干份,印刷厂有甲、乙两种 收费方式,除按印刷份数收取印刷费用外,甲种方式还收取制版费,而乙种 不需要,两种印刷方式的费用y(元)与印刷份数x(份)之间的函数关系如图所 示.
(1)求甲乙两种收费方式的函数关系式; (2)若需印刷100~400份(含100和400)份复习资料,选择哪种印刷方式比 较合算?
解:(1)设购买的文化衫t件,则购买相册(45-t)本, 根据题意,得w=28t+20×(45-t)=8t+900
(2)根据题意,得88tt++990000≥≤11770000--556404,, 解得 30≤t≤32,∴有 3 种购买方案:
方案1:购买30件文化衫、15本相册; 方案2:购买31件文化衫、14本相册; 方案3:购买32件文化衫、13本相册. ∵在w=8t+900中,k=8>0,∴w随t的增大而增大, ∴当t=30时,w取最小值,此时用于拍照的费用最多. ∴为了使拍照的资金更充足,应选择方案1,购买30件文化衫、15本相册
19.3课题学习_选择方案(1)

(1)求购买设备的资金y万元与购买A型x台的函数关系,并 设计该企业有几种购买方案
y=12x+10(10-x)
即 y=2x+100
A型
价格(万元/台)
B型
10
12
பைடு நூலகம்
∵y=2x+100≤105 ∴ x≤2.5
处理污水量(吨/月)
年消耗费(万元/台)
240
1
200
1
又∵x是非负整数 ∴x可取0、1、2 ∴有三种购买方案:
解得
x≥1
又∵x可取0、1、2
∴ x为 1或 2 ∵k=2>0∴y随x增大而增大。 即: 为节约资金,应选购A型1台,B型9台
解后反思
这个实际问题的解决过程中是怎样思考的?
实际问题
设变量 找对应关系
一次函数问题
实际问题的解
解释实 际意义
一次函数问题的解
2 (2)若y1<y2,即3t-45<50,解不等式,得t<31 3 ; 2 (3)若y1>y2,即3t-45>50,解不等式,得t>31 3 .
解决问题
1 令3t-100>120,解不等式,得t>73 3 . 31小时40分 ,选择方案A最省钱; 当上网时间不超过____________ 31小时40分至73小时20分 ,选择方案 当上网时间为__________________________ B最省钱; 73小时20分 当上网时间超过_______________ ,选择方案C最省钱. 1 令3t-100=120,解方程得t =73 3 ;
设照明时间为x小时,则节能灯的总费用为
y
1
=0.5×0.01x+60
设照明时间为x小时,则节能灯的总费用为
19.3梯形(1)公开课件

你发现了什么? 你发现了什么?
等腰
形的
等腰梯形有哪 些性质呢
边 角 对角线 对称 猜 想 两腰相等 ,两腰相等 两底平行, 两底平行 同一底上的两个角相等。 同一底上的两个角相等。 对角线相等。 对角线相等。 边: 不是中心对称图形。 不是中心对称图形。 轴对称图形。 轴对称图形。 角: 对角线 对称
等腰梯形性质
探究等腰梯形的性质: 探究等腰梯形的性质:边、角、对角线、对称性 对角线、
• 1、过等腰梯形ABCD的一个顶点,将该 过等腰梯形ABCD的一个顶点, ABCD的一个顶点 特殊的几何 梯形分割成我们已学过的特殊的 梯形分割成我们已学过的特殊的几何 图形。 图形。 • 2、过等腰梯形ABCD的两个顶点,将该 过等腰梯形ABCD的两个顶点, ABCD的两个顶点 梯形分割成我们已学过的特殊的 特殊的几何 梯形分割成我们已学过的特殊的几何 图形。 图形。
A
D
对角线相等 对角线 (3)对角线相等
AC=BD
B
C
是轴对称图形,上下底中点连线所在的直线是对称轴。 是轴对称图形 对称性 (4)是轴对称图形,上下底中点连线所在的直线是对称轴。
3、我们在研究问题时,可以用哪些方法将梯形问题转化 我们在研究问题时, 成其他图形问题? 成其他图形问题?
通常是把梯形转化为特殊的四边形和三角形。 通常是把梯形转化为特殊的四边形和三角形。可 四边形 采用割 的几何变换方法,来解决梯形问题。 采用割或补的几何变换方法,来解决梯形问题。
A
上底 高
D
下底 (1)平行的两边叫做底 1 平行的两边叫做底
腰
C
腰
B
较短的称作上底,较长的称作下底 较短的称作上底,:梯形的 注意: 注意
19.3 坐标与图形的位置1

A
D
B
C
小结:
建立平面直角坐标系的要求与原则
(1):选原点 (2):画坐标轴 (3):建系利于坐标求
活动一:探究与展示
已知边长为4的正方形,请你建立一个 平面直角坐标系(用尽可能多的方法),并求 出各点的坐标. • 说明: • (1)你是如何建立的平面直角坐标系? D (如何确定的原点和坐标轴)A • (2)各点坐标如何求得?
在等腰三角形ABC中,腰
AB=AC=2√10 ,底边 BC=4,
A
(1)请你在网格图中建立 适当的坐标系,并写出A, B,C的坐标. (2)解释你选择这个坐标 系的理由.
B C
y (0,6) A
y A (2,6)
(-2,0) B
0
C x (2,0)
B 0 (0,0)
C (4,0)x
体现轴对称性
图形在第一象限
【中考· 滨州】如图,正五边形ABCDE放入 某平面直角坐标系后,若顶点A,B,C,D 的坐标分别是(0,a),(-3,2),(b,m),(c, m),则点E的坐标是( C ) A.(2,-3) B.(2,3) C.(3,2) D.(3,-2)
【中考· 福州】如图,在3×3的正方形 网格中有四个格点A,B,C,D,以其 中一点为原点,网格线所在直线为坐标 轴,建立平面直角坐标系,使其余三个 点中存在两个点关于一条坐标轴对称, 则原点是( B ) A.A点 B.B点 C.C点 D. D点
如图,将正方形OABC放在平面直 角坐标系中,O是原点,点A的坐标为(1, 3),则点C的坐标 为( A ) A.(- 3 ,1) B.(-1, 3 ) C.( 3 ,1) D.(- 3 ,-1)
在△ABC中,点A,B,C的坐标分别为 (-1,0),(5,0),(2,5),则△ABC的 形状是( B ) A.直角三角形 B.等腰三角形 C.钝角三角形 D.等边三角形
19.3.1 尺规作图教案
图1图2MN的长,在射线AB上截取就是所要画的线段,如图2所示。
''',答案:已知∠AOB,如图(1),求作:∠A O B作法:第一步:画射线O A''。
第二步:以点适当长为半径画弧,交OA于C,交OB于D.第三步:以点为圆心,以OC长为半径画弧,交O A''于C'。
第四步:以点OD、OE,使OD=OE.的长为半径画弧,在∠四、课堂练习只用无刻度的直尺就能作出的是(1)所示,在________上截取_________2)所示,以点_______为圆心,径作弧,交_______于点_______,交_______:点与直线的位置关系有哪几种?答案:点在直线上和点在直线外。
图1图2图3 图4求作:直线l的垂线,使它经过C。
为圆心,适当长度为半径画弧,交和B为圆心,大于1 2图1 图2和点B为圆心,大于长为半径画弧,两弧相交于点M和N.就是所求作的线段1中,点A(0,8),点B 只用直尺(没有刻度)和圆规,求作一个点P,使点的两边的距离相等应满足什么条件?图1 图2 图3 图4,使BC= (如图2)= (如图3);的垂直平分线且交AB于P,其中上取两点D、E,使),并根据要求填空:,交BC于点F.的关系为互相垂AB=CD,°,求证:BC=BD.,求证:△ABC≌△DCB.求证:△AOP≌△BOP.)∠A=∠D,∠B=∠F;(2)∠A=∠D,AB=DE.∠D,CO=BO,,你能找出一对全等的三角形AB=AC.BAD=∠ABC.求证:∠BAC=∠ABD.DAC,求证:△AB C≌。
HDL 智能系统配置 19.3.17 - 副本
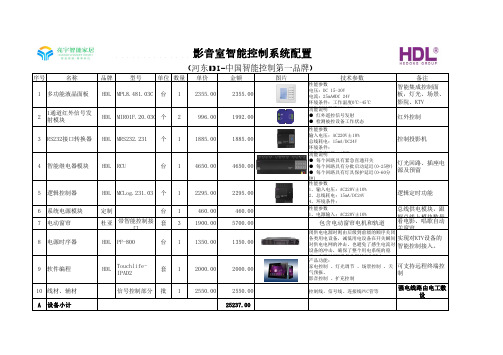
强电线路由电工敷 设
25237.00
B 人工施工费用 总计
(系统布线、安装、调试)A*15%
3750 28987
注:实现功能:1、私人影院智能控制,灯光、电动窗帘、影院音响投影设备控制。 2、私人影院智能控制,带一键启动【影院模式】、【卡拉OK模式】、【日常模式】、【离开模式】 等。 3、可以手机、平板控制。
对供电电网的冲击,也避免了感生电流对 智能控制接入。
设备的冲击,确保了整个用电系统的稳
定,实现对KTV设备的智能控制接入。 产品功能:
家电控制 、灯光调节 、场景控制 、天 可支持远程终端控
气预报、
制
影音控制 、扩充控制
信号控制部分 批 1 2550.00
2550.00
控制线、信号线、连接线PVC管等
金额 2355.00
HDL MIR01F.20.03C 个 2
996.00
1992.00
HDL MRS232.231 个 1 1885.00
1885.00
HDL RCU
台 1 4650.00
4650.00
HDL MCLog.231.03 个 1 2295.00
定制
台1
杜亚 带智能控制接 套 3 口
HDL PF-800
源及预留
钟) 性能参数
1、输入电压:AC220V±10% 2、总线耗电:15mA/DC24V
逻辑定时功能
4、环境条件:
性能工参作数温度0℃-40℃
总线供电模块,跟
1、电源输入:AC220V±10%
包含电动窗帘电机和轨道
据总线上模块数量 看电影、唱歌自动
关窗帘
闭供电电源时则由后级到前级的顺序关闭
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
你能自己写出方式B的上网费y2关于上网时间 t之间的 函数关系式吗? 50, 0≤t≤50; 3t-100,t>50. 方式C的上网费y3关于t之间的函数关系式呢?
y2=
当t≥0时,y3=120.
解决问题
解:设上网时间为t h,方案A,B,C的上 120 网费分别为y1 元,y2 元, y3 元,则
总结归纳
解决含有多个变量的问题时,可以分析这
些变量之间的关系,从中选取一个取值能
影响其他变量的值的变量作为自变量,然
后根据问题的条件寻求可以反映实际问题 的函数,以此作为解决问题的数学模型.
解后反思
这个实际问题的解决过程中是怎样思考的?
实际问题
设变量 找对应关系
一次函数问题
实际问题的解
解释实 际意义
某学校计划在2300元的限额内,租用汽车送 234名学生和6名教师集体外出活动,每辆汽车 上至少有1名教师.现有甲、乙两种大客车,它 们的载客量和租金如表所示:
甲种客车 载客量(单位:人/辆) 45 租金 (单位:元/辆) 400 乙种客车 30 280
(1)保证240名师生有车坐,则车总数不能小 于 6 . 每辆车上至少有1名教师,则汽车总数不 能大 于 6. 6 综合起来可知汽车总数为 .
0≤t≤50; y1=30, 0≤t≤25; y = 50, 2 3t-45,t>25. 3t-100,t>50.
y
y1
y2 y3
y3=120.
结合图象可知: 若0≤t≤ t1时,y1最小;
50 30
t2
t3
O
25
t1
50
75
t
上网时间不超过31小时40 若t1≤t≤t3 时,y2最小; 分,方案A最省钱; 若t>t3时,y3最小 上网时间为31小时40分至 73小时20分,方案B最省钱; 上网时间超过73小时20分, 方案C最省钱.
例 某工程机械厂根据市场要求,计划生产A、
B两种型号的大型挖掘机共100台,该厂所筹生
产资金不少于22400万元,但不超过22500万元,
且所筹资金全部用于生产这两种型号的挖掘机, 所生产的这两种型号的挖掘机可全部售出,此 两种型号挖掘机的生产成本和售价如下表所示: A B 型号 200 240 成本(万元/台) 售价(万元/台) 250 300
(1)该厂对这两种型号挖掘机有几种生产方案? (2)该厂如何生产获得最大利润?
2.某校校长暑假将带领该校市级“三好生”去北京旅 游.甲旅行社说:“如果校长买全票一张,则其余学生可 变式练习 享受半价优惠.”乙旅行社说:“包括校长在内,全部按 全票价的6折优惠.”若全票价为240元. (1)设学生数为 x,甲旅行社收费为 y甲,乙旅行社收费为 y乙,分别计算两家旅行社的收费(建立表达式); zx`````x``k
甲种客车 x 辆 载客量(单位:人/辆) 租金 (单位:元/辆) 45 400
乙种客车 (6-x)辆 30 280
设租用 x 辆甲种客车,则租车费用y(单位: 元)是 x 的函数,即
z```x``x``k
怎样确定 x 的 取值范围呢?
甲种客车 x 辆乙种客车 (6-x)辆 45 30 载客量(单位:人/辆) 400 280 租金 (单位:元/辆) 确定x的范围 确定x的范围
(2)这两个函数的图象如下: 观察图象,可知: 当通话时间为150分时, 选择A或B方案费用一样;
50 40 30
y(元)
y1 = 15+0.2t
● ●
y1 = 0.3t
当通话时间少于150分时, 20 选择B方案费合算; 10 当通话时间多于150分时, O 选择A方案合算.
●
50
100
150 t(分)
另收通话费为0.2元/分;B方案: 零月租费,
通话费为0.3元/分.
(1)试写出A,B两种方案所付话费y(元) 与通话时间t(分)之间的函数关系式; (2)在同一坐标系画出这两个函数的图象, 并指出哪种付费方式合算?
解:(1) A方案: y1 = 15+0.2t(t≥0) ,
B方案: y2 = 0.3t(t≥0).
19.3 课题学习
选择方案
问题1 怎样选取上网收费方式? 问题一:怎样选取上网收费方式 下表给出 A,B,C三种上宽带网的收费方式.
收费方式 月使用费/元 包时上网时间/h 超时费/ (元/min)
A B C
30 50 120
25 50 不限时
0.05 0.05
选择哪种方式能节省上网费?
收费方式
• (1)设装运乙种蔬菜的汽车x辆、装运丙种蔬菜的汽车y辆,由题意得: x+y=8 x+1.5y=11, 解得: x=2 y=6. 答:装运乙种蔬菜的汽车2辆、装运丙种蔬菜的汽车6辆; (2)设装运甲种蔬菜的汽车a辆,装运乙种蔬菜的汽车b辆,则装运丙种蔬菜 的汽车(20-a-b)辆,获得的利润为W百元,由题意得: 2a+b+1.5(20-a-b)=36①W=10a+7b+6(20-a-b)②, 由①,得 b=a-12. 由②,得 W=4a+b+120 W=4a+a-12+120, W=5a+108, ∵k=5>0, ∴W随a的增大而增大. ∵ a≥1 b≥1 20-a-b≥1, ∴13≤a≤15.5, ∵a为整数, ∴当a=15时,W最大=5×15+108=183百元, 装运方案是:甲种蔬菜的汽车15辆,装运乙种蔬菜的汽车3辆,则装运丙 种蔬菜的汽车2辆
当堂练习
1.某单位准备和一个体车主或一国营出租车公司 中的一家签订月租车合同,设汽车每月行驶x 千米, 个体车主收费y1元,国营出租车公司收费为y2元, >1500 时,选用个体车 观察下列图象可知,当x________
较合算.
2、某移动公司对于移动话费推出两种收费
方式: A方案:每月收取基本月租费15元,
月使用费/元
包时上网时间/h
超时费/ (元/min)
A B C
30 50 120
25 50 不限时
0.05 0.05
1.哪种方式上网费是会变化的?哪种不变? 2.在A、B两种方式中,上网费由哪些部分组成? 3.影响超时费的变量是什么? 4.这三种方式中有一定最优惠的方式吗?
问题一:怎样选取上网收费方式——分析问题
由函数可知 y 随 x 增大而增 大,所以 x = 4时 y 最小, 所以租用4辆甲车,2辆乙车.
解:(1)要保证240名师生有车坐,由甲
种客车每辆载客45人可知汽车总数不能
小于6;要使每辆汽车上至少有1名教师,有 6名教师可知汽车总数不能大于6.
综合起来可知汽车总数为6.
(2)若单独租甲种车,需要费用: 400×6=2400(元),不满足总费用2300元的限额. 若租甲、乙两种车,设租用x辆甲种客车,则租用(6-x)辆乙种客车, 则车费y与 x 的函数关系式为y=400x+280(6-
一次函数问题的解
课堂小结
解决方案问题步骤: 1.把实际问题转化为数学函数问题,列出函数关 系式(建立数学模型). 2.通过解不等式或画函数图象的方式确定自变量
的范围.
3.利用一次函数的增减性知识从而选择出最佳方案.
3.如图是甲、乙两家商店销售同一种产品 的销售价 y(元)与销售量 x(件)之间的函 数图象.下列说法, 正确的说法有 ①②③ . (填序号) ①售2件时甲、乙两家售价一样; ②买1件时买乙家的合算; ③买3件时买甲家的合算; ④买1件时,售价约为3元.
收费方式 月使用费/元 包时上网时间/h 超时费/(元/min)
A B
30 50
25 50
0.05 0.05
设月上网时间为t,则方式A、B的上网费y1、 y2都是t的函数,方式c的上网费y3是常量,
收费方式
月使用费/元
包时上网时间/h
超时费/(元/min)
问题一:怎样选取上网收费方式 A 30 25——分析问题 0.05
某学校计划在2300元的限额内,租用汽车送234 名学生和6名教师集体外出活动,每辆汽车上至 少有1名教师.现有甲、乙两种大客车,它们的 载客量和租金如表所示:
载客量(单位:人/辆) 租金 (单位:元/辆) 甲种客车 45 400 乙种客车 30 280
问题1:租车的方案有哪几种? 问题2:若只租甲种车需多少辆?乙种车呢? 问题3:若甲、乙都租,能确定合租车辆的 范围吗?
问题2 怎样租车?
某学校计划在2300元的限额内,租用汽车送 234名学生和6名教师集体外出活动,每辆汽 车上至少有1名教师.现有甲、乙两种大客车, 它们的载客量和租金如表所示:
甲种客车 载客量(单位:人/辆) 45 租金 (单位:元/辆) 400 乙种客车 30 280
(1)共需租多少辆汽车? (2)给出节省费用的租车方案.
(1)为使240名师生有车坐,(2)租车费用不超过2300元,
结合问题的实际意义,你能有几种不同的租车 方案?为节省费用应选择其中的哪种方案?
由x为正整数,可知x 的取值为4或5
由上述可知共有两种方案: 方案一:4辆甲种客车,2辆乙种客车, 除了分别计算两 种方案的租金外, 方案二:5辆甲种客车,1辆乙种客车 , 还有其他选择方 案的方法吗?
在方式A中,超时费一定会产生吗?什么情况 下才会有超时费? 当0≤t≤25时,y1=30; 当t>25时,y1=30+0.05×60(t-25)=3t45.
合起来可写为:
y1=
30, 0≤t≤25; 3t-45, >25.
收费方式
月使用费/元
包时上网时间/h
超时费/(元/min)
A 30 25 0.05 问题一:怎样选取上网收费方式 ——分析问题 B C 50 120 50 不限时 0.05
